1. Introduction
In the natural environment, ice takes various forms, including ice sheets, glaciers, icebergs, ground ice, river and lake ice, and sea ice. The majority (99.5%) of the permanent ice volume on Earth is locked up in ice sheets and glaciers which contains about 70% of Earth’s freshwater. One of the simplest ways to create holes in glaciers is by using thermal hot-point ice drills, also known as hot points, which have a heating element at the bottom to melt the ice [
1]. These drills are full-face (non-coring) drilling tools that can only produce meltwater and the borehole itself.
Hot-point ice drills are used to deploy sensors and other instruments under ice shelves [
2], to measure ice temperatures [
3], geothermal heat flow [
4], variation of firn density with depth [
5,
6] and other scientific purposes. Recently, there has been specific interest in their use in connection with investigations of the subglacial environment on Earth and other bodies in the Solar System [
7,
8,
9,
10,
11].
Thermal hot-point ice drills can be divided into two types based on the configuration of the drill head: (1) designs that use an intermediate fluid heating medium to transfer thermal energy from a surface-based heat source to a downhole drill head, and (2) electrically heated drill heads, in which various types of electric heaters are embedded directly within the drill head structure (
Figure 1). The second type is generally more energy-efficient, as the thermal losses at the interfaces between the heaters and the drill head are typically lower than the combined losses in heat exchangers and long supply lines. In this study, we focus primarily on electrically heated hot-point drilling systems.
At first glance, the thermal drilling process using hot points appears quite simple. Electric power is supplied to the thermal heaters, which in turn heat the drill head. This thermal energy is transferred to the bottom of the borehole, where it heats and melts the ice. A critical issue in hot-point drilling is the refreezing of water in the open hole. In temperate glaciers, where boreholes filled with meltwater can remain open for days, drilling can proceed safely with interruptions in the drilling process and reaming. The deepest hole drilled in this manner reached a depth of 756 m at Salmon Glacier in Canada [
12,
13]. However, in polar glaciers, refreezing occurs rapidly, and several approaches have been proposed to address this issue [
1]. One of the most promising methods is the use of freezing-in instruments with tethered power cables, also known as Philberth probes [
14]. Several recent research projects have focused on implementing this technique [
7,
8,
9,
10,
11].
Optimization of hot-point drill design is crucial for all types of ice drilling operations, and particularly for extraterrestrial missions, where strict constraints on power consumption, weight, and system size apply. The drill head is the key component of a hot-point ice drill, as it is directly responsible for ice melting and largely determines both the overall drilling performance and the characteristics of the entire drill. To evaluate potential drill head designs before committing to physical prototyping or resource-intensive Computer-Aided Engineering (CAE) simulations, it is often reasonable to use analytical models. Several analytical models have been developed to describe thermal penetration into ice and to optimize drilling performance. In this study, four analytical models are reviewed: Shreve, 1962 [
15]; Kudryashov and Shurko, 1982 [
16]; Fomin and Cheng, 1991 [
17]; Talalay et al., 2014 [
18]. Although these models are based on similar physical principles and share many assumptions, they differ in their simplifications, required input parameters, and computational complexity. As a result, each model has specific limitations in practical applications and none offers a universal design solution.
The Shreve (1962) [
15] analytical model is distinguished by the assumption that the ice is initially at the melting point; that is, the model does not account for the energy required to raise the ice temperature to 0 °C. The formulation employs several dimensionless variables. It neglects lateral heat losses to the borehole wall, but the drill head shape can be user-defined, provided it satisfies axial symmetry and smoothness.
The Kudryashov and Shurko (1982) [
16] analytical model was developed specifically for annular (coring) thermal drill heads operating in boreholes filled with antifreeze fluid. The shape of the drill head is included in the formulation, but only influences the flow channel length used in the hydrodynamic analysis. Several input parameters are subject to internal constraints imposed by the model’s structure.
The Fomin and Cheng (1981) [
17] analytical model was developed for the general case of melting of a solid body and is not specifically tailored to ice. Its applicability to ice is achieved through the appropriate selection of thermophysical properties. The model does not account for lateral heat losses to the borehole wall and considers only thermal loading, without including mechanical interaction with the ice. The drill head geometry is limited to a strictly parabolic profile, which is a fundamental assumption of the model. All calculations are carried out in fully nondimensional form.
The Talalay et al. (2014) [
18] analytical model estimates the thermal power required for penetration using a simplified energy balance approach. It assumes a cylindrical melt geometry and uses empirical correction factors to account for borehole enlargement effects. The shape of the drill head is not included in the formulation. The final temperature of meltwater is treated as an input parameter, either defined experimentally or assumed from prior studies.
For ease of comparison, the key input parameters for each model are summarized in
Table 1.
Among the four models, the one proposed by Kudryashov and Shurko offers a notable advantage in terms of input parameter structure. However, it was developed exclusively for annular (coring) thermal drill heads and is therefore not directly applicable to solid (non-coring) configurations used in hot-point thermal drills. To address this limitation, the original model was modified in this study by adjusting the heat transfer component of the formulation to enable its application to solid drill heads. The modified version of the model is presented in the following section. The main conclusions are verified by comparing them with experimental results obtained using the RECoverable Autonomous Sonde (RECAS). The structure and detailed design of the RECAS sonde are described by Sun et al. (2024) [
11]. In the second half of the paper, we propose and discuss some aspects of the optimal design for hot points.
2. Methods
This section presents the adaptation of the analytical model developed by Kudryashov and Shurko (1982) [
16] for application to non-coring thermal drill heads, achieved through modification of the heat transfer formulation. The resulting model establishes analytical relationships between the ROP and the key parameters governing the thermal drilling process.
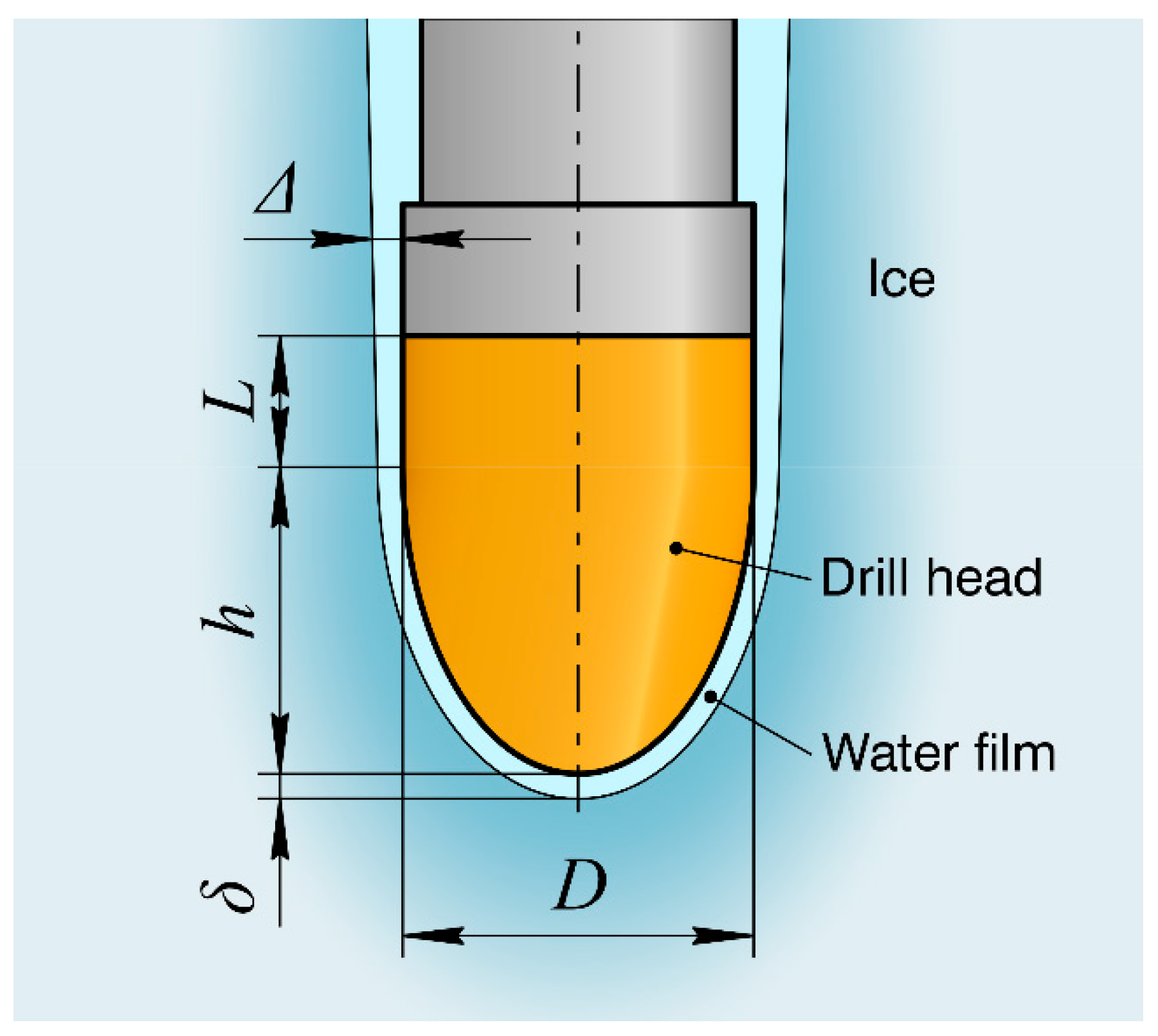
Let us consider a drill head with diameter
D, whose lower part has the shape of a streamlined body of revolution with height
h, and whose lateral surface is cylindrical with height
L. The heater has a specific volumetric heat output
qυ. The surface of the drill head interacts with the ice at the bottom through a continuously forming meltwater film of uniform thickness
δ. The lateral surface interacts with the borehole walls through a thin water layer of thickness Δ. The borehole is completely filled with a water with density
ρw (
Figure 2).
In the following derivations, we use the following assumptions:
a steady-state heat transfer process is considered during thermal drilling;
the heater’s shape is axisymmetric;
heat generated by the internal source within the drill head is uniformly distributed over its surface;
the melting front advances into an infinite, isotropic medium with respect to thermal properties;
ROP is constant;
the flow of meltwater film between the drill head and ice is laminar;
the upper end of the drill head is thermally insulated and does not participate in heat exchange;
the melting point of ice is 0°С;
with increasing borehole depth, only the temperature of the ice changes.
Heat flux at the working surface of the drill head will be:
where
qw is the heating of the meltwater layer between the drill head surface and the borehole bottom (W m
-2);
qm is the heat used for ice melting (W m
-2);
qf is the heat for establishing the temperature field ahead of the moving borehole bottom (W m
-2);
qbw is the heat for warming and melting the borehole lateral walls (W m
-2).
Heat flux directly used for penetration,
qbb, can be estimated as:
where
Ph is the effective thermal power output of the drill head (W);
Qbw is the heat rate spent on warming and melting the lateral borehole walls (W);
A is the projected area of the streamlined section of the drill head surface (m
2).
Amount of heat used for warming and melting the lateral borehole walls is interpreted by Kudryashov and Shurko (1982) [
16] as:
where
D is the diameter of the drill head (m);
th is the temperature of the working surface of the drill head (°С);
λw is the thermal conductivity of water (W m
-1 °C
-1); Δ is the thickness of the water layer between the drill head and the borehole wall (m);
L is the height of the cylindrical part of the drill head (m);
qυ is the specific volumetric heat output of the drill head (W m
-3);
λh is the thermal conductivity of the drill head material (W m
-1 °C
-1).
Projected area of the streamlined section of the drill head surface equals to:
Specific volumetric heat output of the drill head is:
where
h is the height of the streamlined part of the drill head, m;
We define the heat terms according to classical thermophysical equations as:
where
cw is the specific heat capacity of water (J kg
-1 °C
-1);
υ is the ROP (m s
-1);
ρi is the density of ice (kg m
-3).
φ is the latent heat of ice fusion (J kg
-1);
ti is the natural (in-situ) temperature of the ice (°C);
ci is the specific heat capacity of ice (J kg
-1 °C
-1).
Substituting Eq. 3, Eq. 6, Eq. 7 and Eq. 8 into Eq. 2, and solving for
υ, we obtain the dependence of the ROP on the working surface temperature:
A thin meltwater film remains at the contact interface between the drill head and the borehole bottom. Its thickness δ is determined by the hydraulic resistance to water being squeezed out from beneath the drill head by the weight of the drill.
The specific mechanical pressure
рs is balanced by the hydrodynamic pressure
р1 and the hydrostatic pressure
р2 of the continuously moving water film above the drill head surface. These pressures are described by the Darcy-Weisbach equation and the height of the film:
where
λ is the dimensionless hydraulic resistance coefficient of the expelled water;
ρw is the density of water (kg m
-3);
w is the average volumetric flow velocity across the channel cross-section (m s
-1);
g is the gravitational acceleration (m s
-2);
De is the equivalent diameter of the slit channel (m);
s is the length of the flow channel (m).
Specific mechanical pressure exerted by the thermal drill on the borehole bottom in a borehole filled with antifreeze fluid can be estimated as:
where
Рd is the weight of the drill (N);
Vd is the volume of the drill (m
3);
Abb is area of the borehole bottom (m
2).
Equivalent diameter of the slit channel in the case, where the meltwater film thickness
δ is much smaller than the radius of the heater, will be:
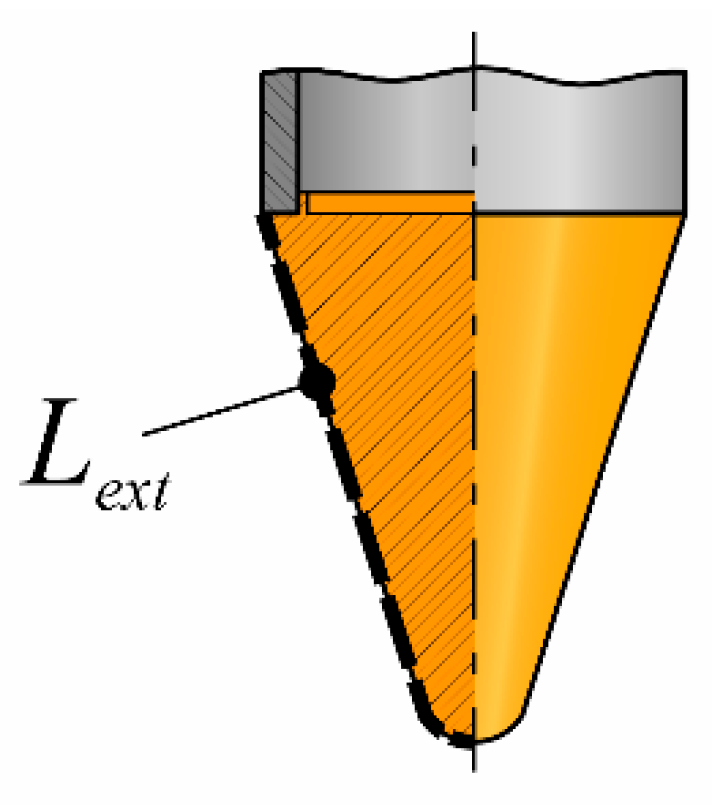
Length of the flow channel can be estimated using the length of the external section of the drill head from the tip to the top edge,
Lext (m) (
Figure 3):
Since the thickness of the meltwater film is very small, the flow regime within it assumed to be laminar. The hydraulic resistance coefficient
λ is given by the Poiseuille law:
where
K is the coefficient accounting for the channel shape;
v is the kinematic viscosity of water in the film (m
2 s
-1).
Since
δ is much smaller than the heater radius, the channel approximates a flat slit, and
K ≈ 96 [
19]. Average volumetric flow velocity across the channel cross-section can be considered as:
Substituting Eq. 12, Eq. 14 and Eq. 15 into equation Eq. 10 and solving for
δ, we obtain:
It should be noted that calculations based on the assumption of laminar water flow in the gap between the drill head and the borehole bottom become unreliable when the specific mechanical pressure approaches the hydrostatic pressure. In this regime, the pressure difference becomes small, the water velocity drops significantly, and although the water film thickness remains low, the flow may no longer be laminar. This may be due to the influence of capillary and surface tension effects, as well as flow instability. Therefore, the calculated ROP under such conditions should not be considered reliable.
Specific heat flux
q is transferred through the water film from the drill head to the borehole bottom. This heat flux provides energy for both ice melting (
qm) and the formation of the temperature field ahead of the melting front (
qf):
where
λw* is effective thermal conductivity of the water film (W m
-1 °C
-1); Nu
∞ is the asymptotic (limiting) Nusselt number. Since the meltwater film thickness
δ is much smaller than the drill head radius, the value Nu
∞ = 3.77 is used, which corresponds to a flat slit geometry.
Substituting Eq. 7, Eq. 8 and Eq. 18 into equation Eq. 17 and solving for
th, we obtain:
Substituting Eq. 9 into Eq. 19, we obtain the dependence of the ROP on all the main determining factors:
The resulting equation is transcendental. It can be solved, for example, using the method of successive approximations. This can be done either with mathematical software or by writing a dedicated utility for the solution. In this study, we used spreadsheet software, where the method of successive approximations was implemented through a custom macro. A description of the example spreadsheet layout is given in Section S1, and the full macro code is provided in Section S2. This spreadsheet is also available in the supplementary materials in .xlsm format.
It should also be noted that this model accounts for lateral heat transfer to the borehole wall using only the cylindrical section of the thermal head. Consequently, the thermal conductivity of the drill head material is used solely for calculating lateral heat losses. If the drill head under consideration does not include a cylindrical section, both the lateral heat losses and the thermal conductivity of the drill head material should be incorporated through empirical correction factors.
4. Thermal Drill Head Design: A Discussion of Key Factors
4.1. General Considerations
This section outlines the most important factors that must be considered when designing a thermal drill head, especially in the early stages of development. Design requirements typically depend on the objectives of the mission. In some cases, the primary goal may be to maximize ROP under specific constraints (e.g., target borehole diameter and a defined borehole-to-drill head clearance). In others, particularly for autonomous or energy-limited operations, achieving high efficiency may take priority. Alternatively, certain applications may require a balance between ROP and energy consumption.
In general, borehole diameter is one of the most critical constraints and should be defined early, as it largely determines the required drill head and the total power. Depending on the type of borehole (open or water-filled), achieving the desired diameter may require additional optimization of the drill head geometry, especially when sidewall heaters are not feasible. A common solution is to include a cylindrical section on the drill head (
Figure 2), which directs heat laterally toward the borehole walls and promote uniform enlargement. The influence of the cylindrical section height on ROP can be evaluated using the analytical model described in
Section 2.
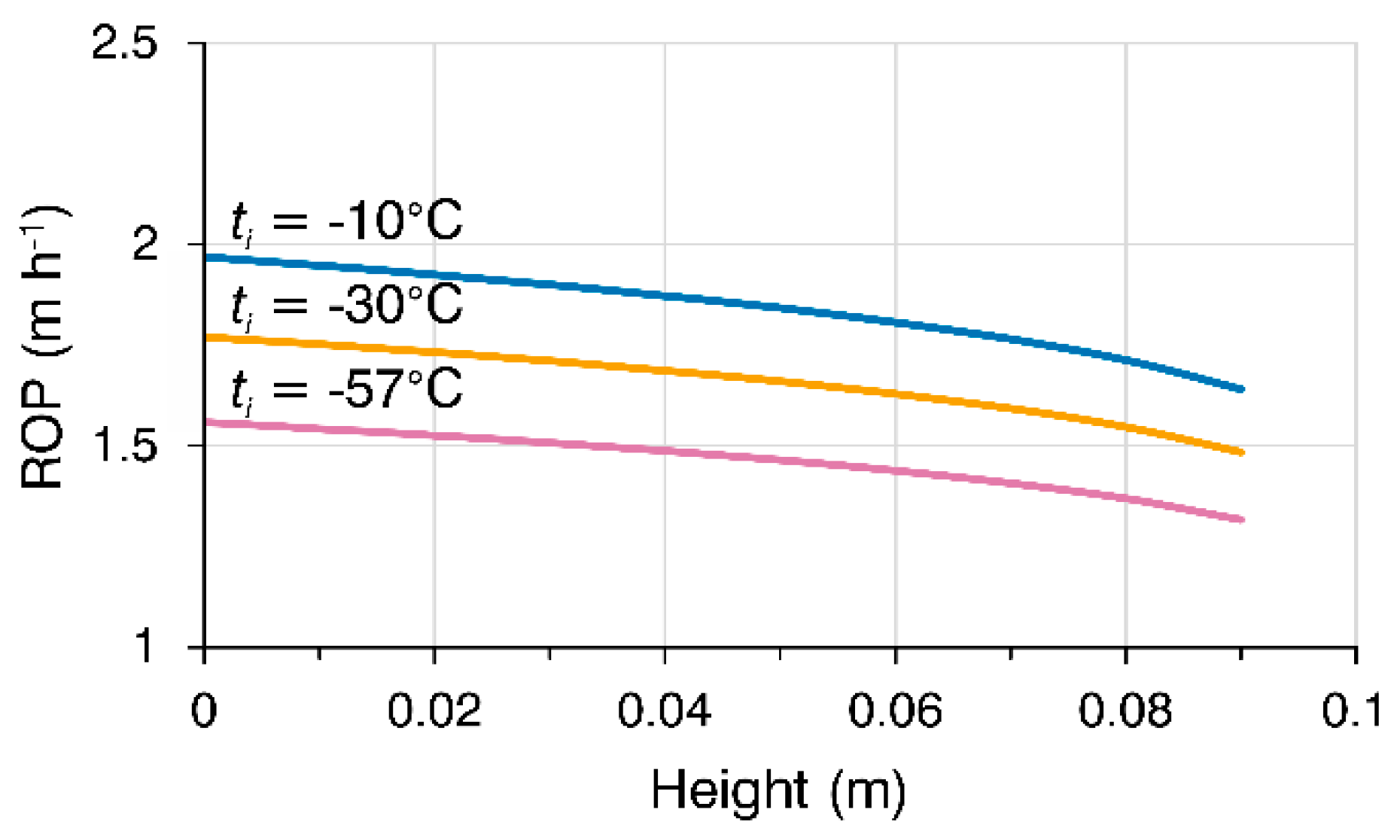
Figure 5 shows dependence of the ROP on height of the cylindrical section of the drill head
L at three different values of ice temperature and constant WOB of 60 N.
The key factors influencing the ROP are input power, WOB, thermal drill head shape, and the design of the heating system. ROP is also affected by the initial temperature of the ice, which cannot be controlled but must be just considered in performance estimation.
4.2. Efficiency
For the purpose of analysis, efficiency in hot-point drilling can be conditionally divided into two components: drill head efficiency and thermal drilling efficiency.
Drill head efficiency ηh characterizes the fraction of the electrical power supplied to the drill head that is converted into useful thermal energy at the interface with the ice. Not all of the input power reaches the melting surface. Internal losses include ohmic losses in the wires and connectors, thermal resistance at the interfaces between heaters and the drill head body, unwanted heat leakage into the internal volume of the assembly, heat accumulation in the bulk material of the drill head and non-uniform heat distribution caused by design constraints. The efficiency of the heating elements themselves must also be considered. For a copper drill head with cartridge heaters, a practical average ηh of 75-80% can be used as an initial assumption.
Thermal drilling efficiency ηd refers to the fraction of thermal energy delivered at the ice-drill interface that is used to melt the minimum volume of ice required to advance the borehole. It is influenced by external losses, including heat dissipation into the meltwater layer, lateral conduction into the surrounding ice, and overheating of the meltwater or adjacent ice beyond the melting point and even up to local boiling. Additionally, the geometry of the drill head influences the distribution of heat flow.
Thermal drilling efficiency can be estimated as:
where
Pm is minimum thermal power theoretically required for ice melting at a given ROP (W), calculated as [
21]:
where Δ
T is temperature difference between initial ice temperature and the melting point.
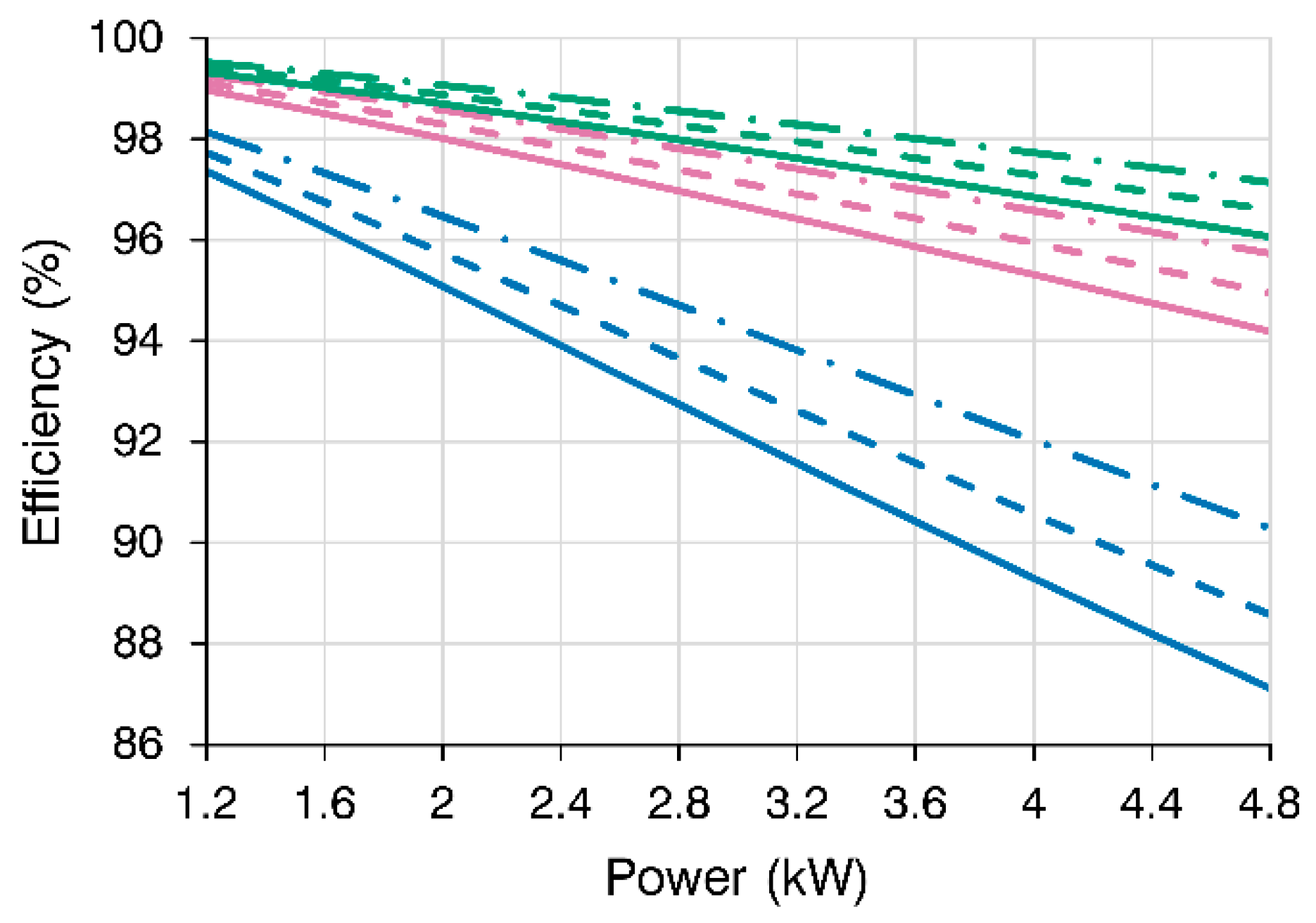
To illustrate the proposed approach, thermal drilling efficiency was calculated for the RECAS-200 drill head geometry and ice properties described in
Section 3. The results are presented in
Figure 6.
The graph shows that thermal drilling efficiency tends to decrease at higher power levels. At the same time, a slight increase in efficiency is observed as the initial ice temperature decreases, since the energy required to raise the ice to the melting point is also considered part of the useful work. Efficiency also increases with higher WOB, although the efficiency gain becomes smaller as WOB rises. It is important to note that the ROP in these calculations is not fixed, but rather determined from the analytical model as the maximum achievable under given conditions.
4.3. Power Requirements
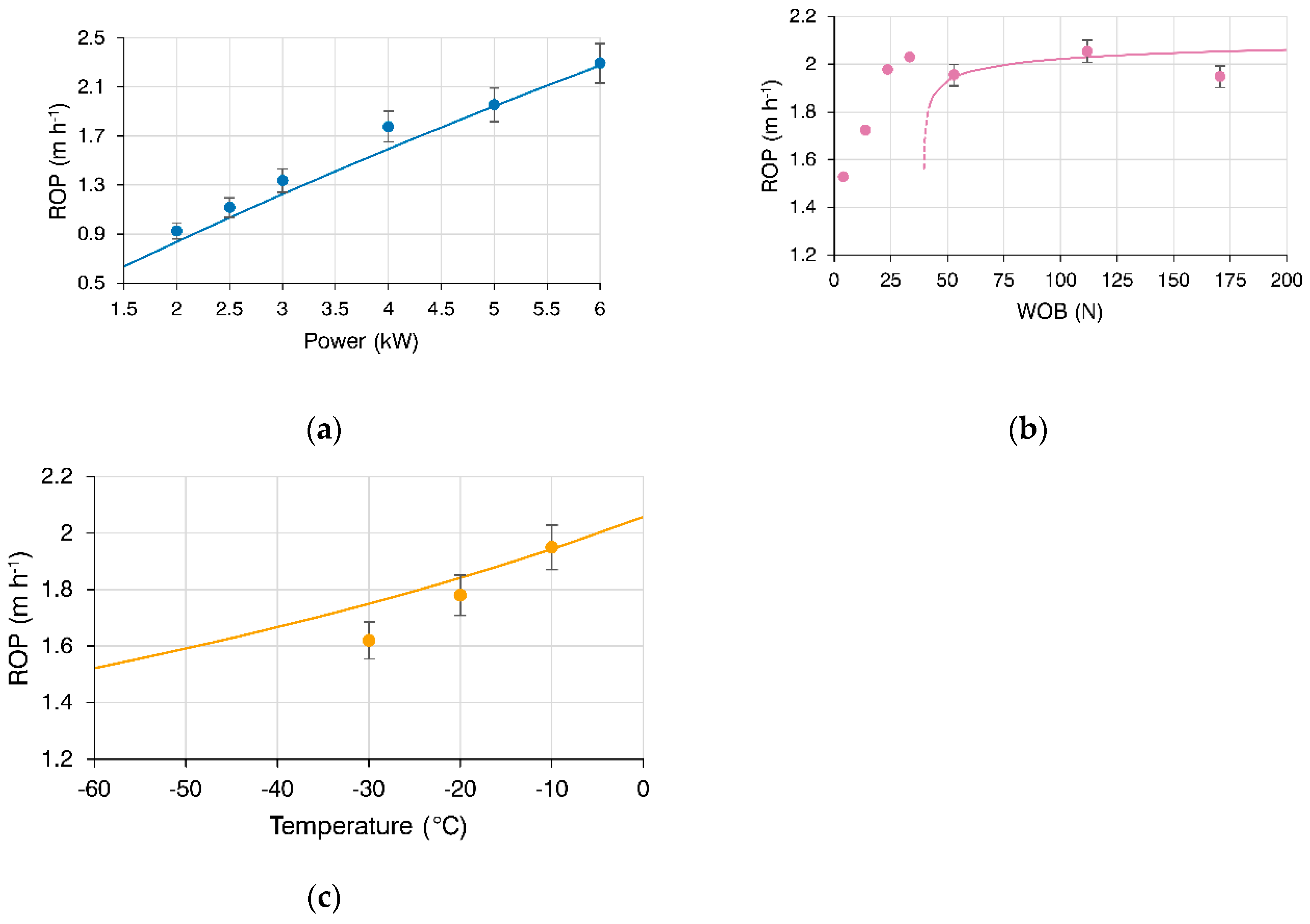
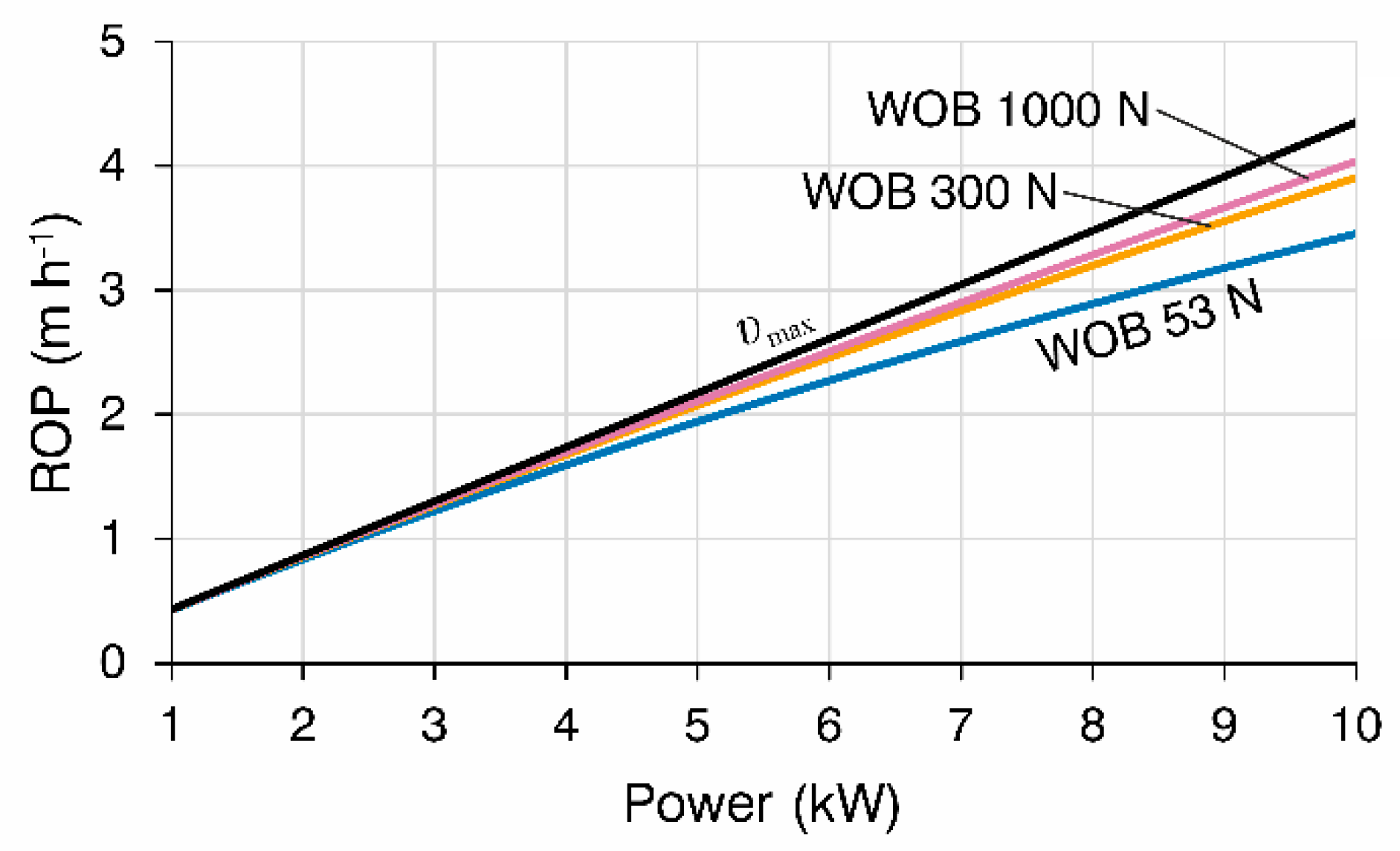
ROP is primarily influenced by the power delivered to the drill head. Within a practical operational range, the relationship is close to linear: higher power generally leads to faster ROPs (
Figure 7).
Despite the intuitive advantage of increasing the supplied power, there is a practical limit to the heat flux that can be transferred to ice without adverse effects. The meltwater film becomes the main barrier to heat transfer, as the thermal conductivity of water (0.58 W m
-1 °C
-1) is much lower than that of ice (2-2.2 W m
-1 °C
-1 at -10 °C) [
22].
The first limiting factor is the boiling point of the meltwater, which depends on the pressure within the water film. The second is the thermal conductivity and other physical properties of the drill head material, as well as its geometry. Theoretically, at sufficiently high ROPs, meltwater film can effectively carry away a relatively high heat flux from the surface of the drill head, until the surface and internal temperatures of the drill head reach levels at which the material begins to lose mechanical strength. According to Mellor (1986) [
23], the maximum sustainable heat flux for a long-life heater is approximately 3 MW m
-2.
The surface temperature required to sustain a given ROP can be estimated using Eq. (19), while the maximum admissible heat flux under specific conditions can be approximated by:
where
Tb is the boiling point of the meltwater (°C).
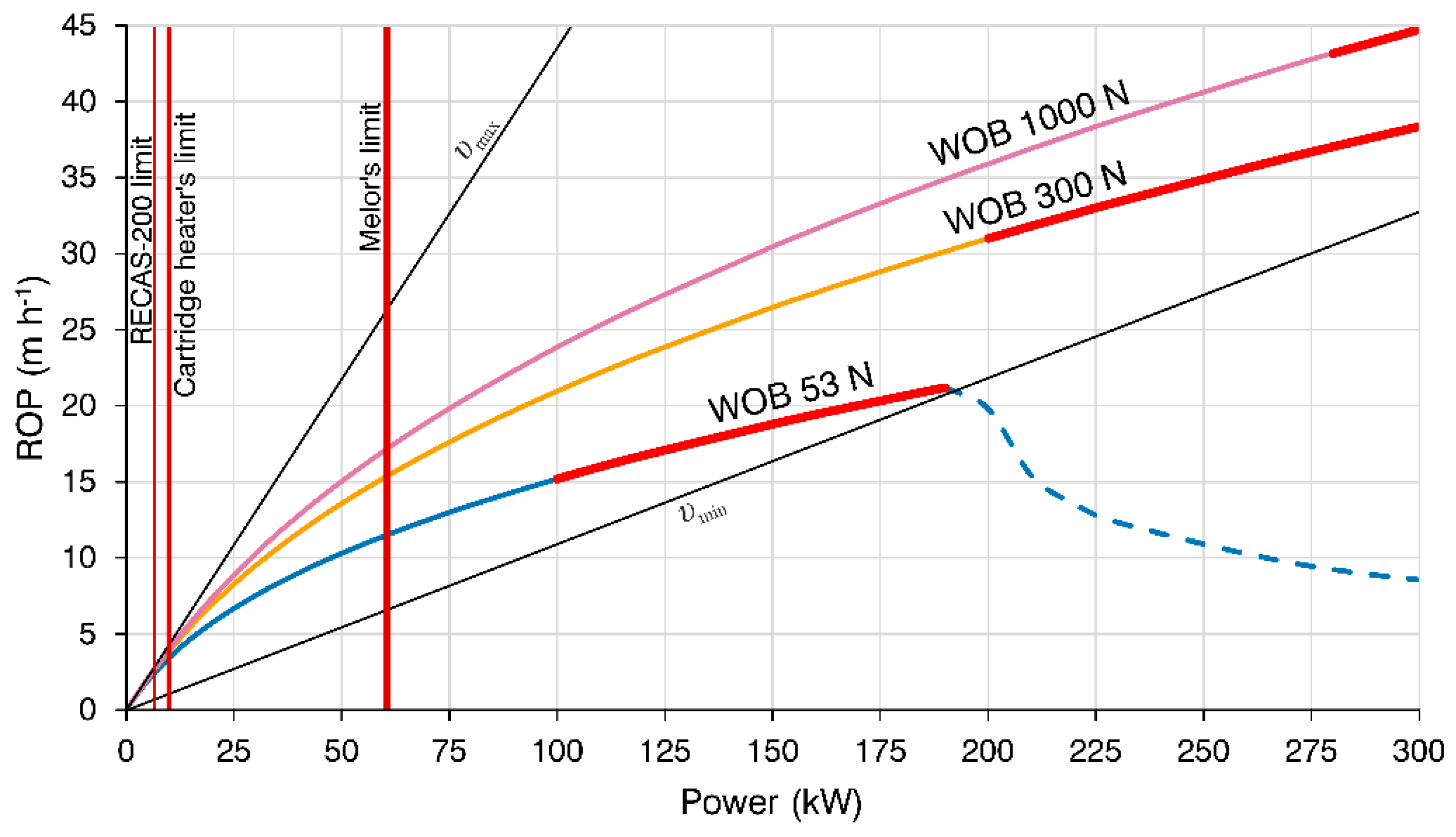
When cartridge heaters are used, the effective heat flux from the drill head surface is typically lower than the rated value of the heaters due to common drill head geometric constraints and internal thermal losses. Although cartridge heaters may offer a surface heat flux of only around 150 kW m-2. Eq. 23 can be used to estimate the minimum required ROP for sufficiently efficient heat removal.
Figure 8 shows ROP curves calculated using the analytical model described in
Section 2. The red segments of the curves indicate regions where the theoretical surface temperature of the drill head exceeds 300 °C – a threshold above which copper begins to lose structural strength. The line labeled
υmax represents the maximum theoretically achievable ROP, calculated from Eq. 22, while
υmin shows the minimum required ROP (Eq. 23). For instance, RECAS-200’s drill head uses sixteen heaters rated at 7.6 kW in total. Assuming 80% efficiency and an active surface area of 0.063 m
2, the resulting heat flux is approximately 96.5 kW m
-2. If the meltwater boiling point is assumed to be 100 °C, the minimal required ROP at maximum power for efficient heat removal would be approximately 0.83 m h
-1. If heat removal is insufficient, one of the two limiting factors described above will inevitably be reached. Additionally, the graph shows that once the calculated ROP drops below
υmin (dashed line), the analytical model becomes invalid.
4.4. WOB
WOB also plays an important role in both ROP and thermal drilling efficiency (
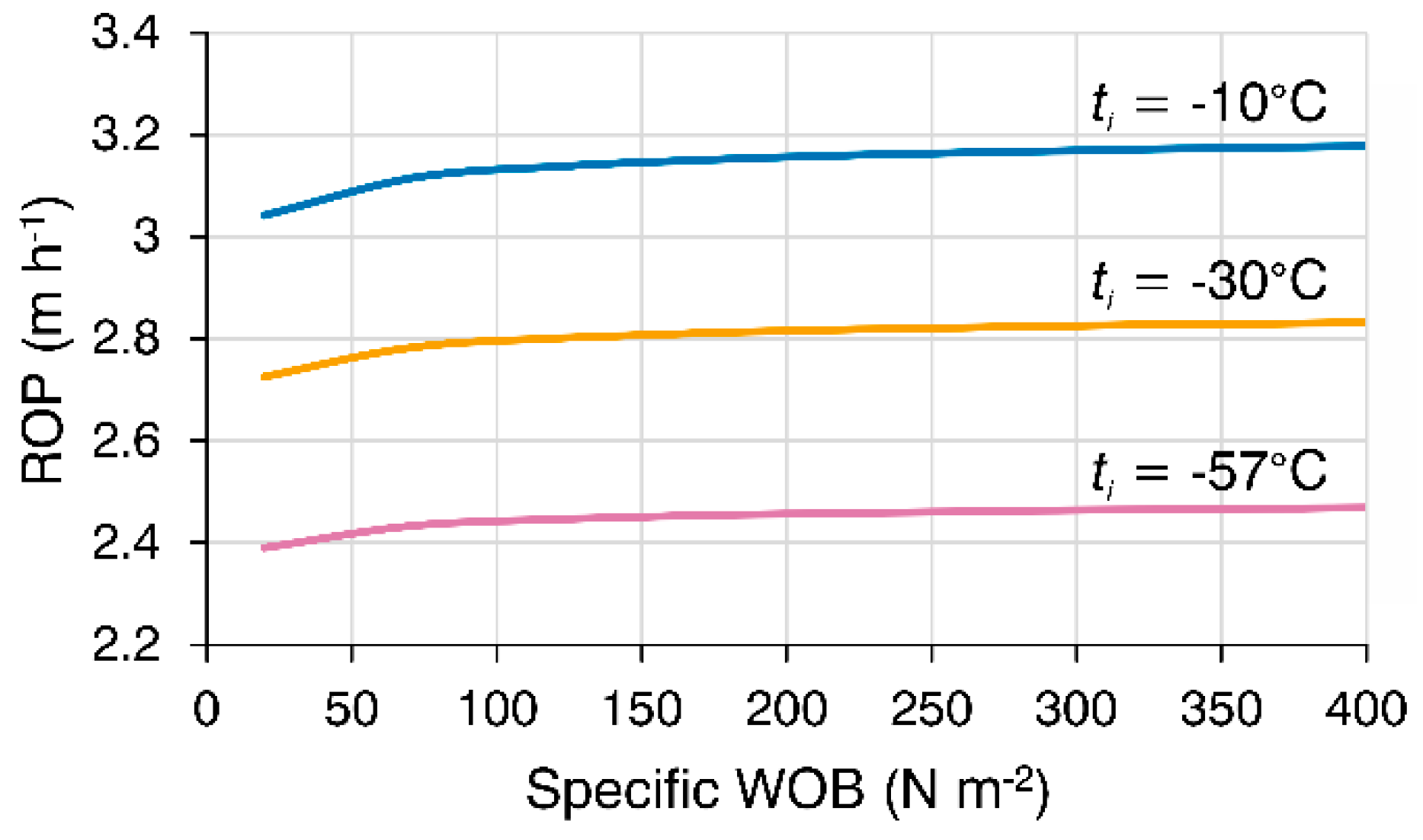
Figure 6, 7 and 8), as it affects the thickness of the meltwater layer at the thermal contact between the drill head surface and the ice. For optimal performance, the WOB should be large enough to ensure intimate contact and minimize the water film. It is also recommended that the applied WOB does not exceed half the total weight of the drill assembly in order to maintain verticality during drilling.
For preliminary estimations of the required WOB it is convenient to use specific load, which is the WOB per unit area of the cross-section of the thermal head. There is a practical limit when increasing the specific load does not result in a significant improvement in ROP (
Figure 9).
An approximate value of WOB sufficient for a specific case can be estimated using the model described in
Section 2. For more precise evaluation, CAE simulations [
3] or experimental studies [
20,
24] may be required.
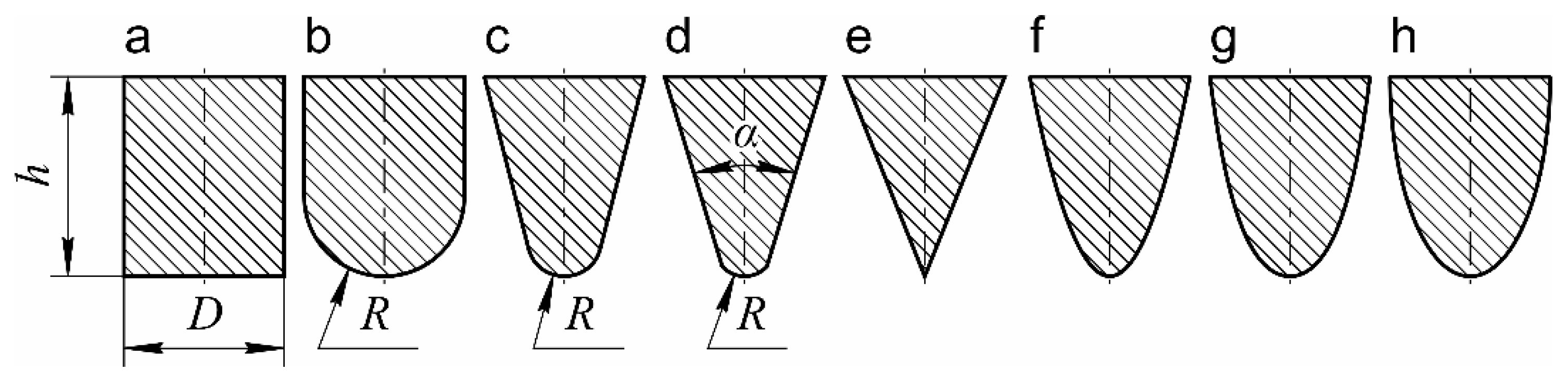
4.5. Thermal Drill Head Shape
Although there are examples of relatively successful projects that employed non-circular cross-sections [
25], the vast majority of thermal drill designs utilize heads shaped as bodies of revolution (
Figure 10). Each of these shapes presents distinct advantages and limitations. The cylindrical shape provides the largest surface area in direct contact with the ice, enabling higher power transfer. Its geometric simplicity also makes it easy to manufacture. However, this configuration has several notable drawbacks: it demonstrates low thermal drilling efficiency, as a significant portion of the heat is directed laterally rather than downward, and it offers neither self-centering capability nor directional stability. Additionally, this shape exhibits the lowest thermal drilling efficiency among standard configurations [
3,
26].
Hemispherical or similar rounded shapes help avoid sharp transitions and reduce the risk of local overheating. However, achieving uniform heat distribution over a curved surface is more complex, thereby increasing the design difficulty. Like the cylindrical shape, hemispherical profiles also lack axial guidance during drilling.
A shape approaching a full cone provides better self-centering and directional stability. The straight walls of a conical form facilitate relatively uniform heat distribution—though not perfectly so. The tip remains the most problematic area: if it becomes a cold spot, penetration slows; if it overheats, the low thermal mass makes it vulnerable to damage. Increasing the cone angle reduces thermal drilling efficiency and leads to higher heat losses, but it can also help minimize thermal disturbance in the surrounding ice [
3].
More complex shapes can also be considered, where the profile is defined by mathematical curves – such as parabola (
Figure 5f), catenary (
Figure 5g), elliptical (
Figure 5h), sinusoidal or power functions, or spline-based profiles. As with rounded shapes, achieving uniform heating across such surfaces remains challenging. According to Pudovkin et al. (1988) [
26], the parabolic profile demonstrated the highest thermal drilling efficiency compared to cylindrical, conical, and hemispherical designs. However, the performance differences between parabolic, full-cone, and hemispherical shapes were relatively minor, which aligns with the findings of Li et al. (2021) [
3].
In parabolic profiles specifically, increasing the elongation (and thus the overall height) generally improves thermal drilling efficiency [
26]. It is likely that the main advantage of a particular curve lies in the total working surface area, which enhances heat transfer and potentially increases ROP. Nevertheless, without detailed thermal-mechanical simulations and field validation, it is difficult to identify a single optimal profile.
An interesting alternative profile was experimentally investigated by Heinen et al (2021) [
7], who tested a thermal drill head with a concave parabolic shape. Despite its unconventional geometry, the experimental results showed performance comparable to more traditional designs, with overall efficiency reaching approximately 80%. One clear advantage of this shape is its compactness, which may be beneficial in systems where space is constrained. However, the concave geometry may also be more susceptible to the accumulation of debris or sediments in the melting zone. As such, this and similar profiles can be considered for applications where compactness is a priority and the drilling depth is relatively shallow.
According to Li et al. (2021) [
3], the drill head shape has only a minor effect on ROP; desired penetration rates can typically be achieved by increasing power input. However, the shape has a significantly stronger influence on thermal drilling efficiency. This limited impact of geometry on ROP is also supported by experimental data from Talalay et al. (2019) [
24].
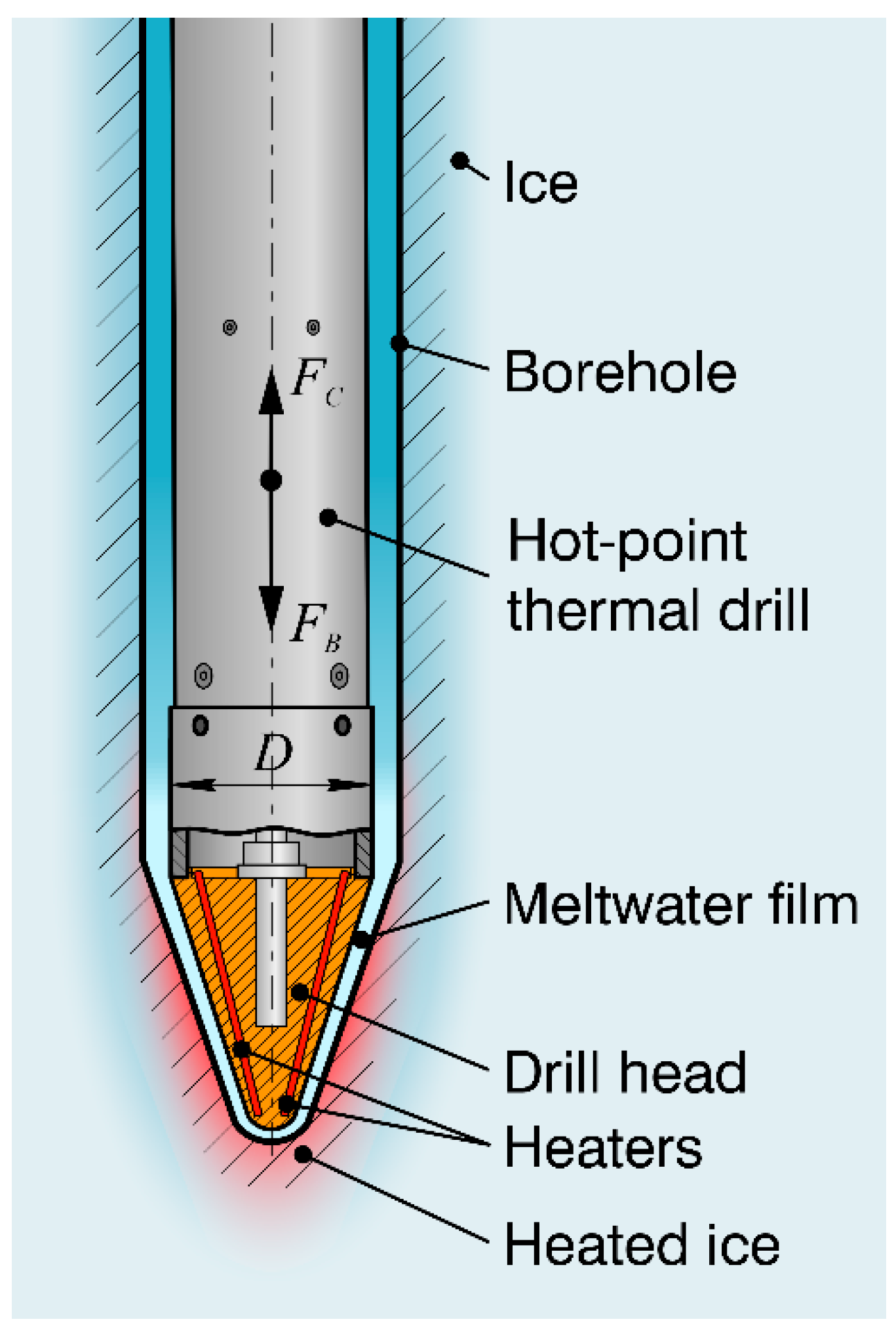
Figure 1.
Schematic of a hot-point thermal drill, except for the upper part with the cable termination. FB is the gravity force on the bit, and FC is the cable tension, which should always be applied to the drill to help maintain the verticality of the borehole.
Figure 1.
Schematic of a hot-point thermal drill, except for the upper part with the cable termination. FB is the gravity force on the bit, and FC is the cable tension, which should always be applied to the drill to help maintain the verticality of the borehole.
Figure 2.
Schematic of the drill head and borehole configuration of hot-point thermal drill.
Figure 2.
Schematic of the drill head and borehole configuration of hot-point thermal drill.
Figure 3.
Example of external section length on RECAS 200 thermal drill head.
Figure 3.
Example of external section length on RECAS 200 thermal drill head.
Figure 4.
Dependence of the ROP of RECAS-200 thermal sonde on: (a) power of the drill head; (b) WOB; (c) temperature of the ice.
Figure 4.
Dependence of the ROP of RECAS-200 thermal sonde on: (a) power of the drill head; (b) WOB; (c) temperature of the ice.
Figure 5.
Influence of the height of cylindrical section on the drill head on the ROP at three different values of ice temperature (initial parameters for the calculations are taken as for the RECAS-200 thermal sonde).
Figure 5.
Influence of the height of cylindrical section on the drill head on the ROP at three different values of ice temperature (initial parameters for the calculations are taken as for the RECAS-200 thermal sonde).
Figure 6.
Dependence of the thermal drilling efficiency on effective power output for three different ice temperatures and WOB values (initial parameters for the calculations are taken from the RECAS-200 thermal sonde configuration; line color corresponds to WOB: blue – 53 N, magenta – 300 N, green – 1000 N; line style corresponds to initial ice temperature: solid – -10 °C, dashed – -30 °C, dash-dotted – -57 °C).
Figure 6.
Dependence of the thermal drilling efficiency on effective power output for three different ice temperatures and WOB values (initial parameters for the calculations are taken from the RECAS-200 thermal sonde configuration; line color corresponds to WOB: blue – 53 N, magenta – 300 N, green – 1000 N; line style corresponds to initial ice temperature: solid – -10 °C, dashed – -30 °C, dash-dotted – -57 °C).
Figure 7.
Dependence of the ROP on power in practical operational range at three different values of WOB (initial parameters for the calculations are taken from the RECAS-200 thermal sonde configuration, ice temperature is -10 °C).
Figure 7.
Dependence of the ROP on power in practical operational range at three different values of WOB (initial parameters for the calculations are taken from the RECAS-200 thermal sonde configuration, ice temperature is -10 °C).
Figure 8.
Dependence of the ROP on power at three different values of WOB (initial parameters for the calculations are taken from the RECAS-200 thermal sonde configuration, ice temperature is -10 °C, meltwater boiling point is 100 °C).
Figure 8.
Dependence of the ROP on power at three different values of WOB (initial parameters for the calculations are taken from the RECAS-200 thermal sonde configuration, ice temperature is -10 °C, meltwater boiling point is 100 °C).
Figure 9.
Dependence of the ROP on specific load at three different values of ice temperature (initial parameters for the calculations are taken as for the RECAS-200 thermal sonde).
Figure 9.
Dependence of the ROP on specific load at three different values of ice temperature (initial parameters for the calculations are taken as for the RECAS-200 thermal sonde).
Figure 10.
Drill head shapes: (a) cylindrical; (b) hemispherical; (c) truncated cone with a rounded tip (continuous); (d) truncated cone with a rounded tip (discontinuous); (e) full cone; (f) parabola; (g) catenary curve; (h) elliptical.
Figure 10.
Drill head shapes: (a) cylindrical; (b) hemispherical; (c) truncated cone with a rounded tip (continuous); (d) truncated cone with a rounded tip (discontinuous); (e) full cone; (f) parabola; (g) catenary curve; (h) elliptical.
Table 1.
Comparison of key input parameters considered in analytical models for ice drilling by contact melting.
Table 1.
Comparison of key input parameters considered in analytical models for ice drilling by contact melting.
| |
Shreve
(1962)
|
Kudryashov and Shurko (1982) |
Fomin and Cheng (1981) |
Talalay et al. (2014) |
| Drill head dimensions |
radius or radii |
radii, height |
radius or radii |
diameter |
| Drill head shape |
✔ |
✔ (flow channel length) |
✔ (strictly parabolic) |
✘ |
| Drill head type |
annular and solid |
annular |
annular and solid |
solid |
| Applied thermal power |
✔ |
✔ |
✔ |
✔ |
| Initial ice temperature |
✘ |
✔ |
✔ |
✔ |
| Rate of penetration (ROP) |
✔ |
✔ |
✔ |
✔ |
| Weight on bit (WOB) |
✔ |
✔ |
✘ |
✘ |
| Other parameters |
- |
drill head’s material thermal conductivity |
- |
water final temperature |