Prerpints.org logo
Preprint
Article

Persistence Landscape based Topological Data Analysis for Personalized Arrhythmia Classification

Altmetrics

Downloads

818

Views

678

Comments

1

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Machine Learning and Biomedical Sensors

Submitted:

01 August 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
Data can be illustrated in shapes, and the shapes could provide insight for data modeling and information extraction. Topological data analysis provides an alternative insight in biomedical data analysis and knowledge discovery with the algebra topology tools. In present work, we study the application of topological data analysis for personalized electrocardiographic signal classification toward arrhythmia analysis. Using phase space reconstruction technique, the signal samples are converted into point clouds for topological analysis facility. With topological techniques the persistence landscapes from the point clouds are extracted as features to perform the arrhythmia classification task. We find that the proposed method is robust to the training set size, with only a training set size of 20% percents, the normal heartbeat class are 100% recognized, ventricular beats for 97.13%, supra-ventricular beats for 94.27% and fusion beats for 94.27% within the corresponding experiments. The property of keeping high performance when using smaller training sample proves that the proposed method is especially applicable to personalized analysis. With the present study, we show that the topological data analysis technique could be a useful tool in biomedical signal analysis, and provide powerful ability in personalized analysis.
Keywords: 
Subject: Computer Science and Mathematics  -   Signal Processing

1. Introduction

Human ECG sensing signals are the observed variables of Electrocardiographic(ECG) signals that reflect cardiac electrical activity over time. The abnormal pattern of ECG signal is associated with cardiac arrhythmia due to severe cardiac risks like stroke, heart failure, and sudden death[1]. Arrhythmia is one of the main tasks that could be induced by aging or different diseases like diabetes, hypertension, and obesity. Recognizing and detecting arrhythmia of the ECG sensor data is one of the main tasks of healthcare applications such as intelligent homes[2], rehabilitation[3], and mobile health[4,5]. Arrhythmia is an irregular heartbeat and is an important event to capture and analyze in modern healthcare systems. In most heart monitoring systems, the automatic detection and classification of the heartbeat signal are one of the most fundamental aspects for conserving life and personalized medicine in today’s growing population. As the Association for the Advancement of Medical Instrumentation (AAMI, Arlington, VA) recommended, the heartbeats could be classified into one of the five ECG patterns: N (normal beats originating in the sinus node), S (supra-ventricular ectopic beats), V (ventricular ectopic beats), F (fusion beats), and Q (unclassifiable beats) for heart monitoring. In this paper, based on N (normal beats originating in the sinus node), S (supra-ventricular ectopic beats), V (ventricular ectopic beats), and F (fusion beats) were used to study the abnormal ECG.
Physiologically, heartbeats exemplify complex systems involving turbulence and space-time wave propagation. The ECG signals collected by different types of sensors can reflect the physiological dynamics of the heart. These signals can be regarded as the observed variables of the dynamic system[6]. The dynamic ECG system will evolve, and the arrhythmia phenomenon represents the abnormal cardiac system. Therefore, the system’s future state can be predicted according to the practical representation information to realize the state monitoring of the ECG system[7]. The feature extracted from the clinical ECG systems is essential to modern arrhythmia systems. Richter et al. pioneered the phase-space reconstruction method to study ECG signals and gave a preliminary description of the morphological properties of ECG signals in phase space[6]. Valenza et al. employed Lyapunov exponents and approximate entropy parameters to study the nonlinear characteristics of heart rate variability in Holter-ECG[8]. The work on Correlation Dimension features of ECG signals to check heart rate variability is formulated in the study of Bolea et al. [9]. Chen et al. used the related tools of Chaos theory to analyze the phase space of ECG signals and extract the corresponding features to realize the identification based on ECG signals[10]. Desai et al. used the feature analysis method of Recurrence Quantification Analysis to learn the modeling and classification of ECG patterns in the state of tachycardia[11]. Other Nonlinear Dynamical System Analysis Techniques, such as Detrended Fluctuation Analysis (DFA)[10] and Poincaré Plot[12], are also used in ECG analysis applications. For the ECG signal with robust chaos, the traditional features cannot represent the nonlinear characteristics of ECG, and some nonlinear features cannot describe the self-organization characteristics of ECG signals. Therefore, we focus on the study of phase-space reconstruction jointly with a recently fast-developing technique of topological data analysis (TDA).
The TDA technique adopts a persistent homology[13,14]tool to describe the point clouds, providing a novel description of the structure of the point clouds and topological properties of the phase space. Topological data analysis theory was first proposed by Gunnar Carlsson et al. and applied to data analysis[15]. The description of simple, complex, and persistent homology tools is abstract. To more intuitively understand the change of state space, Bubenik et al. used the persistence situation function to describe the state complexity when time series changes[16]. Seversky et al.[17]extracted topological imprints from time series to explain features and realize classification problems in standard signals. The nonlinear dynamics analysis with topological descriptions has been used in wheeze detection[18], heart dynamics analysis toward arrhythmia detection[19], gait dynamics analysis toward neurodegenerative disease discrimination[20,21], EEG-based dynamics analysis toward brain state recognition[22], and plenty of time series classification applications[23,24]. TDA provided an alternative viewpoint for signal analysis and enriched the nonlinear dynamical system-based signal processing research. The jointly nonlinear analysis methods could provide essential features for arrhythmia analysis. [6]use time-delay embedding to convert the ECG signal into a 2-D point cloud for cardiac system analysis. In[25], the term topological signal representation was proposed using time-delay embedding and TDA. Besides, Safarbali[26] offered a statistical analysis using the time-of-life phrase in persistent homology of TDA toward the atrial fibrillation nonlinear dynamic analysis, and Dindin[27] used the Betti curves as an alternative feature of the deep learning representations, using in a recognition system with a cascaded modular neural network. TDA constitutes an alternative to traditional statistical methods used in recognition applications. From a nonlinear dynamical system viewpoint, the system’s information can contribute to the machine learning tasks, which depend on entirely different theories than statistical ones. How to incorporate the system information into the machine learning statistical computation framework, a recent topological signature[28,29,30] termed persistence landscape answers. This work illustrates how to use the topological signatures in the arrhythmia classification system.
In this spirit, the main contribution of this work includes:
Based on single lead ECG data set, we adopted a nonlinear dynamic characteristic analysis ECG modeling method to extract nonlinear topological dynamic characteristics of four kinds of ECG signals for abnormal heart rate detection.
Based on the extracted topological features, we set up four experiments and four test set training set ratios for ECG anomaly detection. When only 20% of the samples are used for training, the classification performance of normal heartbeat class is 100% recognized, ventricular beats for 97.13%, supra-ventricular beats 10 for 94.27%, and fusion beats for 94.27%. The experimental results show that TDA is a practical solution for the robust detection of ventricular ectopic and supraventricular ectopic beats that can effectively characterize the nonlinear system of ECG.

2. Materials & Method

2.1. Materials and pre-processing

The method proposed in Section I is applied to the long-term ECG data in the Physionet MIT-BIH Long-Term database (PhysioBank)[31]. The long-term ECG database contains six two-channel ECG signals sampled at 128 Hz per channel with 12-bit resolution and one three-channel ECG sampled at 128 Hz per channel with 10-bit resolution. The seven long-term ECG record IDs are 14046, 14134, 14149, 14157, 14172, 14184, and 15814. We resample the ECG signals to 340 Hz, a typical sampling rate in ECG algorithm studies. The baseline wander (caused by perspiration, respiration, and body movements), power line interference, and muscle noise were removed with a Butterworth filter. Then the filtered ECG signals were segmented into individual heartbeat waveforms based on the detected R peaks. With the extracted R peaks, each 340-point signal is determined in an ad-hoc rule: set the R position as the 141 points, and pull the anterior 140 points and the following 199 points from the original time series. Then the extracted samples are illustrated in Table 1.
We can see that the data samples are severely imbalanced for each record. So we further redesign an experiment with the following settings:
1. Data samples with a limited number are ignored, like the F class in ID 14172 and V in ID 15814;
2. As some samples are ignored, the classification task in ID 14184 and ID 14046 becomes a two-class classification task.
Then we only focus on the 3-class classification task in ID 15814, ID 14134, and ID 14172. For each job, we randomly select the corresponding signal samples to make the signal sample distribution balanced and also for the reduction of computation consumption. As Table 2 illustrated, each task allocations for the signal samples are 1:2:4. For a small sample validation, we designed different experiments with 100 representatives from each class from ID 14172. Next, we will conduct experiments based on the preprocessed data.

2.2. Phase Space Reconstruction

ECG signals are nonlinear and non-stationary time series. When the topological nonlinear dynamic analysis is carried out, the ECG time series can be converted into the corresponding trajectory in the phase space. This process is called phase space reconstruction[32], and the reconstructed phase space is called topological space. In phase space reconstruction, the ECG time series is transformed into a point cloud in abstract phase space by time delay embedding[33,34], and the point cloud is regarded as a collection of vector points. Mathematically, consider the time series of { t 0 , t 1 , ⋯ } , the time delay embedding can be denoted as:
x k = ( t k , t k + τ , ⋯ , t k + ( d − 1 ) τ )
X k is the time series after delay embedding. The state point cloud of the dynamics of a moving system can be represented by the state point set of X = { x 0 , x 1 , x 2 , ⋯ } . Two crucial factors in the PSR stage are the time delay parameter denoted as τ and the dimension indicated as d used to unfold the dynamics in the phase space. Selecting appropriate parameters can improve the robustness of the model. In previous studies, many methods for phase space reconstruction have been proposed, such as average mutual information method[35], relevant strategies for selecting optimal delay parameters[36], methods for determining delay parameters based on geometric information[37] and pseudo-nearest neighbor algorithm[38]. Based on relevant studies[39], it is found that the fixed size remains unchanged, which will not affect the validity of the experimental conclusion. Therefore, based on the principle of the average mutual information method and set size, τ =5 and d =2 are selected as the optimal parameters for delayed embedding in this experiment. As shown in Figure 2, the ECG signal is mapped to the point cloud formed in the image space.

2.3. Persistent Homology

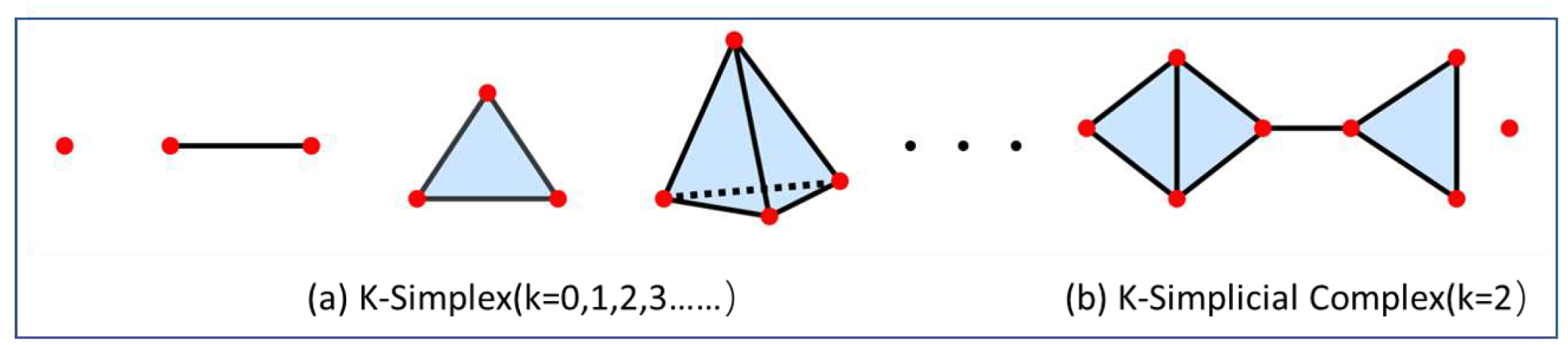
Persistent homology is one of the main tools for topological data analysis, which can be used to analyze point clouds in topological space. The analysis principle uses simple complex sequences to describe the relationship between data points and extract effective topological features[40]. Among them, a simple complex is a data structure that uses geometric objects such as points (0-simplex), lines (1-simplex), triangular surfaces (2-simplex), and tetrahedrons (3-simplex) to splice or glue into the whole topological space(as shown in Figure 1(a)). In higher dimensional space, a shape formed by connecting two or more simplex forms is called a simple complex(as shown in Figure 1(b)). The modeling of persistent homology is to regard a single point in the topological space as a ball with a radius of ϵ . 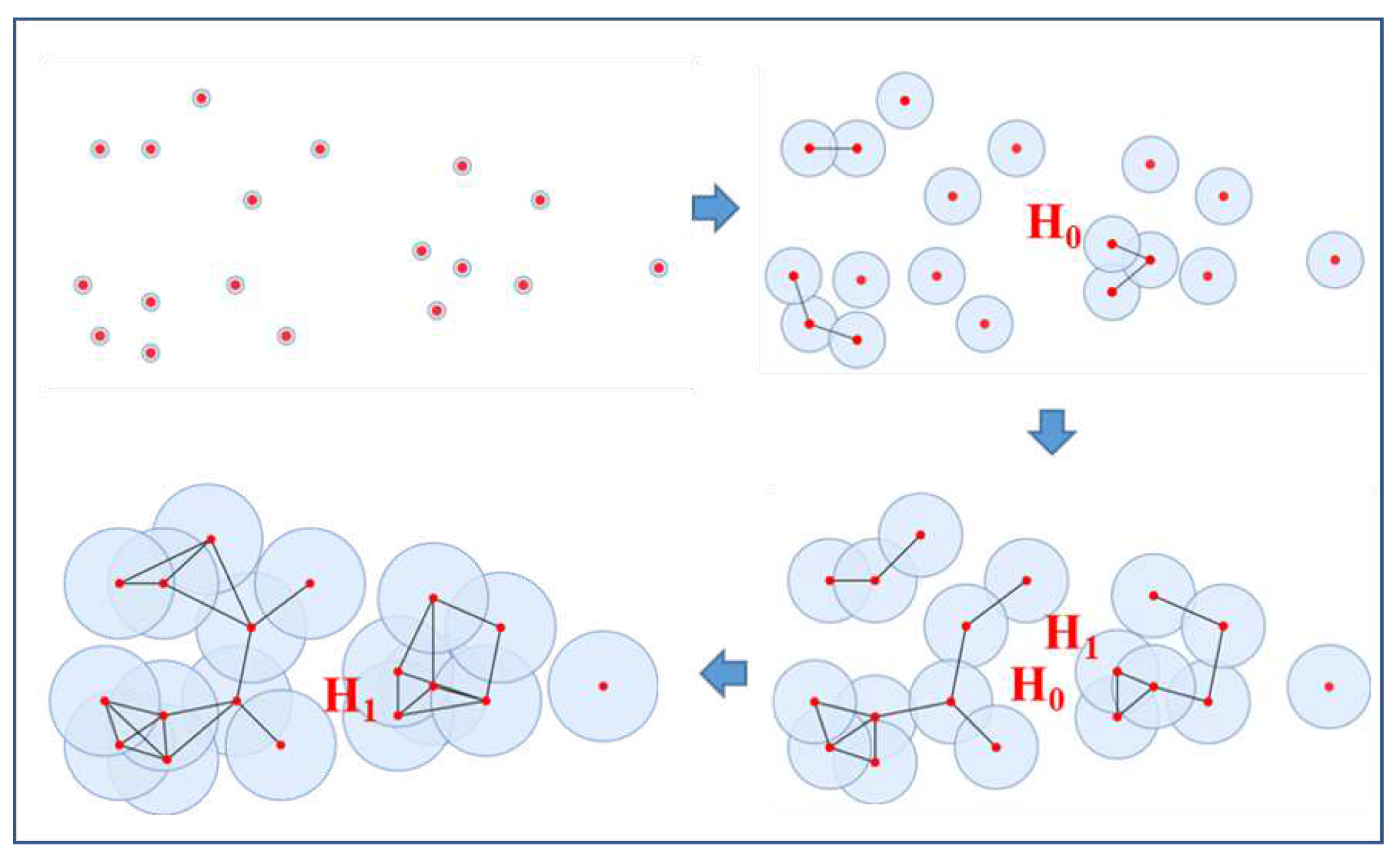Various simple, complex forms can represent the topological properties of different radius balls. The specific construction process is as follows:
1)First, replace the points of { x 1 , x 2 , . . . x m } with the radius-based sphere disks in the 2-dimension case with a radius parameter ϵ , These points can be represented as { B ( x 1 , ϵ ) , B ( x 2 , ϵ ) , . . . B ( x m , ϵ ) } .
2) Then, gradually increase the radius parameter ϵ from 0 to ∞. As the parameter of ϵ gradually increases, the ϵ -spheres collide and merge to form new components and holes, as shown in Figure 2.
3) Finally, all the individual objects of B ( x m , ϵ ) merged into one sphere when the radius of the spheres ϵ increases to ∞.
Preprints 81175 g001
Figure 1. Simplex: (a) the k-simplexes; (b) the combination of simplexes forms a simplicial complex.
Figure 1. Simplex: (a) the k-simplexes; (b) the combination of simplexes forms a simplicial complex.
Preprints 81175 g001
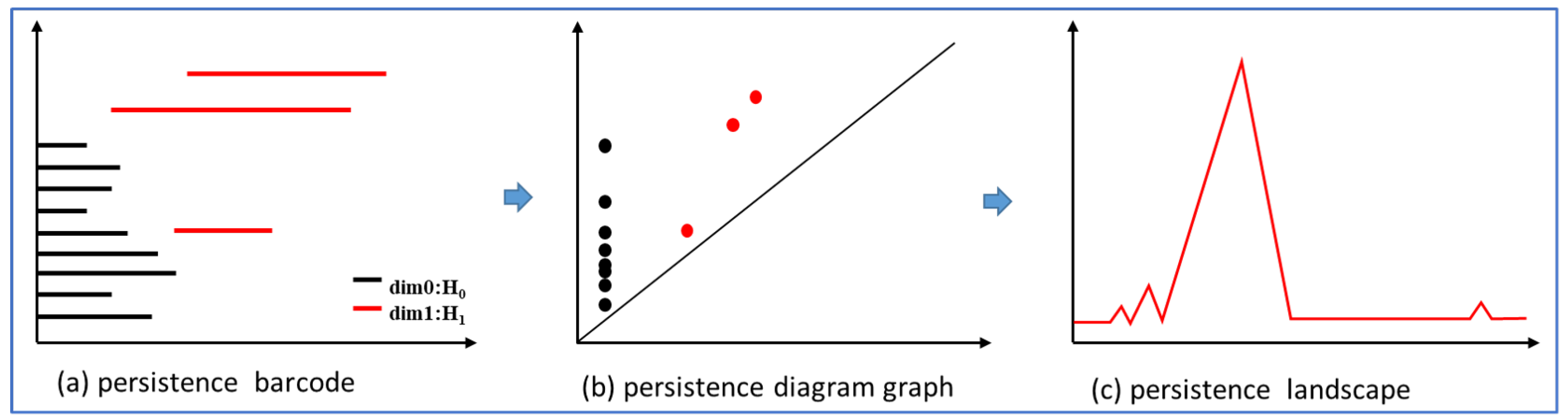
The components and holes appear and disappear in the process of simple-complex construction, as illustrated in Figure 2; the connected components belong to the 0-dimensional homology class H 0 , while the holes belong to the 1-dimensional homology class H 1 as shown in Figure 2. The persistent barcode can record the continuous state of holes[41]. The straight line length represents the survival time of different holes, as shown in Figure 3(a).
Preprints 81175 g002
Figure 2. 2D point cloud modeling process based on persistent homology.
Figure 2. 2D point cloud modeling process based on persistent homology.
Preprints 81175 g002
Preprints 81175 g003
Figure 3. Barcode Illustrations.
Figure 3. Barcode Illustrations.
Preprints 81175 g003

2.4. Topological Feature Extraction

From the perspective of machine learning applications, persistent barcodes generated with the topological method can be considered alternative feature sets. Some applications directly consider the persistent barcode as an estimator in statistics or features[42], i.e., use the barcode intervals as representation. Further, using distance measures like the Bottleneck and Wasserstein distance for comparison, the topological similarity between persistence diagrams for applications in protein binding analysis[43]. Other essential works are distance-based signal classification[44]. In this work, we use the Persistence Landscape as our topological nonlinear features based on the persistence of H 0 and H 1 .
The persistent landscape is transformed from the persistent barcode. Firstly, the persistent barcode can be transformed into a persistence diagram graph with birth indices on the horizontal axis and death indices on the vertical axis in Figure 3(b). The homology α was "born" at b α and "die" at d α which make a pair ( b α , d α ) .
For each birth-death point ( b α , d α ) , a piecewise linear function:
f ( b α , d α ) x − b α , i f x ∈ ( b α , b α + d α 2 ) − x + b α , i f x ∈ ( b α + d α 2 , d α ) 0 , i f x ∉ ( b α , d α )
with which a sequence of functions λ can be given by:
λ ( x ) = k − m a x { f ( b α , d α ) ( x ) | ( b α , d α ) ∈ P k }
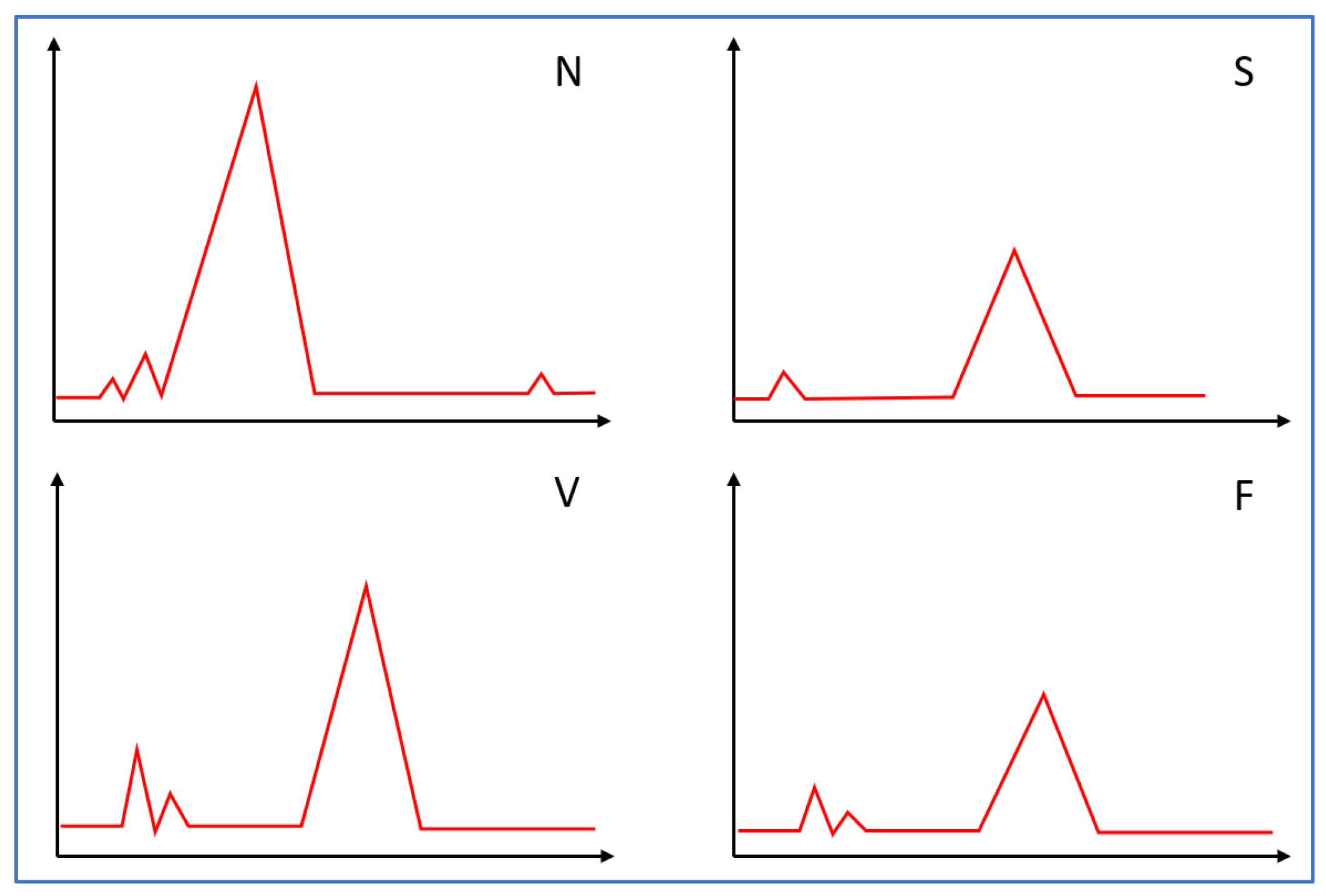
Where the k-max denotes the k-th most enormous value of a function, statistical methods can be involved with the persistence landscape in Banach space. More theory descriptions of persistence landscape can be referred to from[45]. The persistent landscape for the four ECG types is shown in Figure 4.

2.5. Algorithm Evaluation

Based on the nonlinear topological features of ECG, we use the Random forests (RF) classifier to perform the multi-class classification task. RF is an ensemble learning method for classification, widely used in different classification and regression problems. The proposed method could be evaluated as a usual classification task parameters, we calculate the four parameters in confusion matrix: the correct classification number (TP as true positive samples); the false classification number (FN as false negatives); correct normal classification number (TN true negatives); and false classification number (FP as false positives). We use the normalized confusion matrix for the performance evaluation. In the normalized confusion matrix, a row represents an instance of the class with its actual label, and a column represents the predicted class. Then the values of the diagonal elements are the correctly classified proportions. In the meantime, the off-diagonal elements are misclassified information. Then higher values in the diagonal elements mean better results.

3. Results & Discussion

With the experiment’s settings, we evaluated the features of the proposed framework with the random forest classifier. We can see that in Figure 4, the persistence landscapes for each class are distributed differently. With the persistence landscapes for each data sample, we set the experiments with a training partition size of 80%, 60%, 40%, and 20%. The rest of the data samples are treated as testing sets. The performance is evaluated with classification confusion matrixes illustrated in Figure 5.
The proposed method evaluated the classification task for N, V, and F. We can see that the V class was well classified; even with only 20% percent of samples used in the training process, the test result of the V class can achieve 89.35%. The results for the F class recognition, the performance dropped rapidly as the training sample reduced from 70.71% to 58.31%. Table 2 shows that in Exp#1, there are only 992 F samples for evaluation. When the training size is set to 20%, with only about 200 training samples, the recognition rate can still achieve 58.31%.
The experiment results of Exp#1 are shown in the first row of Figure 5. In Exp #1, a 3-class
In the second row of Fig5, for Exp#2, the N, V, and F-oriented 3-class classification task was evaluated. With 20% percent for the training set, the recognition rates of V and F classes achieve 96.31% and 91.97%, respectively. In the third row for Exp#3, the N, S, V oriented 3-class classification task was evaluated, and the recognition rates of V and F are 95.88% and 97.88%, respectively, when training size set into 20%. The fourth row illustrates the results of Exp#4, and we use a small data size; the results also show excellent performance.
This paper introduces a new personalized ECG beat classification and arrhythmia analysis scheme using the algebra topology field’s persistence landscape. This work is the first on the TDA representation persistence landscape applied to the personalized arrhythmia analysis. The project has been proven as an efficient representation of ECG analysis, primarily when used in small training sizes; the technique shows great potential.
Compared to the previous work in ECG classification or arrhythmia analysis. We have the following different settings:
  • In many ECG analysis tasks, they validate the method using a mixture of different patients. However, in this work, we focus more on personalized settings. The reason for this setting is that, for different individuals, the cardiac system could differ from the physiological system. The locations could bring a sample deviation because of the dynamics difference, which departures the purpose of this study.
  • The topological method was used in this study to extract representations that differ from the statistical features’ work. This study is more related to nonlinear signal analysis, which uses TDA instead of other nonlinear parameters.
  • There is a limited study on the small training set experiments; the proposed experiments show that the proposed method could perform well for the arrhythmia analysis task. This specialty could be meaningful for wearable or clinical applications when dealing with a high prediction performance under limited data source conditions.

4. Conclusion

The TDA methods provide alternative insights compared to the statistical features. We show that a TDA-based signal feature, namely persistence landscape, can give useful representation for personalized arrhythmia analysis. The proposed method performs well when dealing with customized arrhythmia analysis in our experiments. We also find that the proposed method is robust to the size of the training set. When dealing with only 20% of the total training dataset, it achieves a 100% accuracy for normal heartbeats, 98.75% for ventricular beats, 95.88% for supra-ventricular moments, and 91.97% for fusion beats. Thus the method can be trained for a single individual, allowing for personalized analysis systems. The study proves that topological data analysis is a representation tool for nonlinear ECG data, which can effectively map the characteristics of the nonlinear dynamic system of ECG. It is a successful attempt at topological data analysis in nonlinear physiological signals and lays a foundation for more complex physiological signal analysis. TDA is an effective tool for biomedical signal analysis with potential applications in personalized data processing.

References

  1. A. S. Go, E. M. Hylek, K. A. Phillips, Y. Chang, L. E. Henault, J. V. Selby, and D. E. Singer, “Prevalence of diagnosed atrial fibrillation in adults: national implications for rhythm management and stroke prevention: the anticoagulation and risk factors in atrial fibrillation (atria) study,” Jama, vol. 285, no. 18, pp. 2370–2375, 2001.
  2. M. M. Baig, H. Gholamhosseini, and M. J. Connolly, “A comprehensive survey of wearable and wireless ecg monitoring systems for older adults,” Medical & biological engineering & computing, vol. 51, pp. 485–495, 2013. [CrossRef]
  3. C. Glaros, D. Fotiadis, A. Likas, and A. Stafylopatis, “A wearable intelligent system for monitoring health condition and rehabilitation of running athletes,” in 4th International IEEE EMBS Special Topic Conference on Information Technology Applications in Biomedicine, 2003. IEEE, 2003, pp. 276–279.
  4. J. Lee, B. A. Reyes, D. D. McManus, O. Maitas, and K. H. Chon, “Atrial fibrillation detection using an iphone 4s,” IEEE Transactions on Biomedical Engineering, vol. 60, no. 1, pp. 203–206, 2012. [CrossRef]
  5. P.-H. Chan, C.-K. Wong, Y. C. Poh, L. Pun, W. W.-C. Leung, Y.-F. Wong, M. M.-Y. Wong, M.-Z. Poh, D. W.-S. Chu, and C.-W. Siu, “Diagnostic performance of a smartphone-based photoplethysmographic application for atrial fibrillation screening in a primary care setting,” Journal of the American Heart Association, vol. 5, no. 7, p. e003428, 2016. [CrossRef]
  6. M. Richter and T. Schreiber, “Phase space embedding of electrocardiograms,” Physical Review E, vol. 58, no. 5, p. 6392, 1998. [CrossRef]
  7. A. S. Al-Fahoum and A. M. Qasaimeh, “A practical reconstructed phase space approach for ecg arrhythmias classification,” Journal of medical engineering & technology, vol. 37, no. 7, pp. 401–408, 2013. [CrossRef]
  8. G. Valenza, P. Allegrini, A. Lanatà, and E. P. Scilingo, “Dominant lyapunov exponent and approximate entropy in heart rate variability during emotional visual elicitation,” Frontiers in neuroengineering, p. 3, 2012. [CrossRef]
  9. J. Bolea, P. Laguna, J. M. Remartínez, E. Rovira, A. Navarro, and R. Bailón, “Methodological framework for estimating the correlation dimension in hrv signals,” Computational and mathematical methods in medicine, vol. 2014, 2014. [CrossRef]
  10. C.-K. Chen, C.-L. Lin, S.-L. Lin, Y.-M. Chiu, and C.-T. Chiang, “A chaotic theoretical approach to ecg-based identity recognition [application notes],” IEEE Computational Intelligence Magazine, vol. 9, no. 1, pp. 53–63, 2014. [CrossRef]
  11. U. Desai, R. J. Martis, U. R. Acharya, C. G. Nayak, G. Seshikala, and R. SHETTY K, “Diagnosis of multiclass tachycardia beats using recurrence quantification analysis and ensemble classifiers,” Journal of Mechanics in Medicine and Biology, vol. 16, no. 01, p. 1640005, 2016. [CrossRef]
  12. Y. Gong, Y. Lu, L. Zhang, H. Zhang, and Y. Li, “Predict defibrillation outcome using stepping increment of poincare plot for out-of-hospital ventricular fibrillation cardiac arrest,” BioMed research international, vol. 2015, 2015. [CrossRef]
  13. H. Edelsbrunner, J. Harer et al., “Persistent homology-a survey,” Contemporary mathematics, vol. 453, no. 26, pp. 257–282, 2008.
  14. N. Otter, M. A. Porter, U. Tillmann, P. Grindrod, and H. A. Harrington, “A roadmap for the computation of persistent homology,” EPJ Data Science, vol. 6, pp. 1–38, 2017. [CrossRef]
  15. G. Carlsson, “Topology and data,” Bulletin of the American Mathematical Society, vol. 46, no. 2, pp. 255–308, 2009.
  16. P. Bubenik et al., “Statistical topological data analysis using persistence landscapes.” J. Mach. Learn. Res., vol. 16, no. 1, pp. 77–102, 2015.
  17. L. M. Seversky, S. Davis, and M. Berger, “On time-series topological data analysis: New data and opportunities,” in Proceedings of the IEEE conference on computer vision and pattern recognition workshops, 2016, pp. 59–67.
  18. S. Emrani, T. Gentimis, and H. Krim, “Persistent homology of delay embeddings and its application to wheeze detection,” IEEE Signal Processing Letters, vol. 21, no. 4, pp. 459–463, 2014. [CrossRef]
  19. B. Safarbali and S. M. R. H. Golpayegani, “Nonlinear dynamic approaches to identify atrial fibrillation progression based on topological methods,” Biomedical Signal Processing and Control, vol. 53, p. 101563, 2019. [CrossRef]
  20. Y. Yan, K. Ivanov, O. Mumini Omisore, T. Igbe, Q. Liu, Z. Nie, and L. Wang, “Gait rhythm dynamics for neuro-degenerative disease classification via persistence landscape-based topological representation,” Sensors, vol. 20, no. 7, p. 2006, 2020. [CrossRef]
  21. Y. Yan, O. M. Omisore, Y.-C. Xue, H.-H. Li, Q.-H. Liu, Z.-D. Nie, J. Fan, and L. Wang, “Classification of neurodegenerative diseases via topological motion analysis—a comparison study for multiple gait fluctuations,” IEEE Access, vol. 8, pp. 96 363–96 377, 2020. [CrossRef]
  22. J. M. Kilner and K. J. Friston, “Topological inference for eeg and meg,” The Annals of Applied Statistics, pp. 1272–1290, 2010.
  23. Y. Umeda, “Time series classification via topological data analysis,” Information and Media Technologies, vol. 12, pp. 228–239, 2017. [CrossRef]
  24. F. A. Khasawneh, E. Munch, and J. A. Perea, “Chatter classification in turning using machine learning and topological data analysis,” IFAC-PapersOnLine, vol. 51, no. 14, pp. 195–200, 2018. [CrossRef]
  25. Z. Zhang, Y. Song, H. Cui, J. Wu, F. Schwartz, and H. Qi, “Topological analysis and gaussian decision tree: Effective representation and classification of biosignals of small sample size,” IEEE Transactions on Biomedical Engineering, vol. 64, no. 9, pp. 2288–2299, 2016. [CrossRef]
  26. B. Safarbali and S. M. R. H. Golpayegani, “Nonlinear dynamic approaches to identify atrial fibrillation progression based on topological methods,” Biomedical Signal Processing and Control, vol. 53, p. 101563, 2019. [CrossRef]
  27. M. Dindin, Y. Umeda, and F. Chazal, “Topological data analysis for arrhythmia detection through modular neural networks,” in Advances in Artificial Intelligence: 33rd Canadian Conference on Artificial Intelligence, Canadian AI 2020, Ottawa, ON, Canada, May 13–15, 2020, Proceedings 33. Springer, 2020, pp. 177–188.
  28. P. Bubenik et al., “Statistical topological data analysis using persistence landscapes.” J. Mach. Learn. Res., vol. 16, no. 1, pp. 77–102, 2015.
  29. P. Bubenik and P. Dłotko, “A persistence landscapes toolbox for topological statistics,” Journal of Symbolic Computation, vol. 78, pp. 91–114, 2017. [CrossRef]
  30. P. Bubenik, “The persistence landscape and some of its properties,” in Topological Data Analysis: The Abel Symposium 2018. Springer, 2020, pp. 97–117.
  31. A. L. Goldberger, L. A. Amaral, L. Glass, J. M. Hausdorff, P. C. Ivanov, R. G. Mark, J. E. Mietus, G. B. Moody, C.-K. Peng, and H. E. Stanley, “Physiobank, physiotoolkit, and physionet: components of a new research resource for complex physiologic signals,” circulation, vol. 101, no. 23, pp. e215–e220, 2000.
  32. M. B. Kennel, R. Brown, and H. D. Abarbanel, “Determining embedding dimension for phase-space reconstruction using a geometrical construction,” Physical review A, vol. 45, no. 6, p. 3403, 1992. [CrossRef]
  33. N. H. Packard, J. P. Crutchfield, J. D. Farmer, and R. S. Shaw, “Geometry from a time series,” Physical review letters, vol. 45, no. 9, p. 712, 1980. [CrossRef]
  34. J. C. Robinson, “Takens’ embedding theorem for infinite-dimensional dynamical systems,” Nonlinearity, vol. 12, pp. 1263–1275, 1999.
  35. A. M. Fraser and H. L. Swinney, “Independent coordinates for strange attractors from mutual information,” Physical review A, vol. 33, no. 2, p. 1134, 1986. [CrossRef]
  36. W. Liebert and H. Schuster, “Proper choice of the time delay for the analysis of chaotic time series,” Physics Letters A, vol. 142, no. 2-3, pp. 107–111, 1989. [CrossRef]
  37. M. T. Rosenstein, J. J. Collins, and C. J. De Luca, “Reconstruction expansion as a geometry-based framework for choosing proper delay times,” Physica D: Nonlinear Phenomena, vol. 73, no. 1-2, pp. 82–98, 1994. [CrossRef]
  38. M. B. Kennel, R. Brown, and H. D. Abarbanel, “Determining embedding dimension for phase-space reconstruction using a geometrical construction,” Physical review A, vol. 45, no. 6, p. 3403, 1992. [CrossRef]
  39. L. M. Pecora, L. Moniz, J. Nichols, and T. L. Carroll, “A unified approach to attractor reconstruction,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 17, no. 1, p. 013110, 2007.
  40. B. Rieck, “Persistent homology in multivariate data visualization,” Ph.D. dissertation, Ruprecht-Karls-Universität Heidelberg, 2017.
  41. S. Emrani, T. Gentimis, and H. Krim, “Persistent homology of delay embeddings and its application to wheeze detection,” IEEE Signal Processing Letters, vol. 21, no. 4, pp. 459–463, 2014. [CrossRef]
  42. B. Safarbali and S. M. R. H. Golpayegani, “Nonlinear dynamic approaches to identify atrial fibrillation progression based on topological methods,” Biomedical Signal Processing and Control, vol. 53, p. 101563, 2019. [CrossRef]
  43. V. Kovacev-Nikolic, P. Bubenik, D. Nikolić, and G. Heo, “Using persistent homology and dynamical distances to analyze protein binding,” Statistical applications in genetics and molecular biology, vol. 15, no. 1, pp. 19–38, 2016.
  44. A. Marchese and V. Maroulas, “Signal classification with a point process distance on the space of persistence diagrams,” Advances in Data Analysis and Classification, vol. 12, pp. 657–682, 2018. [CrossRef]
  45. M. Dindin, Y. Umeda, and F. Chazal, “Topological data analysis for arrhythmia detection through modular neural networks,” in Advances in Artificial Intelligence: 33rd Canadian Conference on Artificial Intelligence, Canadian AI 2020, Ottawa, ON, Canada, May 13–15, 2020, Proceedings 33. Springer, 2020, pp. 177–188.
Preprints 81175 g004
Figure 4. The topological feature for each class.
Figure 4. The topological feature for each class.
Preprints 81175 g004
Preprints 81175 g005
Figure 5. The topological signatures for each class.
Figure 5. The topological signatures for each class.
Preprints 81175 g005
Table 1. The 7 records’detail of MIT-BIH Long Term Dataset.
Table 1. The 7 records’detail of MIT-BIH Long Term Dataset.
Arrhythmia Type
User ID N S V F Total Samples
14046 105,408 2 9,767 95 115,272
14134 38,769 29 9,836 992 49,626
14149 144,548 0 264 0 0
14157 83,422 244 4,369 63 88,098
14172 58,318 1,152 6,529 1 66,000
14184 78,104 39 23,383 11 101,537
15814 91,628 34 9,942 1,744 103,348
Table 2. 4 designed experiments from the MIT-BIH Long-term Database.
Table 2. 4 designed experiments from the MIT-BIH Long-term Database.
Arrhythmia Type
Experiment Number User ID N S V F
Exp #1 14134 3,968 0 1,984 992
Exp #2 15814 6,976 0 3,488 1,744
Exp #3 14172 4,608 1,152 2,304 0
Exp #4 14172 100 100 100 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated