Preprint

Article

Insights of Gravitational Phenomena: A Study Applying Thermodynamic Properties of Gases

Altmetrics

Downloads

970

Views

435

Comments

Supplementary Material

supplementary.docx (3.65MB )

Chithra Piyadasa^*

This version is not peer-reviewed

Submitted:

07 March 2024

Posted:

08 March 2024

You are already at the latest version

Alerts

Abstract

Laboratory experiments and investigations into natural phenomena in this research series have unveiled the presence of a gravitational repulsion force that permeates our environment on both microscopic and macroscopic scales, contingent upon the thermal energy present. This paper presents a study exploring novel properties of gravitational forces among gas molecules, employing principles of thermodynamics. A model has been devised based on the interactions between pairs of gas molecules. While traditional models treat gravitational interaction as a singular force, our experimental approach validates it as the composite of two distinct forces: gravitational repulsion and attraction. By utilizing established experimental data on gas thermodynamics, our model demonstrates robust performance both analytically and experimentally. It verifies the coexistence of gravitational repulsion and attraction forces among gas molecules, showcases their Inverse-Cube relationship with distance, and elucidates the direct proportionality of the repulsion force to absolute temperature. This bridges a crucial gap between energy and fundamental forces. The order of magnitudes of gravitational repulsion and attraction forces are found to be considerably large, contrasting with the low values predicted by classical theory, which results from their amalgamation. Recognizing these forces as substantial in magnitude promises unprecedented outcomes and advancements.

Keywords:

Subject: Physical Sciences - Other

1. Introduction

A study of gravitation forces has been conducted modelling them as two distinct forces of repulsive and attractive nature on gaseous matter. The model has been validated applying experimentally determined and established data utilized in practical thermodynamic applications of mechanical engineering. It is a self-standing model, which requires no fitting into existing models. The presented alternative model could more effectively describe the nature of the universe at both micro and macro levels. The gravitational repulsion concept presented in the series of publications ¹ emanating from this research program, are based on experimental observations and natural phenomena; making neither abstruse assumptions nor explanations.

The present understanding of the Universe is that there are four fundamental interactions (also known as fundamental forces in classical theory): weak (subatomic), strong (subatomic), electromagnetic and gravitational [Table S1 in supplementary information]. None of these fundamental forces is so far defined to be temperature (hence energy) dependent. There are, nevertheless, phenomena observed in nature/universe (e.g.: pressure, expansion, phase change and so on) that are dependent on temperature, which is a manifestation of the thermal energy content. Both gravitational repulsion and attraction forces analytically and experimentally proved, in this research, to be dependent on the thermal energy content, elucidating the inter-relation between energy and fundamental forces. Such findings resonate with ‘Principia Mathematica’² published by Isaac Newton in 1687; see Prepositions XLIII-XLV of Book 1, pp171-182, and ³ among others.

In some literature ³, the gravitational repulsion force is referred to as the antigravitational force. Therefore, we use both these terms in our text to mean the same concept.

Presenting a new scientific revelation that fundamentally challenges our understanding of the universe requires examining the foundations of our present understanding, viz., Newtonian and Einsteinian gravity concepts. The author would, for the benefit of those interested in contextual knowledge, in the supplementary information (supplementary information: Section A), briefly note the following:

Newtonian and Einsteinian gravity concepts, thus highlighting the foundations of our present understanding
Early notions of the gravitational repulsion force and its recent revelations

1.1. Recent Revelation of the Gravitational Repulsion Force:

A series of experiments involving mechanistic laboratory studies ¹ by the author, have shown that the upward motion of matter against the gravitational attraction of the Earth (e.g., the upward movement of iodine in a vacuum ^1d (briefly presented in Section 2) and upward movement water droplets in the air ^{1b, 1c}), happens due to a force acting opposite to gravitational attraction. In that series, the studies on water droplets ^{1b, 1c} confirmed that the force acting opposite to the gravitational attraction is proportional to the internal thermal energy of the droplets. The said tangible experiments lead to the understanding of gravitational repulsion or antigravity force which persists against the gravitational attraction force. It has further been extended that both gravitational repulsion and attraction forces pervade our surroundings both microscopically and macroscopically ^1a; such as condensation of gases, accumulative (flocking together) nature of clouds and accelerating expansion of the Universe.

The discussion so far has briefly indicated why we need a deviation from the existing gravitational models, e.g., Newtonian ‘Law of Universal Gravity’ and Einsteinian ‘EFE’. Also, we need to deviate from a major idealistic assumption made in the kinetic theory of ideal gas, as explained in the next section. Now, our attempt is to develop a relationship for a better understanding of the behavior of gas molecules utilizing the force of repulsive nature on matter; antigravity as revealed in this investigation.

1.2. Challenges of some Major Assumptions in Derivation of the Kinetic Theory of Gas:

As reasoned above, in the derivation of the ideal gas equation, the skepticism is mainly on the idealistic assumption ⁴:

The intermolecular force in the gaseous state is zero and as such molecules exhibit no force among themselves

In deriving the ideal gas equation, one of the most fundamental forces, the gravitational attraction among matter has been overlooked, both among the gas molecules themselves and with the Earth. Such an assumption does not justify the principles of fundamental science. Even though a gas molecule has only a minute quantity of matter, it is susceptible to gravitational forces with all other entities of matter around. Therefore, it may not be prudent to make an assumption to neglect the gravitational forces on gas molecules with entities small or large. It is accepted that the atmosphere around the Earth exists because of the gravitational force of the Earth and this is a major force between the Earth and air molecules. Even Mars with a lower gravitational attraction accommodates an atmosphere of pressure ~ 0.6% (610 Pa) of the Earth atmosphere ⁵. Also, denser atmospheres are found in planets with higher gravity such as Jupiter and Saturn, which hold even light gases such as hydrogen and helium in their atmospheres ⁶.

Another assumption in the kinetic theory that raises skepticism is the “perfectly elastic collision” between gas molecules and the wall (of the container, for example) applied when defining the pressure in a static situation. This definition, especially, would not work when the wall is moving under the pressure force. To move a wall under the pressure force, the energy (momentum) of gas molecules has to be transferred to the wall; which would preclude “perfectly elastic collision”. The mass of an average air molecule is just around 4.8 x 10^-26 kg, which is negligibly small in mass when compared to the mass of a rigid wall where any pressure effect is observed/considered. The movement of such a heavy object (with a rigid surface where the pressure force is experienced) by transferring momentum (energy) of gas molecules is highly unrealistic according to ‘Newton’s Third Law’. It is worth mentioning that the mechanism of momentum/energy transfer via fundamental forces is also not clear.

The postulates of the kinetic molecular theory of ideal gases, further ignore the volume occupied by the molecules of a gas. Real gases, however, show significant deviations from the behavior expected for an ideal gas ⁷, e.g., Van Der Waals Equation. Brief information regarding the behavior of real gas is mentioned in supplementary information - Section B.

Instead of accepting assumptions with challenges as such as above, this research program considers real forces experimentally established. The following section introduces a few previous experiments carried out in this research program, where the Gravitational Repulsion force was discovered in addition to the already known Gravitational Attraction force.

2. Groundbreaking Experiment on Gravitational Repulsion:

The very first experiment ^1a on gravitational repulsion by the author has shown the upward movement of heavy particles (iodine) in a vacuum (details of the experimental set-up can be found in supplementary information: Section C). Therein, the experimental design has eliminated all factors which are believed to be causing the upward movement of particles against the gravitational pull in the air, viz., buoyancy and convective forces. Initially, at room temperature (≈ 25°C), the iodine particles detached from the iodine sample moved downward under the gravitational attraction force with the Earth, and deposited in the bottom part of the paper jacket. When the iodine sample was heated, the experiment revealed that iodine particles move against the gravitational pull in the vacuum as shown in supplementary information Figure S1. The paper ^1a also cites an example from electronic vacuum tubes (also called electronic valves) where evaporated tungsten and thorium particles (heavy metal particles) from the filaments move upwards despite the gravitational pull and the strong radial electric fields, and deposit at the top of the glass tube. These findings substantiate that the gravitational repulsion force acts on matter, similar to the gravitational attraction force.

2.1. Inferences from the Above Iodine Experiment:

In the gravitational repulsion force experimentally observed as described above, the two entities of matter are iodine particles and the Earth. The findings of the said experiment could be summarized as:

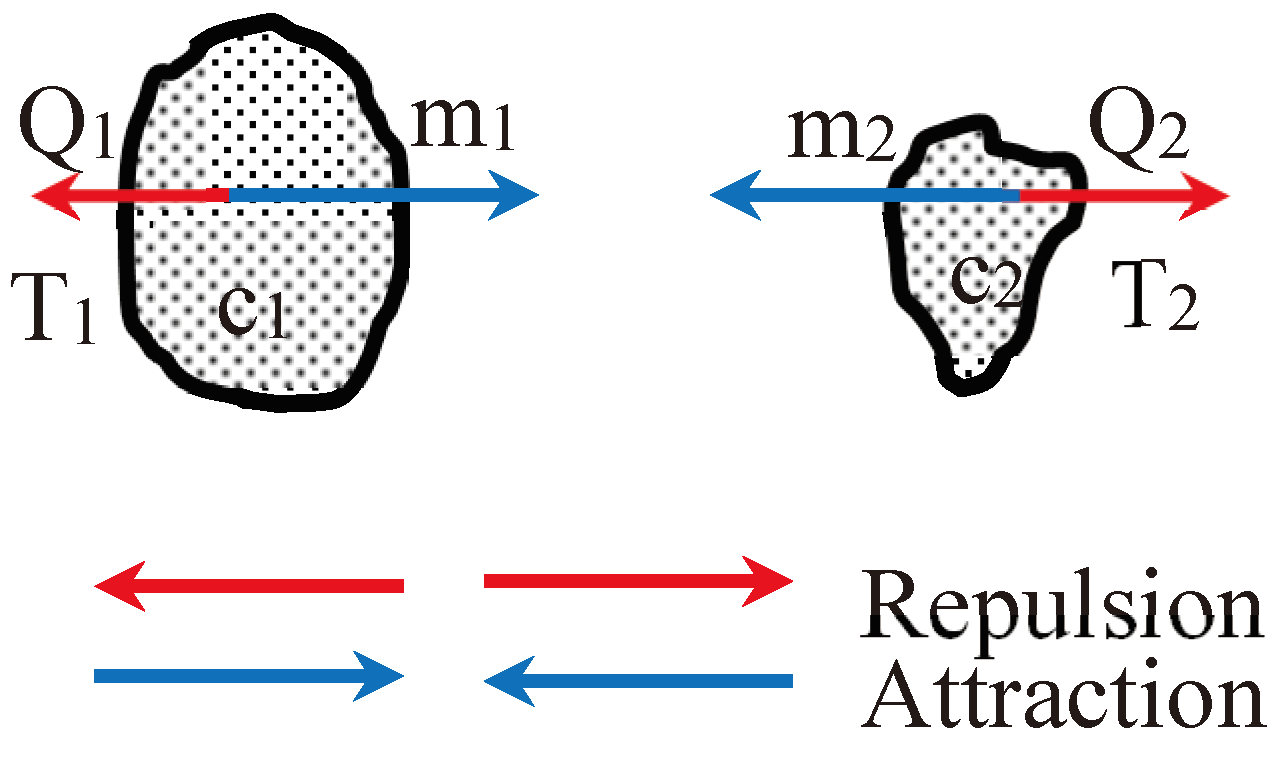
1): There is a repulsion force acting on iodine particles, in the direction opposite to the Earth’s gravitational attraction force.
2): The repulsion force is dependent on the thermal energy of the particle (related to the temperature T, which is a manifestation of the thermal energy Q).

Note:: Heat is thermal energy. According to the classical definition, thermal energy is the net potential energy of the system. The internal energy is the net potential energy + the net kinetic energy of the system. The virial theorem assumes that the average kinetic energy over time, of a stable system consisting of a given number of particles and bound by a potential force, is proportional to the average potential energy over time ⁸. The virial theorem also discusses some possible mechanisms ⁹ dominating stellar contraction due to the gravitational attraction. Our discussion, however, is grounded on a repulsive force dependent on thermal energy which is based only on its potential energy and therefore further engagement with kinetic energy is disregarded in this paper.

Further, other stages in this research program have experimentally demonstrated the existence of a repulsion force between water droplets and the Earth, and that the time-of-fall of a water-droplet in still air increases with the temperature of the droplet ^{1a, 1b}. A similar idea has been predicted for a hypothetical quantum fluid: “that the temperature difference creates a direction in space in which quantum liquids can flow, even against the force of gravity” ⁹ p1950184-1.

2.2. Forces between Two Entities of Matter:

The above summarized points are illustrated in Figure 1, generalized for any two entities of matter.

Reference the arrangement presented in Figure 1, the relationships between two arbitrary entities of matter, with masses m₁, m₂, at absolute temperatures T₁, T₂ and thermal energy contents Q₁, Q₂ are:

1): Based on the conventional gravitational law:

a t t r a c t i o n f o r c e \propto m a s s (m_{1}, m_{2})

(1)

2): Experimental findings presented in the Author’s publication ^1b show that:

r e p u l s i o n f o r c e \propto t h e r m a l e n e r g y (Q_{1}, Q_{2})

(2)

Thermal energy, Q is expressed by definition ¹⁰ as:

Q = m c T

(3)

where c is the specific heat capacity and T is the absolute temperature.

The reason for focusing on the behavior of gases is:

1): The model could be applied to explain certain natural phenomena observed in the atmosphere, some of which have been studied in the previous experiments in this research program [1].
2): Forces at the micro level (between gas molecules) may be generalized to the macro level to explain the behavior of the Universe.

Above mathematical relationships of gravitational repulsion and attraction forces would enable us study the behavior of gases.

3. Alternative Mathematical Model for the Gravitational Repulsion and Attraction Forces, Elucidating Gaseous Behavior:

3.1. Introduction to the Analysis:

A model of the gravitational repulsion force and the gravitational attraction force (Figure 1) is developed herein, considering them as two distinct forces acting between two gas molecules (strictly for gases). Established experimental data ¹¹ on thermodynamic properties of gases are then applied to derive the following models, coefficients and magnitudes pertaining to gravitation:

a): A mathematical model for the gravitational repulsion force
b): A revised mathematical model for the gravitational attraction force
c): Orders of magnitude of both the gravitational repulsion coefficient and the gravitational attraction coefficient
d): Orders of magnitude of both gravitational repulsion and gravitational attraction forces

The analysis is conducted without using idealistic assumptions (such as pointed out in Section 1.2) used in classical theory.

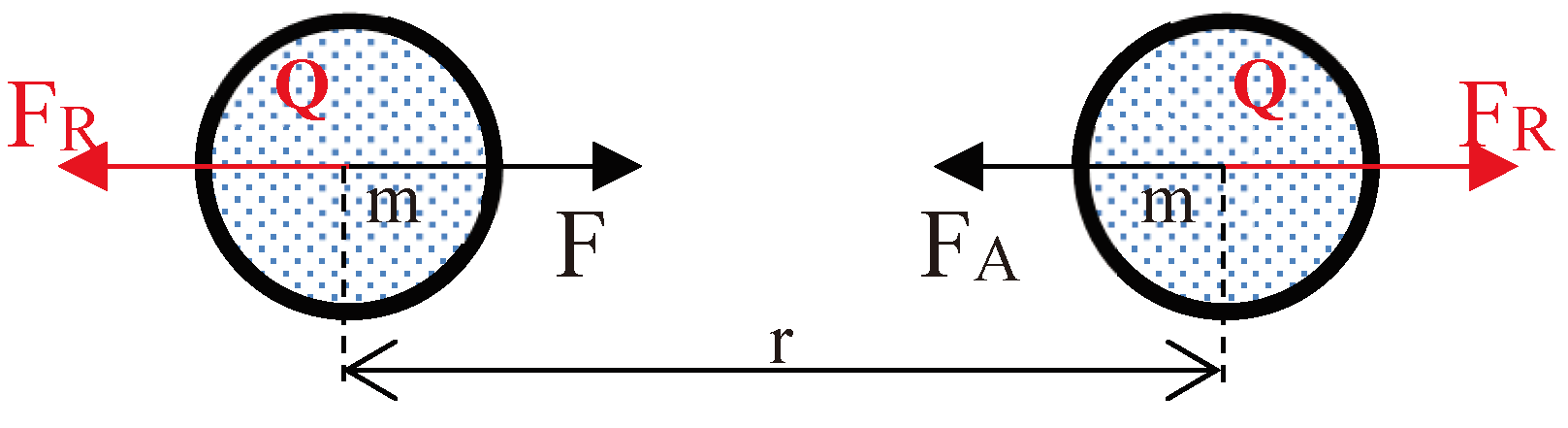
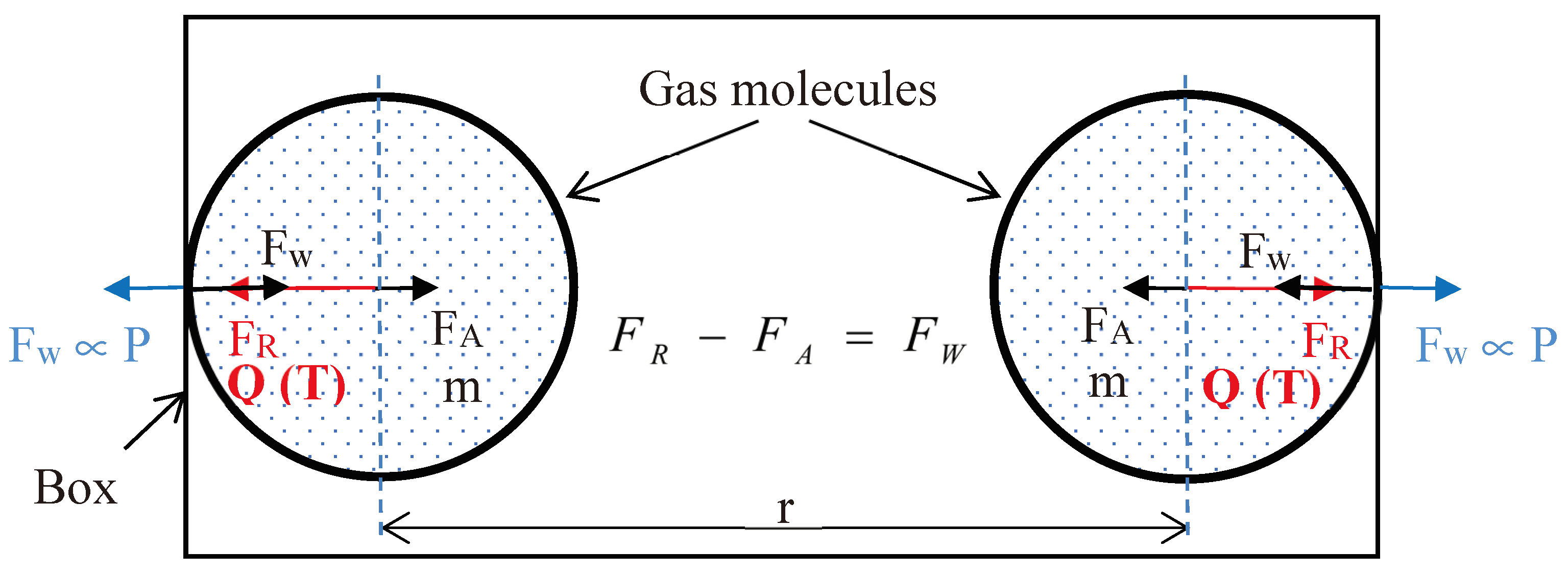
3.2. Forces between Two Gas Molecules:

To analyze the gravitational repulsion force and the gravitational attraction force, strictly for gases, diagram Figure 2 (a version of Figure 1, that better yields to analysis) could be drawn. It depicts two gas molecules in free space; each with mass m, thermal energy content Q, and distance r apart. There exist, gravitational repulsion forces F_R proportionate to their thermal energy contents Q and gravitational attraction forces F_A proportionate to their masses m (Section 2.2). Both forces F_R and F_A are inversely proportionate to r.

Although some phenomena observed in the nature/Universe, e.g., pressure, expansion and phase change, are dependent on temperature, which is a manifestation of the thermal energy content, none of the four fundamental forces in classical theory are considered dependent on thermal energy content/temperature. As presented below, proven both analytically and experimentally, the thermal energy content dependent gravitational repulsion force would elucidate the inter-relation between energy and fundamental forces.

3.3. Mathematical Model for Coefficient of Gravitational Repulsion and Gravitational Attraction:

For the mathematical analysis, consider only these two molecules exist confined within a box at a distance r apart (Figure 3), at a certain pressure (i.e., an outward force F_W exists). The two molecules, hence, are at rest touching the walls of the box, under the gravitational repulsion force (F_R), the gravitational attraction (F_A) and the F_W exerted by the wall. Existence of pressure on the box walls implies that the repulsion force between molecules is greater than the attraction force (F_R > F_A).

For the equilibrium of forces on gas molecules depicted in Figure 3:

F_{R} - F_{A} = F_{W}

(4)

In this situation, Pressure P on the wall (by the two gas molecules) results from the outward force F_W of the system on a unit area; thus: P ∝ F_W

In reality, any small quantity of gas molecules exhibits the same pressure regardless of the number of molecules enclosed. This implies that pressure at any point in the gas is caused by the very basic building block; intermolecular forces.

The intensity of the gravitational attraction force is proportional to the mass m (Equation 1). Under the proposed concept ^1b, the intensity of the gravitational repulsion force is proportional to the thermal energy Q (Equation 2).

Isotropic distribution of the force field of an entity of matter could be considered the same, irrespective of the type of force; whether gravitational repulsion force or gravitational attraction force. The distance r between the two entities of matter is in the denominator of the relationships for both the intensity of the gravitational repulsion force, as well as the intensity of the gravitational attraction force. In the denominator, the power of r is denoted by x, because the distribution of the force field around the molecule with the distance is assumed unknown in the context of gravitational attraction and repulsion. The value of the exponent x is to be derived by applying established experimental data. For the two identical molecules with mass m given in Figure 3, the gravitational attraction force F_A is defined (Equation 1 is modified) as:

F_{A} = G_{A} \frac{m m}{r^{x}} = G_{A} \frac{m^{2}}{r^{x}}

(5)

where, G_A is defined as the ‘Gravitational Attraction Coefficient’.

For the two identical molecules with thermal energy Q given in Figure 3, the gravitational repulsion force, F_R is also defined as:

F_{R} = G_{R} \frac{Q Q}{r^{x}} = G_{R} \frac{Q^{2}}{r^{x}}

(6)

where, G_R is defined as the ‘Gravitational Repulsion Coefficient’.

Thermal energy Q (which contributes to the repulsion force) is defined (Equation 3 is modified) for the calculation of F_R as:

Q = m c T^{y}

(7)

where, c (Note 1 below) is the Specific Heat Capacity, T (Note 2 below) is the absolute temperature and y is the exponent of T. The parameter y as the exponent of T is introduced because the effect of absolute temperature on the thermal energy of an entity is not known in the context of gravitational repulsion. For example, the radiant heat energy is proportional to the power 4 of T in the Stefan–Boltzmann Law ¹². Similarly, the radiant field of antigravity is assumed proportional to the power y of T. The value of the exponent y is to be derived applying established experimental data.

Note 1:: c is further defined for gases ¹⁰ as: c_v (Specific Heat Capacity at constant volume) and c_p (Specific Heat Capacity at constant pressure).
Note 2:: In the classical theories, the thermal energy of a single molecule is considered as its kinetic energy (translational, vibrational, rotational, etc.), and no temperature term is associated. Nevertheless, any matter, regardless of its size, absorbs and emits energy (infrared radiation in the case of thermal energy); Stefan–Boltzmann Law ¹². Gas molecule in the space is also an individual entity having its own characteristic mass and temperature, thus absorbs and emits radiation corresponding to its temperature regardless of its size ¹³.

Solutions for parameters x, y, G_R, G_A, F_R and F_A in Equations (5), (6) and (7) are obtained, considering 3 Situations i, ii and iii (Figure S2 and Section D.1 and Section D.3 in supplementary information), pertaining to Figure 3, to yield Equations (8), (9), (10), (11) and (12). Details are given in supplementary information: Section D.2. Forces acting on two molecules under three different situations, Situations i, ii and iii are depicted in Figure S3 in supplementary information.

3.4. Solutions for Parameters x, G_R, G_A, F_R and F_A:

Equations (5), (6) and (7) give the solution for x as follows:

x = L o g (\frac{α m^{2} - β Q_{1}^{2}}{α m^{2} - β Q_{2}^{2}}) / L o g (\frac{r_{1}}{r_{3}})

(8)

where:

α = \frac{β Q_{1}^{2} - (P_{1} / N_{f})}{m^{2}}

and

β = \frac{P_{2} - P_{1}}{N_{f} (Q_{2}^{2} - Q_{1}^{2})}

General solutions for G_R, G_A, F_R and F_A are given as:

G_{R} = β r^{x}

(9)

G_{A} = α r^{x}

(10)

F_{R} = \frac{G_{R} Q^{2}}{r^{x}}

(11)

F_{A} = \frac{G_{A} m^{2}}{r^{x}}

(12)

To determine the numerical values for x, y, G_R, G_A, F_R and F_A it is necessary to consider the established experimental values of mass, specific heat capacity (either c_v or c_p discussed later in this paper), molecular distance, and pressure of gases at different T and y. As a sample calculation of the said analysis, the established experimental data on thermodynamic properties ¹⁴ of nitrogen N₂ are utilized and presented in this paper. Analysis was repeated utilizing established experimental data on thermodynamic properties ¹⁴ of hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide as well, and all information is available on request. Details of the analysis of nitrogen are presented in supplementary information: Section G.

4. Calculation of x, y, G_R, G_A, F_R and F_A Based on Thermodynamic Properties of Gas:

The focus of this section is to engender a reasonable qualitative and quantitative picture of the combined effect of gravitational repulsion and attraction forces on matter in the gaseous state. Results would be considered and compared with conditions and observations encountered in the nature. Thermodynamic properties of gaseous nitrogen are used in the following sample calculation to elucidate the effect. Established experimental data ¹⁴ (published in 1948) on the gas properties of nitrogen (see supplementary information: File SF1) were applied to Equations 8–12, to calculate the values for x, G_R, G_A, F_R and F_A. See File SF2 and SF2 for the program written in Mathematica to solve the respective parameters. From the said table (File SF1) of the properties of nitrogen with average molecular mass

28.016 \times 1.66054 \times 10^{- 27}

kg/molecule, c_v and c_p at varying temperatures (from 146.65 K to 2888.9 K), were extracted. The detailed calculations are given in supplementary information: Section E. Derivation of P and r values for the calculations of Equations 8-12 are given in supplementary information: Section E.1,

The following results are concluded (see Supplementary information: Section E.2) by the analysis of thermodynamic data using equations 8–12:

x is a constant = 3, regardless of T and y (Figure S4 (a) in supplementary). The significance of this finding will be discussed below.
Behaviors of G_R and G_A (Figures S4 (b) and (c) in supplementary) show that y = 0.5 is a significant point in this analysis.
F_R is linearly proportionate to T at any given value of y (Figure S4 (d) in supplementary information); thus, vindicating the mathematical model Equation 2. Significantly, this result confirms the findings presented in a previous paper ^1b of the series of publications emanating from this research program (see Figure S6 in supplementary information). It states therein, ^1b p148:

In experiment 2, t_f (time-of-fall) of a water-droplet in still air increases with the temperature of the droplet. That is: “The hotter the water-droplet, the slower it falls”.

A significant finding is that, in the linear relationship F_R vs. T, the extrapolated graph intercept near the origin [≈ (0,0)] when y ≈ 0.5 (Figure S7 in supplementary information).

The significance of these numerical values obtained for x, y, G_R, G_A, F_R and F_A are discussed in detail in supplementary information: Section F (Sections F.1, F.2, F.3, F.4, F.5 and F.6 respectively). These findings would be summarized in the Discussion. The impact on G_R and G_A with temperature under both c_v and c_p are also depicted in Figure S5.

4.1. The Gist of the Model and the Outcomes:

A perceptible alternative model of the gravitational repulsion force and the gravitational attraction force has been developed above, considering them as two distinct forces acting on gaseous matter. The development of this model has been presented in Section 3. When established experimental data on nitrogen, hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide were applied, the model performed, yielding significant outcomes. These outcomes were presented in Section 4.

In view of the numerous details, equations, outcomes, etc., of the model presented above, the gist of them all is diagrammatically presented in Figure S6 for the convenience of the reader.

5. Discussion

It is observed that Newtonian and Einsteinian mechanics encounter challenges in explaining certain phenomena seen in laboratory experiments (e.g.: upward motion of heated iodine particles in vacuum) and natural phenomena (e.g.: condensation of gases, accumulative (flocking together) nature of clouds and accelerating expansion of the Universe) ¹. Under these existing models, the gravitational force has been reckoned as a “weak force”. Thus, in deriving the ideal gas equation, one of the most fundamental forces, the gravitational attraction among matter has been overlooked as negligible, both among gas molecules themselves and with the Earth. Such lapses of overlooking the gravitational force among gas molecules as negligible in the classical theory has given an erroneous picture as now revealed by this investigation

The alternative model considering both gravitational repulsion and attraction, presented in this paper, is self-standing; independent of existing idealistic models. This model has been built up without idealistic assumptions such as: “intermolecular force in the gaseous state is zero”, “perfectly elastic collisions”, “consists of a large number of molecules”, “the volume of the molecules is negligibly small” and so on. In fact, there are no idealistic assumptions involved in this model; hence it is closer to reality.

The entire mathematical model presented in this paper has been derived considering the forces of gravitational repulsion and attraction between just two gaseous molecules; the basic building blocks of the gas. Force (net repulsive) between individual gas molecules represents the pressure in the system; a significant deviation from the kinetic theory’s concept of momentum transfer. Hence, the pressure is not identified here as the rate of change of momentum of a number of molecules in a certain mass or volume of the gas, as assumed in the kinetic theory in the derivation of the ideal gas equation.

It should be noted that the above relationships (Equations S11, S12 and 8–12) are developed for the matter in the gaseous state. It is, hence, recommended that future research should focus on analysis of matter in other states, viz., solid, liquid and plasma.

The model has been validated applying experimentally determined and established data ¹⁴ utilized in practical thermodynamic applications of mechanical engineering. The data has been published in 1948, by Joseph Henry Keenan and Joseph Kaye. Applying these data to Equations 8-12, the behavior of x, G_R, G_A, F_R and F_A with respect to T and y were derived and presented in 3D graphs (a), (b), (c), (d) and (e) in Figure S4 in supplementary information.

The result x = 3.0 as presented in the 3D graph Figure S4 (a) contributes new scientific information on the distribution of gravitational force fields that fill up the volume in free space, at the length scale of intermolecular distances for gas molecules. The relationship of gravitational repulsion and attraction forces being inversely proportional to the cube-of-the-distance (r³), interprets the gravitational force distributions as volumetric or solid spherical distributions (4/3 πr³) in free space, rather than the area or surface distributions (4πr²) considered in the classical model. This is a significant departure from the Inverse-Square Law. Inverse-Square Law describes the wave front propagation of energy. In contrast, force fields fill up the volume in the free space. The volumetric distribution or fill-up the free space by the force is more appropriate for understanding; as a force field always exists in a 3D space rather than on a 2D surface.

In the literature on force fields, the inverse proportionality to the cube (Inverse-Cube Law) of the distance is not new. An extra force besides gravity, that is obeying the Inverse-Cube Law, has been mentioned in ‘Principia Mathematica’ ² published by Isaac Newton in 1687; see Prepositions XLIII-XLV of Book 1, pp171-182. It has also been demonstrated ¹⁵ experimentally that, in magnetostatic fields where both poles geometrically coincide, the attraction and the repulsion forces obey the Inverse-Cube Law with the distance. Future research should focus on discerning whether inverse proportionality to the cube-of-the-distance (r³) is more appropriate in applications of fundamental physics.

The analysis presented in this paper signifies that y = 0.5 is a very special value when considering the behaviors of G_R, G_A, F_R and F_A. The most noteworthy points were that, for both c_v and c_p, when y ≈ 0.5:

extrapolation of graphs F_R vs. T cross (0,0)
negative F_A tends to become positive as T approaches 0 K

This was found to be true for all gases considered: nitrogen, hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide; yielding similar results irrespective of atomic mass m. How these results resonate with other empirically established models such as Boyle’s Law, Charles’ Law and Amontons’ Law/Gay-Lussac’s Law will be discussed in a future publication.

In the 3D graphs Figures S4 (b) and (c), both Gravitational Repulsion Coefficient and Gravitational Attraction Coefficient appeared dependent on the temperature T. This result is unexpected, as the temperature dependency of G_A was not previously known. Further to that, as presented in the 3D graphs in Figures S4 (d) and (e), both F_R and F_A are temperature dependent; being gravitational forces, they are fundamental interactions in nature. Significant departure from the existing knowledge is that, the four fundamental interactions (fundamental forces) in classical theory are not defined to be temperature dependent. Existing theories, nevertheless, state that the increase of thermal energy increases the potential energy of the gas molecules; with no mention that a relationship exists between thermal energy (classically known as potential energy) and gravitational forces. Results showed that, the increase of thermal energy increased the repulsion (Equations 2 and 11) between gas molecules. See the graphs of F_R vs. T and F_A vs. T, where, as T increases:

the positive value of F_R increases
the negative value of F_A increases

That implies that the thermal energy is directly proportional to the resultant of F_R and F_A (see Figure S8 in supplementary information), confirming the relationship between energy and fundamental forces. With this revelation, the critical gap between energy and fundamental forces has been filled. Fundamental forces could be more readily linked with observable temperature dependent phenomena (e.g.: pressure, expansion, and so on) in the nature/Universe; thus, enabling better explanations.

In the 3D graph Figure S4 (d), the gravitational repulsion force appeared linearly proportionate to the temperature. This vindicated the experiment conducted in this research program by the Author, presented in paper ^1b. The said experiment demonstrated that the time-of-fall of water droplets is linearly proportionate to the temperature (Figure S6 is drown according to the data given in Table S2 in supplementary information).

Negative values of F_A at elevated temperatures [Figure S4 (e)], together with F_R, cause the gas to have only repulsive forces among molecules. This gives rise to the property that real gases expand infinitely as the available space increases. Such circumstances of all repulsive forces were observed in the other gases studied (hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide) as well (information available on request).

Analysis presented in this paper further shows that as the temperature decreases, repulsion forces decrease and attraction forces increase (from negative at elevated temperatures to close to positive at lower temperatures) between gaseous molecules, thus causing aggregation of atoms/molecules together, i.e., causing condensation of the gas. This finding is significant in a context where the exact fundamental mechanism of condensation has so far not been explained by classical theories.

This program of research has shown that, the so called ‘weak’ gravitational force (Table S1 in supplementary information), is actually the resultant of two extremely large forces, i.e., gravitational repulsion and gravitational attraction, which distinctly act on matter. Newly determined gravitational repulsion and attraction forces between two nitrogen molecules at 305 K are in the order of 10³⁰ times (supplementary information: Section F) greater than the classically calculated gravitational attraction force. It thus reveals that the gravitational repulsion and attraction forces in fact are of similar orders of magnitude as the other three forces in nature. Even though the gravitational repulsion and attraction forces are colossal in magnitude, they are nearly equal, thus nearly in equilibrium in nature and their algebraic sum is a mini (weak) force; hence always observed to be a weak force.

An experiment was referred to in Section 2, where heated iodine particles moved upwards in vacuum against the Earth’s gravitational pull. This was a groundbreaking experiment where the said phenomenon occurred in a situation where all factors which are believed to be causing the upward movement of particles in the air against the gravitational pull, viz., buoyancy and convective forces, are eliminated by the experimental design. Initially, at room temperature (≈ 25°C), the iodine particles detached from the iodine sample moved downward under the gravitational attraction force with the Earth, and deposited in the bottom part of the paper jacket. When the iodine sample was heated, the experiment revealed that the iodine particles move against gravitational pull in the vacuum and deposited in the top part of the paper jacket. In electronic vacuum tubes (called electronic valves) also, evaporated tungsten and thorium particles from filaments move upwards in the absence of air, despite the gravitational pull and strong radial electric fields, and deposit at the top of the glass tube.

The above was a laboratory experiment at a micro scale. The antigravity concept could also be extended to macro level phenomena in the nature such as clouds and the accelerating expansion of the Universe. Review paper by the Author ^1a on the previous papers in this research program states:

In addition to attractive and repulsive forces of water-droplets of a cloud with earth, there exist attractive and repulsive forces among water droplets within the cloud. These forces acting inside the cloud explain the accumulative (flocking together) nature of the cloud which has not been explained by the classical theories. The equilibrium of these two forces will confine the droplets to a certain area as a floccule. The repulsiveness does not allow shrinking and finally collapsing the cloud while the attractive force keeps the droplets together without dispersion. ^1a p4

The above is an ideal example where there is no net outward force (no net pressure exerted outward) among flocculent water droplets. Water droplets behave as a flock under the equilibrium of gravitational repulsion and gravitational attraction forces. The paper ^1b dispelled the classical belief that clouds float due to convection currents, and showed that the force that holds the flocculent water droplets up in the air is “antigravity”. Coexistence of repulsive and attractive forces considered in the theoretical derivations presented in this paper are supported by the mechanism for the existence of clouds deduced in the paper ^1b.

Considering both gravitational repulsion and gravitational attraction on matter and filling the critical gap between energy and fundamental forces, opens doors for more research enabling stronger scientific explanations of observable temperature dependent phenomena, e.g.:

Heavy gas molecules (such as CFC) in the upper atmosphere
Brownian Motion
Condensation/evaporation/sublimation
Expansion/contraction of gas/liquid/solid
and more

The concept of gravitational repulsion and gravitational attraction forces could be further applied at macro level to explain the accelerating expansion of the Universe. Even in our solar system:

… the distance of the Earth’s [sic] from the sun. Various measurements indicate that this distance (or at least the length of the Earth’s semimajor axis) is increasing at the rate of 15 cm per year (plus or minus 4 cm). ¹⁶

Galaxies and other interstellar objects are not in a state of equilibrium as a result of increasing thermal energy content due to various reasons including atomic fission and fusion causing mass-energy conversion (E = mc²). The effect of increasing thermal energy on (a) expanding gas, i.e., at the microscopic level, and (b) expanding universe ^1a, i.e., at the macroscopic level, should be similar. Such mass-energy conversion has dual effects on equilibria in the Universe: (1) increasing thermal energy increases gravitational repulsion forces, while (2) decreasing mass decreases gravitational attraction forces. Gravitational repulsion forces, hence, keep exceeding gravitational attraction forces, thus causing outward expansion of the Universe with acceleration ¹⁷. In essence, gravitational repulsion is a significant force between gas molecules (microscopic level), and could be generalized to explain macroscopic level phenomena, e.g., behavior of the universe ¹⁸, existence of clouds ^1a.

Gravitational repulsion and attraction forces pervade our environments at both micro and macro levels. Once fully understood, such nearly in balance colossal forces offer the prospect of learning to control and manipulate to achieve hitherto unknown results, outcomes and developments. This is another direction for future research. The reader may continue to read more information related to this topic from the content of the preprint ¹⁹.

6. Conclusions

A self-standing alternative mathematical model of gravitational repulsion and attraction forces has been built without idealistic assumptions. It was based on the forces between two gaseous molecules, i.e., the basic building blocks of the gas. The new mathematical model thus derived in this research performed successfully [explaining phenomena and complying with empirical laws] when established experimental data on gas properties of nitrogen, hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide were applied. Gravitational repulsion and attraction forces are inversely proportional to the cube-of-the-distance (r³) between gaseous molecules; thus following an Inverse-Cube relationship; departing from the traditionally accepted Inverse-Square relationship. Gravitational repulsion force is linearly proportional to the thermal energy content (temperature, which is a manifestation of the thermal energy) of the entities of matter. The latter vindicated the observations of the previous experiment conducted in this research program. Gravitational attraction force too is found to be dependent on temperature. Mechanism between energy and fundamental forces being thus revealed, the critical gap between energy and fundamental forces has been filled. The latter opens doors for more research enabling better explanations of observable temperature dependent phenomena. The model could also be applied at the macro level to explain the accelerating expansion of the Universe. The current need is to fully understand the gravitational repulsion and attraction forces, where both are found to be colossal; larger in the order of 10³⁰ times compared to the traditionally known gravitational force between gas molecules. Once these two colossal forces are fully understood, we could control and manipulate them to achieve hitherto unknown outcomes and developments. Such endeavors are where future research should focus.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

All the work has been done by C.P.

Funding

This research received no external funding.

Data Availability

The data that support the findings of this study are available within the article [and its supplementary material]. Additional data that support the findings of this study are available on request from the corresponding author.

Acknowledgments

G. Piyadasa was financially supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada. Financial support given by Harsha Subasinghe and Codegen International (Pvt.) Ltd. are greatly appreciated. The author acknowledges A. Gole and U. Annakkage for continual support of this work. Extensive edits by D. Darshi De Saram and G. S. Palathirathna Wirasinha improved the quality of this paper.

Conflicts of Interest

The author declares no conflict of interest.

Availability of Data and Material

See supplementary information file Section G.

Code Availability

See supplementary data

References

(a) Piyadasa, C. K. G., Antigravity, an answer to nature’s phenomena including the expansion of the universe Advances of High Energy Physics, Special issue : Dark Matter and Dark Energy in General Relativity and Modified Theories of Gravity 2020, 2020 (Dark Matter and Dark Energy in General Relativity and Modified Theories of Gravity (DMDG)), 1-5; (b) Piyadasa, C. K. G., Antigravity, a major phenomenon in nature yet to be recognized. Physics Essays 2019, 32 (2), 10; (c) Piyadasa, C. K. G., Will rising water droplets change science? Canadian Journal of Pure and Applied Sciences 2012, 6 (2), 1991 - 1997; (d) Piyadasa, C. K. G., Antigravity - is it under our nose? Canadian Journal of Pure and Applied Sciences 2011, 5 (2), 1715 - 9997.
Newton, I.; Motte, A.; Machin, J. The Mathematical Principles of Natural Philosophy; Benjamin Motte: Londonm, UK, 1729. [Google Scholar]
(a) Villata, M., CPT symmetry and antimatter gravity in general relativity. Europhysics Letters 2011, 94 (2), 20001; (b) Wanas, M., The Other Side of Gravity and Geometry: Antigravity and Anticurvature. Advances of High Energy Physics 2012, 2012, 10; (c) Fowles, G. R., Introduction to Modern Optics. Dover Publications: New York, 1975; (d) Oikonomou, V. K.; Karagiannakis, N., Study of Antigravity in an Model and in Brans-Dicke Theory with Cosmological Constant. Journal of Gravity 2014, 2014, 625836.
Sonntag, R.E.; Borgnakke, C.; Van Wylen, G.J. Fundamentals of Thermodynamics; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
Haberle, R.M. Solar system/Sun, Atmospheres, Evolution of Atmospheres | Planetary Atmospheres: Mars; Academic Press: Oxford, 2015; pp. 168–177. [Google Scholar]
Atreya, S. K.; Mahaffy, P. R.; Niemann, H. B.; Wong, M. H.; Owen, T. C. , Composition and origin of the atmosphere of Jupiter - an update, and implications for the extrasolar giant planets. Planetary and Space Science 2003, 51, 105. [Google Scholar] [CrossRef]
Cambel, A.B.; Duclos, D P.; Anderson, T.P. Real Gases; Academic Press: Boston, 1963. [Google Scholar]
Singh, A.K. Structure, Synthesis, and Application of Nanoparticles; Academic Press: Boston, 2016; pp. 19–76. [Google Scholar]
Zloshchastiev, K. G. , Temperature-driven dynamics of quantum liquids: Logarithmic nonlinearity, phase structure and rising force. International Journal of Modern Physics B 2019, 33(17), 1950184. [Google Scholar] [CrossRef]
Obert, E.F. Concepts of Thermodynamics; McGraw-Hill: New York, 1960. [Google Scholar]
Keenan, J.H.; Chao, J.; Kaye, J. Gas Tables; John Wiley and sons: New York, 1980; p. 217. [Google Scholar]
Kaiserl. Akademie der Wissenschaften in, W., Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften. Mathematisch-Naturwissenschaftliche Classe. Abt. 2, Mathematik, Physik, Chemie, Mechanik, Meteorologie und Astronomie. 1872, 32 v. (vol. 65-96).
Golovkin, B. G. Physical meaning temperature of gas and separate molecule. World Scientific News 2018, 94(2), 8. [Google Scholar]
Keenan, J. H.; Kaye, J., Gas Tables: Thermodynamic Properties of Air, Products of Combustion and Component Gases, Compressible Flow Function Including Those of Ascher H. Shapiro and Gilbert M. Edelman. J. Wiley: 1948.
Michaud, A. , On The Magnetostatic Inverse Cube Law and Magnetic Monopoles. International Journal of Engineering Research and Development 2013, 7(5), 16. [Google Scholar]
(a) Iorio, L. (a) Iorio, L., Effect of sun and planet-bound dark matter on planet and satellite dynamics in the solar system. Journal of Cosmology and Astroparticle Physics 2010, 2010 (05), 018-018; (b) page, E. T. f. t. a. Dark Matter May Explain the Puzzling Change in Earth-Sun Distance. https://www.technologyreview.com/2010/01/14/206662/dark-matter-may-explain-the-puzzling-change-in-earth-sun-distance/.
Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. , A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551(7678), 85–88. [Google Scholar]
(a) Sidharth, B. G., THE UNIVERSE OF FLUCTUATIONS. International Journal of Modern Physics A 1998, 13 (15), 2599-2612; (b) Riess, A. G.; Filippenko, A. V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P. M.; Gilliland, R. L.; Hogan, C. J.; Jha, S.; Kirshner, R. P.; Leibundgut, B.; Phillips, M. M.; Reiss, D.; Schmidt, B. P.; Schommer, R. A.; Smith, R. C.; Spyromilio, J.; Stubbs, C.; Suntzeff, N. B.; Tonry, J., Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. The Astronomical Journal 1998, 116 (3), 1009-1038; (c) Perlmutter, S.; Aldering, G.; Valle, M. D.; Deustua, S.; Ellis, R. S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Groom, D. E.; Hook, I. M.; Kim, A. G.; Kim, M. Y.; Knop, R. A.; Lidman, C.; McMahon, R. G.; Nugent, P.; Pain, R.; Panagia, N.; Pennypacker, C. R.; Ruiz-Lapuente, P.; Schaefer, B.; Walton, N., Discovery of a supernova explosion at half the age of the Universe. Nature 1998, 391 (6662), 51-54; (d) Lima, J. A. S., Alternative dark energy models: an overview. Brazilian Journal of Physics 2004, 34, 194-200.
Piyadasa, C. K. G., An alternative model of gravitational forces in nature using the combined effects of repulsion and attraction forces on gaseous molecules. PREPRINT (Version 1) available at Research Square 2021, (rs-1173458).

Figure 1. Forces acting between two arbitrary entities with masses m₁, m₂, at absolute temperatures T₁, T₂, specific heat capacities c₁, c₂ and thermal energy contents Q₁, Q₂. There exists repulsion (red arrows) and attraction (blue arrows) forces between them proportional to the thermal energy Q and the mass m, respectively.

Figure 2. Two gas molecules with thermal energy Q and mass m. Each molecule, distance r apart, experiences a gravitational repulsion force F_R and a gravitational attraction force F_A.

Figure 3. Inside the box are two gas molecules, of mass m, containing thermal energy Q (corresponding to their temperature T). The distance between the two molecules is r. Consider that the two molecules are at rest touching the walls of the box. F_R, F_A and F_W are respectively: the repulsion force, the attraction force and the force exerted by the wall. They are in equilibrium (

F_{R} - F_{A} = F_{W}

). Pressure P of the gas (on the wall) results from F_W thus P ∝ F_W.

F_{R} - F_{A} = F_{W}

). Pressure P of the gas (on the wall) results from F_W thus P ∝ F_W.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Insights of Gravitational Phenomena: A Study Applying Thermodynamic Properties of Gases

Abstract

1. Introduction

1.1. Recent Revelation of the Gravitational Repulsion Force:

1.2. Challenges of some Major Assumptions in Derivation of the Kinetic Theory of Gas:

2. Groundbreaking Experiment on Gravitational Repulsion:

2.1. Inferences from the Above Iodine Experiment:

2.2. Forces between Two Entities of Matter:

3. Alternative Mathematical Model for the Gravitational Repulsion and Attraction Forces, Elucidating Gaseous Behavior:

3.1. Introduction to the Analysis:

3.2. Forces between Two Gas Molecules:

3.3. Mathematical Model for Coefficient of Gravitational Repulsion and Gravitational Attraction:

3.4. Solutions for Parameters x, GR, GA, FR and FA:

4. Calculation of x, y, GR, GA, FR and FA Based on Thermodynamic Properties of Gas:

4.1. The Gist of the Model and the Outcomes:

5. Discussion

6. Conclusions

Supplementary Materials

Author Contributions

Funding

Data Availability

Acknowledgments

Conflicts of Interest

Availability of Data and Material

Code Availability

References

MDPI Initiatives

Important Links

Subscribe

3.4. Solutions for Parameters x, G_R, G_A, F_R and F_A:

4. Calculation of x, y, G_R, G_A, F_R and F_A Based on Thermodynamic Properties of Gas: