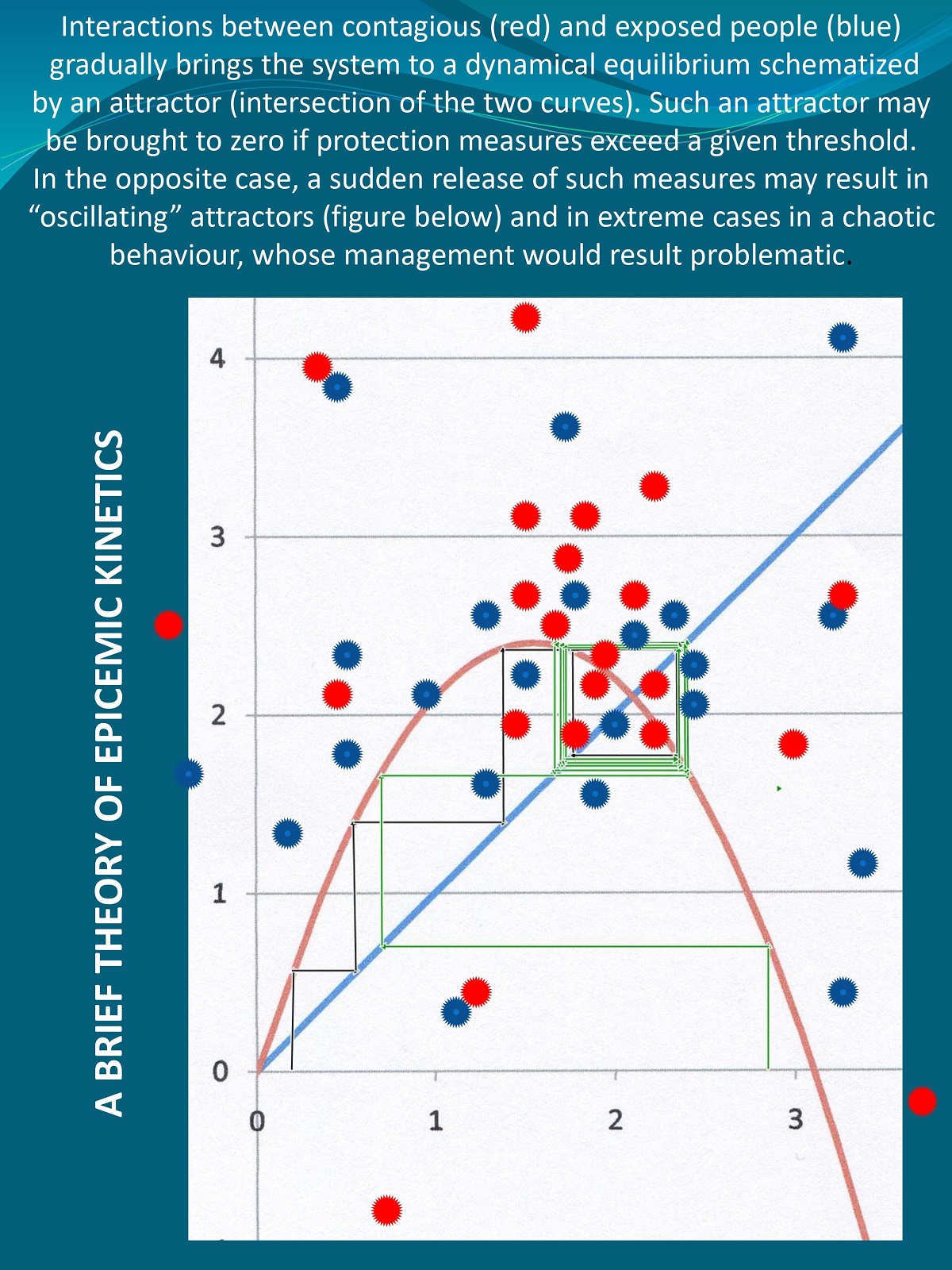
In the context of the COVID-19 epidemic, and on the basis of the Theory of Dynamical Systems, we propose a simple model for the expansion of contagious diseases, with a particular focus on viral respiratory tracts. The infection develops through contacts between contagious and exposed people, with a rate proportional to contact duration and turnover, inversely proportional to the efficiency of protection measures, and balanced by the average immunological response. The obvious initial exponential increase is readily hindered by the size reduction of the exposed population. The system converges towards a stable attractor whose value is expressed in terms of the ratio C/D of contamination vs decay factors. Decreasing this ratio below a critical value leads to a tipping point beyond which the epidemic is over. By contrast, significant values of C/D may bring the system through a bifurcating hierarchy of stable cycles up to a chaotic behaviour.