Submitted:
21 February 2023
Posted:
22 February 2023
You are already at the latest version
Abstract
Abstract: The objective of Peter Chew Triangle Diagram is to clearly illustrate the topic solution of triangle and provide a complete design for the knowledge of AI age. Peter Chew's triangle diagram will suggest a better single rule that allows us to solve any problem of topic solution of triangle simple , directly and more accurately. There are two important rules for solving the topic solution of triangle today [1,2], namely the sine rule and the cosine rule. The sine rule is used to find a non-included angle when are given two sides and a non-included angle or the opposite side angle given when are given two angles and one side. The cosine rule normally is used to find the included angle when are given three sides or the third side when are given two sides and the included angle. Peter Chew Method[3] allow us to find the third side simple and directly when given two sides and a non-included angle. Peter Chew rule [4] allow us to find a non included angle simple, directly and more accurately when given 2 sides and an included angle. Aply Peter Chew Triangle Diagram to Education 4.0 Calculator , Peter Chew Triangle Diagram Calculator allows the Calculator to solve any problems in the topic solution of triangle simple, directly and more accurate. This can be effective in increasing students' interest in using technology while learning mathematics and will help in the learning of mathematics, especially when similar covid-19 issues arise in the future.
Keywords:
Peter Chew Triangle Diagram
; Peter Chew
1. Introduction
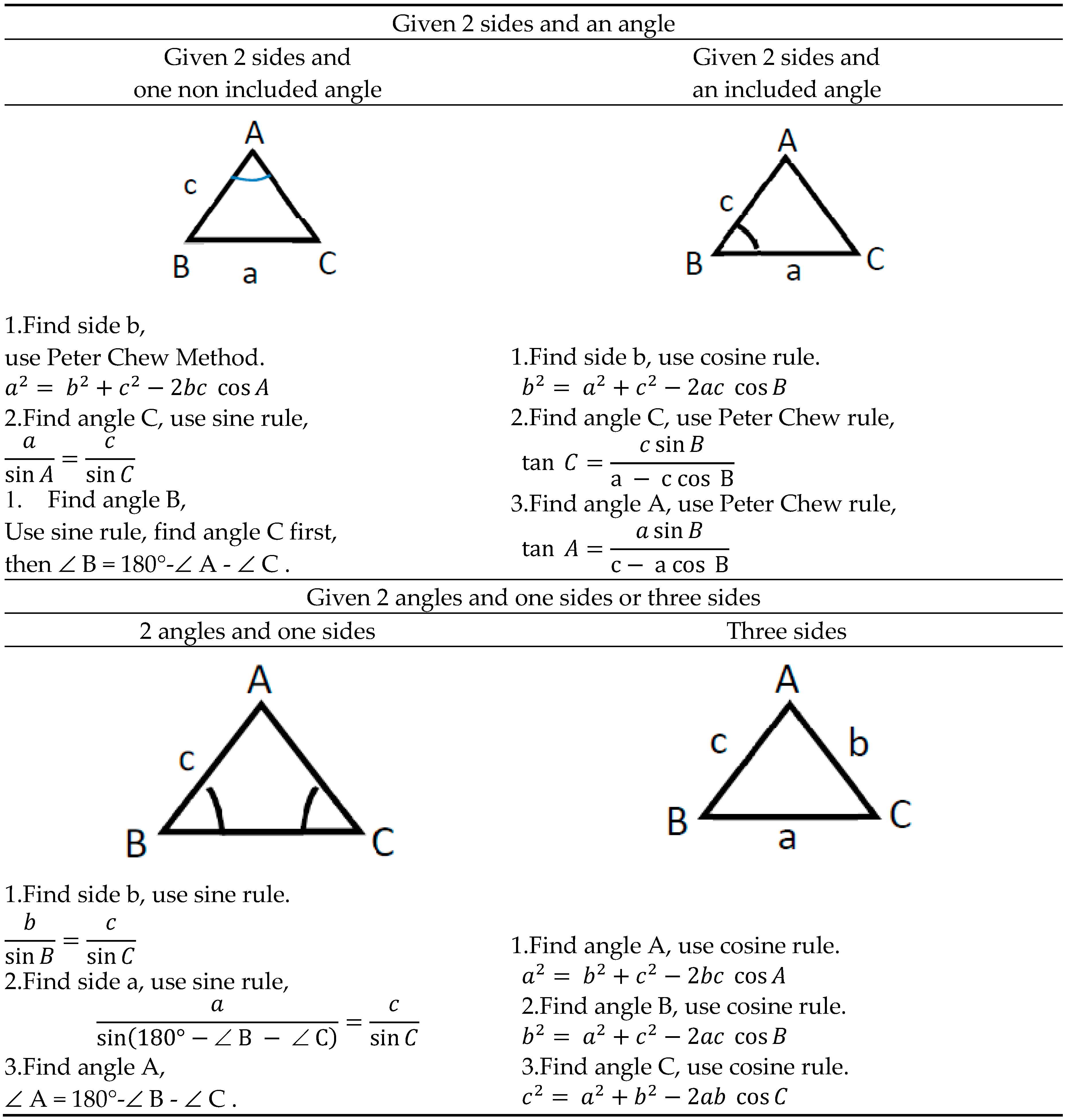
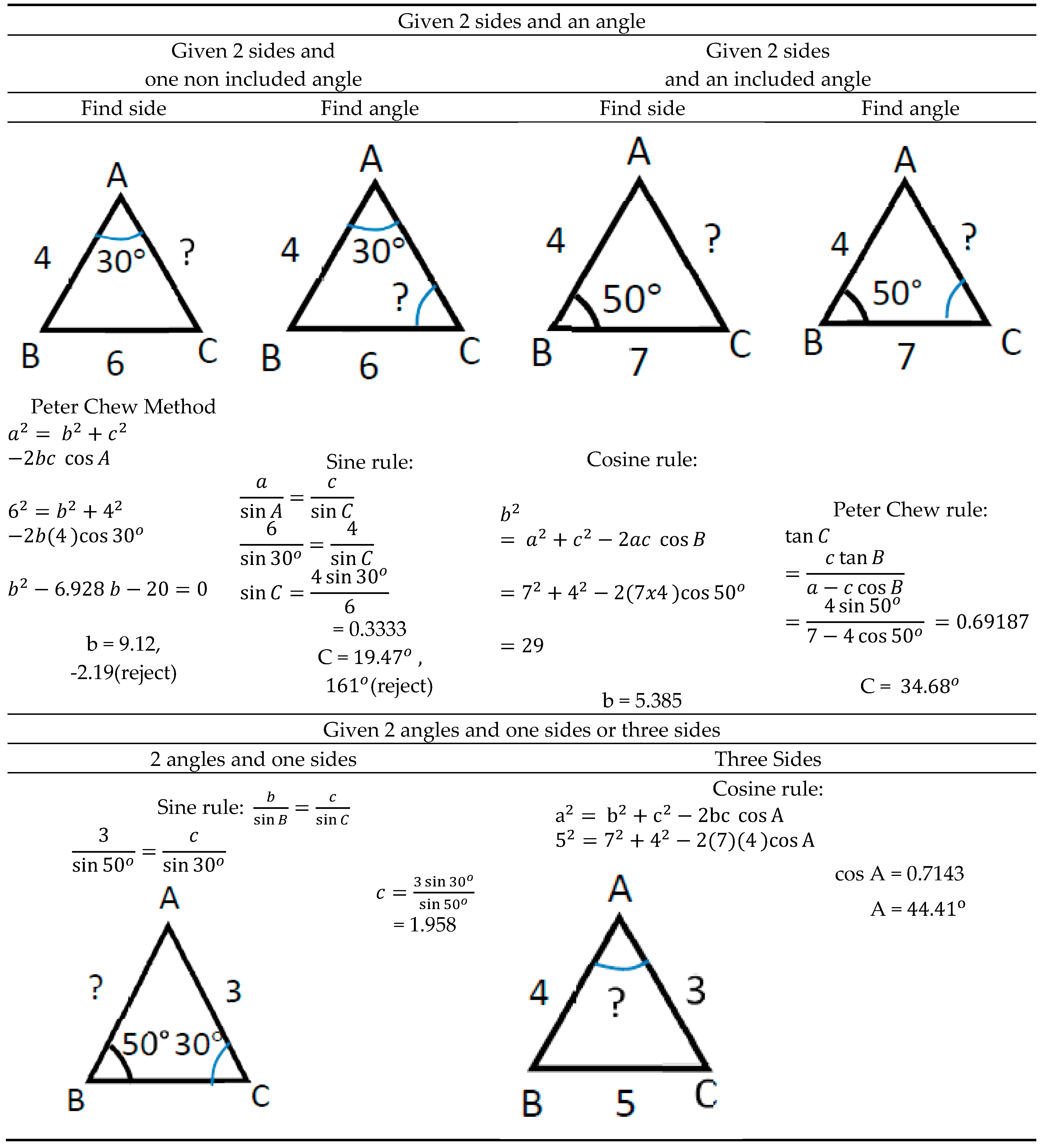
There are two important rules for solving the topic solution of triangle today, namely sine rules and cosine rules . The sine rule is used to find a non-included angle when are given two sides and a non-included angle or the opposite side angle given when are given two angles and one side. The cosine rule normally is used to find the included angle when are given three sides or the third side when are given two sides and the included angle. Peter Chew Method allow us to find the third side simple and directly when given two sides and a non-included angle. Peter Chew rule allow us to find a non included angle simple, directly and more accurately when given 2 sides and an included angle.
2. Peter Chew triangle Diagram
3. Peter Chew triangle Diagram Example solution
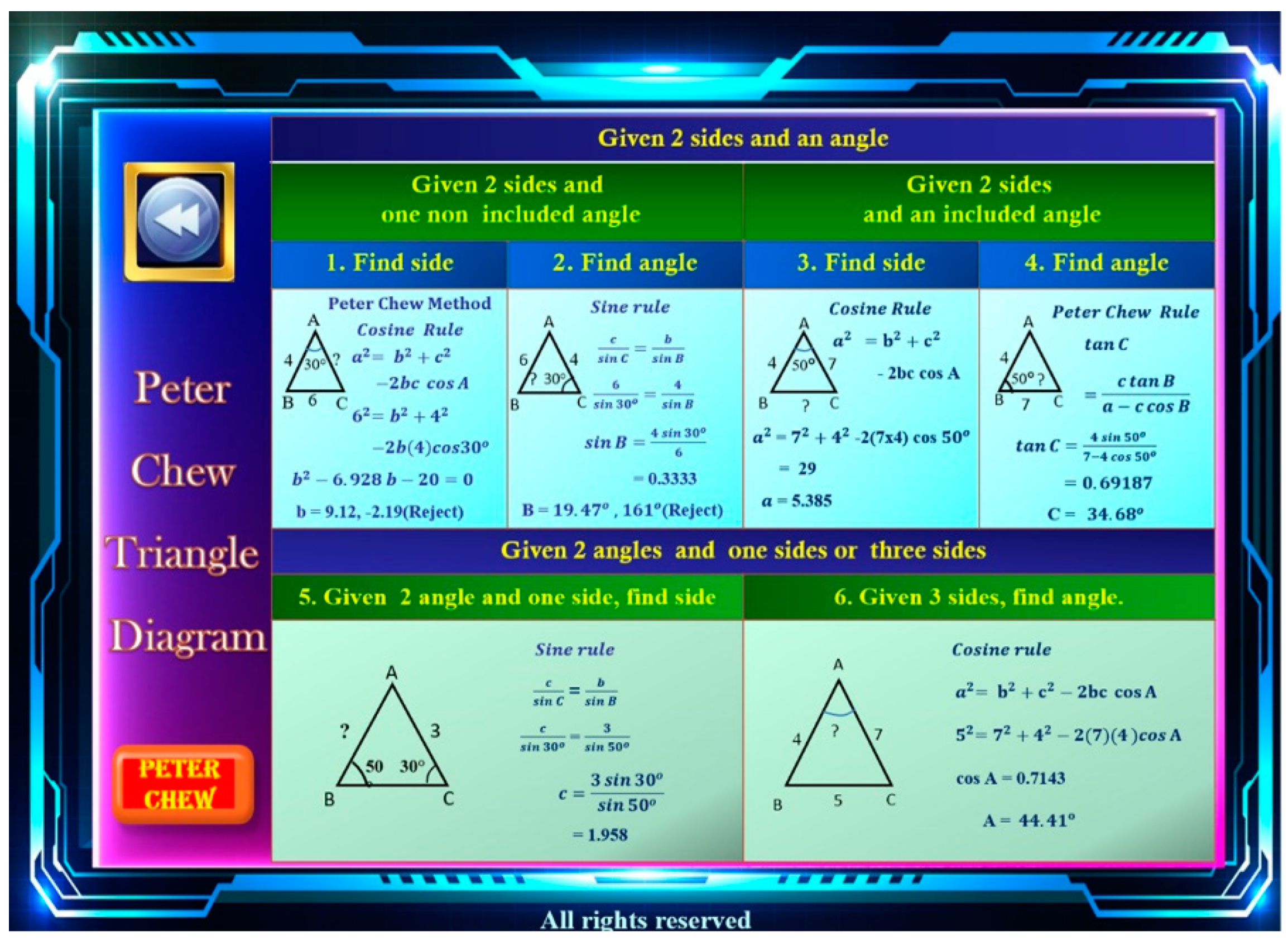
4. The Application of Peter Chew Triangle Diagram
Today's online calculators only contain the knowledge already explained in the book, such as the topic solutions of the triangle rule, sine and cosine rules. For problems that cannot be solved directly by the sine or cosine rules, online calculators such as Wofram alfa and Symbolab cannot help students solve the problem directly. This will result in students not being interested in using technology such as online calculators when learning mathematics. In order to solve the above problems, i create Peter Chew Method , Peter Chew Rule and Peter Chew Triangle Diagram to supplement the necessary information to complete the topic of solution of triangle.
With the help of Peter Chew Method and Peter Chew Rule, Peter Chew Triangle Diagram can guide user to solve all triangle problems with simple solution, only need to use one rule and only once. Aply Peter Chew Triangle Diagram to Education 4.0 Calculator , Peter Chew Triangle Diagram Calculator allows the Calculator to solve any problems in the topic solution of triangle simple, directly and more accurate. This can be effective in increasing students' interest in using technology while learning mathematics and will help in the learning of mathematics, especially when similar covid-19 issues arise in the future.
Main page of Education 4.0 Calculator , Peter Chew Triangle Diagram Calculator
For more information of Education 4.0 Calculator, please refer to the YouTube link https://youtu.be/zSLS1hFh5GI [ Education 4.0 Calculator ].
5. Conclusion
Peter Chew's triangle diagram will suggest a better single rule that enables us to solve any problem topic solution of triangle simple, directly, more easily and more accurately. Peter Chew Triangle Diagram provides a complete design of AI age knowledge for the topic solution of triangle. The application of Peter Chew triangle diagram in the Peter Chew Triangle Diagram Calculator allows the calculator solve any problem in the topic solution of triangle simple, directly and more accurately, which can effectively help the teaching of mathematics, especially when similar covid-19 problems arise in the future. The main goal of Peter Chew's rules and methods is to simplify the solution, which is the same as Albert Einstein's famous quote: Everything should be made as simple as possible, but not simpler.
In addition, Albert Einstein's also quote :
i) If you can't explain it simply you don't understand it well enough,
ii)We cannot solve our problems with the same thinking we used when we created them.
iii) When the solution is simple, God is answering
From the Albert Einstein's quote above, it can be seen that simplifying knowledge is very important.
Acknowledgments
Because the aim of the Peter Chew Triangle Diagram aims to facilitate the teaching and learning of the Topic 'Solution of Triangle ' easily especially during a pandemic such as Covid-19, the Peter Chew Triangle Diagram (preprint) has been published at the World Health Organization (WHO) (Appendix 1) the link to this information is https://pesquisa.bvsalud.org/global-literature-on-novel-coronavirus-2019-ncov/resource/en/ppzbmed-10.20944.preprints202106.0221.v1
Appendix
References
- Xin-She Yang. Engineering Mathematics with Examples and Applications 62 (2017).
- John Bird Engineering Mathematics. Fifth Edition 216 (2007).
- Chew, Peter, Peter Chew Method For Solution Of Triangle (August 29, 2022). Available at SSRN: https://ssrn.com/abstract=4203746. [CrossRef]
- Peter Chew . Peter Chew rule for solution of triangle. Journal of Physics: Conference Series 1411 (2019) 012009 IOP Publishing. Nov2019. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
