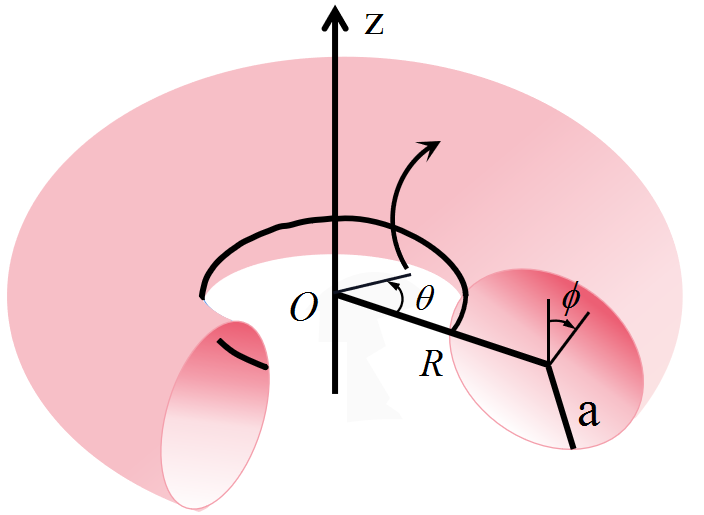
The nonlinear deformation and stress analysis of a circular torus is a difficult undertaking due to its complicated topology and the variation of the Gauss curvature. A nonlinear deformation (only one term in strain is omitted) of Mindlin torus was formulated in terms of the generalized displacement, and a general Maple code was written for numerical simulations. Numerical investigations show that the results obtained by nonlinear Mindlin, linear Mindlin, nonlinear Kirchhoff-Love, and linear Kirchhoff-Love models are close to each other. The study further reveals that the linear Kirchhoff-Love modeling of the circular torus gives good accuracy and provides assurance that the nonlinear deformation and stress analysis (not dynamics) of a Mindlin torus can be replaced by a simpler formulation, such as a linear Kirchhoff-Love theory of the torus, which has not been reported in the literature.