Preprint

Article

An Integral Expression for Pi Obtained by Virtue of Ramanujan’s Approximation in Conoidal Areas: Applications of the Resultant Figure in Engineering

Altmetrics

Downloads

408

Views

677

Comments

Joseph Cabeza Lainez^*

This version is not peer-reviewed

Submitted:

17 February 2023

Posted:

21 February 2023

You are already at the latest version

Alerts

Abstract

unlike the volume, the expression for the surface area of a regular conoid has not yet been obtained by means of direct integration or a differential geometry procedure. As this non-developable form is relatively used in engineering, the difficulty to determine its surface, represents a serious shortcoming for several problems which arise in radiative transfer, lighting and construction, to cite just a few. In order to solve the problem, I conceived the surface as a set of linearly dwindling ellipses which remain parallel to a circular directrix, a typical problem appears when searching the length of such ellipses. I employed a new procedure which, in principle, consists in dividing the surface into infinitesimal elliptic strips to which we have successively applied Ramanujan’s second approximation for the longitude of the ellipse. In this manner, we can obtain the perimeter of any transversal curve pertaining to the said form as a function of the radius of the directrix and the position of the ellipse’s center on the X-axis. Integrating the so-found perimeters of the differential strips for the whole span of the conoid, an unexpected solution emerges through the newly found number psi (ψ) which seems like a refined approximation to the third decimal of Pi but derived from a definite integral equation. As the strips are in truth slanted in the symmetry axis, their width is not uniform and we need to perform some adjustments in order to complete the problem with sufficient precision, but this is discussed separately in the annexes. Relevant implications for mathematical symmetry applied to multifarious architectural and engineering forms can be derived from this finding

Keywords:

Subject: Computer Science and Mathematics - Geometry and Topology

1. Introduction

1.1. Outline of the problem

Since antiquity the meaning of the number Pi has been associated to the length of a circumference, that is, such magnitude, if the diameter of the circumference equates the unit, gives Pi, and accordingly for different measures of the diameter. Even in the Book of Kings of the Olde Testament, when instructions are transferred to build an offering’s laver (known as the brazen or molten sea) of circular design in the Temple of Solomon in Jerusalem, it is mentioned that the perimeter has to be three times the diameter [1] a fair estimate for an ancient time.

This said, could we not try to find, from a scientific point of view, the meaning of different powers of Pi, like for instance, Pi^N?

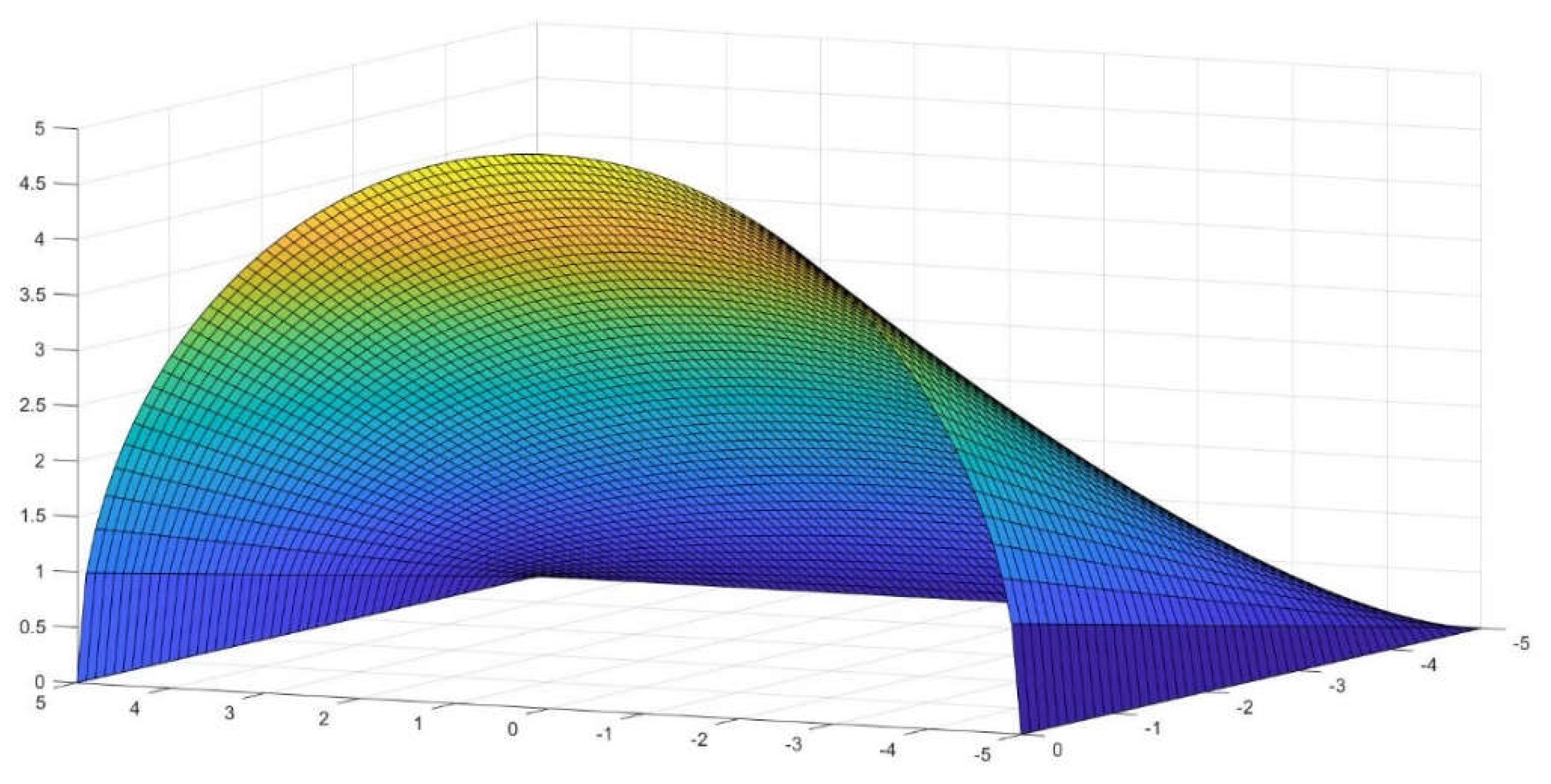
The answer for us is affirmative, and in this article we would discuss the particular case of the second power of π, namely, Pi squared or Pi². Such innovative result emerges when we try to calculate the surface area of a Conoid, a ruled surface generated by parallel straight lines which project from a circumference directrix onto a linear edge (Figs.1 and 2).

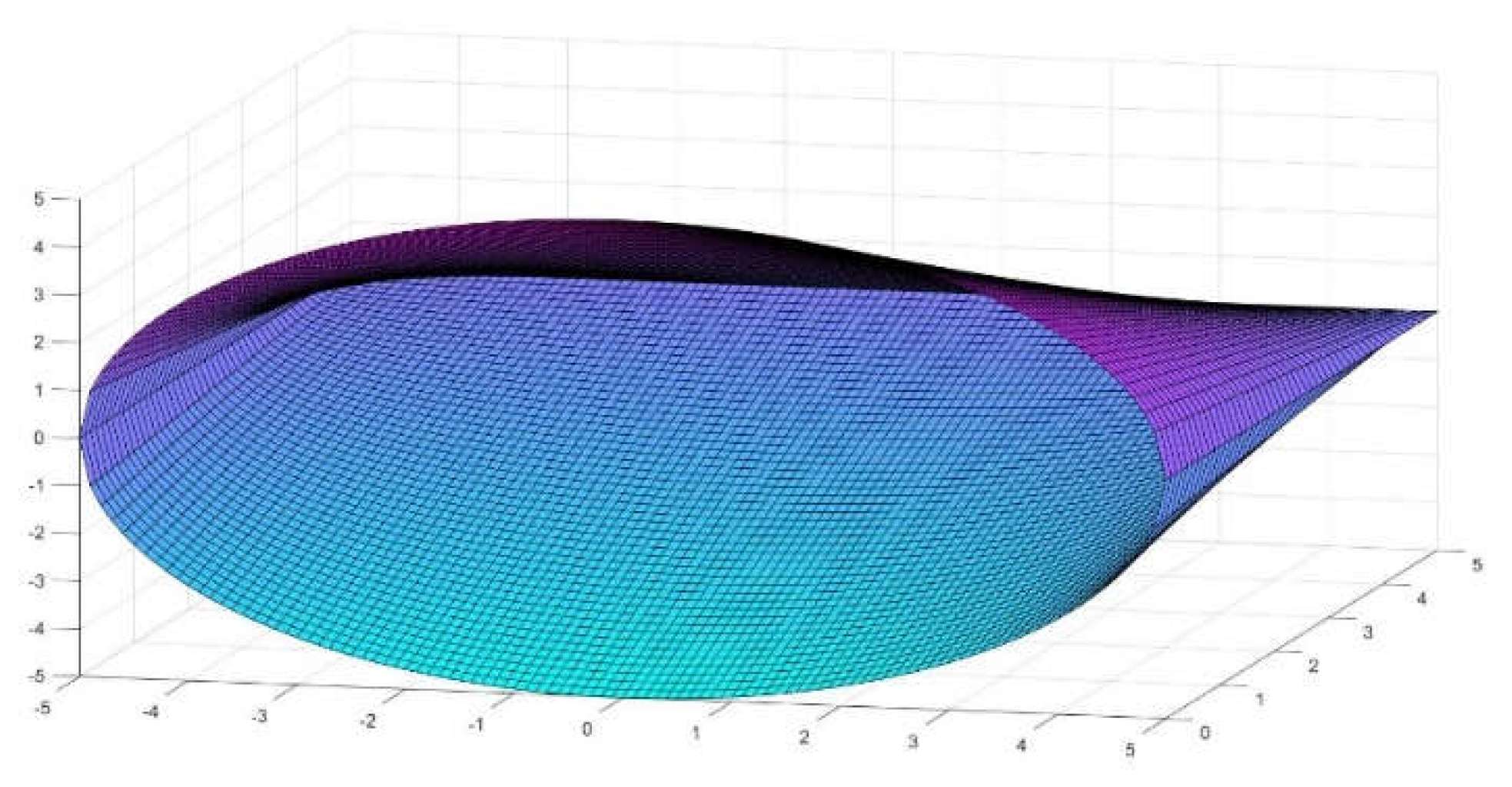
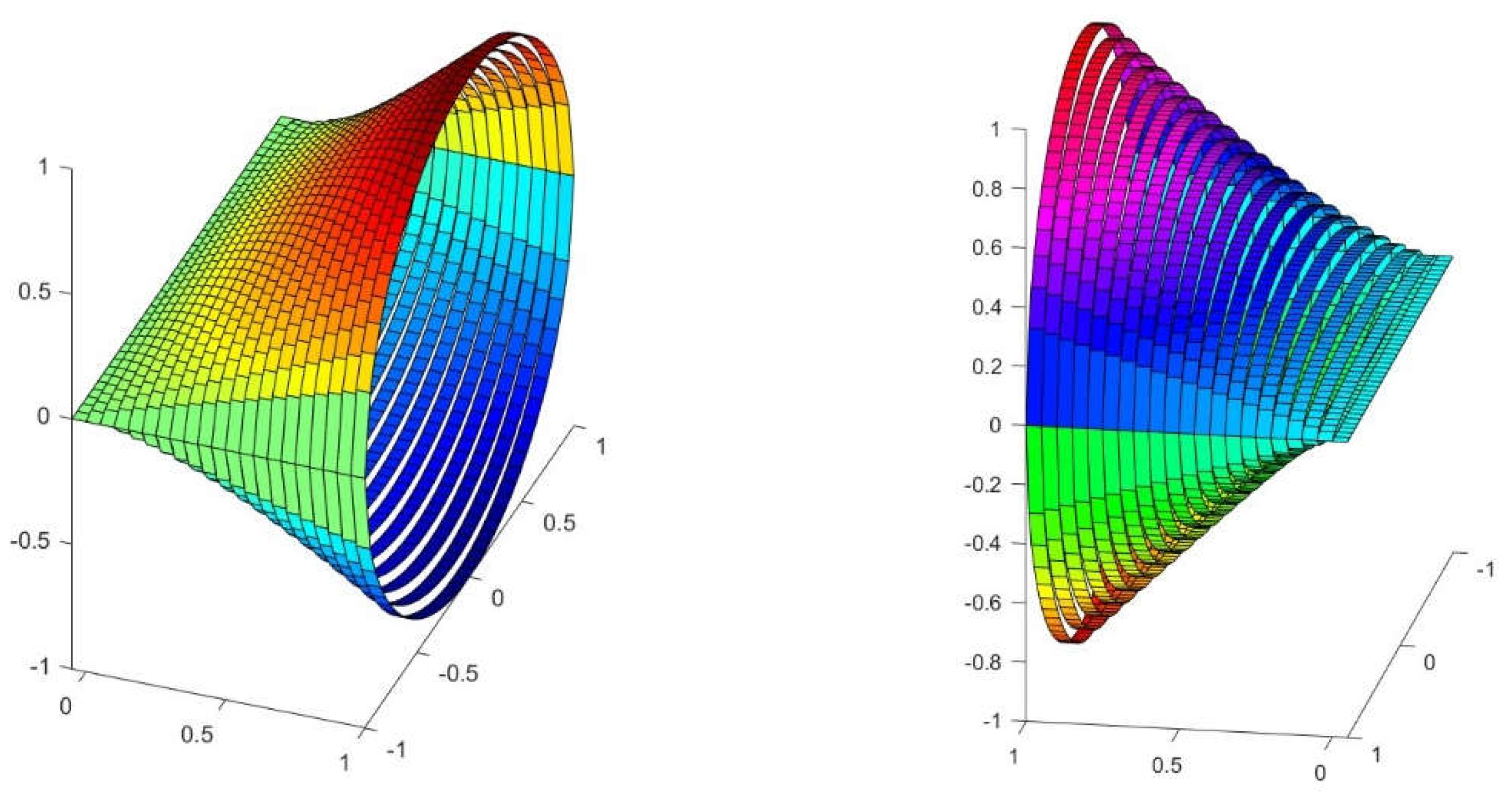
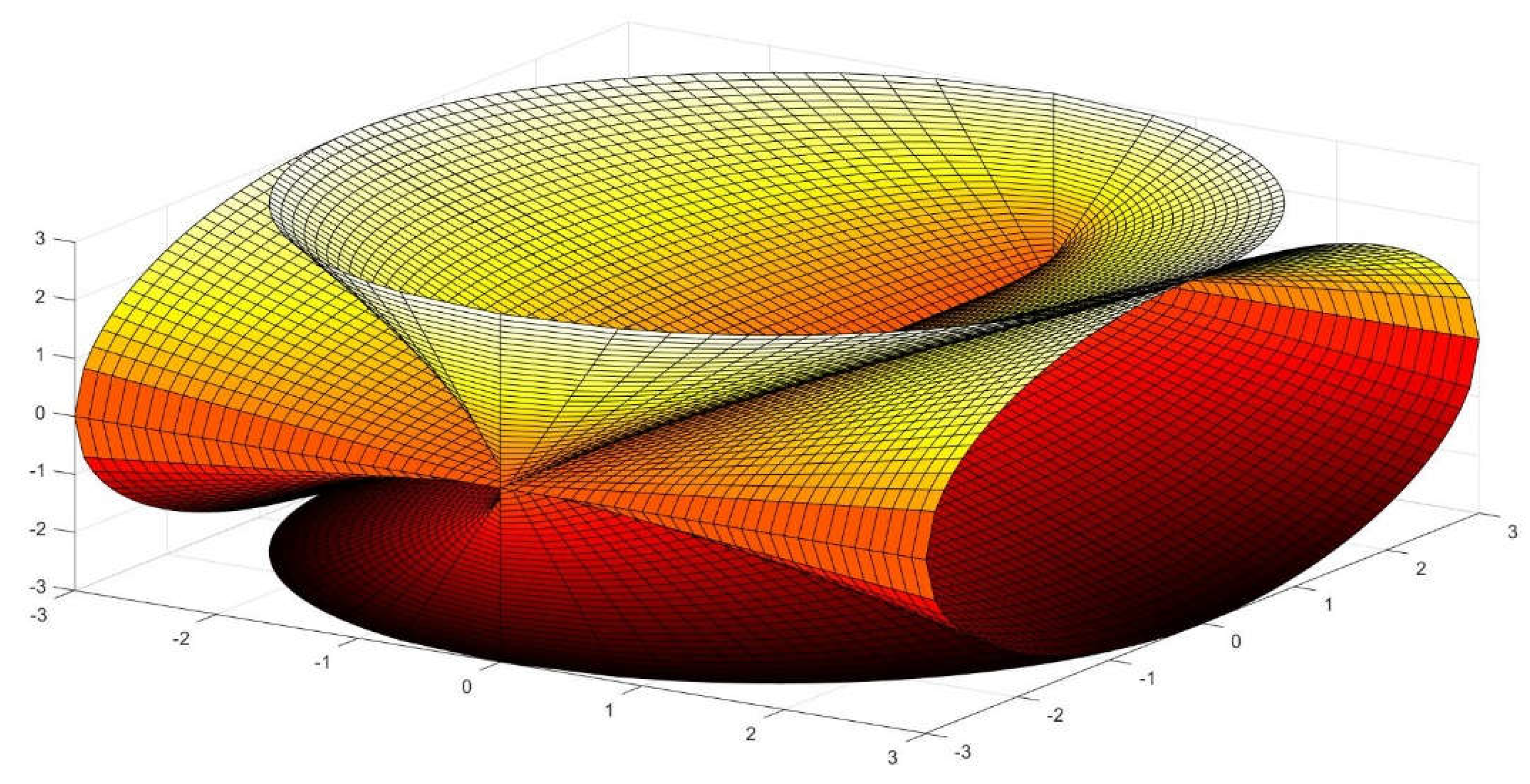
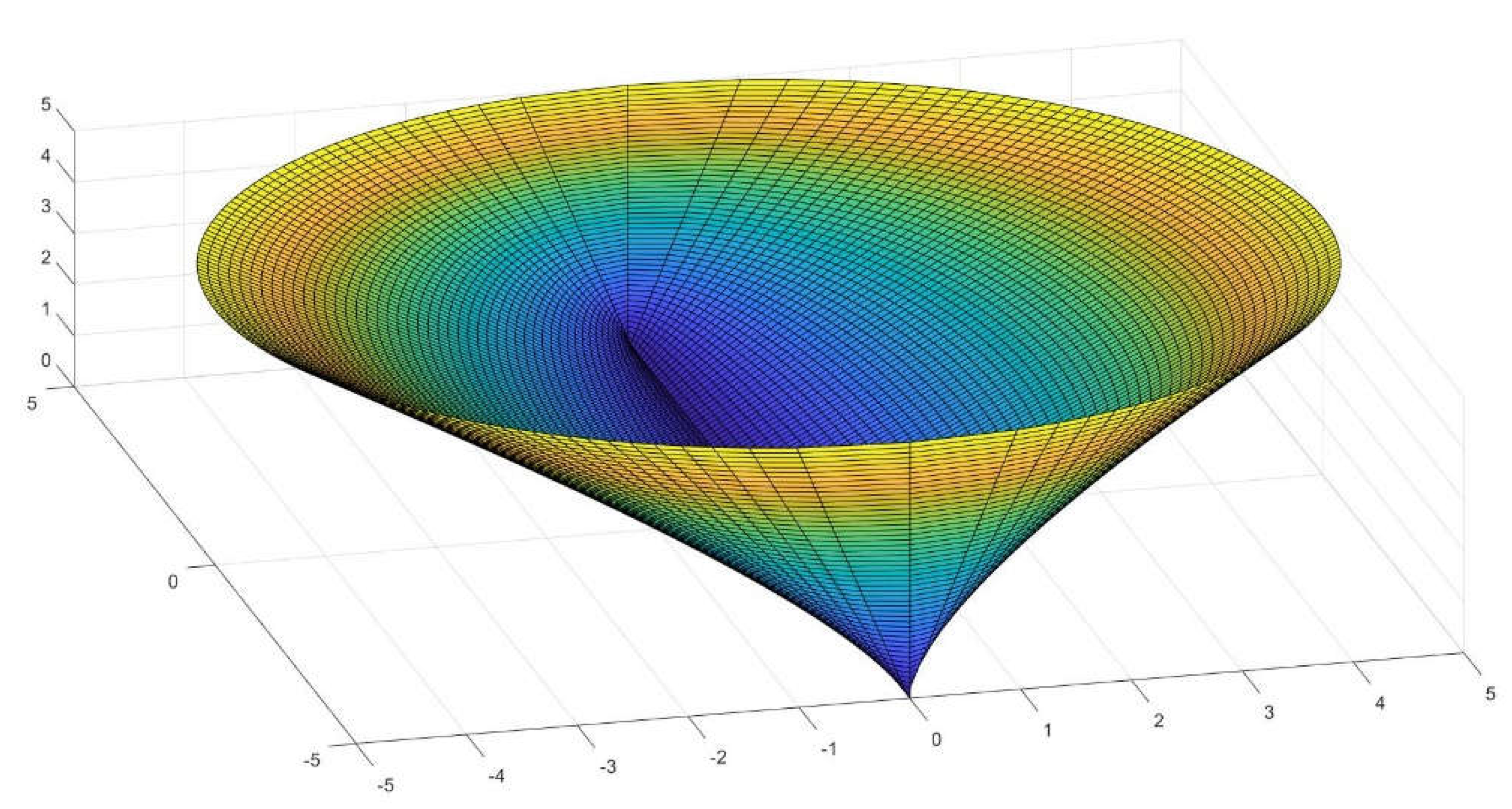
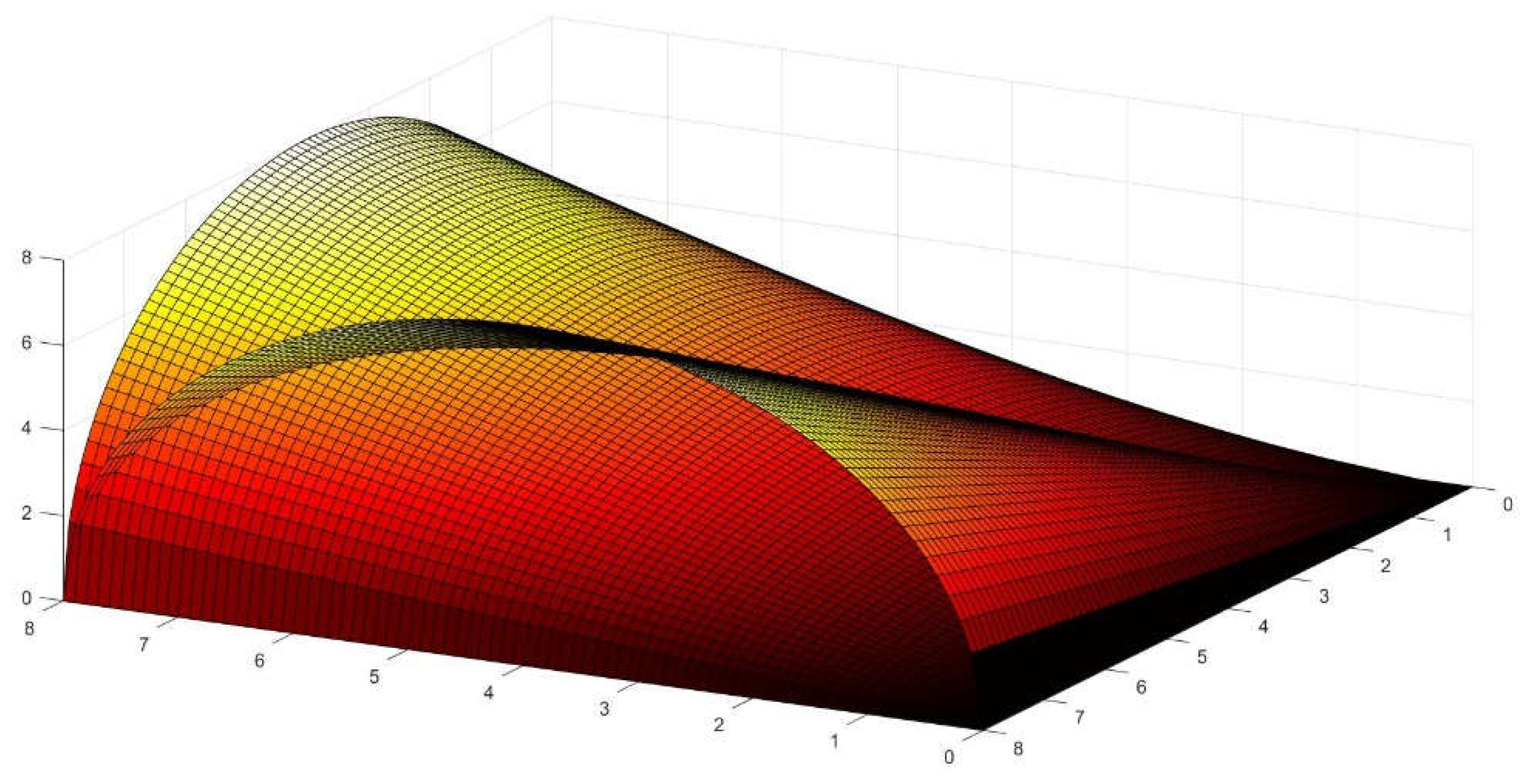
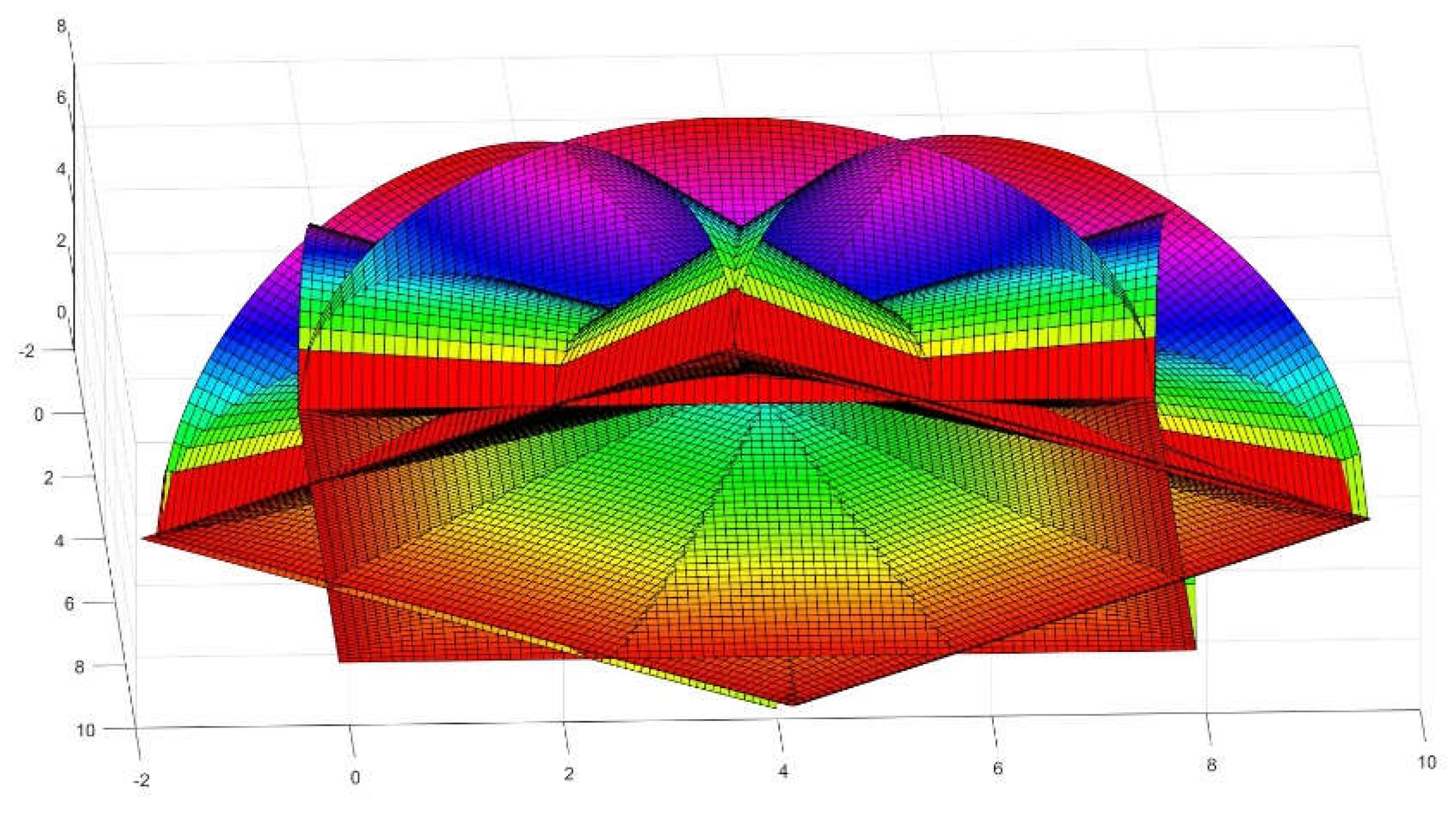
Figure 1. A typical straight conoid with circular directrix, where R=L=5.

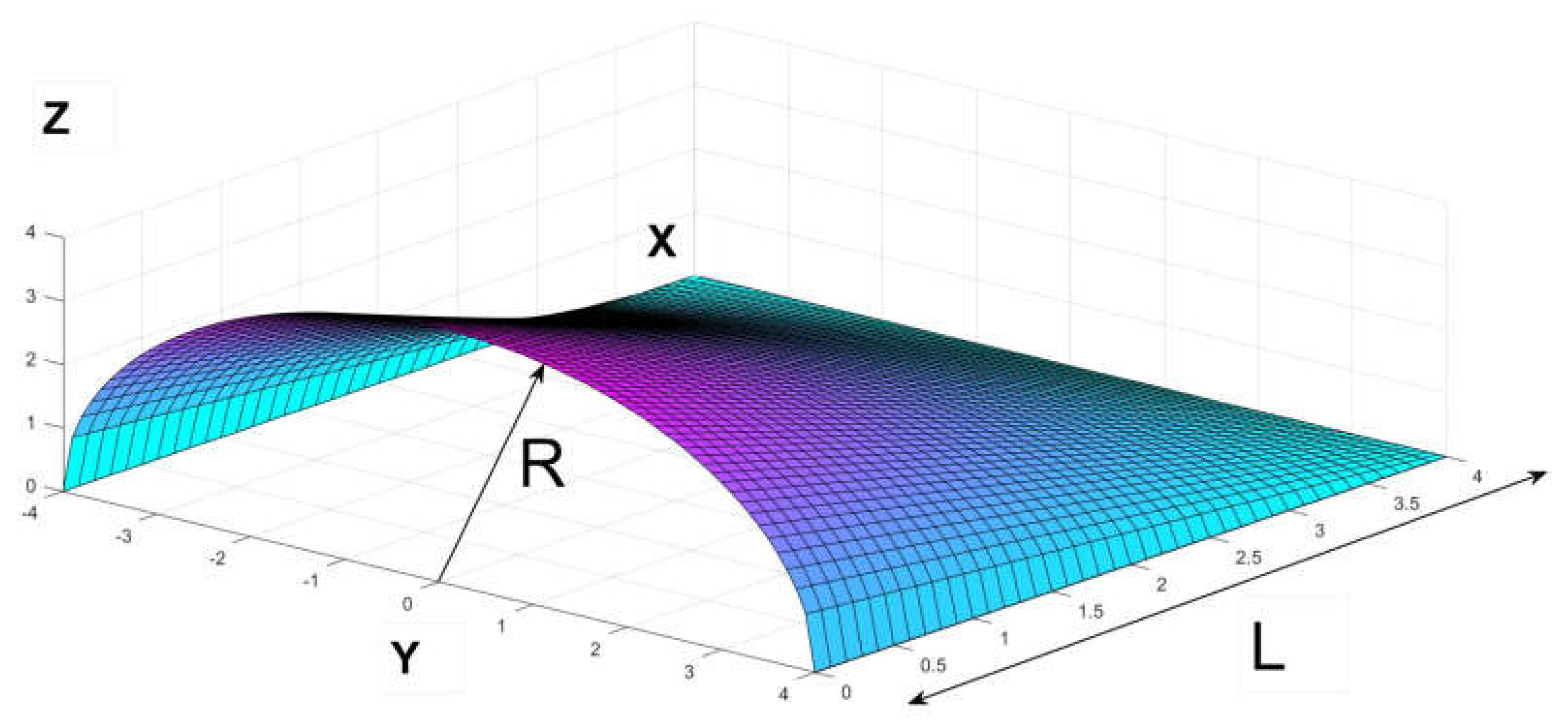
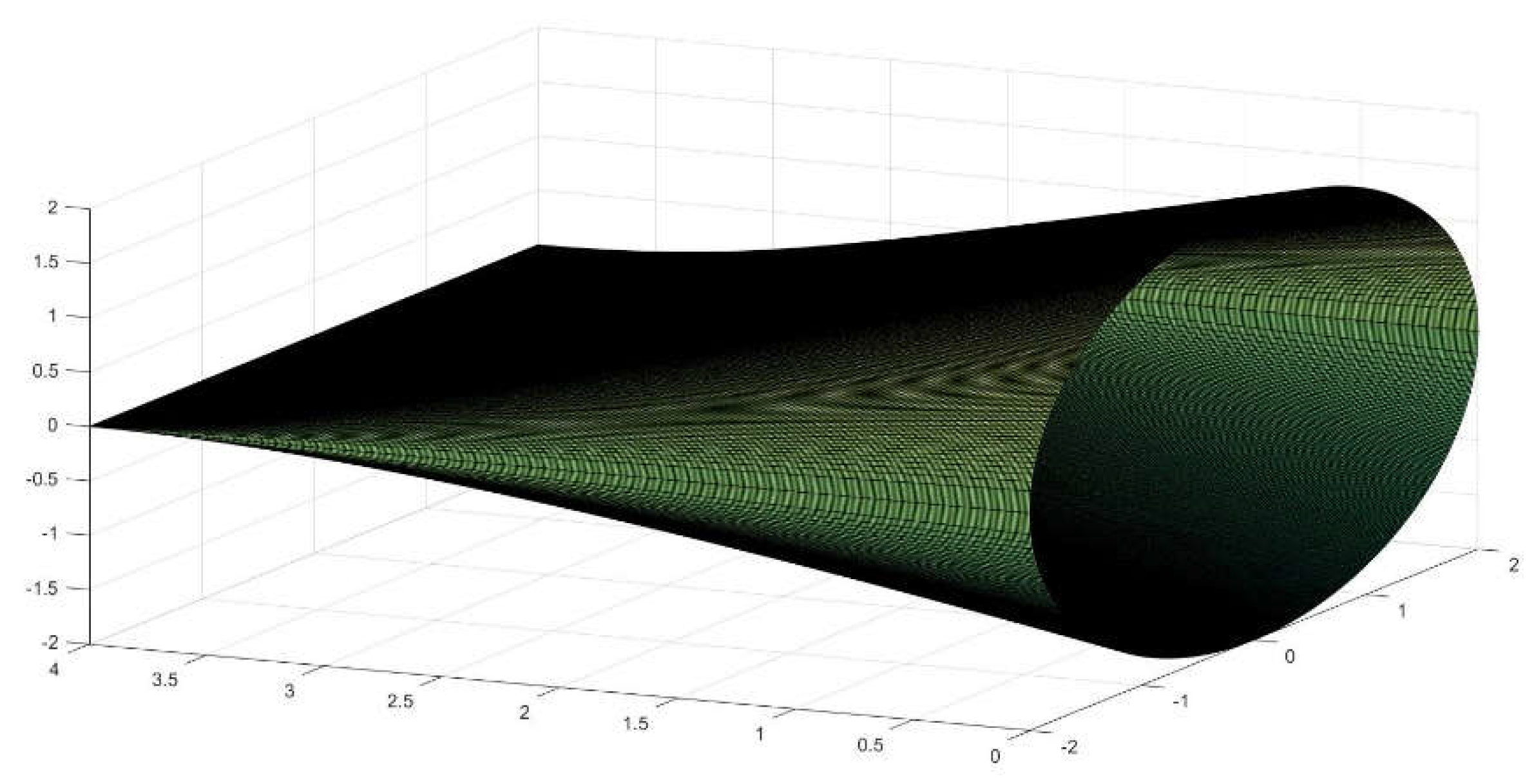
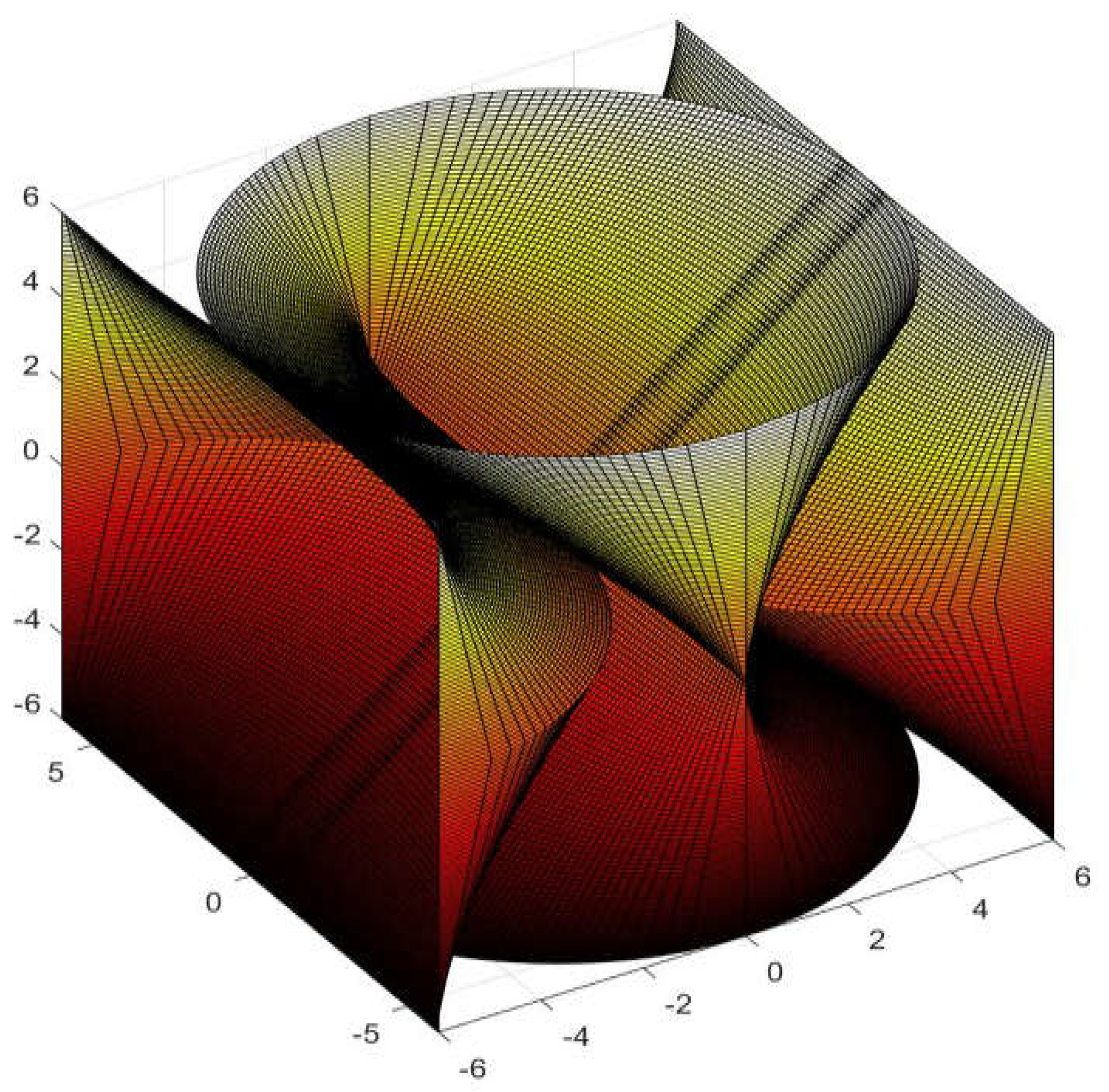
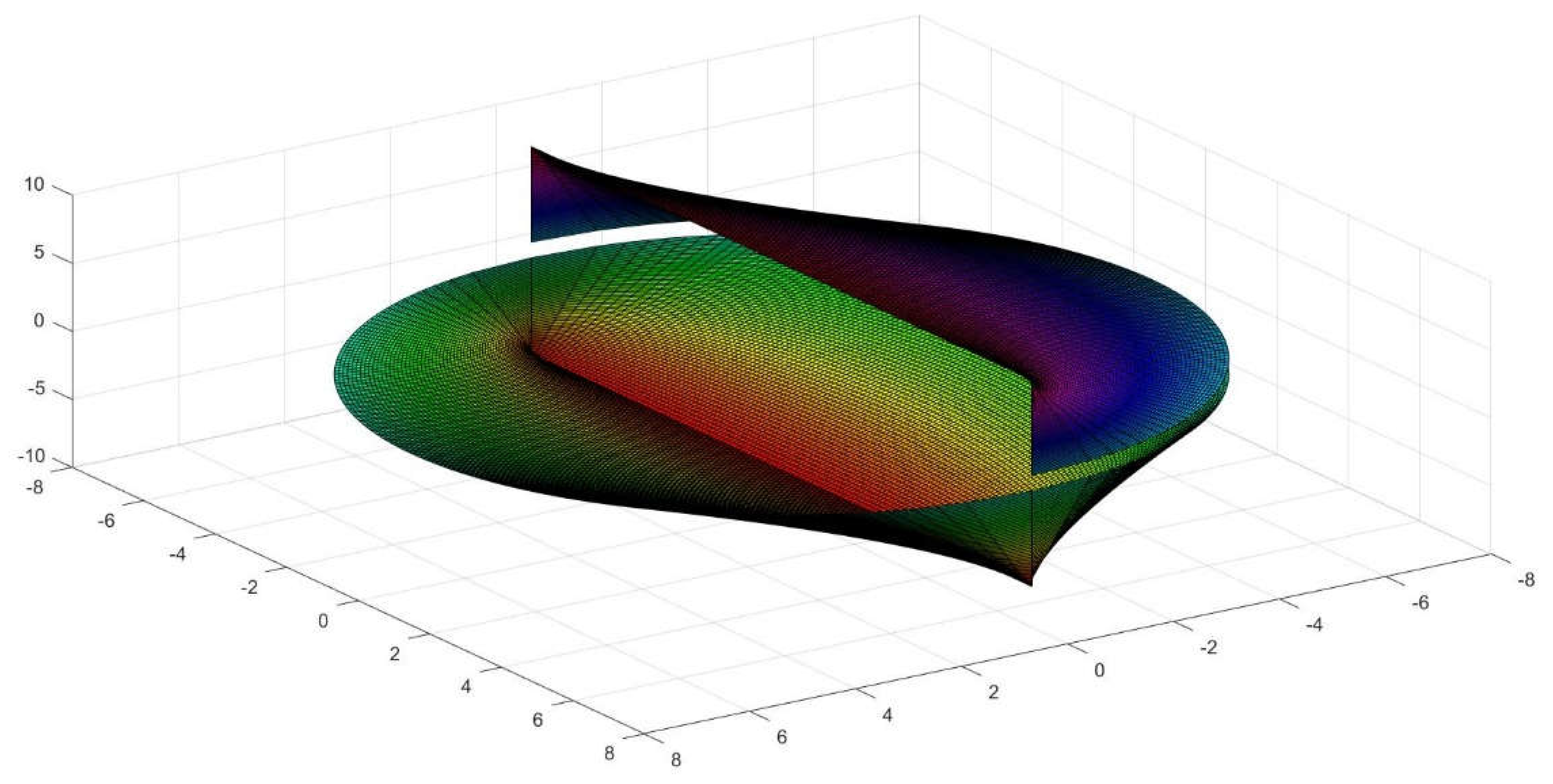
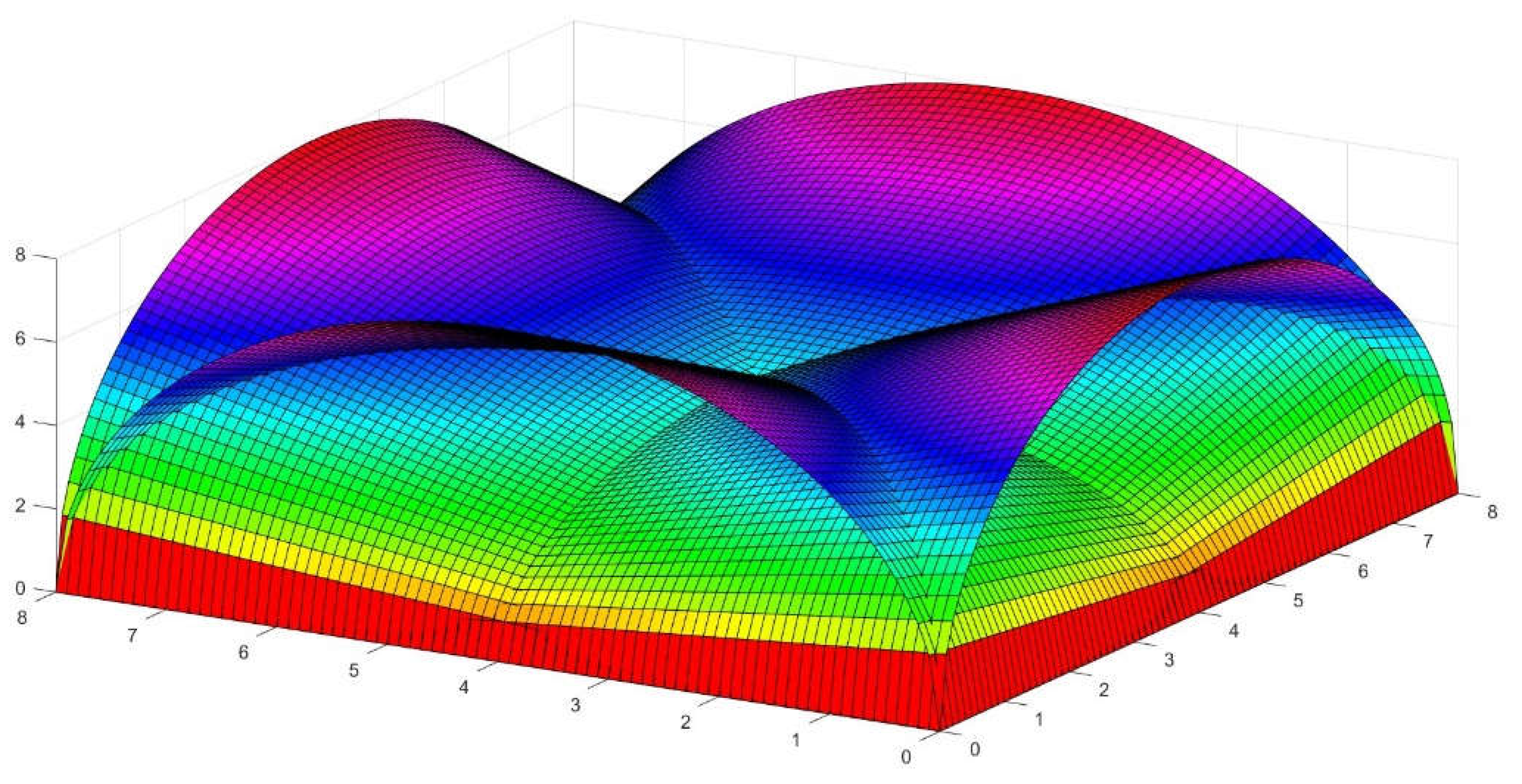
Figure 2. Explanation of the parts of a straight conoid with circular forming line, in this case R=L=4.

The equation that regulates such warped figure for x positive is:

\frac{L^{2} z^{2}}{{(L - x)}^{2}} + y^{2} = R^{2}

(1)

where R stands for the radius of the directrix in the case of a circumference and L is the length in the X direction as drawn in Figure 2. If we assume for convenience L=R, it results that,

\frac{R^{2} z^{2}}{{(R - x)}^{2}} + y^{2} = R^{2}

(2)

To obtain the solution of the lateral area of such surface, after not reaching a conclusion with sundry methods, we have employed Ramanujan’s second approximation for ellipses. [2]

2. Methods and materials

2.1. Resolution of the proposed approximation

In his well-known conjecture to calculate the perimeter of an ellipse, Ramanujan stated that the perimeter (P) of the curve equates:

P = π (3 (a + b) - \sqrt{(3 a + b) (3 b + a))}

(3)

Where a represents the major and b stands for the minor semi-axis. (Figure 3)

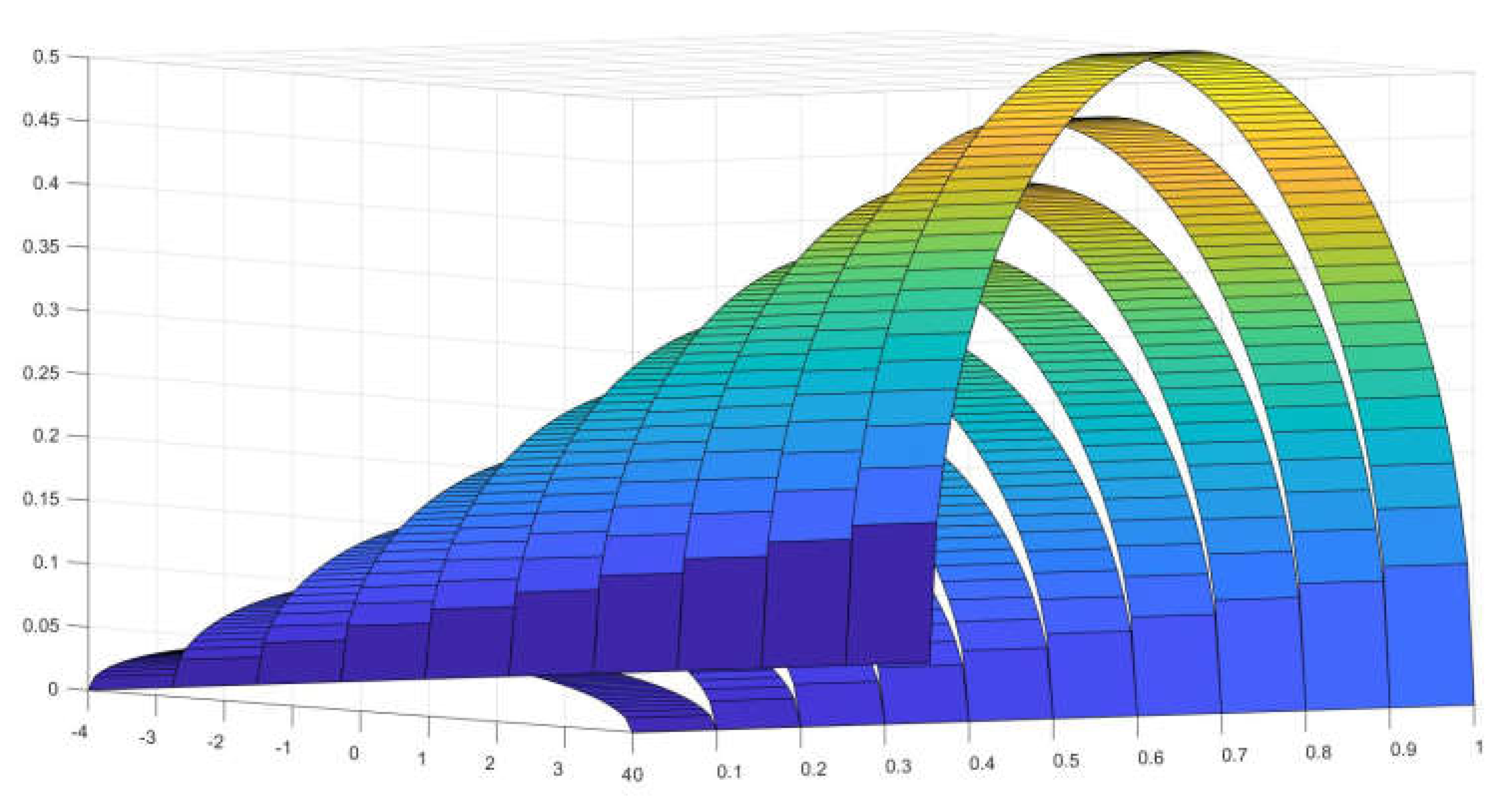
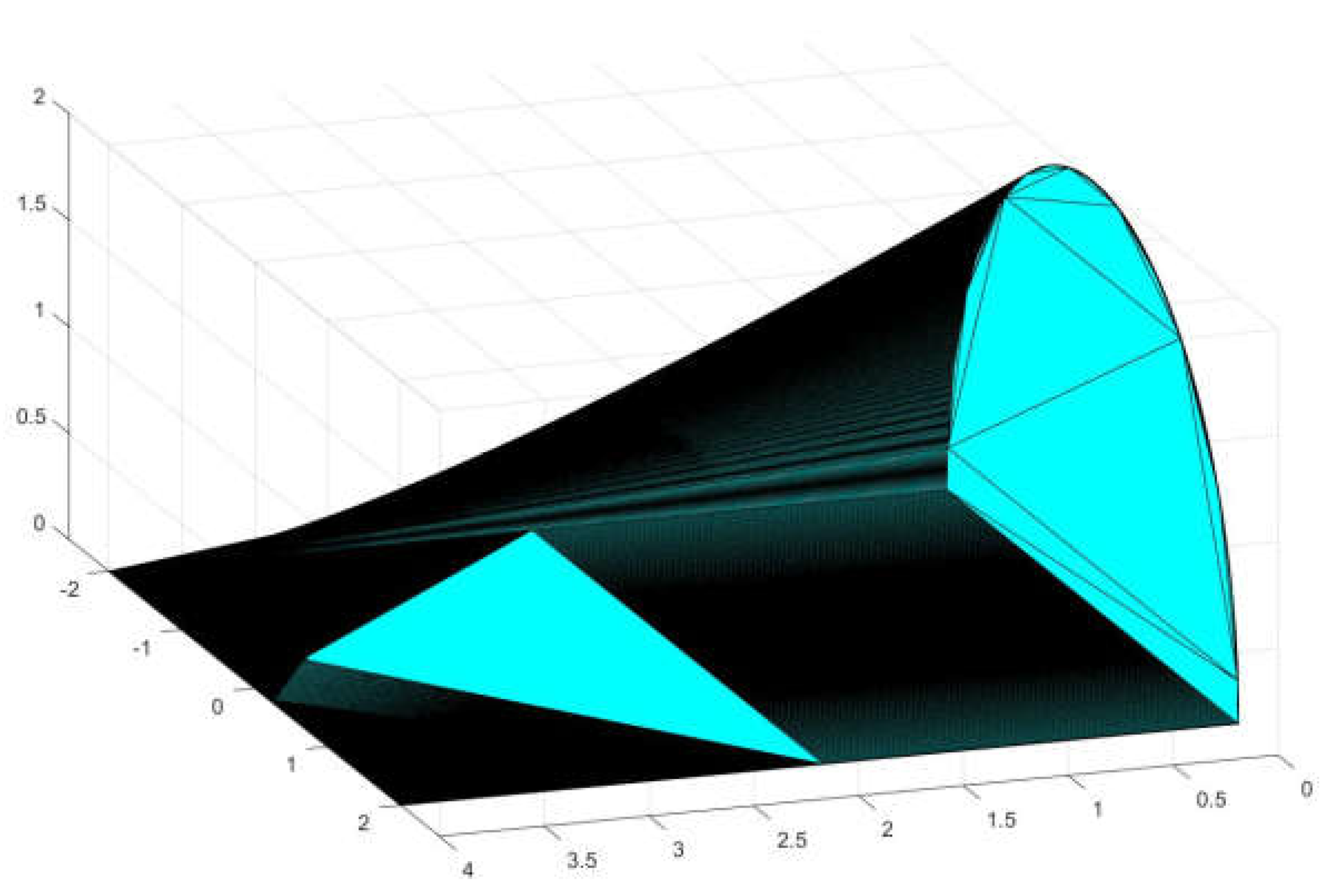
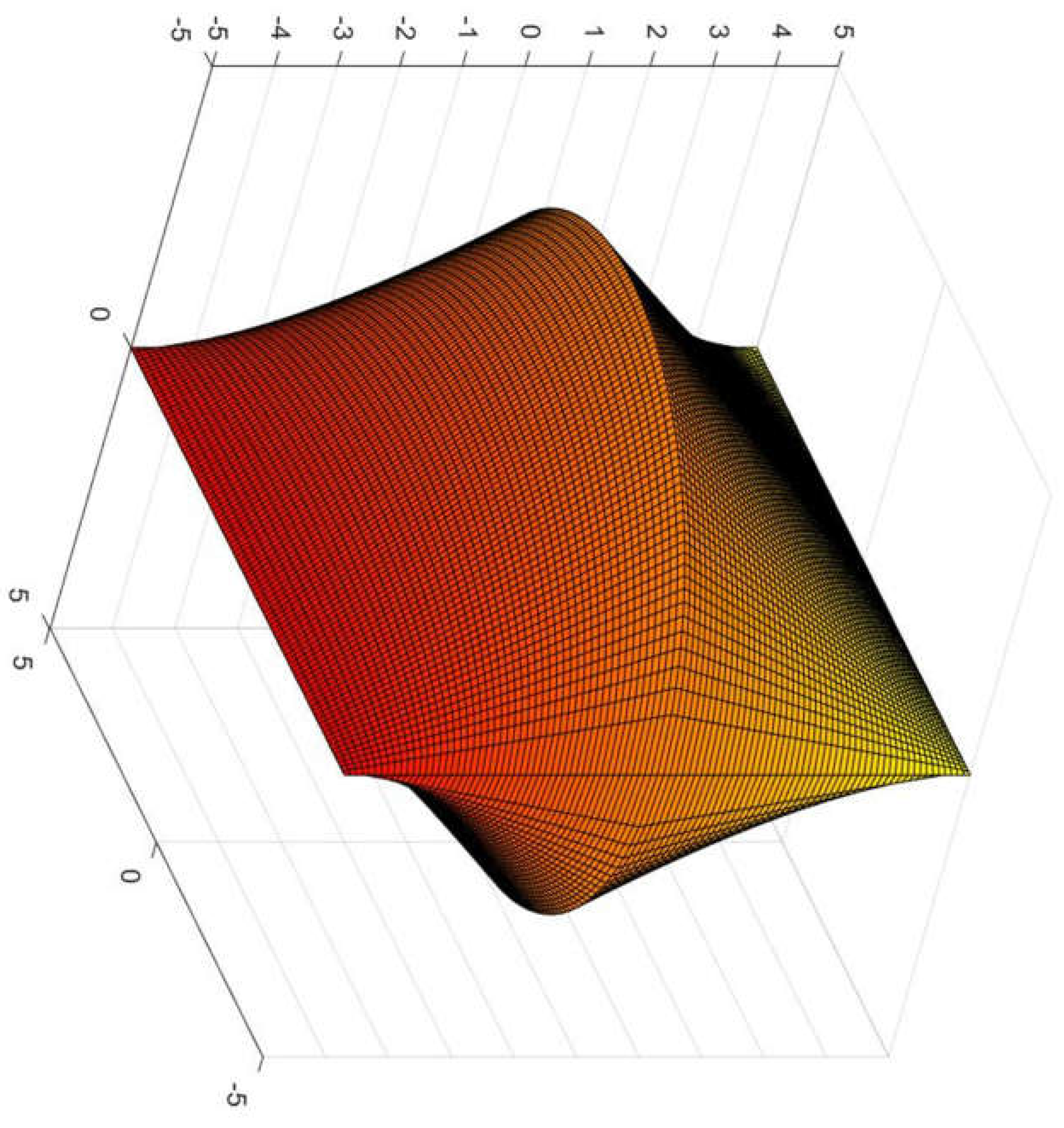
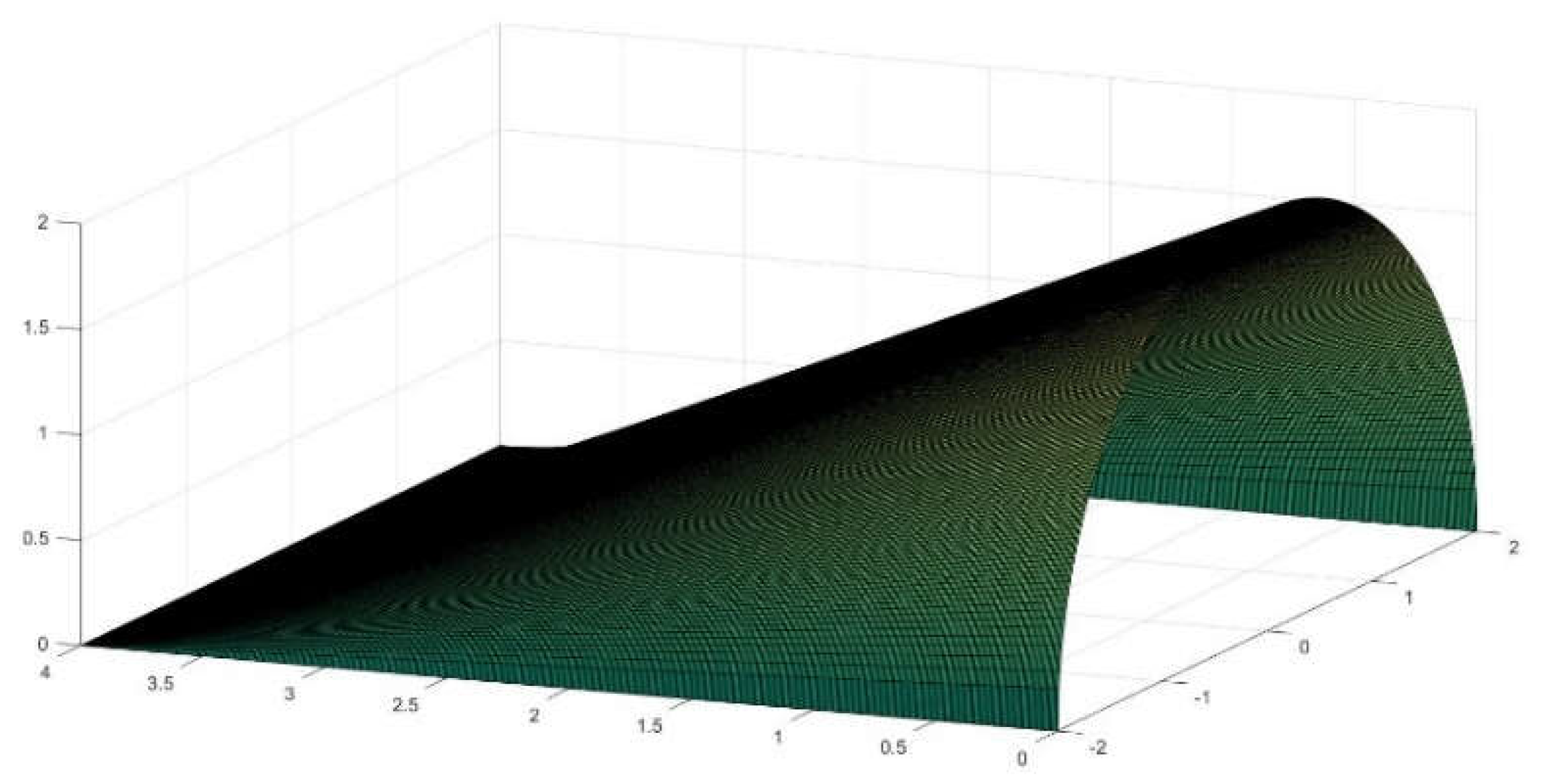
Figure 3. Elliptical straps’ finite approximation for radius 4 and length 1.

Such approximation, is rather easy to handle and it works well for the extreme case of b=0, a straight line, that appears in the limit edge of the conoid and its contour.

For the directrix, we can substitute a for R, the radius of the circumference at the edge.

Thus, a=R and it is easy to demonstrate that, being R/L the tangent of the angle formed by the middle section of the figure, the minor semi-axis equates b=x*R/L

As previously mentioned, R is the radius of the end semicircle and L is the total length and for any x value between 0 and L, we would obtain,

P = π (3 (R + x R / L) - \sqrt{(3 R + \frac{x R}{L}) (\frac{3 x R}{L} + R)}

(4)

And grouping similar terms,

P = π (3 R (1 + x / L) - \sqrt{R (3 + x / L) R (3 x / L + 1)})

(5)

P = π (3 R (1 + x L) - \sqrt{R^2 (3 + x / L) (3 x / L + 1)})

(6)

The half perimeter P₁ yields,

P_{1} = (π / 2) (3 R (1 + x L) - \sqrt{R^2 (3 + x / L) (3 x / L + 1)})

(7)

We can take R out of the whole expression,

P_{1} = (π R / 2) (3 (1 + x L) - \sqrt{(3 + x / L) (3 x / L + 1)})

(8)

And L as well,

P_{1} = (π R / (2 L)) (3 (L + x) - \sqrt{3 x^{2} + 10 L x + 3 L^{2})})

(9)

To obtain the lateral area of the conoid composed by decreasing strips along the central section, we need to perform the integration of,

A_{c} = \frac{π R}{2 L} \int_{0}^{L} [3 L + 3 x - \sqrt{3 x^{2} + 10 L x + 3 L^{2})}] d x

(10)

The first two terms are immediate and give the solution;

I_{1} + I_{2} = {[3 L x + \frac{3 x^{2}}{2}]}_{o}^{L}

(11)

And the final result is for these two terms, applying the limits of integration is,

I_{1} + I_{2} = 3 * L^{2} + \frac{3 L^{2}}{2} = \frac{9 L^{2}}{2}

(12)

This, multiplied by the constants out of the integral yields,

\frac{9 π R L}{4}

;

The third term is slightly more complicated being of the square root type and it involves a logarithmic primitive.

I_{3} = \int_{0}^{L} [\sqrt{3 x^{2} + 10 L x + 3 L^{2}}] d x

(13)

This integral presents the root of an expression of the type a+bx+cx².

As such, it is recommended to find the value of Δ=4ac-b², for this case, 36L²-100 L²= - 64 L²

The solution yields, [3]

I_{3} = {[\frac{6 x + 10 L}{12} \sqrt{3 x^{2} + 10 L x + 3 L^{2}} - \frac{64 L^{2}}{24} (\frac{1}{\sqrt{3}}) \log (2 \sqrt{3 (3 x^{2} + 10 L x + 3 L^{2})} + 6 x + 10 L)]}_{0}^{L}

(14)

And substituting,

I_{3} = [\frac{4 L}{3} (4 L) - \frac{64 L^{2}}{24} (\frac{1}{\sqrt{3}}) \log (2 \sqrt{3 (16 L^{2})} + 16 L)] - [\frac{10 L}{12} \sqrt{3 L^{2}} - \frac{64 L^{2}}{24} (\frac{1}{\sqrt{3}}) \log (2 \sqrt{3 (3 L^{2})} + 10 L)]

(15)

I_{3} = [\frac{16 L^{2}}{3} - \frac{5 \sqrt{3} L^{2}}{6} + (\frac{8 L^{2}}{3 \sqrt{3}}) \log (16 L) - (\frac{8 L^{2}}{3 \sqrt{3}}) \log (8 L \sqrt{(3)} + 16 L)]

(16)

By virtue of the properties of division of the logarithm,

I_{3} = L^{2} [\frac{16}{3} - \frac{5 \sqrt{3}}{6} - (\frac{8}{3 \sqrt{3}}) \log (\frac{\sqrt{3} + 2}{2})]

(17)

And from Eq. 12, the sum of the two previous immediate integrals was,

I_{1} + I_{2} = \frac{9 L^{2}}{2}

(18)

The total result for the so-conceived area, subtracting I₃ from Eq.17 is,

\frac{π R}{2 L} L^{2} [\frac{9}{2} - \frac{16}{3} + \frac{5 \sqrt{3}}{6} + (\frac{8}{3 \sqrt{3}}) \log (\frac{\sqrt{3} + 2}{2})]

(19)

After careful simplification, the Area the conoid based in R and L gives:

I = \frac{π R L}{2} [\frac{27 - 32}{6} + \frac{5 \sqrt{3}}{6} + (\frac{8 \sqrt{3}}{9}) \log (\frac{\sqrt{3} + 2}{2})]

(20)

Which can be reduced to,

I = A = \frac{π R L}{2} [\frac{5 \sqrt{3}}{6} - \frac{5}{6} + (\frac{8 \sqrt{3}}{9}) \log (\frac{\sqrt{3} + 2}{2})]

(21)

And consequently,

A = \frac{π R L}{4} (\frac{1}{9} [15 (\sqrt{3} - 1) + 16 \sqrt{3} l o g (\frac{\sqrt{3} + 2}{2})])

(21)

2.2. Discussion of the findings

The more astounding fact is that the definite integral that we had sought for, when solved gives the number ψ explained in Eq. 25, which can be assimilated to π. Thus;

\int_{0}^{L} [3 L + 3 x - \sqrt{3 x^{2} + 10 L x + 3 L^{2})}] d x = L^{2} \frac{ψ}{2} \approx L^{2} \frac{π}{2}

(22)

\frac{2}{L^{2}} \int_{0}^{L} [3 L + 3 x - \sqrt{3 x^{2} + 10 L x + 3 L^{2})}] d x = ψ \approx π

(23)

π ≅ \frac{2}{L^{2}} \int_{0}^{L} [3 L + 3 x - \sqrt{3 x^{2} + 10 L x + 3 L^{2})}] d x

(24)

It was inconceivable at the beginning of the study that such fancy integral equation when solved would give a value very similar to

π

For a variety of reasons, including its occurrence in the first written text in Grecian alphabet (750 B.C.) at Abu Simbel (Egypt) in stone and also its appearance in the banner of Barbados, homeland to Ms. Rihanna, we have decided to identify the expression inside the parenthesis as ψ, Psi, a letter unique to the Greek language.

ψ = \frac{1}{9} [15 (\sqrt{3} - 1) + (16) \sqrt{3} l o g (1 + \frac{\sqrt{3}}{2})] = 3.140923532703498

(25)

ψ \approx π

(26)

ψ is much alike to

π

up to the third decimal, which is quite surprising and for engineering purposes both numbers can be equated and this will considerably clarify Equation 21 as,

A = \frac{π R L}{4} [ψ \approx π] = \frac{π^{2} R L}{4}

(27)

We find such result remarkable in sundry senses. Firstly, because, ψ is a transcendent irrational number [4], akin to Pi but original in concept and newly derived from pure integration. Secondly, if substituted for Pi in the discussion, it could perhaps improve the accuracy of Ramanujan’s approach and this remains a question open for discussion in future developments.

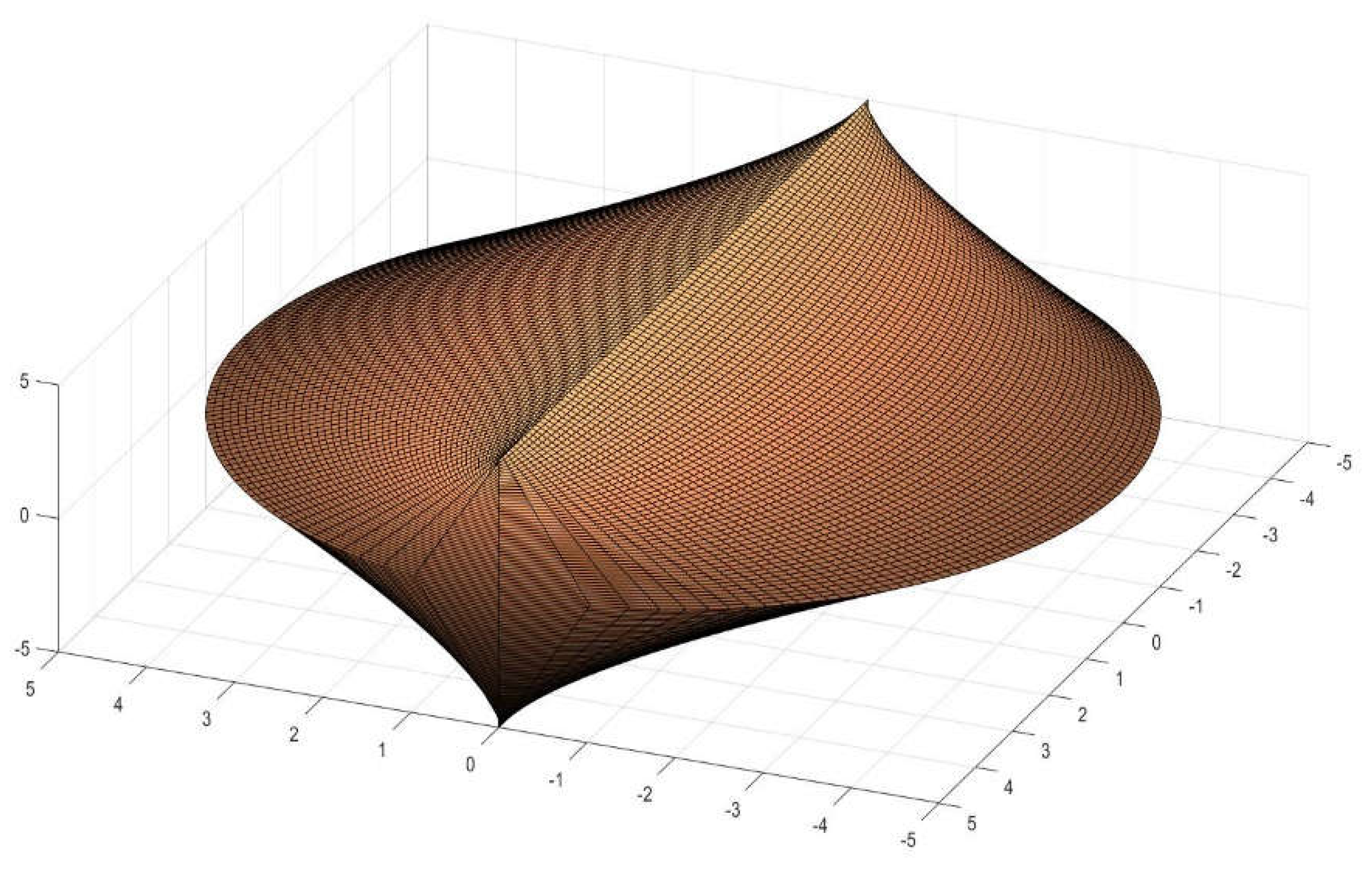
Thirdly, it involves the surprising fact that the area of the figure studied, when complete with the four quarters of conoidal strips, if the radius and the length are taken to the unity, R=L=1 would yield the value of Pi squared or Pi multiplied by itself. The news is that Pi^2, π² has a three-dimensional, non-trivial and distinct meaning that we have found at last (Figure 4 and Figure 5).

2.3. Definition of the Antisphera

A volume composed of four symmetrical opposed sets of conoidal strips as previously defined (radius=1, longitude=1) would have a lateral surface of π², that is Pi squared.

When conceiving such a form, obvious similarities with the sphere come to mind and that it is why we have named this curious figure in Grecian “Antisphera”. The plan of the figure resembles a perfect square of two by two, but the front view is a circle of diameter one and the lateral view is four-pointed star. It constitutes a three-dimensional example of the circle’s quadrature, sought since antiquity [5].

Its equation in continuous form responds to,

\frac{R^{2} z^{2}}{{(\pm (R - x))}^{2}} + y^{2} = R^{2}

(28)

We consider just this to be a noticeable finding to merit diffusion.

However, the principle problem is not completely solved since the parallel infinitesimal strips may not fit perfectly with the curved surface and they would act as a kind of envelope. We have estimated that for engineering purposes this is deemed sufficient when the angle of inclination of the figure, θ, is not too steep (less than π/2.5), but in order to improve accuracy we have calculated a coefficient to take into account the differences of width of the said strips (See Annex 1).

Since we certainly know that at the middle section of the surface, the width of an actual unit section of the conoid is not dx but instead dx/cosθ, we need to take into account this feature and effect an interpolation between both values.

It can be discussed if the variation of the strip is curvilinear or not, but several experimental calculations (See 2.4), estimate that for the time being, this is the preferred approximation for angles under pi/2.5 (other approaches are also being considered for higher values of θ, see Annex 1).

Such coefficient of Cabeza-Lainez, κ, would accordingly be,

κ = \frac{1 + s e c θ}{2} = \frac{1 + c o s θ}{2 c o s θ}

(29)

Where tan(θ) = R/L as θ is the arctangent of the central section of the figure.

Therefore, the final expression to compute the lateral area of this particular surface, Antishpera, with the caveats referred above, produces,

A = \frac{π^{2} R L}{4} \frac{(1 + c o s θ)}{2 c o s θ}

(30)

But if R and L coincide, Eq. 30 is reduced to,

A = \frac{π^{2} R^{2}}{4} \frac{(1 + \sqrt{2})}{2}

(31)

In the case of a new volume that we had defined as Antisphera, (Figure 6), if R is the unit and if we adjoin the four quarters of which it is composed,

A = π^{2} R^{2} \frac{(1 + \sqrt{2})}{2} = π^{2} \frac{(1 + \sqrt{2})}{2}

(32)

Nevertheless, if we should make,

R^{2} = \frac{2}{(1 + \sqrt{2})}

(33)

It would mean that for an Antisphera of precise Radius = 0.9102,

A = π^{2}

(34)

In this fashion, again a new and distinct meaning, has been attributed to the second power of π, by virtue of such elaborate demonstration. This is a non-descript and original finding to assign a three-dimensional meaning to the product of Pi by itself.

In Annex 2 we have compared the lateral area obtained by our method whith other automated surface calculators like Matlab’s Alphashape and Grasshopper’s (Figure 7).

We have also conceived a different procedure to obtain the area of the figure by using the straight lines instead of the ellipses of the conoid. This easier method shall be described in Annex 3.

2.4. Calculations of the area for an elliptic conoid

In 2.1 we had stayed the discussion after attaining the area values for the conoid ending in a circumference, but in a similar manner we can continue to use Ramanujan’s prediction for an ordinate fragment of the same conoid whose extreme is merely an ellipse. For any real number n, the area yields,

A_{e c} = \frac{π R}{2 L} \frac{(1 + c o s θ)}{2 c o s θ} \int_{0}^{n L} [3 L + 3 x - \sqrt{3 x^{2} + 10 L x + 3 L^{2})}] d x

(35)

A_{e c} = \frac{π R L}{216} \frac{(1 + c o s θ)}{2 c o s θ} [9 (18 n (2 + n) - (6 n + 10) \sqrt{n (3 n + 10) + 3} + 10 \sqrt{3}) + 96 \sqrt{3} l o g (\frac{\sqrt{3 n (3 n + 10) + 9} + 3 n + 5}{8})]

(36)

For n=1 the solution is Eq.21.

As before, we have employed the coefficient κ (Eq.29), but we need to be advised that for values of θ nearing π/2.5 the expressions proposed in the annex 1, that is, κ₁ or κ₂ should be introduced in its stead.

2.7. Calculations for the volume of the conoid

As a complement of the theories exposed, the computation of the volume of the conoidal figure by means of the previous integral method is relatively simple and exact. Since the value of the area of an ellipse is πab, and as before, a=R and b= xR/L

V = π R \int_{0}^{n L} [x R / L] d x = \frac{π R^{2} n^{2} L}{2}

(37)

This equates the volume of the equivalent cylinder multiplied by s=n/2.

If n=1 and the limit is L , V=

\frac{π R^{2} L}{2}

(38)

that is half the volume of the equivalent cylinder (as s=½).

Finally, if L=R, the volume gives V=

\frac{π R^{3}}{2}

(39)

making R=1 as in the Antisphera we receive, V=π/2, which is also interesting.

With R=0.9102 as in Eq. 33, the volume reaches, 0.3770π

The volume and area properties in the conoid are smaller than in the cylinder but still larger than the equivalent cone. This will prove advantageous for the sustainability of many different structures and buildings, as the envelope and consequently the energy exchange is less pronounced and the cost of materials is lesser.

The finding of the volume of a conoid is sometimes attributed to Johannes Kepler but to our knowledge the first polymath to deduct it by comparison with the volume of a cone of the same basis, was Camillo Guarino Guarini in his monumental treatise, Euclides Adauctus et Methodicus [5].

In Annex 3, the repercussions for radiative heat transfer inside the figure are discussed.

3. Generation of new figures based on the previous findings

In Section 2, we defined the symmetrical figure composed of four conoids, namely the Antisphera. [Figure 8]

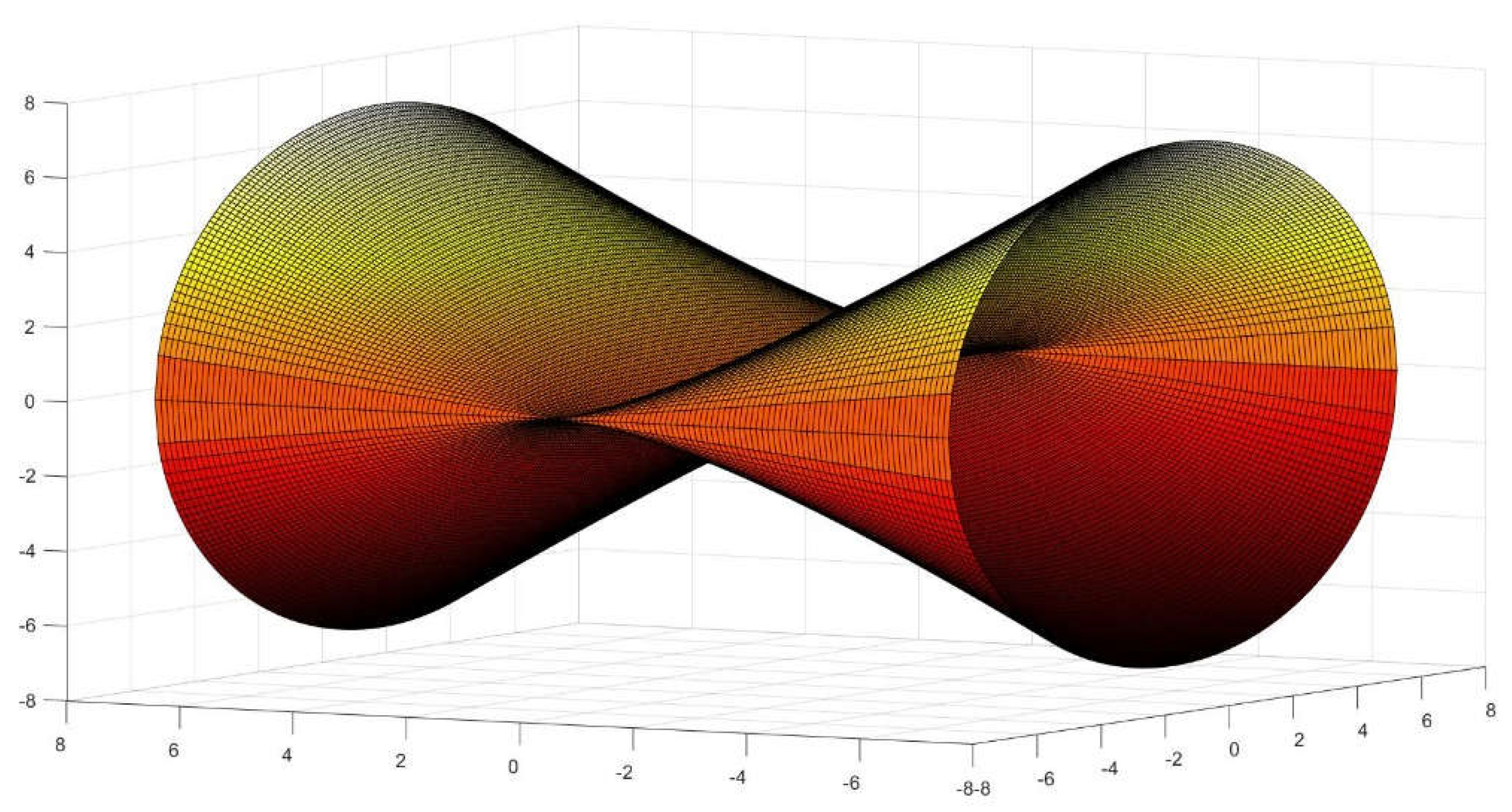
Nevertheless, we have conceived that by altering the symmetry and parts of the previous figure, a series of other interesting bodies derives, maintaining initially the ratio R=L.

The first one is opposed geometrically to the Antisphera because straight lines of the edge intersect at its center plane, which is void. Due to this elusive and somewhat dual nature we have coined the name Dyosphera© for this shape [Figure 9].

In total, the Dyosphera features eight conoidal sections, organized in groups of four, rotated π/2 degrees [Figure 10]

The corresponding Equations are,

\frac{R^{2} z^{2}}{x^{2}} + y^{2} = R^{2}

(40)

Combined with,

\frac{R^{2} x^{2}}{z^{2}} + y^{2} = R^{2}

(41)

The open cavities and sinuous receptacles of this strangely (Figure 11 and Figure 12) symmetrical figure make it particularly suitable for aeronautical and machinery parts. It is also a very stable form because it possesses four circular bases.

Horizontal parts of the Dyosphera, can be adroitly combined with the upper part of the Antisphera [Figure 13], to obtain a different figure that we have called Alosphera©.

In Figure 13, we can see represented the Alosphera, its main feature is that two bases are square and two circular, what makes it suitable por different uses, with straightforward storage of various units and we have come to guess that some cellular growths of different organisms may respond to this evolutive pattern.[13]

The Alosphera is the first Antisymmetric figure that we have identified but, like the Dyosphera, it also presents eight conoids.

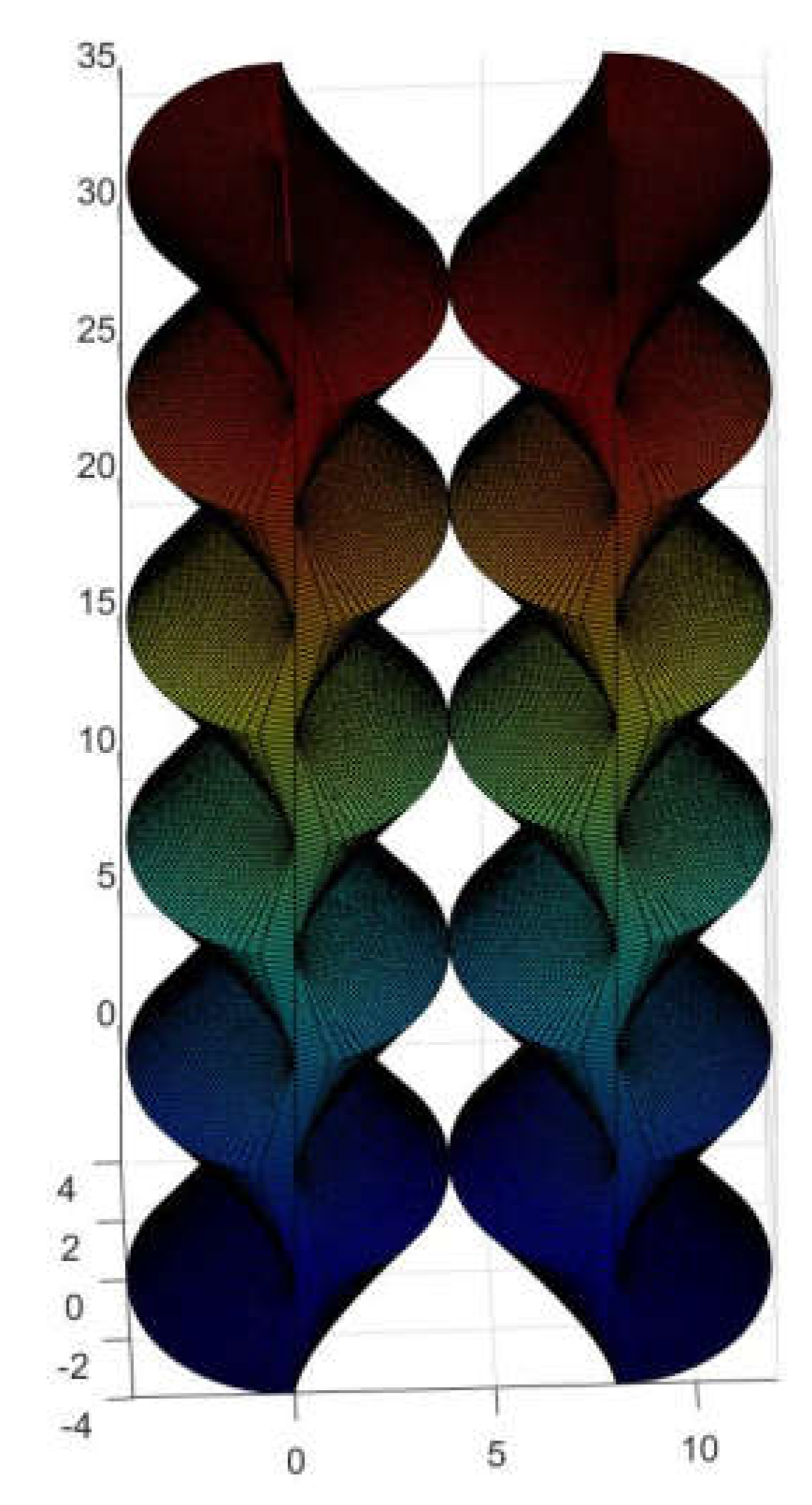
Finally, a very important antisymmetric finding is the Pterasphera [Figure 14].

This body as we shall discuss below is tubular in nature. Being internally connected in its entirety, it is apt for conducting all kinds of fluids in an advantageous manner since for instance it can reduce the velocity and at the same time the noise of transporting the required fluids. Unlike Antisphera it is self-standing and well balanced, which turns it suitable for elongation in the manner of a tower.

4. Future proposals based on the devised form

As a corollary for the theories exposed we will discuss two prospective forms that we have obtained with conoids taking into account evolving technologies. The first one is a system of skylights in which the glazed parts instead of being planar are also conoids (Figure 15). Keeping in mind the discussion on heat and light transfer of Annex 4, this feature presents undoubted advantages [19]. Firstly, the glazing is better shaded and protected by the opaque upper conoid. Secondly, sunlight and heat transmission are modulated by the smooth curves supplementary to the innovative glass properties. In this way the glass surface becomes resistant to severe efforts and collaborates with the general structure.

Such new skylights are weather-resistant, break-proof, safer and cleaner in the absence of maintenance, as dust collection is diminished with the curvature (Figure 16).

The second form consists of an innovative proposal for an amphitheater, music or sports venue (Figure 17).

In this case, being a double conoid, the advantages previously exposed are improved. The sections are closed curves, like the ellipse and the circumference in the brim. Thus, they work as tension rings or girdles to hold the structure together without severe deformations. The bearing capacity of the shape is extreme. The tiers of the amphitheater are the obverse of the external façade, there is no need to superimpose a conical structure inside a cylinder like in the Roman Colosseum or in Spanish bullrings. Among other problems, the ancient structures forced to build massive offload vaults and galleries which transferred severe thrusts to the outer façade. As a result, we have calculated that savings in building materials of this proposed facility could be remarkable.

Still, the structure can be easily constructed with straight beam elements and reinforcements. The foundations are pointing to the soil as in a kind of shard or spear, that means that it will be very stable, safe and simple to develop.

The outer surface of the conoid is not vertical but inclined and so the surroundings of the amphitheater would be self-shaded and rain protected, an interesting feature in many climates.

As for the grandstands, it is not difficult to adapt awnings or other shading systems to the inside area in order to protect the tiers from the rain or the sun (Figure 18)

As mentioned above, the effect of concentration of sound, rather annoying in conventional stadiums will be almost completely avoided due to the convexity of the surface. In reference 6 we have demonstrated this by acoustic ray-tracing procedures. These rely on the finding of the normal to the conoid surface at each point (See Annex 5). The same shading form is being used to protect the remains of Roman amphitheaters that can be found in Andalusia (Spain).

The only remaining questions for modern projects, would be those of selecting the relative heights of the stages and platforms and other design issues like transit within the venue. Nonetheless we believe that our proposal could be another good example of how the conoid-based bodies are able to create a significant volumetric space with a comparatively small enveloping surface, the key is that they offer a high spatial compactness which is usually an added value in terms of heat exchange, costs reduction and sustainability in general.

5. Repercussions for technology based in tubular forms

So far, we have presented scientific design developments that we hope will find a myriad of applications in technological areas like Nautical, Aerospace, Building, Heritage, Retrofit and associated industries or machinery. Such fact attests to the versatility and feasibility of the solutions presented which derive from our mathematical investigation founded in symmetry. In the last part of the research, due to their complexity, the surfaces have been materialized with the help of 3D fabrication procedures to decide on some difficult points of the equations or either on future realizations of the proposals. It is undeniable for us that the results attain the domains of Architectural and Engineering design. Although this will perhaps merit a separate study, we have included here some of the most remarkable findings.

We believe that the implications of this geometrical advance are far-reaching. Due to its internal logic, it would be suitable for biotechnology [13]. Specially the last development, the Pterasphera being of a tubular nature would be prone to fluid transportation. As a spring-like configuration it conjoins flexibility and balance. In Figure 19 and Figure 20 we present examples of possible association and growth in parallel or opposed patterns.

If we analyze the internal section of the tubules (Figure 21) it is composed of two semi-ellipses of varying sizes, but the span is constant at R, the extreme one is a semi-circumference of radius R and the middle horizontal section is a complete ellipse of minor axis R and major axis 2R.

An unusual characteristic is that dimensions of the section are constant but its shape is not (Figure 22). thus the velocity of the fluid inside the tubule can be deftly regulated from the same form. This would offer a clear alternative to reduce the noise level in the ducts or to decant particles in suspension.

The longitudinal central section of the Pterasphera gives a lozenge of horizontal dimensions R and the sides are inclined to the angle (π/2 – θ), with θ = arctan(L/R). The perpendicular distance between inclined sides is of d = Rcos θ.

This characteristic will facilitate insertion in existing rectangular ducts for example in retrofits. Serial fabrication is also simple since the form allows cuboid molds of middle section over 2R x Rcosθ.

In Figure 23, Figure 24 and Figure 25 we present an example of vertical growth of the tubules, resembling vegetal pillars.

We decided to explicate this finding, because of the possibilities that it showcases. For instance, in tower buildings. Vertical connections are always feasible at the middle plane of the column, but the external envelop will benefit from the sun tracking or shading properties already exposed combined with new photic materials of variable transparency (Figure 25 and Figure 26)). In consequence lighting, thermal and acoustic features will considerably improve the existing conditions.

The structure of the so-conceived tower can be as lightweight as desired due to its inner balance and counterweight, the middle section is perfectly rectangular. As we have explained previously, alone or better in groups (Figure 25), it should perform adequately under earthquakes, extreme wind conditions or other unpredictable circumstances.

After several trials we realized that the tubule could be rectified by means of appropriate sections. This is a considerable advance as it permits application not only in ducts but also in tunnels, the author has already launched a proposal for a model tunnel (Figure 27 and Figure 28) illuminated with daylight by PV fixtures. [19].

The speed within the tunnel can be regulated by the form in itself as the lower floor is not entirely planar except the central line, diverse advantages can be gained by this geometrical adaption (Figure 29). Optic and acoustic properties are much enhanced as demonstrated in Annexes 3 and 4 [17].

Recently I have devised a set of n-dimensional crossings for the above tunnels (Figure 30, Figure 31, Figure 32, Figure 33, Figure 34 and Figure 35). Therefore, is entirely possible to construct grids of tunnels that will allow for many different uses in galleries and filtration circuit plants for instance.

I believe that diverse technological fields could have a keen interest in the new forms that I have found both for the macro and micro-scales. It is indeed a leap into a sustainable future based on smart geometries that we hope to see beyond.

7. Conclusions and future aims

We have obtained a new transcendent number that we would call ψ, of a very precise nature which provides a sufficiently accurate value of π. Thanks to Ramanujan’s clairvoyant prediction we have found the approximate lateral area of the conoid, a recurrent form in organic structures whose scientific and technical knowledge was insufficient and desired.

We have shown its utility for the design of many types of aeronautical parts and vessels. Due to its particular geometric properties it can both work for heat-storage or dissipation as the case may be, it performs aptly especially in thermal, luminous and acoustic radiation domains. We have also discussed how the notions that led to this form have evolved since Early Modern Times. All the former make these structures rather sustainable.

Further advantages to be outlined are: it enhances the employ of an engineering and architectural form which can save considerable amounts of materials and building lapses not only when used as cover or roofing in the sense of vaults or domes, but also vertically for cantilevered stadiums and amphitheaters that tend to derive from the cylinder since the Roman Colosseum.

From the building perspective, easy reinforcement for pre-stressed construction and enhanced structural behavior could be other reasons to use them. Self-shading of the structure and built-in protection from weather phenomena are added values and contribute to its durability.

In the process, we have created no less than four new types of figures which present a high potential in many fields. Especially the last one Pterasphera, and its rectified version, owing to its tubular nature can provide interesting developments in tunnels, biotechnology and fluid-conducting devices.

The repertoire of possibilities derived from this geometric finding and exploration appear endless to me.

Overall, the paramount finding hereby exposed is the attribution of a precise meaning for the number π², an achievement that leaves us wondering on the many-fold possibilities for these notions, that is π³, π^N and π elevated to various powers.

Author Contributions

J.M. Cabeza-Lainez has developed and envisioned the whole work. He programmed all the figures and solved all the equations. All faults in this article are necessarily his.

Funding

This research received no external funding.

Acknowledgments

The author would like to express remembrance for the late Dr. Manuel Bendala García who was helpful to me in his academic years.

Conflicts of Interest

The author declares none.

Annex 1

Discussion for higher values of the conoid angle

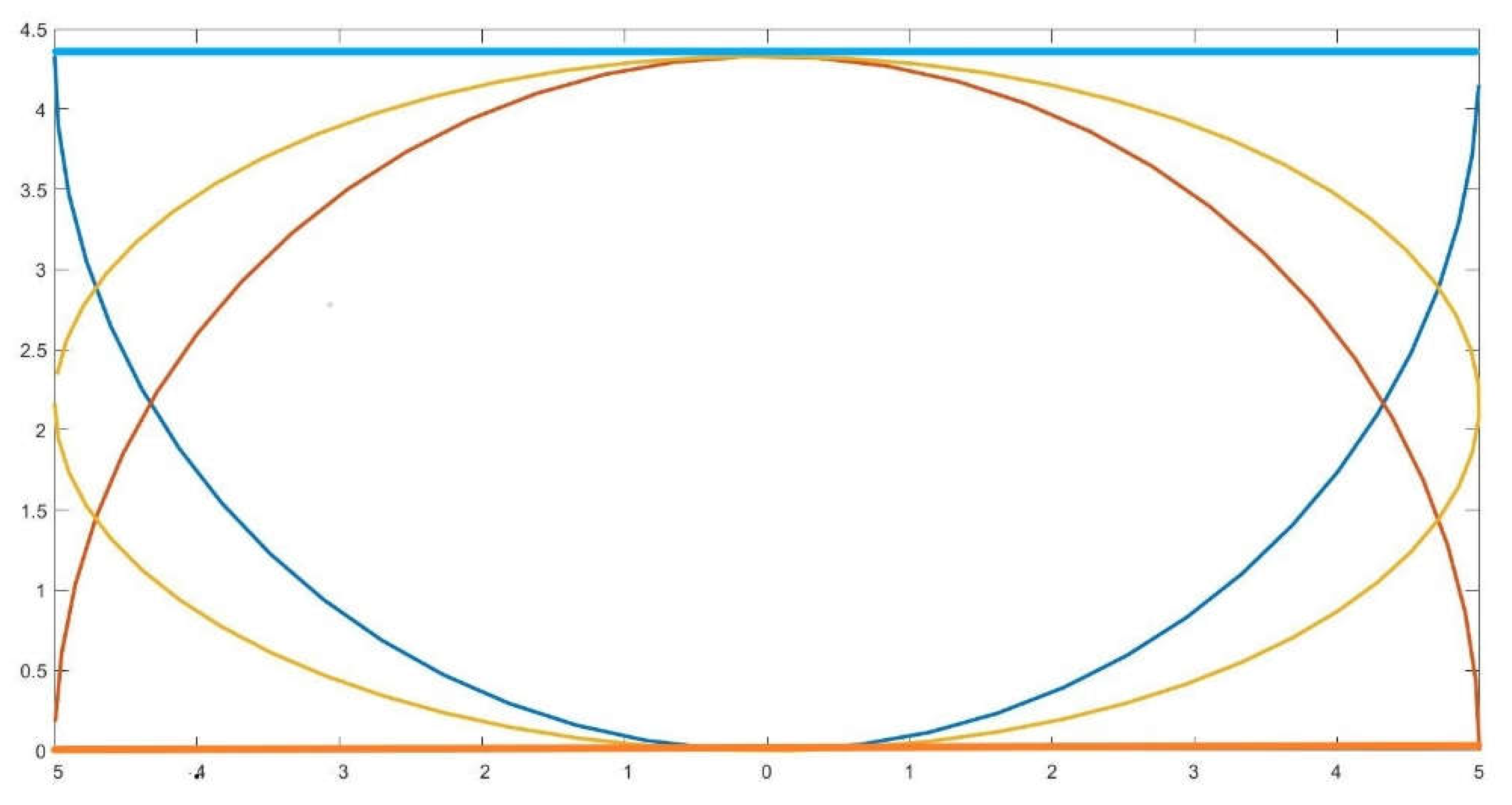
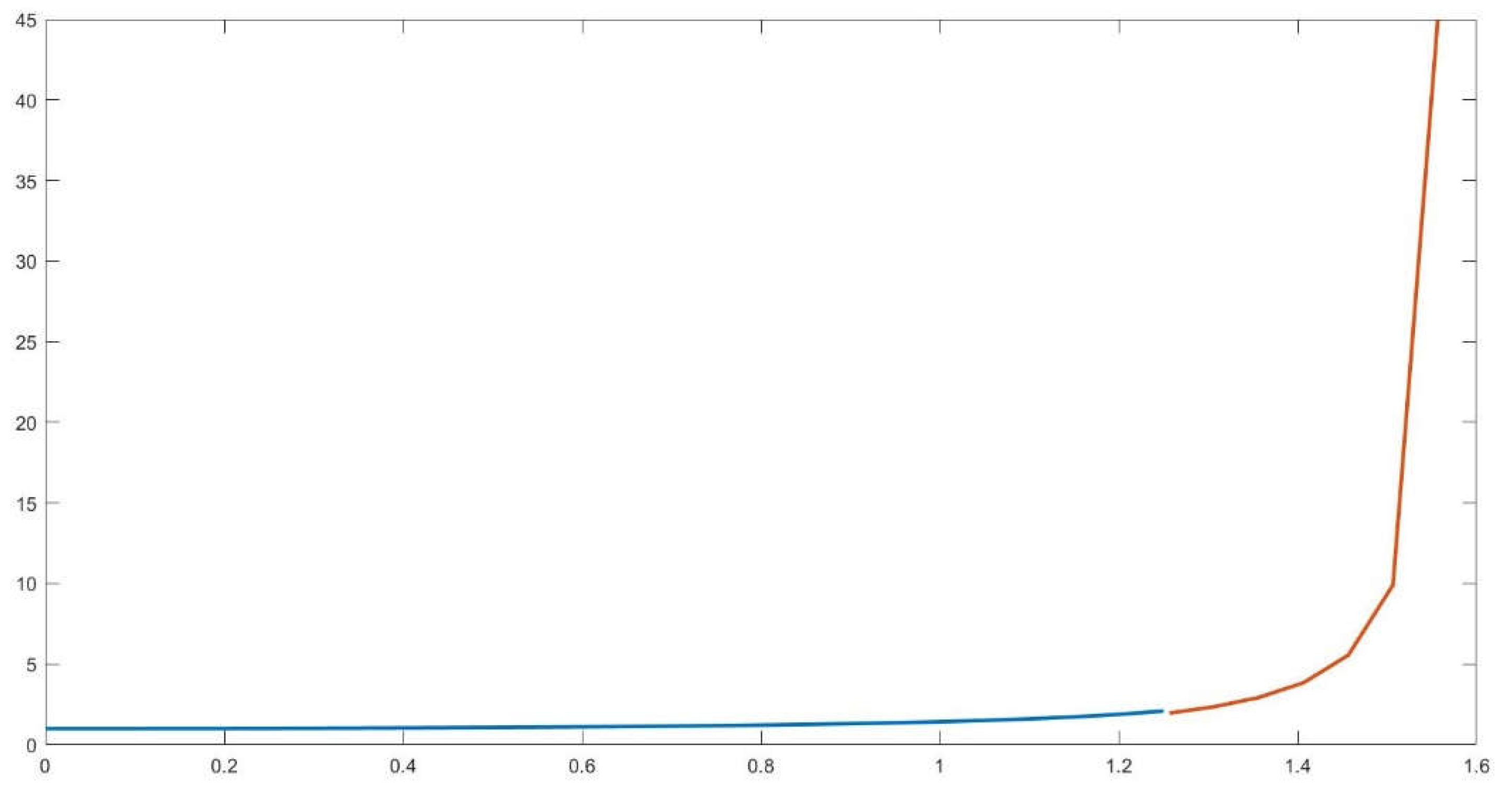
The κ coefficient previously defined must, for coherence, remain over,

κ > \frac{2 t a n θ}{π}

(1)

It is however clear that, for values of θ > 1.25 the former relation may cease to verify (Figure 1)

For lower quantities, the coefficient performs smoothly, since cosθ tends to be one and the same does κ, so our prediction becomes even more accurate.

But for values over pi/2.5, it is convenient to define a new coefficient. We are currently estimating different adjustments to present them in a further development of our theory. In the meantime, a tentative assumption for the value of the area, would be the following,

A = \frac{π^{2} R L}{4} + \frac{π R^{2}}{2} = \frac{π R}{4} (π L + 2 R) = \frac{π^{2} R L}{4} (1 + \frac{2 R}{π L})

(2)

Thus, the new coefficient κ₁ would be,

κ_{1} = 1 + \frac{2 t g θ}{π}

(3)

A suggested experimental refinement of this factor from θ= π/2.5 and onwards is,

κ_{2} = s i n (\frac{π}{2} - θ) + \frac{2 t g θ s i n θ}{π}

(4)

In most problems of engineering, high values of the said angle are rare because they imply that the conoid is very close to the circle or in other words, there is little or no space left inside the surface, which may become contradictory with the nature of spatial design [6].

Annex 2

Subsequently, we have proceeded to compere the aftermath with numerical simulation available, for instance the command Alphashape for computation of areas in Matlab and the graphic interface Grasshopper. The results show a considerable agreement and our findings stay in the middle of the output for both approximate tools (Table 1).

Table 1. Results of computing the area of several conoids by the method proposed by author and with graphic interpolation procedures allowed by the software Grasshopper and the command Alphashape of Matlab.

Radius=L unit	Alpha-Shape	Cabeza Approx.	Grass-Hopper
0.25	0.1958	0.1862	0.1842
0.50	0.7712	0.7446	0.7369
1	3.0726	2.9784	2.9476
2	12.155	11.913	11.790
3	27.734	26.805	26.528
4	48.886	47.654	47.161
5	76.019	74.460	73.690
6	109.27	107.22	106.11
7	148.83	145.94	144.43
8	194.54	190.61	188.64
9	246.41	241.25	238.75
10	304.254	297.841	294.76

More thorough data are being prepared, but the procedure for the graphic interfaces is clumsy and haphazard as a bespoke volume is required every time in order to compute the areas and the mesh of interpolation has to be decided beforehand with frequent hollow regions. This is a clear advantage of our method.

Annex 3. An alternate method to obtain the lateral area of the figure

As we have already noticed the conoid is composed of straight lines parallel to a plan, these have a maximum height at the middle section coincidental with the tangent of the angle R/L and a minimum elevation in the horizontal lines at the extremes.

The length of such straight lines is defined as the hypotenuse of the triangles that appear in different sections of the volume.

h²=L²+z²

(1)

With the same meanings of L,R and z, as before.

But in the circumference of the directrix, z is related to the radius R, as,

z²+y²=R² and, z²= R² -y² for y positive.

The hypotenuse in terms of y will give

h^{2} = L^{2} + R^{2} - y^{2} h = \sqrt{L^{2} + R^{2} - y^{2}}

if we assign a thickness of dy to these inclined lines and integrate from 0 to R, we would find the area of an eight part of the figure, thus,

A = \int_{0}^{R} \sqrt{L^{2} + R^{2} - y^{2}} d y

(2)

Which yields:

A = \frac{1}{2} {[y \sqrt{L^{2} + R^{2} - y^{2}} + (L^{2} + R^{2}) a r c s e n \frac{y}{\sqrt{L^{2} + R^{2}}}]}_{0}^{R}

(3)

Substituting the limits of integration, we would obtain,

A = \frac{1}{2} [R L + (L^{2} + R^{2}) a r c s e n \frac{R}{\sqrt{L^{2} + R^{2}}}]

(4)

If R=L, the total area is,

A = 8 (1 / 2 (R^{2} + 2 R^{2} a r c s e n \frac{R}{R \sqrt{2}})) = 4 R^{2} (1 + π / 2)

(5)

Remembering that for the Antisphera, R=L=1,

A=4((1+π/2)=10.2832

With the previous formula,

A=π^2=9.8696

Both seem coincidental around 10, so it appears to be a good estimate of calculation. However, more developments are required for this procedure.

Annex 4. Radiative exchanges inside the new figures.

Introduction to the problem of surface factors

In previous researches [6], some of which were published in the Buldings and Sustainability journals [7], Cabeza-Lainez defined that the radiative exchange factor for any manifold surface is dependent on the equation:

F_{12} = \frac{1}{A_{1}} [\int_{A_{2}} \int_{A_{1}} \frac{\cos θ_{1} \cos θ_{2}}{{π r}^{2}} {dA}_{1} {dA}_{2}],

(40)

Figure 1. The magnitudes involved in the expression for radiative exchanges due to manifold surface sources.

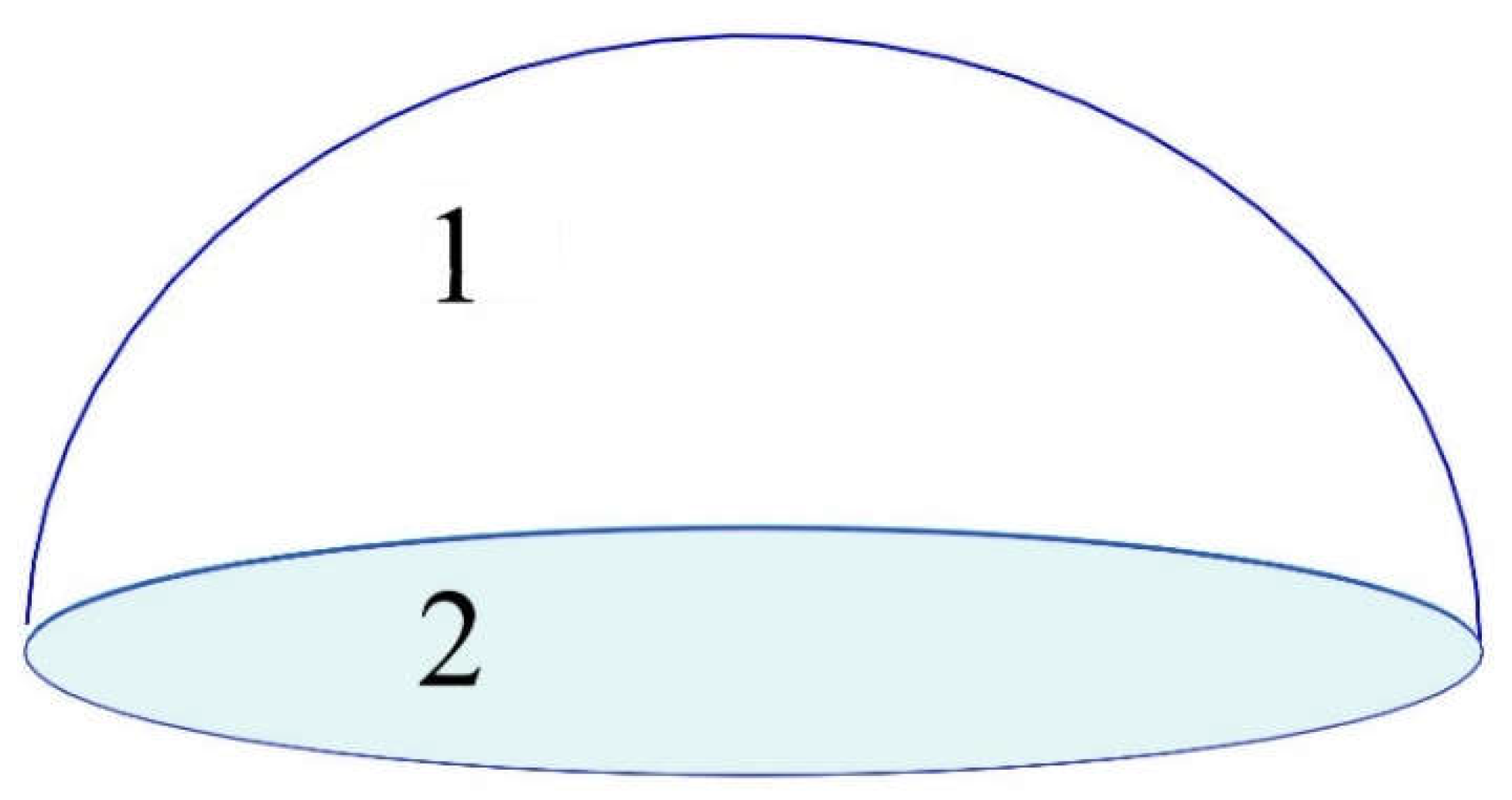
In a volume composed of only two surfaces, the same author established its second principle of radiation [8], which states that in the said situation, the rate of exchange is proportional to the areas of the intervening surfaces. For example, in a hemisphere (see Figure 4.), the respective areas are A₁ =2πR² and A₂= πR².

As such, the corresponding form-factor from the half sphere to its base disc is [8],

Figure 2. The second radiation principle of Cabeza-Lainez form-factors applied to a hemisphere.

F_{12} = \frac{A_{2}}{A_{1}} = \frac{1}{2}

, and the amount of energy from the hemisphere to itself, F₁₁ is also ½ [8].

By the principle of conservation of energy all interchanges must add to 100% or the unity [6].

However, if the disc were topped by a double symmetric conoid, since previous to our finding, we ignored the value of its lateral area, the question remained unbeknownst.

We are finally in the position to respond to this issue with perfect ease. It is opportune to outline that the above integral equation (Eq. 41) is deemed unsolvable for the conoidal geometry. [7]

Figure 3. The second radiation principle of Cabeza-Lainez applied to the form-factor of a double conoid.

The area of this double conoid is,

A = \frac{π^{2} R^{2}}{2} \frac{(1 + \sqrt{2})}{2}

(1)

Example 1

In all the cases where θ=π/4, the relationship between the area of the base circle πR² and the double conoid is precisely,

F_{12} = \frac{A_{2}}{A_{1}} = \frac{4}{π (1 + \sqrt{2})} = 0.527393

(2)

This is the factor from the conoidal top to the circular base and since F₁₁+ F₁₂ =1, the self-factor F₁₁ is then,

F₁₁ = 1- F₁₂ = 1- 0.527393= 0.4726.

(3)

For this particular disposition, the values are not dissimilar from those of the hemisphere, 0.5, but they will need to be included in a standard comparison among radiative shapes described in reference [8].

Let us now discuss a new and more difficult situation for a conoid with radius 2 and length 4. (Figure 4)

Figure 4. The single conoid limited by a rectangular plane and semicircle.

Example 2

In reference [9], Cabeza-Lainez has partly solved Eq. 1 for some circular fragments.

For any vertical circular sector with a center situated in the middle of the edge x of a horizontal rectangle of dimensions, x and y; by virtue of the Cabeza-Lainez seventh principle, [10] the configuration factor from the sector of radius r to a point in the perpendicular rectangle, will be:

Bearing in mind that the sector is comprised between the angles θ₂ and θ₁ and being its radius ras mentioned.

For

t = r^{2} + y^{2} + x^{2}

;

m = \sqrt{x^{2} \sin^{2} θ_{1} + y^{2}}

;

n = \sqrt{x^{2} \sin^{2} θ_{2} + y^{2}}

f_{12} = \frac{y}{2 π} \times (\frac{c o s θ_{1}}{m} a r c t a n \frac{r}{m + \frac{c o s θ_{1} x}{m} (c o s θ_{1} x - r)} - \frac{c o s θ_{2}}{n} a r c t a n \frac{r}{n + \frac{c o s θ_{2} x}{n} (c o s θ_{2} x - r)}) + \frac{y}{4 π x} l n [\frac{(t - 2 c o s θ_{1} r x)}{(t - 2 c o s θ_{2} r x)}]

(4)

In the usual situation of a semicircle the above expression is reduced to,

f_{12} = \frac{1}{2 π} (a r c t a n \frac{r + x}{y} + a r c t a n \frac{r - x}{y}) + \frac{y}{4 π x} [\ln (r^{2} + y^{2} + x^{2} - 2 r x) - l n (r^{2} + y^{2} + x^{2} + 2 r x)]

(5)

By numerical procedures detailed in [7], we extend the above expression to the whole rectangle to find the form factor, whose value is of F₁₂ = 0.1272. It represents fraction of exchange of radiative energy from the horizontal rectangle under the conoid (A₁) to the semi-circular side of the figure (A₂).

The previously unknown area of the conoidA₃, following the above stated formulas (Eq.7) is 20.9042

From the reciprocity principle [6], A₁ F₁₂ = A₂ F₂₁, whence,

F₂₁=(16/2π)0.1272= 0.3239

(6)

Being A₁ and A₂ planar, it is mandatory that [6],

F₁₂+ F₁₃=1

(7)

F₂₁+ F₂₃=1

(8)

And this implies,

F₁₃ =1- 0.1272 = 0.8728

(9)

F23 =1- 0.3239 = 0.6761

(10)

Applying reciprocity again [6], A₃ F₃₁ = A₁ F₁₃ and A₃ F₃₂ = A₂ F₂₃, which yields,

F₃₁= (A₁/ A₃) F₁₃ = (16/20.9042) 0.8728= 0.6680

(11)

F₃₂= (A₂/ A₃) F₂₃ = (2π/20.9042) 0.6761= 0.2032

(12)

By virtue of the principle of conservation of energy [6],

F₃₁+ F₃₂+ F₃₃=1

(13)

F₃₃=1- F₃₁- F₃₂

(14)

Being non planar, the fraction of energy that the radiating conoid exchanges with itself is,

F₃₃ = 1-0.6680-0.2032= 0.1288

(15)

Not merely radiative heat transfer in the figure under study has been solved by this procedure, but also light transmission when it originates at conoidal skylights like those constructed by Ilja Doganoff [11] in 1957 in Bulgaria.

Example 3

If we, as in a sort of check, would double the conoid presented in Ex. 2 and compare in it the factor between a circle (A₂) and (A₁) the enclosing figure, (Figure 5) we would obtain that, since the relation of areas is now 0.3006, the factor from the conoid to the circle is precisely this value, following Cabeza-Lainez’ second principle [8].

Accordingly, the complex self-factor of the conoid to itself yields nothing but,

F₁₁=1-0.3006 = 0.6994

(16)

Figure 5. The three surfaces intervening in Example 2 whose area is calculated by computer graphic interpolation.

In the original half Antisphera, if we remember 3.2, and Ex.1, the same quantity amounted to,

F₁₁ = 1-0.527393= 0.4726

(17)

Such difference can be explained because the area of this new conoid is larger than the previous one since the angle θ is less pronounced (in this case, the length doubles the radius), or in other words more energy is retained under the new configuration.

In the second example discussed of a half-conoid (3.3), involving three surfaces (rectangle, semicircle and conoid), the self-factor was smaller, 0.1288, but a noticeable fact is that even so, it does not reach a fraction of one half of the self-factor for the whole conoid (0.6994/2= 0.3497) of the same dimensions (Ex. 3), as logic would perhaps induce to think Figure 6). This exemplifies the complexity of the solutions because they often appear to rule out common sense [12].

It is important to stress the utmost difficulty of obtaining these entities by any other method, including quadruple integration [7].

Figure 6. The three surfaces intervening in Example 2 whose area is calculated by computer graphic interpolation.

Annex 5

Obtaining the mathematical normal to the conoid surface.

The procedure to extract the normal is first order differentiation of the equation of the surface defined as F(x,y,z). The normal vector is obtained as a differential N = (F_x, F_y, F_z) and in this case, has the value of:

N = (\frac{R^{2} z^{2}}{{(R - x)}^{3}}, y, \frac{R^{2} z}{{(R - x)}^{2}})

(1)

We can trace a vector field with the reflected sound-rays from an emission point to check that they are effectively dispersed in the air and not concentrated [6].

References

The Bible. 1 Kings 7:23. “And he made the Sea of cast bronze, ten cubits from one brim to the other; it was completely round. Its height was five cubits, and a line of thirty cubits measured its circumference”.
Ramanujan, S. Ramanujan’s Collected Works, Chelsea, New York, 1962.
Jeffrey, A.; Dai, H. Handbook of Mathematical Formulas and Integrals; Elsevier Academic Press: Burlington, Massachussets, 2008. [Google Scholar]
Weisstein, Eric W. Trascendent Numbers. In Weisstein, Eric W, ed. MathWorld. Wolfram Research.
Guarini, C. G. Euclides Adauctus et Methodicus Mathematicaque Universalis. 1671. Torino (Italy).
Cabeza-Lainez, J.M. Fundamentos de transferencia radiante luminosa o la verdadera naturaleza del factor de forma y sus modelos de cálculo; Netbiblio; Seville, Spain, 2010.
Salguero-Andújar, F.; Cabeza-Lainez, J.-M. New Computational Geometry Methods Applied to Solve Complex Problems of Radiative Transfer. Mathematics 2020, 8, 2176. [Google Scholar] [CrossRef]
Cabeza-Lainez, J.M.; Pulido-Arcas, J.A. New configuration factors for curved surfaces. Journal of Quantitative Spectroscopy and Radiative Transfer 2012. [CrossRef]
Salguero Andujar, F.; Cabeza-Lainez, J.M. The Problem of Lighting in Underground Domes, Vaults, and Tunnel-Like Structures of Antiquity; An Application to the Sustainability of Prominent Asian Heritage (India, Korea, China). Sustainability 2019, 11, 5865. [Google Scholar] [CrossRef]
Gómez-Gálvez, Pedro; Vicente-Munuera, Pablo; Tagua, Antonio; Forja, Cristina; Castro, Ana M.; Letrán, Marta; Valencia-Expósito,Andrea; Grima,Clara; Bermúdez-Gallardo, Marina (27 July 2018). “Scutoids are a geometrical solution to three-dimensional packing of epithelia”. Nature Communications. 9 (1): 2960. [CrossRef]
Ramswamy, S.G. Design and Construction of Concrete Shell Roofs, 2004.
Cabeza-Lainez, J. et al. Rehabilitación del pabellón Plaza de América de la Exposición Universal de 1992. Revista de Edificación. Ecoconstrucción. 1997. Vol. 27. https://hdl.handle.net/10171/16978.
Peña-García, A. , Cabeza-Lainez, J., “Daylighting of road tunnels through external ground-based light-pipes and complex reflective geometry,” Tunnelling and Underground Space Technology, 131, 104788, 2023. [CrossRef]
Cabeza-Lainez, J.M.; Salguero-Andújar, F.; Rodríguez-Cunill, I. Prevention of Hazards Induced by a Radiation Fireball through Computational Geometry and Parametric Design. Mathematics 2022, 10, 387. [Google Scholar] [CrossRef]
Sasaki, K.; Sznajder, M. Analytical view factor solutions of a spherical cap from an infinitesimal surface. Int. J. Heat Mass Transf. 2020, 163, 120477. [Google Scholar] [CrossRef]

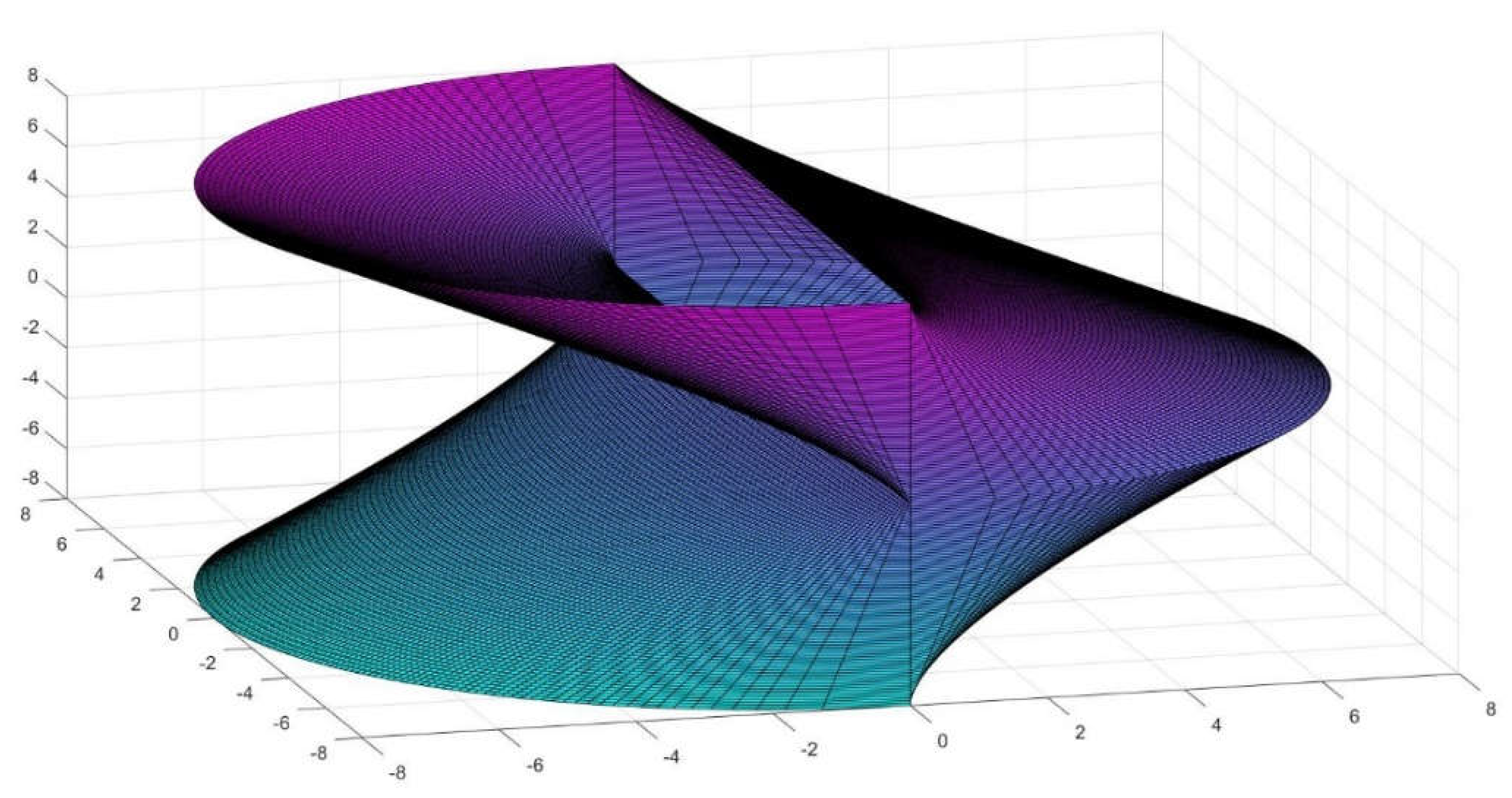
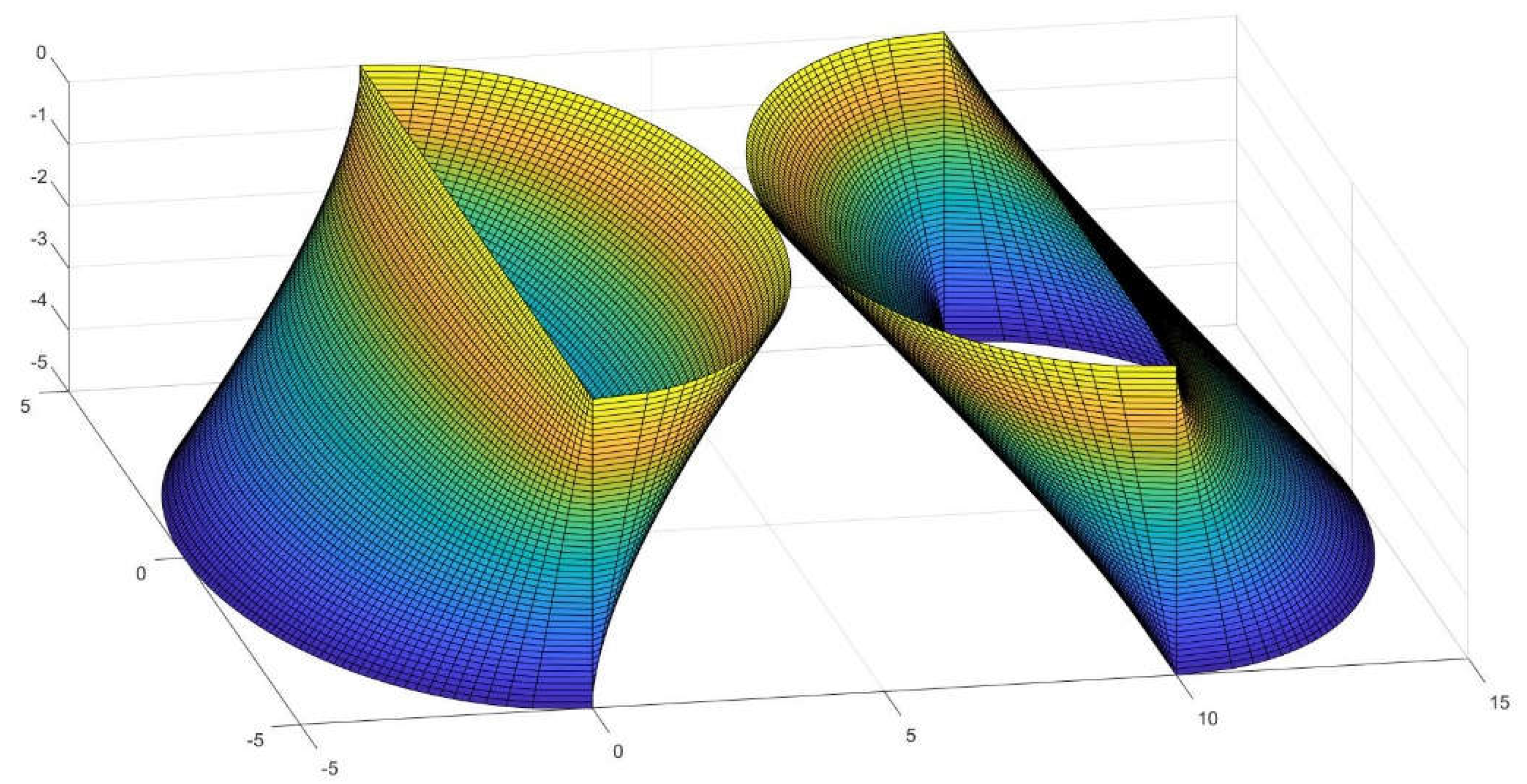
Figure 4. An elemental depiction of the figure whose lateral area equates π² if R and L are one.

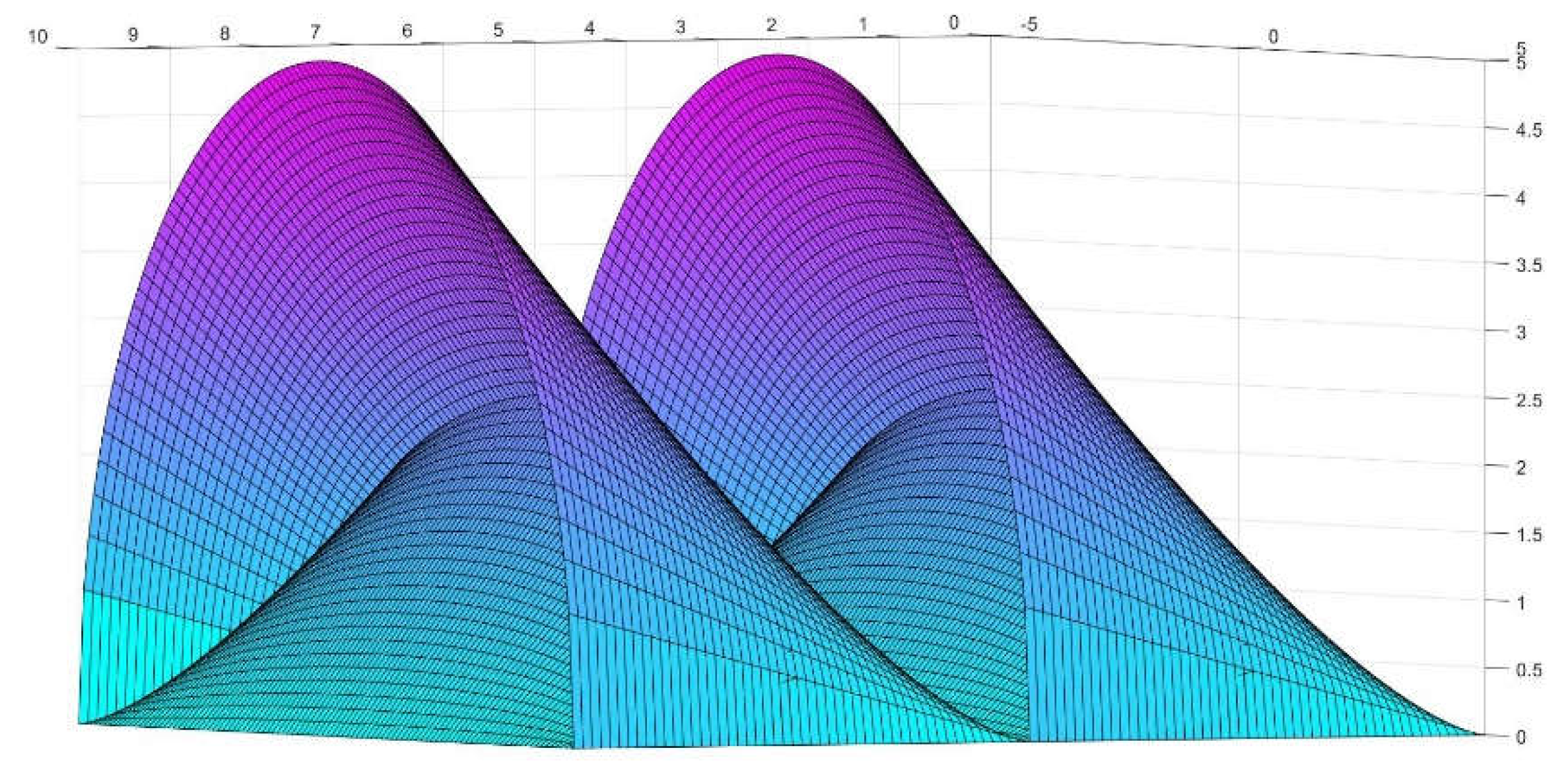
Figure 5. (a). and (b). More refined representation of the figure divided in two halves.

Figure 6. Depiction of the Antisphera for R=5.

Figure 7. Antisphera in bronze by the artist Sergio Portela and in gold by Joseph Cabeza-Lainez.

Figure 8. Three-dimensional rendering of the Antisphera.

Figure 9. The horizontal part of the body known as Dyosphera.

Figure 10. Distorted depiction of the complete Dyosphera.

Figure 11. the Dyosphera in 3D print, detail of interlocks.

Figure 12. The Dyosphera standing on one of its four bases.

Figure 13. The Alopshera.

Figure 14. Initial Section of the Pterasphera.

Figure 15. Outline of proposed Skylights with internal conoid glazing.

Figure 16. 3D print of a conoid used for skylights.

Figure 17. 3-D drawing of the new Amphitheater.

Figure 18. The Amphiteater with proposed retractable shade.

Figure 19. Two parallel Pterasphera tubules.

Figure 20. The same tubules opposed.

Figure 21. Horizontal section of a Pterasphera of major axis 10 and minor 5.

Figure 22. Horizontal extreme (semicircle) and middle sections (ellipse) of a Pterasphera, same area but continuously different form.

Figure 23. A pair of tubules of different height.

Figure 24. Different perspectives of the tubule.

Figure 25. The entwined tubule.

Figure 26. 3D print of the model tubule.

Figure 27. Rectified tubule as a model for tunnels.

Figure 28. Frontal view of the tunnel.

Figure 29. Inside view of the tunnel.

Figure 30. Corner crossing depiction of the tunnel.

Figure 31. Corner of the tunnel grid in 3D print.

Figure 32. Four ways crossing for the tunnels.

Figure 33. 3D model of the central crossing.

Figure 34. Detail of the conoidal crossing.

Figure 35. Proposal for an eightfold conoid crossing.

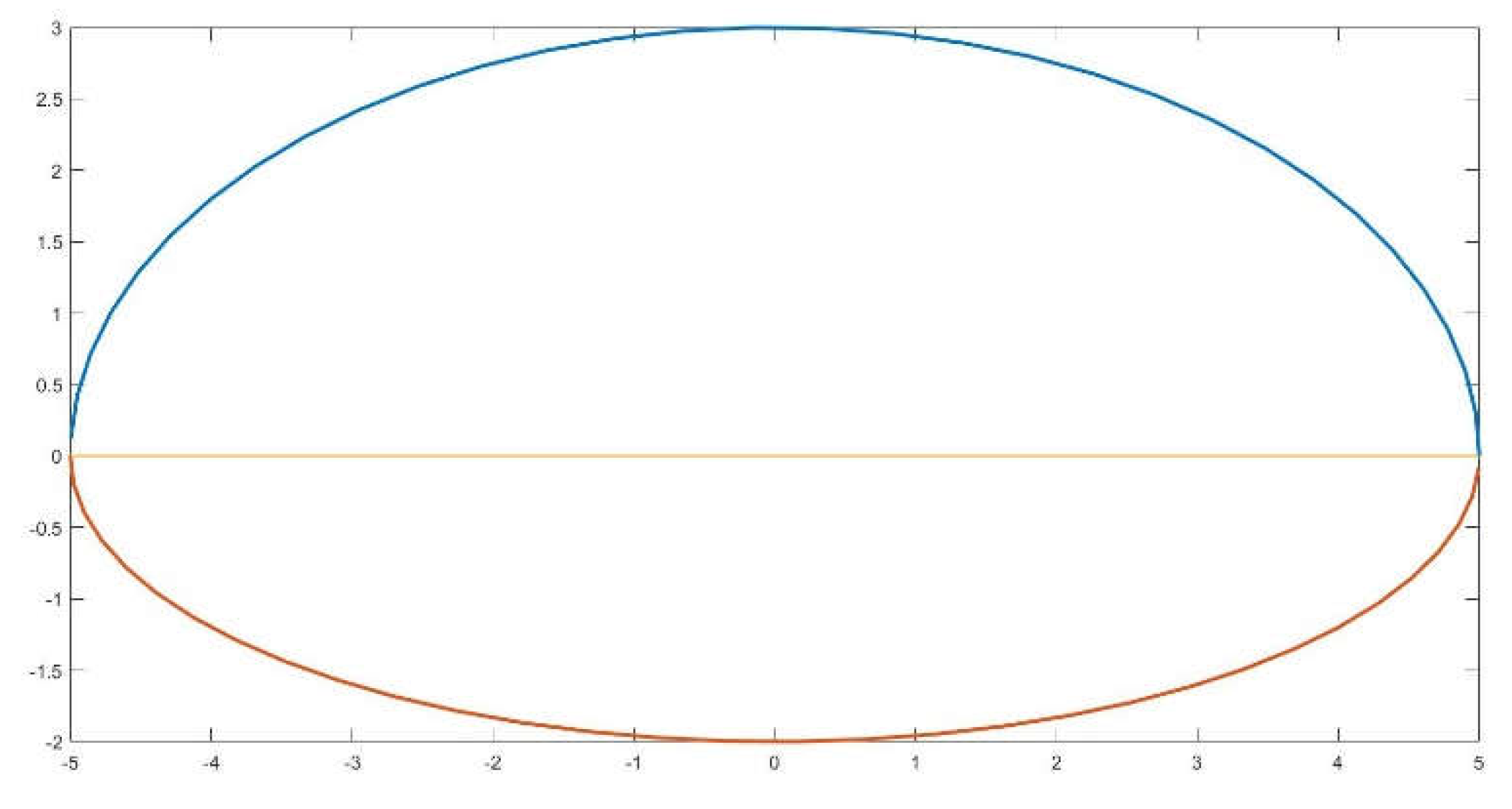
Figure 1. Depiction of Cabeza-Lainez coefficient κ (blue) and limit case (red).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer