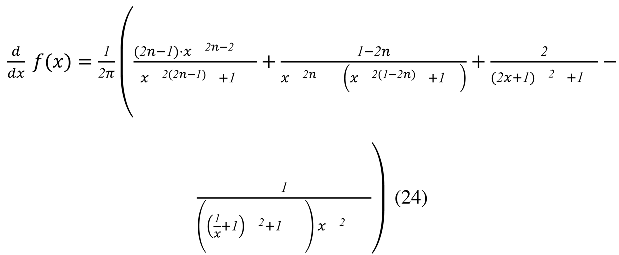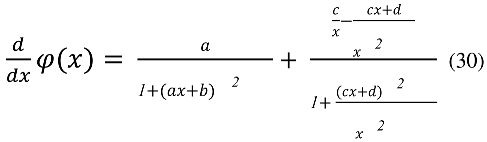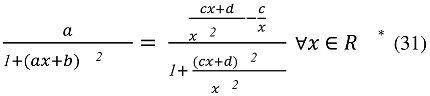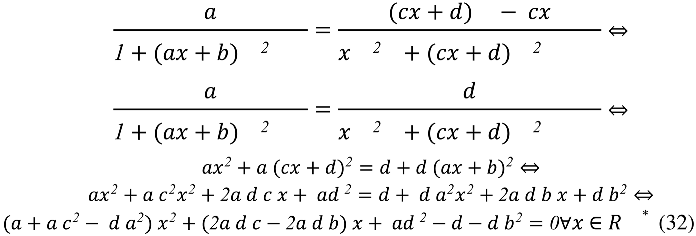A Closed-Form Expression for the Unit Step Function

Preprint

Article

A Closed-Form Expression for the Unit Step Function

Altmetrics

Downloads

328

Views

199

Comments

John Venetis^*

This version is not peer-reviewed

Submitted:

24 February 2023

Posted:

01 March 2023

You are already at the latest version

Alerts

Abstract

In this paper, an analytical form of the Unit Step Function (or Heaviside Step function) is presented. This important function constitutes a fundamental concept of Operational Calculus and is also involved in many other fields of applied and engineering mathematics. In particular, Heaviside Step Function is performed in a very simple manner by the use of a finite number of standard operations, as the summation of six inverse tangent functions. The novelty of this work when compared with other analytical expressions, is that the proposed exact formula contains two arbitrary single - valued continuous functions which satisfy only one restriction. In addition, the proposed representation is not exhibited in terms of miscellaneous special functions, e.g. Bessel functions, Beta function, Logistic function. Besides, it is neither the limit of a function, nor the limit of a sequence of functions with point – wise or uniform convergence. Hence, this formula may be much more practical, flexible and useful in the computational procedures which are inserted into Operational Calculus techniques and other engineering practices.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

The Heaviside step function, or Unit Step Function, which is usually notated by the symbols H or u, is a discontinuous single – valued function, the value of which is zero for negative argument and equal to unity for positive argument [1]. This special function was introduced by Oliver Heaviside, who was an important pioneer in the study of electronics and also made a remarkable contribution to the field of Operational Calculus [2]. A very significant property of this function is that it is capable of being represented either as a piecewise constant function or as a generalized function [1,3]. The Unit Step Function is mainly used in the calculation processes of Control Theory and signal processing in order to represent a signal which switches on at a specified time and stays switched on indefinitely. This function is also implemented together with its derivative, i.e., Dirac delta functions in structural engineering in order to describe various types of structural loads, e.g., off – axis four point bending of simply supported or fully constrained beams. Thus, it is very useful for the necessary calculations dealing with conceptual and embodiment design procedures from the engineering viewpoint.

In the meanwhile, there are many smooth analytic approximations to the Unit Step function as it can be seen in the literature [4–6]. Besides, Sullivan et al. [7] obtained a linear algebraic approximation to this function by means of a linear combination of exponential functions. However, the majority of all these approaches lead to closed – form representations consisting of non - elementary special functions, e.g., Gamma function, Hyperfunction, Error function etc and also most of its exact forms are expressed in terms of generalized integrals or infinitesimal terms, something that complicates the related computational procedures. In Ref. [8] an analytical form of the Unit Step Function was proposed as a summation of two inverse tangent functions. Nonetheless, according to this simplified approach the singularity structure was left ambiguous. Besides, one may point out that a shortcoming of such formulae is that the involved inverse trigonometric functions do not have unique definitions. In addition, in Ref. [9] this special function was explicitly expressed by the aid of purely algebraic representations. The novelty of this work was that the proposed explicit formula is not performed in terms of non-elementary special functions. Moreover, another elegant approximation to Heaviside function in the form of a summation of two logarithmic functions was carried out by Murphy in Ref. [10]. In this work, the author also presented a closed form of Dirac delta function. Also, a nonlinear trigonometric approximation of delta function was exhibited in Ref. [11]. In Ref. [12] Dirac delta function is approached in a rigorous manner by means of integral and series representations, whereas for a detailed study on multi-dimensional Heaviside and Dirac delta functions, one may refer to Ref. [13].

In Ref. [14], Dirac delta function was approached using the nonextensive-statistical-mechanics q-exponential function.

In Ref. [15] the Unit Step Function was obtained by some cumulative distribution functions (e.g., Half-Cauchy and Hyperbolic-secant functions), whilst in Ref. [16] an analogous study was carried out towards the approximation of Unit Step Function by some other cumulative distribution functions.

In Ref. [17] a Hausdorff approximation of Heaviside Step function by means of several sigmoid functions (log–logistic, transmuted log–logistic and generalized logistic functions) was taken into account and in this framework, upper and lower bounds for the Hausdorff distance were derived.

On the other hand, in Ref. [18] a single – valued function was introduced, which was proved to be synonymous with the Unit Step Function. This formula consists of purely algebraic representations and does not contain either generalized integrals or any other infinitesimal quantities. Further, a study on Heaviside and Impulse Function from an engineering point of view is performed in Ref. [19]. Finally, in Ref. [20] an analytical form of the Unit Step Function was proposed as the summation of four inverse tangent functions. This formula constitutes a purely algebraic representation, since it does not contain special functions, generalized integrals or any other infinitesimal quantities.

In the present study, in the sense of Ref. [20] an explicit form of the Unit Step Function is proposed as a summation of six inverse tangent functions. The novelty of this work when compared with other analytical representations, is that the proposed exact formula contains two arbitrarily selected single - valued continuous functions which satisfy only one restriction. In this framework, this formula seems to be flexible and practical and thus may have good prospects towards the computational procedures that concern the applications of Heaviside step function in Operational Calculus, as well as in other engineering practices.

2. Towards an exact form of Heaviside Function

Let us introduce the following single – valued function

f : R^{*} \to R

with

f (x) = \frac{1}{2 π} ((a r c t a n (2 x + 1) + a r c t a n (1 + \frac{1}{x}) + a r c t a n {(x}^{2 n - 1}) + a r c t a n \frac{1}{x^{2 n - 1}}) + \frac{3}{2 π} (a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)}))

(1)

where

g, h

are two single - valued continuous functions such that:

(g \cdot h) (x) > 0, \forall x \in R^{*}

(2)

Actually, the above constraint implies that the values of

g (x)

and

h (x)

always agree in sign and also are never zero.

In this context, both

g (x)

and

h (x)

should be either strictly positive or strictly negative respectively.

3. Claim

The function

f

coincides with Unit Step Function over its domain of definition.

4. Proof

We shall prove that the values of the function

f

vanish for strictly negative arguments and equal unity for strictly positive arguments. To this end, let us focus on the summation:

a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)}

which can be modified as follows:

a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)} = k π + a r c t a n [\frac{\frac{g (x)}{h (x)} + (\frac{h (x) - g (x)}{h (x) + g (x)})}{(1 - \frac{g (x)}{h (x)} \cdot (\frac{h (x) - g (x)}{h (x) + g (x)}))}] \Leftrightarrow a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)} = k π + a r c t a n [\frac{g (x) \cdot (h (x) + g (x)) + h (x) ((h (x) - g (x))}{h (x) ((h (x) + g (x)) - g (x) ((h (x) - g (x))}] \Leftrightarrow a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)} = k π + a r c t a n [\frac{g^{2} (x) + h^{2} (x)}{g^{2} (x) + h^{2} (x)}] \Leftrightarrow a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)} = k π + a r c t a n 1 \Leftrightarrow a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)} = k π + \frac{π}{4}

(3)

where

k

denotes an arbitrary integer variable.

Eqn. (3) informs us that the quantity

(a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)})

does not vary with respect to variable

x

Next, to determine the integer variable

k

one may proceed as follows:

Inequality (2) asserts us that

g (x)

and

h (x)

agree in sign over the set

(- \infty, 0) \cup (0, + \infty)

Let us distinguish the following four cases:

1) g (x) > h (x) > 0

(4)

According to inequality (4) one infers:

\frac{g (x)}{h (x)} > 1

(5)

and

- 1 < \frac{h (x) - g (x)}{h (x) + g (x)} < 0

(6)

Then the following inequalities are evident

\frac{π}{4} < a r c t a n \frac{g (x)}{h (x)} < \frac{π}{2}

(7)

and

- \frac{π}{4} < \arctan \frac{h (x) - g (x)}{h (x) + g (x)} < 0

(8)

and therefore

0 < a r c t a n \frac{g (x)}{h (x)} + a r c t a n \frac{h (x) - g (x)}{h (x) + g (x)} < \frac{π}{2}

(9)

Inequality (9) can be combined with eqn. (3) to yield

0 < k π + \frac{π}{4} < \frac{π}{2}

(10)

Inequality (10) guarantees that the integer variable

k

should vanish.

2) 0 < g (x) < h (x)

(11)

On the basis of inequality (11) one may deduce that:

0 < \frac{g (x)}{h (x)} < 1

(12)

and

0 < \frac{h (x) - g (x)}{h (x) + g (x)} < 1

(13)

Thus according to the same reasoning one may derive the following inequalities

0 < a r c t a n \frac{g (x)}{h (x)} < \frac{π}{4}

(14)

and

0 < \arctan \frac{h (x) - g (x)}{h (x) + g (x)} < \frac{π}{4}

(15)

By adding inequalities (14) and (15) one obtains again inequality (9), which in combination with eqn. (3) warrants that the integer variable

k

should vanish.

3) g (x) < h (x) < 0

(16)

By taking into consideration inequality (18) one infers

\frac{g (x)}{h (x)} > 1

(17)

and

0 > \frac{h (x) - g (x)}{h (x) + g (x)} > - 1

(18)

Hence according to the same reasoning, one obtains the following inequalities

\frac{π}{4} < a r c t a n \frac{g (x)}{h (x)} < \frac{π}{2}

(19)

and

- \frac{π}{4} < \arctan \frac{h (x) - g (x)}{h (x) + g (x)} < 0

(20)

By adding inequalities (19) and (20), one derives again inequality (9), which in combination with eqn. (3) asserts us that the integer variable

k

should vanish.

4) h (x) < g (x) < 0

(21)

According to inequality (25) one may deduce that

0 < \frac{g (x)}{h (x)} < 1

(22)

and

0 < \frac{h (x) - g (x)}{h (x) + g (x)} < 1

(23)

The same procedure as in previous cases, results again in inequality (9), which in combination with eqn. (3) guarantees that the integer variable

k

should vanish.

In continuing, let us calculate the first derivative of

f

with respect to

x

After the necessary algebraic manipulations, it implies that

\frac{d}{d x} f (x) = 0, \forall x \in (- \infty, 0) \cup (0, + \infty)

(25)

Here, one may also pinpoint that since the left sided and right sided limits of the term:

a r c t a n \frac{1}{x^{2 n - 1}}

, letting letting

x

tend to zero) are not equal, the limit of

f (x)

letting

x

tend to zero does not exist.

Sagestively, let us calculate the values of

f (x)

x

= -1 and at

x

= 1 respectively.

Thus we can write out

f (- 1) = \frac{1}{2 π} ((a r c t a n (- 1) + a r c t a n (0) + a r c t a n (- 1) + a r c t a n (- 1)) + \frac{3 π}{4}) \Rightarrow f (- 1) = 0

(26)

On the other hand one may calculate the value

f (1)

as follows

f (1) = \frac{1}{2 π} ((a r c t a n (3) + a r c t a n (2) + a r c t a n (1) + a r c t a n (1)) + \frac{3 π}{4}) \Rightarrow f (1) = 0.625 + 0.375 = 1

(27)

Hence, on the basis of eqns. (26) and (27) in combination with eqn. (25) one may deduce that the continuous function

f

as defined by eqn. (1) coincides with Unit Step function over the set

(- \infty, 0) \cup (0, + \infty) .

5. Discussion

In the previous Section, we proposed an explicit form of Unit Step Function as a summation of six inverse tangent functions. This function coincides with Unit Step function over the set

(- \infty, 0) \cup (0, + \infty) .

However, one may pinpoint that a shortcoming of the single – valued function

f

is that it cannot be defined at

x

=0. Besides, the limit of

f

(

x

) at

x

=0 does not exist, since the left sided and right sided limits of

f

(

x

) letting

x

tend to zero are not equal.

Here, one may also remark that when Heaviside step function

H (x)

is approached by the well – known Logistic function

\frac{L}{1 + E X P (- k (x - x_{0})}

, it is admitted beforehand that

H (0) = \frac{1}{2}

[21].

In addition, one may also observe that a disadvantage of all mathematical formulae consisting of inverse trigonometric functions is that these functions do not have unique definitions [22]. Moreover, one should elucidate that mathematical representations containing such quantities are not appropriate for determining the Dirac function by differentiating the proposed function with respect to variable

x

. For instance, it was shown that the first derivative of

f

with respect to

x

vanishes over the set

(- \infty, 0) \cup (0, + \infty) .

Moreover, one should emphasize that the formula introduced by eqn. (1) does not describe only one function but in fact describes a family of functions, that all have the same property (to be synonymous with Heaviside function) and this is an advantage over the mathematical formula proposed in Ref. [8]. Here, one may also point out that the function

f

introduced by eqn. (1), could take the following simplified form, which can be easily proved that is also synonymous to Heaviside Step Function over the set

(- \infty, 0) \cup (0, + \infty)

f (x) = \frac{1}{π} (a r c t a n (2 x + 1) + a r c t a n (1 + \frac{1}{x})) + \frac{1}{4}

(28)

Further, one may consider a single - valued continuous function

φ : R^{*} \to R

of the following general form

φ (x) = a r c t a n (a x + b) + a r c t a n (\frac{c x + d}{x})

(29)

where a,b,c,d are arbitrary real constants

By differentiating eqn. (29) with respect to

x

one finds

Then by requesting

\frac{d}{d x} φ (x) = 0

over the set

(- \infty, 0) \cup (0, + \infty)

it implies that

or equivalently

Thus the following relations should hold simultaneously

a + a c^{2} - {d a}^{2} = 0

and

2 a d c - 2 a d b

and

{a d}^{2} - d - d b^{2} = 0 (33, a, b, c)

Additionally, one should request

a r c t a n (b - a) + a r c t a n (c - d) \neq a r c t a n (a + b) + a r c t a n (c + d)

(34)

Hence, according to the above statements one may deduce that

φ (x) = A

over the set

(- \infty, 0)

and

φ (x) = B

over the set

(0, + \infty)

where

A, B

are real constants such that

A \neq B

In this context, one may infer that the quantity

\frac{a r c t a n (a x + b) + a r c t a n (\frac{c x + d}{x}) - A}{B - A}

coincides with Heaviside step function over the set

(- \infty, 0) \cup (0, + \infty)

provided that statements (38) and (39) hold.

6. Conclusions

The objective of this theoretical investigation was to introduce an analytical form of the Unit Step function. The proposed formula constitutes a linear combination of six inverse trigonometric functions and therefore does not contain either generalized integrals or any other infinitesimal quantities. In addition, no other special functions are involved (e.g., Gamma function, Complementary Error function etc). The novelty of this work when compared with other analytical representations, is that the proposed exact formula contains two arbitrary single - valued continuous functions which satisfy only one constraint. In this context, it seems to be more flexible and practical and thus may have good prospects towards the computational procedures that concern the applications of Heaviside step function in Operational Calculus, as well as in other engineering practices. Nevertheless, one should pinpoint that a shortcoming of the proposed closed - form expression is that it cannot be defined at

x = 0 .

As a future work, one could propose analytical representations to ramp and signum function by taking into consideration this approach.

Conflicts of Interest

The author declares that there is no conflict of interest regarding the publication of this paper.

References

M. Abramowitz, I.A. and Stegun, Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, Dover Publications INC (1972).
B.J. Hunt, Oliver Heaviside. Phys. Today, Vol. 65, Number 11, pp. 48-55.
R. Bracewell Heaviside’s Unit Step Function, H(x). The Fourier Transform and its Applications, McGraw – Hill (2000).
L. Berg Introduction to the Operational Calculus, North – Holland Publishing Company (1967).
R.P. Kanwal, Generalized Functions Theory and Technique: Theory and Technique. 2nd ed. Boston, MA: Birkhäuser (1998).
J. Spanier, J. K.B. and Oldham The Unit-Step u(x-a) and Related Functions Ch. 8 from: An Atlas of Functions. Washington, DC: Hemisphere, pp. 63-69, 1987.
J. Sullivan, L. Crone and J. Jalickee, Approximation of the Unit Step Function by a Linear Combination of Exponential Functions, Journal of. Approximation Theory, Vol. 28, Number 3, pp. 299 – 308, 1980.
J. Venetis, An analytic exact form of the unit step function, Mathematics and Statistics Vol. 2, Number 7, pp. 235-237, 2014.
J. Venetis, An analytic exact form of the Heaviside step function Advances and Applications in Discrete Mathematics, Volume 22, Number 2, 2019, Pages 153-159.
K. Murphy, Explicit Forms of Discontinuous Functions the Dirac Delta and Irreducible Forms (preprint). https://www.academia.edu/11704122/Explicit_Forms_of_Discontinuous_Functions_the_Dirac_Delta_and_Irreducible_Forms.
X. Xu, Nonlinear trigonometric approximation and the Dirac delta function, Journal of Computational and Applied Mathematics 209 (2006) 234 – 245.
Y.T. Li and R. Wong, Integral and Series Representations of the Dirac Delta Function, Communications on Pure and Applied Analysis,(2013). arXiv:1303.1943.
C. Min and F. Gibou, Robust second-order accurate discretizations of the multi-dimensional Heaviside and Dirac delta functions, Journal of Computational Physics archive, Vol. 227, Issue 22, Nov.(2008), pages 9686-9695.
M. Jauregui and C. Tsallis, New representations of π and Dirac delta using the nonextensive-statistical-mechanics q-exponential function, Journal of Mathematical Physics 51, 063304,(2010).
N. Kyurkchiev, On the Approximation of the step function by some cumulative distribution functions. Compt. rend. Acad. bulg. Sci. Vol. 68, Number 4, pp. 1475–1482, 2015.
V. Kyurkchiev, N. Kyurkchiev, On the Approximation of the Step function by Raised – Cosine and Laplace Cumulative Distribution Functions, European International Journal of Science and Technology Volume 4, Number 2, pp. 75–84, 2016.
Iliev, N. Kyurkchiev, S. Markov, On the approximation of the step function by some sigmoid functions, Mathematics and Computers in Simulation, Volume 133, Number 1, pp. 223-234, 2017.
J. Venetis, Analytic Exact Forms of Heaviside and Dirac Delta Function, Advances in Dynamical Systems and Applications, Vol. 15, Number 1, pp. 115-121, 2020.
Enrique Chicurel-Uziel Unit Step and Impulse Function Equations to Simplify the Solution of Engineering Problems, Journal of Information Sciences and Computing Technologies, Volume 7, Issue 1 2018, pp.654-666.
J. Venetis, An explicit form of Heaviside Step Function, Advances in Dynamical Systems and Applications, Volume 16, Number 2, (2021) pp. 895-900.
I. A. Maron, Problems in Calculus of One Variable, with Elements of Theory, Translated from the Russian by Leonid Levant [Revised from the 1970 Russian Ed.] Mir Publishers, 1973.
Stewart, J., Redline,L., Watson, S.(2001). Algebra and trigonometry, Brooks/Cole Thomson Learning.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Closed-Form Expression for the Unit Step Function

Abstract

1. Introduction

2. Towards an exact form of Heaviside Function

3. Claim

4. Proof

5. Discussion

6. Conclusions

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe