Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds

Preprint

Article

Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds

Altmetrics

Downloads

211

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 February 2023

Posted:

16 February 2023

You are already at the latest version

Alerts

Abstract

Ramsey theory influences the dynamics of mechanical systems, which may be described as abstract complete graphs. We address a mechanical system which is completely interconnected with the two kinds of ideal Hookean springs. The suggested system mechanically corresponds to the cyclic molecules, in which functional groups are interconnected with two kinds of chemical bonds, represented mechanically with two springs k1 and k2. In this paper, we consider a Cyclic system (molecule) built of six equal masses m and two kinds of springs. We pose the following question: what is the minimal number of masses in the such a system in which three masses are constrained to be connected with spring k1 or three masses to be connected with spring k2? The answer to this question is supplied by the Ramsey theory, and it is formally stated as follows: what is the minimal number R3,3? The result emerging from the Ramsey theory is R3,3=6. Thus, in the aforementioned interconnected mechanical system will be necessarily present the triangles (at least one triangle), built of masses and springs. This prediction constitutes the vibrational spectrum of the system. Thus, the Ramsey Theory supplies the selection rules for the vibrational spectra of the cyclic molecules. Symmetrical system built of six vibrating entities is addressed. The Ramsey approach works for 2D and 3D molecules, which may be described as abstract complete graphs. The extension of the proposed Ramsey approach to the systems, partially connected by ideal springs, viscoelastic systems and systems, in which elasticity is of an entropy nature is discussed. “Multi-color systems” built of three kinds of ideal springs are addressed. The notion of the inverse Ramsey network is introduced and analyzed.

Keywords:

Subject: Physical Sciences - Mathematical Physics

1. Introduction

Ramsey theory, is a branch of mathematics/combinatorics that focuses on the appearance of ordered substructures within a structure of a known size. Ramsey theory states that any structure will necessarily contain an orderly substructure [1]. Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colors) of a sufficiently large complete graph [2]. To demonstrate the theorem for two colors (say, blue and orange), let p and q be any two positive integers, the Ramsey theorem states that there exists a least positive integer

R (p, q)

for which every blue-orange link coloring of the complete graph on

R (p, q)

vertices contains a blue clique on p vertices or an orange clique on q vertices. The Schur Theorem, demonstrating for any

r \in N

there is a natural number P such that any r- coloring of

[1, P]

contains x, y , z having the same color such that

x + y = z

exemplifies the Ramsey theorem. One more example is supplied by the van der Waerden’s theorem: colorings of the integers by finitely many colors must have long monochromatic arithmetic progressions [2]. Problems in Ramsey theory typically ask a question of the form: "how big must some structure be to guarantee that a particular property holds?" More specifically, Ron Graham described Ramsey theory as a "branch of combinatorics"[3,4,5]. A simple, popular introduction to the Ramsey theory is found in refs. 2-3. More advanced, rigorous mathematical approach is presented in refs. 4-5. Applications of the Ramsey theory for the theory of communication and decision making are discussed in ref. 6. Interconnection between the Ramsey theory and statistical physics was addressed in ref. 7. One of the most actual problem of the Ramsey theory is calculation of values of the Ramsey numbers for many-vertices systems. Classical Hamiltonian that favors configurations in a way to establish lower bounds on Ramsey numbers was demonstrated [7]. The application of the Ramsey theory to classical thermodynamics was demonstrated in ref. 8. Maps (graphs) built of thermodynamic states were addressed [8]. The Ramsey theory supplies the answer to the following question how large should be a graph describing connections between discrete thermodynamic states to guarantee the appearance of thermodynamic cycles [8]? The application of the Ramsey theory to physical systems, in which attraction and repulsion forces act between, the bodies constituting the system is discussed in ref. 9. The Ramsey theory explains why nature prefers cubic lattices over hexagonal ones for systems built of electric or magnetic dipoles [9].

In the present paper we address the application of the Ramsey theory for the analysis of mechanical systems, which may be represented as complete graphs. Cyclic molecules may be seen as complete graphs [10,11]. Chemical bonds are seen the edges (links) of the graph, which in a very crude approximation may be considered as ideal springs. We demonstrate that the Ramsey theory introduces the “selection rules” for eigenmodes (eigenfrequincies) of the cyclic molecules, treated as completed graphs. Thus, the Ramsey approach to the vibrational spectra of the cyclic molecules becomes possible. The proposed Ramsey approach predicts the Ramsey modes, which are necessarily present in these spectra.

2. Ramsey theory and vibrations of cyclic molecules

2.1. Ramsey theory for the system interconnected by two kinds of ideal springs

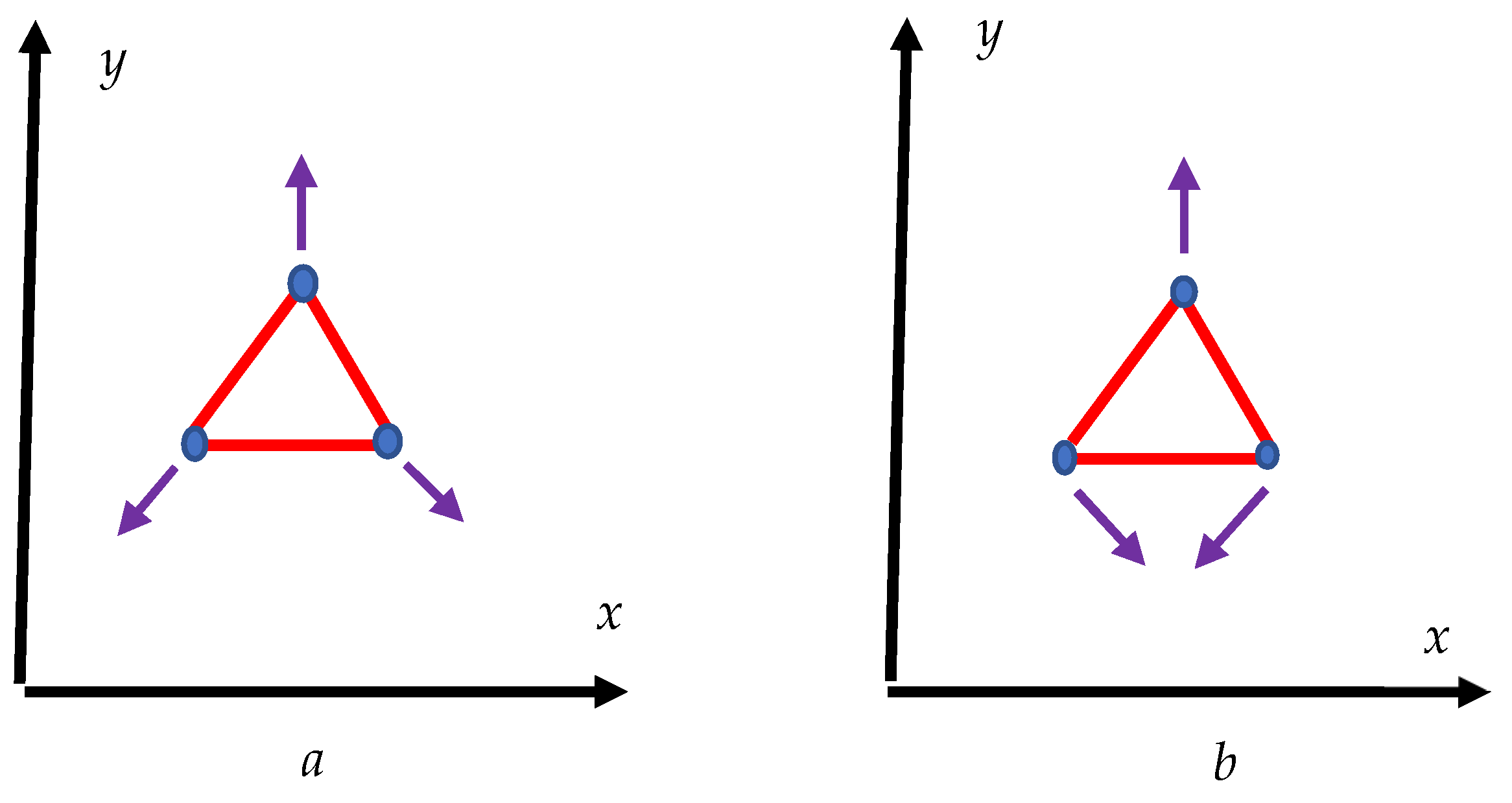
Consider mechanical system built of six identical masses m shown in Figure 1. These masses are connected with two ideal Hookean massless springs

k_{1}

and

k_{2}

as shown in Figure 1. The mechanical system depicted in Figure 1 corresponds to the chemical compound in which two kinds of chemical bonds are present. These bonds are represented by the springs

k_{1}

and

k_{2}

. The bonds form the complete graph, i.e. a graph in which each pair of graph vertices (masses) is connected by an edge (spring/chemical bond). We demonstrate that the Ramsey theory supplied predictions related to the eigenvalues of frequencies of vibrations in the system described in Figure 1. In other words, the Ramsey theory may predict the peculiarities of the vibrational spectrum of the cyclic chemical compound (molecule) corresponding to the mechanical system [10,11], shown in Figure 1. For a sake of simplicity, the masses of the vibrating bodies are taken equal.

The complete graph depicted in Figure 1 is a graph typical for the Ramsey theory. Let us connect the masses interconnected with the spring

k_{1}

with the red; in turn, let us connect the masses interconnected with the spring

k_{2}

with the green line.

We recognize two triangles in Figure 1. The vibrational spectrum of the system shown in Figure 1 will crucially depend on the presence of the triple of double chains of masses. Let us pose the following question: what is the minimal number of masses in the system in which three masses are connected with spring

k_{1}

or three masses are connected with spring

k_{2}

. The answer to this question is supplied by the Ramsey theory, and it is formulated as follows: what is the minimal number

R (3,3) ?

The answer emerging from the Ramsey Theory is:

R (3,3) = 6

. Indeed, we recognize in the example illustrated with Figure 1, that in the molecule built of six point masses, in which the relationships “to be connected by spring

k_{1}

” and “to be connected by spring

k_{2}

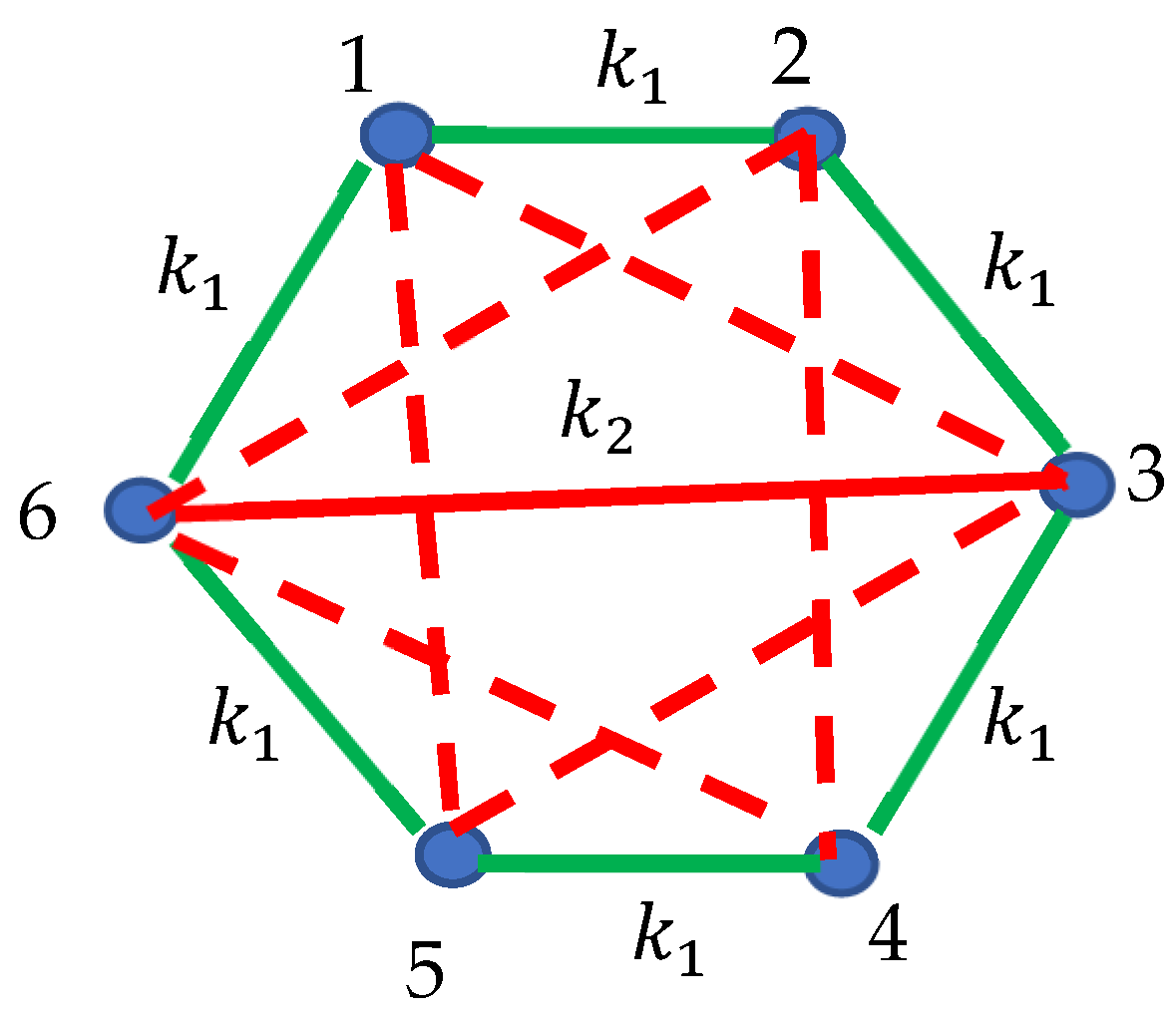
” are necessarily present we find triads of masses connected by the same kinds of springs (at least one triangle-shaped ring chain of masses will be necessarily present in the system of masses completely interconnected one to another). Of course, the quantitative prediction of the eigenfrequency corresponding to the triangle-shaped chain of masses, for the asymmetric system, shown in Figure 1, presents extremely challenging computational problem. 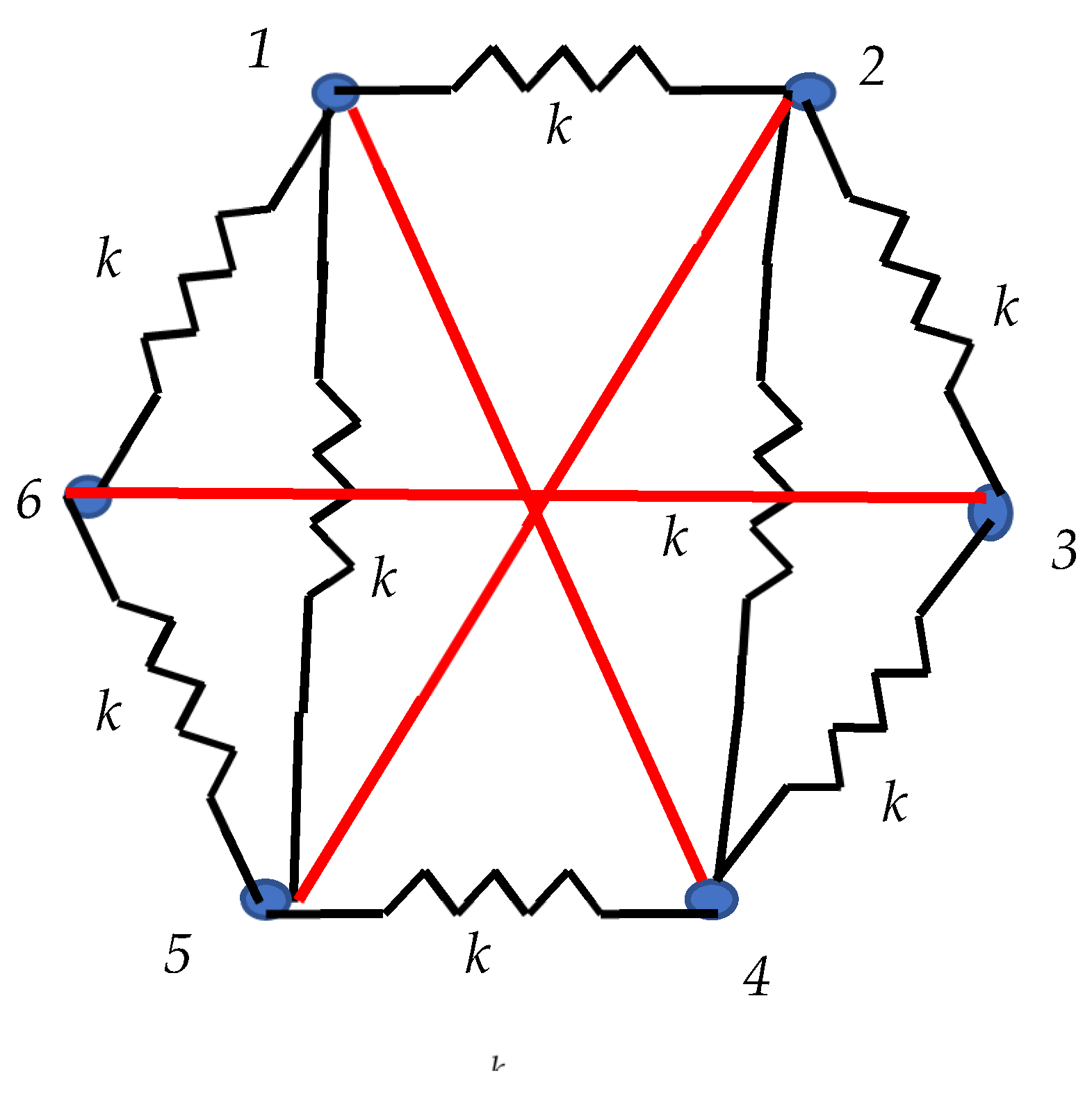This problem becomes solvable for the symmetric plane distribution of masses depicted in Figure 2 (the masses form the regular hexagon).

(green edges) and

k_{2}

(red edges). Two equilateral triangles “153” and “246” are recognized).

Two equilateral triangles, namely “153” and “246” are present within the cyclic “molecule” depicted in Figure 2. These triangles built of the masses m and springs

k_{2}

are shown with the red dashed lines. If harmonic oscillations of the masses connected with the “green” and “red” springs are decoupled (this will take place when

k_{1} ≫ k_{2}

is fulfilled), the eigenvalues of the vibrations occurring within the red dashed triangles are calculated with the standard methods of the classical mechanics [12]. The full spectrum of the eigenfrequencies

ω_{e i g e n}

in this case is given by Eq. 1:

ω_{e i g e n} = (0,0, 0, \sqrt{\frac{3 k_{2}}{2 m}}; \sqrt{\frac{3 k_{2}}{2 m};} \sqrt{\frac{3 k_{2}}{m}})

(1)

Two of aforementioned trivial zero-eigenfrequencies correspond to the x and y translations of the entire system in the XY-plane, and the third one corresponds to the uniform rotation of the entire system about its center of mass. The detailed treatment of the eigenmodes is supplied in Appendix A. In addition, the modes inherent for the ring of “green” springs

k_{1}

should be considered [13,14]. We call these modes the Ramsey modes. It turns out that the Ramsey theory imposes restrictions on the vibrational spectrum of the cyclic mechanical systems, described by complete graphs. In other words, it supplies the “selection rules” for the vibrational spectra of the cyclic molecules, chemical structure of which may be described with the complete graphs [10-11. ). It is noteworthy that

R (2,6) = 6 .

Thus, if we have a molecule, described by a complete graph, which is built of six functional groups, or two or six interconnected groups will necessarily be present in its structure; thus, explaining the formation of the benzene-like ring structures (see Figure 2).

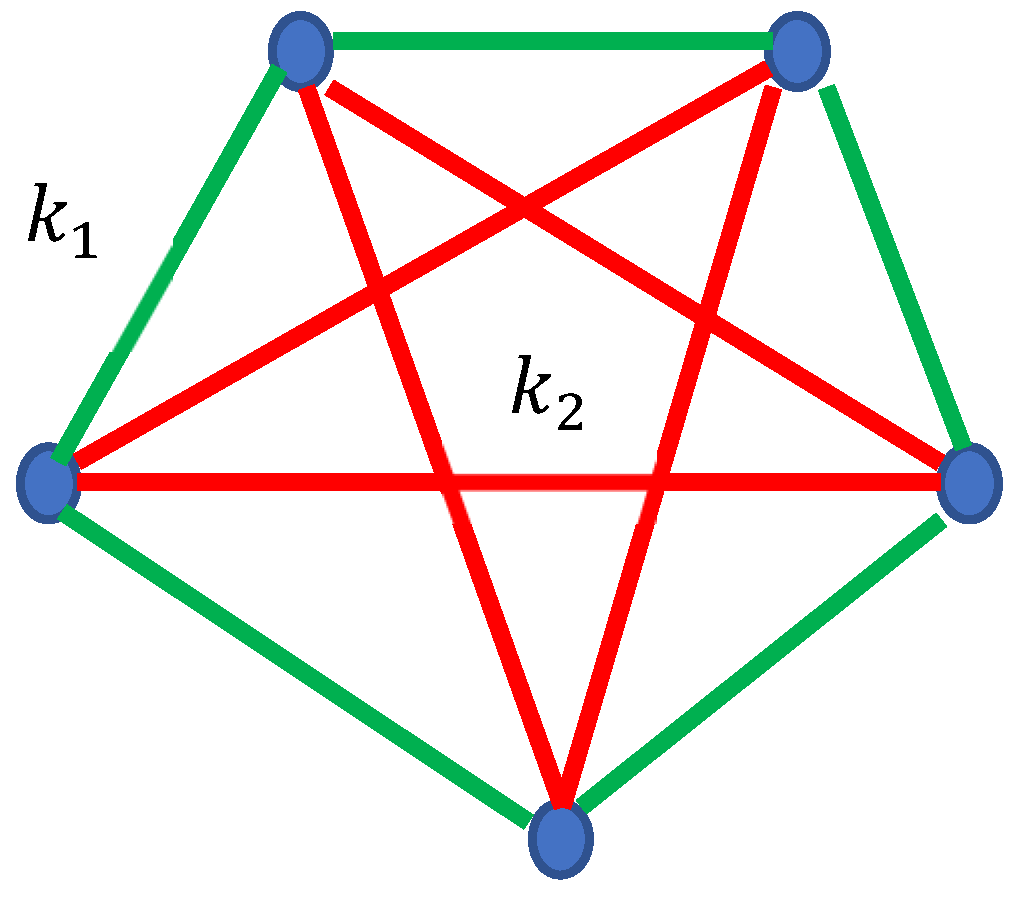
At the same time, eigenfrequencies supplied with Eq. 1 will not necessarily appear in the molecule built of five point masses, shown in Figure 3. Indeed, the triangles built of the springs are not present in these structures, and this conclusion immediately follows from the Ramsey approach:

R (3.3) = 6 > 5 .

(green edges) and

k_{2}

(red edges). No triangles are formed in the springs network. The Ramsey number

R (3.3) = 6 > 5 .

Again, the Ramsey Theorem works as a selection rule for the vibrational spectra of molecules.

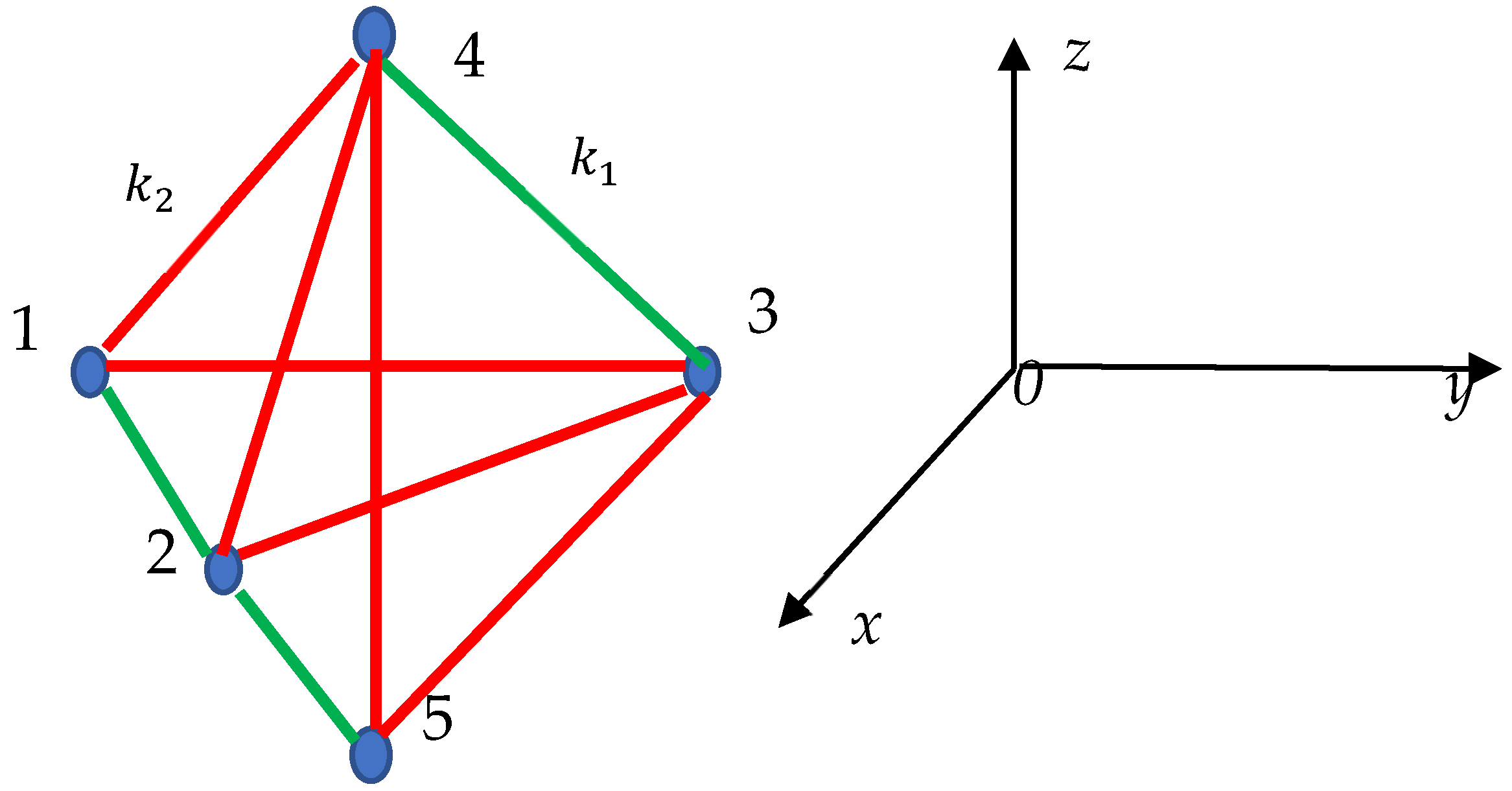
The proposed Ramsey approach is easily extended for the 3D vibrating systems/molecules such as those shown in Figure 4. The molecule shown in Figure 4 is built from two tetrahedrons, denoted “1234” and “1235”. Triangle “123” is located in the plane

(X O Y)

(see Figure 4). Masses placed in the vertices of the tetrahedron are connected with two kinds of springs, the green (

k_{1})

and red (

k_{2}

) ones.

Figure 4 depicts coloring of the 3D system in which no monochrome triangle is present. Thus, eigenmodes supplied with Eq. 1 will not appear in the vibrating system/molecule built of five point masses, shown in Figure 4. This result conforms from the Ramsey approach:

R (3,3) = 6 > 5;

and it works for 3D systems. It is noteworthy, that “springs” connecting the masses may be classic or quantum ones [15].

2.2. Direct and inverse Ramsey networks of ideal springs

It is instructive to introduce the inverse Ramsey networks of ideal springs, namely to replace springs

k_{1}

with strings

k_{2}

, and strings

k_{2}

to replace correspondingly with strings

k_{1} .

We call such a Ramsey network the “inverse graph”; introducing of inverse Ramsey network is possible for any complete source graph. Construction of the “inverse graph” results in replacement of red, links depicted in Figure 1 with the red links and vice versa. Consider the Ramsey structure built of six atoms, such as depicted in Figure 1. Obviously, the total number of triangles in the “direct” (source) and “inverse” Ramsey graphs is the same, thus giving rise to Eq. 2:

t_{r} + t_{g} = t_{r}^{'} + t_{g}^{'}

(2)

where

t_{r} a n d t_{g}

are the numbers of red and green triangles in the source graph;

t_{r}^{'} a n d t_{g}^{'}

are the numbers of red and green triangles in the inverse graph. Eq. 2 represents the “conservation law” for the Ramsey complete networks built of six elements. It is noteworthy, that direct and inverse graphs form the Abelian (commutative group).

2.3. Ramsey theory for the system of vibrating masses partially connected by the ideal springs

It seems from the first glance that the Ramsey theory will be useful only for the systems, completely interconnected by the springs. Thus, the complete graphs, built of springs, such as depicted in Figure 1, Figure 2, Figure 3 and Figure 4 emerge.

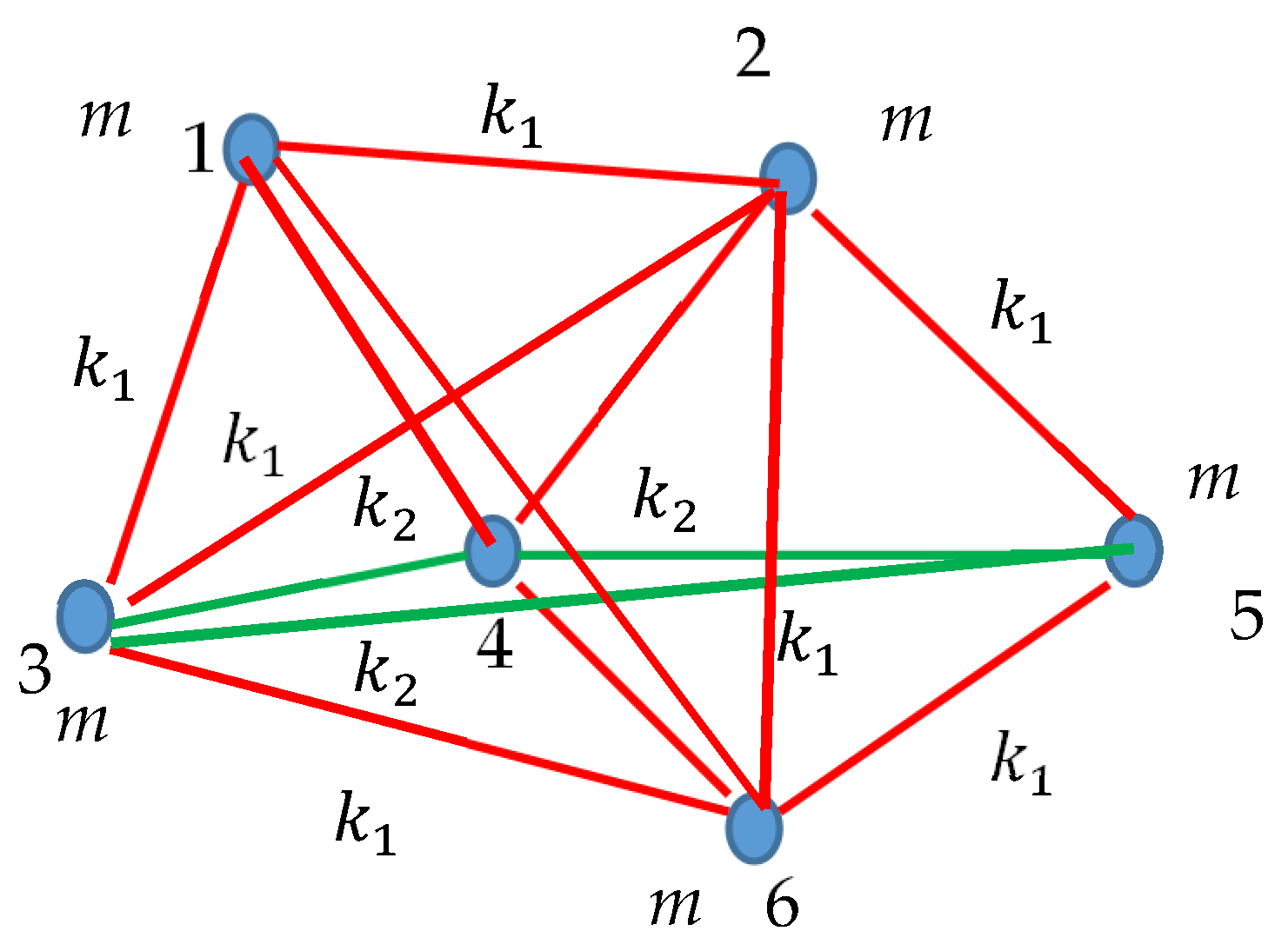
We demonstrate that the Ramsey approach also works for the systems which are partially interconnected by the springs, such as those, shown in Figure 5. Consider the system built of six point masses m connected by ideal springs k as depicted in Figure 5. It should be emphasized that the pairs of masses labeled ”14”, “45” and “36” are not connected by springs (see Figure 5).

Let us connect the masses interacting via spring k with black links, and disconnected masses via red links as shown in Figure 5. Thus, the complete graph built of black and red links emerges. According to the Ramsey theory, at least one “red” or “black” triangle should necessarily appear within the graph. Indeed, black triangles “156” and “234” are present in the graph. The eigen-frequencies inherent for this triangles are

ω_{e i g e n} = (\sqrt{\frac{3 k}{2 m}}; \sqrt{\frac{3 k}{2 m};} \sqrt{\frac{3 k}{m}})

. Thus, we come to the important conclusion, namely: the vibrating systems partially interconnected with the springs may be described with the Ramsey approach.

2.4. Multi-color systems built of ideal springs

The Ramsey approach makes possible the analysis of more complicated cyclic compounds interconnected with the three kinds of ideal springs, denoted

k_{1}, k_{2}

and

k_{3}

. Thus, the analysis of the vibration of such a system is reduced to the Ramsey number

R (3,3, 3)

. It was established that

R (3,3, 3) = 17 .

If harmonic oscillations of the masses are decoupled (this will take place when

k_{1} ≅ k_{2} ≫ k_{3}

is fulfilled), the eigenvalues of the vibrations occurring within the red dashed triangles are calculated with the standard methods of the classical mechanics and they are given by:

ω_{e i g e n} = (\sqrt{\frac{3 k_{3}}{2 m}}; \sqrt{\frac{3 k_{3}}{2 m};} \sqrt{\frac{3 k_{3}}{m}})

2.5. Ramsey model of viscoelasticity

It is also instructive to consider the Ramsey model of viscoelasticity presented in Figure 6 [16,17,18,19]. In this model point masses m are connected with ideal springs k or with viscous elements, quantified by viscosity denoted

η

are connected with ideal springs k or with viscous elements, quantified by viscosity

η

. Viscous joints are colored with red whereas elastic joints are connected with black links.

Elastic links we color with black color, whereas, viscous connections are colored with red. For a sake of simplicity we consider the complete graph, similar to that shown in Figure 5. The Ramsey number

R (3,3)

=6, this the “black” (elastic) or “red” (viscous) triangle will necessary appear in the graph. . Indeed, elastic triangles labeled “156” and “234” are present in the graph. The eigen-frequencies inherent for this triangles are

ω_{e i g e n} = (\sqrt{\frac{3 k}{2 m}}; \sqrt{\frac{3 k}{2 m};} \sqrt{\frac{3 k}{m}})

. Thus, we conclude that the Ramey approach is applicable for modeling of viscoelastic media [16,17,18,19] , namely: the vibrating systems partially interconnected with the springs may be described with the Ramsey approach. Of course, there exists the possibility that no “elastic” triangles will be present in the graph, and only viscous ones will appear. In this case, only eigenvalues of frequencies inherent for pair oscillations of masses will appear in the vibration spectrum of the viscoelastic body.

2.6. Ramsey theory for vibrations of systems in which entropy elasticity is present

The approach presented in Section 2.1 is easily extended to the analysis of the systems in which elasticity of the entropic nature, as it takes place for polymer molecules [20]. Consider cyclic interconnected system built of the identical masses m, such as depicted in Figure 1, in which springs

k_{1}

and

k_{2}

represent elasticity of two kinds of ideal polymer chains. Assume, that red links correspond to ideal polymer chains built of

N_{1}

Kuhn monomers; the Kuhn length of the monomer is denoted

b_{1}

. In turn, green links correspond to ideal polymer chains built of

N_{2}

Kuhn monomers, the Kuhn length of the monomer is labeled

b_{2}

. The entropic string constants of the chains are given by Eq. 3 [20]:

k_{1} = \frac{3 k_{B} T}{N_{1} b_{1}^{2}}; k_{2} = \frac{3 k_{B} T}{N_{2} b_{2}^{2}}

(3)

where

k_{B}

and T are Boltzmann constant and the temperature of polymer chains correspondingly. In the simplest possible configuration of the symmetric polymer molecule, such as depicted in Figure 2 (again springs

k_{1}

and

k_{2}

represent entropic elasticity of ideal polymer chains), in the limiting case of

k_{1} ≫ k_{2}

, we obtain for the spectrum of

ω_{e i g e n} = (0,0, 0, \frac{3}{b_{2}} \sqrt{\frac{3 k_{B} T}{2 N_{2}}}; \sqrt{\frac{3 k_{B} T}{2 N_{2}};} \sqrt{\frac{3 k_{B} T}{N_{2}}})

(4)

Remarkably all of eigen-frequencies scale as:

ω_{e i g e n} ~ \frac{1}{b_{2}}, ω_{e i g e n} ~ \frac{1}{\sqrt{N_{2}}}, ω_{e i g e n} ~ \sqrt{T}

, thus, their values grow as square root from the temperature.

3. Conclusions

Ramsey theory is a branch of combinatorics that predicts the appearance of ordered substructures within a structure of a known size [1,2,3,4,5,6]. Ramsey theory states, under addressing the properties of complete graphs, that any structure will necessarily contain an orderly substructure [1,2,3,4,5,6]. We applied the Ramsey theory for the analysis of the cyclic mechanical systems, in which point masses m are connected with two kinds of ideal springs. Such systems may be seen as complete graphs, in which vertices (point masses) are connected with the edges colored with two colors (i.e. two kinds of springs). We applied the Ramsey theory for these kinds of graphs. These graphs also represent cyclic molecules, in which functional groups are connected by two kinds of chemical bonds [7,8]. Two kinds of springs/chemical bonds in our case are colored with “green” and “red” correspondingly. The Ramsey number for the aforementioned systems is defined as the smallest value of n such that in a group of n point masses either a group of j masses forms a complete network of “red” springs or i masses form a complete network connected by the “green” springs. We formulated the following question: what is the minimal number of masses in the system in which three masses are connected with spring

k_{1}

or three masses are connected with spring

k_{2}

? The answer to this question emerges from the Ramsey Theory, and it is mathematically formalized as follows: what is the minimal Ramsey number

R (3,3) ?

The Ramsey Theory states that is

R (3,3) = 6 .

Thus, within the interconnected mechanical system built of six point masses the triangles (triangle), comprising masses and springs of the same kind will be necessarily present. This prediction constitutes the vibrational spectrum of the system. Thus, the Ramsey Theory supplies the kind of the selection rules for the vibrational spectra of the mechanical systems/cyclic molecules, which may be described by the complete graph. Consider that also

R (2,6) = 6 .

Thus, if we have a molecule, described by a complete graph, which is built of six functional groups, or two or six interconnected groups will necessarily be present in its chemical structure; thus, explaining the formation of the benzene-like ring structures.

The cyclic molecule built of five functional groups interconnected with two kinds of chemical bonds will not necessarily be characterized by the collective modes involving vibration of three point entities. This fact is easily explained within the Ramsey approach

R (3,3) = 6 > 5 .

The calculation of the eigen-frequencies of these systems in the general case poses essential mathematical difficulties.

Symmetrical systems/molecules in turn may be analyzed explicitly. Symmetrical system built of six entities is addressed. The eigenfrequencies inherent for the vibrations of triangles are reported. We call these modes the Ramsey modes of the systems described by complete graphs [7,8]. The introduced approach is easily extended for 3D vibrating systems interconnected by classical/quantum springs, which may be described as abstract complete graphs. The extension of the proposed Ramsey approach to the systems, partially connected by ideal springs, viscoelastic systems and systems, in which elasticity is of an entropy nature is discussed. “Multi-color systems” built of three kinds of springs are addressed. The notion of the inverse Ramsey network is introduced and analyzed. Future work should consider k-partite-graph extensions of Ramsey theory, which correspond to graphs with k sets of nodes which cannot self-interact.

APPENDIX A

Calculation of eigenmodes of system built of the point masses interconnected with ideal springs forming an equilateral triangle

Consider three equal masses connected with ideal springs

k_{2}

. Springs form an equilateral triangle (the side of the triangle is a), as shown in Figure 1A. The center of the masses of the entire system is in rest, considering this fact yields:

x_{1} + x_{2} + x_{3} = 0; y_{1} + y_{2} + y_{3} = 0,

(1A)

where

x_{i}

and

y_{i}

denote the displacement of i-body from equilibrium.

Figure 1A. Modes of the vibrations occurring within a system built from three equal masses m and springs

k_{2}

. Springs form an equilateral triangle.

Figure 1A. Modes of the vibrations occurring within a system built from three equal masses m and springs

k_{2}

. Springs form an equilateral triangle.

The addressed planar system is characterized by six degrees of freedom; hence, it necessarily has six eigenfrequencies; three of these eigenfrequencies equal zero (see Eq. 1). Two of these trivial eigenfrequencies correspond to the x and y translations of the entire system in the XY-plane, and the third one corresponds to the uniform rotation of the entire system about its center of mass. The non-trivial modes are depicted in Figure A1. The mode shown in inset (a) corresponds to the situation when all of the bodies move along the bisectors of the triangle. The Lagrange function corresponding to this mode is supplied by Eq. 2A:

L (x, \dot{x}) = \frac{3 m {\dot{x}}^{2}}{2} - \frac{9 k_{2} x^{2}}{2}

(2A)

Eq. 2A immediately yields (see Eq. 1):

ω_{1 e i g e n} = \sqrt{\frac{3 k_{2}}{m}}

(3A)

One more mode, shown in inset (b) is found from the symmetry considerations. One of the nodes (the upper one in the inset (b)) moves along the bisector of the triangle. The movements of the remaining nodes in this case will be a mirror image of each other in the plane of symmetry of the triangle. The Lagrange function corresponding to this mode is supplied by Eq. 4A (

x_{1}, y_{1} ≪ a

is adopted):

L (x_{1}, y_{1}, {\dot{x}}_{1}) = 4 m {\dot{x}}_{1}^{2} - \frac{9}{4} k_{2} x_{1}^{2} - \frac{27 k_{2} y_{1}^{2}}{4} + \frac{3 \sqrt{3} k_{2} x_{1} y_{1}}{2}

(4A)

The eigenfrequency emerging from this Lagrange function is given by Eq. 5A:

ω_{2 e i g e n} = \sqrt{\frac{3 k_{2}}{2 m}}

(5A)

The symmetry considerations yield (see Eq. 1):

ω_{3 e i g e n} = ω_{2 e i g e n} = \sqrt{\frac{3 k_{2}}{2 m}}

(6A)

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, N. S. and E. B.; methodology, N. S. and E. B.; formal analysis, N. S.; M. F.; S. S. and E. B.; investigation, N. S.; M. F.; S. S. and E. B.; writing—original draft preparation, N. S.; M. F.; S. S. and E. B.

Funding

“This research received no external funding”.

Data Availability Statement

“Not applicable”.

Conflicts of Interest

“The authors declare no conflict of interest.”

References

Ramsey, F.P. On a Problem of Formal Logic. In: Gessel, I., Rota, GC. (eds) Classic Papers in Combinatorics. Modern Birkhäuser Classics. Birkhäuser Boston 2009, pp. 264-286, . [CrossRef]
Katz, M.; Reimann, J. An Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathematical Library Volume: 87; 2018; pp. 1-34.
Graham, R. L.; Spencer, J. H. Ramsey Theory, Scientific American, 1990, 7, 112-117.
Graham, R.; Butler, S. Rudiments of Ramsey Theory (2nd ed.). American Mathematical Society, Providence, Rhode Island, USA, 2015, pp. 7-46.
Graham, R. L.; Rothschild, B. L.; Spencer, J. H. Ramsey theory, 2^nd ed., Wiley-Interscience Series in Discrete Mathematics and Optimization, John Wiley & Sons, Inc., New York, A Wiley-Interscience Publication, 1990, pp. 10-110.
Roberts, F. S. Applications of Ramsey theory. Discrete Appl. Math. 1984, 9 (3), 251-261.
Wouters, J.; Giotis, A.; Kang, R.; Schuricht, D.; Fritz, L. Lower bounds for Ramsey numbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 0332.
Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko Ed. Ramsey theory and thermodynamics, Heliyon, 2023, 9 (2), e13561.
Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko Ed. Universe as a Graph (Ramsey Approach to Analysis of Physical Systems), Preprints 2022, 2022110277. [CrossRef]
Randic, M. On Characterization of Cyclic Structures, J. Chem. Inf. Comput. Sci. 1997, 37, 1063-1071.
Garcia-Domenech, R.; Galvez, J.; de Julia´n-Ortiz, J. V.; Pogliani, L. Some New Trends in Chemical Graph Theory. Chem. Rev. 2008, 108, 1127−1169.
Goldstein, H.; Poole, C. P.; Safko, J. L. Classical Mechanics (3rd ed.). Chapter 6, Addison-Wesley, Menlo Park, USA, 2001.
Collins, J.J.; Stewart, I. A group-theoretic approach to rings of coupled biological oscillators. Biol. Cybern. 1994, 71, 95–103.
Qin, W-X.; Zhang, P-L. Discrete rotating waves in a ring of coupled mechanical oscillators with strong damping. J. Math. Phys. 2009, 50, 052701.
Lievens, S.; Stoilova, N. I.; Van der Jeugt, J. A linear chain of interacting harmonic oscillators: solutions as a Wigner Quantum System, Journal Physics: Conference Ser. 2008, 128, 012028.
Vinogradov, G. V.; Malkin, A. Ya. Rheology of polymers: viscoelasticity and flow of polymers, USSR, Moscow, Mir, 1980.
Sánchez, M.A.G.; Giraldo-Vásquez, D.H.; Sánchez, R.M. Rheometric, transient, and cyclic tests to assess the viscoelastic behavior of natural rubber-based compounds used for rubber bearings. Mater. Today Commun. 2020, 22, 100815.
Breńkacz, L.; Bagiński, P.; Korbicz, J. K. Vibration damping of the anti-vibration platform intended for use in combination with audio/music devices. Journal Vibroengineering, 2020, 22 (3), 578-593.
Christensen, R.Theory of viscoelasticity: an introduction. Chapter 1, Elsevier, Amsterdam, Nl. 2012.
Rubinstein, M.; Colby, R.H. Polymer Physcis, Chapter 2, Oxford University Press, Oxford, UK, 2003.

Figure 1. Cyclic chemical compound represented by the mechanical system forming a complete graph. The system is built of identical masses m interconnected by two kinds springs

k_{1}

and

k_{2}

Figure 1. Cyclic chemical compound represented by the mechanical system forming a complete graph. The system is built of identical masses m interconnected by two kinds springs

k_{1}

and

k_{2}

Figure 2. Equal masses m forming a regular hexagon are interconnected with two kinds of ideal springs denoted

k_{1}

Figure 2. Equal masses m forming a regular hexagon are interconnected with two kinds of ideal springs denoted

k_{1}

Figure 3. Five equal masses m forming a regular pentagon are interconnected with two kinds of ideal springs denoted

k_{1}

Figure 3. Five equal masses m forming a regular pentagon are interconnected with two kinds of ideal springs denoted

k_{1}

Figure 4. 3D systems built of two tetrahedrons “1234” and “1235” is depicted. Masses placed in the vertices of the tetrahedron are connected with two kinds of springs, the green (

k_{1})

and red (

k_{2}

) ones. Triangle “123” is located in the plane

(X O Y)

Figure 4. 3D systems built of two tetrahedrons “1234” and “1235” is depicted. Masses placed in the vertices of the tetrahedron are connected with two kinds of springs, the green (

k_{1})

and red (

k_{2}

) ones. Triangle “123” is located in the plane

(X O Y)

Figure 5. System of six point masses m partially interconnected by identical ideal springs k. masses labeled ”14”, “45” and “36” are not connected by springs. Masses connected by springs are connected with black links; masses which are not joint with the springs are connected with red links. Black triangles “156” and “234” are present in the graph.

Figure 6. The Ramsey model of viscoelastic body is presented. Point masses

m_{i} (i = 1 \dots 6)

Figure 6. The Ramsey model of viscoelastic body is presented. Point masses

m_{i} (i = 1 \dots 6)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds

Abstract

1. Introduction

2. Ramsey theory and vibrations of cyclic molecules

2.1. Ramsey theory for the system interconnected by two kinds of ideal springs

2.2. Direct and inverse Ramsey networks of ideal springs

2.3. Ramsey theory for the system of vibrating masses partially connected by the ideal springs

2.4. Multi-color systems built of ideal springs

2.5. Ramsey model of viscoelasticity

2.6. Ramsey theory for vibrations of systems in which entropy elasticity is present

3. Conclusions

APPENDIX A

Calculation of eigenmodes of system built of the point masses interconnected with ideal springs forming an equilateral triangle

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe