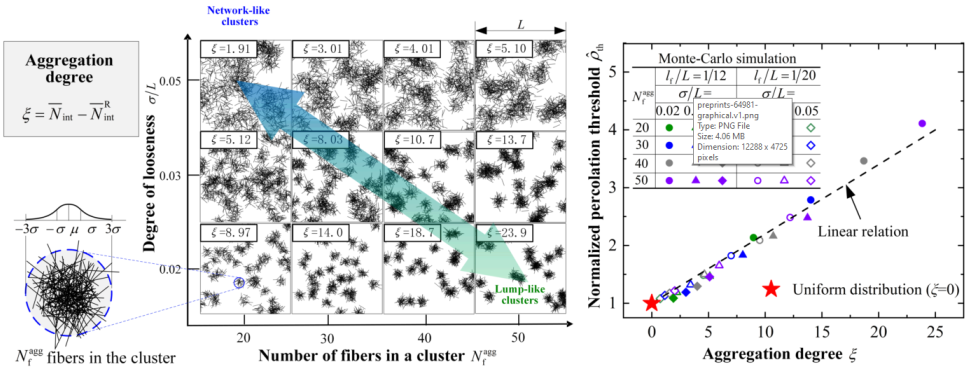
Fiber aggregation in nanocomposites has an important effect on the macroscopic electrical performance. To quantitatively evaluate its effect, an index to characterize the degree of aggregation is imperative, and ideally it should have three features simultaneously, i.e., single-parametric, dimensionless and physically meaningful, applicable to different aggregation topologies, and one-to-one corresponding to material electrical properties. To this end, a new aggregation degree is proposed, which is defined as the average increased number of fibers that connect with each one when fibers aggregate from a uniformly distributed state. This index is applicable to different aggregation topologies from lump-like aggregating clusters to network-like aggregating clusters. This index is proven to only depend on the local features of aggregating clusters, and can be concisely expressed by the characteristic parameters of local structure, via geometric probability analysis and numerical validations. Further, a one-to-one linear relation between the aggregation degree and percolation threshold is established by Monte Carlo simulations, which is independent of the distribution law of the fibers. This work provides a guide to the property characterization, performance prediction and material design of nanocomposites, and also gives a physical insight into the understanding of systems with similar non-uniform distributions.