1. Introduction
The self-weight of the soil layers and the applied external loads cause stresses in the soil. Estimating the distribution and amount of these stresses in the soil is important to solve many problems in geotechnical engineering. These stresses, depend on the soil properties, the intensity of the applied load, and the dimensions of the loaded area. The estimation of the stresses within a soil mass due to applied loads has concerned researchers for many years. Many approaches have been developed using the theory of elasticity to determine the stress distribution in soil. These approaches are similar and the difference between them is the assumptions made to determine the elastic conditions of the soil.
Due to the complex structure of the soil, it is very difficult to make realistic stress-strain analyzes. For this reason, analyzes are usually performed with the assumption that the soil is isotropic and linearly elastic. Therefore, soil properties are defined by two parameters, Elasticity modulus, E, and Poisson’s ratio, µ.
Boussinesq’s [
1] equation is one of the most frequently used and practical equations used to obtain the stress values in the soil due to external loads. This equation was originally developed to calculate the vertical stresses for a point load in a homogeneous, isotropic, weightless, linearly elastic half-space, and then is integrated over the footing area to calculate the stresses under a distributed load. It is often used when stresses and deformations in the soil due to loads applied from circular areas on the soil surface are applied by circular storage silos, foundations, and wheels.
Foster and Ahlvin [
2], and Ahlvin and Ulery [
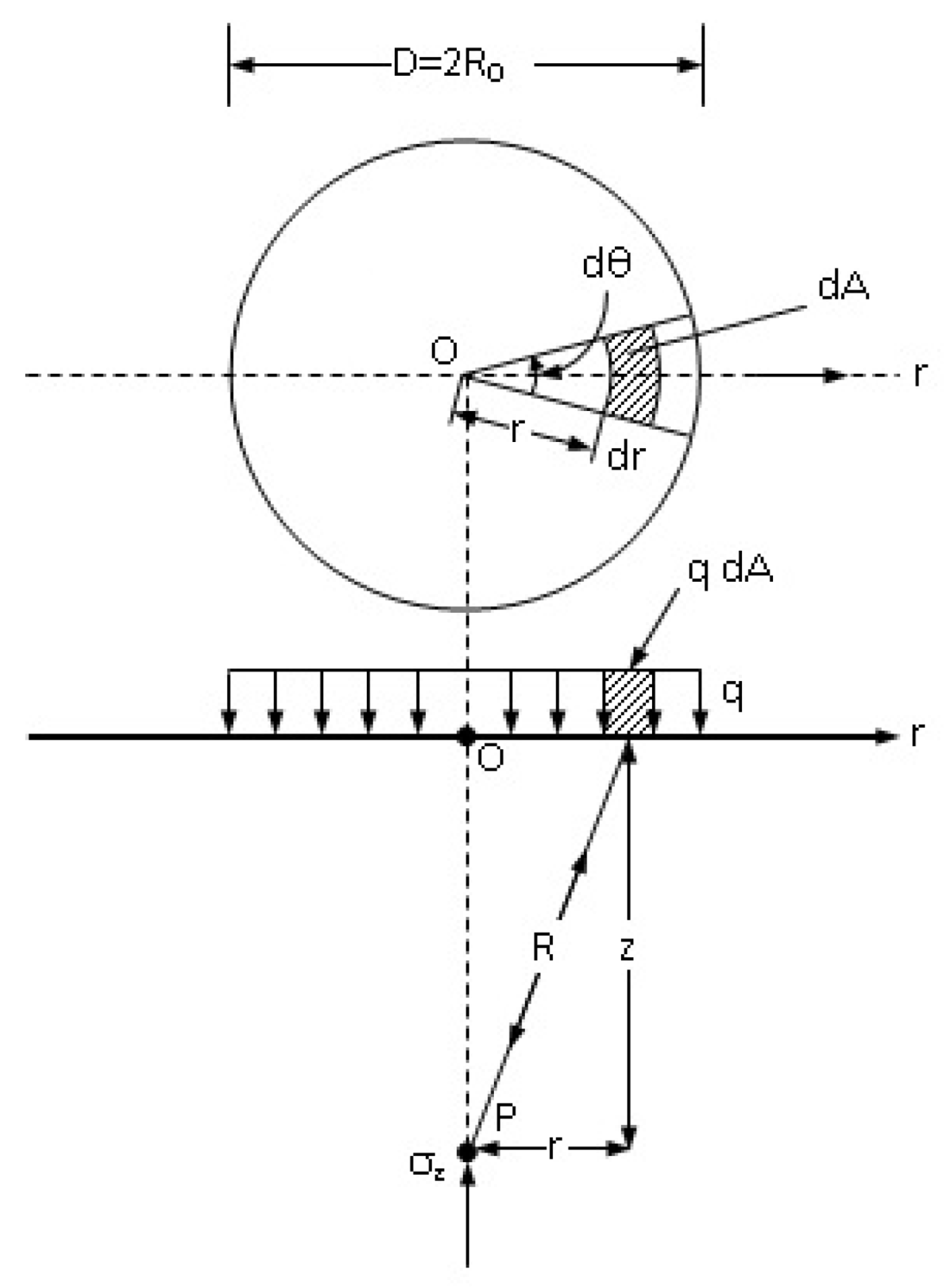
3] carried out studies on the calculation of stress and deformations in a homogeneous and isotropic medium due to loads applied to circular areas. In these studies, simple equations required for calculations and influence diagrams and coefficient tables for use in equations are presented. For the solution of foundation engineering problems, it is very important to know the vertical stresses that occur in the soil due to external loads. The variation of vertical stresses under a uniform load applied to a circular area with respect to the radius of the loaded area and the depth from which the vertical stress value will be calculated is shown in
Figure 1.
In Boussinesq’s [
1] solution, vertical stress distributions are independent of the material properties. In addition, parameters such as the type of soil, density and consistency cannot be taken into account, and there is no difference between the stress distributions in soil types with different properties.
Westergaard [
4] presented an equation for a vertical point load at the surface and discussed the stress functions for plane strain problems. Unlike the Boussinesq solution, the Poisson ratio of the soil medium is required as the material parameter in the Westergaard equations for stress calculations.
Although the soil medium is considered isotropic and homogeneous in the above-mentioned elastic solutions, most soils are neither isotropic nor homogeneous. Previous studies including laboratory experiments and numerical analyzes on the subject have shown that the stress distribution in soils varies significantly depending on the material parameters of the soil. For that reason, it is required to find the vertical stress values experimentally and to compare these with numerical and theoretical solutions. When the previous studies on the vertical stress distribution in soils due to applied loads are examined, it is seen that not enough experimental studies have been performed.
The vertical stress value at any depth of z under the centerline for a uniformly distributed load applied to a circular area is:
The study of Koegler and Scheidig [
5] is considered to be one of the first experimental studies to determine the stress values in soils. In the study, laboratory model tests were carried out to obtain the stress distribution in the sand soil. For this purpose, a sand fill was loaded and stresses at particular depths of horizontal planes were measured with instruments located at measurement depths. Koegler and Scheidig [
5] compared the results obtained from the experimental study with the theoretical solutions and indicated that vertical stress distributions obtained from the experimental study beneath the loaded areas were in good agreement with the predictions from the Boussinesq equations [
6].
In the experimental study carried out by Morgan and Gerard [
7], vertical stresses were measured under model foundations resting on the sand, and it was observed that there was a general agreement with the stress values obtained by elastic solutions.
Burland et al. [
8] examined factors such as non-homogeneity, non-linearity, and anisotropy that affect the vertical stress values and concluded that the Boussinesq solution gives a reasonably accurate vertical stress distribution under a uniformly loaded area for different soil conditions.
In the study by Balakrishna et al. [
9], dimensionless equations are derived to calculate the vertical stress distribution under rigid circular foundations on sands using the elastoplastic approach. The resulting distribution was used to calculate stresses at various points using elastic theory. In the study, the obtained results are presented graphically and compared with the distribution of Boussinesq.
Algin [
10], formulated algebraically the vertical stress distribution below the origin of the linearly distributed Boussinesq loading case. In the study, the equation was evaluated to establish that the current used equation of the uniformly loaded rectangular loading case is valid. This paper concludes that the formula which has been developed is valid.
Lim [
11], carried out a series of laboratory model tests to investigate the Boussinesq’s theory on the vertical stress increment in the sandy soil mass caused by surface loading. The test results were compared with the theoretical values of Boussinesq. The theoretical stress values obtained by the Boussinesq method were always smaller than the test results under the footing, regardless of the depth. Outside of the footing, the values were greater than the stress measured only at the depth of the foundation width. It has been seen that the theoretical and experimental results are close to each other when the depth reaches two and three times the width of the footing. In the study, the measured vertical stress decreased as the applied load increased. These trends were confirmed to be valid for the considered range of the relative density of sand and/or width of the footing. According to the results obtained from the study, it has been seen that if the Boussinesq theory is used, more accurate values can be obtained by correcting the theoretical values using these results.
Keskin et al. [
12] carried out an experimental investigation and compared the results with the numerical and theoretical results. They indicated that vertical stress distributions beneath the uniformly loaded rectangular area show the same characteristics in all methods.
By using Boussinesq displacement potential functions, Onah et al. [
13] determined the vertical stress distribution and vertical displacements under the influence of a uniformly distributed load on a rectangular area, assuming that the soil medium is homogeneous, elastic, and semi-infinite. The results show that the strain-displacement relations for small displacement assumptions and Hooke’s generalized stress-strain laws for linear elastic, isotropic, homogeneous bodies are applied simultaneously to derive the vertical fields from the displacement fields.
Cicek et al. [
14] carried out a study to obtain the vertical stress values beneath the center of continuous foundations resting on geotextile-reinforced soil. At the end of the study, it was observed that when the reinforcement is placed in the soil, the vertical stress values that occurred beneath the centerline of the footing decrease and there is a general agreement between the experimental results and the finite element analysis results at certain depths. However, they found that the vertical stress values obtained experimentally and numerically are different from the vertical stress values obtained theoretically.
Ateş and Şadoğlu [
15] carried out an experimental study to measure the vertical stress increases in the soil due to the applied vertical surface loads. In the study, various tests were carried out with a model strip foundation under plane strain conditions in a reinforced cohesionless soil. They concluded that the relative density of sand is an effective parameter for the stress distribution in soils. However, methods based on the theory of elasticity give very inaccurate results in low relative density reinforced soils.
Gebremariam et al. [
16], investigated the variation in vertical stresses under geosynthetic reinforced walls in a case study. The stress values measured in the field were compared with the theoretically predicted vertical stress values. In the comparison, Boussinesq and approximate 2V:1H methods were used as theoretical methods. As a result of the comparison, it was seen that the stress values obtained by using the 2V:1H method were more conservative for the design, but the stress values obtained by using the Boussinesq method were closer to the experimental stress values measured in the field.
Giwangkara et al. [
17], in their study, investigated the vertical stress distribution under static loads using laboratory model experiments when natural crushed aggregate (NCA) and recycled concrete aggregate (RCA) materials are used as road base material. They stated that the vertical stress values obtained by laboratory model tests are different from the vertical stress values obtained theoretically using Boussinesq’s equations and the material properties change the stress distribution behavior.
Frazee [
18] considered the Boussinesq formula used in the determination of vertical stresses. In the study, new closed solutions are presented in the form of cartesian coordinate functions for different load cases.
Lu et al. [
19], discussed the difficulties of using the Boussinesq method when bedrock is located under a compressible soil layer. In their study, an analytic method has been proposed to solve the plane strain problem under the influence of strip footings. The effects of soil layer thickness on vertical stress and displacements are discussed and the obtained results are compared with the numerical analysis results.
In the study by Useche-Infane et al. [
20], the results of a series of loading tests on a footing model resting on a sandy soil are presented. In the study, the vertical stress values in the soil under the applied loads were measured with a circular footing model. Sand was placed in a circular tank with a diameter of 60 cm and a height of 45 cm, and diaphragm load cells were used to measure the vertical stresses. In the measurements, it was aimed to determine the effect of relative density on the vertical distribution of stresses in the sand. The stresses measured with the load cells were compared with the stress values estimated by the Boussinesq’s method and the results were validated using a finite element model. According to the results obtained from the study, it has been seen that the vertical stress values obtained by the Boussinesq’s method are in an acceptable approximation to the stresses measured with the load cells.
A study was carried out by Singhai and Vikash [
21] on the effect of elastic modulus on vertical stress distribution due to strip loading in elastic half-space. At the end of the study, it has been shown that the elastic modulus of the soil has a significant effect on the vertical stress distribution and settlements.
The purpose of this paper is to present the results of experimental, theoretical, and numerical studies to determine the vertical stress distribution beneath the circular footings on sand. In the experimental study, reduced-scale laboratory tests were conducted using two footings having a different radius to investigate the effect of the footing size on the vertical stresses that occurred in the sand. In the experiments, pressure transducers were used to determine the vertical stress values occurring in the sand due to the circular load applied to the surface, and stress measurements were carried out at certain depths. In the analysis, the soil was modeled as a non-linear elastoplastic material using the Drucker-Prager model available in the ANSYS [
22] program, in two-dimensional axisymmetric and three-dimensional conditions. Also, Hardening Soil model which available in PLAXIS [
23] program was used to investigate the effect of the material model on the vertical stresses in sand due to applied circular load. The results obtained from the experimental study and numerical analyses were compared with Boussinesq’s results.
2. Experimental Investigation
Model tests carried out within the scope of this study were conducted using the experimental setup designed in the Geotechnical Laboratory of Cukurova University Civil Engineering Department. The facility is shown in
Figure 2. Vertical stress measurements at certain depths beneath the centerline of the circular footing were carried out in a reduced-scale, square-shaped test tank with a plan length of 0.7 m, a width of 0.7 m and a height of 0.7 m. In order to prevent lateral movements that may occur during the placement of the sand in the test box and the static loading of the circular footing, the bottom and vertical edges of the test box were stiffened by using angled sections. The front and back surfaces of the test box consist of 8 mm thick glass plate, and the side surfaces consist of 20 mm thick wooden plate. The inner walls of the tank have been smoothed to minimize the friction that may occur on the side surfaces.
Static vertical loads were applied to the model circular footing resting on the sand, with a mechanical jack attached to a loading beam mounted on the test box. Static load values applied to the circular model footing were measured using a comparator and a load ring placed between the jack and the model footing. In the tests, model footings were loaded with loading rate of 1mm/min.
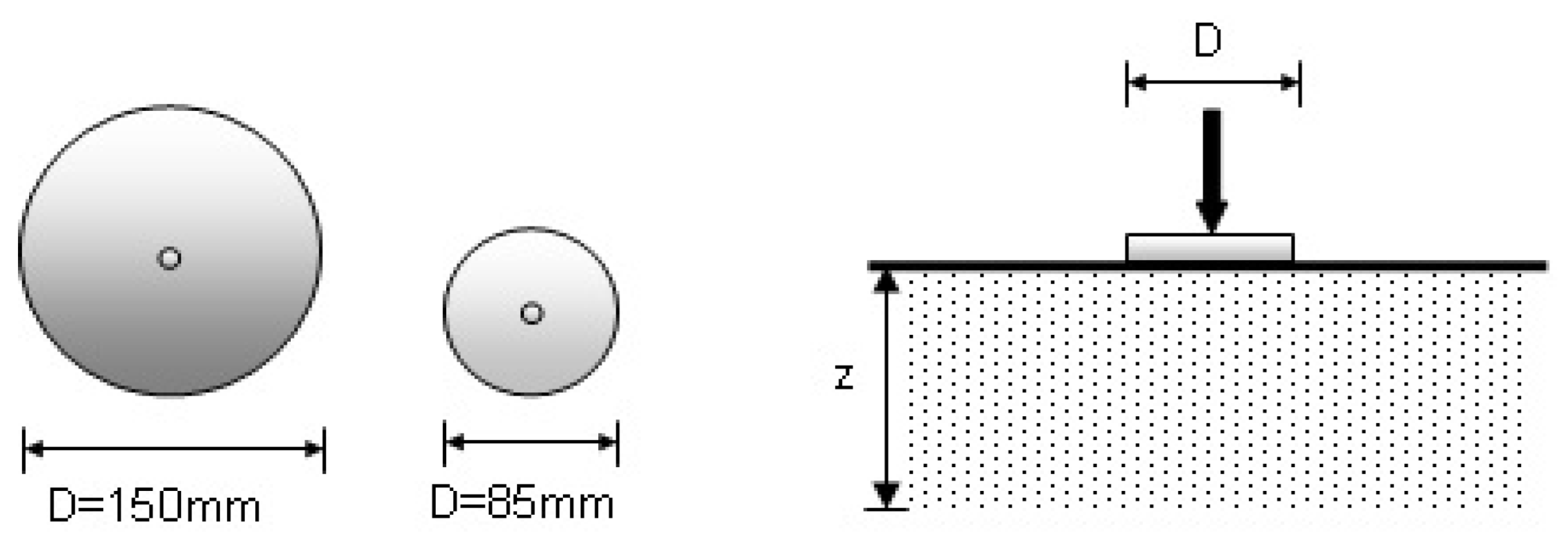
Loading tests were carried out on circular rigid model footings made of steel material. The diameters of the model footings were 85 mm and 150 mm, and the thickness was 20 mm (
Figure 3).
The loads were transferred to the circular model footing by means of a bearing ball. This produces a hinge, which allows the footing to rotate freely as it approaches failure and eliminates any potential moment transfer from the loading system.
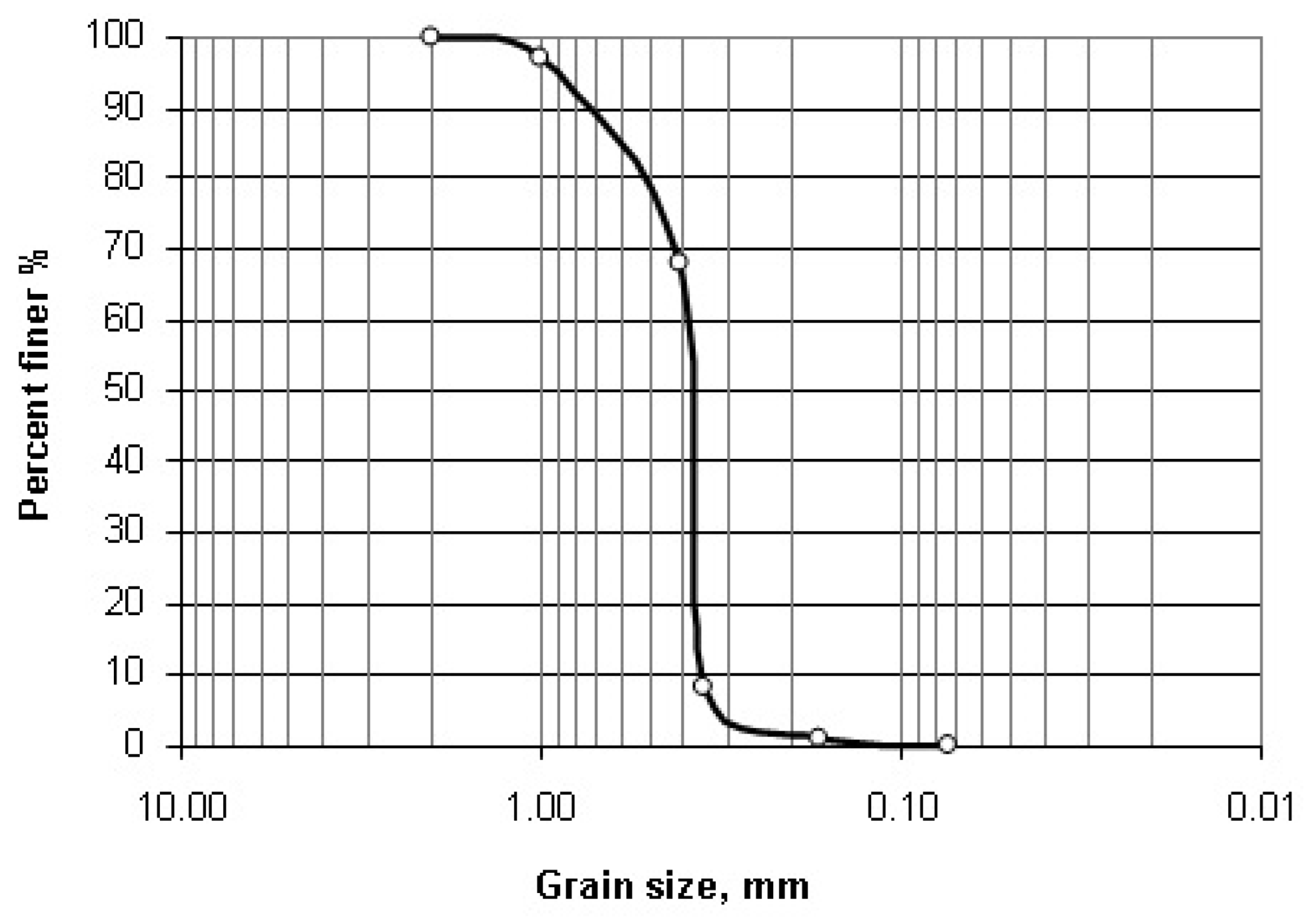
In the experimental study, uniform, clean and fine sand taken from the Seyhan River bed was used as soil. After the sand material was subjected to pre-washing and sieving processes, it was dried in air and a sieve analysis test was carried out to determine the particle size distribution in accordance with ASTM D422-63 [
24]. It is shown in
Figure 4. The classification of the sand material was determined as poorly graded sand (SP) according to the Unified Soil Classification System (USCS). In
Table 1, the general physical properties of the sand used in the experiments are summarized.
Sand material was placed in the test box in 25 mm. thick layers up to the base level of the model footing. Each layer of sand was compacted to a predetermined depth by an electrically operated vibration device. In order to obtain uniform density during compaction and to prevent crushing of sand grains, a 13cm×13cm sized and 2.0cm thick plastic plate is mounted on the tip of the vibration compactor. The glass and wooden sides of the test box were scaled for convenience during the placement of the sand. After compacting each layer of sand, the next lift height was checked using scaled lines on the glass and wood plates of the test box. Following the compaction process was completed and the sand bed was prepared, the areas beneath the circular model footing were leveled carefully. The leveling process was carried out in order to ensure the full contact of the model footing with the sand and the applied load on the model footing to act vertically [
25].
Care was taken to apply the same compression force to each sand layer during the compaction of the sand in the test box to have a uniform density. In the control tests performed on the compacted sand layers, it was determined that the difference between the densities was less than 1%. With the sand compaction technique applied in the experimental study, a uniform relative density of approximately 65% with a unit weight of 17.1 kN/m3 was achieved.
In order to determine the shear strength properties of the sand, which was compacted by layers in the test box, direct shear and consolidated-drained triaxial compression tests were carried out on the samples in accordance with ASTM D3080 [
26]. The estimated internal friction angle was determined to be 41° at the same relative density used in the tests.
To measure the vertical stresses in sand due to the applied circular load, a 100 kPa capacity soil stress transducer was placed in predetermined locations beneath the center of the model footing before the sand bed preparation. The transducer calibrated in the sand before testing was connected to a data logger to measure the stresses. Vertical stresses beneath the center of each footing were measured at three various depths (1.0D, 1.5D, 2.0D; D = diameter of footing). For each test, load-stress readings were taken using a measuring system.
3. Finite Element Analysis
The analysis of the vertical stress values beneath the centerline of the circular footings resting on the sand bed was carried out using the commercially available computer program ANSYS (version 10), which solves with the finite element method. ANSYS is a finite element modeling package program developed to analyze various engineering problems numerically. The ANSYS program allows effective studies in different disciplines such as mechanics, linear or non-linear static, and dynamic structural analysis.
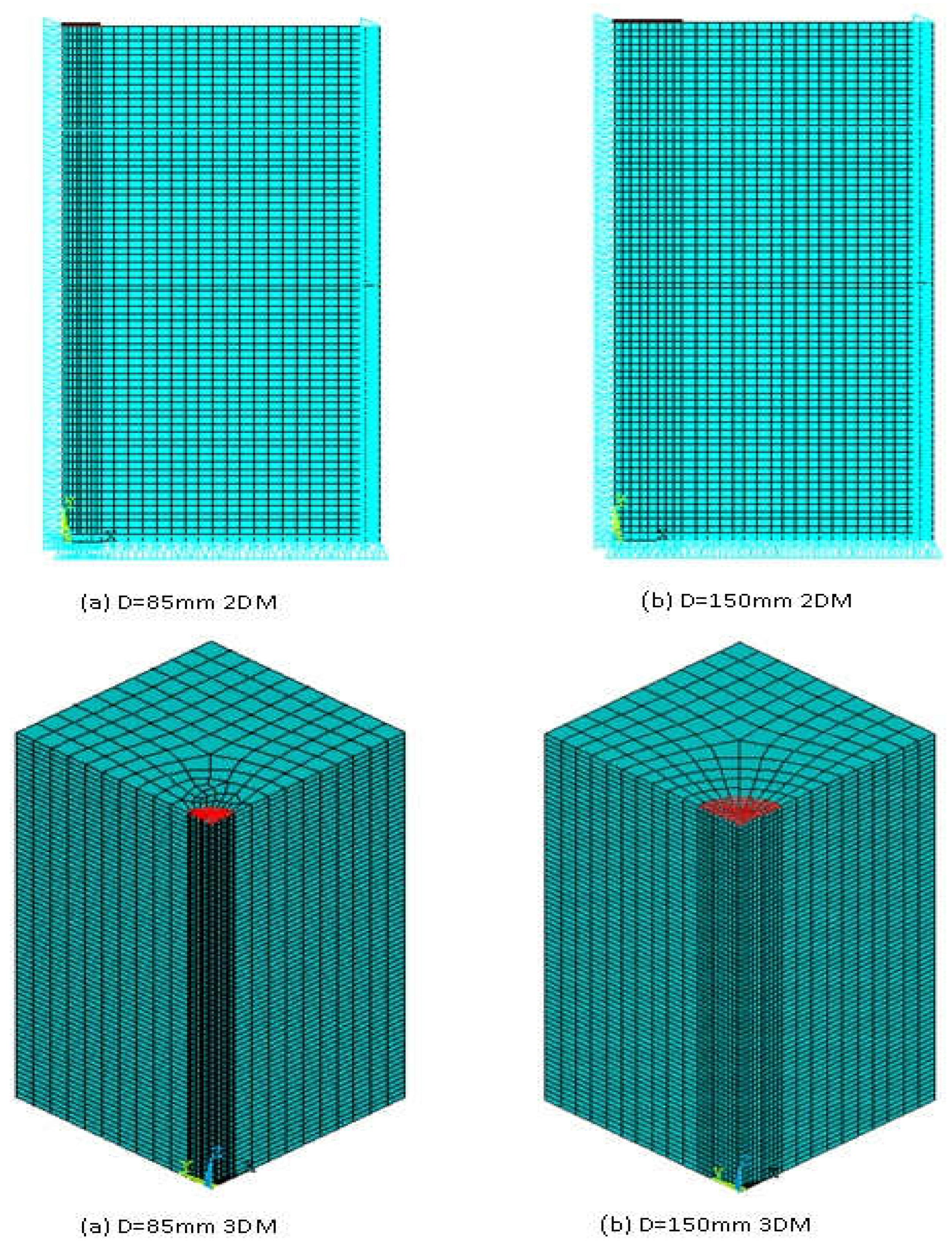
Within the scope of this study, two- and three-dimensional finite element analyses were carried out in order to support the results of the experimental study and to determine the vertical stress distribution in the sand bed subjected to load transferred from circular footing.
Two different models were used for the analyses: the 2D axisymmetric model (2DM) and the 3D model (3DM) with the same dimensions as the model tests setup used in the experimental study. In the numerical study, it was aimed to analyze the effects of 2D and 3D conditions on vertical stress values by analyzing the test setup with 2D axial symmetry and 3D modeling. By using the axisymmetric model in analysis, modeling and analysis time can be greatly reduced compared to an equivalent 3DM.
There are material models such as Mohr-Coulomb, Von Mises, and Drucker-Prager for modeling the soil material numerically. These include the elastic and plastic model parameters such as E (Elasticity modulus), µ (Poisson’s ratio), cohesion c, internal friction angle Ø, and dilatation angle, ψ. Among the mentioned methods, the Drucker-Prager criterion is frequently used in numerical analysis as one of the most suitable in terms of numerical efficiency. In this study, the Drucker–Prager elastoplastic criteria has been used to model sand behavior.
The Drucker-Prager material model in the ANSYS program, the required parameters of elasticity modulus, Poisson’s ratio, and shear strength of the sand were obtained by laboratory experiments performed on the samples taken from the sand in accordance with ASTM D7181-20 [
27] and are presented in
Table 2.
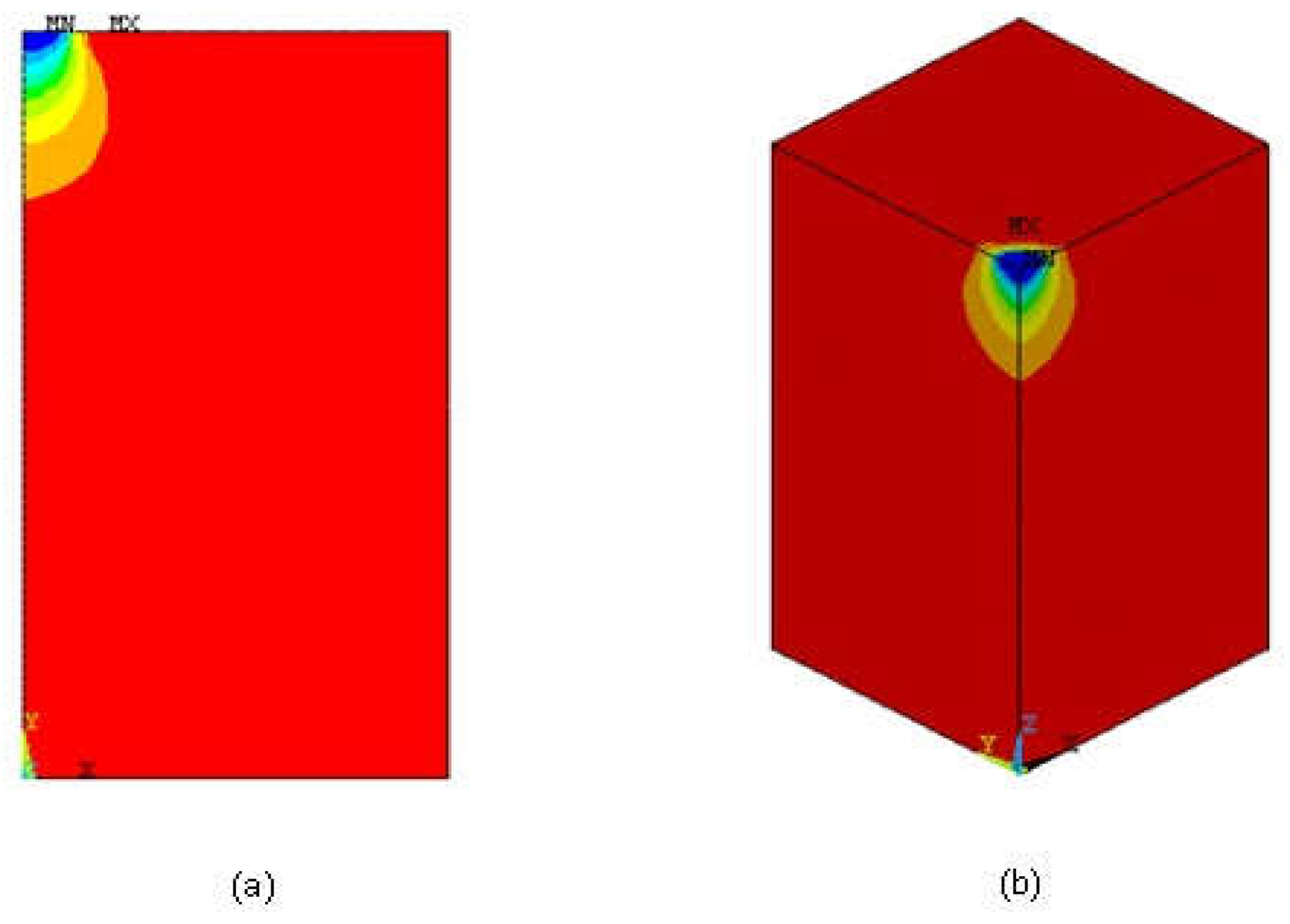
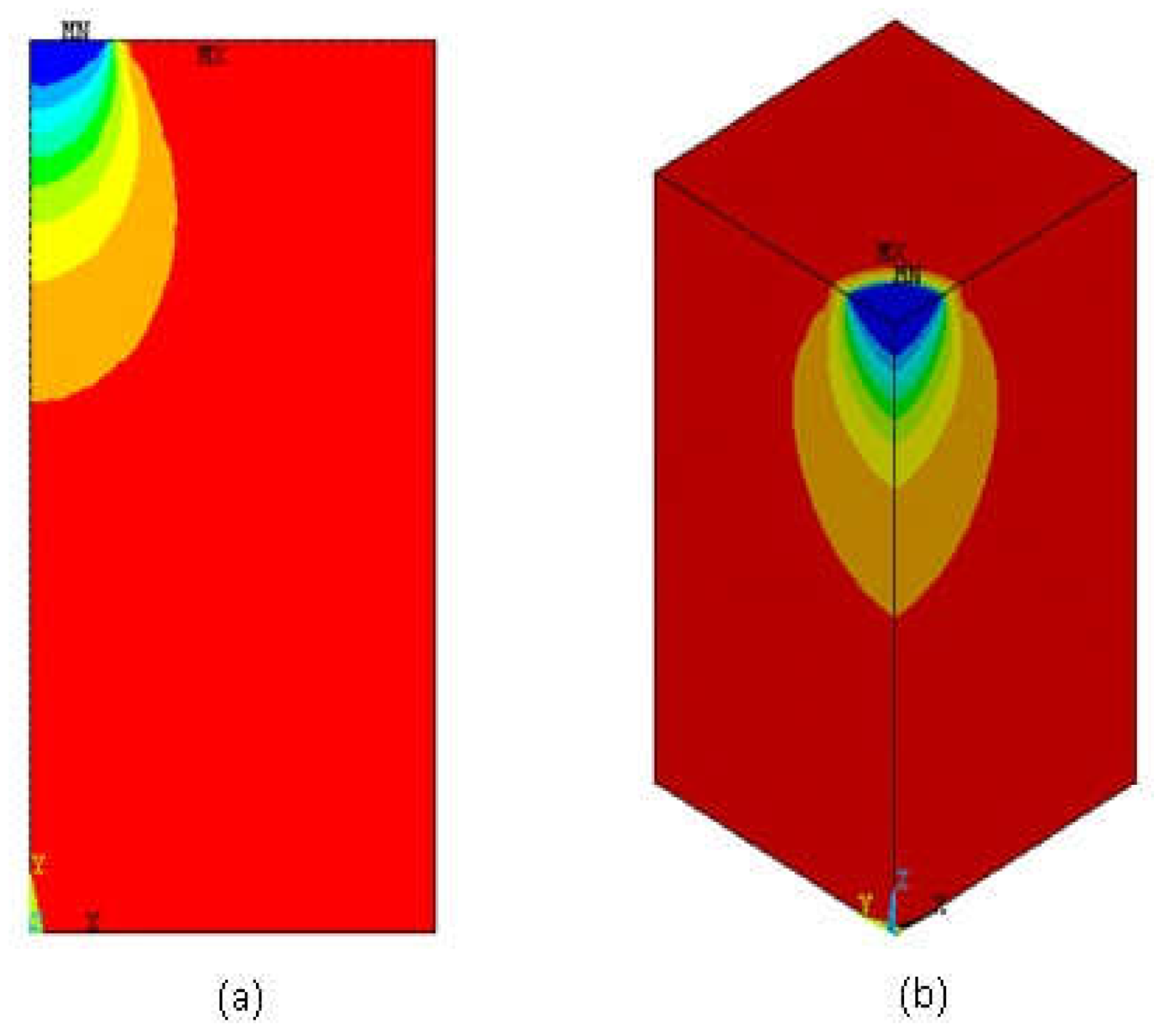
In the analyses, SOLID45 element type was used for the three-dimensional modeling of the soil-footing system (
Figure 5). SOLID45 element type is defined by eight nodes with three degrees of freedom in the x, y, and z directions at each node. The element has plasticity, creep, swelling, stress stiffening, large deflection, and large strain capabilities.
PLANE42 element type is used to model the soil-footing system in 2-D modeling (
Figure 6). The element is suitable for two-dimensional modeling, axial-symmetrical and plane-strain conditions. PLANE42 element type is defined by four nodes having two degrees of freedom in the nodal x and y directions at each node. The PLANE42 element type, similar to the SOLID45 element type, has the capabilities of plasticity, creep, swelling, stress hardening, large deflection, and large strain.
In the numerical study, mesh analyses were performed on the model in order to determine the effects of mesh geometry on the results. In the mesh analysis, it was seen that the geometry of the mesh can affect the vertical stress distribution in the sand beneath the circular footing. As a result of the analyses, a mesh geometry that does not affect the vertical stress distribution was selected and this mesh geometry was used in the subsequent analyses. The mesh used in the study was formed by refining around the areas with the highest stresses located vicinity of the footing (
Figure 7).
Circular area load with the same diameters of footing plates were placed centrally over sand bed in the case of circular footings. The loads were applied in steps, vertically to the soil and symmetrically to the axis, as in the model experiments. In the analysis, the boundary conditions are defined by limiting the displacement in the x and y directions. Accordingly, the y displacements in the x direction and the x displacements in the y direction are constrained.
In addition, the outer boundaries of the analyzed model are also restrained in the x and y directions. The hard layer underlying the sand layer was assumed to be a rigid boundary, so the degrees of freedom in three directions were limited. The geometry, boundary conditions and finite element mesh of the analyzed model are presented in
Figure 7.
Figure 1.
Vertical stress under a uniformly loaded circular area.
Figure 1.
Vertical stress under a uniformly loaded circular area.
Figure 2.
Test set-up: 1) Mechanical jack 2) Proving ring 3) Model plate 4) Datalogger 5) Steel profile 6) Sand bed 7) Reaction beam.
Figure 2.
Test set-up: 1) Mechanical jack 2) Proving ring 3) Model plate 4) Datalogger 5) Steel profile 6) Sand bed 7) Reaction beam.
Figure 3.
Model footings and geometric parameters of model test.
Figure 3.
Model footings and geometric parameters of model test.
Figure 4.
Grain size distribution of the sand.
Figure 4.
Grain size distribution of the sand.
Figure 5.
SOLID45 geometry.
Figure 5.
SOLID45 geometry.
Figure 6.
PLANE42 geometry.
Figure 6.
PLANE42 geometry.
Figure 7.
The geometry of FEM, meshing, and boundary conditions.
Figure 7.
The geometry of FEM, meshing, and boundary conditions.
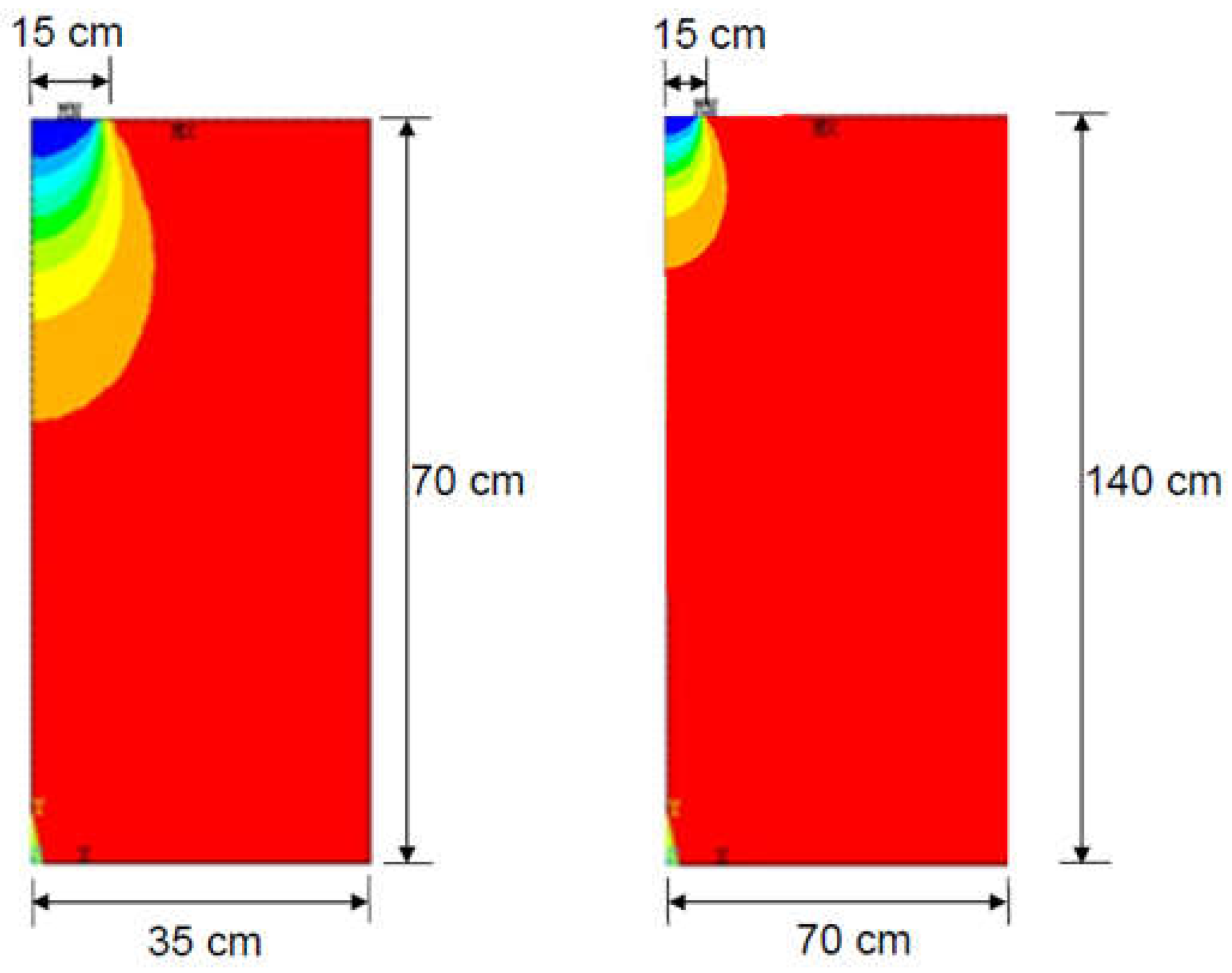
Figure 8.
Vertical stress distribution beneath the 85mm circular footing.
Figure 8.
Vertical stress distribution beneath the 85mm circular footing.
Figure 9.
Vertical stress distribution beneath the 150mm circular footing.
Figure 9.
Vertical stress distribution beneath the 150mm circular footing.
Figure 10.
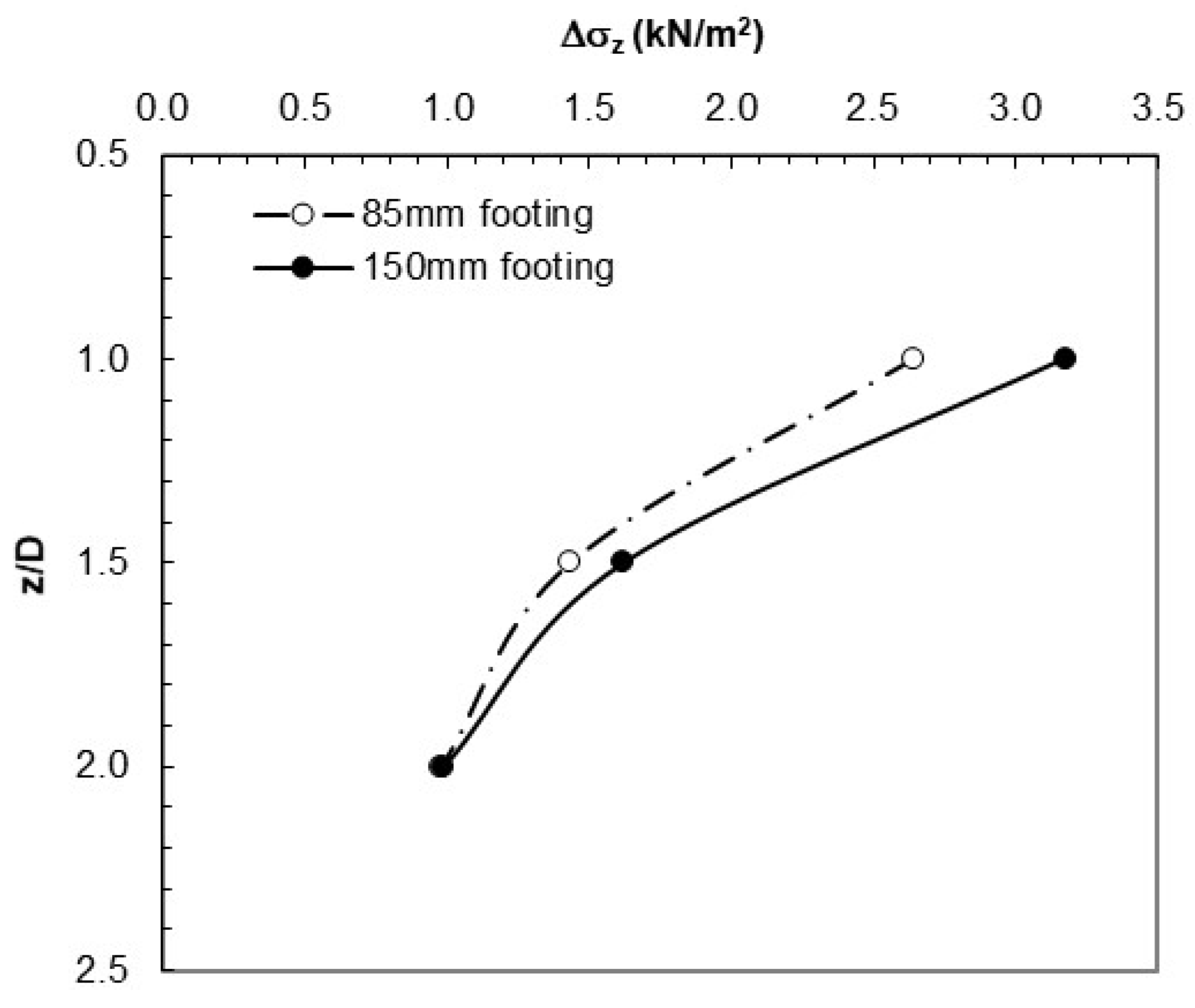
Measured vertical stress values for circular footings.
Figure 10.
Measured vertical stress values for circular footings.
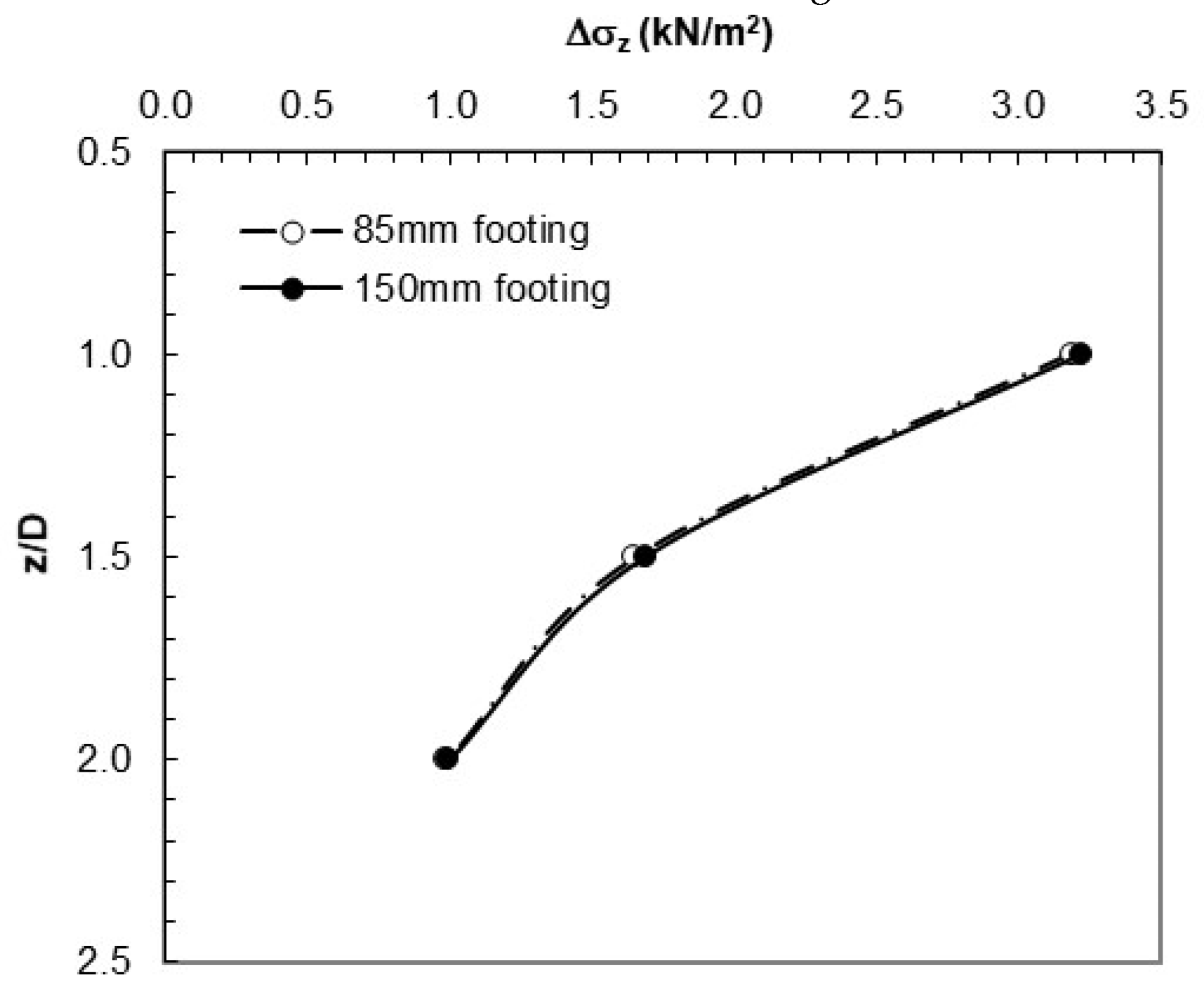
Figure 11.
Vertical stress values obtained from 2DM analysis.
Figure 11.
Vertical stress values obtained from 2DM analysis.
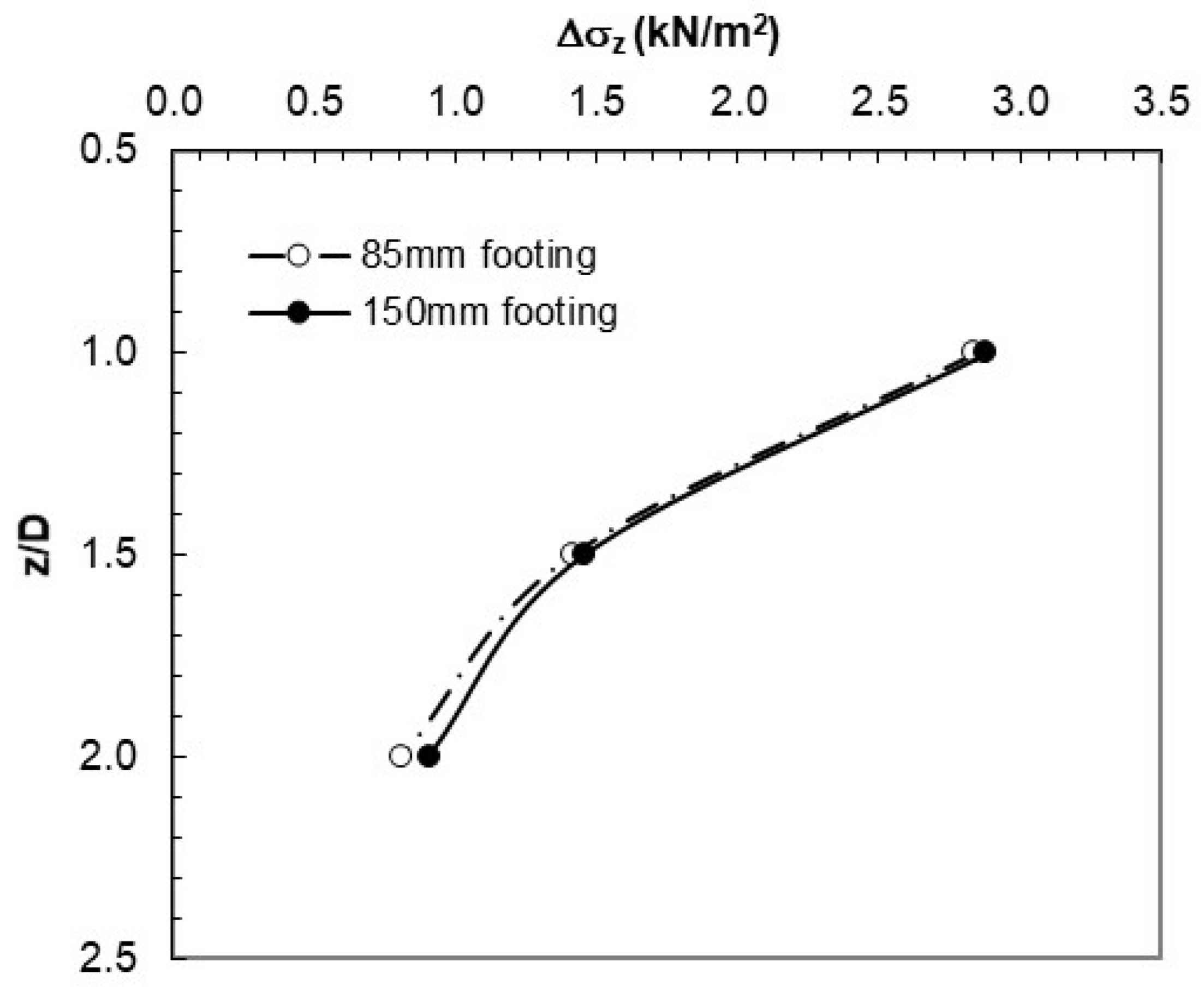
Figure 12.
Vertical stress values obtained from 3DM analysis.
Figure 12.
Vertical stress values obtained from 3DM analysis.
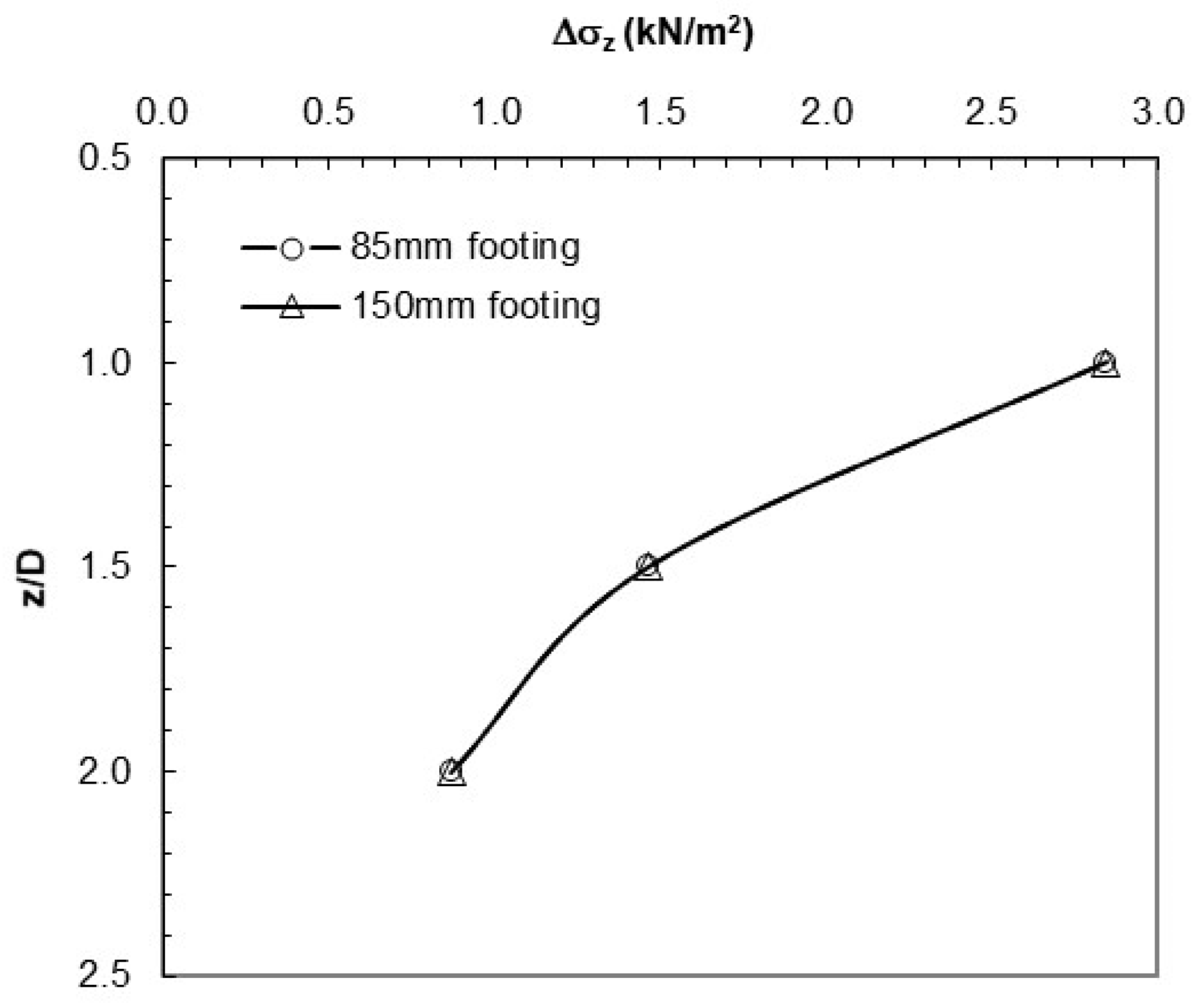
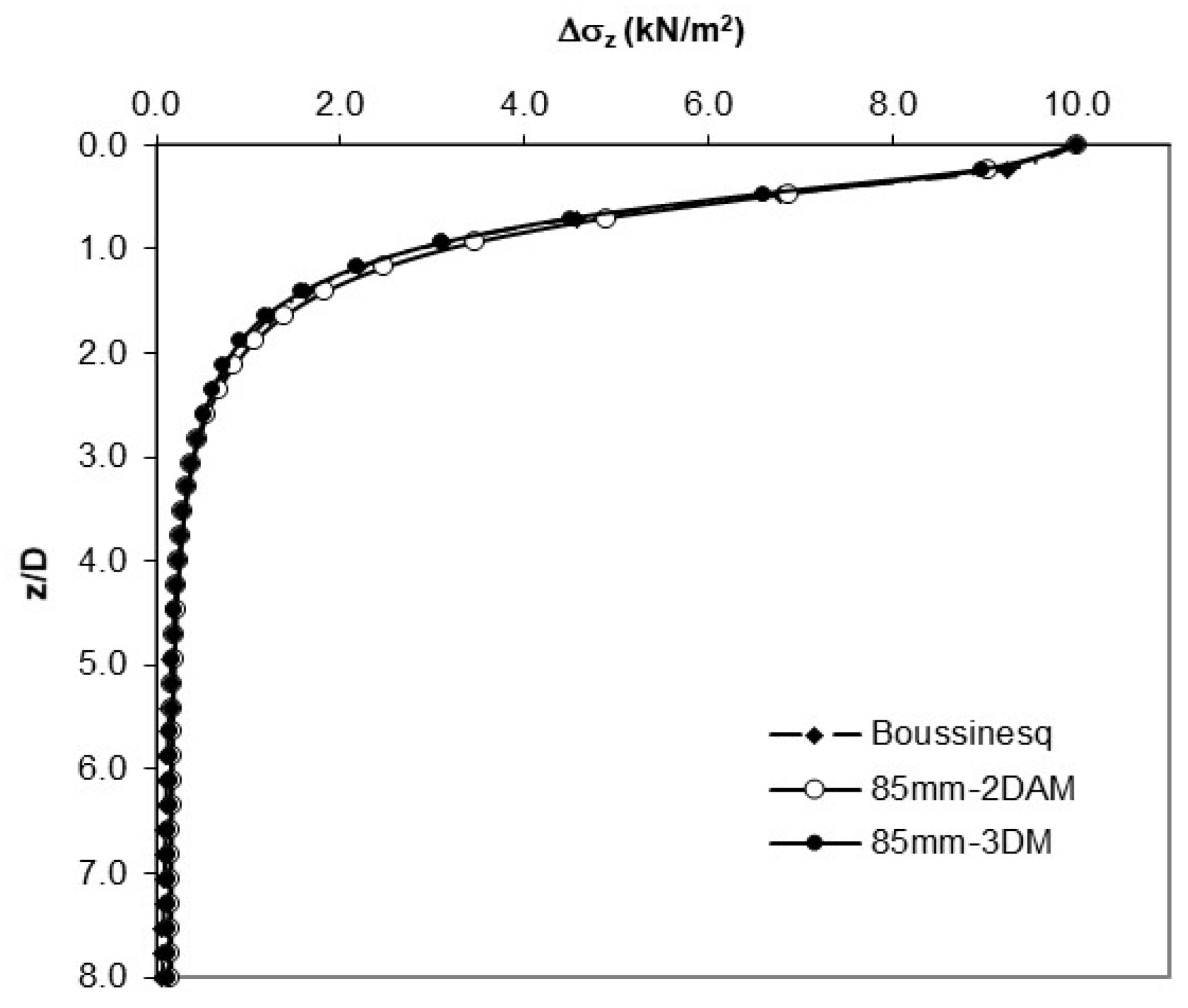
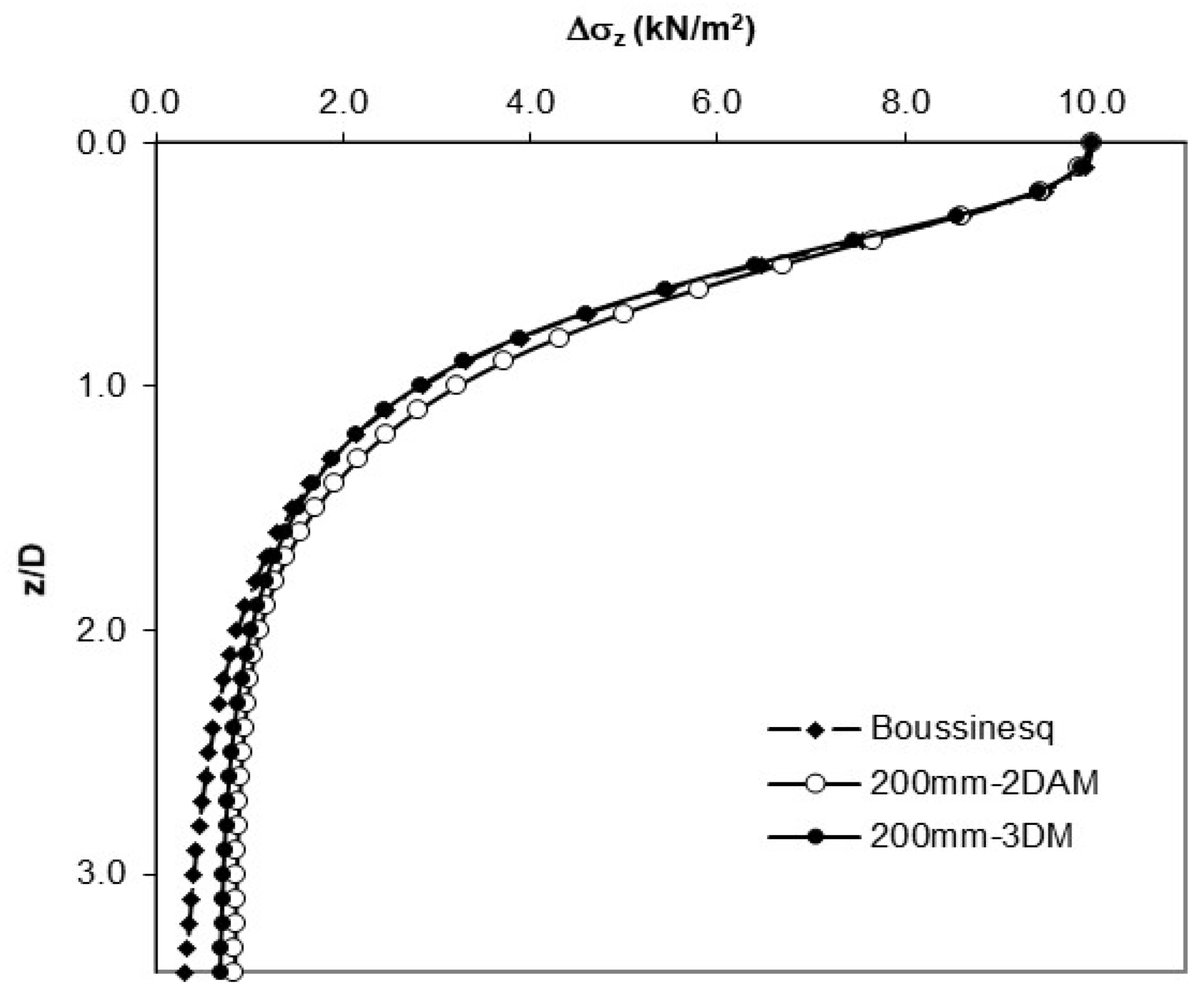
Figure 13.
Vertical stress values obtained from Boussinesq theory.
Figure 13.
Vertical stress values obtained from Boussinesq theory.
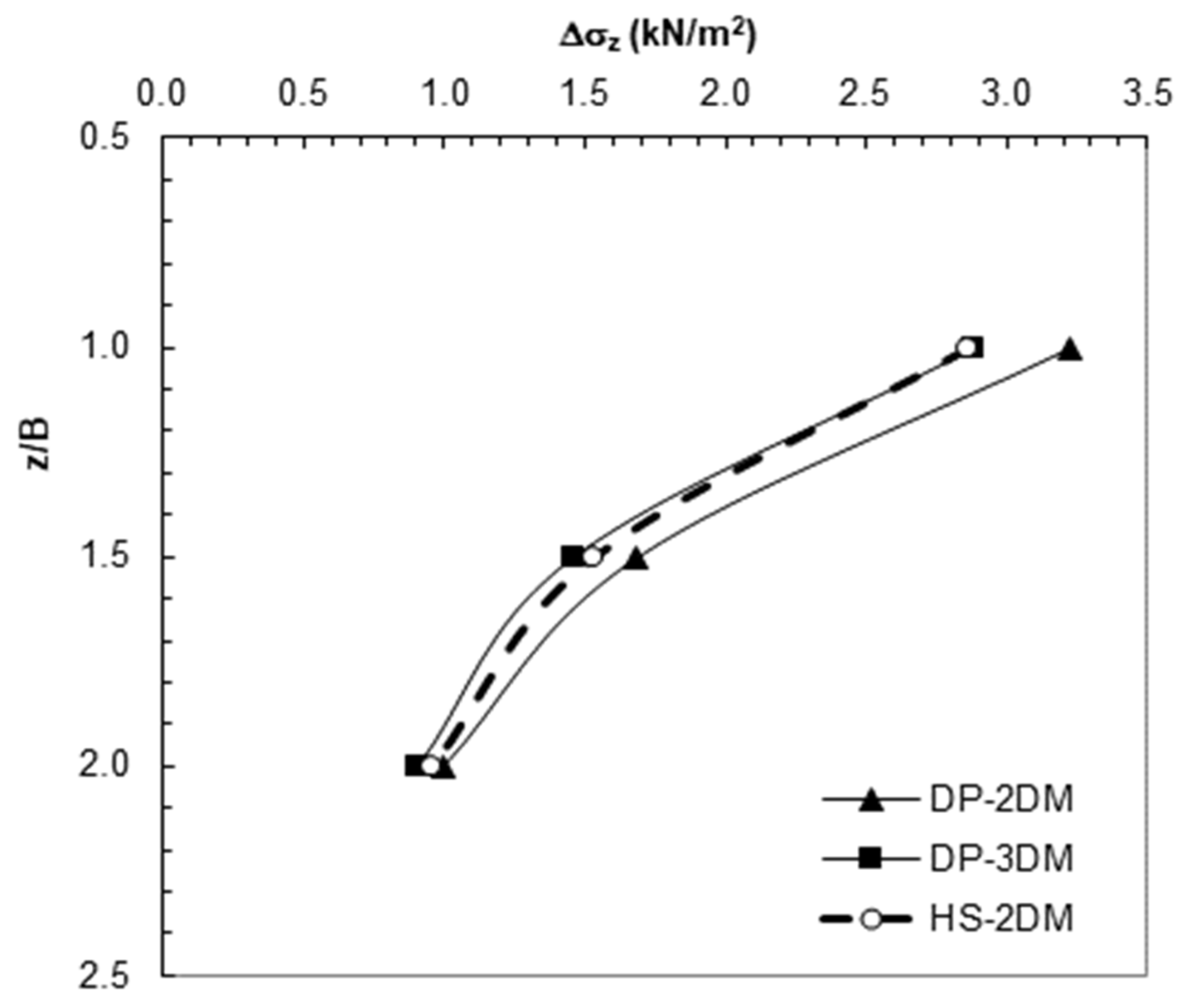
Figure 14.
Vertical stresses with HS and DP models (85 mm footing).
Figure 14.
Vertical stresses with HS and DP models (85 mm footing).
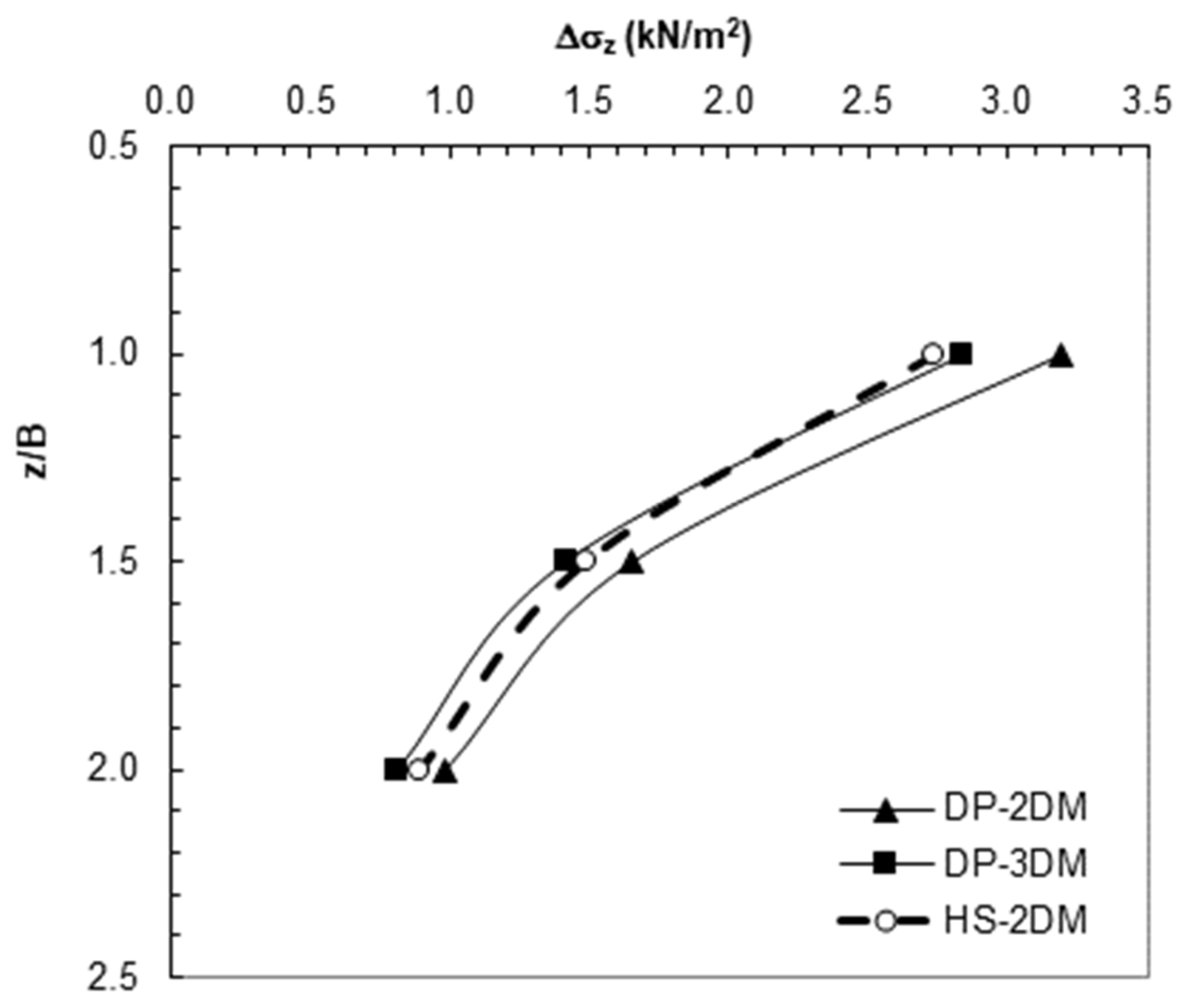
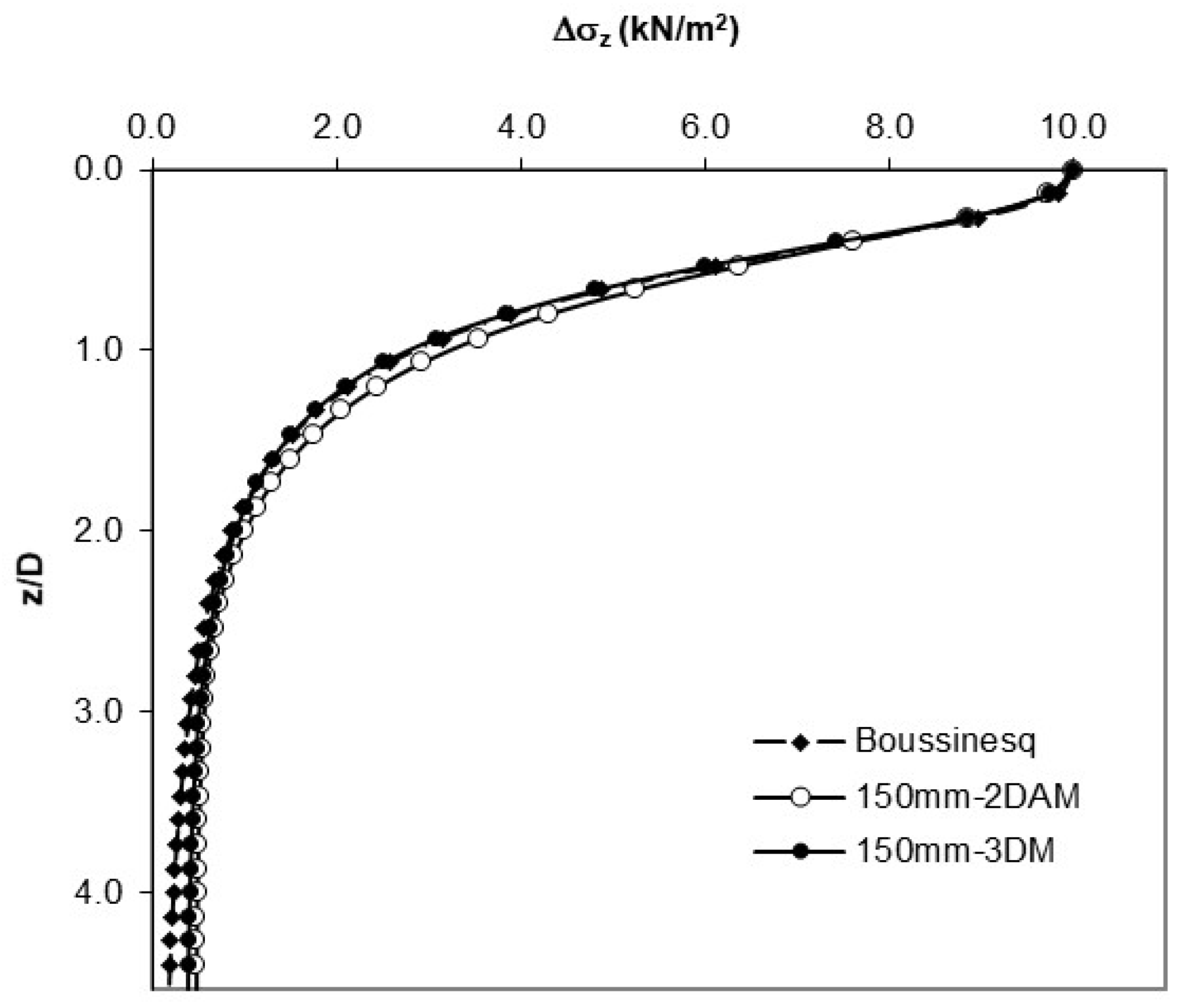
Figure 15.
Vertical stresses obtained with HS and DP models (150 mm footing).
Figure 15.
Vertical stresses obtained with HS and DP models (150 mm footing).
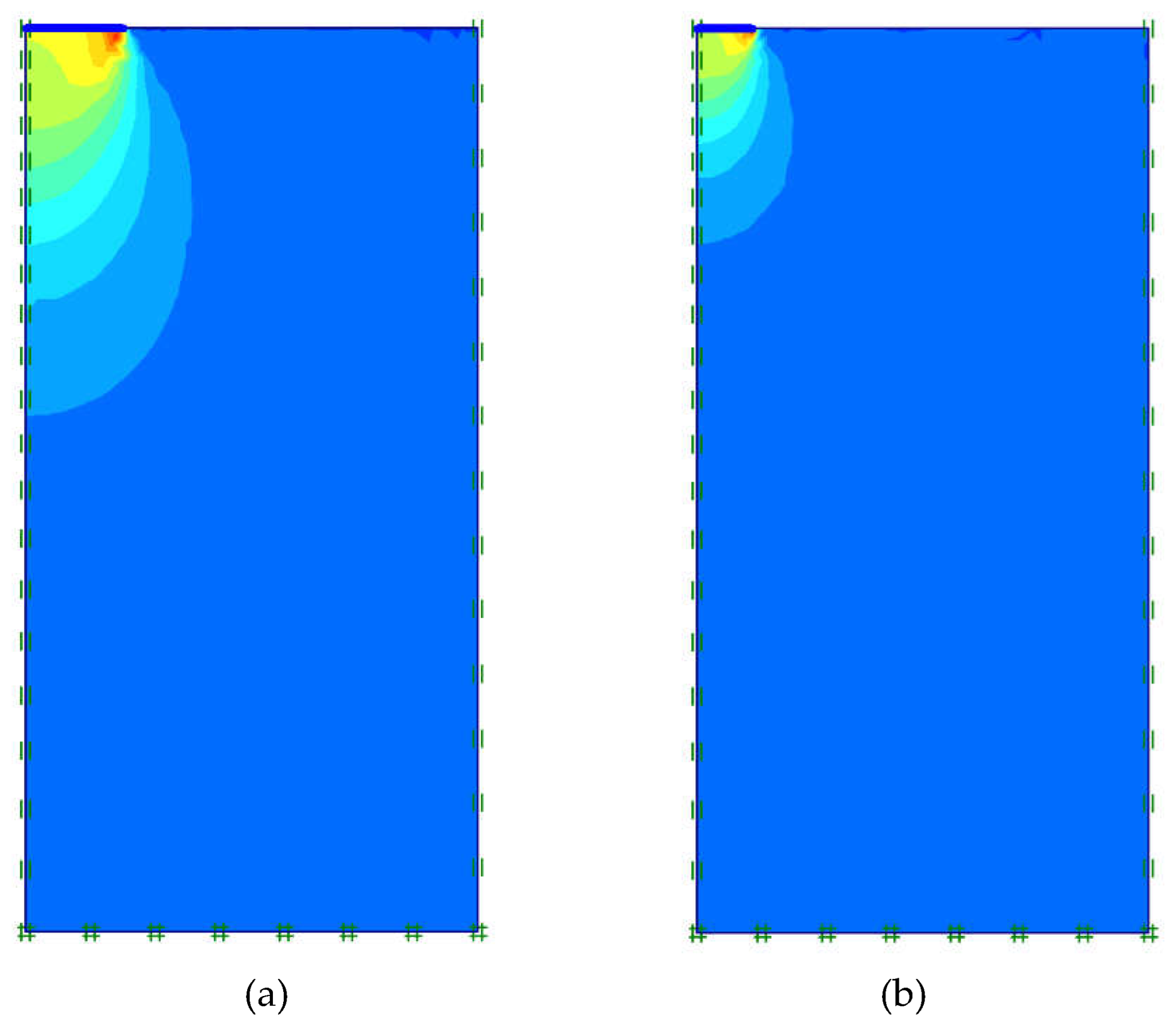
Figure 16.
Vertical stress distribution with HS model (a) 150 mm (b) 85 mm.
Figure 16.
Vertical stress distribution with HS model (a) 150 mm (b) 85 mm.
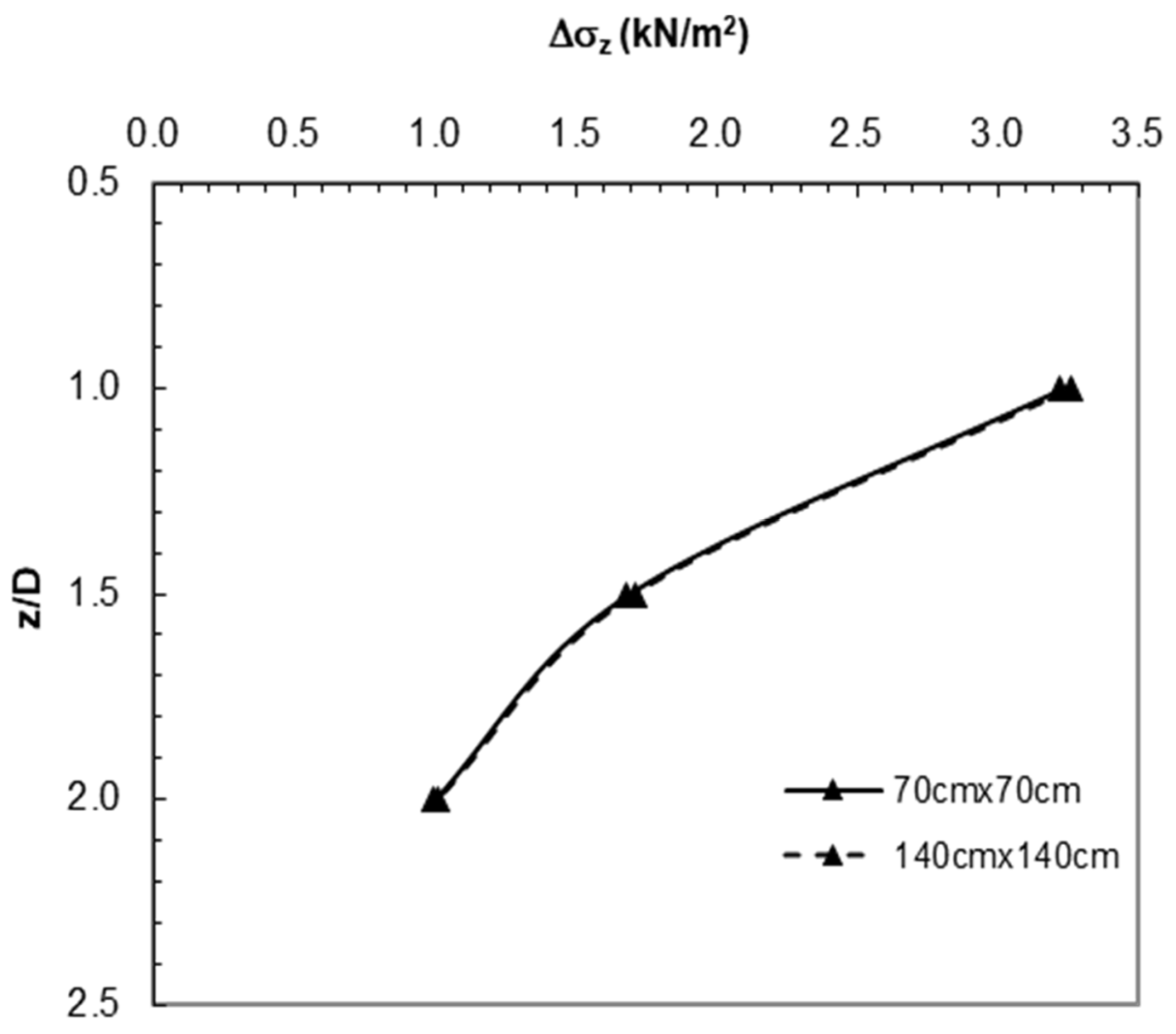
Figure 17.
Vertical stress values obtained from analysis of boundary effect.
Figure 17.
Vertical stress values obtained from analysis of boundary effect.
Figure 18.
Distribution of vertical stresses obtained from analysis of boundary effect.
Figure 18.
Distribution of vertical stresses obtained from analysis of boundary effect.
Figure 19.
Vertical stress distribution (D=85 mm).
Figure 19.
Vertical stress distribution (D=85 mm).
Figure 20.
Vertical stresses beneath the 85mm circular footing(a) 2DM (b) 3DM.
Figure 20.
Vertical stresses beneath the 85mm circular footing(a) 2DM (b) 3DM.
Figure 21.
Vertical stress distribution (D=150mm).
Figure 21.
Vertical stress distribution (D=150mm).
Figure 22.
Vertical stresses beneath the 150mm circular footing (a) 2DM (b) 3DM.
Figure 22.
Vertical stresses beneath the 150mm circular footing (a) 2DM (b) 3DM.
Figure 23.
Vertical stresses distribution (D=200mm).
Figure 23.
Vertical stresses distribution (D=200mm).
Table 1.
Properties of sand bed.
Table 1.
Properties of sand bed.
| Property |
Value |
| Coarse sand percentage (%) |
0.0 |
| Medium sand percentage (%) |
34 |
| Fine sand percentage (%) |
66 |
| D10 (mm) |
0.28 |
| D30 (mm) |
0.36 |
| D60 (mm) |
0.42 |
| Uniformity coefficient, Cu |
1.5 |
| Coefficient of curvature, Cc |
1.1 |
| Specific gravity (kN/m3) |
2.68 |
| Maximum dry unit weight (kN/m3) |
17.6 |
| Minimum dry unit weight (kN/m3) |
15.4 |
| Classification (USCS) |
SP |
Table 2.
Parameters of DP model.
Table 2.
Parameters of DP model.
| Parameters |
Symbol |
Unit |
Value |
| Elasticity modulus |
E |
kN/m2
|
28000 |
| Poisson’s ratio |
μ |
- |
0.20 |
| Cohesion |
c |
kN/m2
|
0.10 |
| Internal friction angle |
Ø |
(°) |
41 |
| Dilatation angle |
ψ |
(°) |
11 |
Table 3.
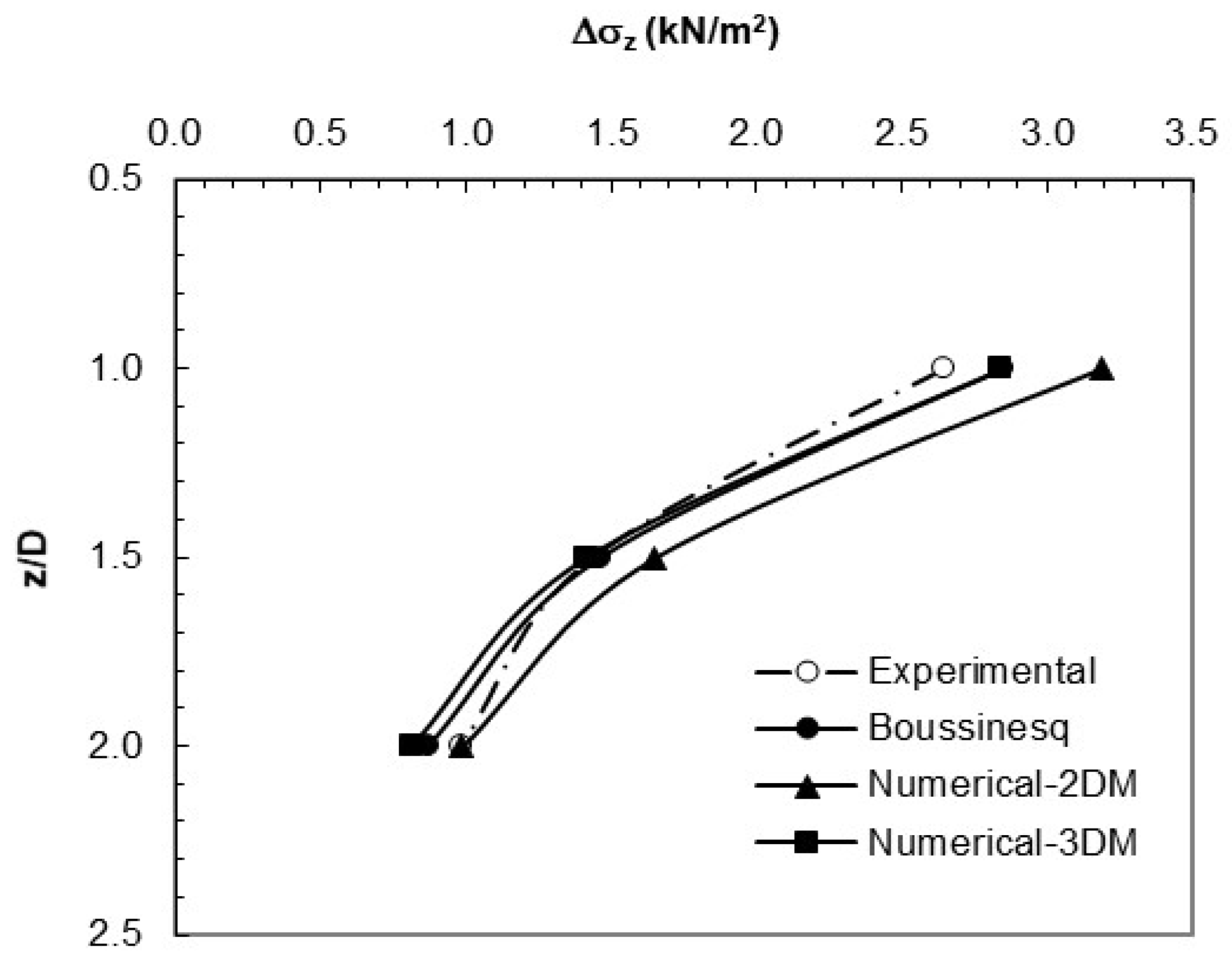
Vertical stress values beneath the centerline of the 85mm circular footing.
Table 3.
Vertical stress values beneath the centerline of the 85mm circular footing.
| Depth, z |
Vertical stresses, Δσz (kN/m2) |
| Experimental |
2DM |
3DM |
Boussinesq |
| 1.0D |
2.65 |
3.19 |
2.84 |
2.85 |
| 1.5D |
1.44 |
1.65 |
1.41 |
1.46 |
| 2.0D |
0.98 |
0.99 |
0.81 |
0.87 |
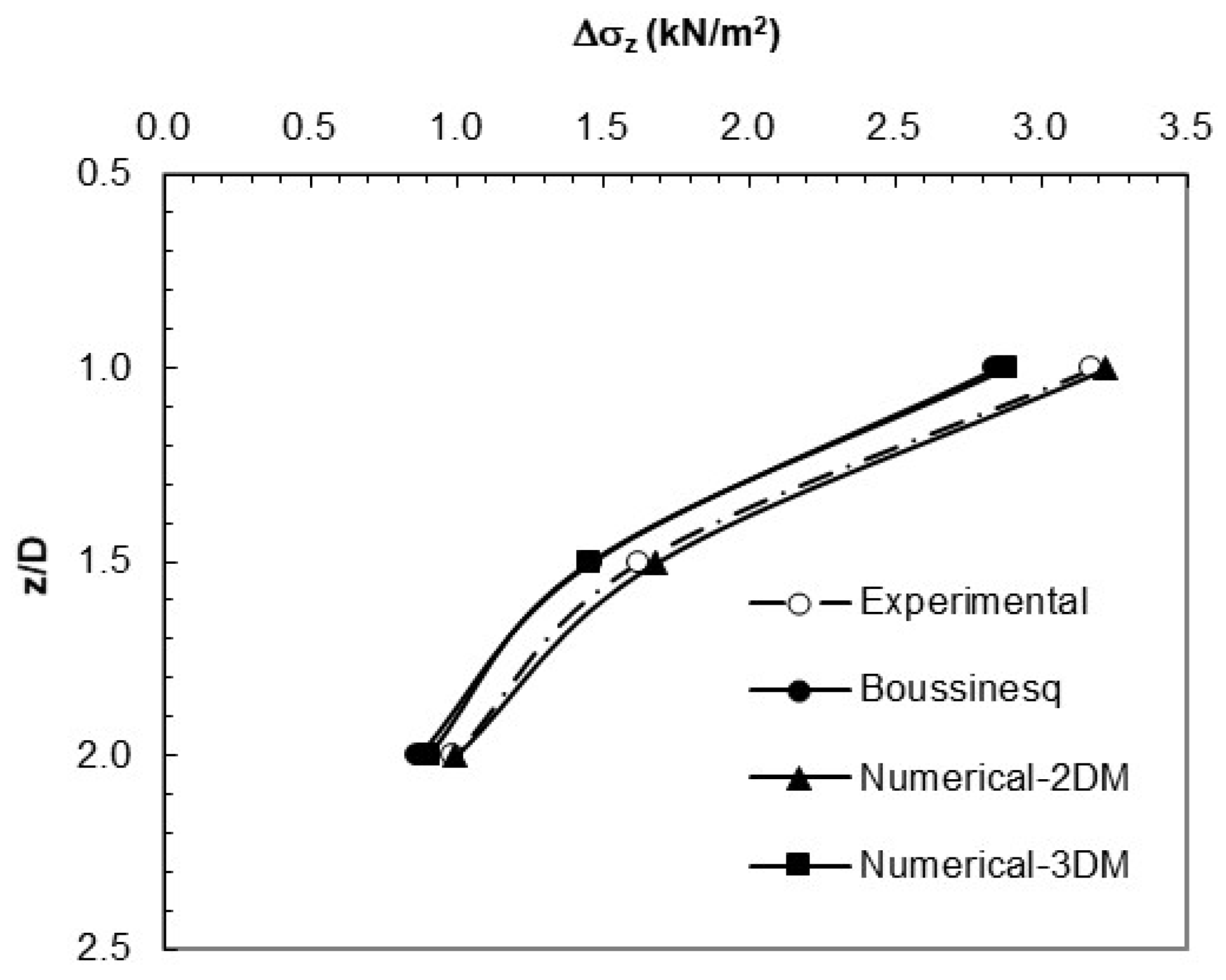
Table 4.
Vertical stress values beneath the centerline of the 150mm circular footing.
Table 4.
Vertical stress values beneath the centerline of the 150mm circular footing.
| Depth, z |
Vertical stresses, Δσz (kN/m2) |
| Experimental |
2DM |
3DM |
Boussinesq |
| 1.0D |
3.18 |
3.22 |
2.88 |
2.85 |
| 1.5D |
1.62 |
1.69 |
1.46 |
1.46 |
| 2.0D |
0.99 |
1.00 |
0.91 |
0.87 |
Table 5.
Parameters of HS model.
Table 5.
Parameters of HS model.
| Parameters |
Symbol |
Unit |
Value |
| Unit weight |
ɣ |
kN/m3
|
17.1 |
| Primary loading stiffness |
|
kN/m2
|
28000 |
| Initial stiffness |
Eoed
|
kN/m2
|
28000 |
| Unloading/reloading stiffness |
Eur
|
kN/m2
|
84000 |
| Cohesion |
c |
kN/m2
|
0.10 |
| Internal friction angle |
Ø |
(°) |
41 |
| Dilatancy angle |
ψ |
(°) |
11 |
| Poisson’s ratio |
μ |
- |
0.20 |