Ensuring Explainability and Dimensionality Reduction in a Multidimensional HSI World for Early XAI-diagnostics of Plant Stress

The work is devoted to the search for effective solutions to the applied problem of early diagnostics of plant stress in the conditions of smart farming and based on modern explicable artificial intelligence (XAI). The study mostly oriented on the theory and practice of XAI, focused on the use of hyperspectral imagery (HSI) and Thermal Infra-Red (TIR) sensor data at the input of a neural network. The first our goal is to build an XAI neural network, explainable due to its structure, the input of which is a datascientist oriented HSI 'explanator', and the output is a biologist oriented TIR 'explanator'. In the middle is SLP-regressor which solves the universal problem of training HSI pixels to temperatures of plants, needed for early plant stress diagnostic. The result can be considered as prototype of a special XAI explanator which is assigned to transform explanator specialized on area 1 onto explanator specialized on area 2. Using this HSI-TIR explanator we ensured the follows: extend HSI data by TIR attribute; providing TIR data for early diagnostic of plant stress; reducing dimensionality HSI needed for TIR training 25 times (from 204 to 8) preserving the same accuracy of temperature prediction (RMSE=0.2-0.3C). This reducing was achieved without using PCA methods. The constructed model is computationally efficient in training: the average training time is significantly less then 1 min (Intel Core i3-8130U, 2.2 GHz, 4 cores, 4 GB). One of the 8 channels, 820 nm, is the leader in correlation with TIR, what allows building local linear temperature prediction functions.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Artificial intelligence (AI) has become the most popular approach to diagnosing plant stress in smart farming. Boldú in a 2018 review [1] noted the widespread use of Deep Learning (DL) in agriculture. Kakogeorgiou, et al. in 2021 [2] and Wei, et al. 2022 [3], showed that DL, gradually adding certain properties of explainability to its arsenal, is becoming more and more used for plant stress and disease diagnostics. At the same time, hyperspectral images (HSI) of plants are widely used as initial data for AI diagnostics.

1.1. HSI as Multidimensional World

A typical HSI occupies hundreds of megabytes of memory, has a complex multi-file structure, and requires special processing software. Each HSI pixel is an n-dimensional channel vector with an almost unique combination of hundreds of channel values. The presence of hundreds of channels in the spectral characteristic of each pixel for HSI gives the object depicted in it hundreds of features and the fundamental possibility of classifying the object by one n-dimensional pixel (signature) even without using context. Dozens of vegetation indices, such as the Normalized Difference Vegetation Index (NDVI), developed in Earth remote sensing (ERS) are also used in the diagnosis of the state of plants and fields. These indices are built on rational combinations of HSI channel values, and their number continues to grow [4,5]. When solving problems of diagnosing the state of plants, indices are usually used instead of HSI, but can also be used together with HSI channels and spectral characteristics of its pixels, sometimes even preferring the latter [6].

Since the advent of HSI, for clustering, segmentation and classification of HSI in remote sensing practice, the ‘Spectral Angle’ measure and the classification procedure with its help began to be used: Spectral Angle Mapper (SAM) Classification. In essence, this coincides with the Fisher criterion for determining separability in a multidimensional space (Grechuka, 2021) [7]. As a result, from the point of view of AI, hyperspectral images form their own multidimensional HSI world, in which both the curse of dimension and the blessing of dimension are necessarily present [8] (Gorban, 2018).

1.2. HSI and AI in Agriculture

The above properties of HSI have made the research and application of HSI constantly expanding [6,9,10,11,12], and applied problems using HSI have become a real testing ground for the development of AI methods and models. For example, Zhang et al. in a 2020 review [12], explored the application of AI for diagnosing plant stresses on HSI data over the past 3 decades. It has been shown that HSI signature data are able to provide recognition of plant diseases with acceptable accuracy, in terms of leaf, stem, ear, and crown. Examples of solutions for images both on the scale of traditional remote sensing and at distances of the order of a meter (s) accessible to UAVs and ground units are given. Publications [6,10,11] reflect the trend towards using “close-range” HSI and high resolution HSI as source data. Sometimes HSI is supplemented with thermal (Thermal IR, TIR) image [11], which is not included in the set of HSI sensors, but is specialized for early stress diagnostics based on an increase in plant temperature [11,13]. Early diagnosis is understood as one that avoids crop losses. The problem of early diagnostics of plant drought stress was also studied in [6]. It was shown that when using several popular classical ML methods, including Multi Layer Perceptron (MLP), the accuracy of plant drought state detection based on the full spectral characteristic of plants HSI, as well as its derivative, turned out to be higher than the accuracy obtained on a combination of 9 vegetation indices. Review [14] over the past almost 25 years is devoted to the development, based on ML and HSI data, of algorithms for detecting the quality of wheat grain protein and its relationship with nitrogen status.

In [9] Schmitter et al. (2017) proposed an original “unsupervised domain adaptation” approach for early detection of plant-drought stress, which also use HSI data. The approach provides the transfer of a neuromodel trained for early detection of the plant-1 stress to the detection of plant-2 stress, using weat and corn as an example. The transfer is carried out on the first principles of plant biology and does not require supervision. The other original method, which use HSI possibilities, was proposed by Pan et al. (2021) [15]. It is the "zero-shot learning" method based on using a high-level feature vector. Such vector ensures the minimization of a dataset required for training, as well as the transfer of training results from one dataset to another, in which some of the categories are missing (or not visible). The high-dimensional spectral HSI characteristics are consided as the source of high-level features.

1.3. Notions of XAI and Explainablity in AI

The number of publications devoted to explainability and explainable artificial intelligence (XAI) has increased significantly in recent years, but there is a noticeable difference in the interpretation of the content of XAI. For example, Zhang et al., which presented in the review [16, Figure 1] the point of view of XAI applicating in diagnostics and surgery, the following scheme was proposed for covering the areas of AI, ML, DL, and XAI: ML entirely belongs to AI, and DL belongs to ML; XAI is the part of AI that overlaps with ML but does not overlap with DL. This vision is consistent with previous publications [17,18,19]. In [18] of Lundberg et al. (2018) build explainable prediction and prevention of hypoxaemia during surgery on objective patient monitoring data, substantiating their importance with the data of Shaply value analysis. In [17] of Lamy, et al. (2019) the authors explain the prediction for breast cancer using a case-based reasoning approach, which is typical for the medicine. In [19] of Antoniadi et al. (2021) the authors draw attention to the lack of explainability in ML-based Clinical Decision Support Systems (CDSS) for the clinicians operating them and insist on its increase. It is understood that for other applications of XAI, clinician means a person who directly uses XAI predictions.

Some works explore XAI as a universal tool [20,21,22,23]. The authors of [20] Wang et al. (2019) proposed an original “Theory-Driven User-Centric” approach for XAI designing. According to him, “explainability” should be oriented towards the user, making it “User-Centric” using the methods of cognitive psychology and the laws of human thinking. The main idea of the approach is expressed by the formula “Understanding Humans Should Inform Explaining AI”.

Vilone and Longo (2020) leading a systematic 81-page review to XAI based on 361 sources [21]. The review contains a detailed study of XAI, including a detailed analysis of concepts related to the concept of explainability, a discussion of explainability attributes, a classification of existing methods and approaches to designing XAI elements and systems. Generalized a state-of-the-art hierarchical framework for XAI design, which includes the following components (from bottom to top): data; modeling; XAI methods; explanators; evaluation.The authors proposed also an alternative ideal vision of XAI as a system of nested components. The central and main focus component is the Explanators (textual, pictoral, rules, dialogue, mix-formats), which is what end-users will ultimately interact with. Then follows: Attributes (comprehensibility, interestingness, persuasiveness...); Modeling (AI connectionist learning, AI symbolic reasoning); Evaluation of explainability (which is realized via interface interaction and human-in-the-loop technic, for designer and end-user). This Explanators-driven XAI concept appear as very interesting on condition if considering Explanators in pair with Data.

Averkin (2021) in the review [22] explores, against the background of modern publications, the possibilities and prospects for the development of XAI in the project “DARPA's explainable artificial intelligence (XAI) program”, presented in the report [24]. This project attracted the attention of the author with its focus on to derive an explainable model from any black box model. For this goal, it is planned to create modified DL methods that study explainable features, and methods that explore more structured, interpretable causal patterns, as well as model induction methods. Maybe it means a reasonable shift of the DL models properties to the side of XAI models properties. The list of modern publications by the author also includes publications of two standards [23,25] on XAI.

The draft NISTIR 8312 (2020) for XAI definition [23] from the National Institute of Standards and Technology (NIST) is more interesting because it offers “Four Principles of Explainable Artificial Intelligence” underlying XAI with an emphasis on human-computer interaction. These principles are: (1) Explanation; (2) Meaningful; (3) Accuracy of explanation; (4) Limits of knowledge (the system must to note any cases for which it was not designed). The principles are independent from the AI area: DL and classical ML, but subject both areas to the same criteria, including the 4th, which is very hard to execute for DL. Their short explanation:

Explanation: Systems deliver accompanying evidence or reason(s) for all outputs.

Meaningful: Systems provide explanations that are understandable to individual users.

Explanation Accuracy: The explanation correctly reflects the system’s process for generating the output.

Knowledge Limits: The system only operates under conditions for which it was designed or when the system reaches a sufficient confidence in its output.

In the examples of providing explainability in the practice of diagnosing plant stress based on DL [2,3], we can speak so far only of partial implementation of three principles, (1) Explanation, (2) Meaningful, and (3) Accuracy of explanation, in order to overcome some of the limitations of the black-box nature of DL models. In examples of providing explainablity based on ML methods [6,13,26], one can see the implementation of the same 3 XAI principles, but with a high degree of content, as well as a part of content of the 4th principle, to which has not yet begun to be given due attention in practice.

2. Materials and Methods

2.1. Materials

An experiment on the early detection of drought stress in plants using wheat as an example was carried out in the biolab of our university. The plants were planted in pots with an average of 16 plants per pot. Plant pots were placed in 3 boxes of 30 pots each. In each box, left 15 pots were watered, and right 15 pots were not watered. The state of the plants during 25 days was regularly recorded every 2-3 days from a height of about 1 m by the following cameras: (1) Specim IQ hyperspectral (HSI) camera (range: 400–1000 nm, spectral resolution: 3 nm, channels: 204; 512 × 512 pix); (2) Testo 885-2 thermal infrared (TIR) camera (320 × 240 pix). The accuracy of the TIR camera is 0.1°C. The total image volume was about 72 GB, mainly comprising HSIs. TIR sensors were chosen to directly record the leaf temperature, an increase in which is the earliest feature of a stress condition.

The differences between non-irrigated and irrigated plants in temperature (according to TIR images) and water loss (%, via plant weighing) were recorded for the 11 days of the experiment: 1st, 3rd, 6th, 8th, 10th, 12th, 14th, 16th, 19th, 22th, and 25th. The following key events and changes in the state of plants were recorded and compared with those of control plants: (1) an increase in the average temperature of plants by 0.2 degrees after 5 days and (2) the beginning of water loss by the plant after 11 days (about 8% of the water volume). The former is the earliest evidence of drought stress, which happens without water loss by plant and visible changes in its green mass. Detection of plant stress before the onset of water loss is a criterion of “early” detection. After 18 days or somewhat later, we observed a depletion of the plant’s compensatory function, as manifested by a break in the line of monotonic temperature increase.

2.2. Construction XAI Early Diagnostics Network with Explanators on the Input Having Only Highdimentional HSI Data as the Source

According to the above publications [21,22,23,24,25], the best guiding idea for building an XAI neural network is the user-centered selection of explanatory features for the XAI system. In our case, the users are agronomists and biologists. According to sources of these knowledge areas, the best explanations are small changes in plant temperature recorded by the TIR sensor. Using HSIs as input data, and be inspired by their using in “Zero-shot learing” method [15], a natural solution for creating explainers is to train n-dimensional HSI pixel signatures on the temperature values. The goal is to build an XAI neural network that is explainable due to its structure, with an HSI 'explanator' as input and a TIR 'explanator' as output. HSI ‘explanator’ should be centered onto data scientists, and TIR ‘explanator’ onto biologist and agroscientists. As a result, such XAI block-explanator solves the universal problem of transformation 'explanator' to 'explanator' and can be used at the input of any network for the early diagnosis of plant stress, as example like in [13] or [26].

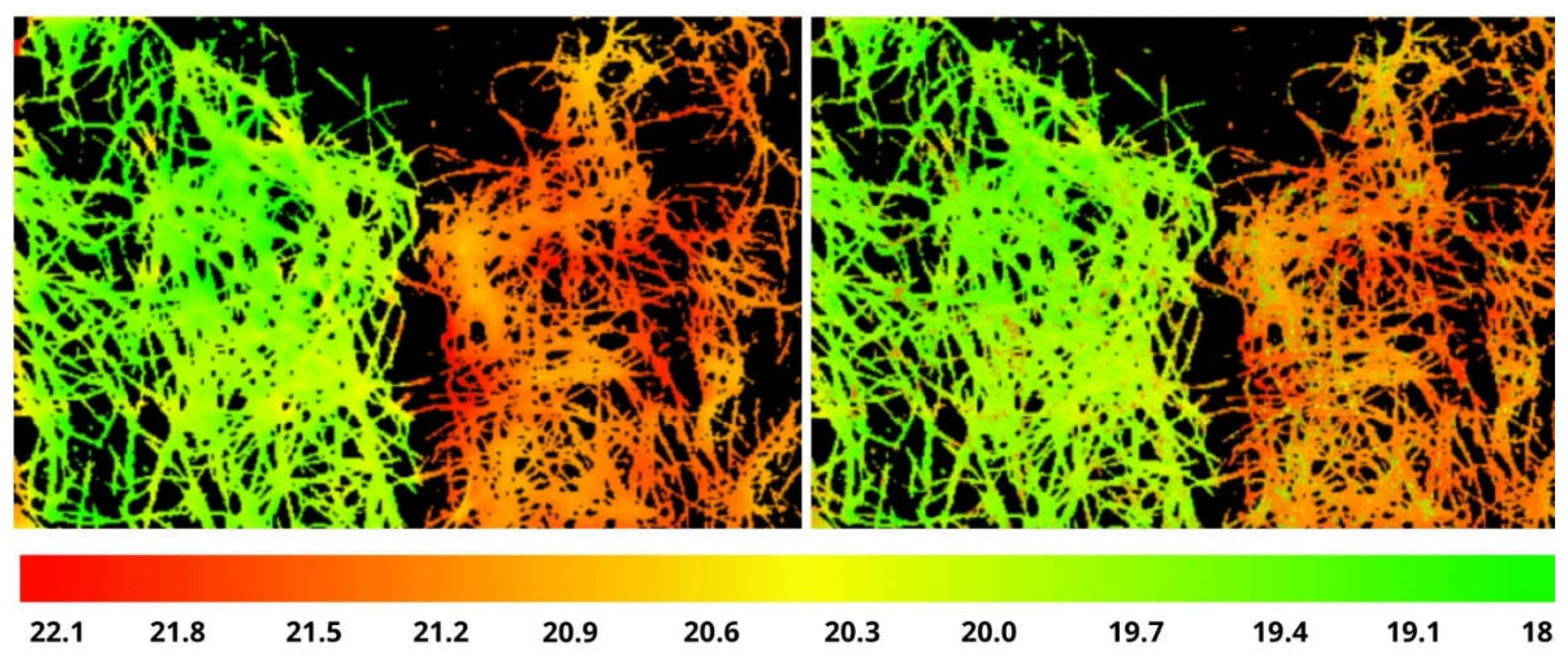
The first experience of training hyperspectral images (HSIs) to the TIR temperatures based on "Zero-Shot Learning" method was taken by our team in [27]. Unfortunately, (1) the achieved RMSE value (0.52°) was not enough for practice, and (2) reconstructed temperature range [18.8°-22.1°] had a significant gap of 1° in the middle due to the same gap in the used original data (1st box at 25th day, as having the widest temperature range, see Figure 1). The training time taken about 1 hour (Intel Core i3-8130U, 2.2 GHz, 4 cores, 4 GB).

2.3. Additional Preprocessing Needed to Split the Plant from the Soil

To solve the problem of training HSI signatures on the temperatures in the temperature range of the experiment, it is necessary to mark up the HSI pixels with the temperatures of the TIR sensor for all key days and enough number pots with plants. To automate of the process, 512×512 resolution HSIs were aligned with 320×240 resolution TIR images using homography transformation. Combining images of significantly different resolutions created additional difficulties: (1) to improve accuracy, alignment was performed not at the level of boxes, but at the level of pots with plants; (2) large pixels of the TIR image appeared along the leaf boundary, simultaneously overlapping the leaf and soil, which generally have different temperatures. To study the correlation of the TIR temperature of a pixel with the HSI channel, and to perform training strictly on pixels that belong entirely to a plant, it is necessary to ensure the separation of plant pixels from others using a special plant mask.

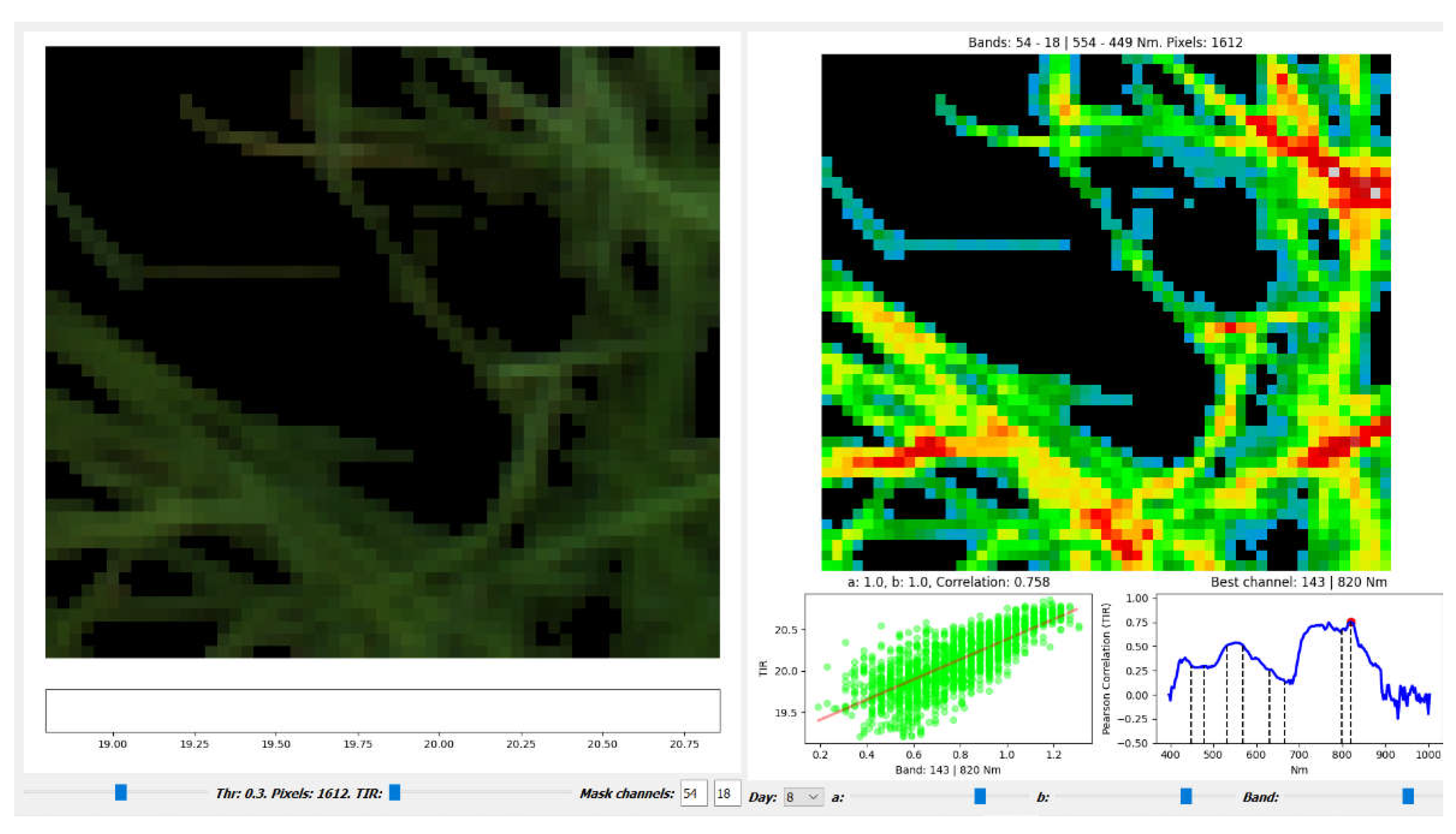
To solve this problem was done the following: 1) based on the vegetation index NDblue (1) introduced in [26], a plant mask controlled by a threshold (thr) is constructed; 2) a special tool for cleaning plant masks has been implemented, which changes the mask by limiting the distance to the linear regression from above and below (a,b parameters), and this tool interface (Figure 2) also.

N D b l u e = \frac{V}{(m a x (V) - m i n (V))}, V = R_{550} - R_{450}, N D b l u e \geq t h r

(1)

On fig. 2 shows potted plants (left) stained with three HSI-channels: R₆₈₀, G₅₅₀ and B₄₈₀. The mask of non-zero values of this image is determined by the threshold value (lower left slider). On the right, a pseudo-color TIR image, for the mask pixels, is visible. Below this image: (1) a plot of HSI and TIR overlay results and a linear regression for the temperature prediction, where the x-axis is the values of the channel selected by the Range slider and the y-axis is the TIR values; (2) сorrelation plot between TIR and all HSI channels for the day of the experiment ("Day" box in the bottom panel), the channel with the best correlation is shown as text above the plot. Using "Band" you can select any channel were you want to apply the values a,b for cleaning. Selected channel is highlighted on the plod by red mark. Correlation estimation is performed using the Pearson Linear Correlation Coefficient (PLCC):

r (x, y) = cov (x, y) / (σ x ⋅ σ y) = E [(x - E x) (y - E y)] / \sqrt{D x} \sqrt{D y} .

(2)

The sliders for a and b parameters is to the right of the Day box. Reducing the parameters a and b further restricts the mask, but increases the correlation coefficient.

Using this tool we can explore a wide range of thresholds [0.1:0.5] for constructing the plant mask, as well as a,b parameters to choose channel(s), which has the best PLCC value to construct a functional TIR (mask-pixel) relationship in terms of PLCC:

y_{i} = E y + \frac{σ_{y}}{σ_{x}} {(x}_{i} - E x),

(3)

were xi – i-th mask-pixel value for current HSI channel, yi – i-th mask-pixel value for TIR.

2.4. Theory and Practice of Feature-Space Dimensionality Reduction in AI-HSI Applications

One of the goals of this work is to explore the possibility of reducing the dimension of the high-level feature vector needed to train HSI signatures on the TIR temperatures. The practical possibility of lowering the HSI dimension in the early diagnosis of plant stress was shown by Agilandeeswari et al. (2022) [28]. They managed to reduce the number of HSI channels used for the task by about 5 times, from 224 to 42-45, using the selection of channels according to efficiency criteria. The criteria were determined from practice and separately for each wave range: in the visible - by the value of the entropy (informativeness) of the channel; in infrared (IR) - according to the value of Normalized Difference Vegetation Index (NDVI); in medium wave IR (SWIR) - by the value of the Modified Normalized Difference Water Index (MNDWI). Selected 14-15 channels from each range. In our case SWIR range is absent.

There are also theoretical and practical reasons for even more significant dimensionality reduction. For example, Allegra et al. (2020) in [29] confirm that a small number of variables is often sufficient to describe locally a high-dimensional data. This minimal number of variables is called the intrinsic dimension of the data (IDD). And such IDD can be viewed as a simple topological feature that is sufficient to implement unsupervised segmentation of multidimensional data.

Even more interesting possibilities are opened by Albergante et al. (2020) [30], confirming the possibility of modeling the internal structure and geometry of a complex multidimensional dataset in the form of an area graph with a low local internal dimension. The ElPiGraph software created during the study has now become part of the Python Package for Intrinsic Dimension Estimation “Scikit-Dimension” [31]. Authors Gorban et al. (2021) in [32] solve the problem of constructing simple correctors that update the properties of the AI system. But it is essential for our study that the authors accept as a working hypothesis that the data can have a rich fine-grained structure with many clusters and corresponding peaks in the probability density. And this hypothesis, workable for the authors, confirms for us the possibility of a sharp decrease in the dimension of the space inside the grain and the efficiency of using local metrics. As an effective tools for local domain coordination were proposed the following: (1) supervised Principal Component Analysis (PCA); (2) semi-supervised PCA; (3) new domain adaptation PCA; (4) transfer component analysis.

2.5. Dimensionality Reduction and Construction of the XAI System Based on HSI-Input-Data as Source of Highlevel Features

We will follow the main ideas of [32], but when choosing local coordinates of low dimension, we will try to choose explainable local coordinate axes instead of using PCA.

We plan to solve the problem of using HSI as input data instead of TIR by 2 ways: (1) investigating whether among the HSI channels there is one(s) that has a high correlation with TIR, close to a functional dependence; (2) training the HSI-pixels to TIR values via using XAI model and "zero-shot learning" [15], that is using found high-level features (H-LFs).

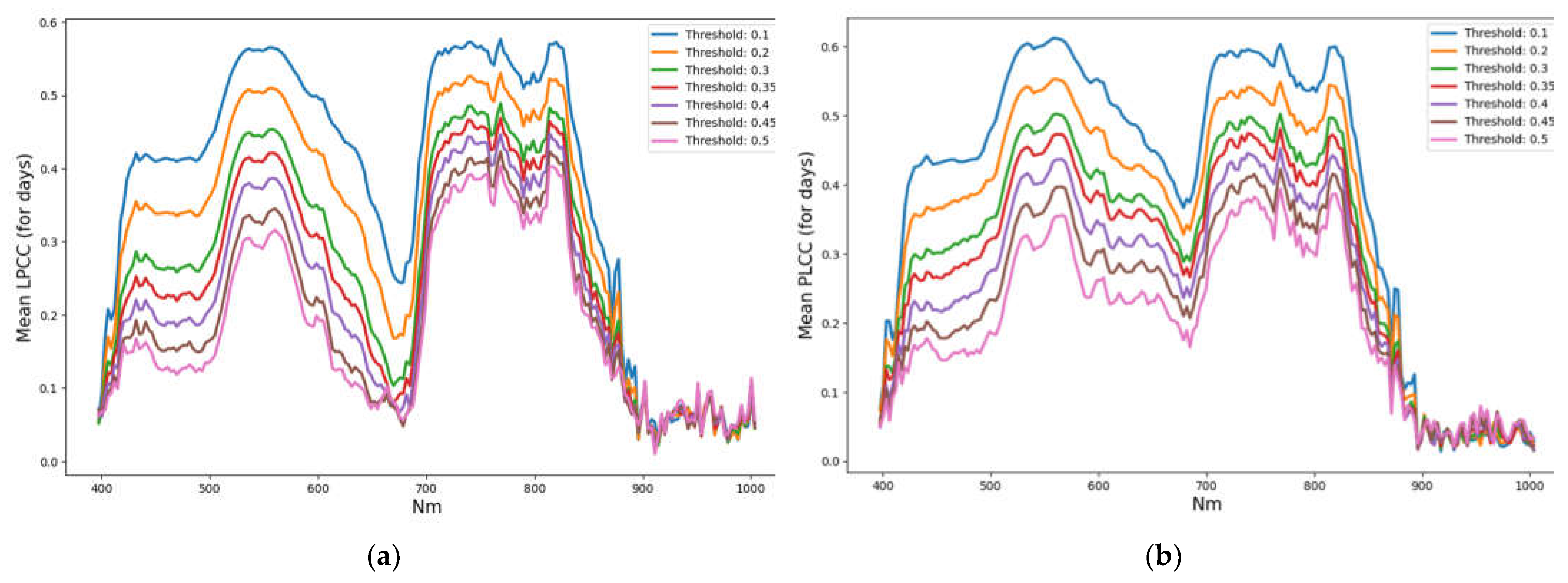
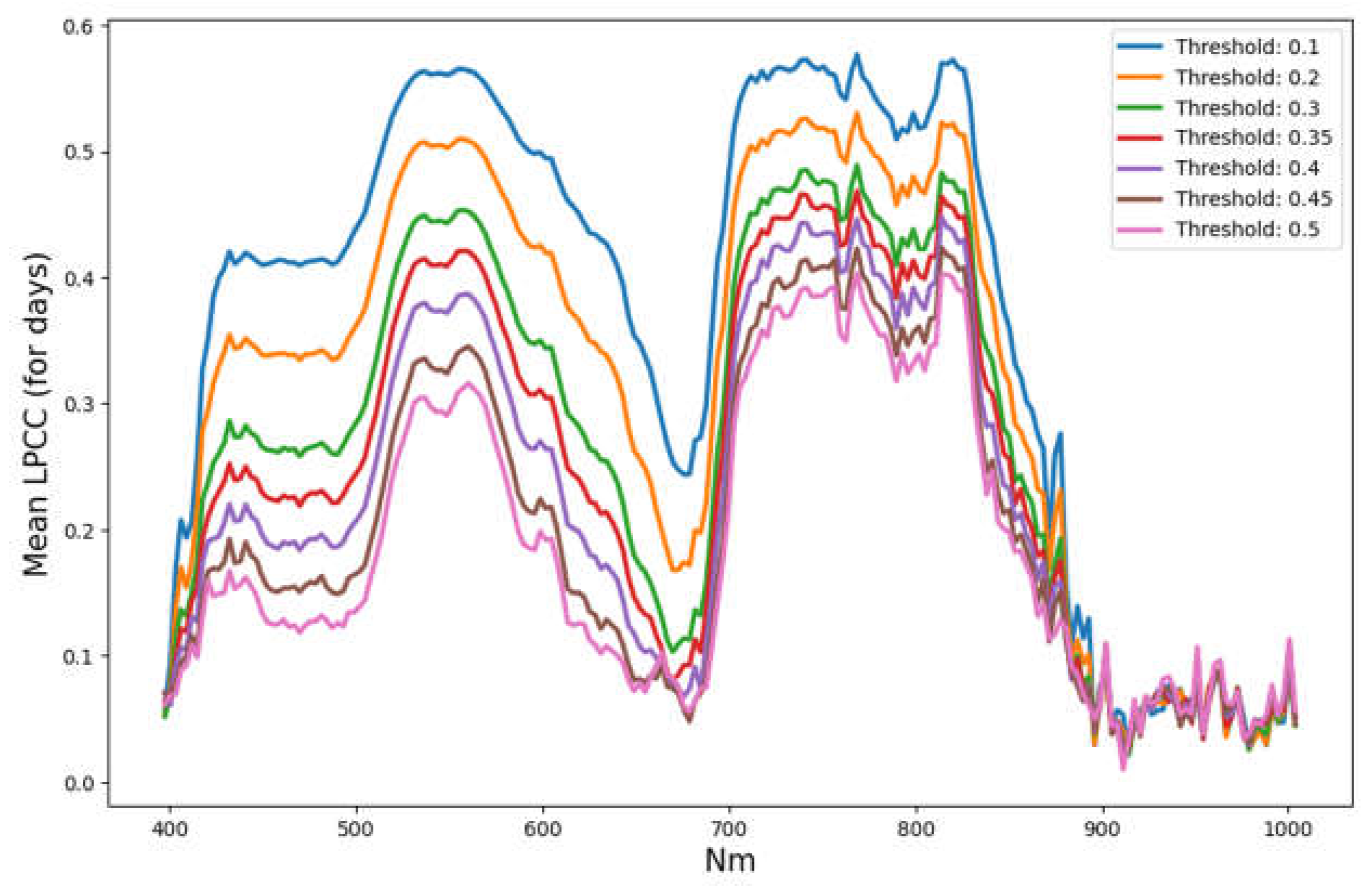
Following these ways we will try to find these high-level features and to minimize the number of HSI-channels needed for the solution. It is most interesting to find a solution to the 2nd problem, which does not depend on the key day, but depends only on the stress state of the plant. Lets form a reduced number of HSI channels on the result of calculation PLCC absolut values averaged over key-days for various threshold values (Figure 3).

It is seen, that curves for different thresholds have very close shapes, which can be characterized by several extremal points near following (channel No/wavelength): 59/570, 117/742, 126/769, 143/820 (4 max). Some widely used vegetation indices (nVI), such as NDVI (Normalized Difference Vegetation Index), GI (Greenness Index), PRI (Photochemical Reflectance Index), and other [9] can be also included as additional features. Together this will only be k=CHextr + nVI channels/indexes (hereinafter channels) instead of 204.

But it is important to note that the real number of local maxima is much more than 4, and they change from one key day to another and in terms of parameters. How many maximums/extrems will be enough for each day and for all days together, and what their types will be, this should be a subject of the study.

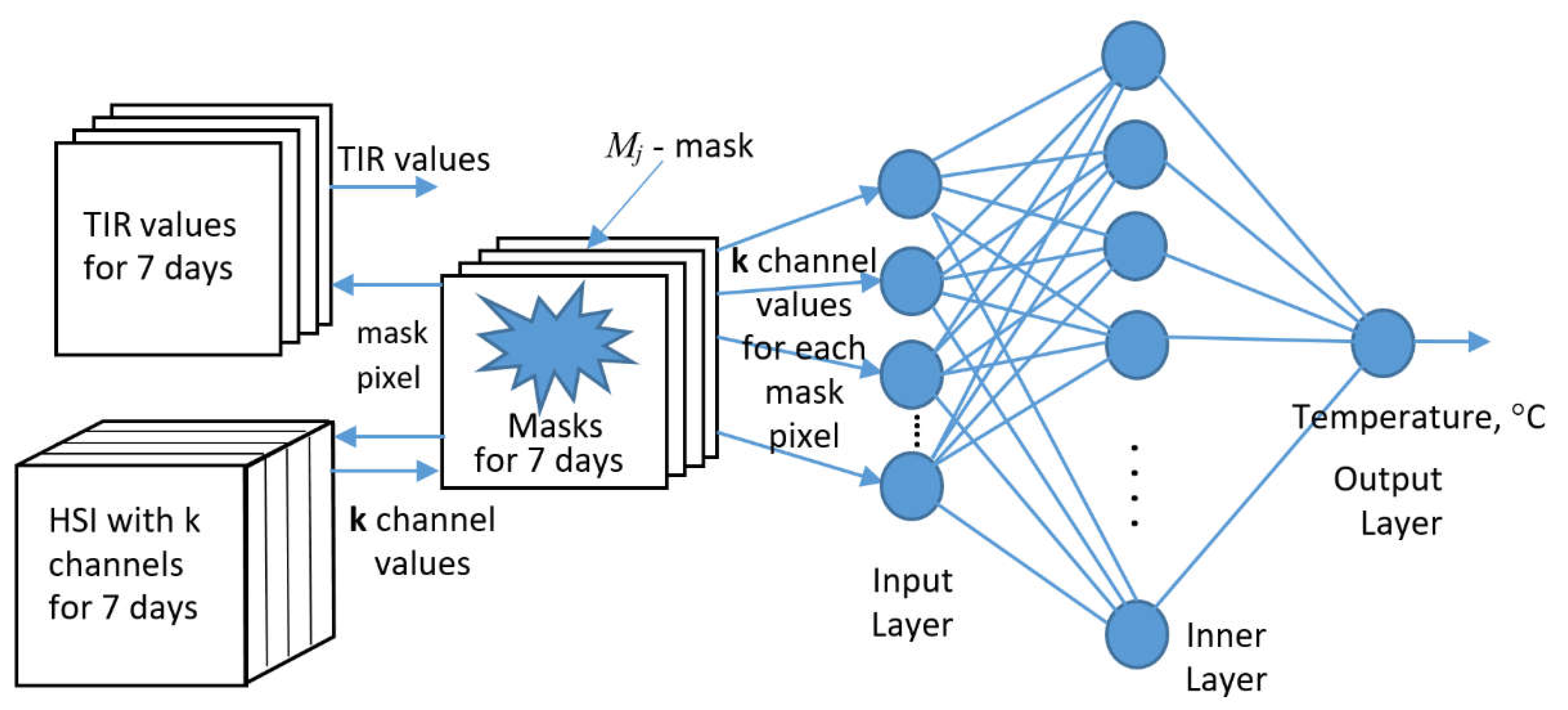
So, for XAI temperature-regressor building we use on its input 3 sources for each of 7 key days: HSI(j), TIR(j) values, and Mask(j), were j is key day number (Fig.4). As base ML-structure for XAI we will use SLP (single-layer peceptron). As an HSI feature input vector for TIR value prediction we will use preliminary selected k HSI channels, which provide to determine the temperature value with a given accuracy. We will solve the problem of k choice in the course of the study.

As XAI output we will use TIR values. The 3rd component Mask, we will use as an organizer of HSI and TIR pixel sampling and parametrization of our study in terms of {thr, a, b} (see Fig.2).

As a preprocessing, a temperature histogram is constructed with the calculation of its statistical characteristics, as well as a pixel and a day for each temperature. It is also important to note that the masks for each key day are different.

As a loss function we considering the RMSE function for deviation predicted temperature from the TIR values under mask for all key-days. In this case loss function must looks like this (4):

R M S E = \sqrt{\sum_{j = 1}^{7} \sum_{m M_{j}} {({p y}_{j m} - y_{j m})}^{2} / n},

(4)

were py_jm – temperature prediction from the channels of the m-th HSI pixel of the j-th day mask Mj,

y_{j m}

- m-th pixel value of TIR mask Mj, n – total number of pixels in 7 masks.

The block diagram of this XAI regressor is shown in Figure 4. Three diagram blocks at the input of the SLP regressor implements the 'HSI explanator' concept for this neural network.

3. Results and Their Discussion

3.1. HSI-Input-Data Dimensionality Reduction via Searching Channels That Has a High Correlation with TIR

In the sequence of 11 days of the experiment, a subsequence of 7 key days {1,3,6,8,12,19,25} was selected, in which qualitative changes in the behavior of plant temperature can occur or are occurring. We also divided box #3 of the dataset into 2 parts: training and testing (Table 1). This was done to check the possibility of transferring the linear dependence (3) built for the 'train'(ing) part of the dataset to the 'test' part.

The PLCC value between TIR and each of the 204 channels is calculated for a set of threshold values that control the plant mask, as shown for ‘train’-ing set in Fig. 3, and for each key day separately. This was done for both the 'train' part and the 'test' part to compare the correlation patterns of these parts with the TIR. Graphs of average PLCC values for the key days of the experiment have noticeable differences, expressed in a noticeable rise in the minimum of the ‘test’ graph on channel 96 (680nm), and with it the entire left part of the graph (see Fig. A1).

The accuracy of the functional dependence of the temperature forecast (3), built on the basis of the fact of a high correlation dependence, was estimated in RMSE values in degrees Celsius (°C).

A study was made of the dependence of PLCC on the threshold value (1) for the plant mask in the range 0.1 ≤ thr ≤ 0.5, with a step of 0.1 for all 7 key days (see Table A1). The table also contains mask statistics for the 'train' part of the TIR and 143 channels to assess their adequacy.

These were determined that:

1) The leaders in correlation with TIR in terms of the sum of PLCC when thr changes are the channels of the NIR range (112-144 channels, and 143 is the leader among them), followed by visible green channels.

2) When the threshold value varies from 0.1 to 0.5, the area of the plant mask decreases approximately linearly, by a factor of 2–4 depending on the day. The area of the plant mask reaches a maximum of 2823 pix (near 7/8 of the image) and a minimum of variation (less than 2 times) on day 12.

3) Each step of increasing the threshold (thr) actually removes soil pixels from the mask first, and then pixels where there is an intersection of soil and plants in different proportions. The value thr=0.4 eliminates almost all mixed pixels, thr=0.5 guarantees that the pixel belongs to the inner part of the sheet.

4) The PLCC value on each day is maximum at thr=0.1 and decreases monotonically by 1.5-3 times with an increase in thr, and by day it is maximum on the first day of the experiment (the maximum for channel 143 is 0.75).

A study was also made of the possibilities of controlling the PLCC and RMSE values for plant leaves (thr = 0.4-0.5) by controlling the parameters a,b with the following results:

1) It has been established that due to filtering the mask with parameters a,b, it is always possible to achieve PLCC values of 0.9 and higher on the leading channels in terms of correlation.

2) The effect of decreasing a,b mask size and on the PLCC value increases non-linearly as high PLCC values are approached

3) With a,b filtering, the correlation (PLCC) curve changes and the maximum correlation channel moves to the 143/820nm channel (Table 2).

4) Finally, there is an HSI channel (143/820nm) that guarantees maximum correlation for the non-zero set of channel pixels and the TIR sensor data (mask pixels).

5) RMSE accuracy close to TIR sensor accuracy (0.1°C) is achievable. An increase in PLCC is positively correlated with an increase in accuracy.

The best results have reached in this direction are demonsrated in the Table 3 (for thr 0.4 ,0.5) and Table A2 (for all thr range).

3.2. Dimensionality Reduction of HSI Input Data to Train Them on TIR Values by Finding the Minimum Set of HSI Channels as a High-Level Feature Vector

The solution of the problem is possible in two formulations: 1) as a set of individual solutions for each of the key days; 2) as a single solution that depends not on the day, but on the objective state of plant leaves, recorded by the HSI camera.

Solution 1 is equivalent to assigning an additional feature, the number of the key day. In this case, we must set this feature for the test dataset as well. Although you can try to use this training result on the other days.

Solution 2 is much more interesting, as it should practically expand the range of the HSI sensor with the capabilities of the TIR sensor. We explored both solutions to compare and better exploit their capabilities.

Solution 1. Since the existence of the 143 HSI channel as the most correlated with TIR was demonstrated in the previous subsection, this channel was tested for efficiency first. To combine training on key days into one process, the number of the key day was added as the second feature. The result of studying the dependence of training accuracy on the threshold value that determines the image mask is shown in Table 4.

We can see that the achieved training accuracy (RMSE value) turned out to be almost independent of the threshold value. Here it is important to consider, that RMSE each time is calculated for current mask area. In reality, RMSE sufficiently depends on a,b, and hence on the area of the mask. Reducing the mask by about 1-2% improves the accuracy by 0.01, and cutting the mask by about half improves the accuracy by about 2 times. However, mask reduction it is also a reduction in the training sequence and its possible diversity. This circumstance may not improve, but worsen the accuracy of the prediction, if there has been a truncation of the real diversity of the data. In general, it can be said that temperature prediction in local 2D coordinate system {143 channel value; day} provides a prediction accuracy of the order of 0.2°C.

Solution 2. This solution is focused on finding the minimum set of HSI channels that able to form a high-level feature vector for training HSI pixels on TIR sensor values. The sampling of TIR and HSI pixels during training can be organized in different ways. The most effective way seems to us to be the preliminary segmentation of TIR images, superimposed with HSI. And segmentation grid should be tied to a grid of temperature values with a step of 0.1°C (the accuracy of TIR sensor). The results of the study are shown in Table 5.

Table 5 shows the results of training on 4 sets of HSI channels, including respectively: 204, 146, 37 and 8 channels. For 204 channels, the whole nature of the dependence on the parameters thr and a,b is shown. It can be seen that for a,b=0.1, the value of train RMSE increases for test RMSE by about 2 times (in the lower rows, by 1.5 times). The ratio of train and test is more stable for a,b=0.5. Therefore, in predicting the real accuracy, one should rely on the data for a,b=0.5.

For the remaining 3 variants, the nature and magnitude of the dependence on thr remain very close. Therefore, only the last 2 lines of similar dependencies are shown. The average values for the Test RMSE column of the full tables for each of the options, respectively: 0.26; 0.21; 0.27; 0.28. This suggests that the found combinations of 37 and 8 channels are almost equivalent to the full set of channels, and the found 8 channels are a necessary high-level feature for successful training of HSI pixels with plant temperatures with an accuracy (RMSE) of the order of 0.3°C. A further decrease in the number or changing in composition of channels leads to an increase in the average RMSE to 0.35°C or more.

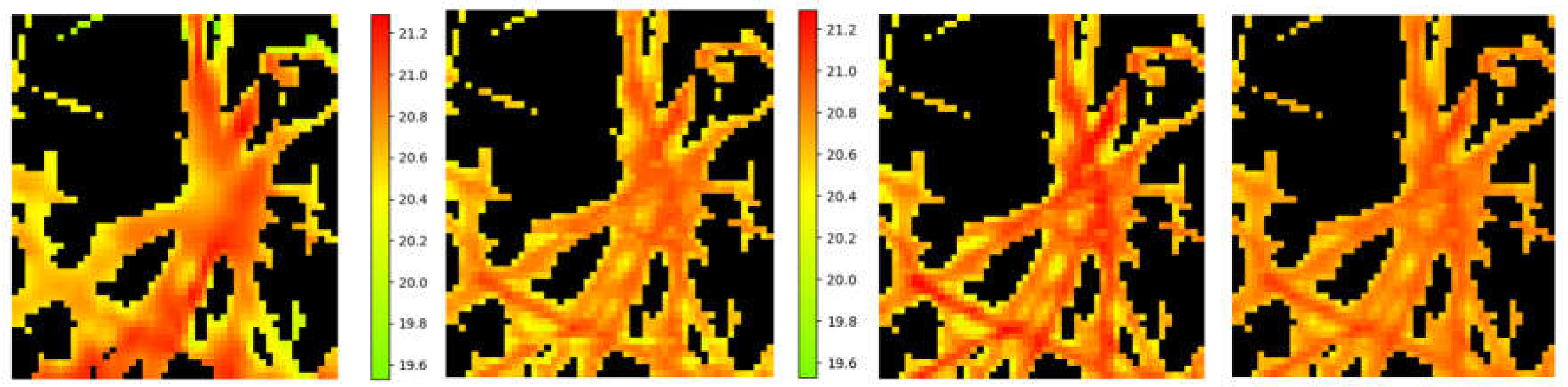
A visual series that deepens the understanding of the obtained results is shown in Figure 5.

4. Conclusion

The results of the search for modern effective solutions to the applied problem of early diagnostics of plant stress using explainable artificial intelligence (XAI) are proposed. Including the analysis of modern publications on the theory and practice of XAI, focused on the use of hyperspectral images (HSI) and Thermal Infra-Red (TIR) images as input data.

Based on this analysis, an XAI neural network was built, which is explainable due to its structure. This network is able to solve the problem of training 204-dimensional HSI pixels to temperatures (TIR sensor values). The purpose of this training is to give any HSI camera an additional TIR channel that will serve as a biologically effective ‘explainator’ for any plant stress early diagnosis network. An example of the implementation of the 'explainator' concept for HSI is shown in the form of a special structure at the input that matches the TIR pixel sample with the sample of days and channels from HSI. The XAI network constructed here can be cosidered as a prototype of a generic XAI explanator or universal XAI-block for an ‘explanator’ propagation, which is assigned to transform explanator specialized on area 1 onto explanator specialized on area 2.

Using the SLP-based XAI regressor, models were trained that are able to predict TIR values with an RMSE accuracy of 0.2-0.3°C using no more than 8 HSI channels. The HSI pixel dimension required to solve the problem with an accuracy of 0.3°C is reduced (dimensionality reduction) from 204 to 8 without using PCA methods, that is, 25 times (which is 5 times higher than in [28]). Data composition of 8 channels in wavelengths (nm): {682, 757, 769, 781, 820, 875, 884, 893}. A channel has been found that has the highest correlation with TIR in terms of PLCC: 143 channel (820nm). The problem of extending the HSI with the temperature attribute of the TIR range with an accuracy of 0.3°С has been solved for the first time.

The constructed model is computationally efficient in training: the training time taken is from 12 to 60 seconds, rarely more on ordinary hardware (Intel Core i3-8130U, 2.2 GHz, 4 cores, 4 GB).

It is planned to continue work in the direction of expanding the application of the model and studying its stability, deepening the explainability of the model.

Author Contributions

Conceptualization and methodology, V.T.; software and validation, M.L, K.P.; formal analysis, M.L.; investigation, E.V., A.G; data curation, M.L.; writing—original draft preparation, M.L.,K.P.; writing—review and editing, V.T.; visualization, M.L.; funding acquisition, V.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Science and Higher Education of the Russian Federation, agreement number 075-15-2020-808.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The used here data of a 25-day experiment on wheat drought with fixation of the state of plants in the control and experimental groups every 2-3 days using three types of sensors (HSI, Thermal IR, RGB) occupy 72.2 GB. The data can be obtained for free using upon request.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Figure A1. Comparison of graphs of average PLCC values by key days of the experiment for 2 datasets of our computational experiment: (a) ‘train’ and (b) ‘test’.

Table A1. Investigation of the correlation between the TIR and values of the 143rd HSI-channel and the accuracy of temperature prediction on mask pixels by the threshold parameter (thr) for the j-th key day (j=1,…,7). The maximum possible Mask for the potted plants is 3136 pixels.

Day (j)	Thre-shold	Mask, pix	Channel, No/nm	PLCC	RMSE, °C	TIR Max	TIR Min	TIR Mean	TIR Std	Chan. Max	Chan. Min	Chan. Mean	Chan. Std
1	0.1	2534	143/820	0.75	0.21	21.5	20.2	20.8	0.23	1.37	0.05	0.53	0.29
1	0.2	2159	143/820	0.70	0.19	21.5	20.3	20.9	0.21	1.37	0.05	0.59	0.27
1	0.3	1702	143/820	0.63	0.19	21.5	20.4	20.9	0.19	1.37	0.16	0.67	0.24
1	0.4	1274	143/820	0.60	0.18	21.5	20.5	21.0	0.18	1.37	0.21	0.74	0.21
1	0.5	867	143/820	0.56	0.17	21.5	20.5	21.0	0.16	1.37	0.32	0.82	0.19

3	0.1	2744	143/820	0.52	0.28	21.5	20.1	20.9	0.23	1.42	0.05	0.49	0.30
3	0.2	2156	143/820	0.41	0.28	21.5	20.1	20.9	0.21	1.42	0.05	0.58	0.27
3	0.3	1643	143/820	0.29	0.29	21.5	20.1	21.0	0.19	1.42	0.16	0.67	0.24
3	0.4	1134	143/820	0.18	0.29	21.5	20.3	21.0	0.18	1.42	0.26	0.77	0.21
3	0.5	700	143/820	0.17	0.26	21.5	20.5	21.0	0.16	1.42	0.42	0.86	0.19

6	0.1	2411	143/820	0.52	0.32	21.6	20.1	20.9	0.24	1.30	0.04	0.57	0.28
6	0.2	2024	143/820	0.45	0.33	21.6	20.1	20.9	0.23	1.30	0.07	0.64	0.25
6	0.3	1633	143/820	0.40	0.32	21.6	20.1	20.9	0.21	1.30	0.11	0.71	0.22
6	0.4	1232	143/820	0.35	0.31	21.6	20.3	21.0	0.21	1.30	0.22	0.77	0.20
6	0.5	824	143/820	0.26	0.32	21.6	20.3	21.0	0.20	1.30	0.33	0.85	0.17

8	0.1	2492	143/820	0.68	0.30	20.9	19.1	20.1	0.30	1.37	0.04	0.62	0.28
8	0.2	2114	143/820	0.63	0.29	20.9	19.3	20.1	0.27	1.37	0.12	0.69	0.24
8	0.3	1761	143/820	0.59	0.28	20.9	19.4	20.2	0.25	1.37	0.19	0.75	0.21
8	0.4	1376	143/820	0.57	0.26	20.9	19.5	20.2	0.24	1.37	0.31	0.81	0.19
8	0.5	952	143/820	0.49	0.26	20.9	19.7	20.3	0.20	1.37	0.38	0.88	0.16

12	0.1	2823	143/820	0.65	0.30	21.4	19.6	20.6	0.30	1.42	0.08	0.70	0.28
12	0.2	2626	143/820	0.61	0.28	21.4	19.8	20.7	0.27	1.42	0.12	0.73	0.25
12	0.3	2359	143/820	0.57	0.26	21.4	19.9	20.7	0.25	1.42	0.20	0.77	0.22
12	0.4	1954	143/820	0.52	0.24	21.4	20.1	20.8	0.21	1.42	0.20	0.83	0.19
12	0.5	1495	143/820	0.47	0.21	21.3	20.2	20.8	0.19	1.42	0.40	0.89	0.17

19	0.1	2367	143/820	-0.54	0.33	22.2	21.2	21.7	0.22	1.59	0.09	0.65	0.30
19	0.2	1940	143/820	-0.49	0.31	22.2	21.2	21.6	0.21	1.59	0.23	0.73	0.27
19	0.3	1546	143/820	-0.49	0.30	22.2	21.2	21.6	0.20	1.59	0.32	0.81	0.25
19	0.4	1124	143/820	-0.43	0.27	22.2	21.2	21.6	0.18	1.59	0.41	0.91	0.22
19	0.5	768	143/820	-0.37	0.25	22.0	21.2	21.5	0.16	1.59	0.59	1.00	0.19

25	0.1	2289	143/820	-0.54	0.35	22.6	21.2	22.0	0.22	1.94	0.17	0.89	0.34
25	0.2	1842	143/820	-0.50	0.34	22.5	21.2	22.0	0.22	1.94	0.28	0.99	0.30
25	0.3	1423	143/820	-0.48	0.33	22.5	21.2	21.9	0.22	1.94	0.39	1.08	0.26
25	0.4	974	143/820	-0.42	0.32	22.4	21.2	21.9	0.21	1.94	0.50	1.19	0.23
25	0.5	588	143/820	-0.38	0.33	22.4	21.2	21.8	0.22	1.94	0.72	1.30	0.20

Table A2. The best accuracies that were achieved using formula (3) for the 143rd channel at all thresholds and small values of a,b in compare with threshold mask area (at a,b=1) and this area without small a,b (out).

Day (j)	Thre-shold	PLCC a,b=1	RMSE ab=1,°C	a	b	Mask, pix	PLCC in	RMSE in, °C	RMSE out, °C	TIR Max	TIR Min	TIR Mean	TIR Std
1	0.1	0.75	0.21	0.1	0.1	1243	0.95	0.14	0.26	21.38	20.45	20.82	0.17
1	0.2	0.70	0.19	0.1	0.1	1110	0.93	0.09	0.26	21.25	20.49	20.85	0.15
1	0.3	0.63	0.19	0.1	0.1	888	0.9	0.08	0.26	21.25	20.58	20.90	0.13
1	0.4	0.60	0.18	0.08	0.08	556	0.91	0.06	0.23	21.25	20.65	20.95	0.11
1	0.5	0.56	0.17	0.06	0.06	316	0.92	0.05	0.2	21.23	20.77	20.99	0.09

3	0.1	0.52	0.28	0.1	0.1	1207	0.92	0.19	0.35	21.50	20.07	20.87	0.23
3	0.2	0.41	0.28	0.08	0.08	735	0.9	0.2	0.32	21.50	20.10	20.92	0.21
3	0.3	0.29	0.29	0.06	0.06	447	0.82	0.2	0.32	21.50	20.10	20.96	0.19
3	0.4	0.18	0.29	0.05	0.05	284	0.64	0.2	0.32	21.50	20.31	21.00	0.18
3	0.5	0.17	0.26	0.04	0.04	141	0.63	0.17	0.29	21.49	20.52	21.04	0.16

6	0.1	0.52	0.32	0.08	0.08	730	0.94	0.16	0.36	21.23	20.58	20.88	0.13
6	0.2	0.45	0.33	0.07	0.07	578	0.93	0.17	0.37	21.18	20.62	20.91	0.11
6	0.3	0.40	0.32	0.05	0.05	353	0.95	0.17	0.35	21.18	20.73	20.94	0.09
6	0.4	0.35	0.31	0.05	0.04	255	0.95	0.17	0.34	21.18	20.77	20.99	0.08
6	0.5	0.26	0.32	0.04	0.04	166	0.9	0.17	0.34	21.18	20.89	21.03	0.05

8	0.1	0.68	0.30	0.1	0.1	887	0.96	0.15	0.36	20.88	19.14	20.05	0.30
8	0.2	0.63	0.29	0.1	0.1	782	0.95	0.13	0.36	20.88	19.29	20.11	0.27
8	0.3	0.59	0.28	0.1	0.1	675	0.94	0.13	0.34	20.88	19.39	20.16	0.25
8	0.4	0.57	0.26	0.1	0.1	559	0.92	0.13	0.32	20.88	19.54	20.22	0.24
8	0.5	0.49	0.26	0.1	0.1	430	0.88	0.15	0.33	20.88	19.69	20.29	0.20

12	0.1	0.65	0.30	0.1	0.1	1063	0.96	0.14	0.37	21.35	19.62	20.64	0.30
12	0.2	0.61	0.28	0.1	0.1	1003	0.95	0.12	0.35	21.35	19.76	20.68	0.27
12	0.3	0.57	0.26	0.1	0.1	921	0.93	0.11	0.33	21.35	19.85	20.71	0.25
12	0.4	0.52	0.24	0.1	0.1	794	0.89	0.09	0.3	21.35	20.09	20.76	0.21
12	0.5	0.47	0.21	0.1	0.1	662	0.84	0.08	0.27	21.33	20.19	20.81	0.19

19	0.1	-0.54	0.33	0.04	0.04	359	-0.99	0.21	0.35	21.86	21.33	21.63	0.13
19	0.2	-0.49	0.31	0.04	0.04	302	-0.98	0.18	0.33	21.81	21.33	21.60	0.11
19	0.3	-0.49	0.30	0.04	0.04	244	-0.98	0.17	0.32	21.76	21.33	21.57	0.11
19	0.4	-0.43	0.27	0.05	0.05	237	-0.95	0.15	0.29	21.73	21.33	21.53	0.09
19	0.5	-0.37	0.25	0.05	0.05	175	-0.91	0.14	0.27	21.65	21.33	21.49	0.07

25	0.1	-0.54	0.35	0.04	0.04	415	-0.98	0.17	0.37	22.23	21.61	22.01	0.10
25	0.2	-0.50	0.34	0.03	0.03	234	-0.98	0.14	0.35	22.17	21.61	21.97	0.09
25	0.3	-0.48	0.33	0.03	0.02	166	-0.99	0.13	0.34	22.13	21.61	21.95	0.09
25	0.4	-0.42	0.32	0.02	0.01	49	-1	0.11	0.33	22.13	21.73	21.90	0.09
25	0.5	-0.38	0.33	0.01	0.01	17	-1	0.11	0.33	21.96	21.67	21.83	0.09

References

Boldú, F.X.P. Deep learning in agriculture: A survey, Computers and Electronics in Agriculture 147 (2018) 70–90. [CrossRef]
Kakogeorgiou, I.; Karantzalos K. Evaluating Explainable Artificial Intelligence Methods for Multi-label Deep Learning Classification Tasks in Remote Sensing. International Journal of Applied Earth Observation and Geoinformation. V. 103, Dec. 2021, 102520, 47pp. [CrossRef]
Wei, K.; Chen, B.; Zhang, J.; Fan, S.; Wu, K.; Liu, G.; Chen, D. Explainable Deep Learning Study for Leaf Disease Classification. Agronomy 2022, 12, 1035. [Google Scholar] [CrossRef]
Liu, Y.; Yue, H. The Temperature Vegetation Dryness Index (TVDI) Based on Bi-Parabolic NDVI-T_s Space and Gradient-Based Structural Similarity (GSSIM) for Long-Term Drought Assessment Across Shaanxi Province, China (2000–2016). Remote Sensing. 2018; 10(6):959. 21pp. [CrossRef]
Kumar, S.; Arya, S.; Jain, K. A SWIR-based vegetation index for change detection in land cover using multi-temporal Landsat satellite dataset. Int. j. inf. tecnol. 14, 2035–2048 (2022). [CrossRef]
Dao, P.D.; He, Y.; Proctor, C. Plant drought impact detection using ultra-high spatial resolution hyperspectral images and machine learning, International Journal of Applied Earth Observation and Geoinformation 102 (2021). [CrossRef]
Grechuka, B.; Gorban, A.N.; Tyukin, I.Y. General stochastic separation theorems with optimal bounds Neural Networks. Volume 138, June 2021, Pages 33-56. [CrossRef]
Gorban, A.N.; Tyukin, I.Y. Blessing of dimensionality: mathematical foundations of the statistical physics of data. Philos Trans R Soc A 2018; 376:20170237. [CrossRef]
Schmitter, P.; Steinrücken, J.; Römer, C.; Ballvora, A.; Léon, J.; Rascher, U.; Plümer, L. Unsupervised domain adaptation for early detection of drought stress in hyperspectral images, ISPRS Journal of Photogrammetry and Remote Sensing 131 (2017) 65–76. [CrossRef]
Shahrimie, M.; Asaari, M. Detection of plant responses to drought using close-range hyperspectral imaging in a high-throughput phenotyping platform, in: 9th Workshop on Hyperspectral Image and Signal Processing : Evolution in Remote, IEEE, Amsterdam, The Netherlands, 2018.
Hernández-Clemente, R.; Hornero, A.; Mottus, M.; Penuelas, J.; González-Dugo, V.; Jiménez, J.C.; Suárez, L. Early diagnosis of vegetation health from high-resolution hyperspectral and thermal imagery: Lessons learned from empirical relationships and radiative transfer modeling, Current Forestry Reports 5 (2019) 169–183. [CrossRef]
Zhang, N.; Guijun, Y.; Pan, Y.; Xiaodong, Y.; Chen, L.; Zhao, C. A review of advanced technologies and development for hyperspectral-based plant disease detection in the past three decades, Remote Sensing 12 (2020) 3188. [CrossRef]
Maximova, I.; Vasiliev, E.; Getmanskaya, A.; Kior, D.; Sukhov, V.; Vodeneev, V.; Turlapov, V. Study of XAI-capabilities for early diagnosis of plant drought, in: IJCNN 2021 : International Joint Conference on Neural Networks, INNS, IEEE, Shenzhen, China, 2021.
Ma, J.; Zheng, B.; He, Y. (2022) Applications of a Hyperspectral Imaging System Used to Estimate Wheat Grain Protein: A Review. Front. Plant Sci. 13:837200. [CrossRef]
Pan, E.; Ma, Y.; Fan, F.; Mei, X.; Huang, J. Hyperspectral Image Classification across Different Datasets: A Generalization to Unseen Categories. Remote Sens. 2021, 13, 1672. [Google Scholar] [CrossRef]
Zhang, Y.; Weng, Y.; Lund, J. Applications of Explainable Artificial Intelligence in Diagnosis and Surgery. Diagnostics 2022, 12, 237. [Google Scholar] [CrossRef] [PubMed]
Lamy, J.-B.; Sekar, B.; Guezennec, G.; Bouaud, J.; Sroussi, B. Explainable artificial intelligence for breast cancer: A visual case-based reasoning approach. Artificial Intelligence in Medicine. 94, 42-53. Epub 2019 Jan 14. PMID: 30871682. [CrossRef]
Lundberg, S.M., Nair, B., Vavilala, M.S., Horibe, M., Eisses, M.J., Adams, T., Liston, D.E., Low, D.K.-W., Newman, S.-F., Kim, J., Lee, S.-I.: Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nature Biomedical Engineering. 2, 749-760 (2018). [CrossRef]
Antoniadi, A.M.; Du, Y.; Guendouz, Y.;Wei, L.; Mazo, C.; Becker, B.A.; Mooney, C. Current Challenges and Future Opportunities for XAI in Machine Learning-Based Clinical Decision Support Systems: A Systematic Review. Appl. Sci. 2021, 11, 5088. 23pp. [CrossRef]
Wang, D.; Yang, Q.; Abdul, A.; Lim, B.Y. Designing Theory-Driven User-Centric Explainable AI. CHI '19: Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems. May 2019. Paper No. 601. 15pp. Glasgow, Scotland UK. [CrossRef]
Vilone, G.; Longo, L. Explainable Artificial Intelligence: a Systematic Review. Okt.2020. 81pp. [CrossRef]
Averkin, A. Explanatory Artificial Intelligence, Results and Prospects. Russian Advances in Fuzzy Systems and Soft Computing: Selected Contributions to the 10th International Conference «Integrated Models and Soft Computing in Artificial Intelligence» (IMSC-2021), May 17–20, 2021, Kolomna, RF. 12pp. https://ceur-ws.org/Vol-2965/paper11.pdf.
Phillips, P.J. et al. Four Principles of Explainable Artificial Intelligence, Draft NISTIR 8312, 2020. [CrossRef]
Gunning, D. DARPA's explainable artificial intelligence (XAI) program. IUI '19: Proceedings of the 24th International Conference on Intelligent User Interfaces, 2019. [CrossRef]
P2976 - Standard for XAI – eXplainable Artificial Intelligence - for Achieving Clarity and Interoperability of AI Systems Design. URL: https://standards.ieee.org/project/2976.
Lysov, M.; Maximova, I.; Vasiliev, E.; Getmanskaya, A.; Turlapov, V. Entropy as a High-Level Feature for XAI-Based Early Plant Stress Detection. Entropy 2022, 24, 1597, 15 pp. [Google Scholar] [CrossRef] [PubMed]
Lysov, M. , Pukhky, K., Turlapov, V. Combined processing of hyperspectral and thermal images of plants in soil for the early diagnosis of drought (2021) CEUR Workshop Proceedings, 3027, pp. 529-541. [CrossRef]
Agilandeeswari, L.; Prabukumar, M.; Radhesyam, V.; Phaneendra, K.L.N.B.; Farhan, A. Crop Classification for Agricultural Applications in Hyperspectral Remote Sensing Images. Appl. Sci. 2022, 12, 1670. [Google Scholar] [CrossRef]
Allegra M, Facco E, Denti F, Laio A, Mira A. Data segmentation based on the local intrinsic dimension. Sci Rep. 2020 Oct 5;10(1):16449. doi: 10.1038/s41598-020-72222-0. PMID: 33020515; PMCID: PMC7536196.
Albergante, L.; Mirkes, E.; Bac, J.; Chen, H.; Martin, A.; Faure, L.; Barillot, E.; Pinello, L.; Gorban, A.; Zinovyev, A. Robust and scalable learning of complex intrinsic dataset geometry via ElPiGraph. Entropy 2020, 22(3), 296. [Google Scholar] [CrossRef] [PubMed]
Bac, J.; Mirkes, E.M.; Gorban, A.N.; Tyukin, I.; Zinovyev, A. Scikit-Dimension: A Python Package for Intrinsic Dimension Estimation. Entropy 2021, 23, 1368. [Google Scholar] [CrossRef] [PubMed]
Gorban, A.N.; Grechuk, B.; Mirkes, E.M.; Stasenko, S.V.; Tyukin, I.Y. (2021) "High-Dimensional Separability for One- and Few-Shot Learning" Entropy 23, no. 8: 1090. [CrossRef]

Figure 1. The original image from TIR sensor in color scale (left), the result of the temperature prediction (right) of (courtesy of the authors [27] Figure 8).

Figure 2. An interface for constructing and examining a plant mask, equipped with the control of the thr,a,b parameters and windows for observing changes in correlation and regression.

Figure 3. PLCC absolut values averaged over key days for various threshold values driving the mask, without any restrictions by a,b parameters (a=b=1). X-axis is wavelength for HSI channels (nm).

Figure 4. The structure of our SLP regressor as an example of the XAI network implementation.

Figure 5. From left to right in the same color scale image for one pot on key day 12: 1) TIR image; 2) the training result of our XAI on 8 channels using a mask with parameters thr=0.4, a,b=0.5; 3) the result of calculation by formula (3) at a,b=1 and RMSE=0.1; 4) the result of calculation by formula (3) at a,b=0.1 and RMSE=0.1.

Table 1. Plant pots included in the 'train' and 'test' parts.

Key day No	1	3	6	8	12	19	25
Train pots No	5	11	9	5	10	5	8
Test pots No	8	8	8	8	8	4	10

Table 2. Examples of accuracy in terms RMSE, which have been reached for different threshold and a,b values.

Day	Best Ch., No/nm	Thre-shold	a	b	Mask, pix	PLCC	RMSE, °C
1	58/566	0.4	1	1	1274	0.616	0.159
1	144/823	0.5	1	1	867	0.57	0.151
1	143/820	0.5	0.1	0.1	483	0.827	0.056
3	55/557	0.4	1	1	1134	0.325	0.207
3	52/549	0.5	1	1	700	0.277	0.194
3	143/820	0.5	0.1	0.1	349	0.48	0.067
6	53/551	0.4	1	1	1232	0.464	0.212
6	118/745	0.5	1	1	824	0.41	0.214
6	143/820	0.5	0.1	0.1	337	0.685	0.058
8	117/742	0.4	1	1	1376	0.596	0.212
8	117/742	0.5	1	1	952	0.496	0.205
8	143/820	0.5	0.15	0.15	590	0.774	0.085
12	142/817	0.4	1	1	1954	0.576	0.198
12	141/814	0.5	1	1	1495	0.537	0.181
12	143/820	0.5	0.1	0.1	662	0.836	0.06
19	145/826	0.4	1	1	1124	-0.465	0.306
19	145/826	0.5	1	1	768	-0.414	0.264
19	143/820	0.4	0.1	0.1	482	-0.795	0.18
25	128/775	0.4	1	1	974	-0.434	0.364
25	143/820	0.5	1	1	588	-0.384	0.371
25	129/778	0.4	0.1	0.1	398	-0.815	0.184
25	116/739	0.5	0.1	0.1	171	-0.828	0.189
25	143/820	0.4	0.05	0.05	166	-0.957	0.189

Table 3. The best accuracies that were achieved using formula (3) for the 143rd channel at thresholds of 0.4, 0.5 and small values of a,b in compare with threshold mask area (at a,b=1) and this area without small a,b (out).

Day (j)	Thre-shold	PLCC a,b=1	RMSE a,b=1,°C	a	b	Mask in,pix	PLCC in	RMSE in, °C	RMSE out, °C
1	0.4	0.60	0.18	0.08	0.08	556	0.91	0.06	0.23
1	0.5	0.56	0.17	0.06	0.06	316	0.92	0.05	0.2
3	0.4	0.18	0.29	0.05	0.05	1134	0.18	0.29	0.32
3	0.5	0.17	0.26	0.04	0.04	700	0.17	0.26	0.29
6	0.4	0.35	0.31	0.05	0.04	255	0.95	0.17	0.34
6	0.5	0.26	0.32	0.04	0.04	166	0.9	0.17	0.34
8	0.4	0.57	0.26	0.1	0.1	1376	0.57	0.26	0.32
8	0.5	0.49	0.26	0.1	0.1	952	0.49	0.26	0.33
12	0.4	0.52	0.24	0.1	0.1	1954	0.52	0.24	0.3
12	0.5	0.47	0.21	0.1	0.1	1495	0.47	0.21	0.27
19	0.4	-0.43	0.27	0.05	0.05	237	-0.95	0.15	0.29
19	0.5	-0.37	0.25	0.05	0.05	175	-0.91	0.14	0.27
25	0.4	-0.42	0.32	0.02	0.01	49	-1	0.11	0.33
25	0.5	-0.38	0.33	0.01	0.01	17	-1	0.11	0.33

Table 4. Investigation of the dependence of training accuracy on the value of the threshold and a,b parameters that together determines the Mask for Train and Test datasets.

Thre-shold	a=b	TrainMask pix	TestMask pix	Train RMSE	Test RMSE	Epoch	Time, sec
0.1	1	16541	17660	0.23	0.22	112	44
0.1	0.5	16121	17333	0.21	0.20	97	37
0.1	0.1	6870	7227	0.15	0.11	188	31
0.2	1	13636	14861	0.26	0.21	236	77
0.2	0.5	13333	14633	0.20	0.20	209	68
0.2	0.1	5769	6207	0.15	0.11	200	29
0.3	1	11146	12067	0.22	0.20	146	39
0.3	0.5	10938	11920	0.21	0.19	79	20
0.3	0.1	4740	5137	0.12	0.11	113	13
0.4	1	8581	9068	0.20	0.20	221	45
0.4	0.5	8465	8985	0.19	0.19	254	52
0.4	0.1	3777	3938	0.09	0.10	225	12
0.5	1	6126	6194	0.19	0.19	106	16
0.5	0.5	6074	6164	0.20	0.18	252	153
0.5	0.1	2762	2828	0.10	0.11	266	41

Table 5. Investigation of the dependence of training accuracy on the value of the threshold and a,b parameters that together determines the Mask for train and test datasets.

Number of channels	Thre-shold	a=b	Train mask,pix	Test mask,pix	Train RMSE,°C	Test RMSE,°C	Epoch	Time, sec
204	0.1	0.5	16121	17333	0.21	0.34	48	35.35
204	0.1	0.1	6870	7227	0.14	0.27	99	34.1
204	0.3	0.5	10938	11920	0.21	0.28	61	37.64
204	0.3	0.1	4740	5137	0.11	0.21	238	61.41
204	0.4	0.5	8465	8985	0.17	0.27	120	66.75
204	0.4	0.1	3777	3938	0.10	0.21	316	57.65
204	0.5	0.5	6074	6164	0.15	0.25	105	48.57
204	0.5	0.1	2762	2828	0.08	0.24	266	46.39
146 (15-160)	0.5	0.5	6074	6164	0.16	0.20	294	98.05
146 (15-160)	0.5	0.1	2762	2828	0.11	0.14	278	33.17
37*	0.5	0.5	6074	6164	0.20	0.25	132	19.19
37*	0.5	0.1	2762	2828	0.14	0.19	207	13.84
8**	0.5	0.5	6074	6164	0.24	0.27	293	34.82
8**	0.5	0.1	2762	2828	0.18	0.21	201	12.14

37* - channels {9, 12, 14, 22, 25, 28, 36, 47, 56, 59, 71, 75, 82, 85, 88, 90, 95, 108, 111, 116, 120, 122, 126, 131, 133, 136, 139, 143, 150, 153, 157, 162, 165, 167, 178, 186, 190} selected as local extremums. 8** - channels {97, 122, 126, 130, 143, 161, 164, 167} selected as average by key days PLCC at thr=0.5, a=b=0.1 on channel 143. Channel-corresponding PLCC values PLCC {0.22, 0.61, 0.67, 0.56, 0.75, 0.21, 0.15, 0.14}.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer