A Different Geometric Approach to the Proof of Fermat’s Last Theorem

Preprint

Article

A Different Geometric Approach to the Proof of Fermat’s Last Theorem

Altmetrics

Downloads

130

Views

133

Comments

Elkhan Beylar Beylarov^*,Ilyas Ravan Hasanov

This version is not peer-reviewed

This preprints belongs to the Topic

Mathematical Modeling

Submitted:

10 January 2023

Posted:

11 January 2023

You are already at the latest version

Alerts

Abstract

This paper presents a new approach to a different proof of "Fermat's Last Theorem.” For the proof of the theorem, it is proposed to use a more straightforward geometrical approach. A special family of curves, the Elba curves, is introduced to facilitate the proof. This approach makes the proof easier to comprehend by mathematicians and those interested in the subject.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

Introduction

Mathematicians have long struggled to solve a theorem that French mathematician Pierre Fermat proposed back in the 17th century, later called "Last Fermat's Theorem" (LFT). Many famous scientists tried to prove the theorem, but they only managed to prove its special cases. Fermat knew the proof of this theorem only for the case of the 4th power. [Edwards, 1980]. Later, Euler, Dirichlet, Legendre, and Lame were able to prove the theorem for certain special cases. The proof of the general case of the theorem was attributed to Andrew Wales, who spent a long enough time solving it (Wiles, 1995). This proof was published in the Annals of Mathematics in 1995, and an issue of the journal contained just this proof. Although Wiles's proof was regarded as a great innovation and the opening of a new page for the history of mathematics, the 130-page proof pushed mathematicians to search for alternative and simpler proofs. This article is one of the attempts to search for a more practical, simple proof of the theorem.

A Brief Literature Review

It is stated that the proof of the last Fermat's theorem, which has not been solved for nearly three centuries, is self-evident only when the power is 4 (Edwards, 1980). Some also note that although Fermat did not write the proof of the theorem, he knew the proof himself (Poulkas, 2020). About a century later, Euler was able to prove the theorem for the case where the power was 3, and two centuries later, Dirichlet and Legendre proved the theorem for the case when the power was 5. Lame demonstrated the theorem for the case where the power was 7. Wels announced that he had proved the theorem in 1993, but after the presentation, it was revealed that there was a flaw in the proof. Wiles presented the final proof of the theorem two years later, in 1995, together with his former student Taylor (Taylor, Wiles, 1995). Wiles and Taylor's proof is very long, some 130 pages. Considering this, later, many mathematicians worked on the existence of more straightforward alternative ways of proof. As an example, we will mention several approaches that have been proposed in recent times. Agofontsev (2012) and Gevorkyan (2020a, 2020b) investigated the theorem for certain cases and obtained some general conclusions. Poulkas (2020) states his results regarding the proof of both LFT and his proposed Generalized Fermat's Theorem (the case when there are n terms in the sum) using number theory. Gevorkyan (2022) presents his results for the proof of the theorem using calculus, number theory, and a geometric approach. In order to contribute to the mathematical literature towards the existence of simpler, alternative proofs of Fermat's Last Theorem, this paper presents a different proof of the theorem using a geometric approach and special types of curves.

Methodology and Used Mathematical Tools

Although certain tools of mathematical analysis and number theory are used to prove the theorem in this article, the geometrical approach is the main focus. A special family of curves called Elba curves is introduced to facilitate the proof.

A New Approach to Theorem Proof, Results, and Their Discussion

There are many different approaches [3] to Fermat's last theorem (FLT). In this study, we will consider an interesting new approach.

Theorem (FLT): For an arbitrary integer n>2, there are not such integers a, b and c (a,b,c>0) satisfying the formula aⁿ + bⁿ = cⁿ [5].

In other words: the indeterminate equation xⁿ + yⁿ = zⁿ has no integer solution for n≥3 [6].

Fermat's theorem can be expressed in a more general way, taking into account not only natural but also negative values of “n.”

Theorem 1: The equation

a^{n} + b^{n} = c^{n}

does not have any solution for n (including negative values of n) in integers (i.e. a, b, c are integers) except n=2 and n=1.

This theorem will be formulated in more detail below as Theorem 3.

It is clear that for n=1 and n=2, there are infinitely many solutions satisfying the equation aⁿ+bⁿ=cⁿ [1]:

With n=2 we get Pythagorean triples 3²+4²=5² or 5²+ 12² = 13² etc.
For n=1 any numbers like 5¹ + 7¹ = 12¹ etc.

As we have already mentioned, positive integers a, b, and c satisfying the equality aⁿ + bⁿ = cⁿ form Pythagorean triples for n=2 [1]. This also means that the numbers that are solutions to the equation are the sides of a right triangle. That is, from them, one can build a triangle, and this triangle will be right-angled. Hence, these numbers satisfy the triangle inequalities:

a+b>c, a+c>b, b+c>a, c-b<a, c-a<b [1]

Theorem 2. Arbitrary positive numbers a, b and c satisfying the equality aⁿ + bⁿ = cⁿ (for n>1) must satisfy the triangle inequalities, i.e., the inequalities a+b>c; a+c>b; b+c>a; c-b<a; c-a<b b-a<c should hold.

In other words, when n>1, the numbers a, b, and c satisfying the equation aⁿ + bⁿ = cⁿ must be the sides of any triangle. For 1<n<2, this triangle will be obtuse, with n=2, it will be right-angled, and for n>2, it will be acute-angled.

To prove it, let us consider three possible cases of expressions a + b and c for positive integers a, b, and c satisfying the equation aⁿ + bⁿ = cⁿ.

1. a+b=c 2. a+b<c 3. a+b>c

1. For a+b=c, raising both sides of the equation to the n-th power, we get:

aⁿ +...+ bⁿ = cⁿ

On the left-hand side of the equation, we get the positive terms of the binomial expansion between the first and last terms. If we subtract the positive terms from the left-hand side of the binomial expansion, then we end up with aⁿ + bⁿ < cⁿ. This contradicts the equation aⁿ + bⁿ = cⁿ. That is, if aⁿ + bⁿ = cⁿ, then the first option, i.e., a+b=c is impossible.

2. If a+b<c, then it is clear that (a+b)ⁿ < cⁿ and aⁿ +...+ bⁿ < cⁿ. Then, if we subtract from the left side of the inequality, the positive terms between the first and the last terms of the binomial expansion, the expression on the left side will get even smaller.

That is, aⁿ + bⁿ << cⁿ, which contradicts the case aⁿ + bⁿ = cⁿ. Therefore, the 2nd case is also impossible.

3. Thus, the 3rd case, i.e. a+b>c, is the only possible one.

3.1. For the case 0<n<1, the triangle inequality is not applied; on the contrary, the following inequalities are applied (Figure 1):

a+b<c; a<c-b and b<c-a

Example: (25)^1/2 + (49)^1/2=(144)^1/2 25+ 49 < 144 etc.

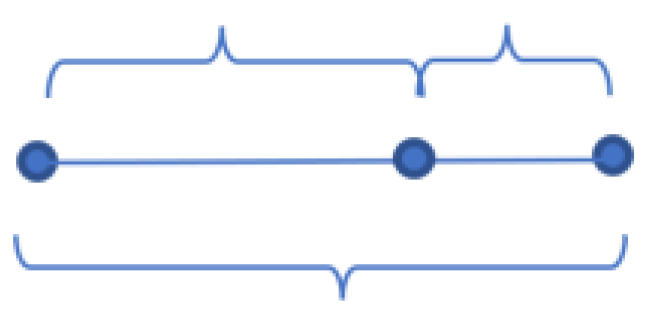
3.2. In the case of n=1, the only possible case is a+b=c. This is expressed by a point located at distances a and b, respectively, from the endpoints on segment c (Figure 2);

Figure 2.

3.3. With 1<n<2, a, b, and c will be the sides of an obtuse-angled triangle (Figure 3);

3.4. With n=2, a, b, and c will be the sides of a right triangle.

3.5. With 2<n, a, b, and c will be the sides of an acute-angled triangle.

Let's consider several theorems and their proofs in the direction of proving Fermat's theorem:

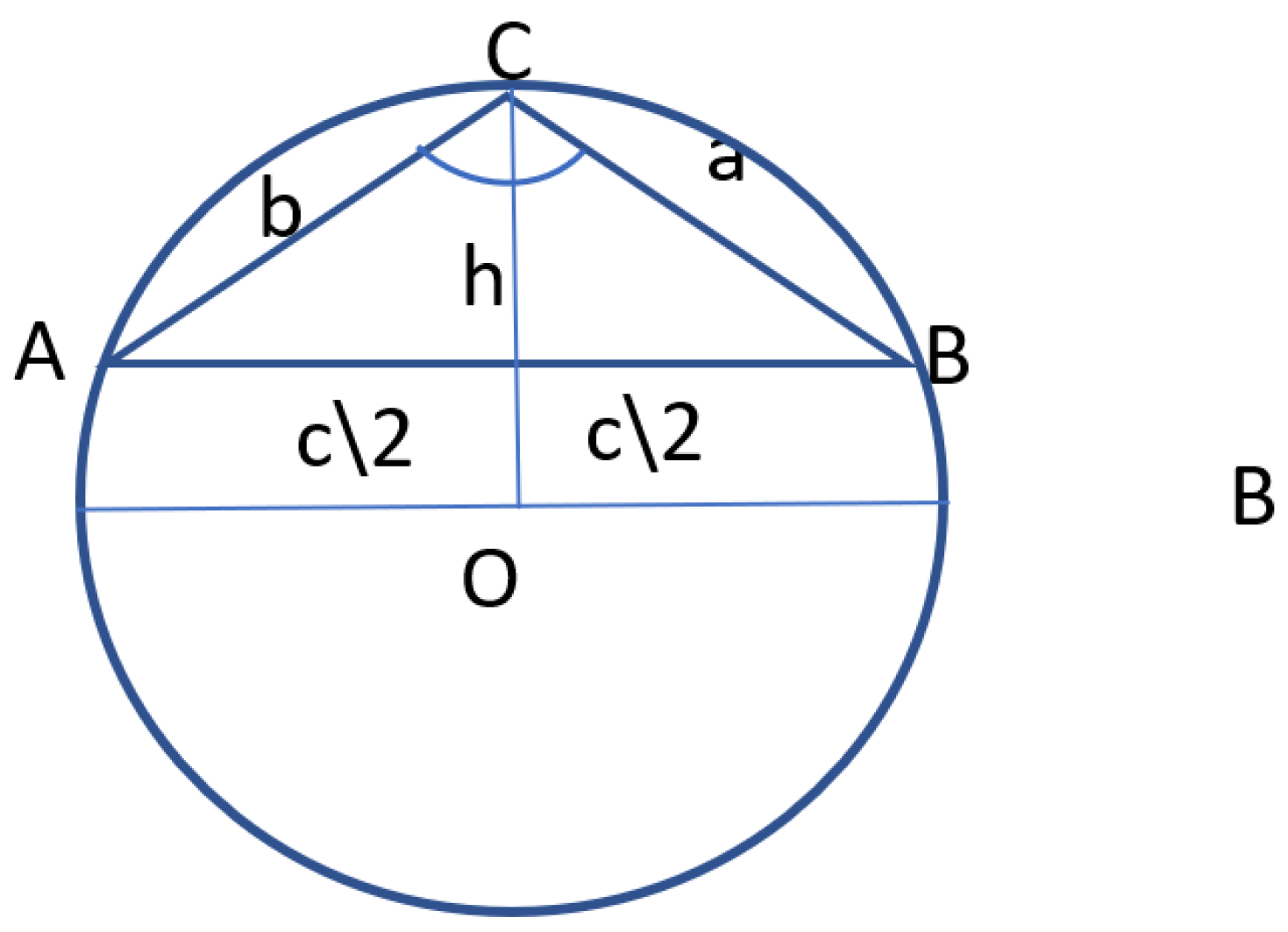
Theorem 3: For arbitrary real numbers 0<a<b<c, there always exist real numbers n>1 and 0<m<1 such that the equations aⁿ + bⁿ = cⁿ and a^m = b^m + c^m are satisfied

Proof: if we divide both sides of the equation by cⁿ, we get

{(\frac{a}{c})}^{n} + {(\frac{b}{c})}^{n} = 1

Here, the function y=

{(\frac{a}{c})}^{x}

is monotonically decreasing (Figure 4, graph 1), and the function y=1-

{(\frac{b}{c})}^{x}

is monotonically increasing (Figure 4, graph 2). Since the domain and image sets of the functions are (-∞,+∞), their graphs must intersect at one point. (See Figure 4.)

For an arbitrary triangle ABC, the abscissa (x) of the intersection point of the graphs of functions y=1-

{(\frac{b}{c})}^{n}

and y=

{(\frac{a}{c})}^{n}

will satisfy the equation a^x+b^x=c^x.

The part of “Theorem 3” related to the equation a^m = b^m + c^m is proved similarly.

Note that in the case of 0<a<b<c, it is impossible to get a real number “k” that satisfies the equation b^k = a^k + c^k. This is because a is less than b, and c is greater than b. For any arbitrary value of k in the expression b^k = a^k + c^k, one of the expressions a^k and c^k will be positive numbers greater than b^k, and the other one less than b^k.

Thus, Theorem 3 is proved.

This means that for any triangle, there are always numbers “n” and “m” such that they satisfy the condition aⁿ + bⁿ = cⁿ for the biggest side, and a^m = b^m + c^m for the smallest side of the triangle.

There is no corresponding number “k” that satisfies the condition b^k = a^k + c^k for the middle side "b" of the triangle.

In our view, the truth of this theorem is one of the most important points complicating the proof of Fermat's theorem in a general form. While so far, attempts have been made to prove that a, b, and c cannot be simultaneous integers or that they cannot be coprime for natural values of n greater than 2 (n>2).

From "Theorem 3," one can see that the search for such contradictions about a, b, c in the equation aⁿ + bⁿ = cⁿ, assuming "n" to be a natural number, will not give any results. The presence of a rational or irrational "n" that satisfies the condition aⁿ + bⁿ = cⁿ for arbitrary a, b, c makes it impossible for there to be a contradiction in this direction.

Note that the correctness of "Theorem 3" requires a change in the direction of the search for the proof of LFT. In other words, Theorem 4 can be formulated as follows:

Theorem 4. There is no integer n greater than 2 (2<n) that satisfies the equation aⁿ+bⁿ=cⁿ for arbitrary integers a, b, c.

Theorem 4" fundamentally differs from "Theorem F" in the formulation of the problem. But the proof of "Theorem 4" will also be the proof of "Theorem F.”

Note. Finding a general formula for "n" that satisfies the condition aⁿ + bⁿ = cⁿ for an arbitrary triangle is a time-consuming technical task. Finding a general formula for "n" is related to the problem of finding the formula for the "logarithm of the sum" (log(f(x) + g(x)) =?). Finding the first will contribute to the solution of the second.

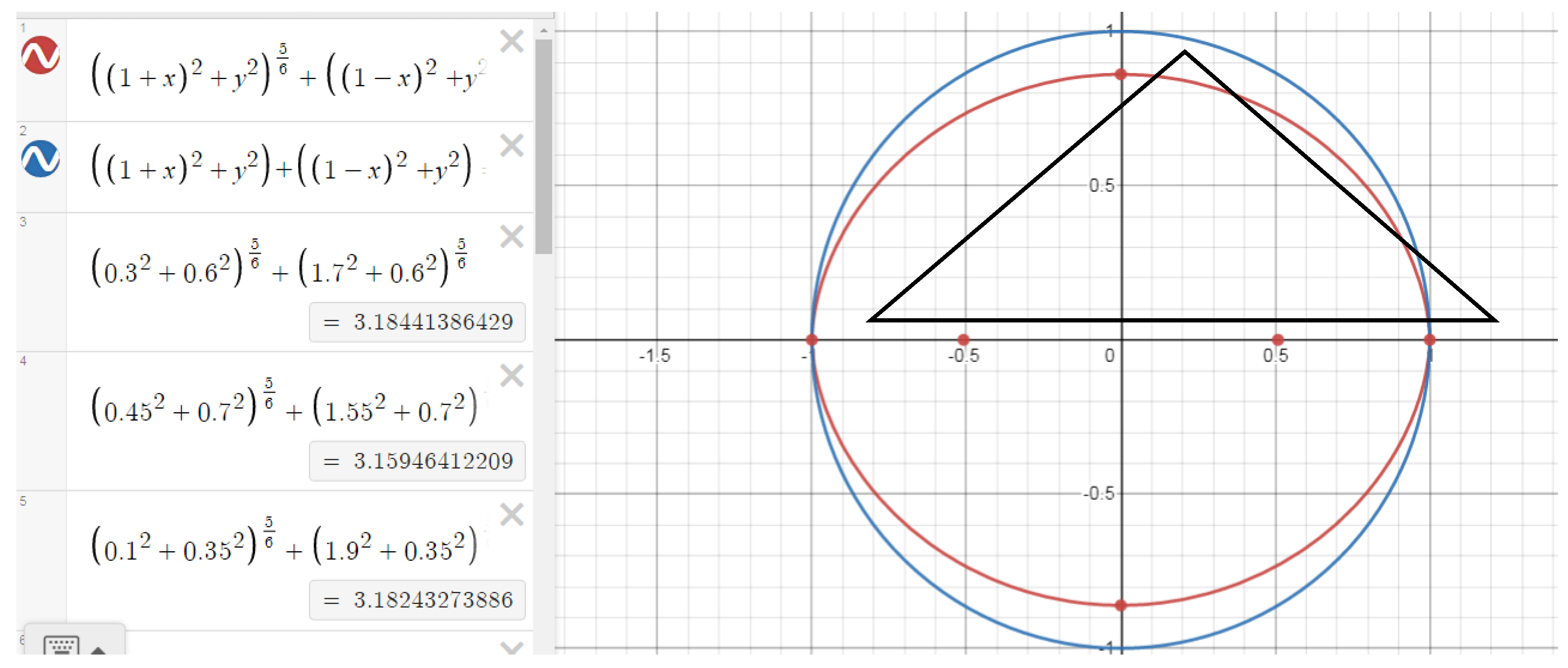
For equilateral triangles, the general formula for n satisfying the condition aⁿ + bⁿ = cⁿ can be obtained as follows:

\frac{c}{2} : a = s i n \frac{C}{2}; c = 2 a s i n \frac{C}{2}; s i n \frac{C}{2} = \frac{c}{2 a} h = a c o s \frac{C}{2}; c o s \frac{C}{2} = \frac{h}{a};

See Figure 5.

Since a=b in an equilateral triangle, we can write the equation aⁿ+bⁿ=cⁿ as: aⁿ+aⁿ=cⁿ

Here we get the following:

2 a^{n} = (2 a {s i n \frac{C}{2})}^{n} \to 1 = 2^{n - 1} {(s i n \frac{C}{2})}^{n} \to 2^{1 - n} = {(s i n \frac{C}{2})}^{n} \to 2^{\frac{1 - n}{n}} = s i n \frac{C}{2};

If we take the logarithm of both sides of this expression to base 2, we get:

\frac{1 - n}{n} = {l o g}_{2} s i n \frac{C}{2} \to \frac{1}{n} - 1 = {l o g}_{2} s i n \frac{C}{2} \to n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}}

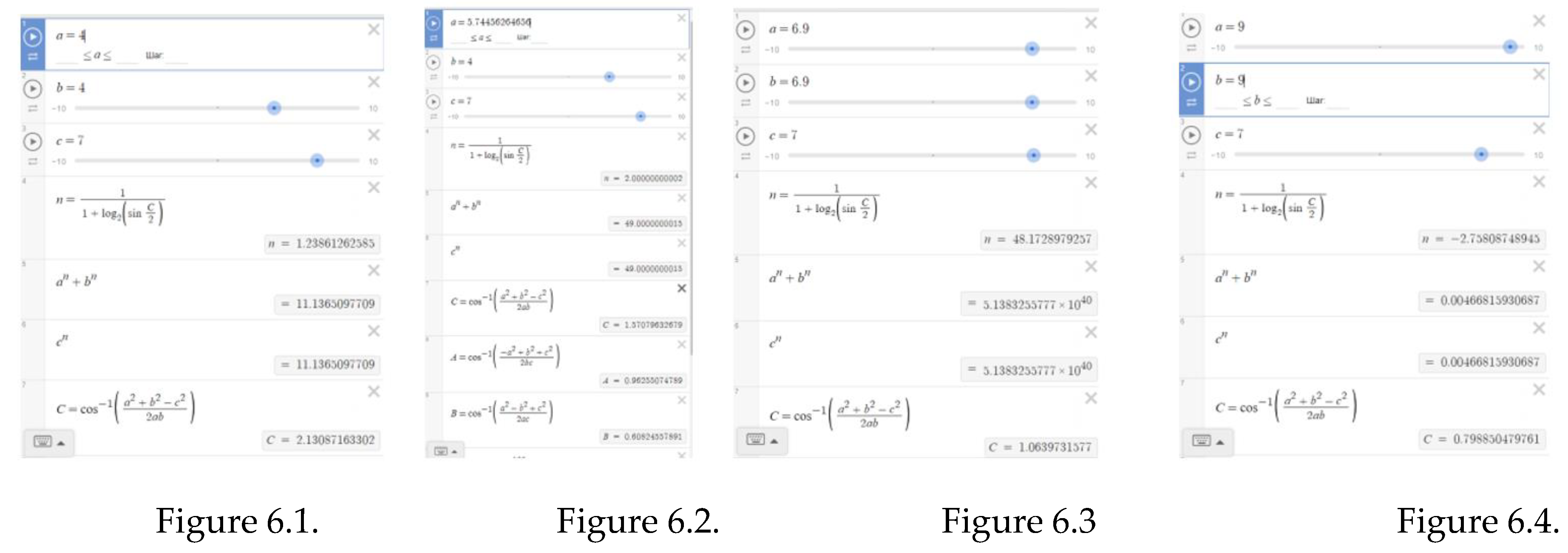
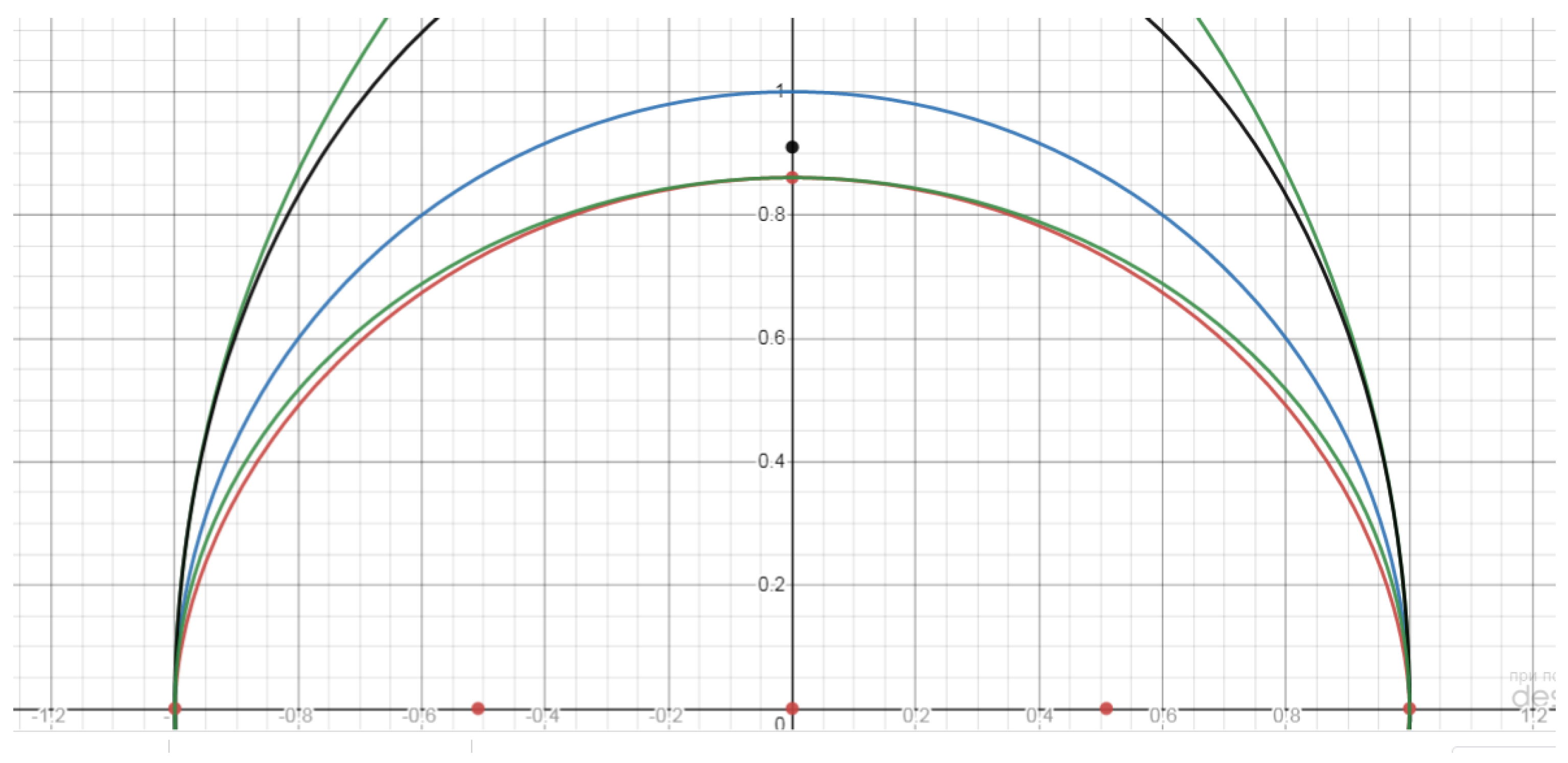
Based on the conducted studies, the following can be noted (see Figure 6.1 - 6.4)

6.1. if C – is an obtuse angle of an equilateral triangle case (Figure 6.1.)

With a=4; b=4; c=7 , according to formula

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}}

n=1.23861262585 and aⁿ+bⁿ=cⁿ=11.1365097709

6.2. The case of approaching to a right triangle (Figure 6.2.)

With a=5.74456264656; b=4; c=7 , according to formula

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}}

n=2.00000000002 and aⁿ+bⁿ=cⁿ=49.0000000015

6.3. As the triangle approaches to an equilateral one, n approaches to infinity (Figure 6.3).

With a=6.9; b=6.9; c=7 , according to formula

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}}

n= 48.1728979257 and aⁿ+bⁿ=cⁿ=5.1383255777x10⁴⁰

6.4. When angle C is acute, the value of n is negative (Figure 6.4).

With a=9; b=9; c=7, according to formula

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}}

n= -2.75808748945 and aⁿ+bⁿ=cⁿ=0.00466815930687

6.5. with a+b=c, n=1.

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}} (B 1)

The formula (B1) is true for arbitrary isosceles triangles, except for equilateral triangles. Since sin30^o=1/2 in the expression (aⁿ+aⁿ=aⁿ) for an equilateral triangle, the denominator of the expression becomes "0" and we get an uncertainty of the form 1/0.

In the following analysis, we will show that the case of an equilateral triangle is also a limiting case for Elba curves (Elkhan Baylarov).

For isosceles triangles, we express the general formula of “n” with the ratio of the sides, with the formula without an angle. If

aⁿ+aⁿ=cⁿ 2aⁿ=cⁿ

If we divide both sides by cⁿ, we get:

2 ({\frac{a}{c})}^{n} = 1

If we take logarithm of both sides to base 2, we get the following:

1 + n \log_{2} \frac{a}{c} = 0 n = - \frac{1}{\log_{2} \frac{a}{c}} (B 2)

Let’s compare formulas (B1) and (B2):

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}}

(B1)

m = - \frac{1}{\log_{2} \frac{a}{c}}

(B2)

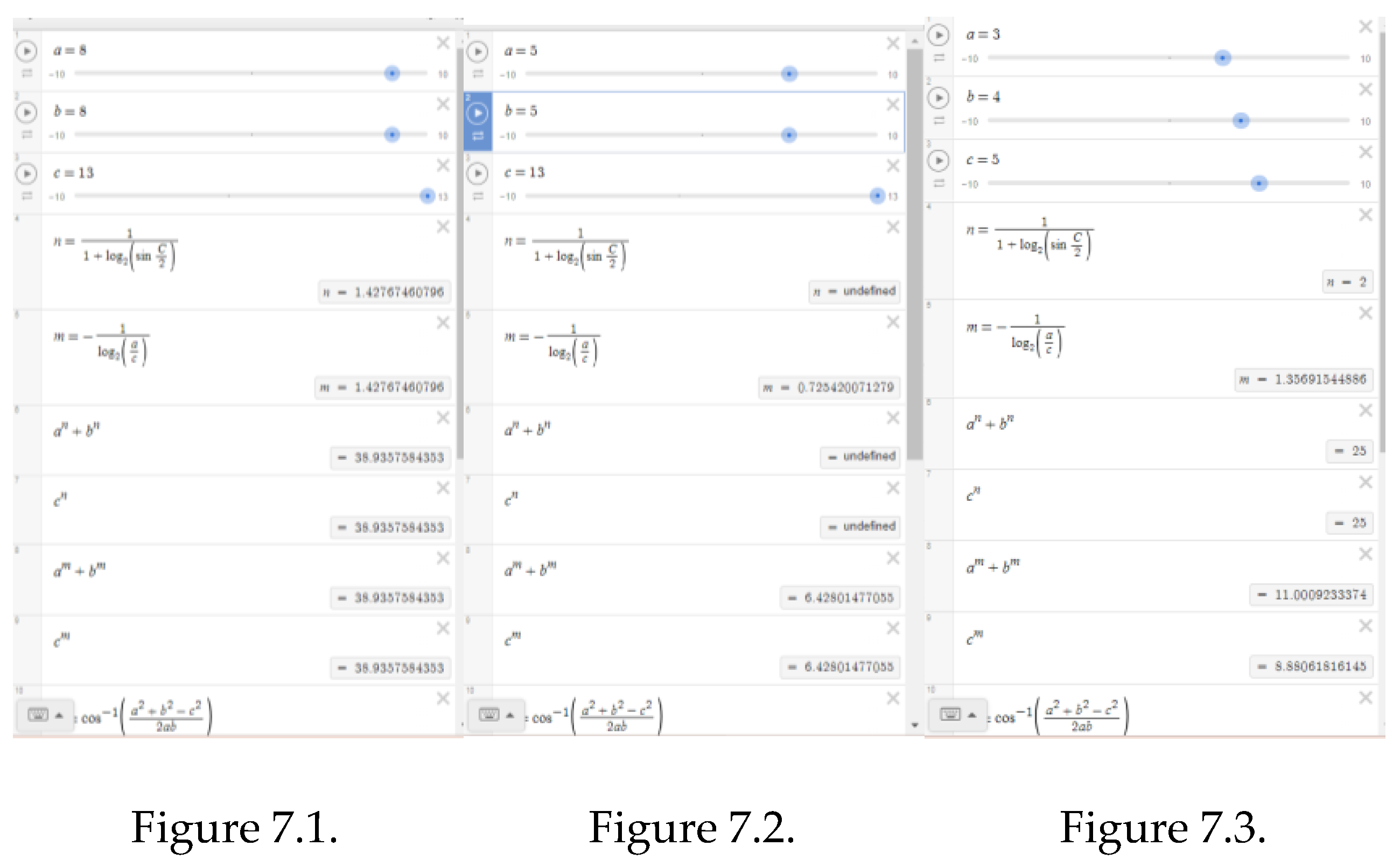
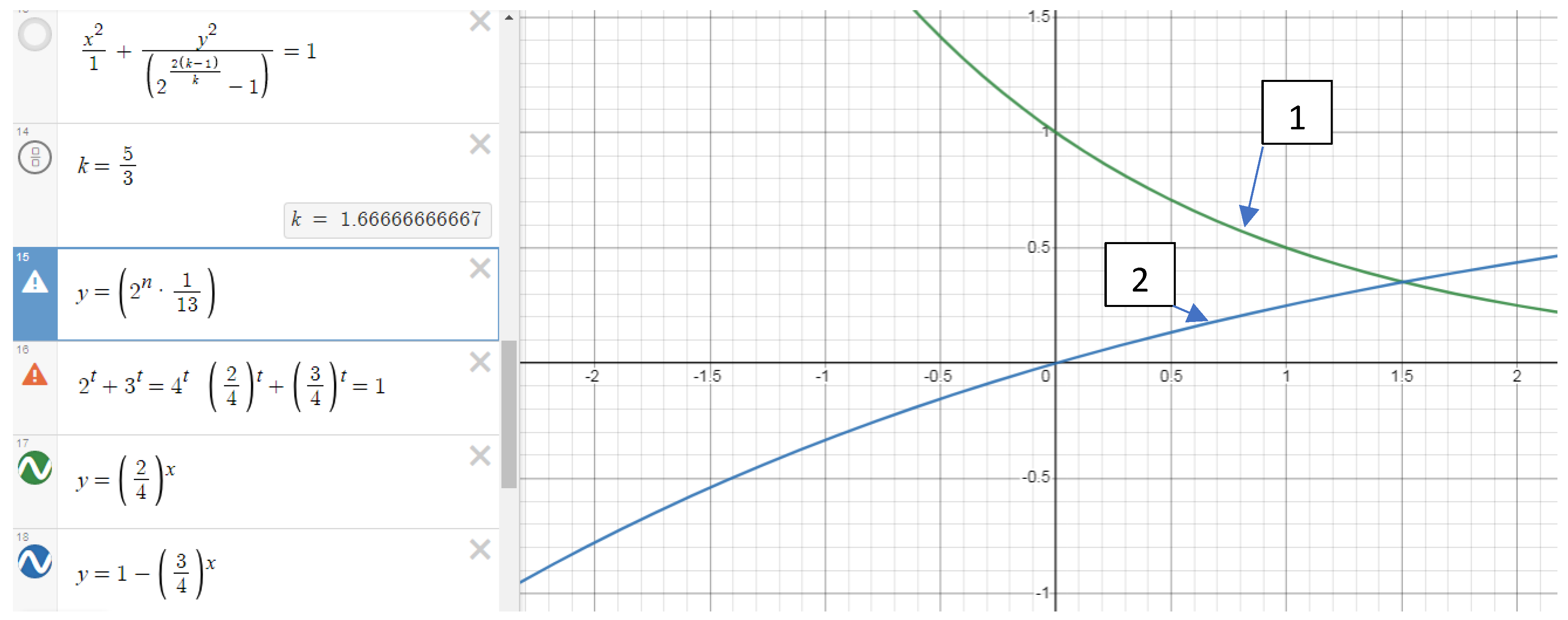
1 For isosceles triangles, both formulas are equally satisfied (Figure 7.1. In the Figure the power of "n", calculated by the formula (B2), is marked with "m" so as not to create contradictions in the Desmos calculator.).

If a=8, b=8, c=13,

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}} = 1.42767460796

(B1)

n = - \frac{1}{\log_{2} \frac{a}{c}} = 1.42767460796

(B2)

Here according to the formulas (B1) and (B2):

aⁿ+bⁿ = 38.9357584353

cⁿ = 38.9357584353

aⁿ+bⁿ=cⁿ

2 When a=b and the numbers a, b, c do not form a triangle, since there is no angle C, formula (B1) cannot be calculated – we get an uncertainty.

But in this case, formula (B2) can be calculated and aⁿ+bⁿ = cⁿ is satisfied.

(Figure 7.2. In the Figure power of "n", calculated by the formula (B2), is marked with "m" so as not to create contradictions in the Desmos calculator).

When a=5, b=5, c=13

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}} = u n c e r t a i n t y

(B1)

n = - \frac{1}{\log_{2} \frac{a}{c}} = - 0.725420071279

(B2)

For “n” calculated by the formula (B1), we get:

aⁿ+bⁿ - uncertainty

cⁿ - uncertainty

For “n” calculated by the formula (B2), we get:

aⁿ+bⁿ = 6.42801477055

cⁿ = 6.42801477055

aⁿ+bⁿ = cⁿ

3 It is strange that although the formula (B1) is written for equilateral triangles, it is also valid for all right triangles - Pythagorean numbers (for n=2).

Because with C=90^o

s i n \frac{C}{2} = \sqrt{\frac{2}{4}} = 2^{- \frac{1}{2}}

and from formula (B1) we get n=2.

However, formula (B2) is not applied for non-isosceles right triangles, (Figure 7.3. In Figure the degree of "n", calculated by the formula (B2), is marked with "m" so as not to create contradictions in the Desmos calculator).

If a=3, b=4, c=5 then

n = \frac{1}{1 + {l o g}_{2} s i n \frac{C}{2}} = 2

(B1)

n = - \frac{1}{\log_{2} \frac{a}{c}} = 1.35691544886

(B2)

For n calculated from formula (B1) we get:

aⁿ+bⁿ = 25

cⁿ = 25

aⁿ+bⁿ=cⁿ

For “n” calculated by formula (B2), we get:

aⁿ+bⁿ = 11.0009233374

cⁿ = 8.88061816145

aⁿ+bⁿ ≠ cⁿ

As odd as it may sound, it is so, and it would be interesting to find out why.

In general, we can formulate "Theorem 5" for triads that can be sides of a triangle.

Theorem 5: For an arbitrary triangle with sides a, b, c, there exists a real number “n” such that aⁿ+bⁿ=cⁿ.

Since this proposition is a special case of Theorem 3, it can be proved in a similar way.

Note that the Pythagorean theorem is a special case of Theorem 5.

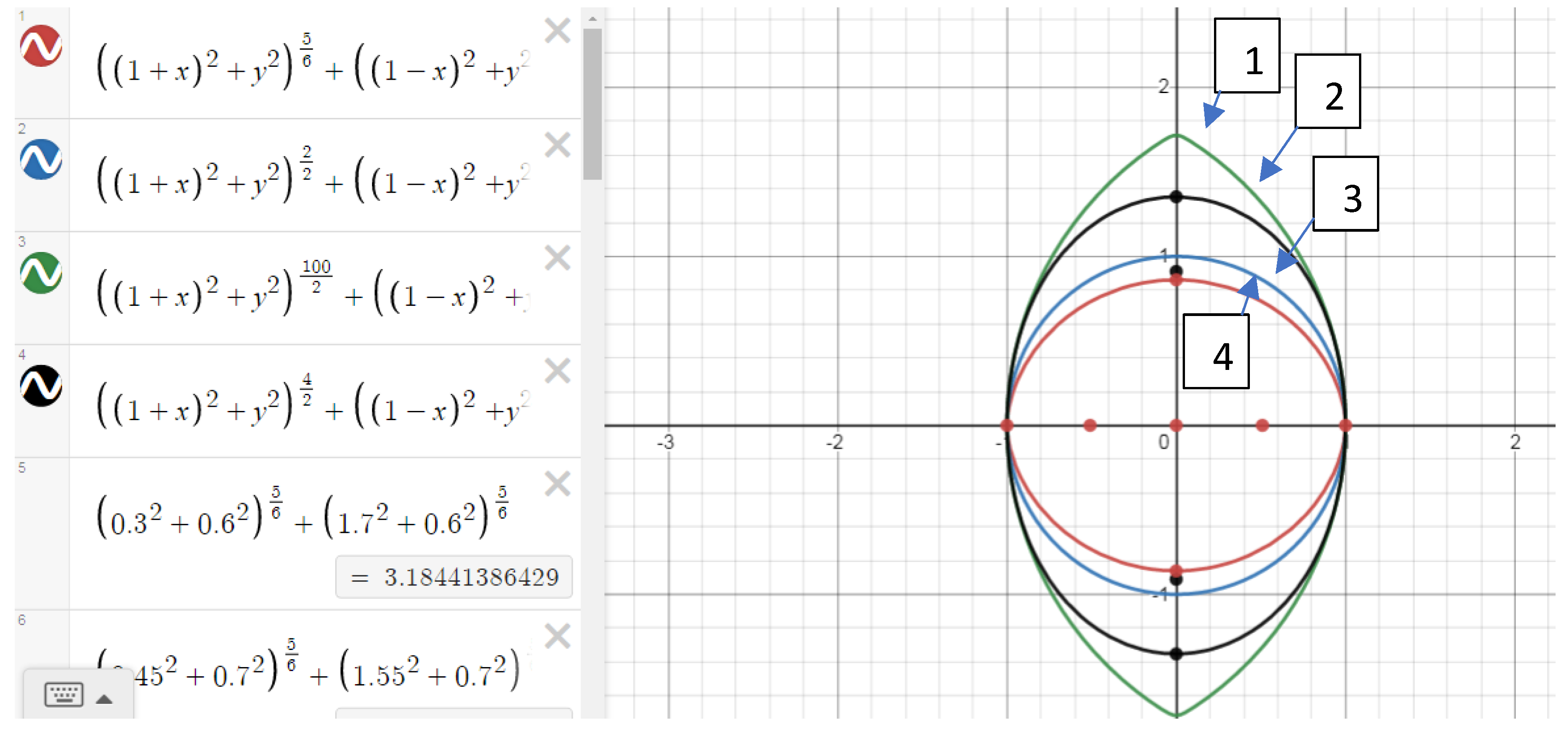
The Elba Curves

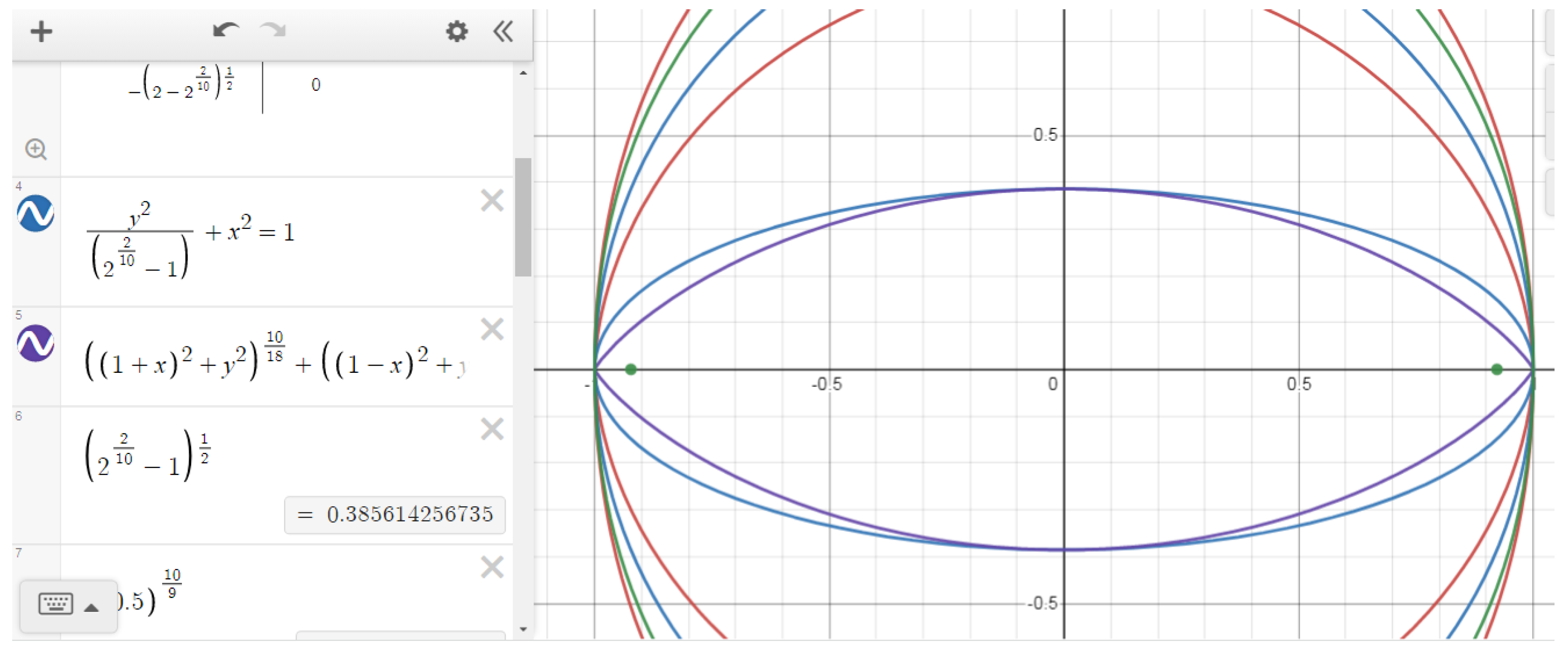
Suppose a, b, c are sides of a triangle and satisfy the condition aⁿ+bⁿ=cⁿ for 1<n<2. Then the solution of the equation (a/c)ⁿ+(b/c)ⁿ=1 with respect to a, b, c will be on the special ellipse-like curves located within a unit circle centered at the origin. We name these family of curves as the Elbe curves (Beylarov E.B.) (Figure 8, graph 2 - ellipse, graph 3 - Elba).

In the case of 1<n<2, the minor semi-axis of Elba curves is less than the radius of the circle, and the major semi-axis is equal to the radius of the circle (Figure 8, graph 3).

In the case of n=2, we get the equation of the unit circle centerd at at origin. (a/c)²+(b/c)²=1. Elba coincides with the unit circle (Figure 8, graph 1).

In the case of 2<n solutions of the equation (a/c)ⁿ+(b/c)ⁿ=1 lie outside of the unit circle centered at the origin, the minor semi-axis is equal to the radius of the circle, the major semi-axis is greater than the radius of the circle, on the an ellipse-like, Elba curve (Figure 9, graphs 1, 2 are the Elbe curves).

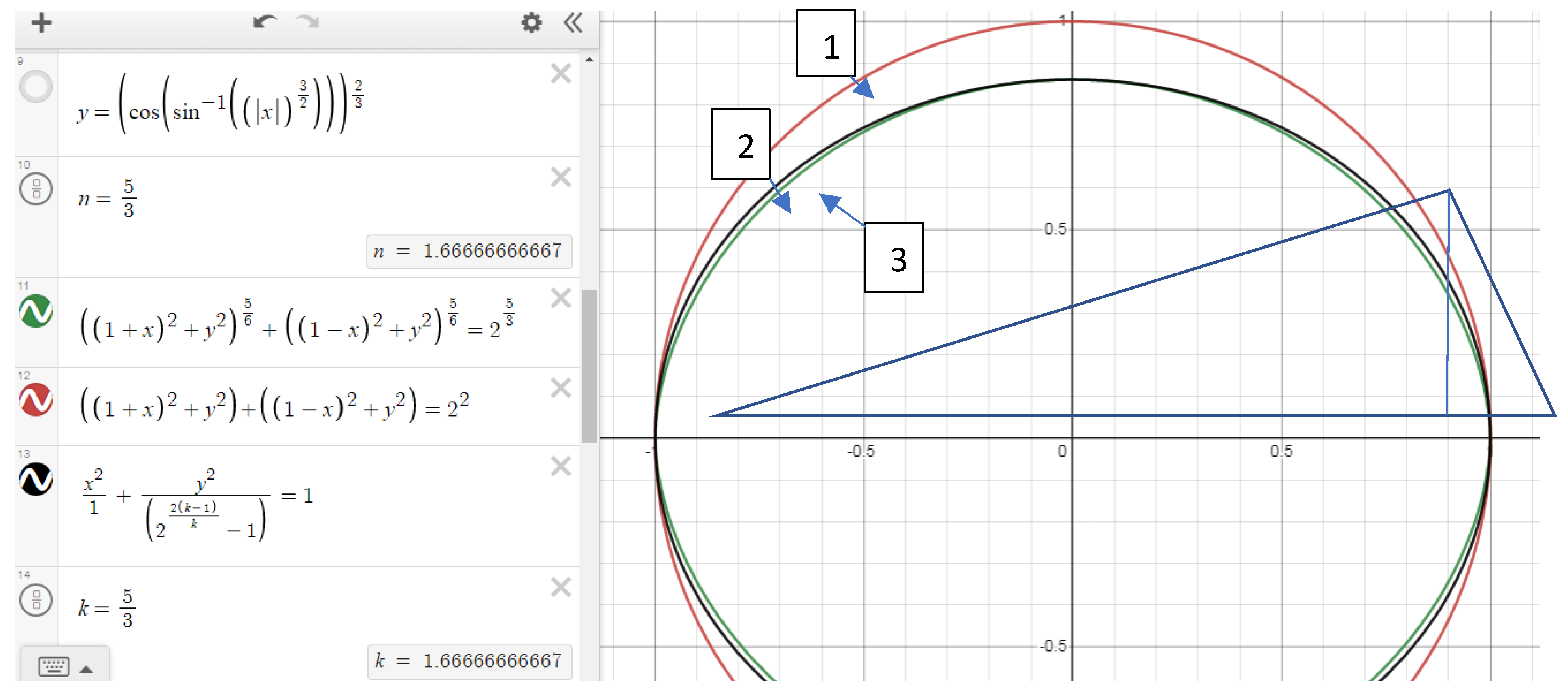
For clarity, hereafter, we will call these curves the Elba curves (Elkhan Beylarova). In Figure 8, the 1st equation is for the Elba, the 2nd equation is for the circle, and the 3rd equation is for the ellipse.

As we already mentioned, although the Elba curve looks like an ellipse with equal major and minor axes, indeed it is a different figure. This can also be seen visually by writing down the corresponding formula of the ellipse with respect to the corresponding semi-axes by observing the graphs.

The Elbe curve is also not a circular arc. This can also be proven by writing the equation of a circle passing through three points.

The angles that subtend the same chord on an arc of a circle are equal, but the angles that subtend the same chord on the Elba differ in magnitude. This is another proof that this is not an arc of a circle.

Note: a) for all right triangles obtained locating the hypotenuse on the diameter of a circle, and moving the vertex on the circle, the sides and the angles adjusent to the base change, but the angle at the vertex (C=90^o) and the n's (n=2) do not change;

b) for the triangles obtained locating the biggest side on a circle’s diameter, and moving the vertex on the Elba, the sides and all angles of the triangle change, but “n” does not change.

For all triangles inside the Elba, n’s that satisfy the condition (a/c)ⁿ+(b/c)ⁿ=1 are fixed.

For further clarity, all the above-mentioned points about Elba curves can also be shown on the coordinate plane.

For example, to build an Elba curve for n=5/3, we would do the following.

Expressing the sides of the triangle in terms of the x, y coordinates, we obtain the Elba equation and its graph for an arbitrary n in the unit circle:

{({(1 + x)}^{2} + y^{2})}^{\frac{n}{2}} + {({(1 - x)}^{2} + y^{2})}^{\frac{n}{2}} = 2^{n}

For n=2 we get an equation of the circle (Figure 8, graph 1):

{({(1 + x)}^{2} + y^{2})}^{1} + {({(1 - x)}^{2} + y^{2})}^{1} = 2^{2}

For n=5/3 we get the equation of the Elba (Figure 8, graph 3):

{({(1 + x)}^{2} + y^{2})}^{\frac{5}{6}} + {({(1 - x)}^{2} + y^{2})}^{\frac{5}{6}} = 2^{\frac{5}{3}}

The curve in the middle, very close to the Elba curve, whose semi-major axis is 1 and whose semi-minor axis is equal to the Elba's minor semi-axis, is a graph of an ellipse. Its equation is shown at the bottom of the figure (Figure 8, graph 2).

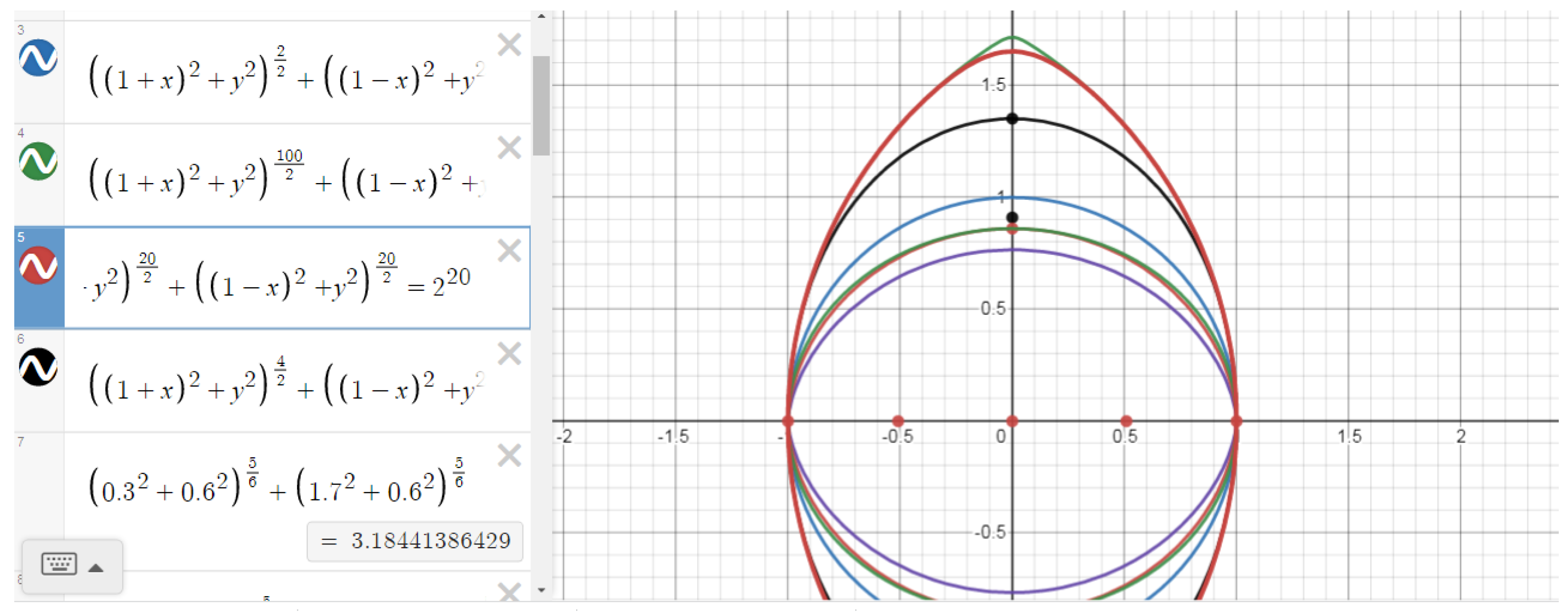
Figure 9 shows graph 1 for n=100; graph 2, for n=4, graph 3, for n=2 circle, graph 4 for n=5/3 – Elba graphs are displayed.

So the circle is also a special case of the Elba with n=2.

Let us show the calculation of the minor semi-axis of the Elba.

Let's use the known equation (a/c)ⁿ+(b\c)ⁿ=1.

For the Elba whose major semi-axis is 1 will have c=2. So,

(a/2)ⁿ+(b/2)ⁿ=1

where a=b

2(a/2)ⁿ=1 → (a/2)ⁿ=1/2 → a/2=(1/2)^1/n → a=2(1/2)^1/n→a=2^(n-1)/n

Therefore, for a unit circle a=b - in the case of an isosceles triangle:

a=b=2^(n-1)^/n

In this case, the minor semi-axis of the Elba will be:

y_x=0= (a²-1²)^1/2=(2^2(n-1)/n-1)^1/2(Figure 9.).

This expression can be obtained easily by assuming x=0 from the equation a²=(1+x)²+y²:

y_x=0²= a²-1² here y_x=0=(2^2(n-1)/n-1)^1/2

In this case, the minor semi-axis of the Elba is y_x=0, and the major semi-axis is x_y=0:

y_x=0= (a²-1²)^1/2=(2^2(n-1)/n-1)^1/2

x_y=0=1

For the minor semi-axis of the Elba within the unit circle, the following can be noted:

1) when n=1 it is "0";

2) In the case of 1<n<2, it is less than the radius of the unit circle, i.e., 1;

3) when n=2 it is equal to 1.

4) In the case of 2<n, it will be greater than 1 (Figure 10).

Lemma 1. When dividing the sides of triangles by the largest side and multiplying by 2, since the largest side is 2, the largest value of the semi-axis on the Y axis of the Elba curves in the positive direction approaches to 3^1/2 (square root of 3) and is approximately equal to 1.73205080757.

Proof: For the largest values of N, when the sides grow and approach to the base, i.e., 2, we get an equilateral triangle. Its height will be h_y² = 2²-1²=3 or h_y = 3^1\2.

This value can be calculated similarly on an arbitrary circle.

Here are some important facts about Elba curves:

For any Elba, in cases where n≠2, n≠1, and c=2, the sides of an isosceles triangle are irrational numbers. Because:

aⁿ+aⁿ=2ⁿ → 2aⁿ=2ⁿ→ aⁿ=2ⁿ:2→aⁿ=2^n-1→ a=2^(n-1)/n

Therefore, the sides of an isosceles triangle in the Elba are irrational in all cases where the side c is an integer or a rational number.

2.: This semi-axis is the height of the corresponding isosceles triangle, and its square is equal to the difference of the square of the side and the square of the half of the base. That is:

Y²_x=0= a²-1²; → Y_x=0²=2^2(n-1)/n-1 → Y_x=0=(2^2(n-1)/n-1)^1/2

This means that the vertical semi-axis of an arbitrary Elba is an irrational number.

3.: The value of the semi-axis of the Elba, along the Y-axis, increases and decreases depending on n.

Let's clarify the dependence of "n" on the vertical axis in Elba.

It is clear that,

tgα=Y_x=0 or tgα=y → tgα=(2^2(n-1)/n-1)^1/2→tg²α=(2^2(n-1)/n-1) → 2^2(n-1)/n= tg²α+1

Here, if we take the logarithm of both sides to base 2, we get:

log₂2^2(n-1)\n= log₂(tg²α+1) →2(n-1)\n= log₂(tg²α+1) →2-2\n= log₂(tg²α+1) →

2- log₂(tg²α+1)=2\n→ n=2\(2- log₂(tg²α+1))(və ya n=1\(1+ log₂cosα))

This shows that in the case of tgα=1, n=2 is obtained, which is the case when the Elba and the circle coincide.

4.: The circle is a special case of the Elba when n=2.

Let us consider some special cases on this issue.

For example, consider the case n=5/3. So: a ^5\3+b^5\3=c^5\3. By dividing boths sides of the equation by c^5\3 and multiplying by 2n, this triangle can be built on the diameter of a unit circle.

Note (Figure 11): for n=5\3 for a triangle that satisfies the condition a ^5\3+b^5\3=c^5\3 we could write the following:

(a\c)^5\3+ (b\c)^5\3=1

a²=(1+x)²+y² (1) → a=((1+x)²+y²))^1\2

b²=(1-x)²+y² (2) → b=((1-x)²+y²))^1\2

From the difference of equations (1) and (2), we get that:

a²-b²=4x;

a²+b²=2+2x²+2y²=2(1+x²+y²)

It would be appropriate to investigate these cases for different values of x and y in the circle, ellipse, and Elba.

(a\c)ⁿ+(b\c)ⁿ=1

For the Elbe, whose semi-major axis is equal to one C=2. Hence, we get (a\2)ⁿ+(b\2)ⁿ=1. From where when a=b, we get:

2(a\2)ⁿ=1 → (a\2)ⁿ=1\2 → a\2=(1\2)^1\n → a=2(1\2)^1\n→a=2^(n-1)\n

Therefore, in a unit circle a=b - the case of an isosceles triangle:

a=b=2^(n-1)\n

In this case, the minor semi-axis of the Elba:

y_x=0= (a²-1²)^1\2=(2^2(n-1)\n-1)^1\2

This expression can be obtained easily by taking x=0 from the equation a²=(1+x)²+y² :

y²_x=0= a²-1² here y_x=0=(2^2(n-1)\n-1)^1\2

In this case, the minor semi-axis of the Elba is y_x=0, and the major semi-axis is x_y=0:

y_x=0= (a²-1²)^1\2=(2^2(n-1)\n-1)^1\2

x_y=0=1

For the semi-focal distance f for the corresponding semi-axial ellipse, we get:

f=(1- y_x=0²)^1\2

For simplicity of calculations and expressions, here, without loss of generality, we can take c = 2 so that the radius of the circle under consideration and the major semi-axis of the corresponding ellipse are equal to one.

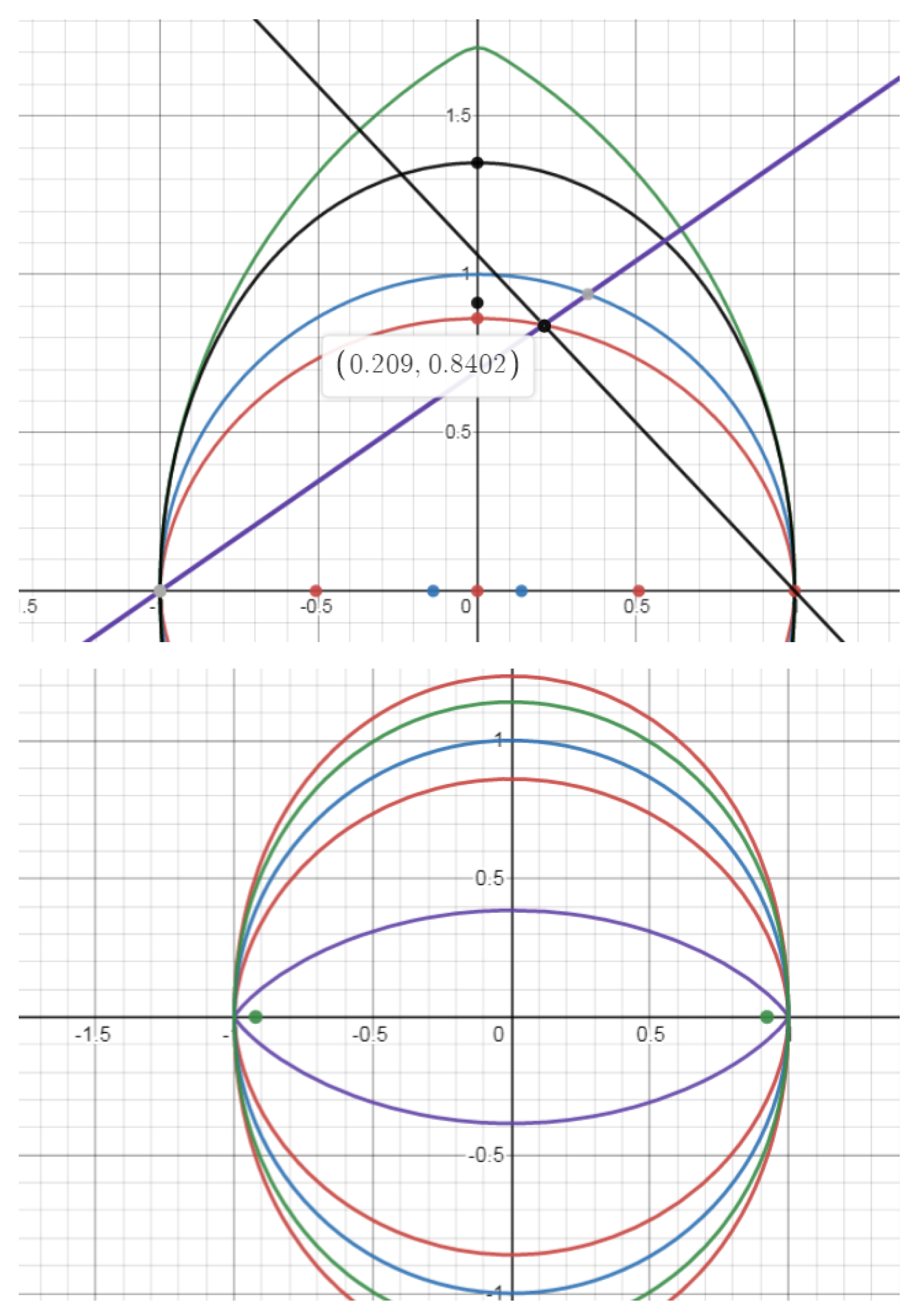
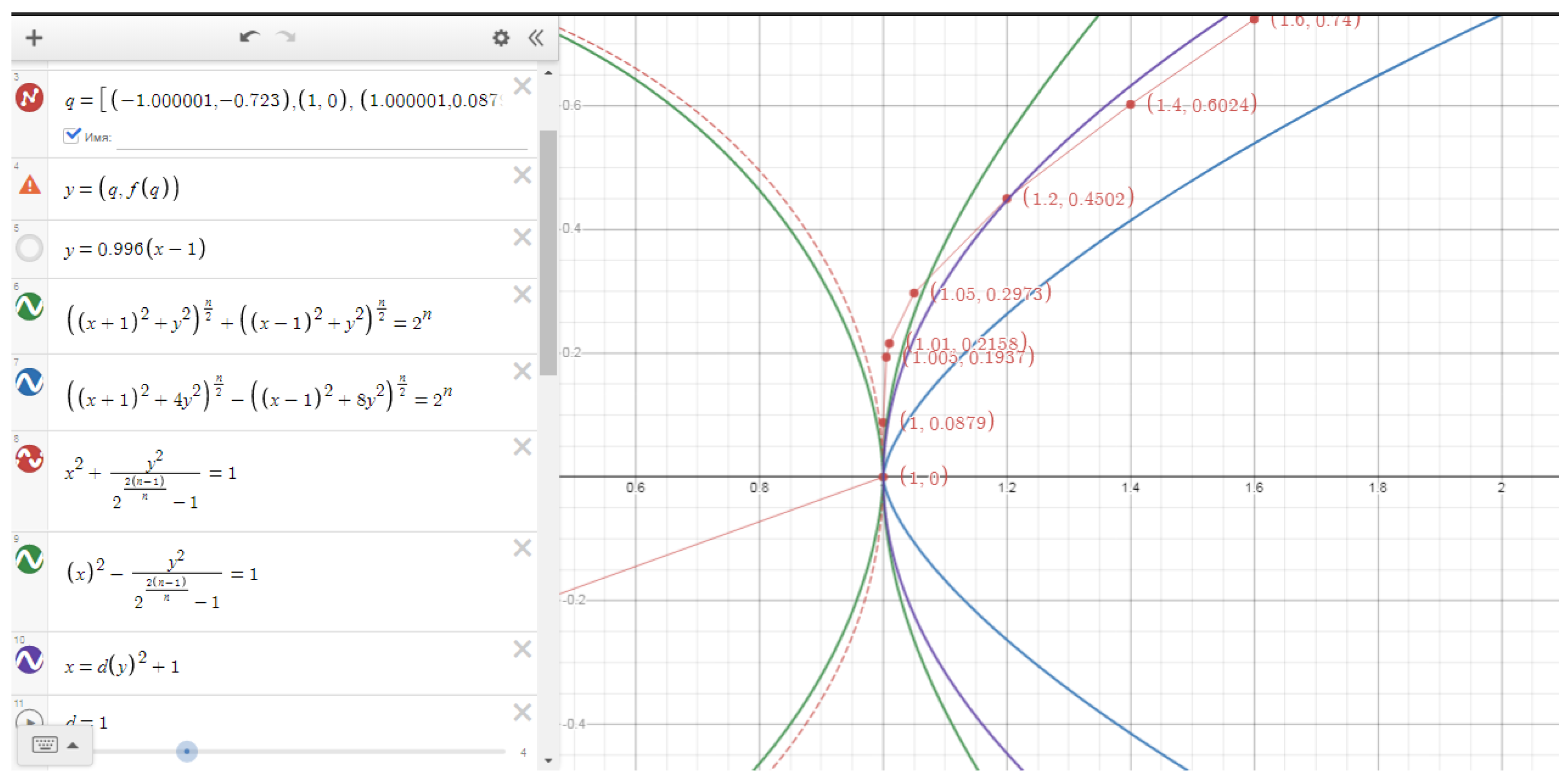
Figure 12 shows the graphical differences between the Elba curve (red) and the ellipse (green), in which the major and minor semi-axes coincide for the case of n=5\3.

Figure 13 demonstrates the graphical differences between the Elba curve (blue) and the ellipse (blue), the major and minor semiaxes of which coincide, for the case of n=10\9.

From a comparison of these two graphs, it can be seen that as the value of n approaches unity, the difference between the ellipse and Elba curves is more clearly observed.

As can be seen from Figure 14, as the value of “n” increases (for example, n=20 in the Figure 14, graph 2), one of the numbers a and b, or both of them (if they are close or equal to each other), approaches to "c.” Of course, since the numbers "α" and "b" are less than the number "c" and the number c remains constant, the graphs will infinitely approach to the Elbe (Figure 14, graph 1) with the largest (here n=100) “n” (Figure 14, graph 1).

Here we would like to raise an interesting question. Figure 15 shows the formulas for transforming Elba and Ellipse into a hyperbola.

Depending on the coefficients of the terms of y² in the Elba formula, the direction of the branches/sides of the curve changes. Studying these cases will reveal interesting facts.

An interesting fact is that a circle is a special case of an ellipse with equal semi-axes. At the same time, the circle is a special case of Elba when n=2. In this case, it is doubtful that there is a connection between the Elba and the ellipse. The discovery of this relation would clarify many characteristics of the Elba curves that would contribute to the solution of Fermat's theorem.

Now let's focus on a few learned facts about the circle, ellipse, and the Elba.

The study showed that:

1): In case 1<n<2, the Elba curve and the ellipse with equal semi-axes are inside the unit circle, and the Elba is inside of the ellipse;
2): in case n=2 Elba, circle and ellipse overlap each other;
3): In the case of 2<n, the ellipse is inside of the Elba, and this situation continues until the value 2<n<4.8... (this is an approximate value).
4): After the value n=4.8... (this is an approximate value), the ellipse again begins to move away from the Elba, and after a certain value, it completely goes beyond its limits.
5): It makes sense to find the logical and geometric explanation of this situation - its meaning, whether such transitions occur at higher values of n.

Although many issues related to Elbe curves have been investigated, we consider it expedient to confine ourselves to their interpretation here. In the following articles, we will clarify these issues and our research on the proof of Fermat’s last theorem.

Note: The problem of proving Fermat's theorem for triangles, by applying the sines theorem shows that the equation aⁿ+ bⁿ=cⁿ and the equation sinⁿα+ sinⁿβ=sinⁿɣ are equally valid, and makes it possible and necessary to use the knowledge about triangles.

Proof of Fermat's Theorem based on solving triangles

Fermat's Last Theorem states that for any natural number, n >2, the equation

a^{n} + b^{n} = c^{n}

has no solutions in non-zero integers

a, b, c

[1].

In the discussions above we showed that the solution to this problem is adequate to finding a triangle ABC with integer sides

a, b, c

, for which

a^{n} + b^{n} = c^{n}

is applied, where the natural number n is greater than two (n>2).

Let us assume that there is Δ ABC with integer sides

a, b, c

, and natural n, where the below equality is applied:

a^{n} + b^{n} = c^{n} (1)

Note 1. Without loss of generality, we can also assume that

a, b, c

are coprime numbers, and a<b<c. At the same time, it is worth mentioning that, the issue with an isosceles triangle is much easier to prove, and in the case of an equilateral triangle, it is obvious that there is not such an n that satisfies (1).

Let us prove that equation (1) under the above conditions can be satisfied only when n=2.

We know that for any triangle, the below expression is true:

a c o s β + b c o s α = c (2)

From (1) and (2) we can assume that

c o s β = \frac{a^{n - 1}}{c^{n - 1}}, c o s α = \frac{b^{n - 1}}{c^{n - 1}} (3)

However, it turns out that this assumption is true only when n=2. In other words, this case is only valid for the right triangle.

Let's check this statement.

c o s β = \frac{a^{n - 1}}{c^{n - 1}} \to \frac{a^{n - 1}}{c^{n - 1}} = \frac{a^{2} + c^{2} - b^{2}}{2 a c} \to 2 a^{n} = c^{n - 2} {(a}^{2} + c^{2} - b^{2}) (4)

From (4) it follows that: 1) either n=2; 2) or a and c have a common factor. The second option contradicts the condition (Note 1).

Hence, in order for n to be greater than two (n>2), the following inequalities should hold:

c o s β \neq \frac{a^{n - 1}}{c^{n - 1}}, c o s α \neq \frac{b^{n - 1}}{c^{n - 1}} (5)

Then the ratios of the corresponding parameters could be denoted as

f_{1}

and

f_{2}

f_{1} = c o s β : \frac{a^{n - 1}}{c^{n - 1}} = c o s β \cdot \frac{c^{n - 1}}{a^{n - 1}}, f_{2} = c o s α : \frac{b^{n - 1}}{c^{n - 1}} = c o s α \cdot \frac{c^{n - 1}}{b^{n - 1}}

We can find the corresponding cosines from the above expressions:

c o s β = \frac{a^{n - 1}}{c^{n - 1}} {\cdot f}_{1}, c o s α = \frac{b^{n - 1}}{c^{n - 1}} {\cdot f}_{2} (6)

Then expression (2) can be written as follows:

a \cdot \frac{a^{n - 1}}{c^{n - 1}} {\cdot f}_{1} + b \cdot \frac{b^{n - 1}}{c^{n - 1}} {\cdot f}_{2} = c

Simplifying this expression, for the triangle being investigated, we get the following:

a^{n} f_{1} + b^{n} f_{2} = c^{n} (7)

But as we know, for the same triangle we assumed that

a^{n} + b^{n} = c^{n}

Therefore, for this triangle we should have:

f_{1} = f_{2} = 1 .

Then we can write the following:

f_{1} = 1 \to c o s β \cdot \frac{c^{n - 1}}{a^{n - 1}} = 1, f_{2} = 1 \to c o s α \cdot \frac{c^{n - 1}}{b^{n - 1}} = 1

Then we get:

\frac{a^{2} + c^{2} - b^{2}}{2 a c} \cdot \frac{c^{n - 1}}{a^{n - 1}} = 1, \frac{b^{2} + c^{2} - a^{2}}{2 a c} \cdot \frac{c^{n - 1}}{b^{n - 1}} = 1 2 a^{n} = c^{n - 2} {(a}^{2} + c^{2} - b^{2}) a n d 2 b^{n} = c^{n - 2} {(b}^{2} + c^{2} - a^{2}) (8)

From (8) we get that: 1) either n=2; 2) or a and c as well as b and c have common factors. Both options contradict the condition (n>2, Note 1).

Note 2. For any real

a, b, c

and natural n,

a < b < c, 2 < n, γ < 90 ⁰

(the angle in front of the side c), the following inequalities are applied for

f_{1} и f_{2}

{1 < f}_{1} < 2 a n d {0 < f}_{2} < 1

If

1 < n < 2 t h e n γ > 90^{0} . I n c a s e o f n = 2, γ = 90^{0}

From the above proven statements, it follows that for any natural number n>2 the equation

a^{n} + b^{n} = c^{n}

has no solutions in non-zero integer coprime numbers

a, b, c

Conclusion

Although some aspects of calculus and number theory are used in the article, a unique approach to the proof of Fermat's Last Theorem is presented mainly utilizing geometrical methods. This approach is more understandable and more straightforward for mathematicians and people interested in the theorem. Of course, we do not claim that the presented method is the simplest and easiest way; we consider it as one of the simple methods. However, our research on the topic continues, and we intend to publish other interesting results that are not directly related to the proof in the form of research articles.

References

Bəylərov E.B., Həsənov İ.R. Həndəsə. Abituriyentlərə kömək, Dərs vəsaiti. Bakı: Təhsil, 2000. 132 s.
Bəylərov E.B., Əlimərdanova X.Y. Üçbucaqlar / Riyaziyyat: İmtahana düşən çətin mövzulara dair ekspert şərhləri. Metodik vəsait. Bak: 2002. TQDK. s.169-174.
Ribenboim Paulo. Fermat’s last theorem for amateurs. 423 p. 1999.
Həsənov İ.R., Bəylərov E.B. Riyaziyyat Olimpiada Məsələləri. Ləman Nəşriyyat Poliqrafiya, Bakı:2015, 448 s.
Velikaya teorema Ferma. Jeyms Trefel. Ensiklopediya. (accessed on 12.18.2022) https://elementy.ru/trefil/21135/Velikaya_teorema_Ferma.
Ивлиев Ю.А. Velikaya teorema Ferma i sovremennaya nauka/ Sovremenniye problemi nauki i obrazovaniye (in Russian). (accessed on 12.18.2022). https://science-education.ru/ru/article/view?id=1642.
Razoblachayem! Velikaya teorema Ferma dokazana? (in Russian) (accessed on 12.18.2022) https://masterok.livejournal.com/1230401.html.
Gevorkyan, Yu. L. (2020a). Chastniy sluchay teoremy Ferma. Trudy IX Mezhdunarodnoy nauchno-prakticheskoy konferentsii “Scientific achievements of modern society”. Liverpul', 418–429.
Gevorkyan, Y. L. (2020b). Fermat’s Theorem. Scientific Journal of Italia "Annali D’Italia”, 1 (8), 7–16. (accessed on 1.1.2023) Available at: https://www.calameo.com/books/006103417d8de062343b8.
Gevorkyan, Y. (2022). Geometric approach to the proof of Fermat’s last theorem. EUREKA: Physics and Engineering, (4), 127-136. (accessed on 1.1.2023) https://doi.org/10.21303/2461-4262.2022.002488.
Poulkas, D.Chr. (2020). A Brief New Proof to Fermat’s Last Theorem and Its Generalization. Journal of Applied Mathematics and Physics, 8, 684-697. (accessed on 1.1.2023). [CrossRef]
Wiles, A. (1995). Modular elliptic curves and Fermat’s last theorem. The Annals of Mathematics, 141 (3), 443. (accessed on 1.1.2023). [CrossRef]
Taylor, R., Wiles, A. (1995). Ring-Theoretic Properties of Certain Hecke Algebras. The Annals of Mathematics, 141 (3), 553. (accessed on 1.1.2023). [CrossRef]
Agafontsev, V. V. (2012). Velikaya teorema Ferma (neobychniy podkhod). Materialy X Mezhdunar. zaoch. nauch.-prakt. konf. «Innovatsii v nauke». Ch. 1. Novosibirsk: Izd-vo Sibirskaya assotsiatsiya konsultantov, 6–10. (accessed on 1.1.2023) available at: https://cyberleninka.ru/article/n/velikaya-teorema-ferma-neobychnyy-podhod.
Edvards, G. (1980). Poslednyaya teorema Ferma. Geneticheskoe vvedenie v algebraicheskuyu teoriyu chisel. Moscow: Mir, 486. (accessed on 1.1.2023 ) Available at: http://www.ega-math.narod.ru/Books/Edwards.htm.

Figure 1.

Figure 3.

Figure 4.

Figure 5.

Figure 8.

Figure 9.

Figure 10.

Figure 11.

Figure 12.

Figure 13.

Figure 14.

Figure 15.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Different Geometric Approach to the Proof of Fermat’s Last Theorem

Abstract

Introduction

A Brief Literature Review

Methodology and Used Mathematical Tools

A New Approach to Theorem Proof, Results, and Their Discussion

The Elba Curves

Proof of Fermat's Theorem based on solving triangles

Conclusion

References

MDPI Initiatives

Important Links

Subscribe