Introduction
Most random phenomena in nature exhibit characteristics of bias. This includes random motion, as such phenomena tend not to occur in a strictly neutral or uniform manner. In a group composed of randomly moving particles, the motions of particles in its sub-groups tend to be biased. Among these biased random motions, several distinct motion processes warrant particular attention. These special motions include particles with a higher probability of movement in a specific direction, while maintaining an equivalent yet lower probability of movement in other directions; particles with greater probabilities of movement toward a point, while maintaining an equivalent yet lower probability of movement in other directions; and biased random processes of particles capable of generating rotation. The study of such phenomena typically begins with the simplest biased random processes.
Biased random processes, akin to the first scenario previously described, have been the subject of extensive research[
5]. The nature of the bias can shape the form of the expression for a random process. For example:
where
denotes a Brownian motion process. In Eq. 1, when the drift (
u) and diffusion (
) terms grow synchronously according to
, geometric Brownian motion will be produced. There will be fractional Brownian motion when particles follow the motion law in Eq. 2.
where
is the regression speed. Additionally, there is a simpler scenario where particles with the same jump speed have a higher probability of moving in a specific direction and equal probabilities of moving in other directions. This is a common biased phenomenon in physics. In a system with constant kinetic energy, it is generally challenging to alter the distribution of particle speeds, while the directions of motion can change more readily. When describing such systems using Eq. 3
the system’s kinetic energy will increase as the drift term
u increases. It is obvious that such an equation does not reflect real scenarios. In contrast, when the drift term
u increases, it may be a better solution to reduce the diffusion term
accordingly. Unfortunately, there is currently no clear quantitative relationship available. This article will delve into this issue in detail and derive a quantitative relationship of Lorentz-like factor between the drift (
u) and diffusion (
) terms. This kind of problem is similar to the problem that the particle speed or time slows down in a moving frame in special relativity. Some researchers
demonstrated the diffusion process (random walk) with a special relativistic effect. However, it is the diffusion or random walk of particles when their speed is affected by the special relativity effect. The case involved in this study is that the particle velocity is determined, and the diffusion in the biased random particle swarm formed by them is restricted by the Lorentz-like factor. They are not the same kind of problem.
In my previous research, I demonstrated the special relativistic-like effect of biased random motion when particles move at a uniform speed of c. This article extends that work by considering particles whose speeds follow a Maxwell distribution with equal average speed c. I establish that such biased random motion retains its special relativistic-like effect. Additionally, I present the corresponding Itô equations and simulate the motion of related examples. My findings offer insights into the intricate relationship between biased random processes and the special relativity effect.
Results and Discussion
Biased Random Walk
In order to elucidate the relationship between the drift and diffusion terms, this study commences with an examination of random walks. Among various biased random walk scenarios, we specifically focus on a situation where the probability of a particle moving in one of the six possible directions in a 3-dimensional space is denoted as
p, while the probability in the remaining five directions is given by
, subject to the condition
. Although the case when
presents an intriguing scenario, it falls outside the purview of this study. Given a particle’s jump speed as
c, the collective or group velocity of all particles can be described by the equation:
This can be expressed equivalently in the form
, where
and
represent 1-dimensional random walks with a jump speed of
. We introduce a 3-dimensional rectangular coordinate system, aligning its (1, 1, 1) direction parallel to the group velocity
. Consequently, the 1-dimensional random walk model along the
-axis, which is one of the three equivalent coordinate axes, is given by:
where
. The corresponding unbiased 1-dimensional random walk model on the
-axis among the three equivalent coordinate axes is
where
. The relative standard deviation of the two 1-dimensional random walk processes along the two equivalent
-axes is
Consider the 3-dimensional random walk vectors, representing velocities, formed by and over a unit time interval. Their magnitudes follow the discrete Maxwell distribution, and the average magnitude is proportional to the standard deviation of any component vector along the equivalent axes. Consequently, the average velocity magnitude of the biased 3-dimensional random walk is times that of its unbiased counterpart, with u defined in Eq. 4 (see Part 1 of the Supplementary Information for the detailed Mathematica code). Evidently, the biased case represents a decelerative process. This also illuminates the relationship between the drift term and the attenuation rate of diffusion in a continuous process with constant energy from an alternative perspective. For a more rigorous depiction of this relationship in continuous time, further proofs are warranted. Yet, directly proving this for a continuous-time stochastic process poses challenges. We can transpose to the following strategy.
Continuous Biased Random Process
When particles in swarm possess speeds governed by a Maxwell distribution with a mean of c, the associated scale parameter for this distribution is . Particles in can be categorized into subgroups , based on their speeds, where each subgroup’s velocity vectors terminate on a series of spheres of radius (). The endpoints of these vectors for particles in are uniformly distributed over the sphere with radius . The number of particles in distributed across these spheres follows a Maxwell distribution with respect to r, with the scale parameter and mean radius . Hence, the scenario where particle speeds are uniformly c can be viewed as a specialized case (). The collective motion characteristics of particles whose velocity vectors terminate on spheres of radius embody the motion traits of particles with speeds dictated by the Maxwell distribution. The particle counts in both and are substantial, with a uniform distribution. When a subgroup of the parent particle swarm—where the magnitudes of the particle velocities follow a Maxwell distribution—moves along the z-axis (with a reference frame based on the parent particle swarm) at an average speed of u, it is equivalent to each sub-particle group () moving along the z-axis with an average speed of .
Let R follow a Maxwell distribution with a scale parameter . Then will follow a Maxwell distribution with a scale parameter . Specifically, along the z-axis, all the component speeds in particle swarm , given by (where ), follow a Maxwell distribution with a mean value of u. Moreover, the standard deviations (where ) of the mixed distributions (we can regard the particles in as a particle swarm possessing a mixed distribution with weight ) across all spherical layers also conform to a Maxwell distribution. For the case along the x- or y-axis, the particles in can also be viewed as a particle swarm possessing a mixed distribution with weight . Adopting a method analogous to that in my previous work, it can be demonstrated that the ratio of the standard deviation of the mixed distribution along the x- or y-axis to that of the unbiased moving particle on the same axis satisfies the relationship , and the ratio of the standard deviation along the z-axis also satisfies this relationship (see Part 2 of the Supplementary Information for the detailed Mathematica code).
Itô Equation of Biased Random Processes
The above results indicate that for particles possessing a group velocity of
u and with speeds following the Maxwell distribution, their speeds within
exhibit a deceleration characterized by a Lorentz-like factor. Despite this change in speed, their distributions still follow the Maxwell distribution within
. This behavior permits their motion to be described by the following Itô equation when viewed from
. It should be noted that the definitions of
and
align with those presented in my previous study
.
where
,
and
are the drift speeds and
;
c is the average speed of particles;
,
and
are Brownian motion processes; and
is their standard deviation. Then, the slice distribution of Eq. 8 is
where
i takes the values 1, 2 and 3, in accordance with the Einstein summation convention. This means that
is equivalent to
. Moreover, the forward equation of Eq. 8 is
where
is the probability of a particle at position
and time
t. This is also a drift-diffusion (or advection-diffusion) equation. Only the diffusion coefficient of this equation is limited by the advection term.
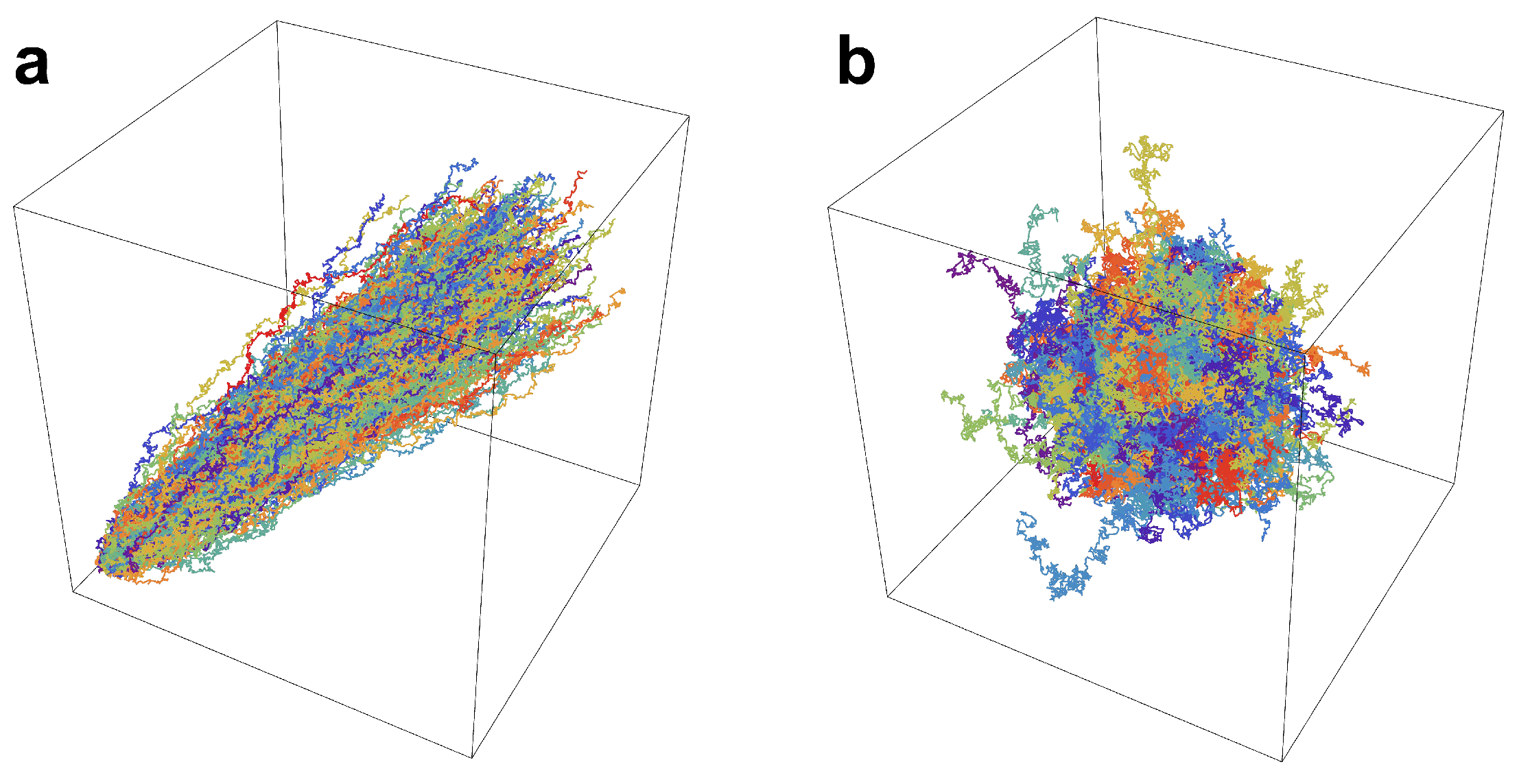
This result (3-dimensional biased Brownian motion) can be simulated by three 1-dimensional biased Brownian motions
. Fig. 1 depicts the trajectories of 300 particles simulated to move randomly over 10 s with a time step of 0.01 s. The randomly moving particles are subject to scenarios with group speeds of 6 (
Figure 1) and 0 (
Figure 1), respectively. Analyzing the diffusion effects, there appears to be no significant difference when compared to an unbiased scenario unaffected by the relativistic-like effect. Further, when considering diffusion velocity, scenarios with a notable group speed show a reduced rate of diffusion.
Conclusions
For a particle swarm composed of particles with a fixed energy, assumed to be in reference frame , the magnitudes of the particle velocities follow a Maxwell distribution with parameter , yielding an average speed of c. When a sub-swarm of particles (assumed to be in reference frame ), exhibits a higher probability of motion in a specific direction and equal yet lower probabilities in other directions (with the group velocity of this sub-swarm denoted as u), as observed from , the velocities of particles within this sub-swarm decelerate, adhering to a pattern determined by the Lorentz-like factor . Consequently, the biased motion of such particles can be described by a set of Itô equations (Eq. 8). Both the time slice distribution and the forward equation for these biased particles differ from those in the reference frame .
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on
Preprints.org Mathematica code for necessary calculation process and graphics. The following file is available free of charge.
Data Availability Statement
All data generated or analysed during this study are included in this published article and its supplementary information files
Acknowledgments
The author is thankful for Wolfram Inc
Conflicts of Interest
There are no conflicts to declare
References
- Tapiero, C.S.; Vallois, P. Run length statistics and the Hurst exponent in random and birth-death random walks. Chaos, Solitons & Fractals 1996, 7, 1333–1341. [Google Scholar]
- Guo, T. Study on the average speed of particles from a particle swarm derived from a stationary particle swarm. Scientific Reports 2021, 11, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Guo, T. Dynamics of stochastic-constrained particles. Scientific Reports 2023, 13, 2759. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Guo, T. The angular speed distribution of randomly moving-particle group. AIP Advances 2022, 12, 045005. [Google Scholar] [CrossRef]
- Codling, E.A.; Plank, M.J.; Benhamou, S. Random walk models in biology. Journal of the Royal society interface 2008, 5, 813–834. [Google Scholar] [CrossRef] [PubMed]
- Debbasch, F.; Chevalier, C. Relativistic stochastic processes. AIP Conference Proceedings. American Institute of Physics, 2007, Vol. 913, pp. 42–48. [CrossRef]
- Dunkel, J.; Hänggi, P. Relativistic brownian motion. Physics Reports 2009, 471, 1–73. [Google Scholar] [CrossRef]
- Hakim, R. Relativistic stochastic processes. Journal of Mathematical Physics 1968, 9, 1805–1818. [Google Scholar] [CrossRef]
- Dunkel, J.; Talkner, P.; Hänggi, P. Relativistic diffusion processes and random walk models. Physical Review D 2007, 75, 043001. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).