Prerpints.org logo
Preprint
Article

Approximation of the Mittag-Leffler functions by Elementary Functions with Physics Applications

Altmetrics

Downloads

142

Views

85

Comments

0

This version is not peer-reviewed

Submitted:

11 January 2023

Posted:

23 January 2023

You are already at the latest version

Alerts
Abstract
In this paper we give approximations to the Mittag-Leffler functions in terms of elementary functions using different methods. This allowed us to establish a practical method we called integerization principle. This principle states that many fractional nonlinear oscillators may be solved by means of the solution to some integer-order Duffing oscillator equation. The accuracy of the obtained results is illsutrated in concrete examples. Formulas for estimating the errors in the approximations are also provided.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction.

Fractional calculus generalizes the differential and integral operators to non-integer orders, for this reason it is also called arbitrary order calculation. This idea is as old as calculus itself, but its development has been largely conditioned by the absence of a physical interpretation and convincing geometry and also by the numerous definition proposals. We could say that it did not have a real development until the second half of the 20th century, that is why we find here a classical and at the same time modern branch of mathematics.
Currently, a large number of articles are published on the subject, and we find applications in most of the sciences, this is because fractional operators are non-local operators, that is, what occurs at a point depends on an average over an interval containing the point, and this makes fractional calculus an exceptional tool for non-local phenomena such as ecological processes such as accumulation of metals, problems of population evolution, problems of radiation, economy, etc. They also play a very important role in relaxation processes such as those associated with viscoelastic materials.
In 1969, the Italian mathematician and physicist Michele Caputo gave a new definition derived from fractional order that allowed to interpret physically the initial conditions of the increasingly numerous applied problems. Caputo (1969) defined the fractional derivative as
D t α x ( t ) = 1 Γ ( 2 − α ) ∫ 0 t x ′ ′ ( s ) d s ( t − s ) α − 1 , 1 < α < 2 . D t α x ( t ) = x ′ ′ ( t ) when α = 2 .
where n − 1 < a < n and f ( n ) ( s ) is an ordinary derivative.
In 1974, the first international conference on Fractional Calculus was held in Connecticut, which served as a stimulus to numerous publications. The second conference took place in 1984 in Scotland, and the third in 1989 in Tokyo. Nowadays it is difficult to find a field of science or engineering that does not consider concepts of the Fractional Calculus, and every year there are several events that show it.
Most nonlinear differential equations do not admit an analytical procedure that describe its solution. For this reason it is necessary to resort to numerical methods such as Runge Kutta, Newton, Euler etc., generally developed in software tools for applications in mathematics and engineering; these methods are a quite practical solution tool that allows approaching in an approximate way the solution of differential equations non linear; another resource contemplated when describing the solution of this type of equations refers to the qualitative information of the general behavior of the solutions that are mactually obtains without solving these equations, basically through methods and geometric analysis. The interest of studying nonlinear differential equations lies mainly in that most physical systems, whether electrical, magnetic, biological, chemical, geological, economic, etc., present a non-linear behavior by nature; the procedure of linearizing the equations segments the knowledge about the behavior of systems around an equilibrium point, while the study of systems by means of of nonlinear theory makes it possible to be aware of the behavior of the system at all points within which it is defined; another reason to study nonlinear systems and differential equations that describe them lies in the existence of natural phenomena and surprising mathematical representations that have no place in linear theory.
Suppose we are given that
D t α x ( t ) + ω 0 2 x ( t ) = 0 , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 ,
The exact solutuion to the i.v.p. (2) reads
x ( t ) = x 0 E α ( − ω 0 2 t α ) + x ˙ 0 t E α , 2 ( − ω 0 2 t α ) ,
where E α ( − t α ) and E α , 2 ( − t α ) are the Mittag-Leffler functions. These functions are defined as follows:
E α ( z ) = ∑ k = 0 ∞ z k Γ ( α k + 1 ) .
E α , β ( z ) = ∑ k = 0 ∞ z k Γ ( α k + β ) .
Our aim is to approximate the Mittag-Leffler functions E α ( − t α ) and E α , 2 ( − t α ) by means of elementary functions. We also will apply the obtained results in the solution of fractional differential equations. The idea is to replace the fractional ode by means of some suitable integer-order oscillator. We will call this method the Integerization Principle.

2. Approximation of Mittag-Leffler functions by means of elementary functions

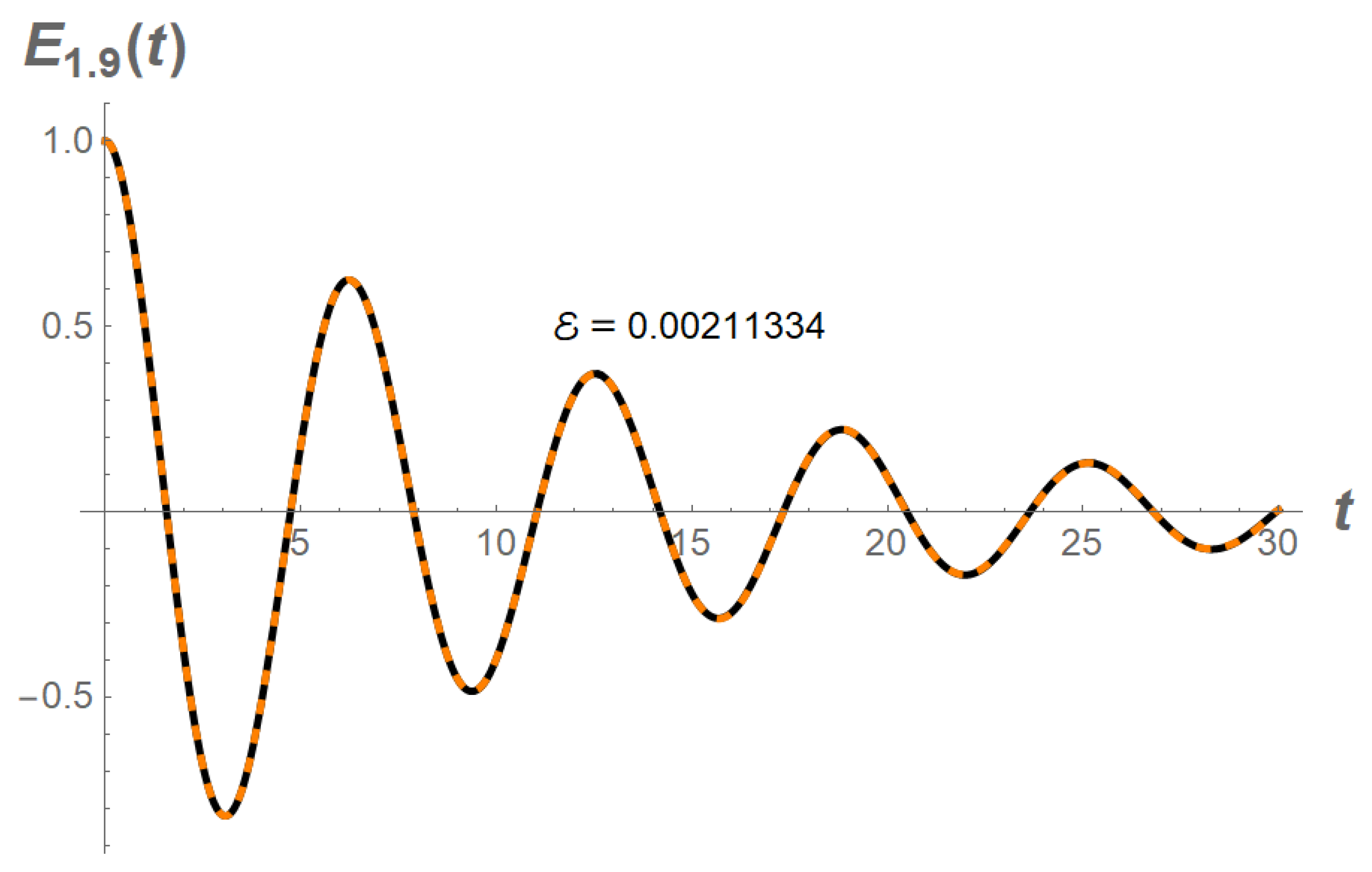
Assume that 1 < α ≤ 2 . Let us consider the Mittag-Leffler function E α ( t ) . To begin with, let α = 1.9 . The function E 1.9 ( t ) is plotted in Figure 1. From that figure we see that the function E 1.9 ( t ) behaves like a damped oscillator. So, we expect thtat this function may be approximated by means of the solution to some damped Duffing equation
x ¨ + 2 ε x ˙ + ( ε 2 + κ 2 ) x + ∑ r = 1 N μ 2 r + 1 x 2 r + 1 = 0 , x ( 0 ) = 1 and x ′ ( 0 ) = 0 .
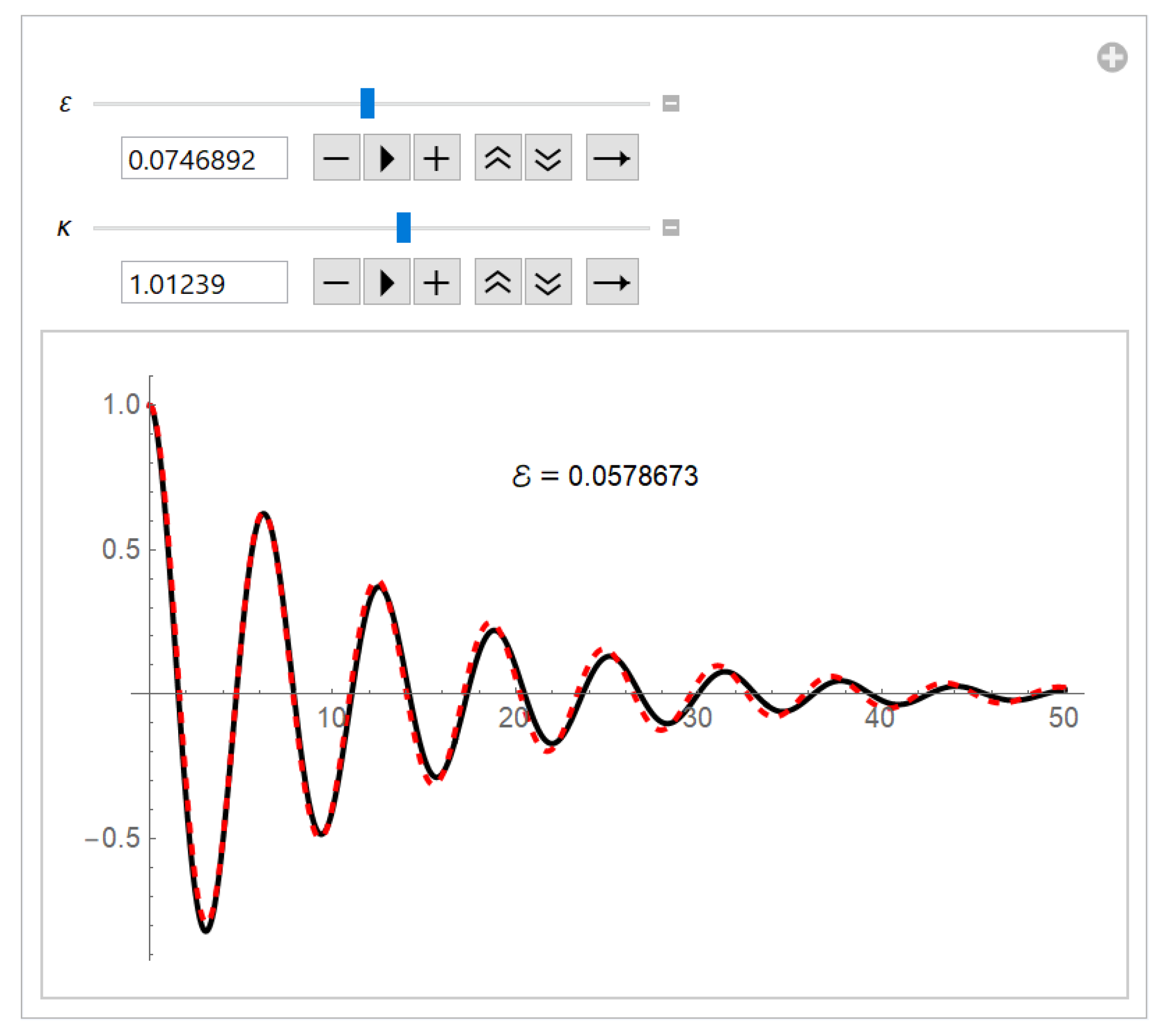
Let us examine several possibilities for the approximation. Choose some positive number T.

2.1. First Method.

We look for suitable positive numbers ε and κ such that E α ( t ) ≈ x ( t ) for 0 ≤ t ≤ T , where
x ¨ + 2 ε x ˙ + ( ε 2 + κ 2 ) x = 0 , x ( 0 ) = 0 and x ′ ( 0 ) = 0 .
The solution to the ode (7) is easy to obtain and it reads
x ε , κ ( t ) = exp ( − ε t ) cos ( κ t ) + ε κ sin ( κ t ) .
We choose the numbers ε and κ so that
F ( ε , κ ) = min ϵ , k E α − x ϵ , k ,
where
E α − x ϵ , k = max 0 ≤ t ≤ T E α ( t ) − x ϵ , k ( t ) .
For example,
E 1.9 ( t ) ≈ x ε , κ ( t ) for ε = 0.0746892 and κ = 1.01239 with error E = 0.0577757 for 0 ≤ t ≤ 100
See Figure 1.
The optimal values for ε and κ are presented in Table 1 and Table 2.
See Figure 2.
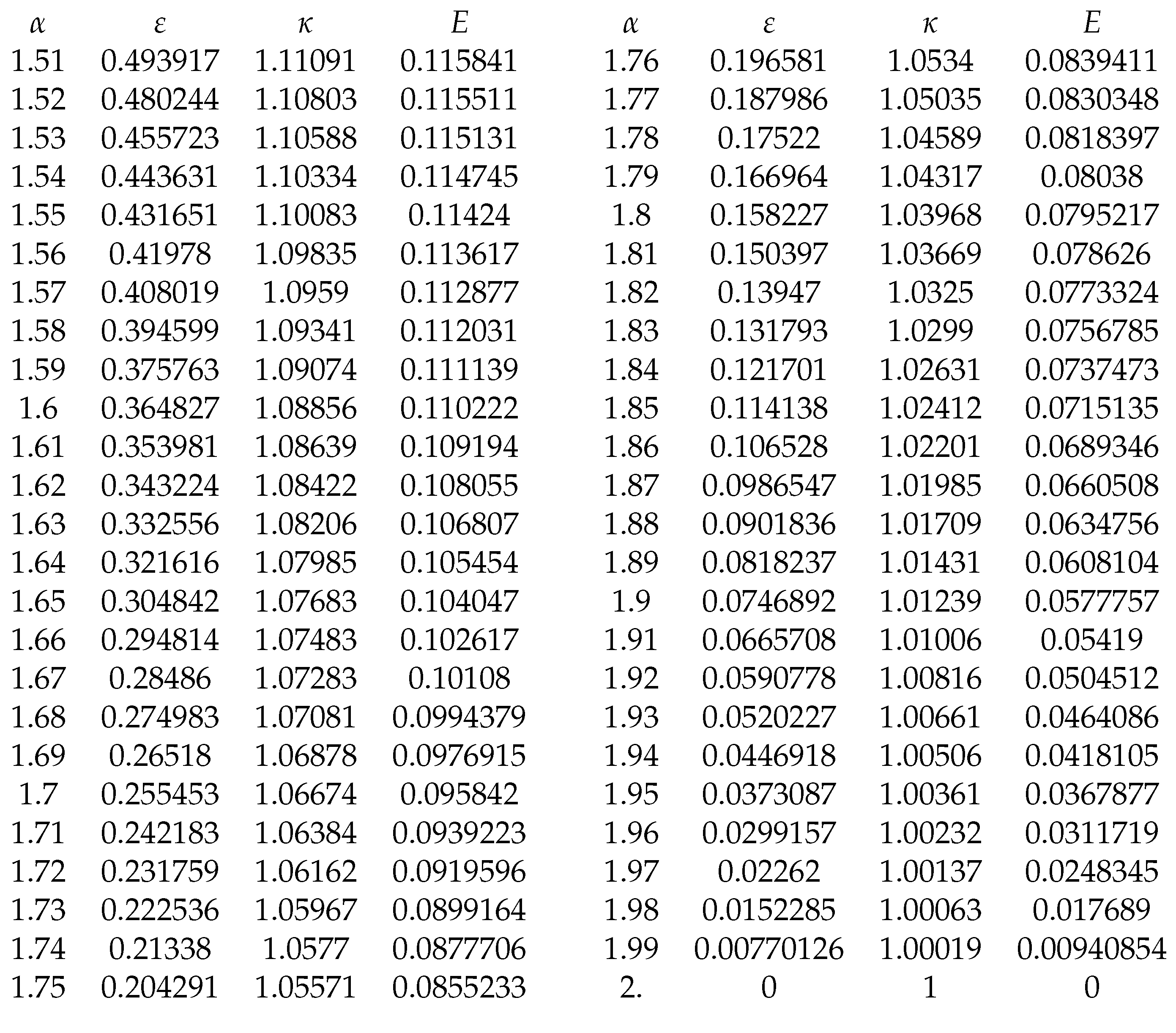
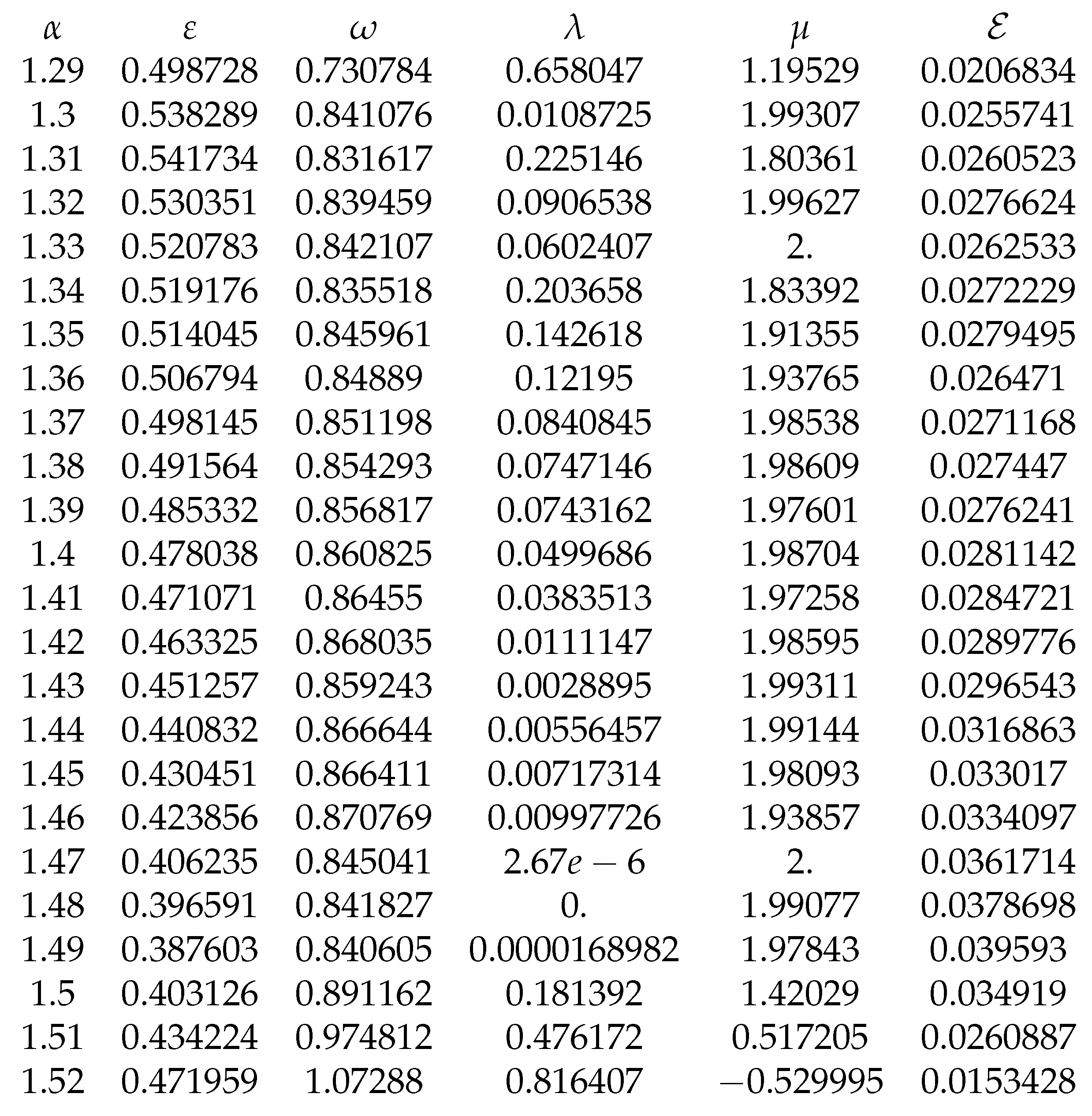
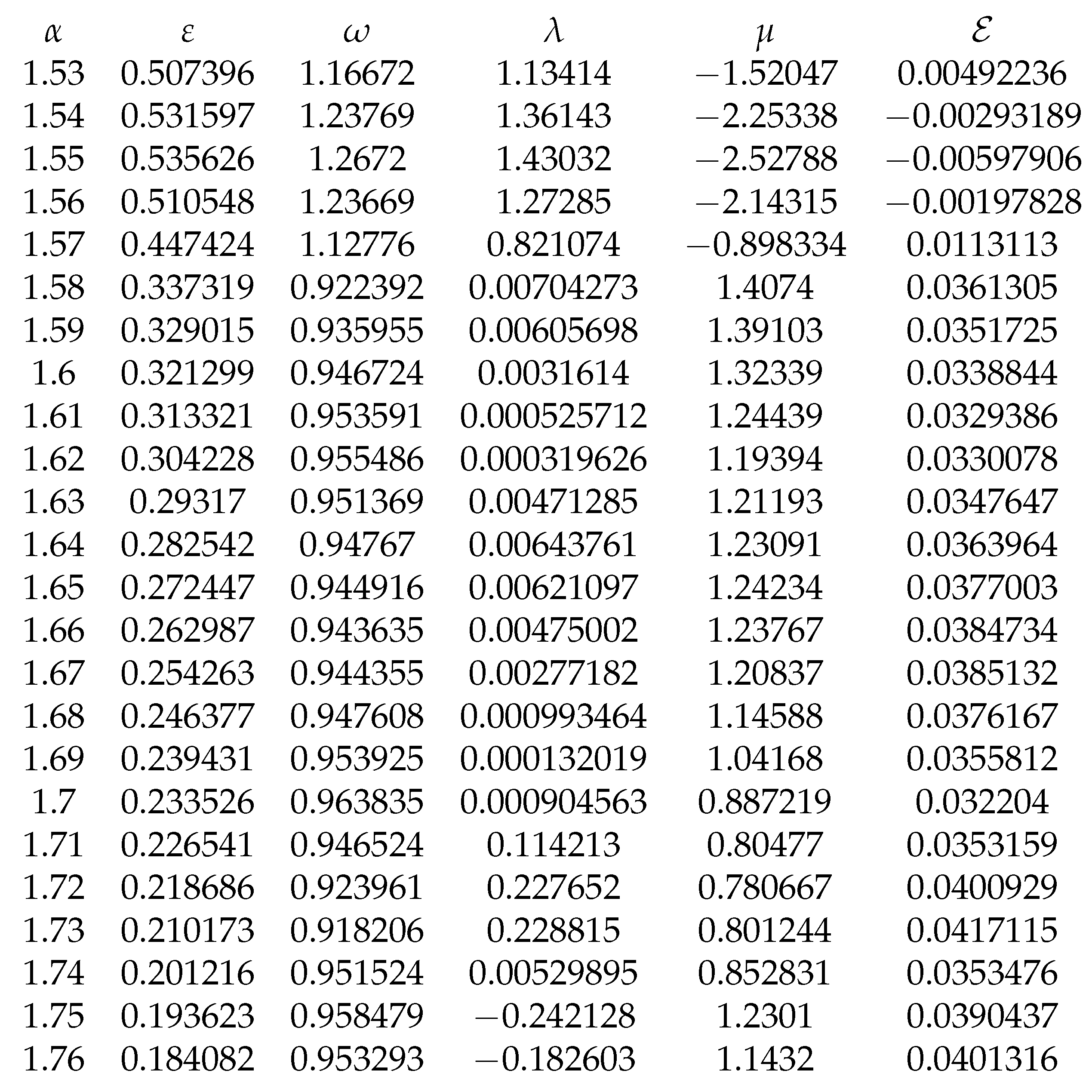
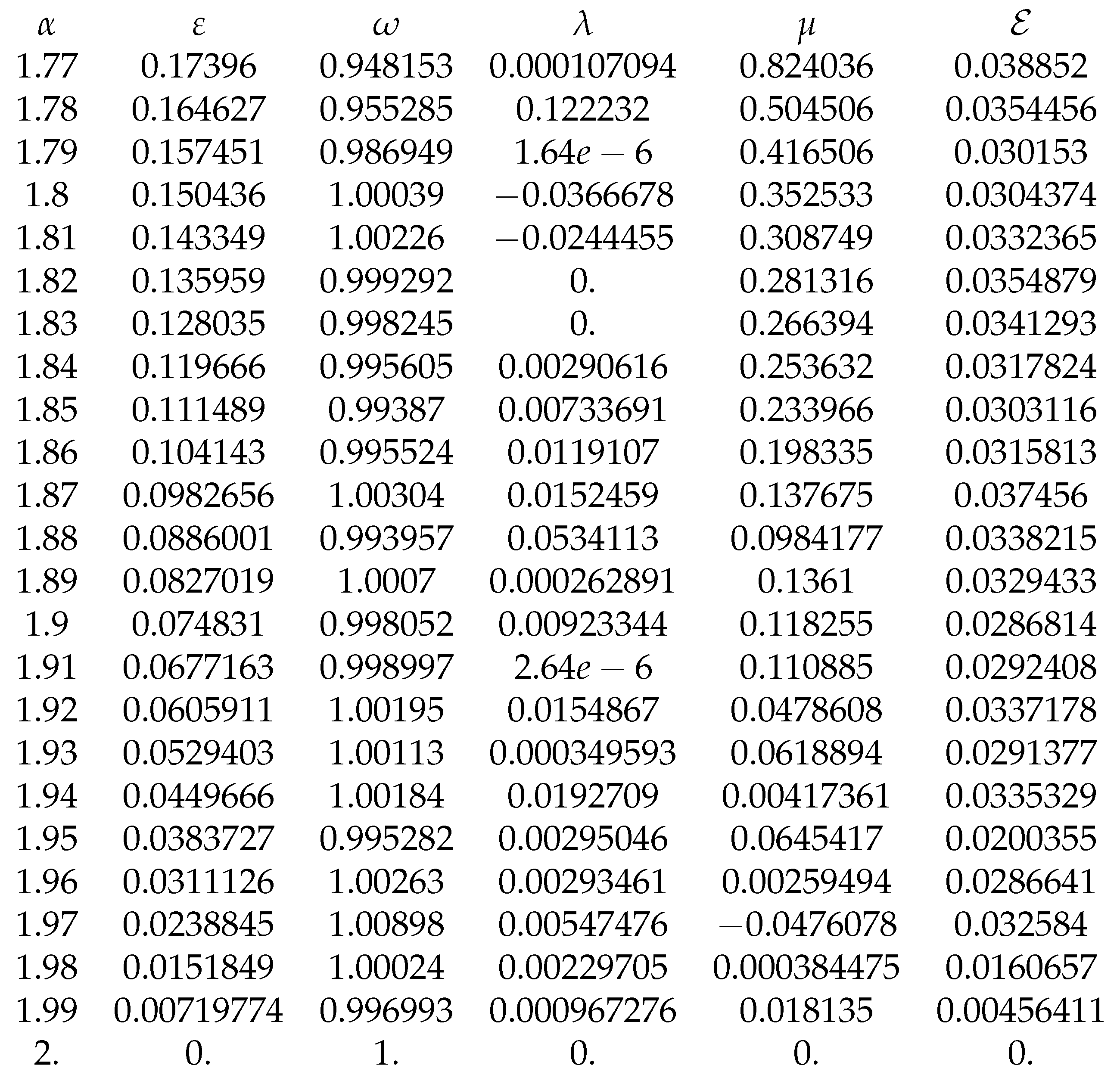
We obtained the following experimental formulas for 1.5 ≤ α ≤ 2 :
E α ( t ) ≈ exp ( − ε t ) cos ( κ t ) + ε κ sin ( κ t ) for 0 ≤ t ≤ 100 , where ε = 38.5892 ( α − 2.2531 ) ( α − 2 ) α 2 − 3.85082 α + 3.84914 α 2 − 2.70744 α + 1.91924 . κ = 153.169 ( 2.22838 − α ) ( α − 1.25676 ) α 2 − 3.98123 α + 4.06822 α 2 − 3.0097 α + 2.38305 . with error E = 158.157 ( α − 2.14235 ) ( α − 2 ) α 2 − 3.53553 α + 3.17211 α 2 − 2.86208 α + 2.06234 .
Thus, the solution (3) to the i.v.p. (2) may be approximated as follows:
x approx ( t ) = c exp − ε ω 0 2 / α t cos κ ω 0 2 / α t + cos − 1 x 0 c , where c = ± 1 κ x ˙ 0 ω 0 − 4 / α 2 ε x 0 ω 0 2 / α + x ˙ 0 + x 0 2 ε 2 + κ 2 .
In particular,
E α , 2 ( t ) ≈ sin ( κ t ) κ t exp ( − ε t ) .
Observe that the function (13) is a solution to the linear ode
x ¨ + 2 ε ω 0 2 / α x ˙ + ( ε 2 + κ 2 ) ω 0 4 / α x = 0 , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 .
This says that the solution to the fractional linear ode
D t α x ( t ) + ω 0 2 x ( t ) = f ( t ) , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 ,
may be approximated by means of the solution to the integer order linear ode
x ¨ + 2 ε ω 0 2 / α x ˙ + ( ε 2 + κ 2 ) ω 0 4 / α x = f ( t ) , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 .

2.2. Second Approach.

We approximate the function E α ( t ) by means of the solution to the following damped Duffing oscillator:
x ¨ + 2 ε x ˙ + ω 2 x + λ x 3 = 0 , x ( 0 ) = 1 and x ′ ( 0 ) = 0 .
The approximate solution to the Duffing oscillator (18) is given by
x ^ ( t ) = exp ( − ε t ) ( cos ( ψ t ) + c sin ( ( t ) ) ) ,
where
ψ ( t ) = 4 ε t w 0 − 2 w 1 e − 2 ε t − w 2 e − 4 ε t + 2 w 1 + w 2 4 ε . w 2 = − w 1 2 2 w 0 , w 1 = 3 λ c 2 + 1 8 w 0 , w 0 = ω 2 − ε 2 . 9 c 5 λ 2 + 18 c 3 λ 2 − 48 c 3 λ w 0 2 + 9 c λ 2 − 48 c λ w 0 2 − 128 c w 0 4 + 128 ε w 0 3 = 0 . c ≈ 128 ε w 0 3 − 9 λ 2 + 48 λ w 0 2 + 128 w 0 4 2 − 729 λ 6 − 73728 λ 2 w 0 6 4 ε 2 + 3 λ + 49152 λ w 0 8 16 ε 2 + 9 λ + 11664 λ 5 w 0 2 − 31104 λ 4 w 0 4 + 2359296 λ w 0 10 + 2097152 w 0 12 .
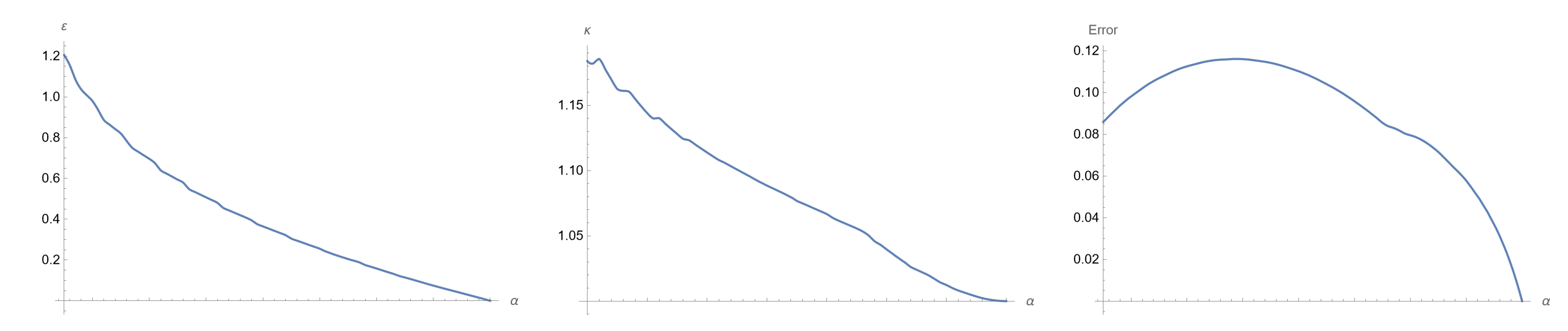
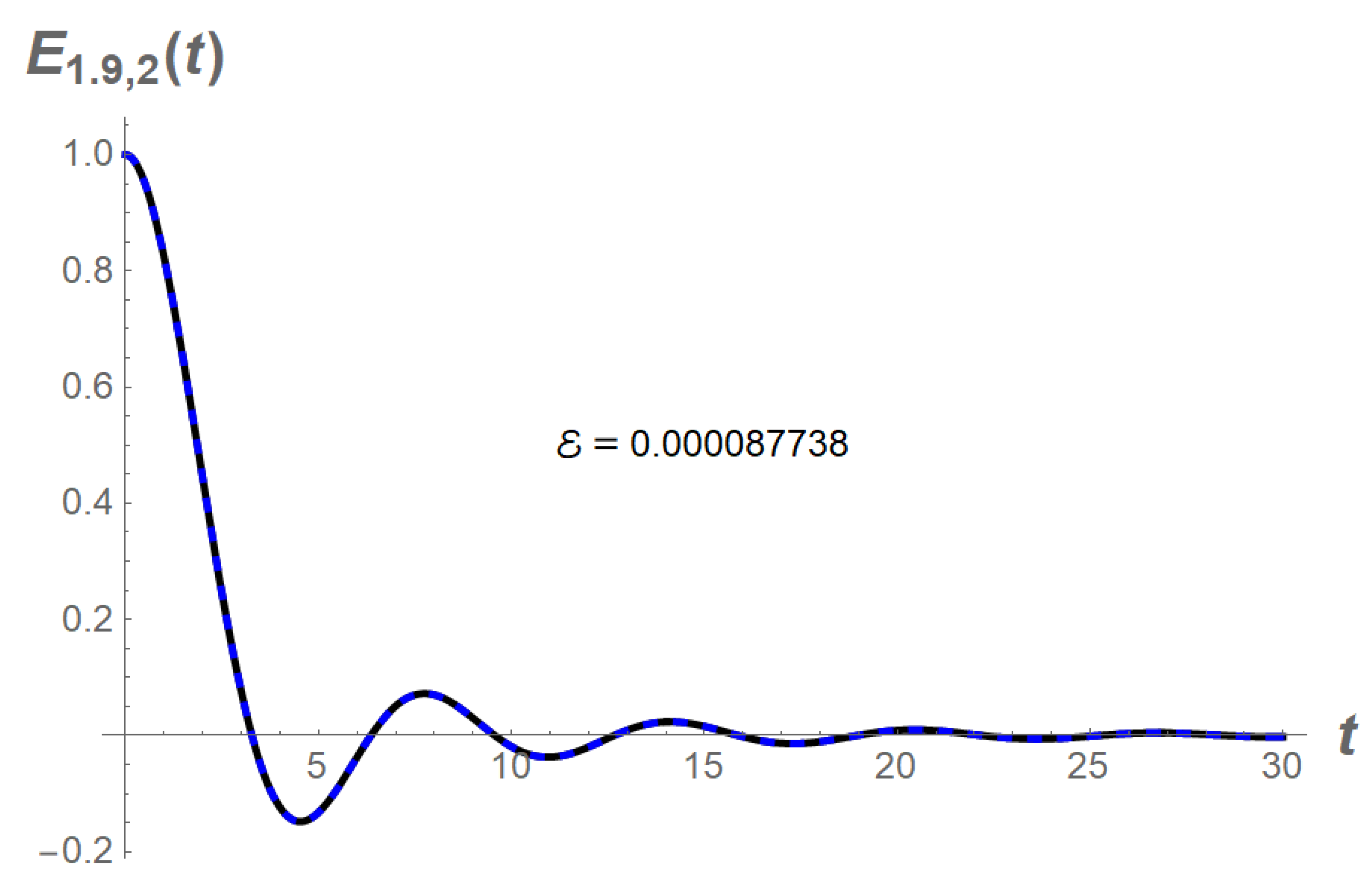
The constants ε , ω and λ are chosen in order to minimize the distance between E α ( t ) and x ^ ( t ) . For example, for α = 1.94 we have
l E α ( t ) ≈ x ^ ( t ) f o r t h e p a r a m e t e r v a l u e s ε = 0.0493409 , ω = 0.987951 , λ = 0.0850072 w i t h e r r o r E = 0.0317695 .
See Figure 3. The approximation reads
x ^ ( t ) = e − 0.0493409 t 0.0484414 sin 0.986718 t + 0.00269236 e − 0.197364 t − 0.328152 e − 0.0986819 t + 0.325459 + cos 0.986718 t + 0.00269236 e − 0.197364 t − 0.328152 e − 0.0986819 t + 0.325459 .
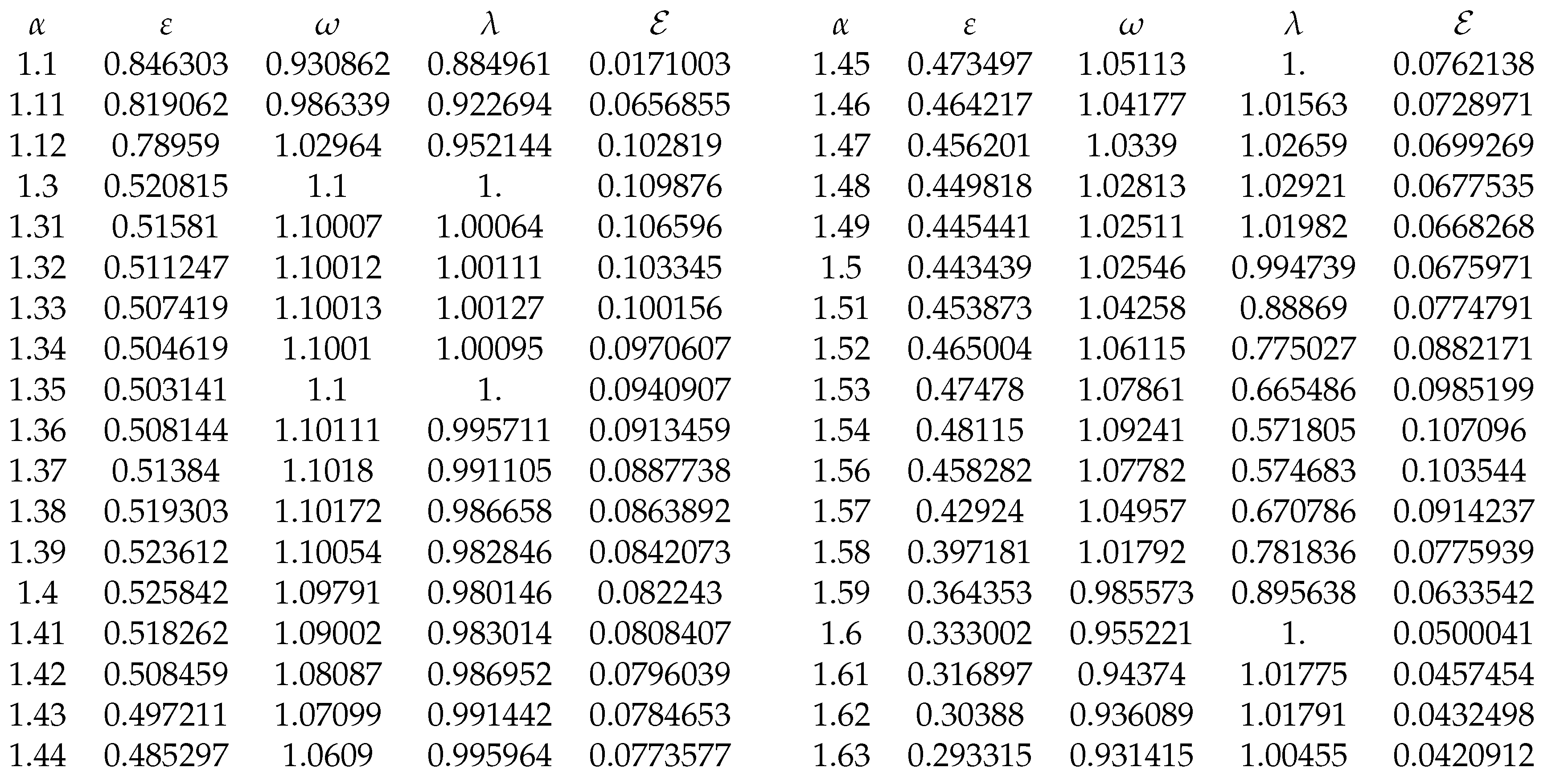
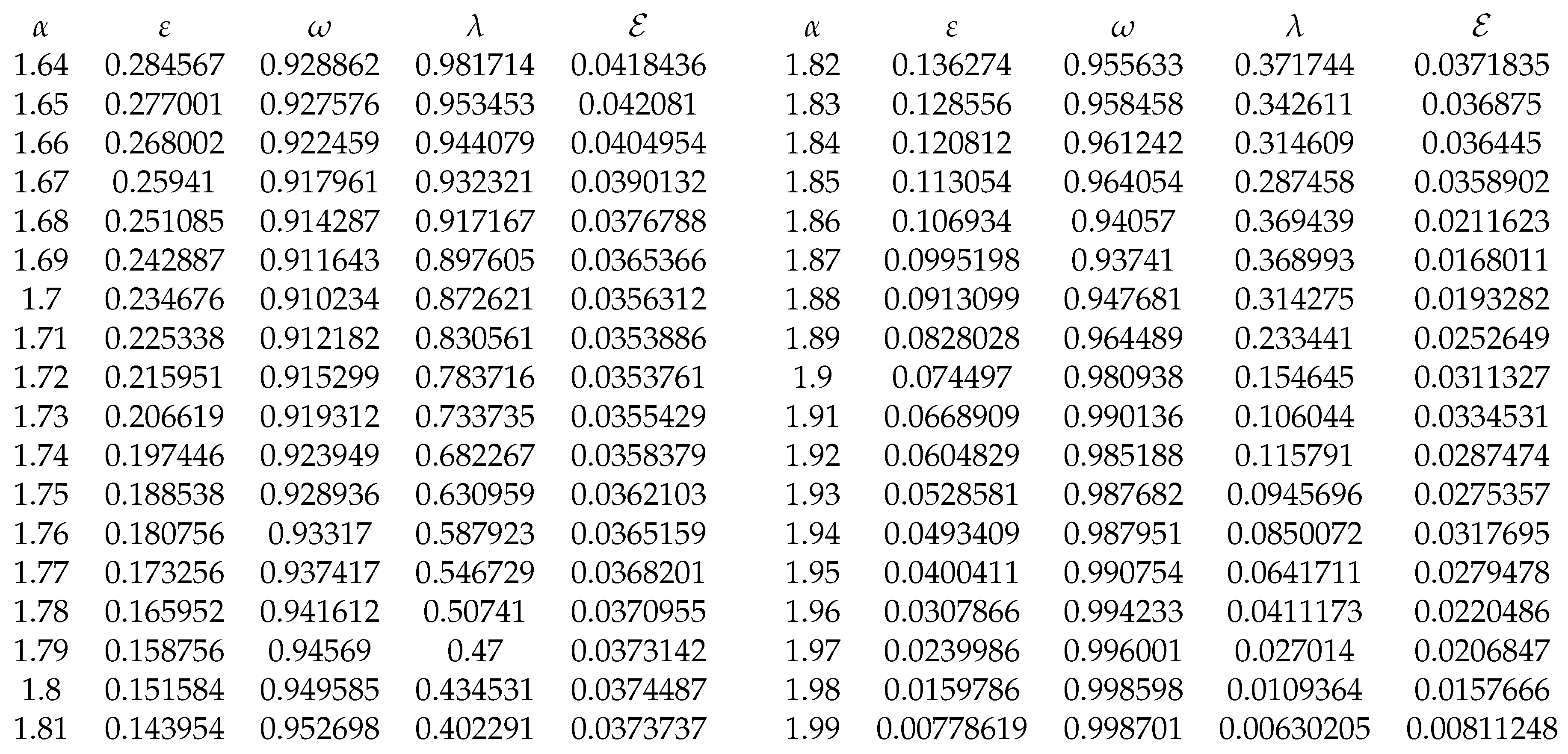
The optimal values for ε , ω and λ are presented in Table 3 and Table 4.

2.3. Third Approach.

We approximate the function E α ( t ) by means of the solution to the following damped cubic-quintic Duffing oscillator:
x ¨ + 2 ε x ˙ + ω 2 x + λ x 3 + μ x 5 = 0 , x ( 0 ) = 1 and x ′ ( 0 ) = 0 .
The approximate solution to the Duffing oscillator (19) is given by
X ^ ( t ) = exp ( − ε t ) cos ψ ( t ) + c sin ψ ( t ) ,
where
ψ ( t ) = 1 4 ε 4 ε w 0 t − 2 w 1 e − 2 ε t − w 2 e − 4 ε t + 2 w 1 + w 2 . w 0 = ω 2 − ε 2 , w 1 = 3 8 w 0 c 2 + 1 λ , w 2 = c 2 + 1 2 128 w 0 3 40 μ w 0 2 − 9 λ 2 . c 5 40 μ w 0 2 − 9 λ 2 + c 3 − 18 λ 2 + 48 λ w 0 2 + 80 μ w 0 2 + c − 9 λ 2 + 48 λ w 0 2 + 40 μ w 0 2 + 128 w 0 4 − 128 ε w 0 3 = 0 . c ≈ 128 ε w 0 3 − 9 λ 2 + 8 w 0 2 ( 6 λ + 5 μ ) + 128 w 0 4 2 − 729 λ 6 + 8192 w 0 8 32 ε 2 ( 3 λ + 5 μ ) + 54 λ 2 + 180 λ μ + 75 μ 2 − 512 w 0 6 144 λ 2 4 ε 2 + 3 λ − 450 λ μ 2 − 125 μ 3 + 1944 λ 4 w 0 2 ( 6 λ + 5 μ ) − 1728 λ 2 w 0 4 18 λ 2 + 60 λ μ + 25 μ 2 + 393216 w 0 10 ( 6 λ + 5 μ ) + 2097152 w 0 12 .
For example, let α = 1.95 . We have
l E α ( t ) ≈ X ^ ( t ) f o r   t h e   p a r a m e t e r   v a l u e s ε = 0.0383727 , ω = 0.995282 , λ = 0.00295046   a n d   μ = 0.0645417 w i t h   e r r o r   E = 0.0200355 .
The approximation reads
X ^ ( t ) = e − 0.0383727 t 0.0377686 sin 0.994542 t − 0.132498 e − 0.153491 t − 0.0145166 e − 0.0767453 t + 0.147015 + cos 0.994542 t − 0.132498 e − 0.153491 t − 0.0145166 e − 0.0767453 t + 0.147015 .
See Figure 4.
The optimal values for ε , ω , λ and μ are presented in Table 5, Table 6, Table 7 and Table 8.

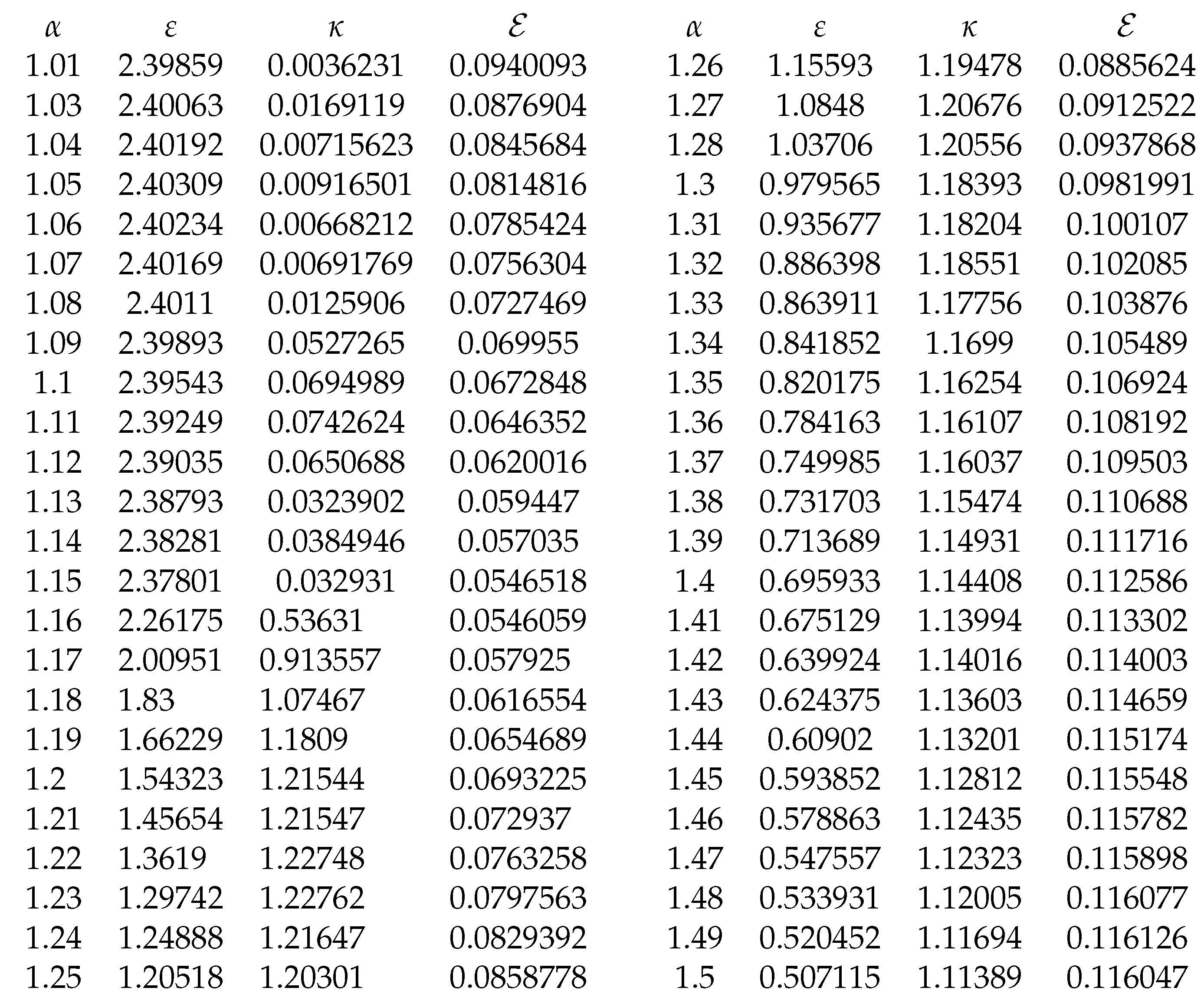
2.4. Fourth Approach.

We approximate the function E α ( t ) by means of the solution to the following damped cubic-quintic-heptic Duffing oscillator:
x ¨ + 2 ε x ˙ + ω 2 x + λ x 3 + μ x 5 + ν x 7 = 0 , x ( 0 ) = 1 and x ′ ( 0 ) = 0 .
The approximate solution to the Duffing oscillator (24) is given by
X ^ ( t ) = exp ( − ε t ) cos ( ψ ( t ) ) + c sin ( ψ ( t ) ) ,
where
ψ ( t ) = 1 12 ε 12 ε t w 0 − 6 w 1 e − 2 ε t − 3 w 2 e − 4 ε t − 2 w 3 e − 6 ε t + 6 w 1 + 3 w 2 + 2 w 3 . w 0 = ω 2 − ε 2 , w 1 = 3 8 w 0 c 2 λ + λ , w 2 = c 2 + 1 2 40 μ w 0 2 − 9 λ 2 128 w 0 3 , w 3 = c 2 + 1 3 27 λ 3 − 120 λ μ w 0 2 + 280 ν w 0 4 1024 w 0 5 . c 7 27 λ 3 − 120 λ μ w 0 2 + 280 ν w 0 4 + c 5 81 λ 3 − 72 λ 2 w 0 2 − 360 λ μ w 0 2 + 320 μ w 0 4 + 840 ν w 0 4 + c 3 81 λ 3 − 144 λ 2 w 0 2 − 360 λ μ w 0 2 + 384 λ w 0 4 + 640 μ w 0 4 + 840 ν w 0 4 + c 27 λ 3 − 72 λ 2 w 0 2 − 120 λ μ w 0 2 + 384 λ w 0 4 + 320 μ w 0 4 + 280 ν w 0 4 + 1024 w 0 6 − 1024 ε w 0 5 = 0 . c ≈ 1024 ε w 0 5 27 λ 3 + 8 w 0 4 ( 48 λ + 40 μ + 35 ν ) − 24 λ w 0 2 ( 3 λ + 5 μ ) + 1024 w 0 6 2 19683 λ 9 + 65536 w 0 14 128 ε 2 ( 48 λ + 80 μ + 105 ν ) + 3456 λ 2 + 1440 λ ( 4 μ + 7 ν ) + 75 ( 8 μ + 7 ν ) 2 − 512 w 0 12 147456 ε 2 λ ( 2 λ + 5 μ ) + 55296 λ 3 + 552960 λ 2 μ + 3600 λ 64 μ 2 − 49 ν 2 − 125 ( 8 μ + 7 ν ) 3 + 4608 λ w 0 10 18432 ε 2 λ 2 + 10368 λ 3 − 75 λ 192 μ 2 + 336 μ ν + 49 ν 2 − 125 μ ( 8 μ + 7 ν ) 2 − 52488 λ 7 w 0 2 ( 3 λ + 5 μ ) + 5832 λ 5 w 0 4 216 λ 2 + 15 λ ( 24 μ + 7 ν ) + 200 μ 2 − 3456 λ 3 w 0 6 756 λ 3 + 945 λ 2 ( 4 μ + ν ) + 225 λ μ ( 12 μ + 7 ν ) + 500 μ 3 + 1728 λ 2 w 0 8 3456 λ 3 + 1800 λ 2 ( 8 μ + 7 ν ) + 75 λ 320 μ 2 + 224 μ ν + 49 ν 2 + 1000 μ 2 ( 8 μ + 7 ν ) + 25165824 w 0 16 ( 48 λ + 40 μ + 35 ν ) + 1073741824 w 0 18 .
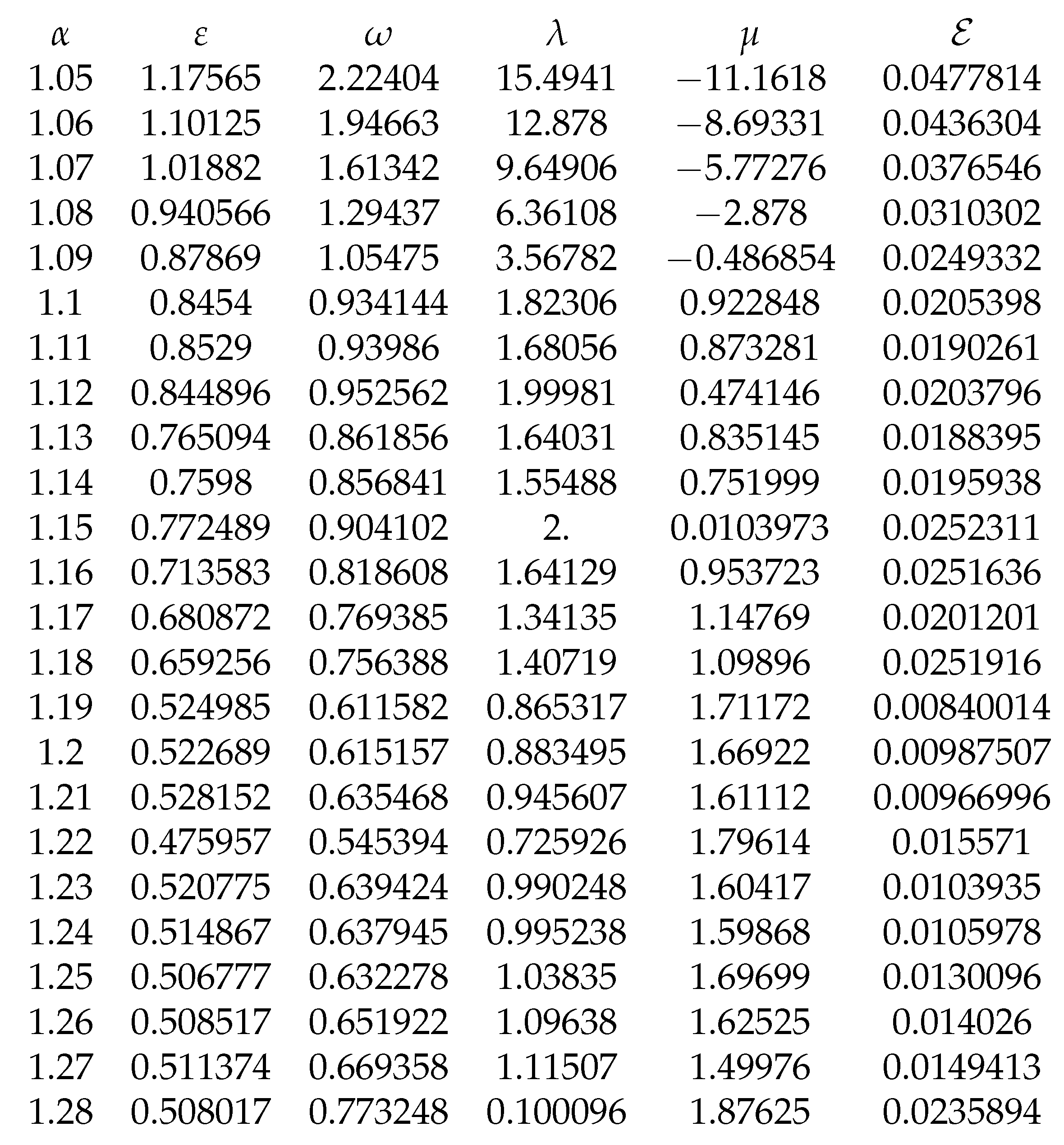
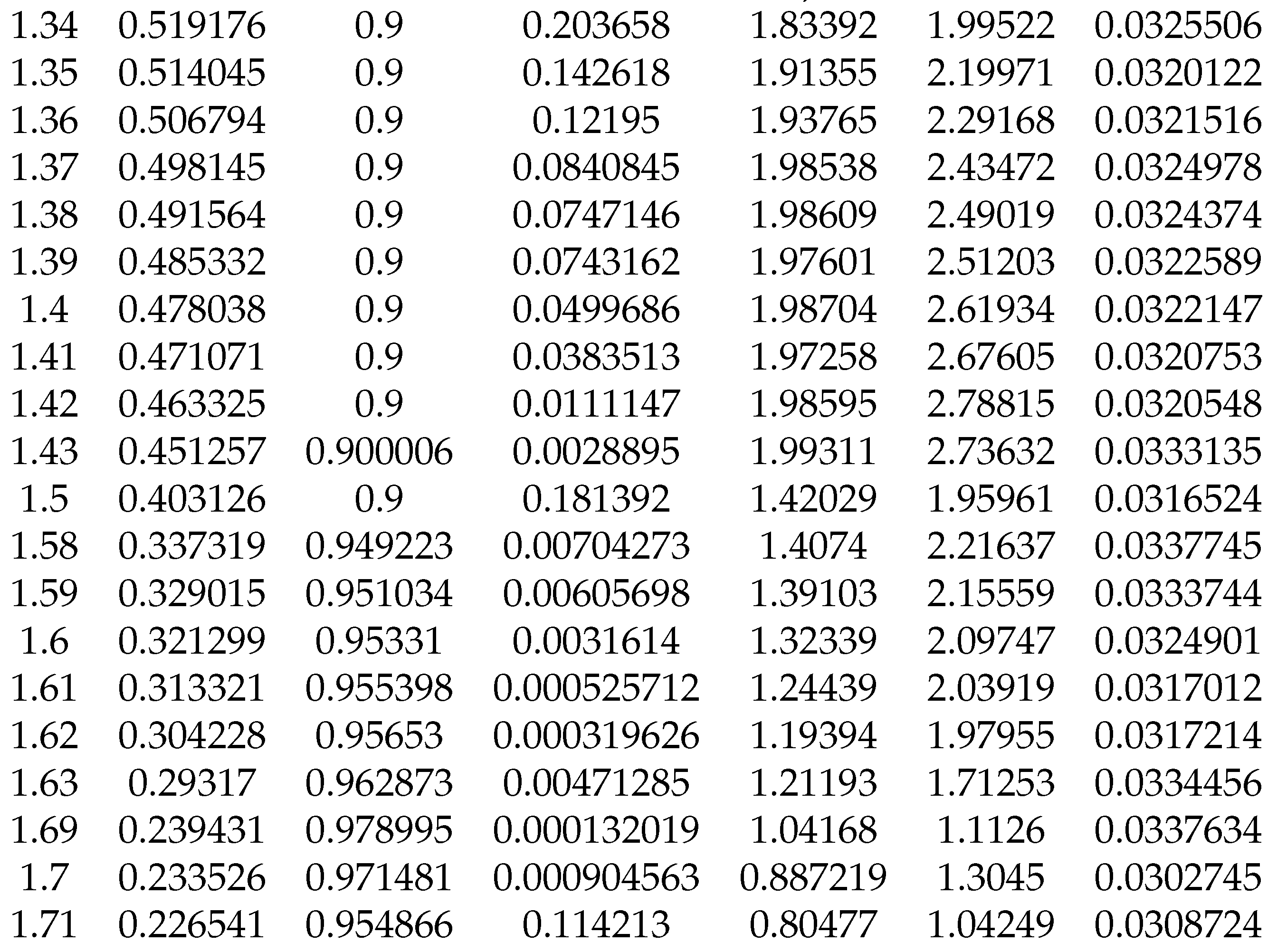
The optimal values for ε , ω , λ , μ and are presented in Table 9 and Table 10.

2.5. Fifth Approach. Polynomial approximation.

Given a continuous function φ ( t ) on [ − 1 , 1 ] we may approximate it by means of a linear combination of Chebyshev polynomials in the form
φ ( t ) ≈ P ( t ) : = ∑ r = 0 N c r T r ( t ) ,
where the constnats c r are determined from the linera system
φ ( ξ j ) = P ( ξ j ) , j = 0 , 1 , 2 , 3 , . . . , N ,
where
ξ 0 = − 1 , ξ N = 1 , ξ N / 2 = 0 and ξ j = cos j + 1 / 2 N + 1 π for 0 < j < N and j ≠ N / 2 .
For example, for N = 5 we have
φ ( t ) ≈ P φ ( t ) : = ∑ r = 0 5 c r T r ( t ) ,
where
c 0 = φ ( 0 ) . c 1 = − 0.174599 φ ( − 1 ) + 0.816497 φ ( − 0.707107 ) − 4.78174 φ ( − 0.258819 ) + 3.8637 φ ( 0 ) + 0.378937 φ ( 0.707107 ) − 0.102802 φ ( 1 ) . c 2 = − 0.5 φ ( − 1 ) + 2 φ ( − 0.707107 ) − 3 φ ( 0 ) + 2 . φ ( 0.707107 ) − 0.5 φ ( 1 ) . c 3 = 1.0238 φ ( − 1 ) − 5.27792 φ ( − 0.707107 ) + 14.3452 φ ( − 0.258819 ) − 11.5911 φ ( 0 ) + 1.69161 φ ( 0.707107 ) − 0.191593 φ ( 1 ) . c 4 = φ ( − 1 ) − 2 φ ( − 0.707107 ) + 2 φ ( 0 ) − 2 φ ( 0.707107 ) + φ ( 1 ) . c 5 = − 1.3492 φ ( − 1 ) + 4.46142 φ ( − 0.707107 ) − 9.56347 φ ( − 0.258819 ) + 7.72741 φ ( 0 ) − 2.07055 φ ( 0.707107 ) + 0.794395 φ ( 1 ) .
Let f ( t ) be a continuous on [ a , b ] function. Define
φ f ( t ) = f b − a 2 t + b + a 2 for − 1 ≤ t ≤ 1 .
Then
f ( t ) ≈ P φ f 2 t b − a − a + b b − a for a ≤ t ≤ b .
Let us apply this technique for approximatingbthe Mittag-Leffler functions.
Example. We have the approximations
l E 1.9 ( t ) ≈ − 7.8941 × 10 − 21 t 20 + 2.33785 × 10 − 18 t 19 − 3.17959 × 10 − 16 t 18 + 2.63053 × 10 − 14 t 17 − 1.47815 × 10 − 12 t 16 + 5.96593 × 10 − 11 t 15 − 1.78388 × 10 − 9 t 14 + 4.01915 × 10 − 8 t 13 − 6.87859 × 10 − 7 t 12 + 8.9635 × 10 − 6 t 11 − 8.88756 × 10 − 5 t 10 + 6.70204 × 10 − 4 t 9 − 3.8524 × 10 − 3 t 8 + 1.68792 × 10 − 2 t 7 − 5.47837 × 10 − 2 t 6 + 1.18961 × 10 − 1 t 5 − 1.52666 × 10 − 1 t 4 + 2.48293 × 10 − 1 t 3 − 6.64595 × 10 − 1 t 2 − 2.41517 × 10 − 3 t + 1 .
and
l E 1.9 , 2 ( t ) ≈ − 4.34152 × 10 − 22 t 20 + 1.3397 × 10 − 19 t 19 − 1.90429 × 10 − 17 t 18 + 1.65206 × 10 − 15 t 17 − 9.77053 × 10 − 14 t 16 + 4.16738 × 10 − 12 t 15 − 1.32279 × 10 − 10 t 14 + 3.17957 × 10 − 9 t 13 − 5.83735 × 10 − 8 t 12 + 8.20778 × 10 − 7 t 11 − 8.83439 × 10 − 6 t 10 + 7.27272 × 10 − 5 t 9 − 4.58522 × 10 − 4 t 8 + 2.21304 × 10 − 3 t 7 − 7.96561 × 10 − 3 t 6 + 1.93654 × 10 − 2 t 5 − 2.78186 × 10 − 2 t 4 + 5.63977 × 10 − 2 t 3 − 2.16129 × 10 − 1 t 2 − 3.05442 × 10 − 3 t + 1 .
See Figure 6.
We obtained the following approximations.

2.6. Mittag Leffler function E α − t α .

For 0 ≤ t ≤ 10 and 1.05 ≤ α ≤ 2 :
E α − t α ≈ − 3.31819 ( α − 2.63795 ) ( α − 2.19825 ) ( α − 0.462826 ) α 2 − 3.44556 α + 3.00567 α 2 − 1.60872 α + 1.11751 t + 9.4249 ( α − 2.63986 ) ( α − 1.17758 ) ( α − 0.593342 ) α 2 − 4.12231 α + 4.25257 α 2 − 1.82145 α + 1.20697 t 2 + − 8.97968 ( α − 2.62418 ) ( α − 2.22066 ) ( α − 1.79894 ) ( α − 1.09393 ) ( α − 0.662815 ) α 2 − 1.92785 α + 1.25783 t 3 + 4.01742 ( α − 2.61737 ) ( α − 2.20703 ) ( α − 1.69479 ) ( α − 1.06394 ) ( α − 0.707285 ) α 2 − 1.99641 α + 1.29223 t 4 + − 0.950677 ( α − 2.60531 ) ( α − 2.16609 ) ( α − 1.63372 ) ( α − 1.05013 ) ( α − 0.73826 ) α 2 − 2.04488 α + 1.31749 t 5 + 0.122174 ( α − 2.58602 ) ( α − 2.12322 ) ( α − 1.59499 ) ( α − 1.04277 ) ( α − 0.760889 ) α 2 − 2.08064 α + 1.33659 t 6 + − 0.00804049 ( α − 2.56221 ) ( α − 2.08505 ) ( α − 1.56918 ) ( α − 1.03844 ) ( α − 0.777908 ) α 2 − 2.10766 α + 1.35122 t 7 + 0.000211896 ( α − 2.5367 ) ( α − 2.0528 ) ( α − 1.55133 ) ( α − 1.03569 ) ( α − 0.790949 ) α 2 − 2.12835 α + 1.36247 t 8 .
For 10 ≤ t ≤ 20 and 1.05 ≤ α ≤ 2 :
E α − t α ≈ − 243804 . ( α − 1.58723 ) ( α − 1.54111 ) ( α − 1.35855 ) ( α − 1.23385 ) ( α − 1.07874 ) ( α − 1.01037 ) ( α − 0.845726 ) + 110862 . ( α − 1.36324 ) ( α − 1.2264 ) ( α − 1.08101 ) ( α − 1.00432 ) ( α − 0.560557 ) α 2 − 3.1297 α + 2.44928 t + − 19807 . ( α − 1.36665 ) ( α − 1.22297 ) ( α − 1.08162 ) ( α − 1.00257 ) ( α − 0.0214421 ) α 2 − 3.12999 α + 2.45035 t 2 + 1630.12 ( α − 1.36945 ) ( α − 1.22108 ) ( α − 1.08186 ) ( α − 1.00176 ) ( α + 1.3272 ) α 2 − 3.12995 α + 2.45056 t 3 + − 36.7302 ( α − 1.37183 ) ( α − 1.21991 ) ( α − 1.08198 ) ( α − 1.0013 ) ( α + 10.5852 ) α 2 − 3.12999 α + 2.45065 t 4 + − 3.94984 ( α − 8.28782 ) ( α − 1.37386 ) ( α − 1.21915 ) ( α − 1.08204 ) ( α − 1.00101 ) α 2 − 3.13029 α + 2.45097 t 5 + 0.342 ( α − 4.40187 ) ( α − 1.37561 ) ( α − 1.21863 ) ( α − 1.08208 ) ( α − 1.00082 ) α 2 − 3.13089 α + 2.45166 t 6 + − 0.010615 ( α − 3.44088 ) ( α − 1.37712 ) ( α − 1.21826 ) ( α − 1.0821 ) ( α − 1.00068 ) α 2 − 3.13176 α + 2.4527 t 7 + 0.00012203 ( α − 3.00628 ) ( α − 1.37841 ) ( α − 1.21798 ) ( α − 1.08212 ) ( α − 1.00058 ) α 2 − 3.13285 α + 2.45406 t 8
For 20 ≤ t ≤ 30 and 1.05 ≤ α ≤ 2 :
E α − t α ≈ 1.66711 × 10 8 ( α − 1.48737 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.58508 α + 3.21328 + − 5.47563 × 10 7 ( α − 1.48737 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.58375 α + 3.21101 t + 7.82832 × 10 6 ( α − 1.48737 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.58244 α + 3.20875 t 2 + − 636231 . ( α − 1.48737 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.58113 α + 3.20652 t 3 + 32149 . ( α − 1.48737 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.57984 α + 3.20431 t 4 + − 1034.23 ( α − 1.48738 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.57856 α + 3.2021 t 5 + 20.6856 ( α − 1.48738 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.57728 α + 3.19991 t 6 + − 0.235189 ( α − 1.48738 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.57601 α + 3.19773 t 7 + 0.00116388 ( α − 1.48738 ) ( α − 1.3924 ) ( α − 1.21666 ) ( α − 1.08216 ) ( α − 1 ) α 2 − 3.57474 α + 3.19554 t 8 .
E = Error = 0.0340668 ( 3.59621 − α ) ( α − 0.997587 ) ( α − 0.316375 ) α 2 − 4.49614 α + 5.09479 α 2 − 3.41703 α + 3.00412

2.7. Mittag Leffler function E α , 2 − t α .

For 0 ≤ t ≤ 10 and 1.05 ≤ α ≤ 2 :
E α , 2 − t α ≈ − 0.278939 ( α − 2.31677 ) ( α − 2.12563 ) ( α + 0.0893733 ) α 2 − 3.59157 α + 3.32862 α 2 − 0.889475 α + 1.39508 t 0.826976 ( α − 2.37246 ) ( α − 1.12366 ) ( α − 0.129251 ) α 2 − 4.13191 α + 4.35456 α 2 − 1.22713 α + 1.33209 t 2 − 0.78555 ( α − 1.84908 ) ( α − 1.05487 ) ( α − 0.245395 ) α 2 − 4.49297 α + 5.05579 α 2 − 1.3987 α + 1.31131 t 3 0.341291 ( α − 2.27376 ) ( α − 2.23048 ) ( α − 1.69824 ) ( α − 1.03336 ) ( α − 0.315277 ) α 2 − 1.50041 α + 1.3013 t 4 − 0.0772279 ( α − 2.35263 ) ( α − 2.10666 ) ( α − 1.63099 ) ( α − 1.02433 ) ( α − 0.359298 ) α 2 − 1.56281 α + 1.29204 t 5 0.00940743 ( α − 2.36727 ) ( α − 2.03824 ) ( α − 1.59441 ) ( α − 1.01982 ) ( α − 0.386893 ) α 2 − 1.60025 α + 1.28059 t 6 − 0.000584189 ( α − 2.36542 ) ( α − 1.98829 ) ( α − 1.57288 ) ( α − 1.01729 ) ( α − 0.403095 ) α 2 − 1.62059 α + 1.26611 t 7 0.0000145004 ( α − 2.35663 ) ( α − 1.95046 ) ( α − 1.55959 ) ( α − 1.01573 ) ( α − 0.41085 ) α 2 − 1.62866 α + 1.2485 t 8 .
For 10 ≤ t ≤ 20 and 1.05 ≤ α ≤ 2 :
E α , 2 − t α ≈ 60943.9 ( α − 2.06184 ) ( α − 1.38175 ) ( α − 1.19821 ) ( α − 1.09657 ) ( α − 0.995747 ) α 2 − 3.11686 α + 2.43632 + − 36159 . ( α − 2.04536 ) ( α − 1.37969 ) ( α − 1.20652 ) ( α − 1.08925 ) ( α − 0.997841 ) α 2 − 3.11793 α + 2.4373 t + 9273.74 ( α − 2.02865 ) ( α − 1.37991 ) ( α − 1.20961 ) ( α − 1.08675 ) ( α − 0.998573 ) α 2 − 3.11906 α + 2.43826 t 2 + − 1342.04 ( α − 2.01202 ) ( α − 1.38072 ) ( α − 1.21123 ) ( α − 1.08549 ) ( α − 0.998941 ) α 2 − 3.1206 α + 2.43983 t 3 + 119.803 ( α − 1.99573 ) ( α − 1.38168 ) ( α − 1.21224 ) ( α − 1.08474 ) ( α − 0.999161 ) α 2 − 3.12255 α + 2.44205 t 4 + − 6.75367 ( α − 1.98001 ) ( α − 1.38264 ) ( α − 1.21292 ) ( α − 1.08425 ) ( α − 0.999304 ) α 2 − 3.12483 α + 2.44481 t 5 + 0.234774 ( α − 1.96503 ) ( α − 1.38354 ) ( α − 1.2134 ) ( α − 1.08391 ) ( α − 0.999404 ) α 2 − 3.12734 α + 2.44795 t 6 + − 0.00460174 ( α − 1.95089 ) ( α − 1.38434 ) ( α − 1.21377 ) ( α − 1.08366 ) ( α − 0.999477 ) α 2 − 3.12998 α + 2.45135 t 7 + 0.0000389484 ( α − 1.93764 ) ( α − 1.38506 ) ( α − 1.21404 ) ( α − 1.08348 ) ( α − 0.999532 ) α 2 − 3.13267 α + 2.45489 t 8
For 20 ≤ t ≤ 30 and 1.05 ≤ α ≤ 2 :
E α , 2 − t α ≈ 1.26462 × 10 6 ( α − 1.48703 ) ( α − 1.39288 ) ( α − 1.21602 ) ( α − 1.08268 ) ( α − 0.999813 ) α 2 − 3.36036 α + 2.82904 + − 351313 . ( α − 1.48714 ) ( α − 1.39271 ) ( α − 1.21619 ) ( α − 1.08251 ) ( α − 0.99988 ) α 2 − 3.32038 α + 2.76052 t + 40872.9 ( α − 1.48716 ) ( α − 1.39267 ) ( α − 1.21618 ) ( α − 1.0825 ) ( α − 0.999888 ) α 2 − 3.26096 α + 2.65869 t 2 + − 2547.21 ( α − 1.68286 ) ( α − 1.48833 ) ( α − 1.4796 ) ( α − 1.39284 ) ( α − 1.21598 ) ( α − 1.08259 ) ( α − 0.999864 ) t 3 + 88.908 ( α − 1.69704 ) ( α − 1.48734 ) ( α − 1.39215 ) ( α − 1.282 ) ( α − 1.21343 ) ( α − 1.08319 ) ( α − 0.999727 ) t 4 + − 1.56062 ( α − 1.70588 ) ( α − 1.48733 ) ( α − 1.39236 ) ( α − 1.21738 ) ( α − 1.08116 ) ( α − 1.00051 ) ( α − 0.765272 ) t 5 + 0.00488049 ( α − 1.71229 ) ( α − 1.48734 ) ( α − 1.3924 ) ( α − 1.21694 ) ( α − 1.08188 ) ( α − 1.00011 ) ( α + 5.24412 ) t 6 + 0.000247386 ( α − 3.46421 ) ( α − 1.7173 ) ( α − 1.48734 ) ( α − 1.39241 ) ( α − 1.21682 ) ( α − 1.08201 ) ( α − 1.00006 ) t 7 + − 2.74 e − 6 ( α − 2.57819 ) ( α − 1.72137 ) ( α − 1.48735 ) ( α − 1.39241 ) ( α − 1.21677 ) ( α − 1.08206 ) ( α − 1.00004 ) t 8 .
E = Error = 0.0340671 ( 3.59618 − α ) ( α − 0.997587 ) ( α − 0.316376 ) α 2 − 4.49615 α + 5.0948 α 2 − 3.41703 α + 3.00412 .

3. Physics Applications.

Suppose we are given that
D t α x ( t ) + x ( t ) + F ( t , x , x ˙ ) = 0 , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 , , 0 ≤ t ≤ T .
We approximate the solution to (44) by means of the solution to the following integer order oscillator:
x ¨ + 2 ε x ˙ + ω 2 x + λ x 3 + μ x 5 + ν x 7 + F ( t , x , x ˙ ) = 0 , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 , 0 ≤ t ≤ T .
The error of this approximation is defined as
E ( x , T ) = max 0 ≤ t ≤ T 1 Γ ( 2 − α ) ∫ 0 t x ′ ′ ( s ) d s ( t − s ) α − 1 + x ( t ) + F ( t , x ( t ) , x ˙ ( t ) ) .
We will refer to this method as Integerization Principle. The oscillator (45) may be easily solved with the aid of the Runge-Kutta methods.

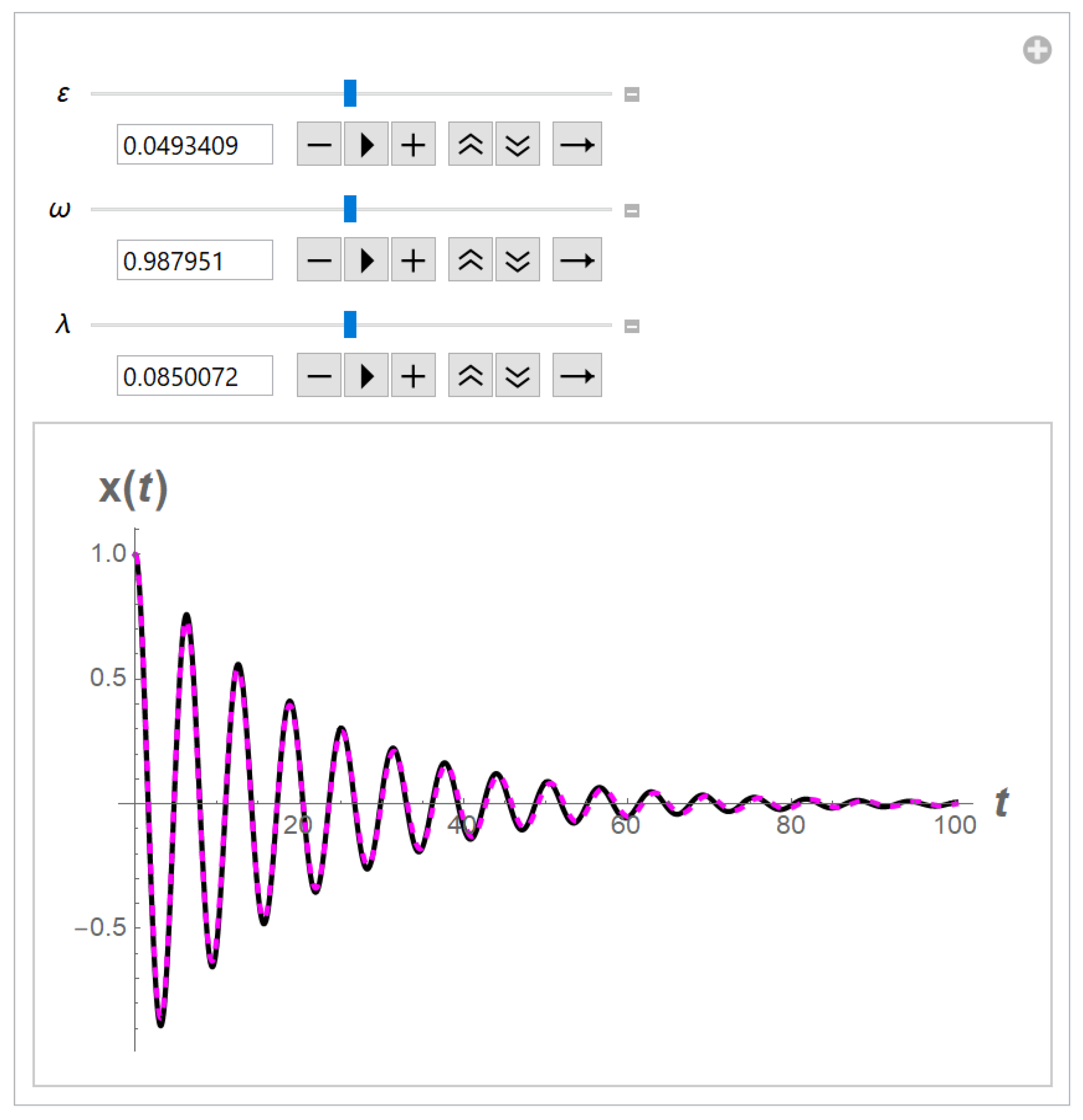
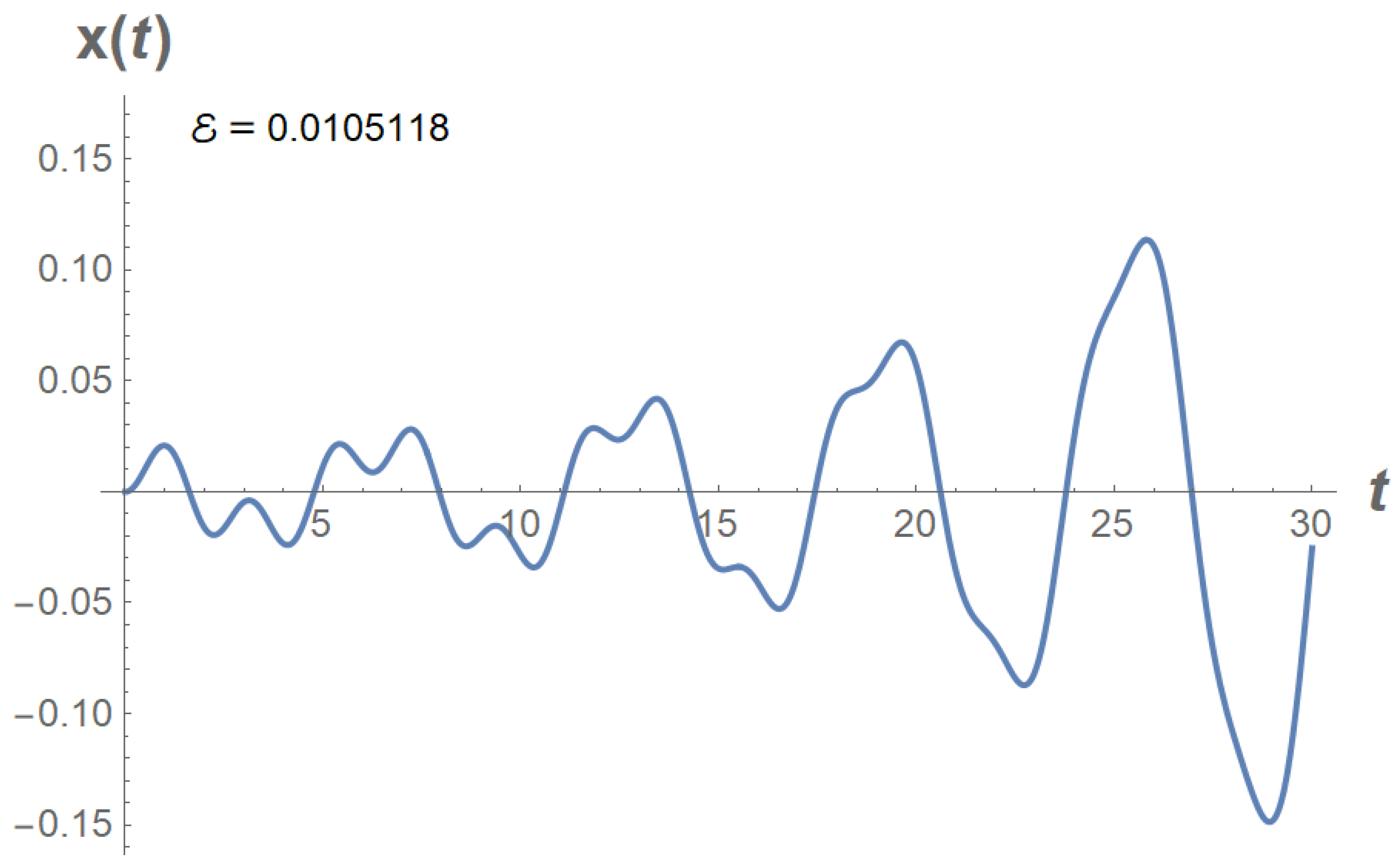
3.1. The fractional Pendulum

Let
D t α x ( t ) + sin ( x ( t ) ) = f ( t ) , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 , , 0 ≤ t ≤ T .
We solve the i.v.p.
x ¨ + 2 ε x ˙ + ω 2 x − 1 / 6 x 3 + 1 / 120 x 5 + λ x 3 + μ x 5 + ν x 7 = f ( t ) , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 , 0 ≤ t ≤ T .
The parameter values ε , ω , λ , μ and ν are obtained from Table 8 and Table 9.
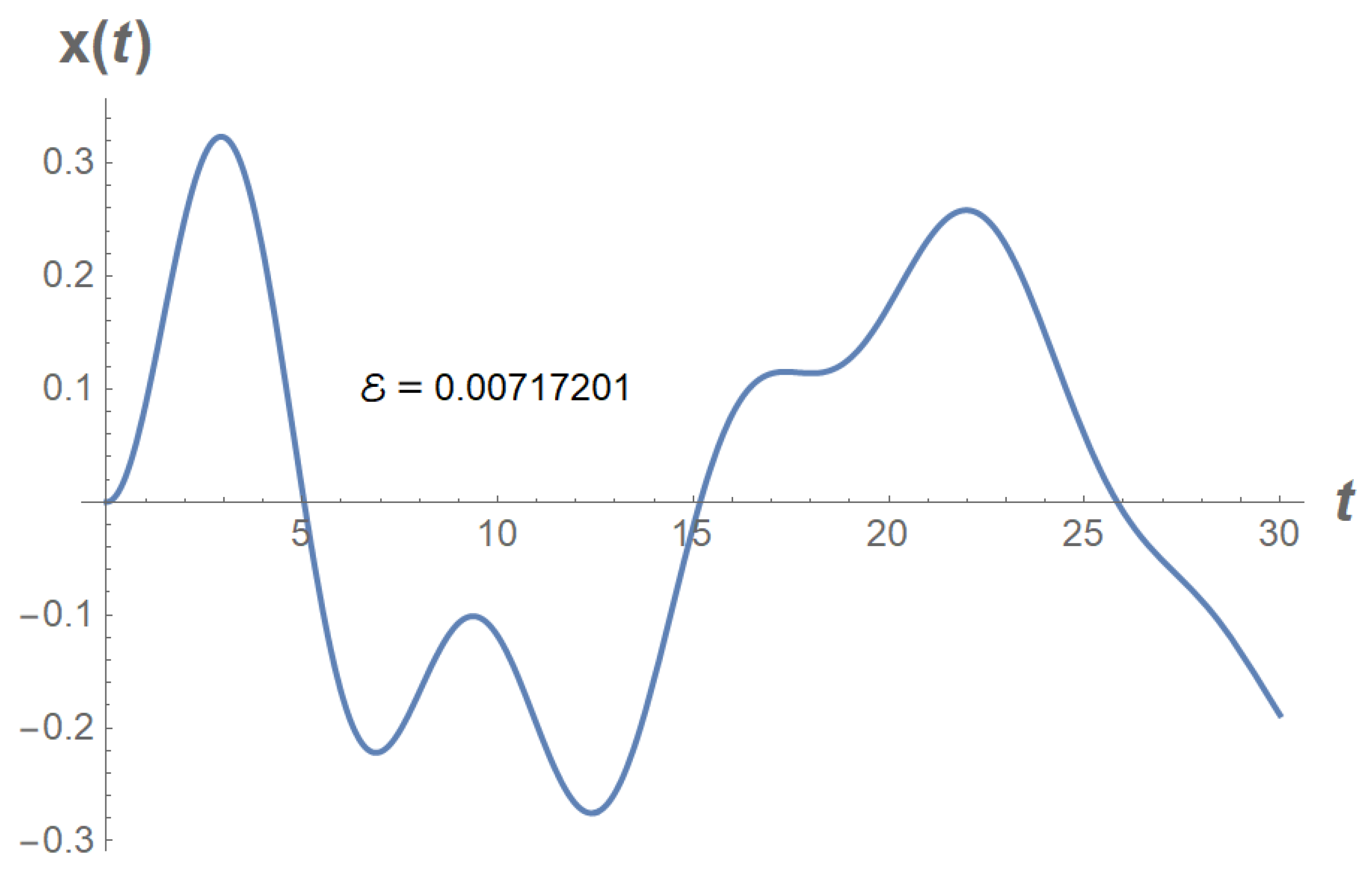
Example. Let
D t 1.9 x ( t ) + sin ( x ( t ) ) = 0.2 cos ( 0.3 t ) , x ( 0 ) = 0 and x ′ ( 0 ) = 0 , 0 ≤ t ≤ 30 .
From Table 9 we get
ε = 0.074831 , ω = 0.991493 , λ = 0.00923344 , μ = 0.118255 , ν = 0.204796 .
We replace the i.v.p. (49) with the i.v.p.
l x ¨ + 0.149662 x ˙ + 0.983059 x − 0.15461 x 3 + 0.126447 x 5 + 0.204796 x 7 = 0.2 cos ( 0.3 t ) . x ( 0 ) = 0 , x ′ ( 0 ) = 0 , 0 ≤ t ≤ 30 .
See Figure 7.

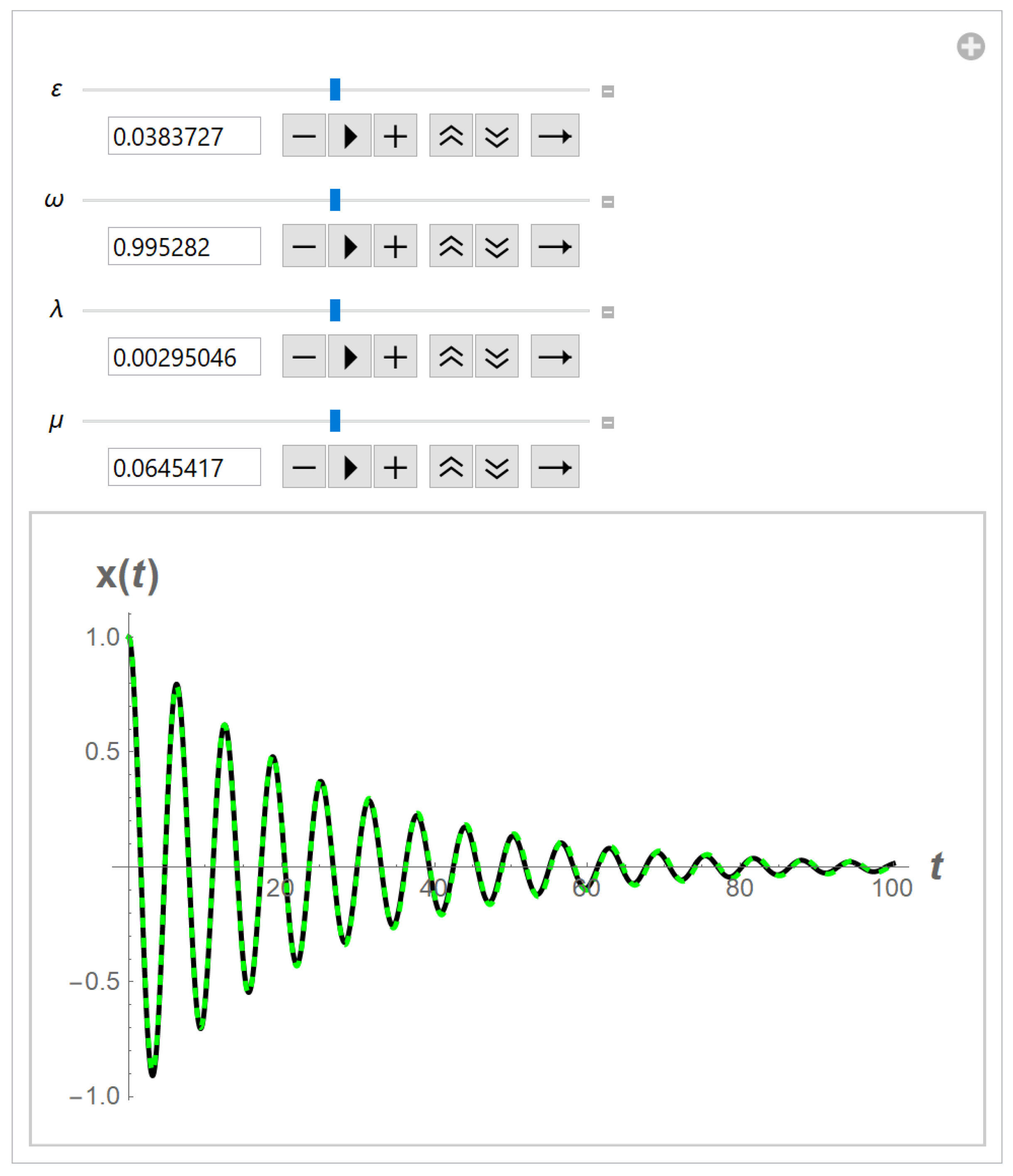
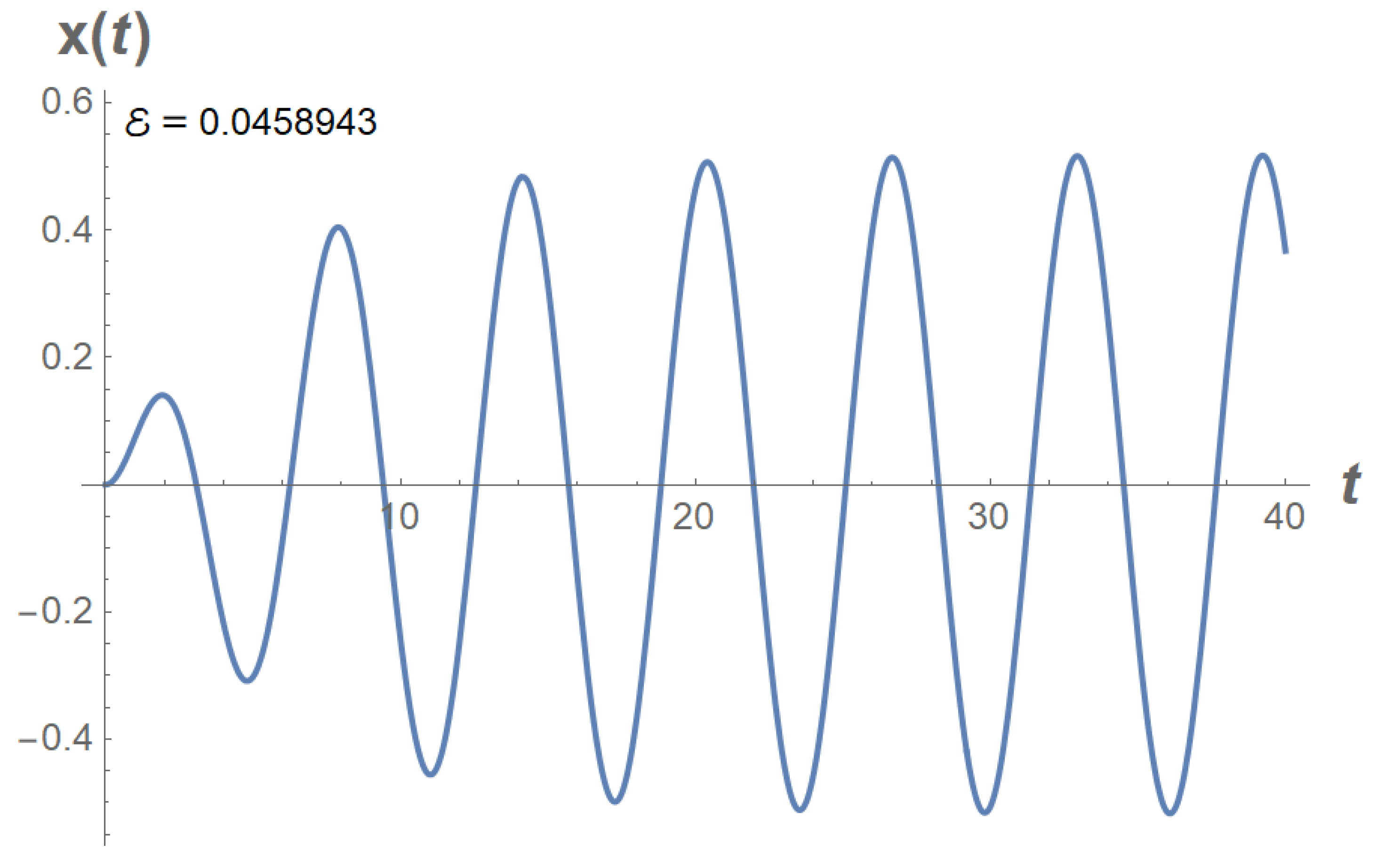
3.2. Fractional Van der Pol oscillator.

Let
D t 1.85 x ( t ) − 0.25 ( 1 − x ( t ) 2 ) x ′ ( t ) + x ( t ) = 0 , x ( 0 ) = 0.5 and x ′ ( 0 ) = 0 , 0 ≤ t ≤ 30 .
Parameter values:
ε = 0.111489 , ω = 0.994873 , λ = 0.00733691 , μ = 0.233966 , ν = 0.338185 .
We solve the following Duffing-Van der Pol oscillator:
l x ′ ′ ( t ) − 0.25 1 − x ( t ) 2 x ′ ( t ) + 0.989773 x ( t ) + 0.222979 x ′ ( t ) + 0.00733691 x ( t ) 3 + 0.233966 x ( t ) 5 + 0.338185 x ( t ) 7 = 0 . x ( 0 ) = 0.5 ∧ x ′ ( 0 ) = 0 , 0 ≤ t ≤ 30 .
See Figure 8.
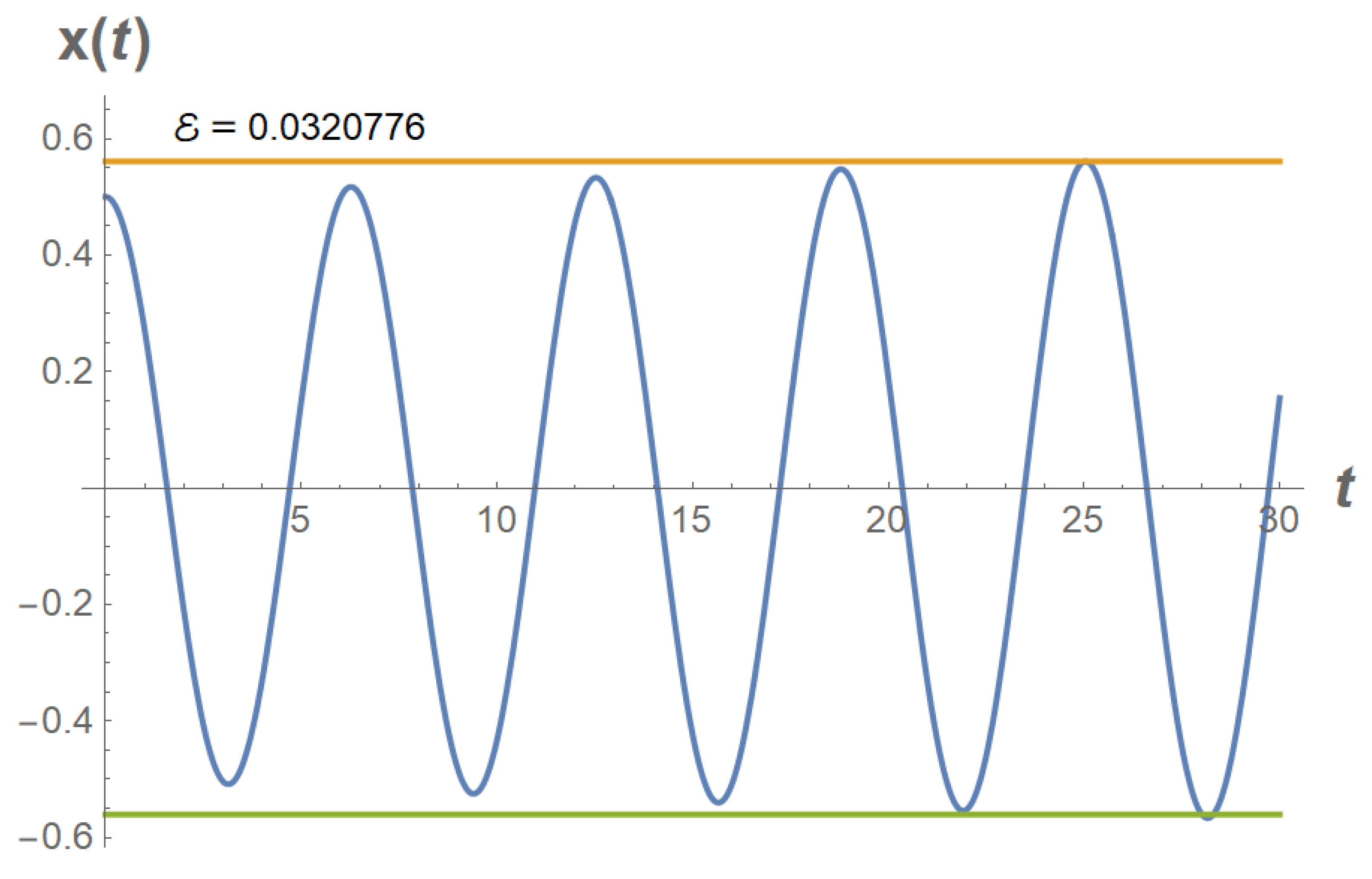
Let now
D t 1.95 x ( t ) − 0.25 ( 1 − x ( t ) 2 ) x ′ ( t ) + x ( t ) = 0.1 cos ( 3 t ) , x ( 0 ) = 0 and x ′ ( 0 ) = 0 , 0 ≤ t ≤ 30 .
Parameter values:
ε = 0.0383727 , ω = 0.996123 , λ = 0.00295046 , μ = 0.0645417 , ν = 0.0804873 .
We solve the following oscillator:
l x ′ ′ ( t ) − 0.25 1 − x 2 x ˙ + 0.0767453 x ˙ + 0.992262 x ( + 0.00295046 x 3 + 0.0645417 x 5 + 0.0804873 x 7 = 0.1 cos ( 3 t ) x ( 0 ) = 0 , x ′ ( 0 ) = 0 , 0 ≤ t ≤ 30
See Figure 9.

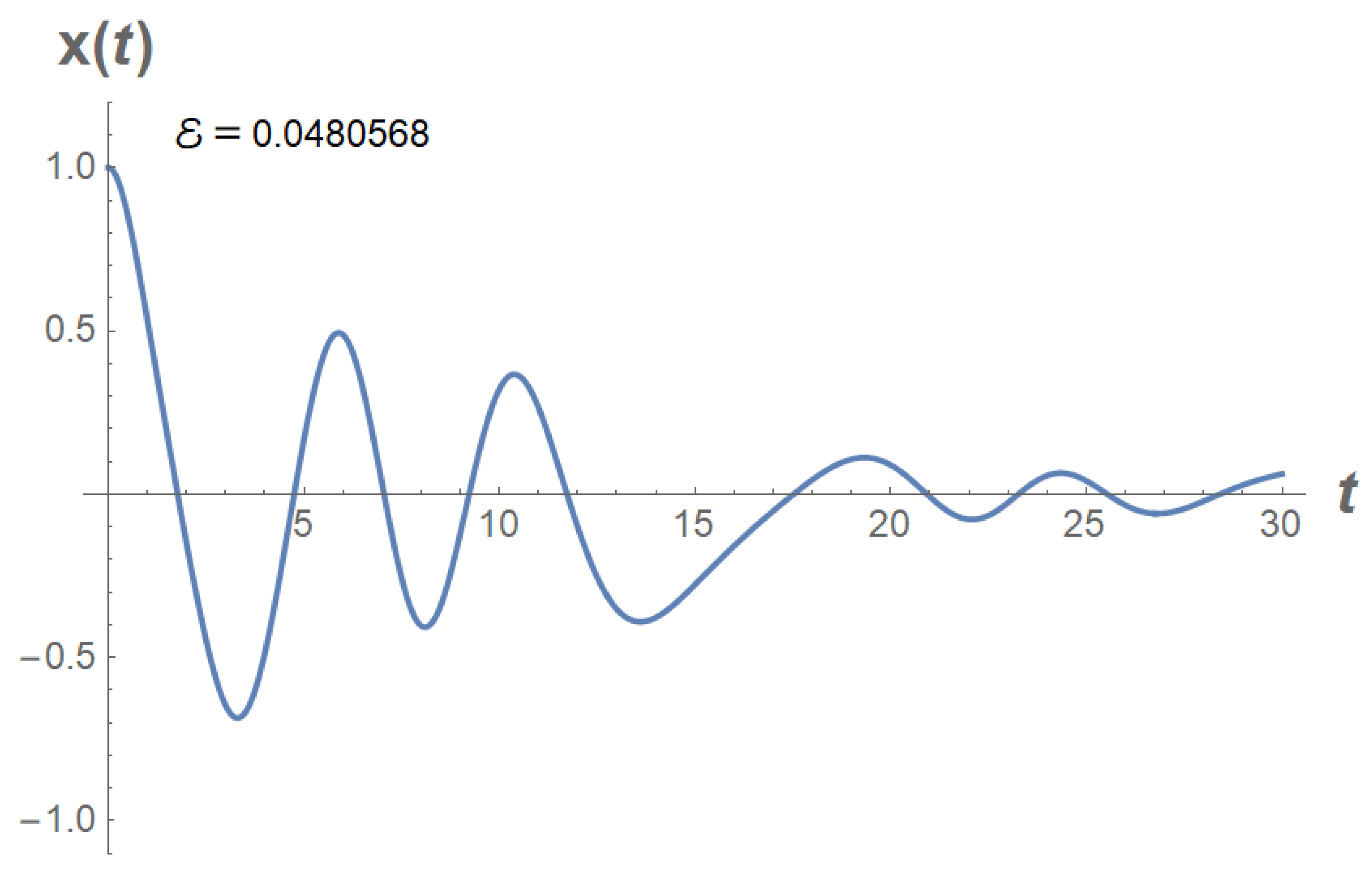
3.3. Fractional linear oscillator.

Suppose we are given that
D t α x ( t ) + x ( t ) = f ( t ) , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 , , 0 ≤ t ≤ T .
We replace this oscillator with the oscilator
x ¨ + 2 ε x ˙ + ω 2 x + λ x 3 + μ x 5 + ν x 7 = f ( t ) , x ( 0 ) = x 0 and x ′ ( 0 ) = x ˙ 0 , , 0 ≤ t ≤ T .
For example, let
D t 1.75 x ( t ) + x ( t ) = 0.2 cos t , x ( 0 ) = 0 and x ′ ( 0 ) = 0 , 0 ≤ t ≤ 40 .
Parameter values:
ε = 0.193623 , ω = 0.995526 , λ = − 0.242128 , μ = 1.2301 , ν = 1.93631 .
We solve the following oscillator:
l x . . + 0.387247 x ˙ + 0.991072 x − 0.242128 x 3 + 1.2301 x 5 + 1.93631 x 7 = 0.2 cos ( t ) x ( 0 ) = 0 , x ′ ( 0 ) = 0 , 0 ≤ t ≤ 40
See Figure 10.

3.4. Fractional Duffing-Mathieu oscillator.

Let us consider the i.v.p.
D t 1.9 x ( t ) + ( 1 − cos ( 0.4 t ) ) + x ( t ) + x 3 ( t ) = 0 , x ( 0 ) = 1 and x ′ ( 0 ) = 0 , 0 ≤ t ≤ 30 .
Parameter values:
ε = 0.074831 , ω = 0.991493 , λ = 0.00923344 , μ = 0.118255 , ν = 0.204796 .
We solve the following oscillator:
l x . . − x cos ( 0.4 t ) + 0.149662 x ˙ + + 0.983059 x + 1.00923 x 3 + 0.118255 x 5 + 0.204796 x 7 = 0 . x ( 0 ) = 1 and x ′ ( 0 ) = 0 , 0 ≤ t ≤ 30 .
See Figure 11.

4. Conclusions.

We gave approximate expression for the Mittag-Leffler functions in terms of elementary functions making use of several appeoaches. This allowed us to establish a method we called integerization principle. We demosntrated in concrete examples the effectiveness of the proposed method. We also may solve other fractional nonlinear oescillators using the integerization principle.

References

  1. A. Belendez, T. Belendez, A. Marquez and C. Neipp. Application of He’s homotopy perturbation method to conservative truly nonlinear oscillators. Chaos, Solitons & Fractals (2008) 770–780.
  2. S. Ghosh, A. Roy and D. Roy. An adaptation of Adomian decomposition for numericanalytic integration of strongly nonlinear and chaotic oscillators. Comput. Methods Appl. Mech. Eng. 196 (2007) 1133–1153.
  3. J.H. He. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 135 (2003) 73–79. Nonlinear Dynamics and Systems Theory, 20 (5) (2020) 568–577 577.
  4. A. Jaradat, M.S.M. Noorani, M. Alquran, and H.M. Jaradat. A Novel Method for Solving Caputo-Time-Fractional Dispersive Long Wave Wu-Zhang System. Nonlinear Dynamics and Systems Theory 18(2) (2018) 182–190.
  5. Z. Denton and J.D. Ramirez. Monotone Method for Finite Systems of Nonlinear RiemannLiouville Fractional Integro-Differential Equations. Nonlinear Dynamics and Systems Theory 18(2) (2018) 130–143. [CrossRef]
  6. Prcious Sibanda and, A. Khidir. A new modification of the HPM for the Duffing equation with cubic nonlinearity. In: Proc. 2011 International Conference on Applied and Computational Mathematics, Turkey, 2011, 139–145.
  7. J. I. Ramos. On the variational iteration method and other iterative techniques for nonlinear differential equations. Appl. Math. Comput. 199 (2008) 39–69.
  8. J. I. Ramos. An artificial parameterdecomposition method for nonlinear oscillators: Applications to oscillators with odd nonlinearities. J. Sound Vib. 307 (2007) 312–329. [CrossRef]
  9. P. D. Ariel, M. I. Syam and Q. M. Al-Mdallal. The extended homotopy perturbation method for the boundary layer flow due to a stretching sheet with partial slip. International Journal of Computer Mathematics 90(9) (2013) 1990–2002. [CrossRef]
  10. M. I. Syam and H. I. Siyyam. Numerical differentiation of implicitly defined curves. J. Comput. Appl. Math. 108(1-2) (1999) 131–144. [CrossRef]
  11. M. Syam. The modified Broyden-variational method for solving nonlinear elliptic differential equations. Chaos, Solitions and Fractals 32(2) (2007) 392–404. [CrossRef]
  12. B. Attili, K. Furati, and M.I. Syam. An efficient implicit Runge-Kutta method for second order systems. Appl. Math. Comput. 178(2) (2006) 229–238. [CrossRef]
  13. P.G. Chhetri and A.S. Vatsala. Generalized Monotone Method for Riemann-Liouville Fractional Reaction Diffusion Equation with Applications. Nonlinear Dynamics and Systems Theory 18(3) (2018) 259–272.
  14. D.J. Sabeg, R. Ezzati, and K. Maleknejad. Solving Two-Dimensional Integral Equations of Fractional Order by Using Operational Matrix of Two-Dimensional Shifted Legendre Polynomials. Nonlinear Dynamics and Systems Theory 18(3) (2018) 297–306.
  15. K.B. Oldham, and J. Spanier. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Courier Corporation, Massachusetts, USA, 2002.
  16. O. Abu Arqub, A. El-Ajou, A. Bataineh and I. Hashim. A representation of the exact solution of generalized Lane Emden equations using a new analytical method. Abstract and Applied Analysis 2013 (2013) 1–10. [CrossRef]
  17. Muhammed, I. Syam. The Modified Fractional Power Series Method for Solving Fractional Undamped Duffing Equation with Cubic Nonlinearity. Nonlinear Dynamics and Systems Theory, 20 (5) (2020) 568–577.
  18. Roman Parovik, 2020. "Mathematical Modeling of Linear Fractional Oscillators," Mathematics, MDPI, vol. 8(11), pages 1-26, October. [CrossRef]
Preprints 67298 g001
Figure 1. The approximation (11).
Figure 1. The approximation (11).
Preprints 67298 g001
Preprints 67298 g002
Figure 2. Pots of ε , κ and Error as functions og α .
Figure 2. Pots of ε , κ and Error as functions og α .
Preprints 67298 g002
Preprints 67298 g003
Figure 3.  
Figure 3.  
Preprints 67298 g003
Preprints 67298 g004
Figure 4.  
Figure 4.  
Preprints 67298 g004
Preprints 67298 g005
Figure 5.  
Figure 5.  
Preprints 67298 g005
Preprints 67298 g006
Figure 6.  
Figure 6.  
Preprints 67298 g006
Preprints 67298 g007
Figure 7.  
Figure 7.  
Preprints 67298 g007
Preprints 67298 g008
Figure 8.  
Figure 8.  
Preprints 67298 g008
Preprints 67298 g009
Figure 9.  
Figure 9.  
Preprints 67298 g009
Preprints 67298 g010
Figure 10.  
Figure 10.  
Preprints 67298 g010
Preprints 67298 g011
Figure 11.  
Figure 11.  
Preprints 67298 g011
Table 1. E α ( t ) ≈ exp ( − ε t ) cos ( κ t ) + ε κ sin ( κ t ) for 0 ≤ t ≤ 100 .
Table 1. E α ( t ) ≈ exp ( − ε t ) cos ( κ t ) + ε κ sin ( κ t ) for 0 ≤ t ≤ 100 .
Preprints 67298 i001
Table 2. E α ( t ) ≈ exp ( − ε t ) cos ( κ t ) + ε κ sin ( κ t ) for 0 ≤ t ≤ 100 .
Table 2. E α ( t ) ≈ exp ( − ε t ) cos ( κ t ) + ε κ sin ( κ t ) for 0 ≤ t ≤ 100 .
Preprints 67298 i002
Table 3.  
Table 3.  
Preprints 67298 i003
Table 4.  
Table 4.  
Preprints 67298 i004
Table 5.  
Table 5.  
Preprints 67298 i005
Table 6.  
Table 6.  
Preprints 67298 i006
Table 7.  
Table 7.  
Preprints 67298 i007
Table 8.  
Table 8.  
Preprints 67298 i008
Table 9.  
Table 9.  
Preprints 67298 i009
Preprints 67298 i010
Table 10.  
Table 10.  
Preprints 67298 i011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated