Prerpints.org logo
Preprint
Article

Non-Local EPR Correlations using Quaternion Spin

Altmetrics

Downloads

723

Views

401

Comments

2

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Theoretical, Quantum and Computational Chemistry

Submitted:

31 March 2023

Posted:

03 April 2023

Read the latest preprint version here

Alerts
Abstract
A statistical simulation is presented which reproduces the correlation obtained from EPR coincidence experiments without non-local connectivity. We suggest that spin carries two complementary properties. In addition to the spin polarization, we identify spin coherence. This spin attribute is anti-symmetric and generates the helicity. In addition this spin has structure formed from two orthogonal magnetic moments. From these, a resonance spin results from their coupling in free flight. Upon encountering a filter, the resonance spin 1 decouples back into two independent spins of $\frac{1}{2}$, with one aligning with the filter and the other randomizing. The process of decoupling the resonance spin is responsible for the quantum correlation which results in the observe violation of Bell's Inequalities. The polarized states give a CHSH value of 2 while the resonance spin give a CHSH value of 1. Coherence can only be formulated by the existence of a bivector which gives a spin the same geometric structure as a photon. Although this work is not about Bell's theorem, we note that there are no hidden variables (HV). The only local variable is the angle that orients a spin on the Bloch sphere, first identified in the 1920's. The new features introduced are changing the spin symmetry from SU(2) to the quaternion group, $Q_8$, and the introduction of a bivector into spin which leads to an element of reality which is anti-Hermitian. The calculations use standard spin algebra, and properties of quaternions.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

Introduction

We consider the correlation obtained from coincidence EPR experiments [1,2,3]. An EPR pair, [4], is defined as two particles that were originally in a singlet state and separated, [5]. In that process, we assume no non-local entanglement persists so the pair forms a product state.
We develop a spin theory which includes a Pauli bivector [6], i σ . From this a spin becomes structured and geometrically equivalent to a photon, (Figure 1), [8] . It has two orthogonal spin 1 2 axes, and in free-flight these couple to give a spin of magnitude of 1, called Q-spin. Upon encountering a field, this decouples back into its spin 1 2 components. We show that the observed violation of Bell’s Inequalities results from the decoupling of the coherent spin of 1 to a spin of 1 2 .
The free-flight wave and the measured particle display wave-particle duality. The complementary property to the measured spin polarization is the helicity, which is destroyed in a polarizing field. In free-flight, a spin is a boson of magnitude 1. When measured it becomes a fermion of 1 2 .
This paper is the third of three in which quaternion spin, or Q-spin, is presented. In the first paper, [8], the Dirac equation is modified to include a bivector, i σ 2 = σ 3 σ 1 which is the origin of helicity and Q-spin. The second paper, [6] shows that its correlation accounts for the observed violation of Bell’s Inequalities (BI).
Here we refer to the usual two state point particle spin 1 2 as Dirac spin,[9], which is symmetric and polarized, in order to distinguish it from Q-spin that carries both polarization and helicity. We first give a step-by-step discussion of the theory which shows that correlation is maintained between EPR pairs by their common orientation upon separation.
A computer simulation is then presented that generates the correlation from both polarization and coherence taking into account the decoupling from the coherent spin 1. As it approach a filter, Q-spin is modeled by two coupled spins resulting in a magnitude of one. The simulation gives a CHSH value or 3 which corresponds to a CHSH = 2 for polarization and a CHSH = 1 for the coherence.
This paper is not primarily about Bell’s Theorem, other than noting it is not violated for each of the two complementary elements of reality. There are no hidden variables, and the only variable, θ , relates the Body Fixed Frame (BFF), denoted by e 1 , e 2 , e 3 , of the structured Q-spin, to the Laboratory Fixed Frame (LFF), X , Y , Z . This variable orients a spin on its Bloch sphere and is explicitly defined and is not hidden. We take the axis of linear momentum to be the laboratory axis Y = e 2 . In the simulation, every EPR pair is counted. Since their are no HV, there can be no loopholes. Except for introducing a physical attribute that is anti-Hermitian, the work uses standard Pauli spin algebra, such as found in many papers, e . g . [5], along with properties of quaternions, [10]. .

Theory

Motiavation

As usual we assume that an EPR pair was initially in a singlet state given by
| Ψ 12 〉 = 1 2 | + 〉 1 | − 〉 2 − | − 〉 1 | + 〉 2
Since coherent states are off-diagonal, ± ∓ , and these are not displayed in the above equation, we use the spin state operator, [11], by taking the outer product of Eq.(1), giving,
ρ 12 = Ψ 12 Ψ 12 = 1 4 I 1 I 2 − σ 1 · σ 2 = 1 2 0 0 0 0 0 1 − 1 0 0 − 1 1 0 0 0 0 0
The resulting matrix can be represented as the tensor product between the two identity matrices, I i and the scalar product between the two Pauli spin vectors. The two diagonal elements of the outer product matrix above describe polarization, whereas the two off-diagonal elements are the coherent terms. The coherent terms are responsible for the entanglement and preclude the product state. If those two coherent states are dropped, then the singlet state becomes a product state,
ρ 12 → drop off - diagonal terms ρ 1 ρ 2 = 1 4 I 1 I 2 − σ 3 1 σ 3 2 = ρ 1 + ρ 2 − + ρ 1 − ρ 2 +
in terms of the tensor product of the two single particle state operators,
ρ i ± = 1 2 I i ± σ 3 i
where σ k i = σ i · e k . We view these state operators as describing the pure states of single particles rather than a statistical ensemble over similarly prepared EPR pairs. Eventually we average over all the different spin orientations, θ , in the simulation. There is no statistical interference between EPR pairs and every pair produces a coincidence event.
Using Eqs.(2) and (3) we obtain the EPR correlation from an entangled state as [6],
E a , b = σ a 1 σ b 2 = a · σ 1 σ 2 · b = a · Tr A , B σ A σ B ρ 12 · b = − a · b = − cos θ a − θ b
Likewise using Eq.(3) the product state gives,
E a , b = Tr 1 σ a 1 ρ 1 Tr 2 σ b 2 ρ 2 = − a · Z Z · b = − cos θ a cos θ b
The basis component, e 3 is chosen to be the usual LFF component Z, giving the two final cosine terms.
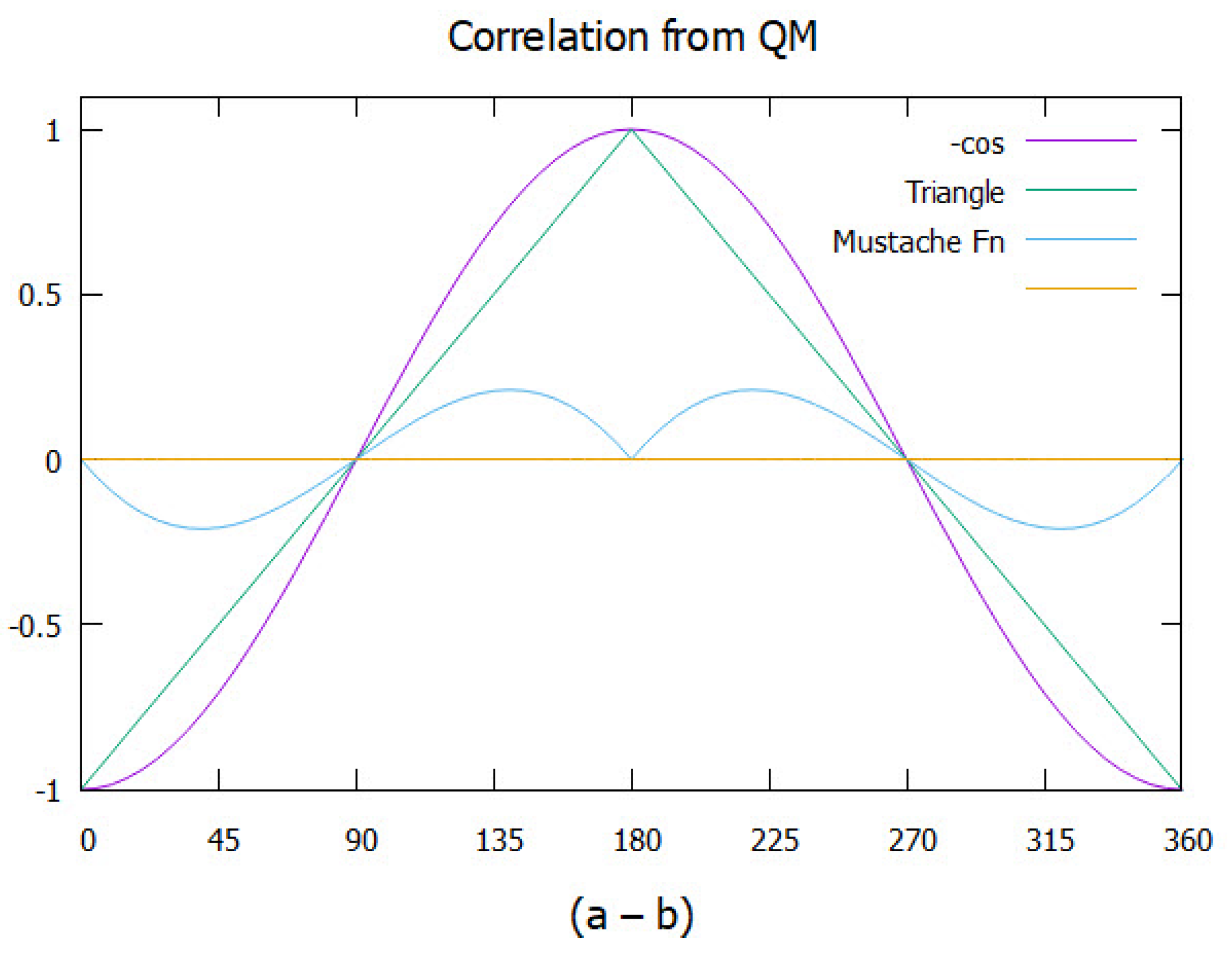
In EPR coincidence experiments, the observed correlation is not consistent with the product state, Eq.(6) but rather gives the full correlation from in Eq.(5). One of the many statements of the EPR paradox [12], is the conclusion that entanglement must be maintained over spacetime. This is justified by Bell’s Theorem, but how such non-local connectivity is maintained is not understood, and defies rational explanation, [13]. [14,15].
In conclusion, if the quantum coherence terms are dropped when an EPR pair separates, the resulting product state does not agree with the experimental results. Including these terms is the purpose of this paper, and we show that they account for the full quantum correlation. That is, the violation is a result of coherence rather than non-local connectivity.

EPR singlet correlation

The correlation arising from an EPR pair, Eq.(5), has the well-known value of CHSH = 2 2 = 2.828 giving the observed violation. This is plotted in (Figure 2) versus ( θ a − θ b ) . The product state given in Eq.(6), does not violate BI with a CHSH = 2. This is displayed in the figure as the triangle. Subtracting the two separates out the part that is responsible for the observed violation of BI, with CHSH = 0.828. We call this the mustache function. Bell’s theorem asserts this correlation can only arise from non-locality, or equivalently that no Local Variable (LV) model can account for the observed violation. In contrast, here we attribute the missing correlation to quantum coherence that was dropped upon particle separation under the assumption of locality.
The figure displays the results from quantum theory. We point out that the simulation presented here from Q-spin gives considerably more correlation than obtained from the standard calculation of a Dirac spin in an entangled state, with CHSH = 2 for the polarization and CHSH = 1 for the coherence. We discuss this difference.

Geometric algebra

The calculations of the correlation given in both Eqs.(5) and (6) involve the trace over the dydic, σ σ . This trace is symmetric requiring 1 2 Tr σ i σ j = δ i j .
One of the most fundamental equations from geometric algebra, [10] expresses a dyadic in terms of the symmetric scalar product and the anti-symmetric wedge product,
ab = 1 2 ab + ba + 1 2 ab − ba = a · b + a ∧ b
Specializing this to the Pauli spin components, we write
σ i σ j = 1 2 σ i σ j + σ j σ i + 1 2 σ i σ j − σ j σ i = 1 2 σ i , σ j + + 1 2 σ i , σ j −
in terms of the anti-commutator and the commutator of these components, , ± . Using the relationship σ i σ j = ε i j k i σ k in terms of the Levi-Civita third rank totally anti-symmetric tensor, requires i = j in the anti-commutator and i ≠ j in the commutator. This leads to the well-known relationship between spin components of
σ i σ j = δ i j + ε i j k i σ k
Note that this expression is complementary since the dyadic cannot be simultaneously symmetric and anti-symmetric (i cannot simultaneously be equal and not equal to j). Only one of the two can occur at any instant.
The anti-symmetric part plays no role in determining the observed spin polarization that depends upon the difference between the two measured spin states, ± , n ^ = ± , θ , ϕ . Here n ^ is unit vector on the Bloch sphere. Motivated by Eq.(9), we defined the hyper-helicity, [6], as a complementary attribute to the coherence,
h ̲ ̲ g = ε ̲ ̲ ̲ · i σ
Using this second rank anti-symmetric and anti-Hermitian operator in the same calculation as given above for the product states, Eq.(6) generates the missing correlation, [6],
a · h ̲ ̲ g 1 · h ̲ ̲ g 2 · b = − sin θ a sin θ b
Of course, added to the product of cosines in Eq.(6), this correlation fully accounts for the -cosine calculated in Eq.(5). This suggests the observe violation of BI is a result of hyper-helicity.

The Dirac equation

Here we summerize the results of reference, [8]. The Dirac equation provides the mathematical basis for spin. If hyper-helicity is an element of reality, it must be consistent with the Dirac equation. Just as Dirac interpreted his four dimensional field as consisting of a matter-antimatter pair of two states each, so should it also give a formal basis for the existence of hyper-helicity.
The Dirac field is represented by the gamma matrices, γ μ , involving time and the three spatial components. The Dirac equation contains no bivector so cannot describe the hyper-helicity. However, a bivector can be introduced by multiplying one gamma matrix by the imaginary number i chosen to be γ ˜ 2 ≡ i γ 2 . This is the only fundamental change introduced in the theory and the solution follows standard methods, [16].
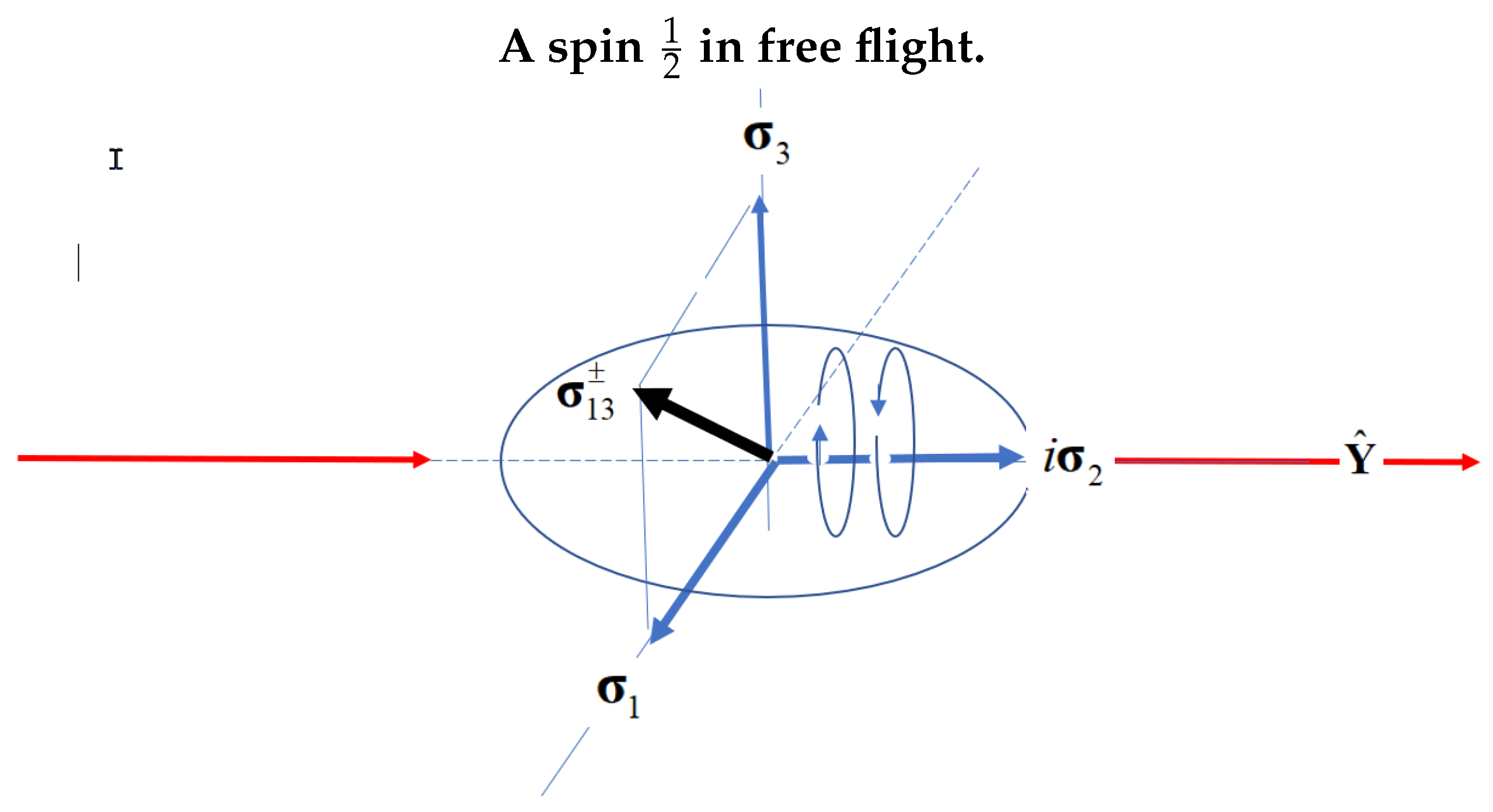
As they must, the gamma matrices still anti-commute but the change to the Pauli spin components in the gamma matrices describes spin in terms of σ 1 , i σ 2 , σ 3 rather than σ 1 , σ 2 , σ 3 . By multiplying by i, the usual spin 1 2 symmetry of SU(2), is changed to being a normal subgroup of the quaternion group, Q 8 . In contrast to the point particle vector description of Dirac spin, the Q-spin displays structure. Now, rather than three spatial components, there are only two, σ 3 , σ 1 . These are two orthogonal Pauli vector components and they give Q-spin a planar 2D structure, (Figure 1). The bivector is no longer a spatial component, but rather is a time, being the frequency of the helicity. The bivector is perpendicular to the two spatial components and, as now discussed, provides the basis for the hyper-helicity.
Introducing the bivector into the Dirac equation renders it non-Hermitian, [8]. It’s two solutions, ψ ± , are mirror states analogous to Dirac’s matter-antimatter description.
We are considering a free particle, and in an isotropic environment, the two spatial components, ( 3 , 1 ) , are indistinguishable, so permuting them with a parity operator P 31 leaves them unchanged. In contrast the bivector is odd to parity, P 31 i σ 2 = P 31 σ 3 σ 1 = − i σ 2 . This directly shows the two solutions are mirror states which reflect under parity, P 31 ψ ± = ψ ∓ , and therefore have no definite parity,[8] themselves.
However, the two mirror states can be combined to give states that are odd and even to parity, Ψ ± = 1 2 ψ + ± ψ − which leads immediately to the separation of spin spacetime, [8], into two distinct parts giving: a two dimension Dirac equation for the two spatial components; and a massless Weyl spinor equation for the bivector. The solution to the Weyl equation is a unit quaternion which spins the 2D spatial plane. The 2D spin states are even to parity while those of the quaternion space are odd to parity.
The quaternion version of the Dirac equation justifies the hyper-helicty as a real attribute of spin which is perpendicular to the 2D spin plane along the LFF Y axis. Taking this as the axis of linear momentum, gives the view in Figure 1 with helicity spinning that axis.
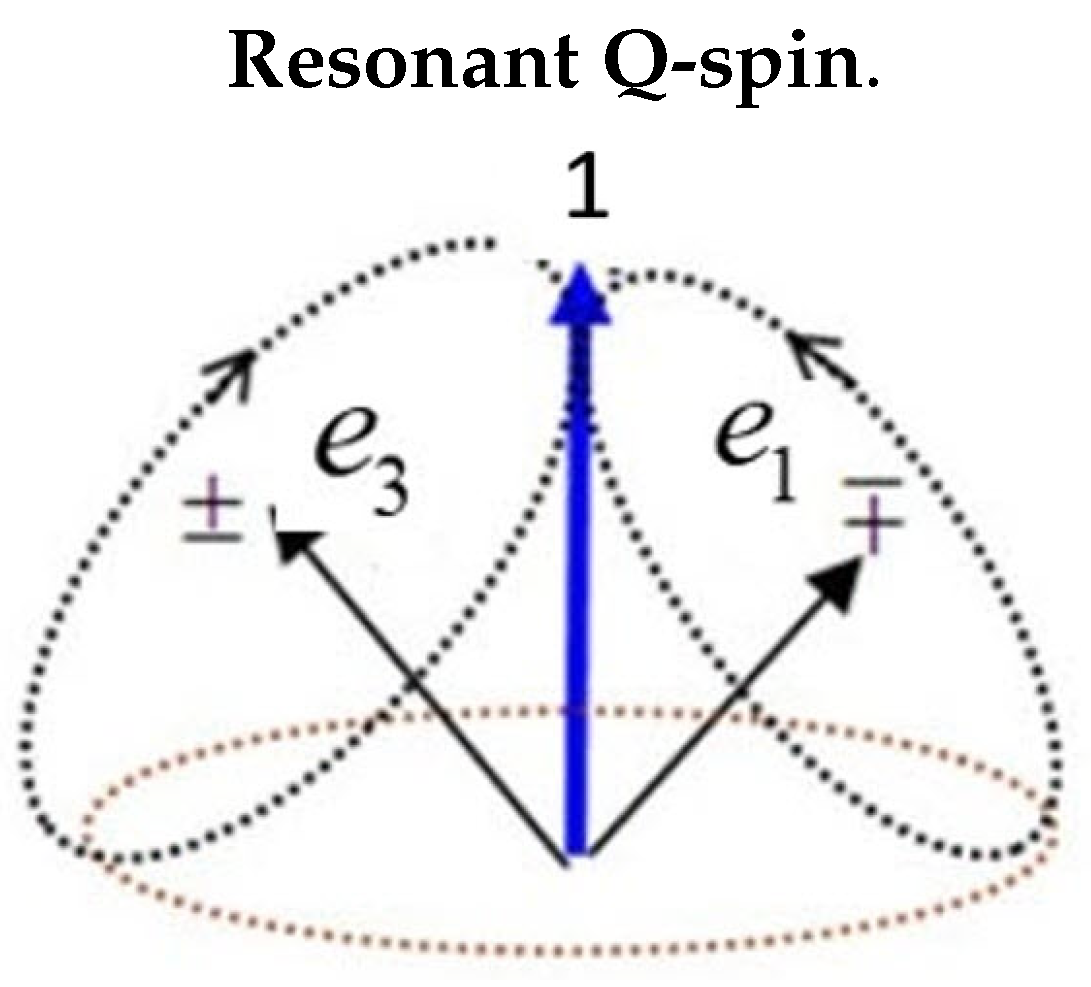
The two orthogonal spatial components, ( 3 , 1 ) , are viewed as two spin 1 2 axes, each carrying a magnetic moment μ . These are the mirror states. The EPR pairs are in free flight from the source up until they encounter their filters. Free-flight helicity and measured polarization impose complementarity on Q-spin.
There are four internal precessions: the helicity about the axis of linear momentum; the two orthogonal spin axes, each with a magnetic moment of μ . In free-flight the two spin 1 2 components must couple to give the forth internal motion of Q-spin, with a magnetic moment of 2 μ , see (Figure 3). As mirror states, the two vectors spin oppositely, thereby constructively generating this spin, [17,18]. However, there is no spin zero component. Although the two spatial components can spin in either direction, producing both ± 1 components, there is no spin zero component because the mirror property would be violated.
In free flight only helicity is manifest since the spinning of the axis of linear momentum averages the resonance spin 1 to zero although it is still present on the particle.
Upon encountering an anisotropic environment due to a filter, the two spin axes, (3,1), are no longer indistinguishable and the mirror property is lost. This leads to the decoupling of Q-spin into its two polarized states of 1 2 . We observe only one since the helicity is transferred to the aligned spin axis which causes its orthogonal twin to average to zero. This recovers Dirac spin which is a measured spin of 1 2 . EPR coincidence experiments observe the transition from a boson in free-flight to a fermion upon measurement.
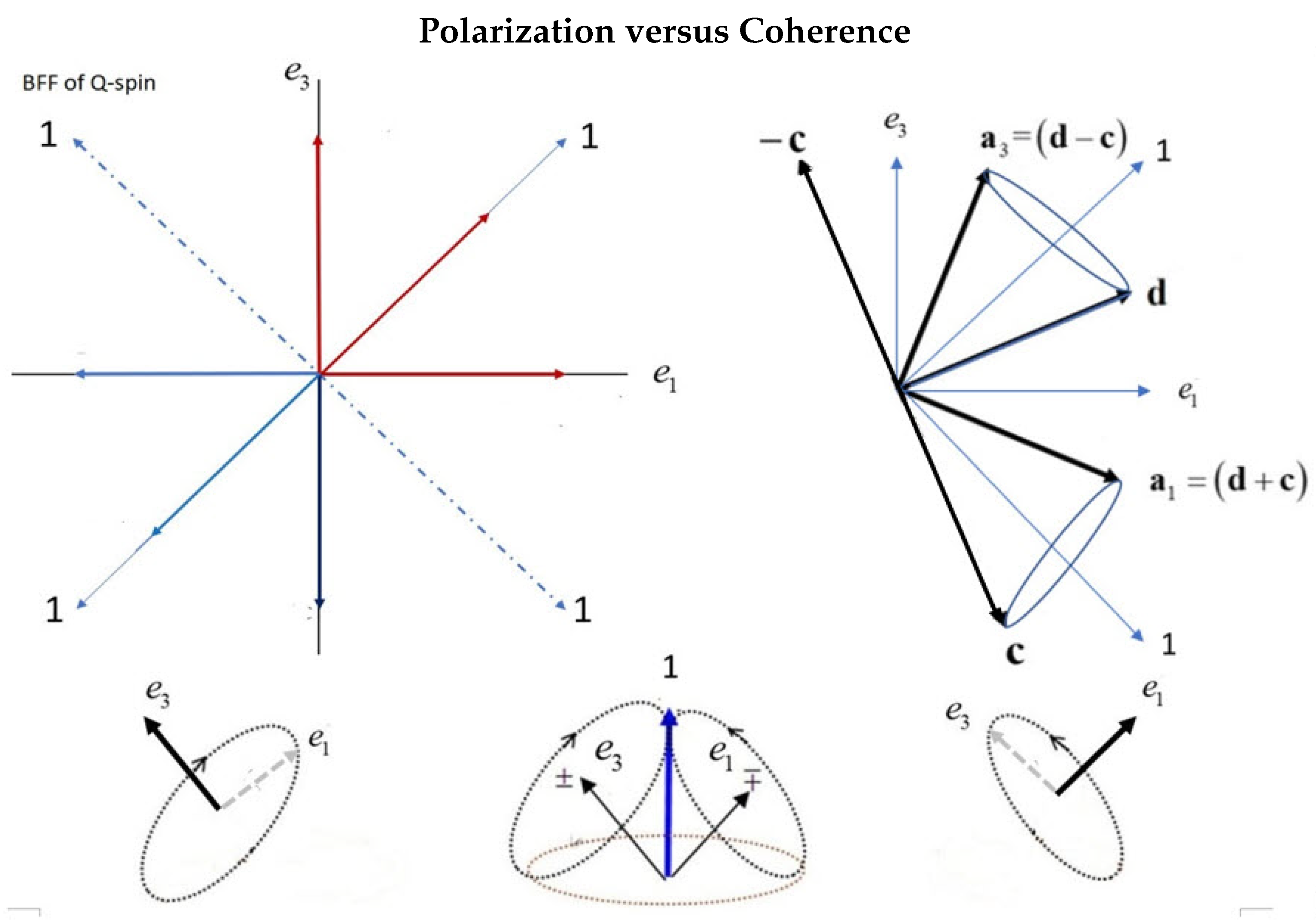
Coherence and polarization are complementary properties of a spin.
Two spin axes on the same particle is a different interpretation than given by Dirac, his being that the mirror states form a matter-antimatter pair.
How the resonant spin decouples depends upon the filter strength and its orientation relative to the resonant spin. This is discussed in the following section.

Application to EPR

Preliminaries

Although complementary, as just discussed, both polarization and coherence states simultaneously exist as attributes of spin. However, only one is manifest at any instant. Just as a dyadic Eq.(9) is the sum of two complementary contributions, so we express Q-spin possessing both properties,
Σ = σ + h ̲ ̲ g = σ + ε ̲ ̲ ̲ · i σ
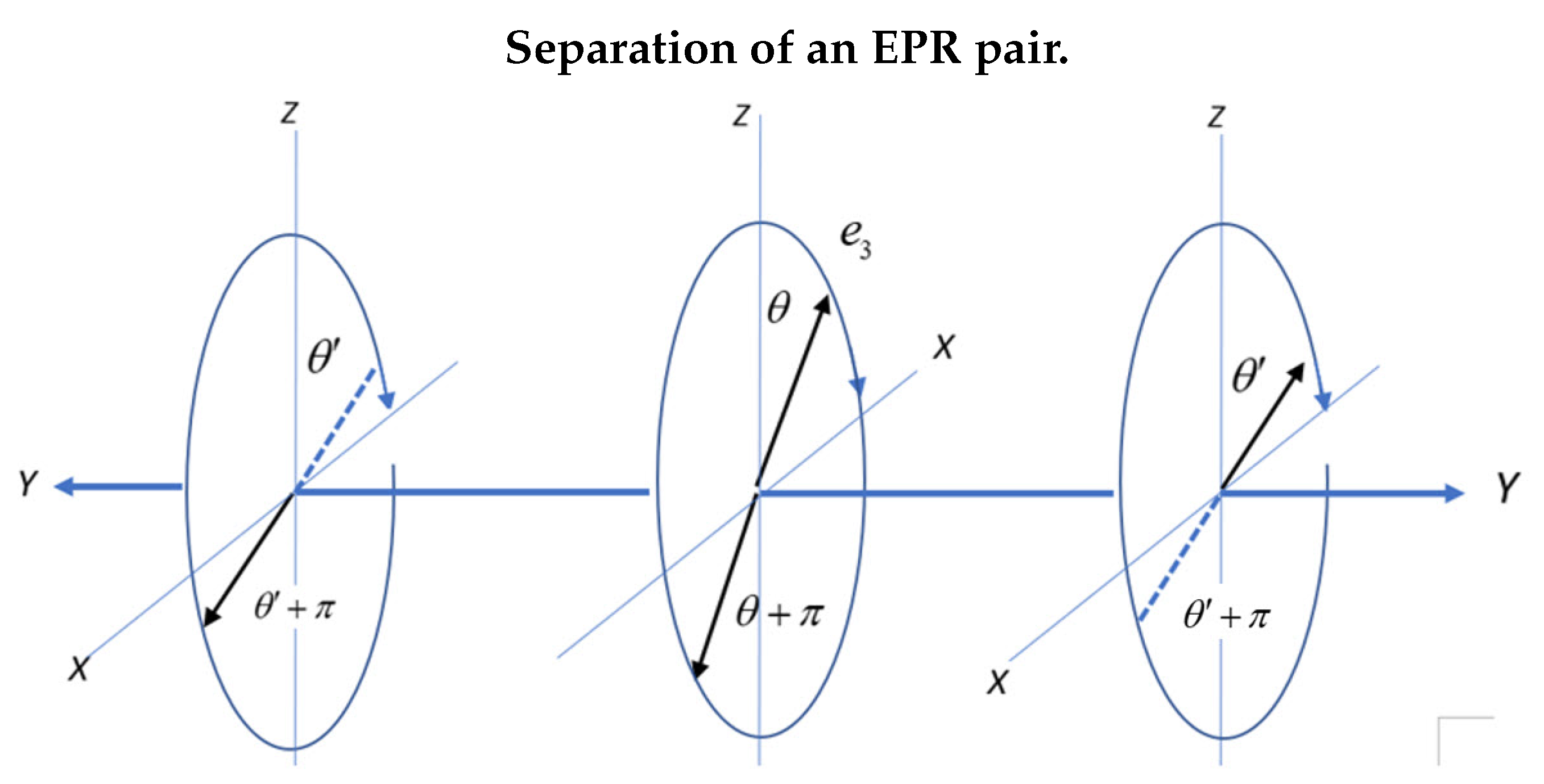
In this section, Q-spin is used to evaluate the correlation between EPR pairs. Initially in a singlet state at the source, they separate and move towards their respective filters. In the process they conserve linear and angular momentum, and helicity, see (Figure 4). The planes depict the separation process with the middle plane displaying the resonance spins of 1 as anti-parallel for Alice and Bob. Alice’s spin moves right and Bob’s moves left. Their initial orientation at the source is set by the angle θ and the axis of linear momentum spins with helicity being either left or right. Bob’s orientation is θ ± π to conserve angular momentum. Both spin around the Y axis in the same direction, thereby maintaining them as anti-parallel in free flight.
Note that Alice and Bob are in opposite frames. Alice is in a right handed frame by the right hand rule and Bob in the left. The two frames are related by complex conjugation, so that whereas they both have the same sense of precession, their helicities are opposite when Bob is viewed from a RH frame.
Since we assume no non-local connectivity between the pairs, we treat only Alice’s spin, with an identical treatment for Bob.

Filter effects

In the following we obtain the correlation from coincidence experiments in different cases. These are determined by the orientation of the filter relative to the coherent Q-spin. Initially in free flight, this spin is probed by the filter and in some cases it easily decouples into its two components, one of which aligns. In other cases, the Q-spin persists while moving into the filter, although it will eventually decouple as it becomes polarized.
The coherent, mustache, correlation requires both Alice and Bob to probe coherent spin simultaneously at both locations, as discussed below.

Polarization

From (Figure 2) the polarizations are given by the triangle. There is no contribution from coherence at multiples of π 2 , indicating that the coherent spin is decoupled at these points. In addition, for all filter settings, the resonance spin is eventually destroyed so polarized correlation is always present.
For polarized states, the helicity term in Eq.(12) is not present. The calculation is unchanged from the product state given in Eq.(6).

Q-spin correlation

In contrast to the state operator for polarized spin, Eq.(6), Q-spin has two orthogonal axes giving Alice’s state operator as
ρ A = 1 2 I A + 1 2 σ 3 A + σ 1 A = 1 2 I A + σ A · r
in the BFF. The vector is defined by,
r = 1 2 e 3 + e 1
From this the expectation values are calculated for the spin axes, e 3 , e 1 using both the symmetric and anti-symmetric contribution, Eq.(12),
a · Σ 1 A = a · σ 1 A + i ε · σ 1 A = + a · e 1 exp + i π 4 Y a · Σ 3 A = a · σ 3 A + i ε · σ 3 A = + a · e 3 exp + i π 4 Y
using a · σ i A = + 1 2 a · e i , and the cross products,
a × e 3 = − 1 2 a · e 1 Y a × e 1 = + 1 2 a · e 3 Y
Q-spins are denoted by Σ i and the two are coupled in free-flight to define the resonance spin of magnitude 1,
Σ 31 ± = 1 2 Σ 3 ± Σ 1
Substituting Eq.(15) give Q-spin in its BFF,
a · σ 31 + = 1 2 a · e 3 exp − i π 4 Y + e 1 + i π 4 Y
The BFF is related to the LFF by,
e 3 = cos θ Z + sin θ X e 1 = − sin θ Z + cos θ X e 2 = Y a = cos θ a Z + sin θ a X
with the filter vector also written in the LFF. Use of these leads to the following expressions,
a · Σ 31 + = 1 2 exp i π 4 − θ a − θ Y = 1 2 exp i π 4 + θ Y exp − i θ a Y = 1 2 cos θ − sin θ exp − i θ a Y + cos θ + sin θ exp i π 2 − θ a Y
The second equality separates the quaternion into a product of a geometric quaternion, and a field quaternion.

Correlation in free-flight

From Equation (15), in the BFF, the resonance spin is oriented by − π 4 from the e 3 axis and by + π 4 from the e 1 axis. They therefore both coincide along the bisector of their quadrant, which is the position of their Q-spin. This is displayed in (Figure 5) giving one of the four Q-spins. Different combinations of ± Σ 31 ± give all four components that bisect the quadrants in (Figure 5). For each specific orientation of the BFF relative to the LFF, a Q-spin can form in any one of the four possible quadrands, and Alice and Bob share opposite quadrants. Once formed, they continue in free-flight after leaving the source and maintain their relative orientations.
Upon separation, Alice and Bob’s spins are anti-correlated by requiring θ → θ ± π for Bob. The correlation is defined as the scalar product between the two resonance spins, being the complex conjugations of either. Remaining in the BFF and in the absence of the filters term, θ a in Eq.(20), the correlation is given by
E free - flight = Σ 31 · Σ 31 * + Σ 31 * · Σ 31 = 1 2 exp i 3 π 4 + θ Y exp i π 4 − θ Y + c . c . = − 1
The correlation is the sum of the contributions from left and right handed helicity, see Eq.(3). As expected, after leaving a common source, in free-flight before encountering filters, the correlation between Alice and Bob is -1 consistent with the two spins remaining anti-parallel and anti-correlated.

Approaching a filter

As the spins of Alice and Bob approach their randomly set filters, the correlation between the two resonance states is
E a , b = a · Σ 31 · Σ 31 * + Σ 31 * · Σ 31 · b = 1 2 exp i 3 π 4 − θ a − θ Y exp i π 4 + θ b − θ Y + c . c . = − cos θ a − θ b
If one of the spins is polarized there is no helicity and only the scalar part of the quaternion is present,
exp i π 4 + θ b − θ Y → no helicity exp + i π 4 Y cos θ b − θ
and only the product state survives even if one spin is coherent,
E a , b = − 1 2 exp i θ a − θ Y cos θ b − θ + c . c . = − cos θ a − θ cos θ b − θ
If a spin is oriented with e 3 = Z then θ = 0 , or if e 3 = X then θ = π 2 and
E a , b = → θ = 0 − cos θ a cos θ b → θ = π 2 − sin θ a sin θ b
To get the full correlation, Eq.(22), Alice and Bob’s spins must both be Q-spins. The lower part of Figure 5 depicts the situations described here. The L and R spins are polarized Dirac spins. Both polarization axes are present, but one is averaged by the spinning. The center figure shows the Q-spin before decoupling.

Interpretation

The second line in Eq.(20) shows the resonance spin, (Figure 3), as viewed from the LFF. The first term is its projection, Eq.(14), onto the laboratory Z axis, and the second term is the projection onto the LFF X axis. Each axis has a field quaternion with angle θ a , and these are shifted between the two axes by π 2 .
Coupling of angular momentum is common in all spectroscopes [19], including transport properties of gases, [20,21]. Coupling of angular momentum depends upon the strength of the applied field relative to the coupling constants. In our case, the resonance spin is stable in free-flight but will eventually decouple as it approaches the filter. At a given distance, the decoupling depends upon the orientation of a spin relative to the filter, and the filter strength relative to the spin coupling strength.
When the orientation of the resonance spin is close to the e 3 or e 1 axes, the spin is more easily polarized than when it lies along the bisected quadrants, see (Figure 5). Such orientation leads to a product state solution, Eqs.(6) and (25).
To visualize the filtering preocess, take (Figure 5) and imagine Alice and Bob’s filter with the same origin and pointing randomly in any direction. An experiment can randomly set the filters to any angles, e . g . , a = − 38 and b = 65 degrees in the BFF. Next rotate BFF in either direction so all values of θ are sampled, and observe how the filters encounter the spins, Dirac spin along ± e 3 and ± e 1 and Q-spin along the four bisectors.
There are generally four cases that vary with θ relative to the filter direction, which are: Both Alice and Bob’s spins are polarized (pol:pol); Alice’s spin is polarized and Bob’s is a Q-spin (pol:coh); Alice’s spin is coherent and Bob’s is a polarized (coh:pol); and both are coherent Q-spins (coh:coh). The first three cases lead to product states, Eq.(24). Only the last case gives the coherent contribution that gives the observed violation of BI, Eq.(20).
With this, we can understand the filter settings in the CHSH inequality that give the maximum correlation and violation of BI. This occurs when the filters at both Alice and Bob are such that both favour Q-spins over the polarized spins. These lie along the bisectors of the quadrants in the BFF. If we choose the relative setting of θ a b to be multiples of π 4 , see (Figure 5), top right, then we can be sure that when Alice encounters regions of high coherence, then so will Bob. The most favourable π 4 wedge lies between 22.5 and 67.5 degrees. Under these conditions, as the BFF orientation is rotated with the filters so set, then when Alice’s coherent axis lies close to the filter, then so must Bob’s. The maximum correlation for the S=CHSH inequality is determined by the filter setting that differ by π 4 , as shown in (Figure 5), and giving,
S = a 1 · d + c + a 3 · d − c = a 1 · d + a 1 · c − a 3 · c + a 3 · d = 2 2
We do not treat the dynamics of the 2D spin approaching the filter, but if the magnetic moment for each spin axis is μ , then the resonance spin has a Larmor precession proportional to 2 μ before it decouples. The Larmor frequency of the resonance spin is twice that of the aligned or polarized spin.

Simulation model

From the discussion above, we distinguish polarization events from coherent events respectively by the presence of the two polarized axes, e 3 and e 1 , or the single axis of the two coupled spins of 1 2 of the Q-spin. From the second line in Eq.(20) the two axes of Q-spin are viewed in the LFF as the superposition of these two axes.
a · Σ 31 + = 1 2 cos θ − sin θ e − i θ a Y + sin θ + cos θ e i π / 2 − θ a Y
This equation re-written from Eq.(20), generates all the simulated correlation presented in this paper.
For polarization coincidences, we choose the real part of either axis of Eq.(27) and simply determine if it spins L (negative) or R (positive) giving a plus or minus click, or vice versa. We use this to calculate the correlation due to the polarizations.
For the coherence part of the simulation, the two field axes, one at Alice and the other at Bob, form the π 4 wedge and this more or less bisects a Q-spin. When the wedge is off-set to the left or right, one axis will be closer to the field direction than the other. The closer one will eventually become polarized. It is important to know which axis will align because they carry opposite spin. It is difficult to imagine that Q-spin could pass the filter intact. Certainly one of the two spin 1 2 axes will become polarized as the filter field increases. We therefore first determine which axis lies closer to the field vector by writing the real parts Eq.(20) as
2 Re A = cos θ − sin θ cos 2 θ a ︷ axis ( Z ) + sin θ + cos θ sin 2 θ a ︷ axis ( X )
and determine the larger axis as the one that will become polarized. With a Larmor precession double that of a polarized spin, the filter angle is doubled to 2 θ a in Eq.(28). From this equation we assume that the larger axis will finally align with the filter,
axis ( X ) < > ︷ ? axis ( Z )
The click events from a polarized spin are determine if the imaginary part of Eq.(27) is positive or negative. In this case, since the larger axis becomes a polarized spin 1 2 , the Larmor precession reverts to that of a spin 1 2 so θ a drops the 2.
2 Im A = cos θ − sin θ sin θ a ︷ R or L spinning + sin θ + cos θ cos θ a ︷ L or R spinning
In the simulation, these relations are used to model the correlation from both polarization and coherence.

Simulation results

The FORTRAN and C code that determines clicks from polarized states and coherent events uses the above algorithms.
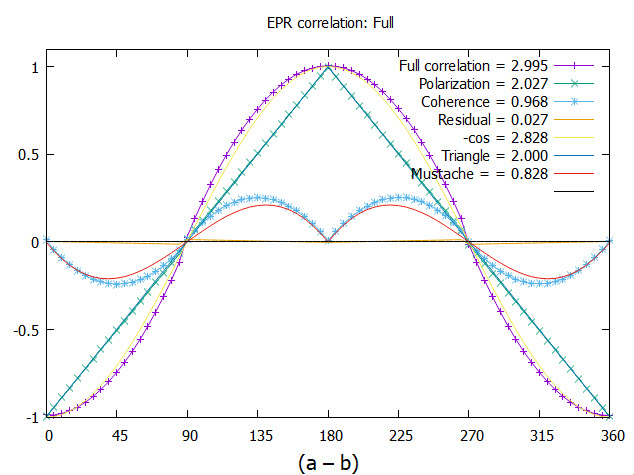
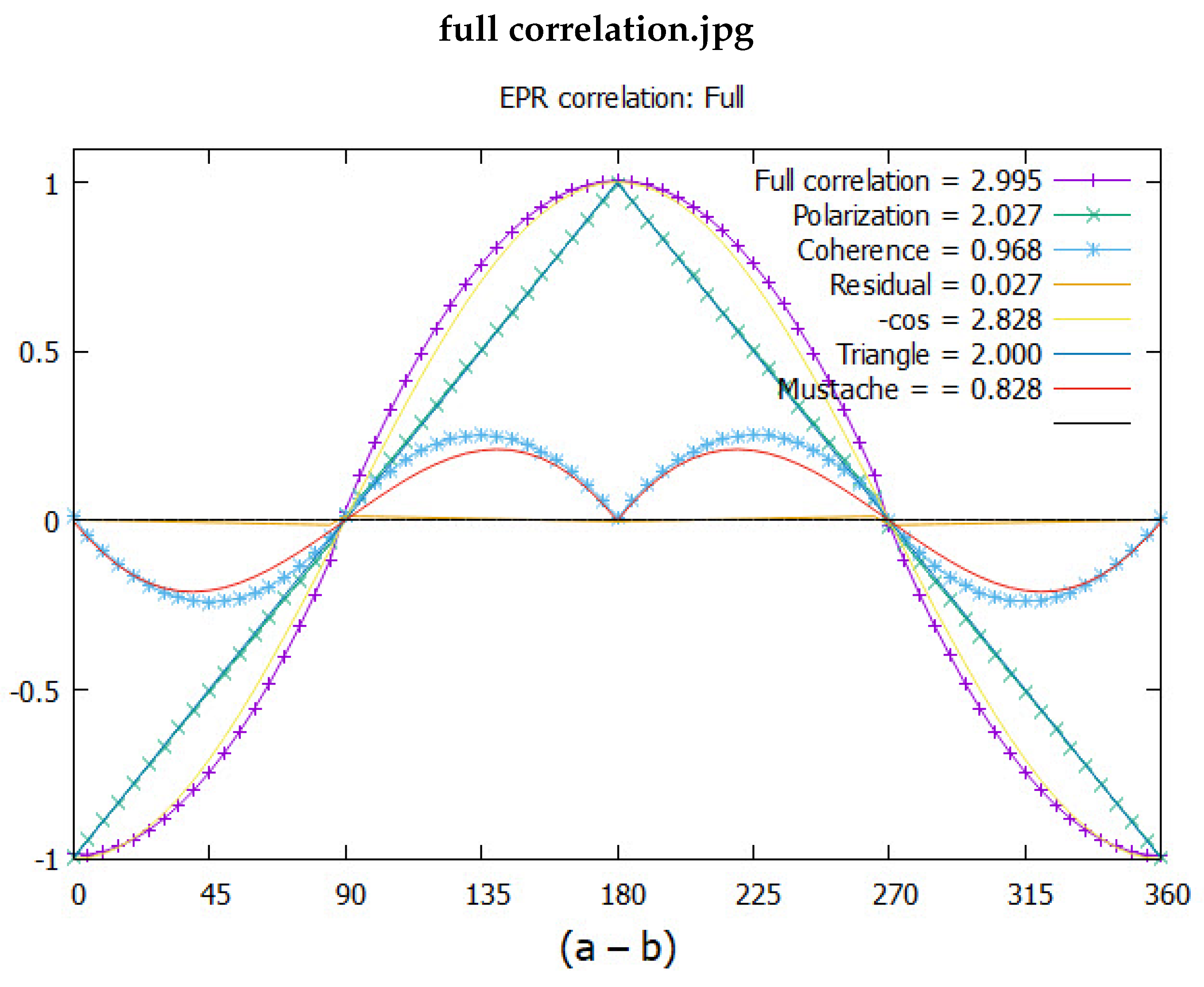
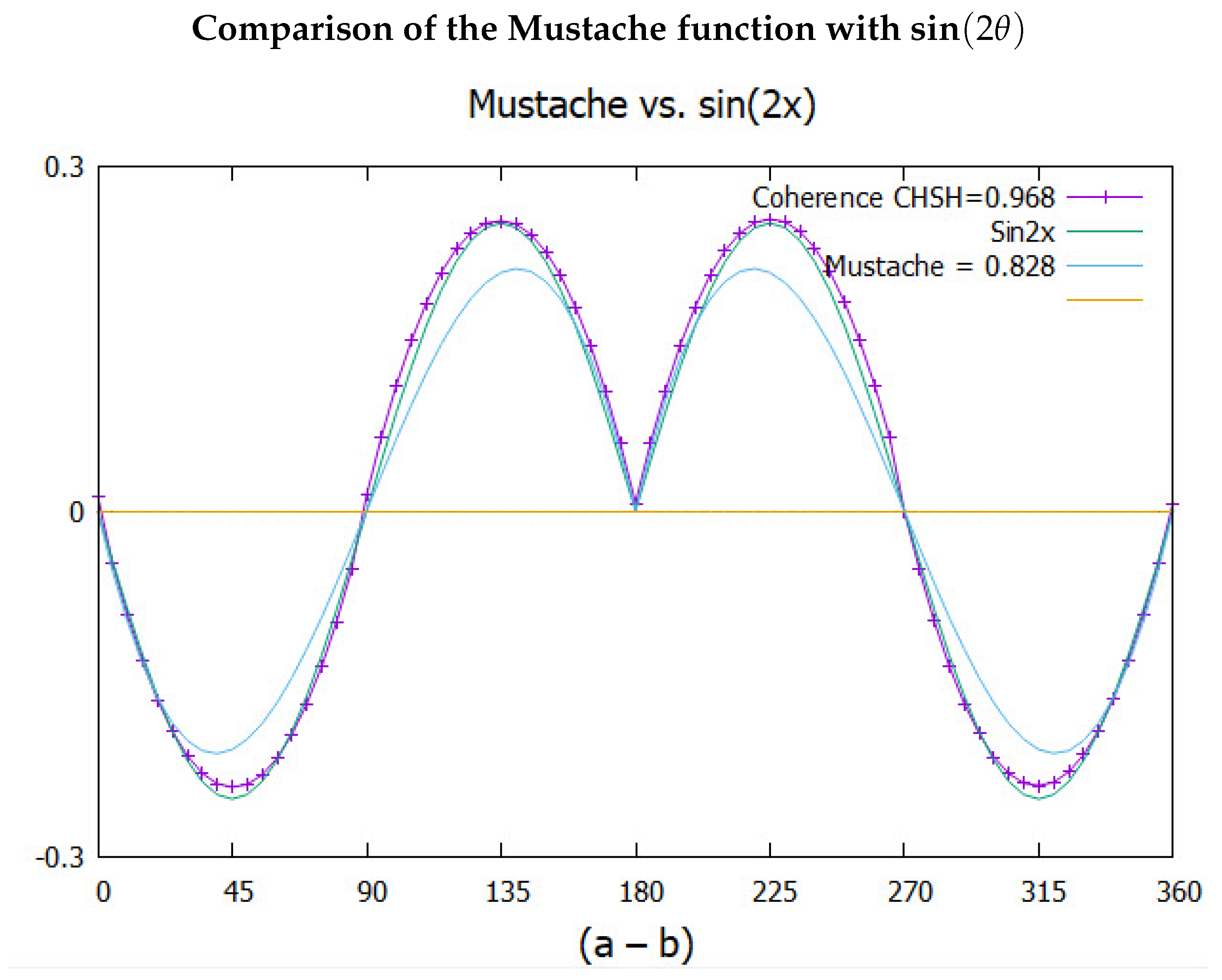
The results are given in Figure (Figure 6). The simulated correlation from either polarization axis gives the polarization as the triangle. The mustache coherence which depends on the couplng of the two axes into one axis, given by ( c f Eq.(27)), is shown in same figure and gives a CHSH = 0.968. The simulation gives more correlation than from quantum theory, CHSH = 0.828
The full simulated plot is the sum of the simulated polarization and the simulated coherence. These give a combined CHSH value of 2.995. Note that this CHSH value is a sum of polarization, 2.027 and coherence, 0.968].
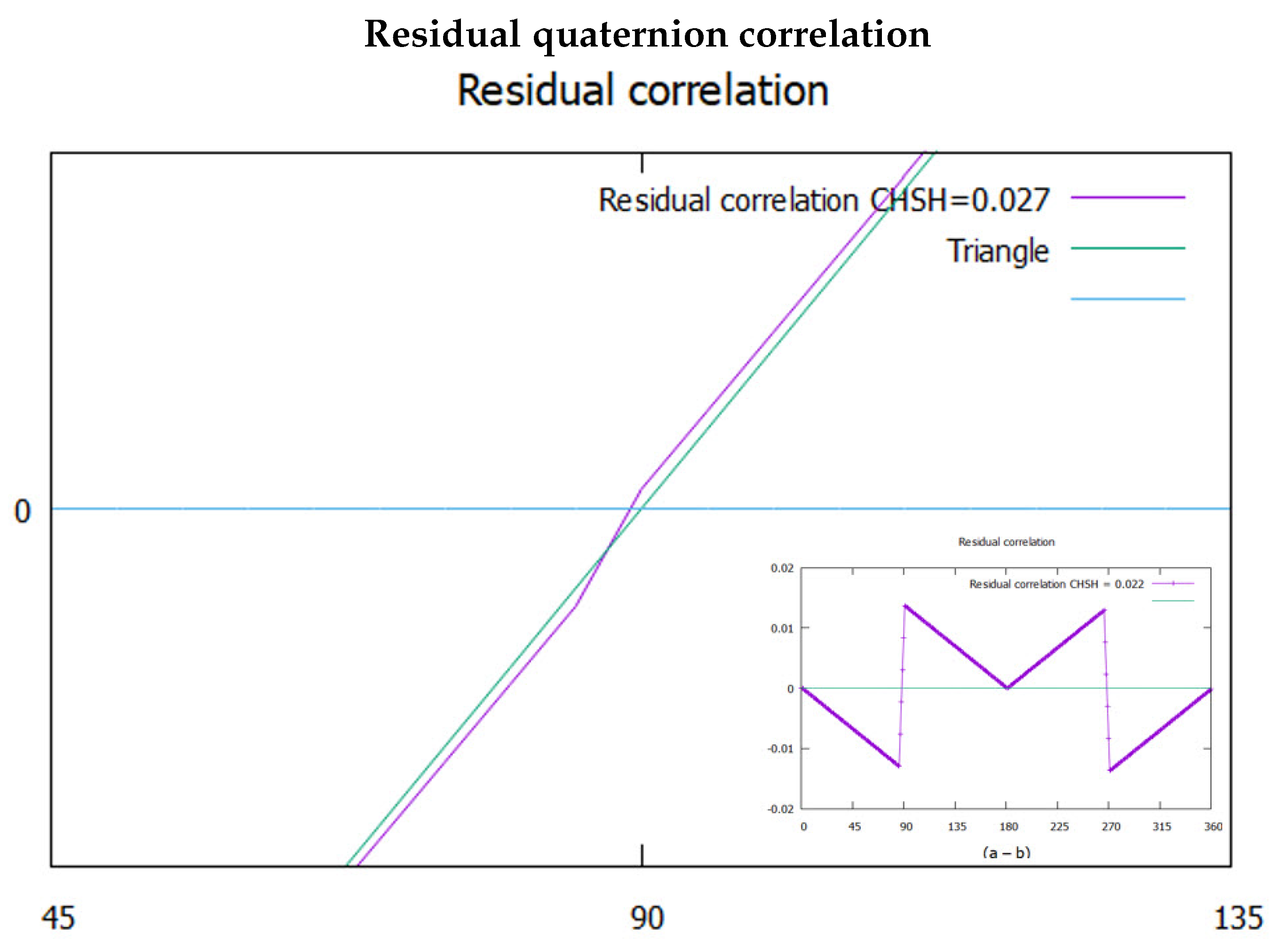
The theoretical CHSH value for polarizations is 2, whereas in (Figure 6) it is 2.027. There is residual correlation that remains as shown in (Figure 7). A cross over occurs close to the horizontal axis. It is hardly discernible. Considering it might be an artifact, various tests did not remove it. This has similar symmetry to the mustache coherence and supports this to be a real feature in the model. From the inset in (Figure 7), there are two discontinuities at π / 2 and 3 π / 2 . Removing these features by moving the middle triangle down gives an inverted triangle, but also gives a CHSH value of zero. The discontinuities, therefore, are necessary for the residue to be physical. We assert this residual contribution to coherence is due to correlation in the polarization states. If confirmed, the polarization exceeds BI, ([7]), by a small amount and violates his theorem ([22].
The CHSH value of 2.995 is larger than that expected from quantum theory 2 2 = 2.828 . In the discussion we argue the 2.995 value results from the way the simulation models the coherences.

Determining the correlation

Polarization and coherence are complementary properties which means that they do not occur simultaneously. The basis for this is Eq.(9). The distribution of these varies with different filter settings as discussed. In the simulation we have not taken that unknown distribution into account. We now address this.
Correlation in EPR coincidence experiments is measured by counting the clicks and organizing them as,
E exp a , b = N e q − N n e N t o t
Here for simplicity, we write the even coincidences as N e q = N + + + N − − and the odd as N n e = N + − + N − + . Note that the value of the observed correlation does not depend upon the total number of clicks, with larger numbers simply improving the accuracy. However in real EPR coincidence experiments the clicks are distributed between the two complementary properties. Although experiment cannot yet distinguish between polarization clicks, p, and coherent clicks, c, we can write the experimentally accumulated clicks in terms of these two correlations,
E exp a , b = N e q p + N e q c − N n e p − N n e c N t o t = N t o t p N t o t N e q p − N n e p N t o t p + N t o t c N t o t N e q c − N n e c N t o t c = p p E p a , b + p c E c a , b
where E p a , b and E c a , b can be identified, and N t o t p = N e q p + N n e p and N t o t c = N e q c + N n e c .
If a filter could be built to distinguish the two contributions then the probabilities of each, p p and p c , give the relative amounts of each contribution at given filter settings. We suggest, as discussed below, the probabilities over all angles that 3/4 of the coincidences are from polarized states and 1/4 from Q-spin.
A filter, in principle, might be constructed by polarizing the beam at the source for both Alice and Bob in some direction, i . e . adjust θ to be the same for all EPR pairs, and then arrange the filters at the detectors at the desired angle relative to the polarized source. Such a pre-filter would distinguish between polarization and coherent states. Additionally the strengths of the applied field can be varied to inhibit or promote decoupling

The mustache function

The quaternion coherence is responsible for the mustache, giving more correlation but a similar structure to the quantum correlation, see (Figure 6). The Q-spin correlation E q , resembles two opposing sine waves which are reflected at π . The following gives a good fit,
E q = − 1 4 sin 2 θ a b 0 ≤ θ a b ≤ π + 1 4 sin 2 θ a b π < θ a b ≤ 2 π
This is plotted in Fig .(Figure 8) along with the simulated data points which match Eq.(33). Also plotted for comparison is the correlation from quantum theory. Note the filter angle is doubled, consistent with a magnetic moment of 2 μ . Note also the prefactor of 1/4. Recall in the interpretation section, there are four types of coincidences: pol:pol, pol:coh, coh:pol: coh:coh. This shows that only 1/4 of the coincidences contribute to the mustache, and 3/4 to the polarization.

Discussion

We find the two complementary properties exist simultaneously. This supports Einstein in the famous Einstein-Bohr debates, [12]. However, only one property can be realized at any instant, thereby supporting Bohr’s notion of complementarity. Coherence and polarization do not commute and are incompatible elements of reality. They influence each other. The spinor spins the polarization; the indistinguishably of the two polarization axes creates the parity for the helicity to know which way to spin.
Table (1) lists four values of the CHSH inequalities. The value of 2 quantifies the Invisible Boundary [23], between polarization and coherence. Quantum theory gives the value of 2 2 which is less than that from the simulation of 2.995, which is close to 3. The value 3 is a result of modeling the three axes of Q-spin: the two polarized and one coherent, suggesting a CHSH = 1 for each axis.
Looking at the simulated coherence, Eq.(33), the prefactor is 1/4. The CHSH values leading to 2.995 are E π 4 = − 0.746 and E 3 π 4 = + 0.758 . This suggests a convergence to 3 / 4 which leads to a CHSH value of 3. This again supports equal contributions from each axis.
Note that the residual quaternion correlation, (Figure 7) has a similar symmetry to (Figure 8) and both are reflected at π , being a consequence of their reflective property.

Spin

In this treatment, non-local entanglement is replaced by helicity. The Dirac spin is replaced with Q-spin. Both these features come from changing the symmetry from SU(2) to Q 8 . The visualization of Q-spin, which is geometrically identical to that of a photon, see (Figure 1), carries a 2D spin plane that forms its own “World Sheet”, [24].
When the Dirac equation is changed to include Q-spin, the two resulting mirror states [8], see (Figure 5) are fundamental particles in Nature. They have no parity, only reflection, but they combine into states of even parity, polarization, and odd parity, coherence.
Spin carries helicity as an element of reality, and quaternions exist in the S 3 hypersphere of four spatial dimensions. Spin extends to this space which is beyond our visualization, but nonetheless it remains an element of reality beyond our dimension. The only part of a quaternion that is visible to us is the stereographic projection from S 3 onto our Minkowski spacetime. From that we can observe an axis spinning and we can account for the observed violation of BI.
According to the treatment here, however, EPR are validated in asserting that quantum theory is incomplete. Quantum mechanics is a theory of measurement but not of Nature. It does not include those higher dimensions of the hyper-sphere, S 3 needed for the coherence, nor does it include anti-Hermitian operators as elements of reality. Nonetheless the treatment here is consistent with the accepted philosophy of the miscroscopic.
In calculating expectation values, the state operator is given by Eq.(13), which includes both polarization axes. We do not include contributions from the helicity in the state operator because it is not physically observable in our spacetime. In the BFF, Q-spin is expressed by Eq.(18) with two axes, e 3 and e 1 projected along the field direction. The magnitude of those projections determine which axis is favoured to align, whereas if both axes are more or less equally projected, the π 4 wedge, then the resonance spin of magnitude 1 is favoured.
To repeat, in free-flight Q-spin acts like a boson and in a perturbing field, it acts like a fermion.

The singlet state

The theory presented here agrees with the usual quantum result of − cos ( θ a − θ b ) and a violation of only 2 2 . This is because our treatment is an example of the Conservation of Geometric Correlation, [6]. Both our treatment and that of quantum theory start from the same entangled singlet state at the source, Eq.(1). Here the two contributions in Eq.(9) are realized at separation. The initial entangled correlation is therefore distributed between a sum of the symmetric and anti-symmetric contributions originally seen in Eq.(8). All the correlation found in the original bound singlet before separation is conserved as see from the − cos in Eq.(22). Our treatment does not change the quantum result but rather gives a mechanism for decomposing the entanglement without requiring it to persist intact after separation.
A simulated value of CHSH = 3 rather than the CHSH = 2 2 from quantum theory gives more correlation from the former. This difference is due to the modeling of Q-spin for the simulation which leads a correlation of CHSH = 1 per axis. Here we suggest why the simulation gives a more accurate accounting for the correlation than from quantum theory.
A singlet state is usually expressed by opposing polarized states which are symmetrized, ↑ ↓ − ↓ ↑ , see Eq.(1). Here a spin has structure and we suggest a singlet state of an electron is more realistically expressed as shown in (Figure 10) where the two magnetic axes are attracted which is balanced by the repulsion of the charges. The helicity now spins the axis as shown. Upon separation, this decomposes into two Q-spins which conserve their reflective properties, throughout. We suggest that after the initial separation, the two settle into trajectories with the disc of polarization spinning along the axis of linear momentum, see (Figure 1), governed by the Intermediate Axis theorem, [25].
Equation 2 shows that the singlet state contains off-diagonal coherent terms which are responsible for the quantum correlation of 2 2 . Using the non-Hermitian states needed to describe Q-spin, Eq.(12), the singlet state can be decomposed into a product of state operators for Alice and Bob, [26],
ρ Ψ 12 − = 1 8 ∑ n 3 , n 1 , = ± 1 I + n 3 σ 3 A + n 1 σ 1 A + n 2 i σ 2 A ⊗ I − n 3 σ 3 B − n 1 σ 1 B + n 2 i σ 2 B
Inserting the Pauli spin matrices and summing the eight terms reproduces the entangled singlet matrix shown in Eq.(2). Some terms cancel in this sum and those are responsible for the difference between quantum theory and the simulation.
Notice that Alice’s two polarization axes are opposite to Bob’s but the two bivectors have the same sign. This is consistent with (Figure 4) which conserves angular momentum and the same sense of precession of the EPR pair after separation. The values of n 1 , n 3 = ± 1 define the quadrants of (Figure 5), whereas n 2 allows for L and R helicity. When an EPR pair separates, it can do so in only one of those eight products in Eq.(34).
This can be demonstrated by taking one component and inserting the Pauli spin matrices. There is one diagonal component and three off-diagonal,
ρ A ρ B = 1 4 I + σ 3 A + σ 1 A + i σ 2 A ⊗ I − σ 3 B − σ 1 B + i σ 2 B = 1 1 0 0 ⊗ 0 0 − 1 1 = 0 0 0 0 0 0 0 0 − 1 − 1 1 1 0 0 0 0
The diagonal component and the − 1 on its left survives the sum over the eight EPR pairs as seen in Eq.(2). The additional two coherent terms express correlation between a polarization state, ± ± and a coherent state, ± ∓ , and these are not present in the final sum that gives the entangled singlet of Eq.(2), because they are canceled by other terms. In the separation into a product state, each contribution contains those additional terms which are missing in the quantum calculation Eq.(5).
We conclude that the singlet state, Eq.(1) is an approximation which misses these terms and this is responsible for the reduced correlation from quantum mechanics as compared to the simulation. Rather than modeling the full singlet state, the simulation uses each component of Eq.(34) as an EPR pair, thereby retaining the components that cancel in the sum. As such, the simulation more closely describes an EPR pair than quantum theory that uses the full singlet state. Each product state reflects the correlation between the three axes, thereby providing more correlation than the usual singlet state, and justifying a CHSH of one per axis.
Finally Eq.(35) is not Hermitian because of the two bivectors which give the helicity in one direction. However there is another term which when combined, makes the two Hermitian,
ρ EPR pair = ρ A ρ B + ρ A † ρ B † = 0 0 − 1 0 0 0 − 1 0 − 1 − 1 2 1 0 0 1 0
and so include both L and R helicities which is consistent with the first line of Eq.(22). There are four possible EPR pairs which correspond to one pair per quadrant in (Figure 5).

Bell

The CHSH form of Bell’s inequalities provides a quantitative measure of correlation. They enables us to separate classical (polarization) from quantum (helicity). Bell’s theorem is distinct from his inequalities and asserts in Bell’s words [22],
If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local.
Although this is an incorrect interpretation by Bell, the mathematics of his theorem is not disputed. The question arises as to how Q-spin can account for the observed correlation without non-local connectivity which directly contradicts the theorem. The reason is complementarity, [27], whereby a spin has two distinct properties, each of which contributes, rather than just the polarization that Bell retained in his classical treatment. In agreement with Einstein, [4] both complementary properties exist on a particle at the same instant. Filters cannot distinguish between the two but if they could, then the complementary property should be evident.
In this work, there are no hidden variables. Nonetheless, we find a CHSH value of 2 for polarization and 1 for coherence, neither of which violates Bell’s theorem. The theorem is misleading, pointing to non-locality as the consequence of the violation, whereas here it is due to the decoupling of the resonance spin. Bell’s theorem states that classical events cannot exceed a CHSH of 2. This is true but only for classical systems. Simply stated, Bell’s Theorem is not applicable to quantum systems. The stark conclusion is that non-locality, which is universally accepted, is replaced by this local treatment that leads to the conclusion that the observed violation is evidence for local realism and not non-locality, [28].
We do not criticize local entanglement and only assert that non-local entanglement is untenable. We view local entanglement as an essential property of quantum theory. Indeed we concur with Schrödinger who famously stated, [29], that entanglement was not “a” but “the” difference from classical. Entanglement is a fundamental property of quantum theory but not of Nature. It simplifies calculations by dropping coherent terms, and the price is missing correlation and structure.
Note however that the simulated CHSH = 2.027 for polarization shows that a local realistic theory can violate BI. We suspect it arises from the canceled terms in forming the singlet. It is of interest to pursue this further.

Conclusions

The existence of Q-spin requires accepting that Nature has reality beyond our spacetime; that there is information lost; [30], and there are properties in Nature we cannot observe. Some limitations of quantum mechanics can be addressed by replacing Dirac spin with Q-spin, and entanglement with helicity.
In the vast majority of cases of interest, spin is not in free flight but is polarized in bonds. Q-spin, however, if accepted, changes our fundamental view of Nature, and requires re-examination of areas of quantum theory that have hitherto relied on non-local connectivity, [1,2,3,30] to [35].
The violation of Bell’s inequalities is not evidence for non-locality, a difficult concept to grasp, but rather evidence for the existence of hyper-helicity and other properties of Nature that are responsible for local realism.

Acknowledgments

The author is grateful to Pierre Leroy, (programmer) and Chantal Roth, PhD (programmer) for their help and patience with simulation methods. I thank Pierre who converted the FORTRAN Program to C. The author also gratefully acknowledges Richard Gill, mathematician, Leiden University, who tenaciously played the role of Devil’s Advocate which helped clarify some aspects of Bell’s theory.

References

  1. Clauser, J. F. , Horne, M. A., Shimony, A., & Holt, R. A. Proposed experiment to test local hidden-variable theories. , Physical review letters 1969, 23, 880. [Google Scholar]
  2. Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804.Aspect, Alain (15 October 1976). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D 1944, 14, 1944–1951.
  3. Weihs, G. , Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters 81(23), 5039.
  4. Einstein, Albert, Boris Podolsky, and Nathan Rosen. “Can quantum-mechanical description of physical reality be considered complete? Physical review, 47.10 (1935): 777.
  5. Greenberger, D. M. , Horne, M. A., Shimony, A., & Zeilinger, A. (1990). Bell’s theorem without inequalities. American Journal of Physics, 58(12), 1131-1143.
  6. Sanctuary, B. Spin with Hyper-helicity. . Preprints 2023, 2023010571. [Google Scholar] [CrossRef]
  7. Bell, John S. “On the Einstein Podolsky Rosen paradox.”. Physics Physique Fizika 1.3 (1964): 195.
  8. Sanctuary, B. Extrinsic Q-spin. Preprints 2023, 2023020055. [Google Scholar] [CrossRef]
  9. Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 117(778), 610-624.
  10. Doran, C. , Lasenby, J., (2003). Geometric algebra for physicists. Cambridge University Press.
  11. Fano, Ugo. “Description of states in quantum mechanics by density matrix and operator techniques.”. Reviews of modern physics 29.1 (1957): 74.
  12. Jammer, M. (1974). Philosophy of Quantum Mechanics. the interpretations of quantum mechanics in historical perspective.
  13. Newton to Bentley, 25 February 1692/3, The Correspondence of Isaac Newton, ed. H. W. Turnbull (Cambridge: Cambridge University Press, 1961.
  14. Einstein, Albert. Born-Einstein Letters 1916-1955: Friendship, Politics and Physics in Uncertain Times. Palgrave Macmillan, 2014.
  15. Mullin, W. J. (2017). Quantum weirdness. Oxford University Press.
  16. Peskin, M. E. Schroeder, D. V. (1995). An Introduction To Quantum Field Theory (Frontiers in Physics), Boulder, CO.
  17. Sanctuary, B. C. “The two dimensional spin and its resonance fringe. arXiv:0707.1763 (2007).
  18. Sanctuary, B. C. “Structure of a spin frac12. r, arXiv:0908.3219 (2009).
  19. Herzberg, Gerhard. Molecular Spectra and molecular structure-Vol I. Vol. 1. Read Books Ltd, 2013.
  20. Turfa, A. F. , Connor, J. N. L., Thijsse, B. J., & Beenakker, J. J. M. (1985). A classical dynamics study of Senftleben-Beenakker effects in nitrogen gas. Physica A: Statistical Mechanics and its Applications 129(3), 439-454.
  21. Sanctuary, B. C. J. M. Beenakker, and J. A. R. Coope. "Influence of nuclear spin couplings on the thermomagnetic torque in HD.". The Journal of Chemical Physics 60.8 (1974): 3352-3353.
  22. Bell, J. S. “Speakable and Unspeakable in Quantum Mechanics” (Cambridge University Press, 1987), 2004. See “Locality in quantum mechanics: reply to critics. Epistemological Letters”, Nov. 1975, pp 2–6.
  23. Wick, David. “The Infamous Boundary: Seven decades of heresy in quantum physics.” Springer Science and Business Media, 2012.
  24. Maldacena, J. , Susskind, L. (2013). Cool horizons for entangled black holes. Fortschritte der Physik, 61(9), 781-811.
  25. Poinsot, Louis. New theory of the rotation of bodies extracted from a memoir read at the Academy of Sciences of the Institute, May 19, 1834 by M. Poinsot. Bachelor, 1834.
  26. Sanctuary, B. C. "Separation of Bell states. arXiv:0705.3657 (2007).
  27. Bohr, Niels. "Can quantum-mechanical description of physical reality be considered complete?.". Physical review 48.8 (1935): 696.
  28. Abellán, Carlos, et al. "Challenging local realism with human choices. arXiv:1805.04431 (2018).
  29. Schrödinger, E. , “Discussion of probability relations between separated systems”. Mathematical Proceedings of the Cambridge Philosophical Society 31 (4): 555–563 (1935). [CrossRef]
  30. Braunstein, Samuel L., and Arun K. Pati. “Quantum information cannot be completely hidden in correlations: implications for the black-hole information paradox.” Physical review letters 98.8 (2007): 080502.
  31. Bennett, C. H. , Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W. K. (1993). Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Physical review letters, 70(13), 1895.
  32. Kim, Y. H. , Yu, R., Kulik, S. P., Shih, Y., & Scully, M. O. (2000). Delayed “choice” quantum eraser. Physical Review Letters, 84(1), 1.
  33. Van Raamsdonk, M. (2010). Building up spacetime with quantum entanglement. General Relativity and Gravitation, 42(10), 2323-2329.
  34. Bashar, M. A. , Chowdhury,M. A., Islam, R., Rahman, M. S., and Das,S. K., “A Review and Prospects of Quantum Teleportation," 2009 International Conference on Computer and Automation Engineering, 2009, pp. 213–217. [CrossRef]
  35. Gisin, N. , Ribordy, G., Tittel, W., Zbinden, H., Quantum cryptography. Reviews of modern physics, 74(1), 145, 2002.
Preprints 70400 g001
Figure 1. Two properties of spin: its polarization perpendicular to its helicity. The helicity is in the direction of propagation and averages out the polarizations.
Figure 1. Two properties of spin: its polarization perpendicular to its helicity. The helicity is in the direction of propagation and averages out the polarizations.
Preprints 70400 g001
Preprints 70400 g002
Figure 2. The full correlation from quantum mechanics, Eq.(5) with CHSH = 2 2 = 2.828 is decomposed into the products state, Eq.(6) with CHSH = 2, and the difference between the two, giving the mustache function with CHSH = 0.828.
Figure 2. The full correlation from quantum mechanics, Eq.(5) with CHSH = 2 2 = 2.828 is decomposed into the products state, Eq.(6) with CHSH = 2, and the difference between the two, giving the mustache function with CHSH = 0.828.
Preprints 70400 g002
Preprints 70400 g003
Figure 3. each of the two polarization axes are spins of 1 2 . They are mirror states that couple to form Q-spin of even parity and spin magnitude 1.
Figure 3. each of the two polarization axes are spins of 1 2 . They are mirror states that couple to form Q-spin of even parity and spin magnitude 1.
Preprints 70400 g003
Preprints 70400 g004
Figure 4. Alice goes right in a RH coordinate frame and Bob goes left in a LH frame. The two spins precess in the same direction, either clockwise or anti-clockwise. Changing Bob’s frame from L to R means the helicity of the two particles is opposite. Note in the center figure that Alice and Bob start off with the same but opposite orientation in the BFF indicated by e 3 .
Figure 4. Alice goes right in a RH coordinate frame and Bob goes left in a LH frame. The two spins precess in the same direction, either clockwise or anti-clockwise. Changing Bob’s frame from L to R means the helicity of the two particles is opposite. Note in the center figure that Alice and Bob start off with the same but opposite orientation in the BFF indicated by e 3 .
Preprints 70400 g004
Preprints 70400 g005
Figure 5. Top Left : Alice’s spin (red lines in the (1,1) quadrant) and Bob’s spin (blue lines in the (-1,-1) quadrant) are oriented anti-parallel in the BFF. All vectors are unit. The superposition of the two axes of spin 1 2 , e 3 and e 1 creates the Q-spin of magnitude 1. Top Right : The heavy black lines indicate the filter settings at Alice and Bob that give the maximum violation of the CHSH inequality. The field wedge of π 4 on either side of the Q-spin mean that both Alice and Bob are simultaneously probing the resonant Q-spin. Bottom: Center, two axes interfering to produce the coherent resonance Q-spin. Depicted on the LHS and RHS are the two possible polarized states of spin 1 2 . The unaligned axes ( e 1 on the left and e 3 on the right) are still there, but are averaged leaving only the polarized state.
Figure 5. Top Left : Alice’s spin (red lines in the (1,1) quadrant) and Bob’s spin (blue lines in the (-1,-1) quadrant) are oriented anti-parallel in the BFF. All vectors are unit. The superposition of the two axes of spin 1 2 , e 3 and e 1 creates the Q-spin of magnitude 1. Top Right : The heavy black lines indicate the filter settings at Alice and Bob that give the maximum violation of the CHSH inequality. The field wedge of π 4 on either side of the Q-spin mean that both Alice and Bob are simultaneously probing the resonant Q-spin. Bottom: Center, two axes interfering to produce the coherent resonance Q-spin. Depicted on the LHS and RHS are the two possible polarized states of spin 1 2 . The unaligned axes ( e 1 on the left and e 3 on the right) are still there, but are averaged leaving only the polarized state.
Preprints 70400 g005
Preprints 70400 g006
Figure 6. Plotting intensity versus the angle difference θ a − θ b The results of the simulation are given by the blue points. The CHSH values are listed. The full correlation is the sum of that from polarization, the triangle, and coherence, the mustache. Note the hardly discernible residual quaternion correlation along the horizontal axis.
Figure 6. Plotting intensity versus the angle difference θ a − θ b The results of the simulation are given by the blue points. The CHSH values are listed. The full correlation is the sum of that from polarization, the triangle, and coherence, the mustache. Note the hardly discernible residual quaternion correlation along the horizontal axis.
Preprints 70400 g006
Preprints 70400 g007
Figure 7. A blow up of the simulated polarization compared to an exact triangle. The insert shows it over 2 π .
Figure 7. A blow up of the simulated polarization compared to an exact triangle. The insert shows it over 2 π .
Preprints 70400 g007
Preprints 70400 g008
Figure 8. The E q function given in Eq.(33) compared to the simulation. Also shown is the correlation from quantum theory.
Figure 8. The E q function given in Eq.(33) compared to the simulation. Also shown is the correlation from quantum theory.
Preprints 70400 g008
Preprints 70400 g009
Figure 9. Values of the CHSH inequalities from classical to Nature.
Figure 9. Values of the CHSH inequalities from classical to Nature.
Preprints 70400 g009
Preprints 70400 g010
Figure 10. A possible structure of a singlet state of an electron showing the attraction of the magnetic axes which is balanced by the repulsion of the two charges.
Figure 10. A possible structure of a singlet state of an electron showing the attraction of the magnetic axes which is balanced by the repulsion of the two charges.
Preprints 70400 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated