Prerpints.org logo
Preprint
Technical Note

Assessment of Wind Speed Statistics in Samaria Region

Altmetrics

Downloads

146

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

23 January 2023

Posted:

31 January 2023

You are already at the latest version

Alerts
Abstract
SStatistical characteristics of the wind speed in Samaria region of Israel have been analyzed by processing 11 years of wind data provided by the Israeli Meteorological Service, recorded at 10 m height above the ground. The cumulative mean wind speed at measurement height was shown to be 4.53 m/s with standard deviation of 2.32 m/s. Prevailing wind direction is shown to be char-acterized by cumulative mean azimuth of 226° with standard deviation of 79.76°. The results were extrapolated to 70-meter height in order to estimate wind characteristics at hub height of a me-dium-scale wind turbine. Moreover, Weibull distribution parameters were calculated annually, monthly and seasonally, demonstrating a good match with histogram-based statistical repre-sentations. Shape parameter of the Weibull distribution was shown to reside within a narrow range of 1.93 to 2.15, allowing us to assume a Rayleigh distribution, thus simplifying wind tur-bines energy yield calculations. The novelty of the current paper is related to gathering wind statistics for a certain area (Samaria) we are not aware of any published statistics regarding wind velocity and direction in this area. The data may be interesting for potential regional wind energy development in which the obtained Weibull distribution can be used in calculations of expected power generation of particular turbines with known power dependence on velocity. We also point out that the fact that realistic wind velocity statistics is well described by an analytic formula (Weibull distribution) is not trivial, and in fact the fit may have been poor.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

During the last decade, wind characteristics and wind power potential have been studied in many countries worldwide [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,61,63,64,65], demonstrating that despite the prolonging global economic crisis, the worldwide wind power ascent continues. The world’s wind power capacity added 38.6 GW in 2009, growing by 32%/year and 38.1 GW in 2010 (24%/year growth), demonstrating 110% growth in three years, to extend total installations up to 197.0 GW. A huge part of this capacity was installed in China with 22.7% of the world wind energy yield (about third of the world year’s additions) and USA with 20.4%, while Germany, Spain and India installing cumulative capacity of 30.9% together [48].
Wind energy became a significant player in the world’s energy market. Global market worth of wind turbine installations in 2009 was around 63 billion US$. About half a million people are now employed, corresponding to GWEC estimates, by the wind industry around the world [49]. Main markets of the wind energy are situated in Asia, North America, and Europe, each of which adds more than 10 GW capacity a year.
Considering the Israeli energy market, the desire to add to the natural gas found, which is a nonrenewable local energy resource has also motivated the state to devote various efforts to the ‘green’ energy research and development, primarily in the area of solar energy. Recently, wind energy drew attention of energy initiatives as well. Yet the wind power amount produced in Israel is diminutive comparing to the continuously growing global market; however, the last steps undertaken by the state are destined to improve the situation.
Israel currently operates a single wind farm in Asanyia Hill in the Golan Heights, with total installed capacity of 6 MW (consisting of ten 600 kW turbines), satisfying the consumption of about 5 thousand families. The wind farm operates around 97% of the time and yields revenue of ~1 million US $ a year. Indeed, wind energy potential of Israel is restricted because of surplus of moderate- or poor-wind velocities’ areas and is limited to the areas with sufficiently constant wind, some of which are being opposed by green groups on landscape conservation grounds. Nevertheless, the state continues efforts for bringing into operation of two more farms with a 50 MW capacity [50].
It is emphasized in the Israel Knesset document that an improved estimate, based on the wind turbines’ technological development, gives a value much more than 500 MW of the Israeli potential wind energy capacity [51]. One of perspective areas for efficient wind technology development, considering its climatic characteristics, is the Samaria region.
It is well known that energy yield of a wind turbine mainly depends on wind energy characteristics and turbine power curve [52,53]. In this paper, statistical characteristics of the wind speed behavior in Ariel (located in Samaria) are derived and investigated, relying on data collected be meteorological station located in Ariel University campus.

2. Materials and Methods

Eleven years of meteorological data (2001-2011), acquired by Ariel Meteorological Station and supplied by the Israeli Meteorological Service were processed. Measurement samples were taken at 10-meter height above the ground and were available at 10 minutes intervals. The city of Ariel is located at 32° 6′ 21.6″ N, 35° 11′ 16.43″ E, in the center of Israel (Figure 1). Ariel Meteorological Station is located inside Ariel University campus at eastern part of the city (Figure 2), residing at 700 m above sea level.
The wind speed data was provided by meteorological station as raw matrix of wind speed ad azimuth versus time at 10 m height, sampled at 10 minutes. In reality, the sample time is much higher than stated and the available data sample is actually an average of tens to thousands of faster samples. An example of monthly wind speed raw data in Ariel represented by 10 minutes samples is shown in Figure 3.
The raw vector is used to extract mean and standard deviation parameters and then can be either transformed into a histogram (discrete probability distribution function – PDF) or fitted to a known PDF, typically of Weibull type, as shown in Figure 4. When creating a histogram, the bins are typically chosen to be 1 m∙s-1 wide to match the resolution of the manufacturer provided turbine power curve data, resulting in the following discrete PDF,
  f H S T ( v ) = f ( v i ) , v i − 0.5 ≤ v < v i + 0.5
where f v i is the magnitude of the histogram bin, centered at v i .
Weibull PDF is defined by two parameters: shape or Weibull modulus (k, dimensionless), and scale (c, m/s for wind speed). The general form of the Weibull PDF is given by:
f W B L ( v ) = k c ( v c ) k − 1 e − ( v c ) k
for positive wind speeds (v > 0) with parameters c and k = related to the site wind speed mean μv and standard deviation σv as [54]:
μ v = c Γ 1 + 1 k
And
σ v = c Γ 1 + 2 k − Γ 2 1 + 1 k
respectively, where:
Γ ( x ) = ∫ 0 ∞ t x − 1 e − t d t
is the complete Gamma function. In case the wind raw data of a site is unavailable, but the mean and standard deviation of the wind speed are given, Weibull PDF is usually assumed, and its parameters are extracted from (4) and (5). In general, several ways to extract Weibull parameters from raw data exist [55]; MATLAB function wblfit was used in this work.
A particular (and very common) case of Weibull PDF is the case where k = 2. It is called Rayleigh PDF and is given by
f R L H ( v ) = 2 v c 2 e − ( v c ) 2
for positive wind speeds (v > 0) with scale parameter c related to the site mean wind speed as
μ v = π 2 c
making (6) to be dependent on average wind speed as [56]:
f R L H ( v ) = π v 2 μ v 2 e − ( π v 2 μ v ) 2
It is worth noting that wind energy resource is typically classified according to average wind speed at 10 m height as shown in Table 1 [56].
Since power in the wind increases with height [57,58], the turbine hub of medium and large-scale wind turbines is usually located a 50 – 150 m height. Therefore, statistical wind parameters must be either measured at hub height or extrapolated from measurements available at smaller heights. In case single height measurements only are available, power law is usually employed to estimate wind speed v 1 at height H 1 as
v 1 v 0 = H 1 H 0 α
where v 0 is the wind speed measurement available at height H 0 and α is the surface roughness dependent friction coefficient [59,60]. Friction coefficient dependence on terrain characteristics is typically determined from Table 2 [56].
According to the above, a software simulator was created receiving meteorological data (excel format) as an input and calculating the following output. Using the wind speed raw data, mean and standard deviation (STD) vales were calculated, followed by Weibull parameters extraction, and plotting respective histograms along with resulting Weibull PDFs. The process was repeated after extrapolating the samples to 70-meter height using friction coefficient of 0.3 according to Table 2. All the results were calculated monthly, annually, and seasonally. As to wind directions, annual Rose diagrams were created for both 10 and 70 m heights.

3. Results

Table 3 and Table 4 summarize yearly and cumulative mean and STD of wind speed and azimuth at 10 and 70 m heights, respectively. It may be concluded that the wind belongs to class 2, according to Table 1.
Table 5 and Table 6 summarize monthly, yearly, and cumulative Weibull parameters of wind speed at 10 and 70 m heights, respectively. It may be concluded that winds in Ariel may be accurately assumed as Rayleigh since the cumulative k is very close to 2.
In order to validate the applicability of Weibull PDF to wind statistics in Ariel, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 present yearly wind speed raw data histograms and Weibull PDFs at both 10 and 70 m heights. Good matching is evident at all figures.
All yearly Weibull PDFs are plotted together in Figure 16 for 10 and 70 m heights, respectively. It may be concluded that wind regime is relatively stable and hence predictable. This is supported by Figure 17, presenting statistical as well as Weibull parameters variations throughout the years at 10 m height.
Weibull parameters were estimated seasonally as well. Winter season in Israel generally takes place from November to January, autumn season - from August to October, spring season - from February and April and summer season from May to July. The results are summarized in Table 7 and Table 8 for 10 and 70 m heights, respectively. Cumulative seasonal PDF plots are given in Figure 18, Figure 19, Figure 20 and Figure 21, respectively.
Another important aspect of wind analysis is prevailing wind direction (azimuth). Eleven years wind direction polar histograms (Rose diagrams) are shown as rose diagram in Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30, Figure 31 and Figure 32 for both 10 and 70 m heights. Cumulative wind rose diagrams are shown in Figure 33. 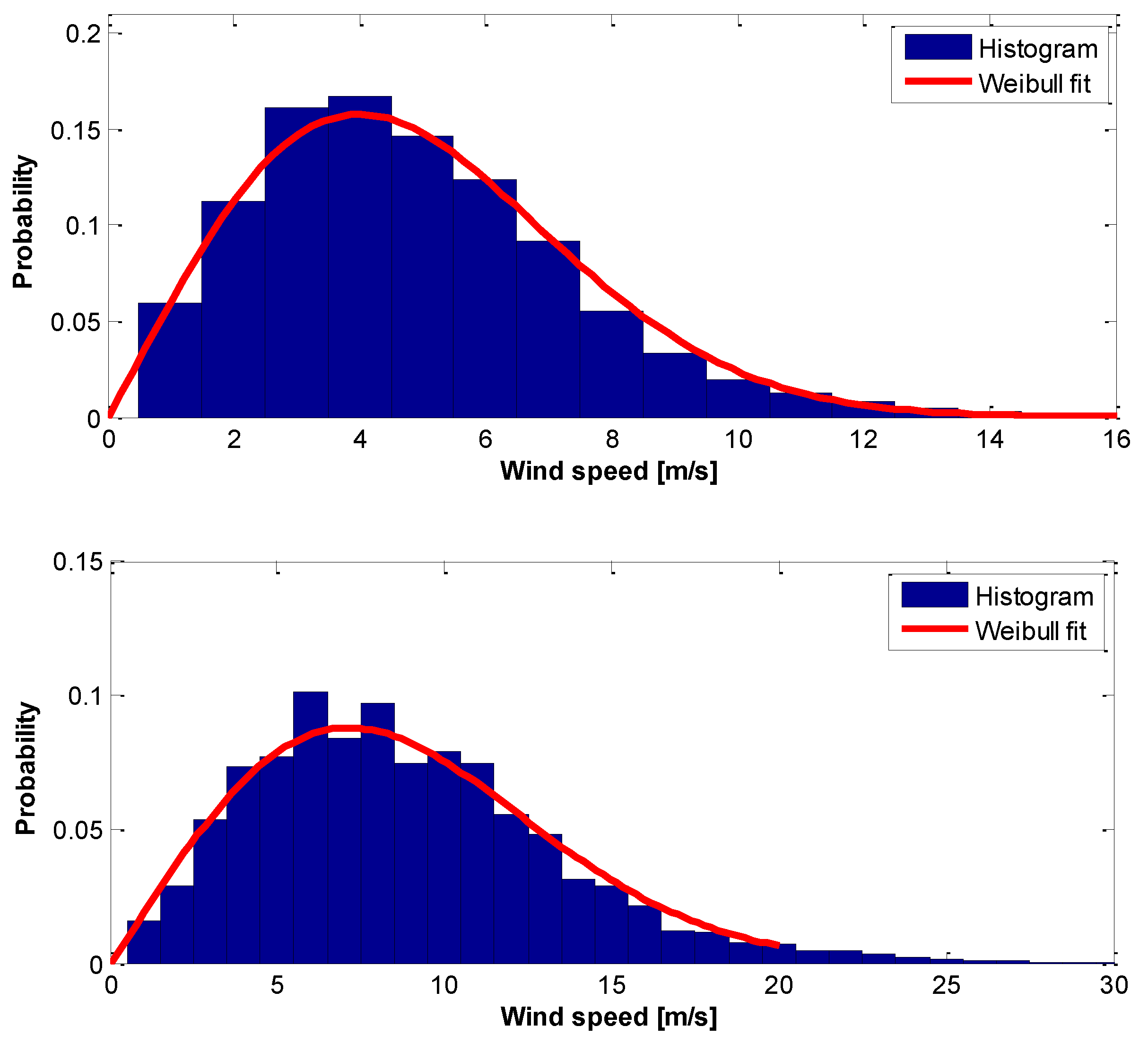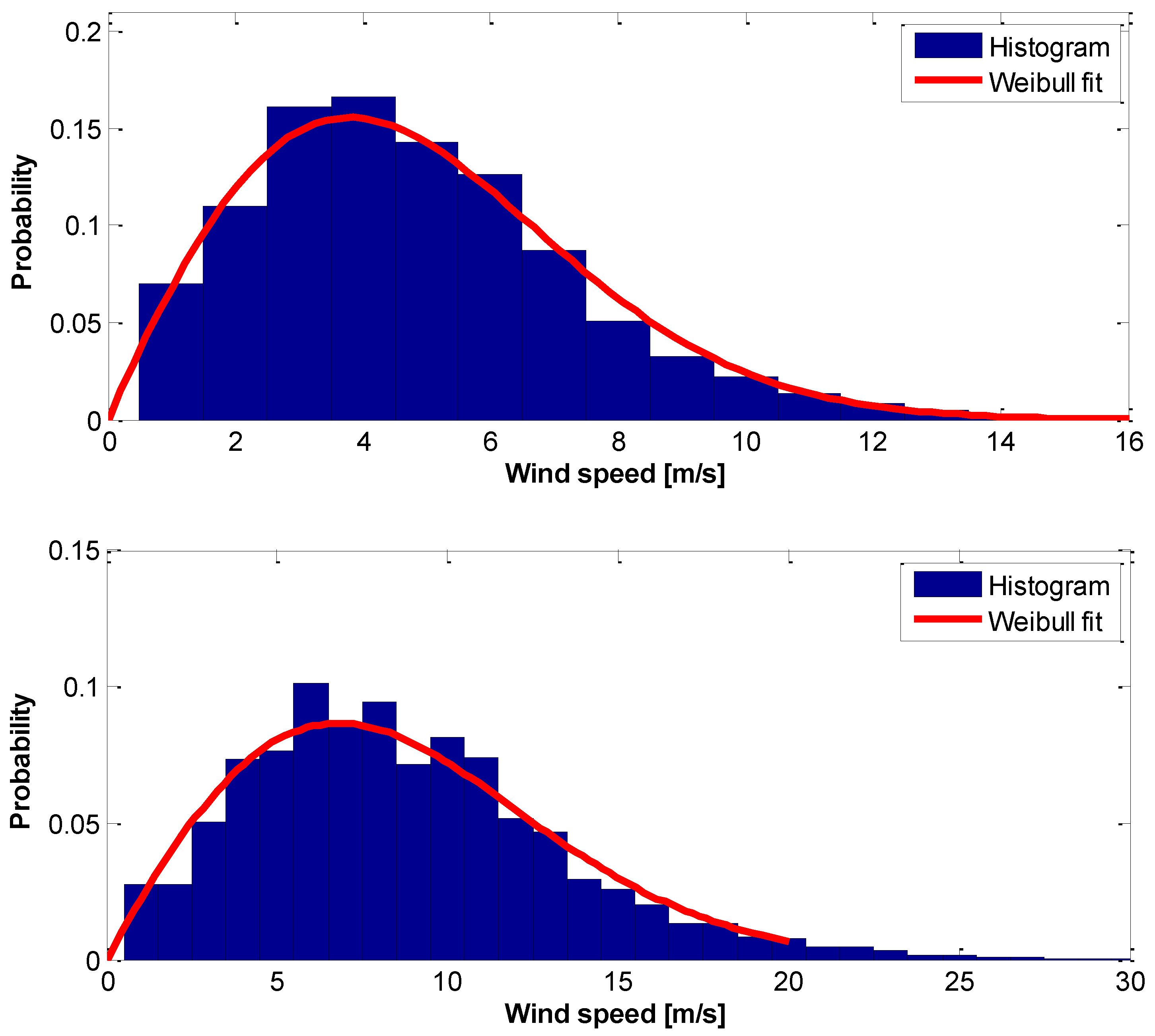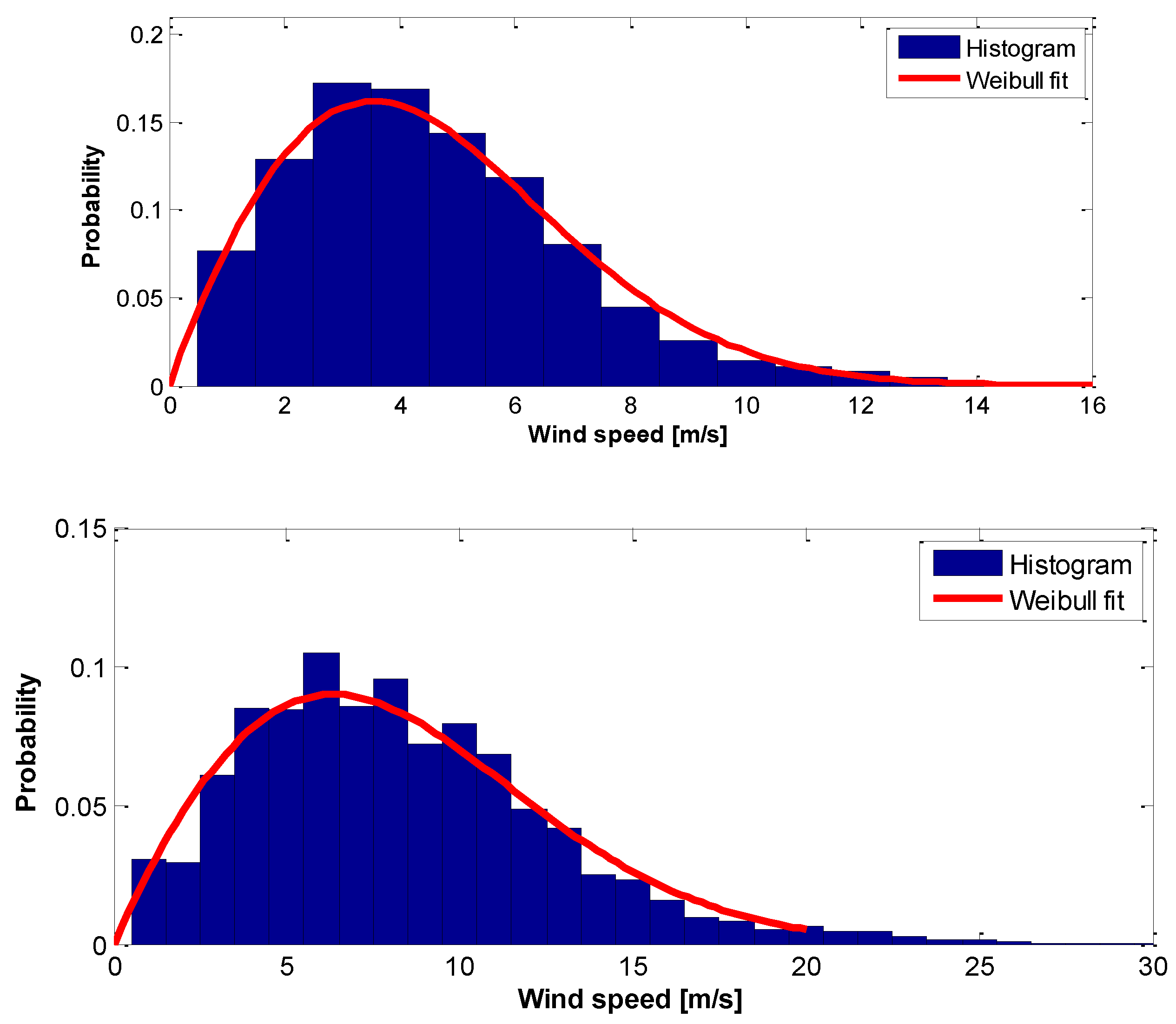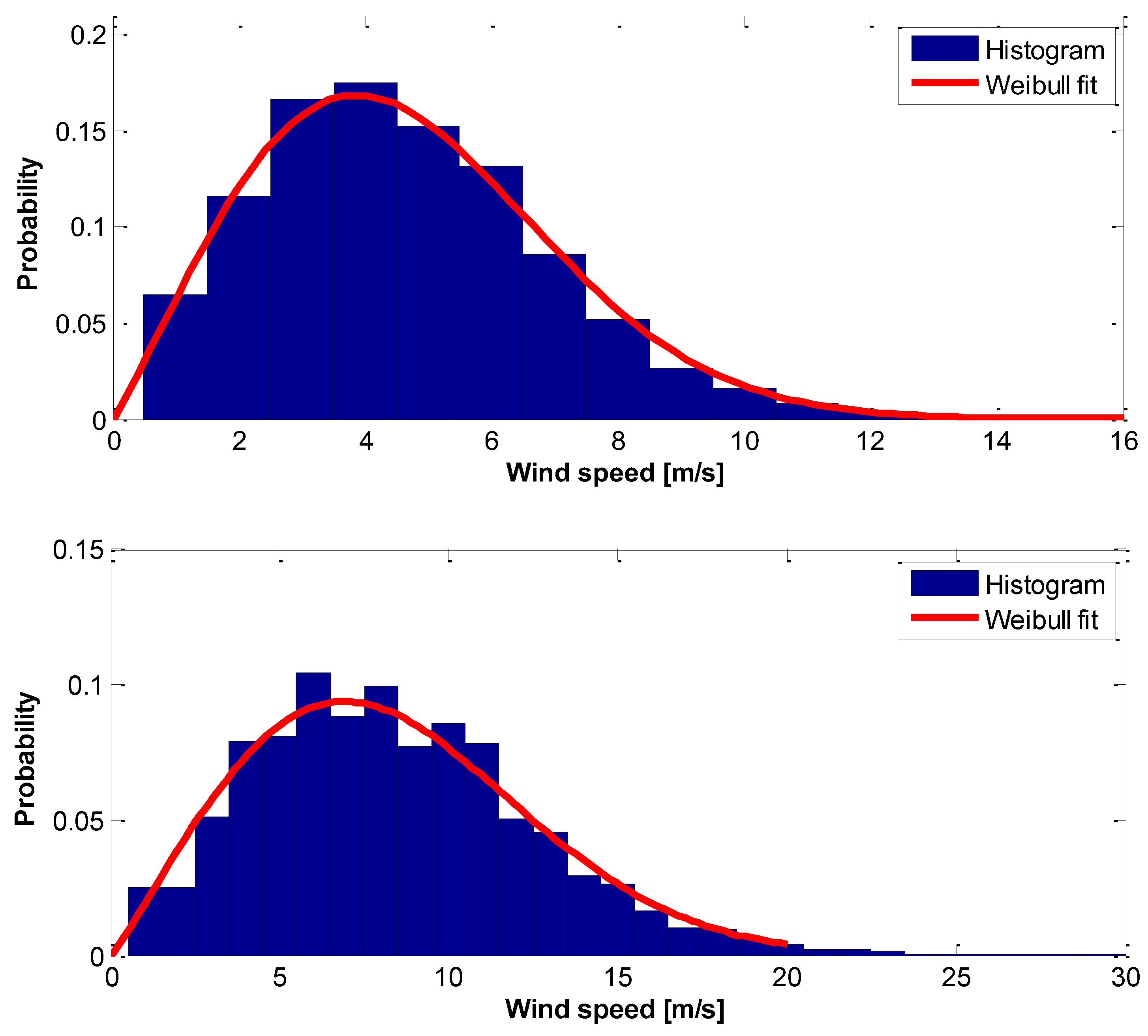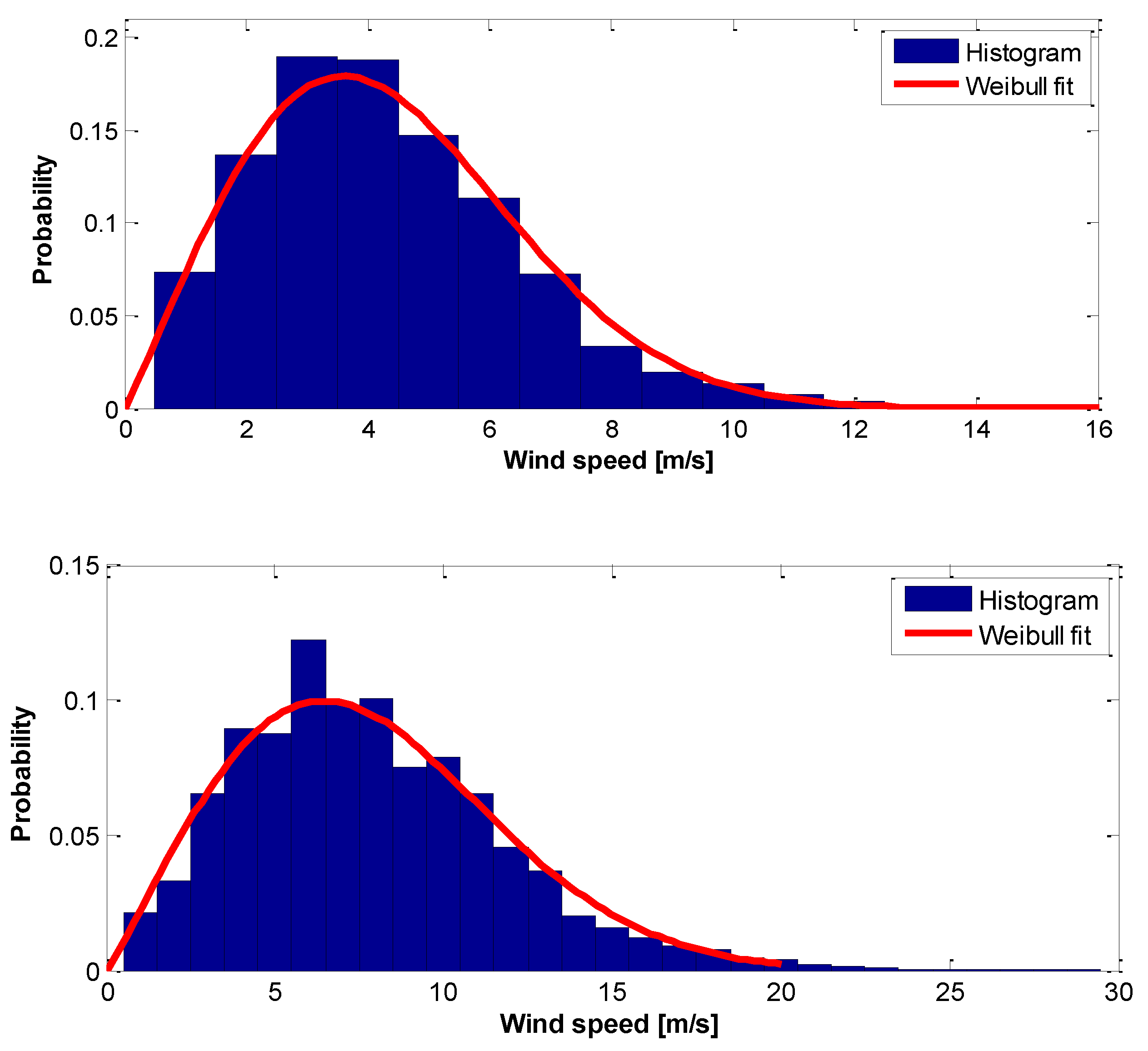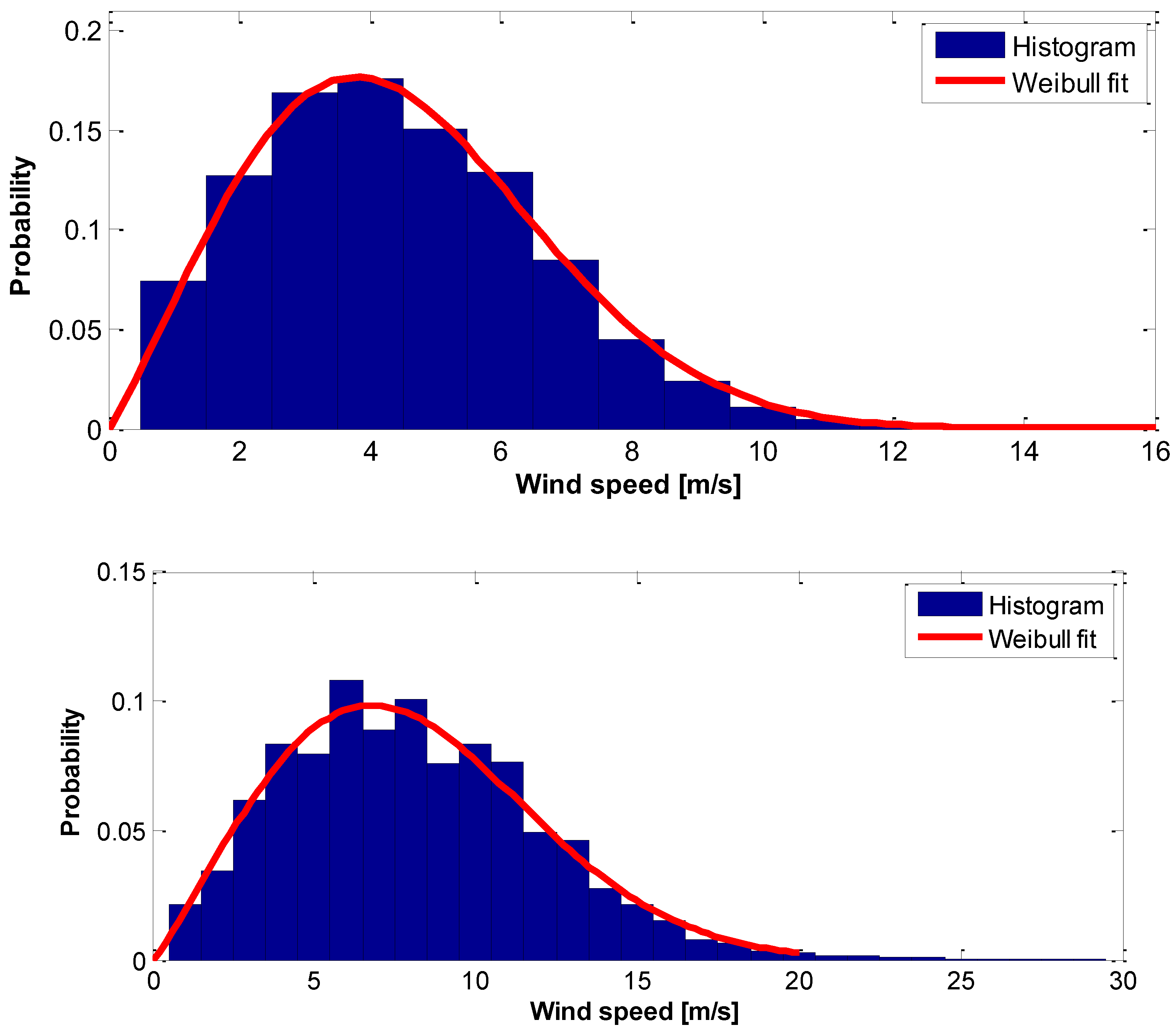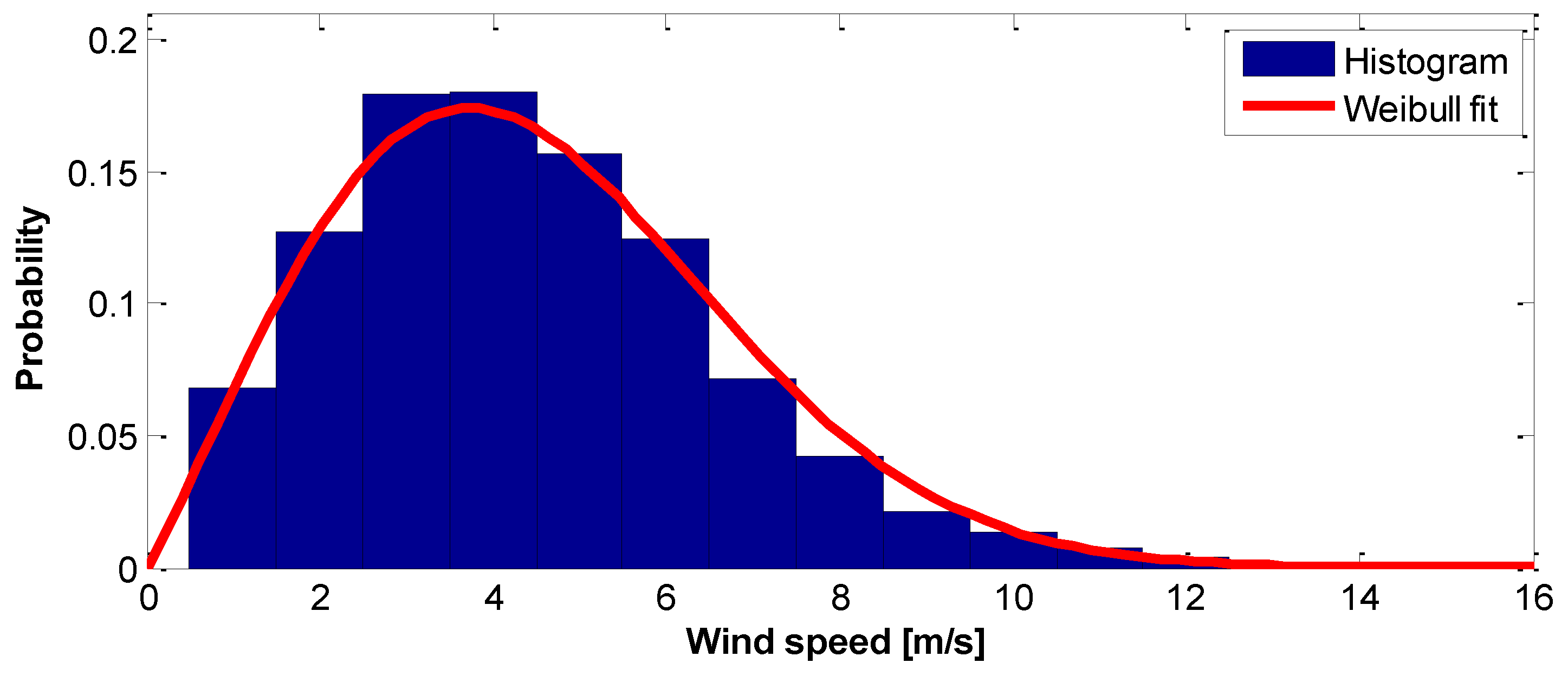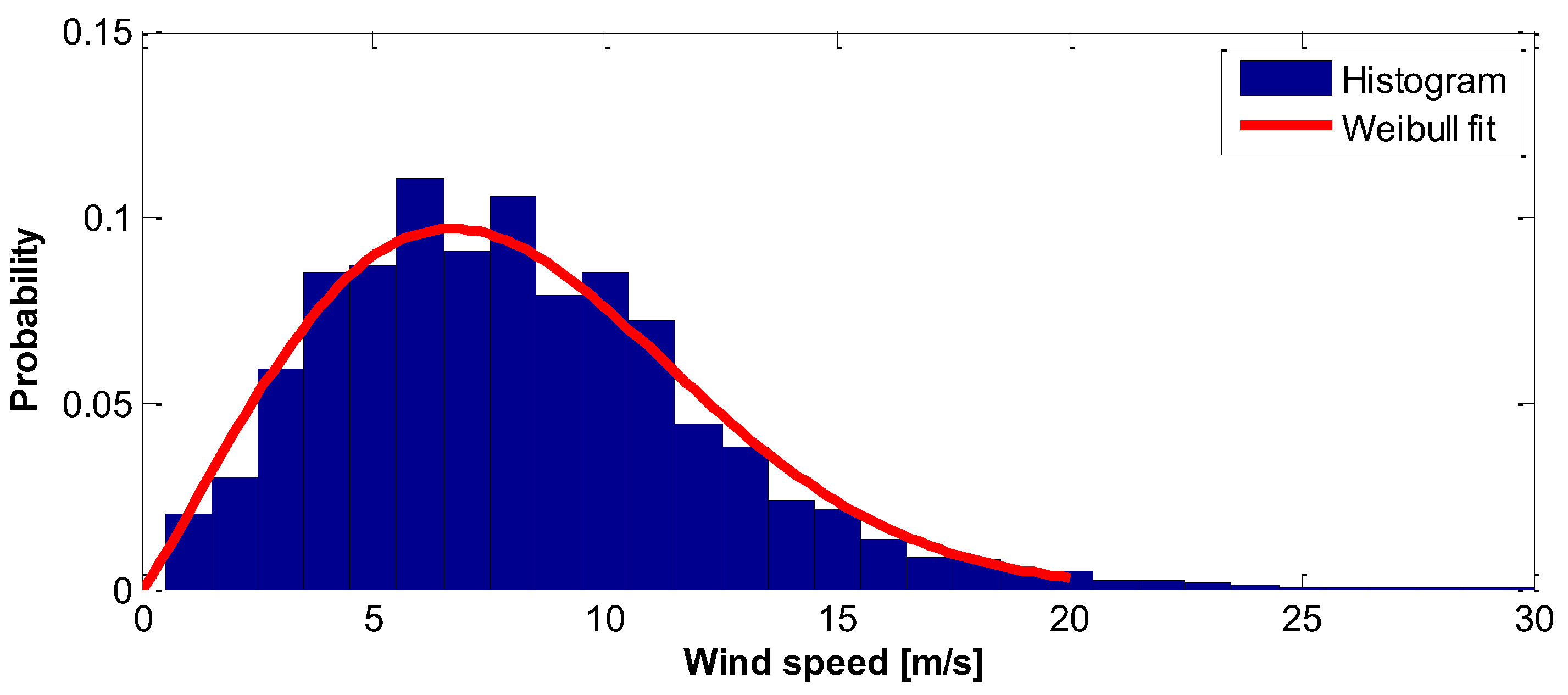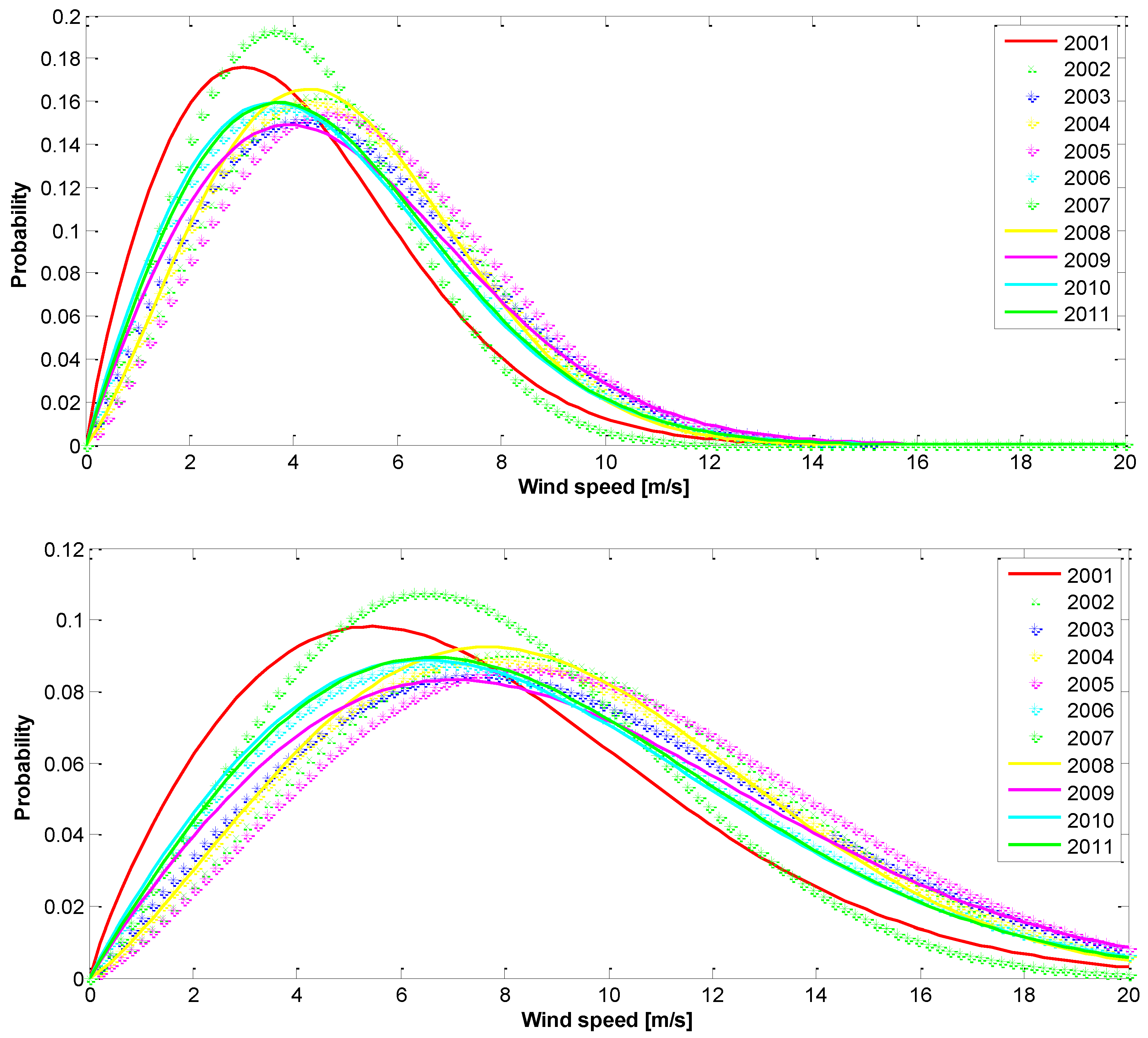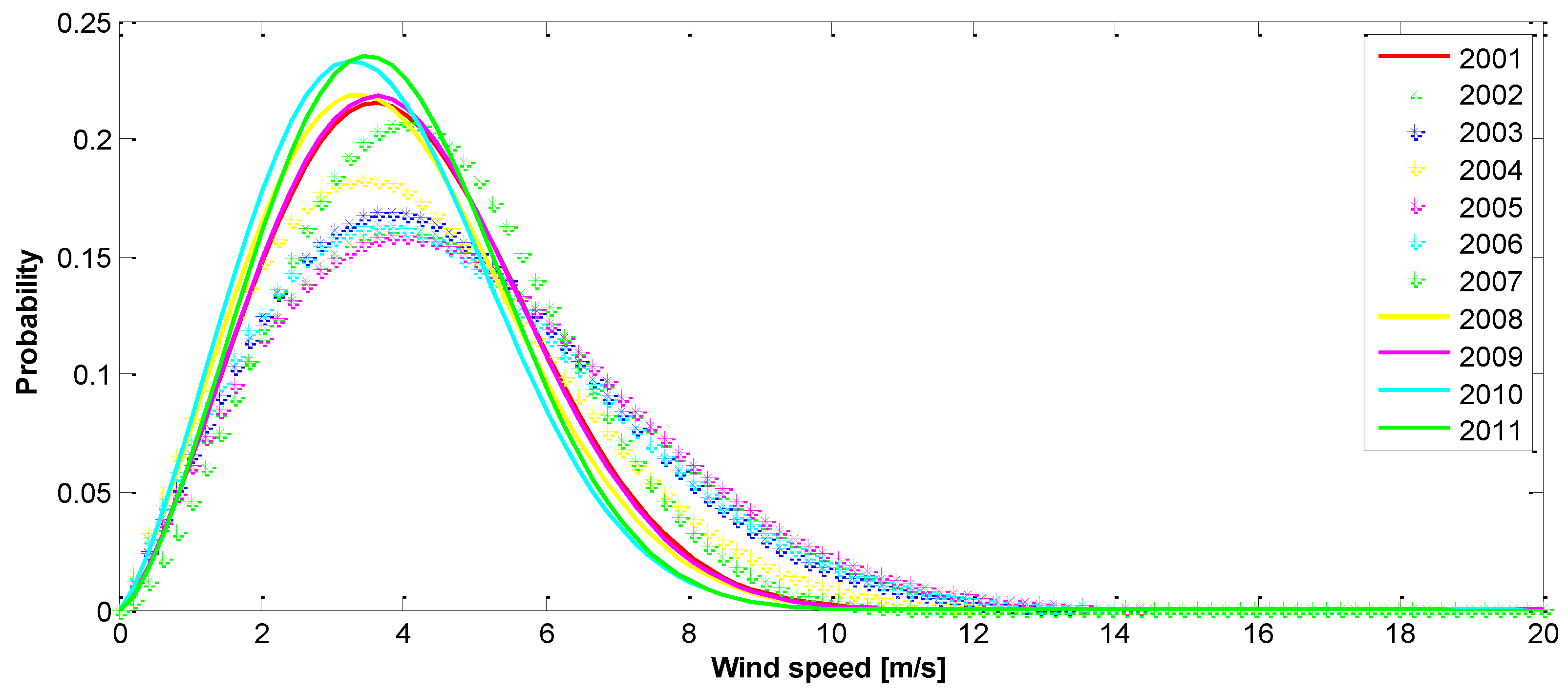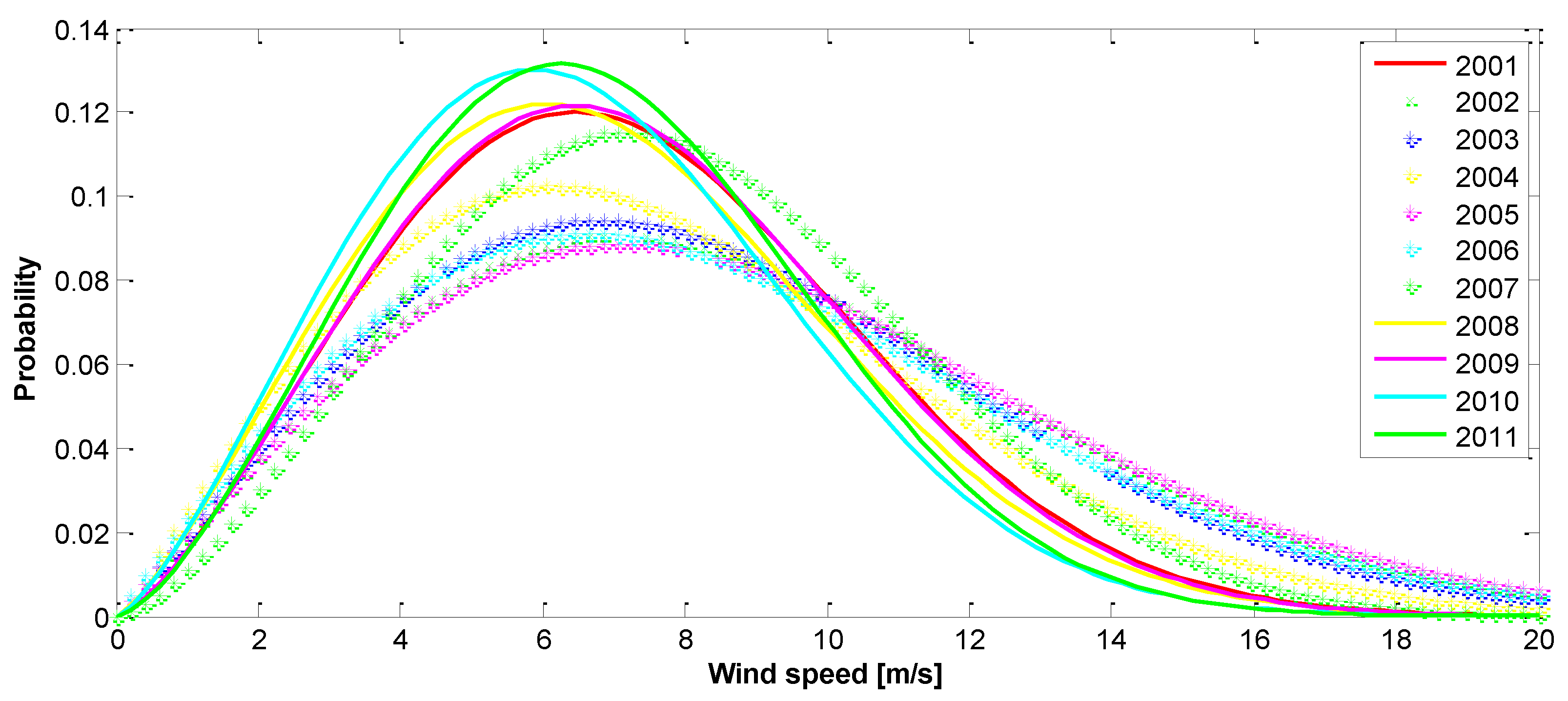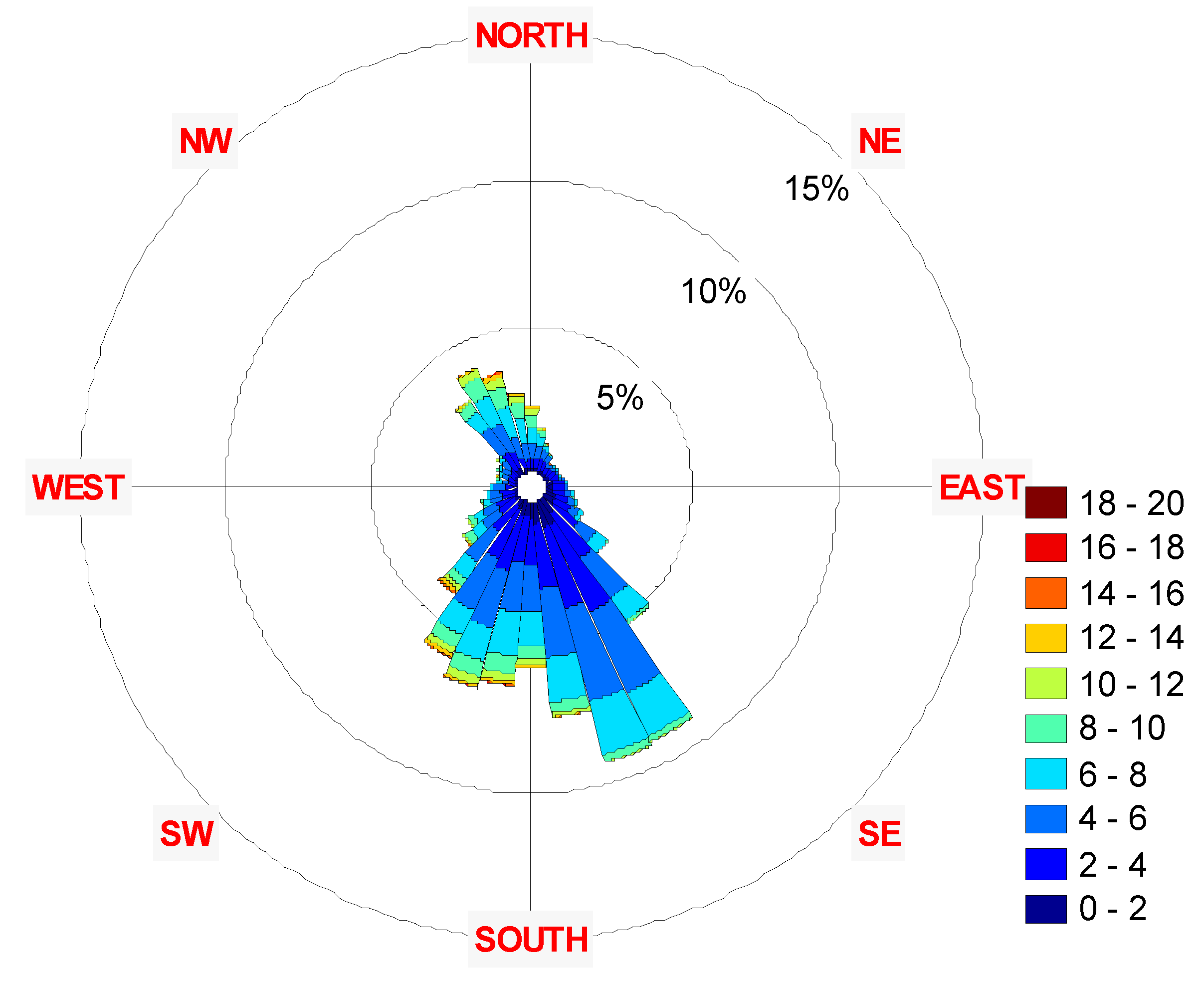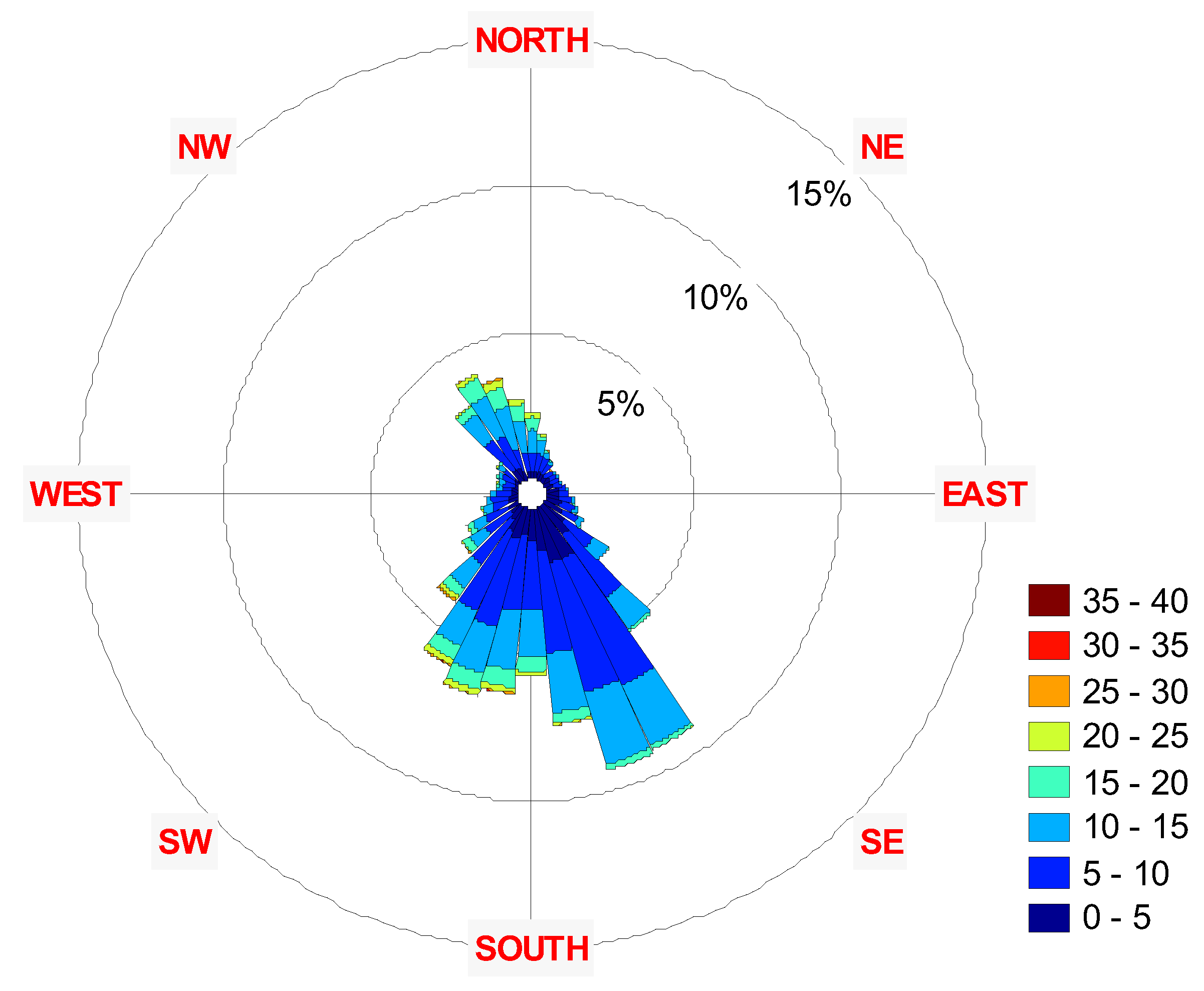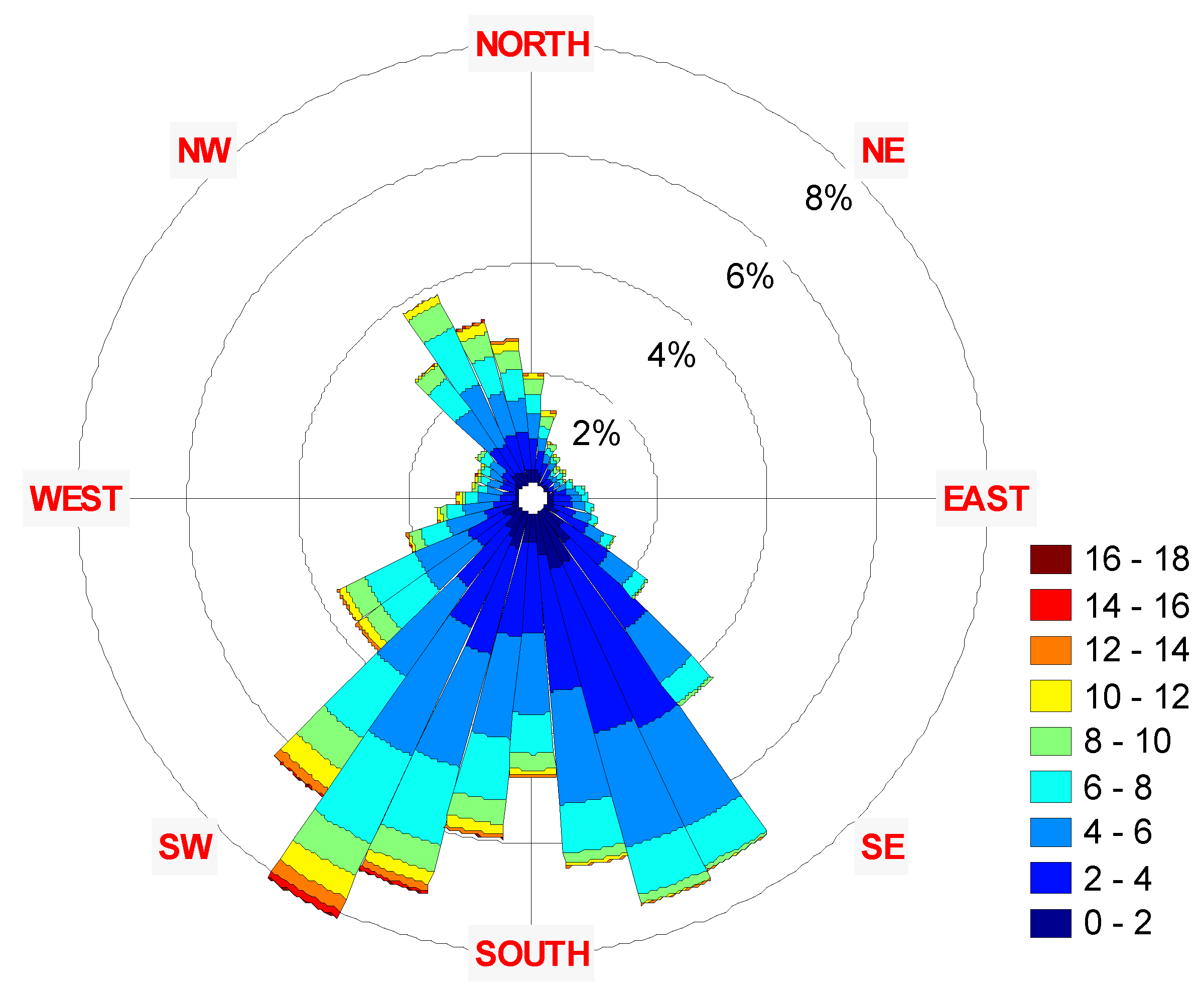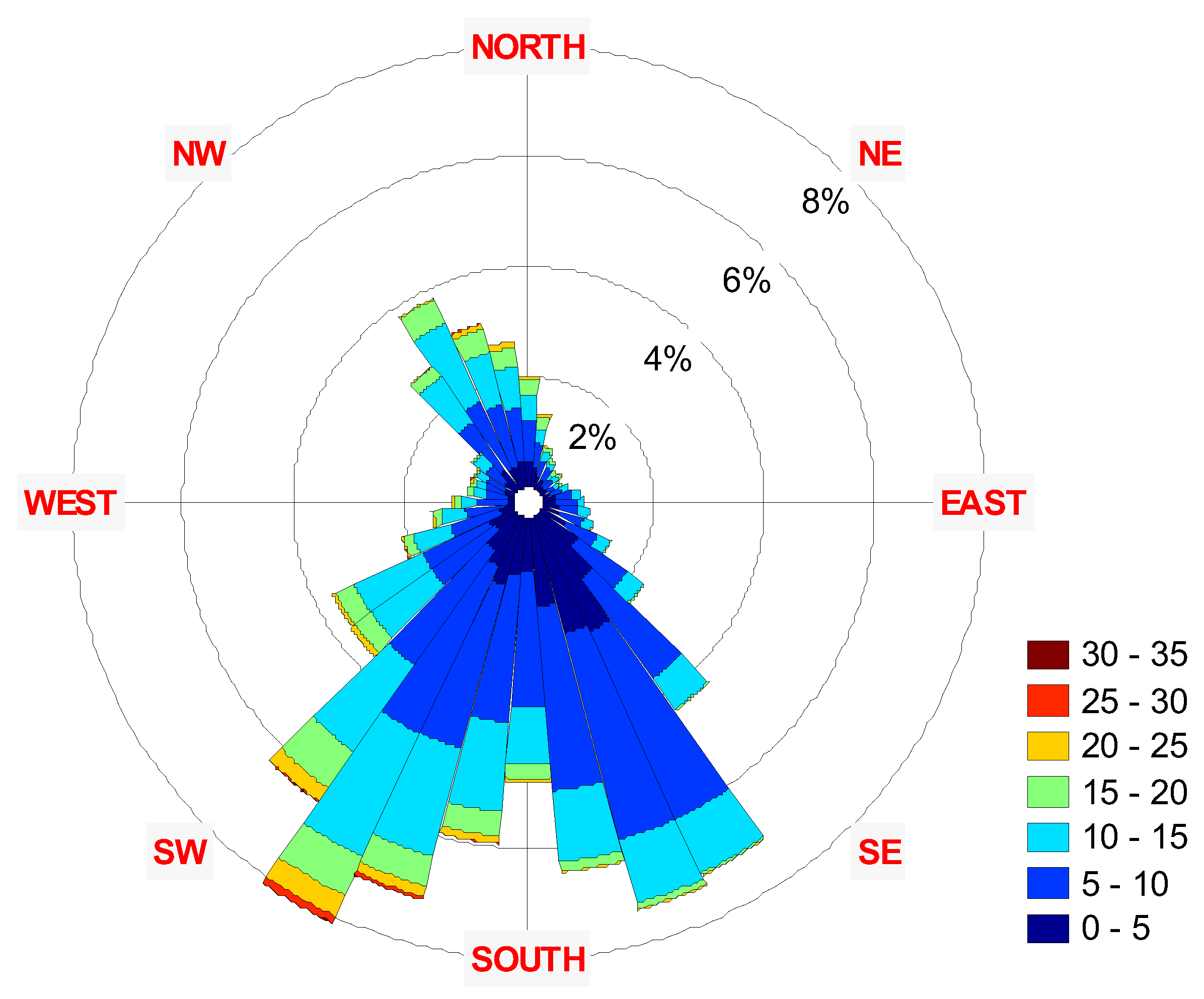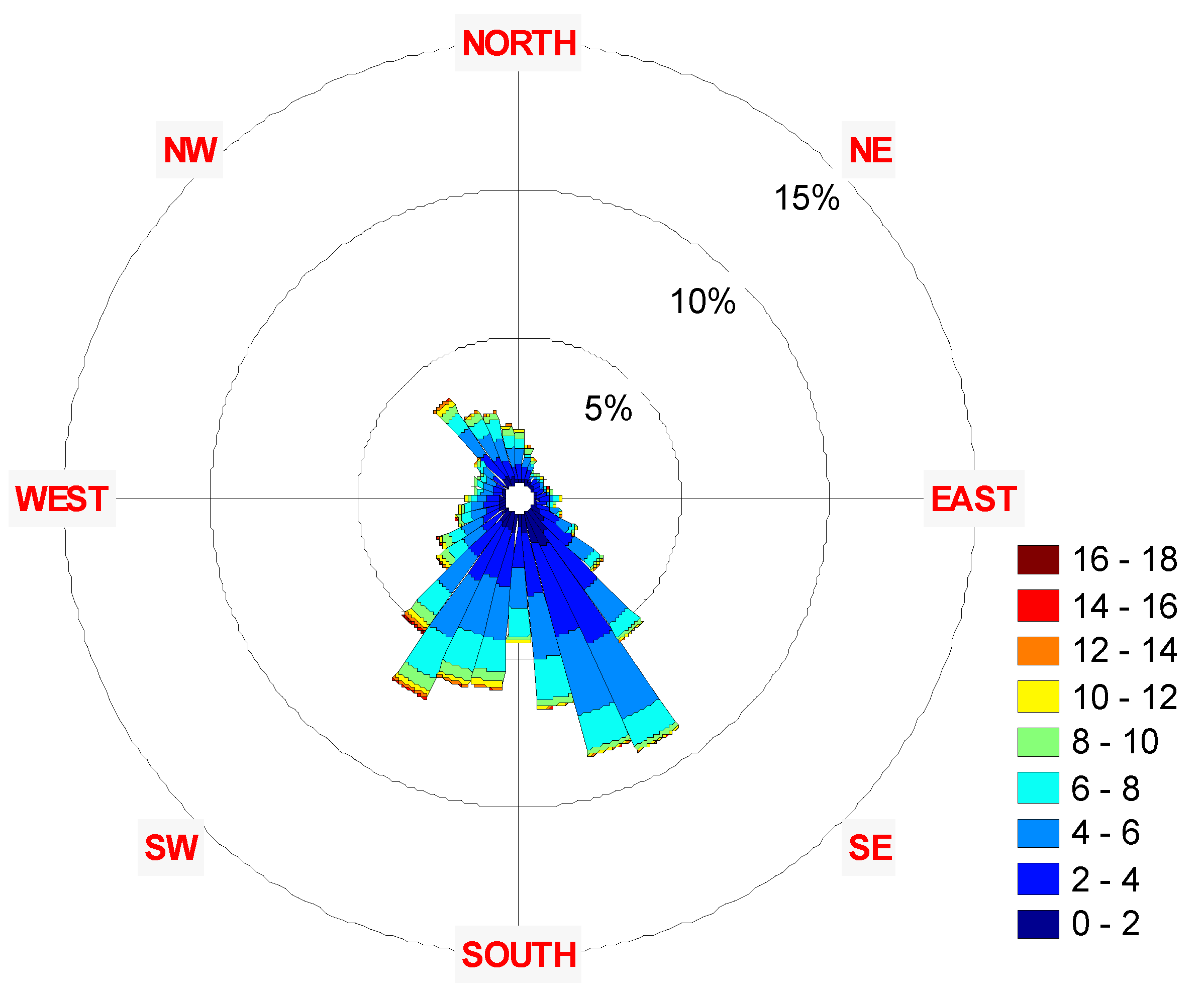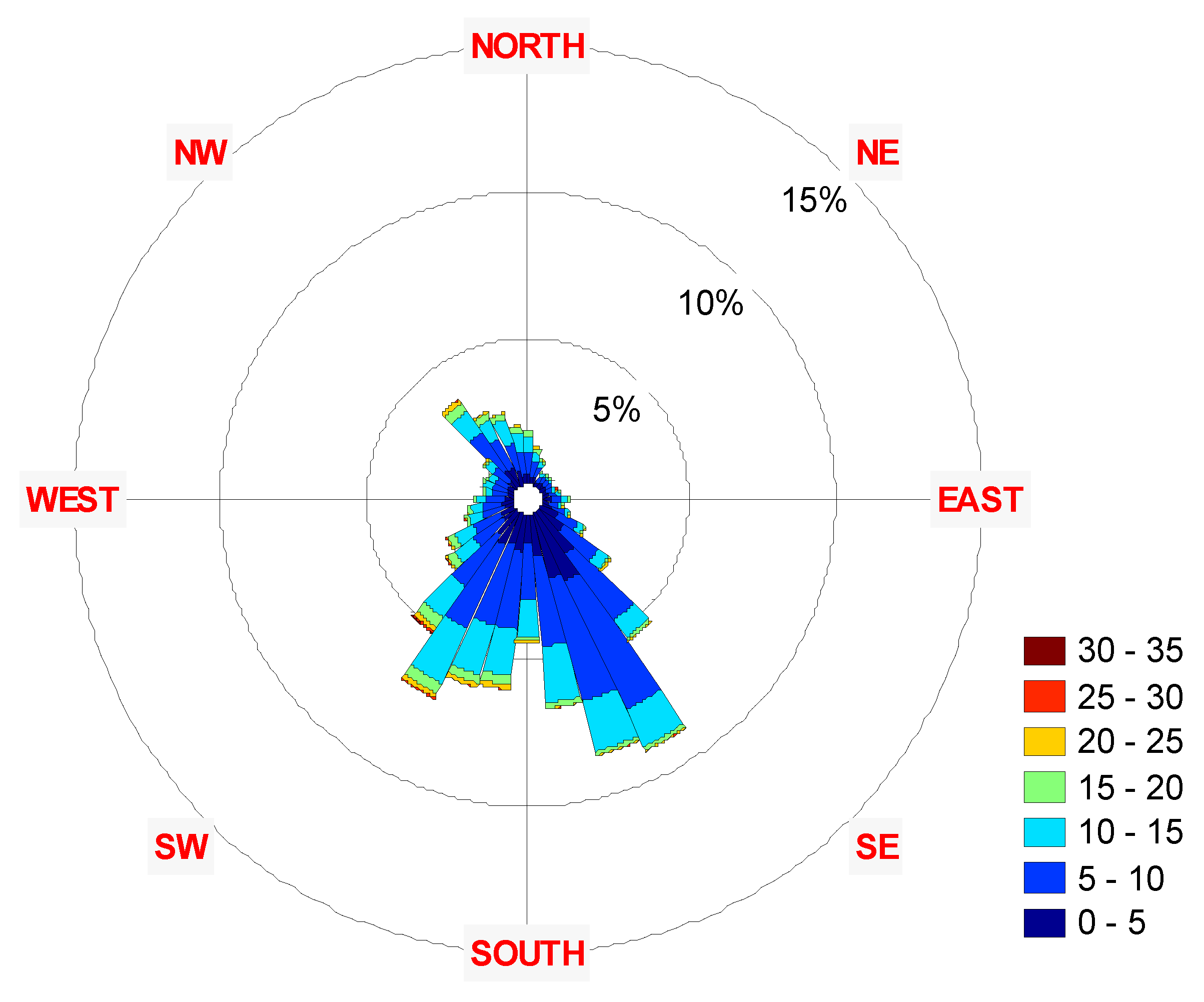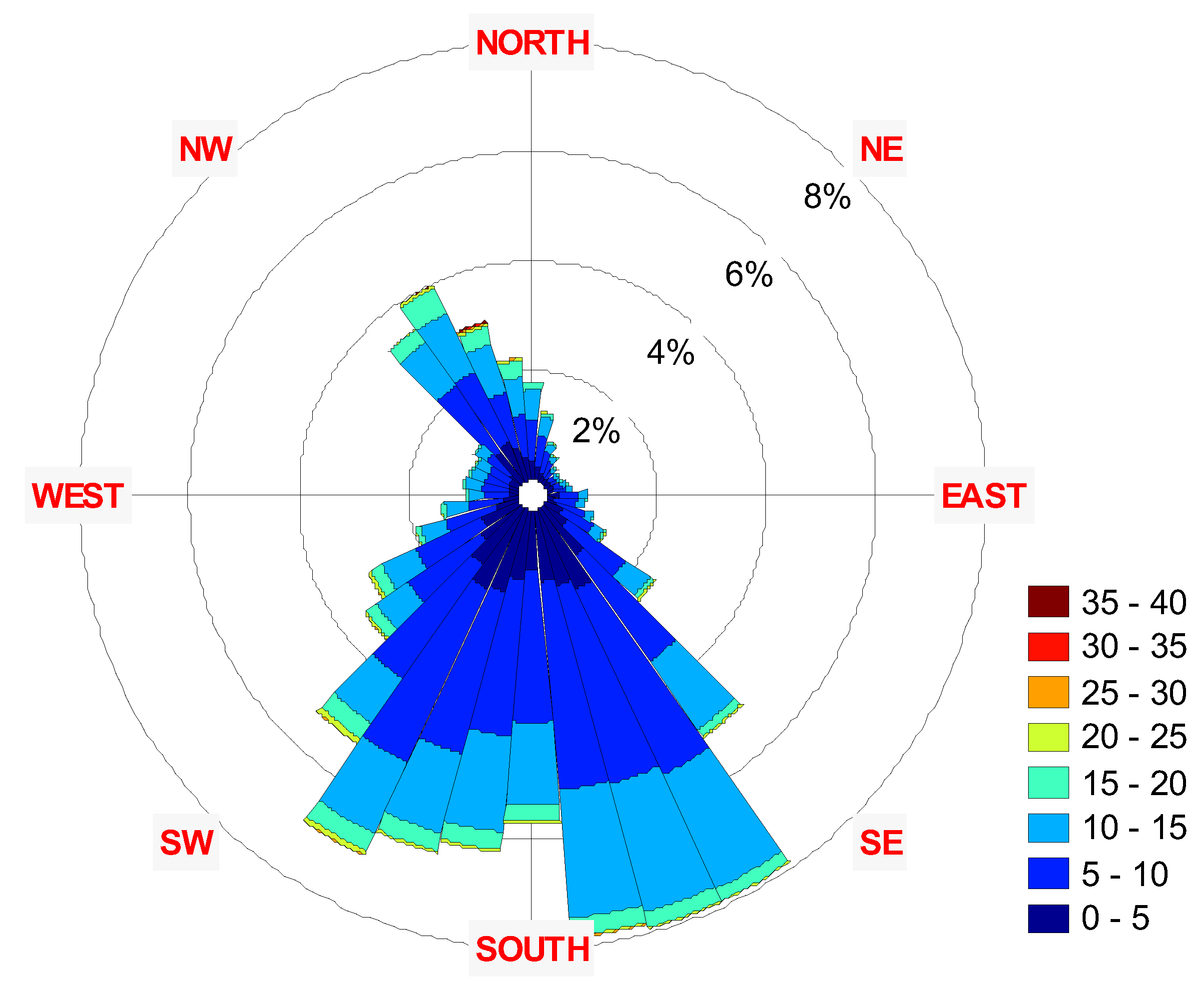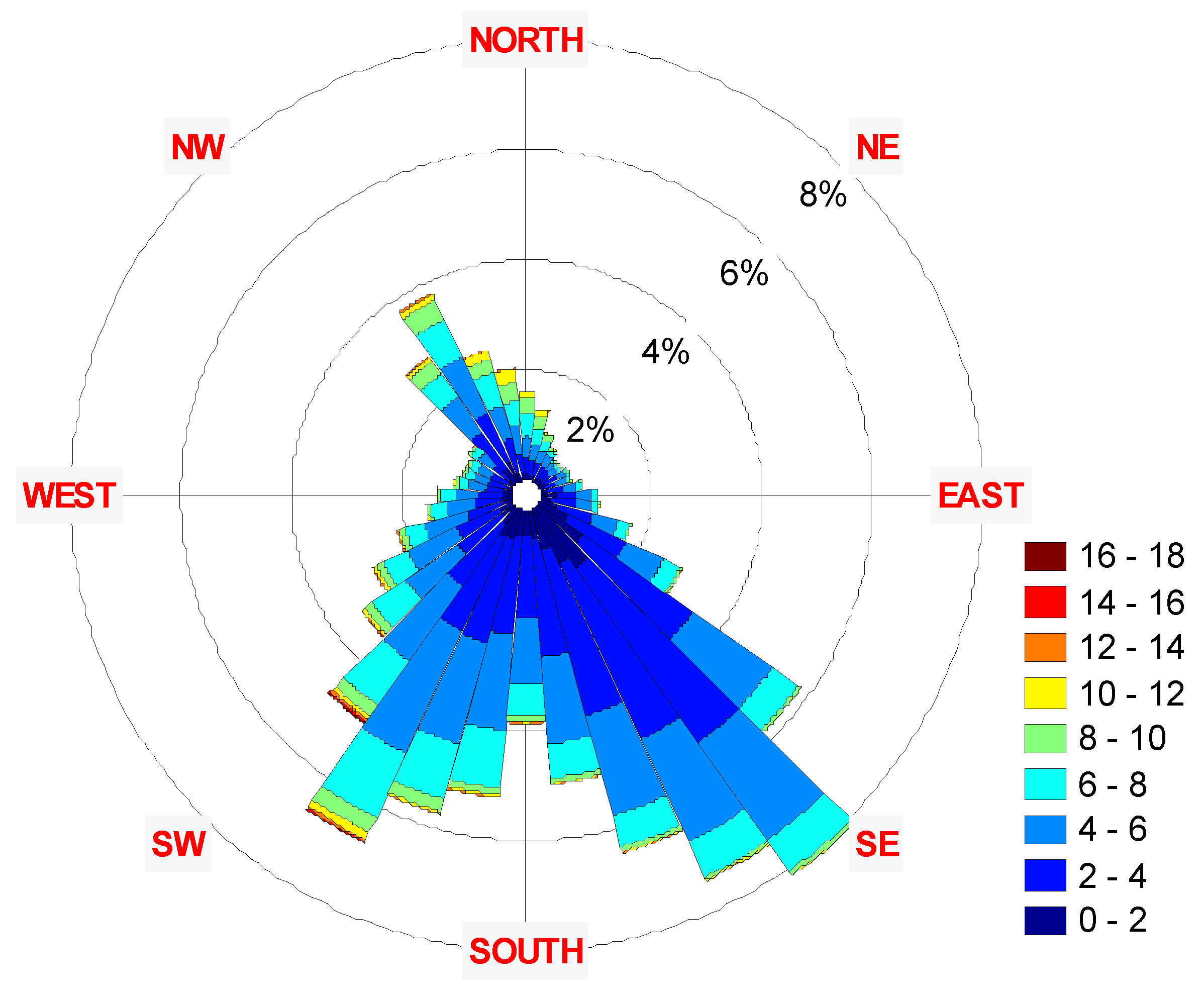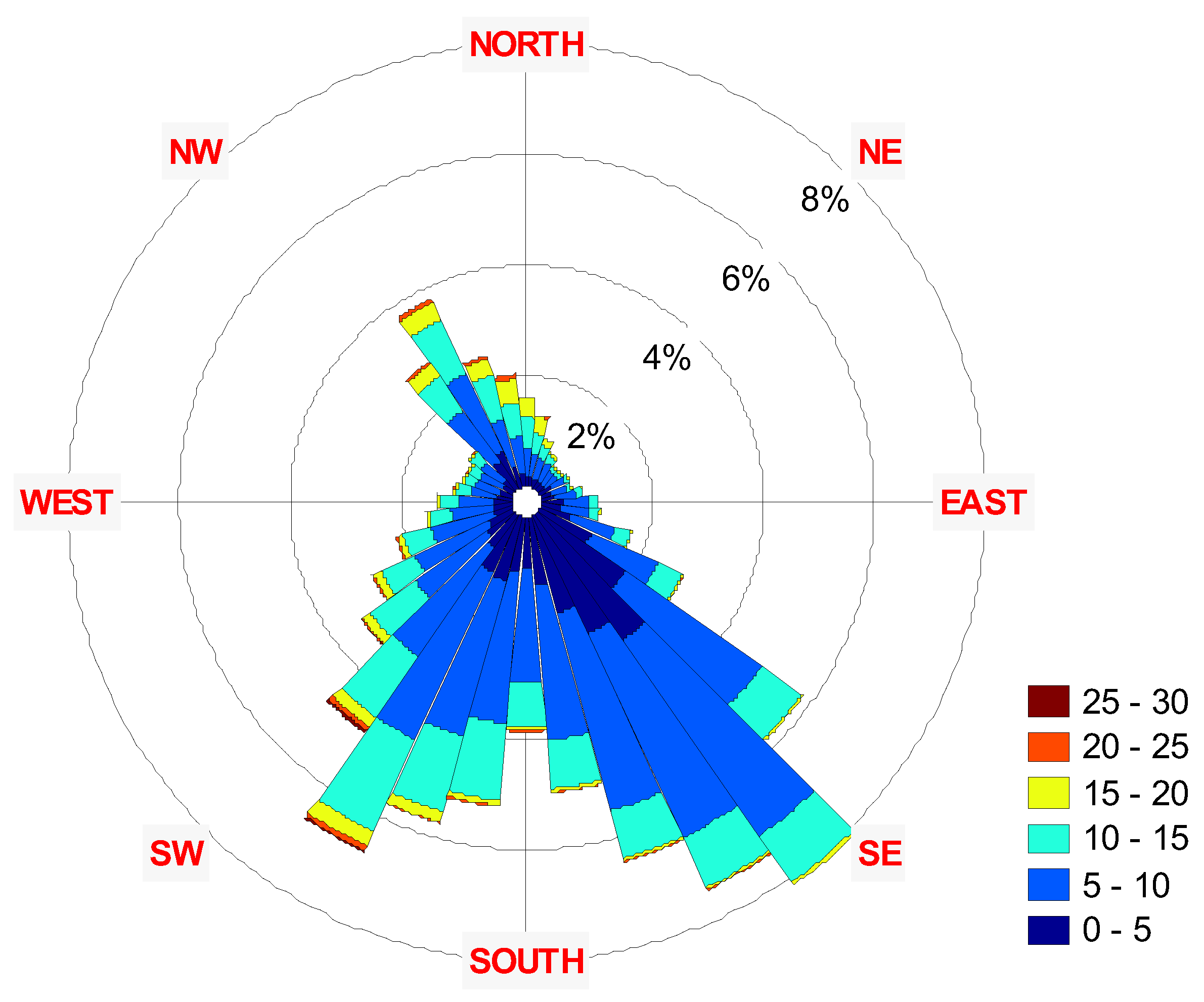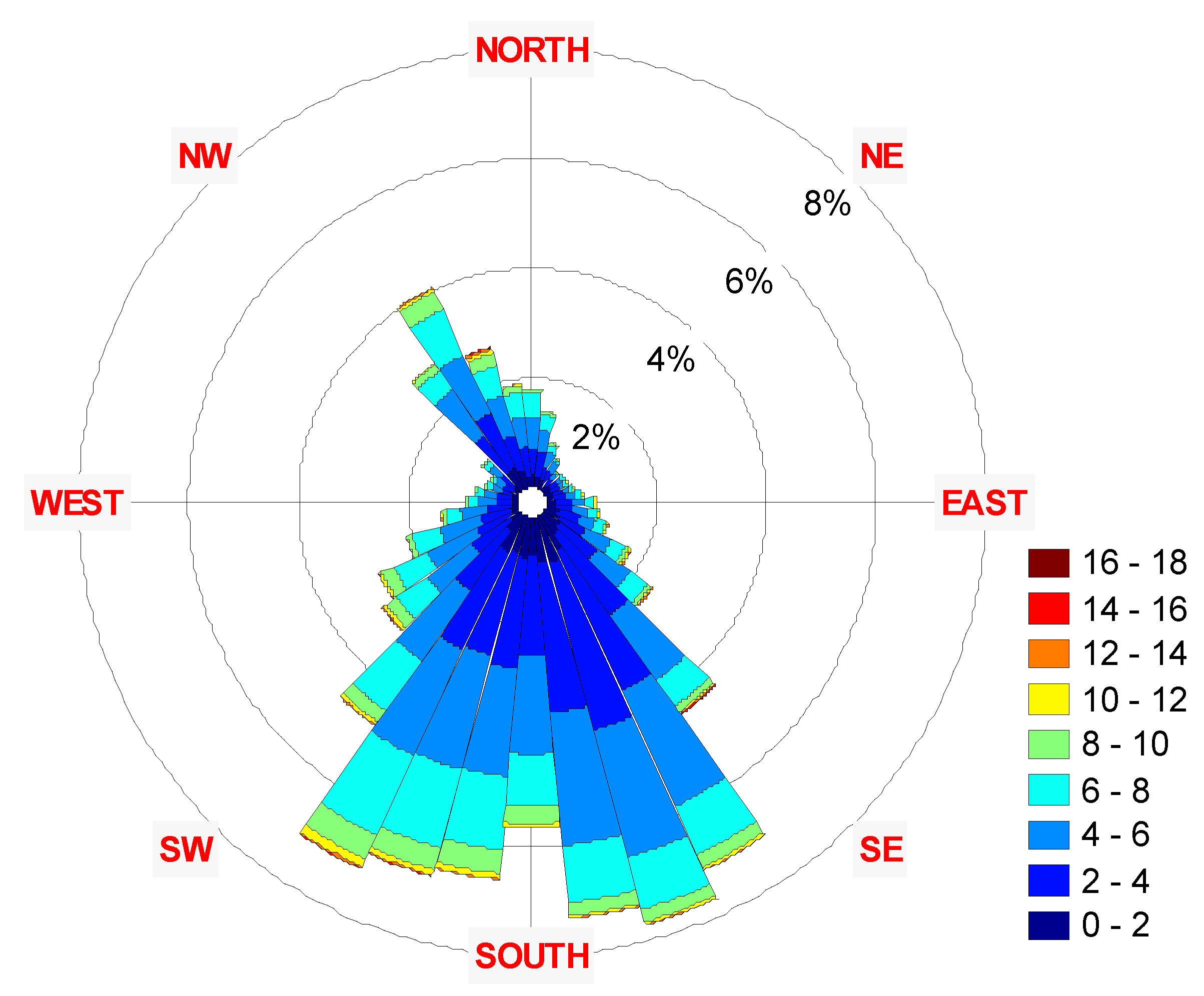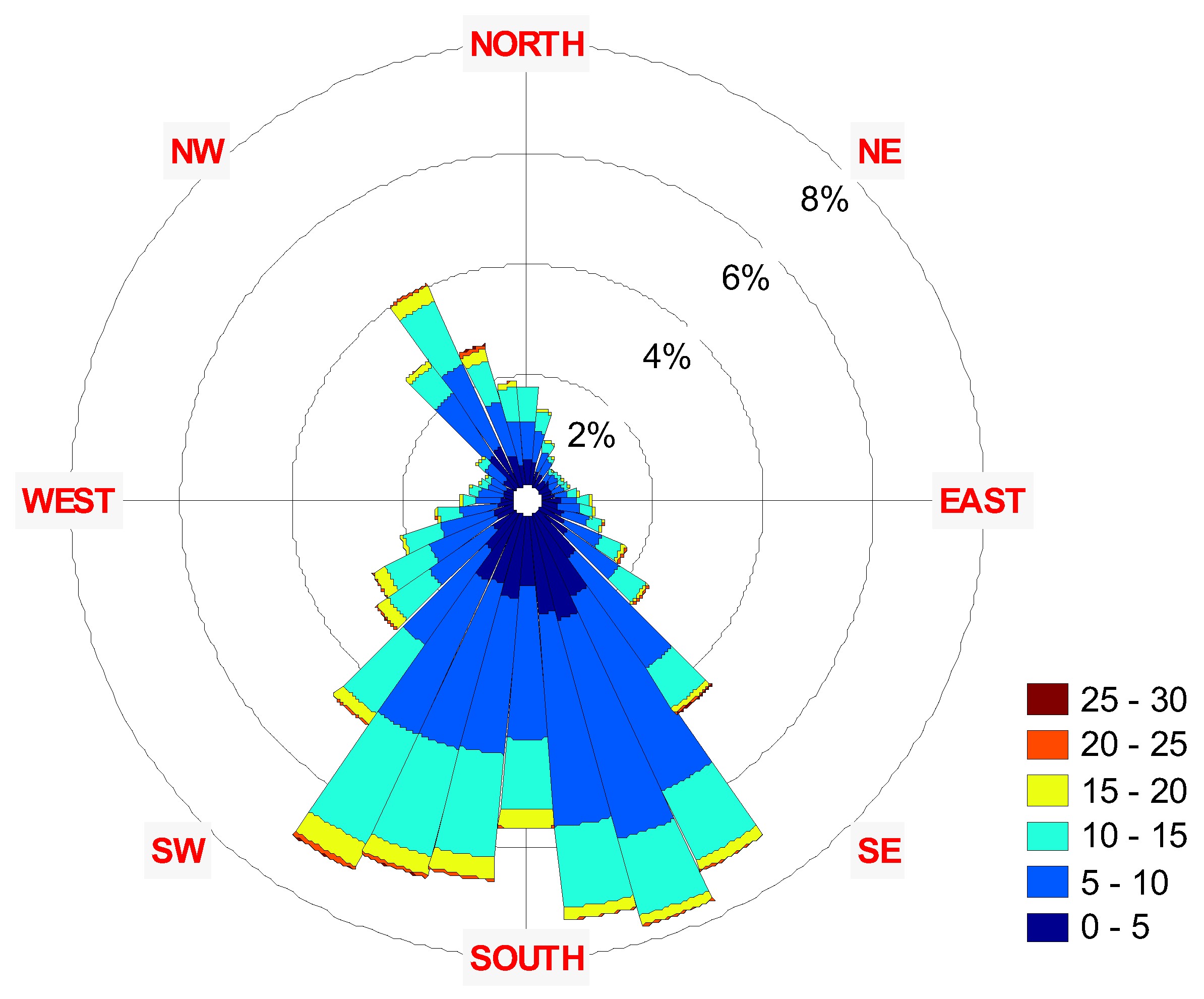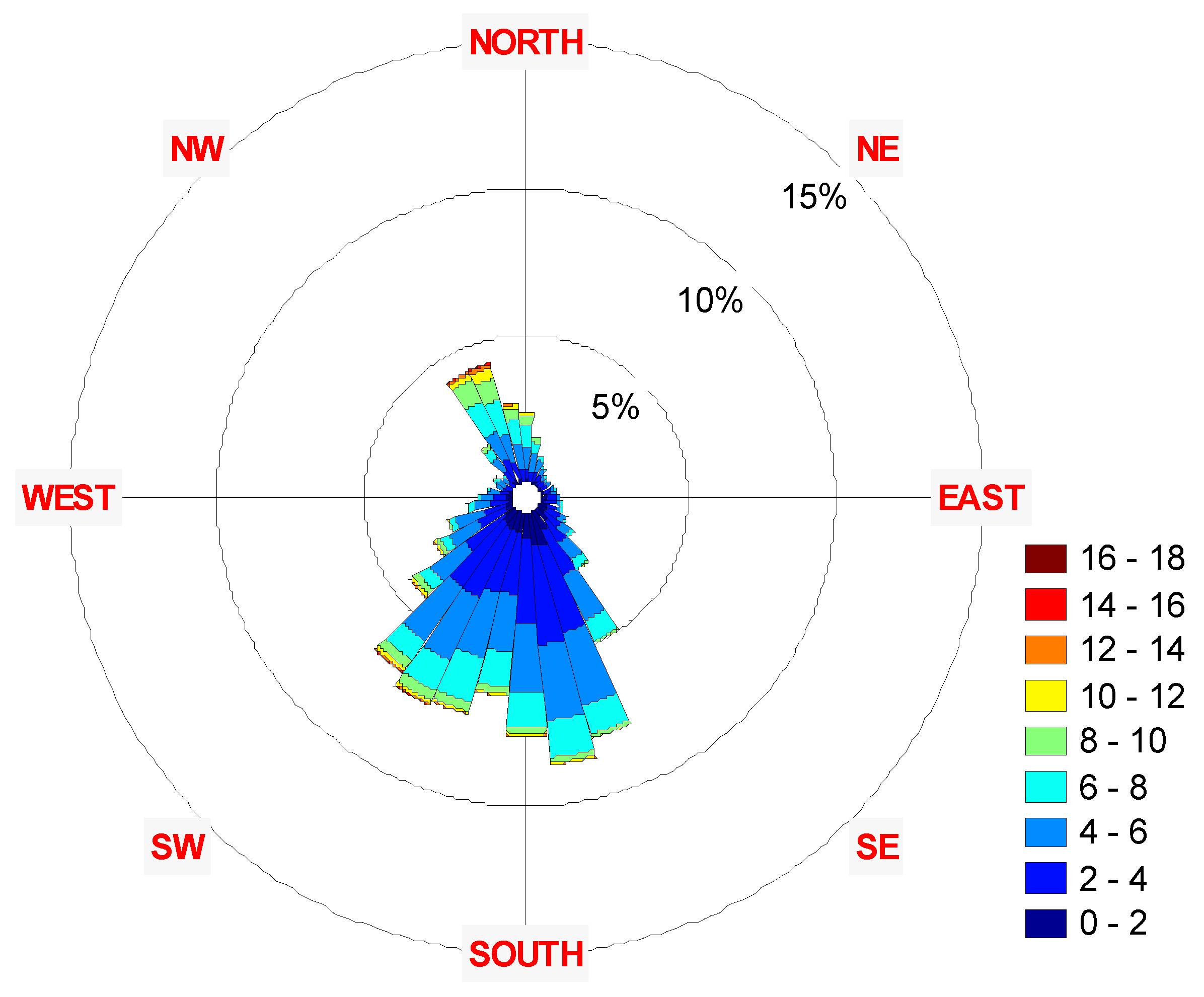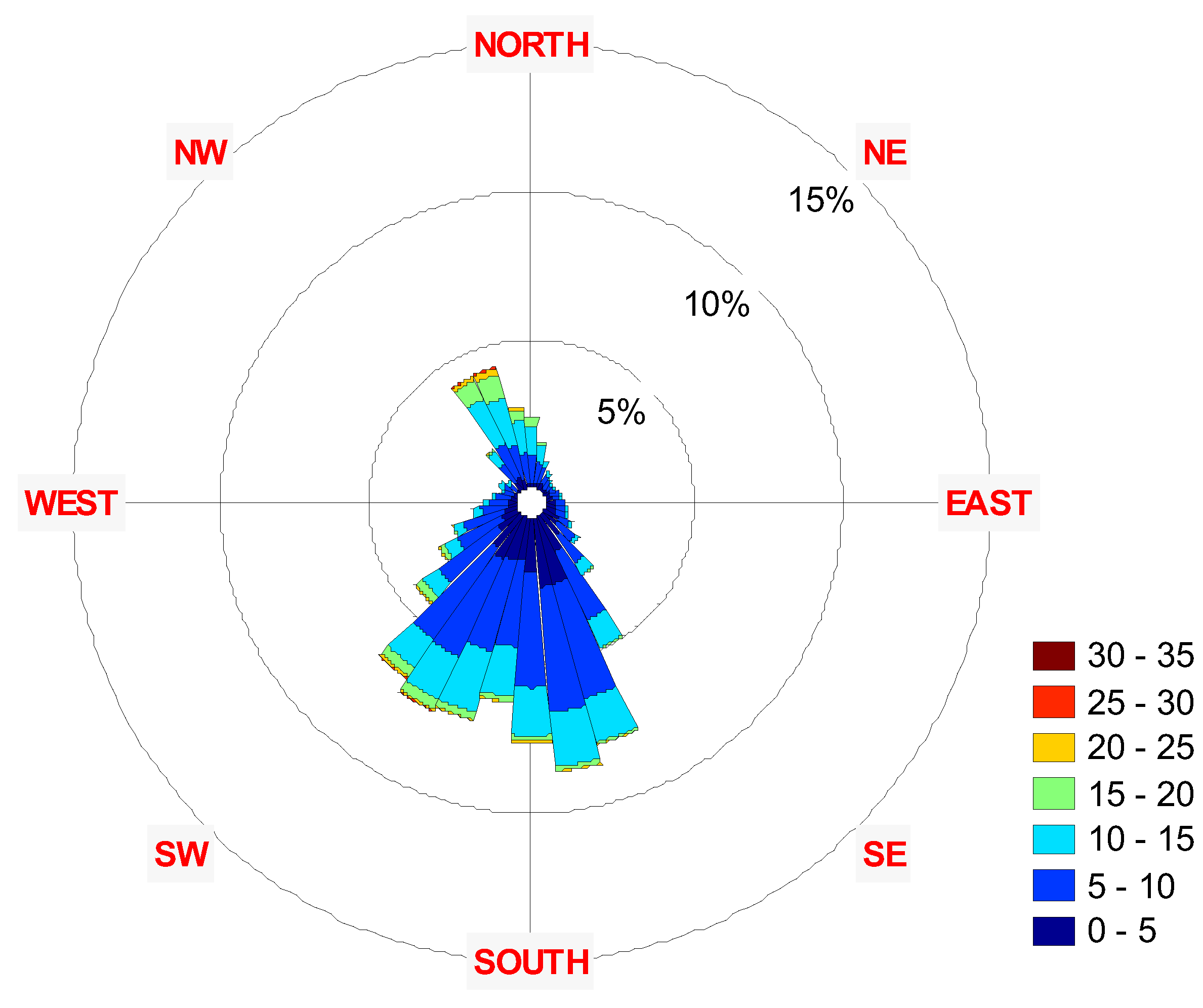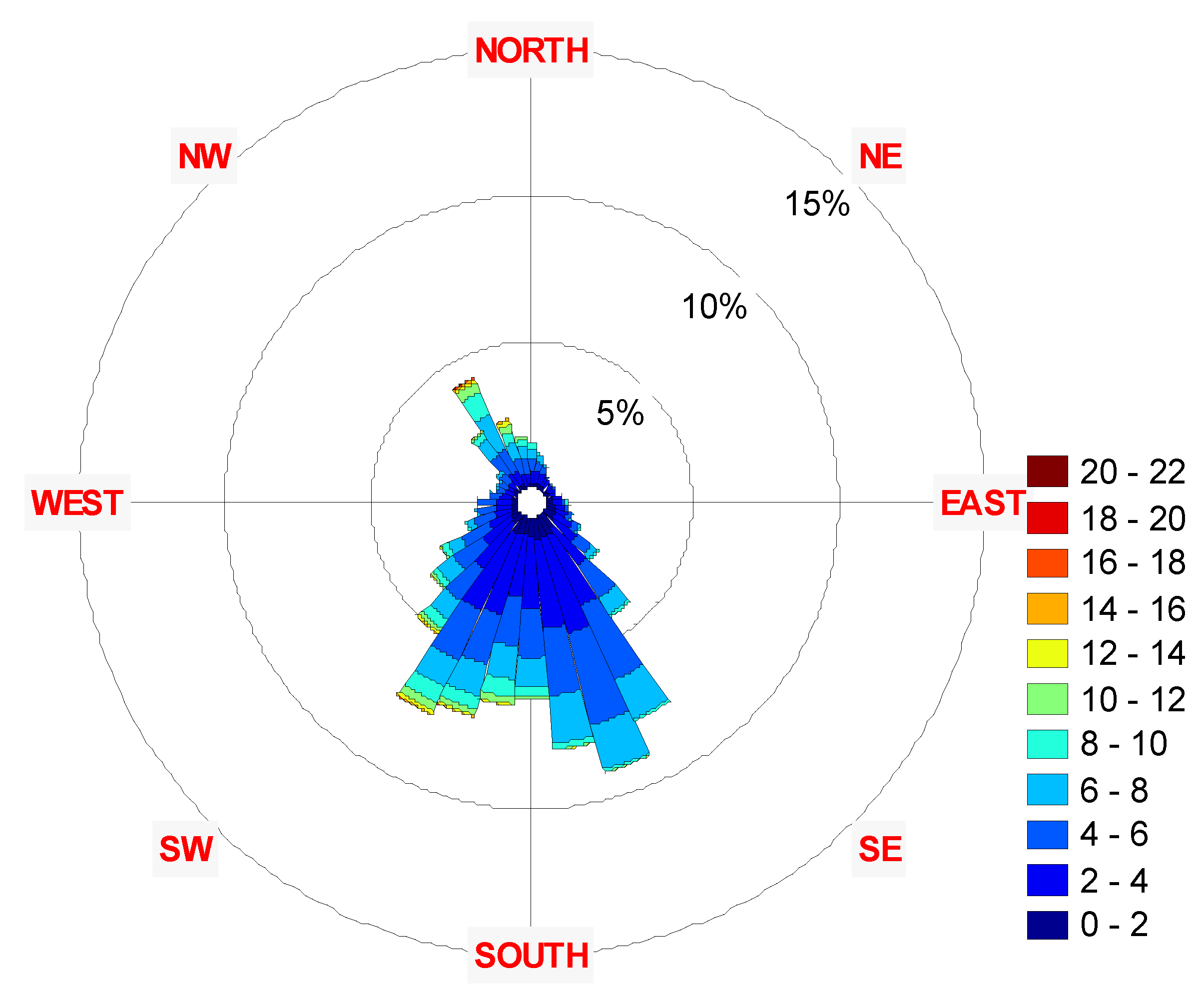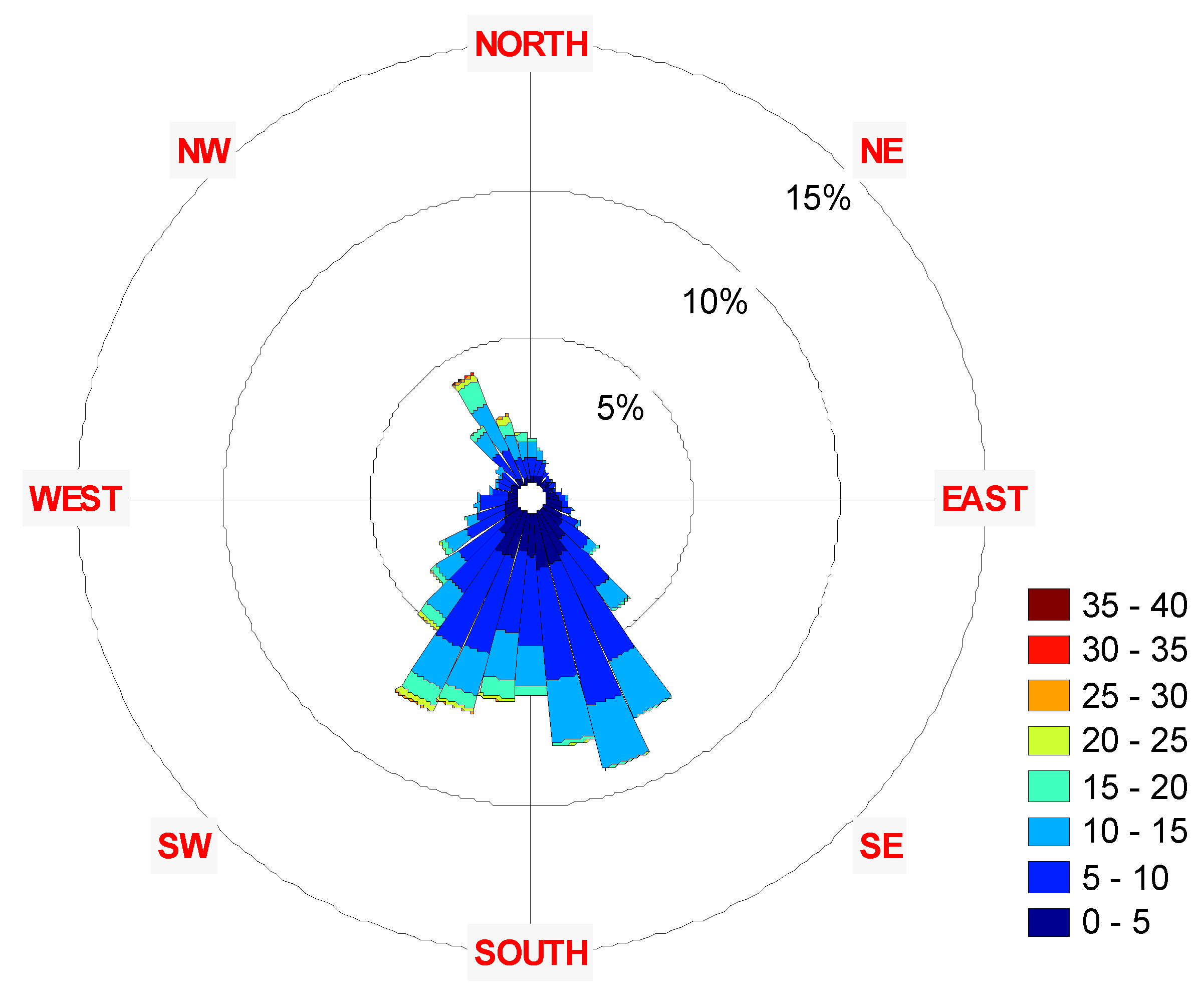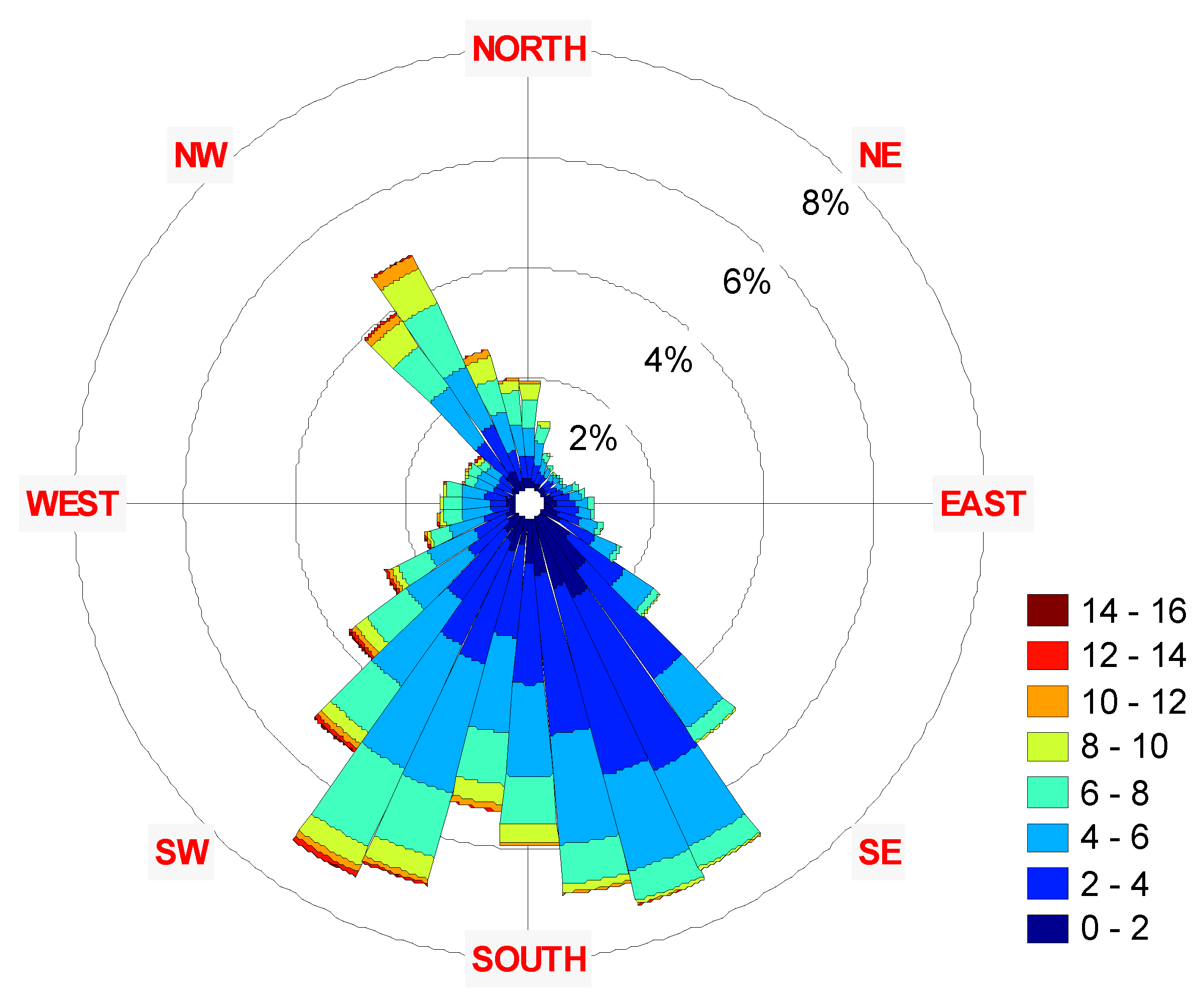It may be concluded that the prevailing wind direction remains relatively stable throughout the years.

4. Wind Power Generation

The power curves of available turbines are described in [66,67], from which three examples are analyzed in this paper and are depicted in Figure 34.
Among the turbines analyzed, the largest is Enercon’s model E101/3000 turbine with a radius of 50.5 m. Hence, we will assume from now on that the hub of the turbine is 70 m. Table 9 will summarize the area and radii of the turbines under study:
For this height, we obtain a speed average of 8.8 m/s. The average of the power and the standard deviation obtained for each turbine are depicted in Table 10, we have used the Weibull distribution to calculate the average power and the power standard deviation.
Table 10 contains the annual economic value of the turbine based on the current price of energy for household consumers in Israel, which is 0.5342 SH for kW hour on January 1, 2023 (before tax), the exchange rate for the same date is 3.5190 SH for one US $. In Israel the price is determined by governmental authorities who strike a balance between the interest of other producers, the cost of transmission and distribution, and the public interest in clean energy.

5. Conclusions

In this work, statistical characteristics, and Weibull parameters of the wind speed in Samaria region have been extracted from 11 years of wind data provided by the Israeli Meteorological Service, acquired at 10 m height above the ground. The cumulative mean wind speed at measurement height was found to be 4.53 m/s with standard deviation of 2.32 m/s. Prevailing wind direction is shown to be characterized by cumulative mean azimuth of 226o with standard deviation of 79.76o. Weibull distribution parameters were calculated yearly, monthly, and seasonally, demonstrating good match with histogram-based statistical representations. Shape parameter of Weibull distribution was shown to reside within narrow range around 2, allowing to assume Rayleigh statistics. The results were extrapolated to 70-meter height in order to estimate wind characteristics at hub height of a medium-scale wind turbine. It was shown that both statistical parameters and wind direction distribution remain relatively constant throughout the years, indicating good prediction potential. The novelty of the current paper is related to gathering wind statistics for a certain area (Samaria), we are not aware of any published statistics regarding wind velocity and direction in this area. The data may be interesting for potential regional wind energy development in which the obtained Weibull distribution can be used in calculations of expected power generation of particular turbines with known power dependence on velocity. We also point out that the fact that realistic wind velocity statistics is well described by an analytic formula (Weibull distribution) is not trivial, and in fact the fit may have been poor.

Author Contributions

Conceptualization, A.Y. and A.K.; methodology, A.K.; software, Y.R.; validation, S.K..; formal analysis, M.B.; investigation, M.B.; resources, A.K.; data curation, A.Y.; writing—original draft preparation, Y.R.; writing—review and editing, A.Y.; visualization, Y.R.; supervision, A.Y. and A.K.; project administration, A.Y. and A.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to thank the Israeli Meteorological Service for providing the Ariel wind raw data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Himri Y, Rehman S, Draoui B, Himri S. Wind power potential assessment for three locations in Algeria. Renewable and Sustainable Energy Reviews 2008; 12:2495 – 2504. [CrossRef]
  2. Thomas, L. Ackera, Susan K. Williamsb, Earl P.N. Duquea, Grant Brummels, Jason Buechler. Wind resource assessment in the state of Arizona: Inventory, capacity factor, and cost. Renewable Energy 2007; 32:1453–1466. [CrossRef]
  3. Laerte de Araujo Lima, Celso Rosendo Bezerra Filho. Wind energy assessment and wind farm simulation in Triunfo - Pernambuco, Brazil. Renewable Energy 2010; 35: 2705-2713. [CrossRef]
  4. Meishen Li, Xianguo Li. Investigation of wind characteristics and assessment of wind energy potential for Waterloo region, Canada. Energy Conversion and Management 2005; 46: 3014–3033. [CrossRef]
  5. Adrian Ilinca, Ed McCarthy, Jean-Louis Chaumel, Jean-Louis Re´tiveau. Wind potential assessment of Quebec Province. Renewable Energy 2003; 28: 1881–1897. [CrossRef]
  6. Zhou Y, Wu W X, Liu G X. Assessment of Onshore Wind Energy Resource and Wind-Generated Electricity Potential in Jiangsu, China. Energy Procedia 2011; 5: 418–422. [CrossRef]
  7. Ahmed Shata A S, Hanitsch R. Electricity generation and wind potential assessment at Hurghada, Egypt. Renewable Energy 2008; 33: 141–148. [CrossRef]
  8. Ahmed Shata Ahmed. Wind energy as a potential generation source at Ras Benas, Egypt. Renewable and Sustainable Energy Reviews 2010; 14: 2167–2173. [CrossRef]
  9. Getachew Bekele, Björn Palm. Wind energy potential assessment at four typical locations in Ethiopia. Applied Energy 2009; 86: 388–396. [CrossRef]
  10. Ravita D Prasad, Bansal R C, Sauturaga M. Wind Energy Analysis for Vadravadra Site in Fiji Islands: A Case Study. IEEE TRANSACTIONS ON ENERGY CONVERSION 2009; 24: 750-757. [CrossRef]
  11. Ioannis Fyrippis, Petros J. Axaopoulos, Gregoris Panayiotou. Wind energy potential assessment in Naxos Island, Greece. Applied Energy 2010; 87: 577–586. [CrossRef]
  12. Vogiatzis N, Kotti K, Spanomitsios S, Stoukides M. Analysis of wind potential and characteristics in North Aegean, Greece. Renewable Energy 2004; 29: 1193–1208. [CrossRef]
  13. Lin Lu, Hongxing Yang, John Burnett. Investigation on wind power potential on Hong Kong islands—an analysis of wind power and wind turbine characteristics. Renewable Energy 2002; 27: 1–12. [CrossRef]
  14. Daoo V J, Panchal N. S, Faby S, Sitaraman V, Krlshnamoorthy T. M. Assessment of wind energy potential of Trombay, Mumbai (19.18N; 72.88E), India. Energy Convers 1998; 13: 1351-1356. [CrossRef]
  15. Mirhosseini M, Sharifi F, Sedaghat A. Assessing the wind energy potential locations in province of Semnan in Iran. Renewable and Sustainable Energy Reviews 2011; 15: 449–459. [CrossRef]
  16. Mostafaeipour, A. Feasibility study of harnessing wind energy for turbine installation in province of Yazd in Iran. Renewable and Sustainable Energy Reviews 2010; 14: 93–111. [CrossRef]
  17. Mostafaeipour A, Sedaghat A, Dehghan-Niri A A, Kalantar V. Wind energy feasibility study for city of Shahrbabak in Iran. Renewable and Sustainable Energy Reviews 2011; 15: 2545–2556. [CrossRef]
  18. Keyhani A, Ghasemi-Varnamkhasti M, Khanali M, Abbaszadeh R. An assessment of wind energy potential as a power generation source in the capital of Iran, Tehran. Energy 2010; 35: 188–201. [CrossRef]
  19. Ouammi A, Dagdougui H, Sacile R, Abdelaziz M. Monthly and seasonal assessment of wind energy characteristics at four monitored locations in Liguria region (Italy). Renewable and Sustainable Energy Reviews 2010; 14: 1959–1968. [CrossRef]
  20. Bivona S, Burlon R, Leone C. Hourly wind speed analysis in Sicily. Renewable Energy 2003; 28:1371–1385. [CrossRef]
  21. Alghoul M A, Sulaiman M Y, Azmi B Z, and Wahab M Adb. Wind Energy Potential of Jordan. International Energy Journal 2007; 8: 71-78.
  22. Kamau J N, Kinyua R, Gathua J K. 6 years of wind data for Marsabit, Kenya average over 14 m/s at 100 m hub height; An analysis of the wind energy potential. Renewable Energy 2010; 35: 1298–1302. [CrossRef]
  23. [23] Islam M R, Saidur R, Rahim N A. Assessment of wind energy potentiality at Kudat and Labuan, Malaysia using Weibull distribution function. Energy 2011; 36: 985 – 992. [CrossRef]
  24. Muzathik A M, Wan Nik W B, Ibrahim M Z, Samo K B. Wind Resource Investigation of Terengganu in the West Malaysia. Wind Engineering 2009; 33: 389–402. [CrossRef]
  25. Mpholo M, Mathaba T, Letuma M. Wind profile assessment at Masitise and Sani in Lesotho for potential off-grid electricity generation. Energy Conversion and Management 2012; 53: 118–127. [CrossRef]
  26. Jaramillo O A, Borja M A. Bimodal versus Weibull Wind Speed Distributions: An Analysis of Wind Energy Potential in La Venta, Mexico. Wind Engineering 2004; 28: 225–234.
  27. Jaramillo O A, Saldan R, Miranda U. Wind power potential of Baja California Sur, Mexico. Renewable Energy 2004; 29: 2087–2100. [CrossRef]
  28. Jaramillo O A, Borja M A. Wind speed analysis in La Ventosa, Mexico: a bimodal probability distribution case. Renewable Energy 2004; 29: 1613–1630. [CrossRef]
  29. Fagbenle R O, Katende J, Ajayi O O, Okeniyi J O. Assessment of wind energy potential of two sites in North-East, Nigeria. Renewable Energy 2011; 36: 1277-1283. [CrossRef]
  30. Ohunakin O S, Adaramola M S, Oyewola O M. Wind energy evaluation for electricity generation using WECS in seven selected locations in Nigeria. Applied Energy 2011; 88: 3197–3206. [CrossRef]
  31. Adaramola M S, Paul S S, Oyedepo S O. Assessment of electricity generation and energy cost of wind energy conversion systems in north-central Nigeria. Energy Conversion and Management 2011; 52: 3363–3368. [CrossRef]
  32. Ohunakin OS, Akinnawonu OO. Assessment of wind energy potential and the economics of wind power generation in Jos, Plateau State, Nigeria. Energy for Sustainable Development 2012; 16: 78–83. [CrossRef]
  33. AL-Yahyai S, Charabi Y, Gastli A, Al-Alawi S. Assessment of wind energy potential locations in Oman using data from existing weather stations. Renewable and Sustainable Energy Reviews 2010; 14: 1428–1436. [CrossRef]
  34. Ullah I, Chaudhry Q, Chipperfield A J. An evaluation of wind energy potential at Kati Bandar, Pakistan. Renewable and Sustainable Energy Reviews 2010; 14: 856–861. [CrossRef]
  35. Safari, B. Modeling wind speed and wind power distributions in Rwanda. Renewable and Sustainable Energy Reviews 2011; 15: 925–935. [CrossRef]
  36. Cabello M, Orza J A G. Wind speed analysis in the province of Alicante, Spain. Potential for small-scale wind turbines. Renewable and Sustainable Energy Reviews 2010; 14: 3185–3191. [CrossRef]
  37. Carta J A, Ramı´rez P, Vela´zquez S. A review of wind speed probability distributions used in wind energy analysis Case studies in the Canary Islands. Renewable and Sustainable Energy Reviews 2009; 13: 933–955. [CrossRef]
  38. Abdeen M, O. On the wind energy resources of Sudan. Renewable and Sustainable Energy Reviews 2008; 12: 2117–2139. [CrossRef]
  39. Tsang-Jung Chang, Yu-Ting Wu, Hua-Yi Hsu, Chia-Ren Chu, Chun-Min Liao. Assessment of wind characteristics and wind turbine characteristics in Taiwan. Renewable Energy 2003; 28: 851–871. [CrossRef]
  40. Dahmouni A W, Ben Salah M, Askri F, Kerkeni C, Ben Nasrallah S. Assessment of wind energy potential and optimal electricity generation in Borj-Cedria, Tunisia. Renewable and Sustainable Energy Reviews 2011; 15:815–820. [CrossRef]
  41. Ali, N. Celik. Review of Turkey’s current energy status: A case study for wind energy potential of Canakkale province. Renewable and Sustainable Energy Reviews 2011; 15: 2743– 2749. [CrossRef]
  42. Onat N, Ersoz S. Analysis of wind climate and wind energy potential of regions in Turkey. Energy 2011; 36: 148-156. [CrossRef]
  43. Eskin N, Artar H, Tolun S. Wind energy potential of Gokceada Island in Turkey. Renewable and Sustainable Energy Reviews 2008; 12: 839–851. [CrossRef]
  44. Ucar A, Balo F. Evaluation of wind energy potential and electricity generation at six locations in Turkey. Applied Energy 2009; 86: 1864–1872. [CrossRef]
  45. Ozgurm A, Arslan O, Kose R, Peker K O. Statistical Evaluation of Wind Characteristics in Kutahya, Turkey. Energy Sources 2009; 31:1450–1463. [CrossRef]
  46. Arslan, O. Technoeconomic analysis of electricity generation from wind energy in Kutahya, Turkey. Energy 2010; 35:120–131. [CrossRef]
  47. Nguyen, KQ. Wind energy in Vietnam: Resource assessment, development status and future implications. Energy Policy 2007; 35:1405–1413. [CrossRef]
  48. Tran VT, Chen TH. Assessing the wind energy for rural areas of Vietnam. International Journal of Renewable Energy Research 2013; 3:423 – 528.
  49. "GWEC, Global Wind Report Annual Market Update". Gwec.net. http://www.gwec.net/index.php?id=180. Retrieved 2011-05-14.
  50. "EWEA - European Wind Energy Association". https://www.ewea.org/index.php?id=1487. Retrieved 2011-05-14.
  51. Israel Ministry of Environmental Protection, “Renewable Energy”. https://www.sviva.gov.il. Retrieved 2014-07-31.
  52. "Wind energy power generation", Background paper written by Orli Lotan, 21.09.05. Knesset, Research and Information Center, Jerusalem, 2005, p. 3 (in Hebrew).
  53. Ditkovich Y, Kuperman A, Yahalom A, and Byalsky M. A generalized approach to estimating capacity factor of fixed speed wind turbines. IEEE Transactions on Sustainable Energy 2013; 3:607 – 608. [CrossRef]
  54. Ditkovich Y, Kuperman A, Yahalom A, Byalsky M. Site-dependent wind turbine performance index. International Journal of Renewable Energy Research 2013; 3:592 – 594.
  55. Ditkovich Y, Kuperman A. Comparison of three methods for wind turbine capacity factor estimation. The Scientific World Journal 2014; 805238: 1 – 7. [CrossRef]
  56. Chang, TP. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application. Applied Energy 2011; 88:272-282. [CrossRef]
  57. Masters, G. Renewable and efficient electric power systems. John Wiley & Sons, New York, 2004.
  58. Kuperman A, Rabinovici R, Weiss G. Torque, and power limitations of a shunt connected inverter based WECS. WSEAS Transactions on Circuits and Systems 2005; 7:684 – 690.
  59. Kuperman A, Rabinovici R, Weiss G. A shunt connected inverter based variable speed wind turbine generation. International Journal of Electromotion 2006; 13:67-72.
  60. Gualtieri G, Secci S. Extrapolating wind speed series vs. Weibull distribution to assess wind resource to the turbine hub height: A case study on coastal location in Southern Italy. Renewable Energy 2014; 62:164-176. [CrossRef]
  61. Gualtieri G, Secci S. Methods to extrapolate wind resource to the turbine hub height based on power law: A 1-h wind speed vs. Weibull distribution extrapolation comparison. Renewable Energy 2013; 43:183-200. [CrossRef]
  62. Sergei Kolesnik, Moshe Sitbon, Asher Yahalom & Alon Kuperman "Assessment of Wind Resource Statistics in Samaria Region" Proceedings of the 16th International Scientific Conference on Engineering for Rural Development, P. 1409-1416, 24-26.05.2017. Jelgava, Latvia.
  63. Hasmat Malik, Nuzhat Fatema, Atif Iqbal, Chapter 8 - Intelligent Data Analytics for Wind Speed Forecasting for Wind Power Production Using Long Short-Term Memory (LSTM) Network, Editor(s): Hasmat Malik, Nuzhat Fatema, Atif Iqbal, Intelligent Data-Analytics for Condition Monitoring, Academic Press, 2021, Pages 165-192, ISBN 9780323855105. [CrossRef]
  64. Panagiotis Triantafyllou, John K. Kaldellis, 2.16 - Wind Power Industry and Markets, Editor(s): Trevor M. Letcher, Comprehensive Renewable Energy (Second Edition), Elsevier, 2022, Pages 497-566, ISBN 9780128197349. [CrossRef]
  65. John, K. Kaldellis, 2.01 - Introduction to Wind Energy, Editor(s): Trevor M. Letcher, Comprehensive Renewable Energy (Second Edition), Elsevier, 2022, Pages 1-12, ISBN 9780128197349. [CrossRef]
  66. Carrillo, C.; Obando Montaño, A.F.; Cidrás, J.; Díaz-Dorado, E. Review of power curve modelling for wind turbines. Renew. Sustain. Energy Rev. 2013, 21, 572–581. Available online: http://grupo_ene.webs.uvigo.es/ (accessed on 17 September 2015). [CrossRef]
  67. Doron Greenberg, Michael Byalsky & Asher Yahalom “Valuation of Wind Energy Turbines Using Volatility of Wind and Price” Electronics 2021, 10, 1098. [CrossRef]
Preprints 67768 g001
Figure 1. The city of Ariel.
Figure 1. The city of Ariel.
Preprints 67768 g001
Preprints 67768 g002
Figure 2. Meteorological station location.
Figure 2. Meteorological station location.
Preprints 67768 g002
Preprints 67768 g003
Figure 3. Typical monthly wind speed raw data.
Figure 3. Typical monthly wind speed raw data.
Preprints 67768 g003
Preprints 67768 g004
Figure 4. Histogram and Weibull PDF fit of wind speed raw data of Figure 3.
Figure 4. Histogram and Weibull PDF fit of wind speed raw data of Figure 3.
Preprints 67768 g004
Preprints 67768 g005
Figure 5. 2001 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 5. 2001 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g005
Preprints 67768 g006
Figure 6. 2002 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 6. 2002 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g006
Preprints 67768 g007
Figure 7. 2003 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 7. 2003 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g007
Preprints 67768 g008
Figure 8. 2004 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 8. 2004 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g008
Preprints 67768 g009
Figure 9. 2005 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 9. 2005 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g009
Preprints 67768 g010
Figure 10. 2006 wind speed data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 10. 2006 wind speed data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g010
Preprints 67768 g011
Figure 11. 2007 wind speed data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 11. 2007 wind speed data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g011
Preprints 67768 g012aPreprints 67768 g012b
Figure 12. 2008 wind speed data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 12. 2008 wind speed data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g012aPreprints 67768 g012b
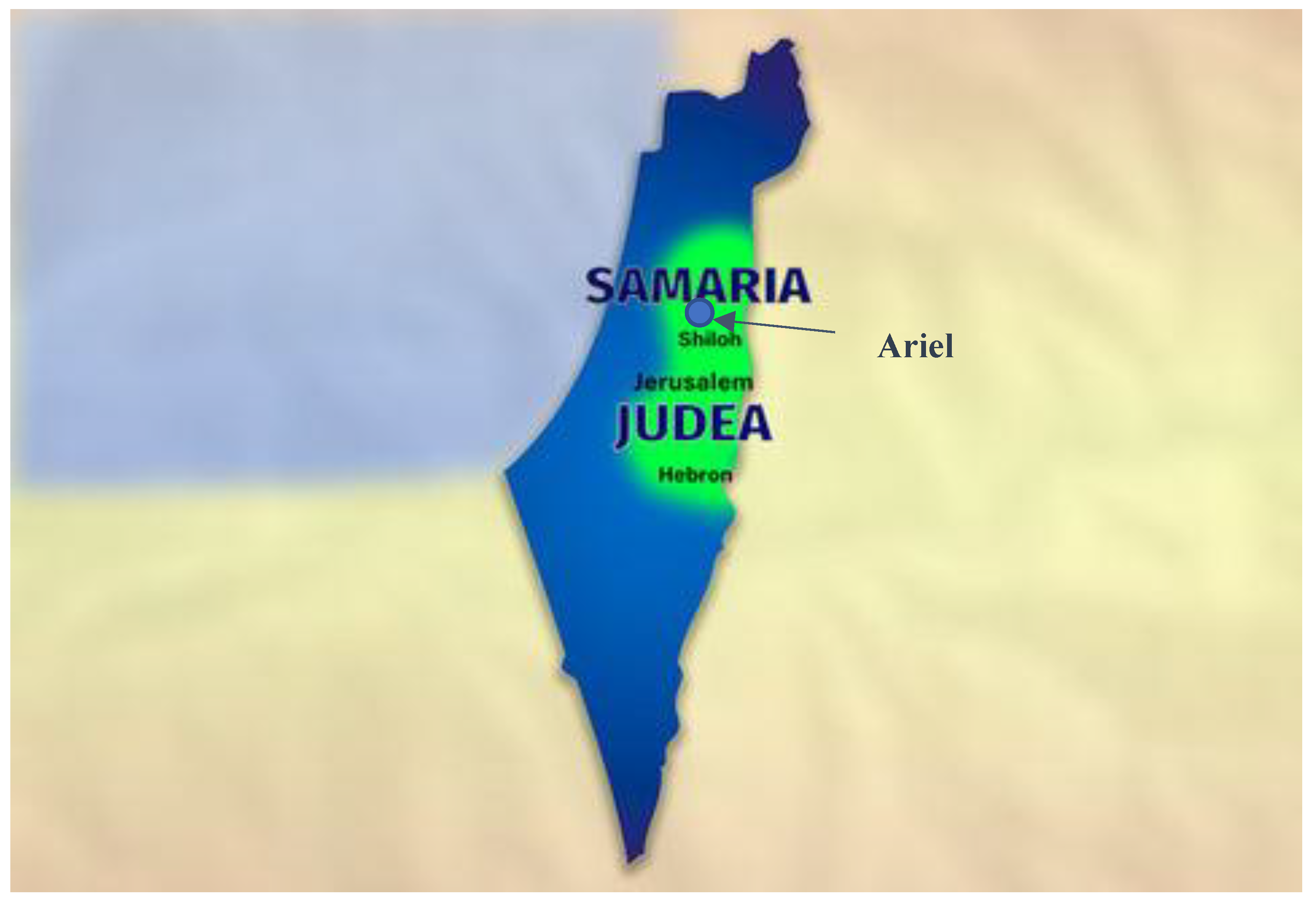
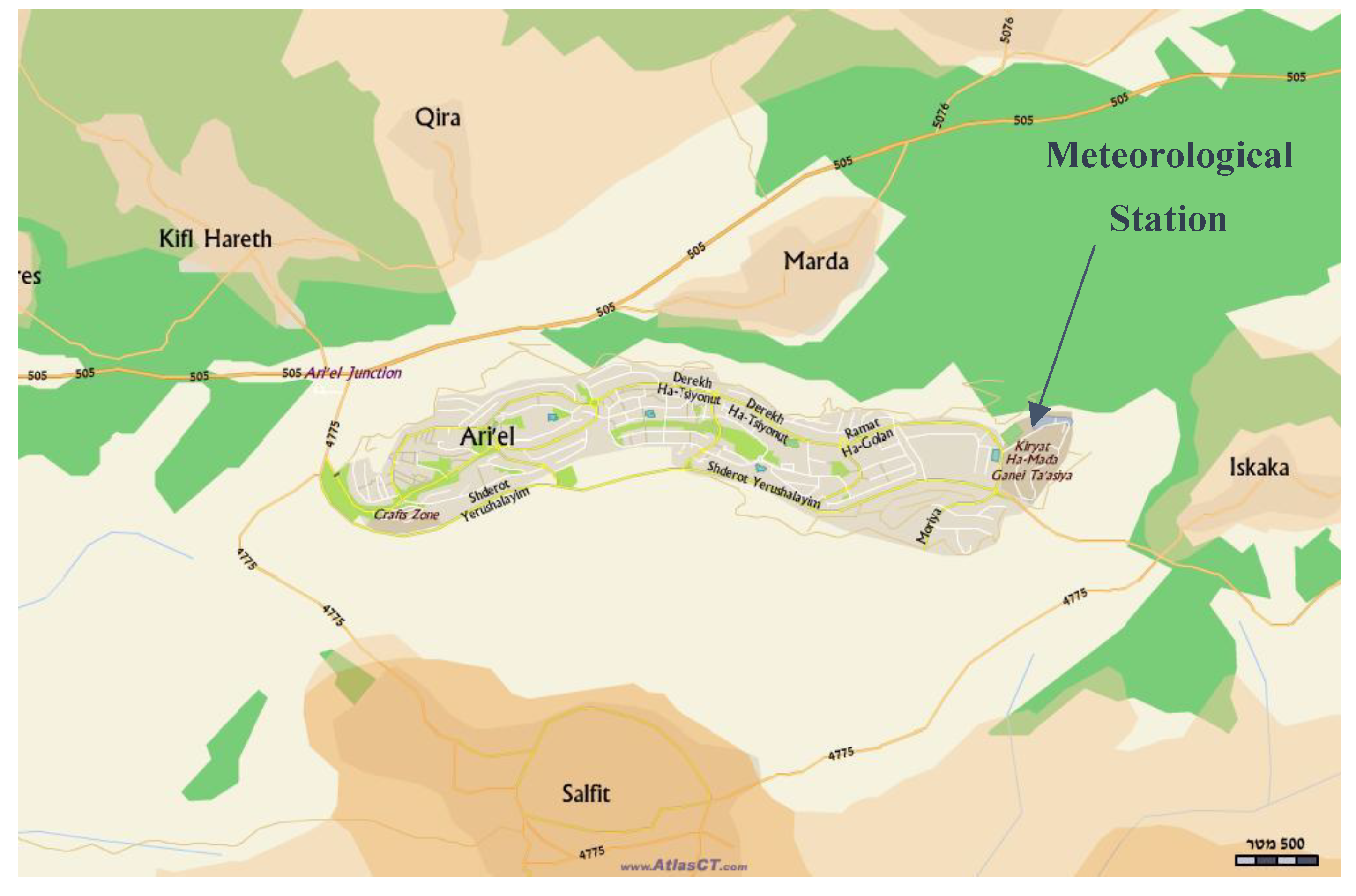
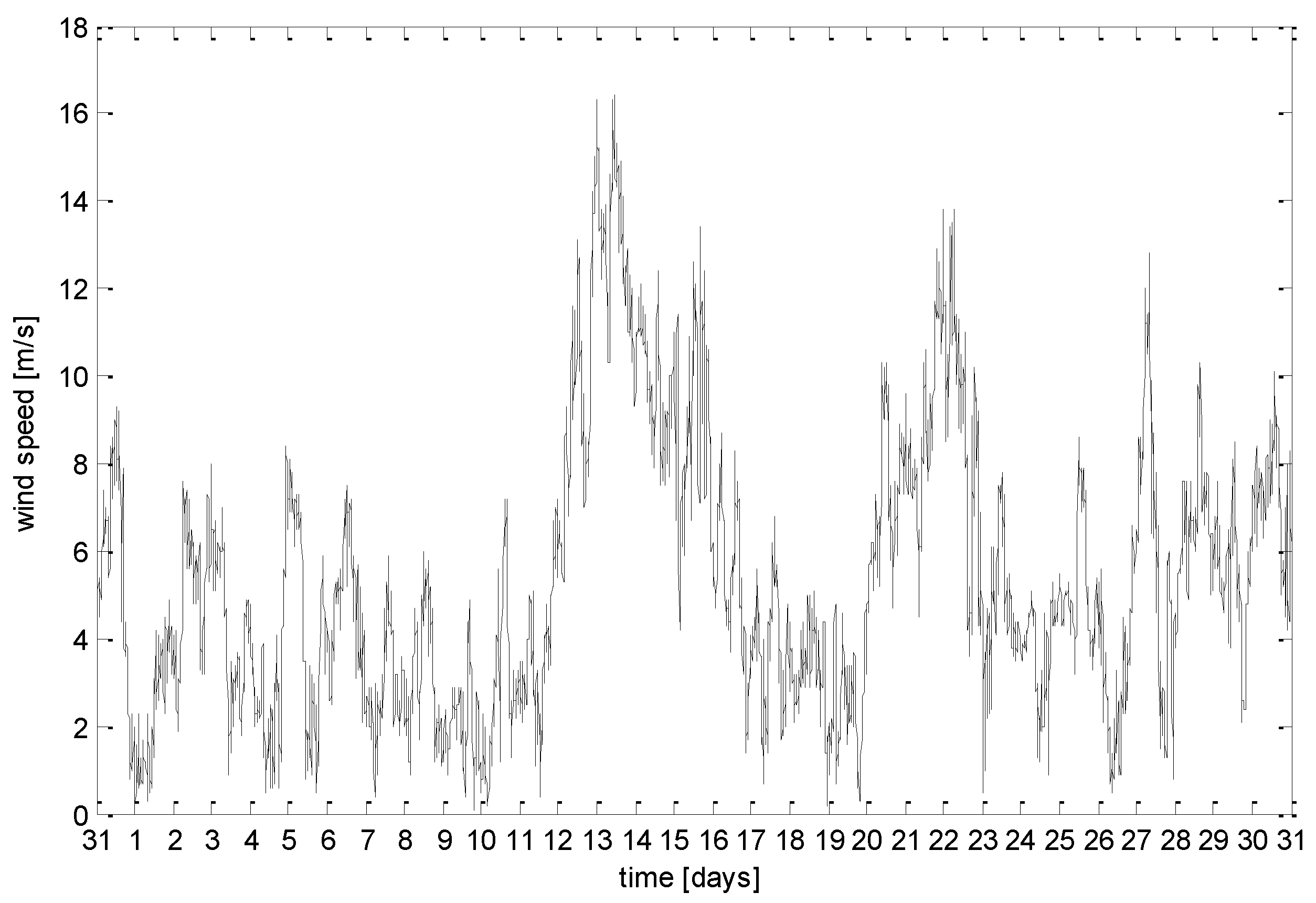
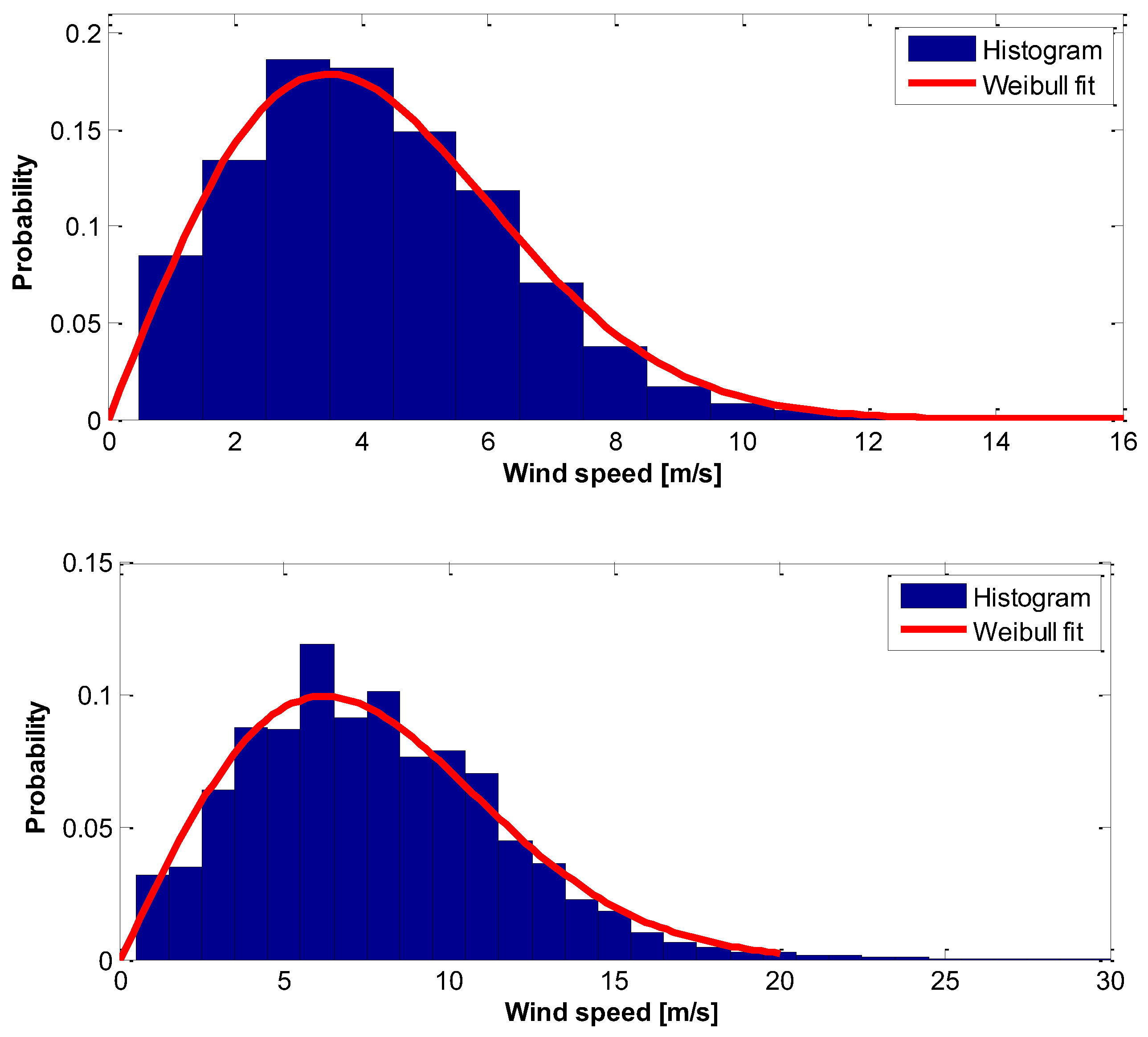
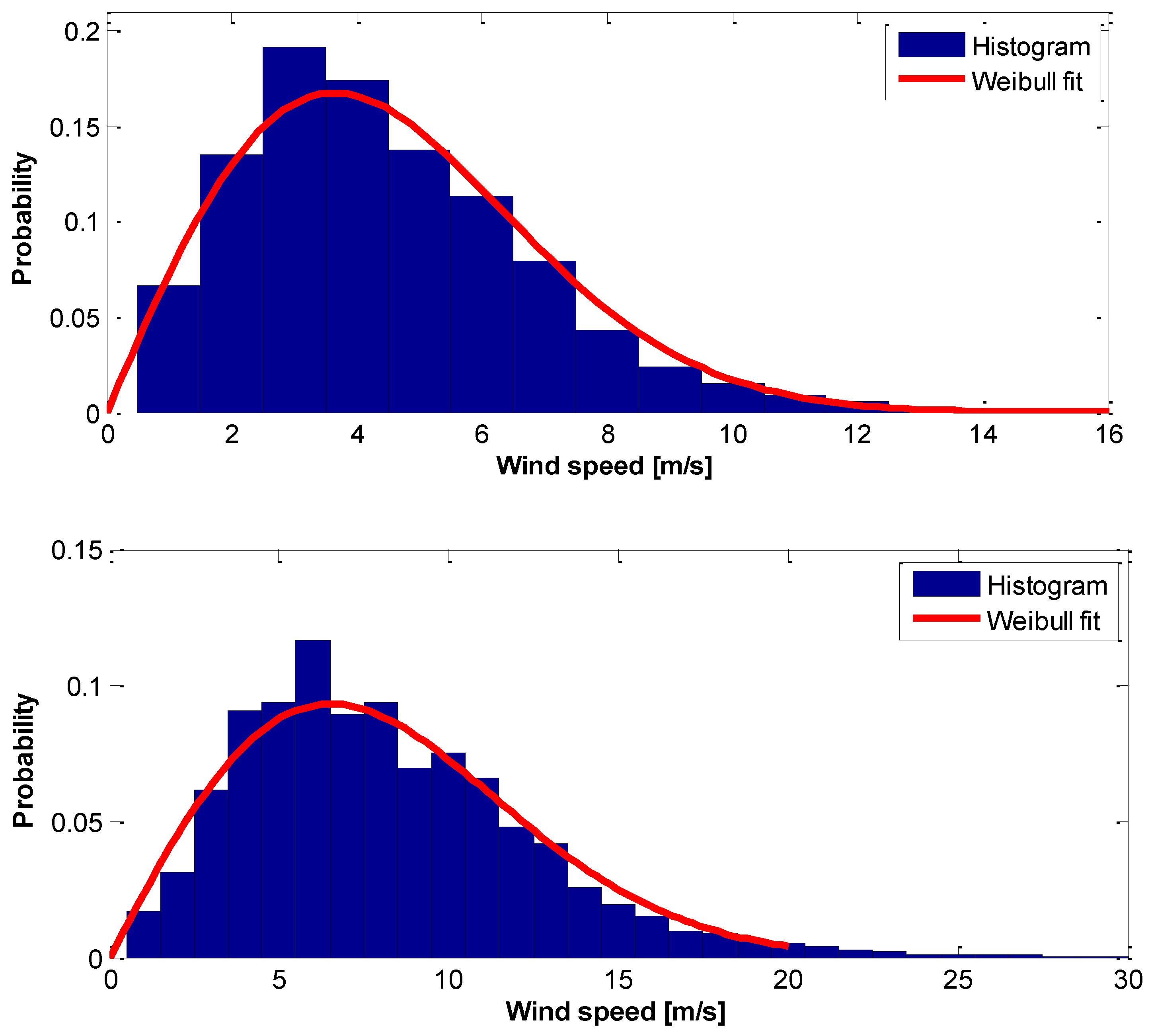
Preprints 67768 g013
Figure 13. 2009 wind speed data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 13. 2009 wind speed data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g013
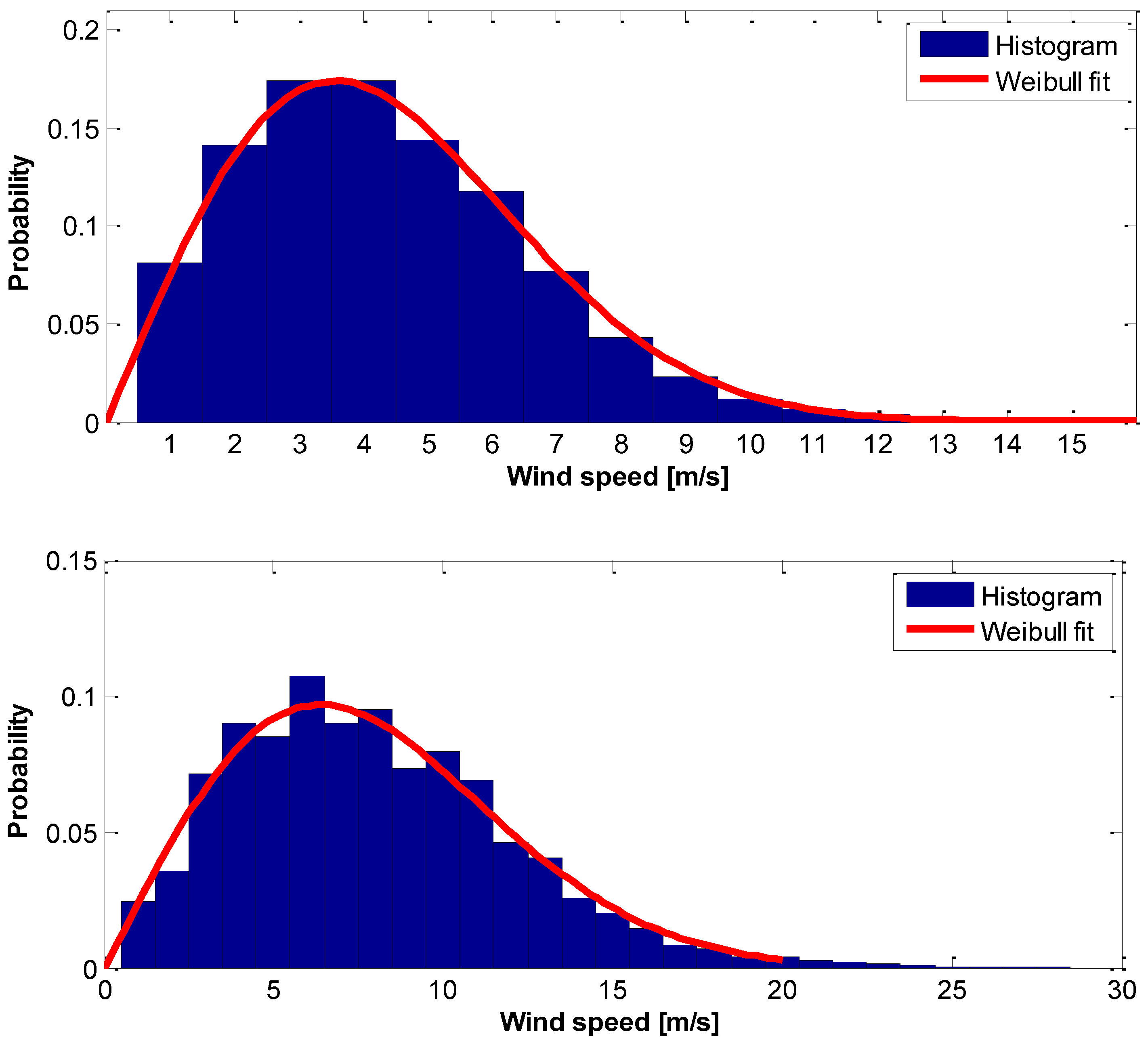
Preprints 67768 g014
Figure 14. 2010 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 14. 2010 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g014
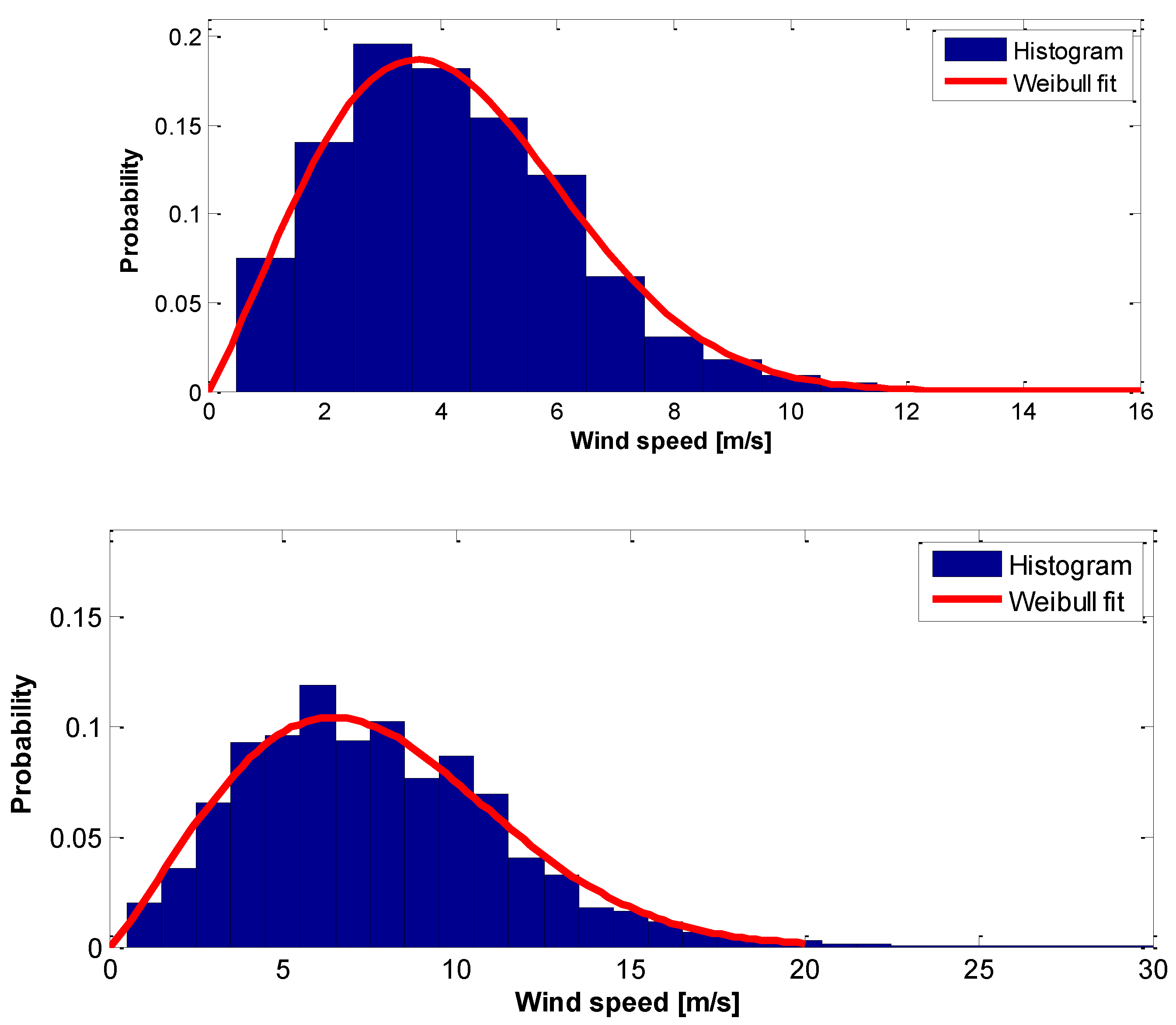
Preprints 67768 g015
Figure 15. 2011 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Figure 15. 2011 wind speed raw data Histogram and Weilbull PDF. Top–10 m height, Bottom–70 m height.
Preprints 67768 g015
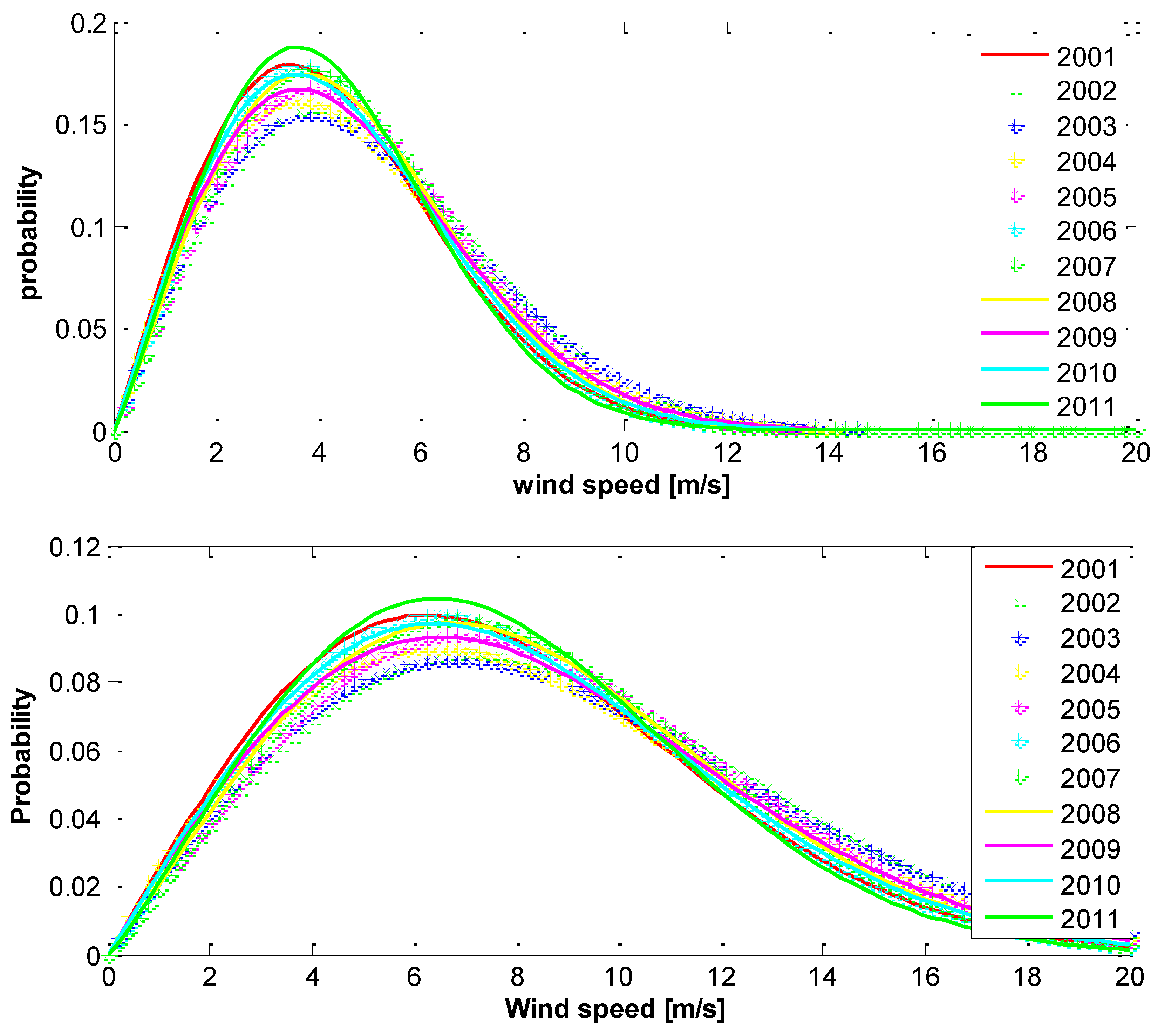
Preprints 67768 g016
Figure 16. 2001-2011 Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Figure 16. 2001-2011 Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Preprints 67768 g016
Preprints 67768 g017aPreprints 67768 g017b
Figure 17. 2001-2011 parameter variations at 10 m. Top–statistical, Bottom–Weibull.
Figure 17. 2001-2011 parameter variations at 10 m. Top–statistical, Bottom–Weibull.
Preprints 67768 g017aPreprints 67768 g017b
Preprints 67768 g018
Figure 18. 2001-2011 spring Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Figure 18. 2001-2011 spring Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Preprints 67768 g018
Preprints 67768 g019aPreprints 67768 g019b
Figure 19. 2001-2011 autumn Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Figure 19. 2001-2011 autumn Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Preprints 67768 g019aPreprints 67768 g019b
Preprints 67768 g020
Figure 20. 2001-2011 summer Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Figure 20. 2001-2011 summer Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Preprints 67768 g020
Preprints 67768 g021
Figure 21. 2001-2011 winter Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Figure 21. 2001-2011 winter Weilbull PDFs. Top–10 m height, Bottom–70 m height.
Preprints 67768 g021
Preprints 67768 g022aPreprints 67768 g022b
Figure 22. 2001 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 22. 2001 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g022aPreprints 67768 g022b
Preprints 67768 g023aPreprints 67768 g023b
Figure 23. 2002 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 23. 2002 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g023aPreprints 67768 g023b
Preprints 67768 g024aPreprints 67768 g024b
Figure 24. 2003 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 24. 2003 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g024aPreprints 67768 g024b
Preprints 67768 g025aPreprints 67768 g025b
Figure 25. 2004 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 25. 2004 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g025aPreprints 67768 g025b
Preprints 67768 g026aPreprints 67768 g026b
Figure 26. 2005 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 26. 2005 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g026aPreprints 67768 g026b
Preprints 67768 g027aPreprints 67768 g027b
Figure 27. 2006 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 27. 2006 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g027aPreprints 67768 g027b
Preprints 67768 g028aPreprints 67768 g028b
Figure 28. 2007 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 28. 2007 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g028aPreprints 67768 g028b
Preprints 67768 g029aPreprints 67768 g029b
Figure 29. 2008 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 29. 2008 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g029aPreprints 67768 g029b
Preprints 67768 g030aPreprints 67768 g030b
Figure 30. 2009 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 30. 2009 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g030aPreprints 67768 g030b
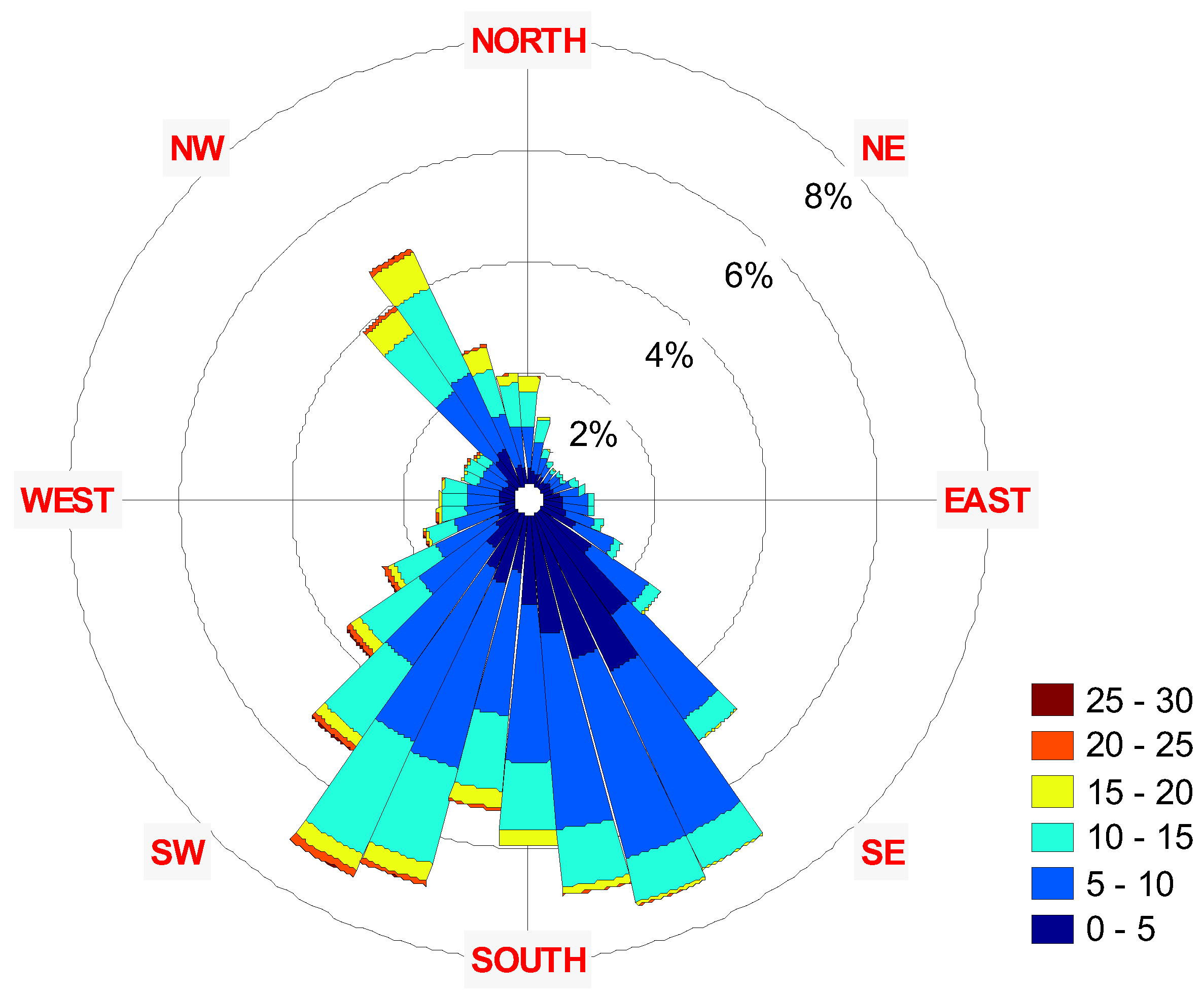
Preprints 67768 g031aPreprints 67768 g031b
Figure 31. 2010 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 31. 2010 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g031aPreprints 67768 g031b
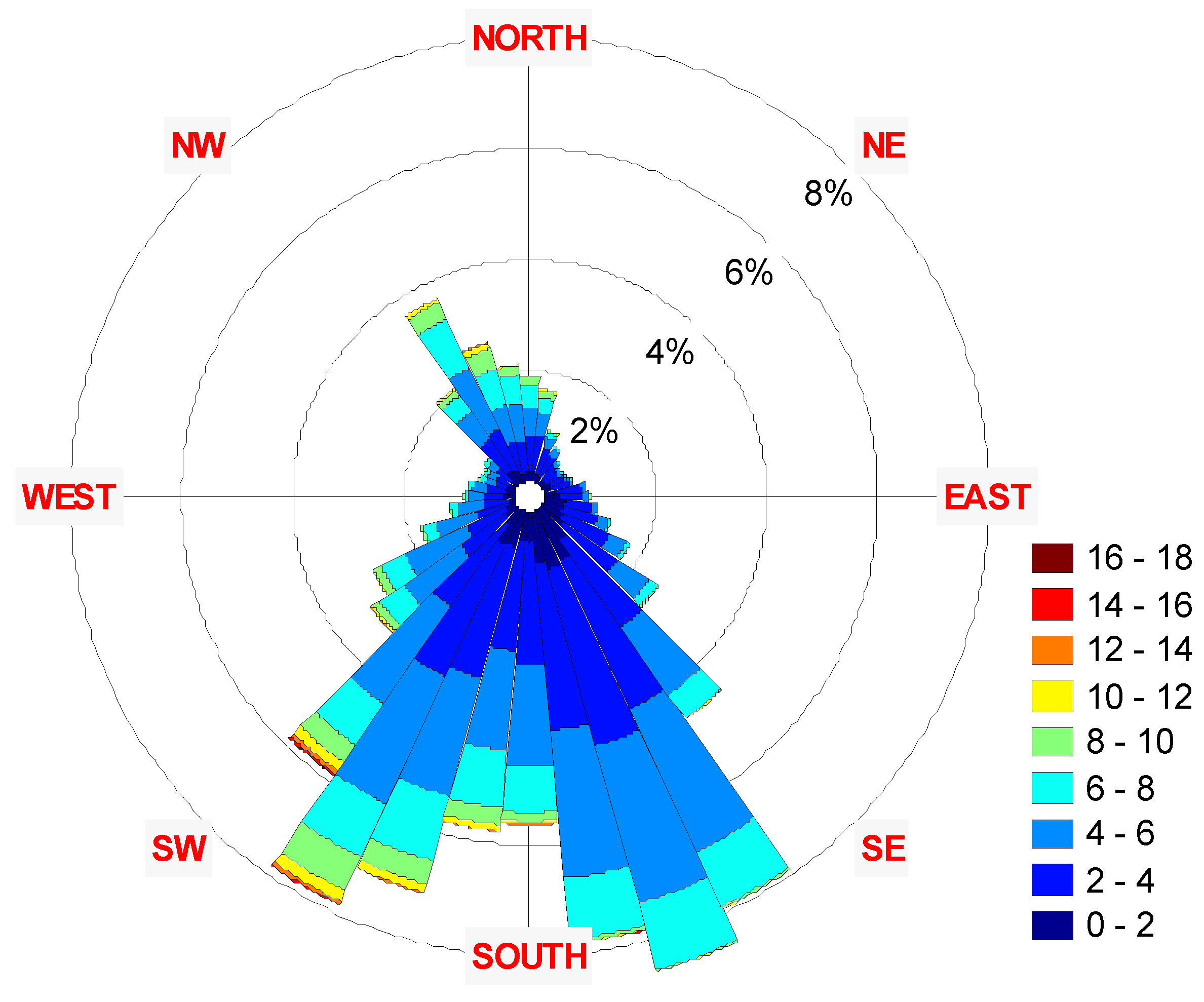
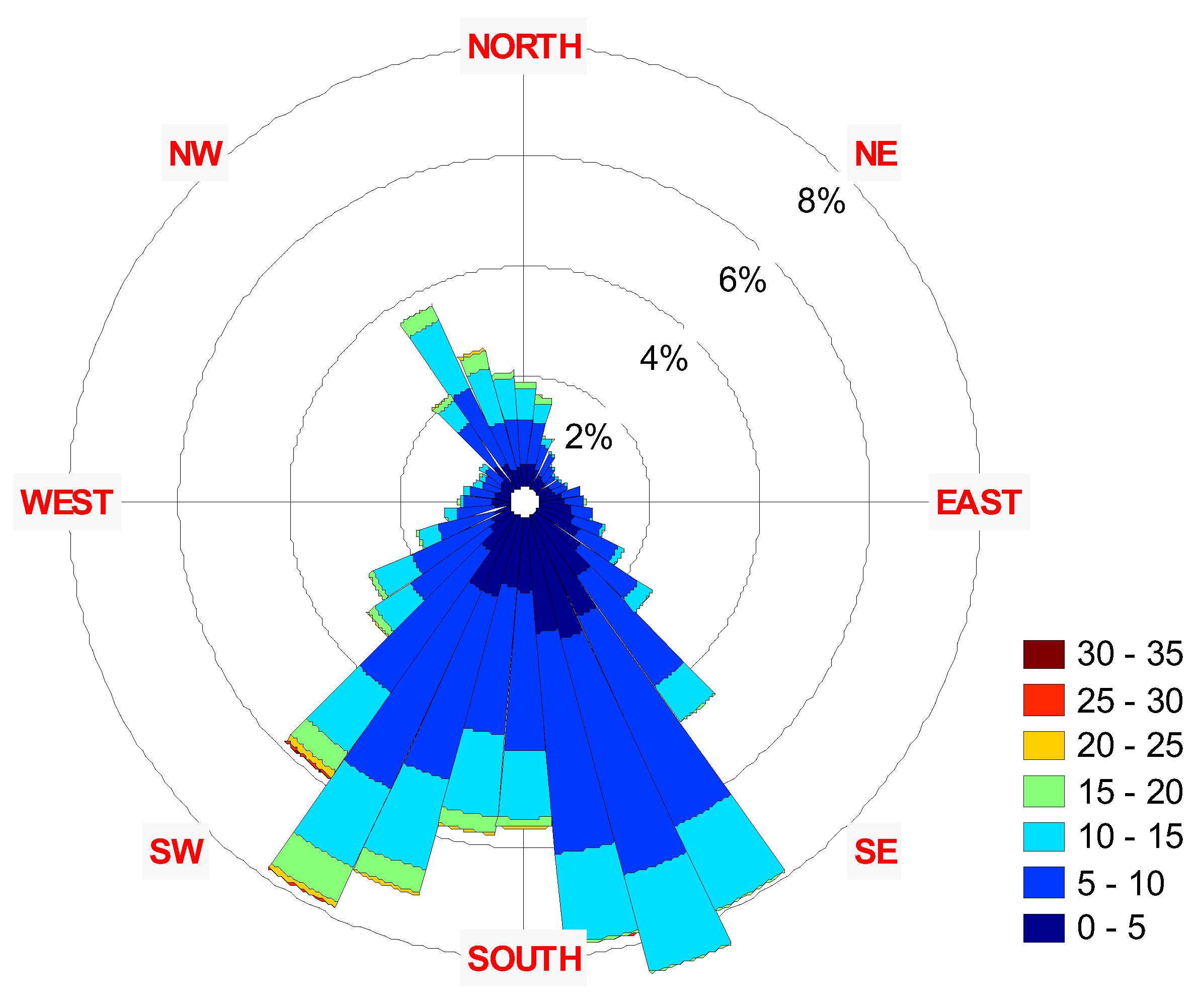
Preprints 67768 g032aPreprints 67768 g032b
Figure 32. 2011 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 32. 2011 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g032aPreprints 67768 g032b
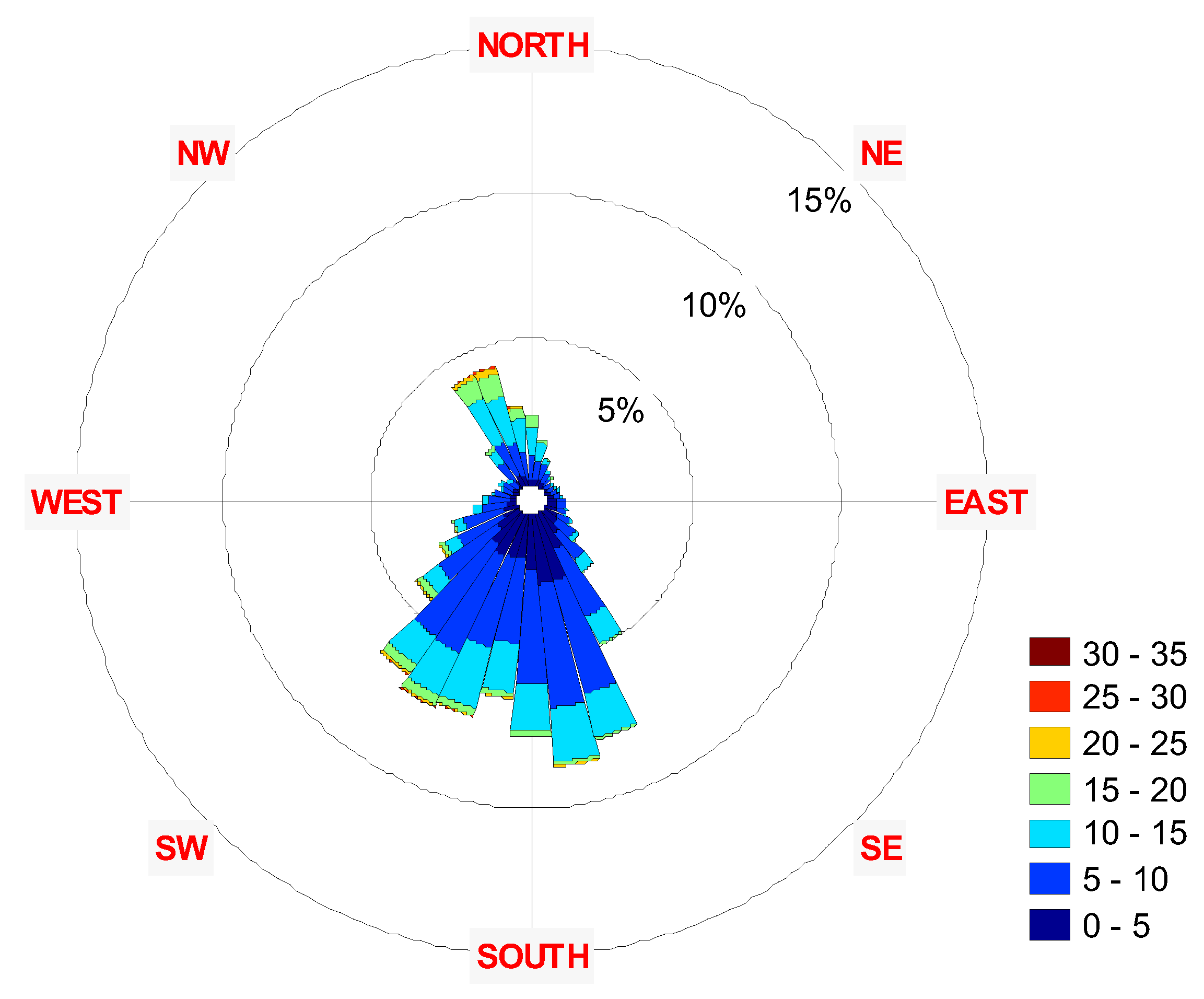
Preprints 67768 g033aPreprints 67768 g033b
Figure 33. 2001-2011 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Figure 33. 2001-2011 wind rose diagrams. Top–10 m height, Bottom–70 m height.
Preprints 67768 g033aPreprints 67768 g033b
Preprints 67768 g034
Figure 34. Power curves of wind turbines [66]. The dashed thick curve is the power curve of Enercon’s model E101/3000 turbine, the thick line is the power curve of AWE’s model 54–900 turbine, and the dashed curve is the power curve of EWT’s model Direct wind 52/750 turbine.
Figure 34. Power curves of wind turbines [66]. The dashed thick curve is the power curve of Enercon’s model E101/3000 turbine, the thick line is the power curve of AWE’s model 54–900 turbine, and the dashed curve is the power curve of EWT’s model Direct wind 52/750 turbine.
Preprints 67768 g034
Table 1. Wind power classification.
Table 1. Wind power classification.
Wind Power
Class		 Average Wind Speed (m/s)
at 10 m Height
1 0 – 4.4
2 4.4 – 5.1
3 5.1 – 5.6
4 5.6 – 6.0
5 6.0 – 6.4
6 6.4 – 7.0
7 7.0– 9.5
Table 2. Friction coefficient dependence in terrain type.
Table 2. Friction coefficient dependence in terrain type.
Terrain Characteristics α
Smooth hard ground, calm water 0.10
Tall grass on level ground 0.15
High crops, hedges and shrubs 0.20
Wooded countryside, many trees 0.25
Small town with trees and shrubs 0.30
Large city with tall building 0.40
Table 3. Yearly and cumulative wind speed statistics at 10 m height.
Table 3. Yearly and cumulative wind speed statistics at 10 m height.
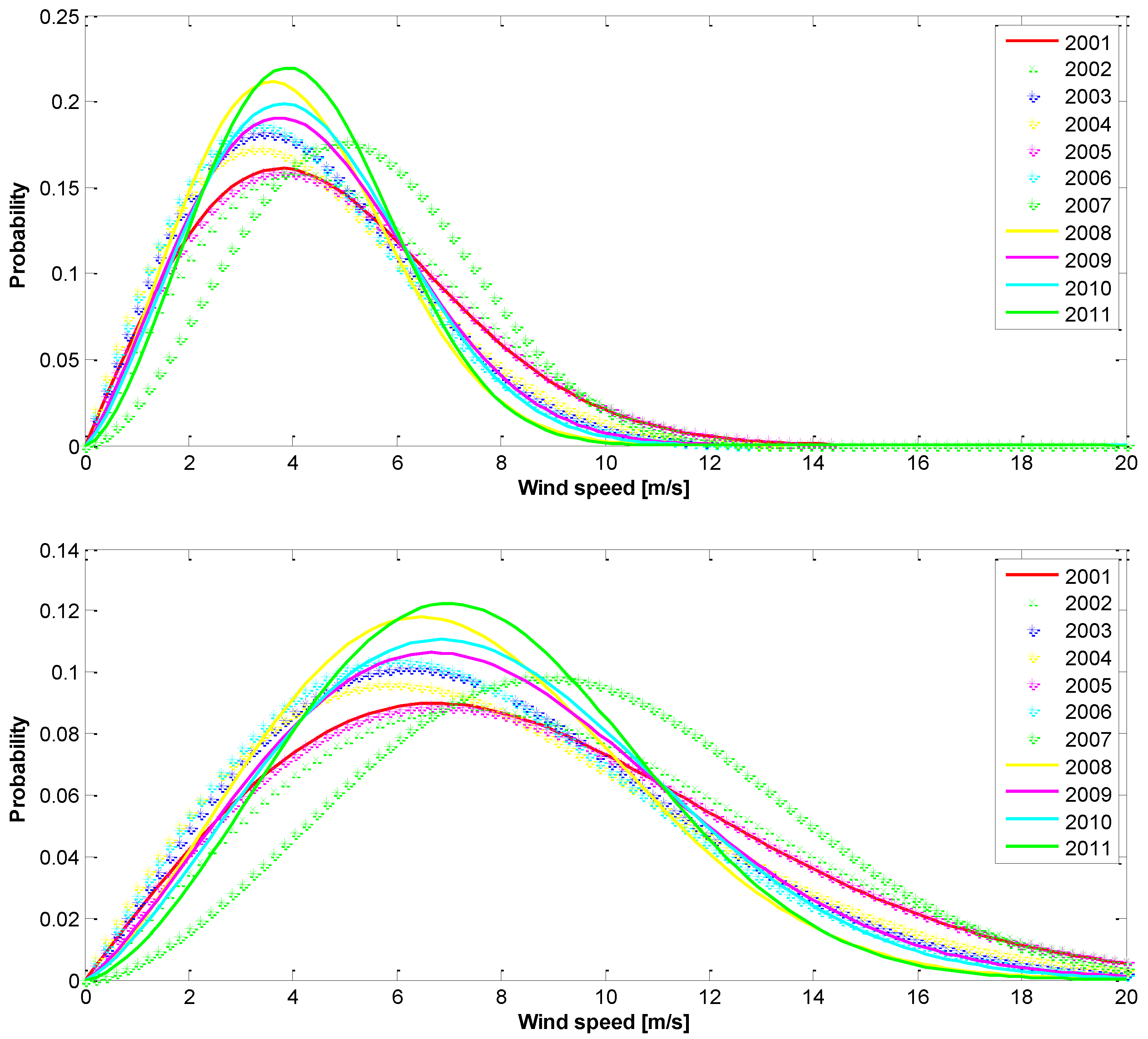
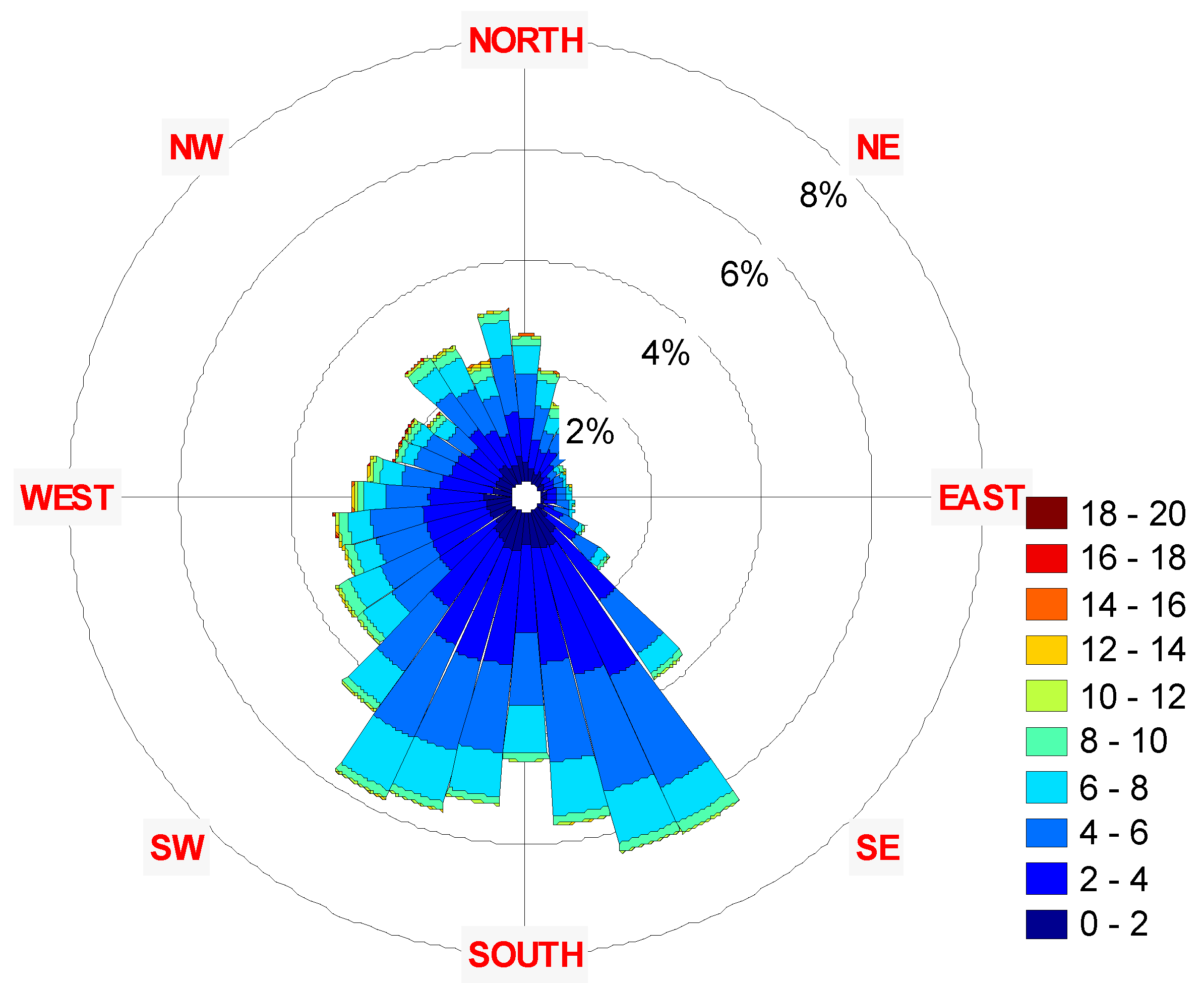
Year Parameter Speed Azimuth
2001 Mean 4.28 209.41
STD 2.21 81.13
2002 Mean 4.89 227.31
STD 2.51 83.03
2003 Mean 4.81 224.15
STD 2.57 78.48
2004 Mean 4.57 228.17
STD 2.49 80.32
2005 Mean 4.64 227.63
STD 2.33 77.45
2006 Mean 4.35 231.65
STD 2.20 83.15
2007 Mean 4.50 228.73
STD 2.21 79.28
2008 Mean 4.50 221.94
STD 2.25 77.23
2009 Mean 4.54 231.31
STD 2.38 75.39
2010 Mean 4.41 225.30
STD 2.27 79.84
2011 Mean 4.26 230.11
STD 2.08 79.28
2001-2011 Mean 4.53 226.00
STD 2.32 79.76
Table 4. Yearly and cumulative wind speed statistics at 70 m height.
Table 4. Yearly and cumulative wind speed statistics at 70 m height.
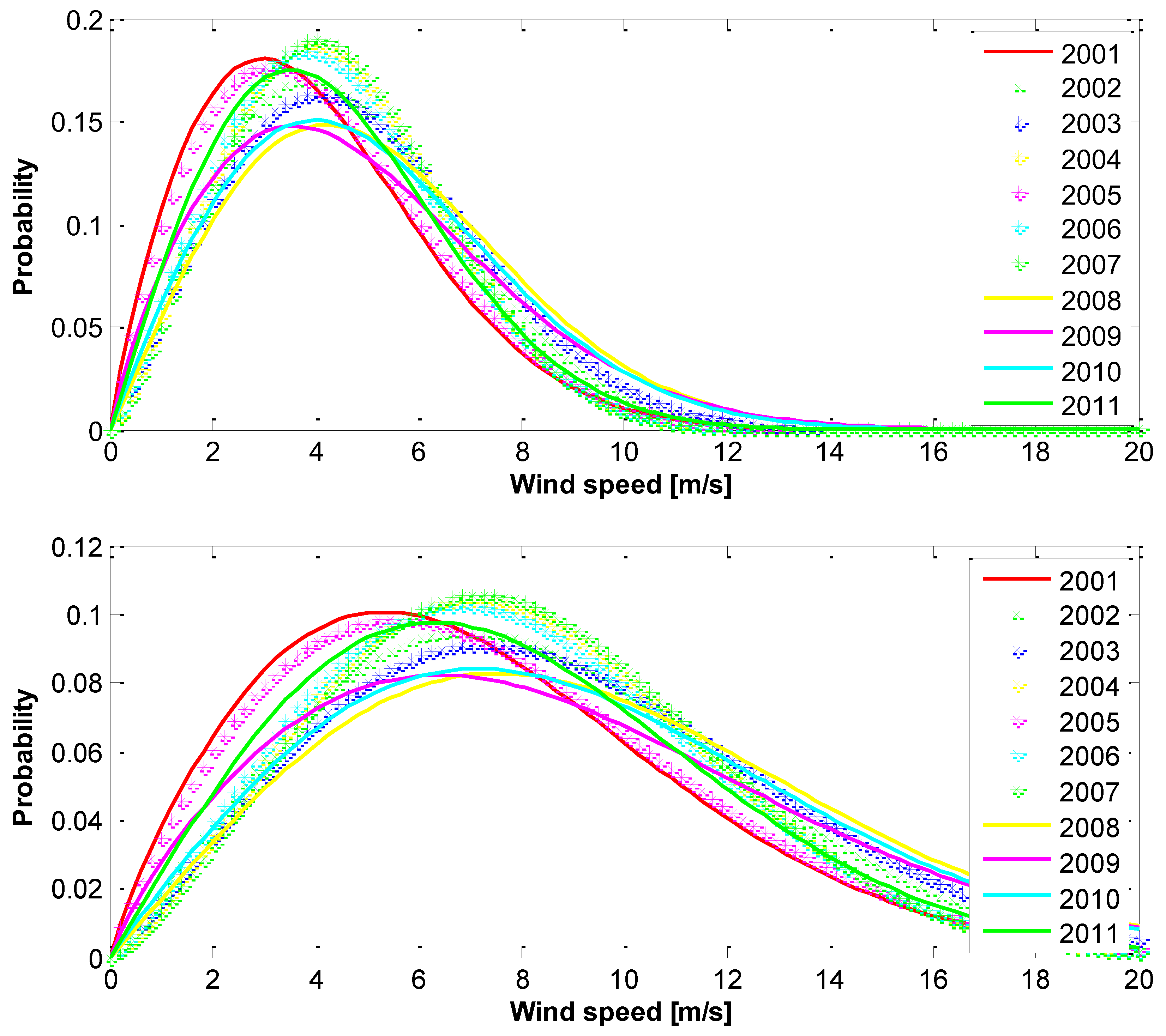
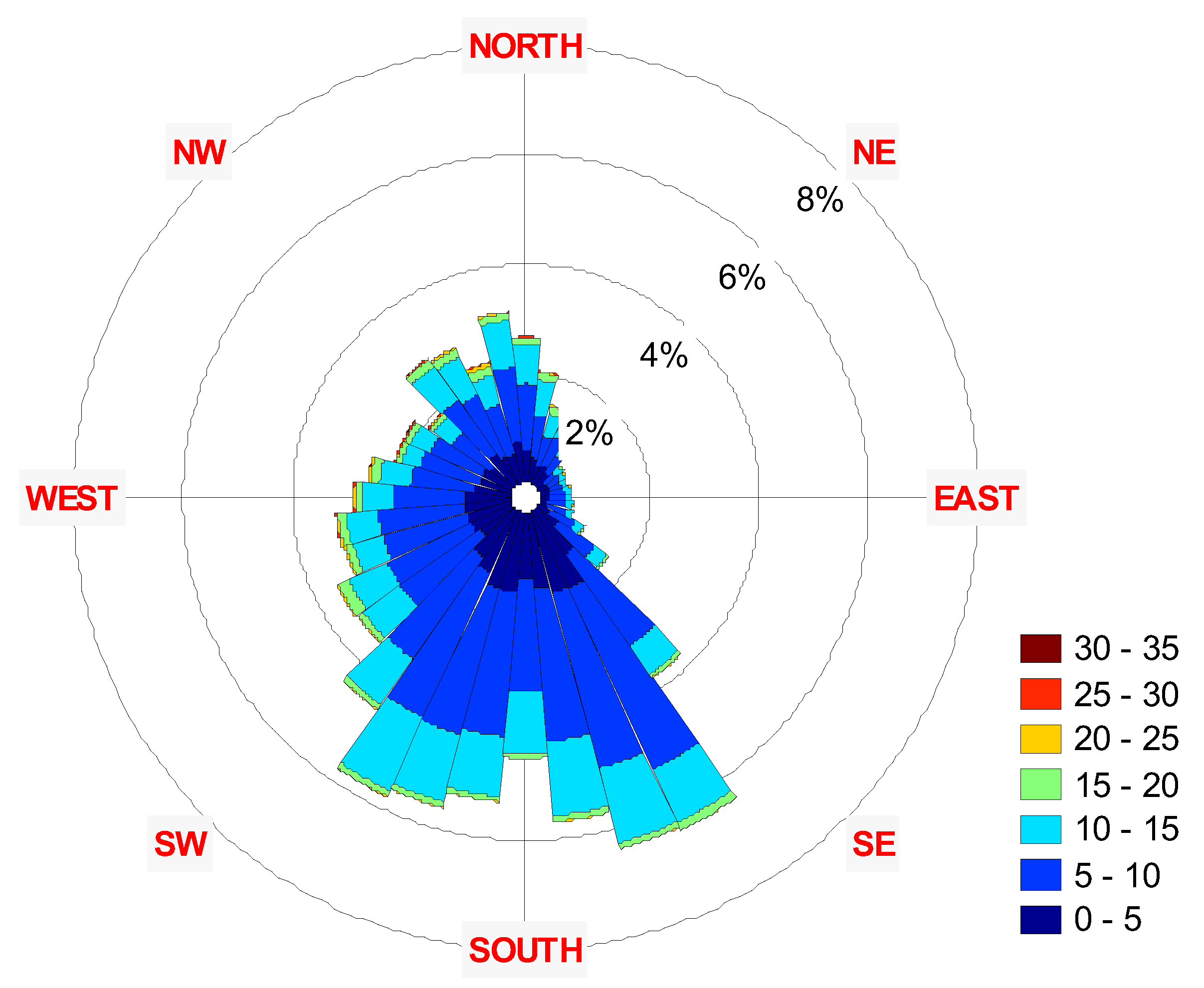
Year Parameter Speed Azimuth
2001 Mean: 7.72 209.41
STD: 3.94 81.13
2002 Mean: 8.78 227.31
STD: 4.50 83.03

2003		 Mean: 8.68 224.15
STD: 4.57 78.48

2004		 Mean: 8.24 228.17
STD: 4.43 80.32

2005		 Mean: 8.37 227.63
STD: 4.15 77.45

2006		 Mean: 7.82 231.65
STD: 3.94 83.15

2007		 Mean: 8.07 228.73
STD: 3.97 79.28

2008		 Mean: 8.07 221.94
STD: 4.04 77.23

2009 		Mean: 8.15 231.31
STD: 4.28 75.39

2010		 Mean: 7.91 225.30
STD: 4.08 79.84
2011 Mean: 7.64 230.11
STD: 3.74 79.28
2001-2011 Mean: 8.13 226.00
STD: 4.17 79.76
Table 5. Monthly, yearly, and cumulative Weibull parameters at 10 m height.
Table 5. Monthly, yearly, and cumulative Weibull parameters at 10 m height.
Preprints 67768 i002
Preprints 67768 i003
Table 6. Monthly, yearly, and cumulative Weibull parameters at 70 m height.
Table 6. Monthly, yearly, and cumulative Weibull parameters at 70 m height.
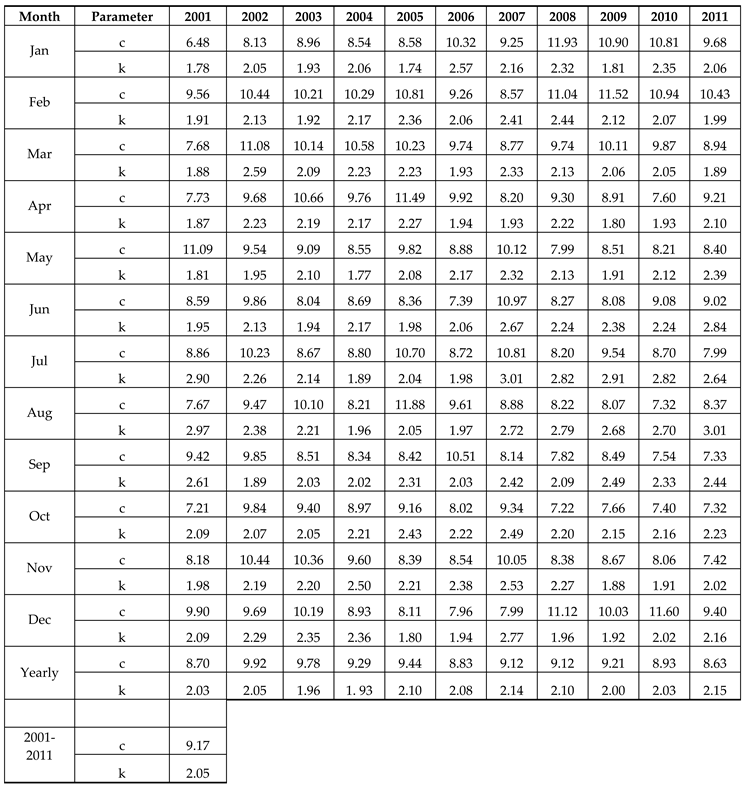Preprints 67768 i001
Table 7. Seasonal variation of Weibull parameters at 10 m height.
Table 7. Seasonal variation of Weibull parameters at 10 m height.
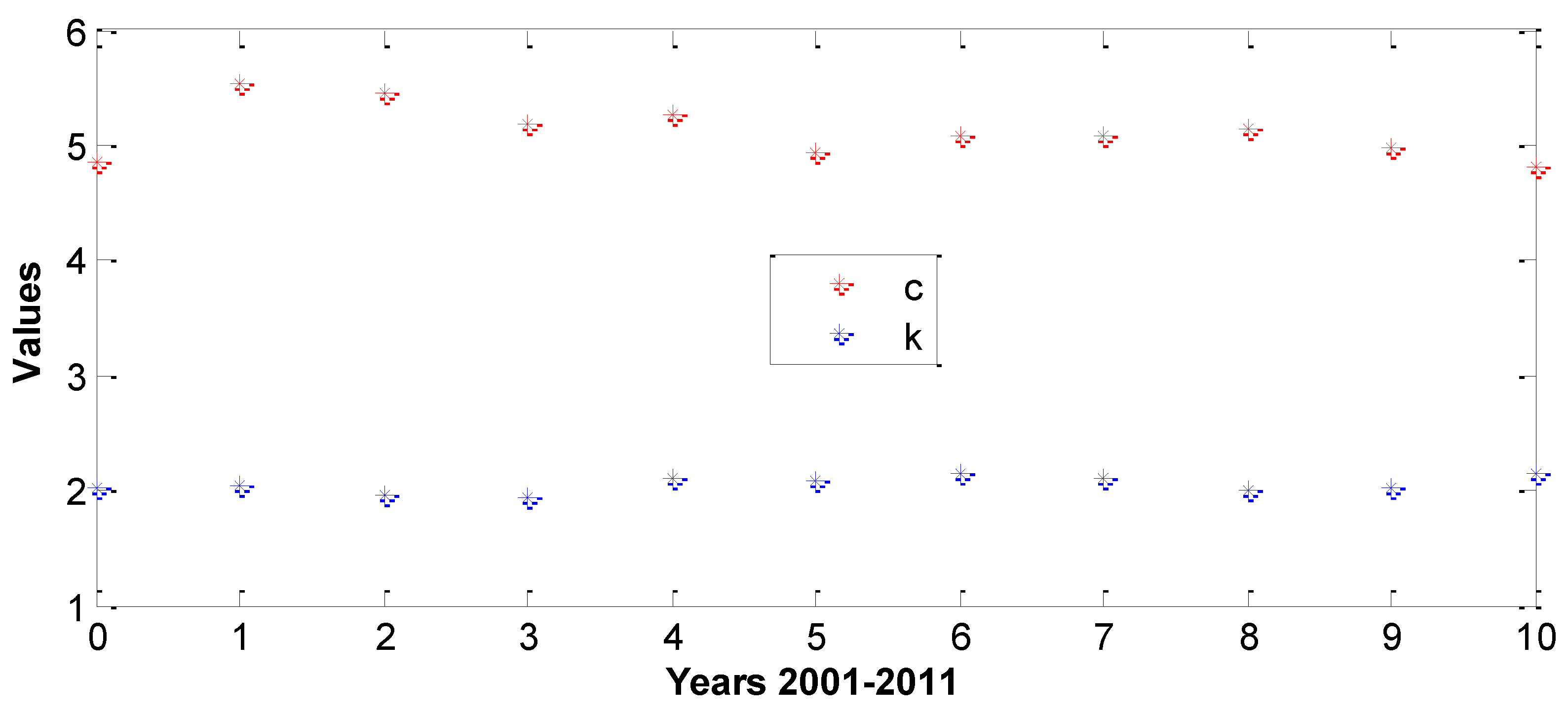
Parameter 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011
winter
Nov-Jan 		c 4.53 5.25 5.48 5.03 4.67 4.99 5.08 5.86 5.51 5.68 4.94
k 1.85 2.12 2.13 2.29 1.88 2.21 2.35 2.04 1.83 1.99 2.02
Spring
Feb-Apr 		c 4.63 5.80 5.77 5.69 6.05 5.38 4.75 5.58 5.66 5.26 5.30
k 1.84 2.29 2.06 2.18 2.26 1.96 2.20 2.23 1.95 1.93 1.97
Summer
May-Jul 		c 5.33 5.58 4.80 4.84 5.37 4.65 5.94 4.55 4.87 4.83 4.72
k 2.00 2.10 2.05 1.92 1.99 2.03 2.62 2.35 2.24 2.34 2.58
Autumn
Aug-Oct 		c 4.53 5.43 5.21 4.75 5.48 5.23 4.90 4.33 4.50 4.14 4.29
k 2.39 2.08 2.08 2.05 2.05 1.99 2.51 2.30 2.41 2.36 2.50
Table 8. Seasonal variation of Weibull parameters at 70 m height.
Table 8. Seasonal variation of Weibull parameters at 70 m height.
Parameter 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011
winter
Nov-Jan 		c 8.12 9.42 9.82 9.03 8.37 8.95 9.11 10.51 9.88 10.18 8.85
k 1.85 2.12 2.13 2.29 1.88 2.21 2.35 2.04 1.83 1.99 2.02
Spring
Feb-Apr 		c 8.31 10.41 10.34 10.21 10.84 9.64 8.52 10.01 10.14 9.44 9.50
k 1.84 2.29 2.06 2.18 2.26 1.96 2.20 2.23 1.95 1.93 1.97
Summer
May-Jul 		c 9.55 10.01 8.60 8.68 9.62 8.34 10.64 8.16 8.73 8.67 8.47
k 2.00 2.10 2.05 1.92 1.99 2.03 2.62 2.35 2.24 2.34 2.58
Autumn
Aug-Oct 		c 8.12 9.73 9.34 8.51 9.83 9.38 8.79 7.76 8.07 7.42 7.68
k 2.39 2.08 2.08 2.05 2.05 1.99 2.51 2.30 2.41 2.36 2.50
Table 9. Wind turbine geometric parameters.
Table 9. Wind turbine geometric parameters.
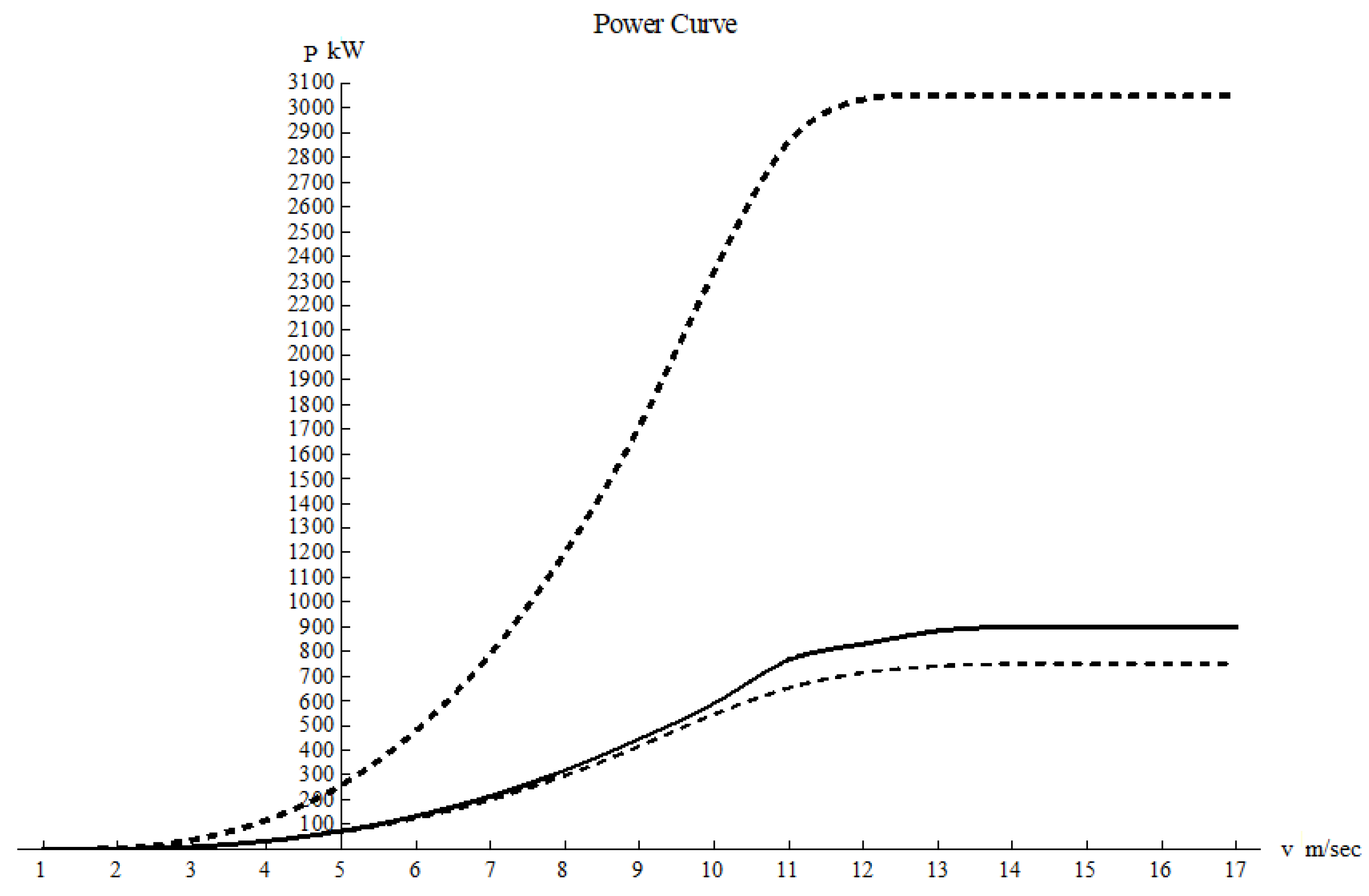
Turbine Enercon’s E101/3000 AWE’s 54–900 EWT’s Directwind 52/750
Area (m2) 8012 2290 2083
Radius (m) 50.5 27 25.75
Table 10. Wind turbine power & economic yield.
Table 10. Wind turbine power & economic yield.
Turbine Enercon‘s E101/3000 AWE’s 54–900 EWT’s Directwind 52/750
Average Power (kW) 1380.97 379.06 333.25
Power Standard Deviation (kW) 1160.94 326.58 275.32
Annual Revenue (Million SH) 6.46 1.77 1.56
Annual Revenue (Million $) 1.84 0.50 0.44
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated