Prerpints.org logo
Preprint
Article

Excited-State Polarizabilities: A Combined Density Functional Theory and Information-Theoretic Approach Study

This version is not peer-reviewed.

Submitted:

02 February 2023

Posted:

07 February 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Accurate and efficient determination of excited-state polarizabilities (α) is an open problem both experimentally and computationally. Following our previous work, [Phys. Chem. Chem. Phys. 2023, 25, 2131−2141], where one can employ simple ground-state density-based functions from the information-theoretic approach (ITA) to accurately and efficiently predict the macromolecular polarizabilities, we aim to predict the lowest excited-state polarizabilities in this work. The philosophy is to use density-based functions to depict the excited-state polarizabilities. As a proof-of-principle application, employing 2-(2′-hydroxyphenyl)benzimidazole and its derivatives as model systems, we have verified that either with the ground-state (S0) or excited-state (S1) densities as input, ITA quantities can be strongly correlated with the excited-state polarizabilities. When the transition densities are considered, both S0 and S1 polarizabilities are in good relationships with some ITA quantities. Furthermore, excitation and emission energies can be predicted based on multivariant linear regression equations of ITA quantities.
Keywords: 
density functional theory
;  
information theory
;  
excited-state polarizability
;  
ESIPT (excited-state intramolecular proton transfer)
Subject: 
Chemistry and Materials Science  -   Physical Chemistry

supplementary.docx (205.74KB )

1. Introduction

Molecular polarizability, especially the static electric dipole polarizability (α), is a fundamental physicochemical property. It reflects the change of a molecule’s dipole moment in a linear-response manner, as resulted from an external electric field perturbation. [1] The experimental determination of excited-state electro-static properties are mainly the Stark spectroscopy or electronic absorption/emission [2,3] method and the flash photolysis time-resolved microwave-conductivity (FP-TMRC) [4,5] technique.
In classical physics, the polarizability can be approximately obtained in terms of the volume of a system. [6,7] For example, many strong correlations have been observed for both atoms and molecules. [8,9,10,11,12,13,14,15,16] It is worthwhile to mention that Tkatchenko and Scheffler (TS) [17] proposed to use atomic volumes and atomic polarizabilities to predict the ground-state polarizabilities for small molecules. Recent progress can be found in ref 18. However, its performance for excited-state systems has not been reported.
In quantum mechanics, the polarizability can be obtained by iteratively solving the coupled-perturbed Hartree–Fock (CPHF) equation [19,20] or its Kohn–Sham DFT (density functional theory) counterpart. [21] Of note, this protocol requires a sufficiently large basis set with polarization and diffuse functions and huge computational costs. Note that the computational barriers can be partly overcome by using some linear-scaling methods. [22,23,24] In addition, machine learning (ML)-based [25,26,27] methods and a regression-based [28] model have been applied to predict the S0 polarizabilities. It is worthy to note that the polarizability can be related to the band gap of HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) in an inverse manner. [29,30,31]
In the literature, only a few studies [32–38] have been reported for the excited-state polarizabilities. This is likely because that accurate predictions of excited-state geometries and molecular properties of large molecules is a tough nut to crack, especially when there are perturbations such as external fields.
Following our previous work where the information-theoretic approach (ITA) quantities are employed to predict the S0 polarizabilities of both small and large molecules, [39,40] here we aim to predict the S1 polarizabilities of 2-(2′-hydroxyphenyl)benzimidazole (HBI, 1) and its derivatives as shown in Figure 1. For 1, it is well-documented [41] that the S0 (Figure 1a) intramolecular proton transfer (IPT) reaction is difficult to take place and the S1 (Figure 1b) or T1 (triplet, not shown) intramolecular proton transfer (ESIPT) process can easily happens. Thus, in this work, only S0 and S1 are considered to reduce the computational cost without compromising the results much. We have found that with the S0 or S1 electron densities as input, ITA quantities can be in good correlations with the excited-state polarizabilities. When the transition densities are considered, both S0 and S1 polarizabilities can be in good relationships with ITA quantities. Furthermore, excitation and emission energies can be predicted based on multiple linear regression equations of ITA quantities. For the first time, we have applied the ITA quantities to predict the excited-state polarizabilities. It is anticipated that this protocol can be readily applied to condensed-phase systems.

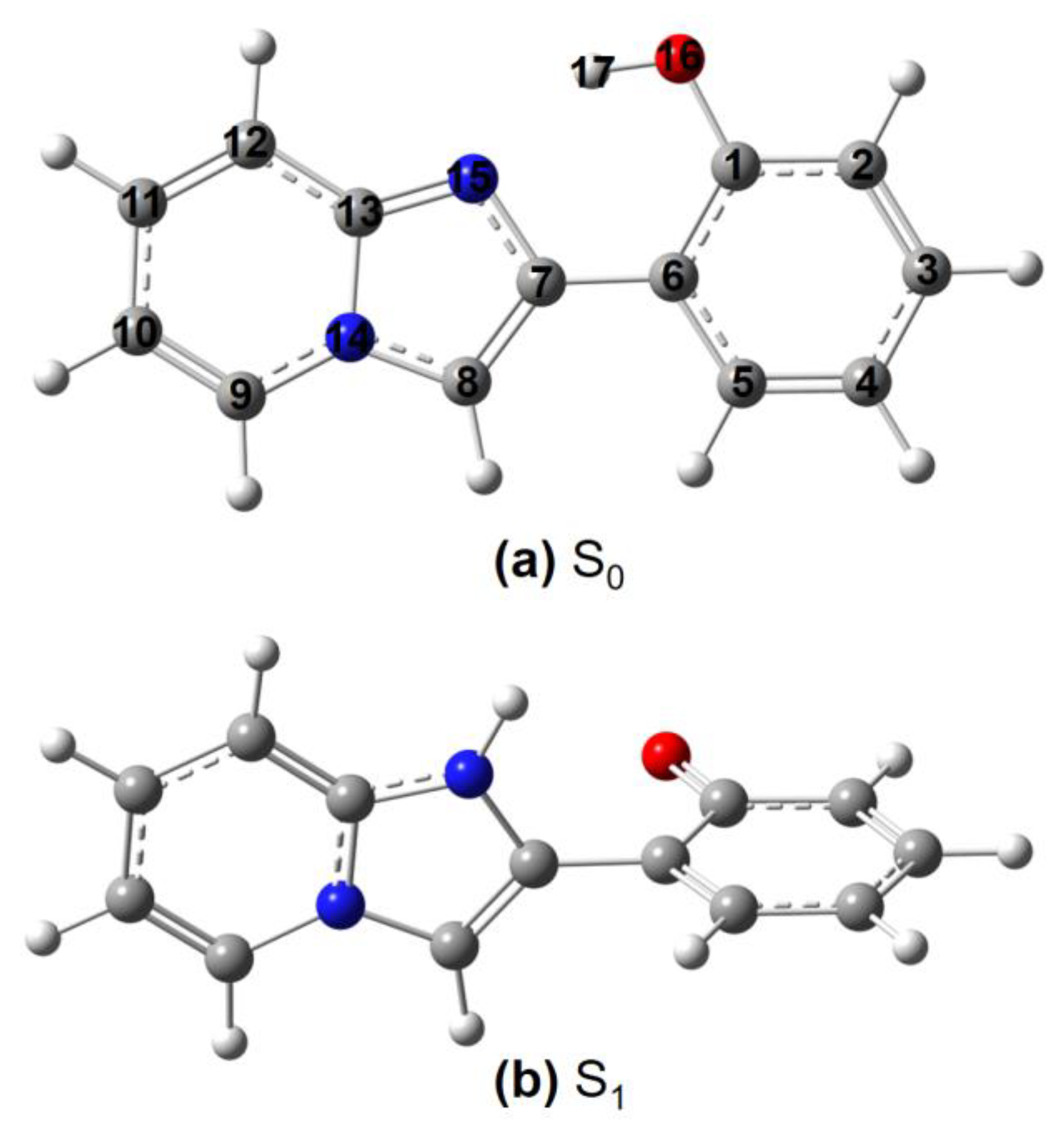
2. Results

Shown in Table 1 are the correlation coefficients (R2) between the S0 polarizabilities (αiso) and ITA quantities, molecular volumes, and quadrupole moments, which are obtained at the CAM-B3LYP/6-311+G(d) level. It is clear from Table 1 that Ghosh−Berkowitz−Parr (GBP) entropy (SGBP), 2nd and 3rd relative Rényi entropy (rR2 and rR3), information gain (IG), G1, G2, and G3, and quadrupole moments (Θiso) are in strong linear relationships with αiso, with R2 > 0.8. However, molecular volumes are in only reasonaly good coorelation with αiso, with R2 = 0.618, indicating that it is not a good descriptor of αiso. Of note, the G3 data have been shown to be strongly correlated with αiso for various systems, among which are 30 planar or quasi-planar bases, [39] 20/40/8000 amino acids/dipeptides/tripeptides, [39] and so on. [40] Also, the Θiso values can be in good relationship with αiso and its theoretical rational can be found in ref 40. However, a solid and sound theoretical verification between G3 and αiso is staill lacking. Overall, the strong correlations can serve as an argument that our computational results are convincing.
Collected in Table 2 are the S1 polarizabilities, the S1 ITA quantities including Shannon entropy (SS), Fisher information (IF), 2nd and 3rd relative Rényi entropy (rR2 and rR3), G2 and G3, molecular volumes (Vol), and quadrupole moments (Θiso), which are obtained at the TD-CAM-B3LYP/6-311+G(d) level. Also given in Table 2 are the correlation coefficients (R2) between the S1 polarizabilities and other quantities at S1. Note that some ITA quantities, well-defined at S0, are numerically ill-behaved at S1 and thus missing. One can see that rR2, rR3, G2, G3, Vol, and Θiso are in good correlations with αiso at S1, with R2 > 0.8. It is intriguing to note that at S1, G3 is still in good correlation with αiso. This is the first time to observe such a phenomenon. However, admittedly, the theoretical foundation lags behind the numerical evidence introduced in this work. Moreover, we have found that for Vol, the correlation coefficient is much stronger at S1 (0.908) than that at S0 (0.618). One possible reason is that the excited-state relaxation expands the volume and polarizability space. Finally, one can discover in Column 4 of IF, 2, 8, and 13 seem to have abnormal values compared with the others. They are all Br-containing, indicating that there may be some regions for heavy atoms where density gradients are numerically ill-behaved at S1. Similar results can also be observed for IF at S0 (see Table 1). Overall, we have unraveled that excited-state densities and molecular properties are mutually entangled.
Now we have shown that ITA quantities can be correlated with αiso either at S0 or S1. It is natural to ask if one can use ITA quantities at S0 to predict αiso at S1. The answer is definitely yes! In Table 3, We have tabulated the correlation coefficients (R2) between the αiso values at S1 and ITA quantities, molecular volumes, and quadrupole moments at S0 as introduced in Table 1. More details can be found in Table S1. Except Shannon entropy (SS), Fisher information (IF), and molecular volumes (Vol), the other quantities at S0 are in good relationships with αiso at S1, with R2 > 0.8. Moving forward, we ask if one can use the transition density (matrix) as input for ITA quantities to correlate with αiso either at S0 or S1. The answer is again yes! Shown in Table 4 are the strong correlations between αiso either at S0 or S1 and ITA quantities with the transition density matrix. Except Shannon entropy (SS) and Fisher information (IF), the other ITA quantities are in strong correlations with αiso either at S0 or S1, with R2 > 0.8. Implication of this part is straightforward that electron-density-based quantities can be used to predict the excited-state properties, such as molecular polarizabilities.
Next, we will compare the αiso data (either at S0 or S1) predicted by the TS formulas as with conventional results as reference. Employing the original Tkatchenko–Scheffler (TS) formula [17] on top of Becke [42] or Hirshfeld [43] partitions, the αiso data (either at S0/S1) are either strongly underestimated or overestimated, with MUE(%) up to –24.90/–21.21 and 6.62/10.82, respectively, as shown in Table 5. It is found that a mean value can reduce the MSE(%) to 16.00/15.23. Moreover, with the new TS formula, [18] the results are not improved but worsened as shown in Table 6. Taken together, we have found that the TS formulas have large room to improve in predicting the S1 polarizabilities.
Finally, we have found that both excitation and emission energies can be predicted on top of multiple linear regression equations of ITA quantities. For example, one can use the transition density matrix as input for ITA quantities to correlate with the excitation energies. Similarly, if the S1 densities are used for ITA quantities, the emission energies can be predicted. Based on the two regression equations,
λfit = 0.32*SS + 0.0027*IF ‒ 0.31*SGBP ‒ 0.85*rR2 + 2.87*rR3 ‒ 27.99*IG + 0.33*G1 ‒ 0.050*G2 + 0.0099*G3,
and
λfit = 0.085*SS + 0.00088*IF + 1.36*rR2 ‒ 1.42*rR3 ‒ 0.080*G2 + 0.038*G3,
we have obtained that the MUEs (mean unsigned error) and the MSEs (mean signed error) are –0.04/0.20 eV and 0.00/0.22 eV for excitation and emission energies, respectively. This indicates that the inaccuracy of this protocol is comparable to that of underlying approximations of DFT. [44,45].

3. Discussion

To accurately and efficiently predict the excited-state polarizabilities is an ongoing issue. Solving standard CPHF/CPKS equations are computationally intensive and the computational costs can be intractable for macromolecular systems. Other algorithms and models available in the literature are normally concerned with the ground-state polarizabilities. Within this context; we proposed to apply some density-based ITA quantities to correlate with αiso at S0/S1. This is inspired by our previous work on predicting the ground-state polarizabilities for small and macromolecular systems. Our tentative results have shown that the protocol should be a promising theoretical tool. More systems along this line need to be considered to make this protocol more robust and applicable. We have to point out when the system under study becomes larger and larger; the molecular wavefunctions (thus electron density) are a tough nut to crack; sometimes computationally intractable. Under these circumstances; we have to resort to linear-scaling electronic structure methods; such as GEBF (generalized energy-based fragmentation method), [46–49] where only small subsystems of a few atoms or groups are treated.
Next, we will look into the TS method, as mentioned previously. We have already found that based upon the Hirshfeld or Becke partition scheme, the original TS formula has an unsatisfactory performance either by overestimating or underestimating the S1 polarizabilities. Apparent reduction of the deviations can be obtained by averaging the two sets of results. The reason behind is unclear at the moment. From the original formula,
α m o l T S − o l d = ∑ A α A e f f = ∑ A α A f r e e V A e f f V A f r e e
one can easily argue that the weights V A e f f V A f r e e may be the root cause of its poor performance, mainly because the atomic polarizabilities α A f r e e   are experimentally determined and computationally verified, as summarized in ref 50. In the same spirit, a revised TS formula,
α m o l T S − n e w = ∑ A α A e f f = ∑ A α A f r e e V A e f f V A f r e e 4 / 3
has witnessed improved performance of predicting the S0 polarizabilities. However, its predicting power has been shown to be far from satisfactory for macromolecules. In this work, we further corroborate that both the original and new TS formulas fail to give a satisfactory description of the S1 polarizability. This indicates that the two formulas are oversimplified and may be system-dependent. Overall, the volume-based are inferior to the density-based ITA quantities.

4. Materials and Methods

4.1. Information-Theoretic Approach Quantities

Shannon entropy SS [51] and Fisher information IF [52] are two cornerstone quantities in information theory. They are defined as Equations (1) and (2), respectively.
S S = − ∫ ρ r l n ρ r d r
I F = ∫ | ∇ ρ ( r ) | 2 ρ ( r ) d r
where ρ r is the electron density and ∇ ρ ( r )   is the density gradient. The physical picture of S S   and I F is clear; the former measures the spatial delocalization of the electron density and the latter gauges the sharpness or localization of the same.
Except the total density, more ingredients, such as kinetic-energy density, can be used to defined an ITA quantity. With both the electron density and the kinetic energy density, Ghosh, Berkowitz, and Parr developed a formula for entropy (SGBP), [53]
S G B P = − ∫ 3 2 k ρ r c + l n t ( r ; ρ ) t T F ( r ; ρ ) d r
where t(r; ρ) and tTF(r; ρ) represent the non-interacting and Thomas–Fermi (TF) kinetic energy density, respectively. Here k, c, and cK are three constants [k, the Boltzmann constant, c = (5/3) +ln(4πcK/3), and cK = (3/10)(3π2)2/3]. Full integration of the kinetic energy density t(r; ρ) leads to the total kinetic energy TS via
∫ t r ; ρ d r = T S
while t(r; ρ) can be obtained from the canonical orbital densities,
t r ; ρ = ∑ i 1 8 ∇ ρ i · ∇ ρ i ρ i − 1 8 ∇ 2 ρ
and tTF(r; ρ) is simply cast in terms of ρ r ,
t T F ( r ; ρ ) = c K ρ 5 / 3 r
Of note, the kinetic-energy density can differ in its form, thus can be used in different contexts. [54,55,56,57,58,59,60,61] But, SGBP satisfies the maximum-entropy requirement from a mathematical viewpoint. [53]
Moving forward, some ITA quantities have been introduced for chemical reactions. As new reactivity descriptors in conceptual density functional theory (CDFT), [62,63,64,65] one example is relative Rényi entropy [66] of order n
R n r = 1 n − 1 l n ∫ ρ n r ρ 0 n − 1 r d r
Information gain [67] (also called Kullback−Leibler divergence or relative Shannon entropy) IG is expressed as follows,
I G = ∫ ρ r l n ρ r ρ 0 r d r
In Equations (7) and (8), ρ0(r) and ρ(r) satisfy the same normalization condition, and ρ0(r) denotes the reference-state density.
Recently, [68] one of the present authors proposed three functions G1, G2, and G3, at both atomic and molecular levels. They are defined as below:
G 3 = ∑ A ∫ ρ A r [ ∇ l n ρ A r ρ A 0 r ] 2 d r
G 1 = ∑ A ∫ ∇ 2 ρ A r ρ A r ρ A 0 r d r
G 2 = ∑ A ∫ ρ A r ∇ 2 ρ A r ρ A r − ∇ 2 ρ A 0 r ρ A 0 r d r
Equations (9)–(11) have been theoretically derived, numerically verified, and have witnessed many applications, as can be found in refs 39, 40, 68, and 69. It is one of our major achievements during the past decade, when we aimed to glue the density functional theory and information theory together in a seamless manner. Because these two theories both can have as electron density as input. Our recent progress along this line can be found in two reviews. [70,71] As another prominent example, we have applied the ITA to appreciate homochirality. [72,73]
Finally, the Hirshfeld’s stockholder approach [43,74–77] is often introduced to partition atoms in a molecule in the literature, as defined in Equation (12),
ρ A r = ω A r ρ r = ρ A 0 r ( r − R A ) ∑ B ρ B 0 r − R A ρ r
Here,   ρ A r is the atomic Hirshfeld density, ω A r is a sharing function, ρ B 0 r − R A is the atomic density of B centered at RA. The sum over all the free atom densities, typically spherically averaged S0 atomic densities, is normally termed the promolecular density. The Stockholder approach is natural in the context of ITA because it is also based on information-theoretic arguments. Alternative partitioning schemes include Becke’s fuzzy atom approach [44] and Bader’s zero-flux atoms-in-molecules (AIM) method. [78]

4.2. Computational Details

All density functional theory (DFT) calculations were performed with the Gaussian 16 [79] package. Default options include ultrafine integration grids and tight self-consistent field convergence, which are adopted to eliminate numerical noises. The ground- and excited-state structural relaxation was fully carried out at the CAM-B3LYP/6-311+G(d) [80,81] and TD-CAM-B3LYP/6-311+G(d) [80,81,82–84] level, respectively, for 27 molecular systems, as shown in Figure 1. The optimized atomic Cartesian coordinates are supplied in the Supplementary Materials. Subsequent harmonic vibrational frequency calculations were executed at the same level and no imaginary frequencies were observed by direct visual inspection. The isotropic polarizabilities [αiso = (αxx + αyy + αzz)/3] and isotropic quadrupole moments [Θiso = (Θxx + Θyy + Θzz)/3], molecular volumes (at 0.001 e/Bohr3 contour surface of electronic density), and molecular wavefunctions were obtained at the CAM-B3LYP/6-311+G(d) level. The Multiwfn 3.8 [85] program was utilized to calculate all ITA quantities at S0 and S1 by using the checkpoint or wavefunction file as the input. The stockholder Hirshfeld partition scheme of atoms in molecules was employed when atomic contributions were concerned. The reference-state density was the neutral atom calculated at the same level of theory as molecules.

Supplementary Materials

The following supporting information can be downloaded at Preprints.org, Excited-state ITA quantities with the transition density matrix as input, the optimized Cartesian coordinates of all systems (S0 and S1).

Author Contributions

Conceptualization, S.L. and D.Z.; data curation, D.Z. and X.H.; formal analysis, D.Z. and X.H.; funding acquisition, D.Z.; project administration, S.L. and D.Z.; supervision, S.L. and D.Z.; writing—original draft, D.Z.; writing—review and editing, S.L. and D.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the start-up funding of Yunnan University and the Yunnan Fundamental Research Projects (grant NO. 202101AU070012).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Acknowledgments

Pratim K. Chattaraj is acknowledged for this invitation.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Buckingham, A.D. Polarizability and hyperpolarizability. Phil. Trans. R. Soc. Lond. A 1979, 293, 239–248. [Google Scholar]
  2. Liess, M.; Jeglinski, S.; Vardeny, Z.; Ozaki, M.; Yoshino, K.; Ding, Y.; Barton, T. Electroabsorption Spectroscopy of Luminescent and Nonluminescent π-Conjugated Polymers. Phys. Rev. B Condens. Matter Mater. Phys. 1997, 56, 15712–15724. [Google Scholar] [CrossRef]
  3. Ponder, M.; Mathies, R. Excited-State Polarizabilities and Dipole Moments of Diphenylpolyenes and Retinal. J. Phys. Chem. 1983, 87, 5090–5098. [Google Scholar] [CrossRef]
  4. Gelinck, G.H.; Piet, J.J.; Wegewijs, B.R.; Müllen, K.; Wildeman, J.; Hadziioannou, G.; Warman, J.M. Measuring the Size of Excitons on Isolated Phenylene-Vinylene Chains: From Dimers to Polymers. Phys. Rev. B Condens. Matter Mater. Phys. 2000, 62, 1489–1491. [Google Scholar] [CrossRef]
  5. De Haas, M.P.; Warman, J.M. Photon-Induced Molecular Charge Separation Studied by Nanosecond Time-Resolved Microwave Conductivity. Chem. Phys. 1982, 73, 35–53. [Google Scholar] [CrossRef]
  6. Condon, E.U. in Handbook of Physics, ed. Condon, E.U. and Odishaw, H. McGraw-Hill, New York, 1958, pp. 4–22.
  7. Jackson, J.D. Classical Electrodynamics, Wiley, New York, 2nd edn, 1975, pp. 60–62.
  8. Dmitrieva, I.K.; Plindov, G.I. Dipole Polarizability, Radius and Ionization Potential for Atomic Systems. Phys. Scr. 1983, 27, 402. [Google Scholar] [CrossRef]
  9. Gough, K.M. Theoretical analysis of molecular polarizabilities and polarizability derivatives in hydrocarbons. J. Chem. Phys. 1989, 91, 2424–2432. [Google Scholar] [CrossRef]
  10. Laidig, K.E.; Bader, R.F.W. Properties of atoms in molecules: Atomic polarizabilities. J. Chem. Phys. 1990, 93, 7213–7224. [Google Scholar] [CrossRef]
  11. Brinck, T.; Murray, J.S.; Politzer, P. Polarizability and volume. J. Chem. Phys. 1993, 98, 4305–4306. [Google Scholar] [CrossRef]
  12. Politzer, P.; Jin, P.; Murray, J.S. Atomic polarizability, volume and ionization energy. J. Chem. Phys. 2002, 117, 8197–8202. [Google Scholar] [CrossRef]
  13. Blair, S.A.; Thakkar, A.J. Relating polarizability to volume, ionization energy, electronegativity, hardness, moments of momentum, and other molecular properties. J. Chem. Phys. 2014, 141, 074306. [Google Scholar] [CrossRef] [PubMed]
  14. Blair, S.A.; Thakkar, A.J. Additive models for the molecular polarizability and volume. Chem. Phys. Lett. 2014, 610–611, 163–166. [Google Scholar] [CrossRef]
  15. Miller, K.J. Additivity Methods in Molecular Polarizability. J. Am. Chem. Soc. 1990, 112, 8533–8542. [Google Scholar] [CrossRef]
  16. Miller, K.J. Calculation of the Molecular Polarizability Tensor. J. Am. Chem. Soc. 1990, 112, 8543–8551. [Google Scholar] [CrossRef]
  17. Tkatchenko, A.; Scheffler, M. Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [PubMed]
  18. Szabó, P.; Góger, S.; Charry, J.; Karimpour, M.R.; Fedorov, D.V.; Tkatchenko, A. Four-Dimensional Scaling of Dipole Polarizability in Quantum Systems. Phys. Rev. Lett. 2022, 128, 070602. [Google Scholar] [CrossRef] [PubMed]
  19. McWeeny, R. Some recent advances in density matrix theory. Rev. Mod. Phys. 1960, 32, 335–369. [Google Scholar] [CrossRef]
  20. Langhoff, W.; Karplus, M.; Hurst, R.P. Approximations to Hartree—Fock Perturbation Theory. J. Chem. Phys. 1966, 44, 505–514. [Google Scholar] [CrossRef]
  21. Colwell, S.M.; Murray, C.W.; Handy, N.C.; Amos, R.D. The determination of hyperpolarisabilities using density functional theory. Chem. Phys. Lett. 1993, 210, 261–268. [Google Scholar] [CrossRef]
  22. Collins, M.A.; Bettens, R.P. Energy-Based Molecular Fragmentation Methods. Chem. Rev. 2015, 115, 5607–5642. [Google Scholar] [CrossRef]
  23. Niklasson, A.M.; Challacombe, M. Density Matrix Perturbation Theory. Phys. Rev. Lett. 2004, 92, 193001. [Google Scholar] [CrossRef] [PubMed]
  24. Weber, V.; Niklasson, A.M.N.; Challacombe, M. Ab Initio Linear Scaling Response Theory: Electric Polarizability by Perturbed Projection. Phys. Rev. Lett. 2004, 92, 193002. [Google Scholar] [CrossRef] [PubMed]
  25. Grisafi, A.; Wilkins, D.M.; Csányi, G.; Ceriotti, M. Symmetry-Adapted Machine Learning for Tensorial Properties of Atomistic Systems. Phys. Rev. Lett. 2018, 120, 036002. [Google Scholar] [CrossRef] [PubMed]
  26. Wilkins, D.M.; Grisafi, A.; Yang, Y.; Lao, K.U.; DiStasio, R.A., Jr.; Ceriotti, M. Accurate molecular polarizabilities with coupled cluster theory and machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 3401–3406. [Google Scholar] [CrossRef] [PubMed]
  27. Nguyen, V.H.A.; Lunghi, A. Predicting tensorial molecular properties with equivariant machine learning models. Phys. Rev. B 2022, 105, 165131. [Google Scholar] [CrossRef]
  28. Amin, M.; Samy, H.; Küpper, J. Robust and Accurate Computational Estimation of the Polarizability Tensors of Macromolecules. J. Phys. Chem. Lett. 2019, 10, 2938–2943. [Google Scholar] [CrossRef] [PubMed]
  29. Unsöld, A. Quantentheorie des Wasserstoffmolekülions und der Born-Landéschen Abstoßungskräfte, Z. Physik 1927, 43, 563–574. [Google Scholar] [CrossRef]
  30. Simón-Manso, Y.; Fuentealba, P. On the Density Functional Relationship between Static Dipole Polarizability and Global Softness. J. Phys. Chem. A 1998, 102, 2029–2032. [Google Scholar] [CrossRef]
  31. Ayers, P.W. The physical basis of the hard/soft acid/base principle. Faraday Discuss 2007, 135, 161–190. [Google Scholar] [CrossRef]
  32. Grozema, F.C.; Telesca, R.; Jonkman, H.T.; Siebbeles, L.D.A.; Snijders, J.G. Excited State Polarizabilities of Conjugated Molecules Calculated Using Time Dependent Density Functional Theory. J. Chem. Phys. 2001, 115, 10014–10021. [Google Scholar] [CrossRef]
  33. Improta, R.; Ferrante, C.; Bozio, R.; Barone, V. The Polarizability in Solution of Tetra-Phenyl-Porphyrin Derivatives in Their Excited Electronic States: A PCM/TD-DFT Study. Phys. Chem. Chem. Phys. 2009, 11, 4664–4673. [Google Scholar] [CrossRef] [PubMed]
  34. Van Der Horst, J.W.; Bobbert, P.A.; De Jong, P.H.L.; Michels, M.A.J.; Siebbeles, L.D.A.; Warman, J.M.; Gelinck, G.H.; Brocks, G. Predicting Polarizabilities and Lifetimes of Excitons on Conjugated Polymer Chains. Chem. Phys. Lett. 2001, 334, 303–308. [Google Scholar] [CrossRef]
  35. Hinchliffe, A.; Sosćun, H.J. Ab Initio Studies of the Dipole Moment and Polarizability of Azulene in Its Ground and Excited Singlet States. Chem. Phys. Lett. 2005, 412, 365–368. [Google Scholar] [CrossRef]
  36. Christiansen, O.; Hättig, C.; Jørgensen, P. Ground and Excited State Polarizabilities and Dipole Transition Properties of Benzene from Coupled Cluster Response Theory. Spectrochim. Acta, Part A 1999, 55, 509–524. [Google Scholar] [CrossRef]
  37. Ye, J.F.; Chen, H.; Note, R.; Mizuseki, H.; Kawazoe, Y. Excess Polarizabilities Upon Excitation from the Ground State to the First Dipole-Allowed Excited State of Diphenylpolyenes. Int. J. Quantum Chem. 2007, 107, 2006–2014. [Google Scholar] [CrossRef]
  38. Orian, L.; Pilot, R.; Bozio, R. In Silico Stark Effect: Determination of Excited-State Polarizabilities of Squaraine Dyes. J. Phys. Chem. A 2017, 121, 1587–1596. [Google Scholar] [CrossRef] [PubMed]
  39. Zhao, D.B.; Liu, S.B.; Chen, D.H. A Density Functional Theory and Information-Theoretic Approach Study of Interaction Energy and Polarizability for Base Pairs and Peptides. Pharmaceuticals 2022, 15, 938. [Google Scholar] [CrossRef] [PubMed]
  40. Zhao, D.B.; Zhao, Y.L.; He, X.; Ayers, P.W.; Liu, S.B. Efficient and accurate density-based prediction of macromolecular polarizabilities. Phys. Chem. Chem. Phys. 2023, 25, 2131–2141. [Google Scholar] [CrossRef] [PubMed]
  41. Purkayastha, P.; Chattopadhyay, N. Role of rotamerisation and excited state intramolecular proton transfer in the photophysics of 2-(2′-hydroxyphenyl)benzoxazole, 2-(2′-hydroxyphenyl)benzimidazole and 2-(2′-hydroxyphenyl)benzothiazole: A theoretical study. Phys. Chem. Chem. Phys. 2000, 2, 203–210. [Google Scholar] [CrossRef]
  42. Becke, A.D. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
  43. Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theoret. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
  44. Parr, R.G.; Yang, W.T. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
  45. Teale, A.M.; Helgaker, T.; Savin, A.; Adamo, C.; Aradi, B.; Arbuznikov, A.V.; Ayers, P.W.; Baerends, E.J.; Barone, V.; Calaminici, P.; et al. DFT exchange: Sharing perspectives on the workhorse of quantum chemistry and materials science. Phys. Chem. Chem. Phys. 2022, 24, 28700–28781. [Google Scholar] [CrossRef] [PubMed]
  46. Li, S.H.; Li, W.; Fang, T. An Efficient Fragment-Based Approach for Predicting the Ground-State Energies and Structures of Large Molecules. J. Am. Chem. Soc. 2005, 127, 7215–7226. [Google Scholar] [CrossRef] [PubMed]
  47. Li, W.; Li, S.H.; Jiang, Y.S. Generalized Energy-Based Fragmentation Approach for Computing the Ground-State Energies and Properties of Large Molecules. J. Phys. Chem. A 2007, 111, 2193–2199. [Google Scholar] [CrossRef]
  48. Li, S.H.; Li, W.; Ma, J. Generalized Energy-Based Fragmentation Approach and Its Applications to Macromolecules and Molecular Aggregates. Acc. Chem. Res. 2014, 47, 2712–2720. [Google Scholar] [CrossRef]
  49. Li, W.; Dong, H.; Ma, J.; Li, S.H. Structures and Spectroscopic Properties of Large Molecules and Condensed-Phase Systems Predicted by Generalized Energy-Based Fragmentation Approach. Acc. Chem. Res. 2021, 54, 169–181. [Google Scholar] [CrossRef] [PubMed]
  50. Schwerdtfeger, P.; Nagle, J.K. Table of static dipole polarizabilities of the neutral elements in the periodic table. Mol. Phys. 2018, 117, 1200–1225. [Google Scholar] [CrossRef]
  51. Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
  52. Fisher, R.A. Theory of statistical estimation. Math. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
  53. Ghosh, S.K.; Berkowitz, M.; Parr, R.G. Transcription of ground-state density-functional theory into a local thermodynamics. Proc. Natl. Acad. Sci. USA 1984, 81, 8028–8031. [Google Scholar] [CrossRef]
  54. Bader, R.F.W.; Preston, H.J.T. The kinetic energy of molecular charge distributions and molecular stability. Int. J. Quantum Chem. 1969, 3, 327–347. [Google Scholar] [CrossRef]
  55. Tal, Y.; Bader, R.F.W. Studies of the energy density functional approach. 1. Kinetic energy. Int. J. Quantum Chem. 1978, 14, 153–168. [Google Scholar] [CrossRef]
  56. Cohen, L. Local kinetic energy in quantum mechanics. J. Chem. Phys. 1979, 70, 788–789. [Google Scholar] [CrossRef]
  57. Cohen, L. Representable local kinetic energy. J. Chem. Phys. 1984, 80, 4277–4279. [Google Scholar] [CrossRef]
  58. Yang, Z.Z.; Liu, S.B.; Wang, Y.A. Uniqueness and Asymptotic Behavior of the Local Kinetic Energy. Chem. Phys. Lett. 1996, 258, 30–36. [Google Scholar] [CrossRef]
  59. Ayers, P.W.; Parr, R.G.; Nagy, Á. Local kinetic energy and local temperature in the density-functional theory of electronic structure. Int. J. Quantum Chem. 2002, 90, 309–326. [Google Scholar] [CrossRef]
  60. Anderson, J.S.M.; Ayers, P.W.; Hernandez, J.I.R. How Ambiguous Is the Local Kinetic Energy? J. Phys. Chem. A 2010, 114, 8884–8895. [Google Scholar] [CrossRef] [PubMed]
  61. Berkowitz, M. Exponential approximation for the density matrix and the Wigner distribution. Chem. Phys. Lett. 1986, 129, 486–488. [Google Scholar] [CrossRef]
  62. Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual Density Functional Theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef]
  63. Johnson, P.A.; Bartolotti, L.J.; Ayers, P.W.; Fievez, T.; Geerlings, P. Charge density and chemical reactivity: A unified view from conceptual DFT. in Modern Charge Density Analysis, ed. Gatti, C. and Macchi, P. Springer, New York, 2012.
  64. Liu, S.B. Conceptual Density Functional Theory and Some Recent Developments. Acta Phys. -Chim. Sin. 2009, 25, 590–600. [Google Scholar]
  65. Geerlings, P.; Chamorro, E.; Chattaraj, P.K.; De Proft, F.; Gázquez, J.L.; Liu, S.B.; Morell, C.; Toro-Labbé, A.; Vela, A.; Ayers, P.W. Conceptual density functional theory: Status, prospects, issues. Theor. Chem. Acc. 2020, 139, 36. [Google Scholar] [CrossRef]
  66. Liu, S.B.; Rong, C.Y.; Wu, Z.M.; Lu, T. Rényi entropy, Tsallis entropy and Onicescu information energy in density functional reactivity theory. Acta Phys. -Chim. Sin. 2015, 31, 2057–2063. [Google Scholar] [CrossRef]
  67. Kullback, S. Information Theory and Statistics; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
  68. Liu, S.B. Identity for Kullback-Leibler divergence in density functional reactivity theory. J. Chem. Phys. 2019, 151, 141103. [Google Scholar] [CrossRef]
  69. Wang, B.; Zhao, D.B.; Lu, T.; Liu, S.B.; Rong, C.Y. Quantifications and Applications of Relative Fisher Information in Density Functional Theory. J. Phys. Chem. A 2021, 125, 3802–3811. [Google Scholar] [CrossRef]
  70. Rong, C.Y.; Wang, B.; Zhao, D.B.; Liu, S.B. Information-Theoretic approach in density functional theory and its recent applications to chemical problems. WIREs Comput. Mol. Sci. 2020, 10, e1461. [Google Scholar] [CrossRef]
  71. Rong, C.Y.; Zhao, D.B.; He, X.; Liu, S.B. Development and Applications of the Density-Based Theory of Chemical Reactivity. J. Phys. Chem. Lett. 2022, 13, 11191–11200. [Google Scholar] [CrossRef] [PubMed]
  72. Liu, S.B. Homochirality Originates from Handedness of Helices. J. Phys. Chem. Lett. 2020, 11, 8690–8696. [Google Scholar] [CrossRef]
  73. Liu, S.B. Principle of Chirality Hierarchy in Three-Blade Propeller Systems. J. Phys. Chem. Lett. 2021, 12, 8720–8725. [Google Scholar] [CrossRef] [PubMed]
  74. Nalewajski, R.F.; Parr, R.G. Information theory, atoms in molecules, and molecular similarity. Proc. Natl. Acad. Sci. USA 2000, 97, 8879–8882. [Google Scholar] [CrossRef]
  75. Ayers, P.W. Information Theory, the Shape Function, and the Hirshfeld Atom. Theor. Chem. Acc. 2006, 115, 370–378. [Google Scholar] [CrossRef]
  76. Parr, R.G.; Ayers, P.W.; Nalewajski, R.F. What Is an Atom in a Molecule? J. Phys. Chem. A 2005, 109, 3957–3959. [Google Scholar] [CrossRef] [PubMed]
  77. Heidar-Zadeh, F.; Ayers, P.W.; Verstraelen, T.; Vinogradov, I.; Vohringer-Martinez, E.; Bultinck, P. Information-Theoretic Approaches to Atoms-in-Molecules: Hirshfeld Family of Partitioning Schemes. J. Phys. Chem. A 2018, 122, 4219–4245. [Google Scholar] [CrossRef] [PubMed]
  78. Bader, R.F.W. Atoms in Molecules: A Quantum Theory. Oxford University Press, Oxford, England, 1990.
  79. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  80. Yanai, T.; Tew, D.; Handy, N. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
  81. McLean, A.D.; Chandler, G.S. Contracted Gaussian-basis sets for molecular calculations. 1. 2nd row atoms, Z=11-18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
  82. Bauernschmitt, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
  83. Furche, F.; Ahlrichs, R. Adiabatic time-dependent density functional methods for excited state properties. J. Chem. Phys. 2002, 117, 7433–7447. [Google Scholar] [CrossRef]
  84. Liu, J.; Liang, W. Analytical Hessian of electronic excited states in time-dependent density functional theory with Tamm-Dancoff approximation. J. Chem. Phys. 2011, 135, 014113. [Google Scholar] [CrossRef]
  85. Lu, T.; Chen, F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
Preprints 68189 g001
Figure 1. Schematic representation of the (a) ground-state (S0) and (b) excited-state (S1) 2-(2′-hydroxyphenyl)benzimidazole (HBI) structure and the atomic numbering. A total of 27 substituted HBI structures are generated, including 1: HBI, 2: 3-Br-HBI, 3: 3-Et2N-HBI, 4: 3-HO-HBI, 5: 3-MeO-HBI, 6: 4-F-HBI, 7: 4-Cl-HBI, 8: 4-Br-HBI, 9: 4-CN-HBI, 10: 4-Me-HBI, 11: 4-MeO-HBI, 12: 10-Cl-HBI, 13: 10-Br-HBI, 14: 10-CN-HBI, 15: 10-Me-HBI, 16: 10-CF3-HBI, 17: 10-Ph-HBI, 18: 12-Ph-HBI, 19: 10-(p-MeO-Ph)-HBI, 20: 10-(p-MeCO2-Ph)-HBI, 21: 12-(p-MeO-Ph)-HBI, 22: 12-(p-MeCO2-Ph)-HBI, 23: 4-Me-10-Cl-HBI, 24: 4-Me-10-CF3-HBI, 25: 10-Ph-12-Ph-HBI, 26: 2-(CH2CH2CH=CH2)-8-(CH2CH2Ph)-HBI, 27: 2-F-3-F-4-F-5-F-HBI. Color code: hydrogen in white, carbon in grey, nitrogen in blue, and oxygen in red.
Figure 1. Schematic representation of the (a) ground-state (S0) and (b) excited-state (S1) 2-(2′-hydroxyphenyl)benzimidazole (HBI) structure and the atomic numbering. A total of 27 substituted HBI structures are generated, including 1: HBI, 2: 3-Br-HBI, 3: 3-Et2N-HBI, 4: 3-HO-HBI, 5: 3-MeO-HBI, 6: 4-F-HBI, 7: 4-Cl-HBI, 8: 4-Br-HBI, 9: 4-CN-HBI, 10: 4-Me-HBI, 11: 4-MeO-HBI, 12: 10-Cl-HBI, 13: 10-Br-HBI, 14: 10-CN-HBI, 15: 10-Me-HBI, 16: 10-CF3-HBI, 17: 10-Ph-HBI, 18: 12-Ph-HBI, 19: 10-(p-MeO-Ph)-HBI, 20: 10-(p-MeCO2-Ph)-HBI, 21: 12-(p-MeO-Ph)-HBI, 22: 12-(p-MeCO2-Ph)-HBI, 23: 4-Me-10-Cl-HBI, 24: 4-Me-10-CF3-HBI, 25: 10-Ph-12-Ph-HBI, 26: 2-(CH2CH2CH=CH2)-8-(CH2CH2Ph)-HBI, 27: 2-F-3-F-4-F-5-F-HBI. Color code: hydrogen in white, carbon in grey, nitrogen in blue, and oxygen in red.
Preprints 68189 g001
Table 1. Correlation coefficient (R2) between the isotropic molecular polarizability (αiso, in Bohr3) and ITA quantities (in a.u.), molecular volume (Vol, in Bohr3/mol), and the isotropic quadrupole moment (Θiso, in a.u.) at S0.
Table 1. Correlation coefficient (R2) between the isotropic molecular polarizability (αiso, in Bohr3) and ITA quantities (in a.u.), molecular volume (Vol, in Bohr3/mol), and the isotropic quadrupole moment (Θiso, in a.u.) at S0.
Index αiso SS IF SGBP rR2 rR3 IG G1 G2 G3 Vol Θiso
1 175.68 96.35 4343.89 746.75 112.64 117.78 1.38 ‒35.34 24.07 139.78 1715.75 ‒87.39
2 200.87 20.66 13967.27 973.91 146.61 151.68 1.36 ‒34.93 23.70 141.74 2073.70 ‒103.29
3 237.32 142.90 5692.80 1016.86 154.03 161.91 2.10 ‒50.98 35.00 196.05 2441.40 ‒115.43
4 182.97 97.74 4793.46 801.56 120.76 126.07 1.45 ‒34.44 22.49 147.78 1855.73 ‒91.79
5 197.76 107.94 5045.63 855.45 129.06 135.01 1.60 ‒39.10 25.75 159.82 1886.74 ‒95.32
6 175.11 92.94 4917.98 801.81 120.62 125.71 1.37 ‒34.55 22.69 144.27 1765.67 ‒93.87
7 188.87 81.70 6524.29 855.22 128.61 133.70 1.37 ‒34.93 22.13 142.27 1959.26 ‒100.99
8 197.51 20.60 13967.06 973.87 146.60 151.67 1.36 ‒34.95 23.67 141.84 1850.09 ‒101.48
9 194.07 102.37 4928.42 829.28 124.78 130.18 1.46 ‒36.68 23.12 151.22 1897.41 ‒106.85
10 189.36 106.46 4595.48 800.72 120.93 126.64 1.53 ‒39.13 25.97 150.98 1931.31 ‒93.18
11 194.81 107.96 5045.77 855.48 129.06 135.02 1.60 ‒39.13 23.71 159.81 1994.38 ‒95.26
12 191.68 81.72 6524.35 855.23 128.60 133.66 1.36 ‒34.98 22.67 142.29 1957.16 ‒105.11
13 200.29 20.66 13967.37 973.93 146.60 151.67 1.36 ‒35.01 22.86 141.85 1980.91 ‒111.96
14 198.88 102.42 4928.71 829.32 124.77 130.16 1.45 ‒36.79 23.62 151.19 1696.49 ‒112.11
15 190.18 106.46 4595.43 800.71 120.93 126.64 1.53 ‒39.12 24.61 151.02 1842.17 ‒94.41
16 191.22 96.42 6318.70 965.73 144.80 150.24 1.46 ‒37.81 23.40 165.13 2064.71 ‒117.92
17 255.95 135.18 5826.22 1017.73 153.69 160.90 1.92 ‒52.71 36.65 192.16 2401.28 ‒125.79
18 246.58 135.11 5826.00 1017.67 153.68 160.90 1.92 ‒52.74 36.93 192.52 2494.60 ‒119.81
19 277.67 146.79 6528.00 1126.45 170.10 178.13 2.14 ‒56.48 38.53 212.18 2819.11 ‒137.35
20 295.24 153.19 7225.20 1222.09 184.32 192.76 2.25 ‒58.90 39.85 226.76 2761.18 ‒154.13
21 268.01 146.71 6527.76 1126.38 170.10 178.12 2.14 ‒56.47 39.11 212.53 2467.93 ‒128.04
22 283.05 153.12 7225.00 1222.03 184.32 192.76 2.25 ‒58.93 39.71 227.00 2913.80 ‒139.45
23 205.46 91.83 6775.95 909.20 136.89 142.52 1.51 ‒38.70 26.44 153.26 1963.41 ‒110.94
24 205.03 106.53 6570.28 1019.70 153.09 159.11 1.61 ‒41.55 26.57 176.20 2201.13 ‒123.83
25 327.20 173.93 7308.31 1288.65 194.73 204.01 2.46 ‒70.08 50.17 244.74 3066.91 ‒156.33
26 320.10 190.84 7330.19 1328.47 201.30 211.70 2.76 ‒74.61 52.80 255.30 3332.26 ‒160.67
27 175.19 82.72 6640.05 966.86 144.50 149.36 1.31 ‒32.94 20.03 158.50 3218.41 ‒108.98
R2 1.000 0.581 0.005 0.859 0.868 0.883 0.927 0.959 0.955 0.931 0.618 0.869
Table 2. Correlation coefficient (R2) between the isotropic molecular polarizability (αiso, in Bohr3) and ITA quantities (in a.u.), molecular volume (Vol, in Bohr3/mol), and the isotropic quadrupole moment (Θiso, in a.u.) at S1.
Table 2. Correlation coefficient (R2) between the isotropic molecular polarizability (αiso, in Bohr3) and ITA quantities (in a.u.), molecular volume (Vol, in Bohr3/mol), and the isotropic quadrupole moment (Θiso, in a.u.) at S1.
Index αiso SS IF rR2 rR3 G2 G3 Vol Θiso
1 166.08 96.94 4345.68 112.73 118.02 23.88 138.16 1784.17 ‒89.93
2 189.81 21.28 13969.19 146.67 151.87 23.61 140.08 1956.89 ‒114.26
3 224.23 143.51 5694.61 154.12 162.16 34.15 194.24 2519.29 ‒126.71
4 174.81 98.36 4795.23 120.83 126.27 22.33 146.07 1862.89 ‒96.38
5 187.84 108.57 5047.40 129.14 135.22 25.53 158.13 1983.35 ‒101.96
6 166.88 93.55 4919.65 120.68 125.87 22.56 142.61 1809.41 ‒97.69
7 182.88 82.29 6525.95 128.66 133.83 23.33 140.53 1948.71 ‒105.58
8 188.20 21.19 13968.88 146.65 151.80 22.97 140.28 1945.05 ‒110.07
9 182.03 103.04 4930.44 124.83 130.34 24.17 149.51 1945.30 ‒110.22
10 178.88 107.05 4597.05 121.02 126.88 26.58 149.31 1919.82 ‒96.99
11 182.81 108.54 5047.21 129.14 135.22 25.57 158.15 1992.00 ‒99.73
12 178.54 82.29 6526.00 128.69 133.90 23.14 140.43 1905.76 ‒103.35
13 186.41 21.24 13968.99 146.69 151.92 23.40 139.90 1961.97 ‒105.81
14 185.73 102.96 4930.10 124.85 130.37 24.33 149.38 1959.21 ‒111.23
15 179.03 107.06 4597.29 121.01 126.87 26.78 149.25 1938.52 ‒94.93
16 178.64 96.95 6320.18 144.88 150.45 23.97 163.21 2040.58 ‒111.79
17 240.42 135.77 5827.95 153.76 161.09 36.81 190.49 2466.79 ‒117.96
18 253.40 135.66 5827.52 153.75 161.08 36.75 190.81 2411.54 ‒120.97
19 260.31 147.38 6529.77 170.17 178.31 39.03 210.40 2664.07 ‒124.40
20 280.48 153.76 7226.84 184.39 192.94 40.08 225.02 2822.78 ‒136.33
21 267.99 147.29 6529.43 170.17 178.33 38.50 210.79 2665.63 ‒128.47
22 327.99 153.50 7225.08 184.32 192.78 39.42 226.35 2798.30 ‒138.46
23 190.90 92.40 6777.37 136.99 142.77 25.46 151.82 2091.13 ‒110.61
24 191.30 107.05 6571.54 153.18 159.32 26.69 174.50 2213.23 ‒119.08
25 331.10 174.16 7307.99 194.72 204.02 48.71 244.76 3050.07 ‒168.67
26 309.58 191.50 7332.09 201.39 211.92 53.05 253.29 3379.72 ‒164.60
27 190.21 83.28 6640.35 144.47 149.29 19.82 157.57 1894.17 ‒115.25
R2 1.000 0.560 0.004 0.861 0.874 0.884 0.917 0.908 0.831
Table 3. Correlation coefficient (R2) between the αiso@S1, and αiso@S0, ITA quantities@S0, Vol@S0, and Θiso@S0.
Table 3. Correlation coefficient (R2) between the αiso@S1, and αiso@S0, ITA quantities@S0, Vol@S0, and Θiso@S0.
αiso SS IF SGBP rR2 rR3
R2 0.941 0.561 0.004 0.855 0.862 0.874
IG G1 G2 G3 Vol Θiso
R2 0.876 0.906 0.896 0.914 0.688 0.814
Table 4. Correlation coefficient (R2) between the αiso@S0/S1 and ITA quantities based on the transition density matrix.
Table 4. Correlation coefficient (R2) between the αiso@S0/S1 and ITA quantities based on the transition density matrix.
R2 SS IF SGBP rR2 rR3 IG G1 G2 G3
αiso@S0 0.580 0.005 0.859 0.868 0.883 0.927 0.959 0.955 0.932
αiso@S1 0.561 0.004 0.855 0.862 0.874 0.873 0.907 0.897 0.914
Table 5. Comparison of molecular polarizabilities (αiso) at S0/S1 predicted by the original TS formula with conventional data as reference.
Table 5. Comparison of molecular polarizabilities (αiso) at S0/S1 predicted by the original TS formula with conventional data as reference.
Index Ground-state (S0) Excited-state (S1)
Becke Hirshfeld avg. Becke Hirshfeld avg.
1 119.84 176.99 148.41 121.05 176.63 148.84
2 228.99 281.15 255.07 228.53 279.36 253.95
3 167.92 250.19 209.05 169.26 249.87 209.56
4 122.82 182.28 152.55 124.20 182.08 153.14
5 132.97 197.56 165.27 134.35 197.34 165.84
6 119.40 177.07 148.24 120.98 177.15 149.06
7 170.42 224.86 197.64 170.23 223.53 196.88
8 229.52 281.83 255.67 227.91 279.02 253.46
9 129.98 189.98 159.98 131.48 190.06 160.77
10 129.77 192.41 161.09 131.17 192.26 161.72
11 132.81 197.40 165.11 134.35 197.35 165.85
12 169.65 224.32 196.98 172.04 224.59 198.32
13 227.44 279.92 253.68 231.41 281.70 256.56
14 130.12 190.12 160.12 131.17 189.61 160.39
15 129.85 192.48 161.16 131.10 192.26 161.68
16 130.63 194.40 162.51 131.24 193.58 162.41
17 167.50 248.17 207.83 168.68 247.78 208.23
18 167.20 248.13 207.66 168.36 247.93 208.14
19 180.67 268.74 224.70 181.79 268.33 225.06
20 190.15 282.83 236.49 191.24 282.39 236.82
21 180.36 268.73 224.55 181.54 268.42 224.98
22 189.86 282.78 236.32 190.76 283.63 237.19
23 179.61 239.76 209.69 182.19 240.24 211.21
24 140.56 209.82 175.19 141.35 209.19 175.27
25 214.86 319.29 267.08 214.84 321.13 267.99
26 226.85 337.95 282.40 228.26 337.38 282.82
27 119.65 177.97 148.81 121.63 179.51 150.57
MUE (%)a –24.90 6.62 –9.14 –21.21 10.82 –5.19
MSE (%)b 28.14 8.10 16.00 26.07 12.63 15.23
aMUE: mean unsigned error.bMSE: mean signed error.
Table 6. Comparison of molecular polarizabilities (αiso) at S0/S1 predicted by the new TS formula with conventional data as reference.
Table 6. Comparison of molecular polarizabilities (αiso) at S0/S1 predicted by the new TS formula with conventional data as reference.
Index Ground-state (S0) Excited-state (S1)
Becke Hirshfeld avg. Becke Hirshfeld avg.
1 119.84 176.99 148.41 121.05 176.63 148.84
2 228.99 281.15 255.07 228.53 279.36 253.95
3 167.92 250.19 209.05 169.26 249.87 209.56
4 122.82 182.28 152.55 124.20 182.08 153.14
5 132.97 197.56 165.27 134.35 197.34 165.84
6 119.40 177.07 148.24 120.98 177.15 149.06
7 170.42 224.86 197.64 170.23 223.53 196.88
8 229.52 281.83 255.67 227.91 279.02 253.46
9 129.98 189.98 159.98 131.48 190.06 160.77
10 129.77 192.41 161.09 131.17 192.26 161.72
11 132.81 197.40 165.11 134.35 197.35 165.85
12 169.65 224.32 196.98 172.04 224.59 198.32
13 227.44 279.92 253.68 231.41 281.70 256.56
14 130.12 190.12 160.12 131.17 189.61 160.39
15 129.85 192.48 161.16 131.10 192.26 161.68
16 130.63 194.40 162.51 131.24 193.58 162.41
17 167.50 248.17 207.83 168.68 247.78 208.23
18 167.20 248.13 207.66 168.36 247.93 208.14
19 180.67 268.74 224.70 181.79 268.33 225.06
20 190.15 282.83 236.49 191.24 282.39 236.82
21 180.36 268.73 224.55 181.54 268.42 224.98
22 189.86 282.78 236.32 190.76 283.63 237.19
23 179.61 239.76 209.69 182.19 240.24 211.21
24 140.56 209.82 175.19 141.35 209.19 175.27
25 214.86 319.29 267.08 214.84 321.13 267.99
26 226.85 337.95 282.40 228.26 337.38 282.82
27 119.65 177.97 148.81 121.63 179.51 150.57
MUE (%)a –28.40 6.77 –10.82 –24.74 11.05 –6.84
MSE (%)b 39.16 15.48 26.74 37.89 16.21 26.41
aMUE: mean unsigned error.bMSE: mean signed error.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

191

Views

59

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated