Submitted:
08 February 2023
Posted:
09 February 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- Introducing a combined mathematical-heuristic-metaheuristic technique for the extraction and simplification of symbolic poles and zeros in OTAs.
- Proposing an enhanced root splitting technique, named ERS, to accurately extract the exact pole/zero expressions.
- Presenting a combined heuristic-metaheuristic algorithm for symbolic pole/zero simplification (named PZSA) utilizing heuristic knowledge available in the circuit model and simulated annealing.
- Programming of the proposed method in a MATLAB m-file, wherein simplified pole/zero equations are automatically generated from the circuit netlist.
- Successfully driving symbolic pole/zero expressions for three OTAs.
2. Literature Review
2.1. Symbolic Simplification Techniques
2.2. Symbolic Pole/Zero Extraction Techniques
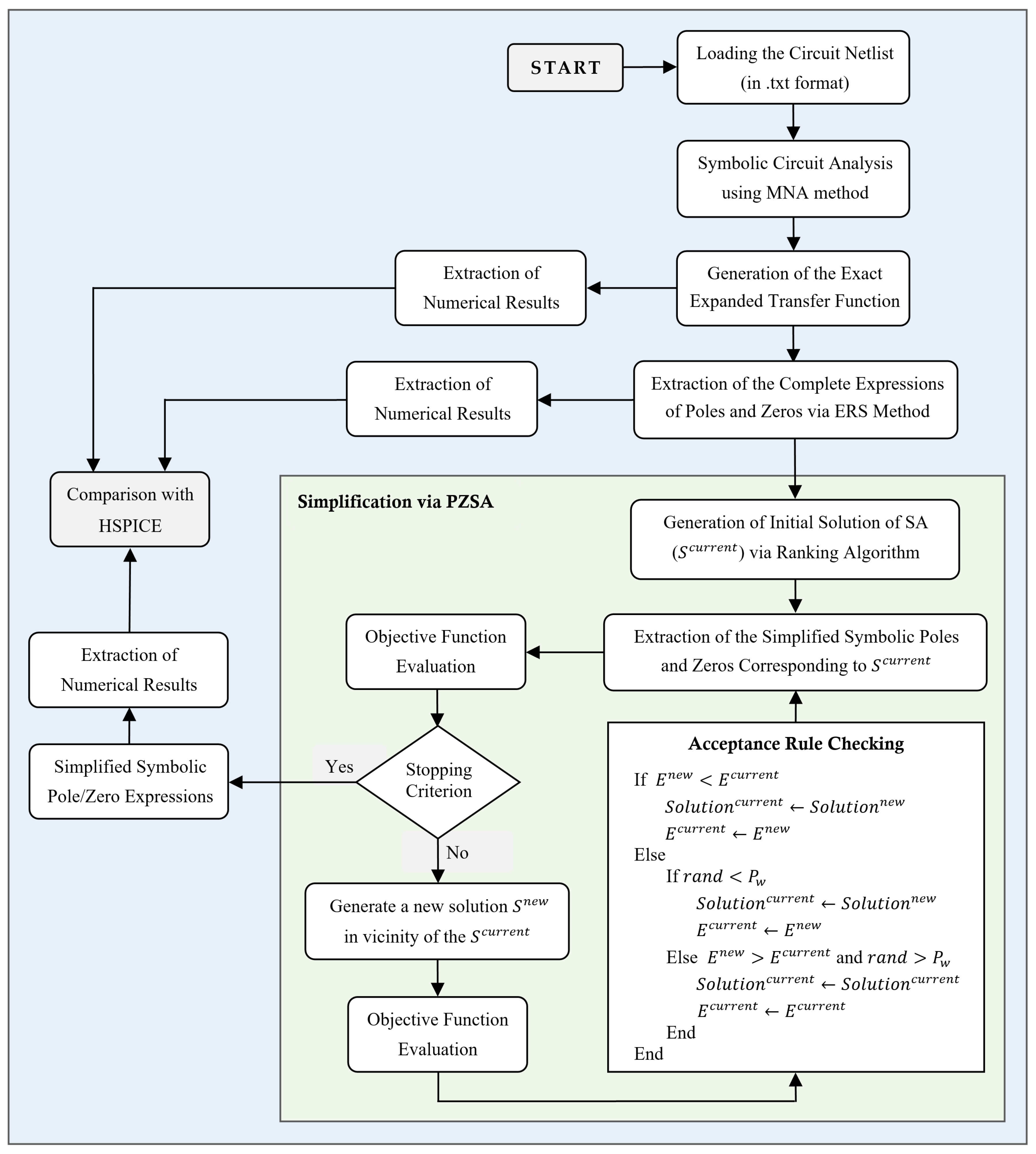
3. Proposed Method
- 1)
- Input circuit netlist is loaded as a text file (in .txt format).
- 2)
- All transistors are replaced via proper small-signal modeling.
- 3)
- The symbolic circuit is solved via a modified nodal analysis (MNA).
- 4)
- The exact transfer function (TF) is achieved in the expanded symbolic form.
- 5)
- Exact expressions of poles and zeroes are derived using ERS.
- 6)
- Numerical results of the exact symbolic pole/zero expressions are stored.
- 7)
- A heuristic algorithm is performed to generate a near-optimal solution utilizing the circuit-based knowledge available in the exact poles and zeroes.
- 8)
- SA is performed to improve further the quality of the heuristic solution, to generate the final simplified symbolic pole/zero expressions.
- 9)
- Numerical results of the obtained simplified symbolic pole/zero expressions are calculated.
- 10)
- Numerical results of the exact and simplified poles/zeros are compared against HSPICE and other simplification algorithms.
3.1. Pole/Zero Extraction via ERS
3.2. Pole/Zero Simplification via PZSA
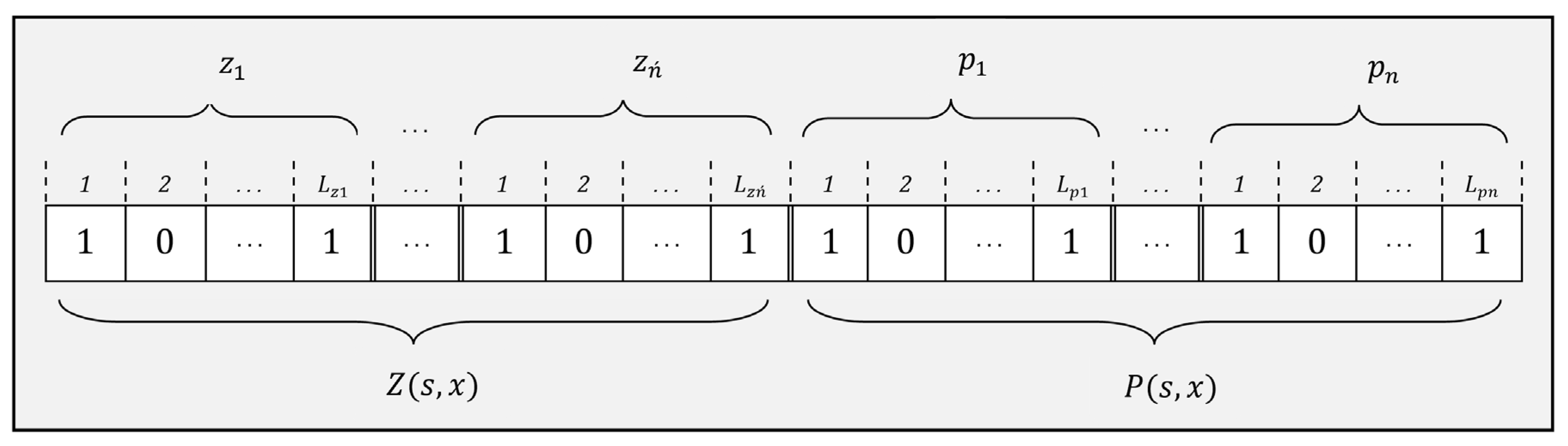
3.2.1. Solution Encoding/Decoding
3.2.2. Generation of the Initial Solution
3.2.3. Objective Function Evaluation
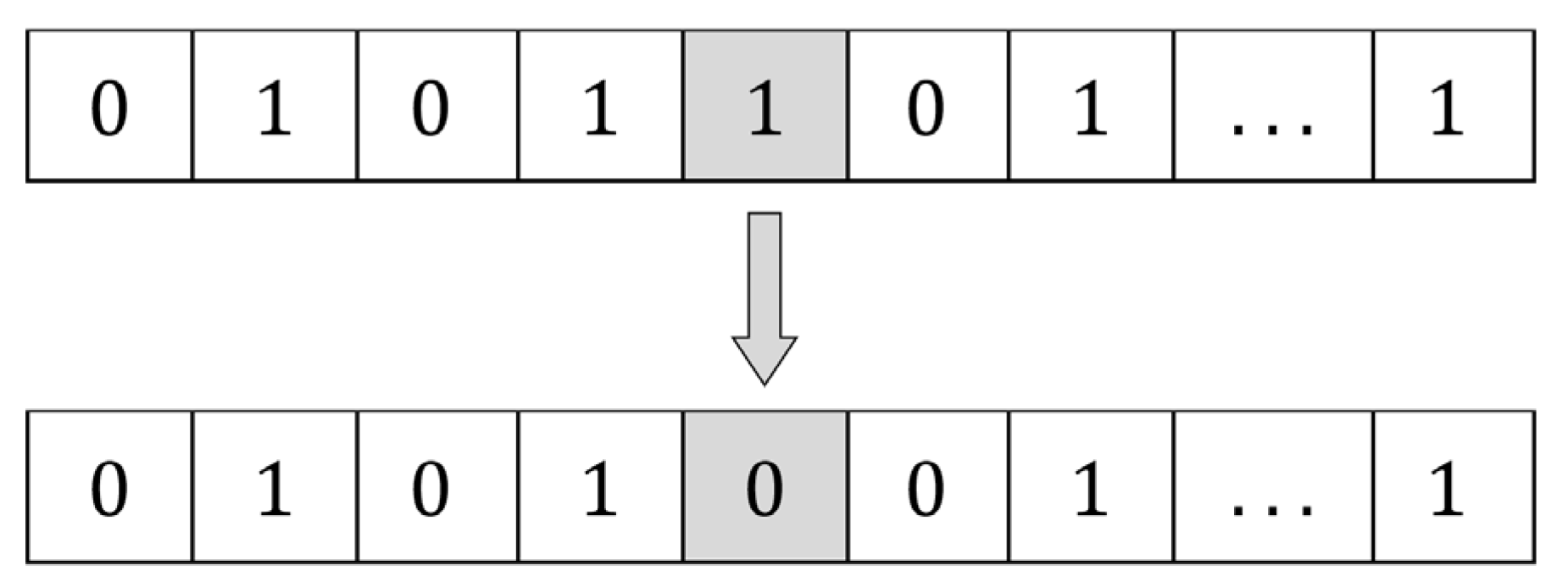
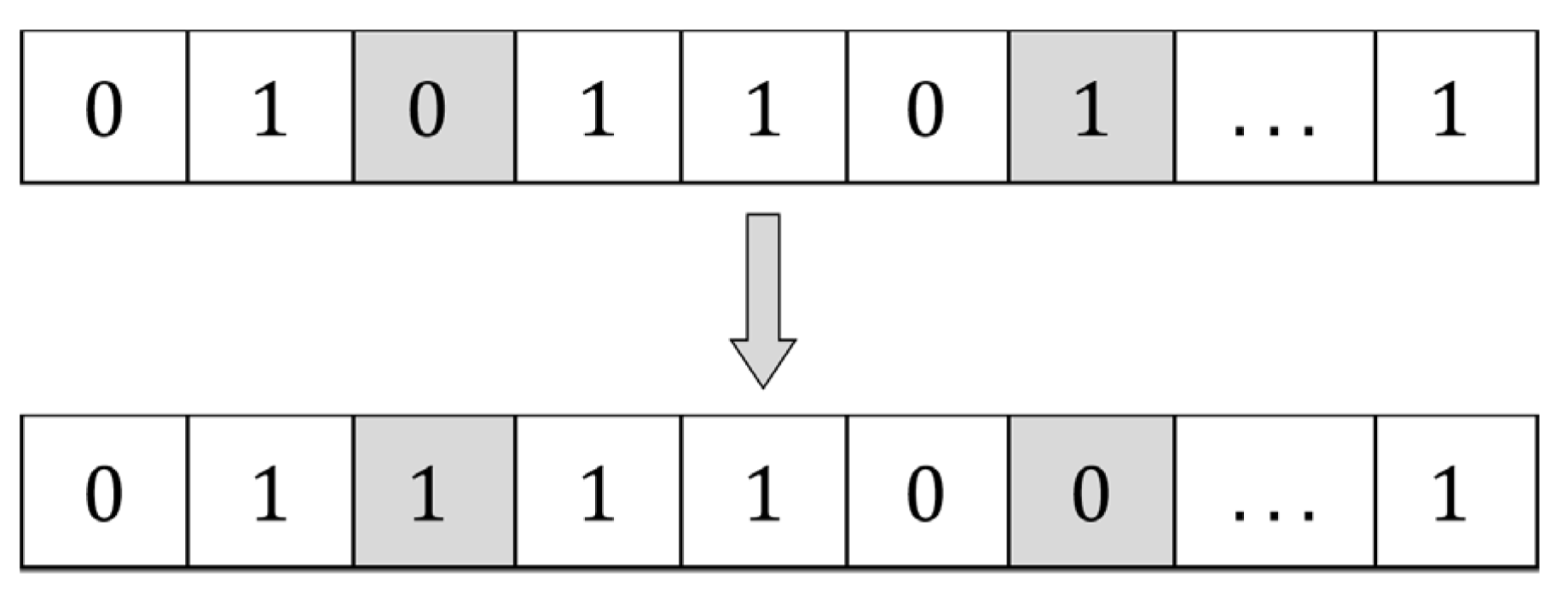
3.2.4. Generation of a New Solution
3.2.5. Acceptance Rule Checking
4. Performance Evaluation
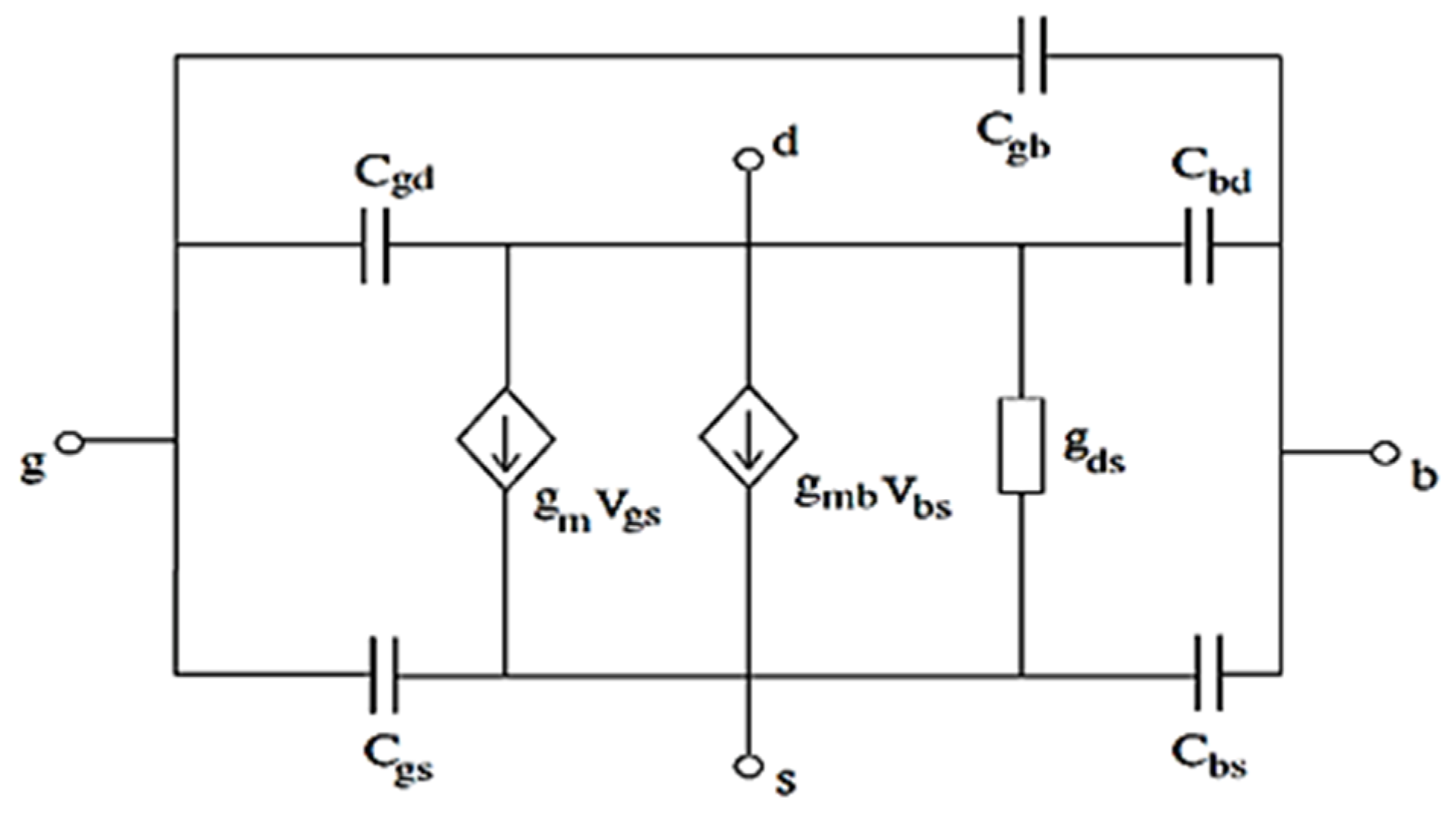
4.1. Results for a Three-Stage Amplifier in the RCgm Model (Circuit 1)
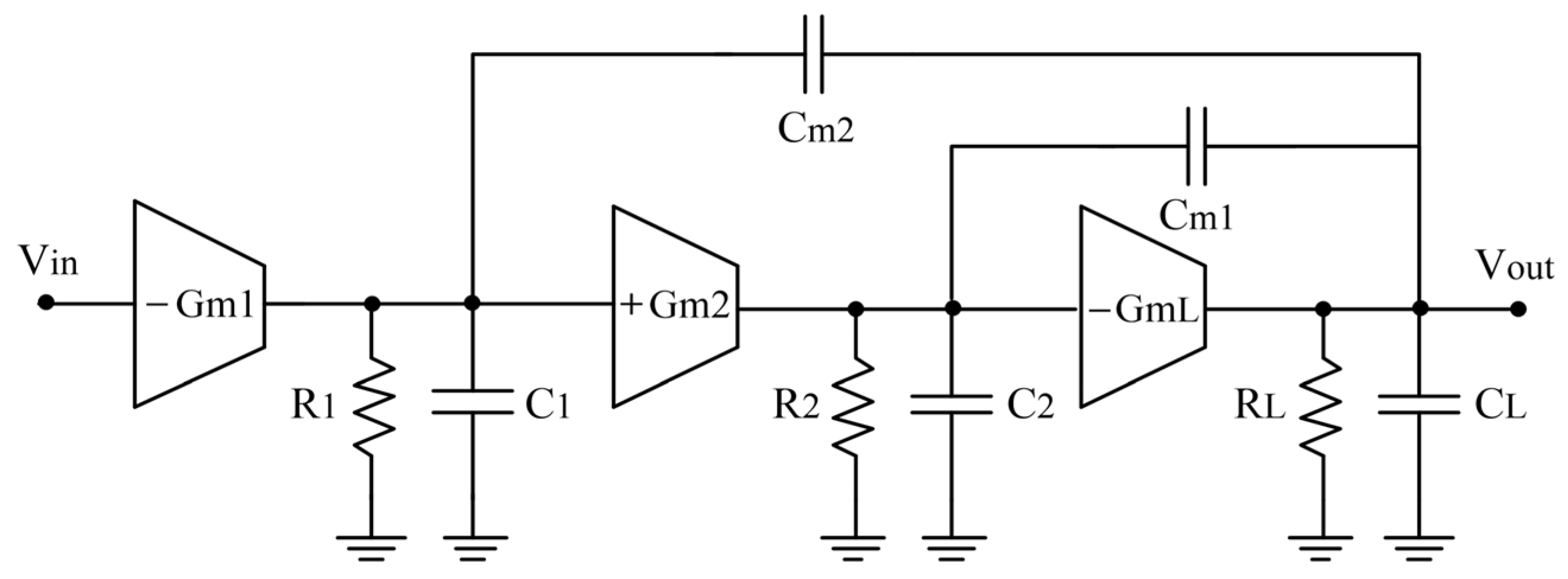
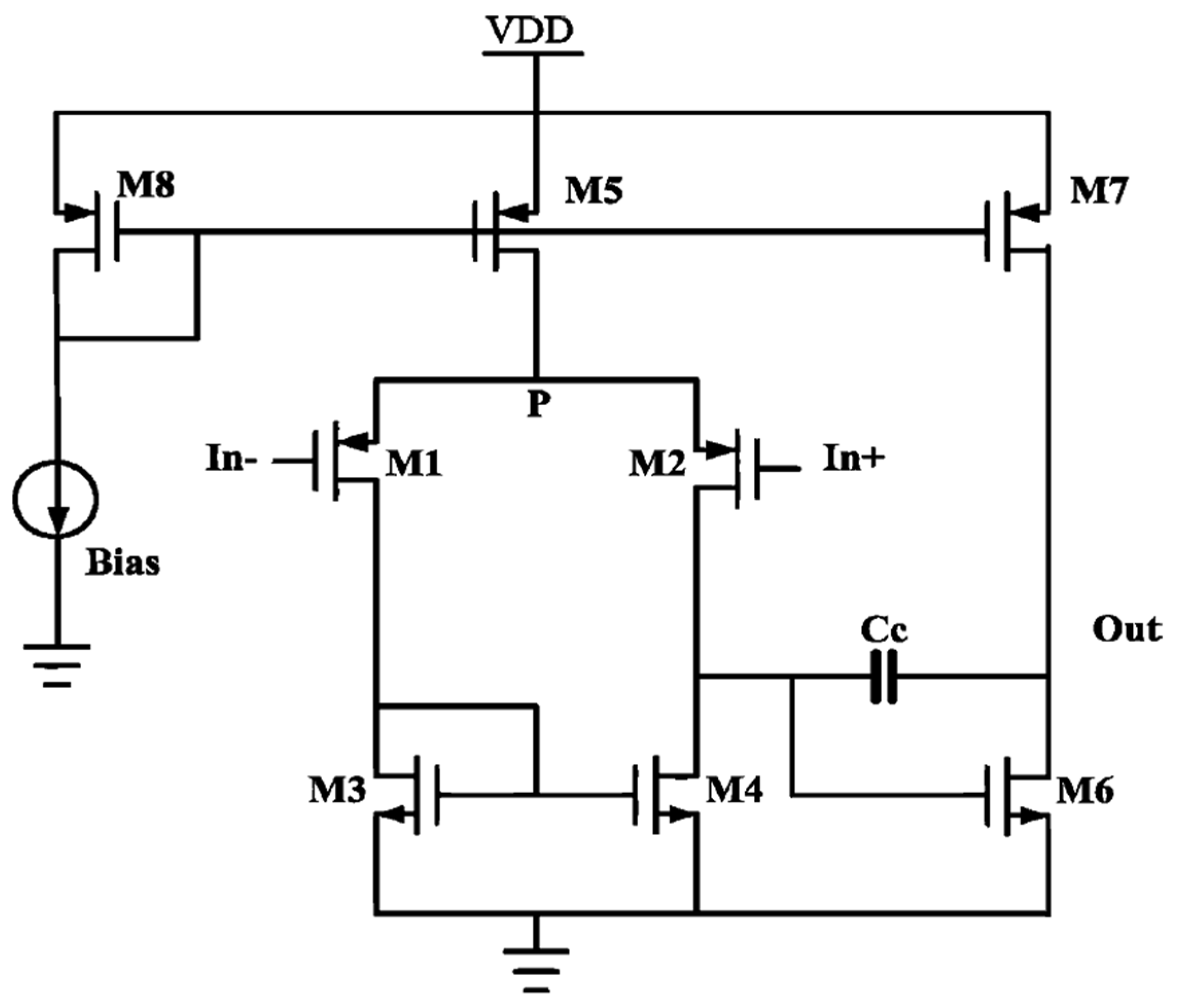
4.2. Results for a Two-Stage Miller Compensated Amplifier (Circuit 2)
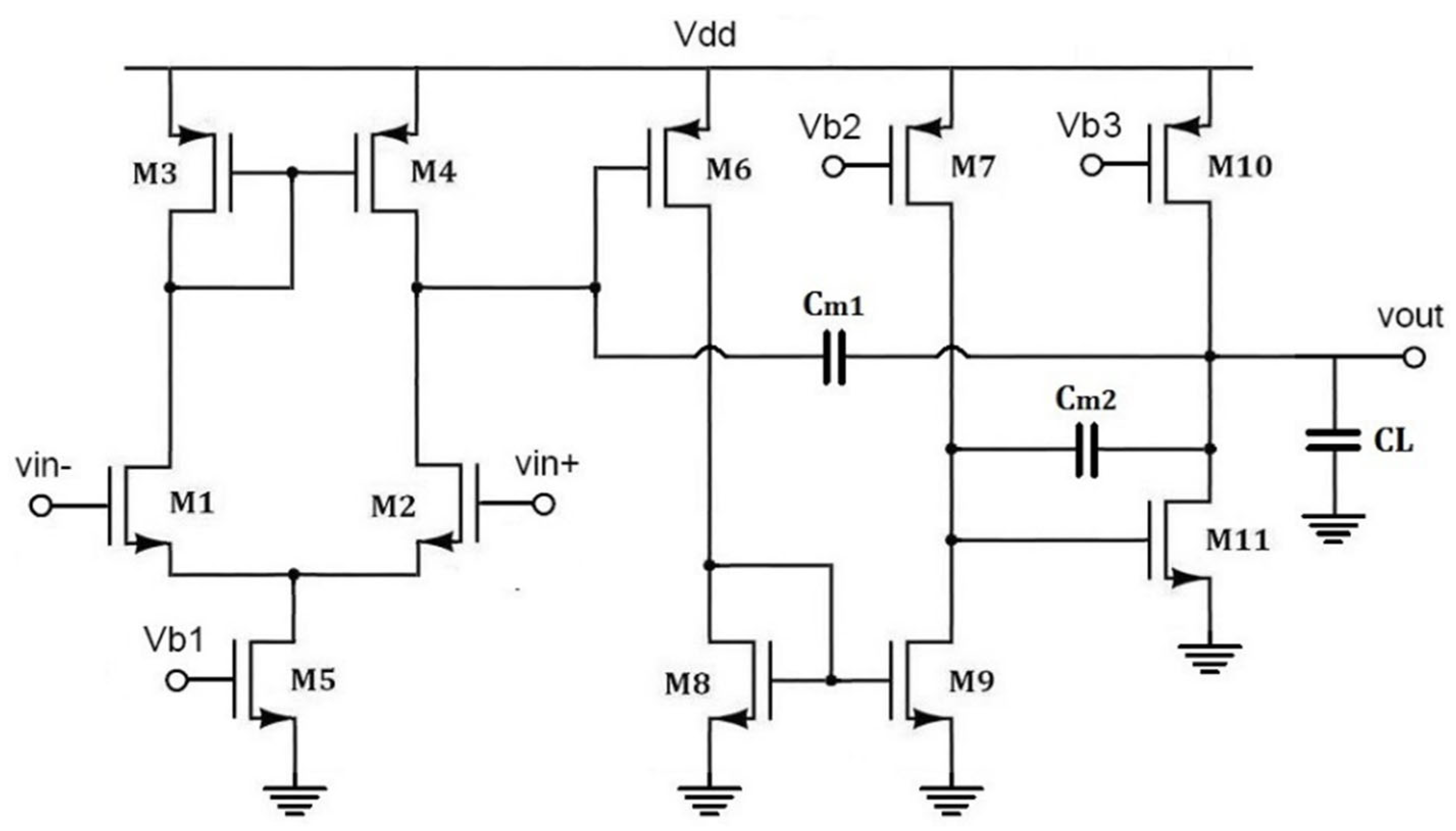
4.3. Results for a Three-Stage Amplifier in Transistor Model (Circuit 3)
4.4. Discussion
- Error-1: the first type of error may occur by comparing HSPICE with the exact expanded TF achieved by MNA. This error may be observed for OTAs described in the transistor level, as HSPICE considers more accurate small-signal modeling for transistors than the simple model in our program (see Figure 5).
- Error-2: the second type of error may be observed when comparing the exact TF with the exact extracted poles/zeroes, because of the simplifications done by the root extraction process via the ERS method.
- Error-3: the third error may occur between exact pole/zero expressions and the simplified ones, due to the simplifications done by PZSA.
5. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Riad, J.; Soto-Aguilar, S.; Estrada-López, J.J.; Moreira-Tamayo, O.; Sánchez-Sinencio, E. Design Trade-Offs in Common-Mode Feedback Implementations for Highly Linear Three-Stage Operational Transconductance Amplifiers. Electronics 2021, 10, 991. [Google Scholar] [CrossRef]
- Rodovalho, L.H.; Toledo, P.; Mir, F.; Ebrahimi, F. Hybrid Inverter-Based Fully Differential Operational Transconductance Amplifiers. Chips 2023, 2, 1–19. [Google Scholar] [CrossRef]
- Akbari, M.; Shokouhifar, M.; Hashemipour, O.; Jalali, A.; Hassanzadeh, A. Systematic design of analog integrated circuits using ant colony algorithm based on noise optimization. Analog. Integr. Circuits Signal Process. 2016, 86, 327–339. [Google Scholar] [CrossRef]
- Ghorbanzadeh, S.; Dehbovid, H.; Ghorbani, A.; Abedi Pahnekolaei, S.M. Design and Analysis of a Two stage Class AB Operational Transconductance Amplifier in 180nm Technology. J. Appl. Dyn. Syst. Control 2022, 5, 35–43. [Google Scholar]
- Akbari, M.; Hussein, S.M.; Hashim, Y.; Khateb, F.; Kulej, T.; Tang, K.T. Implementation of a Multipath Fully Differential OTA in 0.18-μm CMOS Process. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 31, 147–151. [Google Scholar] [CrossRef]
- Aminzadeh, H.; Grasso, A.D.; Palumbo, G. A methodology to derive a symbolic transfer function for multistage amplifiers. IEEE Access 2022, 10, 14062–14075. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Jalali, A. Simplified symbolic transfer function factorization using combined artificial bee colony and simulated annealing. Appl. Soft Comput. 2017, 55, 436–451. [Google Scholar] [CrossRef]
- Grasso, A.D.; Marano, D.; Pennisi, S.; Vazzana, G. Symbolic factorization methodology for multistage amplifier transfer functions. Int. J. Circuit Theory Appl. 2015, 44, 38–59. [Google Scholar] [CrossRef]
- Shi, G.; Tan SX, D.; Tlelo-Cuautle, E. Advanced Symbolic Analysis for VLSI Systems 2014. Springer.
- Hayes, M. Lcapy: symbolic linear circuit analysis with Python. PeerJ Comput. Sci. 2022, 8, e875. [Google Scholar] [CrossRef]
- Dziedziewicz, S.; Warecka, M.; Lech, R.; Kowalczyk, P. Self-Adaptive Mesh Generator for Global Complex Roots and Poles Finding Algorithm. IEEE Trans. Microw. Theory Tech. 2023. [CrossRef]
- Rodriguez-Garcia, J.D.; Guerra, O.; Fernandez, F.V.; Rodriguez-Vazquez, A. Symbolic pole/zero extraction through dedicated SBG/SDG techniques. In Proc. SMACD 1998 (pp. 43–48).
- Gomes, J.L.; Nunes, L.C.; Gonçalves, C.F.; Pedro, J.C. An accurate characterization of capture time constants in GaN HEMTs. IEEE Trans. Microw. Theory Tech. 2019, 67, 2465–2474. [Google Scholar] [CrossRef]
- Cao, H. , Zhang, Y., Han, Z., Shao, X., Gao, J., Huang, et al. Temperature compensation circuit design and experiment for dual-mass MEMS gyroscope bandwidth expansion. IEEE/ASME Trans. Mechatron. 2019, 24, 677–688. [Google Scholar] [CrossRef]
- Coşkun K, Ç.; Hassan, M.; Drechsler, R. Equivalence Checking of System-Level and SPICE-Level Models of Linear Circuits. Chips 2022, 1, 54–71. [Google Scholar] [CrossRef]
- Marin, M.E.; Staicu, C.S.; Gheorghe, A.G.; Constantinescu, F. Generation of state equations for circuits with excess elements. In 2020 International Symposium on Fundamentals of Electrical Engineering 2020, (pp. 1-4). IEEE.
- Noferini, V.; Van Dooren, P. On computing root polynomials and minimal bases of matrix pencils. Linear Algebra Its Appl. 2023, 658, 86–115. [Google Scholar] [CrossRef]
- Moir, T.J. A study on square root control-systems. J. Comput. Appl. Math. 2022, 406, 113938. [Google Scholar] [CrossRef]
- Evnin, O. Melonic dominance and the largest eigenvalue of a large random tensor. Lett. Math. Phys. 2021, 111, 66. [Google Scholar] [CrossRef]
- Gheorghe, A.G.; Constantinescu, F. Pole/Zero Computation for Linear Circuits. In 2012 Sixth UKSim/AMSS European Symposium on Computer Modeling and Simulation 2012, (pp. 477–480).
- Gheorghe, A.G.; Constantinescu, F.; Nitescu, M. Improved LR algorithm for computation of the approximate symbolic pole/zero expressions. In Proc. AFRICON 2013, (pp. 1–4).
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Hennig, E. Symbolic Approximation and Modeling Techniques for Analysis and Design of Analog Circuits. Shaker Verlag: Herzogenrath 2000, Germany.
- Toumazou, C.; Moschytz, G.S.; Gilbert, B. Trade-offs in analog circuit design: the designer's companion. New York: Kluwer Academic Publishers 2014.
- Wierzba, G. , et al. SSPICE-A symbolic SPICE program for linear active circuits. In Midwest Symposium on Circuits and Systems 1989, (pp. 1197–1201).
- Fernandez, F.; Vazquez, A.R.; Huertas, J. Interactive AC modeling and characterization of analog circuits via symbolic analysis. Kluwer J. Analog. Integr. Circuits Signal Process. 1991, 1, 183–208. [Google Scholar]
- Gielen, G.; Walscharts, H.; Sansen, W. ISAAC: a symbolic simulator for analog integrated circuits. IEEE J. Solid-State Circuits 1989, 24, 1587–1597. [Google Scholar] [CrossRef]
- Fakhfakh, M.; Cuautle, E.T.; Fernandez, F.V. Design of analog circuits through symbolic analysis. Sharjah: Bentham Science Publishers, 2012.
- Shokouhifar, M.; Jalali, A. An evolutionary-based methodology for symbolic simplification of analog circuits using genetic algorithm and simulated annealing. Expert Syst. Appl. 2015, 42, 1189–1201. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Jalali, A. Automatic Simplified Symbolic Analysis of Analog Circuits Using Modified Nodal Analysis and Genetic Algorithm. J. Circuits Syst. Comput. 2015, 24, 1–20. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Jalali, A. Evolutionary based simplified symbolic PSRR analysis of analog integrated circuits. Analog. Integr. Circuits Signal Process. 2016, 86, 189–205. [Google Scholar] [CrossRef]
- Panda, M.; Kumar Patnaik, S.; Kumar Mal, A.; Ghosh, S. Fast and optimised design of a differential VCO using symbolic technique and multi objective algorithms. IET Circuits Devices Syst. 2019, 13, 1187–1195. [Google Scholar] [CrossRef]
- Panda, M.; Patnaik, S.K.; Mal, A.K. An efficient method to compute simplified noise parameters of analog amplifiers using symbolic and evolutionary approach. Int. J. Numer. Model. Electron. Netw. Devices Fields 2021, 34, e2790. [Google Scholar] [CrossRef]
- Zhou, R.; Poechmueller, P.; Wang, Y. An Analog Circuit Design and Optimization System with Rule-Guided Genetic Algorithm. IEEE Trans. Comput. -Aided Des. Integr. Circuits Syst. 2022, 41, 5182–5192. [Google Scholar] [CrossRef]
- Sohrabi, M.; Zandieh, M.; Shokouhifar, M. Sustainable inventory management in blood banks considering health equity using a combined metaheuristic-based robust fuzzy stochastic programming. Socio-Econ. Plan. Sci. 2022, 86, 101462. [Google Scholar] [CrossRef]
| Sets / Parameters | Definition |
|---|---|
| Index of poles, | |
| Index of zeroes, | |
| Degree of the denominator within the exact expanded TF | |
| Degree of the numerator within the exact expanded TF | |
| Index of the symbolic terms, | |
| Number of symbolic terms within all pole/zero expressions | |
| Defined frequency bound range for the pole/zero extraction | |
| A binary decision parameter defining whether the -th symbolic term is used or not | |
| Set of poles in the frequency range of | |
| ZeroSet | Set of zeroes in the frequency range of |
| -th pole within the exact expanded TF | |
| -th extracted pole via ERS | |
| -th simplified pole via SA | |
| Mean pole displacements (in %) | |
| -th zero of the exact expanded TF | |
| -th extracted zero via ERS | |
| -th simplified zero via SA | |
| Mean zero displacements (in %) | |
| Maximum allowable pole/zero extraction error via ERS | |
| Maximum allowable pole/zero simplification error via SA |
| Phase | Parameter | Value/Description |
|---|---|---|
| Pole/Zero | in Eqs. (32,33) | 10 % |
| Extraction | 1 Hz | |
| Parameters | 10 × | |
| Maximum iterations | 5 × L | |
| SA | Local search mechanisms | Swap & Exchange |
| Parameters | in Eq. (41) | 10-5 |
| in Eq. (41) | 0 | |
| Objective | in Eq. (35) | 0.999 |
| Function | in Eq. (35) | 0.001 |
| Parameters | in Eqs. (38) and (39) | 20 % |
| Expression | Exact Symbolic | Ref. [34] | Ref. [13] | Ref. [15] | Proposed (Complete) | Proposed (Simplified) |
|---|---|---|---|---|---|---|
| P1 | N/A | N/A | 1 | 10 | 10 | 1 |
| P2 | N/A | N/A | 4 | 26 | 26 | 3 |
| P3 | N/A | N/A | 5 | 25 | 25 | 3 |
| Z1 | N/A | N/A | 2 | 9 | 3 | 2 |
| Z2 | N/A | N/A | 2 | 9 | 4 | 2 |
| Overall Transfer Function | 40 | 10 | N/A | N/A | N/A | N/A |
| Parameter | HSPICE | Exact Symbolic | Ref. [34] | Ref. [13] | Ref. [15] | Proposed (Complete) | Proposed (Simplified) |
|---|---|---|---|---|---|---|---|
| P1 (Hz) | -12.8 | -12.8 | -13.3 | -13.2 | -12.8 | -12.8 | -13.2 |
| P2 (MHz) | -3.19 | -3.19 | -3.49 | -3.19 | -2.96 | -2.96 | -3.18 |
| P3 (MHz) | -40.6 | -40.6 | -36.3 | -43.9 | -43.8 | -43.8 | -39.8 |
| Z1 (MHz) | 2.72 | 2.72 | 2.72 | 3.18 | 3.36 | 3.18 | 3.18 |
| Z2 (MHz) | -18.6 | -18.6 | -18.6 | -15.9 | -17.5 | -15.9 | -15.9 |
| Mean pole displacement (%) | N/A | N/A | 7.8 | 3.8 | 5 | 5 | 1.9 |
| Max pole displacement (%) | N/A | N/A | 10.6 | 8.36 | 7.9 | 7.9 | 3.5 |
| Mean zero displacement (%) | N/A | N/A | 0.03 | 15.9 | 14.7 | 15.8 | 15.9 |
| Max zero displacement (%) | N/A | N/A | 0.04 | 17.1 | 23.6 | 17.1 | 17.1 |
| Expression | Exact Symbolic | Ref. [34] | Ref. [13] | Ref. [15] | Proposed (Complete) | Proposed (Simplified) |
|---|---|---|---|---|---|---|
| P1 | N/A | N/A | 5 | 104 | 104 | 5 |
| P2 | N/A | N/A | 7 | 82 | 82 | 2 |
| Z | N/A | N/A | 4 | 18 | 18 | 2 |
| Overall Transfer Function | 134 | 11 | N/A | N/A | N/A | N/A |
| Parameter | HSPICE | Exact Symbolic | Ref. [34] | Ref. [13] | Ref. [15] | Proposed (Complete) | Proposed (Simplified) |
|---|---|---|---|---|---|---|---|
| P1 (KHz) | -177.1 | -178.5 | -192 | -152.8 | -178.4 | -178.4 | -152.8 |
| P2 (MHz) | -377.4 | -435.4 | -409.1 | -341 | -435.6 | -435.6 | -409.3 |
| Z (MHz) | 407.2 | 409.3 | 409.3 | 409.3 | 409.3 | 409.3 | 409.3 |
| Mean pole displacement (%) | N/A | N/A | 6.8 | 18 | 0.04 | 0.04 | 10.2 |
| Max pole displacement (%) | N/A | N/A | 7.5 | 21.7 | 0.04 | 0.04 | 14.4 |
| Zero displacement (%) | N/A | N/A | 0.01 | 0.01 | 0 | 0 | 0.01 |
| Expression | Exact Symbolic | Ref. [34] | Ref. [13] | Ref. [15] | Proposed (Complete) | Proposed (Simplified) |
|---|---|---|---|---|---|---|
| P1 | N/A | N/A | 29 | 714 | 714 | 9 |
| P2 | N/A | N/A | 21 | 837 | 837 | 3 |
| P3 | N/A | N/A | 23 | 330 | 330 | 3 |
| Z1 | N/A | N/A | 15 | 75 | 75 | 2 |
| Z2 | N/A | N/A | 13 | 105 | 105 | 2 |
| Overall Transfer Function | 1320 | 18 | N/A | N/A | N/A | N/A |
| Parameter | HSPICE | Exact Symbolic | Ref. [34] | Ref. [13] | Ref. [15] | Proposed (Complete) | Proposed (Simplified) |
|---|---|---|---|---|---|---|---|
| P1 (Hz) | -27.7 | -27.9 | -20.6 | -20.5 | -27.9 | -27.9 | -22.8 |
| P2 (MHz) | -1.84 | -1.84 | -2.03 | -2.16 | -1.76 | -1.76 | -2.07 |
| P3 (MHz) | -36.6 | -40.2 | -36.3 | -36.1 | -42.1 | -42.1 | -35.7 |
| Z1 (MHz) | 1.4 | 1.4 | 1.4 | 2.23 | 1.62 | 1.62 | 1.62 |
| Z2 (MHz) | -10.3 | -10.2 | -10.5 | -7.37 | -8.81 | -8.81 | -9.1 |
| Mean pole displacement (%) | N/A | N/A | 15.6 | 18 | 3 | 3 | 14.2 |
| Max pole displacement (%) | N/A | N/A | 26.4 | 26.5 | 4.6 | 4.6 | 18.4 |
| Mean zero displacement (%) | N/A | N/A | 1.7 | 43.5 | 14.8 | 14.8 | 13.5 |
| Max zero displacement (%) | N/A | N/A | 2.9 | 59.3 | 15.9 | 15.9 | 16.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





