A New Principle to Determine the Radiative Heat Transfer in Sphere-related Surfaces

Preprint

Article

A New Principle to Determine the Radiative Heat Transfer in Sphere-related Surfaces

Altmetrics

Downloads

123

Views

Comments

Joseph Cabeza-Lainez^*

This version is not peer-reviewed

Submitted:

13 February 2023

Posted:

15 February 2023

You are already at the latest version

Alerts

Abstract

The exact determination of radiative exchanges between solids and surfaces has been a long sought-for question in heat transfer science. Being the canonical equation that rules such phenomena, a fourfold integral, it is extremely difficult to obtain an accurate solution like a formula or abacus. Over the last thirty years, the author has tried to integrate the canonical expression by sundry procedures and they have published two books and a dozen of articles on the matter, recently by virtue of computational geometry and graphic algorithms as a new way to solve the finite-difference problems that arise on complex geometries. In architectural engineering curved radiant emitters are customary since antiquity, especially in domes and vaults and their oculus, However, a consistent procedure to handle them was not readily available. The principles that are described hereby based on Cabeza-Lainez’ first principle for spherical fragments offer a complete panorama on the manner in which surface sources related or contained in spheres can be interpreted and accounted for without resorting to integration. The main advance is that a variety of unexplained problems of radiative heat transfer, applicable to aerospace engineering, meteorological, architectural and medical sciences can be sorted out as exactly as quickly.

Keywords:

Subject: Physical Sciences - Optics and Photonics

1. Introduction

One of the main objectives of environmental sciences applied to architectural engineering has been to determine how the built environment is transformed due to the physiognomy of the constructions and how the design should be adjusted to obtain an improved climate performance [1]. In other words, how to optimize the design to attain a satisfactory and coherent distribution of available energy. A similar problem appears in aerospace technology and industry for different reasons.

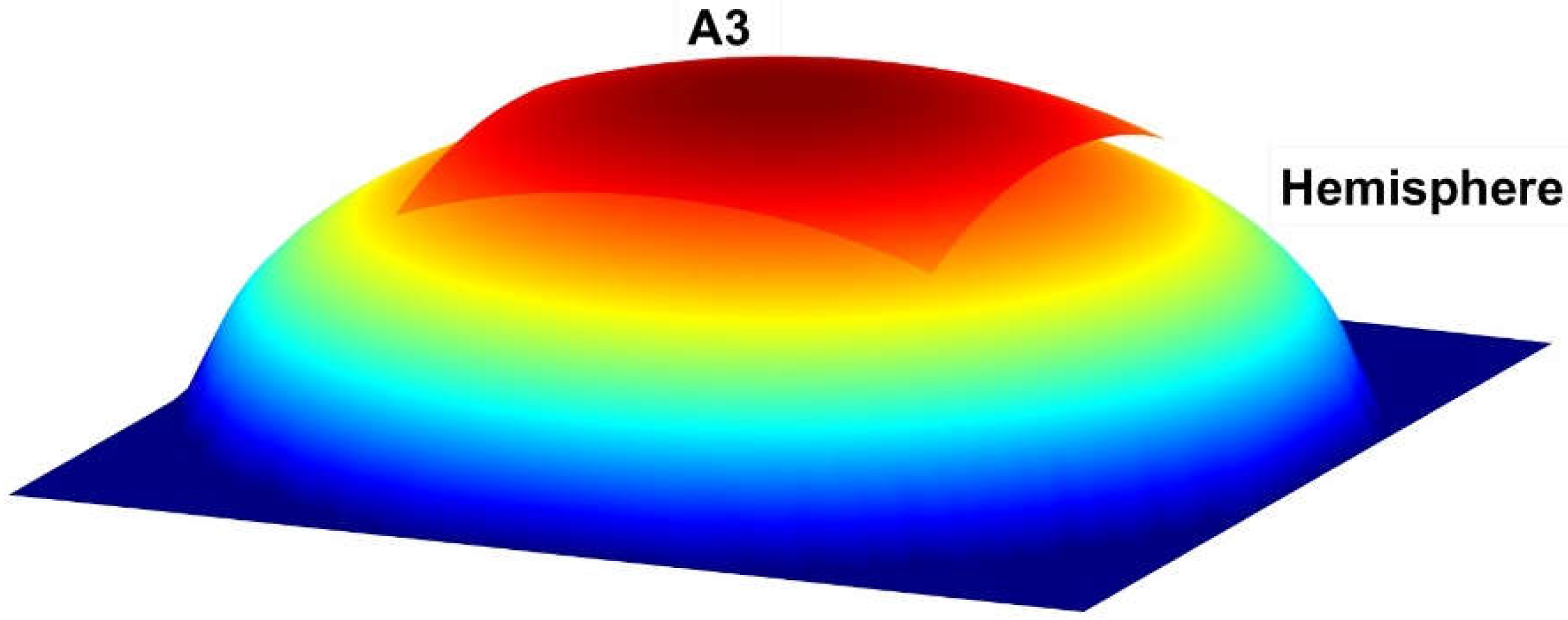
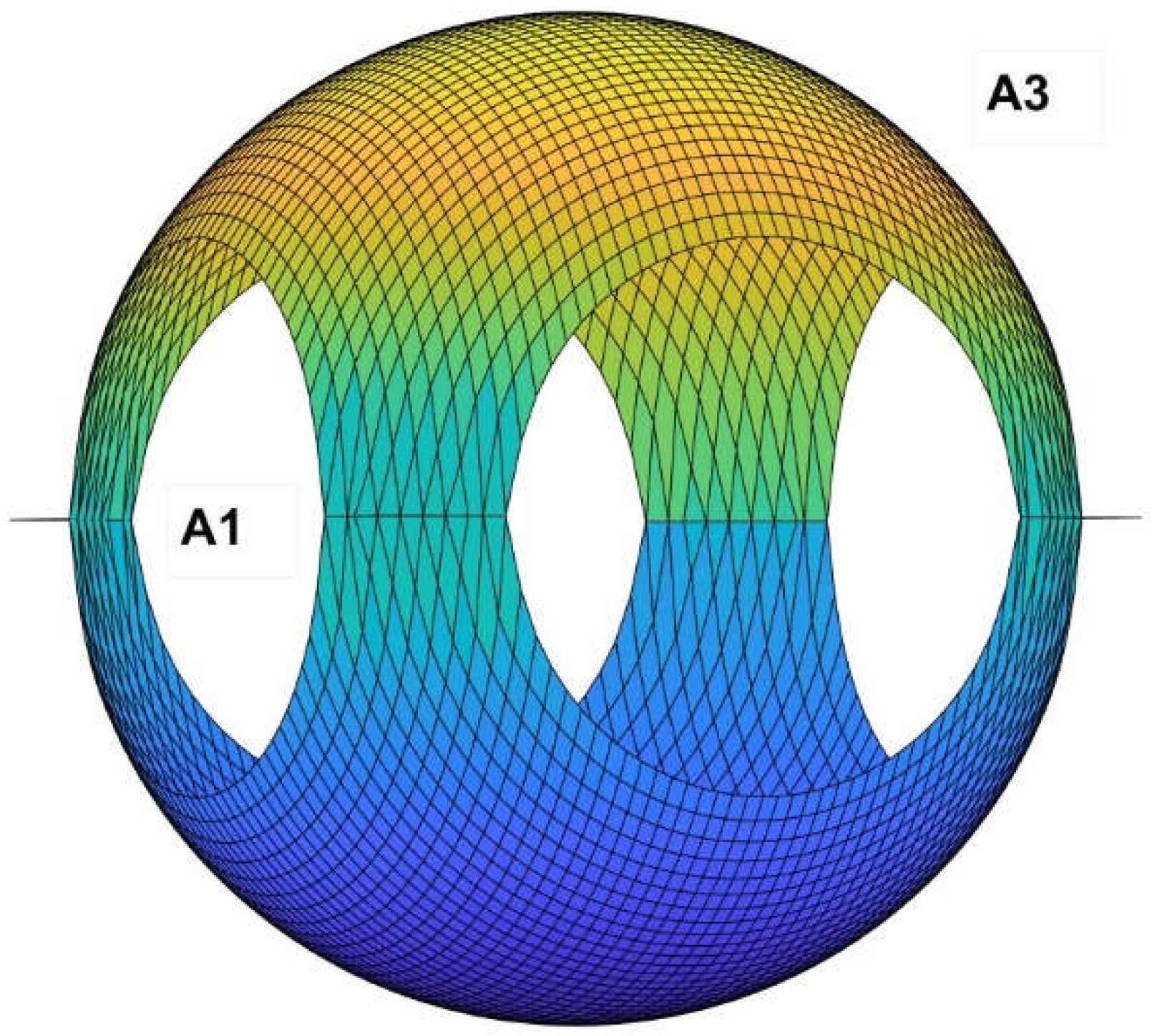
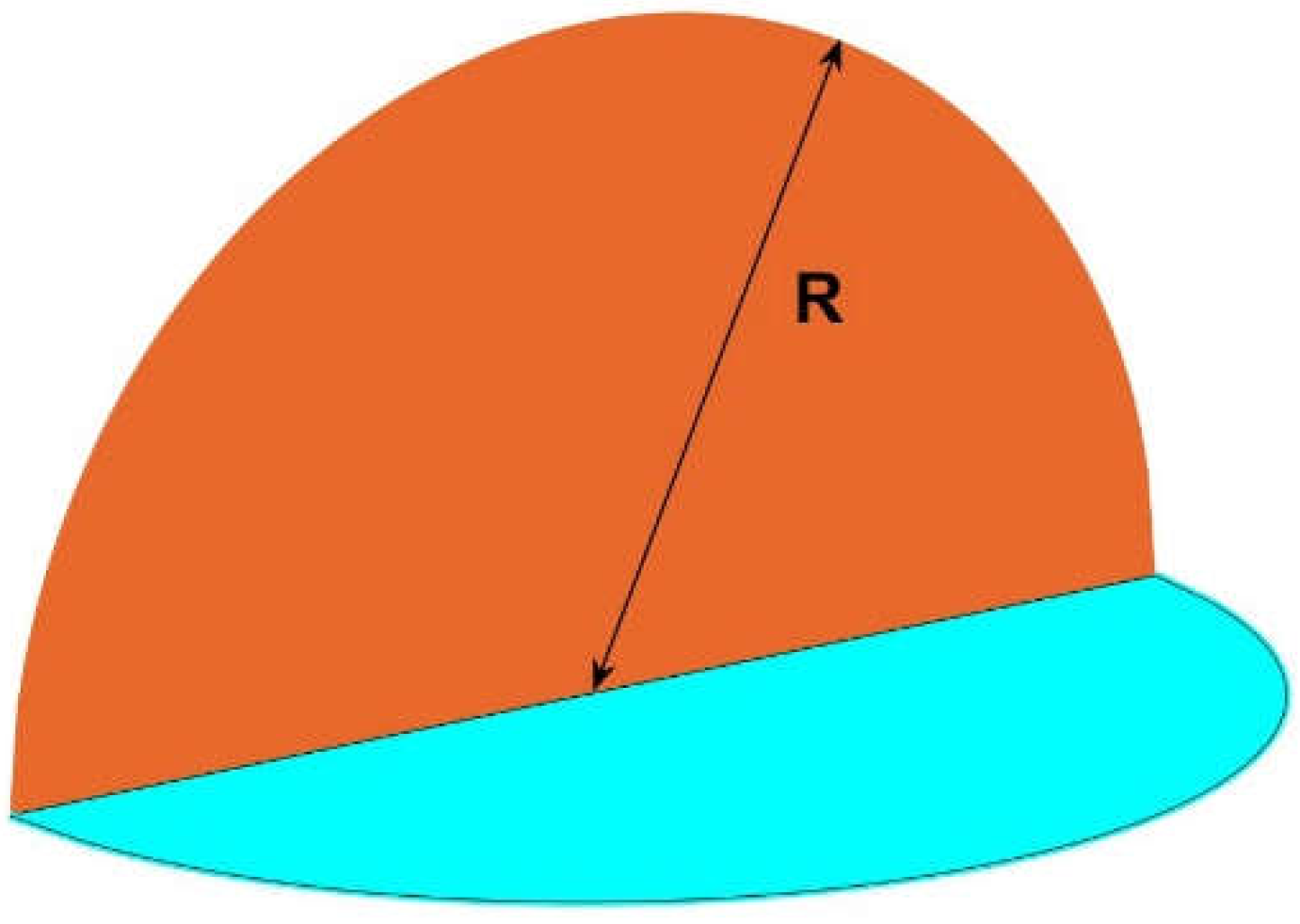
Spherical sources are extremely common in human designs or even natural forms, but their radiative performance in terms of heat transfer was not well-known. In this sense, the first principle of Cabeza-Lainez [2], states that for a spherical surface numbered for convenience A₃, the so-called F₃₃ , that is the fraction of energy emitted by such sphere’s fragment over itself, is defined as the ratio between the area of the said fragment and the whole sphere (Equation (1)), i.e. ½ for a hemisphere, ¼ for a quarter of sphere and successively, due to its simplicity it constituted a paramount finding [3].

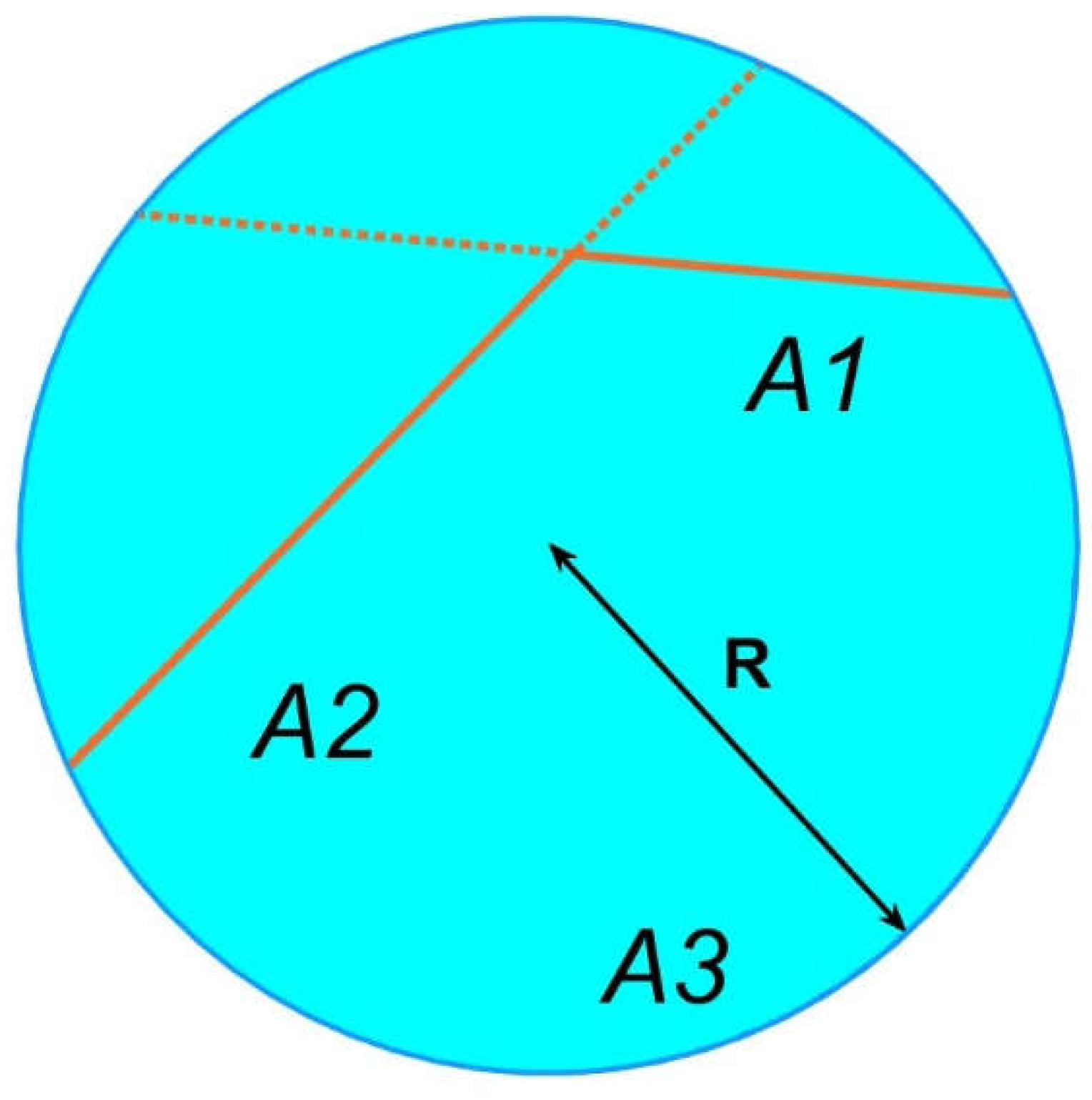
It can be expressed algebraically as:

F_{33} = \frac{A_{3}}{A_{s}} = \frac{A_{3}}{4 π R^{2}}

(1)

Therefore, this extremely complex factor if we were to calculate it with conventional methods equals the area of surface A₃ divided by the total area of the sphere, A₃/A_sphere, as in Figure 1.

The first Cabeza-Lainez principle is compact and deft in the sense that it would be very difficult to solve the canonical expression described in Equation (2) in differential form regardless of the shape of the spherical fragment, [4] while it is almost immediate to find the surface area of the same fragment.

d ϕ_{12} = (E_{1} - E_{2}) \cos θ_{1} \cos θ_{2} \frac{d A_{1} d A_{2}}{π r_{12}^{2}}

(2)

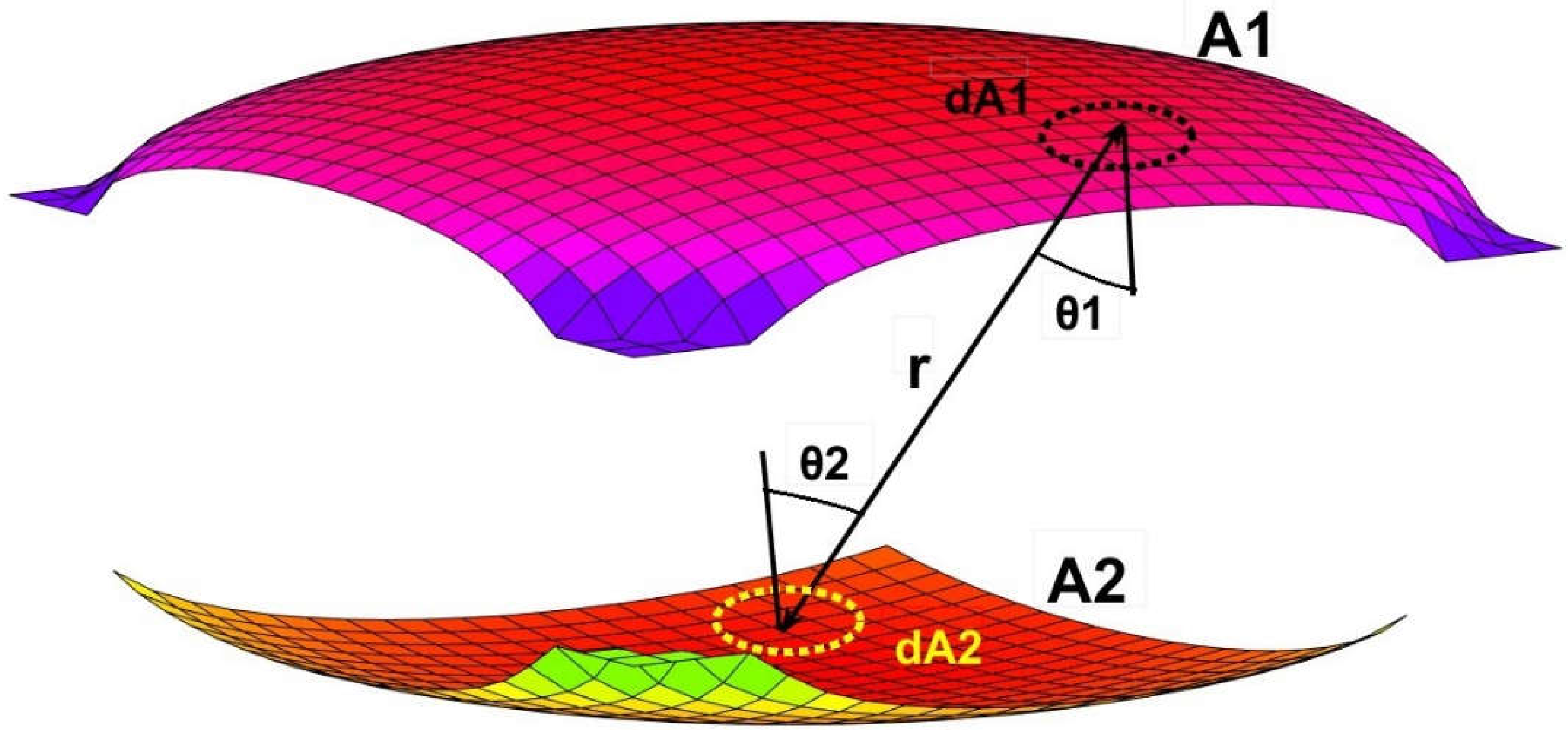
In Equation (2), E₁ and E₂ the amounts of energy (in W/m²) emitted in Lambertian fashion by surfaces 1 and 2.

Figure 2. The magnitudes involved in the expression for radiative exchanges due to manifold surface sources.

Besides θ₁ and θ₂, stand for the inclination angles formed by the perpendiculars to the unit area elements of area dA₁ and dA₂ if r₁₂ is the vector that connects these surfaces dA₁ and dA₂.

Exact and complete solution of equation 2 is reserved, after lengthy calculations, to a few spare geometries, like rectangles and parallel concentric circles [1].

2. Materials and Methods

In most cases the fourfold integration of a volume composed by two curve-edged but planar surfaces, usually circular segments and an enclosing fragment of sphere is not attainable. So far, the author has had to desist after the third round of integration. In the near future some limited result is being obtained by virtue of numerical calculus and computational graphics [5]. Meanwhile, Cabeza-Lainez’ third principle is sufficient to solve the problem for all the volumes specified, regardless of the position of the two planar surfaces, i.e., if they cut each other, they are tangent or not.

We can express such new principle in the following terms. For any couple of planar sections of a sphere (A₁-A₂) that enclose within them a fragment of the same sphere (A₃) and irrespective of their relative position, if they pass or not through the center of the sphere, or even if they possess any tangent point, the form factor from surface 1 to surface 2 can be expressed as:

F_{12} = \frac{A_{1} + A_{2} + A_{3} (F_{33} - 1)}{2 A_{1}} = \frac{1}{2} (1 + \frac{A_{2} - A_{3}}{A_{1}} + \frac{A_{3}^{2}}{A_{s} A_{1}})

(3)

F₃₃ , is the factor of a sphere’s fragment over itself that was defined previously in Cabeza-Lainez’ first principle as the ratio between the area of the said fragment and the whole sphere (Eq.1), which gave ½ for a hemisphere, ¼ for a quarter of sphere and successively; it is written A₃/A_sphere.

A₁ and A₂ are, as defined, the respective areas of surfaces 1, 2 (segments of circle) and A₃ is the comprised fragment of sphere (Figure 3 and Figure 4). Determination of areas 1 and 2 offers no particular problem but finding the surface of a fragment of sphere might require the employ of spherical trigonometry and the internal angles comprised to substitute in the formula of the third principle.

Based on this new and innovative principle, to obtain the form factor is only a matter of knowing the areas of surfaces 1, 2 and 3 which is usually trivial and requires of no integration. We have to note that this principle was discovered by the author in early 2019 but for several reasons it was not published until now although it is mentioned succinctly in reference [6].

3. Proof and Results

The form factor algebra demonstrated elsewhere [1] states that,

F₁₁+ F₁₂+ F₁₃+… F_1N = 1

(4)

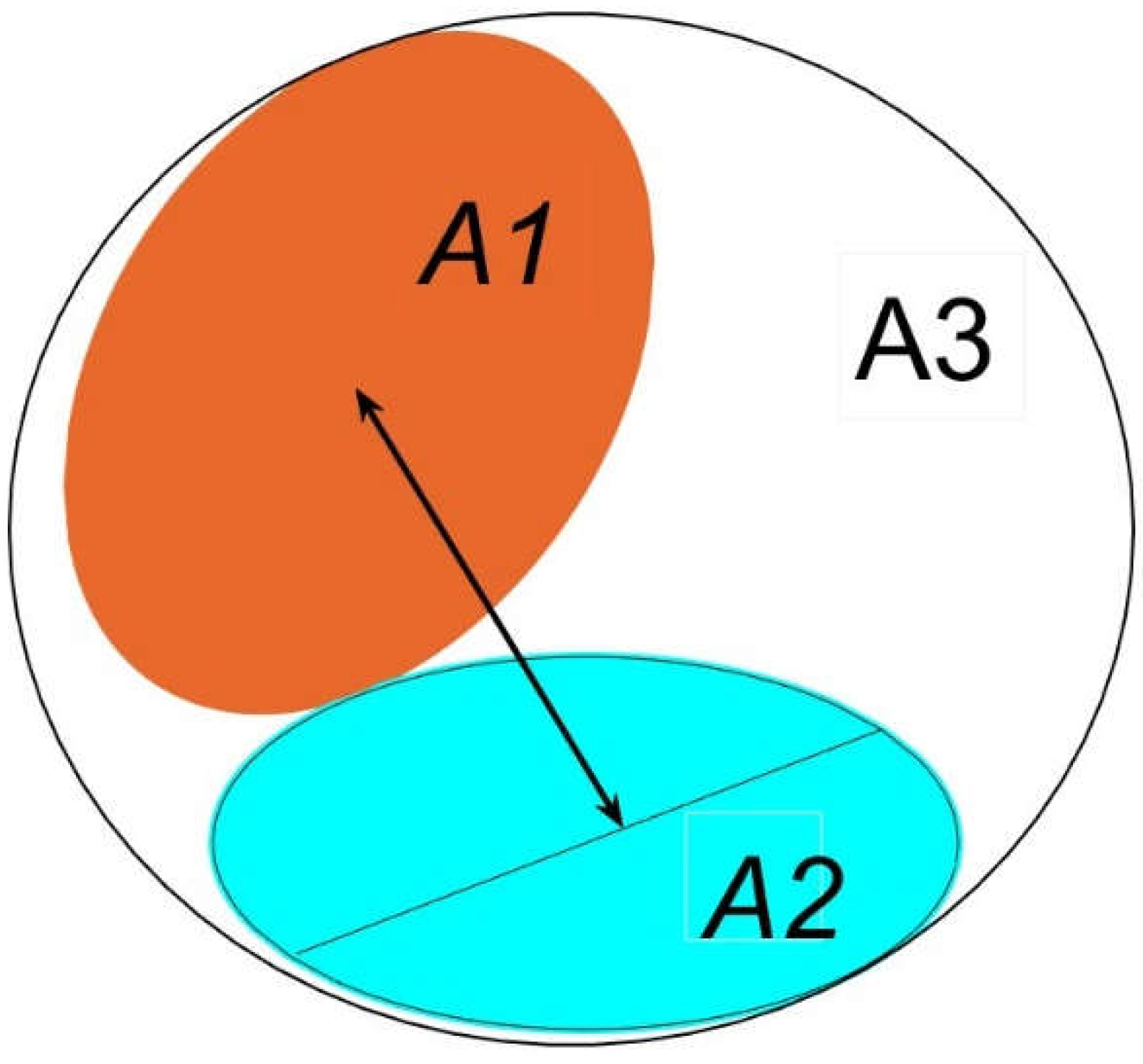
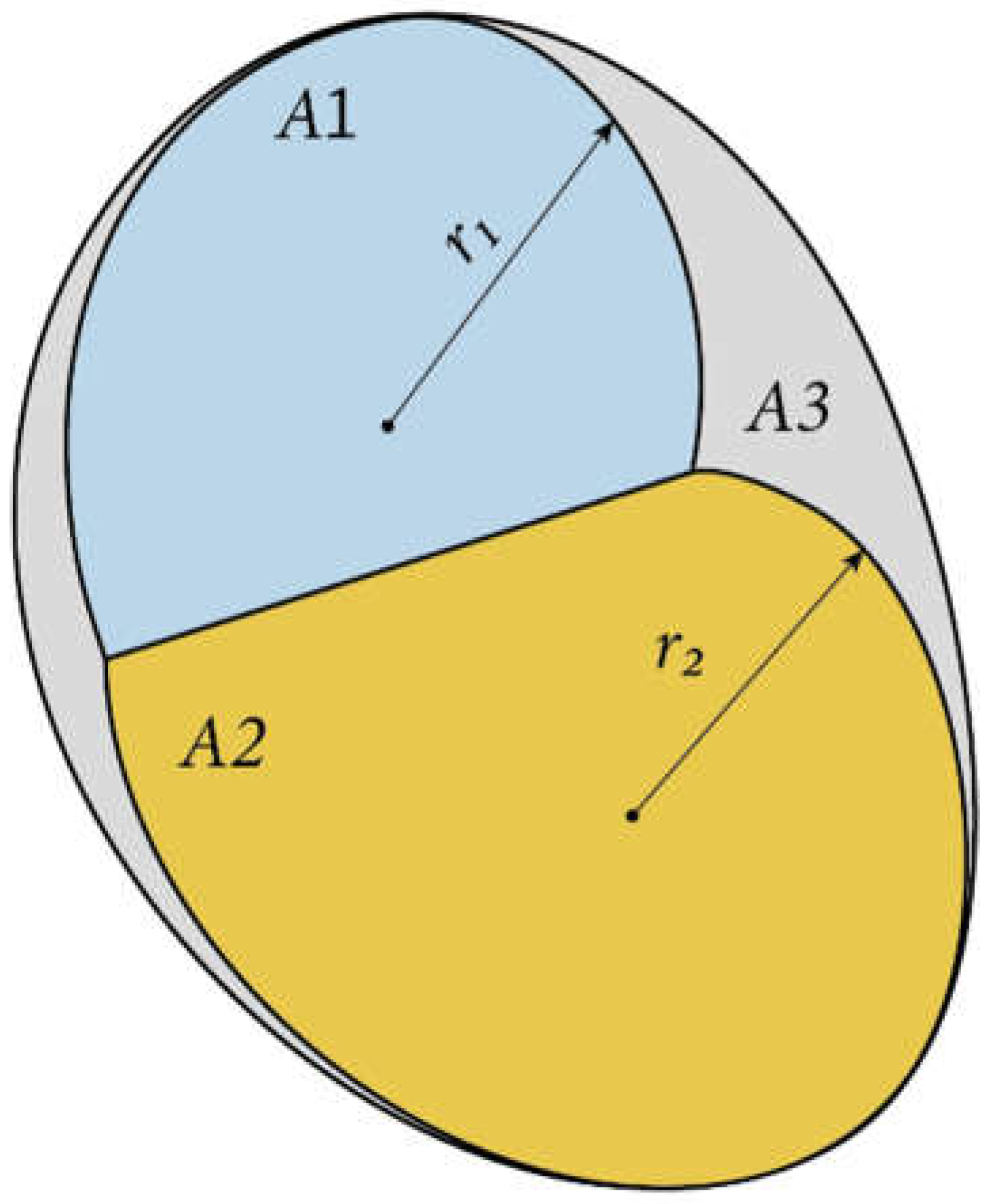
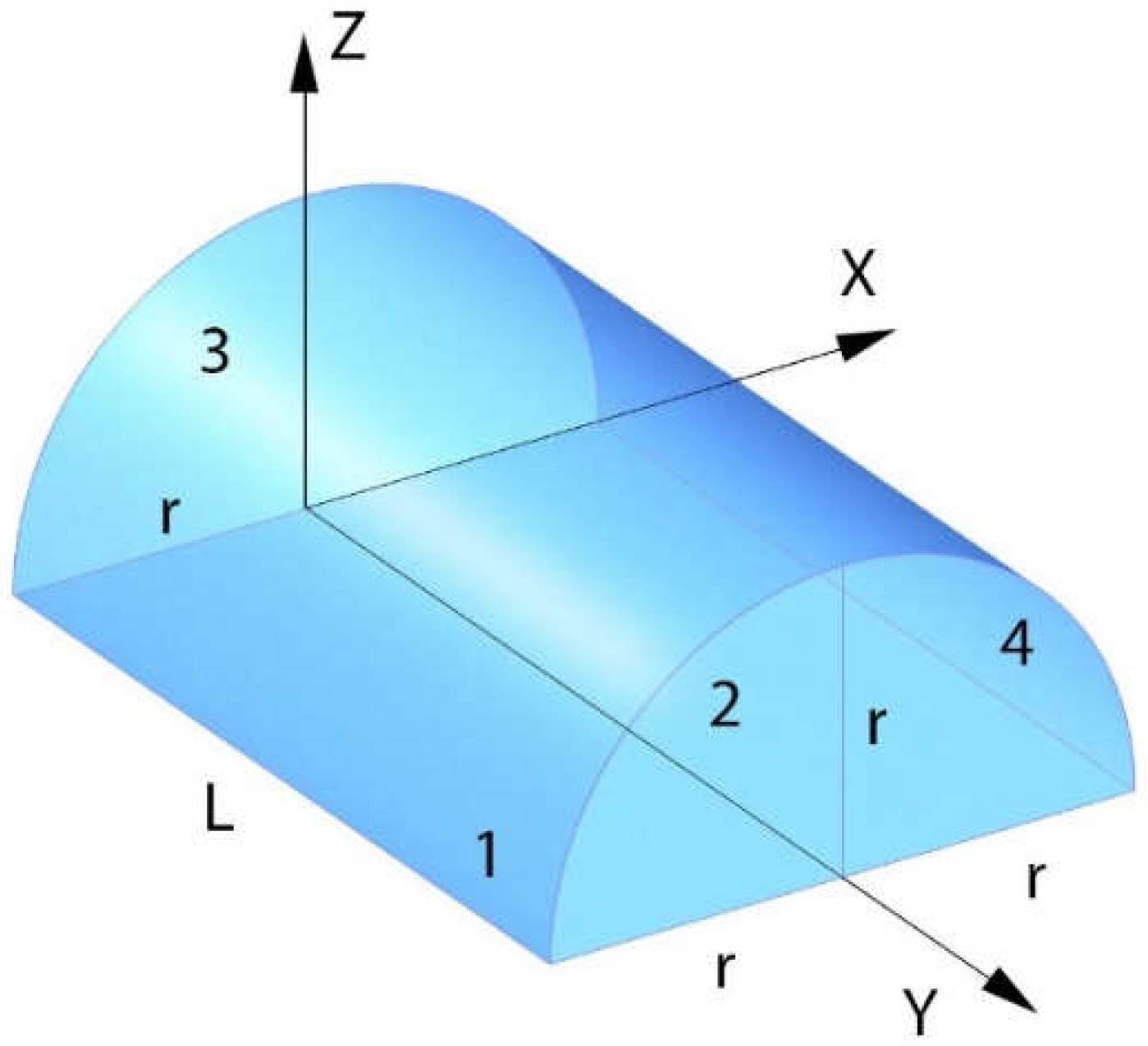
In a volume composed by threes surfaces in the manner previously described (Fig. 5), a fragment of sphere (surface 3) and two limiting planar surfaces (areas 1 and 2), the sole reflexive or self-factor that appears is logically F₃₃, which has been previously defined in Cabeza-Lainez’ first principle of form factors (Eq. 1) as the ratio between the surface area of the fragment of sphere and the total area of the sphere in which surface 3 is contained. F₃₃ is therefore a constant for a given surface which belongs to the sphere.

Figure 5. The three surfaces involved in radiative exchange for the third principle.

In this situation if we apply the above algebra to find the unknown factors, we would find that,

F₃₁+ F₃₂+ F₃₃ = 1;

(5)

F₁₂+ F₁₃ = 1;

(6)

F₂₁+ F₂₃ = 1;

(7)

Consequently,

F₁₂= 1- F₁₃;

(8)

F₂₃= 1- F₂₁;

(9)

F₁₃= 1- F₁₂;

(10)

But the form factor algebra applied to finite surfaces in a closed volume [1] implies that:

A₁F₁₂=A₂F₂₁

(11)

Thus,

F_{32} = \frac{A_{2}}{A_{3}} (1 - F_{21});

(12)

F_{31} = \frac{A_{1}}{A_{3}} (1 - F_{12});

(13)

From Equation (5) we know that,

F₃₁ = 1- F₃₂ -F₃₃;

(14)

Substituting (12) and (13) in (14)

\frac{A_{1}}{A_{3}} (1 - F_{12}) = 1 - \frac{A_{2}}{A_{3}} (1 - F_{21}) - F_{33};

(15)

Also substituting (11) in (15);

\frac{A_{1}}{A_{3}} (1 - F_{12}) = 1 - \frac{A_{2}}{A_{3}} + \frac{A_{1} x F_{12}}{A_{3}} - F_{33};

(16)

Multiplying by A₃ in both terms, we obtain

A_{1} - A_{1} F_{12} = A_{3} - A_{2} + A_{1} F_{12} - A_{3} F_{33};

(17)

And simplifying,

{2 A}_{1} F_{12} = A_{1} + A_{2} - A_{3} + A_{3} F_{33};

(18)

Thus we arrive to,

F_{12} = \frac{1}{2} (1 + \frac{A_{2} - A_{3}}{A_{1}} + \frac{A_{3}}{A_{1}} F_{33});

(19)

As (19) is equal to (3) the expression for the form factor has been demonstrated; QED.

Knowing F₁₂, it is immediate to find F₂₁ by using reciprocity theorem (11)

Consequently, we have arrived to the values of F₂₃ (9), F₁₃ (10), F₃₂ (12) and F₃₁ (13 and 14).

All the unknown factors of the problem are solved with perfect ease for a great variety of shapes previously unexplored.

Ensuing, let us check the form factor due to several typical configurations.

1.: Perpendicular circles within the sphere

We shall begin as is customary with perpendicular circles by virtue of Cabeza-Lainez’ 3^th principle, Figure 6 and Figure 7.

Figure 6 is and extreme case of Figure 7 in which the perpendicular circles have been enlarged to become tangent.

The third principle, that we have seen in Equation (3) states that:

For any couple of planar sections of a sphere (1-2) with a common edge or point the form factor from surface 1 to surface 2 is:

F_{12} = \frac{A_{1} + A_{2} + A_{3} (F_{33} - 1)}{2 * A_{1}} = \frac{1}{2} (1 + \frac{A_{2} - A_{3}}{A_{1}} + \frac{A_{3}^{2}}{A_{s} A_{1}})

(3)

And assuming that the area of the circles has to be πR²/2 and A₁= A₂ , such equation turns out to be:

F_{12} = 1 + \frac{A_{3} (F_{33} - 1)}{2 A_{1}} = 1 + \frac{A_{3}^{2}}{{2 A}_{s} A_{1}} - \frac{A_{3}}{{2 A}_{1}}

In this case, A₃ is found by subtraction of the area of the two identical caps to the sphere, and the area of one segment is π(a²+ h²), being h the height and a the radius of the base circumference of the cap. Theretofore, a=R√2/2 and h=R(1-√2/2),

a^{2} = \frac{R^{2}}{2}; h^{2} = R^{2} (\frac{3}{2} - \sqrt{2}) = \frac{R^{2}}{2} (3 - 2 * \sqrt{2})

A_{3} = 4 π R^{2} - 2 π \frac{R^{2}}{2} (1 + 3 - 2 \sqrt{2}) = 4 π R^{2} - 2 π R^{2} (2 + \sqrt{2}) = π R^{2} (2 \sqrt{2})

and this yields,

A_{3}^{2} = π^{2} R^{4} 8

F_{12} = 1 + \frac{π^{2} R^{4} 8}{8 π R^{2} π R^{2} / 2} - \frac{π R^{2} (2 \sqrt{2})}{π R^{2}}

An thus the sought factor F₁₂ is obtained as,

F_{12} = 1 + 2 - (2 \sqrt{2}) = 3 - 2 \sqrt{2} = 0.1715

This value appears as the radiative exchange in a sort of cube composed of circles which in turn are enclosed in a fragment of sphere. The same value would be obtained for the parallell circles of the same figure. In the real cube of six squares [1], the value of F₁₂ would be, as it is known, 1/5 = 0.2 , a very similar figure which attests to its validity.

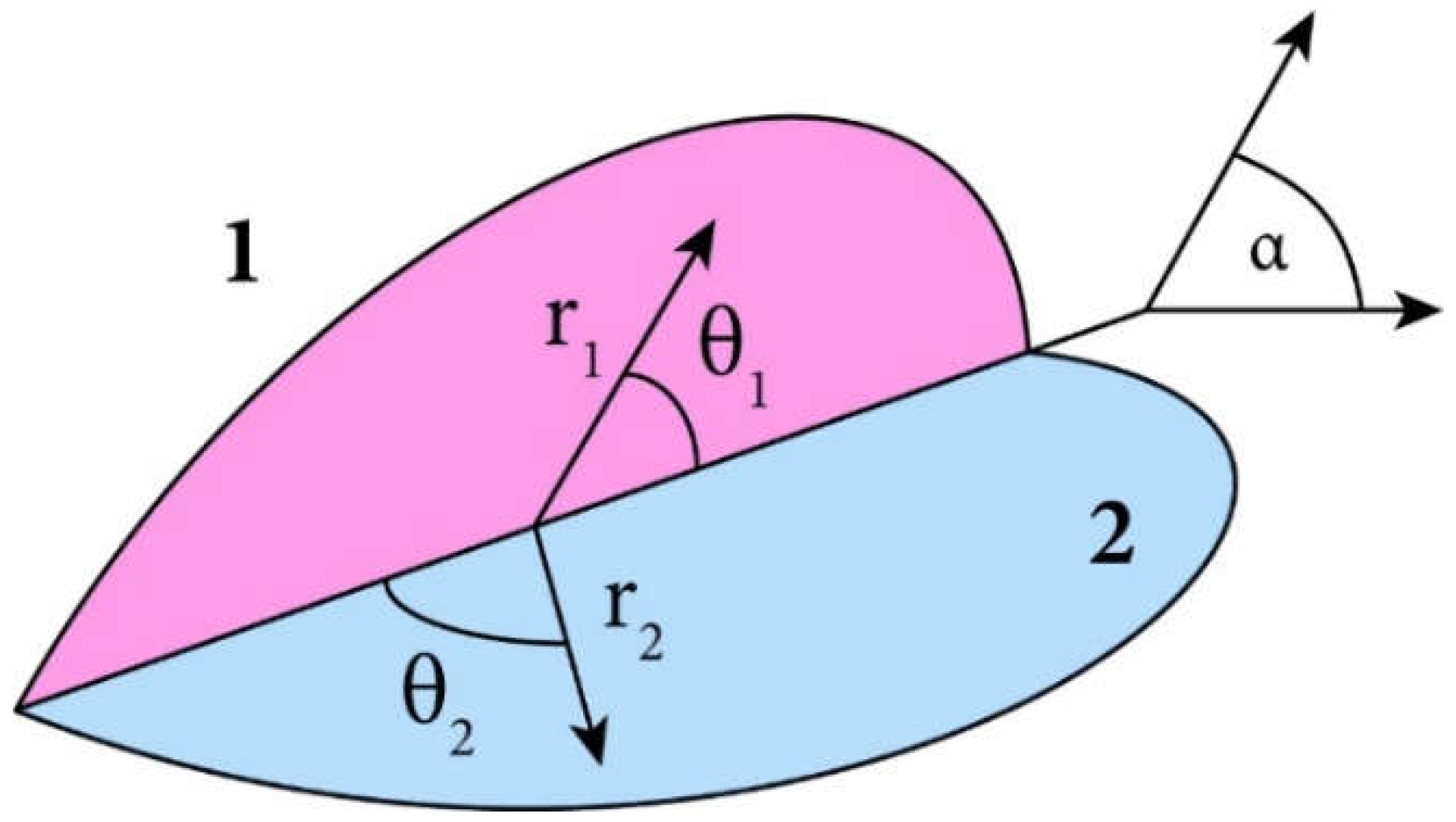
In the fourth principle [2], by logic deduction from the sphere, Cabeza-Lainez was able to obtain the form factor for semicircles of equal radius possessing a common edge, depending on the internal angle formed by the half disks α. Which was at the time a no minor feat. (Fig. 8).

Figure 8. Two semicircles with a common edge.

In this case, the defining equation is,

F_{12} = 1 - \frac{2 α}{π} + {(\frac{α}{π})}^{2}

(20)

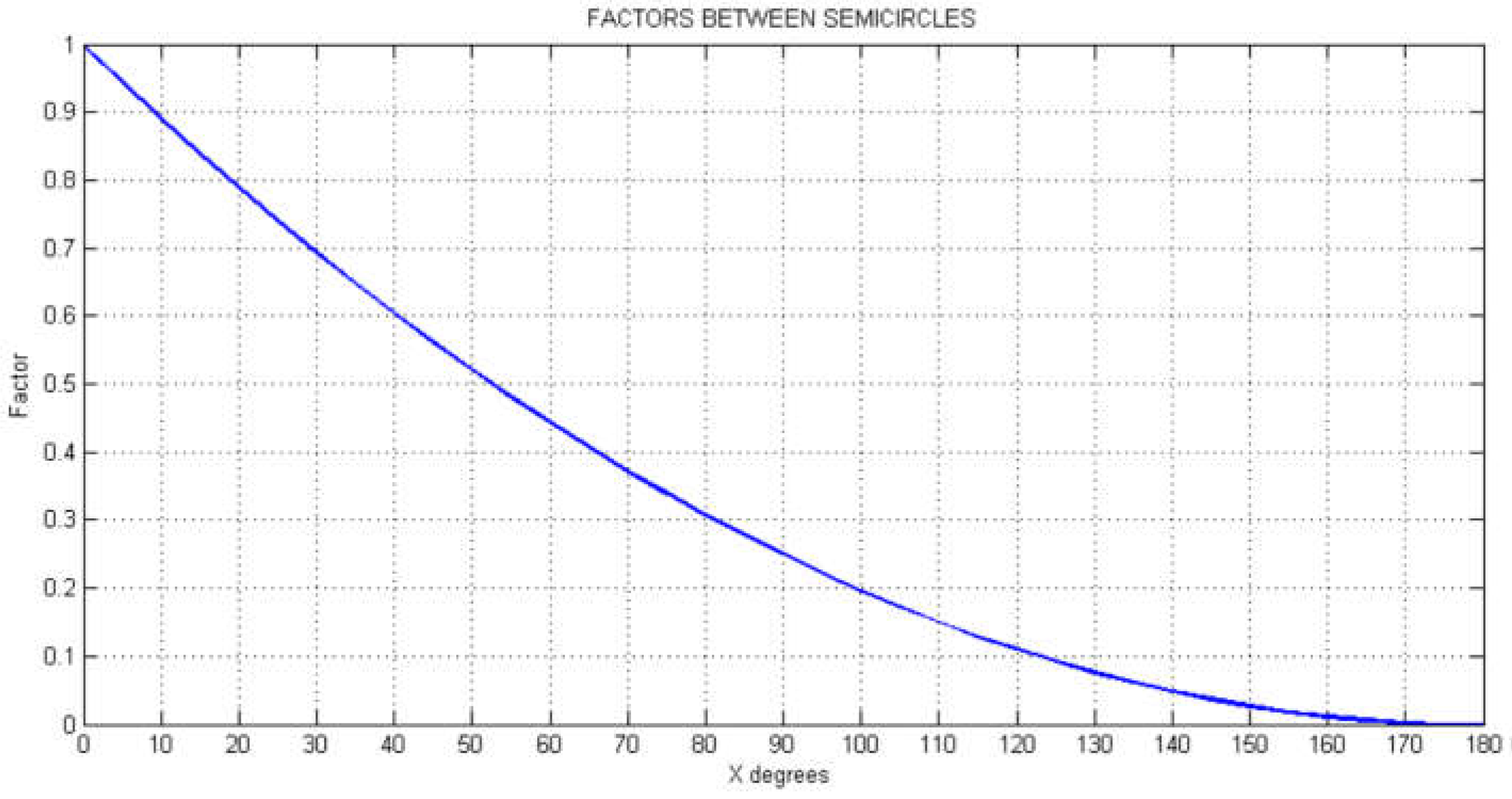
Introducing the parameter p,

p = \frac{α}{π}

The equation, represented in Figure 9 can be expressed as:

F_{12} = 1 - 2 p + p^{2}

(21)

This factor may be seen as something obvious but if we were to look in more detail (Fig. 10),

Figure 10. Radiative exchange between two semicircles forming a common angle α.

The integral equation that we would be forced to solve would be for the semicircles (Eq.22),

F_{12} = \int_{0}^{π} \int_{0}^{π} \int_{0}^{R} \int_{0}^{R} \frac{{(r}_{1}^{2} * r_{2} * s i n θ_{1} * r_{2}^{2} * r_{1} * s i n θ_{2}) d r_{1} d r_{2} d θ_{1} d θ_{2}}{π * {[{(r}_{1}^{2} + r_{2}^{2} + 2 * r_{1} * r_{2} * c o s θ_{1} * c o s θ_{2})]}^{2}}

(22)

Equation 22, which is only valid for α=π/2, describes the unusual complexity of the factor F₁₂ to evaluate the radiative exchanges that occur in figures 8 and 10, such exchanges, are almost impossible to calculate even for the perpendicular angle not to mention any other inclinations, therefore the fourth principle can be considered as a pivotal advance, which is now subsumed in the third principle, as we will show. As it happens, the fourth principle was discovered before the third, but being less general, the author has decided to slightly alter the order.

Let us now proceed to check more examples based on the former.

2.: Calculations for an eighth of sphere.

The area of an octave of a sphere is

A_{3} = 2 α R^{2}

, where α is the angle between two semicircles with a common edge. For the whole sphere α=2π.

In this case α=π/4 and A₃= πR²/2

But we know by virtue of Cabeza’s first principle that

F_{33} = \frac{1}{8}

That means the area of the octave of sphere divided by the total area

And applying the 3^rd principle to this particular case, from Equation (3),

F_{12} = \frac{A_{1} + A_{2} + A_{3} (F_{33} - 1)}{2 A_{1}} = \frac{π R^{2} + π R^{2} / 2 (1 / 8 - 1)}{π R^{2}} = 1 - \frac{7}{16} = \frac{9}{16} = 0.5625

Remember that A₁= A₂ =πR²/2 and subsequently equal to A₃, to find that,

F_{12} = 0.5625

It is exactly the same result that can be obtained with Cabeza’s fourth principle, given that, in the latter expression we found the following (Equation (20)),

F_{12} = 1 - \frac{1}{2} + {(\frac{1}{4})}^{2} = \frac{1}{2} + \frac{1}{16} = \frac{9}{16} = 0.5625

3.: Estimations for a fifth of sphere.

In one fifth of sphere, angle α=2π/5 (72º) and

A_{3} = 4 π R^{2} / 5

F_{12} = \frac{π R^{2} + 4 π R^{2} / 5 (1 / 5 - 1)}{π R^{2}} = 1 - \frac{4}{5} \frac{4}{5} = 1 - \frac{16}{25} = \frac{9}{25} = 0,36

F_{12} = 1 - \frac{4}{5} + {(\frac{2}{5})}^{2} = \frac{1}{5} + \frac{4}{25} = \frac{9}{25}

4.: The case of a fourth of sphere.

If we had applied the same reasoning to a quarter of sphere, we would have obtained,

F_{12} = \frac{A_{1} + A_{2} + A_{3} (F_{33} - 1)}{2 A_{1}} = \frac{π R^{2} + π R^{2} (1 / 4 - 1)}{π R^{2}} = 1 - \frac{3}{4} = \frac{1}{4} = 0.25

Which is already a familiar result by the fourth principle (see Fig.9 for a 90 deg. angle).

This value has also been experimentally verified through numerical calculus by Cabeza-Lainez. It is demonstrated that the value of a form factor between two surfaces is the average of configuration factor from receiving surface source over the whole emitting surface [1]. Such demonstration has been used to check the value of 0.25 previously found(see section 7).

5.: Calculations for a third of sphere

For a third of sphere, angle α=2π/3 and

A_{3} = 4 π R^{2} / 3

F_{12} = \frac{π R^{2} + 4 π R^{2} / 3 (1 / 3 - 1)}{π R^{2}} = 1 - \frac{4}{3} \frac{2}{3} = 1 - \frac{8}{9} = \frac{1}{9} = 0,111

With the fourth principle we would have obtained,

F_{12} = 1 - \frac{4}{3} + {(\frac{2}{3})}^{2} = - \frac{1}{3} + \frac{4}{9} = \frac{1}{9} = 0,111

It is the same result anew.

6.: Null case, half of a sphere.

In the particular case of a hemisphere Equation (3) provides,

F_{12} = \frac{π R^{2} + 2 π R^{2} (1 / 2 - 1)}{π R^{2}} = 1 - 1 = 0

As we already knew and could be expected since both semicircles are in the same plane and constitute a whole circle, no energy can be exchanged between them since they are one and the same planar surface.

It is henceforth clear that the third principle encompasses all the situations appearing in the more limited fourth principle but both are valid depending on the geometry of the case.

7.: Cases obtained by numerical calculus

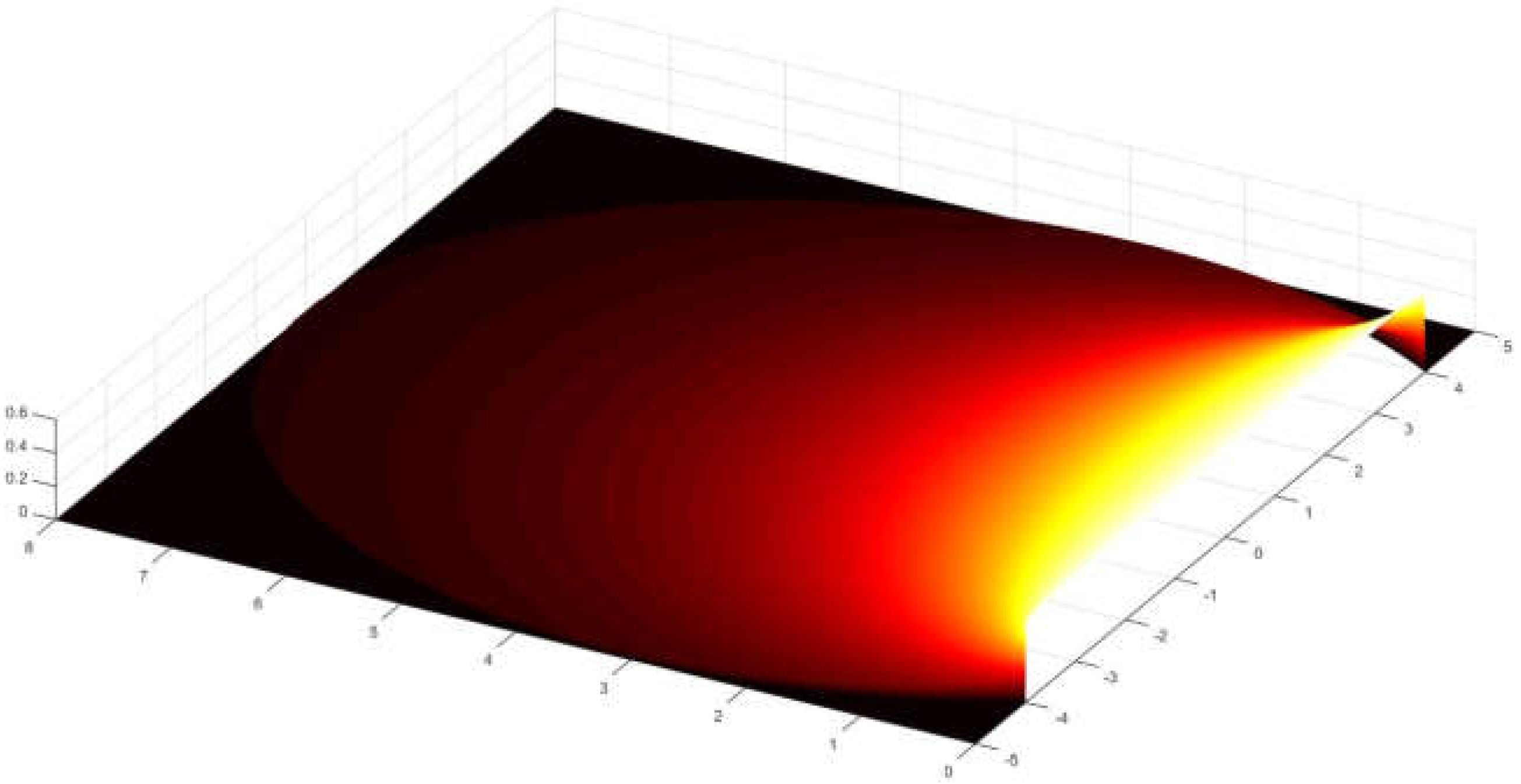
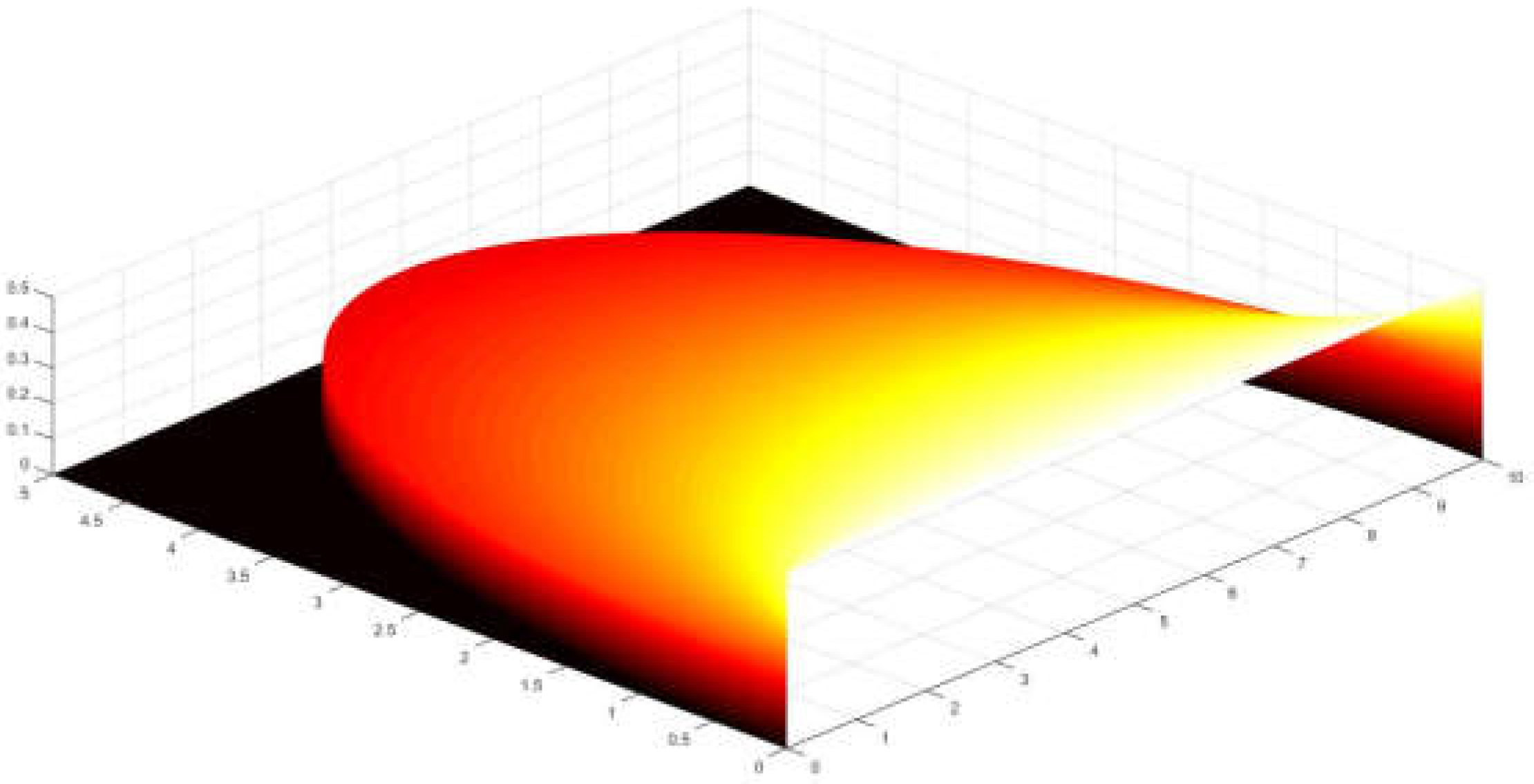
As previously mentioned Cabeza-Lainez was capable of integrating the formula for radiative exchange from a semicircle [3] over a rectangular field in 2013, but it laid dormant until 2018 for a series of calculation and representational difficulties (Equation (23)) (Figure 11).

F_{21} = \frac{1}{2 π} (a r c t a n \frac{r + x}{y} + a r c t a n \frac{r - x}{y}) + \frac{y}{4 π * x} [\ln (r^{2} + y^{2} + x^{2} - 2 r * x) - l n {(r}^{2} + y^{2} + x^{2} + 2 r * x)]

(23)

The meaning of the variables for the spatial directions is given in Figure 12.

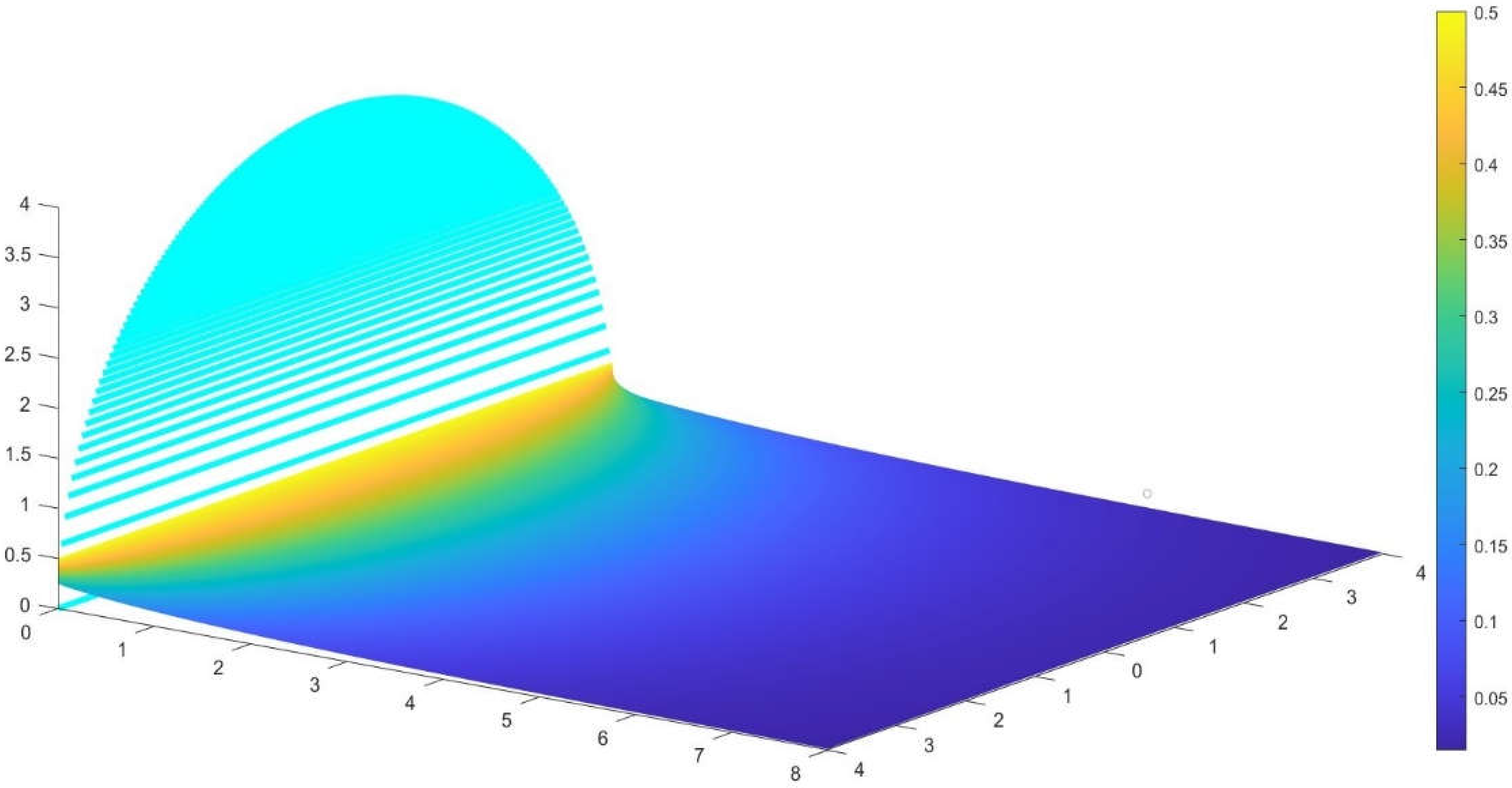
Equation (23) is a point by point distribution over x and y, stemming from the semicircle, but if it is averaged by numerical calculations over the second emitting source, the form factor can be obtained with sufficient accuracy.

The author has used this procedure in a perpendicular semicircle with the same radius (Figure 13 and Figure 14), to find the value of 0.25 obtained theoretically above in Section 4.

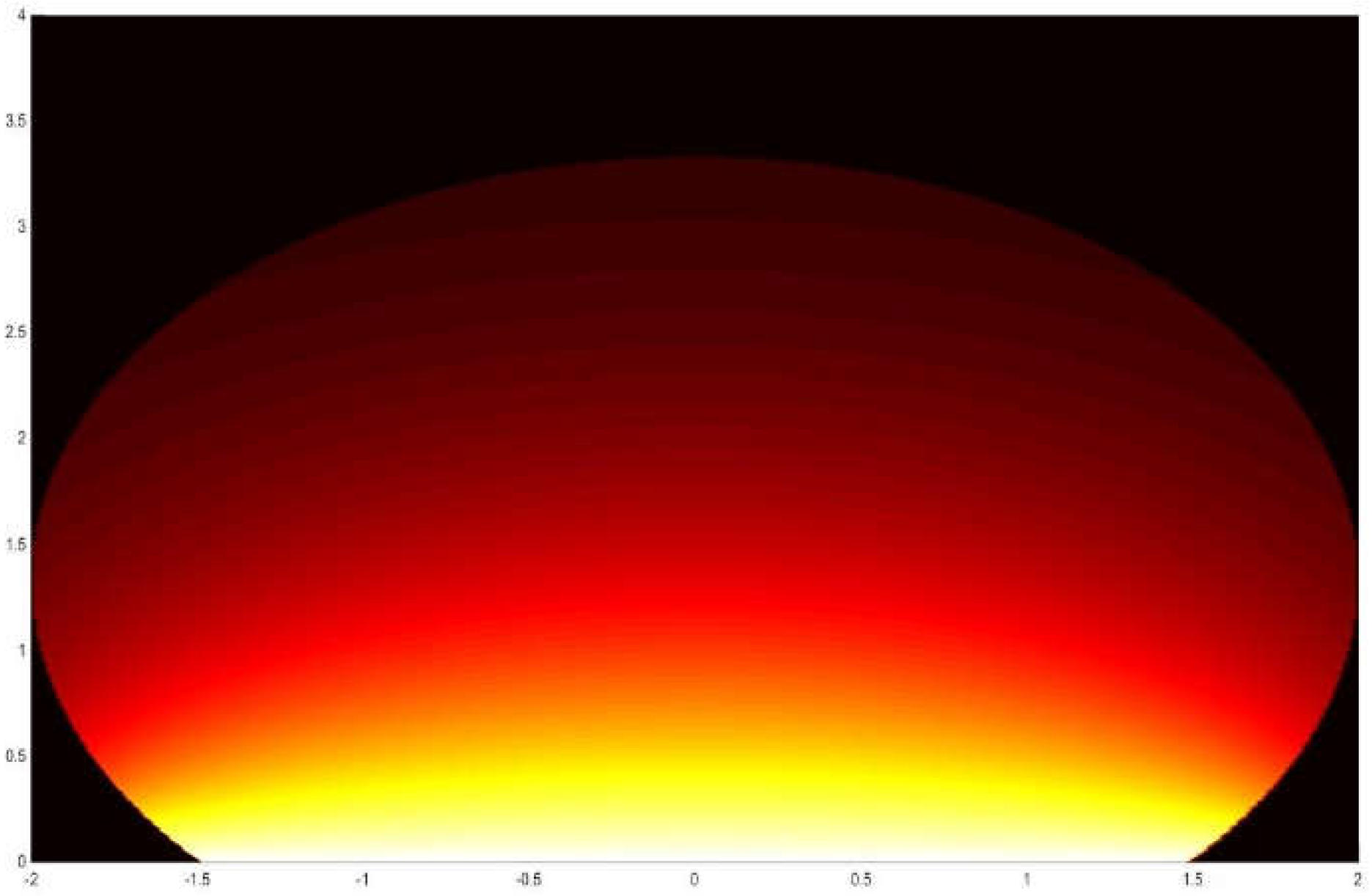
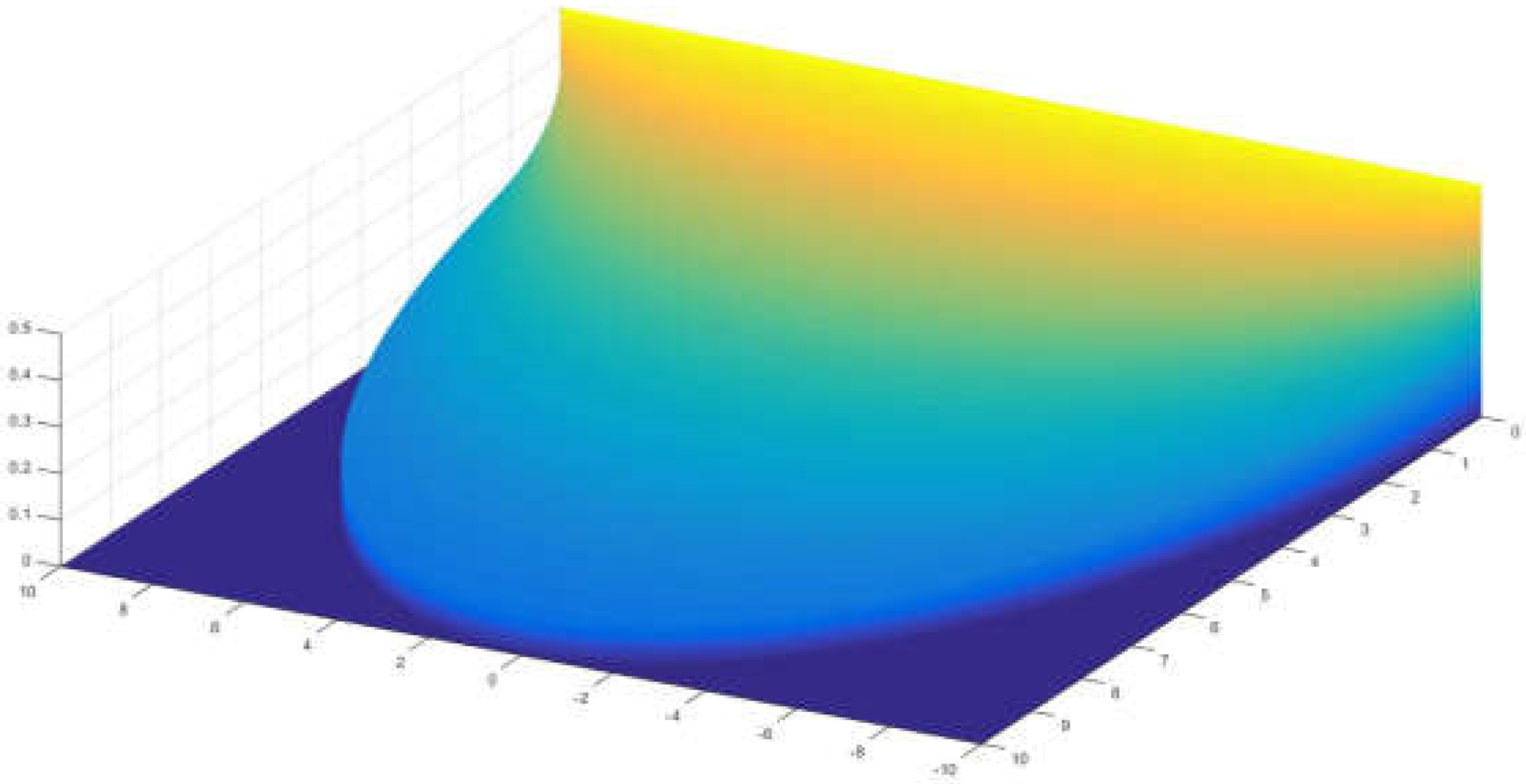
The second example is the form factor between a semicircle and a perpendicular circular segment both contained in a sphere (Figure 15 and Figure 16). The numerical results closely agree with those using the third principle of Cabeza-Lainez.

Unfortunately, for shapes not perpendicular it is not currently possible to obtain a numercial verification although we are working on the issue. Due to the coherence and robust behaviour shown by the third principle in all the former instances we have every reason to believe that it will hold true when an experimental procedure is available in the near future.

Figure 15. Form factor between a semicircle and a circular segment.

Figure 16. Numerical determination of the factor in plan.

4. Complementary Considerations for Inter-Reflections

A first consequence of obtaining the form factors in a volume composed of three surfaces by means of the third principle is that we need to complete the frame with the possibility of inter-reflections between the surfaces involved. This point has also been specifically developed by the author as follows.

The total balance of energy depends on the equation

E_{t o t} = E_{d i r} + E_{r e f}

(24)

where E_dir is the fraction of direct energy and E_ref is the reflected fraction. If these quantities are added, we obtain the global amount of radiation E_tot.

Usually, several surfaces intervene in the process of reflection, and thus a set of expressions can be built. It is possible to introduce a pair of instrumental arrays that we will call F_d and F_r. For the volume enclosed by the three surfaces (see Figure 5), such matrices would have the ensuing form:

F_{d} = (\begin{matrix} 0 & F_{12} ρ_{2} & F_{13} ρ_{3} \\ F_{21} ρ_{1} & 0 & F_{23} ρ_{3} \\ F_{31} ρ_{1} & F_{32} ρ_{2} & F_{33} ρ_{3} \end{matrix})

(25)

F_{r} = (\begin{matrix} 1 & {- F}_{12} ρ_{2} & {- F}_{13} ρ_{3} \\ {- F}_{21} ρ_{1} & 1 & {- F}_{23} ρ_{3} \\ {- F}_{31} ρ_{1} & {- F}_{32} ρ_{2} & 1 \end{matrix})

(26)

with factors F_ij as previously found, yielding the energy transfer between the respective surfaces involved. Here, ρ_i represents the ratio of reflection (direct or otherwise) assigned to a particular element i [1,7].

Notice that in the matrix called F_d (Equation (25)) the third element of the diagonal is not null as the F_ii (with two ii) element has definite values for curved surfaces, unlike the exchange that happens in a cuboid.

If after careful integration by the procedures described in the previous sections, we are able to fix all the elements in Equations (25) and (26), we can establish new expressions (Equations (27)–(29)) in order to correlate the primary direct energy with the one extracted by reflections.

{F_{r} E}_{r e f} = {{F_{d}}_{} E}_{d i r}

(27)

{F_{r d}}_{} = {F_{r}^{- 1} {F_{d}}_{}}_{}

(28)

{E_{r e f}}_{} = {F_{r d}^{} {E_{d i r}}_{}}_{}

(29)

Thus the problem of radiating energy exchanges in the so-defined volume is completely settled.

The second issue that may appear is that as the planar surfaces that we have identified are usually the circular bases of caps belonging to the enveloping sphere, instead of finding the exchanges between the circles we would like to find the exchanges within the said caps.

We could resort to the original integration but we could use as well a new property that we have enunciated although it was not published before.

We have discovered that in certain cases involving circles the form factors have the commutative property, that is, a product of form factors is functional and not only addition.

The second principle of Cabeza-Lainez says that in a volume composed of two surfaces, the form factor exchange is proportional to the ratio of areas between the planar basis and the curved top surfaces [2]. This principle is valid for forms other than the sphere but in the case of a spherical cap as we have here, the form factor depends on the relation between the area of the cap and the area of the base circle.

If we have for instance identified the form factor between two inner circles F₁₂, and then we have the form factor from this circle to the corresponding cap

F_{12}^{1}

, the final factor between the other circle and the said cap F would be the product of the two factors, that is,

F = F_{12} F_{12}^{1}

(30)

5. Discussion

We have established and verified a new unbeknownst principle to find all the exchanges of radiant energy between two planar surfaces that cut a sphere in any way and the resulting fragment of the said sphere and their possible inter-reflections. The principle is original and efficient, some cases covered by it, for instance parallel circles were partially solved earlier in the literature by other more difficult means. These cases had no regard of the radiative transfer between the circles and the surrounding fragment of sphere that we have now settled in an exact manner. Particularly, if the two planar surfaces intersected themselves in any fashion and ceased to be circular to become circular segments such important case was not described at all by the literature, or was termed unsolvable [9] and can only be determined through the third principle of Cabeza-Lainez, hereby presented.

Such finding will have paramount repercussions in various fields of engineering and heat transfer that are not completely foreseeable but we can outline just a few in aerospace technology and building construction. Sundry architectural configurations included the sphere and the circular fragment as an important part of their fenestration or ceiling system (Figures 17 to 1), especially in Heritage or singular buildings. The analysis of thermal acoustic or lighting performance of these features was severely restricted and the possibility to increase energy savings and comfort for the users was almost impeded which subsequently led to its abandonment. With the findings developed we expect that they are better preserved and future developments are implicit for this area.

In aerospace technique parts of the vessels or mechanisms that feature spheres and or circles will experience a more accurate predictions of their performance. Lighting industries will greatly benefit from having an ampler palette of simulation tools to be able to offer more conscious products. This is our yearning for beyond the manuscript.

Figure 17. Ilja Doganoff. Railway Sheds in Bulgaria (1958). Source: Author.

Figure 18. Dome of the church of St. Louis (1730). Seville. Spain. Source: Author.

Figure 19. The Latina Market (1960). Madrid. Spain. Source: Author.

Funding

This article received no external funding.

Acknowledgments

This article is dedicated to the Odajima family. I wish to honor the memory of Prof. Manuel Bendala Garcia.

References

Cabeza-Lainez, J. Fundamentals of luminous radiative transfer: An application to the history and theory of architectural design; Crowley Editions: Seville, Spain, 2006. [Google Scholar]
Cabeza-Lainez, J. New configuration factors for curved surfaces. J. Quant. Spectrosc. Radiat. Transf. 2013, 111, 71–80. [Google Scholar] [CrossRef]
Cabeza-Lainez, J.M.; Pulido-Arcas, J.A. New Configuration Factor between a Circle, a Sphere and a Differential Area al Random Positions. J Quant Spectrosc Radiat Transf 2013, 129, pp. 272–276. [Google Scholar] [CrossRef]
Cabeza-Lainez, J.M.; Salguero-Andújar, F.; Rodríguez-Cunill, I. Prevention of Hazards Induced by a Radiation Fireball through Computational Geometry and Parametric Design. Mathematics 2022, 10, 387. [Google Scholar] [CrossRef]
Salguero-Andújar, F.; Cabeza-Lainez, J.-M. New Computational Geometry Methods Applied to Solve Complex Problems of Radiative Transfer. Mathematics 2020, 8, 2176. [Google Scholar] [CrossRef]
Salguero Andujar, F.; Rodriguez-Cunill, I.; Cabeza-Lainez, J.M. The Problem of Lighting in Underground Domes, Vaults, and Tunnel-Like Structures of Antiquity; An Application to the Sustainability of Prominent Asian Heritage (India, Korea, China). Sustainability 2019, 11, 5865. [Google Scholar] [CrossRef]
Naraghi, M.H. Radiative View Factors from Spherical Segments to Planar Surfaces. J Thermophys Heat Transf 1988, 2, 4, pp. 373-375. [CrossRef]
Cabeza-Lainez, J. Architectural Characteristics of Different Configurations Based on New Geometric Determinations for the Conoid. Buildings 2022, 12, 10. [Google Scholar] [CrossRef]
Moon, P.H.; Spencer, D.E. The Photic Field; The MIT Press: Cambrige, MA, USA, 1981. [Google Scholar]

Figure 1. Hemisphere with fragment of sphere A₃ used to determine F₃₃ as a ratio of the areas.

Figure 3. Profile view of surfaces A_1, A₂ and A₃ forming part of a sphere of radius R.

Figure 4. Imaginary perspective view of A₁ a spherical segment with radius r₁ and A₂ of radius r₂, in concordance with A₃.

Figure 6. Perpendicular circles with a tangent point.

Figure 7. Perpendicular circles in a sphere.

Figure 9. Graphic representation of Cabeza-Lainez fourth principle of form factors between semicircles.

Figure 11. Radiative field generated by a semicircle over and area of 8 m. by 4 m.

Figure 12. The main dimensions used for Equation (23), x, y andr.

Figure 13. Average of the configuration factor from a semicircle over another perpendicular of equal radius.

Figure 14. Graph of numerical calculation between perpendicular semicircles.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A New Principle to Determine the Radiative Heat Transfer in Sphere-related Surfaces

Abstract

1. Introduction

2. Materials and Methods

3. Proof and Results

4. Complementary Considerations for Inter-Reflections

5. Discussion

Funding

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe