Prerpints.org logo
Preprint
Article

The Most Stable Structure of PTB7-Th: DFT Conformational Analysis

Altmetrics

Downloads

174

Views

66

Comments

0

This version is not peer-reviewed

Conjugated Polymers: Preparation, Properties and Applications

Submitted:

11 February 2023

Posted:

16 February 2023

You are already at the latest version

Alerts
Abstract
PTB7-Th is an important donor copolymer used in construction of many organic devices and other industrial applications. In this work, we investigate the structure and energetics of PTB7-Th. We employ density functional theory (DFT) (B3LYP), dispersion corrected DFT (B3LYP-D3) and long-range corrected DFT (CAM-B3LYP, LC-BLYP, and ωB97xD) to analyze the conformational structures and their corresponding energies to determine the lowest energy state of PTB7-Th. The role of the alkane side chains is carefully investigated. Our findings indicate that, when branched ethylhexyl side chains are present, the lowest energy structure of PTB7-Th has fluorine in the same plane and the same side as the double bonded oxygen in the TT-CF part of the monomer and S-C-C-S dihedral angles along the chain backbone are cis-like having values in the range of 20-30 degrees in most cases. Without these side chains the polymer, not unexpectedly, has many near conformational degeneracies.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

For more than three decades now, organic based electric and thermoelectric devices such as organic solar cells (OSCs) [1,2,3,4] and organic light emitting diodes (OLEDs) [5]), and organic wearable products [6] have emerged, due to their superior advantages such as the flexibility, non-toxicity and low cost, as important sources of electrical power and of many other industrial applications. These devices and applications often employ organic polymers as their sole or as one of the materials in their construction. For example, the highly promising bulk heterojunction OSCs use polymers (donors) and fullerenes (acceptors) in their active layers [7]. When fullerenes are replaced with small-molecule (SM) acceptors which are combined with polymer donors, the resulting pairings give rise to the so-called non-fullerene acceptor (NFA) OSCs with much improved efficiencies [8].
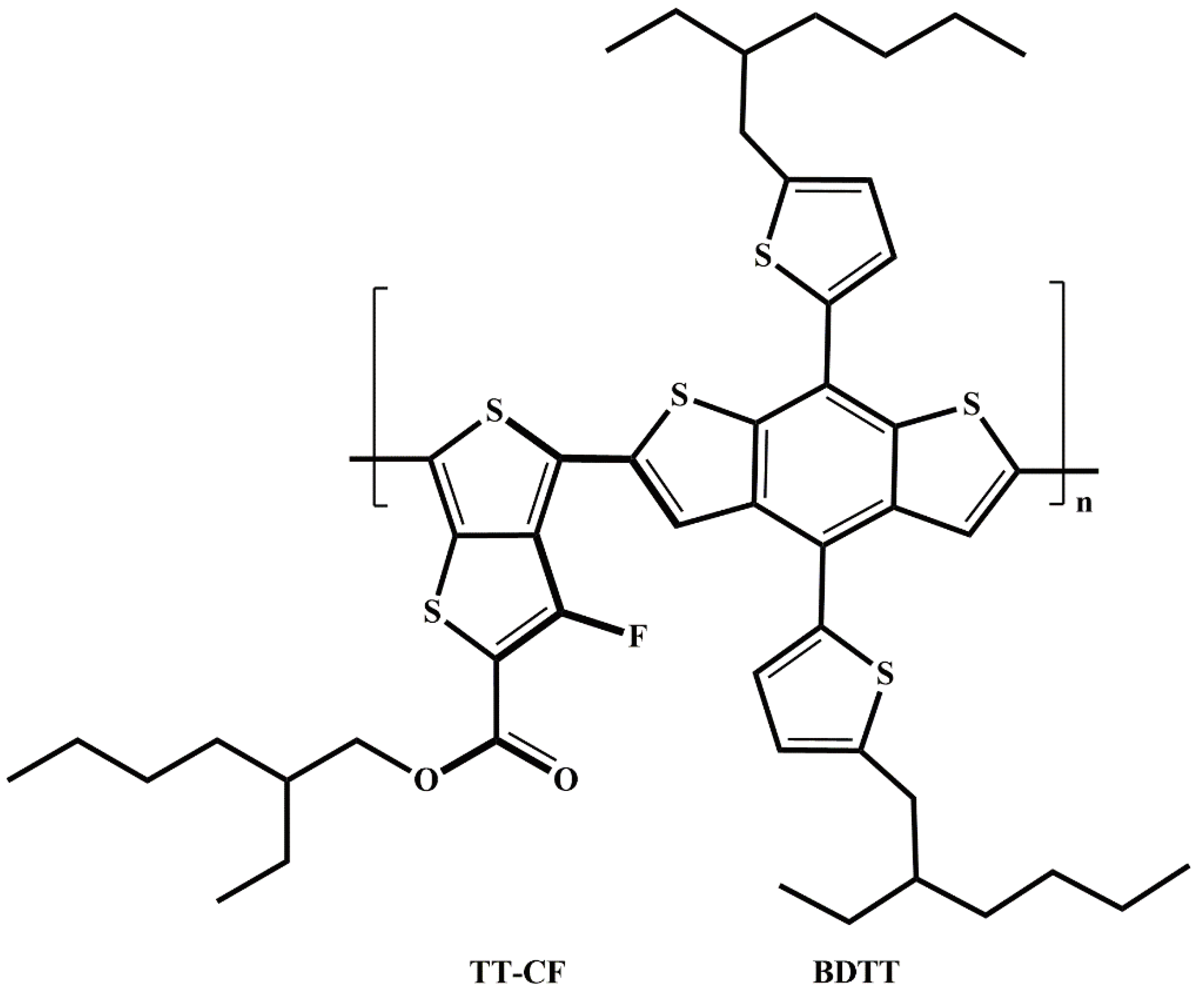
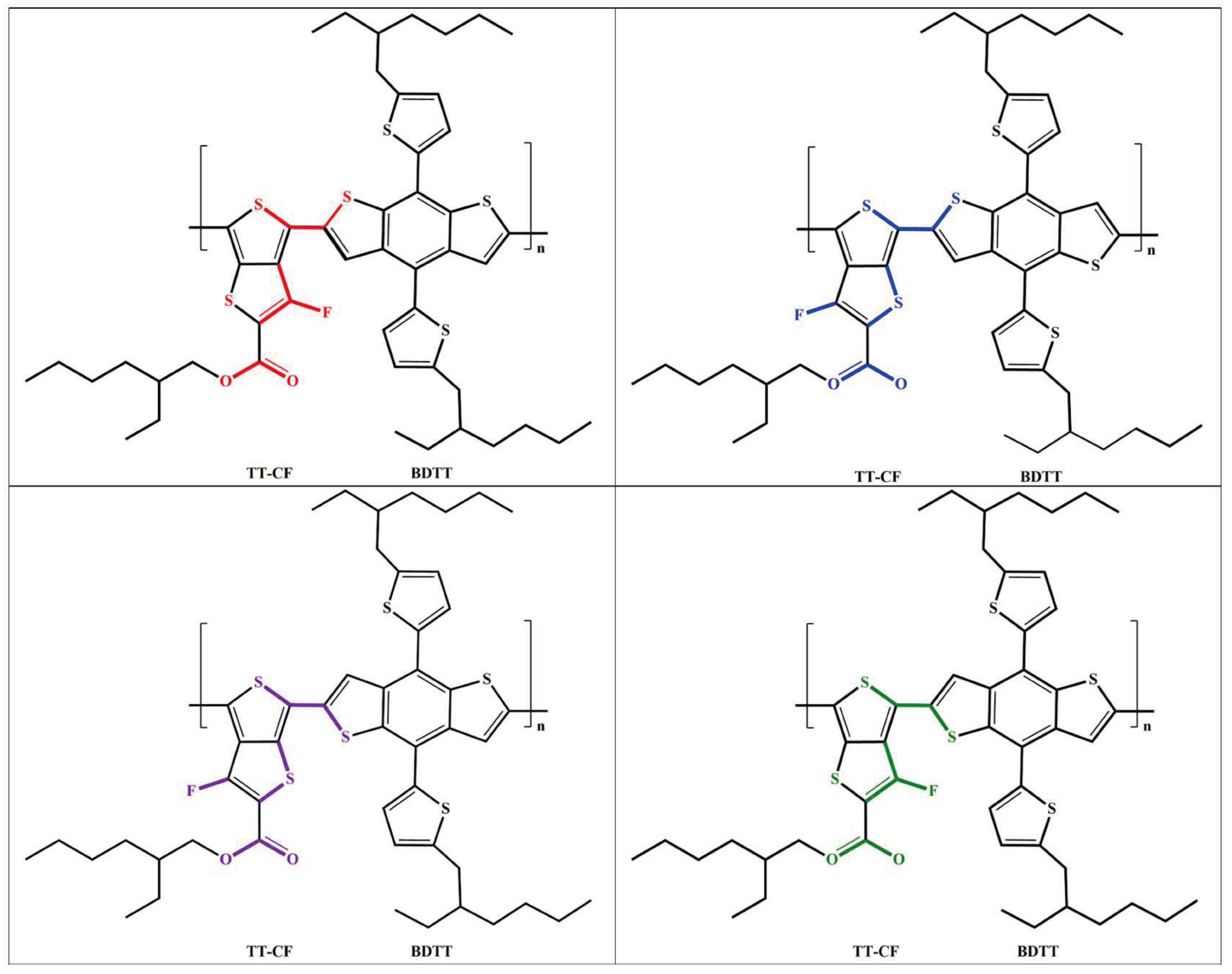
One of the critically important donor polymer (one could say foundational in the history of OSCs) is PTB7-Th [1,9,10] (poly[[4,8-bis[5-(2-ethylhexyl)-2-thienyl]benzo[1,2-b:4,5-b']dithiophene-2,6-diyl][2-[[(2-ethylhexyl)oxy]carbonyl]-3-fluorothieno[3,4-b]thiophenediyl]], also known as PBDTTT-EFT and PCE-10 [9]). PTB7-Th is an example of a low band gap (1.58 eV [8]) donor co-polymer whose monomers consist of donor-acceptor (D-A) parts, i.e. the electron donating alkyl-thienyl-benzodithiophene (BDTT) and the electron accepting thienothiophene with carbonyl and fluorine (F) substituents (TT-CF) units [1] (see Scheme 1). PTB7-Th has oxy-ethylhexyl side chains on TT-CF and thienyl ethylhexyl side groups on BDTT. The thienyl ethylhexyl side groups extend the polymer’s conjugation along the backbone plane giving rise to better interchain π–π overlapping which leads to higher charge mobility of PTB7-Th which, in turn, leads to better device performance [1,2].
The above mentioned and other (experimentally determined) properties of PTB7-Th have been studied extensively (see [1,2,9,10,11,12,13,14,15] a small sample of recent examples). Fewer computational investigations of PTB7-Th have been carried out [15,16,17,18,19]. However, we found that in spite of its importance, the lowest energy structure of PTB7-Th is not unambiguously established in the current scientific literature. This is because, the detailed (conformational) knowledge of its lowest energy structure is not essential for experimental/device investigations. Furthermore, the structure of PTB7-Th used in computational studies (typically involving heterogeneous donor-acceptor pairs) is one without alkyl side chains and often without considering which of its possible many (conformational) structures has the lowest energy.
As a result of this ambiguity, different chemical structures of PTB7-Th are displayed in literature (see examples in Scheme 1). For instance, in the reference [13] the structure of PTB7-Th has sulfur on the same side as the single bonded oxygen in the TT-CF part of the monomer while, in the review [1] the structure of PTB7-Th has fluorine in the same plane as the single bonded oxygen. Also, in some studies (e.g. [8,9]) the S-C-C-S dihedral angle along the chain backbone of PTB7-Th is in a cis-like whereas it is in a trans-like conformation in others (e.g. [10,11,12]). In this work, we address this structural ambiguity of PTB7-Th (as related to its most stable structure) by carrying out the conformational analysis.
It is important to note that, in most organic devices and applications, PTB7-Th is combined with different acceptor materials (SMs, fullerenes or other polymers) [7,8,9,10,11,12,13,14,15,16,17,18,19]. Hence, the understanding of intra- and inter-molecular interactions of the PTB7-Th and PTB7-Th/acceptor blends is critical for the enhanced device performance. This means the most stable structure of PTB7-Th must be determined accurately for the use in its computational/modelling investigations. We have found that the conformational analysis of the relatively large molecular systems (such those employed to model PTB7-Th) must be carried out with the help of a high-level quantum mechanical approach such as DFT since the low-level approaches such Molecular Mechanics (MM) and Molecular Dynamics (MD) give unphysical results for their chemical structures. In this work, we perform a careful (full) DFT conformational study of monomers and dimers of PTB7-Th which we then use to determine the structure and energies of (stable) longer oligomers such as tetramers.
Based on our earlier work [20], DFT/B3LYP [21,22] and dispersion corrected DFT/B3LYP-D3 [23] methods are reliable in determining the electronic structures and conformational energies of organic oligomers mentioned above. We also employ long-range corrected (LC) DFT methods such as CAM-B3LYP [24], LC-BLYP [25] and ωB97xD [26]. Moreover, as mentioned above, most (if not all) of computational studies that are available consider PTB7-Th without (alkyl) side chains [15,16,17,18,19]. Experimental works have illustrated that varying side chains/groups of PTB7-Th (and of other similar conjugated polymers) has a significant effect on device performance [10,27,28,29]. For example, it is well known that length of alkyl side chains may have a negligible effect on energy levels and optical absorption spectra of polymers, but can have profound effect on their aggregation in solution and self-assembly in thin film since side chains can cause steric hindrance and twisting of the conjugated backbone, which in turn could lead to a larger band gap and lower carrier mobility and lower device performance [30,31]. For all of the above reasons, in this work, we carry out the first detailed conformational analysis of PTB7-Th (with model systems that include side chains) and determine its most stable structure using B3LYP, B3LYP-D3 and LC-DFT (CAM-B3LYP, LC-BLYP and ωB97xD) methods. In addition, we extensively study the effect of branched ethylhexyl side chains (henceforth simply referred to as side chains (SdChs)) on the structure and energy of an isolated PTB7-Th oligomers.

2. Computational Approach

Our main theoretical/computational tool that is used to carry out the proposed research is the density functional theory as implemented in Gaussian 16 software [32]. We use the hybrid B3LYP functional [21,22] to determine electric and conformational structures and energies. Experimental studies show that material properties are sensitive (apart from the chemical structure) to their 3D morphology and microstructure. For this reason, weak non-covalent van der Waals forces should be included in our simulations. DFT approach has been extended to include the long-range electron correlations (known as the dispersion forces) which allow for more accurate description of molecular configurations and conformations where the interactions are dominated by the dispersion forces [23]. Hence in addition to DFT/B3LYP, we employ B3LYP-D3 as the dispersion corrected DFT [23] (that (explicitly) includes dispersion C6 (~1/r6) corrections) in our calculations especially those that focus on investigating the effect of the alkane side chain interactions on the polymer structure. In addition, we employ (other) LC-DFT methods (CAM-B3LYP, LC-BLYP and ωB97xD) [24,25,26] in our computational analysis of dimers with SdChs.

3. Conformational Analysis - Most Stable Structure of PTB7-Th

In order to determine the most stable structure of PTB7-Th, we first focus on the determining the lowest energy state of its repeat unit, consisting of a dimer (i.e. two monomers of PTB7-Th), which in turn requires that we begin with studying the conformational states of monomers of PTB7-Th.

3.1. Monomers of PTB7-Th

It is clear from the structure of PTB7-Th (see Scheme 1) that there are two possible chemical geometries for the monomers of PTB7-Th defining two intra-monomer S-C-C-S dihedral angles Φ1 and Φ2 (see Figure 1). In the first case (top part of Figure 1), the TT-CF unit is oriented with fluorine (F) pointing towards the BDTT part (Φ1) and in the second case (bottom part of Figure 1) sulfur (S) is pointing towards the BDTT part (Φ2). In addition to the differences in the orientation of S-C-C-S dihedral angles, the double bonded oxygen (=O) can be rotated and can either be placed on the side of F or the side of S of the TT-CF part of the PTB7-Th monomer. 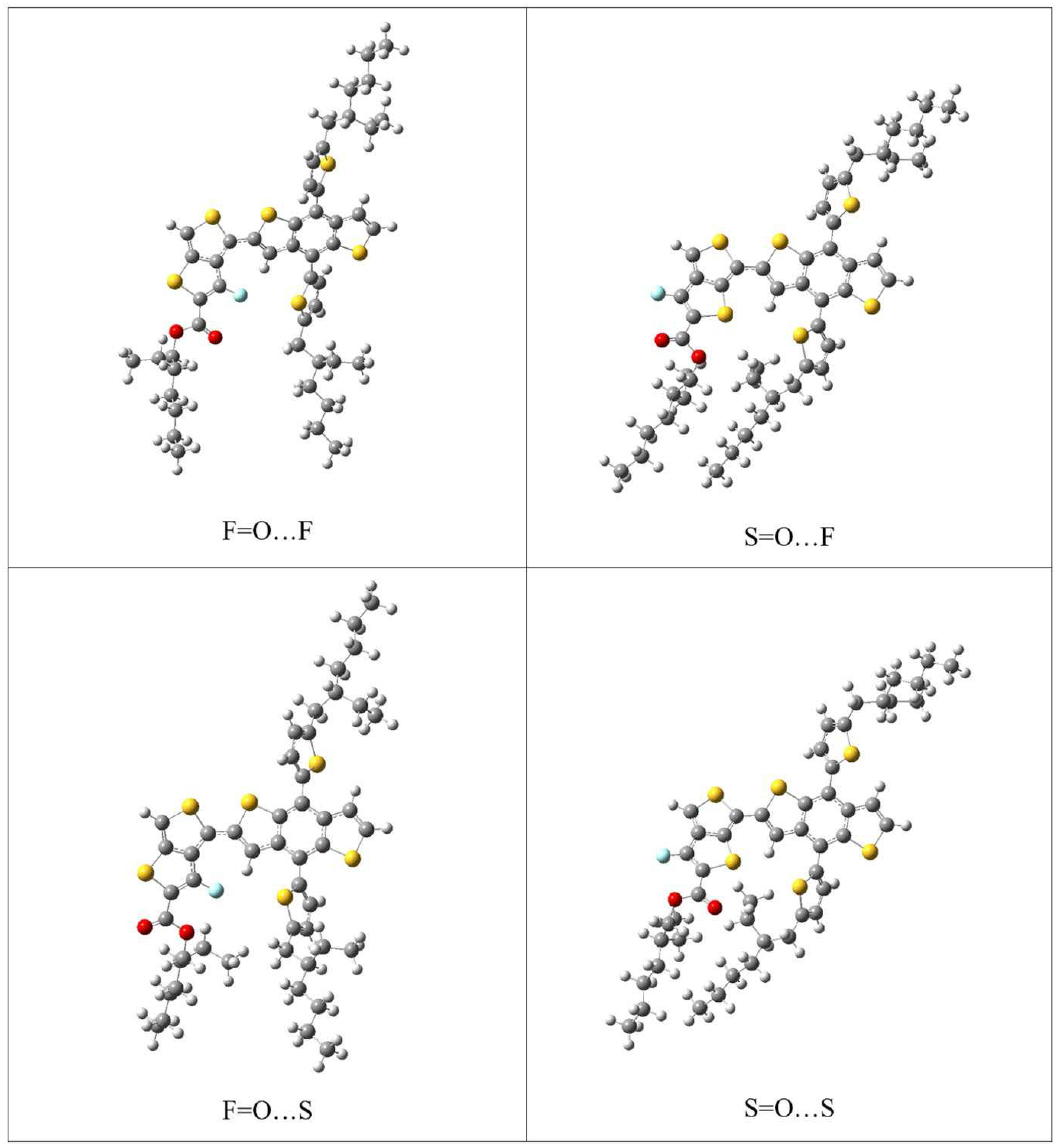Hence we consider four initial structures of the monomers (see again Figure 1): (1) F=O…F meaning F facing in (Φ1) with =O on the same side as F; (2) S=O…F meaning S facing in (Φ2) with =O on the same side as F; (3) F=O…S meaning F facing in (Φ1) with =O on the same side as S; (4) S=O...S meaning S facing in (Φ2) with =O on the same side as S.
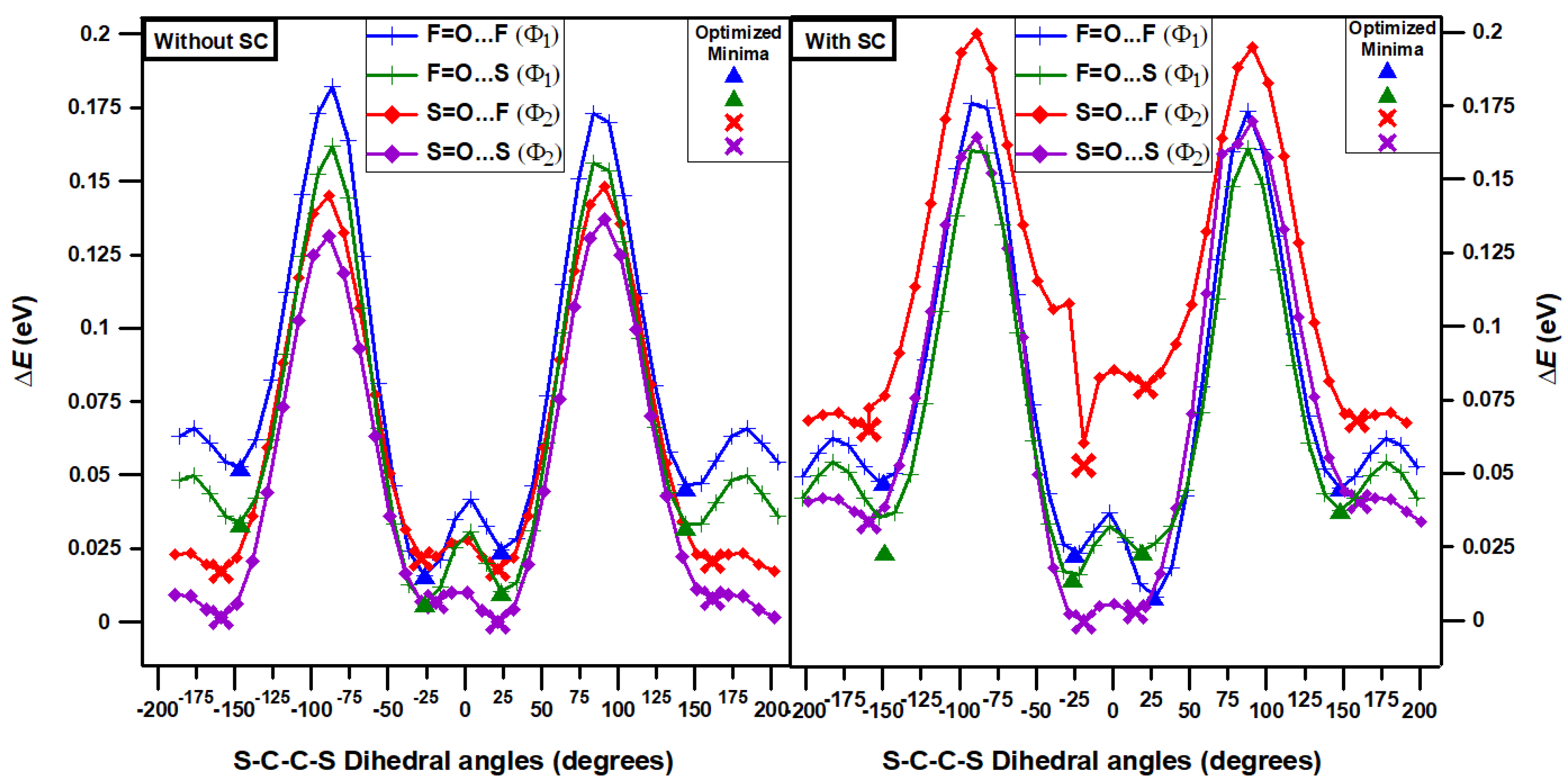
In order to determine the most stable structures of monomers we carry out one dimensional (1D) potential energy curve (PEC) DFT/B3LYP scans for the two S-C-C-S dihedral angles, Φ1 and Φ2, as defined in Figure 1. The scans are performed for the four structures of monomers without and with side chains (SdChs) present (see Scheme 1). Figure 2 illustrates the results of the 1D-PEC scans and of the geometry optimizations near scan minima for monomers. This figure clearly shows that in all cases, the minima are associated with their either cis-like (Φ1 and Φ2 are close to 0°) or trans-like (Φ1 and Φ2 are close to +180° or -180°) conformations. Therefore, their optimized structures will be our focus in this section (see Table 1) and will be used for studying the structures of longer oligomers in the following sections (3.2 and 3.3).
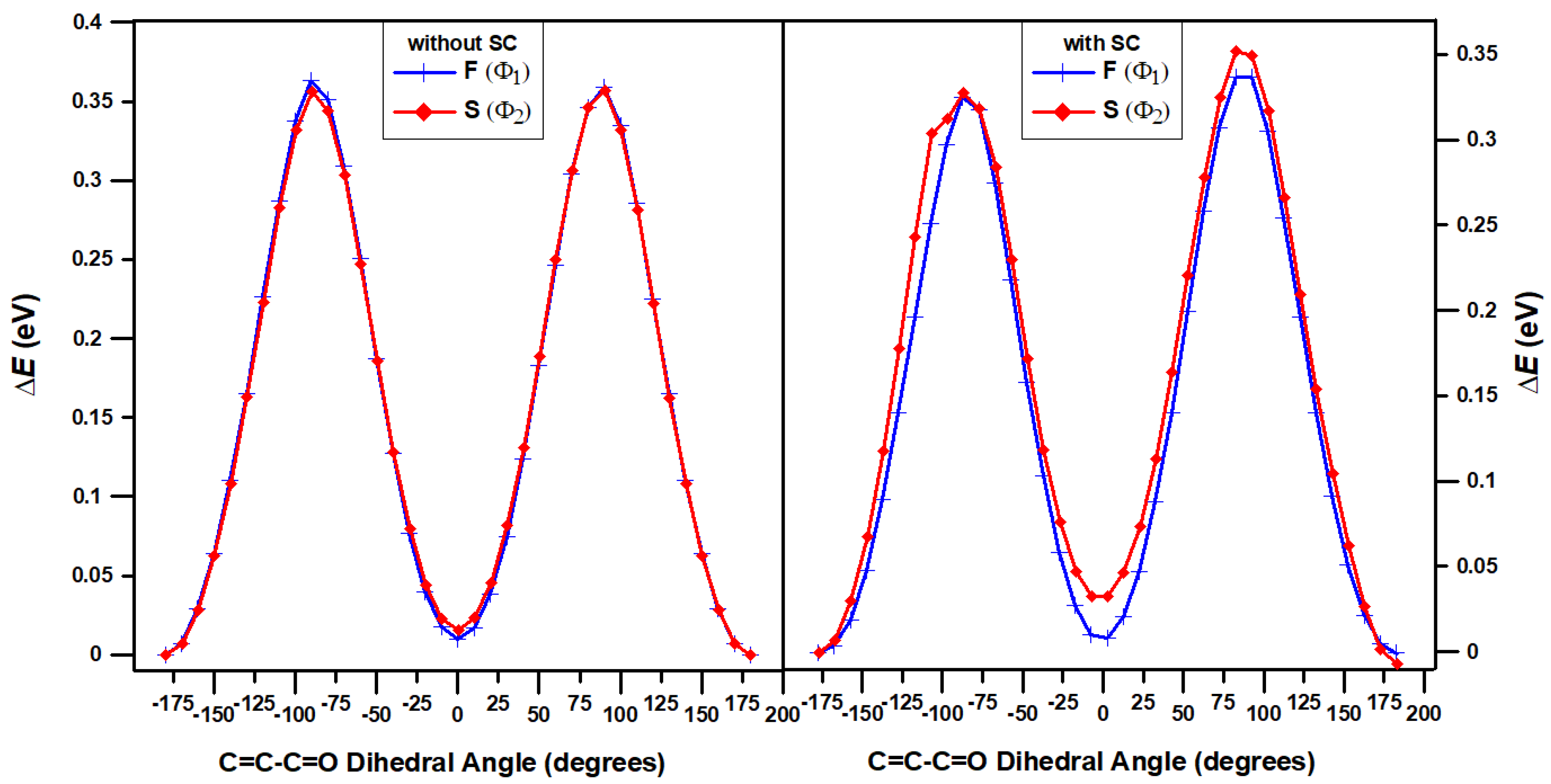
In order to determine more precisely the orientation of a =O relative to S and F of TT-CF part, we have carried out 1D-PEC scans for the C=C-C=O dihedral angles of the two Φ1 and Φ2 structures (see Figure 3). These scans show that =O strongly prefers to be located in plane containing F or S, i.e. be in the plane of TT-CF (and not be either perpendicular or in some other orientation relative to that plane).
Table 1 shows the relative (fully optimized) B3LYP and B3LYP-D3 conformational energy differences of the cis-like and trans-like conformations of PTB7-Th monomers (that were obtained from the results of Figure 2). For the monomers without SdChs, the B3LYP and B3LYP-D3 results show that cis-like S=O…S structure has the lowest energy. However, all of the other (B3LYP and B3LYP-D3) conformations (two trans-like and the other cis-like) for the S=O…S structure have energies that are within 0.02 eV (or less) of the global minimum energy. Meaning that they are all nearly degenerate. Moreover, for the B3LYP calculations, with the exception of trans-like conformations of F=O...S and F=O…F structures, all of the other conformations and structures also have energies within the 0.02 eV of the global minimum. For the B3LYP-D3 computations, the cis-like conformations have energies within 0.02 eV of the global minimum in F=O…S, S=O…F and F=O…F configurations (other conformations have higher relative energies). This means that, both B3LYP and B3LYP-D3 computations indicate that, for the PTB7-Th monomer without SdChs all of the cis-like structures have energies close to the global minimum energy irrespective of whether S or F is facing in and whether =O is on the same side as S or F of the TT-CF unit. In particular, for monomers with F facing in, Φ1 is equal to -26.10° (B3LYP) or -29.04° (B3LYP-D3) in their lowest energy (cis-like) states, and with S facing in, Φ2 is equal to 22.09° (B3LYP) or 25.17° (B3LYP-D3) in their lowest energy (cis-like) states. For these systems trans-like conformations have somewhat higher relative energies. In both (B3LYP and B3LYP-D3) cases energy differences range from 0 to 0.06 eV, which means that dispersion energy does not affect relative energies very much when there are no SdChs present in the monomers.
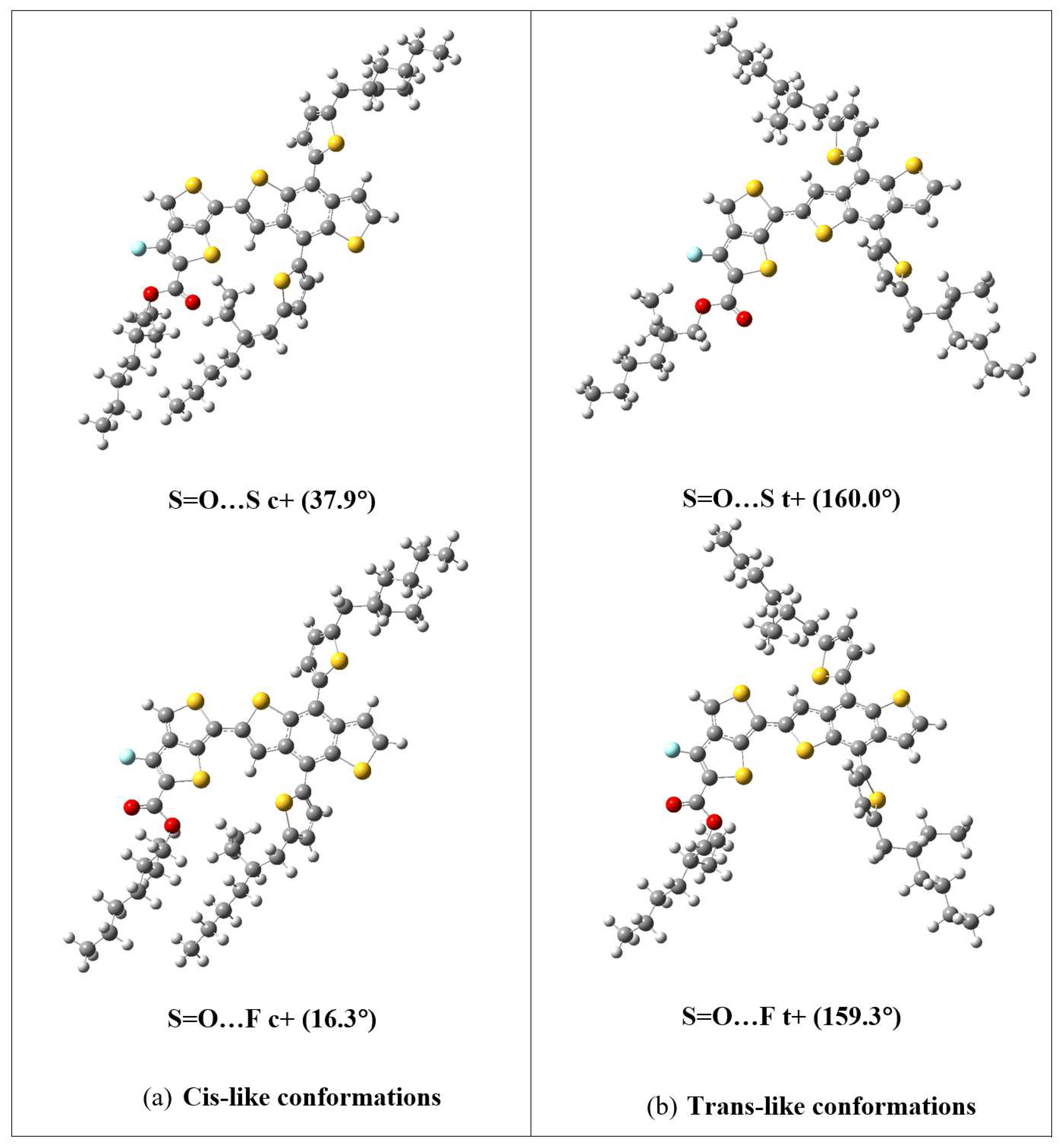
For monomers with SdChs, the B3LYP results show that cis-like (-22.04° and 14.83°) conformations of S=O…S structure have the lowest energies (with differences less than 0.003 eV) which, in turn, are nearly degenerate (energies differ by 0.02 eV or less) with cis-like conformations of F=O…S (-26.37°) and F=O…F (-24.82°, 26.54°), and with trans-like conformation of F=O…S (-148.69°) monomers. It should be noted that for these monomers, the B3LYP relative energy differences range from 0 to 0.08 eV which is again a relatively narrow energy range similar to the case when no SdChs are present as discussed above. The B3LYP-D3 removes many degeneracies, giving S=O…S cis-like (37.94°) as the lowest energy state which is only nearly degenerate (energy difference of 0.02 eV) with the cis-like state (16.26°) of S=O…F. The lowest energy state with F in (which is 0.21 eV above the global minimum) is given by cis-like conformations (-14.71° and 30.36°) of F=O…S monomer. In this case, the B3LYP-D3 relative energy differences range from 0 to 0.33 eV (which are significantly higher compared to the B3LYP results). This indicates that the inclusion of the dispersion energy in the B3LYP-D3 computations introduces stronger intermolecular interactions between SdChs which bring the SdChs closers in the cis-like compared to the trans-like conformations of the monomers (see an example in Figure 4, and Figures S1 and S2 in Supplementary Information (SI) for the remaining B3LYP and B3LYP-D3 optimized geometries of the four conformational sets of monomers with SdChs). In summary, these computations indicate that, for the PTB7-Th monomers with SdChs, the cis-like conformations in S=O…S (B3LYP, B3LYP-D3), S=O…F (B3LYP-D3), and F=O…S and F=O…F (B3LYP) have some of the lowest energies (see their optimized geometries in Figure 5). Figure 5 illustrates again the stronger interactions between SdChs in the B3LYP-D3 cis-like conformations of S=O…S and S=O…F. Based on the above discussion, we expect that since cis-like conformations are preferred in the monomers of PTB7-Th, that they will be preferred in the longer oligomers as well (i.e. the lowest energy state will be cis-like for the whole polymer).

3.2. Repeat Units (Dimers) of 2PTB7-Th

3.2.1. DFT/B3LYP and DFT/B3LYP-D3 results

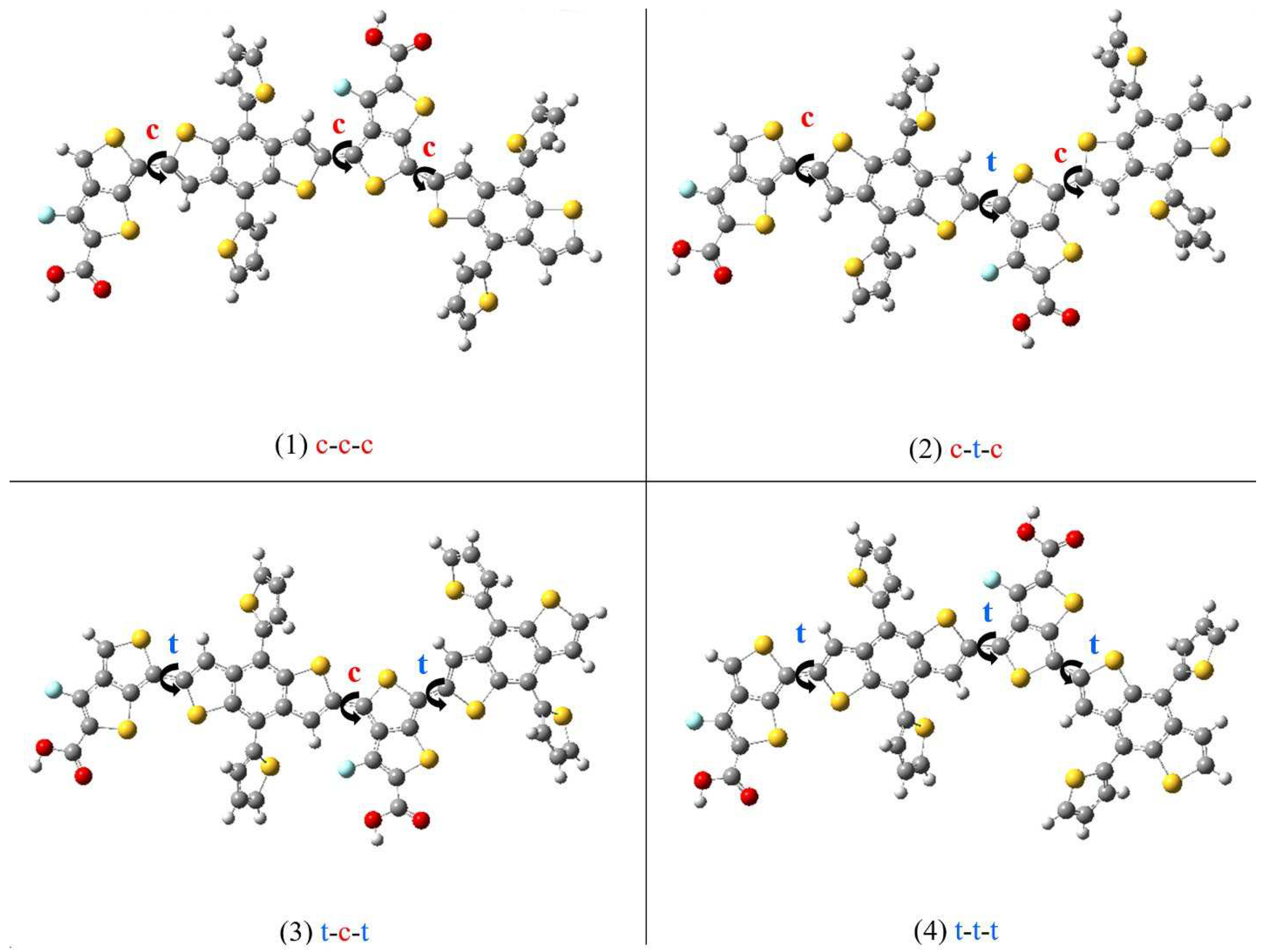
The monomer prediction (as discussed above) is first tested on repeat units (dimers) of PTB7-Th (referred to as 2PTB7-Th). Once again there are four possible configurations for the dimers: (1) S=O...S; (2) S=O…F; (3) F=O…S; (4) F=O…F. Based on the previous results of Figure 2, we expect that these dimer structures will have the low conformational-energy states when the S-C-C-S dihedral angles are either cis-like (c) or trans-like (t). Therefore, we consider the orientation of S-C-C-S dihedral angles of the dimers that can take the form of all-cis (c-c-c) or all-trans (t-t-t) or a mix of both cis and trans (c-t-c and t-c-t). 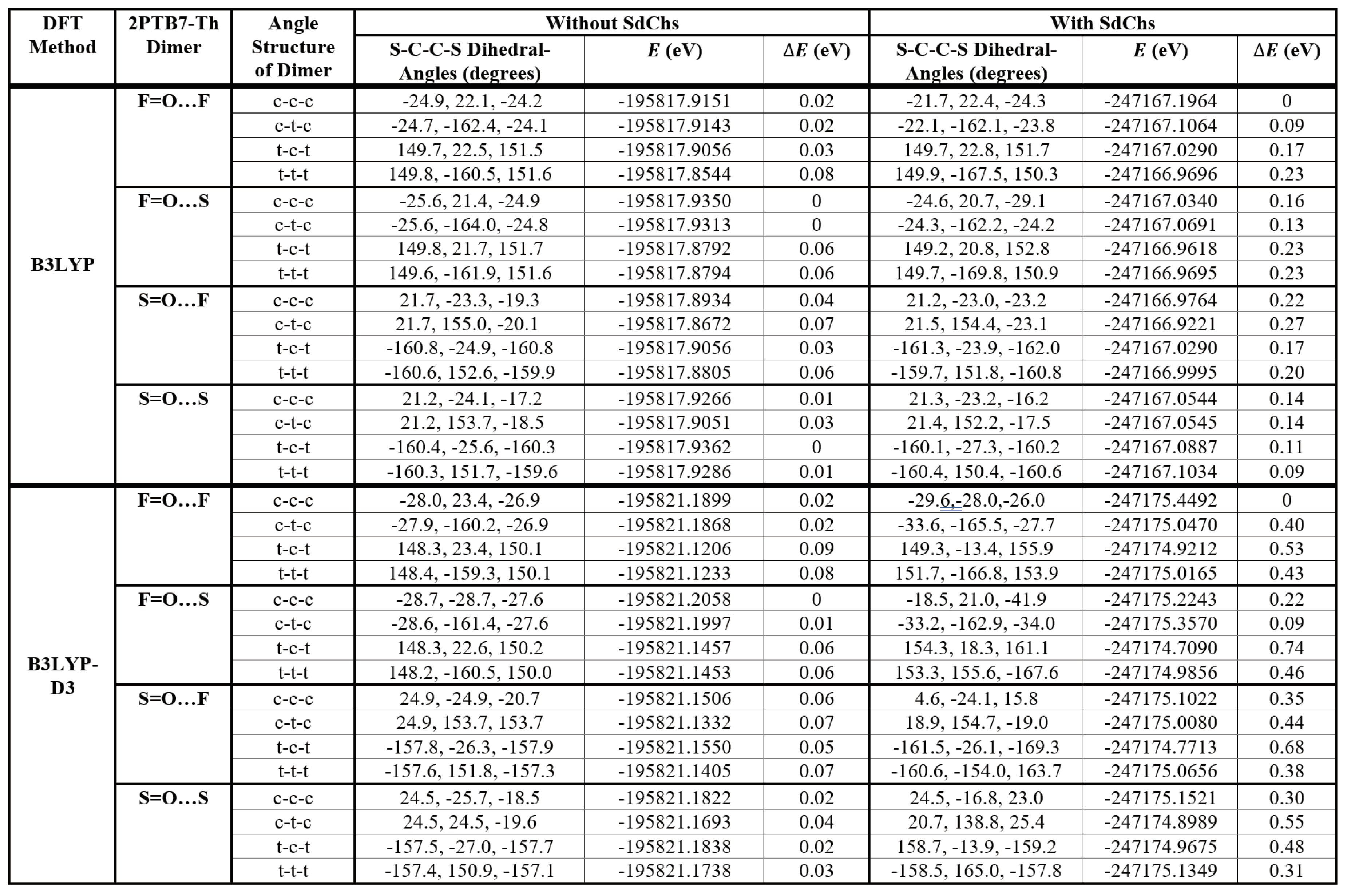Theses four types of S-C-C-S dihedral angles along the backbone chains of 2PTB7-Th are illustrated in Figure 6 for an S=O…S structure as an example. The results of the relative B3LYP and B3LYP-D3 conformational energy differences for the 16 optimized dimers without and with SdChs are given in Table 2.
When SdChs are added, the number of degeneracies is significantly decreased. The representative B3LYP results show that c-c-c conformation of F=O…F dimer has the lowest energy (with the next lowest state having energy 0.09 eV above the global minimum in c-t-c conformation of F=O…F dimer and t-t-t conformation of S=O…S dimer). The B3LYP-D3 results agree with B3LYP computations and give c-c-c conformation of F=O…F dimer as the lowest energy state. Similar to the monomers results in precious section, it is clear that the presence of SdChs has a considerable effect on determining the lowest energy state of 2PTB7-Th. In order to illustrate the behaviour of SdChs, dimers with SdChs are shown in Figures S3 and S4 in SI. For example, Figure S3 (containing B3LYP-D3 results) shows that SdChs in c-c-c conformation of F=O…F dimer has the two pairs of SdChs strongly interacting (see also Figure 9 below). Similarly in the second lowest (B3LYP-D3) energy conformation c-t-c of F=O...S dimer also has two pairs of SdChs strongly interacting. In all of the other conformations, SdChs are relatively far apart from each other and relative energy differences (ranging from 0.2 to 0.7 eV) are considerably above the lowest energy state (this is especially true for all of the S=O...S and S=O…F dimer conformations).
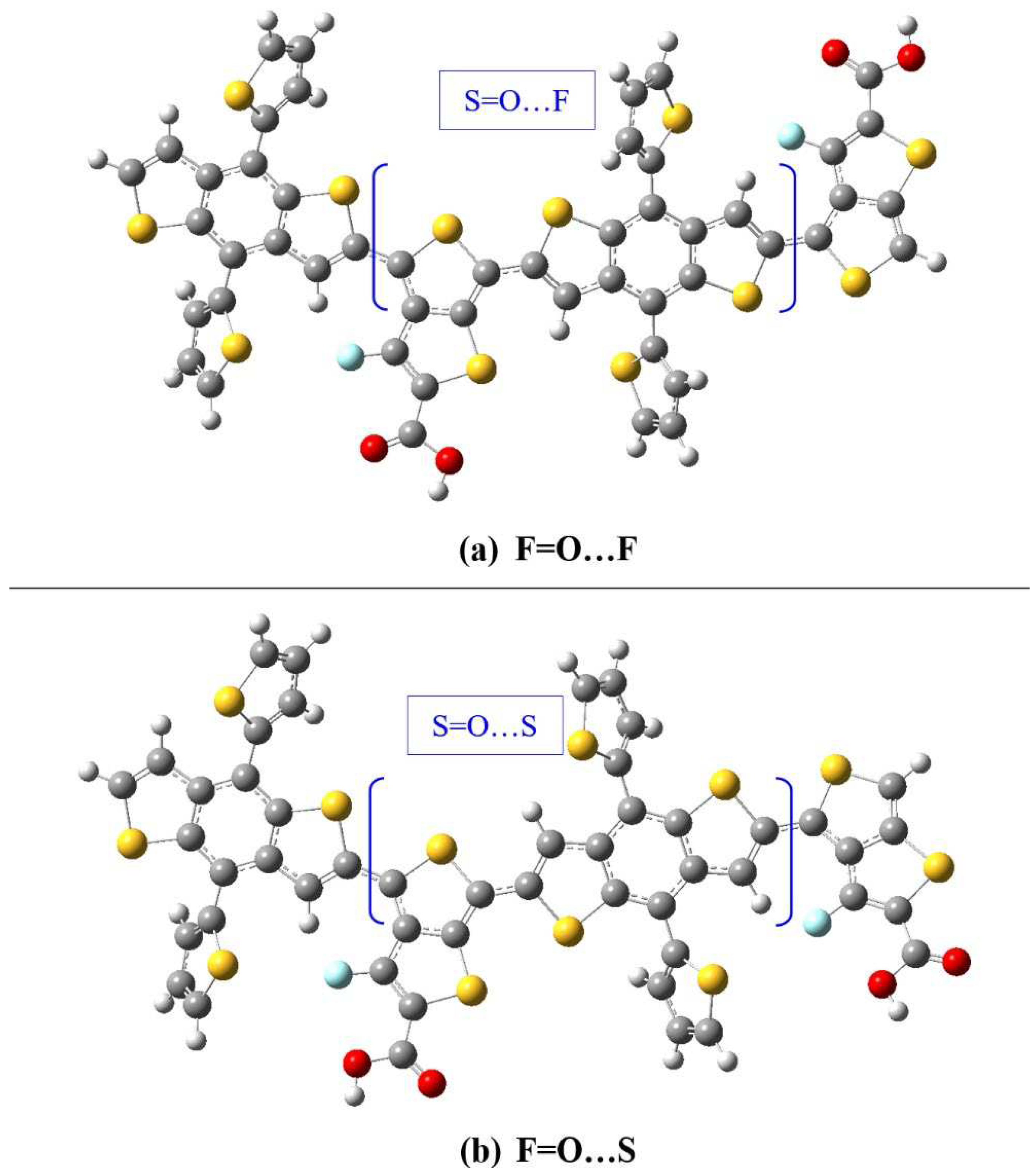
It is interesting to note that the lowest (B3LYP and B3LYP-D3) energy configurations for dimers occur for F=O…F (with SdChs) (c-c-c) and F=O…S (without SdChs) (c-c-c) configurations. This appears to contradict the monomer results which showed that S=O…S and S=O…F structures give the lowest energy. However, it can be noted that dimers can be also equivalently considered as central monomers with end groups (TT-CF and BDTT). In this case the F=O…F (c-c-c) dimer can be equivalently thought of as S=O…F monomer with the TT-CF and BDTT end groups (see Figure 7 (a)). Similarly, F=O…S (c-t-c) dimer can be thought of as S=O…S monomer with the TT-CF and BDTT end groups (see Figure 7 (b)). This does agree with the above-mentioned monomer results (which show that S=O…F and S=O…S monomers tend to have the lowest conformational energies). This analysis shows that the lowest energy configurations/conformations in monomers tend to dominate the dimer results (i.e. the configuration/conformation of central monomer determine dimer’s lowest energy state).
The dimer and monomer computational results also show that most trans-like dihedral angles are close to either +/-150° or +/-160° and cis-like angles are close to +/-20° (ranging from +/-15° to +/-30° in most cases). Moreover, most trans-like conformations for monomers are higher in energy than cis-like conformations and appear to be more or less equivalent in energy irrespective of their configuration. This equivalency of trans-like conformations also appears to be true for dimers (although here larger energy differences are observed, see Table 1 and Table 2 for comparison).

3.2.2. LC-DFT results

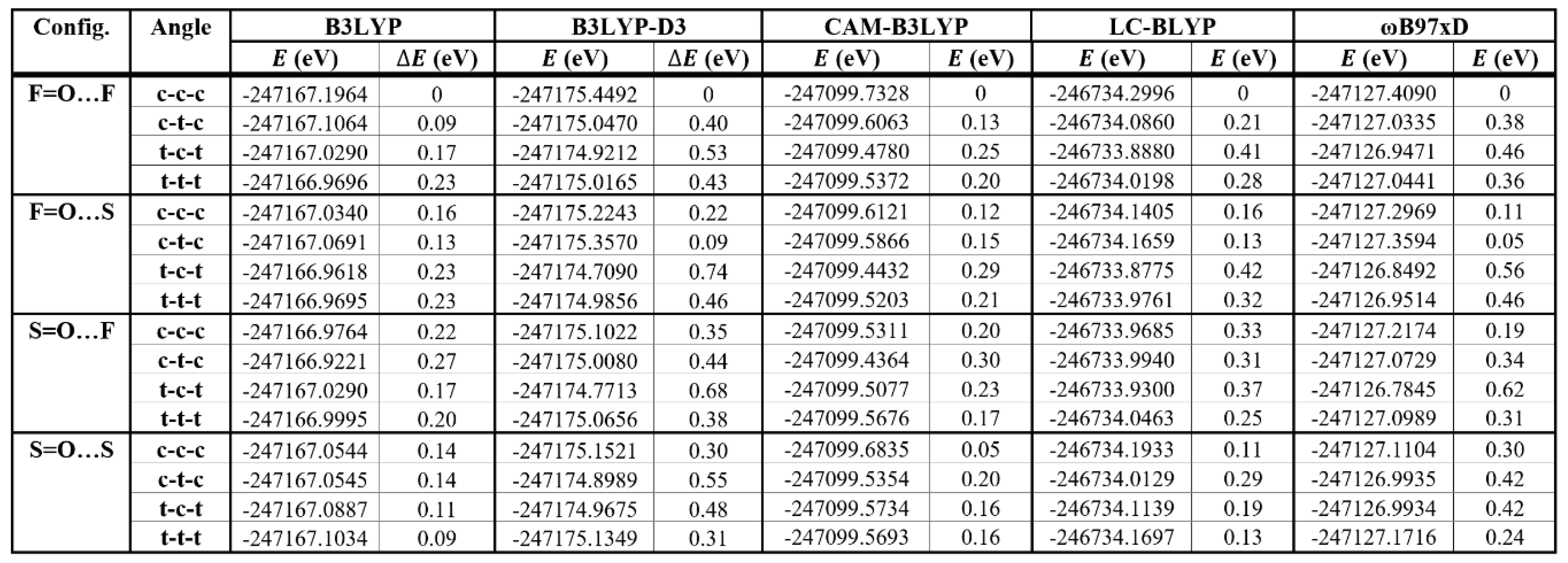
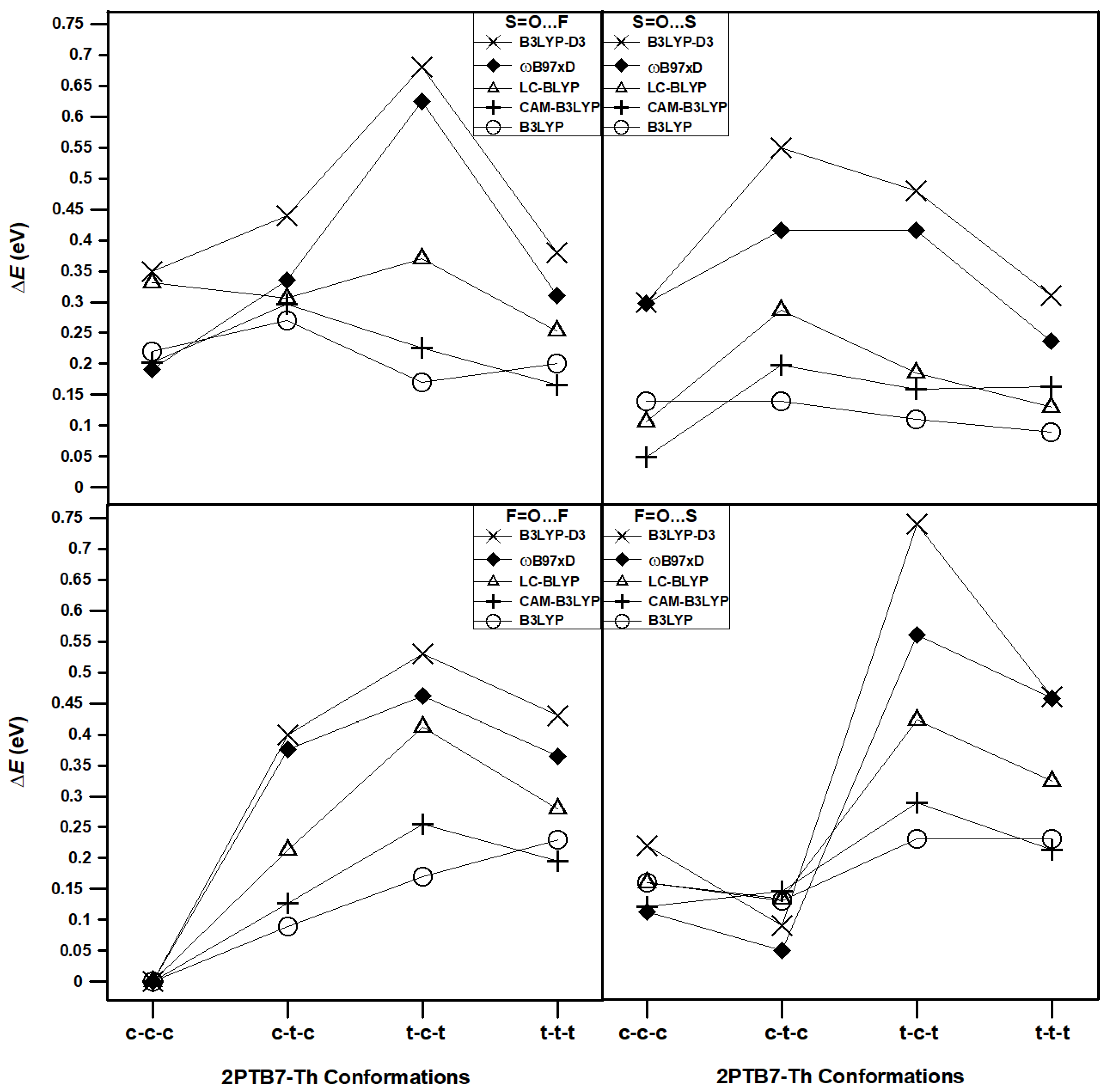
To further verify the conformational behavior of 2PTB7-Th dimers as obtained using B3LYP and B3LYP-D3 in previous subsection, we optimize the 16 configurations of 2PTB7-Th with SdChs using LC-DFT methods (CAM-B3LYP, LC-BLYP and ωB97xD). The results of these computations are given in Table 3. The three LC-DFT methods show that, in most cases, the conformations of 2PTB7-Th with predominantly cis-like S-C-C-S dihedral angles (such as c-c-c and c-t-c) are more favorable (i.e. they have lower total energies) than those with predominantly trans-like dihedral angles (such as t-c-t and t-t-t). This behaviour is particularly evident in the F=O…F and F=O…S configurations. For the S=O…F and S=O…S configurations, conformational energy differences are smaller for those conformations that include all-cis and all-trans S-C-C-S dihedral angles than those that include a mix of cis-like and trans-like S-C-C-S dihedral angles (such as c-t-c and t-c-t). We find that in all cases, for a given LC-DFT method (consistent with the B3LYP and B3LYP-D3 results) the F=O…F all cis (c-c-c) configuration has the lowest total energy. Also consistent with the B3LYP and B3LYP-D3 results, we find no energy degeneracies for the optimized LC-DFT configurations. This is mainly due to the presence of SdChs as discussed in the previous subsection.
In order to illustrate the above results more clearly, the calculated (B3LYP, B3LYP-D3, CAM-B3LYP, LC-BLYP, and ωB97xD) conformational (relative) energy differences for the 16 conformations of 2PTB7-Th are displayed in Figure 8. The hybrid DFT, DFT-D3, and LC- DFT methods, all show similar trend for the results of F=O…F and F=O…S configurations. For the S=O…F and S=O…S configurations there are some differences in trends. In this case, B3LYP-D3 and ωB97xD perform similarly but are somewhat different from B3LYP, CAM-B3LYP and LC-BLYP results. However, in all of these cases, the conformational energy differences are far above the energy of the most stable structure (F=O…F all cis) and hence these differences in trends do not affect our final conclusion of what constitutes the most stable structure of 2PTB7-Th. Hence, we conclude that the three LC-DFT methods confirm our findings as obtained using the B3LYP and B3LYP-D3 functionals. Because of this consistency in the results, the remaining part of this conformational analysis (that will involve energy optimizations of longer oligomers) is carried out with only B3LYP and B3LYP-D3 DFT functionals. This is done primarily for computational expediency.

3.3. Longer Oligomers of PTB7-Th

First, we make a note regarding the naming of longer oligomers (extended dimers). It can be seen from the discussion above that dimer names such as F=O…F etc are somewhat ambiguous. That is, because of the symmetry of the monomers, dimers can be equivalently thought of as central monomer with end groups (e.g. S=O…F monomer in the case of F=O…F dimer). In order to be consistent, we name the longer oligomers based on the initial monomers that were used to build the longer oligomers of PTB7-Th. Appropriate comments regarding their structures and energies will be made as it is needed.
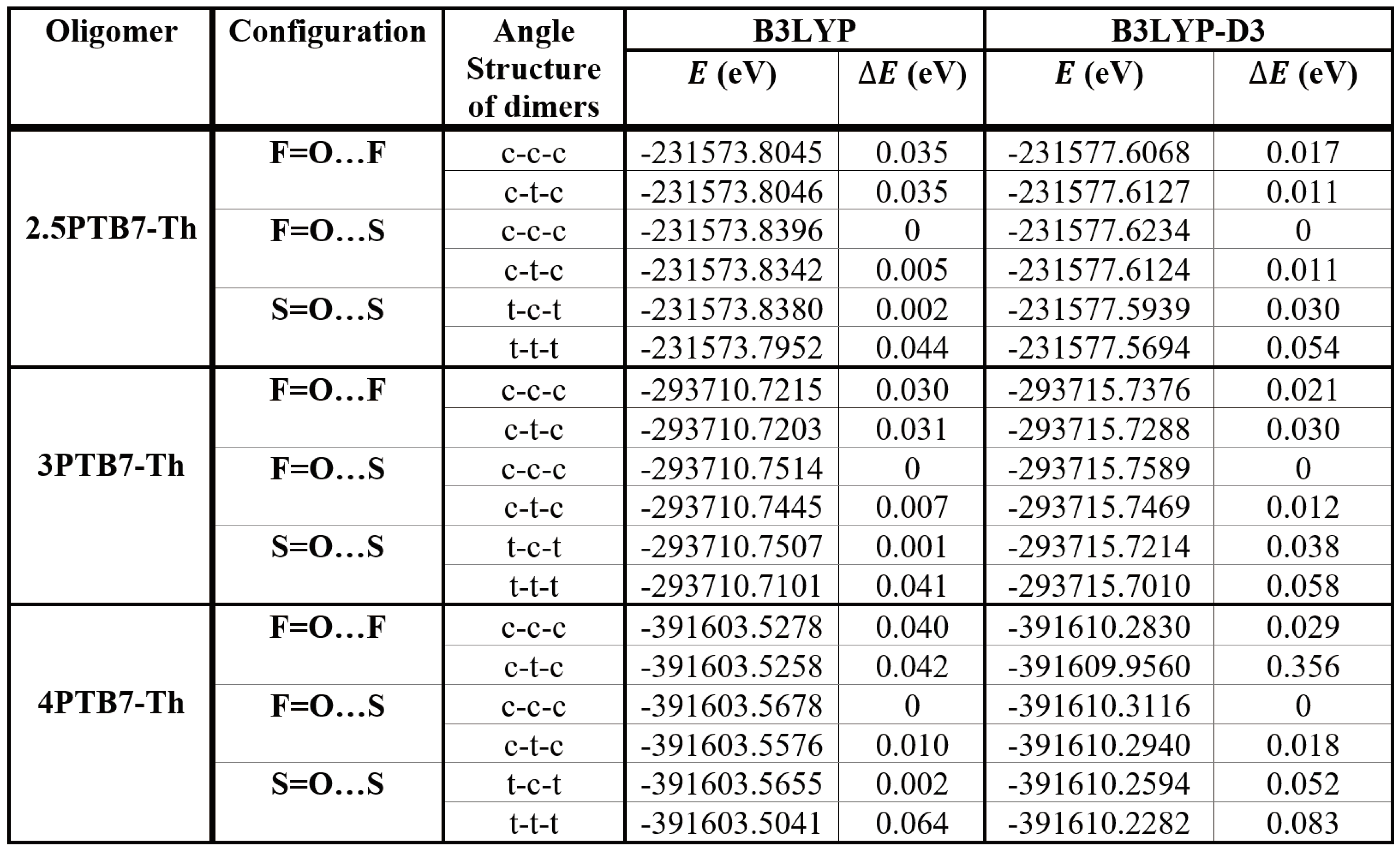
In order to further assess the lowest energy state of PTB7-Th, we carry out conformational analysis of longer oligomers of PTB7-Th. The dimers that exhibited relatively lower conformational energy differences in the previous section 3.2 (such as, for example, F=O...F (c-c-c) and F=O…S (c-t-c)) are extended to two-and-half (2.5) oligomers, trimers and tetramers. They are referred to as 2.5PTB7-Th, 3PTB7-Th, and 4PTB7-Th oligomers, respectively. The 2.5PTB7-Th is purposely selected for its symmetrical structure (that is, for example, its F=O…S configuration can be thought of as consisting of either two F=O…S monomers or equivalently of two S=O…S monomers with a corresponding end group).
Table 4 gives the conformational energy results for the representative longer oligomers without SdChs. The B3LYP and B3LYP-D3 computational data in the table predict that all cis-like conformations of F=O…S configurations of constituent monomers have the lowest energies for the respective oligomers (2.5, trimers and tetramers). There are some near degeneracies in the case of B3LYP results. This is very much consistent with the conformational analysis of the monomers, which predicted that both cis-like conformations of S=O…S and F=O…S configurations have the lowest energies. As described above, it should be noted that for longer oligomers denoted by, say, F=O…S name, the F=O…S or equivalently S=O…S monomers are alternating along the chain backbone with possible end groups (see also Figure 7). Hence, it is expected that all cis-like oligomers without SdChs denoted by S=O…S or F=O…S would produce the lowest energy states.
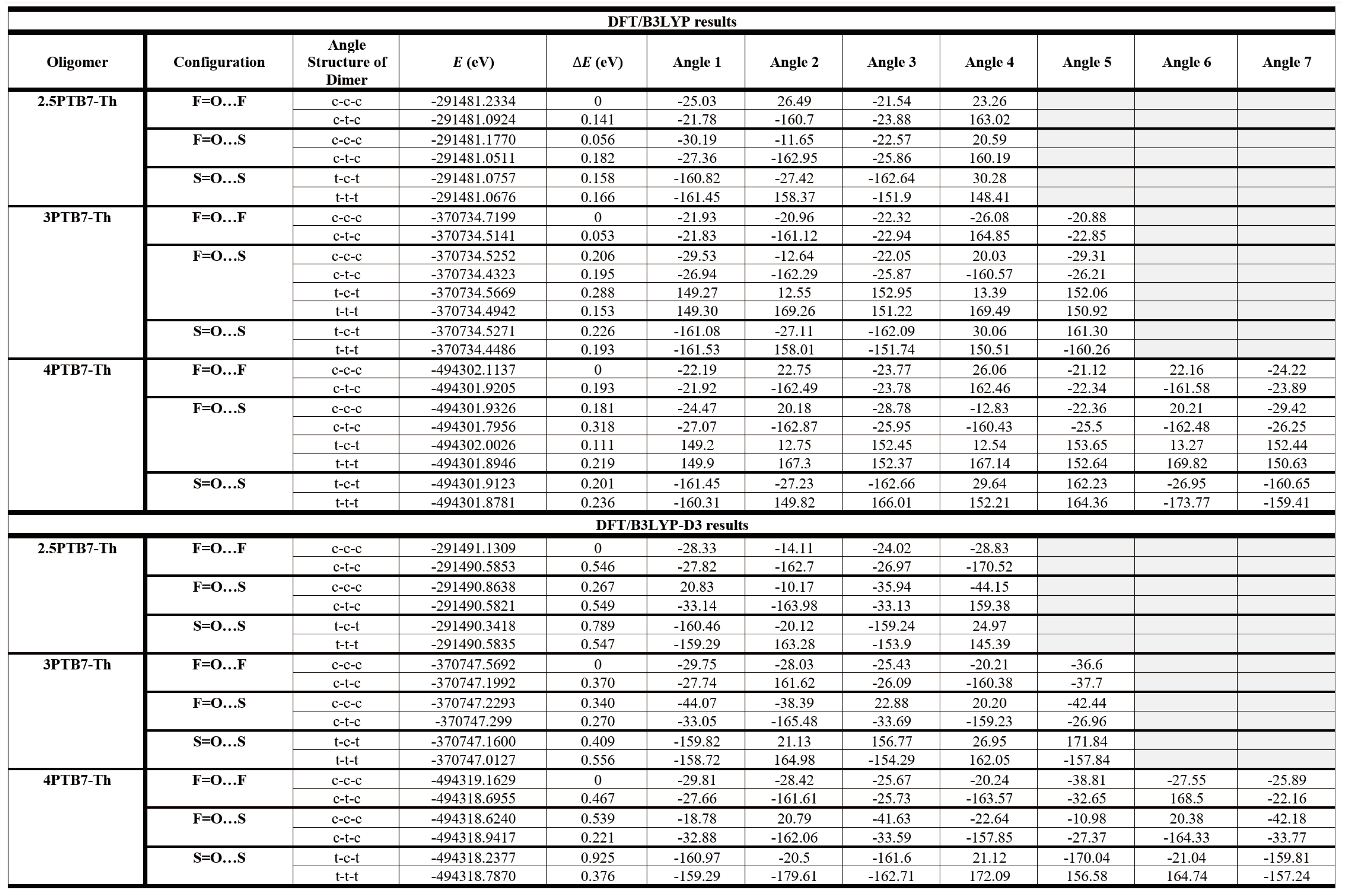
Table 5 presents the B3LYP and B3LYP-D3 energies and the main S-C-C-S dihedral angles along the chain backbones for the representative longer oligomers with SdChs (the optimized structures for all of the oligomers with SdChs are displayed in Figures S5 and S6 in SI). In contrast to the results for oligomers without SdChs, the results of Table 5 show no degeneracies in the conformational energies for all of the studied oligomers with SdChs. This clearly indicates the significant role of SdChs in the conformational energy analysis. The data in Table 5 also show that all cis-like conformations of F=O…F oligomers with SdChs (or equivalently consisting of cis-like S=O…F configurations of constituent monomers) have the lowest energies for all of the representative systems studied (i.e. 2.5 oligomers, trimers and tetramers). These results for the longer oligomers with SdChs are consistent with the dimer results which found that the lowest energy configurations occur for F=O…F (c-c-c) dimers with SdChs. The main conclusion that can be made for both dimers and longer oligomers with SdChs is that the preferred state is an all cis-like conformation with the =O in the plane with F (see optimized geometries in Figure 9). Whereas for longer oligomers without SdChs the =O is located in plane with S in their lowest energy structures.
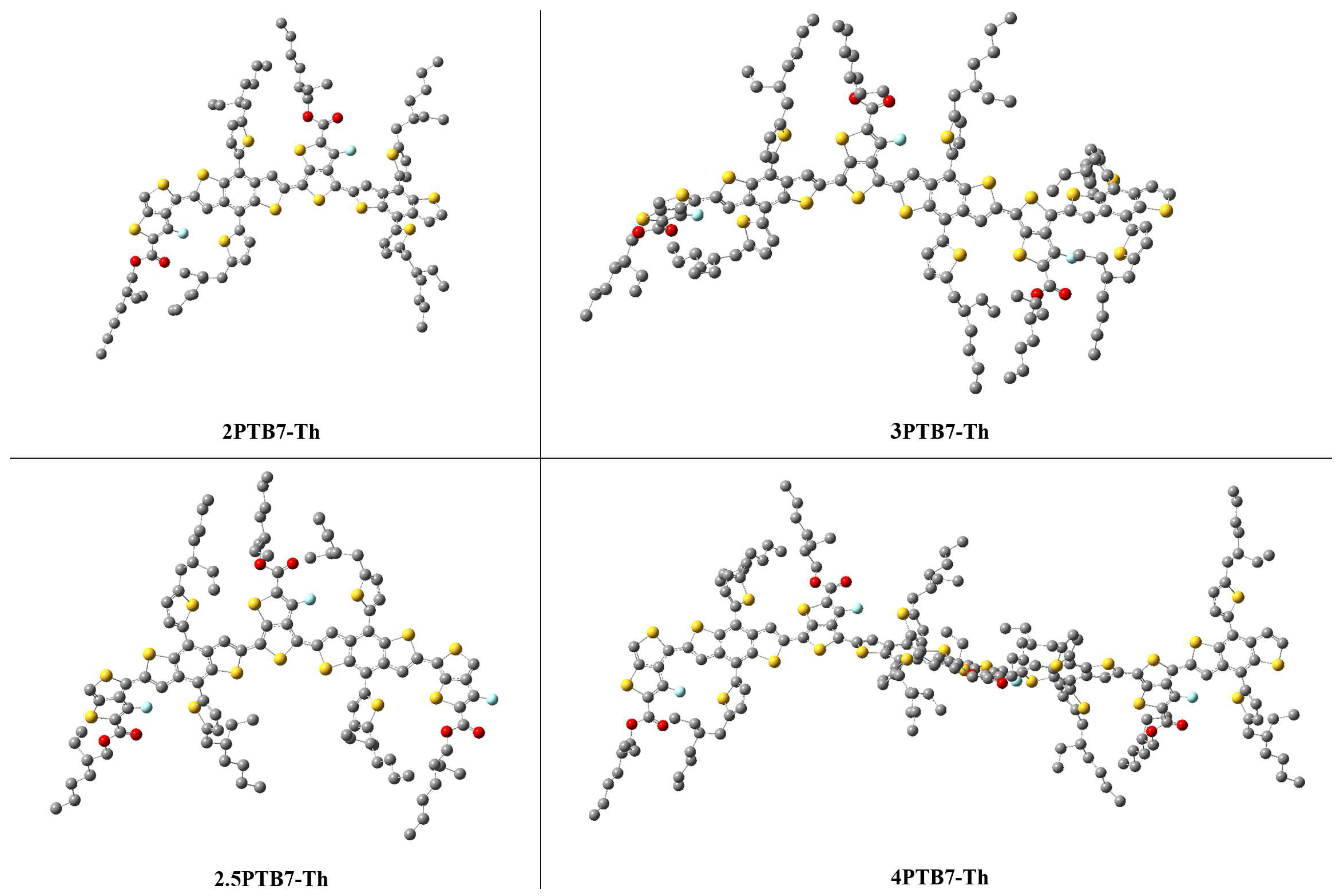
To understand why F=O…F (all cis) structure exhibits the lowest conformational energy, we consider the optimized geometries of the longer studied oligomers as shown in Figure 9. This figure shows that in the all cis-like conformations the SdChs tend to bunch in groups of three along the oligomer backbones. These SdChs intermolecular interactions provide extra (attractive) energy that makes these structures more stable relative to other conformations (where the SdChs are either unevenly distributed on both side of the backbone in mixed conformations or are farther apart in the all trans-like conformations). As an example, we look at the optimized structures of 4PTB7-Th’s as shown in Figure 10 in some greater details. It appears that F=O…F (all cis) 4PTB7-Th displays a slight twist along oligomer chain backbone, which causes a stronger intra-chain interactions within the twisted backbone, thus lowering its conformational energy (see Figure 10 (a)). The backbone twists in all cis-like conformations further enhances the SdChs interactions by bunching them in groups of three as mentioned above. This twist is not present in the geometries of other structures (such as S=O…S (all trans) in Figure 10 (b)). When cis- and trans-like S-C-C-S dihedral angles are mixed (such as c-t-c), the chain backbone bends (see Figure 10 (c) and (d)). We also note that these mixed conformations have an uneven distribution of SdChs (with one side having significantly more SdChs than the other) in comparison to the all cis-like (or all trans-like) conformations.
Preprints 68569 g009
Figure 9. The B3LYP-D3 optimized geometries for the preferred states of the longer oligomers of PTB7-Th (F=O...F, all-cis). Hydrogens are removed for visual clarification.
Figure 9. The B3LYP-D3 optimized geometries for the preferred states of the longer oligomers of PTB7-Th (F=O...F, all-cis). Hydrogens are removed for visual clarification.
Preprints 68569 g009
Table 5 also includes the main S-C-C-S dihedral angles along the chain backbone of the longer oligomers. Similar to dimer and monomer computational results, the longer oligomers also show that most trans-like dihedral angles are close to either +/-150 or +/-160 (ranging from +/-150 to +/-180) and cis-like angles are close to +/-25 (ranging from +/-10 to +/-40). In general, in comparison to oligomers without SdChs there are more fluctuations in dihedral angles (and they tend to be somewhat larger) when SdChs are present due intermolecular interactions between SdChs for both B3LYP and B3LYP-D3 results. Also, due to explicit inclusion of the van der Waals intermolecular energy, B3LYP-D3 dihedral angle values tend to be larger than the corresponding B3LYP values, again due to SdChs interactions (see discussion above). For example, Table 5 show that cis-like angles for longer oligomers with SdChs tend to be closer to 30 (B3LYP-D3) rather than 25 (B3LYP) and similarly B3LYP-D3 trans-like angles tend to be larger by approximately 5 in comparison to the corresponding B3LYP results for oligomers with SdChs.

3.4. Electronic Structure of PTB7-Th

Conformational analysis of the PTB7-Th is the main focus of this paper. However, to verify that our conformational results are physically meaningful, we compare the computed electronic structure (HOMO, LUMO and band gap) values of PTB7-Th with the respective experimental values. The experimentally determined band gap (Eg) of PTB7-Th is 1.59 eV and its HOMO and LUMO energy values estimated to be –5.23 eV and –3.64 eV respectively [1,8,33]. 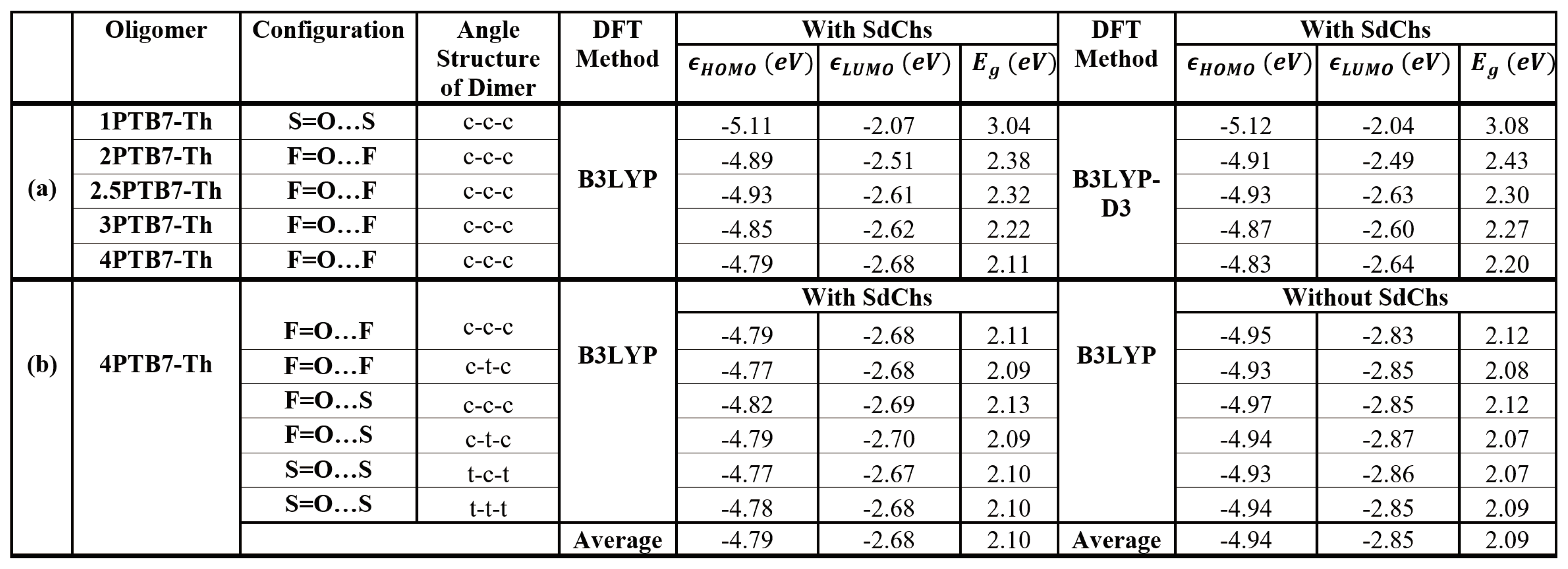Table 6 (a) lists the HOMO and LUMO eigenvalues and band gaps for the most stable DFT/B3LYP and DFT/B3LYP-D3 structures of oligomers from monomers to tetramers as found above (to obtain B3LYP energies from B3LYP-D3 computations, we employ B3LYP-D3 optimized geometries in single point B3LYP calculations). 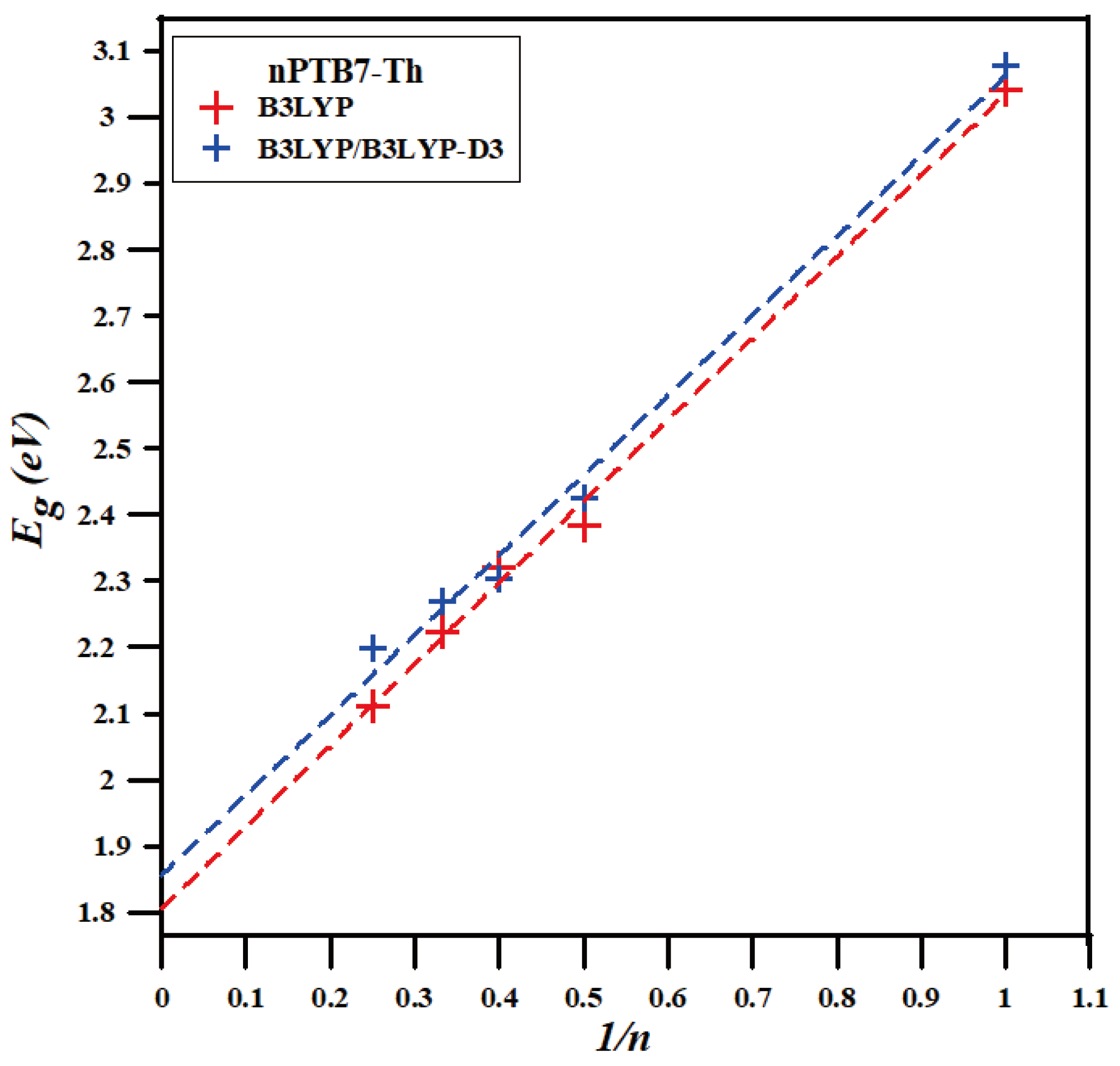Figure 11 estimates the band gap for the infinite chain length (PTB7-Th) polymer by plotting oligomer band gaps as a function of the inverse of their lengths and extrapolating to zero. These extrapolations give value of 1.8 eV and 1.86 eV for the B3LYP and B3LYP-D3 band gap of PTB7-Th respectively. As expected [34], these gas-phase values differ by approximately 0.2 eV from the experimental (bulk phase) value. Hence, we can conclude that our conformational analysis resulted in a structure of PTB7-Th with electronic properties that are in good agreement with the respective experimental results.
In addition, we look at the variation of HOMO and LUMO eigenvalues and band gap energies with the changes in conformation and configuration of the oligomers. We focus on the results for the 4PTB7-Th since it is the longest oligomer we consider (and hence, it can be thought of as the best model for the polymer). Table 6 (b) shows that band gaps (and HOMO and LUMO) values change very little with different conformational changes in 4PTB7-Th. The average value for the band gap is 2.1 eV with HOMO and LUMO eigenvalues are close to – 4.8 eV and – 2.7 eV respectively for all of the tetramers. We also study the effect of SdChs on the electronic structure energies by considering again results for 4PTB7-Th’s. We found that for all of the tetramers without SdChs, HOMO and LUMO eigenvalues are close to – 4.9 eV and – 2.9 eV respectively and the average band gap energy is 2.09 eV. In agreement with our previous findings, alkane (linear or branched) SdChs do not affect significantly the band gap energies and HOMO/LUMO eigenvalues of organic polymers [35].

4. Conclusions

In this work, we carry out an extensive conformational analysis on the PTB7-Th oligomers (ranging from monomers to tetramers) using the DFT-B3LYP, DFT-B3LYP-D3, and LC-DFT (CAM-B3LYP, LC-BLYP, and ωB97xD) computations. The fully geometry optimized conformational energy states were calculated for various orientations of S, F, and =O in the TT-CF part relative to the PBDTT part. Particular attention was paid to the role of branched ethylhexyl SdChs, and the S-C-C-S dihedral angles along the chain backbones of the PTB7-Th oligomers. Our findings show that SdChs remove the degeneracies in the conformational energy calculations of the oligomers without SdChs. The results of B3LYP, B3LYP-D3, CAM-B3LYP, LC-BLYP, and ωB97xD predicted that all cis-like conformation with the S-C-C-S dihedral angles between 20 and 30 (in most cases) with preference for F on the TT-CF part of the monomer being in the same plane and the same side as the =O in the lowest energy (ground) state for PTB7-Th oligomers with SdChs (see Scheme 2). In contrast, for B3LYP and B3LYP-D3 oligomers without SdChs, there is a slight preference for S on the TT-CF part of the monomer to be in the same plane and the same side as the =O in their lowest energy states. The preference of the F=O…F structure over other configurations (such as the S=O…S) is mainly due to their stronger (grouped) SdChs interactions in oligomers with SdChs. Conformations with mix cis- and trans-like dihedral angles along the backbone have an uneven distribution of SdChs (with one side having significantly more SdChs than the other) in comparison to the all cis-like conformations. All trans-like conformations have similar SdChs distributions as all cis-like conformations but they are not energetically preferred for the lowest energy state of PTB7-Th. Finally, DFT electronic structure energies agree well with the corresponding experimental values (e.g. to within expected accuracy of 0.2 eV for band gaps).

Supplementary Materials

SI displays structures of all of the optimized oligomers with SdChs.

Data Availability Statement

The raw/processed data required to reproduce these findings cannot be shared at this time due to technical or time limitations.

Acknowledgments

This research was enabled in part by support provided by Calcul Québec (calculquebec.ca), the Digital Research Alliance of Canada (alliance​can​.ca), and King Abdulaziz University’s High Performance Computing Centre (Aziz Supercomputer) (www.hpcc-kau.com).

References

  1. Zhang, G.; Lin, F.R.; Qi, F.; Heumuller, T.; Distler, A.; Egelhaaf, H.-J.; Li, N.; Chow, P.C.Y.; Brabec, C.J.; Jen, A.K.-Y.; Yip, H.-L. Renewed Prospects for Organic Photovoltaics. Chem. Rev. 2022, 122, 14180–14274. [Google Scholar] [CrossRef]
  2. Wang, Y.; Lee, J.; Hou, X.; Labanti, C.; Yan, J.; Mazzolini, E.; Parhar, A.; Neson, J.; Kim, J.-S.; Li, Z. Recent progress and chanllenges toward highly stable nonfullerene acceptor-based organic solar cells. Adv. Energy Mater. 2020, 2003002–2003043. [Google Scholar]
  3. Inganas, O. Organic Photovoltaics over Three Decades. Advanced Materials 2018, 30, 1800388–1800414. [Google Scholar] [CrossRef]
  4. Hou, J.H.; Inganas, O.; Friend, R.H.; Gao, F. Organic solar cells based on non-fullerene acceptors. Nature Materials 2018, 17, 119–128. [Google Scholar] [CrossRef]
  5. Zou, S.J.; Shen, Y.; Xie, F.M.; Chen, J.D.; Li, Y.Q.; Tang, J.X. Recent advances in organic light-emitting diodes: toward smart lighting and displays. Materials Chemistry Frontiers 2020, 4, 788–820. [Google Scholar] [CrossRef]
  6. Zhao, Y.; Liu, L.; Zhang, F.; Di, C.; Zhu, D. Advances in organic thermolectric materials and devices for smart applications. Smart Mat. 2021, 2, 426–445. [Google Scholar]
  7. Rafique, S.; Abdullah, S.M.; Sulaiman, K.; Iwamoto, M. Fundamentals of bulk heterojunction organic solar cells: An overview of stability/degradation issues and strategies for improvement. Renewable & Sustainable Energy Reviews 2018, 84, 43–53. [Google Scholar]
  8. Gurney, R.S.; Lidzey, D.G.; Wang, T. A review of non-fullerene polymer solar cells: from device physics to morphology control. Reports on Progress in Physics 2019, 82, 036601–036638. [Google Scholar] [CrossRef]
  9. Ye, T.; Jin, S.; Kang, C.; Tian, C.; Zhang, X.; Zhan, C.; Lu, S.; Kan, Z. Comparison study of wide bandgap polymer (PBDB-T) and narrrow bandgap polymer (PBDTTT-EFT) as donor for perylene diimide based polymer solar cells. Front. Chem. 2018, 6, 613–621. [Google Scholar] [CrossRef]
  10. Ye, L.; Zhang, S.Q.; Zhao, W.C.; Yao, H.F.; Hou, J.H. Highly Efficient 2D-Conjugated Benzodithiophene-Based Photovoltaic Polymer with Linear Alkylthio Side Chain. Chemistry of Materials 2014, 26, 3603–3605. [Google Scholar] [CrossRef]
  11. Cui, C.H.; He, Z.C.; Wu, Y.; Cheng, X.; Wu, H.B.; Li, Y.F.; Cao, Y.; Wong, W.Y. High-performance polymer solar cells based on a 2D-conjugated polymer with an alkylthio side-chain. Energy & Environmental Science 2016, 9, 885–891. [Google Scholar]
  12. Zhang, W.J.; Li, Y.R.; Zhu, L.P.; Liu, X.H.; Song, C.J.; Li, X.D.; Sun, X.H.; Fang, J.F. A PTB7-based narrow band-gap conjugated polyelectrolyte as an efficient cathode interlayer in PTB7-based polymer solar cells. Chemical Communications 2017, 53, 2005–2008. [Google Scholar] [CrossRef]
  13. Wang, J.F.; Jia, X.K.; Zhou, J.P.; Pan, L.K.; Huang, S.M.; Chen, X.H. Improved Performance of Polymer Solar Cells by Thermal Evaporation of AgAl Alloy Nanostructures into the Hole-Transport Layer. Acs Applied Materials & Interfaces 2016, 8, 26098–26104. [Google Scholar]
  14. Oh, S.; Song, C.E.; Lee, T.; Cho, A.; Lee, H.K.; Lee, J.C.; Moon, S.J.; Lim, E.; Lee, S.K.; Shin, W.S. Enhanced efficiency and stability of PTB7-Th-based multi-non-fullerene solar cells enabled by the working mechanism of the coexisting alloy-like structure and energy transfer model. Journal of Materials Chemistry A 2019, 7, 22044–22053. [Google Scholar] [CrossRef]
  15. Mehboob, M.Y.; Adnan, M.; Hussain, R.; Irshad, Z. Quantum chemical designing of banana-shaped acceptor materials with outstanding photovoltaic properties for high-performance non-fullerene organic solar cells. Synthetic Metals 2021, 277, 116800–116814. [Google Scholar] [CrossRef]
  16. Ans, M.; Ayub, K.; Muhammad, S.; Iqbal, J. Development of fullerene free acceptors molecules for organic solar cells: A step way forward toward efficient organic solar cells. Computational and Theoretical Chemistry 2019, 1161, 26–38. [Google Scholar] [CrossRef]
  17. Shehzad, R.A.; Iqbal, J.; Khan, M.U.; Hussain, R.; Javed, H.M.A.; Rehman, A.U.; Alvi, M.U.; Khalid, M. Designing of benzothiazole based non-fullerene acceptor (NFA) molecules for highly efficient organic solar cells. Computational and Theoretical Chemistry 2020, 1181, 112833–112844. [Google Scholar] [CrossRef]
  18. Mahmood, A.; Irfan, A.; Wang, J.L. Machine learning and molecular dynamics simulation-assisted evolutionary design and discovery pipeline to screen efficient small molecule acceptors for PTB7-Th-based organic solar cells with over 15% efficiency. Journal of Materials Chemistry A 2022, 10, 4170–4180. [Google Scholar] [CrossRef]
  19. Afzal, Z.; Hussain, R.; Khan, M.U.; Khalid, M.; Iqbal, J.; Alvi, M.U.; Adnan, M.; Ahmed, M.; Mehboob, M.Y.; Hussain, M.; Tariq, C.J. Designing indenothiophene-based acceptor materials with efficient photovoltaic parameters for fullerene-free organic solar cells. Journal of Molecular Modeling 2020, 26, 137–154. [Google Scholar] [CrossRef]
  20. Ayoub, S.A.; Lagowski, J.B. Assessment of the performance of four dispersion-corrected DFT methods using optoelectronic properties and binding energies of organic monomer/fullerene pairs. Computational and Theoretical Chemistry 2018, 1139, 15–26. [Google Scholar] [CrossRef]
  21. Becke, A.D. Density-functional thermochemistry 3. The role of exact exchange. Journal of Chemical Physics 1993, 98, 5648–5652. [Google Scholar]
  22. Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the colle-salvetti correlation-energy formula into a functional of the electron-density. Physical Review B 1988, 37, 785–789. [Google Scholar] [CrossRef]
  23. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. Journal of Computational Chemistry 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  24. Yanai, T.; Tew, D.; Handy, N. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
  25. Iikura, H; Tsuneda, T.; Yanai, T.; Hirao, K. Long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 2001, 115, 3540–44. [CrossRef]
  26. Chai, D.J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–20. [Google Scholar] [CrossRef]
  27. Huo, L.J.; Zhang, S.Q.; Guo, X.; Xu, F.; Li, Y.F.; Hou, J.H. Replacing Alkoxy Groups with Alkylthienyl Groups: A Feasible Approach To Improve the Properties of Photovoltaic Polymers. Angewandte Chemie-International Edition 2011, 50, 9697–9702. [Google Scholar] [CrossRef]
  28. Zhang, S.Q.; Ye, L.; Zhao, W.C.; Liu, D.L.; Yao, H.F.; Hou, J.H. Side Chain Selection for Designing Highly Efficient Photovoltaic Polymers with 2D-Conjugated Structure. Macromolecules 2014, 47, 4653–4659. [Google Scholar] [CrossRef]
  29. Zhang, Z.G.; Li, Y.F. Side-chain engineering of high-efficiency conjugated polymer photovoltaic materials. Science China-Chemistry 2015, 58, 192–209. [Google Scholar] [CrossRef]
  30. Zhao, J.J.; Huang, X.L.; Li, Q.D.; Liu, S.J.; Fan, Z.Q.; Zhang, D.; Ma, S.S.; Cao, Z.X.; Jiao, X.C.; Cai, Y.P.; Huang, F. Shorter alkyl chain in thieno 3,4-c pyrrole-4,6-dione (TPD)-based large bandgap polymer donors - Yield efficient non-fullerene polymer solar cells. Journal of Energy Chemistry 2021, 53, 69–76. [Google Scholar] [CrossRef]
  31. Mamba, S.; Perry, D.S.; Tsige, M.; Pellicane, G. Toward the Rational Design of Organic Solar Photovoltaics: Application of Molecular Structure Methods to Donor Polymers. Journal of Physical Chemistry A 2021, 125, 10593–10603. [Google Scholar] [CrossRef]
  32. Frisch, G.W.T.M.J.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; Li, X.; Caricato, M.; Marenich, A.V.; Bloino, J.; Janesko, B.G.; Gomperts, R.; Mennucci, B.; Hratchian, H.P.; Ortiz, J.V.; Izmaylov, A.F.; Sonnenberg, J.L.; Williams-Young, D.; Ding, F.; Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Zakrzewski, V.G.; Gao, J.; Rega, N.; Zheng, G.; Liang, W.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Throssell, K.; Montgomery, J.A., Jr.; Peralta, J.E.; Ogliaro, F.; Bearpark, M.J.; Heyd, J.J.; Brothers, E.N.; Kudin, K.N.; Staroverov, V.N.; Keith, T.A.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.P.; Burant, J.C.; Iyengar, S.S.; Tomasi, J.; Cossi, M.; Millam, J.M.; Klene, M.; Adamo, C.; Cammi, R.; Ochterski, J.W.; Martin, R.L.; Morokuma, K.; Farkas, O.; Foresman, J.B.; Fox, D.J. (Gaussian, Inc., Wallingford CT 2016).
  33. Liao, S.H.; Jhuo, H.J.; Cheng, Y.S.; Chen, S.A. Fullerene Derivative-Doped Zinc Oxide Nanofilm as the Cathode of Inverted Polymer Solar Cells with Low-Bandgap Polymer (PTB7-Th) for High Performance. Advanced Materials 2013, 25, 4766–4771. [Google Scholar] [CrossRef]
  34. Gierschner, J.; Cornil, J.; Egelhaaf, H.J. Optical bandgaps of pi-conjugated organic materials at the polymer limit: experiment and theory. Adv. Mater. 2007, 19, 173–191. [Google Scholar] [CrossRef]
  35. Ayoub, S.A.; Lagowski, J.B. Side chain effect on conjugated polymer/fullerene interfaces in organic solar cells: a DFT study. Physical Chemistry Chemical Physics 2019, 21, 23978–23995. [Google Scholar] [CrossRef]
Preprints 68569 sch001
Scheme 1. Examples of the different chemical configurations of PTB7-Th found in literature (the differences are colored).
Scheme 1. Examples of the different chemical configurations of PTB7-Th found in literature (the differences are colored).
Preprints 68569 sch001
Preprints 68569 g001
Figure 1. A representation of the four possible structures of PTB7-Th monomers, defining the dihedral S-C-C-S angles Φ1 (top part) and Φ2 (bottom part) and the orientations of =O in TT-CF units. Also defining the naming of monomers as F=O...F etc as shown in the figure (see text for more details). Monomers are shown without SdChs.
Figure 1. A representation of the four possible structures of PTB7-Th monomers, defining the dihedral S-C-C-S angles Φ1 (top part) and Φ2 (bottom part) and the orientations of =O in TT-CF units. Also defining the naming of monomers as F=O...F etc as shown in the figure (see text for more details). Monomers are shown without SdChs.
Preprints 68569 g001
Preprints 68569 g002
Figure 2. 1D-PEC B3LYP scans for monomers of PTB7-Th with and without SdChs.
Figure 2. 1D-PEC B3LYP scans for monomers of PTB7-Th with and without SdChs.
Preprints 68569 g002
Preprints 68569 g003
Figure 3. 1D-PEC B3LYP scans for =O relative to F or S in the TT-CF part of the PTB7-Th monomer with and without SdChs.
Figure 3. 1D-PEC B3LYP scans for =O relative to F or S in the TT-CF part of the PTB7-Th monomer with and without SdChs.
Preprints 68569 g003
Preprints 68569 g004
Figure 4. Representative examples of the intermolecular interactions between SdChs for the cases of (a) cis-like and (b) trans-like within (S=O...S) and (S=O…F) optimized monomer using B3LYP-D3 method.
Figure 4. Representative examples of the intermolecular interactions between SdChs for the cases of (a) cis-like and (b) trans-like within (S=O...S) and (S=O…F) optimized monomer using B3LYP-D3 method.
Preprints 68569 g004
Preprints 68569 g005
Figure 5. The optimized geometries of the lowest-energy cis-like conformations in S=O…S and S=O…F (B3LYP-D3) monomers, and F=O…S and F=O…F (B3LYP) monomers.
Figure 5. The optimized geometries of the lowest-energy cis-like conformations in S=O…S and S=O…F (B3LYP-D3) monomers, and F=O…S and F=O…F (B3LYP) monomers.
Preprints 68569 g005
Preprints 68569 g006
Figure 6. An example of the four types of S-C-C-S dihedral-angles for the 2PTB7-Th (S=O…S) structure. Dimers are shown without SdChs.
Figure 6. An example of the four types of S-C-C-S dihedral-angles for the 2PTB7-Th (S=O…S) structure. Dimers are shown without SdChs.
Preprints 68569 g006
Preprints 68569 g007
Figure 7. The optimized geometries of (a) F=O…F dimer (S=O…F central monomer) and (b) F=O…S dimer (S=O…S central monomer). Dimers are shown without SdChs.
Figure 7. The optimized geometries of (a) F=O…F dimer (S=O…F central monomer) and (b) F=O…S dimer (S=O…S central monomer). Dimers are shown without SdChs.
Preprints 68569 g007
Preprints 68569 g008
Figure 8. Conformational energy differences for the representative 2PTB7-Th conformations and configurations using B3LYP, B3LYP-D3, CAM-B3LYP, LC-BLYP, and ωB97xD methods.
Figure 8. Conformational energy differences for the representative 2PTB7-Th conformations and configurations using B3LYP, B3LYP-D3, CAM-B3LYP, LC-BLYP, and ωB97xD methods.
Preprints 68569 g008
Preprints 68569 g010
Figure 10. Representative examples of the B3LYP-D3 optimized geometries of 4PTB7-Th oligomers. Hydrogens are removed for visual clarification.
Figure 10. Representative examples of the B3LYP-D3 optimized geometries of 4PTB7-Th oligomers. Hydrogens are removed for visual clarification.
Preprints 68569 g010
Preprints 68569 g011
Figure 11. Band gaps of B3LYP and B3LYP-D3 optimized geometries of PTB7-Th oligomers versus the inverse of their chain lengths.
Figure 11. Band gaps of B3LYP and B3LYP-D3 optimized geometries of PTB7-Th oligomers versus the inverse of their chain lengths.
Preprints 68569 g011
Preprints 68569 sch002
Scheme 2. Chemical Composition for the most stable conformation of PTB7-Th monomer.
Scheme 2. Chemical Composition for the most stable conformation of PTB7-Th monomer.
Preprints 68569 sch002
Table 1. S-C-C-S Dihedral Angles, Conformational Energies ( E ), and Conformational Energy Differences ( ∆ E ) for the four conformational sets of PTB7-Th monomers without and with SdChs optimized with B3LYP and B3LYP-D3 methods.
Table 1. S-C-C-S Dihedral Angles, Conformational Energies ( E ), and Conformational Energy Differences ( ∆ E ) for the four conformational sets of PTB7-Th monomers without and with SdChs optimized with B3LYP and B3LYP-D3 methods.
Preprints 68569 i001
Table 2. B3LYP and B3LYP-D3 results for the representative 2PTB7-Th dimers.
Table 2. B3LYP and B3LYP-D3 results for the representative 2PTB7-Th dimers.
Preprints 68569 i002
Table 3. DFT-B3LYP, DFT-B3LYP-D3, and LC-DFT (CAM-B3LYP, LC-BLYP, and ωB97xD) results for the representative 2PTB7-Th dimers with SdChs.
Table 3. DFT-B3LYP, DFT-B3LYP-D3, and LC-DFT (CAM-B3LYP, LC-BLYP, and ωB97xD) results for the representative 2PTB7-Th dimers with SdChs.
Preprints 68569 i003
Table 4. B3LYP and B3LYP-D3 conformational energy results for the representative PTB7-Th oligomers without SdChs.
Table 4. B3LYP and B3LYP-D3 conformational energy results for the representative PTB7-Th oligomers without SdChs.
Preprints 68569 i004
Table 5. B3LYP and B3LYP-D3 conformational energy and S-C-C-S dihedral angle results for the representative PTB7-Th oligomers with SdChs.
Table 5. B3LYP and B3LYP-D3 conformational energy and S-C-C-S dihedral angle results for the representative PTB7-Th oligomers with SdChs.
Preprints 68569 i005
Table 6. HOMO ( ϵ H O M O ) and LUMO ( ϵ L U M O ) eigenvalues, and band gaps ( E g ) calculated using (a) (B3LYP and single point B3LYP on B3LYP-D3 optimized geometries) for the most stable structures of PTB7-Th (from 1PTB7-Th monomer to 4PTB7-Th tetramers), and (b) B3LYP for various configurations of 4PTB7-Th with and without SdChs.
Table 6. HOMO ( ϵ H O M O ) and LUMO ( ϵ L U M O ) eigenvalues, and band gaps ( E g ) calculated using (a) (B3LYP and single point B3LYP on B3LYP-D3 optimized geometries) for the most stable structures of PTB7-Th (from 1PTB7-Th monomer to 4PTB7-Th tetramers), and (b) B3LYP for various configurations of 4PTB7-Th with and without SdChs.
Preprints 68569 i006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated