The concepts of fractional calculus and the related techniques have been gaining momentum in circuit system fields, and an increasing body of evidence suggests that fractional-order characteristics are widely distributed in electronic components. In this paper, we consider the fractional characteristics of non-solid aluminum electrolytic capacitors and focus on the nonlinear dynamic characteristics of peak-current-mode controlled (PCMC) dc-dc boost converters with such components. In the work, we establish a piecewise smooth non-commensurate fractional-order model to describe the converter, in which the fractional-order equivalent impedance model of capacitors is adopted and the detailed control loop is considered. In order to analyze the converter, we use the fractional Adams-Bashforth-Moulton typed method (F-ABM) and stroboscopic map technique to obtain the time-domain solutions and the bifurcation diagram. The results of bifurcation diagrams indicate that, with the change of different parameters, the converter enters chaotic state through period doubling bifurcation. In order to provide empirical evidence for the nonlinear dynamic analysis, we consider both circuit-level simulation and experiments in the work, the results of which further confirm the results of theoretical analysis.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

Introduction

Power electronic converters, such as dc-dc converters, are typical piecewise smooth circuit systems due to the turn-on and turn-off effects of power switches, and their performance is closely related to operation conditions. It is generally believed that, when the load or power source fluctuates, or the parameters of passive components are not properly configured, one may be able to observe nonlinear dynamic phenomena such as bifurcations and chaos in power electronic converters, which are undesired in practical applications [1]. For instance, the active duty ratio of a PCMC dc-dc boost converter is generally limited to less than

0.5

in continuous conduction mode (CCM), because when the ratio exceeds this range, the converter will be in period-2 sub-harmonic oscillation state, so the voltage boost capability is limited in applications [2].

In order to better predict the nonlinear phenomena of power electronic converters and provide design-oriented guidance in practice, lumped parameter models and integer-oder piecewise linear differential equations are widely adopted to describe the the electrical relationship of the state variables of power electronics converters [3]. To analyze the nonlinear behaviours of the converters, one can solve the initial value problem (IVP) of integer-oder ordinary differential equations (ODEs) by both numerical and analytical calculation methods, and use the stroboscopic map technique to sew up the solutions of piecewise linear differential equations [4]. Based on these methods, a large number of researches have been conducted to explore nonlinear dynamic phenomena in power electronic converters, such as those surveyed in literature [5,6,7].

By reviewing the key publications in the related field, one can find that, the parameters of traditional lumped parameter models usually appear in the form of parameter variables (or parameter vector), while in the solving process of IVP, these parameter variables are usually substituted with constant nominal values or the measured constant values under a fixed condition. However, not only the load and power supply may change, but also some other electronic components may experience parameter drift in practice [8,9,10,11]. For instance, non-solid electrolytic aluminum capacitors are widely adopted in power electronic converters, but their capacitance and equivalent series resistance (ESR) can be easily affected by operating frequency, working temperature, and so on. In order to reflect the impacts of parameter variations on the nonlinear characteristic of converters, one can draw bifurcation diagrams by changing the parameters of traditional lumped parameter models, but the model itself cannot reflect the parameter drift of the components. That is to say, traditional models cannot reflect the correlation between the microscopic characteristics of electronic components and the macroscopic electrical characteristics of converter systems. The results obtained by using traditional integer-order models may be biased in practice. Therefore, it is worthwhile to develop more precise and reliable methods to address the aforementioned concerns.

In recent decades, exploring the characteristics of electronic components arouses ever-increasing attention in circuit theory and application fields [12], and a rich source of evidence suggests that the characteristics of electronic components can be more effectively captured by using the concepts of fractional calculus compared to classical calculus-based models [13,14,15], and factional-order impedance (or constant phase elements, CPEs) based models have been widely adopted to describe the characteristics of electronic components, such as inductors [16], ultracapacitors (UCs) [17,18], lithium batteries [19], power MOSFETs [20], and non-solid electrolytic capacitors [21]. Therefore, using this model to bridge the gap between the microscopic characteristics of electronic components and the macroscopic characteristics of circuit systems has become a hot issue in recent years.

In this paper, taking a PCMC dc-dc boost converter as an example, we study the nonlinear characteristics of the converter with a fractional-order output filtering capacitor, and we carried out the following works:

A piecewise smooth non-commensurate fractional-order model is developed for a PCMC dc-dc boost converter, which contains a fractional-order output filtering capacitor and a detailed control loop design based on a type UC3842 PCMC power management chip.
A large-signal stability analysis is performed for the converter, in which the fractional Adams-Bashforth-Moulton typed method (F-ABM) and stroboscopic map technique are applied for tiem-domain calculation, while bifurcation diagrams are obtained for dynamic states justification.
Both circuit-level simulations and experiments are provided to verify the correctness of the theoretical analysis.

To present the above features in detail, the rest of this paper begins with the derivation of the piecewise smooth model of the converter in section II. After that, a detailed nonlinear dynamic characteristic analysis of the converter is provided in section III. Then, in section IV, both the circuit-level simulation platform and experiment prototype are established, and the results are provided for validation and comparison. Finally, conclusion is outlined in Section V.

2. Piecewise Smooth Fractional-Order Model of PCMC DC-DC Boost Converters

2.1. Circuit configuration

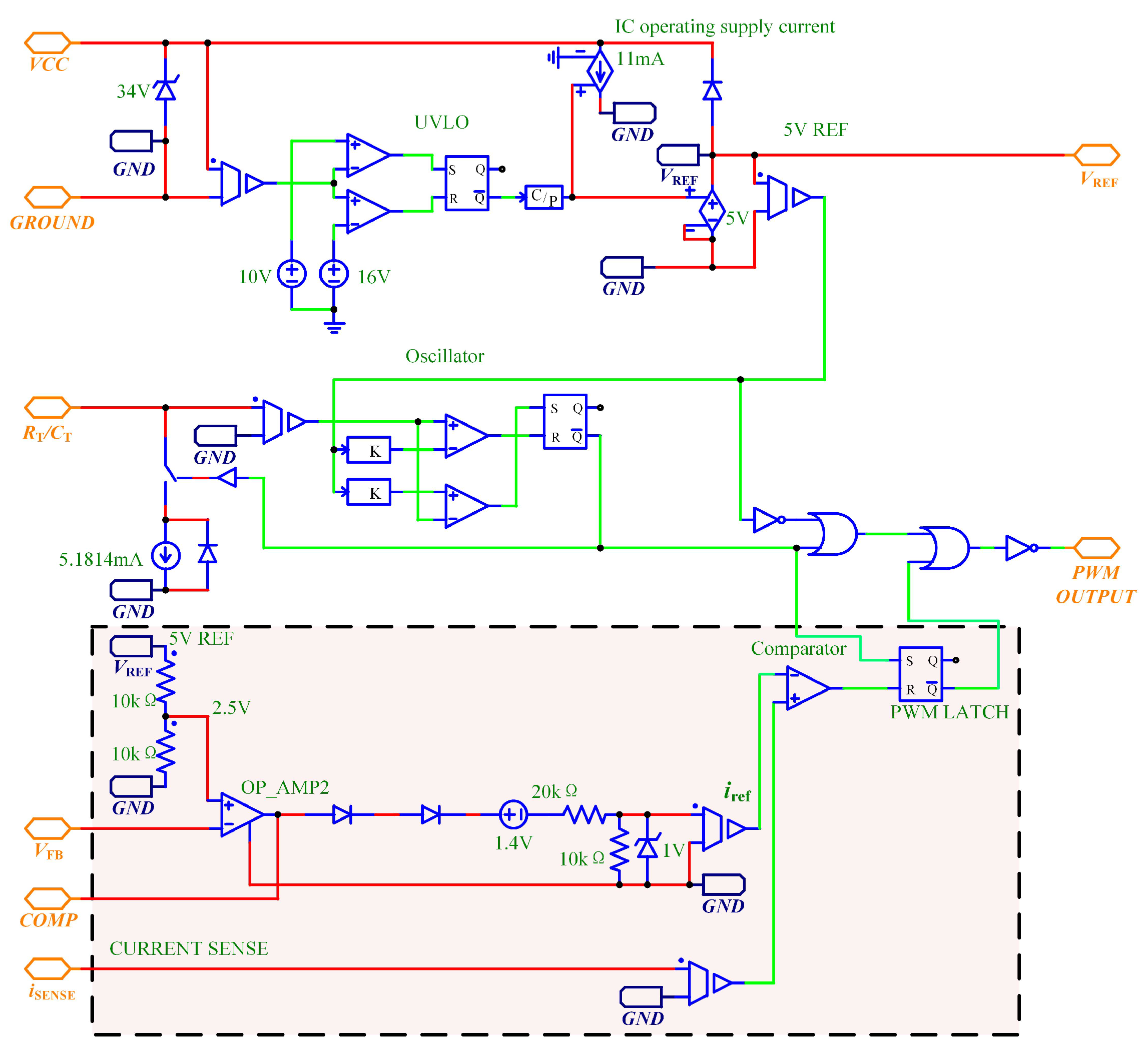
It is a fast and cost effective option to use power management chip to control dc-dc converters in application. In this work, we use a type-UC3842 power management chip, which is a fixed frequency current-mode controllers [21], its internal structure is as depicted in Figure 1.

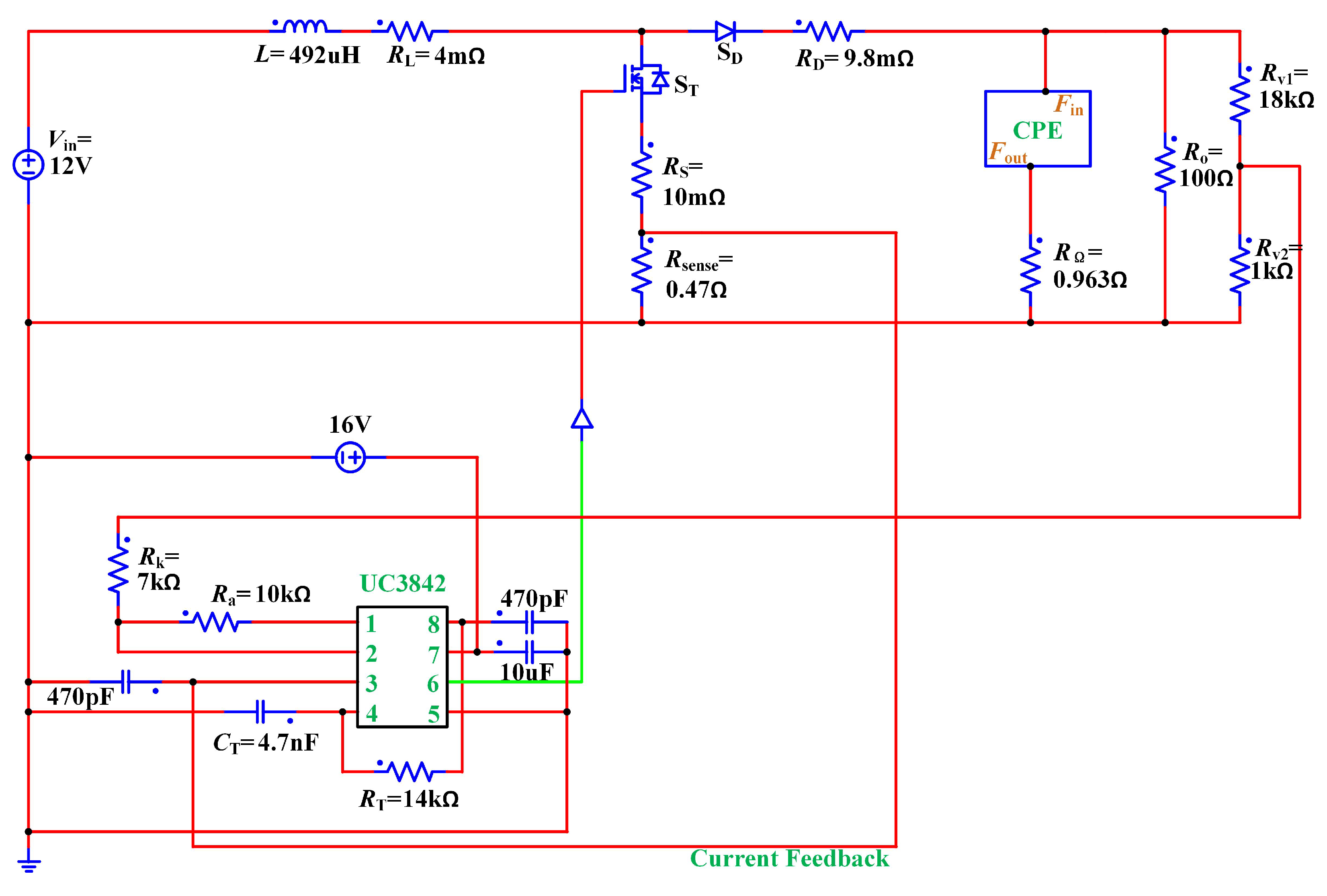
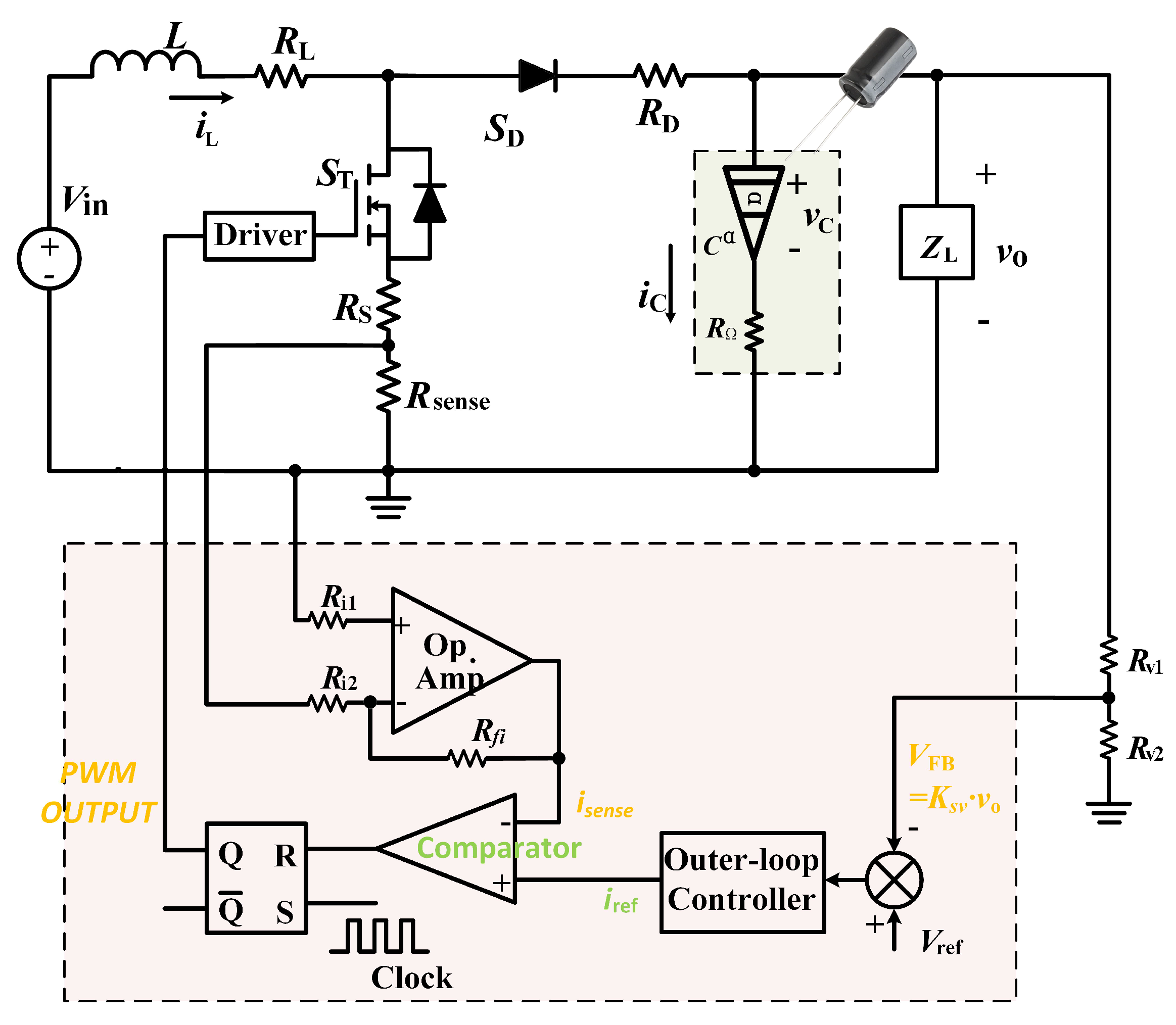
By adopting this chip to a dc-dc boost converter, one can achieve a PCMC design, the schematic diagram of which is depicted in Figure 2.

Note that the output filtering capacitor in Figure 2 is a non-solid electrolytic capacitor. According to a previous work [23], the capacitance and the equivalent series resistance of the capacitor have frequency-related fractional-order characteristics in a wide frequency band. Therefore, we use a fractional-order equivalent impedance model to represent it, where an ideal fractional-order capacitor

C^{α}

(or constant phase element, CPE) is in series with an estimated equivalent series resistance

R_{Ω}

. The symbol C is the nominal capacitance of the capacitor and the symbol

α

is the estimated fractional order of the capacitor.

In addition, note that in both Figure 1 and Figure 2, the two boxes with red background correspond to the same function module. Specifically, there are the same output voltage current sensing unit, inductor current sensing unit, the inner curent loop controller, and the outer voltage loop controller. The inner current loop usually includes an inductor current sensing resistor

R_{s e n s e}

, and a proportional sampling unit is used to sample the inductor current

i_{L}

. The

V_{F B}

pin of the UC3842 chip is connected to a voltage divider composed by two resistors

R_{v 1}

and

R_{v 2}

, which is used to sample the output voltage

v_{o}

. The outer-loop controller can be achieved by configuring the circuit between the

V_{F B}

pin and the

C O M P

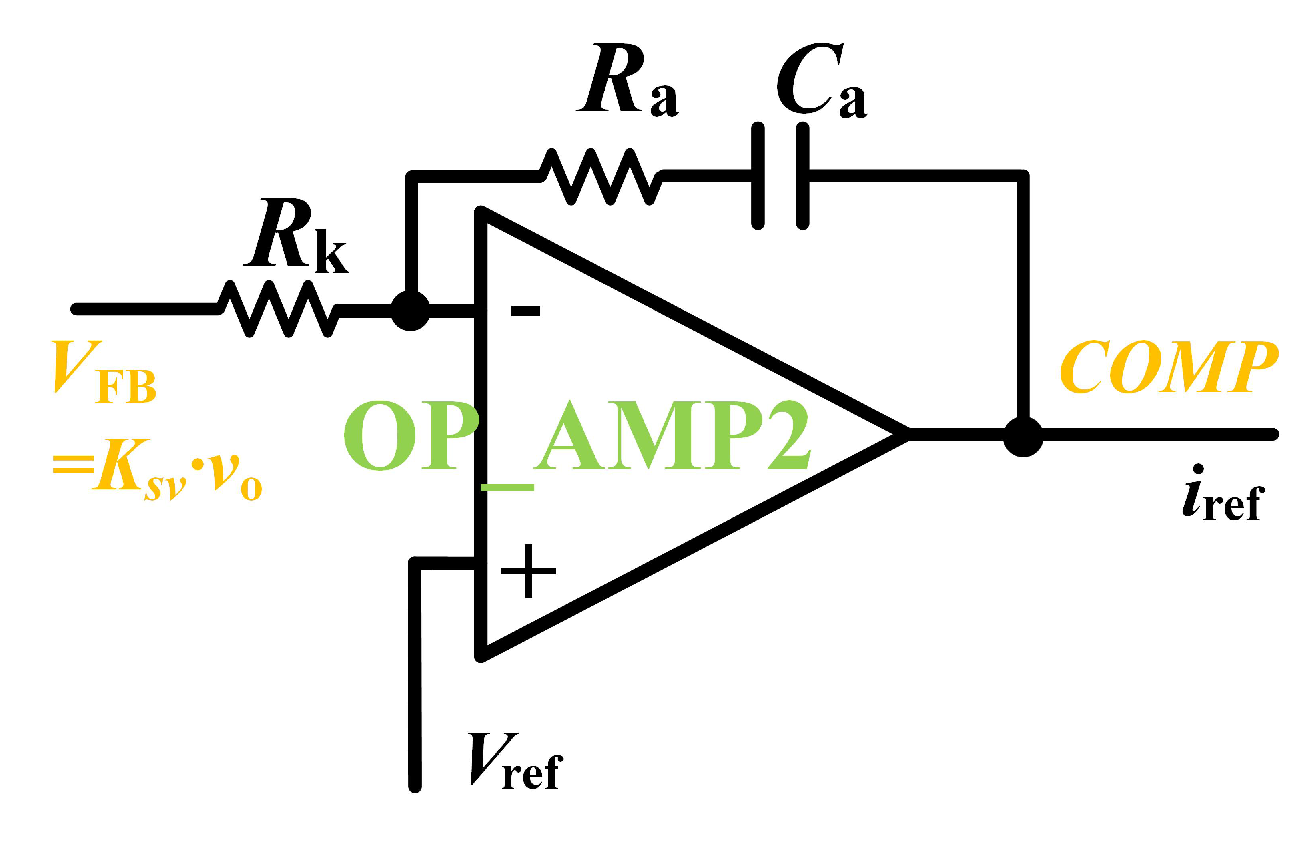
pin of the chip. For example, if one wants to used a typical PI controller in the outer loop, then one can configure the above two pins of the operational amplifier

O P_{A M P 2}

as follows.

According to the above Figure 3, one can deduce the the output of the outer voltage loop, or the reference signal

i_{r e f}

of the inner current loop, as follows.

\begin{matrix} i_{r e f} (t) & = V_{r e f} - R_{a} C_{a} \frac{d v_{a} (t)}{d t} - v_{a} (t) \\ = (1 + \frac{R_{a}}{R_{k}}) V_{r e f} - \frac{R_{a}}{R_{k}} K_{s v} v_{o} (t) + \frac{1}{R_{k} C_{a}} \int [V_{r e f} - K_{s v} v_{o} (t)] d t, \end{matrix}

(1)

If one uses a typical proportional controller for the outer voltage loop, then the the output of the outer voltage loop, or the reference signal

i_{r e f}

of the inner current loop, will be as follows.

\begin{matrix} i_{r e f} (t) = (1 + \frac{R_{a}}{R_{k}}) V_{r e f} - \frac{R_{a}}{R_{k}} K_{s v} v_{o} (t) . \end{matrix}

(2)

in which the symbol

K_{s v}

is the sampling ratio for the output voltage

v_{o}

, the value of which is determined by

R_{v 2} / (R_{v 1} + R_{v 2})

. In addition, one can obtain the values of the proportional and integral coefficients

K_{v p}

and

K_{v i}

are

R_{a} / R_{k}

and

1 / (R_{k} C_{a})

, respectively.

Meanwhile, the sampling current

i_{s e n s e}

is:

i_{s e n s e} (t) = K_{s i} i_{L} (t),

(3)

in which the symbol

K_{s i}

is the sampling ratio for the inductor current

i L

, the value of which is determined by

R_{s e n s e}

R_{f}

R_{i 1}

, and

R_{i 2}

According to the schematic and the working principle, the output of the outer voltage loop is employed as the reference signal

i_{r e f}

of the inner current loop. The comparison result of two signals

i_{s e n s e}

and

i_{r e f}

is sent to an R-S trigger, the output of which is fed to two driving circuits to control the turn-on and off state of two power MOSFETs

S_{T}

and

S_{D}

2.2. Fractional-order piecewiese smooth model

Because of the turn-on and turn-off operations of power MOSFETs

S_{T}

and

S_{D}

, the converter is a typical piecewise smooth dynamic system. If one uses a proportional controller for the outer loop, and takes the inductor current

i_{L}

and the voltage

v_{C}

of the CPE as state variables, the converter will have a state vector of

x (t) = {[i_{L} (t), v_{C} (t)]}^{T r}

, and the switching modes of the converter can be governed by:

Switching mode 1: When the power MOSFETs $S_{T}$ is on and $S_{D}$ is off, the state of the converter can be governed by:

$\{\begin{matrix} \frac{d i_{L} (t)}{d t} = \frac{V_{i n}}{L} - \frac{R_{s e n s e} + R_{L} + R_{S}}{L} i_{L} (t) \\ \frac{d^{α} v_{C} (t)}{d t^{α}} = - \frac{1}{(R_{o} + R_{Ω}) C} v_{C} (t) . \end{matrix}$

(4)
Switching mode 2: When the power MOSFETs $S_{T}$ is off, $S_{D}$ is on, and the inductor current is not 0, the state of the converter can be governed by:

$\{\begin{matrix} \frac{d i_{L} (t)}{d t} = \frac{V_{i n}}{L} - \frac{R_{L} + R_{D}}{L} i_{L} (t) - \frac{R_{o} R_{Ω}}{(R_{o} + R_{Ω}) L} i_{L} (t) - \frac{R_{o}}{(R_{o} + R_{Ω}) L} v_{C} (t) \\ \frac{d^{α} v_{C} (t)}{d t^{α}} = \frac{R_{o}}{(R_{o} + R_{Ω}) C} i_{L} (t) - \frac{1}{(R_{o} + R_{Ω}) C} v_{C} (t) . \end{matrix}$

(5)
Switching mode 3: When the power MOSFETs $S_{T}$ is off, $S_{D}$ is on, and the inductor current is 0, the state of the converter can be governed by:

$\{\begin{matrix} \frac{d i_{L} (t)}{d t} = 0 \\ \frac{d^{α} v_{C} (t)}{d t^{α}} = - \frac{1}{(R_{o} + R_{Ω}) C} v_{C} (t) . \end{matrix}$

(6)

According to the internal structure of Figure 1 and the schematic of Figure 2, when the output of the outer voltage loop is less than

1 V

, the switching condition of switching modes 1 and 2 is:

\begin{matrix} s (t) & = i_{r e f} (t) - i_{s e n s e} (t) \\ = \frac{1}{3} [(1 + \frac{R_{a}}{R_{k}}) V_{r e f} - \frac{R_{a}}{R_{k}} K_{s v} v_{o} (t) - 1.4] - K_{s i} i_{L} (t), \end{matrix}

(7)

in which the term

1.4

corresponds to the forward voltage of two series diodes, which are in series with the output of the voltage controller. In addition, the coefficient

1 / 3

comes from the voltage divider of two resistors

20 k Ω

and

10 k Ω

, which are in series with the two diodes. These details can be found in Figure 1.

When the output of the outer voltage loop is not less than

1 V

, the reference signal

i_{r e f} (t)

will be clamped at

1 V

, and the switching condition of switching modes 1 and 2 will be:

s (t) = 1 - K_{s i} i_{L} (t) .

(8)

At the switching-mode transition time

t_{s}

, the condition of

i_{r e f} (t_{s}) = i_{s e n s e} (t_{s})

is satisfied, thus one can obtain the duty cycle

d (t)

. In steady state, if the converter works in the current continuous mode (CCM), that is, the current does not drop to 0 at the end of switching mode 2, the converter switches between switching modes 1 and 2 periodically.

3. Time-Domain Analysis

To reveal the time-domain performances and nonlinear dynamic characteristics of the PCMC DC-DC boost converter, the state equations 4 to equations 6 should be calculated, which are all fractional-order ordinary differential equations (FO-ODEs). Basically, these FO-ODEs can be generalized by the following following initial value problem (IVP)

\begin{matrix} D_{*}^{q} x = f (x), \\ x (0) = x_{0}, \end{matrix}

(9)

in which the term

q = {[1, α]}^{T r}

is the non-commensurate order vector, the function

f : R^{n} \to R^{n}

, and the operator

D_{*}^{q}

is the differential operator of order q.

3.1. Preliminaries: Principles of Some Related Techniques

To solve the above IVP, this section introduces the principle of fractional Adams-Bashforth-Moulton typed method (F-ABM), and applies the stroboscopic map technique to cope with piecewise smooth situations.

3.1.1. F-ABM calculation method

In case of

- 1 \leq α \leq 1

, according to the definition of F-ABM method [23], the IVP of the fractional-order system of Equation 9 can be determined by:

\begin{matrix} x (n + 1) = x (0) & + \frac{h^{α}}{Γ (2 + α)} f [t_{n + 1}, x^{P} (n + 1)] \\ + \frac{h^{α}}{Γ (2 + α)} \sum_{j = 0}^{n} A_{j, n + 1} f [t_{j}, x (j)], \end{matrix}

(10)

where the term n is any integer and

A_{j, n + 1}

A_{j, n + 1} = \{\begin{matrix} = n^{α + 1} - (n - α) {(n + 1)}^{α}, j = 0 \\ = {(n - j + 2)}^{α + 1} + {(n - j)}^{α + 1} \\ - 2 {(n - j + 1)}^{α + 1}, 1 \leq j \leq n \\ = 1, j = n + 1 \end{matrix}

(11)

The predictor

x^{P} (n + 1)

in Equation 9 is

x^{P} (n + 1) = x_{0} + \frac{1}{Γ (α)} \sum_{j = 0}^{n} B_{j, n + 1} f [t_{j}, x (j)],

(12)

in which the term

B_{j, n + 1}

B_{j, n + 1} = \frac{h^{α}}{α} [{(n + 1 - j)}^{α} - {(n - j)}^{α}] .

(13)

Note that, the term h in equation 10 and equation 13 is a predetermined step size, the value of which is defined according to the switching period

T_{s}

of the converter. In this work, we will set the step size to

1 / 100

of the switching period

T_{s}

, which satisfies the Nyquist sampling theorem.

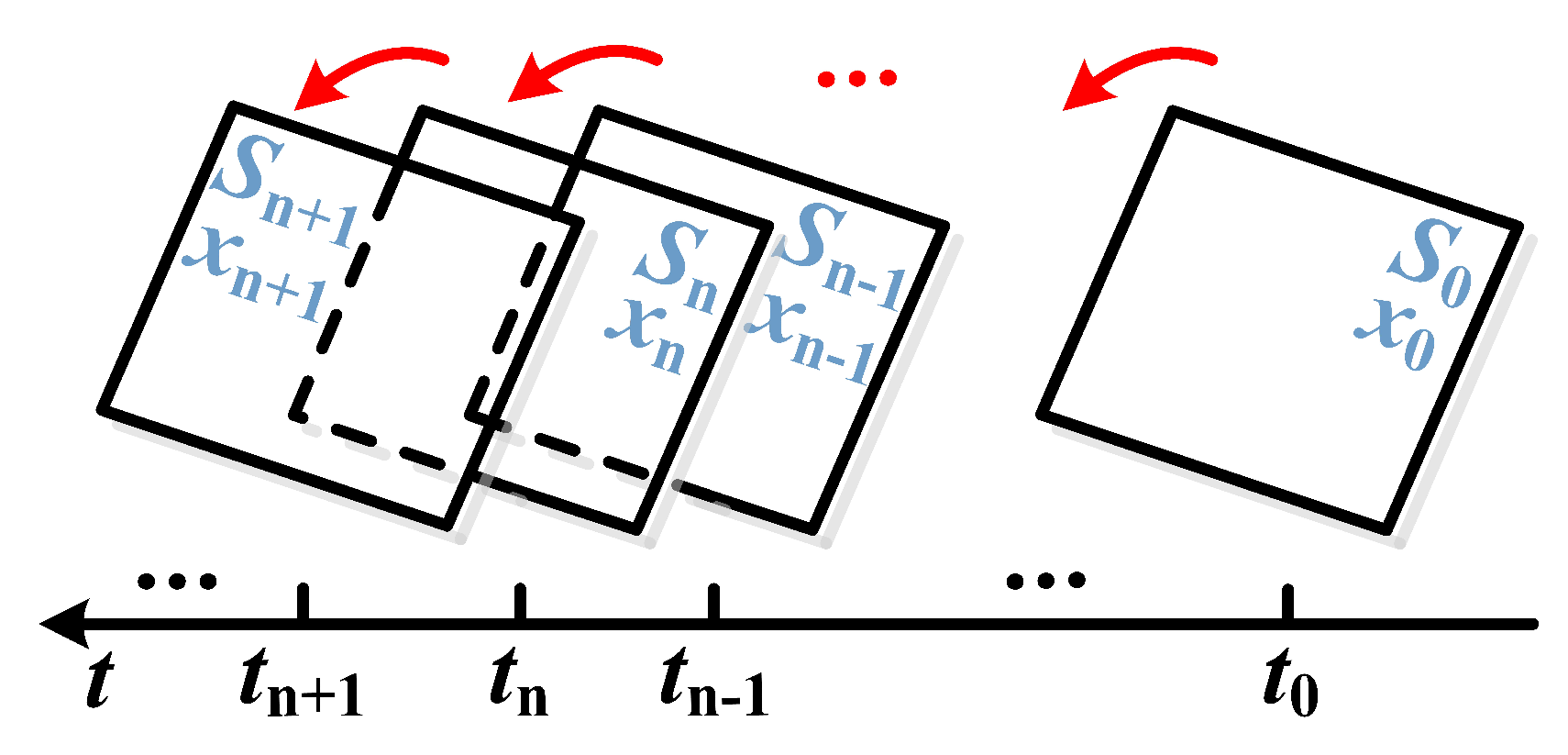
3.1.2. Stroboscopic map technique

As introduced in section 1.2, the state of the converter cycles between switching mode 1 and switching mode 2 in each switching period in CCM. Along with the on- and off operations of power MOSFETs

S_{T}

and

S_{D}

, there are a set of discontinuous points. Accordingly, a technique called stroboscopic map should be employed in calculations. This technique has been widely adopted in the dynamic analysis of piecewise-smooth systems and switching power converters. The principle of stroboscopic map technique is depicted in Figure 4.

By this technique, the dynamic behavior of the converter at each switching mode

S_{n}

will be collected in one switching cycle, that is, the solution

x_{n}

of the previous switching mode at time

t_{n}

will be employed as the initial value of the next switching mode, thus a cycle-by-cycle calculation can be carried out.

3.2. Bifurcation analysis

According to the discrete form of the obtained fractional-order piecewise smooth model, one can carry out the cycle-by-cycle numerical simulation for the converter in Figure 1. In simulation, the parameters are as Table 1.

Note that in the above table, the fractional order

α

and the ESR

R_{Ω}

of the output filtering capacitor are obtained by using a LCR meter and the parameter estimation method developed in [21]. According to Table 1, the sampling ratio

K_{s i}

of inductor current equals to

R_{s e n s e} = 0.1 ~ 0.68

, the sampling ratio

K_{s v}

of the output voltage equals to

R_{v 2} / (R_{v 1} + R_{v 2}) = 0.015 ~ 0.5

, and the proportional coefficient

K_{v p}

of the outer voltage loop controller equals to

R_{a} / R_{k} = 1 ~ 100

Then by using the F-ABM method to calculate equation 4 to equation 6, and by sewing up the solutions of these equations end to end by the stroboscopic map technique, one can obtain the bifurcation diagrams of state variables versus different parameters, such as

i_{L}

versus power supply

V_{i n}

i_{L}

versus load resistance

R_{o}

, and

i_{L}

versus output voltage divider resistance

R_{v 1}

, as depicted in Figure 5.

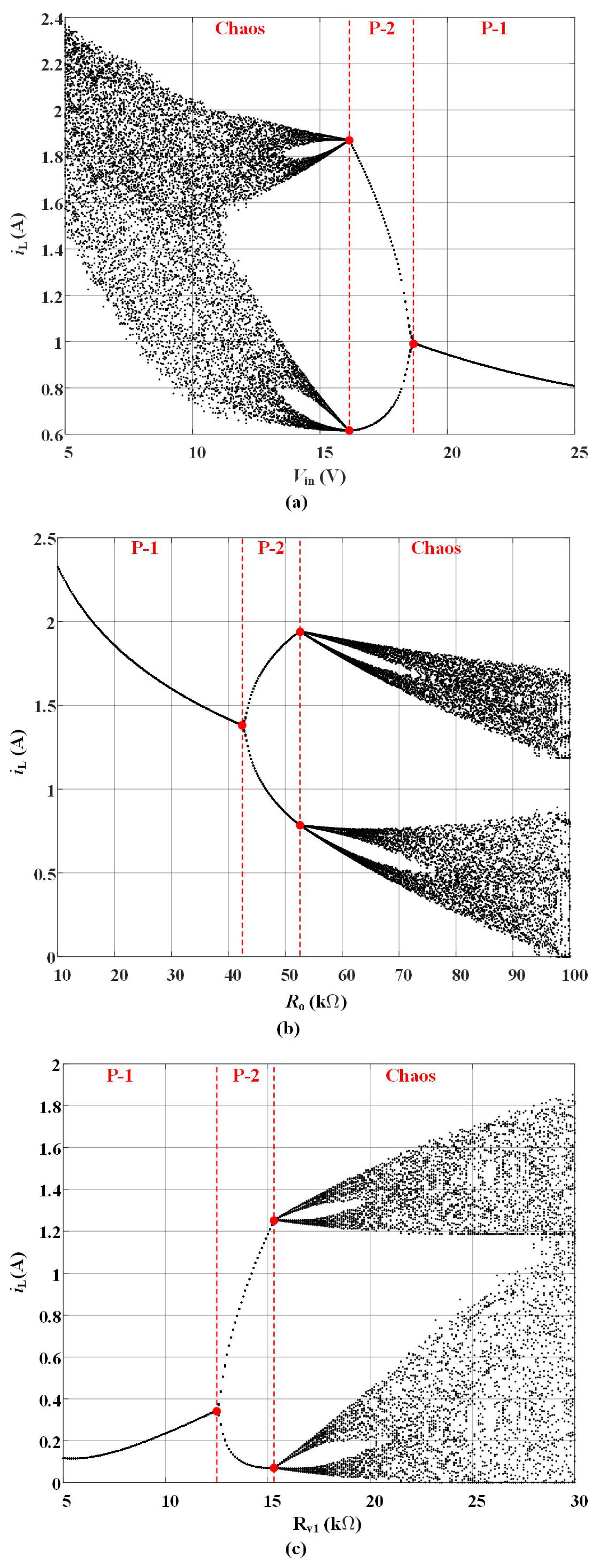
In Figure 5, one can find that, the PCMC dc-dc boost converter enters chaotic state through period-doubling bifurcation in three cases. Specifically, when one set the load resistance

R_{o}

to be

60 Ω

, the compensation resistors of voltage loop controller

R_{k} = 7 k Ω

R_{a} = 10 k Ω

, the voltage divider resistor

R_{v 2} = 1 k Ω

R_{v 1} = 25 k Ω

, and other parameters to be as those listed in Table 1, the converter keeps in chaotic state when the power supply is lower than

16 V

. Increasing the power supply above this value will lead to the converter enters period-2 (P-2) sub-harmonic oscillation state. After around

V_{i n} = 18.8 V

, the converter will be in period-1 (P-1) stable state. As to the load variation situation, when one set the power supply

V_{i n}

to be

15 V

and other parameters as in the previous case, the converter will be in P-1 stable state when the load resistance

R_{o}

is less than

42.6 Ω

. After around

R_{o} = 53 Ω

, the converter enters chaos. In addition in the output-voltage sampling ratio variation situation, when one set the power supply

V_{i n}

to be

15 V

, the load resistance

R_{o}

to be

100 Ω

, and other parameters as in the previous case, the converter will be in P-1 stable state when the resistance

R_{v 1}

is less than

12.6 k Ω

, and the converter will fall into chaos when the resistance

R_{v 1}

is greater than

15.3 k Ω

4. Validation and Comparison

4.1. Circuit-level simulation

In order to validate the results of theoretical analysis, circuit-level simulation is conducted in PSIM software in this section, the schematic of the simulation paltform is as follows:

Figure 6. Circuit-level simulation in PSIM software.

In the above schematic, the PCMC module UC3842 is actually Figure 1, the CPE module, or an ideal order-

0.9615

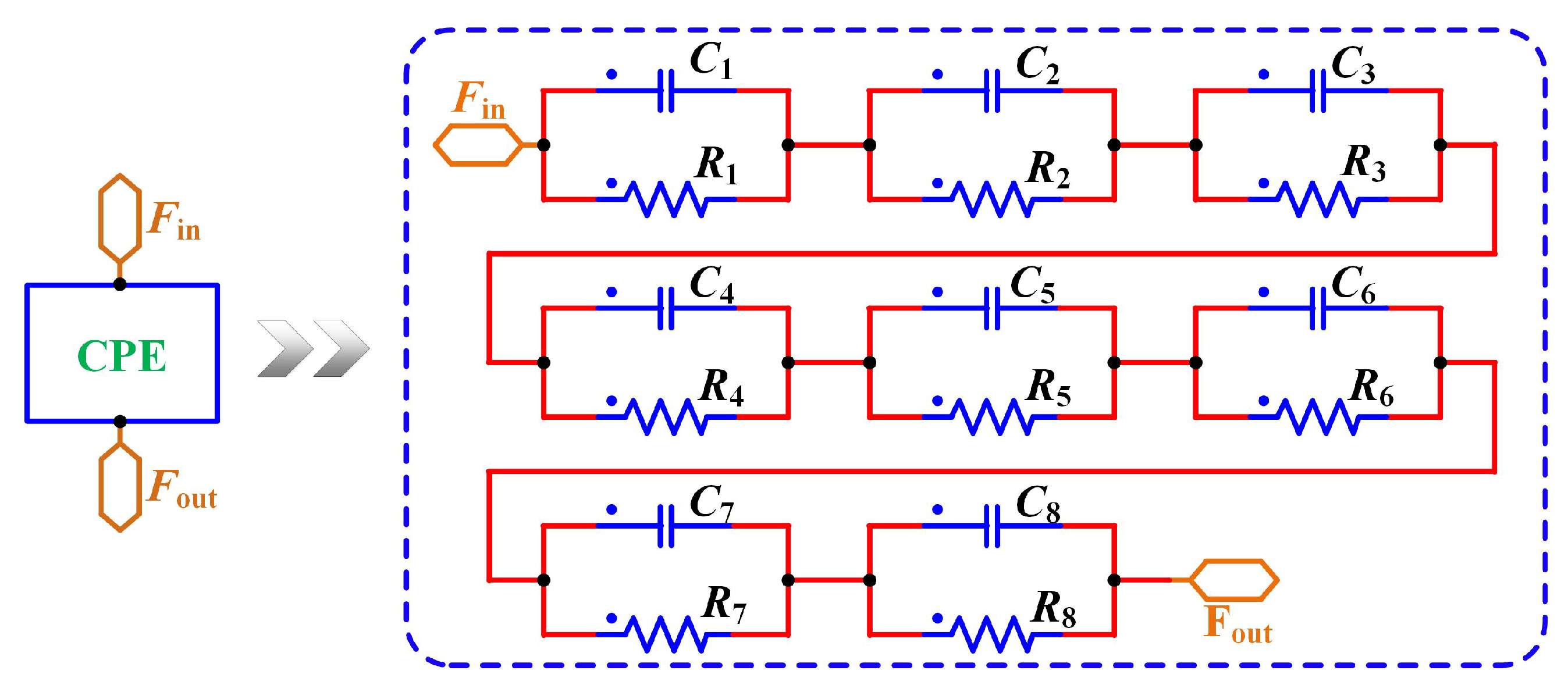
CPE, is constructed based on the rational approximation method, which has been used in a previous work [25]. The details of the rational approximation circuit is as Figure 7, in which the rational approximation circuit of

10 / {(s e c o n d)}^{1 - 0.9615}

CPE contains eight groups of R-C parallel unit. These groups are in series one by one, their vaules are obtained by a frequency-domain approximation method proposed in literature [26,27,28] and the circuit network synthesis method adopted in previous work [25,29], in which we set the approximate phase error is within

1 d B

. The detailed values of the CPE is listed in Table 2.

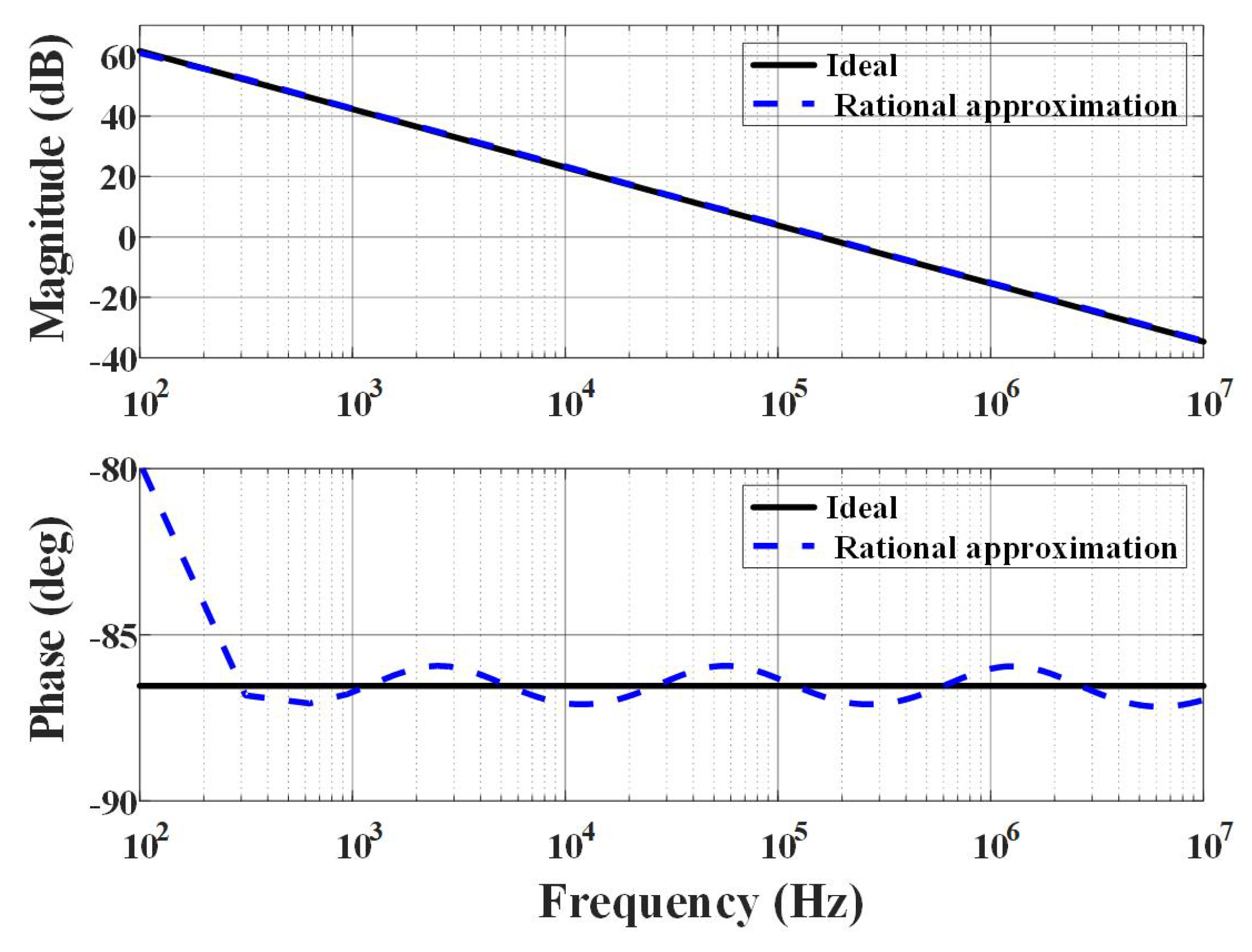
By using the values of

R_{i}

and

C_{i}

listed in the above table, one can plot the Bode diagrams of the constructed CPE, as dipicted in Figure 8, in which the black solid lines represent the ideal order-

0.9615

CPE and the blue dash curves belong to the devices obtained by rational approximation method and synthesis method.

Additionally, one can obtain the theoretical impedance

Z_{i}

and the synthesis impedance

Z_{s}

of the

10 μ F / {(s e c o n d)}^{1 - 0.9615}

capacitor as follows.

\{\begin{matrix} Z_{i} \approx 0.0610 - 1.0072 i \\ Z_{s} \approx 0.0583 - 1.0496 i, \end{matrix}

(14)

respectively. And one can find that the errors of the real part and the imaginary part of the two impedance are

4.39 %

and

4.20 %

, respectively. These error can be reduced by using a lower approximate phase error, but it will lead to an increase in the numbers of

R_{i} C_{i}

units in the chain structure, as those discussed in literature [25] and [29]. It can be seen from Figure 8 and Equation 14 that, both the frequency characteristic curves and two impedance values meet well with each other. It means that the constructed CPE can be used in simulation for validation.

Then one can use the constructed order-

0.9615

CPE in PSIM software to obtain the time-domain results of the PCMC dc-dc boost converter. In the first place, we set the voltage dividing resistor

R_{v 1} = 10 k Ω

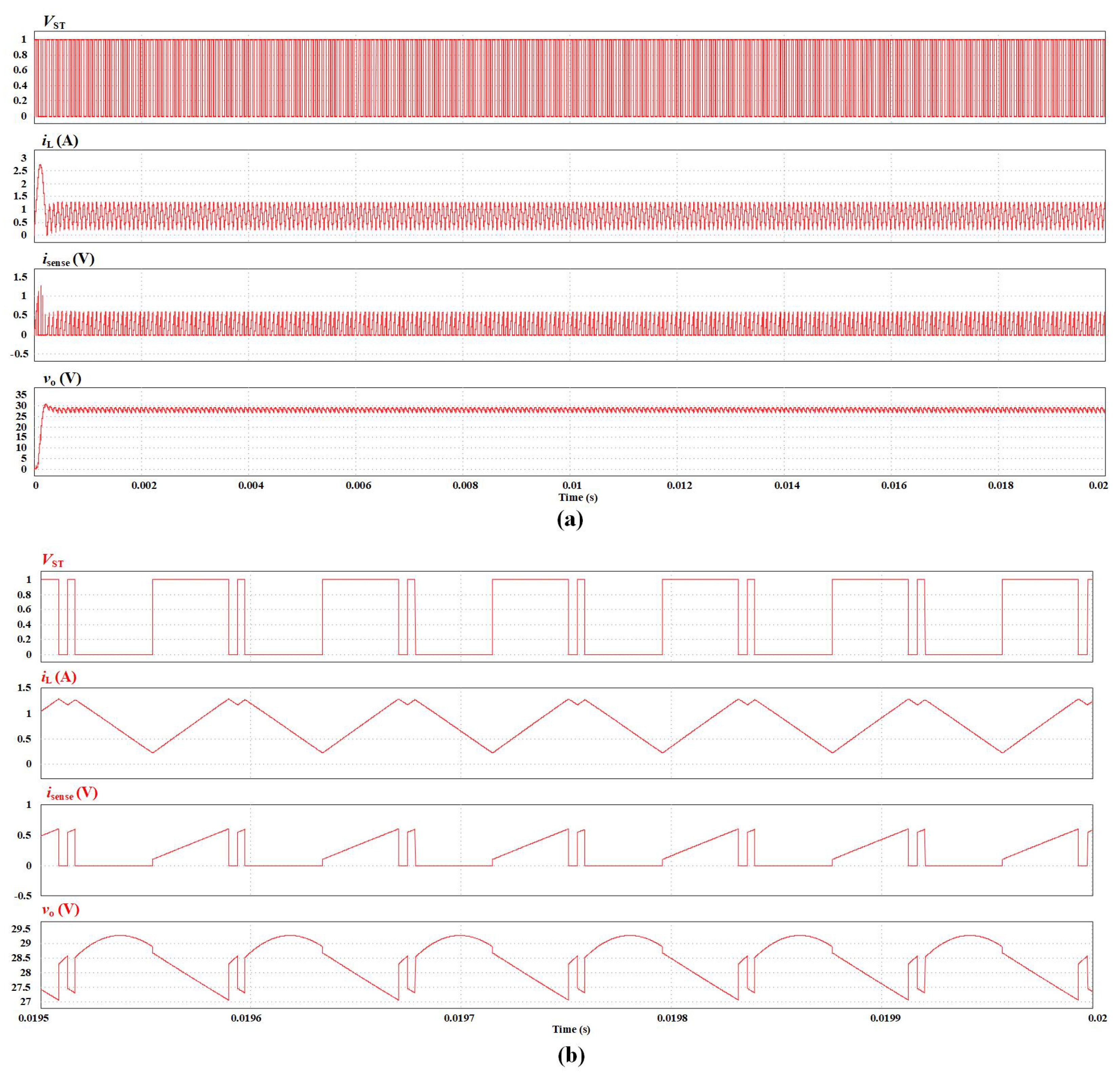
, the time-domain results of circuit-level simulation in PSIM software is as the following Figure 9.

In the figure above, from top to bottom, sub-figures correspond to the G-S voltage of power switch

S_{T}

, the inductor current

i_{L}

, the sampling value of the inductor current

i_{s e n s e}

(which is actually the voltage of

R_{s e n s e}

), and the output voltage

v_{o}

. One can find that, the PCMC dc-dc boost is in P-1 stable state under the configuration of parameters. The result is consistent with the results of bifurcation diagrams.

Then, we set the voltage dividing resistor

R_{v 1} = 12 k Ω

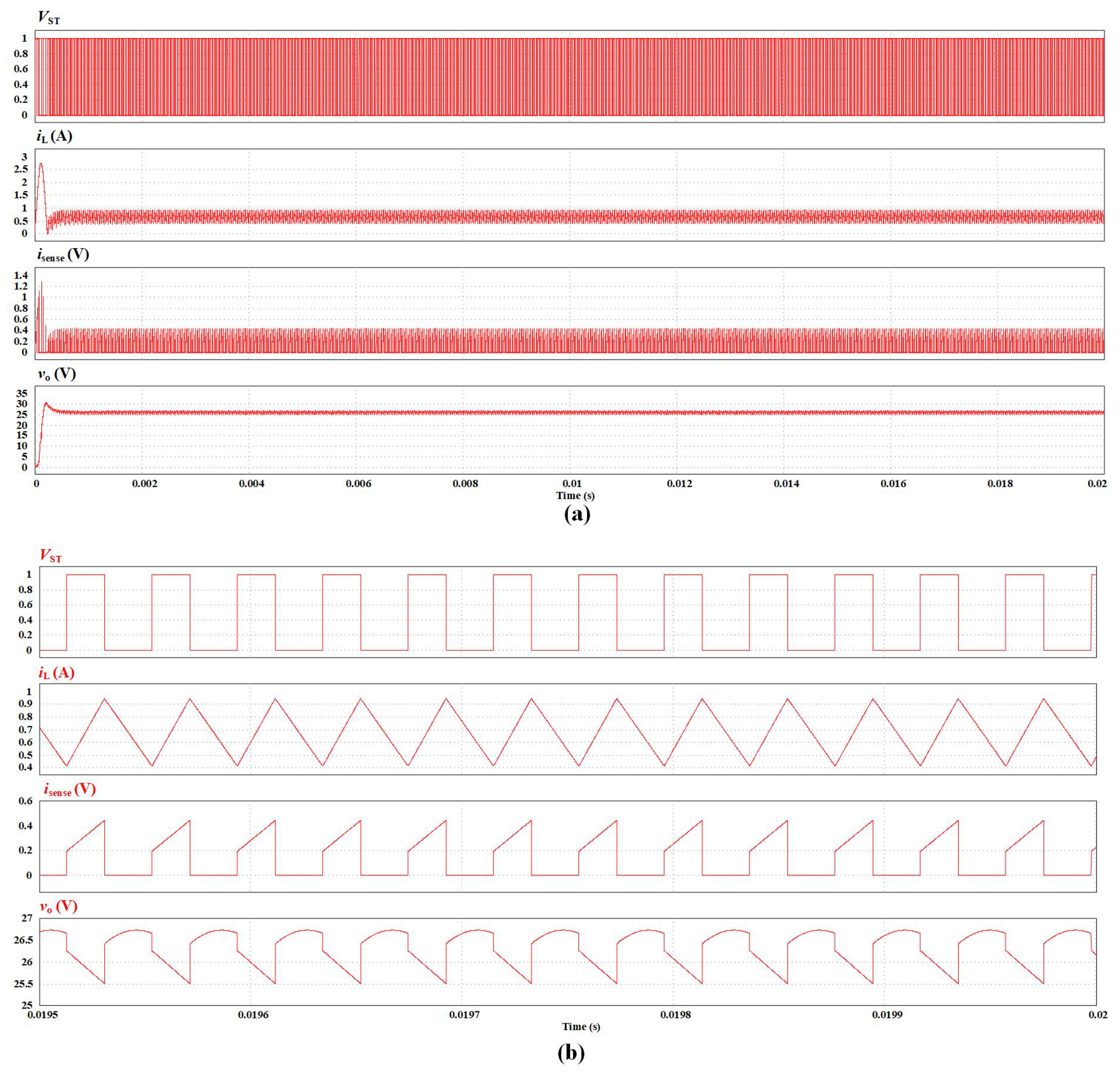
, the time-domain results of circuit-level simulation in PSIM software is as Figure 10.

In Figure 10, from top to bottom, sub-figures correspond to the G-S voltage of power switch

S_{T}

, the inductor current

i_{L}

, the sampling value of the inductor current

i_{s e n s e}

(which is actually the voltage of

R_{s e n s e}

), and the output voltage

v_{o}

. One can find that, the PCMC dc-dc boost is in P-2 sub-harmonic oscillation state under the configuration of parameters. The result is also consistent with the results of bifurcation diagrams.

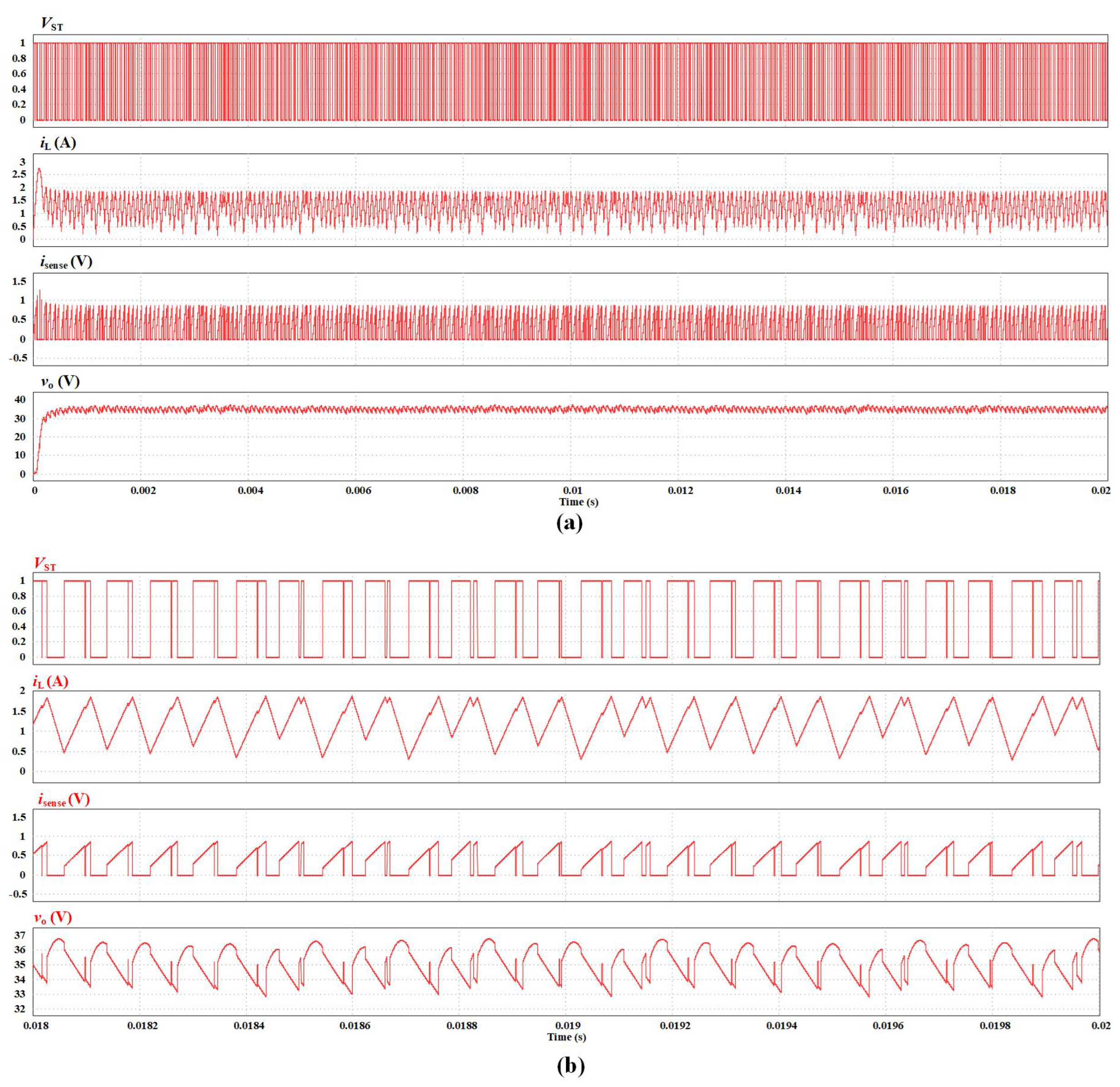
At last, we set the voltage dividing resistor

R_{v 1} = 25 k Ω

, the time-domain results of circuit-level simulation in PSIM software is as Figure 11, in which sub-figures correspond to the G-S voltage of power switch

S_{T}

, the inductor current

i_{L}

, the sampling value of the inductor current

i_{s e n s e}

(which is actually the voltage of

R_{s e n s e}

), and the output voltage

v_{o}

from top to bottom. One can find that, the PCMC dc-dc boost is in chaotic state under the configuration of parameters. The result is also consistent with the results of bifurcation diagrams.

4.2. Experiments

In order to further validate the results of both theoretical analysis and circuit-level simulation, a simple prototype is established in this work, in which a

10 μ F

aluminum electrolytic capacitor is adopted as the output filtering capacitor, a type-IRF640B power MOSFET and a type-1N5008 rectifier diode are exploited as

S_{T}

and

S_{D}

of the converter, and a UC3842 IC is employed to control the dc-dc boost converter. The experiment scene is as follows:

Figure 12. A glimpse of experiment scenes: (a) capacitance measurement scene, (b) experimental prototype.

By rotating the bar of the type-3296 potentiometer on the circuit board to adjust the voltage dividing ratio, one can observe that the PCMC dc-dc boost converter experiences different nonlinear dynamic states.

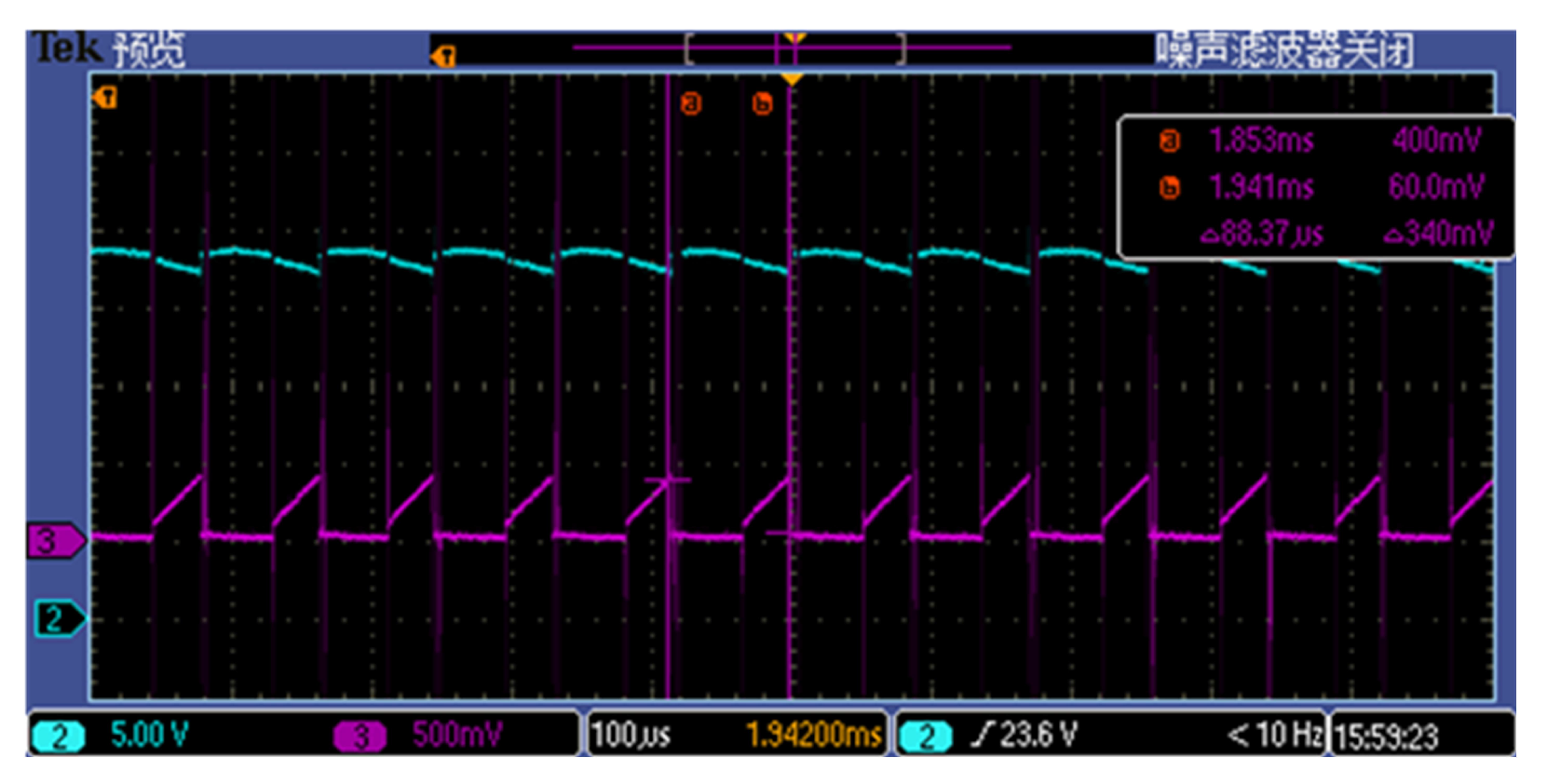
Figure 13. Experiment waveforms of P-1 stable state when the resistance of type-3296 potentiometer is around

1 k Ω

Figure 13. Experiment waveforms of P-1 stable state when the resistance of type-3296 potentiometer is around

1 k Ω

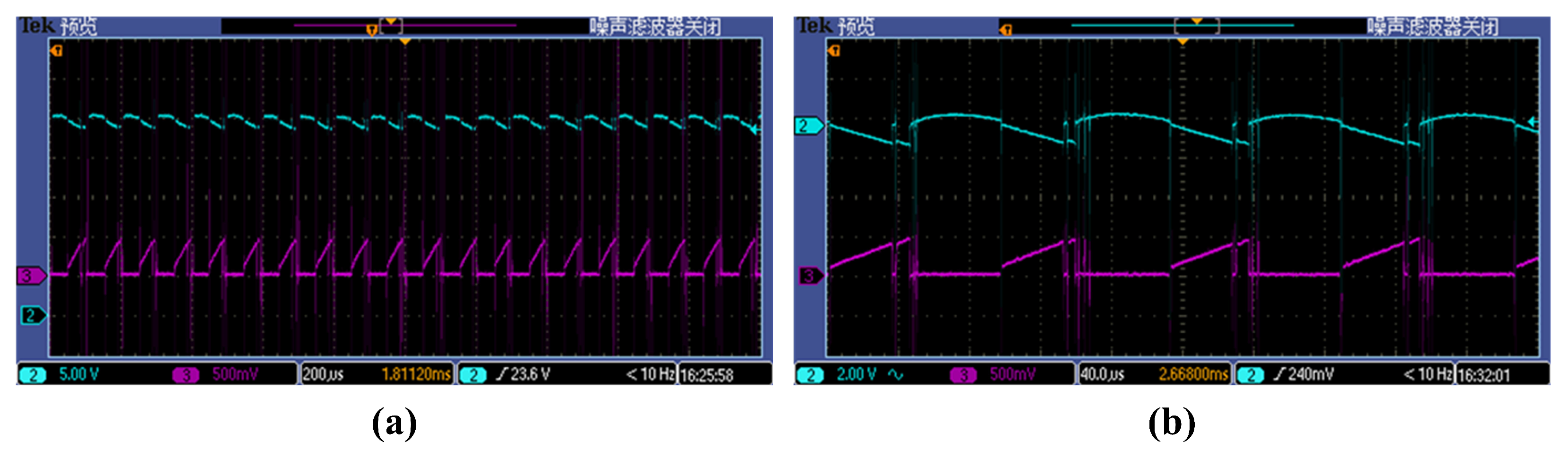
Figure 14. Experiment waveforms of P-2 sub-harmonic oscillation state when the resistance of type-3296 potentiometer is around

1 k Ω

: (a) time-domain waveforms, (b) enlarged peak-to-peak waveforms.

Figure 14. Experiment waveforms of P-2 sub-harmonic oscillation state when the resistance of type-3296 potentiometer is around

1 k Ω

: (a) time-domain waveforms, (b) enlarged peak-to-peak waveforms.

It can be found that experimental waveforms are very similar to the results of circuit-level simulation, and the variation trend is consistent with the results of bifurcation diagrams, which confirm the correctness of theoretical analysis.

5. Conclusions

The concept of fractional-order components and circuit systems has received widespread attention recently. This study appears to be the very few empirical studies on the nonlinear dynamic of real-world fractional-order circuit systems, in which the nonlinear dynamic characteristics of a real-world fractional-order system are objectively measured and evaluated, that is, a PCMC dc-dc boost converter using an aluminum electrolytic capacitor as the output filtering capacitor. Returning to the question posed at the beginning of this paper, it is now possible to state that, the fractional-order piecewise smooth model built in this work can be used for the large-signal stability analysis of the converter, by which one can draw bifurcation diagrams of the converter. The results of bifurcation diagrams emerged as reliable predictors of nonlinear dynamic analysis for the converter, when different parameters change, they can be used to predict the dynamics of the converter. Both circuit-level simulations and experiments have confirmed the correctness of the theoretical analysis. Notwithstanding the relatively limited example, this work offers a reference for the parameter selection and optimal design for power electronic converters which have fractional-order characteristics.

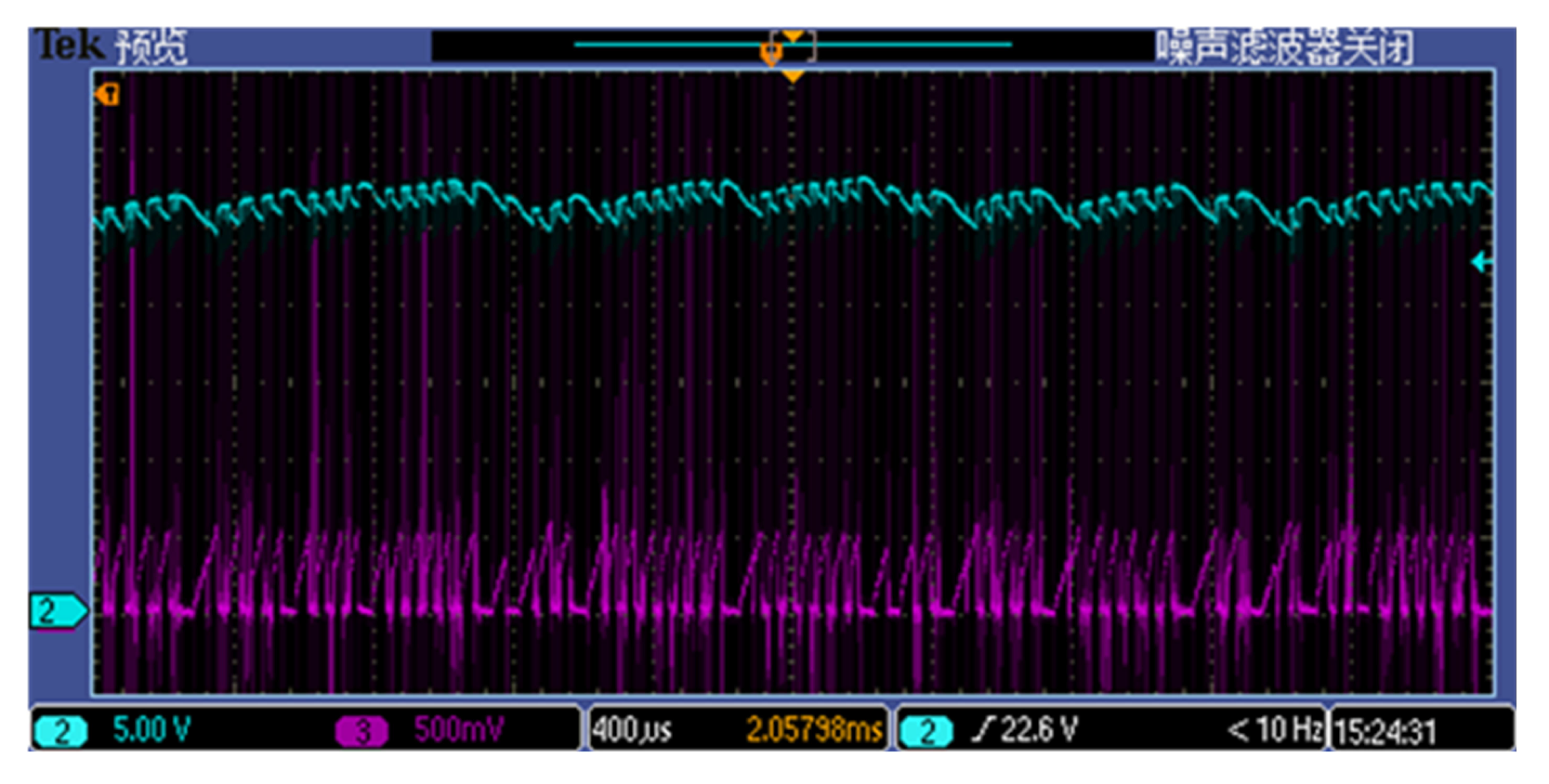
Figure 15. Experiment waveforms of chaotic state when the resistance of type-3296 potentiometer is around

1 k Ω

Figure 15. Experiment waveforms of chaotic state when the resistance of type-3296 potentiometer is around

1 k Ω

Author Contributions

Conceptualization, methodology, writing—original draft preparation, and supervision, Xi Chen; Software, validation, formal analysis, and data curation, Feng Zheng; Validation, resources, data curation, and visualization, Chao Yang; writing—review and editing, and project administration, Hui Ma; writing—review and editing, project administration, and funding acquisition, Binxin Zhu. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Project of Yichang, China (A20-3-014).

Conflicts of Interest

The authors declare no conflict of interest.

References

Tse, C. K.; Xi, L.; Bernardo, M. D. Complex Behavior in Switching Power Converters. Proceedings of the IEEE 2002, 90(5), 768–781. [Google Scholar] [CrossRef]
Chen, Y.; Xie, F.; et al. Improvement of Stability in a PCM-Controlled Boost Converter with the Target Period Orbit-Tracking Method. Electronics 2019, 8(12), 1432. [Google Scholar] [CrossRef]
Chen, Y.; Zhang, B. Equivalent-Small-Parameter Analysis of DC/DC Switched-Mode Converter, 1st ed.; Springer: Singapore 189721, Singapore, 2018; pp. 1–2. [Google Scholar]
Tse, C. K. Design-Oriented Bifurcation Analysis of Power Electronics Systems. In: In, V., Longhini, P., Palacios, A. (eds) Applications of Nonlinear Dynamics. Understanding Complex Systems.; Springer, Berlin, Heidelberg, 2009; pp. 175–187.
Ding, L.; Wong, S. C.; Tse, C. K. Bifurcation Analysis of a Current-Mode-Controlled DC Cascaded System and Applications to Design. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4), 3214–3224. [Google Scholar] [CrossRef]
Aroudi, A.; Haroun, R.; et al. Fast-Scale Stability Analysis of a DC–DC Boost Converter With a Constant Power Load. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 8(4), 549–558. [Google Scholar] [CrossRef]
Ji, H.; Xie, F.; et al. Small-Step Discretization Method for Modeling and Stability Analysis of Cascaded dc–dc Converters With Considering Different Switching Frequencies. IEEE Transactions on Power Electronics, 2022, 37(8), 8855–8872. [Google Scholar] [CrossRef]
Yang, Z.; Xi, L.; Zhang, Y.; Chen, X. An Online Parameter Identification Method for Non-solid Aluminum Electrolytic Capacitors. IEEE Transactions on Circuits and Systems II: Express Briefs 2022, 69(8), 3475–3479. [Google Scholar] [CrossRef]
Wang, K.; Sun, P.; et al. Monitoring Chip Branch Failure in Multichip IGBT Modules Based on Gate Charge. IEEE Transactions on Industrial Electronics, 2023, 70(5), 5214–5223. [Google Scholar] [CrossRef]
Zhu, B.; Liu, Y.; et al. A Family of Bipolar High Step-Up Zeta–Buck–Boost Converter Based on “Coat Circuit”. IEEE Transactions on Power Electronics, 2023, 38(3), 3328–3339. [Google Scholar] [CrossRef]
Zhu, B.; Huang, Y.; et al. High step-up SEPIC converters based on kinds of coat circuit. CSEE Journal of Power and Energy Systems, 2022. early access. [Google Scholar]
Elwakil, A. Fractional-Order Circuits and Systems: An Emerging Interdisciplinary Research Area. IEEE Circuits and Systems Magazines 2010, 10(4), 40–50. [Google Scholar] [CrossRef]
Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications; Academic Press: LONDON, UK, 1998; pp. 124–125. [Google Scholar]
Petráš, I. Fractional-Order Nonlinear Systems; Springer-Verlag: Berlin Heidelberg, 2011; pp. 43–54. [Google Scholar]
Zhang, B.; Shu, X. Fractional-Order Electrical Circuit Theory (CPSS Power Electronics Series), 1st ed.; Springer: Singapore 189721, Singapore, 2022; pp. 39–54. [Google Scholar]
Zhang, L.; Kartci, A.; et al. Fractional-Order Inductor: Design, Simulation, and Implementation. IEEE Access 2021, 9, 73695–73702. [Google Scholar] [CrossRef]
Allagui, A.; Freeborn, T. J.; Elwakil, A. S.; et al. Review of fractional-order electrical characterization of supercapacitors. Journal of Power Sources 2018, 400, 457–467. [Google Scholar] [CrossRef]
Chen, X.; Pei, M. Enhancing parameter identification of electrochemical double layer capacitors by fractional-order equivalent impedance models and Levy flight strategy. International Journal of Circuit Theory and Applications 2022, online. [Google Scholar] [CrossRef]
Zou, C.; Zhang, L.; et al. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. Journal of Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
Huang, Y.; Chen, X. A fractional-order equivalent model for characterizing the interelectrode capacitance of MOSFETs. IEEE COMPEL - The international journal for computation and mathematics in electrical and electronic engineering 2022, 41(5), 1660–1676. [Google Scholar] [CrossRef]
Allagui, A.; Elwakil, A. S.; Fouda, M. E. Revisiting the Time-Domain and Frequency-Domain Definitions of Capacitance. IEEE Transactions on Electron Devices 2021, 68(6), 2912–2916. [Google Scholar] [CrossRef]
ONSENMI, UC3842B: High Performance Current Mode Controllers. Available online: https://www.onsemi.com/pdf/datasheet/uc3842b-d.pdf (accessed on 22 Feb. 2023).
Chen, X.; Xi, L.; et al. Fractional techniques to characterize non-solid aluminum electrolytic capacitors for power electronic applications. Nonlinear Dynamics 2019, 98, 3125–3141. [Google Scholar] [CrossRef]
Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer-Verlag: Berlin Heidelberg, 2010; pp. 195–225. [Google Scholar]
Chen, X.; Chen, Y. A Modeling and Analysis Method for Fractional-order DC-DC Converters. IEEE Transactions on Power Electronics 2017, 32(9), 7034–7044. [Google Scholar] [CrossRef]
Oustaloup, A.; Levron, F.; et al. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Transactions on Circuits and Systems I-Fundamental Theory and Applications 2000, 47(1), 25–39. [Google Scholar] [CrossRef]
Xue, D.; Chen, Y. System Simulation Techniques with MATLAB® and Simulink®, 1st ed.; John Wiley Sons: West Sussex, United Kingdom, 2013; pp. 85–90. [Google Scholar]
Malti, R.; Victor, S.; et al. CRONE Toolbox for system identification using fractional differentiation models. IFAC-Papers OnLine 2015, 48(28), 769–774. [Google Scholar] [CrossRef]
Zhang, Y.; Lian, Z.; et al. An ESR Quasi-Online Identification Method for the Fractional-Order Capacitor of Forward Converters Based on Variational Mode Decomposition. IEEE Transactions on Power Electronics 2022, 37(4), 3685–3690. [Google Scholar] [CrossRef]

Figure 1. Internal structure of UC3842 type current-mode controller chip.

Figure 2. PCMC DC-DC boost Converter.

Figure 3. Implementation of an outer-loop PI controller.

Figure 4. Principle of stroboscopic map technique.

Figure 5. Bifurcation diagrams of inductor current

i_{L}

versus different parameters: (a)

i_{L}

versus power supply

V_{i n}

, (b)

i_{L}

versus load resistance

R_{o}

, (c)

i_{L}

versus output voltage divider resistance

R_{v 1}

Figure 5. Bifurcation diagrams of inductor current

i_{L}

versus different parameters: (a)

i_{L}

versus power supply

V_{i n}

, (b)

i_{L}

versus load resistance

R_{o}

, (c)

i_{L}

versus output voltage divider resistance

R_{v 1}

Figure 7. Rational approximation circuit of

10 / {(s e c o n d)}^{1 - 0.9615}

CPE.

Figure 7. Rational approximation circuit of

10 / {(s e c o n d)}^{1 - 0.9615}

CPE.

Figure 8. Bode diagrams of fractional-order devices with different orders: (a)

C^{β}

with

β = 0.9

Figure 8. Bode diagrams of fractional-order devices with different orders: (a)

C^{β}

with

β = 0.9

Figure 9. Time-domain simulation results by setting

R_{v 1} = 10 k Ω

: (a) the whole operation process from initial state to 0.02s, (b) enlarged plot from 0.0195s to 0.02s.

Figure 9. Time-domain simulation results by setting

R_{v 1} = 10 k Ω

: (a) the whole operation process from initial state to 0.02s, (b) enlarged plot from 0.0195s to 0.02s.

Figure 10. Time-domain simulation results by setting

R_{v 1} = 12 k Ω

: (a) the whole operation process from initial state to 0.02s, (b) enlarged plot from 0.0195s to 0.02s.

Figure 10. Time-domain simulation results by setting

R_{v 1} = 12 k Ω

: (a) the whole operation process from initial state to 0.02s, (b) enlarged plot from 0.0195s to 0.02s.

Figure 11. Time-domain simulation results by setting

R_{v 1} = 25 k Ω

: (a) the whole operation process from initial state to 0.02s, (b) enlarged plot from 0.018s to 0.02s.

Figure 11. Time-domain simulation results by setting

R_{v 1} = 25 k Ω

: (a) the whole operation process from initial state to 0.02s, (b) enlarged plot from 0.018s to 0.02s.

Table 1. Parameters of the PCMC DC-DC Boost converter.

Parameter	Symbol	Value
Power supply	$V_{i n}$	$5 V ~ 20 V$
Reference voltage	$V_{r e f}$	$2.5$ V
Switching frequency	$f_{s}$	$25 k$ Hz
On resistance of power MOSFETs	$R_{S}$	$\approx 10 m Ω$
Inductor	L	$492 μ$ H
Equivalent series resistance of inductor	$R_{L}$	$\approx 4 m Ω$
Load resistance	$Z_{L} = R_{o}$	$10 Ω ~ 100 Ω$
Output filtering capacitor	C	$10 μ$ F
Fractional order of capacitor	$α$	$\approx 0.9615$
Equivalent series resistance of capacitor	$R_{Ω}$	$\approx 0.9630 Ω$
Sampling resistor for inductor current	$R_{s e n s e}$	$100 m Ω ~ 680 m Ω$
Input resistors of current conditioning circuit	$R_{i 1}$ , $R_{i 2}$	$10 k Ω$
Feedback resistors of current conditioning circuit	$R_{f i}$	$10 k Ω$
Output voltage divider resistors	$R_{v 1}$ , $R_{v 2}$	$0.5 k Ω ~ 33 k Ω$
Reference voltage	$V_{r e f}$	$2.5$ V
Compensation resistors of voltage loop controller	$R_{k}$ , $R_{a}$	$1 k Ω ~ 100 k Ω$

Table 2.

R_{i}

and

C_{i}

values of an order-

0.9615

rational approximation circuit.

Table 2.

R_{i}

and

C_{i}

values of an order-

0.9615

rational approximation circuit.

i	$R_{i} (Ω)$	$C_{i} (μ F)$
0	0	0
1	$0.7961 m$	$41.5040$
2	$15.7435 m$	$47.0628$
3	$0.3131$	$53.0628$
4	$6.2286$	$59.8130$
5	$123.9148$	$67.4164$
6	$2.4692 k$	$75.8646$
7	$51.0412 k$	$82.2952$
8	$8.5964 M$	$10.9568$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On Nonlinear Dynamic Characteristics of Peak-Current-Mode Controlled DC–DC Boost Converters with Fractional-Order Output Filtering Capacitor

Abstract

Introduction

2. Piecewise Smooth Fractional-Order Model of PCMC DC-DC Boost Converters

2.1. Circuit configuration

2.2. Fractional-order piecewiese smooth model

3. Time-Domain Analysis

3.1. Preliminaries: Principles of Some Related Techniques

3.1.1. F-ABM calculation method

3.1.2. Stroboscopic map technique

3.2. Bifurcation analysis

4. Validation and Comparison

4.1. Circuit-level simulation

4.2. Experiments

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe