Preprint
Article
Application of Variational AutoEncoder (VAE) Model and Image Processing Approaches in Game Design
Altmetrics
Downloads
142
Views
83
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
28 February 2023
Posted:
01 March 2023
You are already at the latest version
Alerts
Abstract
In recent decades, the Variational AutoEncoder (VAE) model has shown good potential and capabilities in image generation and dimensionality reduction. The combination of VAE and various machine learning frameworks has also worked effectively in different daily life applications, however its possibility and effectiveness in modern game design has seldom been explored nor assessed. The use of its feature extractor for data clustering was minimally discussed in literature neither. This paper first attempts to explore different mathematical properties of the VAE model, in particular, the theoretical framework of the encoding and decoding processes, the possible achievable lower bound and loss functions of different applications; then applies the established VAE model into generating new game levels within two well-known game settings; as well as validating the effectiveness of its data clustering mechanism with the aid of the Modified National Institute of Standards and Technology (MNIST) database. Respective statistical metrics and assessments were also utilized for evaluating the performance of the proposed VAE model in aforementioned case studies. Based on the statistical and spatial results, several potential drawbacks and future enhancement of the established model were outlined, with the aim of maximizing the strengths and advantages of VAE for future game design tasks and relevant industrial missions.
Keywords:
Subject: Computer Science and Mathematics - Data Structures, Algorithms and Complexity
1. Introduction
In the 21st century, enormous mathematical and data analytic techniques and algorithms have been adopted in designing new video games and frames, for the purposes of enhancing teaching and learning processes within virtual environment, pushing the innovation and specialty of gameplay mechanics to its furthest extent, and visualizing game scenes in a human-crafted, realistic and dynamic manner [1,2,3]. The concerned subjects include the investigation of 3-dimensional geometric properties of characters within a particular frame [4], the capturing of geometric transformations and motion in real-time basis [5], the use of simulation games for analyzing and building up complex systems that could better reflect real world conditions [6]. Today, credited with the increment of computing power and resources, the enhancement of capability in terms of data storage, and the massive data volume for simultaneous processing [3], advances in machine learning (ML) and artificial intelligence (AI) approaches are taking place and being widely adopted in different practical disciplines, especially those related to image processing and computer vision, as well as the emergence of generative models. Such new digital era has also promoted the use of these approaches in handling creative and artistic tasks, for example, conditional adversarial neural networks have been applied for generating city maps from a sketch [7]; a Generative Adversarial Network (GAN) model was proposed and established to generate images based on the simple sentence description of an object or a specific scenario [8]; the Game Design via Creative Machine Learning (GDCML) mechanism was utilized for setting up an interface and modules of games and informing new systems [9]. In view of all these success, achieving “computational creativity” in the perspective of video game design has now become a hotspot and new focus; while game companies and developers are seeking ways to adopt ML and AI algorithms, so that the overall production cost of a game or related products can be reduced, at the same time brand new working procedures within the game can also be explored in the long run. A research report published by Netease has reviewed that the incorporation of ML models into game design could reduce the development costs by millions of Renminbi (RMB) dollars [10].
In the early days of video game development, most games were relatively simple and “monotonous”, and were conducted via the “third-person shooting” mode with the aid of electronic machines. In 1962, Steve Russell and several student hobbyists in Massachusetts Institute of Technology (MIT) developed the first ever video game in the world, called Spacewar! [11], and this game was published on the Digital Equipment Corporation (DEC) platform at a later time. Within the historical development stage, Spacewar! was considered as the first highly influential video game, because it motivated the advancement of computing resources, reviewed the difficulties in transferring programs and graphics between computing platforms at different places [11], and stimulated the development of different game genres. In the early 1970s, the first home video game console called the “Magnavox Odyssey” and the first arcade video game called the “Computer Space and Pong” were respectively established. At the earlier stages, despite the effective integration of technology, creativity and computing resources, it is lacking of a uniform standard for classifying game genres in terms of gameplay, but can be generally categorized as in [12]. Some key examples include (1) Action Games that emphasize on physical challenges, particularly the coordination of hands and eyes; (2) First Person Shooter Games that include the use of guns and weapons for competition and fighting against each other from a first-person perspective; (3) Sports and Racing Games, which simulate the practice of sports or racing originated from real or fantastical environments; (4) Simulation Games that describe a diverse super-category of video games, so that real world activities can be effectively simulated and displayed, for example, flight simulation and farming simulation. With the combination of these genres and capabilities in algorithmic design and data analytics, the importance and popularity of arcades and consoles had diminished, and were gradually replaced by games that are compatible on personal computers, smartphones and mobile devices. Some mainstream game platforms in the 21st century are as shown in Table 1. Nowadays, most games released are not limited to a particular genre, for example, “Need for Speed” is considered to be both a Sports and Racing Game, as well as a Simulation Game [13]; while many games can be released on multiple platforms, for example, the “Genshin Impact” is compatible on PC, mobile device and PlayStation simultaneously [14].
Apart from categorizing video games based on their genres and compatible platforms, modern games all consist of three major components, namely (1) the program component; (2) the gameplay component; and (3) the artistic component. Programs form the basis of a video game, which determine the basic structure and logic of the game; gameplay decides how the players and the surrounding environment could interact, from the aspects of designing background settings, battles, balances and stages of the game itself; artistic components lay down what the player can visualize and hear during the gameplay, which can include the design of characters, environmental settings, design of background music and animations, as well as the ways of interaction [18]. In particular, when designers attempt to produce artistic materials that put spice into the attractiveness of the video game, they may either take reference of real world architectural and parametric settings, or create objects and environment that do not exist in reality. This provide possibilities for the utilization and application of image generation techniques within game design processes [19,20]. Designers and scientists have started exploring how ML and combinatorial algorithms could play a systematic role in different levels of game design, for example, data preprocessing, clustering, decoding and encoding, as well as generating attractive and sustainable image outputs of a specific game [21,22,23,24]. Further, a recent concept called “game blending” was adopted by Gow and Coreneli to establish a framework that produces new games from multiple existing games [25], while the Long Short-Term Memory (LSTM) technique has also been applied to blend computer game levels based on Mario and Kid Icarus, then combine with the Variational AutoEncoder (VAE) model to generate more controllable game levels [26,27]. In recent years, Generative Adversarial Network (GAN) models have become popular, and have been incorporated into the framework of generating game levels and images under specific conditions and settings [28,29]. These black-box models allow users to design and generate levels in an automatic manner, thus Schrum et al. [30] utilized such unique features to develop a latent model-based game designing tool; while Torrado et al. [31] investigated the conditional GAN and established a new GAN-based architecture called “Conditional Embedding Self-Attention GAN”, then equipped it with the bootstrapping mechanism for the purpose of generating Role-Playing Games (RPG) levels. All these have shown certain capabilities in generating game levels within specific set-ups. Nevertheless, it is incredibly hard to obtain complete understanding of the internal structure of ML-based models, as well as the statistical properties behind the scene. Thus, it is of utmost importance to develop and explore the use of a mathematical model that can do corresponding tasks, i.e., generate new game levels that are applicable in modern game design and for future extension of the game, but at the same time, users can acquire basic understanding of statistical properties of the model, for example, time complexity, amount of loss during model training process, the relationship between time consumption with size of the input data.
In this study, the effectiveness of the Variational AutoEncoder (VAE) model in image generation within game design was first explored and assessed. It is considered as a deep generative model that consists of a variational autoencoder, which is equipped with a prior and noise distribution. During model training process, which is usually conducted by Expectation-Maximization meta-algorithm, the encoding distribution is “regularized” so that the resulting latent space suffices to generate new and meaningful datasets. Detailed mathematical derivation will be discussed in Section 3, and readers can refer to [32] for more technical details as well. The VAE model was first proposed by Kingma and Welling [33], and has been widely applied in different disciplines, for example, image generation, data classification and dimensionality reduction [34,35,36]. In particular, Vuyyuru et al. has constructed a weather prediction model based on the combination of VAE and Multilayer Perceptrons (MLP) models [37], and Lin et al. attempted to detect the anomaly of office temperature within a prescribed period via LSTM and VAE models [38]. Furthermore, Bao et al. had effectively combined the Convolutional Variational Autoencoder (cVAN) with GAN model to generate human photos by controlling the gender of required figures [39]. All these have demonstrated the systematic and practical usages of the VAE model, therefore we expect that with suitable data processing mechanism, fine-tuning of model parameters, and minimization of loss function during training, selected game functions or level maps could be generated, as a result provide assistance to game developers in the long run, in terms of auxiliary development, designing new games, and enhancing the speed and time complexity of image generation.
Section 2 includes the flowchart of how the VAE model was applied within this study, and the description of datasets used for later case studies. Then, the mathematical theories and statistical properties of the VAE model are outlined in Section 3, and Section 4 showcases some numerical experiments conducted and their corresponding statistical analyses. Section 5 discusses the drawbacks and limitations of current study, as well as some potential future research direction, then a short conclusion is provided in Section 6.
2. Flowchart and Data Sources
2.1. Overview of this study
Figure 1 shows an overall flowchart of the preprocessing and construction of the VAE model adopted in this study. After raw data or attributes were obtained from games or available databases, they were pre-processed to some extent whenever necessary. Upon the application of specific scaling factors within each dimension, these processed datasets could be ingested into a machine, where sufficient amount of datasets will be used for model training. In particular, the variational autoencoder within the VAE model was constructed, and the VAE algorithm was iterated such that the optimization of lower bound was achieved under some constraints, which might depend on the set-up of corresponding game and/or application. Such lower bound was called the “Evidence lower bound (ELBO)”. Further, the loss function during machine learning processes was also minimized, with the aim of estimating the amount of information that have been lost during model training processes. For data clustering applications, an alternative form of loss function was deemed more appropriate than the aforementioned “loss” during training. After fine-tuning all parameters of such a statistical model, the optimized VAE model was used to obtain some graphical outputs after a series of geometric transformations. In this study, we focus on analyzing the relationship between averaged loss figures with the number of epochs; the time complexity with the size of input datasets; the effects of scaling factors etc. Respective statistical figures will be presented either in graphical or tabular formats, as in Section 4.
2.2. Data Sources and Description
Within this study, three different datasets have been used for model training and assessing the effectiveness of the developed VAE model. Each of these datasets has its significance, namely, (1) provide good references for game designers; (2) consist of a “humanistic” character equipped with motion; and (3) practical for image processing and data clustering.
2.2.1. Game Map from Arknights
Arknights is a tower-defense puzzle game developed by Hypergraph [40]. The game was first published in 2019, and soon became popular and welcomed by many citizens in mainland China. In this study, we attempted to generate new maps based on existing game maps extracted from the official site, which could hopefully provide useful reference to game designers, especially in updating of motion and appearance of characters and surrounding spatial features.
A tool called Unity Hub was adopted to dispatch the original game installation package obtained from the official website of Arknights. In total, 180 different game maps were extracted, and Figure 2 shows an example of an original game map image. The size of the original image here is 500 × 500, with 300 pixels per inch (ppi). Detailed documentation of Unity Hub can be found in [41].
2.2.2. Characters from Konachan
The second type of dataset(s) that has been adopted in this study was obtained from the Konachan site, which is an image board site that consists of more than 60,000 different anime or manga wallpapers as at Feb 2023 [42]. Figure 3 shows an example of an anime avatar extracted from this official website. The size of this image is 512 × 512 digits, with 300 ppi.
2.2.3. Modified National Institute of Standards and Technology (MNIST) database
The third type of dataset was extracted from the MNIST database, which was created in 1998. This vast database of handwritten digits has been shown useful in pattern recognition and training various image processing systems for classification, with the aid of convolution neural network techniques [43,44]. This database consists of 60,000 ‘28 × 28 grayscale images’- each of which consists of 10 digits (from 0 to 9, inclusive); along with a test set that consists of 10,000 images [45]. An example is as shown in Figure 4, and within this study, MNIST database was selected to test and validate the effects of clustering, because every data entry has already been pre-labelled with classification labels.
3. Methodologies: Steps of the VAE Model
The important steps and statistical measures of the VAE model are provided in this section, which provide readers a crucial reference of how the VAE model was constructed; the ideas of data preprocessing; and the important parameters that should be controlled (i.e., maximized or minimized) during the machine learning stage.
3.1. Data Preprocessing
First, the raw images were compressed by applying a specific scaling factor, which is defined as the ratio of the length of a side of a desired output image to that of the original image. In this study, a scaling factor of less than 1 was adopted to speed up the machine learning and training processes, at the same time prevent the overflowing of memory.
Afterwards, the compressed images were decolorized using the optimization approach proposed in [46], with the aim of preserving original color contrasts to the best extent. In principle, the VAE model is applicable for handling RGB images, however due to limitations of computer performance, the images obtained from datasets in Section 2 were converted into grayscale styles. Nevertheless, the texture, color contrast and pixel properties were preserved as much as possible, so that the effectiveness of VAE model could be fairly assessed. In this study, the Intel(R) Xeon(R) CPU E5-2670 v3 with 2 processors was adopted, and the system was prescribed as a 64-bit operating system, with 128 GB RAM installed.
As for the Arknights game maps described in Section 2.2.1, since every game map represents only a class label, while only 180 different images could be obtained from the open data source, each of these 180 images was then copied by 10 times, so that a total of 1800 images were ingested into the VAE model, with most of them being grouped as the ‘training set’, and a small pile of these images was considered the ‘testing set’. Further, the 10 versions of each image possess different brightness, contrast and gamma correction factors, so that a total of 1800 class labels could be obtained for statistical analyses.
3.2. Autoencoding, Variational AutoEncoder (VAE) and Decoding Processes
In analyzing large datasets that contain vast amount of features within each observation, Principal Component Analysis (PCA) was widely adopted to visualize multi-dimensional information, by reducing the dimension of the original dataset but keeping the maximum amount of information in the output [47]. However, PCA was only applicable in handling linear surfaces, thus the concept of “autoencoding” came in. An autoencoder is capable of handling both linear and non-linear transformations, which is a model that reduces the dimension of complex datasets via neural network approaches [48]. It adopts backpropagation for learning features at instant time during model training and building stages, thus are more prone to achieve data overfitting when compared with PCA [49]. The structure of an autoencoder is as shown in Figure 5, which includes mainly an encoder for handling input datasets, some codes within the encoding process, and a decoder to produce meaningful outputs.
Denote as the set of all samples in the original dataset, where represents the th sample. The encoder is a function that encodes the original dataset to , i.e., , where the dimension of is significantly less than that of . Afterwards, the simplified dataset is passed onto the decoder, which decodes and outputs . Hence, the decoder is mathematically expressed as . The loss function under arbitrary norm (depending on the type of application) is then used to estimate the closeness between and . If the magnitude of is small, then the model is considered effective. Here, we may assume that the encoded will include most valuable information from , so that suffices to represent the original dataset even after dimensionality reduction has been applied during the model training process. For example, let be an image, where and are the dimensions that store the information of . The overall goal is to train an autoencoder that encodes the image into (i.e., dimensionality reduction), then apply a decoder that reformulates the image as such that the loss function is minimized. In practice, this model will create not only useful attributes of the image, but also unwanted noise components, because the distribution of , as denoted by has not been modelled. To complement such deficiency, the Variational AutoEncoder (VAE) was adopted to first model the probabilistic distribution of , before all useful attributes of are extracted to form a sampling space of and passed into the decoder for image recovery.
Suppose , where I represents an identity matrix, which means that can be regarded as a multi-dimensional random variable that obeys the standard multivariate Gaussian distribution. Denote and as random variables, and the corresponding ith samples are denoted as and respectively. With this set-up, the eventual output is generated by a stochastic process of 2 steps, with being the hidden variable: (1) The prior distribution of is encoded and sampled to obtain , then (2) based on the conditional distribution , a data point or sample is achieved.
As for the decoding process, the samples obtained from the distribution are ingested into the decoder, then the parametrized decoder establishes a mapping that outputs the precise distribution of corresponding to , which is denoted as . To simplify the statistical complexity, we may assume that obeys isotropic multivariate Gaussian distribution for any given , i.e., Equation (1) holds. This means that after is ingested into the decoder, the distribution of can be obtained after fitting and .
By taking into account that , Equation (2) is obtained, where represents the hyper-parameter within our VAE model.
Then, the Maximum Likelihood Estimation (MLE) is applied to estimate based on the observed or inputted dataset . Detailed formulation is as shown in Equation (3).
Generally speaking, the dimension of is very large, while even after dimensionality reduction is conducted, the dimension of is not extremely small. Thus, a sufficiently large amount of samples have to be considered for achieving an accurate estimate of . To cope with this, the posterior distribution has to be introduced in the encoder. Equation (4) shows how the Bayes’ formula can be applied into computing . The procedures here are designed and formulated with reference to the ideas of [50].
Next, the AutoEconding Variational Bayesian (AEVB) algorithm is applied to optimize the parametrized encoder and . Denote as the approximate posterior distribution of the encoder (with parameter ), if , then the encoder can be adopted to obtain the probabilistic distribution of [33]. Since and are of multivariate Gaussian distributions, so is . As a result, it suffices to acquire outputs of and from the encoder to outline the posterior of the generative model. For any sample , should satisfy the distribution as shown in Equation (5).
3.3. Steps of the VAE Model
Based on the methods reviewed and introduced in Section 3.2, the actual steps of the VAE model are outlined as follows (Steps 1 – 4):
Step 1: The encoder was assigned a data point / sample , and parameters of that the latent variable obeys were obtained through neural network methods. Since this posterior distribution is of an isotropic Gaussian distribution, it suffices to find out the parameters and of the Gaussian distribution that obeys. As an example, here may represent some images of orange cats.
Step 2: Based on the parameters and , a sample from the distribution was obtained, which is considered as a similar type of sample as . As an example, represents all cats that are orange in color.
Step 3: Then, the decoder proceeded to fit the likelihood distribution , i.e., when was ingested into the decoder, the parameters of the distribution that obeys could be achieved. Since the likelihood will also obey an isotropic Gaussian distribution, we can denote the output parameters as and . As an example, represents a distribution of images of orange cats.
Step 4: After the statistical parameters of the distribution were acquired, a sequence of data points was obtained via sampling. Nevertheless, most people use as an alternative representation of . An example here is to sample a new orange cat image from a particular distribution of orange cats.
In addition, it is also widely recognized that is an isotropic multivariate Gaussian distribution with fixed variance, which can be mathematically expressed as in Equation (6), where is considered as a hyper-parameter.
The overall graphical structure of the VAE model is as shown in Figure 6.
3.4. Evidence Lower Bound (ELBO) of the VAE Model
After fixing the structure of the VAE model for handling datasets in Section 2, an effective loss function for estimating the information loss during model construction process has to be established. Following the idea of MLE, and the application of variational inference, the likelihood function can be expressed as in Equation (7), and it is bounded below by , which is named the “Evidence Lower Bound (ELBO)”.
Here, the first integral of the last expression in Equation (7) is denoted as , while the second integral is called the KL divergence (also known as relative entropy in information theory), and is denoted by . Since KL divergence is always non-negative, is considered as the lower bound of . Rearranging Equation (7) results in Equation (8) below.
That is, to maximize is equivalent to maximize and to minimize . To minimize , we further assume that the approximate posterior distribution converges to the posterior distribution , which is valid because the encoder should only output meaningful distributions for further retrieval and signal recovery.
Expanding as shown in Equation (9), we have:
Again, the two terms in the last step of Equation (9) have their own physical meanings and implications, where the first integral represents the “latent loss”, and is denoted by ; while the second integral is known as the “reconstruction loss”, and is denoted by the expectation quantity .
Based on our assumption of the VAE model, and both follow Gaussian distribution, therefore, the analytical solution of can be obtained as follows:
Here, represents the relative entropy from to for these two probability distributions defined on the same measurable sample space.
As for the second term, multiple ’s from were sampled to approximate the term , where
Suppose the dimension of every data point is , we can expand as shown in Equation (11) below.
3.5. General Loss Function of the VAE Model
Based on the parameters introduced in Section 3.4, the loss function in Equation (12) should be minimized during the machine learning and model training processes:
In the formula, ’s are actually sampled from , however only one such is needed empirically, therefore, we simply consider the case of , hence Equation (12) can be simplified as Equation (13).
In our study, by considering that is an isotropic multivariate Gaussian distribution with fixed variance, it is reasonable to set as a -dimensional vector, with all elements being 0.5. With that, the corresponding loss function can be expressed as in Equation (14).
Here, represents the ith sample, which acts as the input of the encoder; and are the outputs of the encoder, which act as the parameters of the distribution of ; is sampled from and acts as the input of the decoder; is the output of the decoder, which precisely represents the eventually generated data point .
3.6. Loss Function of the VAE Model in Clustering
As aforementioned, the KL-divergence for and is defined as . Such an expression is only valid when we have the assumptions that is a Gaussian distribution, and both and are conditional Gaussian distributions. If all these hold, the loss of the ordinary VAE model can be obtained by a series of substitutions.
Nevertheless, in the case of data clustering, the hidden variables may not always be continuous variables. Thus, we set the latent variable as , where is a continuous variable that represents a coding vector, and is a discrete variable that represents the category. After updating the latent variable, the resulting KL-divergence is as shown in Equation (15), and such expression is applicable for clustering within the VAE model of this study.
In practice,
Therefore, Equation (15) can be re-written as Equation (17), which can essentially obtain the specific loss function of data clustering by following the procedures outlined in preceding sub-sections.
The formula shown in Equation (17) is also applicable for describing both encoding and decoding procedures. First, a data point or dataset is sampled, which represents an image formed by the original data, then apply to obtain the encoding characteristic, followed by using the cluster that classifies the encoded information or attributes. Next, a category is selected from the distribution , and a random hidden variable is selected from the distribution . Finally, the decoding process can generate new images accordingly. By these theoretical procedures, images with specific class labels and minimized loss can be generated in a systematic manner.
4. Numerical Experiments and Results
4.1. Case Study 1: Generation of Video Game Maps
The Arknights game maps were downloaded from [40], and were preprocessed as in Section 3.1, where a scaling factor of 0.2 was adopted. Further, the number of epochs within the VAE model was pre-set to be 50, which means that each sample in the training dataset will have 50 times to update its internal model parameters. The number “50” was selected to ensure that the error from the model is sufficiently minimized, but at the same time ensuring the affordability of our computing platform [51]. This number of epochs in testing the effectiveness of a model has been adopted in many literature, such as [52,53] for different practical applications, for example, forecasting power demand and the smart utilization of power grids, and the classification of coronavirus. The VAE-based outputs are as shown in Figure 7 and Figure 8, where Figure 7 shows two outputs obtained after the completion of model training within the VAE architecture, and that after mixing process was conducted; while Figure 8 shows the detailed output game map obtained after several original images were mixed together.
As observed from Figure 7, the images generated by the VAE model could retain the characteristics and features of the original image, and a new image could be effectively generated by mixing several original raw images from [40]. The mixing process was feasible (as shown on the right panel of Figure 7). However, when zooming in the output and attempting to visualize the fine details of an image, it was noticed that the sharpness of the output image was rather insufficient, mainly due to the noise components induced during the training process. It is suggested to apply suitable Laplacian sharpening filter or Sobel gradient for spatial enhancement, so that the edges of figures within an image will become more obvious [54]. Nevertheless, the new output images from the VAE model can still serve as good references for game designers when creating new game levels, or adding in new characters and spatial features into a particular video frame.
After obtaining the output images, numerical experiments were conducted to the same dataset for exploring the statistical properties of the VAE model. First, Figure 9 shows one of the most well-known learning curves, with the aim of illustrating the relation between average loss of the ten image-generation process and the number of epochs within the machine learning stage. In general, the average loss of the model decreases as the number of epochs increases, but the rate of decrease of average loss is gradually decreasing with the increase of epochs. Exact statistical figures of average loss within different number of epochs ranging from 1 to 16 (inclusive) are provided in Table 2. The average loss of using 1 epoch was 1259.3, then decreased to 1122.4 and 1025.6 when 2 and 10 epochs were respectively adopted. Continuing such process, it was observed that at the 21st epoch, the average loss would decrease to 999.0; while after 50 epochs, the resulting average loss would be 968.24. In overall, both graphical and statistical results have shown that the VAE model is fit to the training dataset extracted from the game map in [40], and 50 epochs is a reasonable number of epochs to be adopted within the VAE model. With these settings, the average loss figure induced when formulating new game levels or creating new frames or images will become stable and eventually converge to a limiting value.
Apart from investigating the average loss figures, the amount of time consumed for processing the VAE model is also crucial if one wants to extend the current VAE formulation to handle massive big data in the future. Figure 10(a) shows the time consumed for training the VAE model against the number of epochs used. The “time” quantity was obtained by taking the average of 10 times of training, with the use of the same dataset and other external parameters for training purposes. Graphical result shows that by fixing all other conditions, the time consumed for VAE model training is linearly related to the number of epochs imposed. For evaluating the time complexity of the VAE model, the number of attributes (i.e., the size of the ingested dataset) was resampled, and the corresponding dataset was ingested into the VAE model, with 50 epochs used during the training process. Then, the time taken for VAE model training was calculated. Figure 10(b) shows that the R2 value of such linear fit between these 2 quantities is 0.979, which implicates that the time consumed for VAE model training is very likely to be linearly related to data size, thus the time complexity of the VAE model adopted is of O(n).
Further, a scaling factor of 0.2 was adopted in this case study. In order to validate the use of such scaling factor and to further evaluate the performance of the VAE model, we varied the scaling factor from 0.15 to 0.5 (which was affordable by the computing platform). For each scaling factor, 10 trial experiments via the application of VAE model were conducted, and the corresponding time consumed and average loss values were recorded. Figure 11(a) and 11(b) show the respective relationship between time consumed for ten image-generation process / average loss figures among the use of different scaling factors.
As observed, the time consumption is not linearly related to the scaling factor imposed in the VAE model. Instead, the plot shown is almost converging to a quadratic or exponential relationship. Nevertheless, as the scaling factor increased from 0.2 to 0.3, the time consumed would exceed double of the original time; while when a scaling factor of 0.4 was applied to the VAE model, it took 75 s for processing the VAE model and generating an image at the end. In this case study, there are only limited number of game maps, and the data size of each raw game map is . Therefore, if this model is extended to handle a large-scale dataset, say those originated from satellite observations [55,56], then it will take days or even months for data processing; not even extend to datasets with multi-dimensions. Combining this concept with the amount of loss as shown in Figure 11(b), a factor of 0.2 was adopted, because a reasonably low average loss was induced by VAE model, and the computation time for the entire process was not exceptionally long even when dealing with larger input datasets. Further, from Figure 11(b), the R2 value of the resulting linear fit is 0.965, therefore it is of high possibility that the average loss is linearly related to the scaling factor imposed.
Despite obtaining all these meaningful conclusions from the correlations between different statistical quantities, we cannot conclude that when a smaller scaling factor is adopted, the model output must be better and of higher clarity. This is because the loss function derived in Section 3.5 only estimates the information loss when comparing the input and output datasets after both encoding and decoding are conducted, but may have ignored the information loss during the pre-processing stage. In actual industrial applications, the information loss of all aspects should be considered, so that an optimal scaling factor can be selected to balance the quality of outputs and model training efficiency.
4.2. Case Study 2: Generating Anime Avatars via VAE Model
VAE model is not only useful and applicable in generating the mixture of images or combined game levels from an input dataset, but can also be used to obtain new outputs – if we consider a set of images as the input, after encoding and decoding processes, a totally brand-new image can be created as the eventual output. In this case study, a dataset that consists of 60,000 different anime-girls (an example is shown in Figure 3) was ingested into the VAE model, then two possible outputs of the model were as shown in Figure 12.
In principle, the creation of new figures or images is not only limited in grayscale representation, but can also be feasible when colored images are desired. The VAE model can generate different new images simply by altering the training dataset, and our purpose within this case study is merely to illustrate the possibility of using VAE model for generating new datasets. In practice, when colored images are of interests, the computer memory needed will be almost tripled, because the RGB color space requires a 3-dimensional array to record the pixel values (i.e., intensities) of all 3 different colors.
4.3. Case Study 3: Application of VAE Model in Data Clustering
The VAE model is considered as both a generative model and a feature extractor, because it consists of an encoder and a decoder (which is treated as a generator), and the distribution of the latent variable can approximately be encoded as a standard normal distribution. Therefore, the effectiveness of the VAE model in performing data clustering was tested, because in principle, the feature extractor can conduct the task without any external supervision.
In this study, the MINST dataset of handwritten numbers (described in Section 2.2.3) was being used to illustrate the applicability of the VAE model in data clustering. Figure 13(a) shows the sampled numbers “6, 2, 7”, while Figure 13(b) showcases the corresponding numbers generated by the VAE model after data clustering was applied to all numbers shown in Figure 13(a). Obviously, the VAE model had reasonably good performance in terms of data clustering, and was capable of classifying different data types without any supervision, then generating appropriate images that corresponded to the clustered dataset.
Within this case study, 50 epochs were adopted, and the averaged recognition accuracy based on conducting 10 similar experiments via the VAE model was 85.4%. Corresponding training accuracy was around 83.7%. Table 3 shows the averaged accuracy of data clustering when different numbers of epochs was applied.
When the number of epochs increased from 3 to 5, significant improvement with respect to the performance of data clustering was achieved, where the average accuracy increased abruptly from 29.7% to 57.2%. Figure 14 displays the associated graphical relation between the two quantities, which has verified that (1) the average recognition accuracy enhanced as the number of epochs increased; (2) as the number of epochs increased, the increment in average accuracy decreased, and the average accuracy converged to a threshold, which was bounded above by 0.9 within this case study.
In actual gameplay, game designers can make use of the VAE model to recognize specific patterns of images or video frames, for example, the automatic recognition of sketches from game players. On top, the VAE model is also capable of performing data augmentation, which is particularly useful for puzzle games, where players are required to “draw” an object or “write down” an answer. Once the pattern resembles the model answer, the game will treat the player as “correct” and give out an award, or promote the player to more advanced stages of the game. VAE model can be fully utilized to serve related purposes, for example, pattern recognition and the clustering of objects or datasets.
5. Discussions and Limitations
5.1. Deficiencies of a low-dimensional manifold & Tokenization
Although the applicability of VAE model in modern game design, pattern recognition and data clustering was clearly illustrated in this study, there are some room for improvements based on the spatial results obtained from some of our case studies. In particular, in the case study of Arknights, when zooming Figure 8 into details, the image quality at specific pixels or regions could be dissatisfactory. This is because the input image consisted of some discrete pixels or point clouds in a high-dimensional space, and VAE attempted to first compress them into a low-dimensional continuous space (which we denoted as a “latent space”), then restored the original space via the decoding process. It was observed that VAE could work very well when the input dataset is actually a low-dimensional manifold being embedded in a higher-dimensional space [57], however some graphics like that in Arknights are obviously not a low-dimensional manifold itself in nature. This has led to some potential errors within the VAE-based retrieval process. Further, some features of images like texture are relatively hard to be described with low data volume, but texture can indeed play an important role in computer vision applications, for example, surface detection and medical imaging [58], therefore to enhance the quality of outputs from the VAE model in these industrial applications, other deep learning networks and transform-based methods can be adopted to distinguish these features at an early stage, either via the use of a smooth function for transformation, or extract the concerned features in another space, with the aid of wavelet transforms [59], ridgelet transform [60] or a Gabor filter [61]. Then, the corresponding attribute(s) can be combined with the latent space vector in VAE to produce better numerical results, and the information lost during encoding and decoding processes of VAE can be minimized.
Further, in order to filter off the invalid and simplify the useful information from the original input dataset, instead of generating low-dimensional images at all scenarios, researchers have proposed to divide a particular game map into the combination of different map elements or components, then replace these components by some tokens. This process is known as “tokenization”, as described in [62]. Much simplified new images that retain all useful attributes can be constructed, then the prescribed machine learning or VAE model can be used to train these images and produce their combined outputs. In the future, this technique can be incorporated into the existing VAE model for enhancing image resolution and producing images with better quality, especially for images similar to our Case Study 1.
5.2. Image Compression, Clarity of Outputs and Model Training
In the VAE model, a scaling factor has to be applied into raw datasets during the data pre-processing stage. If one excessively compresses the original image, much useful information will be lost, and fine details cannot be effectively kept during the model training stage, which could result in outputs of insufficient clarity. On the other hand, if the compression is not conducted, huge computing resources will be occupied especially when we are handling large-scale datasets, for example, database from ImageNet [63] or remotely sensed imageries for object detection or environmental monitoring [64,65]. In most desktops, the memory is of typically 4G-48G [66], therefore, memory overflow will easily take place, thus limit the overall efficiency and reliability of a model. The time consumed for model training and image retrieval will be excessively long as well. On top, in terms of model training, it took many rounds of experiments and data analytics in order to optimize the hyper-parameters of the VAE model, as a result increase the time consumed in overall. Therefore, it is of utmost importance to strike a balance in between the quality of outputs and the time consumed for generating the outputs via modelling approaches.
For the purposes of game design and creating new game levels, in order to alleviate the problem of insufficient clarity caused by the VAE model, and to avoid the occurrence of “mode collapse” (i.e., only one or several image types will be generated) that often takes place in traditional GAN models, the combination of VAE and GAN models can be adopted. VAE model only consists of one generator, while the GAN model consists of both a generator and a discriminator. These two “machines” will oppose to each other, where the generator is continuously attempting to generate images and frames that can fool the discriminator, such that the probability for a discriminator to make mistakes will be increased; while the discriminator tries its best to distinguish between real and useful data from fake ones via neural network mechanism [67]. As a result, better outputs can be generated after to and fro checking. For enhancing the clarity of images in Case Studies 1 and 2 of this paper, we propose to adopt the VAE model as the generator and simultaneously develop a discriminator to supervise the VAE model, i.e., a combined model of VAE and GAN models is to be established. Thus, the generator of the VAE-GAN model consists of the statistical or probabilistic distribution of the original input dataset, at the same time, it can effectively reduce the training time throughout the entire process, and reduce the probability of suffering from “mode collapse”.
6. Conclusion
In this study, we illustrated the possibility and statistical feasibility of using the combination of VAE model and machine learning strategies for modern game design, with the aid of 3 case studies arising from different nature and applications. The mathematical principles and assumptions of the VAE model, as well as its Evidence Lower Bound (ELBO), loss function during model construction, and loss function in data clustering, were first explored and derived. Then, the VAE model was applied to generate new game maps based on existing maps obtained from Arknights, create and retrieve anime avatars, and cluster a group of MNIST datasets that consist of numerals. The output images and datasets could retain and re-combine information from the inputs to a certain extent, however in the case study of Arknights (Case Study 1), there were room for improvements due to the lack of clarity within the output image, which could essentially represent a new game level in practice.
Some statistical features of the model and relationship between different parameters were also reviewed from these 3 case studies, for example, there is a high possibility that the time complexity of this VAE model is O(n); the loss of the VAE model decreases as the number of epochs applied increases, but the rate of change of such loss is also declining in general; the time consumed for performing VAE model is positively and linearly related to the number of epochs. For preventing memory overflow and saving computing resources, an appropriate scaling factor has been applied to each input dataset or image at the pre-processing stage, and it was found that the time consumed increases as the scaling factor increases, and there is a significant possibility that the loss derived from the loss function is positively and linearly related to such scaling factor.
Despite showing some technical deficiencies in generating new game levels (as reviewed in Case Study 1), the VAE model has shown its capability in data clustering. Further, for image attributes (or data points) with obviously different characteristics or spatial features, the VAE model can successfully distinguish one class from another via the model training process, then generate images of a specific class. On average, the recognition accuracy under 50 epochs is 85.4%, which is considered satisfactory.
Generally speaking, the VAE model is most effective in generating images with a specific graphical pattern, or handling and producing images of low resolution requirements, for example, clouds, grass and distant views in our nature. It is particularly promising in terms of clustering and creating new characters within a game.
In view of the technical shortcoming of the current VAE model, we learnt that the future enhancement should lie on increasing the resolution of images generated, for example via the combination of VAE model with other machine learning mechanisms like GAN and LSTM; ensuring sufficiency with regard to the amount of information in the model training set, so that all output images will contain more useful information and attributes, but at the same time consist of the least amount of noise components. This may be possible by tracing back to the techniques adopted in data pre-processing stages. This study has opened a new window for utilizing the strengths of VAE for future game design missions within the industry, at the same time identifying some potential weaknesses of VAE and proposing potential ways of remedy in the foreseeable future.
Author Contributions
Conceptualization, H.W.L.M. and R.H.; methodology, H.W.L.M. and R.H.; software, R.H.; validation, H.W.L.M. and H.H.F.Y.; formal analysis, H.W.L.M. and R.H.; investigation, H.W.L.M., R.H., H.H.F.Y.; writing—original draft preparation, H.W.L.M. and R.H.; writing—review and editing, H.W.L.M. and H.H.F.Y.; supervision, H.W.L.M.; project administration, H.W.L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Acknowledgments
This paper is an extended and modified version of the master project report of R.H., which is supervised by H.W.L.M.
Conflicts of Interest
The authors declare no conflict of interest. There is no funder involved in this study and this paper.
References
- Moyer-Packenham, P.S.; Lommatsch, C.W.; Litster, K.; Ashby, J.; Bullock, E.K.; Roxburgh, A.L.; Shumway, J.F.; Speed, E.; Covington, B.; Hartmann, C.; Clarke-Midura, J.; Skaria, J.; Westenskow, A.; MacDonald, B.; Symanzik, J.; Jordan, K. How design features in digital math games support learning and mathematics connections. Comput. Hum. Behav. 2019, 91, 316–332. [Google Scholar] [CrossRef]
- Berglund, A.; Berglund, E.; Siliberto, F.; Prytz, E. Effects of reactive and strategic game mechanics in motion-based games. In Proceedings of 2017 IEEE 5th International Conference on Serious Games and Applications for Health (SeGAH), Perth, WA, Australia, 2017; pp. 1–8. [Google Scholar]
- Petrovas, A.; Bausys, R. Procedural Video Game Scene Generation by Genetic and Neutrosophic WASPAS Algorithms. Appl. Sci. 2022, 12, 772. [Google Scholar] [CrossRef]
- Amani, N.; Yuly, A.R. 3D modeling and animating of characters in educational game. J. Phys.: Conf. Ser. 1193 2019, 012025. [Google Scholar] [CrossRef]
- Patoli, M. Z.; Gkion, M.; Newbury, P.; White, M. Real Time Online Motion Capture for Entertainment Applications. In Proceedings of 2010 Third IEEE International Conference on Digital Game and Intelligent Toy Enhanced Learning, Kaohsiung, Taiwan, 2010; pp. 139–145. [Google Scholar]
- Lukosch, H.K.; Bekebrede, G; Kurapati, S; Lukosch, S.G. A Scientific Foundation of Simulation Games for the Analysis and Design of Complex Systems. Simul Gaming. 2018, 49(3), 279–314. [Google Scholar] [CrossRef] [PubMed]
- OpenDotLab, Invisible cities. Available at: https://opendot.github.io/ml4ainvisible-cities/ (accessed on 24 Feb 2023).
- Li, W.; Zhang, P.; Zhang, L.; Huang, Q.; He, X.; Lyu, S.; Gao, J. Object-Driven Text-To-Image Synthesis via Adversarial Training. In Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 2019; pp. 12166–12174. [Google Scholar]
- Sarkar, A.; Cooper, S. Towards Game Design via Creative Machine Learning (GDCML). In Proceedings of IEEE Conference on Games (CoG), Osaka, Japan, 2020; pp. 1–6. [Google Scholar]
- GameLook, Netease game artificial intelligence laboratory sharing: AI technology applied in games. Available at: http://www.gamelook.com.cn/2019/03/353413/ (accessed on 24 Feb 2023).
- History of video games. Available at: https://en.wikipedia.org/wiki/History_of_video_games (accessed on 24 Feb 2023).
- Wang, Q. Video game classification inventory. Culture Monthly. 2018, 4, 30–31. [Google Scholar]
- Need for Speed™ on Steam. https://store.steampowered.com/app/1262540/Need_for_Speed/ (accessed on 24 Feb 2023).
- Genshin Impact. https://genshin.hoyoverse.com/en/ (accessed on 24 Feb 2023).
- Xbox Official Site. https://www.xbox.com/en-HK/ (accessed on 24 Feb 2023).
- PlayStation® Official Site. https://www.playstation.com/en-hk/ (accessed on 24 Feb 2023).
- Nintendo Switch Lite. https://www.nintendo.co.jp/hardware/detail/switch-lite/ (accessed on 24 Feb 2023).
- Game design basics: How to start creating video games. https://www.cgspectrum.com/blog/game-design-basics-how-to-start-building-video-games (accessed on 24 Feb 2023).
- Zhang, B. Design of mobile augmented reality game based on image recognition. J Image Video Proc. 2017, 90. [Google Scholar] [CrossRef]
- Tilson, A.R. An Image Generation Methodology for Game Engines in Real-Time Using Generative Deep Learning Inference Frameworks. Master Thesis, University of Regina, Canada, Jan 2021. [Google Scholar]
- Edwards, G.; Subianto, N.; Englund, D.; Goh, J.W.; Coughran, N; Milton, Z.; Mirnateghi, N.; Ali Shah, S.A. The Role of Machine Learning in Game Development Domain - A Review of Current Trends and Future Directions. In Proceedings of 2021 Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, Australia, 2021; pp. 01–07. [Google Scholar]
- Elasri, M.; Elharrouss, O.; Al-Maadeed, S.; Tairi, H. Image Generation: A Review. Neural Process Lett. 2022, 54, 4609–4646. [Google Scholar] [CrossRef]
- Yin, H.H.F.; Ng, K.H.; Ma, S.K.; Wong, H.W.H.; Mak, H.W.L. Two-State Alien Tiles: A Coding-Theoretical Perspective. Mathematics. 2022, 10(16), 2994. [Google Scholar] [CrossRef]
- Justesen, N.; Bontrager, P.; Togelius, J.; Risi, S. Deep Learning for Video Game Playing. IEEE Transactions on Games. 2020, 12(1), 1–20. [Google Scholar] [CrossRef]
- Gow, J.; Corneli, J. Towards generating novel games using conceptual blending. In Proceedings of the Eleventh Artificial Intelligence and Interactive Digital Entertainment Conference, California, USA, 2015. [Google Scholar]
- Sarkar, A.; Cooper, S. Blending levels from different games using LSTMs. In Proceedings of the AIIDE Workshop on Experimental AI in Games, Canada, 2018. [Google Scholar]
- Sarkar, A.; Yang, Z.; Cooper, S. Controllable level blending between games using variational autoencoders. In Proceedings of the AIIDE Workshop on Experimental AI in Games, Atlanta, Georgia, 2019. [Google Scholar]
- Moghaddam, M.M.; Boroomand, M.; Jalali, M.; Zareian, A.; Daeijavad, A.; Manshaei, M.H.; Krunz, M. Games of GANs: game-theoretical models for generative adversarial networks. Artif Intell Rev. 2023. [Google Scholar] [CrossRef]
- Awiszus, M.; Schubert, F.; Rosenhahn, B. TOAD-GAN: Coherent Style Level Generation from a Single Example. In Proceedings of the Sixteenth AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment (AIIDE-20), Virtual, 2020. [Google Scholar]
- Schrum, J.; Gutierrez, J.; Volz, V.; Liu, J.; Lucas, S.; Risi, S. Interactive evolution and exploration within latent level-design space of generative adversarial networks. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancún, Mexico, 2020. [Google Scholar]
- Torrado, R.E.; Khalifa, A.; Green, M.C.; Justesen, N.; Risi, S.; Togelius, J. Bootstrapping Conditional GANs for Video Game Level Generation. In Proceedings of 2020 IEEE Conference on Games (CoG), Osaka, Japan, 2020. [Google Scholar]
- Cinelli, L.P.; Marins, M.A.; da Silva, E.A.B.; Netto, S. L. Variational Autoencoder. In Variational Methods for Machine Learning with Applications to Deep Networks; Springer: Cham, Switzerland, 2021; pp. 111–149. [Google Scholar]
- Kingma, D. P.; Welling, M. Auto-encoding Variational Bayes. In Proceedings of International Conference on Learning Representations (ICLR), Canada, 2014. [Google Scholar]
- Cai, L.; Gao, H.; Ji, S. Multi-Stage Variational Auto-Encoders for Coarse-to-Fine Image Generation. In Proceedings of the 2019 SIAM International Conference on Data Mining, Alberta, Canada, 2019; pp. 630–638. [Google Scholar]
- Cai, F.; Ozdagli, A.I.; Koutsoukos, X. Variational Autoencoder for Classification and Regression for Out-of-Distribution Detection in Learning-Enabled Cyber-Physical Systems. Appl. Artif. Intell. 2022, 36(1). [Google Scholar] [CrossRef]
- Kaur, D.; Islam, S.N.; Mahmud, M.A. A Variational Autoencoder-Based Dimensionality Reduction Technique for Generation Forecasting in Cyber-Physical Smart Grids. In Proceedings of 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 2021; pp. 1–6. [Google Scholar]
- Vuyyuru, V.A.; Rao, G.A.; Murthy, Y.V.S. A novel weather prediction model using a hybrid mechanism based on MLP and VAE with fire-fly optimization algorithm. Evol. Intel. 2021, 14, 1173–1185. [Google Scholar] [CrossRef]
- Lin, S.; Clark, R.; Birke, R.; Schonborn, S.; Trigoni, N.; Roberts, S. Anomaly Detection for Time Series Using VAE-LSTM Hybrid Model. In Proceedings of 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Virtual and at Barcelona, Spain, 2020; pp. 4322–4326. [Google Scholar]
- Bao, J.; Chen, D.; Wen, F.; Li, H.; Hua, G. CVAE-GAN: Fine-Grained Image Generation through Asymmetric Training. In Proceedings of 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 2017; pp. 2764–2773. [Google Scholar]
- Arknights. https://www.arknights.global/ (accessed on 25 Feb 2023).
- Installing the Unity Hub. https://docs.unity3d.com/2020.1/Documentation/Manual/GettingStartedInstallingHub.html (accessed on 25 Feb 2023).
- konachan.com - Konachan.com Anime Wallpapers. https://konachan.com/ (accessed on 25 Feb 2023).
- Kaplun, V.; Shevlyakov, A. Contour Pattern Recognition with MNIST Dataset. In Proceedings of Dynamics of Systems, Mechanisms and Machines (Dynamics), Omsk, Russian Federation, 2022; pp. 1–3. [Google Scholar]
- Nocentini, O.; Kim, J.; Bashir, M.Z.; Cavallo, F. Image Classification Using Multiple Convolutional Neural Networks on the Fashion-MNIST Dataset. Sensors. 2022, 22, 9544. [Google Scholar] [CrossRef] [PubMed]
- How to Develop a CNN for MNIST Handwritten Digit Classification. https://machinelearningmastery.com/how-to-develop-a-convolutional-neural-network-from-scratch-for-mnist-handwritten-digit-classification/ (accessed on 26 Feb 2023).
- Lu, C.; Xu, L.; Jia, J. Contrast Preserving Decolorization. In Proceedings of IEEE International Conference on Computational Photography (ICCP), Seattle, WA, USA, 2012. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: a review and recent developments. Phil. Trans. R. Soc. A. 2016. 37420150202.. [Google Scholar] [CrossRef] [PubMed]
- Baldi, P. Autoencoders, Unsupervised Learning, and Deep Architectures. J Mach Learn Res. 2012, 27, 37–50. [Google Scholar]
- Balodi, T. 3 Difference Between PCA and Autoencoder With Python Code. https://www.analyticssteps.com/blogs/3-difference-between-pca-and-autoencoder-python-code (accessed on 26 Feb 2023).
- Ding, M. The road from MLE to EM to VAE: A brief tutorial. AI Open. 2022, 3, 29–34. [Google Scholar] [CrossRef]
- Difference Between a Batch and an Epoch in a Neural Network. https://machinelearningmastery.com/difference-between-a-batch-and-an-epoch/ (accessed on 26 Feb 2023).
- Roy, K.; Ishmam, A.; Taher, K.A. Demand Forecasting in Smart Grid Using Long Short-Term Memory. In Proceedings of 2021 International Conference on Automation, Control and Mechatronics for Industry 4.0 (ACMI), Rajshahi, Bangladesh, 2021; pp. 1–5. [Google Scholar]
- Jawahar, M.; Anbarasi L., J.; Ravi, V.; Prassanna, J.; Graceline Jasmine, S.; Manikandan, R.; Sekaran, R.; Kannan, S. CovMnet–Deep Learning Model for classifying Coronavirus (COVID-19). Health Technol. 2022, 12, 1009–1024. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Porwal, R. Combining Laplacian and Sobel Gradient for Greater Sharpening. IJIVP. 2016, 6(4), 1239–1243. [Google Scholar] [CrossRef]
- Ul Din, S.; Mak, H.W.L. Retrieval of Land-Use/Land Cover Change (LUCC) Maps and Urban Expansion Dynamics of Hyderabad, Pakistan via Landsat Datasets and Support Vector Machine Framework. Remote Sensing. 2021, 13(16), 3337. [Google Scholar] [CrossRef]
- Drouyer, S. VehSat: a Large-Scale Dataset for Vehicle Detection in Satellite Images. In Proceedings of IGARSS 2020 - 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 2020; pp. 268–271. [Google Scholar]
- Kalatzis, D.; Eklund, D.; Arvanitidis, G.; Hauberg, S. Variational Autoencoders with Riemannian Brownian Motion Priors. In Proceedings of the 37th International Conference on Machine Learning, Online, PMLR 119. 2020. [Google Scholar]
- Armi, L.; Fekri-Ershad, S. Texture Image Analysis and Texture Classification Methods. Int. J. Image Process. Pattern Recognit. 2019, 2(1), 1–29. [Google Scholar]
- Scheunders, P.; Livens, S.; van-de-Wouwer, G.; Vautrot, P.; Van-Dyck, D. Wavelet-based texture analysis. International Journal on Computer Science and Information Management. 1998, 1(2), 22–34. [Google Scholar]
- Arivazhagan, S.; Ganesan, L.; Kumar, T. S. Texture classification using ridgelet transform. Pattern Recognit. Lett. 2006, 27(16), 1875–1883. [Google Scholar] [CrossRef]
- Idrissa, M.; Acheroy, M. Texture classification using Gabor filters. Pattern Recognit. Lett. 2002, 23(9), 1095–1102. [Google Scholar] [CrossRef]
- Xenopoulos, P.; Rulff, J.; Silva, C. ggViz: Accelerating Large-Scale Esports Game Analysis. Proc. ACM Hum.-Comput. Interact. 2022, 6. No. Chi Play, 238. [Google Scholar] [CrossRef]
- ImageNet. https://www.image-net.org/ (accessed on 28 Feb 2023).
- Xie, D.; Cheng, J.; Tao, D. A New Remote Sensing Image Dataset for Large-Scale Remote Sensing Detection. In Proceedings of 2019 IEEE International Conference on Real-time Computing and Robotics (RCAR), Irkutsk, Russia, 2019; pp. 153–157. [Google Scholar]
- Mak, H.W.L.; Laughner, J.L.; Fung, J.C.H.; Zhu, Q.; Cohen, R.C. Improved Satellite Retrieval of Tropospheric NO2 Column Density via Updating of Air Mass Factor (AMF): Case Study of Southern China. Remote Sensing. 2018, 10(11), 1789. [Google Scholar] [CrossRef]
- Lin, Y.; Lv, F.; Zhu, S.; Yang, M.; Cour, T.; Yu, K.; Cao, L.; Huang, T. Large-scale image classification: Fast feature extraction and SVM training. CVPR 2011. Colorado Springs, CO, USA. 2011; 1689–1696. [Google Scholar]
- Biswal, A. What are Generative Adversarial Networks (GANs). https://www.simplilearn.com/tutorials/deep-learning-tutorial/generative-adversarial-networks-gans (accessed on 28 Feb 2023).
Figure 1.
Overall flowchart of this study, from extraction of original dataset, model construction to statistical analyses.
Figure 1.
Overall flowchart of this study, from extraction of original dataset, model construction to statistical analyses.
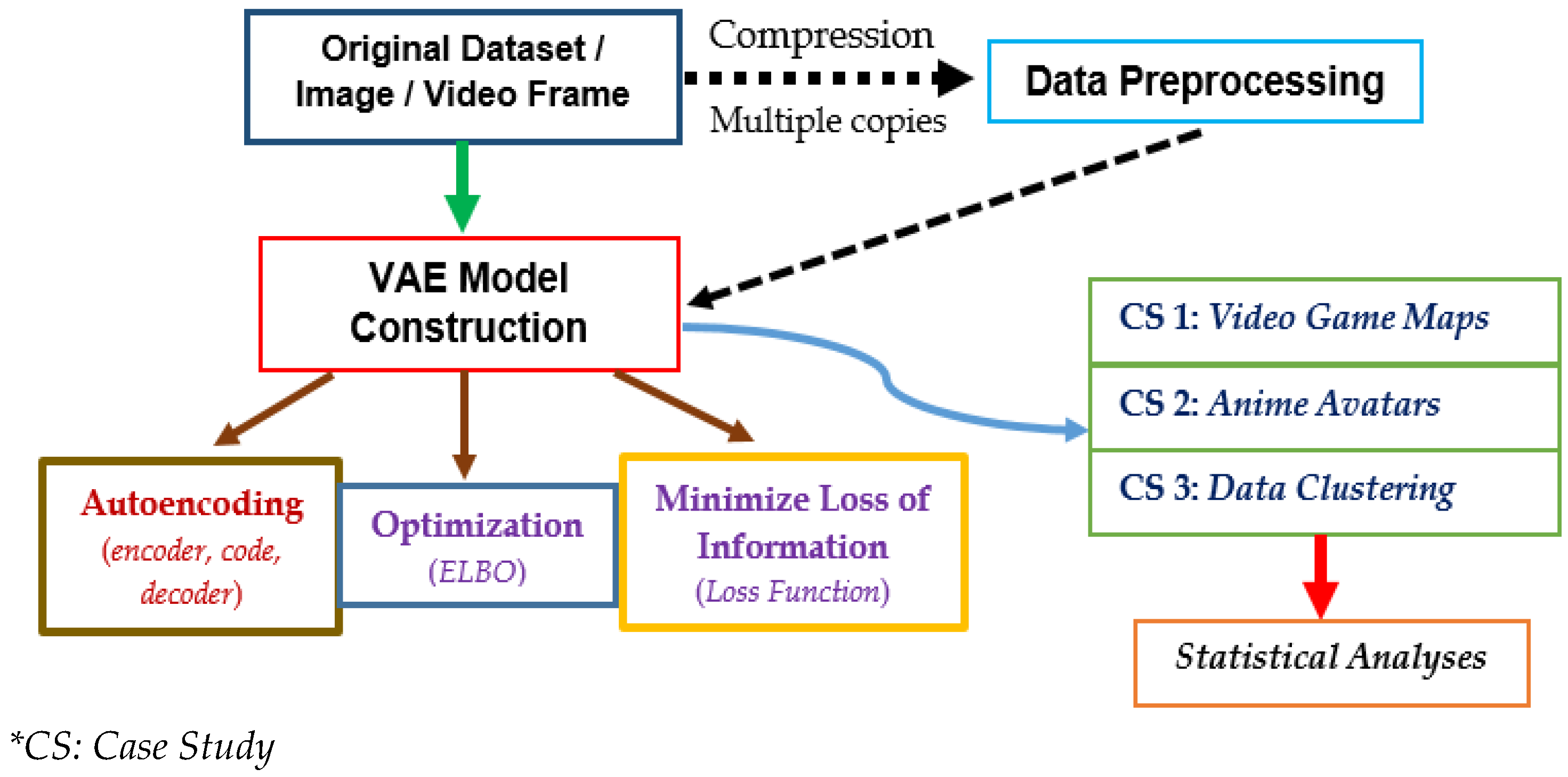
Figure 2.
An example of a game map obtained from Arknights via Unity Hub.
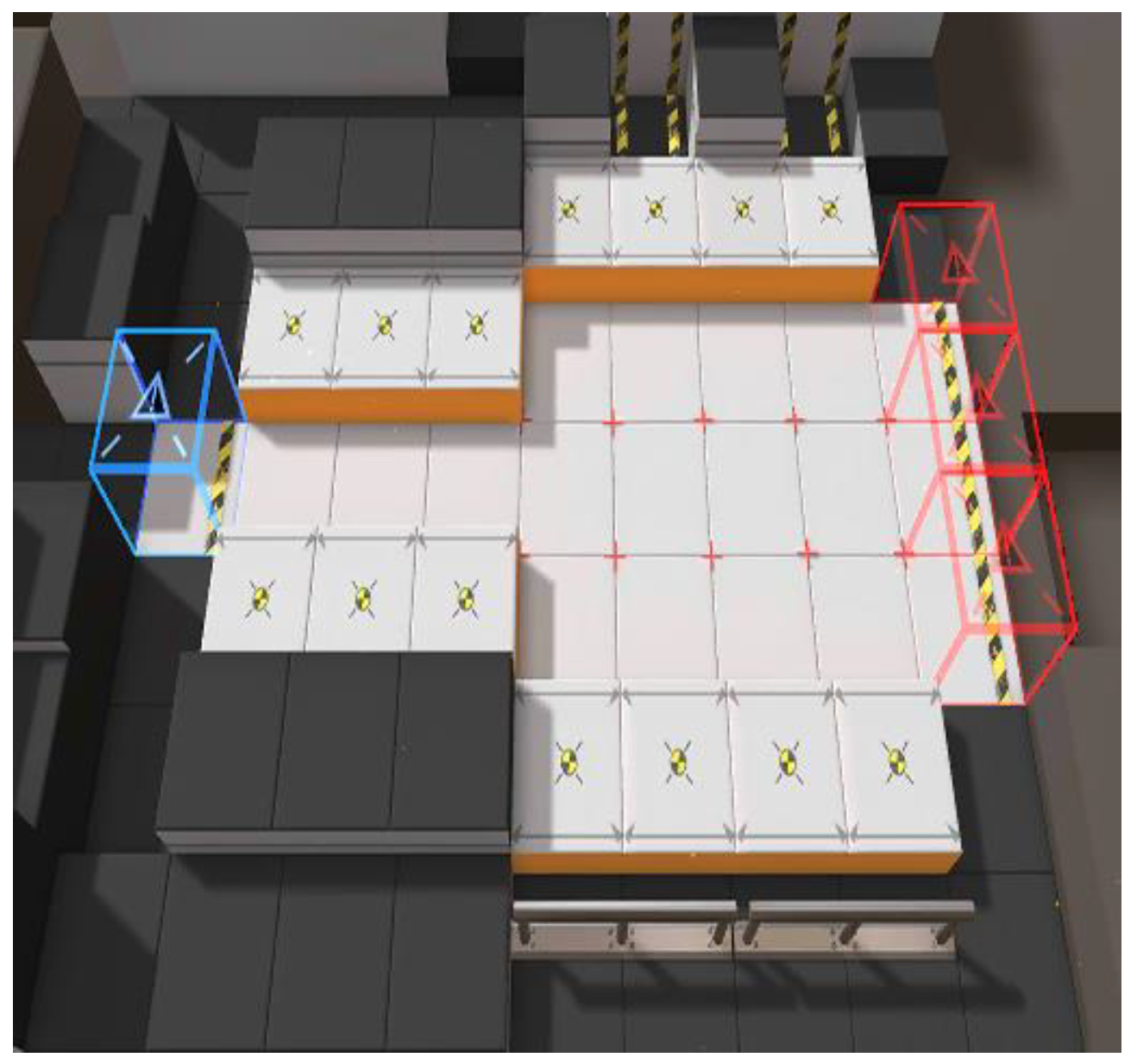
Figure 3.
An example of the anime avatar image, due to [42].
Figure 3.
An example of the anime avatar image, due to [42].

Figure 4.
A grayscale image extracted from the MNIST database.

Figure 5.
Structure of an autoencoder adopted in the VAE model of this study.
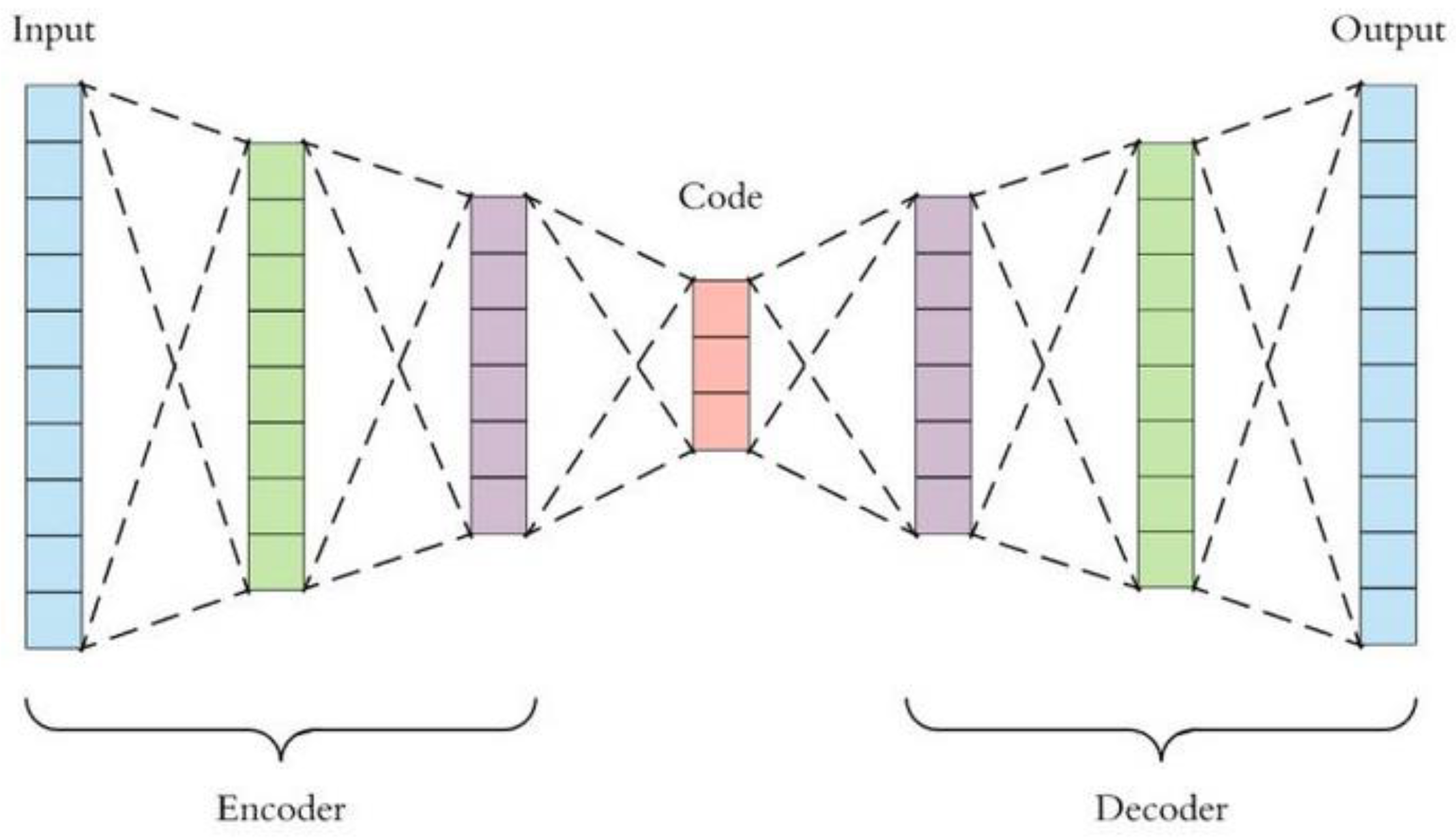
Figure 6.
Graphical representation and steps of the VAE model in this study.
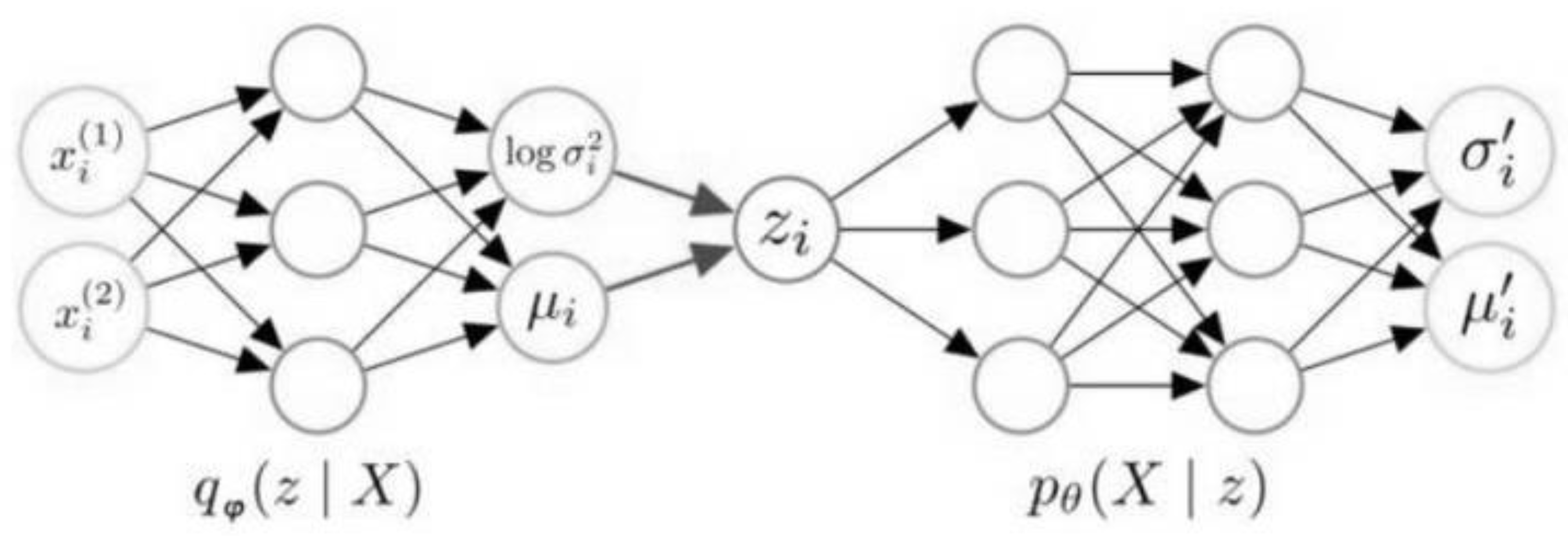
Figure 7.
Resulting output game maps obtained after (a) the training of the VAE model; (b) mixing process (based on raw game maps of Arknights obtained from [40])
Figure 7.
Resulting output game maps obtained after (a) the training of the VAE model; (b) mixing process (based on raw game maps of Arknights obtained from [40])
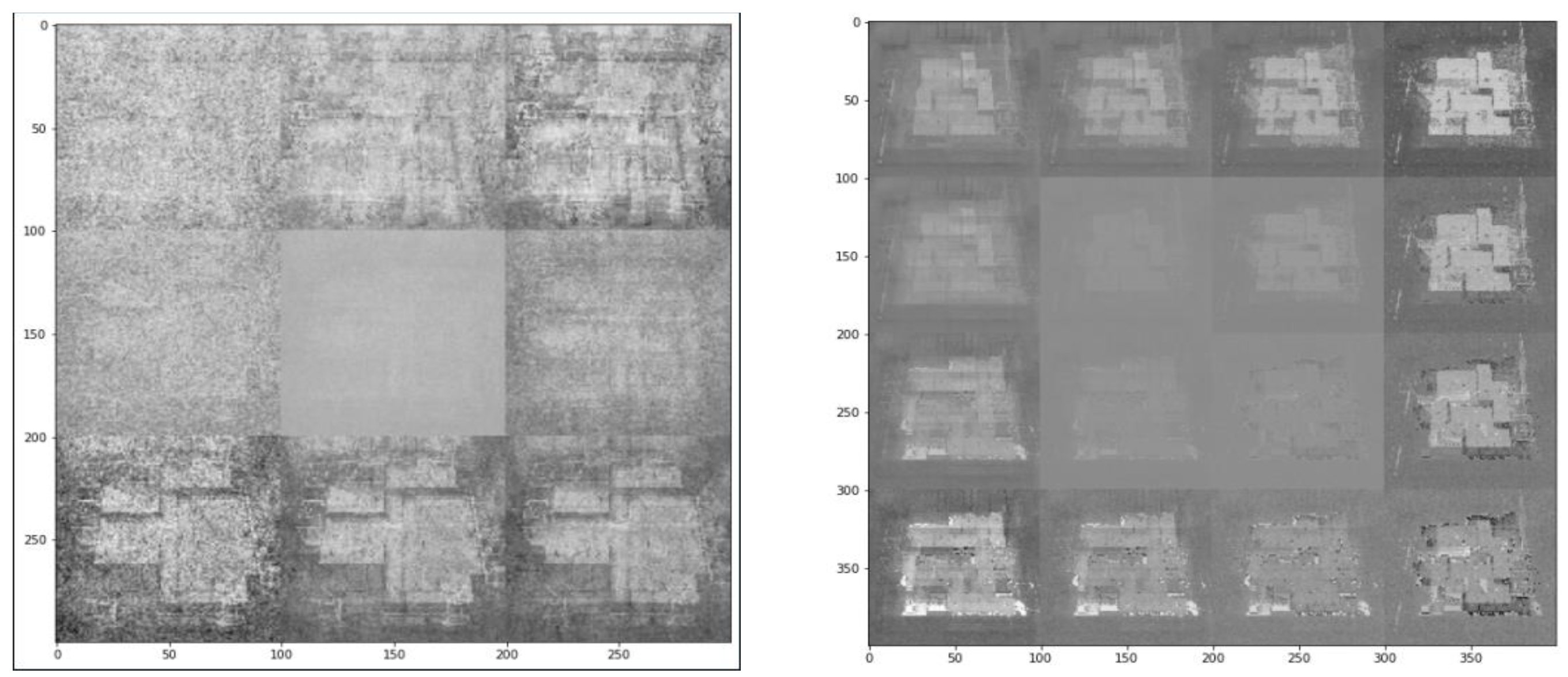
Figure 8.
The zoom-in version of an output game map of Arknights after the mixing of several processed images in VAE model.
Figure 8.
The zoom-in version of an output game map of Arknights after the mixing of several processed images in VAE model.

Figure 9.
Average loss of the ten image-generation process versus number of epochs in Case Study 1.
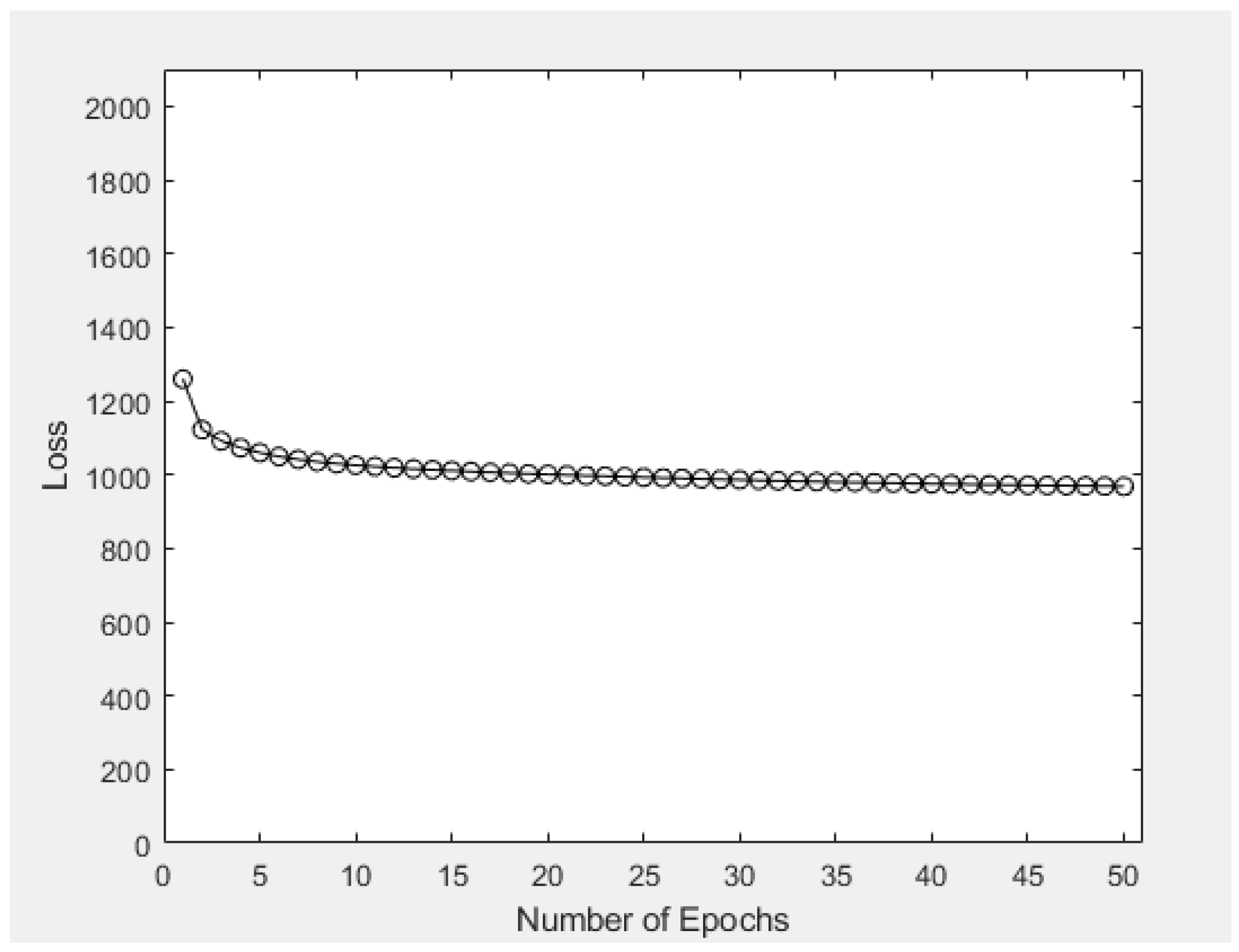
Figure 10.
(a) Time consumed for VAE model training (in s) versus the number of epochs adopted in the model; (b) Time consumed for VAE model training (in s) versus the size of dataset ingested into the model.
Figure 10.
(a) Time consumed for VAE model training (in s) versus the number of epochs adopted in the model; (b) Time consumed for VAE model training (in s) versus the size of dataset ingested into the model.
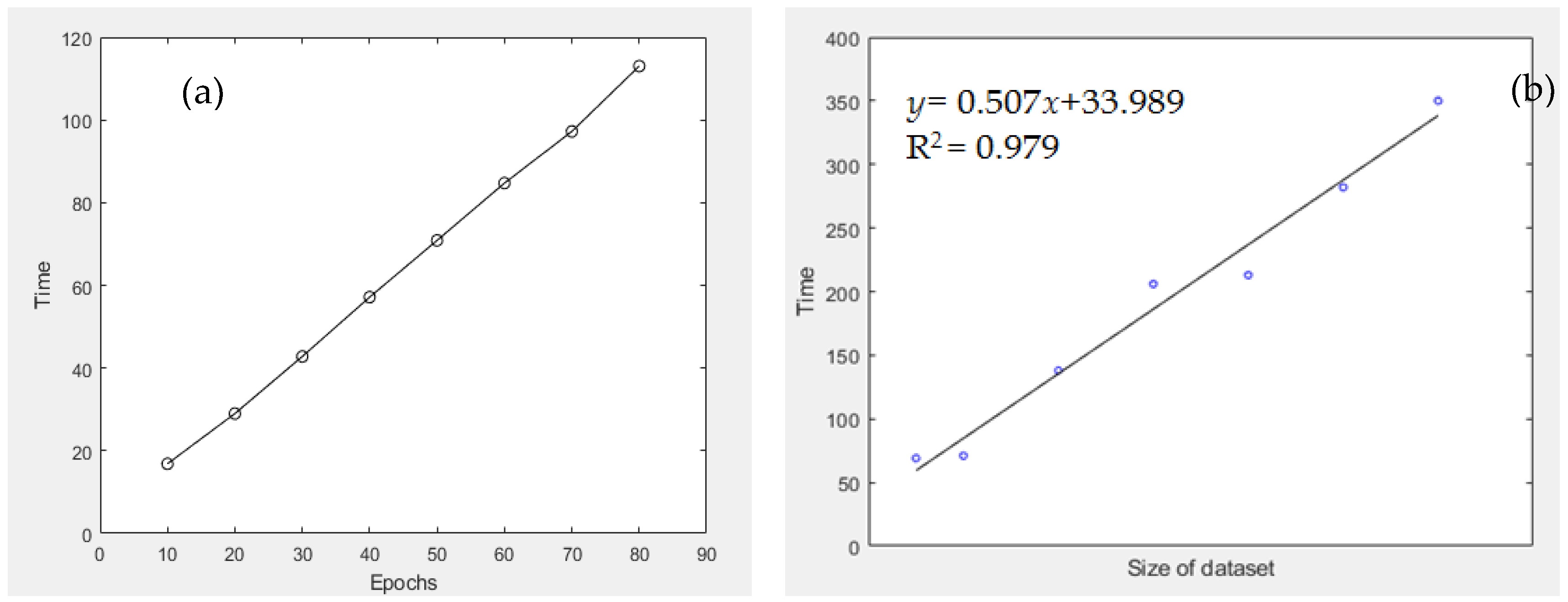
Figure 11.
(a) Time consumed for ten image-generation process (in s) versus scaling factor imposed in the model; (b) Average loss of the ten image-generation process versus scaling factor imposed in the model.
Figure 11.
(a) Time consumed for ten image-generation process (in s) versus scaling factor imposed in the model; (b) Average loss of the ten image-generation process versus scaling factor imposed in the model.
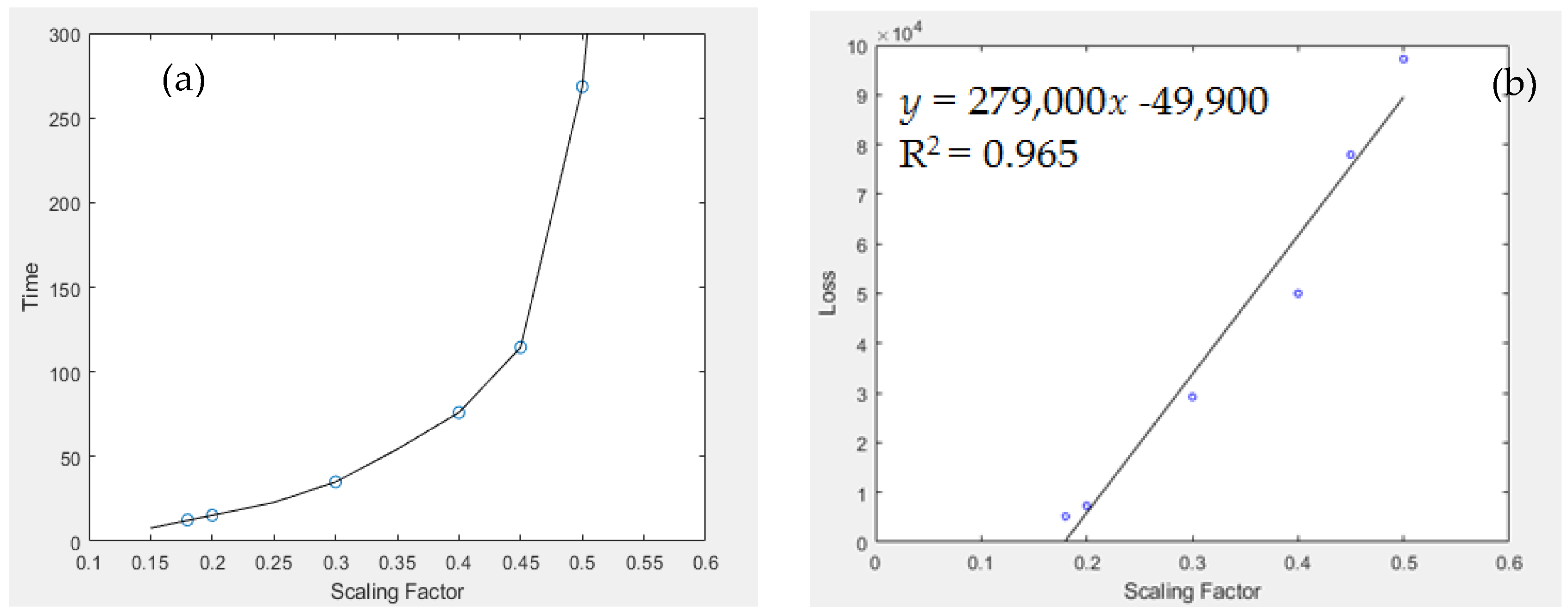
Figure 12.
2 sample output images obtained from the VAE model based on the anime-girl dataset (Section 2.2.2).
Figure 12.
2 sample output images obtained from the VAE model based on the anime-girl dataset (Section 2.2.2).

Figure 13.
(a) Sampled datasets of “6, 2, 7” ingested into the VAE model; (b) Output datasets obtained from the VAE model.
Figure 13.
(a) Sampled datasets of “6, 2, 7” ingested into the VAE model; (b) Output datasets obtained from the VAE model.

Figure 14.
Average recognition accuracy versus the number of epochs used in the model.
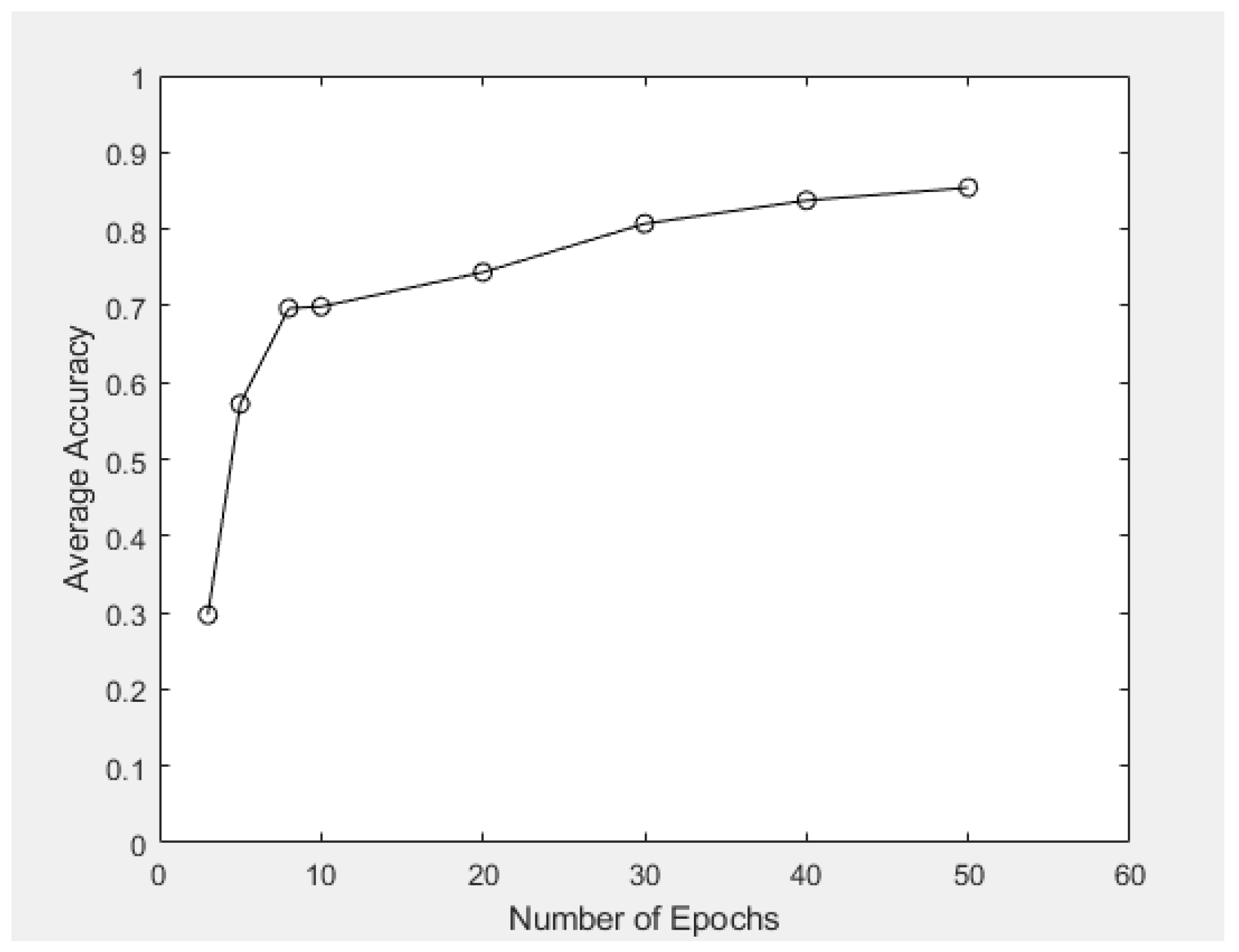
Table 1.
Mainstream game platforms and corresponding compatible device in the 21st century.
| Game Platform | Company | Device |
|---|---|---|
| Personal Computer (PC) | Microsoft | Desktop / Laptop Computers |
| Mobile Phone | Apple, Google, Samsung etc. | Smartphones |
| Xbox [15] | Microsoft | Xbox game console |
| PlayStation (PS) [16] | Sony | PlayStation 1- 5 |
| Switch [17] | Nintendo | Nintendo 3DS / Nintendo Switch |
Table 2.
Statistical figures of average loss at different number of epochs within the VAE model.
| Number of Epochs | Average Loss | Decrease in Average Loss with 1 more epoch |
|---|---|---|
| 1 | 1259.3 | Not applicable |
| 2 | 1122.4 | 136.9 |
| 3 | 1091.5 | 30.9 |
| 4 | 1072.9 | 18.6 |
| 5 | 1059.7 | 13.2 |
| 6 | 1049.2 | 10.5 |
| 7 | 1041.1 | 6.9 |
| 8 | 1034.8 | 6.3 |
| 9 | 1029.8 | 5.0 |
| 10 | 1025.6 | 4.2 |
| 11 | 1021.9 | 3.7 |
| 12 | 1018.7 | 3.2 |
| 13 | 1015.5 | 3.2 |
| 14 | 1013.1 | 2.4 |
| 15 | 1010.7 | 2.4 |
| 16 | 1008.4 | 2.3 |
Table 3.
Relation between average accuracy (%) in data clustering with the number of epochs used in the VAE model.
Table 3.
Relation between average accuracy (%) in data clustering with the number of epochs used in the VAE model.
| Number of epochs | Average Accuracy |
|---|---|
| 3 | 29.7 |
| 5 | 57.2 |
| 8 | 69.7 |
| 10 | 69.9 |
| 20 | 74.3 |
| 30 | 80.7 |
| 40 | 83.7 |
| 50 | 85.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Application of Variational AutoEncoder (VAE) Model and Image Processing Approaches in Game Design
Hugo Wai Leung Mak
et al.
,
2023
Adversarial Variational Autoencoders to Extend and Improve Generative Model
Loc Nguyen
et al.
,
2024
Semi-supervised Adversarial Variational Autoencoder
Ryad Zemouri
,
2020
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









