Prerpints.org logo
Preprint
Article

Mathematical Modeling and Exact Optimizing of University Course Scheduling COnsidering Preferences of Professors

Altmetrics

Downloads

170

Views

80

Comments

0

This version is not peer-reviewed

Submitted:

07 March 2023

Posted:

08 March 2023

You are already at the latest version

Alerts
Abstract
University course scheduling (UCS) is one of the most important and time-consuming issues that all educational institutions face yearly. Most of the existing techniques to model and solve UCS problems have applied approximate methods, which are different in terms of efficiency, performance, and optimization speed. Accordingly, this research aims to apply an exact optimization method to provide an optimal solution to the course scheduling problem. In other words, in this research, an integer programming model is presented to solve the USC problem. In this model, hard and soft constraints include the facilities of classrooms, courses of different levels and compression of students' curriculum, courses outside the faculty and planning for them, and the limited time allocated to the professors. The objective is to maximize the weighted sum of allocating available times to professors based on their preferences in all periods. To evaluate the presented model's feasibility, it is implemented using the GAMS software. Finally, the presented model is solved in a larger dimension using a real data set from a college in China and compared with the current program in the same college. The obtained results show that considering the mathematical model's constraints and objective function, the faculty courses' timetable is reduced from 4 days a week to 3 working days. Moreover, master courses are planned in two days, and the courses in the educational groups do not interfere with each other. Furthermore, by implementing the proposed model for the real case study, the maximum teaching hours of the professors are significantly reduced. The results demonstrate the efficiency of the proposed model and solution method in terms of optimization speed and solution accuracy.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

1. Introduction

Generally, scheduling can be described as allocating a number of events, each with its own characteristics, to the available resources, so that the provided solution does not violate the problem constraints. Among the major applications of the timetabling problem, educational scheduling, sports scheduling, hospital staff scheduling, and transportation schedules can be mentioned [1]. Nowadays, all universities and colleges around the world need to prepare their curriculum at the beginning of each academic semester, so-called university course scheduling (UCS). The UCS problem faces multiple constraints such as the preferences of the professors, the request and expectations of students, the policies of the educational calendar of the institutions, and the available equipment and facilities. Another issue that forces universities to use a method to find a timetable is the limited time for planning. So, there is a need for an efficient method to create a weekly curriculum with high speed and quality in such a way that it meets the needs of professors and students while satisfying the UCS constraints [2].
The UCS problem has been defined as the process of assigning university courses to specific time periods and to classrooms that meet the conditions for a specific number of students and professors during five working days of the week. Educational planners in universities are constantly faced with various resources and limitations in setting the timetable of classrooms, so preparing a timetable taking into account all these limitations in a short time and without interfering with the allocation of resources is not automatic. Moreover, it is not easily possible to apply the necessary changes due to the change in the time of access to resources or the change in the policies of the universities in relation to the laws and planning priorities [4]. On the other hand, with the expansion of the number of faculties in terms of the variety of educational fields, student acceptance, and study levels, it is necessary to provide optimization methods for the UCS problem [5].
The goal of this research is to find an optimal planning method for the timetable of the courses by observing all the conditions for the undergraduate and graduate degrees of the faculty. The main contributions of this research can be summarized as follows:
  • Mathematical modeling and exact optimization of the UCS problem, considering the preferences of professors and reducing empty classrooms in the university.
  • Finding suitable time intervals by observing the minimum distance between the intervals for the courses in each group.
  • Implementing an exact search method to find the best course schedule (placing the courses at the best possible time and place).
  • Successfully performing the proposed mathematical model and solution method for UCS in a real data set from a college in China and comparing the obtained scheduling results with the current program in the same college.
Considering the hard and soft constraints in the USC problem, in this research, a series of new constraints have been applied, such as considering the time of predetermined courses, taking into account the different levels of education and curriculum and time planning for that level, considering the capacity of the classroom and its equipment according to the courses, the non-interference of optional courses, and providing courses in specific periods.
The structure of this research is as follows. In Section 2, a theoretical foundation in the subject field and a review of the literature are presented. In Section 3, the proposed mathematical model is introduced. In Section 4, the evaluation of the results from different simulations is described. Finally, Section 5 concludes this research.

2. Theoretical Foundations of Research and Related Literature

In this section, the definitions of the timetabling problem are described. Moreover, the previous related works are reviewed and analyzed. The scheduling problem has attracted the attention of researchers since 1960, and the work in this field is still ongoing [1]. This issue is particularly important in cases when the resources are extensive and unlimited, and enough time is needed to prepare or update it. In general, the scheduling problem can be considered as an assignment problem, and the schedule is described by a set of sessions that must be assigned to several time intervals and classrooms subject to a group of constraints. Lu et al. [1] optimized the scheduling problem, allocating resources and facilities, taking into account almost the entire set of constraints and desirable goals that have been determined in advance. Shobaki et al. [2] and Burke et al. [3] stated that the scheduling problem is a problem with four parameters: a finite set of times, a finite set of resources, and a finite set of sessions so that a series of constraints as much as possible can be observed.
Among the different types of timetables, educational timetables are studied more from a scientific point of view. This issue is one of the most practical, significant, and time-consuming issues that takes place in all educational centers. As it was noted before, educational scheduling can be defined as an allocation problem that aims to allocate a set of resources (courses, professors, etc.) to a limited number of time intervals [2].

2.1. University Course Scheduling Constraints

Generally, in UCS problems, satisfying the soft constraints to some extent is added to the complexity of the problem, but the hard constraints should certainly be satisfied to reach the desired final solution. For most of the UCS problems, researchers take into account both hard and soft constraints:
  • Hard constraints (HCs) are those constraints that should be followed and must not be violated. HCs guarantee the feasibility of the solution and are usually related to educational or administrative rules that are considered according to the university's needs, the faculty's requests, and the educational system.
  • Soft constraints (SCs) are those limitations that determine the level of efficiency and usefulness of the timetable, which is not required to be exactly applied, and they can be seen as some options for building a high-quality timetable. SCs depend on the request of the planners and can include the opinions of the university staff, professors, and students. It is clear that there may not be a feasible solution that satisfies all the soft constraints, so the optimization models seek to find a solution that minimizes the violation of the soft constraints.
Soft and hard constraints may be handled in different ways in the mathematical model. HCs change the solution space, while SCs cause trade-offs between different solutions. For this reason, considering the integrated soft and hard constraints makes the mathematical model's optimization process more complex. In real-world UCS problems, soft and hard constraints are simultaneously effective [6,7,8,9,10].

2.2. Related Works and Research Gaps

The segmentation of the previous research items can lead to providing a suitable comparison between the most important previous works. Table 1 shows a comparison among 31 papers related to the current research, and the details are provided in Figure 1. By examining all related research items in Table 1 and the data obtained from the graphs in Figure 1, the following research gaps can be recognized:
  • In most papers, the number of hard constraints considered in planning the schedule of university courses is small. Many researchers have worked on the problem of scheduling university courses, and each of them considered constraints in the form of soft constraints. Moreover, the models usually do not take into account many of the constraints that exist in real-world UCS problems, and their results are far from the actual conditions.
  • According to the comparison of the research literature with the existing conditions in real-world universities, it is possible to find some constraints that have not been considered in the previous studies. So, there is a need to efficiently consider these constraints and incorporate them into the problem model.
  • There are some challenging constraints in educational systems, which are less mentioned in the literature. Moreover, most of the existing techniques focus only on satisfying the schedules of professors and courses, and less attention is paid to the preferences of the students.
  • In the past, few articles have dealt with the timing of predetermined courses, presenting them at a specific time, placing optional courses in a group, and not interfering with them. According to the conditions of most universities, some courses are shared between different disciplines, and the time of presentation of these courses is communicated. According to the time set for specific courses, their timing with other courses should also be examined.
  • In the case of the students' constraints, more attention has been paid to the non-interference of the students' programs. Accordingly, it is necessary to consider different levels of education, including holding prerequisite and post-requisite courses simultaneously.
  • In the formulation of the constraints related to the professors, more attention has been paid to the non-interference of the professors' schedules and the planning of courses based on their attendance. To focus on the preferences of professors and reduce their fatigue, some attention should also be paid to this point.
  • To reduce the interference of schedules between different groups of academic fields, the schedule of courses during the week should be compressed as much as possible. Therefore, more classrooms can be freed, and a certain number of classrooms are assigned to the specified group.
In this research, different constraints in the form of hard and soft constraints are considered to propose a mathematical model for the university course schedules. These constraints include the hard and soft constraints related to professors, students, classrooms, and courses. To efficiently solve the proposed UCS model, one wishes to find an optimal solution. On the other hand, time plays an important role in solving this problem. Therefore, in this research, an exact solution method is applied to find an optimal solution to the problem. In the next section, the proposed mathematical model and solution method for the UCS problem are explained in detail.

3. Research Method

The UCS is a problem in which a weekly schedule is designed for university courses. The planning program should be such that the courses are placed in a certain number of classrooms and periods, so that no more than one course is placed in a specific classroom and time period. Different types of this problem exist in different universities according to their rules, requirements, and constraints. Due to the difference in the university standards, a single program cannot be applied to all universities. However, the remarkable issue is the presence of common characteristics for all of them. Among them, we can mention three effective factors in timing, including the professor, the course, and the classroom.
The assumptions of the UCS problem are very dependent on how the courses are presented in the university and how the university resources are used to schedule the classrooms. In order to explain the assumptions, the issue of scheduling classrooms, required resources, and periods to provide courses are examined. In the faculty investigated in this study, one-hour time periods are considered from 8:00 to 19:00. For each one-hour period, 15 minutes, and for two-hour periods, 30 minutes are considered for students to rest and change the classrooms. The number of units of each course determines the time required to present that course. One-unit courses are practical courses. For most of them, the schedule is determined in advance, and a period of time is considered for them. For two-unit courses, it is assumed that a two-hour period is needed. Three-unit courses require a one one-hour period and one two-unit period, preferably not consecutive.

3.1. Defining the Problem of Scheduling Classes

According to the assumptions presented in Section 2, the objectives, constraints, inputs, and outputs of the UCS problem are defined in the following.

3.1.1. Objectives

In the proposed mathematical model, various objectives can be considered, which are described as follows:
1)
Compression of the students’ schedule. One of the main objectives of the UCS problem is to minimize the distance between two consecutive classrooms and the minimum distance traveled by the students. In other words, the schedule of the students should be connected to each other as much as possible, which means that their schedules should have the least gap between courses.
2)
Compression of the classroom schedule. This objective is used to utilize as few classrooms as possible to minimize interference with the rest of the educational groups.
3)
Compression of the professors’ schedule: Another objective is to plan the courses according to the times that the professors have in mind to present the courses. Moreover, it tries to coincide as much as possible with the program of the the professors in such a way that it has the least empty space in the schedule of each professor and the minimum distance traveled by the professors.
4)
Maximize the number of courses to be presented: According to this objective, all the courses should be presented in the semester, so that all students can choose their desired units.

3.1.2. Constraints

In the proposed UCS problem, the hard and soft constraints are related to the professors, the time of the courses, the students, and the classrooms, which are discussed in the following. As different universities may have different requirements, these constraints can be different depending on the type of problem and the goals pursued in each problem. The problem constraints in this study are as follows:
Professors impose the following constraints on the program:
  • Each professor has the ability to teach a specific set of courses.
  • Each professor has specific time periods for giving courses.
  • The maximum allowed teaching hours of the professors must be respected.
  • The Master programs should be as compact as possible.
The courses must be presented in one semester, considering the following constraints:
  • Each course should be presented to the students with unique entries.
  • Courses presented in two sessions must be given as far as possible one day apart.
  • For courses with more than two units, two sessions are held during the week.
  • The timing for predetermined courses has to be considered.
  • The number of class meetings should be held based on the relevant courses and their number of units.
The constraints for the students are as follows:
  • The program for incoming students of a particular year should be held in consecutive time periods as much as possible.
  • The students' program must not be spread among the week as much as possible.
  • The senior students' program should be scheduled as much as possible in two days.
The classrooms should be consistent with the following constraints:
  • Classrooms should be selected based on their capacity (number of persons).
  • Classrooms should be selected based on the required facilities of the course.
  • The time of the classes that are determined outside the faculty should be included in the schedule.
  • The schedule of the classrooms does not interfere with each other.

3.1.3. Inputs

The general information required to set up a schedule in the proposed UCS problem can be described utilizing the following inputs:
Information about professors:
  • Number of professors
  • The name of the courses that each professor will present
  • The attendance times of the professors to present the relevant courses
Information about classrooms:
  • Number of classrooms
  • Classroom capacities
  • Classroom facilities
Information about study groups:
  • Number of working days per week
  • Number of sessions per day
  • Information about reasonable times for the formation of courses

3.1.4. Outputs

The main output of the proposed UCS problem is a timetable that shows the course, professor, day, time, and place for each course. As a case study, this problem has been implemented for the courses presented in the first half of the academic year 2021-2022, in which all the professors, the courses with their presentation time, and the classrooms in which they are to be held are specified.

3.2. Mathematical Model

The proposed UCS model is a timetable based on the characteristics and facilities of the educational institution. This model takes into account the special constraints of the studied university. To formulate the mathematical model subsequently, a list of notations including sets, indices, parameters, and decision variables, are summarized in Table 2.
The integer linear mathematical programming model for the proposed UCS problem can be formulated as follows:
M a x   Z = ∑ c ∑ k ∑ t ∑ r ( w r δ r d t ( X c k t r + Y c k t r ) )
where the objective function Z maximizes the weighted sum of allocating available times to professors based on their preferences in all periods. More specifically, for each professor with a higher weight than others, the curriculum is included as much as possible. The problem constraints can be formulated as follows:
∑ c ∈ C ∑ k ∈ K X c k t r ≤ a r t   ∀ t ∈ T , r ∈ R
∑ c ∈ C ∑ k ∈ K Y c k t ′ r ≤ a r t ′     ∀ t ′ ∈ T ′ , r ∈ R
∑ c ∈ C ∑ k ∈ K X c k t r + ∑ c ∈ C ∑ k ∈ K Y c k t ′ r   ∀ r ∈ R , 2 t ′ − 1 ≤ t ≤ 2 t ′
∑ k ∈ K ∑ t ′ ∈ T ′ Y c k t ′ r + ∑ k ∈ K ∑ t ∈ T X c k t r = b c × β r c   ∀ c ∈ C , r ∈ R
∑ k ∈ K ∑ t ′ ∈ T ′ Y c k t ′ r ≤ β r c   ∀ c ∈ C , r ∈ R
∑ k ∈ K ∑ t ∈ T X c k t r ≤ β r c   ∀ c ∈ C , r ∈ R
∑ c ∈ C ∑ r ∈ R X c k t r ≤ f k t   ∀ k ∈ K , t ∈ T
∑ c ∈ C ∑ r ∈ R Y c k t ′ r ≤ f k t ′   ∀ k ∈ K ∈ T ′
∑ c ∈ C ∑ r ∈ R X c k t r + ∑ c ∈ C ∑ r ∈ R Y c k t ′ r ≤ 1   ∀ k ∈ K , 2 t ′ - 1 ≤ t ≤ 2 t ′
X c k t r ≤ P c k × γ c t   ∀ c ∈ C , k ∈ K , t ∈ T , r ∈ R
Y c k t ′ r ≤ P c k × γ c t ′   ∀ c ∈ C , k ∈ K , t ′ ∈ T ′ , r ∈ R
∑ c ∈ C ∑ k ∈ K ∑ t ∈ T h t d × X c k t r + 2 ∑ c ∈ C ∑ k ∈ K ∑ t ′ ∈ T ′ h t ′ d × Y c k t ′ r ≤ m   ∀ r ∈ R , d ∈ D
∑ r ∈ R ∑ c ∈ C ∑ k ∈ K λ c l × X c k t r ≤ 1   ∀ t ∈ T , l ∈ L    
∑ r ∈ R ∑ c ∈ C ∑ k ∈ K λ c l × Y c k t ′ r ≤ 1   ∀ t ′ ∈ T ′ , l ∈ L
∑ r ∈ R ∑ c ∈ C ∑ k ∈ K λ c l × X c k t r + ∑ r ∈ R ∑ c ∈ C ∑ k ∈ K λ c l × Y c k t ′ r ≤ 1     ∀ l ∈ L , 2 t ′ − 1 ≤ t ≤ 2 t ′    
Constraints (2-4) ensure that each professor will teach only one course in one classroom in each time period. Constraints (5-7) guarantee that each professor r teaches b c hours per week for course c. Constraints (8-10) state that each classroom should be assigned to only one professor and one course in each time period. Constraints (11,12) state that each course should be taught only in classrooms that have appropriate facilities and at times that are possible. Constraint (13) provides the condition that the scheduled time for each professor is at most m hours per day. Constraints (14-16) have been included in order to prevent the simultaneous holding of courses related to the same study group. In the following, the simulation of the model and the evaluation of its results will be discussed to solve the problem of course scheduling.

4. Numerical Results

In order to solve the mathematical model presented for the scheduling problem of university classrooms, the GAMS software (version 24.1) has been used. This software was chosen due to its availability and high ability as a solution for integer programming models. In the following, the results of solving the model are evaluated using the GAMS software. All simulations have been carried out on a PC with 5 GB RAM and 2.6 GHz Core i5 CPU running on windows 10. To validate the model, the parameters mentioned in the proposed model have been selected according to the following specifications.

4.1. Number of Study Units

The parameter b c is used to check the study units. In the following, a day of the week is considered, and scheduling is done for 9 courses ( C ), 3 classrooms ( K ), and 3 professors ( R ). The optimal timetables for all courses are provided in Table 3, Table 4 and Table 5. The number of hours that course c should be held per week includes a one-hour period for single-unit courses and a two-hour period for two-unit courses that must be two hours consecutively (without a break). Moreover, for three-unit courses, two time periods, which include two hours and one hour, are considered. All course units are presented in these intervals, and the time of holding classes and the schedules of the professors do not interfere with each other.

4.2. Maximum Allowed Teaching Hours

The parameter m has been used to determine the maximum teaching time of the professors per day. This parameter is considered in the model due to increasing the productivity and lack of fatigue of professors. In this Section, two days of the week are considered, and then, scheduling is done for 10 courses ( C ), 2 classrooms (K), and 2 professors ( R ). Courses ( C 1 , . . . , C 4 ) are taught by professor R 1 , courses ( C 5 , . . . , C 10 ) are taught by professor R 2 . To check the sensitivity of the model, the professors’ allowed teaching hours are considered to be separately 10 hours and 6 hours, respectively. The optimal schedules of the model for the two professors are given in Table 6 and Table 7, respectively.
In Table 6, the total teaching hours of professor R 1 are 3 and 8 hours on the first and second day, respectively. Moreover, according to Table 7, professor R 2 teaches 7 and 2 hours, respectively. Therefore, in any case, the daily total teaching hours of the professors are less than 10 and 6 hours, respectively. In Table 7, on the first and second day, the total teaching hours of professor R 1 are 5 and 6 hours, respectively, and professor R 2 teaches 3 and 6 hours, respectively. In this case, the total teaching hours of the professors did not exceed 6 hours. As a result, with this parameter, it is possible to reduce or increase the hours allowed for the professors to teach per day.

4.3. Preparation Times of the Professors for Teaching

The parameter a r t has been used to determine the time periods when the professor is ready to present the course. In the university, most of the professors are ready to give courses at certain times for various reasons, such as teaching in other faculties, holding group meetings, etc., and they announce these times to the faculty before the start of the new semester. In this section, a day of the week is considered. Scheduling is done for 9 courses ( C ), 2 classrooms ( K ), and 3 professors ( R ). It is assumed that courses C 1 and C 2 (three units) are taught by professor R 1 , courses C 3 , C 4 , and C 5 (two units) are taught by professor R2, and courses C 6 , C 7 , C 8 , and C 9 (one unit) are taught by professor R 3 . Moreover, time slots are considered from 8:00 to 19:00.
In the results summarized in Table 8, we consider the professors' teaching time as accessible during the day. Moreover, in Table 9, professors R 1 , R 2 , and R 3 , can teach only in the time slots 13-19, 13-15, and 8-12, respectively. In Table 8, the curriculum of the professors is given without constraints. In Table 9, considering that the professors can be present at certain times, their curriculum is described as follows. Master courses of professor   R 1 are scheduled in the afternoon from 13:00 onwards. Master courses of professor R 2 are not scheduled at 13-15 hours, and all master courses of professor R 3 are scheduled in the morning from 8:00 to 10:00. In this way, it is possible to easily add professors' attendance hours for teaching to the model and change professors' teaching time.

4.4. Course and Classroom Matching

The parameter P c k is used to determine the classrooms according to the capacity and facilities and to check the feasibility of presenting the courses in them. Considering that some courses require a video projector and others are offered once every two semesters, such as optional courses, most students must take that course unit in the corresponding semester. So, it is necessary to take these courses in classrooms with the capacity (number of persons) to be presented. For example, a day of the week is considered. Scheduling is done for 9 courses ( C ), 2 classrooms ( K ), and 3 professors ( R ). Assume that courses C 1 and C 2 (three units) are taught by professor R1, courses C 3 , C 4 , and C 5 (two units) are taught by the second professor R 2 , and courses C 6 , C 7 , C 8 , and C 9 (one unit) are taught by professor R3. The professors and classrooms are available at all hours of the day, and time slots are considered from 8:00 to 19:00.
In the results reported in Table 10, all courses can be held in all classrooms without constraints, and in Table 11, courses 1, 2, and 3 must be held in the first classroom, and courses 4, 5, and 6 should be held in the second classroom, and the rest of the courses can be presented in both classrooms. According to the obtained results in Table 11, courses C 1 , C 2 , and C 3 are planned only in the first classroom, and courses C 4 , C 5 , and C 6 in the second classroom due to the need for special facilities and conditions of the classroom and the rest of the courses. Considering that there is no need for special classroom conditions and facilities for courses C 7 , C 8 , and C 9 , they can be planned in both classrooms. Therefore, by considering this parameter in our model, classrooms can be assigned according to the needs of the course.

4.5. Determining the Time of the Courses

The parameter   γ c t is used to determine when the courses can be implemented. Since senior students are mostly working, the courses of these students should be defined as intensively as possible. Some courses such as computing courses that require more concentration, can be planned in the morning. For example, 2 days of the week are considered. Scheduling is done for 12 courses ( C ), 2 classrooms ( K ) and 3 professors ( R ). Assume that courses C 1 , C 2 , C 11 , and C 12 (3, 2, 1, 2 units respectively) by professor R 1 , courses C 3 , C 4 , C 5 and C 6 (two units) by professor R 2 and courses C 7 , C 8 , C 9 and C 10 (3, 2, 1, 1 units, respectively) are taught by professor R 3 . Assuming that professors and classrooms are available at all hours of the day, the time slots are from 8:00 to 19:00. In this part, 3-course groups, are considered. In the first group, there are C 1 , C 2 , C 3 , and C 4 industrial master courses. In the second group, the main specialized courses or computing courses include C 5 , C 6 , C 7 , and C 8 . Other groups include undergraduate courses from semester 1 to semester 8, including C 9 , C 10 , C 11 , and C 12 .
In Table 12, all courses can be held on all days and hours without constraints, while in Table 13, the master course must be held on the first day, and computing and specialized courses must be held on both days from 8:00 to 13:00. Moreover, the rest of the groups can be offered on both days and all hours. Therefore, the optimal schedule of the model changes as follows. Since the master courses should only be presented on the first day, as indicated in Table 13, C1, C 2 , C 3 , and C 4 courses, which are related to the master level, are scheduled on the first day. Courses C 5 , C 6 , C 7 , and C 8 are also related to specialized or calculation courses, which should be presented in the first hours of the day in the morning before 13:00, and the rest of the courses C 9 , C 10 , C 11 , and C 12 , can be held in any time. By using this parameter, it is possible to apply the time of workshop and laboratory courses and other courses that are not held by the faculty. In this case, the general education determines the time of their holding and in coordination with other disciplines in the model ensures it doesn’t interfere with the other courses of that group.

4.6. Classroom Access Time

The parameter f k t is used to determine when the classrooms are available. For example, in some cases, the relevant classroom may not be available at a certain time due to the use of other educational fields and the holding of courses by other educational groups. Therefore, it is not possible to plan for that classroom at a specific time. For example, let us consider a day of the week, at which scheduling is done for 9 courses ( C ), 2 classrooms ( k ), and 3 professors ( R ). Assume that courses C 1 and C 2 (three units) are taught by professor R 1 , courses C 3 , C 4 , and C 5 (two units) are taught by professor R 2 , and courses C 6 , C 7 , C 8 , and C 9 (one unit) are taught by professor R3. The professors are available at all hours of the day and the time slots are from 8:00 to 19:00. In Table 14, all classrooms are available during the day, and in Table 15, classroom K 1 at 8-10 and classroom K 2 class at 10-12 are already available for other educational groups. As seen in Table 14, courses are scheduled without classroom constraints. However, according to the obtained results in Table 15, due to classroom constraints at some times during the day, classroom K 1 at 8-10 and classroom K 2 at 10-12 is not available.

4.7. Determining the Groups

To determine the non-interference of the courses of each semester, the courses related to each educational level are planned in one group. Parameter λ c l is utilized to determine the relationship between courses and groups. For example, the courses of the three semesters of bachelor students should not overlap each other so that the students of the third semester can take all the courses during the semester. This parameter can also be used for the non-interference of optional courses so that the optional courses are considered as one group. Due to the non-interference of the courses of each group selected by this parameter, students can easily take more courses.
For example, a day of the week is considered at which scheduling is done for 9 courses ( C ), 2 classrooms ( K ), and 3 professors ( R ). Assume that courses C 1 and C 2 (three units) are taught by professor R 1 , courses C 3 , C 4 , and C 5 (two units) are taught by professor R 2 , and courses C 6 , C 7 , C 8 , and C 9 (one unit) are taught by professor R3. The professors and classrooms are available at all hours of the day, and time slots are considered from 8:00 to 19:00. In Table 16, all courses are considered without limitations to the study group. However, in Table 17, the courses are in three groups so that courses C 1 , C 6 , and C 9 are of the same semester, the courses C 3 , C 7 , and C 8 are optional, and the optional courses with the same semester (i.e., courses C 2 , C 4 , and C 5 ), should not overlap and are grouped. According to these conditions, the model's optimal timetable can be shown in Table 17. Since the courses C 1 , C 6 , and C 9 belong to the same group, as shown in Table 17, these courses do not have overlapping times. These conditions are also applied to courses C 2 , C 4 , and C 5 , and courses C 3 , C 7 , and C 8 , and the optional courses and courses of the same semester do not overlap. This parameter can be used for any courses that need not interfere with each other.

4.8. Execution Time Analysis

The execution time of the GAMS software (in seconds) to derive the exact solution for different scenarios is provided in Table 18. The first four rows in Table 18 correspond to the obtained results in Sections 4.1 to 4.7, while rows 5-10 report the execution time for synthetic data by increasing the number of courses, classrooms, and professors. The results show a considerable effect of the problem size on the required execution time for deriving the optimal solution.

4.9. Checking the Validity of the Solutions

By comparing the obtained results of solving the proposed model in this study by the GAMS software with the manual programs currently used in the same college, the following points are noteworthy:
  • Speed of obtaining solutions. One of the significant advantages of the proposed model is its computation time. According to the considered solutions, this model is solved in a short and reasonable time.
  • The possibility of analyzing the solutions. In the cases when the program is done manually, by making a small change in the conditions, such as a change in the schedule of the professors, the number of courses, or a change in the classrooms, it is necessary to revise the program again and thus, sometimes one is forced to re-prepare the weekly schedule of the courses, and this requires to spend a long time. However, using the proposed model is possible easily and quickly, and it can be checked with different results together, and then to choose the best one.
  • Solution accuracy and error reduction. Considering that the designed mathematical model reaches an optimal solution and this means that all constraints are satisfied, if the data are entered correctly, the errors that may occur in manual programming will not occur.
  • Proper allocation of classrooms, courses, and time. Comparing the proposed model and the manual model, it can be seen that fewer classrooms have been allocated, and even some classrooms have not been used. For example, in class 10 and class 11, the courses are not offered during the week in these two classes, and the classes are free. Courses are assigned based on the capacity and equipment of the classrooms. The schedule of classrooms is compressed as much as possible during the week. Moreover, the days of the week have decreased from 5 working days to 4 working days.
  • The quality of the obtained schedule. In addition to taking into account the conditions of the faculty of engineering, the designed model tries to reduce the time gaps between the professors, not providing same-group courses at the same time for students, compressing the sessions of students, especially senior students, limiting the teaching time of the professors has increased to 8 hours. If the inputs of the model are entered carefully, the output solution will be very suitable. Therefore, it will lead to the maximum satisfaction of students and professors.

5. Conclusions

In this research, a comprehensive approach was presented to solve the university course scheduling problem. According to the implementation of the proposed method and the analyses that have been carried out, it has been observed that this method is very effective for solving the timetabling problem and accelerating the preparation of the program. It will be used weekly in the university, and all the constraints for creating a timetable considered by the university officials have been met.
The numerical results of this research showed that by presenting a linear model and implementing it in the GAMS software, an optimal solution could be obtained. Considering the constraints of the faculty, including the limited time of professors in the university, the compression of time planning for senior students in two days, the presence of pre-determined courses, etc., led to finding a solution that has considered all aspects of the university course schedule. The scheduling of university courses, i.e., the UCS problem, is basically according to the specific conditions of each educational center, which makes it impossible to use a general model in all university centers. For example, in a particular university, general and specialized classrooms may be held in nearby and distant buildings, or the time of group meetings or professors' consultation time, etc., should be included into the model. According to the proposed model, such conditions can be easily applied to the model.
In the proposed model, while taking into account professors' attendance hours and classroom availability, constraints such as minimizing the interference in students' schedules and compressing sessions, reducing gaps in the schedules of the professors are considered. The presented results of the optimization of the proposed mathematical model have shown that the integration of decision-making regarding the scheduling of university courses can lead to the achievement of a solution that simultaneously considers the preferences of both of the professors and students and also has the highest level of satisfaction. This approach can be used in all universities and educational centers. In order to develop this research further, it is suggested to consider the uncertainty in the important parameters of the mathematical model and implement robust optimization [33] to deal with such uncertainties. Moreover, due to the high complexity of the proposed mathematical model, it is suggested to apply efficient meta-heuristic algorithms such as a firefly algorithm (FFA) [34], whale optimization algorithm (WOA) [35], or pareto-based metaheuristics [36], to handle the complexities of the mathematical model.

Author Contributions

Conceptualization, M.C.; methodology, M.C. and M.S.; software, M.C.; validation, M.C., M.S and F.W.; investigation, M.C.; data curation, M.C.; resources, M.C.; writing—original draft preparation, M.C., M.S., and F.W.; writing—review and editing, M.S. and F.W.; visualization, M.C.; formal analysis, M.S.; supervision, M.S.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used in the study is available with the authors and can be shared upon reasonable requests.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lü, Z.; Hao, J.K. Adaptive tabu search for course timetabling. Eur. J. Oper. Res. 2010, 200, 235–244. [Google Scholar] [CrossRef]
  2. Shobaki, G.; Gordon, V.S.; McHugh, P.; Dubois, T.; Kerbow, A. Register-Pressure-Aware instruction scheduling using ant colony optimization. ACM Trans. Archit. Code Optim. (TACO) 2022, 19, 1–23. [Google Scholar] [CrossRef]
  3. Burke, E.K.; Mareček, J.; Parkes, A.J.; Rudová, H. Decomposition, reformulation, and diving in university course timetabling. Comput. Oper. Res. 2010, 37, 582–597. [Google Scholar] [CrossRef]
  4. Soza, C.; Becerra, R.L.; Riff, M.C.; Coello, C.A. C. Solving timetabling problems using a cultural algorithm. Appl. Soft Comput. 2011, 11, 337–344. [Google Scholar] [CrossRef]
  5. Shiau, D.F. A hybrid particle swarm optimization for a university course scheduling problem with flexible preferences. Expert Syst. Appl. 2011, 38, 235–248. [Google Scholar] [CrossRef]
  6. Gunawan, A.; Ng, K.M.; Poh, K.L. A hybridized Lagrangian relaxation and simulated annealing method for the course timetabling problem. Comput. Oper. Res. 2012, 39, 3074–3088. [Google Scholar] [CrossRef]
  7. Cacchiani, V.; Caprara, A.; Roberti, R.; Toth, P. A new lower bound for curriculum-based course timetabling. Comput. Oper. Res. 2012, 40, 2466–2477. [Google Scholar] [CrossRef]
  8. Basir, N.; Ismail, W.; Norwawi, N.M. A simulated annealing for Tahmidi course timetabling. Procedia Technol. 2013, 11, 437–445. [Google Scholar] [CrossRef]
  9. Bolaji, A.L. A.; Khader, A.T.; Al-Betar, M.A.; Awadallah, M.A. University course timetabling using hybridized artificial bee colony with hill climbing optimizer. J. Comput. Sci. 2014, 5, 809–818. [Google Scholar] [CrossRef]
  10. Fong, C.W.; Asmuni, H.; McCollum, B.; McMullan, P.; Omatu, S. A new hybrid imperialist swarm-based optimization algorithm for university timetabling problems. Inf. Sci. 2014, 283, 1–21. [Google Scholar] [CrossRef]
  11. Badoni, R.P.; Gupta, D.K.; Mishra, P. A new hybrid algorithm for university course timetabling problem using events based on groupings of students. Comput. Ind. Eng. 2014, 78, 12–25. [Google Scholar] [CrossRef]
  12. Al-Yakoob, S.M.; Sherali, H.D. Mathematical models and algorithms for a high school timetabling problem. Comput. Oper. Res. 2015, 61, 56–68. [Google Scholar] [CrossRef]
  13. Babaei, H.; Karimpour, J.; Hadidi, A. A survey of approaches for university course timetabling problem. Comput. Ind. Eng. 2015, 86, 43–59. [Google Scholar] [CrossRef]
  14. Méndez-Díaz, I.; Zabala, P.; Miranda-Bront, J.J. An ILP based heuristic for a generalization of the post-enrollment course timetabling problem. Comput. Oper. Res. 2016, 76, 195–207. [Google Scholar] [CrossRef]
  15. Vermuyten, H.; Lemmens, S.; Marques, I.; Beliën, J. Developing compact course timetables with optimized student flows. Eur. J. Oper. Res. 2016, 251, 651–661. [Google Scholar] [CrossRef]
  16. Soria-Alcaraz, J.A.; Özcan, E.; Swan, J.; Kendall, G.; Carpio, M. Iterated local search using an add and delete hyper-heuristic for university course timetabling. Applied Soft Computing 2016, 40, 581–593. [Google Scholar] [CrossRef]
  17. Bellio, R.; Ceschia, S.; Di Gaspero, L.; Schaerf, A.; Urli, T. Feature-based tuning of simulated annealing applied to the curriculum-based course timetabling problem. Comput. Oper. Res. 2016, 65, 83–92. [Google Scholar] [CrossRef]
  18. Cavdur, F.; Kose, M. A fuzzy logic and binary-goal programming-based approach for solving the exam timetabling problem to create a balanced-exam schedule. Int. J. Fuzzy Syst. 2016, 18, 119–129. [Google Scholar] [CrossRef]
  19. Fonseca, G.H.; Santos, H.G.; Carrano, E.G. Integrating matheuristics and metaheuristics for timetabling. Computers & Operations Research 2016, 74, 108–117. [Google Scholar]
  20. Borchani, R.; Elloumi, A.; Masmoudi, M. Variable neighborhood descent search based algorithms for course timetabling problem: Application to a Tunisian University. Electron. Notes Discret. Math. 2017, 58, 119–126. [Google Scholar] [CrossRef]
  21. Song, K.; Kim, S.; Park, M.; Lee, H.S. Energy efficiency-based course timetabling for university buildings. Energy 2017, 139, 394–405. [Google Scholar] [CrossRef]
  22. Bagger, N.C. F.; Sørensen, M.; Stidsen, T.R. Benders’ decomposition for curriculum-based course timetabling. Computers & Operations Research 2018, 91, 178–189. [Google Scholar]
  23. Akkan, C.; Gülcü, A. A bi-criteria hybrid Genetic Algorithm with robustness objective for the course timetabling problem. Computers & Operations Research 2018, 90, 22–32. [Google Scholar]
  24. Jamili, A.; Hamid, M.; Gharoun, H.; Khoshnoudi, R. Developing a comprehensive and multi-objective mathematical model for university course timetabling problem: a real case study. In Conference proceedings of the international conference on industrial engineering and operations management 2018, Paris, France (Vol. 130).
  25. Junn, K.Y.; Obit, J.H.; Alfred, R.; Bolongkikit, J. A formal model of multi-agent system for university course timetabling problems. In Computational Science and Technology 2019, Kota Kinabalu, Malaysia, 29-30 August 2018 (pp. 215-225). Springer Singapore.
  26. Müller, T.; Rudová, H.; Müllerová, Z. University course timetabling and international timetabling competition 2019. In Proceedings of the 12th International Conference on the Practice and Theory of Automated Timetabling 2019, (Vol. 1, pp. 5-31).
  27. Joolaei, A.; Arabamiri, A.; Nejati Kalate, A.; Farzaneh, F. Basement relief modeling by gravity inversion via Ant Colony Algorithm. Iran. J. Geophys. 2020, 14, 39–54. [Google Scholar]
  28. Tavakoli, M.M.; Shirouyehzad, H.; Lotfi, F.H.; Najafi, S.E. Proposing a novel heuristic algorithm for university course timetabling problem with the quality of courses rendered approach; a case study. Alex. Eng. J. 2020, 59, 3355–3367. [Google Scholar] [CrossRef]
  29. Kenekayoro, P. Incorporating machine learning to evaluate solutions to the university course timetabling problem. arXiv preprint 2020, arXiv:2010.00826, arXiv:2010–00826. [Google Scholar]
  30. Al-Khanak, E.N.; Lee, S.P.; Khan, S.U. R.; Behboodian, N.; Khalaf, O.I.; Verbraeck, A.; van Lint, H. A heuristics-based cost model for scientific workflow scheduling in cloud. Comput. Mater. Contin. 2021, 67, 3265–3282. [Google Scholar] [CrossRef]
  31. Guerriero, F.; Guido, R. Modeling a flexible staff scheduling problem in the Era of Covid-19. Optim. Lett. 2022, 16, 1259–1279. [Google Scholar] [CrossRef] [PubMed]
  32. Savio, A.D.; Balaji, C.; Kodandapani, D.; Sathyasekar, K.; Naryanmoorthi, R.; Bharatiraja, C.; Twala, B. DC Microgrid Integrated Electric Vehicle Charging Station Scheduling Optimization. J. Appl. Sci. Eng. 2022, 26, 253–260. [Google Scholar]
  33. Sohrabi, M.; Zandieh, M.; Shokouhifar, M. Sustainable inventory management in blood banks considering health equity using a combined metaheuristic-based robust fuzzy stochastic programming. Socio-Econ. Plan. Sci. 2022, 101462. [Google Scholar] [CrossRef]
  34. Thepphakorn, T.; Pongcharoen, P. Modified and hybridised bi-objective firefly algorithms for university course scheduling. Soft Computing 2023, 1–38. [Google Scholar] [CrossRef]
  35. Shokouhifar, M.; Sohrabi, M.; Rabbani, M.; Molana, S.M.H.; Werner, F. Sustainable Phosphorus Fertilizer Supply Chain Management to Improve Crop Yield and P Use Efficiency using an Ensemble Heuristic–Metaheuristic Optimization Algorithm. Agronomy 2023, 13, 565. [Google Scholar] [CrossRef]
  36. Tirkolaee, E.B.; Goli, A.; Ghasemi, P.; Goodarzian, F. Designing a sustainable closed-loop supply chain network of face masks during the COVID-19 pandemic: Pareto-based algorithms. J. Clean. Prod. 2022, 333, 130056. [Google Scholar] [CrossRef] [PubMed]
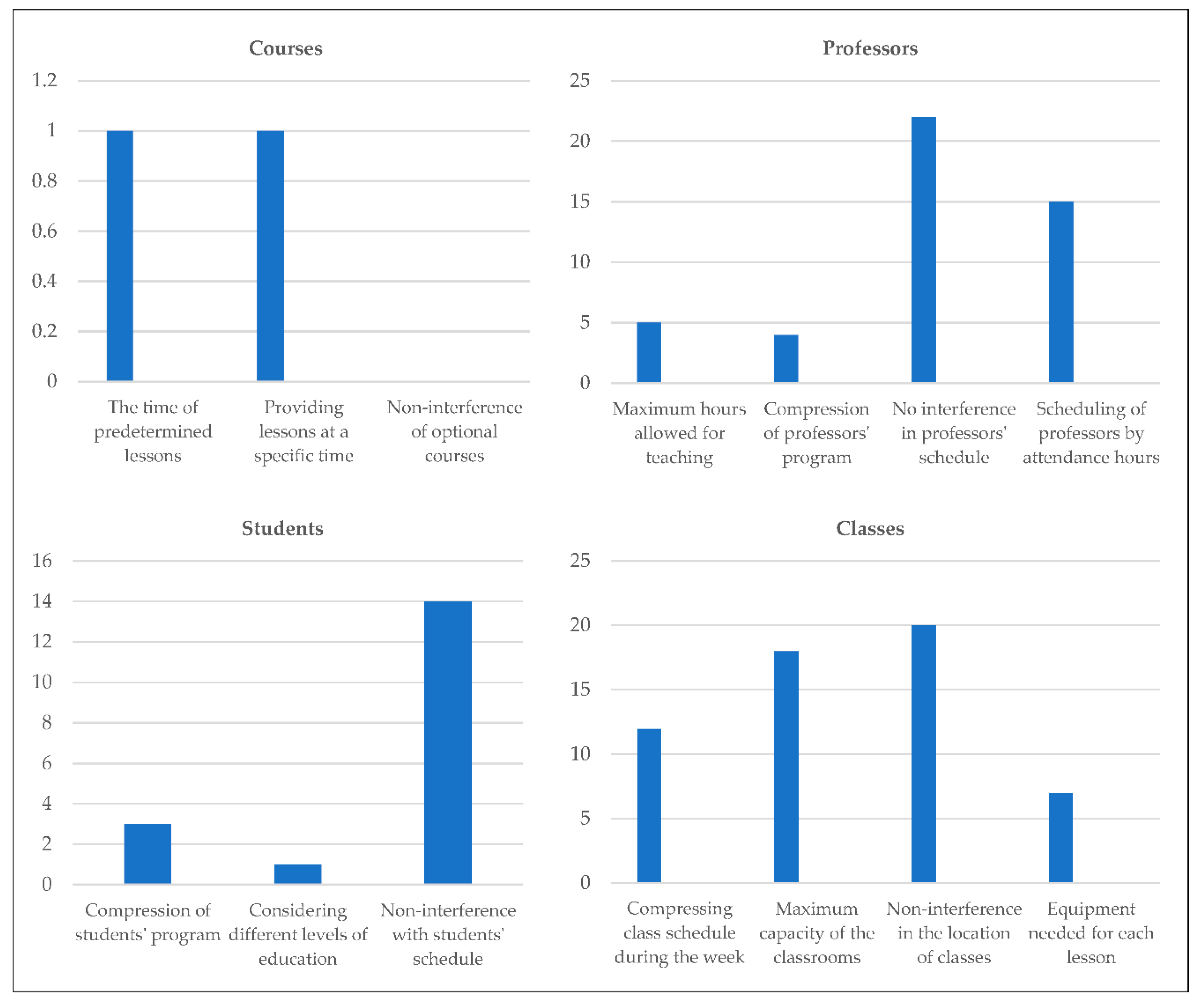
Preprints 69509 g001
Figure 1. Summary of related research items.
Figure 1. Summary of related research items.
Preprints 69509 g001
Table 1. Comprehensive survey of the measures taken in the previous studies.
Table 1. Comprehensive survey of the measures taken in the previous studies.
Reference Year F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15
Lü and Hao [1] 2010 * * * *
Burke et al. [3] 2010 * * * *
Soza et al. [4] 2011 * * * *
Shiau [5] 2011 * * * *
Gunawan et al. [6] 2012 * * * *
Cacchiani et al. [7] 2013 * * * * *
Basir et al. [8] 2013 * * *
Bolaji et al. [9] 2014 * * * *
Fong et al. [10] 2014 * * * *
Badoni and Mishra [11] 2014 * * * *
Al-Yakoob & Sherali [12] 2015 * * * *
Babaei et al. [13] 2015 * * * *
Méndez-Díaz et al. [14] 2016 * * *
Vermuyten et al. [15] 2016 * * * *
Soria-Alcaraz et al. [16] 2016 * * * *
Bellio et al. [17] 2016 * * * *
Cavdur et al. [18] 2016 * * *
Fonseca et al. [19] 2016 * * *
Borchani et al. [20] 2017 * * *
Song et al. [21] 2017 * * *
Bagger et al. [22] 2018 * * * *
Akkan et al. [23] 2018 * * *
Jamili et al. [24] 2018 * * * * * *
Junn et al. [25] 2019 * * *
Müller et al. [26] 2019 * * *
Joolaei et al. [27] 2020 * * * * *
Tavakoli et al. [28] 2020 * * * *
Kenekayoro [29] 2020 * * * * *
Al-Khanak et al. [30] 2021 * * * * * * *
Guerriero et al. [31] 2022 * * *
Savio et al. [32] 2022 * * *
F1:  No interference with optional courses
F2:  Providing courses at a specified time
F3:  Considering the time of predetermined courses
F4:  Planning of professors' courses based on attendance hours
F5:  No interference in professors' schedule
F6:  Compression of professors' program
F7:  Considering the maximum hours allowed for teaching
F8:  Consider the equipment needed for each course
F9:  Non-interference in the location of classes
F10:  The capacity of the classrooms
F11:  Compressing the classroom schedule during the week
F12:  No interference with the students' schedule
F13:  Maximum number of courses for students
F14:  Considering different levels of education
F15:  Compression of students' program
Table 2. List of notations.
Table 2. List of notations.
Sets/Indices Definition
T Set of time intervals of weekdays on which course planning is possible, enumerated by the index t .
K Set of classrooms that are available for the weekly course schedule, enumerated by the index k .
R The collection of professors who teach university courses, enumerated by the index r .
C Set of courses that are planned for the group of students, enumerated by index c.
L Set of study groups that become a special entry for students during a semester, enumerated by index l .
Parameters Definition
b c The number of hours that the c-th course must be held per week (the number of units of course c).
m The maximum time that can be scheduled for a professor on a day in hours.
a r t Binary parameter, which takes the value one, if the r-th professor is ready to present the course in the t-th period, and zero otherwise.
β r c Binary parameter, which takes the value one, if the r-th professor teaches the c-th course.
P c k Binary parameter, which takes the value one, if the c-th course can be held in the k-th class.
γ c t Binary parameter, which takes the value one, if the c-th course can be held at the t-th time.
f k t Binary parameter, which takes the value one if the k-th class is available at the t-th time.
λ c l Binary parameter, which takes the value one, if the c-th course is in the l-th subject group.
h d t Binary parameter, which takes the value one, if the t-th time interval belongs to the d-th day (d=1,2,3,4,5).
w r The weight of the professor r which is a numerical value in the range [0-1], is determined based on some characteristics such as the academic degree, experience, etc.
δ r d t The weight of the time period that expresses the preference of professor r over the interval t from day d.
Decision
Variables 		Definition
X c k t r Binary variable, which takes the value one, if the c-th course is scheduled in the t-th 1-hour interval ( t = 1 ,   2 , . . . . , 50 ) in the k-th class and this course is presented by the professor r .
Y c k t ′ r Binary variable, which takes the value one, if the c-th course is scheduled in the t'-th 2-hour interval ( t ′ = 1,2 , . . . . , 25 ) in the k-th class, and this course is presented by the professor r .
Table 3. Program of one-unit courses.
Table 3. Program of one-unit courses.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 C1
R1		 C2
R1		 C3
R1		 C4
R2		 C5
R2		 C6
R2		 C7
R3		 C8
R3		 C9
R3		 -
K2 - - - - -
K3 - - - - -
Table 4. Program of two-unit courses.
Table 4. Program of two-unit courses.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 - - - - -
K2 C4
R2		 C7
R3		 C1
R1		 C2
R1		 C3
R1
K3 C8
R3		 - C9
R3		 C5
R2		 C6
R2
Table 5. Program of three-unit courses.
Table 5. Program of three-unit courses.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 C1
R1		 C2
R1		 C3
R1		 C4
R2		 C5
R2		 C6
R2		 C7
R3		 C8
R3		 C3
R1		 C4
R2
K2 C4 C7 C1 C2 C3
K3 C8 - C9 C5 C6
Table 6. The maximum allowed teaching time is 10 hours.
Table 6. The maximum allowed teaching time is 10 hours.
Classroom/Time 8-10 10-12 15-13 17-15 19-17
Day 1 K1 C1
R1		 C2
R1		 C3
R1		 - - - C8
R2		 C9
R2		 C10
R2
K2 C6 C7 - - -
Day 2 K1 C1 C2 C3 C4 C5
K2 - - - - -
Table 7. The maximum allowed teaching time is 6 hours.
Table 7. The maximum allowed teaching time is 6 hours.
Classroom/Time 8-10 10-12 15-13 17-15 19-17
Day 1 K1 C1
R1		 C2
R1		 C3
R1		 - - - C1
R1		 C2
R1		 C3
R1
K2 - - C4 - -
Day 2 K1 C1 C2 C3 C5 -
K2 C7 - - - -
Table 8. Teaching time of freelance professors.
Table 8. Teaching time of freelance professors.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 C1
R1 		C2
R1 		- - C6
R2		 C7
R3		 C8
R3		 C9
R3		 -
K2 C3
R2		 C1
R1		 C2
R1		 C4
R2		 C5
R2
Table 9. Times when the professors are available for teaching.
Table 9. Times when the professors are available for teaching.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 - C6
R3		 C5
R2		 C2
R1		 C2
R1		 C1
R1		 C4
R2
K2 C8
R3		 - C7
R3		 C9
R3		 - C3
R2		 C1
R1
Table 10. Conducting courses in all classrooms.
Table 10. Conducting courses in all classrooms.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 C1
R1		 C2
R1		 - - C6
R3		 C7
R3		 C8
R3		 C9
R3		 -
K2 C3 C1 C2 C4 C5
Table 11. Holding courses in a number of special classrooms.
Table 11. Holding courses in a number of special classrooms.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 C2
R1		 C1
R1		 C2 R1 C3 R2 C1 R1 C8
R3		 C7
R3
K2 C6
R3		 - - C9
R3		 - C5 R2   C4
R2
Table 12. Presentation of free courses.
Table 12. Presentation of free courses.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
Day 1 K1 C1
R1		 - C4
R2		 - C7
R3		 C8
R3		 C9
R3		 -
K2 - C12 C1 C2 C3
Day2 K1 C11
R1		 - C9
R3		 C5
R2		 C6
R2		 C10
R3
K2 - - - - -
Table 13. Presentation of courses with the constraint of study groups.
Table 13. Presentation of courses with the constraint of study groups.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
Day 1 K1 C1
R1		 - C4
R2		 - - C10
R3		 C11
R1		 -
K2 - - C1 C2 C3
Day2 K1 C7
R3		 C8
R3		 C5
R2		 C6
R2		 C9
R3		 C10
R3
K2 - - - - -
Table 14. Available classrooms.
Table 14. Available classrooms.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 C1
R1		 C2
R1		 - - C6
R3		 C7
R3		 C8
R3		 C9
R3		 -
K2 C3
R2		 C1
R1		 C2
R1		 C4
R2		 C5
R2
Table 15. The optimal classroom availability in each hour.
Table 15. The optimal classroom availability in each hour.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 - C2
R1		 C1
R1		 C7
R3		 C8
R3		 C1
R1		 C5 R2
K2 C4 R2 - C3
R2		 C6
R3		 C9
R3		 C2 R1
Table 16. Courses without being in a group.
Table 16. Courses without being in a group.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 C1
R1		 C2
R1		 - - C6
R3		 C7
R3		 C8
R3		 C9
R3		 -
K2 C3
R2		 C1
R1		 C2
R1		 C4
R2		 C5
R2
Table 17. Courses classified into several groups.
Table 17. Courses classified into several groups.
Classroom/Time 8-10 10-12 13-15 15-17 17-19
K1 C3 R2 C7
R3		 C1
R1		 C8
R3		 C9
R3		 - C6
R3		 -
K2 C1 R1 C5
R2		 C4
R2		 C2
R1		 - C2 R1
Table 18. Execution time analysis.
Table 18. Execution time analysis.
No. Courses No. Classrooms No. Professors Execution Time (second)
9 3 3 38
10 2 2 40
9 2 3 37
12 2 3 48
10 3 5 63
15 3 5 148
20 3 5 412
20 5 7 637
25 7 10 1150
25 10 10 1533
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated