Decentralized Control for the Cell Power Balancing of a Cascaded Full-Bridge Multilevel Converter

In modern inverter applications, multilevel converters are used thanks to their capability of reducing the passive fi lter volumes, improving the overall THD, sharing the power sources across the several converter cells, and providing a reconfi guration ability in case of failure. However, increasing the number of cells makes more complex the control of the converter. This article proposes a decentralized control technique based on the use of elementary modular controllers, associated with each converter cell and communicating with their close neighbors to obtain the balancing of the powers they supplied. Each modular controller can be dynamically removed or added to allow reconfi guration of the converter for functional safety purpose. This method is applied to a 240V/3A 5-cells Cascaded Full-Bridge Multilevel Converter. The response of the system to load transients and cell voltage disturbances demonstrates the robustness of the proposed decentralized control method. Thanks to the use of modular controllers, the number of levels of the converter can be extended to the order N without adding complexity to its control.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

In the last decades, power electronics have been used in several applications, such as energy conversion and transmission, electrical traction, and storage systems. In all of these cases, the power converters have a key role, converting the energy of the source into a suitable one for the load, which are based on passive elements and switching devices such as MOSFETs or IGBTs [1,2]. For low and medium-voltage applications, MOSFETs and IGBTs are relatively fast and offer the advantage of controlling device turns on and off. However, these switching devices are limited for high power/voltage applications due to their voltage and current maximum value or switching time.

One solution for high power/voltage management is using Multi-Cellular Converters (MCC). The idea of MCCs is to “divide and rule". These converters consist of an arrangement of several cells connected in parallel, in series, or in cascade, allowing the voltage or current distribution at the input or the output. There are many types of MCCs, such as the Flying Capacitor Multilevel Converter (FCMC) [3,4,5,6,7], where the input voltage is distributed among the cell voltages; Cascaded Full Bridge Multilevel Converter (CFBMC) [8,9,10,11,12,13], where the total output voltage is the sum of the output voltage of each Full Bridge (FB); and Multiphase Buck Converter, where its output current is the sum of the leg current [14,15,16]. In all these cases the energy is distributed among the cells, allowing the use of low or medium-power devices for high-power applications. This fact is a great advantage because, normally, low-power devices are faster and more efficient than high-power ones. Therefore, MCCs allow managing high power conversion with low power and fast switching devices. Another feature of the multi-cellular converters is that with suitable frequency modulation techniques [17,18,19,20] it is possible to obtain a much higher output frequency than the MOSFETs or IGBTs switching frequency.

MCCs offer many advantages, however, there are a lot of challenges to be solved for these topologies. One of them is the ability to balance one variable of the cells according to the application. In FCMC, it is very useful that the capacitor voltages are balanced. Well-balanced capacitor voltages produce the supplied power distributed equally in all the cells. Furthermore, it makes a suitable ripple output voltage [3,4,21]. In the case of Multiphase Buck, balancing the leg current produces an appropriate distribution of the output current of the system [16]. For the case of CFBMC, it is possible to balance the output voltages of each FB to maintain equalized the power delivered by each FB [22,23,24,25]. For the same converter, if the sources are batteries, balancing the input current of each FB maintaining well-balanced the charging or discharging of the batteries, making also possible to control their State Of Charge (SOC). All these cell-variables balancing strategies can turn very complicated if the number of cells increases significantly.

Another challenge for Multi-cellular converters is the ability to insert or remove cells during operation [3,15,21,23], allowing to increase the power of the converter or giving a fault tolerance ability.

There exist many controllers that satisfy all these specifications. In [3,21], a control structure is proposed applied for an FCMC, which balances the capacitor voltages, regulates the output current, and allows a cell insertion/removal ability, obtaining interesting results.

The present work applies in the CFBMC the controller proposed in [3,21], develops a mathematical approach of the controller used in this topology, and shows the simulation and experimental results.

Section two describes the topology of the CFBMC and models it. The next section presents a description of the decentralized controller. Then in the fourth section, an in-depth analysis of the controller applied to the CFBMC is shown, presenting the closed-loop and open-loop transfer function and analyzing the bandwidth of the system. In section five, the design of the controller is presented, based on the open loop transfer functions of the system, obtaining, theoretically, the eigenvalues of the system. Then, section six presents the simulation and experimental results with three tests: load step, input voltage step, and cell insertion tests. Finally, the conclusion and future works are presented in the seventh section.

2. Description of the system

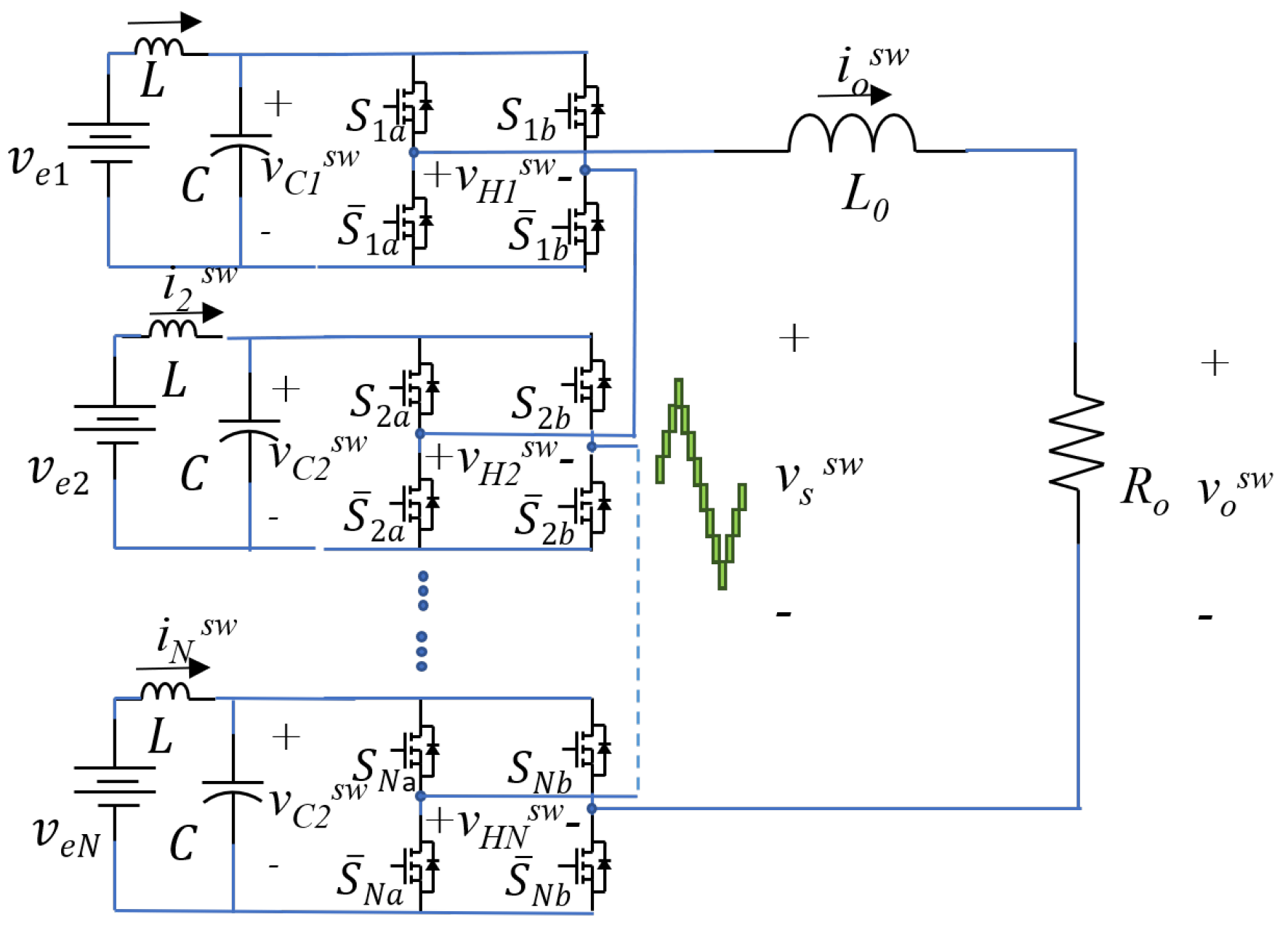
This article proposes an adaptation of a decentralized control applied previously to FCMC in [3,21], now implemented in a CFBMC of N Full-Bridges with inductive filter and resistive load. Figure 1 shows the topology of the converter, using MOSFET as the switching device, where the control is implemented, where

S_{y k}

, represents the position of the high-side switches, 1, if it is in ON state, and 0 if it is in OFF state, for the

k^{t h}

Full-Bridge (FB),

k = 1, 2, \dots, N

y = a

for the left side branch of the

k^{t h}

Full-Bridge and

y = b

for the right side.

\bar{S_{y k}}

is the complementary signal of

S_{y k}

v_{e k}

v_{H k}^{s w}

v_{C k}^{s w}

i_{k}^{s w}

are: the input voltage, the switching output voltage, the switching FB cell input capacitor voltage and the switching FB cell input inductance current of the

k^{t h}

FB, respectively, while

i_{o}^{s w}

and

v_{o}^{s w}

correspond to the output current and voltage of the inverter, respectively. Depending on the position of the switches, the value of

S_{y k}

varies and also the internal cell signals. In order to simplify the equations, a slow variation assumption is made, compared to the switching frequency and an average model can be proposed, where the variable x is the moving average of the

x^{s w}

, and x can be:

v_{H k}

v_{C k}

i_{k}

v_{o}

i_{o}

. In this work, the goal is to balance the moving average of the output voltage of the Full-Bridges,

v_{H k}

, called the Cell Voltage (CV) and to regulate the output current,

i_{o}

, which is the Global Variable (GV) and to provide a means of easily inserting or removing an FB cell without adding complexity to the balancing control system.

Taking into account that the switching current through the output of each Full-Bridge is

i_{o}^{s w}

, and the average is

i_{o}

for all the FB cells, balancing their output voltage is equivalent to balance the power delivered by each cell. According to Figure 1, the dynamic equation of the moving average variable is:

\begin{matrix} {\dot{i}}_{k} & = \frac{1}{L} v_{e k} - R_{L} \frac{1}{L} i_{k} - \frac{1}{L} v_{c_{k}} \end{matrix}

(1a)

\begin{matrix} {\dot{v}}_{C_{k}} & = \frac{1}{C} i_{k} - \frac{1}{C} u_{k} i_{o} \end{matrix}

(1b)

\begin{matrix} \dot{i_{o}} & = \frac{1}{L_{o}} \sum_{k = 1}^{N} v_{c_{k}} u_{k} - \frac{1}{L_{o}} (R_{x} + R_{o}) i_{o} \end{matrix}

(1c)

where

u_{k} = d_{a k} - d_{b k}

d_{y k}

is the duty cycle of

S_{y k}

R_{L}

is the series resistance of the inductance L, and

R_{x}

corresponds to

2 N R_{d s} + R_{L_{o}}

R_{D S}

is the drain-source-ON resistance of the MOSFET and

R_{L_{o}}

is the series resistance of

L_{o}

. The dynamical model of the output voltage of the Full-Bridge,

v_{H k}

is:

v_{H_{k}} = v_{C_{k}} u_{k}

(2)

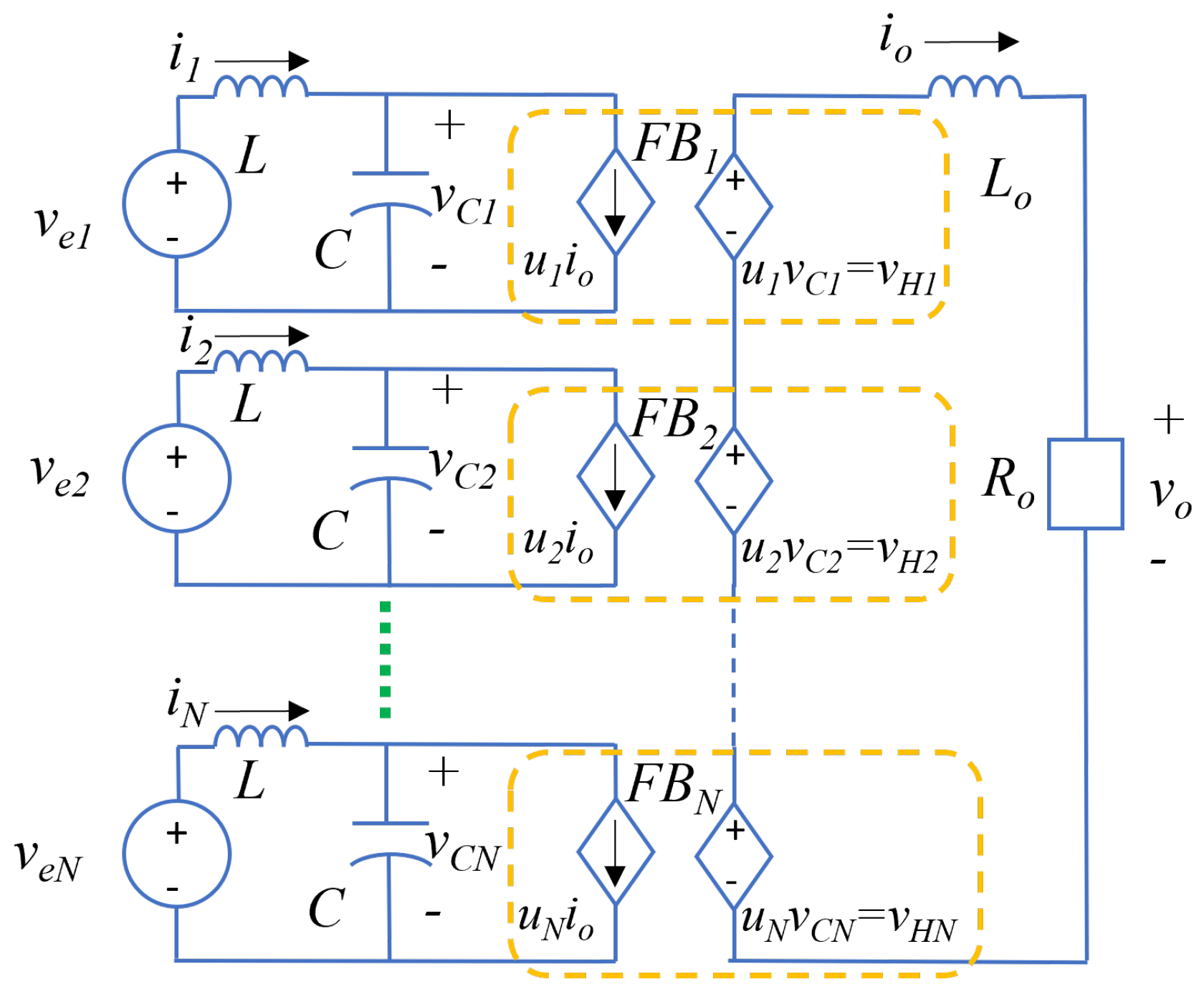
According to (1) and (2) the equivalent circuit of the converter is shown in Figure 2:

Knowing that in the CFBMC all the input voltages have the same nominal value,

v_{e k} = {\bar{v}}_{e} + {\hat{v}}_{e k}

. Hence, according to [12,26], it is possible to simplify the model, considering the oscillation produced by the input filter and the variations in the input voltage as a disturbance. Therefore:

v_{C_{k}} = δ_{v_{C k}} + {\bar{v}}_{e} + {\hat{v}}_{e k}

(3)

Based on (1c) and (3), the converter follows the presented model:

\begin{matrix} \dot{i_{o}} & = \frac{1}{L_{o}} \sum_{k = 1}^{N} ({\bar{v}}_{e} u_{k} + δ_{v_{H k}}) - \frac{1}{L_{o}} (R_{x} + R_{o}) i_{o} \end{matrix}

(4a)

\begin{matrix} v_{H_{k}} & = {\bar{v}}_{e_{k}} u_{k} + δ_{v_{H k}} \end{matrix}

(4b)

where

δ_{v_{H k}} = (δ_{v_{C k}} + {\hat{v}}_{e k}) u_{k}

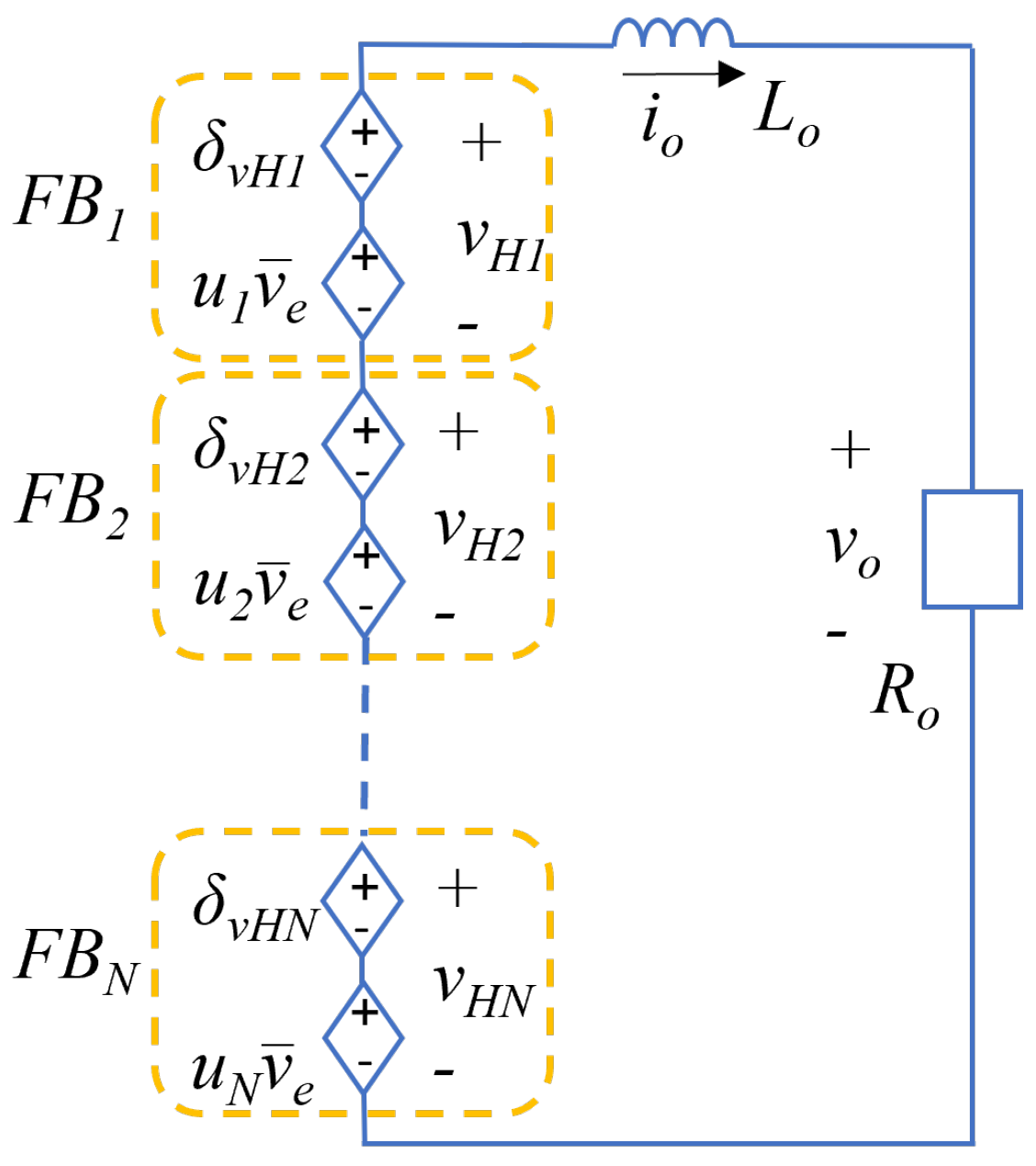
Based on (4), Figure 3 presents the equivalent linear circuit:

Equation (4) represents the linear model of the inverter. Hence, it is possible to express it in Laplace domain:

\begin{matrix} I_{o} (s) & = \frac{1}{L_{o} s + (R_{x} + R_{o})} \sum_{k = 1}^{N} ({\bar{v}}_{e} U_{k} (s) + Δ_{V_{H k}} (s)) \end{matrix}

(5a)

\begin{matrix} V_{H_{k}} (s) & = {\bar{v}}_{e} U_{k} (s) + Δ_{V_{H k}} (s) \end{matrix}

(5b)

Then, expressing it as a matrix form:

\begin{matrix} I_{o} (s) & = G (s) {V_{1}}^{T} ({\bar{v}}_{e} U (s) + Δ_{V_{H}} (s)) \end{matrix}

(6a)

\begin{matrix} V_{H} (s) & = {\bar{v}}_{e} U (s) + Δ_{V_{H}} (s) \end{matrix}

(6b)

where

G (s) = \frac{1}{L_{o} s + (R_{x} + R_{o})}

Δ_{V_{H}} (s) = {[\begin{matrix} Δ_{V_{H_{1}}} (s) & Δ_{V_{H_{2}}} (s) & \dots & Δ_{V_{H_{N}}} (s) \end{matrix}]}^{T}

U (s) = {[\begin{matrix} U_{1} (s) & U_{2} (s) & \dots & U_{N} (s) \end{matrix}]}^{T}

V_{1} = {[\begin{matrix} 1 & 1 & \dots & 1 \end{matrix}]}^{T}

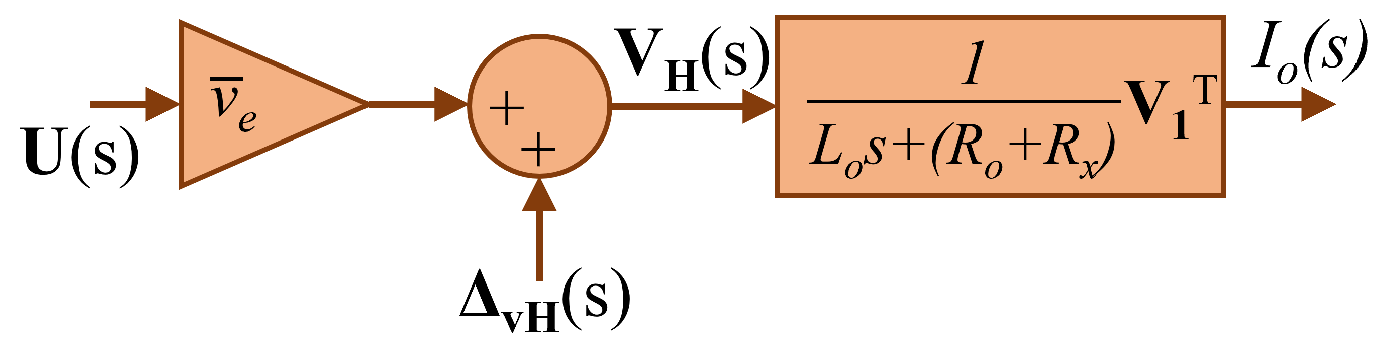
Figure 4 shows the block diagram of (6). Thanks to this model, a decentralized controller used to balance the output voltage of the cells

v_{H k}

is proposed in the next chapter.

3. Description of the decentralized controller

The proposed control loop for this article is based on the controller found in [3,21] that is applied to a FCMC, which shows interesting results. Furthermore, [23] shows a simulation of this controller applied in a grid-tied cascaded multilevel inverter. The presented paper implements the controller to an isolated Cascaded FB Multilevel Inverter, connected to a resistive load with an inductive filter. 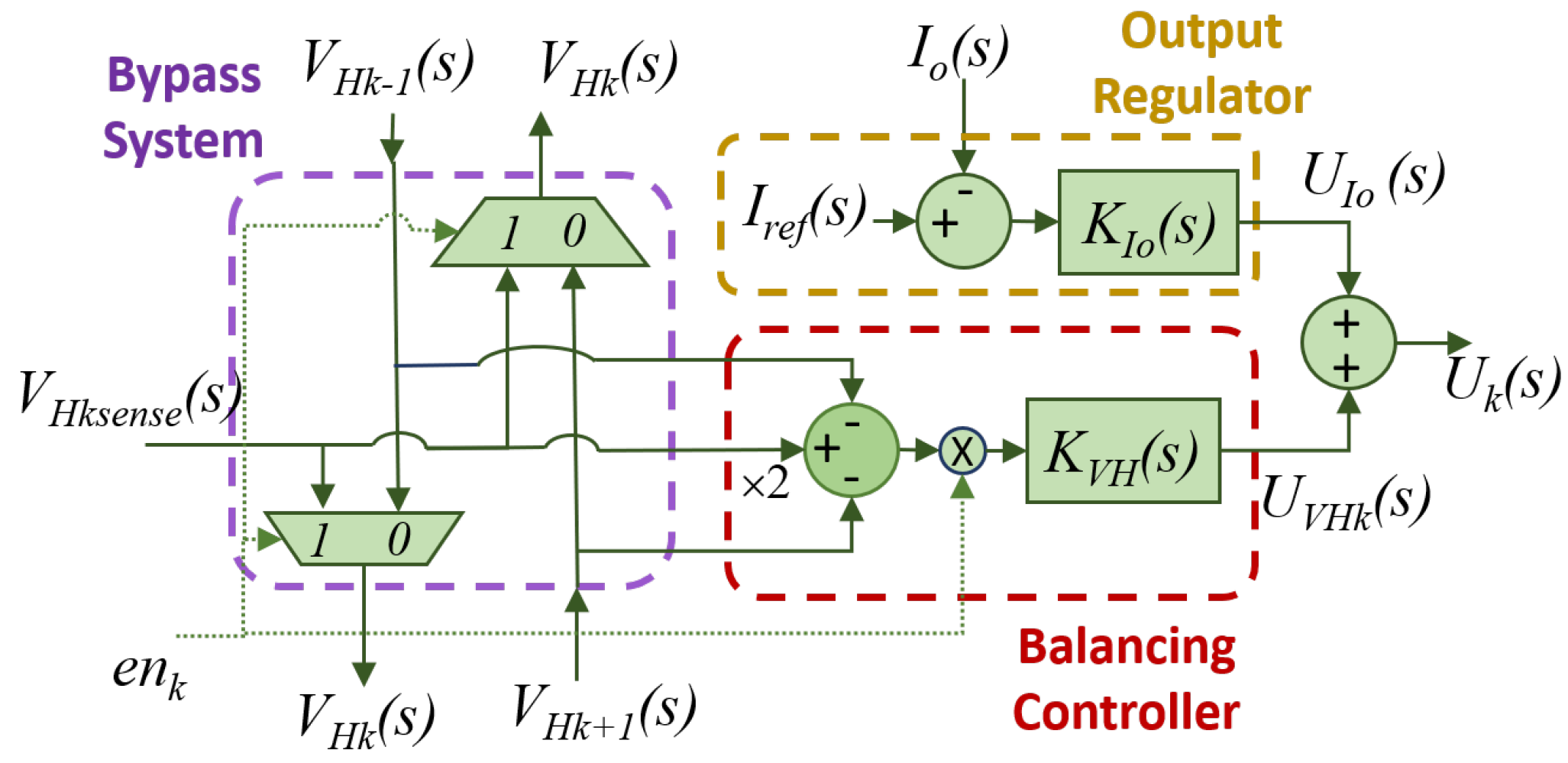Figure 5 shows the proposed control structure.

As Figure 5 shows, the control structure presents three stages: the Bypass system, the Balancing controller and the Output Current regulator.

3.1. The Bypass System

The main goal of this block is to manage the communication between the cells depending on its state (active or inactive, ON or OFF). According to Figure 5, the cell controller receives an enable signal used to turn OFF or ON the FB cell. When the

k^{t h}

FB cell is ON, the bypass system sends

V_{H k s e n s e} (s)

V_{H k} (s)

, which is the signal that is sent to the cell

k + 1

and

k - 1

, respectively. When the

k^{t h}

cell is OFF, the FB is skipped and the value of

V_{H k s e n s e} (s)

is not sent anymore. Instead of that, the cells

k + 1

and

k - 1

receive the values of

V_{H k - 1} (s)

and

V_{H k + 1} (s)

, respectively. This part of the controller allows the insertion or removal of FB cells during operation. However, if a balancing controller is not implemented, each FB cell can supply different power, voltage, or current that could not be the desired one.

3.2. The Output Current Regulator

This part of the controller regulates the output current supplied to the load. It is a typical linear controller,

K_{I_{o}} (s)

, that can be a PI or other regulator, based on the transfer function of the plant. According to Figure 5, the output of the output regulator is defined as:

U_{I_{o}} (s) = K_{I_{o}} (s) (I_{r e f} (s) - I_{o} (s))

(7)

3.3. The Cell Power Balancing Controller

This stage of the control structure is the cell power balancing controller. It compares the values of its output voltage

V_{H k} (s)

with the average value of the output voltages of the neighboring actives FB cells,

V_{H k - 1} (s)

and

V_{H k + 1} (s)

. The error obtained is then canceled by a linear controller,

K_{V H (s)}

, that can be a PI or another type of compensator.

U_{V_{H k}} (s) = K_{V_{H}} (s) (2 V_{H_{k}} (s) - V_{H_{k + 1}} (s) - V_{H_{k - 1}} (s))

(8)

According to (7), (8) and Figure 5, the output of the entire controller is defined as:

\begin{matrix} U_{k} (s) = & U_{I_{o}} (s) + U_{V_{H k}} (s) \end{matrix}

(9a)

\begin{matrix} U_{k} (s) = & K_{I_{o}} (s) (I_{r e f} (s) - I_{o} (s)) + K_{V_{H}} (s) (2 V_{H_{k}} (s) - V_{H_{k + 1}} (s) - V_{H_{k - 1}} (s)) \end{matrix}

(9b)

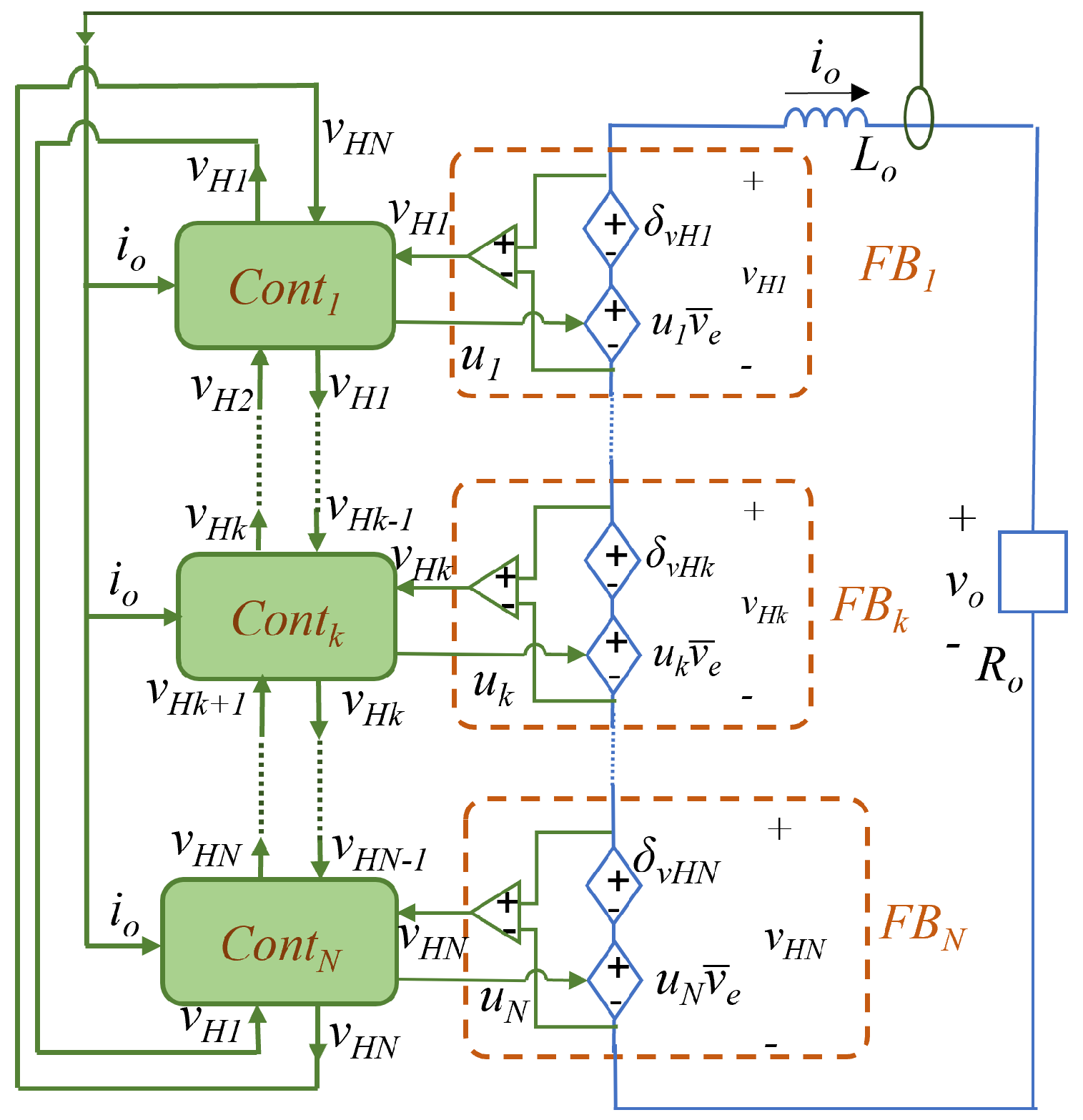
The control method illustrated in Figure 5 is applied to each FB cell. Then the cells are connected together in a closed-loop chain of communications to exchange with their close neighbors the values of their output voltage, as shows Figure 6.

Notice that the

N^{t h}

cell communicates with the 1^st and

N - 1^{t h}

cells, and the 1^st cells are compared with the cell 2^nd and

N^{t h}

, closing the chain of the system.

Expressing (9b) as a matrix form, it follows:

U (s) = K_{I_{o}} (s) (I_{r e f} (s) - I_{o} (s)) V_{1} + K_{V_{H}} (s) D_{i f f} V_{H} (s)

(10)

where

D_{i f f} = [\begin{matrix} 2 & - 1 & 0 & \dots & 0 & - 1 \\ - 1 & 2 & - 1 & ⋱ & ⋮ & 0 \\ 0 & - 1 & 2 & ⋱ & 0 & ⋮ \\ ⋮ & 0 & ⋱ & ⋱ & - 1 & 0 \\ 0 & ⋮ & ⋱ & - 1 & 2 & - 1 \\ - 1 & 0 & \dots & 0 & - 1 & 2 \end{matrix}]

4. Closed-Loop System Analysis

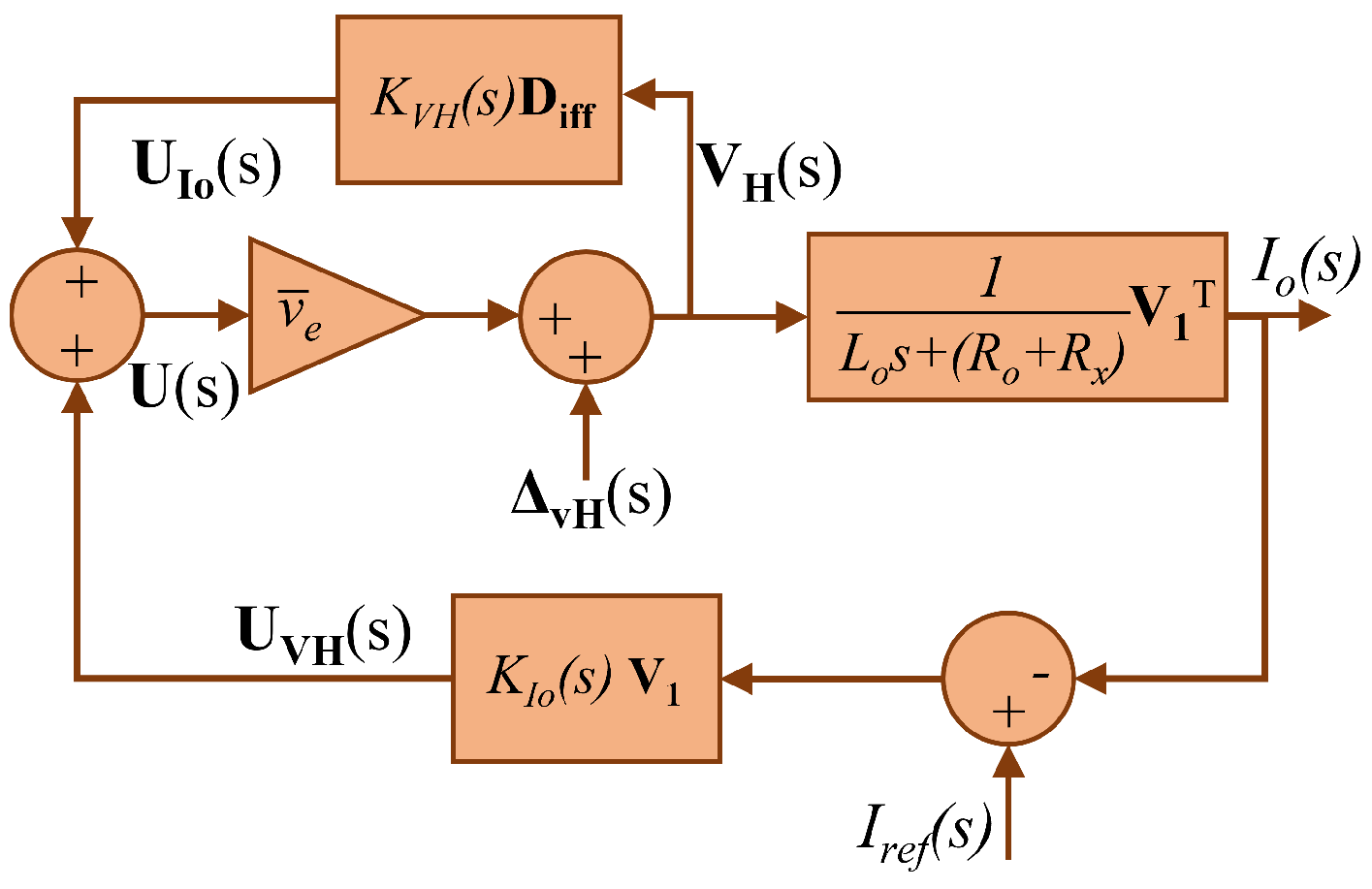
This section shows the mathematical study of the closed-loop system using the proposed controller. The analysis of the transfer functions which comprise the output current regulator and the local balancing controller makes it possible to determine the nature and the parameters of the controllers used. Their design is discussed in the next chapter. The block diagram of the system, and the model of the converter with the controllers is shown in Figure 7.

Thanks to Figure 7, one can determine the open-loop transfer function and the closed-loop transfer function of the output regulator and the ones of the balancing controller.

4.1. Output Current Regulator Analysis

To design the output regulator it is necessary to perform an analyzes the output regulator loop. Hence, inserting the decentralized controller, proposed in (10), into the model of the output current control loop of the inverter, and taking into account that

{V_{1}}^{T} V_{1} = N

and

{V_{1}}^{T} D_{i f f} = 0

, (6a) one obtains:

\begin{matrix} I_{o} (s) = & \underset{F_{o l_{I} o} (s)}{\underset{︸}{\frac{N {\bar{v}}_{e} K_{I_{o}} (s)}{L_{o} s + R_{x o}}}} (I_{r e f} (s) - I_{o} (s)) + \frac{1}{L_{o} s + R_{x o}} {V_{1}}^{T} Δ_{V_{H}} (s) \end{matrix}

(11)

where

R_{x o} = R_{x} + R_{o}

and

F_{o l_{I o}} (s)

is the open-loop transfer function of the output current regulator.

Notice that the term related to the balancing control stage is removed in the transfer function because

D_{i f f}

represents the Laplacian of a graph. Indeed, according to [3,21,23], the sum of the elements of the rows and the sum of the elements of the columns is zero. Because this matrix is post multiplied by

V_{1}

, the results are zero. Based on

F_{o l I o} (s)

, the design of

K_{I_{o}} (s)

is provided in the next section.

In order to get a better understanding of the balancing control loop, it is necessary to analyze the closed-loop transfer function of the output regulator,

F_{c l I o} (s)

, which is defined below.

I_{o} (s) = \underset{F_{c l I o} (s)}{\underset{︸}{\frac{N {\bar{v}}_{e} K_{I_{o}} (s)}{L_{o} s + R_{x o} + N {\bar{v}}_{e} K_{I_{o}} (s)}}} I_{r e f} (s) + \underset{F_{d i s t} (s)}{\underset{︸}{\frac{1}{L_{o} s + R_{x o} + N {\bar{v}}_{e} K_{I_{o}} (s)}}} {V_{1}}^{T} Δ_{V_{H}} (s)

(12)

It shows that the resulting regulated output current is provided by the separate contribution of the current loop

F_{c l_{I o}} (s)

and a disturbance transfer function,

F_{d i s t} (s)

, generated by the oscillations of the input voltage capacitors and the duty cycles of each cell FB.

For the next subsection it should be considered if the output regulator is well designed, when

I_{r e f} (s)

is a step,

I_{r e f} (s) = \frac{I_{a}}{s}

t \to \infty

, means that with

s \to 0

i_{o} (t) = I_{a}

, producing that

F_{c l_{I o}} (s) = 1

when

s \to 0

4.2. Cell Power Balancing Control loop analysis

Now, the balancing control loop has to be analyzed Inserting (10) in (6b), it follows:

V_{H} (s) = {\bar{v}}_{e} K_{V_{H}} (s) D_{i f f} V_{H} (s) + {\bar{v}}_{e} K_{I_{o}} (s) (I_{r e f} (s) - I_{o} (s)) V_{1} + Δ_{V_{H}} (s)

(13)

Inserting (12) in (13), one obtains

\begin{matrix} V_{H} (s) = & {\bar{v}}_{e} K_{V_{H}} (s) D_{i f f} V_{H} (s) + \frac{{\bar{v}}_{e} K_{I_{o}} (s) (L_{o} s + R_{x o})}{L_{o} s + R_{x o} + N {\bar{v}}_{e} K_{I_{o}} (s)} I_{r e f} (s) V_{1} \\ + (I - \frac{{\bar{v}}_{e} K_{I_{o}} (s)}{L_{o} s + R_{x o} + N {\bar{v}}_{e} K_{I_{o}} (s)} V_{1} {V_{1}}^{T}) Δ_{V_{H}} (s) \end{matrix}

(14)

Simplifying:

\begin{matrix} V_{H} (s) = & \underset{F_{o l_{V H}} (s)}{\underset{︸}{{\bar{v}}_{e} K_{V_{H}} (s) D_{i f f}}} {V_{H}}^{'} (s) + \frac{1}{N} F_{c l_{I o}} (s) (L_{o} s + R_{x o}) I_{r e f} (s) V_{1} \\ + (I - \frac{1}{N} F_{c l_{I o}} (s) V_{1} {V_{1}}^{T}) Δ_{V_{H}} (s) \end{matrix}

(15)

where

{V_{H}}^{'} (s)

is the excitation signal. The controller

K_{V_{H}} (s)

is defined based on the desired bandwidth of

F_{o l_{V H}} (s)

, which is directly linked to the eigenvalues of the matrix

D_{i f f}

, then it is described in the next section.

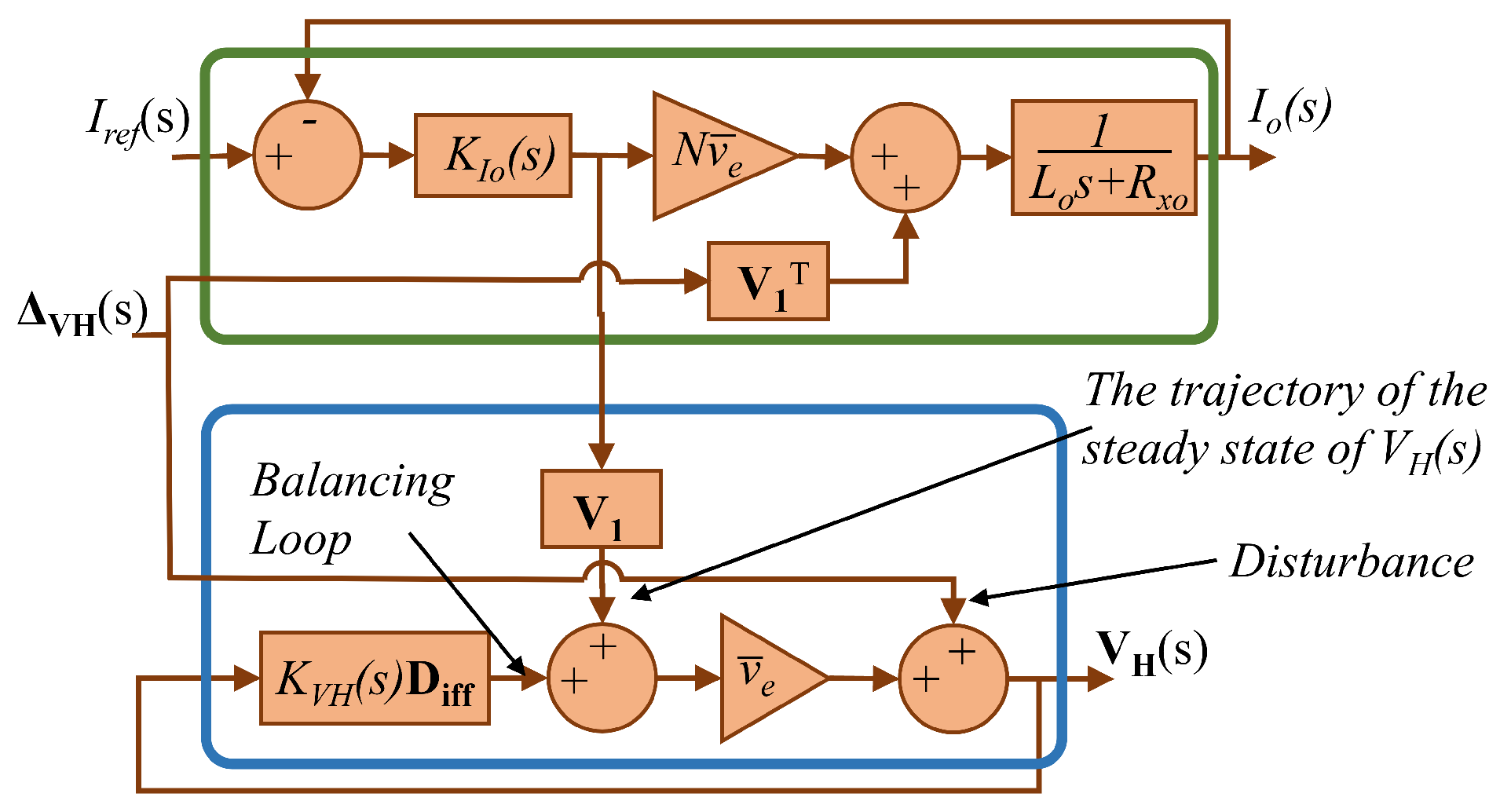
4.3. Global closed-loop analysis

According to (11), and (13), Figure 8 shows the simplified closed-loop block diagram.

Notice that

V_{H} (s)

depends on three inputs, one corresponds to the balancing controller, other depends on the disturbance,

Δ_{V_{H}} (s)

, and the last one depends on the output current loop, which affects all the cell voltages at the same time. Analyzing in steady state, according to (15), when

s \to 0

, if the controller is well designed,

F_{c l I o} (s) = 1

, producing that the trajectory in steady states for

V_{H} (s)

\frac{R}{N} I_{r e f} (s)

5. Design of the controllers

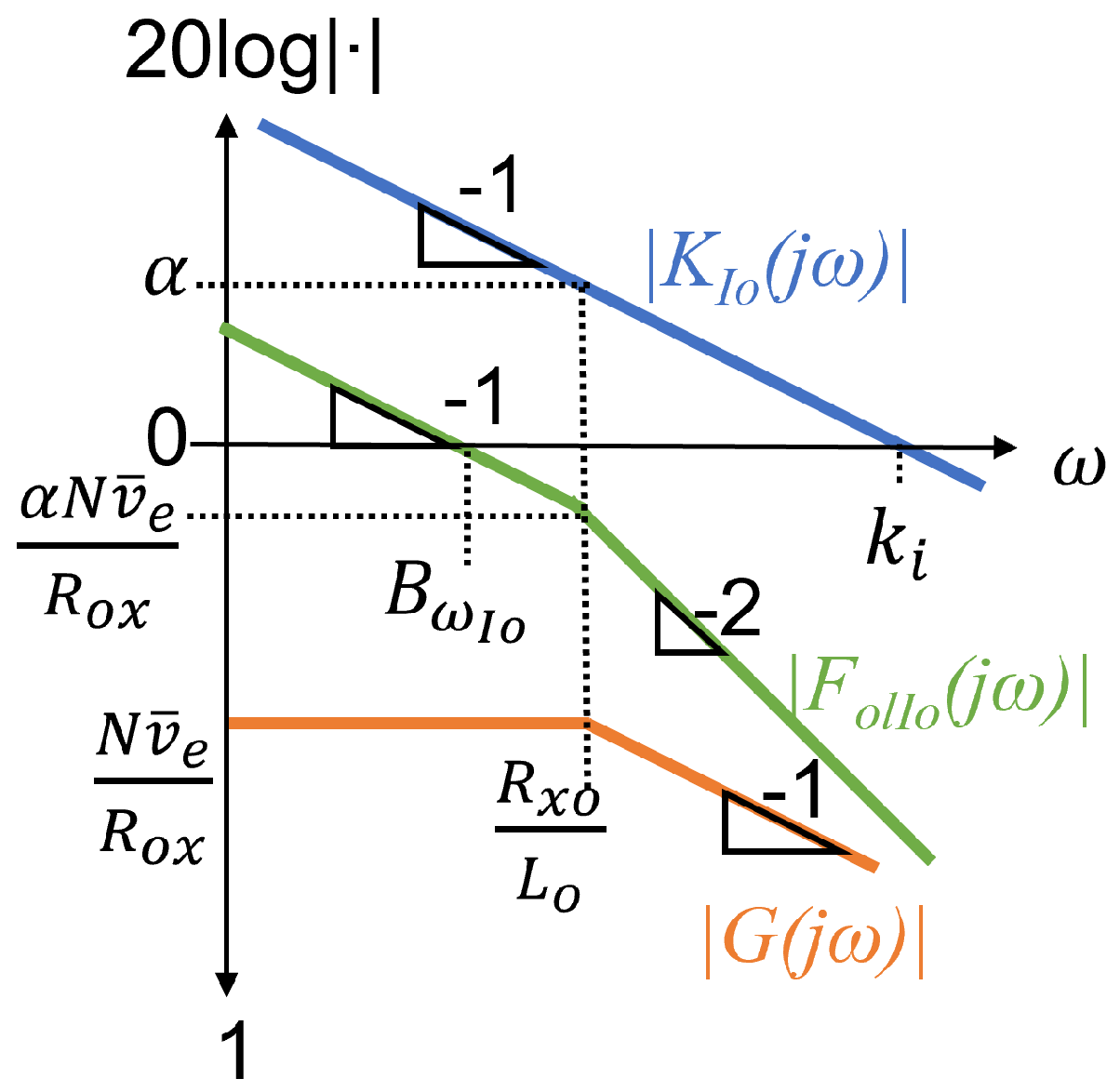
Now, both controllers have to be designed, taking into account some criteria, such as bandwidth of the loops and the correlation of Bode analysis between the two loops.

5.1. Design of the Output Current Regulator

Based on

F_{o l_{I o}} (s)

, for a stable and low bandwidth system, an integral corrector can be proposed for

K_{I o (s)}

, and the chosen controller type for the output current regulator is an Integral (I) controller, hence:

K_{I_{o}} (s) = k_{i} \frac{1}{s}

(16)

The Bode analysis of

F o l_{I_{o}} (s)

K_{I_{o}} (s)

and

G (s)

are shown in Figure 9:

According to Figure 9, it follows:

\begin{matrix} α & = \frac{k_{i} L_{o}}{R_{x o}} \end{matrix}

(17a)

\begin{matrix} \frac{α {\bar{v}}_{e}}{R_{x o}} & = \frac{B_{ω_{I o} L_{o}}}{R_{x o}} \end{matrix}

(17b)

\begin{matrix} k_{i} & = \frac{B_{ω_{I o} R_{x o}}}{N {\bar{v}}_{e}} \end{matrix}

(17c)

where

B_{ω_{I_{o}}}

is the bandwidth of the output regulator, which is fixed ten time less than the switching frequency of the MOSFETs,

f_{s w}

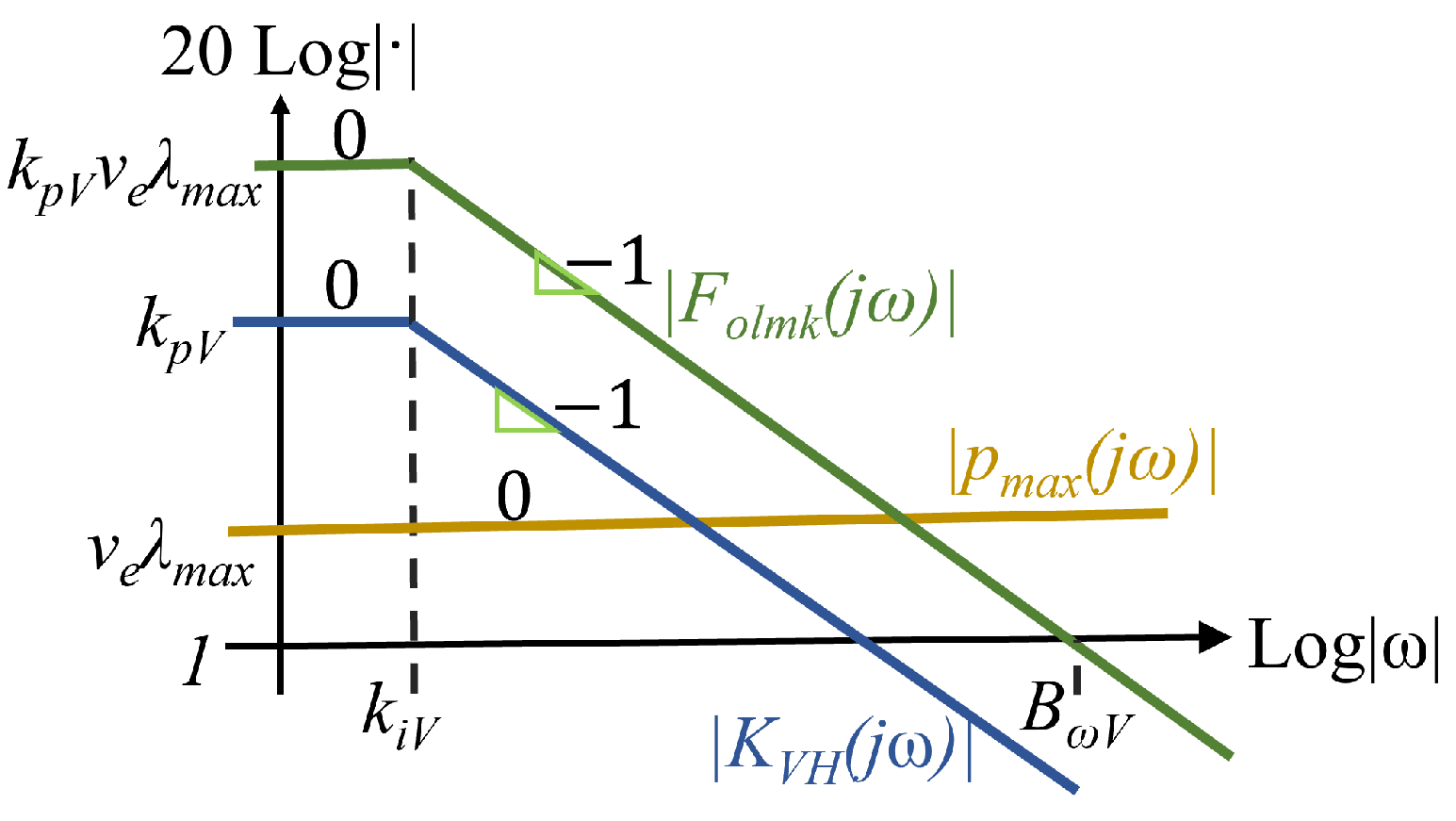
5.2. Design of the cell power balancing controllers

The balancing controller is designed based on the

F_{o l_{V H}} (s)

expression. According to (15),

F_{o l_{V H}} (s) = {\bar{v}}_{e} K_{V_{H}} (s) D_{i f f}

. Then, decomposing

D_{i f f}

in its modal and diagonal matrix,

F_{o l_{V H}} (s)

follows to:

\begin{matrix} D_{i f f} & = V_{e i g} Λ V_{e i g}^{- 1} \end{matrix}

(18a)

\begin{matrix} F_{o l_{V H}} (s) & = V_{e i g} \underset{Π (s)}{\underset{︸}{{\bar{v}}_{e} K_{V_{H}} (s) Λ}} V_{e i g}^{- 1} \end{matrix}

(18b)

where

Λ

and

V_{e i g}

are the Diagonal and Modal matrix of

D_{i f f}

, respectively. It should be noted that one eigenvalue of

D_{i f f}

is equal to 0, because it is a Laplacian of a graph.

\begin{matrix} Λ = [\begin{matrix} λ_{1} & 0 & \dots & 0 \\ 0 & λ_{2} & ⋱ & ⋮ \\ ⋮ & ⋱ & ⋱ & 0 \\ 0 & \dots & 0 & λ_{N} \end{matrix}] & ; λ_{1} = 0 \end{matrix}

(19)

Π (s)

represents the transfer function of the modal response, defined as:

Π (s) = K_{V_{H}} (s) [\begin{matrix} p_{1} (s) & 0 & \dots & 0 \\ 0 & p_{2} (s) & ⋱ & ⋮ \\ ⋮ & ⋱ & ⋱ & 0 \\ 0 & \dots & 0 & p_{N} (s) \end{matrix}]

(20)

where

p_{k} (s) = {\bar{v}}_{e} λ_{k}

Hence the open-loop transfer function of the

k^{t h}

mode is:

F_{o l m_{k}} (s) = {\bar{v}}_{e} λ_{k} K_{V_{H}} (s)

(21)

It should be mentioned that

D_{iff}

corresponds to a circulant matrix

M_{C}

, which is described as:

M_{C} = [\begin{matrix} c_{1} & c_{2} & \dots & c_{N} \\ c_{N} & c_{1} & ⋱ & ⋮ \\ ⋮ & ⋱ & ⋱ & c_{2} \\ c_{2} & \dots & c_{N} & c_{1} \end{matrix}]

(22)

Since

D_{iff}

is a circulant matrix, it is possible to obtain an expression of its eigenvalues. According to [27] the eigenvalues of a circulant matrix are:

λ_{k} = \sum_{n = 1}^{N} c_{n} e^{\hat{j} \frac{2 π (n - 1) (k - 1)}{N}}

(23)

where

\hat{j} = \sqrt{- 1}

It can be observed that for the case of the

D_{iff}

, the coefficients,

c_{k}

s, are:

c_{n} = \{\begin{matrix} 2 & ; n = 1 \\ - 1 & ; n = \{\begin{matrix} 2, & N \end{matrix}\} \\ 0 & ; n = \{\begin{matrix} 3, & 4, & \dots, & N - 1 \end{matrix}\} \end{matrix}

(24)

Therefore, according to (23) and (24), the eigenvalues of

D_{iff}

are defined as:

\begin{matrix} λ_{k} = & c_{1} + c_{2} e^{\frac{2 π (k - 1)}{N} \hat{j}} + c_{N} e^{\frac{2 π (k - 1) (N - 1)}{N} \hat{j}} \\ λ_{k} = & 2 (1 - cos (\frac{2 π (k - 1)}{N})) \end{matrix}

(25)

Notice that the first eigenvalue,

λ_{1}

, is equal to 0, validating that it also represents the Laplacian of a graph. Furthermore, because of the symmetric property of the cosine, the

k^{t h}

eigenvalue is equal to the

{(N + 1 - k)}^{t h}

eigenvalue. Finally, the highest eigenvalue is obtained for

k = \frac{N}{2} + 1

when N is even, and

k = \frac{N \pm 1}{2} + 1

when N is odd. The maximum case is produced when N is even, generating a

λ_{m a x} = 4

. For odd values of N the highest eigenvalue tends to be 4 when N increases. The design of the balancing controller is based on the possible maximum eigenvalue,

λ_{m a x}

, and the minimum eigenvalue,

λ_{m i n} = λ_{1}

, which values are 4 and 0, respectively.

λ_{m i n} = 0

means the system presents a pure integrator that theoretically is stable. However, because of numeric approximations in the implementation, the system may be unstable after a long lapse. For that reason, the selected controller corresponds to a low-pass filter that ensures the stability of the system, with a pole located at a very low frequency. Hence, the proposed controller is:

K_{V H} (s) = k_{p V} (\frac{k_{i V}}{s + k_{i V}})

(26)

In order to determine the parameters of the controller, Figure 10 shows the Bode diagram of

K_{V H} (s)

p_{k} (s)

f_{o l m k} (s)

Based on the Bode diagram of Figure 10, the bandwidth

B_{ω V}

is set using the

k_{p V}

parameter:

\begin{matrix} v_{e} λ_{m a x} k_{p V} & = \frac{B_{ω V}}{k_{i V}} \\ k_{p V} & = \frac{B_{ω V}}{v_{e} λ_{m a x} k_{i V}} \end{matrix}

(27)

The bandwidth,

B_{ω V}

, must be ten times less than the switching frequency

2 π f_{s w}

. Due to that, the converter can work either as an inverter, or as a DC/DC converter, the pole

k_{i V}

is selected ten times less than the operating frequency of the inverter.

6. Results

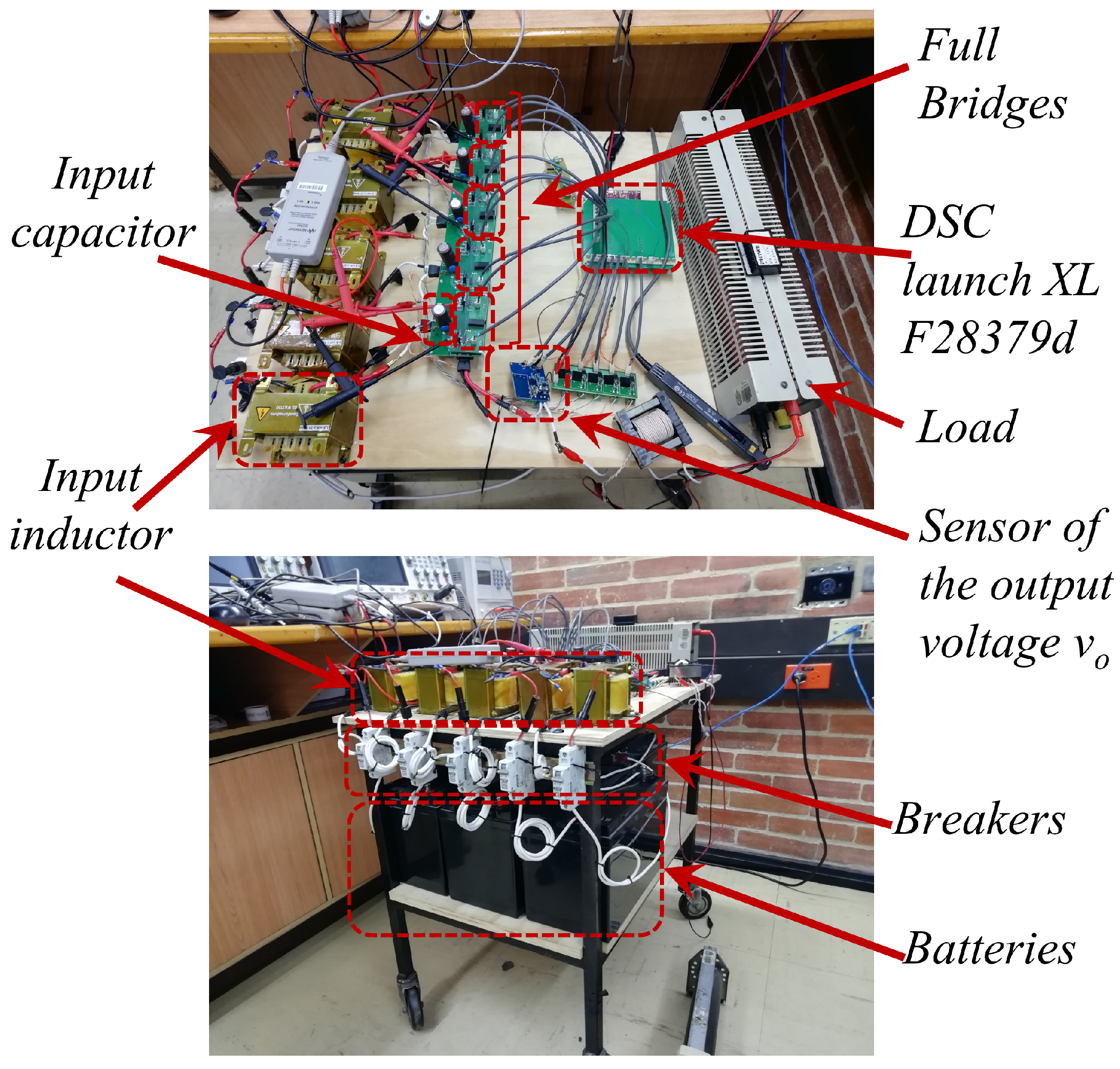
A prototype implements the proposed decentralized controller is now considered. It has been carried out in the laboratory for measurement purpose. The controllers are implemented in a Cascaded Multilevel Inverter of 5 FBs, as shown in Figure 11.

Both simulation and experimental results, developed hereafter, are obtained with the converter working as a DC/AC converter, with three different tests: an input voltage step, a load step and a cell insertion during operation. Furthermore, a modal response simulation is also presented. The parameters of the controllers are shown in Table 1:

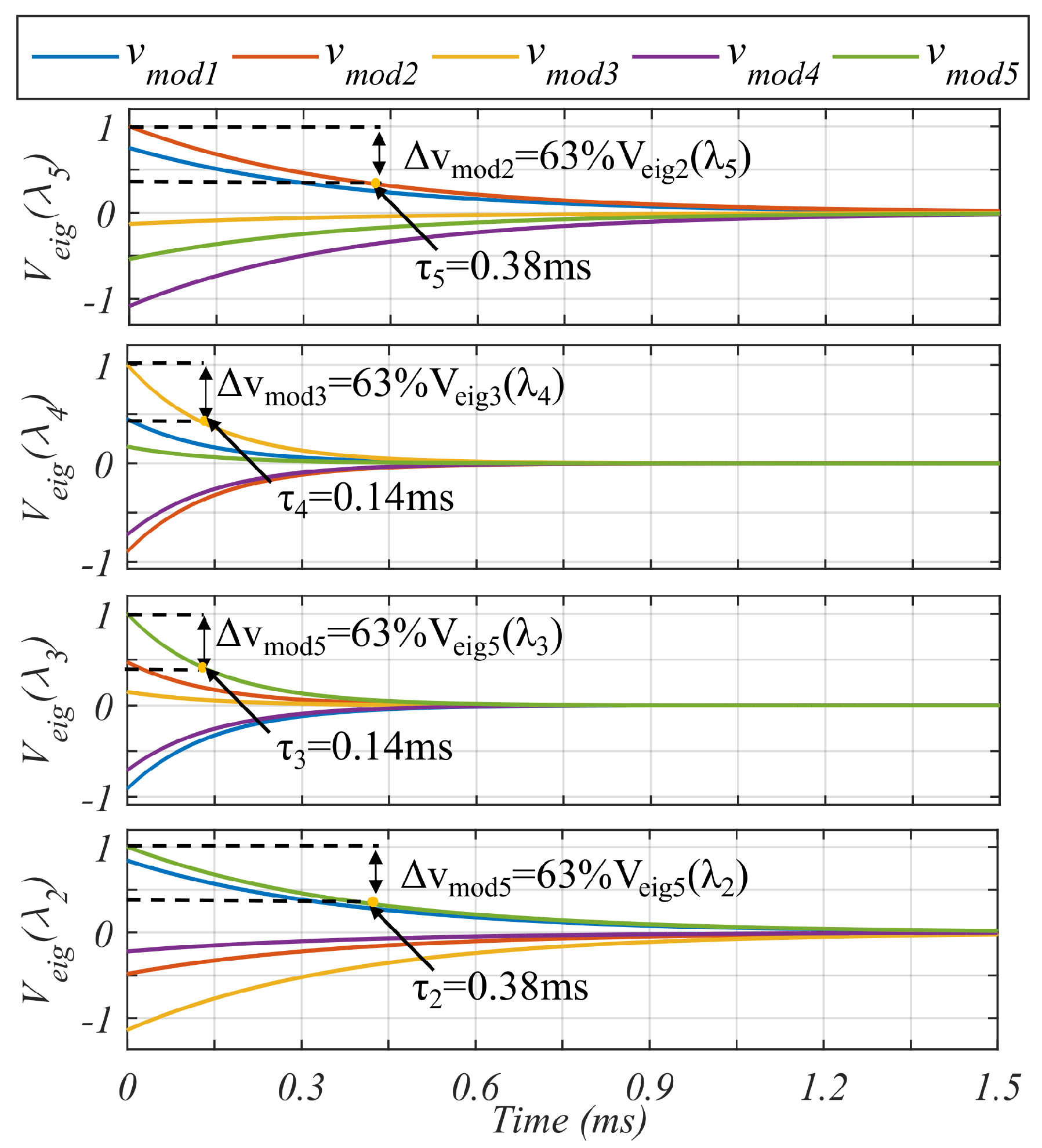
6.1. Modal Response Simulation

This simulation corresponds to the modal respond of the transfer function of the balancing loop. For

N = 5

Λ

corresponds to:

Λ = \frac{\sqrt{5}}{2} \begin{matrix} [c] 0 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5} - 1 & 0 & 0 & 0 \\ 0 & 0 & \sqrt{5} + 1 & 0 & 0 \\ 0 & 0 & 0 & \sqrt{5} + 1 & 0 \\ 0 & 0 & 0 & 0 & \sqrt{5} - 1 \end{matrix}

(28)

Appendix 1 shows the demonstration of these values, which their numeric values are:

{[\begin{matrix} λ_{1} & λ_{2} & λ_{3} & λ_{4} & λ_{5} \end{matrix}]}^{T} = {[\begin{matrix} 0 & 1.38 & 3.62 & 3.62 & 1.38 \end{matrix}]}^{T}

while the modal matrix,

V_{e i g}

, is:

V_{eig} = \begin{matrix} \underset{V_{eig} (λ_{1})}{\underset{︸}{[\begin{matrix} 1.00 \\ 1.00 \\ 1.00 \\ 1.00 \\ 1.00 \end{matrix}}} & \underset{V_{eig} (λ_{2})}{\underset{︸}{\begin{matrix} 1.00 \\ - 0.57 \\ - 1.35 \\ - 0.26 \\ 1.19 \end{matrix}}} & \underset{V_{eig} (λ_{3})}{\underset{︸}{\begin{matrix} 1.00 \\ - 0.52 \\ - 0.16 \\ 0.78 \\ - 1.1 \end{matrix}}} & \underset{V_{eig} (λ_{4})}{\underset{︸}{\begin{matrix} 1.00 \\ - 2.00 \\ 2.23 \\ - 1.61 \\ 0.38 \end{matrix}}} & \underset{V_{eig} (λ_{5})}{\underset{︸}{\begin{matrix} 1.00 \\ 1.33 \\ - 0.18 \\ - 1.44 \\ - 0.72 \end{matrix}]}} \end{matrix}

(29)

Using the eigenvectors as the initial conditions, Figure 12 shows the modal respond of the system.

It is clearly observed that the system is stable and the time response of the modes are very different. Depending on the parameter

k_{p V}

of the decentralized controller, this time response can be adjusted. Table 2 shows a comparison between the theoretical time constants and the ones obtained by simulation.

Notice that given that there are two pairs of similar eigenvalues, there are also two pairs of time constants, meaning that there are two double poles at these time constants. Furthermore, it can be observed that simulated and theoretical values are very similar, validating the performance of the controller.

6.2. Full System Simulation Results

The first simulation test corresponds to a load transient from 95

Ω

to 70

Ω

. Figure 13 shows

v_{s}

and

i_{o}

when the converter works as a DC/AC converter.

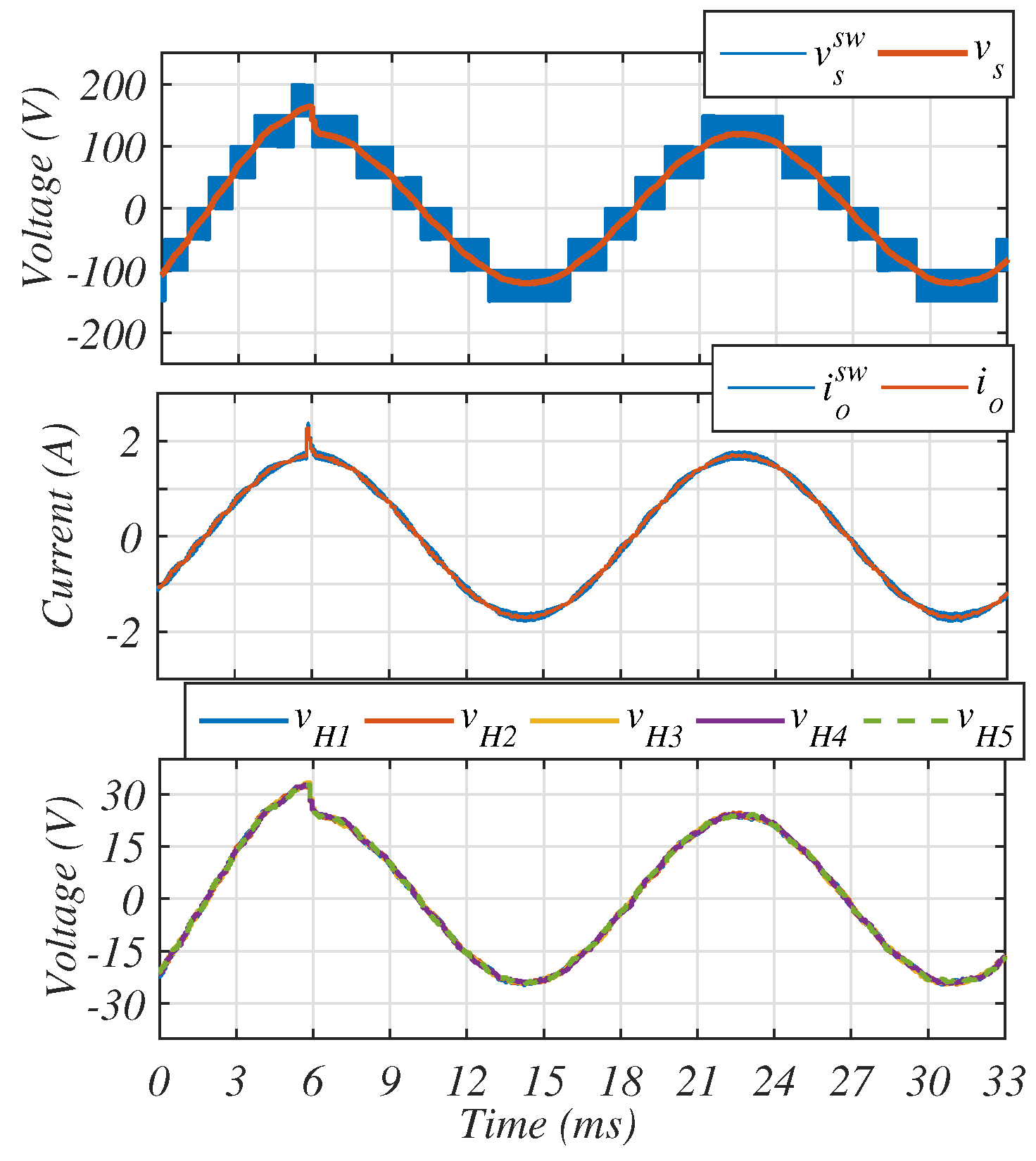
It is observed that before the disturbance occurs, the multilevel converter uses 9 voltage levels. After the disturbance, only 7 levels are required to regulate the output current. Notice also that the CVs are balanced during all the simulation, before and after the disturbance, validating for DC/AC conversion that when a disturbance in the output current occurs, the CVs are not unbalanced, only their common average value are affected. Furthermore, the current is stabilized during a small transient, less than 1 ms.

The next simulation result, shown in Figure 14, corresponds to an input cell voltage disturbance, i.e. a step voltage from 40 to 50V for the inverter with a resistive load of 77

Ω

It should be noted that the voltage disturbance almost affects neither the output current

i_{o}

nor the output voltage

v_{s}

, while the CVs are automatically balanced thanks to the decentralized controllers in only 0.5 ms. Figure 14 also shows that, by nature of the inverter, when one of the input voltages is 40 V, there exists an asymmetric ripple in

i_{o}^{s w}

and

v_{s}^{s w}

and when the input voltage is 50 V, the ripples are equalized. However, in both cases the average output current

i_{o}

and the

v_{H k}

s are well regulated and balanced, respectively.

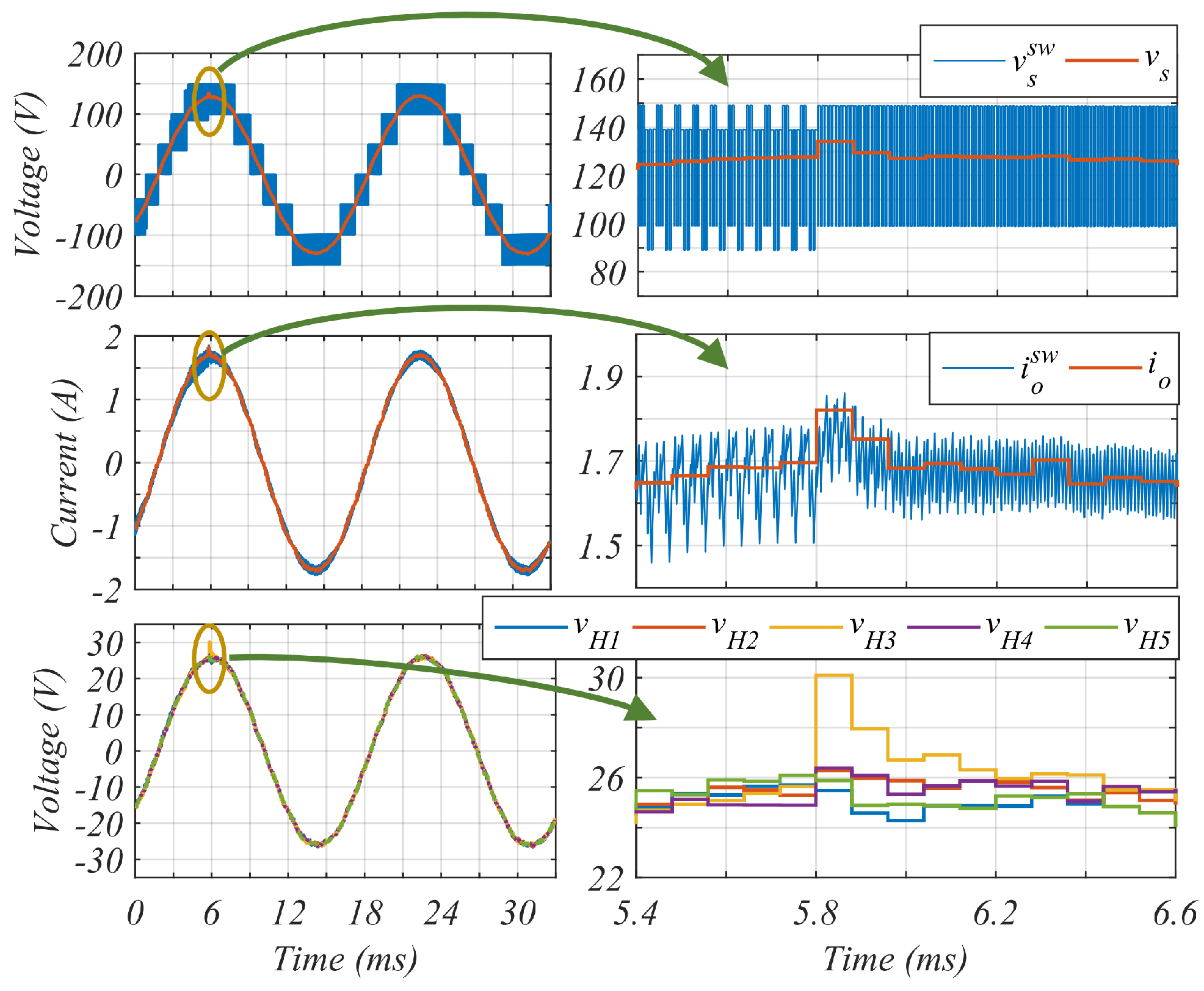
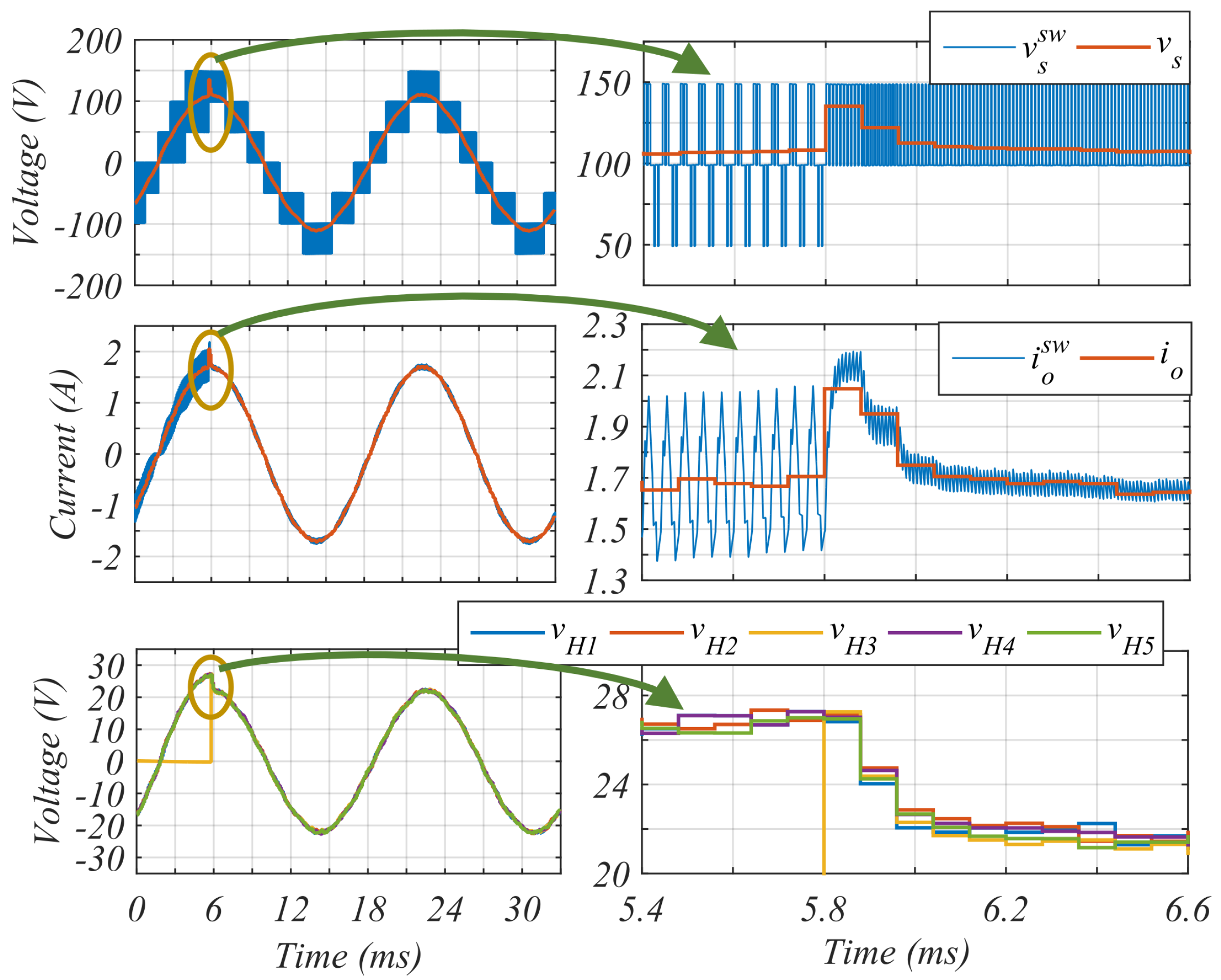
The next simulation corresponds to a cell insertion during operation, going from 4 FBs to 5 FBs, when the converter operates as an inverter. Figure 15 shows the results obtained for the

v_{H k}

i_{o}

and

v_{s}

signals.

It should be noticed that before the cell insertion,

i_{o}

and

v_{s}

present both a high ripple, due to a constant control signal interleaving set for 5 cells, i.e. signal phase. Even if the ripple is high, the average value of the output current is regulated when only 4 cells are activated. When the fifth FB cell is inserted,

i_{o}

presents an overshoot and then it is stabilized in less than 0.25 ms.

v_{H k}

s voltages are balanced when there are 4 FBs and then, when the 5^th cell is inserted, there are auto balanced, reaching a new operation point in 0.25 ms approximately.

This test validates by simulation the three functions of the controller, the balancing of the CV, the regulation of the GV, and the bypass system activation. It can be inferred that all the simulation results are in concordance with the previous theoretical study, producing the expected behavior in terms of reconfigurability, bandwidth and stability for this multilevel converter topology.

6.3. Experimental Results

The experimental results are developed with a prototype composed of a CFBMC of 5 FB, fed by Li-ion Batteries of 48 V, with the parameters described in Table 1. More details related to the construction of the inverter is presented in [28].

In order to compare the simulation and experimental results, the tests developed here are the same than the ones illustrated in the previous simulations.

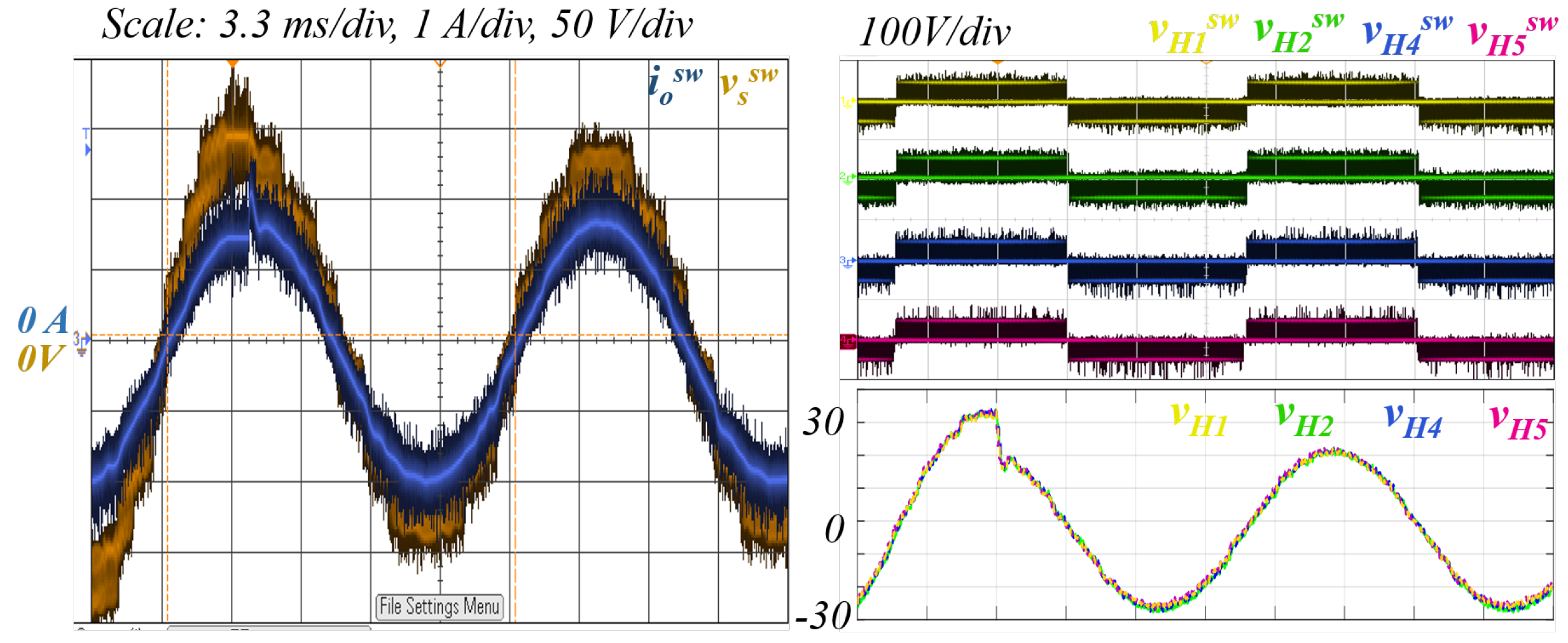
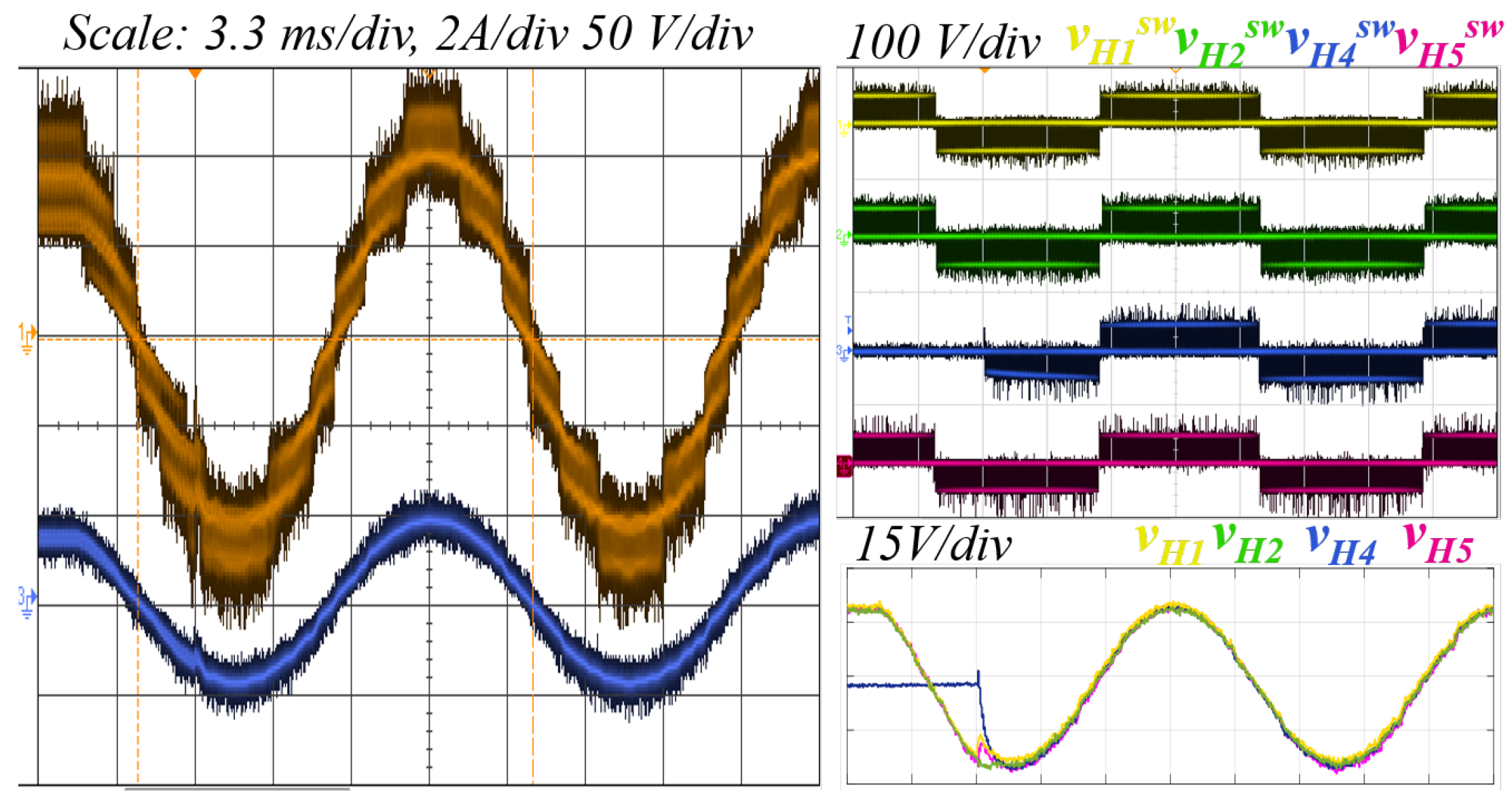
Figure 16 shows the experimental results of first test, corresponding to a load step (or load transient). It can be seen that there exists a concordance with the simulation result of this test, presenting similar overshoot in the current and similar settling time. Moreover, the switching levels of

v_{s}

are the same. Furthermore, as happened in the simulation, the operating points of

v_{H k}

s change in 0.5 ms without any unbalance between them.

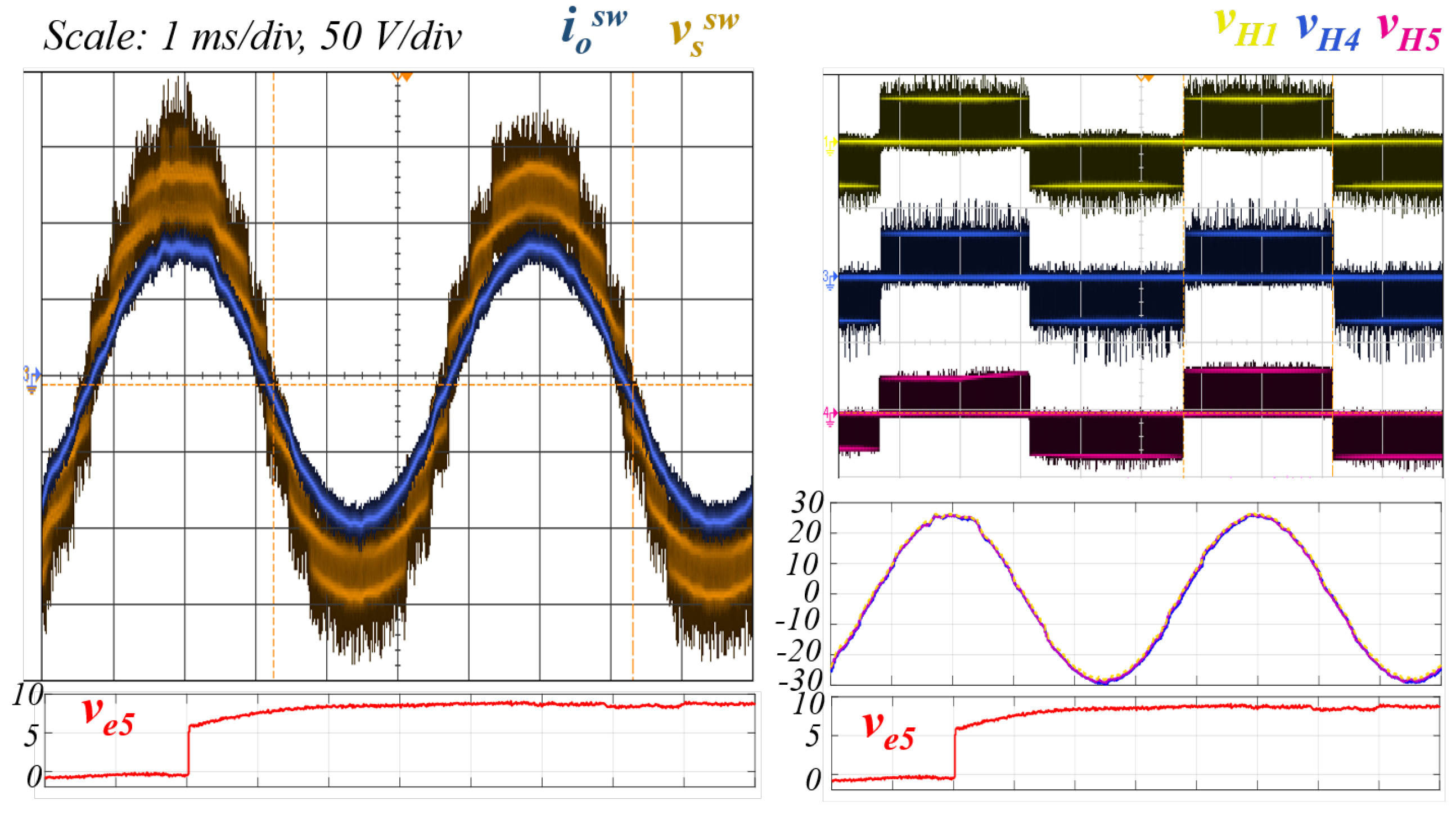
The next result corresponds to the disturbance in one input voltage FB cell. Figure 17 shows the behavior of the output current

i_{o}^{s w}

, the output voltage

v_{s}^{s w}

, the switching output voltage of each FB 1, 4 and 5,

v_{H k}^{s w}

\forall k = {1, 4, 5}

, and their respectively moving average,

v_{H k}

It should be noted that the step voltage is almost not detected in

v_{H}

s. This is because the input filters presented in the converter smooth the effect of the voltage disturbance. Furthermore, it can be observed that during all the experiments

v_{H k}

s voltage are well balanced. This observation also validates the balancing controller, maintaining the same output voltage of each FB cell even when the input voltages change. Additionally, the output current is well regulated.

The next result, presented in Figure 18, corresponds to a FB cell insertion during operation, starting with 4 FB cell and inserting the 5^th FB cell. It is important to note that the current follows the reference during all the experiments, presenting a small transient when the FB cell is inserted. Furthermore, it can be observed that the CVs are well balanced after the insertion, reaching a new operating point with a settling time of 0.6 ms, approximately. These values are in concordance with the predicted time constants of the system and show a strong similarity with the simulation results. This test validates the three stages of the controller, the balancing controller, the GV regulator, and the bypass system.

It can be inferred that all the experimental tests are in concordance with the simulation tests and the theoretical studies developed in this paper, demonstrating the good performance of the controller for this topology.

7. Conclusion

A decentralized control principle for the balancing of the power delivered by the FB cell of a multilevel converter has been shown in this paper.

The decentralized control is composed of several controllers, each associated with a cell of the inverter, which adjust their local control signal by comparing their sensed cell voltage with those of the closest neighbors.

This control method can handle a huge number of cells and makes it possible to obtain a robust system for the case of load transient and cell battery voltages variations.

Moreover, it allows to manage the number of active cells and to carry out reconfiguration during operation. These reconfiguration capability can be useful in case of a cell failure and address functional safety concerns.

Tests of a laboratory prototype help to demonstrate the robustness of the proposed method.

Two future works are in mind with this control method. The first one is the implementation of this controller for balancing the state of charge of the batteries that are the input sources of a CFBMC, and the second future work is the implementation of this control method in a multi-phase buck converter.

8. Appendix

Appendix 8.1. Appendice 1: Demonstration of the eigenvalues

For

N = 5

, the eigenvalues are:

\begin{matrix} λ_{1} = & 2 (1 - cos (0)) \\ λ_{2} = & 2 (1 - cos (\frac{2 π}{5})) \\ λ_{3} = & 2 (1 - cos (\frac{4 π}{5})) \\ λ_{4} = & 2 (1 - cos (\frac{6 π}{5})) \\ λ_{5} = & 2 (1 - cos (\frac{8 π}{5})) \end{matrix}

Using trigonometric identities, follows to:

\begin{matrix} λ_{1} = & 0 \\ λ_{2} = & 2 (1 - cos (\frac{2 π}{5})) \\ λ_{3} = & 2 (1 + cos (\frac{π}{5})) \\ λ_{4} = & 2 (1 + cos (\frac{π}{5})) \\ λ_{5} = & 2 (1 - cos (\frac{2 π}{5})) \end{matrix}

assigning

α = c o s (π / 5)

, and using trigonometric identities follows:

\begin{matrix} λ_{1} = & 0 \\ λ_{2} = & 4 (1 - α^{2}) \\ λ_{3} = & 2 (1 + α) \\ λ_{4} = & 2 (1 + α) \\ λ_{5} = & 4 (1 - α^{2}) \end{matrix}

Hence, obtaining

α

all the eigenvalues are found. Taking into account that

cos (\frac{π}{2}) = 0

cos (2 \frac{π}{5} + (\frac{1}{2}) \frac{π}{5}) = 0

, hence:

cos (2 \frac{π}{5}) cos ((\frac{1}{2}) \frac{π}{5}) - sin (2 \frac{π}{5}) sin ((\frac{1}{2}) \frac{π}{5}) = 0

Using the double and half angle formulas and taking into account that

α = cos (\frac{π}{5})

follows:

Hence:

\begin{matrix} λ_{1} = & 0 \\ λ_{2} = & \frac{\sqrt{5}}{2} (\sqrt{5} - 1) \\ λ_{3} = & \frac{\sqrt{5}}{2} (\sqrt{5} + 1) \\ λ_{4} = & \frac{\sqrt{5}}{2} (\sqrt{5} + 1) \\ λ_{5} = & \frac{\sqrt{5}}{2} (\sqrt{5} - 1) \end{matrix}

References

Mohan, N.; Undeland, T.; Robbins, W.P. Power Electronics: Converters, Applications and Design. 1989.
Rashid, M.H. Power electronics: devices, circuits and applications; Pearson, 2014. [Google Scholar]
Vivert, M.; Cousineau, M.; Ladoux, P.; Fabre, J. Decentralized Controller for the Cell-Voltage Balancing of a Multilevel Flying Cap Converter. In Proceedings of the PCIM Europe 2019; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management; 2019; pp. 1–8. [Google Scholar]
Fabre, J.; Ladoux, P.; Solano, E.; Gateau, G.; Blaquière, J. Full SiC multilevel chopper for three-wire supply systems in DC electric railways. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, 2016, Ship Propulsion and Road Vehicles International Transportation Electrification Conference (ESARS-ITEC); pp. 1–7. [CrossRef]
Fabre, J.; Ladoux, P.; Solano, E.; Gateau, G.; Blaquière, J. MVDC Three-Wire Supply Systems for Electric Railways: Design and Test of a Full SiC Multilevel Chopper. IEEE Transactions on Industry Applications 2017, 53, 5820–5830. [Google Scholar] [CrossRef]
Meynard, T.A.; Foch, H. Multi-level conversion: high voltage choppers and voltage-source inverters. In Proceedings of the PESC ’92 Record. 23rd Annual IEEE Power Electronics Specialists Conference; 1992; pp. 397–403. [Google Scholar] [CrossRef]
Meynard, T.A.; Fadel, M.; Aouda, N. Modeling of multilevel converters. IEEE Transactions on Industrial Electronics 1997, 44, 356–364. [Google Scholar] [CrossRef]
Negash, M.F.; Manthati, U.B. Development of 7-level cascaded H-bridge inverter topology for PV applications. In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techniques, ICEEOT 2016; IEEE: Chennai, Tamil Nadu, India, 2016; pp. 1847–1852. [Google Scholar] [CrossRef]
Vivert, M.; Diez, R.; Cousineau, M.; Bernal Cobaleda, D.; Patino, D.; Ladoux, P. Real-Time Adaptive Selective Harmonic Elimination for Cascaded Full-Bridge Multilevel Inverter. Energies 2022, 15. [Google Scholar] [CrossRef]
Luo, F.L.; Ye, H. Multilevel DC/AC Inverters. In Advanced DC/AC Inverters: Aplications in Renewable Energy; chapter 8; CRC Press: Boca Raton, FL, 2013; pp. 137–154. [Google Scholar]
Luo, F.L.; Ye, H. Trinary Hybrid Multilevel Inverters. In Advanced DC/AC Inverters: Aplications in Renewable Energy; chapter 9; CRC Press: Boca Raton, FL, 2013; pp. 155–205. [Google Scholar]
Vivert, M.; Patino, D.; Diez, R. Modulation Strategy and Controller for Grid-Tied Trinary Hybrid Multilevel Inverter. IEEE Journal of Emerging and Selected Topics in Power Electronics. [CrossRef]
Liu Yu, F.L. Trinary hybrid 81-level multilevel inverter for motor drive with zero common-mode voltage. IEEE Transactions on Industrial Electronics 2008, 55, 1014–1021. [Google Scholar] [CrossRef]
Cousineau, M.; Cougo, B. Interleaved converter with massive parallelization of high frequency GaN switching-cells using decentralized modular analog controller. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE); 2015; pp. 4343–4350. [Google Scholar] [CrossRef]
Le Bolloch, M.; Cousineai, M.; Meynard, T. New Masterless Modular Current-Sharing technique for DC/DC Parallel converters. In Proceedings of the Proceedings of 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010 2010, T3–73–T3–80. [Google Scholar] [CrossRef]
Fabre, J.; Ladoux, P. Parallel Connection of 1200-V/100-A SiC-MOSFET Half-Bridge Modules. IEEE Transactions on Industry Applications 2016, 52, 1669–1676. [Google Scholar] [CrossRef]
Sahoo, S.K.; Bhattacharya, T. Phase-Shifted Carrier-Based Synchronized Sinusoidal PWM Techniques for a Cascaded H-Bridge Multilevel Inverter. IEEE Transactions on Power Electronics 2018, 33, 513–524. [Google Scholar] [CrossRef]
Huang, Q.; Huang, A.Q. Feedforward Proportional Carrier-Based PWM for Cascaded H-Bridge PV Inverter. IEEE Journal of Emerging and Selected Topics in Power Electronics 2018, 6, 2192–2205. [Google Scholar] [CrossRef]
Tengfei Wang.; Yongqiang Zhu. Analysis and comparison of multicarrier PWM schemes applied in H-bridge cascaded multi-level inverters. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, 2010, pp. 1379–1383. [CrossRef]
Arazm, S.; Vahedi, H.; Al-Haddad, K. Phase-shift modulation technique for 5-level packed U-cell (PUC5) inverter. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018); 2018; pp. 1–6. [Google Scholar] [CrossRef]
Vivert, M.; Cousineau, M.; Ladoux, P.; Fabre, J.; Mannes-Hillesheim, M.; Diez, R.; Patino, D. Decentralized Control for Balancing the Cell Voltages of a High Conversion Ratio Flying Capacitor Multilevel Converter. IEEE Journal of Emerging and Selected Topics in Industrial Electronics 2022, 3, 635–646. [Google Scholar] [CrossRef]
Xu, B.; Tu, H.; Du, Y.; Yu, H.; Liang, H.; Lukic, S. A Distributed Control Architecture for Cascaded H-Bridge Converter. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC); 2019; pp. 3032–3038. [Google Scholar] [CrossRef]
Vivert, M.; Patino, D.; Diez, R.; Cobaleda, D.B.; Cousineau, M. Decentralized Controller for a Grid Tied Cascade Multilevel Invert. In Proceedings of the IEEE 3rd Colombian Conference on Automatic Control (CCAC); 2019. [Google Scholar]
Achanta, P.K.; Maksimovic, D.; Ilic, M. Decentralized control of series stacked bidirectional DC-AC modules. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC); 2018; pp. 1008–1013. [Google Scholar] [CrossRef]
He, J.; Li, Y.; Liang, B.; Wang, C. Inverse Power Factor Droop Control for Decentralized Power Sharing in Series-Connected-Microconverters-Based Islanding Microgrids. IEEE Transactions on Industrial Electronics 2017, 64, 7444–7454. [Google Scholar] [CrossRef]
Vivert, M.; Patino, D.; Diez, R. Variation of a sliding mode control applied to a trinary hybrid multilevel inverter. In Proceedings of the 2017 IEEE 3rd Colombian Conference on Automatic Control (CCAC); 2017; pp. 1–6. [Google Scholar] [CrossRef]
Gray, R.M. Toeplitz and circulant matrices: a review; Now Publishers, 2006. [Google Scholar]
Diego Bernal Cobaleda, Miguel Vivert, R.D.G.P. Low-Voltage Cascade Multilevel Inverter with GaN Devices for Energy Storage System. In Proceedings of the 13th IEEE International Conference on Power Electronics and Drive Systems (PEDS 2019), 2019.

Figure 1. Cascaded Full-Bridge Multilevel Converter of N FBs

Figure 2. Equivalent circuit of the average model of the Cascaded Multilevel Converter of N FBs

Figure 3. Equivalent circuit of the linear model of the Cascaded Multilevel Converter of N levels

Figure 4. Block diagram of the linear model of the cascaded FB multilevel converter

Figure 5. Block diagram of the control system computing the local duty-cycle

U_{k} (s)

of the

k^{t h}

cell.

Figure 5. Block diagram of the control system computing the local duty-cycle

U_{k} (s)

of the

k^{t h}

cell.

Figure 6. Block diagram of the linear model of the cascaded FB multilevel converter with the proposed controller in closed-loop chain of communication

Figure 7. Block diagram of the Closed-Loop system with the proposed controller

Figure 8. Simplified closed-loop transfer function of the system

Figure 9. Bode diagram of

G (s)

K_{V H} (s)

and

F_{o l_{I o}} (s)

Figure 9. Bode diagram of

G (s)

K_{V H} (s)

and

F_{o l_{I o}} (s)

Figure 10. Bode diagram of

p_{m a x}

K_{V H} (s)

and

F_{o l m k} (s)

of the CFBC

Figure 10. Bode diagram of

p_{m a x}

K_{V H} (s)

and

F_{o l m k} (s)

of the CFBC

Figure 11. Setup of the Cascaded Full-Bridge Multilevel Inverter

Figure 12. Modal response of the of the CFBMC with the decentralized controller

Figure 13. Load transient test as a DC/AC converter

Figure 14. Input cell voltage step response simulation for the inverter case

Figure 15. FB insertion simulation for blue the inverter case

Figure 16. Load transient experimental test in DC/AC mode

Figure 17. Input cell voltage disturbance experimental test.

Figure 18. FB cell insertion experimental test in DC/AC mode

Table 1. Parameters of the CFBMC

Parameter	Value
Number of FBs N	5
Input Voltage ( $v_{e}$ )	$48 V$
Input Inductance (L)	$1.8 m H$
ESR of L (R)	$200 m Ω$
Input Capacitance (C)	$4 m F$
Drain-Source ON Resistance ( $R_{D S}$ )	$58 m Ω$
Frequency of the inverter (f)	60 Hz
$I_{r e f}$ as an inverter	$1.7 sin (2 π f t) A$
$I_{r e f}$ as a DC/DC converter	$1.7 A$
Switching frequency ( $f_{s w}$ )	12.5 kHz
Load Resistance ( $R_{o}$ )	$60 Ω - 100 Ω$
$k_{i}$	1884 $A^{- 1} s^{- 1}$
$k_{p V}$	39 $V^{- 1} s^{- 1}$
$k_{i V}$	37.7 $r a d s / s$

Table 2. Time constants of the CFBMC

$τ_{k}$	Theoretical (ms)	Simulated (ms)
$τ_{2}$	0.384	0.38
$τ_{3}$	0.146	0.14
$τ_{4}$	0.146	0.14
$τ_{5}$	0.384	0.38

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Decentralized Control for the Cell Power Balancing of a Cascaded Full-Bridge Multilevel Converter

Abstract

1. Introduction

2. Description of the system

3. Description of the decentralized controller

3.1. The Bypass System

3.2. The Output Current Regulator

3.3. The Cell Power Balancing Controller

4. Closed-Loop System Analysis

4.1. Output Current Regulator Analysis

4.2. Cell Power Balancing Control loop analysis

4.3. Global closed-loop analysis

5. Design of the controllers

5.1. Design of the Output Current Regulator

5.2. Design of the cell power balancing controllers

6. Results

6.1. Modal Response Simulation

6.2. Full System Simulation Results

6.3. Experimental Results

7. Conclusion

8. Appendix

Appendix 8.1. Appendice 1: Demonstration of the eigenvalues

References

MDPI Initiatives

Important Links

Subscribe