Submitted:
10 March 2023
Posted:
15 March 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Measurement principle
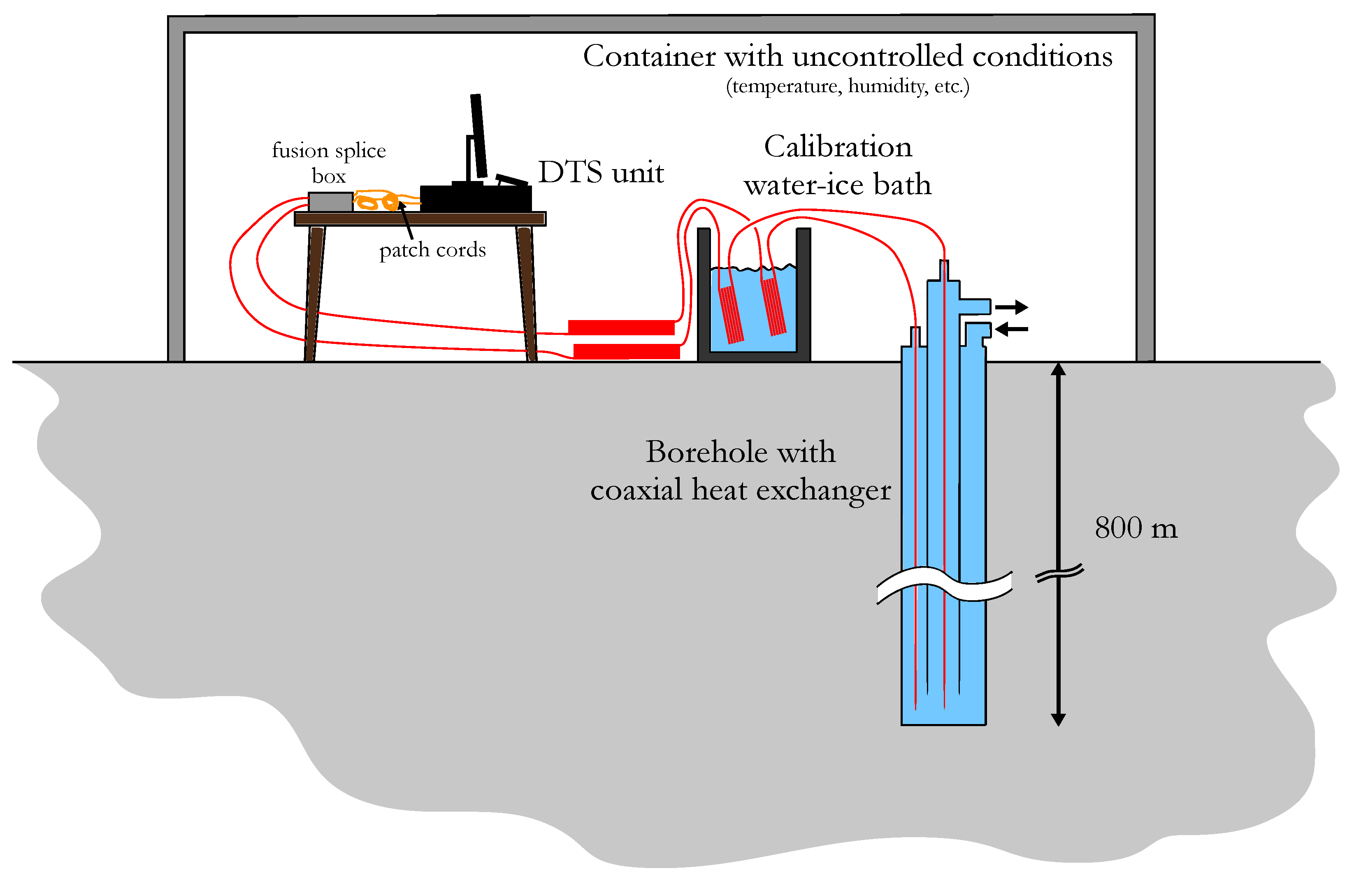
2.2. In-situ DTS configuration
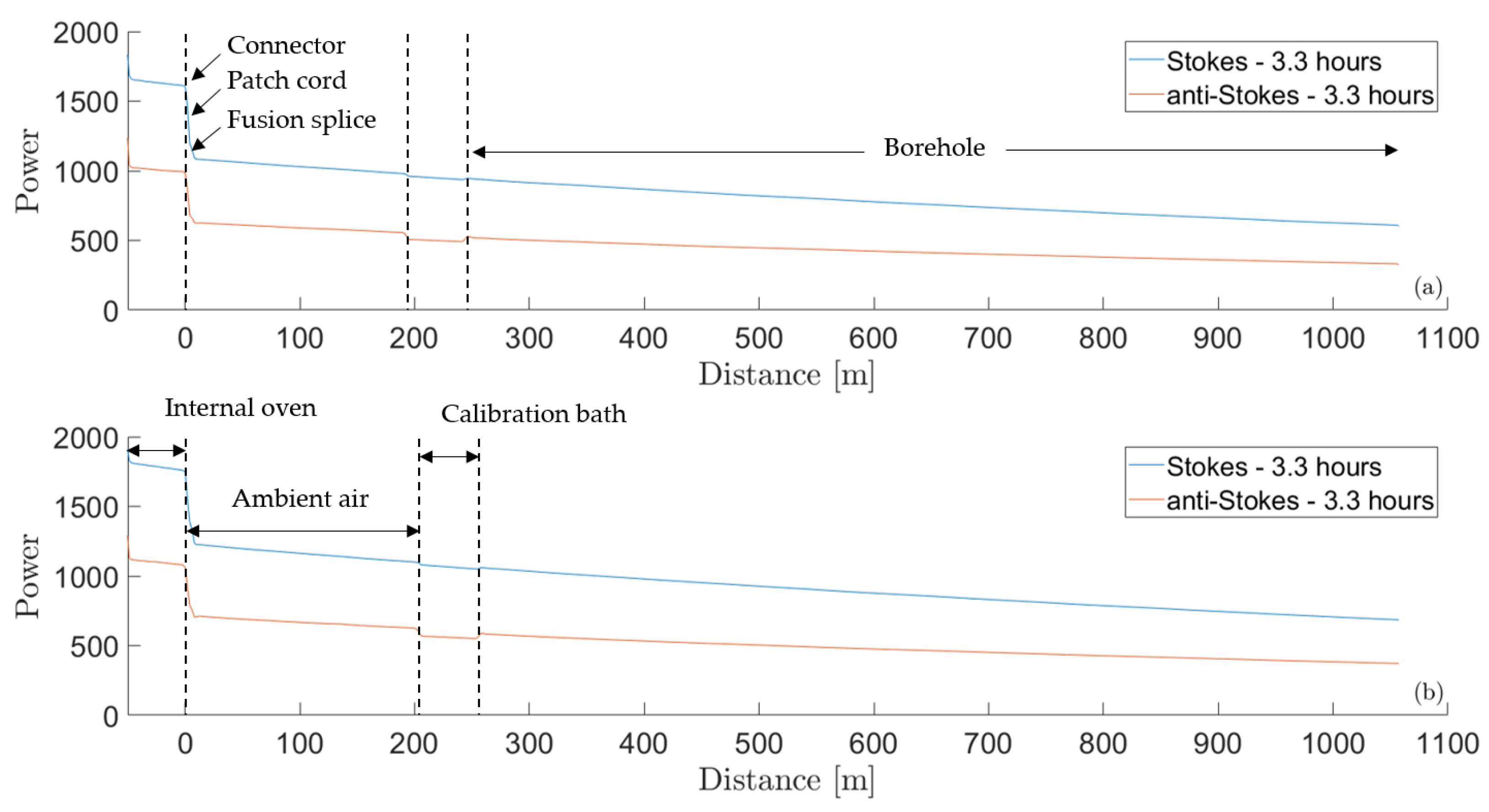
2.3. Correction of temperature drifts
2.4. Calibration
2.5. Uncertainty evaluation
2.5.1. Propagation of error
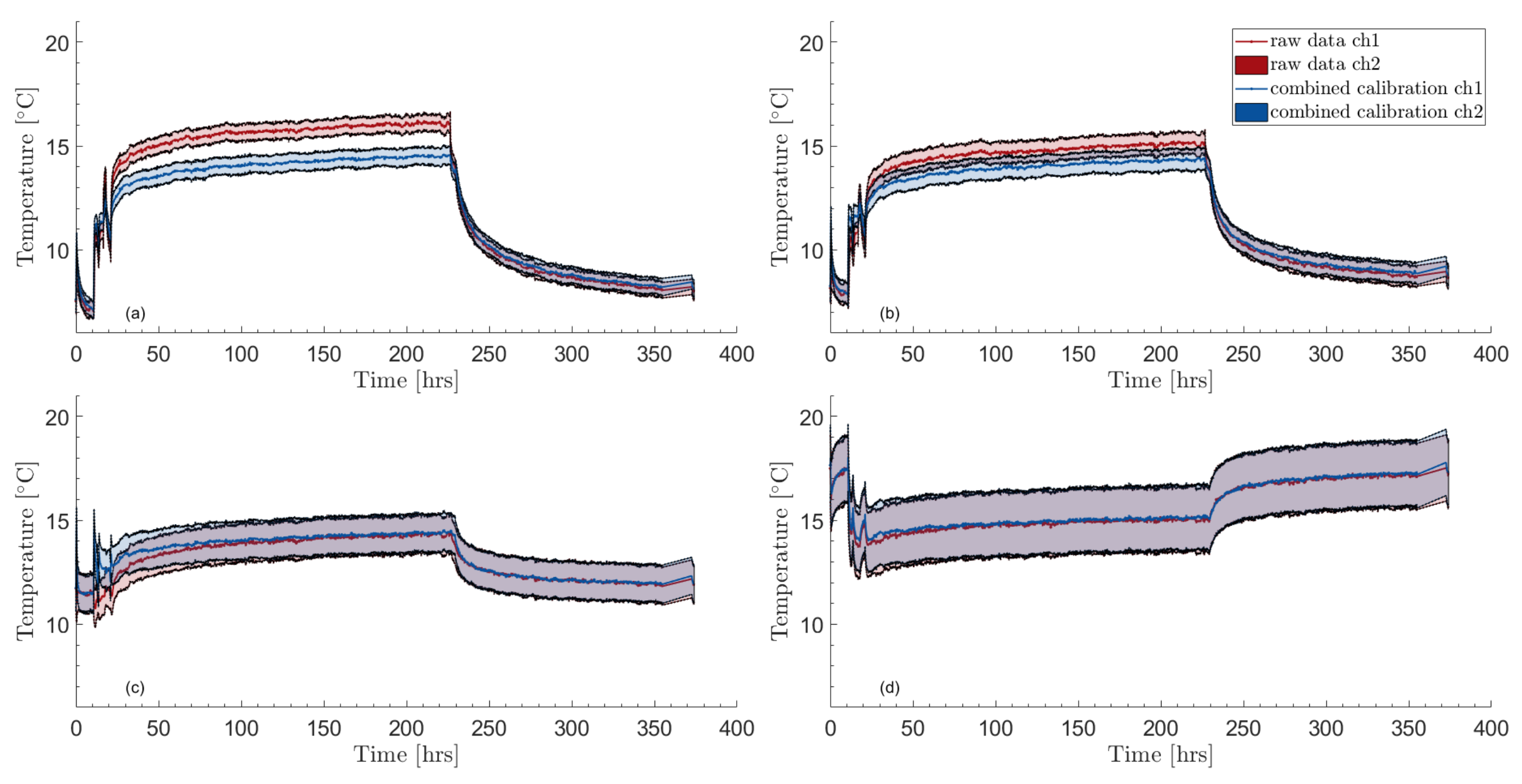
2.5.2. Deviations in bath and bottom conditions
2.5.3. Temperature averaging
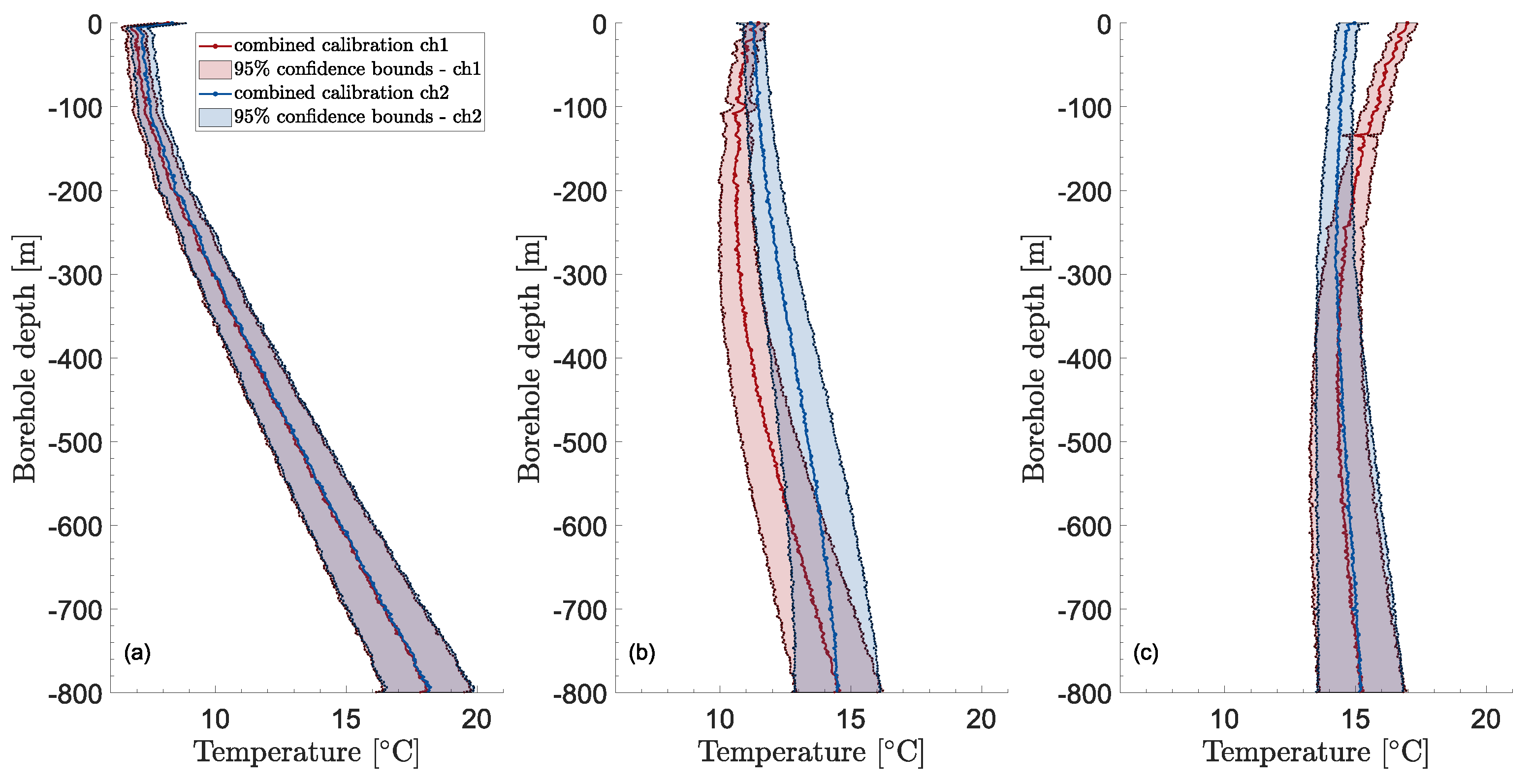
2.5.4. Overall uncertainty, degrees of freedom and extended uncertainty
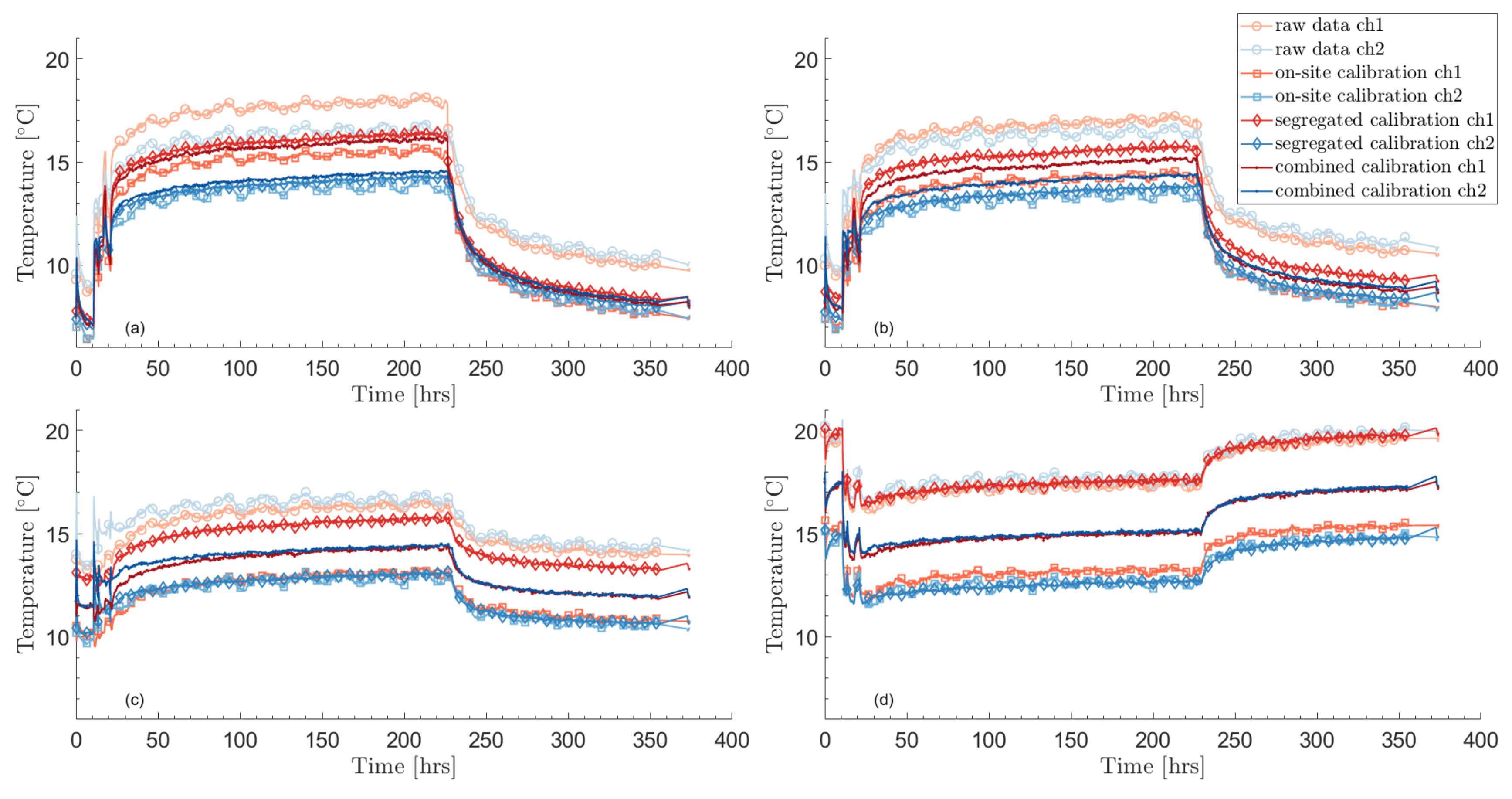
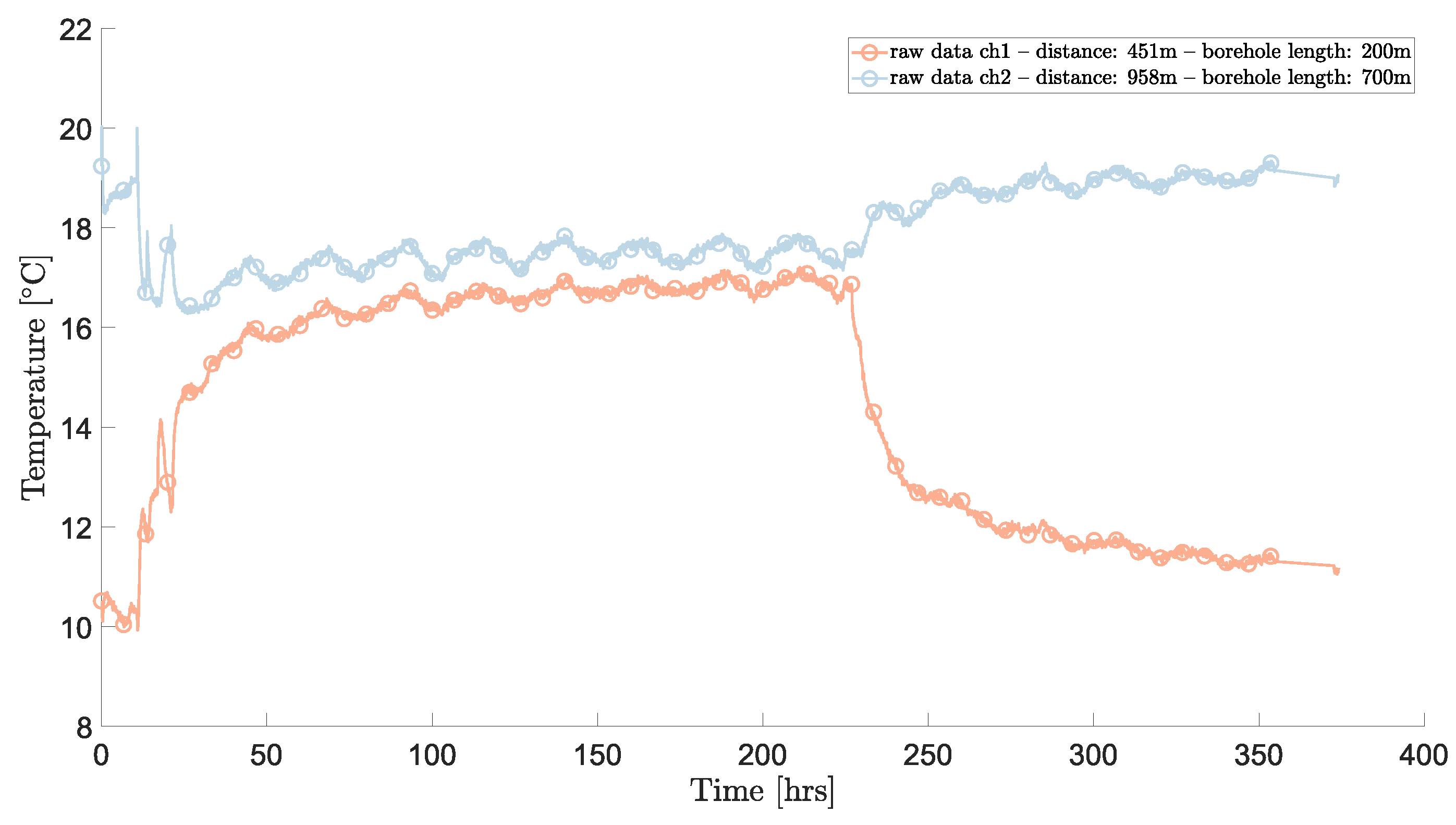
3. Results
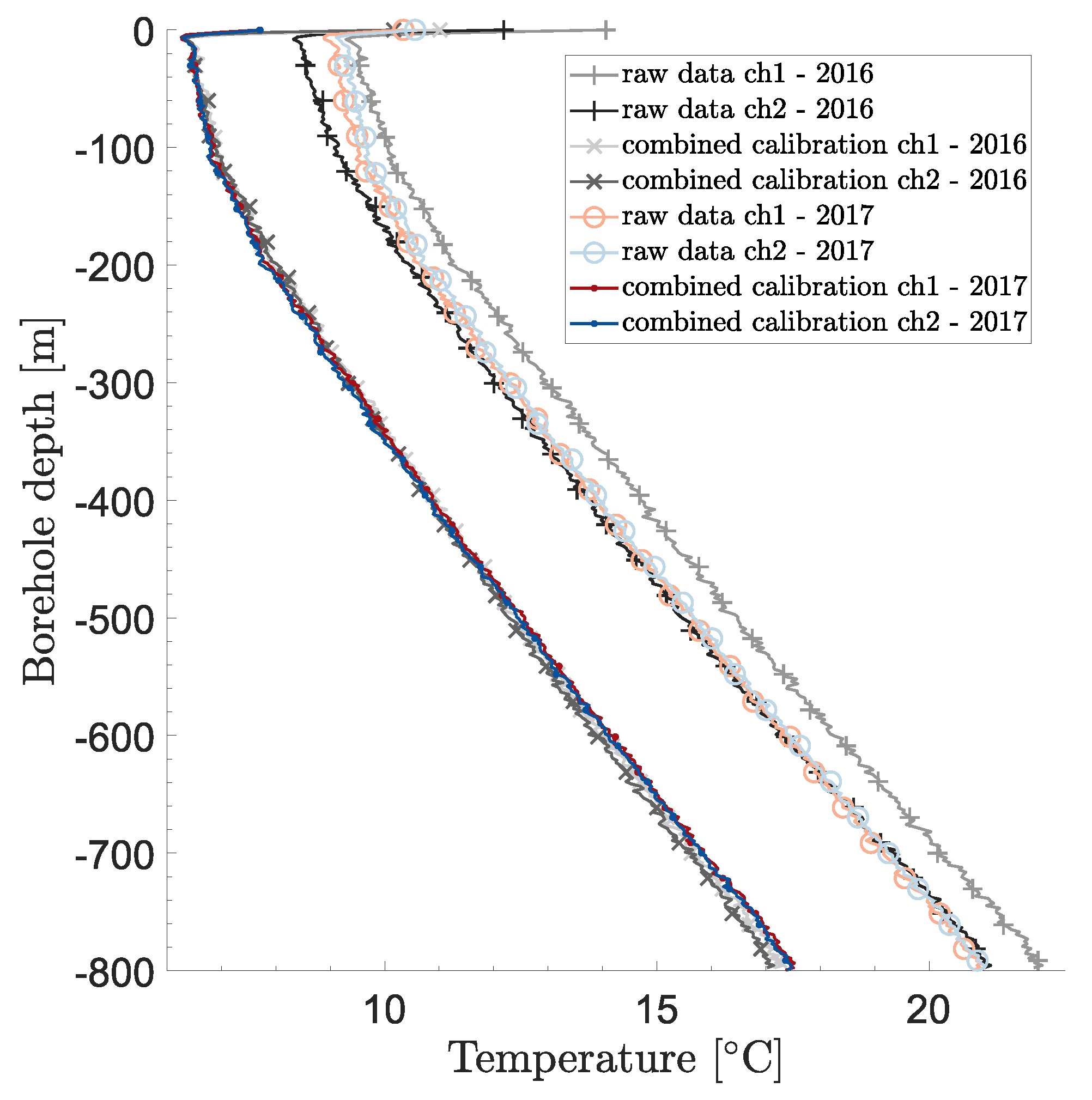
3.1. Correction of temperature drifts and calibration
3.1.1. Verification of the calibration
3.2. Uncertainty evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the correction based on linear regression
References
- Bolognini, G.; Hartog, A. Raman-based fibre sensors: Trends and applications. Optical Fiber Technology 2013, 19, 678–688. [Google Scholar] [CrossRef]
- Hurtig, E.; Großwig, S.; Jobmann, M.; Kühn, K.; Marschall, P. Fibre-optic temperature measurements in shallow boreholes: experimental application for fluid logging. Geothermics 1994, 23, 355–364. [Google Scholar] [CrossRef]
- Selker, J.S.; Thévenaz, L.; Huwald, H.; Mallet, A.; Luxemburg, W.; Giesen, N.v.d.; Stejskal, M.; Zeman, J.; Westhoff, M.; Parlange, M.B. Distributed fiber-optic temperature sensing for hydrologic systems. Water Resources Research 2006, 42. [Google Scholar] [CrossRef]
- Ukil, A.; Braendle, H.; Krippner, P. Distributed Temperature Sensing: Review of Technology and Applications. IEEE Sensors Journal 2012, 12, 885–892. [Google Scholar] [CrossRef]
- Liu, Z.; Kim, A.K. Review of Recent Developments in Fire Detection Technologies. Journal of Fire Protection Engineering 2003, 13, 129–151. [Google Scholar] [CrossRef]
- Toccafondo, I.; Nannipieri, T.; Signorini, A.; Guillermain, E.; Kuhnhenn, J.; Brugger, M.; Pasquale, F.D. Raman Distributed Temperature Sensing at CERN. IEEE Photonics Technology Letters 2015, 27, 2182–2185. [Google Scholar] [CrossRef]
- Curtis, A.; Kyle, P. Geothermal point sources identified in a fumarolic ice cave on Erebus volcano, Antarctica using fiber optic distributed temperature sensing. Geophysical Research Letters 2011, 38. [Google Scholar] [CrossRef]
- Williams, G.R.; Brown, G.; Hawthorne, W.; Hartog, A.H.; Waite, P.C. Distributed temperature sensing (DTS) to characterize the performance of producing oil wells. In Proceedings of the Industrial Sensing Systems. International Society for Optics and Photonics; 2000; Vol. 4202, pp. 39–54. [Google Scholar] [CrossRef]
- Freifeld, B.M.; Finsterle, S.; Onstott, T.C.; Toole, P.; Pratt, L.M. Ground surface temperature reconstructions: Using in situ estimates for thermal conductivity acquired with a fiber-optic distributed thermal perturbation sensor. Geophysical Research Letters 2008, 35. [Google Scholar] [CrossRef]
- Rath, V.; Sundberg, J.; Näslund, J.O.; Liljedahl, L.C. Paleoclimatic inversion of temperature profiles from deep boreholes at Forsmark and Laxemar. Technical Report TR-18-06, Swedish Nuclear Fuel and Waste Management, 2019.
- Pickler, C.; Gurza Fausto, E.; Beltrami, H.; Mareschal, J.C.; Suárez, F.; Chacon-Oecklers, A.; Blin, N.; Cortés Calderón, M.T.; Montenegro, A.; Harris, R. Recent climate variations in Chile: constraints from borehole temperature profiles. 14, 559–575. Publisher: Copernicus GmbH. [CrossRef]
- Khan, A.A.; Vrabie, V.; Beck, Y.L.; Mars, J.I.; D’Urso, G. Monitoring and early detection of internal erosion: Distributed sensing and processing. Structural Health Monitoring 2014, 13, 562–576. [Google Scholar] [CrossRef]
- Coleman, T.I.; Parker, B.L.; Maldaner, C.H.; Mondanos, M.J. Groundwater flow characterization in a fractured bedrock aquifer using active DTS tests in sealed boreholes. Journal of Hydrology 2015, 528, 449–462. [Google Scholar] [CrossRef]
- Read, T.; Bour, O.; Bense, V.; Borgne, T.L.; Goderniaux, P.; Klepikova, M.V.; Hochreutener, R.; Lavenant, N.; Boschero, V. Characterizing groundwater flow and heat transport in fractured rock using fiber-optic distributed temperature sensing. Geophysical Research Letters 2013, 40, 2055–2059. [Google Scholar] [CrossRef]
- Clifford, S.M.; Yoshikawa, K.; Byrne, S.; Durham, W.; Fisher, D.; Forget, F.; Hecht, M.; Smith, P.; Tamppari, L.; Titus, T.; et al. Introduction to the fifth Mars Polar Science special issue: Key questions, needed observations, and recommended investigations. Icarus 2013, 225, 864–868. [Google Scholar] [CrossRef]
- Hurtig, E.; Schrötter, J.; Großwig, S.; Kühn, K.; Orrell, P.; Harjes, B. Borehole temperature measurements using distributed fibre optic sensing. In Proceedings of the Proceedings; 1992. [Google Scholar]
- Sharma, W.S.K.; Seki, A.; Angel, S.M.; Garvis, D.G. Field testing of an optical fiber temperature sensor in a geothermal. Geothermics 1990, 19, 285–294. [Google Scholar] [CrossRef]
- Acuña, J.; Mogensen, P.; Palm, B. Distributed thermal response tests on a multi-pipe coaxial borehole heat exchanger. HVAC&R Research 2011, 17, 1012–1029. [Google Scholar] [CrossRef]
- Acuña, J.; Palm, B. Distributed thermal response tests on pipe-in-pipe borehole heat exchangers. Applied Energy 2013, 109, 312–320. [Google Scholar] [CrossRef]
- Fujii, H.; Okubo, H.; Itoi, R. Thermal response tests using optical fiber thermometers. 2006, Vol. 30 I, pp. 545–551.
- Fujii, H.; Okubo, H.; Nishi, K.; Itoi, R.; Ohyama, K.; Shibata, K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers. Geothermics 2009, 38, 399–406. [Google Scholar] [CrossRef]
- Galgaro, A.; Pasquier, P.; Schenato, L.; Cultrera, M.; Dalla Santa, G. Soil thermal conductivity from early TRT logs using an active hybrid optic fibre system. In Proceedings of the Research Conference Proceedings; 2018. [Google Scholar] [CrossRef]
- Radioti, G.; Delvoie, S.; Charlier, R.; Dumont, G.; Nguyen, F. Heterogeneous bedrock investigation for a closed-loop geothermal system: A case study. Geothermics 2016, 62, 79–92. [Google Scholar] [CrossRef]
- Rolando, D.; Acuna, J.; Fossa, M. Heat extraction distributed thermal response test: A methodological approach and in-situ experiment. In Proceedings of the Research Conference Proceedings; 2017. [Google Scholar] [CrossRef]
- Sakata, Y.; Katsura, T.; Nagano, K. Multilayer-concept thermal response test: Measurement and analysis methodologies with a case study. Geothermics 2018, 71, 178–186. [Google Scholar] [CrossRef]
- Aranzabal, N.; Martos, J.; Stokuca, M.; Mazzotti Pallard, W.; Acuña, J.; Soret, J.; Blum, P. Novel instruments and methods to estimate depth-specific thermal properties in borehole heat exchangers. Geothermics 2020, 86, 101813. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Cheng, Y.; Zhang, Y.; Gao, X.; Shan, K. A Case Study of Field Thermal Response Test and Laboratory Test Based on Distributed Optical Fiber Temperature Sensor. 15, 8101. Number: 21 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef]
- Hakala, P.; Vallin, S.; Arola, T.; Martinkauppi, I. Novel use of the enhanced thermal response test in crystalline bedrock. 182, 467–482. [CrossRef]
- Abuasbeh, M.; Acuna, J. Ates system monitoring project, first measurement and performance evaluation: Case study in Sweden. In Proceedings of the Research Conference Proceedings; 2018. [Google Scholar] [CrossRef]
- Korhonen, K.; Leppaharju, N.; Hakala, P.; Arola, T. Simulated temperature evolution of large BTES - case study from Finland. In Proceedings of the Research Conference Proceedings; 2018. [Google Scholar] [CrossRef]
- McDaniel, A.; Fratta, D.; Tinjum, J.M.; Hart, D.J. Long-term district-scale geothermal exchange borefield monitoring with fiber optic distributed temperature sensing. Geothermics 2018, 72, 193–204. [Google Scholar] [CrossRef]
- Monzó, P.; Lazzarotto, A.; Acuña, J. First Measurements of a Monitoring Project on a Btes System; 2017. [CrossRef]
- Sommer, W.T.; Doornenbal, P.J.; Drijver, B.C.; van Gaans, P.F.M.; Leusbrock, I.; Grotenhuis, J.T.C.; Rijnaarts, H.H.M. Thermal performance and heat transport in aquifer thermal energy storage. Hydrogeology Journal 2014, 22, 263–279. [Google Scholar] [CrossRef]
- Malmberg, M.; Raymond, J.; Perozzi, L.; Gloaguen, E.; Mellqvist, C.; Schwarz, G.; Acuna, J. Development of a thermal conductivity map of Stockholm. In Proceedings of the Research Conference Proceedings; 2018. [Google Scholar] [CrossRef]
- Radioti, G.; Sartor, K.; Charlier, R.; Dewallef, P.; Nguyen, F. Effect of undisturbed ground temperature on the design of closed-loop geothermal systems: A case study in a semi-urban environment. Applied Energy 2017, 200, 89–105. [Google Scholar] [CrossRef]
- Aranzabal, N.; Martos, J.; Steger, H.; Blum, P.; Soret, J. Temperature measurements along a vertical borehole heat exchanger: A method comparison. Renewable Energy 2019, 143, 1247–1258. [Google Scholar] [CrossRef]
- Schüppler, S.; Zorn, R.; Steger, H.; Blum, P. Uncertainty analysis of wireless temperature measurement (WTM) in borehole heat exchangers. Geothermics 2021, 90, 102019. [Google Scholar] [CrossRef]
- Acuña, J. Distributed thermal response tests: new insights on U-pipe and Coaxial heat exchangers in groundwater-filled boreholes. PhD Thesis, KTH Royal Institute of Technology, Stockholm. 2013. OCLC: 940250501.
- Hausner, M.B.; Suárez, F.; Glander, K.E.; Giesen, N.v.d.; Selker, J.S.; Tyler, S.W. Calibrating Single-Ended Fiber-Optic Raman Spectra Distributed Temperature Sensing Data. Sensors 2011, 11, 10859–10879. [Google Scholar] [CrossRef]
- Tyler, S.W.; Selker, J.S.; Hausner, M.B.; Hatch, C.E.; Torgersen, T.; Thodal, C.E.; Schladow, S.G. Environmental temperature sensing using Raman spectra DTS fiber-optic methods. Water Resources Research 2009. [Google Scholar] [CrossRef]
- Vieira, A.; Maranha, J.; Christodoulides, P.; Alberdi-Pagola, M.; Loveridge, F.; Nguyen, F.; Florides, G.; Radioti, G.; Cecinato, F.; Prodan, I.; et al. Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications. Energies 2017, 10, 2044. [Google Scholar] [CrossRef]
- van de Giesen, N.; Steele-Dunne, S.C.; Jansen, J.; Hoes, O.; Hausner, M.B.; Tyler, S.; Selker, J. Double-Ended Calibration of Fiber-Optic Raman Spectra Distributed Temperature Sensing Data. Sensors 2012, 12, 5471–5485. [Google Scholar] [CrossRef] [PubMed]
- Hausner, M.B.; Kobs, S. Identifying and Correcting Step Losses in Single-Ended Fiber-Optic Distributed Temperature Sensing Data. Journal of Sensors 2016. [Google Scholar] [CrossRef]
- McDaniel, A.; Tinjum, J.M.; Hart, D.J.; Fratta, D. Dynamic Calibration for Permanent Distributed Temperature Sensing Networks. IEEE Sensors Journal 2018, PP, 1–1. [Google Scholar] [CrossRef]
- des Tombe, B.; Schilperoort, B.; Bakker, M. Estimation of Temperature and Associated Uncertainty from Fiber-Optic Raman-Spectrum Distributed Temperature Sensing. 20, 2235. Number: 8 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef] [PubMed]
- Ghafoori, Y.; Vidmar, A.; Kryžanowski, A. A Dynamic Calibration of Optical Fiber DTS Measurements Using PEST and Reference Thermometers. 22, 3890. Number: 10 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef] [PubMed]
- Lillo, M.; Suárez, F.; Hausner, M.B.; Yáñez, G.; Veloso, E.A. Extension of Duplexed Single-Ended Distributed Temperature Sensing Calibration Algorithms and Their Application in Geothermal Systems. 22, 3319. Number: 9 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef] [PubMed]
- FIDES cost action 299. Guideline for Use of Fibre Optic Sensors. Technical report, 2009.
- Joint Committee for Guides in Metrology. Evaluation of measurement data — Guide to the expression of uncertainty in measurement. Guide 100, BIPM, IEC, IFCC, ISO, IUPAC, IUPAP, OIML, ILAC, 2008.
- Radioti, G.; Cerfontaine, B.; Charlier, R.; Nguyen, F. Experimental and numerical investigation of a long-duration Thermal Response Test: Borehole Heat Exchanger behaviour and thermal plume in the heterogeneous rock mass. Geothermics 2018, 71, 245–258. [Google Scholar] [CrossRef]
- Monzó, P. Modelling and monitoring thermal response of the ground in borehole fields. PhD Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Parra-Murillo, C.A.; Santos, M.F.; Monken, C.H.; Jorio, A. Stokes–anti-Stokes correlation in the inelastic scattering of light by matter and generalization of the Bose-Einstein population function. Physical Review B 2016, 93, 125141. [Google Scholar] [CrossRef]
- Velez, S.T.; Seibold, K.; Kipfer, N.; Anderson, M.D.; Sudhir, V.; Galland, C. Preparation and Decay of a Single Quantum of Vibration at Ambient Conditions. Physical Review X 2019, 9, 041007. [Google Scholar] [CrossRef]
- Geng, J.; Jin, R.; Xu, J.; Li, X.; Li, Y.; Guo, C.; Wei, G.; Zhang, H. An improved model for the fully distributed temperature single-mode fibre optic sensor based on Raman optical frequency-domain reflectometry. Journal of Optics A: Pure and Applied Optics 2004, 6, 932–936. [Google Scholar] [CrossRef]
- Farahani, M.A.; Gogolla, T. Spontaneous Raman scattering in optical fibers with modulated probe light for distributed temperature Raman remote sensing. Journal of Lightwave Technology 1999, 17, 1379–1391. [Google Scholar] [CrossRef]
- Beier, R.A.; Smith, M.D.; Spitler, J.D. Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis. 40, 79–85. [CrossRef]
- Mazzotti, W.; Firmansyah, H.; Acuña, J.; Stokuca, M.; Palm, B. Newton-Raphson method applied to the time-superposed ILS for parameter estimation in Thermal Response Tests. In Proceedings of the Research Conference Proceedings. [CrossRef]
- Sensornet. Halo DTS datasheet v3.
- Mazzotti Pallard, W.; Lazzarotto, A.; Acuña Sequera, J.; Palm, B. Design methodology for laboratory scale borehole storage: An approach based on analytically-derived invariance requirements and numerical simulations. 87, 101856. [CrossRef]
- Holmberg, H.; Acuña, J.; Næss, E.; Sønju, O.K. Thermal evaluation of coaxial deep borehole heat exchangers. 97, 65–76. [CrossRef]
- Morchio, S.; Fossa, M. Thermal modeling of deep borehole heat exchangers for geothermal applications in densely populated urban areas. 13. [CrossRef]
- Claesson, J. Markvärme: en handbok om termiska analyser. D. 3, D. 3,; Statens råd för byggnadsforskning: Svensk byggtjänst. OCLC: 185671287.
| 1 | For calibration and data acquisition with DTS, it is important to distinguish between single and double-end configurations. Single-ended configurations, in opposition to double-ended configurations, are setups in which the fiber optic cables is connected to the DTS instrument only through one end. For discussions on single versus double-ended configurations, the reader is referred to Tyler et al. [40], Hausner et al. [39] and Hausner and Kobs [43]. The present paper focuses on calibration of single-ended configurations but calibration procedures for double-ended configurations may be found in [42,44,45]. |
| 2 | |
| 3 | It should be noted that calibration baths are not the best metrics for accuracy since they are performed precisely to maximize accuracy within those baths. |
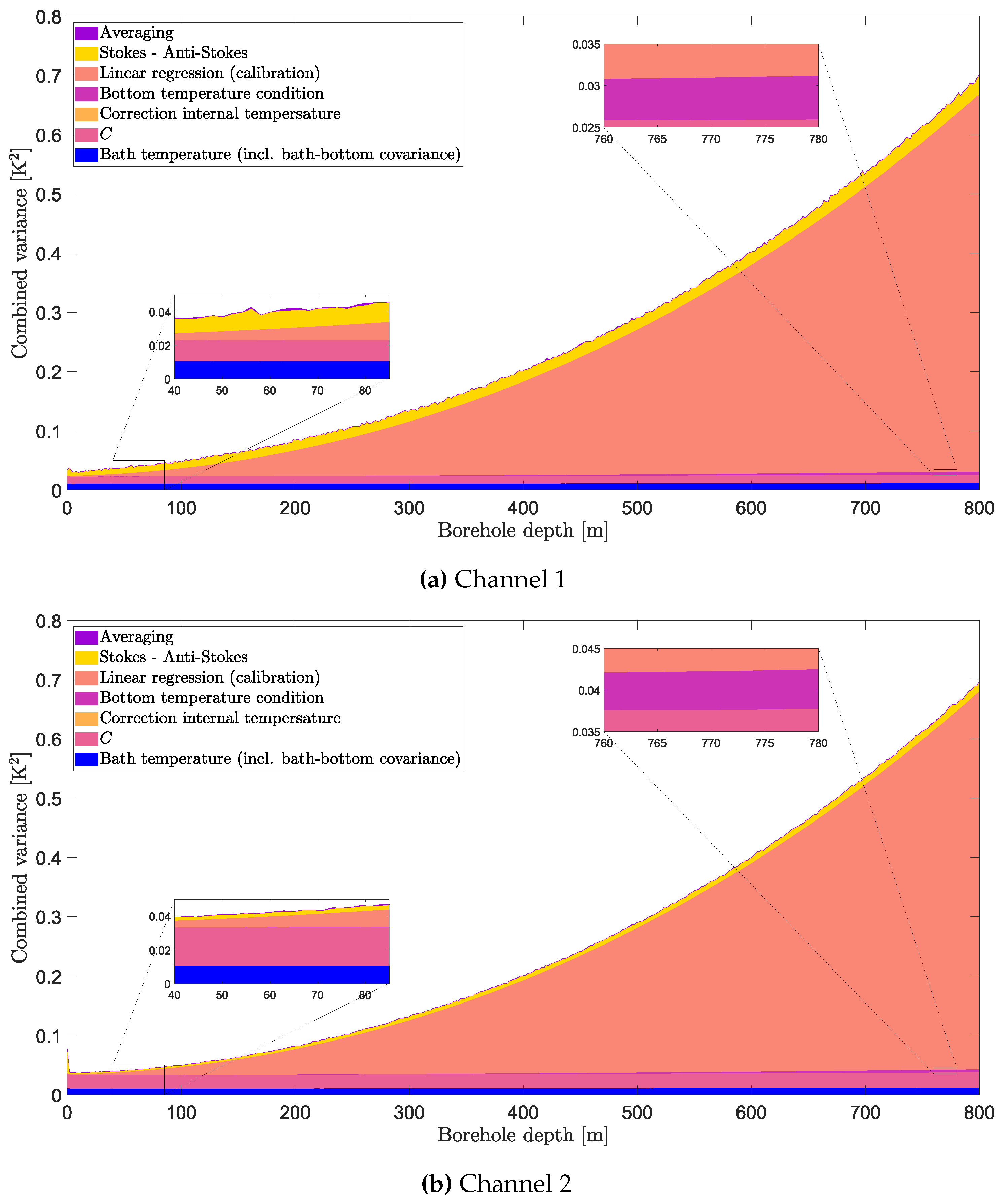
| 4 | For a sampling interval of 2.029 m and a temporal averaging of 5 min. The effective degrees of freedom vary with depth but is in average between 40 and 180. |
| 5 | For a sampling interval of 2.029 m and a temporal averaging of 5 min. The effective degrees of freedom vary with depth but is in average between 40 and 180. |
| 6 | the contribution from the Stokes/anti-Stokes is calculated between averaged periods and do not account for variations within a given averaged period (as these data are not directly available from the DTS instrument) |
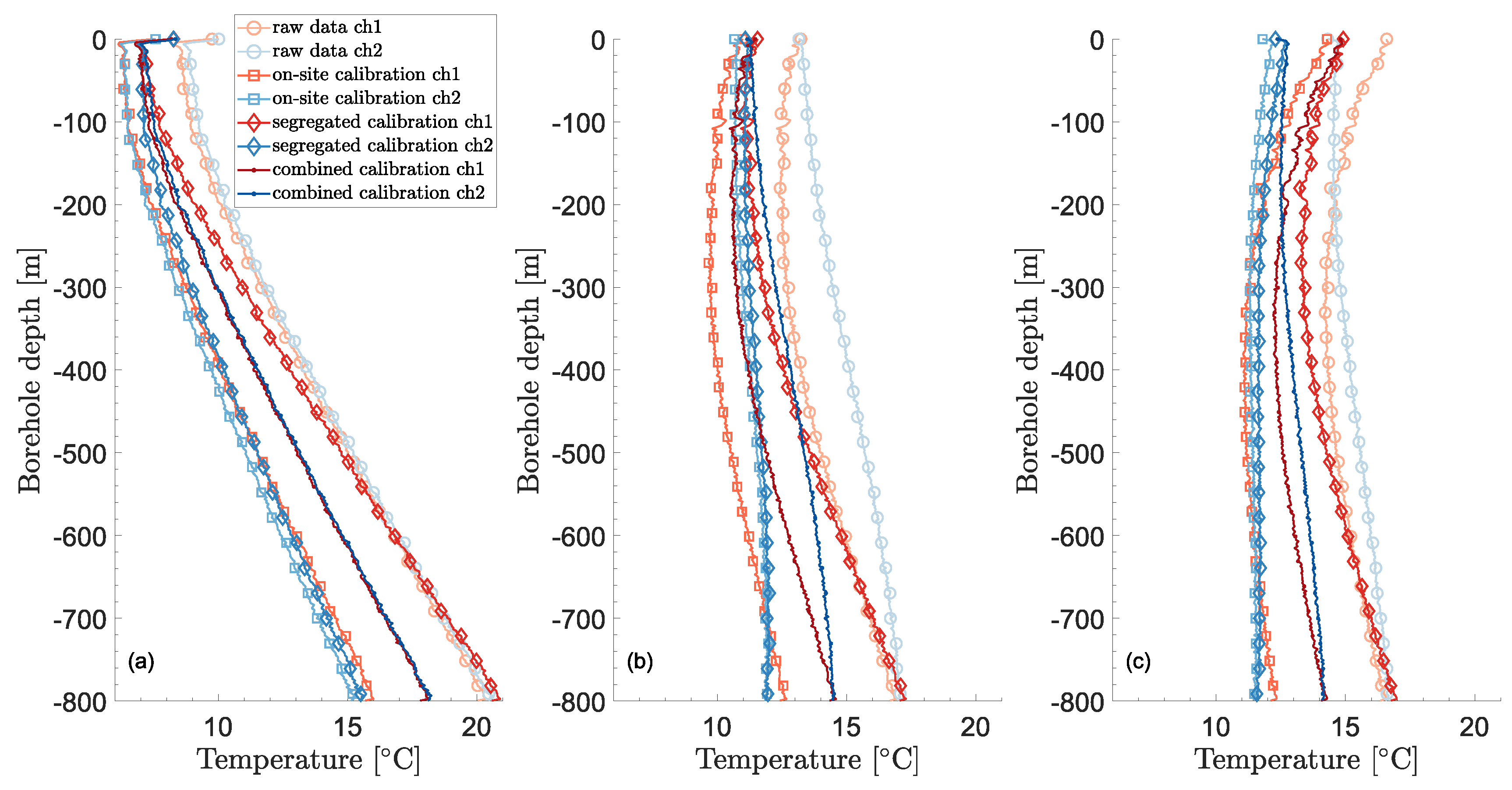
| [] | [-] | [] | [-] | ||
| Raw data (default) | - | - | |||
| On-site calibration | -0.0106 | -0.0106 | |||
| Segregated calibration | -0.0165 | -0.0092 | |||
| Combined calibration | -0.0121 | -0.0137 | |||
| Independent combined calibration (one-year interval) | -0.0104 | -0.0172 |
| [-] | [] | [m] | |||
| 516.4 | -0.0015 | 50 |
| Depth / length [m] | 0 | 10 | 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 |
| Channel 1 [K] | 0.379 | 0.358 | 0.383 | 0.445 | 0.588 | 0.742 | 0.907 | 1.08 | 1.27 | 1.46 | 1.66 |
| Channel 2 [K] | 0.553 | 0.395 | 0.400 | 0.450 | 0.581 | 0.735 | 0.903 | 1.08 | 1.27 | 1.46 | 1.65 |
| Manufacturer’s "resolution" [58] [K] |
0.025 | 0.025 | 0.025 | 0.025 | 0.027 | 0.028 | 0.029 | 0.030 | 0.030 | 0.032 | 0.033 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




