Submitted:
15 March 2023
Posted:
16 March 2023
You are already at the latest version
Abstract
Keywords:
1. INTRODUCTION
2. MATHEMATICAL MODEL OF HYDRAULIC SYSTEM
2.1. Mathematical model of hydraulic system
2.1.1. Mathematical model of water turbine
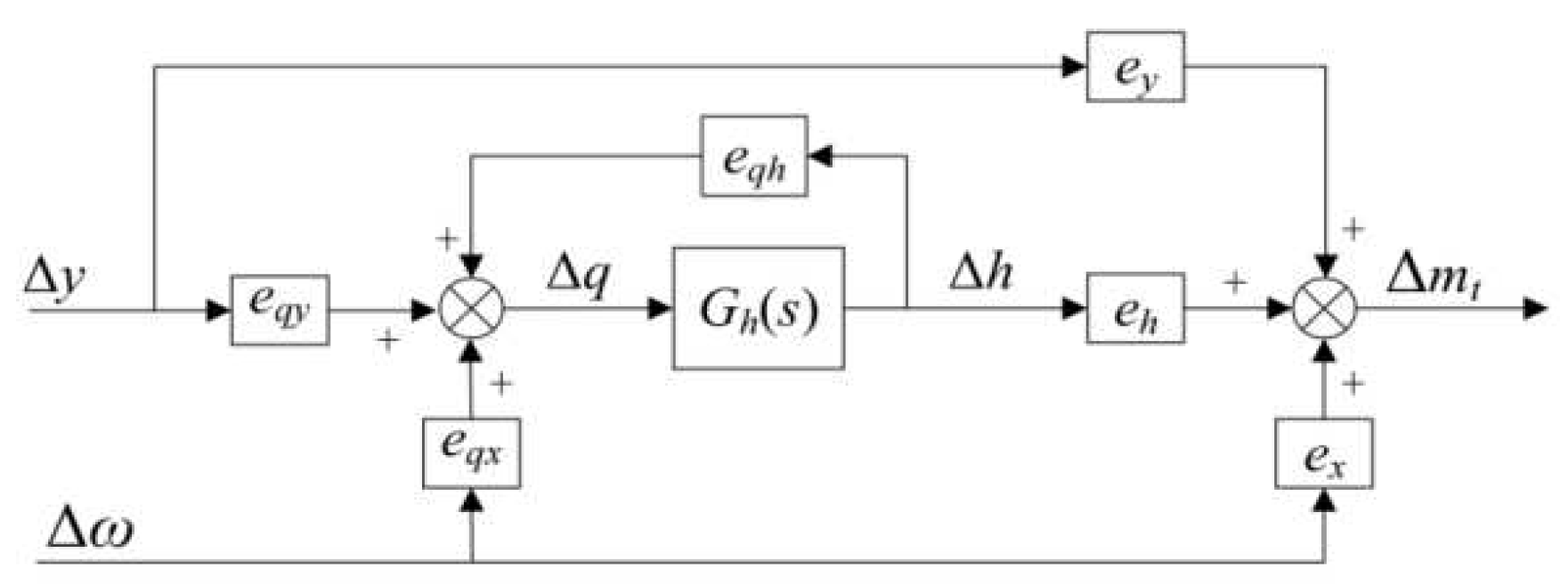
2.1.2. Comprehensive mathematical model of hydraulic system
2.2. Mathematical model of generator
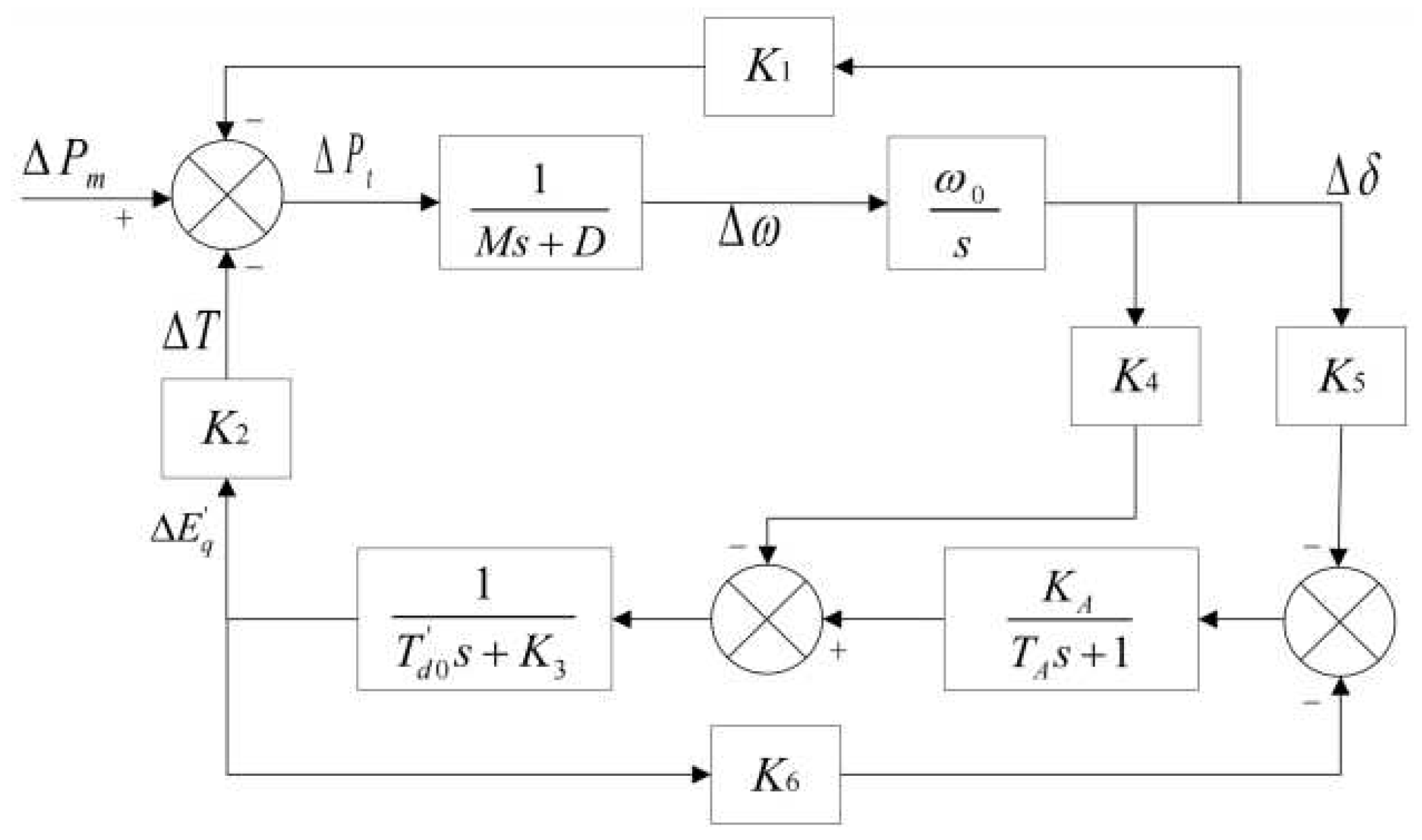
2.3. Mathematical model of regulating system of hydropower unit
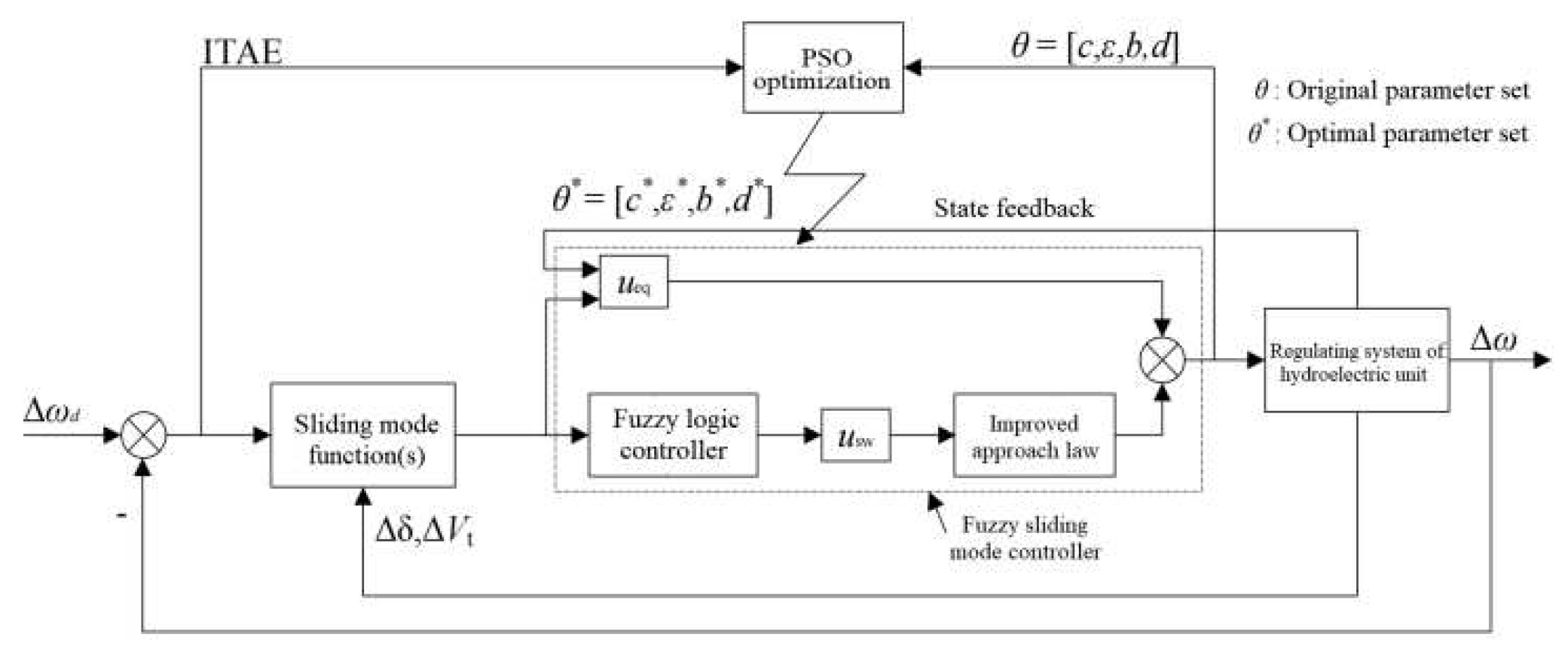
3. DESIGN OF FUZZY SLIDING MODE CONTROLLER FOR REGULATING SYSTEM OF HYDROPOWER UNIT
3.1. Conventional sliding mode controller
3.2. Improved sliding surface
3.3. Control law of fuzzy sliding mode controller combined with fuzzy system
3.4. Design of reaching law
3.5. Control law of regulating system of hydropower unit
3.5.1. Conclusions
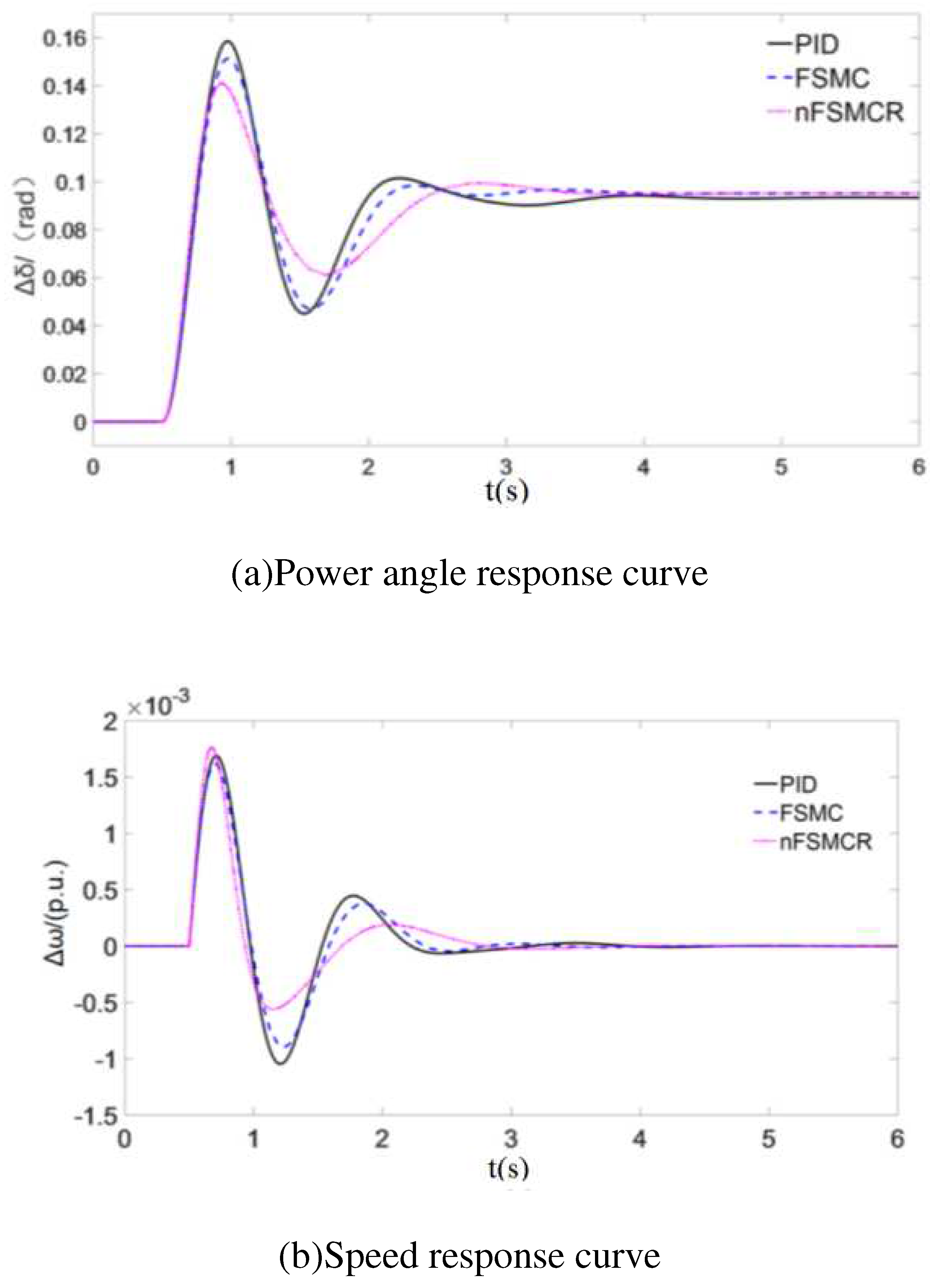
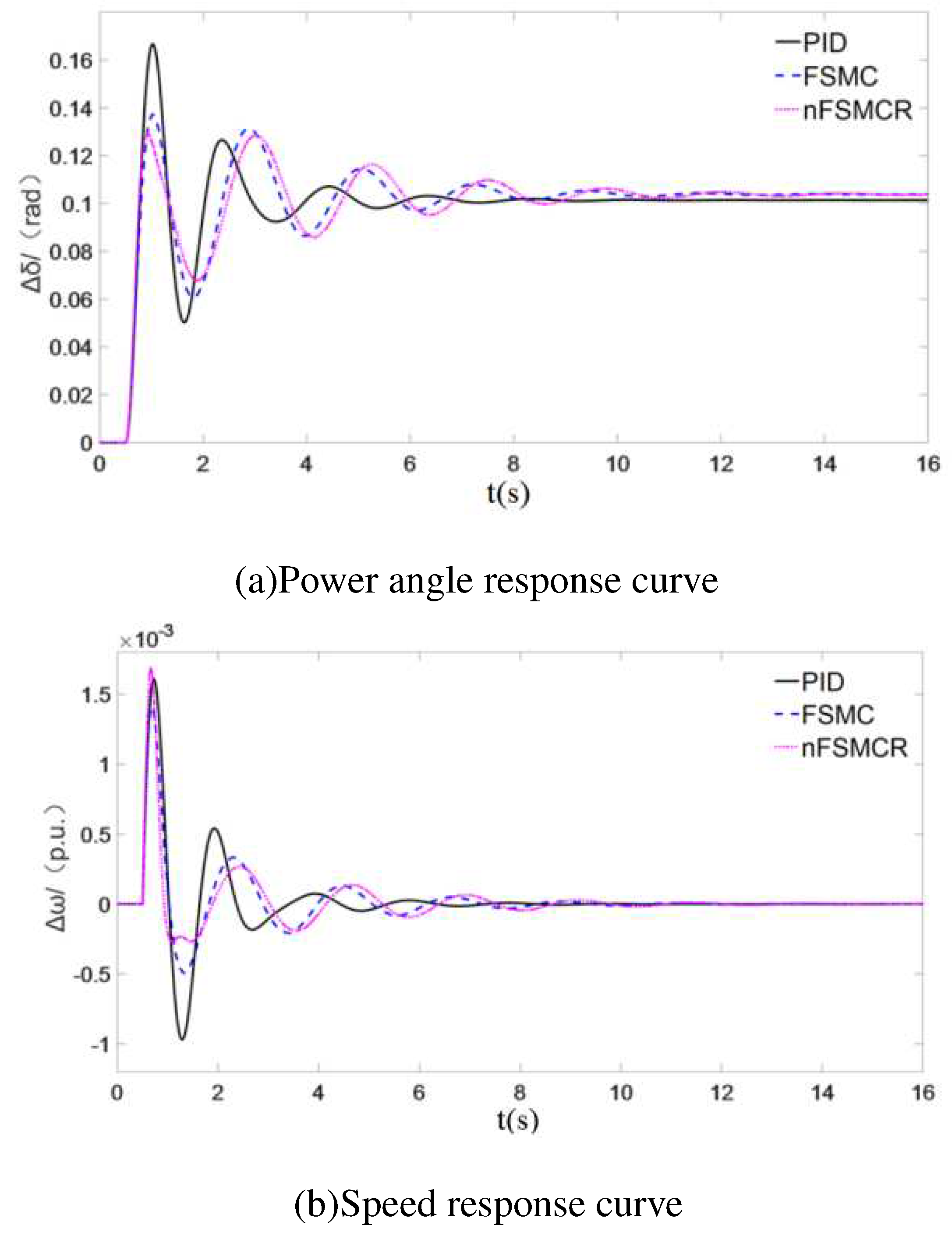
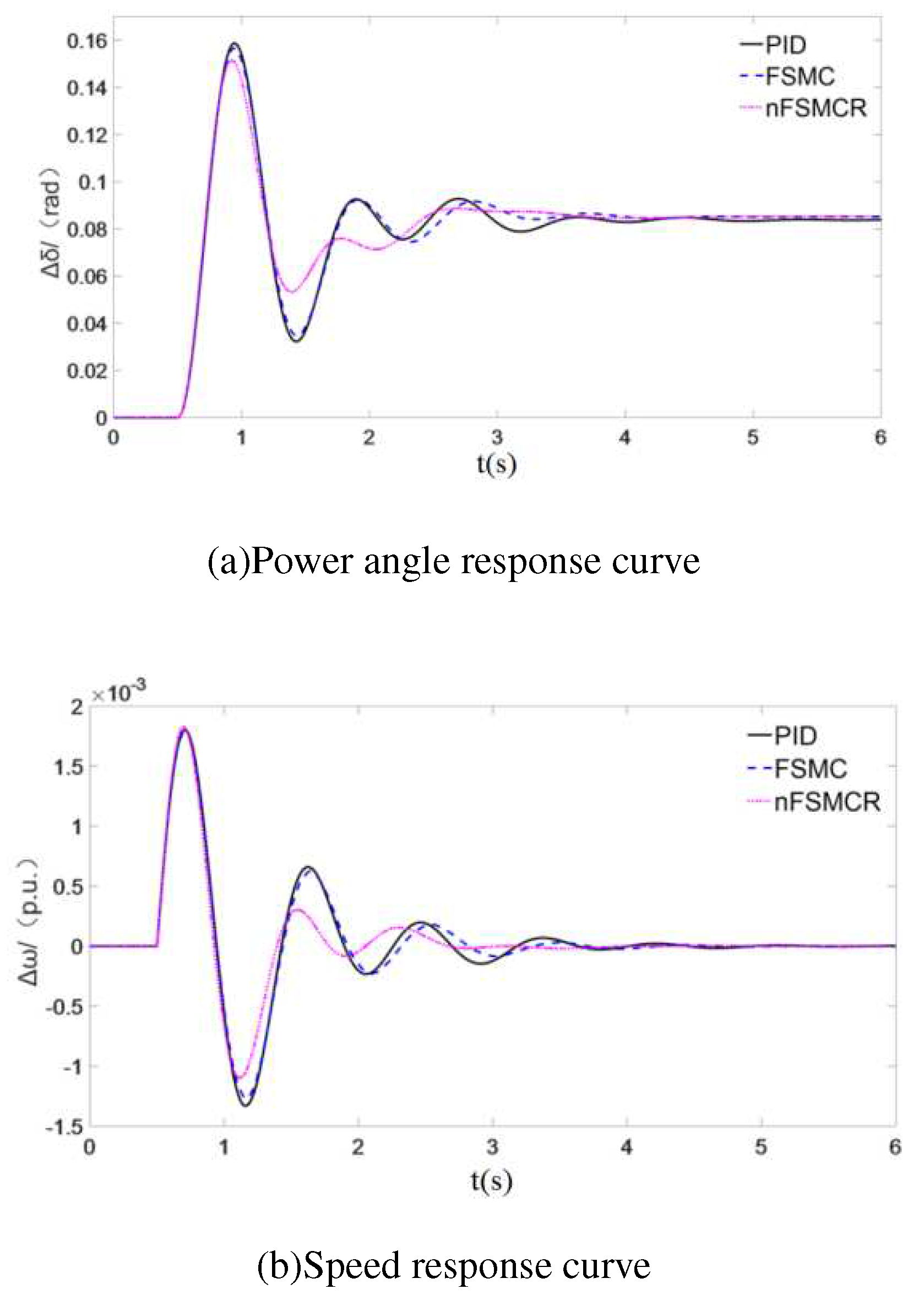
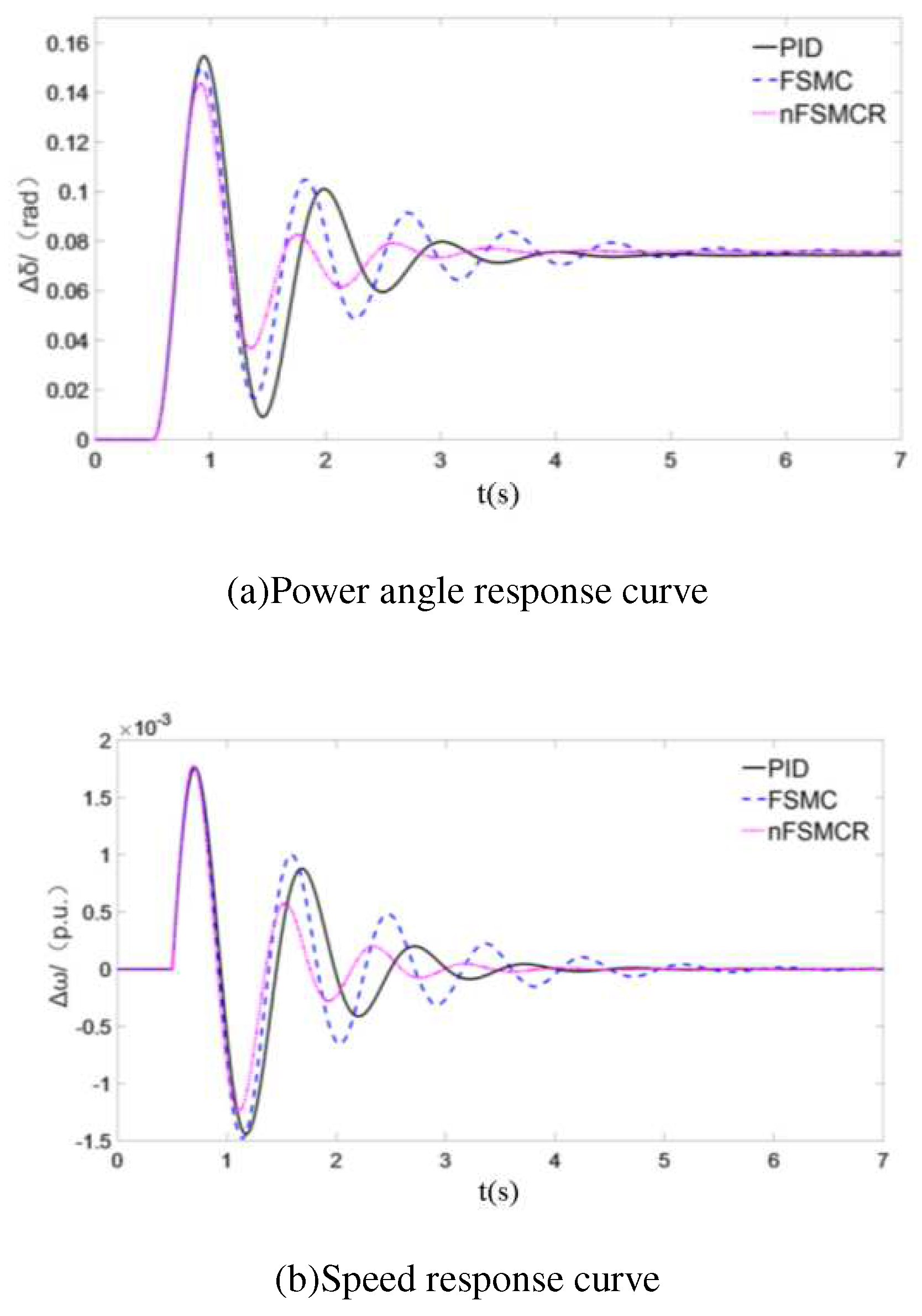
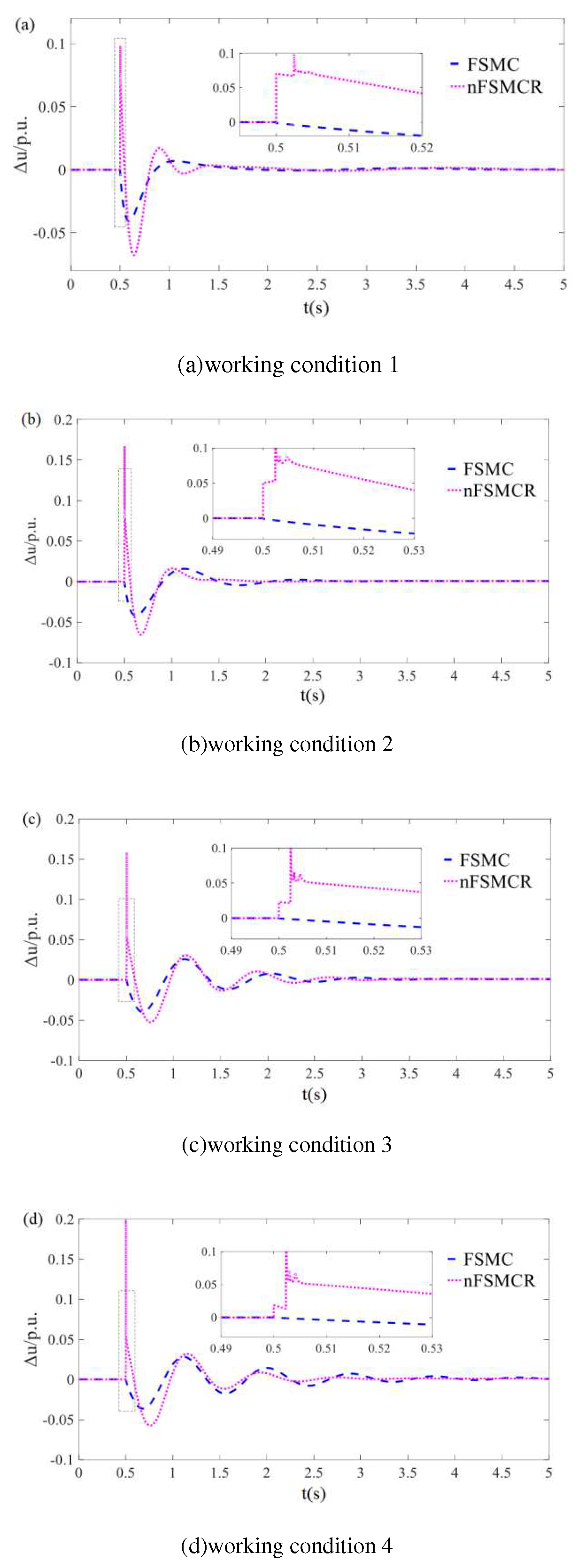
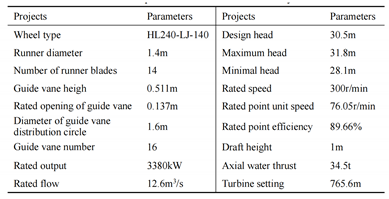
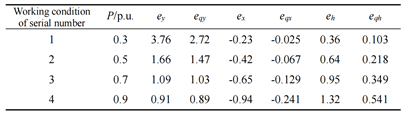
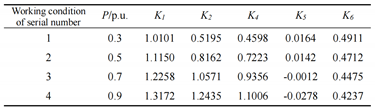
4. COMPARATIVE ANALYSIS OF CONTROLLERS
4.1. Parameter optimization
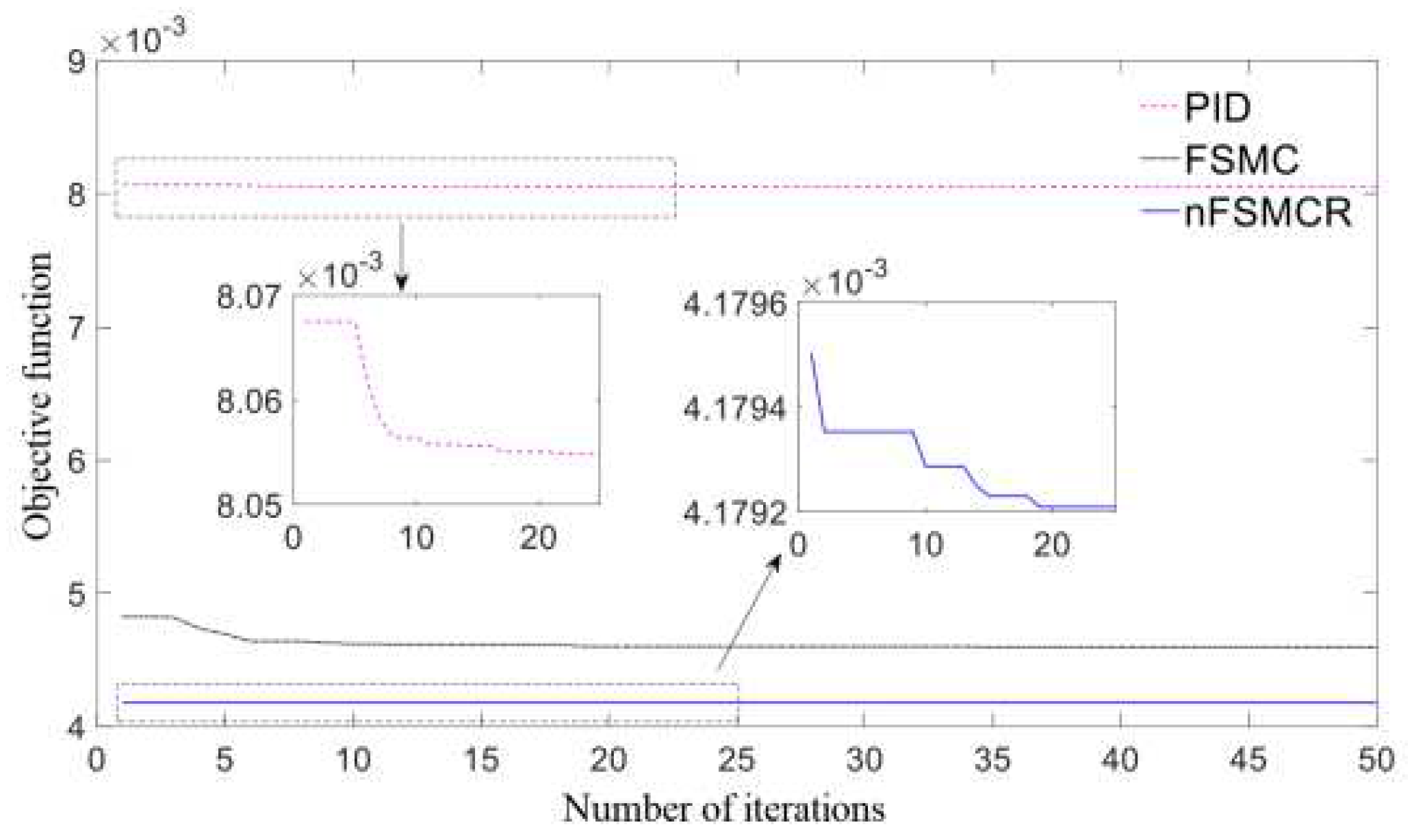
4.2. Simulation comparison
5. CONCLUSIONS
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Corresponding author
NOMENCLATURE
| Hydro-turbine regulating system. | |
| Fuzzy sliding mode controller. | |
| Improved fuzzy sliding mode controller. | |
| Proportion Integration Differentiation. |
References
- S.M.Mozayan,M.Saad,H.Vahedi,et al,“Sliding mode control of PMSG wind turbine based on enhanced exponential reaching law”,IEEE Transactions on Industrial Electronics,vol.63,no.10,pp.6148-6159,Oct.2016. [CrossRef]
- F.Blaabjerg,M.Liserre,K.Ma,“Power electronics converters for wind turbine systems”,IEEE Trans. Ind. Appl.,vol.48,no.2,pp.708-719,Oct.2012. [CrossRef]
- Weijia Yang,Per Norrlund,Chiyung Chung, et al,“Eigen-analysis of hydraulic-mechanical-electrical coupling mechanism for small signal stability of hydro-power plant”,Renewable Energy,vol.115,pp.1014-1025,Jan.2017. [CrossRef]
- Xiaoping Huang,Yufang Zhu,Paniz Vafaei,et al,“An iterative simulation algorithm for large oscillation of the applicable 2D-electrical system on a complex nonlinear substrate”,Engineering with Computers,vol.38,pp.3137–3149,Feb.2021. [CrossRef]
- Diyi Chen,Cong Ding,Younghae Do,et al,“Nonlinear dynamic analysis for a Francis hydro-turbine governing system and its control”,Journal of the Franklin Institute,vol.351,no.9,pp.4596-4618,Sep.2014. [CrossRef]
- P.C.O.Silva,C.Nicolet,P.Grillot,et al,“Assessment of power swings in hydropower plants through high-order modeling and eigenanalysis”,IEEE Transactions on Industry Applications,vol.53,no.4,pp.3345-3354,Nov.2017. [CrossRef]
- Xiaoping Huang,Huadong Hao, Khaled Oslub,et al,“Dynamic stability/instability simulation of the rotary size-dependent functionally graded microsystem”,Engineering with Computers,May 2021. [CrossRef]
- J.I.Sarasua,J.I.Perez-Diaz,J.R.Wilhelmi,et al,“Dynamic response and governor tuning of a long penstock pumped-storage hydropower plant equipped with a pump-turbine and a doubly fed induction generator”,Energy Conversion and Management,vol.106,pp.151-164,Dec.2015. [CrossRef]
- Chaoshun.Li,Nan Zhang,Xinjie Lai,et al,“Design of a fractional-order PID controller for a pumped storage unit using a gravitational search algorithm based on the Cauchy and Gaussian mutation”,Information Sciences,396:162-181,Aug.2017. [CrossRef]
- Yang Zheng,Jianzhong Zhou,Wenlong Zhu, et al,“Design of a multi-mode intelligent model predictive control strategy for hydroelectric generating unit”,Neurocomputing,207:287-299,Sep.2016. [CrossRef]
- H.V.Pico,J.D.Mccalley,A.Angel,et al,“Analysis of very low frequency oscillations in hydro-dominant power systems using multi-unit modelingt”,IEEE Trans. Power Syst.,vol.27,no.4,pp.1906-1915,Nov.2012. [CrossRef]
- Beibei Xu,Feifei Wang,Diyi Chen,et al,“Hamiltonian modeling of multi-hydro-turbine governing systems with sharing common penstock and dynamic analyses under shock load”,Energy Conversion and Management,vol.108,no.15,pp.478-487,Jan.2016. [CrossRef]
- Bin Wang,Jianyi Xue,Fengjiao Wu,et al,“Robust Takagi-Sugeno fuzzy control for fractional order hydro-turbine governing system”,ISA Transactions,65:72-80,Nov.2016. [CrossRef]
- Chang Xu,Dianwei Qian,“Governor design for a hydropower plant with an upstream surge tank by GA-based fuzzy reduced-order sliding mode”,Energies,vol.8,no.12,pp.13442-13457,2015. [CrossRef]
- Lei Chen,Xiaomin Lu,Yong Min,et al,“Optimization of governor parameters to prevent frequency oscillations in power systems”,IEEE Transactions on Power Systems,vol.33,no.4,pp.4466-4474,Jul.2018. [CrossRef]
- Hao Zhang,Diyi Chen,Beibei Xu,et al,“Nonlinear modeling and dynamic analysis of hydro-turbine governing system in the process of load rejection transient”,Energy Conversion and Management,90:128-137,Jan.2015. [CrossRef]
- Huanhuan Li,Diyi Chen,Hao Zhang,et al,“Nonlinear modeling and dynamic analysis of a hydro-turbine governing system in the process of sudden load increase transient”,Mechanical Systems and Signal Processing,80:414-428,Dec.2016. [CrossRef]
- J.Shin,D.Kwak,K.Kwak,“Model predictive path planning for an autonomous ground vehicle in rough terrain,”International Journal of Control,Automation, and Systems,vol.19,no.6,pp.2224–2237,2021. [CrossRef]
- Chaoshun Li,Yifeng Mao,Jiandong Yang,et al,“A nonlinear generalized predictive control for pumped storage unit”,Renewable Energy,114:945-959,2017. [CrossRef]
- Weijia Yang,Per Norrlund,Johan Bladh,et al,“Hydraulic damping mechanism of low frequency oscillations in power systems: Quantitative analysis using a nonlinear model of hydropower plants”,Applied Energy,212:1138-1152,Feb.2018. [CrossRef]
- G.Delille,B.Francois,G.Malarange, “Dynamic frequency control support by energy storage to reduce the impact of wind and solar generation on isolated power system’s inertia”,IEEE Trans.Sustain.Energy,vol.3,no.4,pp.931-939,Oct.2012. [CrossRef]
- C.G.Jiang,J.H.Zhou,S Peng,et al,“Ultra-low frequency oscillation analysis and robust fixed order control design”,International Journal of Electrical Power and Energy Systems,104:269-278,Jan.2019. [CrossRef]
- Bicheng Guo,Jiang Guo.“Feedback linearization and reaching law based sliding mode control design for nonlinear hydraulic turbine governing system”,Energies,vol.12,no.12,pp.1-19,Jun.2019. [CrossRef]
- Xiaohui Yuan,Zhihuan Chen,Yanbin Yuan,et al,“Design of fuzzy sliding mode controller for hydraulic turbine regulating system via input state feedback linearization method”,Energy,vol.91.no.1,pp.173-187,Dec.2015. [CrossRef]
- Yinggan Tang,Xiangyang Zhang,Dongli Zhang,et al,“Fractional order sliding mode controller design for antilock braking systems”,Neurocomputing,111:122-130,Jul.2016. [CrossRef]
- Zhiren Han,Chuang Wei,Simin Du, Zhen Jia,Xinyang Du,“Numerical simulation and experimental research on rubber flexible-die forming limitation with new position-limited backpressure mechanism”,The International Journal of Advanced Manufacturing Technology,vol.116,pp.2183–2196,Jul.2021. [CrossRef]
- N.Pathak,T.S.Bhatti,A.Verma,“Discrete data AGC of hydro-thermal systems under varying turbine time constants along with the power system loading conditions”,IEEE Trans. Ind. Appl.,vol.53,no.5,pp.4998-5013,Sep.2017. [CrossRef]
- A.Salem,H.Van Khang,K.G.Robbersmyr,et al,“Voltage source multilevel inverters with reduced device count:Topological review and novel comparative factors”,IEEE Trans.Power Electron.,vol.36,no.3,pp.2720-2747,Mar.2021. [CrossRef]
- Civalek Ö,Demir C,“A simple mathematical model of microtubules surrounded by an elastic matrix by nonlocal fnite element method”,Appl. Math Comput.,289:335-352,2016. [CrossRef]
- Z.Akhtar,B.Chaudhuri,S.Y.Ron Hui,“Primary frequency control contribution from smart loads using reactive compensation”,IEEE Trans.Smart Grid,vol.6,no.5,pp.2356-2365,Sep.2015. [CrossRef]
- D.Rimorov,I.Kamwa,G.Joos,“Quasi-steady-state approach for analysis of frequency oscillations and damping controller design”,IEEE Trans. Power Syst.,vol.31,no.4,pp.3212-3220,Jul.2016. [CrossRef]
- Xinjie Lai,Chaoshun Li,Wencheng Guo,et al,“Stability and dynamic characteristics of the nonlinear coupling system of hydropower station and power grid”,Communications in Nonlinear Science and Numerical Simulation,79:104919.1-104919.20,Dec.2019. [CrossRef]
- M.A.Fnaiech,F.Betin,G.A.Capolino,et al,“Fuzzy logic and sliding-mode controls applied to six-phase induction machine with open phases”,IEEE Trans.Ind.Electron.,vol.57,no.1,pp.354-364,Jan.2010. [CrossRef]
- A.Moeini,I.Kamwa,“Analytical concepts for reactive power based primary frequency control in power systems”,IEEE Trans.Power Syst.,vol.31,no.6,pp.4217-4230,Nov.2016. [CrossRef]
- Xiaoguang Zhang,Lizhi Sun,Ke Zhao,et al,“Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques”,IEEE Transactions on Power Electronics,vol.28,no.3,pp.1358-1365,Mar.2013. [CrossRef]
 |
 |
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





