Prerpints.org logo
Preprint
Article

Maximizing the Accuracy of Microcomb-Based Microwave Photonic Transversal Signal Processors

Altmetrics

Downloads

165

Views

44

Comments

0

This version is not peer-reviewed

Submitted:

31 March 2023

Posted:

31 March 2023

You are already at the latest version

Alerts
Abstract
Microwave photonic (MWP) transversal signal processors offer a compelling solution for realizing versatile high-speed information processing by combining the advantages of reconfigurable electrical digital signal processing and high-bandwidth photonic processing. With the capability of generating a number of discrete wavelengths from micro-scale resonators, optical microcombs are powerful multi-wavelength sources for implementing MWP transversal signal processors with significantly reduced size, power consumption, and complexity. By using microcomb-based MWP transversal signal processors, a diverse range of signal processing functions have been demonstrated recently. In this paper, we provide a detailed analysis for the processing inaccuracy that are induced by the imperfect response of experimental components. First, we investigate the errors arising from different sources including imperfections in the microcombs, the chirp of electro-optic modulators, chromatic dispersion of the dispersive module, shaping errors of the optical spectral shapers, and noise of the photodetector. Next, we provide a global picture quantifying the impact of different error sources on the overall system performance. Finally, we introduce feedback control to compensate the errors caused by experimental imperfections and achieve significantly improved accuracy. These results provide a guide for optimizing the accuracy of microcomb-based MWP transversal signal processors.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

Ⅰ. INTRODUCTION

Ever-increasing data capacity in the information age is driving the demand for high-speed information processing. In contrast to conventional microwave signal processing based on electronics, that face intrinsic bandwidth bottlenecks [1,2], the use of photonic hardware and technologies to process high-bandwidth microwave signals, or microwave photonic (MWP) processing, can provide speeds orders of magnitude faster [3,4], which is critical for high-speed processing applications [3,4,5,6].
In the past two decades, a range of high speed MWP processors have been demonstrated by employing different optical approaches, in both discrete and integrated form, as optical filtering modules to process microwave signals modulated on a single optical carrier [3,7,8,9,10,11,12,13,14,15,16]. While successful, featuring high performance with dynamic tuning, these approaches provided only single processing functions with limited reconfigurability and fixed parameters. In contrast, MWP transversal signal processers, where the microwave signal is modulated onto multiple optical carriers with adjustable delays and weights before summing via photodetection [17,18], have significant advantages in achieving highly reconfigurable processing [17,18].
For MWP transversal signal processors, a large number of optical carriers forming discrete taps to sample the input microwave signal are needed to achieve a high accuracy. Despite the use of conventional multi-wavelength sources, such as discrete laser arrays [19,20,21] and fiber Bragg grating arrays [22,23,24], to offer the discrete taps, the numbers of available taps they can provide are normally restricted to be < 10 ‒ mainly due to the dramatic increase of the system size, power consumption, and complexity with the tap number. Recent advances in optical microcombs [25,26] provide an effective way to circumvent such problem by generating a large number of wavelengths equally spaced by large microwave bandwidths from single chip-scale devices. This opens new horizons for implementing MWP transversal signal processors with significantly reduced size, power consumption, and complexity. By using microcomb-based MWP transversal signal processors, a range of signal processing functions have been demonstrated recently, first for basic functions including differentiations [27,28], integration [29], and Hilbert transforms [30,31,32], followed by more complex functions such as phase encoding [33], arbitrary waveform generation [34], and computations within the framework of optical neural networks [35,36,37].
For signal processors, processing accuracy is a key parameter. For microcomb-based MWP signal processors, processing errors are induced by both theoretical limitations and imperfect response of system components. Recently, we presented an analysis quantifying the errors induced by theoretical limitations [38]. In this paper, we provide a complementary analysis to that work, focusing on errors induced by experimental imperfections. First, errors arising from imperfect microcomb characteristics, chirp in the electro-optic modulator, chromatic dispersion in the dispersive module, shaping errors of the optical spectral shaper, and noise of the photodetector are investigated. Next, a global picture is presented to show the influence of different error sources by quantifying their contributions to the overall system performance. Finally, we introduce feedback control to compensate errors induced by imperfect response of experimental components, and in doing so we achieve a significant improvement in the processing accuracy. These results are useful for understanding and optimizing the accuracy of microcomb-based MWP transversal signal processors.

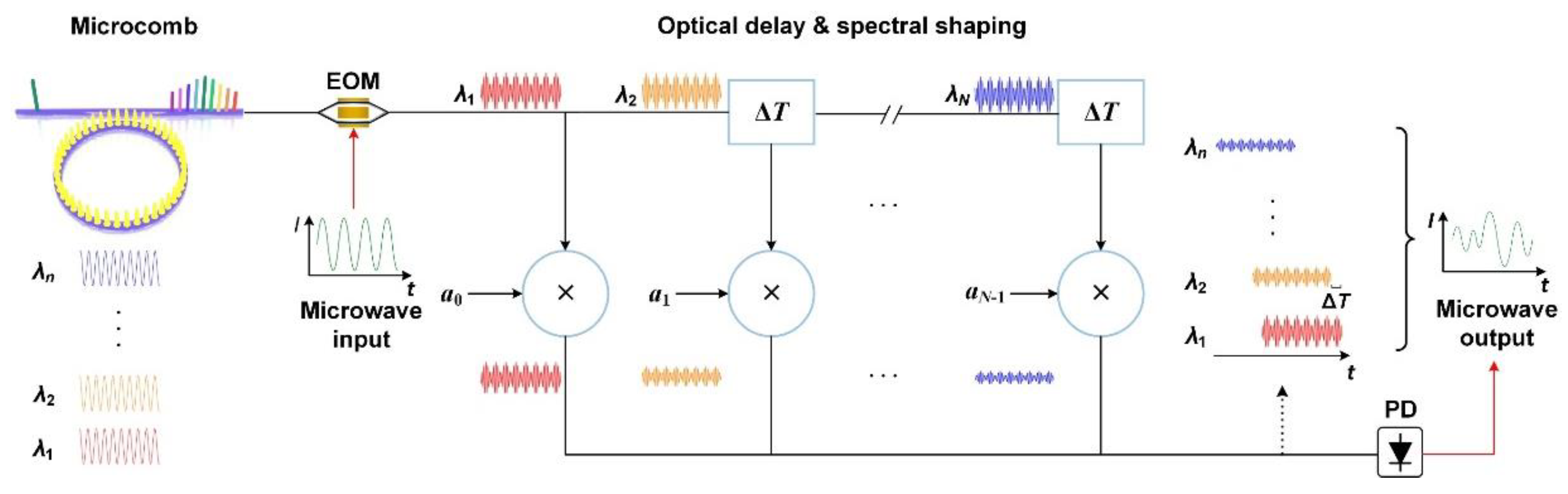
Ⅱ. MICROCOMB-BASED MWP TRANSVERSAL SIGNAL PROCESSORS

Microwave transversal signal processors are implemented based on the transversal filter structure in digital signal processing that features a finite impulse response [37]. Implementing them with photonic technologies yields a significantly increased processing bandwidth compared to their electronic counterparts [17]. Figure 1 shows the schematic diagram and signal processing flow of a typical MWP transversal signal processor. An optical microcomb, serving as a multi-wavelength source, provides a large number of wavelength channels as discrete taps. An input microwave signal is multicast onto each channel via an electro-optic modulator (EOM) to generate multiple microwave signal replicas. Next, time delays between adjacent wavelength channels are introduced by optical delay elements, and the delayed replicas at different wavelength channels are weighted through spectral shaping. Finally, the delayed and weighted replicas are summed via photodetection to generate the final microwave output of the system.
For the MWP transversal signal processor in Figure 1, each of the taps can be regarded as a discrete sample of the system’s impulse response, i.e., the system’s impulse response can be expressed as [17]
H ( t ) = ∑ M - 1 n = 0 a n δ ( t – n Δ T ) ,
where M is the tap number, an (n = 0, 1, 2, …, M-1) is the tap weight of the nth tap, and ΔT is the time delay between adjacent wavelength channels. Therefore, the output microwave signal s(t) can be given by [39]
s ( t ) = f ( t ) * h ( t ) = ∑ M - 1 n = 0 a n f ( t – n Δ T ) ,
where f(t) is the input microwave signal. After Fourier transformation from Eq. (1), the spectral transfer function of the MWP transversal signal processor is
H ( ω ) = ∑ M - 1 n = 0 a n e - j ω n Δ T ,
which shows agreement with the spectral response of a typical microwave transversal filter [39].
As can be seen from Eqs. (1) ‒ (3), by simply altering the tap weights an (n = 0, 1, 2, …, M-1) through comb shaping, different signal processing functions can be achieved without any changes of the hardware [17]. This allows for a high degree of reconfigurability for the MWP transversal signal processor.
Figure 2 shows a schematic of the experimental implementation of the MWP transversal signal processor in Figure 1, which includes a microcomb generation module and a transversal signal processing module. In the microcomb generation module, a continuous-wave (CW) laser, amplified by an erbium-doped fibre amplifier (EDFA) with a polarization controller (PC) to adjust its polarization, is used to pump a high-Q nonlinear microring resonator (MRR) to generate optical microcombs. The output from this module is sent to the transversal signal processing module, which executes the signal processing flow depicted in Figure 1. The processing module involves a PC, an EOM, a spool of single-mode fibre (SMF) as the optical delay module, an optical spectral shaper (OSS) to shape the comb lines, and a balanced photodetector (BPD) for photodetection. The BPD connected to the two complementary output ports of the OSS divides all the wavelength channels into two groups with a phase difference of π, which introduces positive and negative signs onto the tap coefficients an (n = 0, 1, 2, …, M-1) in Eqs. (1) ‒ (3).
For experimentally implemented MWP transversal signal processor in Figure 2, processing errors arise from both theoretical limitations and imperfect response of practical system. The former refers to the theoretical approximation of a continuous impulse response (which corresponds to infinite tap number M) using a practical system with a finite tap number, and was the subject of our previous paper mentioned above [38]. The latter refers to errors induced by imperfect performance of different components, such as the noise of microcomb, chirp of the EOM, second- (SOD) and third-order dispersion (TOD) of the SMF, shaping errors of the OSS, and noise in the BPD.
To quantify the processing errors, the root mean square error (RMSE) is used to compare the deviation between the processor’s output and the ideal result, which is defined as [40]
RMSE = ∑ k i = 1 ( Y I – y i ) 2 k
where k is the number of sampled points, Y1, Y2, …, Yn are the values of the ideal processing result, and y1, y2, …, yn are the values of the output of the microcomb-based MWP transversal signal processors.
Figure 3(a) shows the RMSEs induced by theoretical limitations as a function of tap number M for three different signal processing functions, including first-order differentiation (DIF), integration (INT), and Hilbert transform (HT). These theoretical RMSEs were calculated assuming a perfect response for all the components in Figure 2. As can be seen, the theoretical RMSEs are small for a large tap number M ≥ 80, indicating that the theoretical errors can be greatly reduced by increasing the tap number. Figure 3(b) compares the theoretical and experimentally measured RMSEs for M = 80, showing that the former is much lower, reflecting that experimental errors typically dominate the system performance of microcomb-based MWP transversal signal processors. In the following Section III, we provide a comprehensive analysis of the experimentally induced processing errors, and in Section IV we provide approaches to mitigate these errors.

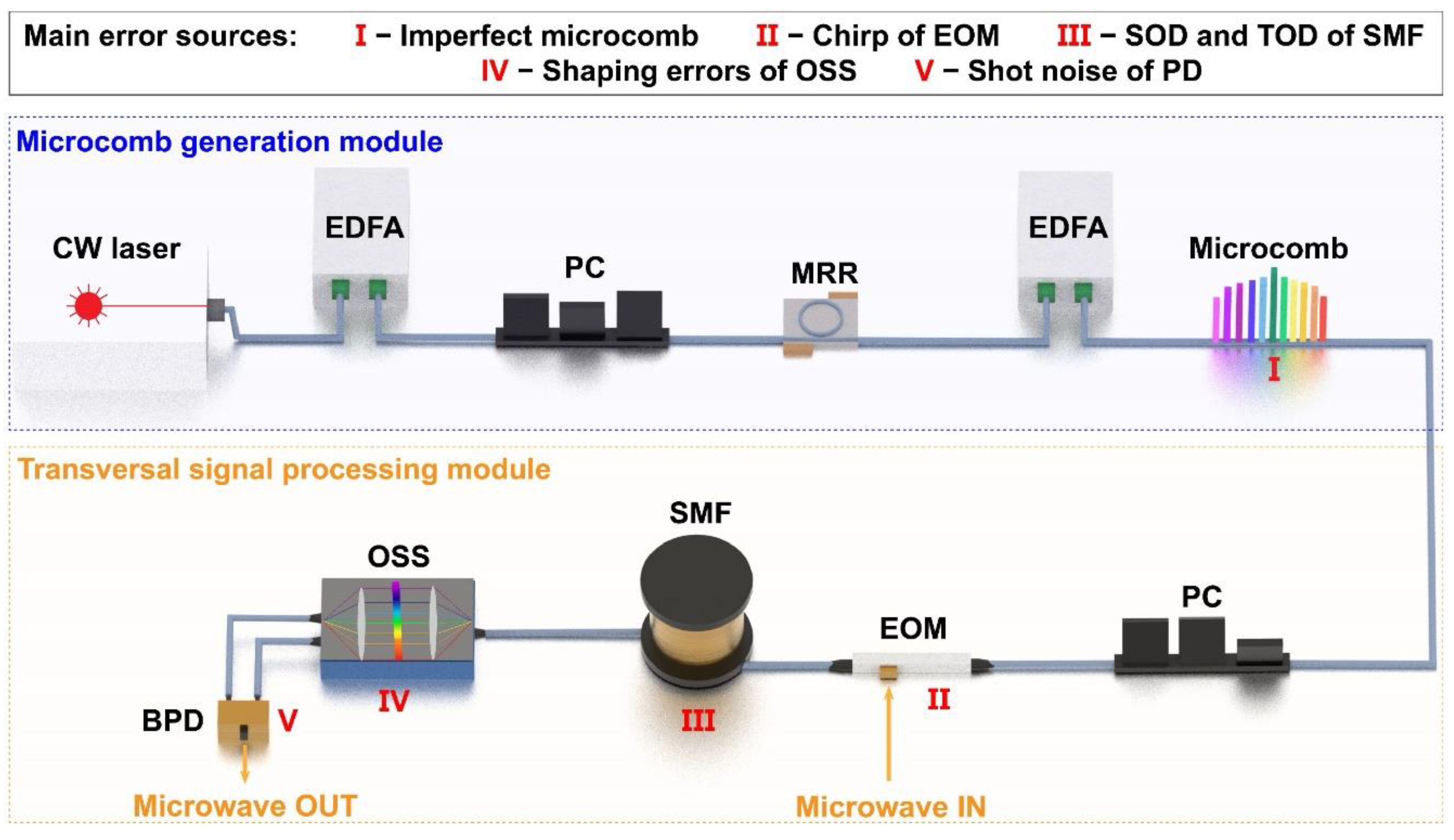
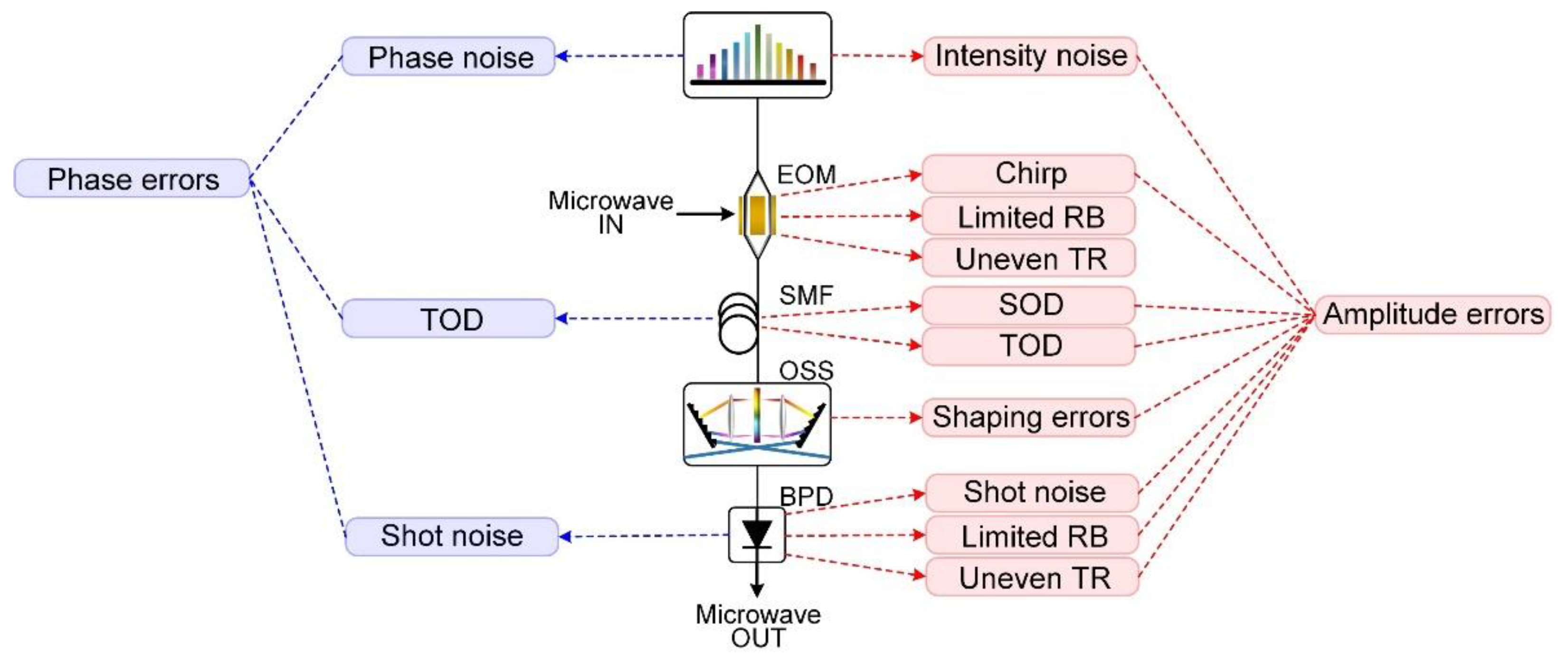
Ⅲ. ERRORS INDUCED BY IMPERFECTIONS OF PRACTICAL SYSTEMS

In this section, we provide a detailed analysis of the processing errors induced by different sources outlined in Figure 2. In subsections A ‒ D, we investigate the influence of specific error sources, assuming the other sources are error-free. In subsection E, we compare the contributions of the different error sources to the overall system performance.
In the following analysis, we use first-order DIF, INT, and HT as examples to quantify the experimentally induced errors. Their spectral transfer functions are given by [27,29,31]
H D I F ( ω ) = j ω ,
H I N T ( ω ) = 1 j ω ,
H H T ( ω ) = { e - j π / 2 , 0 ≤ ω < π e j π / 2 , - π ≤ ω < 0
where j = - 1 and ω is the angular frequency.
For comparison, in our analysis we assume the processors have the same tap number (M = 80), comb spacing (∆λ = 0.4 nm), and length and SOD for the SMF (L = 4.8 km and D2 = 17.4 ps/nm/km). These parameters are the same as those in our previous papers [27,29,31]. The input microwave signal is taken as a Gaussian pulse with a full width at half maximum (FWHM) of ~0.17 ns, whose spectral bandwidth (~5 GHz) is within the processing bandwidth of the signal processors (i.e., FSRMW =1 / (∆λ × L × D2) = ~30 GHz).

A. Influence of the optical microcombs

In this section, we analyze the influence of microcomb imperfections on the system performance for different processing functions. These imperfections generate intensity and phase noise in the comb channels. The intensity noise includes power fluctuations of the comb lines and the intensity noise floor, which mainly arise from photon shot noise and spontaneous emission beat noise [41]. For MWP transversal signal processors, the microcomb intensity noise results in inaccuracy of the tap coefficients, thereby degrading the system accuracy.
To characterize the microcomb intensity noise, the optical signal-to-noise ratio (OSNR) is introduced, which is the ratio of the maximum optical signal to the noise power in each of the comb lines. Figure 4(a) shows the simulated output waveforms from processors that perform DIF, INT, and HT, where flat intensity noise floors are assumed for the microcombs with different OSNRs. For comparison, the ideal processing outcome without theoretical errors, and the results that only account for theoretical errors (corresponding to OSNR = ∞) are also shown. As the OSNR of the comb lines increases from 10 dB to ∞, the processors’ output waveforms match the ideal results better for all three processing functions, reflecting the reduced error achieved by increasing the OSNR. To better reflect the intensity envelop of the microcombs, a sinc-shaped intensity noise floor is introduced. The corresponding results are shown in Figure 4(b), showing a trend similar to that in Figure 4(a).
Figure 4(c) shows the RMSEs between the simulated processors’ output waveforms and the ideal processing results as a function of the OSNR. As expected, for both the flat and sinc-shaped intensity noise floor, the RMSEs decrease with the microcomb OSNR for all three processing functions, showing agreement with the trend in Figure 4(a) and (b). For OSNRs less than 20 dB, the RMSEs decrease more steeply. As the OSNR increases, the decrease in RMSE is more gradual, and there is only a very small reduction in error beyond an OSNR of 20 dB. For the DIF and INT, the RMSE for microcombs with sinc-shaped intensity noise floors is higher than for flat intensity noise floors, whereas the opposite trend is observed for the HT. This reflects the fact that the impact of the microcomb intensity envelope errors depends on the processing function.
The phase noise of microcombs, which manifests as a broadened linewidth, an appearance of multiple repetition-rate beat notes, and a reduction in temporal coherence [42], is affected by several factors, such as the noise of the CW pump as well as the mechanical and thermal noise of the MRR [43,44]. These sources of error are difficult to quantitatively analyze. For mode-locked microcombs with extremely low phase noise, the phase noise induced errors are negligible [35,36]. Therefore, to achieve a high accuracy over long periods, it is necessary to use microcombs with low phase noise, high coherence, and stable mode locking. A number of mode-locking approaches have been reported [17,18]. It is worth noting that even with relatively incoherent microcombs, processors can still achieve an acceptable accuracy because the microcomb mainly serves as a multi-wavelength source and the optical powers of different wavelength channels are detected incoherently by a BPD.

B. Influence of the electro-optic modulator

In Figure 2, an electro-optic modulator is used to modulate the input microwave signal onto different wavelength channels. The most commonly used electro-optic modulators are Mach-Zehnder modulators (MZMs), owing to their high modulation efficiency, low insertion loss, and large operation bandwidth [45]. Due to the asymmetry in the electric field overlap at each electrode [46], practical MZMs not only produce intensity modulation, but also give rise to undesired phase modulation, known as modulation chirp. The chirp leads to distortions in the modulated optical signals, thus resulting in processing errors. Here, we analyze the influence of modulator chirp on the accuracy for different processing functions.
The chirp of a MZM can be characterized by the chirp parameter given by [47]
α = γ 1 + γ 2 γ 1 - γ 2
where γ1 and γ2 are the voltage-to-phase conversion coefficients for the two arms of the MZM. When α = 0 (i.e., γ1 = −γ2), pure intensity modulation is achieved. Figure 5(a) – (c) show the output waveforms from microcomb-based MWP transversal signal processors that perform DIF, INT, and HT for different chirp parameters α. The ideal processing result without theoretical errors and the results that only account for theoretical errors (corresponding to α = 0) are also shown for comparison. For all processing functions the output waveforms approach the ideal results as α decreases from 1 to 0, indicating the reduced system error for a lower modulator chirp.
Figure 5(d) shows the calculated RMSEs versus modulator chirp α. As expected, the RMSE increases with α for all processing functions, which agrees with the trend in Figure 5(a) – (c). We also noted that the impact of the modulation chirp on the system performance is more significant for the DIF and INT functions as compared to the HT.

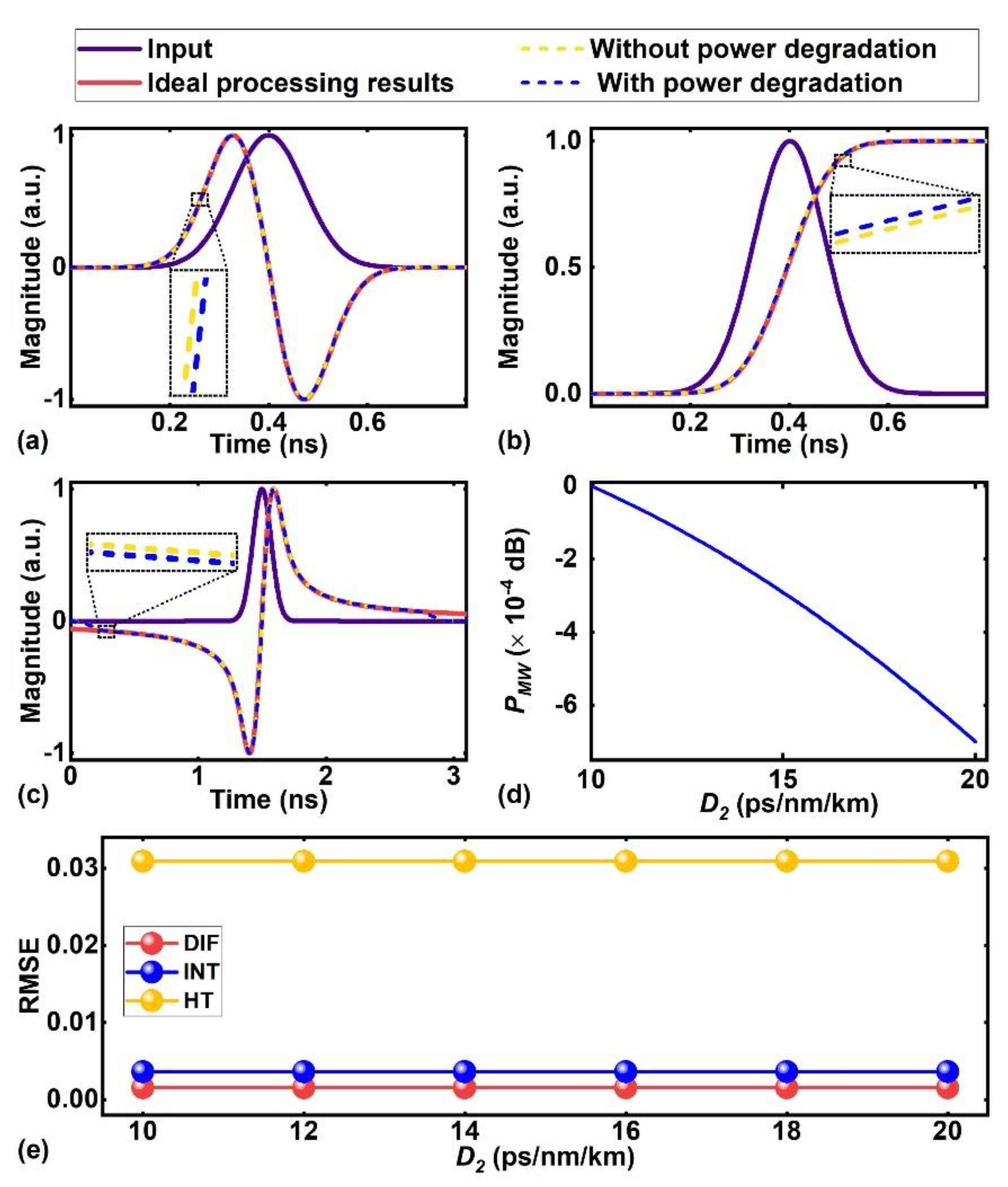
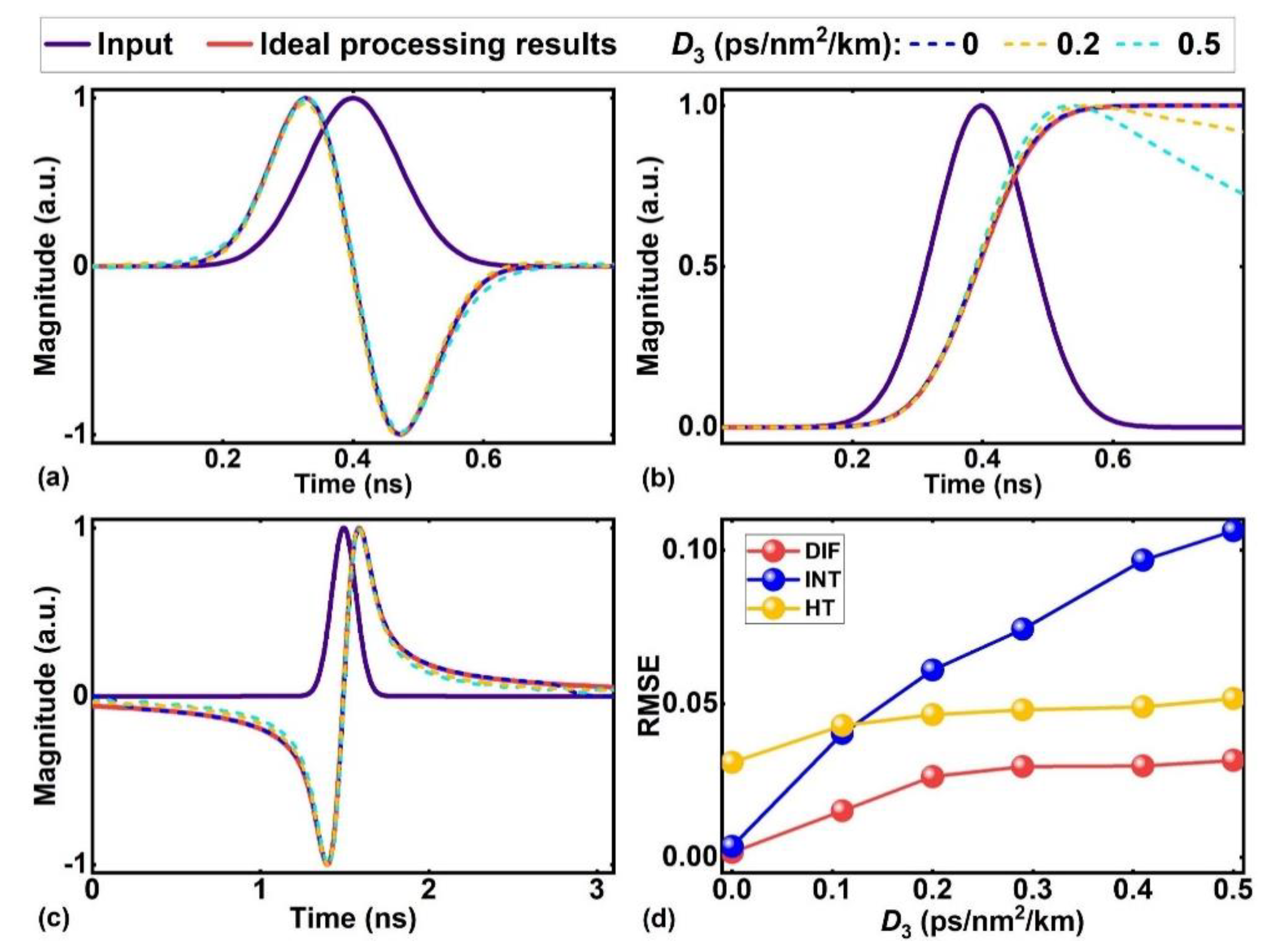
C Influence of the single-mode fibre

In Figure 2, a spool of SMF is employed as the dispersive module of the MWP transversal signal processor, which introduces both amplitude and phase errors due to its chromatic dispersion, including both SOD and TOD. SOD induces a uniform time delay between adjacent taps, which is required for MWP transversal signal processors without alignment errors. However, SOD also introduces a time delay between the modulated sidebands, which leads to a power degradation of the microwave output after photodetection, and hence system errors [48]. On the other hand, the SMF TOD introduces non-uniform time delays between adjacent taps, thus resulting in undesired phase errors. In this section, we analyze the influence of the SMF’s SOD and TOD on the accuracy for different processing functions.
A MZM generates two modulated sidebands, with the output termed a double-sideband (DSB) signal. The SOD of the SMF generates different phase shifts for the two sidebands resulting in different phase shifts between the carrier and the two beat microwave sidebands. Therefore, the final microwave output after photodetection experiences a power degradation, with its power given approximately by [48]
P M W ∝ cos ( π L D 2 c λ c 2 f M W 2 )
where c is the speed of light in vacuum, λc is the center wavelength of each channel, and fMW is the frequency of the input microwave signal.
Figure 6(a) – (c) show the output waveforms from the processors for the DIF, INT, and HT functions, with and without including the power degradation caused by SOD. The SOD parameter is kept constant at D2 = 17.4 ps/nm/km. For all processing functions, there are only slight differences induced by SOD. Figure 6(d) shows the power degradation PMW as a function of D2, which is calculated based on Eq. (9). As can be seen, the power degradation induced by SOD is very small, being < 10-3 dB for D2 = 17.4 ps/nm/km in Figure 6(a) – (c).
Figure 6(e) shows the RMSE as a function of D2, showing that the RMSE only vary very slightly (< 10-4) with D2 for all processing functions, in agreement with Figure 6(a) – (c). These results indicate that although the SOD of SMF induces power degradation of the microwave output, its influence on the system accuracy is very small.
The TOD of the SMF introduces additional non-uniform time delays between the modulated replicas in the wavelength channels, thus resulting in alignment errors in the processing results. The additional time delay of the nth tap is given by [49]
Δ T T O D = D 3 L Δ λ 2 n 2
where D3 is the TOD parameter.
Figure 7(a) – (c) show the output waveforms from processors that perform DIF, INT, and HT, versus the TOD parameter D3. The ideal processing result without theoretical errors and the results that only account for theoretical errors (corresponding to D3 = 0) are also shown for comparison. For all processing functions, the processors’ outputs approach the ideal processing results as D3 decreases from 0.5 ps/nm2/km to zero, indicating that improved accuracy can be achieved for a smaller TOD.
Figure 7(d) shows the RMSE as a function of D3, where, as expected, the RMSE increases with increasing D3 for all functions ‒ agreeing with the trend in Figure 7(a) – (c). The influence of TOD on the system performance is more significant than that of the SOD. We also note that the INT function is more susceptible to errors induced by the TOD as compared to the DIF and HT functions, reflecting that INT has a more stringent requirement for the accuracy of the phase of the different taps.

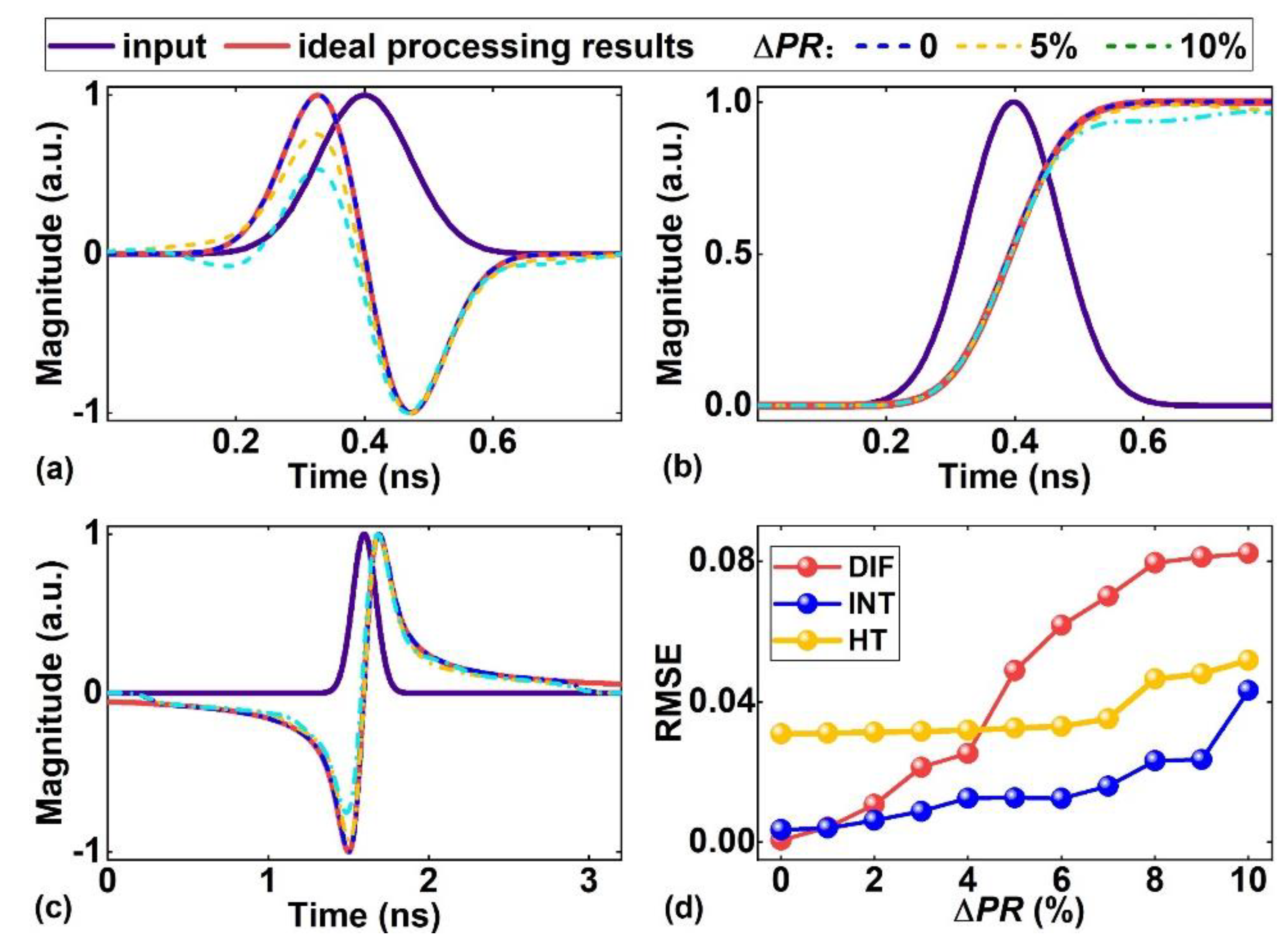
D Influence of optical spectral shapers and photodetectors

In Figure 2, an optical spectral shaper is used as a spectral shaping module to weight the delayed signals across different wavelength channels according to the designed tap coefficients. This is followed by a BPD that sums the delayed and weighted signals to generate the microwave output of the processor. The OSS induces shaping errors, which result in inaccurate tap coefficients and hence output errors. On the other hand, noise and an uneven transmission response of the BPD lead to variations of the power of the microwave output. In this section, we analyze the influence of these error sources for the different processing functions.
We introduce random tap coefficient errors (RTCEs) within a certain percentage range of ∆PR to characterize the shaping errors of the OSS.Figure 8(a) – (c) show the output waveforms from the processors for all functions and for the RTCEs in different ranges, together with the ideal processing result without theoretical errors and the results that only account for theoretical errors (corresponding to ∆PR = 0). For all the three processing functions, the processors’ output waveforms show better agreement with the ideal results for a smaller ∆PR, reflecting an improved accuracy associated with reduced RTCEs.
Figure 8(d) shows the RMSE as a function of ∆PR, showing that the RMSE increases with ∆PR for all functions, agreeing with the trend in Figure 8(a) – (c). The shaping errors of the OSS have a more obvious impact on the accuracy for DIF as compared to the other two functions, indicating that DIF has a more stringent requirement for the accuracy of the tap amplitudes.
In Figure 2, the use of a BPD greatly suppresses the common-mode noise of the optical signal, which largely cancels out the intensity noise caused by the photodetector. Therefore, the errors induced by the BPD mainly come from its limited response bandwidth and uneven transmission response, which introduce additional errors in the tap coefficients after spectral shaping. Similarly, the limited bandwidth and uneven response of the EOM could also introduce additional errors to the tap coefficients before spectral shaping. These errors, together with the shaping errors of the OSS, can be effectively mitigated through feedback control, which will be discussed in section Ⅳ. Finally, we note that the BPD shot noise can induce random power fluctuations in the output microwave signal which limits the lowest achievable phase noise floor [50]. The influence of this on the system performance is similar to the microcomb noise, and can be reduced by using a BPD with higher sensitivity [51].

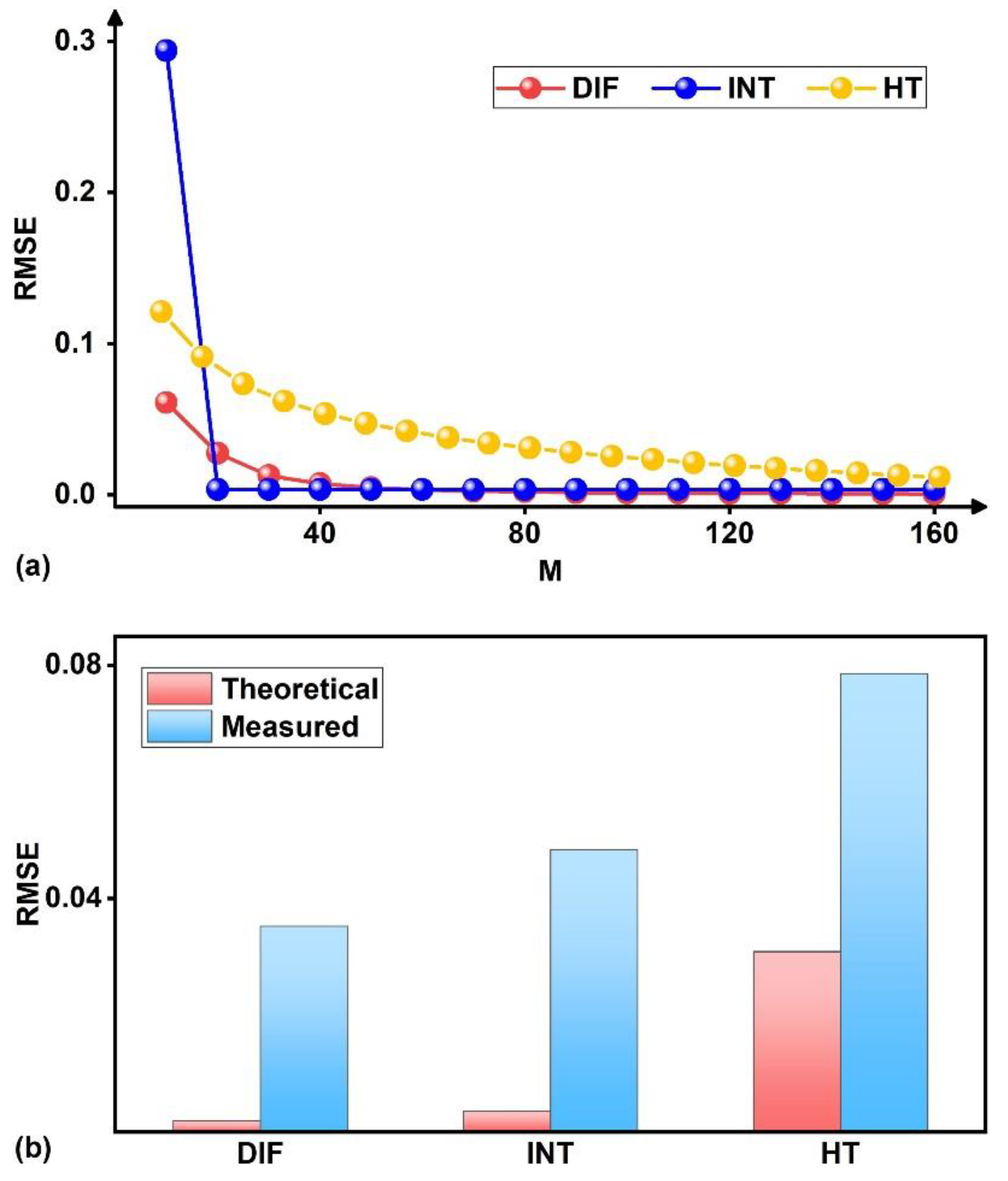
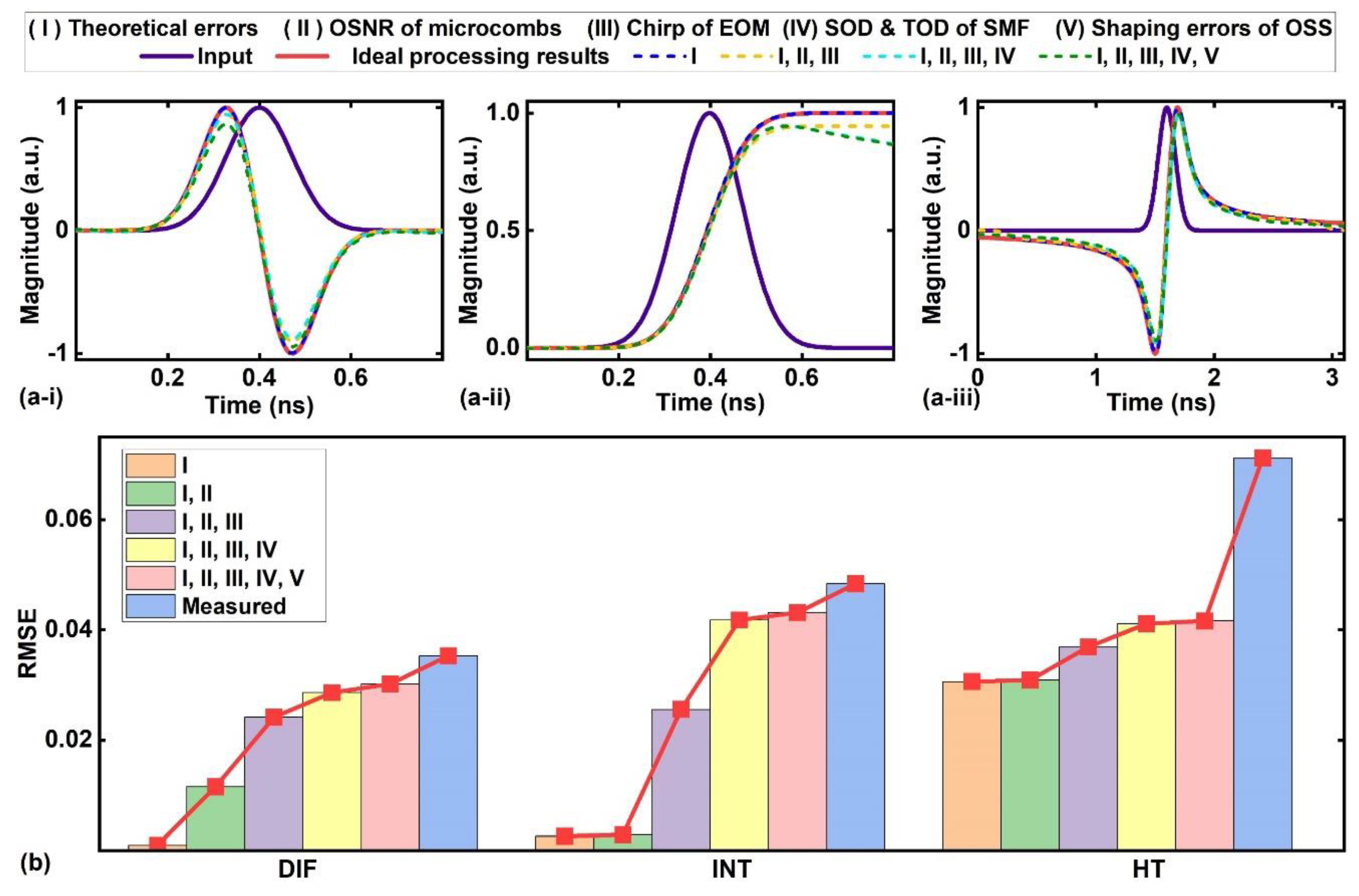
E Contributions of different error sources

In this section, we analyze the contribution of the error sources discussed above to the overall processing errors of microcomb-based MWP transversal signal processors and provide a global picture to show the impact of different error sources.
Figure 9(a) shows the simulated output waveforms for all functions, including errors induced by the sources from I to V in Figure 2, with the ideal results shown for comparison. Based on the measurements and parameters of the components in our previous experiments [27,30,34], the OSNR of the sinc-shaped microcomb, chirp parameter of the EOM, SOD and TOD parameter of the SMF, and range of RTCEs are set to OSNR = 30 dB, α = 0.5, D2 = 17.4 ps/nm/km, D3 = 0.083 ps/nm2/km, and ∆PR = 5%, respectively. As expected, the overall output errors become larger with the accumulation of errors induced by these sources for all processing functions.
In order to quantify the contributions of the different sources of error, we calculate the RMSEs from the simulation results Figure 9(a) and plot them in Figure 9(b). The experimentally measured RMSEs are also shown for comparison. In our simulations, we used the input microwave signal waveform measured by a high-bandwidth real-time oscilloscope to calculate the RMSEs, this can minimize the errors induced by the discrepancy between the experimentally generated and ideal Gaussian pulses. The RMSEs of the simulation results increase with the accumulation of errors, which agrees with the trend in Figure 9(a). There are margins between the RMSEs of the simulation results and the experimental results. They are mainly caused by deviations between the simulation and experiment parameters as well as factors that are not accounted for in our simulation, such as the phase noise of the microcomb, the limited response bandwidth and uneven transmission response of the EOM and BPD, and the shot noise of the BPD. According to Figure 9(b), the system error for the DIF is mainly induced by the microcomb imperfections and EOM chirp. For the INT, the main error sources are the EOM chirp and the SMF TOD. As compared to the DIF and INT, the theoretical errors have a more significant influence on the accuracy for the HT.

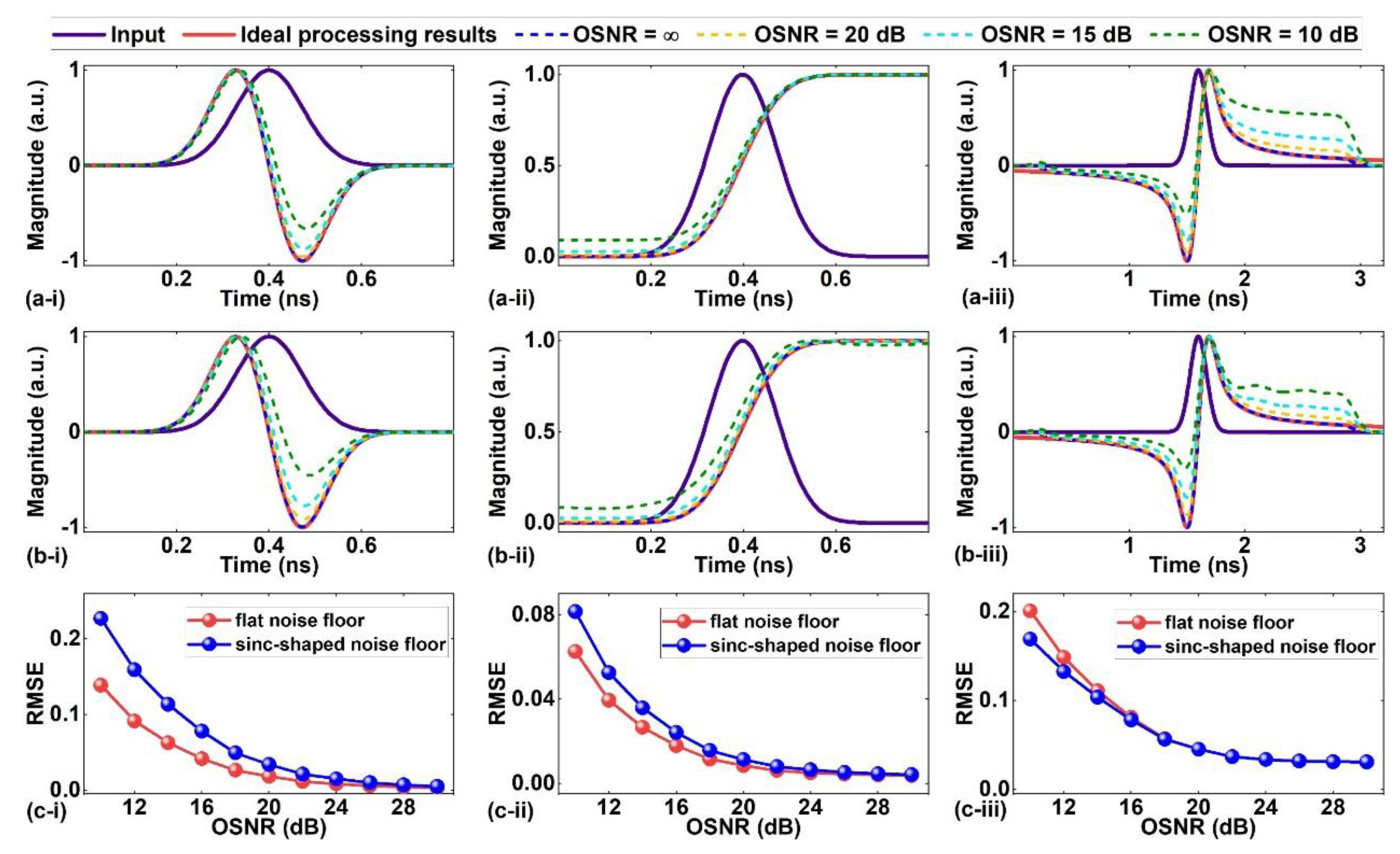
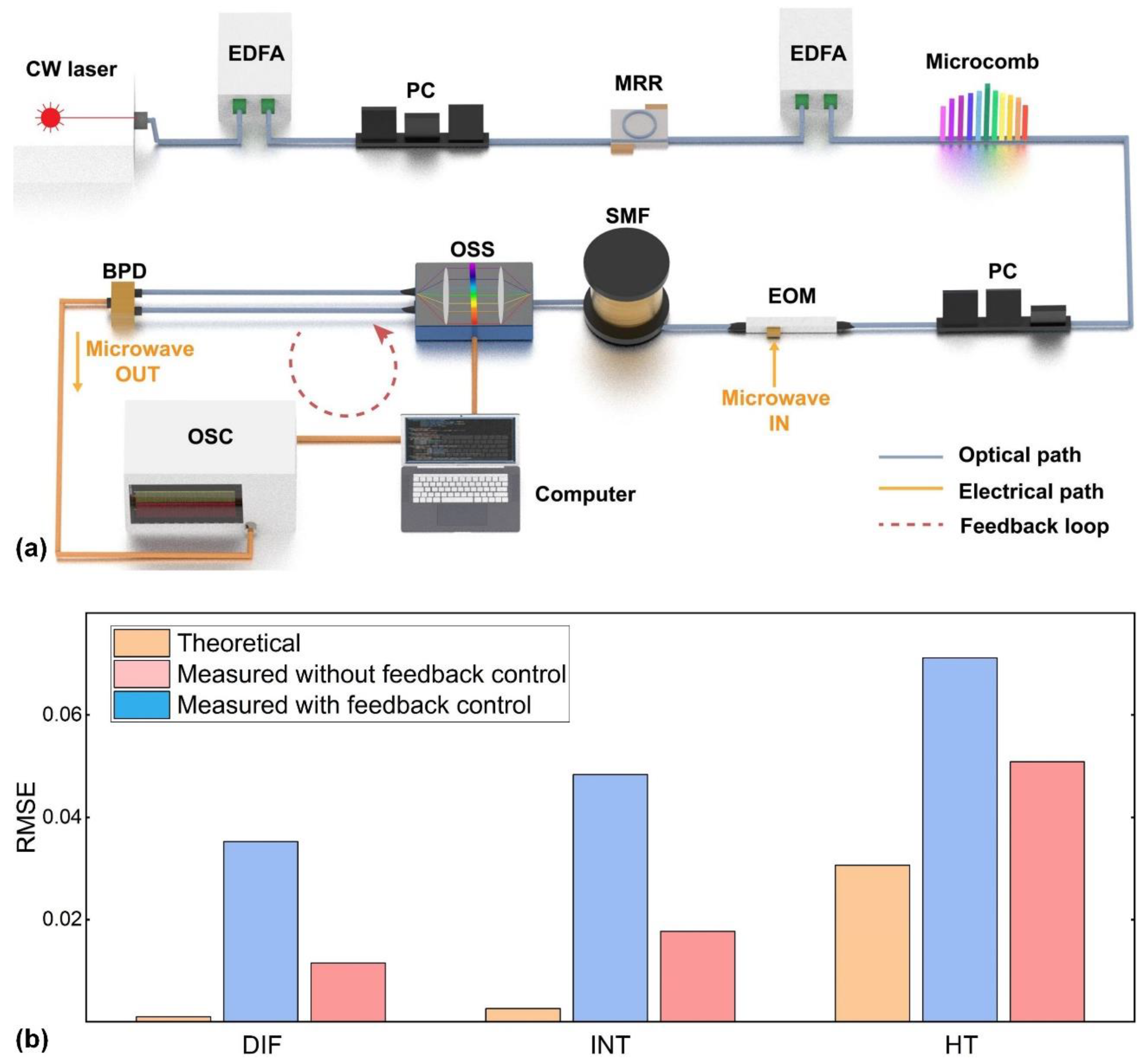
Ⅳ. ERROR COMPENSATION VIA FEEDBACK CONTROL

In this section, feedback control is introduced to compensate for errors induced by the imperfect response of experimental components. The benefit of feedback control is quantitatively analyzed by comparing the system errors with and without feedback control.
As shown in Figure 10, we classify the error sources discussed in Section III into two categories, depending on whether amplitude or phase errors are introduced in the taps. The amplitude and phase errors refer to errors in the tap coefficients (i.e., an in Eqs. (1) ‒ (3)) and time delays (i.e., n∆T in Eqs. (1) ‒ (3)) for different taps, respectively. The sources of amplitude errors include the microcomb intensity noise, EOM chirp, TOD and SOD of the SMF, OSS shaping errors, BPD shot noise, and the bandwidth response of the EOM and BPD. The sources of phase errors include microcomb phase noise, TOD of the SMF, and BPD shot noise. We note that some of the error sources in Figure 10are static or slowly varying, e.g., chirp of EOM, SOD and TOD of SMF, and shaping errors of OSS. In contrast, the fluctuations in the amplitude and phase caused by microcombs and the BPD are normally faster ‒ on the order of 10 GHz.
The static or slowly varying amplitude errors in Figure 10can be compensated for by introducing feedback control to calibrate the designed tap coefficients set for the OSS. Figure 11(a) shows a schematic of a MWP transversal signal processor with feedback control. A feedback control loop including all the components of the signal processor is introduced to calibrate the amplitude of the temporal impulse response of each tap based on the ideal impulse response. During the calibration process, a microwave signal is employed as the input signal to test the impulse response of the processor channel by channel, where the same input microwave signal is modulated onto the corresponding comb line. The intensities of the microwave signals after photodetection are recorded by an oscilloscope and sent to a computer, where they are subtracted from the designed tap weights to generate error signals. Finally, the generated error signals are sent to the OSS to calibrate the attenuation of comb line intensity. After several iterations of the above process, the amplitude errors caused by the non-ideal impulse response of the system can be effectively reduced. Similarly, the static or slowly-varying phase errors can be mitigated by exploiting the programmable phase characteristics of the OSS to compensate the deviation between the measured and desired phase response.
In Figure 11(b), we compare the RMSEs for all functions with and without feedback control. The RMSEs caused by theoretical errors are also shown for comparison. As expected, the measured RMSEs with feedback control are much lower than those measured without calibration and approach the theoretical RMSEs more closely. After calibration, there are still discrepancies between the measured RMSEs and theoretical RMSEs, reflecting that there are still residual errors that cannot be compensated for with feedback control. We infer that these errors are mainly induced by rapidly varying error sources, by deviations between the simulated and experimental parameters, and by the limited resolution of the instruments such as the OSS and oscilloscope.
To further improve the system accuracy, multiple-stage feedback control can be employed. For example, another feedback loop with one more OSS can be introduced in the microcomb generation module to flatten the comb lines of the initially generated microcomb. This allows for uniform wavelength channel link gain and can also reduce the loss control range for the spectral shaping in the transversal signal processing module. Recently, self-calibrating photonic integrated circuits have been demonstrated [52,53], where the impulse response calibration was achieved by incorporating an optical reference path to establish a Kramers-Kronig relationship and then calculate the amplitude and phase errors based on a Fourier transform. This offers new possibilities to achieve precise feedback control in MWP transversal signal processors, [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73] based on optical integrated microcombs. [74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129]

V. CONCLUSIONS

In summary, we analyze the processing errors induced by experimental imperfections for microcomb-based MWP transversal signal processors. We first investigate the errors arising from imperfect microcomb characteristics, EOM chirp, chromatic dispersion in the dispersive module, errors in the optical spectral shaper, and photodetector noise. Next, we present a global picture of the quantitative influence of different error sources on the overall system performance. Finally, we introduce feedback control to compensate for the errors and quantitatively analyze the improvement in the processing accuracy. Our results show that the influence of the error sources varies for the different processing functions studied here, and that these errors can be significantly reduced by introducing feedback control for both static and slowly varying sources of error. This work provides a useful guide for optimizing the performance of microcomb-based MWP transversal signal processors for versatile high-speed information processing applications.

References

  1. J. Capmany et al., “Microwave photonics combines two worlds,” Nat. Photonics, vol. 1, no. 6, pp. 319-330, 2007. [CrossRef]
  2. D. Marpaung et al., “Integrated microwave photonics,” Nat. Photonics, vol. 13, no. 2, pp. 80-90, 2019.
  3. W. Liu et al., “A fully reconfigurable photonic integrated signal processor,” Nat. Photonics, vol. 10, no. 3, pp. 190-195, 2016. [CrossRef]
  4. D. R. Solli et al., “Analog optical computing,” Nat. Photonics, vol. 9, no. 11, pp. 704-706, 2015. [CrossRef]
  5. B. Fischer et al., “Autonomous on-chip interferometry for reconfigurable optical waveform generation,” Optica, vol. 8, no. 10, pp. 1268-1276, 2021. [CrossRef]
  6. H. Arianfard et al., “Sagnac interference in integrated photonics,” Applied Physics Reviews, vol. 10, no. 1, pp. 011309, 2023. [CrossRef]
  7. M. Ferrera et al., “On-chip CMOS-compatible all-optical integrator,” Nat. Commun., vol. 1, no. 1, pp. 29, 2010. [CrossRef]
  8. J. Yao et al., “Fully reconfigurable waveguide Bragg gratings for programmable photonic signal processing,” Journal of Lightwave Technology, vol. 38, no. 2, pp. 202-214, 2019.
  9. W. Zhang et al., “Photonic integrated field-programmable disk array signal processor,” Nat. Commun., vol. 11, no. 1, pp. 1-9, 2020. [CrossRef]
  10. N. K. Berger et al., “Temporal differentiation of optical signals using a phase-shifted fiber Bragg grating,” Opt. Express, vol. 15, no. 2, pp. 371-381, 2007. [CrossRef]
  11. K. A. Rutkowska et al., “Ultrafast all-optical temporal differentiators based on CMOS-compatible integrated-waveguide Bragg gratings,” Opt. Express, vol. 19, no. 20, pp. 19514-19522, 2011. [CrossRef]
  12. F. Liu et al., “Compact optical temporal differentiator based on silicon microring resonator,” Opt. Express, vol. 16, no. 20, pp. 15880-15886, 2008. [CrossRef]
  13. J. Wu et al., “Compact tunable silicon photonic differential-equation solver for general linear time-invariant systems,” Opt. Express, vol. 22, no. 21, pp. 26254-26264, 2014. [CrossRef]
  14. J. Wu et al., “On-Chip Tunable Second-Order Differential-Equation Solver Based on a Silicon Photonic Mode-Split Microresonator,” Journal of Lightwave Technology, vol. 33, no. 17, pp. 3542-3549, 2015. [CrossRef]
  15. A. Zheng et al., “Fractional-order photonic differentiator using an on-chip microring resonator,” Opt. Lett., vol. 39, no. 21, pp. 6355-6358, 2014. [CrossRef]
  16. Zheng et al., “Tunable fractional-order differentiator using an electrically tuned silicon-on-isolator Mach-Zehnder interferometer,” Opt. Express, vol. 22, no. 15, pp. 18232-18237, 2014. [CrossRef]
  17. J. Wu et al., “RF Photonics: An Optical Microcombs’ Perspective,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 24, no. 4, pp. 1-20, 2018.
  18. Y. Sun et al., “Applications of optical microcombs,” Adv. Opt. Photon., vol. 15, no. 1, pp. 86-175, 2023. [CrossRef]
  19. S. Mansoori et al., “RF transversal filter using an AOTF,” IEEE Photonics Technology Letters, vol. 16, no. 3, pp. 879-881, 2004. [CrossRef]
  20. J. Zhang et al., “Photonic true-time delay beamforming using a switch-controlled wavelength-dependent recirculating loop,” Journal of Lightwave Technology, vol. 34, no. 16, pp. 3923-3929, 2016. [CrossRef]
  21. L. Zhang et al., “Photonic true time delay beamforming technique with ultra-fast beam scanning,” Opt. Express, vol. 25, no. 13, pp. 14524-14532, 2017.
  22. G. Yu et al., “High-performance microwave transversal filter using fiber Bragg grating arrays,” IEEE Photonics Technology Letters, vol. 12, no. 9, pp. 1183-1185, 2000. [CrossRef]
  23. D. B. Hunter et al., “Tunable optical transversal filter based on chirped gratings,” Electronics Letters, 31, https://digital-library.theiet.org/content/journals/10.1049/el_19951495, 1995]. [CrossRef]
  24. Y. Liu et al., “Wideband true-time-delay unit for phased array beamforming using discrete-chirped fiber grating prism,” Optics Communications, vol. 207, no. 1-6, pp. 177-187, 2002. [CrossRef]
  25. A. Pasquazi et al., “Micro-combs: A novel generation of optical sources,” Physics Reports, vol. 729, pp. 1-81, 2018. [CrossRef]
  26. L. Chang et al., “Integrated optical frequency comb technologies,” Nat. Photonics, vol. 16, no. 2, pp. 95-108, 2022. [CrossRef]
  27. X. Xu et al., “Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source,” APL Photonics, vol. 2, no. 9, pp. 096104, 2017. [CrossRef]
  28. M. Tan et al., “RF and Microwave Fractional Differentiator Based on Photonics,” IEEE Trans. Circuits Syst. II-Express Briefs, vol. 67, no. 11, pp. 2767-2771, 2020. [CrossRef]
  29. X. Xu et al., “Photonic RF and Microwave Integrator Based on a Transversal Filter With Soliton Crystal Microcombs,” IEEE Trans. Circuits Syst. II-Express Briefs, vol. 67, no. 12, pp. 3582-3586, 2020. [CrossRef]
  30. T. G. Nguyen et al., “Integrated frequency comb source based Hilbert transformer for wideband microwave photonic phase analysis,” Opt. Express, vol. 23, no. 17, pp. 22087-22097, 2015. [CrossRef]
  31. M. Tan et al., “Microwave and RF Photonic Fractional Hilbert Transformer Based on a 50 GHz Kerr Micro-Comb,” Journal of Lightwave Technology, vol. 37, no. 24, pp. 6097-6104, 2019. [CrossRef]
  32. M. Tan et al., “Highly Versatile Broadband RF Photonic Fractional Hilbert Transformer Based on a Kerr Soliton Crystal Microcomb,” Journal of Lightwave Technology, vol. 39, no. 24, pp. 7581-7587, 2021. [CrossRef]
  33. X. Xu et al., “Photonic RF Phase-Encoded Signal Generation With a Microcomb Source,” Journal of Lightwave Technology, vol. 38, no. 7, pp. 1722-1727, 2020. [CrossRef]
  34. M. Tan et al., “Photonic RF Arbitrary Waveform Generator Based on a Soliton Crystal Micro-Comb Source,” Journal of Lightwave Technology, vol. 38, no. 22, pp. 6221-6226, 2020. [CrossRef]
  35. X. Xu et al., “Photonic Perceptron Based on a Kerr Microcomb for High-Speed, Scalable, Optical Neural Networks,” Laser Photon. Rev., vol. 14, no. 10, 2000070, 2020.
  36. X. Xu et al., “11 TOPS photonic convolutional accelerator for optical neural networks,” Nature, vol. 589, no. 7840, pp. 44-51, 2021. [CrossRef]
  37. X. Xu et al., “Microcomb-Based Photonic RF Signal Processing,” IEEE Photonics Technology Letters, vol. 31, no. 23, pp. 1854-1857, 2019. [CrossRef]
  38. Y. Sun et al., “Quantifying the Accuracy of Microcomb-based Photonic RF Transversal Signal Processors,” to be published, IEEE Journal of Selected Topics in Quantum Electronics. Research Square. [CrossRef]
  39. J. Capmany et al., “Discrete-time optical processing of microwave signals,” Journal of Lightwave Technology, vol. 23, no. 2, pp. 702-723, 2005. [CrossRef]
  40. A. Toprak et al., “Impulse noise reduction in medical images with the use of switch mode fuzzy adaptive median filter,” Digital Signal Processing, vol. 17, no. 4, pp. 711-723, 2007. [CrossRef]
  41. P. J. Marchand et al., “Soliton microcomb based spectral domain optical coherence tomography,” Nat. Commun., vol. 12, no. 1, pp. 427, 2021. [CrossRef]
  42. T. Herr et al., “Universal formation dynamics and noise of Kerr-frequency combs in microresonators,” Nat. Photonics, vol. 6, no. 7, pp. 480-487, 2012. [CrossRef]
  43. K. Nishimoto et al., “Investigation of the phase noise of a microresonator soliton comb,” Opt. Express, vol. 28, no. 13, pp. 19295-19303, 2020. [CrossRef]
  44. A. B. Matsko et al., “Noise conversion in Kerr comb RF photonic oscillators,” J. Opt. Soc. Am. B, vol. 32, no. 2, pp. 232-240, 2015. [CrossRef]
  45. Y. Fu et al., “Mach-Zehnder: A Review of Bias Control Techniques for Mach-Zehnder Modulators in Photonic Analog Links,” IEEE Microwave Magazine, vol. 14, no. 7, pp. 102-107, 2013. [CrossRef]
  46. A. Djupsjobacka, “Residual chirp in integrated-optic modulators,” IEEE Photonics Technology Letters, vol. 4, no. 1, pp. 41-43, 1992. [CrossRef]
  47. B. E. Rogers Iii et al., “Characterization and compensation of the residual chirp in a Mach-Zehnder-type electro-optical intensity modulator,” Opt. Express, vol. 18, no. 2, pp. 1166-1176, 2010. [CrossRef]
  48. G. H. Smith et al., “Overcoming chromatic-dispersion effects in fiber-wireless systems incorporating external modulators,” IEEE Transactions on Microwave Theory and Techniques, vol. 45, no. 8, pp. 1410-1415, 1997. [CrossRef]
  49. X. Xu et al., “Photonic microwave true time delays for phased array antennas using a 49 GHz FSR integrated optical micro-comb source Invited,” Photonics Res., vol. 6, no. 5, pp. B30-B36, 2018. [CrossRef]
  50. Ahn et al., “Synchronization of an optical frequency comb and a microwave oscillator with 53&#x2009;&#x2009;zs/Hz1/2 resolution and 10-20-level stability,” Photonics Res., vol. 10, no. 2, pp. 365-372, 2022.
  51. J. Hu et al., “Microwave photonic link with improved phase noise using a balanced detection scheme,” Optics Communications, vol. 370, pp. 1-5, 2016. [CrossRef]
  52. X. Xu et al., “Self-calibrating programmable photonic integrated circuits,” Nat. Photonics, vol. 16, no. 8, pp. 595-602, 2022. [CrossRef]
  53. X. Xu et al., “Phase retrieval of programmable photonic integrated circuits based on an on-chip fractional-delay reference path,” Optica, vol. 9, no. 12, pp. 1401, 2022. [CrossRef]
  54. M. Tan et al, “Orthogonally polarized Photonic Radio Frequency single sideband generation with integrated micro-ring resonators”, IOP Journal of Semiconductors, Vol. 42 (4), 041305 (2021). [CrossRef]
  55. M. Tan et al., “Photonic Radio Frequency Channelizers based on Kerr Optical Micro-combs”, IOP Journal of Semiconductors Vol. 42 (4), 041302 (2021). [CrossRef]
  56. Xu, et al., “Advanced adaptive photonic RF filters with 80 taps based on an integrated optical micro-comb source,” Journal of Lightwave Technology, vol. 37, no. 4, pp. 1288-1295 (2019).
  57. X. Xu, et al., Broadband microwave frequency conversion based on an integrated optical micro-comb source”, Journal of Lightwave Technology, vol. 38 no. 2, pp. 332-338, 2020. [CrossRef]
  58. M. Tan, et al., “Photonic RF and microwave filters based on 49GHz and 200GHz Kerr microcombs”, Optics Comm. vol. 465,125563, Feb. 22. 2020. [CrossRef]
  59. X. Xu, et al., “Broadband photonic RF channelizer with 90 channels based on a soliton crystal microcomb”, Journal of Lightwave Technology, Vol. 38, no. 18, pp. 5116 - 5121, 2020. [CrossRef]
  60. X. Xu, et al., “High performance RF filters via bandwidth scaling with Kerr micro-combs,” APL Photonics, vol. 4 (2) 026102. 2019. [CrossRef]
  61. M. Tan et al, “RF and microwave high bandwidth signal processing based on Kerr Micro-combs”, Advances in Physics X, VOL. 6, NO. 1, 1838946 (2021). [CrossRef]
  62. X. Xu, et al., “Advanced RF and microwave functions based on an integrated optical frequency comb source,” Opt. Express, vol. 26 (3) 2569 (2018). [CrossRef]
  63. Wu, J. et al. RF Photonics: An Optical Microcombs’ Perspective. IEEE Journal of Selected Topics in Quantum Electronics Vol. 24, 6101020, 1-20 (2018).
  64. X. Xu, et al., “Broadband RF channelizer based on an integrated optical frequency Kerr comb source,” Journal of Lightwave Technology, vol. 36, no. 19, pp. 4519-4526, 2018. [CrossRef]
  65. X. Xu, et al., “Continuously tunable orthogonally polarized RF optical single sideband generator based on micro-ring resonators,” Journal of Optics, vol. 20, no. 11, 115701. 2018. [CrossRef]
  66. X. Xu, et al., “Orthogonally polarized RF optical single sideband generation and dual-channel equalization based on an integrated microring resonator,” Journal of Lightwave Technology, vol. 36, no. 20, pp. 4808-4818. 2018. [CrossRef]
  67. Corcoran, et al., “Ultra-dense optical data transmission over standard fiber with a single chip source”, Nature Communications, vol. 11, Article:2568, 2020.
  68. X. Xu et al., “Neuromorphic computing based on wavelength-division multiplexing”, 28 IEEE Journal of Selected Topics in Quantum Electronics Vol. 29 Issue: 2, Article 7400112 (2023). [CrossRef]
  69. Y.Bai et al., “Photonic multiplexing techniques for neuromorphic computing”, Nanophotonics 12 (5): 795–817 (2023). [CrossRef]
  70. Prayoonyong et al., “Frequency comb distillation for optical superchannel transmission”, Journal of Lightwave Technology 39 (23) 7383-7392 (2021). [CrossRef]
  71. M.Tan et al., “Integral order photonic RF signal processors based on a soliton crystal micro-comb source”, IOP Journal of Optics 23 (11) 125701 (2021).
  72. Y. Sun et al., “Performance analysis of microcomb-based microwave photonic transversal signal processors with experimental errors”, Journal of Lightwave Technology Vol. 41 Special Issue on Microwave Photonics (2023).
  73. M. Tan et al., “18 Tb/s photonic digital signal processor for real time video image processing”, Research Square (2023). https://doi.org/10.21203/rs.3.rs-1775424/v.
  74. M.Ferrera et al., “CMOS compatible integrated all-optical RF spectrum analyzer”, Optics Express, vol. 22, no. 18, 21488 - 21498 (2014).
  75. M. Peccianti, et al., “Demonstration of an ultrafast nonlinear microcavity modelocked laser”, Nature Communications, vol. 3, pp. 765, 2012.
  76. A. Pasquazi, et al., “Self-locked optical parametric oscillation in a CMOS compatible microring resonator: a route to robust optical frequency comb generation on a chip,” Optics Express, vol. 21, no. 11, pp. 13333-13341, 2013. [CrossRef]
  77. Pasquazi, et al., “Stable, dual mode, high repetition rate mode-locked laser based on a microring resonator,” Optics Express, vol. 20, no. 24, pp. 27355-27362, 2012.
  78. L. Razzari, et al., “CMOS-compatible integrated optical hyper-parametric oscillator,” Nature Photonics, vol. 4, no. 1, pp. 41-45, 2010. [CrossRef]
  79. M. Ferrera et al., “Low Power CW Parametric Mixing in a Low Dispersion High Index Doped Silica Glass Micro-Ring Resonator with Q-factor > 1 Million”, Optics Express, vol.17, no. 16, pp. 14098–14103 (2009).
  80. M. Kues, et al., “Passively modelocked laser with an ultra-narrow spectral width”, Nature Photonics, vol. 11, no. 3, pp. 159, 2017.
  81. M. Ferrera, et al., “On-chip CMOS-compatible all-optical integrator”, Nature Communications, vol. 1, Article 29, 2010.
  82. A. Pasquazi, et al., “Sub-picosecond phase-sensitive optical pulse characterization on a chip”, Nature Photonics, vol. 5, no. 10, pp. 618-623 (2011). [CrossRef]
  83. M. Ferrera et al.“On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Opt. Express, vol. 19, (23)pp. 23153-23161 (2011).
  84. Bao, C., et al., Direct soliton generation in microresonators, Opt. Lett, 42, 2519 (2017). [CrossRef]
  85. Duchesne et al., “Supercontinuum generation in a high index doped silica glass spiral waveguide,” Optics Express, vol. 18, no, 2, pp. 923-930, 2010.
  86. M. Ferrera, et al., “Low-power continuous-wave nonlinear optics in doped silica glass integrated waveguide structures,” Nature Photonics, vol. 2, no. 12, pp. 737-740, 2008. [CrossRef]
  87. H Bao et al., “Turing patterns in a fiber laser with a nested microresonator: Robust and controllable microcomb generation”, Physical Review Research 2 (2), 023395 (2020). [CrossRef]
  88. A. Pasquazi, et al., “All-optical wavelength conversion in an integrated ring resonator,” Optics Express, vol. 18, no. 4, pp. 3858-3863, 2010.
  89. Pasquazi et al., “Efficient wavelength conversion and net parametric gain via Four Wave Mixing in a high index doped silica waveguide,” Optics Express, vol. 18, no. 8, pp. 7634-7641, 2010.
  90. M. Peccianti et al., “Subpicosecond optical pulse compression via an integrated nonlinear chirper,” Optics Express, vol. 18, no. 8, pp. 7625-7633, 2010. [CrossRef]
  91. Little, B. E. et al., “Very high-order microring resonator filters for WDM applications”, IEEE Photonics Technol. Lett. 16, 2263–2265 (2004). [CrossRef]
  92. Moss, D. J. et al., “New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics”, Nature photonics Vol. 7, 597 (2013). [CrossRef]
  93. H. Bao, et al., Laser cavity-soliton microcombs, Nature Photonics, vol. 13, no. 6, pp. 384-389, Jun. 2019. [CrossRef]
  94. A. Cutrona et al.,“High Conversion Efficiency in Laser Cavity-Soliton Microcombs”, Optics Express Vol. 30, Issue 22, pp. 39816-39825 (2022). https://doi.org/10.1364/OE.470376. [CrossRef]
  95. M.Rowley et al., “Self-emergence of robust solitons in a micro-cavity”, Nature 608 (7922) 303–309 (2022).
  96. R. Holzwarth et al., Phys. Rev. Lett. 85, 2264-2267 (2000).
  97. P. Del’Haye et al., Nature 450, 1214-1217 (2007).
  98. S. A. Diddams et al., Science 369, eaay3676 (2020).
  99. A. L. Gaeta, et al., Nature Photonics 13, 158-169 (2019).
  100. T. J. Kippenberg et al., Science 361 (2018).
  101. X. Xue et al., J. Lightwave Technology 32, 3557 (2014).
  102. P. Trocha et al., Science 359, 887 (2018).
  103. M. G. Suh, and K. J. Vahala, Science 359, 884 (2018).
  104. D. J. Jones et al., Science 288, 635 (2000).
  105. P. Del’Haye et al., Physical Review Letters 107, 063901 (2011).
  106. S. A. Diddams et al., Phys. Rev. Lett. 84, 5102 (2000).
  107. T. Tetsumoto et al., Nature Photonics 15, 516 (2021).
  108. J. Hu et al., Nature Commun. 11, 4377 (2020).
  109. H. Shu et al., Nature 605, 457-463 (2022).
  110. M. G. Suh et al., Nature Photonics 13, 25 (2019).
  111. T. Herr et al., Nature Photonics 8, 145-152 (2014).
  112. T. Herr, and R. A. McCracken, IEEE Photonics Technology Letters 31, 1890 (2019).
  113. A. Fulop et al., Nature Commun. 9 (2018).
  114. P. Marin-Palomo et al., Nature 546, 274 (2017).
  115. J. Riemensberger et al., Nature 581, 164 (2020).
  116. T. Hansson, and S. Wabnitz, Nanophotonics 5, 231 (2016).
  117. S. Fujii et al., Opt. Express 30, 1351 (2022).
  118. J. Pfeifle et al., Nature Photonics 8, 375 (2014).
  119. J. Wang et al., Photonics Res. 8, 1964 (2020).
  120. Obrzud et al., Nature Photonics 13, 31 (2019).
  121. J. Feldmann et al., Nature 589, 52 (2021).
  122. M. G. Suh et al., Science 354, 600-603 (2016).
  123. Wang et al., Nature Communications 4, 1345 (2013).
  124. W. Liang et al., Optics Letters 36, 2290 (2011).
  125. S. B. Papp et al., Phys. Rev. X 3, 031003 (2013).
  126. H. Agha et al., Optics Express 17, 16209-16215 (2009).
  127. S. Levy et al., Nature Photonics 4, 37-40 (2010).
  128. Bao et al., Optics Letters 39, 6126-6129 (2014).
  129. A. Kovach et al., Adv. Opt. Photon. 12, 135-222 (2020).
Preprints 70377 g001
Figure 1. Schematic diagram and signal processing flow of a MWP transversal signal processor with an optical microcomb source. EOM: electro-optic modulator. PD: photodetector.
Figure 1. Schematic diagram and signal processing flow of a MWP transversal signal processor with an optical microcomb source. EOM: electro-optic modulator. PD: photodetector.
Preprints 70377 g001
Preprints 70377 g002
Figure 2. Schematic of a practical microcomb-based MWP transversal signal processor. The main error sources are labelled as I ‒ V. CW laser: continuous-wave laser. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. EOM: electro-optic modulator. SMF: single-mode fibre. OSS: optical spectral shaper. BPD: balanced photodetector. SOD: second-order dispersion. TOD: third-order dispersion.
Figure 2. Schematic of a practical microcomb-based MWP transversal signal processor. The main error sources are labelled as I ‒ V. CW laser: continuous-wave laser. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. EOM: electro-optic modulator. SMF: single-mode fibre. OSS: optical spectral shaper. BPD: balanced photodetector. SOD: second-order dispersion. TOD: third-order dispersion.
Preprints 70377 g002
Preprints 70377 g003
Figure 3. (a) Root mean square errors (RMSEs) induced by theoretical limitation for differentiation (DIF), integration (INT), and Hilbert transformation (HT) as a function of tap number M. (b) Comparison of RMSEs induced by theoretical limitations and practical measured RMSEs for DIF, INT, and HT when M = 80. In (a) ‒ (b), the comb spacing, length of dispersive medium, and second-order dispersion (SOD) parameter are ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively. The input microwave signals are assumed to be Gaussian pulses with a full width at half maximum (FWHM) of ~0.17 ns.
Figure 3. (a) Root mean square errors (RMSEs) induced by theoretical limitation for differentiation (DIF), integration (INT), and Hilbert transformation (HT) as a function of tap number M. (b) Comparison of RMSEs induced by theoretical limitations and practical measured RMSEs for DIF, INT, and HT when M = 80. In (a) ‒ (b), the comb spacing, length of dispersive medium, and second-order dispersion (SOD) parameter are ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively. The input microwave signals are assumed to be Gaussian pulses with a full width at half maximum (FWHM) of ~0.17 ns.
Preprints 70377 g003
Preprints 70377 g004
Figure 4. Influence of microcombs’ intensity noise on errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (b) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (ⅰ) DIF, (ⅱ) INT, and (ⅲ) HT, where the intensity noise floors of the microcombs are (a) flat and (b) sinc-shaped, respectively. Different curves show the results for different optical signal-to-noise ratios (OSNRs) of the comb lines. The ideal processing results are also shown for comparison. (c) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of microcomb’s OSNR. In (a) – (c), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively.
Figure 4. Influence of microcombs’ intensity noise on errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (b) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (ⅰ) DIF, (ⅱ) INT, and (ⅲ) HT, where the intensity noise floors of the microcombs are (a) flat and (b) sinc-shaped, respectively. Different curves show the results for different optical signal-to-noise ratios (OSNRs) of the comb lines. The ideal processing results are also shown for comparison. (c) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of microcomb’s OSNR. In (a) – (c), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively.
Preprints 70377 g004
Preprints 70377 g006
Figure 5. Influence of the modulator chirp on errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (c) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (a) DIF, (b) INT, and (c) HT. Different curves show the results for different chirp parameter α. The ideal processing results are also shown for comparison. (d) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of α. In (a) – (d), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively.
Figure 5. Influence of the modulator chirp on errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (c) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (a) DIF, (b) INT, and (c) HT. Different curves show the results for different chirp parameter α. The ideal processing results are also shown for comparison. (d) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of α. In (a) – (d), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively.
Preprints 70377 g006
Preprints 70377 g006
Figure 6. Influence of SMF’s SOD on errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (c) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (a) DIF, (b) INT, and (c) HT. Different curves show the results with and without the influence of power degradation induced by SOD. The SOD parameter is D2 = 17.4 ps/nm/km. The ideal processing results are also shown for comparison. (d) Power degradation of the output microwave signal PMW as a function of the SOD parameter D2. (e) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of D2. In (a) – (e), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, and length of dispersive medium are M = 80, ∆λ = 0.4 nm, and L = 4.8 km, respectively.
Figure 6. Influence of SMF’s SOD on errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (c) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (a) DIF, (b) INT, and (c) HT. Different curves show the results with and without the influence of power degradation induced by SOD. The SOD parameter is D2 = 17.4 ps/nm/km. The ideal processing results are also shown for comparison. (d) Power degradation of the output microwave signal PMW as a function of the SOD parameter D2. (e) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of D2. In (a) – (e), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, and length of dispersive medium are M = 80, ∆λ = 0.4 nm, and L = 4.8 km, respectively.
Preprints 70377 g006
Preprints 70377 g007
Figure 7. Influence of SMF’s TOD on errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (c) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (a) DIF, (b) INT, and (c) HT. Different curves show the results for different TOD parameter D3. The ideal processing results are also shown for comparison. (d) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of D3. In (a) – (d), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively.
Figure 7. Influence of SMF’s TOD on errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (c) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (a) DIF, (b) INT, and (c) HT. Different curves show the results for different TOD parameter D3. The ideal processing results are also shown for comparison. (d) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of D3. In (a) – (d), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively.
Preprints 70377 g007
Preprints 70377 g008
Figure 8. Influence of shaping errors induced by the OSS on accuracy of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (c) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (a) DIF, (b) INT, and (c) HT. Different curves show the results for different percentage ranges (∆PRs) of random tap coefficient errors (RTCEs). The ideal processing results are also shown for comparison. (d) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of ∆PR. In (a) – (d), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively.
Figure 8. Influence of shaping errors induced by the OSS on accuracy of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) – (c) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (a) DIF, (b) INT, and (c) HT. Different curves show the results for different percentage ranges (∆PRs) of random tap coefficient errors (RTCEs). The ideal processing results are also shown for comparison. (d) Corresponding RMSEs between the ideal results and the processors’ output waveforms as a function of ∆PR. In (a) – (d), the Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively.
Preprints 70377 g008
Preprints 70377 g009
Figure 9. Contributions of different error sources to the overall errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (i) DIF, (ii) INT, and (iii) HT. Different curves show the results after accumulating errors induced by different sources from I to V. The ideal processing results are also shown for comparison. (b) Corresponding RMSEs between the ideal results and the processors’ outputs. The practical measured RMSEs are also shown. In (a) and (b), the microcomb has an OSNR of 30 dB. The chirp parameter, SOD parameter, TOD parameter, and tap coefficient fluctuations are α = 0.5, D2 = 17.4 ps/nm/km, D3 = 0.083 ps/nm2/km, and ∆PR = 5%. The Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, and length of dispersive medium are M = 80, ∆λ = 0.4 nm, and L = 4.8 km respectively.
Figure 9. Contributions of different error sources to the overall errors of differentiation (DIF), integration (INT), and Hilbert transformation (HT). (a) Temporal waveform of Gaussian input pulse and output waveforms from the transversal signal processors performing (i) DIF, (ii) INT, and (iii) HT. Different curves show the results after accumulating errors induced by different sources from I to V. The ideal processing results are also shown for comparison. (b) Corresponding RMSEs between the ideal results and the processors’ outputs. The practical measured RMSEs are also shown. In (a) and (b), the microcomb has an OSNR of 30 dB. The chirp parameter, SOD parameter, TOD parameter, and tap coefficient fluctuations are α = 0.5, D2 = 17.4 ps/nm/km, D3 = 0.083 ps/nm2/km, and ∆PR = 5%. The Gaussian input pulse has a FWHM of ~0.17 ns. The tap number, comb spacing, and length of dispersive medium are M = 80, ∆λ = 0.4 nm, and L = 4.8 km respectively.
Preprints 70377 g009
Preprints 70377 g010
Figure 10. Amplitude and phase errors induced by different components in microcomb-based MWP transversal signal processors. EOM: electro-optic modulator. SMF: single-mode fibre. OSS: optical spectral shaper. BPD: balanced photodetector. RB: response bandwidth. TR: transmission response. SOD: second-order dispersion. TOD: third-order dispersion.
Figure 10. Amplitude and phase errors induced by different components in microcomb-based MWP transversal signal processors. EOM: electro-optic modulator. SMF: single-mode fibre. OSS: optical spectral shaper. BPD: balanced photodetector. RB: response bandwidth. TR: transmission response. SOD: second-order dispersion. TOD: third-order dispersion.
Preprints 70377 g010
Preprints 70377 g011
Figure 11. (a) Schematic of a microcomb-based MWP transversal signal processor with feedback control. CW laser: continuous-wave laser. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. OSS: optical spectral shaper. OSA: optical spectrum analyzer. OC: optical coupler. EOM: electro-optic modulator. SMF: single-mode fibre. BPD: balanced photodetector. OSC: oscilloscope. (b) Comparison of measured RMSEs for DIF, INT, and HT with and without feedback control. The corresponding theoretical RMSEs are also shown for comparison. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively. The input microwave signals are Gaussian pulses with a FWHM of ~0.17 ns.
Figure 11. (a) Schematic of a microcomb-based MWP transversal signal processor with feedback control. CW laser: continuous-wave laser. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. OSS: optical spectral shaper. OSA: optical spectrum analyzer. OC: optical coupler. EOM: electro-optic modulator. SMF: single-mode fibre. BPD: balanced photodetector. OSC: oscilloscope. (b) Comparison of measured RMSEs for DIF, INT, and HT with and without feedback control. The corresponding theoretical RMSEs are also shown for comparison. The tap number, comb spacing, length of dispersive medium, and SOD parameter are M = 80, ∆λ = 0.4 nm, L = 4.8 km, and D2 = 17.4 ps/nm/km, respectively. The input microwave signals are Gaussian pulses with a FWHM of ~0.17 ns.
Preprints 70377 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated