Prerpints.org logo
Preprint
Article

Modelling Microsegregation during Metal Additive Manufacturing: Impact of Dendrite Tip Kinetics and Finite Solute Diffusion

Altmetrics

Downloads

274

Views

196

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 March 2023

Posted:

03 April 2023

You are already at the latest version

Alerts
Abstract
Rapid solidification during metal additive manufacturing (AM) leads to non-equilibrium microsegregation, which can result in the formation of detrimental phases and cracking. Most of the microsegregation models, assume a Scheil-type solidification, where the solidification interface is planar and there exists local equilibrium at the interface along with either zero or infinite solute diffusion in the respective participating phases - solid and liquid. This assumption leads to errors in prediction. One has to account for finite solute diffusion and the curvature at the dendritic tip for more accurate predictions. In this work, we compare different microsegregation models that do and do not consider finite diffusion and dendrite tip kinetics against the experiments. We also propose a method to couple dendrite tip kinetics with the diffusion module (DICTRA®) implemented in Thermo-Calc®. The models which accounted for both finite diffusion and dendrite tip kinetics matched well with the experimental data.
Keywords: 
Subject: Engineering  -   Metallurgy and Metallurgical Engineering

1. Introduction

Metal additive manufacturing (AM) can be used to produce parts with complicated geometries that are not possible to make using traditional manufacturing methods [1]. Due to this advantage, there is interest in utilizing AM to fabricate parts made of commercial alloys that are commonly used in aerospace and biomedical applications [2]. The steep temperature gradients and high cooling rates commonly observed in powder bed fusion processes lead to non-equilibrium segregation [3]. This can lead to the precipitation of detrimental phases either during AM process [4] or during post-processing [5]. These phases can also lead to cracking [3,6]. Non-equilibrium segregation phenomenon can be predicted for a different process parameter combination and the parameters that lead to minimal detrimental phases can be chosen [7].
Solidification during both conventional processes (such as welding and casting) and AM processes lies in the non-equilibrium regime. The lever rule which assumes full equilibrium in solid and liquid is insufficient to describe the microsegregation occurring under such conditions. Scheil-Gulliver model - which is based on the assumption that there is no diffusion in solid and complete mixing in liquid - is commonly used for its ability to predict the upper limit of segregation [8]. In reality, the segregation that occurs generally lies between the values given by the lever rule and the Scheil-Gulliver model. Both models do not consider the effect of microstructure and finite solute diffusion in the participating phases, thus leading to inaccurate predictions.
Brody and Flemings [9] proposed a model to include finite diffusion in the solid. Several authors have improved the model and made modifications to treat the solute diffusion in solid more accurately [10,11]. The effect of dendrite tip curvature on microsegregation is often neglected. Under rapid solidification conditions experienced during AM, the dendrite tip radius is in the order of a few microns and thus, the curvature effect is significant [12]. Flood and Hunt [13] proposed the "Truncated Scheil model" which couples the dendrite tip kinetics with the Scheil model. However, the model does not consider finite diffusion in either solid or liquid. Tong and Beckermann proposed a model to include both finite diffusion and the effect of dendrite tip kinetics [14]. Maguin et al. extended Tong and Beckermann’s model for multicomponent alloys [15]. However, both Tong-Beckermann model and its extension are not coupled with CALPHAD (Calculation of Phase Diagram) databases and assumes constant partition coefficients. Coupling CALPHAD databases to microsegregation models have shown to improve the results and allows to account for second phase formation [16]. DICTRA (DIffusion Controlled TRAnsformation)® module of Thermo-Calc® software has been used to predict microsegregation during solidification [17]. This module which is coupled with thermodynamic and diffusion databases accounts for solute diffusion in both solid and liquid while enforcing a local equilibrium in planar solid-liquid interface [18]."Scheil with solute trapping model" in Thermo-Calc® was introduced to account for deviation in equilibrium at the high solidification velocities experienced during AM [19]. However, it does not consider finite diffusion.
The Phase-field model which assumes a diffuse interface between the participating phases has been developed to simulate microstructure evolution during phase transformations [20]. This allows an efficient way of performing microstructure simulation while including most of the relevant physics. Calphad-coupled two-dimensional phase-field models have been used to predict microsegregation during welding [21] and additive manufacturing [22]. This model accounts for thermodynamic, diffusion and curvature effects thus leading to improved predictions compared to other models [17]. However, the phase-field model remains computationally expensive compared to other 1D models.
Haynes 282 is a γ ′ strengthened Ni-based superalloy and is one of the proposed materials for Advanced Ultra Super Critical (AUSC) power plants [23]. Laser powder bed fused Haynes 282 showed better mechanical properties than its wrought counterpart [24]. Laser deposited Haynes 282 showed segregation of Mo and Ti to the interdendritic region and led to the formation of γ ′ precipitates in as-built condition [25]. Thus, studying the segregation behaviour of Haynes 282 becomes essential.
In this work, we probe the impact of the dendrite tip and the finite diffusion in liquid and solid on the microsegregation prediction. The microsegregation models with and without the above-mentioned effects are applied for the case of laser powder bed fusion (LPBF) of Haynes 282 Ni-based superalloy and compared against experimentally measured segregation values.

2. Experimental Methods

In this work, Haynes 282 alloy powder of the standard composition from Praxair® Co., was used. An EOS M290® machine was used for fabricating 5 mm cube samples. The samples were fabricated under an Ar-gas atmosphere employing a layer thickness of 40 μ m and a hatch spacing of 0.11 mm. Laser power was chosen to be 285 W and a scan speed of 0.96 m/s was used. The fabricated samples were dense with minimal defects. Further details on process parameter optimization can be found in our previous report [22]. The as-built samples were cut from the baseplate using an electric discharge machine (EDM). The microstructural characterization was carried out using a scanning electron microscope (SEM) (Thermofisher Scios®) fitted with a field emission gun source (FEG). For SEM analysis, the sample was prepared using a standard metallographic procedure using silicon grit papers followed by diamond paste (9 to 0.5 micron particle size) and final polish with Vibro-polisher (Buehler VibroMet®) using a colloidal silica suspension. Composition across dendritic and interdendritic regions was analyzed using Transmission Electron Microscope (TEM) (Thermofisher TITAN Themis® 300 KV), fitted with Energy dispersive X-ray spectroscopy (EDS) (Bruker Esprit EDS®). Electron transparent sample for TEM analysis was prepared by extracting a 3 mm disk from the as-built cube. The disks were mechanically grounded to 80 µm thickness. The final specimen were made using twin jet electropolishing (Struers®) with a mixture of CH3OH and 5 vol% perchloric acid at – 238 K.

3. Computational Methods

3.1. Finite Element Modelling

Finite element analysis was performed to predict the solidification conditions (thermal gradient and cooling rate) which will be used for further microsegregation models. Fourier’s heat conduction equation gives the governing equation for heat transfer analysis (Eqn. 1)
∂ ( ρ C p T ) ∂ t = ∇ . ( κ ∇ T ) + Q
where ρ , C p , κ are the density, specific heat, and thermal conductivity of the material, respectively and Q is the heat source term. The thermophysical properties of Haynes 282 used for analysis were obtained from Haynes 282 brochure [26]. For the Finite Element Analysis, commercial software Simcenter 3D®[27] was used to solve the governing equation; the convective and the radiative heat transfer were ignored. The simulation considers a linear motion of laser heat source (single track) along Y direction. The laser heat source was modelled using 3D-conical heat source[28] for volumetric heat distribution as given in Eqn.2
Q = Q o exp ( − 3 r 2 r o 2 )
r o = r e − ( r e − r i ) z e − z z e − z i
Q o = 9 η P e 3 π ( e 3 − 1 ) × 1 ( z e − z i ) ( r e 2 + r e r i + r i 2 )
where P is the laser power, r o is the heat distribution parameter, r e and r i are the radii at the top and the bottom of the conical heat source respectively, z e and z i are the Z coordinates at the top and the bottom of the conical heat source respectively and η is the efficiency. The laser power is taken as 285 W and the scan speed is 0.96 m/s. In this Finite Element Model, the initial temperature of the domain was 353 K, HEXA8 elements of size 20 µm were used only in the fusion zone to account for steep temperature gradients and coarse mesh was used elsewhere. The dimensions of the domain were 5 × 1 × 0.5 mm. The elements and nodes present in the thermal model were 83710 and 64319 respectively.

3.2. Microsegregation Models

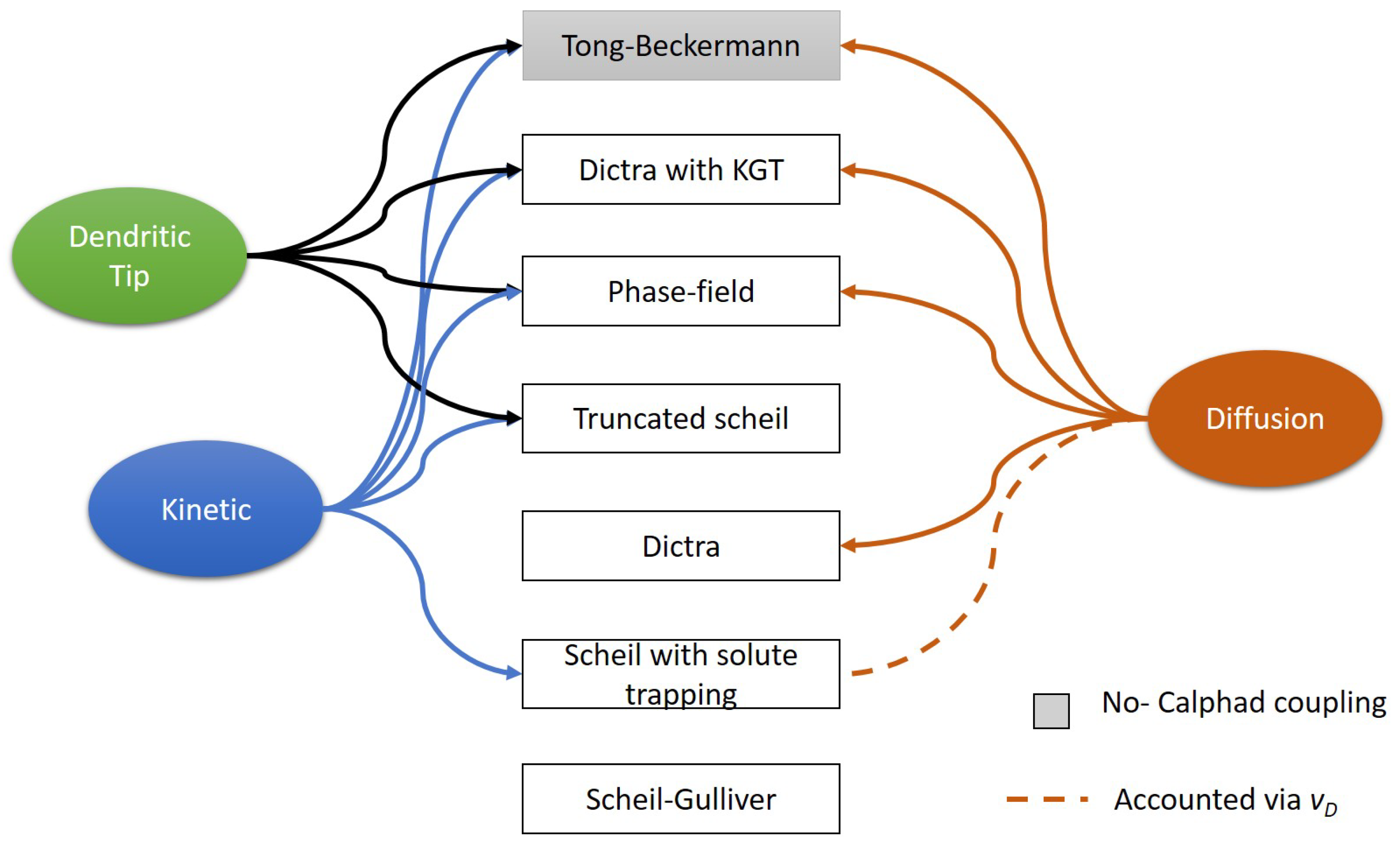
Figure 1 shows the models implemented in this study and the effects considered in each model. Except for the Scheil-Gulliver model, all other models take input from the thermal model either in the form of solidification velocity only or cooling rate only or both thermal gradient and solidification velocity. All the models except the phase-field model are one-dimensional and steady-state models, whereas the phase-field model is a two-dimensional and transient model. In all the models with Calphad coupling, TCNI10 and MOBNI4 databases were used. In this study, Haynes 282 alloy is considered an alloy with 6 elements (Cr=20 wt%, Co= 10 wt %, Mo = 8.5 wt %, Ti = 2.1 wt %, Al = 1.5 wt %, Ni - Remaining). Boron and Carbon are neglected due to their lower concentration.

3.2.1. Scheil-Gulliver model

Scheil-Gulliver model assumes a closed volume element in which no mass flows in or out of the system. No diffusion is assumed to occur in solid, whereas in liquid complete mixing (infinite diffusivity) is assumed. The model also assumes that the solid-liquid interface is planar and local equilibrium prevails at the interface; that is, the equilibrium phase diagram gives the interface compositions. The procedure for calculating the Scheil-Gulliver model via Calphad-based software tools (Thermo-Calc®’s Classical Scheil Model) is outlined below [16]. The calculation starts at the liquidus temperature and the temperature is decreased by an initially specified temperature step. The fraction and composition of the liquid and the solid phases are calculated. An equilibrium calculation is performed using the liquid composition from the previous step as the overall composition and the current step’s temperature. The residual liquid concentration is set the same as the liquid concentration from equilibrium calculations. The increase in the fraction of phase γ is calculated as Δ f γ = f l f γ ′ where f l is the fraction of remaining liquid and f γ ′ is the fraction of phase γ calculated using equilibrium calculations. The phase fraction values are then updated. The procedure is repeated till the fraction of the solid is 0.99.

3.2.2. Scheil model with solute trapping

Scheil model with solute trapping in Thermo-Calc® is based on Aziz and Kaplan’s continuous growth model [29] which calculates the partition coefficient as a function of solidification velocity. Scheil with solute trapping model has the same assumptions as the Scheil-Gulliver model but the partition coefficient is calculated using Aziz and Kaplan’s model. This model relaxes the local equilibrium at interface assumption and accounts for the deviation in equilibrium that occurs during high solidification velocities relevant to additive manufacturing. Aziz and Kaplan’s model uses the diffusive speed ( v D ) which is the ratio of solute diffusivity of liquid and characteristic diffusion distance. The solute diffusivity values are calculated from the mobility databases. Other than computing v D , the liquid is assumed to be completely mixed (infinite diffusivity of liquid) when performing microsegregation calculation.

3.2.3. Dendrite tip calculation

The dendrite tip radius is calculated using Kurz-Giovanola-Trivedi (KGT) model [30]. KGT model has been used extensively to predict the microstructure selection occurring during AM [31]. The model assumes a linearized phase diagram. The set of equations used in this study is given below.
T D = T L + ∑ i ( C L , t i p i m v i − C o i m o i ) − 2 Γ R − v μ k − G D i v
C L , tip i = C o i 1 − ( 1 − k v i ) I v ( P e i )
4 π 2 Γ 1 R 2 + ( 2 ∑ i m v i P e i ( 1 − k v i ) C L , t i p i ξ C i ) ( 1 R ) + G = 0
ξ C i = 1 − 2 k v i 2 k v i − 1 + 1 + 2 π P e i 2
k v i = k o i + v v D 1 + v v D
m v i = m o i × 1 − k v i ( 1 − ln ( k v i / k o i ) 1 − k o i
In Eqn. 5, T D is the temperature of the dendrite tip, T L is the equilibrium liquidus temperature of the alloy, Γ is the Gibbs-Thomson coefficient, μ k is the kinetic coefficient, the second term on the right-hand side of the equation is due to constitutional undercooling, and the next two terms are curvature and kinetic undercoolings respectively. The last term accounts for the cellular growth at low solidification speeds. C L , tip i is the liquid composition at the dendrite tip. Iv ( Pe ) = Pe · exp ( Pe ) · E 1 ( Pe ) is the Ivantsov solution that represents the solute diffusion field ahead of the dendrite , where E1 is the first exponential integral and is computed using ’scipy’ library [32]. Ivantsov solution is a function of the non-dimensional solutal Peclet number which is given by the expression, P e i = V R / 2 D i , where R is the dendrite tip radius, D i is the solute diffusivity in liquid. The expressions for velocity-dependent partition coefficient and liquidus slope is given in Eqns and respectively. Equation is solved iteratively using bisection method for a given thermal gradient (G) and solidification velocities to obtain R and C L , t i p i [33].

3.2.4. Truncated Scheil model

This model proposed by Flood and Hunt [13] assumes during solidification the fraction of solid increases from zero to the value determined by the Scheil-Gulliver model at the temperature corresponding to the dendrite tip temperature. All the assumptions of the Scheil-Gulliver model are valid with an exception that the initial liquid composition and temperature are given by KGT model. Since KGT model, accounts for kinetic effects, this model accounts for both kinetic and dendrite tip effects.

3.2.5. Dictra-Planar model

In this method, DICTRA® module of Thermo-Calc® is used. This model considers a one-dimensional closed volume element. It assumes that the interface is planar (Figure 2(a)) and that there exists local equilibrium at the interface. Since the calculations are coupled to both thermodynamic and mobility databases, the effect of diffusion in solid and liquid is considered. The effect of dendrite tip curvature and the kinetic effect at high solidification velocities are ignored. The flux balance at the interface controls the velocity of the interface. The cooling rate from the thermal model is used as input for the model. The solid phase FCC ( γ ) given by equilibrium composition is assumed to nucleate at one end of the domain. The length of the domain is taken as half of the primary dendrite arm spacing (PDAS) due to the symmetry.

3.2.6. Dictra with KGT model

In this method, the dendrite tip kinetics is coupled with Dictra® module. All the assumptions of Dictra-Planar are kept the same, except how the first solid is initialized. Dictra® normally calculates the initial solid composition using the equilibrium phase diagram. In this case, the initial solid of an infinitesimal thickness (0.5 nm), with the composition of dendrite tip ( C L , tip i × k v i ) is initialized as shown Figure 2. The simulation started with the temperature corresponding to the tip temperature. This approximation can be rationalized based on the arguments from Tong and Beckermann [14] where they considered that at the dendrite tip, f s reaches zero. Thus, at the limit lim f s → 0 C L i = C L , tip i . This approach includes kinetic effect, dendrite tip kinetics and finite diffusion in solid and liquid.

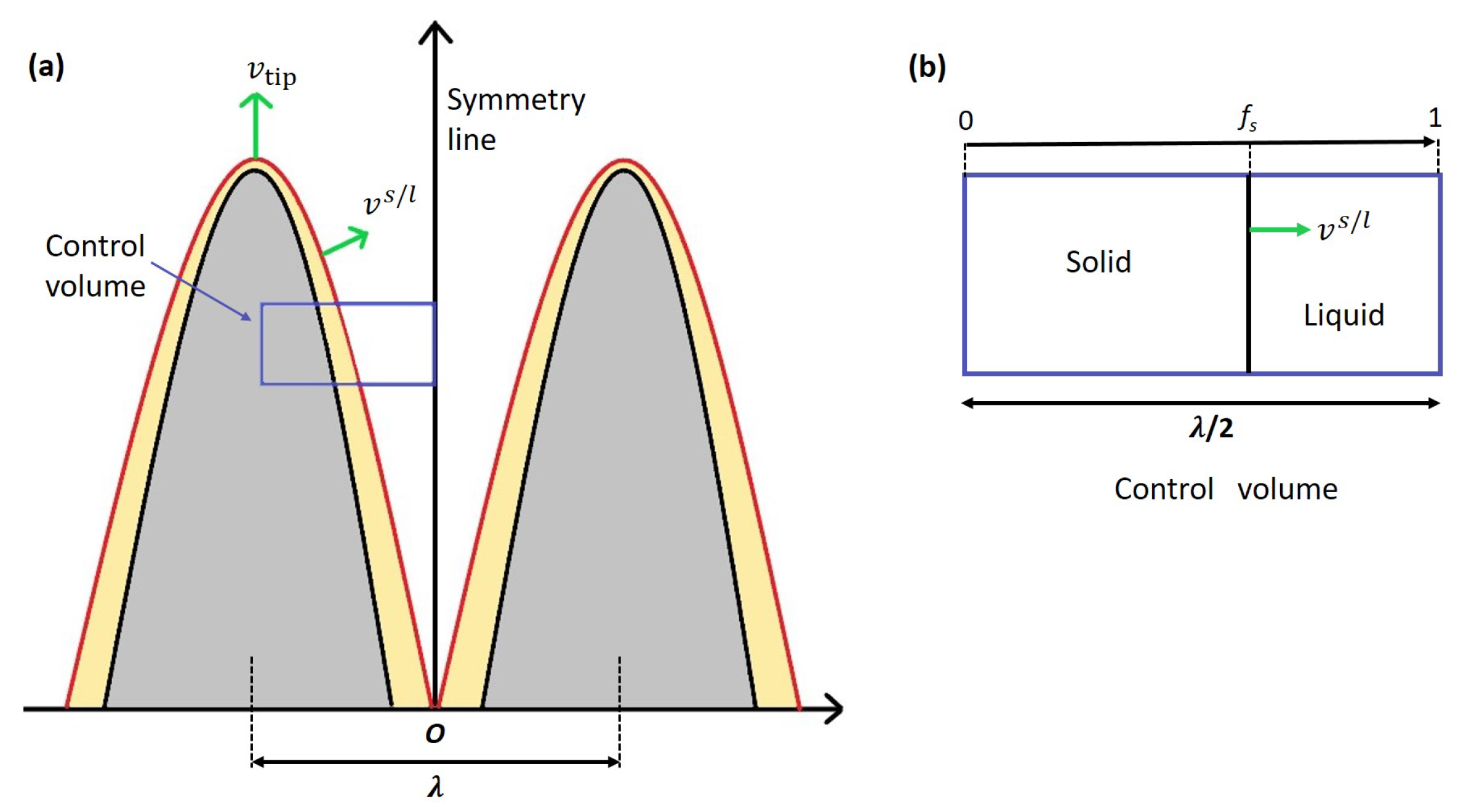
3.2.7. Tong-Beckermann Model

Multicomponent Tong-Beckermann model based on the diffusion layer concept accounts for dendrite tip kinetics and finite diffusion in both solid and liquid [14,15]. A schematic representation of the Tong-Beckermann model is shown in Figure 3.
The model represents the dendritic growth in the direction of the applied thermal gradient (G) and the dendrites are separated by a distance ( λ ). Here only the dendritic envelope is considered. The growth of dendrite and its representation within the control volume is given in Figure 3(a). The red lines indicate the solute boundary layer that develops around the growing dendrite. Appropriate mass balance equations are written for the control volume in Figure 3(b). The velocity of the tip is taken the same as the imposed solidification velocity. The velocity of the solid/liquid interface is calculated based on the parabolic cooling assumption [34]. Based on the above assumptions, the set of ordinary differential equations that represent microsegregation is given by the following equations.
F 1 ( f s ) d C L ( s / l ) i d f s = F 2 ( f s , C L ( s / l ) i , C S ( s / l ) i )
where,
F 1 ( f s ) = 2 β i ′ f s ( 1 − H i ( f s ) ) F 2 ( f s , C L ( s / l ) i , C S ( s / l ) i ) = ( 1 + 6 α i ) ( C o i − C S ( s / l ) i ) + ( C L ( s / l ) i − C o i ) H i ( f s ) f s − 2 β i ′ ( 1 + 6 α i ) ( 1 − H i ( f s ) H i ( f s ) = exp − ( 1 − f s ) / ( 2 β ′ i f s )
The above equations correspond to the multicomponent extension of Tong and Beckermann model proposed by Maguin et al. [15]. Here, the solute diffusion is defined via Fourier number for each species in solid ( α i ) and liquid ( β i ).
α i = D S i t s ( λ / 2 ) 2
β i = D L i t s ( λ / 2 ) 2
Here D S i and D L i are solute diffusivities of element i in solid and liquid respectively. t s is the solidification time and is taken as the ratio of solidification interval and cooling rate. Often secondary arm spacing is used as the characteristic length in solid Fourier number ( α i ) [15]. However, only primary dendrites (cells) form during LPBF of Haynes 282. Hence, PDAS was taken as the characteristic length for both solid and liquid Fourier numbers. The mass balance equations do not satisfy the zero flux boundary condition at the symmetry line and a correction factor( σ ) is used. The corrected Fourier number for liquid is given by Eqn. 14. The corrected Fourier number is arrived at by solving the Eqn. 11 at the limit of f s = 0 .
β ′ i = σ i β i
β ′ i = C o i − C S , tip i 2 ( C L , tip i − C o i )
Eqn. 11 is solved for fraction of solid 0 to 0.99. The ’odeint’ function of ’scipy’ was used to solve the equation. The solid and liquid diffusivities along with the partition coefficients are calculated using Thermo-Calc®.

3.2.8. Phase-field Model

In this current study, phase-field model simulation was carried out using Micress® software [35] which uses multi-phase-field method [20]. In this report, a two-dimensional (2D) domain taken parallel to the build direction was used as the simulation domain. We assume "frozen temperature approximation", that is, the thermal gradient and the cooling rate are constant. These conditions, therefore, depict the evolution of the microstructure in an area that is solidifying under the applied heat conditions at the solidification interface. The simulation starts with a flat solidification interface. Solute diffusion is assumed to be finite in both solid and liquid. A domain size of 6 µm × 13 µm with a grid size of 10 nm is considered and other simulation parameters are the same as used in our previous study [22].

4. Results and Discussion

4.1. As-build microstructure

The backscattered electron (BSE) micrograph taken along the build direction is shown in Figure 4. The micrograph indicates the presence of cellular structures and the absence of secondary arms. The cooling rates ( ≈ 10 6 K/s) and thermal gradients ( ≈ 10 7 K/m) observed in LPBF are very high compared to the values observed in other additive manufacturing techniques [1]. These extreme solidification conditions lead to the presence of only primary dendrites (also called cells). This kind of solidification structure is commonly present under rapid solidification conditions. These structures appear as hexagonal cells if sectioned perpendicular to the growth direction and appear as elongated columns when sectioned parallel to their growth direction. Due to 67° laser rotation in each layer, the temperature distribution is more uniform and as a result, one can observe both these structures next to each other in Figure 4. The regions with the same contrast indicate that they belong to the same grain. It is clear that the cell spacing is close to 1 µm and agrees with the previously reported values [22].
To understand the solidification behaviour, the TEM-EDS map was taken and is shown in Figure 5. From the figure, the segregation of Mo and Ti is evident. The thin elongated regions that are rich in Mo and Ti are the interdendritic regions. Segregation of Mo and Ti to the interdendritic region has been observed in Haynes 282 processed via different manufacturing processes like welding [36], laser deposition [25] and LPBF [37]. The Mo and Ti-rich isolated precipitates in interdendritic regions might be MC-type (Ti,Mo)C carbides. These carbides are called primary carbides and are commonly formed during solidification [38]. However, a few isolated bright regions in Mo and Cr might be due to the presence of M23C6-type Cr23C6 carbides and M6C-type Mo6C carbides [39]. These secondary carbides and are generally formed after aging heat treatment. These carbides might have formed by the in situ heat treatment effect caused by the thermal cycles. However, further investigation is needed to confirm this claim. Additionally, the interdendritic regions are slightly depleted in Co and Ni. Al and Cr are found to be uniformly distributed in both dendritic and interdendritic regions. The isolated Al-rich regions might be due to the presence of Al2O3 and have been observed during LPBF of IN 718[40].

4.2. Thermal Modelling

The temperature distribution calculated using the finite element model is shown in Figure 6. The melt pool dimensions are calculated after steady-state is achieved. The melt pool width and depth are 157 μ m and 90 μ m respectively. The melt pool dimensions measured from the single track experiments in IN 718 alloy match closely with the calculated values [41]. Since the thermophysical properties of IN 718 and Haynes 282 are similar, the melt pool dimensions are also expected to be very close to each other [22]. Moreover, the EOS® optimized process parameters for Haynes 282 and IN 718 alloys are the same [22].
When the Rosenthal solution or the Eager-Tsai model is used, the width of the melt pool will be approximately twice the melt pool depth due to the semi-circular nature of the melt pool. This is possible when the melting takes place purely by conduction mode [42]. In this case, the melt pool is deeper suggesting the mixed (conduction + keyhole) mode melting [41]. The temperature gradient and cooling rate at the bottom of the melt pool are 1.96 × 10 7 K/m and 6.92 × 10 5 K/s respectively. Thus, the solidification velocity which is taken as the ratio of the cooling rate and the thermal gradient is 3.5 cm/s. This solidification velocity, cooling rate and thermal gradient data will be used for dendrite tip and microsegregation calculations.

4.3. Dictra-Planar

The domain size is taken as 500 nm based on the experimental observations and previous reports [22]. A cooling rate of 6.92 × 10 5 K/s which was calculated from the thermal model was used for this calculation. The domain is initialized with liquid having composition same as the overall alloy composition.
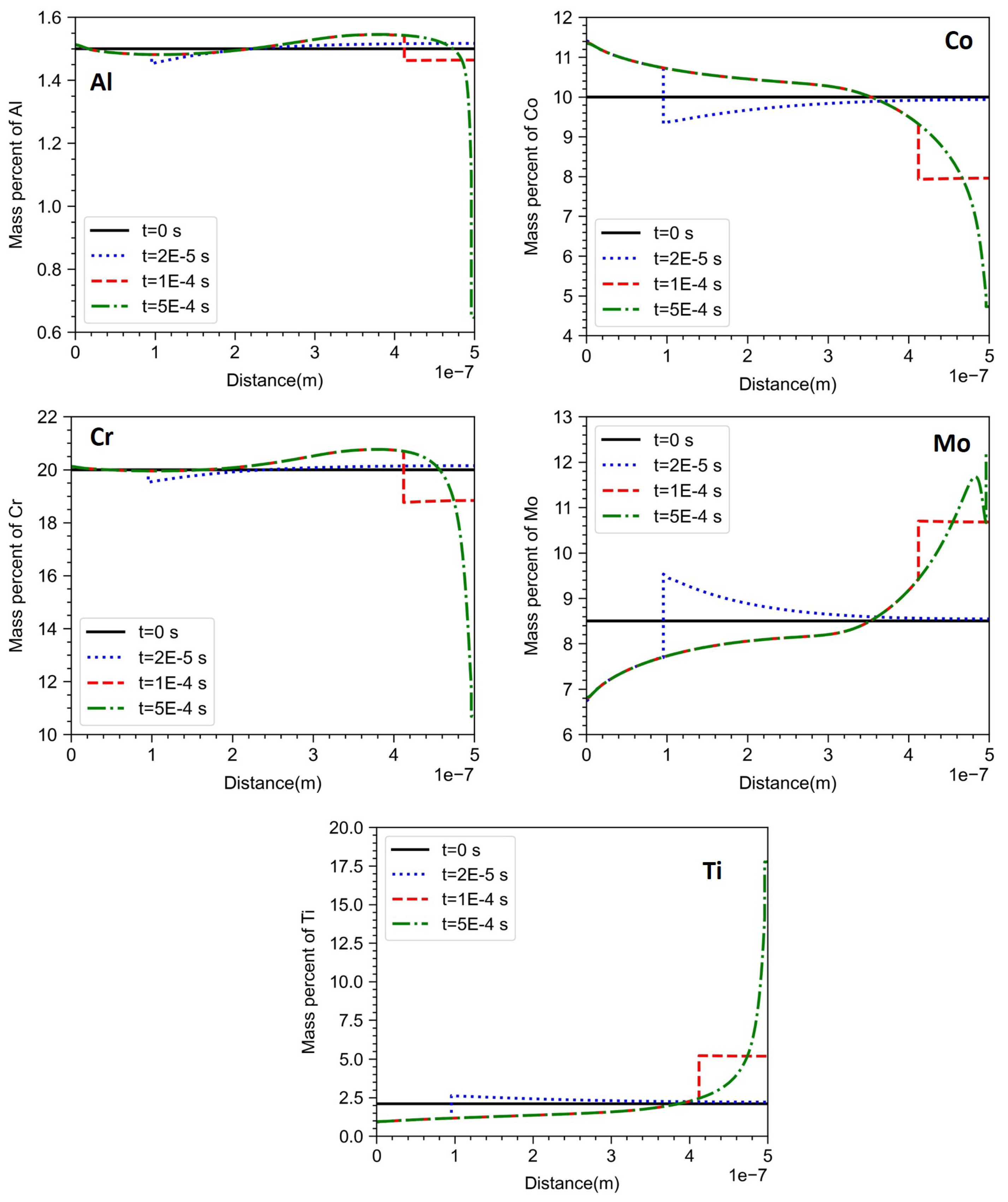
The evolution of the composition profile with time is given in Figure 7. As time proceeds, the solid-liquid interface moves from left to right. Al and Cr show non-monotonous variation in the composition profile. This non-monotonous variation can be obtained only if the non-diagonal terms in the diffusion matrix are considered [43]. At time t = 2 × 10 − 5 s, one can observe the continuous change in the liquid composition from the solid-liquid interface to the end of the domain. This is due to the finite solute diffusion in liquid. Thus, at the initial stage of solidification, the assumption of complete solute mixing in liquid is invalid. However, towards the end of solidification ( t = 1 × 10 − 4 s), the liquid composition is uniform and the assumption of complete solute mixing of liquid is valid. From Figure 7, it is clear that the last solidified region is depleted in Al, Co and Cr, whereas it is enriched with Mo and Ti. In the cases of Mo, Ti and Co, this matches with the experiments; however, for Cr and Al, they are uniformly distributed in dendritic and interdendritic regions.

4.4. Dictra-KGT

The material properties needed for calculating the dendrite tip composition and temperature are given in our previous report [31]. The liquid composition ahead of the tip and velocity-dependent partition coefficients are given in Table 1. The tip temperature was 1621.51 K. The solid composition for initializing the solid region in the Dictra with KGT model was calculated as the product of liquid composition and partition coefficient. The evolution of the composition profile with time is given in Figure 8.
There are differences between the composition profiles obtained from Dictra-Planar and Dictra with KGT Model. From Figure 8, it is clear that near the start of the domain, the composition is different from the equilibrium solid composition. The composition profile remains relatively flat almost till half the domain size as opposed to the continuous variation observed in the case of Dictra-Planar. Towards the end of the domain at the final stage of solidification, the local compositions are close to that one obtained from Dictra-Planar. For the same time step ( t = 2 × 10 − 5 s), the interface in Dictra with KGT model covered 70% of the domain, whereas, in the case of Dictra-Planar model, the interface covered 20% of the domain. Since the flux balance governs the motion of the interface, the change in the initial condition led to a change in the interface position. A quantitative comparison between both models is given in the subsequent section.

4.5. Model comparison

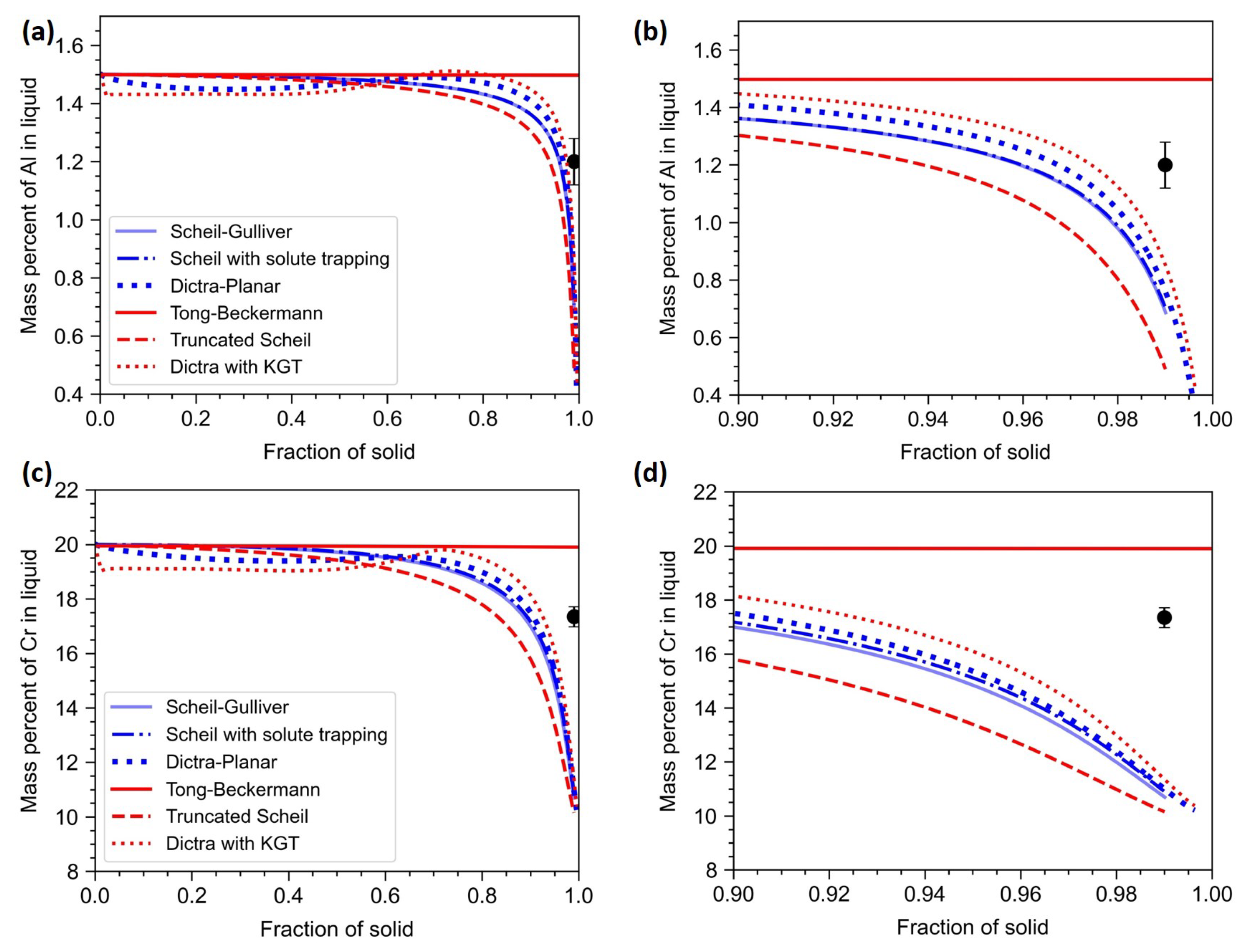
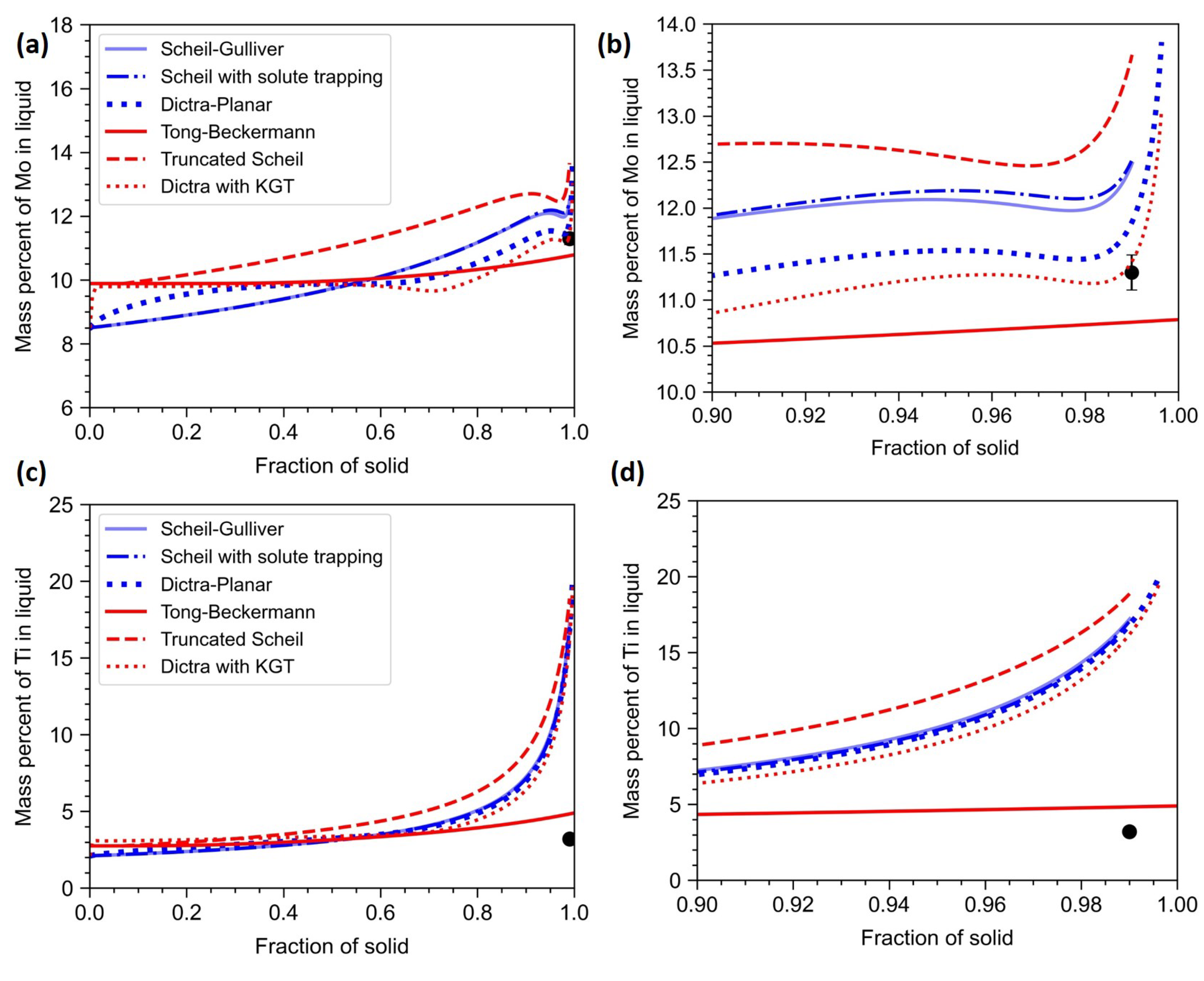
In this section, all the one-dimensional microsegregation models are compared. In Figure 9, the models that account for dendritic tip curvature are plotted in red, whereas the models that assume a planar interface are plotted in blue. The TEM-EDS composition taken at the interdendritic region is considered as the composition at f s = 0.99 , since it is the last solidifying region. The elements are grouped based on their segregation behaviour.
In the case of Al (Figure 9a,b), it is clear that both Scheil-Gulliver and Scheil with solute trapping models gave the same results. The truncated Scheil model overestimates the segregation behaviour. Since the truncated Scheil model assumes a jump condition, the solute is not conserved. The assumption of a jump in the fraction of solid is not physically well-founded and let to discrepancies in the calculation. The incorporation of finite diffusion in solid and liquid improved the prediction. The inclusion of the curvature effect nudged the results in the correct direction. Tong-Beckermann model assumes a constant partition coefficient and the partition coefficients of Al and Cr are close 1.0. Thus, the curve predicted by Tong-Beckermann model is close to a straight line. A quantitative comparison of the models is given in Table 2.
Co has an equilibrium partition coefficient slightly greater than 1.0. Thus, Co is expected to be depleted in interdendritic region. As seen from Figure 10, the observations are very similar to that of Al and Cr. Here Tong-Beckermann model predicted closer values than other models.
Both Mo and Ti have equilibrium partition coefficients less than 1.0. Thus they are enriched in interdendritic region. In the case of Mo (Figure 11(a,b)), there is a better match with experiments. The effect of solute diffusion is significant and both Dictra-Planar and Dictra with KGT models predict close to the experimentally observed with Dictra with KGT model matching more accurately. In the case of Ti (Figure 11(c,d)), there is a large difference between the predicted and the experimental value. This variation is partly because of the formation of TiC in the interdendritic region. Even after accounting for such phase formation, the discrepancy is too high.
From the above results, it is clear that models incorporating both finite solute diffusion and dendrite tip kinetics resulted in better predictions compared to other models. In the Dictra with KGT model, the end of the assumed control volume corresponds to the symmetry line between growing primary dendrite arms. At the terminal stage of solidification, when the boundary layers converge, the zero flux boundary condition can not be enforced at the symmetry line. This can lead to discrepancies in the prediction. However, this issue is addressed in the Tong-Beckermann model via the correction factor or tuning constant ( σ ). These correction factors are calculated from eqns 12,14 and are shown in Table 3. The correction factors depend only on the overall composition and the dendritic tip characteristics. Thus, the dendrite tip curvature directly influences the microsegregation.

4.6. Phase field Model

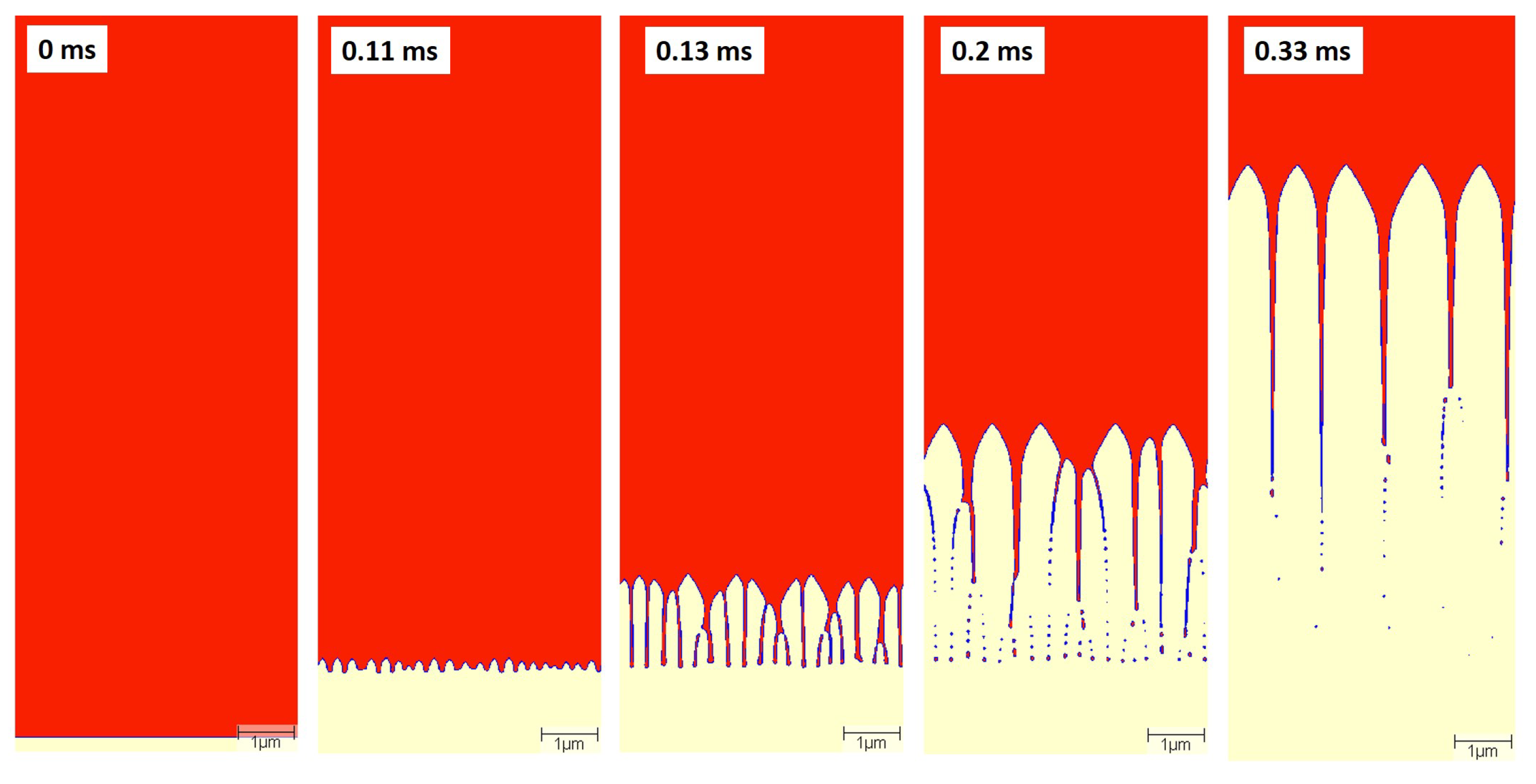
The change in solidification morphologies for the given cooling conditions is given in Figure 12. The liquid phase is shown in red, FCC in white and the interface is shown in blue. The domain was intialized with a flat solid–liquid interface and the evolution of the interface depends on the imposed thermal conditions. As time proceeds, the flat interface becomes unstable, and undulations are formed. These undulations became cellular perturbations. These perturbations develop into steady-state cellular structures with only primary dendrite arms. This cellular arrangement remained unchanged for the rest of the simulation. The primary dendrite arm spacing is calculated to be approximately 1 µm, which agrees with the experimental value.
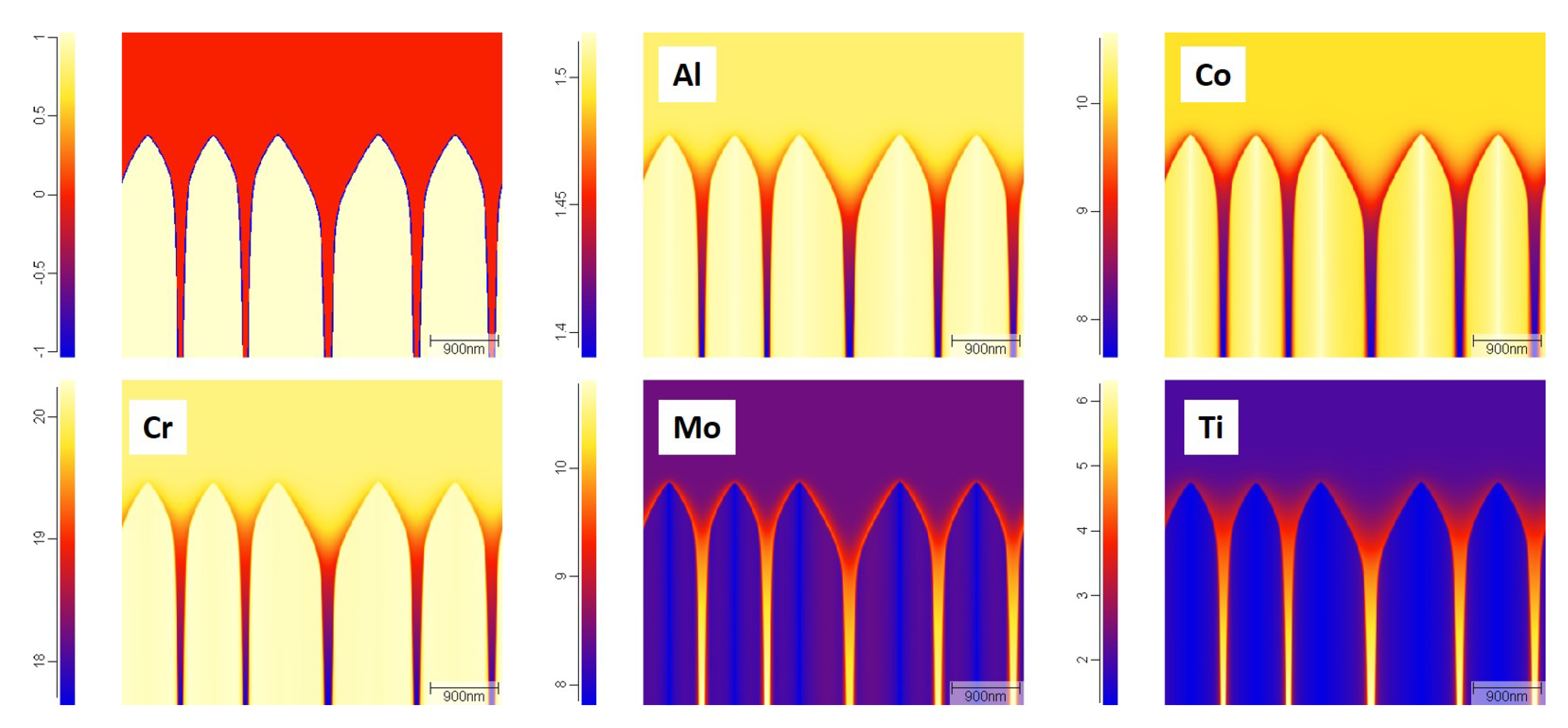
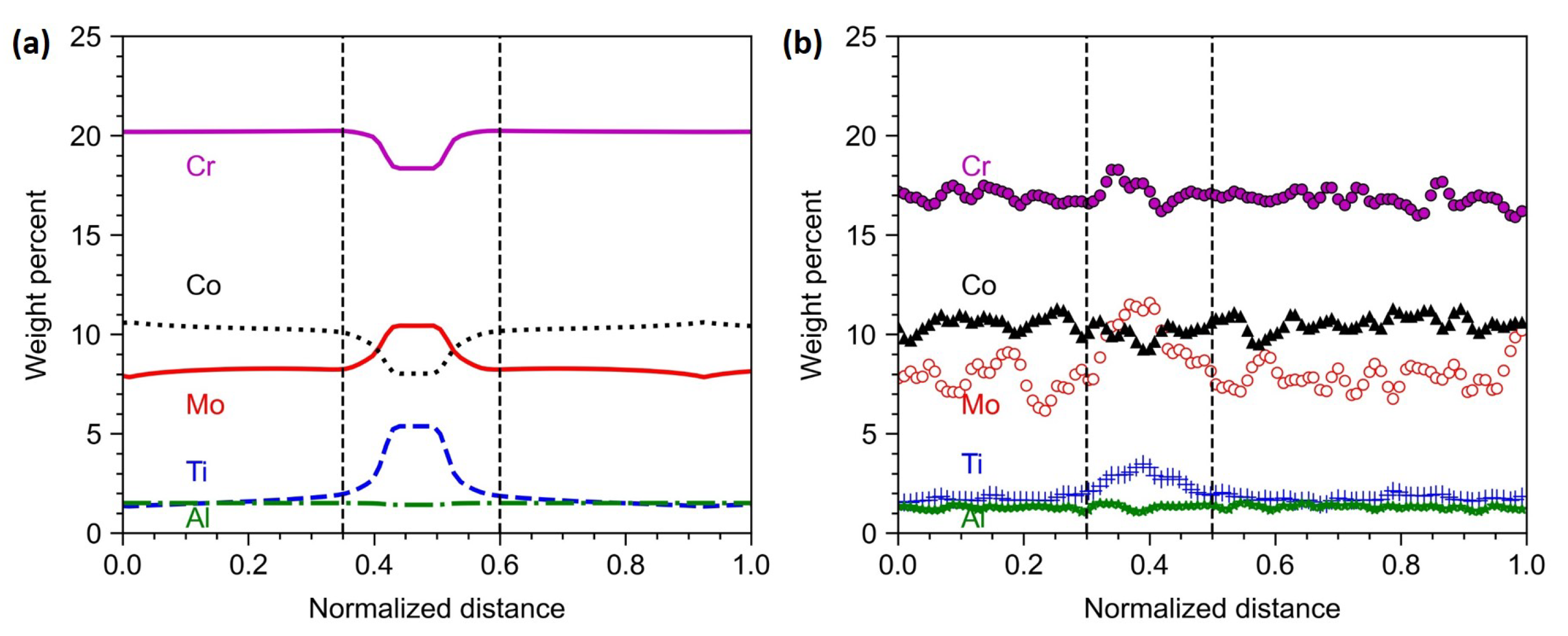
The elemental segregation is shown in Figure 13. From the figure, it can be observed that Ti and Mo enriched to the interdendritic region, while Co and Cr were diminished in the interdendritic region. Al is uniformly distributed. The composition variation across the dendritic and interdendritic regions obtained from phase-field and experiments are shown in Figure 14. It is clear that the phase-field model is able to predict the segregation behaviour during LPBF of Haynes 282. The overall composition of Cr is slightly lower than the ideal value (20 wt.%) and leads to differences in the experimental and simulated values. In all other cases, there is both qualitative and quantitative agreement with the experimental results. This is because most of the physics like anisotropic interfacial energies, dendrite curvature effect and Calphad coupling which were partly or fully ignored in other models are included in the phase-field model. Thus one can consider phase-field models as closer to reality though computationally expensive.

5. Conclusions

In the case of Haynes 282 alloy, including the finite solute diffusion in solid and liquid improves the predictive capability of the microsegregation model. During rapid solidification conditions experienced in additive manufacturing, the dendrite tip curvature influences the solute segregation behaviour and needs to be accounted for accurate prediction of microsegregation. We demonstrated that coupling dendrite tip model with Dictra® showed an improvement in the results. Both the multicomponent Tong-Beckermann and the phase-field models which incorporate the effect of finite solute diffusion and dendrite tip kinetics gave better predictions than other models which ignored these effects.

Author Contributions

Conceptualization, VS.H and G.P.; methodology, VS.H; software, VS.H, L.R; validation, N.B., SK.M.; formal analysis, VS.H, L.R, N.B; investigation, VS.H.; resources, G.P., SK.M; data curation, N.B.; writing—original draft preparation, VS.H.; writing—review and editing, N.B., SK.M., BS.M, G.P; visualization, VS.H, L.R.; supervision, BS.M, G.P; project administration, BS.M, G.P.; funding acquisition, G.P. All authors have read and agreed to the published version of the manuscript.

Funding

This study was funded by the Department of Science and Technology, Government of India, through The National Centre for Clean Coal Research and Development.

Data Availability Statement

https://github.com/ICME-India/Microsegregation

Acknowledgments

The authors would like to acknowledge Dr. D Kesavan, Indian Institute of Technology Palakkad for providing access to the LPBF facility. The authors acknowledge the Advanced Facility for Microscopy and Microanalysis (AFMM), Indian Institute of Science Bangalore, for providing access to SEM and TEM.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. DebRoy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.M.; Wilson-Heid, A.d.; De, A.; Zhang, W. Additive manufacturing of metallic components–process, structure and properties. Progress in Materials Science 2018, 92, 112–224. [Google Scholar] [CrossRef]
  2. Babu, S.S.; Raghavan, N.; Raplee, J.; Foster, S.J.; Frederick, C.; Haines, M.; Dinwiddie, R.; Kirka, M.; Plotkowski, A.; Lee, Y.; others. Additive manufacturing of nickel superalloys: opportunities for innovation and challenges related to qualification. Metallurgical and Materials Transactions A 2018, 49, 3764–3780. [Google Scholar] [CrossRef]
  3. Hariharan, A.; Lu, L.; Risse, J.; Kostka, A.; Gault, B.; Jägle, E.A.; Raabe, D. Misorientation-dependent solute enrichment at interfaces and its contribution to defect formation mechanisms during laser additive manufacturing of superalloys. Physical Review Materials 2019, 3, 123602. [Google Scholar] [CrossRef]
  4. Sridar, S.; Zhao, Y.; Xiong, W. Phase transformations during homogenization of inconel 718 alloy fabricated by suction casting and laser powder bed fusion: a CALPHAD case study evaluating different homogenization models. Journal of Phase Equilibria and Diffusion 2021, 42, 28–41. [Google Scholar] [CrossRef]
  5. Zhang, F.; Levine, L.E.; Allen, A.J.; Stoudt, M.R.; Lindwall, G.; Lass, E.A.; Williams, M.E.; Idell, Y.; Campbell, C.E. Effect of heat treatment on the microstructural evolution of a nickel-based superalloy additive-manufactured by laser powder bed fusion. Acta materialia 2018, 152, 200–214. [Google Scholar] [CrossRef]
  6. Guo, B.; Zhang, Y.; Yang, Z.; Cui, D.; He, F.; Li, J.; Wang, Z.; Lin, X.; Wang, J. Cracking mechanism of Hastelloy X superalloy during directed energy deposition additive manufacturing. Additive Manufacturing 2022, 55, 102792. [Google Scholar] [CrossRef]
  7. Rahul, M.; Agilan, M.; Mohan, D.; Phanikumar, G. Integrated experimental and simulation approach to establish the effect of elemental segregation in Inconel 718 welds. Materialia 2022, 26, 101593. [Google Scholar]
  8. Fisher, D.; Kurz, W. Fundamentals of solidification. Fundamentals of Solidification.
  9. Brody, H.D. Solute redistribution in dendritic solidification. PhD thesis, Massachusetts Institute of Technology, 1965.
  10. Clyne, T.; Kurz, W. Solute redistribution during solidification with rapid solid state diffusion. Metallurgical Transactions A 1981, 12, 965–971. [Google Scholar] [CrossRef]
  11. Kraft, T.; Chang, Y. Predicting microstructure and microsegregation in multicomponent alloys. Jom 1997, 49, 20–28. [Google Scholar] [CrossRef]
  12. Rappaz, M.; David, S.; Vitek, J.; Boatner, L. Development of microstructures in Fe- 15Ni- 15Cr single crystal electron beam welds. Metallurgical Transactions A 1989, 20, 1125–1138. [Google Scholar] [CrossRef]
  13. Flood, S.; Hunt, J. A model of a casting. Applied Scientific Research 1987, 44, 27–42. [Google Scholar] [CrossRef]
  14. Tong, X.; Beckermann, C. A diffusion boundary layer model of microsegregation. Journal of crystal growth 1998, 187, 289–302. [Google Scholar] [CrossRef]
  15. Maguin, V.; Guillemot, G.; Jaquet, V.; Niane, N.; Rougier, L.; Daloz, D.; Zollinger, J.; Gandin, C.A. Finite diffusion microsegregation model applied to multicomponent alloys. IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2019, Vol. 529, p. 012029.
  16. Boettinger, W.J.; Kattner, U.R.; Banerjee, D.K. Analysis of solidification path and microsegregation in multicomponent alloys. Modelling of Casting, Welding and Advanced Solidification Processed-VIII 1998, 1, 159–170. [Google Scholar]
  17. Keller, T.; Lindwall, G.; Ghosh, S.; Ma, L.; Lane, B.M.; Zhang, F.; Kattner, U.R.; Lass, E.A.; Heigel, J.C.; Idell, Y.; others. Application of finite element, phase-field, and CALPHAD-based methods to additive manufacturing of Ni-based superalloys. Acta materialia 2017, 139, 244–253. [Google Scholar] [CrossRef] [PubMed]
  18. Borgenstam, A.; Höglund, L.; Ågren, J.; Engström, A. DICTRA, a tool for simulation of diffusional transformations in alloys. Journal of phase equilibria 2000, 21, 269–280. [Google Scholar] [CrossRef]
  19. Thermo-Calc software, AM. Thermo-Calc. 2021B.
  20. Eiken, J. A phase-field model for technical alloy solidification; Shaker Verlag, 2009.
  21. Agilan, M.; Satyamshreshta, K.; Sivakumar, D.; Phanikumar, G. High-Throughput Experiment and Numerical Simulation to Study Solidification Cracking in 2195 Aluminum Alloy Welds. Metallurgical and Materials Transactions A 2022, 53, 1906–1918. [Google Scholar] [CrossRef]
  22. Hariharan, V.; Pramod, S.; Kesavan, D.; Murty, B.; Phanikumar, G. ICME framework to simulate microstructure evolution during laser powder bed fusion of Haynes 282 nickel-based superalloy. Journal of Materials Science 2022, 57, 9693–9713. [Google Scholar] [CrossRef]
  23. Pike, L. HAYNES® 282 alloy: a new wrought superalloy designed for improved creep strength and fabricability. Turbo Expo: Power for Land, Sea, and Air. American Society of Mechanical Engineers, 2006, Vol. 42398, pp. 1031–1039.
  24. Hariharan, V.; Kaushik, R.; Phanikumar, G.; Murty, B. Tailoring the Crystallographic Texture of Laser Powder Bed Fused Haynes 282 Through Scan Rotation Modification: Simulation & Experiments, 2023. [CrossRef]
  25. Ramakrishnan, A.; Dinda, G. Microstructure and mechanical properties of direct laser metal deposited Haynes 282 superalloy. Materials Science and Engineering: A 2019, 748, 347–356. [Google Scholar] [CrossRef]
  26. Haynes International, 2022. Accessed on , 2023. 15 March.
  27. Software, S.D.I. Simcenter 3D, 2022. Accessed on , 2023. 15 March.
  28. Wu, C.; Wang, H.; Zhang, Y.; others. A new heat source model for keyhole plasma arc welding in FEM analysis of the temperature profile. WELDING JOURNAL-NEW YORK- 2006, 85, 284. [Google Scholar]
  29. Aziz, M.J.; Kaplan, T. Continuous growth model for interface motion during alloy solidification. Acta metallurgica 1988, 36, 2335–2347. [Google Scholar] [CrossRef]
  30. Kurz, W. .; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta metallurgica 1986, 34, 823–830. [Google Scholar] [CrossRef]
  31. Hariharan, V.S.; Murty, B.S.; Phanikumar, G. Interface Response Functions for multicomponent alloy solidification- An application to additive manufacturing, 2023. [CrossRef]
  32. Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; van der Walt, S.J.; Brett, M.; Wilson, J.; Millman, K.J.; Mayorov, N.; Nelson, A.R.J.; Jones, E.; Kern, R.; Larson, E.; Carey, C.J.; Polat, İ.; Feng, Y.; Moore, E.W.; VanderPlas, J.; Laxalde, D.; Perktold, J.; Cimrman, R.; Henriksen, I.; Quintero, E.A.; Harris, C.R.; Archibald, A.M.; Ribeiro, A.H.; Pedregosa, F.; van Mulbregt, P.; SciPy 1. 0 Contributors. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
  33. Haines, M.; Plotkowski, A.; Frederick, C.L.; Schwalbach, E.J.; Babu, S.S. A sensitivity analysis of the columnar-to-equiaxed transition for Ni-based superalloys in electron beam additive manufacturing. Computational Materials Science 2018, 155, 340–349. [Google Scholar] [CrossRef]
  34. Giovanola, B.; Kurz, W. Modeling of microsegregation under rapid solidification conditions. Metallurgical Transactions A 1990, 21, 260–263. [Google Scholar] [CrossRef]
  35. Access, e.V. . Micress 7.1, 2022. Accessed on , 2023. 15 March.
  36. Osoba, L.; Ding, R.; Ojo, O. Microstructural analysis of laser weld fusion zone in Haynes 282 superalloy. Materials Characterization 2012, 65, 93–99. [Google Scholar] [CrossRef]
  37. Shaikh, A.S.; Schulz, F.; Minet-Lallemand, K.; Hryha, E. Microstructure and mechanical properties of Haynes 282 superalloy produced by laser powder bed fusion. Materials Today Communications 2021, 26, 102038. [Google Scholar] [CrossRef]
  38. Matysiak, H.; Zagorska, M.; Andersson, J.; Balkowiec, A.; Cygan, R.; Rasinski, M.; Pisarek, M.; Andrzejczuk, M.; Kubiak, K.; Kurzydlowski, K.J. Microstructure of Haynes® 282® superalloy after vacuum induction melting and investment casting of thin-walled components. Materials 2013, 6, 5016–5037. [Google Scholar] [CrossRef] [PubMed]
  39. Joseph, C.; Persson, C.; Hörnqvist Colliander, M. Precipitation kinetics and morphology of grain boundary carbides in Ni-base superalloy Haynes 282. Metallurgical and Materials Transactions A 2020, 51, 6136–6141. [Google Scholar] [CrossRef]
  40. Xu, J.; Ma, T.; Peng, R.L.; Hosseini, S. Effect of post-processes on the microstructure and mechanical properties of laser powder bed fused IN718 superalloy. Additive Manufacturing 2021, 48, 102416. [Google Scholar] [CrossRef]
  41. Pramod, S.; Kesavan, D. Melting modes of laser powder bed fusion (L-PBF) processed IN718 alloy: Prediction and experimental analysis. Advances in Industrial and Manufacturing Engineering 2023, 6, 100106. [Google Scholar] [CrossRef]
  42. Promoppatum, P.; Yao, S.C.; Pistorius, P.C.; Rollett, A.D. A comprehensive comparison of the analytical and numerical prediction of the thermal history and solidification microstructure of Inconel 718 products made by laser powder-bed fusion. Engineering 2017, 3, 685–694. [Google Scholar] [CrossRef]
  43. Guillemot, G.; Senninger, O.; Hareland, C.A.; Voorhees, P.W.; Gandin, C.A. Thermodynamic coupling in the computation of dendrite growth kinetics for multicomponent alloys. Calphad 2022, 77, 102429. [Google Scholar] [CrossRef]
Preprints 70409 g001
Figure 1. Models used in this study and the effects considered in each model
Figure 1. Models used in this study and the effects considered in each model
Preprints 70409 g001
Preprints 70409 g002
Figure 2. A schematic representation of Dictra-Planar and Dictra with KGT model
Figure 2. A schematic representation of Dictra-Planar and Dictra with KGT model
Preprints 70409 g002
Preprints 70409 g003
Figure 3. A schematic representation of (a) columnar-dendritic growth along with symmetry line (b) Control volume (inspired from [14])
Figure 3. A schematic representation of (a) columnar-dendritic growth along with symmetry line (b) Control volume (inspired from [14])
Preprints 70409 g003
Preprints 70409 g004
Figure 4. BSE micrograph of the as-built sample
Figure 4. BSE micrograph of the as-built sample
Preprints 70409 g004
Preprints 70409 g005
Figure 5. TEM-EDS map showing the dendritic and interdendritic regions
Figure 5. TEM-EDS map showing the dendritic and interdendritic regions
Preprints 70409 g005
Preprints 70409 g006
Figure 6. (a) Trimetric view showing the melt pool and the temperature distribution (b) Top view showing length and width of the melt pool (c) Cross section showing the melt pool width and depth
Figure 6. (a) Trimetric view showing the melt pool and the temperature distribution (b) Top view showing length and width of the melt pool (c) Cross section showing the melt pool width and depth
Preprints 70409 g006
Preprints 70409 g007
Figure 7. Evolution of composition profile with time as predicted by Dictra-Planar Model
Figure 7. Evolution of composition profile with time as predicted by Dictra-Planar Model
Preprints 70409 g007
Preprints 70409 g008
Figure 8. Evolution of the composition profile with time as predicted by Dictra with KGT model
Figure 8. Evolution of the composition profile with time as predicted by Dictra with KGT model
Preprints 70409 g008
Preprints 70409 g009
Figure 9. Comparison of prediction from different microsegregation models for Al and Cr
Figure 9. Comparison of prediction from different microsegregation models for Al and Cr
Preprints 70409 g009
Preprints 70409 g010
Figure 10. Comparison of prediction from different microsegregation models for Co
Figure 10. Comparison of prediction from different microsegregation models for Co
Preprints 70409 g010
Preprints 70409 g011
Figure 11. Comparison of prediction from different microsegregation models for Mo and Ti
Figure 11. Comparison of prediction from different microsegregation models for Mo and Ti
Preprints 70409 g011
Preprints 70409 g012
Figure 12. Microstructure evolution during LPBF
Figure 12. Microstructure evolution during LPBF
Preprints 70409 g012
Preprints 70409 g013
Figure 13. Elemental segregation during solidification
Figure 13. Elemental segregation during solidification
Preprints 70409 g013
Preprints 70409 g014
Figure 14. Composition variation across the dendritic and interdendritic region obtained from (a) phase-field model (b) TEM-EDS line scan
Figure 14. Composition variation across the dendritic and interdendritic region obtained from (a) phase-field model (b) TEM-EDS line scan
Preprints 70409 g014
Table 1. Equilibrium and velocity dependent partition coefficient along with the liquid composition at the dendrite tip obtained from KGT Model results
Table 1. Equilibrium and velocity dependent partition coefficient along with the liquid composition at the dendrite tip obtained from KGT Model results
Elements Equilibrium partition coefficient Kinetic partition coefficient Liquid Composition at tip
Al 1.002 1.002 1.49
Co 1.144 1.143 9.31
Cr 1.005 1.005 19.95
Mo 0.788 0.789 9.88
Ti 0.429 0.431 2.75
Table 2. Comparison of microsegregation models with experiments. Composition of the interdendritic region ( f s = 0.99 ) is given in the table
Table 2. Comparison of microsegregation models with experiments. Composition of the interdendritic region ( f s = 0.99 ) is given in the table
Elements Scheil-Gulliver Scheil with solute trapping Truncated Scheil Dictra-Planar Dictra with KGT Tong - Beckermann Phase-field Experiment
Al 0.69 0.71 0.49 0.76 0.90 1.49 1.42 1.2 ±0.1
Co 4.62 4.69 4.57 4.81 5.05 8.75 8.03 9.7 ± 0.4
Cr 10.7 10.91 10.15 11.0 11.54 19.9 18.36 17.4 ± 0.4
Mo 12.47 12.51 13.67 11.84 11.34 10.76 10.43 11.3 ± 0.2
Ti 17.19 17.01 18.88 16.82 15.78 4.83 5.38 3.2 ± 0.2
Table 3. Correction factor for individual elements used in Tong-Beckermann model
Table 3. Correction factor for individual elements used in Tong-Beckermann model
Elements Correction factor ( σ )
Al 0.7147
Co 0.451
Cr 0.338
Mo 0.5347
Ti 0.4070
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated