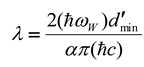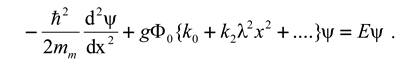Preprint

Article

On the Flavour States and the Mass States of Neutrinos

Altmetrics

Downloads

232

Views

110

Comments

Engel Roza^*

This version is not peer-reviewed

Submitted:

07 April 2023

Posted:

10 April 2023

Read the latest preprint version here

Alerts

Abstract

A structure based analysis of the pion’s decay path reveals that neutrinos can show up in three eigenstates. It requires a proper understanding of the nature of charged leptons, such as why the loss of binding energy stops the lepton generation at the tauon level. The analysis quantifies this binding energy in terms of the weak interaction strength as embodied by the weak interaction boson and the strength of the energetic background field as embodied by the Higgs boson. Next to this it is shown that a reconstruction of Fermi’s neutrino theory allows a quantitative assessment of the Fermi constant straightforwardly from the weak interaction strength. The article ends with the conclusion that neutrino oscillation is not a physical phenomenon, but, instead, a measurement interpretation induced from projecting the statistical behaviour of a multi-particle ensemble onto a single particle.

Keywords:

Subject: Physical Sciences - Nuclear and High Energy Physics

1. Introduction

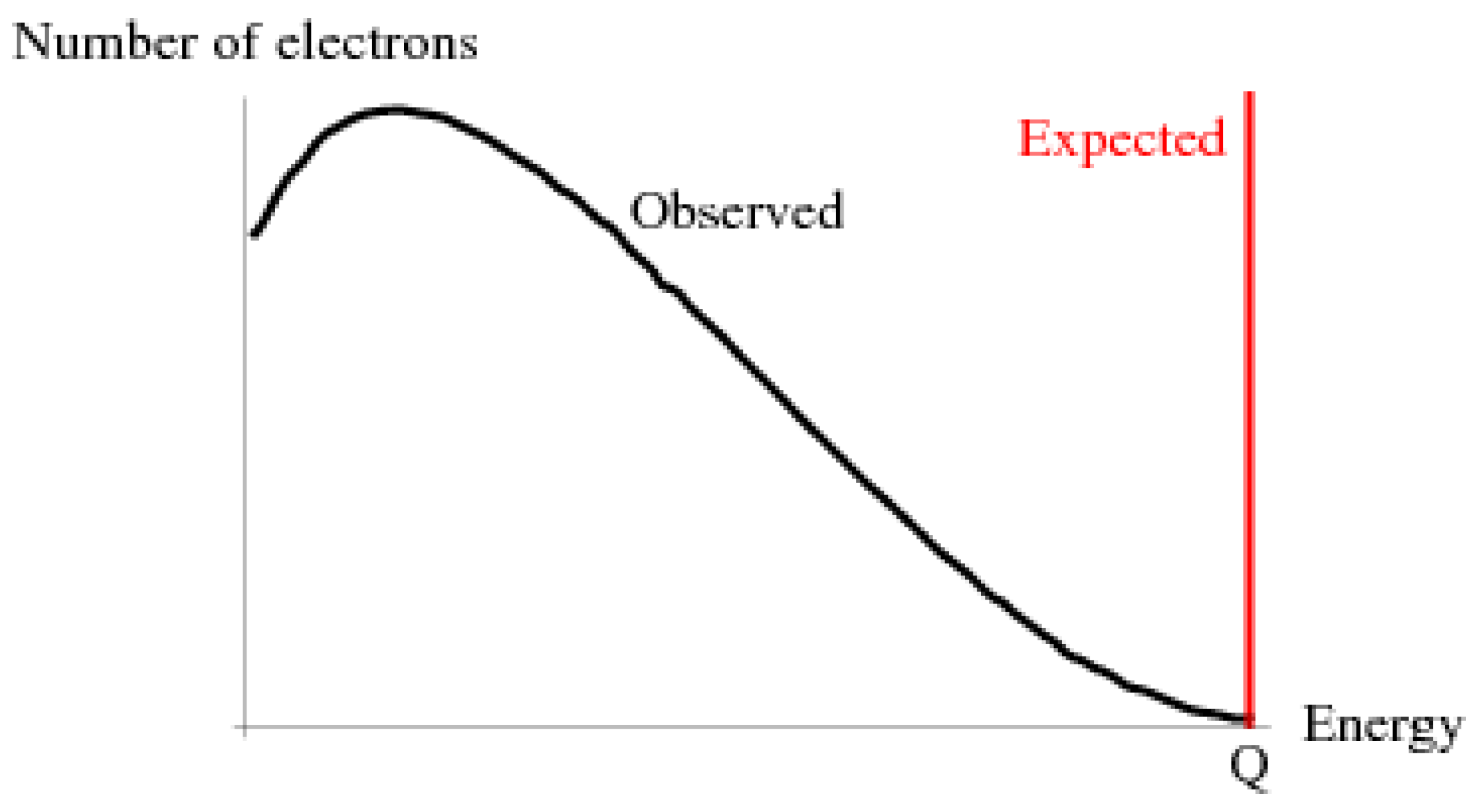
In the history of the development of the theory for particle physics described in previous work [1], the description of a particular dilemma that has pre-eminently been decisive for the current Standard Model has been omitted still. This dilemma has to do with the neutrino, which in that work has been barely described. The history of the neutrino begins with a non-understood phenomenon from the years before 1930. Up to then it was expected that in radioactivity, in which nuclear particles change state, the energy of the decaying particle would be carried away by particles with a discrete energy value. This was clearly the case with alpha radiation carried by Helium atomic nuclei. Curiously, it was not the case with beta radiation carried by electrons. The spectrum of the electron beam turned out to be continuous rather than being discrete, like illustrated in Figure 1.

That was already apparent 1914 from observations by James Chadwick (who became famous in 1930 for the discovery of the neutron) and others. It was a problem that led Wolfgang Pauli in 1927 to formulate a bold hypothesis which he did not dare to publish, but sighing posited in a letter to Hans Geiger and Lise Meitner [2]. Because, unlike some other scientists, including Niels Bohr, he did not want to doubt the law of energy conservation, he suggested in the letter the existence of a particle that eludes observation. That particle should be nearly massless, electrically neutral, and have half-integer spin. He called that particle “neutron”, a name that was changed later into neutrino after Chadwick’s discovery of the neutron. It was Enrico Fermi who took Pauli’s hypothesis seriously and in 1933 developed a theory for beta radiation based on the neutrino existence. Incidentally, the existence of the neutrino was not experimentally confirmed until 1956 by Reines and Cowan [3].

That experiment marks the start of experimental studies on neutrinos. One of the problems, next to identify suitable physical processes to study the interaction of neutrinos with matter, is the issue how to obtain neutrino fluxes large and strong enough to detect the rare events expected from those processes. Reines and Rowan used a nuclear reactor for the purpose. Their experiment got follow-ups by other ionic neutrino experiments, in particular those based upon knowledge captured in the Standard Solar Model. The idea behind those is, that since the energy of the sun is known and since its major energy production mechanism as well, it is possible to calculate the neutrino flux on earth as well. This flux is defined as the number of neutrinos that, each second pass through 1 m square surface perpendicular to the direction to the sun. This would enable to develop experimental evidence not only in qualitative terms, but in quantitative terms as well.

And it did. Most remarkably, however, those experiments revealed an unexpected result [4]. The predicted neutrino count showed a deficit of about 50%-70% with respect the actually measured count. The solar neutrino problem was born. What happened with the neutrinos emitted by the sun? Why would those not be capable to produce the predicted neutrino count? The inevitable answer to the problem is the awareness that neutrinos are subject to changes when they move from to the sun to the detectors on earth. The most simple approach to this problem is the assumption that neutrinos come in different flavours. Because they are produced in co-production with charged leptons, they show a specific flavour determined by the co-produced charged lepton. This hypothesis could be affirmatively tested by making the neutrino detectors in the experimental equipment no longer exclusively sensitive to electron neutrinos. Nevertheless, a major problem remained: the neutrino flow from the sun is produced from nuclear fusion of Hydrogen atoms into Helium nuclei, thereby producing almost exclusively electron neutrinos. How to explain the change of electron neutrinos into a significant amount of other flavours on their route from sun to earth?

Eventually this tantalizing question has resulted into the bold hypothesis, earlier formulated by Pontecorvo in 1957, and later adopted as explanation for the missing neutrinos, that neutrinos are built up by a virtual substructure [5]. Such a virtual substructure would allow neutrino compositions built by three basic eigenstates, different from their flavour states, more or less in the same way as hadrons are composed by quarks. According to this hypothesis, the electron neutrino is in a particular mixture of eigenstates, while a muon neutrino and a tauon neutrino would be in other mixtures. Hypothetically, this would allow oscillations between the flavour states of neutrinos and the loss of coherency would solve the solar neutrino problem.

If substructures are considered as being viable for neutrinos, why would substructures for charged leptons not be viable as well? Why not conceiving the electron, the muon and the tauon as states built by underlying constituents as well? Within the Standard Model the charged leptons are simply considered as elementary particles, and because in the Standard Model everything comes in a three, even a basic question as “why no charged leption beyond the tauon” has remained unanswered. This article is aimed to show how these issues of the constrained lepton generation and the mass and origin of neutrino’s can be highlighted in the structure based model of particle physics, documented in [1].

It will be shown that the view to be developed in this article my help to remove the confusion evoked by the documentation of the Particle Data Group (PDG), which shows two different lists on the mass of neutrinos [6]. The first list summarizes the results of direct measurements on the mass of the neutrino flavours. This list gives values for electron neutrinos (< 1.1 eV), muon neutrinos (< 0.19 MeV) and tauon neutrinos (< 18.2 MeV). The second list summarizes the results of measurements on the basis of Pontecorvo’s formalism. Such measurements allow to establish quantitative values on the sum of three mass states (

\approx

0.15 eV) defined in this formalism.

In the second paragraph of this article it is shown how the structural model for charged and uncharged leptons (neutrinos) evolve from the structural model of mesons as developed in previous work. It is the stepping stone for the explanation of some unrecognized phenomena in the Standard Model of particle physics. The first of these is a proof for the non-understood stop of the lepton generation at the tauon level (paragraph 3). It is shown that this can be traced back to the very same reason as why the quark flavour generation stops at the

b

(ottom) level (topquarks are of a different kind [1]). The fourth paragraph contains a reconstruction of Fermi’s neutrino theory dealing with the break-down of the weak interaction bond in charged leptons. It results into the conclusion that the Fermi constant, which usually is considered as an empirical constant of nature, can be calculated by theory from the weak interaction mechanism. In the fifth paragraph it will be shown why neutrino flavours are composed by eigenstates and how these become manifest as physical mass. The final paragraph contains a discussion on the flavour oscillation phenomenon.

2. Structural models for pion, muon and neutrino

Figure 1 is an illustration of the structural model for a pion as developed by the author over the years [1]. It shows that two quarks are structured by a balance of two nuclear forces and two sets of dipoles. The two quarks are described as Dirac particles with two real dipole moments as the virtue of particular gamma matrices. The vertical one is the equivalent of the magnetic dipole moment of an electron. The (real valued) horizontal dipole moment is the equivalent of the (imaginary valued) electric dipole moment of an electron [7,8].

In a later description, after recognizing that this structure shows properties that match with a Maxwellian description, the quarks have been described as magnetic monopoles in Comay’s Regular Charge Monopole Theory (RCMT). This allows to give an explanation of the quark’s electric charge by assuming that the quarks second dipole moments (the horizontal ones) coincide with the magnetic dipole moments of electric kernels

q_{e}

. This description allows to conceive the nuclear force as the cradle of baryonic mass (the ground state energy of the created anharmomic oscillator) as well as the cradle of electric charge.

The model allows a pretty accurate calculation of the mass spectrum of mesons. It also allows the development of a structural model of baryons including an accurate calculation of the mass spectrum of baryons as well. This calculation relies upon the recognition that the structure can be modelled as a quantum mechanical anharmonic oscillator. Such anharmonic oscillators are subject to excitation, thereby producing heavier hadrons with larger (constituent) masses of their constituent quarks. The increase of baryonic energy under excitation is accompanied with a loss of binding energy between the quarks. This sets a limit to the maximum constituent mass value of the quarks. It is the reason why quarks heavier than the bottom quark cannot exist and why the topquark has to be interpreted different from being the isospin sister of the bottom quark [1].

Because lepton generations beyond the tauon have not been found, they probably don’t exist for the same reason. In such a picture the charge lepton structure would result from the decay loss of the magnetic charges of the kernels in the pion structure under simultaneous replacement by their electric charges. This structure is bound together by an equilibrium of the repelling force between the electric charges and the attraction force between the scalar dipole moments. In spite of its resemblance with the pion structure, its properties are fundamentally different. Whereas the pion consists of a particle and an antiparticle making a boson, the charged lepton consists of two kernels making a fermion. 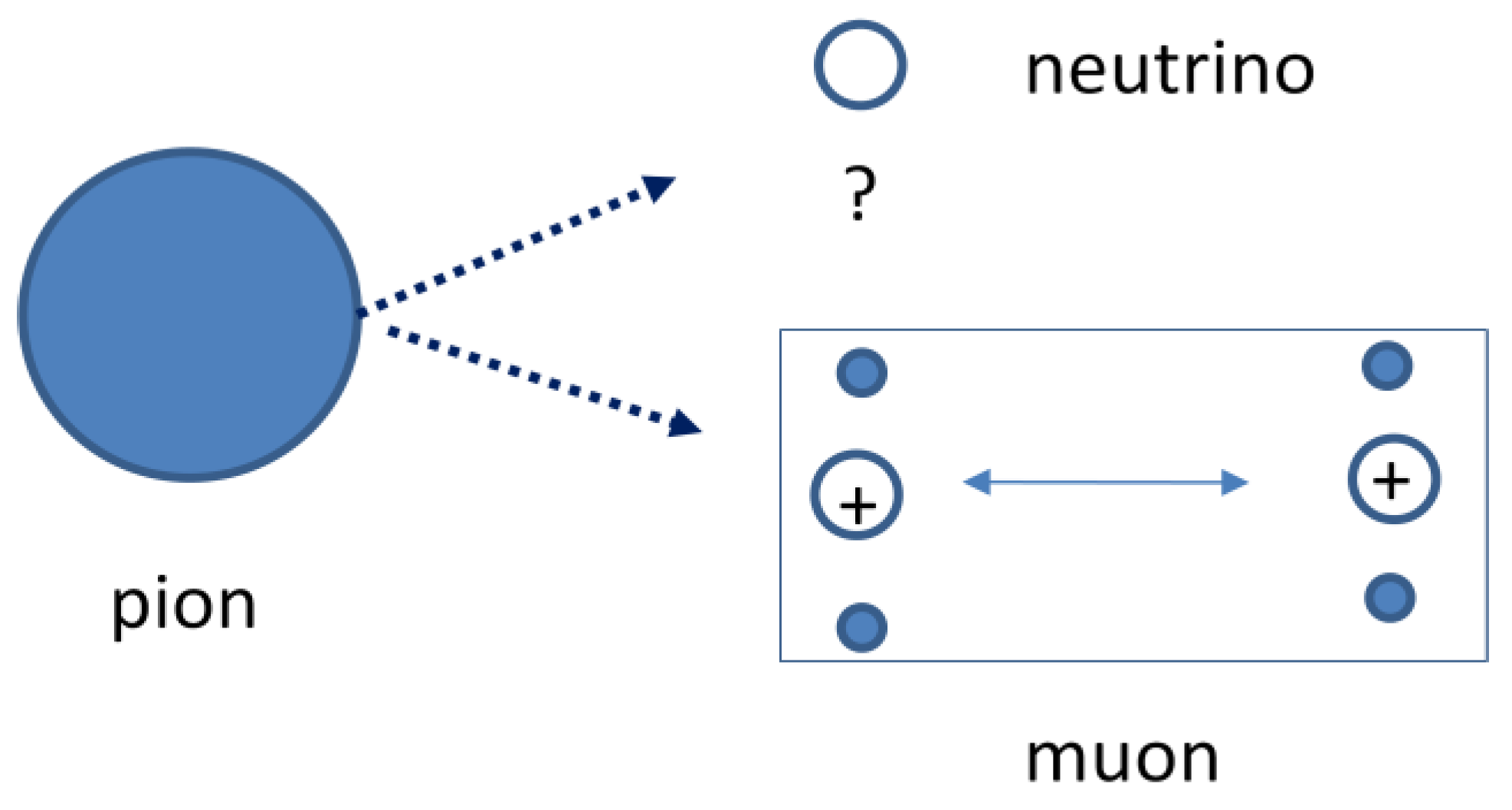Figure 3 shows a naive picture of the decay process. Under decay, the pion will be split up into a muon and a neutrino. In the rest frame of the muon, the muon will obviously contain the electric kernels and some physical mass. The remaining energy will fly away as a neutrino with kinetic energy and some remaining physical mass. Figure 2 shows the model, in which a structureless neutrino is shown next to a muon with a hypothetical substructure.

In this picture the muon is considered to be a half spin fermion in spite of the appearance of two identical kernels in the same structure. Assigning the fermion state to the structure seems being in conflict with the convention to distinguish the boson state from the fermion state by a naive spin count. Instead, a true boson state for particles in conjunction should be based upon the state of the temporal part of the composite wave function. In this particular case, the reversal of the particle state into antiparticle of one of the quarks marks a transformation from the bosonic pion state into the fermionic muon state under conservation of the weak interaction bond.

Let us proceed from the observation that there is no compelling reason why the weak interaction mechanism between a particle and an antiparticle kernel would not hold for two subparticle kernels. In such model, the structure for the charged lepton is similar to the pion one. It can therefore be described by a similar analytical model. Hence, conceiving the muon as a structure in which a kernel couples to the field of another kernel with the generic quantum mechanical coupling factor

g

, the muon can be modeled as a one-body equivalent of a two-body oscillator, described by the equation for its wave function

ψ

- \frac{ℏ^{2}}{2 m_{m}} \frac{d^{2} ψ}{{dx}^{2}} + {U (d + x) + U (d - x)} ψ = E ψ; U (x) = g Φ (x),

(1)

In which

ℏ

is Planck’s reduced constant, 2

d

the kernel spacing,

m_{m}

is the effective mass of the center,

V (x) = U (d + x) + U (d - x)

its potential energy, and

E

the generic energy constant, which is subject to quantization. The potential energy

V (x)

can be derived from a potential

Φ (x)

. Similarly as in the case of the pion quarks, this potential is a measure for the energetic properties of the kernels. It characterized by a strength

Φ_{0}

(in units of energy) and a range

λ^{- 1}

(in units of length: the dimension of

λ

is [m^-1]).

The potential

Φ (x)

of a pion quark has been determined as,

Φ (x) = Φ_{0} \exp (- λ x) (\frac{1}{{(λ x)}^{2}} - g_{m} \frac{1}{λ x}), in which g_{m} \approx 1 / 0.55 \approx 2

(2)

These quantities have more than a symbolic meaning, because in the structural model for particle physics developed so far [1],

λ

has been quantified by

{m^{'}}_{H} = 2 λ ℏ c

, in which

{m^{'}}_{H}

(

\approx

126 GeV) is the energy of the Higgs particle as the carrier of the energetic background field. The quantity

Φ_{0}

has been quantified by

{m^{'}}_{W} = g Φ_{0}

, in which

{m^{'}}_{W}

(

\approx

80.4 GeV) is the energy of the weak interaction boson. An equal expression for the potential

Φ (x)

would make the muon model to a Chinese copy of the pion model.

Instead, we wish to describe the potential

Φ (x)

of the muon kernels as,

Φ (x) = Φ_{0} (\frac{1}{{(λ x)}^{2}} - 2 \frac{1}{λ x}) .

(3)

The rationale for this modification is twofold. In the structural model for the pion, the exponential decay is due to the shielding effect of an energetic background field. If the muon is a true electromagnetic particle, there is no reason why its potential field would be shielded. This may explain why an additional energetic particle is required to compensate for the difference between the shielded and the unshielded potential. This may explain the origin of the neutrino. Why the integer 2 takes the place of the

g_{m}

factor is disused in the Appendix A to this article. Considering that the potential is a measure of energy and that the break-up of a pion into a muon and a neutrino takes place under conservation of energy, it is fair to conclude that the neutrino can be described in terms of a potential function as well, such that

Φ_{m u o n} (x) = Φ_{p i o n} (x) + Φ_{n e u t r i n o} (x) .

(4)

We may even go a step further by supposing that similarly as the muon, the neutrino can be modelled by a composition of two kernels as well. If so, each of these neutrino kernels have a potential function

Φ_{ν} (x)

, such that

Φ_{ν} (x) = Φ_{0} [{\frac{1}{{(λ x)}^{2}} - \frac{2}{λ x}} - \exp (- λ x) {\frac{1}{{(λ x)}^{2}} - \frac{g_{m}}{λ x}}] .

(5)

It is instructive to emphasize that the potential function of a particle, be it a quark, a charged lepton or a neutrino, does not contain any information about its mass. In that respect it is not different from the potential function of a charged particle like an electron. Furthermore it is of interest to emphasize that, like mentioned before, the quantities

Φ_{0}

and

λ

have a physical meaning in quantitative terms.

The muon is not a stable particle. It may lose its weak interaction bond under decay into electrons. Figure 4 shows an interpretation of the process. It shows how the weak interaction boson that binds the pion quarks desintegrates into the muon and the muon neutrino and how the two may recoil into a weak interaction boson that decays into an electron and electron antineutrino. This picture and the description just given evoke two basic questions.

The first one is this. If it is true indeed that the behaviour of the muon can be modelled as an anharmonic oscillator, why would the muon not be subject to a similar excitation mechanism as shown by the pion? The answer is that the muon is subject to excitation indeed, thereby producing the tauon state. Actually, this has been documented in previous work [9]. But, unlike as in the case of pions, it is a single stop. This excitation mechanism will be summarized in the next paragraph. It will be shown that this analysis will give a firm support to the model captured by the equations (2-7).

The second issue is the question how the muon decays into an electron and a neutrino. This has been documented in previous work as well [10]. In this work it has been shown that this can adequately be described in a way as originally proposed by Fermi. Its predictive power, however, has not been properly understood. Also this will be summarized in one of the next paragraphs.

This paragraph is now concluded with the statement that the leptons show up in three generations of charged-uncharged twins. The muon twin is the result of the pion’s loss of its bond with energetic background field . The tauon twin is an excitation and the electron twin is the elementary one.

It might be worthwhile to remark that there is no reason why the picture shown in Figure 4 would not be reversible, like shown by all quantum mechanical processes. It means that the neutrinos may change flavour, although not on their own. An electron neutrino with high energy may recoil with an electron to produce a weak interaction boson that subsequently disintegrates into a muon and an muon antineutrino. This observation, however, does not solve the solar neutrino problem mentioned before, because that problem point to neutrino interactions on their own.

Let us proceed by considering the structure of the charged leptons.

3. The charged leptons

The formulation of the anharmonic oscillators shown by (2-4) does not contain any particular quantum mechanical property. A binomial expansion of the potential energy

V (x)

allows to rewrite the wave equation as,

(6)

The oscillator vibrates with a certain frequency

ω

, subject to the classical relationship,

(7)

Two additional relationships will make the oscillator essentially different from a classical behavior. The first one is based upon the recognition that the major part of the energy is not embodied by the massive component

m_{m}

, but instead by the vibration energy of the oscillator, even to an amount that the massive component is negligible. The second one is based upon the recognition that the bond between the kernels is sustained by the weak interaction boson, such that

ℏ ω = ℏ ω_{W}

. These considerations result into in the additional relationship, derived by a geodesic approach, documented in [11,12].

g Φ_{0} = \frac{k_{2} λ^{2}}{k_{0}^{2}} \frac{{(ℏ c)}^{2}}{m_{m} c^{2}} .

(8)

It is this second relationship that makes a bond that may arise from an equilibrium between two monopole forces and two dipole moment forces essentially different from similar bonds that may arise in classical physics. An example of a classical bond is the one between two electrons sustained by the equilibrium between the repulsive force from their monopoles and the attraction force from their magnetic dipole moments, analyzed by Mikhailichenko [13]. As compared with the weak interaction bond, such a classical bond is extremely weak. Because the derivation of (8) is well documented it will be left beyond the scope of this article. It expresses, though, the birth of the weak interaction. Hence, a few words on its origin might be instructive. It is based upon the awareness that the anharmonic oscillator converts the energy from two potential fields into the ground state energy of the structure that they build. This ground state energy can be interpreted in terms of Einstein’s stress tensor. Hence, this ground state energy represents an amount of baryonic matter. It curves space-time, subject, though, to quantum steps in energy. These energetic quantum steps are (the weak interaction) bosons. In the classical construct of a two-electron bond just mentioned, the spacing between the two particles is too far extended from the quantum mechanical range covered by weak interaction.

By equating

λ^{2}

from the two expressions (7) and (8) we get,

ℏ ω_{W} = 2 g Φ_{0} | k_{0} | .

(9)

Similarly as in the pion case, it will make sense to normalize the wave function equation to,

- α_{0} \frac{d^{2} ψ}{d {x^{'}}^{2}} + V^{'} (x^{'}) = E^{'} ψ,

(10)

in which

α_{0} = \frac{λ^{2} ℏ^{2}}{2 m_{m} g Φ_{0}},

x^{'} = x λ

d^{'} = d λ

E^{'} = \frac{E}{g Φ_{0}}

U^{'} (x^{'}) = \frac{U (λ x)}{g Φ_{0}}

and

V^{'} (x^{'}) = U^{'} (d^{'} + x^{'}) + U^{'} (d^{'} - x^{'}) = k_{0} + k_{2} {x^{'}}^{2} + .......

(11)

In which

k_{0}

and

k_{2}

are dimensionless coefficients that depend on the spacing 2

d

between the quarks. To proceed it is imperative to establish a numerical value for the constant

α_{0}

. From (8) and (11) we have,

α_{0} = \frac{k_{0}^{2}}{2 k_{2}} .

(12)

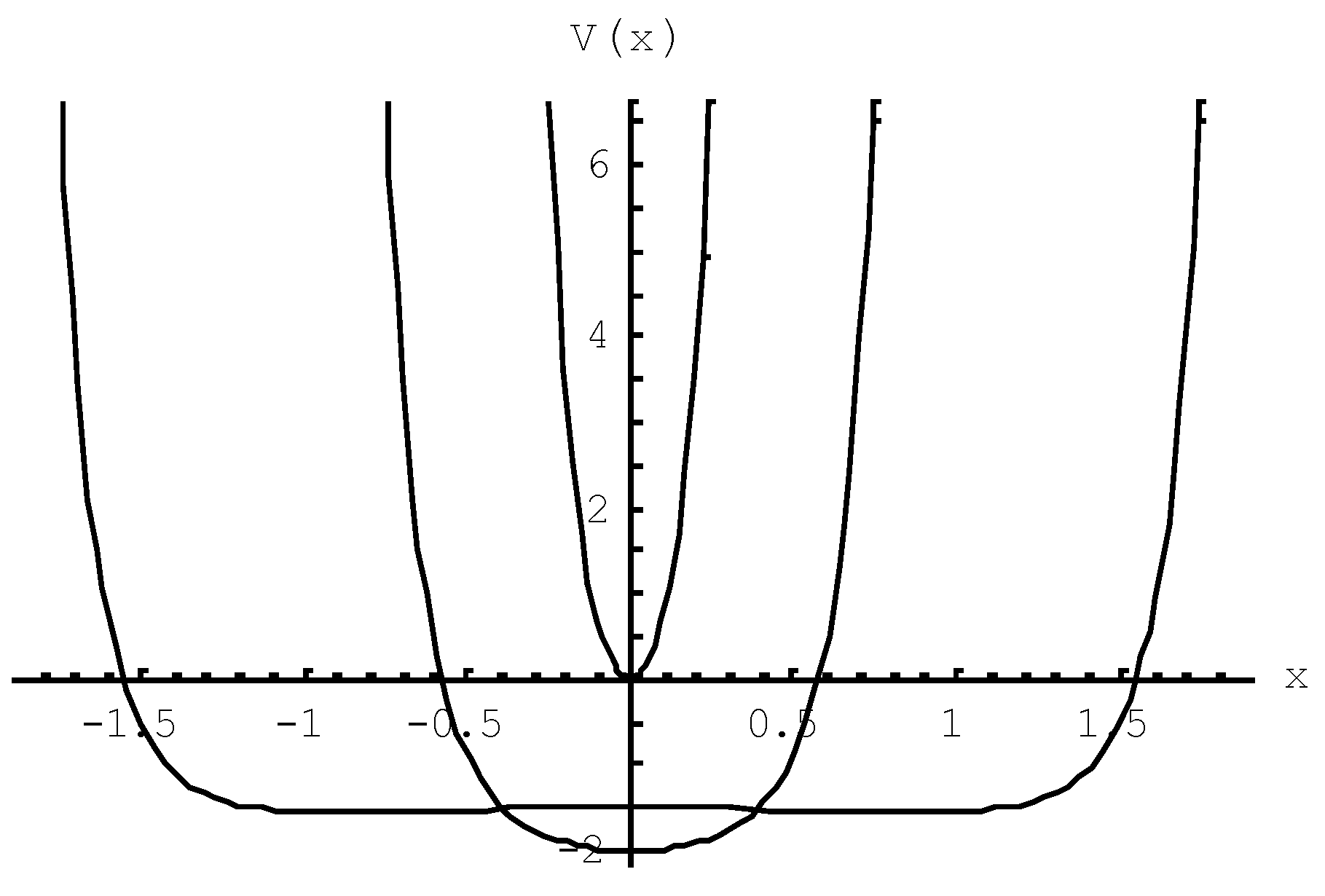
Let us proceed by observing Figure 1. It shows the potential (energy)

V^{'} (x)

of the muon’s center of mass, defined by (1) and (12) as a function of its deviation from the spatial center. Each curve in the figure is characterized by a particular parameter value for the (normalized) spacing

d^{'}

between the poles. There is a clear minimum for

d^{'} = {d^{'}}_{\min}

, an increase of the curvature for

d^{'} < {d^{'}}_{\min}

and a decrease of the curvature for

d^{'} > {d^{'}}_{\min}

. If the two poles are spaced in the state of minimum potential (

d^{'} = {d^{'}}_{\min}

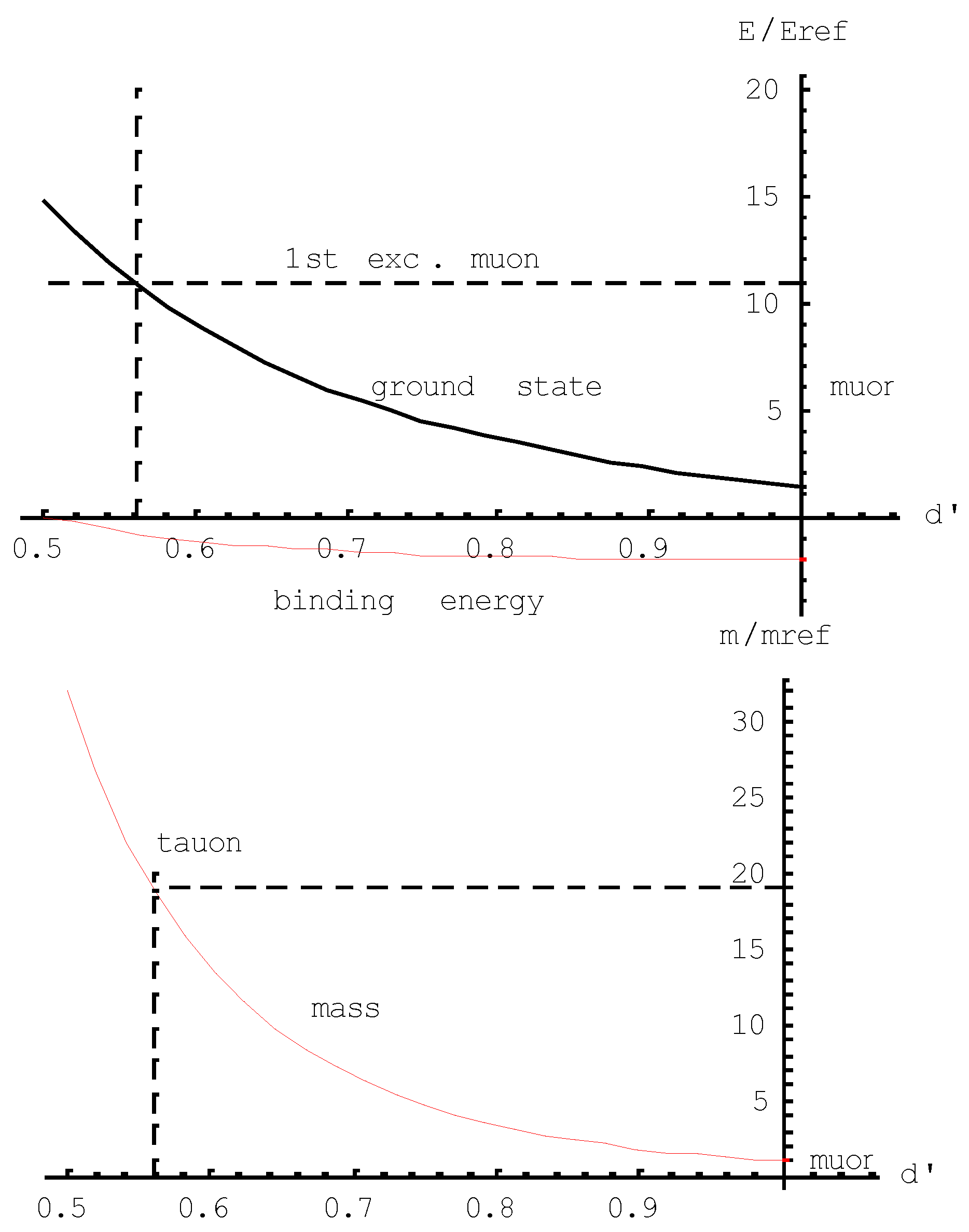
), the vibration energy of the muon is in the ground state. As long as the curves show a minimum with a negative value, the configuration shows an amount of stability-preserving binding energy. It will be clear that the binding energy is lost for narrow spacing. In Figure 2 it is illustrated that the energy constant level of first excitation in ground state may correspond with the ground state energy constant of the configuration at a smaller spacing.

This is the reason why, under excitation conditions, the configuration may jump from the muon state to the tauon state. It will be clear that the jump to the level of second excitation cannot be made under preservation of negative binding energy. Hence, charged leptons beyond the tauon particle are non-existing.

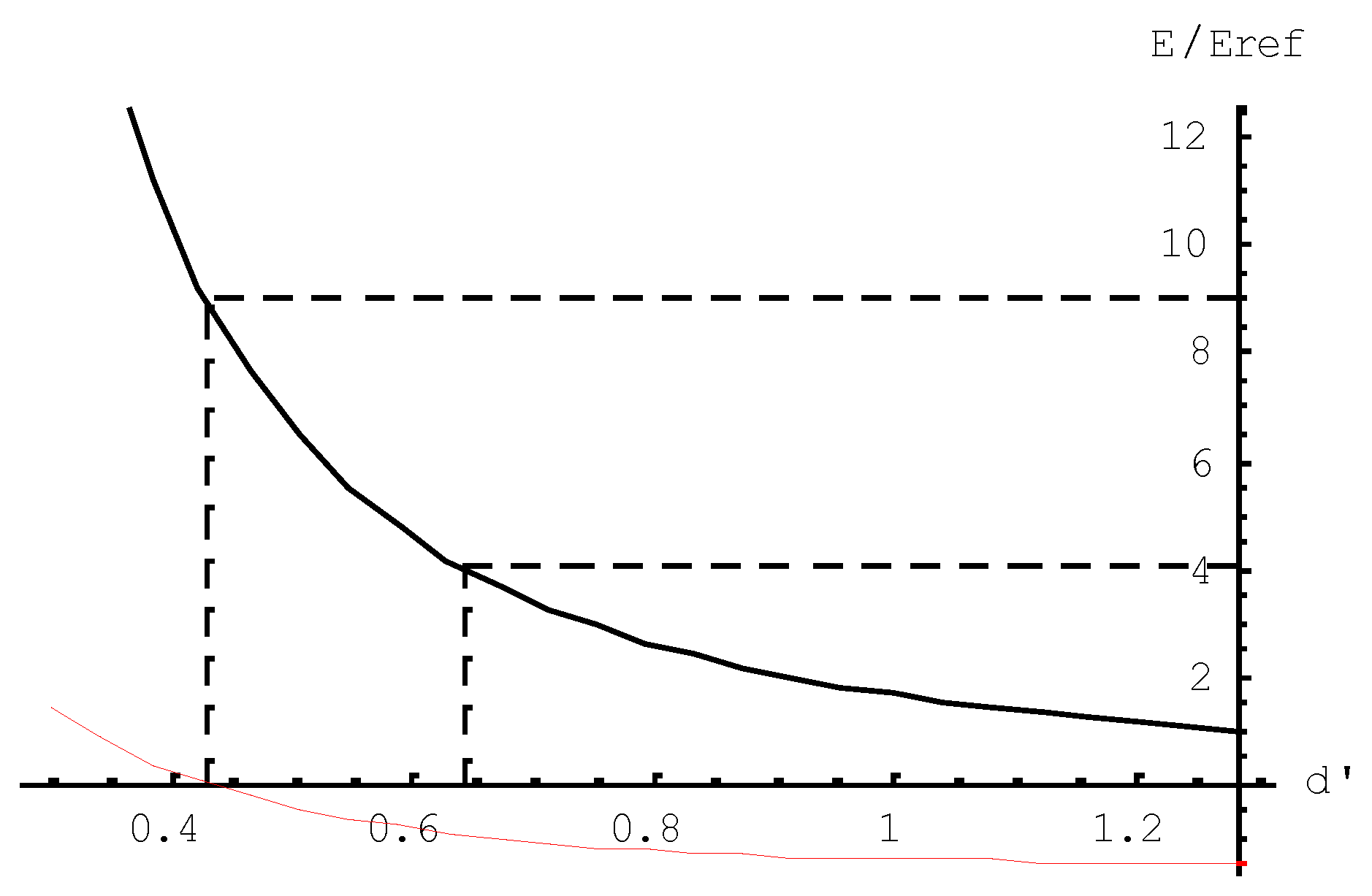
The normalized wave equation allows to calculate by simple computer code the ground state energy as a function of the spacing

d^{'}

. This is shown in the upper part of Figure 3. It also allows to calculate the excitation levels. The dashed line in that part shows the level of first excitation. It may seem as if the energy level of the first excitation is far beyond reasonable physical expectation, because an ideal harmonic oscillator would show at first excitation only three times the ground state value In that respect the picture is somewhat misleading. One should, however, take into consideration that both these values must be established from the bottom level, determined by the binding energy. In this picture the binding energy level in relative amounts is -2, the ground state energy is 1.42 and the first excitation level is 10.9. This makes the excitation to ground state ratio about 3.8. The difference between the factor 3 of the ideal harmonic oscillator shows the effectiveness of the computer code, in which the anharmonic nature of the oscillator is taken into account.

To quantitatively establish the mass relationship between the muon and the tauon, next to the basic relationships (7) and (8) , a third one has to be added. Because the bond between the two kernels is sustained by the weak interaction boson, the spacing 2dλ = 2d^′_min is expected about equal to a half wave length of the weak interaction boson

ℏ ω_{W}

. Hence,

(13)

in which α is a dimensionless correction factor of order 1. Algebraic evaluation on the three basic relationships reveals,

{m^{'}}_{m} = 8 \frac{k_{2}}{| k_{0} |} {(\frac{{d^{'}}_{\min}}{α π})}^{2} ℏ ω_{W} .

(14)

In this picture the mass

m_{m}

has to be considered as the constituent mass of the two kernels. It embodies the energy of the oscillator distributed over the kernels. Similarly as in the case of mesons, this mass is a measure for the rest mass of the lepton. It does not reflect the bare physical (gravitational) mass. The expression allows to relate the rest mass of the tauon with the one of the muon without elaborating of the mass

m_{m}

itself. Even without bothering about the difference between the lab frame and the center-of-mass frame of the pion. The lower part of Figure 3 shows the mass curve as derived from

k_{2} (d^{'})

as a function of

d^{'}

, in which

k_{2} ({d^{'}}_{\min)}) =

1 is taken as the reference. The lower curve shows that, at spacing

d^{'} =

0.56, the relative mass value of the structure amounts to 18.9. This means that the tau particle’s mass is expected being 1.89 GeV/c². This is rather close to the tau particle’s PDG rest mass (1.78 GeV/c²⁾. The difference is due to a slight inaccuracy of the calculation.

For a proper understanding of this “take-over” mechanism it is instructive to point to the relationship between the quantities

Φ_{0}

(strength),

λ^{- 1}

(range) and

g

(coupling factor) that can straightforwardly be derived from (8) and (13), as

g \frac{Φ_{0}}{λ} = \frac{α π ℏ c}{4 | k_{0} | {d^{'}}_{\min}} .

(15)

This ratio is frame independent. It is, however, not an invariant in the sense that quarks or leptons are the same if this quantity is the same. This will be obvious from the consideration that

{d^{'}}_{\min}

is not invariant. The true invariant is the spacing quantity

d

because of its relationship with the invariant weak interaction boson.

It is instructive to emphasize that in the “tauon state” the structure seems being in the same condition as before in the “muon state”, albeit with different values for the major quantities. Hence, the question rises why the mechanism would not allow a bootstrapping effect, which would give rise to a lepton with an eighteen times larger rest mass than the tauon has. It is a question related with the so called “hadronization limit” that pops up in the meson case. This limit prevents the generation of quark flavors heavier than the bottom quark (the out of scale topquark has a different origin and is not part of this question [1]). The short answer to the problem is that bootstrapping stops as soon as the energy gained in excitation is not sufficient enough to compensate for the loss in binding energy. Study of this subtlety is beyond the scope of this article. It is adequately covered in previous work [14].

It is worthwhile as well to note that the excitation mechanism of leptons is somewhat different from that of the mesons. This is due that the lepton structure does not allow an asymmetry between the kernels. While in the lepton structure the two kernels both have the same values for

Φ_{0}

and

λ

, although different for the muon case and the tauon case, the meson excitation mechanism allows asymmetric structures, with different values for

Φ_{0}

and

λ

for quarks in the same structure.

The derived quantitative relationship between the muon’s rest mass and that of the tauon gives a firm to support to the theory of the charged leptons as developed in this paragraph. Let us continue by giving a second proof for its viability.

It would be nice if some more quantitative support could be found for this view. One of the issues is the question why the pion’s energy with a rest mass value of 140 MeV breaks up into the muon’s energy with a rest mass value of about 100 MeV and the neutrino’s energy of about 40 MeV as observed in the lab frame. Curiously, whereas the pion’s energy is distributed over the energy of the muon and the energy of the neutrino, making the pion to the stronger particle, the potential view shows the opposite: the muon’s potential is distributed over the the pion’s one and the neutrino’s one, making the muon to the stronger particle. This confusing picture is due to the antiparticle nature of the neutrino. It means that the neutrino adds its energy to that of the muon to make the energy of the pion. Let us proceed by considering the mass formula (14) in the equivalent format,

{m^{'}}_{m} = 16 k_{2} {(\frac{{d^{'}}_{\min}}{α π})}^{2} g Φ_{0} .

(16)

Because the basic properties

Φ_{0}, λ

and

g

are the same for the pion and the lepton, we may express the ratio of the pion mass over the muon mass as,

\frac{m_{0 π}}{m_{0 μ}} = \frac{k_{2 π}}{k_{2 μ}} \frac{{({d^{'}}_{\min} / α)}_{_{π}}^{2}}{{({d^{'}}_{\min} / α)}_{μ}^{2}} .

(17)

In the rest frame of the muon, the kernels are spaced at

d^{'} = {d^{'}}_{\min} =

1, while the quarks in the (virtual) rest frame of the pion are spaced at

d^{'} = {d^{'}}_{\min} \approx

0.85. In the rest frame of the muon

k_{2} ({d^{'}}_{\min}) =

2, while in the rest frame of the pion

k_{2} ({d^{'}}_{\min}) =

2.74. Inspection of the mass formula (16) shows these different $k_{2}$

values have a major impact on the energy difference between the pion and the muon. Unfortunately, it appears that the different values of

{d^{'}}_{\min}

neutralize the impact. There is, however, still a third factor to be considered. It is the factor

α

in the mass formula. But because the

λ

value for the pion and the muon are the same, we have from (17), eventually

\frac{m_{0 π}}{m_{0 μ}} = \frac{k_{2 π}}{k_{2 μ}} \approx 1.37.

(18)

This ratio is just the same as observed from experimental evidence. Hence, we may conclude that the structural model allows to derive the rest mass of the pion from the rest mass of the pion or the other way around. In the Standard Model the muon is considered as an elementary particle, while the rest mass of the pion is considered as experimental evidence. Relationship by theory has not been established, while, like shown in this text, the structural model allows to do so.

As noted before, neither the potential function for the quark nor the one for the lepton contains any information of their rest masses. In that respect they are not different from electrons. Neither the primary parameter

Φ_{0}

nor the primary parameter

λ

is related with the rest mass of these fermions. The strength parameter

Φ_{0}

is fixed by the weak interaction boson as

{m^{'}}_{W} = g Φ_{0}

. The range parameter

λ

is fixed by the Higgs boson as

{m^{'}}_{H} = 2 λ ℏ c

.. The quantity that ultimately expresses the difference in rest mass is the curvature parameter

k_{2} (d)

, shown by (16).

The calculated result corresponds with a kinematic analysis. Figure 4 illustrates how the pion’s rest mass (139.57 MeV/c²) is splitted upinto the rest mass of the muon (105.66 MeV/c²) and the kinetic energy of the neutrino (33.91 MeV). Some algebraic evaluation [15] shows that, in the rest frame of the muon, the pion gets a slight amount of kinetic energy of 4.12 MeV/c². Stated otherwise: the pion explodes and breaks up into two pieces, a heavy part flying away at low speed and a light part flying away at high speed, such as illustrated in Figure 4.

The kinetic energy of the neutrino can be related with its rest mass because of the relativistic relationship

E_{ν} = \frac{{m^{'}}_{ν}}{\sqrt{1 - v^{2} / c^{2}}} .

(19)

If we would know the neutrino’s velocity, we would be able to calculate the neutrino mass from its kinetic energy. Unfortunately, the only thing known is an estimate of the neutrino mass from direct measurements with, like reported by PDG [6], doubtful reliability. These direct measurements show an upper limit for the muon neutrino mass of

m_{ν μ} <

190 keV/c².

4. Fermi’s theory

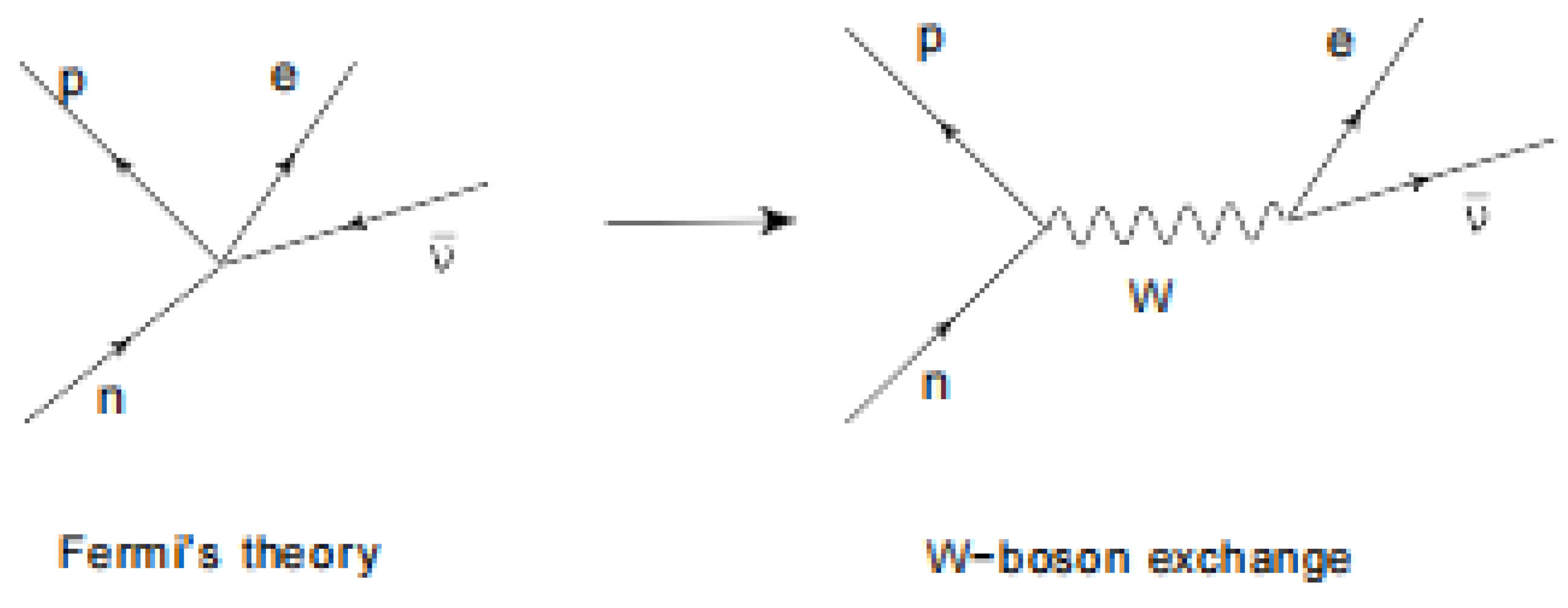
Unfortunately, the excitation model muon-tauon does not hold for the electron-muon relationship. Whereas the muon and the tauon are interrelated because of their internal weak interaction bond, such a bond does not exist for the electron, because the electron is produced as a decay from the muon caused by the loss of this bond. It is instructive to analyze this decay process on the basis of Fermi’s theory, which as forerunner of the weak interaction theory by

W

bosons, describes the origin of the neutrinos as the inevitable consequence from the shape of the energy spectrum of electrons shown in measurements on beta decay.

Fermi’s model is conceptually simple, but rather complex in its implementation. For the purposes of this essay, a simplified representation will suffice, illustrated in the left hand part of Figure 5 . This shows the decay of a neutron into a proton under release of an electron. To satisfy the conservation of energy, the energy difference

E_{0}

between the neutron and the proton must be absorbed by the energy

E

of the electron and the energy

p_{ν} c

of the neutrino moving at about the speed of light. To satisfy momentum conservation, the momentum

P

of the nucleon must be taken over by the momenta

p_{e}

and

p_{ν}

of the electron and neutrino, respectively, so that

E_{0} = E_{e} + p_{ν} c and 0 = P + p_{e} + p_{ν} .

(20)

To explain the occurring energy spectrum of the electron, Fermi has developed the concept of density of states. This is based on the assumption that fermions, such as the electron and the neutrino, despite their pointlike character, require a certain spatial space for their wave function that does not allow a second wave function of a similar particle in the same space. That comes down to respecting the exclusion principle that was posited by Pauli in 1925 in the further development of Niels Bohr’s atomic theory from 1913.

In a simple way, that spatial space is a small cube whose sides are determined by half the wavelength (

L / 2

) of the fermion. A volume

V

contains

N

fermions. So,

N = \frac{V}{{(L / 2)}^{3}} = \frac{8}{{(c T)}^{3}} = \frac{8}{c^{3}} \frac{ω^{3}}{{(2 π)}^{3}} = \frac{8}{{(ℏ c)}^{3}} \frac{{(ℏ ω)}^{3}}{{(2 π)}^{3}} V .

(21)

For a particle in a relativistic state holds

ℏ ω = p c

. In that case, after differentiating,

\frac{d N}{V} = \frac{24}{{(2 π ℏ)}^{3}} p^{2} d p .

(22)

A somewhat more fundamental derivation in terms of a spheric volume split up by solid angles

d Ω

expresses this differential density of states as,

\frac{d N}{V} = \frac{4 π}{{(2 π ℏ)}^{3}} p^{2} d p .

(23)

The difference is about a factor of 2. The difference can be explained, because the roughly derived quantity admits two particles in the interval by taking into account a difference in spin. The differential density of states that can be attributed to the decay product of neutron to proton is equal to the product of the contributions of the electron and of the neutrino, so that

\frac{d n}{V} = \frac{4 π}{{(2 π ℏ)}^{3}} p_{e}^{2} d p_{e} \frac{4 π}{{(2 π ℏ)}^{3}} p_{ν}^{2} d p_{ν} .

(24)

For the differentiated density of states holds,

\frac{1}{V} \frac{d n}{d E_{e}} = {\frac{4 π}{{(2 π ℏ)}^{3}}}^{2} {p_{e}^{2} d p_{e} \frac{d}{d E_{e}} p_{ν}^{2} d p_{ν} + p_{ν}^{2} d p_{ν} \frac{d}{d E_{e}} p_{e}^{2} d p_{e}} .

(25)

For the electron, which is not necessarily in a relativistic state, holds

p_{e}^{2} d p_{e} = \frac{1}{c^{3}} {(E_{e} - m_{e} c^{2})}^{2} d E_{e} .

(26)

Since the neutrinos do not contribute to the spectrum of the electrons, the spectral density of the electrons can be calculated by integrating over the moments of the neutrinos. Hence,

\frac{1}{V} \frac{d n}{d E_{e}} = \frac{1}{4 π^{4} ℏ^{6} c^{3}} {{(E_{e} - m_{e} c^{2})}^{2} d E_{e} \frac{d}{d E_{e}} \int p_{ν}^{2} d p_{ν} + {(E_{e} - m_{e} c^{2})}^{2} \int p_{ν}^{2} d p_{ν} .

(27)

Since the decay occurs from the nucleon in state of rest, the conservation law of momentums prescribes

| p_{ν} | = | p_{e} |

. For the neutrino it then follows that,

p_{ν}^{2} d p_{ν} = p_{e}^{2} d p_{e} .

(28)

It will be clear that the first term in

d n / d E_{e}

is infinitesimally small with respect to the second term and that therefore,

\frac{1}{V} \frac{d n}{d E_{e}} = \frac{1}{4 π^{4} ℏ^{6} c^{6}} {{(E_{e} - m_{e} c^{2})}^{4}} .

(29)

So here

d n

is the number of electrons per m³ in an energy interval between

E_{e}

and

E_{e} + Δ E_{e}

. In terms of energy, therefore,

d W = {(m_{e} c^{2})}^{2} V d n

, so that

\frac{d n}{d E_{e}} = \frac{1}{{(m_{e} c^{2})}^{2} V^{2}} \frac{d W}{d E_{e}} \to \frac{d W}{d E_{e}} = {(m_{e} c^{2})}^{2} V^{2} \frac{1}{4 π^{4} ℏ^{6} c^{6}} {{(E_{e} - m_{e} c^{2})}^{4} .

(30)

This expression can be rewritten as,

\frac{d W}{d E_{e}} = \frac{{G^{'}}_{F}^{2}}{2 π^{3}} {{(E_{e} - m_{e} c^{2})}^{4}

, with

\frac{{G^{'}}_{F}^{2}}{2 π^{3}} = V^{2} {(m_{e} c^{2})}^{2} \frac{1}{4 π^{4} ℏ^{6} c^{6}} \to {G^{'}}_{F} = \frac{V}{\sqrt{2 π}} \frac{m_{e} c^{2}}{{(ℏ c)}^{3}} .

(31)

The relationship takes on a simple form if the decay product is relativistic. This is usually true when muons decay into electrons, because in the major part of the spectrum

E > > m_{e} c^{2}

. In that case,

W_{E} = \frac{{G^{'}}_{F}^{2}}{2 π^{3}} \int_{m_{e} c^{2}}^{E_{0}} {(E_{e} - m_{e} c^{2})}^{4} d E_{e} \approx \frac{{G^{'}}_{F}^{2}}{2 π^{3}} \frac{1}{5} E_{0}^{5}; E_{0} = m_{u} c^{2} .

(32)

The relevance of this expression because clear from Fermi’s “Golden Rule”, which relates the half-life

τ

(in which half of a nuclear particle decays) and the integral

W_{E}

of the decay spectrum,

\frac{1}{τ} = \frac{W_{E}}{ℏ} .

(33)

This expression shows that the lifetime of a nuclear particle is determined by the time it takes to build up the decay spectrum with the total energy value

W_{E}

. Note that the expression resembles Heisenberg’s uncertainty relation,

Δ ι \cdot Δ W_{E} = ℏ .

(34)

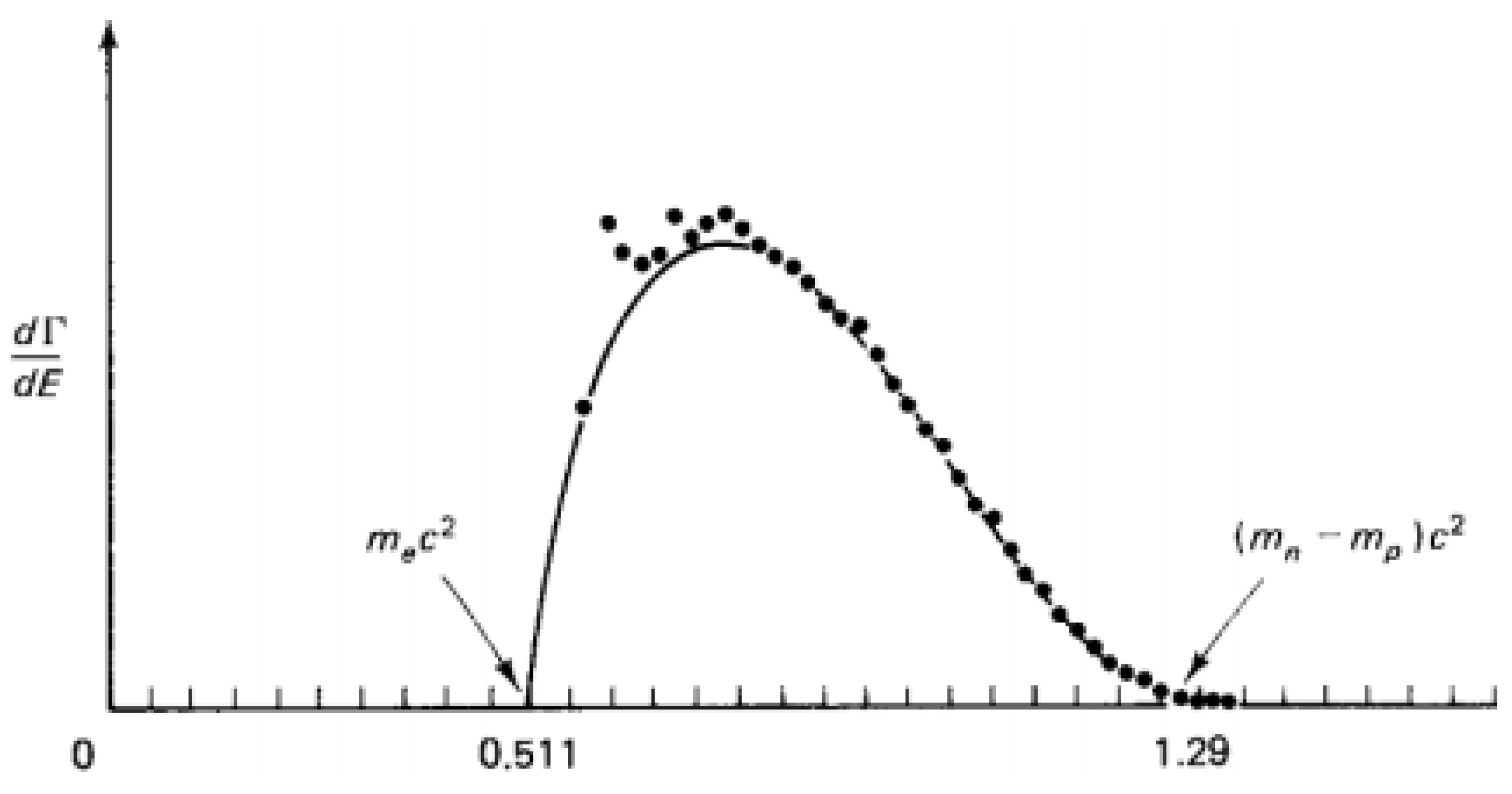
The rule is based on a statistical analysis of the decay process, the details of which can be found in literature [16,17]. The calculated energy density spectrum is shown in Figure 6. The fifth-power shape, which relates the massive energy

m c^{2}

of a nuclear particle to its decay half-life, is known as (Bernice Weldon) Sargent’s law, as formulated empirically in 1933.

It would be nice if it would appear being possible to derive by theory an estimate for the numerical value of

{G^{'}}_{F}

. Let us see if this can be done.

If we would know

V

, the constant

{G^{'}}_{F}

can be calculated. Since the calculation of the density of states assumes the spatial boundary of the wave function of the decay products, it is reasonable to assume that the volume

V

is determined by the spatial boundary of the wave function that fits the energy from which the decay products originate, so that

V = {(\frac{L}{2})}^{3} = {(\frac{c T}{2})}^{3} = {(\frac{c}{2} \frac{2 π}{ω})}^{3} = {(π \frac{ℏ c}{ℏ ω})}^{3}

, and therefore

{G^{'}}_{F} = \frac{π^{3}}{\sqrt{2 π}} \frac{m_{e} c^{2}}{{(ℏ ω_{n p})}^{3}},

(35)

in which

ℏ ω_{n p}

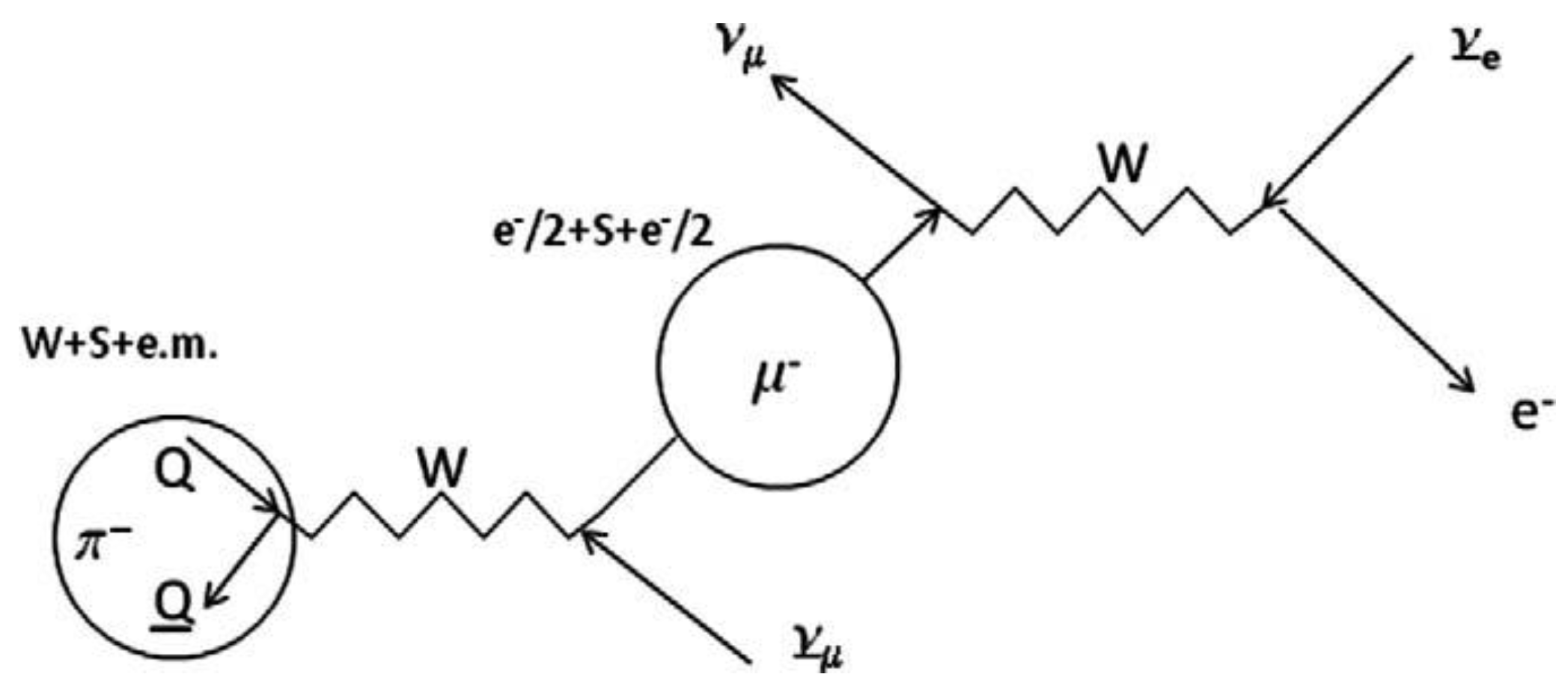
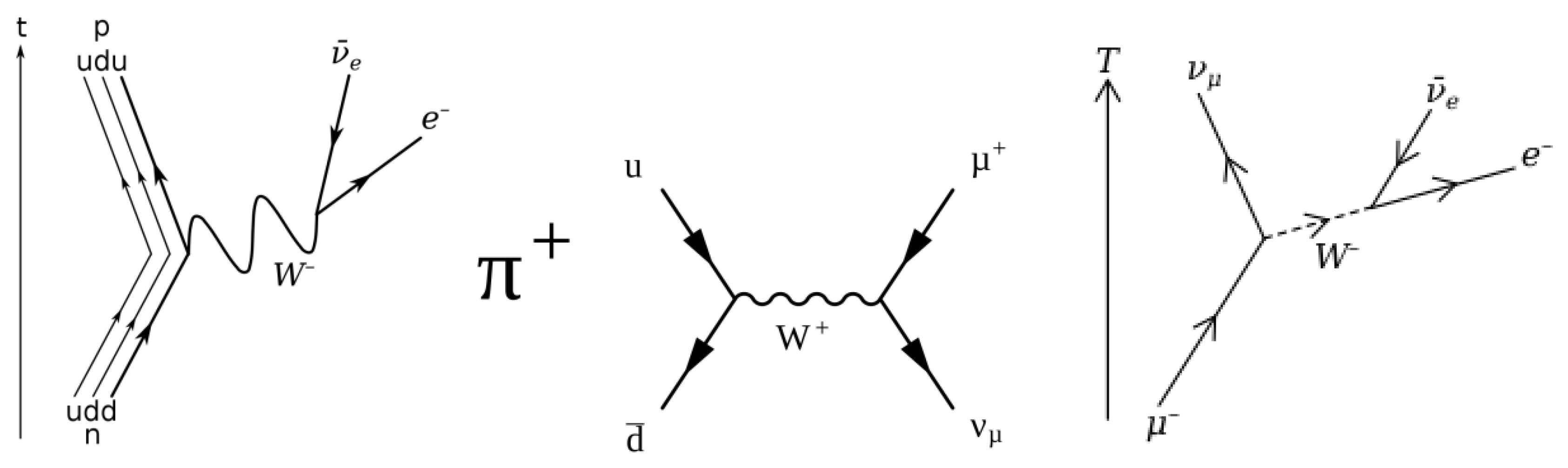
the energy that determines the formation of the decay products. As illustrated in the right-hand part of Figure 5, Fermi’s point contact model has been revised after the discovery of

W

bosons as carriers of the weak force, which is seen as the cause of the decay process. This insight led to the model shown in the right half. Zooming in on it shows that the neutron decay is caused by the change in composition of the nucleon from

u d d \to u d u

. This is shown in the left-hand part of Figure 7. This picture is symbolic, because it suggests that the energy difference between a

u

quark and a

d

quark is determined by a

W

boson, while we know that the free state energy of a boson is 80.4 GeV and there is only a 1.29 MeV mass difference between the

(u d d)

neutron and the

(u d u)

proton.

The figure in the middle gives a more realistic picture of the

W

boson. A positive pion decays in its entirety via a

W

boson into a (positive) muon and a neutrino. It is more realistic, because earlier in this essay we established that the pion moving at about the speed of light has a rest mass of 140 MeV, while it behaves relativisticly as 80.4 GeV prior to its decay into the muon’s rest mass of 100 MeV plus a neutrino energy (that in the rest frame of the muon corresponds to a value of about 40 MeV). A (negative) muon in turn decays into electrons and antineutrons as shown in the right part of the figure. It will be clear from these figures that one

W

boson is not the other. Only the middle image of Figure 7 justifies its energetic picture. Hence, as discussed earlier in the essay, the 140 MeV rest mass of the pion is the non-relativistic equivalent of the 80.4 GeV value of the boson.

These considerations lead us to consider the decay process from pion to muon to be the most suitable one to calculate the constant

{G^{'}}_{F}

. Because the pion decays to a muon, the rest mass of the muon (= 100 MeV) takes the place of the electron before. The energy

ℏ ω_{n p}

from which the decay product arises is the energy of the free state

W

boson, so that

{G^{'}}_{F} = \frac{π^{3}}{\sqrt{2 π}} \frac{m_{u} c^{2}}{{(ℏ ω_{W})}^{3}}; m_{u} c^{2} = 100 MeV; ℏ ω_{W} = 80.4 GeV.

(37)

This makes

{G^{'}}_{F}

= 2.38 10^-6 GeV^-2.

Summarizing:

\frac{1}{τ} = \frac{W_{E}}{ℏ} = (\frac{c}{ℏ c}) W_{E}; W_{E} = \frac{{G^{'}}_{F}^{2}}{10 π^{3}} {(m c^{2})}^{5}; {G^{'}}_{F} = \frac{π^{3}}{\sqrt{2 π}} \frac{m_{u} c^{2}}{{(ℏ ω_{W})}^{3}} .

(38)

This result has a predictive value, because it allows to calculate the decay time of any nuclear radioactive particle from the reference values of, respectively, the weak interaction boson

(ℏ ω_{W} =

80.4 GeV) and the massive energy of the muon (

m_{u} c^{2} =

105 MeV). The result thus calculated for the muon itself is

τ_{μ} =

2.56 x 10^-6 s . This compares rather well with the experimentally established value

τ_{μ} =

2.2 × 10⁻⁶ s reported by the Particle Data Group (PDG) [18].

Let us emphasize that in this text the result is obtained by theory. The canonical theory is less predictive. Instead, the empirical established value of the muon’s half life is invoked for giving an accurate value for Fermi’s constant. The analytical model described in Griffith’s book [17] gives as canonically defined result,

W = \frac{G_{F}^{2}}{192 π^{3}} E_{0}^{5}; E_{0} = m_{u} c^{2} .

(39)

The factor 192 (= 2 x 8 x 12) is the result of integer numerical values that play a role in the analysis. Unlike the predictive model described in this paragraph, this relationship does not allow to calculate the decay time

τ_{μ}

of the muon. Instead, taking the experimentally measured result of this decay time

τ_{μ}

(= 2.1969811 × 10⁻⁶ s ) as a reference, the quantity

G_{F}

, dubbed as Fermi’s constant is empirically established as

G_{F} =

1.106 10^-5 GeV^-2. It confirms the predictive merit of

{G^{'}}_{F}

The theory as described in this text does not allow to relate the rest masses of the muon and the tauon with the rest mass of the electron. Within the Standard Model the three charged leptons are considered as elementary particles. Hence, their rest masses are taken for granted. What has been shown in this text, though, is, that the rest masses of the muon and the tauon are related by theory. Further detailing of the rest mass values requires a link with gravity. For the electron it is the empirical result from Millikan’s classical experiment. In this text it has been shown that the rest mass of the muon is related by theory with the rest mass of the pion. The pion’s rest mass relies upon the rest mass of the quark. Also here, a link with gravity is needed to reveal the true value for the quark’s rest mass. It can be found in [10].

What can be done, though, is trying to measure the mass of the neutrino on the basis of an careful analysis of the spectrum of beta radiation produced by the radioactivity of a suitably chosen element. Figure 6 is suited for explaining the principle. It shows that the endpoint of the graph is characteristic for the maximum energy that an electron may get in the decay process. The difference between the measured energy of the fastest electrons with the theoretical endpoint must be equal to the rest mass of the electron neutrino. The accuracy obtained with KATRIN (KArlsruhe TRItium Neutrino) experiment, has enabled to assess an upper limit for the mass of the electron neutrino, such that

m_{ν} <

0.8 eV/c², [19].

5. The eigenstates of neutrinos

Considering that the tauon is the result of the excitation of the muon modelled as an anharmonic oscillator built up by two kernels, it is worthwhile to consider the possibility that the muon neutrino is subject to excitation as well. We have concluded before that the muon neutrino is built up by two kernels, each having a potential function given by (5). Similarly as in the case of the pion and the muon, the two kernels may compose an anharmonic oscillator that can be described by the wave equation in the general format (1). Similarly as in the muon case, this equation can be written as,

(40)

The only difference so far is that the expansion of the potential function (4) will result in other values for the dimensionless constants

k_{0}

and

k_{2}

. Rewriting (40) in a normalized format gives,

\frac{- {(ℏ c)}^{2} λ}{2 {m^{'}}_{m}} \frac{λ}{g Φ_{0}} \frac{d^{2} ψ}{d {x^{'}}^{2}} + (k_{0} + k_{2} {x^{'}}^{2}) ψ = E^{'} ψ .

(41)

Invoking the relationship (13)

\frac{- (ℏ c) λ}{2 {m^{'}}_{m}} \frac{2 {d^{'}}_{\min}}{α π} \frac{d^{2} ψ}{d {x^{'}}^{2}} + (k_{0} + k_{2} {x^{'}}^{2}) ψ = E ψ,

(42)

And because of the relationship,

λ ℏ c = {m^{'}}_{H}

(43)

- α_{0} \frac{d^{2} ψ}{d {x^{'}}^{2}} + (k_{0} + k_{2} {x^{'}}^{2}) ψ = E ψ; α_{0} = \frac{{m^{'}}_{H}}{{m^{'}}_{m}} \frac{{d^{'}}_{\min}}{α π} .

(44)

Unlike as in the pion case and the muon case, the bond between the kernels is not sustained by weak interaction. This means that it is not allowed to invoke relationship (12). Hence, in the neutrino case we have to cope with an unknown quantity for

α_{0}

, which has a very large value because of the extremely small value of the neutrino’s massive energy

{m^{'}}_{m}

. This difference has a dramatic effect on the shape of the wave function that show up as the solution of the wave equation. The wave equation can be solved numerically with the same computation model as for mesons and the charged leptons. This model with its computer code has been documented in previous work [20].

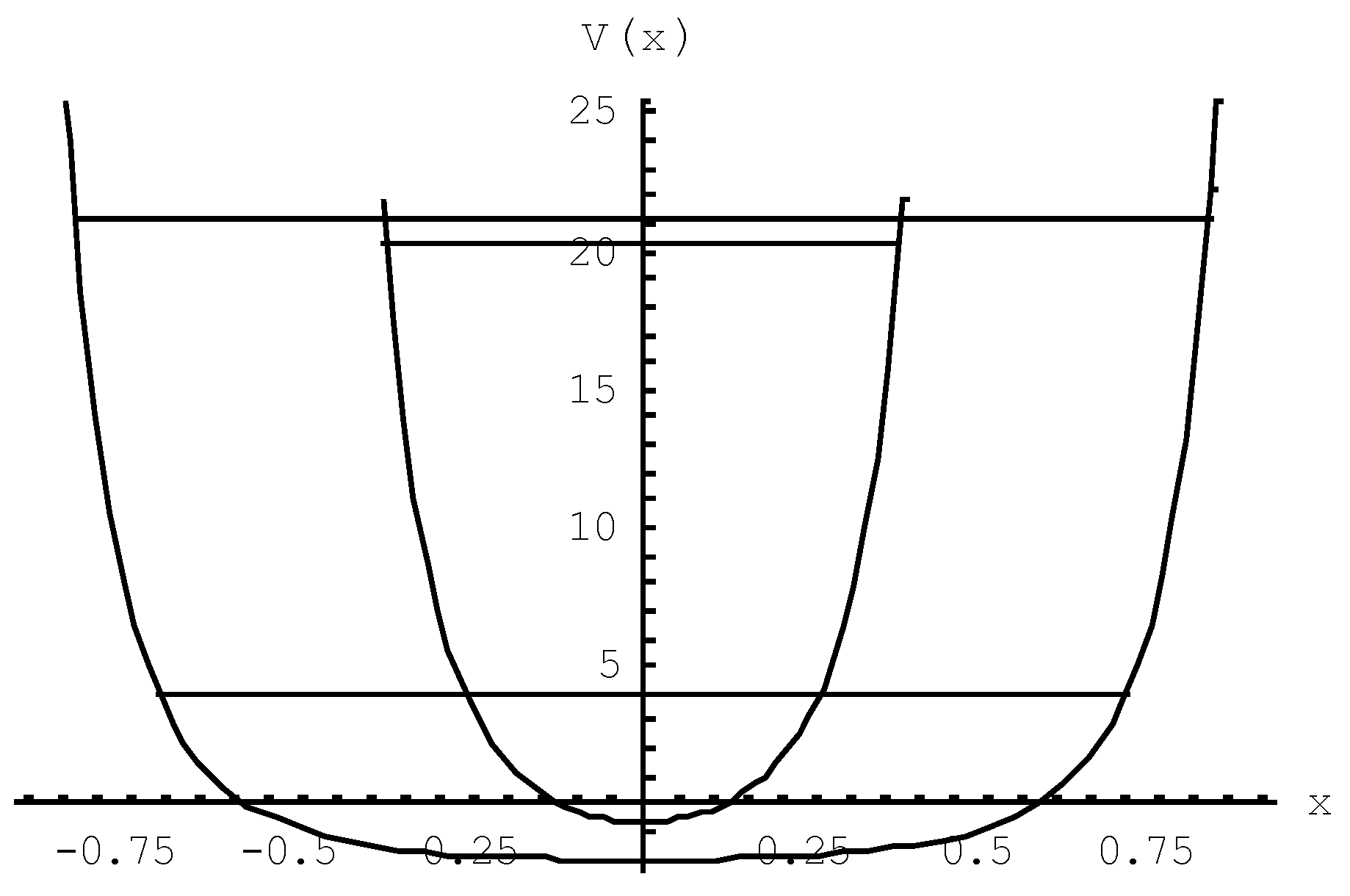
Figure 8 is the equivalent of Figure 3 shown for the charged lepton. It illustrates that the ground state energy of a neutrino with a smaller spacing between the poles equals the energy levels of the first excitation and the second excitation of the neutrino in a minimum state of energy. The implication of this effect is that neutrinos may show up in three different eigenstate modes. The dramatic impact of the

α_{0}

difference between the charged leptons and the neutrinos is illustrated in Figure 9. Whereas the wave function of the charged lepton, similarly as the meson, has the characteristics of a nearly perfect harmonic oscillator, the wave function of the neutrino has the “brick wall” characteristic. Whereas the weak interaction bond gives the inter-pole potential

V (x)

more or less quadratic shape, the loss of weak interaction shapes this potential to a brick wall.

It has to be emphasized that this result is obtained by analysis and a numerical solution of the wave equation. How to interpret this analytical result in physical terms? It seems as if the pion acts under decay as an emitter for energetic standing wave packets, similarly as antennas do in electromagnetic communication. These packets seem to possess a similar kind of coherency as lasers have in radiation of their photons. Because the potential field of the neutrino poles have no other physical parameters apart from

Φ_{0}

as fixed by the weak interaction boson, and

λ

as fixed by the Higgs field, it is fair to conclude that neutrinos will exclusively show up in three modalities, because loss of binding energy will prevent other ones. It is possible to estimate its physical size, because,

d = {d^{'}}_{\min} λ = {d^{'}}_{\min} \frac{ℏ c}{{m^{'}}_{H}} \approx 1.28 (197/126.5) x 10^{- 18} [m]

6. Discussion

This eigenstate model for neutrinos shares quite some characteristics with the present adopted model of neutrinos as in 1957 heuristically proposed Pontecorvo. Quite some questions, though, still remain. It is for instance not clear why neutrinos should interact on their own, making different flavour states, without being influenced by their charged partners. One of the issues to be taken into consideration is the statistical character of particle physics. Taking as an example the break-down of the weak interaction of muons into electrons and neutrinos, one might expect that the produced neutrinos are not only subject to a statistical distribution of their kinetic energy, but that their distribution over the three possible eigenstates is subject to a statistical behaviour as well. While in this view any of the neutrinos will physically be in different defined eigenstates out of three, one may adopt a mathematical description captured in a single matrix, common for all neutrinos in the decay of a specific neutrino flavour, such as done in the now commonly accepted theory of neutrinos [21]. In fact, however, this is no more than a projection of the statistical behaviour of a multi-particle system on a single virtual particle.

Taking this in mind, let us consider the decay process of the pion, once more. There is no reason why the picture shown in Figure 4 would not be reversible, like shown by all quantum mechanical processes. It means that the neutrinos may change flavour, but not on their own. An electron neutrino with high energy may recoil with an electron to produce a weak interaction boson that subsequently disintegrates into a muon and an muon antineutrino. This observation, however, does not solve the solar neutrino problem mentioned before. And that problem is usually tackled by assuming that neutrinos may change for whatever reason flavour on their own under influence their eigenstate behaviour. But why should they do so?

It is in the author’s view quite probable that the answer to this question has to do with an interpretation of experimental evidence. A neutrino can only be detected if it produces its charged lepton partner. Such a production can be understood from the reverse process just described. As compared to the forward mode, the reverse mode is not impossible, but unlikely. This implies that the instrumentation for neutrino detection is based on the counting of rare events over considerable time. A beautiful example is the method used in the Super-Kamiokande experiment, which is based upon the detection of Cherenkov radiation [22]. This radiation is produced by electrons and muons in water that may propagate in water at a faster speed than the light in water does. The radiation profile from electrons and muons produced by the matter interaction between neutrinos and (heavy) water molecules is slightly different. This difference enables to distinguish between electron-neutrinos and muon-neutrinos. The experimental evidence that the sum of the electron-neutrino counts and the muon-neutrino counts is equal to the corresponding calculated amount of solar electron-neutrinos is presently taken as proof that neutrinos change flavours on their own, thereby solving the mystery of the missing solar neutrinos.

Another explanation could be that the production of neutrinos in the reverse decay process is somewhat different from the production of neutrinos in the forward process. Whereas in the forward process the neutrinos are emitted in a certain flavour dependent distribution over the three eigenstates, the production of charged leptons in the reverse process might be selective on eigenstates. This would mean, that flavour changes between neutrinos on their own are non existing. It also implies that the oscillation phenomenon as observed in instrumentation based upon the detection of beat frequencies of propagating neutrino wave functions is not due to physical interaction between the neutrino flavours, but that this phenomenon is a result from non interacting physical eigenstates propagating at slightly different speeds.

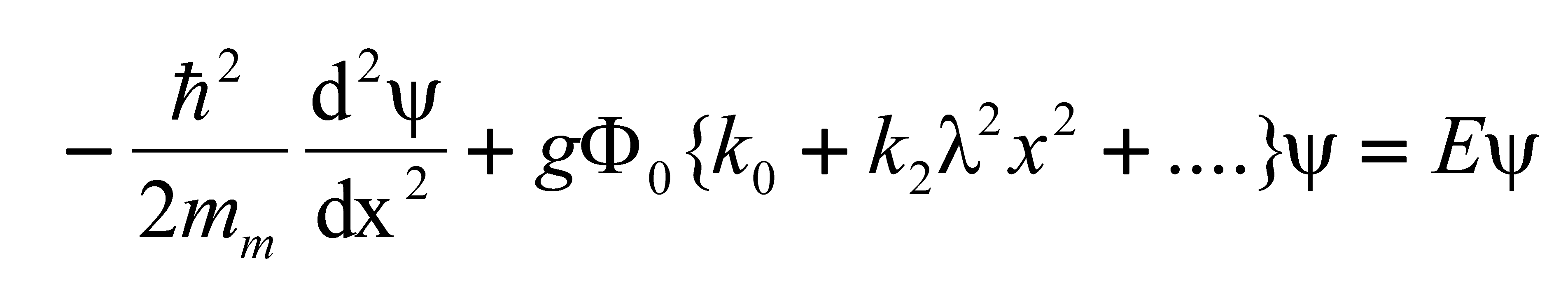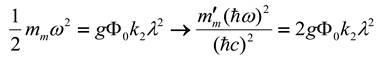Appendix A

The Appendix is meant for explaining the factor 2 in eq. 3 of the plain text. This will be done by describing the correspondences and the differences between a classical bond and the weak interaction bond. An example of the classical bond can be found in [13], in which it is shown how two electrons can compose a stable bond under the balance of electric repulsing between the two electrons and a magnetic attraction between the associated magnetic dipole moments

μ_{m}

. In this classical case, the potential

V (x)

at a distance

x

spaced from the center of the two electrons spaced

2 d

apart can be written as,

V (x) = {Φ (x) + Φ (- x)} / 2, in which

(A1)

Φ (x) = - \int F (x) d x; F (x) = (\frac{A}{{(d + x)}^{2}} - \frac{B}{{(d + x)}^{4}}); A = \frac{e^{2}}{4 π ε_{0}}; B = 3 \frac{μ_{0}}{4 π} μ_{m}^{2}

Hence,

V (x) = \frac{1}{2} (\frac{B}{3 {(d - x)}^{3}} - \frac{A}{d - x} + \frac{B}{3 {(d + x)}^{3}} - \frac{A}{d + x}) .

(A2)

(Check : V (0) = \frac{B}{3 d^{3}} - \frac{A}{d} \to \frac{d V (0)}{d d} = \frac{B}{d^{4}} - \frac{A}{d^{2}} \to d^{2} = \frac{B}{A}).

(A3)

V (x) = \frac{B}{2} {(\frac{1}{3 {(d - x)}^{3}} + \frac{1}{3 {(d + x)}^{3}}) - \frac{A}{B} (\frac{1}{d + x} + \frac{1}{d - x}); \frac{A}{B} = \frac{1}{x_{0}^{2}}

V (x) = \frac{B}{2} {\frac{1}{x_{0}^{3}} (\frac{1}{3 {(d^{'} - x^{'})}^{3}} + \frac{1}{3 {(d^{'} + x^{'})}^{3}}) - \frac{1}{x_{0}^{3}} (\frac{1}{d^{'} + x^{'}} + \frac{1}{d^{'} - x^{'}}); d^{'} = \frac{d}{x_{0}}; x^{'} = \frac{x}{x_{0}} .

V (x) = \frac{A}{2 x_{0}} {(\frac{1}{3 {(d^{'} - x^{'})}^{3}} + \frac{1}{3 {(d^{'} + x^{'})}^{3}}) - (\frac{1}{d^{'} + x^{'}} - \frac{1}{d^{'} - x^{'}}} .

(A4)

This can be written as,

V (x) = U (d + x) + U (d - x); U (x) = \frac{A}{6 x_{0}} (\frac{1}{{x^{'}}^{3}} - \frac{3}{x^{'}})

(A5)

Let us compare this result with the case that

V (x)

in (A-4) has a different format,

V (x) = \frac{1}{2} (\frac{B}{2 {(d - x)}^{2}} - \frac{A}{d - x} + \frac{B}{2 {(d + x)}^{2}} - \frac{A}{d + x}) .

(A6)

This is a generalization of the format of the potential between two quarks or two charged leptons, built up by a far field

\propto 1 / x

and a near field

\propto 1 / x^{2}

. Evaluation of this expression along the same lines as just above, yields

V (x) = U (d + x) + U (d - x); U (x) = \frac{A}{4 x_{0}} (\frac{1}{{x^{'}}^{2}} - \frac{2}{x^{'}})

(A7)

Note the difference with (A5). This explains the reason for the factor 2 in eq.3 of the plain text.

References

E. Roza, “ From black-body radiation to gravity: why quarks are magneiic electrons and why gluons are massive photons”, 0211. Available online: https://www.preprints.org/manuscript/202209.0211/v1.
Available online: 2. https://www.radioactivity.eu.com/site/pages/Neutrino_Hypothesis.htm.
C. L. Cowan, Jr., F. Reines, F. B. Harrison, H. W. Kruse and A. D. McGuire, “Detection of the Free Neutrino: a Confirmation”, Science 124, 103 (1956).
Bahcall, J. N.; Davis Jr, R. Science. 191 (4224): 264–267 (1976).
V.N.Gribov and B.M. Pontecorvo, “Neutrino astronomy and lepton charge,” Phys. Lett. B 28, 493-496 (1969).
Prog. Theor. Exp. Phys. 2020, 083C01 (2020).
E. Roza, “On the second dipole moment of Dirac’s particle”, Found. of Phys. 50, 828 (2020).
E. Roza, “On the second dipole moment of Dirac’s particle”, updated. www.preprints.org 2021. [CrossRef]
E. Roza, “The Impact of Nuclear Spin and Isospin of Dirac Particles on the Mass Spectrum of Leptons”, www.preprints.org 1919.
E. Roza, “ From Black-Body Radiation to Gravity:Why Neutrinos are Left-Handed and Why the Vacuum is not Empty. www.preprints.org 2022. [CrossRef]
E. Roza, A hypothetical H-particle, Phys. Essays, 24, 1 (2011).
E. Roza, The gravitational constant as a quantum mechanical expression, Results in Phys.,6, 149 (2016).
A. Mikhailichenko, “To the Possibility of Bound States between Two Electrons”, Proc. 3rd Int. Particle Accelerator Conf. (IPAC’12), New Orleans, LA, 2792.
E. Roza, On the quark scaling theorem and the polarisable dipole moment of the quark in a scalar field. 2022. Available online: https://www.preprints.org/manuscript/202006.0304/v4.
Available online: http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/piondec.html.
Scattering and Decays From Fermi’s Golden Rule. Available online: https://web2.ph.utexas.edu/~schwitte/PHY362L/QMnote.pdf.
D. Griffiths, Introduction to Elementary Particles, ISBN 3527406018, Wiley (2008).
M. Tanabashi et al. (Particle Data Group), Phys. Rev. D 98, 030001 (2018).
The KATRIN Collaboration. “Direct neutrino-mass measurement with sub-electronvolt sensitivity”, Nat. Phys. 18, 160–166 (2022).
E. Roza, A hypothetical H-particle, Phys. Essays, 24, 1 (2011).
Maki, Z.; Nakagawa, M.; Sakata, S. (1962). ”Remarks on the unified model of elementary particles”. Progress of Theoretical Physics. 28 (5): 870 (1962).
S. Fukuda; et al. , “The Super-Kamiokande detector”, Nuclear Instruments and Methods in Physics Research A, 501 (2–3): 418, (2003).

Figure 1. Expected density spectrum of the electron’s energy in beta radiation (red) and the actually observed one (black).

Figure 2. Hypothetical equivalence of the quark’s polarisable linear dipole moment with the magnetic dipole moment of its electric charge attribute.

Figure 3. The decay of the pion’s atypical dual dipole moment configuration into two typical single dipole moment configurations.

Figure 4. A charged pion decays into a charged lepton (muon) and its associated neutrino because of emission of the vector weakinteraction boson. Subsequently, the muon and the neutrino recoils into a weak interaction boson that subsequently decays into a (Pauli) shower of electrons and antineutrinos.

Figure 1. The potential energy of the muon’s center of mass as a function of spacing between the poles. The stable ground state of the muon occurs at maximum binding energy (V(x) = -2; d’ = 1). The binding energy is lost for spacing d’ = 0.5.

Figure 2. The jump from the muon state to the tauon state is a jump from the first excitation level of the muon state to the ground state of the heavier tauon. It happens at a spacing d’ = 0.56, where the energy constants (not to be confused with the massive energies) match, under preservation of a slight amount of binding energy.

Figure 3. The lower curve shows the dependence of the lepton’s physical mass on the pole spacing. The upper graph shows that the pole spacing of the tau particle is determined by the equilaty in vibration energy of the muon’s first excitation level and the ground state vibration energy of the heavier tau particle. Note that the binding energy of the tau particle is just slightly negative.

Figure 4. The break up of a pion into a (low speed) muon (left) and a (high speed) neutrino (right).

Figure 5. Fermi’s beta decay model with direct coupling versus decay by weak interaction boson.

Figure 6. Electron energy distribution from neutron beta decay, calculated and experimental (dots).. Source: ref. [5,7].

Figure 7. The symbolic representation of the weak decay process by the weak interaction boson.

Figure 8. The pole spacing of the neutrino is determined by the equity in vibration energy of the neutrino’s first excitation level, respectively the second excitation energy from ideal ground state with its the ground state vibration energy at reduced pole spacing..Note that the binding energy (shown in a different scale as the lower curve) just allows three modes of eigenstates.

Figure 9. Comparison of the wave function formats between the charged lepton and the neutrinos. Whereas the wave function of the charged lepton is close to the one of an harmonic quantum mechanical oscillator, the wave function of a neutrino is a non-electromagnetic standing wave packet.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.