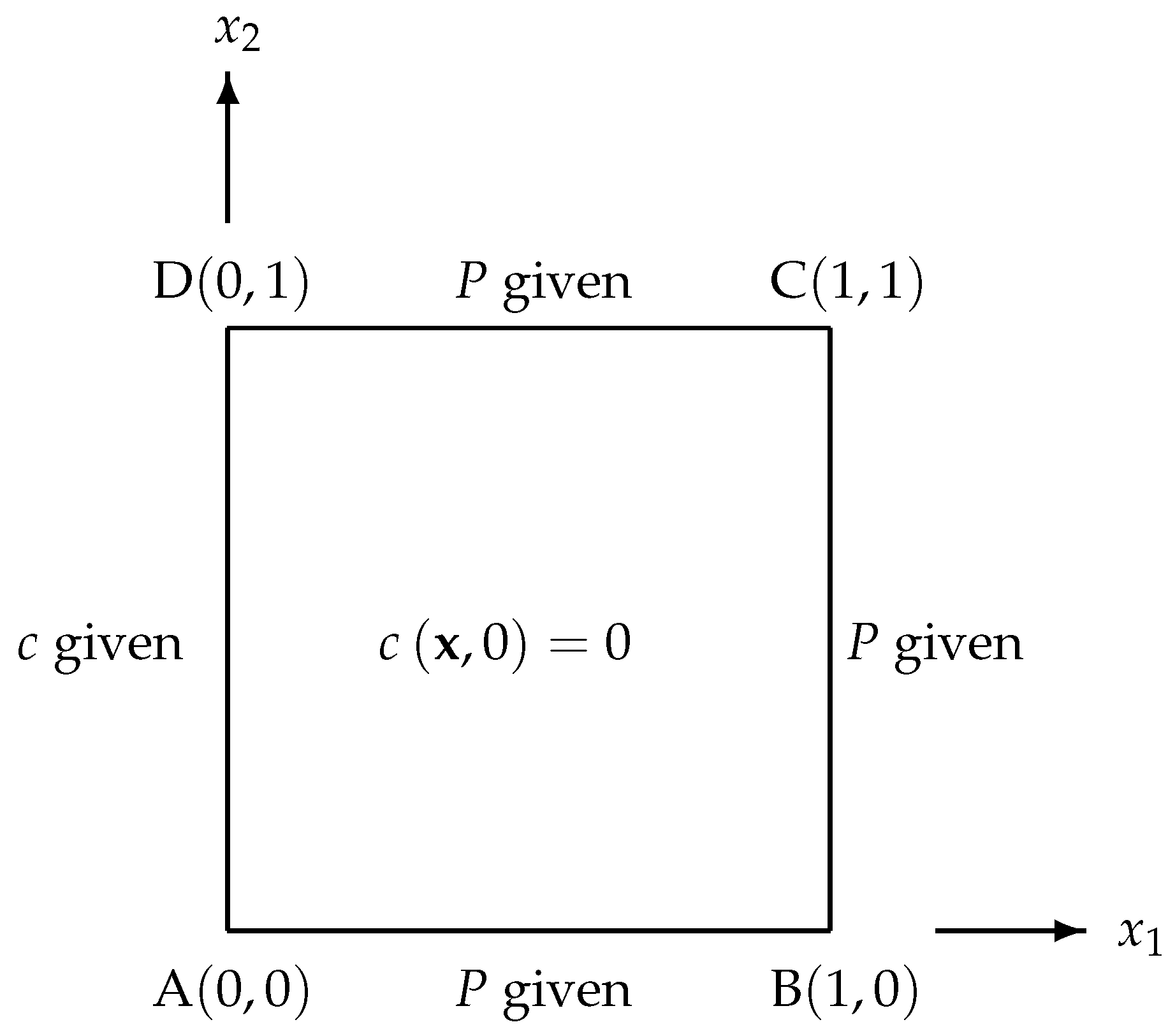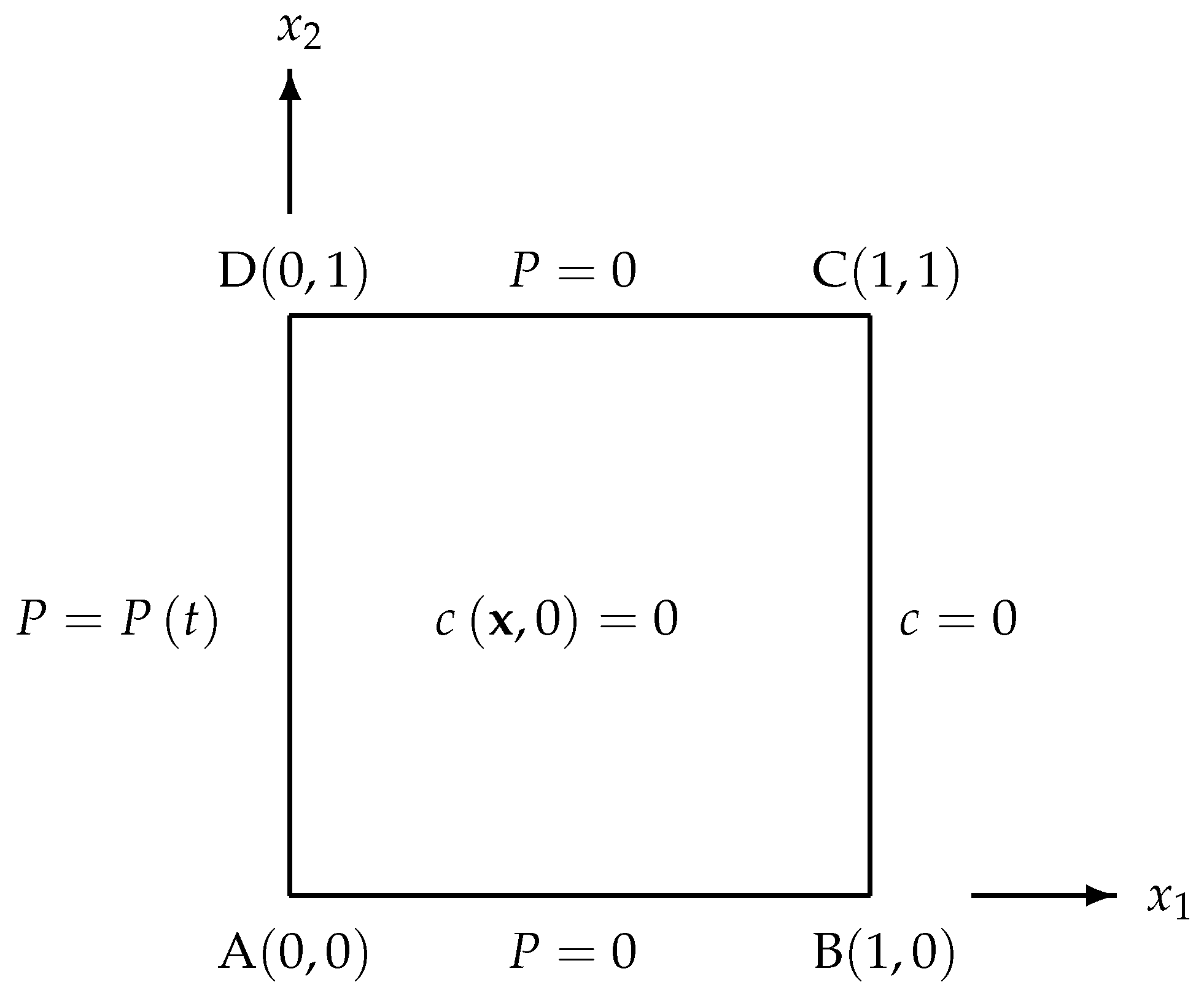Numerical Simulation for Transient Diffusion Convection Reaction Problems of a Class of Anisotropic FGMs

Preprint

Article

Numerical Simulation for Transient Diffusion Convection Reaction Problems of a Class of Anisotropic FGMs

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Mohammad Ivan Azis^*

This version is not peer-reviewed

Submitted:

12 April 2023

Posted:

12 April 2023

You are already at the latest version

Alerts

Abstract

In this paper a combined Laplace transform (LT) and boundary element method (BEM) is used to find numerical solutions to problems of anisotropic functionally graded media which are governed by the transient diffusion-convection-reaction equation. First, the variable coefficients governing equation is reduced to a constant coefficients equation. Then, the Laplace-transformed constant coefficients equation is transformed a boundary-only integral equation. Using a BEM, the numerical solutions in the frame of Laplace transform may then be obtained from this integral equation. Then the solutions are inversely transformed numerically using the Stehfest formula. Some problems considered are those of compressible or incompressible flow, and of media which are quadratically, exponentially and trigonometrically graded materials. The results obtained show that the analysis used to transform the variable coefficients equation into the constant coefficients equation is valid, and the mixed LT-BEM is easy to implement for obtaining the numerical solutions. The numerical solutions are verified by showing their accuracy and steady state. For symmetric problems, the symmetry of solutions is also justified. Moreover, the effect of the anisotropy and inhomogeneity of the material on the solutions are also shown, as to suggest that it is important to take the anisotropy and inhomogeneity into account when doing experimental studies.

Keywords:

Subject: Computer Science and Mathematics - Computational Mathematics

1. Introduction

Over the last ten years, functionally graded materials (FGMs) have become a popular research topic, and many studies have been conducted on FGMs for various applications. FGMs are defined by authors as materials that are inhomogeneous and have properties that change spatially in a continuous manner, such as thermal conductivity, hardness, toughness, ductility, and corrosion resistance.

The diffusion convection reaction (DCR) equation has many applications in engineering, medicine, biology, and ecology. Several studies have been conducted to find numerical solutions to the DCR equation. Some of these studies include Fendoglu et al. [1] in 2018, Wang and Ang [2] in 2018, Sheu et al. [3] in 2000, Xu [4] in 2018, and AL-Bayati and Wrobel [5] in 2019, who considered the DCR equation with constant coefficients. Samec and Škerget [6] in 2004, Rocca et al. [7] in 2005, and AL-Bayati and Wrobel [8,9] in 2018 studied the DCR equation with variable velocity. Martinez et al. [10] used nonstandard finite difference schemes based on Green’s function formulations for reaction-diffusion-convection systems in 2013.

This paper is intended to extend the recently published works [11] on the steady DCR equation to the transient DCR equation for anisotropic functionally graded materials of the form

\frac{\partial}{\partial x_{i}} [d_{i j} (x) \frac{\partial c (x, t)}{\partial x_{j}}] - \frac{\partial}{\partial x_{i}} [v_{i} (x) c (x, t)] - k (x) c (x, t) = α (x, t) \frac{\partial c (x, t)}{\partial t}

(1)

The continuously varying coefficients

d_{i j}, v_{i}, k, α

in (1) respectively represent the anisotropic diffusivity, velocity, decay reaction and change rate coefficients of the medium of interest. Therefore equation (1) is relevant for FGMs. Equation (1) provides a wider class of problems since it applies for anisotropic and inhomogeneous media but nonetheless covers the case of isotropic diffusion taking place when

d_{11} = d_{22}, d_{12} = 0

and also the case of homogeneous media which occurs when the coefficients

d_{i j} (x)

v_{i} (x)

k (x)

and

α (x, t)

are constant.

2. The initial boundary value problem

Referred to the Cartesian frame

O x_{1} x_{2}

we will consider initial boundary value problems governed by (1) where

x = (x_{1}, x_{2})

. The coefficient

[d_{i j}]

(i, j = 1, 2)

is a real positive definite symmetrical matrix. Also, in (1) the summation convention for repeated indices applies, so that explicitly (1) can be written as

\begin{matrix} \frac{\partial}{\partial x_{1}} (d_{11} \frac{\partial c}{\partial x_{1}}) + \frac{\partial}{\partial x_{1}} (d_{12} \frac{\partial c}{\partial x_{2}}) + \frac{\partial}{\partial x_{2}} (d_{12} \frac{\partial c}{\partial x_{1}}) + \frac{\partial}{\partial x_{2}} (d_{22} \frac{\partial c}{\partial x_{2}}) \\ - \frac{\partial}{\partial x_{1}} (v_{1} c) - \frac{\partial}{\partial x_{2}} (v_{2} c) - k c = α \frac{\partial c}{\partial t} \end{matrix}

By knowing the coefficients

d_{i j} (x), v_{i} (x), k (x), α (x, t)

we will seek solutions

c (x, t)

and its derivatives to (1) which are valid for time interval

t \geq 0

and in a region

Ω

R^{2}

with boundary

\partial Ω

which consists of a finite number of piecewise smooth curves. On

\partial Ω_{1}

the dependent variable

c (x, t)

is specified, and

P (x, t) = d_{i j} (x) \frac{\partial c (x, t)}{\partial x_{i}} n_{j}

(2)

is specified on

\partial Ω_{2}

where

\partial Ω = \partial Ω_{1} \cup \partial Ω_{2}

and

n = (n_{1}, n_{2})

denotes the outward pointing normal to

\partial Ω

. The initial condition is

c (x, 0) = 0

(3)

3. The boundary integral equation

We restrict the coefficients

d_{i j}, v_{i}, k, α

to be of the form

\begin{matrix} d_{i j} (x) & = & {\hat{d}}_{i j} g (x) \end{matrix}

(4)

\begin{matrix} v_{i} (x) & = & {\hat{v}}_{i} g (x) \end{matrix}

(5)

\begin{matrix} k (x) & = & \hat{k} g (x) \end{matrix}

(6)

\begin{matrix} α (x, t) & = & \hat{α} (t) g (x) \end{matrix}

(7)

where

g (x)

is a differentiable function,

{\hat{d}}_{i j}, {\hat{v}}_{i}, \hat{k}

are constants and

\hat{α} (t)

is a function of time t. Substitution of (4)-(7) into (1) gives

{\hat{d}}_{i j} \frac{\partial}{\partial x_{i}} (g \frac{\partial c}{\partial x_{j}}) - {\hat{v}}_{i} \frac{\partial (g c)}{\partial x_{i}} - \hat{k} g c = \hat{α} g \frac{\partial c}{\partial t}

(8)

Assume

c (x, t) = g^{- 1 / 2} (x) ψ (x, t)

(9)

therefore use of (4) and (9) in (2) gives

P (x, t) = - P_{g} (x) ψ (x, t) + g^{1 / 2} (x) P_{ψ} (x, t)

(10)

where

P_{g} (x) = {\hat{d}}_{i j} \frac{\partial g^{1 / 2} (x)}{\partial x_{j}} n_{i} P_{ψ} (x, t) = {\hat{d}}_{i j} \frac{\partial ψ (x, t)}{\partial x_{j}} n_{i}

Moreover, equation (8) can be written as

{\hat{d}}_{i j} \frac{\partial}{\partial x_{i}} [g \frac{\partial (g^{- 1 / 2} ψ)}{\partial x_{j}}] - {\hat{v}}_{i} \frac{\partial (g^{1 / 2} ψ)}{\partial x_{i}} - \hat{k} g^{1 / 2} ψ = \hat{α} g \frac{\partial (g^{- 1 / 2} ψ)}{\partial t}

{\hat{d}}_{i j} \frac{\partial}{\partial x_{i}} [g (g^{- 1 / 2} \frac{\partial ψ}{\partial x_{j}} + ψ \frac{\partial g^{- 1 / 2}}{\partial x_{j}})] - {\hat{v}}_{i} (g^{1 / 2} \frac{\partial ψ}{\partial x_{i}} + ψ \frac{\partial g^{1 / 2}}{\partial x_{i}}) - \hat{k} g^{1 / 2} ψ = \hat{α} g (g^{- 1 / 2} \frac{\partial ψ}{\partial t})

{\hat{d}}_{i j} \frac{\partial}{\partial x_{i}} (g^{1 / 2} \frac{\partial ψ}{\partial x_{j}} + g ψ \frac{\partial g^{- 1 / 2}}{\partial x_{j}}) - {\hat{v}}_{i} (g^{1 / 2} \frac{\partial ψ}{\partial x_{i}} + ψ \frac{\partial g^{1 / 2}}{\partial x_{i}}) - \hat{k} g^{1 / 2} ψ = \hat{α} g^{1 / 2} \frac{\partial ψ}{\partial t}

Use of the identity

\frac{\partial g^{- 1 / 2}}{\partial x_{i}} = - g^{- 1} \frac{\partial g^{1 / 2}}{\partial x_{i}}

implies

{\hat{d}}_{i j} \frac{\partial}{\partial x_{i}} (g^{1 / 2} \frac{\partial ψ}{\partial x_{j}} - ψ \frac{\partial g^{1 / 2}}{\partial x_{j}}) - {\hat{v}}_{i} (g^{1 / 2} \frac{\partial ψ}{\partial x_{i}} + ψ \frac{\partial g^{1 / 2}}{\partial x_{i}}) - \hat{k} g^{1 / 2} ψ = \hat{α} g^{1 / 2} \frac{\partial ψ}{\partial t}

Rearranging and neglecting some zero terms gives

g^{1 / 2} ({\hat{d}}_{i j} \frac{\partial^{2} ψ}{\partial x_{i} \partial x_{j}} - {\hat{v}}_{i} \frac{\partial ψ}{\partial x_{i}}) - ψ ({\hat{d}}_{i j} \frac{\partial^{2} g^{1 / 2}}{\partial x_{i} \partial x_{j}} + {\hat{v}}_{i} \frac{\partial g^{1 / 2}}{\partial x_{i}}) - \hat{k} g^{1 / 2} ψ = \hat{α} g^{1 / 2} \frac{\partial ψ}{\partial t}

So that if g satisfies

{\hat{d}}_{i j} \frac{\partial^{2} g^{1 / 2}}{\partial x_{i} \partial x_{j}} + {\hat{v}}_{i} \frac{\partial g^{1 / 2}}{\partial x_{i}} - λ g^{1 / 2} = 0

(11)

where

λ

is a constant, then the transformation (9) brings the variable coefficients equation (1) into a constant coefficients equation

{\hat{d}}_{i j} \frac{\partial^{2} ψ}{\partial x_{i} \partial x_{j}} - {\hat{v}}_{i} \frac{\partial ψ}{\partial x_{i}} - (λ + \hat{k}) ψ = \hat{α} \frac{\partial ψ}{\partial t}

(12)

Taking the Laplace transform of (9), (10), (12) and applying the initial condition (3) we obtain

ψ^{*} (x, s) = g^{1 / 2} (x) c^{*} (x, s)

(13)

P_{ψ^{*}} (x, s) = [P^{*} (x, s) + P_{g} (x) ψ^{*} (x, s)] g^{- 1 / 2} (x)

(14)

{\hat{d}}_{i j} \frac{\partial^{2} ψ^{*}}{\partial x_{i} \partial x_{j}} - {\hat{v}}_{i} \frac{\partial ψ^{*}}{\partial x_{i}} - (λ + \hat{k} + s {\hat{α}}^{*}) ψ^{*} = 0

(15)

By using Gauss divergence theorem, equation (15) can be transformed into a boundary integral equation

\begin{matrix} η (ζ) ψ^{*} (ζ, s) & = & \int_{\partial Ω} \{P_{ψ^{*}} (x, s) Φ (x, ζ) - [P (x) Φ (x, ζ) \\ + Γ (x, ζ)] ψ^{*} (x, s)\} d S (x) \end{matrix}

(16)

where

P_{v} (x) = {\hat{v}}_{i} n_{i} (x)

For 2-D problems the fundamental solutions

Φ (x, ζ)

and

Γ (x, ζ)

for are given as

\begin{matrix} Φ (x, ζ) & = & \frac{ρ_{i}}{2 π D} exp (- \frac{\dot{v} \dot{R}}{2 D}) K_{0} (\dot{μ} \dot{R}) \\ Γ (x, ζ) & = & {\hat{d}}_{i j} \frac{\partial Φ (x, ζ)}{\partial x_{j}} n_{i} \end{matrix}

where

\begin{matrix} \dot{μ} & = & \sqrt{{(\dot{v} / 2 D)}^{2} + [(λ + \hat{k} + s {\hat{α}}^{*}) / D]} \\ D & = & [{\hat{d}}_{11} + 2 {\hat{d}}_{12} ρ_{r} + {\hat{d}}_{22} (ρ_{r}^{2} + ρ_{i}^{2})] / 2 \\ \dot{R} & = & \dot{x} - \dot{ζ} \\ \dot{x} & = & (x_{1} + ρ_{r} x_{2}, ρ_{i} x_{2}) \\ \dot{ζ} & = & (ζ_{1} + ρ_{r} ζ_{2}, ρ_{i} ζ_{2}) \\ \dot{v} & = & ({\hat{v}}_{1} + ρ_{r} {\hat{v}}_{2}, ρ_{i} {\hat{v}}_{2}) \\ \dot{R} & = & \sqrt{{(x_{1} + ρ_{r} x_{2} - ζ_{1} - ρ_{r} ζ_{2})}^{2} + {(ρ_{i} x_{2} - ρ_{i} ζ_{2})}^{2}} \\ \dot{v} & = & \sqrt{{({\hat{v}}_{1} + ρ_{r} {\hat{v}}_{2})}^{2} + {(ρ_{i} {\hat{v}}_{2})}^{2}} \end{matrix}

where

ρ_{r}

and

ρ_{i}

are respectively the real and the positive imaginary parts of the complex root

ρ

of the quadratic equation

{\hat{d}}_{11} + 2 {\hat{d}}_{12} ρ + {\hat{d}}_{22} ρ^{2} = 0

and

K_{0}

is the modified Bessel function. Use of (13) and (14) in (16) yields

η g^{1 / 2} c^{*} = \int_{\partial Ω} \{(g^{- 1 / 2} Φ) P^{*} + [(P_{g} - P_{v} g^{1 / 2}) Φ - g^{1 / 2} Γ] c^{*}\} d S

(17)

Equation (17) provides a boundary integral equation for determining the numerical solutions of

c^{*}

and its derivatives at all points of

Ω

. The derivative solutions

\partial c^{*} / \partial ξ_{1}

and

\partial c^{*} / \partial ξ_{2}

can be determined using the following equations

\begin{matrix} \frac{\partial c^{*}}{\partial ζ_{1}} & = & g^{- 1 / 2} [\int_{\partial Ω} \{(g^{- 1 / 2} \frac{\partial Φ}{\partial ζ_{1}}) P^{*} + [(P_{g} - P_{v} g^{1 / 2}) \frac{\partial Φ}{\partial ζ_{1}} - g^{1 / 2} \frac{\partial Γ}{\partial ζ_{1}}] c^{*}\} d S - c^{*} \frac{\partial g^{1 / 2}}{\partial ζ_{1}}] \\ \frac{\partial c^{*}}{\partial ζ_{2}} & = & g^{- 1 / 2} [\int_{\partial Ω} \{(g^{- 1 / 2} \frac{\partial Φ}{\partial ζ_{2}}) P^{*} + [(P_{g} - P_{v} g^{1 / 2}) \frac{\partial Φ}{\partial ζ_{2}} - g^{1 / 2} \frac{\partial Γ}{\partial ζ_{2}}] c^{*}\} d S - c^{*} \frac{\partial g^{1 / 2}}{\partial ζ_{2}}] \end{matrix}

Knowing the solutions

c^{*} (x, s)

and its derivatives

\partial c^{*} / \partial x_{1}

and

\partial c^{*} / \partial x_{2}

from (17), the numerical Laplace transform inversion technique using the Stehfest formula is then employed to find the values of

c (x, t)

and its derivatives

\partial c / \partial x_{1}

and

\partial c / \partial x_{2}

. The Stehfest formula is

\begin{matrix} c (x, t) & ≃ & \frac{ln 2}{t} \sum_{m = 1}^{N} V_{m} c^{*} (x, s_{m}) \\ \frac{\partial c (x, t)}{\partial x_{1}} & ≃ & \frac{ln 2}{t} \sum_{m = 1}^{N} V_{m} \frac{\partial c^{*} (x, s_{m})}{\partial x_{1}} \\ \frac{\partial c (x, t)}{\partial x_{2}} & ≃ & \frac{ln 2}{t} \sum_{m = 1}^{N} V_{m} \frac{\partial c^{*} (x, s_{m})}{\partial x_{2}} \end{matrix}

(18)

where

\begin{matrix} s_{m} & = & \frac{ln 2}{t} m \\ V_{m} & = & {(- 1)}^{\frac{N}{2} + m} \sum_{k = [\frac{m + 1}{2}]}^{min (m, \frac{N}{2})} \frac{k^{N / 2} (2 k)!}{(\frac{N}{2} - k)! k! (k - 1)! (m - k)! (2 k - m)!} \end{matrix}

Possible multi-parameter solutions

g^{1 / 2} (x)

to (11) are

\begin{matrix} g^{1 / 2} (x) & = & \begin{matrix} \{\begin{matrix} constant, λ = 0 \\ exp (β_{0} + β_{i} x_{i}), {\hat{d}}_{i j} β_{i} β_{j} + {\hat{v}}_{i} β_{i} - λ = 0 \end{matrix} \end{matrix} \end{matrix}

(19)

If the flow is incompressible, that is the divergence of the velocity is zero, then

\frac{\partial v_{i} (x)}{\partial x_{i}} = 0

Therefore the governing equation (1) reduces to

\frac{\partial}{\partial x_{i}} [d_{i j} (x) \frac{\partial c (x, t)}{\partial x_{j}}] - v_{i} (x) \frac{\partial c (x, t)}{\partial x_{i}} - k (x) c (x, t) = α (x) \frac{\partial c (x, t)}{\partial t}

Also, from (5) we obtain

\frac{\partial v_{i} (x)}{\partial x_{i}} = 2 g^{1 / 2} (x) {\hat{v}}_{i} \frac{\partial g^{1 / 2} (x)}{\partial x_{i}} = 0

so that

{\hat{v}}_{i} \frac{\partial g^{1 / 2} (x)}{\partial x_{i}} = 0

Therefore equation (11) reduces to

{\hat{d}}_{i j} \frac{\partial^{2} g^{1 / 2}}{\partial x_{i} \partial x_{j}} - λ g^{1 / 2} = 0

(20)

Thus, for incompressible flow, possible multi-parameter functions

g^{1 / 2} (x)

satisfying (20) are

\begin{matrix} g^{1 / 2} (x) & = & \begin{matrix} \{\begin{matrix} β_{0} + β_{i} x_{i}, λ = 0 \\ cos (β_{0} + β_{i} x_{i}) + sin (β_{0} + β_{i} x_{i}), {\hat{d}}_{i j} β_{i} β_{j} + λ = 0 \\ exp (β_{0} + β_{i} x_{i}), {\hat{d}}_{i j} β_{i} β_{j} - λ = 0 \end{matrix} \end{matrix} \end{matrix}

(21)

4. Numerical examples

We will examine multiple analytical and non-analytical test problems to demonstrate the accuracy and effectiveness of the mixed Laplace transform and boundary element method used in deriving the boundary integral equation (17). We will also analyze the efficiency, accuracy, and consistency of the combined LT-BEM method.

We assume each problem belongs to a system which is valid in given spatial and time domains and governed by equation (1). The system also is assumed to satisfy the initial condition (3) and some boundary conditions as mentioned in Section 2. The characteristics of the system which are represented by the coefficients

d_{i j} (x), v_{i} (x), k (x), α (x, t)

in equation (1) are assumed to be of the form (4), (5), (6) and (7). They represents respectively the diffusivity or conductivity, the velocity of flow existing in the system, the reaction coefficient and the change rate of the unknown or dependent variable

c (x, t)

Standard BEM with constant elements is employed to obtain numerical results. For a simplicity, a unit square depicted in Figure 1 and Figure 11 will be taken as the geometrical domain for all problems. A number of 320 elements of equal length, namely 80 elements on each side of the unit square, are used.

A FORTRAN script is developed to compute the numerical solutions. A subroutine that evaluates the values of the coefficients

V_{m}, m = 1, 2, \dots, N

of the Stehfest formula in (18) for any number N is embedded in the script. Table 1 shows the values of

V_{m}

for

N = 6, 8, 10, 12

resulted from the subroutine.

4.1. A test problem

The problems will consider three types of inhomogeneity functions

g (x)

, namely exponential function of the form (19) with compressible flow, and quadratic and trigonometric functions of the form (21) with incompressible flow. For all test problems we take coefficients

{\hat{d}}_{i j}

and

\hat{k}

{\hat{d}}_{i j} = [\begin{matrix} 1 & 0.35 \\ 0.35 & 0.25 \end{matrix}] \hat{k} = 0.5

and a set of boundary conditions (see Figure 1)

P is given on side AB, BC, CD

c is given on side AD

For each problem, numerical solutions c and the derivatives

\partial c / \partial x_{1}

and

\partial c / \partial x_{2}

are sought at

19 \times 19

interior points

(x_{1}, x_{2}) = \{. 05, . 1, . 15, \dots, . 9, . 95\} \times \{. 05, . 1, . 15, \dots, . 9, . 95\}

and 9 time-steps

t = . 0004, \frac{π}{8}, \frac{π}{4}, \frac{3 π}{8}, \frac{π}{2}, \frac{5 π}{8}, \frac{3 π}{4}, \frac{7 π}{8}, π

. The value

t = . 0004

is the approximating value of

t = 0

as the singularity of the Stehfest formula. The individual relative error

E_{I}

at each interior point and the aggregate relative error

E_{A}

of the numerical solutions are computed using the formulas

\begin{matrix} E_{I} & = & |\frac{c_{n, i} - c_{a, i}}{c_{a, i}}| \\ E_{A} & = & {[\frac{\sum_{i = 1}^{19 \times 19} {(c_{n, i} - c_{a, i})}^{2}}{\sum_{i = 1}^{19 \times 19} c_{a, i}^{2}}]}^{\frac{1}{2}} \end{matrix}

where

c_{n}

and

c_{a}

are the numerical and analytical solutions c or the derivatives respectively.

4.1.1. Case 1

First, we suppose that the function

g (x)

is an exponential function

g^{1 / 2} (x) = exp (1 + 0.15 x_{1} - 0.25 x_{2})

that is, the material under consideration is an exponentially graded material. We choose

\begin{matrix} {\hat{v}}_{i} & = & (1, 1) \\ \hat{α} (t) & = & 0.192625 t \end{matrix}

so that the system has a compressible flow. In order for

g (x)

to satisfy (19) then

λ = - 0.088125

. The analytical solution

c (x, t)

for this problem is

c (x, t) = \frac{t exp [- (0.2 x_{1} + 0.3 x_{2})]}{exp (1 + 0.15 x_{1} - 0.25 x_{2})} .

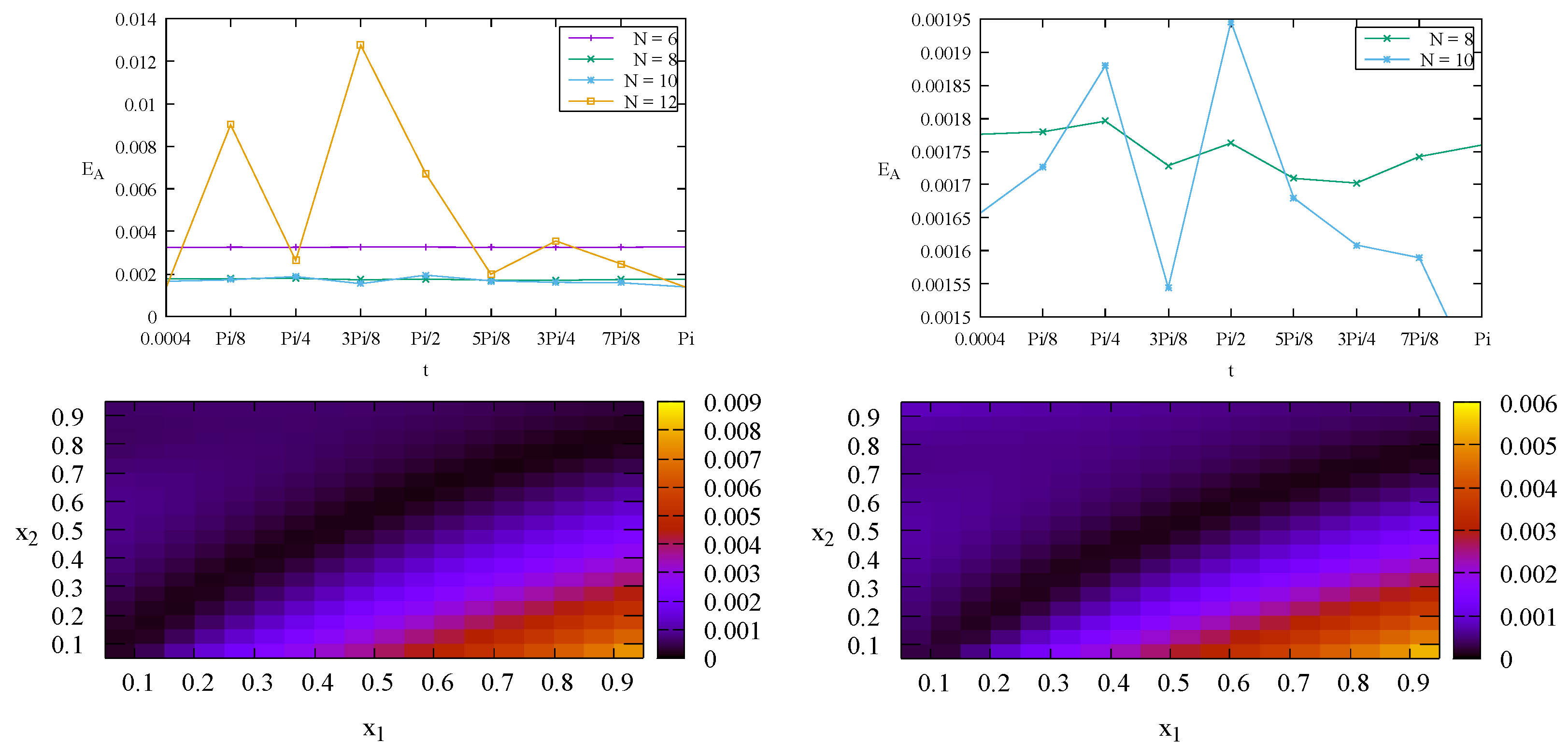
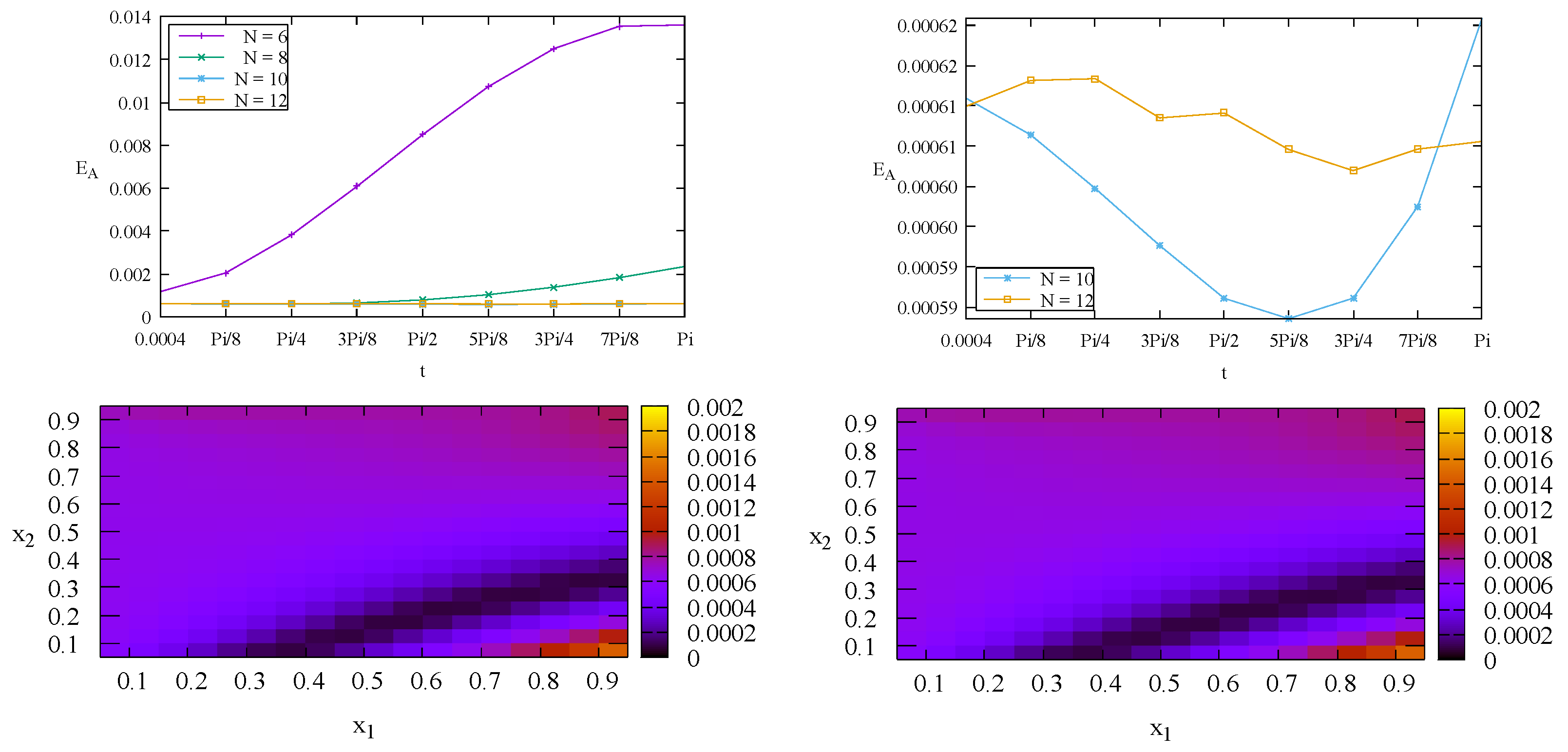
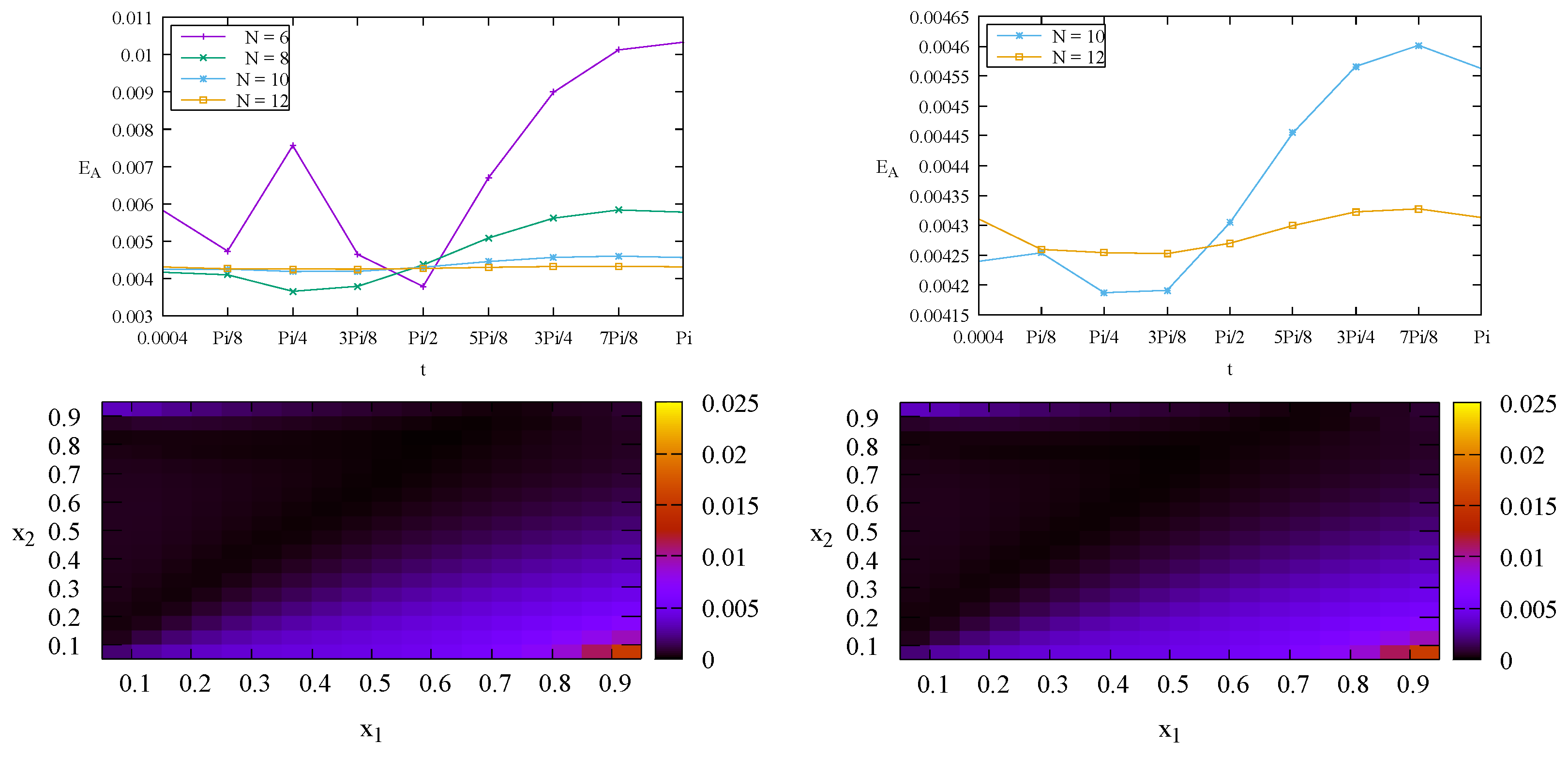
Figure 2 (top row) shows the aggregate relative errors

E_{A}

of the numerical solutions c obtained using

N = 6, 8, 10, 12

for the Stehfest formula (18). It indicates convergence of the Stehfest formula when the value of N changes from

N = 6

N = 10

. For this specific case (Case 1) the value of N is optimized at

N = 10

. Increasing N to

N = 12

does not give more accurate solutions. According to Hassanzadeh and Pooladi-Darvish [12] increasing N will increase the accuracy up to a point, and then the accuracy will decline due to round-off errors. Bottom row of Figure 2 depicts individual relative errors

E_{I}

for the

19 \times 19

interior points at time

t = π / 2

(left) and

t = π

(right) with

N = 10

as the optimized value of N. It indicates that the errors

E_{I}

decreases as t changes from

t = π / 2

t = π

. This result agrees with the result of the aggregate relative error

E_{A}

in the top row of Figure 2.

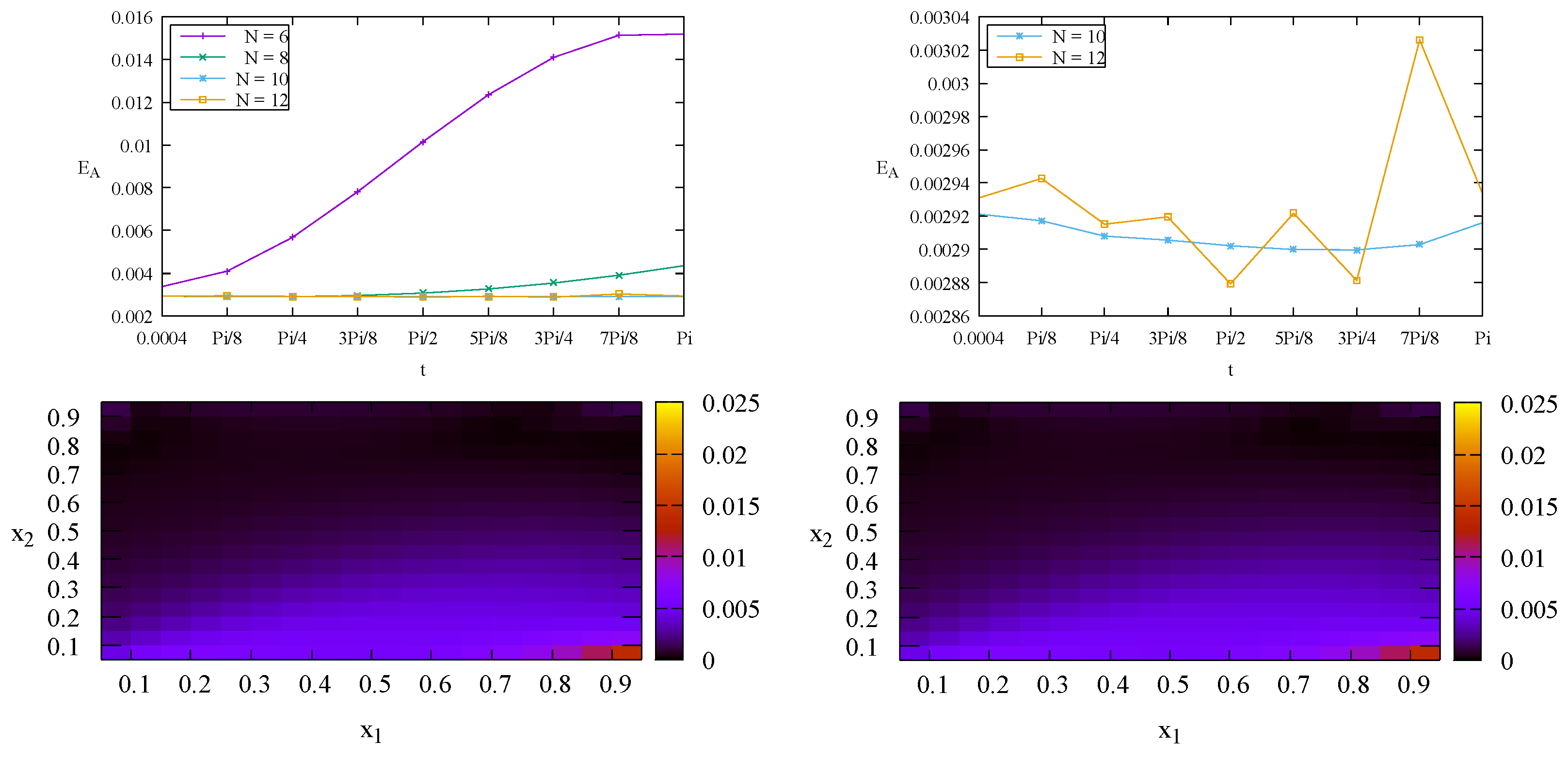
For the derivative solution

\partial c / \partial x_{1}

, Figure 3 (top row) shows that

N = 6

is the optimized value of N for the aggregate relative errors

E_{A}

. Bottom row of Figure 3 depicts individual relative errors

E_{I}

with

N = 6

. It indicates that the errors

E_{I}

stay steady as t changes from

t = π / 2

t = π

. This result agrees with the result of the aggregate relative error

E_{A}

in the top row of Figure 3.

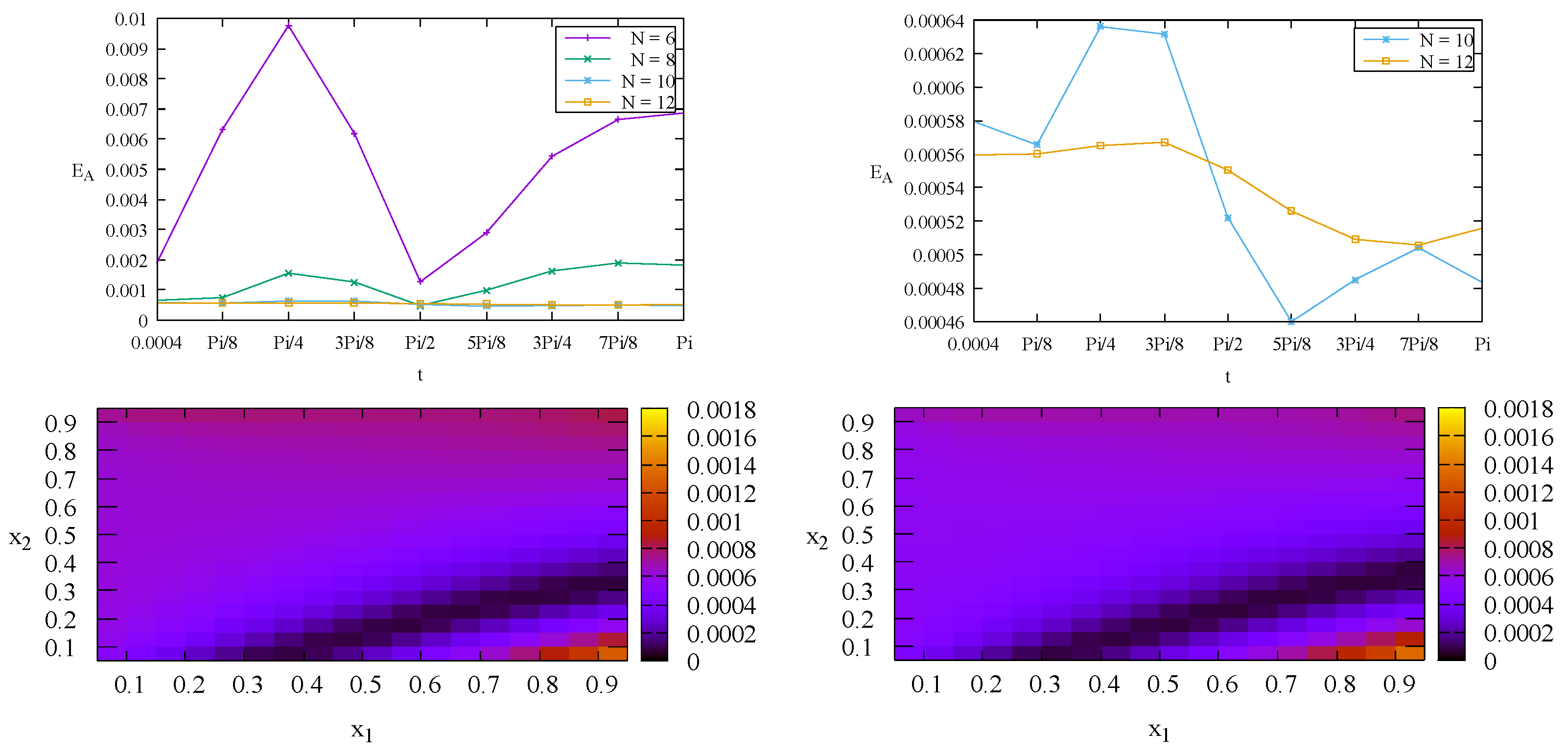
Whereas for the derivative solution

\partial c / \partial x_{2}

, Figure 4 (top row) shows that

N = 10

is the optimized value of N for the aggregate relative errors

E_{A}

. Bottom row of Figure 4 depicts individual relative errors

E_{I}

with

N = 10

4.1.2. Case 2

Next, we choose an analytical solution

c (x, t) = \frac{exp [- (0.2 x_{1} + 0.3 x_{2})]}{1 + 0.15 x_{1} - 0.25 x_{2}} sin \sqrt{t}

Suppose the function

g (x)

and the coefficients are

\begin{matrix} g^{1 / 2} (x) & = & 1 + 0.15 x_{1} - 0.25 x_{2} \\ {\hat{v}}_{i} & = & (1, 0.6) \\ \hat{α} (t) & = & - 0.031 \sqrt{t} tan (\sqrt{t}) \end{matrix}

Therefore the considered system involves a quadratically graded material with an incompressible flow. From (21) we have the parameter

λ = 0

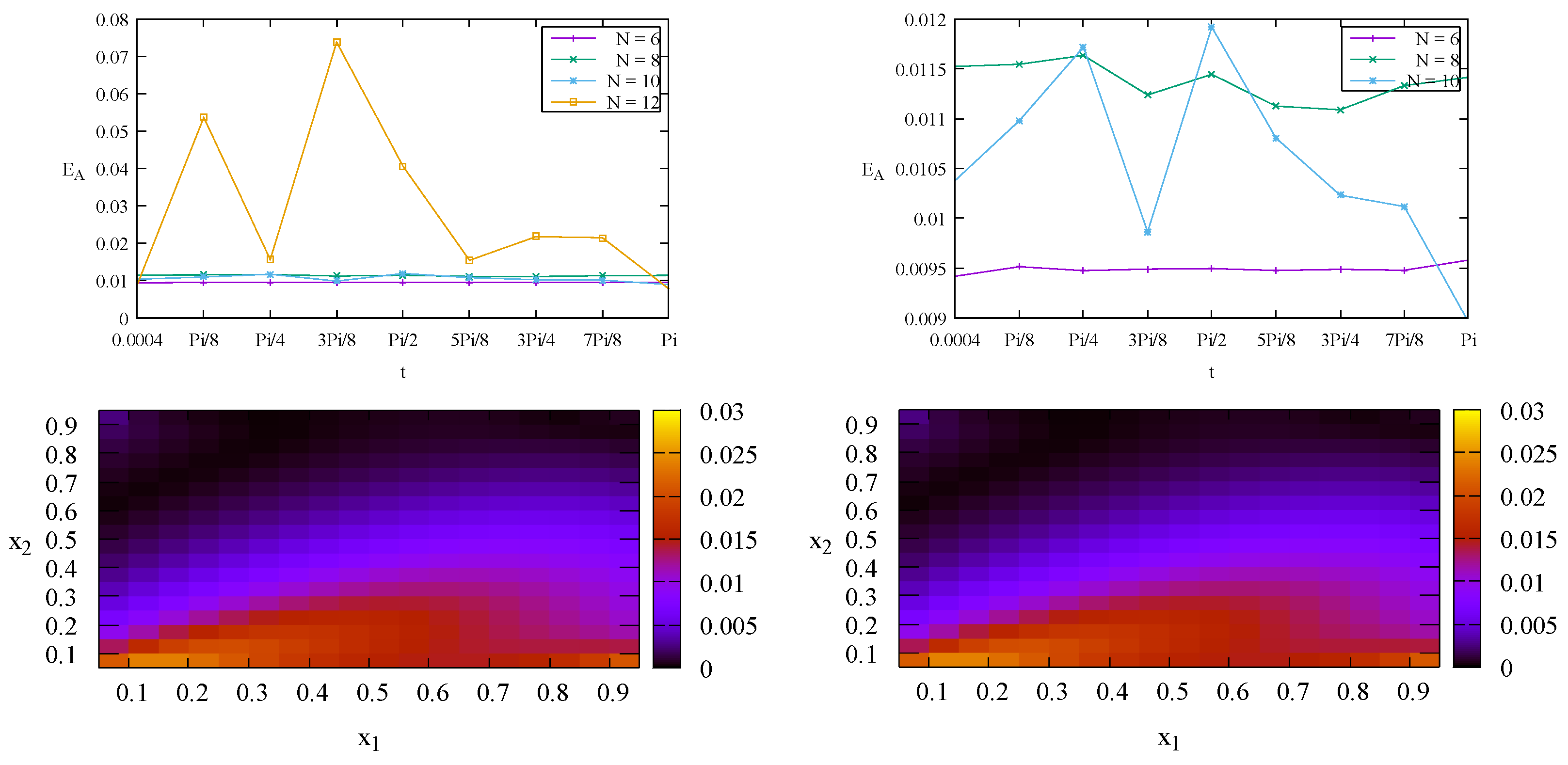
Figure 5 (top row) indicates that

N = 10

is the optimized value of N for the aggregate relative errors

E_{A}

of the numerical solutions c. Increasing N to

N = 12

gives worse solutions. Bottom row of Figure 5 depicts individual relative errors

E_{I}

with

N = 10

N = 10

is also the optimized value of N for the aggregate relative errors

E_{A}

of the numerical solutions

\partial c / \partial x_{1}

. This results is shown in Figure 6 (top row). Bottom row of Figure 6 depicts individual relative errors

E_{I}

with

N = 10

Whereas for the derivative solution

\partial c / \partial x_{2}

, Figure 7 (top row) shows that

N = 6

is the optimized value of N for the aggregate relative errors

E_{A}

. Bottom row of Figure 7 depicts individual relative errors

E_{I}

with

N = 6

4.1.3. Case 3

Now, we consider a trigonometrically graded material with a grading function

g^{1 / 2} (x) = cos (1 + 0.15 x_{1} - 0.25 x_{2})

We choose

{\hat{v}}_{i} = (1, 0.6), \hat{α} (t) = 0.003625 [1 - exp (t)]

so that the system has an incompressible flow. From (21) we have

λ = - 0.011875

. The analytical solution

c (x, t)

for this problem is

c (x, t) = \frac{exp [- (0.2 x_{1} + 0.3 x_{2})] [1 - exp (- t)]}{cos (1 + 0.15 x_{1} - 0.25 x_{2})}

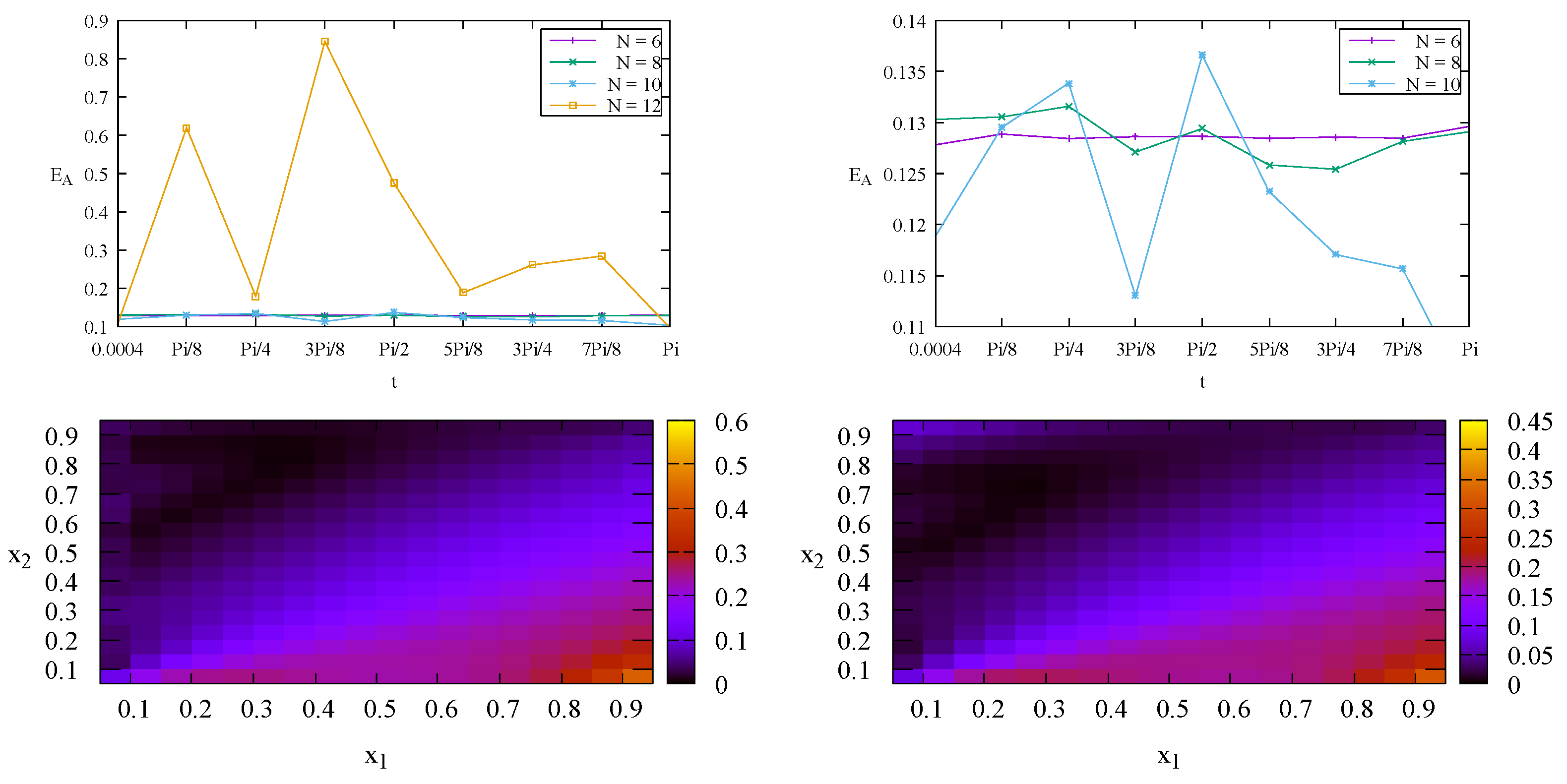
Based on the results in Figure 8, Figure 9 and Figure 10 (top rows) we assume that

N = 12

is the optimized value for the aggregate relative errors

E_{A}

of the solutions c and the derivatives

\partial c / \partial x_{1}

and

\partial c / \partial x_{2}

. The corresponding individual relative errors

E_{I}

are shown at the bottom row of each figure.

4.2. A problem without analytical solution

Further, we will show that the anisotropy and inhomogeneity of materials give impacts on the solutions. We will use

{\hat{d}}_{i j}, {\hat{v}}_{i}, \hat{k}, g^{1 / 2} (x)

in Case 3 of Problem Section 4.1 for this problem, which are

\begin{matrix} {\hat{d}}_{i j} & = & [\begin{matrix} 1 & 0.35 \\ 0.35 & 0.25 \end{matrix}] \\ {\hat{v}}_{i} & = & (1, 0.6) \\ \hat{k} & = & 0.5 \\ g^{1 / 2} (x) & = & cos (1 + 0.15 x_{1} - 0.25 x_{2}) \end{matrix}

We choose

\hat{α} (t) = 1

As we aim to show the impacts of the anisotropy and inhomogeneity of the material, we need to consider the case of homogeneous material and the case of isotropic material. We assume when the material is homogeneous then

g^{1 / 2} (x) = 1

and for an isotropic material is under consideration then

{\hat{d}}_{i j} = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}]

The boundary conditions are (see Figure 11)

P = 0

on side AB

c = 0

on side BC

P = 0

on side CD

P = P (t)

on side AD

where

P (t)

is associated with four cases, namely

Case 1:	$P (t) = 1$
Case 2:	$P (t) = exp (- t)$
Case 3:	$P (t) = t$
Case 4:	$P (t) = t / (t + 0.01)$

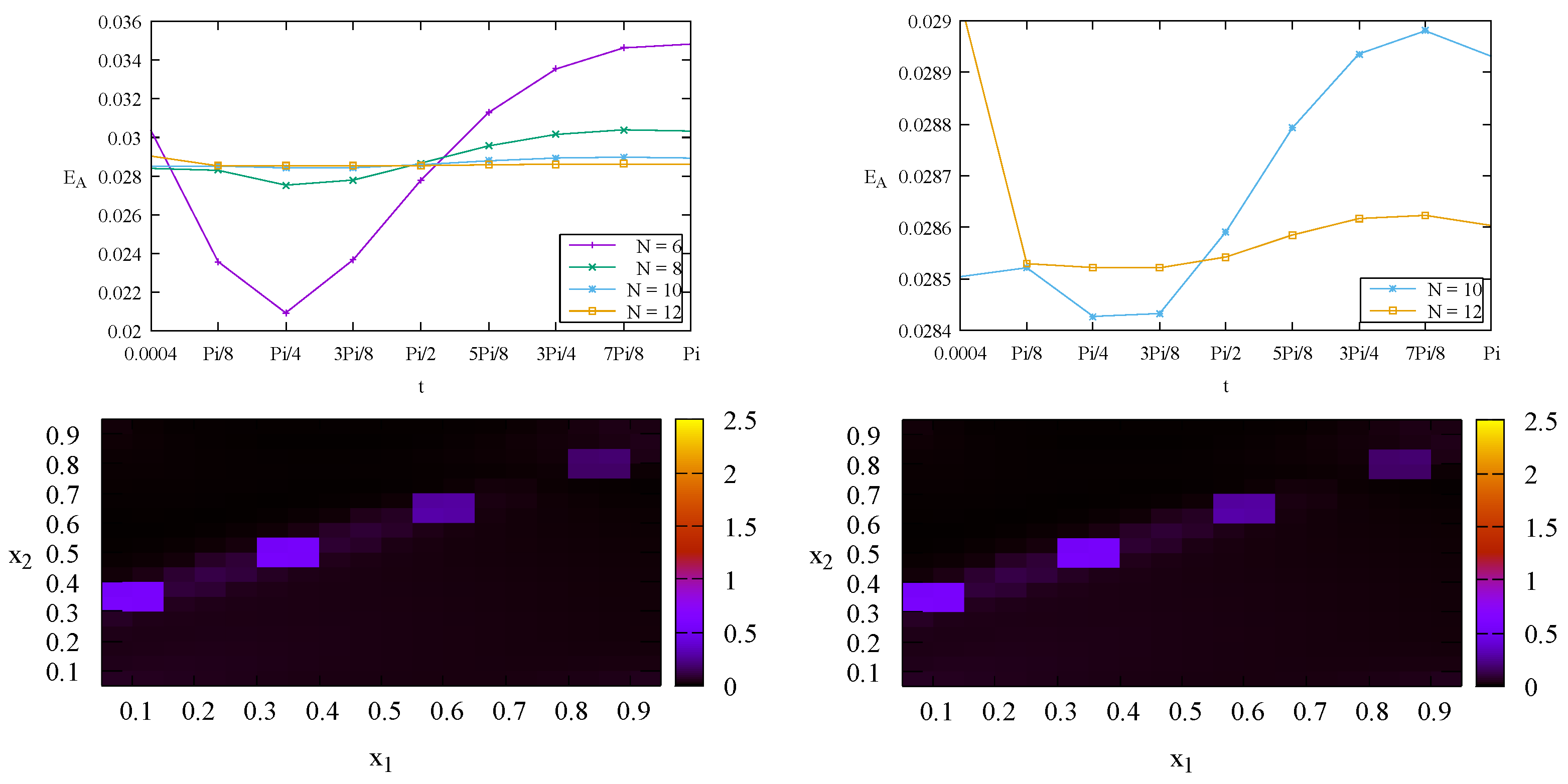
Figure 12 shows for all cases when the material is isotropic and homogeneous the solutions

c (0.5, 0.3, t)

and

c (0.5, 0.7, t)

coincide. This is to be expected as the problem is geometically symmetric at

x_{2} = 0.5

when the material is isotropic and homogeneous. The results in Figure 12 also indicate that the anisotropy and inhomogeneity of the material give effects on the solutions. Moreover, as also expected, the variation of the solution with respect to t mimics the time function

P (t)

as the boundary condition on side AD.

Whereas, the results in Figure 13 show that the Case 1 of

P (t) = 1

and Case 4 of

P (t) = t / (t + 0.01)

have the same steady state solution. This is to be expected as

P (t) = t / (t + 0.01)

will converge to 1 when t approaches infinity.

5. Conclusion

Several problems for a class of anisotropic FGMs (quadratically, exponentially and trigonometrically graded materials) have been solved using a combined BEM and Laplace transform. From the results of the considered problems in Section 4.1 and Section 4.2, we may conclude that the analysis of reduction to constant coefficients equation (in Section 3) for deriving the boundary-only integral equation (17) is valid, and the BEM and Stehfest formula is appropriate for solving such problems as defined in Section 2. Moreover, the results of the test problem in Section 4.1 show the accuracy of the method, whereas the results of the problem in Section 4.2 exhibit the consistency of the numerical solutions. The effect of the inhomogeneity and anisotropy of materials as well as the obtained steady-state solutions are as expected.

Funding

The APC was funded by Hasanuddin University, Makassar, Indonesia.

Data Availability Statement

The data that supports the findings of this study are available within the article.

Acknowledgments

This work is supported by Hasanuddin University and Ministry of Education, Culture, Research, and Technology of Indonesia.

Conflicts of Interest

The author declares that there is no conflicts of interest for publishing the manuscript.

Abbreviations

The following abbreviations are used in this manuscript:

FGM	Functionally Graded Material
BEM	Boundary Element Method
LT	Laplace Transform
DCR	Diffusion Convection Reaction

References

Fendoglu, H.; Bozkaya, C.; Tezer-Sezgin, M. DBEM and DRBEM solutions to 2D transient convection-diffusion-reaction type equations. Eng. Anal. Boundary Elem. 2018, 93, 124–134. [Google Scholar] [CrossRef]
Wang, X.; Ang W-T. A complex variable boundary element method for solving a steady-state advection–diffusion–reaction equation. Appl. Math. Comput. 2018, 321, 731–744. [Google Scholar] [CrossRef]
Sheu, T.W.H.; Wang, S.K.; Lin, R.K. An Implicit Scheme for Solving the Convection–Diffusion–Reaction Equation in Two Dimensions. J. Comput. Phys. 2000, 164, 123–142. [Google Scholar] [CrossRef]
Xu, M. A modified finite volume method for convection-diffusion-reaction problems. Int. J. Heat Mass Transfer 2018, 117, 658–668. [Google Scholar] [CrossRef]
AL-Bayati, S.A.; Wrobel, L.C. Radial integration boundary element method for two-dimensional non-homogeneous convection–diffusion–reaction problems with variable source term. Eng. Anal. Boundary Elem. 2019, 101, 89–101. [Google Scholar] [CrossRef]
Samec, N.; Škerget, L. Integral formulation of a diffusive–convective transport equation for reacting flows. Eng. Anal. Boundary Elem. 2004, 28, 1055–1060. [Google Scholar] [CrossRef]
Rocca, A.L.; Rosales, A.H.; Power, H. Radial basis function Hermite collocation approach for the solution of time dependent convection–diffusion problems. Eng. Anal. Boundary Elem. 2005, 29, 359–370. [Google Scholar] [CrossRef]
AL-Bayati, S.A.; Wrobel, L.C. The dual reciprocity boundary element formulation for convection-diffusion-reaction problems with variable velocity field using different radial basis functions. Int. J. Mech. Sci. 2018, 145, 367–377. [Google Scholar] [CrossRef]
AL-Bayati, S.A.; Wrobel, L.C. A novel dual reciprocity boundary element formulation for two-dimensional transient convection–diffusion–reaction problems with variable velocity. Eng. Anal. Boundary Elem. 2018, 94, 60–68. [Google Scholar] [CrossRef]
Hernandez-Martinez, E.; Puebla, H.; Valdes-Parada, F.; Alvarez-Ramirez, J. Nonstandard finite difference schemes based on Green’s function formulations for reaction–diffusion–convection systems. Chem. Eng. Sci. 2013, 94, 245–255. [Google Scholar] [CrossRef]
Azis, M.I. Standard-BEM solutions to two types of anisotropic-diffusion convection reaction equations with variable coefficients. Eng. Anal. Boundary Elem. 2019, 105, 87–93. [Google Scholar] [CrossRef]
Hassanzadeh, H.; Pooladi-Darvish, M. Comparison of different numerical Laplace inversion methods for engineering applications. Appl. Math. Comput. 2007, 189, 1966–1981. [Google Scholar] [CrossRef]

Figure 1. The boundary conditions for Problem 4.1

Figure 2. Top: The aggregate relative error

E_{A}

of the numerical solutions c with

N = 6, 8, 10, 12

for Case 1 (left) and zoom-in view for

N = 8, 10

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 10

Figure 2. Top: The aggregate relative error

E_{A}

of the numerical solutions c with

N = 6, 8, 10, 12

for Case 1 (left) and zoom-in view for

N = 8, 10

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 10

Figure 3. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{1}

with

N = 6, 8, 10, 12

for Case 1 (left) and zoom-in view for

N = 6, 8, 10

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 6

Figure 3. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{1}

with

N = 6, 8, 10, 12

for Case 1 (left) and zoom-in view for

N = 6, 8, 10

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 6

Figure 4. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{2}

with

N = 6, 8, 10, 12

for Case 1 (left) and zoom-in view for

N = 6, 8, 10

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 10

Figure 4. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{2}

with

N = 6, 8, 10, 12

for Case 1 (left) and zoom-in view for

N = 6, 8, 10

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 10

Figure 5. Top: The aggregate relative error

E_{A}

of the numerical solutions c with

N = 6, 8, 10, 12

for Case 2 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 10

Figure 5. Top: The aggregate relative error

E_{A}

of the numerical solutions c with

N = 6, 8, 10, 12

for Case 2 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 10

Figure 6. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{1}

with

N = 6, 8, 10, 12

for Case 2 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 10

Figure 6. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{1}

with

N = 6, 8, 10, 12

for Case 2 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 10

Figure 7. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{2}

with

N = 6, 8, 10, 12

for Case 2. Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 6

Figure 7. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{2}

with

N = 6, 8, 10, 12

for Case 2. Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 6

Figure 8. Top: The aggregate relative error

E_{A}

of the numerical solutions c with

N = 6, 8, 10, 12

for Case 3 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 12

Figure 8. Top: The aggregate relative error

E_{A}

of the numerical solutions c with

N = 6, 8, 10, 12

for Case 3 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 12

Figure 9. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{1}

with

N = 6, 8, 10, 12

for Case 3 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 12

Figure 9. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{1}

with

N = 6, 8, 10, 12

for Case 3 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 12

Figure 10. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{2}

with

N = 6, 8, 10, 12

for Case 3 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 12

Figure 10. Top: The aggregate relative error

E_{A}

of the numerical solutions

\partial c / \partial x_{2}

with

N = 6, 8, 10, 12

for Case 3 (left) and zoom-in view for

N = 10, 12

(right). Bottom: The individual relative errors

E_{I}

t = π / 2

(left) and

t = π

(right) with

N = 12

Figure 11. The boundary conditions for Problem 4.2.

Figure 12. Solutions

c (0.5, 0.3, t)

and

c (0.5, 0.7, t)

for all cases of Problem Section 4.2

Figure 12. Solutions

c (0.5, 0.3, t)

and

c (0.5, 0.7, t)

for all cases of Problem Section 4.2

Figure 13. Solutions

c (0.5, 0.5, t)

for Case 1 and 4 of Problem Section 4.2

Figure 13. Solutions

c (0.5, 0.5, t)

for Case 1 and 4 of Problem Section 4.2

Table 1. Values of

V_{m}

of the Stehfest formula for

N = 6, 8, 10, 12

Table 1. Values of

V_{m}

of the Stehfest formula for

N = 6, 8, 10, 12

$V_{m}$	$N = 6$	$N = 8$	$N = 10$	$N = 12$
$V_{1}$	1	$- 1 / 3$	$1 / 12$	$- 1 / 60$
$V_{2}$	$- 49$	$145 / 3$	$- 385 / 12$	$961 / 60$
$V_{3}$	366	$- 906$	1279	$- 1247$
$V_{4}$	$- 858$	$16394 / 3$	$- 46871 / 3$	$82663 / 3$
$V_{5}$	810	$- 43130 / 3$	$505465 / 6$	$- 1579685 / 6$
$V_{6}$	$- 270$	18730	$- 236957.5$	$1324138.7$
$V_{7}$		$- 35840 / 3$	$1127735 / 3$	$- 58375583 / 15$
$V_{8}$		$8960 / 3$	$- 1020215 / 3$	$21159859 / 3$
$V_{9}$			$164062.5$	$- 8005336.5$
$V_{10}$			$- 32812.5$	$5552830.5$
$V_{11}$				$- 2155507.2$
$V_{12}$				$359251.2$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Numerical Simulation for Transient Diffusion Convection Reaction Problems of a Class of Anisotropic FGMs

Abstract

1. Introduction

2. The initial boundary value problem

3. The boundary integral equation

4. Numerical examples

4.1. A test problem

4.1.1. Case 1

4.1.2. Case 2

4.1.3. Case 3

4.2. A problem without analytical solution

5. Conclusion

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe