Prerpints.org logo
Preprint
Article

Rapid In Vitro Assessment of Antimicrobial Drug Effect Bridging Clinically Relevant Pharmacokinetics: A Comprehensive Methodology

Altmetrics

Downloads

116

Views

23

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 April 2023

Posted:

13 April 2023

You are already at the latest version

Alerts
Abstract
Rapid in vitro assessment of antimicrobial drug efficacy under clinically relevant pharmacokinetic conditions is an essential element of both drug development and clinical use. Here we present an overview of a novel integrated methodology for rapid assessment of such efficacy, particularly against emergence of resistant bacterial strains, as jointly researched by the authors in recent years. This methodology enables rapid in vitro assessment of antimicrobial efficacy of a single or multiple drugs in combination, following clinically relevant pharmacokinetics. The proposed methodology entails (a) automated collection of longitudinal time-kill data in an optical-density instrument; (b) processing of collected time-kill data with the aid of a mathematical model to de-termine optimal dosing regimens under clinically relevant pharmacokinetics for a single or mul-tiple drugs; and (c) in vitro validation of promising dosing regimens in a hollow fiber system. Proof-of-concept of this methodology through a number of in vitro studies is discussed. Future directions for refinement of optimal data collection and processing are discussed.
Keywords: 
Subject: Medicine and Pharmacology  -   Medicine and Pharmacology

1. Introduction

Rapid assessment of antimicrobial drug efficacy in clinically relevant pharmacokinetic conditions is fundamental for both new drug development and clinical drug use [1]. This need is particularly pressing for resistant strains, as they pose a serious threat for human health [2]. Assessing the effect of drugs on pathogenic bacteria can be typically measured in vitro through exposure of a bacterial population to (one or more) drugs at various time-invariant concentrations over a period of time. The number of live cells in the bacterial population at distinct points in time can be typically assessed by quantitative culture (plating) methods [3]. This widely used as this simple approach is, it provides limited data, as plating can realistically be performed only at a few time points during a corresponding experiment (see [4] and references therein). As a result, simple indicators of drug efficacy against bacterial strains, such as the minimum inhibitory concentration (MIC), area under the curve (AUC), and others, are in widespread use [5,6,7]. Unfortunately such indicators often fail at predicting therapeutic outcomes under realistic pharmacodynamic and pharmacokinetic conditions [1,8], particularly when a bacterial population comprises subpopulations of varying degrees of resistance [9,10,11,12,13]. More detailed pharmacodynamic models could provide a better picture of drug efficacy [14]. However, developing such models from scant measurements based on plating is not practical.
An obvious way to address this issue would be to collect more measurements of bacterial population size at densely spaced time points during drug exposure. Accomplishing this by plating would be practically infeasible, particularly in situations where time or resources are limited yet reliable results are needed quickly, e.g. in a clinical setting. Among a number of in principle feasible options (e.g. quantitative polymerase chain reaction (PCR) [15,16], fluorescence microscopy [17,18], enzyme-linked immunosorbent assay (ELISA) [19], fluorescence-based microplate reader [20,21,22], flow cytometry (FCM) [17,23,24], or fiber-based fluorescence spectroscopy [25]), a long known efficient potential alternative to plating would be to take measurements of sample turbidity (cloudiness) by optical density methods (spectrophotometry) [26,27,28]. While optical density measurements rely on well established principles (of light propagation through a liquid) and can easily provide a virtually continuous real-time stream of data in a modern instrument, they have a serious limitation: they count both live and dead cells of a bacterial population in a suspension, as both kinds of cells block/absorb light, thus affecting the resulting optical signal. As a result, optical density measurements are routinely taken only in studies focusing on growing populations of cells (e.g. to study contamination) and, until recently, have not been applied to shrinking populations, the very focus of time-kill experiments with bacterial populations exposed to drugs.
This limitation was removed in a series of recent publications that are the main focus of this paper. Specifically, we present a synthesis of individual prior results, which collectively constitute a novel integrated methodology that straddles the span from in vitro longitudinal time-kill data (capturing the drug effect on a bacterial population) to the design of therapeutic dosing regimens for drugs following clinically relevant pharmacokinetics. While this methodology is still undergoing refinements, there is already a body of work at a stage mature enough for direct use, hence worth communicating.
In the rest of the paper, we summarize in Materials and Methods the basic elements of the proposed methodology referred to above, and present in Results a selection of basic outcomes presented in literature. Finally, we discuss potential improvements and extensions of this methodology.

2. Materials and Methods

The essence of the methodology referred to lies in the use of data-driven mathematical modeling tools which extract useful information from longitudinal time-kill data collected in an optical density instrument. Implementation of this methodology entails the following elements:
  • Automated collection of longitudinal optical density measurements of several bacterial cell suspensions in an optical density instrument, each suspension exposed to a single or multiple drugs at a time-invariant concentration.
  • Feeding of the data collected in the previous step to a mathematical model, to estimate the kill rate of the least susceptible bacterial population as a function of drug concentration.
  • Use of the drug-concentration-dependent kill rate estimate from the previous step to design dosing regimens predicted to eradicate a bacterial population exposed to a drug following clinically relevant pharmacokinetics.
  • Validation test of promising dosing regimens from the previous step in an in vitro hollow fiber infection model mimicking human pharmacokinetics.
We elaborate on each of the above elements next.

2.1. Longitudinal Optical Density Measurements of Bacterial Cell Suspension under Drug Exposure

In a spectrophotometer, a cell population in suspension is placed in a transparent cuvette and light is shone to it. Because cells impart turbidity (cloudiness) to the suspension as they absorb and scatter light, the intensity of transmitted light is lower than the intensity of the incident light. Comparing the two intensities provides a quantitative assessment of the number of the cells in suspension (optical density). Optical density is roughly proportional to the biomass in the cell suspension in a given range that is specific to the cell type. The simplicity and ability to generate abundant longitudinal data have made spectrophotometry the method of choice for measurements of bacterial growth in related applications. The inherent drawback of spectrophotometry, as already mentioned, is its inability to distinguish between live and dead cells, a limitation of utmost importance in time-kill experiments [29]. Indeed, whereas in bacterial growth experiments live cells quickly far outnumber dead cells, time-kill experiments experience the reverse. In fact, bacterial populations with resistant subpopulations may exhibit interesting behavior, as depicted in Figure 1, adapted from [29]. This figure indicates that for successive multiples of drug concentrations the number of live cells, N live , may qualitatively exhibit pure growth, delayed growth, decline followed by regrowth or delayed regrowth, and finally continued decline Figure 1a. However, what optical density measurements will indicate is a set of curves for the total number of cells (comprising both live and dead cells), N total , that never decline, as shown in Figure 1b.
It is this inherent limitation of optical density instruments that is addressed by the integrated mathematical modeling methodology presented here, as detailed in subsequent sections.
In addition to the above inherent limitation, secondary issues with optical density instruments may arise from multiple difficulties in reliably translating optical density to number of bacterial cells. The following examples are representative of systematic error sources: To extend their dynamic range, many optical density instruments change measurement method from scattering to absorption, based on a threshold value of bacterial concentration, thus possibly introducing calibration errors [30]; Dead cells decompose over time, thus changing the optical signature of the cell suspension and making corresponding adjustments necessary; Concentration of cells in suspension used in the instrument may not be uniform, if mixing is not adequate, thus biasing measurements; A number of antibiotics, such as fluoroquinolones, can induce morphological changes to exposed bacteria (e.g. filaments at concentrations close to the MIC) thus inadvertently changing again the optical signature observed. Nevertheless, results show remarkable robustness of the proposed mathematical modeling method based on optical density data [29,30]. Of course, it is also reasonable to expect that improvements in optical density instruments will help improve the applicability of the proposed method.

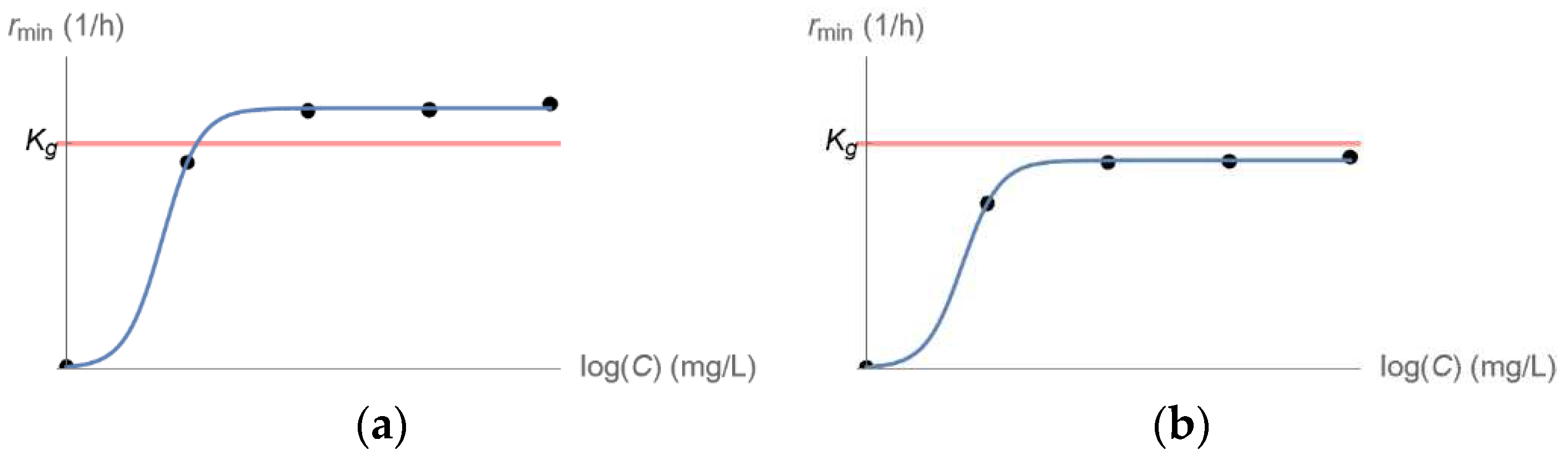
2.2. Kill Rate Estimation of Least Susceptible Bacteria as a Function of Drug Concentration

The study of bacterial population dynamics has a long history [31], with a variety of mathematical models used for corresponding quantitative descriptions [14,32]. At the core of these models is the elementary differential equation d N live / d t = K g N live t or its counterpart for a saturating bacterial population d N live / d t = K g N live t 1 − N live / N max , where K g is the physiological growth rate and N max the upper bound of the growing bacterial population [33]. Exposure to bactericidal drugs adds a killing term r N live to the right-hand side of the preceding equations, where r is the kill rate, dependent on drug concentration C . A typical expression for the kill rate is
r = K C H C H + C 50 H
where H is the Hill exponent of sigmoidicity [9,34,35,36]. For typical time-kill experiments with time-invariant C , solution of the differential equation d N live / d t = K g − r N live t is N live t = N live 0 exp ⁡ K g − r t , which corresponds to a straight line of slope K g − r in a plot of log ⁡ N live t vs. t .
As conceptually useful as such linear plots are, most practical situations of bacterial populations exposed to drugs involve subpopulations of varying susceptibility to the drug(s), corresponding of a distribution of values of r ≥ 0 over a bacterial population at any given drug concentration C [9,10]. The result is curves rather than straight lines for log ⁡ N live t , as depicted for example in Figure 1a. For such cases it was shown [11,12] that the size N live ( t ) of a heterogeneous bacterial population exposed to one or more drugs at time-invariant concentration C is well captured by the equation
ln ⁡ N l i v e t N 0 = K g − r m i n t + λ e − a t − 1 − − ln ⁡ 1 + K g N l i v e 0 N m a x ∫ 0 t exp ⁡ K g − r m i n τ + λ e − a τ − 1 d τ
and the kill rate average and variance over time are well captured by the equations
μ t = r m i n + μ 0 − r m i n exp ⁡ − μ 0 − r m i n λ t = = r m i n + λ a e − a t
σ ( t ) 2 = μ 0 − r m i n 2 λ e x p − μ ( 0 ) − r m i n λ t = = λ a 2 e − a t
where
N l i v e t is the live bacterial population size with initial value N 0 ;
K g is the physiological net growth rate of the entire bacterial population, common for all subpopulations;
r m i n is the kill rate induced by the antibiotic on the most resistant (least susceptible) subpopulation;
N m a x is the maximum size of a bacterial population reaching saturation under growth conditions;
μ t is the kill rate average over the bacterial population at time t ;
σ t 2 is the kill rate variance over the bacterial population at time t ;
λ > 0 , a > 0 are constants associated with the initial decline of the average kill rate of the population, and correspond to the Poisson distributed variable ( r − r m i n ) / a with average and variance equal to λ . Note that no assumptions about the mechanisms that confer bacterial resistance have been made to derive the above Equations (2)–(4).
The parameters K g ,   r m i n ,   λ ,   a ,   N m a x that appear in Equation (2) can be estimated by regression, assuming enough values of N live ( t ) are available. The preceding statement immediately justifies why plating methods for measurement of N live ( t ) are impractical for estimation of K g ,   r m i n ,   λ ,   a ,   N m a x : At least 10-20 data points would be needed for reasonable parameter estimates [9,10].
This limitation, posed by plating-based measurements, is overcome by the optical density-based methods discussed, which can routinely generate measurements every minute or so. However, as already mentioned, there measurements are of N total rather than of N live . To make measurements of N total usable in parameter estimation, the following equation was derived [29]:
N t o t a l t N 0 = e λ e − a t − 1 + K g − r m i n t + + e − λ λ K g − r m i n a K d + r m i n a ∫ λ e − a t λ z − 1 + r m i n − K g a e z d z + ∫ λ e − a t λ z r m i n − K g a e z d z
when N 0 ≪ N max , typical for time-kill experiments. (The full expression for N 0 not far from N max is shown in [29].) In fact, it may be numerically simpler and conceptually insightful to use the following two differential equations (from which Equation (5) is derived for N 0 / N max ≈ 0 ) in parameter estimation based on measurements of N total t :
d N l i v e d t = − K g N l i v e t N m a x + K g − r m i n − λ a e − a t N l i v e t ≈ K g − r m i n − λ a e − a t N l i v e t
d N t o t a l d t = K g 1 − N l i v e t N m a x + K d N l i v e t ≈ K g + K d N l i v e t
where K d is the natural death rate of bacterial cells.
Equations (6) and (7) shed light to the nature of the parameter estimation problem:
First, estimates of K g ,   K d can be obtained from a simple time-growth experiment ( C = 0 ) for which there is no drug-induced kill rate, i.e. r min = 0 and λ = 0 , by default. Then, estimates of N live t are reasonably well obtained from Equation (7), provided that d N total / d t can be estimated with reasonable accuracy. It is for this purpose that optical density-based measurements of N total ( t )  at closely spaced points in time become crucial, as they allow a reasonably accurate estimation of d N total / d t , hence of N live t via Equation (7), and finally of the parameters r m i n , λ ,   a via standard regression using Equation (6).
Of the parameters estimated via the exercise just described, the one critical for dosing regimen design is r min , the kill rate of the least susceptible (most resistant) subpopulation. (Note that in long enough time-kill experiments, Equation (3) immediately suggests that the average kill rate, μ t , quickly tends to r min .) The importance of r min stems from the fact that for complete eradication of a bacterial population exposed to a drug at concentration C it is necessary and sufficient that
r min > K g
i.e. the kill rate of the least susceptible bacterial subpopulation should be greater than the corresponding population growth rate (see Equation (5) and discussion in [29]). The dependence of r min on C is typically considered to follow the form of Equation (1), as shown qualitatively in Figure 2, which depicts qualitatively a fit of Equation (1) to values of r min estimated from time-kill experiments at distinct drug concentrations C . It is noted that counterparts of Equation (1) can be fit to effective concentrations concerning multiple drugs, but this pharmacodynamics issue [37,38,39] is beyond the scope of this paper. The outcome of fitting r min to C is crucial for designing effective dosing regimens under clinically relevant pharmacokinetics, as will be discussed in the next section.

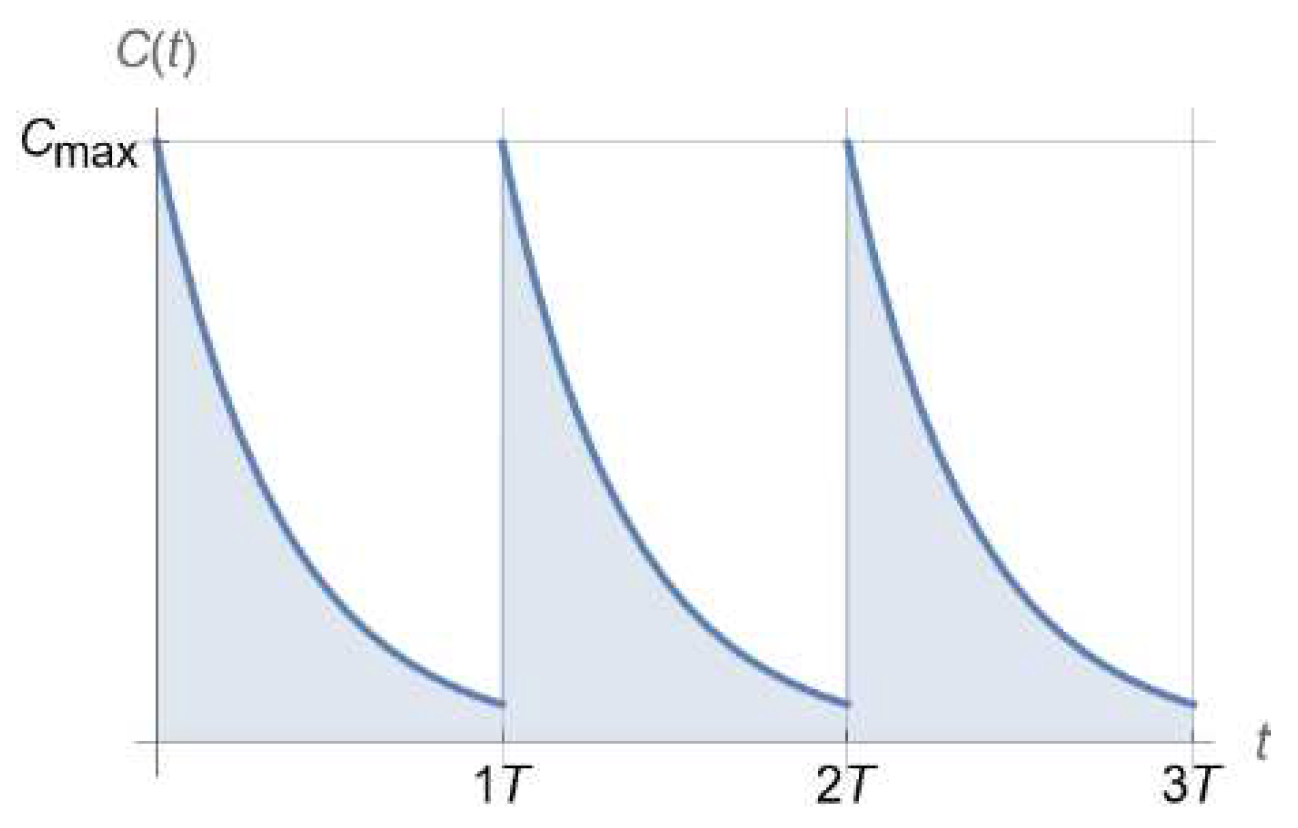
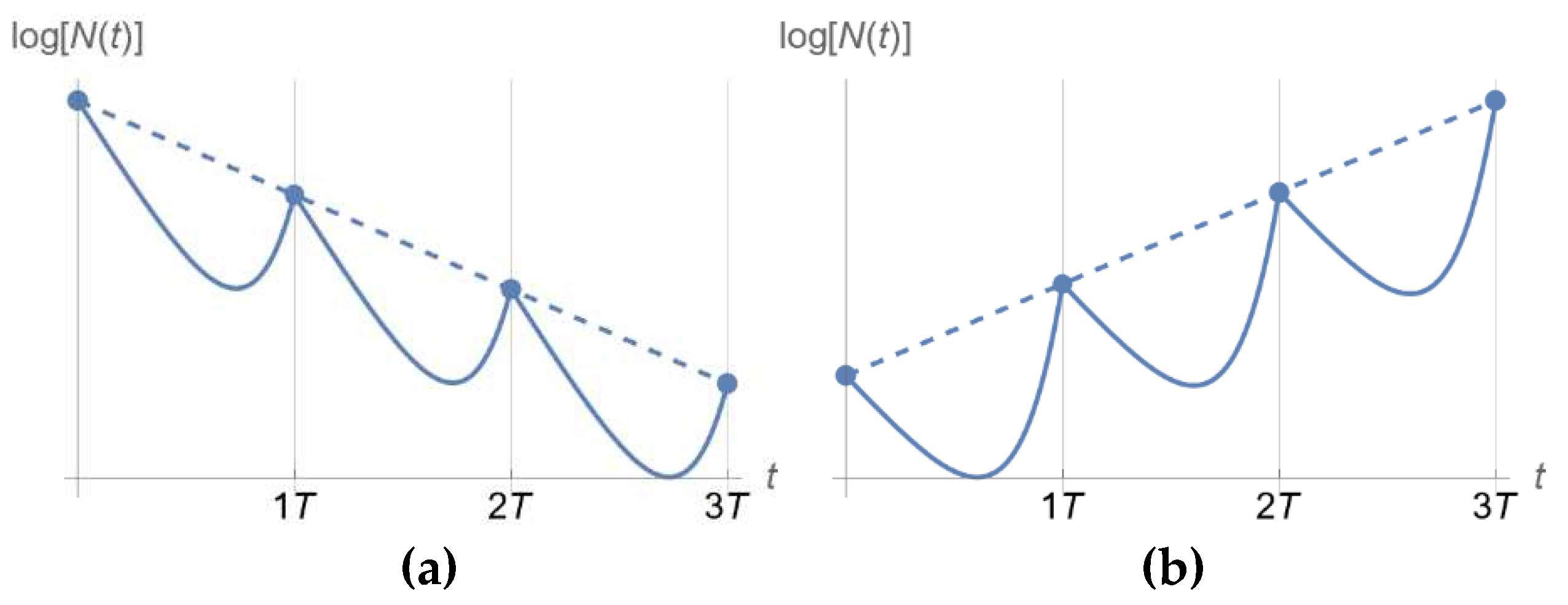
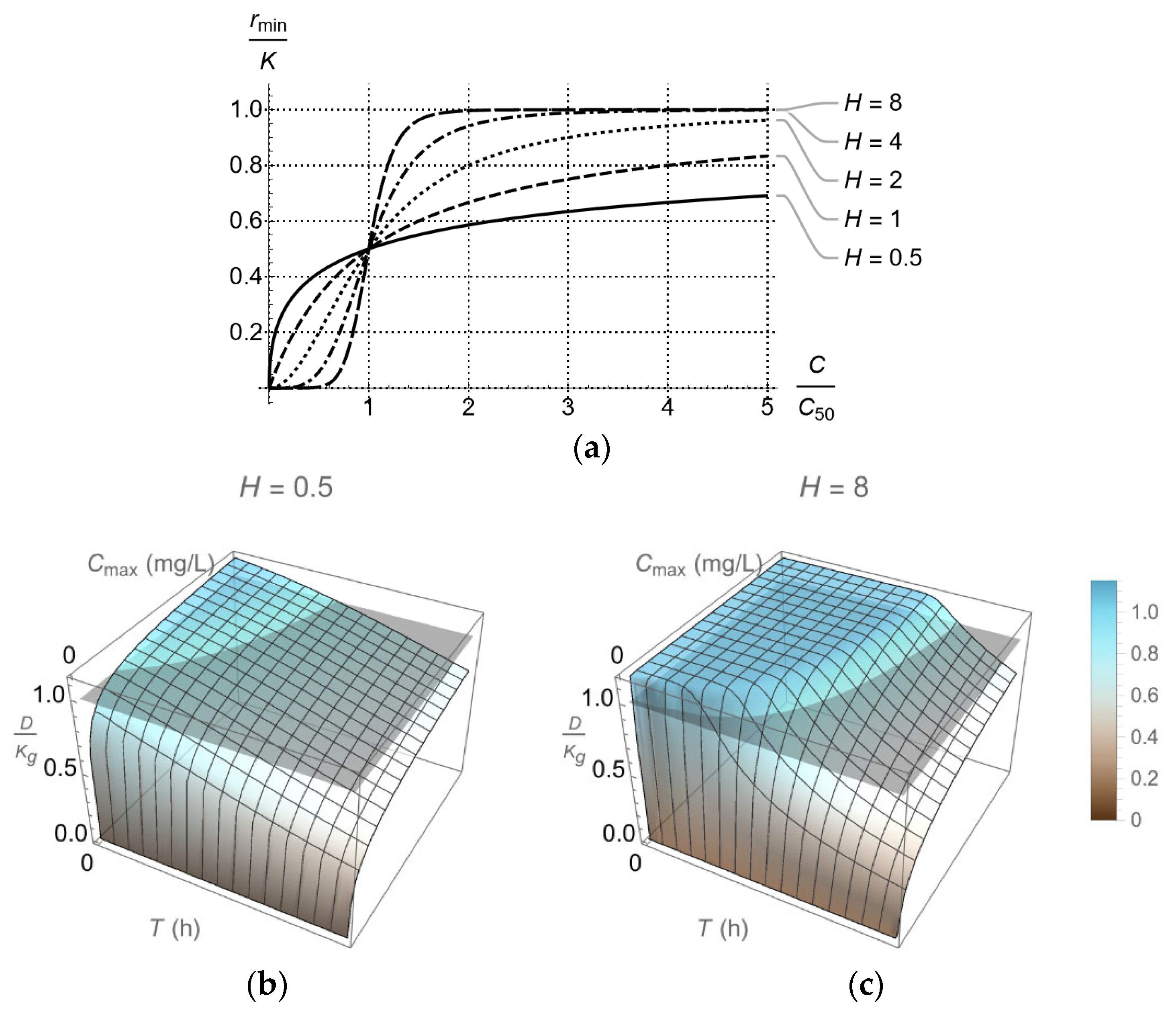
2.3. Dosing Regimen Design for Bacterial Eradication under Clinically Relevant Pharmacokinetics

The preceding discussion in Section 2.1 and Section 2.2 is concerned with pharmacodynamics (PD), i.e. the bactericidal effect of a drug at a certain concentration. This knowledge is one of the two fundamental components of pharmacology for antimicrobial therapy [1]. The second fundamental component is pharmacokinetics (PK), i.e. the absorption, distribution, and metabolism / elimination of drugs. In this section we describe how pharmacodynamic information, as acquired by the approach described in the previous two sections, can be combined with related pharmacokinetics, for design of effective drug dosing regimens.
For periodic drug administration and subsequent elimination Figure 3 shows a typical profile of drug concentration C t .
The profile of Figure 3 may produce one of the two outcomes shown in Figure 4 for a homogeneous microbial population [40].
It can be shown [40] that outcome (a) of Figure 4, i.e. elimination of a bacterial population by drug administration following the PK profile of Figure 3, is predicted if and only if
D ≝ 1 T ∫ 0 T r min C η d η > K g
for the least susceptible bacterial subpopulation.
Equation (9) is the main outcome of this section and can be used to complete a dosing regimen design that ensures, with confidence, that D > K g . It provides a direct link between PK and PD, as drugs with the same PD but different PK or with the same PK and different PD will generally result in different D , hence will require different dosing regimens to achieve similar bactericidal outcomes. A detailed investigation of this aspect is provided in [40] and, in a broader context, in [4]. Qualitatively, what one can expect when selecting C max and T for a dosing regimen accommodating the PK of a drug with half-life t 1 / 2 (Figure 3) depends on all three parameters K , C 50 , and H of r min (see Equation (1)). Of these parameters, H determines how sigmoidal r min is (Figure 5a) and ultimately whether the drug exhibits time-dependent or concentration-dependent behavior [1]. The resulting D / K g qualitatively follows the patterns shown in Figure 5b,c, which provide link between PK and PD for corresponding drugs.

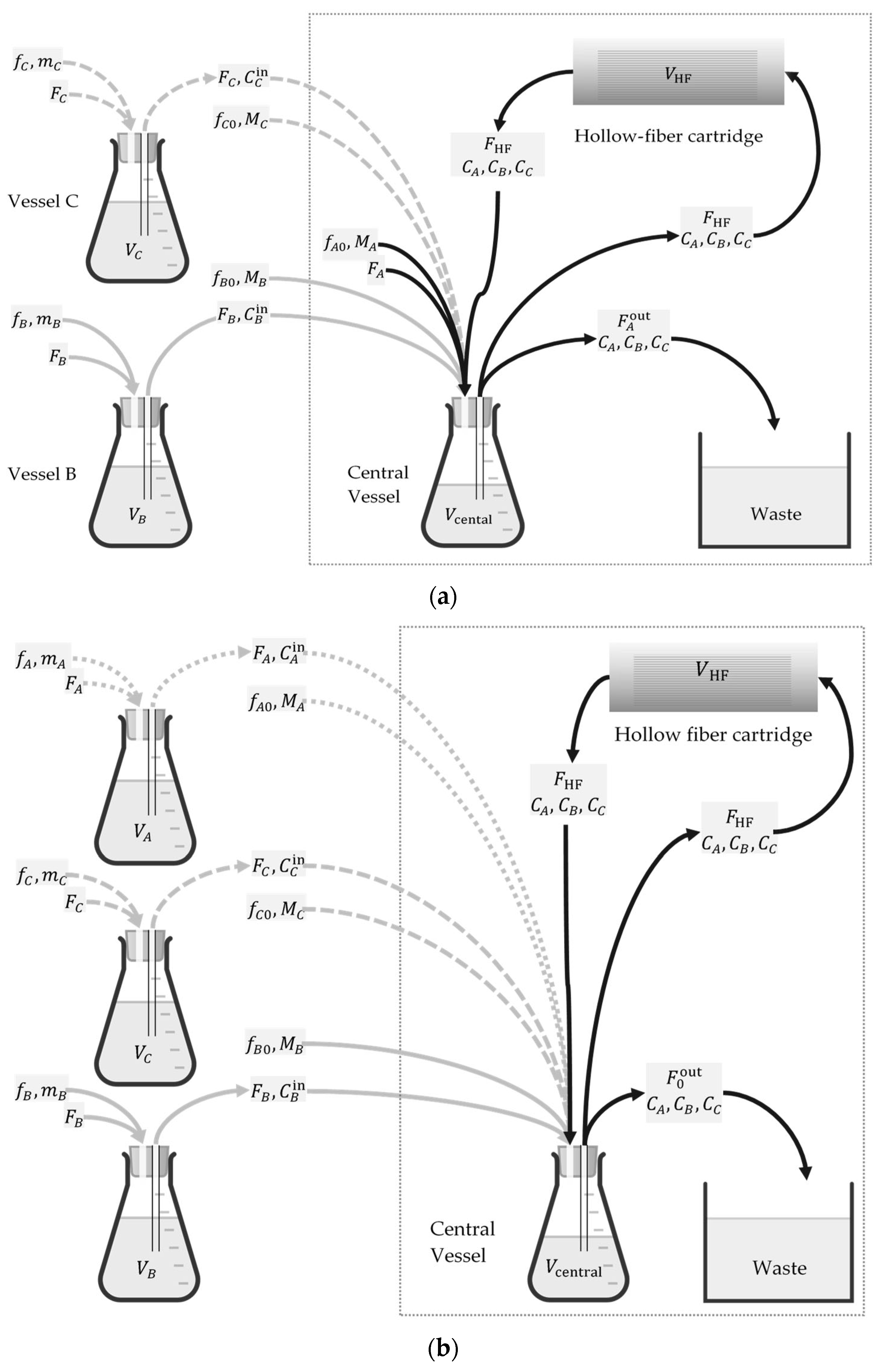
2.4. Validation Test of Promising Dosing Regimens in an In Vitro Hollow Fiber Infection Model

While the preceding methodology can use optical density measurements from time-kill experiments to rapidly design dosing regimens expected to be effective under realistic pharmacokinetics, there is inherent uncertainty in such expectations [37,38,39]. In vitro testing in a hollow-fiber infection model (HFIM, Figure 6) [41,42] can be used to test whether expected outcomes under realistic pharmacokinetics will indeed be achieved [43,44,45]. Simple HFIM designs for a single drug (in terms of both structure and design parameter values) were heuristically extended in the 1980s to designs for two drugs with different pharmacokinetics [41,46]. However, recent developments in treatment of multidrug resistant bacterial infections [47,48,49,50,51] have made it necessary to test three or even more drugs in an HFIM before a corresponding combination is put to clinical use [37,52,53]. This made it necessary to advance the state of the art in HFIM design. A comprehensive new design method was developed in [54], where (a) new configurations beyond the standard in-series configuration of [41,46] were developed (Figure 6), (b) explicit formulas were derived for setting design parameters to values that result in desired pharmacokinetics for each drug in the hollow fiber cartridge, and (c) even for two drugs, an entire family of designs beyond Blaser’s [46] was provided. In addition to making designs for three or more drugs feasible, these advancements substantially improved flexibility for satisfaction of design objectives and constraints in an HFIM.

3. Results

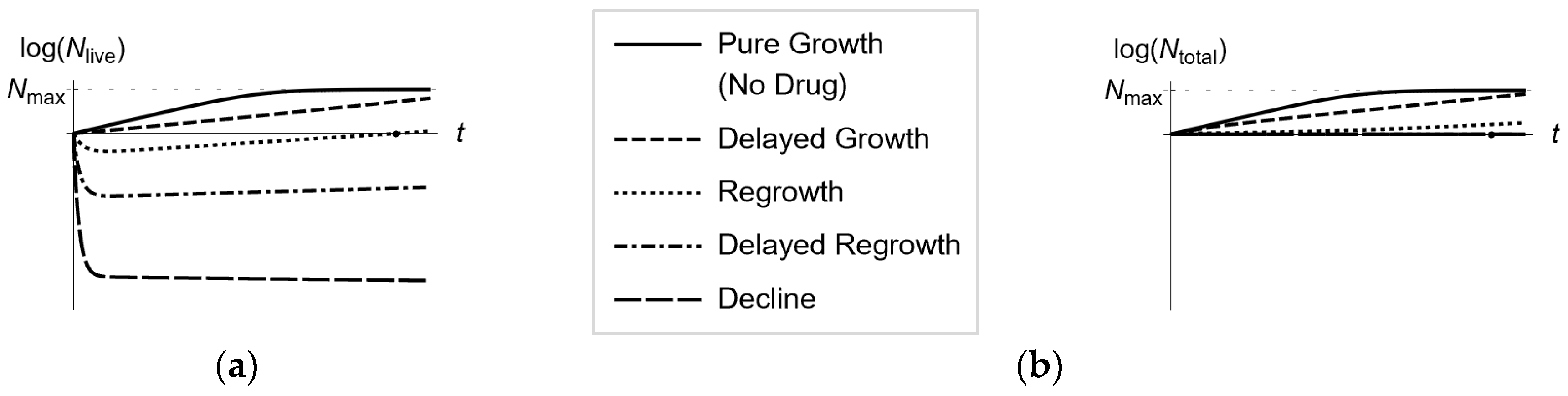
3.1. Longitudinal Optical Density Measurements of Bacterial Cell Suspension under Drug Exposure

Proof of concept was provided in [29] for the information extraction capabilities of model-based analysis of longitudinal optical density measurements from a bacterial suspension exposed to antibiotics in time-kill experiments, as outlined in Section 2.1. In [29], levofloxacin in fourfold dilutions was used against Acinetobacter baumannii, ATCC BAA747. Longitudinal measurements of the bacterial population size (of the kind shown in Figure 1b for both live and dead cells) were collected by an optical density instrument (BacterioScan model 216Dx) at the early stages of its development at the time. Even though the instrument could not explicitly report declining population patterns for live cells, as explained in Section 2.1, the model-based analysis of optical density data for both live and dead cells could reconstruct the live cell population over time with remarkable fidelity, correctly estimating live population decline and subsequent long-term regrowth patterns from data of as little duration as six hours. These patterns were confirmed with separate plating-based measurements, validating the credibility of the method and suggesting its potential use in dosing regimen design for clinically relevant pharmacokinetics, as discussed next.

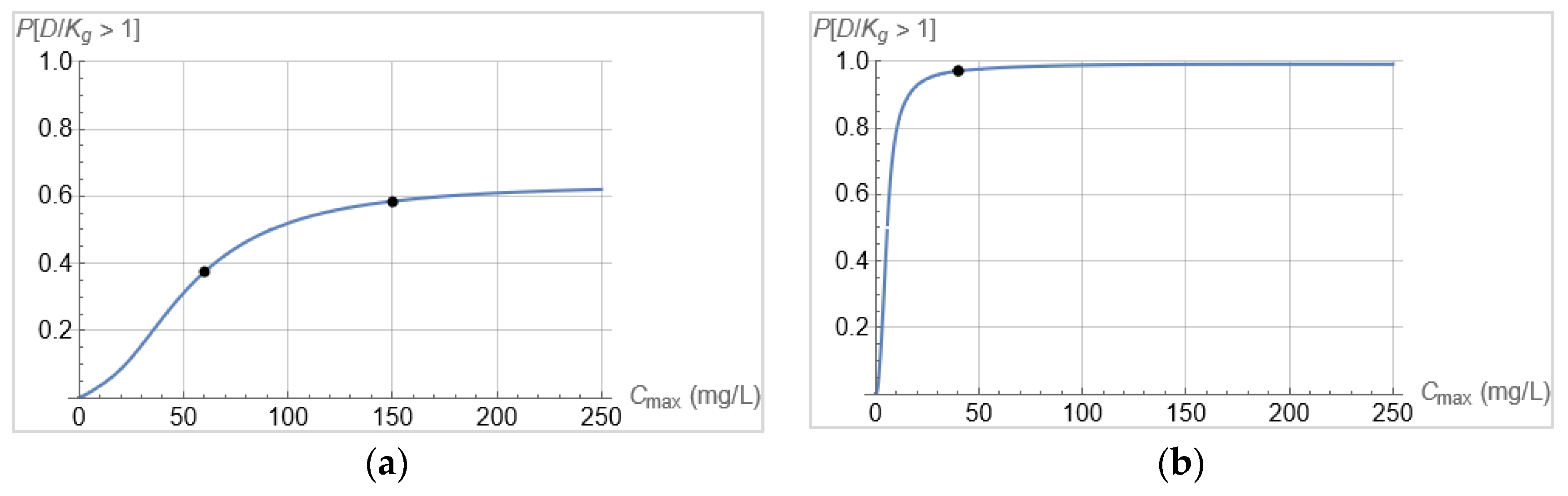
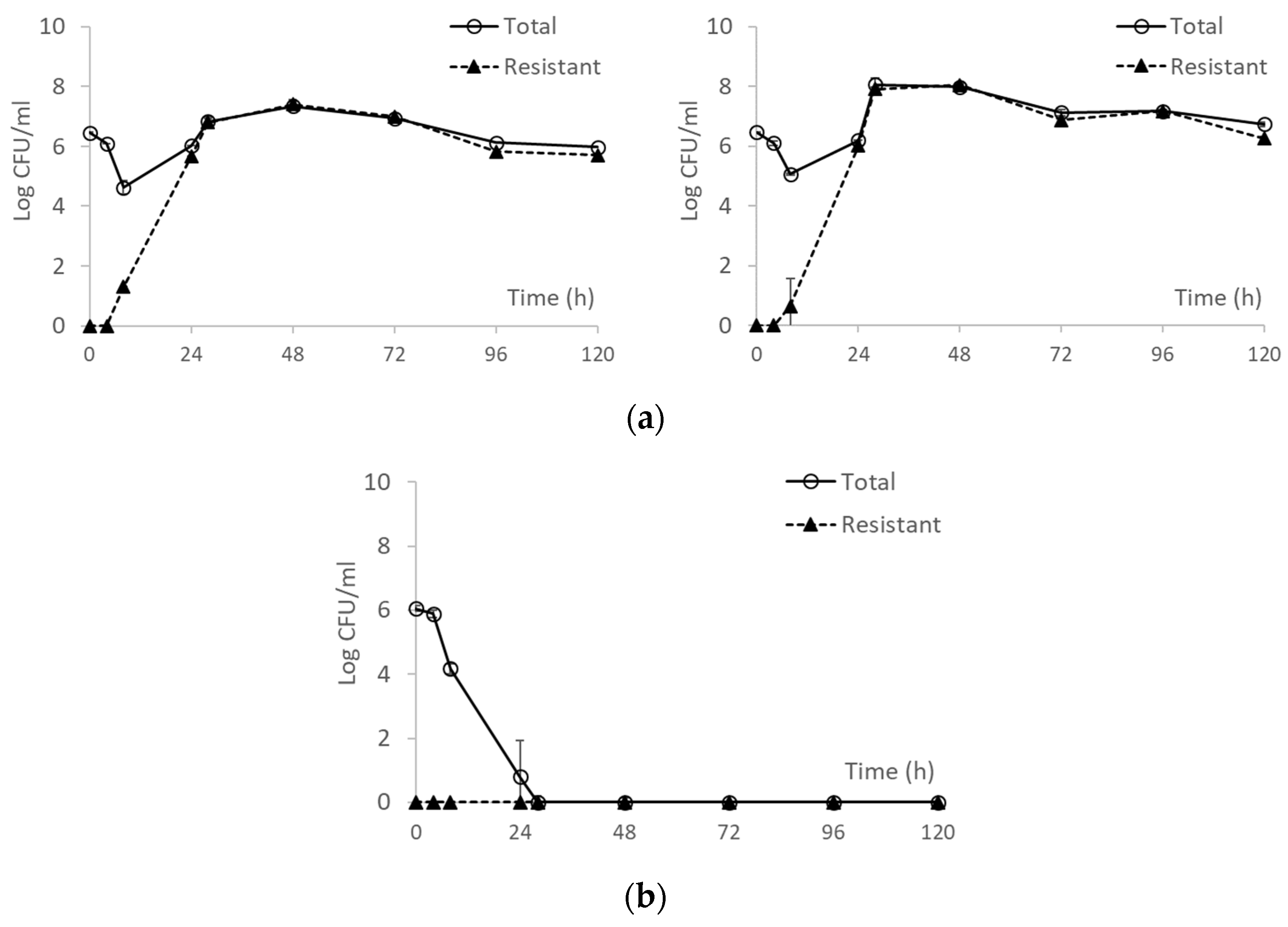
3.2. From Optical Density Measurements to dosing Regimen Design for Clinically Relevant Pharmacokinetics

The suitability of the proposed model-based methodology to start from optical density time-kill measurements and eventually guide individualized dosing regimen design for clinically relevant pharmacokinetics, was experimentally validated in vitro in [30]. In that study, longitudinal optical density measurements were collected using the same instrument as in Section 3.1. In corresponding time-kill experiments, Acinetobacter baumannii, ATCC BAA747, was exposed to fourfold dilutions of (a) ceftazidime and of (b) ceftazidime/amikacin in concentrations ratio 2:1. Model-based data analysis was performed for both cases, considering periodic injections every T = 8 h with subsequent exponential drug decline corresponding to half-life of t 1 / 2 = 2.5 h . The design parameter left to choose for both cases was C max , the peak concentration of ceftazidime (Figure 3). The outcome of the model-based analysis is summarized in Figure 7. In that figure it is indicated that ceftazidime alone is not very likely to suppress the entire bacterial population, even at high concentrations (Figure 7a). By contrast, the ceftazidime/amikacin 2:1 combination has very high likelihood of suppression even at modest concentrations.
The predictions of Figure 7 were experimentally tested in an in vitro hollow-fiber infection model, using C max = 60 ,   150   mg / L (Figure 3) for case (a) and C max ,   ceftazidime / C max ,   amikacin = 40 / 20   ( mg / L ) / ( mg / L ) for case (b). The outcomes are shown Figure 8, where confirmation of predictions is evident.

4. Discussion and Conclusions

This results presented highlight the potential for clinicians to use the proposed method for individualized dosing regimen design. The utility of the proposed method can be further consolidated and expanded with additional future work. Potential items to study include
  • Instrumentation improvements that may improve the quality of the data (reduction of systematic error).
  • A wider range of clonally diverse bacteria.
  • Bacteria with various resistance mechanisms.
  • Different antibiotics, particularly with pharmacodynamics and pharmacokinetic differences.
  • Combination therapy, particularly the interplay between pharmacodynamics and pharmacokinetics.
  • Automation of computations through software development.
  • Testing of in vivo relevance in animal infection models.

5. Patents

A US patent application has been filed for the method presented here [55].

Author Contributions

As this paper reviews prior results in a comprehensive way, both authors contributed equally to corresponding tasks.

Funding

The Institute of Allergy and Infectious Diseases of the National Institutes of Health under award number R01AI140287-05 supported the research reported in this publication. 100% of the project costs were financed with Federal money. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Funding sources had no involvement in study design; in the collection, analysis and interpretation of data, nor in the writing of the report nor in the decision to submit the article for publication.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Craig, W.A. State-of-the-Art Clinical Article: Pharmacokinetic/Pharmacodynamic Parameters: Rationale for Antibacterial Dosing of Mice and Men. Clin. Infect. Dis. 1998, 26, 1–10. [Google Scholar] [CrossRef] [PubMed]
  2. Dadgostar, P. Antimicrobial Resistance: Implications and Costs. Infect. Drug Resist. 2019, 12, 3903–3910. [Google Scholar] [CrossRef] [PubMed]
  3. Sanders, E.R. , Aseptic Laboratory Techniques: Plating Methods. J. Vis. Exp. 2012, e3064. [Google Scholar]
  4. Tam, V.H.; Nikolaou, M. A Novel Approach to Pharmacodynamic Assessment of Antimicrobial Agents: New Insights to Dosing Regimen Design. PLOS Comput. Biol. 2011, 7, e1001043. [Google Scholar] [CrossRef] [PubMed]
  5. Andrews, J.M. , Determination of minimum inhibitory concentrations. J. Antimicrob. Chemother., 2001. 48: p. 5-16.
  6. Mouton, J.W.; Dudley, M.N.; Cars, O.; Derendorf, H.; Drusano, G.L. Standardization of pharmacokinetic/pharmacodynamic (PK/PD) terminology for anti-infective drugs: an update. J. Antimicrob. Chemother. 2005, 55, 601–607. [Google Scholar] [CrossRef] [PubMed]
  7. Wiegand, I.; Hilpert, K.; Hancock, R.E.W. Agar and broth dilution methods to determine the minimal inhibitory concentration (MIC) of antimicrobial substances. Nat. Protoc. 2008, 3, 163–175. [Google Scholar] [CrossRef] [PubMed]
  8. Vogelman, B.; Craig, W.A. Kinetics of antimicrobial activity. J. Pediatr. 1986, 108, 835–840. [Google Scholar] [CrossRef]
  9. Giraldo, J.; Vivas, N.M.; Vila, E.; Badia, A. Assessing the (a)symmetry of concentration-effect curves: empirical versus mechanistic models. Pharmacol. Ther. 2002, 95, 21–45. [Google Scholar] [CrossRef]
  10. Lipsitch, M.; Levin, B.R. The population dynamics of antimicrobial chemotherapy. Antimicrob. Agents Chemother. 1997, 41, 363–373. [Google Scholar] [CrossRef]
  11. Bhagunde, P.R.; Nikolaou, M.; Tam, V.H. Modeling heterogeneous bacterial populations exposed to antibiotics: The logistic-dynamics case. AIChE J. 2015, 61, 2385–2393. [Google Scholar] [CrossRef]
  12. Nikolaou, M.; Tam, V.H. A New Modeling Approach to the Effect of Antimicrobial Agents on Heterogeneous Microbial Populations. J. Math. Biol. 2005, 52, 154–182. [Google Scholar] [CrossRef]
  13. Tam, V.H.; Nikolaou, M. A Novel Approach to Pharmacodynamic Assessment of Antimicrobial Agents: New Insights to Dosing Regimen Design. PLOS Comput. Biol. 2011, 7, e1001043. [Google Scholar] [CrossRef] [PubMed]
  14. Mueller, M.; de la Peña, A.; Derendorf, H. Issues in Pharmacokinetics and Pharmacodynamics of Anti-Infective Agents: Kill Curves versus MIC. Antimicrob. Agents Chemother. 2004, 48, 369–377. [Google Scholar] [CrossRef] [PubMed]
  15. Kralik, P.; Ricchi, M. A Basic Guide to Real Time PCR in Microbial Diagnostics: Definitions, Parameters, and Everything. Front. Microbiol. 2017, 8, 108. [Google Scholar] [CrossRef] [PubMed]
  16. Ricchi, M.; Bertasio, C.; Boniotti, M.B.; Vicari, N.; Russo, S.; Tilola, M.; Bellotti, M.A.; Bertasi, B. Comparison among the Quantification of Bacterial Pathogens by qPCR, dPCR, and Cultural Methods. Front. Microbiol. 2017, 8, 1174. [Google Scholar] [CrossRef] [PubMed]
  17. Wang, Y.; Hammes, F.; De Roy, K.; Verstraete, W.; Boon, N. Past, present and future applications of flow cytometry in aquatic microbiology. Trends Biotechnol. 2010, 28, 416–424. [Google Scholar] [CrossRef]
  18. Hasan, M.; Alam, M.W.; Wahid, K.A.; Miah, S.; Lukong, K.E. A Low-Cost Digital Microscope with Real-Time Fluorescent Imaging Capability. PLOS ONE 2016, 11, e0167863. [Google Scholar] [CrossRef]
  19. Gracias, K.S.; McKillip, J.L. A review of conventional detection and enumeration methods for pathogenic bacteria in food. Can. J. Microbiol. 2004, 50, 883–890. [Google Scholar] [CrossRef]
  20. Pascaud, A.; Amellal, S.; Soulas, M.-L.; Soulas, G. A fluorescence-based assay for measuring the viable cell concentration of mixed microbial communities in soil. J. Microbiol. Methods 2009, 76, 81–87. [Google Scholar] [CrossRef]
  21. Feng, J.; Wang, T.; Zhang, S.; Shi, W.; Zhang, Y. An Optimized SYBR Green I/PI Assay for Rapid Viability Assessment and Antibiotic Susceptibility Testing for Borrelia burgdorferi. PLOS ONE 2014, 9, e111809. [Google Scholar] [CrossRef]
  22. Alakomi, H.-L.; Mättö, J.; Virkajärvi, I.; Saarela, M. Application of a microplate scale fluorochrome staining assay for the assessment of viability of probiotic preparations. J. Microbiol. Methods 2005, 62, 25–35. [Google Scholar] [CrossRef] [PubMed]
  23. Ou, F.; McGoverin, C.; Swift, S.; Vanholsbeeck, F. Absolute bacterial cell enumeration using flow cytometry. J. Appl. Microbiol. 2017, 123, 464–477. [Google Scholar] [CrossRef] [PubMed]
  24. Imade, G.E.; Badung, B.; Pam, S.; Agbaji, O.; Egah, D.; Sagay, A.S.; Sankalé, J.-L.; Kapiga, S.; Idoko, J.; Kanki, P. Comparison of a New, Affordable Flow Cytometric Method and the Manual Magnetic Bead Technique for CD4 T-Lymphocyte Counting in a Northern Nigerian Setting. Clin. Vaccine Immunol. 2005, 12, 224–227. [Google Scholar] [CrossRef] [PubMed]
  25. Guo, R.; McGoverin, C.; Swift, S.; Vanholsbeeck, F. A rapid and low-cost estimation of bacteria counts in solution using fluorescence spectroscopy. Anal. Bioanal. Chem. 2017, 409, 3959–3967. [Google Scholar] [CrossRef]
  26. Mytilinaios, I.S. , Magdi; Schofield, Hannah K.; Lambert, Ronald J. W., Growth curve prediction from optical density data. Int. J. Food Microbiol., 2012. 154(3): p. 169-176.
  27. López, S.; Prieto, M.; Dijkstra, J.; Dhanoa, M.; France, J. Statistical evaluation of mathematical models for microbial growth. Int. J. Food Microbiol. 2004, 96, 289–300. [Google Scholar] [CrossRef]
  28. McMeekin, T.A. , et al., Predictive Microbiology: Theory and Application. 1993, New York: Wiley.
  29. Kesisoglou, I.; Tam, V.H.; Tomaras, A.P.; Nikolaou, M. Discerning in vitro pharmacodynamics from OD measurements: A model-based approach. Comput. Chem. Eng. 2021, 158, 107617. [Google Scholar] [CrossRef]
  30. Kesisoglou, I.; Eales, B.M.; Merlau, P.R.; Tam, V.H.; Nikolaou, M. Deciphering longitudinal optical-density measurements to guide clinical dosing regimen design: A model-based approach. Comput. Methods Programs Biomed. 2022, 227, 107212–107212. [Google Scholar] [CrossRef]
  31. Schaechter, M. A brief history of bacterial growth physiology. Front. Microbiol. 2015, 6, 289–289. [Google Scholar] [CrossRef]
  32. Baranyi, J., T. A. Roberts, and P. McClure, A non-autonomous different equation to model bacterial growth. Food Microbiology, 1993. 10: p. 43-59.
  33. Verhulst, P.F. , Resherches mathematiques sur la loi d'accroissement de la population. Nouveaux memoires de l'academie royale des sciences, 1845. 18: p. 1-41.
  34. Jusko, W.J. Pharmacodynamics of Chemotherapeutic Effects: Dose-Time-Response Relationships for Phase-Nonspecific Agents. J. Pharm. Sci. 1971, 60, 892–895. [Google Scholar] [CrossRef]
  35. Wagner, J. Kinetics of pharmacologic response I. Proposed relationships between response and drug concentration in the intact animal and man. J. Theor. Biol. 1968, 20, 173–201. [Google Scholar] [CrossRef]
  36. Hill, A.V. , The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J. Physiol., 1910. 40: p. iv-vii.
  37. Tamma, P.D.; Cosgrove, S.E.; Maragakis, L.L. Combination Therapy for Treatment of Infections with Gram-Negative Bacteria. Clin. Microbiol. Rev. 2012, 25, 450–470. [Google Scholar] [CrossRef] [PubMed]
  38. Gloede, J. , et al., In vitro pharmacodynamic models to determine the effectof antibacterial drugs. J. Antimicrob. Chemother., 2010. 65: p. 186-201.
  39. Doern, C.D. When Does 2 Plus 2 Equal 5? A Review of Antimicrobial Synergy Testing. J. Clin. Microbiol. 2014, 52, 4124–4128. [Google Scholar] [CrossRef] [PubMed]
  40. Nikolaou, M.; Schilling, A.N.; Vo, G.; Chang, K.-T.; Tam, V.H. Modeling of Microbial Population Responses to Time-Periodic Concentrations of Antimicrobial Agents. Ann. Biomed. Eng. 2007, 35, 1458–1470. [Google Scholar] [CrossRef]
  41. Blaser, J., B. Stone, and S. Zinner, Two compartment kinetic model with multiple artificial capilary units. J. Antimicrob. Chemother., 1985. 15: p. 131-137.
  42. Bulitta, J.B.; Hope, W.W.; Eakin, A.E.; Guina, T.; Tam, V.H.; Louie, A.; Drusano, G.L.; Hoover, J.L. Generating Robust and Informative Nonclinical In Vitro and In Vivo Bacterial Infection Model Efficacy Data To Support Translation to Humans. Antimicrob. Agents Chemother. 2019, 63. [Google Scholar] [CrossRef] [PubMed]
  43. Cadwell, J. , The hollow fiber infection model: Principles and practice. Arch. Clin. Microbiol., 2017. 08.
  44. Bao, L.; Liu, B.; Lipscomb, G.G. Entry mass transfer in axial flows through randomly packed fiber bundles. AIChE J. 1999, 45, 2346–2356. [Google Scholar] [CrossRef]
  45. De Bartolo, L.; Salerno, S.; Curcio, E.; Piscioneri, A.; Rende, M.; Morelli, S.; Tasselli, F.; Bader, A.; Drioli, E. Human hepatocyte functions in a crossed hollow fiber membrane bioreactor. Biomaterials 2009, 30, 2531–2543. [Google Scholar] [CrossRef] [PubMed]
  46. Blaser, J. In-vitro model for simultaneous simulation of the serum kinetics of two drugs with different half-lives. J. Antimicrob. Chemother. 1985, 15, 125–130. [Google Scholar] [CrossRef]
  47. Siwakoti, S.; Subedi, A.; Sharma, A.; Baral, R.; Bhattarai, N.R.; Khanal, B. Incidence and outcomes of multidrug-resistant gram-negative bacteria infections in intensive care unit from Nepal- a prospective cohort study. Antimicrob. Resist. Infect. Control. 2018, 7, 114. [Google Scholar] [CrossRef]
  48. Wang, M.; Wei, H.; Zhao, Y.; Shang, L.; Di, L.; Lyu, C.; Liu, J. Analysis of multidrug-resistant bacteria in 3223 patients with hospital-acquired infections (HAI) from a tertiary general hospital in China. Bosn. J. Basic Med Sci. 2019, 19, 86–93. [Google Scholar] [CrossRef]
  49. Jain, A.; Roy, I.; Gupta, M.K.; Kumar, M.; Agarwal, S.K. Prevalence of extended-spectrum β-lactamase-producing Gram-negative bacteria in septicaemic neonates in a tertiary care hospital. J. Med Microbiol. 2003, 52, 421–425. [Google Scholar] [CrossRef]
  50. Pop, V. , et al., Multidrug Resistant Gram Negative Bacteria in a Long Term Care Facility: Prevalence and Risk Factors. J. Am. Geriatr. Soc., 2008. 56(7).
  51. Saeed, S., A. Naim, and P. Tariq, A study on prevalance of multi-drug-resistant gram negative bacteria. Int. J. Biol. Biotech. 2007, 4, 71–74. [Google Scholar]
  52. Tängdén, T. Combination antibiotic therapy for multidrug-resistant Gram-negative bacteria. Upsala J. Med Sci. 2014, 119, 149–153. [Google Scholar] [CrossRef] [PubMed]
  53. Karakonstantis, S.; I Kritsotakis, E.; Gikas, A. Pandrug-resistant Gram-negative bacteria: a systematic review of current epidemiology, prognosis and treatment options. J. Antimicrob. Chemother. 2020, 75, 271–282. [Google Scholar] [CrossRef] [PubMed]
  54. Kesisoglou, I.; Eales, B.M.; Ledesma, K.R.; Merlau, P.R.; Tam, V.H.; Wang, W.; Nikolaou, M. Simultaneous in vitro simulation of multiple antimicrobial agents with different elimination half-lives in a pre-clinical infection model. Comput. Chem. Eng. 2021, 155. [Google Scholar] [CrossRef]
  55. Nikolaou, M.; Tam, V.H.; Kesisoglou, I. Optical based methods for determining antimicrobial dosing regimens. US Patent App. 17/636,079, 2023. [Google Scholar]
Preprints 70967 g001
Figure 1. Qualitative patterns of the number of live (a) and dead (b) bacterial cells in suspension exposed to time-invariant antibiotic concentrations in multifold dilutions. Bacterial subpopulations of varying degrees of drug resistance are considered. As drug concentration is set at increasingly higher values, the bacterial population response over time exhibits the five patterns shown. Note that while the number of live cells may decline (a), the total number of cells (both live and dead) will never decline (b). An optical density instrument can only produce the curves in (b). A central focus of this paper is to summarize a mathematical model-based methodology for obtaining the curves of in (a) from the curves in (b).
Figure 1. Qualitative patterns of the number of live (a) and dead (b) bacterial cells in suspension exposed to time-invariant antibiotic concentrations in multifold dilutions. Bacterial subpopulations of varying degrees of drug resistance are considered. As drug concentration is set at increasingly higher values, the bacterial population response over time exhibits the five patterns shown. Note that while the number of live cells may decline (a), the total number of cells (both live and dead) will never decline (b). An optical density instrument can only produce the curves in (b). A central focus of this paper is to summarize a mathematical model-based methodology for obtaining the curves of in (a) from the curves in (b).
Preprints 70967 g001
Preprints 70967 g002
Figure 2. Fit of Equation (1) to values of r min estimated from time-kill experiments with a bacterial population exposed to distinct drug concentrations C . (a) Eradication of the entire bacterial population is predicted for high enough drug concentrations C . (b) No drug concentration C can eliminate the entire bacterial population.
Figure 2. Fit of Equation (1) to values of r min estimated from time-kill experiments with a bacterial population exposed to distinct drug concentrations C . (a) Eradication of the entire bacterial population is predicted for high enough drug concentrations C . (b) No drug concentration C can eliminate the entire bacterial population.
Preprints 70967 g002
Preprints 70967 g003
Figure 3. Clinically relevant pharmacokinetics of drug injection every T time units at peak concentration C max for a drug with corresponding half life t 1 / 2 .
Figure 3. Clinically relevant pharmacokinetics of drug injection every T time units at peak concentration C max for a drug with corresponding half life t 1 / 2 .
Preprints 70967 g003
Preprints 70967 g004
Figure 4. Qualitatively distinct outcomes of a homogeneous bacterial population exposed to a drug following the PK in Figure 3, depending on D / K g (Equation (9)). (a) Bacterial population decline for D / K g > 1 . (b) Bacterial population growth for D / K g < 1 .
Figure 4. Qualitatively distinct outcomes of a homogeneous bacterial population exposed to a drug following the PK in Figure 3, depending on D / K g (Equation (9)). (a) Bacterial population decline for D / K g > 1 . (b) Bacterial population growth for D / K g < 1 .
Preprints 70967 g004
Preprints 70967 g005
Figure 5. (a) Bactericidal rate of drugs following concentration-dependent ( H ≪ 1 ) or time-dependent ( H ≫ 1 ) activity [1], as captured by the Hill exponent H in Equation (1). (b) Qualitative dependence of D / K g (compared to 1) on design parameters T (period of injection) and C max (peak drug concentration) associated with a dosing regimen following the pharmacokinetic pattern of Figure 3 for a drug of corresponding half-life. (c) Similar to (b), the only difference being the Hill factor H (8 vs. 0.5).
Figure 5. (a) Bactericidal rate of drugs following concentration-dependent ( H ≪ 1 ) or time-dependent ( H ≫ 1 ) activity [1], as captured by the Hill exponent H in Equation (1). (b) Qualitative dependence of D / K g (compared to 1) on design parameters T (period of injection) and C max (peak drug concentration) associated with a dosing regimen following the pharmacokinetic pattern of Figure 3 for a drug of corresponding half-life. (c) Similar to (b), the only difference being the Hill factor H (8 vs. 0.5).
Preprints 70967 g005
Preprints 70967 g006
Figure 6. In vitro hollow fiber infection model for testing the effectiveness of three drugs following different pharmacokinetics. Design parameters shown take values according to the formulas developed in [54]. (a) In-series configuration: adds vessels B, C to the basic central vessel of the single-drug design. (b) In-parallel configuration: adds vessels A, B, C to the basic central vessel of the single-drug design, offering additional flexibility on the range of pharmacokinetics to be simulated in vitro. The framed areas in (a) and (b) refer to the basic design for a single drug. Each framed area along with vessel B and associated streams corresponds to Blaser’s long known configuration [41,46] for two drugs. Figure reproduced from [29].
Figure 6. In vitro hollow fiber infection model for testing the effectiveness of three drugs following different pharmacokinetics. Design parameters shown take values according to the formulas developed in [54]. (a) In-series configuration: adds vessels B, C to the basic central vessel of the single-drug design. (b) In-parallel configuration: adds vessels A, B, C to the basic central vessel of the single-drug design, offering additional flexibility on the range of pharmacokinetics to be simulated in vitro. The framed areas in (a) and (b) refer to the basic design for a single drug. Each framed area along with vessel B and associated streams corresponds to Blaser’s long known configuration [41,46] for two drugs. Figure reproduced from [29].
Preprints 70967 g006
Preprints 70967 g007
Figure 7. Probability of satisfaction of Equation (9) for bacterial exposure to (a) ceftazidime, and (b) ceftazidime and amikacin at mass ratio 2:1. In both cases drugs were injected every T = 8 h with subsequent exponential decline of concentration from its peak of C max , with corresponding half-life of t 1 / 2 = 2.5 h . Selected for testing in the in vitro HFIM were C max = 60 ,   150   mg / L for case (a) and C max ,   ceftazidime / C max ,   amikacin = 40 / 20   ( mg / L ) / ( mg / L ) for case (b) with corresponding probabilities 59%, 38%, and 98%, respectively. Figure reproduced from [30].
Figure 7. Probability of satisfaction of Equation (9) for bacterial exposure to (a) ceftazidime, and (b) ceftazidime and amikacin at mass ratio 2:1. In both cases drugs were injected every T = 8 h with subsequent exponential decline of concentration from its peak of C max , with corresponding half-life of t 1 / 2 = 2.5 h . Selected for testing in the in vitro HFIM were C max = 60 ,   150   mg / L for case (a) and C max ,   ceftazidime / C max ,   amikacin = 40 / 20   ( mg / L ) / ( mg / L ) for case (b) with corresponding probabilities 59%, 38%, and 98%, respectively. Figure reproduced from [30].
Preprints 70967 g007
Preprints 70967 g008
Figure 8. (a) Bacterial response to two ceftazidime dosing regimens in the hollow fiber infection model. Ceftazidime equivalent to 1   g ( C max = 60   mg / L ) and 2.5   g ( C max = 150   mg / L ) administered every 8   h , as shown in Figure 3. Data shown as mean + / − standard deviation. (b) Bacterial response to a combination of ceftazidime and amikacin ( 2 : 1 mass ratio). Ceftazidime equivalent to 0.67   g and amikacin equivalent to 5   mg / kg administered every 8   h , as shown in Figure 3. Data shown as mean + / − standard deviation. Figure reproduced from [30].
Figure 8. (a) Bacterial response to two ceftazidime dosing regimens in the hollow fiber infection model. Ceftazidime equivalent to 1   g ( C max = 60   mg / L ) and 2.5   g ( C max = 150   mg / L ) administered every 8   h , as shown in Figure 3. Data shown as mean + / − standard deviation. (b) Bacterial response to a combination of ceftazidime and amikacin ( 2 : 1 mass ratio). Ceftazidime equivalent to 0.67   g and amikacin equivalent to 5   mg / kg administered every 8   h , as shown in Figure 3. Data shown as mean + / − standard deviation. Figure reproduced from [30].
Preprints 70967 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated