Prerpints.org logo
Preprint
Article

Effect of High Energy Ball Milling Time on the Density and Mechanical Properties of W-7%Ni-3%Fe Alloy

Altmetrics

Downloads

131

Views

58

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 April 2023

Posted:

18 April 2023

You are already at the latest version

Alerts
Abstract
The present work was aimed at the investigation of effect of High Energy Ball Milling (HEBM) time on the sintering kinetics, structure, and properties of heavy tungsten alloy (HTA) W-7%Ni-3%Fe. The HTA samples were obtained from the nanopowders (20-80 nm) by conventional liquid phase sintering (LPS) in hydrogen and by Spark Plasma Sintering (SPS) in vacuum. The HTA density was shown to depend on the HEBM time non-monotonously that originates from the formation of non-equilibrium solid solutions in the W-Ni-Fe systems during HEBM. The SPS kinetics of the HTA nanopowders was shown to have a two-stage character, the intensity of which depends on the Coble diffusion creep rate and on the intensity of diffusion of the tungsten atoms in the crystal lattice of the -phase. The kinetics of sintering of the initial submicron powders have a single-stage character originating from the intensity of the grain boundary diffusion in the -phase. The dependencies of the hardness and of the yield strength on the grain sizes were found to obey the Hall-Petch relation. The hardness, strength, and dynamic strength in the compression tests of the fine-grained tungsten alloys obtained by SPS and LPS were studied.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Heavy tungsten alloys (HTAs) of the W-Ni-Fe system with the W contents over 85-90% have a number of unique characteristics: simultaneous increased density, strength, and plasticity at room temperature [1,2,3,4,5], high characteristics of dynamic strength [6,7], high radiation resistance, etc. The industrial tungsten alloys with 90-95%W obtained by conventional liquid-phase sintering (LPS) have the density of 17-19 g/cm3, the ultimate strength up to 1000 MPa, and elongation to failure up to 25-30% at room temperature. Additional strain strengthening allows improving the ultimate strength up to 1400-1600 MPa preserving satisfactory ductility [8,9,10,11]. These features make HTAs interesting for various construction applications as well as interesting object for investigations of the effect of the interphase boundaries on the mechanical properties of the alloys [12,13,14,15].
It is worth noting that the technologies of strain hardening of the HTAs have approached the limits of their capabilities at present. For further improving the properties of the HTA, modern technologies of powder metallurgy are used often [16,17] including the additive manufacturing methods [18,19,20] and microwave sintering method [21]. Modern methods of fabrication of nanopowder compositions W-Ni-Fe are being developed extensively [5,18,22].
The analysis of the literature shows Spark Plasma Sintering (SPS) to be one of promising methods of fabricating the HTAs [23,24,25,26,27]. An opportunity to vary main process parameters affecting the microstructure parameters of the HTAs most essentially (the heating rate, the temperature and time of sintering, the magnitude of the pressure applied, etc.) directly in the course of sintering provides a great flexibility to SPS method in controlling the mechanical properties of the HTAs. An opportunity of sintering the materials at very high heating rates (up to 2500 oC/min) is an important feature of SPS technology, which allows reducing the grain growth rate [23,27]. The fine-grained HTAs obtained by SPS have simultaneously high strength and hardness [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44] (Table A1, see Appendix A).
Joint application of High Energy Ball Milling (HEBM) and SPS is one of promising methods of further improving the mechanical properties of the HTAs [1,2,8,9,12,13,14,15,16,17]. This allows ensuring an outstanding increase in the strength and hardness of the HTAs (Table A1, see Appendix A). It is interesting to note that the results of [27,28,33,39] evidence the possibility of formation of strongly supersaturated solid solution of tungsten in the γ-phase based on nickel during HEBM that leads to an additional acceleration of sintering of the W-based nanopowders. The formation of the supersaturated solid solution of tungsten atoms in the γ-phase leads to manifestation of some unexpected effects. The effect of non-monotonous dependence of the density on the sintering temperature [28,29,35,43,44,45] as well as the effect of reduction of the activation energy of sintering of the nanopowders [45] deserve high attention. One should note separately the effect of decreasing of the density of the tungsten alloys sintered from mechanically activated nanopowders [33,39,45], the nature of which remains unclear now. Also, the effect of nonmonotonous (with a maximum) dependencies of the HTA density on the time of preliminary HEBM of the powders observed in [45] is interesting.
From the practical viewpoint, the result of increase in the hardness, the static strength and the dynamic one of the HTAs obtained by SPS is important.
The analysis of the literature shows that the W-7%Ni-3%Fe alloys obtained by SPS from nanopowders (tHEBM = 20 min) have a higher dynamic strength as compared to the coarse-grained alloys [42,46]. The decreasing of the grain sizes was noted to result in simultaneous increase in the static strength, the dynamic one, and in the penetration depth of a HTA sample into a steel barrier. At the throwing speed of 1194 m/s, the penetration depth reached 15.2 mm whereas for the coarse-grained HTAs this magnitude varied from 9.4 to 12.8 mm at similar testing regimes [46]. The formation of strongly supersaturated solid solution in the γ-phase may be one of the origins of manifestation of increased dynamic strength of the HTAs. In our opinion, it allows increasing the strength of the interphase (α-γ)-boundaries and, as a consequence, ensuring additional increase in the strength of HTAs.
The investigation of the effect of the HEBM time (tHEBM) of the powders on the density, microstructure parameters, and mechanical properties of heavy tungsten alloy W-7%Ni-3%Fe obtained by SPS was the main goal of the present work.

2. Materials and Methods

The object of investigations was W-7%Ni-3%Fe alloy. The chemical compositions of the initial powders α-W, β-Ni, and α-Fe are presented in Table 1. The mean particle sizes in the initial powders α-W, β-Ni, and α-Fe according to Fischer were R0 = 0.8 μm, 20 μm, and 11 μm respectively.
The initial coarse-grained compositions were obtained by mixing the powders α-W, β-Ni, and α-Fe in a FRITSCH® Pulverisette 6 planetary ball mill (Idar-Oberstein, Germany). The mixing time was 15 h, the mixing rate was 100 rpm. HEBM of the compositions W-7%Ni-3%Fe was performed in APF-3 high energy planetary mill (Russia). The acceleration of the milling bodies was 60g, the mixing rate was 1450 rpm. The containers and milling balls of 6-10 mm in diameter were made from industrial alloy W-7%Ni-3%Fe. The mass ratio of the balls and the powders was 10:1. HEBM with the durations of 5, 10, 20, and 40 min was performed in argon ambient with addition of ethanol. To minimize the heating of the powders, HEBM was performed in several stages each 5 min long.
The HTA samples were obtained by conventional sintering in hydrogen (Method I) and by SPS (Method II).
To obtain the HTA samples by Method I, the nanopowders were pressed into the samples of 30 mm in diameter and 5-6 in height in advance. The uniaxial pressing by the pressure of 150 MPa was performed at room temperature in a steel mold. The sintering was performed in a two-stage regime: Stage I – heating with the rate 25 oC/min up to 950 oC and holding for 2 h for the reduction of the powders and removing oxygen; Stage II – heating up to the sintering temperature (1250, 1300, 1350, and 1400 oС) in 100 min and holding for ts = 1 h. The accuracy of measuring the temperature was ±6 oC. After sintering, the samples were subjected to annealing in vacuum (10-5 Torr) at 1000 oС, 2 h. As the reference samples, the coarse-grained alloys W-7%Ni-3%Fe obtained by sintering the coarse-grained powder compositions in hydrogen were used.
Method II was implemented using Dr. Sinter model SPS-625 setup (SPS SYNTEX Inc., Japan). The sintering of the samples of 30 mm in diameter and 4-4.5 mm in height was performed in vacuum (6 Pa) when applying a uniaxial pressure of 70 MPa. A single-stage sintering regime was used – heating with the rate of 100 oC/min up to the sintering temperature (1200 oC). The uniaxial pressure was applied simultaneously with the beginning of heating up. The holding at the sintering temperature was absent (ts = 0 min). The temperature was measured by an optical pyrometer Chino IR-AH (Japan) focused onto the surface of the graphite mold. The uncertainty of the temperature measurement was ±5 oC. As the reference samples, the nanopowders after HEBM subjected to annealing in hydrogen at 900 oC, 1 h in advance (before SPS) were used.
In the course of heating up, the effective shrinkage (Leff, mm) and shrinkage rate (Seff, mm/s) of the nanopowders were measured using a dilatometer. The contribution of the thermal expansion (L0, mm) of the graphite mold and punch was taken into account on the base of the results of experiments with empty mold. The temperature curves of shrinkage of the nanopowders (L, mm) were calculated according to the formula: L(T) = Leff(T) – L0(T).
The residual graphite was removed from the surfaces of the sintered samples of 30 mm in diameter by waterjet cleaning. The mechanical grinding was performed using Struers Secotom 10 setup, polishing – Buehler Automet 250 setup. In the course of mechanical treatment, the layers of ~300-350 μm, were removed from the sample surfaces, which an increased carbon concentration can be observed in due to high temperature interaction of the material with the graphite mold [47,48].
The microstructure investigations of the alloys were carried out using Leica IM DRM optical metallographic microscope, Jeol JSM-6490 scanning electron microscope (SEM), and TESCAN Vega 2 SEM with Oxford Instruments INCA 350 EDS microanalyzer. The density of the samples was measured by hydrostatic weighting in distilled water using Sartorius CPA balance. The uncertainty of measuring the density was ± 0.01 g/cm3. The magnitude of the theoretical density was accepted to be equal to ρth = 17.245 g/cm3. The analysis of the chemical composition was performed using Ultima 2 ICP atomic-emission spectrometer and Leco RHEN-602 analyzer. The X-ray diffraction (XRD) phase analysis was performed using Shimadzu XRD-700 diffractometer (CuKα emission, λ = 1.54056 Å, scan rate 0.5 o/min, exposure 2 s). The phase analysis of the samples was performed by Rietveld method. The contribution of the apparatus broadening into the XRD peaks was taken into account according to [45]. The analysis of internal stresses and calculation of the sizes of coherent scattering regions were performed by Williamson-Hall method [49].
To study the mechanical properties of the sintered samples, the stress-relaxation testing technique was used allowing determining the magnitudes of the macroelasticity stress (lattice friction stress) (σ0) and of the yield strength (σy) in the compression tests [45]. To measure σ0 and σy, the cylindrical samples of 3 mm in diameter and 6 in height were used. The uncertainties of measuring σ0 and σy were ±20 MPa. The microhardness (Hv) of the alloys was measured using HVS-1000 hardness tester at the load of 1 kg.
The magnitude of compressive dynamic ultimate strength (Ys) was investigated by Kolsky bar method using Hopkinson split rod at the strain rate of ~103 s-1 [50]. An example of a dynamic strain curve of a tungsten alloy is presented in Figure 1. The ballistic characteristics of the material were determined by measuring the penetration depth (H) of the sample of 3 mm in diameter and 25 mm long (Figure 2a) into a steel target of 30 in thickness. The penetration depth of the sample was measured on the metallographic cross-section with Leica IM DRM optical microscope using Good Grains software (Figure 2b). The uncertainty of determining the magnitude of H was ± 0.01 mm. The steel hardness was 27-30 HRC. The samples were accelerated with a 12 mm two-stage gas gun powered by compressed air. The impact angle of the sample with the steel plate was 90o. The test procedure was described in [46]. The samples for testing were cut out from the central parts of the workpieces of 30 mm in diameter by spark cutting in distilled water.

3. Results

3.1. Investigation of the Powders`

Figure 3 presents the images of the powders of W-7%Ni-3%Fe compositions in the initial state, after mixing in the FRITSCH® Pulverisette 6 planetary ball mill (32 h, Figure 3a) and after HEBM for different processing times (Figure 3b–f).
As one can see in the images presented in Figure 3, large enough micron-sized agglomerates consisting of several tens nanoparticles having splinter shapes (Figure 4a) or round one (Figure 4b) form in the course of HEBM.
The results of the XRD phase analysis shows the decrease in the intensity and broadening of the XRD peaks of α-W to take place in the course of HEBM (Figure 5a). No peaks corresponding to iron and nickel were visible in the XRD curves. It allows suggesting a strong fragmentation of the Ni and Fe particles to take place during HEBM.
A shift of the tungsten peaks towards greater diffraction anglers was observed (Figure 5b). The (110) α-W peak position in the initial coarse-grained powder corresponds to the diffraction angle 2Θmax = 40.26o ± 0.02o. After МА during tHEBM = 40 min, the (110) α-W XRD peak shifted by ~0.08-0.12o up to 2Θmax = 40.34-40.38o. According to Wulff-Bragg’s equation (2dhkl = nλCu·sin2Θhkl), this evidences the compressive internal stress fields to form in the tungsten nanoparticles in the course HEBM that leads to a decrease in the interplanar distances dhkl.
Note that one can see an asymmetry of the tungsten XRD peaks in Figure 5b – the (110) α-W peaks are broadened stronger towards greater diffraction angles 2Θ. After HEBM during 40 min, the half width at half maximum (HWHM) of the (110) α-W peak at small diffraction angles was Θ-0.5 ~ 0.30-0.32o whereas the one at large diffraction angles Θ-0.5 ~ 0.42-0.44o. In the initial state, the (110) α-W peaks were highly symmetric (Θ-0.5 ~ Θ+0.5 ~ 0.06-0.10o). According to [45], this result means that the nanoparticles after HEBM have a core-shell structure – a strain-induced dissolving of nickel and iron atoms in the surface layers of the α-W nanoparticles takes place during HEBM. It leads to the formation of the internal compressive stress fields in the surface layers of the α-W nanoparticles and, as a consequence, to the broadening of the α-W peaks towards greater diffraction angles.
The calculations of the coherent scattering region sizes (DXRD) according to Williamson-Hall model shows DXRD to decrease from ~80-100 nm down to ~20-25 nm with increasing tHEBM from 5 up to 40 min. The estimates obtained evidence the agglomerates shown in Figure 3 to consist of several tens or hundred tungsten particles in average.
It is worth to pay attention to a non-monotonous character of the dependence of the micro strain of the tungsten crystal lattice (ε) calculated according to Williamson-Hall method on the HEBM time. As one can see in Figure 5c, the maximum value εmax ~ 9·10-3 was achieved after 20 min of HEBM. At further increasing of the HEBM time, the magnitude of ε decreased down to ~ 6·10-3. So far, one can conclude essential compressive internal stress fields to form in the tungsten nanoparticles in the course of HEBM that leads to a strong distortion of the α-W crystal lattice (see [51]).
The investigations of the chemical composition have shown that the oxygen concentration in the nanopowders after HEBM reached 1.5-1.55%. These results agree qualitatively with the ones of [52] where an increase in the oxygen concentration in the tungsten powders after HEBM was observed also. After annealing in hydrogen at 900 oC (1 h), the oxygen concentration in the nanopowders decreased down to 0.8-0.95%. The parameters of the XRD peaks of α-W did not change after annealing in hydrogen.

3.2. Sintering the Nanopowders in Hydrogen

The investigations of the macrostructure of the samples have shown that the sintering of the nanopowders at 1450 at 1500 oC leads to formation of large pores (Figure 6). This leads to a decrease in the density of the samples sintered from the mechanically activated nanopowders (Table 3). Sintering at lower temperatures (1250, 1300, and 1350 oC) did not result in formation of the macropores. No macropores were observed when sintering the coarse-grained powders.
The chemical reaction of hydrogen with oxygen adsorbed on the nanopowder particle surfaces is the most probable origin of the macropore formation. This reaction goes with formation of water vapor: 2H2 + O2 = 2H2O (see [53]). The removing of the water vapor from the nanopowders pressed in advance is difficult that leads to an increase in the gas pressure inside the micropores and, as a consequence, to the formation of large macropores at elevated temperatures. The second factor promoting the macropore formation can be more intensive diffusion of hydrogen in the nanostructured HTAs. The investigations of the chemical composition have shown the hydrogen concentration in the samples sintered from the nanopowders reaches 83-97 ppm (Ts = 1450-1500 oC) while in the samples sintered from the coarse-grained powders, the hydrogen concentration varied from 2.6 to 11 ppm.
Table 2 presents the results of investigations of the density and mean grain sizes for the W-7%Ni-3%Fe alloy samples sintered in hydrogen at different temperatures. Figure 7 presents the microstructure of the HTA samples sintered in hydrogen from the coarse-grained powders and nanopowders.
The analysis of the results presented shows the increasing of the sintering temperature up to 1250 and 1400 oC to result in a smooth increase in the mean tungsten particle sizes up to ~1 μm and ~3-5 μm, respectively (Figure 7b,d). The mean grain sizes in the samples sintered from the nanopowders were less than the ones in the samples sintered from the coarse-grained powders but the alloy microstructure was nonuniform enough.
The macroscopic inhomogeneities of the specimen microstructure were observed at the initial stages of sintering at the sintering temperatures 1150-1200 oC (Figure 8a,b). The presence of such inhomogeneities may be caused by the presence of large agglomerates in the nanopowders after HEBM. The degree of the structure inhomogeneity decreases with increasing sintering temperature (Figure 8c).
The XRD phase analysis results shows the increasing of the sintering temperature to result in an increase in the intensity of the α-W XRD peaks; the asymmetry and the broadening of the peaks decrease essentially.
The increase in the mean grain sizes with increasing HTA sintering temperature from 1250 oC up to 1400 oC leads to worsening of the mechanical properties of the alloy – the hardness decreased from 7.9 down to 6.9 GPa, the macroelasticity stress – from 960 down to 300 MPa, and the yield strength – from 1370 down to 620 MPa. Note that the mechanical properties of the samples sintered from the nanopowders at Ts = 1250 and 1300 oC were better considerably than the ones of the samples sintered from the coarse-grained powders (Table 2). Further increasing of the annealing temperature (over 1350 oC) leads to a considerable decrease in the differences in the mechanical characteristics of the samples sintered from the coarse-grained and nanopowders.

3.3. Spark Plasma Sintering

Figure 9 presents the temperature curves of the shrinkage (Figure 9a,b) and the ones of the shrinkage rate (Figure 9c,d) of the nanopowders. Table 3 presents the results of investigations of the microstructure, density, and mechanical properties of these ones.
The analysis of the curves L(T) presented in Figure 9a shows the intensive shrinkage of the nanopowders to begin at lower temperatures as compared to the initial coarse-grained powders. The increasing of the HEBM time from 5 up to 20 min leads to a shift of the temperature of beginning of the intensive shrinkage stage from ~780-800 oC down to ~720 oC with simultaneous increase in the maximum shrinkage Lmax from ~2.6-2.7 mm up to 3.6-3.7 mm. The temperature of the end of the intensive shrinkage stage increases weakly with increasing tHEBM from 5 up to 20 min. Further increasing of the HEBM time up to 40 min leads to an increasing of the temperature of beginning of the intensive shrinkage stage up to ~750 oC and to decreasing of Lmax down to ~3.0-3.1 mm. Similar character of the dependence Lmax(tHEBM) was observed for the annealed nanopowders (Figure 9b).
As one can see in Figure 9b, the increasing of the HEBM time leads to a shift of the curve S(T) towards lower temperatures and to an increase in the maximum shrinkage rate Smax. As one can see in Figure 9b, the maximum shrinkage rate for the coarse-grained powders was observed at the temperatures ~1060-1080 oС; the shrinkage rate at that was Smax ~10-2 mm/s. The increasing of the HEBM time up to 20-40 min leads to increasing of Smax up to ~(1.1-1.2) 10-2 mm/s and to decreasing of the temperature corresponding to the maximum of the curve S(T) up to 850-890 oС. In the case of the annealed nanopowders, the maximum shrinkage rate Smax ~(1.3-1.4) 10-2 mm/s was observed at the sintering of the nanopowders subjected HEBM for 20 min.
The annealing in hydrogen affects the curves L(T) essentially and, to less extent, the curves S(T). Comparing Figure 9a and Figure 9b shows the annealing in hydrogen to result in an increasing of the shrinkage of the initial coarse-grained powders. The scale of increasing of the maximum shrinkage Lmax for the annealed nanopowders was ~0.1-0.15 mm and depended on the HEBM time weakly. The annealing of the nanopowders in hydrogen leads to an insufficient decrease in the temperature corresponding to the maximum of the curve S(T) and to weak increasing of the maximum shrinkage rate Smax.
It is interesting to note that the densities of the samples depend on the HEBM time non-monotonously. As one can see from Table 3, the increasing of tHEBM from 0 up to 20 min leads to a decrease in the density from 16.97 down to 15.68 g/cm3. After HEBM for 40 min, the densities of the samples increased up to 16.78 g/cm3. The dependence of density on the HEBM time for the samples sintered from the annealed nanopowders has similar character. It should be stressed here that the annealing resulted in an increase in the densities of the sintered samples in ~0.1-0.2 g/cm3.
The analysis of the results presented in Table 4 shows the increasing of the HEBM time leads to a decrease in the mean grain sizes in the alloys sintered at 1200 oC. The mean grain sizes in the alloys sintered from the annealed and non-annealed powders were close to each other (Figure 10).
The HTAs obtained by SPS have a uniform enough microstructure (Figure 10 and Figure 11), which few large grains are present in. These grains are the recrystallized microstructure areas with minimal γ-phase content (Figure 11). Such large grains were observed in the samples obtained from the nanopowders with tHEBM ≥ 10 min most often. The volume fraction and sizes of the abnormally large grains in the samples sintered from the annealed nanopowders were smaller considerably than the ones in the samples sintered form the non-annealed nanopowders (Figure 10). This result allows suggesting the presence of the agglomerates after HEBM and increased oxygen concentration in the nanopowders to be the most probable origins of the appearing of the abnormally large grains.
Figure 12 presents the results of XRD phase analysis of the samples obtained by SPS from the nanopowders. The analysis of the XRD curves presented shows the broadening of the α-W peaks in the sintered samples to be much lower than the one in the nanopowders after HEBM. The asymmetry of the α-W XRD peaks in the sintered samples was absent while the peak positions 2Θmax was shifted towards smaller diffraction angles as compared to the one in the nanopowder. No essential differences in the characteristics of the (110) α-W peaks for the samples sintered from the nanopowders subjected to HEBM of different times were observed (Figure 12b,c). This evidences the intragranular stresses formed in the tungsten powders during HEBM to relax in the course of sintering.
The low-intensity γ-phase peaks are visible in the XRD curves of the sintered samples. Such peaks were absent in the XRD curves of the nanopowders after HEBM (Figure 12b,c). The characteristics of the XRD peaks from the γ-phase almost do not depend on the HEBM time (Figure 12b,c).

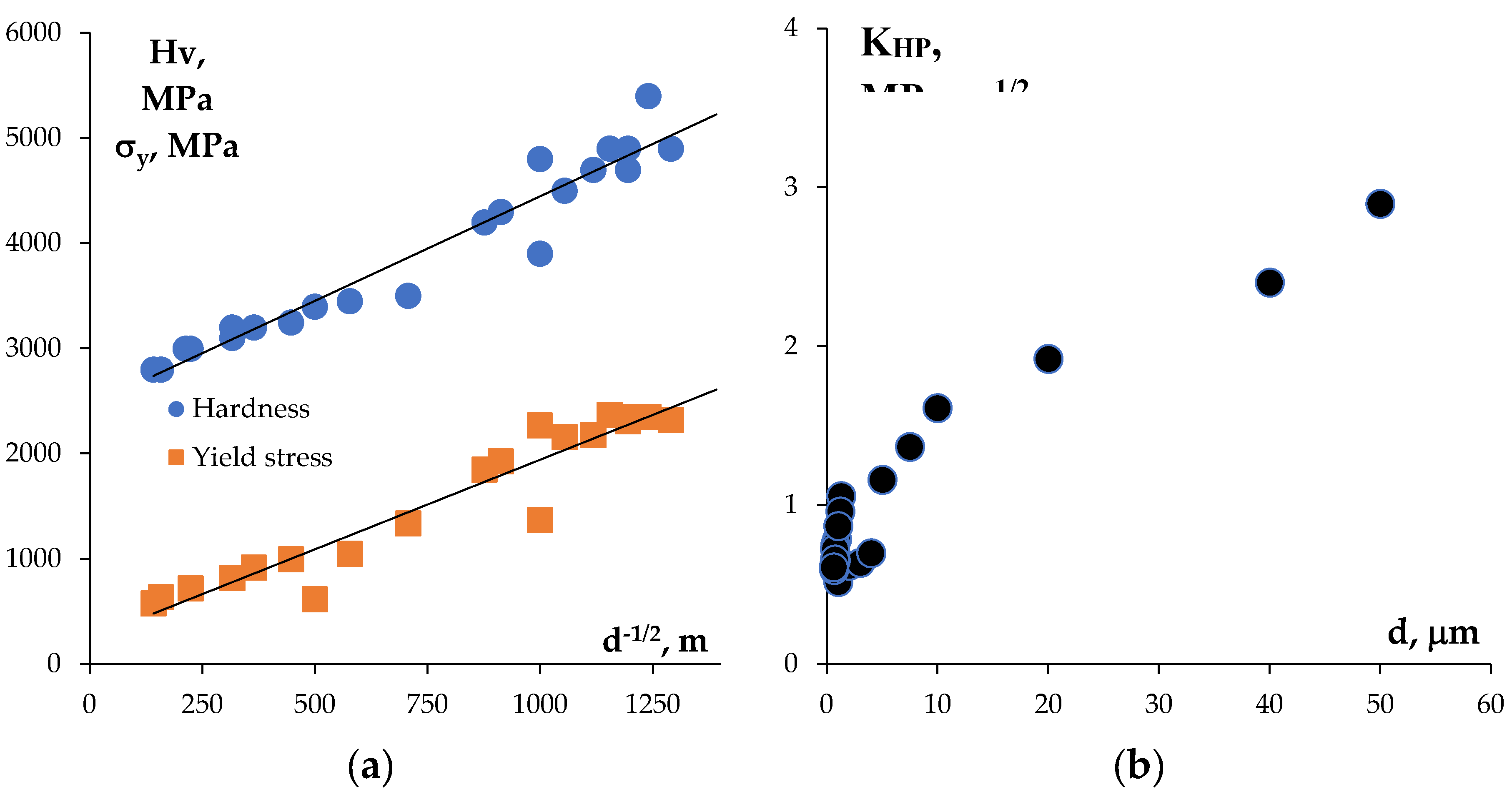
4. Discussion

The nonmonotonous dependence of the density of the samples obtained by SPS on the HEBM time (Figure 13) is one of the most interesting results obtained in the present work. The decrease in the alloy density from 98.4% down to 90.9% for the samples sintered from the non-annealed nanopowders and from 98.7% down to 94.6% for the ones sintered from the annealed nanopowders was observed when increasing HEBM time from 0 up to 20 min.
Note that large pores were absent in the microstructure of the sintered samples. The comparison of the microstructure of the samples sintered from the coarse-grained powders and from the nanopowders after tHEBM = 20 min (Figure 8 and Figure 9) did not reveal any essential increase in the sizes and volume fraction of the pores. So far, one can conclude that the decrease in the density of the alloy sintered from the nanopowders originates not from the increase in the volume fraction of the pores but from other factors. This conclusion is supported indirectly by the analysis of the curves L(T) and S(T) presented in Figure 7. As it has been shown above, the maximum values of the shrinkage Lmax and of the shrinkage rate Smax were observed in the case of SPS of the powders subjected to HEBM for 20 min.
To answer the question of the origin of the non-monotonous dependence of the density on the HEBM time, let us analyze the SPS mechanisms of the W-Ni-Fe nanopowders. First, it is worth noting that the characteristic sintering temperature Ts = 1200 oC is ~0.4Tm(W) and, according to [54], the diffusion intensity and the strain rate in tungsten are very low. (Here Tm(W) = 3695 K is the melting point of tungsten [54]).
As one can see in Figure 9a,b, the curve L(T) has usual three-stage character: the shrinkage of the nanopowders is finished almost completely within the intensive shrinkage stage (Stage II) in the temperature range from 750-800 oC to 1000-1050 oC. The intensity of shrinkage of the nanopowders within the third stage of sintering (Тs > 1000-1050 oC), which the grain growth occurs at often is very low.
The analysis of the compaction kinetics of the nanopowders at Stage II can be made using Young-Cutler model [55] developed for the analysis of the compaction curves of the fine-grained powders in the continuous heating regime. The Young-Cutler model [55] describes the initial stage of non-isothermic sintering of spherical particles in the conditions of simultaneous volume and grain boundary diffusion as well as plastic deformation processes. According to [55], the slope of the dependence ln(T∂ε/∂T) – Tm/T corresponds to the effective activation energy of the non-isothermic sintering process mQs2 where m is a numerical coefficient depending on the diffusion mechanism, Tm = Tm(Ni) = 1723 K is the melting point of the γ-phase [1,2]. The magnitude of m = 1/3 for the case of the grain boundary diffusion, m = 1/2 for the case of the volume diffusion in the crystal lattice, m = 1 for the case of the creep of the material [55].
The dependencies ln(T·∂ε/∂T) – Tm/T are presented in Figure 14. As one can see in Figure 14, the dependencies ln(T·∂ε/∂T) – Tm/T have usual two-stage character that confirms the correctness of application of the Young-Cutler model to analyze the sintering kinetics of the W-Ni-Fe alloy. The values of the effective sintering activation energy at the intensive shrinkage stage (mQs2) are presented in Table 4. The mean uncertainty of determining the activation energy mQs2 was ±0.2 kTm.
Table 4. SPS activation energies of nanopowders W-7%Ni-3%Fe.
Table 4. SPS activation energies of nanopowders W-7%Ni-3%Fe.
Nanopowders after HEBM Nanopowders after HEBM
and annealing in hydrogen
tHEBM,
min		 Stage II Stage III Stage II Stage III
mQs2,
kTm 		m Qs2,
kTm / kJ/mol		 Qs3,
kTm / kJ/mol		 mQs2,
kTm 		m Qs2,
kTm / kJ/mol		 Qs3,
kTm / kJ/mol
0 3.9 1/3 11.7 / 167 16.1 / 230 3.2 1/3 9.6 / 137 17.2 / 246
5 6.5 1 6.5 / 93 17.8 / 255 5.9 1 5.9 / 84 15.4 / 221
10 6.0 6.0 / 86 19.1 / 273 4.9 4.9 / 70 14.7 / 210
20 5.2 5.2 / 75 18.9 / 271 4.6 4.6 / 65 15.8 / 226
40 7.0 7.0 / 100 19.2 / 275 6.4 6.4 / 92 16.8 / 240
In the case of the coarse-grained powders, the magnitude of the effective SPS activation energy mQs2 was close to the activation energy of the grain boundary diffusion in nickel (Qb(Ni) = 115 kJ/mol [54]) at m = 1/3. This allows suggesting the kinetics of high-speed sintering of the coarse-grained powders W-7%Ni-3%Fe at the intensive shrinkage stage to be controlled by the intensity of the grain boundary diffusion in the γ-phase.
A good correspondence of the SPS activation energy of the nanopowders to the data on the activation energy of the diffusion processes reported in the literature was observed for m = 1 (Table 4). The value of m = 1 allows concluding the sintering kinetics of the nanopowders W-7%Ni-3%Fe to be determined by the Coble creep intensity. This conclusion agrees qualitatively with M.F. Ashby deformation-mechanism maps [54], in which the SPS regimes used in the present work correspond well to the creep area for nickel (stress σ = 70 MPa ~ 9⋅10-4G where G = 78.9 GPa [54] is the shear modulus for nickel, temperature 1200 oС). In our opinion, large lengths of the grain boundaries in the sintered materials is the origin of the realization of Coble creep mechanism in SPS of nanopowders since no intensive grain growth takes place at this sintering stage yet. Note also that the decreasing of the grain sizes would lead to an essential increase in the creep rate in the metal materials [56]. Note also that Coble creep is one of main compaction mechanisms in SPS of WC [57], WC-Co [58,59], and YAG:Nd-W [60] nanopowders.
Note that sometimes lower values of the activation energy of the grain boundary diffusion in fine-grained nickel are reported in the literature as well. In particular, the creep activation energy of 110-115 kJ/mol and the activation energy of the grain boundary diffusion of ~66 kJ/mol were reported for ultrafine-grained nickel with the grain sizes 0.3-0.5 μm [61].
The annealing of the nanopowders in hydrogen leads to a decrease in the SPS activation energy (Table 4). In our opinion, it originates from, first of all, the reduced concentration of oxygen adsorbed on the nanopowder particle surfaces. This leads to an increase in the diffusion creep rate in the nanopowders W-7%Ni-3%Fe at elevated temperatures. Thin tungsten oxide layers, which can form on the W nanoparticle surfaces when heating in vacuum can be another origin of decrease in the creep rate. The oxide nanoparticles located at the tungsten grain boundaries can lead to a decrease in the creep rate at the second SPS stage.
In the high temperature range, the slope of the dependence ln(T·∂ε/∂T) – Tm/T (Figure 14) becomes negative. It means that one has to use another approach to estimate the sintering activation energy in the higher temperature range. According to [62], one can estimate the activation energy at this stage using the model of diffusion dissolving of pores located near the grain boundaries in the fine-grained materials. The correctness of application of this procedure was demonstrated earlier in [45,60,63,64]. The activation energy at the non-isothermic sintering stage Qs3 can be determined from the slope of the dependence ρ(T)/ρth in the double logarithmic axes ln(ln(α⋅ρ/ρth/(1-ρ/ρth)) – Tm/T where α is the coefficient of compaction when pressing (α = 0.45 for nanopowders α-W) (Figure 15). The mean uncertainty of determining the activation energy Qs3 was ±1.5 kTm. The calculated values of Qs3 are presented in Table 4. For the annealed nanopowders, the value of Qs3 was ~2-3 kTm less than the one for the mechanically activated nanopowders.
The calculated values of the SPS activation energy correspond well to the activation energy of heterodiffusion of the tungsten atoms in the γ-phase (taking into account the corrections for the decrease in the activation energy of the grain boundary diffusion in the fine-grained materials [65]). Available data on sintering activation energies of W-Ni-Fe tungsten alloys give dramatically different values; Qs for W-8.4Ni-3.6Fe alloy is 250 kJ/mol according to [66], whereas reference [67] gives Qs = 367 kJ/mol for W-8.4Ni-3.6Fe alloy and 480 kJ/mol for 95W-3Ni-2Fe. In [68], the SPS activation energy for the fine-grained alloy W-5.6%Ni-1.4%Fe was shown to depend on the heating rate – at V < 30 oC/min the magnitude of Qs = 454 kJ/mol, at V > 200 oC/min the magnitude of Qs = 200 kJ/mol. The diffusion activation energy for 181W in nickel crystal lattice is Qv ~268-309 kJ/mol [8,69]. In the cases of the volume diffusion in the Ni-W system and in the γ-Fe-W one, the values of Qv are 295-306 kJ/mol and 268 kJ/mol, respectively [70,71]. So far, one can conclude the compaction of the W-Ni-Fe nanopowders at high temperatures to be determined by the intensity of the heterodiffusion of the tungsten atoms in the crystal lattice of the γ-phase.
Summarizing the results of analysis, one should stress that the intensive shrinkage of the mechanically activated nanopowders W-7%Ni-3%Fe goes at low temperatures and is characterized by small values of compaction activation energy. In our opinion, low activation energy of sintering in nanopowder materials is the origin of the reduction of the activation energy of sintering of the W-Ni-Fe nanopowders.
According to the theory of the nonequilibrium grain boundaries [65], the increasing of the free (excess) volume of the grain boundaries Δα is the origin of the decrease in the activation energy of the grain boundary diffusion in the strongly deformed fine-grained metals and alloys. The magnitude of Δα is proportional to the density of orientation mismatch dislocations (OMDs) captured by the grain boundaries during severe plastic deformation. In the course of HEBM, the grinding of the γ-phase particles with the FCC lattice is difficult due to high ductility of these ones. In the course of HEBM, the grinding of the γ-phase particles and the accumulation of the OMDs at the grain boundaries take place [65]. The diffusion permeability of the γ-phase grain boundaries after HEBM appears to be higher than the one of “conventional” grain boundaries in the γ-phase formed during sintering individual γ-phase particles to each other. The enhanced diffusion permeability of the nonequilibrium grain boundaries to accelerated diffusion of the tungsten atoms in the γ-phase, and to enhanced Coble creep rate. These factors will lead to a decrease in the SPS activation energy of the nanopowders W-Ni-Fe.
The second factor promoting the decrease in the activation energy of the SPS of nanopowders can be the nonequilibrium state of their crystal lattice.
As it has been shown above, the asymmetric distortion of the (110) α-W XRD peak towards higher reflection angles after HEBM was observed. In our opinion, it means that the crystal lattice constant in the surface layers of the W particles appears to be smaller than the one in the central parts of the W particles. So far, the asymmetry of the (110) α-W XRD peak originates from the increase in the concentrations of the Ni and Fe atoms in the surface layers of the α-W particles. the concentrations of the Ni and Fe atoms in the surface layers of the α-W nanoparticles and from the increase in the concentration of the W atoms in the γ-phase particles with the nonequilibrium grain boundaries.
Tungsten is known to have a high solubility in nickel. At elevated temperatures, the concentration of the W atoms in the γ-phase can reach 25-28% [4]. Partial dissolving of the α-W nanopowders in the γ-phase takes place during sintering that leads to a decrease in the density of the sintered W-Ni-Fe samples. This process can be accelerated by larger specific surface area of the α-W nanoparticles, strong distortion of the crystal lattice in the surface layers of the α-W nanoparticles, and high diffusion permeability of the γ-phase nonequilibrium grain boundaries.
Now, let us consider the origins of the non-monotonous dependence of the density of the W-7%Ni-3%Fe alloy on the HEBM time (Figure 13). This effect was observed, in particular, for the nanopowders annealed in hydrogen and, consequently, its nature is not related to the oxidation of the nanopowders in the course of storing.
The primary origin of the decrease in the alloy density is the strain-stimulated dissolving of the W atoms in the γ-phase lattice during HEBM. This effect can have a considerable scale for the W-7%Ni-3%Fe alloy since the volume fraction of the γ-phase in this alloy exceeds 20%. The increasing of the HEBM time lead to an increase in the volume fraction of the tungsten particles dissolved in the γ-phase. The decrease in the initial density of the W-Ni-Fe nanopowders would lead to a decrease in the final density of the alloy at given sintering regimes provided all other conditions being equal.
It is worth noting that the acceleration of the grain boundary diffusion processes and the increase in the creep rate should lead to an increase in the rate of solid phase sintering of the W-Ni-Fe nanopowders. This effect would compensate partly the negative effect of HEBM on the density of the W-7%Ni-3%Fe alloy.
The question of the origins of the increase in the SPS activation energy at long HEBM times (tHEBM = 40 min) is more complex. In our opinion, this effect is caused simultaneously by three factors.
First, it is worth noting that the intensity of the strain-induced dissolving of the tungsten particles can decrease at long HEBM times due to the achievement of the solubility limit of W in the γ-phase. In this case, the increasing of the HEBM time leads to an increase in the creep rate due to an increase in the nonequilibrium degree of the grain boundaries in the γ-phase and a decrease in the grain sizes in the alloy.
The analysis of the XRD phase analysis results shows that the micro-strain of the α-W crystal lattice begins to decrease after 40 min of HEBM (Figure 5b). This effect can originate from the decrease in the concentrations of the Ni and Fe atoms in the surface layers of the α-W nanoparticles as well as from the decrease in the dislocation density in the α-W particles. The heating of the powders during HEBM is the most probable origin of this effect. The increase in the temperature during HEBM will reduce the distortion degree of the α-W crystal lattice and, as a consequence, the tendency of the nanoparticles to dissolving in the strongly deformed γ-phase. It will lead in an increase in the density of the tungsten alloy.
The increase in the density of agglomerates after 40 min of HEBM is the third probable origin. The increase in the density of agglomerates can originate from the intensive plastic deformation of the tungsten nanoparticles during HEBM as well as from the heating of the samples. The increase in the packing density of the nanoparticles inside the agglomerates will lead to an increase in the initial density of the powder composition W-Ni-Fe and, as a consequence, will provide an opportunity to achieve a higher final density of the tungsten alloy when sintering in the same conditions.
Finally, let us discuss briefly the results of investigations of the mechanical properties of the HTAs. As one can see in Figure 16a, the dependencies of hardness and yield strength on the grain size can be described by Hall-Petch relation with a good accuracy. Traditionally, the dependence of the strength characteristics on the grain size in the coarse-grained HTAs is suggested to have more complex character. In particular, the magnitudes of the ultimate strength and of the yield strength in the tension tests depend strongly on the volume fraction of the γ-phase particles as well as on the relations of the lengths of the intergranular boundaries W-W and the ones of the interphase boundaries W-γ [5,11,31,32]. The realization of Hall-Petch effect in the ultrafine-grained HTAs can be a consequence of considerably greater lengths of the grain boundaries that leads to the proportional decrease in the sizes (thicknesses) of the interphase boundaries α-W - γ-phase.
Knowing the magnitudes of the yield strength σy, of the macroelasticity stress σ0, and of the grain size d one can calculate Hall-Petch coefficient according to the formula KHP = (σy - σ0)⋅d1/2 for each alloy reflected in Table 2 and Table 3. Figure 16b presents the dependence of KHP on the grain size. As one can see in Figure 16b, the increasing of the sintering temperature and the grain growth lead to an increase in Hall-Petch coefficient. The maximum magnitudes of KHP were achieved in the HTAs sintered at 1450 and 1500 oC (Table 2). In our opinion, this evidences an increase in the adhesion strength of the interphase boundaries with increasing sintering temperature. The increasing of the concentration of the W atoms in the γ-phase can also contribute additionally into the increase in KHP.
No essential differences in the magnitudes of KHP for the alloys obtained from the non-annealed and annealed nanopowders were observed. This allows suggesting the differences in the strength characteristics of the HTAs observed to originate from, first of all, the differences in the grain sizes.

5. Conclusions

1. High Energy Ball Milling (HEBM) of the W-Ni-Fe powders leads to grinding of the tungsten particles and to formation of supersaturated solid solution of W atoms in the γ-phase. After the HEBM, the W nanoparticles have a core – shell structures, which have high concentrations of Ni and Fe atoms in the surface layers of the α-W nanoparticles. This leads to broadening and asymmetry of the α-W XRD peaks.
2. The SPS kinetics for initial fine powders W-7%Ni-3%Fe is governed by the intensity of grain boundary diffusion in the γ-phase. SPS was shown to allow obtaining the samples with increased density, small grain sizes (~1.2-1.3 μm), and increased hardness (4.2-4.3 GPa) as compared to the samples obtained by conventional sintering the fine-grained powders in hydrogen.
3. The SPS kinetics of the nanopowders has two-stage character owing to intensive diffusion Coble creep in the low temperature range and intensive diffusion of W atoms in the crystal lattice of the γ-phase at elevated temperatures. The SPS activation energy in the low heating temperature range is small that originates from the nonequilibrium state of the grain boundaries in the γ-phase with an increased density of defects arising during the HEBM. The recrystallization process in the γ-phase is a possible origin of the change of the diffusion mechanism responsible for the intensity of the nanopowder compaction process in SPS.
4. The relative density of HTAs obtained by SPS was shown to depend on the HEBM time non-monotonously (with a minimum). It was suggested that the effect of reduction of the density is caused by the formation of strongly supersaturated solid solutions of Ni and Fe in the tungsten particles.
5. Annealing the nanopowders in hydrogen was shown to result in a decrease in the sintering activation energy and in an increase in the density of the sintered HTAs. It originates from the decreasing of the oxygen concentration in the nanopowders and an increasing of the Coble diffusion creep rate in SPS.
6. The dependencies of the yield strength and of the hardness on the grain size is described by Hall-Petch equation with a good accuracy. The maximum values of Hall-Petch coefficient were observed for the alloys sintered in hydrogen at elevated temperatures (1450, 1500 oC). This originates from a high adhesion strength of the interphase boundaries as well as probably from the increased concentration of the tungsten atoms in the γ-phase.

Author Contributions

Conceptualization, N.V.M.1 and A.V.N.; methodology, N.V.M.1 and A.V.N.; formal analysis, N.V.M.1, V.N.C. and A.V.N.; investigation, N.V.M.1, N.V.M.2, A.M.B., A.R.F., M.S.B., E.A.L., N.V.S.; resources, V.N.C.; data curation, N.V.M.1 and A.V.N.; writing—original draft preparation, N.V.M.1, V.N.C. and A.V.N.; writing—review and editing, N.V.M.1, V.N.C. and A.V.N..; visualization, N.V.M.1 and A.V.N.; supervision, V.N.C.; project administration, N.V.M.1; funding acquisition, N.V.M.1 All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Russian Science Foundation, grant number 22-79-10080.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

LPS—conventional liquid phase sintering; CG—coarse-grained (alloy); GB—grain boundary; HTA—heavy tungsten alloy; HEBM—high energy ball milling; MA—mechanical activation; OMDs—orientation mismatch dislocations; SEM—scanning electron microscopy; SPS—Spark Plasma Sintering; UFG—ultrafine-grained (alloy); XRD—X-ray diffraction (phase analysis).

Appendix A

Table A1. Microstructure parameters and mechanical properties of HTAs obtained by SPS / FAST.
Table A1. Microstructure parameters and mechanical properties of HTAs obtained by SPS / FAST.
Ref. Alloy (wt.%) SPS modes Characteristics of the HTA Note 2
Ts,
oC		 V,
oC/min		 P,
MPa		 ts,
min		 Density
(ρ)		 d, μm Mechanical properties 1
[22] W-4Ni-2Co-1Fe 1200- 1400 - 30 6 16.78 g/cm3 0.34 84.3 HRA
σts = 968 MPa		 R0 = 120 nm
tHEBM = 15 h, 226 r/min
[23] W-5.6Ni-1.4Fe 1230 90 50 0 16.3 g/cm3 (~92%) 0.72 No data R0 = 6 nm
tHEBM = 40 h, 226 rpm.
Add: Ni2W4C, Fe6W6C
[24] W-5.6Ni-1.4Fe 1410 90 30 0 99.4% ~2 No daa R0 = 2.44 μm
[25] W-5.6Ni-1.4Fe 1360 380 30 0 94.8% 6.0 σy = 1050 MPa
σb = 1580 MPa
418 HV1 		R0 = 2.44 μm
[26] W-5.6Ni-1.4Fe 1400 105 30 2 ~98% 4.4 σb = 1700 MPa
418 HV1 		-
+ cyclic heat treatment 1400 oC ~98% ~6 σb = 1780 MPa
489 HV1
[27] W-7Ni-3Fe 1150 100 50 8 96.12% 5-10 σb = 1020 MPa
68-69 HRA		 R0 =1-3 μm 3
tHEBM = 5 h, 266 rpm.
Add: WC, NiW
[28] W-5.6Ni-1.4Fe 1320 90 30 0-45 ~96% 4-7 No data R0 = 2.44 μm
[29] W-2Mo-7Ni-3Fe 1200 100 50 8 96.42% 4-5 σb = 922 MPa
73.8 HRA		 R0 =1-3 μm 3
tHEBM = 40 h, 800 rpm.
Add: NiW, Ni2W4C, WC
[30] W-8Ni-2Fe 1000 100 30 0 80.84% 10-20 σy = 586 MPa
σb = 975 MPa
63 HRA		 D90 =6.3 μm3
tHEBM = 40 h, 260 rpm
W-8Ni-2Fe-6Mo 84.61% 5-20 σy = 784 MPa
σb = 1025 MPa
65 HRA
W-8Ni-2Fe-12Mo 86.34% 10-20 σy = 825 MPa
σb = 1120 MPa
68 HRA
W-8Ni-2Fe-18Mo 93.12% 10-20 σy = 950 MPa
σb = 1160 MPa
72 HRA
W-8Ni-2Fe-24Mo 94.25% 15-20 σy = 998 MPa
σb = 1250 MPa
75 HRA
[31] W-7Ni-3Fe 1100 100 30 2 68.57% 11.45 σy = 475 MPa
138 HV0.5 		D90 =6.2 μm3
tHEBM = 30 min (in the mortar)
W-7Ni-3Fe-0.25La2O3 87.95% 10.66 σy = 497 MPa
357 HV0.5
W-7Ni-3Fe-0.50La2O3 76.83% 9.76 σy = 822 MPa
370 HV0.5
W-7Ni-3Fe-0.755La2O3 75.51% 8.88 σy = 952 MPa
397 HV0.5
W-7Ni-3Fe-1La2O3 70.44% 7.89 σy = 1110 MPa
533 HV0.5
[32] W-7Ni-3Fe-0.5SiC 1400 100 50 5 93.95% 10-20 σy = 1068 MPa
443 HV0.5 		R0 = 10 μm 3
tHEBM = 1 h + pressed
600 MPa
W-7Ni-3Fe-1SiC 90.98% 5-20 σy = 810 MPa
458 HV0.5
W-7Ni-3Fe-1.5SiC 85.05% 5-20 σy = 708 MPa
532 HV0.5
W-7Ni-3Fe-2SiC 82.86% 5-10 σy = 729 MPa
564 HV0.5
[33] W-7Ni-3Fe 1000 100 50 8 ~93% < 1 σy = 954.5 MPa
79.3 HRA		 R0 = 2.3-2.7 μm 3
tHEBM = 40 h, 266 rpm
1250 ~87% 3-5 σy = 353.6 MPa
63.8 HRA
[34] W-2Mo-6Ni-2.5Fe
-1.5Co		 1000 100 50 8 90.68% ~2 σb = 595 MPa
76.14 HRA		 R0 =1-3 μm 3
tHEBM = 20 h, 220 rpm
1250 98.93% 5.4 σb = 1040 MPa
71.43 HRA
[35] W-5.6Ni-2.4Fe 1400 100 30 - ~84.8% 12.3 σy = 686 MPa
σt = 975 MPa
385 HV0.5 		R0 = 10 μm 3
tHEBM = 1 h
Add: Ni-W
W-5.6Ni-2.4Fe-0.5Co 93.365 11.56 σy = 770 MPa
σt = 961 MPa
455 HV0.5
W-5.6Ni-2.4Fe-1Co ~90.5% 9.48 σy = 1300 MPa
σt = 1508 MPa
467 HV0.5
W-5.6Ni-2.4Fe-1.5Co ~87% 9.68 σy = 1080 MPa
σt = 1330 MPa
471 HV0.5
W-5.6Ni-2.4Fe-2Co ~83% 11.1 σy = 1000 MPa
σt = 1256 MPa
499 HV0.5
[36] W-21Ni-9Fe 1250 100 40 4 98.6 ~10 σt = 890 MPa
25.6 HRC		 tHEBM = 4 h,
400 rpm
[37] W-5.6Ni-1.4Fe 1050-1100 100 50 5 98.12 0.871 σb = 987 MPa
84.3 HRA		 R0 =100 nm3
tHEBM = 6 h,
300 rpm
[38] W-2Mo-7Ni-3Fe 1150 100 50 8 No data ~2 σb = 390.1 MPa
69-70 HRA		 R0 =1-3 μm 3
tHEBM = 40 h,
266 rpm
Add: Ni2W4C
1 σts – transverse rupture strength, σb – bending strength, σy – yield strength, σt – tensile strength. 2 R0 is the initial particle size, Add – there are auxiliary phases in the specimens. 3 the initial particle size of the α-W.

References

  1. Green, E.C.; Jones, D.J.; Pitkin, W.R. Developments in high-density alloys. Proc. Symp. Powder Metall. 1954, 58, 253–256. [Google Scholar]
  2. Krock, R.; Shepard, H. Mechanical behavior of the two-phase composite tungsten-nickel-iron. Trans. Metall. Soc. AIME 1963, 227, 1127–1134. [Google Scholar]
  3. Das, J.; Rao, G.A.; Pabi, S.K. Microstructure and mechanical properties of tungsten heavy alloys. Mater. Sci. Eng. A. 2010, 527, 7841–7847. [Google Scholar] [CrossRef]
  4. Povarova, K.B.; Makarov, P.V.; Ratner, A.D.; Zavarzina, E.K.; Volkov, K.V. VNZH-90-type heavy alloys. I. Eff. Alloying Cond. Fabr. Tungsten Powders Their Struct. Prop. Sintered Alloys. Russ. Metall. 2002, 4, 39–48. (In Russian) [Google Scholar]
  5. Sahin, Y. Recent progress in processing of tungsten heavy alloys. J. Powder Technol. 2014, 764306. [Google Scholar] [CrossRef]
  6. Ishchenko, A.N. Afanas’eva, S.A.; Belov, N.N.; Burkin, V.V.; Galsanov, S.V.; Kasimov, V.Z.; Kudryavtsev, V.A.; Lipatnikova, Y.D.; Martsunova, L.S.; Rogaev, K.S.; Sammel’, A.Y.; et al. Destruction features of impactors made of a porous alloy based on tungsten with reinforcing filler when interacting with armored obstacles. Tech. Phys. 2020, 65, 414–419. [Google Scholar] [CrossRef]
  7. Luo, R.; Huang, D.; Yang, M.; Tang, E.; Wang, M.; He, L. Penetrating performance and “self-sharpening” behavior of fine-grained tungsten heavy alloy rod penetrators. Mater. Sci. Eng. A 2016, 675, 262–270. [Google Scholar] [CrossRef]
  8. Ravi Kiran, U.; Panchal, A.; Sankaranarayana, M.; Nandy, T.K. Tensile and impact behavior of swaged tungsten heavy alloys processed by liquid phase sintering. Int. J. Refract. Met. Hard Mater. 2013, 37, 1–11. [Google Scholar] [CrossRef]
  9. Ravi Kiran, U.; Sambasiva Rao, A.; Sankaranarayana, M.; Nandy, T.K. Swaging and heat treatment studies on sintered 90W-6Ni-2Fe-2Co tungsten heavy alloy. Int. J. Refract. Met. Hard Mater. 2012, 33, 113–121. [Google Scholar] [CrossRef]
  10. Gong, X.; Fan, J.L.; Ding, F.; Song, M.; Huang, B.Y.; Tian, J.M. Microstructure and highly enhanced mechanical properties of fine-grained tungsten heavy alloy after one-pass rapid hot extrusion. Mater. Sci. Eng. A 2011, 528, 3646–3652. [Google Scholar] [CrossRef]
  11. Yu, Y.; Zhang, W.; Chen, Y.; Wang, E. Effect of swaging on microstructure and mechanical properties of liquid-phase sintered 93W-4.9(Ni,Co)-2.1Fe alloy. Int. J. Refract. Met. Hard Mater. 2014, 44, 103–108. [Google Scholar] [CrossRef]
  12. Das, J.; Kiran, U.R.; Chakraborty, A.; Prasad, N.E. Hardness and tensile properties of tungsten based heavy alloys prepared by liquid phase sintering technique. Int. J. Refract. Met. Hard Mater. 2009, 27, 577–583. [Google Scholar] [CrossRef]
  13. Mazilkin, A.A.; Straumal, B.B.; Protasova, S.G.; Bulatov, M.F.; Baretzky, B. Pseudopartial wetting of W/W grain boundaries by the nickel-rich layers. Mater. Lett. 2017, 192, 101–103. [Google Scholar] [CrossRef]
  14. Luo, J.; Gupta, V.K.; Yoon, D.H.; Meyer, H.M. Segregation-induced grain boundary premelting in nickel-doped tungsten. Appl. Phys. Lett. 2005, 87, 231902. [Google Scholar] [CrossRef]
  15. Fortuna, E.; Sikorsky, K.; Kurzydlowski, K.J. Experimental studies of oxygen and carbon segregation at the interfacial boundaries of a 90W-7Ni-3Fe tungsten heavy alloy. Mater. Charact. 2004, 52, 323–329. [Google Scholar] [CrossRef]
  16. Krasovskii, P.V.; Samokhin, A.V.; Fadeev, A.A.; Sinayskiy, M.A.; Sigalev, S.K. Alloying effects and composition inhomogeneity of plasma-created multimetallic nanopowders: A case study of the W-Ni-Fe ternary system. J. Alloys Compd. 2018, 250, 265–275. [Google Scholar] [CrossRef]
  17. Parabhu, G.; Kumar, N.A.; Sankaranarayana, M.; Nandy, T.K. Tensile and impact properties of microwave sintered tungsten heavy alloys. Mater. Sci. Eng. A 2014, 607, 63–70. [Google Scholar] [CrossRef]
  18. Gryaznov, M.; Samokhin, A.; Chuvil’deev, V.; Fadeev, A.; Alekseev, N.; Shotin, S.; Dorofeev, A.; Zavertyaev, A. Method of W-Ni-Fe composite spherical powder production and the possibility of its application in Selective Laser Melting technology. Metals 2022, 12, 1715. [Google Scholar] [CrossRef]
  19. Chen, H.; Ye, L.; Han, Y.; Chen, C.; Fan, J. Additive manufacturing of W-Fe composites using laser metal deposition: Microstructure, phase transformation, and mechanical properties. Mater. Sci. Eng. A 2021, 811, 141036. [Google Scholar] [CrossRef]
  20. Chen, H.; Zi, X.; Han, Y.; Dong, J.; Liu, S.; Chen, C. Microstructure and mechanical properties of additive manufactured W-Ni-Fe-Co composite produced by selective laser melting. Int. J. Refract. Met. Hard Mater. 2020, 86, 105111. [Google Scholar] [CrossRef]
  21. Liu, W.; Ma, Y.; Zhang, J. Properties and microstructural evolution of W-Ni-Fe alloy via microwave sintering. Int. J. Refract. Met. Hard Mater. 2012, 35, 138–142. [Google Scholar] [CrossRef]
  22. Krasovskii, P.V.; Samokhin, A.V.; Fadeev, A.A.; Sinayskiy, M.A.; Sigalev, S.K. Alloying effects and composition inhomogeneity of plasma-created multimetallic nanopowders: A case study of the W-Ni-Fe ternary system. J. Alloys Compd. 2018, 750, 265–275. [Google Scholar] [CrossRef]
  23. Tokita, M. Progress of Spark Plasma Sintering (SPS): Method, Systems, Ceramics Applications and Industrialization. Ceramics 2021, 4, 160–198. [Google Scholar] [CrossRef]
  24. Mukasyan, A.S.; Rogachev, A.S.; Moskovskikh, D.O.; Yermekova, Zh.S. Reactive spark plasma sintering of exothermic systems: A critical review. Ceram. Int. 2022, 48, 2988–2998. [Google Scholar] [CrossRef]
  25. Munir, Z.A.; Anselmi-Tamburini, U.; Ohyanagi, M. The effect of electric field and pressure on the synthesis and consolidation materials: A review of the spark plasma sintering method. J. Mater. Sci. 2006, 41, 763–777. [Google Scholar] [CrossRef]
  26. Olevsky, E.; Dudina, D. Field-Assisted Sintering. Springer Int. Publ., 2018. [CrossRef]
  27. Chuvildeev, V.N.; Panov, D.V.; Boldin, M.S.; Nokhrin, A.V.; Blagoveshchensky, Yu.V.; Sakharov, N.V.; Shotin, S.V.; Kotkov, D.N. Structure and properties of advanced materials obtained by Spark Plasma Sintering. Acta Astronaut. 2015, 109, 172–176. [Google Scholar] [CrossRef]
  28. Li, X.; Xin, H.; Hu, K.; Li, Y. Microstructure and properties of ultra-fine tungsten heavy alloys prepared by mechanical alloying and electric current activated sintering. Trans. Nonferrous Met. Soc. China 2010, 20, 443–449. [Google Scholar] [CrossRef]
  29. Hu, K.; Zheng, D.; Li, Y. SPS densification behavior of W-5.6Ni-1.4Fe heavy alloy powders. Rare Met. 2011, 30, 581–587. [Google Scholar] [CrossRef]
  30. Hu, K.; Li, X.-q.; Yang, Ch.; Li, Y.-y. Densification and microstructure evolution during SPS consolidation process in W-Ni-Fe system. Trans. Nonferrous Met. Soc. China 2011, 21, 493–501. [Google Scholar] [CrossRef]
  31. Li, Y.; Hu, K.; Li, X.; Qu, Sh. Fine-grained 93W-5.6Ni-1.4Fe heavy alloys with enhanced performance prepared by spark plasma sintering. Mater. Sci. Eng. A 2013, 573, 245–252. [Google Scholar] [CrossRef]
  32. Li, X.; Hu, K.; Qu, Sh.; Yang, Ch. 93W-5.6Ni-1.4Fe heavy alloys with enhanced performance prepared by cyclic spark plasma sintering. Mater. Sci. Eng. A 2014, 599, 233–241. [Google Scholar] [CrossRef]
  33. Xiang, D.P.; Ding, L.; Li, Y.Y.; Chen, G.B.; Zhao, Y.W. Preparation of fine-grained tungsten heavy alloys by spark plasma sintered W-7Ni-3Fe composite powders with different ball milling time. J. Alloys Compd. 2013, 562, 19–24. [Google Scholar] [CrossRef]
  34. Hu,K. ; Li, X.; Qu, S.; Li, Y. Spark-Plasma Sintering of W-5.6Ni-1.4Fe heavy alloys: Densification and grain growth. Metall. Mater. Trans. A 2013, 44, 923–933. [Google Scholar] [CrossRef]
  35. Xiang, D.P.; Ding, L.; Li, Y.Y.; Chen, X.Y.; Zhang, T.M. Fabricating fine-grained tungsten heavy alloy by spark plasma sintering of low-energy ball-milled W-2Mo-7Ni-3Fe powders. Mater. Sci. Eng. A 2013, 578, 18–23. [Google Scholar] [CrossRef]
  36. Prasad, B.S.L.; Annamalai, R. A study of molybdenium addition on W-Ni-Fe based heavy alloys sintered with spark plasma sintering. Bull. Pol. Acad. Science. Tech. Sci. 2019, 67, 167–172. [Google Scholar] [CrossRef]
  37. AyyappaRaj, M.; Yadav, D.; Agrawal, D.K.; Rajan, R.A.A. Microstructure and mechanical properties of spark plasma-sintered La2O3 dispersion-strengthened W-Ni-Fe alloy. Rare Met. 2020. [Google Scholar] [CrossRef]
  38. Chaurasia, J.K.; Muthuchamy, A.; Patel, P.N.; Annamalai, A.R. Densification of SiC particle reinforced W-Ni-Fe heavy alloy composites through conventional and Spark Plasma Sintering. Trans. Indian Inst. Met. 2017, 70, 2185–2191. [Google Scholar] [CrossRef]
  39. Ding, L.; Xiang, D.P.; Li, Y.Y.; Li, C.; Li, J.B. Effects of sintering temperature on fine-grained tungsten heavy alloy produced by high-energy ball milling assisted spark plasma sintering. Int. J. Refract. Met. Hard Mater. 2012, 33, 65–69. [Google Scholar] [CrossRef]
  40. Ding, L.; Xiang, D.P.; Pan, Y.L.; Li, Y.Y. Mechanical properties and microstructural evolution of Mo-Co-co-strengthened W-Ni-Fe alloys by spark plasma sintering. J. Alloys Compd. 2017, 712, 593–598. [Google Scholar] [CrossRef]
  41. Senthilnathan, N.; Raja Annamalai, A.; Venkatachalam, G. Microstructure and mechanical properties of spark plasma sintered tungsten heavy alloys. Mater. Sci. Eng. A 2018, 710, 66–73. [Google Scholar] [CrossRef]
  42. Wu, Y.; Li, Y.; Yu, D. Fine-grained W-Ni-Fe heavy alloys prepared by Spark Plasma Sintering. Mater. Sci. Forum 2016, 849, 745–752. [Google Scholar] [CrossRef]
  43. Jingang, Z.; Weimin, W.; Wei, J.; Qianglong, H.; Aiang, W.; Lin, T.; Kai, Y. Ultrafine grain tungsten heavy alloys with excellent performance prepared by Spark Plasma Sintering. J. Wuhan Univ. Technol. – Mater. Sci. Ed. 2020, 35, 393–398. [Google Scholar] [CrossRef]
  44. Ding, L.; Xiang, D.P.; Li, Y.Y.; Zhao, Y.W.; Li, J.B. Phase, microstructure and properties evolution of fine-grained W-Mo-Ni-Fe alloy during spark plasma sintering. Mater. Des. 2012, 37, 8–12. [Google Scholar] [CrossRef]
  45. Chuvil’deev, V.N.; Nokhrin, A.V.; Boldin, M.S.; Baranov, G.V.; Sakharov, N.V.; Belov, V.Yu.; Lantsev, E.A.; Popov, A.A.; Melekhin, N.V.; Lopatin, Yu.G.; Blagoveshchenskiy, Yu.V.; Isaeva, N.V. Impact of mechanical activation on sintering kinetics and mechanical properties of ultrafine-grained 95W-Ni-Fe tungsten heavy alloys. J. Alloys Compd. 2019, 773, 666–688. [Google Scholar] [CrossRef]
  46. Bragov, A.M.; Chuvil’deev, V.N.; Melekhin, N.V.; Filippov, A.R.; Konstantinov, А.Y.; Sakharov, N.V. Dynamic strength of heavy 90W-7Ni-3Fe alloy produced by Spark Plasma Sintering. Phys. Mesomech. 2019, 22, 307–312. [Google Scholar] [CrossRef]
  47. Dudina, D.V.; Bokhonov, B.B.; Ukhina, A.V.; Anisimov, A.G.; Mali, V.I.; Esikov, M.A.; Batraev, I.S.; Kuznechik, O.O.; Pilinevich, L.P. Reactivity of materials towards carbon of graphite foil during Spark Plasma Sintering: A case study using Ni-W powders. Mater. Lett. 2016, 168, 62–67. [Google Scholar] [CrossRef]
  48. Bokhonov, B.B.; Ukhina, A.V.; Dudina, D.V.; Anisimov, A.G.; Mali, V.I.; Batraev, I.S. Carbon uptake during Spark Plasma Sintering: Investigation through the analysis of the carbide “footprint” in a Ni-W alloy. RSC Adv. 2015, 98, 80228–80237. [Google Scholar] [CrossRef]
  49. Williamson, G.K.; Hall, W.M. X-ray line broadening from aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
  50. Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Society. Sect. B 1949, 62, 676–700. [Google Scholar] [CrossRef]
  51. Savenko, V.I.; Toropov, Y.P.; Chernyshev, V.V.; Malkin, A.I. Microstructure and properties of surface-modified tungsten powders mechanically activated in different media. Phys. Met. Metallogr. 2017, 118, 1066–1072. [Google Scholar] [CrossRef]
  52. Duan, B.; Zhou, T.; Yang, G.; Yang, D.; Wang, D. Microstructures and properties of 90W-4Ni-6Mn alloy prepared by vacuum sintering. Mater. Res. Express 2020, 7, 036522. [Google Scholar] [CrossRef]
  53. Farooq, S.; Kemp, P.B.; German, R.M.; Base, A. Effect of initial oxygen content and sintering atmosphere dew point on the properties of tungsten based heavy alloys. Int. J. Refract. Met. Hard Mater. 1989, 8, 236–243. [Google Scholar]
  54. Frost, H.J.; Ashby, M.F. Deformation-mechanism maps; Pergamon Press: London, UK, 1982; 328p. [Google Scholar]
  55. Young, W.S.; Culter, I.B. Initial sintering with constant rates of heating. J. Am. Ceram. Soc. 1970, 53, 659–663. [Google Scholar] [CrossRef]
  56. Coble, R. A model for boundary diffusion controlled creep in polycrystalline materials. J. Appl. Phys. 1963, 34, 1679–1682. [Google Scholar] [CrossRef]
  57. Lantsev, E.A.; Malekhonova, N.V.; Nokhrin, A.V.; Chuvil’deev, V.N.; Boldin, M.S.; Blagoveshchenskiy, Yu.V.; Andreev, P.V.; Smetanina, K.E.; Isaeva, N.V.; Shotin, S.V. Influence of oxygen on densification kinetics of WC nanopowders during SPS. Ceram. Int. 2021, 47, 4294–4309. [Google Scholar] [CrossRef]
  58. Lantsev, E.A.; Malekhonova, N.V.; Nokhrin, A.V.; Chuvil’deev, V.N.; Boldin, M.S.; Blagoveshchenskiy, Yu.V.; Andreev, P.V.; Smetanina, K.E.; Isaeva, N.V.; Murashov, A.A. Spark plasma sintering of fine-grained WC hard alloys with ultra-low cobalt content. J. Alloys Compd. 2021, 857, 157535. [Google Scholar] [CrossRef]
  59. Lantcev, E.; Nokhrin, A.; Malekhonova, N.; Boldin, M.; Chuvil’deev, V.; Blagoveshchenskiy, Y.; Isaeva, N.; Andreev, P.; Smetanina, K.; Murashov, A. A study of the impact of graphite on the kinetics of SPS in nano- and submicron WC-10%Co powder compositions. Ceramics 2021, 4, 331–363. [Google Scholar] [CrossRef]
  60. Golovkina, L.S.; Orlova, A.I.; Nokhrin, A.V.; Boldin, M.S.; Lantsev, E.A.; Chuvil’deev, V.N.; Sakharov, N.V.; Shotin, S.V.; Zelenov, A.Yu. Spark Plasma Sintering of fine-grained ceramic-metal composites YAG:Nd-(W,Mo) based on garnet-type oxide Y2.5Nd0.5Al5O12 for inert matrix fuel. J. Nucl. Mater. 2018, 511, 109–121. [Google Scholar] [CrossRef]
  61. Kolobov, Y.R.; Grabovetskaya, G.P.; Ivanov, K.V.; Girsova, N.V. Effect of the grain-boundary state and grain size on the mechanisms of creep of submicrocrystalline nickel. Phys. Met. Metallogr. 2001, 91, 532–537. (in Russian). [Google Scholar]
  62. Chuvil’deev, V.N.; Boldin, M.S.; Dyatlova, Ya.G.; Rumyantsev, V.I.; Ordanyan, S.S. A comparative study of hot pressing and Spark Plasma Sintering of Al2O3-ZrO2-Ti(C,N) powders. Inorg. Mater. 2015, 51, 1047–1053. [Google Scholar] [CrossRef]
  63. Chuvil’deev, V.N.; Blagoveshchenskiy, Y.V.; Nokhrin, A.V.; Boldin, M.S.; Sakharov, N.V.; Isaeva, N.V.; Shotin, S.V.; Belkin, O.A.; Popov, A.A.; Smirnova, E.S.; et al. Spark plasma sintering of tungsten carbide nanopowders obtained through DC arc plasma synthesis. J. Alloys Compd. 2017, 708, 547–561. [Google Scholar] [CrossRef]
  64. Golovkina, L.S.; Orlova, A.I.; Nokhrin, A.V.; Boldin, M.S.; Chuvil’deev, V.N.; Sakharov, N.V.; Belkin, O.A.; Shotin, S.V.; Zelenov, A.Y. Spark Plasma Sintering of fine-grain ceramic-metal composites based on garnet-structure oxide Y2.5Nd0.5Al5O12 for Inert Matrix Fuel. Mater. Chem. Phys. 2018, 214, 516–526. [Google Scholar] [CrossRef]
  65. Segal, V.M.; Beyerlein, I.J.; Tome, C.N.; Chuvil’deev, V.N.; Kopylov, V.I. Fundamentals and Engineering of Severe Plastic Deformation; Nova Science Publishers: New York, NY, USA, 2010; 542p. [Google Scholar]
  66. Blaine, D.C.; Park, S.J.; Suri, P.; German, R.M. Application of work-of-sintering concepts in powder metals. Metall. Mater. Trans. A 2006, 37, 2827–2835. [Google Scholar] [CrossRef]
  67. Park, S.J.; Johnson, J.L.; Wu, Y.; Kwon, Y.-S.; Lee, S.; German, M.R. Analysis of the effect of solubility on the densification behavior of tungsten heavy alloys using the master sintering curve approach. Int. J. Refract. Met. Hard Mater. 2013, 37, 52–59. [Google Scholar] [CrossRef]
  68. Hu, K.; Li, X.; Qu, S.; Li, Y. Effect of heating rate on densification and grain growth during spark plasma sintering of 93W-5.6Ni-1.4Fe heavy alloys. Metall. Mater. Trans. A 2013, 44, 4323–4336. [Google Scholar] [CrossRef]
  69. Larikov, L.N.; Yurchenko, Y.F. Diffusion in metals and alloys; Naukova dumka: Kiev, 1987; 509p. (In Russian) [Google Scholar]
  70. Park, S.M.; Martin, J.M.; Guo, J.F.; Johnson, J.L. Densification behavior of tungsten heavy alloy based on master sintering curve concept. Metall. Mater. Trans. A 2006, 37, 2837–2848. [Google Scholar] [CrossRef]
  71. Seith, W. Diffusion in Mettallen. Platzwechselreaktionen; Springer Verlag: Berlin/Heidelberg, Germany, 1955; 381p. [Google Scholar]
Preprints 71220 g001
Figure 1. Typical stress – strain and strain rate – strain curves for a tungsten alloy sample recorded in a dynamic compression test according to Kolsky bar method.
Figure 1. Typical stress – strain and strain rate – strain curves for a tungsten alloy sample recorded in a dynamic compression test according to Kolsky bar method.
Preprints 71220 g001
Preprints 71220 g002
Figure 2. Tungsten alloy samples for testing (a) and example of measuring the sample penetration depth into the steel target (b).
Figure 2. Tungsten alloy samples for testing (a) and example of measuring the sample penetration depth into the steel target (b).
Preprints 71220 g002
Preprints 71220 g003
Figure 3. SEM images of W-7%Ni-3%Fe powder agglomerates for different HEBM: times (a) 0 min; (b) 5 min; (с) 10 min; (d) 20 min; (e, f) 40 min.
Figure 3. SEM images of W-7%Ni-3%Fe powder agglomerates for different HEBM: times (a) 0 min; (b) 5 min; (с) 10 min; (d) 20 min; (e, f) 40 min.
Preprints 71220 g003
Preprints 71220 g004
Figure 4. SEM images of the nanoparticles in the powder agglomerates 90%W-7%Ni-3%Fe for different HEBM times: (a) tHEBM = 10 min; (b) tHEBM = 40 min.
Figure 4. SEM images of the nanoparticles in the powder agglomerates 90%W-7%Ni-3%Fe for different HEBM times: (a) tHEBM = 10 min; (b) tHEBM = 40 min.
Preprints 71220 g004
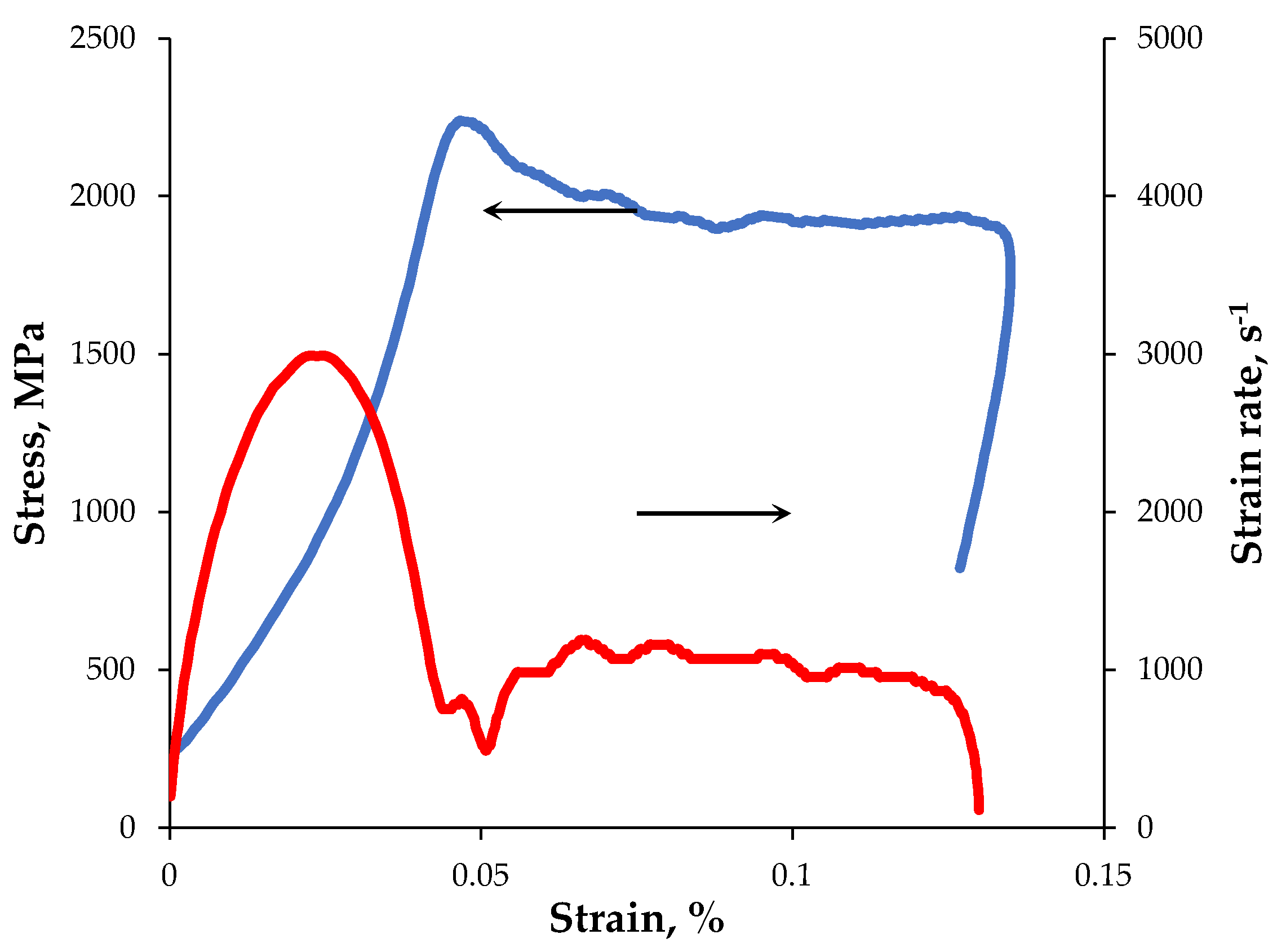
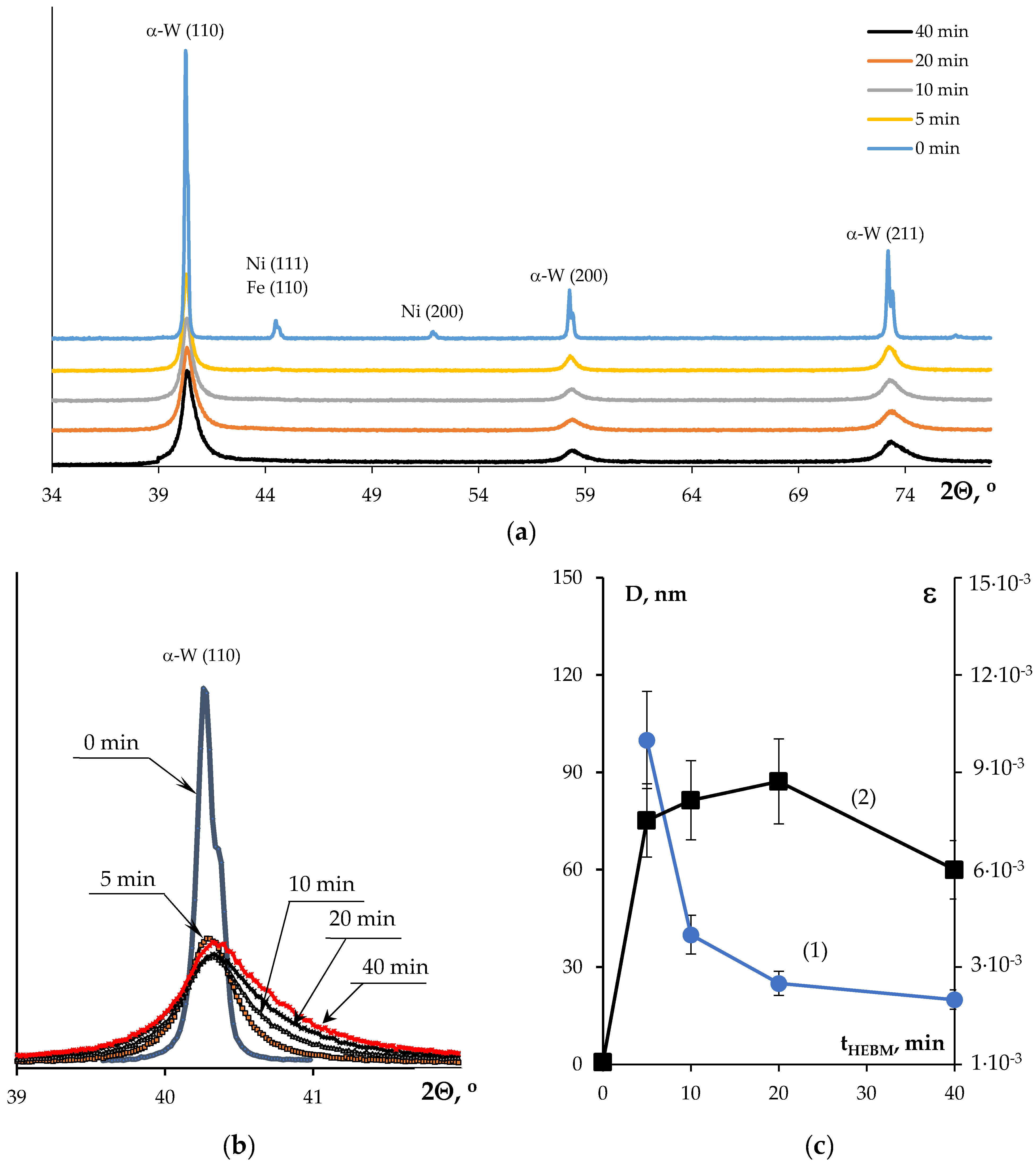
Preprints 71220 g005
Figure 5. Results of XRD phase analysis of the powders 90%W-7%Ni-3%Fe: (а) overview XRD curves after different HEBM times; (b) effect of the HEBM time on the broadening of the (110) α-W pears [45]; (c) effect of the HEBM time on the CSR size (1) and on the magnitude of the micro strain of the α-W crystal lattice (2) [45].
Figure 5. Results of XRD phase analysis of the powders 90%W-7%Ni-3%Fe: (а) overview XRD curves after different HEBM times; (b) effect of the HEBM time on the broadening of the (110) α-W pears [45]; (c) effect of the HEBM time on the CSR size (1) and on the magnitude of the micro strain of the α-W crystal lattice (2) [45].
Preprints 71220 g005
Preprints 71220 g006
Figure 6. Appearance of the W-7%Ni-3%Fe alloy samples sintered in hydrogen from the nanopowders obtained by HEBM. Sintering temperature: (a) 1450 oС; (b) 1500 oС.
Figure 6. Appearance of the W-7%Ni-3%Fe alloy samples sintered in hydrogen from the nanopowders obtained by HEBM. Sintering temperature: (a) 1450 oС; (b) 1500 oС.
Preprints 71220 g006
Preprints 71220 g007
Figure 7. Microstructure of W-7%Ni-3%Fe alloy sintered from coarse-grained (a, c, e) and nanopowder (tHEBM = 20 min) (b, d, f). Sintering temperature Ts = 1250 oC (a, b), 1400 oC (c, d).
Figure 7. Microstructure of W-7%Ni-3%Fe alloy sintered from coarse-grained (a, c, e) and nanopowder (tHEBM = 20 min) (b, d, f). Sintering temperature Ts = 1250 oC (a, b), 1400 oC (c, d).
Preprints 71220 g007
Preprints 71220 g008
Figure 8. Microstructure of the W-7%Ni-3%Fe alloy sintered from the nanopowder (tHEBM = 20 min) at the temperatures 1150 oC (a), 1200 oC (b), and 1400 oC (с).
Figure 8. Microstructure of the W-7%Ni-3%Fe alloy sintered from the nanopowder (tHEBM = 20 min) at the temperatures 1150 oC (a), 1200 oC (b), and 1400 oC (с).
Preprints 71220 g008
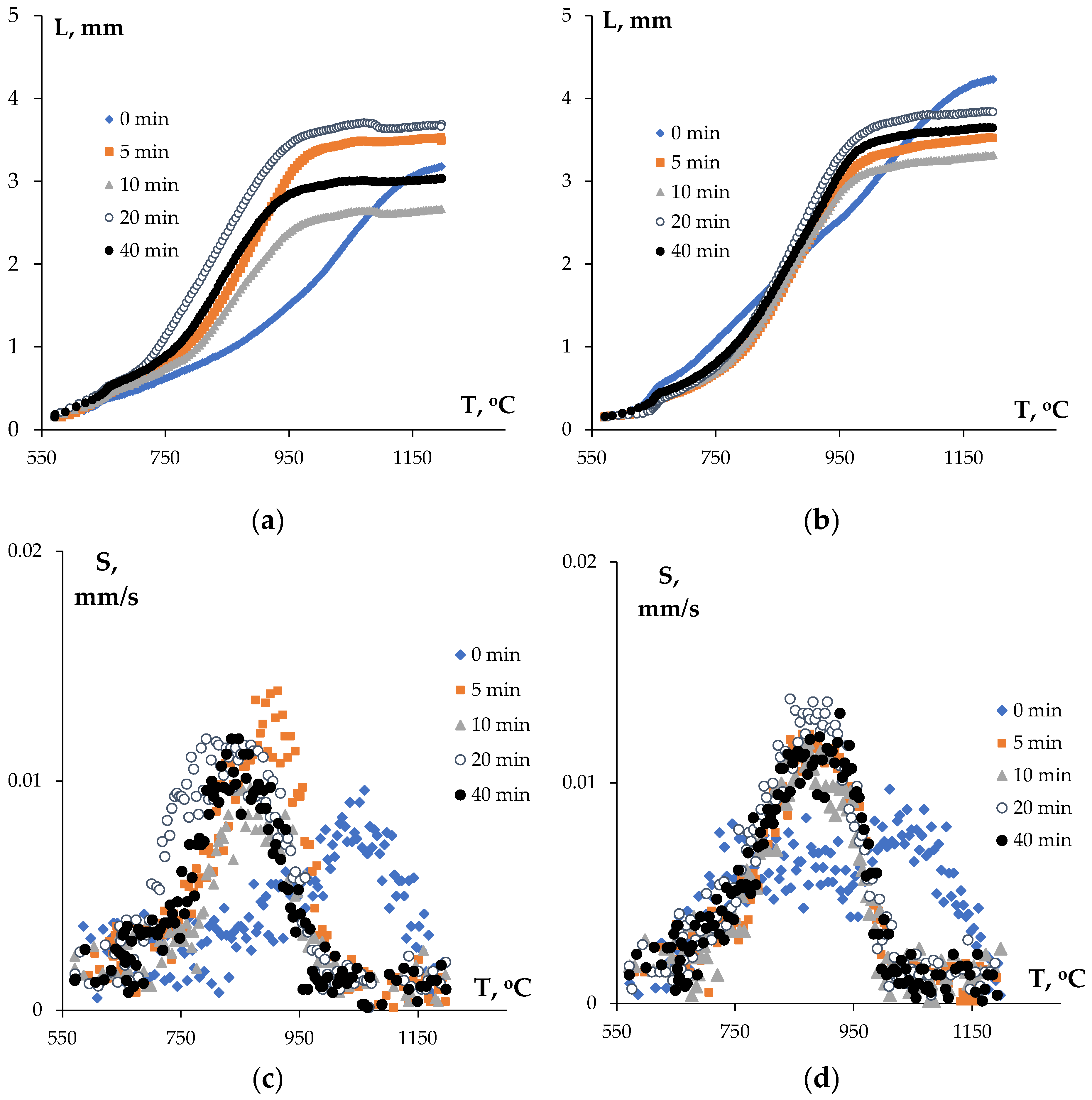
Preprints 71220 g009
Figure 9. Temperature curves of shrinkage (a, b) and shrinkage rate (c, d) for the W-7%Ni-3%Fe nanopowders after HEBM (a, c), and after HEBM and annealing in hydrogen (b, d).
Figure 9. Temperature curves of shrinkage (a, b) and shrinkage rate (c, d) for the W-7%Ni-3%Fe nanopowders after HEBM (a, c), and after HEBM and annealing in hydrogen (b, d).
Preprints 71220 g009
Preprints 71220 g010
Figure 10. Microstructure of the W-7%Ni-3%Fe alloy obtained by SPS at 1200 oC from non-annealed (а, c, e) and annealed (b, d, f) nanopowders. HEBM time: (a, b) 0 min; (c, d) 10 min; (e, f) 40 min.
Figure 10. Microstructure of the W-7%Ni-3%Fe alloy obtained by SPS at 1200 oC from non-annealed (а, c, e) and annealed (b, d, f) nanopowders. HEBM time: (a, b) 0 min; (c, d) 10 min; (e, f) 40 min.
Preprints 71220 g010
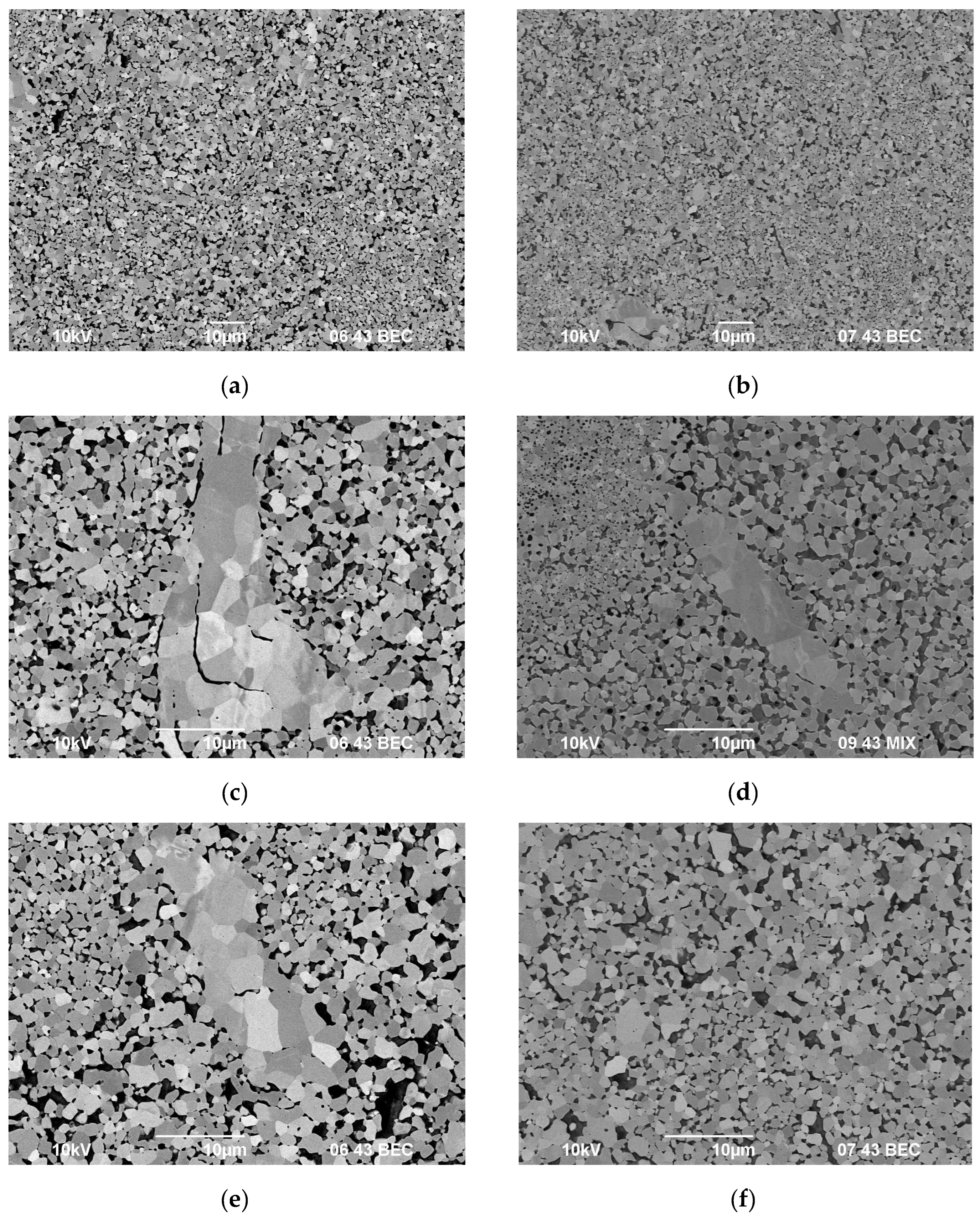
Preprints 71220 g011
Figure 11. Microstructure of the samples obtained by SPS from the annealed (a) and non-annealed (b) nanopowders after HEBM (tHEBM = 40 min). The areas with the abnormally large grains in the microstructure of the W-7%Ni-3%Fe alloy obtained by SPS at 1200 oC from non-annealed (с, d, e) and annealed (f) nanopowders: (c) tHEBM = 10 min, (d) tHEBM = 20 min; (e, f) tHEBM = 40 min.
Figure 11. Microstructure of the samples obtained by SPS from the annealed (a) and non-annealed (b) nanopowders after HEBM (tHEBM = 40 min). The areas with the abnormally large grains in the microstructure of the W-7%Ni-3%Fe alloy obtained by SPS at 1200 oC from non-annealed (с, d, e) and annealed (f) nanopowders: (c) tHEBM = 10 min, (d) tHEBM = 20 min; (e, f) tHEBM = 40 min.
Preprints 71220 g011
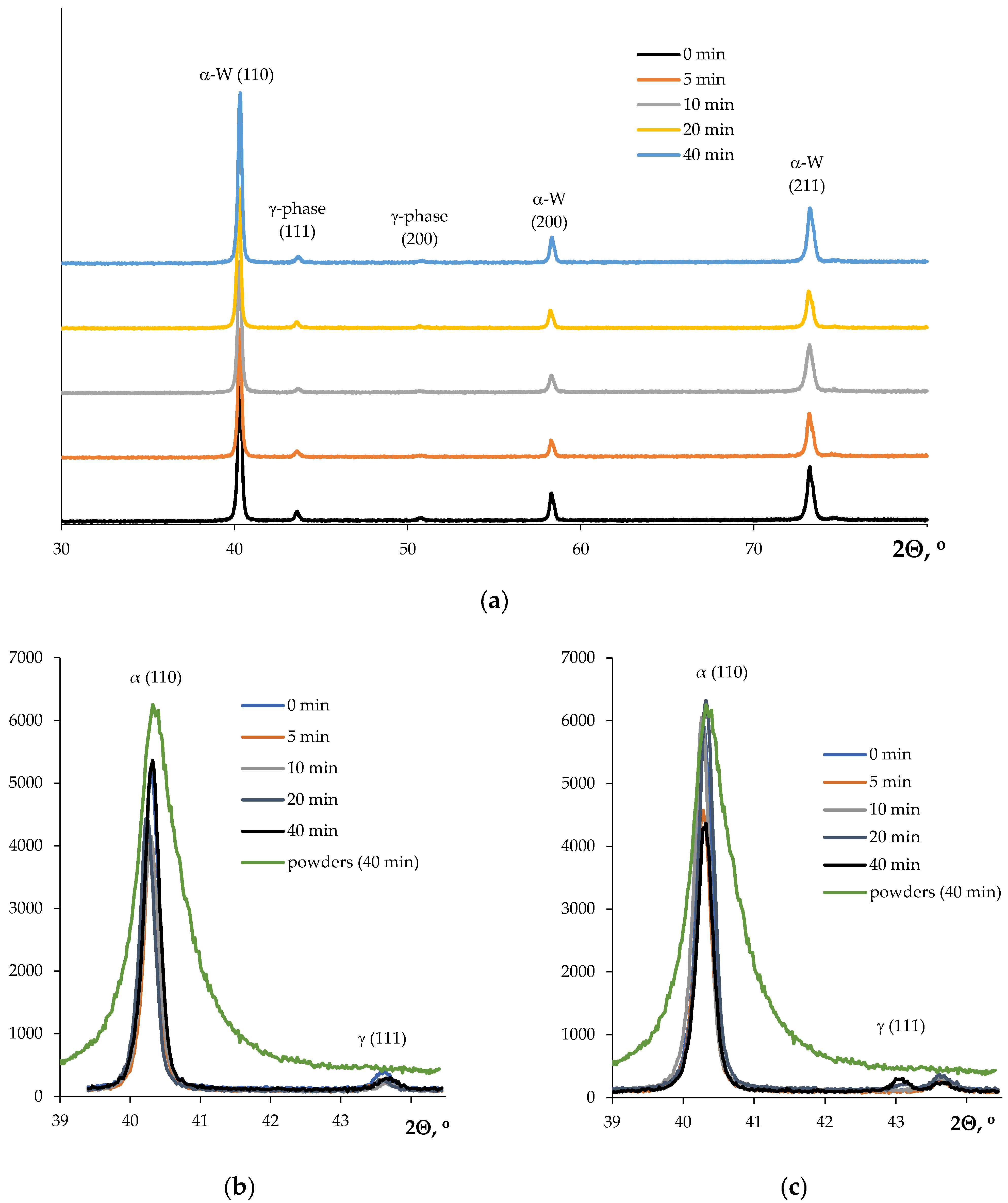
Preprints 71220 g012
Figure 12. Results of XRD analysis of the W-7%Ni-3%Fe alloy obtained by SPS at 1200 oC. Effect of the HEBM time on the parameters of the (100) α-W peak in the samples sintered from the non-annealed (a) and annealed nanopowders (b).
Figure 12. Results of XRD analysis of the W-7%Ni-3%Fe alloy obtained by SPS at 1200 oC. Effect of the HEBM time on the parameters of the (100) α-W peak in the samples sintered from the non-annealed (a) and annealed nanopowders (b).
Preprints 71220 g012
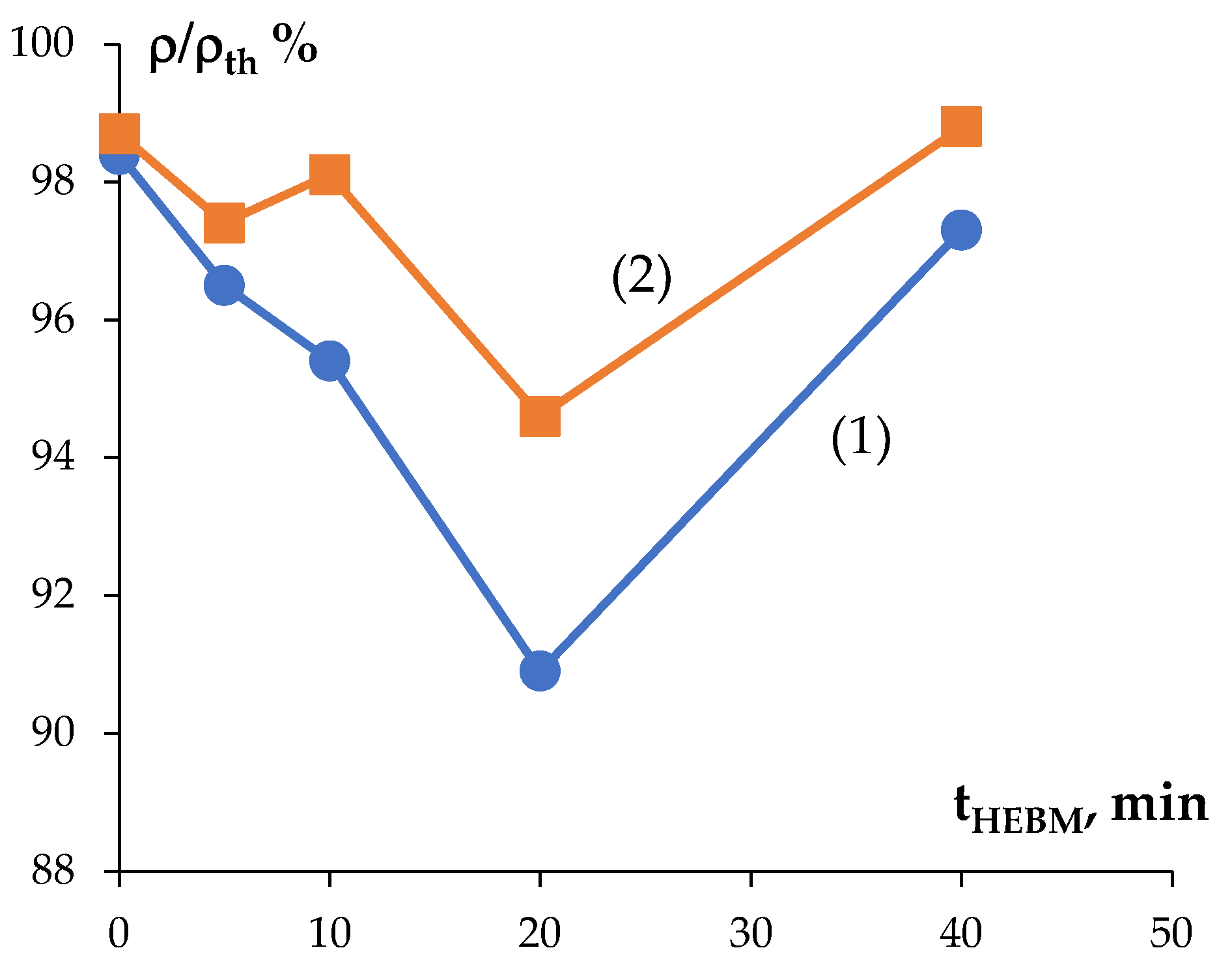
Preprints 71220 g013
Figure 13. Dependencies of relative density of the W-7%Ni-3%Fe alloy sintered at 1200 oC on the HEBM time: (1) – densities of the samples sintered from the non-annealed nanopowders; (2) – densities of the samples sintered from the annealed nanopowders.
Figure 13. Dependencies of relative density of the W-7%Ni-3%Fe alloy sintered at 1200 oC on the HEBM time: (1) – densities of the samples sintered from the non-annealed nanopowders; (2) – densities of the samples sintered from the annealed nanopowders.
Preprints 71220 g013
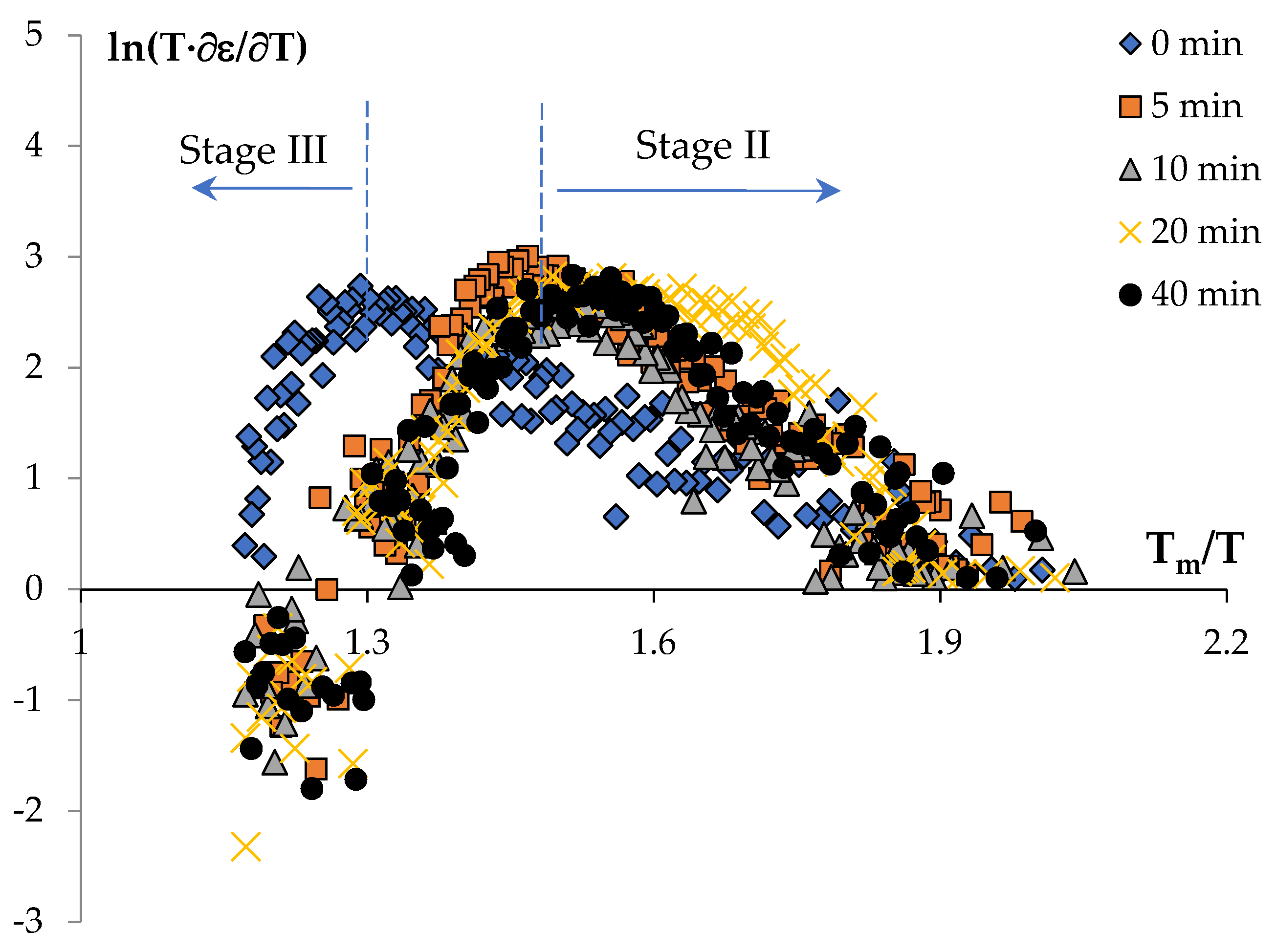
Preprints 71220 g014
Figure 14. Dependencies (T·∂ε/∂T) – Tm/T for the W-7%Ni-3%Fe alloy. Analysis of the compaction mechanisms of the non-annealed nanopowders at Stage II.
Figure 14. Dependencies (T·∂ε/∂T) – Tm/T for the W-7%Ni-3%Fe alloy. Analysis of the compaction mechanisms of the non-annealed nanopowders at Stage II.
Preprints 71220 g014
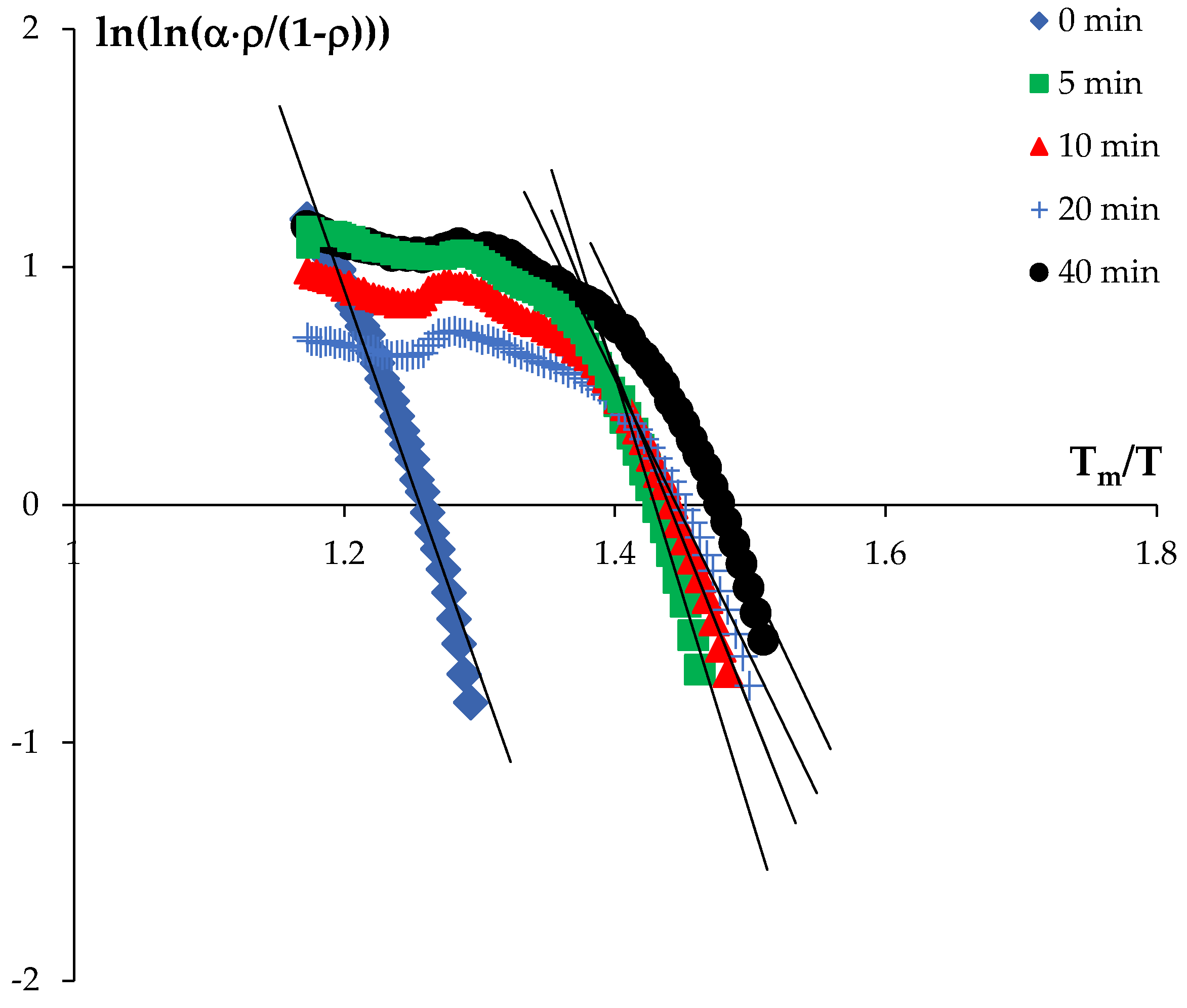
Preprints 71220 g015
Figure 15. Dependencies ln(ln(α⋅ρ/ρth/(1-ρ/ρth)) – Tm/T for non-annealed nanopowders W-7%Ni-3%Fe.
Figure 15. Dependencies ln(ln(α⋅ρ/ρth/(1-ρ/ρth)) – Tm/T for non-annealed nanopowders W-7%Ni-3%Fe.
Preprints 71220 g015
Preprints 71220 g016
Figure 16. Analysis of investigations of the mechanical properties of the HTAs 90%W-7%Ni-3%Fe: (a) dependencies of the hardness and of the yield strength on the grain size; (b) dependence of Hall-Petch coefficient on the grain size. Analysis of the results presented in Table 2 and Table 3.
Figure 16. Analysis of investigations of the mechanical properties of the HTAs 90%W-7%Ni-3%Fe: (a) dependencies of the hardness and of the yield strength on the grain size; (b) dependence of Hall-Petch coefficient on the grain size. Analysis of the results presented in Table 2 and Table 3.
Preprints 71220 g016
Table 1. Chemical composition of initial powders (wt.%).
Table 1. Chemical composition of initial powders (wt.%).
Powders O Fe C S P Ni Co Si Cu Mo Mn
α-W 8⋅10-2 2⋅10-2 1⋅10-2 - 5⋅10-3 1⋅10-2 - 5⋅10-3 1⋅10-2 4.5⋅10-2 2⋅10-3
β-Ni 3⋅10-1 1.5⋅10-3 1⋅10-1 6⋅10-4 1⋅10-3 - 7⋅10-4 1⋅10-3 1⋅10-3 - 3⋅10-4
α-Fe 2⋅10-1 - 4.8⋅10-2 4⋅10-3 - - - 1⋅10-2 - - -
Table 2. Microstructure characteristics and mechanical properties of the W-7%Ni-3%Fe alloy samples obtained from the nanopowders by sintering in hydrogen.
Table 2. Microstructure characteristics and mechanical properties of the W-7%Ni-3%Fe alloy samples obtained from the nanopowders by sintering in hydrogen.
Characteristics of alloy obtained from coarse-grained powders Characteristics of alloy obtained from nanopowders
Ts, oC ρ,
g/cm3 		d,
μm		 σ0,
MPa		 σy,
MPa		 Hv,
GPa		 Ys,
MPa		 H,
mm		 ρ,
g/cm3 		d,
μm		 σ0,
MPa		 σy,
MPa		 Hv,
GPa		 Ys,
MPa		 H,
mm
1250 17.94 5-10 520 1150 4.2 1830 3.8 17.79 1-3 960 1540 7.9 1900 5.1
1300 18.02 ~5-10 460 990 4.2 1700 4.15 17.93 1-3 1000 1340 7.5 2050 4.68
1350 18.06 ~10 290 790 4.1 1650 4.23 17.95 1-3 860 1200 7.2 1870 3.72
1400 18.14 ~20 230 740 4.0 1640 4.05 17.49 3-5 300 740 6.9 1500 3.1
1450 18.11 40-45 220 600 3.8 1590 3.7 17.05 1 ~10 - - 6.5 - -
1500 18.06 ~50 200 690 3.6 1580 3.2 16.87 1 ~22 - - 6.2 - -
1 The density was measured by measuring the mass and geometrical sizes of the samples.
Table 3. Microstructure characteristics and mechanical properties of the W-7%Ni-3%Fe alloy samples obtained by SPS from nanopowders (Ts = 1200 oC).
Table 3. Microstructure characteristics and mechanical properties of the W-7%Ni-3%Fe alloy samples obtained by SPS from nanopowders (Ts = 1200 oC).
Characteristics of alloy obtained from non-annealed nanopowders Characteristics of alloy obtained from annealed nanopowders
tHEBM, min ρ, g/cm3 d, μm σ0, MPa σy, MPa Hv, GPa Ys, MPa H, mm ρ, g/cm3 d, μm σ0, MPa σy, MPa Hv, GPa Ys, MPa H, mm
0 16.97 1.3 920 1850 4.2 - 4.9 17.02 1.2 1050 1930 4.3 - 5.1
5 16.64 0.9 1330 2160 4.5 2280 5.8 16.79 1.0 1400 2270 4.8 2350 5.1
10 16.45 0.8 1450 2180 4.7 - 5.7 16.92 0.7 1520 2310 4.9 - 5.4
20 15.68 0.7 1500 2370 4.8 - 5.7 16.31 0.6 1610 2350 5.3 - 6.6
40 16.78 0.7 1480 2350 4.7 2480 5.6 17.04 0.6 1530 2320 4.9 2630 6.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated