Prerpints.org logo
Preprint
Article

Urban Network Percolation and Traffic Dynamics: Causality Relationships in Numerical Experiments

Altmetrics

Downloads

234

Views

177

Comments

0

This version is not peer-reviewed

Submitted:

18 April 2023

Posted:

20 April 2023

You are already at the latest version

Alerts
Abstract
It was recently shown that urban networks might exhibit two different critical points, one for the percolation of congested links through the network, and another one for the flow of vehicles through the network. It was observed that the percolation critical point happens after the flow critical point, where network throughput is maximized. This result is important because if a causal relationship exists between these two processes, it can be leveraged for improving control methods to avoid network collapse. This paper presents the results of numerical experiments to understand the possible causal relationship between the percolation and flow processes by focusing on the relative timing between the two critical points. The goal is to understand the impacts of important factors such as: (i) urban network type: long- and short-block networks, (ii) signal timing control type: fixed, random, responsive, and (iii) route choice: turning proportions at intersections. We find that the threshold density $k^*_c$ to determine if a link is congested has the main impact on the timing of the percolation transition, where lower values trigger earlier transitions. This implies that $k^*_c$ can be set such that the percolation transition happens before the flow critical point, opening the door for improved congestion management strategies. If $k^*_c$ is set to the average network critical density, maximum network throughput happen simultaneously with the percolation transition. Surprisingly, it appears that these results, and more generally, the relationship between the percolation and flow processes is independent of (i) and (ii) above.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

Recent advances in our understanding of urban congestion both at the empirical [1,2,3], and theoretical levels [4] give support to the hypotheses that urban networks exhibit the type of critical behavior typically found in complex systems. Complexity science emerged in the mid-eighties to understand physical systems composed of a large number of particles/agents that interact locally [5]. The rules governing these local interactions are typically very simple, yet they produce complicated, chaotic and unpredictable dynamics, which cannot be tackled with our traditional tools based on calculus and statistics. The critical behavior of phase transitions is a major source of complexity in many physical systems including traffic flow, with power-law dynamics due to a fractal underlying structure that renders the system scale invariant near the critical point. Evidence of such critical behavior in urban networks was already conjectured in [6,7], where percolation phase transitions [8] and self-organized criticality (SOC) [9] are suggested as guiding frameworks. In particular, SOC was suspected since the mid-nineties [6,10] as a mechanism of network collapse caused by conventional traffic management strategies seeking to maximize the flow. Indeed, they showed that these policies make the system more unpredictable and hard to control as a consequence of (i) guiding the system to the flow critical point, and (ii) extending the area of the network subject to critical conditions.
A second critical point, however, was recently conjectured in [11] describing the percolation of congested links through the network (i.e., the percolation critical point). Using calibrated mesoscopic simulation networks from real cities, [11] showed that using the observed critical density of each link, k c (the density that maximizes the flow for each individual link) as the threshold/critical density to determine the general traffic state of a link k c * (e.g., congested vs. uncongested), the critical percolation point happens *after* the flow critical point (i.e., the SOC critical point of maximum network throughput).
This paper presents an alternative conjecture for k c whereby the timing of the two critical points can be reversed so that the percolation transition happens *before* the SOC critical point that will inevitably lead to network collapse. This result is important because if a causal relationship exists, it can be leveraged for control and avoid network collapse. Our conjecture is based on the results of a large number of numerical experiments to understand the possible causal relationship between the percolation and flow processes. We focus on the relative timing between the two critical points as a function of important factors such as: (i) urban network type: long- and short-block networks, (ii) signal timing control type: fixed, random, responsive (iii) route choice: turning proportions at intersections.
The remainder of the paper is organized as follows. Section 2 presents empirical evidence of critical behavior on urban networks, most of which appeared only very recently. Section 3 explains the methods for carrying out the numerical experiments, while Section 4 presents the results. Finally, a discussion and outlook are included in Section 5.

2. Evidence of Network Criticality

This section presents a short overview of the empirical and theoretical evidence of criticality in urban networks.
It appears that the first indications of criticality in traffic flow go back to [6,10]. Using ideas from the theory of percolation phase transitions and the [12] cellular automata model (NaSch model) for numerical experiments, the critical exponent of jam durations was found to be very close to τ = 3 / 2 and suggested the relationship with the first return time of a one-dimensional random walk. Shortly after, the same authors [13] presented numerical evidence of SOC on a simple network and argued that conventional traffic control would tend to enlarge the area of the network under criticality. They suggested that an effective management strategy would be to force the system away from criticality through less efficient traffic management. Their conjecture was based on the large travel time variance observed near the critical state on a simulated network, but other properties of SOC systems were not verified. Notice that recently [4] formalized the criticality definition of the kinematic wave model using the variational theory of traffic flow [14].
Surprisingly, the impact of SOC in the field of traffic flow theory has been underwhelming [15,16]. Apart from [13,17,18] who present some numerical evidence of SOC on networks, it appears that the subject has gone largely under the radar. One reason might be that the main insight from the early works [6,10] was that SOC in the NaSch model emerges only in ”cruise-control” mode, where random perturbations are only allowed in congested traffic states. This apparent dependence on the rule details might have been interpreted as the absence of a universality class in traffic flow, implying that SOC might not be an intrinsic property of traffic flow, but just of particular models.
It is perhaps because of this confusion in the literature that it took almost 2 decades to observe the first empirical evidence of criticality, with [19] reporting a 1/f power spectra over all loop-detectors from the City of London, indicating long spatio-temporal correlations typical of a critical system, conjectured to be a consequence of emerging spatial synchronization of queues. No evidence was found to correlate this synchronization to signal traffic control.
[18] used simulation tools on several networks of large cities and identified three states of urban traffic, free flow, traffic jam, and gridlock, separated by two transitions: the appearance of the first bottlenecks and the collapse of the system. They also observed similarities with directed percolation phase transitions.
The relation between network traffic dynamics and percolation theory [8] was first described in [20]. They define a network link as functional when its normalized speed exceeds a given threshold, and analyzed the structure of the resulting connected components of the network (clusters). They observed that the size of the largest cluster exhibits a sharp discontinuity at a given threshold, the critical threshold, indicating a phase transition. This discontinuity coincides with the second largest cluster reaching its maximum, as in percolation theory.
More recently, the authors of a series of 3 papers [1,2,3] have used percolation analysis on high-resolution GPS datasets of urban traffic in several Chinese megacities. They found strong evidence of critical behavior, as expected, but also observed the following: (i) [2] has revealed that urban networks in China exhibit a phase transition characterized by a power law behavior with a percolation critical exponent τ ≈ 2.3 for a large number of working days in 2015. This robustness of the critical exponent led the authors to conclude that urban networks exhibit SOC as a consequence of the interactions between supply and demand, and that they are analogous to the BTW sand pile model. (ii) [1] re-examined the data in [2] and found two modes of critical behavior, one mode during non-rush hours or days off with τ ≈ 2.3 , and another mode for rush hours with τ ≈ 2.1 . (iii) [3] found three network regimes: a global functional regime and a metastable hysteresis-like regime, followed by a global collapsed regime. These results suggest the existence of a nonequilibrium phase transition between a state where congestion is localized to another state where congestion occurs over the whole network during rush hours. Here we note that (i) the percolation critical exponents τ ≈ 2.1 − 2.3 reported in the literature are consistent with the universality classes to be explored in this proposal (see Table 1), and (ii) our preliminary results dictate that similar exponents can be obtained with a microscopic simulation on the grid networks.

3. Methods

This section describes all the ingredients needed to formulate our problem, including the traffic flow model to describe the behavior of vehicles, the type of network, the vehicle routing assumptions and the traffic signal configuration.
The numerical examples are based on the simplest microscopic network model able to reproduce critical behavior, first described in [21]. The traffic flow model is the elementary cellular automata (CA) rule 184 [5], known to be the most efficient computational method to obtain the exact solution of the kinematic wave model (or LWR model) [22,23] with a triangular flow-density fundamental diagram [24,25]. Accordingly, here both the free-flow speed and the wave speed are equal to 1, implying that the link saturation flow is 1/2, the link critical density k c is also 1/2, and the link jam density is 1, without loss of generality. In a CA model, each lane of the road is divided into small cells i = 1 , 2 , … ℓ the size of a vehicle jam spacing, where cell ℓ is the most downstream cell of the lane. The value in each cell can be either “1” if a vehicle is present and “0” otherwise. The network corresponds to a grid network of bidirectional streets with one lane per direction and with a traffic light on all intersections. To attain spatial homogeneity, the network is defined on a torus where each street can be thought of as a ring road where all intersections have 4 incoming and 4 outgoing approaches; see Figure 1. Vehicle routing is assumed to be fully adaptive to avoid unrealistic bifurcations in the MFD [26]. Bifurcation takes place when drivers cannot clear the intersection because the downstream link in their route is jammed. If the driver does not adapt and change his/her route, the jam propagates even faster, eventually leading to gridlock, with a portion of the links in the network being jammed, and the rest being empty. As this type of bifurcations are not common in real networks, we employ the full adaptive assumption not only for parsimony but also because it gives a useful benchmark. Future studies could vary the percentage of drivers that are adaptive, as some literature suggests that the benefits of adaptive driver quickly decrease once 50% or more of the drivers behave adaptively [27]. Here, the full adaptability is implemented using random routing: A driver reaching the stop line, say Mary, will choose to turn with probability p or keep going straight with probability 1 − p . If Mary decides to turn, she will turn left, right or U-turn with equal probability. If two or more vehicles are bound for the same approach during a time step, the tie is broken randomly. If the downstream approach is blocked then Mary will not move during that time step, and will repeat the same selection process during the next time step, discarding any information about prior trials. Traffic signals operate under the simplest possible setting with only red and green phases (no lost time, red-red, yellow, nor turning phases). All the control policies consider here are incremental in the sense that decisions are taken every g time steps, which can be interpreted as a minimum green time: After the completion of each green time of length g, the controller decides whether to prolong the current phase or to switch light colors. The following signal control policies will be used as baseline in this paper:
  • FIX: fixed signal timing, 50-50 split,
  • LQF: “longest queue first” gives the green to the direction with the longest queue; it is a greedy method used here as a proxy for the “best” control,
  • RND: “random” control gives the green with equal probability to both directions, akin to no control.
We parametrize the space of all grid networks by λ and p. With this, we are able to compare LQF and RND control for a given λ by setting a minimum green time g in the simulation as:
g   = 2 l / λ l / λ     for   FIX   and   LQF   (1a) for   RND                                     (1b)
Each experiment is as follows: Given parameters λ , p, an initial density k 0 ∈ ( 0 , 1 ) and a signal timing strategy, we load the network at a constant rate so that after T cycles the density reaches a final value k 1 . The aggregation time is a traffic signal cycle (given by 2 g with g ae per (1)), which is used to compute the average network flow and density to plot the macroscopic fundamental diagram (MFD), and to report individual link densities for the percolation analysis. For percolation, we only need to define the parameter k c * , a density threshold value that is used to define congested vs. uncongested clusters.

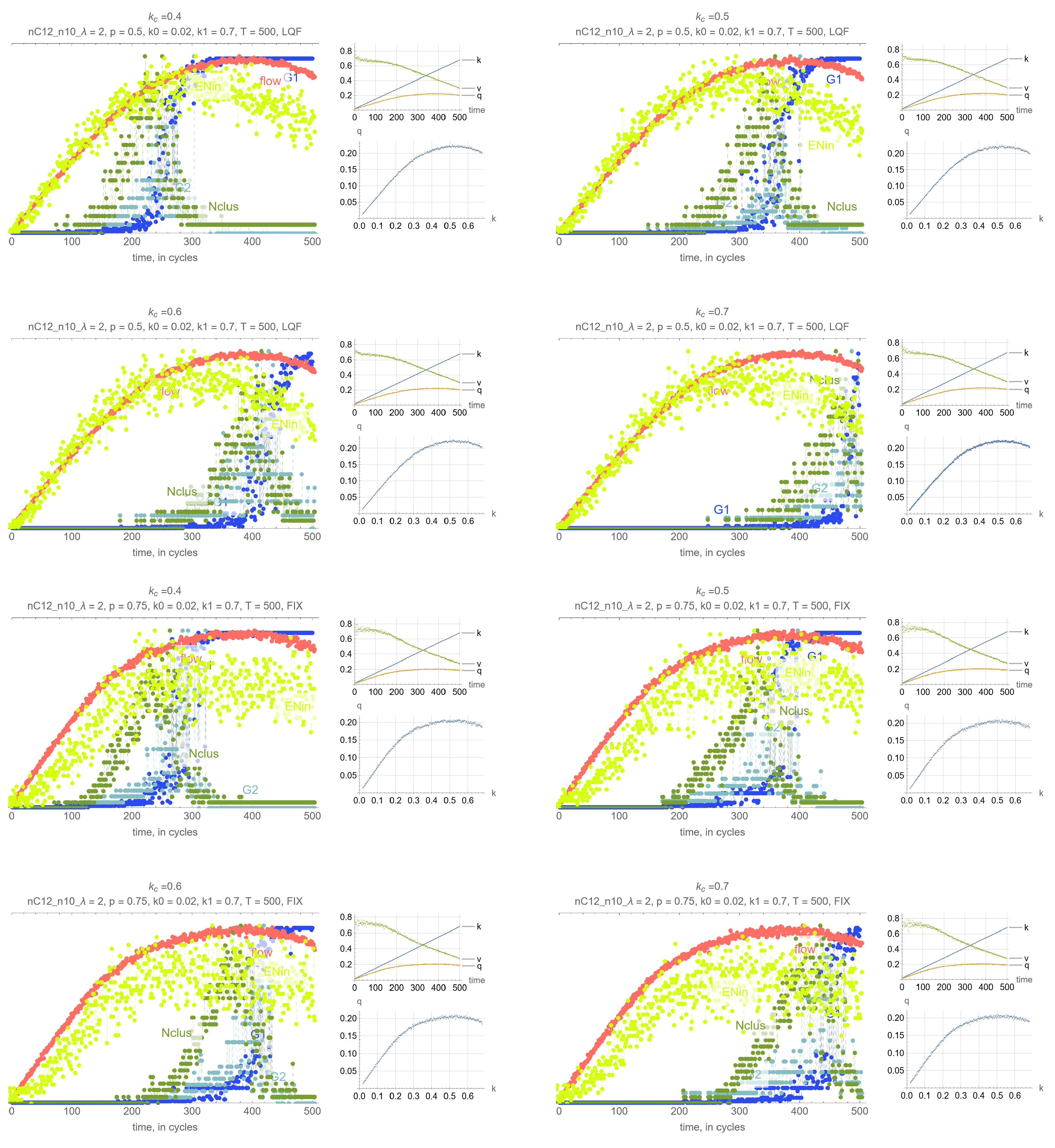
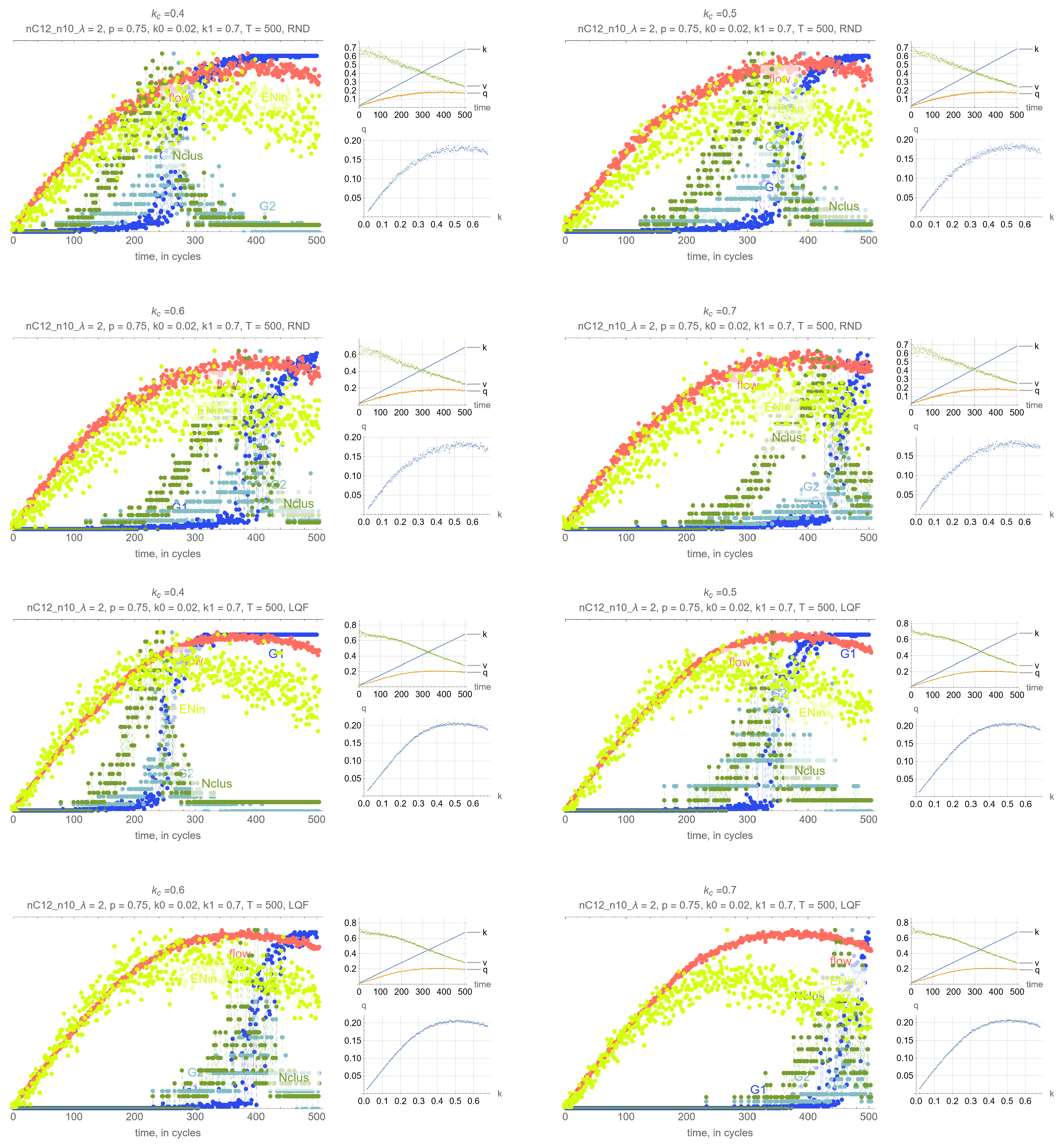
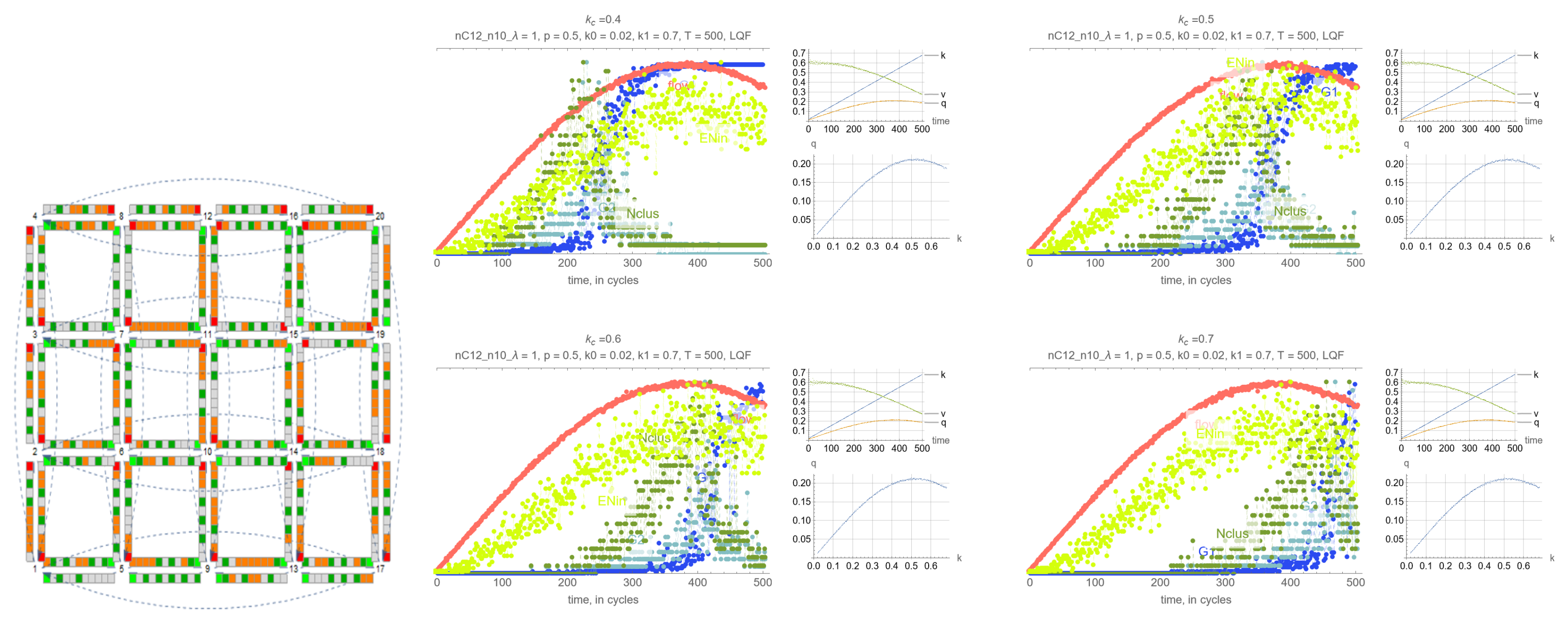
4. Results

The following results are based on a large number of experimental output, such as the ones in Figure, for different network parameters λ , p , percolation parameter k c * , and the three baseline signal control methods. Apart from the macroscopic traffic data monitored every cycle, i.e., flow, density and speeds, we include EN i n , the average number of cars across all intersections that are delayed when merging. The percolation-related variables tracked include:
  • G 1 : size of the largest connected component (cluster)
  • G 2 : size of the 2nd largest component (cluster)
  • N c l u s : number of clusters
Figure 1 (Right) shows 4 output panels from numerical experiments for a particular parameter combination, each with a different random seed. The appendix includes similar output for all other parameter combinations considered in this paper. Based on these output, we can draw the following remarks:
R-1 
Effects of k c * . Perhaps unsurprisingly, the threshold density k c * has the main impact on the timing of the percolation transition, where lower values of k c * lead to earlier percolation transitions. Therefore, one can leverage this remark so that the percolation transitions happens before the SOC critical point and avoid network collapse.
R-2 
Synchrony of critical points. If k c is set to the MFD critical density, maximum network throughput and the percolation transition happen simultaneously.
R-3 
Synchrony of percolation variables. G 1 , G 2 and N c l u s exhibit the phase transition at the same time.
R-4 
Possible precursors. The maximum value of N c l u s always precedes the percolation phase transition, by an amount that depends on network parameters mostly, but which can be too small in some cases to be effective. More promising perhaps is EN i n , the average number of cars across all intersections that are delayed when merging, whose maximum precedes the maximum flow critical point perhaps more consistently than N c l u s . This, however, is not a percolation-related variable, but clearly reflects the traffic conditions in the system, and could be very useful for traffic control.
R-4 
Effects of network parameters. Surprisingly, it appears that these results, and more generally, the relationship between the percolation and flow processes is independent of the network type and signal control. The only exception appears to be short-block networks with low turning probability and LQF signal control, λ = 1 / 2 , p = 0.1 + LQF in the figure, where one can see that the percolation transitions happens before the maximum flow

5. Discussion

Through the use of simplified urban network modeling, this paper gives strong evidence that a suitable setting for the parameter k c * , possibly link-dependent, is able to reverse the timing between the percolation transition in the SOC transition as observed recently in [11]. This result is important because it means that one can have the percolation transition happen before the point of maximum flow, which can be leveraged for control purposes. Adopting k c * values that are lower than k c leads to the identification of clusters that are not congested (as per the definitions associated with the fundamental diagram at the link level) but close to congestion. Tracking then the percolation-related metrics for those clusters, allows us to anticipate the SOC transition. Interestingly enough, it appears that the system does exhibit the percolation behavior independently of the values of k c * (at least within reasonable bounds for k c * ). This should be further verified by looking at the cluster size distribution at criticality. Other precursor variables were identified such as the number of clusters or the number of delayed vehicles, but modifying the percolation transition timing via k c * seems a simpler alternative at this point.
The question remains as to what is the “correct” timing for these transitions. At first glance one would expect the critical point to be unique such that all relevant phase transitions happen in synchrony. The evidence in [11] is strong in showing us otherwise, and efforts should be made to understand the network mechanisms behind this result for better congestion management.
The impacts of the traffic flow model used should also be investigated. It has been argued [4,28] that criticality in traffic flow can only be described realistically using a microscopic framework, even in the case of MFD inspired modeling [29]. In fact, the lack of awareness regarding the critical behavior in traffic flow prevalent today in our community [21] can be explained by our use of aggregated models such as the cell transmission model or any PDE-inspired numerical solution method. Upon aggregation, it is argued, the chaotic behavior near criticality is lost, as initial conditions have been aggregated and therefore the sensitivity to initial conditions is lost. This can have the effect of slowing down the propagation of congestion through the network, compared to a fully microscopic model. A sequel to this paper will address this important issue.
Finally, it would be good to have a final paragraph.

Acknowledgments

This research was partially funded by NSF Award #193245 and by the NYUAD Center for Interacting Urban Networks (CITIES), funded by Tamkeen under the NYUAD Research Institute Award CG001.

Appendix A. Simulation Output Figures

For each combination of parameters λ ∈ ( 1 / 2 , 1 , 2 ) , p ∈ ( 0.1 , 0.5 , 0.75 ) and a signal timing strategy, a total of 4 Monte Carlo simulations are performed and shown below, each corresponding to a different value of the threshold density k c * ∈ ( 0.4 , 0.5 , 0.6 , 0.7 ) . Starting with an initial density k 0 = 0 we load the network at a constant rate so that after T = 500 cycles the density reaches a final value k 1 = 0.7 . Each panel below consists of three figures. The large figure is a time series of all the variables being tracked as a function of time. The two smaller figures on its side give the traffic variable time series and the MFD observed during that particular simulation run, respectively.
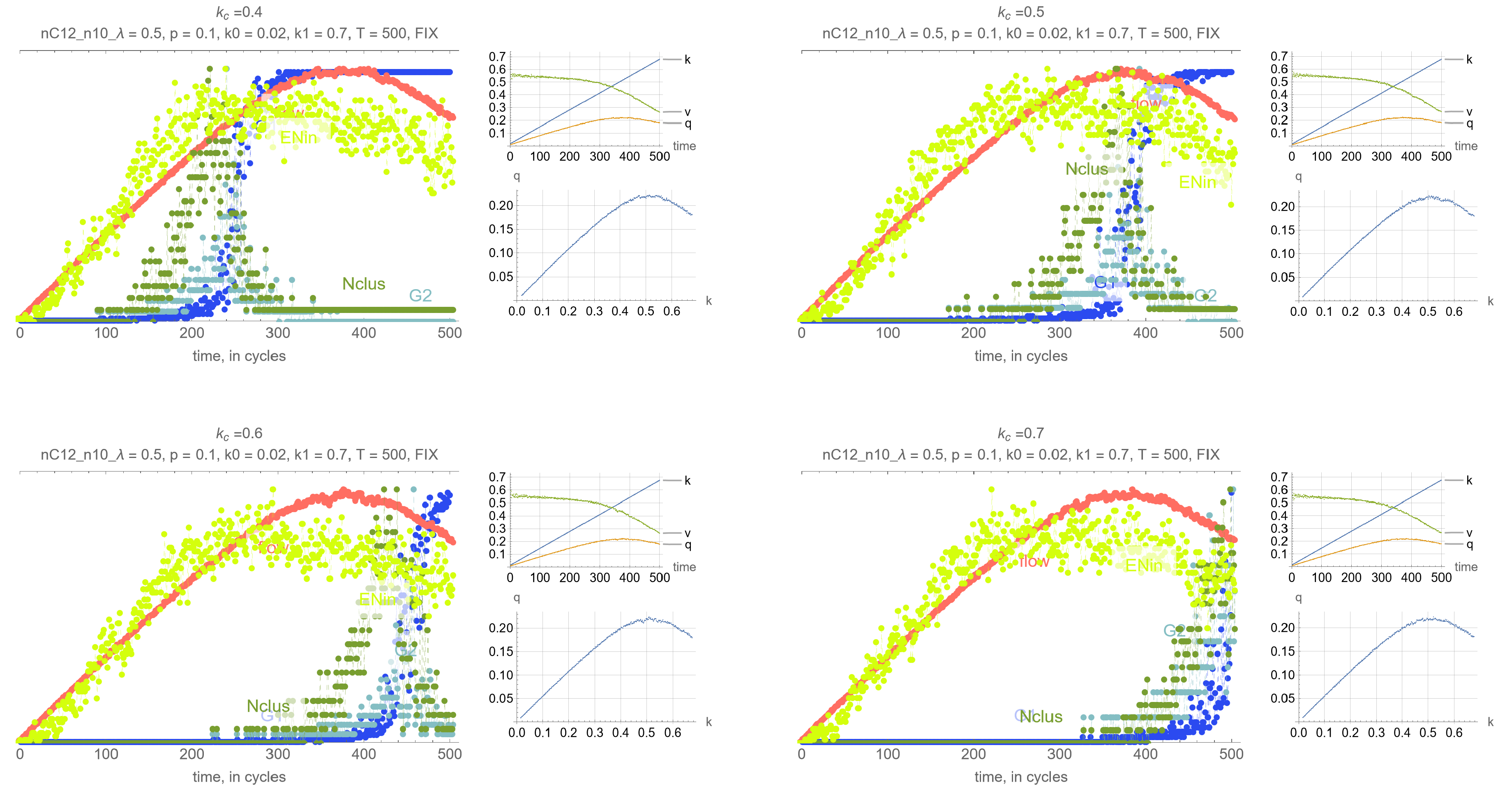
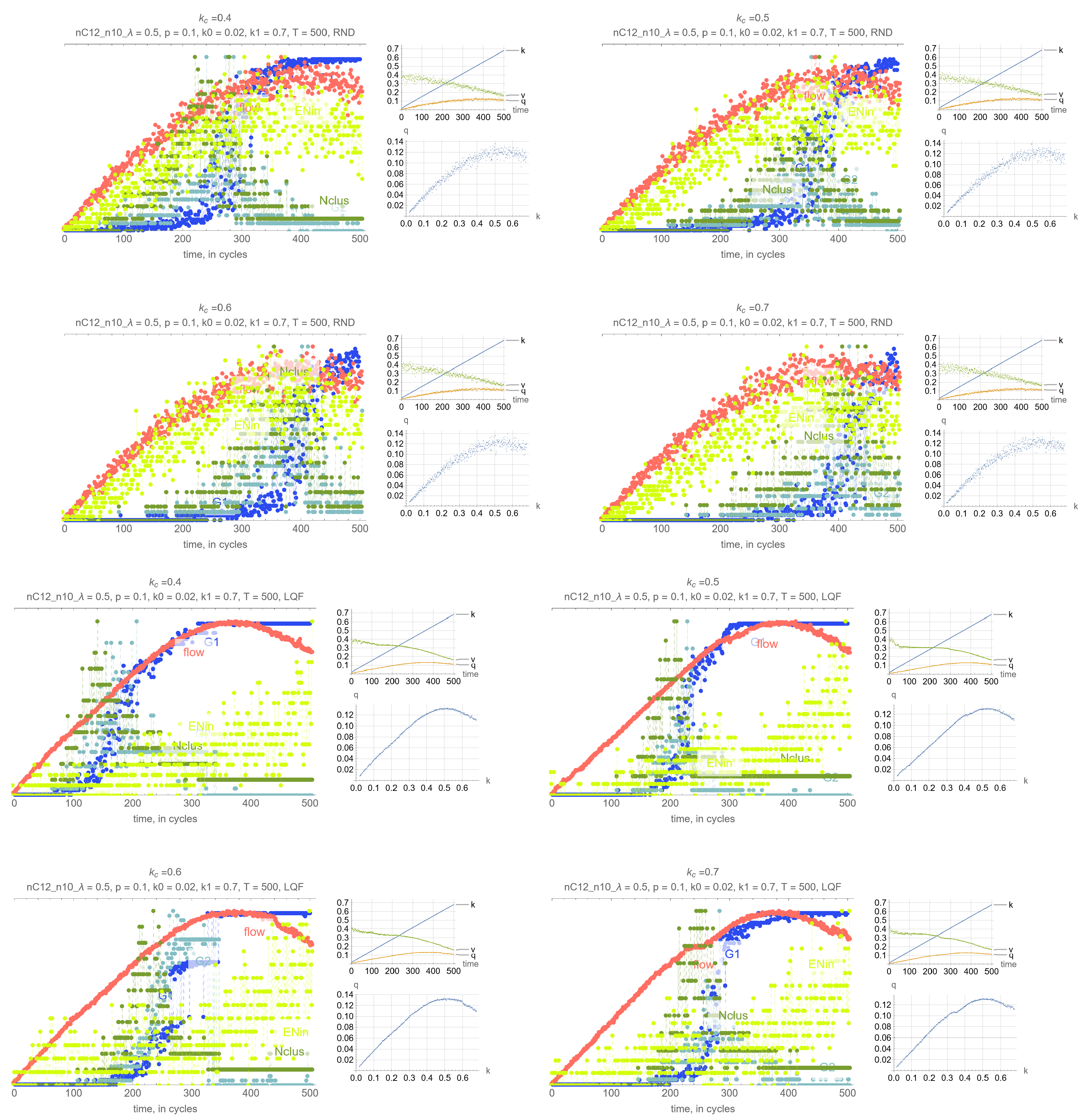
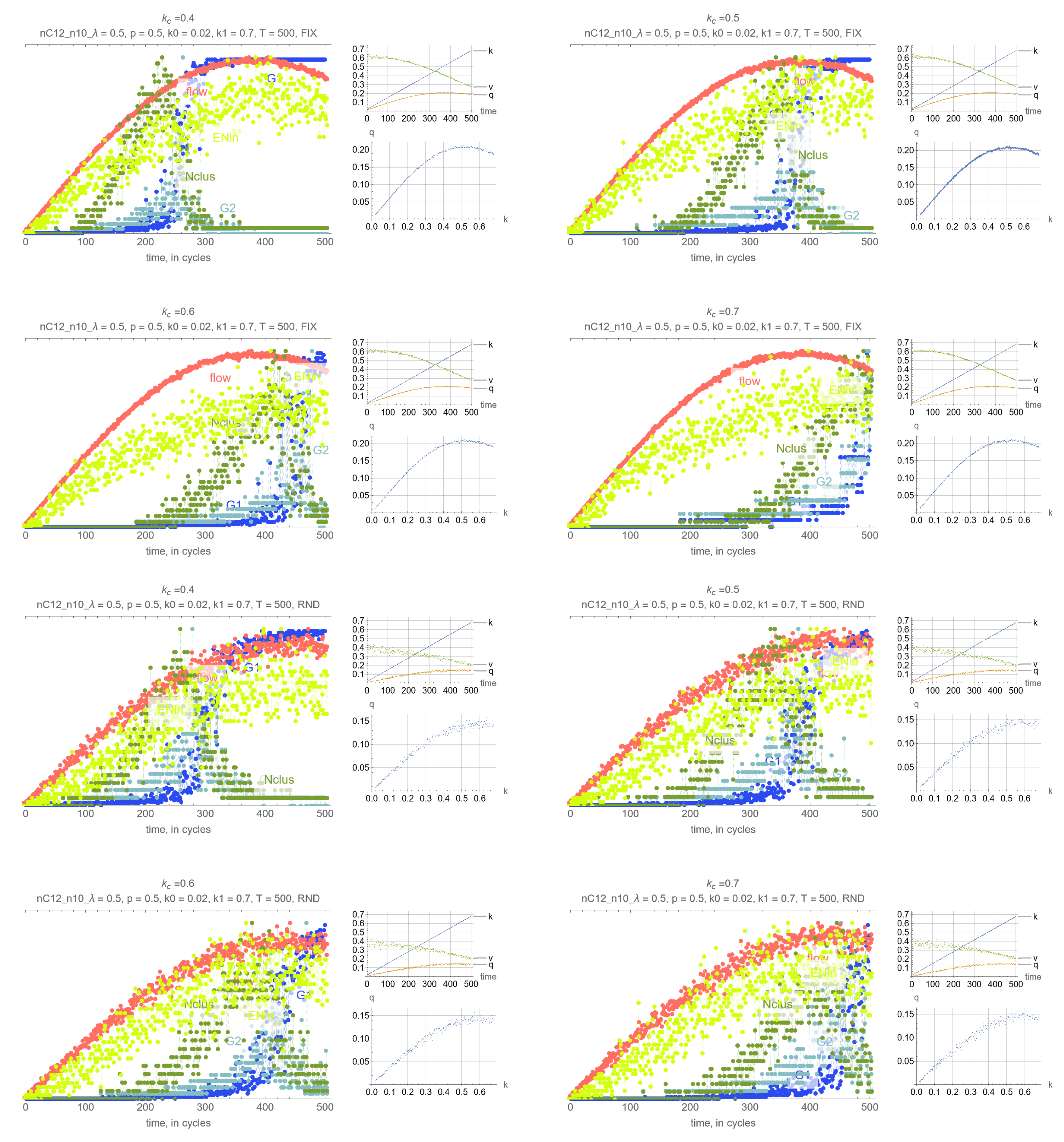
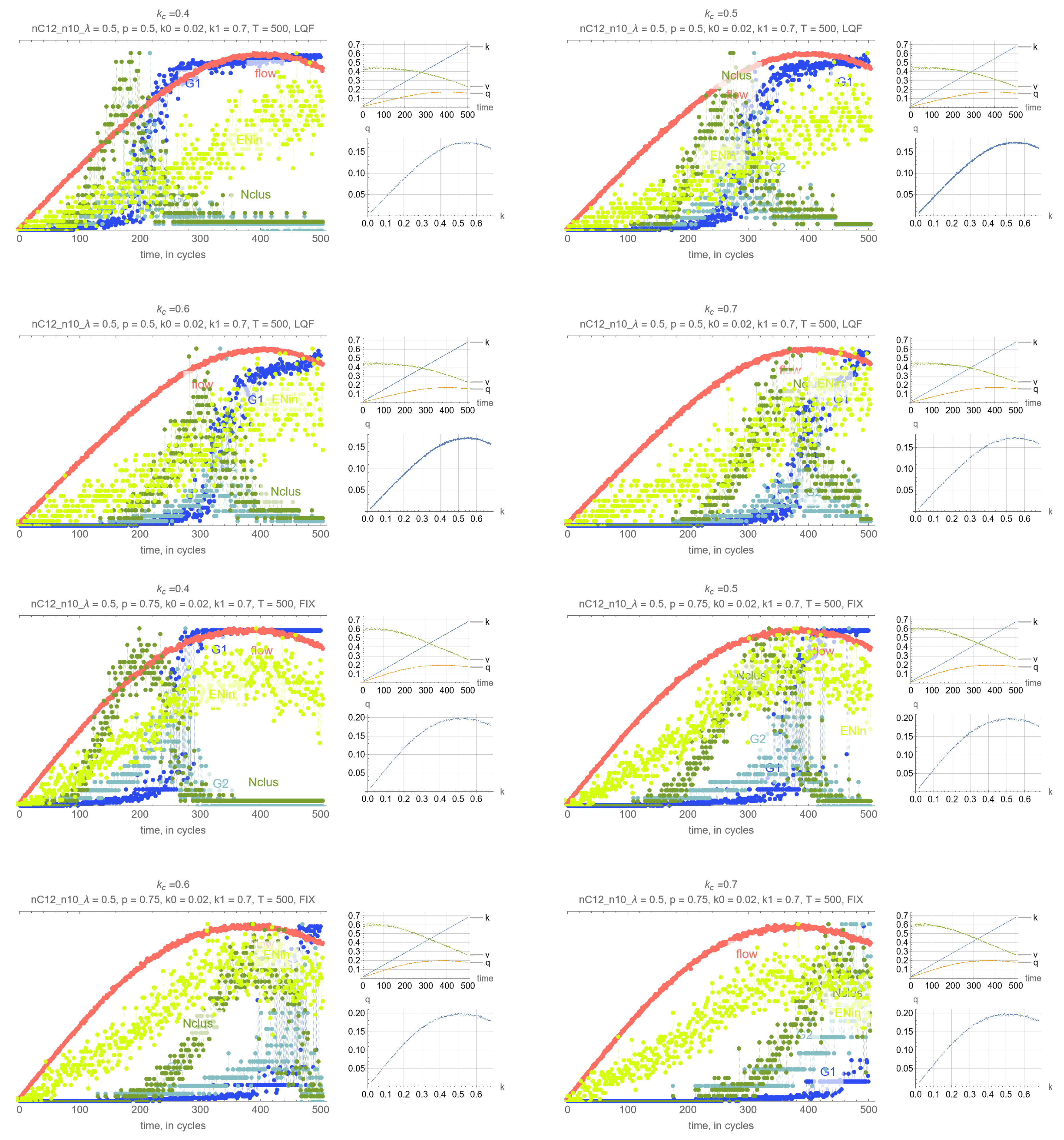
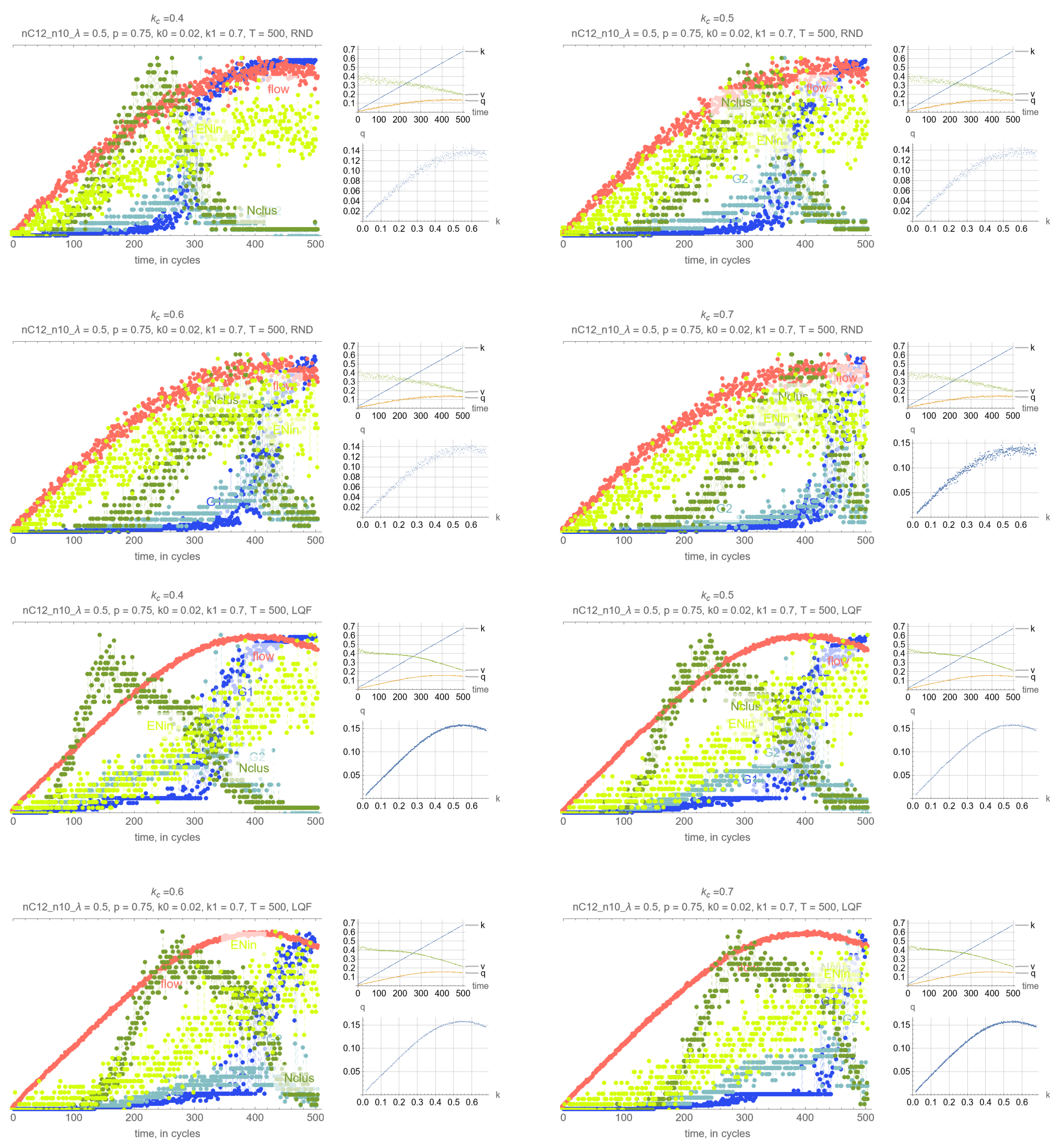
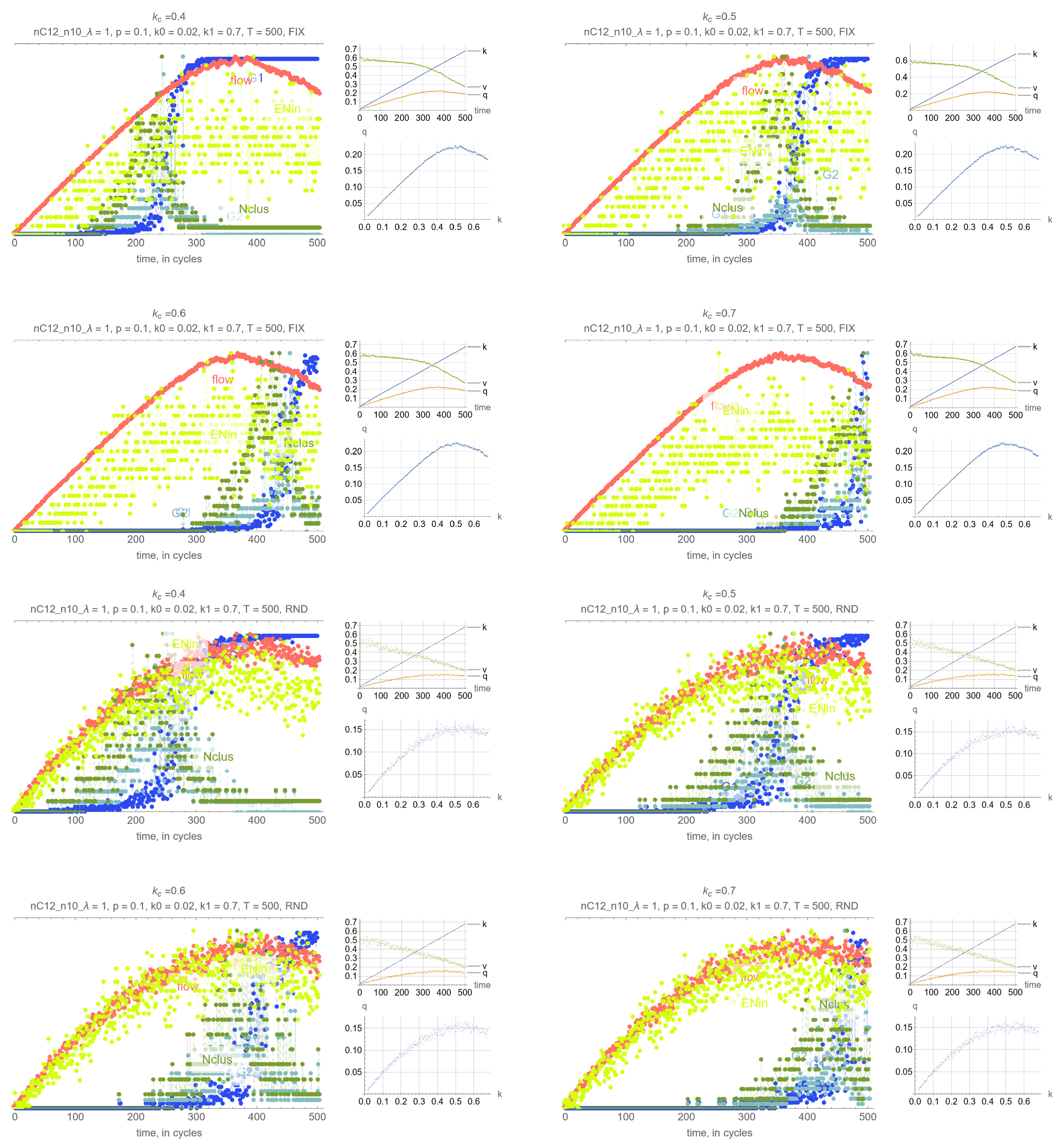
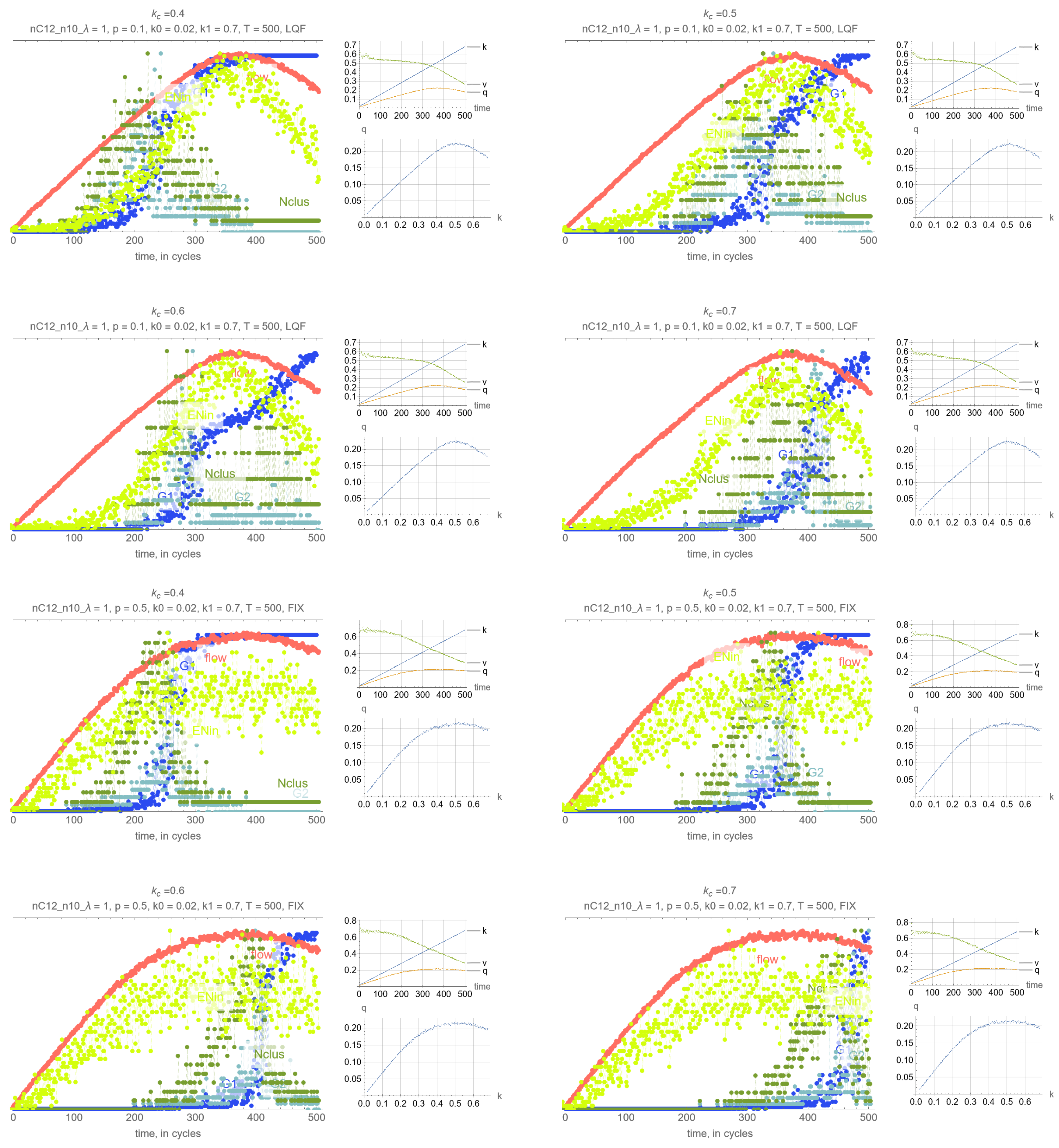
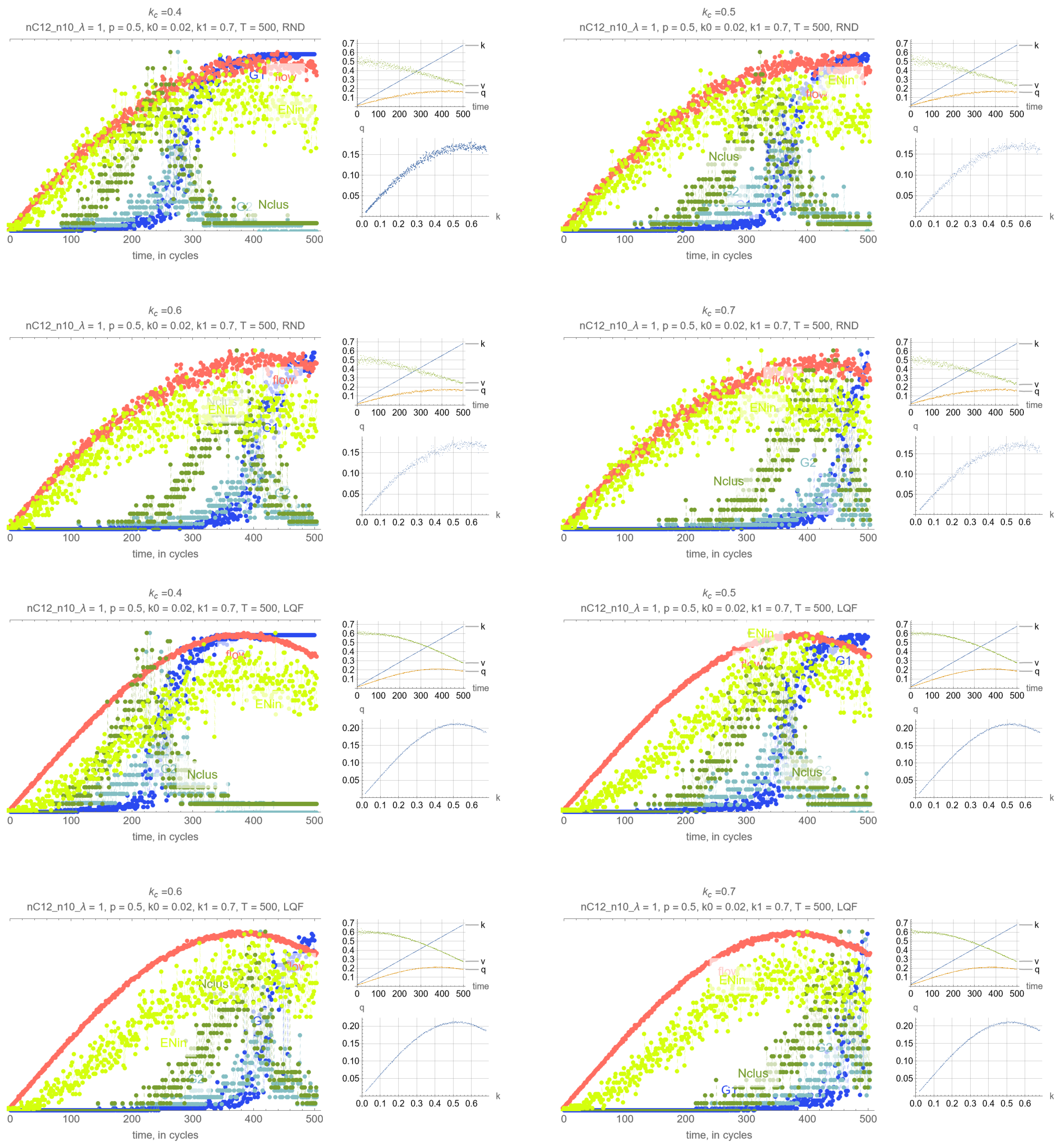
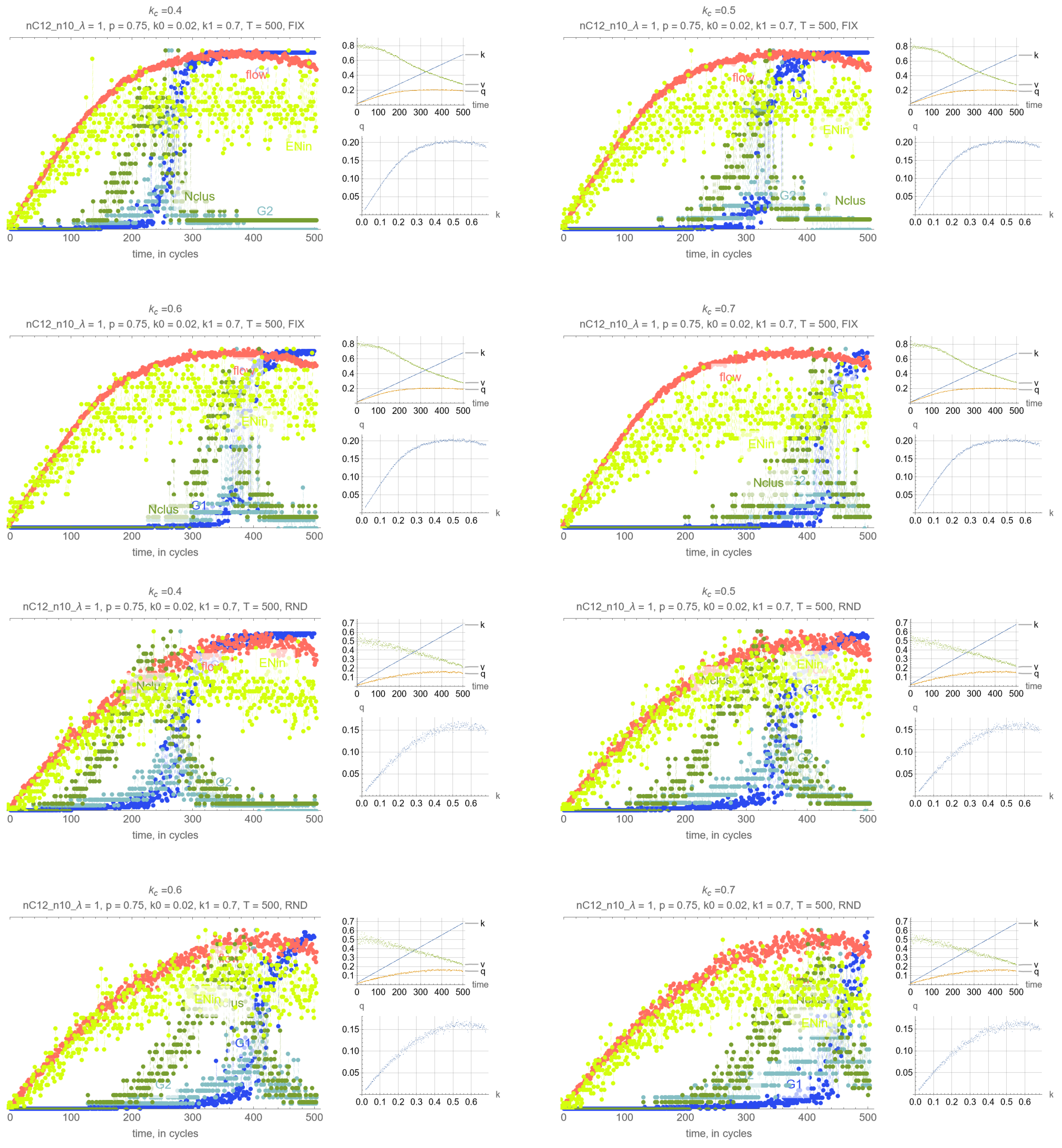
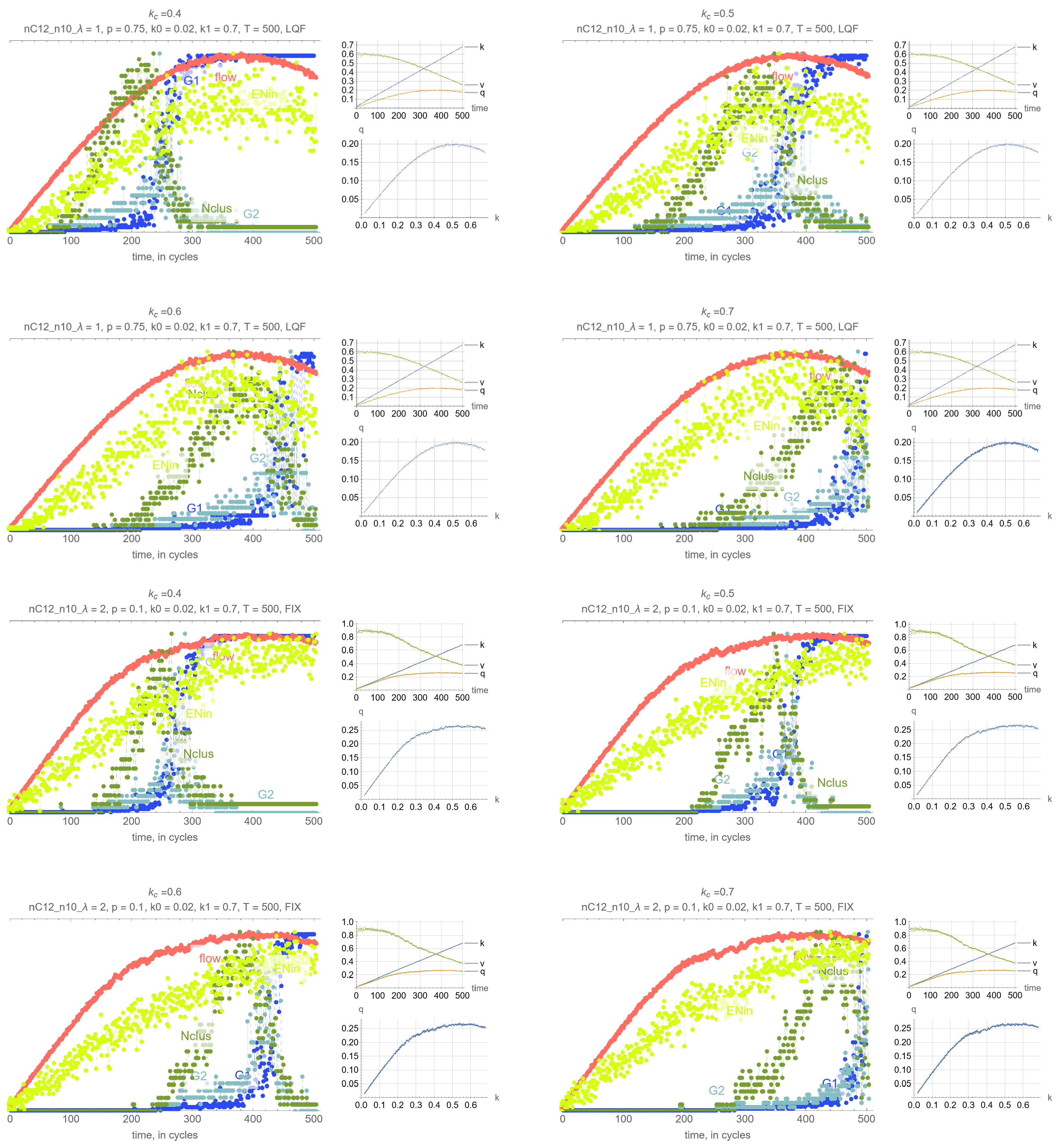
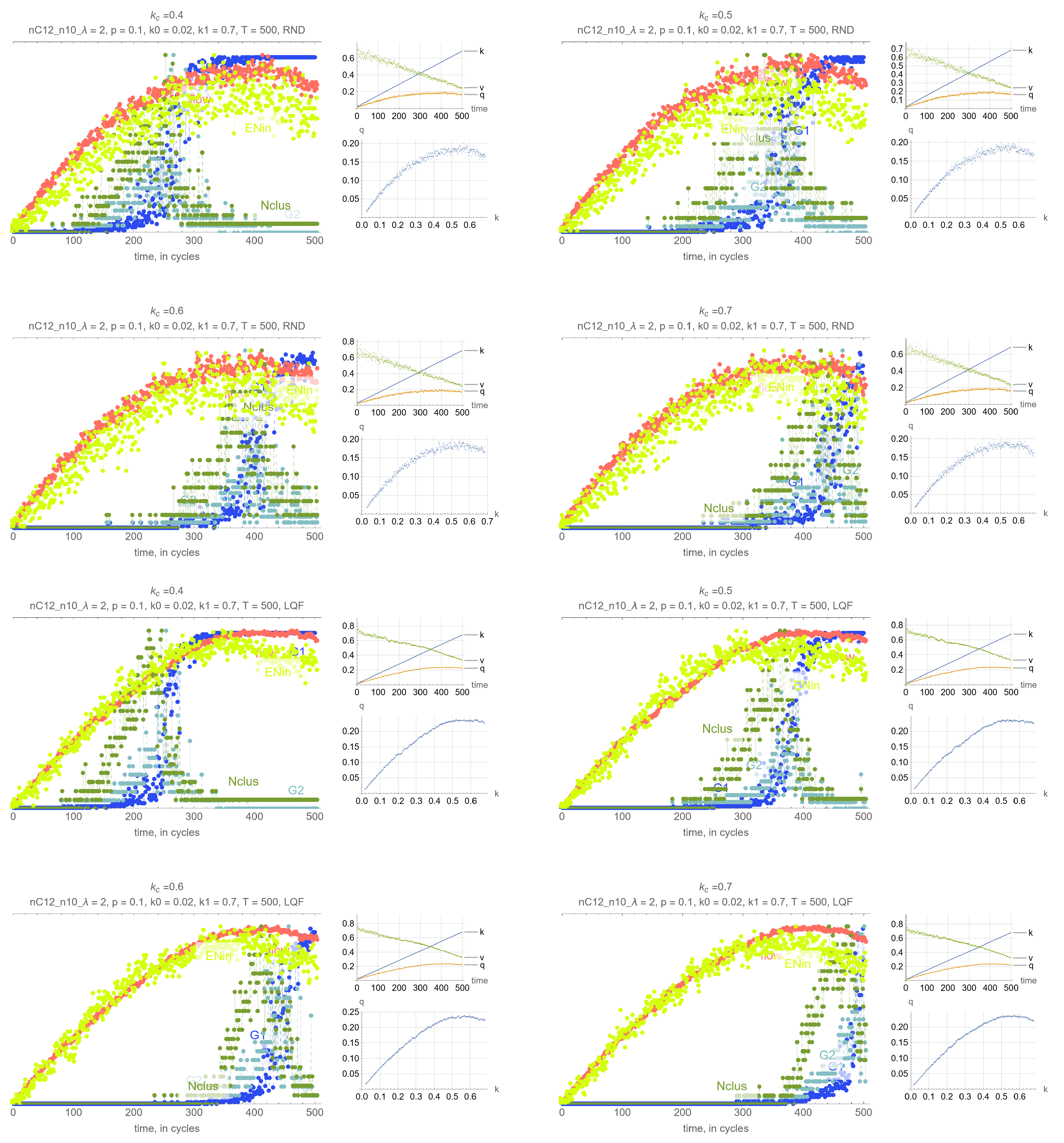
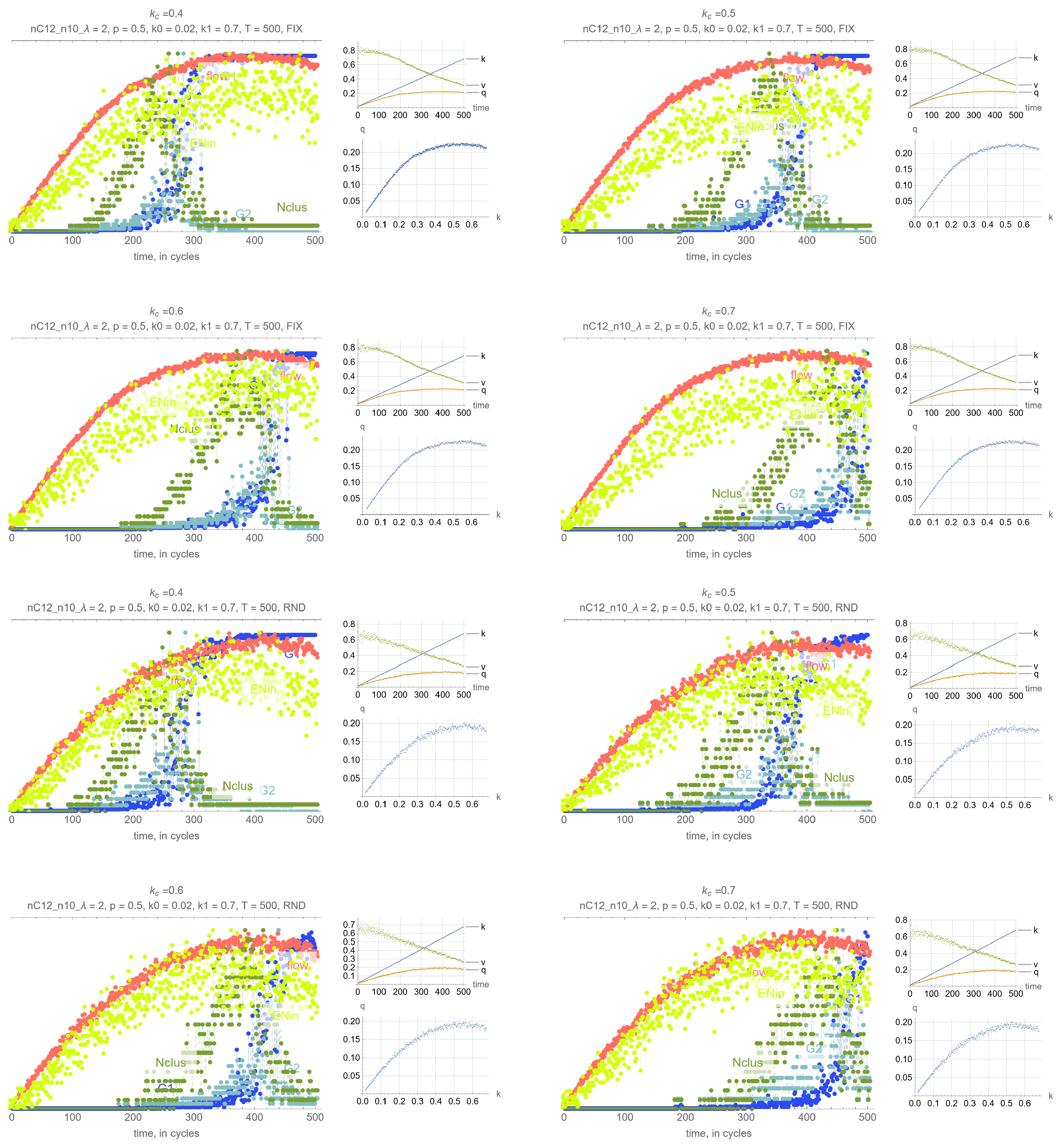
Preprints 71324 i001Preprints 71324 i002Preprints 71324 i003Preprints 71324 i004Preprints 71324 i005Preprints 71324 i006Preprints 71324 i007Preprints 71324 i008Preprints 71324 i009Preprints 71324 i010Preprints 71324 i011Preprints 71324 i012Preprints 71324 i013Preprints 71324 i014

References

  1. Zeng, G.; Li, D.; Guo, S.; Gao, L.; Gao, Z.; Stanley, H.E.; Havlin, S. Switch between critical percolation modes in city traffic dynamics. Proc. Natl. Acad. Sci. USA 2019, 116, 23–28. [Google Scholar] [CrossRef] [PubMed]
  2. Zhang, L.; Zeng, G.; Li, D.; Huang, H.J.; Stanley, H.E.; Havlin, S. Scale-free resilience of real traffic jams. Proc. Natl. Acad. Sci. usa 2019, 116, 8673–8678. [Google Scholar] [CrossRef] [PubMed]
  3. Zeng, G.; Gao, J.; Shekhtman, L.; Guo, S.; Lv, W.; Wu, J.; Liu, H.; Levy, O.; Li, D.; Gao, Z.; et al. Multiple metastable network states in urban traffic. Proc. Natl. Acad. Sci. usa 2020, 117, 17528–17534. [Google Scholar] [CrossRef] [PubMed]
  4. Laval, J.A. Self-organized criticality of traffic flow: Implications for congestion management technologies. Transp. Res. Part C Emerg. Technol. 2023, 149, 104056. [Google Scholar] [CrossRef]
  5. Wolfram, S. Cellular automata as models of complexity. Nature 1984, 311, 419. [Google Scholar] [CrossRef]
  6. Nagel, K.; Paczuski, M. Emergent traffic jams. Phys. Rev. E 1995, 51, 2909. [Google Scholar] [CrossRef]
  7. Nagel, K.; Wagner, P.; Woesler, R. Still flowing: Approaches to traffic flow and traffic jam modeling. Oper. Res. 2003, 51, 681–710. [Google Scholar] [CrossRef]
  8. Stauffer, D.; Aharony, A. Introduction to Percolation Theory; CRC press, 2018. [Google Scholar]
  9. Bak, P.; Chen, K.; Creutz, M. Self-organized criticality in the’Game of Life. Nature 1989, 342, 780–782. [Google Scholar] [CrossRef]
  10. Paczuski, M.; Nagel, K. Self-organized criticality and 1/f noise in traffic. In Traffic and Granular Flow; World Scientific: Singapore, 1996; p. 73. [Google Scholar]
  11. Ambühl, L.; Menendez, M.; González, M.C. Understanding congestion propagation by combining percolation theory with the macroscopic fundamental diagram. Commun. Phys. 2023, 6, 26. [Google Scholar] [CrossRef]
  12. Nagel, K.; Schreckenberg, M. A cellular automaton model for freeway traffic. J. De Phys. I 1992, 2, 2221–2229. [Google Scholar] [CrossRef]
  13. Nagel, K.; Rasmussen, S.; Barrett, C.L. Network Traffic as a Self-Organized Critical Phenomena; Technical report; Los Alamos National Lab.: NM, USA, 1996. [Google Scholar]
  14. Daganzo, C.F. A Variational Formulation of Kinematic Wave Theory: Basic theory and complex boundary conditions. Transp. Res. Part B 2005, 39, 187–196. [Google Scholar] [CrossRef]
  15. Nagel, K. Personal communication, 2021.
  16. Schadschneider, A. Personal communication, 2021.
  17. Rieser, M.; Nagel, K. Network breakdown “at the edge of chaos” in multi-agent traffic simulations. Eur. Phys. J. B 2008, 63, 321–327. [Google Scholar] [CrossRef]
  18. Olmos, L.E.; Çolak, S.; Shafiei, S.; Saberi, M.; González, M.C. Macroscopic dynamics and the collapse of urban traffic. Proc. Natl. Acad. Sci. USA 2018, 115, 12654–12661. [Google Scholar] [CrossRef] [PubMed]
  19. Petri, G.; Expert, P.; Jensen, H.J.; Polak, J.W. Entangled communities and spatial synchronization lead to criticality in urban traffic. Sci. Rep. 2013, 3, 1798. [Google Scholar] [CrossRef] [PubMed]
  20. Li, D.; Fu, B.; Wang, Y.; Lu, G.; Berezin, Y.; Stanley, H.E.; Havlin, S. Percolation transition in dynamical traffic network with evolving critical bottlenecks. Proc. Natl. Acad. Sci. USA 2015, 112, 669–672. [Google Scholar] [CrossRef]
  21. Laval, J.; Zhou, H. Congested urban networks tend to be insensitive to signal settings: Implications for learning-based control. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24904–24917. [Google Scholar] [CrossRef]
  22. Lighthill, M.J.; Whitham, G.B. On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 229, 317–345. [Google Scholar]
  23. Richards, P.I. Shock waves on the highway. Oper. Res. 1956, 4, 42–51. [Google Scholar] [CrossRef]
  24. Newell, G.F. A simplified car-following theory: A lower order model. Transp. Res. Part B Methodol. 2002, 36, 195–205. [Google Scholar] [CrossRef]
  25. Laval, J.A.; Chilukuri, B.R. Symmetries in the kinematic wave model and a parameter-free representation of traffic flow. Transp. Res. Part B Methodol. 2016, 89, 168–177. [Google Scholar] [CrossRef]
  26. Daganzo, C.F.; Gayah, V.V.; Gonzales, E.J. Macroscopic relations of urban traffic variables: Bifurcations, multivaluedness and instability. Transp. Res. Part B Methodol. 2011, 45, 278–288. [Google Scholar] [CrossRef]
  27. Mühlich, N.; Gayah, V.; Menendez, M. Use of microsimulation for examination of Macroscopic Fundamental Diagram hysteresis patterns for hierarchical urban street networks. Transp. Res. Rec. 2015, 2491, 117–126. [Google Scholar] [CrossRef]
  28. Laval, J. Traffic Flow as a Simple Fluid: Towards a Scaling Theory of Urban Congestion. Preprints 2022, 2022060377. [Google Scholar] [CrossRef]
  29. Laval, J.A. Effect of the trip-length distribution on network-level traffic dynamics: Exact and statistical results. Transp. Res. Part C Emerg. Technol. 2023, 148, 104036. [Google Scholar] [CrossRef]
Preprints 71324 g001
Figure 1. Left: Example 4 × 5 traffic network. The connecting links to form the torus are shown as dashed directed links; we have omitted the cells on these links to avoid clutter. Each segment has ℓ = 10 cells; an additional cell has been added downstream of each segment to indicate the traffic light color. Right: 4 output panels from numerical experiments for a particular parameter combination, each with a different random seed. Each panel consists of three figures. The large figure is a time series of all the variables being tracked as a function of time (the size of the largest component and the second largest component, the number of clusters, the average number of cars across all intersections that are being delayed when merging, and the MFD flow). The two smaller figures on its side give the traffic variable time series and the MFD observed during that particular simulation run, respectively.
Figure 1. Left: Example 4 × 5 traffic network. The connecting links to form the torus are shown as dashed directed links; we have omitted the cells on these links to avoid clutter. Each segment has ℓ = 10 cells; an additional cell has been added downstream of each segment to indicate the traffic light color. Right: 4 output panels from numerical experiments for a particular parameter combination, each with a different random seed. Each panel consists of three figures. The large figure is a time series of all the variables being tracked as a function of time (the size of the largest component and the second largest component, the number of clusters, the average number of cars across all intersections that are being delayed when merging, and the MFD flow). The two smaller figures on its side give the traffic variable time series and the MFD observed during that particular simulation run, respectively.
Preprints 71324 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated