Prerpints.org logo
Preprint
Article

Electro-elastic Modeling of Multi-Step Transitions in two Elastically Coupled and Sterically Frustrated 1D Spin-Crossover Chains

Altmetrics

Downloads

127

Views

64

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 April 2023

Posted:

21 April 2023

You are already at the latest version

Alerts
Abstract
1D spin crossover (SCO) solids which convert between the low-spin (LS) and the high-spin (HS) states are widely studied in the literature due to their diverse thermal and optical characters which allows obtaining many original behaviors, such as large thermal hysteresis, incomplete spin tran-sitions, as multi-step spin transitions with self-organized states. In the present work, we investigate the thermal behaviors of a system of two-elastically coupled 1D mononuclear chains, using the electro-elastic model, by including an elastic frustration in the nearest neighbors (nn) bond length distances of each chain. The chains are made of SCO sites that are coupled elastically through springs with their nn and next-nearest neighbors. The elastic inter-chain coupling includes diagonal springs, while the nn inter-chains distance is fixed to that of the high-spin state. The model is solved using MC simulations, performed on the spin states and the lattice distortions. When we only frustrate the first chain, we found a strong effect on the thermal-dependence of the HS fraction of the second chain, whose, by lowering its transition temperature which is also accompanied with the appearance of a significant residual HS fraction at low temperature. In the second step, we frustrate both chains by imposing different frustration rates and found that, for high frustration values, the thermal dependence of the total HS fraction exhibits three step and even four step spin transitions. The careful examination of the spin state structures in the plateau regions revealed the existence of special antiferro-elastic structure of type LSLS-HSHS-LSLS-HSHS along the first chain, and HSHS-LSLS-HSHS-LSLS along the second, also showing that the two chains seem to be antifer-ro-elastically coupled. This type of organization is interesting, because it anticipates the possible existence of periodic structures made of alternate 1D antiferro-like HS-LS strings coupled in the ferro-like fashion along the interchain direction in the 2D case.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Spin crossover materials SCO represent a fascinating generation of switchable molecular solids, offering serious applications, in molecular electronic, for the development of a new electronic devices, such as, molecular sensors, displays, nonvolatile memories, and reversible switches [1,2,3,4,5]. Among them, The most studied objects are iron (II)-based SCO solids [1,5,6,7,8,9,10,11,12], characterized by their electronic character which confers them the property to convert from a diamagnetic low spin state ( L S ,   e g 0 t 2 g 6 ,   S = 0 ) to a paramagnetic high spin state ( H S ,   e g 2 t 2 g 4 ,   S = 2 ) upon change of a external stimuli, as temperature, pressure [13], light [14,15,16,17,18], static electric field [19,20] and magnetic field [21]. The SCO phenomena are possible when the central iron atom is surrounded by nitrogen atom in octahedral symmetry. In addition, when the energy gap between the LS and the HS states, is in of the order of magnitude of the thermal, electric, magnetic and light energy.
At the molecular level, this transition is accompanied by a volume change of octahedral cage of 3%, while, the change of the Fe-ligand distances is almost 10% [7]. This volume change is delocalized over all the crystal, through elastic strain, leading to long-range interactions [22].
From the experimental point of view, the thermally-induced SCO transition may appear through several types: (i) continuous spin transitions [23], (ii) discontinuous first-order transitions [24], (iii) incomplete transitions [25] with residual HS fractions and (iv) multi-step spin transitions [26,27,28,29,30].
From the theoretical point of view, several models have been used to describe the multi-step transition. The most famous are based on the Ising-like models combining competing ferro- and antiferro-like interactions [31,32], which were solved using mean-field theory or by the Monte Carlo simulations. Later on, several works have been published related with the modeling of the multi-step transitions phenomena in SCO systems, based on electro-elastic descriptions, and elastic frustration concept, resulting from the presence of antagonist steric effects, as in Ref [33], where the authors studied the effect of an elastic frustration injected along the diagonals in a 2D lattice.
In a previous work [34], we have studied the thermal properties of an elastically-frustrated 1D isolated SCO chain. Where, the frustration was introduced between the nnn distances, leading to antagonist effects between the nn and nnn equilibrium distances, along the thermal transition between the LS and the HS states, and in Ref [35], we investigate the thermal properties of 1D binuclear chain. The elastic frustration is injected in the nn equilibrium distances, inside the binuclear units, where usually the bonds are more rigid that the inter-binuclear bonds. In the present contribution, we extend our model [35], to study the effect of an elastic frustration for a system made of two elastically coupled 1D SCO chains, each containing N=120 sites. As previously explained, the frustration is injected in the equilibrium distance inside each binuclear unit. However, the sites constituting the binuclear interact with their neighbors from consecutive binuclear sites. In addition, the two chains are also coupled along their diagonal directions. The simulations have been performed using Monte Carlo method running on spins and lattice positions accounting for the change of the chain size along the spin transition.
The manuscript is organized as follows. Sec. 2 introduces the model Hamiltonian and the details of the simulations. In Sec. 4, we present the results in the case of only one frustrated chain, while the other remains free from any elastic frustration. In Sec. 5, we frustrate the second chain too and study the thermal properties for the two coupled chains for various frustrations rates of the two chains. In Sec. 6 we conclude and outline some possible extensions of the present model.

2. The electro-elastic Model

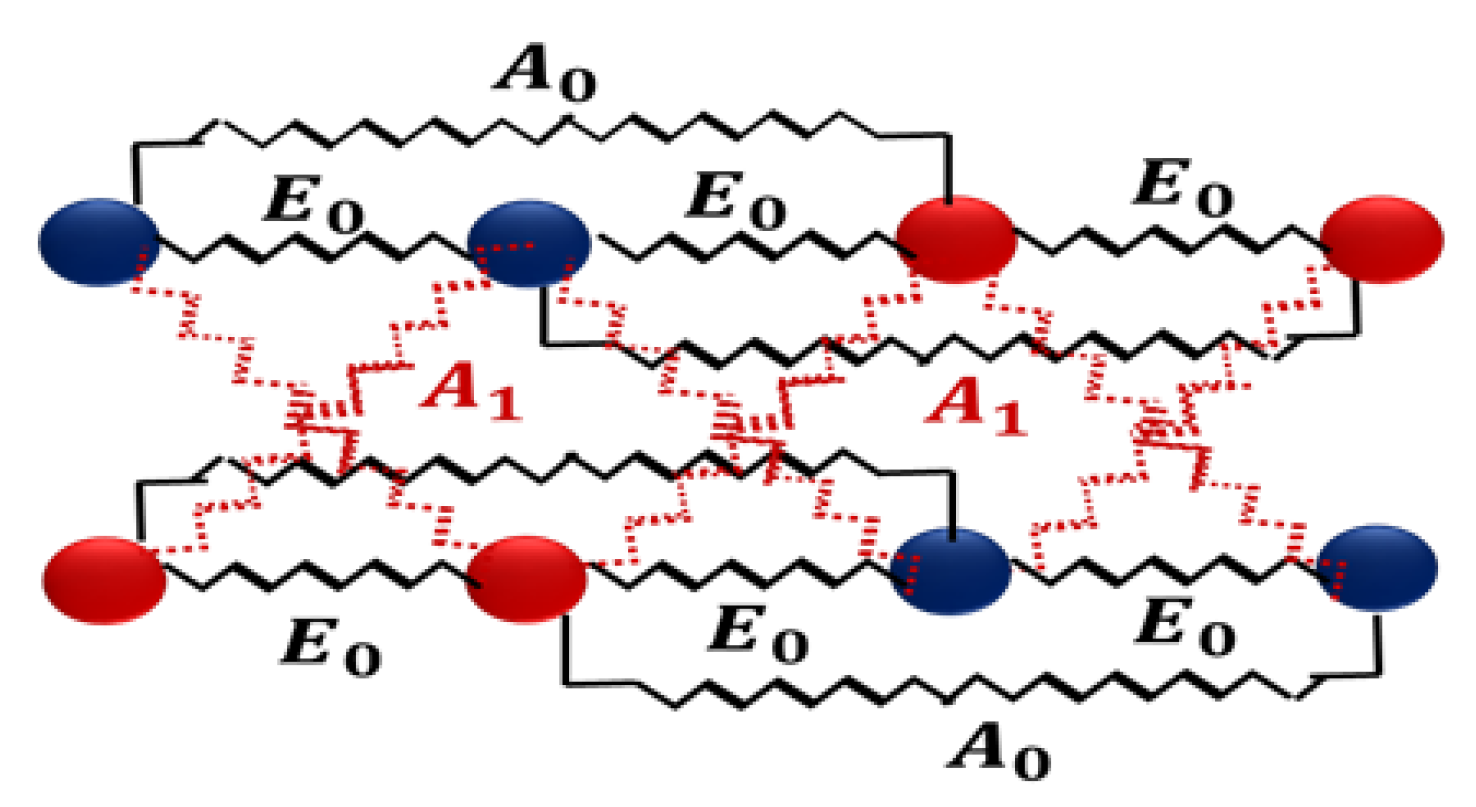
In this work, we will study and simulate the thermal induced transition, of a model system made of two elastically-frustrated 1D SCO chains, of size N=120 atoms, elastically connected by springs along the diagonal directions. In each chain, the atoms (sites) can occupy two states, namely low spin (LS), and high spin (HS), to which we associate a fictitious spin state S , whose eigenvalues are respectively, S = − 1 (LS) and S = 1 (HS). The lattice sites are coupled by springs, and are constrained to move only along the direction of the chains (ie x directions). Thus the atoms do not move along the y directions, and therefore during the simulations we had fixed the distance between the two chains (according to y) to R H H = 1.2 n m . In each chain, the sites are coupled elastically to their nearest neighbors (nn) by a spring of elastic constant E 0 and to their next nearest neighbors (nnn) by a spring of elastic constant, A 0 .
The two chains are coupled elastically along the diagonal directions by another spring of elastic constant A 1 , as shown in Figure 1.
In this model, the bond lengths distances between the sites depend on the spin states of the connected sites. The equilibrium distances between two nn sites i and i + 1 are noted R n n ( S 1 , i , S 1 , i + 1 ) , for the first chain numbered by index 1, and R n n S 2 , i , S 2 , i + 1 for the second chain numbered by index 2. The dependence of the equilibrium bond lengths (i.e., the lattice parameters of the chain) on the spin states ( S l , i and S l , i + 1 , l = 1,2 ) of the neighboring i and i + 1 sites is written so as to ensure a bigger length of the chain in the HS state in comparison that of the LS state.
The Hamiltonian describing this system of two coupled 1D chains, taking accounting for the electronic and elastic degrees of freedom [36,37,38,39,40], writes:
H = H 1 + H 2 + H 12 ,
where, H 1 , H 2 are the respective energetic contributions of the first, the second chain, while H 12 accounts for the elastic interaction between the two chains. Their expressions are given as follows:
H 1 = 1 2 ∑ i = 1 N x ∆ 0 − k B T l n g   S 1 , i + E 0 ∑ i = 1 N x ( x 1 , i − x 1 , i + 1 ) − R 0 S 1 , i , S 1 , i + 1 2 + A 0 ∑ i = 1 N x ( x 1 , i − x 1 , i + 2 ) − R 0 ' S 1 , i , S 1 , i + 2 2 ,
H 2 = 1 2 ∑ i = 1 N x ∆ 0 − k B T l n g   S 2 , i + E 0 ∑ i = 1 N x ( x 2 , i − x 2 , i + 1 ) − R 0 S 2 , i , S 2 , i + 1 2 + A 0 ∑ i = 1 N x ( x 2 , i − x 2 , i + 2 ) − R 0 ' S 2 , i , S 2 , i + 2 2 ,
H 12 = ∑ i ≠ j N x A 1 d 12 − 2 R n n S 1 , i , S 2 , i 2 ,
where, d 12 = ( x 2 , i + 1 − x 1 , i ) 2 + R 0 H H 2 .
The first terms of H 1 and H 2 in Eqs. (2) and (3) stand for the electronic contributions of the ligand fields energy ∆ 0 at 0K, while the temperature-dependent term – k B T l n g , accounts for the entropic effects originating from the difference of effective electronic and vibrational degeneracies originating from the intra-molecular vibrations and lattice phonons as well as on the contributions of the spin state changes along the spin transition. The second and the third terms of Hamiltonian H 1 and H 2 , describe the elastic interactions between the nearest (nn) and next nearest-neighbors (nnn), respectively. Here, the elastic constants E 0 and A 0 are assumed, for simplicity, as independent of spins ( S i ) and position ( x i ) variables.
In this model the nn (resp. nnn) ( 1 , i ) and ( 1 , i + 1 ) [resp. ( 1 , i ) and ( 1 , i + 2 ) ] sites of the first chain with corresponding spins S 1 , i and S 1 , i + 1 (resp. S 1 , i and S 1 , i + 2 ) are linked through springs, whose bond-lenghts at equilibrium are noted R 0 S 1 , i , S 1 , i + 1 [resp. R 0 ' S 1 , i , S 1 , i + 2 ] . Similarly, for the second chain, we denote by ( 2 , i ) and ( 2 , i + 1 ) [resp. ( 2 , i ) and ( 2 , i + 2 ) ] the nn (resp. nnn i and i + 1 (resp. i and i + 2 ). Their corresponding spins noted S 2 , i and S 2 , i + 1 [resp. S 2 , i and S 2 , i + 2 ] are linked through springs, whose bond lengths at equilibrium are noted R 0 S 1 , i , S 1 , i + 1 [resp. R 0 ' S 1 , i , S 1 , i + 2 ].
In each chain, the atoms are constrained to move only along the x direction. Let us denoted by R 0 H H = R ( + 1 , + 1 ) , R 0 L L = R ( − 1 , − 1 ) , and R 0 H L = R + 1 , − 1 the respective nn equilibrium distances between the HS-HS, LS-LS and HS-LS sites. For simplicity, we consider here that R 0 H L = R 0 H H + R 0 L L 2 , wich means that the equilibrium distance between HS and LS states is exactly equal to the average distance between those of LS-LS and HS-HS configurations.
Within this, it is quite easy to demonstrate that for the two chains, the general expressions of the nn and nnn equilibrium distances connect to the spin states through the simple formulas:
R 0 S l , i , S l , i + 1 = R 0 H L + δ R 4 ( S l , i + S l , i + 1 ) ,
R 0 ' S l , i , S l , i + 2 = 2 R 0 H L + δ R 2 S l , i + S l , i + 2 ,
where l = 1,2 stands for the chain number and the quantity δ R = R 0 H H − R 0 L L is the lattice parameter misfit between the pure LS and the HS phases.
The idea of the elastic frustration, which is at the heart of this paper, assumes the existence of a lattice mismatch between the nn and the nnn equilibrium distances inside the chains. In a previous work [35], we studied the effect of such elastic frustration in an isolated 1D SCO chain by introducing the elastic frustration only between LS-LS and LS-HS neighbors.
In the present model, we extend these investigations to two coupled frustrated chains, while keeping, as in the previous study, the HS state free for any elastic frustration, in the two chains. Thus, in addition we imposed the elastic frustration between the nn and the nnn distances for the HS-LS and LS-LS configurations, we only consider the diagonal elastic coupling between the two chains.
The elastic frustration consists here in the existence of antagonist equilibrium distances between the nn and nnn along the chains in the previously mentioned configurations. Since no transverse displacement is allowed in these simulations, once frustrated the system will not be able to relax the excess of stress. In practice, the elastic frustration is introduced in the nn equilibrium distance between sites ( l , i ) , ( l , i + 1 ) , l = 1,2 , in the two chains respectively, as follows:
R S l , i , S l , i + 1 = R S l , i , S l , i + 1 + δ R ξ l 2 1 − S l , i + S l , i + 1 2 ,
Here, ξ l   l = 1,2 expresses the frustration strength for the two chains.
Thus, according to Eq. (7), in the case of three consecutive LS-LS-LS sites in chain 1, for example, the equilibrium nn distances are equal to R ( − 1 , − 1 ) = R 0 L L + δ R ξ 1 , while the nnn equilibrium distance, which is still given by Eq. (6), is R ' = 2 R 0 L L ≠ 2 R 0 L L + δ R ξ 1 . Consequently, a bond length misfit does exist between these two quantities, since the “atoms” can move only along the x directions. Within this frustration, the system will optimize its total elastic energy by moving the atoms and the final mechanical equilibrium will clearly depend on the nn and nnn elastic constants as well as on the coupling between the chains.
To perform the present simulations, we use in each chain, the following values for the non-frustrated nn equilibrium bond length distances: R 0 L L = 1.0 n m , R 0 H H = 1.2 n m and R 0 H L = 1.1 n m , which leads to the lattice misfit between the LS and HS phases, δ R = 0.2 n m . The elastic constants have been fixed to E 0 = 24000 K . n m − 2 = 24 m e v . Å − 2 for the nn interactions along the chains, to A 0 = 0.1 E 0 for the nnn elastic interactions within the same chain, and to A 1 = 0.05 E 0 for the diagonal inter-chain interactions. We recall that the nn distance between the chains is kept constant and equal to that of the HS state in order to enforce the atoms to move along the x-direction in both chains. The value of the ligand-field energy is taken equal to Δ 0 = 450 K , and that of the degeneracy ratio is such as l n g = 5 . This value leads to the entropy change, Δ S = 41 J . K . m o l − 1 , a value which is in fair agreement with experimental finding of calorimetry [41].

3. Results and discussions

In this section, we are interested in the thermodynamic properties of this set of two coupled chains. For that, we determine the thermal-dependence of the usual macroscopic order parameters describing the spin transition, which are: (i) the HS fractions, n H S 1 and n H S 2 , of the chains 1 and 2, which connect to the corresponding average magnetization < S > l ( l = 1 , 2 ) through Eq. (8), and (ii) the average intra-chains and inter-chains bond length distances < d > l . Here, we calculate these parameters for each chain, which are denotes as n H S l for the HS fraction of the l t h chain, and < d > l were l = 1,2 stands for the chain number. On the other hand, we also define the distance, < d > 12 , as the average diagonal bond length between the two chains, while their shortest distance is fixed here to that of the HS bond length distance, R 0 H H . The previous quantities can be simply expressed as:
n H S l = 1 + m l 2 = 1 + < S l > 2 ,
< d > l = ∑ i = 2 N α x l , i − x l , i + 1 N x − 1   ,
< d > 12 = ∑ i = 1 N α x 1 , i − x 2 , i 2 + R 0 H H 2 2 N x − 1  
where l = 1,2 stands for the chain number, and < S l > is the average spin value of the l t h chain, while x l , i − x l , i + 1 [resp and x l , i − x l , i + 2 ] are the nn (resp nnn) distances between neighboring sites. The total HS fraction is then given by:
n H S = n H S 1 + n H S 2 ,
The Hamiltonian (1) is solved numerically by Monte Carlo (MC) technique running on spins and positions variables, in view of its complex structure. Here, we aim to study its thermal properties, considering the respective frustration strengths of the two chains ξ 1 and ξ 2 , as control parameters.
When starting the simulations, we first prepare the system in the HS phase (which is not frustrated by construction) by fixing all the spins to S i = + 1 and all nn [resp. nnn] lattice distances equal to R 0 H H (resp. 2 R 0 H H ).
The MC simulations are performed on two-coupled chains, each of them containing 120 sites. The sites are visited randomly while the MC procedure is performed on both spin and lattice position variables, in a sequential way. The stochastic algorithm is performed as follows: for a site i randomly selected, with spin S i = ± 1 and position, x i , a new spin value S i ' = − S i is set without position change. This spin change is updated, using Metropolis transition rates, and whatever the result of this first process (accepted or rejected spin change), the whole lattice is systematically relaxed mechanically by a slight motion of nodes (selected randomly) with a quantity δx = 0.05, which is much smaller than the smallest equilibrium distance R 0 L L between the sites. This procedure of the lattice relaxation is repeated 10 times for each spin flip. Afterward, a new site is randomly selected and we repeat the procedure. Once all nodes of the lattice are visited for the spin change, we define such step as the unit of the Monte Carlo step “MCS”. In the present simulations, the thermal properties are calculated by changing the temperature by 1K step. At each temperature, we perform 2500 MCS to reach the equilibrium state and we use 2500 other MCS for the statistics. Within this procedure, each site is displaced 2500 times for 1 MCS. So, at each temperature, each spin state and lattice position are updated 6 ×107 times, respectively. We have checked that increasing the simulation time does not affect the final results, which ensures that we reached the stationary state for spin and lattice position variables.

4. Frustration of the first chain

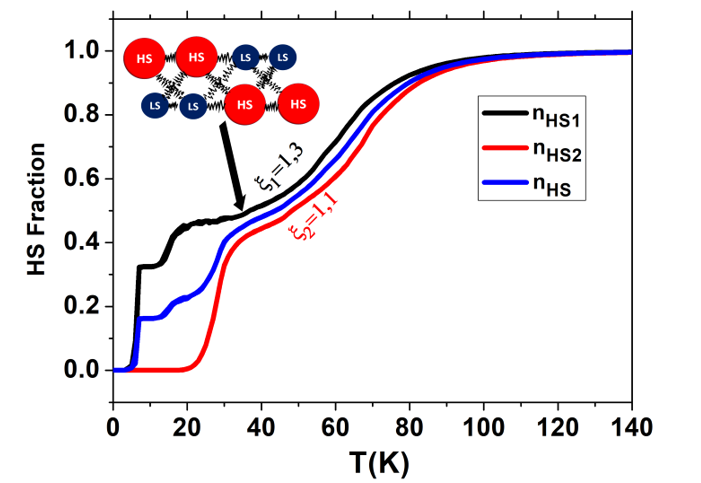
In the first step, we impose an elastic frustration between the nn and nnn equilibrium distances solely in the first chain, and we let the second without frustration. Our objective here is to investigate the effect of the frustration of the first chain on the thermal properties of the second chain, for several frustration parameter ξ 1 ranging from 0 to 1.3, while ξ 2 = 0 .
The obtained results are summarized in Figure 2, where Figure 2a, displays the thermal dependence of the HS fraction n H S 1 of the first chain for different values of the ξ 1 . In the absence of frustration ( ξ 1 = 0 ) , one obtains a hysteretic first-order transition of width ∆ T = 8.4 K . This result may be found quite surprising for a 1D chain. However, the elastic interactions generate infinite long-range interactions between the spin states and so the system belongs to mean-field universality class as demonstrated by Miyashita and al. [42], which then allows obtaining long-lived metastable states around the transition temperatures on heating and cooling.
When the elastic frustration comes into play (i.e., ξ 1 ≠ 0 in Figure 2a), the HS fraction of the first chain, is shifted to the low temperature regions, and the thermal transition transform from first order transition with hysteresis to a continuous two- step transition with a large plateau around n H S 1 = 0.5 . In Figure 2b, we depict the corresponding thermal dependence of the HS fraction, n H S 2 , of the second chain. In absence of frustration in chain 1, the transformation between the HS and the LS states of the second chain is exactly the same as that of the first chain. This is well understood when examining Hamiltonians (2) and (3) which are equivalent for ξ 1 = ξ 2 . In contrast, when we frustrate the first chain, a symmetry breaking occurs between the two Hamiltonians, since exchanging the indexes 1 by 2 and vice versa does not keep the total Hamiltonian invariant. Thus, the two chains are expected to have different behaviors. Indeed, the second chain feels a strong elastic strain that deforms the HS fraction curve by decreasing the transition temperature, which is accompanied with the emerging of humps along the transition, for small HS fractions from ξ 1 = 0.3 , announcing the existence of a slight two-step transition. Interestingly, above some critical value ξ 1 located in the interval 0.6-0.8, the 2nd chain experiences an incomplete spin transition on the HS fraction, with the presence of the residual HS fraction at low temperature which increases with the frustration rate ξ 1 .
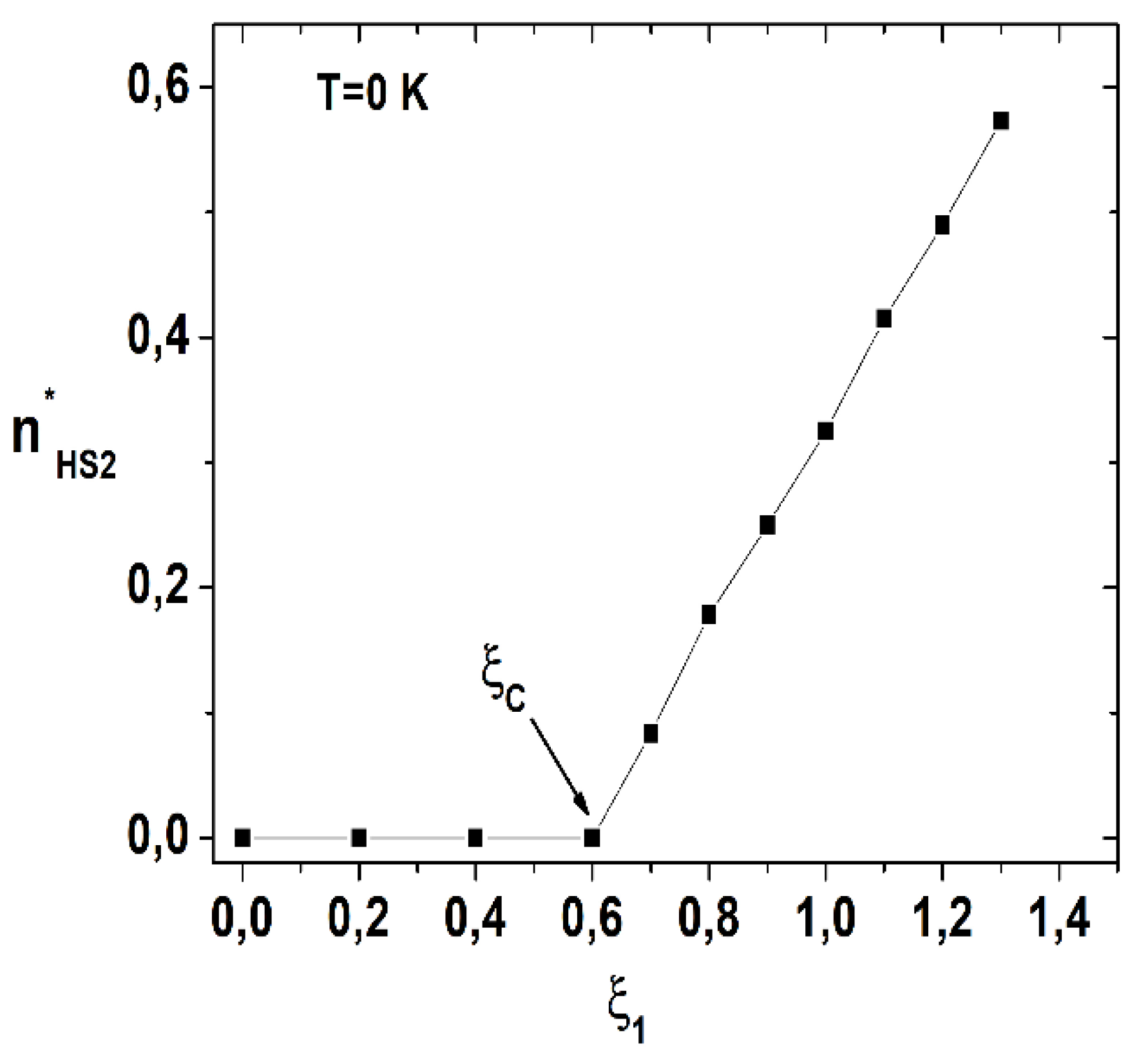
Figure 3. Summarizes the ξ 1 -dependence of this residual HS fraction, denoted n H S 2 at low temperatures ( T = 0 K), derived from MC simulations running on spin and distortion. The results clearly indicate the existence of a threshold value ξ C ≅ 0.6 , above which the LS state is no more the stable state in the second chain, while the first chain is still in the LS state. Remarkably, the residual fraction n H S 2 linearly increases with the frustration rate ξ 1 .
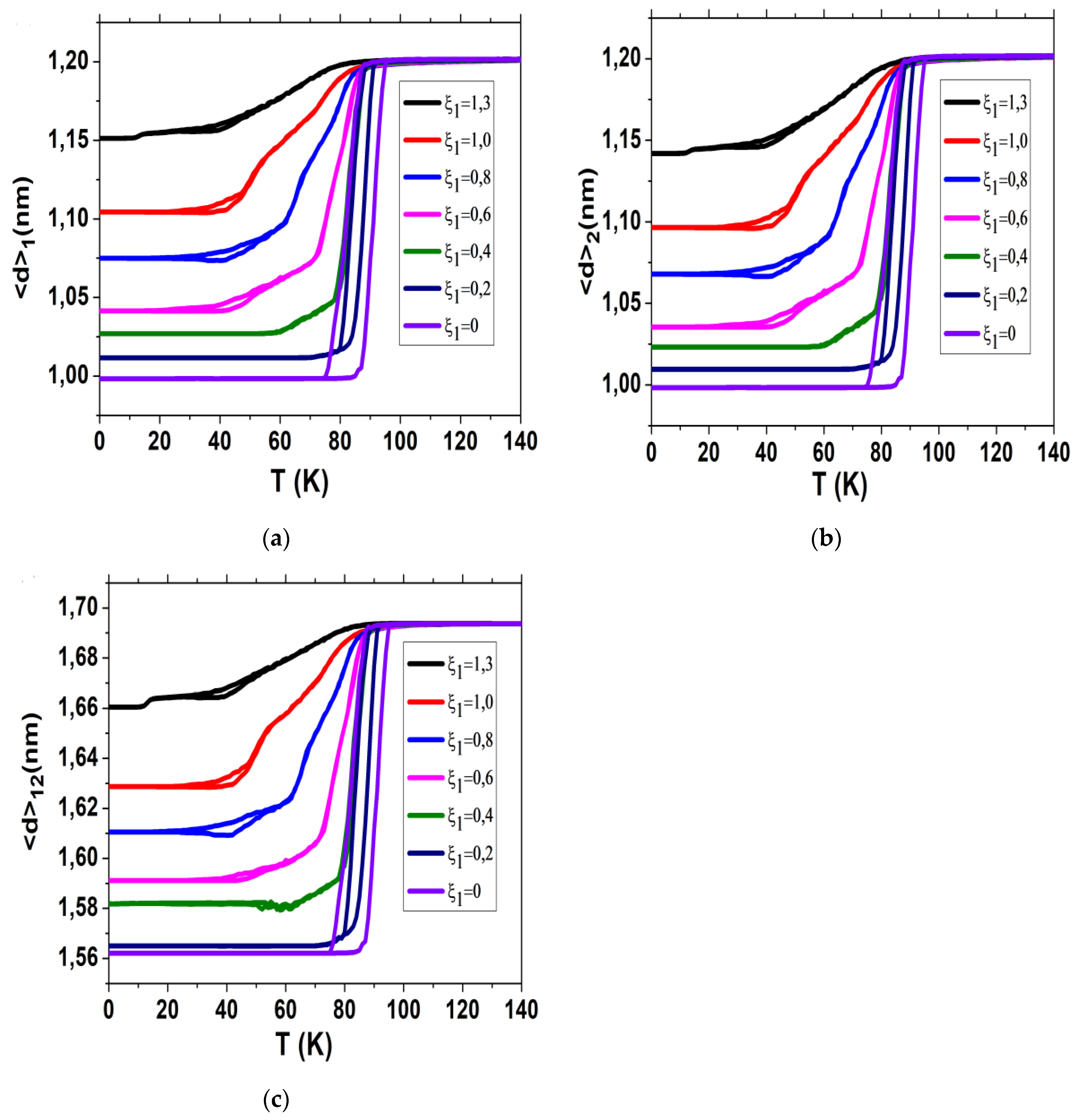
To understand the origin of the two-step (resp. incomplete) transitions appearing in chain 1 (resp. 2) of Figure 2b for large ξ 1 ( > 0.6 ) values, we plot in Figure 4 a-c the corresponding thermal behaviors of the average nn lattice bond lengths < d > 1 , < d > 2 , and < d > 12 . Interestingly, it is immediately remarked that as soon as ξ 1 is nonzero, the average low-temperature bond lengths < d > 1 , < d > 2 , and < d > 12 become bigger than their LS state values. 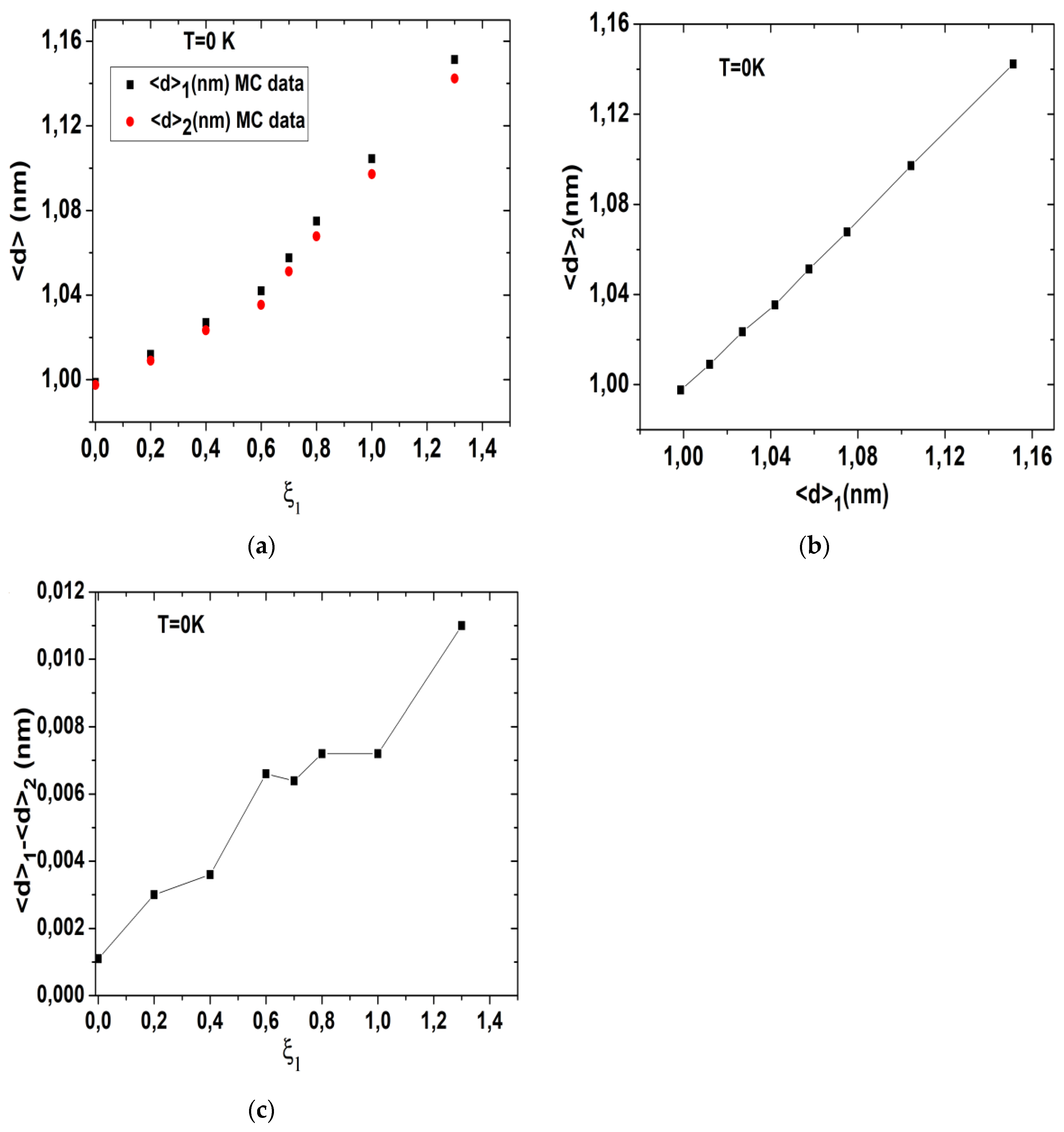As a result, ξ 1 induces a negative internal pressure in the lattice. However, this negative pressure is bigger for chain 1 than for chain 2. Indeed, a careful inspection of the curves of Figure 4a,b shows as well as those of Figure 5a, where we compare the low-temperature values of < d > 1 and < d > 2 as function of ξ 1 , demonstrates that at 0 K, one has < d > 1 always bigger than < d > 2 , and the difference < d > 1 − < d > 2 even increases as ξ 1 increases (Figure 5c). However, contrary to the thermal behaviors of the HS fractions of the two chains, given in Figure 2a-b, the corresponding average nn bond lengths < d > 1 and < d > 2 show very similar temperature dependence trends. However, it is important to keep in mind that the elastic frustration is only injected in chain 1. As a result, in the LS state for example, all equilibrium distances of chain 1 become bigger than those of LS, which forces the chain to expand. However, since the latter is coupled to the second chain by imposing all nn interchain distances as invariant (see Figure 1), this leads to an additional frustration for both chains. Therefore, the intermediate plateaus obtained in chain 2 are caused by the behavior of the first chain which experiences a stronger elastic frustration than the second chain.
When we analyze Figure 3 and Figure 4 and correlate the electronic and the elastic properties of the lattice, we find that when < d > 1 exceeded < d > 1 = R H L = 1.1 n m (see black curve in Figure 4a) for at ξ 1 = 1.0, a plateau starts to emerge in the thermal dependence of n H S 1 in Figure 2a and concomitantly with the appearance of nonzero residual HS fraction in the 2nd chain (Figure 2b). On the other hand, this proves again that the second chain (Figure 4b) seems to follow the same behavior as that the first one, although the values of the average parameter < d > 2 differ slightly from those of < d > 1 when the frustration rate ξ 1 increases due to the elastic coupling between the two chains. In Figure 4c the diagonal bond length < d > 12 between the two chains also follows the same trends with temperature as < d > 1 and < d > 2 except for the behavior of < d > 12 at 0 K which present some differences with those of < d > 1 and < d > 2 .
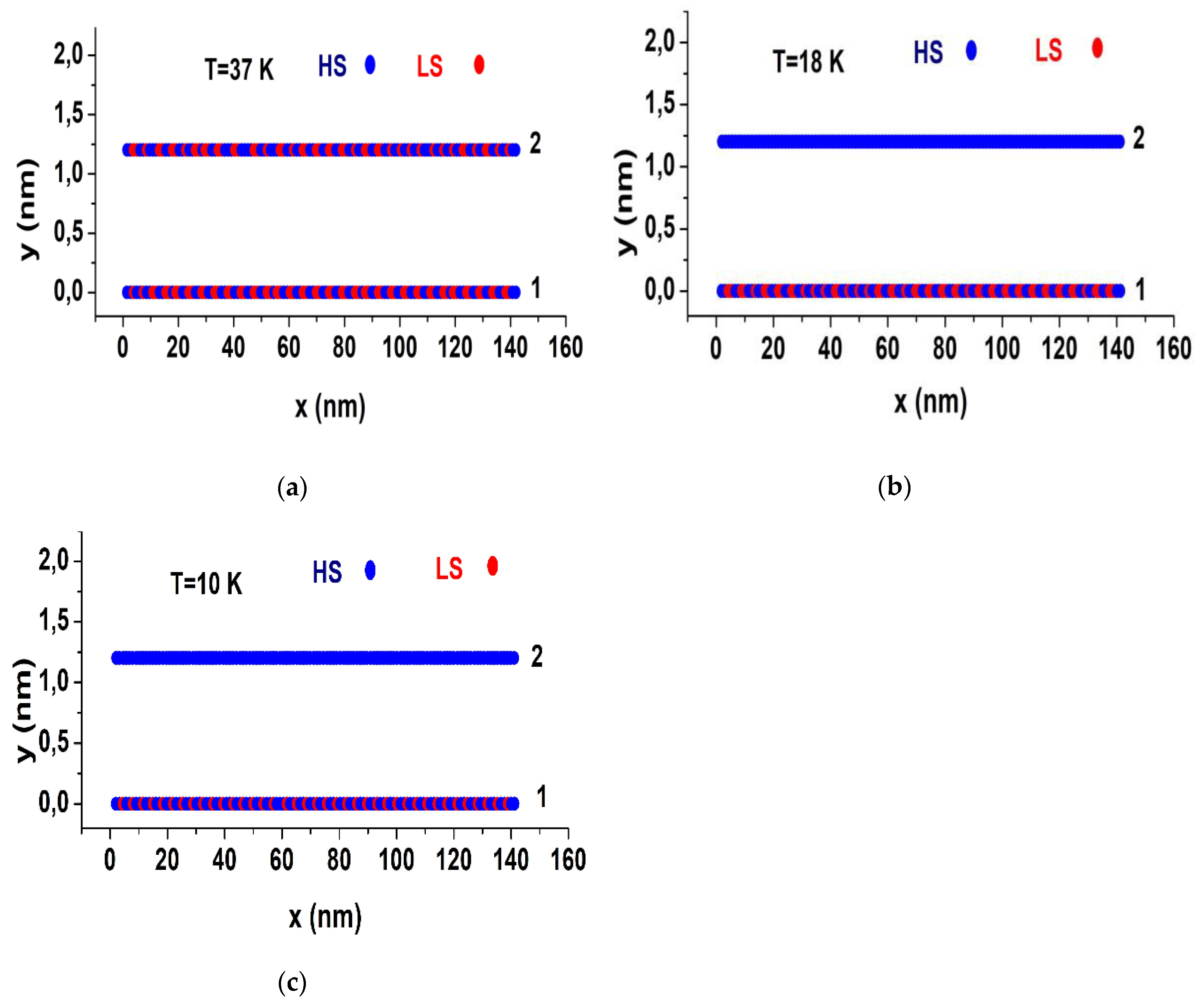
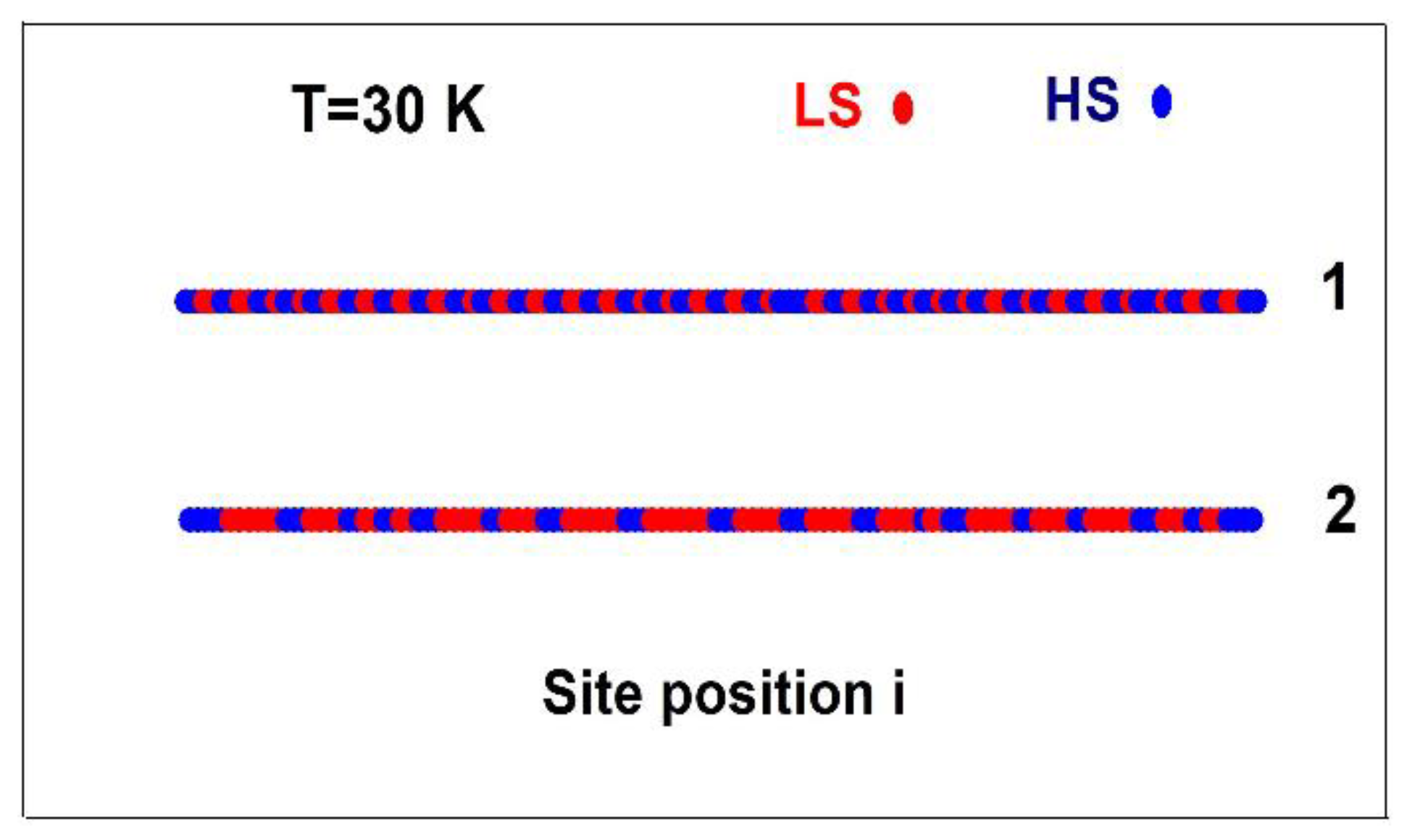
To provide more insights about the organization mode of the spin states inside the plateau region, we plotted in Figure 6, the spatial configurations of the spin states (red dots = HS and blue dots = LS) inside the lattice along the two-step thermal transition (see Figure 2a) of the first chain, for the frustration rate value, ξ 1 = 1.3. An undeniable evidence of the presence of an ordered LS-LS-HS-LS-HS… state, noted for simplicity L2H2, is observed in the plateau region in the interval 25 ≤ T ≤ 40 K. In the same Figure 6, we depict the corresponding spatial configurations of the spin states along the thermal transition of the second chain (black curve of Figure 2b), which is characterized by the emergence of a residual fraction n H S 2 ∼ 2 3 at low temperature, where an ordered state LS-LS-HS-HS-HS-HS-, noted for simplicity L2H4 is also obtained. In addition, it is important to notice for both self-organized states, the presence of antiphase boundaries, since the symmetric configurations, H2L2… and resp. H4L2… have the same energies as L2H… and L2H4…, respectively. Interestingly, the self-organization of the spin states is accompanied with that of the nn distances along the chains. 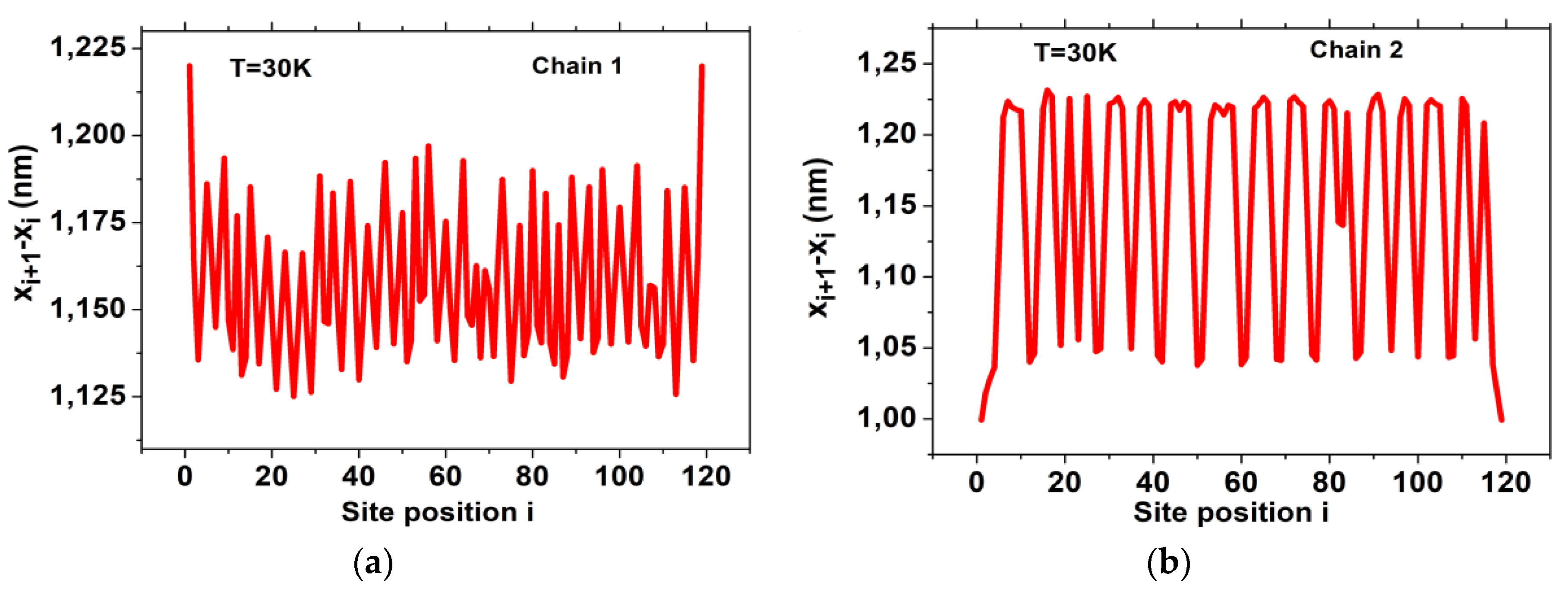To check this aspect, we draw in Figure 7a the behavior of the interatomic distance, d x = x i + 1 − x i , along the direction of the first chain at 30 K. A periodic modulated curve, leading to the oscillating sequence d H H , d H L , d L L distances, perturbed at some points by the presence of the phase boundaries, is obtained, in good agreement with H2L2 structure of Figure 6a. Similarly, the dependence of nn bond length d x = x i + 1 − x i along the x-direction for the second chain (Figure 7b) also gives a periodic modulated structure which confirms the L2H4 self-organized state of Figure 6b, since the nn distances follow the periodic sequence, d H H , d H H , d H H , d H L , d L L .

5. Both chains are frustrated

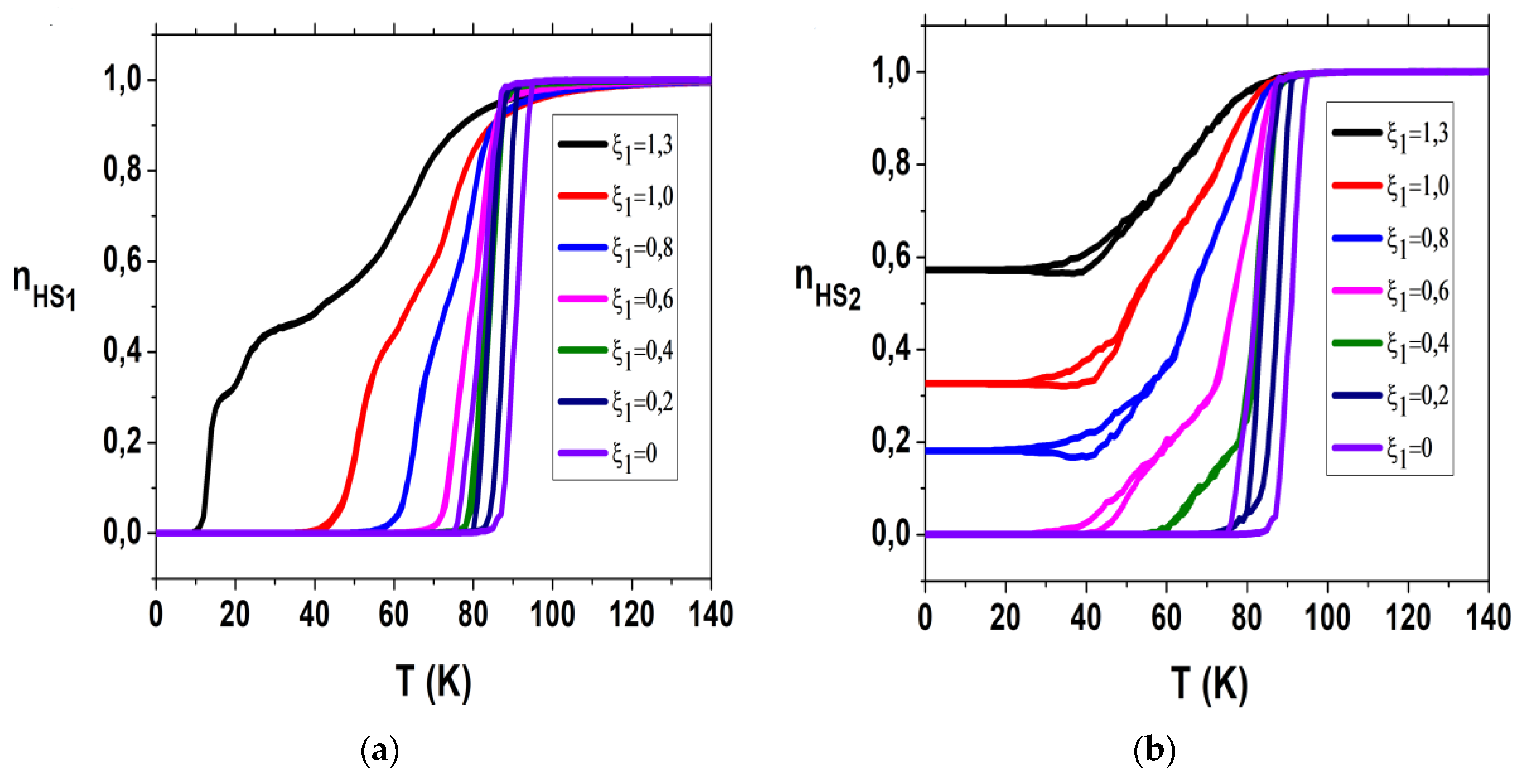
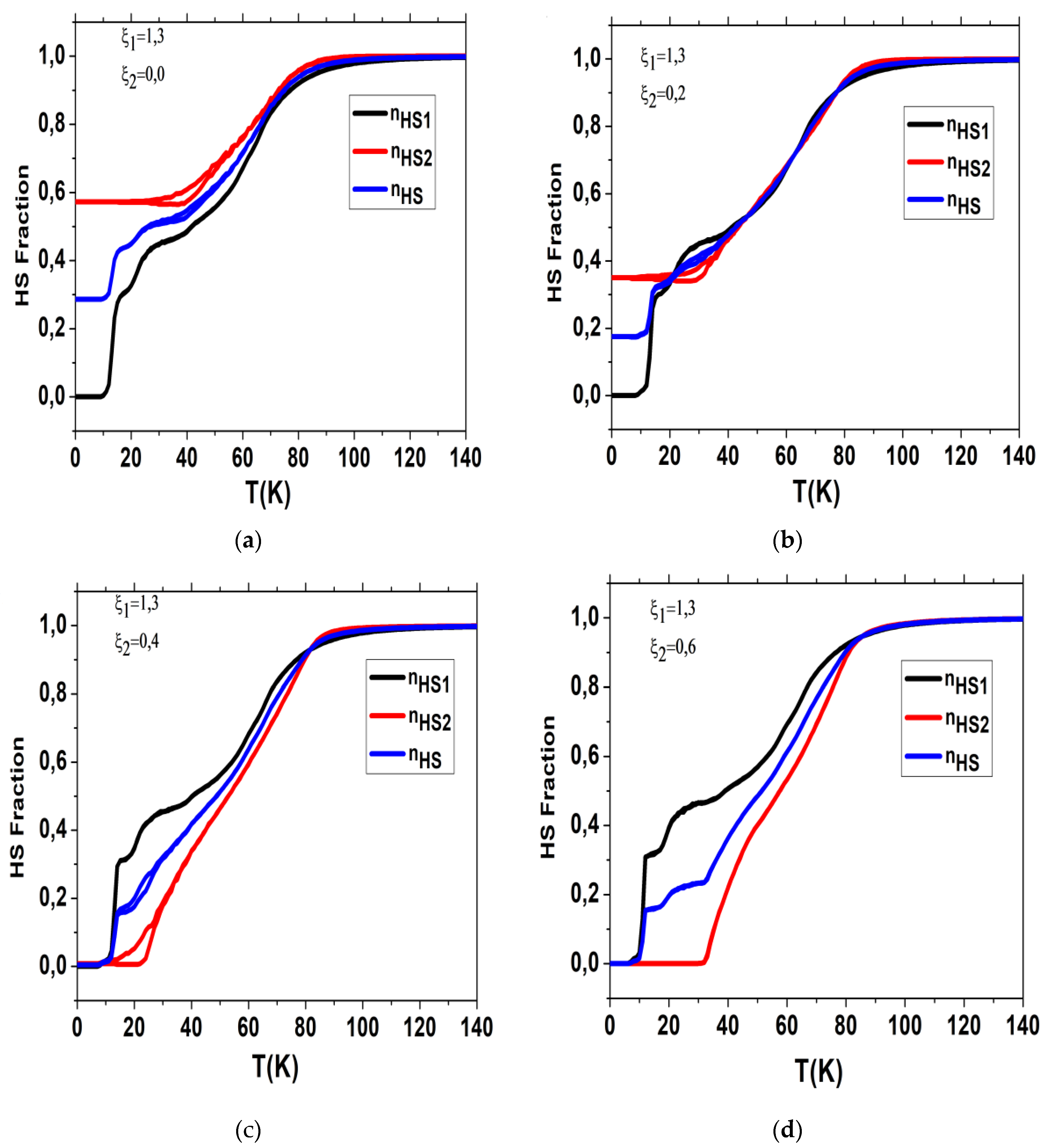
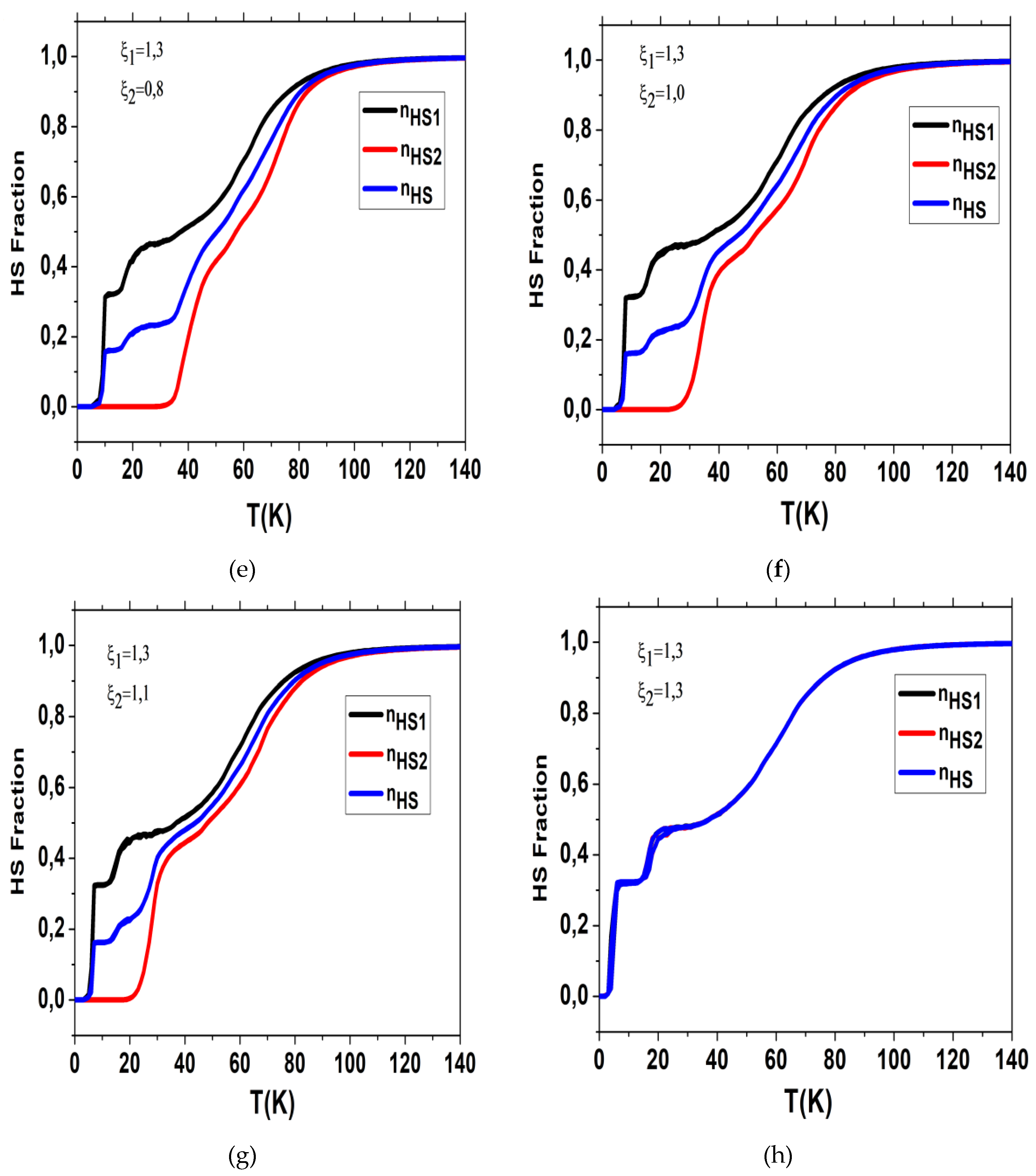
Now we study the general situation where both chains are frustrated according to Eq. (7), with respective frustration rates, ξ 1 and ξ 2 , in such a way to cause antagonist distances between nn and nnn sites. Our objective here is to investigate the thermal behavior of each chain subsystem, with respect to the values of the frustrations ξ 1 and ξ 2 in order to investigate the mechanical interplay between them through their nn and nnn interchain interactions.
For that, we fix ξ 1 = 1.3 and we vary ξ 2 from 0 to 1.1. In both chains, only the nn distances are subject to frustration for LS-LS and LS-HS configurations as we did for the first chain in Sec. 4.
The results of the MC simulations are summarized in Figure 8 where we report the thermal behaviors of the HS fractions of each chain as well as their average bond lengths for various ξ 2 values. In Figure 8a, we recall for comparison the case already presented in Figure 2a of ξ 1 = 1.3 and ξ 2 = 0 (black curve), which results in the occurrence of a double-step transition with a plateau around n H S 1 = 0.5 for the first chain, and the incomplete transition with a residual HS fraction at low temperature n H S 2 ≃ 2 3 in the second chain. When the frustration of the second chain comes into play, the value of the HS fraction, n H S 2 , at low temperature of the second chain decreases gradually from the value 0.38 for ξ 2 = 0.2 (Figure 8b) to reach the value n H S 2 = 0 (LS) for ξ 2 = 0.4 (Figure 8c), with the emergence of a first plateau around n H S = 0.5 for the total HS fraction (blue curve in Figure 8c). When ξ 2 exceeds the value 0.6 (see Figure 8e), a second plateau starts to emerge in the thermal dependence of total HS fraction n H S around n H S = 0.25 . For higher frustration values the thermal dependence of the HS fraction exhibits a three step (Figure 8f–h) and even four step spin transitions for ξ 2 = 1.1 (Figure 8g), with the emergence of several plateaus in the total HS fraction (blue curve in Figure 8g). For ξ 1 = ξ 2 = 1.3 the two chains become equivalent and the thermal-dependences of their HS fractions become exactly the same as it appears clearly in Figure 8h.
Preprints 71537 g009
Preprints 71537 g009
To obtain a clearer view of the organization mode of the spin states inside the plateau regions, we plotted in Figure 9 the spatial configurations of the spin states (red dots = HS and blue dots = LS), for the first and the second chain respectively, inside the lattice along the thermal transition of the three-step behavior corresponding to Figure 8g, obtained for ξ 1 = 1.3 and ξ 2 = 1.1 , at T=37, 18 and 10 K respectively.
The first snapshot (Figure 9a) corresponding to the highest plateau at n H S ≅ 0.5 depicts the presence of a special antiferromagnetic-like structure LL-HH-LL-HH made of dimerized spin states organization along the two chains. 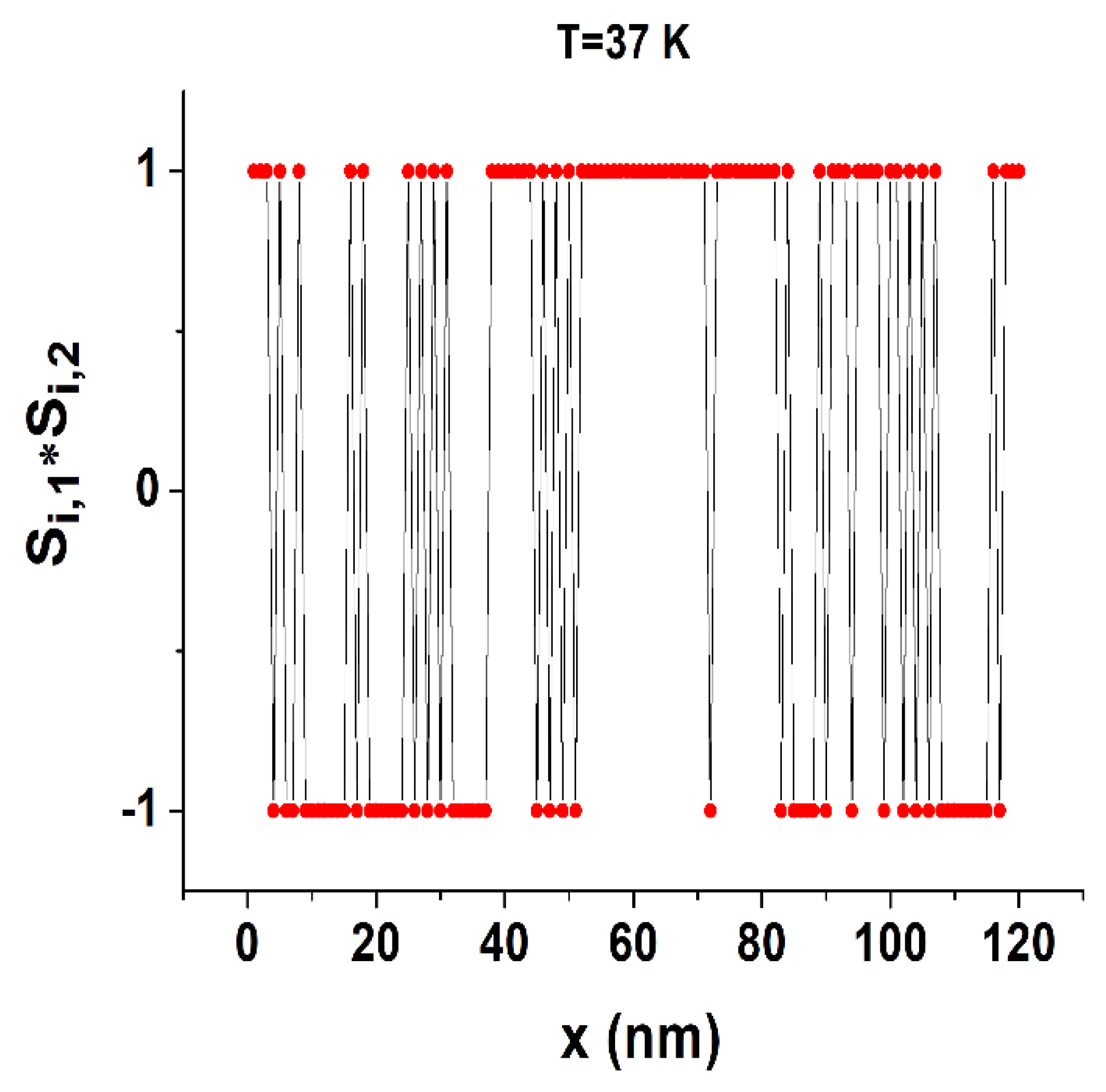This structure is consistent with the n H S value, but it is clearly different from the usual antiferromagnetic-like HLHLHL structures obtained by Ising models in the literature, except for the case of frustrated nnn Ising model combining competing nearest and next-nearest exchange interactions [30,31]. In addition, the two chains seem to be antiferromagnetically coupled. However, the presence of antiphase boundaries highlighted by the green squares in the first chain induces some disorder due to the energetic equivalence of the LL-HH-LL... and the HH-LL-HH configurations. To confirm these facts, we present in Figure 10 the spatial-dependence of the spin products S i , 1 × S i , 2 of two sites of the same rank i, belonging to different chains for the temperature T = 37 K. There, we observe the presence of an antiferromagnetic-like organization between the two chains in the intervals 5 ≤ x ≤ 35 , 82 ≤ x ≤ 90 nm and 110 ≤ x ≤ 120 while ferromagnetic-like organizations ( S i , 1 × S i , 2 = + 1 ) are obtained for 35 ≤ x ≤ 80 nm and 90 ≤ x ≤ 110 nm . .
For the second snapshots (Figure 9b), an antiferromagnetic-like structure LL-HH-LL-HH… emerges along the first chain at T = 18 K while a full LS state subsists along the second chain, leading to an average HS fraction equal to 1/3, in agreement with Figure 8g. For the third snapshot, (Figure 9c), obtained at 10 K, the first chain self organizes with the special structure L-HH-L-HH… which displays a periodic alternation of antiferro- ferro short-range ordering while the 2nd chain is fully LS a situation which is also consistent with the results of Figure 8g.

6. Conclusion

1D spin crossover solids are widely studied in the literature due to their specific anisotropic character which allows many original behaviors, such as large thermal hysteresis, incomplete spin transitions as well as multi-step spin transitions. Therefore, they represent excellent objects of study for theoreticians due to their one-dimensional character, which presupposes a simple implementation and rapid calculations when they are modeled. In previous works [33,34], we have studied the origin of multi-step transitions in an isolated 1D binuclear SCO chain, by means of the electro-elastic in which we included an elastic frustration in the intra-binuclear nn bond length distances. In the present work, we have extended our model to investigate the thermal behaviors of a system of two-elastically coupled mononuclear chains. Each chain is made of SCO sites that are coupled elastically through spring with their nearest and next-nearest neighbors. The elastic inter-chain coupling includes diagonal springs, while the nn inter-chains distance is assumed as invariant. As a result, the atoms in both chains can only move along the longitudinal directions, which then imposes a strong constraint or a geometrical frustration during the expansion and the contraction of the chains, corresponding respectively to transitions into the HS and LS states. In addition, specific frustrations, related to the existence of antagonist nn and nnn distances are injected in the chains. At the end, the model is solved using MC simulations, performed on the spin states and the lattice positions. The obtained results can be summarized as follows. We frustrate only the nn bond lengths of the first chain, with elastic frustration strength parameter ξ 1 , we demonstrate that the thermal-dependence of the HS fraction curve of the second chain strongly deforms by decreasing its transition temperature which is accompanied with the appearance of a significant residual HS fraction at low temperature, whose amount linearly increases with the rate of frustration, ξ 1 . The interplay between the two chains is clearly due to the elastic strength generated by the elastic interaction along their diagonal directions.
In the second step, we frustrated both chains by imposing different frustration rates, ξ 1 and ξ 2 . We found that, for higher frustration values in the two chains, the thermal dependence of the HS total fraction exhibits a three step and even four step spin transitions, with the emergence of several plateaus in the total HS fraction. Moreover, the analysis of the spatial organization of the spin states in intermediate states revealed the existence of several unexpected and complex configurations in the case of strong and different elastic frustration rates in the two chains. These results also significantly depend on temperature. Thus, while for identical values of the frustration rates, ξ 1 and ξ 2 , the two chains are equivalent since the thermal dependence of their HS and bond-length are the same, an important difference takes place for ξ 1 ≠ ξ 2 . Indeed, in this particular case, new types of self-organizations of the spin states are obtained, such as HH-LL-HH-LL… for the 1st chain and LL-HH-LL-HH… for the second chain. This type of organization is interesting and open the way for a new type of self-organization of the spin states for systems with a higher number of chains.
The extension of the present model to investigate the effect of the frustration on the dynamics of the LS to HS photo-excitation mechanism of these coupled chains through LIESST [43,44,45,46] (Light-Induced Spin State Trapping) is very instructive. Moreover, the analysis of isothermal relaxation of the metastable photo-induced HS state, searching for evidence of multi-step relaxation processes, reminiscent of the thermal behavior of the system, deserves to be considered in a near future.

Acknowledgments

This project has received financial support from the CNRS through the MITI interdisciplinary programs through its exploratory research program, as well as from the ANR project Mol-CoSM No. ANR-20-CE07-0028-02, the Universities of Versailles and Paris-Saclay-UPSAY. We thank all of them for their strong support.

Conflicts of Interest

The authors declare no competing financial interest.

References

  1. Phan, H.; Benjamin, S.M.; Steven, E.; Brooks, J.S.; Shatruk, M. Photomagnetic Response in Highly Conductive Iron(II) Spin Crossover Complexes with TCNQ Radicals. Angew. Chem. Int. Ed, 2015, 54, 823. [Google Scholar] [CrossRef]
  2. Ohkoshi, S.I.; Tokoro, H. Photomagnetism in Cyano-Bridged Bimetal Assemblies. Acc. Chem. Res, 2012, 45, 1749. [Google Scholar] [CrossRef]
  3. Coronado, E.; Galán-Mascarós, J.R.; Monrabal-Capilla, M.; García-Martínez, J.; Pardo-Ibáñez, P. Bistable Spin-Crossover Nanoparticles Showing Magnetic Thermal Hysteresis near Room Temperature. Adv. Mater, 2007, 19, 1359. [Google Scholar] [CrossRef]
  4. Kahn, O.; Jay-Martinez, C. Spin-Transition Polymers: From Molecular Materials. Toward Memory Devices Science, 1998, 279, 44. [Google Scholar]
  5. Gütlich, P.; Hauser, A.; Spiering, H. Thermal and Optical Switching of Iron(II) Complexes. Angew. Chem. Int. Ed, 1994, 33, 2024–2054. [Google Scholar] [CrossRef]
  6. Phan, H.; Benjamin, S. M.; Steven, E.; Brooks, J. S.; Shatruk, M. Photomagnetic Response in Highly Conductive Iron(II) Spin- Crossover Complexes with Tcnq Radicals. Angew. Chem., Int. Ed, 2015, 54, 823−827. [Google Scholar] [CrossRef]
  7. Gütlich, P.; Hauser, A.; Spiering, H. Thermal and Optical Switching of Iron(II) Complexes. Angew. Chem., Int. Ed Engl, 1994, 33, 2024−2054. [Google Scholar] [CrossRef]
  8. Gütlich, P.; Goodwin, H. A. Spin Crossover in Transition Metal Compounds Iron(II); Springer: Berlin, 2004; Volume 233, pp. 234–235. [Google Scholar]
  9. Olguín, J.; Brooker, S. Spin Crossover Active Iron(II) Complexes of Selected Pyrazole-Pyridine/Pyrazine Ligands. Coord. Chem. Rev, 2011, 255, 203−240. [Google Scholar] [CrossRef]
  10. Gütlich, P.; Gaspar, A. B.; Garcia, Y. Spin State Switching in Iron Coordination Compounds. Beilstein. J. Org. Chem, 2013, 9, 342−391. [Google Scholar]
  11. Li, Z. Y.; Dai, J. W.; Shiota, Y.; Yoshizawa, K.; Kanegawa, S.; Sato, O. Multi-Step Spin Crossover Accompanied by Symmetry Breaking in an Fe(III) Complex: Crystallographic Evidence and DFT Studies. Chem. Eur. J, 2013, 19, 12948−12952. [Google Scholar] [CrossRef]
  12. Olguín, J.; Brooker, S. Spin crossover active Iron(II) complexes of selected pyrazole-pyridine/pyrazine ligands. Coord. Chem. Rev, 2011, 255, 203–240. [Google Scholar]
  13. Jureschi, C.M.; Linares, J.; Rotaru, A.; Ritti, M.H.; Parlier, M.; Dîrtu, M.M.; Wolff, M.; Garcia, Y. Pressure Sensor via Optical Detection Based on a 1D Spin Transition Coordination Polymer. Sensors, 2015, 15, 2388–2398. [Google Scholar] [CrossRef] [PubMed]
  14. Decurtins, S.; Gütlich, P.; Hasselbach, K.M.; Hauser, A.; Spiering, H. Light-induced excited-spin-state trapping in Iron(II) spin-crossover systems. Optical spectroscopic and magnetic susceptibility study. Inorgan. Chem, 1985, 24, 2174–2178. [Google Scholar] [CrossRef]
  15. Hauser, A. Reversibility of light-induced excited spin state trapping in the Fe(ptz)6(BF4)2, and the Zn1-xFex(ptz)6(BF4)2 spin-crossover systems. Chem. Phys. Lett. 1986, 124, 543–548. [Google Scholar] [CrossRef]
  16. Hauser, A.; Adler, J.; Gütlich, P. Light-induced excited spin state trapping (LIESST) in [ Fe(2-mephen)3]+2 embedded in polymer matrices. Chem. Phys. Lett, 1988, 152, 468–472. [Google Scholar] [CrossRef]
  17. Gütlich, P.; Garcia, Y.; Goodwin, H.A. Spin crossover phenomena in Fe(II) complexes. Chem. Soc. Rev, 2000, 29, 419–427. [Google Scholar] [CrossRef]
  18. Hauser, A. Light-Induced Spin Crossover and the High-Spin Low-Spin Relaxation in Spin Crossover in Transition Metal Compounds. Chem, T.C., Ed.; Springer: New York, NY, USA, 2004, 234, 155–198. [Google Scholar]
  19. Mahfoud, T.; Molnar, G.; Bonhommeau, S.; Cobo, S.; Salmon, L.; Demont, P.; Tokoro, H.; Ohkoshi, S.; Boukheddaden, K.; Bousseksou, A. Electric-Field-Induced Charge-Transfer Phase Transition: A Promising Approach Toward Electrically Switchable Devices. J. Am. Chem. Soc, 2009, 131, 15049–15054. [Google Scholar] [CrossRef]
  20. Rotaru, A.; Dugay, J.; Tan, R.P.; Guralskiy, I.A.; Salmon, L.; Demont, P.; Carrey, J.; Molnar, G.; Respaud, M.; Bousseksou, A. Nanoelectromanipulation of Spin Crossover Nanorods: Towards Switchable Nanoelectronic. Devices. Adv. Mater, 2013, 25, 1745–1749. [Google Scholar] [CrossRef]
  21. Prins, F.; Monrabal-Capilla, M.; Osorio, E.A.; Coronado, E.; van der Zant, H.S. Room-Temperature Electrical Addressing of a Bistable Spin-Crossover Molecular System. Adv. Mater, 2011, 23, 1545–1549. [Google Scholar] [CrossRef]
  22. Slimani, A.; Boukheddaden, K.; Varret, F.; Oubouchou, H.; Nishino, M.; Miyashita, S. Microscopic spin-distortion model for switchable molecular solids: Spatiotemporal study of the deformation field and local stress at the thermal spin transition. Phys. Rev B, 2013, 87, 014111. [Google Scholar] [CrossRef]
  23. Moussa, N.O.; Ostrovskii, D.; Garcia, V.M.; Molnár, G.; Tanaka, K.; Gaspar, A.B.; Real, J.A.; Bousseksou, A. Bidirectional photoswitching of the spin state of iron(II) ions in a triazol based spin crossover complex within the thermal hysteresis loop. Chem. Phys. Lett, 2009, 477, 156–159. [Google Scholar] [CrossRef]
  24. Shepherd, H.J.; Rosa, P.; Fallis, I.A.; Guionneau, P.; Howard, J.A.K.; Goeta, A.E. Structural origin of the gradual spin transition in a mononuclear iron(II) complex. Phys. Chem. Solids, 2012, 73, 193–197. [Google Scholar] [CrossRef]
  25. Takahashi, K.; Mori, H.; Kobayashi, H.; Sato, O. Mechanism of reversible spin transition with a thermal hysteresis loop in [FeIII(qsal)2][Ni(dmise)2] · 2CH3CN: Selenium analogue of the precursor of an Fe(III) spin-crossover molecular conducting system. Polyhedron, 2009, 28, 1776. [Google Scholar] [CrossRef]
  26. Fedaoui, D.; Bouhadja, Y.; Kaiba, K.; Guionneau, P.; Létard, J. Complexation of 2,6-Bis(3-pyrazolyl)pyridine–Bis(thiocyanato)iron(II) with a Bridging 4,40-Bipyridine: A New Example of a Dinuclear Spin Crossover Complex. Eur. J. Inorg. Chem, 2008, 7, 1022–1023. [Google Scholar] [CrossRef]
  27. De Gaetano, Y.; Jeanneau, E.; Verat, A.Y.; Rechignat, L.; Bousseksou, A.; Matouzenko, G.S. Ligand-Induced Distortions and Magneto-Structural Correlations in a Family of Dinuclear Spin Crossover Compounds with Bipyridyl-Like Bridging Ligands. Eur. J. Inorg. Chem 2013, 1015–1023. [Google Scholar] [CrossRef]
  28. Sciortino, N.F.; Scherl-Gruenwald, K.R.; Chastanet, G.; Halder, G.J.; Chapman, K.W.; Létard, J.F.; Kepert, C.J. Hysteretic Three-Step Spin Crossover in a Thermo-and Photochromic 3D Pillared Hofmann-type Metal–Organic Framework. Angew. Chem. Int. Ed. Engl, 2012, 124, 10301–10305. [Google Scholar] [CrossRef]
  29. Romstedt, H.; Spiering, H.; Gütlich, P. Modelling of two step high spinlow spin transitions using the cluster variation method. J. Phys. Chem. Solids, 1998, 59, 1353–1362. [Google Scholar] [CrossRef]
  30. Li, Z.Y.; Dai, J.W.; Shiota, Y.O.; Yoshizawa, K.; Kanegawa, S.; Sato, O. Multi-Step Spin Crossover Accompanied by SymmetryBreaking in an Fe(III) Complex: Crystallographic Evidence and DFT Studies. Chemistry. 2013, 19, 12948–12952. [Google Scholar] [CrossRef]
  31. Bousseksou, A.; Nasser, J.; Linares, J.; Boukheddaden, K.; Varret, F. Ising-like model for the two-step spin-crossover. J. Phys. I Fr, 1992, 2, 1381–1403. [Google Scholar] [CrossRef]
  32. Boukheddaden, K.; Linares, J.; Codjovi, E.; Varret, F.; Niel, V.; Real, J.A. Dynamical ising-like model for the two-step spin-crossover systems. J. Appl. Phys, 2003, 93, 7103–7105. [Google Scholar] [CrossRef]
  33. Paez-Espejo, M.; Sy, M.; Boukheddaden, K. Elastic Frustration Causing Two-Step and Multistep Transitions in Spin-Crossover Solids: Emergence of Complex Antiferroelastic Structures. J. Am. Chem. Soc, 2016, 138, 3202–3210. [Google Scholar] [CrossRef] [PubMed]
  34. Traiche, R.; Sy, M.; Boukheddaden, K. Elastic Frustration in 1D Spin-Crossover Chains: Evidence of Multi-Step Transitions and Self-Organizations of the Spin States. J. Phys. Chem. C, 2018, 122, 4083–4096. [Google Scholar] [CrossRef]
  35. Traiche, R.; Oubouchou, H.; Boukhedaden, K. Elastic Modeling of Two-Step Transitions in Sterically Frustrated 1D Binuclear Spin-Crossover Chains. Symmetry, 2021, 13, 1836. [Google Scholar] [CrossRef]
  36. Boukheddaden, K.; Traiche, R.; Oubouchou, H.; Linares, J. Multistep Relaxations in a Spin-Crossover Lattice with Defect: A Spatiotemporal Study of the Domain Propagation. Magnetochemistry, 2016, 2, 17. [Google Scholar] [CrossRef]
  37. Singh, Y.; Oubouchou, H.; Nishino, M.; Miyashita, S.; Boukheddaden, K. Elastic-frustration-driven unusual magnetoelastic properties in a switchable core-shell spin-crossover nanostructure. Phys. Rev. B, 2020, 101, 054105. [Google Scholar] [CrossRef]
  38. Ndiaye, M.; Belmouri, N.; Linares, J.; Boukheddaden, K. Elastic Origin of the Unsymmetrical Thermal Hysteresis in Spin Crossover Materials: Evidence of Symmetry Breaking. Symmetry, 2021, 13, 828. [Google Scholar] [CrossRef]
  39. Di-Scala, N.; Belmouri, N.; Paez-Espejo, M.; Boukheddaden, K. ; Explaining the origin of the orientation of the front transformation in spin-transition crystals. Phys. Rev. B, 2022, 106, 144107. [Google Scholar] [CrossRef]
  40. Affes, K.; Singh, Y.; Boukheddaden, K. ; Electro-Elastic Modeling of Thermal Spin Transition in Diluted Spin-Crossover Single Crystals. Int. J. Mol. Sci. 2022, 23, 13854. [Google Scholar] [CrossRef]
  41. De Gaetano, Y.; Jeanneau, E.; Verat, A.Y.; Rechignat, L.; Bousseksou, A.; Matouzenko, G.S. Ligand-Induced Distortions and Magneto-Structural Correlations in a Family of Dinuclear Spin Crossover Compounds with Bipyridyl-Like Bridging Ligands. Eur. J. Inorg. Chem, 2013, 2013, 1015–1023. [Google Scholar] [CrossRef]
  42. Miyashita, S.; Konishi, Y.; Nishino, M.; Tokoro, H.; Rikvold, P.A. Realization of the mean-field universality class in spin-crossover materials. Phys. Rev. B Condens, Matter Mater. Phys. 2008, 77, 014105. [Google Scholar] [CrossRef]
  43. Decurtins, S., et al., Light-induced excited-spin-state trapping in iron(II) spin-crossover systems. Optical spectroscopic and magnetic susceptibility study. Inorganic Chemistry, 1985, 24, 2174–2178. [CrossRef]
  44. Decurtins, S., et al., New examples of light-induced excited spin state trapping (LIESST) in iron( II ) spin-crossover systems. Journal of the Chemical Society. Chemical Communications, 1985, 7, 430–432.
  45. Desaix, A., et al., Light-induced bistability in spin transition solids leading to thermal and optical hysteresis. The European Physical Journal B – Condensed Matter and Complex Systems 1998, 6, 183–193. [CrossRef]
  46. Létard, J.F., et al., Structural, Magnetic, and Photomagnetic Studies of a Mononuclear Iron(II) Derivative Exhibiting an Exceptionally Abrupt Spin Transition. Light-Induced Thermal Hysteresis Phenomenon. Inorg. Chem, 1998, 37, 4432–4441. [CrossRef]
Preprints 71537 g001
Figure 1. Schematic view of the interaction configurations of selected sites among the two 1D coupled SCO chains considered in this study.
Figure 1. Schematic view of the interaction configurations of selected sites among the two 1D coupled SCO chains considered in this study.
Preprints 71537 g001
Preprints 71537 g002
Figure 2. a) Thermal dependence of the HS fraction n H S 1 of the first chain for different values of the elastic frustration strength, ξ 1 , showing the occurrence of first-order transition for ξ 1 < 0.6 and continuous multi-step transitions for higher ξ 1 values. b) Corresponding thermal dependence of the HS fraction n H S 2 of the second chain showing similar behavior with the presence at low-temperature of a residual HS fraction for ξ 1 > 0.6 . .
Figure 2. a) Thermal dependence of the HS fraction n H S 1 of the first chain for different values of the elastic frustration strength, ξ 1 , showing the occurrence of first-order transition for ξ 1 < 0.6 and continuous multi-step transitions for higher ξ 1 values. b) Corresponding thermal dependence of the HS fraction n H S 2 of the second chain showing similar behavior with the presence at low-temperature of a residual HS fraction for ξ 1 > 0.6 . .
Preprints 71537 g002
Preprints 71537 g003
Figure 3. Low-temperature (0 K), frustration rate ξ 1 -dependence of the residual HS fraction, n H S 2 * , of the second chain, derived from Figure 2b. Notice the existence of a threshold value ξ C ≅ 0.6 above which n H S 2 * linearly increases with ξ 1 .
Figure 3. Low-temperature (0 K), frustration rate ξ 1 -dependence of the residual HS fraction, n H S 2 * , of the second chain, derived from Figure 2b. Notice the existence of a threshold value ξ C ≅ 0.6 above which n H S 2 * linearly increases with ξ 1 .
Preprints 71537 g003
Preprints 71537 g004
Figure 4. Thermal dependences of the average nn distances for various elastic frustration strength ξ 1 a) < d > 1 for the first chain, b) < d > 2 for the second, and c) < d > 12 between the two chains corresponding to Figure 2. All figures show a monotonous increase of the relaxed lattice parameter of the LS state (i.e., < r i j > at 0 K) as ξ 1 increases.
Figure 4. Thermal dependences of the average nn distances for various elastic frustration strength ξ 1 a) < d > 1 for the first chain, b) < d > 2 for the second, and c) < d > 12 between the two chains corresponding to Figure 2. All figures show a monotonous increase of the relaxed lattice parameter of the LS state (i.e., < r i j > at 0 K) as ξ 1 increases.
Preprints 71537 g004
Preprints 71537 g005
Figure 5. a) Relaxed nn distance, < d > 1 , < d > 2 , in the LS state vs elastic frustration strength, ξ 1 , showing the appearance of a slight difference between their values at 0K, which increases as function of ξ 1 b) Plot of < d > 2 vs < d > 1 showing a fair correlation. c) Dependence of < d > 1 − < d > 2 as function of ξ 1 at 0 K.
Figure 5. a) Relaxed nn distance, < d > 1 , < d > 2 , in the LS state vs elastic frustration strength, ξ 1 , showing the appearance of a slight difference between their values at 0K, which increases as function of ξ 1 b) Plot of < d > 2 vs < d > 1 showing a fair correlation. c) Dependence of < d > 1 − < d > 2 as function of ξ 1 at 0 K.
Preprints 71537 g005
Preprints 71537 g006
Figure 6. Snapshots of the spatial distribution of the spin states of the first chain, showing an antiferromagnetic-like organization of type L2H2 in the plateau region of the black curve of Figure 2a at T = 30 K and ξ 1 = 1.3 , and the corresponding Snapshots of the second chain, showing an antiferromagnetic-like organization of type L2H4 of the black curve of Figure 2b at T = 30 K and ξ 1 = 1.3 .
Figure 6. Snapshots of the spatial distribution of the spin states of the first chain, showing an antiferromagnetic-like organization of type L2H2 in the plateau region of the black curve of Figure 2a at T = 30 K and ξ 1 = 1.3 , and the corresponding Snapshots of the second chain, showing an antiferromagnetic-like organization of type L2H4 of the black curve of Figure 2b at T = 30 K and ξ 1 = 1.3 .
Preprints 71537 g006
Preprints 71537 g007
Figure 7. a) Space-dependence of the nn bond length, in the plateau region corresponding to the snapshot of Figure 6a, along the first chain showing a spatial modulation, corresponding to a perfect L2-H2-L2-H2… structure. b) Similar plot for the 2nd chain, corresponding the snapshot of Figure 6b, depicting a spatial modulation of the nn bond length denoting a periodic spin state organization of type L2H4-L2H4... The model parameters are the same as those of Figure 4, except for ξ 1 = 1.3 and T = 30 K.
Figure 7. a) Space-dependence of the nn bond length, in the plateau region corresponding to the snapshot of Figure 6a, along the first chain showing a spatial modulation, corresponding to a perfect L2-H2-L2-H2… structure. b) Similar plot for the 2nd chain, corresponding the snapshot of Figure 6b, depicting a spatial modulation of the nn bond length denoting a periodic spin state organization of type L2H4-L2H4... The model parameters are the same as those of Figure 4, except for ξ 1 = 1.3 and T = 30 K.
Preprints 71537 g007
Preprints 71537 g008aPreprints 71537 g008b
Figure 8. MC results of the thermal dependence of the HS fraction of the first chain nHS1, second chain n H S 2 , and the average fraction n H S , of Hamiltonian (1) for different values of the elastic frustrations strengths, ξ 1 , and ξ 2 showing the occurrence of multi-step transitions. ξ 1 has been fixed to 1.3 in all figures. From a) to h) ξ 2 = 0 0, 0.2 , 0.4 , 0.6 , 0.8, 1.0 1.1 and 1.3, respectively.
Figure 8. MC results of the thermal dependence of the HS fraction of the first chain nHS1, second chain n H S 2 , and the average fraction n H S , of Hamiltonian (1) for different values of the elastic frustrations strengths, ξ 1 , and ξ 2 showing the occurrence of multi-step transitions. ξ 1 has been fixed to 1.3 in all figures. From a) to h) ξ 2 = 0 0, 0.2 , 0.4 , 0.6 , 0.8, 1.0 1.1 and 1.3, respectively.
Preprints 71537 g008aPreprints 71537 g008b
Preprints 71537 g009
Figure 9. Selected snapshots of the spatial distribution of the spin states of two coupled SCO chains of 120 sites, corresponding to Figure 8g. An antiferromagnetic-like organizations in the plateau regions of the black and red curves of Figure 8g are obtained for a) T = 37 K, b) T = 18 K and c) T = 10 K. The model parameters are the same as those of Figure 8g, where ξ 1 = 1.3 and ξ 2 = 1.1 .
Figure 9. Selected snapshots of the spatial distribution of the spin states of two coupled SCO chains of 120 sites, corresponding to Figure 8g. An antiferromagnetic-like organizations in the plateau regions of the black and red curves of Figure 8g are obtained for a) T = 37 K, b) T = 18 K and c) T = 10 K. The model parameters are the same as those of Figure 8g, where ξ 1 = 1.3 and ξ 2 = 1.1 .
Preprints 71537 g009
Preprints 71537 g010
Figure 10. The product S i , 1 × S i , 2 as a function of the sites positions of two coupled chains of 120 sites, corresponding to Figure 8g at T = 37K. Notice the clear coexistence of alternate ferromagnetic ( S i , 1 × S i , 2 = + 1 ) and antiferromagnetic-like ( S i , 1 × S i , 2 = − 1 ) inter-chains orders. The model parameters are the same as those of Figure 8g, where for ξ 1 = 1.3 and ξ 2 = 1.1 .
Figure 10. The product S i , 1 × S i , 2 as a function of the sites positions of two coupled chains of 120 sites, corresponding to Figure 8g at T = 37K. Notice the clear coexistence of alternate ferromagnetic ( S i , 1 × S i , 2 = + 1 ) and antiferromagnetic-like ( S i , 1 × S i , 2 = − 1 ) inter-chains orders. The model parameters are the same as those of Figure 8g, where for ξ 1 = 1.3 and ξ 2 = 1.1 .
Preprints 71537 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated