Prerpints.org logo
Preprint
Article

Ordinary Muon Capture on 136Ba: Comparative Study Using the Shell Model and pnQRPA

Altmetrics

Downloads

109

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 April 2023

Posted:

25 April 2023

You are already at the latest version

Alerts
Abstract
In this work, we present a study of ordinary muon capture (OMC) on 136Ba, the daughter nucleus of the 136Xe double beta decay (DBD). OMC rates to low-lying nuclear states (below 1 MeV of excitation energy) in 136Cs are assessed by using both the interacting shell model (ISM) and the proton-neutron quasiparticle random-phase approximation (pnQRPA). We also add the chiral two-body (2BC) meson-exchange currents and use an exact Dirac wave function for the captured s-orbital muon. OMC can be viewed as a complementary probe of the wave functions in 136Cs, the intermediate nucleus of the 136Xe DBD. At the same time OMC can be considered as a powerful probe of the effective values of the weak axial-type couplings in a 100-MeV momentum-exchange region relevant for the neutrinoless DBD. The present work represents the first attempt to compare the ISM and pnQRPA results for the OMC on a heavy nucleus by including also the exact muon wave function and the 2BC. Sensitivity estimates of the present and future neutrinoless DBD experiments will clearly benefit from the future OMC measurements through the OMC calculations similar to the present one.
Keywords: 
Subject: Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

Neutrinoless double beta decay (NDBD) has been one of the key issues in nuclear and particle physics since many decades [1,2,3,4]. A number of experiments are trying to measure this hypothetical process [5] and numerous nuclear-structure calculations have tried and are trying to address the associated nuclear matrix elements (NME) (for a comprehensive list, see [1,4,5]). In particular, several efforts to compute these NME have been done in the interacting shell model (ISM) (see, e.g., [6,7,8,9]) and proton-neutron quasiparticle random-phase approximation (pnQRPA) (see, e.g., the reviews [5,10]). The theory estimates for NDBD are pestered by sizable discrepancies between the NME—which enter the NDBD rate in second power—obtained with different nuclear many-body methods [5]. Furthermore, there is an additional uncertainty related to the possible need of quenching the Gamow-Teller type of spin-isospin operator σ τ , which dominates the NDBD NME. Since g A multiplies this operator, the quenching of σ τ by a quenching factor q can be interpreted also as quenching of g A in terms of g A eff = q g A bare , where we take g A bare = 1.27 as the bare value of g A , obtained from the beta decay of a free neutron (there have been many measurements, see, e.g., [11]). A lot of work has been done within the ISM and pnQRPA communities in order to seek for appropriate quenching in the context of low-momentum exchange beta and two-neutrino double-beta decays [12]. However, the situation at higher momentum exchange is less clear [13]. The need of quenching is a result of deficiencies in the nuclear many-body methods used in the calculations and of the omission of the two-body meson-exchange currents, as discussed exhaustively for light nuclei in [14].
The above-mentioned work on the effective value of g A concerns processes with momentum exchanges between the involved lepton(s) and the nucleus within the range of a few MeV 1. Contrary to this, the momentum exchanges involved in the NDBD are of the order of 100 MeV. This means that one cannot use the obtained results for the quenching related to the meson-exchange currents directly for the NDBD, but one has to evolve those to higher momentum exchanges, like first done in [13] implementing the chiral two-body currents (2BC) in the Gamow-Teller type of transitions. Recently, these two-body currents were implemented in the nuclear ordinary muon capture (OMC) formalism of Morita and Fujii [15] in [16] for the light nucleus 24 Mg.
OMC is able to probe nuclear wave functions within wide ranges of energies and spins of nuclear excitations, relevant for the NDBD [17,18]. At the same time, OMC can be used to probe the effective values of both g A and g P , the induced pseudoscalar coupling, in a momentum-exchange region typical for the NDBD [19]. In addition, comparison of the muon-capture and NDBD matrix elements shows clear correlations as shown in [18,20].
As mentioned above, 2BC were implemented in [16] for the OMC on 24 Mg. There ISM results were compared with those of an ab initio method, the valence-space in-medium similarity renormalization group (VS-IMSRG). Here we want to extend the ISM study to a heavy-nucleus case, 136 Ba, the final nucleus of the 136 Xe NDBD. The nucleus 136 Xe is highly important in terms of NDBD measurements [21,22,23,24]. In the present work, we compare the ISM- and pnQRPA-computed partial OMC rates with each other and study the effects of the 2BC on them for final states below some 1 MeV of excitation energy in 136 Cs. This energy range is accessible to the present state-of-the-art OMC experiments, like the one of the MONUMENT Collaboration [25].

2. Theoretical framework

Ordinary muon capture (OMC), as differentiated explicitly from its radiative counterpart, on the even-even nucleus 136 Ba populates the final states in the odd-odd nucleus 136 Cs according to the schematic
μ − + 136 Ba ( 0 g . s . + ) → ν μ + 136 Cs ( J f π ) ,
where a negative muon ( μ − ) is captured by the ground state of 136 Ba, leading to the final states J f π in 136 Cs, where J is the angular momentum and π the parity. At the same time a muon neutrino ν μ is emitted.

2.1. Bound-muon s-orbital wave function

Here we compute the OMC rates by using the formalism of Morita and Fujii [15]. In this formalism it is straightforward to implement the exact Dirac wave function of the muon, as described in detail in [16]. The Dirac wave function can be written as
ψ μ ( κ , μ ; r ) = ψ κ μ ( μ ) = − i F κ ( r ) χ − κ μ ( r ^ ) G κ ( r ) χ κ μ ( r ^ ) ,
where G κ and F κ are the radial wave functions of the bound state [15] and χ κ μ are normalized spherical spinors. The index κ is related to the orbital quantum number l in the following manner
l = κ and j = l − 1 2 for κ > 0 l = − κ − 1 and j = l + 1 2 for κ < 0 .
After being stopped in the outer shells of an atom, the negative muon transits to the lowest atomic orbital, the 1 s 1 / 2 state, which corresponds to κ = − 1 and μ = ± 1 / 2 . The corresponding large and small components of the bound-muon wave function, G − 1 and F − 1 , of Equation (2) can be numerically solved from the Dirac wave equations in the Coulomb field created by the nucleus [16]. Here we assume a nucleus with a uniform spherical charge distribution with a charge radius R c = r 0 A 1 / 3 , with r 0 = 1.2 fm and A being the nuclear mass number. The large component of the wave function accounts for the major part of the physics of the captured muon, while the small part accounts only for some 1% of the wave function, see e.g. Figure 1 in Ref. [16]. Hence, we can safely neglect the small part. The G − 1 part can be compared with the Bethe-Salpeter (BS) equation [26] for a point nucleus:
G − 1 = ( 2 Z / a 0 ) 3 2 1 + γ 2 Γ ( 2 γ + 1 ) 2 Z r a 0 γ − 1 e − Z r / a 0 .
In Figure 1 we display the exact Dirac s-orbital wave function (large component) and its various degrees of approximation for 136 Ba. In the figure it can be seen that the point-nucleus exact wave function and its BS approximation are quite close to each other, except at very short distances r ≲ 3 fm. Contrary to this, the exact finite-nucleus Dirac wave function deviates considerably from the other two, especially within the nucleus (the gray band in the figure). This is a much more drastic effect than the corresponding one for a light nucleus, such as 24 Mg (see Figure 1 of [16]).

2.2. Muon-capture rates

The calculation of the OMC rates is done using the Morita-Fujii formalism [15] and its extension developed in Refs. [27,28] in order to treat small OMC rates in a more reliable way. The OMC rate of the process (1) can be expressed as
W = 2 P ( 2 J f + 1 ) 1 − q m μ + A M q 2 ,
where the momentum exchange (q value) can be expressed as
q = ( m μ − W 0 ) 1 − m μ 2 ( m μ + A M ) .
Here J f is the final-state spin-parity, M the average nucleon mass and m μ ( m e ) the rest mass of the muon (electron). The threshold energy W 0 = M f − M i + m e + E X contains M i and M f as the masses of the initial and final nuclei and E X the excitation energy of the final nuclear state in 136 Cs. The rate function P contains the nuclear matrix elements, phase-space factors and combinations of the weak couplings g A (axial-vector coupling), g P (induced pseudoscalar coupling) and g M = 1 + μ p − μ n (induced weak-magnetism coupling), where μ p and μ n are the anomalous magnetic moments of the proton and the neutron. In the present work we use the Goldberger-Treiman partially conserved axial-vector-current (PCAC) value for the ratio of the two axial-type couplings:
g P / g A = 2 M q q 2 + m π 2 ≈ 6.8 ,
where m π = 138.04 MeV is the pion rest mass. Unless otherwise indicated, we adopt the free-neutron value g A = 1.27 in our calculations. Explicit expressions for the rate function P, containing all the next-to-leading-order terms, can be found in all detail in [28] and we do not repeat those expressions in this article. It should be noted that at low excitation energies, as considered in the present work, W 0 / m μ ≪ 1 and hence the nuclear matrix elements in P depend only weakly on the excitation energy E X of the nuclear state.

2.3. Chiral two-body currents

We take the effect of the 2BC into account by making the replacements
g A → ( 1 + δ a ( q 2 ) ) g A
and
g P → 1 − q 2 + m π 2 q 2 δ a P ( q 2 ) g P ,
where the 2BC contributions δ a ( q 2 ) and δ a P ( q 2 ) are approximated by the normal-ordered one-body part of the chiral two-body currents, as done in [29]. The normal ordering is done with respect to a Fermi-gas reference state with density ρ . In the present work we take the involved integrals in δ a ( q 2 ) and δ a P ( q 2 ) to be those of [30] with the density range ρ = 0.09 − 0.11 fm − 3 . We use the same values of the involved constants as in [29], as done also in [31]. For the low-energy constants (LEC) c 1 , c 3 , c 4 , c 6 and c D involved in the currents, we use the values listed in Table V of [29]. The constant c D was in [29] adjusted so that the axial-vector correction δ a ( q 2 ) corresponds to the typical 20 − 30 % axial-vector quenching (or g A eff = 0.89 − 1.02 in terms of an effective coupling) at q = 0 MeV: the pair ( ρ = 0.09 fm − 3 , c D = − 6.08 ) giving the most quenching and ( ρ = 0.11 fm − 3 , c D = 0.3 ) the least. We use the ranges of δ a ( q 2 ) and δ a P ( q 2 ) produced by these parameter choices for quantifying the uncertainties of our computed OMC rates. The corresponding 2BC are displayed in Figure 2 where the relevant momentum-exchange region is indicated by a vertical band. For the excitation-energy region discussed in the present work the momentum exchanges are contained within the interval q OMC = 101.5 − 102.6 MeV and the 2BC contributions within the intervals δ a ( q 2 ) = − ( 0.210 − 0.211 ) and δ a P ( q 2 ) = 0.178 − 0.180 .
The corrections coming from the inclusion of the 2BC at the relevant momentum-exchange region correspond to a range g A eff ( q OMC ) = 0.88 − 1.00 of quenched values of the weak axial coupling and a range of g P eff ( q OMC ) = 5.04 − 5.43 of quenched values of the induced pseudoscalar coupling.

2.4. Many-body methods

In the present work, we use the interacting shell model (ISM) [32] and the proton-neutron quasiparticle random-phase approximation (pnQRPA) [33] to compute the ground-state wave function of 136 Ba and the ground and excited states of 136 Cs. There are several earlier ISM calculations of DBD characteristics of the 136 Xe– 136 Cs– 136 Ba triplet of nuclei [6,7,8,9]. In these calculations the jj55pn model space with the single-particle orbitals 2 s 1 / 2 , 1 d 3 / 2 , 1 d 5 / 2 , 0 g 7 / 2 and 0 h 11 / 2 was adopted for both protons and neutrons. Here we adopt the same model space and use the sn100pn [34] interaction whose Hamiltonian consists of neutron-neutron ( n n ) , proton-neutron ( p n ) and proton-proton ( p p ) interactions, with the latter containing the Coulomb interaction. The single-particle energies are -9.68, -8.72, -7.34, -7.24, and -6.88 MeV for the proton and -9.74, -8.97, -7.62, -7.31, and -7.38 MeV for the neutron 0 g 7 / 2 , 1 d 5 / 2 , 2 s 1 / 2 , 1 d 3 / 2 and 0 h 11 / 2 orbitals, respectively [34]. In [8] a quenching factor q = 0.45 was used for the spin-isospin operator σ τ , and in [6,7,9] q = 0.74 . The latter quenching corresponds to a value g A eff = 0.93 of the effective value of the axial-vector coupling. We adopt this value of g A eff in this work, as benchmarked by the three mentioned ISM calculations and preferred by the quenching through the 2BC, the associated g A eff interval discussed at the end of Section 2.3. In the actual ISM computations we use the NuShellX@MSU code with its interaction libraries [35].
The pnQRPA is known to be a theory which correctly accounts for the gross features of spin-isospin strength functions, e.g. in (p,n) and (n,p) reactions [4]. The problem with the pnQRPA is the fine structure of, e.g., the low-lying states in odd-odd nuclei. In the present study, we want to test the capabilities of pnQRPA in producing the low-energy excitation spectrum in 136 Cs by comparison of its results with those of the ISM. We use the same large no-core single-particle bases for protons and neutrons as in [36]. These bases are based on Coulomb-corrected Woods-Saxon potential [37] and slightly modified in the vicinity of the respective Fermi surfaces. All the basic features of the pnQRPA are covered in detail in [33] so that we do not want to go into these details in this article. It suffices to know that the pnQRPA is based on the BCS theory of superconductivity and the pairing strengths for the protons and neutrons are obtained from the matching with the observed proton and neutron separation energies in the reference even-even nucleus [33], in this case 136 Ba. Furthermore, we use the method of Ref. [38] to divide the renormalization of the effective two-body Bonn-A G-matrix interaction [39] into particle-hole and particle-particle parts by using the effective adjustable strength parameters g ph and g pp , known as the particle-hole and particle-particle strength parameters, respectively. The particle-hole parameter, g ph , is typically adjusted to the centroid energy of the Gamow-Teller giant resonance (GTGR) in the adjacent odd-odd nucleus of the even-even reference nucleus. Here we resort to the same recipe and adjust it to the known GTGR energy in 136 Cs [36] to obtain the value g ph = 1.18 .
In Ref. [36], a refined method concerning the g pp parameter was adopted: following the original idea put forth in [40], a scheme called partial isospin restoration (PIR) was adopted. In the present work we follow the PIR by multiplying the isoscalar ( T = 0 ) and isovector ( T = 1 ) parts of the particle-particle matrix elements of the G-matrix by the strength parameters g pp T = 0 and g pp T = 1 , respectively. The isovector strength is adjusted such that the Fermi part of the two-neutrino double-beta-decay (TNDBD) NME, corresponding to the transition 136 Xe → 136 Ba , vanishes, leading to a partial isospin restoration of the T = 1 proton-neutron, proton-proton and neutron-neutron pairing channels. The isoscalar strength is subsequently varied to reproduce the measured half-life of the mentioned TNDBD transition [41].

3. Results and discussion

First, we perform benchmark calculations in both the ISM and pnQRPA omitting the 2BC contributions and using the free-nucleon value g A = 1.27 and the corresponding pseudoscalar coupling g P = 8.64 following from the Goldberger-Treiman relation (7). In the pnQRPA calculations, we adjust the particle-particle parameters via the PIR scheme. We use the shorthand notations sm-1BC and qrpa-1BC for these methods in the following. Then, we perform more realistic calculations taking into account the missing 2BC and the deficiencies of the many-body methods. We perform four different evaluations of the OMC rates, naming them as:
sm-2BC:
We perform an ISM calculation using the sn100pn interaction [34] by quenching the free axial-vector couplings g A = 1.27 and g P = 8.64 by the 2BC according to Equations (8) and (9).
sm-phen:
We perform an ISM calculation like above but this time we use the phenomenologically obtained quenched value g A eff = 0.93 [9] and the value g P eff = 6.32 obtained through the Goldberger-Treiman relation (7).
qrpa-2BC:
We use the pnQRPA method as described in Section 2.4 and quench g A and g P by the 2BC using Equations (8) and (9). We use the PIR scheme and adjust the isoscalar strength to a value g pp T = 1 = 0.86 in order to achieve the partial isospin restoration and then we adjust the isoscalar strength to the values g pp T = 0 = 0.65 ( g pp T = 0 = 0.67 ) in order to reproduce the TNDBD half-life t 1 / 2 ( 2 ν ) = ( 2.18 ± 0.05 ) · 10 21 yr [41] using the effective coupling g A eff = 0.89 ( g A eff = 1.02 ) corresponding to the free-nucleon value g A = 1.27 quenched by the zero-momentum-transfer correction δ a ( 0 ) through Equation (8) with parameters ρ = 0.09 fm − 3 and c D = − 6.08 ( ρ = 0.11 fm − 3 and c D = 0.30 ) .
qrpa-phen:
Again, we use the pnQRPA method like above but use as the particle-particle strength the value g pp T = 0 = g pp T = 1 = 0.7 obtained from the extensive survey of the β -decay and TNDBD half-lives within the mass range A = 100 − 136 in [42]. We adopt the effective coupling g A eff = 0.83 resulting from the so-called linear g A model of the same work. This value is somewhat below the range of values g A eff = 0.89 − 1.02 corresponding to the axial-vector correction δ a ( 0 ) at zero-momentum transfer. The corresponding effective pseudoscalar coupling is g P eff = 5.64 as obtained through the Goldberger-Treiman relation (7). The value g A eff = 0.83 can be considered to account for both the missing two-body currents at q = 0 MeV and the deficiencies of the many-body approach in the spirit of [14]. However, it does not take into account the momentum dependence of the two-body currents.
A summary of the values of all the involved couplings and parameters is made in Table 1. We only consider OMC rates to states with angular momenta J ≤ 5 since OMC rates to states of higher angular momenta are negligible.
We start by comparing the calculated ISM and pnQRPA excitation spectra of 136 Cs with the experimental one, the results being shown in Figure 3. The pnQRPA calculations are done according to the scheme qrpa-2BC and qrpa-phen. Here it is worth noting that there are three sets of the pnQRPA-computed energies based on the three different values of the ( g pp T = 0 , g pp T = 1 ) pairs used in the pnQRPA calculations. Here we plot just one set of energies in the qrpa-2BC scheme since the two sets of energy are almost identical. From Figure 3 it can be seen that the density of both the ISM- and pnQRPA-computed states is quite the same, higher than the density of the measured ones. It is in fact remarkable that both theories predict so similar low-energy spectra with pnQRPA able to reproduce the density of the ISM states. The density of the experimental spectrum is smaller than predicted by the computations, probably due to difficulties in observing some of the states.
The results of the OMC calculations are presented in Table 2 (ISM results) and Table 3 (pnQRPA results). In Table 2, the first column displays the spin-parity of the final state and the second column its excitation energy in MeV (in order of increasing energy). The third to fifth columns give the ISM-computed OMC rates in units of 10 3 1/s. The third column (1BC) corresponds to an ISM calculation without the 2BC contribution and the fourth column corresponds to the same calculation with the 2BC contribution included (the sm-2BC calculational scheme). The fifth column lists the OMC rates obtained by using the phenomenological sm-phen calculational scheme. Table 3 has a similar structure but now there are two sets of qrpa-2BC energies (column 2) corresponding to the two sets of LEC used in our calculations, and the set of qrpa-phen energies in column 3. Columns 4 − 6 list the OMC rates obtained by using the schemes qrpa-1BC, qrpa-2BC and qrpa-phen.
The first observation from columns three and four of Table 2 and Table 3 is that the two-body currents, included either via the 2BC corrections δ a ( q 2 ) and δ a P ( q 2 ) or phenomenologically via effective couplings, affect the OMC rates considerably, on average by some (30-40)%, but even up to almost 50% in some cases. Comparison of the ISM-computed and pnQRPA-computed OMC rates with each other indicates that in both models the most important contributions come from the 1 + , 2 + , 2 − and 3 + states. Quantitatively, the correspondence of the OMC rates between the four schemes is quite reasonable for the 2 − , 4 + and 4 − states, the 4 1 − and 4 2 − states seemingly switched in energy between the ISM and pnQRPA models. The total rates to these states are 41.5 (53.3), 9.29 (10.5), 14.3 (18.4) for the sm-2BC scheme, 44.4, 9.78, 15.0 for the sm-phen scheme, 26.6 (26.0), 20.8 (22.6), 31.8 for the qrpa-2BC scheme and 14.2, 20.39, 21.2 for the qrpa-phen scheme in units of 10 3 1/s, respectively. A quantitative comparison for the 1 + and 2 + state would give the total OMC rates of 4.79 (6.19), 32.7 (38.1) for the sm-2BC scheme, 5.18, 34.9 for the sm-phen scheme, 243 (303), 211 (240) for the qrpa-2BC scheme and 207, 201.1 for the qrpa-phen scheme in units of 10 3 1/s, respectively, indicating that the pnQRPA states are able to catch more collectivity of these states, in particular for the 1 1 + state which is quite collective in the pnQRPA.
In order to relate the pnQRPA results to previous measurements one can take a look at the computations done in Ref. [28]. There the rates of the OMC on several double-beta daughter nuclei, in particular on 136 Ba, were computed by using large no-core single-particle spaces and the effective Bonn-A potential, quite like in the present work. In those calculations the effective values g A eff = 0.80 and g P eff = 7.0 were adopted which are values close to those of our qrpa-phen scheme and not far from our qrpa-2BC calculational scheme. This makes the three computations very well comparable, in particular for the OMC on 136 Ba, but also for 76 Se where experimental data exists. In Table V of [28] the pnQRPA-computed OMC rates to final states in 76 As, below some 1 MeV of excitation like in the present work, were compared with the corresponding experimental ones, and a surprisingly good correspondence was found. There the total rate for the OMC to the 0 + , 1 + , 1 − , 2 + , 2 − , 3 + , 3 − , 4 + and 4 − final states in 76 As was 665 × 10 3 1/s in experiment and 675 × 10 3 1/s in the pnQRPA. These total OMC rates are in line with the total OMC rates of ( 674 − 807 ) × 10 3 1/s and 592 × 10 3 1/s of our qrpa-2BC and qrpa-phen calculational schemes, respectively. In particular, both in the experiment and in the pnQRPA calculation of [28] the 1 + rate was the larges one with the values 218 × 10 3 1/s for the experiment and 237 × 10 3 1/s for the pnQRPA, well comparable with our ( 243 − 303 ) × 10 3 1/s and 207 × 10 3 1/s in the qrpa-2BC and qrpa-phen calculational schemes. In [28] also the OMC to 2 − states was strong, some 10 times stronger than in the present calculations, since the role of 2 − states in p f -shell nuclei is quite pronounced [4].
The measured total rate in 136 Ba, including all the possible final states, features 11100 × 10 3 1/s [44]. This means that the OMC rate to states below 1 MeV accounts for some 1.5 % of the total rate for the sm-2BC scheme, 1.4 % of the total rate for the sm-phen scheme, 6 − 7 % of the total rate for the qrpa-2BC scheme and 5.3 % of the total rate for the qrpa-phen scheme, thus being below 10 % but still non-negligible. This highlights the importance of comparison with the potential future experimental data and the emerging implications for the virtual NDBD transitions below some 1 MeV of excitation in the intermediate nucleus of a double-beta triplet of nuclei.
In the end, it would be highly interesting to compare the presently computed OMC rates to individual final states and the total OMC rate below 1 MeV with the future experimental results by the MONUMENT Collaboration [45]. This will open up the possibility to probe the nuclear wave functions within the considered 1 MeV excitation-energy interval in 136 Cs. At the same time, we can gain information on the value of both g A and g P , the weak axial coupling and the induced pseudoscalar coupling, in a momentum-exchange range relevant for the NDBD [19]. This gained information helps improve the precision of the nuclear matrix elements of the NDBD and thus reflects to the sensibility estimates of the presently running and future NDBD experiments.

4. Conclusions

In the present work we compute the rates of the ordinary muon capture on 136 Ba to low-lying nuclear states (below some 1 MeV of excitation energy) in 136 Cs, 136 Ba being the daughter nucleus of the 136 Xe double-beta decay. The capture rates are computed by using the interacting shell model (ISM) and the proton-neutron quasiparticle random-phase approximation (pnQRPA). Also the chiral two-body meson-exchange currents and the exact s-orbital Dirac wave function of the captured muon are used in the numerical computations. The computed energy spectra and the capture rates below 1 MeV of excitation in 136 Cs are surprisingly similar for both the ISM and the pnQRPA, the experimental low-energy spectrum being less dense. The chiral two-body currents reduce the capture rates by some (30-40)% on average and the summed capture rates below 1 MeV of excitation in 136 Cs account for some (1-7)% of the total measured capture rate, thus being potentially a sizable portion of the total capture rate. Comparison of the capture rates with the future experimental data opens up possibilities for accessing the wave functions of the low-energy states in 136 Cs and the effective values of the weak axial-type couplings, relevant for the neutrinoless double beta decay of 136 Xe, and beyond.

Author Contributions

Ordinary muon capture rates and pnQRPA calculations, P.G.; parameter values and supervision of the computations L.J; calculation of the relativistic muon wave function, J.K; nuclear shell-model calculations, M.R; original idea of the project, coordination and supervision of the computations, writing of the first draft of the paper, J.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Academy of Finland grants No. 314733, No. 320062, and No. 345869, and by Arthur B. McDonald Canadian Astroparticle Physics Research Institute. TRIUMF receives federal funding via a contribution agreement with the National Research Council of Canada.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Suhonen, J.; Civitarese, O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Physics Reports 1998, 300, 123–214. [Google Scholar] [CrossRef]
  2. Vergados, J.D.; Ejiri, H.; Šimkovic, F. Neutrinoless double beta decay and neutrino mass. Int. J. Mod. Phys. E 2016, arXiv:hep-ph/1612.02924]25, 1630007. [Google Scholar] [CrossRef]
  3. Engel, J.; Menéndez, J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Reports on Progress in Physics 2017, 80, 046301. [Google Scholar] [CrossRef] [PubMed]
  4. Ejiri, H.; Suhonen, J.; Zuber, K. Neutrino-nuclear responses for astro-neutrinos, single beta decays and double beta decays. Physics Reports 2019, 797. [Google Scholar] [CrossRef]
  5. Agostini, M.; Benato, G.; Detwiler, J.A.; Menéndez, J.; Vissani, F. 2022; arXiv:hep-ex/2202.01787].
  6. Caurier, E.; Nowacki, F.; Poves, A.; Retamosa, J. Shell Model Studies of the Double Beta Decays of 76Ge, 82Se, and 136Xe. Phys. Rev. Lett. 1996, 77, 1954–1957. [Google Scholar] [CrossRef]
  7. Caurier, E.; Menéndez, J.; Nowacki, F.; Poves, A. Influence of Pairing on the Nuclear Matrix Elements of the Neutrinoless ββ Decays. Phys. Rev. Lett. 2008, 100, 052503. [Google Scholar] [CrossRef]
  8. Caurier, E.; Nowacki, F.; Poves, A. Shell Model description of the ββ decay of 136Xe. Physics Letters B 2012, 711, 62–64. [Google Scholar] [CrossRef]
  9. Horoi, M.; Brown, B.A. Shell-Model Analysis of the 136Xe Double Beta Decay Nuclear Matrix Elements. Phys. Rev. Lett. 2013, 110, 222502. [Google Scholar] [CrossRef]
  10. Suhonen, J.; Civitarese, O. Double-beta-decay nuclear matrix elements in the QRPA framework. Journal of Physics G: Nuclear and Particle Physics 2012, 39, 085105. [Google Scholar] [CrossRef]
  11. Märkisch, B.; Mest, H.; Saul, H.; Wang, X.; Abele, H.; Dubbers, D.; Klopf, M.; Petoukhov, A.; Roick, C.; Soldner, T.; Werder, D. Measurement of the Weak Axial-Vector Coupling Constant in the Decay of Free Neutrons Using a Pulsed Cold Neutron Beam. Phys. Rev. Lett. 2019, 122, 242501. [Google Scholar] [CrossRef]
  12. Suhonen, J.T. Value of the Axial-Vector Coupling Strength in β and ββ Decays: A Review. Frontiers in Physics 2017, 5. [Google Scholar] [CrossRef]
  13. Menéndez, J.; Gazit, D.; Schwenk, A. Chiral Two-Body Currents in Nuclei: Gamow-Teller Transitions and Neutrinoless Double-Beta Decay. Physical Review Letters 2011, 107. [Google Scholar] [CrossRef]
  14. Gysbers, P.; Hagen, G.; Holt, J.; Jansen, G.; Morris, T.; Navrátil, P.; Papenbrock, T.; Quaglioni, S.; Schwenk, A.; Stroberg, S.; Wendt, K. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nature Physics 2019, 15, 1. [Google Scholar] [CrossRef]
  15. Morita, M.; Fujii, A. Theory of Allowed and Forbidden Transitions in Muon Capture Reactions. Phys. Rev. 1960, 118, 606–618. [Google Scholar] [CrossRef]
  16. Jokiniemi, L.; Miyagi, T.; Stroberg, S.R.; Holt, J.D.; Kotila, J.; Suhonen, J. Ab initio calculation of muon capture on 24Mg. Phys. Rev. C 2023, 107, 014327. [Google Scholar] [CrossRef]
  17. Kortelainen, M.; Suhonen, J. Ordinary muon capture as a probe of virtual transitions of ββ decay. Europhysics Letters 2002, 58, 666. [Google Scholar] [CrossRef]
  18. Kortelainen, M.; Suhonen, J. Nuclear muon capture as a powerful probe of double-beta decays in light nuclei. Journal of Physics G: Nuclear and Particle Physics 2004, 30, 2003. [Google Scholar] [CrossRef]
  19. Siiskonen, T.; Hjorth-Jensen, M.; Suhonen, J. Renormalization of the weak hadronic current in the nuclear medium. Phys. Rev. C 2001, 63, 055501. [Google Scholar] [CrossRef]
  20. Jokiniemi, L.; Suhonen, J. Comparative analysis of muon-capture and 0νββ-decay matrix elements. Phys. Rev. C 2020, 102, 024303. [Google Scholar] [CrossRef]
  21. Asakura, K.; others. Search for double-beta decay of 136Xe to excited states of 136Ba with the KamLAND-Zen experiment. Nucl. Phys. A 2016, arXiv:hep-ex/1509.03724]946, 171–181. [Google Scholar] [CrossRef]
  22. Albert, J.B.; Anton, G.; Badhrees, I.; Barbeau, P.S.; Bayerlein, R.; Beck, D.; Belov, V.; Breidenbach, M.; Brunner, T.; Cao, G.F.; Cen, W.R.; Chambers, C.; Cleveland, B.; Coon, M.; Craycraft, A.; Cree, W.; Daniels, T.; Danilov, M.; Daugherty, S.J.; Daughhetee, J.; Davis, J.; Delaquis, S.; Der Mesrobian-Kabakian, A.; DeVoe, R.; Didberidze, T.; Dilling, J.; Dolgolenko, A.; Dolinski, M.J.; Fairbank, W.; Farine, J.; Feyzbakhsh, S.; Fierlinger, P.; Fudenberg, D.; Gornea, R.; Graham, K.; Gratta, G.; Hall, C.; Hansen, E.V.; Hoessl, J.; Hufschmidt, P.; Hughes, M.; Jamil, A.; Jewell, M.J.; Johnson, A.; Johnston, S.; Karelin, A.; Kaufman, L.J.; Koffas, T.; Kravitz, S.; Krücken, R.; Kuchenkov, A.; Kumar, K.S.; Lan, Y.; Leonard, D.S.; Li, G.S.; Li, S.; Licciardi, C.; Lin, Y.H.; MacLellan, R.; Michel, T.; Mong, B.; Moore, D.; Murray, K.; Nelson, R.; Njoya, O.; Odian, A.; Ostrovskiy, I.; Piepke, A.; Pocar, A.; Retière, F.; Rowson, P.C.; Russell, J.J.; Schmidt, S.; Schubert, A.; Sinclair, D.; Stekhanov, V.; Tarka, M.; Tolba, T.; Tsang, R.; Vogel, P.; Vuilleumier, J.L.; Wagenpfeil, M.; Waite, A.; Walton, T.; Weber, M.; Wen, L.J.; Wichoski, U.; Wrede, G.; Yang, L.; Yen, Y.R.; Zeldovich, O.Y.; Zettlemoyer, J.; Ziegler, T. Search for Neutrinoless Double-Beta Decay with the Upgraded EXO-200 Detector. Phys. Rev. Lett. 2018, 120, 072701. [Google Scholar] [CrossRef]
  23. Shimizu, I.; Chen, M. Double Beta Decay Experiments With Loaded Liquid Scintillator. Frontiers in Physics 2019, 7. [Google Scholar] [CrossRef]
  24. Kharusi, S.; Anton, G.; Badhrees, I.; Barbeau, P.; Beck, D.; Belov, V.; Bhatta, T.; Breidenbach, M.; Brunner, T.; Cao, G.; Cen, W.; Chambers, C.; Cleveland, B.; Coon, M.; Craycraft, A.; Daniels, T.; Darroch, L.; Daugherty, S.; Davis, J.; Ziegler, T. Search for Majoron-emitting modes of Xe 136 double beta decay with the complete EXO-200 dataset. Physical Review D 2021, 104. [Google Scholar] [CrossRef]
  25. The MONUMENT Collaboration, see the Contribution List of the MEDEX’22 Workshop, Prague, Czech Republic, -17, 2022. https://indico.utef.cvut.cz/event/32/contributions. 13 June.
  26. Bethe, H.; Salpeter, E. Quantum Mechanics of One- and Two-Electron Atoms; Academic Press, New York, 1959.
  27. Jokiniemi, L.; Suhonen, J.; Ejiri, H.; Hashim, I. Pinning down the strength function for ordinary muon capture on 100Mo. Physics Letters B 2019, 794, 143–147. [Google Scholar] [CrossRef]
  28. Jokiniemi, L.; Suhonen, J. Muon-capture strength functions in intermediate nuclei of 0νββ decays. Phys. Rev. C 2019, 100, 014619. [Google Scholar] [CrossRef]
  29. Hoferichter, M.; Menéndez, J.; Schwenk, A. Coherent elastic neutrino-nucleus scattering: EFT analysis and nuclear responses. Phys. Rev. D 2020, 102, 074018. [Google Scholar] [CrossRef]
  30. Klos, P.; Menéndez, J.; Gazit, D.; Schwenk, A. Large-scale nuclear structure calculations for spin-dependent WIMP scattering with chiral effective field theory currents. Phys. Rev. D 2013, 88, 083516. [Google Scholar] [CrossRef]
  31. Jokiniemi, L.; Romeo, B.; Soriano, P.; Menéndez, J. Neutrinoless ββ-decay nuclear matrix elements from two-neutrino ββ-decay data. Physical Review C 2022, arXiv:nucl-th/2207.05108]107, 044305. [Google Scholar] [CrossRef]
  32. Caurier, E.; Martínez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–488. [Google Scholar] [CrossRef]
  33. Suhonen, J. From Nucleons to Nucleus: Concepts of Microscopic Nuclear Theory; Theoretical and Mathematical Physics, Springer: Berlin, Germany, 2007. [Google Scholar] [CrossRef]
  34. Brown, B.A.; Stone, N.J.; Stone, J.R.; Towner, I.S.; Hjorth-Jensen, M. Magnetic moments of the 21+ states around 132Sn. Phys. Rev. C 2005, 71, 044317. [Google Scholar] [CrossRef]
  35. Brown, B.; Rae, W. The Shell-Model Code NuShellX@MSU. Nuclear Data Sheets 2014, 120, 115–118. [Google Scholar] [CrossRef]
  36. Jokiniemi, L.; Ejiri, H.; Frekers, D.; Suhonen, J. Neutrinoless ββ nuclear matrix elements using isovector spin-dipole Jπ=2- data. Phys. Rev. C 2018, 98, 024608. [Google Scholar] [CrossRef]
  37. Bohr, A.; Mottelson, B.R. Nuclear Structure; Vol. I, Benjamin: New York, 1969. [Google Scholar]
  38. Suhonen, J.; Taigel, T.; Faessler, A. pnQRPA calculation of the β+/EC quenching for several neutron-deficient nuclei in mass regions A = 94–110 and A =146–156. Nuclear Physics A 1988, 486, 91–117. [Google Scholar] [CrossRef]
  39. Holinde, K. Two-nucleon forces and nuclear matter. Physics Reports 1981, 68, 121–188. [Google Scholar] [CrossRef]
  40. Šimkovic, F.; Rodin, V.; Faessler, A.; Vogel, P. 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys. Rev. C 2013, 87, 045501. [Google Scholar] [CrossRef]
  41. Barabash, A. Precise Half-Life Values for Two-Neutrino Double-β Decay: 2020 review. Universe 2020, 6, 159. [Google Scholar] [CrossRef]
  42. Pirinen, P.; Suhonen, J. Systematic approach to β and 2νββ decays of mass A=100-136 nuclei. Phys. Rev. C 2015, 91, 054309. [Google Scholar] [CrossRef]
  43. ENSDF database. http://www.nndc.bnl.gov/ensdf/.
  44. Suzuki, T.; Measday, D.F.; Roalsvig, J.P. Total nuclear capture rates for negative muons. Phys. Rev. C 1987, 35, 2212–2224. [Google Scholar] [CrossRef]
  45. The MONUMENT collaboration. Work in progress.
1
Note: in the present work we use the convention c = 1 for compactness of presentation.
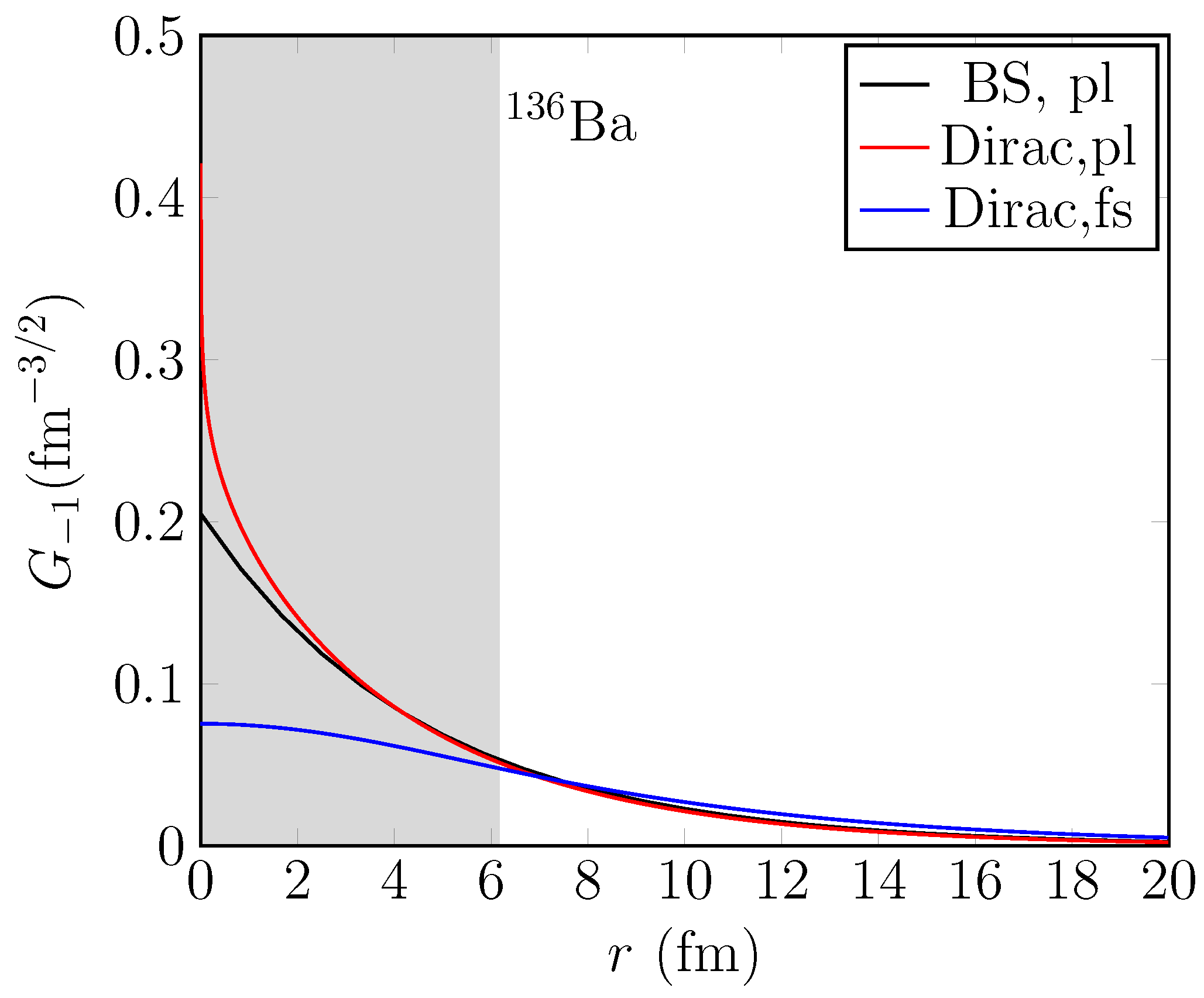
Preprints 71805 g001
Figure 1. Comparison of the large component of the exact muon wave function for a finite nucleus with a uniform spherical charge distribution (blue line) with a corresponding one for a point-like nucleus (red line) and its Bethe-Salpeter (BS) approximation (black line). The gray band denotes the range inside the nucleus.
Figure 1. Comparison of the large component of the exact muon wave function for a finite nucleus with a uniform spherical charge distribution (blue line) with a corresponding one for a point-like nucleus (red line) and its Bethe-Salpeter (BS) approximation (black line). The gray band denotes the range inside the nucleus.
Preprints 71805 g001
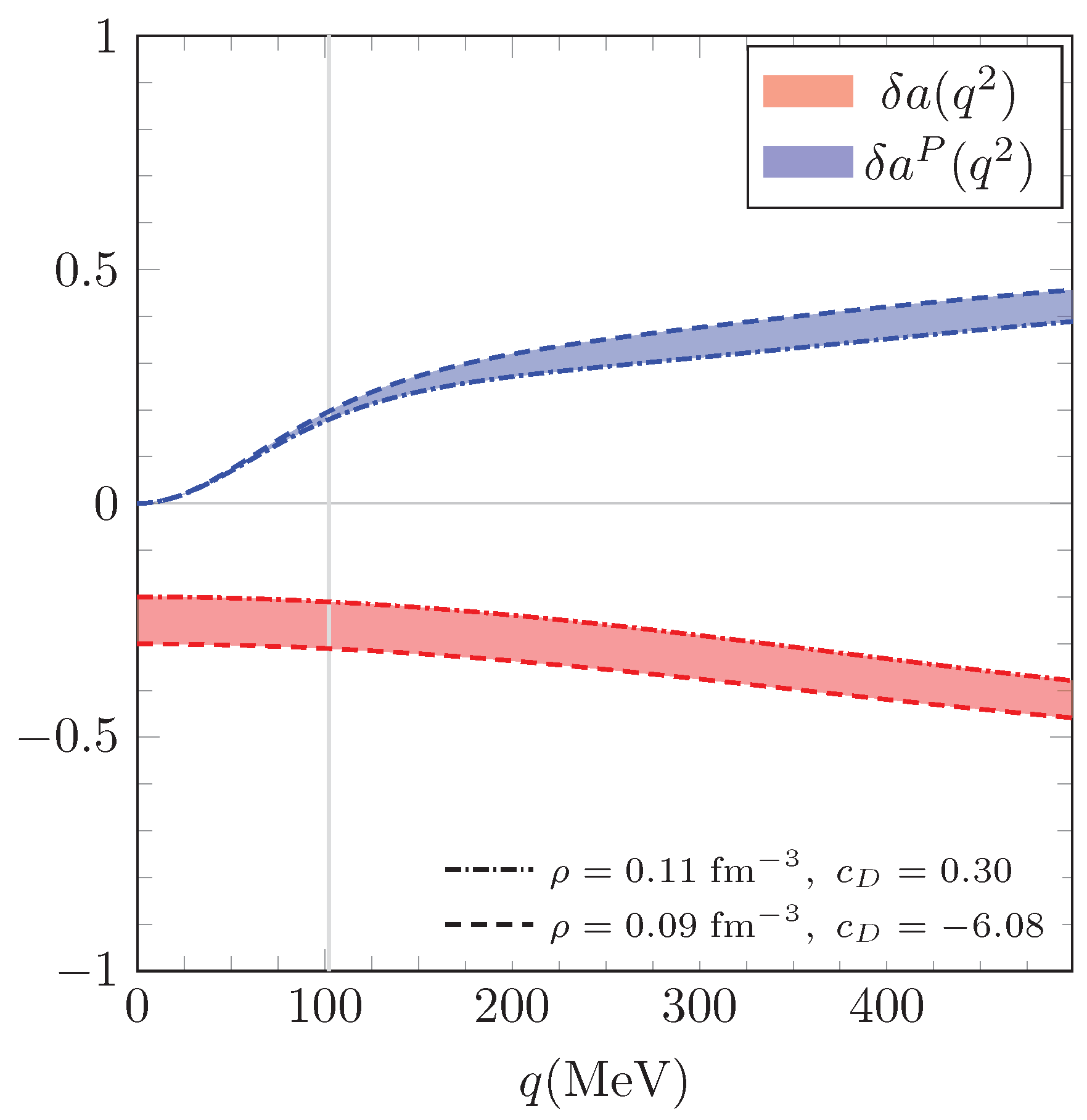
Preprints 71805 g002
Figure 2. Two-body currents used in the present work as functions of momentum exchange. The dashed lines denote the currents obtained by ρ = 0.09 fm − 3 and c D = − 6.08 and the dotted those obtained with ρ = 0.11 fm − 3 and c D = 0.30 . The typical momentum-exchange region of the transitions considered in the present work is denoted by a vertical gray band.
Figure 2. Two-body currents used in the present work as functions of momentum exchange. The dashed lines denote the currents obtained by ρ = 0.09 fm − 3 and c D = − 6.08 and the dotted those obtained with ρ = 0.11 fm − 3 and c D = 0.30 . The typical momentum-exchange region of the transitions considered in the present work is denoted by a vertical gray band.
Preprints 71805 g002
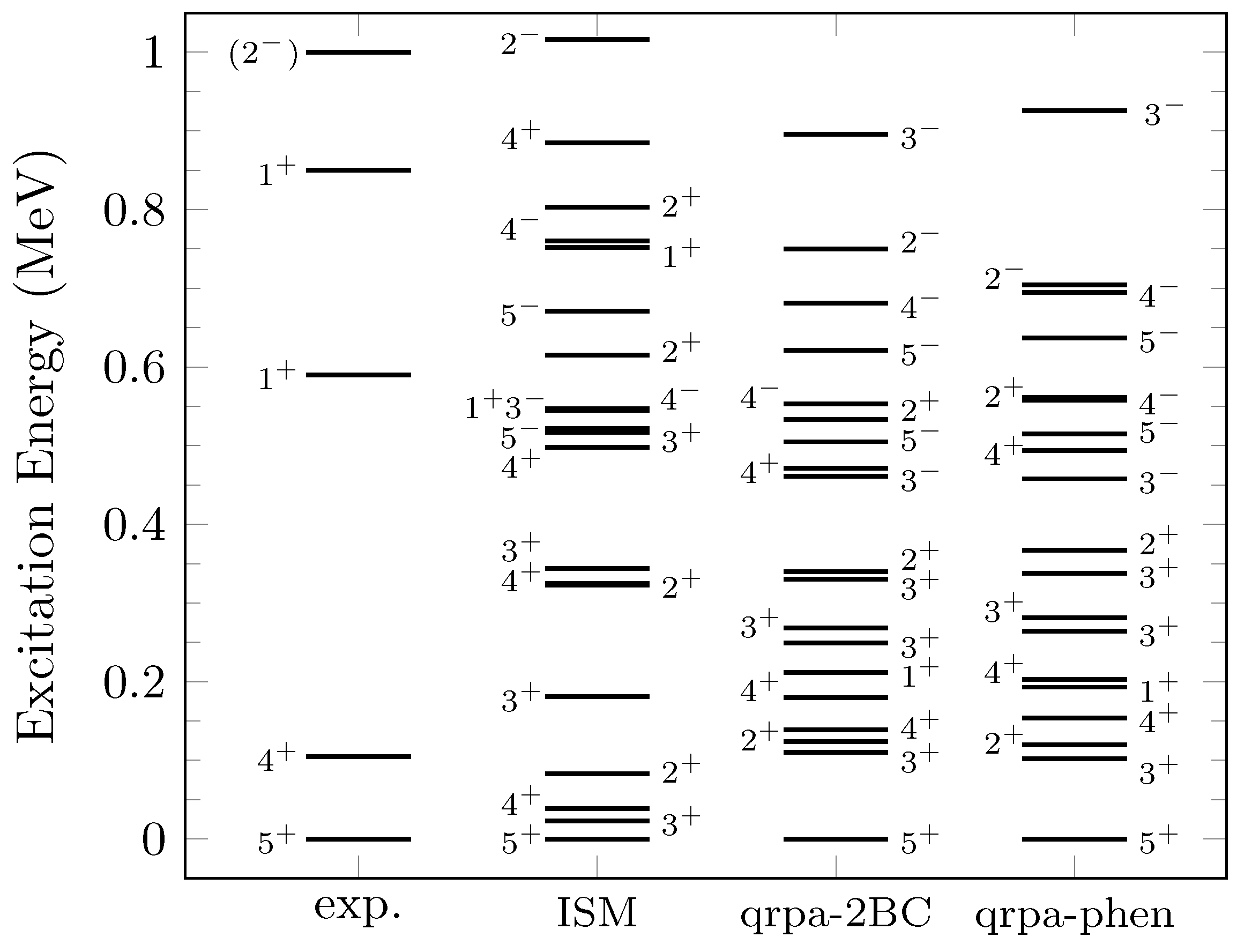
Preprints 71805 g003
Figure 3. Excitation-energy spectrum of 136 Cs. A comparison between the experimental spectrum and those computed by using the ISM and pnQRPA is shown. The experimental spectrum is taken from the ENSDF database [43]. Only states with angular momenta J ≤ 5 are considered.
Figure 3. Excitation-energy spectrum of 136 Cs. A comparison between the experimental spectrum and those computed by using the ISM and pnQRPA is shown. The experimental spectrum is taken from the ENSDF database [43]. Only states with angular momenta J ≤ 5 are considered.
Preprints 71805 g003
Table 1. Values of the weak axial couplings, the Fermi-gas density ρ , the LEC c D and pnQRPA parameters used in our calculations.
Table 1. Values of the weak axial couplings, the Fermi-gas density ρ , the LEC c D and pnQRPA parameters used in our calculations.
sm-1BC and sm-2BC sm-phen qrpa-1BC qrpa-2BC qrpa-phen
g PP T = 0 - - 0.69 0.65 0.67 0.7
g PP T = 1 - - 0.86 0.86 0.86 0.7
g ph - - 1.18 1.18 1.18 1.18
g A 1.27 0.93 1.27 1.27 1.27 0.83
g P / g A 6.8 6.8 6.8 6.8 6.8 6.8
ρ 0.09 0.11 - - 0.09 0.11 -
c D -6.08 0.30 - - -6.08 0.30 -
Table 2. ISM-computed energies (second column) and OMC rates (third to fifth columns) to the final states (f) of spin J and parity π (first column) with angular momenta J ≤ 5 . The bottom line summarizes the total OMC rates below some 1 MeV as summed over the OMC rates listed in colums three to five. The lower (upper) limits in column four correspond to the Fermi-gas density ρ = 0.09 fm − 3 and the low-energy constant c D = − 6.08 ( ρ = 0.11 fm − 3 and c D = 0.3 ), the rest of the LEC being equal in the two sets.
Table 2. ISM-computed energies (second column) and OMC rates (third to fifth columns) to the final states (f) of spin J and parity π (first column) with angular momenta J ≤ 5 . The bottom line summarizes the total OMC rates below some 1 MeV as summed over the OMC rates listed in colums three to five. The lower (upper) limits in column four correspond to the Fermi-gas density ρ = 0.09 fm − 3 and the low-energy constant c D = − 6.08 ( ρ = 0.11 fm − 3 and c D = 0.3 ), the rest of the LEC being equal in the two sets.
OMC Rate ( 10 3 1 / s )
J f π E(MeV) sm-1BC sm-2BC sm-phen
5 1 + 0.000 0.0647 0.0661 (0.0836) 0.0433
3 1 + 0.023 4.02 2.75 (3.36) 2.60
4 1 + 0.039 1.50 1.36 (1.40) 1.37
2 1 + 0.083 10.6 5.62 (6.99) 6.18
3 2 + 0.181 12.0 6.24 (8.08) 6.66
2 2 + 0.225 20.1 12.8 (15.00) 13.7
3 3 + 0.244 4.94 2.48 (3.23) 2.71
4 2 + 0.323 5.83 3.50 (4.17) 3.78
4 3 + 0.498 6.00 4.34 (4.83) 4.54
3 4 + 0.517 31.2 16.8 (21.5) 17.9
5 1 − 0.522 0.645 0.371 (0.451) 0.404
3 1 − 0.545 16.1 8.85 (11.0) 9.73
1 1 + 0.545 9.01 4.67 (6.03) 5.03
4 1 − 0.547 24.0 13.0 (16.7) 13.7
2 3 + 0.615 18.2 12.5 (14.2) 13.2
5 2 − 0.671 0.251 0.190 (0.208) 0.198
1 2 + 0.752 0.285 0.123 (0.163) 0.146
4 2 − 0.760 2.22 1.31 (1.65) 1.32
2 4 + 0.803 2.49 1.74 (1.95) 1.83
4 4 + 0.885 0.143 0.0865 (0.103) 0.0933
2 1 − 1.016 78.6 41.5 (53.3) 44.4
Sum ( 10 3 1 / s ) 248 140 (174) 150
Table 3. pnQRPA-computed energies for the qrpa-2BC scheme (second column) and the qrpa-phen scheme (third column), and OMC rates (fourth to sixth columns) to the final states (f) of spin J and parity π (first column) with angular momenta J ≤ 5 . The bottom line summarizes the total OMC rates below 1 MeV as summed over the OMC rates listed in colums four to six. The two energies in column 2 and the lower (upper) limits in column five correspond to the Fermi-gas density ρ = 0.09 fm − 3 and the low-energy constant c D = − 6.08 ( ρ = 0.11 fm − 3 and c D = 0.3 ), the rest of the LEC being equal in the two sets.
Table 3. pnQRPA-computed energies for the qrpa-2BC scheme (second column) and the qrpa-phen scheme (third column), and OMC rates (fourth to sixth columns) to the final states (f) of spin J and parity π (first column) with angular momenta J ≤ 5 . The bottom line summarizes the total OMC rates below 1 MeV as summed over the OMC rates listed in colums four to six. The two energies in column 2 and the lower (upper) limits in column five correspond to the Fermi-gas density ρ = 0.09 fm − 3 and the low-energy constant c D = − 6.08 ( ρ = 0.11 fm − 3 and c D = 0.3 ), the rest of the LEC being equal in the two sets.
OMC Rate ( 10 3 1 / s )
J f π E(MeV) qrpa-2BC E(MeV) qrpa-phen qrpa-1BC qrpa-2BC qrpa-phen
5 1 + 0.000 0.000 0.902 0.491 ( 0.601 ) 0.483
3 1 + 0.110 ( 0.107 ) 0.102 3.04 1.74 ( 2.19 ) 1.51
2 1 + 0.124 ( 0.122 ) 0.120 133 102 ( 111 ) 93.3
4 1 + 0.139 ( 0.144 ) 0.154 10.0 8.81 ( 9.34 ) 8.96
1 1 + 0.227 ( 0.213 ) 0.193 443 243 ( 303 ) 207
4 2 + 0.180 ( 0.179 ) 0.203 12.4 8.76 ( 9.61 ) 8.25
3 2 + 0.249 ( 0.254 ) 0.264 11.6 7.93 ( 10.8 ) 3.49
3 3 + 0.268 ( 0.273 ) 0.281 156 85.6 ( 108 ) 77.5
3 4 + 0.330 ( 0.332 ) 0.338 12.2 9.50 ( 11.9 ) 5.34
2 2 + 0.340 ( 0.346 ) 0.367 88.3 49.0 ( 60.2 ) 50.1
3 1 − 0.461 ( 0.459 ) 0.458 48.0 28.9 ( 34.4 ) 25.8
4 3 + 0.471 ( 0.477 ) 0.494 4.19 3.24 ( 3.60 ) 3.18
5 1 − 0.505 ( 0.509 ) 0.515 1.20 0.825 ( 0.933 ) 0.775
4 1 − 0.553 ( 0.555 ) 0.558 1.60 1.04 ( 1.19 ) 0.596
2 3 + 0.533 ( 0.538 ) 0.561 87.1 60.0 ( 68.3 ) 57.7
5 2 − 0.621 ( 0.624 ) 0.637 0.017 0.0135 ( 0.0149 ) 0.0178
4 2 − 0.681 ( 0.686 ) 0.695 43.1 24.1 ( 30.6 ) 20.5
2 1 − 0.750 ( 0.725 ) 0.704 27.3 26.6 ( 26.0 ) 14.2
3 2 − 0.896 ( 0.901 ) 0.926 20.5 12.7 ( 15.1 ) 12.9
Sum ( 10 3 1 / s ) 1103 674 ( 807 ) 592
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated