Measurement of the Acoustic Relaxation Absorption Spectrum of CO₂ Using an Optical Fiber DBR Laser

1. Introduction

Ultrasonic gas sensing technology is an integration technique of gas sensing with ultrasonic sensor, which has two main technical branches depending either on acoustic velocity or acoustic relaxation absorption.

As early as the late 19th century, Fritz Haber used sound velocity change to assess the presence of hydrogen in the air during underground mining or a burning gas whistle [1, 2]. Polturak used the acoustic travel time (time of flight) method to measure sound in propane and ethylene binary gas mixture, and reached a relative high sensitivity of 0.008% [3]. The Cassini-Huygens spacecraft used sound velocity to calculate changes in methane concentration in Titan's atmosphere as a function of altitude [4]. These methods are only applicable to the concentration detection of binary gas mixtures due to considering a single sound propagation characteristic parameter, velocity, and become complicated when more than three components involved in mixed gases. Since sound velocity cannot provide enough information, another important parameter, sound absorption coefficient, came into sight. Tours, et al [5]. proposed a tri-component gas detection approach using both sound velocity and acoustic absorption at a time in 1985, but considered only the classical absorption rather than acoustic relaxation absorption led by molecular relaxation process. In 2003, Phillips et al [6]. introduced the theory of simultaneous measurement of sound velocity and attenuation to achieve the measurement of ternary gas concentration. The product of sound velocity and sound absorption coefficients is called acoustic relaxation absorption coefficient, which can be used for three or four-element gas detection.

Measurement of the acoustic transmission spectrum is the other technical solution for ultrasonic gas sensing, which collects relevant information of multi-component gases from both acoustic absorption and acoustic velocity spectrum, i.e., a practical method for the measurement of acoustic absorption spectrum is a prerequisite for gas sensing. The absorption curves of most excitable gases (non-mono-atomic or molecular gases) cover the frequency range of 10~10⁸ Hz at room temperature and pressure [7]. Current consumer ultrasonic transducers are only launched at one frequency, besides a few with kilohertz bandwidth. A large number of acoustic transducers at different frequencies are required to cover the entire frequency spectral line to be measured [8]. Therefore, a wide band ultrasonic sensor with a flat response would be preferred. Since the ultrasonic transmitter is not able to be replaced at present, an alternative approach adjusted the ambient pressure, which is inversely proportion to the relaxation frequency of gas molecules [9], an alternative approach adjusted the ambient pressure to obtain the whole sound propagation spectrum with a transmitter and a DBR fiber laser is proposed in this paper.

Compared with piezoelectric transducer, cantilever beam, tuning fork and other ultrasonic sensors, the newly emerged optical fiber ultrasonic sensors have advantages of small size, wide bandwidth, and high sensitivity [10]. In 2017, Gang et al. [11] proposed a miniature compact Michelson interferometer, which completed a highly sensitive detection of 100~300 kHz ultrasound wave using a gold film deposit fiber tip. Another Fabry-Perot interferometer (FPI) ultrasonic transducer achieved noise equivalent sound pressure as low as 2 Pa and a bandwidth of -6 dB greater than 22.5 MHz, but the consistency is an issue for FPI ultrasonic sensor, Moreover, its demodulation usually depends on a narrow linewidth tunable laser with high cost[12]. An ultrasonic sensor based on a micro fiber MZI is proposed [13], whose noise equivalent sound pressure and the highest detectable frequency reached 0.15 kPa and 40 MHz. Restoration of the acoustic absorption curve of gas needs to measure the ultrasonic waves in the kHz ~ MHz frequency range, which increasingly attenuates in gas with frequency and requires a more sensitive sensor to respond to the weak ultrasonic signal.

Compared with other optical ultrasonic sensors, a DBR fiber laser sensor has the merits of narrow line width (usually less than a few kilohertz), high output power and stability, which would derive further benefits from interferometric demodulation, low noise and its high sensitivity. A DBR fiber laser composed of a piece of active optical fiber between two fiber gratings written in pair is proposed as the ultrasonic sensing element, which is capable of detecting the wavelength shift affected by weak sound pressure. The applied ultrasonic wave can be recognized by continue detecting the optical frequency variation, which is capable of a noise equivalent sound pressure as low as 45 Pa and frequency up to 100 MHz using the phase demodulation technology based on a non-equilibrium M-Z interferometer [14]. Guan Baiou et al. reported a photoacoustic imaging application of fiber laser bent into different diameters to achieve ultrasonic response with different spatial resolution [15]. In 2022, Guan’s team developed a miniaturized photoacoustic endoscope system with noise equivalent pressure density (NEPD) below 1.5 mPa/Hz^1/2, and measurement range from 5 to 25 MHz [15].

This paper presents a DBR fiber laser sensor of gas concentration through restoring the gas acoustic propagation curve, which makes up for the shortcomings of fixed frequency and relative low sensitivity of current consumer ultrasonic transducers. In section 2, ultrasonic response and sensing model of the DBR fiber laser are discussed before applying to the relaxation absorption coefficient measurement and calibration. Section 3 experimentally demonstrates the reconstruction process of the relaxation absorption curve and concentration measurement of CO₂ using the DBR fiber laser ultrasonic sensor.

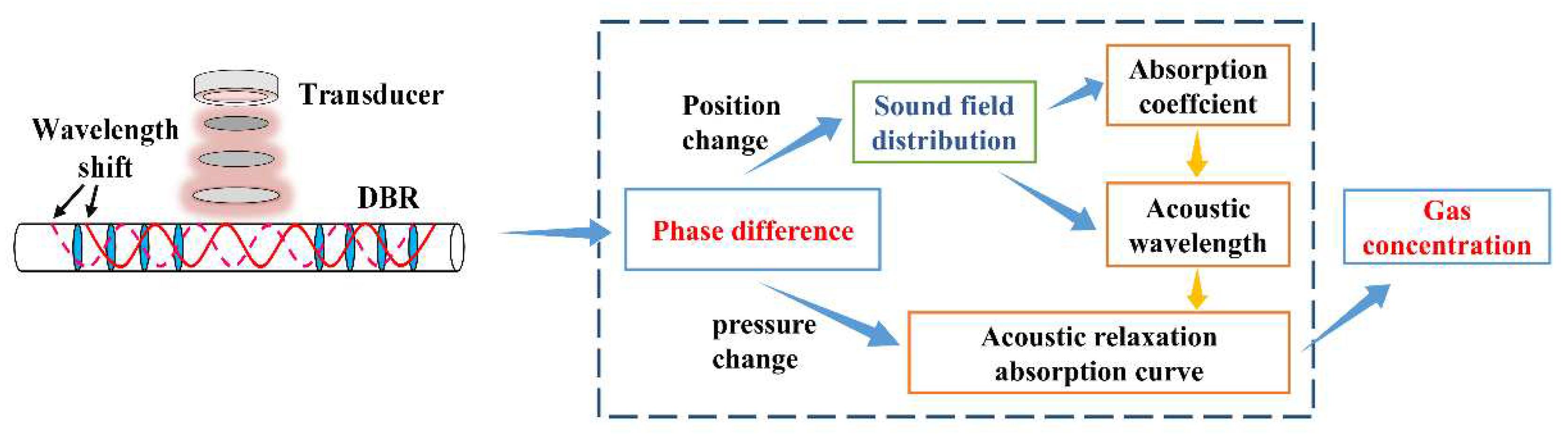
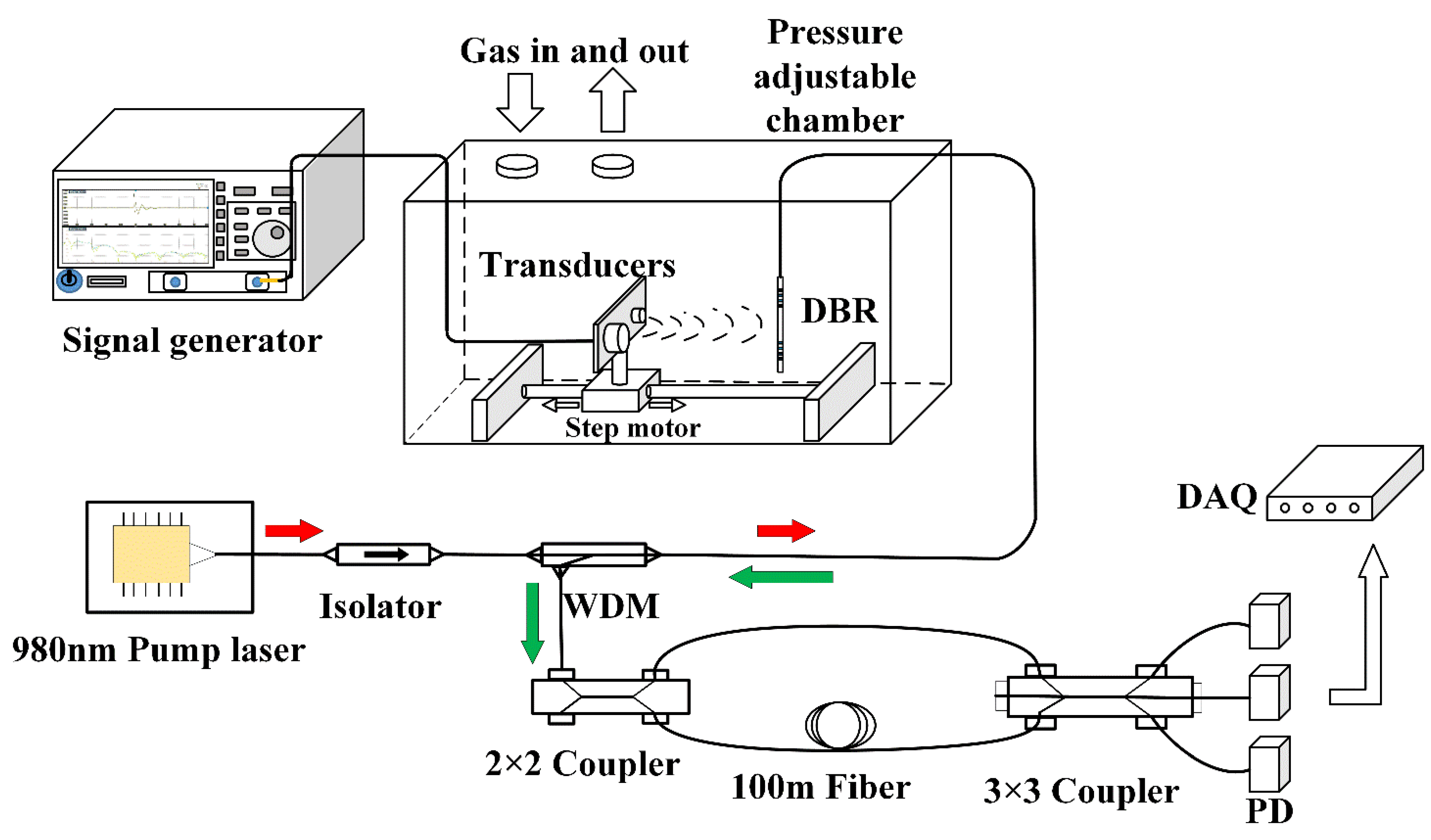
2. Ultrasonic sensing model of the DBR fiber laser

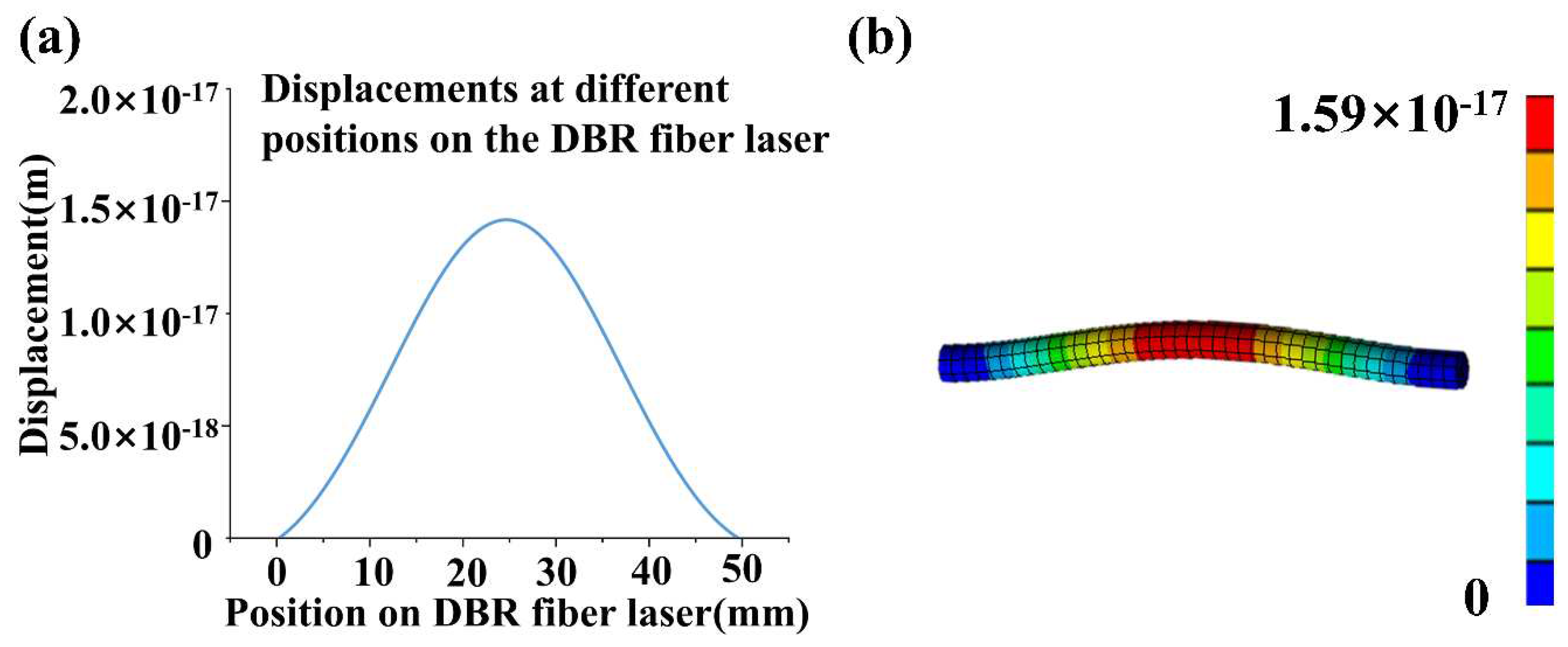
2.1. Response of the DBR fiber laser to ultrasonic wave

A DBR fiber laser consists of a pair of fiber Bragg gratings (FBGs) and a piece of Er-doped fiber in between works as a sensing unit. The process of a soundwave applying to the DBR fiber laser changing the cavity length and in turn the laser wavelength, which involves two physical effects, elastic deformation and photoelastic effect of the DBR fiber laser, so the induced strain of the DBR fiber laser under ultrasonic wave needs to be figured out before sensor modelling. In this work, the displacement of the DBR fiber laser is obtained by solving partial differential equation of one-dimensional vibration of the optical fiber, and numerically proved by the finite element simulation.

Figure 1 illustrates the gas detection scheme proposed in this paper. Transmitting transducers generate ultrasonic waves of several specific frequencies, which are received by the DBR fiber laser.

As a kind of mechanical wave, ultrasonic wave acting on the DBR fiber laser follows the wave theory of a string and generates longitudinal stress waves propagating along the fiber axis, which produces axial strain on the DBR fiber laser. Considering the DBR fiber laser as a thin rod consisting of several segments, longitudinal displacement of each segment leads to compression or elongation of its adjacent segments.

Assuming the ultrasonic wave as a plane wave emitted from the transducer, the acoustic sound pressure of z direction (perpendicular to the fiber axis) p(z) can be written as the following.

where p₀ is the sound pressure at the transmitter, $\alpha$ is the attenuation coefficient.

Assuming the DBR fiber laser is an uniform bar, and u(x, t) is the displacement perpendicular to the fiber axis at position x and time t of the DBR fiber laser. The vibration equation has an expression as:

In Equation (2), v is the velocity of sound in the optical fiber. The displacement on the DBR fiber laser caused by the continuous force of ultrasonic waves presents as u(x, t), and the sound pressure p modulates the sensor’s geometry, which leads to wavelength shift of the DBR fiber laser.

Equation (3) is one dimensional vibration equation of the DBR fiber laser, in which, m is a positive integer, d is the fiber segment length under ultrasonic wave, L is the length of the DBR fiber laser, v₀ is the initial velocity of the fiber vibration, p_m$\left(\tau \right)$ is the sound pressure acting on DBR fiber laser, which is proportional to p(z) in Equation(1).

Figure 2 illustrates the displacement distribution of the DBR fiber laser under ultrasonic sound pressure of 2 Pa and 25 kHz according to Equation (3).

25 kHz ultrasonic wave is launches perpendicularly to the axis of the DBR fiber laser, the two ends of which are fixed. The ultrasonic wave acting on the DBR fiber laser sets to 2 Pa, and covers fiber segment length of 20 mm.

Figure 2a plots the displacement distribution of the DBR fiber laser by solving the vibration equation as well as the finite element simulation results (Figure 2b). The center node has the maximum displacement about 1.5×10^-17 m for the DBR fiber laser length of 48 mm.

The wavelength shift of the DBR fiber laser caused by ultrasonic wave can be deduced from the obtained displacement. Since p is a function of the ultrasonic frequency, the wavelength shifts of the DBR fiber laser under 25 kHz (black square), 40 kHz (red dot), 112 kHz (blue up triangle), 200 kHz (green down triangle) and 300 kHz (purple diamond) ultrasonic wave are compared in Figure 3. In Figure 3, the maximum wavelength shift of the DBR fiber laser increases with the ultrasonic source strength which is proportional to the sound pressure applied to the DBR fiber laser at a specific frequency and decreases while the ultrasonic frequency increases.

The DBR fiber laser is essentially the sensing unit and subjected to sound pressure. The cavity length changes with the applied ultrasonic wave, then results in the wavelength shift of the DBR fiber laser. In Figure 3, the intensity of the ultrasonic wave is indicated by the source strength. For ultrasonic waves of a certain frequency, the wavelength shift of the DBR fiber laser is proportional to the intensity of the sound source, and decreases with the frequency of the sound source increase, which results from the faster attenuation of the ultrasonic wave at higher frequency. Since better linearity of the DBR fiber lasers sensing system brings with smaller systematic error in gas detection, the response linearity of the DBR fiber lasers sensing system is experimentally demonstrated in section 2.2.

The DBR fiber laser has two specific frequencies to be determined, the resonance frequency and the theoretical maximum response frequency that limited by the geometry of the DBR fiber laser. Using the equation of string vibration, resonant frequency $f_m=mv/2L,m=1,2,3\dots$ When the density and Young's modulus of the communication fiber are chosen, the sound velocity in the DBR fiber laser is about 5570 m/s. So the frequency response of the fundamental mode is around 58 kHz. The fundamental vibration mode has the maximum amplitude, which is inversely proportional to m square (m is the order of harmonic mode). On the other hand, only the axial strain needs to be considered when the ultrasonic wavelength is much larger than the diameter of the DBR fiber laser (125m). Therefore, the frequency response of the DBR fiber laser in CO2 reaches above 2 MHz, (the wavelength of the sound wave and the response bandwidth increase while the molar mass of the gas decreases), which fully meets the experimental requirements.

The output light frequency f_light of the DBR fiber laser depends on its cavity geometry written as follow:

where Q is the positive integer, c is the velocity of light, n is the refractive index of the fiber, L is length of the DBR fiber laser.

The relation of output frequency, cavity length and refractive index of the DBR fiber laser has an expression as the derivative of Equation (4):

ΔL, Δn, Δf_light, Δ_light are the variation of cavity length, refractive index change caused by photoelastic effect, the frequency shift and the wavelength shift of the DBR fiber laser. For convenience, frequency variation rewrites in the form of relative wavelength shift as Equation (6).

According to Hooke's law, the strain tensor of the DBR fiber laser in an uniform sound field can be expressed as:

Where E is the Young's modulus of the DBR fiber laser, μ is the poisson ratio. By substituting Equation (7) into Equation (6), the relative sound pressure sensitivity K_DBR of the DBR fiber laser can be obtained:

As can be seen from equation (8), the sound pressure sensitivity of the DBR fiber laser depends on the effective elastic coefficient p₁₁ and p_12, Young's modulus and Poisson ratio of the DBR fiber laser can be effectively improved by selecting appropriate materials for packaging.

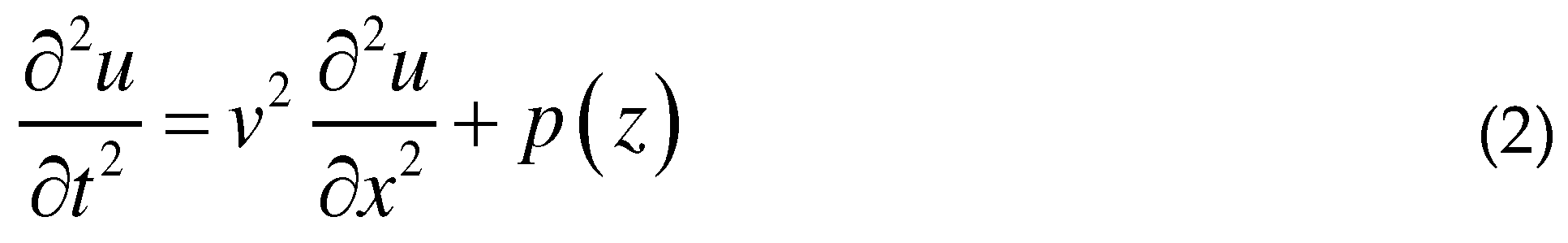
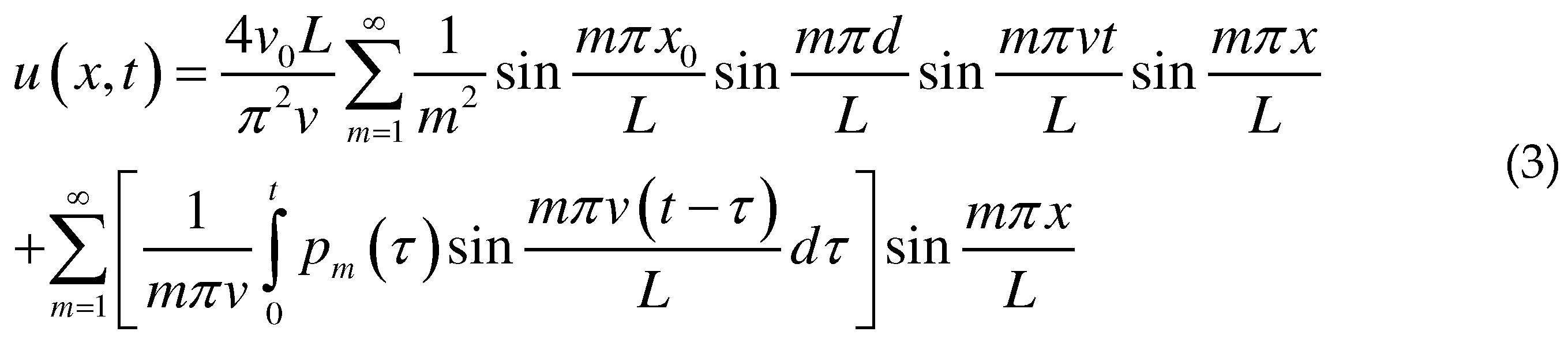
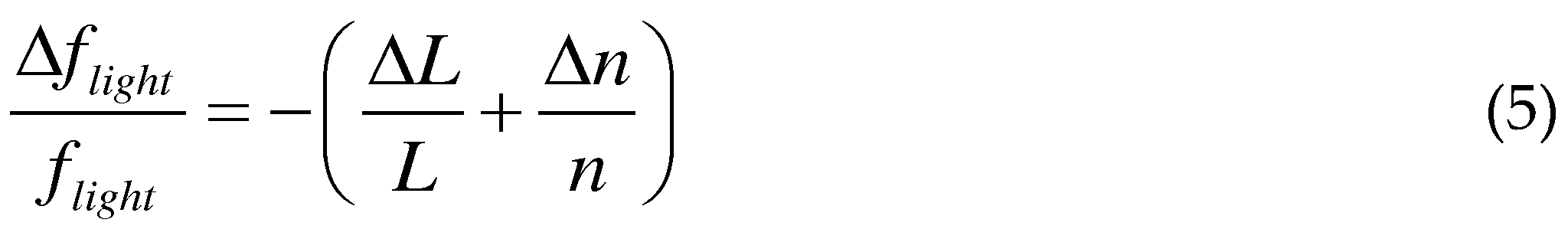
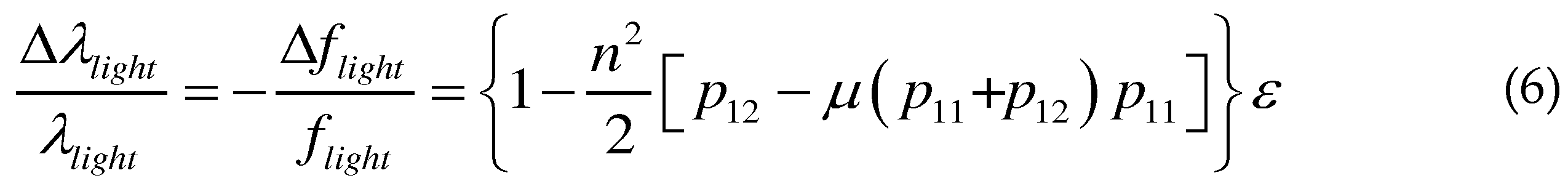
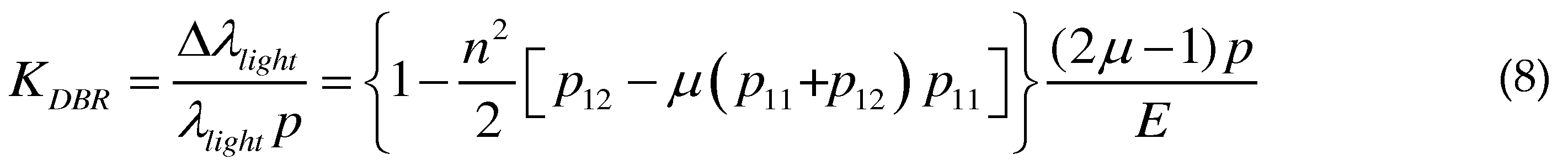
2.2. Ultrasonic wave sensing model of the DBR fiber laser.

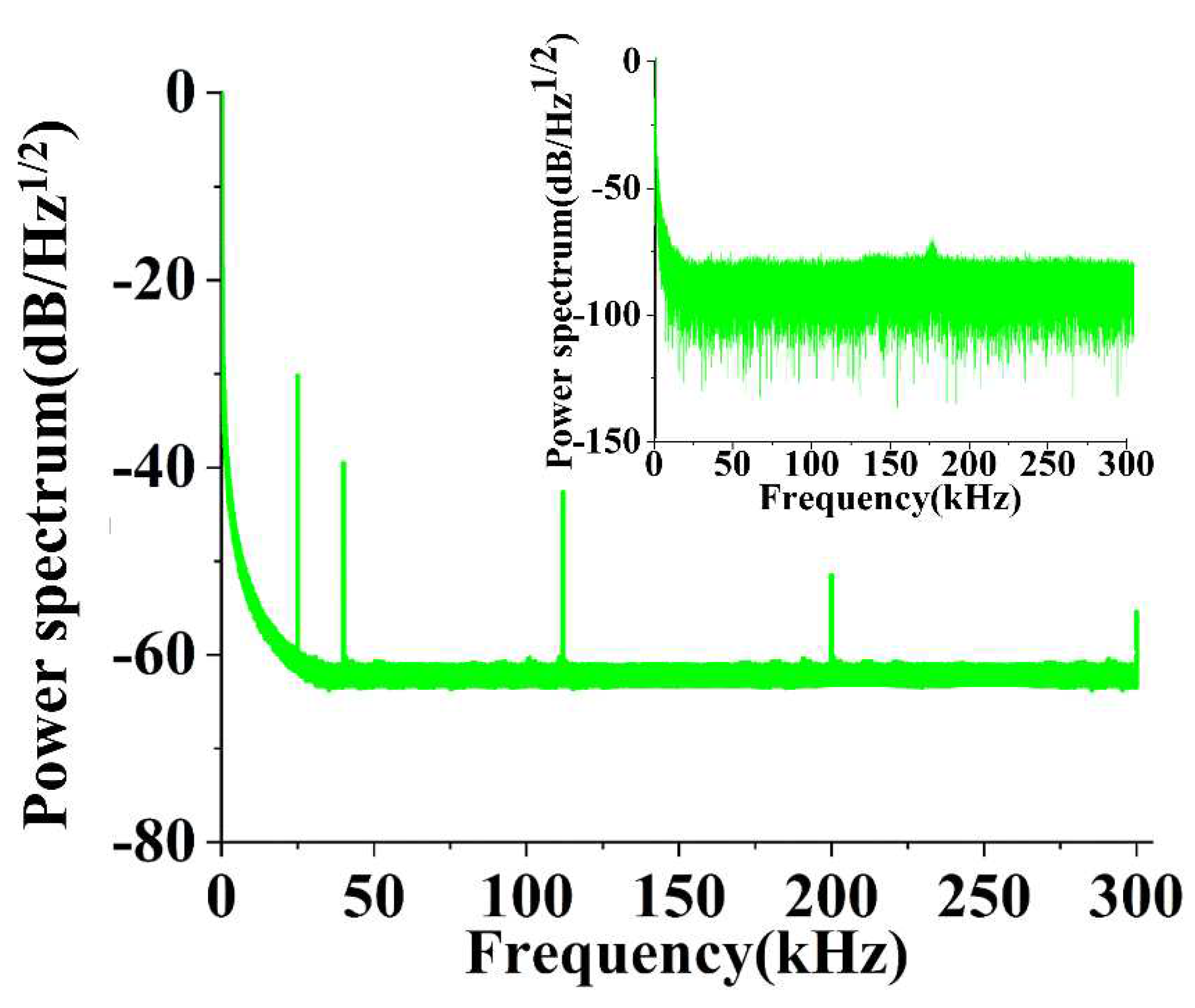
2.2.1. The optical interrogation signal of the DBR fiber laser.

Assuming the operating wavelength of the DBR fiber laser is ₀, and the wavelength shift is Δ(t). The corresponding phase difference introduced by the NE-MZI has an expression as:

Where L_OPD is optical path difference of the NE-MZI, and Δt is the phase difference caused by the wavelength shift of the DBR fiber laser, i.e., the demodulation signal recorded in the experiments. The ultrasonic response comparison of the DBR fiber laser with the ultrasonic transducer takes advantage of the proportional relation between the applied sound pressure and the output voltage of ultrasonic transducer under the same frequency and circumstance pressure. The DBR fiber laser is placed right in front of the receiving transducer facing the transmitting transducer. The phase difference proves to be proportional to the sound pressure applied onto the DBR fiber laser. The demonstration scheme and results are plotted in Figure 4.

Figure 4 a is the experimental scheme of the demonstration experiment, Figure 4b shows the influences of the ambient pressure on the ultrasonic noise power of the DBR fiber laser output. The noise power increases with the ambient pressure, and is much smaller than the ultrasonic signal power. Noise will affect the accuracy of ultrasonic measurement, so the noise signal is subtracted during ultrasonic measurement. Figure 4 c and d are the sample experimental spectrums of phase difference to transducer output voltages for 25 kHz and 300 kHz ultrasonic wave. Figure 4 shows the phase difference of the DBR fiber laser changes linearly with the ultrasonic pressure, and the linear correlation coefficients of the experimental results are over 0.99.

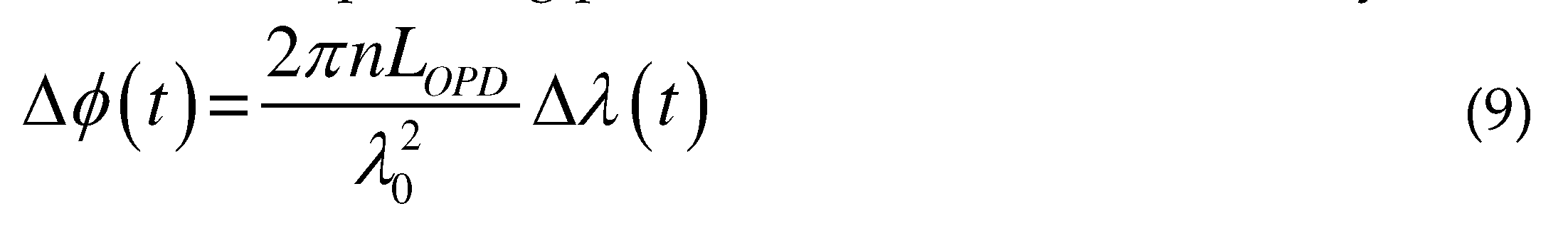
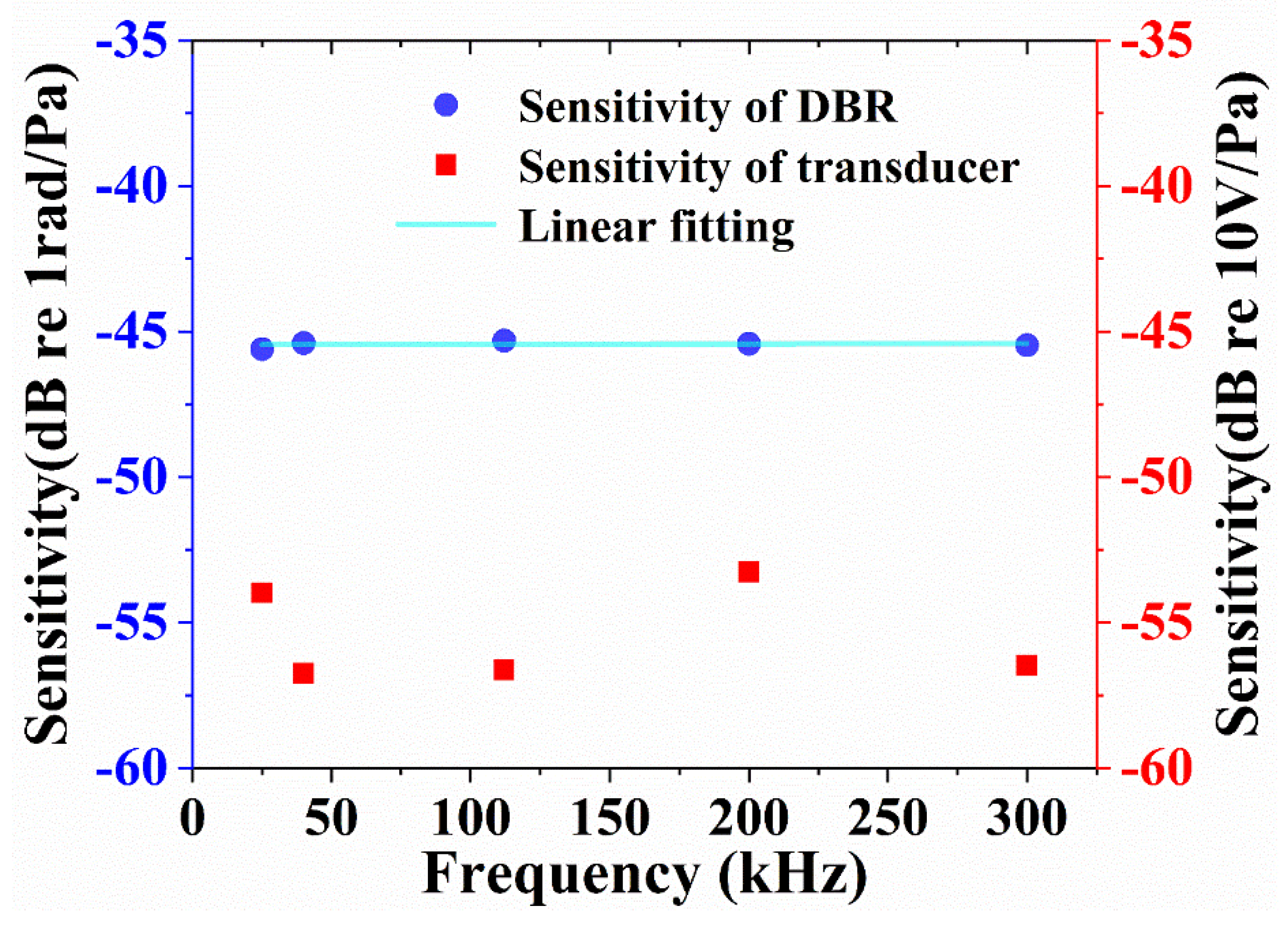
2.2.2. Calibration of the ultrasonic response of the DBR fiber laser.

Since it is the first time to measure the ultrasonic sound pressure quantitively using a DBR fiber laser, the ultrasonic response of the proposed DBR fiber laser system needs tested and compared with their corresponding transducers at five ultrasonic frequencies of our applications.

Figure 5 shows the optical responses of the DBR fiber laser to five sampling ultrasonic waves between 20 to 300 kHz at 25, 40, 112, 200 and 300 kHz, where the ultrasonic waves launched at five frequencies are tested simultaneously. And the inlet plots the background noise without ultrasonic signal applied.

The background noise power is relative large at lower frequency (for example, raising to -50dB/Hz^1/2 below 1 kHz), decreases with the frequency increase, and below -75 dB/Hz^1/2 after 15 kHz, where the noise equivalent sound pressure(NESP) reaches about -80 dB/Hz^1/2. However, the noise power raises to -60 dB/Hz^1/2 at 20 kHz as the ultrasonic wave launched. Therefore, calibration is necessary for the DBR fiber laser before sensing application.

Five piezoelectric transducers of 25 kHz, 40 kHz, 112 kHz, 200 kHz and 300 kHz are chosen for the sensitivity calibration of the DBR fiber laser. The results are shown in Figure 6.

Figure 6 shows the sensitivity of the DBR fiber laser and transducers over the frequency range from 25 to 300 kHz. The average sensitivity of the DBR fiber laser is -45.4 dB, and relatively flat over the ultrasonic range. By now, the DBR fiber laser system is ready for ultrasonic detection and gas sensing.

3. Measurement of the acoustic relaxation absorption and concentration of CO₂ with the DBR fiber laser ultrasonic sensor.

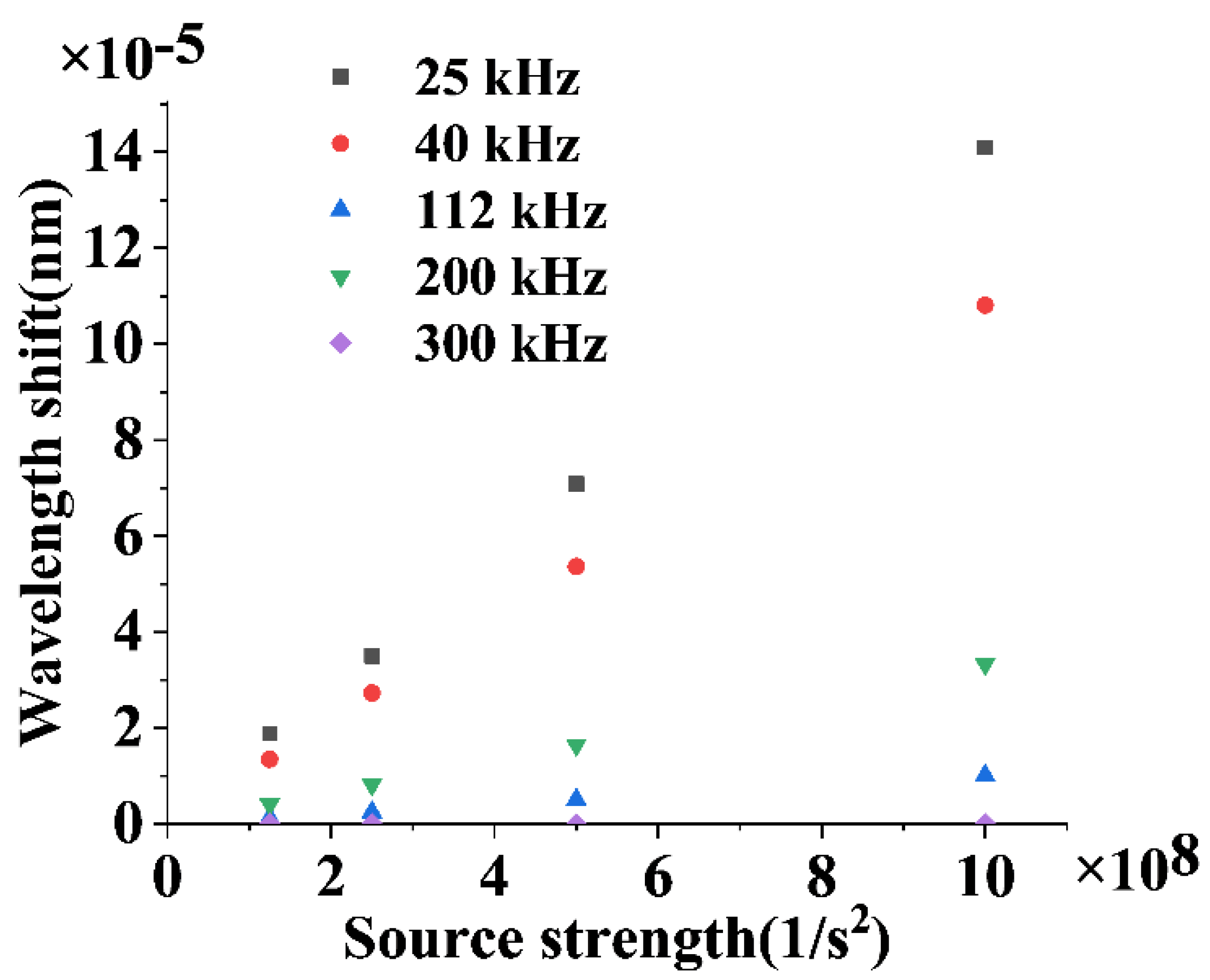
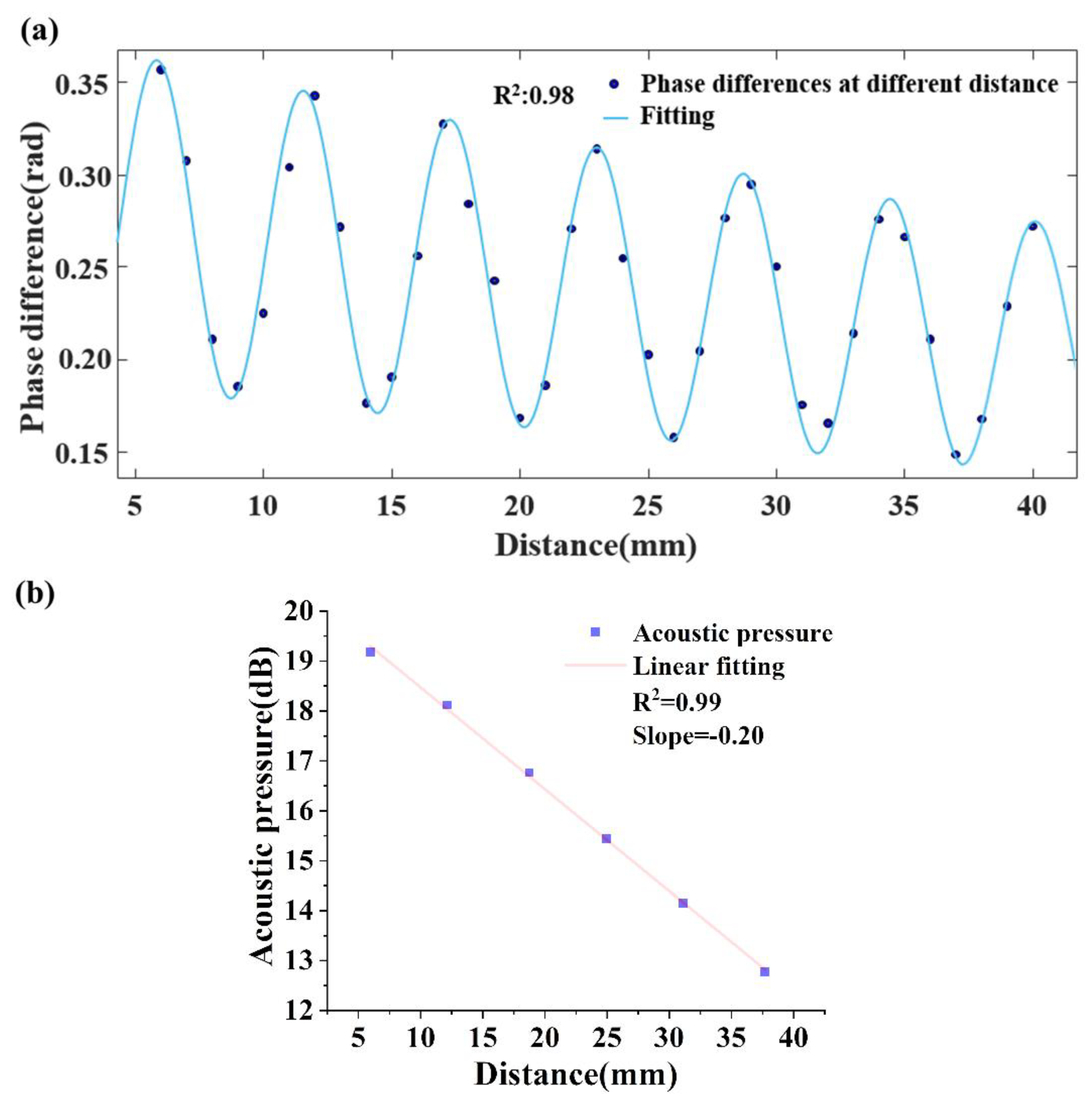
3.1. Measurement of the acoustic relaxation absorption at a specific frequency.

Relaxation frequency and the corresponding intensity of the absorption curve are the unique characteristics of a specific gas and generally used to identify the unknown composition of a gas mixture. The composition or concentration of a certain gas in the mixture can be identified with the sound velocity spectrum or the absorption spectrum, which depends on the number of components in the mixture. Characteristic frequency, absorption coefficient and sound velocity of the measured gas can be evaluated from the comparison of the reconstruction spectrum with the theoretical or published experimental ultrasonic spectral data of gases [17]. Since the transmitting transducers find no substitutes at present, the experiment chooses a decompression gas chamber to simulate the main molecular relaxation process.

Figure 7 illustrates the experimental system proposed in this paper. A pressure tunable gas chamber ranging from 0.01 to 1 atm is designed for the acoustic absorption spectrum measurement. Transmitting transducers embedded in a plate fixed on a step motor emit ultrasonic waves of 25 and 40kHz, which are received by the DBR fiber laser. The output signal of the DBR fiber laser feeds into a NE-MZI through a wavelength division multiplexer (WDM), and interrogates the phase difference and corresponding wavelength shift of the DBR fiber laser under applied ultrasonic wave using the 3×3 coupler method, which effectively improves the sensitivity of the system.

In the gas chamber, the DBR fiber laser is placed on the path and axially perpendicular to the direction of the ultrasonic emission. Since the diameter of optical fiber is much smaller than the ultrasonic wavelength, reflection from the fiber is no concern of our experiments. An aluminum plate places next to the DBR fiber laser on the opposite side of the transmitting transducer to form an effective standing wave.

CO₂ is a popular validation gas in reduction studies of acoustic relaxation absorption spectrum. Acoustic absorption measures first for the reconstruction of the acoustic relaxation absorption curve of CO₂. According to Clapeyron equation, a decreasing chamber pressure is equivalent to an increasing ultrasonic frequency. Since the effective relaxation frequency of the acoustic relaxation absorption curve of 100% CO₂ locates at 40 kHz, an ultrasonic transducer of 25 kHz is a better choice to satisfy the measurement of the relaxation absorption spectrum of CO₂, where f/p is controlled by adjusting the chamber pressure. The distance between the transmitting transducer and the DBR fiber laser varies between 30~100 mm to satisfy the far field prerequisite for ultrasonic attenuation coefficient measurement.

The incidence ultrasonic wave is reflected on the receiving transducer/aluminum plate and interferes with its reflected counterpart, thus sound field is a superposition of sound absorption and interference. According to the classical definition of sound absorption coefficient in Equation (10), acoustic pressure need to be obtained along the direction of ultrasonic emission at various distances, where the transmitting transducer moves on a linear guide rail controlled by a step-motor from 30 mm (distance to the DBR fiber laser) to 100 mm, and records the output phase difference of the DBR fiber laser sensor every 1 mm.

Where α is the absorption coefficient, U1 and U2 are the output voltages of the receiving transducer obtained in the positions L1 and L2 respectively. The output voltage U is also defined as a product of sound pressure sensitivity kt and intensity p. Equation (10) clears that the absorption coefficient α is independent of the sensitivity of the sensor kt, for a specific ultrasonic frequency and only determined by the gas characteristics. Therefore, the absorption coefficient α keeps the same no matter either a transducer or a DBR fiber laser sensor is used for testing as long as the f/p keeps the same. The sensitivity determines the lowest detectable acoustic pressure or the noise equivalent sound pressure, so the measurement precision of acoustic attenuation coefficient improves with the sensitivity.

Testing results of the 25kHz sound field distribution recovered by the DBR fiber laser sensor is plotted in Figure 8a. Based on the linear relation of phase difference and acoustic pressure and Equation (10), a diagram of peak pressures level in Figure 8a to the distance and its linear fitting are shown in Figure 8b, and the slope of which is divided by 20 is equal to the absorption coefficient of the gas, where the phase difference variation limits to a linear zone because of the weak ultrasonic absorption.

From Figure 8a, the standing sound wave field produced by the superposition of the incident and reflected ultrasonic waves shows a tendency of oscillation decline. According to Equation (10) and the direct conversion relationship between sound pressure and sound pressure level, the slope of the fitting line in Figure 8b divided by 20 is acoustic absorption coefficient α, and equals to 0.01 dB/mm. The ultrasonic wavelength  is 11.3 mm, the acoustic relaxation absorption coefficient  is 0.113. Following the same process to get the acoustic relaxation absorption coefficients at various frequencies by tuning the gas chamber pressure, the acoustic relaxation absorption spectrum is recovered.

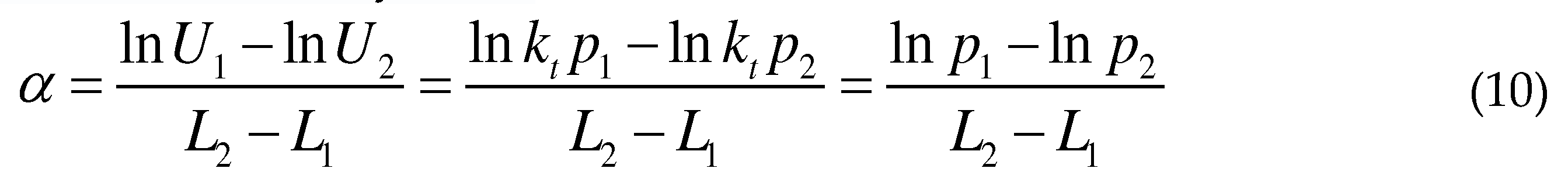
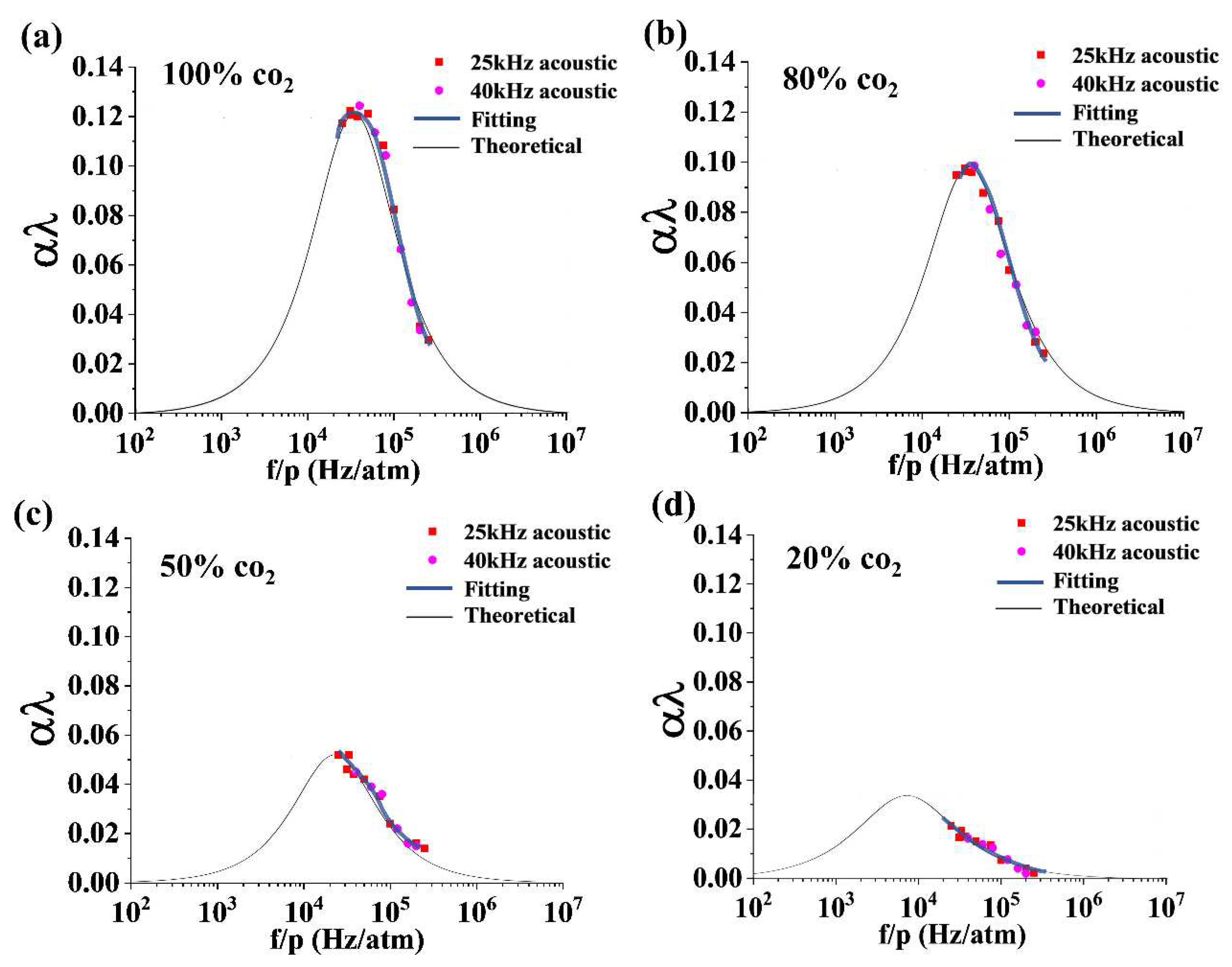
3.2. Measurement results of the absorption spectrum of CO₂.

To restore the gas relaxation absorption spectrum, ultrasonic attenuation coefficients over a wide range of f/p need to be obtained through a series of measurements with various pressures. The acoustic attenuation increases with the pressure of gas chamber decreases. And the minimum detectable sound pressure of the DBR fiber laser sensor determines the minimum chamber pressure in the experiments. A smaller detectable sound pressure means even lower applicable chamber pressure and wider frequency bandwidth, and the reconstruction of the acoustic relaxation absorption spectrums get more precise.

A group of experiments are carried with the gas chamber pressure tuning between 0.1 to 1.0 atm for CO₂ concentrations of 100%, 80%, 50%, 20%. Measurements use two ultrasonic transducers of 25 kHz and 40 kHz as the emitting sources and the DBR fiber laser as the sensing probe. Repeating the test steps in section 3.1, acoustic relaxation absorption coefficients are obtained corresponding to a series of f/p around the effective relaxation frequency. The acoustic relaxation absorption spectrum of 100% CO₂ is restored by the fitting spectrum of 25 kHz (red square) and 40 kHz (pink round) results in Figure 9a, and similar fitting curves are plotted in Figure 9b, c and d respectively for CO₂ concentration of 80%, 50%, 20%. The black solid curves are theoretical curves corresponding to the four CO₂ concentrations.

In Figure 9a, the experimental acoustic relaxation absorption spectrum slightly deviates from the theoretical spectrum of 100% CO₂, which leads to an error of 0.82% of concentration. In Figure 9b, the deviation of the experimental spectrum from the theoretical leads to an error of 0.84%. For 50% and 20% CO₂, the errors are 1.26% and 1.32%, respectively. While the relaxation absorption coefficient decreases with the concentration of CO₂, the measurement error of the corresponding acoustic relaxation absorption spectra increases. On the other side, it shows that measurement taken as close as possible to the absorption peak frequency will gives better precision.

4. Discussion and conclusion

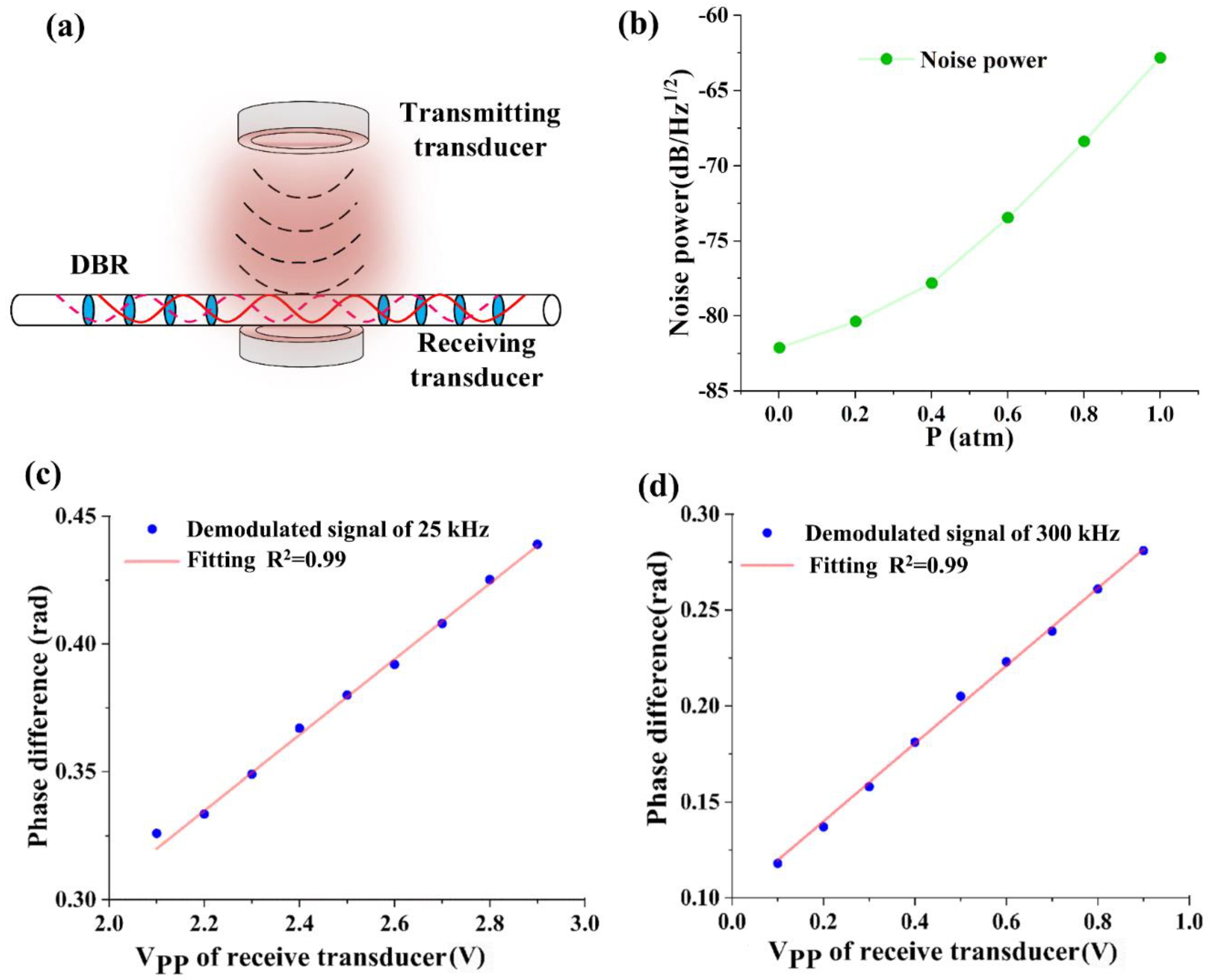
4.1. Systematic error results from variation with f/p.

The deviation of the experimental results from the theoretical model increasing with f/p, i.e. higher frequency, might stem from several factors. First, the acoustic impedance mismatch of the transducer in gas affects both acoustic generation and detection and result in a decreasing signal to noise ratio (SNR) with frequency increasing. Second, any foreign molecules present in the gas chamber (for example, gas leaking from the vacuum pump) may induce multiple molecular relaxation pathways leading to possible broadening of the acoustic relaxation absorption spectrum. These issues might also be responsible for the generally larger standard deviations at low pressures. In general, raising the f/p ratio leads to a larger measurement error of the relaxation absorption coefficient.

4.2. The temperature and pressure instability of the gas chamber and compensation.

Pressure instability of the gas chamber is mainly related to poor tightness and circumstance temperature variation. The air tightness of the gas chamber affects not only the f/p ratio during measurement, but also the acoustic relaxation absorption coefficient. When the gas chamber pressure drops below 1 kPa, the average pressure variation in the gas chamber is about 3Pa/10min, where 10 minutes is the time of one complete test, indicating an error of the f/p ratio caused by the gas chamber pressure increases about 0.003% every 10 minutes. During the measurement of the acoustic relaxation absorption coefficient, temperature varies less than 0.01 K every 10 minutes in the gas chamber, results in a sound velocity error of about 0.002% and f/p error of 0.033%. Therefore, temperature is compensated for 293 K, and the pressure of the gas chamber was corrected accordingly.

In brief, a novel optical approach using a DBR fiber laser is proposed to measure the acoustic absorption coefficient over a wide frequency band and application of reconstruction of the acoustic relaxation absorption spectra of CO₂ with various concentrations. With a relative wide and flat frequency response, the DBR fiber laser sensor measures and restores a full acoustic relaxation absorption spectrum of CO₂ using a decompression gas chamber between 0.1 and 1 atm to accommodate the main molecular relaxation processes, and interrogates with a non-equilibrium Mach-Zehnder interferometer to gain a phase noise power about -80 dB/Hz^1/2. Combined with the gas sensing approach based on ultrasonic velocity, the DBR fiber laser sensor is a promising candidate for analysis of ternary or quaternary gases.