Prerpints.org logo
Preprint
Communication

Building Local Correlation Models for Analytical Pricing

Altmetrics

Downloads

138

Views

18

Comments

0

This version is not peer-reviewed

Submitted:

26 April 2023

Posted:

27 April 2023

You are already at the latest version

Alerts
Abstract
This short paper reveals a simple methodology to create local-correlation models suitable for the closed-form pricing of multi-asset financial derivatives. The multivariate models are built to ensure two conditions, first, marginals follow desirable processes, e.g. we choose the Geometric Brownian Motion (GBM), popular for stock prices. Second, the payoff of the derivative should follow a desired one dimensional process. These conditions lead to a specific choice of the dependence structure, in the form of a local-correlation model. Two popular multi-asset options are entertained, a spread option and a basket option.
Keywords: 
Subject: Business, Economics and Management  -   Finance

1. Introduction

Since the introduction of the Geometric Brownian Motion (GBM) in one-asset derivative pricing Black and Scholes (1973), many theoretical works have tried, with little success, to extend these convenient closed-form solutions to the context of multi-asset derivatives. One key reason is that multidimensional stochastic processes are built from Brownian motions, therefore, even in the favorable scenario of a Gaussian process with non-path dependent financial derivatives, the price of the product would depend on the multivariate Gaussian distribution. This is, expected value calculations are doomed to multivariate integrals, solvable numerically of via simulations. For more advanced processes, e.g., stochastic covariance model (see Gouriéroux (2006) for the Wishart, and Escobar and Gschnaidtner (2018) for the PCSV), the price of multi-asset products is rarely analytical, closed-form solutions are available for Affine and Quadratic models via multivariate Fourier transform methods or simulations (see Fonseca et al. (2007) and Cheng et al. (2019)). The modelling limitations in multidimensions has also contributed to the absence of path-dependent multi-asset products (see He et al. (1998); Götz et al. (2014) and Escobar et al. (2014) for rare analytical pricing), in contrast to the popularity of the one-asset path-dependent counterpart e.g. barrier options, and lookback options, see Rubinstein (1991).
This paper uses standard techniques from Ito’s calculus to design multidimensional processes, in particular, correlation structures, capable of producing analytical solutions for the calculations of specific expectations. These expectations are chosen as the prices of meaningful multi-assets financial derivatives, e.g. spread options and basket options. The perspective introduced here can be extended to not only advanced products like path-dependent derivatives, but also to advanced models on the marginal like constant elasticity of volatility or stochastic volatility models.
This work benefits from the well-known notion of local-variance and local-correlation, adapting the latter conveniently. A popular example of a local-variance stochastic process is the constant elasticity of volatility model (CEV), see Cox (1975). CEV treats volatility as a function of both the current asset level and time while permitting analytical solutions for derivative pricing. On the other hand, the literature on multivariate CEV models (e.g. local-covariance or multivariate local-variance) is scarce and mostly based on numerical approximations (see Cont and Deguest (2013) and Bayer and Laurence (2014)). As for local correlations, Langnau (2009) provides evidence of local correlation under the risk-neutral measure using basket options but it does not aim at analytical solutions. Carmona and Sun (2012) targets spread options with no analytical solution either.
The main results of the paper are provided in the next section, where the general setting is described first, and then the cases of a spread option model and a basket option model are defined and studied.

2. Setting and Methodology

Let all the stochastic processes introduced in this paper be defined on a complete probability space ( Ω , F , P , { F t } t ∈ [ 0 , T ] ) , where { F t } t ∈ [ 0 , T ] is a right-continuous filtration generated by standard Brownian motions Z i , t , i = 1 , 2 (BMs).
Assume a financial market consisting of 2 risky assets with the following stochastic differential equations (SDE):
d S 1 , t S 1 , t = μ 1 d t + σ 1 d Z 1 , t P = r + λ 1 σ 1 d t + σ 1 d Z 1 , t P , d S 2 , t S 2 , t = μ 2 , t d t + σ 2 ρ t d Z 1 , t P + 1 − ρ t 2 d Z 2 , t P = r + λ 1 σ 2 ρ t + λ 2 σ 2 1 − ρ t 2 d t + σ 2 ρ t d Z 1 , t P + 1 − ρ t 2 d Z 2 , t P
where μ 1 , μ 2 , σ 1 , σ 2 are scalars, and ρ t represents the instantaneous correlation between S 1 and S 2 , hence bounded by -1 and 1. The correlation is assumed a function of time and the stocks underlying, which explains the term "local correlation".
The model above is commonly referred as the dynamic of stock prices under the historical measure. This dynamic is not helpful for the pricing of financial derivatives, a change to a risk-neutral measure is required. Let us assume a simple of change of measure defined by d Z i , t P = d Z i , t − λ i d t , leading to:
d S 1 , t S 1 , t = r d t + σ 1 d Z 1 , t , d S 2 , t S 2 , t = r d t + σ 2 ρ t d Z 1 , t + 1 − ρ t 2 d Z 2 , t
where r is the free rate of interest.
Given the boundness of the process ρ t , there exists a unique strong solution for the SDE under the two measures by simply applying Lipschitz and linear Growth conditions (see Karatzas and Shreve (2012)).
Let us now assume a contingent claim, i.e. financial derivative, on the underlyings, with payoff G ( X 1 , T , X 2 , T , K ) , where X i , T = S i , u u = t T represents the history of the underlying stock, i = 1 , 2 , from today t till maturity T, and K is a scalar. Examples of this payoff are:
Call option on F : G ( X 1 , T , X 2 , T , K ) = F ( X 1 , T , X 2 , T ) − K + Put option on F : G ( X 1 , T , X 2 , T , K ) = K − F ( X 1 , T , X 2 , T ) + Barrier option on F : G ( X 1 , T , X 2 , T , K ) = 1 F ( X 1 , T , X 2 , T ) > K Lookback option on F : G ( X 1 , T , X 2 , T , K ) = K − min t ≤ u ≤ T F ( X 1 , u , X 2 , u ) +
where x + = x 1 x > 0 and F ( X 1 , T , X 2 , T ) could be any function of the underlyings, for instance:
Spread : F ( X 1 , T , X 2 , T ) = a 1 S 1 , T − a 2 S 2 , T Basket : F ( X 1 , T , X 2 , T ) = a 1 S 1 , T + a 2 S 2 , T Best of : F ( X 1 , T , X 2 , T ) = max S 1 , T , S 2 , T Worst of : F ( X 1 , T , X 2 , T ) = min S 1 , T , S 2 , T Average : F ( X 1 , T , X 2 , T ) = ∫ t T S 1 , u d u + ∫ t T S 2 , u d u
The objetive of this paper is to compute the correlation structure implied by assuming the process Y t = F ( X 1 , t , X 2 , t ) follows a predetermined stochastic process of the form:
d Y 1 , t Y 1 , t = r d t + σ Y d Z 3 , t ,
where σ Y could be a function of time and the underlying Y t , and Z 3 , t is a standard Brownian motion. Such structure for Y could allow for closed-form pricing of the contingent claim, which is usually unfeasible in multi-asset products.
The next section will show how the idea can be implemented for two cases (Spread and Basket options), and the kind of correlation structure it generates.

3. Results.

In this section we will explore two financial derivatives of interest to practitioners, the spread option and a basket option.

3.1. Pricing Spread options.

We want to create a correlation structure such that the spread option process Y t = a 1 S 1 , t − a 2 S 2 , t follows the Gaussian process 1:
d Y t = r Y t d t + σ 3 , t d Z 3 , t ,
where a 1 and a 2 are scalars to ensure a 1 S 1 , t and a 2 S 2 , t are comparable in value, e.g. a i = 1 S i , 0 , and σ 3 , t is assumed deterministic to facilitate the closed-form pricing of options 2. Note, there is an implicit constraint on σ 3 , t coming from the boundeness of correlations, this is:
a 1 σ 1 − a 2 σ 2 ≤ σ 3 , t ≤ a 1 σ 1 + a 2 σ 2
Applying Ito’s to Y t = a 1 S 1 , t − a 2 S 2 , t :
d Y t = r Y t d t + a 1 σ 1 S 1 , t d Z 1 , t − a 2 σ 2 S 2 , t ρ t d Z 1 , t + 1 − ρ t 2 d Z 2 , t = r Y t d t + a 1 σ 1 S 1 , t − a 2 σ 2 S 2 , t ρ t 2 + a 2 2 σ 2 2 S 2 , t 2 1 − ρ t 2 d Z 3 , t
Therefore we impose the condition a 1 σ 1 S 1 , t − a 2 σ 2 S 2 , t ρ t 2 + a 2 2 σ 2 2 S 2 , t 2 1 − ρ t 2 = σ 3 , t 2 . Solving for ρ t :
ρ t = min max a 1 σ 1 2 a 2 σ 2 S 1 , t S 2 , t + σ 2 a 2 2 σ 1 a 1 S 2 , t S 1 , t − σ 3 , t 2 2 a 1 a 2 σ 1 σ 2 1 S 1 , t S 2 , t , − 1 , 1
The constraint on ρ t implies that the joint behaviour of the stocks is limited to a constrained region of the space. To see this, for simplicity, let us take σ 1 = σ 2 = σ , a 1 = a 2 = 1 , the model force the stocks to stay within the following bounds:
σ 3 σ < S 1 , t + S 2 , t , − σ 3 σ < S 1 , t − S 2 , t < σ 3 σ
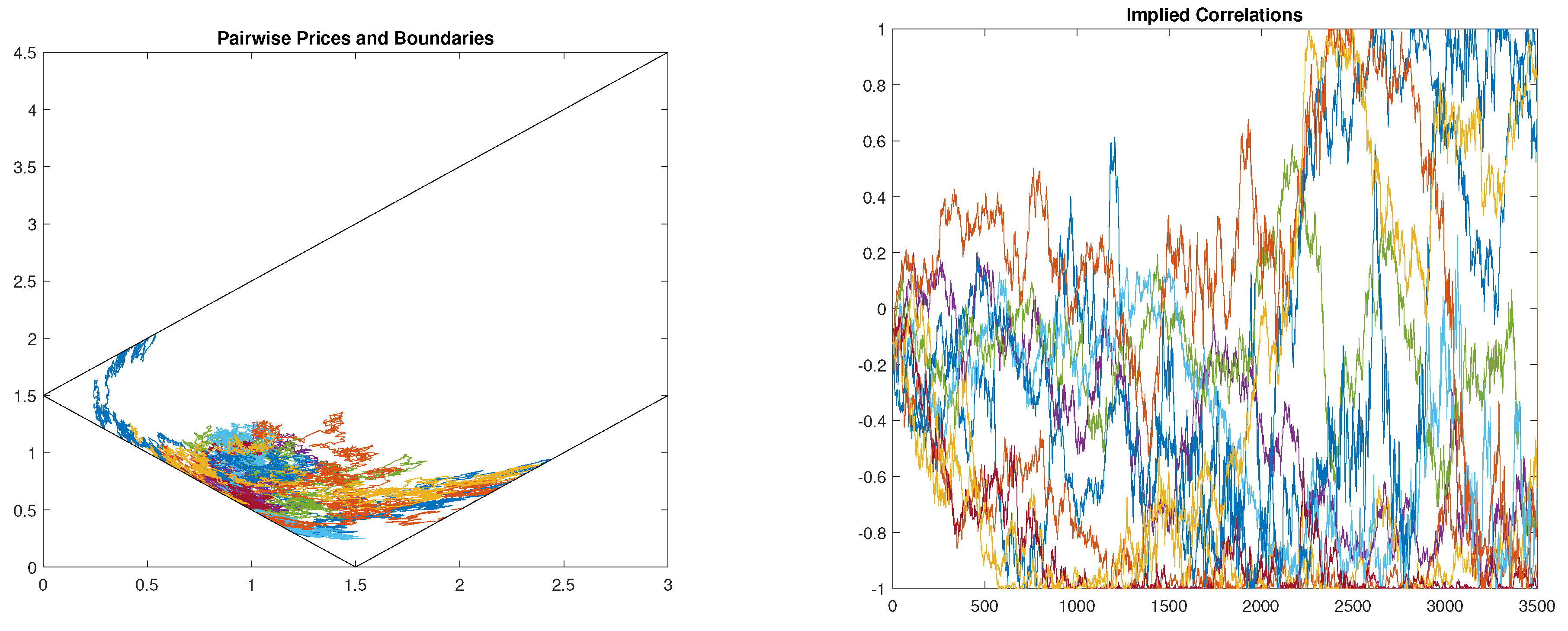
Figure 1 shows 10 simulated paths of ( S 1 , t , S 2 , t ) together with the contained region where the pair is defined. The figure also plot the local correlations implied by the simulated paths. For this simulation we generate 3,500 daily prices with σ 1 = σ 2 = 0.2 (i.e. 20% annual volatility), r = 0 , S 1 , 0 = S 2 , 0 = 1 and σ 3 = 0.3 .
The marginals of this model are GBM, hence the pricing of one-asset products remain the same as in the Black-Scholes-Merton (BSM) setting. The benefit of our model is that the price of spread options would be similar to that of BSM formulas, this is (call spread):
E t e − r ( T − t ) S 1 , T − S 2 , T − K + = E t e − r ( T − t ) Y T − K + = e − r ( T − t ) σ Y 2 e − 0.5 μ Y − K σ Y 2 + ( K + σ Y μ Y ) N μ Y − K σ Y
where N ( · ) is the Gaussian cumulative distribution function, and we have used that Y T is normal with mean μ Y = Y t e r ( T − t ) and variance
σ Y 2 = ∫ t T σ 3 , t 2 exp 2 r s − t d s = σ 3 2 e 2 r ( T − t ) − 1 2 r
Other derivatives on Y T can be also priced in closed form thanks to its Gaussian distribution, for instance, put spread options, and products depending on min 0 ≤ t ≤ T Y t or max 0 ≤ t ≤ T Y t , e.g. Barrier options, lookback options.

3.2. Pricing 2-dim Basket options.

We now aim at the correlation structure such that Y t = S 1 , t + S 2 , t follows the GBM process:
d Y t = r Y t d t + σ 3 , t Y t d Z 3 , t ,
Applying Ito’s to Y t :
d Y t = r Y t d t + σ 1 S 1 , t d Z 1 , t + σ 2 S 2 , t ρ t d Z 1 , t + 1 − ρ t 2 d Z 2 , t = r Y t d t + σ 1 S 1 , t + σ 2 S 2 , t ρ t 2 + σ 2 2 S 2 , t 2 1 − ρ t 2 d Z 3 , t
As before, the condition is σ 1 S 1 , t + σ 2 S 2 , t ρ t 2 + σ 2 2 S 2 , t 2 1 − ρ t 2 = σ 3 , t 2 Y t 2 , and the solution for ρ t :
ρ t = min max σ 3 , t 2 S 1 , t + S 2 , t 2 − σ 1 2 S 1 , t 2 − σ 2 2 S 2 , t 2 2 σ 1 S 1 , t σ 2 S 2 , t , − 1 , 1
The model force the stocks to stay within a viable region, for instance, let us take σ 1 = σ 2 = σ . With S i > 0 , and σ 3 , t 2 < σ 2 (otherwise the region is empty) we obtain:
2 σ 2 + σ 3 , t 2 σ 2 − σ 3 , t 2 > S 1 , t 2 + S 2 , t 2 S 1 , t S 2 , t , S 1 , t 2 + S 2 , t 2 S 1 , t S 2 , t > − 2
Let us denote a = σ 2 + σ 3 , t 2 σ 2 − σ 3 , t 2 > 0 , then we obtain the viable region:
S 1 , t a − a 2 − 1 < S 2 , t < S 1 , t a + a 2 − 1
Note, the region leads to an implicit upper bound on the actual correlation, to see this note
ρ t = σ 3 , t 2 − σ 2 2 σ 2 S 1 , t 2 + S 2 , t 2 S 1 , t S 2 , t + σ 3 , t 2 σ 2
where σ 3 , t 2 − σ 2 2 σ 2 < 0 , S 1 , t 2 + S 2 , t 2 S 1 , t S 2 , t > 2 , hence the maximum correlation is: σ 3 , t 2 σ 2 + σ 3 , t 2 − σ 2 σ 2 = 2 σ 3 , t 2 − σ 2 σ 2 < 1 .
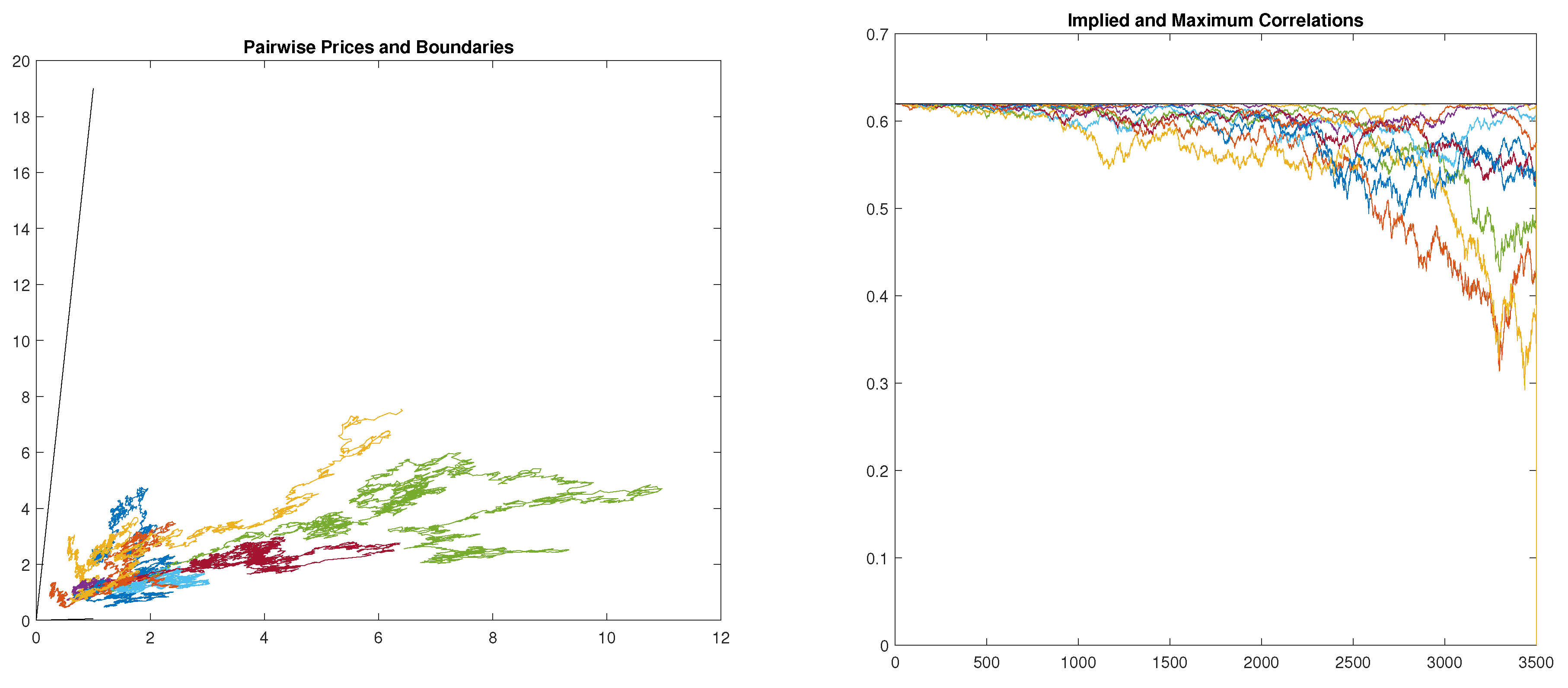
Figure 2 shows 10 simulated paths of ( S 1 , t , S 2 , t ) together with the contained region where the pair is defined. The figure also plot the local correlations implied by the simulated paths. For this simulation we generate 3,500 daily prices with σ 1 = σ 2 = 0.2 (i.e. 20% annual volatility), r = 0.04 , S 1 , 0 = S 2 , 0 = 1 and σ 3 = 0.18 .
As before, the marginal of this model are GBM with all its benefit for pricing one-asset products. On the other hand, the price of basket options would be similar to that of BSM formulas. For simplicity, let us take σ 3 , t = σ 3 :
E t e − r ( T − t ) S 1 , T + S 2 , T − K + = E t e − r ( T − t ) Y T − K + = Y t N d 1 + e − r ( T − t ) K N d 2
where d 1 = 1 σ 3 T − t ( ln Y t K + ( r + 0.5 σ 3 2 ) ( T − t ) ) , d 2 = d 1 − σ 3 T − t .
Other derivatives on Y T can be also priced in closed form thanks to the GBM connection, for instance, put basket options, and products depending on min 0 ≤ t ≤ T Y t or max 0 ≤ t ≤ T Y t , e.g. Barrier options, lookback options.

4. Discussion

As highlighted in the introduction, this paper provides a methodology to define multivariate processes with convenient marginal and dependence structure in continuous-time. For simplicity of presentation we focused on two dimensions (two assets) with GBM marginals and two special derivatives, basket and spread options, where the contingent claims are modelled as either a GBM or an OU with time dependent volatilities.
The results obtained for the two cases considered are promising in terms of the level of realism of the correlation structures generated as well as the region of feasible joint stock prices.
The concept presented here could be extended in many directions. First, we could have assumed contingent claims processes ( Y t ) that follow CEV or stochastic volatility (SV) models (for instance models for Y t like in Beckers (1980), and Heston (1993) ), enriching the dynamics of the implied correlation structure. A CEV model looks like:
d Y t = r Y t d t + σ 3 Y t β d Z 3 , t ,
While a SV model would be:
d Y t = r Y t d t + σ t Y t d Z 3 , t , d σ t = κ θ − σ t d t + δ σ t d Z 4 , t
We could also consider other type of options, in particular, Barrier and path-dependent products, which would be solvable even for the SV case mentioned above (see Lipton (2001) for closed-form solutions).
Higher dimensions, i.e. more than two assets, is also feasible, particularly with a single local correlation using a CAPM construction as follows:
d S 1 , t S 1 , t = r d t + σ 1 d Z 1 , t , d S i , t S i , t = r d t + σ i ρ t d Z 1 , t + 1 − ρ t 2 d Z i , t , i = 2 , . . , n
With n > 2 asset, we enter into more complex derivatives like the world of mountain range products, collateralized debt obligations, collateralized fund obligations and structured products (see Escobar and Olivares (2013); Escobar et al. (2010); Escobar et al. (2018) and Ansejo et al. (2006)), which would likely be solvable in closed-form thanks to the convenient correlation structure. More than a single local correlation is also viable and worth exploring, this could be handled with a one factor model and n correlations ρ i , t , i = 1 , . . . , n :
d S 1 , t S 1 , t = r d t + σ 1 d Z 1 , t , d S i , t S i , t = r d t + σ i ρ i , t d Z 1 , t + 1 − ρ i , t 2 d Z i , t , i = 2 , . . , n

Funding

This research received no external funding.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is available upon request.

References

  1. Ansejo, Unai, Marcos Escobar, Aitor Bergara, and Luis Seco. 2006. Correlation breakdown in the valuation of collateralized fund obligation. The Journal of Alternative Investments 9(3), 77–88.
  2. Bayer, Christian and Peter Laurence. 2014. Asymptotics beats monte carlo: The case of correlated local vol baskets. Communications on Pure and Applied Mathematics 67(10), 1618–1657. [CrossRef]
  3. Beckers, S. 1980. The constant elasticity of variance model and its implications for option pricing. The Journal of Finance 35(3), 661–673. [CrossRef]
  4. Black, Fischer and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of political economy 81(3), 637–654.
  5. Carmona, René, and Youhong Sun. 2012. Implied and local correlations from spread options. Applied Mathematical Finance. [Google Scholar]
  6. Cheng, Yuyang, Marcos Escobar-Anel, and Zhenxian Gong. 2019. Generalized mean-reverting 4/2 factor model. Journal of Risk and Financial Management 12(4), 159. [CrossRef]
  7. Cont, Rama and Romain Deguest. 2013. Equity correlations implied by index options: estimation and model uncertainty analysis. Mathematical Finance: An International Journal of Mathematics, Statistics and Financial Economics 23(3), 496–530. [CrossRef]
  8. Cox, J. 1975. Notes on option pricing in constant elasticity of variance diffusions. Technical report, Stanford University Working paper.
  9. Escobar, Marcos, Sebastian Ferrando, and Xianzhang Wen. 2014. Barrier options in three dimensions. International Journal of Financial Markets and Derivatives 3(3), 260–292. [CrossRef]
  10. Escobar, Marcos, Barbara Götz, Luis Seco, and Rudi Zagst. 2010. Pricing a cdo on stochastically correlated underlyings. Quantitative Finance 10(3), 265–277. [CrossRef]
  11. Escobar, Marcos and Christoph Gschnaidtner. 2018. A multivariate stochastic volatility model with applications in the foreign exchange market. Review of Derivatives Research 21, 1–43.
  12. Escobar, Marcos and Pablo Olivares. 2013. Pricing of mountain range derivatives under a principal component stochastic volatility model. Applied Stochastic Models in Business and Industry 29(1), 31–44. [CrossRef]
  13. Escobar, Marcos, Sven Panz, and Rudi Zagst. 2018. Pricing multiple barrier derivatives under stochastic volatility. Journal of Computational Finance 24(2). [CrossRef]
  14. Fonseca, José Da, Martino Grasselli, and Claudio Tebaldi. 2007. Option pricing when correlations are stochastic: an analytical framework. Review of Derivatives Research 10, 151–180. [CrossRef]
  15. Götz, Barbara, Marcos Escobar, and Rudi Zagst. 2014. Closed-form pricing of two-asset barrier options with stochastic covariance. Applied Mathematical Finance 21(4), 363–397. [CrossRef]
  16. Gouriéroux, Christian. 2006. Continuous time wishart process for stochastic risk. Econometric Reviews 25(2-3), 177–217. [CrossRef]
  17. He, Hua, William P Keirstead, and Joachim Rebholz. 1998. Double lookbacks. Mathematical Finance 8(3), 201–228.
  18. Heston, S.L. 1993. A Closed-form Solution for Options with Stochastic Volatility with Applications to Bond and Currency options. Rev. Financ. Stud. 6(2), 327–343. [CrossRef]
  19. Karatzas, Ioannis and Steven Shreve. 2012. Brownian motion and stochastic calculus, Volume 113. Springer Science & Business Media.
  20. Langnau, Alex. 2009. Introduction into" local correlation modelling". arXiv preprint arXiv:0909.3441. [Google Scholar]
  21. Lipton, Alexander. 2001. Mathematical methods for foreign exchange: a financial engineer’s approach. World Scientific.
  22. Rubinstein, Mark. 1991. Breaking down the barriers. Risk 4, 28–35.
1
This is not a classical Ornstein-Uhlenbeck due to r > 0
2
Other structures would be feasible for our purposes, for instance, CEV models (e.g. Cox (1975)), or stochastic volatility models like Heston (1993)
Preprints 71947 g001
Figure 1. The figure show 10 simulations of pairwise stocks prices (left side) and implied correlation paths (right side) for the spread option model.
Figure 1. The figure show 10 simulations of pairwise stocks prices (left side) and implied correlation paths (right side) for the spread option model.
Preprints 71947 g001
Preprints 71947 g002
Figure 2. The figure show 10 simulations of pairwise stocks prices (left side) and implied correlation paths (right side) for the basket option model.
Figure 2. The figure show 10 simulations of pairwise stocks prices (left side) and implied correlation paths (right side) for the basket option model.
Preprints 71947 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated