Aluminum Bronze Crystallization on Deformed Base during Electron Beam Additive Manufacturing

To obtain a given structure in 3D building-up modes, it is necessary to use optimal surfacing modes that determine the amount of heat input in local areas. For this purpose, aluminum bronze was surfacing onto a deformed base and the structure and its characteristics in the surfacing and heat-affected zones were studied by the EBSD method. The heterogeneity of the formation of the structure in each selected zone is established, which indicates the heterogeneity of heat input in local areas of the material in one mode of surfacing. For typical cases of crystallization, a molecular dynamics simulation of crystallization processes with different heat input to the base with characteristics specified based on experimental data was carried out. It has been established that the amount of heat input determines the degree of melting and the inherited defectiveness of growing crystals. The formation of misorientation boundaries and crystallization centers of new grains is determined by the conditions of joint growth of grains with given crystallographic parameters of the computational model. Numerical calculations agree with the experimentally observed results.

Keywords:

Subject: Chemistry and Materials Science - Metals, Alloys and Metallurgy

1. Introduction

Additive manufacturing (AM), including direct metal deposition (DED) and powder bed fusion, are popular alternative methods for producing parts that have gained significant popularity in various industries in recent times [1,2,3,4]. Each of these methods has its own characteristics and limitations and can be used for printing a certain range of materials [5,6].

The main sources of heat in AM are most often: laser beam, electron beam (EB), plasma and arc. The use of an electron beam as an energy source in AM has been known since the end of the 20th century and is the most attractive in terms of high performance and work in a vacuum chamber. In addition, the electron beam has a sufficiently high energy density, which significantly speeds up the printing process and eliminates unnecessary production costs [7].

In addition, recently there have been frequent cases of using methods that combine the parameters of several AM methods. The article [8] demonstrates the use of a combined additive printing method, which combines the supply of powder and wire. Using the CuAl–WC system as an example, it was studied how the concentration and particle size of the reinforcing material affect the microstructure characteristics and tribological properties of the resulting composite material.

An attractive point of additive technologies is that when they are used, it is possible to control the grain morphology and the structure of printed materials. It is possible to predict the mechanical properties of the resulting material using variations in the surfacing mode. By carrying out intermediate deformation, it becomes possible to get rid of large columnar grains formed under the influence of a temperature gradient during layer-by-layer deposition of the material [9,10,11].

Aluminum bronze, which has a number of attractive properties, is popular in a number of engineering applications, such as the oil and gas and petrochemical industries, aviation, and shipbuilding [12,13].

The generally accepted approach to improve the functional characteristics of aluminum bronzes is their heat treatment [14]. The change in the structure of aluminum bronze can be associated with phase transformations that occur in the presence of temperature effects. Thus, it was shown in [15] that during the annealing of aluminum bronze obtained by electron beam additive manufacturing (EBAM) in the temperature range of 400°C, 675°C, and 800 + 400°C, the decomposition of the β'-phase led to a decrease in the tensile strength and increasing plasticity. The article [16] describes in detail how heat input affects the formation of growth structures, and how the mechanical properties of Al bronze grown by the EBAM method depend on this parameter. In [17], it is shown how an equiaxed structure formed by static recrystallization was obtained using thermal and thermomechanical treatments for aluminum bronze samples obtained by AM. Rolling, friction stir processing, hot isostatic pressing, shot-peening are also applicable to samples obtained by wire arc additive manufacturing, selective laser melting or EBAM to influence the structure and mechanical properties [18,19,20]. The authors of the review [21] described in detail the features of DED, concluding that post-processing has a positive effect in a number of cases. The most frequent course of events under such impacts are phase transformations and recrystallizations. In [22], using a model experiment as an example, a positive effect of interlayer impact treatment on the mechanical characteristics of CuAl7 bronze obtained by EBAM was shown. In particular, the use of interlayer impact treatment promotes the formation of equiaxed recrystallized grains with annealing twin boundaries.

The molecular dynamics (MD) method is often used as a tool for studying the mechanisms of materials crystallization [23,24,25,26,27]. A detailed review of methods for modeling the characteristics of microstructures in the additive production of metals is given in [28]. Interesting results presented by Vo, Truong Quoc and Kim, Bo Hung in [29] on thermal and energy management for additive manufacturing. Li-li Zhou et al. [30] present the results of MD simulations, which make it possible to improve understanding of the crystallization process of FCC alloys during rapid cooling. Gurmeet Singh et al. in [31] on the relationship between the parameters of the additive process and the crystal structure on the example of copper, they state that it is possible to avoid defects with slow cooling. The molecular dynamics method is one of the applicable methods for predicting detailed grain morphology [32]. Although MD simulation is associated with the use of large computational resources, it provides information on the structural features of the material, including helping to trace the crystallographic dependences of growth [33]. It becomes possible to trace the interaction of a melt drop with the crystallographic orientation of the substrate grains and the regularities in the formation of stacking faults and twins [34].

During surfacing, the process of grain growth depends on technological parameters, the main role of which is to control the conditions of crystallization. By changing technological parameters, it is possible to regulate the temperature, change the rate of heating, cooling and temperature gradient. Regular heating during the application of each subsequent layer creates conditions for the redistribution of defects and recrystallization in the underlying layers. Accounting for structural changes in these layers is important in order to evaluate the mechanical properties of the product as a whole. Therefore, researchers [22] turn to the variant of grain refinement by intermediate deformation during surfacing. In this regard, it seems appropriate to experimentally study the process of surfacing on a preliminarily deformed base and evaluate the possibilities of modeling the processes occurring in the heat-affected zone of the deformed base and the surfaced part by the molecular dynamics method.

2. Materials and Methods

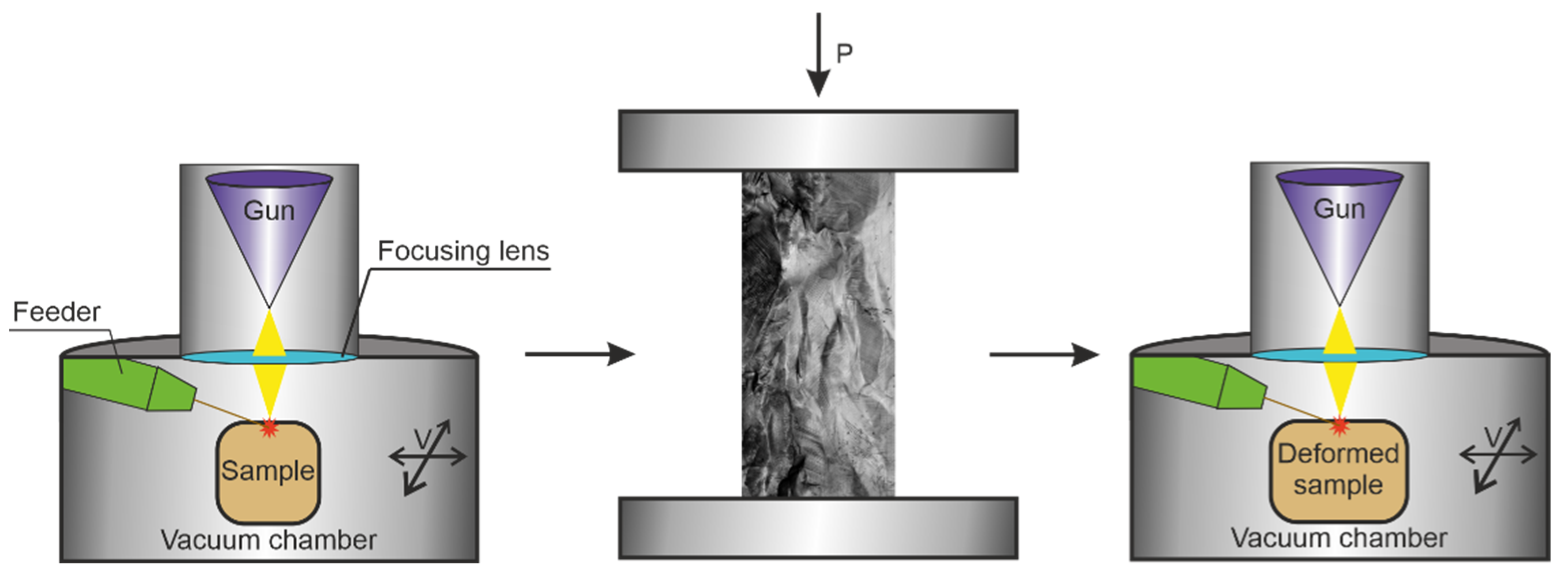
The object of research is samples of aluminum bronze containing 7.5 wt.% aluminum (Cu-13 at.% Al). A work piece obtained by 3D electron-beam building-up in a vacuum. Building-up was carried out on a laboratory installation of ISPMS SB RAS. Additive production modes: the electron beam accelerating potential—30 kV; the beam current—30 mA; the spot size—4.5 mm; the beam sweep frequency—1000 Hz; the heat input—0.22 kJ/mm. Surfacing was carried out by a zigzag motion of the table relative to the gun in layers along programmed transitions to a new layer in a time of 30 s. The product obtained by 3D surfacing was deformed by compression by 0.75 nominal strain. Then, the layers were deposited on the prepared surface according to similar modes. The sequence of operations is shown in Figure 1.

The resulting workpiece had the following dimensions: length ~30 mm, width ~25 mm, height ~18 mm. The sample cut from the workpiece the following dimensions: length ~16 mm, width ~7 mm, height ~6 mm. The size of the surface for investigation is 7×16 mm². The orientation of the surface is parallel to the direction of movement of the melt spot. The long side of the sample was oriented perpendicular to the building-up layers. The sample cut out by electrical discharge machining. The surface of the samples for the study was prepared according to a standard technique, including polishing on abrasive paper and polishing suspensions. The final stage of preparation was the surface ion milling with a low-energy ion beam on a SEMPrep2 device (Technoorg Linda Co. Ltd., Budapest, Hungary). The grain orientations and grain boundary misorientations have been studied by electron backscatter diffraction (EBSD) method (Instrument Nordlys, Oxford Instruments, High Wycombe, UK) mounted on a Tescan Mira 3 LMU scanning electron microscope (TESCAN ORSAY HOLDING, Brno, Czech Republic). HKL Channel 5 software (Oxford Instruments, High Wycombe, UK) is used for an analysis of the EBSD data [35]. EBSD investigation was carried out with the equipment of Tomsk Regional Core Shared Research Facilities Center of NR TSU. Center was supported by the Ministry of Science and Higher Education of the Russian Federation Grant no. 075-15-2021-693 (no. 13.RFC.21.0012).

3. EBSD Crystallographic Analysis of Grains Obtained by Electron Beam Surfacing

In this section, the results of morphological and crystallographic analyzes of the aluminum bronze grain structure after surfacing on a deformed base are considered. Surfacing was carried out by the electron-beam method using aluminum bronze wire in the same modes before and after deformation.

An overview image of the transition area from the deformed part of the sample to the deposited layers is shown in Figure 2 (X is the direction perpendicular to the deposited layers from the base, located on the left). According to the structure relative to the boundary between the deformed and deposited material, we distinguish three zones: the heat affected zone, the remelting zone and the deposited alloy zone. The heat affected zone highlighted in the figure extends to 7…8 mm and is characterized by areas of return, partial and complete primary recrystallization, as well as an area of secondary recrystallization. Deformed grains are observed outside the heat affected zone.

An overview image (size 4x4 mm²) gives us an idea of the heterogeneity of the development of the substructure in depth and in the direction of surfacing. The thickness of each deposited layer is approximately 0.5…1 mm. A remelting layer separates the surfacing layers. The thickness of the remelting layer reaches 200 μm. When a new layer is deposited, we observe crystallization processes with the formation of fine grains (R on Figure 2) or continued growth of columnar grains in the direction of a new maximum temperature gradient (D on Figure 2). Columnar grains change their slope following the thermal field during surfacing when the direction of movement of the workpiece relative to the electron gun changes during surfacing of the next layer. The marking of the grains in the colors of the inverse polar figure indicate the predominant orientation of individual grains and groups of grains in different parts of the deposited zone relative to the chosen orientation of the laboratory coordinate axis. Fine and medium-sized grains represent the structure of the remelting zone at the boundary with the deformed material. This zone is limited on one side by a layer of secondarily recrystallized isometric grains, and on the other side by deposited grains. Moreover, the first deposited layer has a finer-grained structure than the subsequent layer with more ideal columnar grains. Conventionally, they are named as unstable and stable zones.

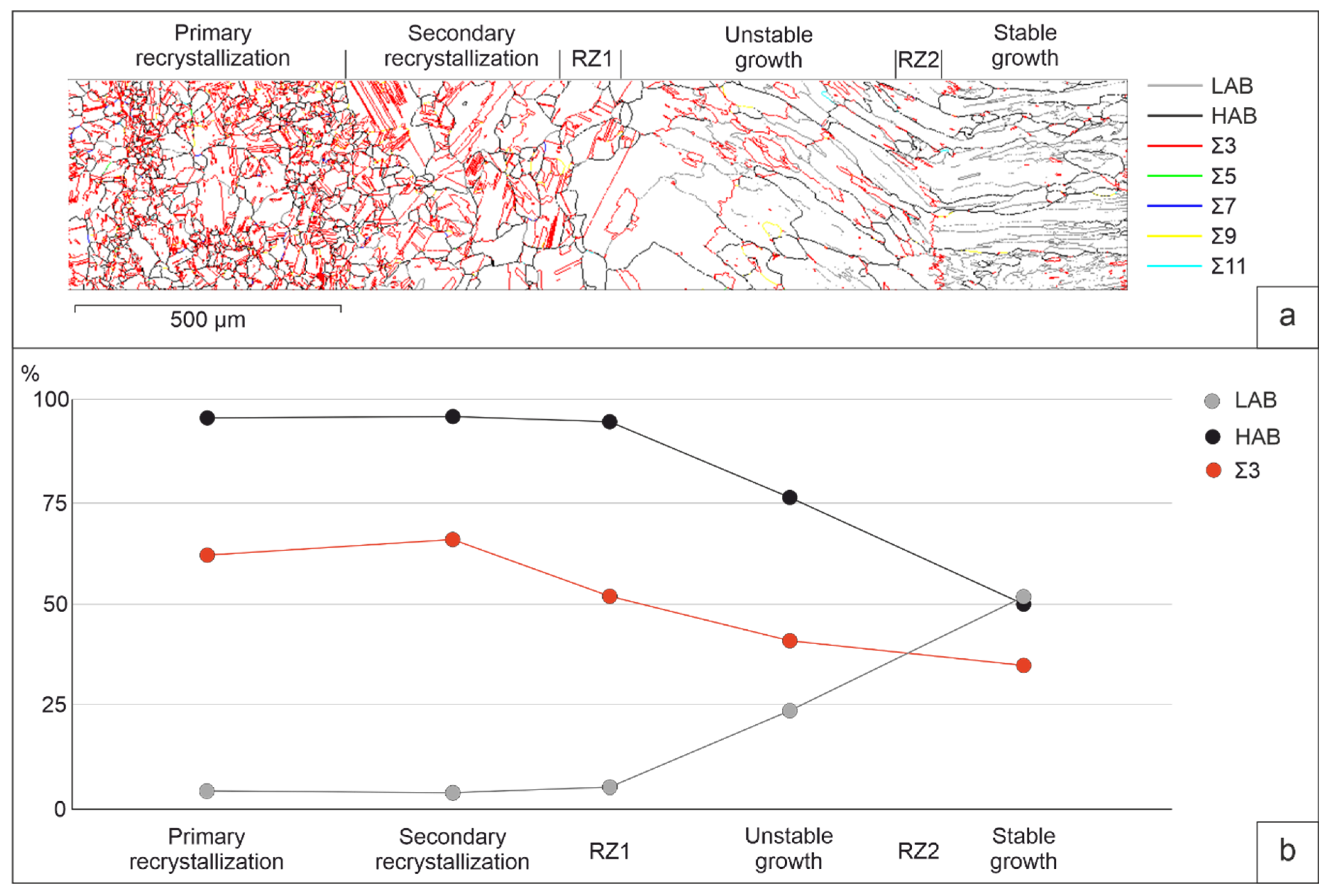
The main difference in the structure lies in the difference in the polycrystal’s grains morphology. The crystallography of grains (texture) and the characteristics of the grain-boundary ensemble associated with the misorientation angle and the crystallographic orientation of the rotation axis differ. It is possible to distinguish the proportions of low-angle (LAB) and high-angle (HAB) boundaries, special type boundaries (CSL). 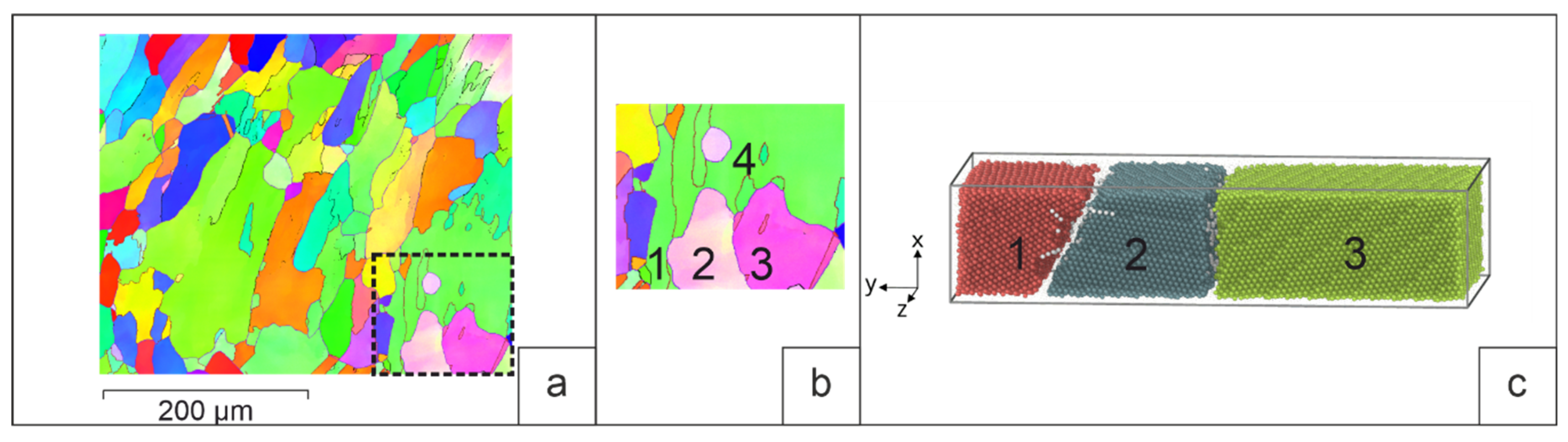Figure 3 is section A on Figure 2 for a more detailed description of the structure.

The orientation grains maps in colors IPF (Figure 3, a-c) give an idea of the grains orientation related to the deposition direction (X-axis) and to the lateral faces of the bar (Y and Z axes). Predominant crystallographic orientation of grains relative to these directions, identified based on IPF. Primary recrystallization of aluminum bronze leads to the formation of numerous fine grains. First, they are formed along the boundaries of groups of deformed grains. In the zones of primary and secondary recrystallization, as well as in the zones of remelting, the preferential grain orientation is not observed. However, in the zones of the deposited area, there is a tendency for the cubic orientation to predominate. In neighboring parallel sections, the preferred orientation and sequence of orientation changes may be different (Figure 2).

The analysis of grain boundaries is of particular interest. Figure 4 gives an idea of the grain boundaries types. The qualitative picture is illustrated by the boundary map (Figure 4, a) and the change in the proportion of boundaries in the area of heat affected zones and deposited zones (Figure 4, b). Separation of LAB and HAB was carried out according to the misorientation value of 15°. The formation of low-angle boundaries is observed in the system of columnar grains of deposited layers. Apparently, this is due either to the incompatibility of the growth of neighboring grains, or to thermal stresses arising in the deposited layers after surfacing. The share of HAB decreases in the deposited layers, while LAB increases. More than half of the HAB are of a CSL. These are the Σ3, boundaries, which are 60° misorientation boundaries around the <111> axis. Their main part is the annealing twins boundaries inside the grains. CSL Σ9, rotate 38.94° around the <110> axis. They make up a few percent of all high-angle boundaries. A large number of CSL are formed in the heat affected zone. Their share decreases by almost two times with a stable growth of columnar grains in the surfacing zone.

Thus, the experimental data provide information about the processes of thermal influence on the deformed base during surfacing and the new grains growth. Data on crystallographic orientation and types of boundaries are the initial data for the problem of molecular dynamics simulation.

4. Model Description

Simulation was performed by the molecular dynamics method using the LAMMPS software package [36]. The interatomic interaction of the selected materials was described by the interatomic potential constructed within the second nearest neighbor modified embedded-atom method (2NN-MEAM) that developed for binary aluminum (Al) alloys applicable from room temperature to the melting point [37]. The equations of atomic motion were integrated using the Verlet velocity method. The OVITO software [38] was used to visualize and analyze the faulted structure. The internal structure was studied using the polyhedral template matching (PTM) method [39]. This method allows you to determine the crystal lattice in which the atom is located, according to its nearest environment, and to calculate the orientation of the lattice relative to the laboratory coordinate system. Based on these data, various grains can be distinguished in a polycrystalline sample.

The simulation objects were groups of grains from selected areas of a Cu-13% at.% Al aluminum bronze sample obtained by 3D surfacing. The crystallographic parameters of these grains were taken from the results of the EBSD analysis. It was assumed that the grain boundaries were located perpendicular to the image plane. The simulation was carried out for two cases: a) surfacing on a base with a crystallization structure (preliminary deposited layer) and b) surfacing on a deformed base.

4.1. Surfacing on a base with a crystallization structure.

The deposition of the molten Cu-13%at.%Al alloy was carried out on a polycrystalline substrate 5×22×11 nm in size. During crystallization, two cases were considered. In the first case, a melt drop with a temperature of 1500K interacts with the base grains, which play the role of seed elements during crystallization (grains 1, 2 and 3 on Figure 5 is the selected site B on Figure 2). Heat was removed only from the side of the base. In the second case, an additional crystallization center is formed inside the melt drop. To do this, after the contact of the substrate with the drop, a part of the drop volume (4×4×5 nm) is replaced by a crystal structure with a certain orientation (grain 4 on Figure 5, b). The sample in this case is cooled from the side of the base and from the side of the new grain. The simulation of heat removal was set by setting the atoms of a 3nm thick layer near the substrate and the atoms of the crystallization center in a drop of additional viscous forces, the value of which was calculated by the formula F=-kV, here V is the atomic velocity, k is the proportionality coefficient. To prevent the drop material from getting past the sample, “virtual” walls of the simulated system were set. The walls were located at a distance of 0.5 nm from the sample surface.

4.2. Surfacing on a deformed base.

The role of heat input during surfacing was simulated by the process of interaction of a molten drop with a cold base 12×36×12 nm in size, consisting of three deformed grains. Based on the results of the crystallographic analysis of the sample, a typical group of three deformed grains was selected, which served as the basis for setting the parameters for simulation. The parameters of the initial structure of the base were set based on the analysis of the orientation map of the sample obtained by the EBSD method. The faulted structure of grains was created by plastic deformation in a model experiment [34]. Its structure after deformation is shown in Figure 6. The interaction of the base with a drop of different temperatures was simulated: near the melting temperature of aluminum bronze T=1380K (overheating by 50 degrees), as well as at temperatures of 1500K and 2000K. Heat removal was set from the side of the base.

Thus, the considered cases correspond to the processes of crystallization of the first layer on the deformed base, the second and subsequent layers deposited on the crystallized layer. The sequences of structural changes in the "drop-base" system are determined by the patterns of heating and cooling of the components in this system. The indicator of this process is the temperature-related velocity of the atoms.

5. Results of Simulation and Comparison with Experiment

5.1. Surfacing on a base with a crystallization structure.

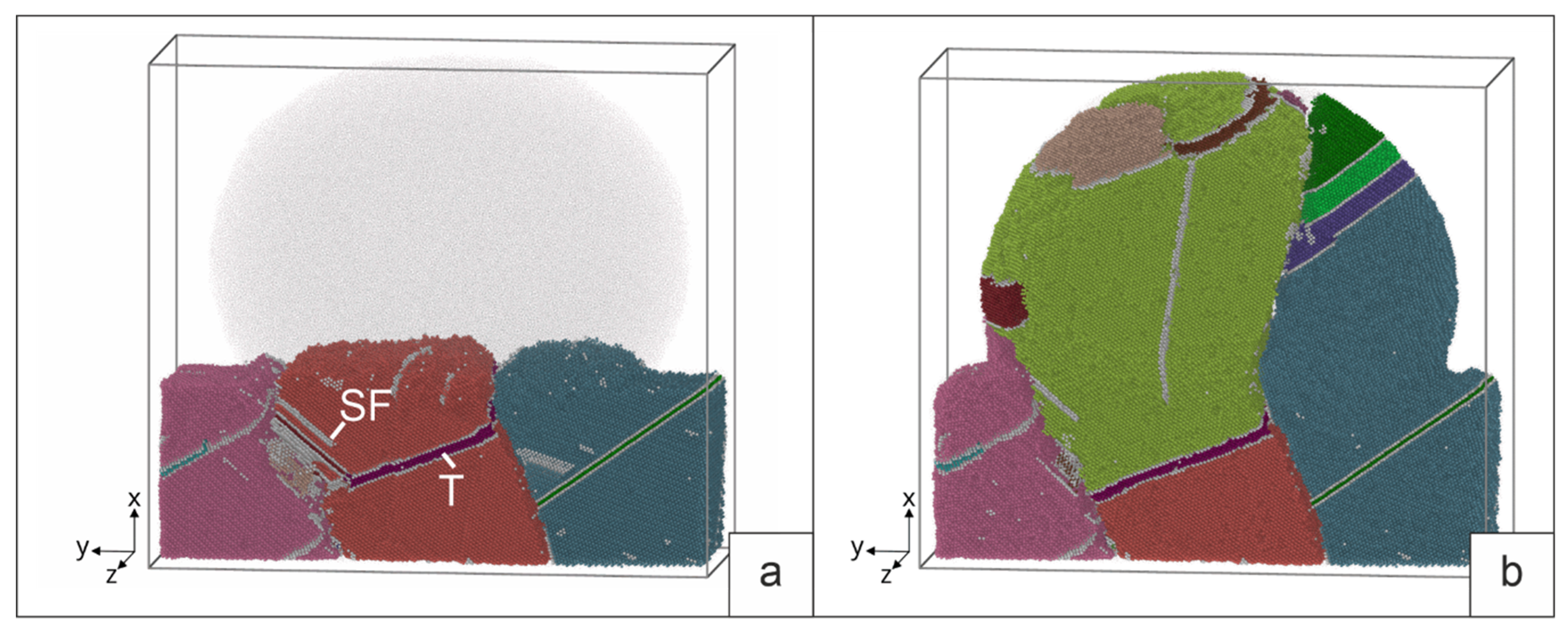
The structure of the sample obtained by deposition of a molten drop on a polycrystalline substrate with grain orientation 1-3 (Figure 5) at the moment of maximum melting is shown in Figure 7a. Figure 7b illustrates the result of a process simulation with an additional crystallization nucleus in a melt drop. During heat removal, the melt drop cools down and crystallizes (Figure 7c, d). In the first case, grain growth occurs due to the growth of grains 1, 2, and 3 of the base. In the second case, a grain in a drop crystallizes simultaneously (grain 4). Stacking faults (SF) are formed in growing grains (SF on Figure 7c, d). Along with the main grains of crystallization, the orientation of which is set at the initial moment, twins are formed (T on Figure 7c). Satisfactory agreement with the experimental patterns of grain crystallization is observed. For example, we see the growth of the twin (T1) at the grain boundary on Figure 7c and the similar formation of the twin (T1) at the grain boundary on Figure 7e. In general, if we take into account the limited volume of simulation in MD, the qualitative patterns in the modeling of crystallization and those observed in the process of surfacing are very similar.

During crystallization, the largest number of twins is observed in the central grain, the growth of which must be consistent with the growth of neighboring grains. Note that in the case of the presence of an additional center of crystallization (grain 4) in the drop, the number of SF and twins in the contact zone of four grains is also maximum. We see a similar picture in the crystallization grains of the deposited layer.

5.2. Surfacing on a deformed base.

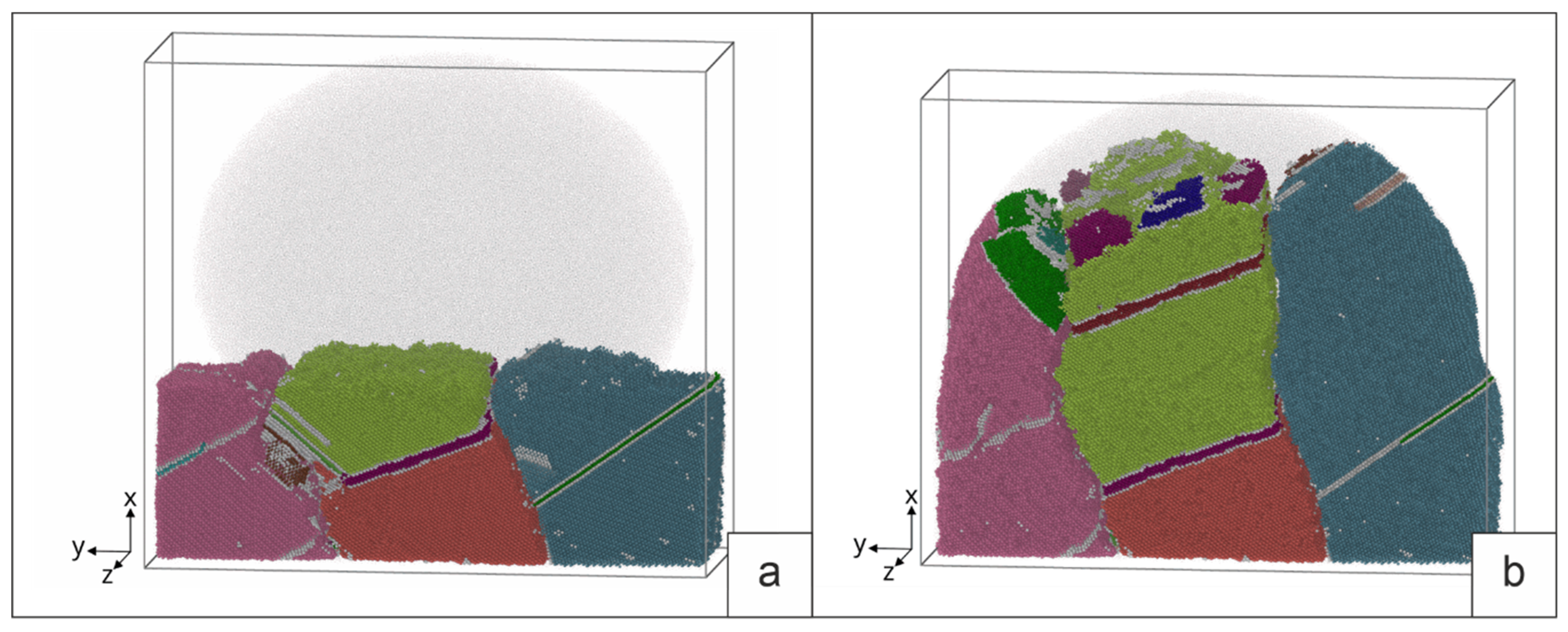
Let us consider the results of simulation of the interaction of a melt drop with a deformed base for different drop temperatures. The initial structure of the deformed three grains is shown in Figure 6. Figure 8 shows the nature of the interaction of a drop with a temperature of 1380 K with a three grains base. Disappearance of the fraction of stacking faults formed during deformation is observed. Due to the low temperature of the melt, some stacking faults remain, while the drop propagates to a limited part of the surface. This causes the grains to grow unevenly. Of the three grains, only two form elongated grains in the direction of the temperature gradient. In the process of crystallization, the formation of stacking faults and twins (SF and T on Figure 8b) is observed, the latter being predominant. During crystallization, the boundaries between grains change their orientation. The predominant growth is observed in the central grain. During crystallization, the boundaries between grains change their orientation. The predominant growth is observed in the central grain.

An increase in the heating temperature of the drop to 1500 K promotes an increase in the contact area of the drop with the surface and a deeper heating of the base. The temperature becomes sufficient for the partial melting of the surface and the disappearance of the upper SF in individual grains (Figure 9 a). The formation of SF, twins, and growth of initial grains is observed during crystallization (Figure 9 b). Twins and SF, as a rule, have orientations similar to their orientations in the original grains. When grains grow, the boundaries also deviate from the initial orientation. The growth of grains in this case is uniform, according to the grain structure of the base.

Intensive spreading of the drop over the base surface and significant melting of the base is observed during the interaction of a melt drop with a temperature of 2000 K. Single SF remain near the substrate (Figure 10, a). During cooling, twins are formed only at the end of crystallization and the amount of SF is small. Deviations of grain boundary planes from the initial orientation are observed.

Thus, the results of the numerical experiment revealed that, depending on the ratio of the heat of the melt and the volume of the base, as a heat-absorbing element, different crystallization structures could be realized. The more perfect the base material, the less SF and growth twins will be in the crystallization structure. The appearance of the observed defects at the final stage of crystallization is apparently due to the uncoordinated growth of adjacent grains. Twinning is a mechanism for changing the orientation of grains during their growth. The main direction of growth corresponds to the maximum temperature gradient. The growth rate is influenced by the amount of melt inflow and the absence of interference from neighboring grains. During crystallization, the influence of crystallization centers inside the melt cannot be ruled out, along with crystallization from the base grains, from which the most intensive heat removal is carried out. The results of crystallization simulation by the MD method are in qualitative agreement with the experimentally observed character of grain growth.

4. Discussion

One of the main factors affecting the structure of the material during crystallization in the process of surfacing metallic materials is the amount of heat input and the rate of dissipation of this heat. Important is the volume of the crystallizing melt and structural factors that determine the number and role of crystallization centers. Let us note some works being carried out in this direction. Liu Y et al. [40] on the Ti-22Al-25Nb alloy showed that a change in the deposition rate noticeably affects the characteristics of the microstructure (grain size, texture, and other parameters). By controlling the surfacing rate, it is possible to obtain the necessary structural parameters that determine the optimal mechanical properties.

Filippov et al. [16] studies have been carried out on aluminum bronze surfacing using varying heat input. Technological regimes were established under which the grain size increases and the transition from equiaxed to columnar grain structure occurs. It is shown that grain growth is inhibited by fast heat removal and low heat input. The considered experiments explain the main patterns of structural changes observed by us during surfacing on a deformed base in various parts of the remelting zone.

The surfacing technology used involves filling the layer area with parallel lines in a zigzag or sequential pattern of their overlay. At the same time, adjacent sections are subjected to reheating and (or) remelting to different overheating temperatures above the melting point. This circumstance was reflected in the simulation modes by setting different temperatures of the melt drop. At a lower temperature of 1380K, in addition to a moderate degree of melting of the base, there is a limitation in the spreading of the melt over the surface of the base. This agrees with the data on the variation in heat input. Authors [16,40] note the presence of areas of poor penetration with increased porosity. Increasing the temperature avoids these undesirable effects. Using temperatures of 1500K and 2000K in modeling, good interaction between the melt and the base is achieved. An increase in temperature in this interval affects the inheritance of faults from the base through the depth of remelting. This circumstance must be taken into account when choosing the heat temperature. The design of the experiment in this work does not allow revealing these effects in pure form, since the repeated heating and cooling cycle when applying each subsequent layer makes its own impact.

Regularities of crystallographic growth during surfacing are considered. For this, the calculation model was based on the crystallographic parameters of a group of grains and the crystallization process was simulated. Grain growth was assumed in the direction of the maximum heat gradient. The upper crystallizing grains served as an indicator of the process and were compared with the structure of the upper grains on the orientation map of the selected area. The simulation shows a good agreement with the experiment regarding the sites of twin nucleation. It should be noted here that at the moment the method for determining the boundary plane requires the construction of a 3D orientation map, which was not carried out in this work. Therefore, the assignment of the boundary plane during simulation may differ from that observed experimentally in the selected area.

Summing up the discussion of the results, we note the good possibilities of MD method for modeling crystallization processes, taking into account the spatial and temporal limitations imposed by computing power.

5. Conclusions

Experimental studies of surfacing of aluminum bronze on a deformed base showed a difference in the structure in each selected layer (zone). The revealed structural difference is explained from the point of view of the local heat inputs heterogeneity, which are repeated remelting to different overheating temperatures and a thermal heating and cooling cycle with different parameters for different areas.

The revealed experimental regularities were used as the basis for the creation of simulated MD objects and modes for conducting a numerical experiment. The formation of a crystallization structure during surfacing of aluminum bronze on a deformed base was traced at temperatures of 1380, 1500, and 2000 K (different heat input with the same heat removal scheme). The deformation structure was created by compressing the workpiece by a numerical experiment using the MD method. A simulation of a melt drop on an undeformed base has been carried out. Two variants of crystallization are considered: only on a base and with a crystallization center inside a melt drop.

The numerical experiment made it possible to establish that the amount of heat input affects the degree of melting, leading to the destruction of the faulted structure of the deformed base. In this case, subsequent crystallization is accompanied by a difference in the defectiveness of growing crystals. The fewer defects there were in the base, which plays the role of a seed, the fewer defects in growing crystals. It has been established that crystal growth is accompanied by a change in the orientation of microregions. The considered case of modeling showed that in this case, boundaries of general and special types are formed. Statistical consideration of misorientation boundaries and literature data indicate a low density of special boundaries in the deposited layers. We experimentally found that low-angle boundaries with a misorientation angle of up to 15 degrees are more favorable for the consistent growth of neighboring grains. The simulation showed that during the growth of grains, a change in the direction of grain growth along the line of maximum heat removal is observed. This is manifested during surfacing. The slope of the columnar grains changes in the direction of the electron beam along the weld. The simulation qualitatively agrees with the experimental data on the localization of the sites of new grains formation during crystallization.

Thus, carrying out a natural and numerical experiment made it possible to reveal the effect of thermal input on the features of a local change in the structure during heating in the process of surfacing new layers of aluminum bronze on a deformed base. Showed the agreement between the results of MD simulation and experimental results and the prospects for a numerical experiment.

Author Contributions

Conceptualization, D.V.L. and A.Y.N.; writing — original draft preparation, D.V.L. and A.Y.N.; software, A.Y.N. and A.A.B.; writing—review and editing, A.A.B.; experiment D.V.L. and O.S.N. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation (Project 20-72-10184; link to information about the Project: https://rscf.ru/en/project/20-72-10184/).

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.

Conflicts of Interest

The authors declare no conflict of interest.

References

Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive Manufacturing of Metals. Acta Mater. 2016, 117, 371–392. [CrossRef]
Clare, A.T.; Mishra, R.S.; Merklein, M.; Tan, H.; Todd, I.; Chechik, L.; Li, J.; Bambach, M. Alloy Design and Adaptation for Additive Manufacture. J. Mater. Process. Technol. 2022, 299, 117358. [CrossRef]
DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive Manufacturing of Metallic Components – Process, Structure and Properties. Prog. Mater. Sci. 2018, 92, 112–224. [CrossRef]
Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal Additive Manufacturing in Aerospace: A Review. Mater. Des. 2021, 209, 110008. [CrossRef]
Lalegani Dezaki, M.; Serjouei, A.; Zolfagharian, A.; Fotouhi, M.; Moradi, M.; Ariffin, M.K.A.; Bodaghi, M. A Review on Additive/Subtractive Hybrid Manufacturing of Directed Energy Deposition (DED) Process. Adv. Powder Mater. 2022, 1, 100054. [CrossRef]
Wong, K. V.; Hernandez, A. A Review of Additive Manufacturing. ISRN Mech. Eng. 2012, 2012, 1–10. [CrossRef]
Heinl, P.; Rottmair, A.; Körner, C.; Singer, R.F. Cellular Titanium by Selective Electron Beam Melting. Adv. Eng. Mater. 2007, 9, 360–364. [CrossRef]
Moskvichev, E.N.; Shamarin, N.N.; Filippov, A. V. Friction and Wear Perfomance of WC Reinforced Aluminum Bronze Produced by EBAM Technique. Russ. Phys. J. 2023, 65, 1598–1604. [CrossRef]
Zhang, C.; Chen, F.; Huang, Z.; Jia, M.; Chen, G.; Ye, Y.; Lin, Y.; Liu, W.; Chen, B.; Shen, Q.; et al. Additive Manufacturing of Functionally Graded Materials: A Review. Mater. Sci. Eng. A 2019, 764, 138209. [CrossRef]
Taufik, M.; Jain, P.K. Role of Build Orientation in Layered Manufacturing: A Review. Int. J. Manuf. Technol. Manag. 2013, 27, 47. [CrossRef]
Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive Manufacturing (3D Printing): A Review of Materials, Methods, Applications and Challenges. Compos. Part B Eng. 2018, 143, 172–196. [CrossRef]
Olakanmi, E.O.; Cochrane, R.F.; Dalgarno, K.W. A Review on Selective Laser Sintering/Melting (SLS/SLM) of Aluminium Alloy Powders: Processing, Microstructure, and Properties. Prog. Mater. Sci. 2015, 74, 401–477. [CrossRef]
Wolf, T.; Fu, Z.; Körner, C. Selective Electron Beam Melting of an Aluminum Bronze: Microstructure and Mechanical Properties. Mater. Lett. 2019, 238, 241–244. [CrossRef]
Xu, X.; Zhao, H.; Hu, Y.; Zong, L.; Qin, J.; Zhang, J.; Shao, J. Effect of Hot Compression on the Microstructure Evolution of Aluminium Bronze Alloy. J. Mater. Res. Technol. 2022, 19, 3760–3776. [CrossRef]
Zykova, A.; Panfilov, A.; Chumaevskii, A.; Vorontsov, A.; Gurianov, D.; Savchenko, N.; Kolubaev, E.; Tarasov, S. Decomposition of Β′-Martensite in Annealing the Additively Manufactured Aluminum Bronze. Mater. Lett. 2023, 338, 134064. [CrossRef]
Filippov, A.; Shamarin, N.; Moskvichev, E.; Savchenko, N.; Kolubaev, E.; Khoroshko, E.; Tarasov, S. Heat Input Effect on Microstructure and Mechanical Properties of Electron Beam Additive Manufactured (EBAM) Cu-7.5wt.%Al Bronze. Materials (Basel). 2021, 14, 6948. [CrossRef]
Khoroshko, E.; Filippov, A.; Tarasov, S.; Shamarin, N.; Moskvichev, E.; Fortuna, S.; Lychagin, D. V.; Kolubaev, E. Strength and Ductility Improvement through Thermomechanical Treatment of Wire-Feed Electron Beam Additive Manufactured Low Stacking Fault Energy (SFE) Aluminum Bronze. Metals (Basel). 2020, 10, 1568. [CrossRef]
Gussev, M.N.; Sridharan, N.; Thompson, Z.; Terrani, K.A.; Babu, S.S. Influence of Hot Isostatic Pressing on the Performance of Aluminum Alloy Fabricated by Ultrasonic Additive Manufacturing. Scr. Mater. 2018, 145, 33–36. [CrossRef]
Neto, L.; Williams, S.; Ding, J.; Hönnige, J.; Martina, F. Mechanical Properties Enhancement of Additive Manufactured Ti-6Al-4V by Machine Hammer Peening. In Advanced Surface Enhancement. INCASE 2019. Lecture Notes in Mechanical Engineering; Itoh, S., Shukla, S., Eds. Springer: Singapore, 2020; pp. 121–132. [CrossRef]
Kalashnikova, T.; Chumaevskii, A.; Kalashnikov, K.; Knyazhev, E.; Gurianov, D.; Panfilov, A.; Nikonov, S.; Rubtsov, V.; Kolubaev, E. Regularities of Friction Stir Processing Hardening of Aluminum Alloy Products Made by Wire-Feed Electron Beam Additive Manufacturing. Metals (Basel). 2022, 12, 183. [CrossRef]
Liu, M.; Kumar, A.; Bukkapatnam, S.; Kuttolamadom, M. A Review of the Anomalies in Directed Energy Deposition (DED) Processes & Potential Solutions - Part Quality & Defects. Procedia Manuf. 2021, 53, 507–518. [CrossRef]
Filippov, A. V.; Khoroshko, E.S.; Shamarin, N.N.; Kolubaev, E.A.; Tarasov, S.Y. Use of Impact Treatment for Structural Modification and Improvement of Mechanical Properties of CuAl7 Bronze Obtained by Electron Beam Additive Manufacturing (EBAM). Russ. Phys. J. 2023. [CrossRef]
Zhang, Y.; Jiang, S. Atomistic Mechanisms for Temperature-Induced Crystallization of Amorphous Copper Based on Molecular Dynamics Simulation. Comput. Mater. Sci. 2018, 151, 25–33. [CrossRef]
Shabib, I.; Miller, R.E. Deformation Characteristics and Stress–Strain Response of Nanotwinned Copper via Molecular Dynamics Simulation. Acta Mater. 2009, 57, 4364–4373. [CrossRef]
Dmitriev, A.I.; Nikonov, A.Y.; Österle, W. Molecular Dynamics Sliding Simulations of Amorphous Ni, Ni-P and Nanocrystalline Ni Films. Comput. Mater. Sci. 2017, 129, 231–238. [CrossRef]
Mo, Y.F.; Tian, Z.A.; Liu, R.S.; Hou, Z.Y.; Wang, C.C. Structural Evolution during Crystallization of Rapidly Super-Cooled Copper Melt. J. Non. Cryst. Solids 2015, 421, 14–19. [CrossRef]
Choudhuri, D.; Majumdar, B.S. Structural Changes during Crystallization and Vitrification of Dilute FCC-Based Binary Alloys. Materialia 2020, 12, 100816. [CrossRef]
Li, J.; Zhou, X.; Brochu, M.; Provatas, N.; Zhao, Y.F. Solidification Microstructure Simulation of Ti-6Al-4V in Metal Additive Manufacturing: A Review. Addit. Manuf. 2020, 31, 100989. [CrossRef]
Vo, T.Q.; Kim, B.H. Molecular Dynamics Study of Thermodynamic Properties of Nanoclusters for Additive Manufacturing. Int. J. Precis. Eng. Manuf. Technol. 2017, 4, 301–306. [CrossRef]
Zhou, L.; Yang, R.; Tian, Z.; Mo, Y.; Liu, R. Molecular Dynamics Simulation on Structural Evolution during Crystallization of Rapidly Super-Cooled Cu50Ni50 Alloy. J. Alloys Compd. 2017, 690, 633–639. [CrossRef]
Singh, G.; Waas, A.M.; Sundararaghavan, V. Understanding Defect Structures in Nanoscale Metal Additive Manufacturing via Molecular Dynamics. Comput. Mater. Sci. 2021, 200, 110807. [CrossRef]
Francois, M.M.; Sun, A.; King, W.E.; Henson, N.J.; Tourret, D.; Bronkhorst, C.A.; Carlson, N.N.; Newman, C.K.; Haut, T.; Bakosi, J.; et al. Modeling of Additive Manufacturing Processes for Metals: Challenges and Opportunities. Curr. Opin. Solid State Mater. Sci. 2017, 21, 198–206. [CrossRef]
Cooke, S.; Ahmadi, K.; Willerth, S.; Herring, R. Metal Additive Manufacturing: Technology, Metallurgy and Modelling. J. Manuf. Process. 2020, 57, 978–1003. [CrossRef]
Nikonov, A.; Lychagin, D.; Bibko, A.; Novitskaya, O. Simulation of Deformation and Growth during Surfacing of Aluminum Bronze Nanograins. Lett. Mater. 2022, 12, 354–359. [CrossRef]
CHANNEL 5, General Introduction, Oxford Instruments HKL. p. 475. 2007. Available online: www.oxinst.com.
Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [CrossRef]
Mahata, A.; Mukhopadhyay, T.; Asle Zaeem, M. Modified Embedded-Atom Method Interatomic Potentials for Al-Cu, Al-Fe and Al-Ni Binary Alloys: From Room Temperature to Melting Point. Comput. Mater. Sci. 2022, 201, 110902. [CrossRef]
Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [CrossRef]
Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust Structural Identification via Polyhedral Template Matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [CrossRef]
Liu, Y.; Shan, Z.; Yang, X.; Jiao, H.; Huang, W. Effect of Scanning Strategies on the Microstructure and Mechanical Properties of Ti-22Al-25Nb Alloy Fabricated through Selective Laser Melting. Metals (Basel). 2023, 13, 634. [CrossRef]

Figure 1. Stages of sample preparation.

Figure 2. The orientation grains map relative to the X axis in colors IPF and the main types of boundaries.

Figure 3. The orientation grains maps in colors IPF (a-c) and preferred crystallographic orientations of the zones relative to the X, Y and Z axes.

Figure 4. The maps of LAB, HAB and CSL-Σ3 boundaries (a) and their share in the identified zones (b).

Figure 5. Area selected for simulation (b) on the orientation map (a) (section B in Figure 2) and the structure of the model before interaction (c) (1-4 are grains whose parameters were put into the model). Here and below the colors show the atoms belonging, according to PTM, to different grains. Small dots show atoms that do not have a definite crystal structure (melt, interfaces, structural faults, etc.). Atoms located at the sites of the HCP lattice are marked in white.

Figure 6. Three-grain model structure after deformation before interaction with a melt drop.

Figure 7. The structural changes during the interaction of a drop of melted aluminum bronze with the crystallized base (a, b) and subsequent crystallization (c, d) compared to orientation maps relative to the X (e) and Y (f) axes.

Figure 8. The structural changes during the interaction of a drop of melted aluminum bronze with the deformed base (a) and subsequent crystallization (b) (the drop temperature 1380K).

Figure 9. The penetration by a drop of melted aluminum bronze of the deformed base (a) and its subsequent crystallization (b) (the drop temperature 1500K).

Figure 10. The melting of the deformed base (a) with the melting drop having a temperature of 2000 and subsequent crystallization of the drop (b).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer