A Review: On the Density of Quantum States for a Three-Dimensional System

Preprint

Review

A Review: On the Density of Quantum States for a Three-Dimensional System

Altmetrics

Downloads

171

Views

240

Comments

Muhammad Feroz Khan^*

S. S. Islam^*

Muhammad Feroz Khan^*

S. S. Islam^*

This version is not peer-reviewed

Submitted:

26 April 2023

Posted:

29 April 2023

You are already at the latest version

Alerts

Abstract

The elegance of mathematical models in quantum mechanics has often been seen with awe, and especially frustration. Nonetheless, the mathematical physics of quantum mechanics is fascinating beyond measure. And fortunately, there are quite baffling things about quantum mechanics that showed us what we never thought could be seen, making it simpler to figure out the behavior of physical systems without having to delve into the subtleties of the subject. In this paper, we present a review on the density of quantum states in an intuitive fashion that is easily comprehensible to undergraduate students with an elementary background in physics.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

Numerous applications in quantum mechanics require the conceptual yet mathematical notion of density of states, as found in various places in physics. Moreover, the notion is somewhat unique and technically the work has been done before. Therefore our purpose is not to enumerate all different connotations of density of states used in physics but to interpret the concept in context to old formulations in quantum and condensed matter physics. The concept of density of states in “solid-state physics", which is based on the foundations of “quantum mechanics" and by far is the biggest single sub-field of “condensed matter physics", has revolutionized the way we understand the electronic and optical properties of materials. It’s a way to access the infinitesimal world of solids, allowing us to explore their vast yet hidden properties and unveil their remarkable behavior. Physicists have gained deeper insights into the fundamental nature of solids and their role in shaping our technological world, as it has paved the way for countless innovations, from faster and more efficient computers to lighter and more robust materials to state-of-the-art and more effective medical treatments. The concept is really awe-inspiring as it opened up new frontiers in our understanding which led to countless advances in science and tech [1,2].

The density of states (DOS) is a measure of the number of available quantum states for a given energy in a multi-dimensional system. It is a fundamental concept in the study of quantum and condensed matter physics, which provides absolutely necessary information about the behavior of a material at the microscopic level. The density of states (DOS) is not just a simple mathematical function, but it’s significance lies in unraveling the mysteries of quantum science. Now for instance, imagine you have a container filled with particles, each with a discrete energy level. The DOS is like a map of all the existing energy levels in the container, showing you how many particles can occupy each level. Just like a map of a city can give you an idea of how densely populated each neighborhood is, the DOS gives you an idea of how densely populated each energy level is. In simple terms, the DOS is akin to a map that leads physicists and engineers to an intelligible design, devising a realizable framework of the future [3,4].

In the next section, we will derive the mathematical expression for the density of states using the concept of reciprocal and real spaces. It becomes imperative to briefly explain these two terms before proceeding further. Here is a simple explanation: In real-space, the position and behavior of particles are represented by their coordinates in the three-dimensional space. Whereas, in reciprocal space, the behavior of the particles is represented by wave vectors, which are linked to the spatial wave patterns of the particles. Reciprocal-space is usually represented in terms of a wave vector k, which is a vector in the three-dimensional space that describes the wave nature of a particle. In “reciprocal-space", the properties of the particles in “real-space" can be studied more easily since the behavior of the particles is characterized by the wave vectors rather than their coordinates. This information in reciprocal-space is used to produce a visual description that provides insights into the nature and internal structure of the particles in real-space [5].

2. Mathematical Derivation

Consider an electron in a three-dimensional bounded region of space. Assume that the finite region of space has dimensions,

L_{x} \times L_{y} \times L_{z}

and within the space

V (r) = 0

.1 The three-dimensional time-independent Schrödinger’s equation is (e.g., [3,6,7,8])

(- \frac{ℏ^{2}}{2 m} \nabla^{2} + V (r)) ψ (r) = E ψ (r)

(1)

and can be rewritten as

(- \frac{ℏ^{2}}{2 m} \nabla^{2}) ψ (r) = E ψ (r)

(2)

- \frac{ℏ^{2}}{2 m} (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}) ψ (x, y, z) = E ψ (x, y, z)

(3)

The above equation (3) can be solved using the method of separation of variables, by simply assuming that the wave function can be written in product form, [6,7]

ψ (x, y, z) = ψ_{x} (x) ψ_{y} (y) ψ_{z} (z)

(4)

Substituting (4) into (3), and dividing through by

ψ_{x} (x) ψ_{y} (y) ψ_{z} (z)

, we have

(\frac{1}{ψ_{x} (x)} \frac{\partial^{2} ψ_{x} (x)}{\partial x^{2}} + \frac{1}{ψ_{y} (y)} \frac{\partial^{2} ψ_{y} (y)}{\partial y^{2}} + \frac{1}{ψ_{z} (z)} \frac{\partial^{2} ψ_{z} (z)}{\partial z^{2}} + \frac{2 m E}{ℏ^{2}}) = 0

(5)

(\frac{1}{ψ_{x} (x)} \frac{\partial^{2} ψ_{x} (x)}{\partial x^{2}} + \frac{1}{ψ_{y} (y)} \frac{\partial^{2} ψ_{y} (y)}{\partial y^{2}} + \frac{1}{ψ_{z} (z)} \frac{\partial^{2} ψ_{z} (z)}{\partial z^{2}} + k^{2}) = 0

(6)

where k^{2} is a constant

The equation (6) is valid, if for all possible values of

x, y, and z

, each of the three terms involving

ψ_{x} (x), ψ_{y} (y) and ψ_{z} (z)

is equal to a constant. Let the constant related with first term, second term and third term be

- k_{x}^{2}, - k_{y}^{2} and - k_{z}^{2}

, respectively [6,7]. Then,

\begin{matrix} \frac{1}{ψ_{x} (x)} \frac{\partial^{2} ψ_{x} (x)}{\partial x^{2}} = - k_{x}^{2} \\ \frac{1}{ψ_{x} (x)} \frac{\partial^{2} ψ_{x} (x)}{\partial x^{2}} + k_{x}^{2} = 0 \\ ψ_{x} (x) & = C_{1} s i n (k_{x} x) + C_{2} c o s (k_{x} x) \end{matrix}

(7)

\begin{matrix} \frac{1}{ψ_{y} (y)} \frac{\partial^{2} ψ_{y} (y)}{\partial y^{2}} = - k_{y}^{2} \\ \frac{1}{ψ_{y} (y)} \frac{\partial^{2} ψ_{y} (y)}{\partial y^{2}} + k_{y}^{2} = 0 \\ ψ_{y} (y) & = C_{3} s i n (k_{y} y) + C_{4} c o s (k_{y} y) \end{matrix}

(8)

\begin{matrix} \frac{1}{ψ_{z} (z)} \frac{\partial^{2} ψ_{z} (z)}{\partial z^{2}} = - k_{z}^{2} \\ \frac{1}{ψ_{z} (z)} \frac{\partial^{2} ψ_{z} (z)}{\partial z^{2}} + k_{z}^{2} = 0 \\ ψ_{z} (z) & = C_{5} s i n (k_{z} z) + C_{6} c o s (k_{z} z) \end{matrix}

(9)

where we must have2 [6,7,9]

\begin{matrix} k = k_{x} \hat{i} + k_{y} \hat{j} + k_{z} \hat{k} \\ k^{2} & = k_{x}^{2} + k_{y}^{2} + k_{z}^{2} = \frac{2 m E}{ℏ^{2}} \end{matrix}

(10)

Simply put, the three-dimensional problem is now reduced to three one-dimensional particle-in-a-box model problems [7]. For an electron confined to a finite region of space,

L_{x y z}

with an infinite confining potential such that,

V (r) = 0 (inside) and V (r) = \infty (outside)

, the wave function must vanish on the boundaries of the bounded region3 [9].

Continuity of wave function,

ψ (r)

x = 0, y = 0, and z = 0

requires that (e.g., [6,10,11])

\begin{matrix} ψ_{x} (x = 0) = 0 \\ ψ_{y} (y = 0) = 0 \\ ψ_{z} (z = 0) = 0 \end{matrix}

(11)

The wave function solution, then becomes

ψ (r) = ψ (x, y, z) = C_{0} s i n (k_{x} x) s i n (k_{y} y) s i n (k_{z} z)

(12)

where

k_{x}, k_{y}, and k_{z}

are the wave numbers in the

x, y, and z

directions, and

C_{0}

is the product of the remaining three constants.

Again, continuity of wave function,

ψ (r)

at the boundaries of the bounded region

i . e ., at x = L_{x}, y = L_{y}, and z = L_{z}

requires that (e.g., [6,10,11])

\begin{matrix} ψ_{x} (x = L_{x}) = 0 \\ ψ_{y} (y = L_{y}) = 0 \\ ψ_{z} (z = L_{z}) = 0 \end{matrix}

(13)

The overall wave function solution, then gives us certain allowed values of

k_{x, y, z}

such that, (e.g., [7,9,11,12,13])

\begin{matrix} k_{n_{x}} = \frac{n_{x} π}{L_{x}}, k_{n_{y}} = \frac{n_{y} π}{L_{y}}, k_{n_{z}} = \frac{n_{z} π}{L_{z}} \\ where n_{x, y, z} = 1, 2, 3, \dots \end{matrix}

(14)

We now have three wave numbers,

k_{n_{x}}, k_{n_{y}}, and k_{n_{z}}

with each one corresponding to a distinct integer quantum number.4 The wave vector

k

can be rewritten as

\begin{matrix} k & = k_{n_{x}} \hat{i} + k_{n_{y}} \hat{j} + k_{n_{z}} \hat{k} \end{matrix}

(15)

Allowed energy levels can be yielded from (10) and (15) as, [6,9,14]

\begin{matrix} E_{k_{n_{x, y, z}}} & = \frac{ℏ^{2}}{2 m} ({k_{n_{x}}}^{2} + {k_{n_{y}}}^{2} + k_{n_{z}}^{2}) \\ E_{k_{n_{x, y, z}}} & = \frac{ℏ^{2}}{2 m} ({(\frac{n_{x} π}{L_{x}})}^{2} + {(\frac{n_{y} π}{L_{y}})}^{2} + {(\frac{n_{z} π}{L_{z}})}^{2}) \end{matrix}

(16)

\begin{matrix} E_{k_{n_{x, y, z}}} & = \frac{ℏ^{2} π^{2}}{2 m} ({(\frac{n_{x}}{L_{x}})}^{2} + {(\frac{n_{y}}{L_{y}})}^{2} + {(\frac{n_{z}}{L_{z}})}^{2}) \end{matrix}

(17)

The density of states or DOS, is defined as the total number of allowed quantum states per unit volume per unit energy over an energy interval

d E

(e.g., [3,6,7,8,9,15]). Quantum states refer to the different possible configurations of a quantum system. These configurations are described by a set of quantum numbers that represent the properties of the system [6,13,16]. Energy states, on the other hand, refer to the specific energy levels that a quantum system can occupy. The DOS is typically expressed in terms of energy states, but can also be expressed in terms of quantum states.

However, the DOS is based on the fact that each energy state corresponds to a certain number of quantum states [17,18,19,20]. This relationship between quantum states and energy states is crucial in understanding the electronic and optical properties of the materials, which the DOS often ascertains [2,21,22,23].

Now, in order to derive an expression for the density of states, we will first determine the number of quantum states per unit volume of the three-dimensional reciprocal-space. The wave function solutions obtained from the above assumed mathematical model can now be mapped onto a three-dimensional reciprocal-space as distinct points, where each point represents an allowed quantum state, as shown in Figure 1. For more details, we refer reader to Refs. [3,7,9,12,24]. Here, it is important to note that we will be taking advantage of the large number of states involved and introduce an infinitesimal error, accounting for trivial wave function solutions when

k_{n_{x}}, k_{n_{y}}, or k_{n_{z}} = 0

5, as shown in Figure 1 [7,25].

The space between any two consecutive points can be given as6 [7,9]

\begin{matrix} k_{n_{x} + 1} - k_{n_{x}} = (n_{x} + 1) \frac{π}{L_{x}} - n_{x} \frac{π}{L_{x}} = \frac{π}{L_{x}} \\ k_{n_{y} + 1} - k_{n_{y}} = (n_{y} + 1) \frac{π}{L_{y}} - n_{y} \frac{π}{L_{y}} = \frac{π}{L_{y}} \\ k_{n_{z} + 1} - k_{n_{z}} = (n_{z} + 1) \frac{π}{L_{z}} - n_{z} \frac{π}{L_{z}} = \frac{π}{L_{z}} \end{matrix}

(18)

A smallest cube of volume, V can be formed by connecting 8 such points in the reciprocal-space, given by

V = \frac{π^{3}}{L_{x} L_{y} L_{z}}

(19)

It can be seen from Figure 2 that, one-eighth of each point is contained within the volume of the aforementioned cube. Consequently, the number of points that can be found inside this cube of volume V, is

1 / 8 \times 8 = 1

point.

Now, it is obvious that one point or one quantum state is contained within a volume, V. In other words, the volume occupied by a single quantum state is simply equal to the volume of the aforementioned cube, then the number of quantum states per unit volume in the reciprocal-space, can be easily deduced from Table 1.

Let us now consider a sphere of radius, k centered at origin in the reciprocal-space, in an attempt to visualize the allowed energies given by the

E - k

relation in (16).

Again, consider another sphere of an incremental radius,

k + d k

, denoting the energy interval

d E

, see Figure 3. The incremental volume between the two spheres can be obtained as following,

V = \frac{4}{3} \cdot π ({(k + d k)}^{3} - {(k)}^{3})

V = \frac{4}{3} \cdot π ((k^{3} + d k^{3} + 3 k^{2} d k + 3 k d k^{3}) - (k^{3}))

but d k^{2} and d k^{3} have no physical meaning, therefore

V = \frac{4}{3} \cdot π (3 k^{2} d k) = 4 π k^{2} d k .

The number of quantum states within the incremental volume of the reciprocal-space can be expressed as7

\begin{matrix} g (k) d k = \frac{1}{8} \cdot \frac{1}{π^{3} / L_{x} L_{y} L_{z}} \cdot 4 π k^{2} d k \times 2 \end{matrix}

(20)

where, a factor 2 is being multiplied as a single quantum state can be occupied by two electrons with opposite spins.8

\begin{matrix} g (k) d k = \frac{L_{x} L_{y} L_{z}}{π^{3}} \cdot π k^{2} d k \end{matrix}

(21)

where,

L_{x} L_{y} L_{z}

is the volume of the three-dimensional system in real-space.

From equation (21), our objective of determining the number of quantum states per unit volume of the reciprocal-space, is accomplished. The expression obtained is in terms of the magnitude of wave vector, k and therefore, we’ll now consider the relation between the magnitude of wave vector, k and the momentum, p to modify the expression in terms of energy, E9 (e.g., [4,26,27,28,29,30,31,32,33,34]).

\begin{matrix} k = \frac{p}{ℏ} \end{matrix}

(22)

Simply, the

E - k

relation is

E = \frac{p^{2}}{2 m} = \frac{ℏ^{2}}{2 m} \cdot k^{2}

\begin{matrix} k^{2} = \frac{2 m E}{ℏ^{2}} \end{matrix}

(23)

Taking first derivative of (23) with respect to k

2 k \cdot d k = \frac{2 m}{ℏ^{2}} \cdot d E

d k = \frac{m}{ℏ^{2}} \cdot \frac{1}{k} \cdot d E

\begin{matrix} d k & = \frac{m}{ℏ^{2}} \cdot \frac{ℏ}{{(2 m E)}^{1 / 2}} \cdot d E \end{matrix}

\begin{matrix} d k & = \frac{m}{ℏ} \cdot \frac{1}{{(2 m E)}^{1 / 2}} \cdot d E \end{matrix}

(24)

The spheres of radii k and

k + d k

simply corresponds to associated energy levels E and

E + d E

. Substituting (23) and (24) into (21), results in the total number of energy states within the incremental volume in the energy interval

d E

[3,7,12].

\begin{matrix} g (E) d E = \frac{L_{x} L_{y} L_{z}}{π^{2}} \cdot (\frac{2 m E}{ℏ^{2}}) \cdot (\frac{m}{ℏ} \cdot \frac{1}{{(2 m E)}^{1 / 2}} \cdot d E) \end{matrix}

(25)

\begin{matrix} g (E) d E = L_{x} L_{y} L_{z} \cdot \frac{{(2 m^{3})}^{1 / 2}}{π^{2} ℏ^{3}} \cdot E^{1 / 2} \cdot d E \end{matrix}

(26)

Dividing through by the volume of the three-dimensional system, we obtain the total number of states per unit volume in real-space as

\begin{matrix} g (E) d E = \frac{1}{π^{2}} \cdot \frac{{(2 m^{3})}^{1 / 2}}{ℏ^{3}} \cdot E^{1 / 2} \cdot d E \end{matrix}

(27)

The number of quantum states per unit volume per unit energy, or the density of quantum states in a three-dimensional system is

\begin{matrix} g (E) = \frac{{(2 m^{3})}^{1 / 2}}{π^{2} ℏ^{3}} \cdot E^{1 / 2} \end{matrix}

(28)

This is the expression for the density of quantum states given in most standard textbooks without complete derivation.

3. Conclusions

In conclusion, the DOS is a powerful tool for understanding the behavior of materials. By mapping the number of available quantum states for each energy level, scientists gain deep insights into a material’s distinct properties such as thermal conductivity, electrical conductivity, specific heat capacity and magnetism and can predict it’s behavior in different states and circumstances. Notably, the calculation of DOS in real materials is often more sophisticated than the free electron model as it is influenced by certain factors such as lattice vibrations, impurities, and the existence of band gaps [2,4]. Despite this complexity, the calculation of DOS remains crucial for understanding and characterizing the properties of real materials.

Acknowledgments

The first author is deeply grateful to Prof. (Dr.) S. S. Islam for arousing his interest in solid-state electronics and is thankful to Dr. Manika Khanuja for her quintessential guidance and words of encouragement.

Conflicts of Interest

The authors declare no conflict of interest.

References

Dick, R. Advanced Quantum Mechanics: Materials and Photons; Graduate Texts in Physics, Springer International Publishing, 2021.
Simon, S.H. The Oxford solid state basics; OUP Oxford, 2013.
Brennan, K. The Physics of Semiconductors: With Applications to Optoelectronic Devices; The Physics of Semiconductors: With Applications to Optoelectronic Devices, Cambridge University Press, 1999. [Google Scholar]
Street, R.A. , The electronic density of states. In Hydrogenated Amorphous Silicon; Cambridge Solid State Science Series, Cambridge University Press, 1991; p. 62–94. [CrossRef]
King, A.; Sapoval, B.; Hermann, C. Physics of Semiconductors; Springer New York, 2003.
Hanson, G. Fundamentals of Nanoelectronics; Pearson/Prentice Hall, 2008.
Pierret, R. Advanced Semiconductor Fundamentals; Modular series on solid state devices, Prentice Hall, 2003.
Streetman, B.; Banerjee, S. Solid State Electronic Devices; Always Learning, Pearson Education Limited, 2015.
Neamen, D. Semiconductor Physics And Devices; McGraw-Hill Education, 2011.
Van Zeghbroeck, J. Principles of Semiconductor Devices; Bart Van Zeghbroeck, 2011.
Ghatak, A.; Lokanathan, S. Quantum Mechanics:Theory and Applications; Macmillan Publishers India Limited, 2004.
Mishra, U.; Singh, J. Semiconductor Device Physics and Design; Springer, 2008.
Manasreh, O. Introduction to Nanomaterials and Devices; Wiley, 2011.
Schubert, E. Physical Foundations of Solid-State Devices; E. Fred Schubert, 2022.
Islam, S. Semiconductor Physics and Devices; Oxford University Press, 2005.
Eisberg, R.; Eisberg, R.; Resnick, R.; Caldwell, D.; Derringh, E.; Christman, J. Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles; Number v. 1 in Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles, Wiley, 1985.
Zawadzki, W. SEMICONDUCTOR PHYSICS | Band Structure and Optical Properties. In Encyclopedia of Modern Optics; Guenther, R.D., Ed.; Elsevier: Oxford, 2005; pp. 432–438. [Google Scholar] [CrossRef]
Marchiori, R. 8 - Mathematical Fundamentals of Nanotechnology. In Nanostructures; Da Róz, A.L.; Ferreira, M.; de Lima Leite, F.; Oliveira, O.N., Eds.; William Andrew Publishing, 2017; pp. 209–232. [CrossRef]
Lehmann, G.; Taut, M. On the numerical calculation of the density of states and related properties. physica status solidi (b) 1972, 54, 469–477. [Google Scholar] [CrossRef]
Kittel, C.; McEuen, P.; Sons, J.W. . Introduction to Solid State Physics; John Wiley & Sons, 2019.
Chelikowsky, J.R.; Wagener, T.J.; Weaver, J.H.; Jin, A. Valence- and conduction-band densities of states for tetrahedral semiconductors: Theory and experiment. Phys. Rev. B 1989, 40, 9644–9651. [Google Scholar] [CrossRef] [PubMed]
Sachs, M. Solid State Theory; Through the magic window, Dover Publications, 1974.
Sze, S.; Lee, M. Semiconductor Devices: Physics and Technology; Semiconductor Devices, Physics and Technology, Wiley, 2012.
Singh, J. Semiconductor Devices : Basic Principles; Wiley India Pvt. Limited, 2007.
Ilouno, J.; Gesa, F.N.; Okpara, N. Assessment of Energy and Density of States of Three Dimensional Quantum Structure (Bulk) 2018.
Omar, M. Elementary Solid State Physics: Principles and Applications; Addison-Wesley series in solid state sciences, Addison-Wesley Publishing Company, 1993.
Dekker, A. Solid State Physics; Textbook Publishers, 2003.
Sengupta, A.; Sarkar, C. Introduction to Nano: Basics to Nanoscience and Nanotechnology; Engineering Materials, Springer Berlin Heidelberg, 2016.
Haus, J. 11 - Nanophotonic devices. In Fundamentals and Applications of Nanophotonics; Haus, J.W., Ed.; Woodhead Publishing, 2016; pp. 341–395. [CrossRef]
Blood, P. SEMICONDUCTOR PHYSICS | Quantum Wells and GaAs-Based Structures. In Encyclopedia of Modern Optics; Guenther, R.D., Ed.; Elsevier: Oxford, 2005; pp. 9–21. [Google Scholar] [CrossRef]
Wasserman, A. Effective Mass✩. In Reference Module in Materials Science and Materials Engineering; Elsevier, 2017. [CrossRef]
Mitin, V.; Kochelap, V.; Stroscio, M. Introduction to Nanoelectronics: Science, Nanotechnology, Engineering, and Applications; Cambridge University Press, 2012.
Ward, D.W.; Volkmer, S.M. How to derive the schrodinger equation. arXiv 2006, arXiv:physics/0610121. [Google Scholar]
Huang, X. How did Schrödinger obtain the Schrödinger equation. arXiv 2012, arXiv:1206.0055. [Google Scholar]

1	In three-dimensional rectangular coordinates, vector r is a position vector, from the origin to some point in space, and is commonly expressed in the terms of standard unit vectors in the $x, y, and z$ directions, as $r = x \hat{i} + y \hat{j} + z \hat{k}$ .
2	Assuming that, $k = \| k \|$ .
3	It is important to note that, we are considering only the hard-wall case with non-periodic boundary conditions, but the results with periodic boundary conditions are quite similar.
4	Each unique set of three quantum numbers $(n_{x}, n_{y}, n_{z})$ , along with a spin quantum number, $m_{s}$ , fundamentally describes the state of a quantum particle, primarily an electron.
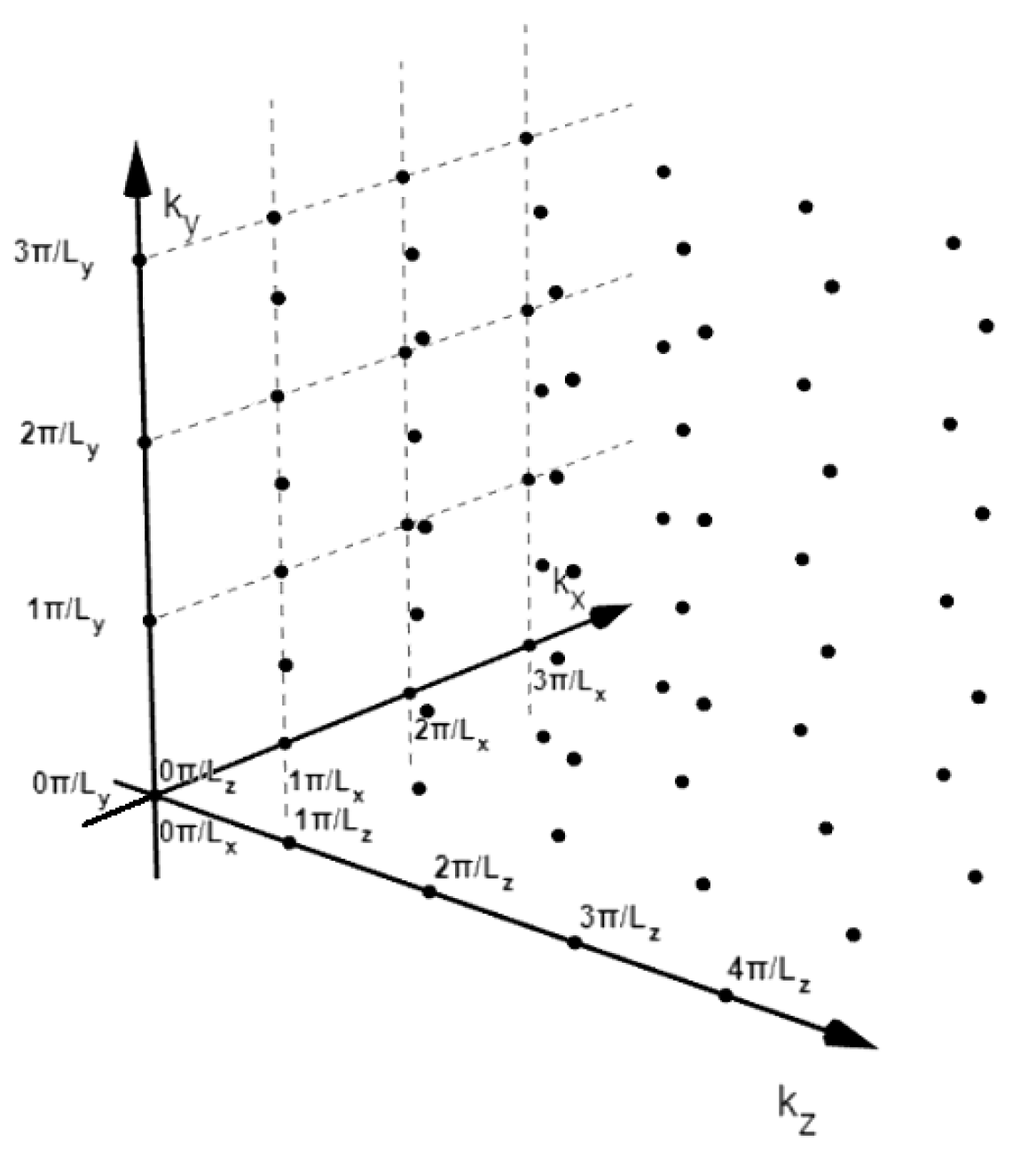
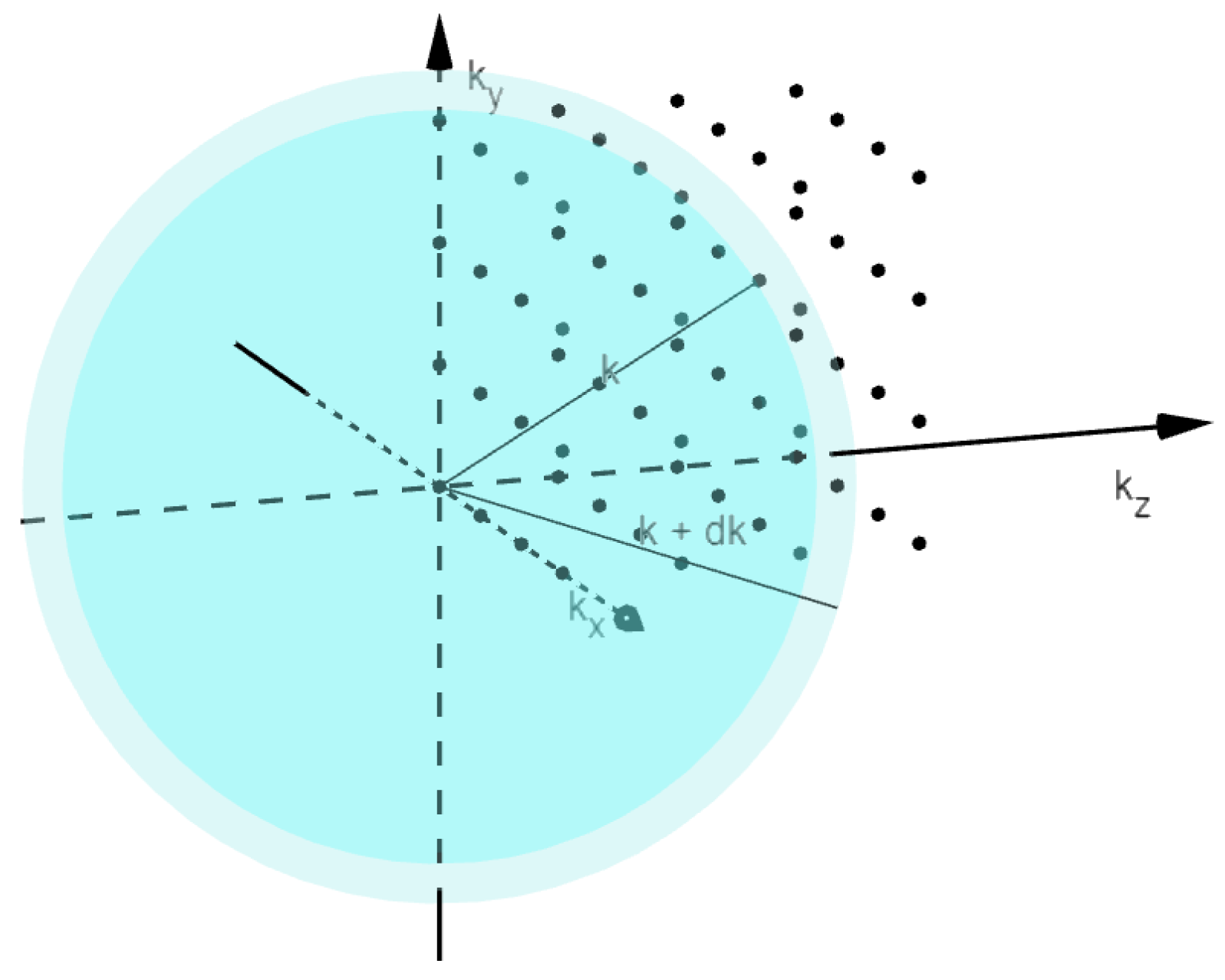
5	Notably, all of the mathematical developments have been made, keeping in mind the objective of determining the number of allowed quantum states per unit volume of the reciprocal-space.
6	The quantum states are being referred to as points in the reciprocal-space.
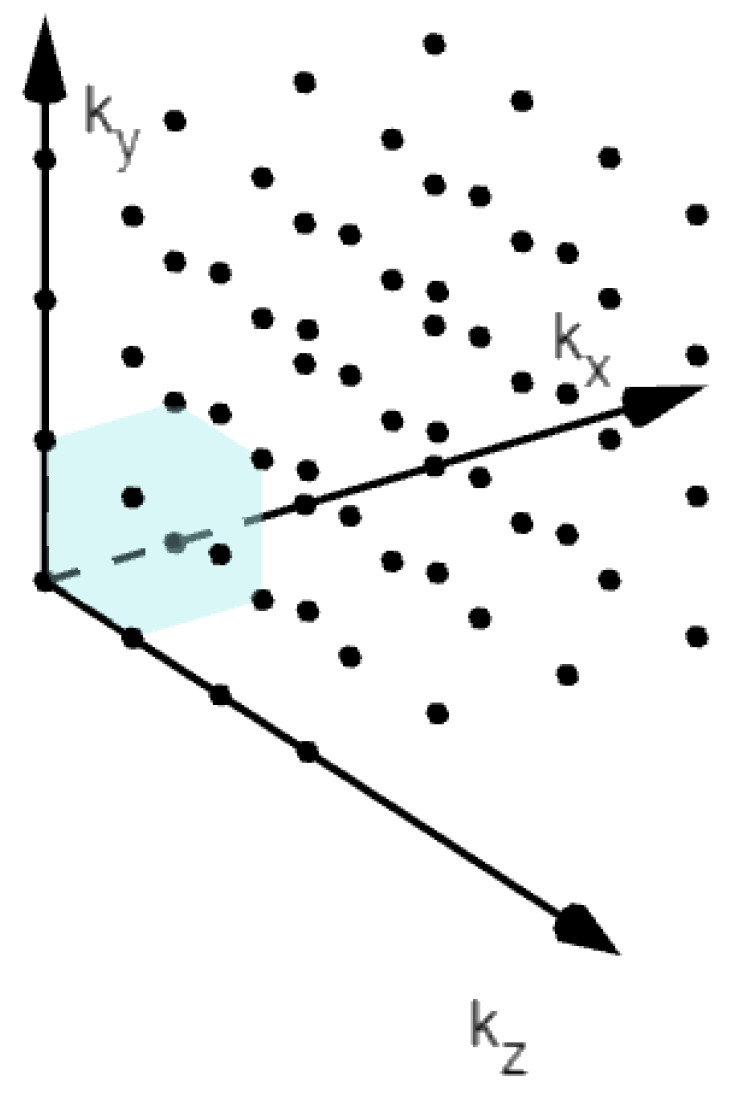
7	Here, considering only the first octant (or positive one-eighth) of the three-dimensional reciprocal-space.
8	Taking into account, an individual quantum state for an individual electron.
9	Assuming that, $k = \| k \|$ .

Figure 1. Allowed quantum states and their associated energy levels in the reciprocal-space.

Figure 2. Smallest volume in the reciprocal-space.

Figure 3. Spheres of radii k and

k + d k

corresponding to energy levels E and

E + d E

Figure 3. Spheres of radii k and

k + d k

corresponding to energy levels E and

E + d E

Table 1. Number of quantum states within a given volume of the reciprocal-space.

# Quantum States	Volume
1	$\frac{π^{3}}{L_{x} L_{y} L_{z}}$
$\frac{1}{π^{3} / L_{x} L_{y} L_{z}}$	1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Review: On the Density of Quantum States for a Three-Dimensional System

Abstract

1. Introduction

2. Mathematical Derivation

3. Conclusions

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe