1. Introduction

2. Materials and Methods

2.1. Case Study

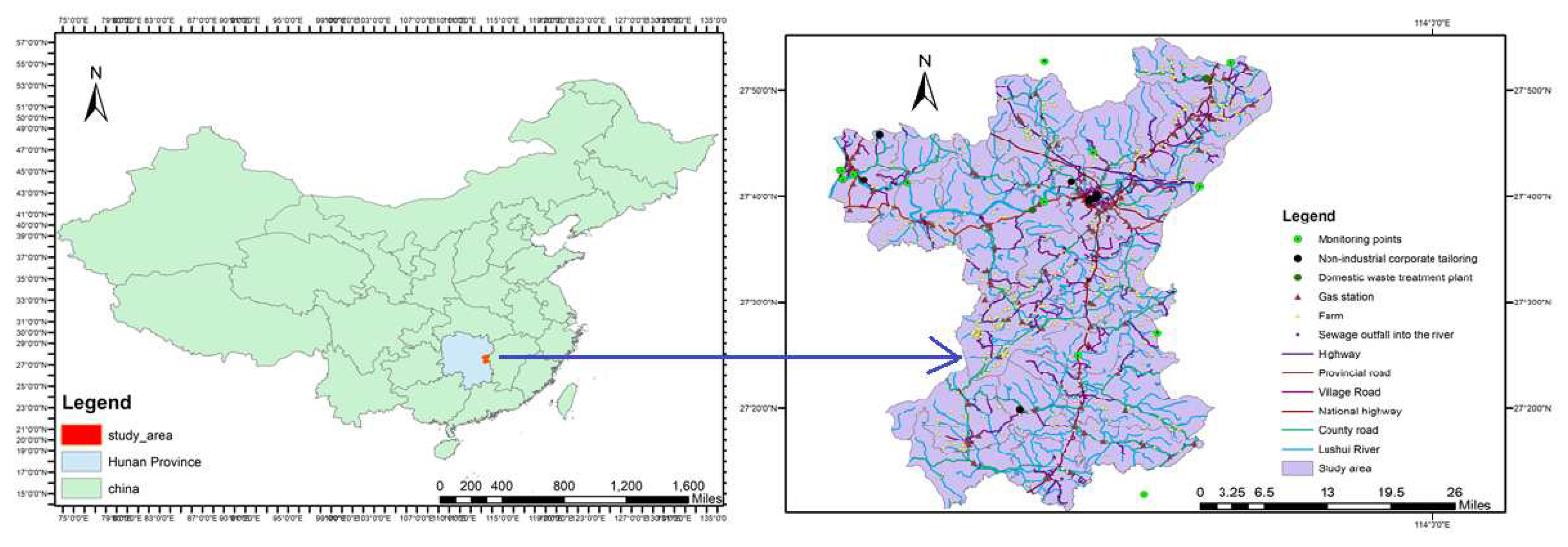
Our study area is in the Lushui River, part of a watershed in Zhuzhou, Hunan Province, China. Its area is around 5675 km2, covering 2278 km2 in Jiangxi and 3397 km2 in Hunan. Lushui is a part of the Zhuzhou City River and Liling City Mother River. It is a fertile, densely populated land rich in products and with rapid economic development. Our research area is a part of the Lushui River; it is a local mother river established in Hunan Province and is a model of integrated watershed management in the Hunan and Jiangxi border regional cooperation demonstration area. It is a relatively intact small watershed, a typical example of ensuring stable water quality and timely completion of an inter-provincial model river under increasing national emphasis on the environment.

Based on ensuring water safety, the reciprocal of population, GDP, water environmental capacity, and pollutant discharge intensity are selected to represent economic, social, and environmental factors, respectively. And we used the Gini coefficient method to calculate the allocation of COD, AN, and TP discharge permit in Lushui Basin. Then, according to the current situation of pollution load in each control unit of Lushui River, its reduction is analyzed and discussed, and corresponding pollution control measures are proposed. It is expected to put forward scientific suggestions for water quality management.

Figure 1. Overview of the study area.

Figure 1. Overview of the study area.

2.2. Description of Discharge Permit Allocation

The research on discharge permit allocation began in the United States in the 1960s with emissions trading, which is significant for management planning and reducing pollution sources. The optimal allocation scheme should be based on the current status of pollutant emissions. Social, economic, environmental, and other factors are allocated [12,13].

Total amount control is divided into three categories: target total amount control, capacity total amount control, and industry total amount control [14]. Currently, the total amount of control implemented in China is the total target amount of control. During the "12th Five Year Plan” period, China expanded the selection range of pollutants regarding pollutant emission reduction indicators and added nitrogen oxides and ammonia nitrogen based on COD and sulfur dioxide. Regarding the allocation mode of the total amount control indicators, China mainly adopts the form of level-by-level allocation from high to low. After a comprehensive national balance, China has developed a national plan to control total pollutant emissions and allocated pollutant emission control targets to provinces, autonomous regions, and municipalities directly under the central government. At this level, the environmental protection management department distributes the control objectives to each prefecture-level city, divides them into counties, districts, and key pollution sources, and conducts annual inspections and assessments. As a result of this allocation method, many problems are also hidden.

First, although the total allocation index is based on the current emissions, it does not comprehensively consider the differences in natural factors, economic development level, atmospheric environmental capacity, environmental function zoning, and other aspects in different regions. Second, setting the total amount allocation target does not consider the difference in pollution reduction potential in the different areas. Implementing the total amount target of enterprises with significant differences in industrial structure and production mode is challenging, and it isn't easy to complete the emission reduction task. At present, researchers at home and abroad have done a lot of in-depth research on the total amount distribution method of pollutants and have made significant progress in the total amount control of pollutants. However, the research on the fairness of distribution results in the actual distribution process is unsatisfactory. In combination with the development of different industries in different regions, fairness should be the first principle to be followed in the total amount distribution process. However, this principle is often evaded in the actual distribution process, or the regional fairness of target distribution is only qualitative analysis. With the development of the total amount control technology and the in-depth study of the total amount allocation method, combined with the requirements of regional development, economic transformation, national development policies, and other aspects, the application of the principle of fairness in the total amount allocation has been paid more and more attention. As mentioned above, the allocation of the total amount target is not only related to the economic development of each region but also affects the interests of different pollutant discharge units. A fair and reasonable total amount allocation scheme can meet the interests of other subjects. It has an excellent guiding role for pollutant discharge units to improve their environmental protection awareness and increase their enthusiasm for pollution control. Therefore, fair distribution is the key to implementing total amount distribution and the smooth performance of total amount control [15].

Aiming at the current situation where it is challenging to balance fairness and benefits in the current pollutant index allocation method, this paper introduces the environmental Gini coefficient into the discharge permit allocation. It selects four representative indicators according to the EGC method, such as land area, population, water environmental capacity, and gross domestic production (GDP) to represent social factors, economic factors, water environmental factors, and other factors, respectively, and to construct a wastewater discharge permit allocation model [16,17].

2.2.1. Water Environmental Capacity Connotation

• Concept and classification;

Water environmental capacity refers to the total pollution load that a water body can bear under certain hydrological conditions and water quality objectives to ensure the function and use of the water environment [17,18,19]. The research on water environmental capacity in China mainly refers to the pollution load of water bodies, that is, the diffusion and dilution of water bodies' pollutants. Therefore, water quality models are needed to simulate the changes of pollutants in water bodies and then determine the amount of pollutants received by water bodies according to water quality objectives, pollutant characteristics, pollution discharge methods, and their space-time distribution. According to different application mechanisms, water environmental capacity can be divided into different types from different perspectives and aspects [20,21]:

(1) Classification according to water environmental objectives

The capacity of environmental water management refers to the allowable pollutant holding capacity of the water quality target based on the standard value of pollutants in the water body. Its influencing factors include natural factors, social factors, economic factors, and the level of governance under certain technical conditions. The capacity of environmental water management is mainly related to water quality objectives, hydrological design conditions, and sewage discharge methods. Therefore, the function of the water environment can be utilized to change the water quality target requirements or the hydrological conditions by adjusting engineering measures to achieve the objective of changing the capacity of water environmental management. Natural water environmental capacity refers to the allowable pollutant holding capacity of the water quality target based on the background value of the water body pollutants. Unlike the environmental water management capacity, it is not affected by human and social factors but only related to natural factors, reflecting the ability of the water body to receive pollutants on the premise of ensuring human health and aquatic ecology, and has a certain objectivity.

(2) Classification according to pollutant degradation mechanism

The dilution capacity of the water environment refers to the pollution load in the water body environment when the concentration of pollutants in the effluent reaches the water function requirements through mixing and dilution. It can be divided into two categories: constant dilution capacity and random dilution capacity. Therefore, the environmental capacity of self-purification refers to the amount of pollutants the water body can self-purify. And when it meets the functional requirements of water quality through biochemical reactions such as photolysis, hydrolysis, and biodegradation, as well as physical processes such as sedimentation, adsorption, and migration, it is the essential component of water environmental capacity.

• Basic Features;

(1) Imbalance: the water's environmental capacity is generally aimed at a specific pollutant. Due to the different properties of pollutants, there are particular differences in the migration and transformation laws in the water body, which leads to the various pollutants in the water's environmental capacity under the same conditions. The capacity of the water environment is different (or unbalanced). For example, the water environmental capacity of toxic organics is relatively low, while that of aerobic organics is very high.

(2) Resource: water environmental capacity is also a natural resource with a specific value, mainly manifested in the fact that the water itself can maintain a certain amount of pollutants and play the role of storage and buffering to meet the requirements of human production and life for water environmental functions, and also It can partially replace the manual purification of sewage, thereby saving the cost of water pollution treatment.

(3) Watershed: on the whole, lakes, rivers, and other water bodies are generally located in the basin systems of different scales, with a certain degree of system or unity, mainly manifested in the relationship between water areas and land areas, the relationship between left shore and right shore, and the relationship between upstream and downstream. Therefore, each water area's water environmental capacity must be reasonably coordinated and allocated from the perspective of the basin.

(4) Regional: due to different natural conditions (such as hydrology, meteorology, etc.), the ability of water bodies to purify pollutants in other regions is also different in a specific regional water environmental capacity. At the same time, the water environmental capacity is also affected by human factors, mainly as follows: human activities have a significant impact, water pollution is severe, and water environmental capacity is small, especially for rivers near cities, their water environmental capacity may almost be lost; On the contrary, the human activities impacts are weak, the water pollution is light, and the water environmental capacity is large.

• Influencing factors ;

According to the above essential characteristics of the capacity of the water environment, the influencing factors of the capacity of the water environment [22,23] can be summarized into the following four aspects:

(1) Water characteristics

The research on water environmental capacity is based on the water characteristics of water bodies. Different types of water bodies have other hydrological and water quality features and physical, chemical, and biological purification capabilities for pollutants, which leads to specific differences in water environmental capacity.

(2) Nature of pollutants

Due to the different physical and chemical properties of various pollutants, their migration and transformation laws in water bodies are different, and their impacts on human health and aquatic ecology are also different. At the same time, pollutants can also affect and interact with each other, which is mainly reflected in the fact that the change in the water environmental capacity of a specific pollutant may cause a difference in the capacity of the water environment of another pollutant. Therefore, when determining the water environmental capacity of various pollutants, it is necessary to combine the constraints to obtain the optimal value.

(3) Environmental function requirements

The connection between water environmental function requirements and the water environmental capacity is mainly shown as follows: low water quality target requirements, large water environmental capacity; conversely, high water quality target requirements, small water environmental capacity.

(4) Sewage discharge method

The location of pollutant discharge, discharge methods, and their temporal and spatial distribution can directly impact water's environmental capacity. Under the same conditions, the capacity of the water environment of the river center discharge is more significant than the shore discharge. And the capacity of the water environment of the continuous discharge is more important than the instantaneous discharge. The water environmental capacity of the dispersed discharge is more significant than that of the centralized discharge. Therefore, the difference in the sewage discharge method will directly lead to different capacities of water environmental.

• Water environmental capacity calculation;

Based on the "Environmental Quality Standard for Surface Water Value" (GB3838-2002), the water environment functional zone division and water quality indicators of Lushui River were analyzed. As a result, three total capacity control parameters (COD, AN, and TP) were identified. There are three methods for calculating the environmental capacity of water: the analytical formula method, the system optimization analysis method, and the trial-and-error method, each of which has advantages and disadvantages [24]. Firstly, the water environmental capacity is obtained using parameters calibrated on the WASP model. And then, the trial-and-error method adjusted COD, AN, and TP pollution load values until the water quality predictions reached the target [24,25]. Previous studies describe the specific steps (Nicolas et al., 2021) [25].

Table 1. Results of water environmental capacity (tons/year).

Table 1. Results of water environmental capacity (tons/year).

Segments	AN			COD			TP
	Dry	Normal	Wet	Dry	Normal	Wet	Dry	Normal	Wet
Seg-1	367	469	571	10,998	14,073	17,148	73	94	114
Seg-2	599	709	650	17,975	21,287	19,513	120	142	130
Seg-3	398	449	481	11,944	13,482	14,428	80	90	96
Seg-4	2858	4517	6173	85,738	135,526	185,195	571	903	1234
Seg-5	343	528	414	10,289	15,847	12,417	68	106	83
Seg-6	256	432	428	7687	12,949	12,831	51	86	85
Total	367	469	571	10,998	14,073	17,148	73	94	114

Seg= Segment.

2.3. Allocation of Discharge Permit Method

2.3.1. Gini Coefficient Concept

The concept of the EGC was first proposed by the Italian economist Gini in the early 20th century based on the Lorenz curve to be used in analyzing the degree of balance and differences in income distribution among households [25,26,27]. Many approaches exist to solve the EGC, such as direct calculation, regression curves, population segmentation, etc. [28]. This paper uses the trapezoidal area method to calculate the Gini coefficient. This method is easy to understand, and the calculation process is simple and convenient. The EGC is a ratio between 0 and 1 and is a standard economic indicator of income inequality or wealth distribution [29]. The lower the Gini coefficient, the more equal the society is.

A higher EGC implies a lower degree of equality. A value of 0 indicates absolute equality, while 1 signifies unequal. EGC is obtained from the Lorenz curve, which plots the cumulative percentage of household income against the cumulative percentage of the population, ranked from lowest to highest [30]. EGC equals the ratio of area A to area A plus B on the graph, as shown in Figure 5. It can be obtained using the following equation (Brown 1994):

$$G=1-\sum _{i=1}^n(X_i-X_{i-1})(Y_i+Y_{i-1})$$

(1)

G is the EGC based on population and other indicators; Xi is the indicator cumulative percentage; Yi is the pollutants cumulative percentage; n is the number of allocated areas; when i=1, (Xi-1, Yi-1) is considered as (0, 0).

The principles of the EGC method can be extended to areas beyond economics. For example, Lu Yuantang et al. (2013) developed the connotation of the EGC, innovatively applied it to environmental resources, and calculated the resource and EGC of SO2 and COD emissions in China in 2009 [31]. Niu Zhiguang et al. (2018) established a model with the minimization of the EGC as the objective function to develop a regional equitable allocation scheme for water pollutants [32]; Wu Lijun et al. (2011) also used the EGC in the allocation of total water pollutant emissions in the Jiujiang River basin. Population, land area, and regional GDP were used as evaluation factors to calculate the respective EGC and evaluate their fairness from different perspectives [33]. It can be seen that the EGC has been involved in the study of total pollutants up to now. When studying the total water pollution discharge in China, Zhanfeng Dong pointed out that the EGC method is directly used for the whole distribution [34]. However, it is assumed that the EGC is used to evaluate the results of a given distribution scheme. In this case, it cleverly avoids the drawbacks of the EGC method in the total direct distribution. Also, it plays an advantage in the fairness of the assessment and distribution. Thus, the EGC method has a certain rationality in assessing the fairness of the existing distribution scheme.

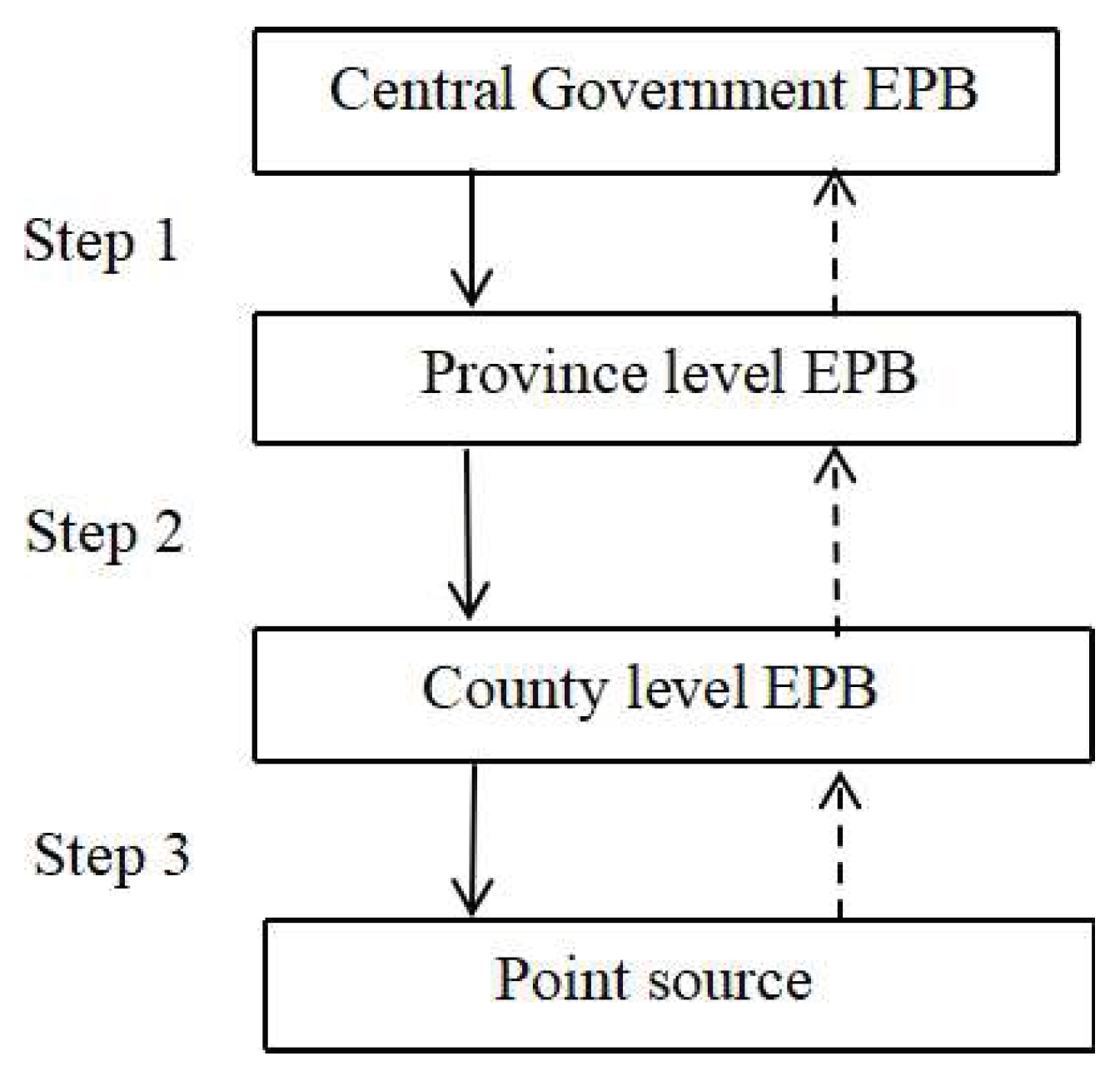
The Chinese wastewater discharge control structure can be classified into four phases, and there are stages in wastewater discharge permit allocation, as shown in Figure 3. The highest level of wastewater governance is the central government's Environmental Protection Office (EPA), which has the authority to establish the total number of wastewater discharge permits in each province. In the first stage, each provincial EPA obtains the entire wastewater discharge permit from the central EPA. In the second step, the provincial EPA will issue a wastewater discharge permit to each district EPA. The allocation in the second step is the concern of this study. In the final step, the county EPBs, which local governments directly manage, will issue discharge permits to each point source. This permit allocation is part of the “Eleventh Five-Year Plan” for Water Resources Management in China, a five-year plan. In China, provincial water resource management plans will be revised every five years.

In contrast, county EBPs can revise their water control plans annually based on local conditions. Nonetheless, non-point source control is also critical in water resource governance; policymakers have technical issues incorporating non-point sources into the wastewater discharge permit system. Each allocation process is accompanied by consultation and feedback from lower levels of management. In Figure 2, the solid line is the direction of the control, and the dashed line is the direction of the feedback.

This study uses the Lorenz curve to assign emission permits. The multiple criteria representing the land area, population, GDP, and environmental capacity are on the X-axis, while the emission permits are on the Y-axis. The Lorenz curve is shown in Figure 2.

Figure 2. EGC calculation using the Lorenz curve.

Figure 2. EGC calculation using the Lorenz curve.

Figure 3. Wastewater discharge management structure in China.

Figure 3. Wastewater discharge management structure in China.

Table 2. Standards for dividing the average degree of income allocation.

Table 2. Standards for dividing the average degree of income allocation.

Gini Coefficient Range	The Average Degree of Income Allocation
0 < G ≤ 0.2	Absolute average
0.2 < G ≤ 0.3	Comparatively average
0.3 < G ≤ 0.4	Relatively reasonable
0.4 < G ≤ 0.6	Large gap
G > 0.6	Wide gap

2.3.2. Multi-Indicators Based on the EGC

As mentioned above, wastewater discharge permits can be considered a resource, and the balance between "efficiency" and "equity" is an essential issue in their allocation. Thus, in this research, we introduce EGC to determine the inequality of this "resource." Various indicators are chosen to indicate "efficiency" and "equality." If the EGC of emission permit allocation is smaller, the distribution will be more equal and efficient.

The EGC uses grouped data from each region to calculate the Gini coefficient rather than from each point source. The EGC method is very familiar to the AR-Gini technique used by Druckman and Jackson to measure resource inequality in each district [35].

In this article, EGC explores the expansion of the original Gini coefficient from a single indicator to a multi-indicator system reflecting economic, environmental, and social factors. When using the EGC method, the following points should be considered in a comprehensive manner when selecting reasonable evaluation indicators:

(1) The feasibility of selecting indicators, which should be easily accessible and operational;

(2) The selected indicators should be scientific, should be related to the natural source environment, and can better reflect the current situation of pollutant emissions in each region;

(3) The selected indicators should have a strong representation. The environmental Gini coefficient index should be determined from environmental capacity and social and economic factors to allocate the total amount of pollution emission.

Thus, in this study, the EGC method selected four indicators, including water environmental capacity, land area, population, and gross domestic product (GDP); the specifics of these four indicators are as follows:

The population is a social indicator. As indicated earlier, wastewater discharge permits are a shared resource or asset; therefore, everyone in the basin has an equal right to them. In a Lorenz curve, the population of each district is on the X-axis, and the wastewater discharge is on the Y-axis. Minimizing the EGC will allow people in the basin to have equal access to discharge permits, and that's what "equality" is all about.

GDP is a commonly used economic indicator that can indicate local economic development. One implication of the "efficiency" concept is that allocating emission allowances will encourage more efficient consumption of "resources." The faster the economy grows, the higher the level of development. Therefore, there should be some emphasis on the total allocation of pollutants. GDP should be the primary indicator for assessing economic factors. Thus, each region is considered a "whole company" in the distribution. According to their historical data, GDP is on the X-axis of the Lorenz curve, while wastewater emissions are on the Y-axis. The minimization of the EGC means that the allocation of wastewater discharge permits will be based on the GDP contribution. At the same time, more "resource" efficient districts could receive larger discharge permits than their current wastewater discharges.

On the other hand, economic development is a significant concern of the local government. EBP can be supported by local governments for total wastewater control if wastewater control does not hinder economic growth. A GDP based on the allocation of discharge permits can also ensure that areas with higher GDP receive a more significant allocation of discharge permits than other areas. The most developed regions can support the allocation plan, significantly influencing basin water management planning and implementation.

The capacity of the water environment is an indicator of environmental tolerance and self-purification effectiveness [36]. In particular, the capacity of the water environment used in this research is the largest total mass that can be sustained by streams and rivers while maintaining good water quality. In the Lorenz curve, the X-axis is the capacity of the water environment, and the Y-axis is the wastewater discharge. As implied by the "efficiency" principle, discharge permits are assigned to reduce environmental impacts to low levels, so wastewater control must depend on natural purification capacity. Minimizing the EGC will allocate discharge permits based on the environmental capacity allocation of each area. The water capacity of streams and rivers in the basin can be effectively depleted.

Land area is the indicator incorporated in the EGC, and future factors are considered. In the Lorenz curve, the X-axis is the land area of each district, and the Y-axis is the wastewater discharge. Minimizing the EGC will lead to an equal distribution of discharge permits based on land area. Land area was chosen as an indicator for three reasons. First, land area in permit allocation is a precursor to non-point source wastewater treatment because land area is directly related to non-point source pollution. Water resource governance will involve non-point source governance, such as total wastewater control and wastewater discharge permit trading systems. Second, as water environmental capacity, land area defines the purification capacity of terrestrial ecosystems such as wetlands and marshes. In contrast, land area is used concerning rainfall and is an essential source of water resources in a basin. Third, a larger land area often implies that the area has the capacity for development in terms of population, industry, or economy.

For the population and the GDP data in each control unit, We received the number of people based on each township data calculation from the Liling city statistics bureau official website, Zhuzhou City Statistics official website, technical plan report for improving Lushui water quality, and analysis report on water environmental problems in the Shahe River basin.

2.3.3. Gini Coefficient Allocation Method Steps

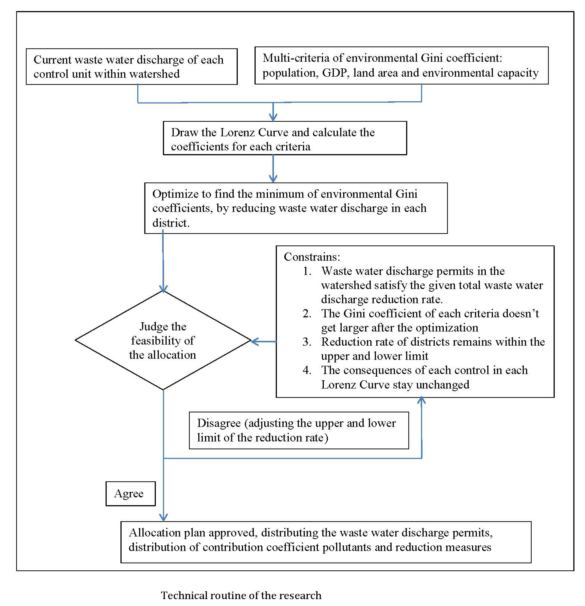
According to the allocation process studied by EGC, the allocation procedure can be presented as including the following four optimization steps:

(1) Conduct pilot research using the actual wastewater discharge as the initial condition for optimization;

(2) Calculation of the Lorenz curve for the actual wastewater discharge and calculation of the EGC using four indicators;

(3) Based on a given wastewater discharge reduction rate, the wastewater discharge permit allocation for each region within the watershed is optimized to obtain the minimum sum EGC for each indicator. The optimization has several constraints. For example, the wastewater discharge permits for the entire watershed should be consistent with the total control plan. Each EGC will only become smaller during the optimization process. The reduction rate of wastewater discharge in each region is within the upper and lower limits. After optimization, the results of each part of the Lorenz curve remain the same. In summary, the optimization process can be described by the following equation.

Object of optimization:

$$min\sum _{j=1}^4{G}_j$$

(2)

$$G_j=1-\sum _{i=1}^n(X_{j(i)}-X_{j(i-1)})(Y_i+Y_{i-1})$$

(3)

Limit to

Wastewater discharge total mass control:

$$P=Wx(1-q)$$

(4)

Gini coefficient constrain:

$$G_j\le G_{0\left(j\right)}$$

(5)

Each district wastewater discharge reduction rate:

$$S_i=(1-p_i{)xS}_{0\left(i\right)}$$

(6)

$$p_{i0}\le p_i\le p_{i1}$$

(7)

The district's consequence in the Lorenz curve:

$$K_{j\left(i\right)}=\frac{S_i}{M_{j\left(i\right)}}$$

(8)

Where G is the Gini coefficient; j is one of the four indicators of EGC; i is the control unit number in the watershed; G_j is the EGC of indicator j after optimization; X_{j (i)} is the cumulative percentage of indicator j in control unit i; Y_i is the cumulative percentage of wastewater discharge after reduction optimization, i.e., the discharge permit of control unit i; S_i is the total water pollutant discharge permit of the control unit i; S_{0( i)} is the current wastewater discharge, G_o(j) is the original Gini coefficient of indicator j and current wastewater discharge; p_i is the wastewater discharge reduction rate of control unit i; p_i0 and p_i1 are the lower and upper limits of wastewater discharge reduction rate of each control unit; M_j(i) is the value of indicator j in partition i, K_j(i) is the wastewater discharge permit of unit indicator j in control unit i after allocation, and n is the number of control units in the watershed.

Discuss the optimization results with the LEPs in each control unit to confirm their feasibility. If the results are unacceptable, the abatement rate should be adjusted, and the optimization process should be repeated. The flow chart of the environmental Gini method is shown in Figure 4.

2.3.4. Contribution Coefficient Calculation

The EGC is used as an assessment method to evaluate the equity of regional pollutant emission distribution. Its fairness is compared among various indicators without individual fairness [37]. If the economic contribution of a control unit is lower than the proportion of resource consumption or pollutant emissions, the control unit will violate the equity of the distribution of other control units; if the economic contribution of a control unit is greater than the proportion of its pollutant emissions, the control unit contributes to the equity of other control units. It reduces the burden of pollutants on other control units [38]. Therefore, the contribution factor can be used as a basis for assessing the equity among control units [39] and is calculated as follows:

$${CC}_j=(M_{ij}/M_j)/(W_i/W)$$

(9)

Where CC_j is the contribution coefficient based on indicator j when indicator j is environmental capacity, GDP, population, and land area, CC_j denotes the economic contribution coefficient (green contribution coefficient GCC), environmental capacity contribution coefficient, population contribution coefficient, and land area contribution coefficient, respectively. M_ij is the value of indicator j for the ith administrative division (control unit). M_j is the value of indicator j in the study area. M_ij/M_j is the contribution factor of indicator j in the ith administrative division; W_i is the pollutant emission in the ith administrative division; W is the total pollutant emission in the river area; W_i/W is the contribution factor of pollutant emission in the ith administrative division.

If CC_j>1, it means that the contribution of indicator j is more significant than the contribution of pollutant emissions, which is more equitable; if CC_j<1, it means that the contribution of pollutant emissions is greater than the contribution of indicator j, which is less acceptable, where the smaller the CC_j, the less equitable it is. The average contribution of the three indicators is called the average contribution coefficient, which can reflect social, economic, and, to some extent, natural resource factors. The EGC reflects the internal equity of pollution load distribution within a given unit. The contribution coefficient is the external influence between control units and can be used to distinguish external equity [40].

3. Results

3.1. Calculation Results of Allocation of the Discharge Permit

In 2020, the total emissions of COD, AN, and TP of Lushui River were 344328.48 tons, 10247.26 tons, and 3531.48 tons, respectively. The Lushui River basin was divided into 06 control units to which total quality control permits were issued. This study demonstrates how emission permits were assigned to each control unit using the EGC method.

First, Lorenz curves were plotted, and EGCs were calculated based on COD, AN, and TP emissions for each control unit in 2020. The results are shown in Table 7, Table 8 and Table 9. For example, the EGCs based on land area for COD, AN, and TP are 0.30, 0.26, and 0.23, respectively. The same step can be followed to calculate other EGCs.

Secondly, the EGC of each indicator was optimized and bounded. Considering the total reduction rate of wastewater discharge after optimization, the upper and lower limits of wastewater discharge reduction rate for each control unit were 0% and 20%, respectively. The optimization results and final discharge permit allocations are presented in Table 10. Table 7, Table 8 and Table 9 show the EGCs for each indicator before and after optimization.

Table 3. Basic information of each indicator.

Table 3. Basic information of each indicator.

Control Units	Land Area (km2)	Population(10000)	GDP100 Million RMB	Discharge (Tons/Year)			% Environmental Capacity
				COD	AN	TP
CU-1	543.31	7.95	369.52	17029.44	272.825	82.782	6.816
CU-2	89.01	33.92	60.53	15339.636	257.754	55.923	9.490
CU-3	549.84	4.08	122.92	9466.056	109.929	95.422	6.43
CU-4	187.75	1.68	41.97	104531.328	1814.791	1045.865	65.63
CU-5	837.84	16.06	43.61	10328.04	155.892	40.392	6.22
CU-6	581.00	4.56	395.14	8916.804	131.925	28.540	5.40

CU= Control Unit.

Table 4. COD water discharge Gini coefficient calculation based on the land area (2020 Year).

Table 4. COD water discharge Gini coefficient calculation based on the land area (2020 Year).

Control Units	Land Area (km2)	COD Discharge (Tons/Year)	Cumulative %		Gini Coefficient
			Land Area	COD Discharge
CU-6	581.00	8916.804	20.83	5.384	0.316
CU-3	549.84	9466.056	40.55	11.100
CU-5	837.84	10328.04	70.59	17.336
CU-2	89.01	15339.636	73.79	26.598
CU-1	543.31	17029.44	93.27	36.881
CU-4	187.75	104531.328	100.00	100
Total	2,788.75	165611.304

Table 5. AN water discharge Gini coefficient calculation based on the land area (2020 Year).

Table 5. AN water discharge Gini coefficient calculation based on the land area (2020 Year).

Control Units	Land Area (km2)	AN Discharge (Tons/Year)	Cumulative %		Gini Coefficient
			Land Area	AN Discharge
CU-6	581.00	131.925	20.83	4.809	0.66
CU-3	549.84	109.929	40.55	8.816
CU-5	837.84	155.892	70.59	14.499
CU-2	89.01	257.754	73.79	23.896
CU-1	543.31	272.825	93.27	33.842
CU-4	187.75	1814.791	100.00	100
Total	2,788.75	2743.119

Table 6. TP water discharge Gini coefficient calculation based on the land area（2020 Year).

Table 6. TP water discharge Gini coefficient calculation based on the land area（2020 Year).

Control Units.	Land Area (km2)	TP Discharge (Tons/Year)	Cumulative %		Gini Coefficient
			Land Area	TP Discharge
CU-6	581.00	28.540	20.83	2.115	0.75
CU-3	549.84	95.422	40.55	9.189
CU-5	837.84	40.392	70.59	12.184
CU-2	89.01	55.923	73.79	16.329
CU-1	543.31	82.782	93.27	22.466
CU-4	187.75	1045.865	100.00	100
Total	2,788.75	1348.926

Table 7. COD environmental Gini coefficient based on multi-indicators.

Table 7. COD environmental Gini coefficient based on multi-indicators.

Criteria	Land Area (km2)	Population	GDP	Environmental Capacity	Total Coefficient
Before the optimization	0.64	0.31	0.63	0.01	1.59
After the optimization	0.30	0.21	0.45	0.002	0.962
Variation	0.34	0.1	0.18	0.008	0.628

Table 8. AN environmental Gini coefficient based on multi-indicators.

Table 8. AN environmental Gini coefficient based on multi-indicators.

Criteria	Land Area (km2)	Population	GDP	Environmental Capacity	Total Coefficient
Before the optimization	0.68	0.36	0.67	0.021	1.731
After the optimization	0.26	0.32	0.32	0.02	0.92
Variation	0.94	0.68	0.99	0.041	2.651

Table 9. TP environmental Gini coefficient based on multi-indicators.

Table 9. TP environmental Gini coefficient based on multi-indicators.

Criteria	Land Area (km2)	Population	GDP	Environmental Capacity	Total Coefficient
Before the optimization	0.74	0.29	0.76	0.12	1.91
After the optimization	0.31	0.27	0.37	0.08	1.03
Variation	1.05	0.56	1.13	0.2	2.94

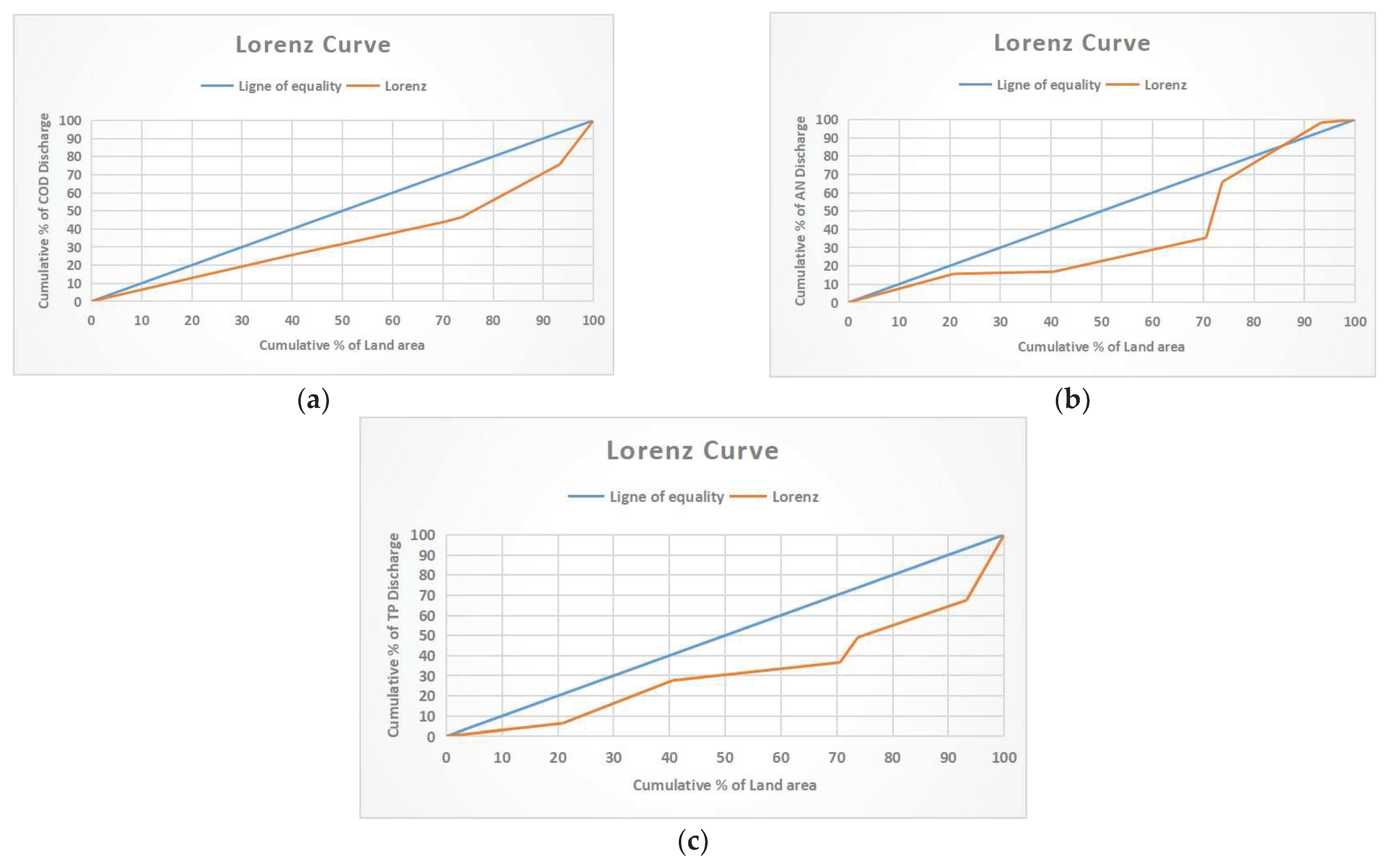
Figure 5. (a–c) Lorenz curve of COD, AN, and TP discharge permit based on Land area after optimization.

Figure 5. (a–c) Lorenz curve of COD, AN, and TP discharge permit based on Land area after optimization.

Table 10. Allocation of COD, AN, and TP discharge permit in each control unit.

Table 10. Allocation of COD, AN, and TP discharge permit in each control unit.

Control Units	Allocation Discharge Permit
	COD	AN	TP
CU-6	6916.804	131.925	26.540
CU-3	6466.056	9.929	79.422
CU-5	9328.04	155.892	38.392
CU-2	1239.636	257.754	49.923
CU-1	15001.44	272.825	80.782
CU-4	12531.328	14.791	65.865
Total	51483.304	843.119	340.926

Figure 6. (a–c) Distribution of COD, AN, and TP discharge permit in each control unit after optimization.

Figure 6. (a–c) Distribution of COD, AN, and TP discharge permit in each control unit after optimization.

3.2. Analysis of Contribution Coefficient Results

According to the calculation formula of the contribution coefficient, we can further understand the composition characteristics of the pollutant emission inequity and analyze the reasons for the overall inequity. The Gini coefficient selects environmental capacity, GDP, population, and land area indicators as evaluation indicators, and the contribution coefficients of each control unit to the pollution emission are calculated to examine the distribution of unfair factors using the GIS spatial analysis techniques to investigate the distribution of unfair factors that cause pollution inequity. The contribution coefficient is assumed to be greater than 1.0. In this case, this means that the contribution of the indicator is greater than the contribution of the pollutant emissions (COD, AN, and TP), which indicates relative equity; if the contribution coefficient is less than 1.0, it means that the contribution of the indicator is less than the contribution of the pollutant emissions, which is relatively less equitable. The smaller the contribution coefficient, the less fairness. After considering the social, economic, land area, natural resources, and other factors, the contribution coefficient can reflect fairness to a certain extent. 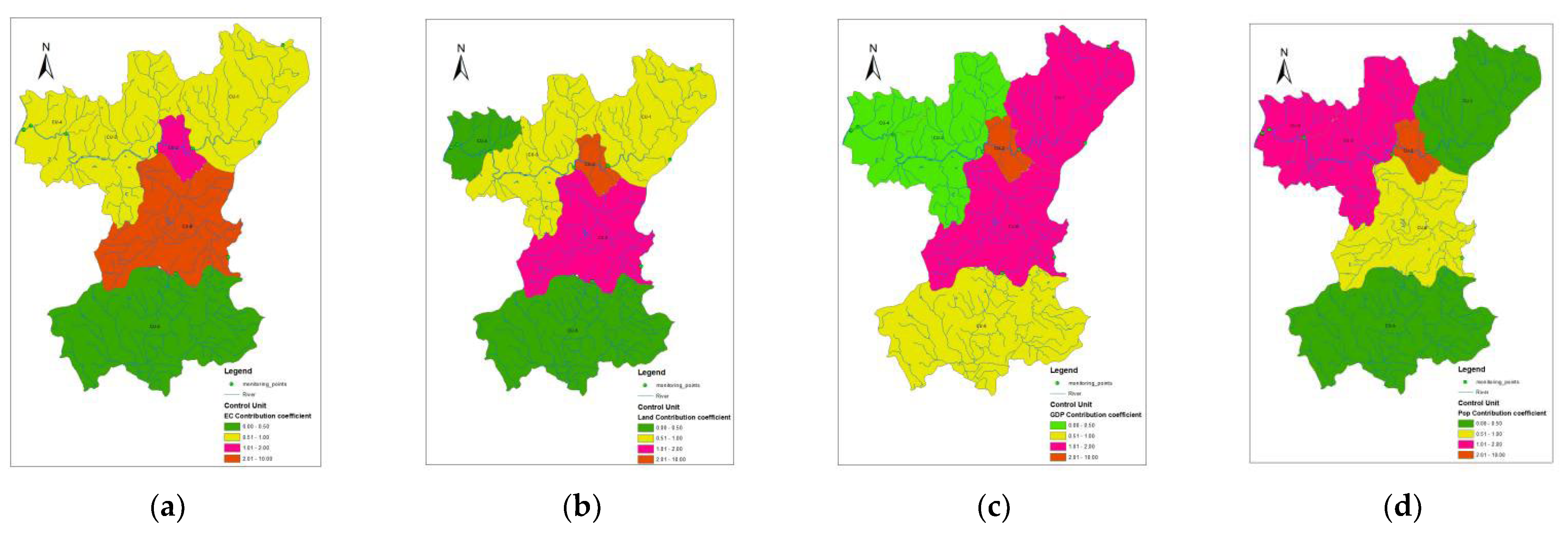Table 11 and Figure 7, Figure 8 and Figure 9a–d) show the contribution coefficients of COD, AN, and TP of Rushui River based on four indicators.

Table 11. COD, AN, and TP contribution coefficient in Lushui River based on the four indicators.

Table 11. COD, AN, and TP contribution coefficient in Lushui River based on the four indicators.

Control Unit	COD				AN				TP
	EC	Land	GDP	Pop	EC	Land	GDP	Pop	EC	Land	GDP	Pop
CU-6	0.52	2.00	7.10	0.43	0.35	1.33	2.44	0.29	1.30	5.02	9.22	1.09
CU-3	3.76	11.51	2.08	2.17	5.46	16.74	10.09	3.16	2.44	7.49	4.52	1.41
CU-5	0.52	2.49	0.67	1.61	0.34	1.62	0.23	1.05	0.32	1.53	0.22	0.99
CU-2	0.53	0.18	0.63	1.88	0.31	0.10	0.19	1.10	3.30	1.11	12.43	11.71
CU-1	0.39	1.11	3.47	0.45	0.21	0.60	1.10	0.24	1.44	4.10	7.53	1.66
CU-4	1.63	0.17	0.06	0.76	37.41	3.84	2.32	17.54	0.99	0.10	0.06	0.47

EC= Environmental capacity; Pop= population; CU: control unit.

Figure 7. (a–d) Distribution of COD contribution coefficient in Lushui River based on the four indicators.

Figure 7. (a–d) Distribution of COD contribution coefficient in Lushui River based on the four indicators.

Figure 8. (a–d) Distribution of AN contribution coefficient in Lushui River based on the four indicators.

Figure 8. (a–d) Distribution of AN contribution coefficient in Lushui River based on the four indicators.

Figure 9. (a–d) Distribution of TP contribution coefficient in Lushui River based on the four indicators.

Figure 9. (a–d) Distribution of TP contribution coefficient in Lushui River based on the four indicators.

4. Discussion

5. Conclusions

References

1. Bosi, S.; Seegmuller, T. Optimal cycles and social inequality: What do we learn from the Gini index? Research in Economics 2006, 60, 35. [Google Scholar] [CrossRef]
2. Lin, W.; Fu, G. Equitable planning and its application in regional water environmental comprehensive improvement planning[J]. Pollution Control Technology 1994, 7, 4–8. [Google Scholar]
3. Xiaoya, Zhang Wanshun, Wang Yan; et al. Hierarchical analysis of the allocation of pollutants in a specific region of Taihu Lake in the distribution of pollutants in the particular region of Taihu Lake[J]. Journal of China Institute of Water Resources and Hydropower Research 2011, 9, 155–160.
4. Gao, Z.; Pang, T.; Zhao, W.; et al. The optimization model of surface water pollution allocation based on equity and efficiency[J]. Anhui Agricultural Science 2012, 40, 8255–8257. [Google Scholar]
5. Burn Durn, D.H.; Mcbean, E.A. Optimization modeling of water quality in an uncertain environment [J]. Water Resources Research 1985, 21, 934–940. [Google Scholar] [CrossRef]
6. Deng, Y.X.; Zheng, B.H.; Fu, G.; et al. Study the total water pollutant load allocation in the Changjiang (Yangtze River) Estuary and adjacent seawater area[J]. Estuarine, Coastal and Shelf Science 2010, 86, 331–336. [Google Scholar] [CrossRef]
7. Wu, W.; Jiang, H.; Duan, Y.; et al. Optimization of water pollution load distribution in control units based on environmental Gini coefficient [J]. China Population, Resources and Environment 2017, 27, 8–16. [Google Scholar]
8. Darkwah, K.A.; Nortey, E.N.N.; Lotsi, A. Estimating the Gini coefficient for the log-normal income distribution using the Lorenz curve[J]. Springer Plus 2016, 5, 1–9. [Google Scholar]
9. Aalami, M.T.; Nourani, V. Fazaeli, H. Developing a surface water resources allocation model under risk conditions with a multi-objective optimization approach[J]. Water Supply 2020, 20, 1167–1177. [Google Scholar] [CrossRef]
10. Jin, J.; Wang, J.X.; Max, Y.; et al. Equality of medical health resource allocation in China based on the Gini coefficient method [J]. Iranian Journal of Public Health 2015, 44, 445–457. [Google Scholar]
11. Zhang, X.C.; Wang, F.L. Life-cycle carbon emission assessment and permit allocation methods: A multi-region case study of China population construction sector[J]. Ecological Indicators 2017, 72, 910–920. [Google Scholar] [CrossRef]
12. Zheng, X.; Xia, T.; Yang, X.; et al. The land Gini coefficient and its application for land use structure analysis in China[J]. PLoSOne 2013, 8, e76165. [Google Scholar] [CrossRef] [PubMed]
13. Fang, Y. Allocation of Total Water Pollutant Emissions in the Jiulong River Basin Based on Gini Coefficient Method Research [J]. Environmental Science and Management 2012, 37, 30–35. [Google Scholar]
14. Zhang Hui, Xi Beidou, Gao Rutai, etc. Calculation of Water Environmental Capacity and Upstream Capacity of Baiyangdian Lake Quantity allocation [J]. Journal of Environmental Engineering Technology 2012, 2, 313–318.
15. Tian Guangyu, Liu Zhan, Liu Hao; et al. Yongding. River Based on Ecological Characteristics of River Environment Domain Integrated Governance and Management [J]. China Water Conservancy 2019, 42–44.
16. Shao Zhejiang, Liu Lian, Wang Tao. Main river pollutants in Zhangjiakou's upper reaches of the Yongding River Source Analysis [J]. Environmental Pollution and Prevention 2020, 42, 204–211.
17. Meng Qinxian, Wu Binglin, Shen Jianfei; et al. Environmental Gini Coefficient in Water Pollution of Suining City Application in Total Quantity Allocation [J]. Sichuan Environment 2015, 34, 74–77.
18. Yang Rui. Research on the allocation of total sulfur dioxide in Shaanxi Province based on the environmental Gini coefficient method [D]. Xi'an: Northwest University, 2016.
19. Qin Dilan, Wei Anlei, Lu Shaoyong; et al. Dongting Lake Area Based on Environmental Gini Coefficient Total Allocation of water pollution [J]. Environmental Science Research 2013, 26, 8–15.
20. Meng Xiangming. Applying the Gini coefficient method in the total allocation of water pollutants [D]. Tianjin: Tianjin University, 2007.
21. Li Hao, Nan Ling. Initial drainage basin emission rights allocation based on environmental Gini coefficient [J]. People's Yellow River, 2014, 36, 56–59.
22. Pei Ling. Evaluation and Optimization of Equity in Total Water Pollutant Allocation: A Case Study of Chongqing City For example [D]. Chongqing: Chongqing University, 2014.
23. Li Yang, Wei Haiyan. Gini coefficient of resources and environment in Shaanxi Province and degree of ecological realization Analysis [J]. Hunan Agricultural Science 2010, 51–54.
24. Wang, J.; Lu, Y.; Zhou, J.; et al. China's Resource and Environmental Gini Based on GDP Coefficient Analysis [J]. Chinese Environmental Science 2006, 26, 111–115. [Google Scholar]
25. Zhai, T.; Guo, J.; Ou, M.; etc. Construction Land in Jiangsu Province Based on Gini Coefficient Research on Total Quantity Allocation [J]. China Population, Resources and Environment 2015, 25, 84–91. [Google Scholar]
26. Tian, P.; Fang, X.; Wang, F.; etc. Based on the minimization model of environmental Gini coefficient Optimization of Total Water Pollutant Allocation: Take the Zhangjiagang Plain Water Network Area as an Example [J]. China Environmental Science 2014, 34, 801–809. [Google Scholar]
27. Xie, G.; Peng, Y.; Li, B.; et al. TMDL Plan and Comprehensive Treatment of Small Watershed Pollution Research on Theoretical Thinking: Taking the Shandong Section of the East Line of the South to North Water Diversion Project as an Example for Pollution Control [J]. Agricultural Mechanization Research 2006, 28, 189–192. [Google Scholar]
28. Ye, C.; Gu, J. Application of the Gini coefficient method in the total allocation of water pollutants [J]. Journal of Xihua University (Natural Science Edition), 2010, 29, 87–91. [Google Scholar]
29. Zhong, X.; Zhang, W.; Li, M. Resource and Environmental Base of Guangdong Province Based on Ecological Capacity Calculation and Analysis of Ni Coefficient: Discussion with Zhang Yinbo et al. [J]. Journal of Ecology 2008, 28, 4486–4493. [Google Scholar]
30. Gan, X.; Wang, S.; Zhao, L.; et al. Analysis of the Gini coefficient of environmental resources in Sichuan Province [J]. Sichuan Environment 2015, 34, 111–116. [Google Scholar]
31. Hao, S. Optimal allocation method and water pollution load tracing application in plain river network area [D]. Beijing: University of the Chinese Academy of Sciences, 2016.
32. He, W.; Liu, D.; Wang, C. Are Chinese provincial carbon emissions allowances misallocated over 2000–2017? Evidence from an extended Gini-coefficient approach. Sustainable Production and Consumption 2022, 29, 564–573. [Google Scholar] [CrossRef]
33. Hu, Z.; Chen, Y.; et al. Optimal allocation of regional water resources: From a perspective of equity-efficiency tradeoff. Resources. Conservation and Recycling 2016, 109, 102–113. [Google Scholar] [CrossRef]
34. Jiang, H.Q.; Shao, X.; et al. A study of the allocation of carbon emission permits among the provinces of China based on fairness and efficiency. Sustainability 2017, 9, 2122–2138. [Google Scholar] [CrossRef]
35. Li, A.; Yuan, Q.; et al. Equality in river pollution control in China. Science of the Total Environment 2021, 777, 146105. [Google Scholar] [CrossRef] [PubMed]
36. Wu, W.; Jiang, H.Q.; et al. The control unit's total water pollutant load distribution application is based on the environmental Gini coefficient. China Population, Resources and Environment 2017, 5, 8–16. (In Chinese) [Google Scholar]
37. Zhou, S.; Du, A.; et al. Applying the environmental Gini coefficient in allocating water governance responsibilities: A Taihu Lake Basin, China case study. Water Science and Technology, 2015, 71, 1047–1055. [Google Scholar] [CrossRef] [PubMed]
38. Zhang, B.; Liu, H.; Yu, Q.; et al. Equity-based optimization of regional water pollutant discharge amount allocation: A case study in the Tai Lake Basin[J]. Journal of Environmental Planning and Management 2012, 55, 885–900. [Google Scholar] [CrossRef]
39. Darkwah, K.A.; Nortey, E.N.; Lotshi, A. Estimation of the Gini coefficient for the log-normal income distribution using the Lorenz curve[J]. Springer Plus 2016, 5, 1–9. [Google Scholar]
40. Wu, L.; Jiang, H.Q.; et al. The control unit's total water pollutant load distribution application is based on the environmental Gini coefficient. China Population, Resources and Environment 2017, 5, 8–16. (In Chinese) [Google Scholar]