Prerpints.org logo
Preprint
Article

Mechanical and Viscoelastic Properties of Carbon Fiber Epoxy Composites with Interleaved Graphite Nanoplatelet Layer

Altmetrics

Downloads

142

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 May 2023

Posted:

08 May 2023

You are already at the latest version

Alerts
Abstract
The use of interleaving material with viscoelastic properties is one of the most effective solutions to improve the damping capacity of CFRP laminates. Improving composite damping without threatening mechanical performance is challenging and the use of nanomaterials should lead to the target. In this paper, the effect of a nanostructured interlayer based on Graphite Nanoplatelets (GNPs) on the damping capacity and fracture toughness of CFRP laminates has been investigated. High-content GNP/Epoxy (70wt/30wt) coating was sprayed on the surface of CF/Epoxy prepregs at two different areal weight (10 and 40 g/m2) and incorporated at the middle-plane of a CFRP laminate. The effect of the GNP areal weight on viscoelastic and the mechanical behaviour of the laminates was investigated. Coupons with low-areal weight GNP interlayer showed a 25% increase in damping capacity with a trivial reduction of the elastic modulus. Moreover, a reduction in interlaminar shear strength (ILSS) and fracture toughness (both mode I and mode II) was observed in the composites with GNPs interlayer. GNPs alignment and degree of compaction reached during process were found as key parameters on material performances. By increasing the areal weight a mitigation on the mechanical performances drop was achieved (-15%).
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Due to the trend towards high-speed, lightweight, automated, and multifunctional aerospace vehicles, the problems of induced vibration and noise are becoming increasingly relevant. Carbon fibre-reinforced polymer (CFRP) composites are commonly used in weight-sensitive structural applications concerning standard metallic structures due to their high stiffness-to-weight ratio [1]. Composites must satisfy the high requirement for vibration and noise reduction in the case of aeronautical vehicles, but also damage resistant and damage tolerant. Thus, many efforts have been made by worldwide researchers to improve the fracture toughness and ductility of thermoset matrix composites without significantly adding weight or reducing in-plane mechanical properties.
Different strategies to improve the passive damping of composites include the use of hybrid fibres [2,3] or high viscoelastic polymeric matrix [4,5] as interleaving damping materials [6,7]. The latter approach is based on the addition of a dissipative core, embedded within the laminate. Viscoelastic materials are suitable for this application, thanks to their inherent capacity to dissipate vibrational energy [8,9]. The sandwich-like architecture induces greater interlaminar stresses within the soft viscoelastic layer due to the stiffness gradient, then dissipation gain due to the capability of the viscoelastic material. The vibration energy is dissipated by the shearing motion of the viscoelastic layer as the base structure vibrates in flexure. Interlaminar stresses generally arise at lamina interfaces in composite laminates, the existence of these interlaminar stresses means that part of the total energy dissipation in a laminate will be due to interlaminar damping.
However, the addition of an interlayer usually deteriorates the elastic properties of the material [10,11]. Improving the damping and the interlaminar fracture toughness of composite materials and maintaining high stiffness and strength is challenging.
Nanomaterials can effectively increase the mechanical performances of polymers both in terms of elastic modulus and damping, thanks to the energy dissipation that occurs at the interface with the matrix [12]. 1D/2D nanomaterials can simultaneously improve composite damping and mechanical properties [13]. Nanoparticles with a lamellar (2D) structure, such as graphene and its analogues (graphene oxide, GO, graphene nanoplatelets, GNP, etc.), can significantly improve the damping capabilities of nanocomposites [14,15] and also fracture toughness [16]. The nanoparticle shape factor and content can influence the mechanical behaviour of nanocomposites and in particular the damping factor (tanδ) [17]. Hybrid composites can be designed by integrating damping features based on the use of appropriately chosen filler, capable of improving the passive dissipation performance of the material [18]. Specifically, GNPs are known to have exceptional mechanical properties, including high stiffness, strength, and toughness, which make them attractive candidates for reinforcement in composite materials. Due to the 2D nature and high specific area of graphene, it was found a significant increase in mode-I fracture toughness of polymers at extremely low loadings of nanoplatelets thanks to strong interfacial bonds and improved load transfer and crack resistance [19]. Ahmadi-Moghadam et al. [20] found that GNPs could effectively and efficiently enhance the mode-I fracture toughness of the epoxy resin, but not the mode-II fracture toughness, due to nanoparticle/matrix debonding and the absence of filler-bridging.
Although nanofillers could improve the toughening mechanism of polymers when added to FRPs the enhancement in fracture toughness is uncertain. Liu et al. [21] found that if the fracture toughness of a resin is improved by 100%, then the improvement of mode I fracture toughness of FRPs is most likely far below 100%. An increase of both GIC and GIIC was found by Quan et al. [22] in the case of CFRP interleaved with MWCNT- doped Polyphenylene-sulfide (PPS) veils with 0.5 g/m2 density, while a reduction of –11% GIC in the case of GNPs/PPS veil of the same density due to agglomeration that inhibits PPS fibre/epoxy adhesion. On the same path, Nagi et al. [23] investigated the effect of mode I and mode II interlaminar fracture toughness of CFRP laminates with GNP interleaves. The continuous GNPs interlayer (with 0.43 g/m2 density) enhances the mode-II fracture toughness of CFRP by 40% but reduces mode-I toughness by –31%. Improvement (+42%) in interlaminar shear strength of the CFRP was found by Wang et al. [24] after introducing 10 wt% GNP/silicon carbide nanowires (SiCnw) interleaves. The effect of nanofiller content was investigated by Moustapha Sarr et al. [25], who found an improvement of 28% in the interlaminar fracture toughness GIic in cellulose nanofiber (CNF) in glass fibre/epoxy composites with the addition of 0.05 wt% CNF, and a reduction of 10% in the case of 0.10 wt% of CNF due to the incomplete impregnation of GF with epoxy resin caused by the thicker CNF layer at the interfacial laminates. Similarly, Korbelin et al. [26] investigated the dependence on the interlayer thickness of interlaminar energy release rate under mode I and mode II loadings of few-layer graphene-modified CFRP with interlayer thicknesses varying from ultra-thin-ply (30 g/m2) to thick-ply (240 g/m2), showing a significant improvement of fracture toughness with respect to the neat CFRP in both cases. Inal et al. [11] reviewed the interlaminar fracture toughness of composite laminates with particle fillers and non-woven fibre veils, showing that processing techniques such as coating, spraying or growing/grafting the particles on fibre preforms/prepregs can minimise the particle loading to enhance interlaminar fracture toughness.
In this paper, the influence of the areal weight of high-content GNPs interleaves on the damping and fracture toughness of CF/Epoxy laminates was investigated. GNPs/Epoxy coatings, with a nominal content of 70 wt% of GNPs, have been deposited onto the prepregs’ surface using a spray process. Symmetric laminates have been fabricated by introducing the functionalized prepreg as a central ply in the stacking process. The effect of interlayer thickness has been investigated by considering two different coating weights of 10 and 40 g/m2. The viscoelastic behaviour of the CFRP laminates has been investigated to evaluate the effect of the interleaves on damping performance. Additionally, the effect of the addition of GNPs interleaves on the damage tolerance of CFRP composite has been investigated, by mode I and mode II interlaminar fracture toughness and interlaminar shear strength (ILSS).

2. Materials and Methods

2.1. Integration of GNP high content layer onto carbon fiber prepreg

GNPs/Epoxy coating with a nominal weight ratio of 70/30 has been deposited on the surface of carbon fibre prepregs. Two-dimensional GNPs, with a high aspect ratio, called G2Nan (lateral size of 30 μm and thickness of 14 nm) and an Epoxy resin HexFlow® RTM6 are employed in this study. Caron fibre/epoxy prepreg was purchased from Krempel. The 2x2 twill 3k prepreg is composed of a KGBD 2508 fibre (56% w/w) in an intermediate modulus epoxy with a 120°C cure temperature and a Tg (glass transition temperature) of 140°C.
A spray deposition process is employed for coating the prepreg surface. Firstly, GNPs are dispersed in acetone by ultra-sonication and mixed with a solution of epoxy diluted in acetone previously prepared [15,27]. Then obtained paste is deposited directly on the carbon fibre KGBD 2508 prepreg (30x30 cm) using a semiautomatic tri-axes pantograph, as shown in Figure 1. Finally, the material is dried at room temperature all night to let the solvent evaporate. Coating with two different areal weights, low-weight GNP interlayer (LW-GNP) of 10 g/m2 and high-weight GNP interlayer (HW-GNP) of 40 g/m2 have been considered in this study (Figure 2). The areal weight of the coating has been managed by controlling the number of deposition cycles during the spraying process. Each deposition cycle corresponds to a nominal areal weight of 10 g/m2.

2.2. Manufacturing of hybrid carbon fiber epoxy composites

Large composite panels were prepared by stacking 16 plies of KGBD 2508 prepreg with a [(90/+45/-45/0)2]S stacking sequence. The GNP-coated prepreg has been stacked at the 8th ply (mid-section), to ensure symmetry, as indicated in Figure 3a. Panels were cured in an autoclave under vacuum on a flat mould (Figure 3b), with the additional pressure of 3 bar and heated at a rate of 3°C min to 100°C for 120 minutes and subsequently post-cured at 140°C for 60 minutes. Moreover, to create an initial crack for Mode I and II fracture testing, a 13 μm Teflon film was included between the 8th and 9th plies, across the top 65 mm of the sheet (Figure 3c). Panels with LW-GNP and HW-GNP interlayers have been fabricated. A reference panel, without the GNP interlayer, has been fabricated for comparison. All fabricated samples are listed in Table 1.

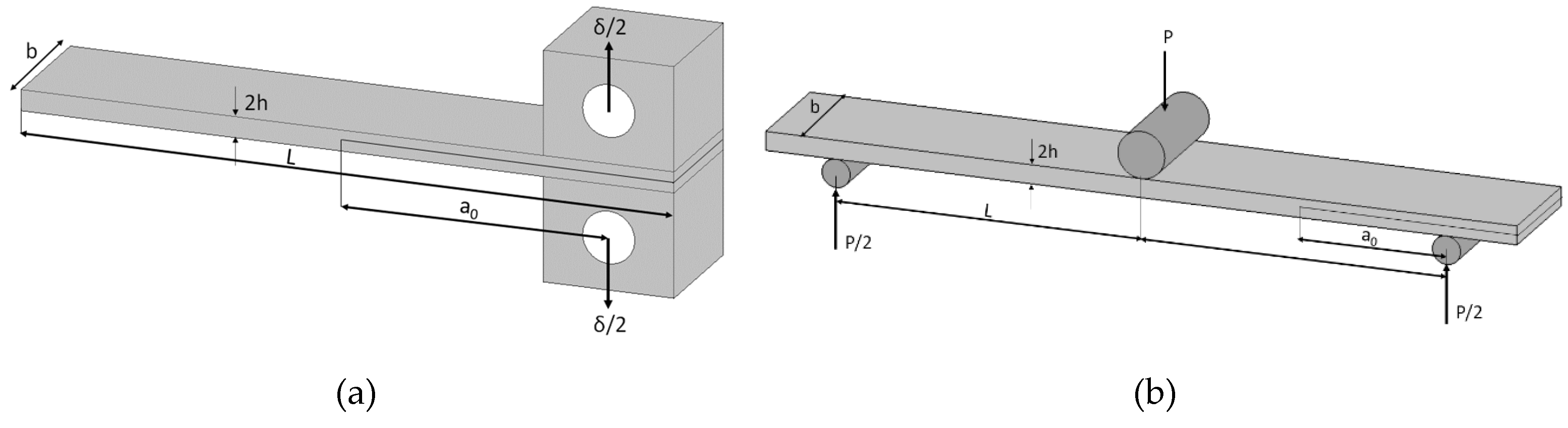
2.3. Experiremental Characterization

Thermogravimetric analysis (TGA) (TA Instruments Q500) was conducted to evaluate the real filler/matrix composition of the coating. Measurements were performed in an inert atmosphere, using nitrogen gas, with a temperature ramp of 10°C/min from room temperature to 800 °C, according to the ASTM E1131. The weight loss is evaluated at 600°C.
The thermal properties of the material were investigated by differential scanning calorimetry (DSC) using the DSC Discovery instrument. Each specimen was heated and cooled twice from 0 to 300°C at a rate of 10°C/min.
Dynamic mechanical analysis (DMA) was employed to measure to assess the viscoelastic behaviour of the laminates. A TA Instruments Q800 DMA equipped with a 3-point bending clamp was used to perform a temperature sweep from 30 to 200°C at a heating rate of 3°C/min and a frequency of 1 Hz and considering an initial amplitude of 20 μm. Three tests were performed for each sample to ensure the repeatability of the result. Data are elaborated according to the ASTM D790 standard for the flexural behaviour of composites [28].
Finally, the composite specimens were cut by diamond saw from the manufactured plates to perform ILSS, Mode I and Mode II fracture tests, using an Instron 68TM-50 universal testing apparatus.
The ILSS of composites was determined using the short beam shear (SBS) test method following the ASTM D2344 standard. The interlaminar shear is generated indirectly through the three-point bending of specimens in the SBS method. The tested specimens were compliant with the dimensions 36x12xh mm3 where h was the actual thickness of the specimens. Three SBS samples were tested for each condition (REF, LW-GNP and HW-GNP). The ILSS (MPa) values were calculated by equation (1):
I L S S = 3 P m a x 4 b h
where Pmax (N) is the maximum load, b (mm) is the sample width, and h (mm) is the actual thickness of specimens.
For Mode I fracture, composite specimens were prepared according to ASTM D5528 std. with dimensions 125x25x4.0 mm3, and an initial crack of 65 mm (Figure 4a). The edges of Double cantilever beams (DCBs) samples were painted with a white correctional fluid to improve crack visibility, and markings were added to track crack growth to the nearest millimetre. Steel loading blocks were glued to the ends of the sample beams using a cyanoacrylate adhesive. The bonding surface of the specimen has been lightly scrabbed with sandpaper and then wiped clean with methylethylketone (MEK) to remove any contamination.
Three DCB samples were tested for each condition (REF, LW-GNP and HW-GNP).
Mode I fracture toughness, GIc, was calculated using the modified beam theory (MBT). MBT assumes a beam with no rotation at the reaction front. The test beam was loaded in displacement control mode (2 mm/min), from the loading blocks until the crack front propagated about 20 mm, before unloading. The beam theory expression for the strain energy release rate (GIc, kJ/m2) of a DCB is as follows:
G I c = 3 P δ 2 b a
where P (N) is the load, δ (mm) is the load point displacement, b (mm) is the sample width, and a (mm) is the crack length at fracture.
Mode II fracture was tested according to ASTM D7905 std. on specimens with dimensions of 160x25x4 mm3, and an initial crack of 45 mm. three beams were tested for each condition. Mode II interlaminar fracture toughness, GIIc, was measured on a 3-point bending fixture as shown in Figure 4b. End notch flexure (ENF) beams were set such that the crack tip was fixed distance from one of the support rollers (a0= 30 mm) and loaded at 1 mm/min. The Mode II interlaminar fracture toughness, GIIc (kJ/m2), is given by the equation:
G I I c = 9 a 0 2 P δ 2 b 2 L 3 + 3 a 0 3
where P (N) is the critical load, a0 (mm) is the initial crack length, δ (mm) is the load point displacement, L (mm) is the half span and b (mm) is the beam width.

3. Results and Discussion

3.1. Characterisation of graphene-coated prepreg

The actual areal weight of the coating has been estimated to be 15 and 59 g/m2 for LW-GNP and HW-GNP respectively, as reported in Table 2. The actual value has been computed by measuring the difference in weight of the samples before and after the spray deposition process.
Figure 5 shows the DSC curves of analysis conducted on the prepreg samples and referred to the prepreg resin weight, which is the only reactive part of the system. In the pictures, a first peak located at 145°C is found for all samples, which is associated with the resin of the Krempel prepreg. The peak area does not significantly modify in the case of functionalized prepreg with respect to the reference. An increase of +3% was found in the case of LW-GNP and a decrease of -6% in the case of HW-GNP. This indicates that the spray deposition step does not affect the resin reactivity.
Also, a second peak, located at 280°C is found in the case of LW-GNP and HW-GNP prepregs, which is associated with the RTM6 resin of the coating. The intensity of the peak is very low, due to the small amount of polymer present in the material.

3.2. Characterisation of functionalized laminates

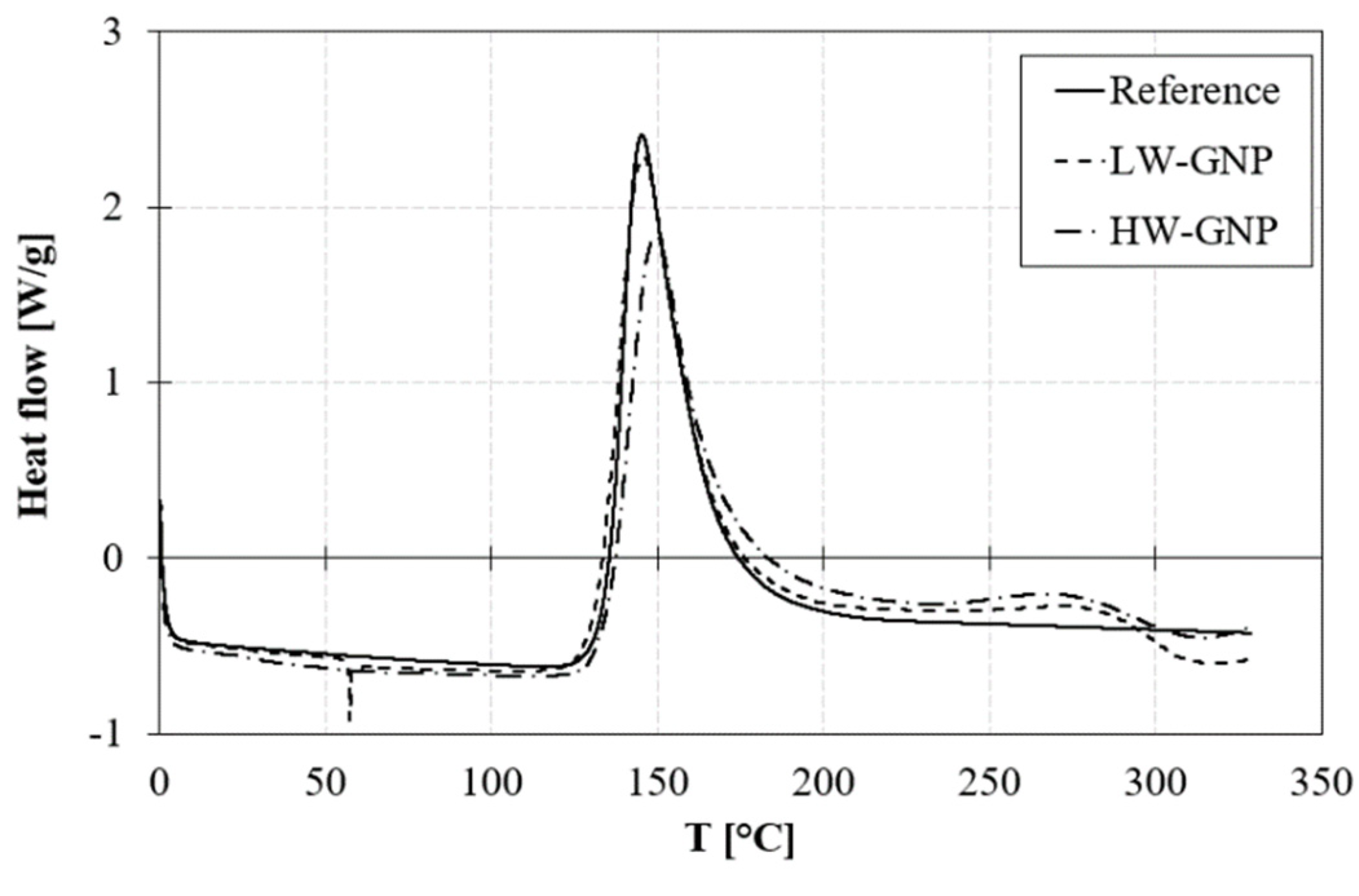
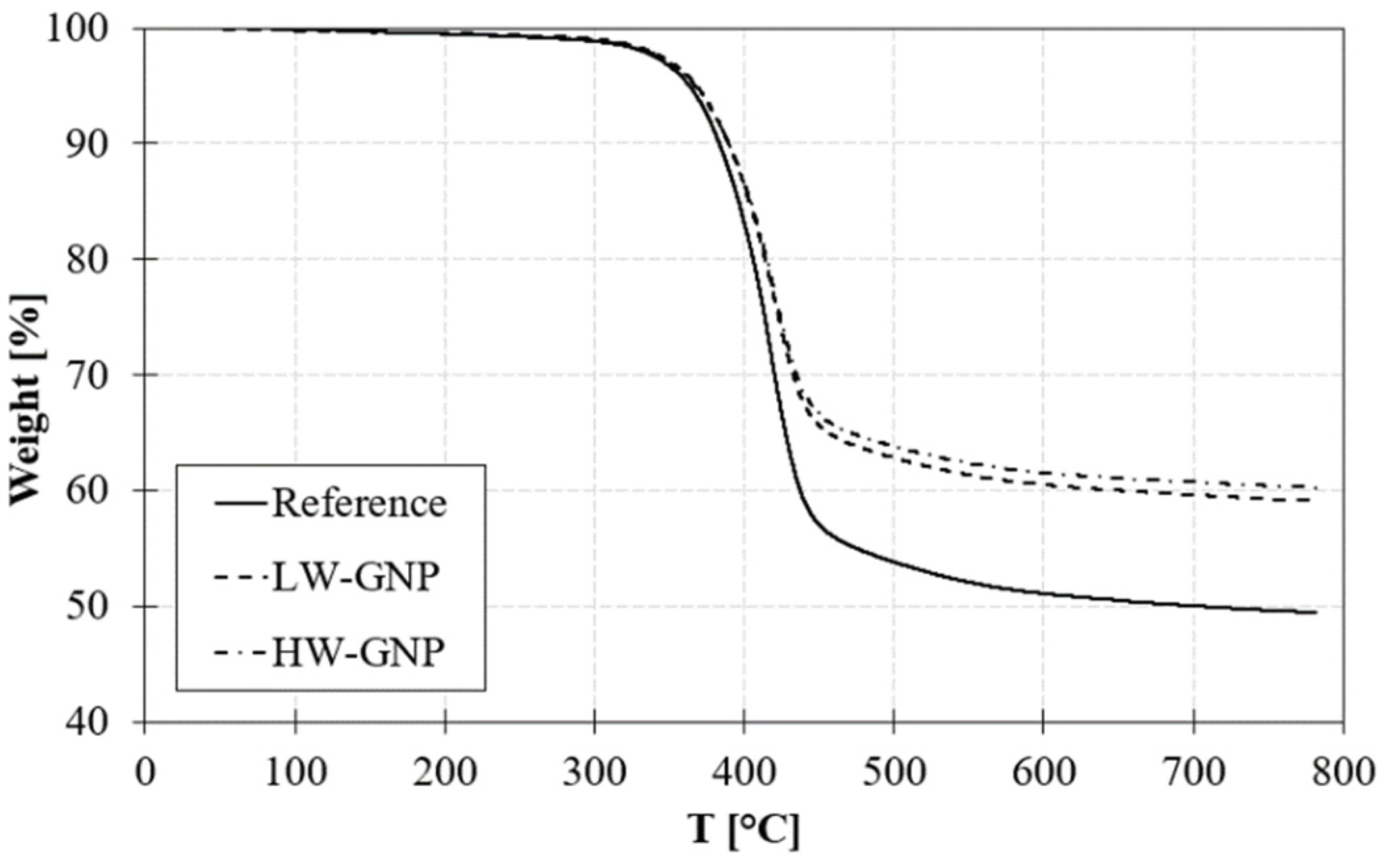
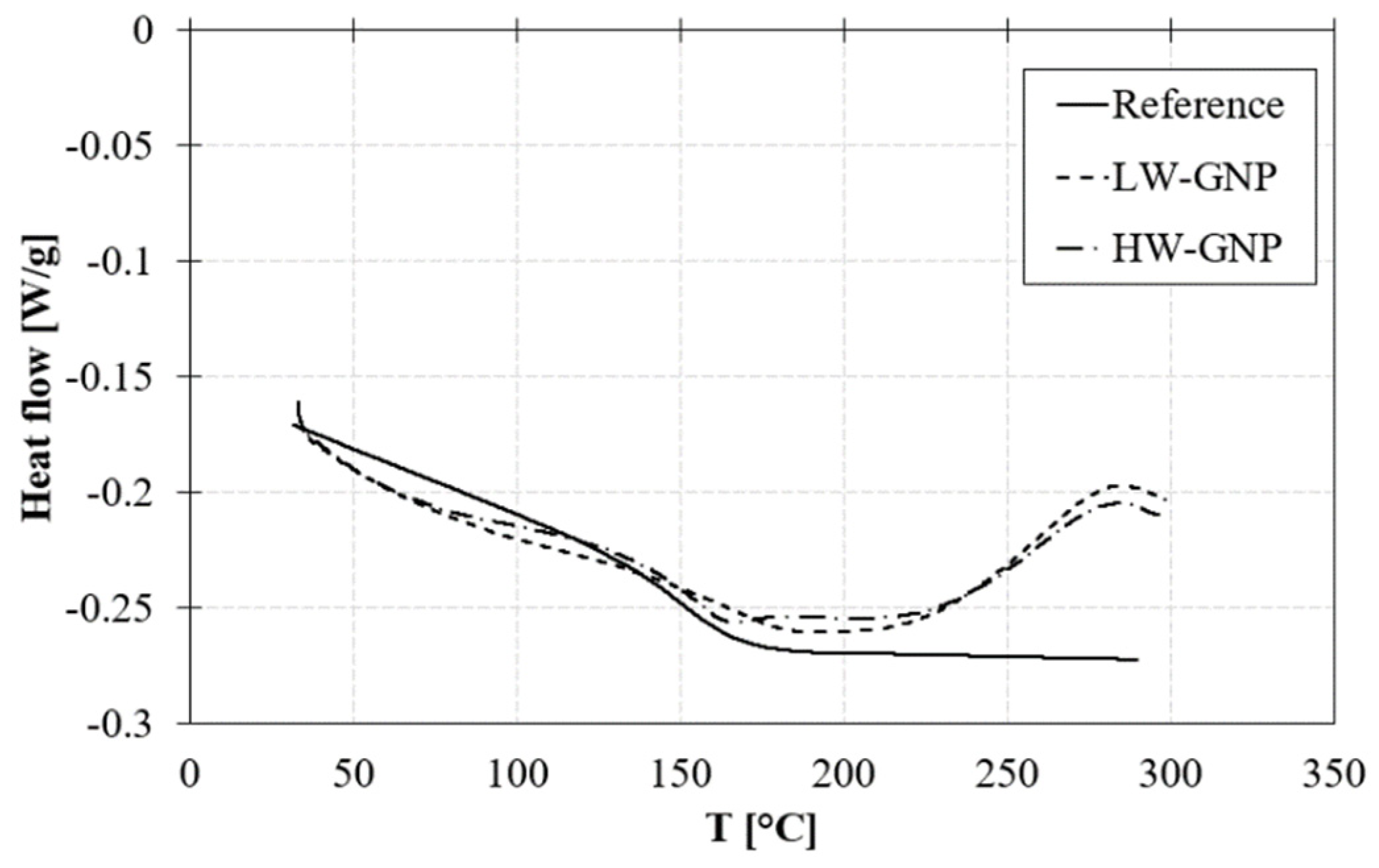
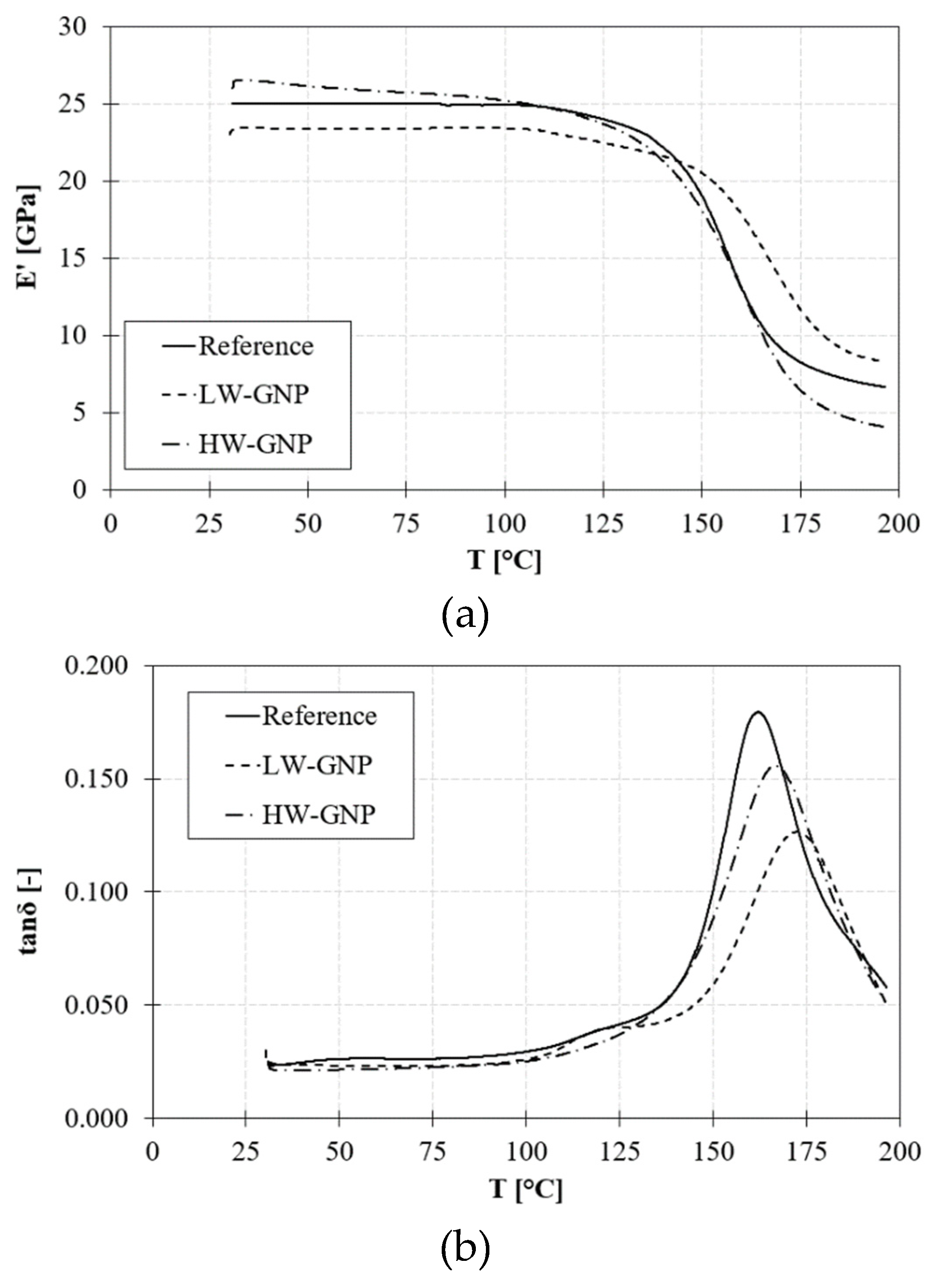
3.2.1. TGA, DSC and DMA results

Figure 6 shows the thermal degradation of laminates. A weight loss of 5% occurs at 370°C for all samples and the weight residue at 600°C is 50% for the reference sample and 60% for LW-GNP and HW-GNP samples.
DSC curves on cured laminates, referred to the Krempel resin weight, (Figure 7) confirm the complete curing of the epoxy resin of Krempel, due to the absence of the reticulation peak at 145°C. Nevertheless, the small peak at 280°C, for LW-GNP and HW-GNP samples, indicates that the RTM6 resin is not completely cured.
The glass transition temperature (Tg) is not affected by the incorporation of GNPs. It slightly reduces by about 4% in the case of laminates with interleaved GNP layers regardless of the areal weight of the coating. The same trend is found for the Tg obtained from DMA analysis, as reported in Table 3.
The bending stiffness of the material increases when a thick interleaved layer is included in the laminate. In fact, the storage modulus (E’) slightly decreases (-7%) in the case of LW-GNP with respect to the reference and increases by +3% in the case of HW-GNP laminates at room temperature (Figure 8a).
The damping capacity of the material (tanδ) increases by +25% when a low-areal weight GNP interlayer is added. A lower increase of tanδ (+6%) is also shown for the HW-GNP sample (Figure 8b). On the contrary, at high temperatures, the peak damping parameter (tan δ peak) slightly decreases with the incorporation of GNPs in the interlaminar region, especially for the LW-GNP sample.

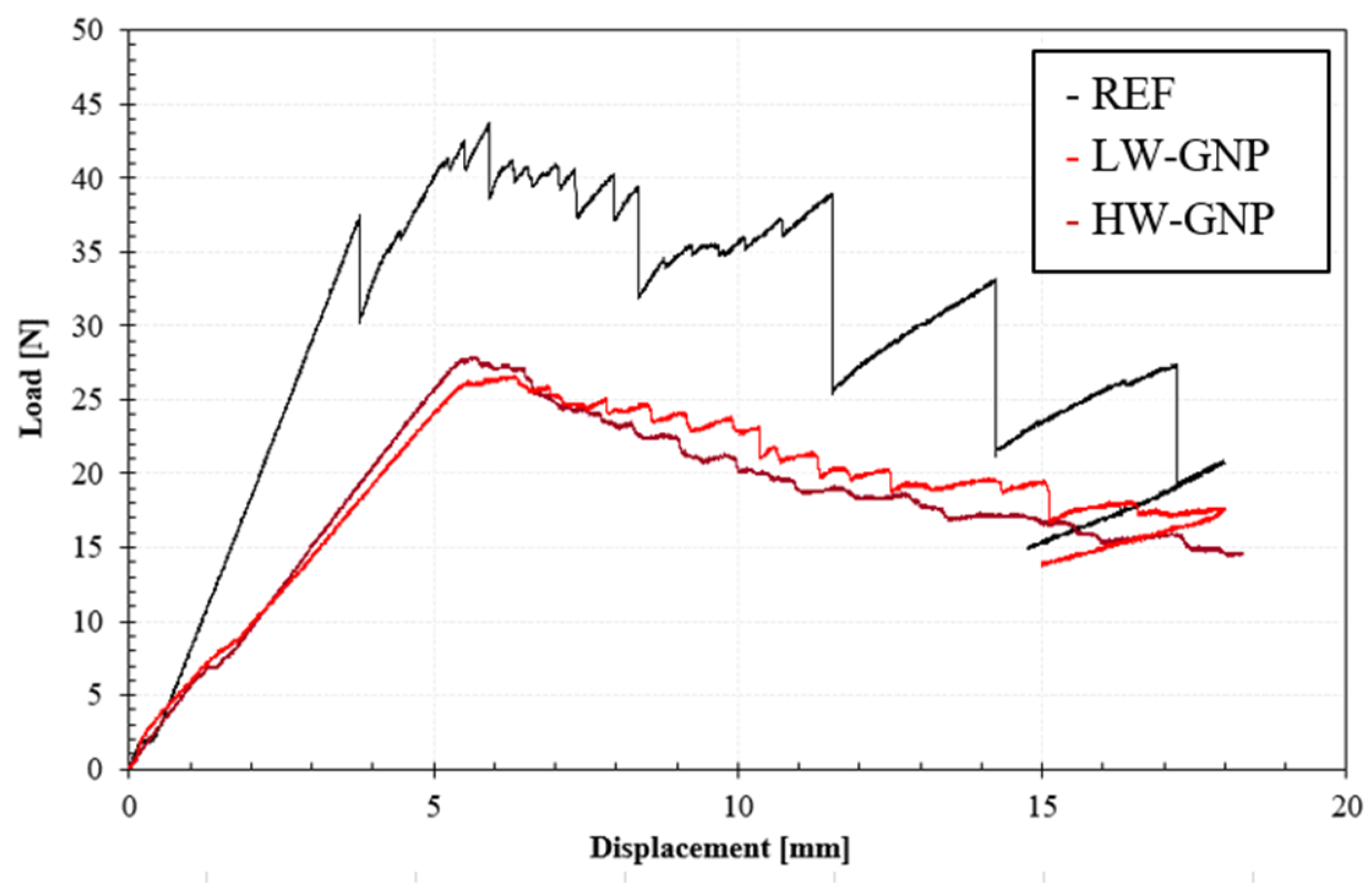
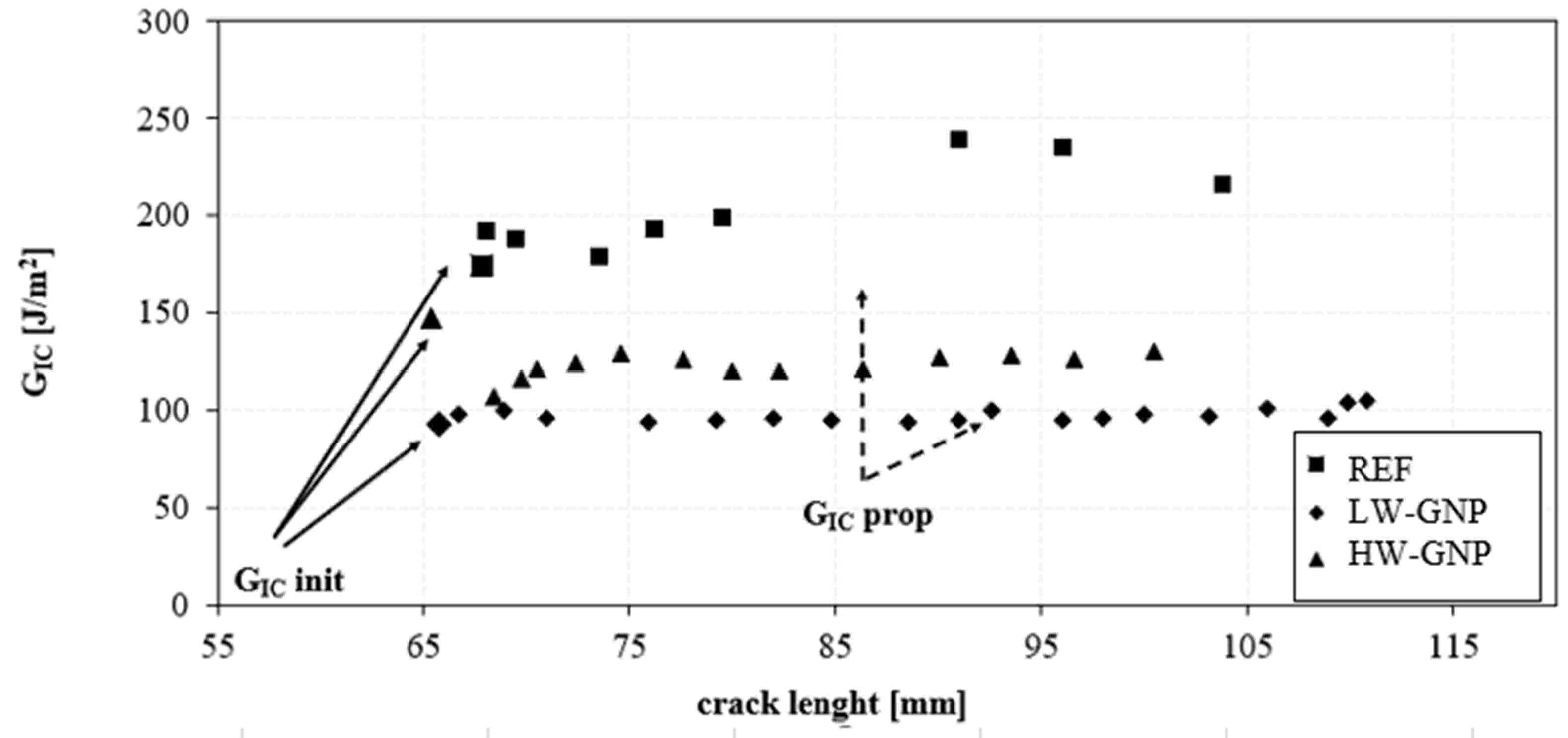
3.2.2. Interlaminar properties

The results of interlaminar shear strength, and mode I and mode II fracture toughness of tested samples are reported in Table 4.
With increasing coating areal weight, the GNPs layer becomes thicker, preventing the epoxy resin from impregnating the CF fibres at the interface. This results in low interfacial adhesion. The ILSS reduces both in the case of LW-GNP and HW-GNP samples with respect to the reference. A higher reduction of -46% is found in the case of the high-areal weight GNP layer.
Figure 9 shows the relation between applied load and displacement for REF laminates, LW-GNP and HW-GNP. The curve modifies in the case of GNPs interleaved samples with respect to the reference CFRP panel. Nevertheless, no significant differences are found between samples with a low and high-areal weight interlayer. Initially, all the curves show an increase in load. After the initial increase in load, there is a large decrease marking the initiation of crack growth. This is again followed by a certain increase in load, only in the case of the reference, before it again starts decreasing. A noticeable difference in crack propagation pattern is shown for LW-GNP and HW-GNP samples: the crack initiation happens at higher displacement but at a much lower load level. With the addition of GNPs, the crack growth is much smoother than the reference sample, where many maxima–minims are shown, meaning that the crack propagation is unstable. This behaviour is due to a consistent resistance offered by cross-bridging between the GNPs and increases with increasing interlayer areal weight.
According to Eq. (2), the mode I fracture toughness (GIc) is calculated and the results are reported in Table 4. The relationship between mode I fracture toughness (GIc) and the increment of the crack length is shown in Figure 10. Mode I fracture toughness increases with the crack length as shown in the Figure 10.
The first value of GIc (on initiation) indicates the energy required for the initial crack extension and is defined as the point of sudden decrease of load. The increase of GIc with crack length is mainly due to fibre bridging that happens on the fracture surface and is indicated as GIc on propagation (averaged over the first 25 mm of crack extension).
The results confirm that the mode I fracture toughness of the REF is higher than the samples with the GNP interlayer. The reduction in the mode I toughness values can be attributed to the suppression of the fibre bridging. Additionally, the mode I fracture toughness of the HW-GNP is higher than LW-GNP, these results confirm that the GIC is dependent on the area areal weight of the GNP interlayer.
Results for the end-notch flexural testing of the reference and GNP-treated CFRP are reported in Table 4. The mode II fracture toughness is calculated according to Eq. (3). A significant reduction is shown for LW-GNP and HW-GNP samples with respect to the reference.

3.3. Morphology of fracture propagation

Table 5 shows the micrographs of testes samples. Micrographs on ILSS-tested samples show that, unlike the reference sample, the fracture occurs within the GNPs interlayer for both LW-GNP and HW-GNP, resulting in a cohesive fracture.
From the ENF and DCB tested samples (Figure 11 and Figure 12), both in the case of reference and LW-GNP samples, the fracture is cohesive. Whereas, in the case of the HW-GNP sample, the fracture propagation occurs at the interface between the GNPs layer and the adjacent CF/epoxy layer.

4. Discussion

The thickness of the GNP interlayer has been estimated by barbaric Optical Microscopy. The thickness of the GNPs interlayer increases with the increasing coating areal weight, being 140 μm in the case of the LW-GNP sample and 320 μm in the case of HW-GNP, there is no evidence of the diffusion of nanoparticles within the carbon fiber layers. Although the areal weight of the GNP coating is four times higher in HW-GNP compared to LW-GNP, the ratio between the two interlayer thicknesses is 2, due to the effect of compaction pressure during manufacturing of laminates (Figure 13).
Table 6 summaries the main properties (E’, tanδ, ILSS, GCI, GCII) of all samples analysed at room temperature.
From the results of DMA analysis, it is found that the elastic behaviour of CF/epoxy laminates is not significantly affected by the high content GNPs interlayer since the storage modulus varies in a small range (-7%, +3%). On the contrary, the dissipative behaviour of the laminates increases by +25% in the case of LW-GNP and +6% in the case of HW-GNP interlayers. The GNPs interlayer acts as a soft layer improving the dissipation of vibrational energy of the laminates [4] . Thanks to the high gradient stiffness (from CF/Epoxy to GNP/Epoxy layer), greater interlaminar stresses are concentrated in the GNP layer, which dissipates energy through interlaminar damping [29].
However, the interlaminar fracture of both low- and high-areal weight GNP interlayer decreases with respect to the CF/epoxy laminate. In ILSS the tensional state is mainly governed by the transverse shear load. Results demonstrate a worsening effect of the nanofiller as the areal weight increases due to the fact the shear stresses, proportional to the section area, decrease as the thickness of the interlayer increases (Table 5).
Similar effects are found on the fracture toughness of the composites. The mechanism through which interlayered GNPs can affect composites' mode I fracture toughness is dual, both improving the fracture toughness of resin and acting as crack bridging [20]. As the crack propagates through the composite, the GNPs interlayer contributes to uniformly distributing the load, as shown in the load-displacement curve, where a smoother and more stable trend is reported for LW-GNP and HW-GNP samples compared to the reference. The high surface area of the GNPs can promote the creation of a large number of microcracks which can help to absorb energy and prevent uncontrollable failure of the composite material. In well aligned 2D nanoplatelets composites failures should occur at different dimensional scales: at the interface with the carbon fiber, within the GNP layer separating nanoparticles and failures within GNP particles.[30] However, the mode I fracture toughness reduces by -40% and -15% in the case of LW-GNP and HW-GNP samples respectively compared to the reference. This reduction may be due to the orientation of the nanoplatelets in the fibre-reinforced specimens. The spray deposition process of a high-loaded GNPs coating promotes the nanoplatelets’ alignment on the surface of the prepreg. In addition, the confinement induced by the fibre layers (before the resin cure), due to the vacuum and external pressure applied on the mould during fabrication contributes to the nanoplatelets alignment, especially near the interfaces [31]. The higher is the alignment achieved during deposition, the lower is the capability of nanoparticle to diffuse inside the CFRP layers preventing the GNPs from bridging. In fact in the case of the low-areal weight interlayer (Figure 12) the fracture toughness is weak.. In the LW-GNP sample, the crack propagates in the planar direction of the laminate through the GNP layer. On the contrary, in the HW-GNP sample, the crack initially propagates in the middle section of the GNPs layer and then deviates to the deposition interface. The different behaviour observed for low and high areal weight is clearly associated with the nanoplatelet's alignment. The preparation of LW-GNP deposition on CFRP facilitates a well aligned assembly of GNP resulting in a poor fracture toughness. While the preparation of HW-GNPs required multiple spray stages which promote the rise of misalignement on the GNP stacking, therefore the nanoplatelets’ alignment is reduced, and a random orientation is favoured within the GNPs layer. In this case, a crack bridging effect is barely activated leading to a lower decrease of GIC (-15%) is found.
The fracture surfaces confirm the role of GNP dispersion state on the final performances. The Figure 14 show for each samples the dispesion state, the right side is the layer where the GNPs have been deposited. In the case of LW the GNP stacking is well ordered and the effect of the compression between layers (upper and lower) is clearly visible. While in the case of HW, the GNP layer losses its alignment. It is worth to notice that in both the cases the fracture propagates inside the GNP layer (Figure 12).
Similarly, ENF results showed a significant reduction of mode II fracture toughness. The evaluation of fracture and toughening mechanisms under mode-II fracture is relatively more challenging when compared to mode-I fracture. When a crack, originally in the mode-II state, starts propagating, it often changes to opening mode (i.e., mode-I fracture) [31]. Therefore, shortly after the crack propagation starts, the observed fracture surface patterns become very similar to those observed for mode-I fracture.
The crack propagation path (Figure 11) in mode II loading shows a global behaviour similar to the double cantilever, even if the presence of a thick layer in the case of HW samples gives rise to an initial failure path related to intensification around the initial delamination corner, and subsequently propagates along GNP layer thicknesssuggesting that the tensional state is more similar to a mixed-mode fracture mechanism rather than mode II [31].

5. Conclusions

In this work, the effect of the high-loaded GNPs interlayer on the mechanical and fracture behaviour of CFRP laminates has been investigated. The influence of layer thickness (i.e., areal weight) has been studied. GNPs interlayer offers improvement in the dissipation mechanism, without affecting the elastic modulus of the laminate, thanks to the intrinsic damping capacity of high aspect ratio GNPs and the high gradient stiffness between the CF/Epoxy layer and the GNP/Epoxy layer. However, the presence of interleaves does not improve the interlaminar fracture toughness of laminates. The mode I fracture tends to take place in a cohesive way through the GNP layer in the case of the LW-GNP sample, and at the interface with the deposited GNP layer in the case of the HW-GNP sample. Mode II fracture follows the same propagation crack as Mode I since GIC/GIIC<1.
The obtained results suggest that the spray deposition technology is suitable to realize functional layer (Epoxy/CF prepregs modified with GNP layer depositions) at different areal weights improving the damping of CF/epoxy composites, however fracture mechanics requires further investigation to preserve the initial performances.
Future works are aimed to simultaneously improve the damping and fracture toughness by modifying the areal weight and/or the GNPs content/aspect ratio. Furthermore, the effect of the interlayer on thermal and electrical conductivities will be investigated.

Author Contributions

Conceptualization, A.M. and F.C.; methodology, B.P. and A.M..; investigation, F.C, B.P., and C.S.; data curation, A.P. and M.E.; writing—original draft preparation, F.C: and B.P..; writing—review and editing, A.M. and M.G.; supervision, A.M..; funding acquisition, A.P. and M.G.. All authors have read and agreed to the published version of the manuscript.

Funding

This research was carried out in the framework of the project MUSAICO, grant number F/190014/01-02/X44, founded by the Italian Government. Data.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Soutis, C. Carbon Fiber Reinforced Plastics in Aircraft Construction. Mater. Sci. Eng. A 2005, 412, 171–176. [Google Scholar] [CrossRef]
  2. Ni, N.; Wen, Y.; He, D.; Yi, X.; Zhang, T.; Xu, Y. High Damping and High Stiffness CFRP Composites with Aramid Non-Woven Fabric Interlayers. Compos. Sci. Technol. 2015, 117, 92–99. [Google Scholar] [CrossRef]
  3. Beylergil, B.; Tanoglu, M.; Aktas, E. Mode-I Fracture Toughness of Carbon Fiber/Epoxy Composites Interleaved by Aramid Nonwoven Veils. Steel Compos. Struct 2019, 31, 113–123. [Google Scholar]
  4. Martone, A.; Antonucci, V.; Zarrelli, M.; Giordano, M. A Simplified Approach to Model Damping Behaviour of Interleaved Carbon Fibre Laminates. Compos. Part B Eng. 2016, 97, 103–110. [Google Scholar] [CrossRef]
  5. Kishi, H.; Kuwata, M.; Matsuda, S.; Asami, T.; Murakami, A. Damping Properties of Thermoplastic-Elastomer Interleaved Carbon Fiber-Reinforced Epoxy Composites. Compos. Sci. Technol. 2004, 64, 2517–2523. [Google Scholar] [CrossRef]
  6. Ouyang, Q.; Wang, X.; Yao, Y.; Liu, L. Improved Damping and Mechanical Properties of Carbon Fibrous Laminates with Tailored Carbon Nanotube/Polyurethane Hybrid Membranes. Polym. Polym. Compos. 2021, 29, 1240–1250. [Google Scholar] [CrossRef]
  7. Zhu, X.; Li, Y.; Yu, T.; Zhang, Z. Enhancement of the Interlaminar Fracture Toughness and Damping Properties of Carbon Fiber Reinforced Composites Using Cellulose Nanofiber Interleaves. Compos. Commun. 2021, 28, 100940. [Google Scholar] [CrossRef]
  8. Akbolat, M.Ç.; Katnam, K.B.; Soutis, C.; Potluri, P.; Sprenger, S.; Taylor, J. On Mode-I and Mode-II Interlaminar Crack Migration and R-Curves in Carbon/Epoxy Laminates with Hybrid Toughening via Core-Shell Rubber Particles and Thermoplastic Micro-Fibre Veils. Compos. Part B Eng. 2022, 238, 109900. [Google Scholar] [CrossRef]
  9. Chen, Q.; Wu, F.; Jiang, Z.; Zhang, H.; Yuan, J.; Xiang, Y.; Liu, Y. Improved Interlaminar Fracture Toughness of Carbon Fiber/Epoxy Composites by a Combination of Extrinsic and Intrinsic Multiscale Toughening Mechanisms. Compos. Part B Eng. 2023, 252, 110503. [Google Scholar] [CrossRef]
  10. Ni, N.; Wen, Y.; He, D.; Yi, X.; Zhao, Z.; Xu, Y. Synchronous Improvement of Loss Factors and Storage Modulus of Structural Damping Composite with Functionalized Polyamide Nonwoven Fabrics. Mater. Des. 2016, 94, 377–383. [Google Scholar] [CrossRef]
  11. İnal, O.; Katnam, K.B.; Potluri, P.; Soutis, C. Progress in Interlaminar Toughening of Aerospace Polymer Composites Using Particles and Non-Woven Veils. Aeronaut. J. 2022, 126, 222–248. [Google Scholar] [CrossRef]
  12. Cilento, F.; Martone, A.; Giordano, M. Insights on Shear Transfer Efficiency in “ Brick-and-Mortar ” Composites Made of 2D Carbon Nanoparticles. Nanomaterials 2022, 12. [Google Scholar] [CrossRef] [PubMed]
  13. Domun, N.; Paton, K.R.; Blackman, B.R.K.; Kaboglu, C.; Vahid, S.; Zhang, T.; Dear, J.P.; Kinloch, A.J.; Hadavinia, H. On the Extent of Fracture Toughness Transfer from 1D/2D Nanomodified Epoxy Matrices to Glass Fibre Composites. J. Mater. Sci. 2020, 55, 4717–4733. [Google Scholar] [CrossRef]
  14. Wang, J.; Jin, X.; Li, C.; Wang, W.; Wu, H.; Guo, S. Graphene and Graphene Derivatives Toughening Polymers: Toward High Toughness and Strength. Chem. Eng. J. 2019, 370, 831–854. [Google Scholar] [CrossRef]
  15. Cilento, F.; Martone, A.; Pastore Carbone, M.G.; Galiotis, C.; Giordano, M. Nacre-like GNP/Epoxy Composites: Reinforcement Efficiency Vis-à-Vis Graphene Content. Compos. Sci. Technol. 2021, 211, 108873. [Google Scholar] [CrossRef]
  16. Park, Y.T.; Qian, Y.; Chan, C.; Suh, T.; Nejhad, M.G.; Macosko, C.W.; Stein, A. Epoxy Toughening with Low Graphene Loading. Adv. Funct. Mater. 2015, 25, 575–585. [Google Scholar] [CrossRef]
  17. Wang, J.; Li, C.; Zhang, X.; Xia, L.; Zhang, X.; Wu, H.; Guo, S. Polycarbonate Toughening with Reduced Graphene Oxide: Toward High Toughness, Strength and Notch Resistance. Chem. Eng. J. 2017, 325, 474–484. [Google Scholar] [CrossRef]
  18. Zhang, H.; Liu, Y.; Kuwata, M.; Bilotti, E.; Peijs, T. Improved Fracture Toughness and Integrated Damage Sensing Capability by Spray Coated CNTs on Carbon Fibre Prepreg. Compos. Part A Appl. Sci. Manuf. 2015, 70, 102–110. [Google Scholar] [CrossRef]
  19. Huang, S.; Fu, Q.; Yan, L.; Kasal, B. Characterization of Interfacial Properties between Fibre and Polymer Matrix in Composite Materials – A Critical Review. J. Mater. Res. Technol. 2021, 13, 1441–1484. [Google Scholar] [CrossRef]
  20. Ahmadi-Moghadam, B.; Taheri, F. Fracture and Toughening Mechanisms of GNP-Based Nanocomposites in Modes I and II Fracture. Eng. Fract. Mech. 2014, 131, 329–339. [Google Scholar] [CrossRef]
  21. Liu, K.; Macosko, C.W. Can Nanoparticle Toughen Fiber-Reinforced Thermosetting Polymers? J. Mater. Sci. 2019, 54, 4471–4483. [Google Scholar] [CrossRef]
  22. Quan, D.; Mischo, C.; Binsfeld, L.; Ivankovic, A.; Murphy, N. Fracture Behaviour of Carbon Fibre/Epoxy Composites Interleaved by MWCNT- and Graphene Nanoplatelet-Doped Thermoplastic Veils. Compos. Struct. 2020, 235, 111767. [Google Scholar] [CrossRef]
  23. Nagi, C.S.; Ogin, S.L.; Mohagheghian, I.; Crean, C.; Foreman, A.D. Spray Deposition of Graphene Nano-Platelets for Modifying Interleaves in Carbon Fibre Reinforced Polymer Laminates. Mater. Des. 2020, 193, 108831. [Google Scholar] [CrossRef]
  24. Wang, F.; Wang, B.; Zhang, Y.; Zhao, F.; Qiu, Z.; Zhou, L.; Chen, S.; Shi, M.; Huang, Z. Enhanced Thermal and Mechanical Properties of Carbon Fiber/Epoxy Composites Interleaved with Graphene/SiCnw Nanostructured Films. Compos. Part A Appl. Sci. Manuf. 2022, 162, 107129. [Google Scholar] [CrossRef]
  25. Moustapha Sarr, M.; Kosaka, T. Effect of Cellulose Nanofibers on the Fracture Toughness Mode II of Glass Fiber/Epoxy Composite Laminates. Heliyon 2023, 9, e13203. [Google Scholar] [CrossRef] [PubMed]
  26. Körbelin, J.; Kötter, B.; Voormann, H.; Brandenburg, L.; Selz, S.; Fiedler, B. Damage Tolerance of Few-Layer Graphene Modified CFRP: From Thin-to Thick-Ply Laminates. Compos. Sci. Technol. 2021, 209. [Google Scholar] [CrossRef]
  27. Cilento, F.; Curcio, C.; Martone, A.; Liseno, A.; Capozzoli, A.; Giordano, M. Effect of Graphite Nanoplatelets Content and Distribution on the Electromagnetic Shielding Attenuation Mechanisms in 2D Nanocomposites. J. Compos. Sci. 2022, 6, 257. [Google Scholar] [CrossRef]
  28. ASTM D 790-17, Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials1 2017.
  29. Brittain, R.; Liskiewicz, T.; Morina, A.; Neville, A.; Yang, L. Diamond-like Carbon Graphene Nanoplatelet Nanocomposites for Lubricated Environments. Carbon N. Y. 2023, 205, 485–498. [Google Scholar] [CrossRef]
  30. Morits, M.; Verho, T.; Sorvari, J.; Liljeström, V.; Kostiainen, M.A.; Gröschel, A.H.; Ikkala, O. Toughness and Fracture Properties in Nacre-Mimetic Clay/Polymer Nanocomposites. Adv. Funct. Mater. 2017, 27, 1605378. [Google Scholar] [CrossRef]
  31. Reinforced, N.; Fiber, G. Interlaminar Fracture Behavior of Nanoclay Reinforced Glass Fiber Composites. 2008, 42. [CrossRef]
Preprints 72942 g001
Figure 1. Spray deposition process of GNP coating on CFRP prepreg.
Figure 1. Spray deposition process of GNP coating on CFRP prepreg.
Preprints 72942 g001
Preprints 72942 g002
Figure 2. The surface of (a) prepreg (reference), (b) LW – GNP coated prepreg; (c) HW – GNP coated prepreg.
Figure 2. The surface of (a) prepreg (reference), (b) LW – GNP coated prepreg; (c) HW – GNP coated prepreg.
Preprints 72942 g002
Preprints 72942 g003
Figure 3. Lamination sequence (a); vacuum bagging and autoclave process (b); CFRP panels with interleaved GNP layer (c).
Figure 3. Lamination sequence (a); vacuum bagging and autoclave process (b); CFRP panels with interleaved GNP layer (c).
Preprints 72942 g003
Preprints 72942 g004
Figure 4. Mode I DCB (a) and Mode II ENF (b) testing configuration.
Figure 4. Mode I DCB (a) and Mode II ENF (b) testing configuration.
Preprints 72942 g004
Preprints 72942 g005
Figure 5. DSC curves in the heating phase (10°C/min) for uncured prepregs samples.
Figure 5. DSC curves in the heating phase (10°C/min) for uncured prepregs samples.
Preprints 72942 g005
Preprints 72942 g006
Figure 6. TGA curves of cured laminate samples.
Figure 6. TGA curves of cured laminate samples.
Preprints 72942 g006
Preprints 72942 g007
Figure 7. DSC curves in the heating phase (10°C/min) for cured laminate samples.
Figure 7. DSC curves in the heating phase (10°C/min) for cured laminate samples.
Preprints 72942 g007
Preprints 72942 g008
Figure 8. Storage modulus (a) and tanδ (b) of laminates samples.
Figure 8. Storage modulus (a) and tanδ (b) of laminates samples.
Preprints 72942 g008
Preprints 72942 g009
Figure 9. Load-displacement curves for representative fracture Mode I tests of reference CF/epoxy composites and LW-GNP and HW-GNP ones.
Figure 9. Load-displacement curves for representative fracture Mode I tests of reference CF/epoxy composites and LW-GNP and HW-GNP ones.
Preprints 72942 g009
Preprints 72942 g010
Figure 10. GIC values for the REF, LW-GNP and HW-GNP specimens.
Figure 10. GIC values for the REF, LW-GNP and HW-GNP specimens.
Preprints 72942 g010
Preprints 72942 g011
Figure 11. Micrographs of tested samples: ENF fractures of (a) REF; (b) LW-GNP; (c) HW-GNP.
Figure 11. Micrographs of tested samples: ENF fractures of (a) REF; (b) LW-GNP; (c) HW-GNP.
Preprints 72942 g011
Preprints 72942 g012
Figure 12. Micrographs of tested samples: DCB fractures of (a) REF; (b) LW-GNP; (c) HW-GNP.
Figure 12. Micrographs of tested samples: DCB fractures of (a) REF; (b) LW-GNP; (c) HW-GNP.
Preprints 72942 g012
Preprints 72942 g013
Figure 13. Specimen micrographs, the GNP layer is higligthed by a dot line (a) REF – no GNP; (b) LW-GNP – 140 microns; (c) HW-GNP – 320 microns.
Figure 13. Specimen micrographs, the GNP layer is higligthed by a dot line (a) REF – no GNP; (b) LW-GNP – 140 microns; (c) HW-GNP – 320 microns.
Preprints 72942 g013
Preprints 72942 g014
Figure 14. Fracture surfaces for mode I specimens. (a) LW-GNP, (b) HW-GNP layer.
Figure 14. Fracture surfaces for mode I specimens. (a) LW-GNP, (b) HW-GNP layer.
Preprints 72942 g014
Table 1. List of samples.
Table 1. List of samples.
Sample Lamination
sequence		 Filler/matrix
content [wt/wt]		 Number of deposition cycles Coating areal weight [g/m2]
REF [(90/+45/-45/0)2]S - 0 -
LW-GNP [(90/+45/-45/0)2]S* 80/20 1 10
HW-GNP [(90/+45/-45/0)2]S* 80/20 4 40
* coated prepreg at the mid-section
Table 2. DSC results on prepreg.
Table 2. DSC results on prepreg.
Actual areal weight
[g/m2]		 Tpeak
[°C]		 Peak area
[J/g]
REF - 145.13 394.80
LW-GNP 15 145.31 405.68
HW-GNP 59 148.70 371.43
Table 3. Results of test conducted on laminates.
Table 3. Results of test conducted on laminates.
Tg,DSC
[°C]		 Tg,DMA
[°C]		 E’
[GPa]		 ΔE’*
[%]		 tanδ
[-]		 Δtanδ*
[%]
REF 151.9±0.5 159.4±2.4 25.1±1.6 - 0.024±0.001 -
LW-GNP 145.1±0.7 166.7±0.8 23.2±2.0 -7 0.030±0.007 +25
HW-GNP 145.9±0.2 164.4±0.7 26.1±2.5 +3 0.025±0.005 +6
*Δ refers to the variation of the parameter with respect to the reference value.
Table 4. Results of ILLS, DCB, and ENF tests conducted on laminates.
Table 4. Results of ILLS, DCB, and ENF tests conducted on laminates.
ILSS
[MPa]		 ΔILSS*
[%]		 GIC, initial
[J/m2]		 ΔGIC, intial*
[%]		 GIC, propagation
[J/m2]		 ΔGIC, propagation *
[%]		 GIIC
[J/m2]		 ΔGIIC*
[%]
REF 63.1±0.3 - 174±29 - 199±12 - 1642±206 -
LW-GNP 38.2±1.4 -40 92±10 -47 101±8 -49 532±56 -67
HW-GNP 34.5±0.4 -46 147±29 -15 128±10 -36 206±5 -87
*Δ refers to the variation of the parameter with respect to the reference value.
Table 5. Micrographs of tested samples (bulk and ILSS fractures).
Table 5. Micrographs of tested samples (bulk and ILSS fractures).
REF LW-GNP HW-GNP
Bulk Preprints 72942 i001 Preprints 72942 i002 Preprints 72942 i003
ILSS Preprints 72942 i004 Preprints 72942 i005 Preprints 72942 i006
Table 6. Comparison of main properties of REF, LW-GNP and HW-GNP samples.
Table 6. Comparison of main properties of REF, LW-GNP and HW-GNP samples.
Property @RT REF LW-GNP HW-GNP
E’ [GPa] 25.1±1.6 23.2±2.0 26.1±2.5
tanδ [-] 0.024±0.001 0.030±0.007 0.025±0.005
ILSS [MPa] 63.1±0.3 38.2±1.4 34.5±0.4
GCI [J/m2] 174±29 92±10 147±29
GCII [J/m2] 1642±206 532±56 206±5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated