Predictive Cell-Culture Time-Evolution Based on Electric Models

Preprint

Article

Predictive Cell-Culture Time-Evolution Based on Electric Models

Altmetrics

Downloads

118

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts

Abstract

The cell concentration measurement on a culture assay using bioimpedance is a very useful tool, but it is complex to translate impedance to cell concentration values. The purpose of this work is to find a method to obtain in real time the cell concentration values for a given cell-culture assay using an oscillator as the measurement circuit. From a basic cell-electrode model, enhanced models of the cell culture immersed in a saline solution (culture medium) can be derived. These models can be used in a fitting routine to real time estimation of the cell concentration in a cell culture, using the oscillation frequency and amplitude delivered by measurement circuits proposed by the authors. Based on real experimental data (frequency and amplitude of oscillations) obtained by connecting the cell culture to an oscillator as a load, the fitting routine is simulated, and real time data of cell concentration is achieved. These results are compared with concentration data found by traditional optical methods for counting. In addition, the error obtained is divided and analyzed in two parts: in the first part of the experiment (when the few cells are adapting to the culture medium) and the second part of the experiment (when the cells grow exponentially until they completely cover the well).Low error values are obtained in the growth phase of the cell culture (the relevant phase), therefore the results obtained are considered to be promising, proving that the fitting routine is valid, and that the cell concentration can be measured in real time using an oscillator.

Keywords:

Subject: Engineering - Bioengineering

1. Introduction

In recent years, a lot of research has been focused on growth monitoring of a cell-culture (CC) assay for the development of a non-invasive, cheap and robust technique [1,2,3,4,5]. Biomedical setups focused to toxicology assays [6], cancer characterization experiments [7,8], biochemical [9], immune-assays [10], stem cells differentiation protocols [11], etc., seek to quantify the number of cells for characterizing a diversity of research objectives and techniques [12,13]. The modeling of a biological sample (BS) allows to know its electrical behavior and several useful parameters. In many cases these models are not useful by themselves to obtain the required result. For this reason, the main purposes of this work are to improve the existing models and to develop an automatic procedure to obtain in real time (RT) the concentration of a CC.

ECIS (electrical cell-substrate impedance sensing) technique senses the electrical response generated on a BS ([14,15]), the CC, when it is excited with an alternating current or voltage electrical source at several frequencies, as consequence of its conductivity properties. The current-voltage relationship, or Ohm’s law, returns an impedance value with a real part and an imaginary part, the so-called Bioimpedance (BI). Since the current applied to the BI must be very low, the ECIS technique requires precise and robust electronics [16]. The CC is immersed in an ionic solution, the culture medium, and the cells of the CC settle on the substrate of the culture well, where the electrodes are placed. The ideal use of this technique would be to inject a signal whose amplitude and frequency are set at their optimum values, i.e., the values most sensitive to a change in BI. In this way, the value of the BI is obtained, but to understand its value, a model of the electrical behavior of an electrode immersed in an ionic solution must be used. There are some works focused on modeling BI by solve electrical system equations [1,5] or performing finite elements simulations [17,18] of the whole system, which comprises CC and electrodes.

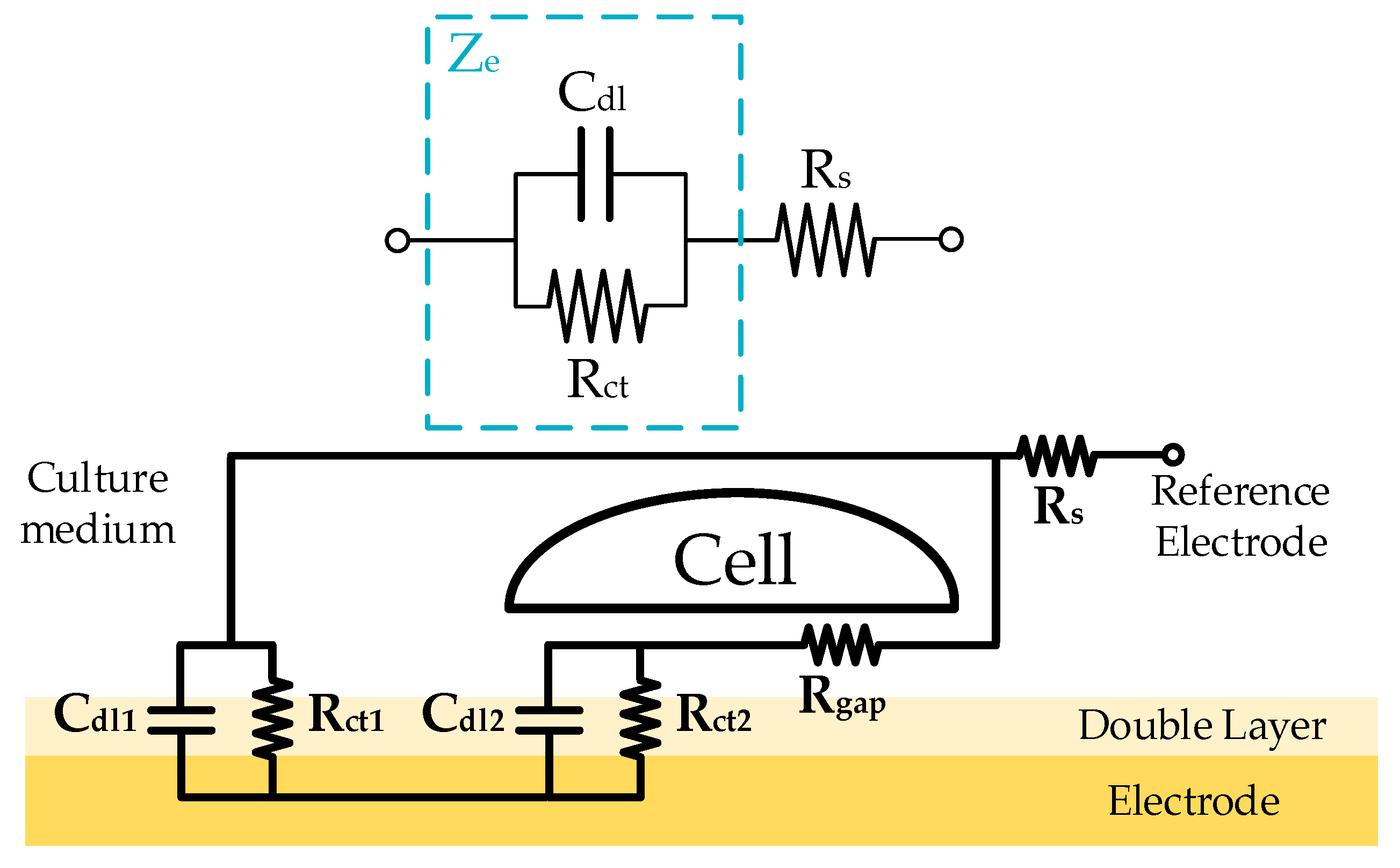
Reference [5] models the electrochemical behavior of an electrode immersed in an ionic solution. The electrical behavior of an electrode immersed in an ionic solution is modeled as a resistance (R_ct) in parallel with a capacitor (C_dl), whose total impedance is Z_e (Figure 1a). Spreading resistance (R_s) is the opposition to current flow through saline solution in contact with electrode. When CC growths, it covers the electrode as a cell layer. The cell layer, act as an impedance whose effects is added to the effect of the electrode. In that way, the real electrical behavior of the cell-electrode (CE) system has been reported in [19]. Figure 1b shows the layout of the electrical model components in a real CC. The electrical model presents the division of R_ct and C_dl in two parallel branches, modeling the electrode area (A_e) covered by cells (A_C) and not covered by cells (A_nC).

Since cell growth is the main parameter to measure, the electrical model must include a parameter that acts as an indicator of cell growth. This parameter is the fill-factor (ff), which is the percentage of electrode area covered by cells in %1, i.e., if A_c = A_e the value of ff is 1, but if A_c = 0 the value of ff is 0. In that way R_ct1, C_dl1, R_ct2 and C_dl2 (electrode model parameters covered and not covered by cells) are defined by the next expressions:

\begin{matrix} R_{c t 1} = \frac{R_{c t}}{1 - f f} C_{d l 1} = C_{d l} \cdot (1 - f f) \\ R_{c t 2} = \frac{R_{c t}}{f f} C_{d l 2} = C_{d l} \cdot f f \end{matrix}

(1)

The TF which models the CE impedance is obtained by solving the circuit of Figure 1b. Equation (2) shows the BI TF, Z_CE (s), which has been parameterized.

\begin{matrix} Z_{C E} (s) = \frac{k_{2} \cdot s^{2} + k_{1} \cdot \frac{ω_{0 z}}{Q} \cdot s + k_{0} \cdot ω_{0 z}^{2}}{s^{2} + \frac{ω_{0 z}}{Q} \cdot s + ω_{0 z}^{2}} \\ k_{2} = R_{s} k_{1} = R_{s} + \frac{R_{g a p} \cdot R_{c t 1}}{2 \cdot R_{g a p} + R_{c t 1} + R_{c t 2}} k_{0} = R_{s} + \frac{R_{c t 1} \cdot (R_{g a p} + R_{c t 2})}{R_{g a p} + R_{c t 1} + R_{c t 2}} \\ ω_{0 z} = \sqrt{\frac{R_{g a p} + R_{c t 1} + R_{c t 2}}{R_{g a p} \cdot {(C_{d l} \cdot R_{c t})}^{2}}} Q = ω_{0 z} \cdot \frac{R_{g a p} \cdot C_{d l} \cdot R_{c t}}{2 \cdot R_{g a p} + R_{c t 1} + R_{c t 2}} \end{matrix}

(2)

This is the basic model, the Single-Electrode Well (SEW) model, considers that electrodes under the cell is a unique big electrode. On this work, two more models (improvements of the SEW model) are proposed, which consider the real electrode composed by 10 microelectrodes and 1 large reference electrode: Real-Electrode Well (REW) model and Fractional-Order Well (FEW) model.

This work is based on the measurements obtained for the author works [19]. In these, the measuring circuit is an oscillator. From the frequency and amplitude of oscillation, which varies with ff, it is desired to obtain the cell concentration in real time (RT), by using the Barkhausen stability criterion (BSC), which is the mathematical condition that the closed-loop feedback system must fulfill to obtain sustained oscillations.

The objective of the presented work is to evaluate the impact of proposed electric models for cell cultures and electrodes, on the description of assays time evolution, in such a way that it will be possible to predict the cell number and density from initial time of the experiment, until its confluence phase. The work presented in the next will describe the electric models employed by us, and the computer algorithms developed to make real-time predictions for cell-culture status.

2. Material and Methods

On this work, the combination of model fitting, the use of the Oscillation-Based Test (OBT) as a sensor and the minimization of a cost function (CF) have the main target of predict ff values, and cell concentration in real-time (RT), i.e., during a real growth experiment of a CC assay. First, a routine will be designed (based on the previous work [20]) in which a real experiment is simulated and the value of ff is predicted at each moment, as well as the cell concentration. This routine will be tested using the REW and FO REW electrical models on data obtained from experiment with three cell lines.

The first cell line is formed by Chinese hamster ovarian fibroblasts: This cell line is identified as AA8 (American Type Culture Collection). This sample is immersed in McCoy’s medium supplemented with 10 % (v/v) foetal calf serum; 2 mM L-glutamine, 50 μg/ml streptomycin and 50 U/ml penicillin.

The second and third biological samples under test are two Mouse neuroblastoma cell lines. The N2a cell line and its cell line stably expressing wildtype human amyloid precursor protein, N2a-APP. Cells were cultured in medium consisting of 50% DMEM High glucose (Biowest) and 50% Opti-MEM (Gibco) supplemented with 10% (v/v) foetal bovine serum (FBS) (Gibco), 2 mM L-glutamine, 50 μg/ml streptomycin and 50 U/ml penicillin (Sigma-Aldrich). N2a-APP was also supplemented with 0.4% Geneticin (Gibco).

Figure 2. 8W10E PET Applied BioPhysics electrodes. Eight separated wells with ten circular biocompatible gold microelectrodes of 250 μm diameter, and a large reference electrode with an area approximately 400 larger than each circular microelectrode.

All cell lines were maintained at 37° C in a humidified atmosphere with 5% CO2 and they were routinely subcultured. Different initial number of cells (N_ini) was seeded for our experiments: 2500, 5000 and 10000 cells. The AA8 experiments start with a N_ini of 2500 cells in wells 1 and 3, 5000 cells in wells 4 and 5, and 10000 cells in wells 7 and 8. On the other hand, the N2a and N2aAPP experiments start with a N_ini of 2500 cells in wells 2 and 6, 5000 cells in wells 3 and 7, and 10000 cells in wells 4 and 8. The employed culture-wells are commercial from Applied Biophysics (model 8W10E PET) [21]. It contains eight separated wells with ten circular biocompatible gold microelectrodes of 250 μm diameter each.

2.1. Bioimpedance Modelling

2.1.1. Real-Electrode Well Model (11 Electrodes)

REW model considers the real electrode structure, 10 microelectrodes and one big reference electrode. Figure 3 shows the block diagram of the REW model, between voltage V_CE and ground. There are 10 microelectrodes, e₁ to e₁₀, and the reference electrode, e_r. Each electrode is composed by the model of the electrode of Figure 1. The only difference is the value of the reference electrode parameters, since depend on the area of the electrode. To reduce the complexity of the model, it can be used the relationship between the parameters of the microelectrode model and the reference electrode model (it is considered that R_gap takes the same value for microelectrodes and reference electrode). The relationship between R_ct and R_ctr (reference electrode R_ct parameter), C_dl and C_dlr (reference electrode C_dl parameter), and R_s and R_sr (reference electrode R_s parameter) can be derived from [5] as,

\begin{matrix} \frac{R_{c t r}}{R_{c t}} = \frac{R_{c t}^{'}}{A_{r e}} \frac{A_{e}}{R_{c t}^{'}} \to R_{c t r} = R_{c t} \frac{A_{e}}{A_{r e}} [Ω] \\ \frac{C_{d l r}}{C_{d l}} = \frac{C_{d l}^{'} \cdot A_{e r}}{C_{d l}^{'} \cdot A_{e}} \to C_{d l r} = C_{d l} \frac{A_{r e}}{A_{e}} [F] \\ \frac{R_{s r}}{R_{s}} = \frac{ρ \cdot \sqrt{π}}{4 \cdot \sqrt{A_{r e}}} \frac{4 \cdot \sqrt{A_{e}}}{ρ \cdot \sqrt{π}} \to R_{s r} = R_{s} \sqrt{\frac{A_{e}}{A_{r e}}} [Ω] \end{matrix}

(3)

where A_re is reference electrode area, and ρ is the electrolyte resistivity of the saline solution. Since the A_e ⁄ A_re factor is repeated, can be defined k_e as k_e = A_e ⁄ A_re. Therefore, the parameters of the electric model of the reference electrode are:

R_{c t r} = R_{c t} \cdot k_{e} C_{d l r} = \frac{C_{d l}}{k_{e}} R_{s r} = R_{s} \cdot \sqrt{k_{e}}

(4)

Using the relationships between parameters of the microelectrodes model and reference electrodes model, Z_well (s) can be defined as TF of the REW model. It is composed by a gain, one pole and one zero. The TF is very complex, but can be simplified for the case of ff→0 (electrode empty of cells) and ff→1 (electrode full of cells, or confluence phase), and obtain the pole, zero and gain expressions for both cases:

\begin{matrix} p_{f f \to 0} = \frac{- 1}{C_{d l} R_{c t}} z_{f f \to 0} = - \frac{R_{c t} \cdot (1 + 10 \cdot k_{e}) + R_{s} \cdot (1 + 10 \cdot \sqrt{k_{e}})}{C_{d l} R_{c t} R_{s} \cdot (1 + 10 \cdot \sqrt{k_{e}})} \\ p_{f f \to 1} = \frac{- 1}{C_{d l} R_{c t}} z_{f f \to 1} = - \frac{R_{c t} \cdot (1 + 10 \cdot k_{e}) + R_{s} \cdot (1 + 10 \cdot \sqrt{k_{e}}) + 11 \cdot R_{g a p}}{C_{d l} R_{c t} \cdot (R_{s} \cdot (1 + 10 \cdot \sqrt{k_{e}}) + 11 \cdot R_{g a p})} \\ k_{w e l l}^{f f \to 0} = R_{c t} \cdot (\frac{1}{10} + k_{e}) + R_{s} \cdot (\frac{1}{10} + \sqrt{k_{e}}) \\ k_{w e l l}^{f f \to 0} = R_{c t} \cdot (\frac{1}{10} + k_{e}) + R_{s} \cdot (\frac{1}{10} + \sqrt{k_{e}}) + 11 \cdot \frac{R_{g a p}}{10} \end{matrix}

(5)

Working with the equations of poles and zeros, the values of R_ct and C_dl for ff→0 and ff→1 are derived:

\begin{array}{l} R_{c t}^{f f \to 0} = - \frac{R_{s} \cdot (1 + 10 \cdot \sqrt{k_{e}}) \cdot (p_{f f \to 0} - z_{f f \to 0})}{p_{f f \to 0} \cdot (1 + 10 \cdot k_{e})} \\ C_{d l}^{f f \to 0} = - \frac{1 + 10 \cdot k_{e}}{R_{s} \cdot (1 + 10 \cdot \sqrt{k_{e}}) \cdot (p_{f f \to 0} - z_{f f \to 0})} \\ R_{c t}^{f f \to 1} = - \frac{(R_{s} \cdot (1 + 10 \cdot \sqrt{k_{e}}) + 11 \cdot R_{g a p}) \cdot (p_{f f \to 0} - z_{f f \to 0})}{p_{f f \to 0} \cdot (1 + 10 \cdot k_{e})} \\ C_{d l}^{f f \to 1} = - \frac{1 + 10 \cdot k_{e}}{(R_{s} \cdot (1 + 10 \cdot \sqrt{k_{e}}) + 11 \cdot R_{g a p}) \cdot (p_{f f \to 0} - z_{f f \to 0})} \end{array}

(6)

To improve the fitting, it is considered that R_s parameter changes with ff , as described in work [19]. Then R_s is splited on two terms R_si and ΔR_s, and

R_{s} (k) = R_{s i} + {f f}^{n} (k) ∙ Δ R_{s}

. The expression means that when ff→0, R_s takes a value of R_si, and the value of ff on each moment k increments the value of R_s.

2.1.2. Fractional Order Model

Fractional Order (FO) models are based on the premise that the order of a differential operator can be non-integer. It can be defined the FO Constant Phase element (CPE), which is used to is used to perform the characterization of electrodes for bioimpedance measurement of animal tissue. In combination with the reference [22], CPE can substitute the C_dl term on the REW model to obtain a FO model. Capacitors of the CE model are replaced by CPE described with FO operators,

X_{C_{d l 1}} = \frac{1}{s^{α_{1}} C_{d l 1}} X_{C_{d l 2}} = \frac{1}{s^{α_{2}} C_{d l 2}}

(7)

where α₁ and α₂ are the FO order of the reactances

X_{C_{d l 1}}

and

X_{C_{d l 2}}

. Then, as in previous section, the TF for the cases ff→0 and ff→1 can be obtained:

\begin{array}{l} Z_{w e l l}^{f f \to 0} (λ_{1}) = k_{w e l l}^{f f \to 0} \frac{p_{f f \to 0}}{z_{f f \to 0}} \frac{λ_{1} + z_{f f \to 0}}{λ_{1} + p_{f f \to 0}} \\ Z_{w e l l}^{f f \to 1} (λ_{2}) = k_{w e l l}^{f f \to 1} \frac{p_{f f \to 1}}{z_{f f \to 1}} \frac{λ_{2} + z_{f f \to 1}}{λ_{2} + p_{f f \to 1}} \\ where λ_{n} = s^{α_{n}} 0 < α_{n} < 2 \end{array}

(8)

Note that, when ff→0, α₂ has no influence in the system behavior, and, when ff→1, α₁ has any influence in the system behavior. Since changes on α₁ and α₁ modified the slope of magnitude and phase of frequency response ΔR_s ([19]) becomes redundant and can be removed from the FO model. Due to the high complexity of the model (cross products of α₁ and α₂), the model is implemented in a different way than the previous section. REW model has been implemented completely to obtain its parameters, while FO models are, in this case, implemented in a transitional mode. This means that, considering that the pole is constant for any value of ff, a transition from

z_{f f \to 0}

z_{f f \to 0}

and from

k_{w e l l}^{f f \to 0}

k_{w e l l}^{f f \to 1}

is implemented using ff to change from

Z_{w e l l}^{f f \to 0} (λ_{1})

Z_{w e l l}^{f f \to 1} (λ_{2})

. Then, the implemented model is:

Z_{w e l l} (λ_{1,} λ_{2}) = k_{w e l l} \frac{p}{z} \frac{λ + z}{λ + p}

(9)

where

p = p_{f f \to 0} = p_{f f \to 1}

and,

\begin{array}{l} z = (1 - f f) \cdot z_{f f \to 0} + f f \cdot z_{f f \to 1} \\ k_{w e l l} = (1 - f f) \cdot k_{w e l l}^{f f \to 0} + f f \cdot k_{w e l l}^{f f \to 1} \\ λ = (1 - f f) \cdot λ_{1} + f f \cdot λ_{2} \end{array}

(10)

2.3. Cost Function

During the RT estimation, the models previously described receive the values of oscillation frequency and amplitude (

f_{C E}

and

a_{C E}

) and return the value of ff and cell concentration. On the next section, the process to use the model to predict ff on real time is explained, but this task need a way to obtain some parameter (including ff) from the BSC. The BSC is the mathematical condition that the closed-loop feedback system must fulfill to obtain sustained oscillations. An oscillator must meet some conditions to get self-sustained oscillation, being one that should include a linear part, G(s = jω) in Laplace domain, and a non-linear part, N(a_osc, f_osc), where G is the transfer function of the linear part of the circuit, s is the Laplace operator, j is imaginary unit and ω_osc is the oscillation frequency on rad/s being its value ω_osc = 2πf_osc, and N is the linearized model of the non-linear part of the circuit (an electronic comparator on the present work). Note that f_osc and a_osc are not the same variables as

f_{C E}

and

a_{C E}

, but f_osc and a_osc can be easily estimated using some internal gains of the oscillator circuit. As the objective of this work is not to explain in detail the oscillator circuit, the calculation of the oscillating variables will not be explained in detail, since their computation is trivial. Then, according to the BSC, the condition the circuit must meet is:

f (a_{o s c}, f_{o s c}) \equiv 1 + G (s = j ω_{o s c}) \cdot N (a_{o s c}, f_{o s c}) = 0

(11)

where f(a_osc, f_osc) is a complex function that depends on f_osc and a_osc. This function can be rewritten as:

f (a_{o s c}, f_{o s c}) = h_{1} (a_{o s c}, f_{o s c}) + j \cdot h_{2} (a_{o s c}, f_{o s c})

(12)

where h₁ and h₂ are the real and imaginary parts of f(a_osc, f_osc). The main goal of using BSC is obtaining the oscillation parameters. Then, since oscillation condition function must be equal to 0, in phasorial form, the condition is:

\begin{matrix} f (a_{o s c}, f_{o s c}) \equiv h ∠ φ = 0 ∠ 0 º \\ h = \sqrt{h_{1}^{2} + h_{2}^{2}} = 0 \\ φ = \tan^{- 1} (\frac{h_{2}}{h_{1}}) = 0 º \end{matrix}

(13)

where h and φ are, respectively, the module and angle of f(a_osc, f_osc) and must be equal to 0 and 0° to meet this condition. There are now the equations of the real part and the imaginary part of the BSC, which must be satisfied in order to have self-sustained oscillations. Using these equations two parameters of the system could be obtained if all others were known, but in this case, for the ff estimation process, this is not possible. Therefore, a cost function will be minimized to ensure that the BSC is satisfied, so that the values of more than two model parameters can be obtained on each moment in combination with the fitting routine (next section). The best way found to meet the condition is to use the module of the complex number h(a_osc, f_osc). Then, the CF can be defined as:

h (a_{o s c}, f_{o s c}) \equiv \sqrt{h_{1} {(a_{o s c}, f_{o s c})}^{2} + h_{2} {(a_{o s c}, f_{o s c})}^{2}}

(14)

The fact of h₁(a_osc, f_osc) and h₂(a_osc, f_osc) are squared assures they cannot compensate each other.

2.3. Fitting Routine

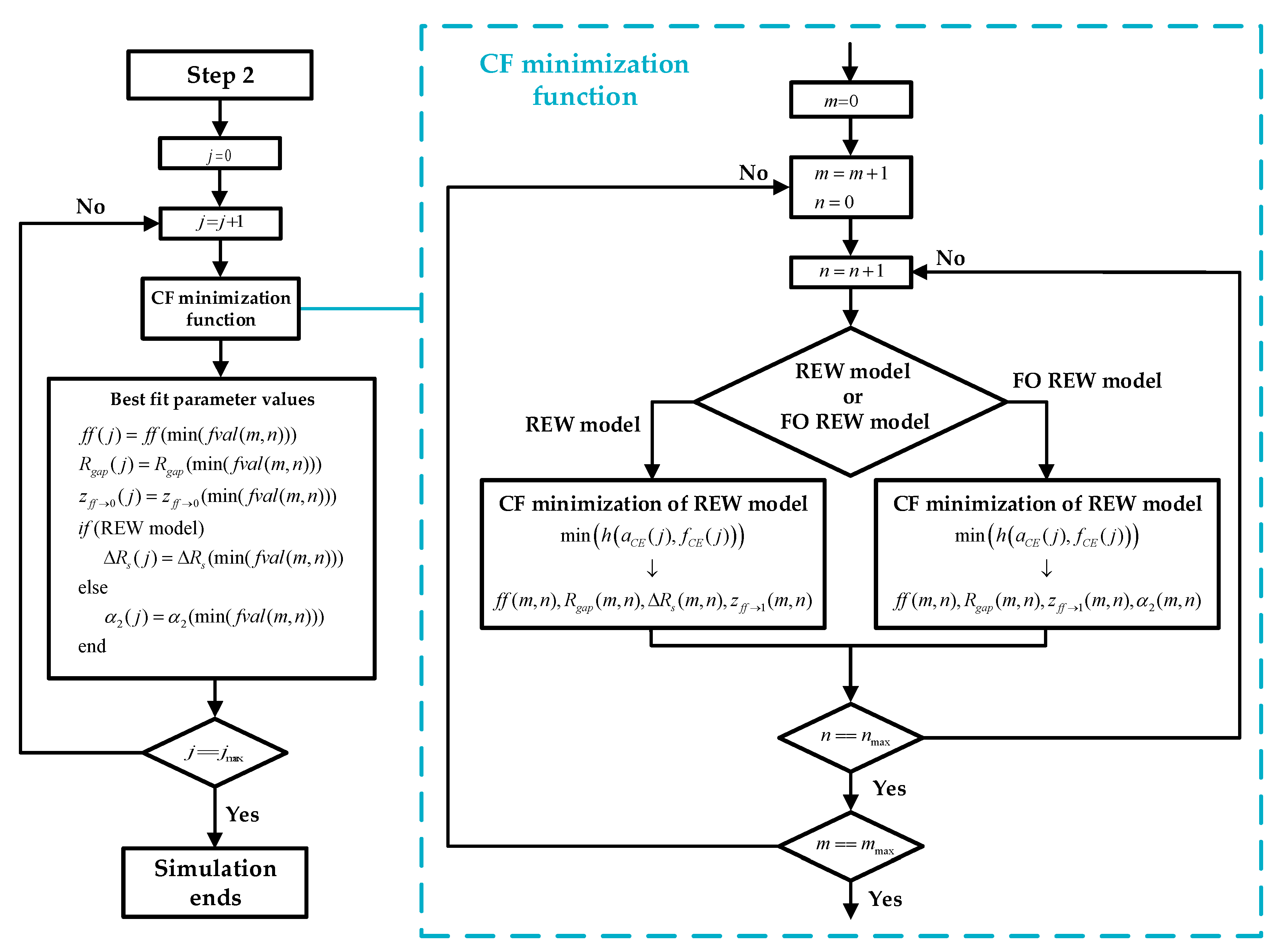
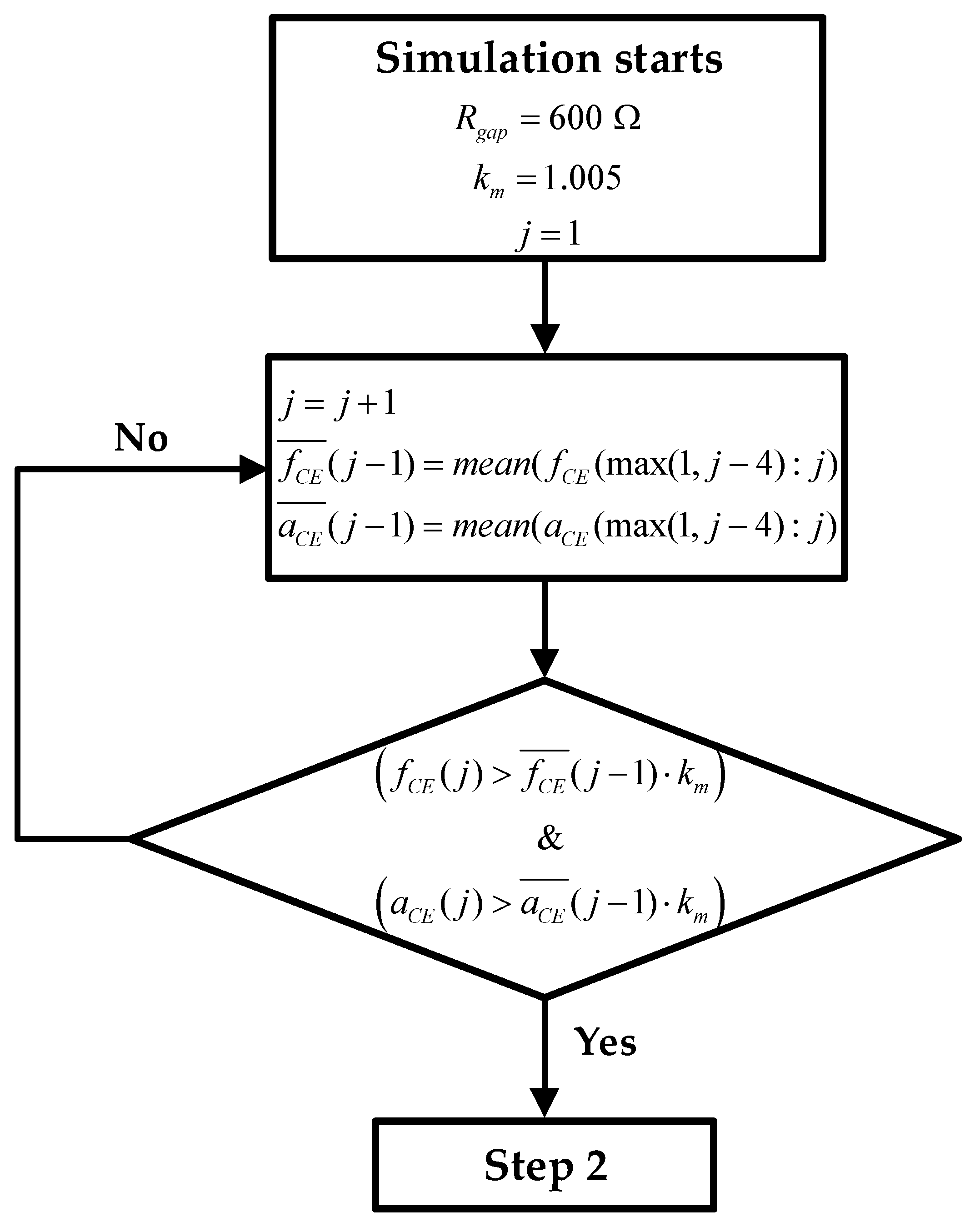
The key problem of knowing ff at each time of a real experiment is that the values of oscillation frequency and amplitude (

f_{C E}

and

a_{C E}

) when well is totally covered by cells (

f f \to 1

) are not available. That is, you can estimate the parameters of the models at the beginning of the experiment, where there is any cell in the well (

f f \to 0

) , but there are certain parameters that have no influence on the behavior of the system at this point. These parameters are R_gap,

z_{f f \to 1}

, ΔR_s (for the REW model), and also α₂ (for the FO REW model). The designed routine is as follows:

1.: Estimate initial values of f_CE and a_CE: Figure 4 shows the block diagram of the step 1, where the initial routine is presented in graphic form. During the first hours or days of the experiment, the mean of the last 5 values of $f_{C E}$ and $a_{C E}$ measured is calculated ( $\bar{f_{C E}}$ and $\bar{a_{C E}}$ ). As the sampling time (time between measurements) is 1 h, the average of the last 4 hours is taken together with the values just obtained. After each measurement, after calculating the mean, a check is performed to verify whether the values obtained are greater than the mean of the new measurement plus a margin (k_m = 1.005). If this condition is met, showed in (15), the lowest $\bar{f_{C E}}$ and $\bar{a_{C E}}$ are stored as minimum values. Figure 4 also defines the initial value of R_gap and the value of the constant k_m. Note that the index j is the time index, and goes from 1 to j_max. During the calculation of $\bar{f_{C E}}$ and $\bar{a_{C E}}$ j is incremented from 1 until (15) is satisfied. j_max is the maximum value of j, and its value is defined by the number of measurements taken during the real experiment.

$(f_{C E} (j) > \bar{f_{C E} (j - 1)} \cdot k_{m}) & (a_{C E} (j) > \bar{a_{C E} (j - 1)} \cdot k_{m})$

(15)
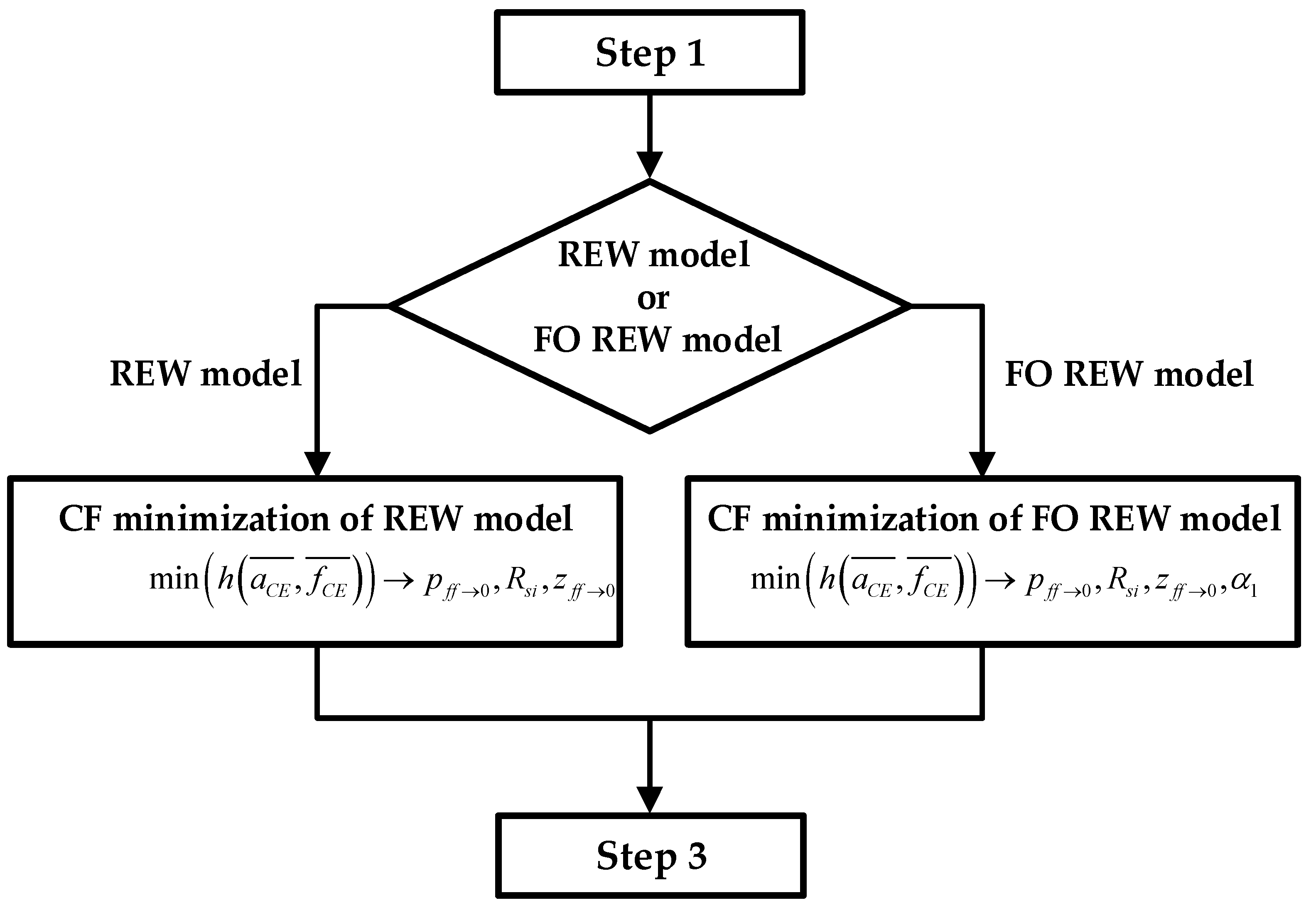
3.: Computation of the initial parameters of the electrical models: Using the minimum $\bar{f_{C E}}$ and $\bar{a_{C E}}$ estimated in the previous step, the initial parameters of the electrical models are fitted. The prediction is performed using the method of CF minimization. For the REW model the parameters p_(ff→1) (which met that p_(ff_→0₎ ≈ p_(ff→1)), R_si and z_(ff→0) are calculated, and the values of R_ct^(ff→0) and C_dl^(ff→0) can be derived from these using the two top equations of (6). For the FO REW model the parameters p_(ff→1) (which met that p_(ff→0) ≈ p_(ff→1)), R_s, z_(ff→0) and α₁ are calculated, and the values of R_ct^(ff→0) and C_dl^(ff→0) can be derived from these using also (6). The initial parameters calculated are the same for all t(j), and therefore they are not re-estimated during the simulation. The whole process of estimating the initial parameters is illustrated in the Figure 6 block diagram, which starts from the results of Step 1 and ends at the beginning of the third and last step.
3.: Real-time estimation of ff: The last step and the goal is to predict in RT the parameter ff. The computation of ff, once the initial parameters of the models are obtained (previous step), is performed for all the previous measurements and for all the measurements that will be performed until the end of the experiment. Figure 5 describes the whole prediction process.

Figure 5. Step 3: Block diagram of step 3 of RT simulation. Describe, after obtaining the initial parameters, the simulation process from j = 1 to j = j_max.

Figure 6. Step 2: Block diagram of step 2 of RT simulation, whose target is to find the initial parameters (

f f \to 0)

using the values of

\bar{f_{C E}}

and

\bar{a_{C E}}

.First, the time index j is initialized to start the estimation of ff from j = 1 to j = j_max. The minimization attempts to obtain the values for each j-measure of the parameters: ff, R_gap, z_(ff→1) and ΔR_s (for the REW model), : ff, R_gap, z_(ff→1) and α₂ (for the FO REW model) using

f_{C E} (j)

and

a_{C E} (j)

Figure 6. Step 2: Block diagram of step 2 of RT simulation, whose target is to find the initial parameters (

f f \to 0)

using the values of

\bar{f_{C E}}

and

\bar{a_{C E}}

f_{C E} (j)

and

a_{C E} (j)

For this purpose, a loop is used to increment the index j from 1 to j_max. Inside the loop, for each value of j, the CF minimization function is used to obtain the candidate values of the parameters to be calculated that obtain a lower f_val value (minimum value of h(a_osc, f_osc)). These candidate values are indexed by the indices m (from 1 to m_max) and n (from 1 to n_max). m and n index are internal to the CF minimization function, so the parameters computed inside the function (ff, R_gap, etc.) indexed with m and n are not the same as the parameters outside the function. When the parameters with the best f_val are obtained, among all, the ones with the lowest f_val are chosen and assigned as the values taken by the parameters for time j. Inside CF minimization function, the first step is to define the bounds of these parameters, which are shown in (3.2). ff bounds changes for each j-estimations, but the bounds of the others parameters remain constant for all j-estimations depending on the experience collected in the previous sections of this work.

\begin{matrix} f f^{b o u n d s} (j) = [\begin{matrix} f (j - 1) - 0.2 & f f (j - 1) + 0.2 \end{matrix}] \\ R_{g a p}^{b o u n d s} = [\begin{matrix} 0.1 & \infty \end{matrix}] z_{f f \to 1}^{b o u n d s} = [\begin{matrix} 10^{3} & 10^{5} \end{matrix}] \\ Δ R_{s}^{b o u n d s} = [\begin{matrix} - R_{s}^{f f \to 0} & 4 \cdot R_{s}^{f f \to 0} \end{matrix}] α_{2}^{b o u n d s} = [\begin{matrix} 0.9 & α_{1} \end{matrix}] \end{matrix}

(16)

CF minimization is performed using as initial values those shown in (3.3). As can be seen,

R_{g a p}^{i n i}

and

z_{f f \to 1}^{i n i}

have four and two initial values, respectively. The index m moves along the vector

R_{g a p}^{i n i}

(from 1 to m_max = 4) and the index n moves along

z_{f f \to 1}^{i n i}

(from 1 to n_max = 2). This is due to the fact that for each j-estimation several minimizations of the CF are performed, as many as possible combinations of the initial values, i.e., eight minimizations. The main purpose of this approach is to find the point that achieves the lowest f_val, in a robust and computationally time efficient way. As a result, a matrix of values is obtained at each time j for each of the estimated parameters. This process is performed for each value of j, after which, when exiting the function and as already explained, the values of the parameters for which f_val is minimum are chosen (note that there is an f_val for each value of the matrix m×n, and there is a matrix m×n for each value of j).

\begin{matrix} f f^{i n i} (j) = f f (j - 1) \\ R_{g a p}^{i n i} = [\begin{matrix} 10 & 100 & 10^{3} & 10^{4} \end{matrix}] \\ z_{f f \to 1}^{i n i} = [\begin{matrix} 10^{3} & 10^{4} \end{matrix}] \\ Δ R_{s}^{i n i} = 0 α_{2}^{i n i} = 1 \end{matrix}

(17)

The steps described above are applied for each value of j for each well of each cell line, performing simulations that do not consider the future values of f_CE and a_CE, using the REW and FO REW models. The following section shows the results of this simulation procedure of the real CC assay experiments, which predicts the cell concentration in RT.

3. Results

The RT simulation method is finally designed to be implemented in a prototype to report the ff and cell concentration values after each measurement. As the required sampling time is 1 h, the time to perform all the necessary mathematical operations is not a critical point. This means that the computation time of the initial parameters, the ff, and other parameters for each measurement, is not a critical problem.

The metric used to determine the level of accuracy of the method is the error in the calculation of the cell concentration. From traditional optical counting methods, the cell concentration could be obtained (defined as C_trad), getting one concentration value per day (time step of 24 h). C_trad is compared with the cell concentration obtained in RT (C_sim). C_sim is obtained using the following expression,

C_{s i m} (j) = \frac{(f f_{s i m} (j) \frac{A_{w e l l}}{A_{c}})}{A_{w e l l}}

(18)

where ff_sim is the vector of ff values obtained from RT simulation, C_sim is the cell concentration calculated using ff_sim, A_c is the cell area and A_well is the well area. It is also desired to compare C_trad with the ideal concentration (C_i), which would be obtained if there were any error on the ff RT estimation. The error in the estimation of the ff will be measured with respect to the deviation from its ideal final value. It is considered that for the maximum ff obtained in the simulation, the error is the difference between the maximum value obtained and the maximum value that ff should reach, i.e., a value of 0.99. Thus, it is possible to calculate the real ff curve that should have been obtained for each well using the following equation,

\begin{matrix} f f_{i} (j) = k_{f f} \cdot f f_{s i m} (j) \\ k_{f f} = \frac{0.99}{\max (f f_{s i m})} \end{matrix}

(19)

where ff_i is the vector of theoretically real values of ff and k_ff is the factor applied to ff_sim to obtain ff_i. Then, C_i is derived as follows,

C_{i} (j) = \frac{(f f_{i} (j) \frac{A_{w e l l}}{A_{c}})}{A_{w e l l}}

(20)

The metrics for measuring accuracy are the mean relative error on the cell concentration (e_rm), in percent (%), defined as follows,

\begin{matrix} e_{r m . s i m} = \sum_{j_{t r a d}} \frac{| C_{s i m} (j_{t r a d}) - C_{t r a d} (j_{t r a d}) |}{C_{t r a d} (j_{t r a d})} \\ e_{r m . i} = \sum_{j_{t r a d}} \frac{| C_{i} (j_{t r a d}) - C_{t r a d} (j_{t r a d}) |}{C_{t r a d} (j_{t r a d})} \end{matrix}

(21)

where j_trad is the index of the cell concentration obtained by traditional optical method.

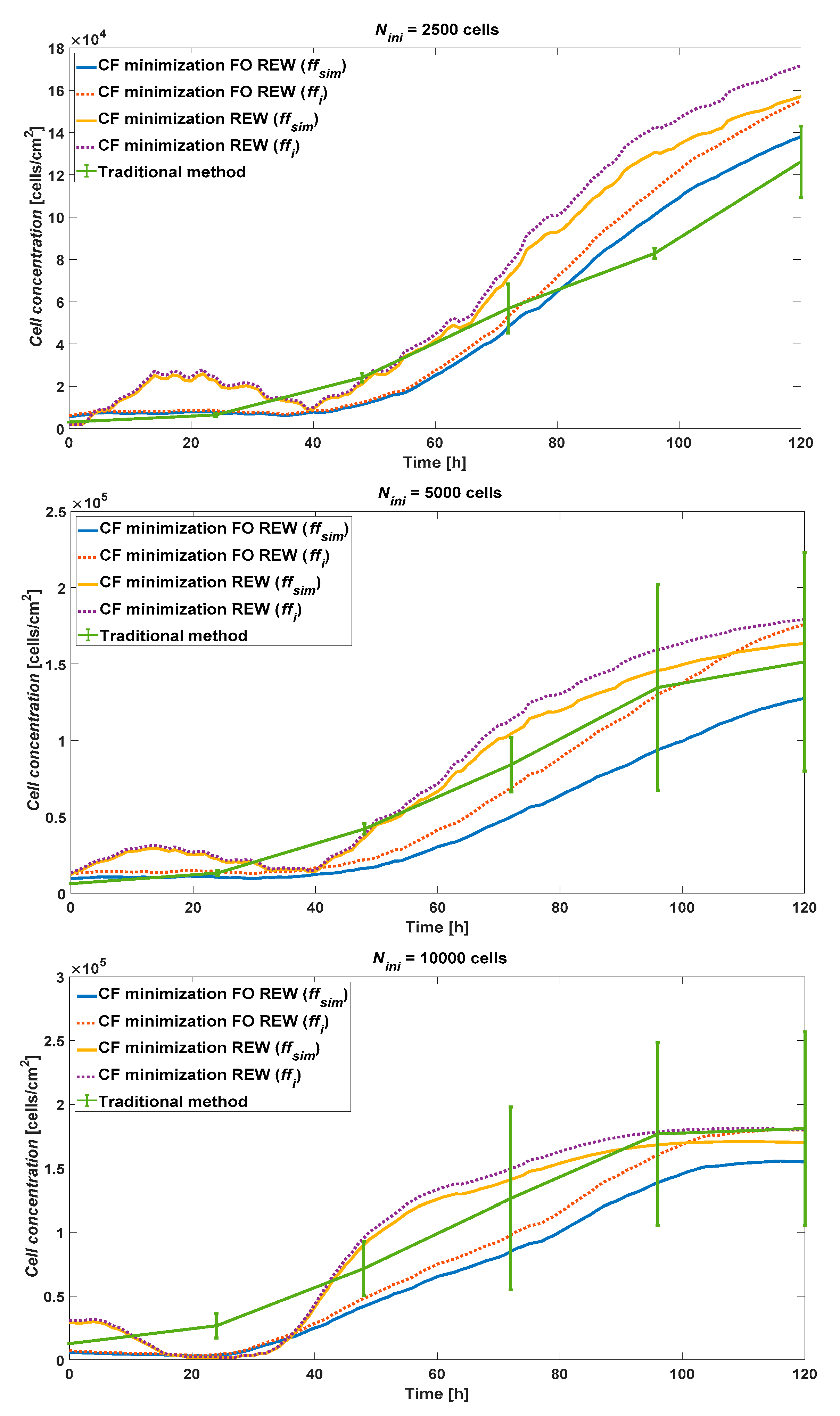
As example, Figure 7 shows the cell concentration estimated in the RT simulation for N_ini of 2500, 5000 and 10000 cells using the experimental data obtained from AA8 cell line. Lines blue and red present the cell concentration obtained by using the FO REW model using ff_sim and ff_i respectively. Lines yellow and purple present the cell concentration obtained by using the REW model using ff_sim and ff_i respectively. The last line, in green, present the cell concentration obtained using the traditional optical counting method. As can be seen, the FO REW model performs a little worse than the REW model on the final point (t = 120 h). In addition, the graph also shows that the higher the initial concentration, the more accurate the cell concentration estimation method.

The main results (and conclusions) are obtained from the mean relative error data. Then, the RT simulation results of the three cell lines used on the present work (AA8, N2a and N2aAPP) must be compared. The data will be analyzed and compared, as well as divided into sections of the experiment. There are two main sections (time windows) of interest: the initial section, where the cells adapt to the culture medium and adhere to the bottom of the well (ff→0), and the section from the beginning of growth (exponential phase) to the saturation phase of the well (ff→1).

Table 1 shows the e_rm of the cell concentration for the three cell lines of the whole experiment.

Table 2 shows the e_rm of the cell concentration for the three cell lines. The error shown is the e_rm of the cell concentration curves during the first hours and/or days of the experiment, i.e., from the time the CC assay is seeded until the moment when it starts to grow significantly (beginning of the exponential phase). On the first simulation period, e_rm are larger than the total e_rm (Table 1). Specifically, the REW model returns much larger errors than the FO REW, since it does not obtain good results for low ff.

The opposite case is the e_rm for the second part of the simulation, which are detailed in the Table 3. The e_rm in the second half of the simulation is much lower than in the first half. The most notable difference is found in the simulations using the REW model, since there is a large difference in error between the first and second frame, with the second one providing much better results (at the accuracy level of FO REW model). Another point to note is that, in general, better results are obtained at higher N_ini. Finally, it should be pointed out that the first section of the simulation is not as important in terms of predicting ff and cell concentration. Therefore, these data are quite acceptable, and provide a useful starting point for an improvement in the models and the method of simulation and parameter computation.

Separate analysis of the two zones of the experiment has provided interesting results. The cell concentration of a CC assay can be estimated in RT by connecting the CC assay as a load to an OBT. The errors are still large, but with some improvements of the algorithm, and of the OBT measurement prototype, the error should be greatly reduced. Also, must be notice that the e_rm obtained, in terms of cell concentration, depends on the cell line, because the lines with a lower A_c (N2a and N2aAPP) reach much larger error values than the cell line with a higher A_c (AA8).

3. Conclusions

The method of minimization of a CF has been used to obtain the optimal values of the model parameters that meet the BSC for each value of f_CE and a_CE. Due to the complexity of the used models (REW and FO REW) it is not easy to achieve good enough fitting results, since there is a considerable number of parameters to calculate at each moment, and small variations in one of them can make the value of the parameter ff differs from its real value. In addition, the f_CE and a_CE data for some cell lines are worse than the data for others, due to small voltage signals for amplitudes, as the prototype measurement is still in the experimental phase. Even with these difficulties, it has been possible to successfully estimate the RT cell concentration present in a CC assay, although with a certain margin of error. Considering the variability of cell concentration, and the studies performed up to now, it can be considered that the results are promising and good, being a useful method, but should be improved in future works.

It has been proved that the cell concentration can be obtained in real-time during the performance of a cell growth experiment employing the methodology described in this work. The errors found, while significant, can be reduced by improving the measurement circuit and the algorithm for calculating the cell concentration.

Author Contributions

JAS, PP, PD: Experimental data acquisition; PD, GH, AY: Experimental design an implementation. JAS, PP, GH: Hardware development and test; JAS, AY, GH, P and PD: paper writing and editing; PD: Cell culture assay, supervision and advising. JASV, PP: Software and data processing. All authors have read, review and agreed to the published version of the manuscript.

Funding

This work was supported in part by the project: Optimización de los procesos de diferenciación en células madre y tumorales basada en electroestimulación (E-CELL). Proyectos de Generación de Conocimiento de la AEI. Referencia: PID2021-122529OB-I00. 2022-2025, and also by the project: Sistema de medida y electroestimulación para aplicaciones de diferenciación y motilidad celular, Project US-1380661, I+D+i FEDER Andalucía 2014-2020.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Available.

Data Availability Statement

All the experimental data are measured from cell cultures supported by the project. The data are available if required.

Conflicts of Interest

The authors declare no conflict of interest.

References

Giaever, I.; Keese, C.R. Use of Electric Fields to Monitor the Dynamical Aspect of Cell Behavior in Tissue Culture. IEEE Trans. Biomed. Eng. 1986, BME-33, 242–247. [Google Scholar] [CrossRef] [PubMed]
Khalil, S.; Mohktar, M.; Ibrahim, F. The Theory and Fundamentals of Bioimpedance Analysis in Clinical Status Monitoring and Diagnosis of Diseases. Sensors 2014, 14, 10895–10928. [Google Scholar] [CrossRef] [PubMed]
Lu, Y.Y.; Huang, J.J.; Cheng, K.S. The design of electrode-array for monitoring the cellular bioimpedance. IEEE Symposium on Industrial Electronics & Applications 2009. [Google Scholar]
Lei, K. Review on Impedance Detection of Cellular Responses in Micro/Nano Environment. Micromachines 2014, 5, 1–12. [Google Scholar] [CrossRef]
Borkholder, D. A. Cell based biosensors using microelectrode. Stanford University, 1998. [Google Scholar]
Pradhan, R.; Mandal, M.; Mitra, A.; Das, S. Monitoring cellular activities of cancer cells using impedance sensing devices. Sensors Actuators B Chem. 2014, 193, 478–483. [Google Scholar] [CrossRef]
Daza, P.; Olmo, A.; Cañete, D.; Yúfera, A. Monitoring living cell assays with bio-impedance sensors. Sensors Actuators B Chem. 2013, 176, 605–610. [Google Scholar] [CrossRef]
Abdolahad, M.; Shashaani, H.; Janmaleki, M.; Mohajerzadeh, S. Silicon nanograss based impedance biosensor for label free detection of rare metastatic cells among primary cancerous colon cells, suitable for more accurate cancer staging. Biosens. Bioelectron. 2014, 59, 151–159. [Google Scholar] [CrossRef]
Lourenço, C.-F.; Ledo, A.; Laranjinha, J.; Gerhardt, G.A.; Barbosa, R.M. Microelectrode array biosensor for high-resolution measurements of extracellular glucose in the brain. Sensors Actuators B Chem. 2016, 237, 298–307. [Google Scholar] [CrossRef]
Dibao-Dina, A.; Follet, J.; Ibrahim, M.; Vlandas, A.; Senez, V. Electrical impedance sensor for quantitative monitoring of infection processes on {HCT}-8 cells by the waterborne parasite Cryptosporidium. Biosens. Bioelectron. 2015, 66, 69–76. [Google Scholar] [CrossRef]
Reitinger, S.; Wissenwasser, J.; Kapferer, W.; Heer, R.; Lepperdinger, G. Electric impedance sensing in cell-substrates for rapid and selective multipotential differentiation capacity monitoring of human mesenchymal stem cells. Biosens. Bioelectron. 2012, 34, 63–69. [Google Scholar] [CrossRef] [PubMed]
12. Hosseini SN, Das PS, Lazarjan VK, Gagnon-Turcotte G, Bouzid K, Gosselin B. Recent Advances in CMOS Electrochemical Biosensor Design for Microbial Monitoring: Review and Design Methodology. IEEE Trans Biomed Circuits Syst. 2023. [CrossRef]
Sara Abasi, John R. Aggas, Guillermo G. Garayar-Leyva, Brandon K. Walther, and Anthony Guiseppi-Elie, Bioelectrical Impedance Spectroscopy for Monitoring Mammalian Cells and Tissues under Different Frequency Domains: A Review, ACS Measurement Science Au 2022, 2, 495–516. [CrossRef]
Giaever, I.; Keese, C.R. Micromotion of mammalian cells measured electrically. Proc. Natl. Acad. Sci. U. S. A. 1991, 88, 7896–7900. [Google Scholar] [CrossRef] [PubMed]
Wegener, J.; Keese, C.R.; Giaever, I. Electric cell-substrate impedance sensing (ECIS) as a noninvasive means to monitor the kinetics of cell spreading to artificial surfaces. Exp. Cell Res. 2000, 259, 158–166. [Google Scholar] [CrossRef] [PubMed]
Grimnes, S.; Martinsen, O.G. Bioimpedance and Bioelectricity Basics, 3rd Ed. ed; Elsevier: Oslo, 2013. [Google Scholar]
Huang, X.; Nguyen, D.; Greve, D.W.; Domach, M.M. Simulation of Microelectrode Impedance Changes Due to Cell Growth. IEEE Sensors J. 2004, 4, 576–583. [Google Scholar] [CrossRef]
Olmo, A.; Yúfera, A. Computer simulation of microelectrode-based bio-impedance measurements with COMSOL. Third International Conference on Biomedical Electronics and Devices 2010, 178–182. [Google Scholar]
Serrano, J.A.; Huertas, G.; Maldonado-Jacobi, A.; Olmo, A.; Pérez, P.; Martín, M.; Daza, P.; Yúfera, A. “An Empirical-Mathematical Approach for Calibration and Fitting Cell-Electrode Electrical Models in Bioimpedance Tests. Sensors, 2018, 18, 2354. [Google Scholar] [CrossRef] [PubMed]
Serrano, J.A.; Perez, P.; Huertas, G.; Yúfera, A. Alternative General Fitting Methods for Real-Time Cell-Count Experimental Data Processing. IEEE Sens. J. 2020, 20, 15177–15184. [Google Scholar] [CrossRef]
“Applied Biophysics.” http://www.biophysics.com/ (accessed 5 November 2020). 5 November.
Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-order Systems and Controls. Fundamentals and Applications. 2010. [Google Scholar]

Figure 1. a) Model of electrode immersed on an ionic solution. b) Basic cell-electrode model.

Figure 3. Real-electrode well (REW) model of the well. It has ten microelectrodes (e₁ to e₁₀) and one big reference electrode (e_r).

Figure 4. Step 1: Block diagram of step 1 of RT simulation, whose target is to find the mean around the

f_{C E}

and

a_{C E}

minimums.

Figure 4. Step 1: Block diagram of step 1 of RT simulation, whose target is to find the mean around the

f_{C E}

and

a_{C E}

minimums.

Figure 7. AA8 cell line cell concentration comparison between RT simulation using FO REW model (obtained from ff_sim in blue and ff_i in red) and REW model (obtained from ff_sim in yellow and ff_i in purple), and traditional counting method (green ).

Table 1. Cell concentration mean relative error, in %.

N_ini	2500			5000			10000
Line	AA8	N2a	Na2APP	AA8	N2a	Na2APP	AA8	N2a	Na2APP
$e_{r m . s i m}^{R E W} [%]$	59.37	372.52	396.43	37.56	154.33	219.13	46.40	83.80	25.51
$e_{r m . i}^{R E W} [%]$	68.47	430.92	443.78	46.70	173.84	271.15	49.79	91.49	22.31
$e_{r m . s i m}^{F O R E W} [%]$	33.34	205.13	238.65	36.79	100.82	102.22	40.70	56.00	45.56
$e_{r m . i}^{F O R E W} [%]$	41.04	275.54	276.67	31.61	129.35	135.65	31.19	55.11	30.58

Table 2. Cell concentration mean relative error, in %, before to start the CC assay growth (t < 40 h).

N_ini	2500			5000			10000
Line	AA8	N2a	Na2APP	AA8	N2a	Na2APP	AA8	N2a	Na2APP
$e_{r m . s i m}^{R E W} [%]$	120.6	1082.9	946.0	88.8	390.4	515.9	111.1	200.2	31.4
$e_{r m . i}^{R E W} [%]$	128.9	1252.4	1056.6	101.1	472.5	616.7	118.6	230.6	25.6
$e_{r m . s i m}^{F O R E W} [%]$	52.5	518.6	535.4	38.5	176.4	229.2	69.7	78.9	62.2
$e_{r m . i}^{F O R E W} [%]$	68.3	771.4	629.5	55.2	327.9	295.9	64.1	117.4	52.5

Table 3. Cell concentration mean relative error, in %, after to start the CC assay growth (t > 40 h).

Line	AA8	N2a	Na2APP	AA8	N2a	Na2APP	AA8	N2a	Na2APP
$e_{r m . s i m}^{R E W} [%]$	28.7	17.3	30.0	11.9	36.3	21.3	14.0	25.6	21.6
$e_{r m . i}^{R E W} [%]$	38.3	20.2	35.2	19.5	24.5	40.8	15.4	21.9	20.1
$e_{r m . s i m}^{F O R E W} [%]$	23.8	48.4	40.8	35.9	63.0	17.6	26.2	44.5	34.5
$e_{r m . i}^{F O R E W} [%]$	27.4	27.6	41.4	19.8	30.1	28.8	14.8	23.9	15.9

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Predictive Cell-Culture Time-Evolution Based on Electric Models

Abstract

1. Introduction

2. Material and Methods

2.1. Bioimpedance Modelling

2.1.1. Real-Electrode Well Model (11 Electrodes)

2.1.2. Fractional Order Model

2.3. Cost Function

2.3. Fitting Routine

3. Results

3. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe