Prerpints.org logo
Preprint
Article

Advanced Video-Based Processing for Low-Cost Damage Assessment of Buildings under Seismic Loading in Shaking Table Tests

Altmetrics

Downloads

114

Views

73

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts
Abstract
The paper explores the potential of a low-cost advanced video-based technique for the assessment of structural damage induced to buildings by seismic loading. A low-cost high-speed video camera was utilized for motion magnification (MM) processing of footages of a two-story reinforced concrete frame building subjected to shaking table tests. The damage after seismic loading was estimated by analyzing the dynamic behavior (i.e. in terms of modal parameters) and the structural deformations of the building in the MM videos. The results by MM were compared for method validation to damage assessment obtained by the analyses of conventional accelerometers and high-precision optical markers tracked by a passive 3D motion capture system. Also, 3D laser scanning to obtain an accurate survey of the building geometry before and after the seismic tests was carried out. In particular, accelerometers were also processed and analyzed by using several stationary and non-stationary techniques with the aim to analyze the linear behavior of the undamaged structure and the nonlinear structural behavior during damaging shaking table tests. The proposed MM-based procedure provided accurate estimate of the main modal frequency and the damage location through the analysis of modal shapes, which were confirmed by advanced analyses of accelerometric data.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

In recent years the application of image-based techniques to structural monitoring has raised increasing interest [1,2,3]. From the one hand, digital image and video processing methods and vision technologies have seen remarkable advancements at more affordable costs thanks to the development of advanced materials for hardware equipment and to improvements of new algorithms for more powerful and robust processing [4,5,6,7,8]. On the other hand, conventional methods for structural monitoring usually require a rather difficult and costly equipment setup comprising the positioning of a relatively limited number of expensive sensors (e.g., accelerometers, velocimeters etc.) in the measurement points of the structure, which need to be physically reachable by human operators, sometimes even with safety concerns [9]. Furthermore, when using a limited number of sensors, it becomes crucial to locate them at proper positions on the structure to optimize response. To this aim a great deal of research has been conducted on optimal sensor placement using a variety of placement techniques and criteria [10]. Video-based methods like motion capture systems (MCS) that require the use of fiducial markers proved very effective in laboratory tests [11,12] but substantially have similar issues for markers positioning, even if markers are typically cheaper than conventional sensors. This issue is completely overcome through video-based methods that are able to monitor the whole structure or most of it without fiducial markers. For the above reasons, improving the capability of extracting parameters related to the structures health from footages taken from a distance by video cameras may play a crucial role for low-cost and safe monitoring of structures.
So far, conventional methods based on accelerometers and seismographs still provide undoubtedly much higher accuracy and reliability of results than video-based methods. However, video-based methods can contribute to help managing structures and infrastructures with more flexible and affordable monitoring systems.
In this context, particularly interesting are the potentialities of the Motion Magnification (MM) method [13] and related advanced processing technics [14], which permit to amplify and analyze the imperceptible movements of the objects in a video. In fact, most conventional methods for structural health monitoring (SHM) are based on sensors able to record the movements in the structure, e.g., static deformations or ambient vibrations [15]. In particular, the analysis of ambient vibration motions is widely used to perform the modal analysis of the structure, as the modal parameters can be easily related to the evolution of the state of damage of the buildings [16]. This essentially motivates the recent remarkable efforts to improve the MM algorithms and the related video processing methods to extract the modal parameters from footages of structures. Some authors explored the potentialities of MM video-based methods for modal analysis by using high-speed high-resolution high-cost cameras obtaining encouraging results in laboratory experiments [17]. Subsequently, also the use of low-cost equipment and consumer-grade cameras (CGCs) was explored both in laboratory and outdoor environments with less accurate but still interesting results in terms of rough estimate of the main modal frequency [18]. Such studies demonstrated that low-speed cameras (typically at 24-30 fps) can actually detect the modal frequencies lower than 3 Hz, even in outdoor environment. Such low level of frequencies is common for the main modal frequency of most structural typologies. However, the quality of the used equipment still plays a decisive role, in particular in terms of video resolution and speed, but also the camera dynamic range and optics are quite important in relation to the lighting conditions during the acquisitions [18]. It is also worth noting that by now some common smartphones and CGCs already offer the possibility to take videos at 1080p or even 4K resolution standards at 60 fps or even 120 fps with a cost of 1 k$ or less.
Nonetheless, the present study makes an effort to get a further step forward by extracting also the modal shape associated with the identified modal frequency by MM analysis of videos taken with relatively low-cost and low-quality equipment. The interest about monitoring the modal shape is that its curvature changes can be used to locate the damage in the structure with higher accuracy than operational deformed shapes [19,20]. In particular, the modal curvature was successfully used to locate the damage arising in framed structures [21]. In these studies, though, curvature was defined through interstory deformations with the aim at identifying the most damaged floors, while video-based methods can generalize these concepts to locate damage at any point in the structure.
The proposed MM-based procedure was validated by experimental application to a 2/3-scaled two-story mockup of a reinforced concrete (RC) framed building, representative of a widely common construction typology on the Italian territory. The mockup was tested on shaking table reproducing a recent Italian earthquake.
In order to validate the results obtained by the proposed procedure, a variety of other sensors and methods were also used in the experiment. In particular, the building was instrumented with conventional accelerometers and high-precision optical markers tracked by a passive 3D MCS. Also, the building geometry was accurately surveyed by 3D laser scanning before and after the seismic tests.
Accelerometric recordings were processed and analyzed by using several stationary and non-stationary techniques with the aim to evaluate the linear behavior of the undamaged structure and the nonlinear structural behavior during damaging shaking table tests. In terms of linear and nonlinear modal parameters, results retrieved by using the band variable filter [21], based on the Stockwell Transform [22,23], and the Short Time Impulse Response Function (STIRF) [24] highlighted the importance of using the time-frequency analyses to study the response of damaging structures also with the aim to better evaluate the health condition of the monitored structure.

2. Proposed MM-Based Procedure

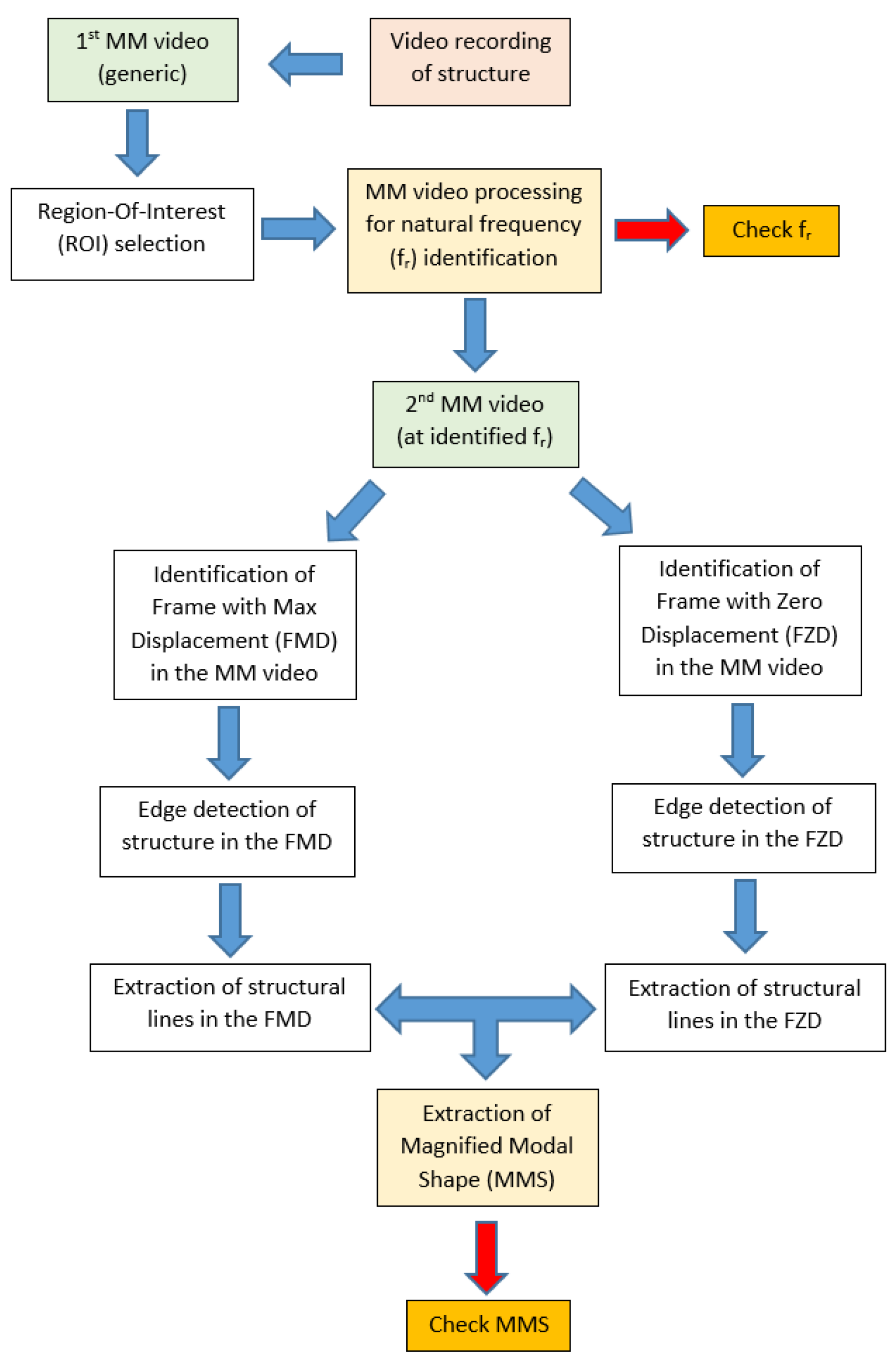
The proposed procedure comprises different processing steps. In Figure 1 the essential flowchart of the proposed procedure is illustrated.
A video camera records a footage of just a few minutes of the object. In the second step, the video is processed by a software tool provided by the Computer Science and Artificial Intelligence Laboratory at the Massachusetts Institute of Technology (MIT-CSAIL). The phase-based MM version (PBMM) of the algorithm implemented in this software was used [25]. It can be summarized that the main parameters to be set are the frequency range and the amplification factor. The frequency range indicates the group of frequencies whose magnification will be enhanced with respect to the others. However, precise specifications about their tuning are lacking, as the MIT researchers themselves warn. Therefore, it is advisable to collect as much information as possible on the studied object, especially about the frequency range of interest entering a frequency range and the required level of amplification within that range. An excessive amplification or a too large frequency range produces disturbing image distortion and noise. Therefore, a trade-off between noise and amplification is always necessary. The duration T of the video is inversely correlated to the frequency resolution in the frequency domain: the larger T, the better the frequency resolution. Unfortunately, a large T means a much longer elaboration time. Moreover, taking into account the Shannon-Nyquist theorem, the camera frame rate (fps) becomes an important parameter. It is suggested, however, to adopt a significant data oversampling to compensate possible aliasing phenomena.
Then, an appropriate Region-Of-Interest (ROI) is selected for analysis in the frequency domain. In fact, the whole full-resolution image could be theoretically processed, but it would be computationally uselessly heavy, as not all pixels in the image provide equally significant information. So, the choice of an efficient ROI is crucial for an efficient identification of the modal frequencies. On the one hand, the ROI should contain a portion of the studied structure with the highest image contrast with respect to the background so that structural motion is captured with highest accuracy. To this purpose, image entropy criterion can provide useful indications [26]. On the other hand, the best results can be obtained by points of the structure with the highest expected displacements associated to the considered modal shapes. Without going into details about the several existing optimal sensor placement approaches [10], the ROI selection can be treated following somewhat similar approaches. However, contrarily to conventional sensor placement, the ROI size, shape and position can be easily changed at any time with great flexibility so that an optimal ROI can be found manually by a few attempts. Nonetheless, it is highly recommendable to preliminarily calculate the expected mode shapes of the structure by finite element analysis (FEA), which provides useful indications to guide the ROI selection. Moreover, ROI size should consider the available computational resources, as the bigger the ROI, the higher the computational time. Finally, the ROI shape is a rectangle that should be as flat as possible in the direction orthogonal to the main motion direction.
Values of pixels extracted from the ROI are processed in the frequency domain, typically by Power Spectral Density (PSD), to identify the main frequencies. Once the pixel time-series are extracted from the magnified video, they are averaged and processed just as the usual standard signals. The somewhat smooth appearance of the PSD depends on the short time span of the video that decreases the PSD frequency resolution. Instances of this procedure can be easily found in the literature, see for example [27].
After identification of fr, a new MM video is produced with passband filter centered on fr and with a sufficiently large amplification factor α so that the MM video actually visualizes the structure moving according to the modal shape.
This latter MM video is then processed by searching for the Frame with Maximum Displacement (FMD) and Frame with Zero Displacement (FZD) of the studied structure. The FMD is assumed as the best frame to identify the modal shape, while the FZD represents the undeformed structure and is used as reference. FZD might be identified as a frame with minimum displacements, as no frame will possibly have zero displacements, given the unavoidable noise in the image.
At this point, the FMD and FZD undergo further processing. Preparatory image processing steps, which essentially make the image structural lines more evident, might include color adjustment and contrast maximization. Then, an inverted edge detection algorithm [28] is applied in order to enhance the main structural lines in the image (e.g., lines of columns and floor slabs etc.). Such lines are extracted from both FMD and FZD. The relative displacements between corresponding structural lines in FMD and FZD are calculated to obtain a Magnified Modal Shape (MMS), which can be demagnified by dividing by α to get an estimate of the real modal shape.

3. Lab Experimentation

The experiment was carried out at the seismic hall of the ENEA Casaccia Research Center, near Rome, Italy, using a 4 m x 4 m, 6 degrees-of-freedom (DOFs) shaking table. The shaking table was used for seismic testing of a 2/3-scaled two-story mockup of a framed weakly RC building. It was designed in accordance to the Italian code and standards of the 1960s and 1970s, when a large part of the Italian building stock was designed during the real estate “boom” of the post-war reconstruction, so that it nowadays represents one of the most widely common construction typologies on the Italian territory [29]. The building mockup was designed to resist only to vertical loads according to the Italian codes of that time.
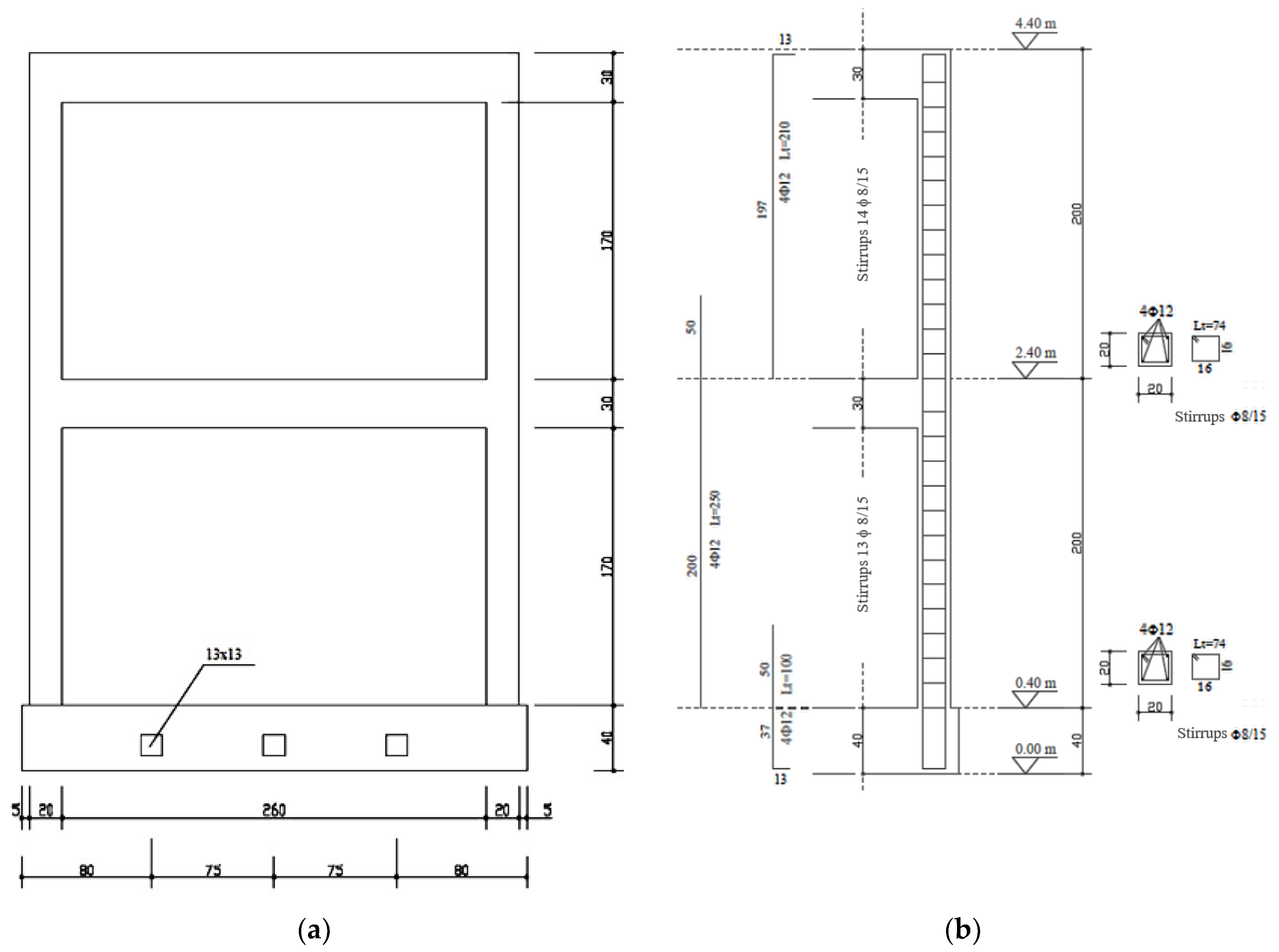
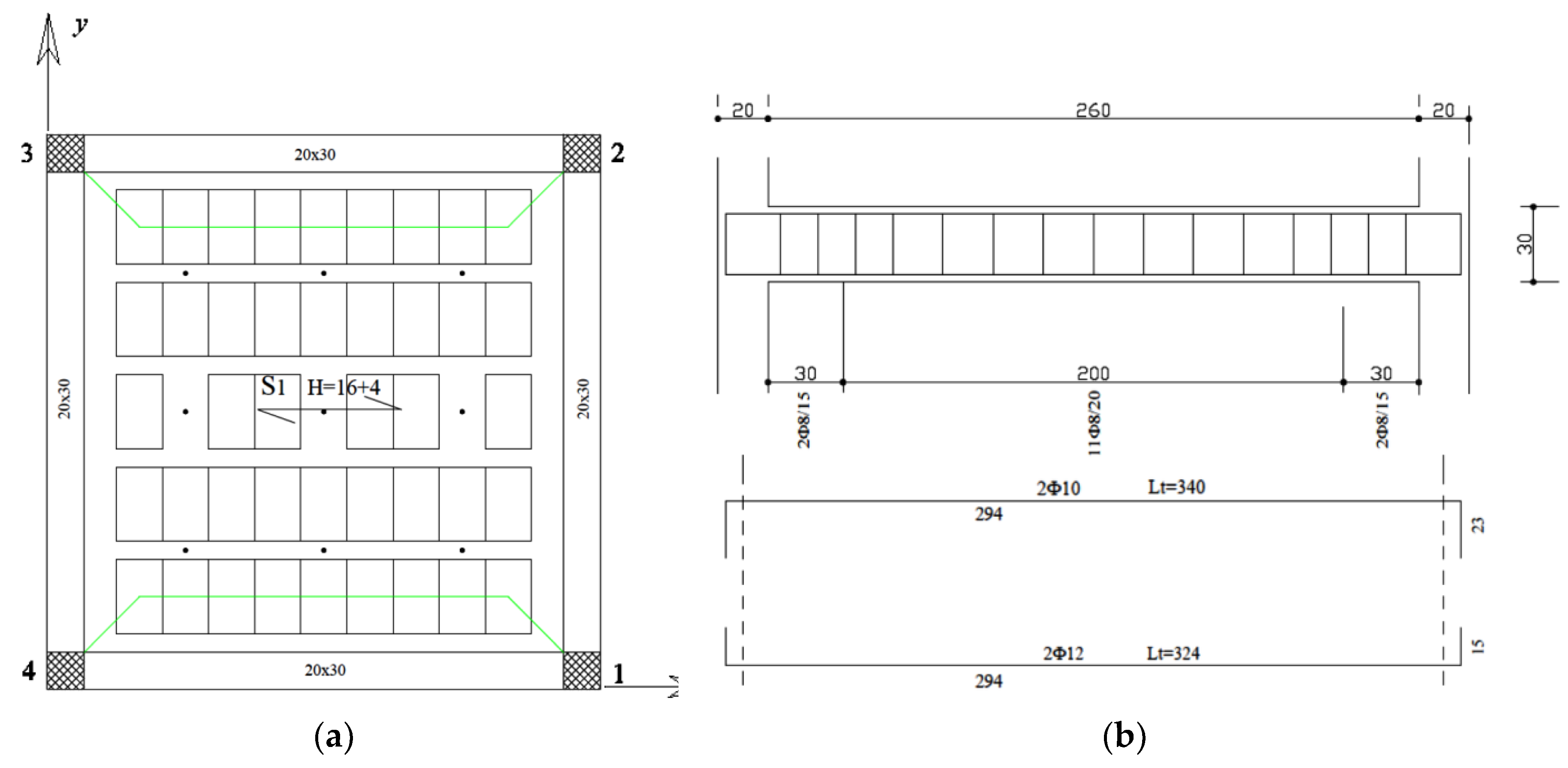
As for the material properties, the utilized concrete has a characteristic compressive strength of 20 MPa and the steel bars have a tensile characteristic yield strength of 450 MPa. Extracts of the design drawings and the dimensions of the tested mockup are illustrated in Figure 2. Also, the slabs were typical of common Italian building stock, they were built as one-way ribbed floor slabs (design drawing in Figure 3) and lightened through the use of hollow clay bricks, floor slab weight was about 21 kN. The overall mass of the building was about 150 kN. An additional load of 12 kN was located on each floor through steel plates placed in nine positions according to a 3 x 3 matrix. The configuration of the additional load was like shown in Figure 4a with slight eccentricity with respect to the building center of mass.
After positioning on the shaking table, the building base was fixed to the table and a 3D geometry survey by laser scanner was carried out. Four stations placed near each building column were acquired (Figure 4b). This acquisition was repeated after the end of the shaking table tests.
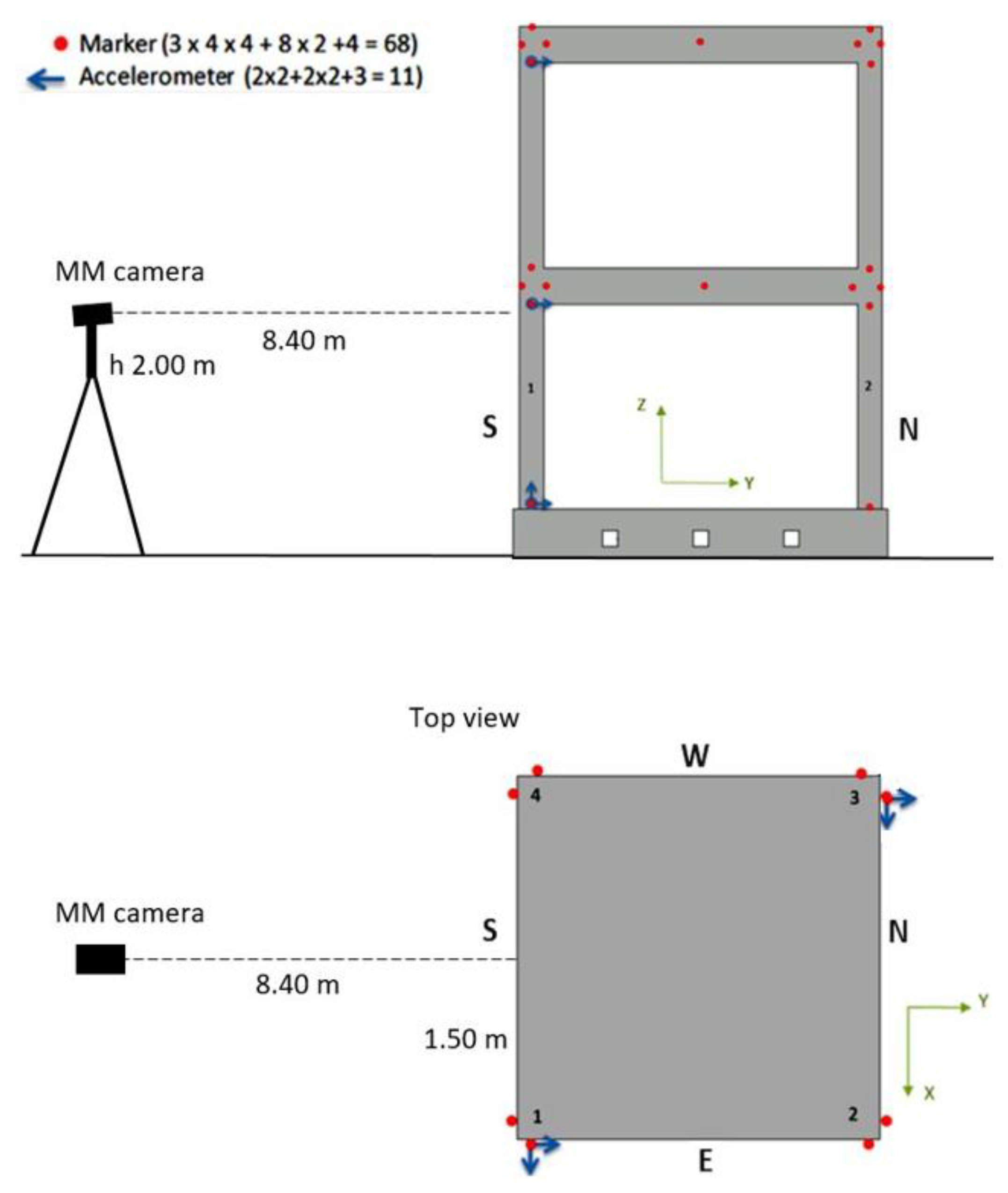
Several instruments were utilized to acquire motion data of the structure positioned on the shaking table (Figure 4c). In particular, the positions of the MM camera, as well as of the accelerometers and of the markers of an optical 3D MCS are illustrated in Figure 5. For nomenclature of measurement points, the building columns were named from 1 to 4 counterclockwise, and building facades were named S, E, N and W according to Cardinal points.
The camera used for MM acquisitions mounted a CMOS sensor Onsemi PYTHON 1300 with full resolution of 1280 x 1024 pixels (1264 x 1016 pixels in color mode) and maximum frame rate of 210 fps with reduced resolution (Figure 6a).
The optical 3D MCS is based on Vicon technology with a constellation of 13 near-infrared (NIR) cameras positioned at safe distance around the shaking table (see Figure 6b). 3D motion capture NIR cameras acquired with 5 Mpixel at 200 fps the position of 68 markers located on the building mockup. The used markers are simple 25-mm diameter plastic balls covered with retro-reflecting coating. They were substantially placed at the base of each column, at the column-beam joints and in the center of both floors’ beams. The system measured the markers position with accuracies of about 0.03 mm and 0.15 mm in terms of root-mean-square (RMS) error in static and dynamic (seismic) conditions, respectively. The used accelerometers were PCB 3701G3FA3G whose broadband capacitive sensors have 3 g peak measurement range. They were acquired at sampling frequency of 200 Hz. Eleven accelerometer channels were positioned at each floor and at specimen base as shown in Figure 5a.
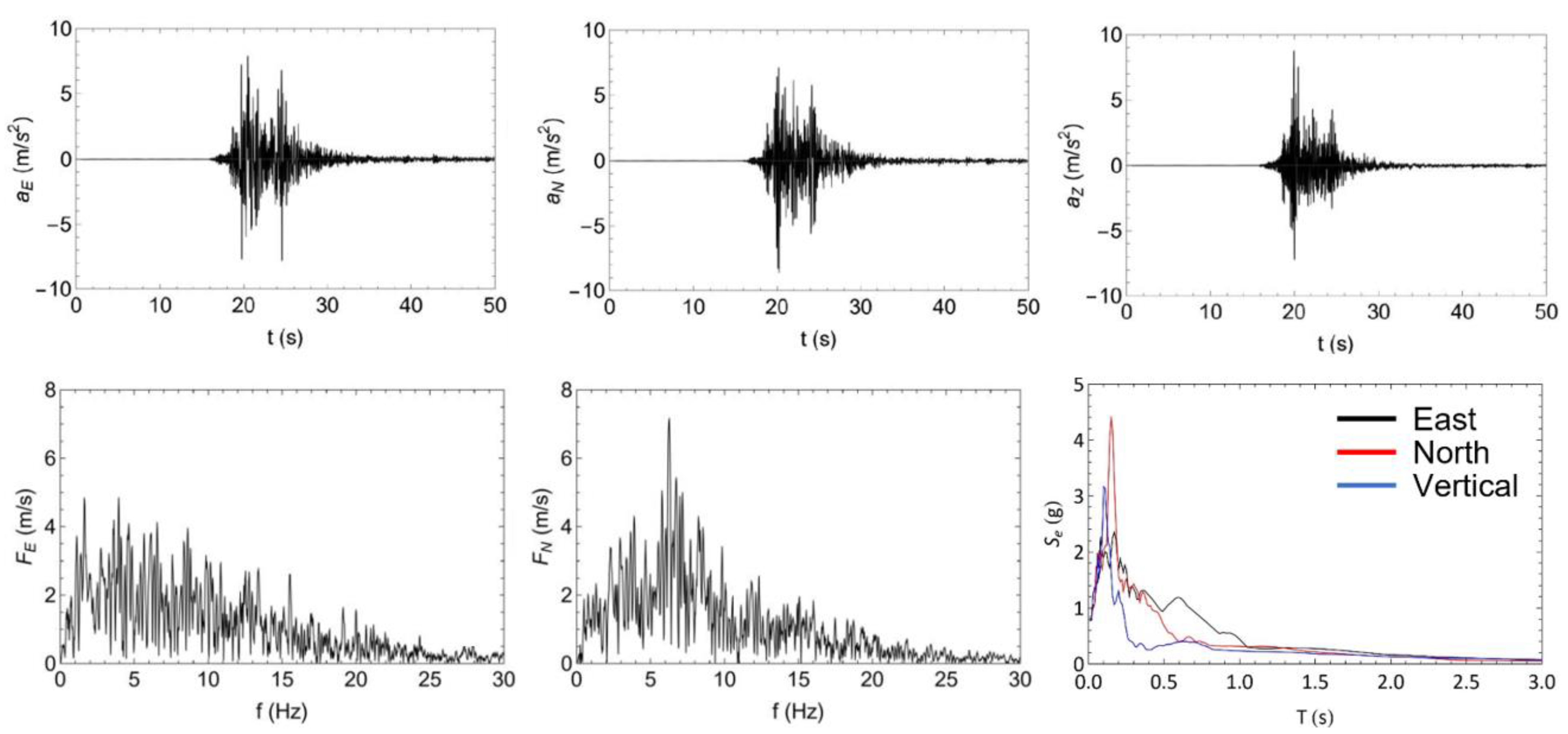
The seismic input was based on the earthquake occurred on 30 October 2016, the largest event in the context of the Central Italy seismic sequence 2016-2017, with estimated magnitude of Mw 6.5 that struck 6 km north of Norcia at 07:40 local time (06:40 UTC). In particular, the shake recorded at the Savelli seismic station (NRC, Lat 42.72492 Lon 13.12578 WGS84, soil type A) located near Norcia (Figure 7), was considered. This was scaled in acceleration in order to obtain the NRC tests (see shaking table sequence in Table 1), with increasing step of 0.1 g of peak ground acceleration (PGA) up to the natural shake with 0.87 g of PGA. Each seismic test was intercalated with dynamic identification tests with white-noise frequency spectrum (also known as ‘random’ tests) at 0.05 g of PGA (Rnd tests in Table 1). The seismic test NRC_100 was repeated to assess damage degradation with same earthquake. The two random tests Rnd_10 and Rnd_11 were executed for checking repeatability of modal identification by MM at different camera parameters. All tests were triaxial.

4. Numerical Modelling and Analysis

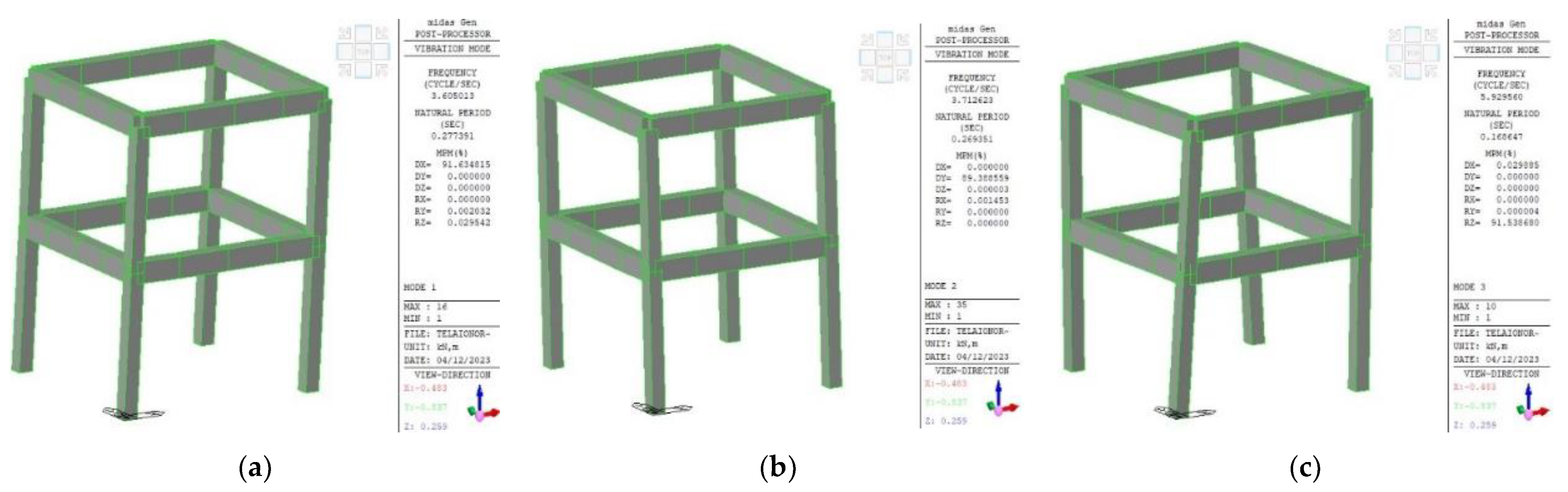
The dynamic behavior of the structure was evaluated by Finite Element models to select coherently the seismic input for the shaking-table test. The software Midas Gen was used for the purpose. Beam elements with six degrees of freedom per node were used. The floors were not directly modeled, assuming a rigid diaphragm behavior with mass and its rotary inertia evaluated separately and applied to the center of mass of each floor. For vertical action, the mass of the floor has been applied to the nodal point of the structure. The mass and inertia of the floor also include the additional point masses placed on the floors to simulate live loads, six of 100 kg and three of 200 kg.
The first analyzes were conducted assuming the design values for the concrete Young modulus, taken from the standards: Ec = 29.96 GPa; subsequently, the model was updated considering Ec = 27.95 GPa, derived from the experimental evaluation of the concrete strength.
However, the analysis of experimental dynamic data from the first random test (Rnd_01), which is representative of the undamaged structure, has shown much lower frequency values than those derived from the initial linear FE model (see Table 2). Instead, a good agreement was obtained by assuming a cracked flexural stiffness in the model, as is reasonable according to the technical codes for seismic analyses, even in the case of service limit states. Therefore, Ec was finally assumed equal to 20 GPa and reduced inertia of structural members was adopted. More in detail, we considered stiffness ratios of 0.7 for columns, 0.64 and 0.4 for x-directed and y-directed beams, respectively. The difference attributed to beams is related to the different contributions of the one-way floor. Figure 8 shows the first three mode shapes and their associated frequencies after updating the linear model.
For the non-linear analyses, a Mander constitutive model [30] was adopted for concrete and a Menegotto-Pinto [31] for steel. Therefore, three zones characterized concrete members: i) not confined for the cover, ii) confined for the core of the columns, iii) confined for the core of the beams. Uncracked initial stiffness was considered in this case. A concrete unconfined strength of fc = 22,217 MPa and a steel yielding strength of fy = 450 MPa were considered.
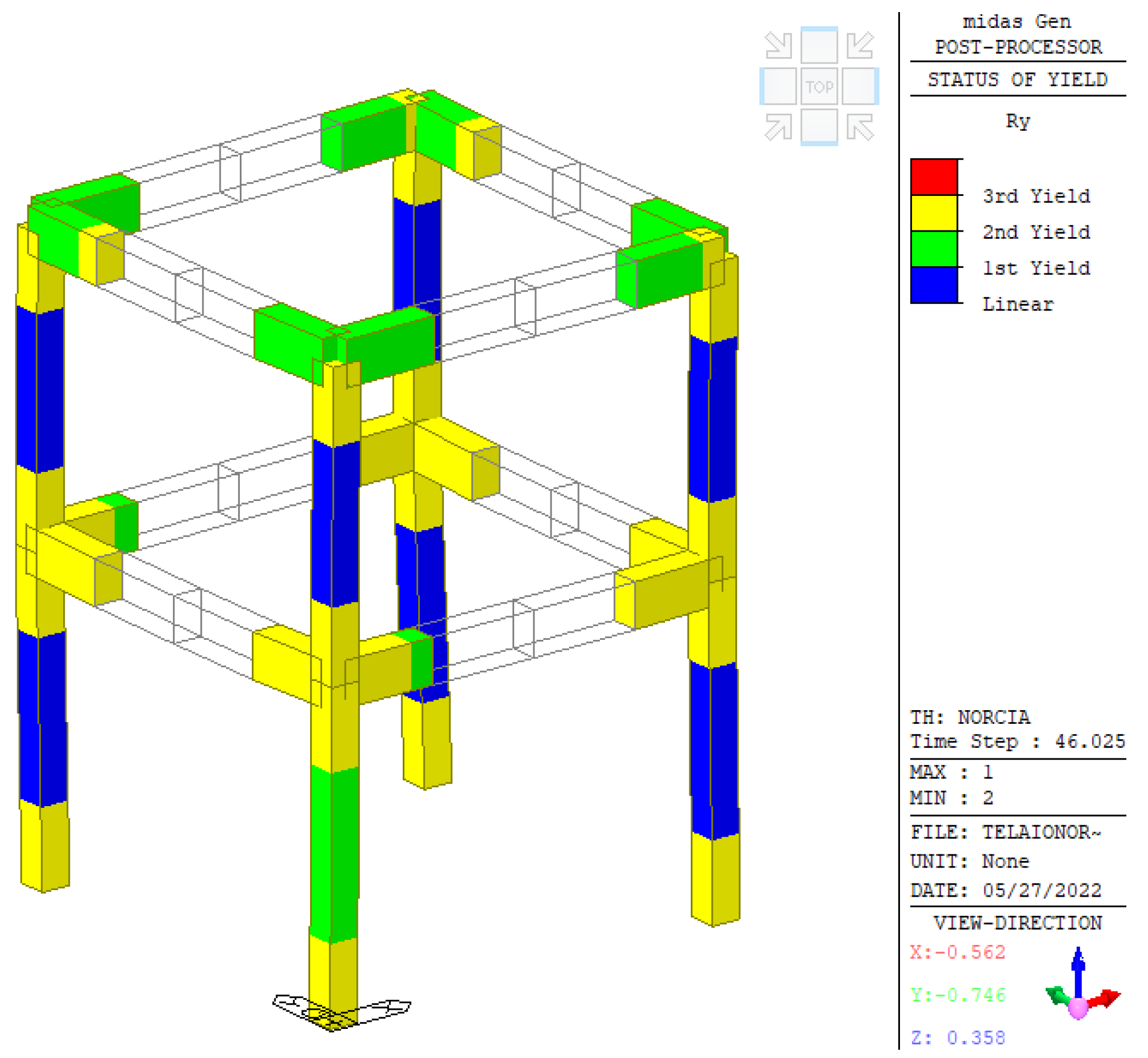
The seismic analysis was performed by direct integration of the equations of motion using the earthquake recorded at the Savelli station in Norcia, 30 October 2016 (NRC_100). The final state of the plastic zones due to rotation around the y-axis in the local reference of the element is shown in Figure 9. No collapse was to be expected, but the structure is expected to exhibit serious damage, according to the objectives of the test. Concerning the top of one column, some details of the result are reported in Figure 10 which shows the partial cracking of the concrete at the end of the analysis with scaled input with factor 0.1, which is approximately corresponding to NRC_01g.

5. Experimental Data Processing

5.1. MM-Based Video Processing

Only the videos acquired during the Rnd tests were taken into account, because the MM algorithm works well when motion is very small. Strong motion videos, such as in seismic tests are not appropriate for MM processing, as they induce abnormal distortion to the final MM video. However, here the aim is to extract damage indications from real structures subject to ambient vibration, so Rnd are more representative of such conditions. In particular, Rnd_02, Rnd_06 and Rnd_11 were acquired in HD mode (1264 x 1016) at 50 fps, while all the other Rnd tests were acquired in LD mode (632 x 508) at 150 fps.
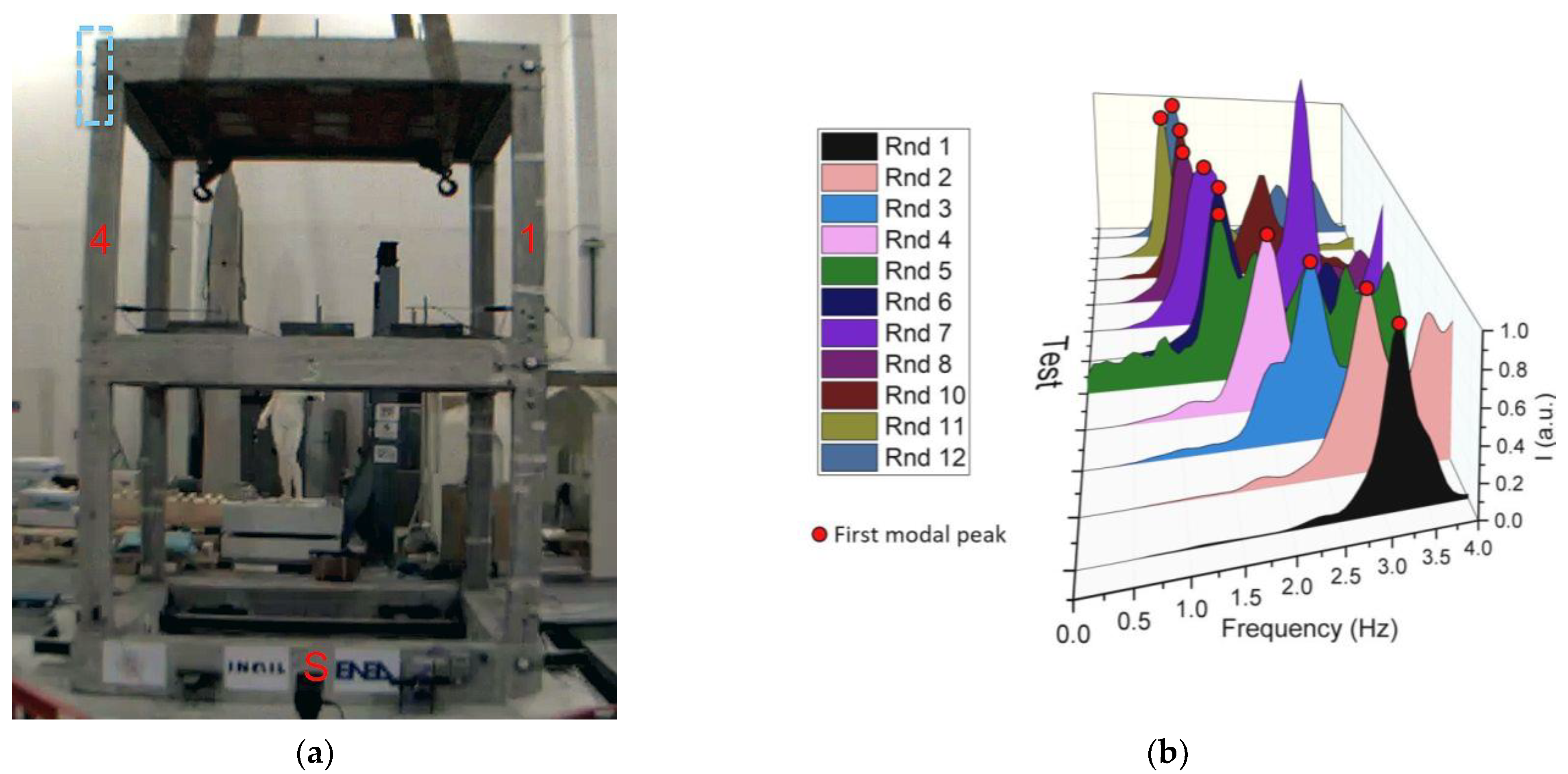
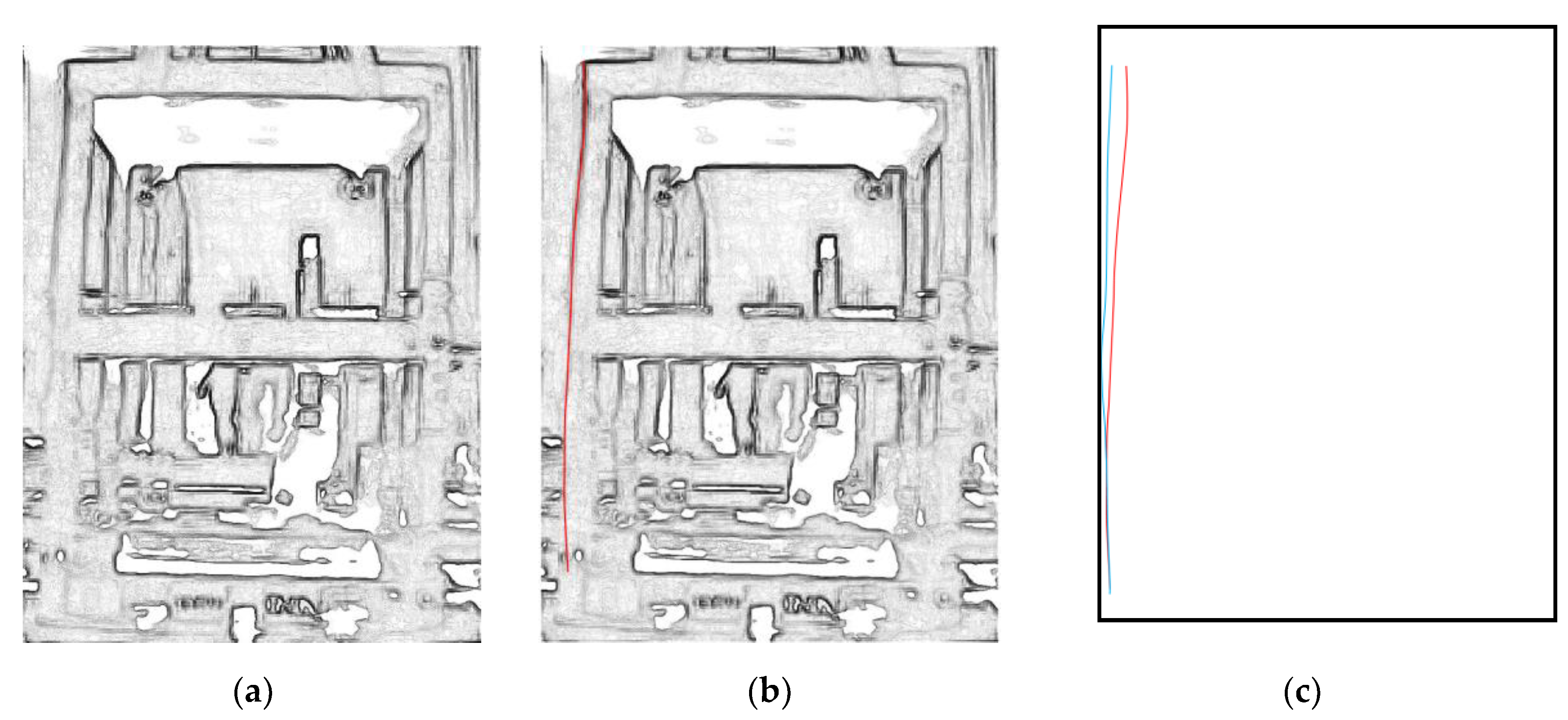
After preliminary FEA of the tested structure, the ROI was selected as depicted in Figure 11a in order to detect the first bending mode in x direction. The selected ROI focuses on top of column 4, where contrast with the background is the highest. The ROI’s shape is such as to sense motion mainly in x direction. The ROI’s pixels were analyzed in the frequency domain and the PSD was calculated for each Rnd test, whose first peak was identified (Figure 11b).
An MM video was produced for each Rnd test with FIR passband filter with window centered on the identified first frequency and bandwidth of ±0.2 Hz, while α was equal to 100. The MM videos were then processed by searching for the frame with the maximum mean value of displacements within the ROI, which was assumed as the FMD of the MM video. The frame with the minimum mean value of displacements within the ROI was assumed as the FZD of the MM video. FMDs and FZDs were processed by color adjustment and contrast maximization. Then, the invert edge detection algorithm was applied to outline the main structural lines of columns and floor slabs (Figure 12a). In particular, the column lines were considered for first modal shape identification, as it is expected to be an x-direction bending mode (Figure 12b). The column lines were digitized with 100 points (one point each 4 cm, for a total height of 400 cm). The relative displacements in x-direction between the corresponding structural lines in FMD and FZD were calculated to extract the modal shape (Figure 12c).

5.2. Optical 3D MCS Markers

Displacement data from the markers were processed for extraction of modal parameters and for monitoring of structural deformations. In particular, markers data of Rnd tests were processed by experimental modal analysis (EMA) techniques through Multi-Input-Multi-Output (MIMO) method. In fact, the four markers at the column base were considered as input signals, while all the other markers on the structure were considered as output signals. More specifically, the H1 estimator of the Frequency Response Function (FRF) was calculated according to the common formulation:
H 1 ω = S i o ω S i i ω
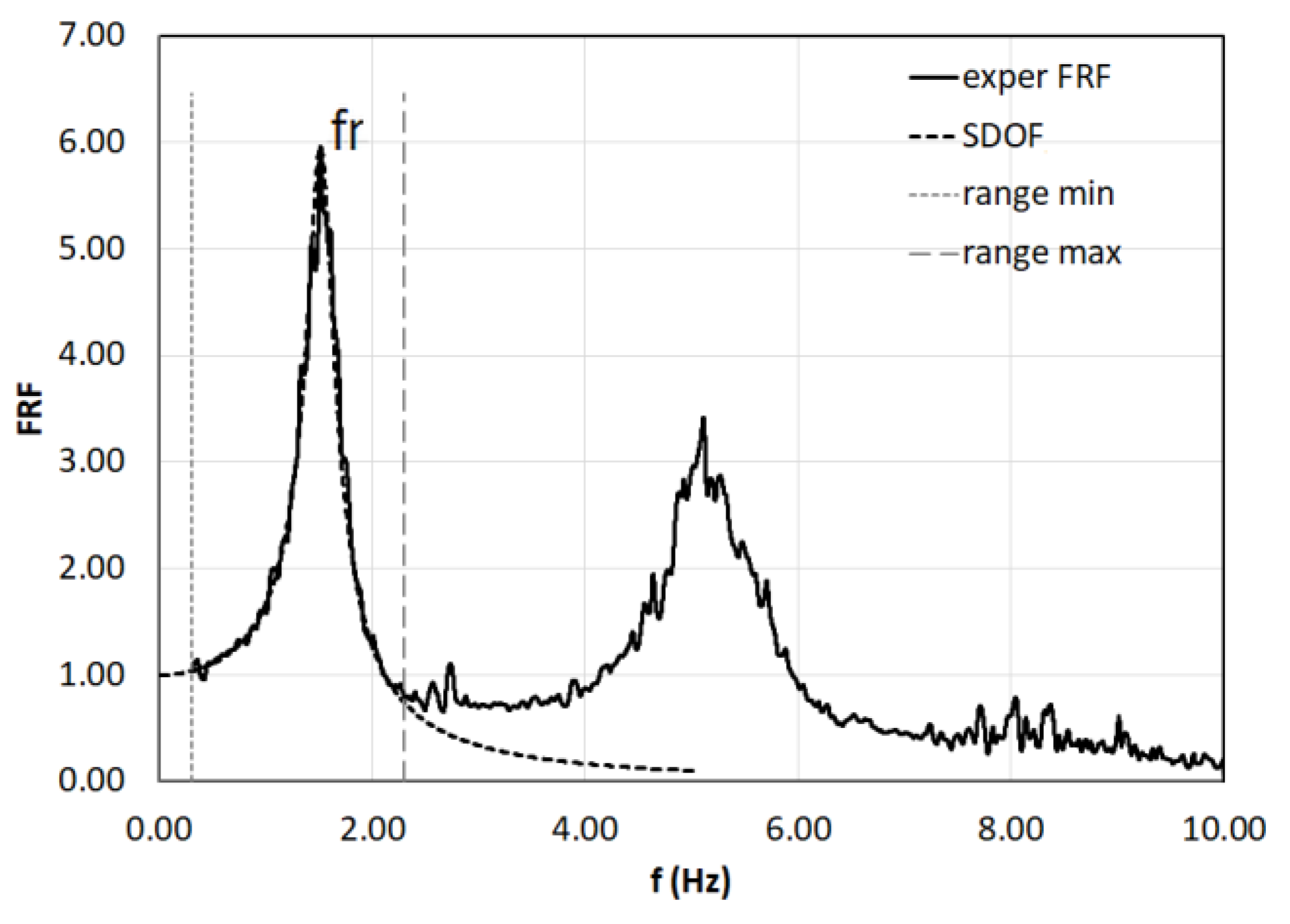
where Sio is the cross power spectrum of input and output signals respectively, Sii is the auto power spectrum of input signals and ω is the angular frequency, calculated as 2π·f, where f is the frequency. The H1 estimator obtained by markers data is then compared with the theoretical single-degree-of-freedom (SDOF) response by curve-fitting method for accurate extraction of the resonance frequency (Figure 13).
Also, the modal shape was calculated by filtering the markers displacements at the identified modal frequency. A 4th-order Butterworth passband filter with window centered on the identified first frequency and bandwidth of ±0.2 Hz was applied.
Relative displacements between markers in x and y directions during the seismic tests were used to obtain the interstory drift at first and second floor with respect to the markers at the columns bases. The interstory drift can be defined as the relative translational displacement between two consecutive floors and is widely considered an important engineering demand parameter and indicator of structural performance [32].
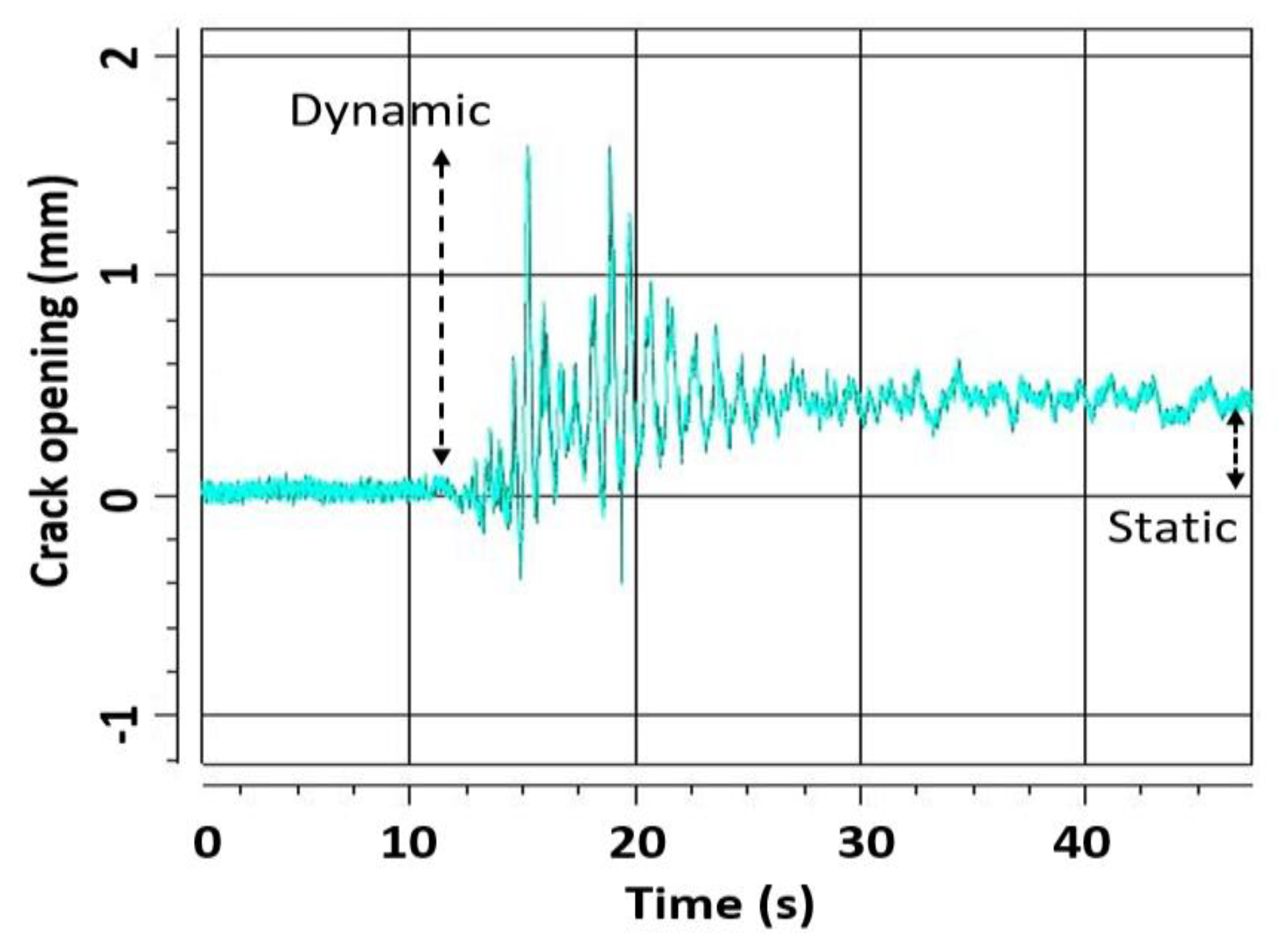
The distances between markers were also investigated to detect structural deformations and, notably, the cracks opening and width [33]. In particular, in Figure 14 the typical behavior of a crack opening during a seismic shake is depicted. The cracks typically open and close during the shake (dynamic condition) and eventually remain residually open at the end of the test (static condition) when permanent plastic deformation of the structure is achieved. Markers can detect cracks width in both dynamic and static conditions so as to accurately characterize the cracks behavior.

5.3. Advanced Accelerometers Processing

In addition to conventional EMA processing of Rnd tests, the accelerometers data of seismic tests were also processed through more advanced techniques. In particular, the nonlinear structural behavior of the mockup structure has been analyzed performing frequency (Smoothed Amplitude Fourier Spectra) and time-frequency analyses (by using the Stockwell Transform [22] and the band-variable filter [21]) considering the relative floor accelerations.
  • In order to analyze accelerometric data referred to the shaking table tests performed by using the Rnd and Norcia inputs (see Table 1), all records were first modified by the following processes: baseline correction;
  • Trends removal;
  • 0.1-25 Hz band-pass filter;
  • Smoothing with a Tukey window.
All data refer to the accelerations recorded by the sensors described within the Figure 5 at columns 1 and 3. The relative accelerations have been evaluated considering as reference stations those located at the base of the model for each horizontal direction. Then, considering only the random tests, amplitude spectra and related modulus have been evaluated by using the following relationship:
A r ω = ∫ − ∞ + ∞ a r t · e − i ω t d t
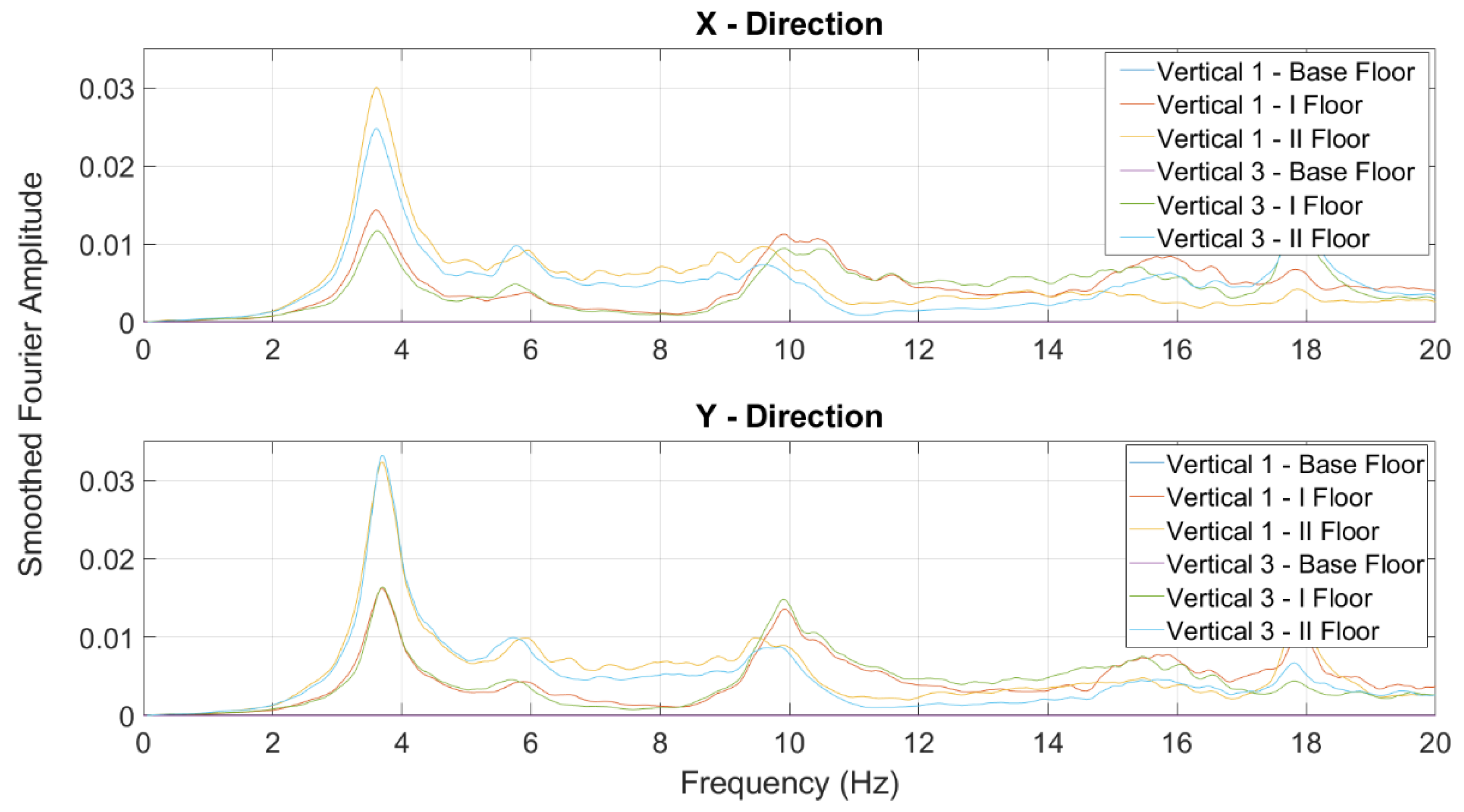
where a r represents the relative floor acceleration. The modulus of relative acceleration spectra A r ω have been smoothed using a 75 points moving average filter implemented in Matlab ®. Figure 15 shows the Smoothed Amplitude Fourier Spectra evaluated on the experimental model, considering data acquired during the test NRC_01g. The same results have also been used to evaluate the mode shapes associated to the first fundamental modal frequencies related to the x and y directions.
It is worth noting that spectral characteristics evaluated using this kind of approach are representative of stationary behavior of the model. In damaging conditions structural modal frequencies change over time during the strong motion phase, then linear modal parameters may not be fully representative of the state of the health of damaged structure. Then, for a damaging structure time-frequency analyses allow to better evaluate the damage state providing the frequency changes instant by instant.
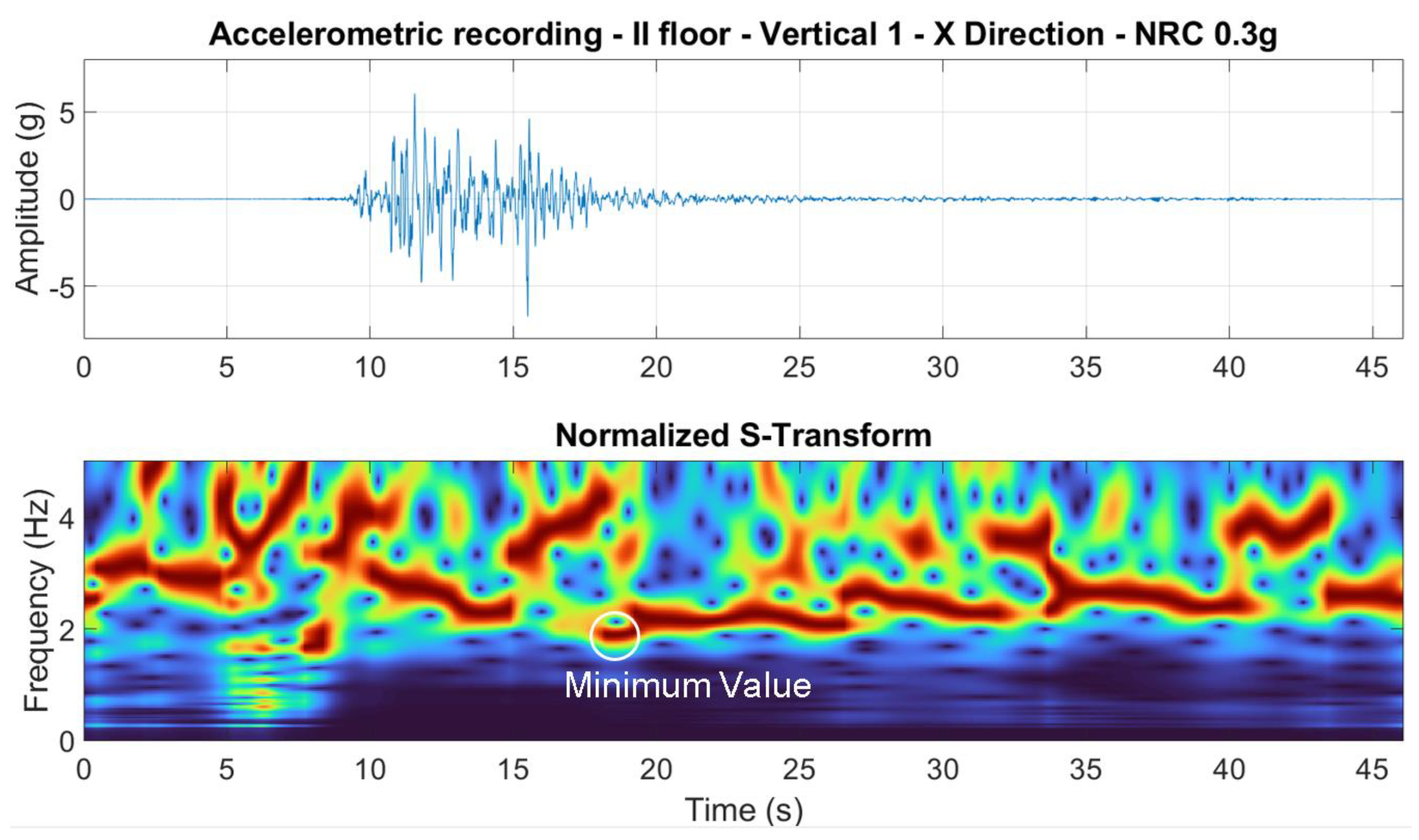
With the aim to evaluate the minimum value of the modal frequencies exhibited by the structure during non-stationary phase, ST analyses have been performed on each top floor accelerometric recordings (along both x and y direction). The ST has been evaluated by using the following relationship [22]:
A r τ , f = f 2 π ∫ − ∞ + ∞ a r ( t ) · e − ( τ − t ) 2 · f 2 2 · e − i · 2 · π · f · t d t
where t is time, f is frequency and τ is a parameter controlling the position of Gaussian window along the time axis. An example of application of the ST is presented in Figure 16 and it is related to the test where the NRC_0.3g earthquake has been applied.
ST analysis allow to evaluate the fundamental frequency variation of the structure during the strong motion test. Along x direction, the minimum value of the fundamental frequency exhibits by the structure during the NRC_0.3g test is equal to 1.86 Hz. Similar results have been retrieved by using the STIRF [24] analyses on the same accelerometric recording, here not show for sake of briefly. More detail about the nonlinear behavior of the structure exhibits during shaking table tests are reported in Results section.

6. Results

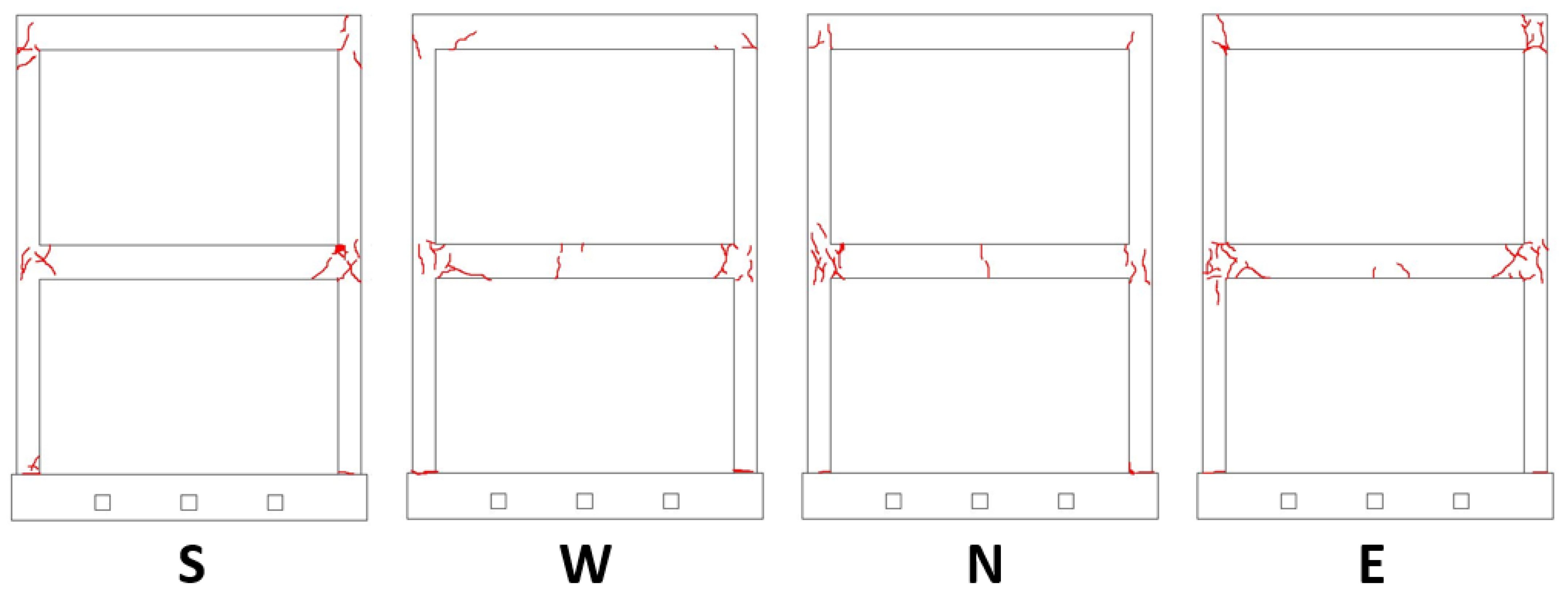
After the shaking table tests, a visual inspection was carried out in order to assess the crack pattern and state of damage of the structure. The visible cracks were essentially concentrated at the beam-column joints of first floor (Figure 17). Fewer cracks were also visible at beam-column joints of second floor (Figure 18). Only a limited amount of small cracks arose at the columns base.
The surveyed cracks positions, orientation, size and openings, were considered to assess the damage grade of the structure. Initially, the damage grade was detected according to the “Agibilita’ e Danno nell’Emergenza Sismica (AeDES)” (“Building Operability and Damage during the Post-earthquake Emergency”) survey form, which is used by the Italian Civil Protection for assessing usability and damage of buildings after earthquakes [34]. Then, the damage was also assessed in the European Macroseismic Scale of 1998 (EMS98) [35] using damage grades conversion table proposed by [36]. The damage resulted between D3 and D4 for vertical members (columns) and D1 for horizontal members (beams and floors).
The distance between 3D MCS markers was monitored to assess the cracks opening and width. Table 3 summarizes the distribution of cracks and their width NRC_100 shaking table tests. The analysis of markers distances substantially confirmed that cracks distribution and severity was concentrated at first floor beam-column joints. In particular, the number of crack at first floor with width higher than 1 mm was more than the double of those detected at the second floor.
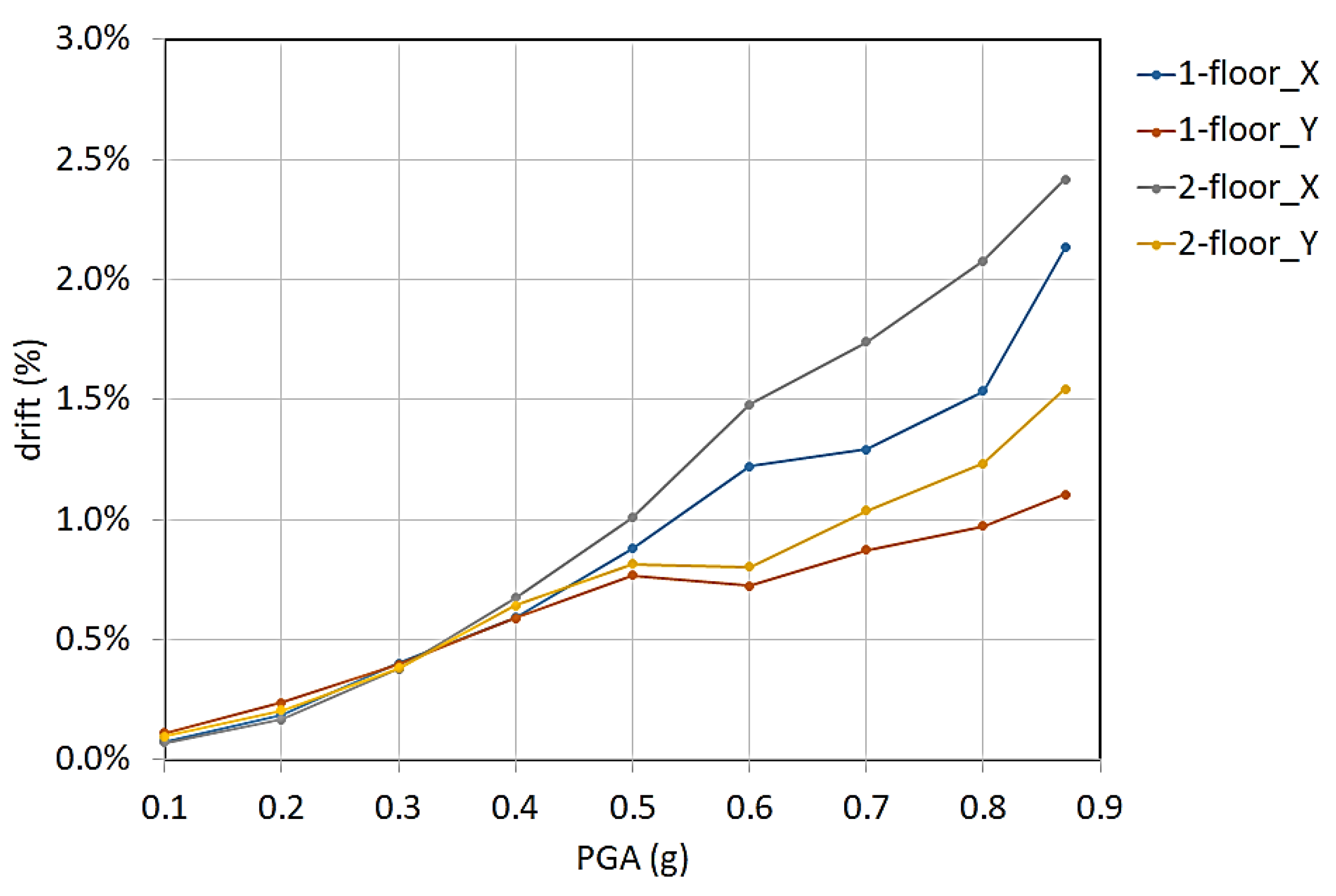
The interstory drift calculated by markers during shaking table sequence is reported in Figure 19. First and second floor drifts were very similar for PGA lower than 0.4 g. Then, the second floor drift in x-direction resulted the largest until the final seismic test. The second floor drift is substantially due to the behavior of the base of the second floor columns, which constitutes the upper part of the first floor beam-column joints.
The 3D laser scanning survey after the seismic tests confirmed that deformation of the structure concentrated at beam-column joints, causing substantial rotation of columns, while floor slabs did not exhibited relevant deformations and remained essentially undamaged.
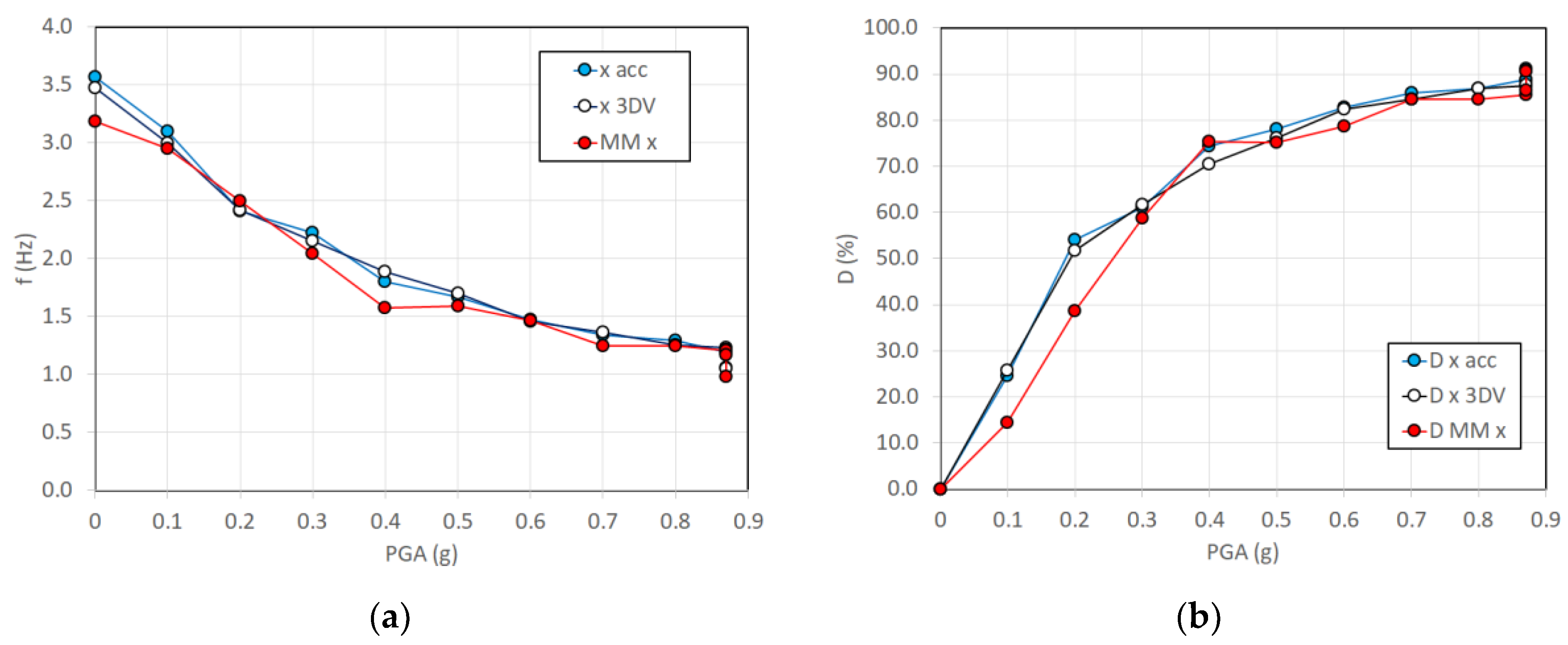
In Figure 20a the comparison of the fr estimates in Rnd tests by accelerometers, markers and MM videos is depicted vs the PGA of the previous shaking table test. In order to assess the state of damage of the structure, a damage index D can be formulated based on the fr according to the following equation:
D = 100 1 − f r f 0 2
where fo is the first modal frequency in Rnd_01, which was performed before the seismic tests, so that it is representative of the undamaged structure. Figure 20b shows the estimated D values.
Table 4 summarizes the estimated values of fr and the corresponding errors with reference to the frequencies obtained by the accelerometers, assumed as the most conventional and consolidated method. The markers of the used 3D MCS reported errors from -0.10 to +0.08 Hz with an RMS error of 0.06 Hz. The MM-based estimates gave errors between -0.38 and +0.11 Hz with an RMS error of 0.16 Hz with higher camera speed (150 fps) but LD camera resolution. When using HD mode resolution and low speed (50 fps), the error in the MM estimate of fr were in the range -0.08 to -0.22 Hz with RMS error of 0.07 Hz. It is interesting noting that MM results at 50 fps, which are more representative of CGCs, are slightly better than at higher speed (150 fps), indicating that when the studied frequencies do not require high speed acquisitions, the pixel resolution seems to play a more relevant role. In addition, MM slightly underestimated the fr identified by accelerometers, providing negative average error values (-0.08 Hz and -0.15 Hz with LD and HD mode respectively). This can be probably due to the MM algorithm, which affects the correct timing of motions.
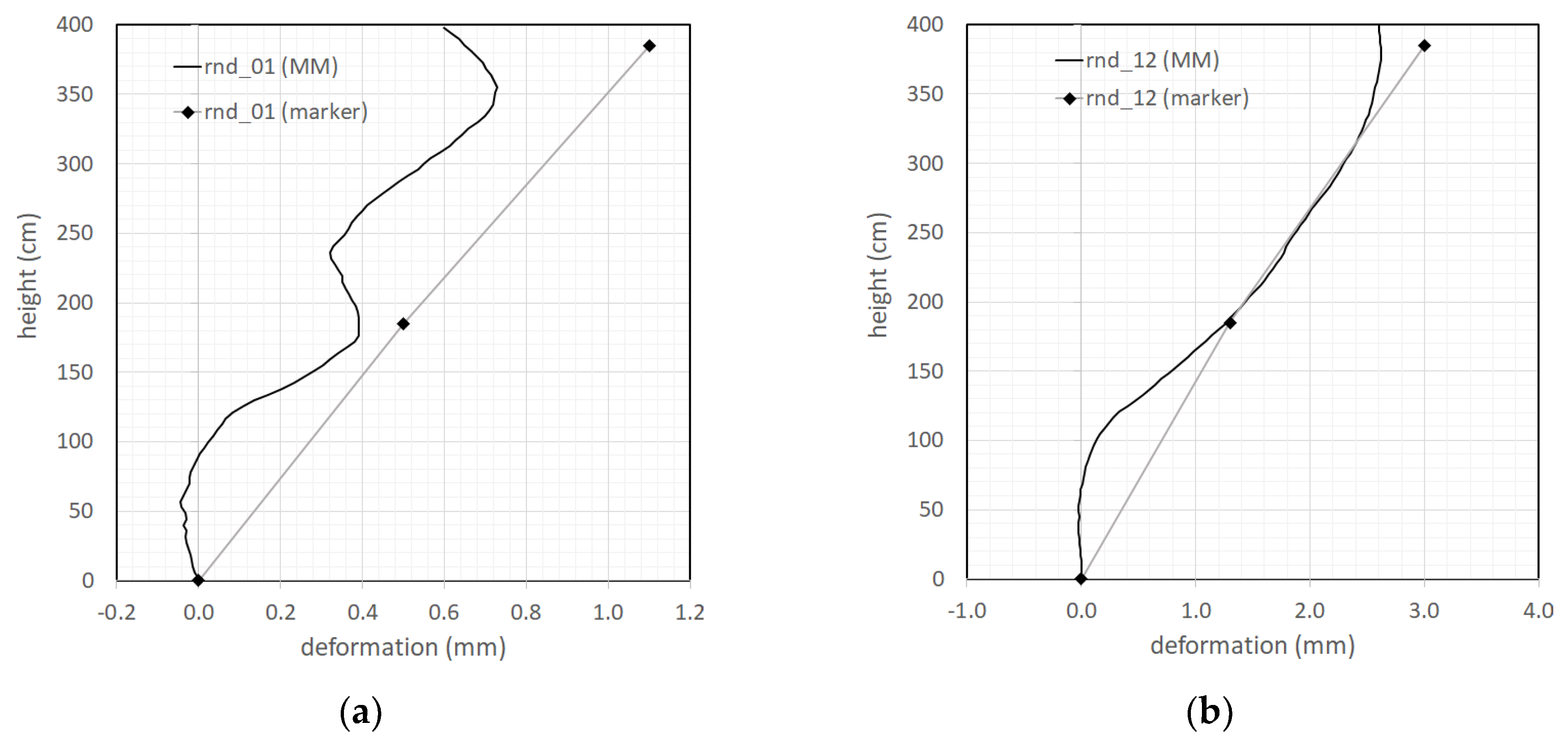
The first modal shape obtained by MM videos and 3D MCS markers are illustrated in Figure 21. Here the modal shape during tests Rnd_01 (undamaged structure) and Rnd_12 (final damaged condition) can be compared. Modal shape was characterized by markers at only three measurement positions (base, first floor and second floor), because marker locations were mainly concentrated at beam-column joints to monitor cracking where most damage was expected. Of course many more markers could be used on columns. However, the number of usable markers are limited in comparison to the positions detectable by video pixels. In fact, the modal shape by MM video was obtained by digitizing 100 points, meaning one point each 4 cm in height. In Figure 21a it is extremely evident the effect of beam-column joints, especially in terms of relation between the flexural stiffness of beams and columns. As it is often the case in low-rise and mid-rise buildings, the relative stiffness of frame members lies in between the flexural-type and the shear-type behavior. As a consequence, both beams and columns bend in double curvature, which typically gives an almost shear type response. Moreover, the rotational flexibility of columns at the base of the building is determined by the degree of fixity at structure base. The slight negative rotation detected at structure base and both beam-column joints of first and second floors can partially due to non-perfectly vertical positioning of the MM camera. However, such rotations are in the order of 0.1 mm in 50 cm, which is very small. In Figure 21b it is interesting noting that the double curvature at first floor beam-column joint disappears completely in the test Rnd_12, which is the effect of advanced damage of the joint that is unable to efficiently connect columns and first floor beam. Curvature at structure base and second floor are still visible, but clearly reduced with respect to initial undamaged condition in Rnd_01, indicating more limited damage.
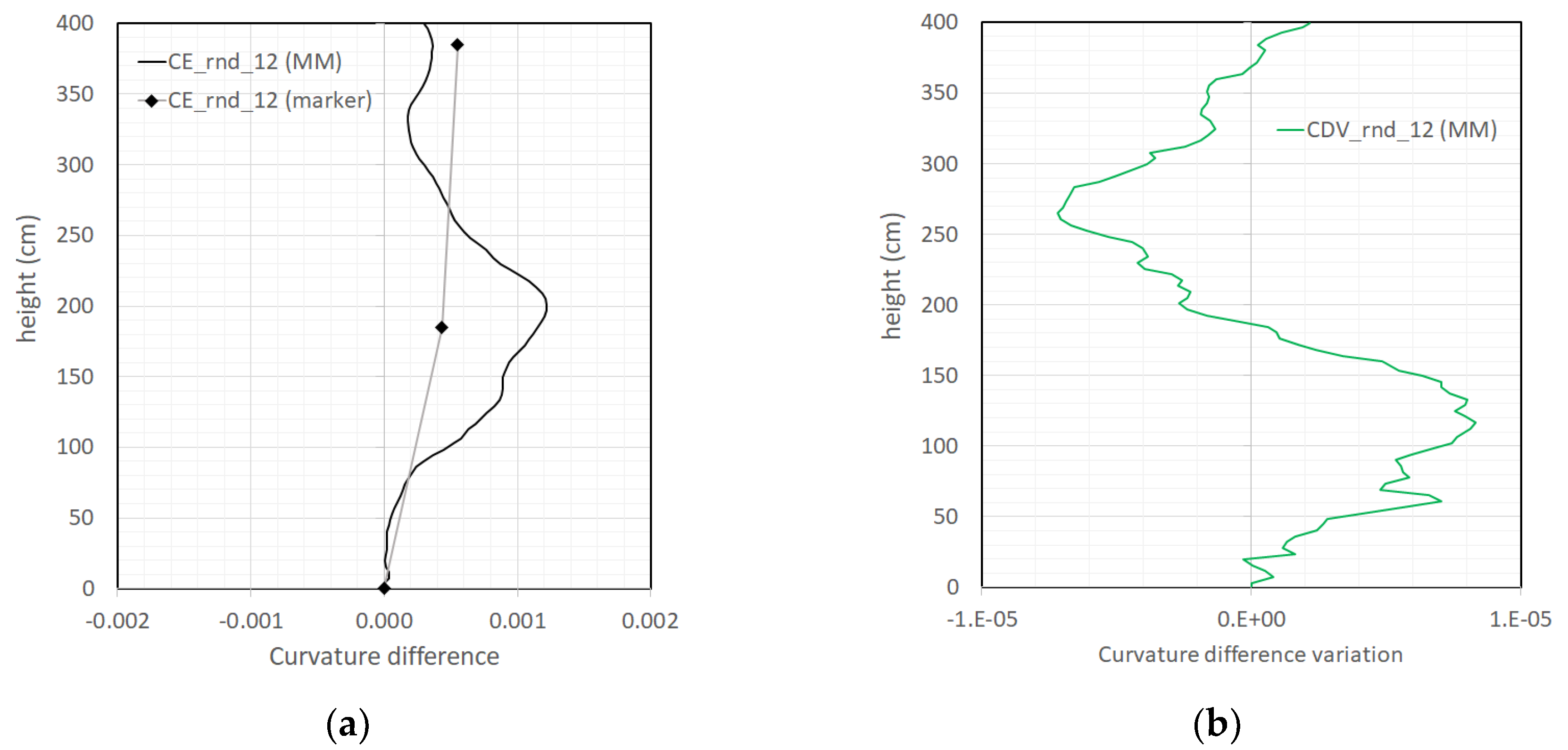
In Figure 22a the analysis of the evolution of first modal shape is illustrated in terms of curvature difference between Rnd_01 and Rnd_12. As a confirmation, curvature difference by MM shows higher values in correspondence of the first floor beam-column joint, locating with remarkable accuracy the main damage.
Location of damage seems even more accurately indicated by the zero crossings of the curvature difference variation in Figure 22b, even if zero crossings cannot provide an estimate of damage severity.
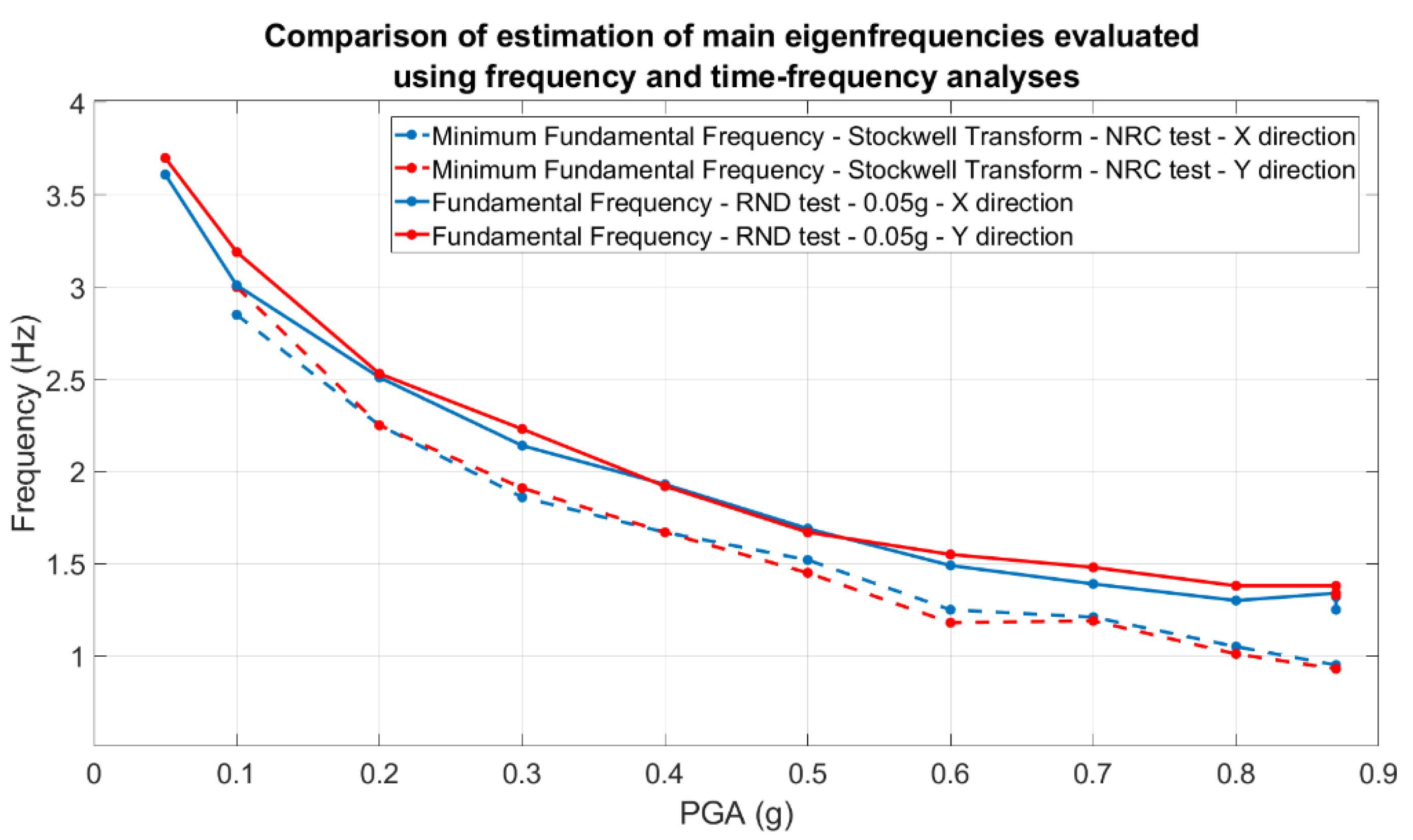
The modulus of Fourier spectra of the relative accelerometric Rnd recordings acquired on the top floor the main modal frequencies was evaluated on both x and y directions. Using the NRC accelerometric recordings, time-frequency ST analyses have been performed with the aim to evaluate the minimum value of fundamental frequency exhibited by the structure during each shaking table test. In Figure 23 a comparison among estimated modal frequencies along x and y directions have been proposed.
It is worth noting that the higher the level of structural damage, the greater the difference between the structural natural frequencies estimated using the random tests (stationary behavior) and those evaluated using the Stockwell transform during the strong motion phase.
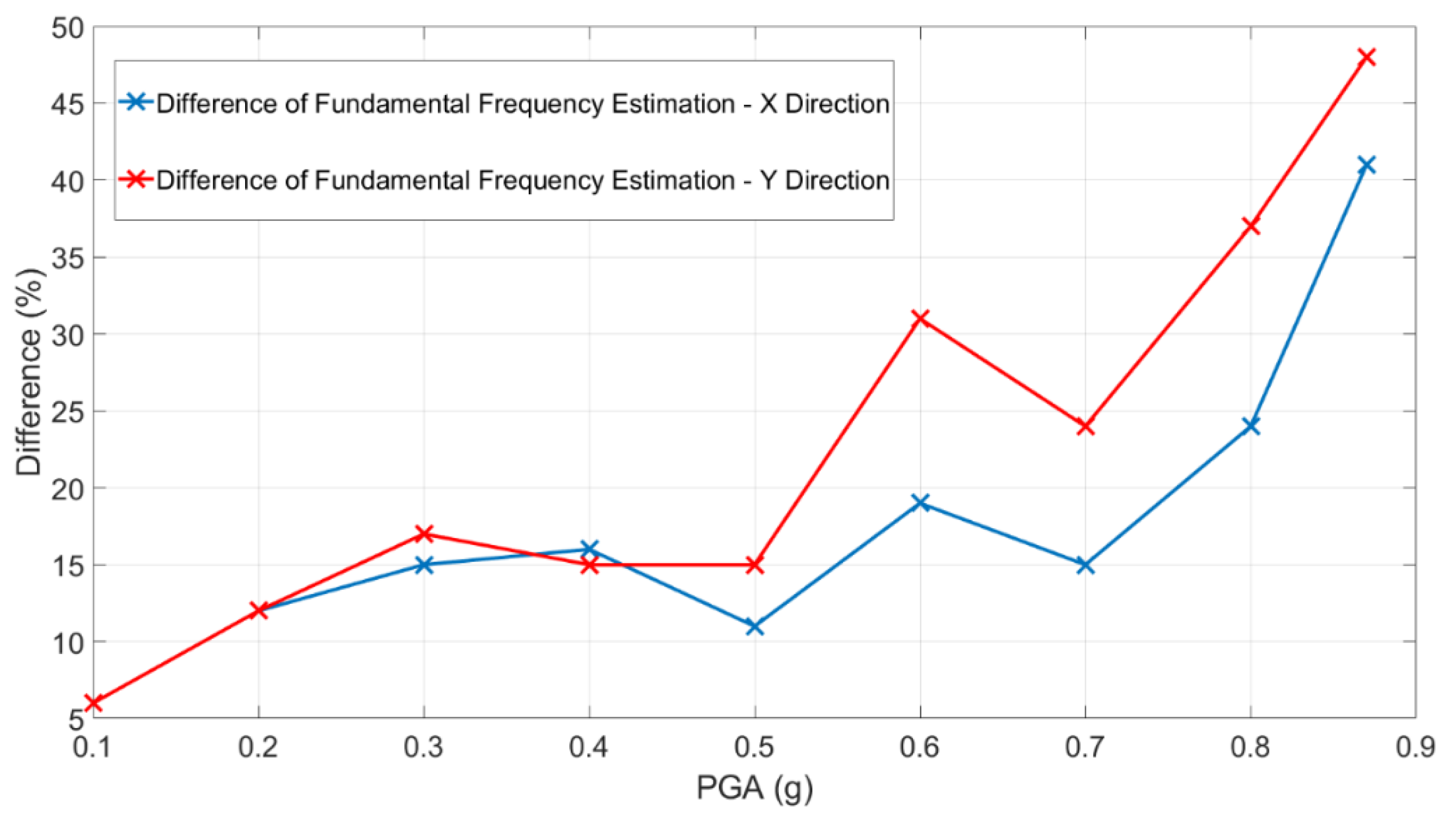
Considering the modal frequencies values depicted in Figure 23, in Figure 24 the differences are quantified as a function of nominal PGA.
Analyzing the results shown in Figure 23 and Figure 24, the importance of using time-frequency analysis techniques emerges to correctly evaluate the structural modal frequencies of damaging structure and, consequently, correctly estimate the relative structural damage. 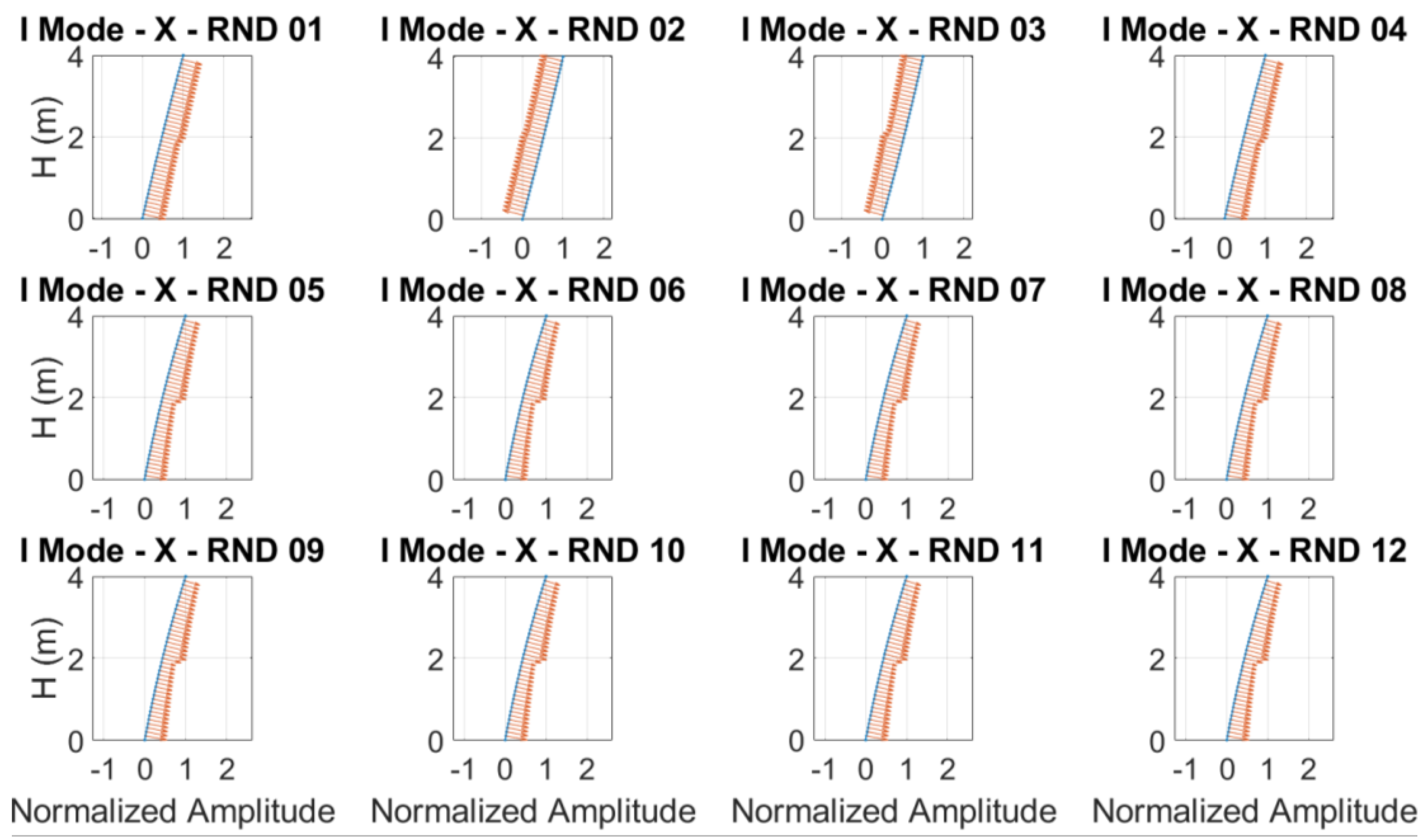Using the performed random tests, the fundamental mode shape evolution relative to the x direction has been evaluated and depicted within the Figure 25.
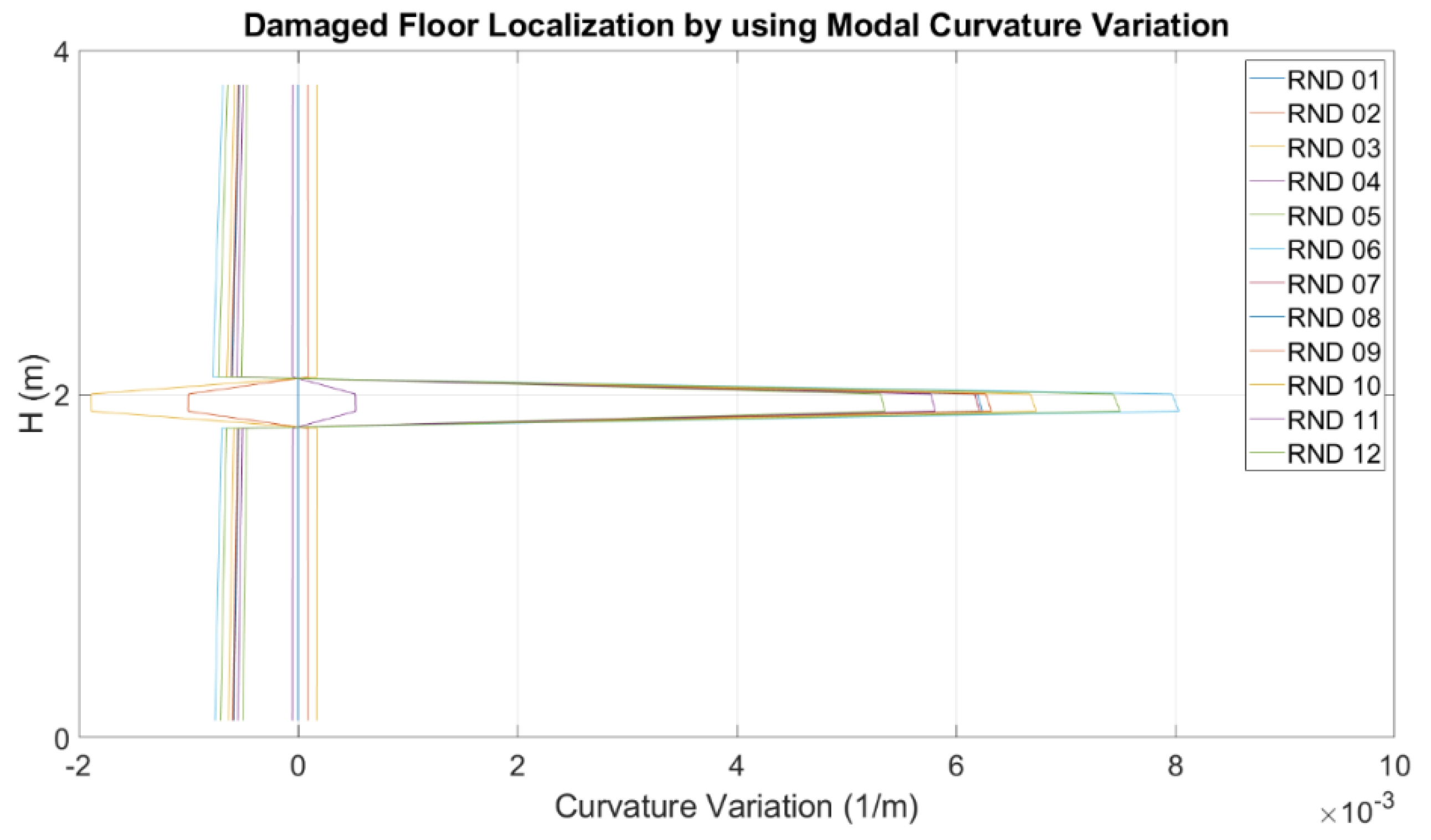
Curvature variation has been evaluated on interpolated mode shapes retrieved by using piecewise cubic Hermite interpolating polynomial: most damaged floor is the first floor. Results obtained for each random test in terms of curvature variation confirm what was found in the laboratory by traditional visual inspections and by using MM-based technique.
In order to identify the most damaged floor by using the accelerometric dataset, the curvature variations have been evaluated by using the procedure described in [23,37,38] and showed in Figure 26.

7. Conclusions

The present work proposed an MM-based procedure to assess the state of damage of a framed RC building by low-cost video-based equipment and processing. The proposed procedure was validated through shaking table experiments reproducing the damage induced on a typical Italian building typology subject to a recent earthquake. In particular, the MM-based procedure aimed at extracting the most relevant modal parameters (frequencies and shapes) for the structural health monitoring of buildings.
The results obtained by the proposed procedure were compared for validation with methods utilizing more conventional and consolidated measurement systems, including accelerometers, 3D laser scanner and an optical 3D MCS.
The advanced analyses of accelerometers data focused on the detection of structural damage using both natural frequencies and mode shape variations. The former were evaluated using the Stockwell Transform on NRC accelerometric recordings. Differences greater than 40% with respect to the natural frequencies obtained using Rnd recordings were evaluated, at least for the most damaged conditions. Mode shape variations, on the other hand, were evaluated using Rnd data, calculating curvature parameters on interpolated mode shapes recovered using piecewise cubic Hermite interpolating polynomial. Results obtained for each random test in terms of curvature variation located the most damage at the first floor.
Also 3D laser scanner surveys and markers displacements of the optical 3D MCS gave confirmation of the location of the main damage at first floor.
The 3D laser final survey detected the main deformations of the structure at beam-column joints, while floor slabs resulted substantially undeformed. In addition, the 3D MCS markers relative displacements revealed that the number and the width of the main cracks concentrated at first floor beam-column joints. Besides, through the markers relative displacements the structural damage was also evaluated by the evolution of the interstory drifts in the seismic tests. Modal frequencies by markers data were also calculated and resulted in good accordance with accelerometers data.
As for the estimates of modal frequency, the proposed MM-based procedure provided results with reasonable accuracy and repeatability with respect to the results obtained analyzing accelerometric recordings in stationary conditions. The MM-based estimates had quite similar errors with either higher camera speed (150 fps) but LD camera resolution and using HD mode resolution and low speed (50 fps). This latter acquisition setup configuration, which can be considered more representative of low-cost and CGCs typical camera parameters, provided even slightly better accuracy than acquisition at higher speed (150 fps), proving that already reasonably affordable cameras have speed levels appropriate for detecting common building frequencies.
The results in terms of detection and analysis of modal shape curvature after seismic shocks was probably the most relevant and interesting, because of their potential of locating the damage in the structure. The MM-based procedure accurately located the main structural damage. It was detected in the first floor beam-column joints, as was found even by traditional visual inspections and in remarkable accordance with advanced methods of analysis of accelerometers data, 3D laser surveys and 3D MCS markers. Moreover, mode shapes could be obtained by image analysis with greater definition (given its raster nature) than by sparse sensors placed in the structure, which makes the video-based procedure a method with high potential even for more complex structural typologies than just framed building.

Supplementary Materials

The following supporting information can be downloaded at: https://eneait-my.sharepoint.com/personal/antonino_cataldo_enea_it/_layouts/15/onedrive.aspx?ga=1&id=%2Fpersonal%2Fantonino%5Fcataldo%5Fenea%5Fit%2FDocuments%2FMAC4PRO%20random%20tests&view=0; All MM-processed videos available.

Author Contributions

Conceptualization, V.F. and I.R.; methodology, V.F. and I.R.; software, A.C. (Antonino Cataldo), F.S. and V.F.; validation, A.C. (Antonino Cataldo), I.R., A.T., A.C. (Alessandro Colucci), F.C.P. and R.D.; formal analysis, I.R., F.C.P. and R.D.; investigation, A.C. (Antonino Cataldo), I.R., A.T. and A.C. (Alessandro Colucci); data curation, A.C. (Antonino Cataldo), V.F., I.R, F.C.P. and R.D.; writing—original draft preparation, I.R, F.C.P. and R.D.; writing—review and editing, I.R.; visualization, I.R.; supervision, I.R.; project administration, A.M.; funding acquisition, C.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors appreciated the contribution of colleagues and researchers who cooperated within the MAC4PRO (Manutenzione intelligente smart maintenance di impianti industriali e opere civili mediante tecnologie di monitoraggio 4.0 e approcci prognostici) project.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Payawal, J.M.G.; Kim, D.K. Image-Based Structural Health Monitoring: A Systematic Review. Appl. Sci. 2023, 13, 968. [Google Scholar] [CrossRef]
  2. Ye, X.W.; Dong, C.Z.; Liu, T. A Review of Machine Vision-Based Structural Health Monitoring: Methodologies and Applications. J. Sensors 2016, 7103039. [Google Scholar] [CrossRef]
  3. Feng, D.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection – A review. Engineering Structures 2018, 156, 105–117. [Google Scholar] [CrossRef]
  4. Lee, J.; Fukuda, Y.; Shinozuka, M.; Cho, S.; Yun, C. Development and application of a vision-based displacement measurement system for structural health monitoring of civil structures. Smart Struct. Syst. 2007, 3, 373–384. [Google Scholar] [CrossRef]
  5. Zona, A. Vision-based vibration monitoring of structures and infrastructures: An overview of recent applications. Infrastructures 2021, 6, 4. [Google Scholar] [CrossRef]
  6. Wu, T.; Tang, L.; Shao, S.; Zhang, X.Y.; Liu, Y.J.; Zhou, Z.X. Cost-effective, vision-based multi-target tracking approach for structural health monitoring. Meas. Sci. Technol. 2021, 32, 125116. [Google Scholar] [CrossRef]
  7. Bao, Y.; Tang, Z.; Li, H.; Zhang, Y. Computer vision and deep learning-based data anomaly detection method for structural health monitoring. Struct. Health Monit. 2018, 18, 401–421. [Google Scholar] [CrossRef]
  8. Dong, C.Z.; Celik, O.; Catbas, F.N.; Obrien, E.; Taylor, Su. A Robust Vision-Based Method for Displacement Measurement under Adverse Environmental Factors Using Spatio-Temporal Context Learning and Taylor Approximation. Sensors 2019, 19, 3197. [Google Scholar] [CrossRef]
  9. Medhi, M.; Dandautiya, A.; Raheja, J.L. Real-Time Video Surveillance Based Structural Health Monitoring of Civil Structures Using Artificial Neural Network. Journal of Nondestructive Evaluation 2019, 38, 63. [Google Scholar] [CrossRef]
  10. Kammer, D.C.; Tinker, M.L. Optimal placement of triaxial accelerometers for modal vibration tests. Mechanical Systems and Signal Processing 2004, 18, 29–41. [Google Scholar] [CrossRef]
  11. Kalybek, M.; Bocian, M.; Nikitas, N. Performance of Optical Structural Vibration Monitoring Systems in Experimental Modal Analysis. Sensors 2021, 21, 1239. [Google Scholar] [CrossRef]
  12. De Canio, G.; de Felice, G.; De Santis, S.; Giocoli, A.; Mongelli, M.; Paolacci, F.; Roselli, I. Passive 3D motion optical data in shaking table tests of a SRG-reinforced masonry wall. Earthquakes and Structures 2016, 40, 53–71. [Google Scholar] [CrossRef]
  13. Wadhwa, N.; Chen, J.G.; Sellon, J.B.; Wei, D.; Rubinstein, M.; Ghaffari, R.; Freeman, D.M.; Büyüköztürk, O.; Wang, P.; Sun, S.; et al. Motion microscopy for visualizing and quantifying small motions. Proc. Natl. Acad. Sci. USA 2017, 114, 11639–11644. [Google Scholar] [CrossRef]
  14. Smieja, M.; Mamala, J.; Praznowski, K.; Cieplinski, T.; Szumilas, Ł. Motion Magnification of Vibration Image in Estimation of Technical Object Condition-Review. Sensors 2021, 21, 6572. [Google Scholar] [CrossRef]
  15. Balageas, D.; Fritzen, C.P.; Güemes, A. Structural Health Monitoring, 2010, ISTE Ltd., pp. 1–495.
  16. Roselli, I.; Malena, M.; Mongelli, M.; Cavalagli, N.; Gioffrè, M.; De Canio, G.; de Felice, G. Structural health monitoring by ambient vibration testing of the ‘Ponte delle Torri’ of Spoleto during the 2016–2017 Central Italy seismic sequence. Int. J. Civ. Struct. Health Monit. 2018, 8, 199–216. [Google Scholar] [CrossRef]
  17. Harmanci, Y.E.; Gülan, U.; Holzner, M.; Chatzi, E. A Novel Approach for 3D-Structural Identification through Video Recording: Magnified Tracking. Sensors 2019, 19, 1229. [Google Scholar] [CrossRef]
  18. Fioriti, V.; Roselli, I.; Cataldo, A.; Forliti, S.; Colucci, A.; Baldini, M.; Picca, A. Motion Magnification Applications for the Protection of Italian Cultural Heritage Assets. Sensors 2022, 22, 9988. [Google Scholar] [CrossRef]
  19. Pandey, A.K.; Biswas, M.; Samman, M.M. Damage Detection from Changes in Curvature Mode Shapes. Journal of Sound and Vibration 1991, 145, 321–332. [Google Scholar] [CrossRef]
  20. Limongelli, M.P. The modal surface interpolation method for damage localization. J. Phys.: Conf. Ser. 2017, 842, 012004. [Google Scholar] [CrossRef]
  21. Ditommaso, R.; Mucciarelli, M.; Ponzo, F.C. Analysis of non-stationary structural systems by using a band-variable filter. Bull. Earthq. Eng. 2012, 10, 895–911. [Google Scholar] [CrossRef]
  22. Stockwell, R.G. , Mansinha L., Lowe R.P. Localization of the complex spectrum: the S transform. IEEE Trans Signal Process 1996, 44, 998–1001. [Google Scholar] [CrossRef]
  23. Ditommaso, R.; Ponzo, F. C.; Auletta, G. Damage detection on framed structures: modal curvature evaluation using Stockwell Transform under seismic excitation. Earthq Eng & Eng Vib 2015, 14, 265–274. [Google Scholar]
  24. Ditommaso, R.; Ponzo, F.C. Automatic evaluation of the fundamental frequency variations and related damping factor of reinforced concrete framed structures using the Short Time Impulse Response Function (STIRF). Eng. Struct. 2015, 82, 104–112. [Google Scholar] [CrossRef]
  25. Wadhwa, N.; Rubinstein, M.; Durand, F.; Freeman, W.T. Phase-based video motion processing. Proceedings of ACM Trans Graphics (SIGGRAPH 2013), Anaheim, Ca, USA, 21-25 July 2013. [Google Scholar]
  26. Fioriti, V.; Roselli, I.; Tatì, A.; Romano, R.; De Canio, G. Motion Magnification analysis for structural monitoring of ancient constructions. Meas. J. Int. Meas. Confed. 2018, 129, 375–380. [Google Scholar] [CrossRef]
  27. Fioriti, V.A.; Roselli, I.; De Canio, G. Modal Identification from Motion Magnification of Ancient Monuments Supported by Blind Source Separation Algorithms. Proceedings of COMPDYN 2019, 7th ECCOMAS, Crete, Greece, 24–26 June 2019. [Google Scholar]
  28. Tian, R.; Sun, G.; Liu, X.; Zheng, B. Sobel Edge Detection Based on Weighted Nuclear Norm Minimization Image Denoising. Electronics 2021, 10, 655. [Google Scholar] [CrossRef]
  29. Petruzzelli, F.; Iervolino, I. NODE: a large-scale seismic risk prioritization tool for Italy based on nominal structural performance. Bull. Earthquake Eng. 2021, 19, 2763–2796. [Google Scholar] [CrossRef]
  30. Mander, J.B.; Priestley, J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
  31. Menegotto, M.; Pinto, P.E. Method of analysis of cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under normal force and bending. Preliminary Report IABSE 1973, 13. [Google Scholar]
  32. Skolnik, D.A.; Wallace, J.W. Critical Assessment of Interstory Drift Measurements. Journal of Structural Engineering 2010, 136, 1574–1584. [Google Scholar] [CrossRef]
  33. Roselli, I.; De Canio, G.; Rossi, M.; Calderini, C.; Lagomarsino, S. Relative displacements of 3D optical markers for deformations and crack monitoring of a masonry structure under shaking table tests. International Journal of Computational Methods and Experimental Measurements 2019, 7, 350–362. [Google Scholar] [CrossRef]
  34. DPC, GNDT, and SSN, 2000. 1st Level Form for Damage Evaluation, Quick Interventions and Usability of Buildings in the Seismic Emergency (05/2000 rel.), Italy.
  35. ESC Working Group, 1998. Macroseismic Scales: European Macroseismic Scale 1998. GeoForschungs Zentrum, Potsdam, Germany.
  36. Augenti, N.; Cosenza, E.; Dolce, M.; Manfredi, G. Masi, A.; Samela, L. Performance of School Buildings during the 2002 Molise, Italy. Earthquake Spectra 2004, 20, S257–S270. [Google Scholar] [CrossRef]
  37. Iacovino, C.; Ditommaso, R.; Ponzo, F.; Limongelli, M. The Interpolation Evolution Method for damage localization in structures under seismic excitation. Earthq. Eng. Struct. Dyn. 2018, 47, 2117–2136. [Google Scholar] [CrossRef]
  38. Ditommaso, R., Iacovino, C., Auletta, G., Parolai, S., & Ponzo, F. C. Damage detection and localization on real structures subjected to strong motion earthquakes using the curvature evolution method: the Navelli (Italy) case Study. Applied Sciences 2021, 11, 6496.
Preprints 73051 g001
Figure 1. Flowchart of proposed video-based MM processing and analysis method.
Figure 1. Flowchart of proposed video-based MM processing and analysis method.
Preprints 73051 g001
Preprints 73051 g002
Figure 2. Tested structure: (a) Building dimensions (cm); (b) Steel reinforcement of columns.
Figure 2. Tested structure: (a) Building dimensions (cm); (b) Steel reinforcement of columns.
Preprints 73051 g002
Preprints 73051 g003
Figure 3. Detail of tested structure floor: (a) top view of slab; (b) Steel reinforcement of beam.
Figure 3. Detail of tested structure floor: (a) top view of slab; (b) Steel reinforcement of beam.
Preprints 73051 g003
Preprints 73051 g004
Figure 4. Test setup: (a) additional load mass and geometry; (b) 3D geometry survey by laser scanner; (c) final setup ready for shaking table tests.
Figure 4. Test setup: (a) additional load mass and geometry; (b) 3D geometry survey by laser scanner; (c) final setup ready for shaking table tests.
Preprints 73051 g004
Preprints 73051 g005
Figure 5. Instrumentation positions in lateral (up) and top (bottom) views.
Figure 5. Instrumentation positions in lateral (up) and top (bottom) views.
Preprints 73051 g005
Preprints 73051 g006
Figure 6. Instrumentation setup: (a) MM camera acquisition station; (b) top view of the acquisition geometry of optical 3D MCS NIR cameras (white triangles).
Figure 6. Instrumentation setup: (a) MM camera acquisition station; (b) top view of the acquisition geometry of optical 3D MCS NIR cameras (white triangles).
Preprints 73051 g006
Preprints 73051 g007
Figure 7. Characterization of reference input accelerograms of seismic NRC shaking table tests (record NRC station, 30 October 2016, 06:40 UTC, Norcia, Italy).
Figure 7. Characterization of reference input accelerograms of seismic NRC shaking table tests (record NRC station, 30 October 2016, 06:40 UTC, Norcia, Italy).
Preprints 73051 g007
Preprints 73051 g008
Figure 8. First three modal shapes: (a) first bending mode in x-direction; (b) first bending mode in x-direction; (c) first torsional mode.
Figure 8. First three modal shapes: (a) first bending mode in x-direction; (b) first bending mode in x-direction; (c) first torsional mode.
Preprints 73051 g008
Preprints 73051 g009
Figure 9. Yielding state at the end of the analysis with unscaled seismic input (NRC_100).
Figure 9. Yielding state at the end of the analysis with unscaled seismic input (NRC_100).
Preprints 73051 g009
Preprints 73051 g010
Figure 10. Analysis of column top at seismic input with scale factor 0.1: (a) tension; (b) compression.
Figure 10. Analysis of column top at seismic input with scale factor 0.1: (a) tension; (b) compression.
Preprints 73051 g010
Preprints 73051 g011
Figure 11. Video processing by motion magnification (MM): (a) selected ROI (blue dotted line) of the South (S) side of column 4; (b) identification of the first mode peaks in the frequency domain for all white noise Rnd shaking table tests.
Figure 11. Video processing by motion magnification (MM): (a) selected ROI (blue dotted line) of the South (S) side of column 4; (b) identification of the first mode peaks in the frequency domain for all white noise Rnd shaking table tests.
Preprints 73051 g011
Preprints 73051 g012
Figure 12. Video processing for modal shape extraction: (a) FMD after edge detection; (b) identification of the structural line of column 4 (red line) in FMD; (c) extracted structural line of column 4 from FMD (red line) and from FZD (blue line).
Figure 12. Video processing for modal shape extraction: (a) FMD after edge detection; (b) identification of the structural line of column 4 (red line) in FMD; (c) extracted structural line of column 4 from FMD (red line) and from FZD (blue line).
Preprints 73051 g012
Preprints 73051 g013
Figure 13. Identification of the first modal frequency (fr) by FRF of markers data (exper FRF).
Figure 13. Identification of the first modal frequency (fr) by FRF of markers data (exper FRF).
Preprints 73051 g013
Preprints 73051 g014
Figure 14. Typical crack opening during seismic test. The shake starts at time 11 s.
Figure 14. Typical crack opening during seismic test. The shake starts at time 11 s.
Preprints 73051 g014
Preprints 73051 g015
Figure 15. Smoothed Amplitude Fourier Spectra evaluated for the RND_01 test.
Figure 15. Smoothed Amplitude Fourier Spectra evaluated for the RND_01 test.
Preprints 73051 g015
Preprints 73051 g016
Figure 16. Stockwell Transform evaluated for the NRC_0.3g test and related to column 1, second floor and x direction.
Figure 16. Stockwell Transform evaluated for the NRC_0.3g test and related to column 1, second floor and x direction.
Preprints 73051 g016
Preprints 73051 g017
Figure 17. Detail of damage at beam-column joints of first floor (numbers indicate the columns).
Figure 17. Detail of damage at beam-column joints of first floor (numbers indicate the columns).
Preprints 73051 g017
Preprints 73051 g018
Figure 18. Crack pattern at the end of seismic tests.
Figure 18. Crack pattern at the end of seismic tests.
Preprints 73051 g018
Preprints 73051 g019
Figure 19. Interstory drifts (1-floor and 2-floor) in x and y directions vs shaking table PGA.
Figure 19. Interstory drifts (1-floor and 2-floor) in x and y directions vs shaking table PGA.
Preprints 73051 g019
Preprints 73051 g020
Figure 20. First modal frequency fr of tested structure calculated by markers data (3DV), accelerometers (acc) and motion magnification (MM) in x-direction: (a) evolution of fr in white noise random tests during shaking table sequence; (b) corresponding damage index D%.
Figure 20. First modal frequency fr of tested structure calculated by markers data (3DV), accelerometers (acc) and motion magnification (MM) in x-direction: (a) evolution of fr in white noise random tests during shaking table sequence; (b) corresponding damage index D%.
Preprints 73051 g020
Preprints 73051 g021
Figure 21. First modal shape calculated by MM and by markers in x-direction: (a) modal shape extracted by test ‘rnd_01’; (b) modal shape extracted by test ‘rnd_12’.
Figure 21. First modal shape calculated by MM and by markers in x-direction: (a) modal shape extracted by test ‘rnd_01’; (b) modal shape extracted by test ‘rnd_12’.
Preprints 73051 g021
Preprints 73051 g022
Figure 22. Analysis of first modal shapes: (a) modal shape curvature difference (CE) between test ‘rnd_12′ and test ‘rnd_01′; (b) corresponding curvature difference variation (CDV).
Figure 22. Analysis of first modal shapes: (a) modal shape curvature difference (CE) between test ‘rnd_12′ and test ‘rnd_01′; (b) corresponding curvature difference variation (CDV).
Preprints 73051 g022
Preprints 73051 g023
Figure 23. Comparison of main structural modal frequencies evaluated using random tests (stationary values of modal frequencies) and Stockwell Transform (minimum value of modal frequencies).
Figure 23. Comparison of main structural modal frequencies evaluated using random tests (stationary values of modal frequencies) and Stockwell Transform (minimum value of modal frequencies).
Preprints 73051 g023
Preprints 73051 g024
Figure 24. Difference of estimation of structural modal frequencies using random tests (stationary values of modal frequencies) and Stockwell Transform (minimum value of modal frequencies).
Figure 24. Difference of estimation of structural modal frequencies using random tests (stationary values of modal frequencies) and Stockwell Transform (minimum value of modal frequencies).
Preprints 73051 g024
Preprints 73051 g025
Figure 25. Fundamental mode shape and related curvature vectors evaluated along x direction by using random tests.
Figure 25. Fundamental mode shape and related curvature vectors evaluated along x direction by using random tests.
Preprints 73051 g025
Preprints 73051 g026
Figure 26. Damage level localization by using the modal curvature variation.
Figure 26. Damage level localization by using the modal curvature variation.
Preprints 73051 g026
Table 1. Shaking table testing sequence.
Table 1. Shaking table testing sequence.
Test Test type Nominal PGA (g) Notes
Rnd_01 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_01g Seismic triaxial 0.10 11% PGA scaled 30 Oct. 2016 shake, Norcia, Italy
Rnd_02 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_02g Seismic triaxial 0.20 23% PGA scaled 30 Oct. 2016 shake, Norcia, Italy
Rnd_03 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_03g Seismic triaxial 0.30 34% PGA scaled 30 Oct. 2016 shake, Norcia, Italy
Rnd_04 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_04g Seismic triaxial 0.40 45% PGA scaled 30 Oct. 2016 shake, Norcia, Italy
Rnd_05 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_05g Seismic triaxial 0.50 57% PGA scaled 30 Oct. 2016 shake, Norcia, Italy
Rnd_06 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_06g Seismic triaxial 0.60 69% PGA scaled 30 Oct. 2016 shake, Norcia, Italy
Rnd_07 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_07g Seismic triaxial 0.70 80% PGA scaled 30 Oct. 2016 shake, Norcia, Italy
Rnd_08 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_08g Seismic triaxial 0.80 91% PGA scaled 30 Oct. 2016 shake, Norcia, Italy
Rnd_09 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_100 Seismic triaxial 0.87 Full 30 October 2016 shake, Norcia, Italy
Rnd_10 White noise triaxial 0.05 Dynamic identification test, 2 min duration
Rnd_11 White noise triaxial 0.05 Dynamic identification test, 2 min duration
NRC_100b* Seismic triaxial 0.87 Full 30 October 2016 shake, Norcia, Italy
Rnd_12 White noise triaxial 0.05 Dynamic identification test, 2 min duration
* Repetition of NRC_100.
Table 2. First three modal frequencies by linear model with initial and cracked stiffness.
Table 2. First three modal frequencies by linear model with initial and cracked stiffness.
Mode Frequency (Hz)
with initial stiffness		 Frequency (Hz)
with cracked stiffness		 Mode type
1 5.125 3.605 Bending in x-direction
2 5.127 3.713 Bending in y-direction
3 8.101 5.930 Torsional
Table 3. Cracks opening and width in dynamic conditions during test NRC_100.
Table 3. Cracks opening and width in dynamic conditions during test NRC_100.
Cracks location Sum of cracks width (mm)1 Number of cracks with width > 1 mm1 Cracks widest opening (mm)1
Floor 1 88.2 39 9.9
Floor 2 54.1 19 3.4
1 Calculated by 3D MCS markers distances.
Table 4. Estimated fr values and errors by 3D MCS markers data (3DV) and motion magnification (MM) with respect to accelerometer data (acc).
Table 4. Estimated fr values and errors by 3D MCS markers data (3DV) and motion magnification (MM) with respect to accelerometer data (acc).
Estimated fr (Hz) Error (Hz) MM camera parameters
Test acc 3DV MM 3DV MM fps resolution px
Rnd_01 3.57 3.48 3.19 -0.09 -0.38 150 632 x 508
Rnd_02 3.10 3.00 2.95 -0.10 -0.15 50 1264 x 1016
Rnd_03 2.42 2.42 2.50 0.00 0.08 150 632 x 508
Rnd_04 2.23 2.15 2.05 -0.07 -0.18 150 632 x 508
Rnd_05 1.81 1.89 1.58 0.08 -0.23 150 632 x 508
Rnd_06 1.67 1.70 1.59 0.03 -0.08 50 1264 x 1016
Rnd_07 1.48 1.46 1.47 -0.02 -0.01 150 632 x 508
Rnd_08 1.34 1.37 1.25 0.03 -0.09 150 632 x 508
Rnd_09 1.29 1.26 1.25 -0.03 -0.04 150 632 x 508
Rnd_10 1.19 1.23 1.21 0.04 0.02 150 632 x 508
Rnd_11 1.20 1.22 0.98 0.02 -0.22 50 1264 x 1016
Rnd_12 1.07 1.06 1.17 -0.01 0.10 150 632 x 508
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated