Prerpints.org logo
Preprint
Article

Experiments on Steam Injection Into Preformed Steam Chambers of Various Shapes for Maximum Condensate Recovery

This version is not peer-reviewed.

Submitted:

09 May 2023

Posted:

10 May 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Recently, in a previous study, we have experimentally shown the existence of an optimal injected steam mass flow rate, per unit length, ϕopt, which produces the maximal recovery of con- densate in a preformed steam chamber with an elliptical cross section of horizontal semi-major axis. Mutatis mutandis, in this work we present experimental studies in preformed steam chambers, one elliptical and the other circular. In both cases, we also have found the existence of unique optimal values. These configurations try to recreate the steam condensation, at a given time lapse, as it would occur during the growth stage of the steam-assisted gravity drainage (SAGD) process, a method used in the recovery of heavy and extra-heavy oil from homogeneous reservoirs. Finding the optimal mass flow rates in actual recovery process could become useful in the design of optimized SAGD processes.
Keywords: 
Subject: 
Engineering  -   Energy and Fuel Technology

1. Introduction

One of the most efficient thermal methods in the recovery of heavy and extra heavy oil from reservoirs is the steam-assisted gravity drainage (SAGD) technique, which was proposed and developed by Butler et al [1,2,3,4] in the 1980’s. The SAGD process involves the injection of hot steam, at constant pressure, into the reservoir through an horizontal upper pipe and the extraction of condensates and water/oil emulsions through the parallel pipe located beneath the injection pipe. Incidentally, there are estimations that heavy oil reserves account for more than 70% of the world’s oil reserves [5]. SAGD operations require large amounts of water (for instance, in Canada, approximately 179 million m3 of fresh water was used in 2009 for oil sands-related extractive activities [6]) along with a significant energy consumption. According to some calculations, losses represent more than 50% of the energy used in SAGD [7]. Finally, a number of efforts have been made to recover and clean the water produced in the free water phase and in the water/oil emulsion, contained in the recovered fluids [8,9].
In the search for a strong reduction of the injected water and the wasted energy, it is crucial to understand the main physical mechanisms and conditions that control the efficient production of condensates [10,11,12,13,14,15]. For instance, some numerical [12,13] and experimental [14,15] studies suggest that it is possible to control the well spacing, the well placement or the injection temperature [13] in order to optimize the oil production of heavy oil reservoirs.
By means of a simple theoretical model for a homogeneous reservoir [10], we also found an optimal (dimensionless) injected steam mass flow rate, per unit length, ϕ o p t , that yields the maximal recovery of condensates or water/oil emulsions, at a given time-lapse. We predicted that this optimal value depends on the shape of the steam chamber edge, the physical properties of the reservoir, the operating parameters, including the wells spacing and placement, and the boiling and reservoir temperatures, all of them measured at a given time period of the growing stage of the chamber.
Following these latest ideas, in a recent experimental study [16], the steam injection at various mass flow rates was carried out inside a preformed steam chamber, made of glass beads occupying an elliptical space (with horizontal semi-major axis), in an iron slab of considerable mass. By analyzing the cumulative amounts of injected steam and recovered condensates, during a short time-lapse, we identified the optimal flow rate. Then, a posteriori, we proceeded through visual and infrared images of such optimal process to track the motion of the condensation front until it reaches the cold solid edge (which is assumed to represent the region where the oil behaves as a solid), similarly, the time evolution of the temperature field was measured until there was no appreciable change. This method allowed us to determine when a steady-state of the steam injection was reached for a specific injected mass flow rate.
In this work we report new experimental studies related to the steam injection into preformed steam chambers of elliptical (with vertical semi-major axis) and circular cross-sectional shapes, to highlight their corresponding efficiency in the production of condensates. The use of preformed chambers embedded in highly massive slabs was conceived as an experimental set-up that reproduces the main physical characteristics of the SAGD process. Moreover, in an real life monitoring of the steam chamber formed in the oil sand layer in the lower Cretaceous McMurray formation, it was shown that the temperature distribution of the steam chamber evolved from a nearly elliptical with a horizontal semi-major axis to another ellipse with a vertical semi-major axis [17].
It is important comment that, perhaps due to the seminal works of Butler [1,2,3,4], many theoretical and experimental works have reported the steam injection in terms of volume flow rates (see for instance [7,11,14,18,19]). However, measuring gas flow using a volumetric flow meter, temperature and pressure measurement are required, along with the gas density, to convert volumetric flow to mass flow. One of the advantages of measuring gas mass flow, is that the mass does not change with temperature or pressure. Mass flow measurement is known to offer more reliable, accurate, and more repeatability data when compared with volumetric flow methods. Consequently, our main results for gas or liquid flows, will be given in terms of mass flow rates.
To reach our goals, the division of this work is as follows: in the next Section we provide the analytical expressions describing the shape of the chambers studied in the experiments. Also, we briefly discuss the main physical parameters involved in the determination of the optimal recovery of the condensates. Later on, in Section 3, the experimental set-up will be presented. There, we will discuss the evolution of the transient condensation fronts in the elliptical and circular steam chambers and later on we will report measurements of the temperature fields in the chambers to also determine the steady-state phase change temperatures, close to the steam chamber edges. In Section 4, the injected steam and the accumulated quantities of recovered condensates allows us to present, in a dimensionless form, the plots of the recovery efficiency of condensates for the elliptical and circular steam chambers. Finally, in Section 5, the main conclusions and limitations of this study will be presented.

2. Preformed steam chambers and parameters governing the steam flow

2.1. Preformed steam chambers

Our theoretical model focuses on the steam flow radially injected from the injection pipe into a porous steam chamber of permeability K and the recovery of the condensed water, due to gravity drainage, at the lower recovery pipe [10]. We justify this approach given that in the actual SAGD process, the injected steam displaces the oil, leading to the formation of a steam-saturated zone partially depleted of oil, the steam chamber, around the injection pipe.
In order to gain physical insight into the main mechanisms of heat and mass transfer within the steam chamber we consider, as in the theoretical model, nearly two-dimensional preformed chambers as those sketched in Figure 1.
The limit of the steam chamber is the edge of the chamber, where a thin layer of mean thickness δ consisting of a water/oil emulsion drains by gravity towards the production pipe, and beyond this layer, there is a region where the highly viscous oil saturating the rest of the reservoir behaves as a solid. We assume, by using cylindrical coordinates, that within given time lapse, the chamber edge has the form r = R c ( θ ) , with the symmetry condition expressed as R c ( θ ) = R c ( − θ ) , where 0 ≤ θ ≤ π / 2 and θ is measured clockwise from the upper vertical axis ( θ = 0 ) to the lower vertical axis ( θ = π / 2 ).
In Figure 1 we depict the cross-sections of two preformed elliptical chambers with different orientation and one preformed circular chamber, all of them centered at the origin O, where the injection pipe is also placed (red dot). In the scheme of Figure 1(a) the ellipse has a horizontal semi-major axis, meanwhile the ellipse in the scheme of Figure 1(b) has a vertical semi-major axis, finally the scheme of the circular chamber is shown in Figure 1(c). The generic equation describing the shape of the edges of the preformed steam chambers is
R c θ = a b a 2 cos 2 θ + b 2 sin 2 θ 1 / 2 .
The corresponding values of a and b, for each edge in Figure 1, are given in Table 1. In the specific case of the circular chamber its radius is R = a = b = 0.10 m, We chose these edge shapes for ease of machining and, as aforementioned, due to the actual formation of both previously described elliptically shaped steam chambers [17]. It is worth mentioning that in a previous work [16], we already have analyzed the steam injection into the elliptical steam chamber of Figure 1(a), and it is referred here to contrast with the new results obtained for the other two steam chamber designs as well as to emphasize the importance of the shape of the steam chamber on the efficiency of the recovery of condensates.
Table 1. Values the geometrical parameters of Eq. (1).
Table 1. Values the geometrical parameters of Eq. (1).
Shape of chamber edge a(m) b(m)
Ellipse (horizontal semi-major axis) 0.157 0.105
Ellipse (vertical semi-major axis) 0.105 0.157
Circumference 0.10 0.10
The elliptical steam chamber of Figure 1(b) is materially the same as that of Figure 1(a), which was manufactured, in a cast iron slab with a height of 0.50 m, a length of 0.36 m and thickness of 0.041 m. To enclose the porous layer between two glass plates, the hollow elliptical space in the slab was filled with glass beads (soda lime) of diameter d = 0.6 mm. With these data we reported in [16] that the mean porosity is φ ≈ 0.40 and the permeability is K ≈ 3 . 55 × 10 − 8 m2. These same values are assumed to be valid for the porous medium in the circular steam chamber since the same glass beads were used in such a case.
To facilitate the optical and infrared visualization of the steam flow in the steam chamber, we placed on each side of the chamber, plates of transparent armored glass of elliptical shapes 0.013 m thick, thus, the chamber is l = 0.015 m deep, which is also the length of the steam diffuser used to radially and evenly distribute the hot steam. The armored glasses were selected to prevent an explosive rupture caused by the thermal stresses and because they were subject to multiple cycles of use.
For the elliptical steam chamber the distance between O and P is H = 0.14 m. At O the diffuser has an external radius of R I = 7 × 10 − 3 m; meaning that the dimensionless radius is ϵ = R I / H = 0.05 , the radius of the orifice of recovery, which is open to atmosphere, is the same as R I . The bores drilled to embed the diffuser in the glass plate and the recovery port were machined only on the rear glass plate.
In the case of the circular steam chamber, Figure 1(c), the chamber was embedded in a slab 0.51 m high, 0.51 m long and 0.064 m thick. In this case the porous layer was enclosed in between two Plexiglas plates 0.011 m thick, hence the chamber has a depth of l = 0.029 m and matches the length for the steam diffuser. Here, the distance between O and P is H = 0.07 m, the radius of the diffuser of steam was R I = 5 × 10 − 3 m which is the same for the recovery orifice, consequently, now we have that ϵ = R I / H = 0.07 .

2.2. Parameters of the steam flow in SAGD

Similar to our theoretical treatment [10], it was assumed that the injected steam condenses in a thin layer, close to the chamber edge r = R c , see Figure 1. If the condensate is mainly composed of water, then it has dynamic viscosity μ w , density ρ w and both of them will be characterized at temperature T b , the boiling temperature of the phase change.
The governing equations for the steady state flows of steam and condensate, valid for a short time lapse of the SAGD process, yield several dimensionless physical parameters, whose values will be directly related to the shape of the steam chamber edge, R c θ , and to the conditions for which the optimum mass flow rate occurs [10]. Such parameters are
S = c p T b L , T I T b , ϵ = R I H , Π = ρ w 2 K g H L μ w k e T b T b − T R T b ,
here c p , is the steam specific heat, L, the latent heat of condensation and k e , the effective thermal conductivity of the steam saturated medium, will be taken according to the temperature T b . Other important quantities are g, the acceleration due to gravity, T I and T R , the temperatures of the steam at injection and at the edge of the steam chamber, respectively.
The physical meaning of the dimensionless group of parameters given in (2) are discussed in [10], but in summary: S is the parameter that measures the ratio of the steam enthalpy (heat energy at a constant pressure) to the latent heat (heat released per unit mass when the substance condenses), the value of T I / T b amounts to the ratio between the injection temperature T I with respect to the phase change temperature T b , ϵ is the radius of the injection pipe scaled with H and the dimensionless parameter Π is related to the dimensionless optimal mass flow rate, per unit length, ϕ o p t = ϕ o p t * / ( k e T b / L ) , where ϕ o p t * is the dimensional optimal mass flow rate per unit length. An analysis of the relation between Π and ϕ o p t establishes as Π increases, ϕ o p t also increases [10]. We notice in (2) that an increase of Π (and consequently an increase of ϕ o p t ) occurs if T R / T b decreases. In this sense, a substantial difference between T b and T R improves the condensates recovery. However, also it was found that if the injection temperature T I is large, the heat flux that reaches the condensation front from the steam leads to a decrease of ϕ o p t . The dimensionless condensate film thickness δ ′ , was estimated to be δ ′ = μ w ϕ * / ρ w 2 g K H and for the optimal case it is δ o p t ′ = μ w ϕ o p t * / ρ w 2 g K H .
Finally, it was found theoretically and experimentally [10,16] that if the dimensionless injected flow rate is larger than ϕ o p t , then a fraction of the steam rapidly reaches the production pipe, without condensing inside the chamber. Conversely, if the injected flow rate is smaller than ϕ o p t , then a large amount of the steam condensates very rapidly and it drains to the production pipe without reaching the edge. The value of ϕ o p t separates these undesirable conditions and must be given as a function of the parameters (2). Many of these claims will be backed by current experimental results.

3. Experiments of steam injection into elliptical and circular chambers

3.1. Steam chambers

For the continuous steam injection into the preformed steam chambers we used the same steam generator described in our previous experimental study [16]. In Figure 2 we schematically show the cast iron slab, enclosing the circular steam chamber, which is mounted on a support structure and, at the rear of the chamber, the jet nozzle is connected to a radial diffuser. We used optic and IR cameras to visualize, in real time, the motion of fluid, and the isotherms distribution, whenever possible.
In the current experiments, initially the preformed steam chamber contains the air-saturated porous medium consisting of dry glass beads at room temperature T r o o m = 293.15 ± 1 K, which is the same as that of the metallic slab. For the case when the optimal mass flow rate has been determined, after the injection at different flow rates, we carefully observed through the treatment of digital images the displacement process of the condensation front, that eventually reaches the edge of the chamber. After the condensate reaches the edge, it will drains toward the recovery pipe at the bottom pipe. In Figure 3 we show the elliptical (Figure 3(a)) and circular (Figure 3(b)) preformed steam chambers used in the current study.
The procedure followed to inject specific amounts of saturated steam was reported elsewhere [16], it was based on the method of direct contact condensation of steam jets [20,21]. Consequently, the injected steam mass is always known m ( t ) as well as the mass flow rate m · = d m / d t . Through a thermocouple located within the chamber, right at the injection orifice, we found that for all the cases the injection temperature was T I = 365.15 ± 1 K, thus, the absolute injection pressure was p I = 75.68 kPa [22]. In the next Section, we report results of the transient evolution before the flow reaches a steady state, first for the elliptical steam chamber and then for the circular chamber.

3.2. Transient steam flow in an elliptical steam chamber

A digital image subtraction treatment was applied to photographs taken every 12 s during experiments where the optimal steam injection  ϕ o p t * was reached. In Figure 4 we present different stages of the evolution of the front within the elliptical steam chamber with vertical semi-major axis, we show the evolution of the condensation front from the central diffuser upto the chamber edge. In Figure 4(a) the advancement of the condensation front is nearly radial, and in Figs. 4(c) and 4(d) we observed that the condensation front first reaches the regions close to θ = π / 2 and θ = 3 π / 2 , and finally, the front reaches the top ( θ = 0 ) and lower ( θ = π ) regions.
Neither the evolution of the condensation front nor the transient evolution of the temperature distribution were considered in our theoretical model, however both aspects become relevant in experiments because they involves the thermalization process of the preformed steam chamber. In the plot of Figure 5 we show the time evolution of the dimensionless front r f ( θ ) / H along the horizontal ( θ = π / 2 ) and vertical ( θ = 0 ) axes. The curve fits for both cases correspond to power laws of the form r f / H ∼ t n where n = 0.29 ± 0.01 if θ = 0 and n = 0.34 ± 0.01 if θ = π / 2 . Moreover, in the same figure, it is observed that the rate of change of r f ( θ = 0 ) / H is larger than r f ( θ = π / 2 ) / H , due to the influence of the buoyancy of steam. In contrast, when a hot liquid is injected into a similar geometry, at a constant flow rate, q, the Darcy velocity of the front close to the injection pipe, v r , evolves as v r = d r f / d t = q / 2 π r f , which yields that r f / H ∼ t 0.5 [23].
At the same time, the time-dependent temperature distributions in the preformed steam chamber during the steam injection, see Figure 6, were obtained by using an infrared camera model FLIR SC660, which has a high performance infrared system within the long wave spectral range, in between 7.5 − 13 μ m. It should be mentioned that, the temperature scales in the thermographies 6(a)-6(d) need to be corrected with methods of radiation exchange of surfaces [24], it was done knowing the thickness and the physical properties (density and refractive index values) of the observation window made from soda lime glass that allows the visualization of the steam flow and temperature distributions.
In Figure 7 we show of the plot of the dimensionless temperature distribution T θ = π / 2 / T b along r ( θ = π / 2 ) / H , for two different time instants. In said plot, data was collected from termographies of Figure 6(c) and 6(d), which have 340 s apart, however they apparently are very similar to each other. Accordingly, the correction of the temperature values, necessary due to the radiation exchange mentioned earlier, were carried out resulting in the data presented in the plot. For completeness, the data measured and used in the construction of plot of Figure 7 were T b ≈ 350.45 ± 1 K (defined as the temperature value where the slope suddenly changes), T I = 365.15 ± 1 K and H = 0.14 m. Notice that the close similarity between the dimensionless temperature distributions in said plot provides evidence of a steady-state regime being reached. The mean temperature T R / T b m e a n = 0.906 was determined at the chamber edge r ( θ = π / 2 ) / H = a / H = 0.75 where a, is given in Table 1.

3.3. Transient steam flow in a circular steam chamber

We now present experimental results similar to those of the previous Subsection, but now for circular cross-sections; all data was obtained for the corresponding optimal injected mass flow of steam, ϕ o p t * . In Figure 8 we show the evolution plot of the condensation front as it approaches to the chamber edge. In Figure 9 we present the plot of the evolution along then vertical line r ( θ = 0 ) / H (dashed red curve ) and along the horizontal r ( θ = π / 2 ) / H (dashed black curve). Now, the exponents of the power law r f / H ∼ t n are n = 0.51 ± 0.02 if θ = 0 and n = 0.46 ± 0.02 if θ = π / 2 . These exponents indicate, as can be seen in Figure 8, that the initial fronts are nearly circular and behaves as the power law for hot water injection [23].
Following the study of the thermalization of the preformed circular steam chamber, we provide four thermographies for the indicated time instants. Through Figure 10(c) and 10(d) we notice that, at the bottom, a water accumulation (liquid pool) appears as a consequence of the recovery orifice (black dots in said figures) being located 0.03 m above the lower edge of the chamber. It is apparent that similar cases could occur in actual SAGD processes, and, therefore, the experimental visualization of this case becomes of interest [25].
From Figs. 10(c)-(d) it is evident the existence of several horizontal isotherms in the confined aquifer, and this has a double effect: first, it releases heat onto the iron slab by conduction at temperatures lower than T b ; second, the condensate coming from the upper parts of the chamber edge must go through a liquid region (close to the red isotherm) where the shear stress limits its speed thus causing the flow rate at the recovery orifice to drop.
Finally, two temperature measurements along the horizontal line r ( θ = π / 2 ) were taken 430 s apart, see Figure 11. The corresponding boiling temperatures were T b = 358.4 ± 1 K for the dashed black curve and T b = 360.4 ± 1 K for the dashed red curve. It is possible that the slight temperature reduction at t = 1080 s could be caused by the continuous heat transfer to the solid slab, as can be observed in Figure 10(d).

4. Optimal injected mass flow rates in the steam chambers

The aim of the current work is to demonstrate that, once the steady-state conditions have been reached, different shapes of the chamber edge yield unique values of the dimensionless optimal mass flow rate per unit length ϕ o p t = ϕ o p t * / ( k e T b / L ) . To reach this goal we measured, during a given time period Δ t , the accumulated mass of injected steam and the corresponding recovered mass of water, because, as it has been argued before, this last quantity must be proportional to the drained oil at the recovery orifice, in experiments with oil-saturated steam chambers. We also need to mention that in some cases, due to an inefficient condensation of steam close to the edge of the steam chamber, in addition to the output water, an unrecoverable amount of steam is released into the atmosphere as a hot turbulent jet of steam that is bent round upwards by the gravitational field. Along with these measurements, the mass flow rate of injected steam per unit length, is also known, ϕ * = m · I s / l .
For the preformed elliptical chambers we injected steam at T I = 365.15 ± 1 K, we repeated each injection experiment three times and the injection and recovery cycle in this case lasts Δ t = 1800 s. The amount of steam injected during a time period Δ t , is quantified as m S I = m I s · Δ t , meanwhile the mass of water recovered in the same period is m W R , and the mass flow rate of water recovered is m · W R = m W R / Δ t . A measure of the efficiency of the steam injection can be estimated through the factor of recovery efficiency, e r , defined as the ratio of the mass of water recovered to the mass of injected steam
e r = m W R m S I ,
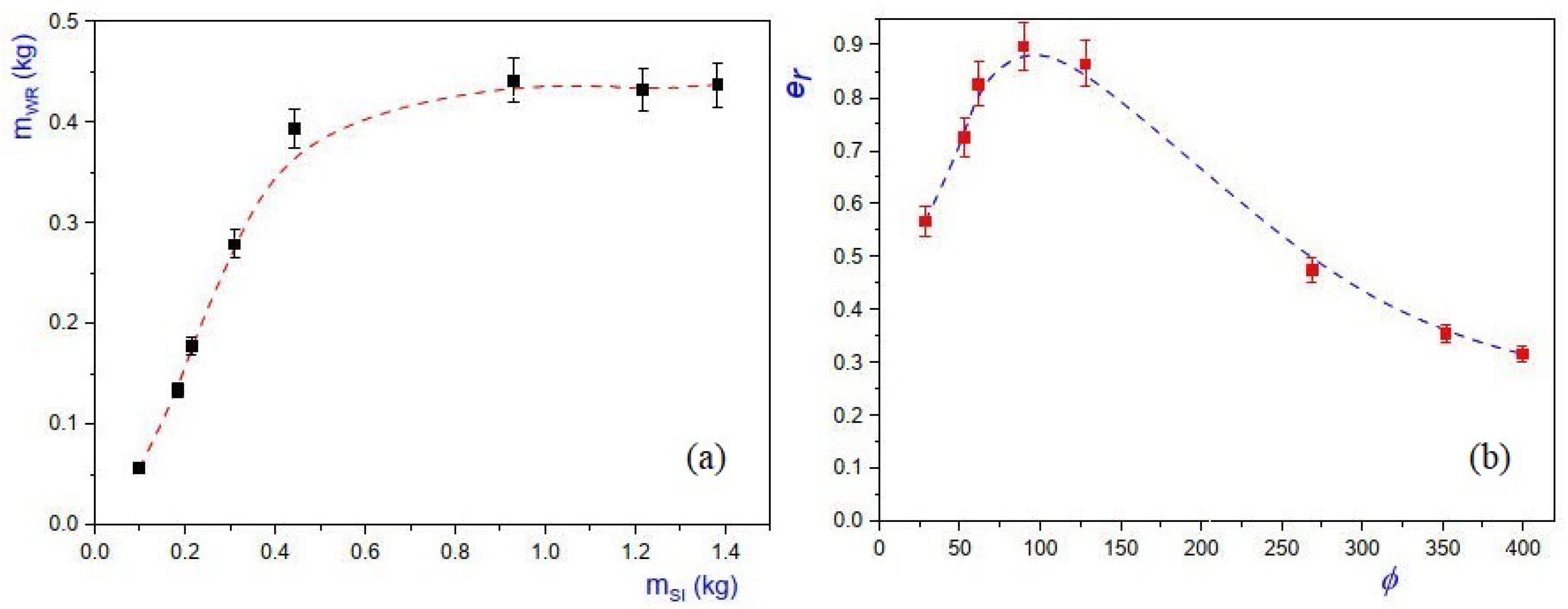
In Figure 12(a) we show the plot of the mass of water recovered m W R , as a function of the mass of the injected steam m S I and in Figure 12(b) the plot of the recovery efficiency e r , as function of the dimensionless injected mass flow rate per unit length ϕ o p t , is given. Clearly, from the plot of Figure 12(b) it can be concluded that the dimensionless injected optimal mass flow rate per unit length is ϕ o p t = 89.58 and at this value the recovery efficiency is close to 90%, i.e., e r ≈ 0.9 .
We emphasize that the plots for the transient flow in the elliptical chamber, given in Figs 4-7, were selected once the optimal mass flow rate of recovered water was determined. Knowledge of the optimal value helps to get, from Figure 7, an estimate of the value of the boiling temperature T b ≈ 350.45 ± 1 K, we also know from experiments that T I = 365.15 ± 1 K. For completeness, other data measured includes the mean temperature of the reservoir T R / T b m e a n = 0.96 and the dimensionless radius is ϵ = R I / H = 0.04 . The water dynamic viscosity and density at temperature T b have the values μ w = 0.355 × 10 − 3 Pa·s, ρ w = 972.44 kg/m3 and the latent heat is L = 2315 . 1 kJ/kg, meanwhile the effective thermal conductivity of the steam saturated medium (with thermal conductivity of the glass beads k s = 1.4 W/m·K and thermal conductivity of the steam k f = 23 × 10 − 3 W/m·K) is k e = 0.849 2 W/m·K and the specific heat of the steam at T b is c p = 1.951 kJ/kg·K [26]. Consequently the dimensionless parameter given in (2) are: S = 0.295 , Π = 98939 and T I / T b = 1 . 04 , the dimensionless condensate film thickness for the optimal mass flow rate is δ o p t ′ = 0.85 × 10 − 4 .
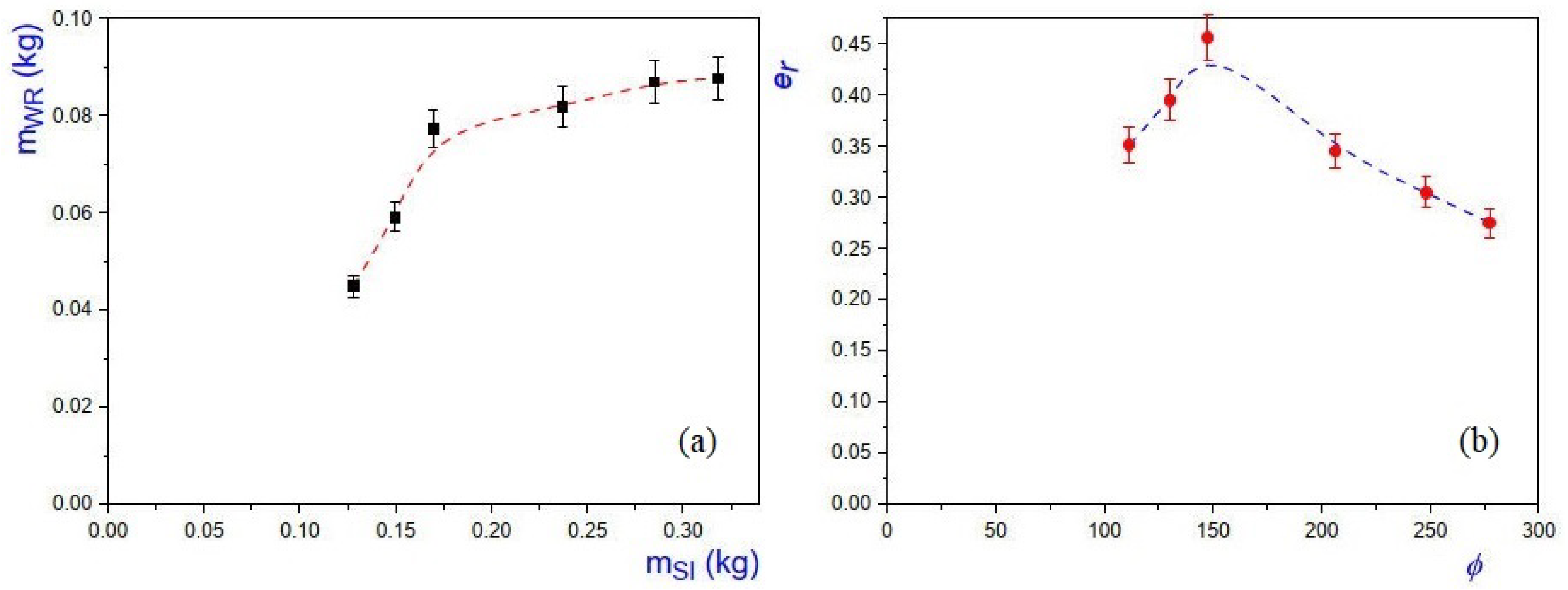
For the circular chambers steam was injected during Δ t = 300 s and in Figure 13(a) we present the plot of the mass of water recovered m W R , as a function of the mass of the steam injected m S I . In Fig. 13(b) we provide the plot of the recovery efficiency e r , as function of the dimensionless injected mass flow rate per unit length ϕ , we found that the optimal dimensionless mass flow rate per unit length is ϕ o p t = 147.65 and the recovery factor is e r ≈ 0.45 .
In this case, from Figure 11 we found the boiling temperature to be T b ≈ 358.4 ± 1 K, T I = 365.15 ± 1 K. The other data measured were and H = 0.07 m, the mean temperature of the reservoir T R / T b m e a n = 0.96 and the dimensionless radius is ϵ = R I / H = 0.07 . The water dynamic viscosity and density at temperature T b have the values μ w = 0 . 302 × 10 − 3 Pa·s and ρ w = 967.95 kg/m3 and the latent heat is L = 2294 . 3 kJ/kg, meanwhile the effective thermal conductivity of the steam saturated medium is k e = 0.849 W/m·K and the specific heat of the steam at T b is c p = 1.951 kJ/kg·K [26]. Consequently the dimensionless parameter given in (2) are: S = 0.295 , Π = 98939 and T I / T b = 1 . 02 . In this case the dimensionless condensate film thickness for the optimal mass flow rate is estimated as δ o p t ′ = 1.18 × 10 − 4 .
In summary, plots 12(a) and 13(a) confirm the prediction of the theoretical model [10]: that if the injected mass flow rate is larger than ϕ o p t , then a fraction of the steam reaches the production pipe without condensing inside the chamber; meaning that in an actual exploitation under a SAGD process, considerable amounts of steam are wasted. Even more, the model also predicts that if the injected flow rate is smaller than ϕ o p t , then the steam cools down and condenses rapidly, before it reaches the chamber wall, thus explaining the production of water between 45-65% of the mass of injected steam, for low flow rates in the elliptic chamber and 35-43% in the circular chamber. In conclusion, the cases when ϕ is far from ϕ o p t imply, for real processes, that a large amount of water and energy are wasted.
It should be mentioned that, by following the evolution of the condensation front we can confirm that the condensation must occur at the steam chamber edge (Figs. 4 and 8), however in our experiments the condensate water wets the cast iron edge [27] of the preformed steam chamber. Such conditions produce a substrate coated with a water film that absorbs the water drops contacting the film [28]. On the contrary, in actual SAGD processes, the condensate water does not wets the steam chamber edge which essentially is in the base oil phase, i.e., both fluids are immiscible, however, the produced fluids in the SAGD recovery method have been reported to be in emulsion form (the most common range of emulsified water in light crudes (> 20 API) of 5–20 vol% and 10–35 vol% in heavier crudes (< 20 API) [29,30], this shows that emulsification is more severe in hydrocarbon recovery from the heavy crude reservoirs). Recent studies have shown that when an aqueous drop contacts an immiscible oil film, it displays complex interfacial dynamics. When the spreading factor is positive, upon contact, the oil spreads onto the drop’s liquid–interface, first forming a liquid bridge whose curvature drives an apparent drop spreading motion and later engulfs the drop [28]. Consequently, more careful studies correlating both types of liquid films will be performed in order to complement our experiments in preformed steam chambers.

5. Conclusions

In this work, we have experimentally studied the water gravity drainage due to the condensation of steam injected into steam chambers of elliptical with vertical semi-major axis and circular shape. For these experiments, we injected steam at various mass flow rates, into cold and dry steam chambers, which allowed us to find that in fact, there exist an optimal dimensionless mass flow rate per unit length, ϕ o p t (measured during short time periods), for which the production of condensate is maximum. We show that the optimal value also depends on the cross-sectional shape of the steam chamber. For instance, we found that an elliptic chamber with vertical semi-major axis has an efficiency close to 90% meanwhile, a circular chamber reaches 45%. Also, in a recent work we found that if the steam chamber has an elliptical shape with horizontal semi-major axis, then the recovery efficiency reaches 85% [16]. These findings suggest that the shape of the chamber edge has a considerable influence on the efficiency of the steam chambers. In the case of the circular steam chamber an aquifer was formed due to the elevation of the recovery pipe from the lower edge of the steam chamber, this setting influences the heat distribution and perhaps this factor considerably limits the efficiency of this chamber. Also, the conditions for the stability of the film, i.e., the transition to dripping of the inverted draining film under an curved surface, requires further investigation at the optimal mass flow rate.

Author Contributions

Design and performance of experiments: A.M., D.B.G., A.L.-V., B.C.-M., and G.P.; modeling: A.M., A.L.-V. and G.P.; writing and revision: A.M., D.B.G., A.L.-V., B.C.-M., and G.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available from the corresponding author upon request. The data are not publicly available as we do not have a publicly accessible repository.

Acknowledgments

A.M. acknowledges the support from CONACYT and Universidad Politecnica de Madrid to the project “Fundamental models for the thermal methods of steam injection in EOR”. He also appreciates the enormous support of F.J. Higuera and A. Liñan, who guided him through a large part of this work.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Butler, R.M.; Stephens, D.J. The gravity drainage of steam-heated heavy oil to parallel horizontal wells. J. Can. Pet. Techno. 1981, 22, 90–96. [Google Scholar] [CrossRef]
  2. Butler, R.M. A new approach to the modelling of steam-assisted gravity drainage. J. Can. Pet. Techno. 1985, 24, 42–51. [Google Scholar] [CrossRef]
  3. Chung, K.H.; Butler, R.M. Geometrical effect of steam injection on the formation of emulsions in the steam-assisted gravity drainage process. J. Can. Pet. Techno.
  4. Butler, R.M. Thermal Recovery of Oil and Bitumen, Prentice Hall; New Jersey, USA 1991.
  5. Hein, F.J. Geology of bitumen and heavy oil: an overview. J. Pet. Sci. Eng. 2017, 154, 551–563. [Google Scholar] [CrossRef]
  6. Canadian Association of Petroleum Producers (CAPP), Upstream Dialogue. The facts on: Oil Sands, 2009, 1–21.
  7. Voskov, D.; Zaydullin, R.; Lucia, A. Heavy oil recovery efficiency using SAGD, SAGD with propane co-injection and STRIP-SAG, Comp. Chem. Engn. 2016, 88, 115-125, and references therein.
  8. Heins, B.; Xiao, X.; Deng-chao, Y. , New technology for heavy oil exploitation wastewater reused as boiler feedwater, Petrol. Explor. Develop. 2008, 35, 113–117. [Google Scholar]
  9. Guirgis, A.; Gay-de-Montella, R.; Faiz, R. Treatment of produced water streams in SAGD processes using tubular ceramic membranes, Desalination 2015, 358, 27–32. 358.
  10. Higuera, F.J.; Medina, A. A. A simple model of the flow in the steam chamber in SAGD oil recovery. In Supercomputing. ISUM 2019. Communications in Computer and Information Science; Torres, M., Klapp, J., Eds.; Springer: Cham, Switzerland, 2019; Volume 1151. [Google Scholar]
  11. Bublik, S.; Semin, M. Numerical simulation of phase transitions in porous media with three-phase flows considering steam injection into the oil reservoir, Computation 2022, 10, 205.
  12. Fernandez, B.; Ehlig-Economides, C.A.; Economides, M.J. Multilevel Injector/Producer Wells in Thick Heavy Crude Reservoirs, Paper SPE 53950, In 1999 SPE Latin American and Caribbean Petroleum Engineering Conference, Caracas, Venezuela, 99. 19 April.
  13. Siavashi, M.; Garusi, H.; Derakhshan, S. Numerical simulation and optimization of steam-assisted gravity drainage with temperature, rate, and well distance control using an efficient hybrid optimization technique, Numer. Heat Transf. Part A: Applications, 2017, 72, 721–744. 72.
  14. Tao, L.; Xu, L.; Yuan, X.; Shi, W.; Zhang, N.; Li, S.; Si, S.; Ding, Y.; Bai, J.; Zhu, Q.; Du, H. 2021; 6.
  15. Tao, L.; Yuan, X.; Cheng, H.; Li, B.; Huang, S.; Zhang, N. Experimental study on well placement optimization for steam-assisted gravity drainage to enhance recovery of thin layer oil sand reservoirs, Geofluids 2021, Article ID 9954127.
  16. Martínez-Gómez, J.E.; Medina, A.; Higuera, F. J.; Vargas, C. A. Experiments on water gravity drainage due to steam injection into elliptical steam chambers, Fluids 2022, 7, 206.
  17. Gao, Y.; Fan, T.; Gao, J.; Li, H.; Dong, H.; Ma, S.; Yue, Q. Monitoring of steam chamber in steam-assisted gravity drainage based on the temperature sensitivity of oil sand, Petrol. Explor. Develop. 2021, 48, 1411–1419. [Google Scholar] [CrossRef]
  18. Purkayastha, S.N. ; Gates, Gates, I.D.; Trifkovic, M. Real-time multivariable model predictive control for steam-assisted gravity drainage, AIChE J. 2018, 64, 3034–3041.
  19. Zhang, Q.; Kang, X.; Liu, H.; Dong, X.; Wang, J. Breccia interlayer effects on steam-assisted gravity drainage performance: experimental and numerical study, J. Petrol. Explor. Prod. Technol. 2022, 12, 613–629. [Google Scholar] [CrossRef]
  20. Chun, M-H. ; Kim, Y-S.; Park, J-W. An investigation of direct condensation of steam jet in subcooled water. Int. Comm. Heat Mass Transfer 1996, 23, 947–958. [Google Scholar] [CrossRef]
  21. Kim, H.Y.; Bae, Y.Y.; Song, C.H.; Park, J.K.; Choi, S.M. Experimental study on stable steam condensation in a quenching tank. Int. J. Energy Res. 2001, 25, 239–252. [Google Scholar] [CrossRef]
  22. Miller, S. Methods for computing the boiling temperature of water at varying pressures, Bull. Amer. Meteor. Soc. 2017, 98, 1485–1491. [Google Scholar] [CrossRef]
  23. Medina, A.; Higuera, F.J.; Pliego, M.; Gomez, G. Temperature profiles due to continuous hot water injection into homogeneous fluid-saturated porous media through a line source. Rev. Mex. Fís. 2021, 67, 365–368. [Google Scholar] [CrossRef]
  24. Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat And Mass Transfer; John Wiley & Sons: New Jersey, USA, 2006. [Google Scholar]
  25. Banerjee, M.; Hascakir, B. Design of flow control devices in steam-assisted gravity drainage (SAGD) completion. J. Petrol. Explor. Prod. Technol. 2018, 8, 785–797. [Google Scholar] [CrossRef]
  26. Properties of Saturated Steam - SI Units. [online] Available at: https://www.engineeringtoolbox.com/saturated-steam-properties-d_101.html [Accessed ]. 6 May.
  27. Somlyai-Sipos, L; Baumli, P. Wettability of Metals by Water. Metals 2022, 12, 1274. [Google Scholar] [CrossRef]
  28. Zhao, C.; Kern, V.R.; Carlson, A.; Lee, T. Engulfment of a drop on solids coated by thin and thick fluid films. J. Fluid Mech. 2023, 958, A41. [Google Scholar] [CrossRef]
  29. Velayati, A.; Nouri, A. Emulsification and emulsion flow in thermal recovery operations with a focus on SAGD operations: A critical review. Fuel 2020, 267, 267. [Google Scholar] [CrossRef]
  30. Kokal, S.L. Crude oil emulsions: A state-of-the-art review. SPE Prod. Facil. 2005, 20, 5–13. [Google Scholar] [CrossRef]
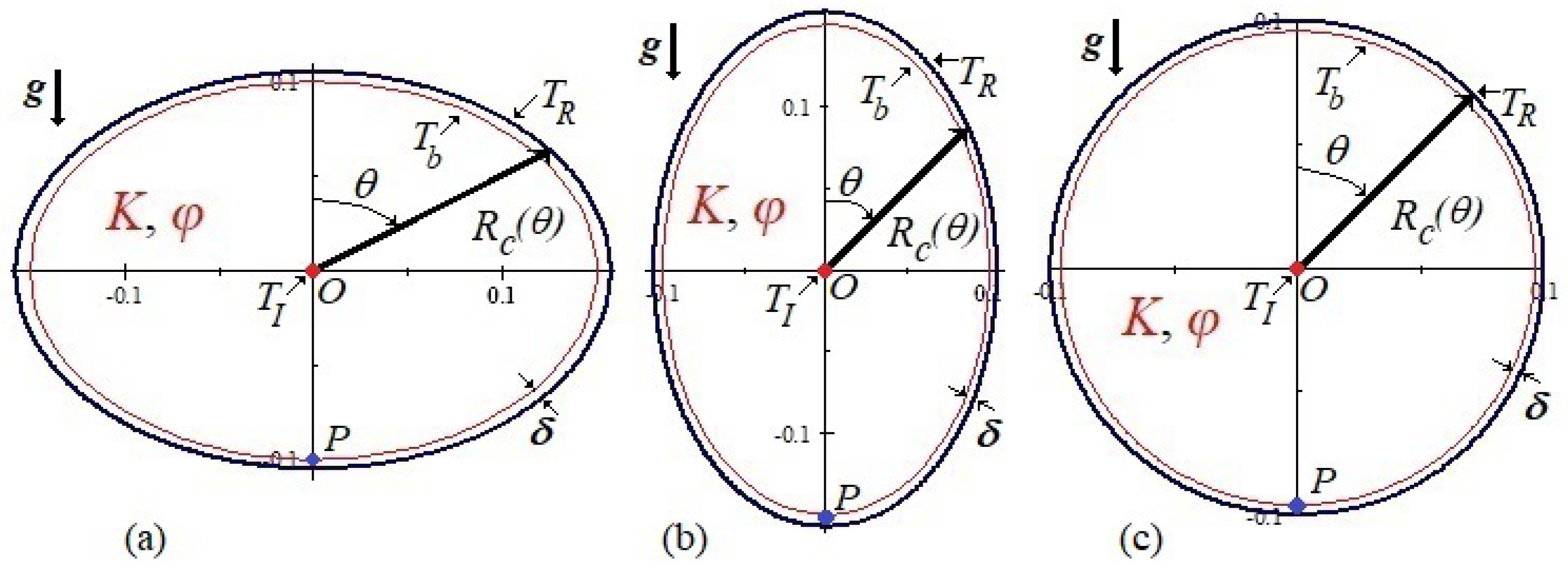
Preprints 73216 g001
Figure 1. Schematics of the cross-sectional regions of the preformed steam chambers with the injection pipe (red dot) at the center and the recovery pipe (blue dot) lying at the bottom. All chambers have symmetric shapes with a generic equation of the edge, r = R c ( θ ) , given by Eq. (1): (a) ellipse with horizontal semi-major axis, (b) ellipse with vertical semi-major axis and (c) circumference. Through the thin layer of mean thickness δ , the water/oil emulsion drains by gravity to the production pipe. Scales on the axes are in meters.
Figure 1. Schematics of the cross-sectional regions of the preformed steam chambers with the injection pipe (red dot) at the center and the recovery pipe (blue dot) lying at the bottom. All chambers have symmetric shapes with a generic equation of the edge, r = R c ( θ ) , given by Eq. (1): (a) ellipse with horizontal semi-major axis, (b) ellipse with vertical semi-major axis and (c) circumference. Through the thin layer of mean thickness δ , the water/oil emulsion drains by gravity to the production pipe. Scales on the axes are in meters.
Preprints 73216 g001
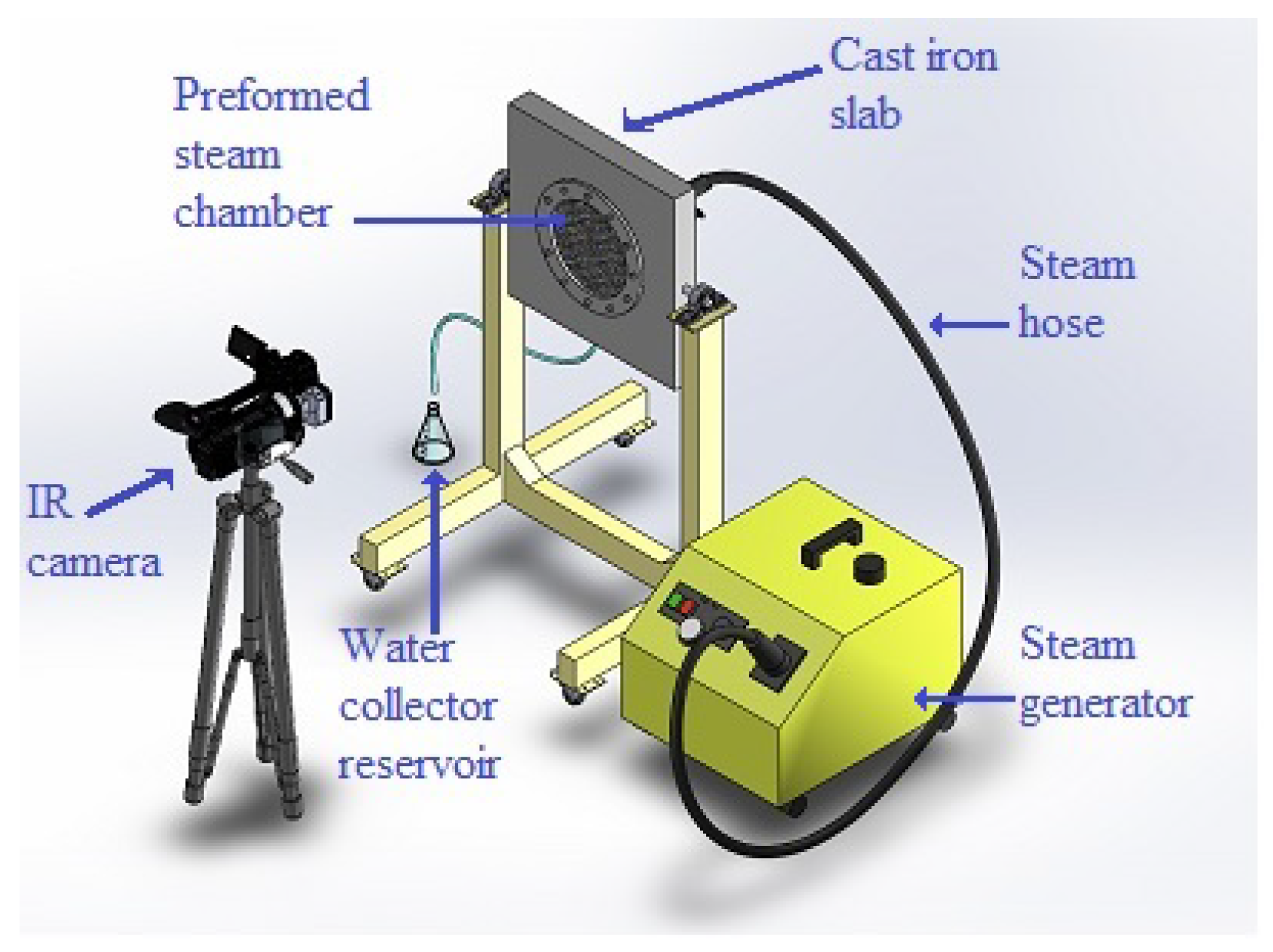
Preprints 73216 g002
Figure 2. Experimental set-up for the real time observation of steam injection into a preformed steam chamber enclosed in a metallic slab.
Figure 2. Experimental set-up for the real time observation of steam injection into a preformed steam chamber enclosed in a metallic slab.
Preprints 73216 g002
Preprints 73216 g003
Figure 3. Pictures of the preformed steam chambers filled with glass beads with a nominal diameter of 6 mm: (a) elliptical chamber and (b) circular chamber. The injection and recovery orifices were placed at the back plates.
Figure 3. Pictures of the preformed steam chambers filled with glass beads with a nominal diameter of 6 mm: (a) elliptical chamber and (b) circular chamber. The injection and recovery orifices were placed at the back plates.
Preprints 73216 g003
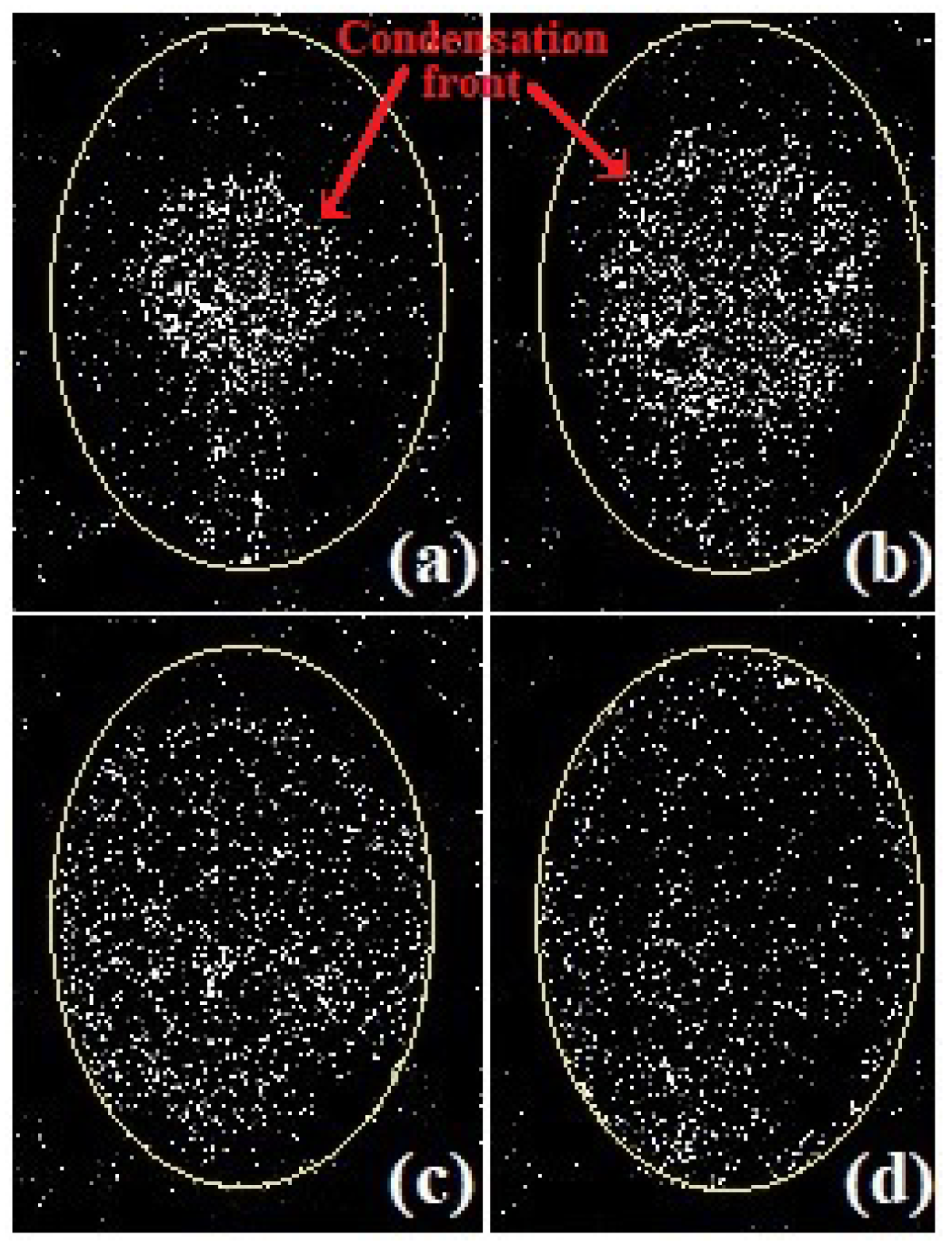
Preprints 73216 g004
Figure 4. Images of the evolution of the condensation fronts during steam injection into an elliptical preformed chamber at T r o o m = 293.15 ± 1 K. In this case, the condensation front was made visible by digital image substraction. The front is visible at (a) t = 36 s, (b) t = 108 s, (c) t = 288 s, and (d) t = 468 s, at this last instance, the front eventually reaches all places of the edge of the steam chamber.
Figure 4. Images of the evolution of the condensation fronts during steam injection into an elliptical preformed chamber at T r o o m = 293.15 ± 1 K. In this case, the condensation front was made visible by digital image substraction. The front is visible at (a) t = 36 s, (b) t = 108 s, (c) t = 288 s, and (d) t = 468 s, at this last instance, the front eventually reaches all places of the edge of the steam chamber.
Preprints 73216 g004
Preprints 73216 g005
Figure 5. Plots of the dimensionless condensation front r f ( θ , t ) / H along the vertical ( θ = 0 ) and horizontal ( θ = π / 2 ) simmetry lines for different times. In this case H = 0.14 m, as referred in Section 2. Some measurements were made from images in Figure 4.
Figure 5. Plots of the dimensionless condensation front r f ( θ , t ) / H along the vertical ( θ = 0 ) and horizontal ( θ = π / 2 ) simmetry lines for different times. In this case H = 0.14 m, as referred in Section 2. Some measurements were made from images in Figure 4.
Preprints 73216 g005
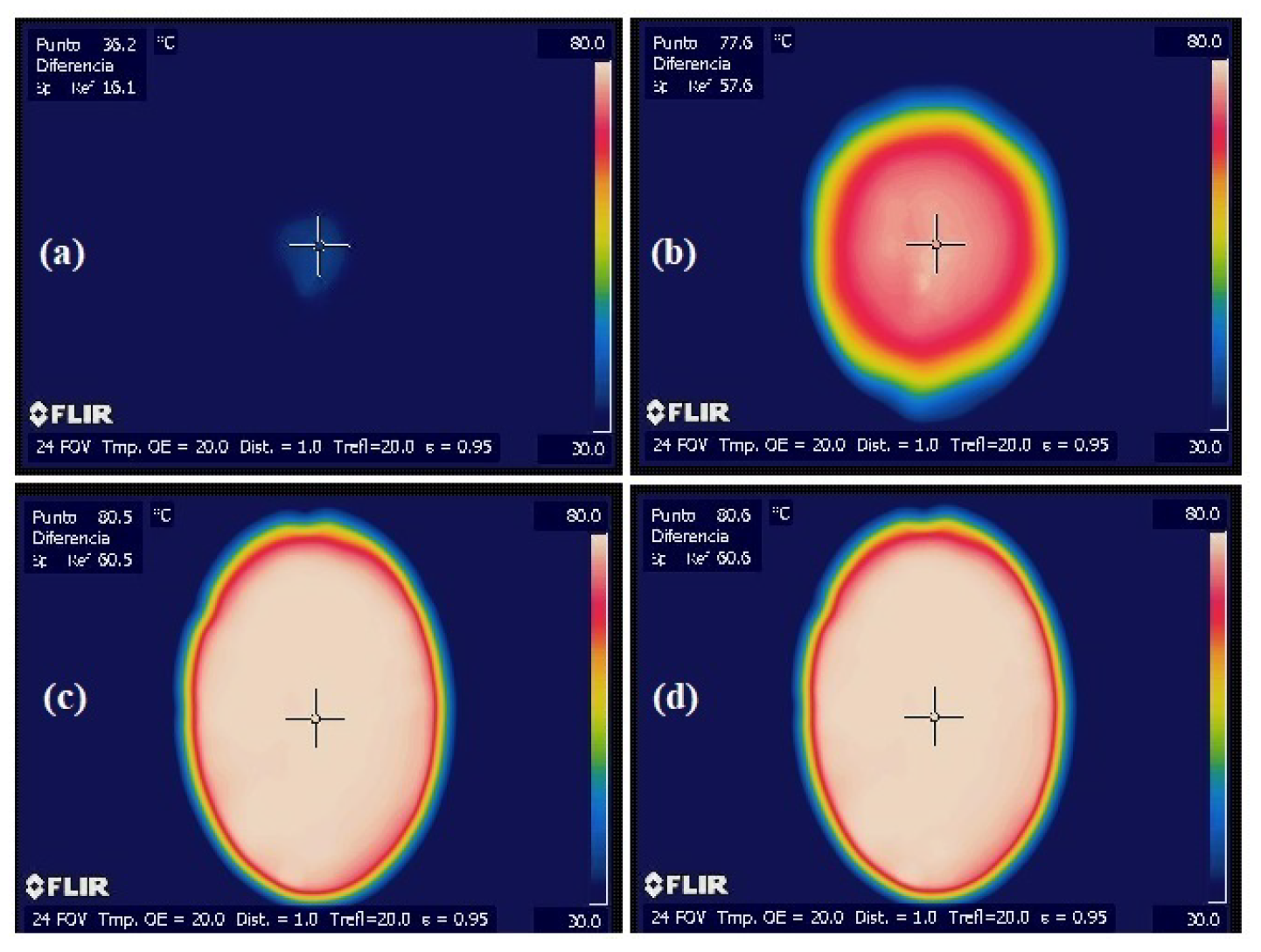
Preprints 73216 g006
Figure 6. Thermographies obtained at different moments after the injection start-up into the steam chamber: (a) t = 30 s , (b) t = 460 s, (c) t = 1310 s, and (d) t = 1650 s. Notice that there is no appreciable difference between thermographies (c) and (d) (c) and (d). This means that a steady-state regime for the temperature distribution was practically reached.
Figure 6. Thermographies obtained at different moments after the injection start-up into the steam chamber: (a) t = 30 s , (b) t = 460 s, (c) t = 1310 s, and (d) t = 1650 s. Notice that there is no appreciable difference between thermographies (c) and (d) (c) and (d). This means that a steady-state regime for the temperature distribution was practically reached.
Preprints 73216 g006
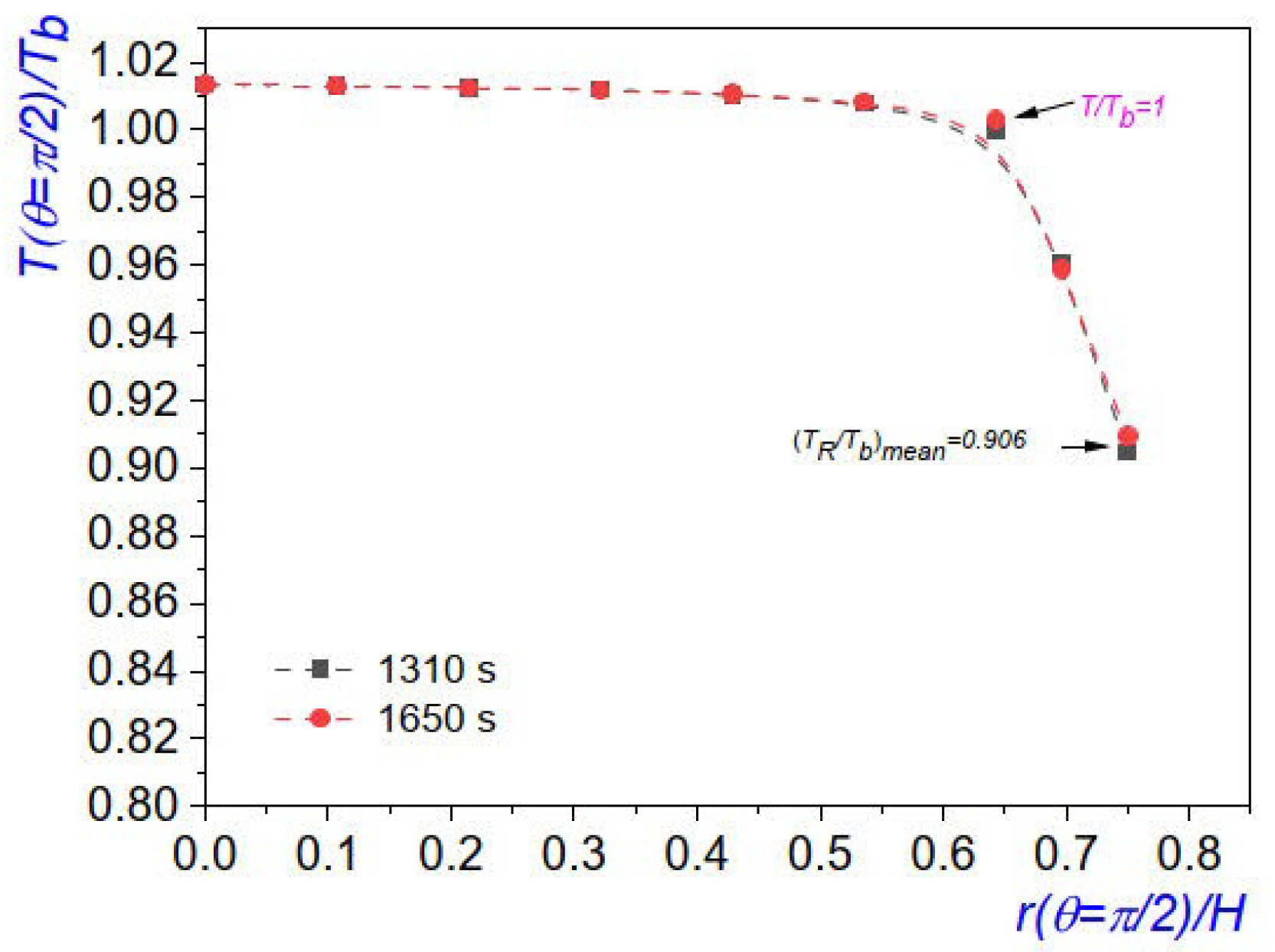
Preprints 73216 g007
Figure 7. Dimensionless temperature distributions in the elliptic steam chamber, along r ( θ = π / 2 ) which were obtained from the thermographies of Figs. 6(c) and 6(d). The temperature at the chamber edge, T R was located at r / H = a / H = 0.75 . The error bars are of the same size as symbols.
Figure 7. Dimensionless temperature distributions in the elliptic steam chamber, along r ( θ = π / 2 ) which were obtained from the thermographies of Figs. 6(c) and 6(d). The temperature at the chamber edge, T R was located at r / H = a / H = 0.75 . The error bars are of the same size as symbols.
Preprints 73216 g007
Preprints 73216 g008
Figure 8. Pictures obtained through image subtraction of the evolution of the condensation front (indicated by the arrows) during steam injection into the preforemed circular steam chamber. Images correspond to (a) t = 12 s, (b) t = 40 s, (c) t = 78 s, and (d) t = 107 s after the injection start-up.
Figure 8. Pictures obtained through image subtraction of the evolution of the condensation front (indicated by the arrows) during steam injection into the preforemed circular steam chamber. Images correspond to (a) t = 12 s, (b) t = 40 s, (c) t = 78 s, and (d) t = 107 s after the injection start-up.
Preprints 73216 g008
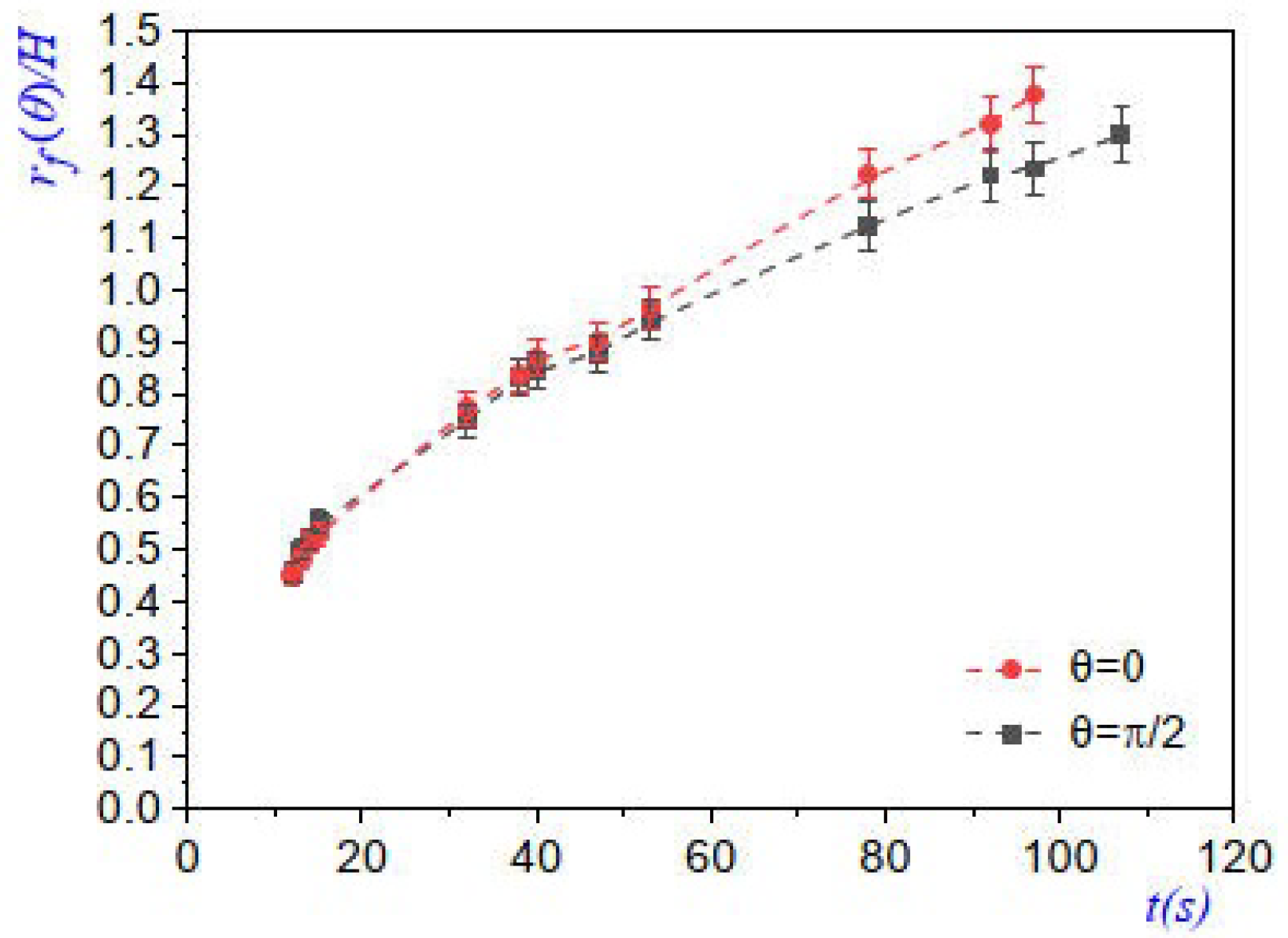
Preprints 73216 g009
Figure 9. Plots of the displacement of the condensation front r f ( θ , t ) / H versus t, along the vertical ( θ = 0 ) and horizontal ( θ = π / 2 ) axes for different time instants. Some measurements were taken from images in Figure 8.
Figure 9. Plots of the displacement of the condensation front r f ( θ , t ) / H versus t, along the vertical ( θ = 0 ) and horizontal ( θ = π / 2 ) axes for different time instants. Some measurements were taken from images in Figure 8.
Preprints 73216 g009
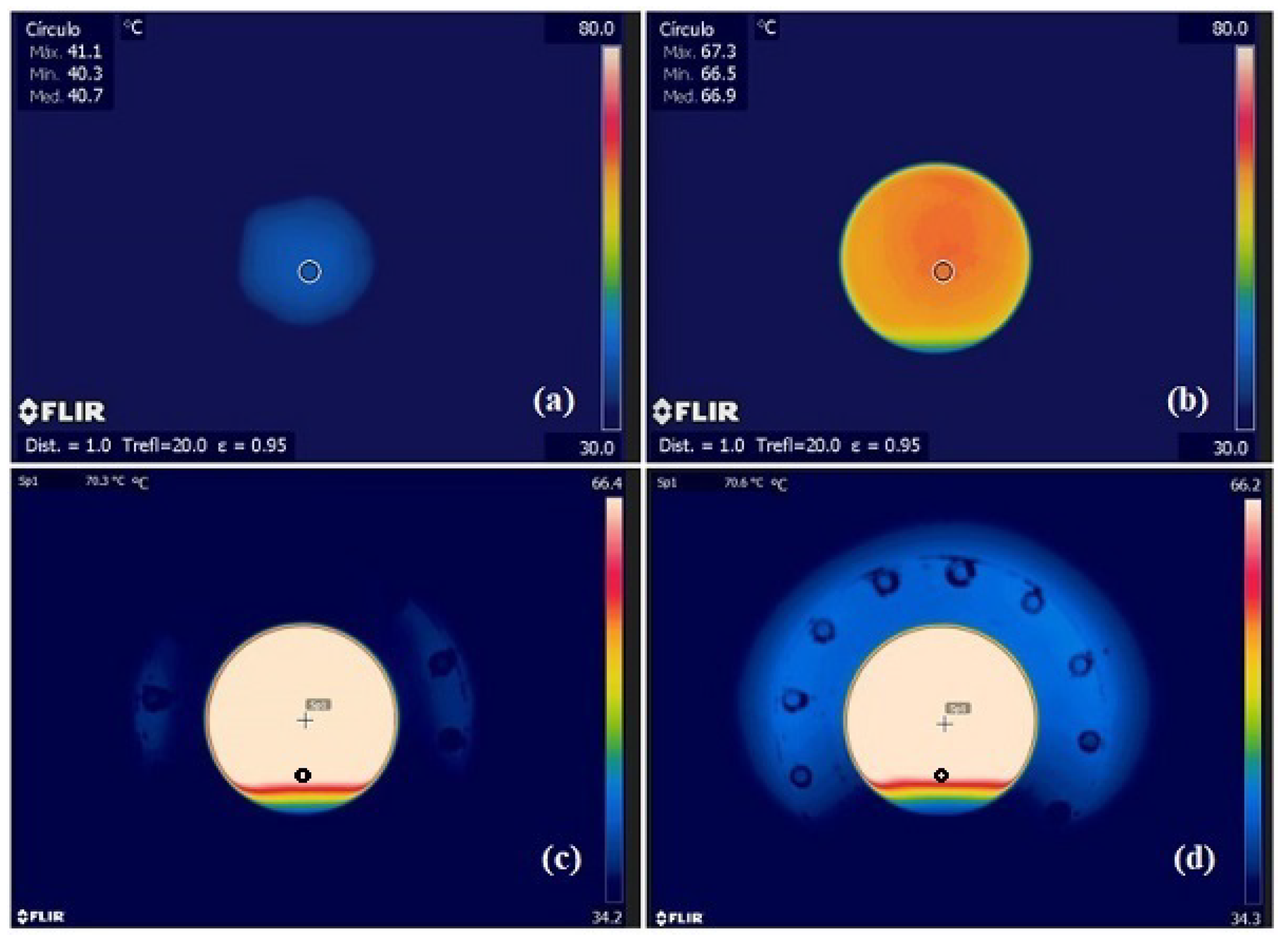
Preprints 73216 g010
Figure 10. Termographies taken during the transient steam injection into the circular preformed steam chamber. These thermographies were taken (a) t = 40 s, (b) t = 360 s, (c) t = 650 s, and (d) t = 1080 s after the injection start-up.
Figure 10. Termographies taken during the transient steam injection into the circular preformed steam chamber. These thermographies were taken (a) t = 40 s, (b) t = 360 s, (c) t = 650 s, and (d) t = 1080 s after the injection start-up.
Preprints 73216 g010
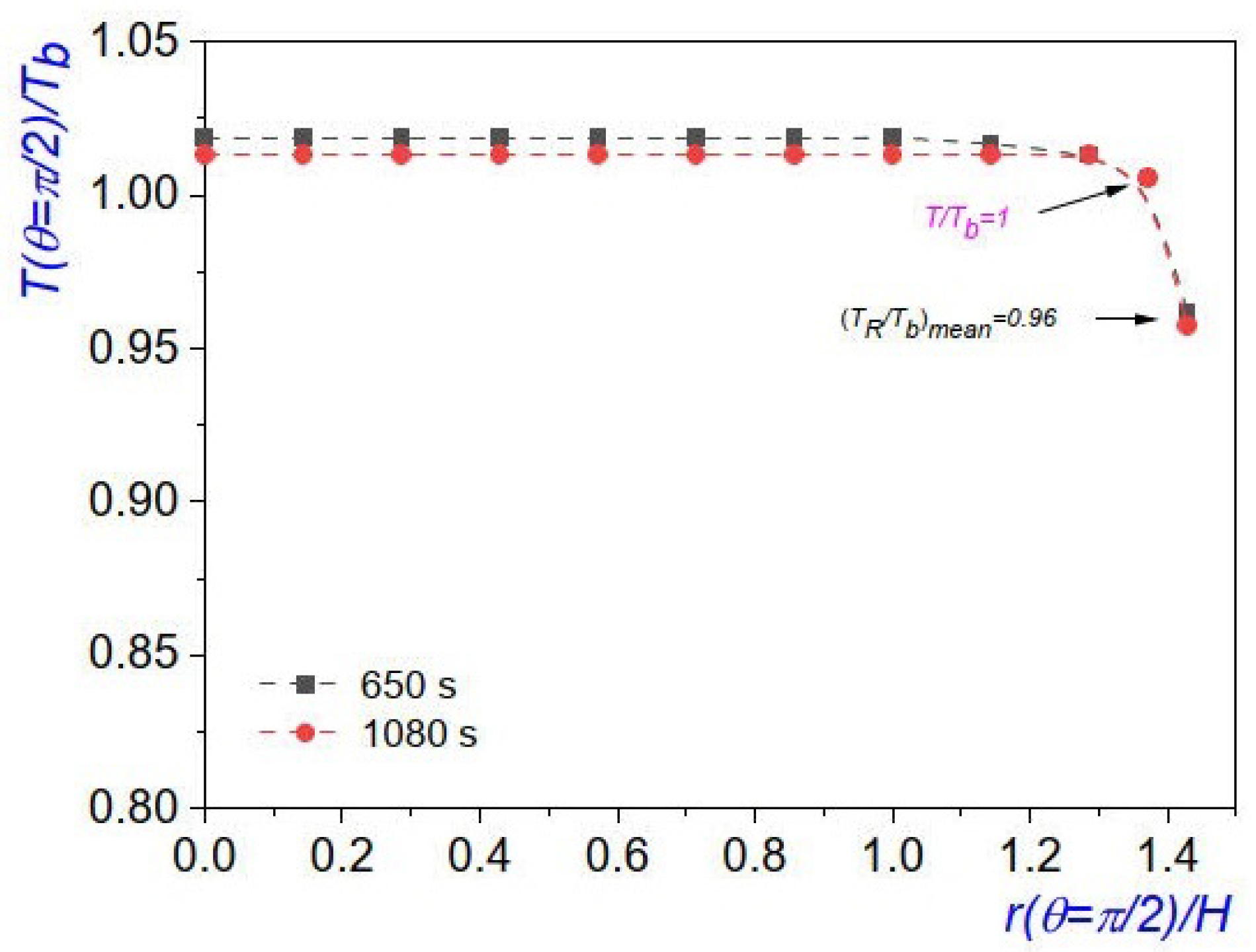
Preprints 73216 g011
Figure 11. Temperature distribution in the circular chamber, along r ( θ = π / 2 ) , they were extracted from the thermographies of Figs. 10(c) and 10(d). For the dashed black curve T b = 358.4 K and for the dashed red curve T b = 360.4 K. These thermographies were taken 430 s, apart. The error bars are of the same size as the symbols.
Figure 11. Temperature distribution in the circular chamber, along r ( θ = π / 2 ) , they were extracted from the thermographies of Figs. 10(c) and 10(d). For the dashed black curve T b = 358.4 K and for the dashed red curve T b = 360.4 K. These thermographies were taken 430 s, apart. The error bars are of the same size as the symbols.
Preprints 73216 g011
Preprints 73216 g012
Figure 12. (a) Plot of recovered water mass m W R versus the injected steam mass m S I in the elliptical chamber; data was taken during time lapse Δ t = 1800 s after the injection start-up, (b) dimensionless plot of e r versus ϕ , where the occurrence of an optimum value can be observed at ϕ o p t = 89.58 . The dashed curve is used as a visual guide and the error bars correspond to 5%.
Figure 12. (a) Plot of recovered water mass m W R versus the injected steam mass m S I in the elliptical chamber; data was taken during time lapse Δ t = 1800 s after the injection start-up, (b) dimensionless plot of e r versus ϕ , where the occurrence of an optimum value can be observed at ϕ o p t = 89.58 . The dashed curve is used as a visual guide and the error bars correspond to 5%.
Preprints 73216 g012
Preprints 73216 g013
Figure 13. (a) Plot of recovered water mass m W R versus the injected steam mass m S I , in the circular steam chamber, in this case data was taken during time lapse Δ t = 300 s after the injection start-up. (b) Plot of e r versus ϕ , where the occurrence of an optimum value can be observed at ϕ o p t = 147.65 . The dashed curve is used as a visual guide.
Figure 13. (a) Plot of recovered water mass m W R versus the injected steam mass m S I , in the circular steam chamber, in this case data was taken during time lapse Δ t = 300 s after the injection start-up. (b) Plot of e r versus ϕ , where the occurrence of an optimum value can be observed at ϕ o p t = 147.65 . The dashed curve is used as a visual guide.
Preprints 73216 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated