Prerpints.org logo
Preprint
Article

Turbulence Kinetic Energy and High-order Moments of Veloc-ity Fluctuations of Flows in the Presence of Submerged Vegetation in Pools

Altmetrics

Downloads

131

Views

58

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 May 2023

Posted:

11 May 2023

You are already at the latest version

Alerts
Abstract
In the presence of aquatic plants in streams, a variety of flow structures have been reported. Re-sults of earlier investigations indicated that the hydrodynamic features of flows in rivers, and streams are influenced by a wide range of submerged and non-submerged vegetation. In the pre-sent study, eight experiment runs were conducted in two artificial pools built in a laboratory flume to assess the flow structures across vegetation cover. The slopes for entrance and exit sec-tions of these two pools are of 5 and 10 degrees, respectively. A patch of artificial grass covered the entire pool area over the gravel bed. The effect of stream flow velocity was investigated by considering two aspect ratios of 2 and 2.7. Also, distributions of flow velocity, Reynolds normal and shear stresses, turbulence intensities, turbulent kinetic energy (TKE), and higher-order mo-ments of velocity fluctuations have been investigated. By means of quadrant analysis, it is found that the skewness coefficients of velocity profiles are significant parameters to evaluate. Based on skewness values for the bursting processes, along the pool entrance section with a smaller slope, the contribution of sweep motion occurs in a more restricted zone above the canopy, and this im-plies that the ejection motion occurs in a pool entrance section with a higher slope. Immediately above the vegetation canopy, the dominant process is the sweep motion of bursting events. Whereas, at the upstream boundary of the vegetation patch, an outward motion with slightly pos-itive value occurs; and around the downstream boundary of the vegetation patch, the isotropic turbulence appears at the boundary of the vegetation and gravel bed. Over the vegetation canopy in the pool, less mixing eddies result in lower Reynolds shear stress values, and thus the turbulent flow becomes weak with lower turbulent kinetic energy (TKE). Because of the shallow flow in an artificial channel with an aspect ratio less than five and the availability of vertical non-zero ve-locity components, secondary currents become stronger in the channel. Consequently, there is a divergence from a linear dispersion of Reynolds shear stress.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

In wetland environments, streams are commonly filled with either partially or fully submerged diverse aquatic plants, such as grasses, shrubs, and bushes. Both vegetated and non-vegetated zones in these streams significantly influence the hydrodynamic features of flow, such as velocity distributions, turbulence intensity, and coherent structures, as well as mass and momentum exchange. In previous studies, a variety of research works have been published with respect to these flow structures [1,2,3,4].
Due to the interaction of the vegetated zone and main channel, the vertical distribution profile of the streamwise velocity follows a “S”-shape, which is caused by the secondary currents in a narrow channel created by riparian vegetation. In fact, an S-shaped velocity profile indicates that there are two vertical mixing layers where coherent structures caused by the development of vertical shear, correlating variations in longitudinal and vertical velocity. The characteristics of the horizontal coherent structures near the vegetation boundary and main flow interface are also influenced by secondary transversal velocity, and different inclination directions of these coherent structures are observed at different depths corresponding to the local transversal velocity [5]. Furthermore, zones of accelerating and decelerating flows in a river are generated due to the changes of its depth and width. Given the significant impact of these flow regimes on turbulence generation and sediment transport, a variety of river topographies, particularly pools and riffles, would be developed [6,7,8,9]. To assess the effects caused by a vegetation canopy and a pool bed, turbulence structures and coherent motions of the bursting process have been investigated in the present study. The Monami, a coherent wave phenomenon caused by plants, is indeed a result of the interaction between vegetation and flow coherent motions, which even promotes the vertical transport of momentum [10]. Mass and momentum exchange are affected by the Monami's phenomenon on the drag discontinuity that extends from the submerged-vegetation zone to the overflow zone [11]. It should assess how the bursting events in the boundary layers are related to the Monami phenomena around the vegetation canopy in the mixing layer of the flow, which applies to fully formed canopy flows.
To investigate turbulence structures above the vegetation canopy, the turbulent kinetic energy (TKE) should be examined, and then the shear and wake generation can be estimated [12]. It should be noted that the wake production is the horizontal average of the product of the local variations of Reynolds stresses and velocity gradients. As reported by previous researchers, the shear velocity in the presence of vegetation yields more turbulent energy than that caused by the wake of vegetation, except for those zones around the edge of vegetation patches [13,14]. Besides, the presence of vortexes leads to an increase in the TKE [3,15,16,17]. In 2D flows in channels with the emergent vegetation elements, instabilities caused by horizontal vortexes at the downstream edge of an vegetation patch play a dominant role on flow structures [18,19]. In the presence of a vegetation canopy layer in a flow, an analogy between the canopy layer and the flow's mixing layer has been reported [20].
In the near-bed region, by means of the quadrant analysis, the occurrence probabilities are dominated by the presence of sweep motions and depend on the thickness density of the vegetation patch which causes a larger wake zone in the emergent region over the canopy. The majority of reported studies focused on evaluating the structures of coherent flows above a vegetation patch. In the present study, coherent flow structures have been investigated at the upstream of the vegetation patch, across the entire vegetation patch in a pool (compared to those in a pool without a vegetation patch), and at the vegetation canopy boundary. It has been found that the motion of ejections appears behind the vegetation patch. The dominant bursting process in flows over vegetation canopy belongs to the periodic occurrence of sweep and ejection events. Varieties of research works have been conducted to study the interactions between strong vortices above vegetation canopies and quadrant occurrences [12,21,22,23]. The study of high-order moments of velocity fluctuations u' and w', also known as skewness fluctuations sk u and   sk w , can derive factors that provide useful information about asymmetry in streams [19]. In other words, a non-zero skewness of velocity fluctuations in the streamwise and vertical directions indicates an asymmetric probability density function (PDF) of the considered variable, which is associated with quadrant bursting events [24,25,26].
In praxctice, engineers are keen on the estimation of low resistance along the pool in the present of vegetation, since resistance changes along different sections of a pool including both entrance and exit slopes as well as different location of a vegetation patch. Reported researches show that no focus was done to investigate the details of flow structures including 3D velocity component distributions, 3D turbulence intensities, TKE distributions, quadrant analysis at the trailing edge of vegetation patch (where the flow reach to gravel along a stream) and spectral analysis for different slopes and regions along the bedform. This study focuses on the role that different bursting events play in the boarder of vegetation and gravel in a 3D bedform. It is to know what happen in trailing edge of vegetation patch over a bedform and how this affects the turbulence features and their distributions. Also, it is necessary to know the validation of Kolomogrove -5/3 law in 3D bedform in the presence of vegetation patch in channel bed.

2. Materials and Methods

In the present study, the desired two pool bed-forms were built in a laboratory flume, which is 8-m long, 0.4-m wide, and 0.6-m deep. One was built with a constant slope of 5 degrees, while the other was built with a slope of 10 degrees for both the entrance and exit slopes. All experiments have been conducted in both gravel pool-bed and vegetated pools (Figure 1). For this experimental study, each desired pool bed-form was placed in a channel position to ensure that the flow is under fully developed condition. To avoid the effects of the downstream tailgate, the 1.5-m long pool was built at a distance of 4.5 meters from the entrance of the flume. The tailgate located downstream end of the flume was used to control the flow depth and set it to the desired values of 20 cm and 15 cm (Table 1). The median diameter of sediments ( d 50 ) in the pool bed for all the experiments was calculated to be ( d 50 = 10.4 mm) using one hundred random samples of the grains. The grain size distributions were relatively non-uniform according to the geometric standard deviation σ g = ( d 84 / d 16 ) 0.5 , where d 16 and d 84 are 16th and 84th percentile of particle-size distribution, respectively [22]. In this study, the geometric standard deviation is smaller than 1.4, and implies that the grain size distribution is non-monotonous [21]. Figure 2 shows the grain size distribution curve and sediment characteristics for this experiment, in which G r is the granulation coefficient, D g depicts the average particle size, C c indicates the curvature coefficient, and C u represents the uniformity coefficient. The vegetation selected for this experimental study was a 2-cm tall artificial grass patch that covers the entire pool section in the flume [23]. Table 1 summarizes data collected from all experimental runs. The experiments in the presence of a 5-degrees pool bed were conducted for two different discharges of 10.5 and 40.5 lit/s; the experiments in the presence of a 10-degrees slope were carried out for two different aspect ratios (w/h; channel width to water depth) of w/h=2 and 2.7. Along with the aforementioned information, Table 1 also presents the flow Froude number; Fr = [ U / ( gH ) 0.5 ] , and the flow Reynolds number; Re [ = UH / ϑ m ] , where H is the water depth, U is mean velocity, and ϑ m is the flow viscosity.
An electromagnetic flowmeter installed at the water pipe entering the flume was used to measure flow discharge. A Nortek Vectrino Acoustic Doppler Velocimeter (ADV) was used to measure the instantaneous three-dimensional velocity components. For each experimental run, the ADV (acoustic Doppler velocimeter) was used to measure the flow velocity at the distance of z=2 mm from the bed to 50 mm below the water surface. Even though some data were filtered to remove outliers, the majority of the velocity data collected in this study was examined with high SNR (signal to noise ratio) and correlation. Data for experiment Run 8 was collected to investigate secondary currents along the channel's second axis, which was 10 cm from the flume sidewall, whereas data for all the other experiment runs was obtained along the flume's center line (20 cm from the flume side wall).

3. Results

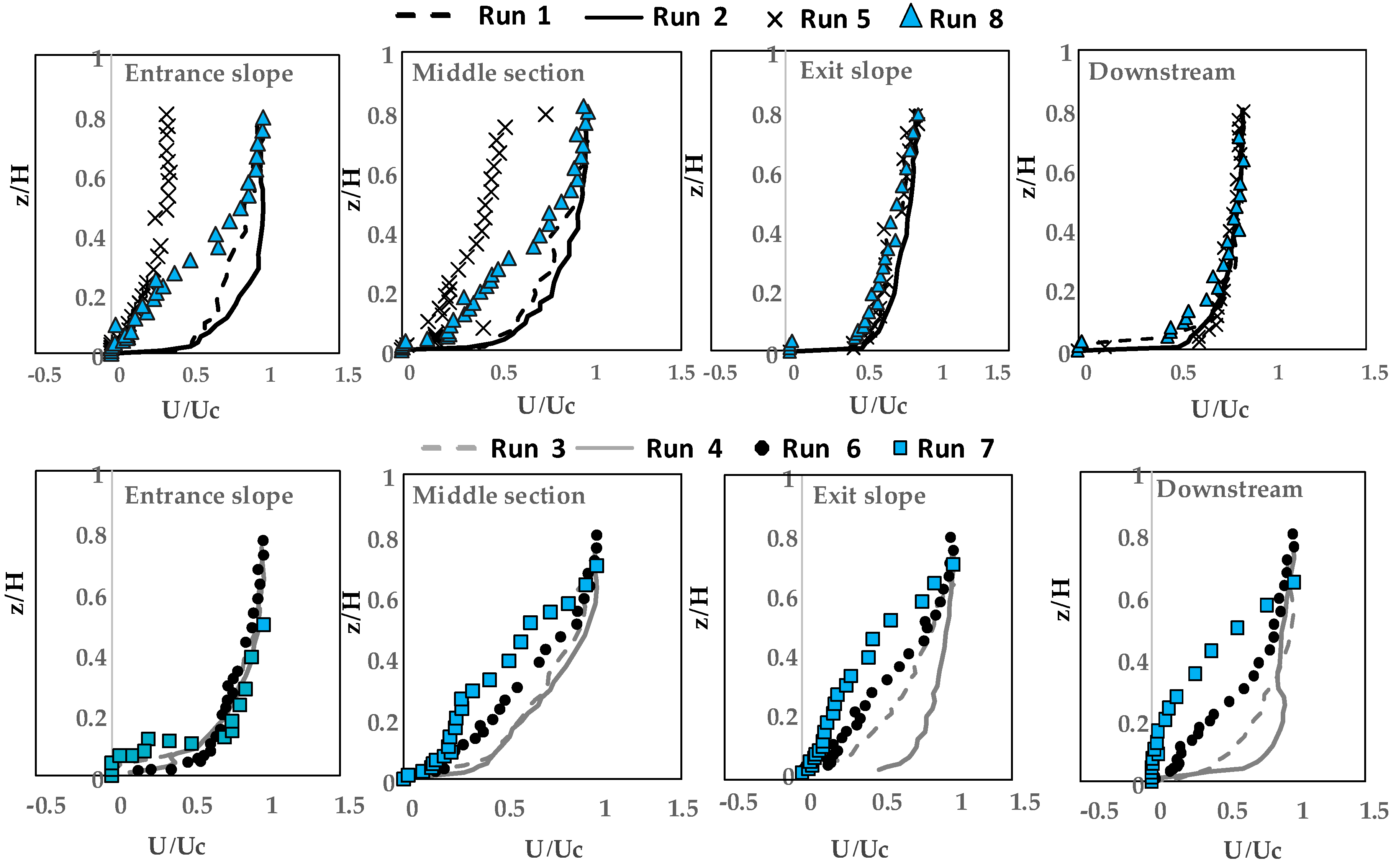
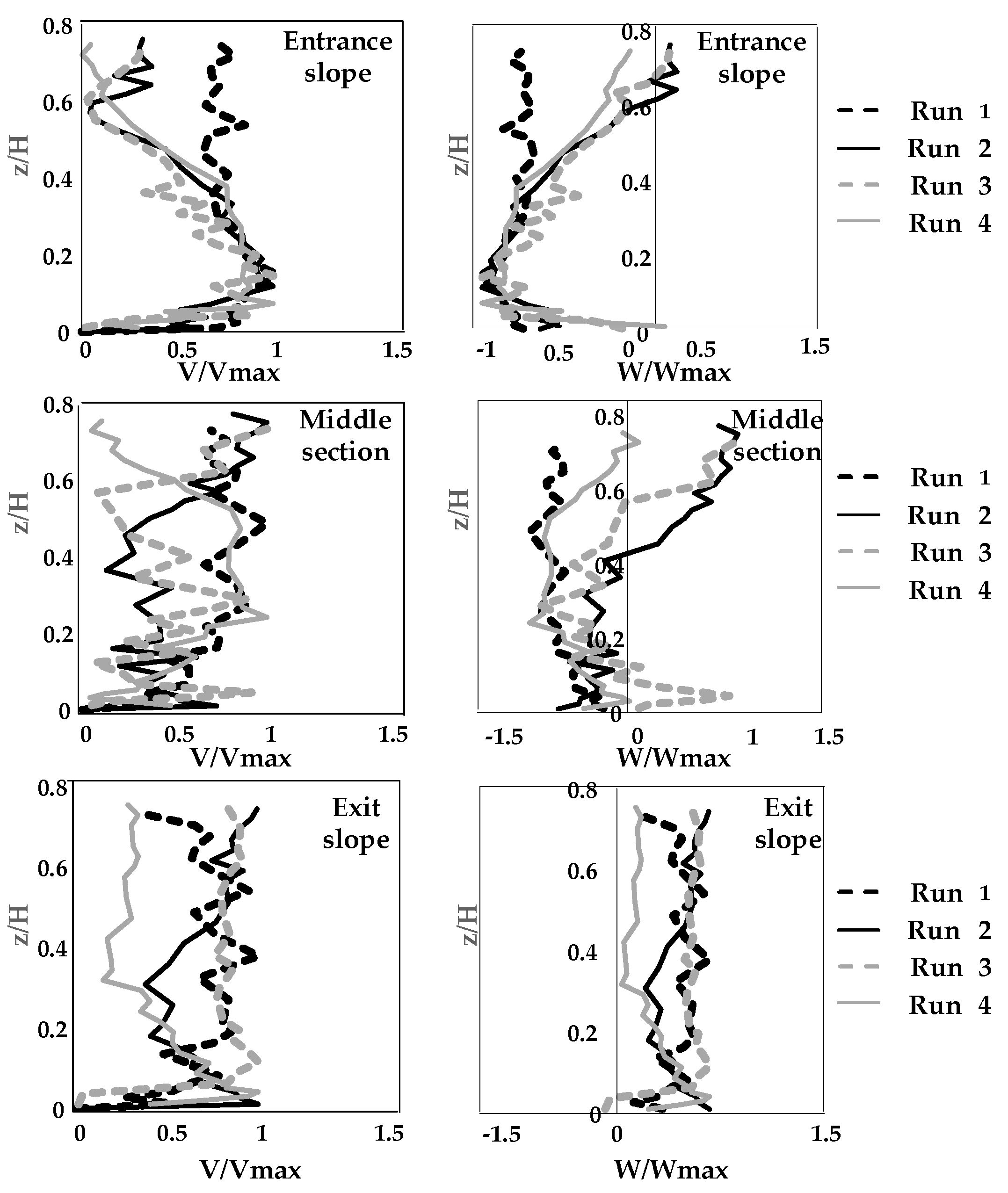
3.1. Velocity Distribution

As showed in Figure 3, the stream-wise velocity (x direction) profiles are displayed for all experimental runs. At each measurement point, by respectively dividing the maximum flow velocity (uc) of each profile and the total flow depth (H), the flow velocity and distance from the bed (z) at this point are converted into dimensionless velocity (u/uc) and flow depth (z/H), respectively. For flow with a low aspect ratio (flume width/flow depth < 5), the location of the maximum velocity may fluctuate due to the influence of secondary currents. However, with a greater aspect ratio (more than 5), this effect is hardly noticeable [22]. If the aspect ratio is less than 5 and the dip phenomena occurs, as reported in the previous studies, the flow will be three-dimensional [25,27]. Neither negative velocities nor flow separation at the bed of both entrance and exit section of pools could be recorded because of the limitations of the ADV. The relative velocity profiles for flow in pools with different slopes are very similar, as showed in Figure 3. Yet, velocities of flow in the pool with a slope of 10-degrees are slower than those with a slope of 5-degrees. In a decelerating flow, the near-bed velocities are lower than those at water surface, and this discrepancy increases in the streamwise direction. This outcome agree with that reported by other researchers [28].
The effect of decelerating flow is still present in the pool's middle section, preventing a uniform flow from developing. In the accelerating flow, velocity increases near the bed and drops near the water surface as flow continues along the exit section. This flow pattern confirms the results of other researchers [6,29]. Unlike a vegetated stream, a stream with a gravel bed generates more mixing flow all over the bed, resulting in the decrease in velocity, which makes flow separation more likely. Despite the aspect ratios is less than 5, no evident for the velocity dip phenomenon is observed within the range of flow depth of z/h < 0.6. Nevertheless, the highest flow velocity has been observed below the water surface at a flow depth of z/H > 0.6 along the decelerating flow section when the entrance slope is 5 degree (Figure 3). As the flow enters the pool region, the maximum flow velocity moves toward the water surface in the zone of flow depth of z/h > 0.8. This finding agrees well with reported result that the dip phenomenon occurs at a distance up to 0.67H (or dip parameter) from the bed for uniform flow with a hydraulic rough bed[26]. According to some earlier studies, the value of the dip parameter for non-uniform flows is 0.22H [25]. In a gravel bed river with flexible submerged vegetation patches and 3D bed-forms, this value is up to 0.8H [30]. However, the findings of theoretical investigations based on the Navier-Stokes equations demonstrate that the value of the dip parameter in the accelerating flows is higher than that in both uniform and decelerating flows [31].
In this study, in the zone above the vegetated canopy up to the depth of z/H < 0.1 in the pool, the velocity fluctuation is dominantly dependent on the drag force caused by the vegetation, and the viscous shear stress has only a minor impact on the velocity profile, leading to minimal changes in the velocity profile in this region. The velocity profile in the upper layer of the flow (z/H > 0.1) increased gradually with the flow depth (z/H). By increasing the aspect ratio, the presence of vegetation canopy inside the pool can result in the "S" shaped distribution profiles of velocity. This is true for both the pool entry and exit sections with a slope of 10 degrees (decreasing the water depth from 20 cm to 15 cm). In fact, the velocity gradient in the upper layer of the flow approaches null; the velocity gradient reaches the maximum in the middle and close to the bed, and the velocity distribution follows the logarithmic function. This outcome supports the findings of prior research [25]. Moreover, contrary to what was found in earlier research, the dimensionless flow velocities in the outer zone of the decelerating flow section (z/h > 0.2) are not necessarily higher than those in the accelerating flow section [23,32,33]. To further assess the impacts of secondary currents on the characteristics of flow in pool with presence of vegetation, flow velocity components in other two directions (span-wise v, and vertical direction w) are shown for four experimental runs in Figure 4.
The presence of both positive and negative values of velocity profiles in both span-wise and vertical directions indicates the pattern of secondary currents [23,25]. While the average vertical velocity is negative in the decelerating and middle sections of the pool reveals the occurrence of downward flow, the positive values of vertical velocities in the accelerating section indicate the inclination of flow toward the water surface. The opposing effect of accelerating and decelerating stream portions on secondary currents along the pool bed has been noted by a number of researchers, which lead the flow convergence in the entrance slope and flow divergence in the exit slope section of the flow [23,29]. Despite the fact that in a balanced flow, it is not always the case that the vertical velocity is downward in an accelerating flow, and upward in a decelerating flow [32].The convergence and divergence pattern of flow in the deceleration and acceleration sections is in agreement with field investigations and experimental studies [8,34,35,36].

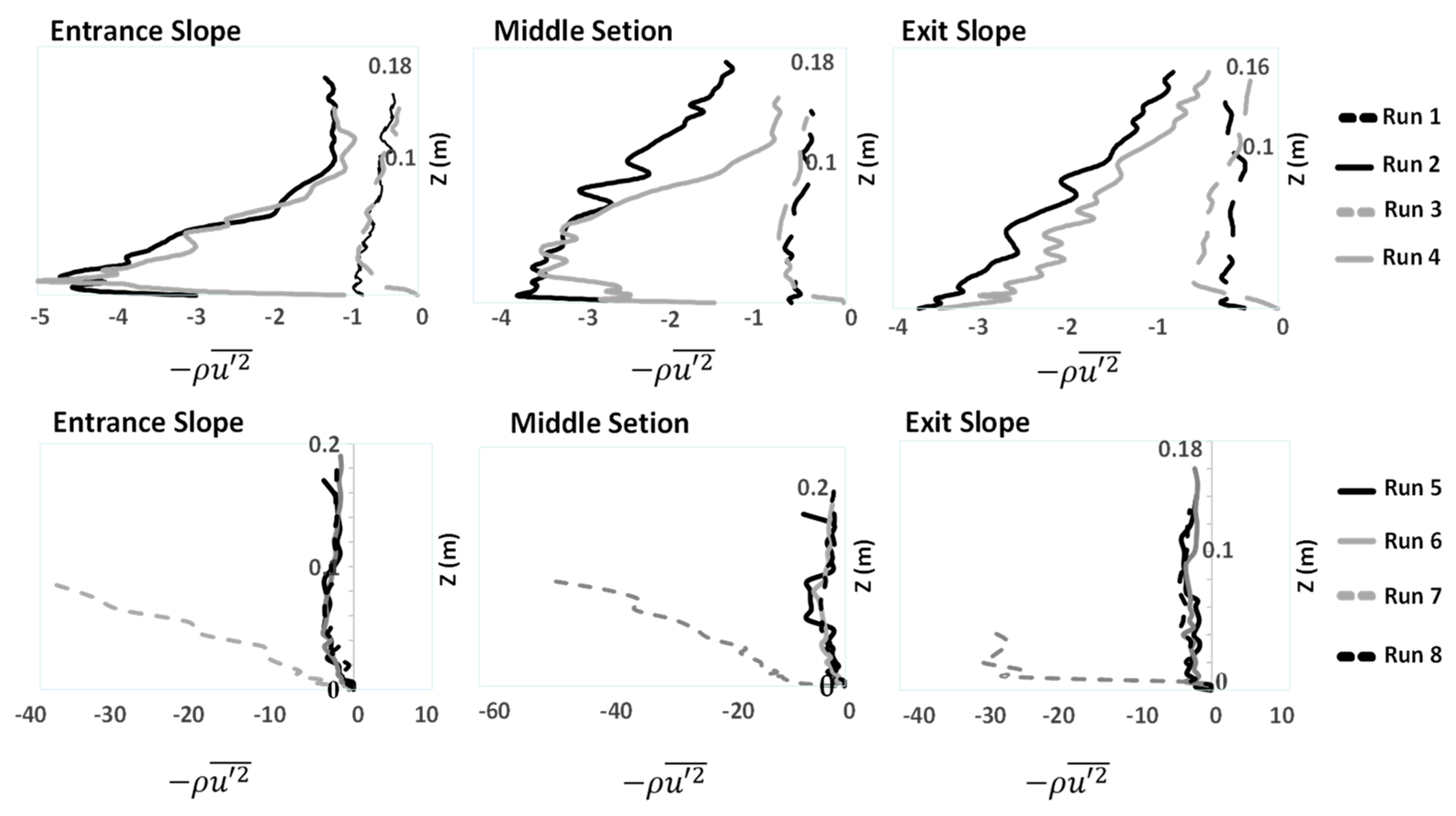
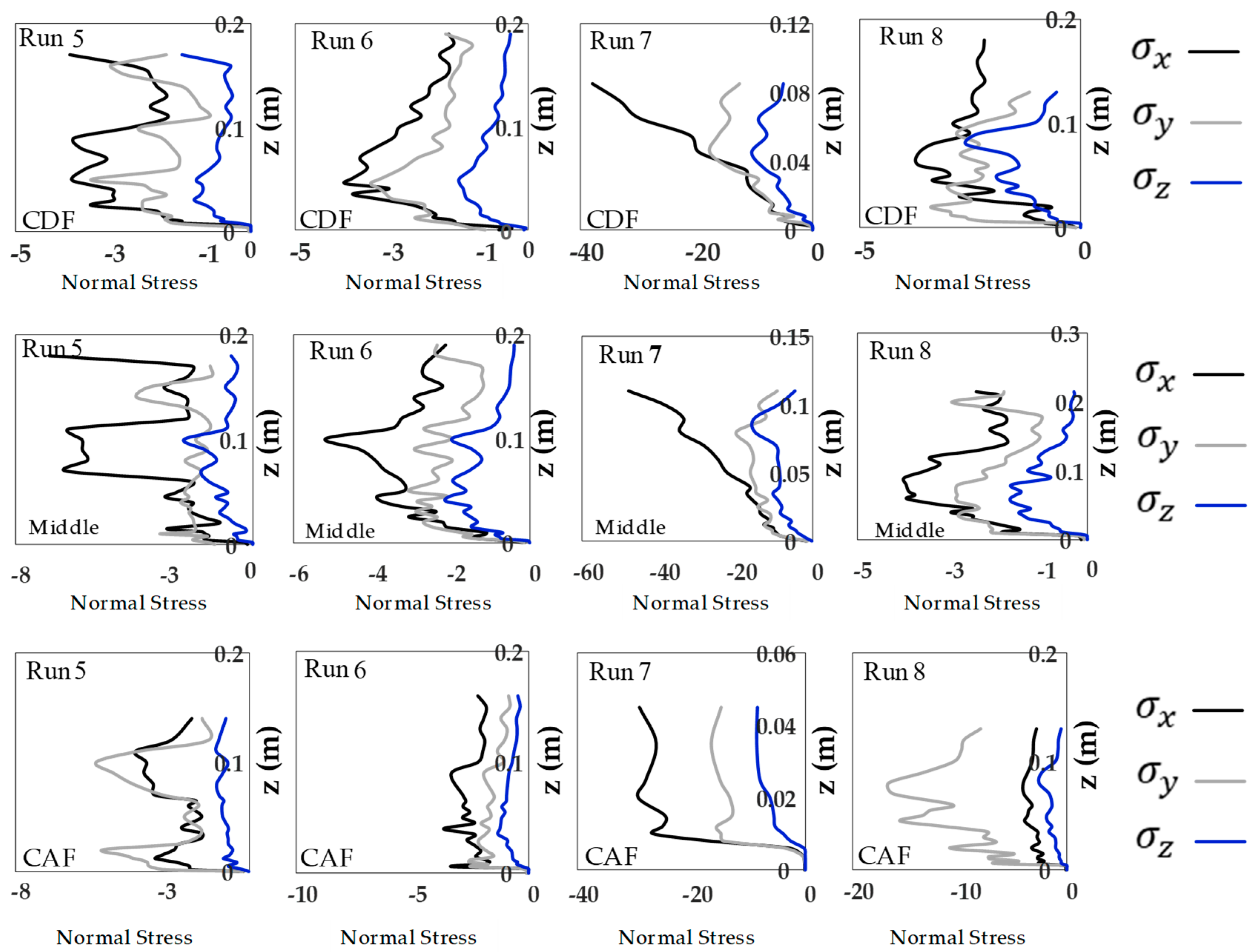
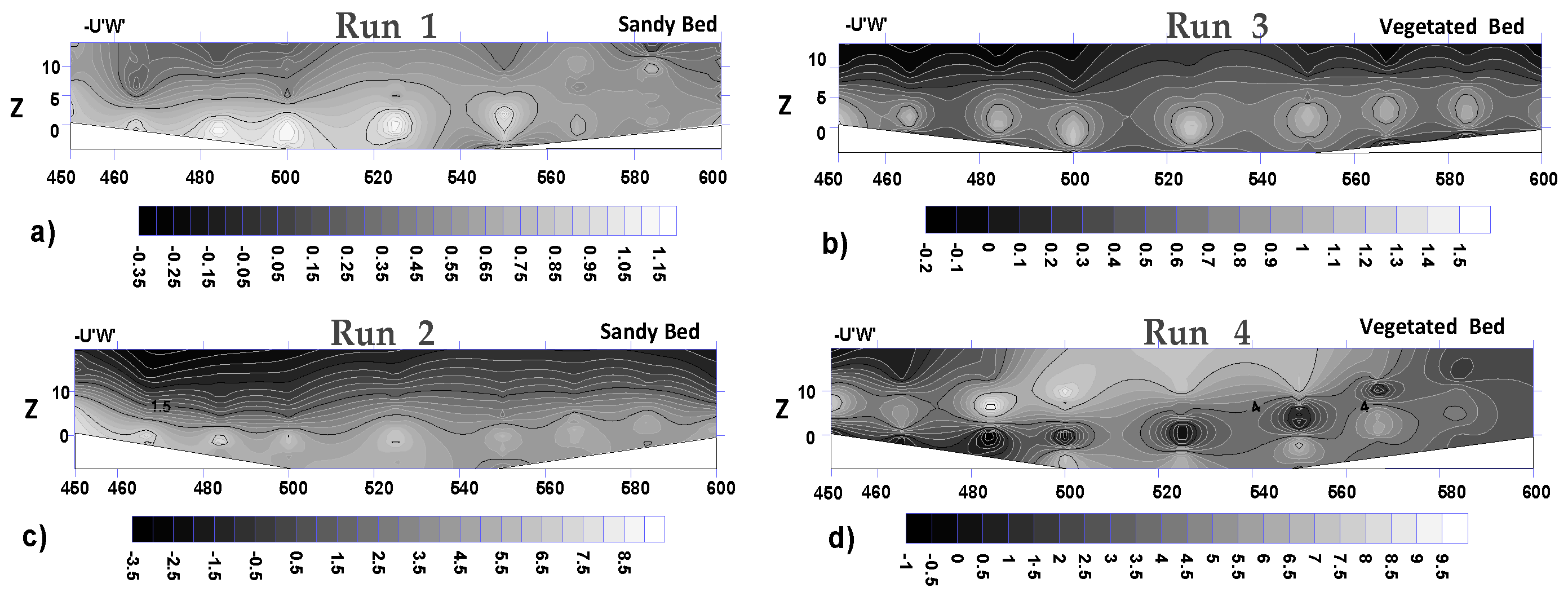
3.2. Reynolds Normal and Shear Stress Distributions

In this study, using the following Equations 1, the dimensional Reynolds normal stresses have been estimated at three locations (entrance, middle, and exit sections) along the pool bed, which depicted in Figure 5.
σ x = - ρ u ' 2 ¯   ,   σ y = ρ v ' 2 ¯   ,   σ z = ρ w ' 2 ¯
Under a constant flow discharge, the normal stresses on the pool bed with vegetation patch are clearly greater than those on the bear gravel-surface. The magnitude of normal stress decreases as the flow rate rises. Also, the magnitude of normal stress decreases as the bed slope angle rises. Additionally, when aspect ratio rises, the magnitude of normal stress becomes small at the water surface. This phenomenon happens due to a stronger secondary current in shallower flows (w/h = 2.7). For experimental Runs 5 to 8 conducted using experiment setup 2 (10-degrees slope), the magnitudes of normal stresses in three directions of the flow are showed in Figure 6. Results indicate that the levels of normal stress are higher in stream-wise direction than those in both lateral and vertical directions. However, the magnitude of stream-wise normal stresses were disturbed in three directions, due to the presence of secondary currents resulted in different roughness between the bed and the banks. Therefore, the Reynolds normal stress distributions are affected by the difference of roughness (gravel or vegetation) and bedform slopes. This makes difficult to provide a general pattern for the distribution of Reynolds normal stress in the bedforms in the present of vegetation cover.
In Figure 7, Reynolds Shear Stresses( − ρ u ' w ' ¯ ) showed in Eq. 2 are normalized with the squared friction velocity u * 2 , in which u * is shear velocity calculated from the velocity profiles near the bed, follow the logarithmic law showed in Eq. 3. Wherein k is the von Karman coefficient, which is equal to 0.41, z 0   is the reference bed level varies with the roughness height of the bed material. In both uniform and non-uniform flows, it has been claimed that the inner zone of each velocity can be extended to a relative depth of z/ z 0 = 0.2 [32].
u ′ w ′ ¯ = 1 N ∑ i = 1 N ( u − u - ) ( w − w - )  
u   u * = 1 k ln z z 0
In the presence of vegetation canopy in the pool bed, four experimental runs have been conducted. The dimensionless Reynolds Shear Stress (RSS) profiles are displayed in Figure 7 along the flow depth. If the channel bed is smooth, the RSS distribution is often linear. The rough sub-layer near to the bed may cause the Reynolds stress distribution to grow up to 20% of the flow depth before decreasing [37]. Results of present study indicate that the secondary currents are intensified due to the presence of the vegetation canopy, the non-zero vertical velocities, and the smaller values of aspect ratio less than 5. Several researches have demonstrated that the secondary currents in shallow flows cause the shear stress distribution to deviate from the expected linear shape [29,38,39]. The RSS has been investigated and showed in Figure 7 for the case when vegetation is present in the pool bed. In order to demonstrate the various trends of Reynolds stress under different experimental settings, results of four experimental runs have been prersented in Figure 7. Depending on the variation in the flow velocities, location of the maximum shear stress can be observed in the upstream portion of the channel, which is located in the zone close to the channel bed within the distance of z/H < 0.15, reveals that the RSS values completely be affected by the roughness elements and relative submergence (H/ d 50 ) [40]. The positive RSS values close to water surface supports the existence of the dip phenomenon. The greater the slope of the pool entrance section (Runs 6, and 7) is, the higher the Reynolds stress values are induced along the flow. Also, the shear stress reduced toward the water's surface as the flow depth increased, and its distribution profile appears a convex shape. Moreover, the positive pressure gradient (also known as the reverse pressure gradient) and the negative pressure gradient (also known as the favorable pressure gradient), have an impact on the Reynolds stress distribution in the decelerating and accelerating flows, respectively[21]. The shear stress profiles in the middle pool section do not exhibit a tendency toward a linear shape, suggesting that the flow is not homogeneous there. In the presence of a vegetation patch in the pool, the increased flow velocity lead to the increease in the shear stress values in the zone of z/H < 0.2 due to higher turbulence intensities. For all experimental runs, the maximum shear stress inside the middle pool section occurred away from the channel bed depending on the flow velocity and slopes of entrance and exit sections, specifically the maximum RSS is observed at the depth of z/H = 0.25 in the middle part of the flow (Run 3, 4, and 6) [21,23,29]. However, the impact of secondary currents resulted from the increase in the aspect ratio has the opposite effect on the location of the maximum shear stress and is shifted toward the water surface (Run 7). For the same flow discharge, as the results showed from Runs 3 and 6, with the increase in the slope of the entrance section (namely, with the decrease in flow velocities), the RSS values increased in the zone of z/H < 0.5 (except for the middle pool section).
Due to significant disturbances resulted from bed forms and roughness, the shape of shear stress distribution profiles in the downstream section of the pool differs from that in the upstream section of the pool. Negative Reynolds stresses are also observed sometimes, as illustrated in Figure 7. Most likely, this is resulted from the flow being transmitted to each component's wake zone by vegetation-induced drag. Nonetheless, the previous investigations in the presence of vegetation and bed morphologies also reported the existence of negative RSS values [41]. These results demonstrated that, even if the sweep and ejection events result in positive RSS values in the flow field, the outward and inward events in the bursting process might be responsible for the negative stresses.
In some places, particularly in the zones that the flow was accelerating, the RSS value increased dramatically. It may be explained that when the flow is accelerated or even the channel bed has a larger slope, the turbulent velocity components undergo some changes, as indicated in Figure 7 and Figure 8. Moreover, the distribution of flow responds more strongly and more quickly to the changes in bed slope near the channel's side walls than it does near the channel's centerline (Figure 8). It has been observed from Figure 9 that, over the garvel pool bed, the highest Reynolds stress region grows to the end of the middle section of the pool. However, with a lower flow discharge, the presence of vegetation resulted in an obvious decrease in the shear stress (Run 3). While, with the higher flow discharge, the vegetated canopy minimizes shear stresses on the entrance slope, the zone with the greatest stress is only visible in the middle section of the pool bed (Run 4).

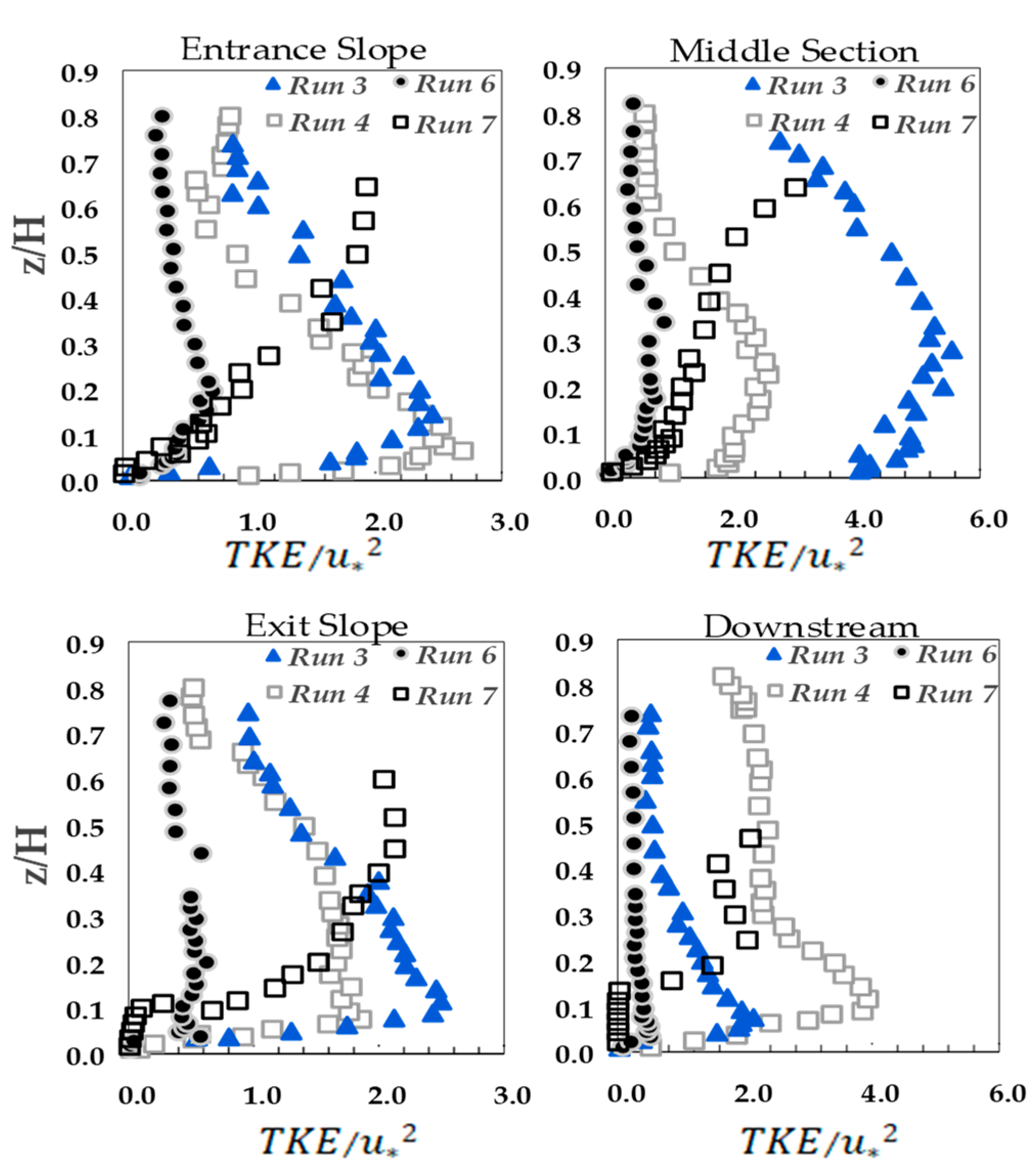
3.3. Turbulence Kinetic Energy (TKE)

As seen in Fig.3 the velocity profile in the inner layer of the flow is almost constant due to the significant wake effects resulted from the vegetation canopy; this zone exhibits negligibly little vertical momentum transmission although it may occasionally appears with a slightly contour-gradient. This inner layer zone is comparable to the "emergent" vegetated open-channel flow studied by previous researchers, which refer to the "longitudinal exchange zone", with a negligibly small vertical momentum transport [4,42,43,44]. In the mixing layer, due to the vertical transfer of momentum, the unstable inflection-point of velocity is induced by secondary currents. The logarithmic law is used to describe the turbulence structure in this zone. Figure 10 represents the variation of dissipation rate of turbulent kinetic energy (TKE = 0.5 c 2 ρ [ u ' 2 ¯ + v ' 2 ¯ + w ' 2 ¯ ] ), normalized with the squared friction velocity ( u * 2 ) , with respect to flow depth in central pool section where vegetation patch presents. In the mixing layer of flow at the canopy part, the turbulent diffusion has an obvious impact on the turbulence kinetic energy (TKE) budget
Figure 10 shows that the great TKE values are observed at different locations in several flow sections. The energy losses are reduced, i.e., as the entrance slope increases, the pressure losses per unit length of the bed are reduced, leading to lower RSS values [20]. In fact, the mixing eddies resulted from the velocity gradient over the vegetation canopy decreased, and the reduction of the entrance slope of a pool leads to turbulence becomes weaker. The profiles of TKE values do not follow a convex shape, as it is considered for Run 7 due to both large entrance and exit slopes of the bedform, indicating a significant role of bedform geometry on the TKE distribution. In addition, due to stronger secondary currents and higher turbulence velocity, an increase in flow velocity by reducing flow depth resulted in larger TKE values in Run 7.
The maximum TKEvalue is predicted to occur generally in a zone that is relatively close to the bed (z/h < 0.2), since the production of Von Karman vortexes is typically associated with the occurrence of TKE values that peak a severe distortion in the velocity profile [10]. Moreover, other studies have revealed lower ranges for the wake zone in streams with broad and heavily submerged vegetation as well as in streams with a broad, partially submerged vegetation in bed. Results of the present study support the existence of a small wake zone over the vegetation canopy [2,14] only for the small bedform slopes (Runs 3 and 4).

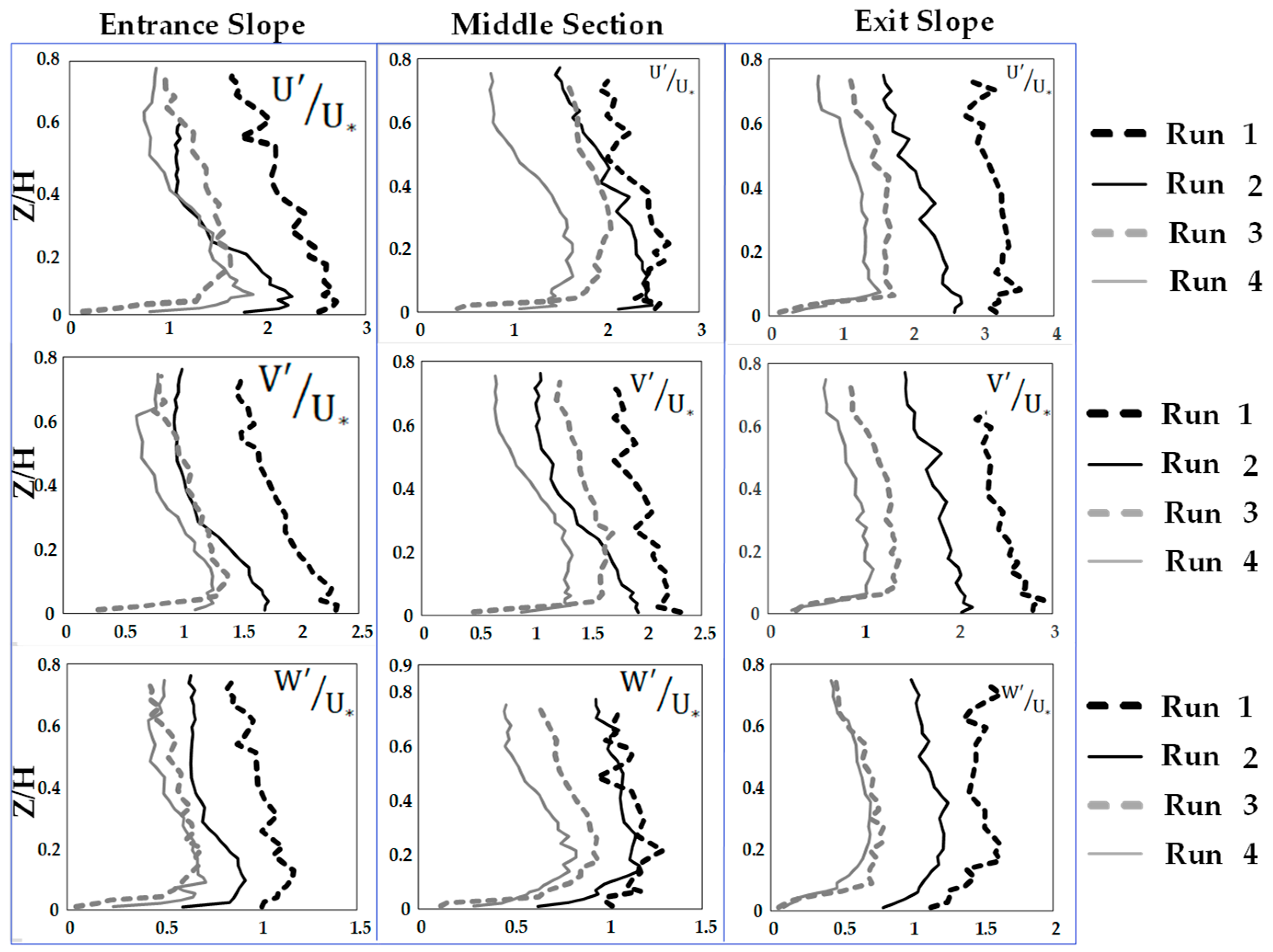
3.4. Turbulence Intensities

By calculating the root mean square (RMS) of flow velocities, turbulence intensity is displayed in Figure 12 to show the values of intensities for pool setup 1. It has been found that the vertical turbulence intensity is highest in the upper layer above the canopy of vegetation, about in the zone of z/H < 0.2, while stream-wise and lateral turbulence intensities reach their maximum just above the canopy of vegetation.
Research results showed that the maximum intensity of streamwise turbulence (u’) occurs just above the canopy, while the maximum intensity of vertical turbulence occurs rather just below the emergent canopy. Due to the non-uniformity of flow in experiments, the values of u’, in particular, exhibit convex shape rather than a concave one, which deviates from the exponential law proposed by Nezu (1977) [45]. This suggests that vegetation considerably modifies the equilibrium state of turbulent kinetic energy and thus, the redistribution of turbulence intensities. In fact, it should be noted that the isotropic turbulence inside of vegetation (including the vegetation stems and canopy) occurs when there is a strong wake of turbulence over those objects. As a result, the wake caused by vegetation elements may cause convex patterns of turbulence intensities in a cascade process [46]. Similar convex-shaped distribution of turbulence intensity has been reported in studies of aquatic canopies [47,48].
It appears that the presence of vegetation has a considerable impact on kinetic energy and the distribution of turbulence intensities [18,47]. As showed in Figure 12, results imply that the slope angle of the channel bed may have an impact on the maximum disturbance intensity. The maximum amount of disturbance along the accelerating section of the flow has greater values than that along the decelerating section. The zone of the inner layer with the largest turbulence intensities can be seen around the zone of z/H < 0.2, while in the central region of the flow it appeared to be in the zone of z/H < 0.4. These zones (or flow depths) are also thought to be the spots where shear stress is at its highest. Instead of the accelerating flow, the decelerating flow intensifies the turbulence and increase Reynolds shear stress, indicating that flow structures are affected by the non-uniformity of the flow [38].

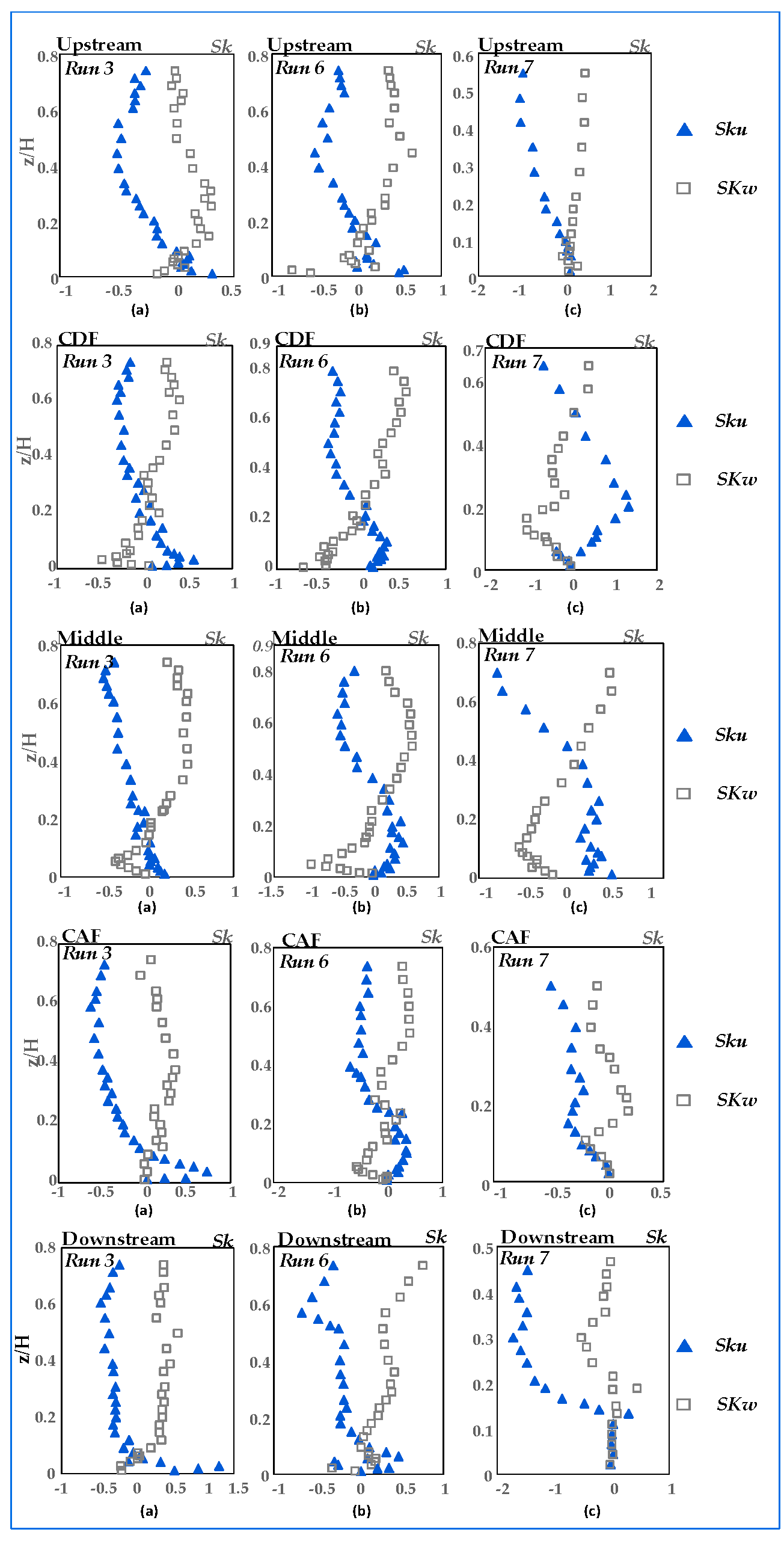
3.5. Skewness Coefficients

Skewness coefficients ( sk u and sk w ) of velocity fluctuations are the third central moment of the factors u’ and w’, which include positive, negative, or zero values in turbulent flows. Asymmetry in a flow field can be better understood by looking at skewness factors [19]. A positive skewness means that the variable u’ is more likely to take on a large positive value than large negative one. In fact, a non-zero skewness of velocity fluctuations in the stream-wise and vertical directions, indicates an asymmetric probability density function (PDF) of the considered variable, namely, the dominated processes in one direction are more possible than in the other one depending on the symptom of the statistics.
The positive skewness indicates that the PDF (probability density function) has a longer tail for u’ > 0 than that for u’ < 0. A zero-skewness value shows an isotropic or homogenous turbulence. The outward motion of the flow is a result of the positive values of u’ and c in bursting process occurrences, the sweep motion is recognized with the positive value of u’, and negative value w’ generally corresponds to the flow stream over the vegetation canopy (often denotes the flow stream above the vegetation canopy). However, the ejection motion of the bursting phenomenon, which has a positive value for w’ and negative value for u’, along with the sweep motion have been observed over smooth walls in boundary layer [49,50]. Lastly, the flow has been recognized to be moving inward if both u’ and w’ have negative values. This organized motion known as the "Monami" was observed by other researchers who examined coherent eddies over aquatic flexible vegetation canopies. The possible explanation is that instability of the inflection-point of velocity profiles is responsible for the generation of Monami coherent eddies in the presence of flexible vegetation in flows. This implies that coherent eddies like ejections and sweeps will resonate with the flexible vegetation [43].
Figure 13 displays the skewness for measured velocity fluctuations ( sk u and( sk w ) from experiments based on data collected from experimental Runs 3, 6, and 7 along the upstream, entrance slope through the decelerating flow (CDF), middle-pool section, and exit sections which leads to the accelerating flow (CAF) of the pool while maintaining the same flow rate and vegetation canopy. The sweep motion is the major event right above the gravel grains in the zone of z/H < 0.1 in the upstream region of the pool, where the fluctuations of flow velocity mostly depend on two parameters, flow depth (H), and median grain size of bed material ( d 50 )(Runs 3 and 6). To precisely study flow dynamics, data was collected at the boundary of gravel and vegetation patch at the upstream portion of the pool, as showed in Figure 13C.
One can see from Figure 13 that sk u just has slightly positive values at point c together with a positive sk w value, where vegetation patch begins at the gravel border, implying that the outward motion has occurred closely above the gravel barrier in the zone of z/H < 0.1.
Along the decelerating part of the flow (CDF), sweep motion appears above the vegetation canopy in the inner layer of the flow in the zone of z/H < 0.2, while the modification of the entrance slope doesn’t lead to a change of the zone for the occurrence of the sweep motion in the stream (Runs 3 and 6). However, by adjusting the aspect ratio in the flow (Run 7, from w/H = 2 to 2.7; w/H < 5), sweep phenomenon has been seen in a higher layer of the stream in the zone of z/H < 0.5, indicating that the change of flow velocity results in the occurrences of bursting events. By increasing the slope of the entrance section of the pool, a larger region for the sweep phenomenon is resulted, while a higher sweep zone (z/H < 0.4) has been observed by altering the aspect ratio. The sweep motion has been noticed just above the vegetation canopy in the acceleration section of the flow. However, a larger zone of sweep motion has been generated because of the modification of the slope of the exit section of a pool.

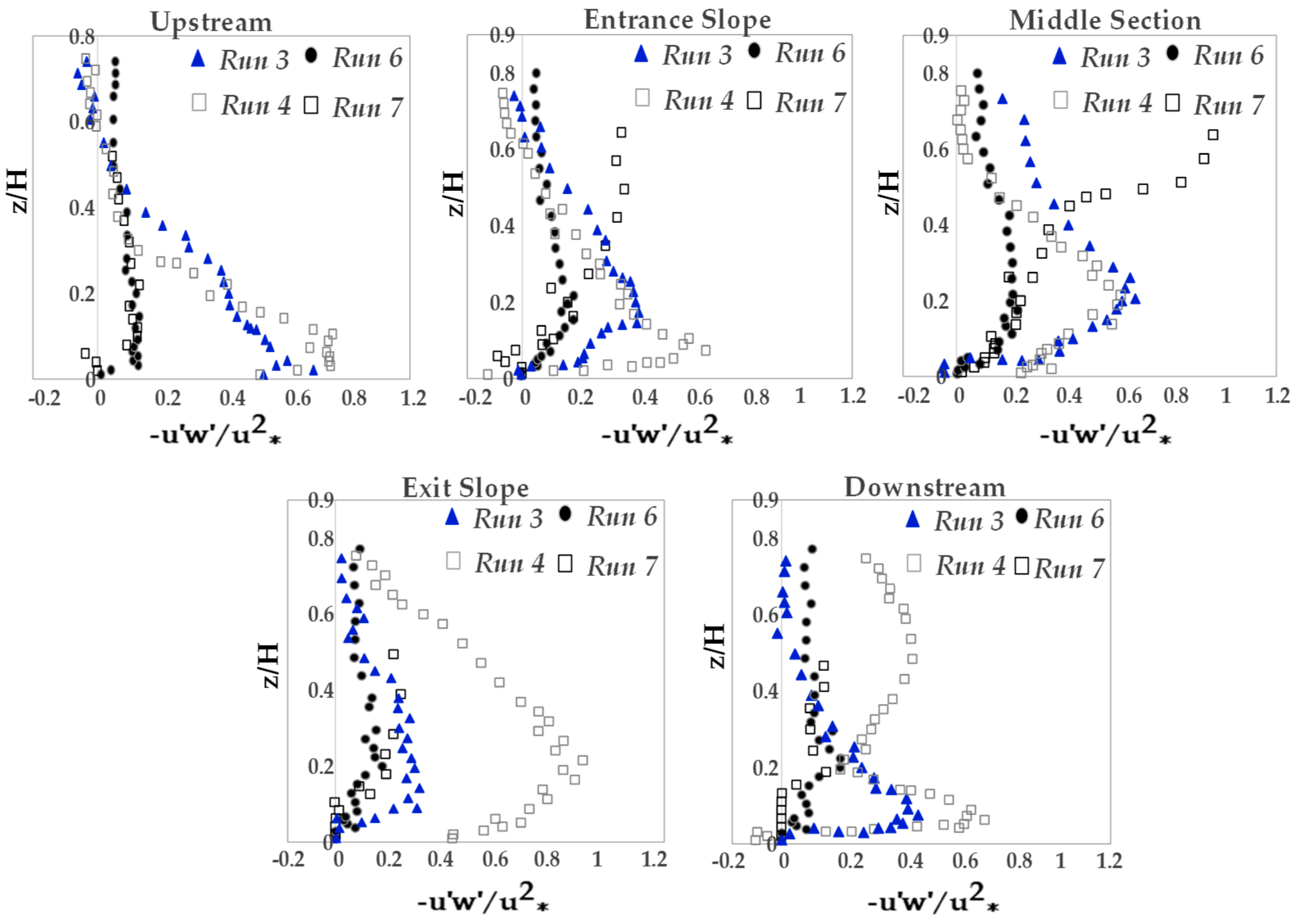
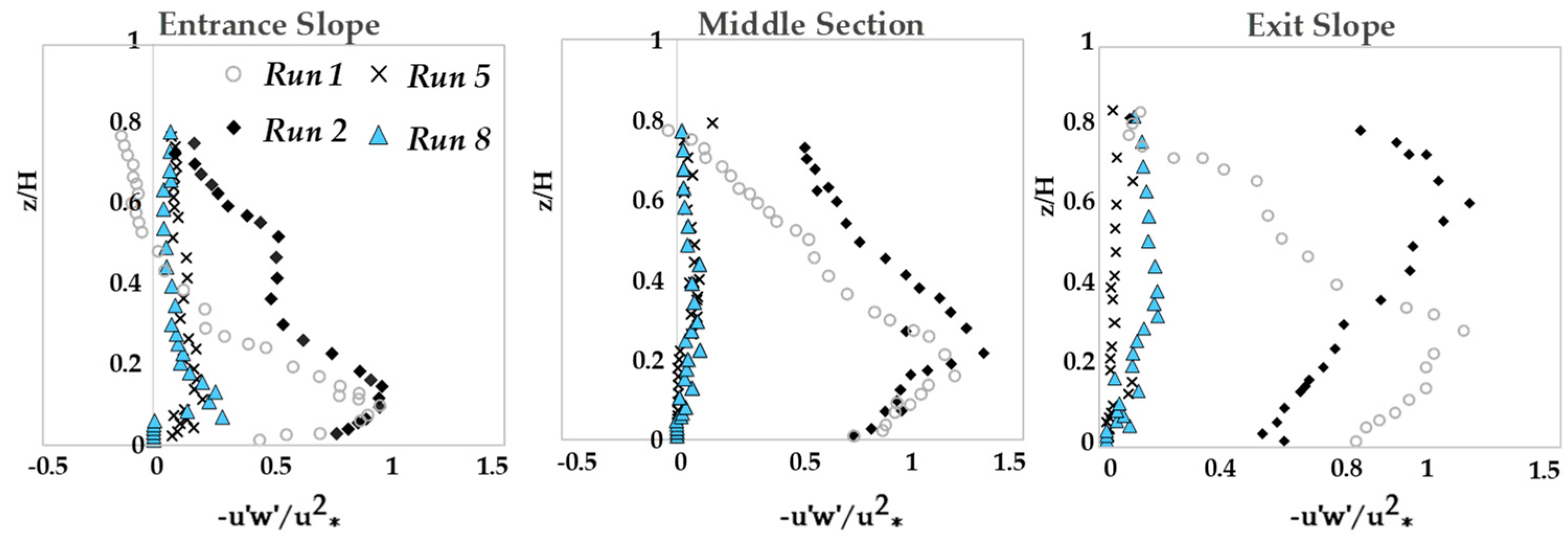
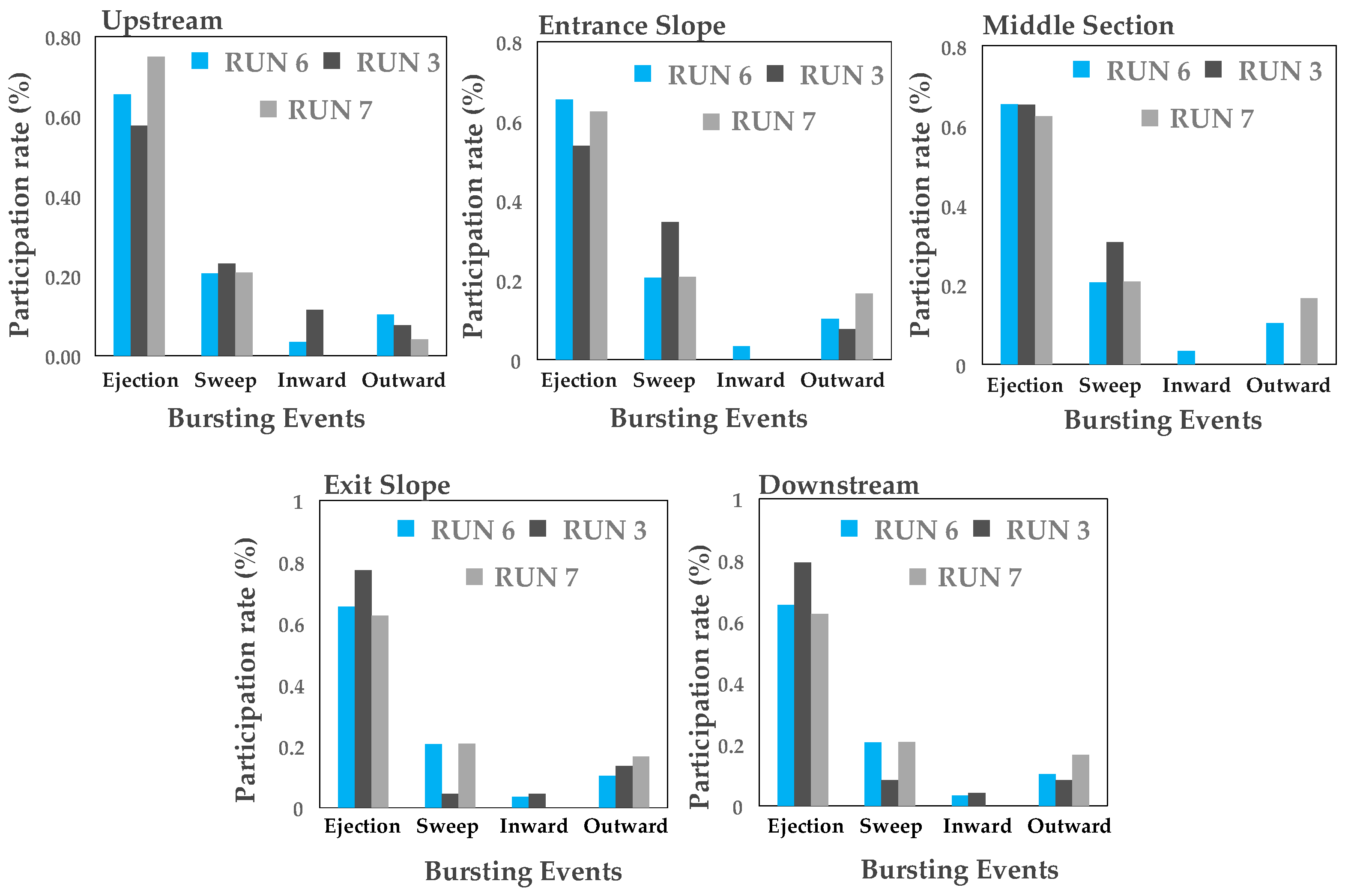
3.6. Quadrant Analysis

The presence vegetation patch over bedform plays a role on the flow structures. However, this aspect of fluvial hydraulic has less been considered by researchers. This part of study especially focus on the boarder of vegetation and grave. This is important question what happen in trailing edge of vegetation over a pool and how this affects the turbulence features and their distributions. It appears that the sweep motion is the primary event of the flow downstream of the pool (trailing edge of vegetation), where the flow reaches the gravel bed again. Nonetheless, according to result of experiment Run 7, the isotropic event often occurs near the boundary between the vegetation patch and gravel bed (trailing edge of vegetation patch). The contribution of each quadrant event is presented in Figure 14, indicating the dominant role of the ejection motion in the bursting process of the flow, and the sweep motion as the second dominant event in the stream.

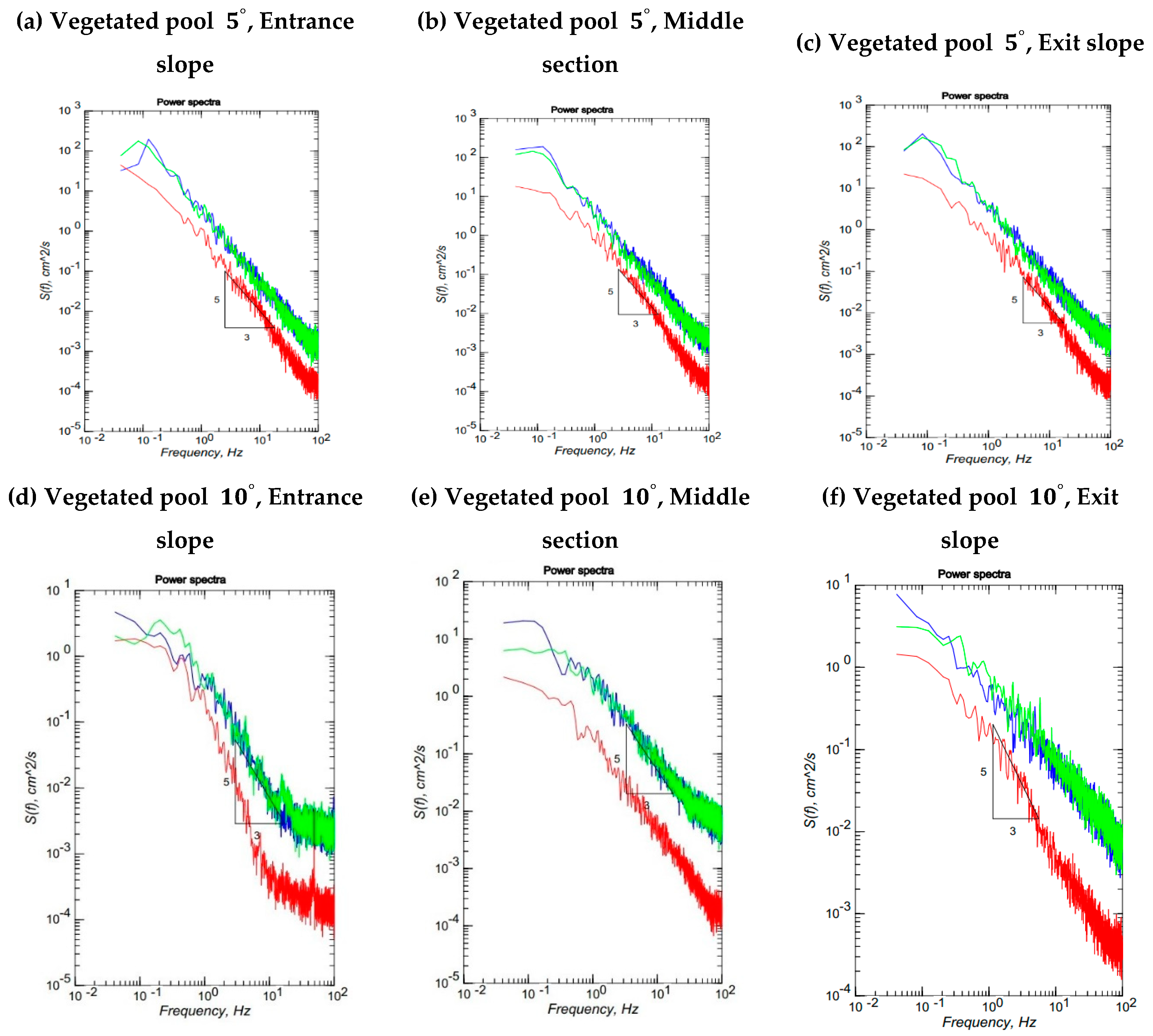
3.7. Spectral Analysis

Spectral analysis has been done for velocity components along the bedform at the same points which are located at 6 mm from the vegetation cover along the entrance slope, middle section, and the exit slope of the pool. The distance of 6 mm from the vegetation cover is selected in this study, since we want to compare results of this study to those of other studies such as Najafabadi et al. (2018)[51]. Power spectral densities of velocity components in Figure 15 are presented for three velocity components; stream-wise velocity is presented as blue curves; spanwise velocity components as green curves and vertical velocity components as red curves. Figure 15 shows a slightly deviation in the Kolmogorov’s -5/3 power law for the vertical velocity component from the inertial sub-range with the presence of a smaller bed slope, but it is generally valid. The slight deviation is resulted from rigid vegetation on the bed that limits its effect to near the vegetation. In addition, the Kolmogorov scale may mainly represent a balance between the kinetic and viscous energy in the flow field, and not necessarily an eddy scale, which could explain this discrepancy in velocity deviation of the Kolmogorov law. Najafabadi et al. (2018) reported that the Kolmogorov’s -5/3 power law is prominent only at the deepest point of bedform. However, our study shows that the law rests universal for the trailing edge of vegetation of 3D bedform as it is reported for 2D pool with 3D flow in a laboratory experiment over the gravel bed[51].
Figure 15 shows that the shedding frequency falls between 1.8 and 4 Hz. However, Nepf (1999) claimed that this range for is (1.8 - 3.6 Hz) for a random of cylinder as emergent vegetation [52], but (1.0 – 1.8 Hz) reported by Lacy and Roy (2007)[53]. Over the gravel bed between the vegetation patches, Afzalimehr et al. (2021) pointed out this range is from 3.0 to 7.7 Hz) [54].This comparison shows that the shedding frequency is affected by the changes in bedform slope as well as the presence of 3D bedforms and vegetation patches, revealing higher values than those reported in literature.

4. Disscusions

In this section, a comparison of results of this study to those of Nepf and Ghisalberti (2008)[4] and Wang el al. (2022) [50] has been presented in order to clarify contribution of the present research. In the study ofNepf and Ghisalberti (2008), they did not consider the 3D bedforms effect and a dense vegetation patch without flexibility but they considered plant stems as rigid circular cylinders with a specific distance between the rigid circular cylinders. Thus, the turbulent structure in their study is completely different from that of the present study. Nepf and Ghisalberti (2008) could investigate the flow structures under top of vegetation because the setup of vegetation stems was spaced apart, and this type of setting enabled to collect data inside the vegetation region using a ADV. A comparison of Reynolds stress (RS) distribution reported by Nepf and Ghisalberti (2008) and that obtained in the present study shows that the location of bedform (entrance, middle and exit sections) plays a significant role in the RS distribution, and thus leads to different results. For example, the Reynolds stress distribution in the study of Nepf and Ghisalberti (2008) (Figure 5 in the study of of Nepf and Ghisalberti (2008)) displays a clear convex distribution. In the present study, however, the RS distribution depends on the entrance slope of the pool and vegetation cover. As showed in some profiles the negative RS values are due to different contribution of bursting events and the role of the 3D bedform in the generation of secondary currents. In some runs (Rune 7 in the middle section of Figure 7), the RS has an increasing trend rather than a decreasing trend toward the water surface. Their objective to investigate the RS distribution was to identify the effect of vegetation deflection on producing a smaller vegetation height under a stronger flow condition. In this study, it is emphasized that no data are able to collect inside the vegetation patch due to a very thin vegetation layer and no change in vegetation flexibility. However, Nepf and Ghisalberti (2008) investigated flexible canopies, where the passage of the vortices of Kelvin-Helmholtz generated a wave called as monami showing a progressive wave along the canopy interface. Furthermore, they reported that the stem geometry plays a significant role in turbulent flow structures. In the present study, however, we investigate the interaction of vegetation cover without rigid stems and with no flexibility at important locations such as trailing edge of vegetation patch. Results of this study indicate that the application of the specific (constant) values of velocity and Reynolds stress for all parts of a bedform will lead to incorrect estimation of hydraulic parameters (e.g., resistance).
Wang el al. (2022) compared the influences of flexible vegetation to those of rigid vegetation on the flow velocity, and found that vegetation tilt has little effect on difference between flow velocity the inside and that of vegetation canopy as well as the turbulence structure in the flow. However, this study does not consider velocity structure inside the thin vegetation layer. Results of this study indicate that the bedform slopes (entrance and exit sections), vegetation patch and the location of pool (entrance, middle and exit sections) affects the velocity distribution. Results of the spectral analysis show that the Kolomogrove -5/3 law over 3D vegetation patch rests valid as it is for 2D pool and 3D flows. Wang et al (2022) worked over the flat bed with vegetation with the height of 0.2 and 0.1 m and arranged vegetation elements in five rows in the streamwise direction and nine rows in the spanwise direction (there is a distance between pellets) where the flow passes through the vegetation stems. By comparing the TKE values in the flow with inclined rigid vegetation to those with vertical rigid vegetation, they found that the TKE in the former case is obviously smaller than that with vertical rigid vegetation. Wang et al. (2022) investigated the energy spectra at the height of the vegetation canopy directly above a row of plants and in the middle of two rows of plants. They reported that that the Kolmogorov's −5/3 scaling law is satisfied in the inertial subrange of flow with rigid vegetation. However, they haven’t investigated the validation of this law at the trailing edge of 3D vegetation patch.

5. Conclusions

The flow in any rivers in arid and semi-arid regions decreases dramatically during summer. As a consequence, vegetation patches develop in different parts of rivers. When water level increases in these rivers during spring, fall and winter, hydraulic condition in rivers with the presence of vegetation patches is completely different from that without the presence of vegetation. Thus, some hydraulic parameters including velocity, Reynolds stress may be over- or under-estimated due to the presence of vegetation patches in channels. To better understand the variation of the hydraulic parameters along 3D vegetation patch, experiments have been carried out in a laboratory flume with an artificial bedform. Two slopes of 5 and 10 degrees for both entrance and exit sections of pools have been utilized. Following results have been drawn with respect to the distribution of velocity profiles, Reynolds normal and shear stress, TKE, turbulence intensities, skewness coefficients and bursting process.
1)
In general, results of this study show that the bedform slopes of both entrance and exit sections, vegetation patch and the location of pool (entrance, middle and exit section) affects the velocity, Reynolds shear stresses, TKE distribution and the contribution of each bursting events on the turbulent flow structures. Results show that, with the entrance and exit slope of 10 dgree, the TKE distribution has no specific form (Run 7). However, with the small entrance and exit slope of 5 degree (Runs 3 and 4), a convex TKE distribution is observed with the maximum value near the bed. Results of the quadrant analysis reveals the bursting events at the trailing edge of vegetation patch where the flow leaves vegetation patch to gravel bed displays different distributions comparing to other locations along the 3D vegetation patch. This difference plays a significant role in estimating flow resitance in open channls. The validation of the spectral anaysis of the Kolmogorov power law for different bedforms slopes has been conducted.
2)
The Reynolds normal stress in the stream-wise direction is greater than those in both lateral and vertical directions. There is a disruption of normal stress values in the stream-wise direction due to the presence of secondary currents generated due to different roughness of the channel bed and sidewalls of the flume. Therefore, the different roughness and bed slope influence the normal Reynolds stress distributions. In the stream-wise direction of the flow, the region with the highest Reynolds shear stress (RSS) moves away from the bed. The RSS values in the zone of z/H > 0.5 decreases as the bed slope increases. A decrease in the reverse pressure gradient and the favorable pressure gradient affects the distribution of Reynolds stresses in both decelerating flow zone (entrance section of a pool) and accelerating flow zone (exit section of a pool). When the entrance slope of the pool is smaller, the distribution of Reynolds stress is more regular toward the water surface.
3)
The quadrant analysis in this sudy focus on the role of different bursting events at the trailing edge of the vegetation patch where the flow leaves the vegetation patch to the gravel bed. Results clarified that both ejections and sweeps govern the turbulence structures and coherent motions at the trailing edge of the vegetation patch. The presence of the vegetation patch as well as the variation of both entrance and exit slopes of pools generate the non-uniformity of the flow, increase the turbulence intensity and TKE in downstream section of the vegetation patch. The sweep motion occurs in a narrower zone above the vegetation canopy. The sweep motions of bursting events are the dominant process directly above the vegetation canopy, while the outward motion with slightly positive values has been observed at the leading edge of the vegetation patch.
4)
The Kolmogorov -5/3 power law rests valid for the 3D vegetation patch. The geometry of bedform including both entrance and exit slopes of a pool does not influence this law compared to the presence of a vegetation patch in a flat bed.
5)
The shedding frequency is affected by the changes in the bedform slopes and the presence of vegetation, revealing higher values than those reported in literature.

References

  1. Poggi, D.; Katul, G.; Albertson, J. A note on the contribution of dispersive fluxes to momentum transfer within canopies. Boundary-layer meteorology. 2004. 111: p. 615-621. [CrossRef]
  2. Folkard, A.M. Hydrodynamics of model Posidonia oceanica patches in shallow water. Limnol. Oceanogr. 2005. 50(5): p. 1592-1600. [CrossRef]
  3. Zong, L.; Nepf, H. Flow and deposition in and around a finite patch of vegetation. Geomorphology. 2010. 116(3-4): p. 363-372. [CrossRef]
  4. Nepf, H.; Ghisalberti, M. Flow and transport in channels with submerged vegetation. Acta Geophys. 2008. 56(3): p. 753-777. [CrossRef]
  5. Shi, H.; Zhang, J.; Huai, W. Experimental study on velocity distributions, secondary currents, and coherent structures in open channel flow with submerged riparian vegetation. Adv. Water Res. 2023: p. 104406. [CrossRef]
  6. MacVicar, B.J.; Rennie, C.D. Flow and turbulence redistribution in a straight artificial pool. Water Resour. Res. 2012. 5(2). [CrossRef]
  7. Richards, K. The morphology of riffle-pool sequences. Earth Surf. Process. 1976. 1(1): p. 71-88. [CrossRef]
  8. Sawyer, A.M.; Pasternack, G.B.; Moir, H.J.; Fulton, A.A. Riffle-pool maintenance and flow convergence routing observed on a large gravel-bed river. Geomorphology. 2010. 114(3): p. 143-160. [CrossRef]
  9. Thompson, D.M., The role of vortex shedding in the scour of pools. Adv. Water Resour. 2006. 29(2): p. 121-129. [CrossRef]
  10. Chen, Z.; Ortiz, A.; Zong, L.; Nepf, H. The wake structure behind a porous obstruction and its implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 2012. 48(9). [CrossRef]
  11. Liu, C.; Nepf, H. Sediment deposition within and around a finite patch of model vegetation over a range of channel velocity. Water Resour. Res. 2016. 52(1): p. 600-612. [CrossRef]
  12. Ortiz, A.C.; Ashton, A.; Nepf, H. Mean and turbulent velocity fields near rigid and flexible plants and the implications for deposition. J. Geophys. Res: Earth Surf. 2013. 118(4): p. 2585-2599. [CrossRef]
  13. Zong, L.; Nepf, H. Vortex development behind a finite porous obstruction in a channel. J. Fluid Mech. 2012. 691: p. 368-391. [CrossRef]
  14. Liu, C.; Hu, Z.; Lei, J.; Nepf, H. Vortex structure and sediment deposition in the wake behind a finite patch of model submerged vegetation. J. Hydraul. Eng. 2018. 144(2): p. 04017065. [CrossRef]
  15. Raupach, M.R.; Finnigan, J.J.; Brunet, Y. Coherent eddies and turbulence in vegetation canopies: the mixing-layer analogy. Boundary-Layer Meteorology. 1996: p. 351-382. [CrossRef]
  16. Okamoto, T.A.; Nezu, I. Spatial evolution of coherent motions in finite-length vegetation patch flow. Environ. Fluid Mech. 2013. 13(5): p. 417-434. [CrossRef]
  17. Houra, T.; Tsuji, T.; Nagano, Y. Effects of adverse pressure gradient on quasi-coherent structures in turbulent boundary layer. Int. J. heat fluid flow. 2000. 21(3): p. 304-311. [CrossRef]
  18. Ghisalberti, M.; Nepf, H.M. Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res. 2002. 107(C2): p. 3-1-3-11. [CrossRef]
  19. Kumar, P.; Sharma, A. Experimental investigation of 3D flow properties around emergent rigid vegetation. Ecohydrol. 2022. 15(8): p. e2474. [CrossRef]
  20. Kazem, M.; Afzalimehr, H.; Sui, J. Characteristics of turbulence in the downstream region of a vegetation patch. Water. 2021. 13(23): p. 3468. [CrossRef]
  21. Nosrati, K.; Afzalimehr, H.; Sui, J. Interaction of Irregular Distribution of Submerged Rigid Vegetation and Flow within a Straight Pool. Water. 2022. 14(13): p. 2036. [CrossRef]
  22. Afzalimehr, H.; Barahimi, M.; Sui, J. Non-uniform flow over cobble bed with submerged vegetation strip. Proc. ICE–Water Manag. 2019, 172, 86–101. [CrossRef]
  23. Parvizi, P.; Afzalimehr, H.; Sui, J.; Raeisifar, H.R.; Eftekhari, A.R. Characteristics of Shallow Flows in a Vegetated Pool—An Experimental Study. Water. 2023. 15(1): p. 205. [CrossRef]
  24. Nezu, I.; Nakagawa, H.; Jirka, G.H. Turbulence in open-channel flows. J. Hydraul. Eng. 1994. 120(10): p. 1235-1237.
  25. Kironoto, B.; Graf, W.H.; Reynolds. Turbulence characteristics in rough uniform open-channel flow. P. I. Civil Eng-Mar En. 1994. 106(4): p. 333-344. [CrossRef]
  26. Bassey, O.B.; Agunwamba, J. Derived Models for the Prediction of Cole’s and Dip Parameters for Velocity Gradients Determination in Open Natural Channels. 1998.
  27. Liu, M.; Huai, W.; Ji, B. Characteristics of the flow structures through and around a submerged canopy patch. Physic. Fluids. 2021. 33(3): p. 035144. [CrossRef]
  28. Fazlollahi, A.; Afzalimehr, H.; Sui, J. Effect of slope angle of an artificial pool on distributions of turbulence. Int. J. Sediment Res. 2015. 30(2): p. 93-99. [CrossRef]
  29. MacVicar, B.J.; Rennie. C.D. Lateral distribution of turbulence and secondary currents in non-uniform open channel flow. In Proceedings of the 33rd IAHR Congress: Water Engineering for a Sustainable Environment Hydraulics, Vancouver, BC, Canada, 9–14 August 2009; pp. 1908–1915.
  30. Afzalimehr, H.; Nosrati, K.; Kazem, M. Resistance to Flow in a Cobble-Gravel Bed River with Irregular Vegetation Patches and Pool-Riffle Bedforms (Case study: Padena Marbor River). Ferdowsi Civ. Eng.(JFCEI). 2021. 2: p. 35-50.
  31. Green, J.C. Comparison of blockage factors in modelling the resistance of channels containing submerged macrophytes. River Res. Appl. 2005. 21(6): p. 671-686. [CrossRef]
  32. Song, T.; Chiew, Y. Turbulence measurement in nonuniform open-channel flow using acoustic Doppler velocimeter (ADV). J. Eng. Mech. 2001. 127(3): p. 219-232. [CrossRef]
  33. Coles, D., The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1956. 1(2): p. 191-226. [CrossRef]
  34. MacWilliams, Jr.; Wheaton, J. M.; Pasternack, G. B.; Street, R. L.; Kitanidis, P. K. Flow convergence routing hypothesis for pool-riffle maintenance in alluvial rivers. Water Resource Res. 2006. 42(10). [CrossRef]
  35. MacVicar, B.; Roy, A. Hydrodynamics of a forced riffle pool in a gravel bed river: 1. Mean velocity and turbulence intensity. Water Resources Res. 2007. 43(12). [CrossRef]
  36. Clifford, N.; Richards, K. The reversal hypothesis and teh maintenance of riffle-pool sequences: A review and field appraisal. In Lowland floodplain rivers. Geomorphological perspectives. 1992. p. 43-70.
  37. Kironoto, B.; Graf, W.H.; Reynolds. Turbulence characteristics in rough non-uniform open-channel flow. Proc. Inst. Civ. Eng.-Water Marit. Energy. 1995, 112, 336–348. [CrossRef]
  38. Yang, S.Q.; Chow, A.T. Turbulence structures in non-uniform flows. Adv. Water Resources. 2008. 31(10): p. 1344-1351. [CrossRef]
  39. Barahimi, M.; Sui, J. Effects of Submerged Vegetation Arrangement Patterns and Density on Flow Structure. Water. 2023. 15(1): p. 176. [CrossRef]
  40. McLean, S.; Nikora, V. Characteristics of turbulent unidirectional flow over rough beds: Double averaging perspective with particular focus on sand dunes and gravel beds. Water Resources Res. 2006. 42(10). [CrossRef]
  41. Kabiri, F.; Afzalimehr, H.; Sui, J. Flow structure over a wavy bed with vegetation cover. Int. J. Sediment Res. 2017. 32(2): p. 186-194. [CrossRef]
  42. Nepf, H.M.; Vivoni, E. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. Ocean. 2000. 105(C12): p. 28547-28557.
  43. Nezu, I.; Sanjou, M. Turburence structure and coherent motion in vegetated canopy open-channel flows. J. Hydr-Environ. Res. 2008. 2(2): p. 62-90. [CrossRef]
  44. Shivpure, V.; Devi, T.B.; Kumar, B. Turbulent characteristics of densely flexible submerged vegetated channel. ISH J Hydraul Eng. 2016. 22(2): p. 220-226. [CrossRef]
  45. Nezu, I. Turbulence intensities in open channel flows. in Proceedings of the Japan Society of Civil Engineers. J. JSCE.1977. 261. 61-76. (In Japanese).
  46. Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000. 32(1): p. 519-571. [CrossRef]
  47. Wilson, C. A. M. E.; Stoesser, T.; Bates, P. D.; Batemann Pinzen, A., Open channel flow through different forms of submerged flexible vegetation. J. Hydraul. Eng. 2003. 129(11): p. 847-853. [CrossRef]
  48. Neary, V.S.; Constantinescu, S.G.; Bennett, S.J.; Diplas, P. Effects of Vegetation on Turbulence, Sediment Transport, and Stream Morphology. J. Hydraul. Eng. 2012, 138, 765–776. [CrossRef]
  49. Adrian, R.J., Meinhart, C.D.; Tomkins, C.D.Vortex organization in the outer region of the turbulent boundary layer. J. fluid Mech. 2000. 422: p. 1-54. [CrossRef]
  50. Wang, J.; He, G.; Dey, S.; Fang, H. Influence of submerged flexible vegetation on turbulence in an open-channel flow. Journal of Fluid Mechanics, 2022. 947, A31. [CrossRef]
  51. Najafabadi, E.F.; Afzalimehr, H.; Rowiński, P.M. Flow structure through a fluvial pool-riffle sequence–Case study. J. Hydro-environment Res. 2018. 19: p. 1-15. [CrossRef]
  52. Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water resources res, 1999. 35(2): p. 479-489. [CrossRef]
  53. Lacey, R.J.; Roy, A.G. A comparative study of the turbulent flow field with and without a pebble cluster in a gravel bed river. Water Resources Res. 2007. 43(5). [CrossRef]
  54. Afzalimehr, H.; Riazi, P.; Jahad, M.; Singh, VP. Effect of vegetation patches on flow structures and the estimation of friction factor. ISH J. Hydraul Eng, 2021. 27. p. 390-400. [CrossRef]
Preprints 73356 g001
Figure 1. Experimental Set up. a) The hydraulic flume; b) The gravel pool bed-form; c) The gravel grains; d) The vegetated pool bed-form; e) The artificial grass used in the experiments.
Figure 1. Experimental Set up. a) The hydraulic flume; b) The gravel pool bed-form; c) The gravel grains; d) The vegetated pool bed-form; e) The artificial grass used in the experiments.
Preprints 73356 g001
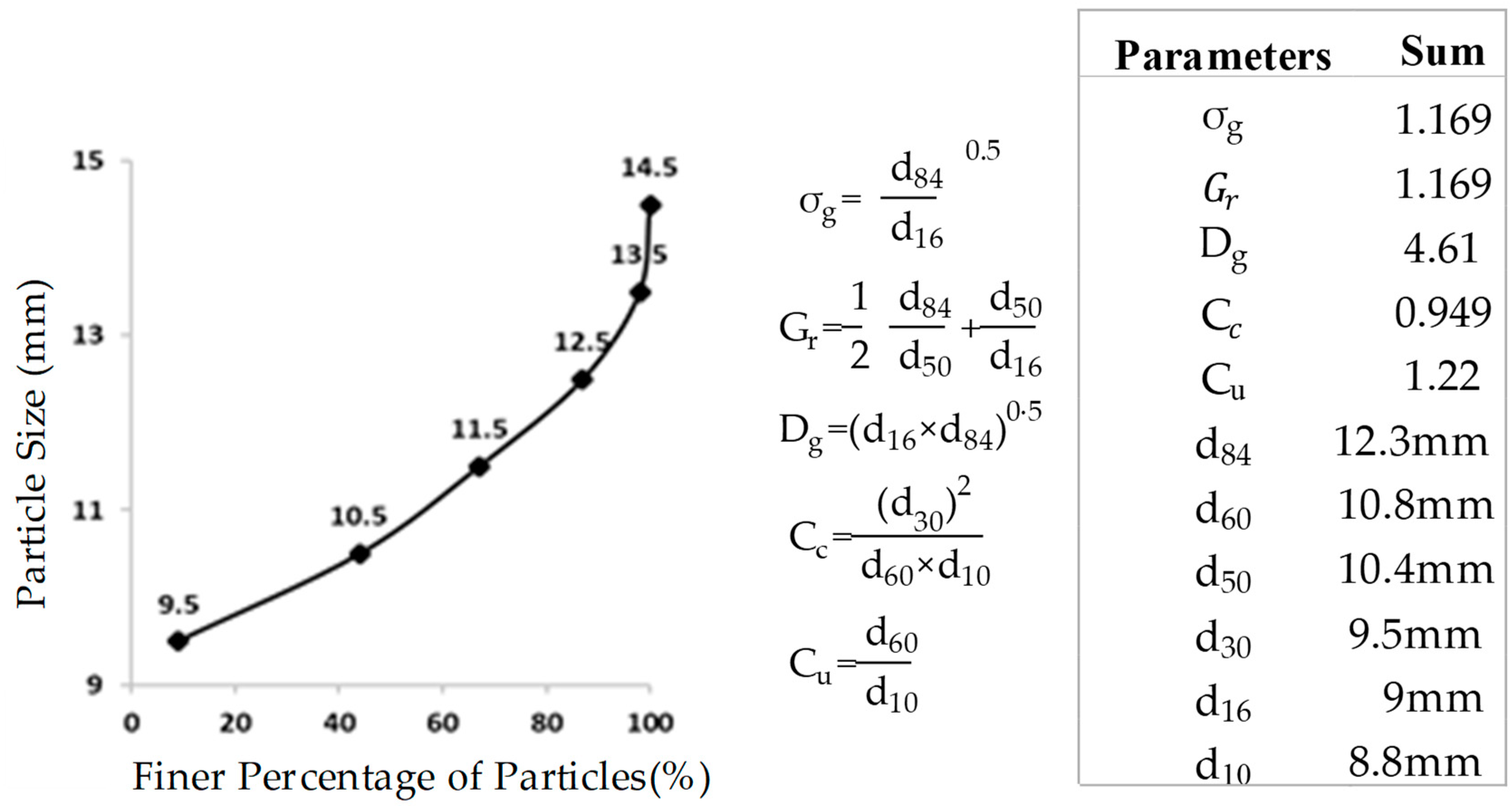
Preprints 73356 g002
Figure 2. The grain size distribution curve and sediment characteristics.
Figure 2. The grain size distribution curve and sediment characteristics.
Preprints 73356 g002
Preprints 73356 g003
Figure 3. Distributions of stream-wise velocity profiles.
Figure 3. Distributions of stream-wise velocity profiles.
Preprints 73356 g003
Preprints 73356 g004
Figure 4. Span-wise and vertical velocity profiles.
Figure 4. Span-wise and vertical velocity profiles.
Preprints 73356 g004
Preprints 73356 g005
Figure 5. Dimensional Reynolds Normal Stress.
Figure 5. Dimensional Reynolds Normal Stress.
Preprints 73356 g005
Preprints 73356 g006
Figure 6. Dimensional Reynolds normal stress in three directions (CDF represents the decelerating flow along the entrance slope, Middle represents the mid-section of the pool, CAF represents accelerating flow along the exit slope).
Figure 6. Dimensional Reynolds normal stress in three directions (CDF represents the decelerating flow along the entrance slope, Middle represents the mid-section of the pool, CAF represents accelerating flow along the exit slope).
Preprints 73356 g006
Preprints 73356 g007
Figure 7. Reynolds Shear Stress distribution profiles in the presence of vegetation.
Figure 7. Reynolds Shear Stress distribution profiles in the presence of vegetation.
Preprints 73356 g007
Preprints 73356 g008
Figure 8. Reynolds Shear Stress distribution profiles at three points of the pools.
Figure 8. Reynolds Shear Stress distribution profiles at three points of the pools.
Preprints 73356 g008
Preprints 73356 g009
Figure 9. Reynolds Shear Stress contour distributions: a. Run 1; b. Run 3; c. Run 2; d. Run 4.
Figure 9. Reynolds Shear Stress contour distributions: a. Run 1; b. Run 3; c. Run 2; d. Run 4.
Preprints 73356 g009
Preprints 73356 g010
Figure 10. Turbulence Kinetic Energy.
Figure 10. Turbulence Kinetic Energy.
Preprints 73356 g010
Preprints 73356 g011
Figure 11. Stream-wise velocity profiles (Run 7).
Figure 11. Stream-wise velocity profiles (Run 7).
Preprints 73356 g011
Preprints 73356 g012
Figure 12. Turbulence intensities for the case of pool setup-1.
Figure 12. Turbulence intensities for the case of pool setup-1.
Preprints 73356 g012
Preprints 73356 g013
Figure 13. Skewness coefficients. (CDF represents the decelerating flow along the entrance slope, Middle represents the mid-section of the pool, CAF represents accelerating flow along the exit slope).
Figure 13. Skewness coefficients. (CDF represents the decelerating flow along the entrance slope, Middle represents the mid-section of the pool, CAF represents accelerating flow along the exit slope).
Preprints 73356 g013
Preprints 73356 g014
Figure 14. Bursting process.
Figure 14. Bursting process.
Preprints 73356 g014
Preprints 73356 g015
Figure 15. Spectral analysis.
Figure 15. Spectral analysis.
Preprints 73356 g015
Table 1. Experimental Conditions.
Table 1. Experimental Conditions.
Pool setup Runs. Entrance
Slope		 Exit
Slope		 H ( c m ) Pool-Bed
Material		 U(m/s) Q
( lit / s ) 		F r R e 10 4 w/h
Setup 1 Run 1 5° 5° 20 Gravel Bed 0.125 10.5± 0.1 0.09 2.5 2
Run 2 5° 5° 20 Gravel Bed 0.5 40.5± 0.1 0.13 10 2
Run 3 5° 5° 20 Vegetated Canopy 0.125 10.5± 0.1 0.09 2.5 2
Run 4 5° 5° 20 Vegetated Canopy 0.5 40.5± 0.1 0.13 10 2
Setup 2 Run 5 10° 10° 20 Gravel Bed 0.125 10.5± 0.1 0.09 2.5 2
Run 6 10° 10° 20 Vegetated Canopy 0.125 10.5± 0.1 0.09 2.5 2
Run 7 10° 10° 15 Vegetated Canopy 0.125 10.5± 0.1 0.09 2.5 2.67
Run 8 10° 10° 20 Vegetated Canopy 0.125 10.5± 0.1 0.09 2.5 2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated