Prerpints.org logo
Preprint
Article

Effective Quantization Evaluation Method of Functional Movement Screening with Improved Gaussian Mixture Model

Altmetrics

Downloads

109

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 May 2023

Posted:

12 May 2023

You are already at the latest version

Alerts
Abstract
Background: Functional Movement Screening (FMS) allows for rapid assessment of an individual’s physical activity level and timely detection of sports injury risk. However, traditional functional movement screening often requires on-site assessment by experts, which is time-consuming and prone to subjective bias. Therefore, the study of automated functional movement screening has become increasingly important. Methods: In this study, we propose an automated assessment method for FMS based on the improved Gaussian Mixture Model (GMM). First, the oversampling of minority samples is conducted, the movement features are manually extracted from the FMS dataset collected with two Azure Kinect depth sensors, then we train the Gaussian mixture model with different scores (1 point, 2 points, 3 points) of feature data separately, finally, we conducted FMS assessment by the Maximum Likelihood estimation. Results: The improved GMM has a higher scoring accuracy (Improved GMM:0.8) compared to other models (Traditional GMM=0.38, Adaboost.M1=0.7, Naïve-Bayes=0.75), and the scoring results of improved GMM have a high level of agreement with the expert scoring (kappa=0.67). Conclusions: The results show that the proposed method based on the improved Gaussian mixture model can effectively perform the FMS assessment task and it is potentially feasible to use depth cameras for FMS assessment.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Functional imbalances of the body can easily lead to sports injuries in individuals during exercise. It not only negatively affects an individual’s physical and mental health, but may also lead to decreased athletic performance, which in turn may also negatively affect their lives and even lead to fear of exercise. Therefore, it is important to improve the functional movement. Functional Movement Screening (FMS) is a screening instrument used to assess an individual’s exercise capacity and potential risk of sports injury. It has been widely used in the fields of sports training and rehabilitation. For example, Sajjad et al. used FMS to assess sports performance and musculoskeletal pain in college students [1]; Li et al. used FMS assessment to reduce knee injuries in table tennis players [2]. On-site evaluation is the most common method in FMS. The expert observes each subject’s movement. However, on-site evaluation is time-consuming and labor intensive, the subjectivity of expert affects the accuracy of the results.
Researchers have experimented with other functional movement data collection methods to address these issues. Shuai et al. used seven 9-axis Inertial Measurement Units (IMU) method to collect joint angle information of functional movements [3]; Vakanski et al. used the Vicon motion capture system to collect joint angle and joint position information of functional movements [4]; Wang et al. collect video data of FMS assessment movements by using two 2D cameras with different viewpoints [5]. Although these devices have high-precision motion capture capabilities and enable fast and accurate assessments by analyzing large amounts of motion data, traditional motion capture systems such as IMU, Vicon and OptiTrack require invasive operations such as tagging or wearing sensors on the subject [6,7,8], which is not only tedious but may also interfere with the subject’s movements. At the same time, the high price of these devices limits their popularity and diffusion in fields such as sports medicine and rehabilitation therapy [9]. As the field of movement quality assessment continues to evolve, some methods of data acquisition using depth cameras are beginning to emerge. Cuellar et al. used the Kinect V1 depth camera to collect 3D skeletal data for standing shoulder abduction, leg lift and arm raise [10]. Capecci et al. used the Kinect V2 depth camera to capture 3D skeletal data and video of healthy subjects and patients with motor disabilities performing squats, arm extensions, and trunk rotations [11]. Depth cameras are able to measure the depth information (RGB-D) of each pixel and use depth information to generate 3D scene models compared with conventional 2D cameras. This makes depth cameras more precise in distance measurement and spatial analysis, therefore it is more suitable for fields such as human activity recognition and movement quality assessment. In addition, Depth cameras are also affordable and have the advantages of being non-invasive, portable, and low-cost [12].
In recent years, with continuing progress and development of artificial intelligence, some automated FMS measurement methods have emerged. Andreas et al. proposed a CNN-LSTM model to achieve the classification of functional movements [13]. Duan et al. used a CNN model to classify the electromyographic (EMG) signals of functional movements, in which the classification accuracy of squat, stride, and straight lunge squat was 91 % , 89 % , and 90 % , respectively [14]. The deep learning algorithms can automatically extract a set of movement features, which can improve the accuracy of activity recognition. However, it requires a large amount of training data, which is time-consuming, and the network structure of deep learning models are more complex and less interpretable. Meanwhile, better results have been achieved in the field of movement quality assessment by training multiple weak classifiers to form a strong classifier in machine learning methods. The automated FMS assessment method based on Adaboost.M1 classifier proposed by Wu et al [15]. FMS assessment can be achieved by training weak classifiers and combine them into a strong classifier. Bochniewicz et al. used a random forest model to assess the arm movements of stroke patients by randomly selecting samples to form multiple classifiers [16]. The classification labels were then predicted by a voting method using a minority-majority approach. This method requires a smaller amount of data and is based on the interpretability of a machine learning method with manually extracted features.
In summary, we proposed an automated FMS assessment method based on an improved Gaussian mixture model in this study. First, we performed feature extraction on the FMS dataset collected with two Azure Kinect depth sensors, then the features with different scores (1 point, 2 points, 3 points) are trained separately in a Gaussian mixture model. Finally, FMS assessment can be achieved by performing maximum likelihood estimation. The results show that the improved Gaussian mixture model has better performance compared to the traditional Gaussian mixture model. It provides fast and objective evaluation with real-time feedback. In addition, we further explore the application of datasets acquired using depth cameras in the field of FMS and validate the feasibility of FMS assessment based on depth cameras.

2. Materials and Methods

2.1. Manual Features in FMS Assessment

Manual feature extraction is a common approach in machine learning-based movement quality assessment, it transforms raw data into a set of representative features for machine learning algorithms. Manual feature extraction usually requires the knowledge and experience of domain experts to select features relevant to the target task, converted into numerical or discrete variables for training and classification of machine learning algorithms. Manual feature extraction has many advantages. First, because the human-selected features are highly interpretable, they can provide meaningful references for subsequent data analysis. Second, manual feature extraction is controllable and can be adjusted according to actual requirements, thus improving movement classification accuracy and generalization ability [17].
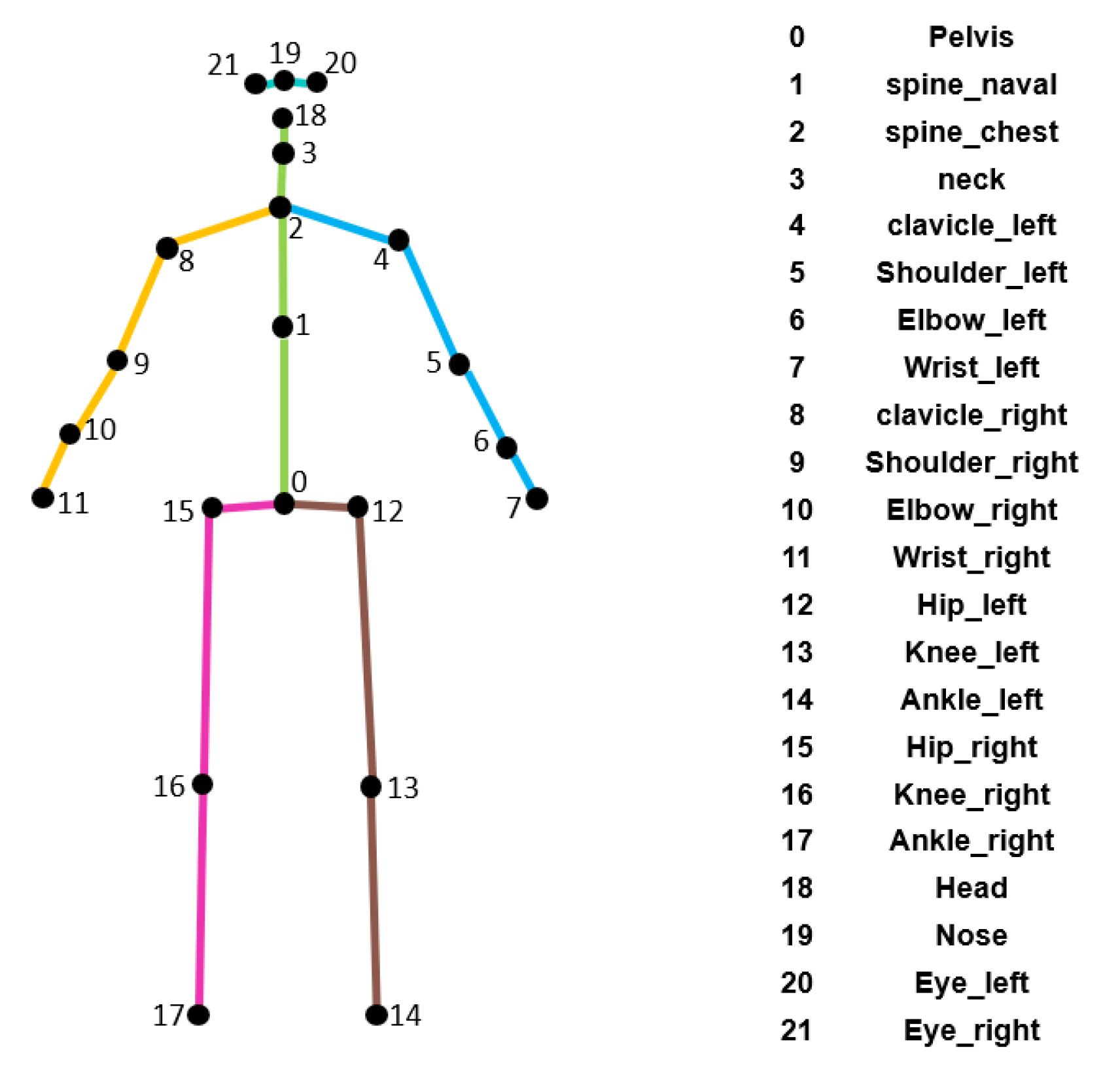
We drew on the functional movement screening methods of Gray Cook, Lee Burton, and the scoring criteria of our experts to manually extract a set of informative and easily interpretable features in this study [18,19,20]. These features contain the key motion characteristics of each FMS, including joint angles and joint spacing, which are critical to the development of effective machine learning-based FMS assessment models. The skeleton joint points are shown in Figure 1. We describe in detail the calculation method of the automatic evaluation metrics for each movement in this section.
In conclusion, manual feature extraction plays a key role of bridging the gap between domain-specific knowledge and deep learning-based automatic feature extraction, which can significantly improve the performance and robustness of machine learning-based FMS assessment.

2.1.1. Deep squat

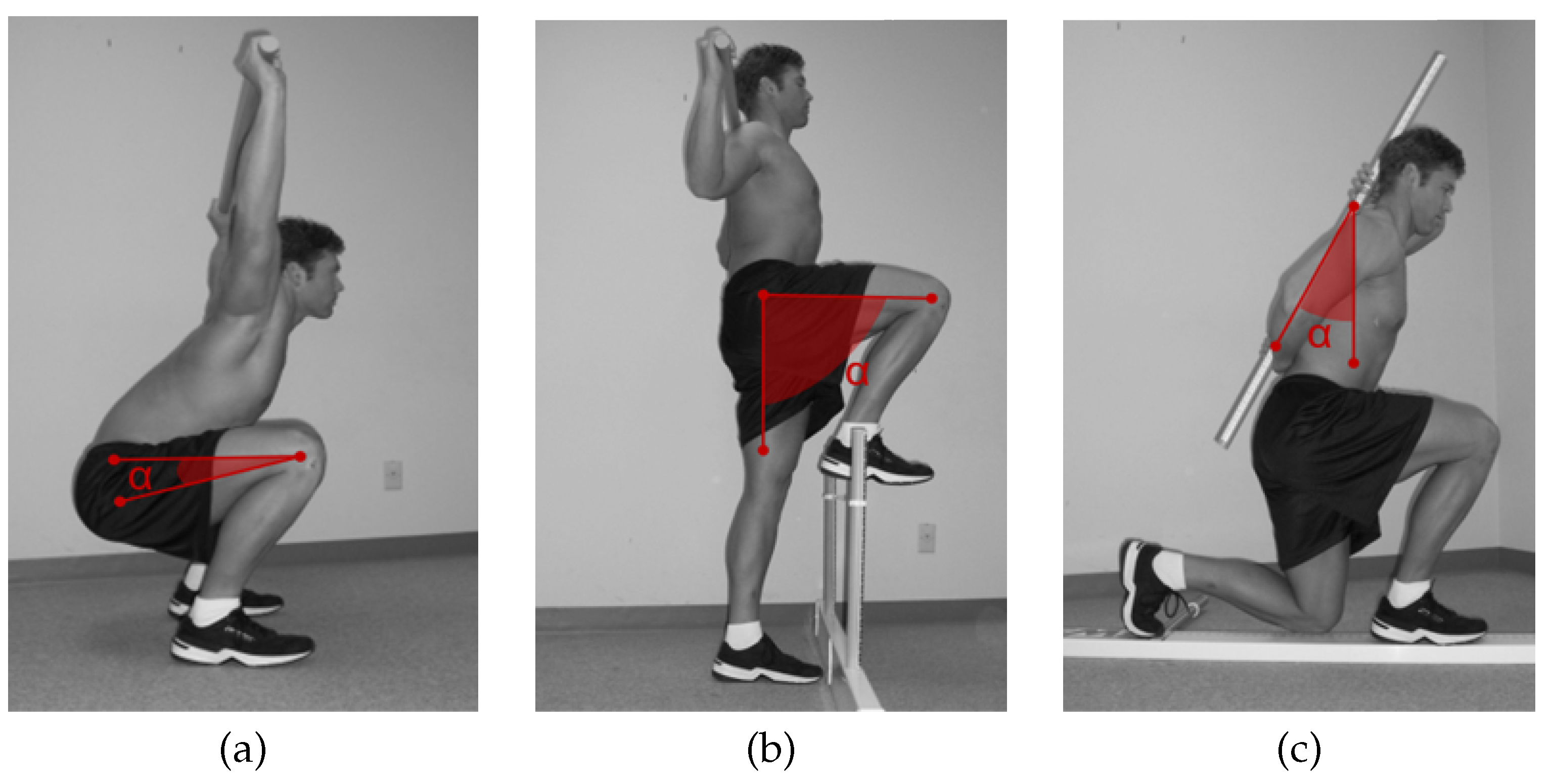
The angle between the thigh and the horizontal plane is defined as the angle between the vector along the left thigh hip joint point to the knee joint point and the horizontal plane during movement.The thigh angle is calculated as the angle between a vector connecting the left thigh hip joint and knee joint and a horizontal vector. K ( X k , Y k , Z k ) and H ( X h , Y h , Z h ) represent the 3D coordinates of the knee joint and hip joint. α is shown in Figure 2a.
K H → = X k − X h , Y k − Y h , Z k − Z h
The thigh angle is given by
α = arccos K H → · h → | K H → | | h → |
where K H → is the left thigh vector (joint 12, joint 13) and h → = ( 1 , 0 , 0 ) is the horizontal vector.

2.1.2. Hurdle step

The raised leg angle is calculated as the angle between a vector connecting the raised leg hip joint and knee joint and a normal vector. H ( X h , Y h , Z h ) and A ( X a , Y a , Z a ) represent the 3D coordinates of the hip joint and ankle joint. α is shown in Figure 2b.
H A → = X a − X h , Y a − Y h , Z a − Z h
The raised leg angle is given by
α = arccos H A → · V → | H A → | | V → |
where H A → is the raised leg vector (joint 12, joint 14) and V → = ( 0 , 1 , 0 ) is the vertical vector.

2.1.3. In-line lunge

The trunk angle is calculated as the angle between a vector connecting the spine chest joint and pelvis joint and a normal vector. S ( X s , Y s , Z s ) and P ( X p , Y p , Z p ) represent the 3D coordinates of the spine chest joint and pelvis joint. α is shown in Figure 2c.
S P → = X p − X s , Y p − Y s , Z p − Z s
The trunk angle is given by
α = arccos S P → · V → | S P → | | V → |
where S P → is the trunk vector (joint 2, joint 0) and V → = ( 0 , 1 , 0 ) is the vertical vector.

2.1.4. Shoulder mobility

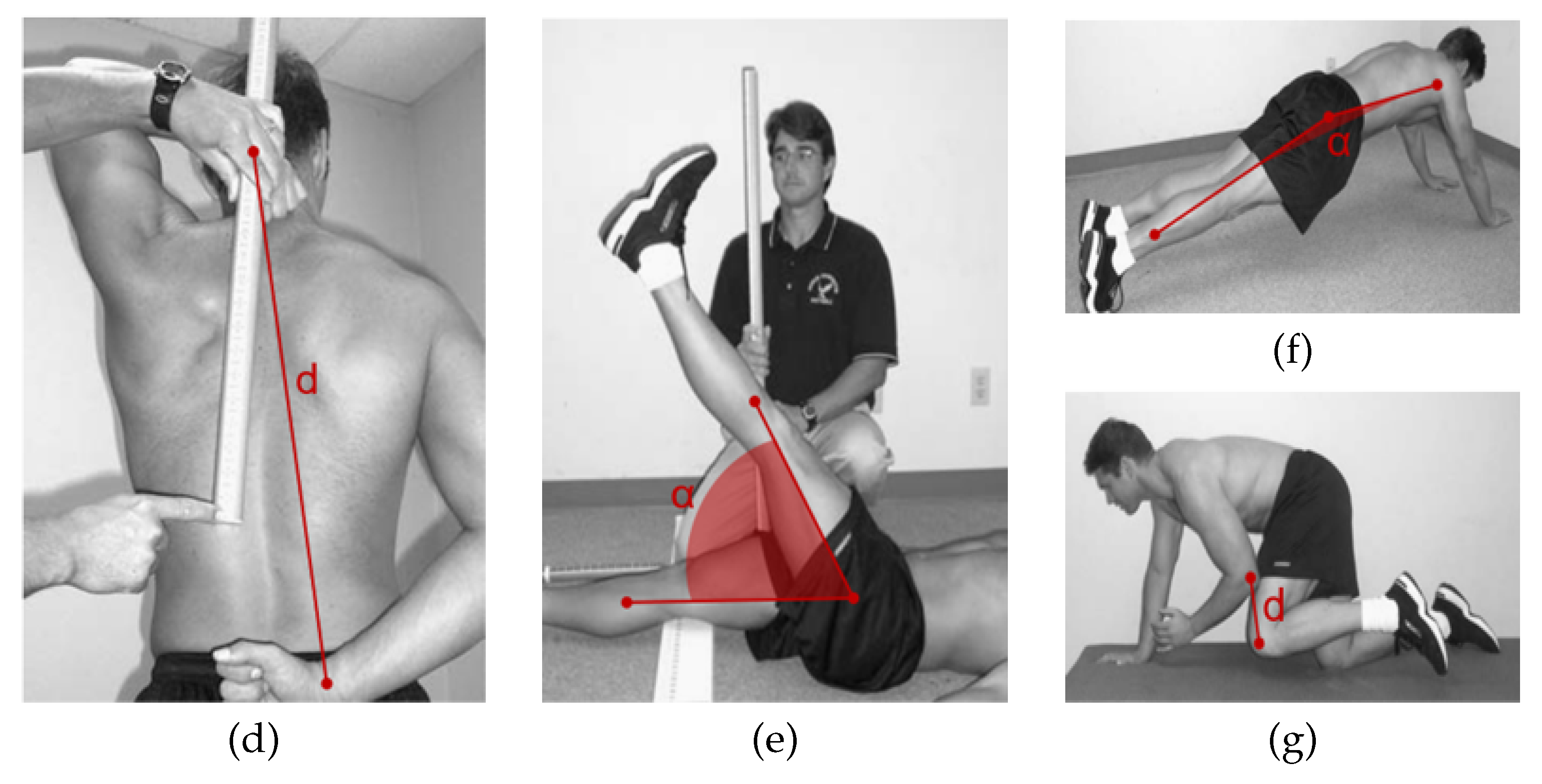
The wrist distance is the minimum distance between the left wrist joint and the right wrist joint. W l X l , Y l , Z l and W r X r , X r , X r represent the 3D coordinates of the left wrist joint and the right wrist joint. d is shown in Figure 2d. The wrist distance is given by
d = X r − X l 2 + Y r − Y l 2 + Z r − Z l 2

2.1.5. Active straight raise

The raised leg angle is calculated as the angle between a vector connecting the hip joint and ankle joint and a horizontal vector. H ( X h , Y h , Z h ) and A ( X a , Y a , Z a ) represent the 3D coordinates of the hip joint and ankle joint. α is shown in Figure 2e.The raised leg angle is given by
α = arccos H A → · h → | H A → | | h → |

2.1.6. Trunk stability

The angle between trunk and thigh is calculated as the angle between a vector connecting the spine chest joint and pelvis joint and a vector connecting the hip joint and ankle joint. α is shown in Figure 2f. The angle between trunk and thigh is given by
α = arccos P S → · H A → | P S → | | H A → |

2.1.7. Rotary stability

The distance between the elbow joint and the ipsilateral or contralateral knee joint is the distance between the moving elbow joint and the moving knee joint.
E l X e l , Y e l , Z e l , K l X k l , Y k l , Z k l and K r X k r , Y k r , Z k r represent the 3D coordinates of the left elbow joint, left knee joint and right knee joint. d is shown in Figure 2g. The distance between the elbow joint and the ipsilateral knee joint is given by
d = X k l X k r − X e l 2 + Y k l Y k r − Y e l 2 + Z k l Z k r − Z e l 2

2.2. Improved Gaussian Mixture Model

The Gaussian mixture model(GMM) is composed of k sub-Gaussian distribution models, which are the hidden variables of the mixture model, and the probability density function of the Gaussian mixture model is formed by linear summation of these Gaussian distributions [21,22]. A model is chosen randomly among the k Gaussian models according to the probability. The probability distribution of the Gaussian mixture model can be described as follows:
p ( x ) = ∑ K = 1 K φ i N x ∣ μ i , σ i
where φ i is the coefficient ( φ i ⩾ 0 , ∑ K = 1 K φ i = 1 ) . N ( x ∣ μ i ) is the probability density function of the Gaussian distribution, and the associated parameters indicate that there are k Gaussian models, each with 3 parameters, namely the mean μ i , the variance σ i , and the generation probability φ i . The sample data is generated by its Gaussian probability density function N ( x ∣ μ i ) after model selection.
N x ∣ μ i , σ i = 1 σ i 2 π exp − x − μ i 2 2 σ i 2
The maximum likelihood function method is used to train the Gaussian mixture model. The likelihood function can be expressed as follows:
L = ∏ i = 1 L p x i ∣ φ
where L is the number of samples in the dataset, x is the data object ( i = 1 , 2 , 3 ⋯ N ) and p(x) denotes the probability of data sample generation in the Gaussian mixture model. The mixed model with maximum likelihood is calculated as follows:
log L = ∑ i = 1 N P x i ∣ φ = ∑ i = 1 N log ∑ k = 1 K α i N x ∣ φ i
The Gaussian mixture model can not acquire the derivative, the EM algorithm is used to solve the best parameters of the model according to the maximized likelihood function in the training phase of the GMM model, the mixture probability φ k , the mean μ k and the covariance σ i , until the convergence of the model.
However, the use of a single GMM as a classifier in movement quality assessment has certain drawbacks. First, it may oversimplify the complexity of motion data and affect the model performance [23,24]. Second, the sensitivity to noisy data and statistics outliers is a weak feature of a single Gaussian mixture model, which reduces the model accuracy [25]. Meanwhile, promising results have been achieved in the movement quality assessment by combining weak classifiers into a strong classifier in the machine learning methods. Several studies have confirmed the validity of this method. For example, Wu proposed an automated FMS assessment method based on Adaboost.M1 classifier, which trains different weak classifiers for the FMS dataset collected by IMU, and then combines these weak classifiers to form a powerful classifier for FMS [15]. In addition, Bochniewicz evaluated the arm movements of stroke patients using a random forest model with randomly selected samples to form multiple classifiers, and then used a minority-majority approach to predict the classification labels through a voting method [16]. Therefore, we proposed an automated FMS assessment method based on the idea of combining three Gaussian mixture models into a strong classifier in this study.
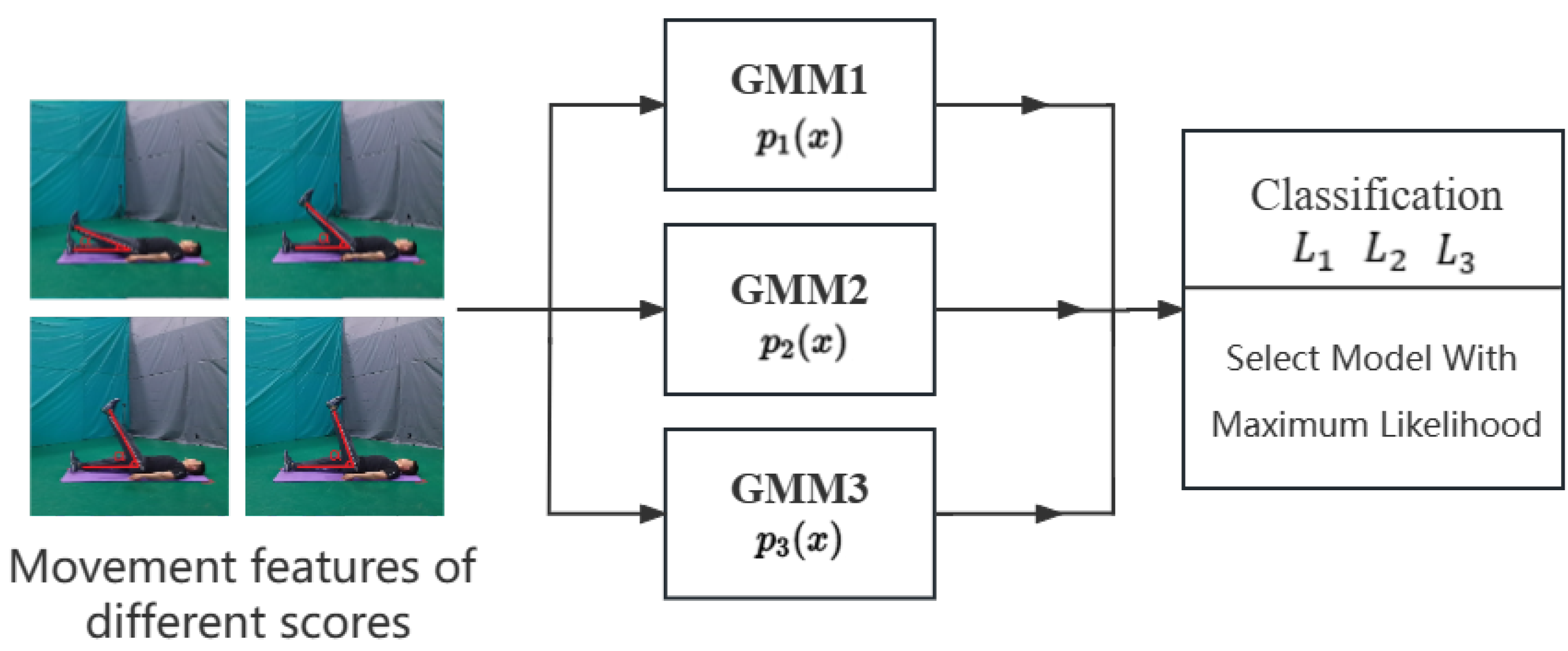
As shown in Figure 2, Firstly, a Gaussian mixture model is trained separately for the movement features with different scores to obtain the Gaussian mixture model probability distributions of 1point, 2 points, and 3 points ( p 1 ( x ) , p 2 ( x ) , p 3 ( x ) ) . Next, the feature data with unknown scores are modeled using each of the 3 Gaussian mixture models, and finally maximum likelihood estimation is performed to obtain the evaluation results. We evaluated the performance of the new classifier by comparing it with three basic classifiers, including the traditional Gaussian mixture model [26], Naïve Bayes [27] and Adaboost.M1 classifier [15].

2.3. Statistical Analysis

In this experiment, we contrasted three traditional machine learning methods (GMM, Naïve-Bayes, Adaboost.M1) to evaluate the scoring ability of the improved GMM. Due to the analysis of experimental results, we used scoring accuracy, confusion matrix and Kappa statistic to evaluate the performance of our proposed models. For the task of FMS movement assessment, scoring accuracy can visually reflect the scoring performance of each model. The confusion matrix can show the difference between the predicted results and the expert scores, the diagonal element values of the matrix represent the consistency between the prediction results and the actual measurements, and the non-diagonal element values of the matrix denote wrong predictions. The kappa coefficient is used to assess the degree of agreement between the model scoring results and the expert scoring results [28].
k = P o − P e 1 − P e
where P o is defined as the sum of the number of samples correctly in each category divided by the total number of samples, which is the overall classification accuracy. We assume the number of correctly samples in each category a 1 , a 2 ⋯ , a m , and the number of predicted samples in each category a 1 , a 2 ⋯ , a m . The total number of samples is n, P e is obtained by dividing the sum of the "product of the actual value and predicted value" for all categories by the square of the total number of samples.
P e = a 1 × b 1 + a 2 × b 2 + ⋯ + a m × b m n × n
The value of kappa usually lies between 0 and 1. Typically, kappa values of 0.0–0.2 are considered a slight agreement, 0.2–0.4 a fair agreement, 0.4–0.6 a moderate agreement, 0.6–0.8 a substantial agreement, and > 0.8 an almost perfect agreement.
For the evaluation of the performance on different movements, we also use the F1-Measure to evaluate the performance of the model, we adopt the micro-averaged F1(miF1), macro-averaged F1(maF1) and weighted-F1 simultaneously.

3. Results and Discussion

We conduct an experimental study using a dataset acquired by a depth camera to validate the effectiveness of the proposed improved Gaussian mixture model. First, the used dataset is introduced. Then, we contrast three classifiers to evaluate the performance of the improved Gaussian mixture model. (Traditional Gaussian mixture model, Naïve-Bayes and Adaboost.M1). Finally, we analyze the effect of skeleton data and feature data on FMS assessment respectively.

3.1. Dataset

This study used the FMS dataset proposed by Xing et al [29]. This dataset is collected from 2 Azure Kinect depth cameras and covered 45 subjects between the ages of 18 and 59 years. The dataset consists of functional movement data which is divided into left and right side movements, including deep squat, hurdle step, in-line lunge, shoulder mobility, active straight raise, trunk stability push-up and rotary stability. In order to improve the accuracy and stability of the data, the researcher used two depth cameras with different viewpoints to collect the movement data of the subjects. The dataset contains both skeletal data and image information.
The Azure Kinect depth sensor has better quality and accuracy of data compared to depth cameras, such as Kinect V1, Kinect V2, and Real Sense, thus it offers the possibility of machine learning and other methods for tasks such as human motion recognition and movement assessment [31,32,33,34,35]. In addition, the dataset not only provides strong support for the functional movement assessment and rehabilitation training, but also provides technical support and data sources for the research and applications in the fields of intelligent fitness and virtual reality.
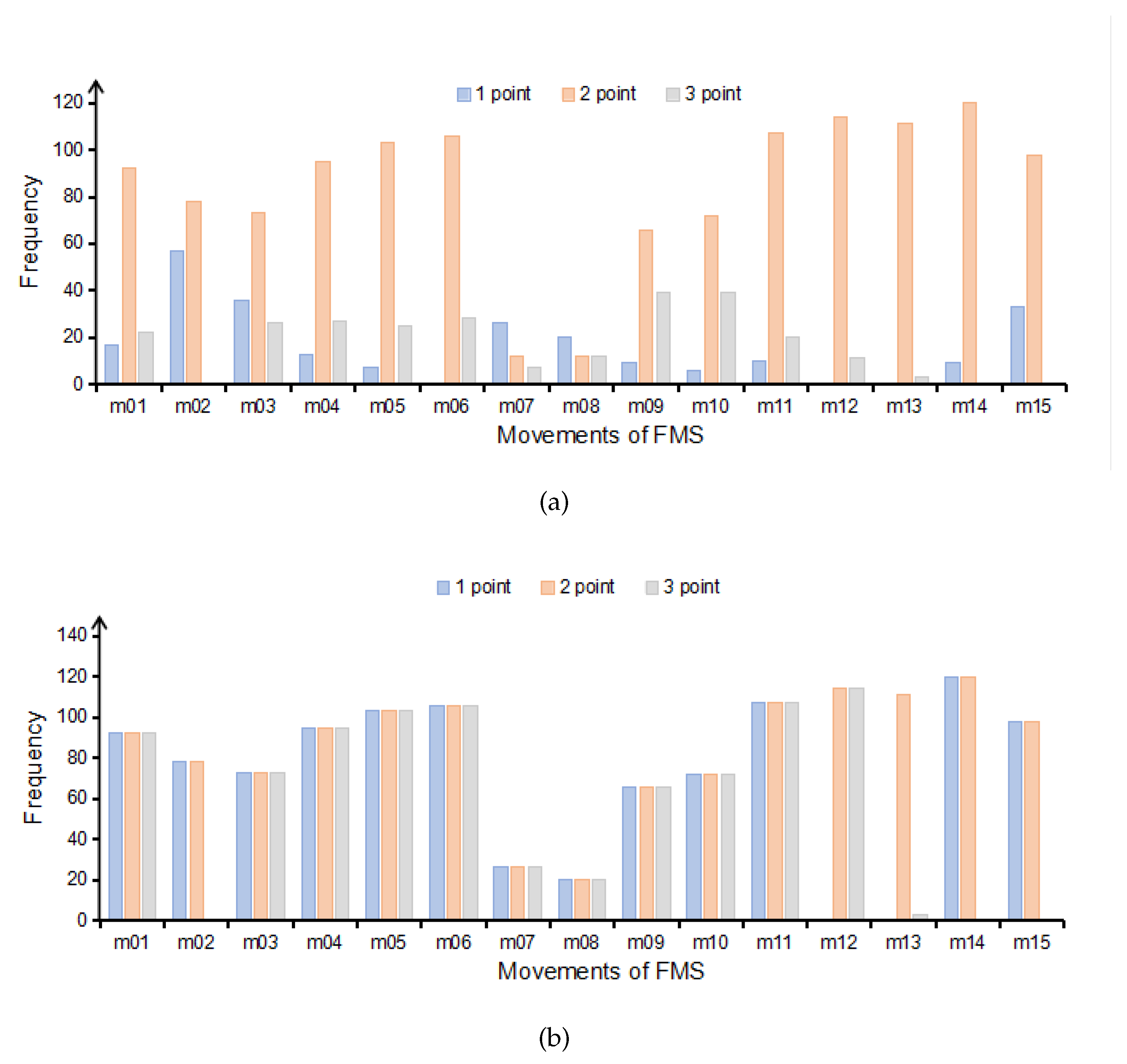
The 3D skeleton data acquired by the frontal depth camera are used in this experiment. The score distribution of each movement is shown in Figure 11a.
As shown in Figure 4a, for example, the number of 2 score is much larger than the number of 1 and 3 scores in m11, due to the uneven distribution of FMS scores, which may decrease the performance of some machine learning models. Although the model has a high overall accuracy rate, 1points and 3points have low accuracy rate. Therefore, in order to avoid this situation, the problem of unequal distribution of each movement in the dataset needs to be addressed. The experiment uses the Borderline SMOTE oversampling algorithm, which is a variant of SMOTE algorithm [35]. The algorithm synthesizes new samples using only the minority boundary samples and considers the category information of the neighbor samples, avoiding the poor classification results caused by the overlapping phenomenon in the traditional SMOTE algorithm. Borderline-SMOTE method divides the minority samples into 3 categories (Safe, Danger and Noise), and oversamples only the minority samples of the Danger category.
After Borderline SMOTE pre-processing, the expert score uniform distribution of FMS movements is also realized, as shown in Figure 4b. However, the distribution of m13 is still uneven. In order to avoid impacts on the experimental results, m13 is not tested in the subsequent experiments. The movements in the dataset are divided into the left side and the right side except for m01, m02 and m11, both sides have the same movement type and movement repetitions. In order to facilitate the targeted analysis and processing of the movement data, we only analyze the movements of the left side of the body. In summary, the movements used for this experiment include m01, m03, m05, m07, m09, m11, m12, m14.

3.2. Evaluation of the Performance on Different Methods

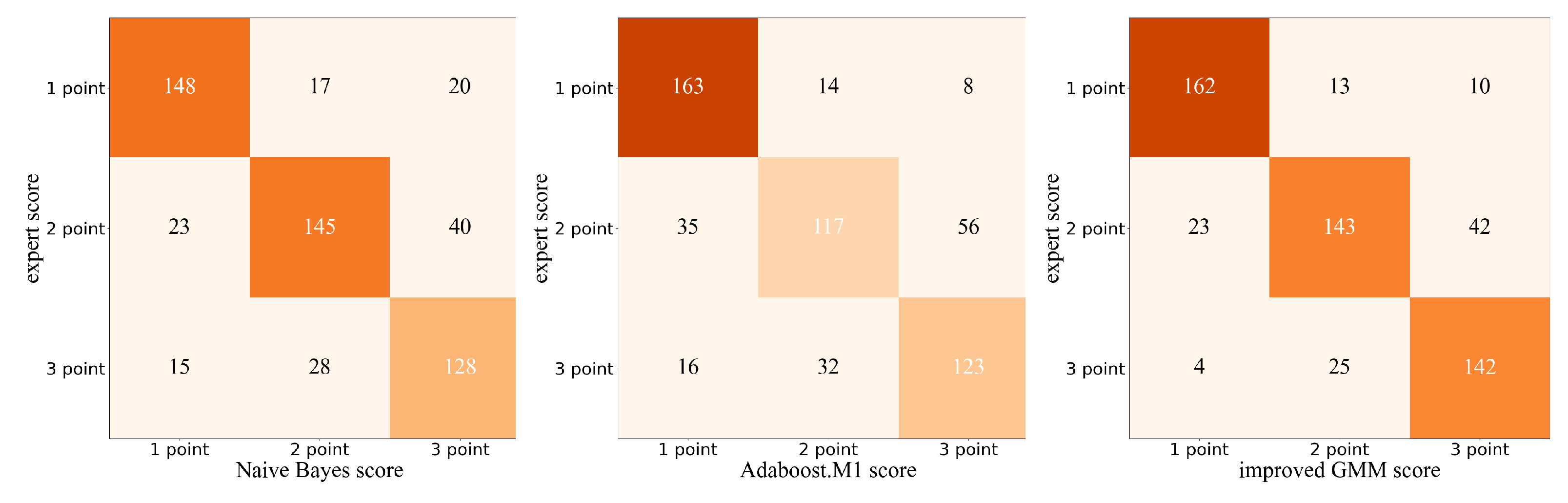
The machine learning model can predict each test action as a score of 1-3. To analyze more detailed results about the scoring performance of the improved GMM, we further visualize the confusion matrix based on the expert scoring and the automatic scoring. Figure 5 shows the confusion matrix obtained by the Naïve Bayes-based method, Adaboost.M1-based method and improved GMM-based method. In this study, we consider expert scoring as the gold standard, and we combined the scoring results for each test action. From Figure 12, we can observe that the misclassified samples are prone to be predicted as a score close to its true score, 1-point samples are more likely to be wrongly predicted as 2 points than 3 points, and 3 points samples are more likely to be wrongly predicted as 2 points than 1 point, among these, the most errors occur when 2 points samples are predicted as 3 points samples.
Table 1 shows the scoring of the Naive-Bayes, Adaboost.M1, improved Gaussian mixture model (GMM) and traditional GMM. The accuracy of improved GMM is higher than Naïve-Bayes, Adaboost.M1 and traditional GMM, and the improved GMM has the highest agreement. In general, the FMS assessment based on the improved GMM model outperformed Naïve Bayes and Adaboost.M1. The results indicate that the improved GMM yields considerable improvement over the traditiona GMM.

3.3. Evaluation of the Performance on Different movements

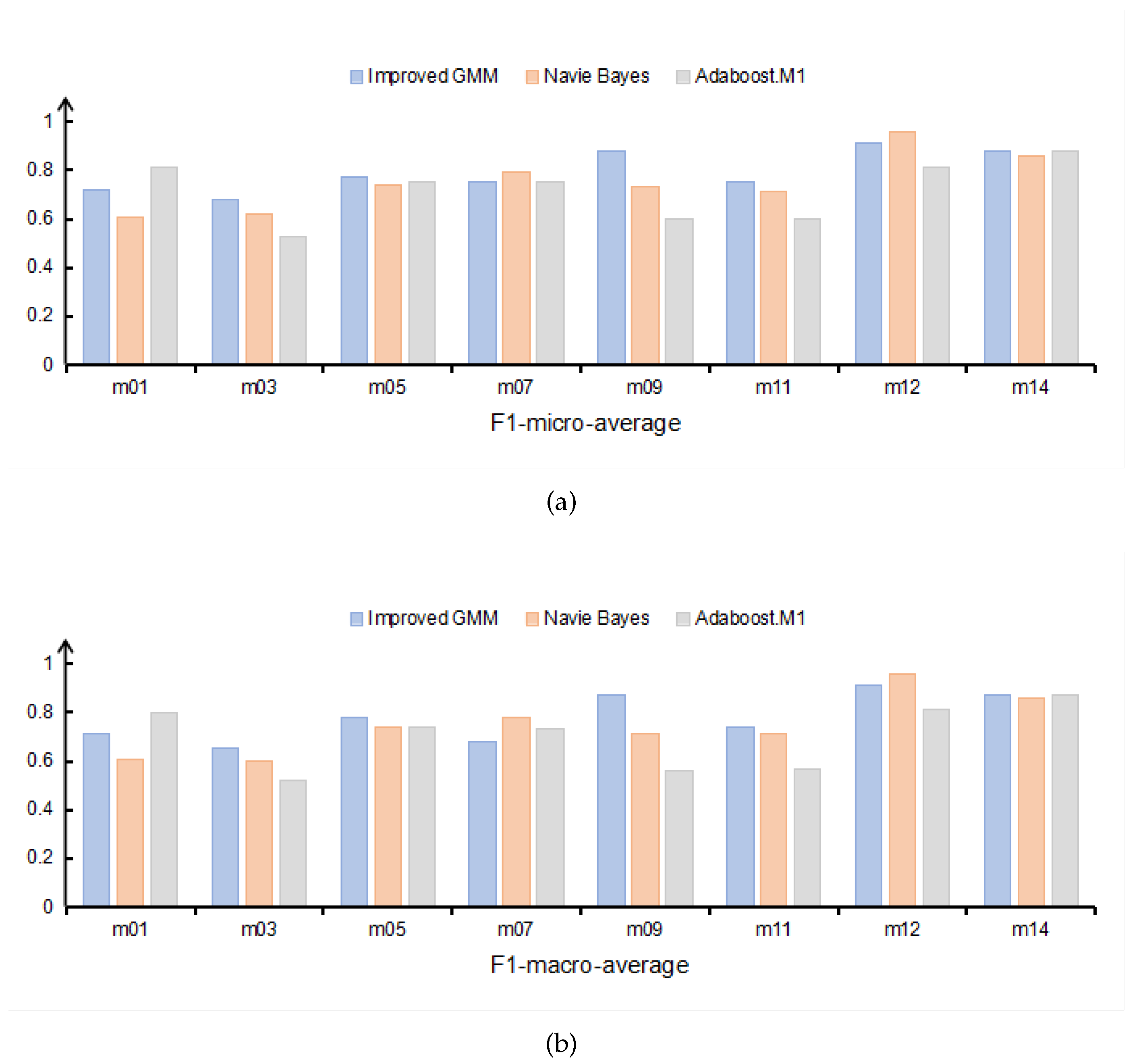
We further investigate the model performance for each FMS test individually, Figure 6a,b show the F1-micro-average and F1-macro-average for FMS movements on different methods. For all three models, we find that improved GMM-based model has better overall performance compared to Naïve Bayes-based model and Adaboost.M1-based model. Specifically, improved GMM-based model is performing better than other methods in the four movements (m03, m05, m09, m11), the performance of three methods is essentially the same in the two movements (m07, m14).

3.4. Comparison of Accuracy before and after Data Balancing

We also compare FMS performance using the original unbalanced feature data (Figure 4a) and balanced feature data after the oversampling pre-processing (Figure 4b) in this research. As shown in Table 2, the average accuracy of balanced distribution of feature data is 0.8, while the average accuracy of unbalanced distribution of feature data is only 0.62, which indicates that the balanced features perform better in the FMS assessment. The scoring accuracy of the balanced movement features is greatly improved compared with unbalanced movement features. The imbalance will cause the performance of the classifier to be biased towards the majority samples due to the unbalanced sample size. Using sampling processing can improve the balance of the training data by increasing the number of samples, thus effectively avoiding this bias. The balanced features after oversampling pre-processing not only reflect the FMS movement quality more comprehensively, but also the accuracy of the classifier is significantly improved.

3.5. Comparison of Performance between Features and Skeleton Data

In the present study, we compare the performance of the manual feature extraction method and the skeleton data-based method in FMS assessment. As shown in Table 3, the manual feature extraction method has better performance in FMS assessment. Compared with the skeleton data-based method, the manual feature extraction method can capture the key features of the FMS movement more accurately, thus assessing the quality of the movement more accurately. The manual feature extraction method circumvents the impact of skeleton data quality differences on action scoring to a certain extent because the skeleton data are screened and cleaned through bespoke processing. In addition, the manual feature extraction method has good interpretability, which helps us better understand the FMS movement quality. Specifically, the manual feature extraction method generally scores each action with higher accuracy than the skeleton data-based method, for example, the scoring accuracy of m09 improved from 0.44 to 0.88. The average accuracy of the manual feature extraction method is 0.8, while the average accuracy of the skeleton data-based method is only 0.63, indicating that the manual feature extraction method has better performance in the FMS assessment.

4. Conclusion

In this study, we propose an automated FMS assessment method based on an improved Gaussian mixture model using the FMS dataset captured by the Azure Kinect depth camera. The experimental results show that our method has a high scoring accuracy in this dataset and a high agreement between the scores and the expert scores compared to the other methods. Thus, the improved Gaussian mixture model-based method can be applied to FMS assessment, while there is some potential for functional movement assessment using depth cameras. This method should be tested on different datasets to improve the performance of machine learning methods and achieve more accurate prediction results in future studies.

References

  1. Mohammadyari, S.; Aslani, M.; Zohrabi, A. J. J. o. m. m. The effect of eight weeks of injury prevention program on performance and musculoskeletal pain in Imam Ali Military University students. Journal of Military Medicine 2022, 23(5), 444–455. [Google Scholar]
  2. Li, X. J. R. B. d. M. d. E. , Application of physical training in injury rehabilitation in table tennis athletes. Journal Abbreviation 2022, 28, 483–485. [Google Scholar]
  3. Shuai, Z.; Dong, A.; Liu, H.; Cui, Y. J. S., Reliability and Validity of an Inertial Measurement System to Quantify Lower Extremity Joint Angle in Functional Movements.Journal Abbreviation, 2022, 22, (3), 863.
  4. Vakanski, A.; Jun, H.-p.; Paul, D.; Baker, R. J. D., A data set of human body movements for physical rehabilitation exercises. Journal Abbreviation, 2018, 3, (1), 2.
  5. Wenbo, W.; Chongwen, W. J. C.; Engineering, E., A skeleton-based method and benchmark for real-time action classification of functional movement screen.Journal of Military Medicine, 2022, 22,102, 108151.
  6. Luinge, H. J.; Veltink, P. H.; Baten, C. T. J. J. o. b., Ambulatory measurement of arm orientation. Journal of Military Medicine,2007, 40, (1), 78-85.
  7. Lepetit, K.; Hansen, C.; Mansour, K. B.; Marin, F. J. C. M. i. B.; Engineering, B., 3D location deduced by inertial measurement units: a challenging problem.Journal of Military Medicine, 2015, 18, (S1), 1984-1985.
  8. Lin, Z.; Zecca, M.; Sessa, S.; Bartolomeo, L.; Ishii, H.; Takanishi, A. In Development of the wireless ultra-miniaturized inertial measurement unit WB-4: Preliminary performance evaluation,2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2011, 6927-6930.
  9. Pfister, A.; West, A. M.; Bronner, S.; Noah, J. A. J. J. o. m. e.; technology, Comparative abilities of Microsoft Kinect and Vicon 3D motion capture for gait analysis. Journal of Military Medicine, 2014, 38, (5), 274-280.
  10. Cuellar, M. P.; Ros, M.; Martin-Bautista, M. J.; Le Borgne, Y.; Bontempi, G. In An approach for the evaluation of human activities in physical therapy scenarios, Mobile Networks and Management: 6th International Conference, MONAMI 2014, Würzburg, Germany, September 22-26, 2014, Revised Selected Papers 6, 2015; Springer: 2015; pp 401-414.
  11. Capecci, M.; Ceravolo, M. G.; Ferracuti, F.; Iarlori, S.; Monteriu, A.; Romeo, L.; Verdini, F. J. I. T. o. N. S.; Engineering, R., The KIMORE dataset: KInematic assessment of MOvement and clinical scores for remote monitoring of physical REhabilitation.Journal of Military Medicine 2019, 27, (7), 1436-1448.
  12. Eichler, N.; Hel-Or, H.; Shmishoni, I.; Itah, D.; Gross, B.; Raz, S. In Non-invasive motion analysis for stroke rehabilitation using off the shelf 3d sensors, 2018 International Joint Conference on Neural Networks (IJCNN), 2018; IEEE: 2018; pp 1-8.
  13. Spilz, A.; Munz, M. J. S., Automatic Assessment of Functional Movement Screening Exercises with Deep Learning Architectures. 2022, 23, (1), 5.
  14. Duan, L. J. R. B. d. M. d. E., Empirical analysis on the reduction of sports injury by functional movement screening method under biological image data. 2021, 27, 400-404.
  15. Wu, W.-L.; Lee, M.-H.; Hsu, H.-T.; Ho, W.-H.; Liang, J.-M. J. A. S., Development of an automatic functional movement screening system with inertial measurement unit sensors. 2020, 11, (1), 96.
  16. Bochniewicz, E. M.; Emmer, G.; McLeod, A.; Barth, J.; Dromerick, A. W.; Lum, P. J. J. o. S.; Diseases, C., Measuring functional arm movement after stroke using a single wrist-worn sensor and machine learning. 2017, 26, (12), 2880-2887.
  17. Nanni, L.; Ghidoni, S.; Brahnam, S. J. P. R. , Handcrafted vs. non-handcrafted features for computer vision classification. 2017, 71, 158–172. [Google Scholar]
  18. Cook, G.; Burton, L.; Kiesel, K.; Rose, G.; Brynt, M. J. C. S. A., CA: On Target Publications, Movement: Functional movement systems: Screening, assessment. 2010, 73-106.
  19. Cook, G.; Burton, L.; Hoogenboom, B. J. N. A. j. o. s. p. t. N., Pre-participation screening: the use of fundamental movements as an assessment of function–part 1. 2006,1, (2), 62.
  20. Cook, G.; Burton, L.; Hoogenboom, B. J. N. A. j. o. s. p. t. N., Pre-participation screening: The use of fundamental movements as an assessment of function–Part 2. 2006,1, (3), 132.
  21. Ververidis, D.; Kotropoulos, C. J. I. t. o. s. p., Gaussian mixture modeling by exploiting the Mahalanobis distance. 2008, 56, (7), 2797-2811.
  22. Reynolds, D. A. J. E. o. b., Gaussian mixture models. 2009, 741, 659-663.
  23. Figueiredo, M. A. T.; Jain, A. K. J. I. T. o. p. a.; intelligence, m., Unsupervised learning of finite mixture models. 2002, 24, (3), 381-396.
  24. Terejanu, G.; Singla, P.; Singh, T.; Scott, P. D. J. J. o. g., control,; dynamics, Uncertainty propagation for nonlinear dynamic systems using Gaussian mixture models. 2008,31, (6), 1623-1633.
  25. Xu, L.; Jordan, M. I. J. N. c., On convergence properties of the EM algorithm for Gaussian mixtures. 1996,8, (1), 129-151.
  26. Williams, C.; Vakanski, A.; Lee, S.; Paul, D. J. M. e.; physics, Assessment of physical rehabilitation movements through dimensionality reduction and statistical modeling. 2019, 74, 13-22.
  27. Putra, D.; Ihsan, M.; Kuraesin, A.; Daengs, G. A.; Iswara, I. In Electromyography (EMG) signal classification for wrist movement using naïve bayes classifier, Journal of Physics: Conference Series, 2019; IOP Publishing: 2019; p 012013.
  28. McHugh, M. L. J. B. m., Interrater reliability: the kappa statistic. 2012, 22, (3), 276-282 .
  29. Xing, Q.-J.; Shen, Y.-Y.; Cao, R.; Zong, S.-X.; Zhao, S.-X.; Shen, Y.-F. J. S. D., Functional movement screen dataset collected with two azure kinect depth sensors. 2022, 9, (1), 104.
  30. Jo, S.; Song, S.; Kim, J.; Song, C. J. S., Agreement between Azure Kinect and Marker-Based Motion Analysis during Functional Movements: A Feasibility Study. 2022, 22, (24), 9819.
  31. Yeung, L.-F.; Yang, Z.; Cheng, K. C.-C.; Du, D.; Tong, R. K.-Y. J. G.; posture, Effects of camera viewing angles on tracking kinematic gait patterns using Azure Kinect, Kinect v2 and Orbbec Astra Pro v2. 2021, 87, 19-26.
  32. Albert, J. A.; Owolabi, V.; Gebel, A.; Brahms, C. M.; Granacher, U.; Arnrich, B. J. S., Evaluation of the pose tracking performance of the azure kinect and kinect v2 for gait analysis in comparison with a gold standard: A pilot study. 2020, 20, (18), 5104.
  33. Özsoy, U.; Yıldırım, Y.; Karaşin, S.; Şekerci, R.; Süzen, L. B. J. J. o. S.; Surgery, E., Reliability and agreement of Azure Kinect and Kinect v2 depth sensors in the shoulder joint range of motion estimation. 2022, 31, (10), 2049-2056.
  34. Tölgyessy, M.; Dekan, M.; Chovanec, Ľ. J. A. S., Skeleton tracking accuracy and precision evaluation of Kinect V1, Kinect V2, and the azure kinect. 2021, 11, (12), 5756.
  35. Han, H.; Wang, W.-Y.; Mao, B.-H. In Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning, Advances in Intelligent Computing: International Conference on Intelligent Computing, ICIC 2005, Hefei, China, August 23-26, 2005, Proceedings, Part I 1, 2005; Springer: 2005; pp 878-887.
Preprints 73414 g001
Figure 1. The skeleton structure used in our methods.
Figure 1. The skeleton structure used in our methods.
Preprints 73414 g001
Preprints 73414 g002aPreprints 73414 g002b
Figure 2. Characteristic indicators of different movements in this study. (A) Deep squat; (B) hurdle step; (C) in-line lunge; (D) shoulder mobility; (E) active straight raise; (F) Trunk stability; (G) Rotary stability.
Figure 2. Characteristic indicators of different movements in this study. (A) Deep squat; (B) hurdle step; (C) in-line lunge; (D) shoulder mobility; (E) active straight raise; (F) Trunk stability; (G) Rotary stability.
Preprints 73414 g002aPreprints 73414 g002b
Preprints 73414 g003
Figure 3. The structure of improved Gaussian mixture model.
Figure 3. The structure of improved Gaussian mixture model.
Preprints 73414 g003
Preprints 73414 g004
Figure 4. (a) Expert score distribution of FMS movements.(b) Expert score distribution of FMS movements based on Borderline-SMOTE.
Figure 4. (a) Expert score distribution of FMS movements.(b) Expert score distribution of FMS movements based on Borderline-SMOTE.
Preprints 73414 g004
Preprints 73414 g005
Figure 5. Confusion matrix for per-level assessment in FMS assessment.
Figure 5. Confusion matrix for per-level assessment in FMS assessment.
Preprints 73414 g005
Preprints 73414 g006
Figure 6. (a) F1-micro-average of FMS movements.(b) F1-macro-average of FMS movements.
Figure 6. (a) F1-micro-average of FMS movements.(b) F1-macro-average of FMS movements.
Preprints 73414 g006
Table 1. Overall comparisons of different methods in FMS assessment.
Table 1. Overall comparisons of different methods in FMS assessment.
Methods Accuracy maF1 weighted-maF1 Kappa Level of Agreement
Naïve Bayes 0.75 0.75 0.71 0.6 Moderate
Adaboost.M1 0.72 0.7 0.71 0.55 Moderate
Traditional GMM 0.38 0.34 0.35 0.1 Poor
Improved GMM 0.8 0.77 0.79 0.67 Good
Table 2. Improved GMM scoring accuracy before and after data balancing.
Table 2. Improved GMM scoring accuracy before and after data balancing.
Feature data before balance Feature data after balance
ID 1 2 3 1 2 3
m01 0.86 0.48 0.25 0.86 0.63 0.71
m03 0.45 0.49 0.57 0.77 0.37 0.88
m05 0 0.67 0.29 0.97 0.69 0.68
m07 1 0 0 0.5 0.56 1
m09 0.8 0.74 0.64 0.95 0.8 0.89
m11 0.67 0.69 0 0.85 0.56 0.84
m12 0.8 0.67 0.88 0.94
m14 0.5 0.83 0.92 0.83
Averge accuracy 0.62 0.8
Table 3. Improved GMM scoring accuracy based on skeleton data.
Table 3. Improved GMM scoring accuracy based on skeleton data.
m01 m03 m05 m07 m09 m11 m12 m14 Average accuracy
0.36 0.39 0.68 0.7 0.44 0.73 0.88 0.86 0.63
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated