Prerpints.org logo
Preprint
Article

Intrinsic Coherence Length Anisotropy in Nickelates, and Some Pnictides and Chalcogenides Superconductors

Altmetrics

Downloads

96

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 May 2023

Posted:

12 May 2023

You are already at the latest version

Alerts
Abstract
Nickelate superconductors, R1-xAxNiO2 (where R is a rare earth metal and A = Sr, Ca), experimentally discovered in 2019 exhibit many unexplained mysteries as the existence of a superconducting state with Tc (up to 18 K) in thin films and its absence in bulk materials. Another unexplained mystery of nickelates is their temperature-dependent upper critical field, Bc2T, which can be nicely fitted to two-dimensional (2D) models; however the deduced film thickness, dsc,GL, exceeds the physical film thickness, dsc, by a manifold. To address the latter, it should be noted that 2D models assume that dsc is less than the in-plane and out-of-plane ground state coherence lengths, dsc<ξab0 and dsc<ξc0, respectively, and, in addition, that the inequality ξc0<ξab0 satisfies. Analysis of the reported experimental Bc2T data showed that at least one of these conditions does not satisfy for R1-xAxNiO2 films. This implies that nickelate films are not 2D superconductors, even despite though that the superconducting state is observed only in thin films. Based on this, here we proposed analytical three dimensional (3D) model for global data fit of in-plane and out-of-plane Bc2T in nickelates. The model is based on a heuristic expression for temperature dependent coherence length anisotropy: γξT=γξ01-1a×TTc, where a>1 is a unitless free-fitting parameter. The proposed expression for γξT, perhaps, has a much broader application because it has been successfully applied to bulk pnictide and chalcogenide superconductors.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

High-temperature superconductivity in Nd1-xSrxNiO2 nickel oxide was experimentally discovered by Li et al [1] in 2019, while the first theoretical report in which the oxidation state of Ni+ was established to be a condition under which nickelates become similar to cuprates (and what was made by Li et al [1]) was published by Anisimov et al [2] in 1999. This experimental discovery initiated further theoretical and experimental studies on R1-xAxNiO2 (where R is rare earth, and A = Sr, Ca) thin films [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50] and bulk [51]. It is widely accepted point of view that the superconducting state in nickelates is exhibited only in thin films [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51], with a thickness of d s c ≲ 15   n m . This is one of the primary mysteries in nickelate superconductors.
Another unexplained mystery of nickelates is the temperature dependence of the upper critical field, B c 2 T . For instance, when this fundamental field is measured for applied field oriented in perpendicular direction to the (00L) planes of the film (which will be designated as B c 2 , p e r p T , herein), the dependence can be nicely fitted to the Ginzburg-Landau (GL) model [23,36]:
B c 2 , p e r p T = ϕ 0 2 π 1 ξ a b 2 T = ϕ 0 2 π 1 − T T c ξ a b 2 0 ,
where ϕ 0 is superconducting flux quantum, and ξ a b 0 is ground state in-plane coherence length. When external field oriented in parallel direction to the (00L) planes of the film (which will be designated as B c 2 , p a r a T ), the dependence reported by many research groups can be nicely fitted to the two-dimensional Ginzburg-Landau (2D-GL) model [36,52,53]:
B c 2 , p a r a T = ϕ 0 2 π 12 d s c , G L 1 ξ a b T = ϕ 0 2 π 12 d s c , G L 1 − T T c ξ a b 0 ,
where d s c , G L is the film thickness associated with the use of Eq. 2 for data fit.
This result should be interpreted as direct evidence of 2D superconductivity in nickelates, supporting the experimental observation that the superconducting state is observed only in thin films of nickelates. However, the deduced film thickness d s c , G L (from the B c 2 , p e r p T and B c 2 , p a r a T data fit to Eqs. 1,2 [23]) by to 2-3 times exceeds the physical film thickness d s c [23]. Here we found that identical problem, i.e. d s c ≇ d s c , G L , does exist for nearly all nickelate films, for which experimental data was reported.
To resolve this issue, here we pointed out that the derivation of Eq. 2 [52] is based on the assumption that physical film thickness d s c is much less than the ground-state coherence length ξ 0 of the superconductor, which means that for anisotropic superconductors:
d s c ≪ ξ a b 0 ,
d s c ≪ ξ c 0 ,
where ξ c 0 is the out-of-plane coherence length. In addition, there is another hidden assumption for the derivation of Eq. 2, which is:
ξ c 0 < ξ a b 0 .
As shown below, at least one of these conditions (Eq. 3-5) is not satisfied for the studied nickelate films. From this, we concluded that there is an incident, that B c 2 , p a r a T data of nickelate films is nicely approximated by square root of independent variable of two-fluid model:
B c 2 , p a r a T ∝ 1 − T T c ,
and the deeper physics behind this dependence should be determined.
In this paper, we propose to resolve this problem by accepting the fact that the superconductivity in nickelates is a three-dimensional (3D) phenomenon and, thus, the upper critical field should be described by standard 3D Ginzburg-Landau equations:
{ (7) B c 2 , p e r p T = ϕ 0 2 π 1 ξ a b 2 T = ϕ 0 2 π 1 − T T c ξ a b 2 0 (8) B c 2 , p a r a T = ϕ 0 2 π 1 ξ c T 1 ξ a b T = ϕ 0 2 π 1 ξ a b T γ ξ T 1 ξ a b T = ϕ 0 2 π γ ξ T 1 − T T c ξ a b 2 0
where γ ξ T = ξ a b T ξ c T denotes the temperature-dependent coherence length anisotropy. By experimenting with many analytical functions, we found a remarkably simple and robust heuristic expression for γ ξ T , which surprisingly enough can also be applied to iron-based superconductors:
γ ξ T = ξ a b T ξ c T = ξ a b 0 ξ c 0 1 1 − 1 a × T T c = γ ξ 0 1 1 − 1 a × T T c ,
where a is a free-fitting parameter (varies within a narrow range of 1.2 < a < 2.3 for all studied superconductors).

2. The upper critical field definition

Before Eqs. 7-9 will be applied for B c 2 T data fit, we should clarify the definition of the B c 2 T , because different research groups define this fundamental field using different criteria.
In many reports on nickelates, the upper critical field, B c 2 T , and, as a direct consequence of it, the coherence length, ξ T , were defined/deduced from the magnetoresistance curves, R T , B , by utilizing 50% of normal state resistance criterion, i.e. R T R n o r m T = 0.5 (it should be noted that some research groups [49] utilized the criterion of R T R n o r m T → 1.0 , which returns the most overestimated T c and B c 2 T and the most underestimated ξ a b 0 and ξ c 0 values).
However, in direct experiments performed by Harvey et al [35], it was shown that the diamagnetic response in nickelate films is always appeared at temperature well below the zero-resistance temperature, T c , z e r o (see, for instance, Figure 2 in Ref. 35). Because diamagnetism is essential and unavoidable property of the superconducting state, the definition of the fundamental superconducting field (i.e., the upper critical field, B c 2 T ) at the condition at which the superconducting state does not exist (and thus neither the Abrikosov’s vortices, nor the phase coherence of the order parameter and the amplitude coherence of the order parameter exist) is incorrect. The definition by R T R n o r m T = 0.5 , or, by any other similar ratios, except R T R n o r m T → 0 , causes many confusions, and the most notable one is the claim that the Pauli limiting field is violated in practically all thin film superconductors [36,54,55]. However, the primary reason for this miserable violation is the definition of the upper critical field, B c 2 T , by the criterion at which the superconducting state does not yet exist.
It should be reaffirmed that because the upper critical field, B c 2 T , is defined as the magnetic flux density at which the superconducting state collapses and the diamagnetism is essential property of the superconducting state, the definition of the B c 2 T should be made based on the disappearance of diamagnetic response or, if it is impossible to measure, by the R T R n o r m T → 0 criterion. However, it should be mentioned that these definitions have been implemented in very few studies [56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74].
Based on remarkably overestimated B c 2 T values, defined by R T R n o r m T = 0.5 or R T R n o r m T → 1 [49,54,55,75,76,77,78], and very broad resistive transition width in some thin film superconductors, new effects/phenomena can be claimed (for instance, the Pauli limiting field violation [36,54,55,75,76,77,78]). However, these new effects/phenomena can be explained by the misinterpretation of the thermodynamic fluctuations of the phase and the amplitude of the order parameter in superconductors with low charge carrier density [79,80,81] as the superconducting state. A strongly fluctuating Fermi sea is not an ordered superconducting condensate, where amplitude and phase coherence have been established across the entire sample. Based on this, it is incorrect to apply basic interpretations developed for superconducting condensate (at which non-zero Meissner response should exist or, at least, zero resistance can be measured in experiment) to a system with strong local fluctuations in space and time, which are manifested as several percent drop in the resistance.
In addition to the aforementioned report by Harvey et al [35] on R0.8Sr0.2NiO2 (R = La, Pr, Nd), there are several reports performed on other perfect single-phase superconductors, in which the diamagnetic response was detected at T c , d i a − o n s e t which is not above (and in many cases well below) the temperature at which the resistance drops to zero, that is T c , d i a − o n s e t ≤ T c , z e r o [35,82,83,84,85,86,87,88,89,90]. These rare, but high quality, experimental reports provide additional evidence for the need to define the B c 2 T by at least the R T R n o r m T → 0 criterion, which is the most accurate experimental value for the superconducting state collapses/emerges if only resistive measurements have been performed for the given sample. This B c 2 T definition has been implemented, but, again, in very rare studies [81,87,91,92,93] in comparison with majority of studies, where B c 2 T was defined by 0.5 ≤ R T R n o r m T < 1 criterion (see, for instance, Refs. [94,95]).
It is interesting to note that Mandal et al [84] defined B c 2 T as by T c , d i a − o n s e t (and for this definition, the derived B c 2 0 = 3.79   T ) as well, as by R T R n o r m T = 0.5 criterion (and for this definition, the derived B c 2 0 = 5.44   T ) for bulk Zr2Ir single crystal. This result demonstrates that B c 2 0 defined by R T R n o r m T = 0.5 criterion can be overestimated by a factor of 1.4.
However, for Nd0.775Sr0.225NiO2 nickelate films, this difference is much larger, shown in Figure 4 in Ref. 23, where the difference between B c 2 , p e r p T defined by R T = 6   K R n o r m T = 6 K = 0.5 and by R T = 6   K R n o r m T = 6   K = 0.01 is approximately five times (the subscripts perp and para are for the direction of the applied magnetic field to the surface of the films). A much larger difference between B c 2 T defined by different R T R n o r m T criteria was reported by Xiang et al [22] for Nd0.8Sr0.2NiO2 thin films. These observed differences for nickelate films are much larger in comparison with bulk Zr2Ir [87] and bulk FeSe [71] which both exhibit similar T c ≅ 7   K value and where the difference in B c 2 T defined by different R T R n o r m T criteria is about 40%.
Recently, independent direct confirmation that T c , d i a − o n s e t < T c , z e r o in the nickelate films has been reported by Zeng et al [45], who observed the inequality for films with thickness 5.5   n m ≤ d s c ≤ 15.2   n m [45].
Based on the above, in this report, we defined the B c 2 T as the lowest possible R T , B R n o r m T , B = 0 criterion, which can be applied to given experimental R T , B datasets (which depend on signal/noise ratio, and other real-world experimental issues).

3. Results

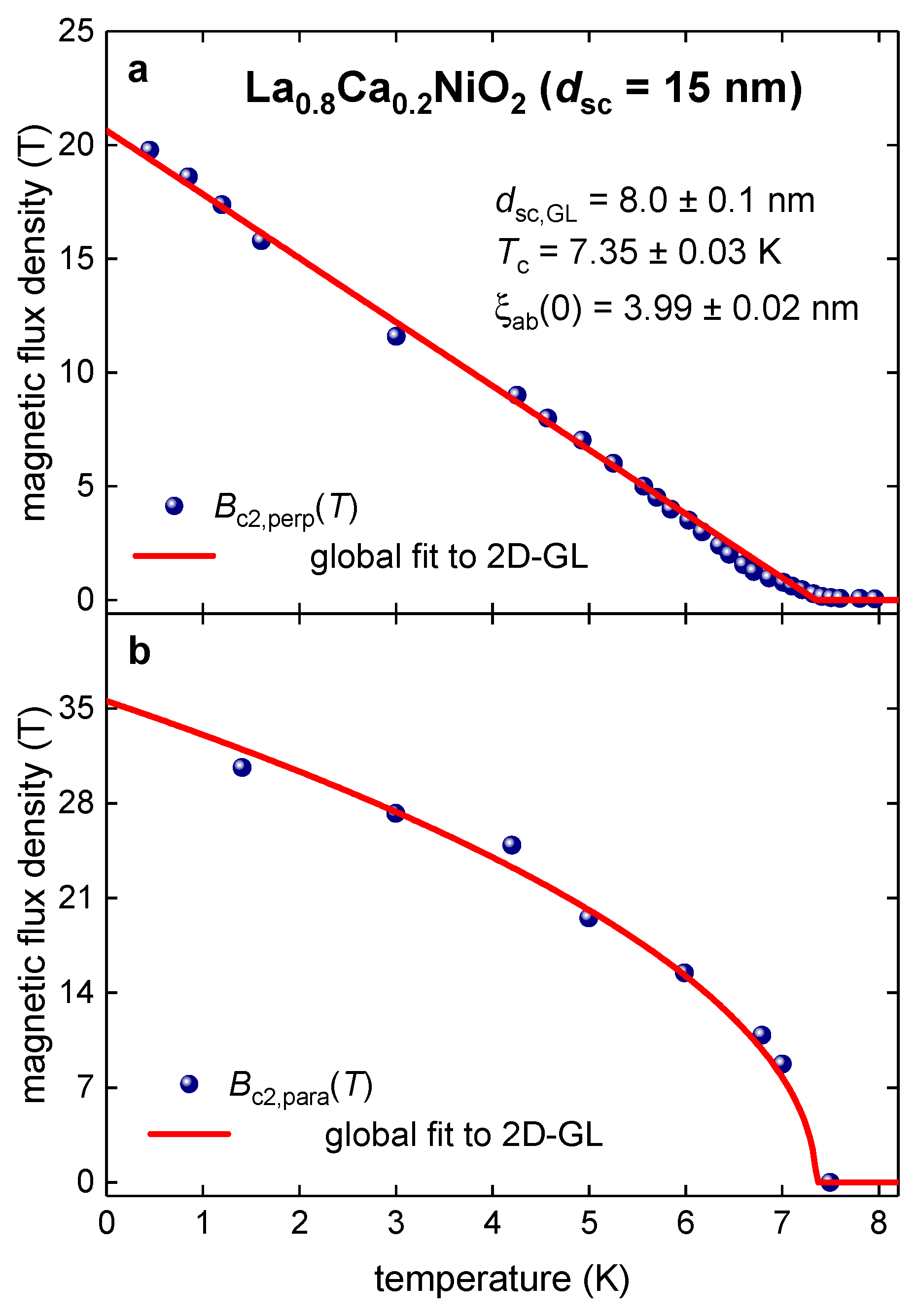
3.1. La0.8Ca0.2NiO2 film

Chow et al [36] reported B c 2 , p e r p T and B c 2 , p a r a T datasets for La0.8Ca0.2NiO2 film (which has a physical thickness d s c = 15   n m ) defined by R T , B R n o r m T , B = 0 = 0.10 , R T , B R n o r m T , B = 0 = 0.50 , and R T , B R n o r m T , B = 0 = 0.90 criteria. By following our discussion in the previous section, in Figure 1 we showed reported B c 2 , p e r p T and B c 2 , p a r a T datasets defined by R T , B R n o r m T , B = 0 = 0.10 criterion and global data fit to 2D-GL model (Eqs. 1,2). The fit quality is high and the fitting parameters have low mutual dependence. However, deduced film thickness, d s c , G L = 8.0 ± 0.1   n m , by nearly two times different from physical film thickness d s c = 15   n m , which is a manifestation of general problem associated with utilization of Eqs. 1,2 for nickelate films [23], as we discussed above.
It should be noted that the deduced ξ a b 0 = 3.99 ± 0.02   n m is much smaller than any of the two film thicknesses:
ξ a b 0 ≅ 4   n m < d s c , G L = 8   n m ,
ξ a b 0 ≅ 4   n m   ≪ d s c = 15   n m ,
Considering that there is an expectation that ξ c 0 ≲ ξ a b 0 , Eqs. 10,11 imply that Eqs. 1,2 cannot be used to fit B c 2 T data for this film, because it is not thin.
In Figure 2 we show the same reported B c 2 , p e r p T and B c 2 , p a r a T datasets (as shown in Figure 1) and the global data fit to our model (Eqs. 7-9).
The fit quality is high (Figure 2) and the mutual dependence of the parameters is low. Deduced coherence lengths are ξ a b 0 = 4.01 ± 0.03   n m and ξ c 0 = ξ a b 0 γ ξ 0 = 2.64   n m . These values agree with our assumption that the film exhibits three dimensional (3D) superconductivity:
ξ c 0 ≅ 2.6   n m < ξ a b 0 ≅ 4   n m   ≪ d s c = 15   n m ,
In Figure 2(c), we show the calculated temperature-dependent anisotropy of the coherence length, γ ξ T = γ ξ 0 1 1 − 1 a × T T c , where all γ ξ T values for temperatures in the range of T c ≤ T < a × T c are shown by the dotted line.
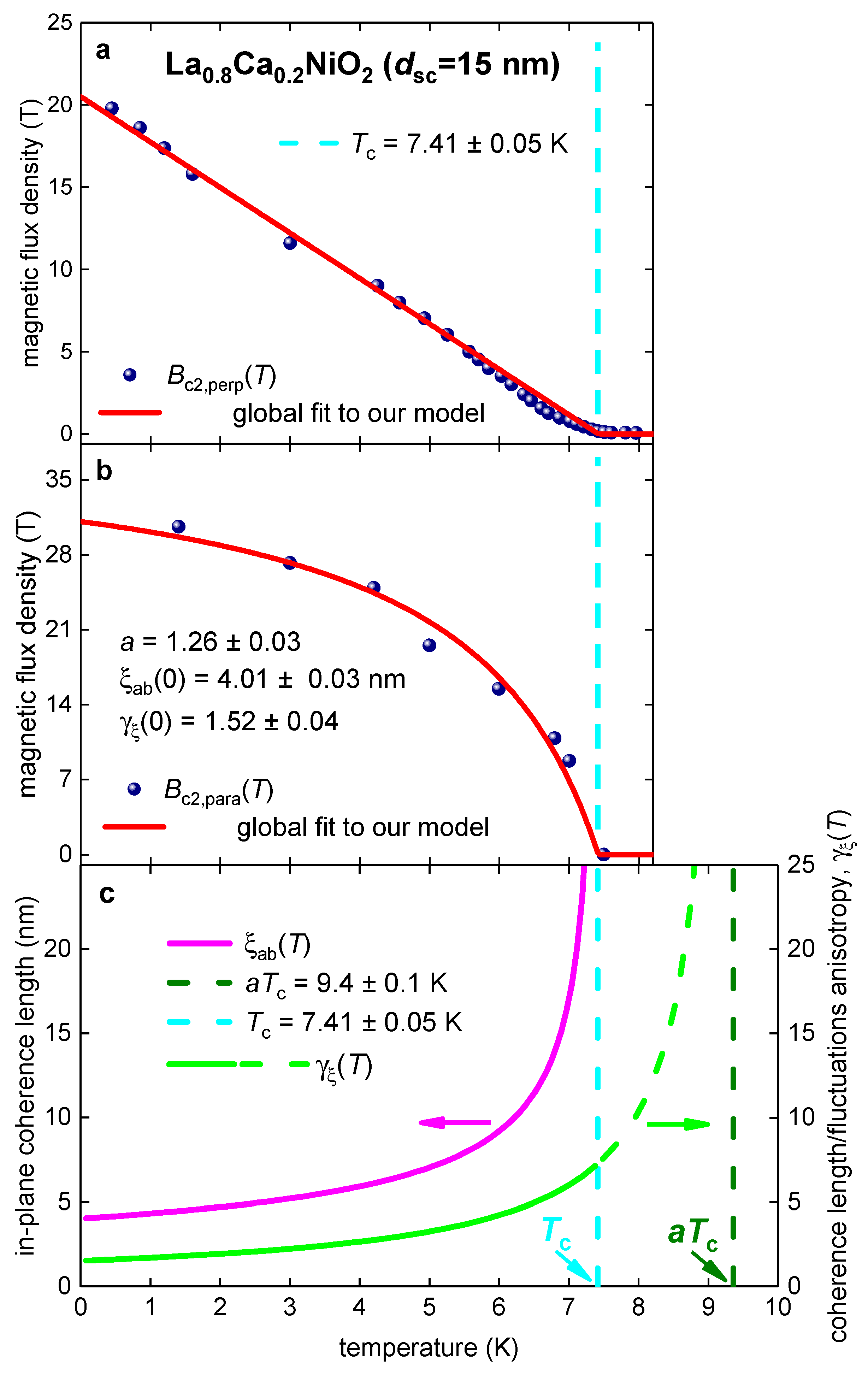
Preprints 73480 g002
Figure 2. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for La0.8Ca0.2NiO2 film with physical thickness d s c = 15   n m . Raw data reported by Chow et al [36]. Deduced parameters are: T c = 7.41 ± 0.05   K , ξ a b 0 = 4.01 ± 0.03   n m , γ ξ 0 = 1.52 ± 0.04 , a = 1.26 ± 0.03 . The goodness of fit is (a) 0.9963 and (b) 0.9832. The 95% confidence bands are indicated by pink shaded areas.
Figure 2. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for La0.8Ca0.2NiO2 film with physical thickness d s c = 15   n m . Raw data reported by Chow et al [36]. Deduced parameters are: T c = 7.41 ± 0.05   K , ξ a b 0 = 4.01 ± 0.03   n m , γ ξ 0 = 1.52 ± 0.04 , a = 1.26 ± 0.03 . The goodness of fit is (a) 0.9963 and (b) 0.9832. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g002
Physical meaning of this part of the γ ξ T curve we discussed in the Discussion section, however in short, it can be mentioned, that the anisotropy should also exist for the phase and the amplitude fluctuations of the order parameter above the transition temperature, T c . Because all nickelates exhibit reasonably wide resistive transitions, similar to other unconventional superconductors (such as cuprates [80] and pnictides [96]), we can propose that a × T c value can be interpreted as the onset of the superconducting fluctuations, T f l u c , in the given material, T f l u c = a × T c [77,78,79,96,97].
Thus, our interpretation of the T f l u c = a × T c is based on the assumption that there is a universal temperature dependence for the anisotropy of the superconducting order parameter and of the fluctuations of this order above the superconducting transition, which, at least from the first glance, looks like a reasonable assumption.

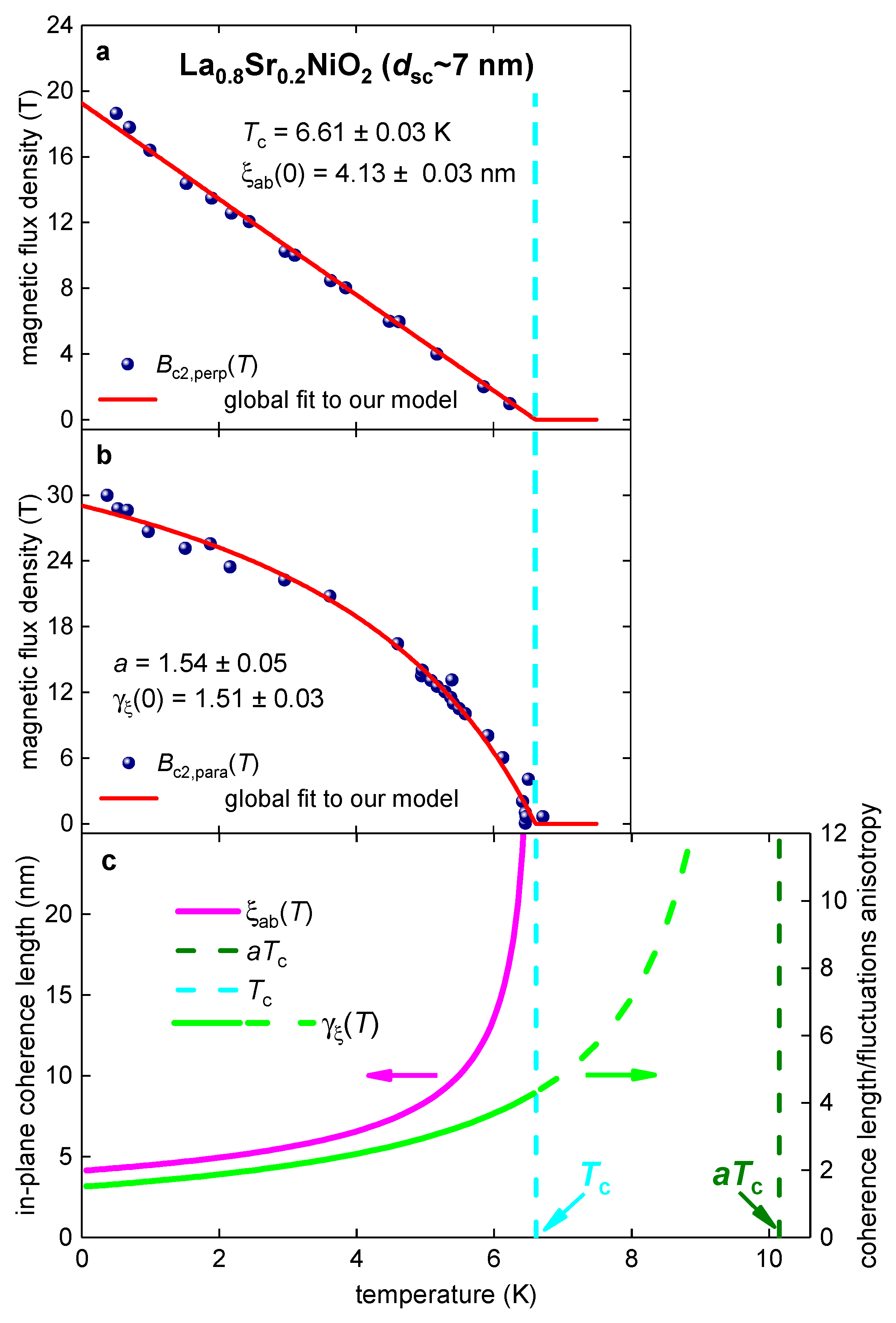
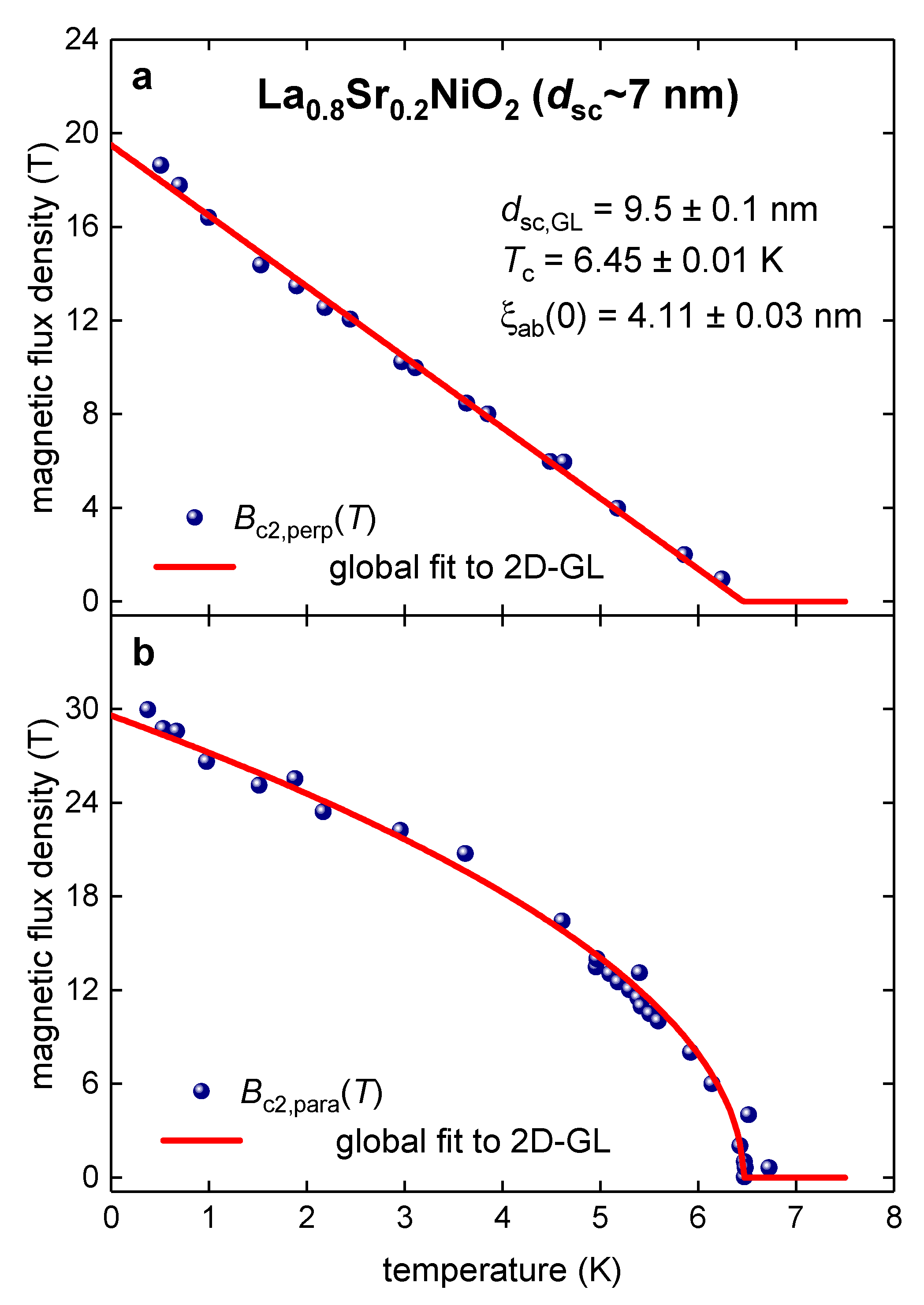
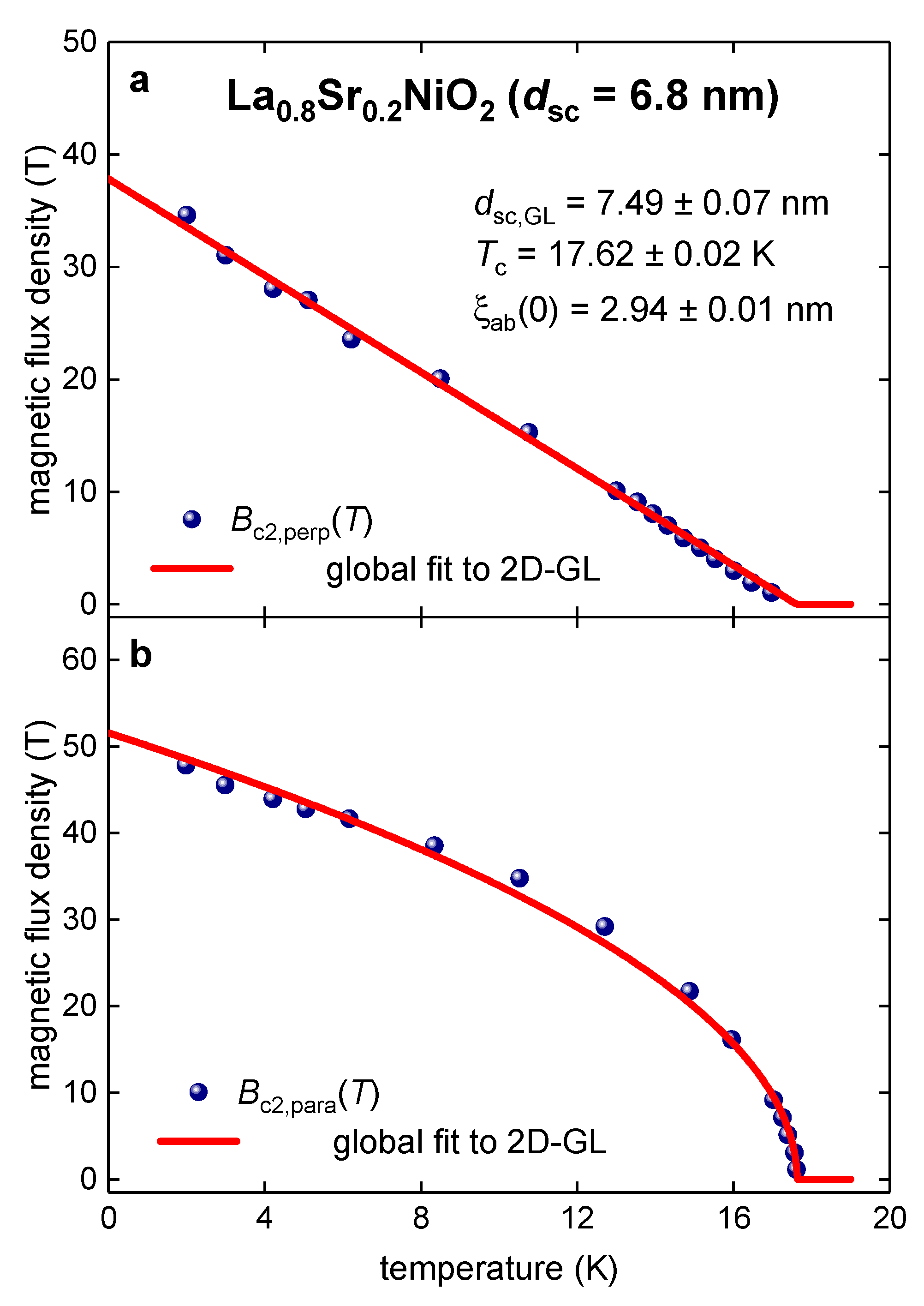
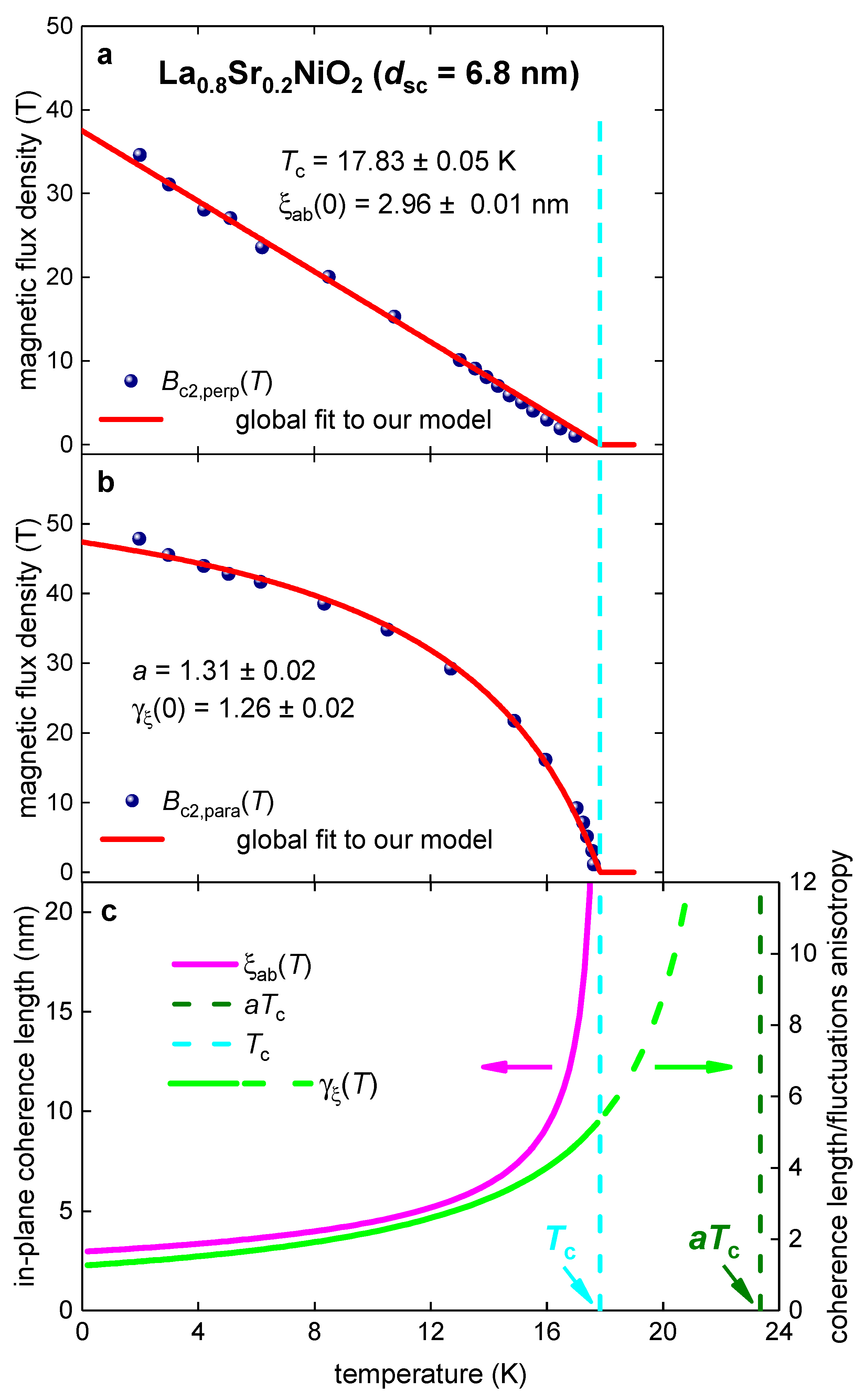
3.2. La0.8Sr0.2NiO2 film

Wang et al [98] reported B c 2 , p e r p T and B c 2 , p a r a T datasets for La0.8Sr0.2NiO2 film (which has a physical thickness d s c ~ 7   n m ) defined by R T , B R n o r m T , B = 0 = 0.50 criterion. In Figure 3 we show reported B c 2 , p e r p T and B c 2 , p a r a T datasets and global data fit to the 2D-GL model (Eqs. 1,2).
The quality of fit is high, and parameters have low mutual dependence. However, the deduced film thickness, d s c , G L = 9.5 ± 0.1   n m , exceeds physical film thickness d s c = 7   n m (Figure 3), and, in addition, the inequality of:
ξ a b 0 ≅ 4   n m < d s c ~ 7   n m < d s c , G L = 9.5   n m ,
shows that the 2D-GL model cannot be used for the analysis (because the film is not sufficiently thin), despite a good fit quality.
In Figure 4 we show the same B c 2 , p e r p T and B c 2 , p a r a T datasets (as shown in Figure 3), which were fitted to our model (Eqs. 7-9). The fits quality is high (Figure 4), and the mutual dependence of the parameters was low. Deduced coherence lengths are ξ a b 0 = 4.13 ± 0.03   n m and ξ c 0 = ξ a b 0 γ ξ 0 = 2.74   n m . These values agree with the assumption of our model that the film exhibits 3D superconductivity:
ξ c 0 ≅ 2.7   n m < ξ a b 0 ≅ 4.1   n m < d s c ~ 7   n m ,
In Figure 4(c), we show the calculated temperature-dependent anisotropy of the coherence length: γ ξ T = γ ξ 0 1 1 − 1 a × T T c , where all γ ξ T values for temperatures in the range of T c ≤ T < a × T c are shown by the dotted line.
Preprints 73480 g004
Figure 4. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for La0.8Sr0.2NiO2 film with physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: T c = 6.61 ± 0.03   K , ξ a b 0 = 4.13 ± 0.03   n m , γ ξ 0 = 1.51 ± 0.03 , a = 1.54 ± 0.05 . The goodness of fit is (a) 0.9959 and (b) 0.9897. The 95% confidence bands are indicated by pink shaded areas.
Figure 4. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for La0.8Sr0.2NiO2 film with physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: T c = 6.61 ± 0.03   K , ξ a b 0 = 4.13 ± 0.03   n m , γ ξ 0 = 1.51 ± 0.03 , a = 1.54 ± 0.05 . The goodness of fit is (a) 0.9959 and (b) 0.9897. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g004
In Figure 4(c), we show the calculated temperature-dependent anisotropy of the coherence length: γ ξ T = γ ξ 0 1 1 − 1 a × T T c , where all γ ξ T values for temperatures in the range of T c ≤ T < a × T c are shown by the dotted line.

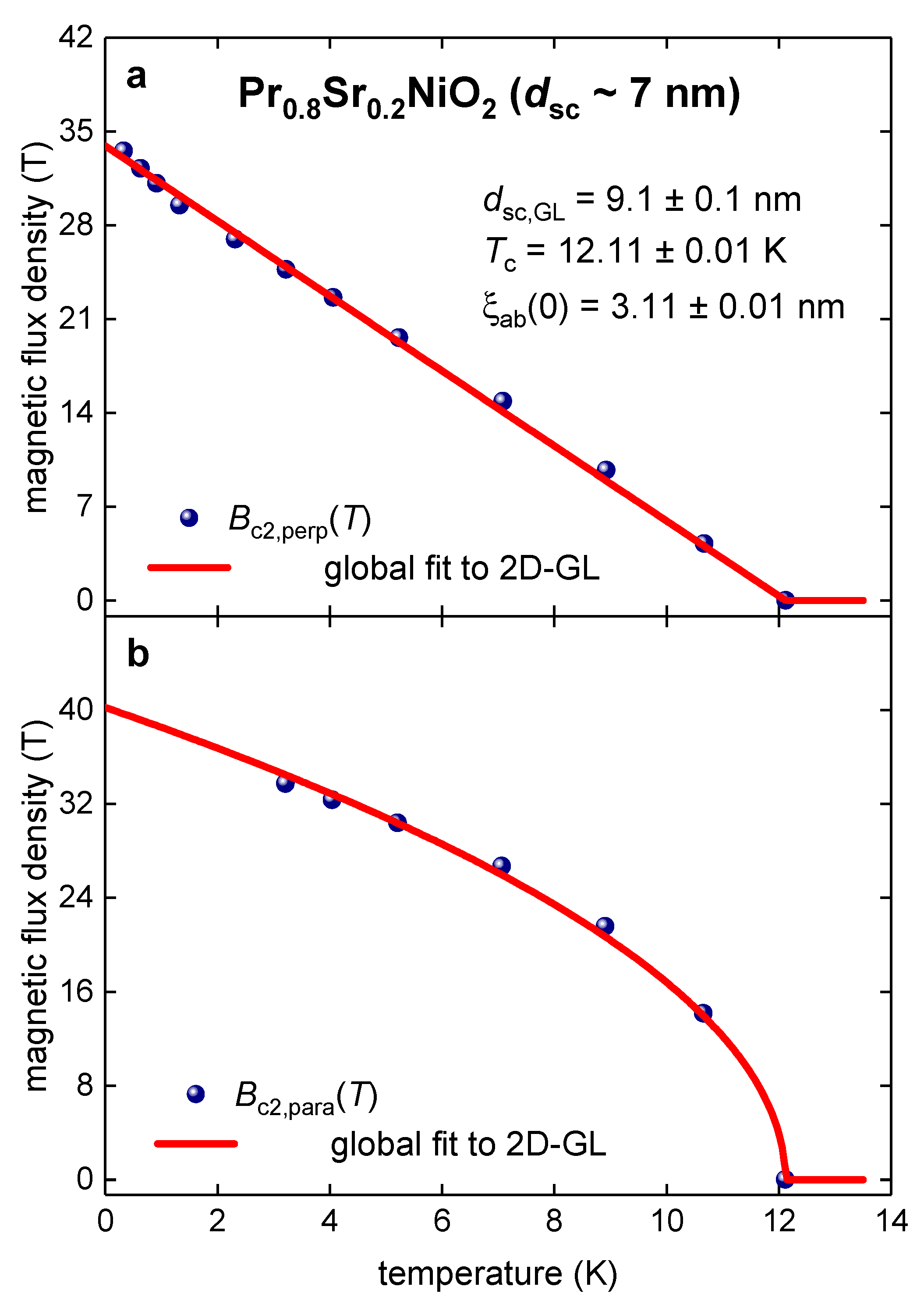
3.3. Pr0.8Sr0.2NiO2 film

Wang et al [98] reported B c 2 , p e r p T and B c 2 , p a r a T datasets for Pr0.8Sr0.2NiO2 film (which has a physical thickness d s c ~ 7   n m ) defined by R T , B R n o r m T , B = 0 = 0.50 criterion. In Figure 5 we show reported B c 2 , p e r p T and B c 2 , p a r a T datasets and global data fit to the 2D-GL model (Eqs. 1,2).
In Figure 6 we show the same B c 2 , p e r p T and B c 2 , p a r a T datasets (as shown in Figure 5), which were fitted to our model (Eqs. 7-9).
Overall, inequalities (similar to those obtained for the other nickelates (Eqs. 10-14)) were revealed for the Pr0.8Sr0.2NiO2 film:
ξ a b 0 ≅ 4   n m < d s c ~ 7   n m < d s c , G L = 9.5   n m ,

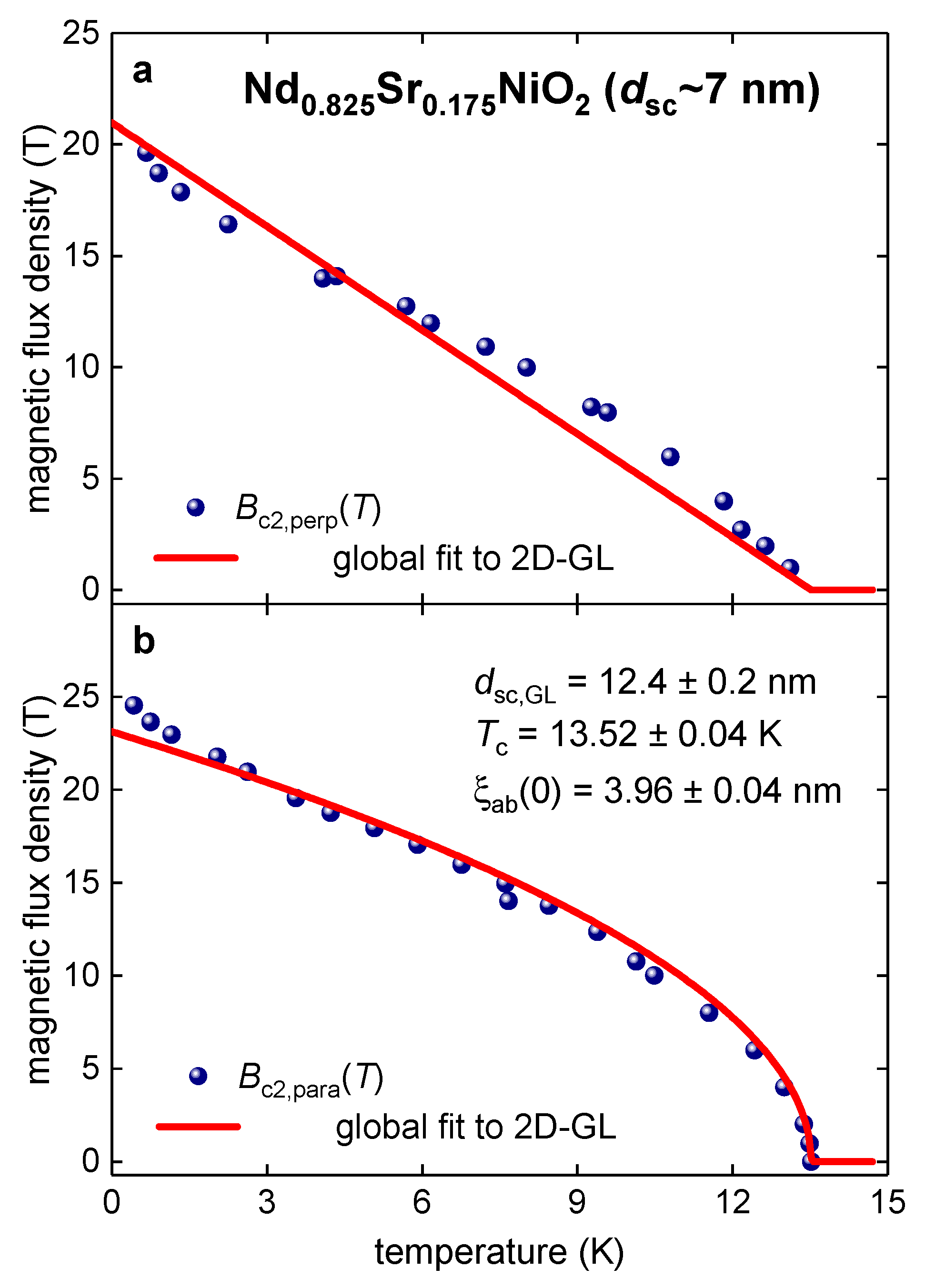
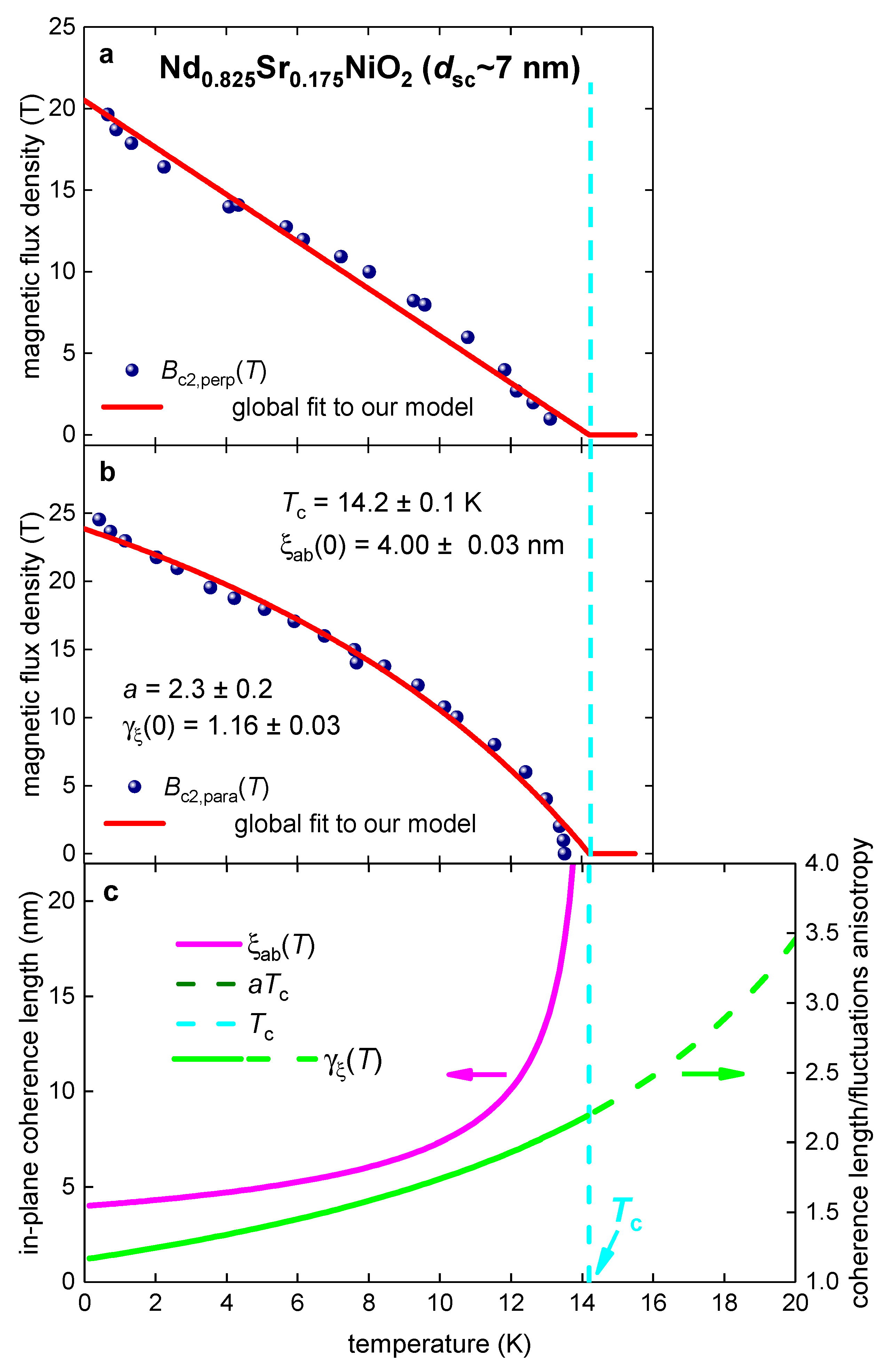
3.4. Nd0.825Sr0.175NiO2 film

Wang et al [98] reported B c 2 , p e r p T and B c 2 , p a r a T datasets for Nd0.825Sr0.175NiO2 film (which has a physical thickness d s c ~ 7   n m ) defined by R T , B R n o r m T , B = 0 = 0.50 criterion. In Figure 7 we show reported B c 2 , p e r p T and B c 2 , p a r a T datasets and global data fit to the 2D-GL model (Eqs. 1,2).
In Figure 8, we show the same B c 2 , p e r p T and B c 2 , p a r a T datasets (as shown in Figure 7) which were fitted to our model (Eqs. 7-9). Deduced inequalities:
ξ c 0 ≅ 3.4   n m < ξ a b 0 ≅ 4.0   n m < d s c ~ 7   n m ,
confirmed the 3D superconductivity of the Nd0.825Sr0.175NiO2 film.

3.5. La0.8Sr0.2NiO2 film

Now we return to the La0.8Sr0.2NiO2 compound, for which Wei et al [70] recently reported the record high-superconducting transition temperature for nickelates. Wei et al [70] also reported B c 2 , p e r p T and B c 2 , p a r a T datasets defined by R T , B R n o r m T , B = 0 = 0.01 , R T , B R n o r m T , B = 0 = 0.50 , and R T , B R n o r m T , B = 0 = 0.90 criteria. Despite our understanding that B c 2 T should be defined by the lowest possible R T , B R n o r m T , B = 0 criterion, in Figs. 9,10 we analysed the B c 2 T data defined by R T , B R n o r m T , B = 0 = 0.50 criterion [70] to make it possible to compare parameters deduced for the La0.8Sr0.2NiO2 film in Section 3.2 (Figs. 3,4). The film thickness is d s c ~ 6.8   n m [70], which is practically the same as the one in report by Wang et al [98]. In Figure 9 we show B c 2 T data and global data fit to the 2D-GL model (Eqs. 1,2).
In Figure 10, we show the same B c 2 , p e r p T and B c 2 , p a r a T datasets (as show in Figure 9), which were fitted to our model (Eqs. 7-9). Deduced inequalities:
ξ c 0 ≅ 3.4   n m < ξ a b 0 ≅ 4.0   n m < d s c ~ 7   n m ,
confirm the 3D superconductivity of the La0.8Sr0.2NiO2 film.
In the following sections, we demonstrate that the high quality fit of B c 2 , p e r p T and B c 2 , p a r a T datasets to Eqs. 1,2 cannot be considered as evidence for 2D superconductivity because we obtained high-quality fits to Eqs. 1,2 for B c 2 T data for bulk iron-based superconductors (IBS).
IBS were experimentally discovered by Hosono’s group [99,100] more than 15 years ago, and to the best of our knowledge, there has been no proposal for an analytical expression for the temperature-dependent coherence length anisotropy, γ ξ T , to this family of superconductors. Here, we show that our 3D model (Eqs. 7-9) can be extended to IBS materials.

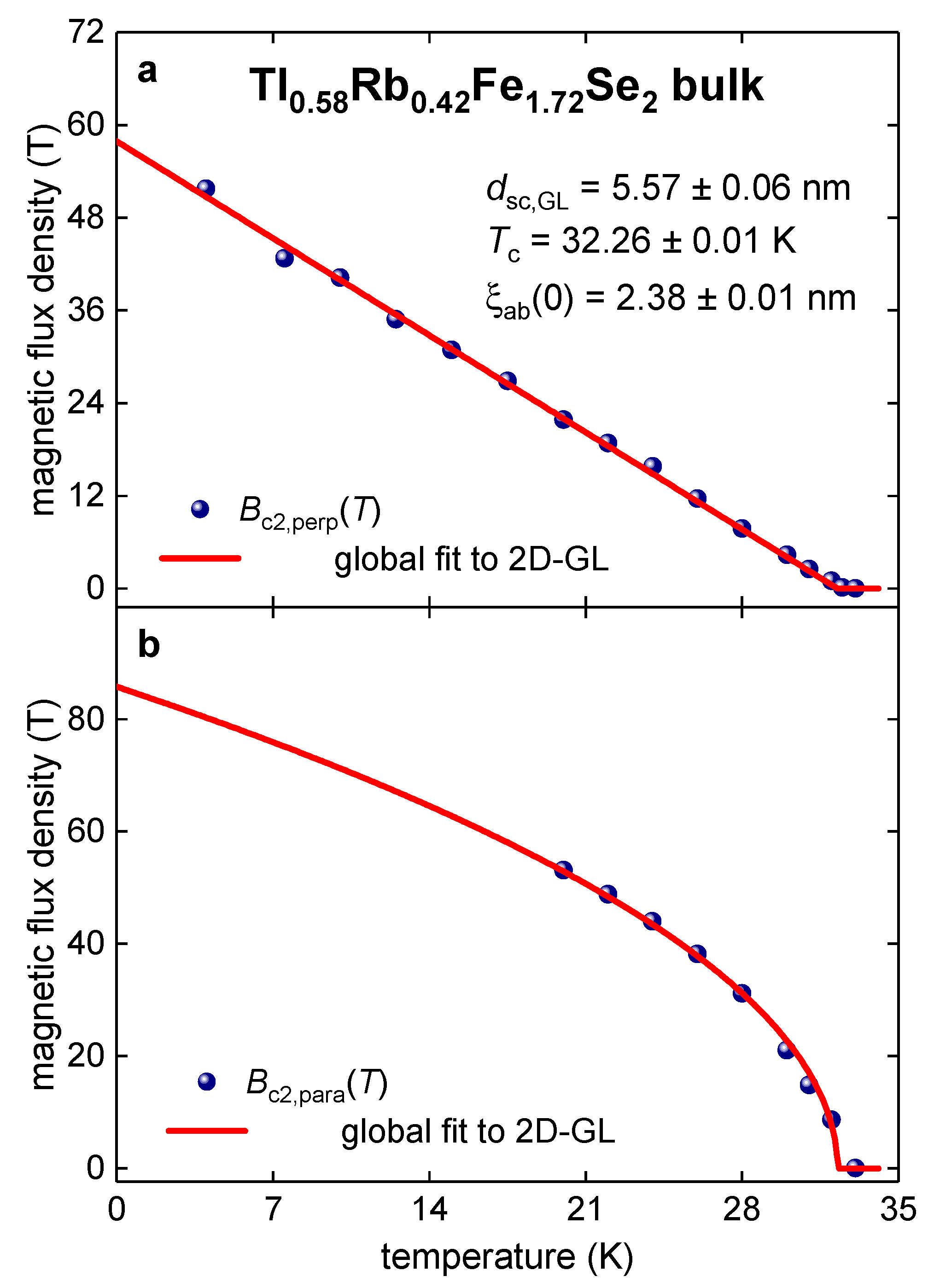
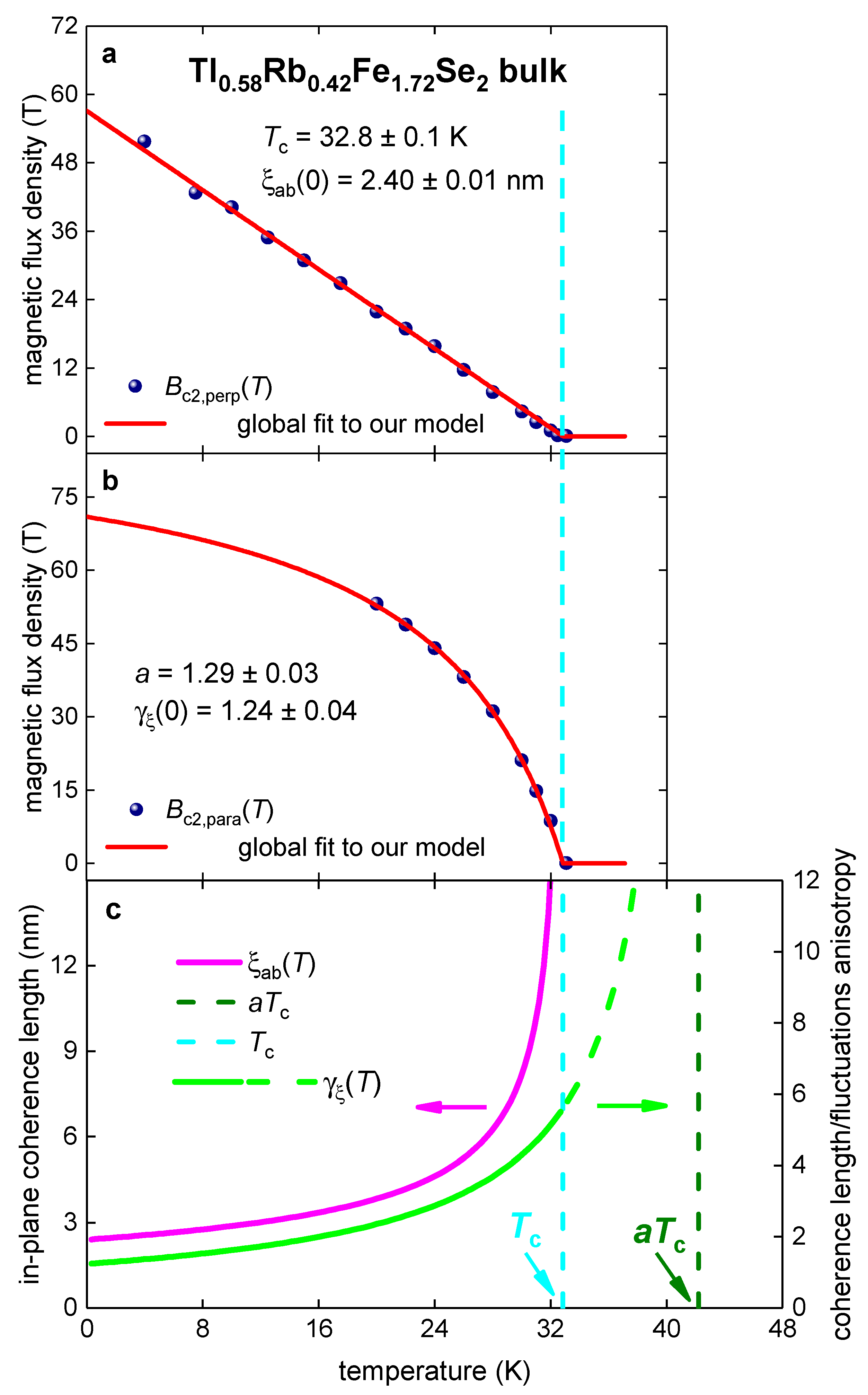
3.6. Bulk Tl0.58Rb0.42Fe1.72Se2

Jiao et al [101] reported R T , B p e r p and R T , B p a r a datasets for bulk single crystal Tl0.58Rb0.42Fe1.72Se2. These authors [101] derived extrapolative values for B c 2 , p e r p T and B c 2 , p a r a T defined by R T , B R n o r m T , B = 0 → 0.0 and R T , B R n o r m T , B = 0 → 1.0 criteria. Because these datasets do not represent values measured in the experiment, in Figs. 11,12 we analysed datasets deduced by R T , B R n o r m T , B = 0 = 0.50 criterion, which represent the measured values.
In Figure 11, we fitted B c 2 , p e r p T and B c 2 , p a r a T datasets to Eqs. 1,2 to prove that high-quality fits to the 2D model can be obtained (and, even, “the thickness” of the superconductor, d s c , G L , can be deduced) for B c 2 T data measured for bulk anisotropic superconductors.
This implies (Figure 11) that the thickness, d s c , G L , of the “2D superconductor” can be deduced from B c 2 , p e r p T and B c 2 , p a r a T datasets measured for bulk superconductors (see, for instance, Figure 11) by utilizing the widely used [53] Eqs. 1,2 proposed by Tinkham in the 1960-s [52,102].
Thus, we argue that Eqs. 1,2 are incorrect for use in data analysis because these equations represent reasonably flexible fitting functions, which can be used for smooth data approximation for some superconductors. However, one parameter in these equations, that is d s c , G L , which exhibits a unit of length, does not have any physical meaning for bulk superconductors.
This implies that traditional interpretation (see, for instance, Ref. 23) that the violation of the following equation:
d s c ≅ d s c , G L ,
in thin film superconductors (including, atomically thin superconductors) should indicate that there is a deep underlying physical effect (for instance, spin-orbit scattering [103,104]), cannot be found to be valid.
In Figure 12 we show the B c 2 , p e r p T and B c 2 , p a r a T datasets for Tl0.58Rb0.42Fe1.72Se2 which were fitted to Eqs. 7-9. Fits have high quality.
a = 1.29 ± 0.03 ,
γ ξ 0 = 1.24 ± 0.04 ,
were within the same ranges as those deduced for the nickelate films (Figs. 2,4,6,8,10). This is an evidence that the nickelates exhibit 3D superconductivity.
However, Figure 12 demonstrates that the 3D model (Eqs. 7-9) can be extended to broader range of superconductors, in particular, on bulk chalcogenides. To demonstrate this, in the next section we apply Eqs. 7-9 on another bulk single crystal chalcogenide superconductor, Fe1.11Te0.6Se0.4 [105].

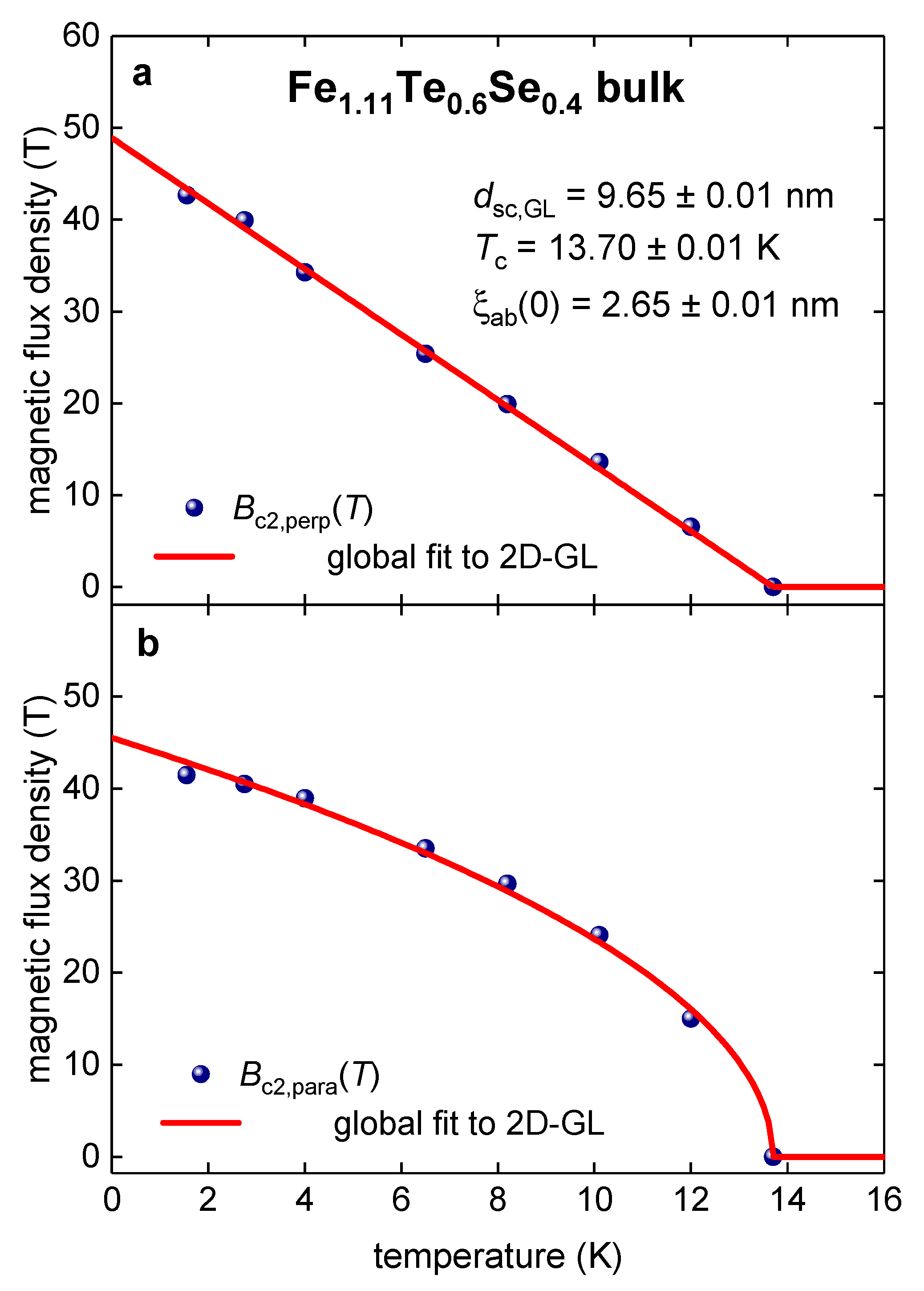
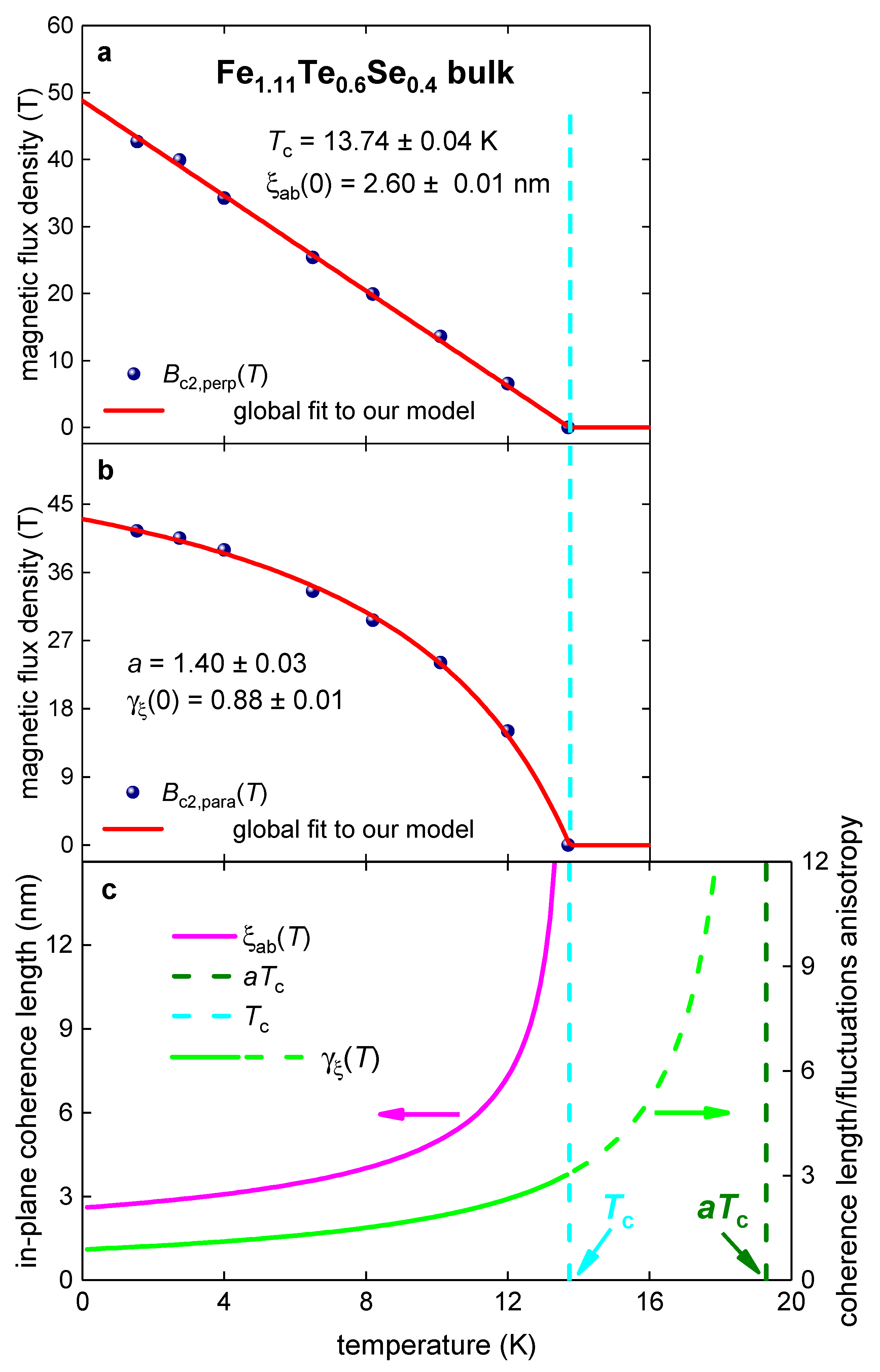
3.7. Bulk Fe1.11Te0.6Se0.4

Fang et al [105] reported B c 2 , p e r p T and B c 2 , p a r a T datasets for bulk single crystal Fe1.11Te0.6Se0.4 [105] defined by R T , B R n o r m T , B = 0 = 0.50 criterion. In Figure 13 we fitted B c 2 , p e r p T and B c 2 , p a r a T datasets to Eqs. 1,2 to demonstrate that high-quality fits to the 2D-GL model can be obtained.
Figure 13 shows that “the thickness of the 2D superconductor”, d s c , G L , of several nanometers (i.e. within a typical range usually deduced for thin film superconductors, including nickeltaes) can be deduced from the fit for this bulk anisotropic superconductor.
In Figure 14 we show the same B c 2 , p e r p T and B c 2 , p a r a T datasets (as shown in Figure 13), which were fitted to Eqs. 7-9. The deduced parameters are in the expected ranges.
However, the ground state anisotropy of the coherence length is less than unity:
γ ξ 0 = 0.88 ± 0.01 < 1.0   ,
It should be noted that γ ξ 0 < 1.0 was reported for several iron-based superconductors, and this topic has been discussed (see, for instance Refs. [106,107]).
Owing to the novelty of our model is the Eq. 9, in the following sections we show that the experimental γ ξ T = B c 2 , p a r a T B c 2 , p e r p T dependences measured for pnictide bulk superconductors can be fitted to Eq. 9, which confirms the validity of the proposed model (Eq. 9).

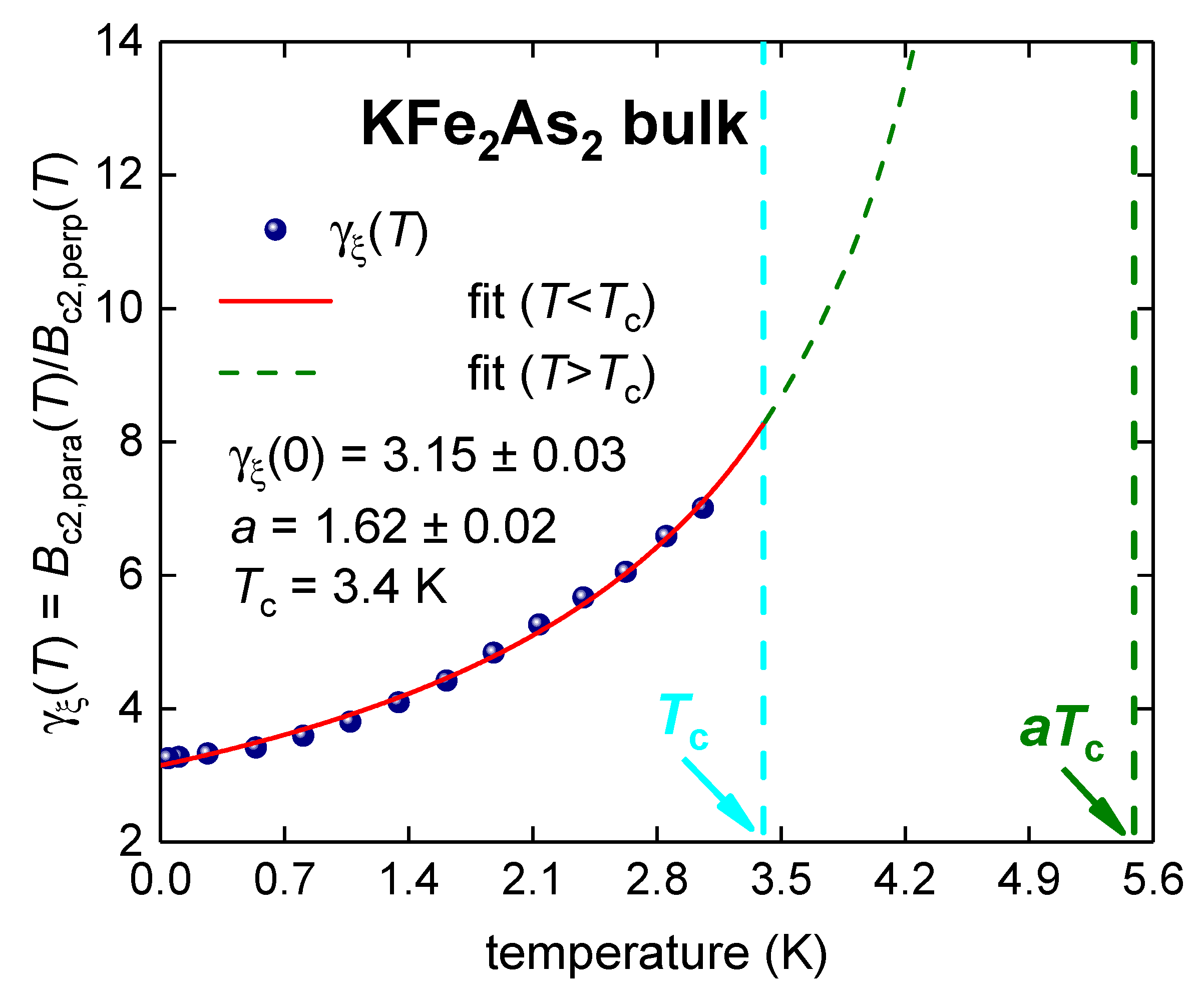
3.8. Bulk KFe2As2

Zocco et al [108] reported B c 2 , p e r p T , B c 2 , p a r a T , and γ ξ T = B c 2 , p a r a T B c 2 , p e r p T datasets for bulk single crystal pnictide KFe2As2 superconductor. In Figure 15, the reported γ ξ T dependence is fitted to Eq. 9 (for this fit, we fixed the transition temperature to the value observed in the experiment, T c = 3.4   ( f i x e d ) ).
The fit has high quality and low parameter dependence. The deduced parameters (Figure 15) are within the ranges reported above for nickelates and chalcogenides.

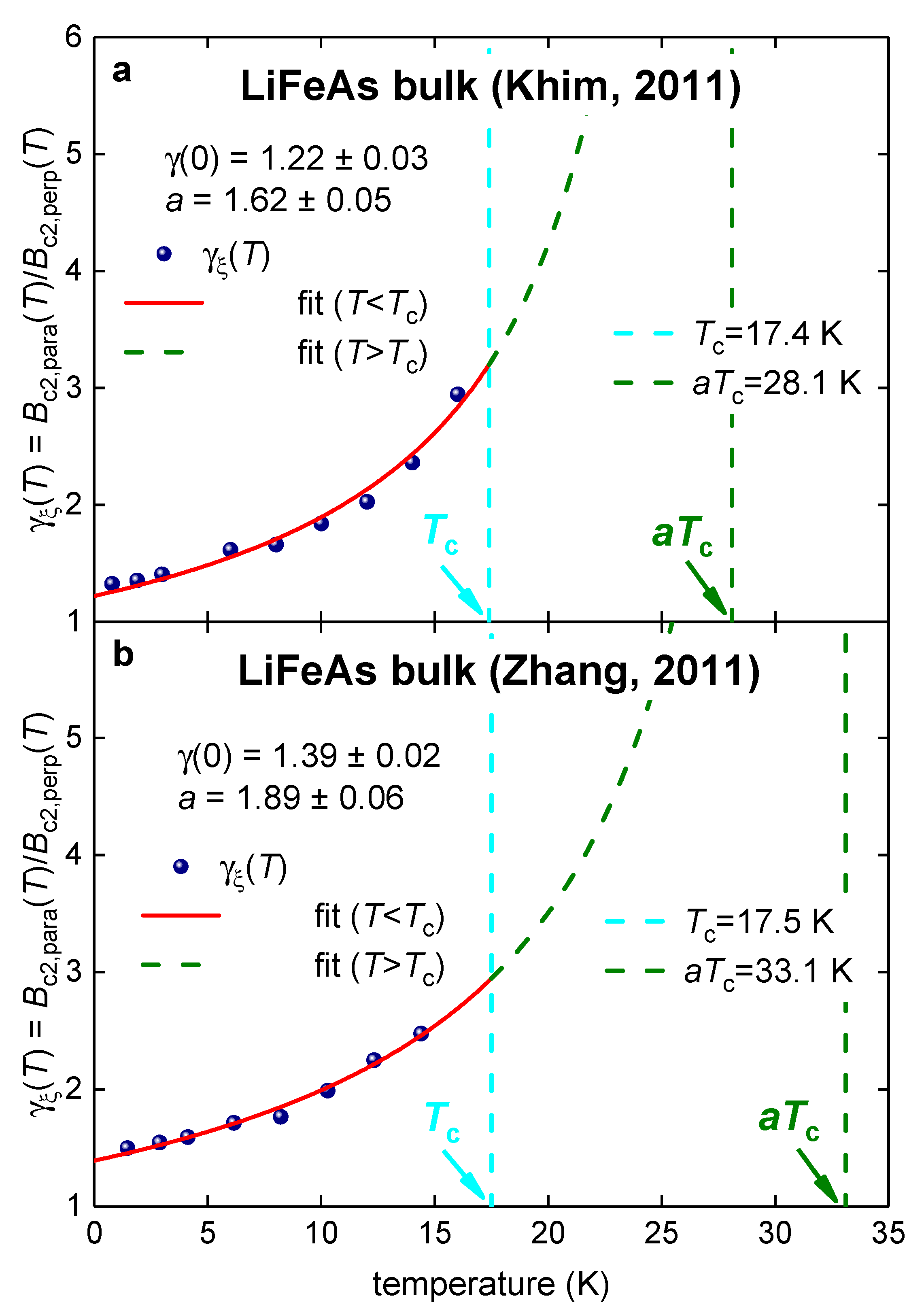
3.9. Bulk LiFeAs

Khim et al [109] and Zhang et al [110] reported B c 2 , p e r p T , B c 2 , p a r a T , and γ ξ T = B c 2 , p a r a T B c 2 , p e r p T datasets for bulk single crystal pnictide LiFeAs superconductor. In Figure 16 we show the fits of the reported γ ξ T to Eq. 9 (for this fit, we set the transition temperature to the value observed in the experiments).
The fits have a high quality and low parameters dependence. The deduced parameters for two datasets reported by independent research groups are close to each other, within acceptable levels of parameter deviations.

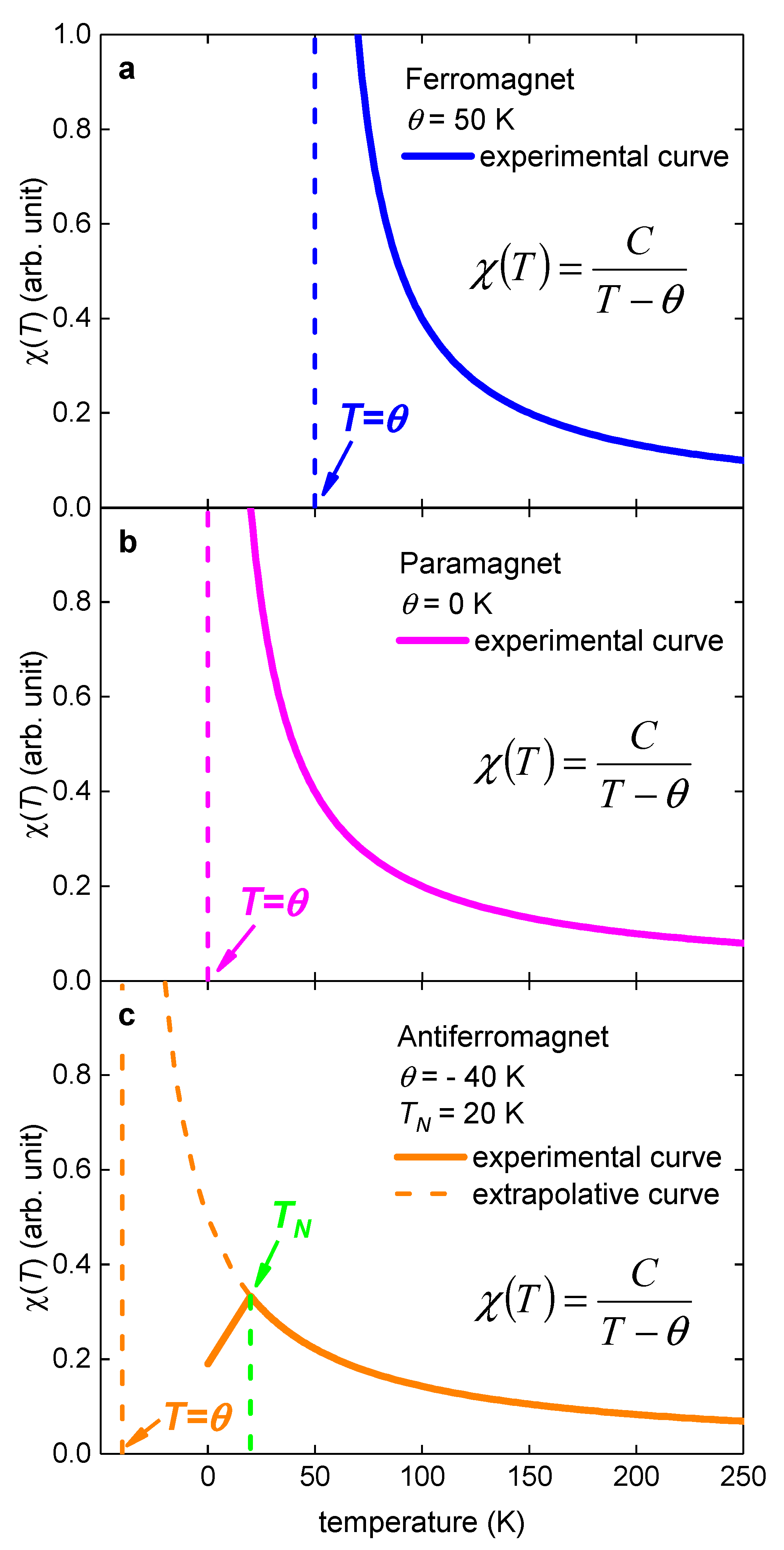
4. Discussion

The physical origin of our model (which is primarily based on Eq. 9) can be understood based on an analogy with the temperature-dependent DC magnetic susceptibility, χ T , in antiferromagnetic materials [111,112]. The temperature-dependent χ T in any material obeys the Curie-Weiss law (Figure 17):
χ T = C T − θ ,
where θ is Curie-Weiss temperature, and C is Curie constant.
In the schematic representations of Eq. 21 in Figure 17, there are three types of magnetic materials that primarily depend on the sign of the Curie-Weiss temperature:
In the schematic representations of Eq. 21 in Figure 17, there are three types of magnetic materials that primarily depend on the
  • θ > 0   K for ferromagnetic materials;
  • θ = 0   K for paramagnetic materials;
  • θ < 0   K for antiferromagnetic materials.
To be consistent with the form of Eq. 21, we can rewrite Eq. 9:
γ T = a T c γ 0 a T c − T = − a T c γ 0 T − a T c = − C T − θ ,
where C = a T c γ 0 , and θ = a T c .
Despite the negative sign (in K units) of the Curie-Weiss temperature, θ , for antiferromagnetic materials, this value represents one of the fundamental constant of the antiferromagnet, which quantifies the strength of the antiferromagnetic interaction in the material.
In antiferromagnetic materials, the χ T would obey the Curie-Weiss law down to very low temperatures, T → 0   K (Figure 17,c), however, at the Neel temperature, T N > 0   K , a phase transition occurs, and the χ T does not obey the Curie-Weiss law at T < T N .
In our model, γ T would obey the Eq. 9 up to high temperatures, T → a T c , however, at T = T c a superconductor-normal state phase transition occurs, and γ T becomes undefined at T > T c . However, the latter does not mean that a T c does not represent any physical value for the material, and our current interpretation of this value is that T = a T c represents the threshold temperature for the appearance of the anisotropy in the fluctuations of the order parameter in superconductor.
It should also be stressed that our model (Eqs. 7-9) utilizes the simplistic GL expression for the temperature-dependent in-plane coherence length:
ξ a b T = ξ a b 0 1 − T T c ,
However, it would be more accurate to use the Werthamer-Helfand-Hohenberg (WHH) theory [113] or its advanced version developed for two-band superconductors by Gurevich [114]. This type of advanced analysis, in conjunction with high-field experimental studies, has been implemented in several studies on IBS [115,116] and nickelates [23].
However, the high flexibility of primary WHH functions (exhibited several parameters, especially for the two-band model), and the nonexistence of WHH functions for T > T c , makes it impossible to extract a simple analytical expression, similar to Eq. 9, for the temperature dependence of the coherence length anisotropy, γ T , which we proposed herein. That is, the fact that:
ξ a b T T → T c → ∞ ,
ξ c T T → T c → ∞ ,
does not exclude the following:
γ ξ T = ξ a b T ξ c T T → T c ≠ ∞ .
The rigorous mathematical expression for the primary message of this study is as follows:
∀ T a T c < 1 ,   ∃   γ ξ T ∈ R > 0 ,
where the standard mathematical symbols are used.
In this regard, the simple heuristic expression for γ ξ T (proposed herein (that is Eq. 9)) might be modified to be more accurate (and unfortunately, more complicated); however, our primary message that the anisotropy of the thermodynamic fluctuations in anisotropic superconductors (exhibiting low charge carrier density) is established at some temperature T = a T c ( a > 1 ) above the entire superconducting transition temperature, T c , should remain unchanged.
All superconductors exhibit the second fundamental characteristic length which is the London penetration depth, λ T . In anisotropic superconductors, the λ T also has two components, which are in-plane London penetration depth, λ a b T , and out of plane London penetration depth, λ c T . We expect that the same approach, to the described herein for γ λ T , should be applied for the temperature dependent London penetration depth anisotropy, γ λ T = λ a b T λ c T [72,117,118,119]. However, as the model development, as data analysis, as the discussion of this topic are far beyond the frames of the current study.

4. Conclusion

In this study, we analyzed the temperature dependence of the upper critical field anisotropy and the coherence length anisotropy, γ ξ T , in nickelate superconductors for which we proposed simple heuristic expression (Eq. 9) within the 3D Ginzburg-Landau model. The proposed expression for γ ξ T (Eq. 9) is also applicable to some chalcogenide and pnictide superconductors.

Funding

This research was funded by the MINISTRY OF SCIENCE AND HIGHER EDUCATION OF THE RUSSIAN FEDERATION, grant number No. АААА-А18-118020190104-3 (theme “Pressure”). The research funding from the Ministry of Science and Higher Education of the Russian Federation (Ural Federal University Program of Development within the Priority-2030 Program) is gratefully acknowledged. The APC was funded by MDPI.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. D. Li, K. Lee, B. Y. Wang, M. Osada, S. Crossley, H. R. Lee, Y. Cui, Y. Hikita, and H. Y. Hwang. Superconductivity in an infinite-layer nickelate. Nature 2019, 572, 624–627. [Google Scholar]
  2. V. I. Anisimov, D. Bukhvalov, and T. M. Rice. Electronic structure of possible nickelate analogs to the cuprates. Phys. Rev. B 1999, 59, 7901. [Google Scholar] [CrossRef]
  3. Y. Nomura, M. Hirayama, T. Tadano, Y. Yoshimoto, K. Nakamura, and R. Arita. Formation of a two-dimensional single component correlated electron system and band engineering in the nickelate superconductor NdNiO2. Phys. Rev. B 2019, 100, 205138. [Google Scholar] [CrossRef]
  4. S. Zeng, C. S. Tang, X. Yin, C. Li, M. Li, Z. Huang, J. Hu, W. Liu, G. J. Omar, H. Jani, Z. S. Lim, K. Han, D. Wan, P. Yang, S. J. Pennycook, A. T. S. Wee, and A. Ariando. Phase diagram and superconducting dome of infinite layer Nd1-xSrxNiO2 thin films. Phys. Rev. Lett. 2020, 125, 147003. [Google Scholar]
  5. M. Osada, B. Y. Wang, B. H. Goodge, K. Lee, H. Yoon, K. Sakuma, D. Li, M. Miura, L. F. Kourkoutis, and H. Y. Hwang. A superconducting praseodymium nickelate with infinite layer structure. Nano Letters 2020, 20, 5735. [Google Scholar]
  6. Q. Gu, Y. Li, S. Wan, H. Li, W. Guo, H. Yang, Q. Li, X. Zhu, X. Pan, Y. Nie, and H.-H. Wen. Single particle tunnelling spectrum of superconducting Nd1-xSrxNiO2 thin films. Nature Communications 2020, 11, 6027. [Google Scholar] [CrossRef]
  7. E. F. Talantsev. Classifying superconductivity in an infinite-layer nickelate Nd0.8Sr0.2NiO2. Results in Physics 2020, 17, 103118. [Google Scholar] [CrossRef]
  8. Y. Wang, C.-J. Kang, H. Miao, and G. Kotliar. Hund's metal physics: From SrNiO2 to LaNiO2. Phys. Rev. B 2020, 102, 161118. [Google Scholar] [CrossRef]
  9. D. Li, B. Y. Wang, K. Lee, S. P. Harvey, M. Osada, B. H. Goodge, L. F. Kourkoutis, and H. Y. Hwang. Superconducting dome in Nd1-xSrxNiO2 infinite layer films. Phys. Rev. Lett. 2020, 125, 027001. [Google Scholar]
  10. M. Jiang, M. Berciu, and G. A. Sawatzky. Critical nature of the Ni spin state in doped NdNiO2. Phys. Rev. Lett. 2020, 124, 207004. [Google Scholar] [CrossRef]
  11. F. Lechermann. Late transition metal oxides with infinite-layer structure: Nickelates versus cuprates. Phys. Rev. B 2020, 101, 081110. [Google Scholar] [CrossRef]
  12. X. Wu, D. D. Sante, T. Schwemmer, W. Hanke, H. Y. Hwang, S. Raghu, and R. Thomale. Robust dx2-y2-wave superconductivity of infinite-layer nickelates. Phys. Rev. B 2020, 101, 060504. [Google Scholar] [CrossRef]
  13. A. S. Botana and M. R. Norman. Similarities and differences between LaNiO2 and CaCuO2 and implications for superconductivity. Phys. Rev. X 2020, 10, 011024. [Google Scholar]
  14. H. Sakakibara, H. Usui, K. Suzuki, T. Kotani, H. Aoki, and K. Kuroki. Model construction and a possibility of cupratelike pairing in a new d9 nickelate superconductor (Nd,Sr)NiO2. Phys. Rev. Lett. 2020, 125, 077003. [Google Scholar] [CrossRef]
  15. M. Kitatani, L. Si, O. Janson, R. Arita, Z. Zhong, and K. Held. Nickelate superconductors - a renaissance of the one-band Hubbard model. npj Quantum Materials 2020, 5, 59. [Google Scholar] [CrossRef]
  16. P. Adhikary, S. Bandyopadhyay, T. Das, I. Dasgupta, and T. Saha-Dasgupta. Orbital-selective superconductivity in a two-band model of infinite-layer nickelates. Phys. Rev. B 2020, 102, 100501. [Google Scholar] [CrossRef]
  17. Z. Wang, G.-M. Zhang, Y.-f. Yang, and F.-C. Zhang. Distinct pairing symmetries of superconductivity in infinite-layer nickelates. Phys. Rev. B 2020, 102, 220501. [Google Scholar] [CrossRef]
  18. P. Werner and S. Hoshino. Nickelate superconductors: Multiorbital nature and spin freezing. Phys. Rev. B 2020, 101, 041104. [Google Scholar] [CrossRef]
  19. Y. -H. Zhang and A. Vishwanath. Type-II t - J model in superconducting nickelate Nd1-xSrxNiO2. Phys. Rev. Research 2020, 2, 023112. [Google Scholar] [CrossRef]
  20. F. Lechermann. Multiorbital processes rule the Nd1-xSrxNiO2 normal state. Phys. Rev. X 2020, 10, 041002. [Google Scholar]
  21. Leonov, S. L. Skornyakov, and S. Y. Savrasov. Lifshitz transition and frustration of magnetic moments in infinite-layer NdNiO2 upon hole doping. Phys. Rev. B 2020, 101, 241108. [Google Scholar] [CrossRef]
  22. Y. Xiang, Q. Li, Y. Li, H. Yang, Y. Nie, and H.-H. Wen. Physical properties revealed by transport measurements for superconducting Nd0.8Sr0.2NiO2 thin films. Chinese Physics Letters 2021, 38, 047401. [Google Scholar] [CrossRef]
  23. B. Y. Wang, D. Li, B. H. Goodge, K. Lee, M. Osada, S. P. Harvey, L. F. Kourkoutis, M. R. Beasley, and H. Y. Hwang. Isotropic Pauli-limited superconductivity in the infinite layer nickelate Nd0.775Sr0.225NiO2. Nature Physics 2021, 17, 473–477. [Google Scholar] [CrossRef]
  24. B. H. Goodge, D. Li, K. Lee, M. Osada, B. Y. Wang, G. A. Sawatzky, H. Y. Hwang, and L. F. Kourkoutis. Doping evolution of the Mott-Hubbard landscape in infinite-layer nickelates. Proceedings of the National Academy of Sciences 2021, 118, e2007683118. [Google Scholar] [CrossRef]
  25. A. S. Botana, F. Bernardini, and A. Cano. Nickelate superconductors: An ongoing dialog between theory and experiments. Journal of Experimental and Theoretical Physics 2021, 132, 618–627. [Google Scholar] [CrossRef]
  26. F. Lechermann. Doping-dependent character and possible magnetic ordering of NdNiO2. Phys. Rev. Materials 2021, 5, 044803. [Google Scholar] [CrossRef]
  27. X. Wan, V. Ivanov, G. Resta, I. Leonov, and S. Y. Savrasov. Exchange interactions and sensitivity of the Ni two-hole spin state to Hund's coupling in doped NdNiO2. Phys. Rev. B 2021, 103, 075123. [Google Scholar] [CrossRef]
  28. C. -J. Kang and G. Kotliar. Optical properties of the infinite-layer La1-xSrxNiO2 and hidden Hund's physics. Phys. Rev. Lett. 2021, 126, 127401. [Google Scholar] [CrossRef] [PubMed]
  29. H. Lu, M. Rossi, A. Nag, M. Osada, D. F. Li, K. Lee, B. Y. Wang, M. Garcia-Fernandez, S. Agrestini, Z. X. Shen, E. M. Been, B. Moritz, T. P. Devereaux, J. Zaanen, H. Y. Hwang, Ke-Jin Zhou, and W. S. Lee. Magnetic excitations in infinite-layer nickelates. Science 2021, 373, 213–216. [Google Scholar]
  30. Q. Lin, P. Villar Arribi, G. Fabbris, A. S. Botana, D. Meyers, H. Miao, Y. Shen, D. G. Mazzone, J. Feng, S. G. Chiuzb_aian, A. Nag, A. C. Walters, M. Garcia-Fernandez, K.-J. Zhou, J. Pelliciari, I. Jarrige, J. W. Freeland, J. Zhang, J. F. Mitchell, V. Bisogni, X. Liu, M. R. Norman, and M. P. M. Dean. Strong super-exchange in a d9- nickelate revealed by resonant inelastic x-ray scattering. Phys. Rev. Lett. 2021, 126, 087001. [Google Scholar]
  31. Leonov. Effect of lattice strain on the electronic structure and magnetic correlations in infinite-layer (Nd,Sr)NiO2. Journal of Alloys and Compounds 2021, 883, 160888. [Google Scholar] [CrossRef]
  32. P. Choubey and I. M. Eremin. Electronic theory for scanning tunneling microscopy spectra in infinite layer nickelate superconductors. Phys. Rev. B 2021, 104, 144504. [Google Scholar] [CrossRef]
  33. X. -R. Zhou, Z.-X. Feng, P.-X. Qin, H. Yan, X.-N. Wang, P. Nie, H.-J. Wu, X. Zhang, H.-Y. Chen, Z.-A. Meng, Z.-W. Zhu, Z.-Q. Liu. Negligible oxygen vacancies, low critical current density, electric-field modulation, in-plane anisotropic and high-field transport of a superconducting Nd0.8Sr0.2NiO2/SrTiO3 heterostructure. Rare Met. 2021, 40, 2847–2854. [Google Scholar]
  34. E. Chow, S. K. 34. E. Chow, S. K. Sudheesh, P. Nandi, S. W. Zeng, Z. T. Zhang, X. M. Du, Z. S. Lim, Elbert E. M. Chia, and A. Ariando. Pairing symmetry in infinite-layer nickelate superconductor. arXiv, arXiv:2201.10038.
  35. S. P. Harvey, B. Y. 35. S. P. Harvey, B. Y. Wang, J. Fowlie, M. Osada, K. Lee, Y. Lee, D. Li, and H. Y. Hwang. Evidence for nodal superconductivity in infinite-layer nickelates. arXiv, arXiv:2201.12971.
  36. E. Chow, K. Y. 36. E. Chow, K. Y. Yip, M. Pierre, S. W. Zeng, Z. T. Zhang, T. Heil, J. Deuschle, P. Nandi, S. K. Sudheesh, Z. S. Lim, Z. Y. Luo, M. Nardone, A. Zitouni, P. A. van Aken, M. Goiran, S. K. Goh, W. Escoffier, and A. Ariando, Pauli-limit violation in lanthanide infinite-layer nickelate superconductors. arXiv, arXiv:2204.12606.
  37. Fowlie, M. Hadjimichael, M. M. Martins, D. Li, M. Osada, B. Y. Wang, K. Lee, Y. Lee, Z. Salman, T. Prokscha, J.-M. Triscone, H. Y. Hwang, and A. Suter. Intrinsic magnetism in superconducting infinite-layer nickelates. Nature Physics 2022, 18, 1043–1047. [Google Scholar] [CrossRef]
  38. H. Chen, A. Hampel, J. Karp, F. Lechermann, and A. Millis. Dynamical mean field studies of infinite layer nickelates: Physics results and methodological implications. Front. Phys. 2022, 10, 835942. [Google Scholar] [CrossRef]
  39. C. Lu, L.-H. Hu, Y. Wang, F. Yang, and C. Wu. Two-orbital model for possible superconductivity pairing mechanism in nickelates. Phys. Rev. B 2022, 105, 054516. [Google Scholar] [CrossRef]
  40. T. Y. Xie, Z. Liu, Chao Cao, Z. F.Wang, J. L. Yang, and W. Zhu. Microscopic theory of superconducting phase diagram in infinite-layer nickelates. Phys. Rev. B 2022, 106, 035111. [Google Scholar] [CrossRef]
  41. 41. Jiang. Characterizing the superconducting instability in a two-orbital d-s model: insights to infinite-layer nickelate superconductors. arXiv, arXiv:2201.12967.
  42. Karp, A. Hampel, and A. J. Millis. Superconductivity and antiferromagnetism in NdNiO2 and CaCuO2: A cluster DMFT study. Phys. Rev. B 2022, 105, 205131. [Google Scholar] [CrossRef]
  43. A. Kreisel, B. M. 43. A. Kreisel, B. M. Andersen, A. T. Roemer, I. M. Eremin, and F. Lechermann. Superconducting instabilities in strongly-correlated infinite-layer nickelates. arXiv, arXiv:2202.11135.
  44. G. Krieger, L. Martinelli, S. Zeng, L. E. Chow, K. Kummer, R. Arpaia, M. Moretti Sala, N. B. Brookes, A. Ariando, N. Viart, M. Salluzzo, G. Ghiringhelli, and D. Preziosi. Charge and spin order dichotomy in NdNiO2 driven by the SrTiO3 capping layer. Phys. Rev. Lett. 2022, 129, 027002. [Google Scholar]
  45. S. W. Zeng, X. M. Yin, C. J. Li, L. E. Chow, C. S. Tang, K. Han, Z. Huang, Y. Cao, D. Y. Wan, Z. T. Zhang, Z. S. Lim, C. Z. Diao, P. Yang, A. T. S. Wee, S. J. Pennycook, and A. Ariando. Observation of perfect diamagnetism and interfacial effect on the electronic structures in infinite layer Nd0.8Sr0.2NiO2 superconductors. Nature Communications 2022, 13, 743. [Google Scholar]
  46. C. C. Tam, J. Choi, X. Ding, S. Agrestini, A. Nag, M. Wu, B. Huang, H. Luo, P. Gao, M. García-Fernández, L. Qiao, and K.-J. Zhou. Charge density waves in infinite-layer NdNiO2 nickelates. Nature Materials 2022, 21, 1116–1120. [Google Scholar]
  47. Rossi, M. Osada, J. Choi, S. Agrestini, D. Jost, Y. Lee, H. Lu, B. Y. Wang, K. Lee, A. Nag, Y.-D. Chuang, C.-T. Kuo, S.-J. Lee, B. Moritz, T. P. Devereaux, Z.-X. Shen, J.-S. Lee, K.-J. Zhou, H. Y. Hwang, W.-S. Lee. A broken translational symmetry state in an infinite-layer nickelate. Nature Physics 2022, 18, 869–873. [Google Scholar]
  48. G. A. Pan, D. F. Segedin, H. LaBollita, Q. Song, E. M. Nica, B. H. Goodge, A. T. Pierce, S. Doyle, S. Novakov, D. C. Carrizales, A. T. N'Diaye, P. Shafer, H. Paik, J. T. Heron, J. A. Mason, A. Yacoby, L. F. Kourkoutis, O. Erten, C. M. Brooks, A. S. Botana, and J. A. Mundy. Superconductivity in a quintuple-layer square-planar nickelate. Nature Materials 2022, 21, 160–164. [Google Scholar]
  49. N. Wang, M. W. Yang, Z. Yang, K. Y. Chen, H. Zhang, Q. H. Zhang, Z. H. Zhu, Y. Uwatoko, L. Gu, X. L. Dong, J. P. Sun, K. J. Jin, and J.-G. Cheng. Pressure-induced monotonic enhancement of Tc to over 30 K in superconducting Pr0.82Sr0.18NiO2 thin films. Nature Communications 2022, 13, 4367. [Google Scholar]
  50. L. E. Chow, K. L. E. Chow, K. Rubi, K. Y. Yip, M. Pierre, M. Leroux, X. Liu, Z. Luo, S. Zeng, C. Li, M. Goiran, N. Harrison, W. Escoffier, S. K. Goh, A. Ariando. Dimensionality control and rotational symmetry breaking superconductivity in square-planar layered nickelates. arXiv. [CrossRef]
  51. Q. Li, C. He, J. Si, X. Zhu, Y. Zhang, and H.-H. Wen. Absence of superconductivity in bulk Nd1−xSrxNiO2. Communications Materials 2020, 1, 16. [Google Scholar] [CrossRef]
  52. Tinkham. Introduction to Superconductivity, 2nd ed. (McGraw Hill, New York, 1996), pp. 141–143.
  53. H. Matsuoka, M. Nakano, T. Shitaokoshi, T. Ouchi, Y. Wang, Y. Kashiwabara, S. Yoshida, K. Ishizaka, M. Kawasaki, Y. Kohama, T. Nojima, and Y. Iwasa. Angle dependence of Hc2 with a crossover between the orbital and paramagnetic limits. Physical Review Research 2020, 2, 012064. [Google Scholar]
  54. Y. Cao, J. M. Park, K. Watanabe, T. Taniguchi, P. Jarillo-Herrero. Pauli-limit violation and re-entrant superconductivity in moiré graphene. Nature 2021, 595, 526–531. [Google Scholar] [CrossRef]
  55. Y. Saito, T. Nojima, Y. Iwasa. Highly crystalline 2D superconductors. Nat. Rev. Mater. 2017, 2, 16094. [Google Scholar]
  56. V. Buntar, F. M. Sauerzopf, H. W. Weber, J. E. Fischer, H. Kuzmany, and M. Halushka. Mixed-state parameters and vortex pinning in single-crystalline K3C60 fullerene superconductors. Phys. Rev. B 1997, 56, 14128–14137. [Google Scholar] [CrossRef]
  57. G. K. Perkins, J. Moore, Y. Bugoslavsky, L. F. Cohen, J. Jun, S. M. Kazakov, J. Karpinski and A. D. Caplin. Superconducting critical fields and anisotropy of a MgB2 single crystal. Supercond. Sci. Technol. 2002, 15, 1156–1159. [Google Scholar] [CrossRef]
  58. Zehetmayer, M. Eisterer, J. Jun, S. M. Kazakov, J. Karpinski, A. Wisniewski, and H. W. Weber. Mixed-state properties of superconducting MgB2 single crystals. Phys. Rev. B 2002, 66, 052505. [Google Scholar] [CrossRef]
  59. F. Honda, S. 59. F. Honda, S. Kobayashi, N. Kawamura, S. Kawaguchi, T. Koizumi, Y. J. Sato, Y. Homma, N. Ishimatsu, J. Gouchi, Y. Uwatoko, H. Harima, J. Flouquet, and D. Aoki. Pressure-induced structural transition and new superconducting phase in UTe2. arXiv, arXiv:2211.02361.
  60. S. Kasahara, H. Suzuki, T. Machida, Y. Sato, Y. Ukai, H. Murayama, S. Suetsugu, Y. Kasahara, T. Shibauchi, T. Hanaguri, and Y. Matsuda. Quasiparticle nodal plane in the Fulde-Ferrell-Larkin-Ovchinnikov state of FeSe. Phys. Rev. Lett. 2021, 127, 257001. [Google Scholar]
  61. C. C. Zhao, L. S. C. C. Zhao, L. S. Wang, W. Xia, Q. W. Yin, J. M. Ni, Y. Y. Huang, C. P. Tu, Z. C. Tao, Z. J. Tu, C. S. Gong, H. C. Lei, Y. F. Guo, X. F. Yang, and S. Y. Li. Nodal superconductivity and superconducting domes in the topological Kagome metal CsV3Sb5. arXiv:2102. 0835. [Google Scholar] [CrossRef]
  62. T. Tayama, A. Harita, T. Sakakibara, Y. Haga, H. Shishido, R. Settai, and Y. Onuki. Unconventional heavy-fermion superconductor CeCoIn5: dc magnetization study at temperatures down to 50 mK. Physical Review B 2002, 65, 180504. [Google Scholar] [CrossRef]
  63. D. Y. Yan, M. Yang, C. X. Wang, P. B. Song, C. J. Yi, Y. G. Shi. Superconductivity in centrosymmetric topological superconductor candidate TaC. Superconductor Science and Technology 2021, 34, 035025. [Google Scholar] [CrossRef]
  64. D. Yan, et al. Superconductivity and Fermi-surface nesting in the candidate Dirac semimetal NbC. Physical Review B 2020, 102, 205117. [Google Scholar] [CrossRef]
  65. Y. Li, et al. Critical magnetic fields of superconducting aluminum-substituted Ba8Si42Al4 clathrate. Journal of Applied Physics 2015, 117, 213912. [Google Scholar] [CrossRef]
  66. F. Buta, M. Bonura, D. Matera, G. Bovone, A. Ballarino, S. C. Hopkins, B. Bordini, X. Chaud, and C. Senatore. Very high upper critical fields and enhanced critical current densities in Nb3Sn superconductors based on Nb–Ta–Zr alloys and internal oxidation. Journal of Physics: Materials 2021, 4, 025003. [Google Scholar]
  67. Y. Skourski, G. Fuchs, P. Kerschl, N. Kozlov, D. Eckert, K. Nenkov, K.-H. Mueller. Magnetization and magneto-resistance measurements of bulk YBa2Cu3O7-x in pulsed magnetic fields up to 50 T. Physica B 2004, 346–347, 325–328. [Google Scholar]
  68. C. L. Zhang, X. He, Z. W. Li, S. J. Zhang, B. S. Min, J. Zhang, K. Lu, J. F. Zhao, L. C. Shi, Y. Peng, X. C. Wang, S. M. Feng, R. C. Yu, L. H. Wang, V. B. Prakapenka, S. Chariton, H. Z. Liu, C. Q. Jin. Superconductivity above 80 K in polyhydrides of hafnium. Materials Today Physics 2022, 27, 100826. [Google Scholar]
  69. S. I. Vedeneev, B. A. Piot, D. K. Maude, A. V. Sadakov. Temperature dependence of the upper critical field of FeSe single crystals. Phys. Rev. B 2013, 87, 134512. [Google Scholar] [CrossRef]
  70. W. Wei, W. 70. W. Wei, W. Sun, Y. Sun, Y. Pan, G. Jin, F. Yang, Y. Li, Z. Zhu, Y. Nie, Z. Shi. Large upper critical fields and dimensionality crossover of superconductivity in infinite-layer nickelate La0.8Sr0.2NiO2. arXiv, arXiv:2304.14196.
  71. H. Zhang, W. Zhong, Y. Meng, B. Yue, X. Yu, J.-T. Wang, and F. Hong. Superconductivity above 12 K with possible multiband features in CsCl-type PbS. Phys. Rev. B 2023, 107, 174502. [Google Scholar] [CrossRef]
  72. R. Gupta, D. Das, C. H. Mielke, III, Z. Guguchia, T. Shiroka, C. Baines, M. Bartkowiak, H. Luetkens, R. Khasanov, Q. Yin, Z. Tu, C. Gong, and He. Lei. Microscopic evidence for anisotropic multigap superconductivity in the CsV3Sb5 kagome superconductor. npj Quantum Materials 2022, 7, 49. [Google Scholar]
  73. B. -B. Ruan, L.-W. Chen, Y.-Q. Shi, J.-K. Yi, Q.-S. Yang, M.-H. Zhou, M.-W. Ma, G.-F. Chen, and Z.-A. Ren. Superconductivity in Mo4Ga20As with endohedral gallium clusters. arXiv 2023, arXiv:2305.02838. [Google Scholar]
  74. T. Shang, J. 74. T. Shang, J. Meng, X. Y. Zhu, H. Zhang, B. C. Yu, Z. X. Zhen, Y. H. Wang, Y. Xu, Q. F. Zhan, D. J. Gawryluk, and T. Shiroka. Fully-gapped superconductivity with preserved time-reversal symmetry in NiBi3 single crystals. arXiv, arXiv:2305.03278.
  75. Y. Xing, et al. Quantum Griffiths singularity of superconductor-metal transition in Ga thin films. Science 2015, 350, 542–545. [Google Scholar] [CrossRef]
  76. S. C. de la Barrera, et al. Tuning Ising superconductivity with layer and spin–orbit coupling in two-dimensional transition-metal dichalcogenides. Nat Commun 2018, 9, 1427. [Google Scholar] [CrossRef]
  77. Y. Liu, et al. Anomalous quantum Griffiths singularity in ultrathin crystalline lead films. Nature Communications 2019, 10, 3633. [Google Scholar] [CrossRef]
  78. J. M. Park, Y. Cao, L.-Q. Xia, S. Sun, K. Watanabe, T. Taniguchi, and P. Jarillo-Herrero. Robust superconductivity in magic-angle multilayer graphene family. Nature Materials 2022, 21, 877–883. [Google Scholar] [CrossRef]
  79. L. N. Bulaevskii, V. L. Ginzburg, A. A. Sobyanin. Macroscopic theory of superconductors with small coherence length. Physica C 1988, 152, 378–388. [Google Scholar] [CrossRef]
  80. V. J. Emery, S. A. Kivelson. Importance of phase fluctuations in superconductors with small superfluid density. Nature 1995, 374, 434–437. [Google Scholar] [CrossRef]
  81. A. Larkin, V. A. Larkin, V. Varlamov. Theory of Fluctuations in Superconductors (Oxford University Press, Oxford, 2005).
  82. T. He, Q. Huang, A. P. Ramirez, Y. Wang, K. A. Regan, N. Rogado, M. A. Hayward, M. K. Haas, J. S. Slusky, K. Inumara, H. W. Zandbergen, N. P. Ong, and R. J. Cava. Superconductivity in the non-oxide perovskite MgCNi3. Nature 2001, 411, 54–56. [Google Scholar]
  83. J. Chen, L. Jiao, J. L. Zhang, Y. Chen, L. Yang, M. Nicklas, F. Steglich, and H. Q. Yuan. BCS-like superconductivity in the noncentrosymmetric compounds NbxRe1-x (0.13 < x < 0.38). Phys. Rev. B 2013, 88, 144510. [Google Scholar]
  84. J. Pan, W. H. Jiao, X. C. Hong, Z. Zhang, L. P. He, P. L. Cai, J. Zhang, G. H. Cao, and S. Y. Li. Nodal superconductivity and superconducting dome in the layered superconductor Ta4Pd3Te16. Phys. Rev. B 2015, 92, 180505. [Google Scholar] [CrossRef]
  85. D. Adroja, A. Bhattacharyya, P. K. Biswas, M. Smidman, A. D. Hillier, H. Mao, H. Luo, G.-H. Cao, Z. Wang, and C. Wang. Multigap superconductivity in ThAsFeN investigated using μSR measurements. Phys. Rev. B 2017, 96, 144502. [Google Scholar] [CrossRef]
  86. Zhou, Y. Sun, C. Y. Xi, Z. S. Wang, J. L. Zhang, Y. Zhang, Y. F. Zhang, C. Q. Xu, Y. Q. Pan, J. J. Feng, Y. Meng, X. L. Yi, L. Pi, T. Tamegai, X. Xing and Z. Shi. Disorder-robust high-field superconducting phase of FeSe single crystals. Phys. Rev. B 2021, 104, L140504. [Google Scholar] [CrossRef]
  87. M. Mandal, C. Patra, A. Kataria, D. Singh, P. K. Biswas, J. S. Lord, A. D. Hillier, and R. P. Singh. Superconducting ground state of nonsymmorphic superconducting compound Zr2Ir. Phys. Rev. B 2021, 104, 054509. [Google Scholar] [CrossRef]
  88. Z. Ryżyńska, J. R. Chamorro, T. M. McQueen, P. Wiśniewski, D. Kaczorowski, W. Xie, R. J. Cava, T. Klimczuk, and M. J. Winiarski. RuAl6 - An endohedral aluminide superconductor. Chem. Mater. 2020, 32, 3805–3812. [Google Scholar]
  89. T. Takenaka, K. Ishihara, M. Roppongi, Y. Miao, Y. Mizukami, T. Makita, J. Tsurumi, S. Watanabe, J. Takeya, M. Yamashita, K. Torizuka, Y. Uwatoko, T. Sasaki, X. Huang, W. Xu, D. Zhu, N. Su, J.-G. Cheng, T. Shibauchi, K. Hashimoto. Strongly correlated superconductivity in a copper-based metal-organic framework with a perfect kagome lattice. Science Advances 2021, 7, eabf3996. [Google Scholar]
  90. X. Gui and R. J. Cava. LaIr3Ga2: A superconductor based on a Kagome lattice of Ir. Chemistry of Materials 2022, 34, 2824–2832. [Google Scholar] [CrossRef]
  91. J. Wang, T. J. Wang, T. Ying, J. Deng, C. Pei, T. Yu, X. Chen, Y. Wan, M. Yang, W. Dai, D. Yang, Y. Li, S. Li, S. Iimura, S. Du, H. Hosono, Y. Qi, J.-g. Guo. Superconductivity in an orbital-reoriented SnAs square lattice: A case study of Li0.6Sn2As2 and NaSnAs, Angewandte Chemie (International Edition) accepted; doi.org/10.1002/anie.202216086.
  92. F. H. Yu, D. H. Ma, W. Z. Zhuo, S. Q. Liu, X. K. Wen, B. Lei, J. J. Ying, and X. H. Chen. Unusual competition of superconductivity and charge-density-wave state in a compressed topological kagome metal. Nature Communications 2021, 12, 3645. [Google Scholar] [CrossRef]
  93. Y. Sun, Z. Shi, and T. Tamegai. Review of annealing effects and superconductivity in Fe1+yTe1-xSex superconductors. Supercond. Sci. Technol. 2019, 32, 103001. [Google Scholar] [CrossRef]
  94. J. Yuan, et al. Scaling of the strange-metal scattering in unconventional superconductors. Nature 2022, 602, 431–436. [Google Scholar] [CrossRef] [PubMed]
  95. Y. Saito, J. Ge, K. Watanabe, T. Taniguchi, and A. F. Young. Independent superconductors and correlated insulators in twisted bilayer graphene. Nature Physics 2020, 16, 926–930. [Google Scholar] [CrossRef]
  96. E. F. Talantsev, W. P. Crump, J. G. Storey, J. L. Tallon. London penetration depth and thermal fluctuations in the sulphur hydride 203 K superconductor. Annalen der Physik 2017, 529, 1700197. [Google Scholar]
  97. J. L. Tallon and E. F. Talantsev. Compressed H3S, superfluid density and the quest for room-temperature superconductivity. J. Supercond. Nov. Magn. 2018, 31, 619–624. [Google Scholar] [CrossRef]
  98. B. Y. Wang, T. C. 98. B. Y. Wang, T. C. Wang, Y.-T. Hsu, M. Osada, K. Lee, C. Jia, C. Duffy, D. Li, J. Fowlie, M. R. Beasley, T. P. Devereaux, I. R. Fisher, N. E. Hussey, H. Y. Hwang. Rare-earth control of the superconducting upper critical field in infinite-layer nickelates. arXiv, arXiv:2205.15355.
  99. Y. Kamihara, H. Hiramatsu, M. Hirano, R. Kawamura, H. Yanagi, T. Kamiya, and H. Hosono. Iron-based layered superconductor. LaOFeP. J. Am. Chem. Soc 2006, 128, 10012–10013. [Google Scholar] [CrossRef] [PubMed]
  100. Y. Kamihara, T. Watanabe, M. Hirano, and H. Hosono. Iron-based layered superconductor La[O1-xFx]FeAs (x = 0.05−0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef]
  101. L. Jiao, Y. Kohama, J. L. Zhang, H. D. Wang, B. Maiorov, F. F. Balakirev, Y. Chen, L. N. Wang, T. Shang, M. H. Fang, and H. Q. Yuan. Upper critical field and thermally activated flux flow in single-crystalline Tl0.58Rb0.42Fe1.72Se2. Phys. Rev. B 2012, 85, 064513. [Google Scholar] [CrossRef]
  102. F. Harper, M. Tinkham. The mixed state in superconducting thin films. Phys. Rev. 1968, 172, 441–450. [Google Scholar] [CrossRef]
  103. X. S. Wu, P. W. Adams, Y. Yang, and R. L. McCarley. Spin proximity effect in ultrathin superconducting Be–Au bilayers. Phys. Rev. Lett. 2006, 96, 127002. [Google Scholar] [CrossRef]
  104. M. B. Shalom, M. Sachs, D. Rakhmilevitch, A. Palevski, and Y. Dagan. Tuning spin–orbit coupling and superconductivity at the SrTiO3/LaAlO3 interface: a magnetotransport study. Phys. Rev. Lett. 2010, 104, 126802. [Google Scholar] [CrossRef]
  105. M. Fang, J. Yang, F. F. Balakirev, Y. Kohama, J. Singleton, B. Qian, Z. Q. Mao, Hangdong Wang, and H. Q. Yuan. Weak anisotropy of the superconducting upper critical field in Fe1.11Te0.6Se0.4 single crystals. Phys. Rev. B 2010, 81, 020509. [Google Scholar] [CrossRef]
  106. Y. Sun, Z. Shi, T. Tamegai. Review of annealing effects and superconductivity in Fe1+yTe1-xSex superconductors. Supercond. Sci. Technol. 2019, 32, 103001. [Google Scholar] [CrossRef]
  107. J. L. Zhang, L. Jiao, Y. Chen, H. Q. Yuan. Universal behavior of the upper critical field in iron based superconductors. Frontiers of Physics 2011, 6, 463–473. [Google Scholar] [CrossRef]
  108. D. A. Zocco, K. Grube, F. Eilers, T. Wolf, and H. v. Löhneysen. Pauli-Limited Multiband Superconductivity in KFe2As2. Phys. Rev. Lett. 2013, 111, 057007. [Google Scholar] [CrossRef]
  109. S. Khim, B. Lee, J. W. Kim, E. S. Choi, G. R. Stewart, and K. H. Kim. Pauli-limiting effects in the upper critical fields of a clean LiFeAs single crystal. Phys. Rev. B 2011, 84, 104502. [Google Scholar] [CrossRef]
  110. J. L. Zhang, L. Jiao, F. F. Balakirev, X. C. Wang, C. Q. Jin, and H. Q. Yuan. Upper critical field and its anisotropy in LiFeAs. Phys. Rev. B 2011, 83, 174506. [Google Scholar]
  111. C. Kittel. Introduction to Solid State Physics, Seventh Ed (John Wiley and Sons, Inc., New York, 1957).
  112. S. Mugiraneza, and A. M. Hallas. Tutorial: a beginner’s guide to interpreting magnetic susceptibility data with the Curie-Weiss law. Communications Physics 2022, 5, 95. [Google Scholar] [CrossRef]
  113. R. Werthamer, E. Helfand, and P.C. Hohenberg. Temperature and purity dependence of the superconducting critical field, Hc2. III. Electron spin and spin–orbit effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
  114. A. Gurevich. Enhancement of the upper critical field by nonmagnetic impurities in dirty two-gap superconductors. Phys. Rev. B 2003, 67, 184515. [Google Scholar] [CrossRef]
  115. J. Hänisch, K. Iida, F. Kurth, E. Reich, C. Tarantini, J. Jaroszynski, T. Förster, G. Fuchs, R. Hühne, V. Grinenko, L. Schultz, and B. Holzapfel. High field superconducting properties of Ba(Fe1-xCox)2As2 thin films. Scientific Reports 2015, 5, 17363. [Google Scholar]
  116. Y. Pan, Y. 116. Y. Pan, Y. Sun, N. Zhou, X. Yi, J. Wang, Z. Zhu, H. Mitamura, M. Tokunaga, Z. Shi. Novel anisotropy of upper critical fields in Fe1+yTe0.6Se0.4. arXiv, arXiv:2305.04515.
  117. R. Prozorov, M. A. Tanatar, R. T. Gordon, C. Martin, H. Kim, V. G. Kogan, N. Ni, M.E. Tillman, S. L. Bud’ko, P. C. Canfield. Anisotropic London penetration depth and superfluid density in single crystals of iron-based pnictide superconductors. Physica C 2009, 469, 582–589. [Google Scholar] [CrossRef]
  118. V. G. Kogan, R. Prozorov, and A. E. Koshelev. Temperature-dependent anisotropies of upper critical field and London penetration depth. Physical Review B 2019, 100, 014518. [Google Scholar] [CrossRef]
  119. D. Torsello, E. Piatti, G. A. Ummarino, X. Yi, X. Xing, Z. Shi, G. Ghigo, and D. Daghero. Nodal multigap superconductivity in the anisotropic iron-based compound RbCa2Fe4As4F2. npj Quantum Materials 2022, 7, 10. [Google Scholar] [CrossRef]
Preprints 73480 g001
Figure 1. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the La0.8Ca0.2NiO2 film with a physical thickness d s c = 15   n m . The raw data were reported by Chow et al [36]. Deduced parameters are: d s c , G L = 8.0 ± 0.1   n m , T c = 7.35 ± 0.03   K , ξ a b 0 = 3.99 ± 0.02   n m . The goodness of fit is (a) 0.9975 and (b) 0.9907. The 95% confidence bands are indicated by pink-shaded areas.
Figure 1. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the La0.8Ca0.2NiO2 film with a physical thickness d s c = 15   n m . The raw data were reported by Chow et al [36]. Deduced parameters are: d s c , G L = 8.0 ± 0.1   n m , T c = 7.35 ± 0.03   K , ξ a b 0 = 3.99 ± 0.02   n m . The goodness of fit is (a) 0.9975 and (b) 0.9907. The 95% confidence bands are indicated by pink-shaded areas.
Preprints 73480 g001
Preprints 73480 g003
Figure 3. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the La0.8Sr0.2NiO2 film with a physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: d s c , G L = 9.5 ± 0.1   n m , T c = 6.45 ± 0.01   K , ξ a b 0 = 4.11 ± 0.03   n m . The goodness of fit is (a) 0.9964 and (b) 0.9837. The 95% confidence bands are indicated by pink-shaded areas.
Figure 3. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the La0.8Sr0.2NiO2 film with a physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: d s c , G L = 9.5 ± 0.1   n m , T c = 6.45 ± 0.01   K , ξ a b 0 = 4.11 ± 0.03   n m . The goodness of fit is (a) 0.9964 and (b) 0.9837. The 95% confidence bands are indicated by pink-shaded areas.
Preprints 73480 g003
Preprints 73480 g005
Figure 5. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the Pr0.8Sr0.2NiO2 film with a physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: d s c , G L = 9.1 ± 0.1   n m , T c = 12.11 ± 0.01   K , ξ a b 0 = 3.11 ± 0.03   n m . The goodness of fit is (a) 0.9982 and (b) 0.9976. The 95% confidence bands are indicated by pink shaded areas.
Figure 5. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the Pr0.8Sr0.2NiO2 film with a physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: d s c , G L = 9.1 ± 0.1   n m , T c = 12.11 ± 0.01   K , ξ a b 0 = 3.11 ± 0.03   n m . The goodness of fit is (a) 0.9982 and (b) 0.9976. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g005
Preprints 73480 g006
Figure 6. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for Pr0.8Sr0.2NiO2 film with physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: T c = 12.15 ± 0.04   K , ξ a b 0 = 3.12 ± 0.01   n m , γ ξ 0 = 1.06 ± 0.02 , a = 1.31 ± 0.03 . The goodness of fit is (a) 0.9984 and (b) 0.9985. The 95% confidence bands are indicated by pink shaded areas.
Figure 6. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for Pr0.8Sr0.2NiO2 film with physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: T c = 12.15 ± 0.04   K , ξ a b 0 = 3.12 ± 0.01   n m , γ ξ 0 = 1.06 ± 0.02 , a = 1.31 ± 0.03 . The goodness of fit is (a) 0.9984 and (b) 0.9985. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g006
Preprints 73480 g007
Figure 7. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the Nd0.825Sr0.175NiO2 film with a physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: d s c , G L = 12.4 ± 0.2   n m , T c = 13.52 ± 0.04   K , ξ a b 0 = 3.96 ± 0.04   n m . The goodness of fit is (a) 0.9658 and (b) 0.9909. The 95% confidence bands are indicated by pink-shaded areas.
Figure 7. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the Nd0.825Sr0.175NiO2 film with a physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: d s c , G L = 12.4 ± 0.2   n m , T c = 13.52 ± 0.04   K , ξ a b 0 = 3.96 ± 0.04   n m . The goodness of fit is (a) 0.9658 and (b) 0.9909. The 95% confidence bands are indicated by pink-shaded areas.
Preprints 73480 g007
Preprints 73480 g008
Figure 8. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for Nd0.825Sr0.175NiO2 film with physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: T c = 14.2 ± 0.1   K , ξ a b 0 = 4.00 ± 0.03   n m , γ ξ 0 = 1.16 ± 0.03 , a = 2.3 ± 0.2 . The goodness of fit is (a) 0.9846 and (b) 0.9900. The 95% confidence bands are indicated by pink shaded areas.
Figure 8. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for Nd0.825Sr0.175NiO2 film with physical thickness d s c ~ 7   n m . Raw data reported by Wang et al [98]. Deduced parameters are: T c = 14.2 ± 0.1   K , ξ a b 0 = 4.00 ± 0.03   n m , γ ξ 0 = 1.16 ± 0.03 , a = 2.3 ± 0.2 . The goodness of fit is (a) 0.9846 and (b) 0.9900. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g008
Preprints 73480 g009
Figure 9. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the La0.8Sr0.2NiO2 film with a physical thickness d s c = 6.8   n m . Raw data reported by Wei et al [70]. Deduced parameters are: d s c , G L = 7.49 ± 0.07   n m , T c = 17.62 ± 0.02   K , ξ a b 0 = 2.94 ± 0.01   n m . The goodness of fit is (a) 0.9978 and (b) 0.9962. The 95% confidence bands are indicated by pink shaded areas.
Figure 9. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for the La0.8Sr0.2NiO2 film with a physical thickness d s c = 6.8   n m . Raw data reported by Wei et al [70]. Deduced parameters are: d s c , G L = 7.49 ± 0.07   n m , T c = 17.62 ± 0.02   K , ξ a b 0 = 2.94 ± 0.01   n m . The goodness of fit is (a) 0.9978 and (b) 0.9962. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g009
Preprints 73480 g010
Figure 10. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for La0.8Sr0.2NiO2 film with physical thickness d s c = 6.8   n m . Raw data reported by Wei et al [70]. Deduced parameters are: T c = 17.83 ± 0.05   K , ξ a b 0 = 2.96 ± 0.01   n m , γ ξ 0 = 1.26 ± 0.02 , a = 1.31 ± 0.02 . The goodness of fit is (a) 0.9965 and (b) 0.9976. The 95% confidence bands are indicated by pink shaded areas.
Figure 10. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for La0.8Sr0.2NiO2 film with physical thickness d s c = 6.8   n m . Raw data reported by Wei et al [70]. Deduced parameters are: T c = 17.83 ± 0.05   K , ξ a b 0 = 2.96 ± 0.01   n m , γ ξ 0 = 1.26 ± 0.02 , a = 1.31 ± 0.02 . The goodness of fit is (a) 0.9965 and (b) 0.9976. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g010
Preprints 73480 g011
Figure 11. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for bulk single crystal Tl0.58Rb0.42Fe1.72Se2. The raw data reported by Jiao et al [101]. Deduced parameters are: d s c , G L = 5.57 ± 0.06   n m , T c = 32.26 ± 0.01   K , ξ a b 0 = 2.38 ± 0.01   n m . The goodness of fit is (a) 0.9986 and (b) 0.9968. The 95% confidence bands are indicated by pink-shaded areas.
Figure 11. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for bulk single crystal Tl0.58Rb0.42Fe1.72Se2. The raw data reported by Jiao et al [101]. Deduced parameters are: d s c , G L = 5.57 ± 0.06   n m , T c = 32.26 ± 0.01   K , ξ a b 0 = 2.38 ± 0.01   n m . The goodness of fit is (a) 0.9986 and (b) 0.9968. The 95% confidence bands are indicated by pink-shaded areas.
Preprints 73480 g011
Preprints 73480 g012
Figure 12. The global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for bulk single crystal Tl0.58Rb0.42Fe1.72Se2. The raw data reported by Jiao et al [101]. Deduced parameters are: T c = 32.8 ± 0.1   K , ξ a b 0 = 2.40 ± 0.01   n m , γ ξ 0 = 1.24 ± 0.04 , a = 1.29 ± 0.03 . The goodness of fit is (a) 0.9984 and (b) 0.9994. The 95% confidence bands are indicated by pink shaded areas.
Figure 12. The global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for bulk single crystal Tl0.58Rb0.42Fe1.72Se2. The raw data reported by Jiao et al [101]. Deduced parameters are: T c = 32.8 ± 0.1   K , ξ a b 0 = 2.40 ± 0.01   n m , γ ξ 0 = 1.24 ± 0.04 , a = 1.29 ± 0.03 . The goodness of fit is (a) 0.9984 and (b) 0.9994. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g012
Preprints 73480 g013
Figure 13. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for bulk single crystal Fe1.11Te0.6Te0.4. Raw data reported by Fang et al [105]. Deduced parameters are: d s c , G L = 9.65 ± 0.01   n m , T c = 13.70 ± 0.01   K , ξ a b 0 = 2.65 ± 0.01   n m . The goodness of fit is (a) 0.9986 and (b) 0.9966. The 95% confidence bands are indicated by pink-shaded areas.
Figure 13. (a) B c 2 , p e r p T and (b) B c 2 , p a r a T data and global fit to the 2D-GL model (Eqs. 1,2) for bulk single crystal Fe1.11Te0.6Te0.4. Raw data reported by Fang et al [105]. Deduced parameters are: d s c , G L = 9.65 ± 0.01   n m , T c = 13.70 ± 0.01   K , ξ a b 0 = 2.65 ± 0.01   n m . The goodness of fit is (a) 0.9986 and (b) 0.9966. The 95% confidence bands are indicated by pink-shaded areas.
Preprints 73480 g013
Preprints 73480 g014
Figure 14. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for bulk single crystal Fe1.11Te0.6Se0.4. Raw data reported by Fang et al [105]. Deduced parameters are: T c = 13.74 ± 0.04   K , ξ a b 0 = 2.60 ± 0.01   n m , γ ξ 0 = 0.88 ± 0.01 , a = 1.40 ± 0.03 . The goodness of fit is (a) 0.9988 and (b) 0.9989. The 95% confidence bands are indicated by pink shaded areas.
Figure 14. Global fit to our model (Eqs. 7-9) for (a) B c 2 , p e r p T , (b) B c 2 , p a r a T , and (c) deduced ξ a b T and γ ξ T for bulk single crystal Fe1.11Te0.6Se0.4. Raw data reported by Fang et al [105]. Deduced parameters are: T c = 13.74 ± 0.04   K , ξ a b 0 = 2.60 ± 0.01   n m , γ ξ 0 = 0.88 ± 0.01 , a = 1.40 ± 0.03 . The goodness of fit is (a) 0.9988 and (b) 0.9989. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g014
Preprints 73480 g015
Figure 15. γ ξ T data and fit to Eq. 9 for single crystal pnictide KFe2As2 superconductor. Raw data reported by Zocco et al [108]. Deduced parameters are: T c = 3.4   ( f i x e d ) , γ ξ 0 = 3.15 ± 0.03 , a = 1.62 ± 0.02 . The goodness of fit is 0.9963. The 95% confidence bands are indicated by pink shaded areas.
Figure 15. γ ξ T data and fit to Eq. 9 for single crystal pnictide KFe2As2 superconductor. Raw data reported by Zocco et al [108]. Deduced parameters are: T c = 3.4   ( f i x e d ) , γ ξ 0 = 3.15 ± 0.03 , a = 1.62 ± 0.02 . The goodness of fit is 0.9963. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g015
Preprints 73480 g016
Figure 16. γ ξ T data and fit to Eq. 9 for single crystal pnictide KFe2As2 superconductor. (a) Raw data reported by Khim et al [109]. Parameters are: T c = 17.4   ( f i x e d ) [109], γ ξ 0 = 1.22 ± 0.03 , a = 1.62 ± 0.05 . The goodness of fit is 0.9777. (b) Raw data reported by Zhang et al [110]. Parameters are: T c = 17.5   ( f i x e d ) [110], γ ξ 0 = 1.39 ± 0.02 , a = 1.89 ± 0.06 . The goodness of fit is 0.9871. The 95% confidence bands are indicated by pink shaded areas.
Figure 16. γ ξ T data and fit to Eq. 9 for single crystal pnictide KFe2As2 superconductor. (a) Raw data reported by Khim et al [109]. Parameters are: T c = 17.4   ( f i x e d ) [109], γ ξ 0 = 1.22 ± 0.03 , a = 1.62 ± 0.05 . The goodness of fit is 0.9777. (b) Raw data reported by Zhang et al [110]. Parameters are: T c = 17.5   ( f i x e d ) [110], γ ξ 0 = 1.39 ± 0.02 , a = 1.89 ± 0.06 . The goodness of fit is 0.9871. The 95% confidence bands are indicated by pink shaded areas.
Preprints 73480 g016
Preprints 73480 g017
Figure 17. Schematic representation of the DC magnetic susceptibility χ T obeys the Curie-Weiss law for (a) ferromagnetic, (b) paramagnetic, and (c) antiferromagnetic materials. θ is Curie-Weiss temperature (the analogue value in our model is a T c ), C is Curie constant (the analogue value in our model is a T c × γ ξ 0 ), T N is Neel temperature (the analogue value in our model is T c ).
Figure 17. Schematic representation of the DC magnetic susceptibility χ T obeys the Curie-Weiss law for (a) ferromagnetic, (b) paramagnetic, and (c) antiferromagnetic materials. θ is Curie-Weiss temperature (the analogue value in our model is a T c ), C is Curie constant (the analogue value in our model is a T c × γ ξ 0 ), T N is Neel temperature (the analogue value in our model is T c ).
Preprints 73480 g017
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated