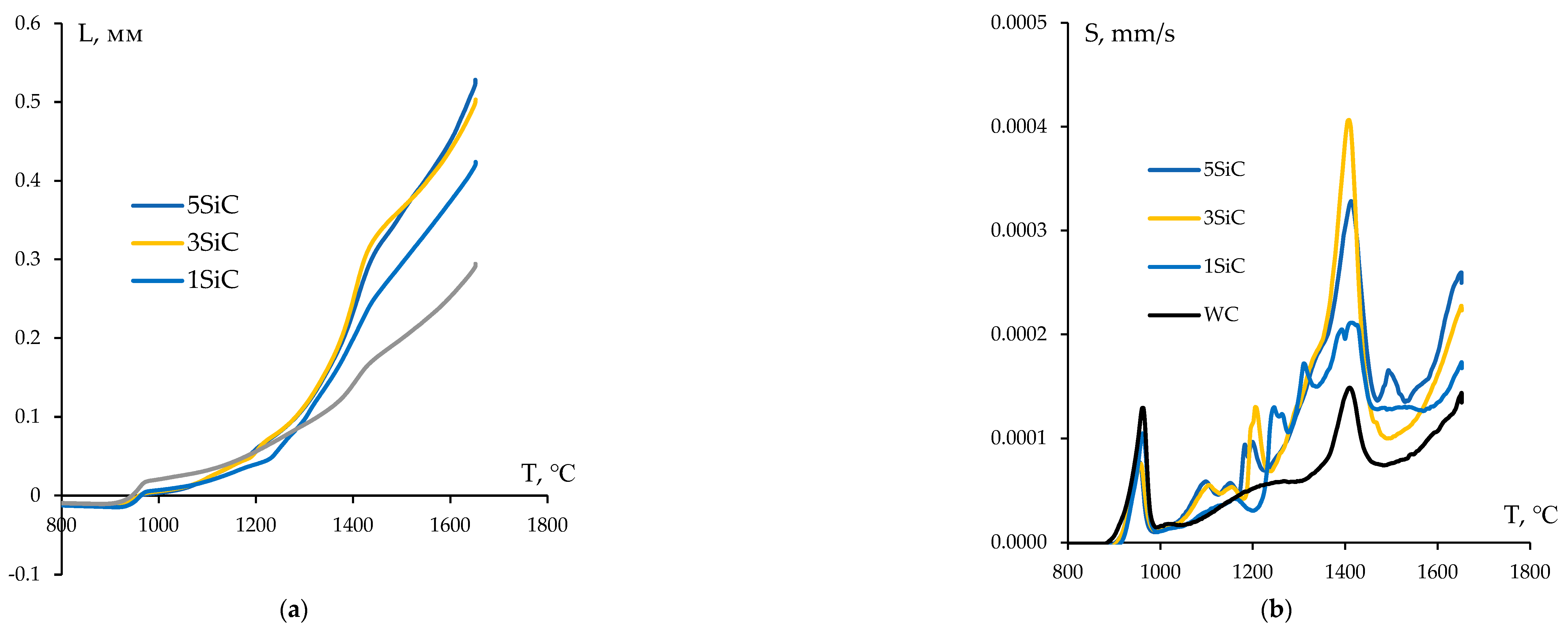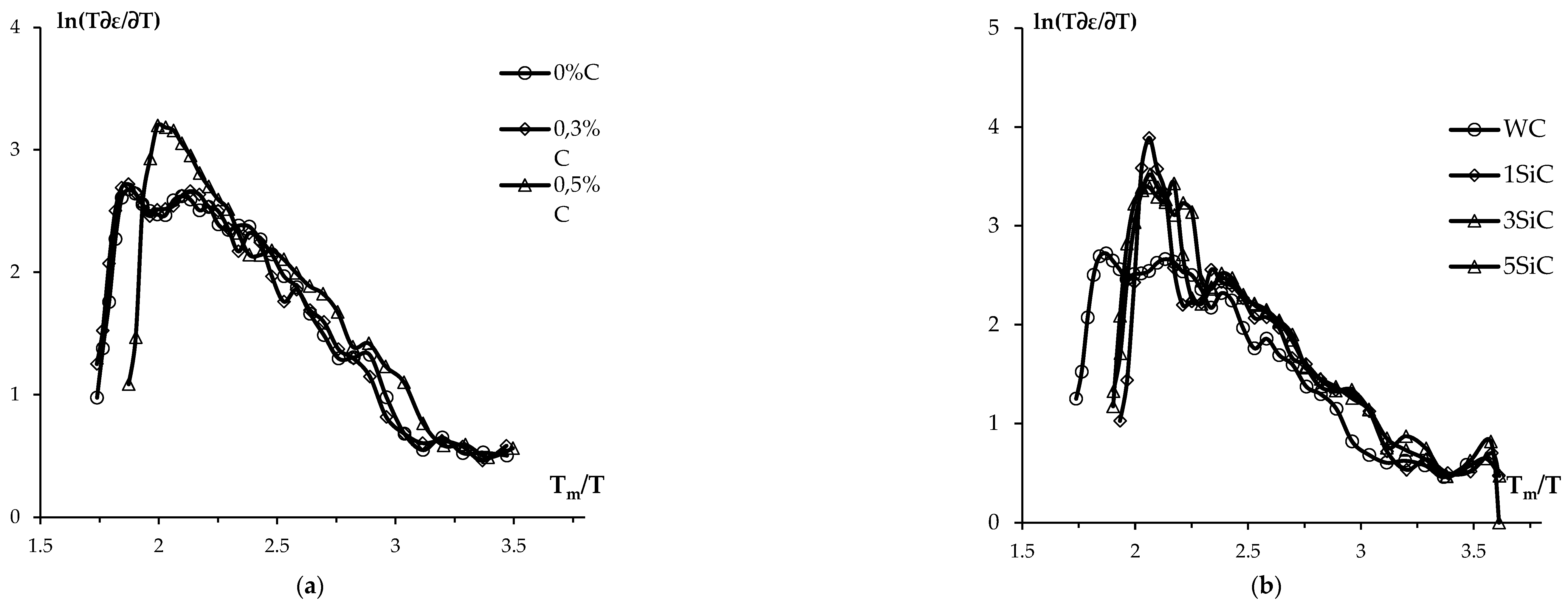Prerpints.org logo
Preprint
Article

Combined Effect of SiC and Carbon on Sintering Kinetics, MI-Crostructure and Mechanical Properties of Fine-Grained Binder-Less Tungsten Carbide

Altmetrics

Downloads

119

Views

35

Comments

0

Submitted:

15 May 2023

Posted:

15 May 2023

You are already at the latest version

Alerts
Abstract
This paper investigates the density, phase composition, microstructure and mechanical properties (microhardness, fracture toughness) of binderless WC + SiC ceramics obtained by conventional pressureless sintering (CPS) and Spark Plasma Sintering (SPS). α-WC nanopowders obtained by DC arc plasma chemical synthesis and β-SiC powders have been used as raw materials. The content of SiC particles was 1, 3, 5% wt. Excess graphite (0.3, 0.5% wt.) was added to α-WC nanopowders to decrease the volume fraction of W2C particles that negatively affect the mechanical properties of ceramics. WC + 1% wt. SiC + 0.3% wt. C ceramics are shown to have a homogeneous fine-grained microstructure, high relative density, increased microhardness and Palmquist fracture toughness. The CPS and SPS activation energies of WC + SiC nanopowders at an intensive shrinkage stage are determined using the Young-Cutler model. The effect of carbon and SiC particles on the CPS and SPS activation energies of tungsten carbide nanopowders has been analyzed. The CPS activation energies of WC, WC + C and WC + SiC + C nanopowders are shown to be closer to the carbon diffusion activation energy along α-WC grain boundaries. The SPS activation energies of WC and WC + SiC nanopowders turn out to be lower than the carbon grain boundary diffusion activation energy of α-WC.
Keywords: 
Subject: Chemistry and Materials Science  -   Ceramics and Composites

1. Introduction

WC-Co hard alloys with increased fracture toughness and satisfactory strength are widely used in machine tool engineering for the production of metal cutting tools (MCT) [1,2,3]. Liquid-phase sintering is generally used to obtain WC-Co hard alloys [1,4,5]. This technology stands out since it ensures a uniform distribution of the fusible phase in the bulk of the material. New hard alloys of WC-Ni [1,4] and WC-Fe [4] type as well as other hard alloys are produced in the same way. Fine-grained hard alloys with 6-10% Co are characterized by HV = 18-22 GPa and Palmquist fracture toughness coefficient of 10-14 MPa·m1/2.
At present, fine-grained ceramics based on binderless tungsten carbide are of great interest. The key feature of WC-based ceramics is the combination of high hardness (HV > 30 GPa) and increased fracture toughness coefficient (KIC > 4-5 MPa·m1/2) [6,7]. Besides, tungsten carbide has a high melting point, high elastic modulus and high corrosion resistance. Such a combination of properties enables binderless tungsten carbide to be used to manufacture MCT designed for finishing engineering structural materials. It is noteworthy that binderless WC-based ceramics produced by conventional pressureless sintering (CPS) have low density and poor mechanical properties.
Particles of oxides, carbides and nitrides are added to WC-based ceramics to improve the mechanical properties [5,8,9]. Preliminary studies suggest far-reaching prospects for dispersion-hardened WC-SiC ceramics with increased strength and hardness [10,11,12]. The introduction of dispersed SiC particles into tungsten carbide is expected to increase its strength and fracture toughness and will allow to control the friction coefficient, which is an important feature for MCT.
The general task of this paper is to produce and study ultrafine-grained (UFG) WC-SiC ceramics with varying carbon content. Tungsten monocarbide has a very narrow homogeneity area in the W-C diagram [2], so even a slight carbon concentration deviation from the equilibrium concentration (С0 = 6.14% wt.) leads to the formation of W2C particles that impair the mechanical properties of ceramics. The carbon concentration in WC decreases during sintering. This is due to the fact that oxygen atoms interact with carbon atoms in the WC lattice [2,6]. This leads to the formation of W2C particles. Besides, it should be noted that excess carbon concentrations lead to the formation of graphite particles that further reduce the mechanical properties of WC-based ceramics [6]. Therefore, optimizing carbon concentrations in WC-based ceramics is a relevant task with practical implications.
Plasma chemical synthesis of tungsten monocarbide nanopowders [13] and spark plasma sintering (SPS) [2,14,15,16,17,18,19,20,21,22,23] have been used to produce ceramics for the goals of this study. We reckon that these technologies combined will help to further improve the mechanical properties of WC-based ceramics by forming a high-density UFG microstructure. One of the crucial SPS advantages is the possibility to sinter ceramics at high heating rates (up to 2500℃/min), which allows to limit grain growth and obtain materials with grains extremely small in size [15,17,23]. Earlier studies have shown promising prospects of applying plasma chemical synthesis of WC nanoparticles and SPS jointly to obtain UFG WC-based ceramics with advanced mechanical properties [6,14,24].
This study aims to investigate the peculiarities of flash sintering of WC-SiC ceramics with varying carbon content, as well as to research the effect of sintering modes on the microstructure parameters, phase composition and mechanical properties of WC-SiC ceramics.

2. Materials and Methods

Binderless tungsten carbide and WC+SiC ceramics based on α-WC nanopowders make up the target of this research.
α-WC nanopowders have been obtained by DC arc plasma chemical synthesis followed by hydrogen annealing at 1050℃ (3 h) (see [13]). 0.3 and 0.5% wt. of colloidal graphite and 1, 3, 5% wt. of β-SiC nanopowders with an average particle size of 45-55 nm (as follows from the manufacturer’s certificate of Alfa Aesar, Germany) were added to the α-WC nanopowder. The powders were mixed in a Pulverisette 6 planetary mill at room temperature in 45-60 ml of isopropyl alcohol. To reduce grinding yield, milling pots and balls (∅ 1.6 mm, 150 g) made of WC-Co solid carbide were used. The weight of each powder batch totaled 50 g. To reduce the degree of agglomeration, the powders were subjected to a two-step ultrasonic treatment with UP200Ht (Hielscher UP 200 Ht) before mixing. To that end, the required amount of SiC and/or graphite powder was added to the isopropyl alcohol, and the resulting suspension was subjected to ultrasound for 5 min. Then, the required amount of WC nanopowder and an additional amount of isopropyl alcohol were added to the suspension. After that, the WC + SiC + C suspension was subjected to ultrasonic treatment for 10 min at room temperature and stirred in a Pulverisette 6 planetary mill at 150 rpm for 6 h. To prevent excessive heating, interruptions of 1 min/h were made with a simultaneous reversal of rotation. The resulting suspension was placed in a Binder vacuum drying chamber and dried at 50℃ and 100 mbar for 2 h.
The average particle size of the powders (RBET) was calculated based on the specific surface area (Ssp) measured using the BET method: RBET = 6/(ρth⋅Ssp), where ρth = 15.44 g/cm3 – theoretical density of tungsten monocarbide. The specific surface area of the powders was measured using a TriStar 3000 analyzer (Micrometrics). The oxygen and carbon concentrations were measured using a CS-600 Leco analyzer.
The cylindrical samples of 12 mm in diameter and 5-6 mm high were sintered using Dr. Sinter model SPS-625. Sintering was carried out in vacuum (6 Pa) in graphite molds with an inner diameter of 12.8 mm. Graphite foil placed between the samples and the inner surface of the mold was used to make the adherence of the sample to the mold tighter. The temperature was controlled by a CHINO IR-AH optical pyrometer focused on the surface of the graphite mold. The temperature accuracy was ±20℃. The dilatometer as part of Dr. Sinter model SPS-625 was used to determine the effective shrinkage temperature dependence of powders Leff(Т). To account for the contribution of the mold thermal expansion L0(T), an experiment on heating empty molds was performed. The true shrinkage value (L) was determined from the formula: L(T) = Leff(T) – L0(T) (see [25]).
Two sintering modes were used in this study.
Mode I: sintering of tungsten carbide powders in a continuous heating mode at a heating rate of 10 and 100 ℃/min up to a point when shrinkage is complete (Ts). Sintering took place under uniaxial stress of 70 MPa applied simultaneously with the start of heating. The holding time at Ts was 0 and 3 min, respectively. In addition, the effects of degassing at 950℃ for 15 min and powder prepressing under 350 MPa were studied. Prepressing of powders was carried out in a steel mold with an inner diameter of 12 mm using a Sorokin hydraulic press. A detailed description of the sintering modes is presented below in Table 1 and Figure 1.
Mode II: SPS of WC + С and WC + SiC + C powders weighing 6 g in a continuous heating mode at 50 ℃/min up to Ts. The holding time at Ts was 0, 3 and 30 min, respectively.
The samples together with the setup were cooled down to room temperature.
A Linseis L75VS1750C high-temperature dilatometer was used to analyze the kinetics of the initial sintering stage. Dilatometer studies were performed under minimum stress of the lower punch of 500 mN. The heating rate was 10℃/min; the samples were heated up to 1650℃. The samples together with the dilatometer were cooled down to room temperature. The temperature was controlled using a B-type thermocouple (platinum-rhodium), the samples were heated using MoSi2 heaters. The dilatometric shrinkage-temperature curves were recorded in argon at a purge rate of 25 ml/min.
The microstructure of powders and ceramics was studied using a TESCAN VEGA 2 scanning electron microscope (SEM) with an Oxford Instruments INCA 350 energy dispersive (EDS) microanalyzer and a Jeol JEM-2100F transmission electron microscope (TEM). X-ray diffraction (XRD) analysis was carried out with a Shimadzu XRD-7000 diffractometer (CuKα, step size of 0.04°, holding time of 2 s). The Rietveld method was applied to quantitative phase analysis. The accuracy of determining the content of α-WC, W2C and β-SiC particles was ±0.5% wt. Initial phase parameters were taken from the ICSD and PDF-2 database.
The Vickers hardness (HV) of ceramics was measured with a Qness A60+ hardness tester. The load totaled 10 kg. The minimum fracture toughness coefficient (KIC) was calculated based on the Palmquist model by the longest radial fracture. When calculating KIC, the elastic modulus of ceramics was taken as E = 710 GPa. The average inaccuracy of HV and KIC was ±0.2 GPa and ±0.2 MPa·m1/2, respectively.
The density of the samples (ρ) was measured by hydrostatic weighing using Sartorius CPA 225D scales. When calculating relative density (ρ/ρth), the theoretical density of binderless tungsten carbide was taken as ρth = 15.77 g/cm3, the theoretical density of W2C carbide was 17.15 g/cm3, the theoretical density of SiC was 3.21 g/cm3. The inaccuracy of relative density (ρ/ρth) was ±0.2%, while that of absolute density was 0.05 g/cm3.
Prior to investigating the microstructure, phase composition and mechanical properties, the samples were mechanically polished to eliminate a ~300-350 µm thick carburized layer formed as a result of carbon diffusing from the graphite mold onto the surface of the ceramic sample (see [24]).

3. Results

3.1. Characteristics of initial powders

Figure 2a,b show electron microscope images of plasma chemical powders of tungsten carbide. Figure 2a proves that the powders form agglomerates of a few microns in size, which consist of individual nanoparticles of ~100 nm. The average particle size of α-WC measured with the ВЕТ method is RBET = 95 nm. Ring X-ray diffraction patterns (Figure 2a) and the results of PEM investigations (Figure 2b) testify that WC nanopowders have a crystalline structure. Twins are observable throughout the nanopowders (Figure 2b), and a thin amorphous layer (Figure 2b), which is probably tungsten oxide, is present on the surface of WC nanopowders. This conclusion qualitatively corresponds to [26,27]. We reckon that a surface oxide layer triggers stronger agglomeration of WC nanopowders (Figure 2a).
According to the XRD results, the plasma chemical nanopowders consist entirely (100%) of the α-WC phase (PDF No. 00-051-0939); no peaks corresponding to other phases (W2C, α-WC, α-W etc.) were found (Figure 3). The X-ray peaks are strongly broadened, which is a common effect for nanopowders.
Figure 2c,d show images of WC + SiC powder compositions. Stirring allows for a homogeneous distribution of silicon carbide particles, which appear dark gray in Figure 2c,d. There are peaks corresponding only to the α-WC phase in XRD patterns of WC + SiC powders. No peaks corresponding to β-SiC were detected (Figure 3). This is attributed to the fact that the corundum number for the most intense peak (111) of the β-SiC phase (2θ ≈ 35.6°) is 2.5 and overlaps with one of the most intense α-WC peaks (100) (2θ ≈ 36.6°). With the β-SiC silicon carbide content (PDF No. 00-029-1129) being low, the intensity of its peaks in XRD patterns goes down to the background level.

3.2. Sintering of α-WC nanopowders

Figure 4 shows temperature curves for shrinkage L(t) and shrinkage rate S(t) of WC powders. These L(T) curves have a classical three-stage character (see [24]): slight compaction at the initial stage when temperatures are under 950℃ (Stage Ⅰ), intensive compaction in the medium temperature range from 950 to 1400℃ (Stage Ⅱ), low-intensity compaction at high temperatures (max 1500℃) with a shrinkage rate tending to a minimum. For heating modes 1, 2, 3, 5, the maximum shrinkage value (Lmax) is ~7 mm. In modes 4 and 6, Lmax decreases to ~5-5.5 mm as a result of initial prepressing of 350 MPa (Table 1).
The temperature curve for powder shrinkage rates in modes 1-4 is characterized by two maxima at 1000 and 1350℃. Maximum shrinkage rates at 1000 and 1350℃ reach 0.02 mm/s and 0.016 mm/s, respectively. Shrinkage rates go down to minimum values (~2⋅10-3 mm/s) for modes 5 and 6 because of a decrease in heating rates from 100℃/min (for modes 1-4) to 10℃/min.
Table 1 shows that the ceramics No.2 have the highest density. A slowdown in heating rates from 100 to 10℃/min decreased shrinkage completion temperatures from 1520 to 1440℃ (at ts = 0 min) and reduced the relative density of ceramics from 98.59 to 97.69%. An increase in the holding time to ts = 3 min raises the density of ceramics from 98.59 to 99.06%. Degassing at 950℃ (15 min) has no significant effect on the density of sintered samples (Table 1). The density of ceramics sintered from prepressed powders within the measurement error (±0.03%) coincides with the density of ceramics sintered from powders that have not been prepressed.
Figure 5 shows the microstructure of the sintered tungsten carbide samples. SPS mode variations obviously lead to no significant changes in the microstructure of the samples. The ceramics have a homogeneous UFG microstructure with an average grain size of ~100-200 nm. Some samples show meso- and microstructural heterogeneity (Figure 5d,e), the presence of which is probably due to a high degree of agglomeration in initial powders.
Figure 6 presents XRD results of the ceramic samples sintered using different SPS modes (Table 1). The analysis of these XRD results shows that the minimum W2C particles content is observed in the ceramics No. 2 (Table 1). Degassing at 950℃, during which adsorbed oxygen interacts with carbon, leads to an increase in the W2C particles content to ~8% wt. Sintering rates going down from 100 to 10℃/min increased the W2C particles content from 7 to 7.7-8.3% wt.
As follows from Table 1, the best combination of hardness and fracture toughness was obtained in ceramic sample No. 1: HV = 28.7 GPa, KIC = 5.0 MPa·m1/2. Degassing and a decrease in heating rates from 100 to 10℃/min reduces hardness to 27.4-27.9 GPa and fracture toughness to 4.2-4.3 MPa·m1/2, respectively.

3.3. Effect of graphite on sintering kinetics of tungsten carbide nanopowders

To study the effect of excess carbon on the compaction kinetics, phase composition and mechanical properties of ceramics, 0.3 and 0.5% graphite was added to the α-WC nanopowder. To ensure correct comparisons and to reduce the degree of agglomeration, the initial α-WC nanopowder was subjected to additional processing in a planetary mill.
XRD results prove that only peaks corresponding to the α-WC hexagonal tungsten monocarbide phase (PDF No. 00-051-0939) are present in XRD patterns of WC-C powder compositions (Figure 3). The average particle size of α-WC powders does not change during mixing.
Figure 7 shows the results of dilatometric studies of the temperature curves for shrinkage and shrinkage rate. These L(T) curves show that powder stirring resulted in higher shrinkage values. The S(T) curve shows three peaks: the first peak of 960-1000℃; the second peak of 1400℃; the beginning of the third peak is observable as well (Figure 7b). It is worth noting that temperature-shrinkage curves for the WC + 0.5% C nanopowder differ from L(T) dependences for other powders. With the same initial powder mass, maximum shrinkage is much higher than that of WC and WC + 0.3% C nanopowders (Figure 7a). Besides, the S(T) curve is different for the WC + 0.5% C nanopowder (Figure 7b). The S(T) dependence for the WC + 0.5%C nanopowder peaks at ~950℃, which is associated with degassing, another peak occurs at ~1620℃. There is no peak at ~1400℃ in the S(T) dependence for the WC + 0.5% C nanopowder (Figure 7b).
Figure 8 shows temperature curves for shrinkage L(t) and shrinkage rate S(t) of WC + C powders. These dependences have a classical three-step character (see Section 3.1). The introduction of 0.3% C into the α-WC nanopowder leads to no noticeable change in its compaction kinetics, while the introduction of 0.5% C causes a shift of the L(T) curve to lower temperatures (Figure 8): the intensive shrinkage completion temperature (Stage II) goes down by 100℃ to reach 1400℃. With the graphite concentration growing from 0.3 to 0.5%, Lmax increases from 5.9 to 6.4 mm, while Smax increases from 1.5·10-2 to 2.6·102 mm/s. It should also be noted that the S(T) dependences for powders with 0.5% graphite have a more complex character than those for WC and WC + 0.3% C powders. In the case of powders without graphite and with 0.3% C, the S(T) curve shows two distinct peaks at 1150 and 1375℃. During SPS of WC + 0.5% C nanopowders, there is a monotonic increase in shrinkage rates to 2.7⋅10-2 mm/s at 1250℃ followed by a sharp decrease in shrinkage rates to 1.3⋅10-3 mm/s at 1375℃.
Table 2 shows that ceramics made of binderless tungsten carbide have high relative density (≥ 99.5%). The introduction of 0.3% and 0.5% graphite reduces the relative density of ceramics to ~98.7% and ~97.7%, respectively.
Figure 9 shows the results of SEM of ceramics with varying graphite content. Microstructural examination shows that an increase in graphite concentrations from 0 to 0.5% wt. leads to abnormally large grains of 50-100 µm long (see also [6,7]). An increase in the isothermal holding time from 0 to 3 min during sintering of WC and WC + 0.3% C samples leads to a slight increase in the average grain size by 50-100 nm. An increase in the holding time to 30 min resulted in an increase in the average grain size to 3 μm for WC ceramics and to 5.5 μm for WC + 0.3% С ceramics (Figure 9). An increase in the holding time from 0 to 30 min during sintering of WC + 0.5% C samples leads to an increase in abnormal grain size to 200 μm (Figure 9). Abnormally large grains in WC + 0.5% C samples after holding for 30 min occupy practically all the ceramic thin section area (Figure 9).
The analysis of XRD patterns shown in Figure 10 proves that sintered WC and WC + 0.3% C ceramics are two-phase.
There are peaks corresponding to the W2C phase in XRD patterns of sintered ceramics (Figure 10). The W2C phase content in the ceramics sintered from the α-WC nanopowder without adding graphite is ~7.5 wt.% and does not depend on the time of isothermal exposure. With an increase in the graphite concentration to 0.3%, the amount of W2C particles decreases to ~2.5%, while in ceramics with 0.5% graphite there are no peaks corresponding to the W2C phase in XRD patterns (Figure 10).
Ceramics made of the α-WC nanopowder are characterized by hardness HV = 27.8 GPa and fracture toughness coefficient KIC = 4 MPa·m1/2 (see Table 2). An increase in isothermal holding time from 0 to 30 min reduces HV to 25.3 GPa and increases KIC to 5 MPa·m1/2. The introduction of 0.3% graphite into the nanopowders and, consequently, a decrease in W2C, raises HV to 28.8 GPa with a simultaneous decrease in KIC to 3.6 MPa·m1/2. Ceramics with the addition of 0.5% graphite have low hardness (HV = 11-12 GPa) and increased fracture toughness coefficient KIC (up to 9 MPa·m1/2). Longer isothermal holding times reduce the hardness of WC + C ceramics and slightly increase KIC (Table 2).

3.4. Sintering of α-WC nanopowders

Figure 11 shows temperature curves for shrinkage L (Figure 11a) and shrinkage rate S (Figure 11b) of WC + SiC powders obtained using a dilatometer. As follows from Figure 11a, an increase in the SiC content leads to a slight increase in shrinkage. The S(T) curves for WC + SiC powders show two maxima at 900℃ and 1400℃. The maximum shrinkage rate at 900℃ is almost independent of the SiC content, while Smax at 1400℃ increases along with an increase in the SiC content.
Figure 12 shows temperature curves for shrinkage L and shrinkage rate S of WC + SiC powders with an addition of 0.3% graphite during SPS. As follows from Figure 12, an increase in the SiC content from 1 to 5% does not change the shrinkage kinetics of tungsten carbide nanopowders. The optimal sintering temperature for WC + SiC + 0.3%C powders is 1350℃, which is 150℃ lower than the shrinkage completion temperature of the WC nanopowder. The L(T) curves for WC + SiC ceramics have a classic three-stage character: slight densification at low temperatures of 600-1000℃ (Stage I), intense shrinkage in the medium temperature range of 1000-1270℃ (Stage II) and, again, weak shrinkage change in the temperature range of 1270-1350℃ (Stage III).
The S(T) curve for tungsten carbide powders with an addition of 0.3% C has one maximum at ~1000℃ (Figure 12). The S(T) curves for WC + SiC + 0.3% C powders have a more complicated nature: two shrinkage rate maxima (Smax(1), Smax(2)) are observed at ~1000℃ (Smax(1)) and 1250℃ (Smax(2)) (Figure 12). As the SiC content increases to 5%, the maximum shrinkage rate Smax(2) increases from 10-2 to 4·10-2 mm/s at 1250-1300℃; maximum powder shrinkage increases from 5.8 to 7.3 mm (Figure 11).
The research findings on density, phase composition, microstructure and mechanical properties of WC + SiC ceramics are summarized in Table 3.
Table 3 shows that SPS allows for high relative density ρ/ρth of WC + SiC ceramics. The density of binderless tungsten carbide samples with 0.3% graphite after holding for 3 min at the maximum sintering temperature is 99.1%. An increase in the SiC content to 5% reduces the relative density of ceramics to 95.1%. Longer isothermal holding time raises the density of WC + SiC + 0.3%C ceramics, and in ceramics with a higher content of silicon carbide particles this effect is even more pronounced (Table 3).
Figure 13 shows the results of electron microscopy of the WC + SiC + 0.3% C ceramics microstructure. As follows from Figure 13, an increase in the SiC content from 1 to 5 % in ceramics leads to a noticeable increase in the volume fraction of black areas. The average size of these areas is ~0.1-0.2 μm, which is comparable in size to SiC particles that form small agglomerates (Figure 2d). In WC + 1% SiC + 0.3% C ceramics, there is a marked increase in abnormally large grains. An increase in the SiC content to 3 and 5% reduces the share of abnormally large grains, whereas the average matrix grain size rises to 0.5 μm.
An increase in the holding time (ts) at Ts = 1350℃ raises the average grain size in ceramics and increases the volume fraction of abnormally large grains (Figure 13). It should be noted that when ts increases from 3 to 30 min in the microstructure of WC + 0.3% C and WC + 1% SiC + 0.3% C ceramics, the size and volume fraction of abnormal grains growing in crystallographically preferred directions are observed to increase. An increase in the isothermal holding time ts for ceramics with 3 and 5% SiC does not lead to abnormally large grains, but there is a fairly noticeable increase in the average matrix grain size (Figure 13).
Generalized XRD results show that no peaks corresponding to the W2C phase are observed in XRD patterns of WC + SiC + 0.3% C ceramics (Figure 10). In the WC + 0.3% C tungsten carbide sample sintered under identical conditions, 2.4% wt. W2C is present. No peaks corresponding to any Si-bearing phases are observed in XRD patterns.
WC + SiC ceramics have sufficiently high mechanical properties. UFG WC + 1% SiC + 0.3% С samples have the following characteristics: hardness HV = 19.1 GPa, fracture toughness coefficient KIC = 5.2 MPa·m1/2, relative density 97.4%. A further increase in the content of SiC particles to 3 and 5% leads to no noticeable increase in hardness, but contributes to a slight decrease in fracture toughness KIC. Images in Figure 14 show that fracture tips have a branching character, meaning that fractures are predominantly distributed along grain boundaries.

4. Discussion

As shown in the Results section, the L(T) curves during SPS have a three-stage character: low-temperature Stage I, at which the compaction intensity is low, intense shrinkage at Stage II, and high-temperature Stage III, at which the shrinkage rate changes slowly again (Figure 3 and Figure 6). The processes occurring at each of the stages are described in sufficient detail in classical monographs on sintering (see, for example, [28,29,30,31]), so we will not dwell on this here.
Let us identify diffusion mechanisms that control nanopowder compaction at each of the SPS stages and dilatometric heating.
The kinetics of nanopowders compaction at the intensive compaction stage (Stage II) can be analyzed using the Young-Cutler model [32], which describes the initial stage of non-isothermal sintering of spherical particles accompanied by simultaneous processes of volume and grain boundary diffusion as well as plastic deformation:
ε 2 ( ε / t ) = ( 2,63 γ Ω D v ε / k T d 3 ) + ( 0,7 γ Ω b D b / k T d 4 ) + ( A p ε 2 D / k T )
where ε – shrinkage, t – time, γ – free energy, Dv – volume diffusion coefficient, Db – grain boundary diffusion coefficient, d – grain size, p – stress, D – diffusion coefficient during plastic deformation. According to [32,33], the slope of ln(T∂ε/∂T) – Tm/T dependence corresponds to the effective activation energy of the sintering process mQs2, where m is a numerical coefficient that depends on the diffusion mechanism (m = 1/3 for grain boundary diffusion, m = ½ for lattice diffusion, m = 1 for viscous flow (creep), Tm = 3053 K – tungsten monocarbide melting temperature).
Figure 15 show ln(T∂ε/∂T) – Tm/T dependences for tungsten carbide samples with varying graphite content (Figure 15a) and WC + SiC + 0.3% C ceramics (Figure 15b). For all ceramics, ln(T∂ε/∂T) – Tm/T dependences have a typical two-stage character, which indirectly testifies to the validity of the Young-Cutler model (see [32]). It may be further noted that the correctness of applying this approach while analyzing temperature-shrinkage dependences during SPS of WC and WC-Co powders was demonstrated in [24,34].
The average values of the effective SPS activation energy for WC + C ceramics at Stage II (mQs2) are presented in Table 2; the accuracy of the effective activation energy mQs2 is ± 0.3 kTm. Table 2 shows that an increase in the graphite content from 0 to 0.5% leads to an increase in mQs2 from 1.3 to 2.3 kTm. At m = 1/3 [32], the SPS activation energy at Stage II Qs2 varies from 4.9 to 6.9 kTm (124 – 175 kJ/mol). The SPS activation energy values appear to be lower than those of the carbon grain boundary diffusion activation energy in tungsten monocarbide (240 kJ/mol [35] ~9.1 kTm).
The effective activation energy for sintering WC + SiC ceramics is mQs2 ~2.0-2.2 kTm (Table 3). At m = 1/3 [32], the SPS activation energy for WC + SiC ceramics at Stage II is Qs2 = 6.0-6.6 kTm (152 – 167 kJ/mol). Thus, the SPS activation energy values for WC + SiC ceramics appear to be lower than those of the carbon grain boundary diffusion activation energy in tungsten monocarbide.
Now let us analyze the results of dilatometric studies. Figure 16 show ln(T∂ε/∂T) – Tm/T dependences for tungsten carbide samples with varying graphite content (Figure 16a) and WC + SiC + 0.3% C ceramics (Figure 16b). The dilatometric curves ln(T∂ε/∂T) – Tm/T have a two-stage character. For binderless tungsten carbide, the effective CPS activation energy is mQs2 ~ 3.6 kTm. Similar effective sintering activation energy values (mQs2 ~ 3.6-4 kTm) are observed for tungsten carbide with 0.3 and 0.5% wt. graphite. At m = 1/3, the CPS activation energy values are 10.8-12 kTm (272-303 kJ/mol) and close to the table value of the carbon grain boundary diffusion activation energy in tungsten carbide (~9.1 kTm (240 kJ/mol [35])). The findings indicate that low SPS activation energy values in the medium heating temperatures range (Stage II) are mostly caused by the effect that applied voltage has on the intensity of WC nanoparticles rearrangement and slippage.
The effective CPS activation energy values for WC + SiC + 0.3% C ceramics (Figure 14) are mQs2 ~ 5-5.8 kTm. At m = 1/3, the CPS activation energy for WC + SiC + 0.3% C ceramics is Qs2 = 15-17.4 kTm (379-439 kJ/mol). These values appear to be bigger than those of the carbon grain boundary diffusion activation energy in tungsten carbide and approach those of the 14С diffusion activation energy in the tungsten carbide lattice. At the same time, it should be noted that the dilatometric curves ln(T∂ε/∂T) – Tm/T for WC + SiC + C ceramics are more complicated in nature, therefore, it is difficult to pin down the CPS activation energy.
Let us analyze SPS mechanisms for ceramics at high temperatures. At high heating temperatures, the slope of ln(T∂ε/∂T) – Tm/T dependence becomes negative (Figure 15 and Figure 16). It means that in order to estimate the SPS activation energy for WC-based ceramics at Stage III (Qs3), other approaches are required.
According to [25], the activation energy at Stage III can be estimated using the diffusion model of dissolving pores located along grain boundaries in UFG materials. The applicability of this procedure for tungsten carbide was previously demonstrated in [14,24]. In line with the model described in [25], the sintering activation energy Qs3 is determined by the slope of ρ(T)/ρth dependence in double logarithmic coordinates ln(ln(α⋅ρ/ρth/(1-ρ/ρth)) – Tm/T, where α = 0.33 – compaction coefficient of α-WC nanopowders (Figure 17). The average accuracy of determining the activation energy Qs3 is ± 1 kTm.
ln(ln(αρ/ρth/(1-ρ/ρth)) – Tm/T dependence for tungsten carbide at Stage III can be accurately plotted with a straight line (Figure 17). The introduction of SiC particles into the WC nanopowder leads to a shift in the above dependences towards higher temperatures, but the character of dependences (slope and monotonicity) does not change with an increase in the SiC content. The SPS activation energy for WC + SiC samples is Qs3 = 10-12 kTm (253-304 kJ/mol) (see Table 2). These values turn out to be close to those of the 14С volume diffusion in tungsten monocarbide (~ 355 kJ/mol [35]). We reckon that one of the reasons for an increase in the SPS activation energy and a change in the sintering mechanism is an intensive grain growth in tungsten carbide with an increased graphite content (see Figure 9).
As follows from Figure 17, a two-stage character of ln(ln(α⋅ρ/ρth/(ρ/ρth-1)) – Tm/T dependence is observed for WC + SiC ceramics. The SPS activation energy for WC + SiC ceramics at Stage III-1 in the low heating temperatures range is Qs3(1) ~ 10-13 kTm, which is close to the carbon volume diffusion activation energy in tungsten monocarbide. At higher temperatures, at the final sintering stage, the SPS activation energy decreases to Qs3(2) ~ 5-6 kTm. We reckon that the SPS activation energy at the final high temperature heating stage (Stage III-2, see Figure 17) reduces due to a decrease in the W2C phase, the presence of which triggers abnormal grain growth and slows down the sintering process.

5. Conclusions

1.
Prepressing of tungsten carbide nanopowders (350 MPa), reduction of heating rates from 100 to 10℃/min as well as degassing at 950 ℃ are shown to lead neither to an increase in density nor to changes in the microstructure of tungsten carbide samples. Fine-grained binderless tungsten carbide ceramics with relative density of ~99% were obtained by heating nanopowders at 10 ℃/min to 1520 ℃, with exposure at this temperature lasting for 3 min. The ceramic is characterized by high mechanical characteristics: hardness HV = 28.7 GPa and fracture toughness coefficient KIC = 5.0 MPa·m1/2.
2.
When carbon concentration in tungsten carbide nanopowders increases, shrinkage curves during SPS shift towards lower temperatures. Tungsten carbide with an increased carbon content demonstrates an abnormal grain growth, which leads to a noticeable decrease in mechanical characteristics of the ceramics. During SPS of tungsten carbide nanopowders, the addition of 0.3% graphite is optimal since it helps to deintensify the formation of undesirable W2C particles. The introduction of 0.3% graphite into the nanopowders increases the hardness of tungsten carbide to 28.8 GPa with a simultaneous decrease in fracture toughness to KIC = 3.6 MPa·m1/2.
3.
WC + SiC + 0.3% С samples with high relative density (95.4-98.1%) were obtained by SPS. These ceramics have a homogeneous UFG microstructure with a grain size of 0.1-0.2 μm and improved mechanical properties. The introduction of SiC particles into the plasma chemical tungsten carbide nanopowder reduces the shrinkage completion temperature during SPS by ~150℃ and allows to reduce the volume fraction of abnormally large grains. The compaction kinetics of WC + SiC + 0.3% C powders has a three-stage character; the powder sintering kinetics at Stage II (medium temperatures) and Stage III (high temperatures) is controlled by grain boundary and volume carbon diffusion in tungsten carbide, respectively. UFG WC + 1% SiC + 0.3% C ceramic samples have the following characteristics: hardness HV = 19.1 GPa, fracture toughness coefficient KIC = 5.2 MPa·m1/2, relative density 97.4%.

Author Contributions

Conceptualization, E.L., P.A. and A.N.; methodology, A.N., P.A. and V.C.; formal analysis, A.N. and V.C.; investigation, E.L., P.A., M.B., A.M.; G.S.; K.S.; Y.B.; N.I. and N.T.; data curation, E.L., A.N. and P.A.; writing—original draft preparation, A.N. and V.C.; writing—review and editing, A.N. and V.C.; supervision, V.C.; project administration, P.A.; funding acquisition, P.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation, grant No. 22-73-10175. TEM microstructure studies were carried out using the equipment provided by the Center Collective Use “Materials Science and Metallurgy” of the National University of Science and Technology “MISIS” with the financial support from the Ministry of Science and Higher Education of the Russian Federation (grant No. 075-15-2021-696).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Panov, V.S.; Chuvilin, A.M. Technology and Properties of Sintered Hard Alloys and Their Products; MISIS: Moscow, Russia, 2001; p. 428. (In Russian) [Google Scholar]
  2. Kurlov, A.S.; Gusev, A.I. Tungsten Carbides. Structure, Properties and Application in Hardmetals; Springer: Cham, Switzerland, 2013; p. 242. [Google Scholar] [CrossRef]
  3. Kramer, G.S. Strength of hard alloys; Metallurgy: Moscow, Russia, 1971; p. 247. (In Russian) [Google Scholar]
  4. Tretyakov, V.I. Fundamentals of metal science and technology of production of sintered hard alloys; Metallurgy: Moscow, Russia, 1976; p. 527. (In Russian) [Google Scholar]
  5. Wachowicz, J.; Dembiczak, T.; Stradomski, G.; et al. Properties of WC-Co composites produced by the SPS method intended for cutting tools for machining of wood-based materials. Materials 2021, 14, 2618. [Google Scholar] [CrossRef] [PubMed]
  6. Sun, J.; Zhao, J.; Huang, Z.; et al. A Review on Binderless Tungsten Carbide: Development and Application. Nanomicro Lett. 2020, 12, 13. [Google Scholar] [CrossRef] [PubMed]
  7. Cha, S.I.; Hong, S.H. Microstructures of binderless tungsten carbides sintered by spark plasma sintering process. Mater. Sci. Eng. A 2003, 356, 381–389. [Google Scholar] [CrossRef]
  8. Sivaprahasam, D.; Chandrasekar, S.B.; Sundaresan, R. Microstructure and mechanical properties of nanocrystalline WC-12Co consolidated by spark plasma sintering. Int. J. Refract. Met. Hard Mater. 2007, 25, 144–152. [Google Scholar] [CrossRef]
  9. Eriksson, M.; Radwan, M.; Shen, Zh. Spark plasma sintering of WC, cemented carbide and functional graded materials. Int. J. Refract. Met. Hard Mater. 2013, 36, 31–37. [Google Scholar] [CrossRef]
  10. Nino, A.; Nakaibayashi, Y.; Sugiyama, S.; et al. Microstructure and Mechanical Properties of WC-SiC Composites. Mater. Trans. 2011, 52, 1641–1645. [Google Scholar] [CrossRef]
  11. Nino, A.; Sekine, T.; Sugawara, K.; et al. Effect of Added Cr3C2 on the Microstructure and Mechanical Properties of WC–SiC Ceramics. Key Eng. Mater. 2015, 656–657, 33–38. [Google Scholar] [CrossRef]
  12. Nino, A.; Nakaibayashi, Y.; Sugiyama, S.; et al. Effect of Mo2C addition on the microstructures and mechanical properties of WC–SiC ceramics. Int. J. Refract. Met. Hard Mater. 2017, 64, 35–39. [Google Scholar] [CrossRef]
  13. Isaeva, N.V.; Blagoveshchenskii, Yu.V.; Blagoveshchenskaya, N.V.; et al. Preparation of nanopowders of carbides and hard-alloy mixtures applying low-temperature plasma. Russ. J. Non-Ferr. Met. 2014, 55, 585–591. [Google Scholar] [CrossRef]
  14. Chuvil’deev, V.N.; Blagoveshchenskii, Yu.V.; Nokhrin, A.V.; et al. Spark plasma sintering of tungsten carbide nanopowders obtained through DC arc plasma synthesis. J. Alloys Compd. 2017, 708, 547–561. [Google Scholar] [CrossRef]
  15. Tokita, M. Progress of Spark Plasma Sintering (SPS) Method, Systems, Ceramics Applications an Industrialization. Ceramics 2021, 4, 160–198. [Google Scholar] [CrossRef]
  16. Olevsky, E.A.; Dudina, D.V. Field-Assisted Sintering: Science and Applications; Springer: Cham, Switzerland, 2018; p. 425. [Google Scholar] [CrossRef]
  17. Zheng, D.; Li, X.; Li, Y.; et al. ZrO2 (3Y) toughened WC composites prepared by spark plasma sintering. J. Alloys Compd. 2013, 572, 62–67. [Google Scholar] [CrossRef]
  18. Wang, J.; Zuo, D.; Zhu, L.; et al. Effects and influence of Y2O3 addition on the microstructure and mechanical properties of binderless tungsten carbide fabricated by spark plasma sintering. Int. J. Refract. Met. Hard Mater. 2018, 71, 167–174. [Google Scholar] [CrossRef]
  19. Kumar, A.N.; Watabe, M.; Kurokawa, K. The sintering kinetics of ultrafine tungsten carbide powders. Ceram. Int. 2011, 37, 2643–2654. [Google Scholar] [CrossRef]
  20. Ren, X.; Peng, Z.; Wang, Ch.; et al. Effect of ZrC nano-powder addition on the microstructure and mechanical properties of binderless tungsten carbide fabricated by spark plasma sintering. Int. J. Refract. Met. Hard Mater. 2015, 48, 398–407. [Google Scholar] [CrossRef]
  21. Demirskyi, D.; Borodianska, H.; Agrawal, D.; et al. Peculiarities of the neck growth process during initial stage of spark-plasma, microwave and conventional sintering of WC spheres. J. Alloys Compd. 2012, 523, 1–10. [Google Scholar] [CrossRef]
  22. Poetschke, J.; Richter, V.; Holke, R. Influence and effectivity of VC and Cr3C2 grain growth inhibitors on sintering of binderless tungsten carbide. Int. J. Refract. Met. Hard Mater. 2012, 31, 218–223. [Google Scholar] [CrossRef]
  23. Munir, Z.A.; Anselmi-Tamburini, U.; Ohyanagi, M. The effect of electric field and pressure on the synthesis and consolidation materials: A review of the spark plasma sintering method. J. Mater. Sci. 2006, 41, 763–777. [Google Scholar] [CrossRef]
  24. Lantsev, E.A.; Malekhonova, N.V.; Chuvil’deev, V.N.; et al. Study of high-speed sintering of fine-grained hard alloys based on tungsten carbide with ultralow cobalt content: Part I. Pure tungsten carbide. Inorg. Mater. Appl. Res. 2022, 13, 761–774. [Google Scholar] [CrossRef]
  25. Chuvildeev, V.N.; Boldin, M.S.; Dyatlova, Ya.G.; et al. Comparative Study of Hot Pressing and High-Speed Electropulse Plasma Sintering of Al2O3 / ZrO2 / Ti(C,N) Powders. Russ. J. Inorg. Chem. 2015, 60, 987–993. [Google Scholar] [CrossRef]
  26. Krasovskii, P.V.; Malinovskaya, O.S.; Samokhin, A.V.; et al. XPS study of surface chemistry of tungsten carbides nanopowders produced through DC thermal plasma/hydrogen annealing process. Appl. Surf. Sci. 2015, 339, 46–54. [Google Scholar] [CrossRef]
  27. Krasovskii, P.V.; Blagoveshchenskii, Yu.V.; Grigorovich, K.V. Determination of oxygen in W-C-Co nanopowders. Inorg. Mater. 2008, 44, 954–959. [Google Scholar] [CrossRef]
  28. Rahaman, M.N. Ceramic processing and sintering, 2nd ed.; Marcel Dekker: New York, USA, 2003; p. 876. [Google Scholar] [CrossRef]
  29. Coble, R.L. Sintering Crystalline Solids. I. Intermediate and Final State Diffusion Models. J. Appl. Phys. 1961, 32, 787–792. [Google Scholar] [CrossRef]
  30. Johnson, D.L. New Method of Obtaining Volume, Grain-Boundary, and Surface Diffusion Coefficients from Sintering Data. J. Appl. Phys. 1969, 40, 192–200. [Google Scholar] [CrossRef]
  31. Kingery, W.D.; Berg, M. Study of the Initial Stages of Sintering Solids by Viscous Flow, Evaporation-Condensation, and Self-Diffusion. J. Appl. Phys. 1955, 26, 1205–1212. [Google Scholar] [CrossRef]
  32. Young, W.S.; Culter, I.B. Initial sintering with constant rates of heating. J. Am. Ceram. Soc. 1970, 53, 659–663. [Google Scholar] [CrossRef]
  33. Nanda Kumar, A.K.; Watabe, M.; Kurokawa, K. The sintering kinetics of ultrafine tungsten carbide powders. Ceram. Int. 2011, 37, 2643–2654. [Google Scholar] [CrossRef]
  34. Lantsev, E.A.; Chuvildeev, V.N.; Nokhrin, A.V.; et al. Kinetics of Spark Plasma Sintering of WC–10% Co Ultrafine-Grained Hard Alloy. Inorg. Mater. Appl. Res. 2020, 11, 586–597. [Google Scholar] [CrossRef]
  35. Buhsmer, C.; Crayton, P. Carbon self-diffusion in tungsten carbide. J. Mater. Sci. 1971, 6, 981–988. [Google Scholar] [CrossRef]
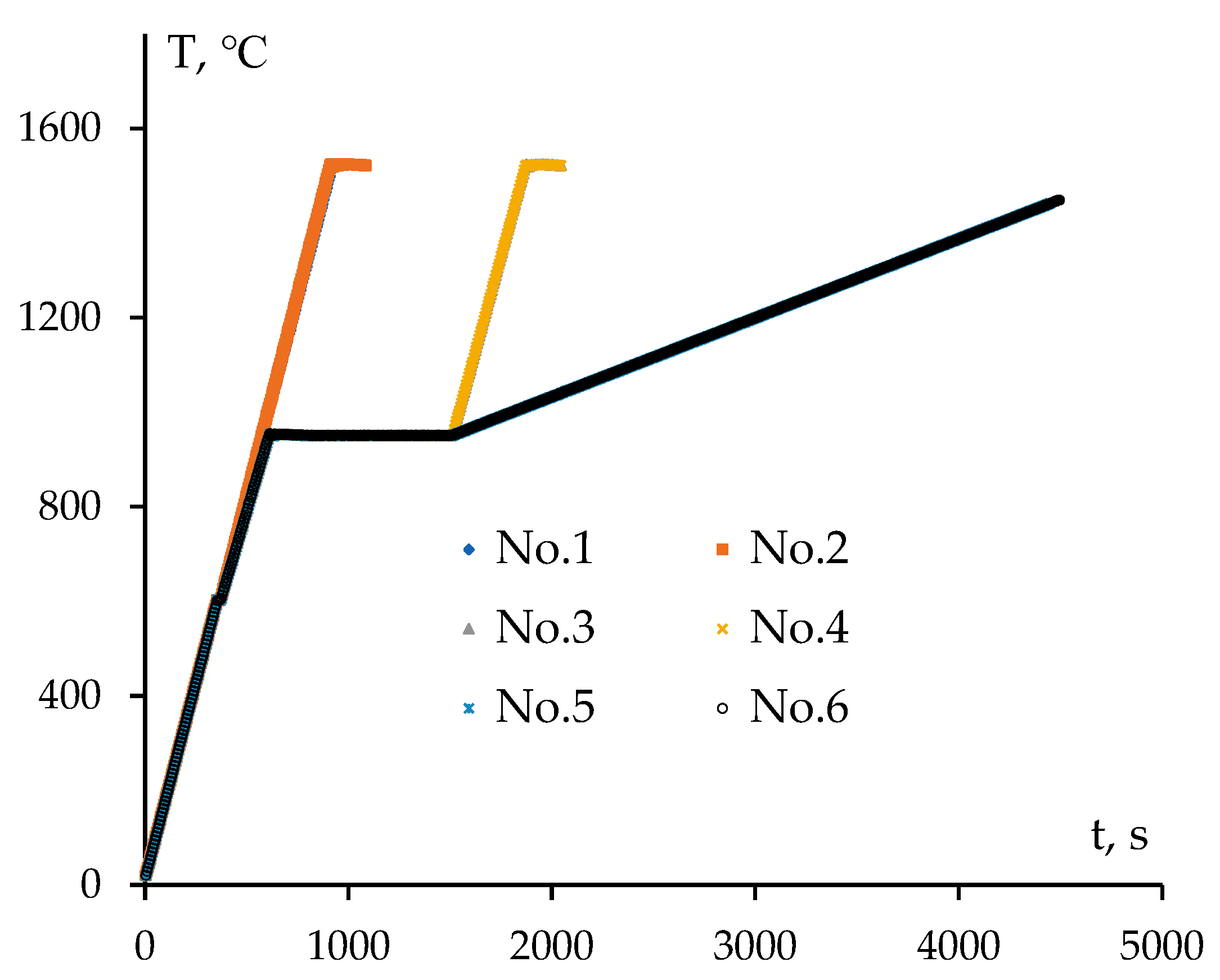
Preprints 73629 g001
Figure 1. Temperature-time diagram of heating powders during SPS.
Figure 1. Temperature-time diagram of heating powders during SPS.
Preprints 73629 g001
Preprints 73629 g002
Figure 2. Electron microscope images of WC powders (a, b), WC + 3% SiC (c) and WC + 5% SiC (d).
Figure 2. Electron microscope images of WC powders (a, b), WC + 3% SiC (c) and WC + 5% SiC (d).
Preprints 73629 g002
Preprints 73629 g003
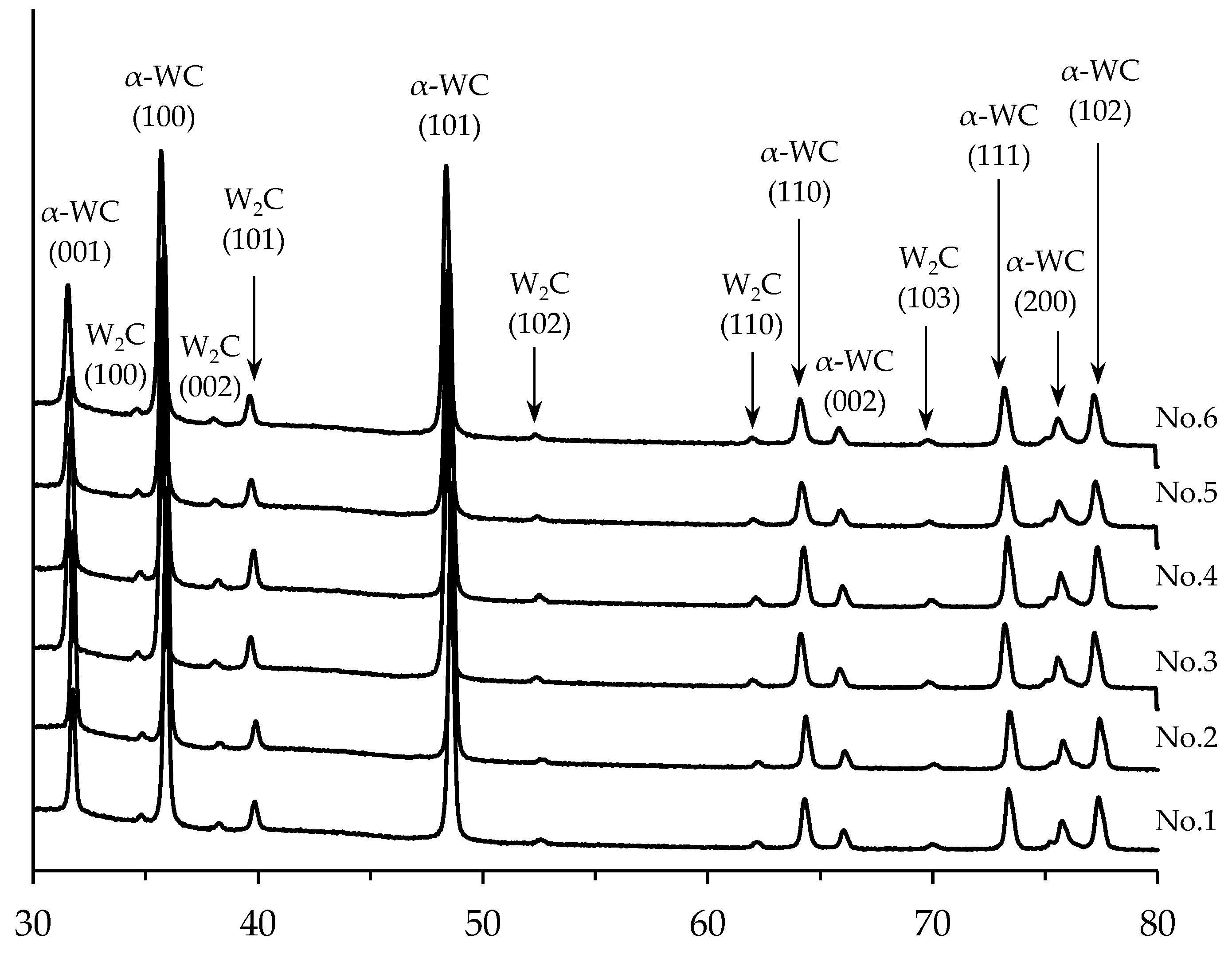
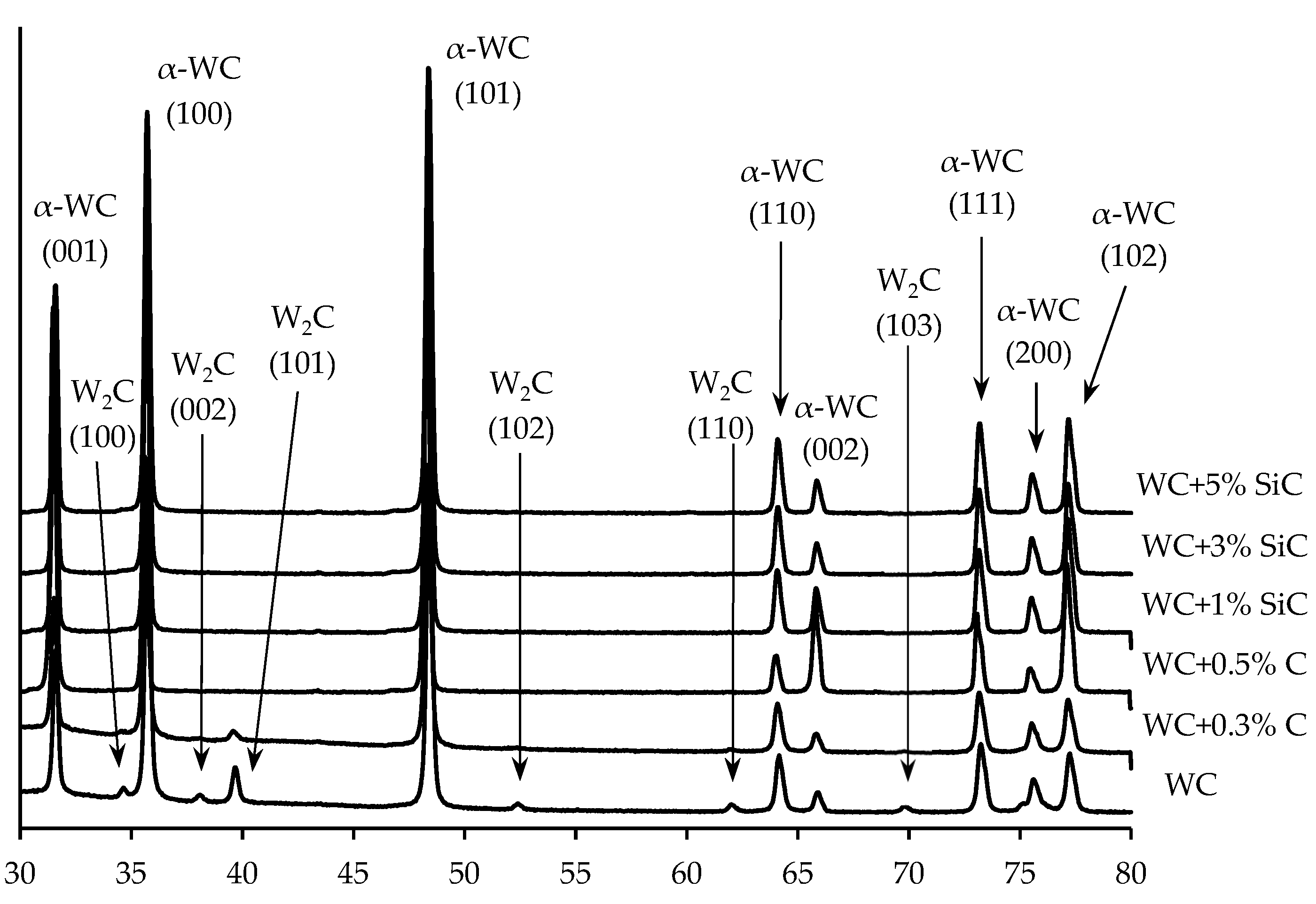
Figure 3. XRD results of WC + SiC and WC + C powders.
Figure 3. XRD results of WC + SiC and WC + C powders.
Preprints 73629 g003
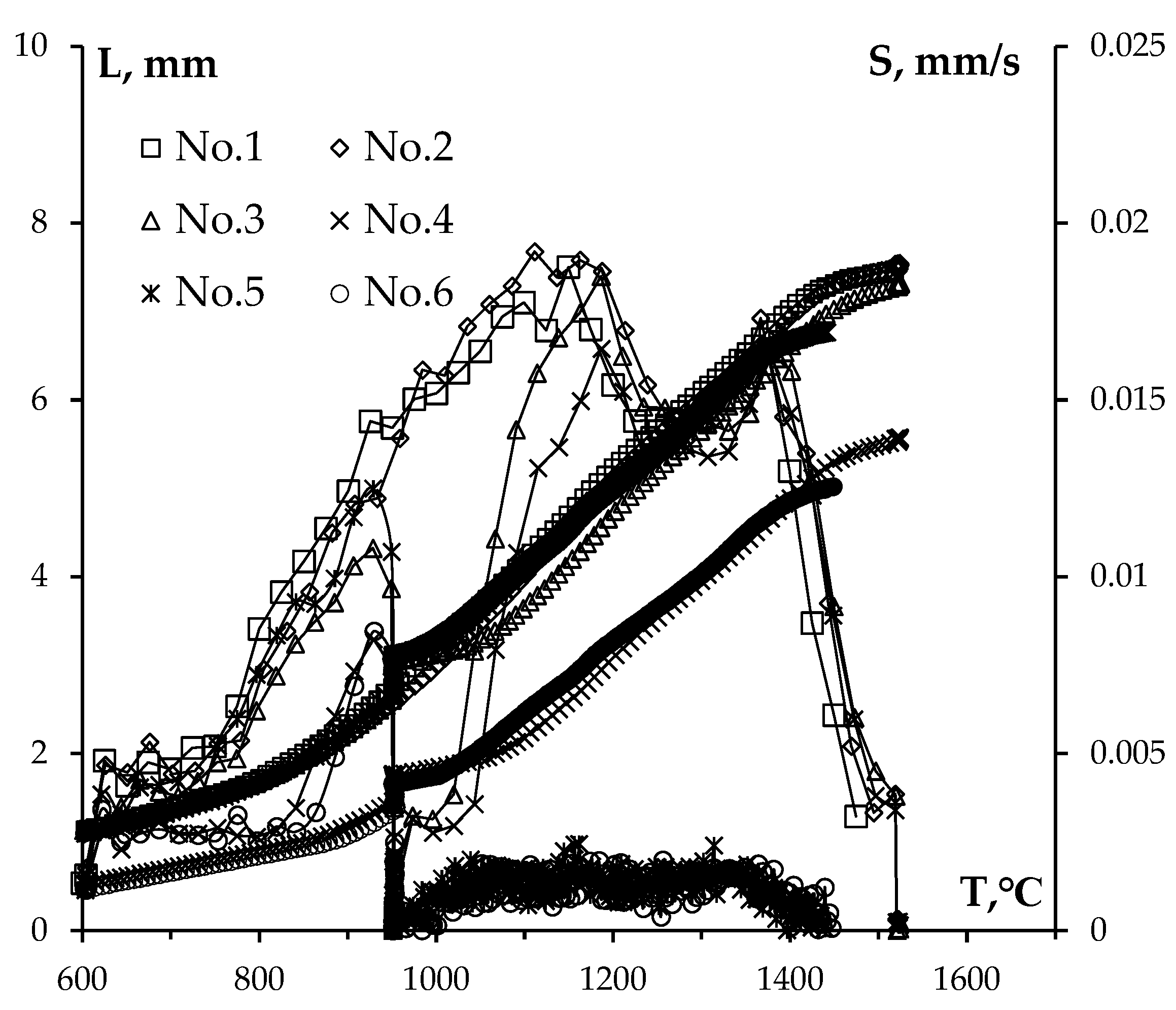
Preprints 73629 g004
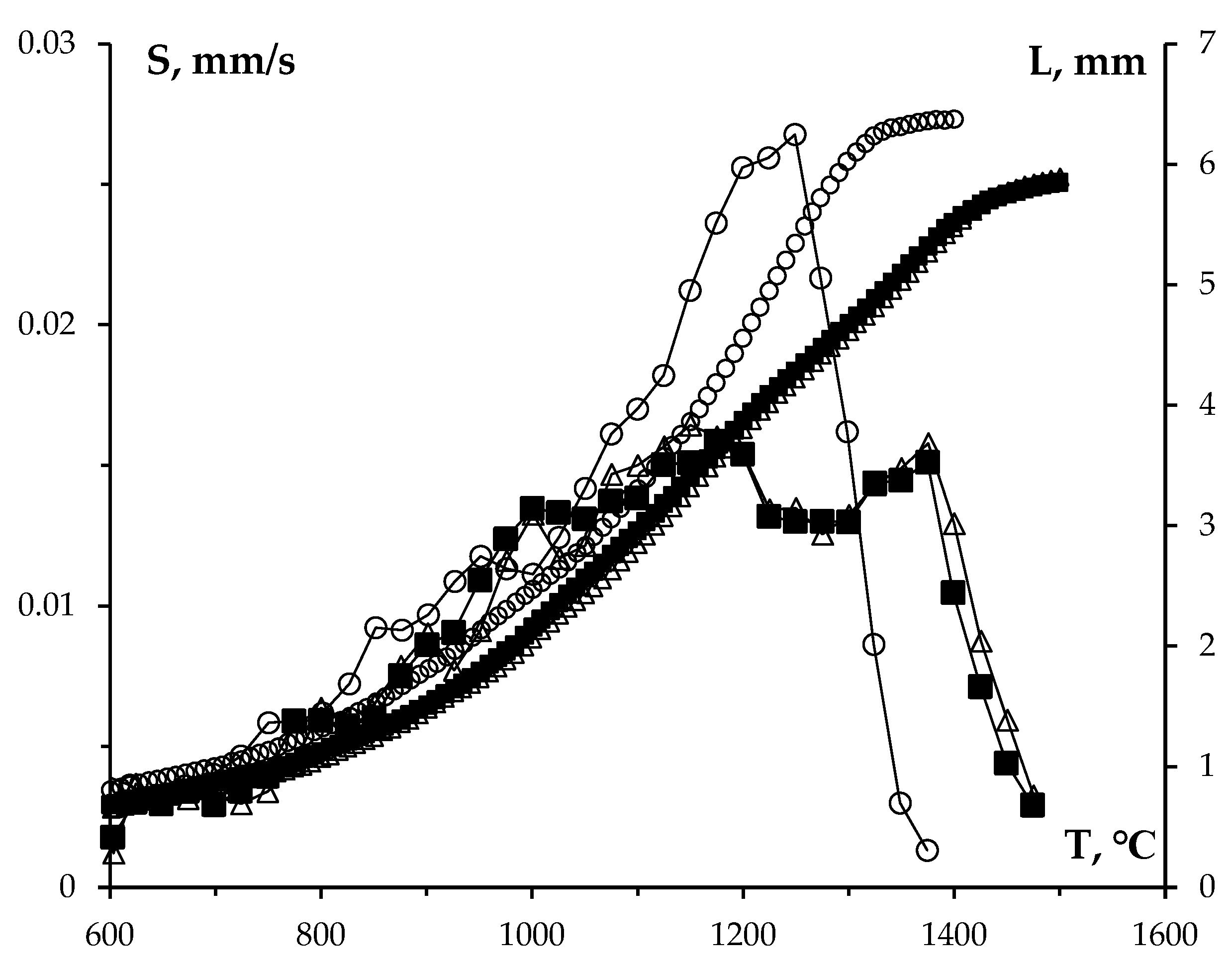
Figure 4. Temperature curves for shrinkage L and shrinkage rate S of WC powders. Numbers in the chart stand for powder numbers (see Table 1).
Figure 4. Temperature curves for shrinkage L and shrinkage rate S of WC powders. Numbers in the chart stand for powder numbers (see Table 1).
Preprints 73629 g004
Preprints 73629 g005
Figure 5. Microstructure of ceramics #1 (a), #2 (b), #3 (c), #4 (d), #5 (e), #6 (f) sintered using different SPS modes (Table 1). SEM.
Figure 5. Microstructure of ceramics #1 (a), #2 (b), #3 (c), #4 (d), #5 (e), #6 (f) sintered using different SPS modes (Table 1). SEM.
Preprints 73629 g005
Preprints 73629 g006
Figure 6. XRD results of tungsten carbide samples. Mode I. Curve numbers stand for ceramic numbers (see Table 1).
Figure 6. XRD results of tungsten carbide samples. Mode I. Curve numbers stand for ceramic numbers (see Table 1).
Preprints 73629 g006
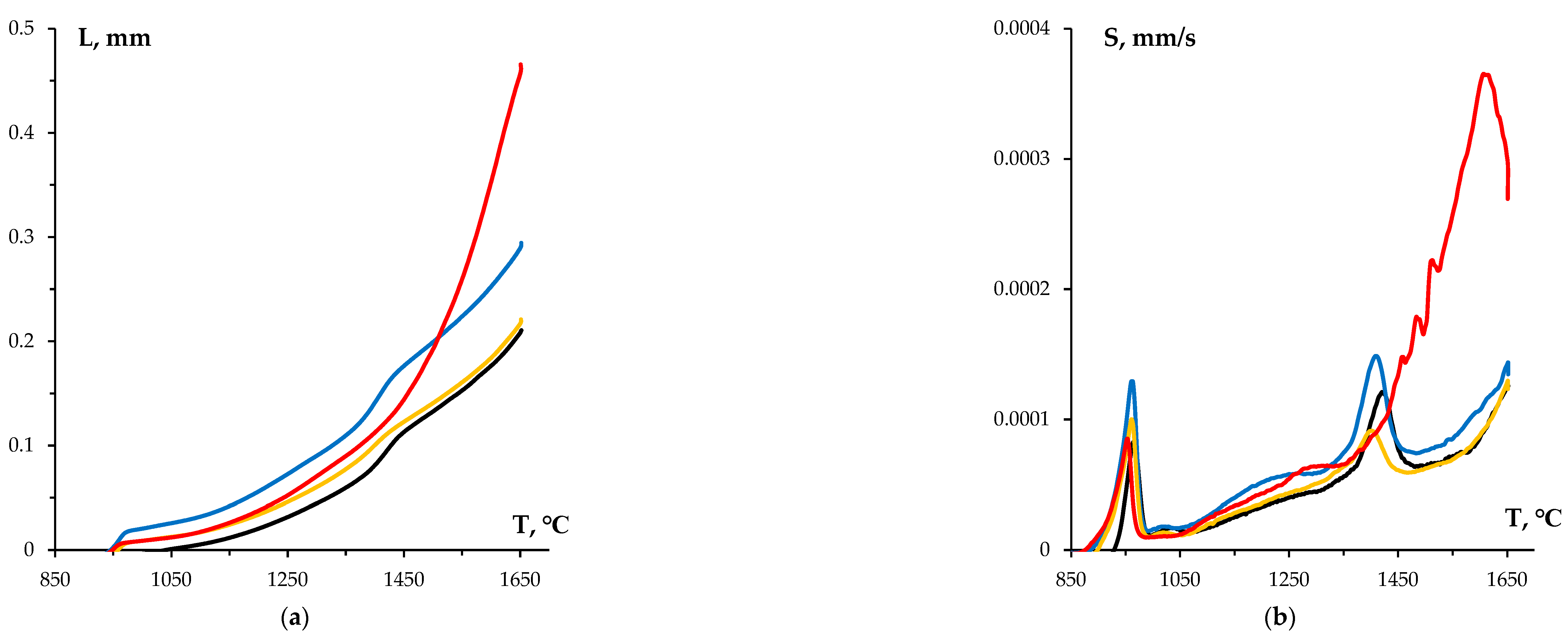
Preprints 73629 g007
Figure 7. Results of dilatometric studies of WC sintering kinetics. Temperature curves for shrinkage (a) and shrinkage rate (b) of tungsten carbide powders with varying graphite content: the black line stands for the initial WC nanopowder, the blue line shows the WC nanopowder after treatment in a planetary mill, the orange line denotes WC + 0.3% C, while the red line indicates WC + 0.5% C.
Figure 7. Results of dilatometric studies of WC sintering kinetics. Temperature curves for shrinkage (a) and shrinkage rate (b) of tungsten carbide powders with varying graphite content: the black line stands for the initial WC nanopowder, the blue line shows the WC nanopowder after treatment in a planetary mill, the orange line denotes WC + 0.3% C, while the red line indicates WC + 0.5% C.
Preprints 73629 g007
Preprints 73629 g008
Figure 8. Temperature curves for shrinkage L and shrinkage rate S of WC powders with varying graphite content: ■ – 0%, ▲ – 0.3%, ● – 0.5%.
Figure 8. Temperature curves for shrinkage L and shrinkage rate S of WC powders with varying graphite content: ■ – 0%, ▲ – 0.3%, ● – 0.5%.
Preprints 73629 g008
Preprints 73629 g009aPreprints 73629 g009b
Figure 9. Microstructure of WC (a, b, c), WC + 0.3% C (d, e, f) and WC + 0.5% C (g, h, i) ceramics with different holding times at Ts: 0 min (a, d, g), 3 min (b, e, h) and 30 min (c, f, i). SEM.
Figure 9. Microstructure of WC (a, b, c), WC + 0.3% C (d, e, f) and WC + 0.5% C (g, h, i) ceramics with different holding times at Ts: 0 min (a, d, g), 3 min (b, e, h) and 30 min (c, f, i). SEM.
Preprints 73629 g009aPreprints 73629 g009b
Preprints 73629 g010
Figure 10. XRD results for WC ceramics with varying graphite content and WC + SiC + 0.3% C ceramics with varying SiC particles content.
Figure 10. XRD results for WC ceramics with varying graphite content and WC + SiC + 0.3% C ceramics with varying SiC particles content.
Preprints 73629 g010
Preprints 73629 g011
Figure 11. Results of dilatometric studies of the CPS kinetics of WC + SiC powders. Temperature dependences for shrinkage (a) and shrinkage rate (b) in tungsten carbide powders with varying SiC content.
Figure 11. Results of dilatometric studies of the CPS kinetics of WC + SiC powders. Temperature dependences for shrinkage (a) and shrinkage rate (b) in tungsten carbide powders with varying SiC content.
Preprints 73629 g011
Preprints 73629 g012
Figure 12. Dependencies of shrinkage L (shaded markers) and shrinkage rate S (light markers) on heating temperatures of WC + 0.3% C powders with varying SiC content: ● – 0%, ♦ - 1%, ■ – 3%, ▲ – 5% SiC.
Figure 12. Dependencies of shrinkage L (shaded markers) and shrinkage rate S (light markers) on heating temperatures of WC + 0.3% C powders with varying SiC content: ● – 0%, ♦ - 1%, ■ – 3%, ▲ – 5% SiC.
Preprints 73629 g012
Preprints 73629 g013aPreprints 73629 g013b
Figure 13. Microstructure of WC + 0.3% C ceramics with 1% (a, b, c), 3% (d, e, f), 5% SiC (g, h, i) obtained by SPS exposed for ts = 0 min (a, d, g), 3 min (b, e, h) and 30 min (c, f, i) at Ts = 1350℃. SEM.
Figure 13. Microstructure of WC + 0.3% C ceramics with 1% (a, b, c), 3% (d, e, f), 5% SiC (g, h, i) obtained by SPS exposed for ts = 0 min (a, d, g), 3 min (b, e, h) and 30 min (c, f, i) at Ts = 1350℃. SEM.
Preprints 73629 g013aPreprints 73629 g013b
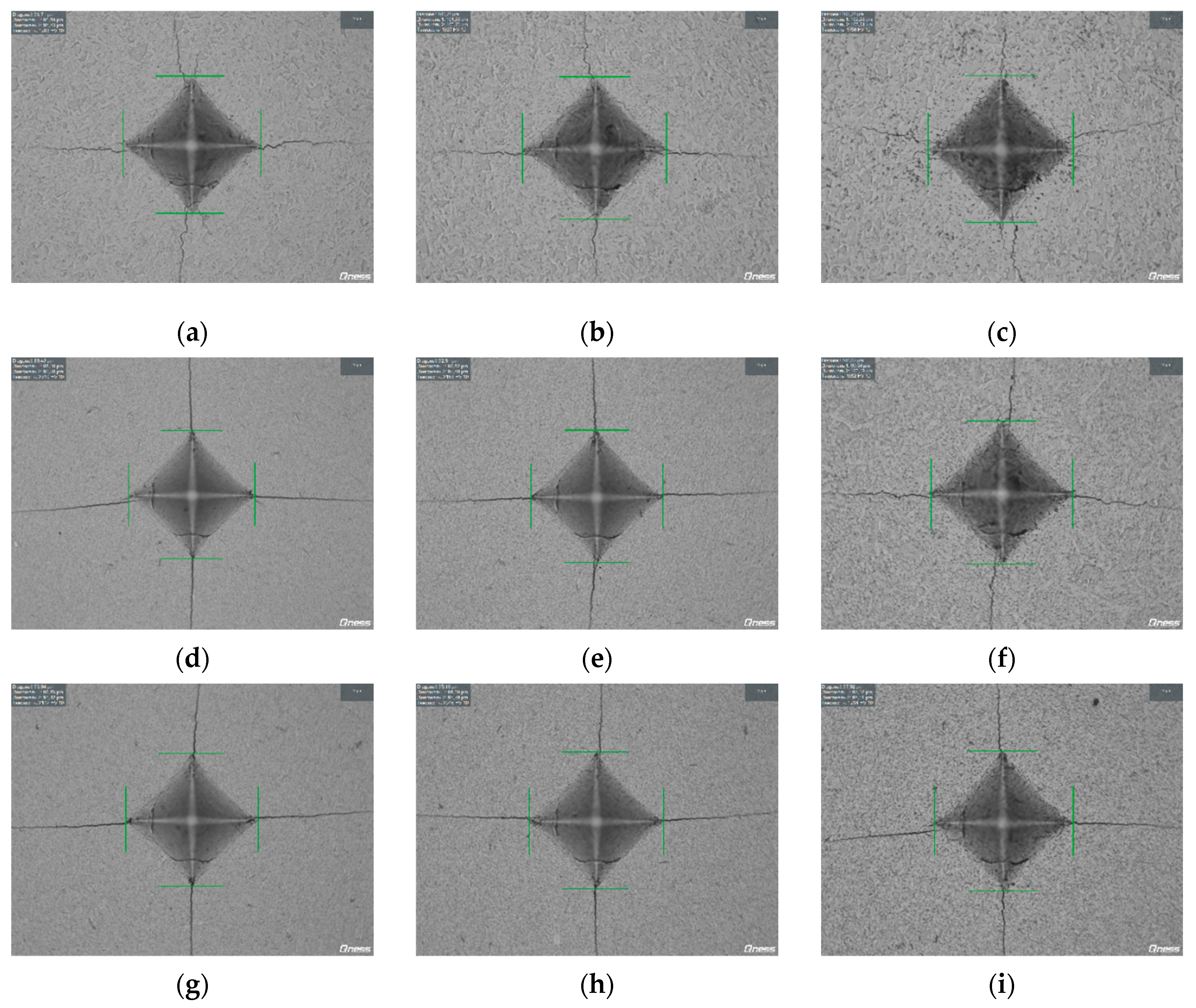
Preprints 73629 g014
Figure 14. Hardness indentation images during hardness and fracture toughness tests of WC + 0.3% C ceramics with 1% (a, b, c), 3% (d, e, f), 5% SiC (g, h, i) obtained by SPS with isothermal holding for ts = 0 min (a, d, g), 3 min (b, e, h) and 30 min (c, f, i) at Ts = 1350℃. SEM.
Figure 14. Hardness indentation images during hardness and fracture toughness tests of WC + 0.3% C ceramics with 1% (a, b, c), 3% (d, e, f), 5% SiC (g, h, i) obtained by SPS with isothermal holding for ts = 0 min (a, d, g), 3 min (b, e, h) and 30 min (c, f, i) at Ts = 1350℃. SEM.
Preprints 73629 g014
Preprints 73629 g015
Figure 15. Temperature-shrinkage curves for WC-C (a) and WC + SiC (b) powders in ln(T∂ε/∂T) – Tm/T coordinates. SPS activation energy calculation for Stage II. For Figure 15a: Graphite content: ● – 0.5%, ▲ – 0.3%, ■ – 0%. For. Figure 15b: SiC content: ● – 0%, ♦ - 1%, ■ – 3%, ▲ – 5%.
Figure 15. Temperature-shrinkage curves for WC-C (a) and WC + SiC (b) powders in ln(T∂ε/∂T) – Tm/T coordinates. SPS activation energy calculation for Stage II. For Figure 15a: Graphite content: ● – 0.5%, ▲ – 0.3%, ■ – 0%. For. Figure 15b: SiC content: ● – 0%, ♦ - 1%, ■ – 3%, ▲ – 5%.
Preprints 73629 g015
Preprints 73629 g016
Figure 16. Temperature-shrinkage curves for WC-C powders in ln(T∂ε/∂T) – Tm/T coordinates. CPS activation energy calculation for Stage II. Dilatometric data analysis.
Figure 16. Temperature-shrinkage curves for WC-C powders in ln(T∂ε/∂T) – Tm/T coordinates. CPS activation energy calculation for Stage II. Dilatometric data analysis.
Preprints 73629 g016
Preprints 73629 g017
Figure 17. Dependences of compaction on heating temperature in ln(ln(αρ/ρth/(1-ρ/ρth) – Tm/T coordinates for WC ceramics with varying graphite content (a) and for WC + SiC + 0.3% С ceramics with silicon carbide particles content (b). For Figure 17a: ■ – 0%, ▲ – 0.3%, ● – 0.5%. For Figure 17b: : ● – 0%, ♦ - 1%, ■ – 3%, ▲ – 5%. SPS activation energy calculation at Stage III.
Figure 17. Dependences of compaction on heating temperature in ln(ln(αρ/ρth/(1-ρ/ρth) – Tm/T coordinates for WC ceramics with varying graphite content (a) and for WC + SiC + 0.3% С ceramics with silicon carbide particles content (b). For Figure 17a: ■ – 0%, ▲ – 0.3%, ● – 0.5%. For Figure 17b: : ● – 0%, ♦ - 1%, ■ – 3%, ▲ – 5%. SPS activation energy calculation at Stage III.
Preprints 73629 g017
Table 1. Sintering modes and characteristics of tungsten carbide samples. Mode I.
Table 1. Sintering modes and characteristics of tungsten carbide samples. Mode I.
Ceramics No. 1 2 3 4 5 6
Powder characteristics
Carbon concentration, % wt. 6.26
Oxygen concentration, % wt. 0.64
α-WC content, % wt. 100
SPS modes
Stress during prepressing, MPa 0 0 0 350 0 350
Applied stress, MPa 70 70 70 70 70 70
Heating rate, ℃/min 100 100 100 100 10 10
Holding time at 950℃, min 0 0 15 15 15 15
Sintering completion temperature Ts, ℃ 1520 1520 1520 1520 1440 1440
Holding time at Ts, min 0 3 3 3 0 0
Ceramics characteristics
W2C content, % wt. 7.4 7.0 7.5 7.8 7.7 8.3
Absolute density, g/cm3 15.65 15.71 15.71 15.71 15.50 15.55
Relative density, % 98.59 99.06 98.97 98.98 97.69 97.93
Grain size d, µm 0.1 0.1 0.1 0.1 0.1 0.1
HV, GPa (±0.2) 28.7 28.0 27.9 27.4 28.0 27.4
KIC, MPa·m1/2 (±0.2) 5.0 4.9 4.4 4.9 4.2 4.3
Table 2. Characteristics of sintered WC-C samples.
Table 2. Characteristics of sintered WC-C samples.
C, % wt. t, min Ts, ℃ ρ/ρth, %
(±0.05%)		 d, μm W2C, % wt. HV, GPa
(±0.2)		 KIC, MPa·m1/2 (±0.2) SPS activation energy
mQsII, kTm (kJ/mol) QsIII, kTm (kJ/mol)
0 0 1500 99.4 0.1 7.5 27.8 4.0 1.3 (33) 11.0 (279)
3 99.7 0.15 28.2 3.9
30 99.6 3.0 25.3 5.0
0.3 0 1500 98.5 0.1 2.5 28.8 3.6 2.0 (51) 13.0 (330)
3 99.1 0.2 27.6 4.1
30 98.6 5.5 24.1 5.2
0.5 0 1400 97.7 22 0 12.9 9.0 2.3 (58) 12.0 (304)
3 97.7 85 12.3 8.
30 97.9 200 11.7 8.5
Table 3. Characteristics of WC + SiC + 0.3% graphite.
Table 3. Characteristics of WC + SiC + 0.3% graphite.
SiC, % wt. t, min Ts, ℃ ρ/ρth, %
(±0.05%)		 d, μm W2C, % wt. HV, GPa (±0.2) KIC, MPa·m1/2 (±0.2) SPS activation energy
mQsII, kTm (kJ/mol) QsIII, kTm (kJ/mol)
1 0 1350 97.4 7 0 19.2 5.9 2.2 (56) 10.0 (250)
3 97.3 10 18.1 6.1
30 97.7 16 17.3 6.2
3 0 1350 95.5 0.5 0 22.6 3.8 2.2 (56) 12.0 (304)
3 95.4 1.2 21.1 4.1
30 96.7 12 18.3 4.4
5 0 1350 95.1 0.3 0 21.5 3.9 2.15 (55) 10.0 (250)
3 96.1 1 20.1 4
30 95.8 3.2 18.7 4.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated