A MATLAB/GUI for Photovoltaic Modules Performance Simulations Based on Two-Diode Model

Preprint

Article

A MATLAB/GUI for Photovoltaic Modules Performance Simulations Based on Two-Diode Model

Altmetrics

Downloads

419

Views

168

Comments

Liomnis Osorio,

Marco Rivera^*,

Víctor Tuninetti

,Yoalbys Retirado Mediaceja,

,Yoalbys Retirado Mediaceja,

Patrick Wheeler

This version is not peer-reviewed

Submitted:

12 May 2023

Posted:

15 May 2023

You are already at the latest version

Alerts

Abstract

Manufacturers of photovoltaic modules do not provide all the information necessary to predict their performance under different climatic conditions. This forces the development of mathematical models of behavior and the application of mathematical methods for the calculation of their associated parameters. A toolbox called PVMSim implemented in MATLAB/GUI is proposed in this paper. PVMSIm provides models allowing the simulation of photovoltaic modules. A two-diode model is used to represent the effect of irradiance and temperature on the V-I and V-P characteristic curves. The accuracy of PVMSim has been vaildated by applying the models to two mono-crystalline and multi-crystalline solar modules of different power ratings and manufacturers. The model PVMSim model accuracy was verified against the manufacturer’s datasheet. This paper shows that this tool is useful for designers and professionals who require an intuitive graphical interface for fast and accurate modeling, simulation and sizing of photovoltaic systems.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The International Renewable Energy Agency (IRENA) reported that in 2022, growth in wind and solar power led to the highest annual increase in renewable generation capacity, together accounting for 90% of all net renewable additions in 2022 [1]. Globally, all renewables increased renewable generation capacity by 295 GW (+9.6%), while Photo-Voltaic (PV) energy continued to lead capacity expansion, with a world increase of 192 GW (+22%) [2]. The highest growth in installed capacity of solar energy was registered in China (+86.0 GW), the United States (+17.6 GW), India (+13.5 GW), Brazil (+9.9 GW), the Netherlands (+ 7.7 GW), Germany (+7.2 GW) and Japan (+4.6 GW) [1,2].

To study the energy production of a single solar module or a PV installation with many modules, it is advisable to have simulation models to allow estimation of the amount of energy that might be produced for different climate conditions and configurations of installation [3]. Therefore, it is important to know the energy performance of PV modules, and to predict, through modeling and simulation, their response to possible operating scenarios [4].

Crystalline silicon (c-Si) PV modules are currently the most widely commercialized [5], these modules are composed of cells connected in series and parallel [6]. Manufacturers provide in the datasheets the power, voltage and current values under Standard Test Conditions (STCs), defined by:

25^{\circ} C

of cell temperature (

T c

1000 W / m^{2}

of irradiance (G) and

1.5 G

of air mass (

A M

) [7,8,9]. However, this information is not sufficient to perform a simulation that delivers reliable predictions about the output power under different operating conditions. As an alternative to STC, the datasheets also provide Nominal Operating Conditions (NOC), defined by:

G = 800 W / m^{2}

20^{\circ} C

of ambient temperature (

T_{a}

), wind speed

v = 1 m / s

and

T_{c, N O C T} \approx 45^{\circ} C

, the latter is known as the Nominal Operating Condition Temperature (NOCT) [10,11]. However environmental conditions are never ideal, so more representative models of the PV modules are needed, including the unknown internal parameters that are not found in the datasheet.

In order to extract these internal parameters of c-Si PV cells, mathematical models based on the one-diode equivalent circuit (that ideally consists of a diode, resistors, and a current source) [12], with its variants of two-diode and three-diode have considered [13,14,15]. Two models for photovoltaic cell modeling are often used: the one-diode model and the two-diode model with five and seven internal parameters respectively [16]. Using these models it is possible to obtain the characteristic current-voltage (V-I) curves, which are very important for monitoring, controlling and evaluating the performance of PV systems. The accuracy of the models depends on the number of internal parameters and the number of diodes [12]. The methods for extraction of the internal parameters are complicated, due to the number of variables involved and the non-linear behaviour of the model equations [17]. However, the MATLAB GUIDE can be used to calculate the internal parameters of the PV modules, in an intuitive, simple and transparent way for both the one-diode or two-diode models [18].

The MATLAB’s Toolbox GUIDE has been used to model the cells and PV modules in many applications. Some researchers have developed an easy and simple Graphical User Interface (GUI) to create and modify PV device models and simulate the device operation in arbitrary conditions easily [19], also to use for sizing on-grid [20] and off-grid [21] PV systems. This method uses mathematical models that represent the energy processing in PV, considering the different components such as solar generators, inverters, electrical cable connections and batteries [22,23,24,25]. Some authors have presented a GUI for continuous real-time monitoring of PV modules based on the V-I and V-P characteristics curves at different geographic sites. Typically, the GUI is integrated with LabVIEW software to allow monitoring of the variables [26,27]. Other authors have developed a GUI for educational purposes [18,28], allowing a user friendly, sequential interaction between the user (student) and the latent knowledge, the user can add information about the power generation capacity and energy requirement in a given rural or urban region. It also serves as educational support in electrical and/or mechanical engineering courses [14]. It has also been demonstrated that students trained using the GUI tool easily can understand the concept of a PV solar module and their electrical parameters [15].

A GUI has also been used for solar radiation forecasting, the calculation of incident radiation to the tilted module and the prediction of energy generated by the PV module [29]. A neural network approach to the performance prediction of PV modules has also been considered. Here the feed-forward neural networks have been used to predict I-V curve parameters as a function of input irradiance and temperature [30]. Other uses consider calculating arrays for partial shading conditions, using a generalized analytical approach to model the PV module [31] and calculating the partial shading effects on PV arrays [32]. These studies all use a GUI Toolbox for analyzing different factors such as atmospheric conditions and the configuration of PV modules and cells.

The aim of this paper is to demonstrate a Toolbox called PVMSim (PV + Matlab + Simulator), created in MATLAB’s GUIDE. This Toolbox allows the analysis of the electrical properties of silicon-based PV modules in a very intuitive way. Specifically, it determines the seven parameters of the two-diode model based on the information provided in the datasheet, using modeling algorithms established in the scientific literature. To prove the validity of the implemented GUI, the methods were applied to two PV modules with different power and technologies. The results were validated using the electrical parameters from the datasheet and the V-I curves obtained with the PVsyst® v7.3.1 software as reference.

This paper is organized as follows: in Section 2, the two-diode equivalent model used for internal parameter extraction and the flowcharts of PVMSim blocks are explained. Section 3, presents case studies of PV module modeling of mono-crystalline and multi-crystalline silicon technologies. In Section 4 explains some advantages of the GUI and mathematical models. Finally, Section 5 concludes with the main findings and contributions to the field of study.

2. Materials and Methods

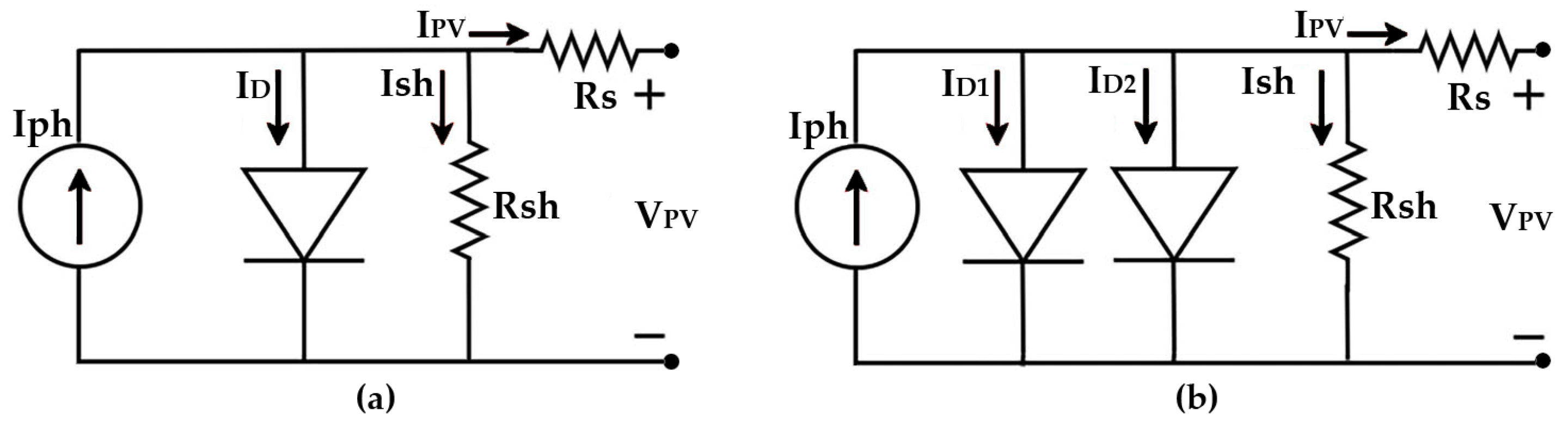
2.1. Equivalent circuit of the PV cell based on the two-diode model

Figure 1 shows the circuits most commonly used to represent the behavior of photovoltaic modules under the effect of varying irradiance and temperature. Both schemes have two resistances, one series-connected and the other one connected in parallel.

The equation for the current I produced by the photovoltaic panel in these two equivalent circuits, can be calculated by applying the Kirchhoff laws and the mathematical model of the Shockley diode [33,34,35]. The one-diode model, shown in Figure 1(a), has five unknown internal parameters as shown in Equation (1) [36].

I = I_{p v} - I_{o} [e x p (\frac{V + I \cdot R_{s}}{n \cdot V_{t}}) - 1] - (\frac{V + I \cdot R_{s}}{R_{s h}})

(1)

The unknown parameters are the photocurrent generated by the incident light

I_{p v}

(A), the reverse saturation diode current

I_{o}

(A), equivalent parallel resistance

R_{s h}

(

Ω

), equivalent series resistance

R_{s}

(

Ω

) and quality factor of the diode n (adimensional). The output voltage V (V) of the module is known,

V_{t} = N_{s} \cdot k \cdot T / q

is the thermal voltage, and

N_{s}

represents cells connected in series, k is the Boltzmann constant [

1.3806503 \cdot 10^{- 23} J / K

], T is the temperature of the p-n junction (

^{\circ} C

) and q is the electron charge [

1.60217646 \cdot 10^{- 19} C

]. This one-diode model is one of the most commonly reported in scientific literature [36,37,38,39,40]. Equation (1) can also be presented in the form of Equation (2).

I = I_{p v} - I_{o} [e x p (\frac{V + I \cdot R_{s}}{n \cdot (N_{s} \cdot k \cdot T / q)}) - 1] - (\frac{V + I \cdot R_{s}}{R_{s h}})

(2)

The two-diode model, shown in Figure 1(b), has seven unknown internal parameters in the output current, as shown in Equation (3).

I = I_{p v} - I_{o 1} [e x p (\frac{V + I \cdot R_{s}}{n_{1} \cdot V_{t 1}}) - 1] - I_{o 2} [e x p (\frac{V + I \cdot R_{s}}{n_{2} \cdot V_{t 2}}) - 1] - (\frac{V + I \cdot R_{s}}{R_{s h}})

(3)

I_{o 1}

is the saturation current (A) of diode 1 due to diffusion and

I_{o 2}

is the saturation current (A) of diode 2 due to recombination effect [35]. In addition, due to two-diode model, the quality factors for both diodes are required (

n_{1}

and

n_{2}

). Equation (3) originates the V-I and V-P curve shown in Figure 2 where three main points were shown: short circuit

(0, I_{s c})

M P P (V_{m p p}, I_{m p p})

, and open circuit

(V_{o c}, 0)

The extraction of the unknown internal parameters is requierd so that they can be substituted in Equation (3), to obtain the V-I and V-P curves and consequently the electrical parameters of the PV module. The two-diode model is more complex, but allows more accurate results than the one-diode model. This is especially evident when the operating conditions of the module highly vary from STC [12]. Furthermore, the two-diode model improves modeling modules of different silicon technologies: multi-crystalline, mono-crystalline and thin-film [12,13,14,37].

2.2. Mathematical model of reverse saturation diode current

The equation for the current generated by the photovoltaic module (

I_{p v}

) can be expressed as a function of temperature and irradiance, as indicated in Equation (4) [36,41].

I_{p v} = [I_{p v S T C} + K_{i} \cdot (T - T_{S T C})] - (\frac{G}{G_{S T C}})

(4)

I_{p v S T C}

is the current generated at STC (A),

K_{i}

is the temperature/current coefficient (

% /^{\circ} C

), T is the temperature of the p-n junction in the analyzed operating conditions (

^{\circ} C

) and

T_{S T C} = 25^{\circ} C

is the temperature at STC. G is the irradiation level in the analyzed operating conditions (

W / m^{2}

) and

G_{S T C} = 1000 W / m^{2}

is the irradiation level at STC.

The saturation diode current

I_{o}

(A) is dependant on temperature and is calculated according to Equation (5), where

E g

is the energy in the semiconductor gap band (

e V

) and

I_{o S T C}

is the salutation diode current (A) at STC [36].

I_{o} = I_{o S T C} \cdot {(\frac{T_{S T C}}{T})}^{3} \cdot e x p [\frac{q \cdot E_{g}}{n \cdot k} \cdot (\frac{1}{T_{S T C}} - \frac{1}{T})]

(5)

The saturation diode current under STC

I_{o S T C}

is calculated by equation (6).

I_{o S T C} = \frac{I_{S T C}}{[e x p (\frac{V_{o c S T C}}{n \cdot V_{T S T C}}) - 1]}

(6)

The accuracy of the calculated saturation diode current

I_{o}

at STC can be improved by using Equation (7) instead of Equation (6) [36]. The temperature/voltage ratio

K_{v}

is included, which is also found in the datasheet provided by the manufacturer. Thus, this will matche with the calculated open circuit voltage

V_{o c}

, provided by the manufacturer in the datasheet, for a wide range of operrating temperatures.

I_{o S T C} = \frac{I_{S T C} + K_{i} \cdot (T - T_{S T C})}{[e x p (\frac{V_{o c S T C} + K_{v} \cdot (T - T_{S T C})}{n \cdot V_{T S T C}}) - 1]}

(7)

To simplify the calculation, it is assumed that both saturation diode currents

I_{o 1}

and

I_{o 2}

are equal, therefore Equation (8) can be used [41].

I_{o 1 S T C} = I_{o 2 S T C} = \frac{I_{S T C} + K_{i} \cdot (T - T_{S T C})}{[e x p (\frac{V_{o c S T C} + K_{v} \cdot (T - T_{S T C})}{(\frac{n_{1} + n_{2}}{p}) \cdot V_{T S T C}}) - 1]}

(8)

With Equation (8), the computing time used in the iteration is considerably simplified and the solution can be obtained analytically. Quality factors

n_{1}

and

n_{2}

represent the diffusion and recombination of the current respectively. According to Shockley’s diffusion theory, the diffusion current

n_{1}

is equal to unity. However, the decision of the value

n_{2}

is flexible. Based on extensive simulations, it is found that if

n_{2} = 1.2

, improve the model accuracy is observed [42]. Currently, it’s still used this assignment [43,44], with which accurate V-I curves are obtained for varied conditions. It is also assumed that

(n_{1} + n_{2}) / p = 1

and therefore the value of

p \geq 2.2

[41,42]. Based on these assumptions, Equation (8) can be rewritten as shown in Equation (9).

I_{o 1 S T C} = I_{o 2 S T C} = \frac{I_{S T C} + K_{i} \cdot (T - T_{S T C})}{[e x p (\frac{V_{o c S T C} + K_{v} \cdot (T - T_{S T C})}{V_{T S T C}}) - 1]}

(9)

This generalization avoids the ambiguity of having to select

n_{1}

and

n_{2}

values. In this way, the calculation of the

I_{p v}

I_{o 1}

I_{o 2}

n_{1}

and

n_{2}

parameters is expedited, leading to decreased computation time. Replacing Equation (9) in Equation (3), gives Equation (10) that simplifies the two-diode model [4,16,41,45,46,47].

I = I_{p v} - I_{o} [e x p (\frac{V + I \cdot R_{s}}{V_{t}}) + e x p (\frac{V + I \cdot R_{s}}{(p - 1) \cdot V_{t}}) + 2] - (\frac{V + I \cdot R_{s}}{R_{s h}})

(10)

In Equation (10), the value of I can be calculated for the range of values of

0 ⩽ V ⩽ V_{o c}

. This means that the number of points of the V-I curve is calculated from

V o c / (s t e p = 0.1)

. To calculate the power of PV arrays as shown in the Figure 3, structured by s x p modules, where s are the modules connected in series and p are the modules connected in parallel, it’s assumed that

I = p \cdot I

;

V = s \cdot V

;

R_{s} = R_{s} \cdot \frac{s}{p}

and

R_{s h} = R_{s h} \cdot \frac{s}{p}

in the Equation (10). Also, it is necessary to calculate

R_{s}

and

R_{s h}

using iterative methods.

2.3. Method for $R_{s}$ and $R_{s h}$ computation

R_{s}

and

R_{s h}

can be calculated simultaneously according to an established method [41,42]. Using this method, the maximum power

P_{m p p}

is adjusted until the calculated maximum power point

P_{m a x C}

matches the maximum power point value of the manufacturer’s datasheet

P_{m a x E}

. The coincidence between

P_{m a x C}

and

P_{m a x E}

will be possible if the value of

R_{s}

is increased iteratively while being calculated simultaneously. From Equation (10) the value of

R_{s h}

is calculated at the maximum power point, obtaining the expression shown in Equation (11).

R_{s h} = \frac{V_{m p p S T C} + I_{m p p S T C} \cdot R_{s}}{I_{p v} - I_{o} \cdot [e x p (\frac{V_{m p p S T C} + I_{m p p S T C} \cdot R_{s}}{V_{T}}) + e x p (\frac{V_{m p p S T C} + I_{m p p S T C} \cdot R_{s}}{(p - 1) \cdot V_{T}}) + 2] - \frac{P_{m a x E}}{V_{m p p S T C}}}

(11)

V_{m p p S T C}

is the voltage amplitude (V) at the maximum power point. The initial condition of series-connected resistance is assumed to be zero and the initial condition of parallel-connected resistance can be estimated using Equation (12).

R_{s o} = 0; R_{s h o} = \frac{V_{m p p S T C}}{I_{s c S T C} - I_{m p p S T C}} - \frac{V_{o c S T C} - V_{m p p S T C}}{I_{m p p S T C}}

(12)

Equation (12) describes the initial value of

R_{s h}

, which is the slope of the line segment between the short circuit current

I_{s c}

and the maximum power point

P_{m p p}

. For each iteration, the value of

R_{s h}

can be calculated simultaneously according to Equation (11). When the seven unknown parameters have been determined, the output current I is calculated using the Newton-Raphson method for values of

0 ⩽ V ⩽ V_{o c}

. This algorithm can be used to calculate the values of

R_{s}

and

R_{s h}

For the PVMSim case, the computation process stops when the condition

| P_{m a x C} - P_{m a x E} | ⩽ 0.01

is reached. The accuracy of this algorithm has been demonstrated by several researchers, where the I-V and P-V curves are obtained by computer simulation [18,20,22,48].

2.4. PV conversion efficiency

PVMSim calculates the parameters that determine the efficiency of the PV module. These are Fill Factor

F F

and

η

F F

is calculated by Equation (13).

F F = \frac{V_{m p p} \cdot I_{m p p}}{V_{o c} - I_{s c}}

(13)

F F

is a parameter determining the maximum power (adimensional). It can be graphically represented as "square" or the largest area of the rectangle that is adjusted on the I-V curve (gray color) as shown in Figure 4. In general, value ranges for fill factor are from 0.4 to 0.8 and take the value of 1 only in ideal PV modules [49,50,51]. The

V_{m p p}

I_{m p p}

V_{o c}

and

I_{s c}

values are required.

The efficiency can be correlated with the operating temperature

T_{c}

. The PV cell only converts a small amount of the radiation it receives into electrical energy, the rest is dissipated as heat [52]. The electrical efficiency

η

is expressed as a function of the

T_{c}

through the linear relationship shown in Equation (14) [53].

η = η_{S T C} \cdot [1 - β_{S T C} \cdot (T_{c} - T_{S T C})]

(14)

η_{S T C}

is the module’s efficiency (%),

β_{S T C}

is the temperature coefficient of power (

% /^{\circ} C

). These parameters and

T_{S T C}

are available from the datasheet. This correlation has been widely accepted, and for this reason, it appears in experimental investigations for different environmental conditions [54,55,56].

T_{c}

is a variable that is not commonly measured but can be calculated by applying mathematical models that correlate some weather variables. Many common models correlate three climate variables:

T_{a}

, G and v. The

T_{a}

can be obtained from in situ measurements or climate dataset such as NASA [57] or some software such as PVsyst [58,59,60,61]. Various methods can be used to calculate the

T_{c}

of PV cells from the available

T_{a}

measurements [17,62]. In the case of PVMSim,

T_{c}

is calculated by the Equation (15) [63], this is a simple implicit expression used by manufacturers to define the NOCT parameter [17]. This equation is widely used by researchers as a reference in current

T_{c}

prediction studies [64,65,66].

T_{c} = T_{a} + (N O C T - 20) \cdot \frac{G}{800}

(15)

G is the incident irradiance on the surface of the PV module. Substituting T from Equation (4) for

T_{c}

from Equation (15), the effect of

T_{a}

and G on the PV efficiency is obtained. For the simulations done in this paper, weather data from the NASA dataset were used [57]. These data are in hourly profile, which means that 144 values are available daily for each meteorological variable. The power is calculated hourly and the energy daily output is displayed on the plot, calculated by the sum of

P_{m a x C}

as a function of time.

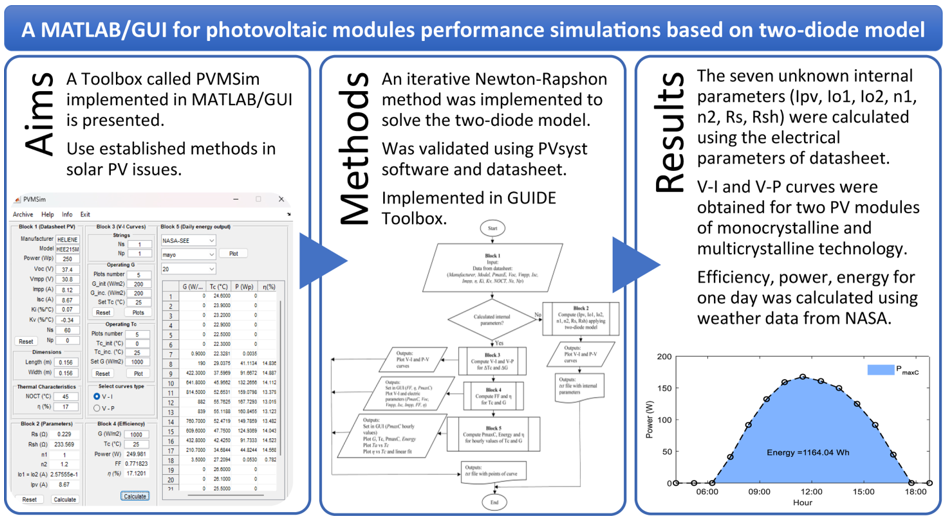
2.5. Methods and implemented algorithm of PVMSim

The PVMSim Toolbox is shown in Figure 5, in MATLAB (2020b) Toolbox GUIDE and through scripts, the methods were programmed.

This toolbox consists of five GUI’s Blocks:

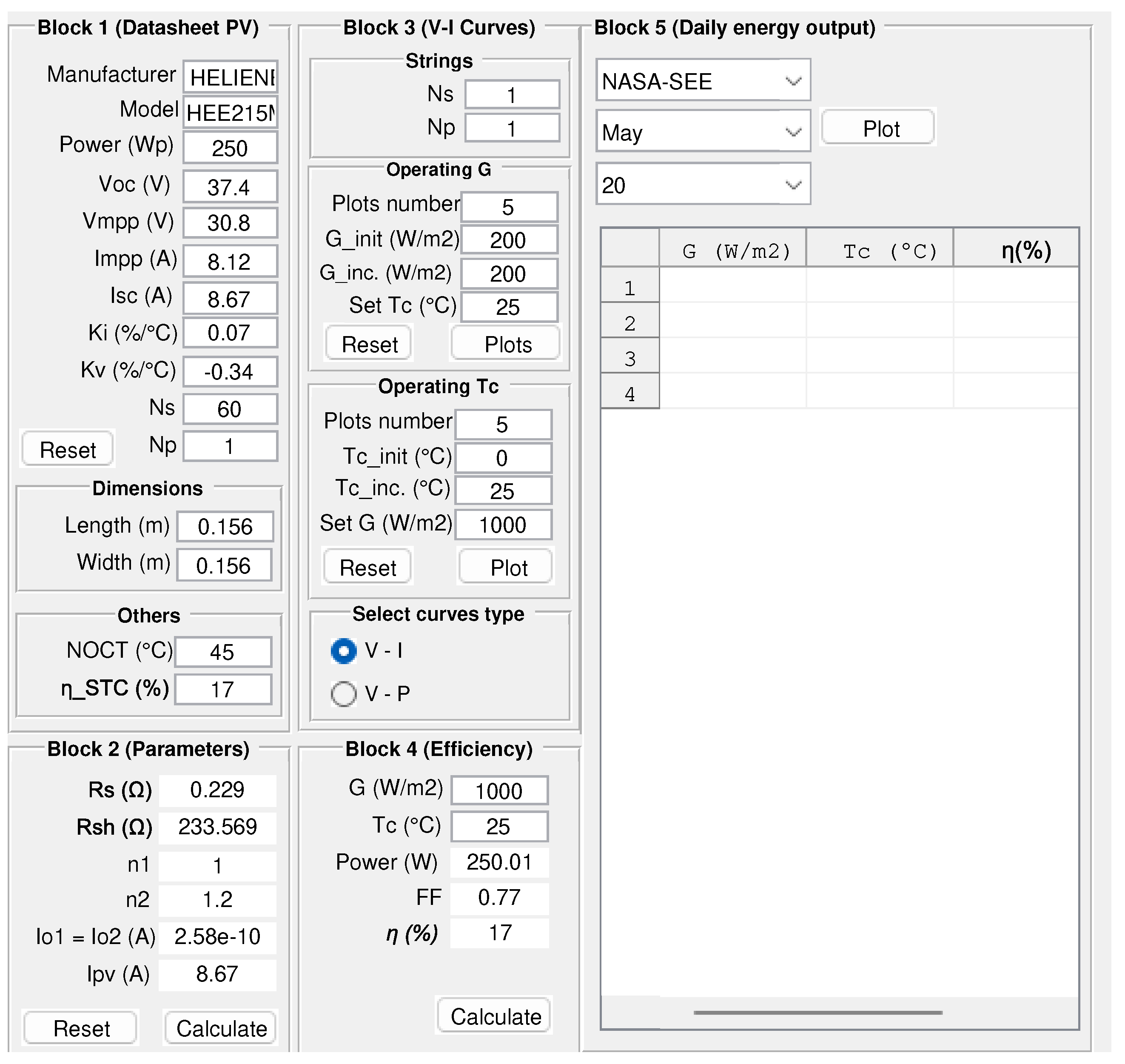
GUI’s Block 1: input data of manufacturer’s datasheet, it is important to add all the values of the electrical parameters for the STC and NOC, also the mechanical data such as dimensions of PV cells, no Editbox of this block can be left incomplete.
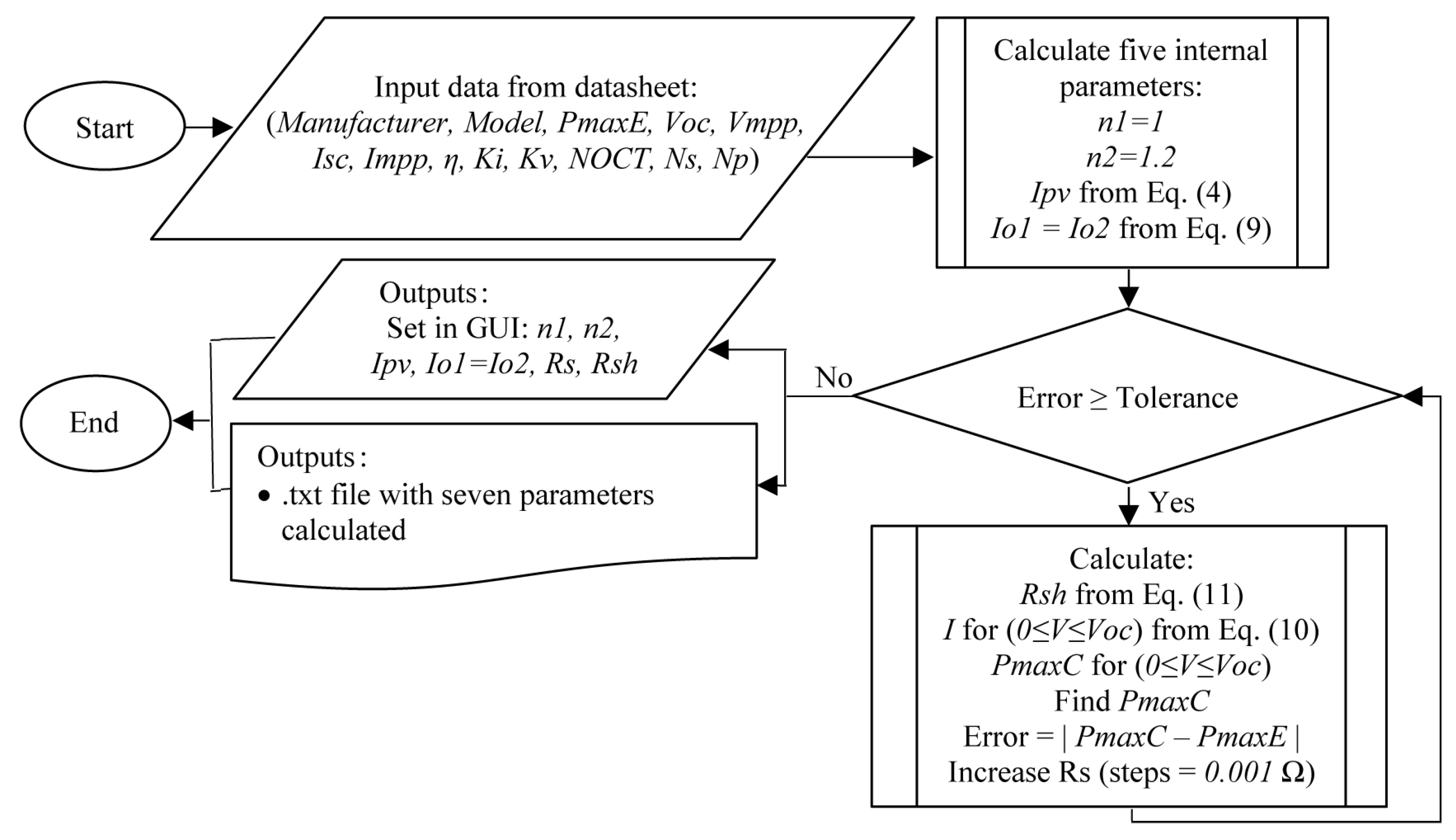
GUI’s Block 2: the modeling algorithm of this block is shown in Figure 6. By Pushbutton (Calculate), the defined process of extracting the seven unknown internal parameters of the PV module begins, through the iterative method of Newton-Raphson, using the two-diode model and applying the methods described above. Once the calculations are completed and the defined tolerance is reached, the values of the parameters are displayed in the Textboxs. No data in this block is entered.
GUI’s Block 3: the simulation algorithm of this block is shown in Figure 7. First, the number of PV modules per string is entered, and the modules connected in series and in parallel must be defined. Then the number of I-V curves and P-V curves are going to be plotted, and the variation of the irradiance and the temperature of the PV cells must also be specified. By pushbutton (Plot) the corresponding curves are obtained. Finally, the points used for the plotted curves are automatically saved in a .txt file.
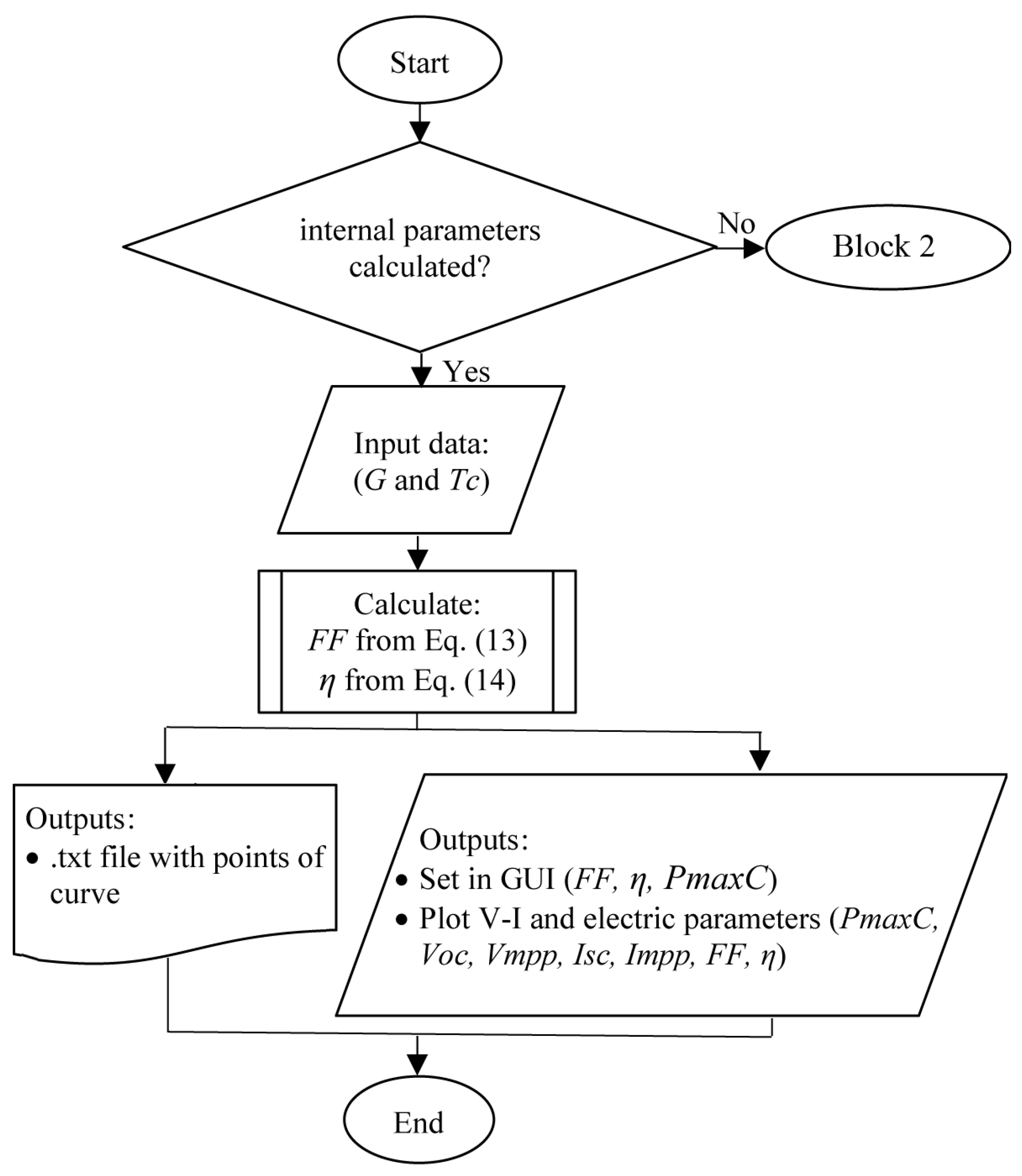
GUI’s Block 4: The simulation algorithm of this block is shown in Figure 8. Calculates and plots the fill factor $F F$ and $η$ numerical values, and plot a single I-V curve with the electrical parameters corresponding to that simulation. Input data of G and $T_{c}$ must be entered for the simulation.
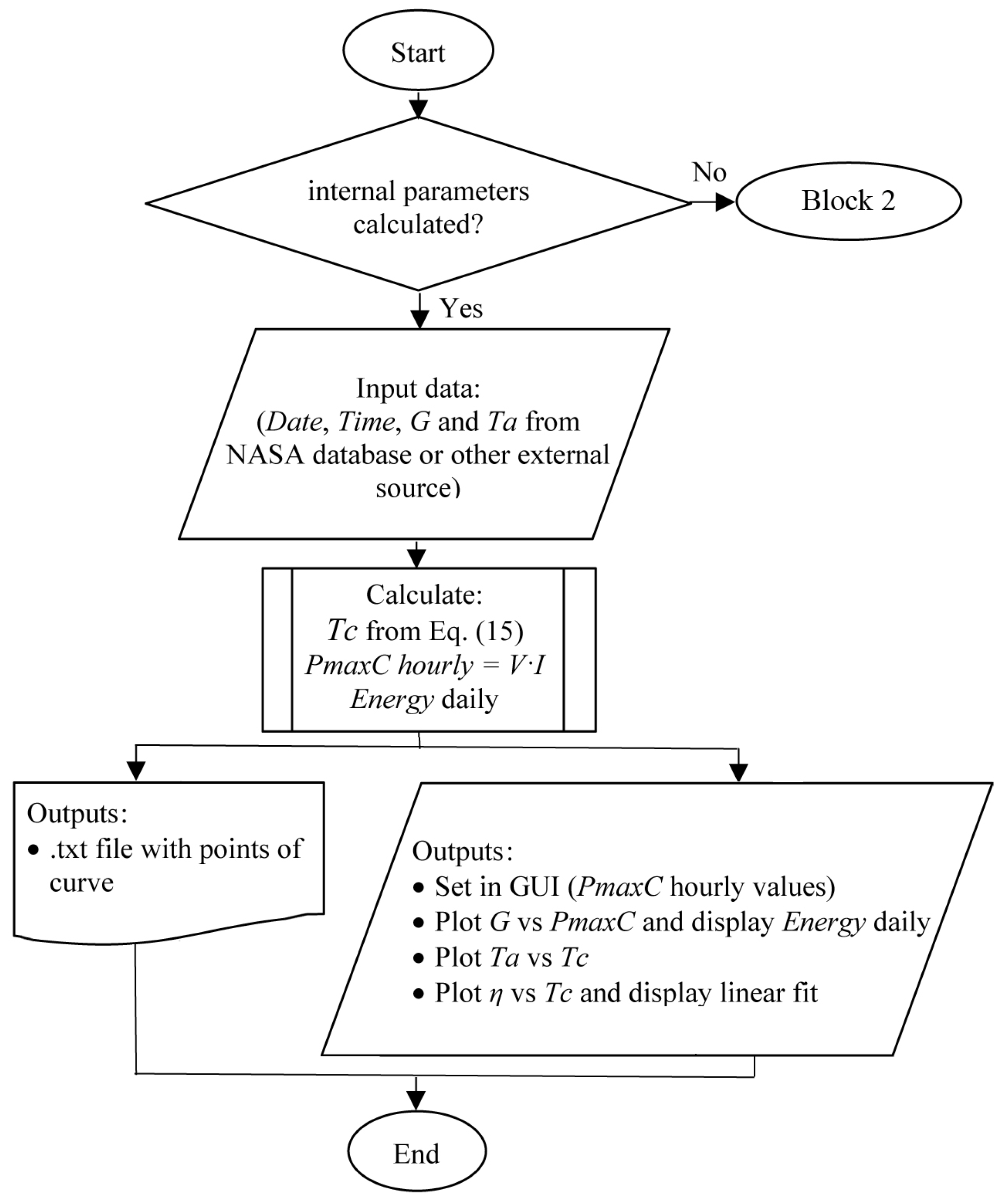
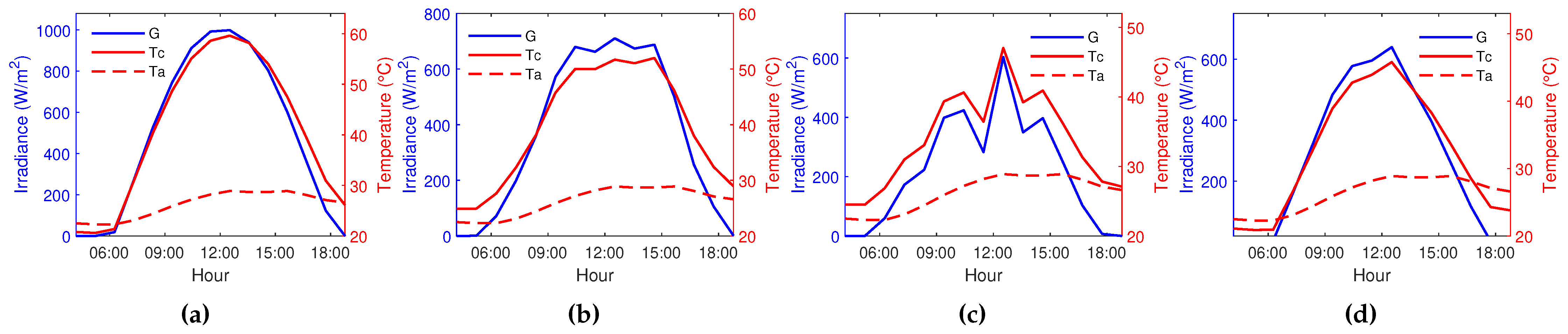
GUI’s Block 5: the calculation algorithm of this block is shown in Figure 9. Plot $P_{m a x C}$ , G, $T_{c}$ , $T_{a}$ and $η$ for the effect of climatic conditions of a given region, within a date selected by the user. To obtain the power values at each hour of the day, PVMSim imports a file in .txt format, with the annual records of the geographic site analyzed. In this case, the data provided by NASA is imported [57]. This data is commonly used for this type of simulation [48,67]. In this block, the hourly data of $P_{m a x C}$ , $T_{c}$ , G and $η$ is also exported to a .txt file.

In order to assess the robustness of the two-diode model, the Mean Absolute Error (MAE) was calculated using Equation (16). The internal parameters are compared with the datasheet parameters and also those obtained by PVsyst.

M A E = \frac{1}{n} \cdot \sum_{i = 1}^{n} | X_{i, P V M S i m} - X_{i, P V s y s t} |

(16)

Subscript

P V M S i m

is equivalent to the data calculated by PVMSim, while the subscript

P V s y s t

is equivalent to the data obtained in PVsyst.

3. Results

For to validate the methods defined in the previous section, two cases were simulated: mono-crystalline silicon HEE215MA68 and multi-crystalline silicon SW150polyR6A PV modules. These PV modules are of different power levels and made by different manufacturers. Table 1 shows the electrical parameters for the STC and NOC. These parameters are also available in the datasheet, hence these variables are used to validate the internal parameter extraction method for the two-diode model.

3.1. Extracting unknown internal parameters

In the GUI’s Block 2 in PVMSim the methodology shown in Figure 6 is used. Upon completion of the extraction of the seven unknown internal parameters, Figure 10 shows the variations of the electrical parameters. The curves are explained as follows:

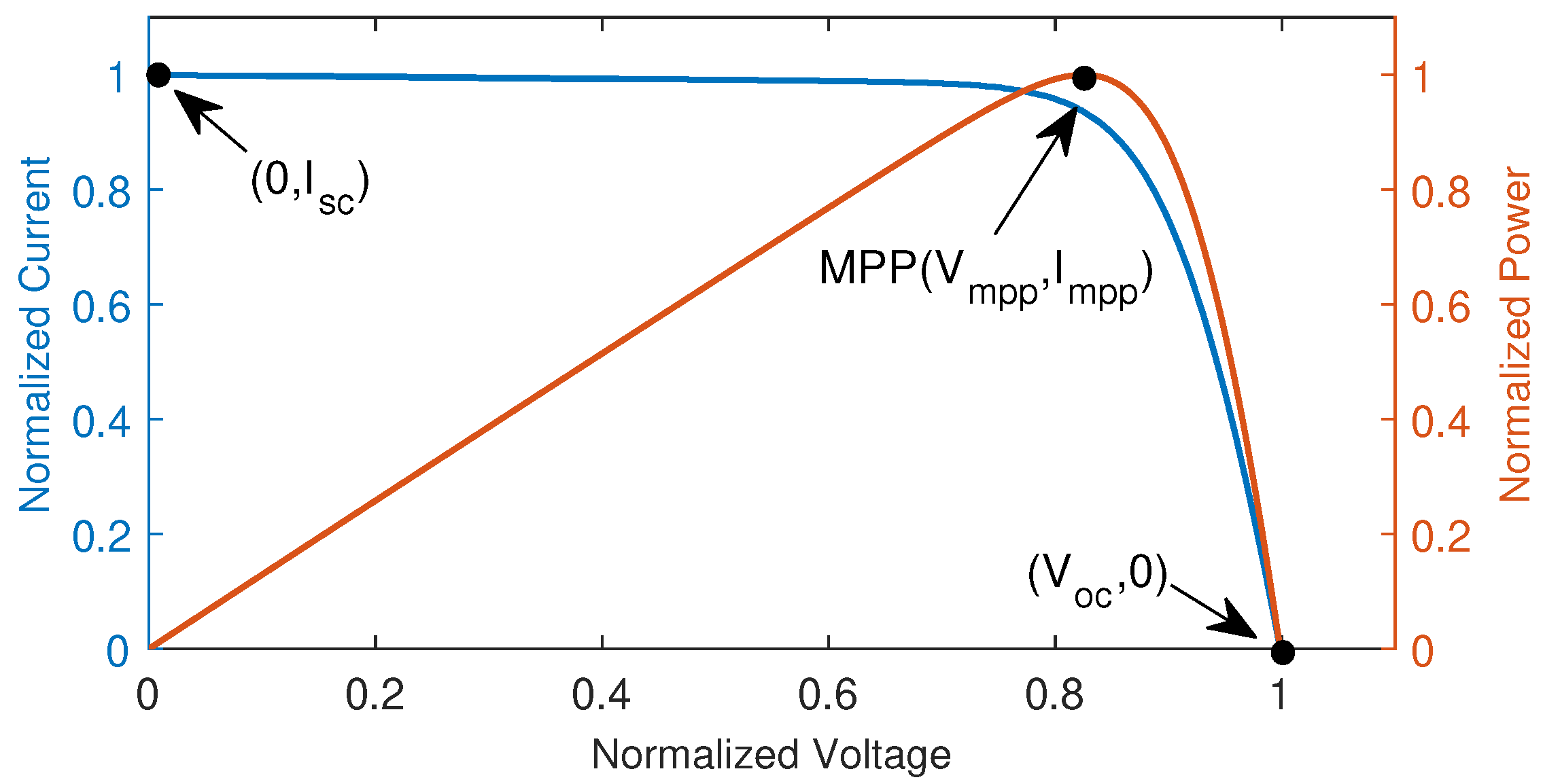
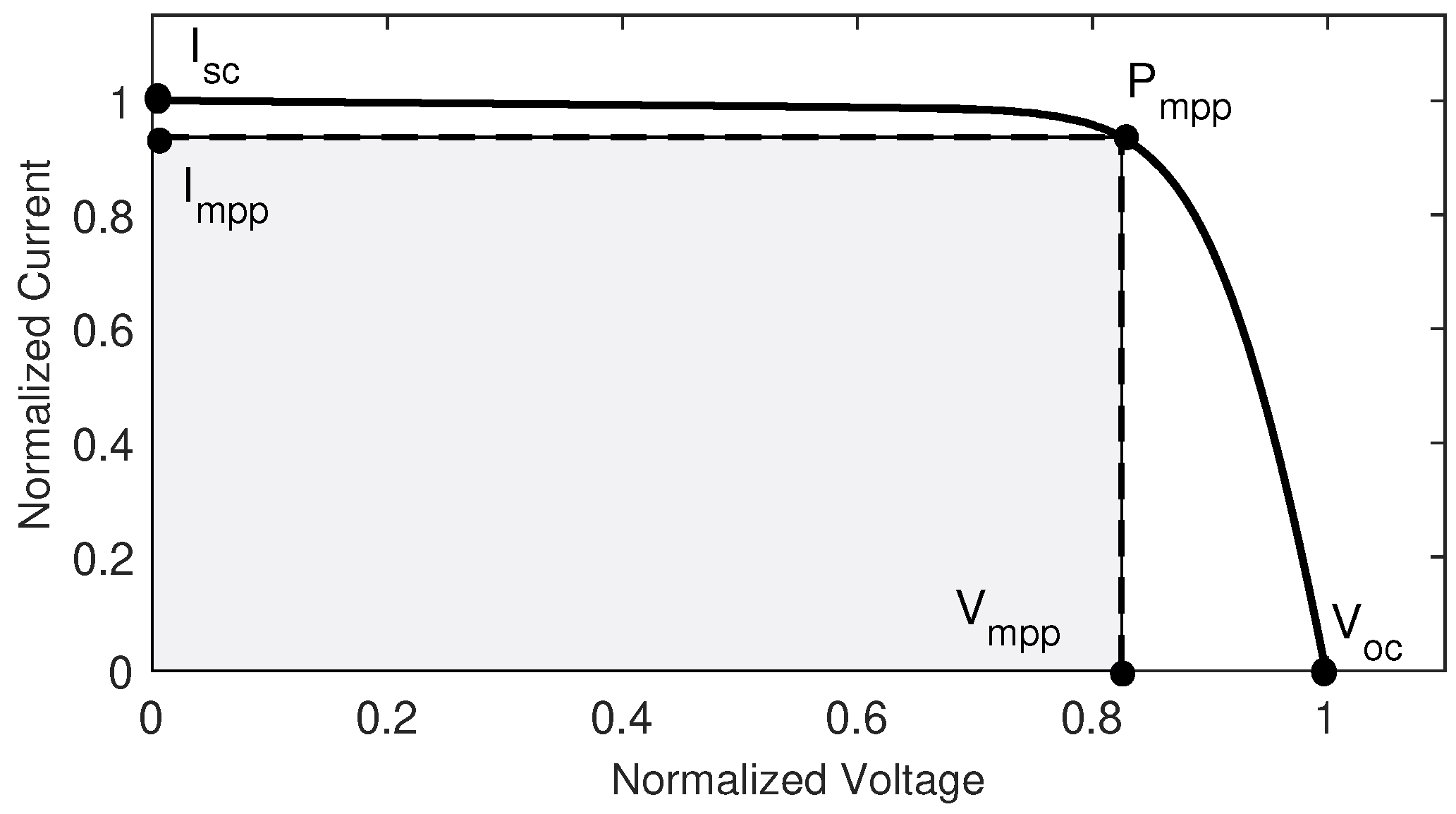
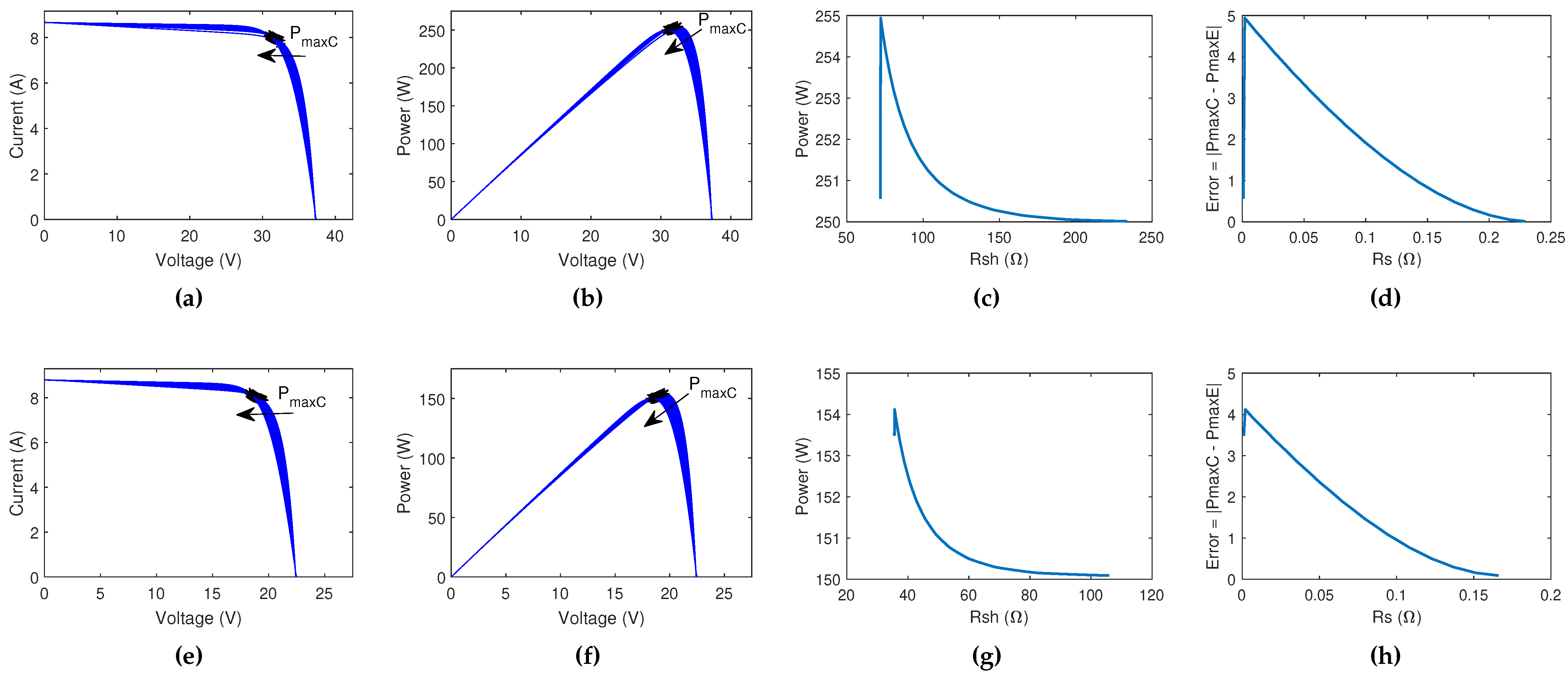
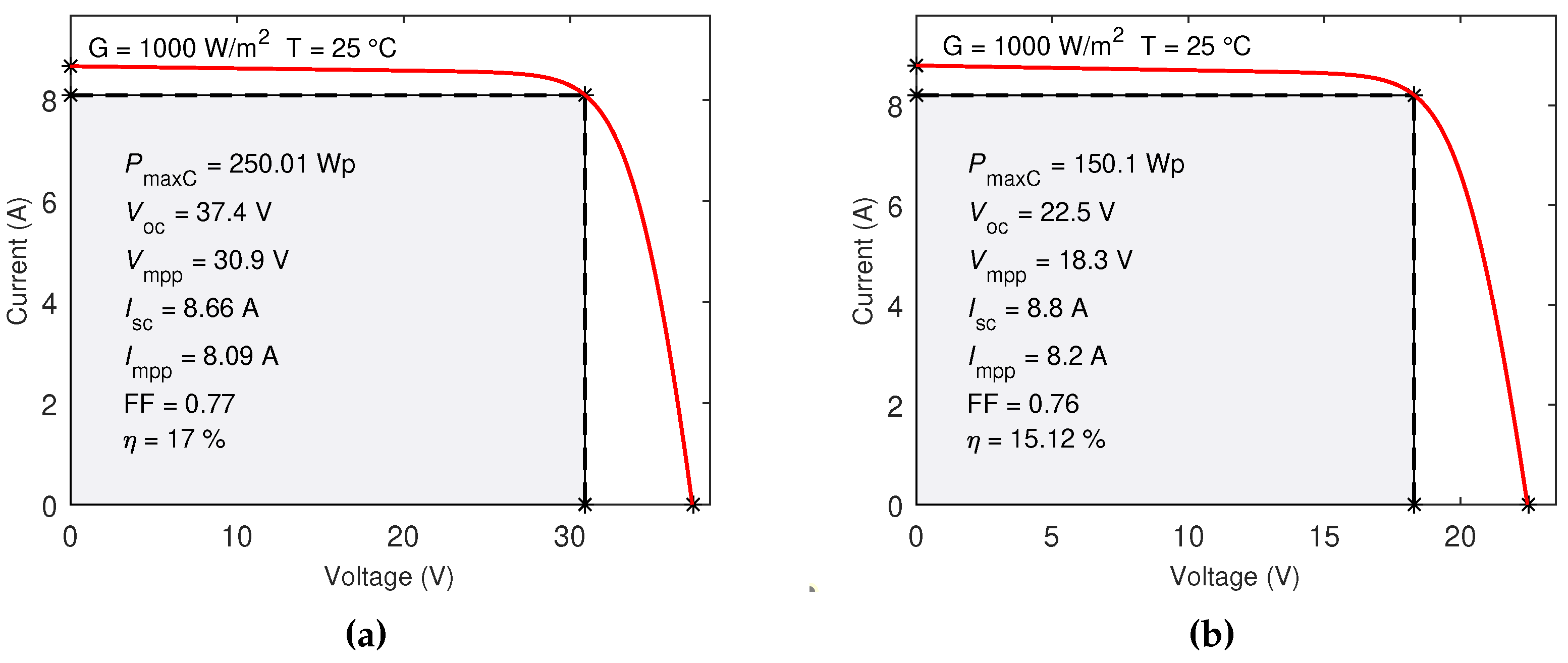
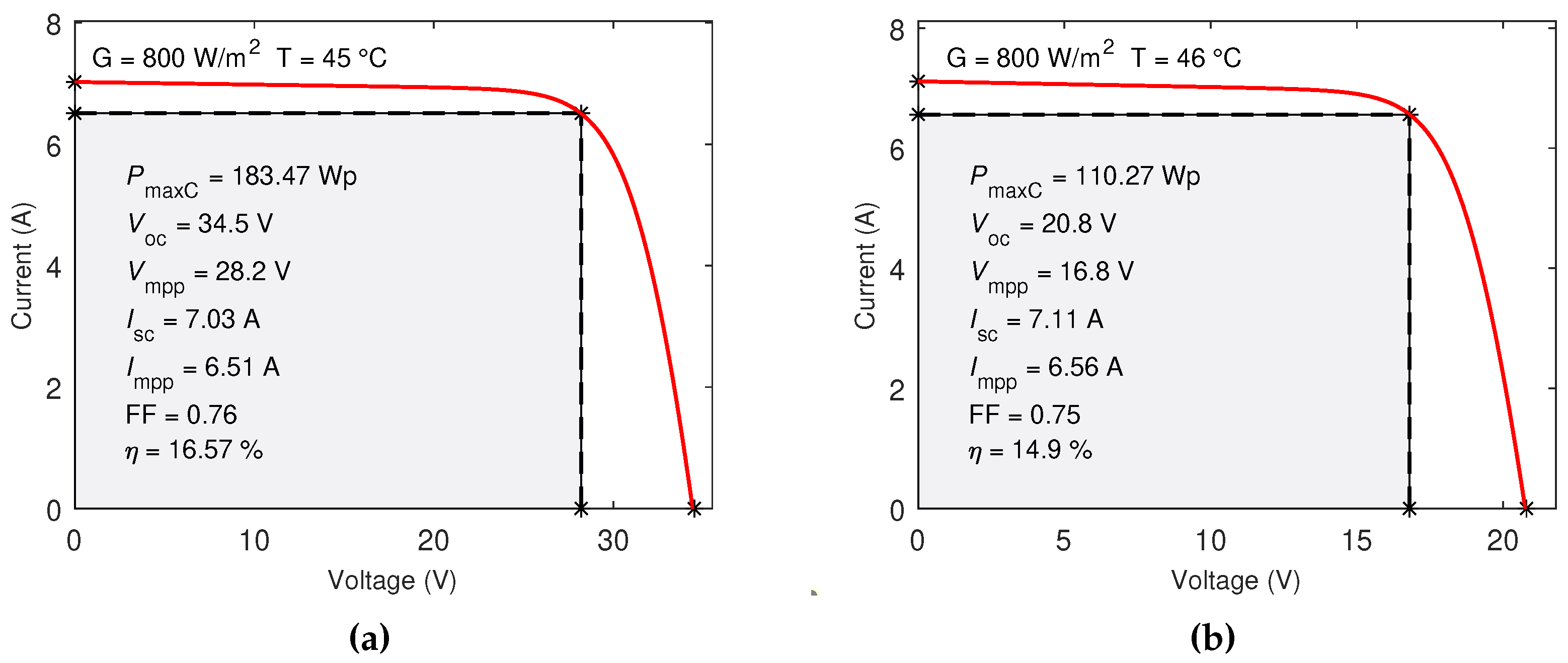
I-V (a,e) and P-V (b,f) characteristic curves show the movement of $P_{m a x C}$ . The maximum power of the PV modules is available in the datasheets, with a tolerance for STC. For the analyzed PV modules, the tolerance are $3 %$ and $2 %$ for HEE215MA68 and SW150polyR6A, respectively. It is important to take this data into account to analyze the accuracy of the algorithm for extracting the unknown internal parameters in Figure 7. The black asterisks represent the $P_{m a x C}$ , while the arrow indicates the direction of movement of the V-I and V-P curves.
Curves in the plot (c,g) show the variation of $P_{m a x C}$ according to the variation of the value of $R_{s h}$ . The algorithm starts the iterative method with values of $P_{m a x C}$ greater than the value of $P_{m a x E}$ . For the PV HEE215MA68 module, the value of $R_{s h o} = 72 Ω$ while for the SW150polyR6A the value of $R_{s h o} = 35.58 Ω$ . The value of $R_{s h}$ is increased (Equation (11) until the stop condition is reached.
Curves in the plot (d,h) begin with the value of $R_{s o} = 0 Ω$ (Equation (12)), then this value is increased with $s t e p s = 0.001 Ω$ until the stop condition is reached.
The modeling algorithm reaches the stopping condition when $| P_{m a x C} - P_{m a x E} | \leq 0.01$ for STC.

Before a simulation can be run, PVMSim validates that the internal parameters have been calculated. The seven parameters calculated for the two-diode model (GUI’s Block 2) are shown in Table 2. Once the program calculates and displays the internal parameters, the I-V and P-V characteristics curves can be simulated in GUI’s Block 3, 4 or 5 as needed.

To validate the calculated internal parameters, the manufacturer’s data of each PV module was used. Table 3 shows the MAE for the electrical parameters found using the two-diode model for STC and NOC.

The MAE errors shown in Table 3 shows the precision of the methodology used. The results are considered to be very accurate, with parameter

P_{m a x C}

remaining within the tolerance range defined by the manufacturer, while the other electrical parameters also perform well, remaining the

F F

and

η

according to their respective PV technologies, such as shown in Section 3.3.

Another way to validate the performance of PVMSim is using the professional software PVsyst as a reference [70]. PVsyst uses the one-diode model like Figure 1(a) with five unknown internal parameters (

R_{s}, R_{s h}, I_{o}, I_{p v}, n

) of the Equation (1) and it’s applied to design and size PV systems. Table 4 shows the

P_{m a x C}

values obtained by the PVsyst and PMVSim for different values of G and

T_{c}

, which are the most common available in the datasheet for the PV modules for countries at any latitude in the world.

Using PVsyst as a reference, both PV modules present good precision according to the values of the MAE errors. For irradiance values close to STC and NOC, the MAE error is lower. For low irradiance levels (

G < 400 W / m^{2}

) it’s difficult to predict the

V_{o c}

value and therefore the

P_{m a x C}

[40]. For different values of

T_{c}

, the PVMSim also performs well, obtaining zero error in both cases for STC. Note that as the

T_{c}

values increase, the value of the MAE increases; previous studies based on experimental measurements have shown that for temperature values far from STC conditions (

T_{c} > 50^{\circ} C

) the prediction of

V_{o c}

and

P_{m a x C}

is less accurate [42,46,47].

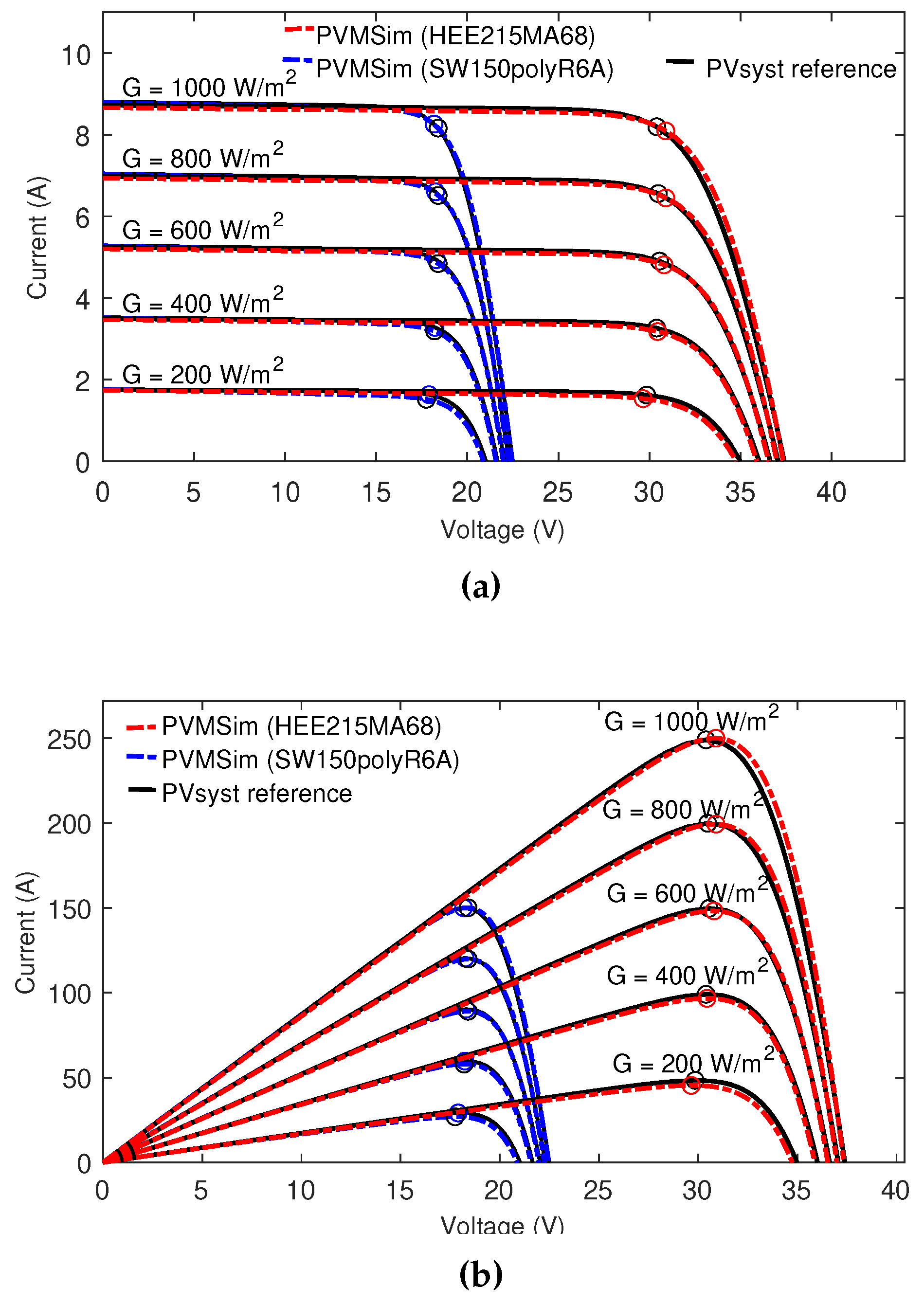
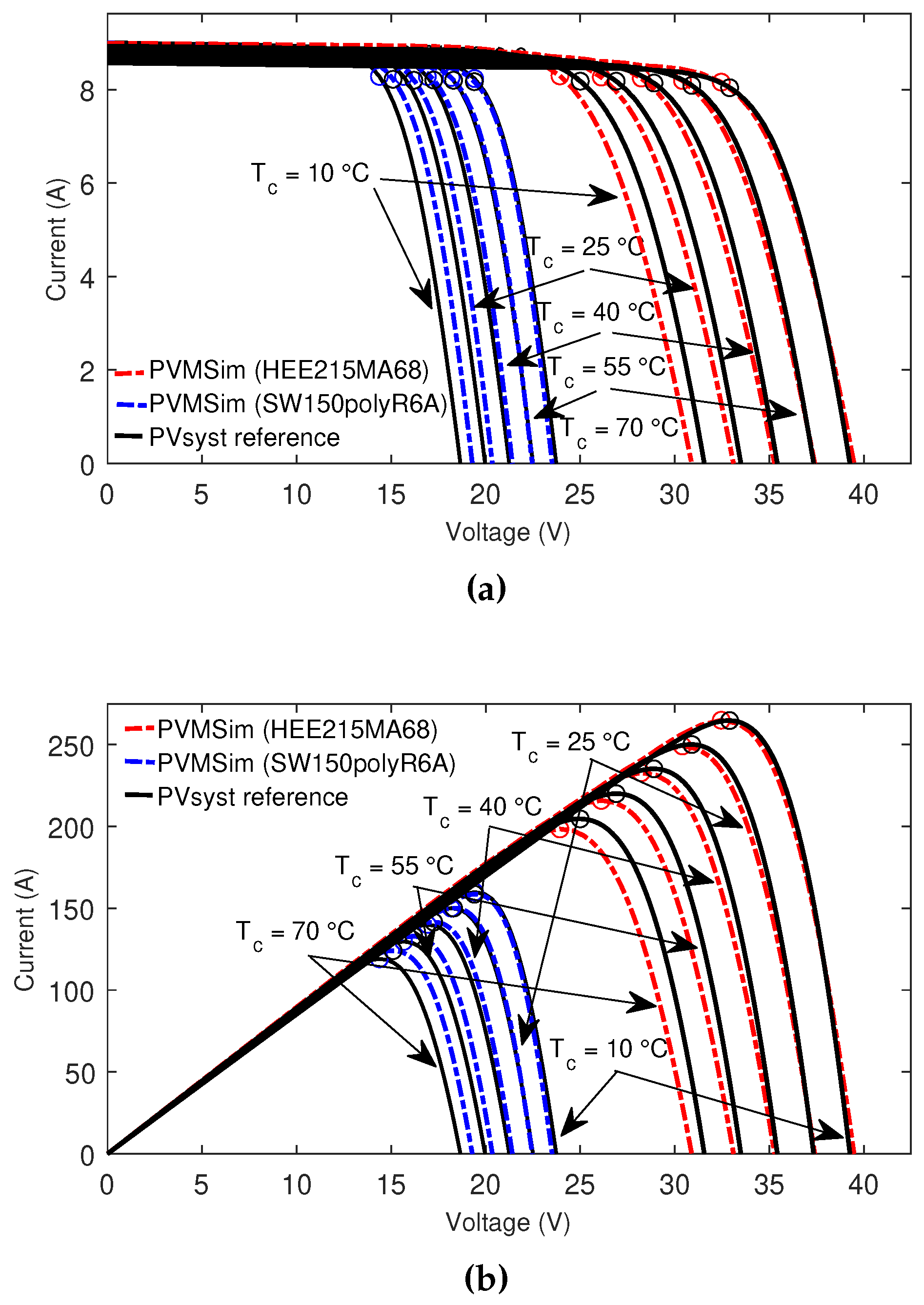
3.2. Simulating the effect of irradiance and temperature

After validating the accuracy of the methodology used to extract the internal parameters, in GUI’s Block 3 of PVMSim the effect of G and

T_{c}

on the power of the PV modules can be simulated using the methodology shown in Figure 7. Figure 11 and Figure 12 show V-I and V-P curves for the different levels of G and

T_{c}

given in Table 4. These plots not only show the correlation of

P_{m a x C}

, but also between

I_{s c}

V_{o c}

and all points on the curve.

Variations in irradiance cause notable variations in short-circuit current

I_{s c}

, while variations in PV cell temperature affect open-circuit voltage

V_{o c}

. In both cases, the maximum power is affected. PVMSim allows any number of characteristic curves to be obtain as required by the user of the application. The points of the curve can be saved in

. t x t

files, for future modeling in MATLAB or to be used in other software.

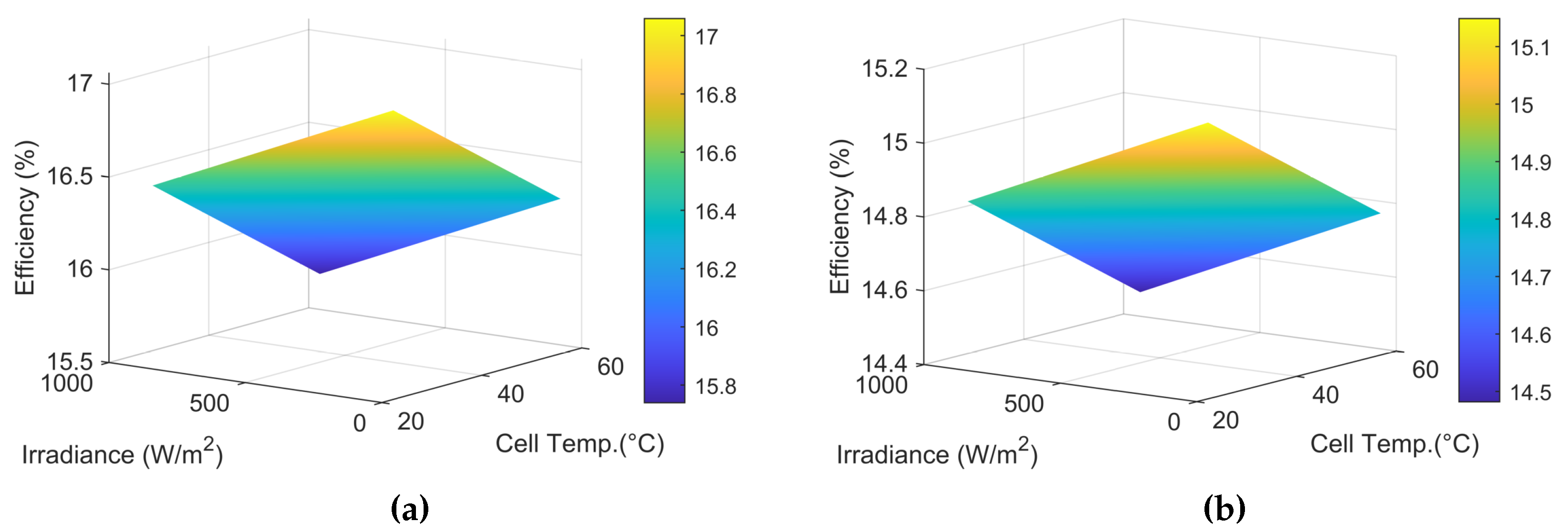
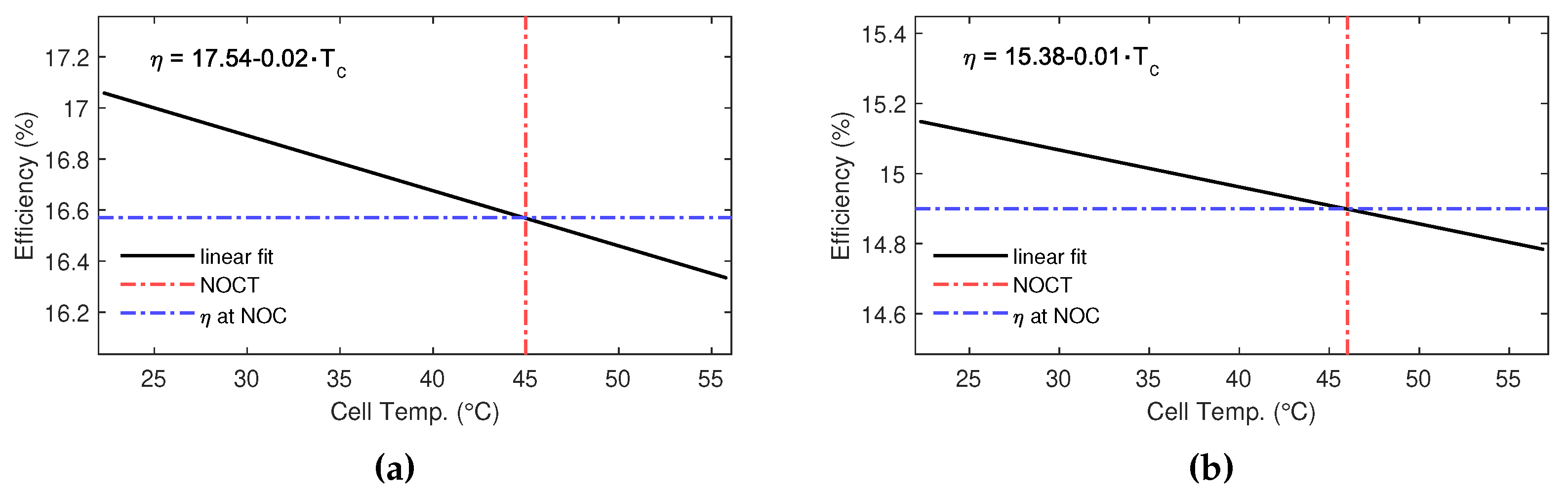
3.3. Predictions of PV efficiency

Using the methodology shown in Figure 8, the theoretical efficiency of the PV module can be calculated. The data in Table 3 is shown in the plots given in Figure 13 and Figure 14, respectively. These figures were obtained in GUI’s Block 4 of PVMSim, gray color depicts the area that is occupied by fill factor

F F

. The I-V characteristic curve is shown in red color for the irradiance and temperature values of operation. The black asterisks represent the calculated electrical parameters.

The

F F

and

η

are not specified in the datasheet of the sample PV modules. However, Figure 13 and Figure 14 shows the values of these parameters obtained by the two-diode model for STC and NOC, respectively. Note that for both cases,

η

is different and

F F

has a difference of 0.01, although these PV modules are of different power and manufacturer, the size of the cells and the silicon technology is decisive. For the NOC, the

P_{m a x C}

decreases as

T_{c}

increases, consequently, the

η

and the

F F

decrease.

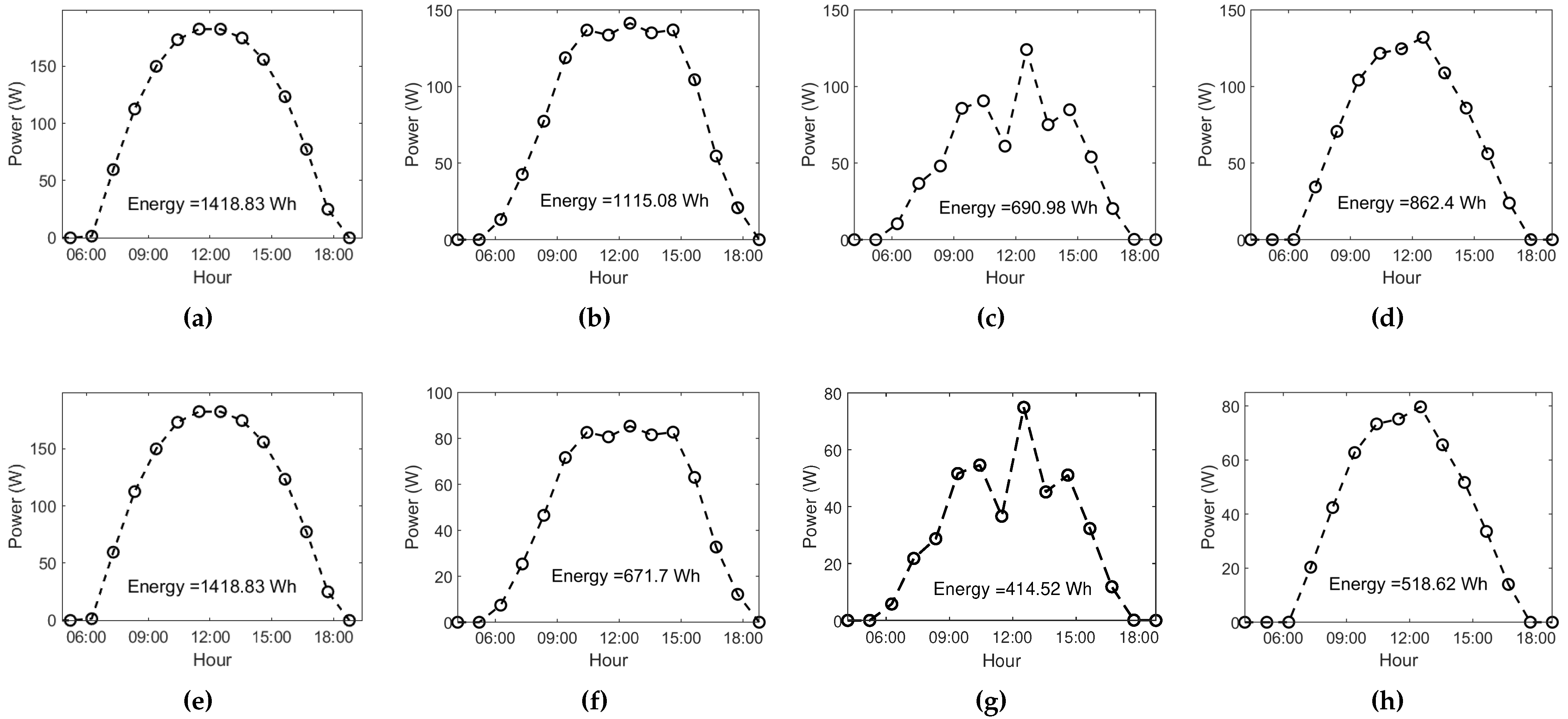
3.4. Obtaining daily energy output

In GUI’s Block 5 of the PVMSim, the predictions of the daily output power and energy are shown, using the methodology given in Figure 9. For the aims of this paper, Santiago de Cuba was chosen to simulate the behavior of PV modules, located in geographic coordinates: latitude 20,0051° N, longitude -75,7711° W, elevation 98 m. Simulations for the days were selected from the NASA dataset: summer solstice day (June 21), autumn equinox (March 21), spring equinox (September 21) and winter solstice (December 21). Figure 15 shows the different evolutions of G,

T_{a}

and

T_{c}

, such as: sunny day (March), partly cloudy day with irregular radiation (September) and partly cloudy day with regular radiation (June and December).

From Figure 15 it can be seen how

T_{a}

and G affects

T_{c}

according to Equation (15), varying from 6:00 hours to 18:00 hours, reaching the maximum levels at 13:00 hours. Table 5 shows the effect of

T_{a}

and G on

P_{m a x C}

and

η

(Equation (14)) at 13:00 hours, for each day chosen.

Figure 16 shows the evolution of maximum power point hourly and daily energy output calculated as the cumulative sum of

P_{m a x C}

, during the chosen day.

Figure 17 shows a plot with the effect of G and

T_{c}

on the PV conversion efficiency, for every month of the year. HEE215MA68 registered levels performance of

16.42 % < η < 17 %

; while the SW150polyR6A registered levels performance of

14.83 % < η < 15.12 %

Figure 18 shows the linear correlation of the

η

T_{c}

calculated from Equation (15). The red vertical line indicates the NOCT value while the blue horizontal line indicates the

η

for NOC.

Therefore, the model can predict that the increase of

1^{\circ} C

T_{c}

has an approximate decreasing effect of

- 0.02

and

- 0.01

in the efficiency of HEE215MA68 and SW150polyR6A, respectively. This plot helps to improve the prediction of

η

for different climatic conditions at the PV module installation site.

4. Discussion

PVMSim is a MATLAB tool that offers a graphical interface that is easily integrated as a Toolbox. In addition, it allows the intuitive modeling and simulation of PV modules. It has the advantage that only the parameters from the datasheet are needed as input data, as well as a meteorological dataset (optional, if is desired to know the daily energy production and the effect of G and

T_{a}

on the

η

). The Toolbox is useful for obtaining important data that can be used in more complex modeling, or as part of more comprehensive algorithms where the extraction of unknown internal parameters is included.

GUI’s Block 1 includes the data on the electrical parameters that are usually available in the datasheet provided by the manufacturer and can also be downloaded from the official website. These data are electrical data (PmaxE, Voc, Vmpp, Impp, Isc, NOCT, η, Ki, Kv) and mechanical data (length and width). Some previous studies contemplate the use of other data, such as measurements of V-I curves [40]. The principal advantage of this block is that all the data necessary for the extraction of unknown internal parameters are available and easily accessible to users.

GUI’s Block 2 introduces an algorithm for the extraction of internal parameters that uses the two-diode method, which has been validated for its robustness by several previous studies [41,48]. Also, this method is used as a reference to know the accuracy of new, complex and modern methods [46,71]. This block includes the Newton-Raphson iterative method, in order to obtain the V-I characteristic curve as close as possible to the curve of the STC of the datasheet, where the value of

P_{m a x C}

reaches its minimum error below a tolerance

\leq 0.01

with respect to

P_{m a x E}

provided by the manufacturer. Simulations have shown that this method is successful for high irradiance values (

400 W / m^{2}

1000 W / m^{2}

), for lower values (below

400 W / m^{2}

) it is less accurate. These results are in agreement with other studies where similar data sets were obtained [41]. This study considered mono-crystalline (HEE215MA68) and multi-crystalline (SW150polyR6A) silicon PV module models, but it has been shown that, in general, this method is very robust for modeling these technologies and also thin-film silicon [42].

There are other methods for the extraction of internal parameters. Recent studies have used the one-diode method [36,72,73] and three-diode [74,75]. However, this method was chosen because it is very efficient and accurate. In addition, it has been proven effective for a wide range of commercial silicon-based PV technologies [42]. Currently and for the next 5 years, PV modules based on crystalline silicon technology will be the market leaders, representing almost 95% of world production [76]. The algorithm used, iteratively calculates the maximum power point until the manufacturer’s

P_{m a x E}

value is obtained, which considerably improves PV string design and sizing studies. Other studies consider the use of the one-diode model also serves the same purpose when precision is not important.

Due to the non-linearity of the model, the computational calculations are not straightforward. In order to improve the precision in the extraction of the unknown internal parameters, other methods can be used, such as optimization techniques and models based on artificial intelligence [12,17]. However, this takes more computational time.

In GUI’s Block 3, the results were compared with the PVsyst, demonstrating that the effect of G and

T_{c}

on the PV modules are in the range of professional software simulations that are commonly used worldwide. The metrics are thus demonstrated, with low MAE errors. Users can simulate as many curves as desired to perform analysis, design and sizing of PV systems.

In GUI’s Block 4, the electrical parameters of the PV module are calculated and displayed in the plot, which also includes

F F

and

η

, which are not provided by the manufacturer. This block is useful to find out the efficiency of a specific PV module for the conditions of the installation site. It allows performance for STC to be extrapolated to local performance for conditions anywhere in the world. This block could be of interest to researchers with a special interest in analyzing of

F F

loss depending on the

T_{c}

for the industrial silicon solar cells [77], limitations of

F F

in heterojunction PV cells [78], assessment the performances and the energy production under various values of

T_{a}

and G as well as the correlation between the

F F

and the weather condition [79]. The Equation (15) could be changed to another method that adds other meteorological parameters (i.e.,

T_{a}

, G, wind speed and relative humidity) in order to improve the prediction of

F F

and

η

, but would require prior experimental analysis at the PV installation site.

GUI’s Block 5 simulates the effect of G and

T_{a}

P_{m a x C}

T_{c}

and

η

throughout the chosen day. The results shown in the plots in Figure 15 are only for during the hours of Sun. This block has the advantage of importing the weather data from a

. t x t

file, which does not limit the source of the data. For this study, the NASA data source was used [57], but users can import climate data measured in situ. Using the tab as separator, the

. t x t

file must be structured as follows:

1^st column: date and time 01/01/2022 0:00:00
2^nd column: irradiance value G ( $W / m^{2}$ )
3^th column: ambient temperature value $T_{a}$ ( $^{\circ} C$ )

Santiago de Cuba (a province in the eastern region of Cuba considered as a study case), has a predominantly humid tropical climate. It is common for the PV modules to reach the operating values presented in Figure 15 and then

η

decreases to less than 2% (Figure 18). The results of this block are consistent with other experimental study in the same region of Cuba, in situ measurements based, in which it was proved that for a six months study, the efficiency dropped to 1.9% during the day with the temperature in the range of

17^{\circ} C < T_{c} < 67^{\circ} C

[58].

PVMSim make MATLAB easy to use, eliminating the need of uses scripts or Simulink programming. There are other similar GUIs in MATLAB documented in previous studies, in which different characteristics of PV modules were analyzed, both in their intrinsic operation, as well as in real-time supervision, performance under certain operating conditions or technical-economic reliability [18,25,26,67]. It is also common to use other platforms such as Python that integrate with the MATLAB platform [80,81,82]. The choice of one or another platform often depends on the knowledge and skill of the user.

With PVMSim is not possible to identify the PV module that best suit a specific PV project or a specific geographical area. Like other professional software such as PVsyst, SAM, HOMER, the user is responsible for choosing the PV module that best suits their design or sizing needs, and then modeling or simulating the operating conditions of the system’s location. The PV project under evaluation must previously define the PV module. For this reason, the user must study the market to determine the PV module that best suits their requirements.

5. Conclusions

In this paper, the Matlab’s PVMSim Toolbox was presented. This tool is useful for modeling the characteristics of silicon-based PV modules, as well as for simulating the effect of irradiance and temperature on the PV conversion efficiency.

The methods were validated with two PV modules of different silicon technologies, mono-crystalline (HEE215MA68) and multi-crystalline (SW150polyR6A), the results led to the following conclusions:

In Block 1, only the electrical parameters and dimensions of the PV cell from the manufacturer’s datasheet are needed to solve the two-diode model, without the need for field measurements.
In Block 3, the Newton-Raphson iterative method applied to solve the two-diode modeling provided accurate results for extraction of the seven unknown internal parameters ( $I_{p v}$ , $I_{o 1}$ , $I_{o 2}$ , $n_{1}$ , $n_{2}$ , $R_{s}$ , $R_{s h}$ ) for the two PV modules investigated. For STC conditions, MAE=0.01 and MAE=0.1 errors were obtained for HEE215MA68 and SW150polyR6A respectively, at the maximum power point, evidenced that the iterative method calculates $P_{m a x C}$ according to the tolerance defined by the manufacturer.
In Block 4, the methodology applied for the plotting of the V-I and V-P characteristic curves, $η$ and $F F$ , allows obtaining them at different irradiance and temperature levels other than STC and NOC laboratory conditions.
In Block 5, the effect of weather parameters (G and $T_{a}$ ) on electrical parameters ( $P_{m a x C}$ , $V_{o c}$ , $V_{m p p}$ $I_{s c}$ , $I_{m p p}$ , $F F$ , $η$ ) was simulated using a NASA dataset. Therefore, the daily energy produced is calculated.
Finally, PVMSim is a useful Toolbox for users to model and simulate the PV modules silicon-based, for any weather conditions. This GUI-based tool allows interaction with the other complementary toolboxes of MATLAB that offer a wide variety of engineering and research applications.

Author Contributions

Conceptualization, L.O. and Y.R.M.; methodology, L.O. and M.R.; code programming, L.O.; validation, L.O., M.R. and Y.R.M.; formal analysis, L.O.; investigation, L.O.; writing—original draft preparation, L.O., M.R. and P.W.; writing—review and editing, L.O., M.R. and V.T.; visualization, L.O., M.R. and V.T.; supervision, M.R., Y.R.M., V.T. and P.W.; funding acquisition, M.R. and P.W.

Funding

This research was funded by ANID/ ATE220023 Project; FONDECYT Regular Research Project 1220556; CLIMAT AMSUD 21001, FONDAP SERC Chile 15110019 and Doctorate of Engieering Macrofacultad I2030.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data are available on request to the authors.

Acknowledgments

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

IRENA. Renewable Capacity Highlights-20 March 2023. https://www.irena.org/Publications/2023/Mar/Renewable-capacity-statistics-2023, accessed on April 10, 2023.
IRENA. Renewable capacity statistics 2023, International Renewable Energy Agency, Abu Dhabi. https://www.irena.org/Publications/2023/Mar/Renewable-capacity-statistics-2023, accessed on April 18, 2023.
Sarquis Filho, E.A.; Fernandes, C.A.F.; da Costa Branco, P.J. A complete framework for the simulation of photovoltaic arrays under mismatch conditions. Solar Energy 2021, 213, 13–26. [CrossRef]
Abbassi, A.; Ben Mehrez, R.; Touaiti, B.; Abualigah, L.; Touti, E. Parameterization of photovoltaic solar cell double-diode model based on improved arithmetic optimization algorithm. Optik 2022, 253, 168600. [CrossRef]
Tao, M.; Fthenakis, V.; Ebin, B.; Steenari, B.M.; Butler, E.; Sinha, P.; Corkish, R.; Wambach, K.; Simon, E.S. Major challenges and opportunities in silicon solar module recycling. Progress in Photovoltaics: Research and Applications 2020, 28, 1077–1088. [CrossRef]
Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. Journal of applied physics 1961, 32, 510–519. [CrossRef]
Schwingshackl, C.; Petitta, M.; Wagner, J.E.; Belluardo, G.; Moser, D.; Castelli, M.; Zebisch, M.; Tetzlaff, A. Wind effect on PV module temperature: Analysis of different techniques for an accurate estimation. Energy Procedia 2013, 40, 77–86. [CrossRef]
Munoz, M.A.; Alonso-García, M.C.; Vela, N.; Chenlo, F. Early degradation of silicon PV modules and guaranty conditions. Solar Energy 2011, 85, 2264–2274. [CrossRef]
Kinsey, G.S. Solar cell efficiency divergence due to operating spectrum variation. Solar Energy 2021, 217, 49–57. [CrossRef]
Umoette, A.T.; Ubom, E.A.; Akpan, I.E. Comparative Analysis of Three NOCT-Based Cell Temperature Models. International Journal of Systems Science and Applied Mathematics 2016, 1, 69. [CrossRef]
Duffie, J.A.; Beckman, W.A.; McGowan, J. Solar Engineering of Thermal Processes . American Journal of Physics 1985, 53, 382–382. [CrossRef]
Venkateswari, R.; Rajasekar, N. Review on parameter estimation techniques of solar photovoltaic systems. International Transactions on Electrical Energy Systems 2021, 31, 1–72. [CrossRef]
Houssein, E.H.; Zaki, G.N.; Diab, A.A.Z.; Younis, E.M. An efficient Manta Ray Foraging Optimization algorithm for parameter extraction of three-diode photovoltaic model. Computers & Electrical Engineering 2021, 94, 107304. [CrossRef]
Ridha, H.M.; Hizam, H.; Gomes, C.; Heidari, A.A.; Chen, H.; Ahmadipour, M.; Muhsen, D.H.; Alghrairi, M. Parameters extraction of three diode photovoltaic models using boosted LSHADE algorithm and Newton Raphson method. Energy 2021, 224, 120136. [CrossRef]
Castro, R.; Silva, M. Experimental and theoretical validation of one diode and three parameters–based pv models. Energies 2021, 14. [CrossRef]
Huang, C.M.; Chen, S.J.; Yang, S.P. A Parameter Estimation Method for a Photovoltaic Power Generation System Based on a Two-Diode Model. Energies 2022, 15, 1–16. [CrossRef]
Siddiqui, M.U.; Siddiqui, O.K.; Alquaity, A.B.; Ali, H.; Arif, A.F.; Zubair, S.M. A comprehensive review on multi-physics modeling of photovoltaic modules. Energy Conversion and Management 2022, 258, 115414. [CrossRef]
Almaktoof, A.; Shebani, N.; Elfallah, A. GUI-PV Application Tool for Teaching Performance of PV System using MATLAB-Graphical User Interface Environment. In Proceedings of the 2021 IEEE 1st International Maghreb Meeting of the Conference on Sciences and Techniques of Automatic Control and Computer Engineering MI-STA, 2021, pp. 447–451. [CrossRef]
Shekoofa, O.; Wang, J.; Luo, Y.; Sun, C.; Xiong, B. PVSIM-GUI, a characterization tool for parameter extraction, modeling and simulation of pv devices. In Proceedings of the 31st European Photovoltaic Solar Energy Conference and Exhibitation, 2015, pp. 2249–52.
Figueiredo, G.; Macêdo, W.; Pinho, J.T. Computational tool for sizing and assessment of grid-connected photovoltaic systems. Energy Procedia 2014, 57, 168–177. [CrossRef]
Belhaouas, N.; Khechafi, S.; Mehareb, F.; Aseem, H.; Bensalem, S.; Hadj Arab, A. Electrical Standalone PV System Sizing with Graphic User Interface (GUI) based on UTE C15-712-2 Guide. Proceedings of 2019 7th International Renewable and Sustainable Energy Conference, IRSEC 2019 2019. [CrossRef]
Aprilianti, K.P.; Baghta, N.A.; Aryani, D.R.; Jufri, F.H.; Utomo, A.R. Potential assessment of solar power plant: A case study of a small island in Eastern Indonesia. IOP Conference Series: Earth and Environmental Science 2020, 599. [CrossRef]
Noor, S.Z.; Zaini, S.; Omar, A.M. Design of graphical user interface development environment software for sizing of Grid Connected Photovoltaic (GCPV) system. International Journal of Engineering and Technology(UAE) 2018, 7, 145–150. [CrossRef]
Da Silva, J.R.C.; Pacheco, G.M. Open source software development in matlab for sizing photovoltaic systems. 2018 13th IEEE International Conference on Industry Applications, INDUSCON 2018 - Proceedings 2019, pp. 256–262. [CrossRef]
Hassan, M.U.; Saha, S.; Haque, M.E. PVAnalytX: A MATLAB toolkit for techno-economic analysis and performance evaluation of rooftop PV systems. Energy 2021, 223, 120074. [CrossRef]
Salim, S.; Ohri, J. Monitoring and Analysis of Solar PV based on GUI. In Proceedings of the 2020 First IEEE International Conference on Measurement, Instrumentation, Control and Automation (ICMICA), 2020, pp. 1–4. [CrossRef]
Ruchira.; Sao, A.; Patel, R.N.; Sinha, S.K. GUI Supported Experimental Investigation of Central Inverter and Microinverter Integrated with 1kW PV System. 3rd International Conference and Workshops on Recent Advances and Innovations in Engineering, ICRAIE 2018 2018, 2018, 1–6. [CrossRef]
Bilu, A.C.; Durusu, A.; Dogansahin, K.; Kekezoglu, B. A new educational software package for photovoltaic system feasibility: PVGUI. International Journal of Electrical Engineering Education 2019. [CrossRef]
Bektas, S.C.; Cakmak, R.; Altas, I.H. Design of a MATLAB GUI for Day Ahead Forecasting of PV Panel Power. Proceedings - 2019 Innovations in Intelligent Systems and Applications Conference, ASYU 2019 2019, pp. 3–7. [CrossRef]
Mittal, M.; Bora, B.; Saxena, S.; Gaur, A.M. Performance prediction of PV module using electrical equivalent model and artificial neural network. Solar Energy 2018, 176, 104–117. [CrossRef]
Kermadi, M.; Chin, V.J.; Mekhilef, S.; Salam, Z. A fast and accurate generalized analytical approach for PV arrays modeling under partial shading conditions. Solar Energy 2020, 208, 753–765. [CrossRef]
Mahmood, R.S.; Yaqoob Javed, M.; Tariq, A.R.; Rizvi, S.N.R.; Cheema, K.M.; Waqas, M. A Comprehensive approach to Study Double Diode Model and Shading Effects on Photovoltaic Arrays. Proceedings - 2020 23rd IEEE International Multi-Topic Conference, INMIC 2020 2020. [CrossRef]
Lorenzo, E.; Araujo, G.; Cuevas, A.; Egido, M.; Minano, J.; Zilles, R. Solar Electricity: Engineering of Photovoltaic Systems. Ed., PROGENSA 1994, p. 316.
Cubas, J.; Pindado, S.; De Manuel, C. Explicit expressions for solar panel equivalent circuit parameters based on analytical formulation and the lambert W-function. Energies 2014, 7, 4098–4115. [CrossRef]
Meyer, E.L. Extraction of Saturation Current and Ideality Factor from Measuring Voc and Isc of Photovoltaic Modules. International Journal of Photoenergy 2017, 2017. [CrossRef]
Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Transactions on Power Electronics 2009, 24, 1198–1208. [CrossRef]
Lo Brano, V.; Orioli, A.; Ciulla, G.; Di Gangi, A. An improved five-parameter model for photovoltaic modules. Solar Energy Materials and Solar Cells 2010, 94, 1358–1370. [CrossRef]
Farivar, G.; Asaei, B. Photovoltaic module single diode model parameters extraction based on manufacturer datasheet parameters. PECon2010 - 2010 IEEE International Conference on Power and Energy 2010, pp. 929–934. [CrossRef]
Piliougine, M.; Guejia-Burbano, R.A.; Petrone, G.; Sánchez-Pacheco, F.J.; Mora-López, L.; Sidrach-de Cardona, M. Parameters extraction of single diode model for degraded photovoltaic modules. Renewable Energy 2021, 164, 674–686. [CrossRef]
Chaibi, Y.; Salhi, M.; El-jouni, A.; Essadki, A. A new method to extract the equivalent circuit parameters of a photovoltaic panel. Solar Energy 2018, 163, 376–386. [CrossRef]
Ishaque, K.; Salam, Z.; Syafaruddin. A comprehensive MATLAB Simulink PV system simulator with partial shading capability based on two-diode model. Solar Energy 2011, 85, 2217–2227. [CrossRef]
Ishaque, K.; Salam, Z.; Taheri, H. Simple, fast and accurate two-diode model for photovoltaic modules. Solar Energy Materials and Solar Cells 2011, 95, 586–594. [CrossRef]
Aoun, N.; Bouchouicha, K.; Bailek, N. Seasonal Performance Comparison of Four Electrical Models of Monocrystalline PV Module Operating in a Harsh Environment. IEEE Journal of Photovoltaics 2019, 9, 1057–1063. [CrossRef]
Al-Masri, H.M.K.; Magableh, S.K.; Abuelrub, A.; Saadeh, O.; Ehsani, M. Impact of Different Photovoltaic Models on the Design of a Combined Solar Array and Pumped Hydro Storage System. Applied Sciences 2020, 10. [CrossRef]
Franzitta, V.; Orioli, A.; Di Gangi, A. Assessment of the usability and accuracy of two-diode models for photovoltaic modules. Energies 2017, 10. [CrossRef]
Chennoufi, K.; Ferfra, M.; Mokhlis, M. An accurate modelling of Photovoltaic modules based on two-diode model. Renewable Energy 2021, 167, 294–305. [CrossRef]
Meng, Z.; Zhao, Y.; Tang, S.; Sun, Y. An efficient datasheet-based parameters extraction method for two-diode photovoltaic cell and cells model. Renewable Energy 2020, 153, 1174–1182. [CrossRef]
Morcillo-Herrera, C.; Hernández-Sánchez, F.; Flota-Bañuelos, M. Method to calculate the electricity generated by a photovoltaic cell, based on its mathematical model simulations in MATLAB. International Journal of Photoenergy 2015, 2015. [CrossRef]
Richter, A.; Hermle, M.; Glunz, S.W. Reassessment of the limiting efficiency for crystalline silicon solar cells. IEEE Journal of Photovoltaics 2013, 3, 1184–1191. [CrossRef]
Leilaeioun, M.; Holman, Z.C. Accuracy of expressions for the fill factor of a solar cell in terms of open-circuit voltage and ideality factor. Journal of Applied Physics 2016, 120. [CrossRef]
Fernández-Solas, Á.; Montes-Romero, J.; Micheli, L.; Almonacid, F.; Fernández, E.F. Estimation of soiling losses in photovoltaic modules of different technologies through analytical methods. Energy 2022, 244. [CrossRef]
Green, M.; Blakers, A.; Shi, J.; Keller, E.; Wenham, S. High-efficiency silicon solar cells. IEEE Transactions on Electron Devices 1984, 31, 679–683. [CrossRef]
Skoplaki, E.; Boudouvis, A.; Palyvos, J. A simple correlation for the operating temperature of photovoltaic modules of arbitrary mounting. Solar Energy Materials and Solar Cells 2008, 92, 1393–1402. [CrossRef]
Kamuyu, W.C.L.; Lim, J.R.; Won, C.S.; Ahn, H.K. Prediction model of photovoltaic module temperature for power performance of floating PVs. Energies 2018, 11. [CrossRef]
Mukisa, N.; Zamora, R.; Lie, T.T. Analysis of Solar Cell Temperature Models used in Solar Photovoltaic Simulating Softwares. 2019 IEEE PES GTD Grand International Conference and Exposition Asia, GTD Asia 2019 2019, pp. 124–129. [CrossRef]
Appelbaum, J.; Maor, T. Dependence of PV Module Temperature on Incident Time-Dependent Solar Spectrum. Applied Sciences 2020, 10. [CrossRef]
Stackhouse, P. NASA POWER|Data Access Viewer. https://power.larc.nasa.gov/data-access-viewer/, accessed on March 26, 2023.
Osorio Laurencio, L.; Retirado-Mediaceja, Y.; Yero, R.P.; Ramos, R. Assessing different models to estimate photovoltaic monocrystalline modules operating temperature using weather data. https://rie.cujae.edu.cu/index.php/RIE/article/view/705/858, accessed on February 13, 2023.
Patchali, T.E.; Ajide, O.O.; Matthew, O.J.; Salau, T.A.; Oyewola, O.M. Generation of meteorological year for the assessment of photovoltaic systems performance in Togo, West Africa. Scientific African 2022, 16, e01171. [CrossRef]
Sun, T.; Shan, M.; Rong, X.; Yang, X. Estimating the spatial distribution of solar photovoltaic power generation potential on different types of rural rooftops using a deep learning network applied to satellite images. Applied Energy 2022, 315, 119025. [CrossRef]
Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The National Solar Radiation Data Base (NSRDB). Renewable and Sustainable Energy Reviews 2018, 89, 51–60. [CrossRef]
Santiago, I.; Trillo-Montero, D.; Moreno-Garcia, I.; Pallarés-López, V.; Luna-Rodríguez, J. Modeling of photovoltaic cell temperature losses: A review and a practice case in South Spain. Renewable and Sustainable Energy Reviews 2018, 90, 70–89. [CrossRef]
Ross, R.; Smokler, M.I. Flat-Plate solar array project final report,. Volume VI: Engineering Sciences and Reliability, Report DOE/JPL-1012-125; JPL: California, United States of America, 1986.
Bailek, N.; Bouchouicha, K.; Hassan, M.A.; Slimani, A.; Jamil, B. Implicit regression-based correlations to predict the back temperature of PV modules in the arid region of south Algeria. Renewable Energy 2020, 156, 57–67. [CrossRef]
Silva, D.D.; Marson, V.; de Souza, R.R.; de Oliveira, J.D.; Silva, J.B.C.; Cardoso, E.M. A new predictive model for a photovoltaic module’s surface temperature. Energy Reports 2022, 8, 15206–15220. [CrossRef]
Yolcan, O.O.; Kose, R. Photovoltaic module cell temperature estimation: Developing a novel expression. Solar Energy 2023, 249, 1–11. [CrossRef]
Alexis Alvarado Silva, C.; Mejia Vasquez, O.; Orlando Gamarra-Rosado, V. Development of a Virtual Learning Module Using Graphic Interface for Remote Teaching of Photovoltaic Systems. ACM International Conference Proceeding Series 2021, pp. 46–52. [CrossRef]
HELIENE. Helios Energy Europe S.L. Photovoltaics Modules. https://avdira-solar.eu/pdf/heliene/215m_en.pdf, accessed on March 12, 2023.
SolarWorld. Sunmodule SW 150 poly R6A. https://www.enfsolar.com/Product/pdf/Crystalline/57733963c96c5.pdf, accessed on February 20, 2023.
PVsyst. PVsyst S.A. - official website. https://www.pvsyst.com, accessed on February 13, 2023.
Meng, Z.; Zhao, Y.; Tang, S.; Sun, Y. An efficient datasheet-based parameters extraction method for two-diode photovoltaic cell and cells model. Renewable Energy 2020, 153, 1174–1182. [CrossRef]
Xu, J.; Zhou, C.; Li, W. Photovoltaic single diode model parameter extraction by dI/dV-assisted deterministic method. Solar Energy 2023, 251, 30–38. [CrossRef]
Toledo, F.J.; Galiano, V.; Blanes, J.M.; Herranz, V.; Batzelis, E. Photovoltaic single-diode model parametrization. An application to the calculus of the Euclidean distance to an I–V curve. Mathematics and Computers in Simulation 2023. [CrossRef]
Qais, M.H.; Hasanien, H.M.; Alghuwainem, S.; Loo, K.; Elgendy, M.; Turky, R.A. Accurate Three-Diode model estimation of Photovoltaic modules using a novel circle search algorithm. Ain Shams Engineering Journal 2022, 13, 101824. [CrossRef]
Garip, Z. Parameters estimation of three-diode photovoltaic model using fractional-order Harris Hawks optimization algorithm. Optik 2023, 272, 170391. [CrossRef]
Benda, V.; Cerna, L. A Note on Limits and Trends in PV Cells and Modules. Applied Sciences 2022, 12. [CrossRef]
Min, K.H.; Kim, T.; Kang, M.G.; Song, H.e.; Kang, Y.; Lee, H.S.; Kim, D.; Park, S.; Lee, S.H. An Analysis of Fill Factor Loss Depending on the Temperature for the Industrial Silicon Solar Cells. Energies 2020, 13. [CrossRef]
Serenelli, L.; Martini, L.; Menchini, F.; Izzi, M.; de Cesare, G.; Condorelli, G.; Gerardi, C.; Muñoz, D.; Tucci, M. Selective contacts and fill factor limitations in heterojunction solar cells. Progress in Photovoltaics: Research and Applications 2021, 29, 876–884. [CrossRef]
Raillani, B.; Ouali, H.A.L.; Amraqui, S.; Moussaoui, M.A.; Mezrhab, A. Analyze and Study on Photovoltaic Parameters of Mono-Crystalline Silicon Solar Cell. In Proceedings of the 2019 International Conference on Intelligent Systems and Advanced Computing Sciences (ISACS), 2019, pp. 1–5. [CrossRef]
Stein, J.S.; Holmgren, W.F.; Forbess, J.; Hansen, C.W. PVLIB: Open source photovoltaic performance modeling functions for Matlab and Python. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), 2016, pp. 3425–3430. [CrossRef]
Theristis, M.; Livera, A.; Micheli, L.; Jones, C.B.; Makrides, G.; Georghiou, G.E.; Stein, J.S. Modeling nonlinear photovoltaic degradation rates. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), 2020, pp. 0208–0212. [CrossRef]
Driesse, A.; Theristis, M.; Stein, J.S. PV Module Operating Temperature Model Equivalence and Parameter Translation. In Proceedings of the 2022 IEEE 49th Photovoltaics Specialists Conference (PVSC), 2022, pp. 0172–0177. [CrossRef]

Figure 1. Equivalent circuit of a photovoltaic module (a) one-diode and (b) two-diode.

Figure 2. Typical (normalized) V-I and V-P characteristic curve of a PV cell.

Figure 3. Typical structure of PV arrays.

Figure 4. Typical (normalized) V-I characteristic curve of a PV cell and plot of

F F

by the gray rectangular area.

Figure 4. Typical (normalized) V-I characteristic curve of a PV cell and plot of

F F

by the gray rectangular area.

Figure 5. Main screen of the Toolbox PVMSim.

Figure 6. Algorithm for extraction of internal parameters (GUI’s Block 2 of PVMSim).

Figure 7. Algorithm for obtaining characteristic curves (GUI’s Block 3 of PVMSim).

Figure 8. Algorithm for obtaining and plot

F F

and

η

values (GUI’s Block 4 of PVMSim).

Figure 8. Algorithm for obtaining and plot

F F

and

η

values (GUI’s Block 4 of PVMSim).

Figure 9. Algorithm for obtaining performance PV daily (GUI’s Block 5 of PVMSim).

Figure 10. Curves obtained from GUI’s Block 2 of PVMSim. I-V and P-V characteristic curves obtained from the numerical compute of the

R_{s}

and

R_{s h}

values: (a-d) HEE215MA68 and (e-h) SW150polyR6A.

Figure 10. Curves obtained from GUI’s Block 2 of PVMSim. I-V and P-V characteristic curves obtained from the numerical compute of the

R_{s}

and

R_{s h}

values: (a-d) HEE215MA68 and (e-h) SW150polyR6A.

Figure 11. Curves obtained from GUI’s Block 3 of PVMSim. Plot of V-I and V-P curves for variable values of G and constant at

T_{c} = 25^{\circ} C

. The circle marks represent the

P_{m a x C}

Figure 11. Curves obtained from GUI’s Block 3 of PVMSim. Plot of V-I and V-P curves for variable values of G and constant at

T_{c} = 25^{\circ} C

. The circle marks represent the

P_{m a x C}

Figure 12. Curves obtained from GUI’s Block 3 of PVMSim. Plot of V-I and V-P curves for variable values of

T_{c}

and constant at

G = 1000 W / m^{2}

. The circle marks represent the

P_{m a x C}

Figure 12. Curves obtained from GUI’s Block 3 of PVMSim. Plot of V-I and V-P curves for variable values of

T_{c}

and constant at

G = 1000 W / m^{2}

. The circle marks represent the

P_{m a x C}

Figure 13. I-V curves including electrical parameters for STC, obtained from GUI’s Block 4 of PVMSim.

F F

represented by the rectangular area of gray color: (a) HEE215MA68 and (b) SW150polyR6A.

Figure 13. I-V curves including electrical parameters for STC, obtained from GUI’s Block 4 of PVMSim.

F F

represented by the rectangular area of gray color: (a) HEE215MA68 and (b) SW150polyR6A.

Figure 14. I-V curves including electrical parameters for NOC, obtained from GUI’s Block 4 of PVMSim.

F F

represented by the rectangular area of gray color: (a) HEE215MA68 and (b) SW150polyR6A.

Figure 14. I-V curves including electrical parameters for NOC, obtained from GUI’s Block 4 of PVMSim.

F F

represented by the rectangular area of gray color: (a) HEE215MA68 and (b) SW150polyR6A.

Figure 15. Evolution of G and

T_{c}

during the chosen days: (a) March 21, (b) June 21, (c) September 21 and (d) December 21.

Figure 15. Evolution of G and

T_{c}

during the chosen days: (a) March 21, (b) June 21, (c) September 21 and (d) December 21.

Figure 16. Curves obtained from GUI’s Block 5 of PVMSim. Evolution of the

P_{m a x C}

and daily energy output: (a-d) HEE215MA68 and (e-h) SW150polyR6A.

Figure 16. Curves obtained from GUI’s Block 5 of PVMSim. Evolution of the

P_{m a x C}

and daily energy output: (a-d) HEE215MA68 and (e-h) SW150polyR6A.

Figure 17. Curves obtained from GUI’s Block 5 of PVMSim. Variation of

η

according to the evolution of G and

T_{c}

: (a) HEE215MA68 and (b) SW150polyR6A.

Figure 17. Curves obtained from GUI’s Block 5 of PVMSim. Variation of

η

according to the evolution of G and

T_{c}

: (a) HEE215MA68 and (b) SW150polyR6A.

Figure 18. Curves obtained from GUI’s Block 5 of PVMSim. Linear fit of the

η

T_{c}

: (a) HEE215MA68 and (b) SW150polyR6A.

Figure 18. Curves obtained from GUI’s Block 5 of PVMSim. Linear fit of the

η

T_{c}

: (a) HEE215MA68 and (b) SW150polyR6A.

Table 1. Electric parameters extracted from datasheet of analyzed PV modules [68,69].

	HEE215MA68		SW150polyR6A
Parameter	STC	NOC	STC	NOC
$P_{m a x} (W)$	250±3%	183	150±2%	110.1
$V_{o c} (V)$	37.40	34.5	22.5	20.5
$V_{m p p} (V)$	30.3	27.7	18.3	16.6
$I_{s c} (A)$	8.72	7.25	8.81	7.17
$I_{m p p} (A)$	8.22	6.7	8.27	6.62
$β (% /^{\circ} C)$	-0.34	-	-0.31	-
$N O C T (^{\circ} C)$	-	45	-	46

Table 2. Seven internal parameters of PV modules calculated with PVMSim.

No	Parameter	HEE215MA68	SW150polyR6A
1 and 2	$I_{o 1} = I_{o 2} (A)$	$2.57 e - 10$	$2.45 e - 10$
3	$I_{p v} (A)$	8.67	8.81
4	$n_{1}$	1	1
5	$n_{2}$	1.2	1.2
6	$R_{s} (Ω)$	0.229	0.166
7	$R_{s h} (Ω)$	233.569	105.973

Table 3. Metrics of the calculated electrical parameters by PVMSim at STC and NOC.

		HEE215MA68				SW150polyR6A
Condition	Parameter	Datasheet	PVMSim	MAE	Datasheet	PVMSim	MAE
	$P_{m a x C} (W)$	250	250.01	0.01	150	150.1	0.1
STC	$V_{o c} (V)$	37.4	37.4	0	22.5	22.5	0
	$I_{s c} (A)$	8.72	8.66	0.06	8.81	8.8	0.01
	$P_{m a x C} (W)$	183	183.47	0.47	110.1	110.27	0.17
NOC	$V_{o c} (V)$	34.5	34.5	0	20.5	20.8	0.30
	$I_{s c} (A)$	7.25	7.03	0.22	7.17	7.11	0.06

Table 4. Metrics of the

P_{m a x C} (W)

calculated at different values of G and

T_{c}

Table 4. Metrics of the

P_{m a x C} (W)

calculated at different values of G and

T_{c}

		HEE215MA68				SW150polyR6A
Condition	Value	PVsyst	PVMSim	MAE	PVsyst	PVMSim	MAE
	$200 W / m^{2}$	48.35	45.40	2.95	29.13	27.00	2.13
	$400 W / m^{2}$	99.08	96.69	2.39	59.74	58.09	1.65
$T_{c} = 25^{\circ} C$	$600 W / m^{2}$	149.76	148.21	1.55	90.30	89.17	1.13
	$800 W / m^{2}$	199.88	199.39	0.49	120.50	119.89	0.61
	$1000 W / m^{2}$	249.10	250.01	0.91	150.10	150.10	0
	$10^{\circ} C$	264.81	264.60	0.21	159.89	158.56	1.36
	$25^{\circ} C$	249.10	250.01	0.91	150.10	150.10	0
$G = 1 k W / m^{2}$	$40^{\circ} C$	232.76	235.13	2.37	140.02	141.52	1.50
	$55^{\circ} C$	215.86	219.98	4.12	129.67	132.85	3.18
	$70^{\circ} C$	198.41	204.56	6.15	119.07	124.08	5.01

Table 5. Effect of

T_{a}

and G on

T_{c}

P_{m a x C}

and

η

at peak solar hour (13:00 hours).

Table 5. Effect of

T_{a}

and G on

T_{c}

P_{m a x C}

and

η

at peak solar hour (13:00 hours).

PV Module	Parameter	21^th March	21^th June	21^th Sept.	21^th Dec.
HEE215MA68	$G (W / m^{2})$	998.7	710.3	602.7	639.5
	$T_{a} (^{\circ} C)$	28.4	29.5	28.2	25.8
	$T_{c} (^{\circ} C)$	59.61	51.7	47.03	45.78
	$P_{m a x C} (W)$	182.51	141.28	124.08	132.06
	$η (%)$	16.25	16.44	16.52	16.55
SW150polyR6A	$G (W / m^{2})$	998.7	710.3	602.7	639.5
	$T_{a} (^{\circ} C)$	28.4	29.5	28.2	25.8
	$T_{c} (^{\circ} C)$	60.86	52.58	47.79	46.58
	$P_{m a x C} (W)$	110.13	85.33	74.9	79.66
	$η (%)$	14.74	14.83	14.88	14.89

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A MATLAB/GUI for Photovoltaic Modules Performance Simulations Based on Two-Diode Model

Abstract

1. Introduction

2. Materials and Methods

2.1. Equivalent circuit of the PV cell based on the two-diode model

2.2. Mathematical model of reverse saturation diode current

2.3. Method for R s and R s h computation

2.4. PV conversion efficiency

2.5. Methods and implemented algorithm of PVMSim

3. Results

3.1. Extracting unknown internal parameters

3.2. Simulating the effect of irradiance and temperature

3.3. Predictions of PV efficiency

3.4. Obtaining daily energy output

4. Discussion

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.3. Method for $R_{s}$ and $R_{s h}$ computation